Figures and data in A functional model of adult dentate gyrus neurogenesis

Figures
Tables
Additional files

6 figures, 1 table and 6 additional files

Figures

Figure 1 with 1 supplement

Download asset Open asset

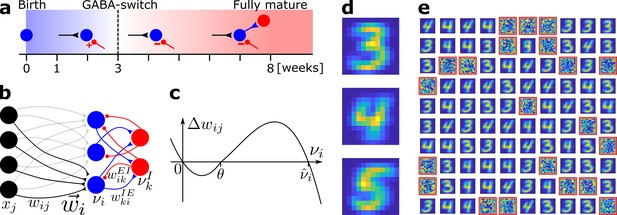
Network model and pretraining.

(a) Integration of an adult-born DGC (blue) as a function of time: GABAergic synaptic input (red) switches from excitatory (+) to inhibitory (−); strong connections to interneurons develop only later; glutamatergic synaptic input (black), interneuron (red). (b) Network structure. EC neurons (black, rate x_j) are fully connected with weights $w_{i j}$ to DGCs (blue, rate $ν_{i}$ ). The feedforward weight vector ${\vec{w}}_{i}$ onto neuron $i$ is depicted in black. DGCs and interneurons (red, rate $ν_{k}^{I}$ ) are mutually connected with probability $p_{I E}$ and $p_{E I}$ and weights $w_{k i}^{I E}$ and $w_{i k}^{E I}$ , respectively. Connections with a triangular (round) end are glutamatergic (GABAergic). (c) Given presynaptic activity $x_{j} > 0$ , the weight update $Δ w_{i j}$ is shown as a function of the firing rate $ν_{i}$ of the postsynaptic DGC with LTD for $ν_{i} < θ$ and LTP for $θ < ν_{i} < {\hat{ν}}_{i}$ . (d) Center of mass for three ensembles of patterns from the MNIST data set, visualized as 12 × 12 pixel patterns. The two-dimensional arrangements and colors are for visualization only. (e) One hundred receptive fields, each defined as the set of feedforward weights, are represented in a two-dimensional organization. After pretraining with patterns from MNIST digits 3 and 4, 79 DGCs have receptive fields corresponding to threes and fours of different writing styles, while 21 remain unselective (highlighted by red frames).

Figure 1—figure supplement 1

Download asset Open asset

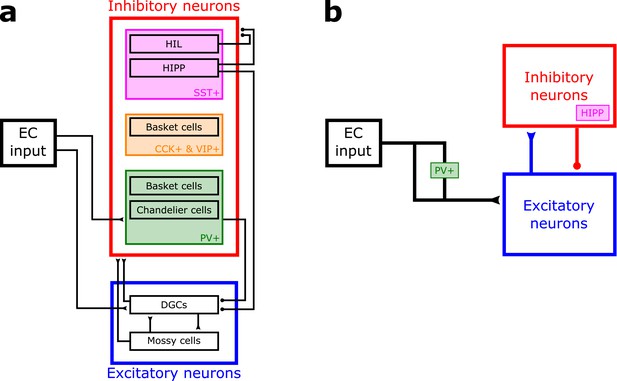
Dentate gyrus network.

(a) The dentate gyrus circuitry is complex, with two main types of excitatory cells: dentate granule cells (DGCs, the principal cells) and Mossy cells, as well as many different types of inhibitory cells, including somatostatin-positive (SST+) cells (magenta), cells expressing cholecystokinin (CCK) and vasoactive intestinal polypeptide (VIP) (orange), and parvalbumin-positive (PV+) cells (green). This tentative schematic of the main aspects of known circuitry neglects the anatomical location of the cells (e.g. granular layer, molecular layer, hilus) and simplifies cell types and connections. For references, see Introduction of main text. HIL: hilar interneurons, HIPP: hilar-perforant-path-associated interneurons, EC: entorhinal cortex. (b) Simplification of the network that we use in our model implementation. EC input does not project to inhibitory neurons in our model, but it is known that it provides feedforward inhibition to DGCs through PV+ cells. We model this by normalizing the input patterns. Lateral inhibition in our model corresponds to the experimentally observed feedback inhibition from HIPP cells.

Figure 2 with 2 supplements

Download asset Open asset

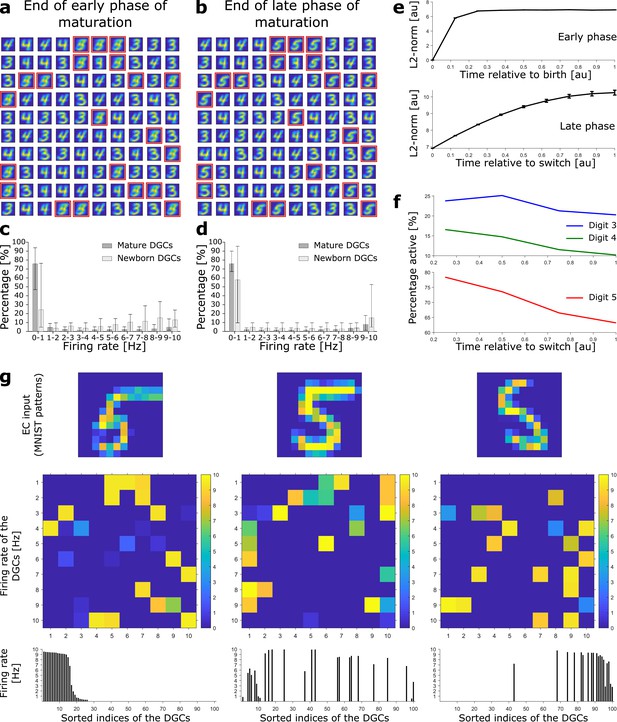
Newborn DGCs become selective for novel patterns during maturation.

(a) Unselective neurons are replaced by newborn DGCs, which learn their feedforward weights while patterns from digits 3, 4, and 5 are presented. At the end of the early phase of maturation, the receptive fields of all newborn DGCs (red frames) show mixed selectivity. (b) At the end of the late phase of maturation, newborn DGCs are selective for patterns from the novel digit 5, with different writing styles. (**c, d**) Distribution of the percentage of model DGCs (mean with 10th and 90th percentiles) in each firing rate bin at the end of the early (c) and late (d) phase of maturation. Statistics calculated across MNIST patterns (‘3’s, ‘4’s, ‘5’s). Percentages are per subpopulation (mature and newborn). Note that neurons with firing rate < 1 Hz for one pattern may fire at medium or high rate for another pattern. (e) The L2-norm of the feedforward weight vector onto newborn DGCs (mean ± SEM) increases as a function of maturation indicating growth of synapses and receptive field strength. Horizontal axis: time = 1 indicates end of early (top) or late (bottom) phase (two epochs per phase, $η = 0.0005$ ). (f) Percentage of newborn DGCs activated (firing rate > 1 Hz) by a stimulus averaged over test patterns of digits 3, 4, and 5 as a function of maturation. (g) At the end of the late phase of maturation, three different patterns of digit 5 applied to EC neurons (top) cause different firing rate patterns of the 100 DGCs arranged in a matrix of 10-by-10 cells (middle). DGCs with a receptive field (see b) similar to a presented EC activation pattern respond more strongly than the others. Bottom: Firing rates of the DGCs with indices sorted from highest to lowest firing rate in response to the first pattern. All three patterns shown come from the testing set, and are correctly classified using our readout network.

Figure 2—figure supplement 1

Download asset Open asset

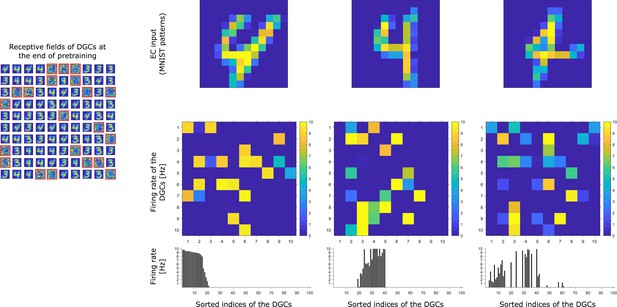
Activity of 100 model DGCs in response to different patterns.

At the end of pretraining, three different patterns of digit 4 applied to EC neurons (top) cause different firing rate patterns of the 100 DGCs arranged in a matrix of 10-by-10 cells (middle). DGCs with a receptive field (left: 10-by-10 grid of receptive fields) similar to a presented EC activation pattern respond more strongly than the others. Bottom: Firing rates of the DGCs with indices sorted from highest to lowest firing rate in response to the first pattern. All three patterns shown come from the testing set and are correctly classified using our readout network.

Figure 2—figure supplement 2

Download asset Open asset

Receptive fields of DGCs.

(a) Several novel digits can be learned simultaneously. After pretraining as in Figure 1e, unresponsive neurons are replaced by newborn DGCs. When patterns from digits 3, 4, 5, and 6 are presented in random order, newborn DGCs exhibit after maturation receptive fields with selectivity for the novel digits 5 and 6. (b) Several novel digits can be learned sequentially. After pretraining with digits 3 and 4, 10 randomly selected unresponsive neurons are replaced by newborn DGCs. Patterns from digits 3, 4, and 5 are presented in random order, while newborn DGCs mature and develop selectivity for the novel digit 5, with different writing styles. Later, the eleven remaining unresponsive neurons of the network are replaced by newborn DGCs. When patterns from the novel digit 6 are presented intermingled with patterns from digits 3, 4, and 5, the newborn DGCs develop selectivity for digit 6.

Figure 3

Download asset Open asset

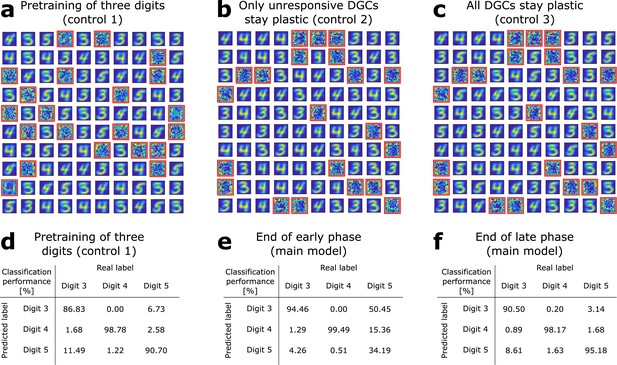
The GABA-switch guides learning of novel representations.

(a) Pretraining on digits 3, 4, and 5 simultaneously without neurogenesis (control 1). Patterns from digits 3, 4, and 5 are presented to the network while all DGCs learn their feedforward weights. After pretraining, 79 DGCs have receptive fields corresponding to the three learned digits, while 21 remain unselective (as in Figure 1e). (b) Sequential training without neurogenesis (control 2). After pretraining as in Figure 1e, the unresponsive neurons stay plastic, but they fail to become selective for digit 5 when patterns from digits 3, 4, and 5 are presented in random order. (c) Sequential training without neurogenesis but all DGCs stay plastic (control 3). Some of the DGCs previously responding to patterns from digits 3 or 4 become selective for digit 5. (**d–f**) Confusion matrices. Classification performance in percent (using a linear classifier as readout network) for control 1 (d) and for the main model at the end of the early (e) and late (f) phase; Figure 2a,b.

Figure 4 with 2 supplements

Download asset Open asset

Novel patterns expand the representation into a previously empty subspace.

(a) Left: The DGC activity responses at the end of the early phase of maturation of newborn DGCs are projected on discriminatory axes. Each point corresponds to the representation of one input pattern. Color indicates digit 3 (blue), 4 (green), and 5 (red). Right: Firing rate profiles of three example patterns (highlighted by crosses on the left) are sorted from high to low for the pattern represented by the orange cross (inset: zoom of firing rates of DGCs with low activity). (b) Same as (a), but at the end of the late phase of maturation of newborn DGCs. Note that the red dots around the orange cross have moved into a different subspace. (c) Example patterns of digit 5 corresponding to the symbols in (a) and (b). All three are accurately classified by our readout network. (d) Evolution of the mean (± SEM) of the projection of the activity upon presentation of all test patterns of digit 5.

Figure 4—figure supplement 1

Download asset Open asset

Receptive fields of the DGCs in a larger network with $N_{D G C} = 700$ (all other parameters unchanged).

After pretraining with digits 3 and 4, all 275 unresponsive DGCs (highlighted by the red/magenta squares) are replaced by newborn DGCs. Newborn DGCs follow a two-step maturation process while patterns from digits 3, 4, and 5 are presented to the network. At the end of maturation, most newborn DGCs represent different prototypes of the novel digit 5. Two of them (highlighted in magenta) became selective for digit 4.

Figure 4—figure supplement 2

Download asset Open asset

Receptive fields of the DGCs in a larger network with $N_{D G C} = 700$ (all other parameters unchanged), when only a fraction of unresponsive units are replaced by newborn DGCs.

Out of the 275 unresponsive DGCs after pretraining with digits 3 and 4 (highlighted by the red/magenta squares), 119 are replaced by newborn DGCs (highlighted by the magenta squares), to mimic the experimental observation that only a fraction of DGCs are newborn DGCs. Newborn DGCs follow a two-step maturation process while patterns from digits 3, 4 and 5 are presented to the network. At the end of maturation, newborn DGCs represent different prototypes or features of the novel digit 5. The remaining unresponsive units (highlighted by the red squares) are available to be replaced later by newborn DGCs so as to learn further tasks.

Figure 5

Download asset Open asset

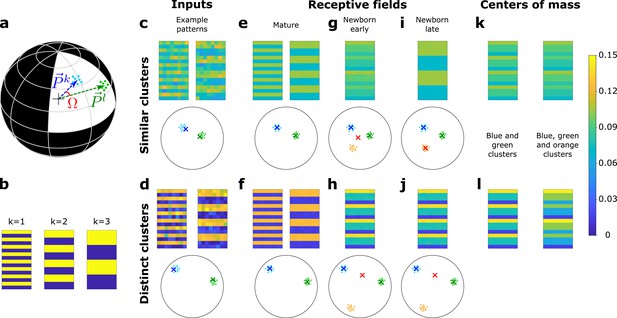
A newborn DGC becomes selective for similar but not distinct novel stimuli.

(a) Center of mass of clusters $k$ and $l$ of an artificial data set ( ${\vec{P}}_{k}$ and ${\vec{P}}_{l}$ , respectively, separated by angle Ω) are represented by arrows that point to the surface of a hypersphere. Dots represent individual patterns. (b) Center of mass of three clusters of the artificial data set, visualized as 16 × 8 pixel patterns. The two-dimensional arrangements and colors are for visualization only. (**c, d**) Example input patterns (activity of 16 × 8 input neurons) from clusters 1 and 2 for similar clusters (c, $s = 0.8$ ), and distinct clusters (d, $s = 0.2$ ). Below: dots correspond to patterns, crosses indicate the input patterns shown (schematic). (**e, f**) After pretraining with patterns from two clusters, the receptive fields (set of synaptic weights onto neurons 1 and 2) exhibit the center of mass of each cluster of input patterns (blue and green crosses). (**g, h**) Novel stimuli from cluster 3 (orange dots) are added. If the clusters are similar, the receptive field of the newborn DGC (red cross) moves toward the center of mass of the three clusters during its early phase of maturation (g), and if the clusters are distinct toward the center of mass of the two pretrained clusters (h). (**i, j**) Receptive field after the late phase of maturation for the case of similar (i) or distinct (j) clusters. (**k, l**) For comparison, the center of mass of all patterns of the blue and green clusters (left column) and of the blue, green, and orange clusters (right column) for the case of similar (k) or distinct (l) clusters. Color scale: input firing rate $\vec{x}$ or weight ${\vec{w}}_{i}$ normalized to $|| {\vec{w}}_{i} || = 1 = || \vec{x} ||$ .

Figure 6 with 1 supplement

Download asset Open asset

Maturation dynamics for similar patterns.

(a) Schematics of the unit hypersphere with three clusters of patterns (colored dots) and three scaled feedforward weight vectors (colored arrows). After pretraining, the blue and green weight vectors point to the center of mass of the corresponding clusters. Patterns from the novel cluster (orange points) are presented only later to the network. During the early phase of maturation, the newborn DGC grows its vector of feedforward weights (red arrow) in the direction of the subspace of patterns which indirectly activate the newborn cell (dark grey star: center of mass of the presented patterns, located below the part of the sphere surface highlighted in grey). (b) During the late phase of maturation, the red vector turns toward the novel cluster. The symbol φ indicates the angle between the center of mass of the novel cluster and the feedforward weight vector onto the newborn cell. (c) The angle φ decreases in the late phase of maturation of the newborn DGC if the novel cluster is similar to the previously stored clusters. Its final average value of $φ \approx {0.4}^{\circ}$ is caused by the jitter of the weight vector around the center of mass of the novel cluster.

Figure 6—figure supplement 1

Download asset Open asset

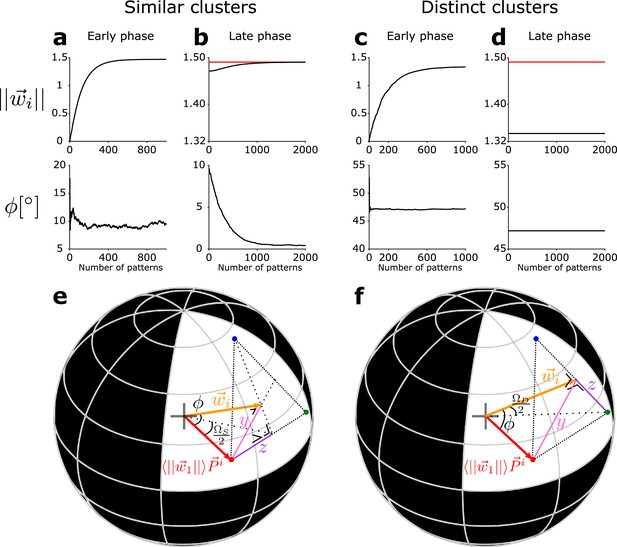
Evolution of the feedforward weight vector onto the newborn DGC.

(**a–d**) The total synaptic strength $|| {\vec{w}}_{i} || = \sqrt{\sum_{j} {(w_{i j})}^{2}}$ of the weight vector onto the newborn DGC (top row), and of its angular separation φ with the center of mass of the novel cluster (bottom row), as a function of the number of pattern presentations. (**a, b**) The three clusters are similar ( $s = 0.8$ ). (**c, d**) The three clusters are distinct ( $s = 0.2$ ). Early phase of maturation (**a, c**), late phase of maturation (**b, d**). The red line shows the mean value of the synaptic strength of the mature DGCs. (**e, f**) Schematic drawing for the analytical computations. The L2-norm of the weight vector ${\vec{w}}_{i}$ onto the newborn DGC at the end of the early phase of maturation, and its angle φ with the center of mass of the novel cluster, for (e) similar clusters ( $s = 0.8$ ) and (f) distinct clusters ( $s = 0.2$ ). The sphere has a radius $⟨ || {\vec{w}}_{1} || ⟩$ . The centers of mass of the first two clusters (represented by the two mature DGCs) projected onto the hypersphere are represented by the blue and green dots. The red dot represents the projection of the center of mass of the novel cluster, ${\vec{P}}^{i}$ , onto the hypersphere.

Tables

Table 1

Parameters for the simulations.

	Biologically plausible network		Simplified network
Network	$N_{E C} = 144$	$N_{I} = 25$	$N_{E C} = 128$	$N_{D G C} = 3$
Network	$N_{D G C} = 100$ (Figures 1–4)
	$N_{D G C} = 700$ (Figure 4—figure supplement 1–2)
Connectivity	$w_{I E} = 1$	$w_{E I} = - \frac{1}{p_{E I} N_{I}}$	$w_{r e c} = - 1.2$
Connectivity	$p_{I E} = 0.9$	$p_{E I} = 0.9$
Dynamics	$τ_{m} = 20$ ms	$τ_{inh} = 2$ ms	$τ_{m} = 20$ ms
Dynamics	$L = 0.5$	$p^{*} = 0.1$
Plasticity	$α_{0} = 0.05$	$β = 1$	$α_{0} = 0.03$	$β = 1$
	$γ_{0} = 10$	$θ = 0.15$	$γ_{0} = 1.65$	$θ = 0.15$
	$ν_{0} = 0.2$	$γ = 9.85$	$γ = 1.5$
Numerical simulations	$Δ t = 0.1$ ms	$η = 0.01$	$Δ t = 1$ ms	$η = 0.01$
Numerical simulations	$η_{b} = 0.01$

Additional files

Supplementary file 1 Classification performance for random combinations of digits. The classification performance (P₀, P₁, P₂) is defined as the percentage of correctly classified patterns on the test set. The numbers m n + q (first column) indicate that MNIST digits m and n are used for pretraining (second column); m, n and q are used for pretraining (third column); or m and n are used for pretraining, and patterns from digit q added after neurogenesis (fourth column). $P_{2} - P_{1}$ (last column) is used for evaluating the contribution of neurogenesis to classification performance.: https://cdn.elifesciences.org/articles/66463/elife-66463-supp1-v2.tex
Download elife-66463-supp1-v2.tex
Supplementary file 2 Comparison of networks with different numbers of inhibitory neurons. The number of excitatory neurons is $N_{D G C} = 100$ for all three networks, and there are $N_{I}$ inhibitory neurons. The case with $N_{I} = 25$ is the one presented in the main text. All other network parameters are unchanged (including $p^{*}$ ). Each network is pretrained once with digits 3 and 4. The percentage of active neurons (firing rate > 1 Hz) for each testing pattern of the corresponding digit is given (mean ± standard deviation), as well as the classification performance over all testing patterns from the trained digits.: https://cdn.elifesciences.org/articles/66463/elife-66463-supp2-v2.tex
Download elife-66463-supp2-v2.tex
Supplementary file 3 Network with 700 DGCs (expansion factor from EC to dentate gyrus of about 5) compared to the case with $N_{D G C} = 100$ as in the main text. All other network parameters are unchanged. Each network is pretrained with digits 3 and 4. Note that only a subset of neurons responsive to digit 3 (or 4) get active (firing rate > 1 Hz) for a given pattern 3 (or 4). Classification performance is evaluated over all test patterns from the trained digits. Top: after pretraining; bottom: late phase, after adding patterns from digit ‘5’. Either all unresponsive cells (Figure 4—figure supplement 1), or only a fraction of these (Figure 4—figure supplement 2), have been replaced by newborn model cells. For the network with 700 DGCs, about 16-18% of DGCs are activated upon presentation of a digit 3 or 4 or 5 (about 112-126 model DGCs). If 119 newborn DGCs are plastic during presentation of the novel digit 5 (middle column), these can become selective for prototypes of digit 5 (Figure 4—figure supplement 2) yielding a good classification performance while keeping 156 unresponsive DGCs available for future tasks. If only 35 newborn DGCs are available, classification performance is lower (right column).: https://cdn.elifesciences.org/articles/66463/elife-66463-supp3-v2.tex
Download elife-66463-supp3-v2.tex
Supplementary file 4 Classification performance with plastic mature DGCs. Top: Using the main neurogenesis network with $N_{D G C} = 100$ DGCs, we keep the learning rate of newborn DGCs at $η = 0.01$ , but now set the learning rate of mature DGCs to nonzero values ( $η_{mature} > 0$ ) throughout maturation of newborn DGCs. This enables us to vary the level of remaining plasticity in mature DGCs. The number of newborn DGCs that undergo neurogenesis ( $N_{newborn} = 21$ ) is the same as in the main text. Overall classification performance for digits 3, 4, and 5 ( $P$ ) is computed at the end of the late phase of maturation of newborn DGCs, as well as the classification performance for digit 3 (P₃), digit 4 (P₄) and digit 5 (P₅). Bottom: Same with the extended neurogenesis network with $N_{D G C} = 700$ . The number of newborn DGCs is either set to $N_{newborn} = 119$ (corresponding to 17% of newborn DGCs), or $N_{newborn} = 35$ (corresponding to 5% of newborn DGCs). The results with $η_{mature} = 0$ from the main text are repeated here for convenience.: https://cdn.elifesciences.org/articles/66463/elife-66463-supp4-v2.tex
Download elife-66463-supp4-v2.tex
Supplementary file 5 Comparison of the neurogenesis model and the random initialization model for different input dimensionalities. The simplified model with $s = 0.8$ (similar input clusters) is used. Pretraining with two clusters and subsequent learning of a novel cluster 3 (Neuro.) was performed in the same way as reported in the main text. After full maturation of the newborn DGC (two epochs), its weights were fixed, and patterns of a novel cluster 4 were introduced as well as another newborn DGC, and so on until all seven clusters were learned. Reconstruction errors were computed at the end of learning of all seven clusters, and compared with two cases where newborn DGCs do not undergo a two-phase maturation during their 2 epochs of learning, always stay plastic, and are born with a randomly initialized feedforward weight vector: one where the L2-norm of the weight vector starts at a low value of 0.1 (RandInitL.), and one where the L2-norm starts at 1.5, which is the upper bound for the length of the weight vector (RandInitH.). We compare the reconstruction error between the neurogenesis model and the random initialization models for different values of the effective input dimensionality (PR), which depends on the concentration parameter (κ) used when creating the artificial dataset. The results with the dataset used in the main text ( $κ = 10^{4}$ , PR =11) are reported here for comparison.: https://cdn.elifesciences.org/articles/66463/elife-66463-supp5-v2.tex
Download elife-66463-supp5-v2.tex
Transparent reporting form: https://cdn.elifesciences.org/articles/66463/elife-66463-transrepform-v2.docx
Download elife-66463-transrepform-v2.docx