Non-linear dimensionality reduction on extracellular waveforms reveals cell type diversity in premotor cortex
Figures
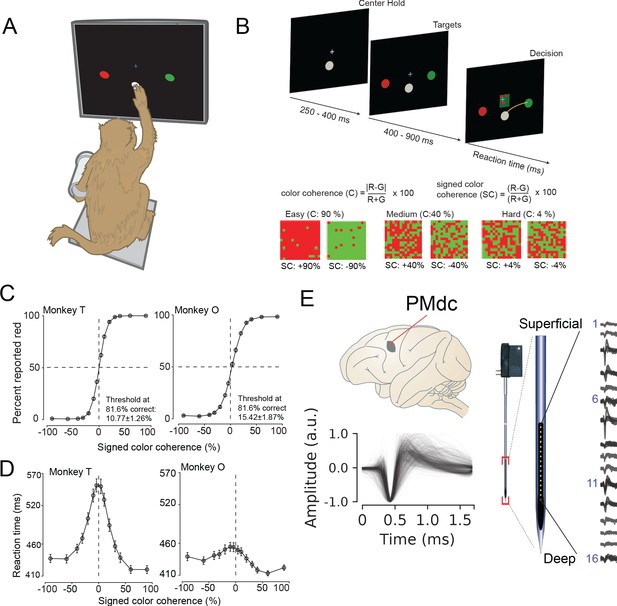
Recording locations, waveform shapes, techniques, task, and discrimination behavior.
(A) An illustration of the behavioral setup in the discrimination task. The monkey was seated with one arm free and one arm gently restrained in a plastic tube via a cloth sling. An infrared-reflecting (IR) bead was taped to the forefinger of the free hand and was used in tracking arm movements. This gave us a readout of the hand’s position and allowed us to mimic a touch screen. (B) A timeline of the decision-making task (top). At bottom is defined the parametrization of difficulty in the task in terms of color coherence and signed color coherence (SC). (C) Average discrimination performance and (D) Reaction time (RT) over sessions of the two monkeys as a function of the SC of the checkerboard cue. RT plotted here includes both correct and incorrect trials for each session and then averaged across sessions. Gray markers show measured data points along with 2 × S.E.M. estimated over sessions. For many data points in (C), the error bars lie within the marker. X-axes in both (C), (D) depict the SC in %. Y-axes depict the percent responded red in (C) and RT in (D). Also shown in the inset of (C) are discrimination thresholds (mean ± S.D. over sessions) estimated from a Weibull fit to the overall percent correct as a function of coherence. The discrimination threshold is the color coherence at which the monkey made 81.6% correct choices. Seventy-five sessions for monkey T (128,989 trials) and 66 sessions for monkey O (108,344 trials) went into the averages. (E) The recording location in caudal PMd (top); normalized and aligned isolated single-unit waveforms (n = 625, 1.6 ms each, bottom); and schematic of the 16-channel Plexon U-probe (right) used during the behavioral experiment.
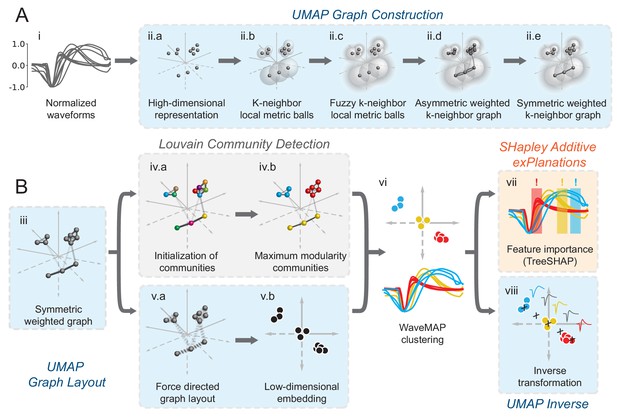
Schematic of WaveMAP.
(A) WaveMAP begins with UMAP which projects high-dimensional data into lower dimension while preserving local and global relationships (see Figure 2—figure supplement 1A for an intuitive diagram). Normalized average waveforms from single units (i) are passed to UMAP (McInnes et al., 2018) which begins with the construction of a high-dimensional graph (ii). In the high-dimensional space (ii.a), UMAP constructs a distance metric local to each data point (ii.b). The unit ball (ball with radius of one) of each local metric stretches to the 1st-nearest neighbor. Beyond this unit ball, local distances decrease (ii.c) according to an exponential distribution that is scaled by the local density. This local metric is used to construct a weighted graph with asymmetric edges (ii.d). The 1-nearest neighbors are connected by en edge of weight 1.0. For the next -nearest neighbors, this weight then falls off according to the exponential local distance metric (in this diagram with some low weight connections omitted for clarity). These edges, and , are made symmetric according to (ii.e). (B) The high-dimensional graph (iii) captures latent structure in the high-dimensional space. We can use this graph in Louvain community detection (Louvain, iv) (Blondel et al., 2008) to find clusters (see Figure 2—figure supplement 1B for an intuitive diagram). In Louvain, each data point is first initialized as belonging to its own ‘community’ (iv.a, analogous to a cluster in a metric space). Then, in an iterative procedure, each data point joins neighboring communities until a measure called ‘modularity’ is maximized (iv.b, see Supplemental Information for a definition of modularity). Next, data points in the same final community are aggregated to a single node and the process repeats until the maximal modularity is found on this newly aggregated graph. This process then keeps repeating until the maximal modularity graph is found and the final community memberships are passed back to the original data points. We can also use this graph to find a low-dimensional representation through a graph layout procedure (v). The graph layout proceeds by finding a ‘low energy’ configuration that balances attractive (shown as springs in v.a) and repulsive (not shown) forces between pairs of points as a function of edge weight or lack thereof. This procedure iteratively minimizes the cross-entropy between the low-dimensional and high-dimensional graphs (v.b). The communities found through Louvain are then combined with the graph layout procedure to arrive at a set of clusters in a low-dimensional embedded space (vi). These clusters (vi, top) can be used to classify the original waveforms (vi, bottom). To investigate ‘why’ these data points became clusters, each cluster is examined for locally (within-cluster) important features (SHAP Lundberg and Lee, 2017), (vii) and globally important trends (UMAP inverse transform, viii). Not shown is the classifier SHAP values are calculated from. The diagrams for the graph construction and layout are based on UMAP documentation and the diagram for Louvain community detection is based on Blondel et al., 2008. Figure 2—figure supplement 1: An intuitive diagram of local and global distance preservation in UMAP and a schematic of the Louvain clustering process.
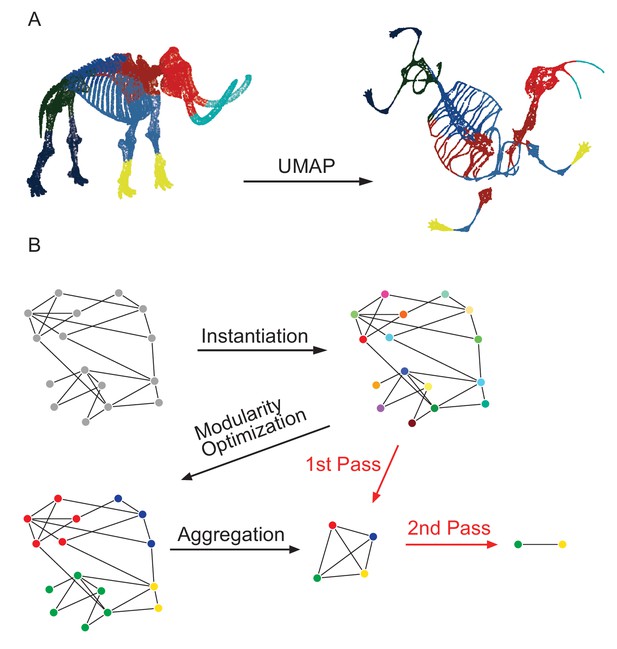
Diagrams of UMAP and Louvain community detection.
(A) A demonstration of UMAP projection on a 3D point cloud skeleton of a wooly mammoth. Local and global structures are incorporated and projected into lower dimension. This preservation of information is evident in the maintained structure of individual bone shapes and sensible spatial relationships between the body parts. Idea from M. Noichl (https://github.com/MNoichl/UMAP-examples-mammoth-; Noichl, 2019) and mammoth skeleton from the Smithsonian Institute’s Smithsonian 3D (https://3d.si.edu/). (B) The Louvain community detection algorithm is applied to weighted symmetric graphs and proceeds in three steps which are said to be one ‘pass’ of the algorithm: (1) each node is assigned to its own cluster; (2) each node is randomly moved into a neighboring cluster and if modularity increases, it becomes a member of that cluster; (3) once modularity no longer increases, each cluster is collapsed into one node. This process repeats for multiple passes until modularity no longer increases. The final cluster memberships are then passed back to the data points on the original graph.
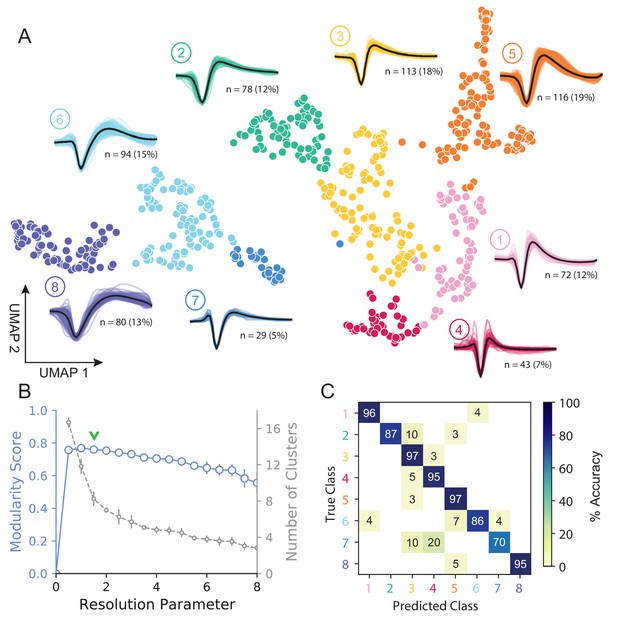
UMAP and Louvain clustering reveal a robust diversity of averaged single-unit waveform shapes.
(A) Scatter plot of normalized EAP waveforms in UMAP space colored by Louvain cluster membership. Adjacent to each numbered cluster (① through ⑧) is shown all member waveforms and the average waveform shape (in black). Each waveform is 1.6 ms. Percentages do not add to 100% due to rounding. (B) Louvain clustering resolution parameter versus modularity score (in blue, axis at left) and the number of clusters (communities) found (in gray, axis at right). This was averaged over 25 runs for WaveMAP using 25 random samples and seeds of 80% of the full dataset at each resolution parameter from 0 to 8 in 0.5 unit increments (a subset of the data was used to obtain error bars). Each data point is the mean ± S.D. with many S.D. bars smaller than the marker size. Green chevrons indicate the resolution parameter of 1.5 chosen and its position along both curves. (C) The confusion matrix of a gradient boosted decision tree classifier with 5-fold cross-validation and hyperparameter optimization. The main diagonal shows the held-out classification accuracy for each cluster and the off-diagonals show the misclassification rates for each cluster to each other cluster. The average accuracy across all clusters was 91%. Figure 3—figure supplement 1: A stability analysis of WaveMAP clustering showing solutions are stable with respect to random seed, random data subset, and in an ensembled version of Louvain. Figure 3—figure supplement 2: Different amplitude normalizations have similar effect but this processing is essential to WaveMAP extracting meaningful structure. Figure 3—figure supplement 3: Pre-processing waveform data with principal component analysis does not alter WaveMAP results.
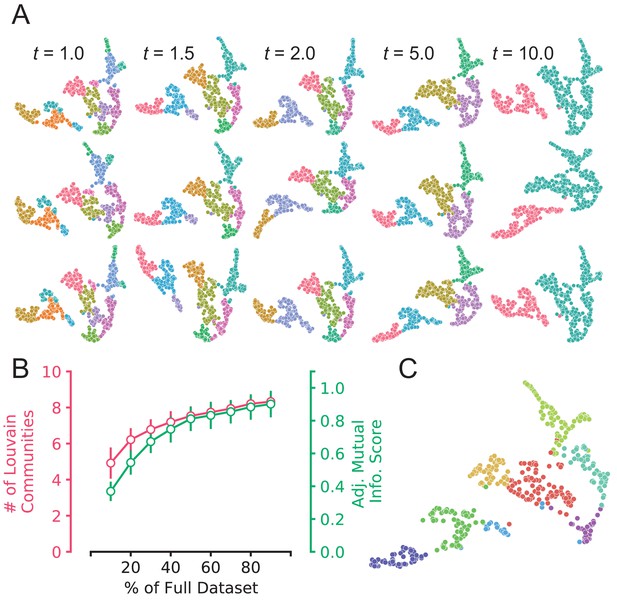
Stability analysis of WaveMAP: (A) WaveMAP instantiated with three different UMAP random seeds (each row is a different seed) and Louvain resolution parameters.
(B) The mean ± S.D. number of clusters (Louvain communities; in red) produced by WaveMAP and adjusted mutual information score (in green) across 100 random samples at various proportions of the full dataset. Number of clusters and adjusted mutual information (AMI) are omitted for 100% of the data because the number of clusters is equal to our result and thus AMI is 1.0 by definition of it being itself. (C) Ensemble clustering on graphs (ECG) is also applied to the UMAP graph. This also produced eight clusters.
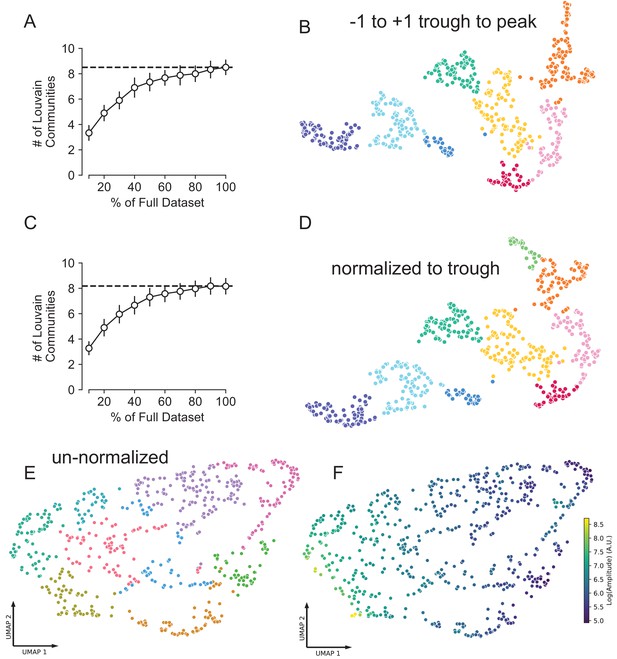
Different amplitude normalizations have similar effect but are essential for meaningful WaveMAP structure.
(A) As in Figure 3—figure supplement 1B, the number of Louvain communities found across various random subsets and random seeds. The mean number of clusters shown on the full dataset with a dashed line. (B) The WaveMAP clusters on waveforms with ±one trough to peak normalization (used in the paper). (C) The same random subsetting and random seed strategy in (A) applied to waveform data normalized to trough depth. (D) WaveMAP clusters applied to waveform data normalized to trough depth. (E) Un-normalized waveforms were passed through WaveMAP with the same parameters used previously. (F) Each waveform in the projected UMAP space found in (E) is colored according to the amplitude (log of the difference between maximum and minimum values).
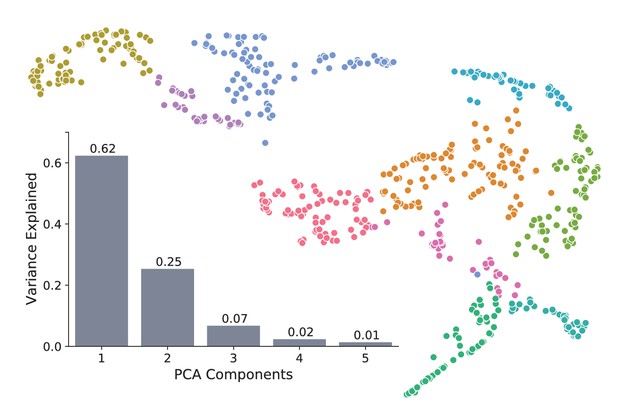
Pre-processing with PCA does not alter WaveMAP structure: the full dataset was pre-processed with principal component analysis (PCA) and projected into the space of the first three principal components.
The scree plot, with explained variance above each bar, shows that the dataset is low-dimensional with 94% of the variance explained in three components. The clustering on the right was produced by applying WaveMAP to the embedded dataset and is very similar to those produced by WaveMAP on data without pre-processing.
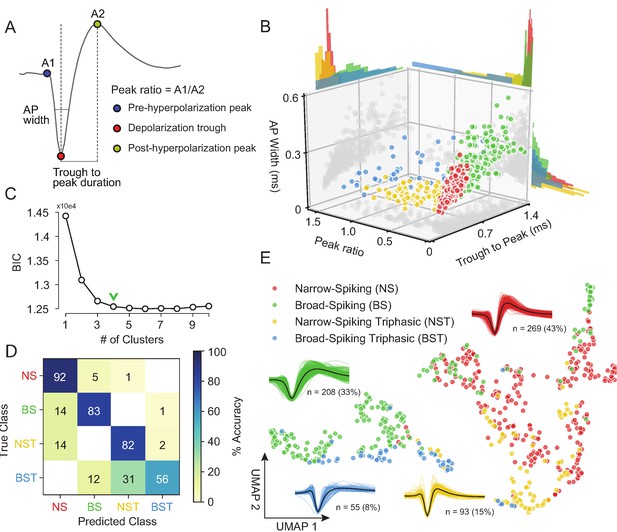
Gaussian mixture model clustering on specified features fails to capture the breadth of waveform diversity.
(A) The three EAP waveform landmarks used to generate the specified features passed to the GMM on a sample waveform.  is the pre-hyperpolarization peak (A1);
is the pre-hyperpolarization peak (A1);  is the depolarization trough; and
is the depolarization trough; and  is the post-hyperpolarization peak (A2). (B) A three-dimensional scatter plot with marginal distributions of waveforms and GMM classes on the three specified features in (A). Narrow-spiking (NS) are in red; broad-spiking (BS) in green; narrow-spiking triphasic (NST) in yellow; and broad-spiking triphasic (BST) types are in blue. Trough to peak was calculated as the time between
is the post-hyperpolarization peak (A2). (B) A three-dimensional scatter plot with marginal distributions of waveforms and GMM classes on the three specified features in (A). Narrow-spiking (NS) are in red; broad-spiking (BS) in green; narrow-spiking triphasic (NST) in yellow; and broad-spiking triphasic (BST) types are in blue. Trough to peak was calculated as the time between  and
and  ; peak ratio was determined as the ratio between the heights of
; peak ratio was determined as the ratio between the heights of  and
and  (A1/A2); and AP width was determined as the width of the depolarization trough
(A1/A2); and AP width was determined as the width of the depolarization trough  using the MLIB toolbox (Stuttgen, 2019). (C) The optimal cluster number in the three-dimensional feature space in (B) was determined to be four clusters using the Bayesian information criterion (BIC) (Trainito et al., 2019). The number of clusters was chosen to be at the ‘elbow’ of the BIC curve (green chevron). (D) A confusion matrix for a gradient boosted decision tree classifier with 5-fold cross-validation with hyperparameter optimization. The main diagonal contains the classification accuracy percentages across the four GMM clusters and the off-diagonal contains the misclassification rates. The average accuracy across classes was 78%. (E) The same scatter plot of normalized EAP waveforms in UMAP space as in Figure 3A but now colored by GMM category. Figure 4—figure supplement 1: We show that WaveMAP clusterings are more consistent across random data subsets than either DBSCAN on t-SNE or a GMM on PCA. Figure 4—figure supplement 2: GMMs fail to full capture the latent structure in the waveforms.
using the MLIB toolbox (Stuttgen, 2019). (C) The optimal cluster number in the three-dimensional feature space in (B) was determined to be four clusters using the Bayesian information criterion (BIC) (Trainito et al., 2019). The number of clusters was chosen to be at the ‘elbow’ of the BIC curve (green chevron). (D) A confusion matrix for a gradient boosted decision tree classifier with 5-fold cross-validation with hyperparameter optimization. The main diagonal contains the classification accuracy percentages across the four GMM clusters and the off-diagonal contains the misclassification rates. The average accuracy across classes was 78%. (E) The same scatter plot of normalized EAP waveforms in UMAP space as in Figure 3A but now colored by GMM category. Figure 4—figure supplement 1: We show that WaveMAP clusterings are more consistent across random data subsets than either DBSCAN on t-SNE or a GMM on PCA. Figure 4—figure supplement 2: GMMs fail to full capture the latent structure in the waveforms.

WaveMAP clusterings are more consistent than either DBSCAN on t-SNE or a GMM on PCA.
(A) At top, DBSCAN (eps = 3, n_neighbors = 15) was applied to t-SNE’s projected space (perplexity = 30) over the full dataset producing 10 clusters. Parameters were chosen to produce similar structure to WaveMAP to facilitate comparison. At bottom, a Gaussian mixture model (n_components = 4, replicates = 25) is applied to the three-dimensional projected space (94% variance explained) produced by the first three principal components of the full dataset (GMM on PCA). The number of clusters chosen was by selecting the value at the elbow (green arrow) of a BIC ± S.D. vs. number of clusters plot shown in the inset. (B) Adjusted mutual information scores (AMI; mean ± S.E.M.) for 100 random sample clusterings of both WaveMAP, DBSCAN on t-SNE, and GMM on PCA. Standard error of the mean bars are smaller than marker size. The AMI was calculated by constructing a ‘reference’ clustering by applying the respective method to the full dataset and then compared to the clusterings produced by random subsamples. (C) A jittered strip plot showing the AMI for 100 random subsets using each method. Subsets were randomly sampled from 40% (left) and 90% (right) of the full dataset. Gray boxes correspond to the data points surrounded by gray boxes in (B).
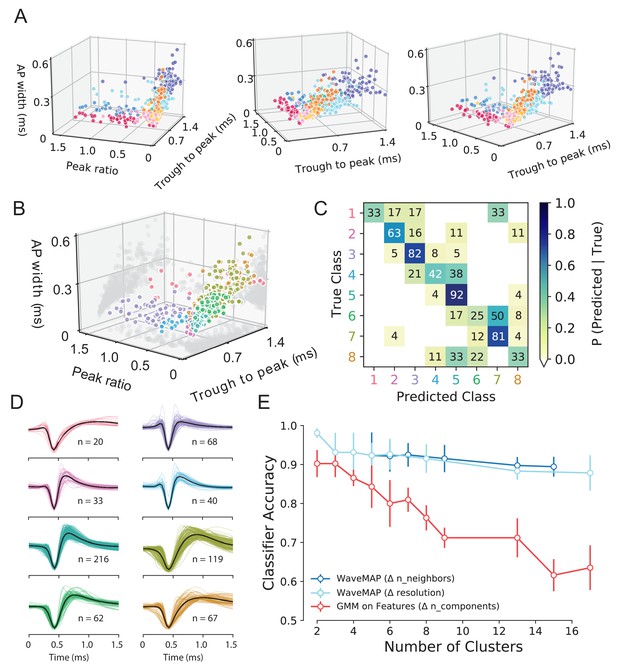
Comparison of GMM and UMAP in the constructed feature space.
(A) Three views of the eight WaveMAP clusters shown in the constructed feature space. The clusters maintain some structure but are largely mixed and linearly inseparable. (B) A GMM instantiated with eight clusters in the constructed feature space of Figure 4B. (C) Confusion matrix for a gradient boosted decision tree classifier with the same hyperparameters as the one trained on four GMM classes (see hyperparameters in Table 1). Numbers listed are in percent accuracy on the main diagonal and misclassification rate percentage on the off-diagonals against held-out data. (D) Each cluster of waveforms in the eight class GMM with average waveforms in black. (E) Both WaveMAP and a GMM on features were used on the full dataset to generate results of various cluster number and a gradient boosted decision tree (hyperparameters optimized to the four-class GMM) was trained on each. Shown is the classifier accuracy (mean ± S.D.) across stratified k-folds (k = 5) and various cluster number from 2 to 16. In dark blue, we generated WaveMAP mappings of different cluster number by changing the n_neighbors parameter associated with UMAP; in light blue, we generated WaveMAP mappings of various cluster number by changing resolution associated with Louvain. In red, we changed the n_components for the Gaussian mixture model.

WaveMAP provides interpretable representations that both validate and extend known and unknown features importances.
(A) WaveMAP applied to the EAP’s as in Figure 3A but overlaid with a grid of test points (black x’s, top) spanning the embedded space. At bottom, the inverse UMAP transform is used to show the predicted waveform at each test point. For each x above, the predicted waveform is shown, plotted, and assigned the color of the nearest cluster or in gray if no cluster is nearby. Note that there exists instability in the waveform shape (see waveforms at corners) as test points leave the learned embedded space. (B) The mean absolute SHAP values for 10 time points along all waveforms subdivided according to the SHAP values contributed by each WaveMAP cluster. These SHAP values were informed by applying path-dependent TreeSHAP to a gradient boosted decision tree classifier trained on the waveforms with the WaveMAP clusters as labels. In the inset, all waveforms are shown and in gold are shown the time points for which the SHAP values are shown on the left. Each vertical line is such that the most opaque line contains the greatest SHAP value across WaveMAP clusters; the least opaque, the smallest SHAP value. (C) Each averaged WaveMAP waveform cluster is shown with the three time points containing the greatest SHAP values for each cluster individually. As before, the SHAP value at each time point is proportional to the opacity of the gray vertical line also shown as a bar graph at left. Figure 5—figure supplement 1: WaveMAP implicitly captures waveform features (such as trough to peak or AP width) without the need for prior specification.
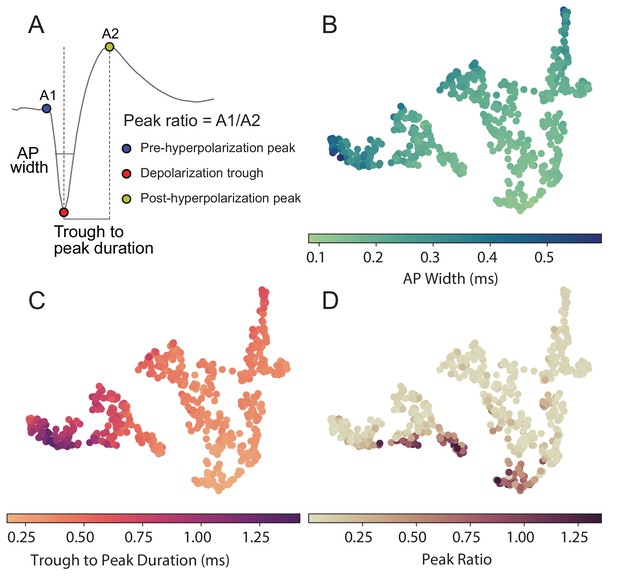
WaveMAP implicitly captures waveform features without the need for specification.
(A) Three waveform shape features used in traditional clustering approaches. The three EAP waveform landmarks used to generate the specified features passed to the GMM on a sample waveform.
 is the pre-hyperpolarization peak (A1);
is the pre-hyperpolarization peak (A1);  is the depolarization trough; and
is the depolarization trough; and  is the post-hyperpolarization peak (A2). AP width is the distance in time between the falling and rising phase of the depolarization trough at its full-width half minimum. The trough to peak duration is the distance between the minimum of the depolarization trough and the peak of the post-hyperpolarization peak. The peak ratio is the height (above zero) of the pre-hyperpolarization peak over the height (again, above zero) of the post-hyperpolarization peak. The same diagram as in Figure 4A but repeated here. (B, C, D) The waveform data points in the projected UMAP space and color coded according to their AP width, trough to peak duration, and peak ratio, respectively.
is the post-hyperpolarization peak (A2). AP width is the distance in time between the falling and rising phase of the depolarization trough at its full-width half minimum. The trough to peak duration is the distance between the minimum of the depolarization trough and the peak of the post-hyperpolarization peak. The peak ratio is the height (above zero) of the pre-hyperpolarization peak over the height (again, above zero) of the post-hyperpolarization peak. The same diagram as in Figure 4A but repeated here. (B, C, D) The waveform data points in the projected UMAP space and color coded according to their AP width, trough to peak duration, and peak ratio, respectively.
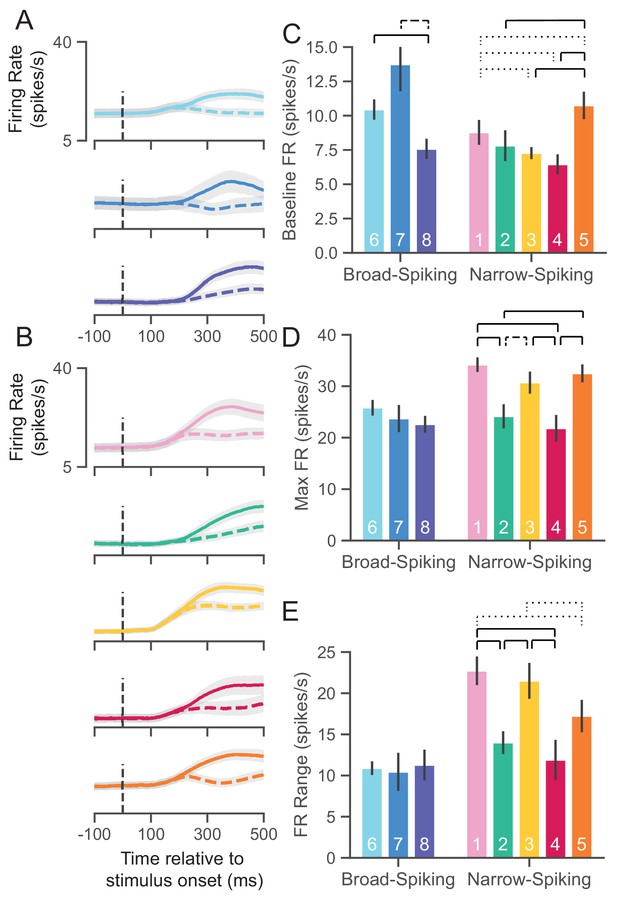
UMAP clusters exhibit distinct physiological properties.
(A) Stimulus-aligned trial-averaged firing rate (FR; spikes/s) activity in PMd for broad-spiking WaveMAP clusters. The traces shown are separated into trials for PREF direction reaches (solid traces) and NONPREF direction reaches (dashed traces) and across the corresponding WaveMAP clusters. Shaded regions correspond to bootstrapped standard error of the mean. Dashed vertical line is stimulus-onset time. (B) The same plots as in (A) but for narrow-spiking WaveMAP clusters. (C) Baseline median FR ± S.E.M. for the neurons in the eight different classes. Baselines were taken as the average FR from 200 ms of recording before checkerboard stimulus onset. (D) Median maximum FR ± S.E.M. for the neurons in the eight different clusters. This was calculated by taking the median of the maximum FR for each neuron across the entire trial. (E) Median FR range ± S.E.M. calculated as the median difference, per neuron, between its baseline and max FR. ---- p < 0.05; ---- p < 0.01; ---- p < 0.005; Mann-Whitney U test, FDR adjusted. Figure 6—figure supplement 1: GMM clusters are less physiologically distinguishable than WaveMAP clusters.
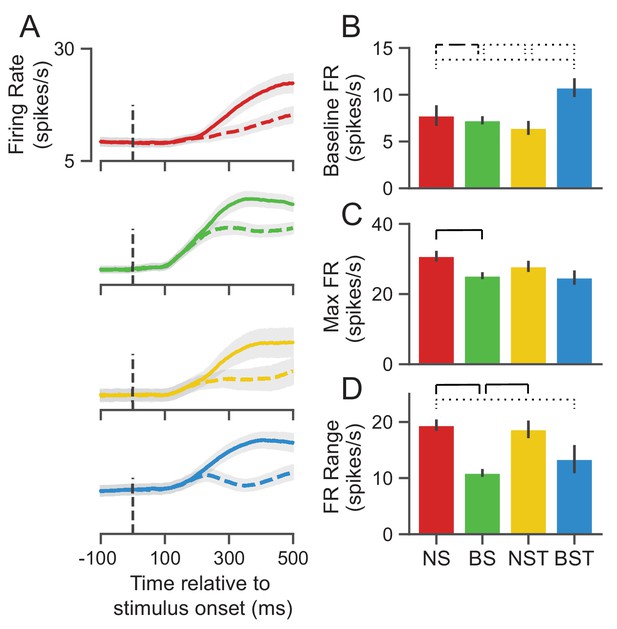
GMM clusters are less physiologically distinguishable than WaveMAP clusters.
(A) Stimulus-aligned trial-averaged firing rate activity in PMd for GMM clusters. As in Figure 6, the traces are separated into PREF and NONPREF trials with solid and dashed lines respectively. Shaded regions correspond to bootstrapped standard error of the mean (S.E.M.). The dashed vertical line denotes the stimulus-onset time. (B) Baseline median firing rates (FR) ± S.E.M. for the four GMM clusters. Baselines were calculated as the average firing rate during the first 200 ms of the trial. (C) Median maximum FRs ± S.E.M. for the neurons in the four GMM clusters. This was caculated by taking the median of the maximum FR for each neuron across the entire trial. (D) Median FR range ± S.E.M. calculated as the median difference, per neuron, between its baseline and max FR. ---- p < 0.05; ---- p < 0.01;—— p < 0.005; Mann-Whitney U test, FDR adjusted.
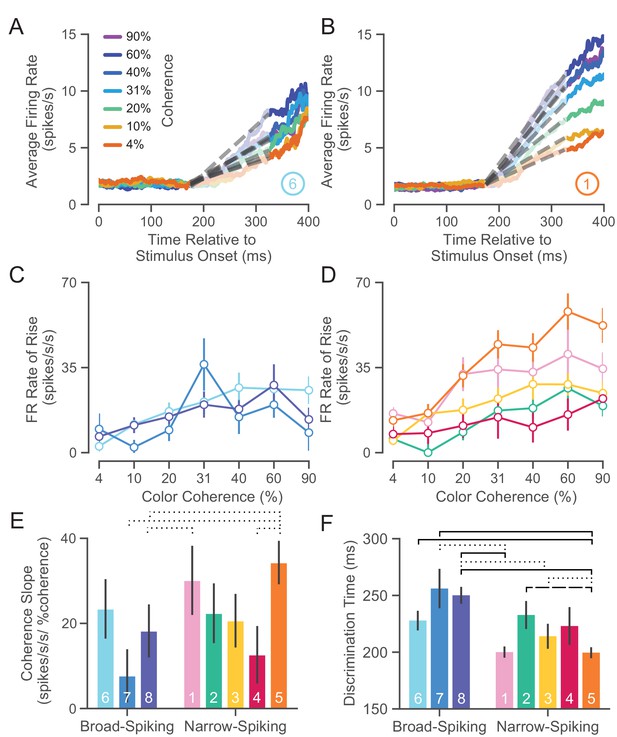
UMAP clusters exhibit distinct functional properties.
(A) Average firing rate (FR) over time for ⑥ (used as a sample broad-spiking cluster) across trials of different color coherences. The gray-dashed lines indicate the linear regression lines used to calculate the FR rate of rise. (B) Average FR over time for ① (used as a sample narrow-spiking cluster) across different color coherences. (C) FR rate of rise vs. color coherence for broad- and (D) narrow-spiking clusters. Error bars correspond to standard error of the mean across trials. (E) Bootstrapped median color coherence slope is shown with the bootstrapped standard error of the median for each cluster on a per-neuron basis. Coherence slope is a linear regression of the cluster-specific lines in the previous plots C and D. (F) Median bootstrapped discrimination time for each cluster with error bars as the bootstrapped standard error of the median. Discrimination time was calculated as the the amount of time after checkerboard appearance at which the choice-selective signal could be differentiated from the baseline FR (Chandrasekaran et al., 2017). dotted line p < 0.05; dashed line p < 0.01; solid line p < 0.005; Mann-Whitney U test, FDR adjusted.
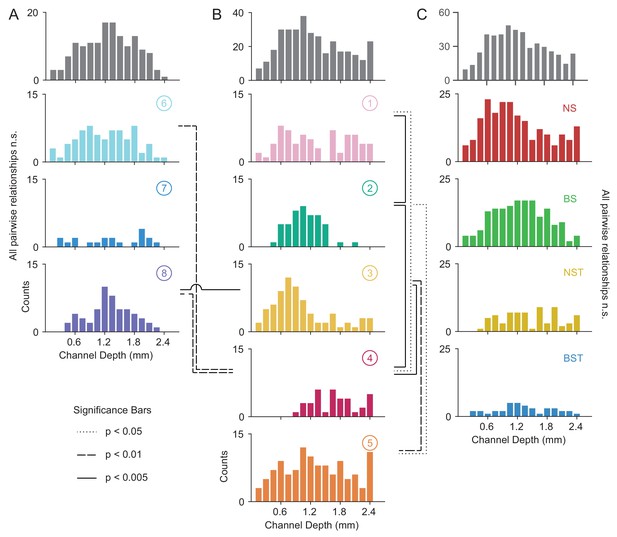
Laminar distribution of WaveMAP waveform clusters.
(A, B) The overall histogram for the broad- and narrow-spiking waveform clusters are shown at top across cortical depths on the left and right respectively (in gray); below are shown histograms for their constituent WaveMAP clusters. These waveforms are shown sorted by the cortical depth at which they were recorded from the (0.0 mm [presumptive pial surface] to 2.4 mm in 0.15 mm increments). Broad-spiking clusters were generally centered around middle layers and were less distinct in their differences in laminar distribution. Narrow-spiking clusters are shown on the right and were varied in their distribution with almost every cluster significantly varying in laminar distribution from every other. (C) Depth histograms for all waveforms collected (top, in gray) and every GMM cluster (below). dotted line p < 0.05; dashed line p < 0.01; solid line p < 0.005; two-sample Kolmogorov-Smirnov Test, FDR adjusted. Figure 8—figure supplement 1: Composite figure showing each WaveMAP cluster with waveform, physiological, functional, and laminar distribution properties.
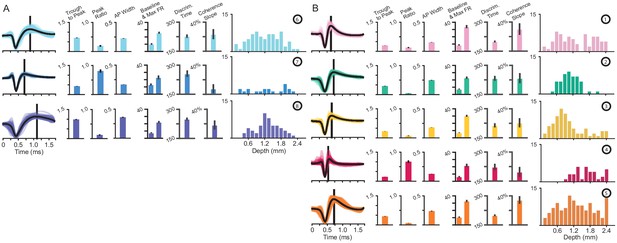
Detailed summary of each UMAP cluster and features.
(A, B) A detailed summary of broad- (A) and narrow-spiking (B) cluster waveform shapes, physiological measures, and laminar distribution. Each waveform shape is shown at left with the average waveform shown as a black trace. The average post-hyperpolarization peak position is shown with a black line. The three waveform features used in the GMM classification (Figure 4A) are shown in the middle as the mean ± S.E. The baseline and max FR for each cluster are subsequently shown in spikes/s (median ± bootstrap S.E.). Functional properties, discrimination time and coherence slope, are shown in milliseconds and spikes/s/s/% coherence (both shown in median ± bootstrap S.E.). Laminar distributions are also shown with each column in the histogram being the number of each waveform found at each channel location. Channels are spaced every 0.15 mm apart from 0.0 to 2.4 mm.

Anatomical labeling of three inhibitory interneuron types in PMd.
(A) Sample maximum intensity projection of immunohistological (IHC) staining of rostral PMd calbindin-positive (CB+) interneurons in blue. Note the many weakly-positive excitatory pyramidal neurons (arrows) in contrast to the strongly-positive interneurons (arrowheads). Only the interneurons were considered in stereological counting. In addition, only around first 1.5 mm of tissue is shown (top of layer V) but the full tissue area was counted down to the 2.4 mm (approximately the top of white matter). Layer IV exists as a thin layer in this area. Layer divisions were estimated based on depth and referencing Arikuni et al., 1988 (Arikuni et al., 1988). (B) Sample maximum intensity projection of IHC staining of PMd calretinin-positive (CR+) and parvalbumin-positive (PV+) interneurons in yellow and fuschia respectively. The same depth of tissue and layer delineations were used as in (A). (C, D, E) Stereological manual counts (Schmitz et al., 2014) (mean ± S.D.) of CB+, CR+, PV+ cells in PMd, respectively. Counts were collected from six specimens, each with all three IHC stains, and with counts normalized to each sample. Source files for this figure are available on Dryad (https://doi.org/10.5061/dryad.z612jm6cf).
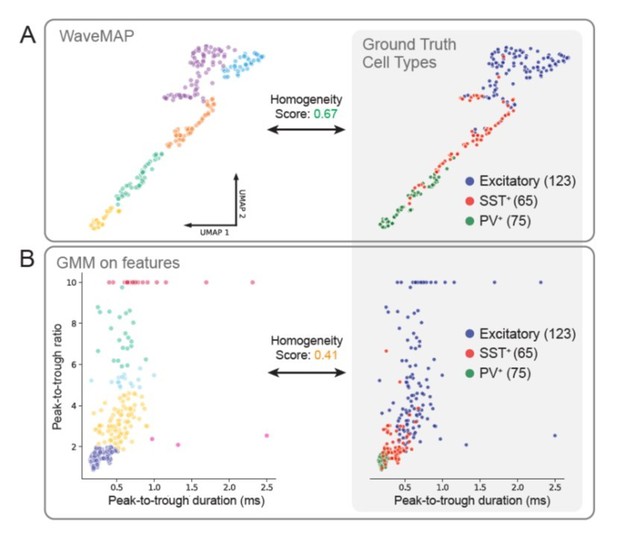
WaveMAP clusters align closer to ground truth cell types than GMM on features.
(A) At left, WaveMAP was applied to juxtacelluar waveforms of known cell type (Yu et al., 2019) withthe same parameters as in the manuscript. Cell types were identified through optogenetic-tagging and histochemical verification. At right, the ground truth cell types are displayed in the UMAP projected space. Homogeneity score for WaveMAP was 0.67. (B) At left, a Gaussian mixture model is applied in the feature space that appears in Figure 1D of (Yu et al., 2019); VIP-positive neurons were excluded for relatively lowcounts (n = 8) and some excitatory cells with very large peak-to-trough ratio were capped at a value of 10. At right, the ground truth cell types are shown in the feature space. Homogeneity score for the GMM on features was 0.41.
Tables
Non-default model hyperparameters used.
| Function | Function name | Parameters | Value |
|---|---|---|---|
| UMAP Algorithm (Python) | umap.UMAP | n_neighbors min_dist random_state metric | 20 0.1 42 ’euclidean’ |
| Louvain Clustering (Python) | cylouvain.best_partition | resolution | 1.5 |
| UMAP Gradient Boosted Decision Tree (Python) | xgboost.XGBClassifier | max_depth min_child_weight n_estimators learning_rate objective rand_state | 4 2.5 100 0.3 ’multi:softmax’ 42 |
| GMM Gradient Boosted Decision Tree (Python) | xgboost.XGBClassifier | max_depth min_child_weight n_estimators learning_rate objective seed | 10 2.5 110 0.05 ’multi:softmax’ 42 |
| 8-Class GMM Gradient Boosted Decision Tree (Python) | xgboost.XGBClassifier | max_depth min_child_weight n_estimators learning_rate objective seed | 2 1.5 100 0.3 ’multi:softmax’ 42 |
| Gaussian Mixture Model (MATLAB) | fitgmdist | k start replicates statset(’MaxIter’) | 4 ’randsample’ 50 200 |
| DBSCAN (Python) | sklearn.cluster.DBSCAN | eps min_samples | 3 15 |
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Primary antibody | Rabbit anti-calbindin D-28k (polyclonal) | Swant | Cat#: CB38 RRID:AB_10000340 | 1:2000 dilution |
| Primary antibody | Rabbit anti-calretinin D-28k (polyclonal) | Swant | Cat#: 7697 RRID:AB_2619710 | 1:2000 dilution |
| Primary antibody | Guinea pig anti-parvalbumin (polyclonal) | Swant | Cat#: GP72 RRID:AB_2665495 | 1:2000 dilution |
| Secondary antibody | Donkey anti-rabbit Alexa 546 | ThermoFisher | Cat#: A10040 RRID:AB_2534016 | 1:200 dilution |
| Secondary antibody | Donkey anti-guinea pig Alexa 546 | Jackson | Cat#: 706-545-148 RRID:AB_2340472 | 1:200 dilution |
Additional files
-
Source code 1
MATLAB code and Python notebook for replicating all figures and figure supplements in the manuscript.
- https://cdn.elifesciences.org/articles/67490/elife-67490-code1-v4.zip
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/67490/elife-67490-transrepform-v4.docx





