A coupled mechano-biochemical model for cell polarity guided anisotropic root growth
- Centro de Biotecnología y Genómica de Plantas, Universidad Politécnica de Madrid (UPM)—Instituto Nacional de Investigación y Tecnología Agraria y Alimentaria (INIA), Spain
- Institute of Science and Technology (IST), Austria
Figures
Figure 1 with 5 supplements
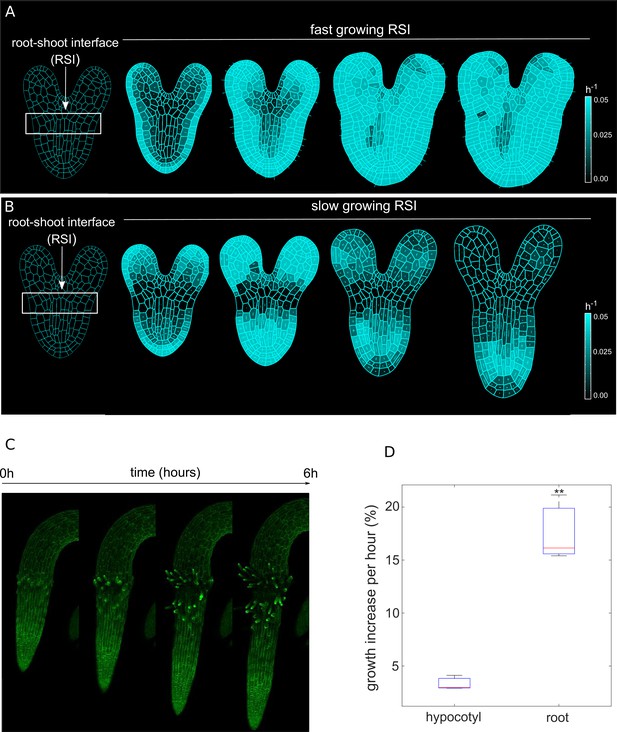
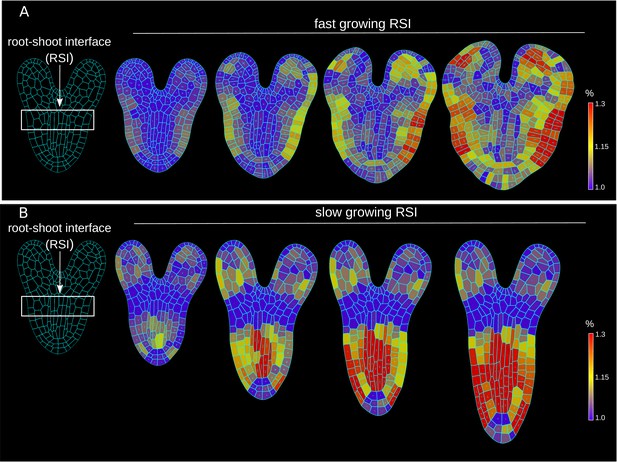
Differential cell growth at the RSI produces the emergent anisotropic expansion of the root.
(A, B) Simulated root growth mechanics with uniform growth rates at the RSI (A). The RSI and the root are allowed to grow at the same rate, producing an isotropic growth pattern. (B) Simulated root outgrowth by assuming differential growth rate at the RSI. The root grows anisotropically since the growing cell deformation causes the gradual AF stabilization orthogonal to this deformation. All the cells are allowed to grow at the same rate (purely mechanical model). Simulations have been run for 300 time steps. The white lines represent the principal directions of growth. (C) Screenshots from time-lapse imaging of growing radicle with PIP-GFP plasma membrane marker (Zhu et al., 2019) for a total time of 6 hr (six time points). (D) Size increase per hour (in %) for adjacent organs radicle (root) and hypocotyl quantified from the time-lapse confocal imaging of three independent plants (n = 3). **p-value = 0.0015 a one-way ANOVA with post-hoc Tukey’s HSD.
-
Figure 1—source data 1
Source data used to generate Figure 1D.
- https://cdn.elifesciences.org/articles/72132/elife-72132-fig1-data1-v2.xlsx
Figure 1—figure supplement 1
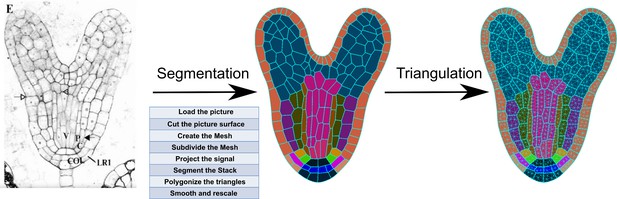
Overview of schematic procedure for the segmentation of microscopy images of an A.
thaliana embryo into a detailed mesh using MorphoGraphX.
Figure 1—figure supplement 2
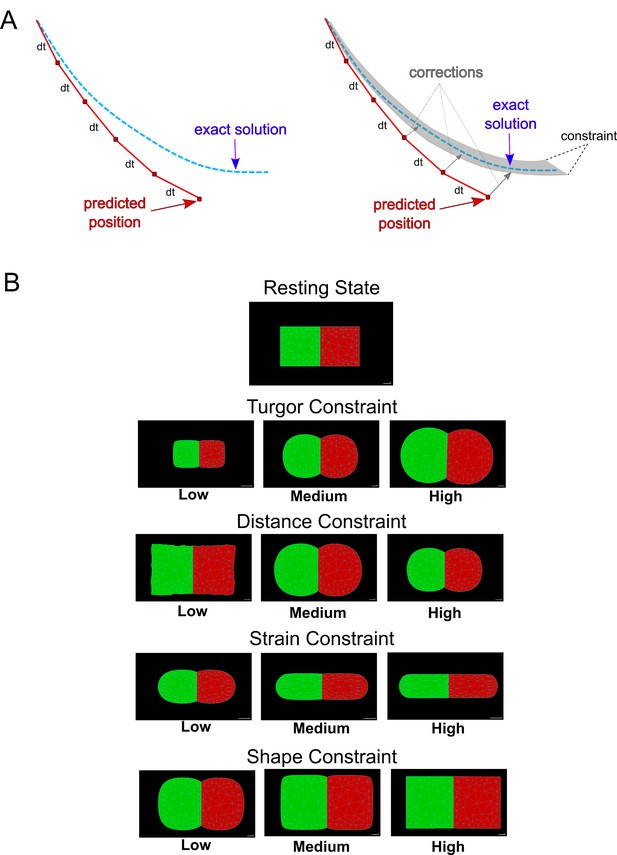
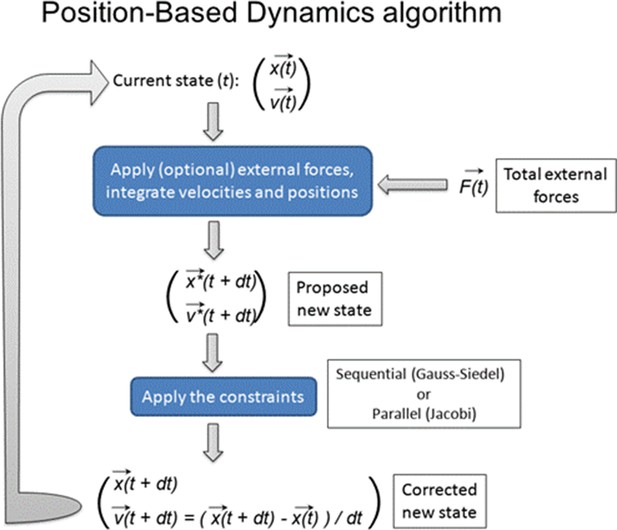
Position-Based Dynamics schematics (A) Comparison between force-based methods (left panel) and PBD (right panel).
In contrast to the typical force-based methods, PBD skips the velocity layer and calculates an object’s positions according to the set of constraints. (B) Schematic examples of PBD constraints. A simple template comprising two square-shaped triangulated cells: simulations demonstrate the effect of projecting each of the PBD constraints onto the cellular mesh.
Figure 1—figure supplement 3
Effect of differential cell growth at the RSI on emergent cell growth anisotropy.
(A, B) (A) Simulated root outgrowth with uniform growth rates at the RSI. (B) Simulated root outgrowth by assuming differential growth rates at the RSI. Cell coloring indicates the AF strength. In both simulations, the chemical effect of auxin on cell growth is not included and all the cells are allowed to grow at the same rate. The simulation has been run for 300-time steps. The white lines represent the principal directions of growth.
Figure 1—figure supplement 4
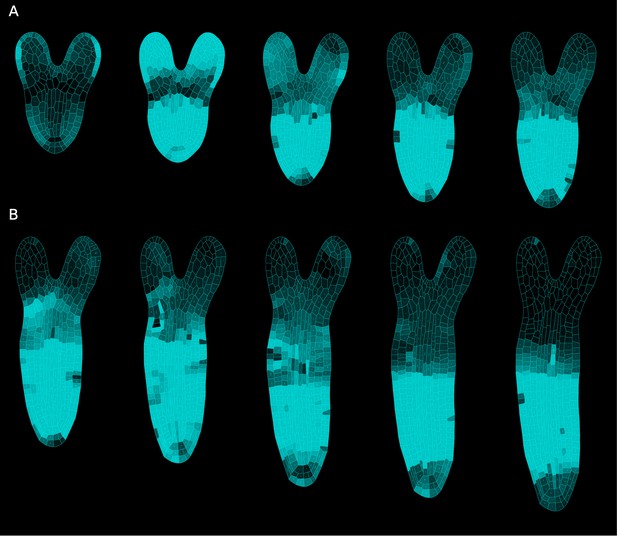
Testing the robustness of the proposed symmetry-breaking model by removing the differential growth between tissues later during the simulation.
(A) Reference root growth simulation as described in Figure 1A. (B) Subsequent steps of the simulation are shown in (A) after the gradual introduction of uniform growth at the RSI. Anisotropy is maintained even after the differential cell growth assumption is relaxed.
Figure 1—video 1
Differential cell growth at the embryo RSI produces anisotropic expansion of the root - movie related to Figure 1.
The left section displays the root development with uniform growth at RSI. The right section shows simulated root outgrowth by assuming a differential growth rate at the RSI.
Figure 2 with 9 supplements
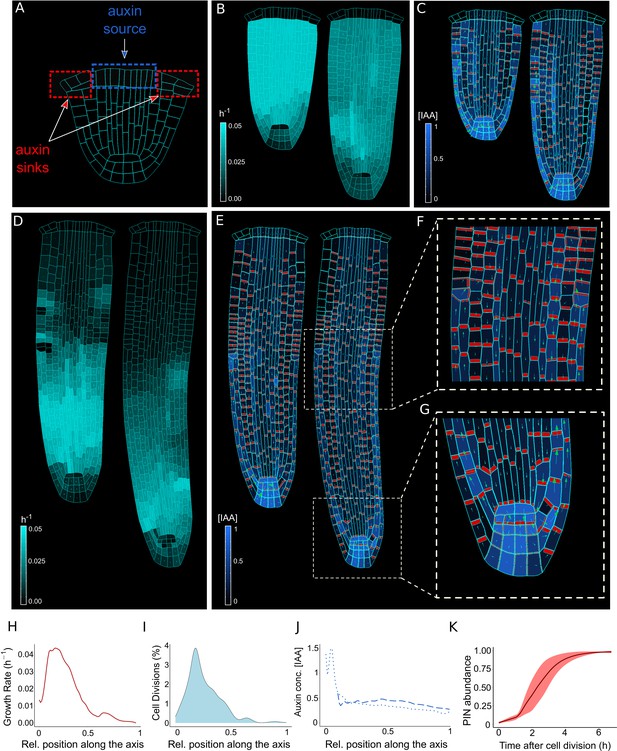
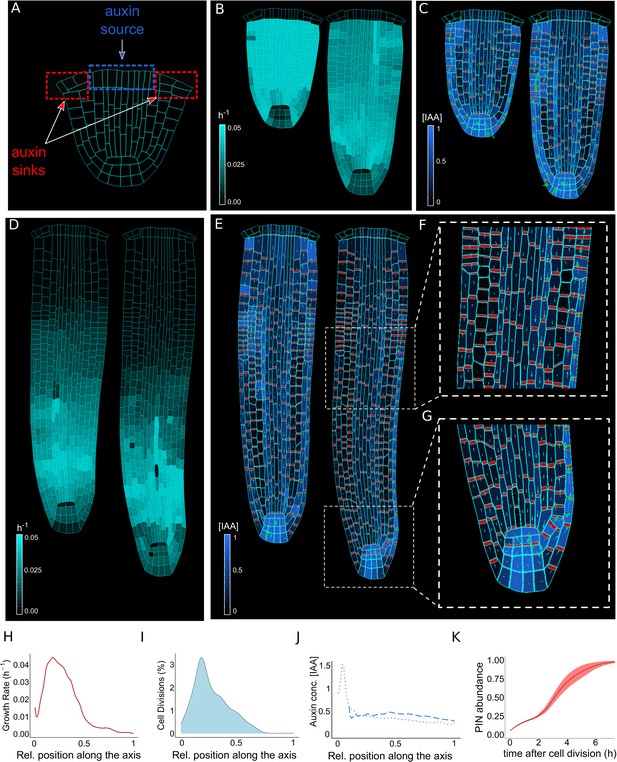
The model reproduces realistic root meristem geometry, auxin distribution, and PINs polar localizations using auxin flux scenario.
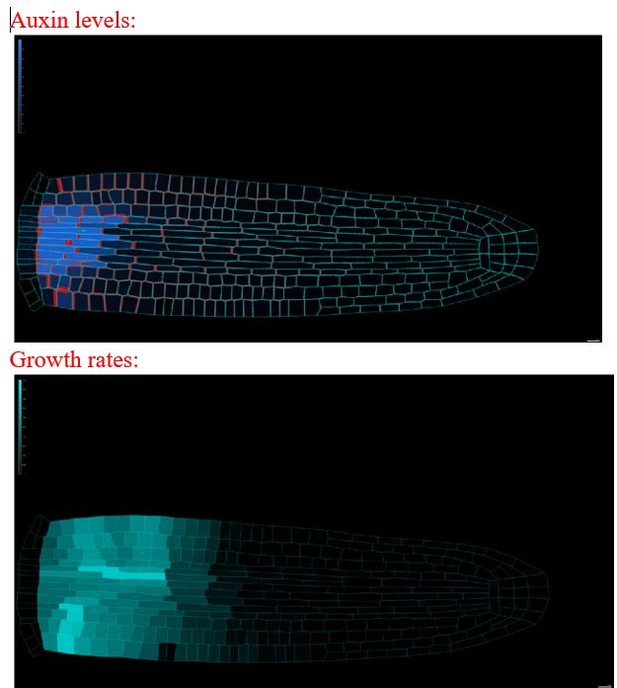
(A) Initial embryonic set point. Locations of auxin influx (auxin source, blue) and evacuation (auxin sinks, red) from the embryo are shown. (B, D) Model simulations predict a time evolution of cell growth rates (bright cyan color) and principal growth directions (white lines). Ongoing cell division events are marked by black regions. (C, E) Dynamics of auxin distribution (blue color), auxin flow direction (arrows,) and PIN localizations (red). (F, G) Zoom on basal meristem (F) and root apical meristem (G). The model correctly reproduces very detailed PINs localizations including bipolar PIN2 localization in the cortex (F). (H–J) Profiles of average values of interest across all cell files along the longitudinal axis. (H) Growth rate profile along the root axis. The fastest-growing region is located in the apical meristem as observed experimentally (Bassel et al., 2014). (I) Cell division frequencies along the root axis. The majority of cell divisions occur in the apical meristem. (J) Auxin concentration in the vascular tissues (dashed blue line) and auxin concentration in the non-vascular tissues (external tissues and the root tip, dotted blue line) along the root axis. Most of the auxin is concentrated in the root tip as observed in experiments (Overvoorde et al., 2010). Time-lapse profile of PINs re-localization on the membranes after cell division event. PINs re-localization is completed in approximately 5–6 hr after cell division (Glanc et al., 2018). All simulations have been run until 1500 time steps were reached.
-
Figure 2—source data 1
Source data used to generate Figure 2H-K.
- https://cdn.elifesciences.org/articles/72132/elife-72132-fig2-data1-v2.xlsx
Figure 2—figure supplement 1
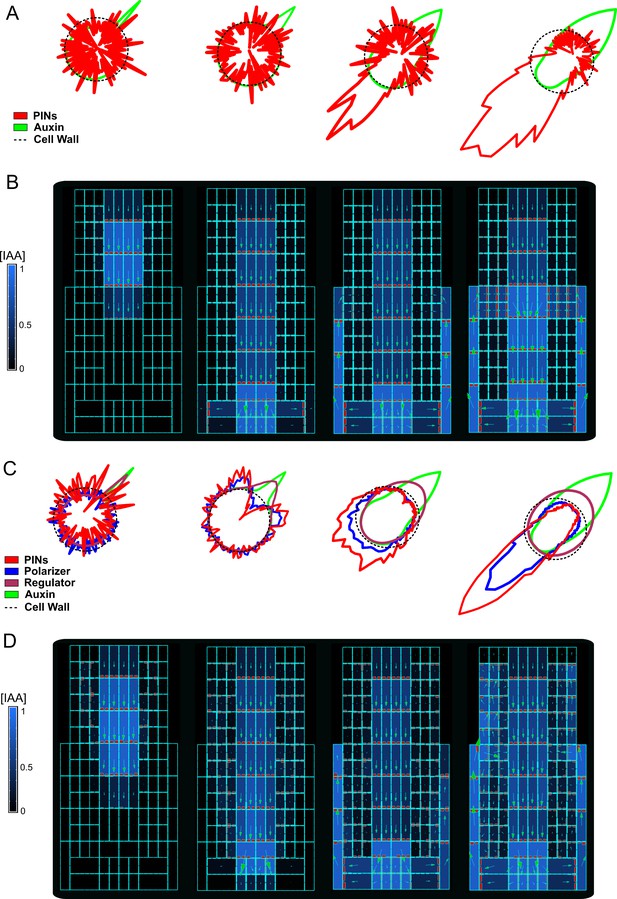
Comparison between ‘auxin-flux’ and ‘regulator-polarizer’ models for PIN polarization.
(A) Single-cell model simulation of the ‘auxin-flux’ model. In this simple single-cell model, there are only two species of molecules: auxin (light green line) and PINs (red line). The auxin-flux model follows a simple rule: auxin application on one side of the cell wall (dotted line) induces PINs polarization on the other side of the cell. (B) Model simulation using the ‘auxin-flux’ model (A) on a simplified root-like grid structure. The ‘auxin-flux’ method is capable of producing a realistic auxin flow inside the grid. Auxin was initially applied to the central cells of the top layer of the grid. (C) Single-cell model simulation of the ‘regulator-polarizer’ method. This model represents a molecular expansion of the ‘auxin-flux’ model (A). This model includes four molecular species: auxin (light green line), PINs (red line), a regulator (dark green line), and a polarizer (blue line). Auxin application on one side of the cell wall (dotted line) induces recruitment of regulators proteins which inhibits the PIN polarizer pushing it towards the opposite side of the cell surface. The polarizer in turn fosters the recruitment of PINs molecules on that side of the cell. (D) Model simulation with the ‘regulator-polarizer’ method (C) on a simplified root-like grid structure. The ‘regulator-polarizer’ model was capable of producing an auxin flow inside the root. Auxin was initially applied to the central cells of the top layer of the grid.
Figure 2—figure supplement 2
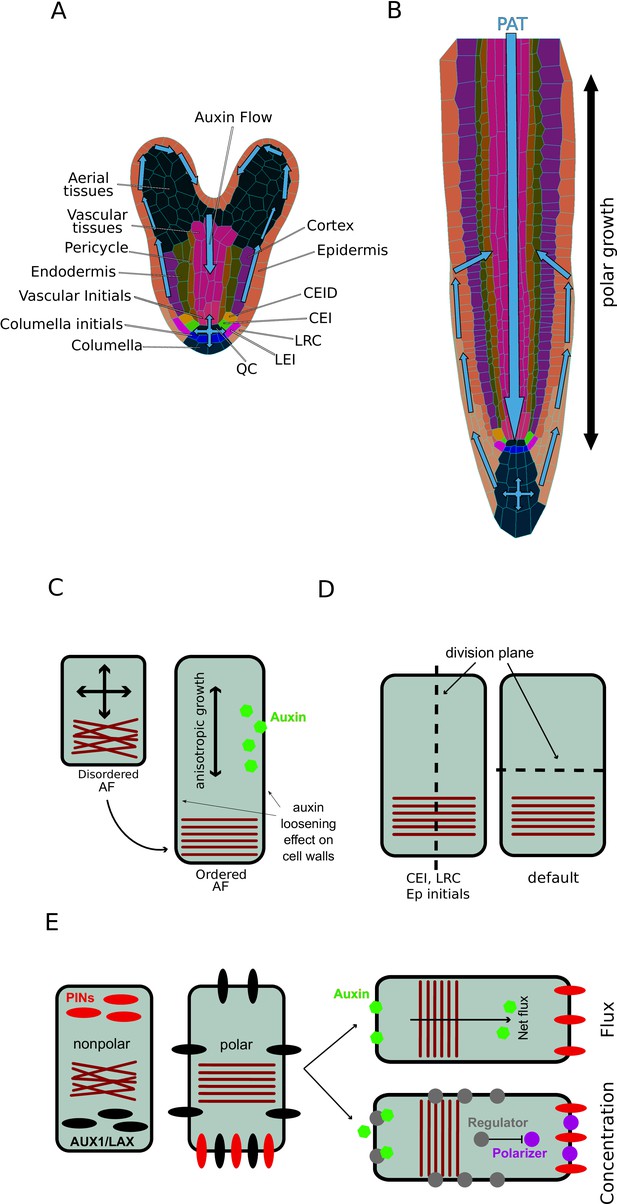
Model schematics.
(A) Digitized microscopy image of an A. thaliana heart-stage embryo processed through MorphoGraphX (Barbier de Reuille et al., 2015). Cell types are shown with different colors, while predicted auxin flow direction is depicted with the arrow. (B) Schematics of a mature A. thaliana root. The direction of auxin transport is visualized with blue arrows. Growth anisotropy is depicted with a bidirectional black arrow. (C) Cells are under constant internal turgor pressure. Auxin induces cell walls relaxation and allows cell expansion. Mechanical deformation(strain) imposed on root cell walls forces the reorganization of the anisotropy factor (AF), which in turn maintains the anisotropic growth. (D) Cell division occurs according to the cell polarity defined by the AF vector. Cell division plane is orthogonal to cell polarity; exceptions to this rule are cortex/endodermis and LRC/epidermis initials. (E) PINs localization is defined by AF orientation and auxin flux direction. Auxin feedback on PINs localization is determined by two equivalent mechanisms; the total auxin flux through the plasma membrane (the ‘auxin-flux’ model) or inhibition of PIN polarizer (e.g. kinase) through an auxin-driven regulator (e.g. phosphatase) (the ‘regulator-polarizer’ model).
Figure 2—figure supplement 3
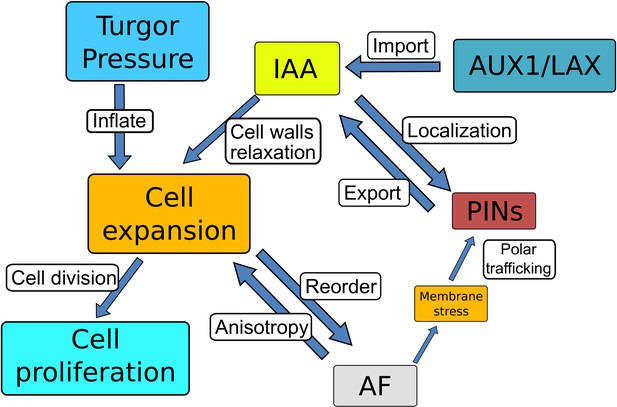
Schematic diagram of the root model.
The diagram shows the main components of the current model and their connections: The turgor pressure forces isotropic cell expansion driven by cell wall relaxation induced by intracellular auxin. Cell expansion causes mechanical deformation of the cell walls that triggers anisotropy factor (AF) reorganization. AF restricts cell expansion along the axis, producing anisotropic growth. Cells divide once the cell area has reached a specific threshold. AF alignment maintains PIN polarity (i.e. by causing the membrane bending stress), reinforcing the auxin-dependent PINs polarization. Polar PINs efflux carriers and non-polar AUX/LAX influx carriers mediate the auxin distribution along the root.
Figure 2—figure supplement 4
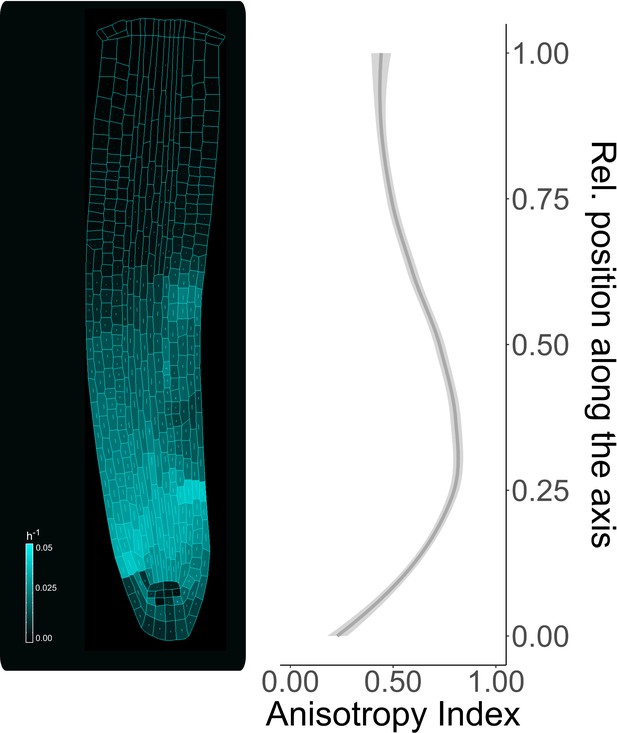
Anisotropy index measured along the proximo-distal axis.
Individual cells growth rate during model simulation (left figure) and anisotropy index along the root axis (right plot). The anisotropy index has been calculated as the ratio of growth directions. A high anisotropy index indicates a greater tendency of the cell for the anisotropic growth, in contrast to a lower index which denotes a cell tendency toward isotropic growth. The simulation has been run for 1500 time steps.
-
Figure 2—figure supplement 4—source data 1
Source data used to generate Figure 2—figure supplement 4.
- https://cdn.elifesciences.org/articles/72132/elife-72132-fig2-figsupp4-data1-v2.xlsx
Figure 2—figure supplement 5
The model can reproduce realistic root meristem geometry, auxin distribution, and PINs localization using the ‘regulator-polarizer’ model scheme.
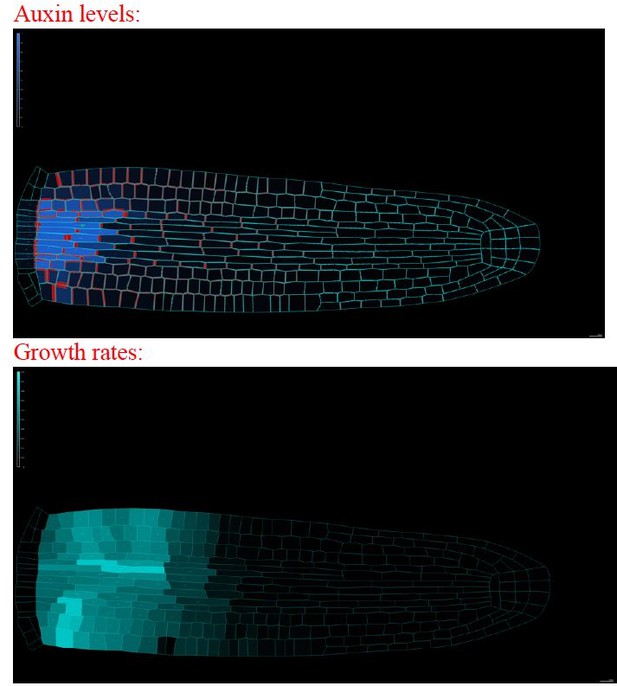
(A) Initial embryonic set point. Locations of auxin influx (auxin source, blue) and evacuation (auxin sinks, red) from the embryo are shown. (B, D) Model simulations predict a time evolution of cell growth rates (bright cyan color) and principal growth directions (white lines). Ongoing cell division events are marked by black regions. (C, E) Dynamics of auxin distribution (blue color), auxin flow direction (arrows), and PIN localization (red). (F, G) Zoom on basal meristem (F) and apical meristem (G) of the root. The model correctly reproduces very detailed PINs localizations including bipolar PIN2 localization in the cortex (F). (H–J) Profiles of average values of interest across all cell files along the longitudinal axis. (H) Growth rate profile along the root axis. The fastest-growing region is located in the apical meristem as observed experimentally (Bassel et al., 2014). (I) Cell division frequencies along the root axis. The majority of cell divisions occur in the apical meristem. (J) Auxin concentration in the vascular tissues (dashed blue line) and auxin concentration in the non-vascular tissues (external tissues and the root tip, dotted blue line) along the root axis are shown. Most of the auxin is concentrated in the root tip as observed in experiments (Overvoorde et al., 2010). Time-lapse profile of PINs re-localization on the membranes after cell division event. PINs re-localization is completed in approximately 5–6 hr after cell division (Glanc et al., 2018). The full simulation has been run for 1500 time steps.
-
Figure 2—figure supplement 5—source data 1
Source data used to generate Figure 2—figure supplement 5H-K.
- https://cdn.elifesciences.org/articles/72132/elife-72132-fig2-figsupp5-data1-v2.xlsx
Figure 2—figure supplement 6
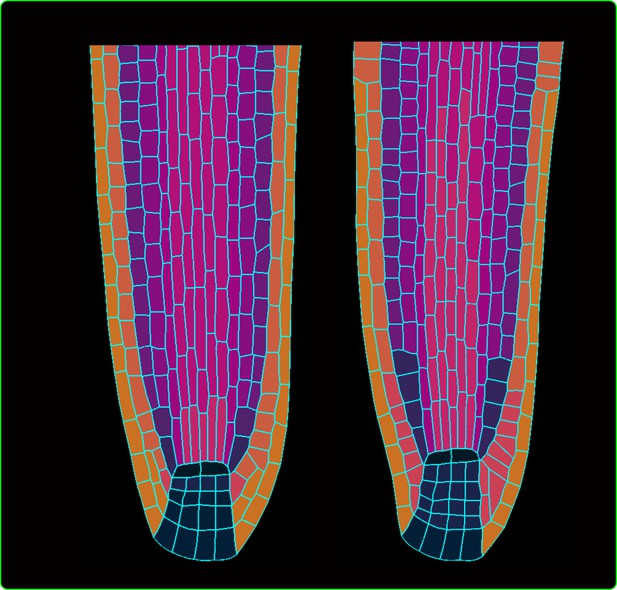
Cell division rule testing.
The wild-type simulation (left) versus root simulations where specific rules for the stem cell niche are removed from the model (right).
Figure 2—figure supplement 7
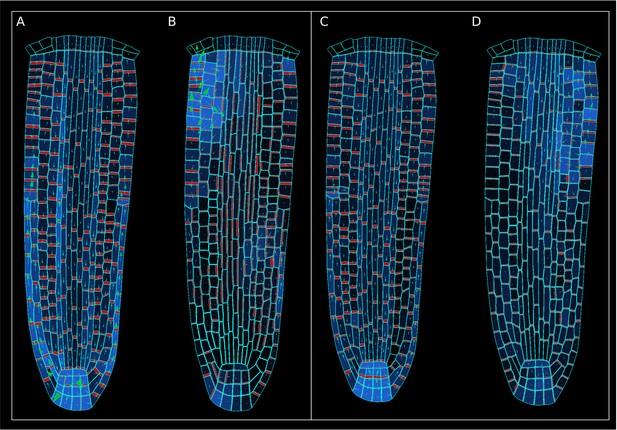
Comparison between the reference model with an alternative model simulation in which the contribution of the anisotropy factor (AF) to PIN localization is omitted at the start the of simulation, using the ‘auxin-flux’ (A–B) and the ‘regulator-polarizer’ (C–D) models, respectively.
In these simulations (B–D) the auxin maximum does not form due to disrupted PIN subcellular localizations.
Figure 2—video 1
Model simulations obtained with the auxin-flux model, related to Figure 2.
The upper simulation displays auxin distribution (blue color), auxin flow direction (arrows), and PIN localizations (red). The lower simulation displays cell growth rate (bright cyan color) and principal growth directions (white lines).
Figure 2—video 2
Model simulations obtained with the regulator-polarizer model, related to Figure 2—figure supplement 5.
The upper simulation displays auxin distribution (blue color), auxin flow direction (arrows), and PIN localization (red). The lower simulation displays cell growth rate (bright cyan color) and principal growth directions (white lines).
Figure 3 with 1 supplement
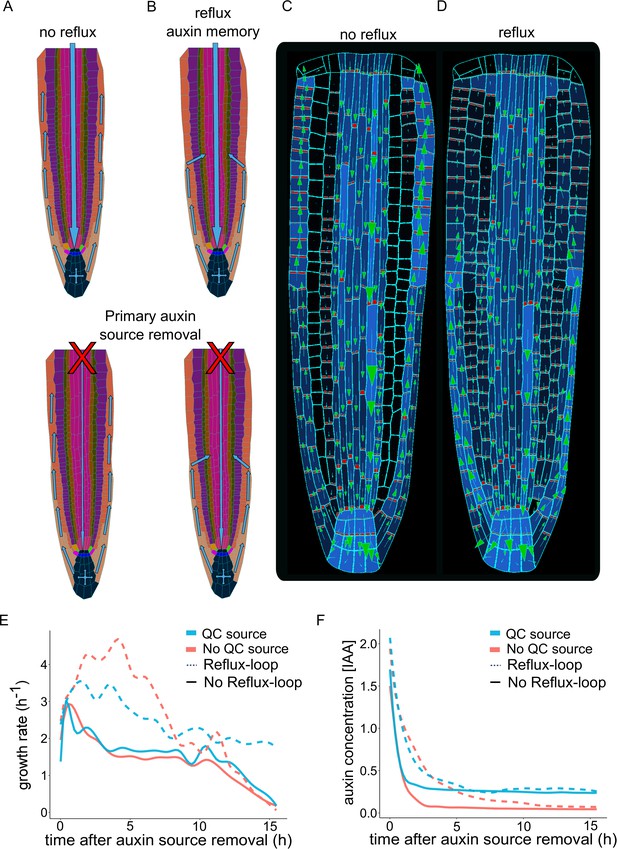
Independent root growth requires auxin reflux and local auxin production.
(A–D) Schematics (A and B) and model simulations (C and D) with the disabled auxin reflux-loop (A, C) or wild-type-like scenario with self-emerging reflux (B, D). Only the in reflux scenario auxin moves from the epidermis back into the vascular tissues sustaining the long-term root growth. (E) Growth rate profiles of model simulations after primary auxin source removal, in four different scenarios. The plot shows the total root growth rate over time. In the absence of an auxin reflux-loop, the root is unable to sustain growth for a long period (solid lines) even if a secondary auxin source in the root tip was introduced (solid blue line). On the contrary, the presence of an auxin reflux-loop sustains the root growth for prolonged periods (dotted lines), further augmented by the presence of a secondary auxin source in the root tip (dotted blue line). (F) Auxin concentration profiles of model simulations after primary auxin source removal. The plots show the average radial auxin concentration among the root cells. In the absence of an auxin reflux-loop, the average auxin concentration in the root quickly drops to zero (solid red line). Alternatively, the presence of an auxin reflux-loop allows the root to maintain an auxin reserve for prolonged periods (dotted blue line). The presence of a secondary auxin source in the root tip preserves an auxin reservoir and sustains root growth in the long term (blue lines). The model simulations have been run for 1000 time steps.
-
Figure 3—source data 1
Source data used to generate Figure 3E and F.
- https://cdn.elifesciences.org/articles/72132/elife-72132-fig3-data1-v2.xlsx
Figure 3—video 1
Model simulations with the enabled/disabled auxin reflux-loop and with/without local auxin production in the QC, related to Figure 3.
Figure 4 with 2 supplements
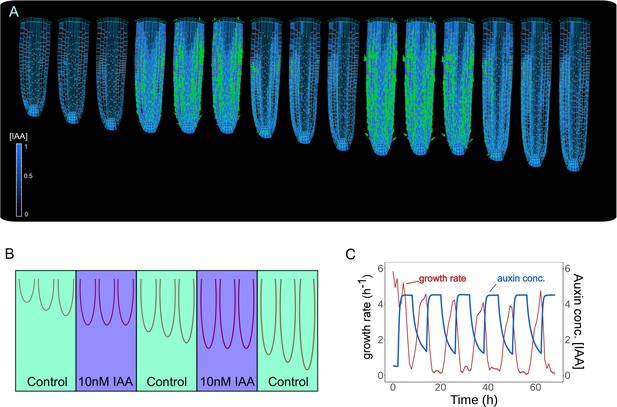
Model predictions reproduce reversible inhibition of root growth by externally applied auxin.
(A) Successive application of external auxin in model simulations according to a predefined cycle. Root growth is inhibited by the introduction of high amounts of auxin and subsequently restored after the external application is stopped as seen in experiments (Fendrych et al., 2018). (B) Schematic of the in silico experiment. To simulate auxin treatment as described in Fendrych et al., 2018, we introduced external auxin inside the root (by inducing excessive auxin synthesis at individual cell level) at predefined time points to inhibit root growth and subsequently removed to allow root growth re-establishment. (C) Time-lapse profile of root growth rate (red line) and average cell auxin concentrations (blue line). The cycles of external auxin applications inhibit and restore root growth, respectively. The simulation has been run for 1500 time steps.
-
Figure 4—source data 1
Source data used to generate Figure 4C.
- https://cdn.elifesciences.org/articles/72132/elife-72132-fig4-data1-v2.xlsx
Figure 4—figure supplement 1
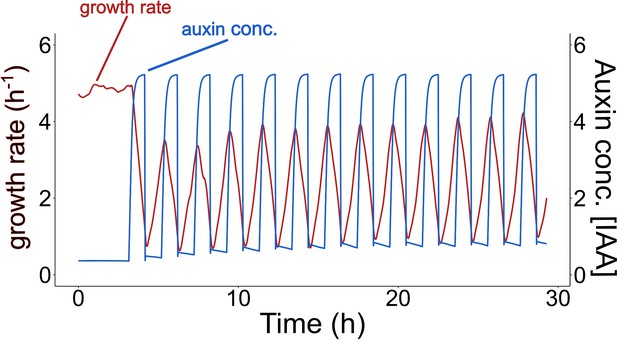
The reversible inhibition of root growth by external auxin applications.
Successive applications of 10 nM of external auxin in model simulations according to a predefined cycle of 1 hr.
-
Figure 4—figure supplement 1—source data 1
Source data used to generate Figure 4—figure supplement 1.
- https://cdn.elifesciences.org/articles/72132/elife-72132-fig4-figsupp1-data1-v2.xlsx
Figure 4—video 1
Successive application of external auxin in model simulations according to a predefined cycle, related to Figure 4.
Root growth is inhibited by the introduction of high amounts of auxin and subsequently restored after the external application is stopped.
Figure 5 with 10 supplements
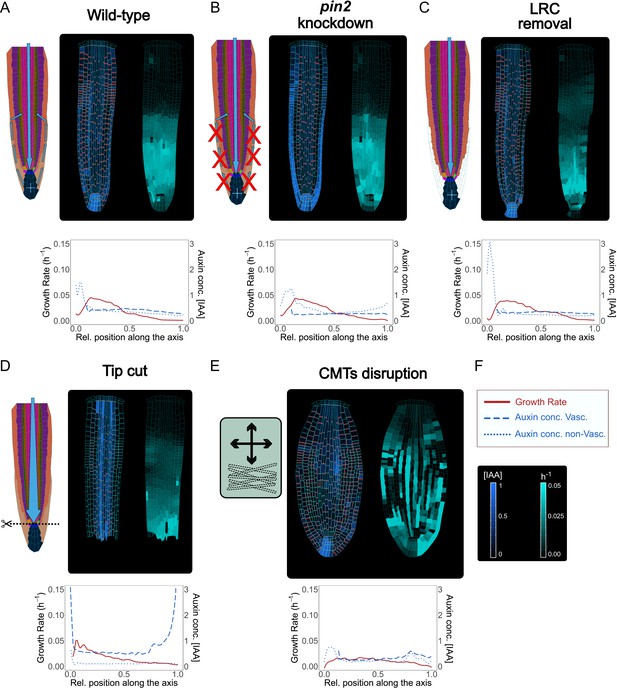
Model simulations recapitulate experimentally observed phenotypes through genetic, pharmacological, and mechanical perturbations.
(A) Reference model simulation of the wild-type scenario. The figure displays a schematic representation of the auxin flow inside the root (left picture), cell growth rate (right picture). The bottom graph shows the profiles of auxin concentration in the vascular tissues (dashed blue line), auxin concentration in the non-vascular tissues (dotted blue line,) and growth rate (red line) along the root axis. (B) Model simulation of the pin2 knockdown mutant. In silico pin2 mutant shows strongly reduced PINs expression in the lateral root cap, epiderm, is, and cortex. Note that acropetal auxin flow is severely affected and auxin tends to accumulate in the lateral tissues as observed in experiments (Dhonukshe et al., 2010). (C) Mechanical removal of lateral root cap resulted in the strong accumulation of auxin inside the root tip, largely because auxin cannot flow anymore shootward through outermost tissues whereas growth rate was not significantly affected. (D) Simulation of root tip cutting. Removing the root tip results in a general increase of auxin level in the central vascular tissues, as a consequence of the disappearance of acropetal auxin flow. PINs localization in the external tissues is also affected due to the loss of incoming auxin flow. (E) Simulated CMTs disruption (i.e. oryzalin treatment or similar) on root growth and polarity. CMTs disruption was simulated by inducing a fast degradation of the anisotropy factor. Cells lose polarity and growth anisotropy, causing the root to expand and bulge radially as observed in experiments (Baskin et al., 1994). Notice that the top cell row is considered to be a static attachment of the root to the substrate and therefore its growth is not affected during the simulation. (F) Legend and scale bars of auxin concentration and cell growth rate. ‘Auxin conc. Vasc.’ indicates auxin concentration in the vascular central tissues (the vascular cells and the pericycle), while ‘Auxin conc. non-Vasc.’ indicates auxin concentration in the remaining external tissues and the root tip. The simulations have been run for 1500 time steps.
-
Figure 5—source data 1
Source data used to generate Figure 5A-E.
- https://cdn.elifesciences.org/articles/72132/elife-72132-fig5-data1-v2.xlsx
Figure 5—figure supplement 1
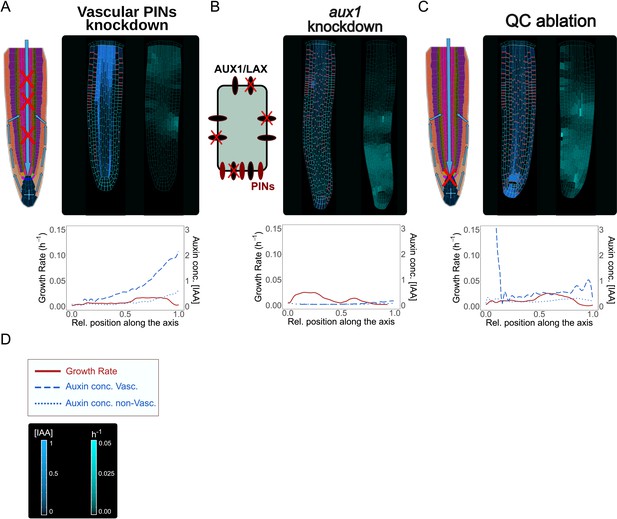
Model simulations recapitulate some of the experimentally observed phenotypes, related to Figure 5.
(A) Model simulations of the vascular PINs reduction. PINs expression was reduced in the vascular tissues, pericycle, and endodermis, to maintain 10 % PIN activity. The model predicts that auxin levels in the root are strongly depleted as the hormone flow is severely affected by PIN down-regulation. (B) Simulated aux1 knockdown mutant. AUX/LAX expression was reduced by 90 % in every cell. This simulated mutant present decreased auxin levels and root growth. (C) Model simulations of QC ablation. Removing the QC cells results in an increase of auxin level in the vascular initial cells above the ablated QC. The model simulations display the disappearance of acropetal auxin flow, as much less auxin each and accumulate in the root tip. (D) Legend and scale bars of auxin concentration and cell growth rate. ‘Auxin conc. Vasc.’ indicated auxin concentration in the vascular central tissues (the vascular cells and the pericycle), while ‘Auxin conc. non-Vasc.’ indicates auxin concentration in the remaining external tissues and the root tip. All simulations have been run for 1500 time steps.
-
Figure 5—figure supplement 1—source data 1
Source data used to generate Figure 5—figure supplement 1A–1C.
- https://cdn.elifesciences.org/articles/72132/elife-72132-fig5-figsupp1-data1-v2.xlsx
Figure 5—figure supplement 2
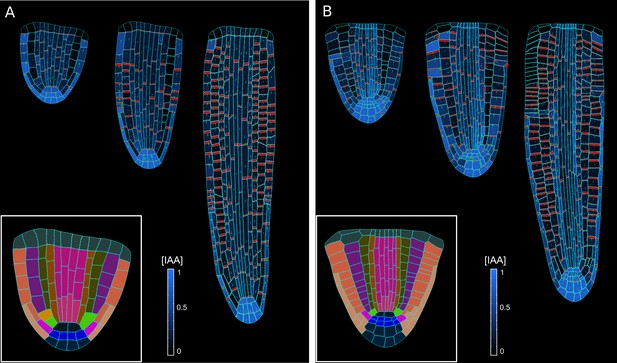
Model simulations using alternative wild-type embryo templates.
(A, B) Embryo templates extracted from the following studies Nieuwland et al., 2016 (A); Scheres et al., 1994 (B). The particular choice of an initial embryo template has no impact on the emergence of root growth and auxin distribution. The simulations have been run for 1500 time steps.
Figure 5—figure supplement 3
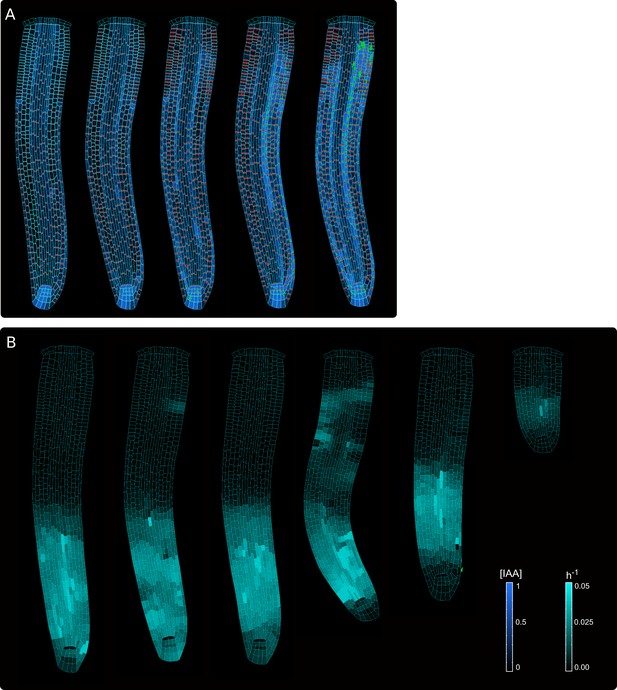
Model parameters sensitivity.
(A) Model testing for parameter kP, the coefficient of contribution for auxin flow to PIN sensitivity (Equation. 14). The values tested are (from the left to right): 0, 1, 3 (default wild-type), 4, and 5. (B) Model testing for parameter K1auxin, the auxin-induced cell wall relaxation coefficient (Equation. 27). The values tested are (from the left to right): 0.005, 0.01, 0.05 (default wild-type), 0.1 and 0.2. The simulations have been run for 1500 time steps.
Figure 5—video 1
Model simulations of the pin2 knockdown mutant, related to Figure 5B.
In silico pin2 mutant shows strongly reduced PINs expression in the lateral root cap, epidermis, and cortex.
Figure 5—video 2
Model simulations of the vascular PINs reduction, related to Figure 5—figure supplement 1A.
Figure 5—video 3
Model simulations of the aux1 knockdown mutant, related to Figure 5—figure supplement 1B.
AUX/LAX expression was reduced by 90 % in each cell.
Figure 5—video 4
Model simulation of QC ablation, related to Figure 5—figure supplement 1C.
Removing the QC cells results in an increase of auxin level in the vascular initial cells just above the ablated QC.
Figure 5—video 5
Model simulation of lateral root cap ablation, related to Figure 5C.
Mechanical removal of LRC resulted in the strong accumulation of auxin inside the root tip, largely because auxin cannot flow anymore shootward through outermost tissues whereas growth rate was not significantly affected.
Figure 5—video 6
Model simulations of root tip cutting, related to Figure 5D.
Figure 5—video 7
Model simulation of mechanics disruption on root growth and polarity, related to Figure 5E.
Scheme 1
Process diagram.
Scheme 2
Position-based dynamics algorithm.
Author response image 1
Author response image 2
Tables
Table 1
Model parameters.
| Parameter | Description | Value | Unit |
|---|---|---|---|
| Mechanical model component | |||
| RAF | AF reorientation rate | 0.02 | h–1 |
| DAF | AF degradation rate | 0.01 | h–1 |
| Auxin transport model component | |||
| bIAA | basal auxin production rate | 0* | nM/h |
| DIIAA | auxin diffusion rate in the intercellular space | 1 | μm2/h |
| dIAAb | basal auxin degradation rate | 0.0125, Perianez-Rodriguez et al., 2021 | nM/h |
| dIAAMax | maximum auxin degradation rate coefficient | 0.125 | h–1 |
| KIAAMax | coefficient for half-max auxin degradation | 5 | nM |
| KAUX1 | coefficient of auxin importing rate by AUX/LAX | 1 | μm/h |
| KPIN | coefficient of auxin export rate by PIN | 1.4, Mironova et al., 2010 | μm/h |
| bAUX1 | AUX/LAX basal expression | 1 | nM/h |
| AUX1expr | auxin-induced AUX/LAX maximal expression | 30 | nM/h |
| AUX1K | auxin-induced AUX/LAX half-max expression | 0.01 | nM |
| AUX1tr | AUX/LAX trafficking rate | 1 | h–1 |
| AUX1Max | maximum concentration of AUX/LAX | 2 | nM |
| AUX1MaxMem | maximum concentration of AUX/LAX on membrane sections | 15 | nM |
| dAUX1 | AUX/LAX degradation rate | 0.08 | h–1 |
| bPIN | PIN basal expression | 0.2, Mironova et al., 2010 | nM/h |
| PINexpr | auxin-induced PIN maximal expression | 50 | nM/h |
| PINK | auxin-induced PIN half-max expression | 0.05 | nM |
| PINtr | PIN trafficking rate | 1 | h–1 |
| PINMax | maximum PIN concentration inside the cell | 2 | nM |
| PINMaxMem | the maximum concentration of PIN on membrane sections | 15 | nM |
| dPIN | PIN degradation rate | 0.08, Mironova et al., 2010 | h–1 |
| dPINmax | maximum PIN degradation rate on membranes | 0.8 | h–1 |
| kAF | coefficient for AF orientation contribution to PIN sensitivity | † | - |
| kP | coefficient for auxin flow contribution to PIN sensitivity | 3 | - |
| kAFP | coefficient for interaction AF orientation+ auxin flow contribution to PIN sensitivity | 3 | - |
| kG | coefficient for cell geometry contribution to PIN sensitivity | 3 | - |
| Kaf | half-max AF orientation contribution to PIN sensitivity | 0.5 | - |
| Kgeom | half-max cell geometry contribution to PIN sensitivity | 0.5 | - |
| PIN polarization parameters | |||
| Kflux | auxin-flux half-max contribution on PIN sensitivity | 0.1 | nM μm |
| bREG | regulator basal expression | 10 | nM/h |
| bPOL | polarizer basal expression | 10 | nM/h |
| dPOL | regulator decay rate | 0.08 | h–1 |
| dREG | polarizer decay rate | 0.08 | h–1 |
| Kregtr | regulator base trafficking rate | 1 | h–1 |
| Kpoltr | polarizer base trafficking rate | 0.01 | h–1 |
| Dreg | regulator diffusion rate | 1 | μm2/h |
| Dpol | polarizer diffusion rate | 0.1 | μm2/h |
| KdispPOL | polarizer displacement rate | 10 | h–1 |
| KregIAA | regulator auxin-induced half-max trafficking rate | 0.01 | nM |
| KpolIAA | polarizer auxin-induced half-max trafficking rate | 0.01 | nM |
| KregGradT | regulator max trafficking rate activation by auxin gradient | 1 | nM/h |
| KregGradK | regulator auxin gradient-induced half-max trafficking rate | 1 | nM |
| KpolIP | half-max value of polarizer contribution on PIN sensitivity | 0.1 | nM |
| Auxin-dependent root growth parameters | |||
| kEMax | cell wall maximum stiffness | 1 | - |
| K1auxin | half-max cell wall relaxation coefficient by auxin | 0.05 | nM |
| K2auxin | half-max cell wall stiffening coefficient by auxin | 3 | nM |
-
*
auxin basal expression is set to zero for the default wild type model. However, when local production in the QC is necessary, the value is set to 10.
-
†
this parameter is set to 0 in the default model and included in the formulas only for completeness.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
A coupled mechano-biochemical model for cell polarity guided anisotropic root growth
eLife 10:e72132.
https://doi.org/10.7554/eLife.72132
