Empirical single-cell tracking and cell-fate simulation reveal dual roles of p53 in tumor suppression

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

410 views

Version of Record published: October 13, 2022 (This version)
Accepted Manuscript updated: September 20, 2022 (Go to version)
Accepted Manuscript published: September 20, 2022 (Go to version)
Accepted: September 13, 2022
Received: July 27, 2021
Preprint posted: May 10, 2018 (Go to version)

1. Of interest
Dynamic organization of cerebellar climbing fiber response and synchrony in multiple functional components reduces dimensions for reinforcement learning

Huu Hoang, Shinichiro Tsutsumi ... Keisuke Toyama

Research Article Sep 27, 2023
Further reading

Abstract
Editor's evaluation
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

The tumor suppressor p53 regulates various stress responses via increasing its cellular levels. The lowest p53 levels occur in unstressed cells; however, the functions of these low levels remain unclear. To investigate the functions, we used empirical single-cell tracking of p53-expressing (Control) cells and cells in which p53 expression was silenced by RNA interference (p53 RNAi). Here, we show that p53 RNAi cells underwent more frequent cell death and cell fusion, which further induced multipolar cell division to generate aneuploid progeny. Those results suggest that the low levels of p53 in unstressed cells indeed have a role in suppressing the induction of cell death and the formation of aneuploid cells. We further investigated the impact of p53 silencing by developing an algorithm to simulate the fates of individual cells. Simulation of the fate of aneuploid cells revealed that these cells could propagate to create an aneuploid cell population. In addition, the simulation also revealed that more frequent induction of cell death in p53 RNAi cells under unstressed conditions conferred a disadvantage in terms of population expansion compared with Control cells, resulting in faster expansion of Control cells compared with p53 RNAi cells, leading to Control cells predominating in mixed cell populations. In contrast, the expansion of Control cells, but not p53 RNAi cells, was suppressed when the damage response was induced, allowing p53 RNAi cells to expand their population compared with the Control cells. These results suggest that, although p53 could suppress the formation of aneuploid cells, which could have a role in tumorigenesis, it could also allow the expansion of cells lacking p53 expression when the damage response is induced. p53 may thus play a role in both the suppression and the promotion of malignant cell formation during tumorigenesis.

Editor's evaluation

This article examines the role of p53 in cell division by using a combination of live-cell imaging, cell tracking, and simulations. Overall, the results are extensively and transparently documented and are of interest to cell biologists studying cell division, cell death, and p53.

https://doi.org/10.7554/eLife.72498.sa0

Introduction

The p53 gene is mutated in >50% of cancers (Kandoth et al., 2013; Hollstein et al., 1991; Petitjean et al., 2007), and loss of p53 function is considered to be involved in tumor progression, thereby defining TP53 as a tumor suppressor gene (Boutelle and Attardi, 2021; Levine, 2019). The cellular functions mediated by p53 are mainly related to its cellular levels, which increase in response to stress, thus activating various mechanisms, for example, cell cycle arrest, cell senescence, cell death, and DNA damage responses (Levine, 2019; Kastenhuber and Lowe, 2017; Lavin and Gueven, 2006; Vogelstein et al., 2000; Hafner et al., 2019). Given that cell cycle arrest, cell senescence, and cell death could lead to the removal of the damaged cells, these processes could act to suppress tumor formation (Kastenhuber and Lowe, 2017; Livingstone et al., 1992; Kastan et al., 1991; Clarke et al., 1993; Lowe et al., 1993; Campisi, 2005; Rufini et al., 2013).

p53 levels are regulated via a mechanism mediated by Mdm2, which constantly degrades p53 by ubiquitination to maintain a low level. p53 accumulation occurs when Mdm2 activity is suppressed by stress-induced phosphorylation, which inhibits its ubiquitination activity, resulting in inhibition of p53 degradation (Boutelle and Attardi, 2021; Kastenhuber and Lowe, 2017; Lavin and Gueven, 2006; Haupt et al., 1997; Honda et al., 1997; Kubbutat et al., 1997). These observations suggest that increased stress levels are required to elevate p53 levels sufficiently to allow it to exert its tumor suppressor function. Maintaining a background low level of p53 may thus have evolved as a means of allowing cells to respond quickly to stress. Alternatively, given that removing p53 by gene silencing increases the efficiency of induced pluripotent stem cell formation (Guo et al., 2014), maintaining low levels of p53 in unstressed cells per se may have functional implications. In this regard, it has been suggested that low levels of p53 activity may be required to respond to a broad spectrum of stress (Vousden and Lane, 2007) through suppression of apoptosis and regulation of metabolisms (Boutelle and Attardi, 2021; Kastenhuber and Lowe, 2017; Kruiswijk et al., 2015; Lassus et al., 1996). If low levels of p53 indeed play a role in regulating cellular functions, it is plausible that loss of these functions could be involved in tumorigenesis. However, the effects of loss of low levels of p53 on cell characteristics remain unclear.

In this study, we silenced the expression of low levels of p53 using small interfering RNA (siRNA) and investigated the effects of this loss on the frequency of induction of cellular events using single-cell tracking to detect rare cellular events and creating a cell-lineage database revealing the fates of individual cells. Cell lineages can be generated by lineage-reconstruction approaches; however, these assume that all cell divisions are bipolar (Chow et al., 2021; Chapal-Ilani et al., 2013; Zafar et al., 2020), and thus cannot be used to analyze lineages, including cells that undergo cell death, multiple cell division, and cell fusion. To overcome this problem, we developed a single-cell-tracking method that can detect cell death, multipolar cell division, and cell fusion events in individual cells, thus allowing the generation of accurate cell-lineage data. In addition to silencing, we also used the alkylating agent, N-methyl -N′-nitroso-N-nitrosoguanidine (MNNG), which acts as a DNA-damaging agent by generating methylated bases (Wood, 1996; Jacobs and Schär, 2012; Lindahl, 1990; Satoh and Lindahl, 1992; Lindahl et al., 1995). Among MNNG-induced methylated bases, O⁶-methylguanine, which acts as a premutagenic DNA lesion that induces a G:C to A:T transversion mutation, is repaired by O⁶-methylguanine methyltransferase, and 7-methylguanine, which causes the induction of cell death through the formation of DNA breaks, is repaired by base excision repair (Wood, 1996; Jacobs and Schär, 2012; Lindahl, 1990; Satoh and Lindahl, 1992; Lindahl et al., 1995). It has been reported that MNNG can increase p53 levels in cells (Lindahl et al., 1988; Kim et al., 2005) and activate DNA repair processes that are not related to p53. We, therefore, studied how the fate trajectories of wild-type and p53-silenced cells were affected by p53-mediated and non-mediated processes at single-cell resolution. Furthermore, because single-cell tracking can reveal spatiotemporal information on individual cells, we used this information to simulate the fates of individual cells beyond the empirical limit of cell culture by developing a cell-fate simulation algorithm.

Our results obtained by single-cell tracking and cell-fate simulation suggest that the low levels of p53 in unstressed cells play a role in suppressing the induction of cell death and cell fusion, which may lead to multipolar cell division and the production of aneuploid progeny. Cell-fate simulation analysis revealed that some aneuploid progeny derived from p53-silenced (p53 RNAi) cells could propagate in an environment dominated by p53-expressing (Control) cells, while p53 RNAi cells per se were unable to gain an advantage over Control cells in terms of population expansion. In contrast, the balance of expansion between Control and p53 RNAi cells was altered by induction of the damage response by MNNG, resulting in the relative expansion of p53 RNAi cells. Thus, although low levels of p53 could act as a tumor suppressor by inhibiting the formation of aneuploid cells, this role could largely depend on the status of the cell population harboring the cells with impaired p53 function, and the stress-damaged environment.

Results

System to investigate the functional implications of maintaining low levels of p53 in unstressed cells

We developed a system to determine whether the low levels of p53 retained in unstressed cells had a functional role in suppressing changes in cell characteristics. We, therefore, performed concurrent video recordings of A549 p53 proficient lung carcinoma cells treated with scrambled siRNA or p53 siRNA (Control and p53 RNAi cells, respectively) and analyzed cells using single-cell tracking. Distinct from other single-cell analyses, for example, single-cell transcriptomics, which reveal the characteristics of individual cells at a certain moment in time, data obtained by single-cell tracking include information on spatiotemporal changes for individual cells, thus revealing the changes in cell population characteristics over time. Furthermore, because tracking of individual cells allows cellular events to be detected regardless of the frequency of their occurrence, the response of a cell population can be delineated at single-cell resolution with higher accuracy compared with analyses based on the average responses of a cell population.

The first step in single-cell-tracking analyses is the generation of a long-term live-cell imaging video recording continuous cell movement. Images, typically 2300 × 2300 pixel area (1200 × 1200 µm), were acquired every 10 min (Figure 1). Phototoxicity, which can damage cells during long-term live-cell imaging, was minimized by using differential interference contrast (DIC) imaging with near-infrared light. The single-cell-tracking videos were then started by selecting cells referred to as progenitors in the video images at a tracking time of 0 min, and single-cell tracking of these progenitors and their progeny was performed using our previous computerized single-cell-tracking analysis system (Sato et al., 2018). This system created fully automated live-cell imaging videos (up to 16 videos concurrently) and carried out image segmentation, automated single-cell tracking, database creation, data analysis, and archiving. Because we excluded any data related to progenitors or progeny that moved out of the field of view, the resulting single-cell-tracking data contained complete information for progenies derived from progenitors produced during the single-cell-tracking period. The resulting single-cell-tracking data thus contained the position of each cell at every time point in an image, the type of events that occurred in a cell (bipolar cell division, tripolar cell division, tetrapolar cell division [tripolar and tetrapolar cell divisions were defined as multipolar cell division], cell death, and cell fusion [see Figure 1—figure supplement 1 for still images of bipolar cell division, multipolar cell division, cell death, and cell fusion; corresponding videos have been deposited in Dryad]), and the relationships of a cell to its parent and offspring cells. To organize single-cell-tracking data, each progenitor and its progeny was assigned a unique ID, that is, a cell-lineage number. In this study, a group of cells (a progenitor and its progeny cells) with the same ID is referred as to a cell lineage. A unique cell number was also assigned to each cell constituting a cell lineage, and a database composed of multiple cell-lineage data is referred as to a cell-lineage database. We then used the cell-lineage database to perform quantitative bioinformatics analysis (Figure 1) at the single-cell and cell-lineage levels. Cell population-level analysis could also be performed by collecting data for cells that belonged to different cell lineages.

Figure 1 with 6 supplements see all

Download asset Open asset

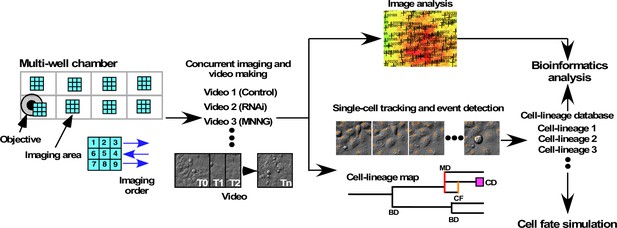
System for investigating the functional role of maintaining low cell levels of p53.

A549 cells were cultured on multi-well chamber slides and the areas of interest were scanned. Cells were treated with scrambled siRNA or p53 siRNA in the presence or absence of various doses of MNNG, and the cell responses were monitored to generate live-cell imaging videos. The videos were used for imaging and single-cell tracking, starting immediately after MNNG treatment. Progenitors were selected from the image designated as tracking time 0 min (T0), and the progenitors and their progeny were tracked empirically. Cell-lineage database comprised tracking results for one progenitor and their progeny, and any events that occurred in the cells. A cell-lineage map was generated from the database to represent the proliferation profile of a progenitor and its progeny through bipolar cell division (BD), multipolar cell division (MD), cell fusion (CF), and cell death (CD). If any progeny moved out from the areas of interest, data related to the lineage of that was not included in the cell-lineage database. Quantitative bioinformatics analysis was performed using the database, which was also used to develop a cell-fate simulation algorithm.

Some information in the cell-lineage database could be visually represented as a cell-lineage map (Figure 1), containing multidimensional information, for example, number of progeny produced from a progenitor, type, and time of events that occurred in a cell or in all cells comprising the lineage, and the length of time between events. Quantitative bioinformatics analyses were performed to analyze specific aspects of the information. Furthermore, given that the information stored in a cell-lineage database can reveal a pattern of events that occurred in the cell, cell lineage, and cell population, we used this information to simulate the fates of cells by developing a cell-fate simulation algorithm.

Quantitation of cell numbers, areas, and densities

First, we prepared uniform cell cultures for siRNA treatment using plated cells occupying ~90% of the culture surface, where >99% of cells were attached to other cells. As shown in Figure 1—figure supplement 2a, the number of cells/µm² increased linearly while the average cell surface area was reduced, confirming that the number of cells could increase continuously in a linear manner during video monitoring. To visualize this increase, density maps were also created at each imaging time point (Figure 1—figure supplement 2b for still images and Figure 1—video 1) by assigning a value of 1 to pixels within a 20-pixel diameter (10.43 µm) of the position of the cell (Figure 1—figure supplement 2c). Cell positions were determined using data recorded in the cell-lineage database, and the pixel was assigned the sum of the number of overlapped areas. When a cell was close to other cells, the number of overlaps (i.e., the sum) increases, representing the cell density in an area. These sums were converted into a heat map, which showed an increase in density during video monitoring (Figure 1—figure supplement 2b and Figure 1—video 1).

Minimum number of cell lineages required to build a cell-lineage database

We then determined the minimum number of cell lineages (i.e., number of progenitors to be tracked) needed per experiment to build a cell-lineage database. For this purpose, we first constructed 485 cell lineages by performing single-cell tracking using 485 progenitor Control cells and then randomly selected 50, 80, 120, 140, and 240 cell lineages from the 485 cell lineages to generate cell-lineage databases containing the selected number of lineages. This selection was repeated three times for triplicate analysis for each cell-lineage database. Variation in the rate of cell population expansion was then evaluated by calculating the total number of cells at each time point using the cell-lineage databases. The results for the 50, 80, 120, 140, and 240 cell lineages are shown in Figure 1—figure supplement 3a–e. For example, the variation in the number of cells at the 4000 min-determined cell-lineage database containing 50 cell lineages (Figure 1—figure supplement 3a, black bar) was 51 cells, and the variations became constant (7.5–6.0 cells for 150–240 cell lineages) when >240 cell lineages were used (Figure 1—figure supplement 3f). This suggests that 240 cell lineages are sufficient for reproducible single-cell-tracking analysis, and we therefore used 335 cell lineages to create a cell-lineage database.

Determination of length of time for single-cell tracking following siRNA and/or MNNG treatment

We determined the length of time required for single-cell tracking following siRNA transfection. Because transfection can be monitored by observing the accumulation of particles (transfection reagents) in cells (Figure 1—figure supplement 4a, DIC), we quantitated the number of particles in an area of the cell culture by extracting particles with a grayscale value >150/255 from the video image and counted the number of particles with a size of 5–30 pixels (Figure 1—figure supplement 4a, Particles, and Figure 1—video 2). The number of particles started to increase at about 1200 min (20 hr) after transfection and peaked at 3750 min (62.5 hr) (Figure 1—figure supplement 4b). Western blotting analysis performed 48 hr after transfection confirmed silencing of p53 (Figure 1—figure supplement 4c; Scrambled siRNA vs. p53 siRNA, ~70% reduction), the expression of low levels of p53 (Scrambled siRNA, 0 μM MNNG), and the occurrence of p53 stabilization by exposure of cells to 7 µM MNNG (Scrambled siRNA, 5.8-fold increase). Based on these parameters, we applied a 30 min pulse of MNNG treatment after the start of particle accumulation (Figure 1—figure supplement 4b; 1740 min [29 hr] after transfection). Single-cell tracking was started at the end of MNNG treatment and continued for 4000 min (66.7 hr), by which time the number of particles was reduced to 70% of that at the peak.

Notably, the degree of p53 silencing may vary among cells, and it is possible that only certain groups of cells may respond to silencing. This technique cannot reveal the level of silencing within the individual cells, but the data for the population as a whole can reveal differences, providing a clue to the function of the low levels of p53.

Analysis of rates of cell population expansion of Control and p53 RNAi cells, and cells treated with MNNG using cell-counting and single-cell-tracking approaches

The lowest levels of p53 could occur in unstressed cells (Boutelle and Attardi, 2021; Kastenhuber and Lowe, 2017; Lavin and Gueven, 2006; Haupt et al., 1997; Honda et al., 1997; Kubbutat et al., 1997). To gain insights into the functions of such low levels of p53, we analyzed the expansion rate of a p53 RNAi cell population and their response to MNNG exposure. The rate of cell population expansion, often referred to as the cell growth curve, has generally been measured by counting cells at certain time intervals. We therefore initially determined the rate of expansion using a classical, cell-counting approach (count cell numbers every 1000 min) and compared the results with those obtained by single-cell-tracking analysis (every 10 min) to evaluate the accuracy of the analysis (Figure 2). For the cell-counting approach, cell population expansion curves were determined manually by counting cells present in images of live-cell imaging videos every 100 time points (1000 min). To this end, images corresponding to every 100 time points were divided into 25 (5 × 5) squares (~512 × 512 pixels per square, 266.24 × 266.24 µm per square), and the number of cells within a square was counted (Figure 2—figure supplement 1). We used three independently generated videos and randomly selected 15 squares. The results of counting of Control and p53 RNAi cells are summarized in Figure 2a and b, respectively. The rates of expansion of the Control and p53 RNAi cells and their responses to MNNG exposure were also compared (Figure 2c–f). There was no significant difference in the expansion rates of Control and p53 RNAi cells (Figure 2c). There was also no significant difference in the expansion rates of Control cells and Control cells exposed to 1 µM MNNG (MNNG1) (Figure 2a, Control vs. MNNG1), while the expansion rate of p53 RNAi cells exposed to 1 µM MNNG (p53 RNAi-MNNG1) was reduced relative to Control cells exposed to MNNG1 (MNNG1) and p53 RNAi cells (Figure 2b and d). When the dose of MNNG was increased to 3 µM (MNNG3), the expansion rate of MNNG3 cells was reduced relative to Control cells (Figure 2a) but was higher than that of p53 RNAi-MNNG3 cells (Figure 2e, MNNG3, and p53 RNAi-MNNG3). At the highest MNNG dose used in this study (7 µM, MNNG7), at which significant accumulation of p53 was observed (Figure 1—figure supplement 4c), the rates of expansion of both the MNNG7 and p53 RNAi-MNNG7 cell populations were significantly reduced compared with non-exposed Control and p53 RNAi cells, respectively, but p53 RNAi cells were significantly less sensitive to the MNNG dose than Control cells (Figure 2f). These results suggest that cells with different sensitivities to MNNG compared with Control cells were generated by silencing the low levels of p53. Furthermore, the relative sensitivities of Control and p53 RNAi cells to different doses of MNNG differed, further suggesting that these p53 RNAi cells did not respond linearly to the different doses of MNNG.

Figure 2 with 1 supplement see all

Download asset Open asset

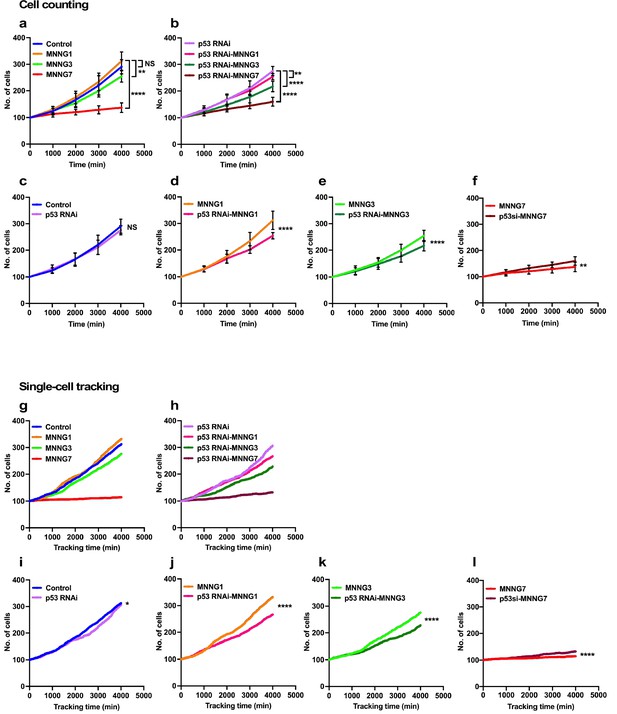
Cell population expansion rates determined by cell-counting and single-cell-tracking analysis.

Control (a) and p53 RNAi (b) cells were exposed to 1, 3, and 7 µM MNNG (Control and p53 RNAi cells exposed to those doses of MNNG are referred to as MNNG1, MNNG3, MNNG7, p53 RNAi-MNNG1, p53 RNAi-MNNG3, and p53 RNAi-MNNG7, respectively). (**a–f**) Images were divided into a 5 × 5 squares and cell population expansion curves were determined by counting the number of cells in a square (~512 × 512 pixels) at 1000 min intervals (see Figure 2—figure supplement 1). Fifteen squares were selected from three independently generated videos. Expansion curves were compared as follows: Control vs. p53 RNAi (c), MNNG1 vs. p53 RNAi-MNNG1 (d), MNNG3 vs. p53 RNAi-MNNG3 (e), and MNNG7 vs. p53 RNAi-MNNG7 (f) cells. Student’s t-test (**c–f**) and ordinary one-way ANOVA (Tukey’s) (**a, b**) were performed (n = 15), and standard errors are shown. Cell population expansion curves of Control (g) and p53 RNAi (h) cells were determined using a cell-lineage database. Single-cell tracking was performed for 4000 min with videos acquired at 10 min intervals (n = 399). The number of cells every 10 min was extracted and plotted. Cell population expansion curves were compared as follows: Control vs. p53 RNAi (i), MNNG1 vs. p53 RNAi-MNNG1 (j), MNNG3 vs. p53 RNAi-MNNG3 (k), and MNNG7 vs. p53 RNAi-MNNG7 (l) cells. (**i–l**) The data were analyzed by Student’s t-tests in the following approach. The difference in cell numbers between n and n + 10 min was calculated (e.g., if the numbers of cells at 10 and 20 min were 100 and 103, the difference was 3). Because the total number of imaging points was 400, the 399 differences in time points can be calculated. Those differences for Control and p53 RNAi cells and those exposed to MNNG were used for the statistical analyses. (**a–f, i–l**) NS, nonsignificant, *p<0.05, **p<0.01, ***p<0.001, ****p<0.0001.

Figure 2—source data 1 Cell population expansion rates determined by cell-counting and single-cell-tracking analysis. Data used in Figure 2.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig2-data1-v3.xlsx
Download elife-72498-fig2-data1-v3.xlsx

These results revealed how cell population size was influenced by p53 silencing and/or MNNG treatment. However, this approach could not provide information on how each cell responded to the treatment or how the response affected the size of the cell population. We then analyzed cell-lineage databases obtained by single-cell tracking, given that the database contains information on events such as cell death, fusion, and division, which influence the cell population expansion, at single-cell resolution. Because the cell-lineage database generated by tracking contained information on individual cells at each time point in the images (every 10 min), the total number of cells every 10 min was plotted in Figure 2g–l (videos of the single-cell-tracking processes, cell-lineage maps, and cell-lineage data have been deposited in Dryad). Single-cell-tracking analysis and cell counting yielded similar results (Figure 2g and h); the relative differences in the rates of cell expansion between the Control and p53 RNAi cells, and those treated with MNNG, were consistent between the counting and single-cell-tracking results (Figure 2j–l). Regarding the comparison between Control and p53 RNAi cells, although counting every 1000 min showed no significant differences, single-cell tracking, which can survey the cell number every 10 min, revealed that the population expansion rate of p53 RNAi cells was significantly lower than that of Control cells, confirming that the single-cell-tracking analysis approach produced equivalent results to the cell-counting approach (Figure 2c and i). However, in contrast to the classical counting approach, which only represents the number of cells at a certain time point, cell-lineage databases contain additional spatiotemporal information at single-cell resolution, which could allow a more detailed analysis of how the cell population is expanded or reduced, what type of cellular events were induced, and how they impacted the phenotype of a cell population with reduced p53 expression or DNA damage stress. We therefore conducted further analyses to gain insights into the Control and p53 RNAi cell populations and those exposed to MNNG using computer-assisted single-cell analysis.

Analysis of reproductive ability of cells using cell-lineage database

Cell populations are known to be composed of cells with different reproductive abilities (Puck et al., 1956), and the overall rate of cell population expansion (Figure 2) is thus often influenced by the relative reproductive abilities of the cells within the population. Cell population expansion curves per se do not provide any insights regarding the reproductive abilities of individual cells to allow the impact of such variations in the cell population to be assessed. We therefore further revealed the characteristics of Control, p53 RNAi, and MNNG-exposed cell populations by analyzing the reproductive abilities of the different cells comprising each cell population.

To this end, we sorted each cell lineage into groups (Figure 3a). Given that the reproductive ability of a cell could be represented by the number of cells (progenitor and its progeny) comprising a cell lineage, we calculated the total number of cells comprising each cell lineage and sorted them according to the number (the example cell lineages shown in Figure 3a are composed of 5 and 13 cells). We grouped cell lineages that produced 1–2, 3–4, 5–6, 7–8, 9–10, 11–12, 13–14, and 15–16 cells as groups A, B, C, D, E, F, G, and H, respectively. The lineages in Figure 3a, left and right, were therefore sorted as groups C and G, respectively.

Figure 3

Download asset Open asset

Number of progeny produced from a progenitor.

(a) Example cell lineages are shown. If a cell lineage was composed of one progenitor (1) and four progenies (2–5) (a: left), the cell lineage was grouped as C (5–6). Similarly, if a cell lineage was composed of one progenitor (1) and 12 progenies (2–13) (b: right), the lineage was grouped as G (13–14). Cells that underwent multipolar cell division, cell death, and cell fusion were also included in this analysis. (**b, c**) The total number of cells belonging to each group was calculated. For example, if five cell lineages were composed of three cells (group B), the number of cells in group B was 5 × 3 = 15, which could represent the number of cells with the reproductive ability to produce three cells within 4000 min of culture in a cell population. (b) Control cells and cells exposed to MNNG. (c) p53 RNAi cells and cells exposed to MNNG.

Figure 3—source data 1 Number of progeny produced from a progenitor. Data used in Figure 3.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig3-data1-v3.xlsx
Download elife-72498-fig3-data1-v3.xlsx

The total number of cells in each group was then calculated (Figure 3b and c). For example, if 20 cell lineages were composed of 11 cells (group G), the total number shown in the group G column would be 220 cells. The columns in Figure 3b and c thus represent the composition of cells that could have different reproductive abilities, categorized as A–H. In the case of Control cells, most cell lineages belonged to group D (7–8 cells), which accounted for 45% of the total number of Control cells (Figure 3b). Most p53 RNAi cell lineages also belonged to group D, but the number of cells with higher reproductive ability , that is, group F (11–12 cells), was increased relative to Control cells (Control: 33 cells vs. p53 RNAi: 143 cells), which might represent a change induced by silencing the low levels of p53 (Figure 3c). The number of cell lineages in group D was increased in the MNNG1 compared with the Control population (Control: 798 cells vs. MNNG1: 1057 cells), while the number of corresponding lineages in p53 RNAi-MNNG1 cells was reduced to 596 cells compared with p53 RNAi 823 cells (Figure 3b). This difference may reflect the difference in cell population expansion rates between MNNG1 and p53 RNAi-MNNG1 cells (Figure 2j). Because MNNG is a cytotoxic agent, it could reduce the number of cells with a higher reproductive ability and increase cells with a lower reproductive ability. Indeed, the numbers of group B cell lineages were increased in MNNG3 and p53 RNAi-MNNG3 cells, but MNNG3 cells could maintain a higher ability to expand relative to p53 RNAi-MMNG3 cells, because of the larger content of group D cell lineages (645 cells vs. 435 cells) (Figure 3b and c). Most lineages in MNNG7 and p53 RNAi-MNNG7 cells were groups A and B. However, p53 RNAi-MNNG7 cells still contained group C and D lineages, which could allow the cell population to recover from the impact of 7 μM MNNG treatment. These results suggest that the Control cells did not respond to different doses of MNNG in a simple dose–response manner and that silencing the low levels of p53 also differentially affected the response patterns. Multipolar cell division, cell death, and cell fusion, which could have a negative impact on the cell proliferation rate, could likely be involved in determining the response patterns, and we therefore further analyzed the impact of p53 silencing and MNNG exposure on these events.

Impact of p53 silencing and MNNG treatment on cell death, multipolar cell division, and cell fusion

It has been reported that multipolar cell division occurs at a frequency of 1–10% of all cell divisions in established cultured cell lines (Ganem et al., 2009; Sato et al., 2016). Cell death could be a less-frequent event in a growing cell population, except in the presence of a cytotoxic agent. Although cell fusion is often induced during differentiation, for example, myogenesis, it is rarely induced in a growing cell population. These events would thus be expected to occur less frequently than bipolar cell division. As noted above (Figure 1—figure supplement 3f), more than 240 cell lineages were sufficient for reproducible single-cell-tracking-based analysis of a cell population expansion curve, which mainly represents the number of cell divisions, that is, bipolar cell divisions. Although we started with 335 progenitors to perform single-cell-tracking analysis, it was not clear if tracking this number of progenitors and their progeny would produce enough multipolar cell division, cell death, and cell fusion events for statistical analysis. To this end, we first generated reference data by visually examining the videos and counting the numbers of multipolar cell division and cell death events in three videos to gain an overview of the frequencies of these events in the entire fields of view, and compared the results with those obtained using single-cell-tracking analysis (Figure 4). Notably, cell fusion was not included in the counting analysis because it was difficult to detect by visual examination.

Figure 4 with 1 supplement see all

Download asset Open asset

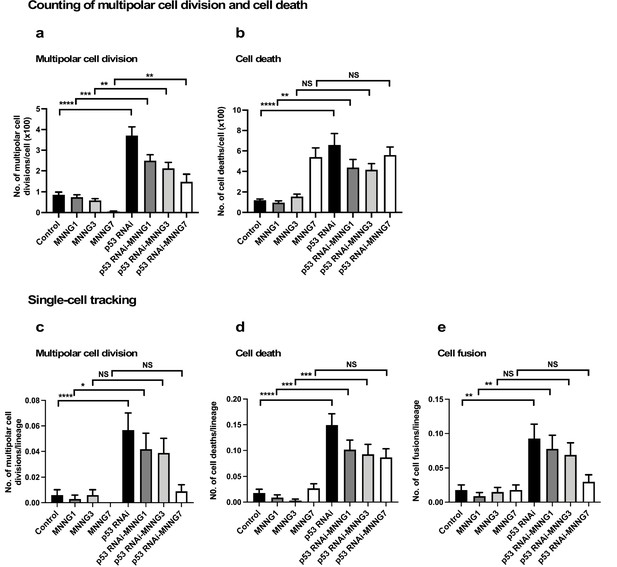
Analysis of multipolar cell division, cell death, and cell fusion using counting and single-cell-tracking analysis.

Control and p53 RNAi cells were exposed to 1, 3, and 7 µM MNNG. The numbers of multipolar cell division (a) and cell death (b) events that occurred during the tracking time (4000 min) were determined by counting those events recorded in a video. Each time point of image was divided into four areas (Figure 4—figure supplement 1), and three independently generated videos were used. Thus, counting was performed in 12 squares (n = 12). The numbers of multipolar cell division (c), cell death (d), and cell fusion (e) events that occurred during the tracking time (4000 min) were determined using single-cell-tracking and cell-lineage database (n = 335). (**a–e**) Statistical analysis was performed by ordinary one-way ANOVA (Tukey’s). NS, non-significant, *p<0.05, **p<0.01, ***p<0.001, ****p<0.0001. Standard errors are shown.

Figure 4—source data 1 Analysis of multipolar cell division, cell death, and cell fusion using counting and single-cell-tracking analysis. Data used in Figure 4.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig4-data1-v3.xlsx
Download elife-72498-fig4-data1-v3.xlsx

For counting, each time point of the video image was divided into four squares (Figure 4—figure supplement 1a), and cell death and multipolar cell division events were marked. p53 silencing significantly increased multipolar cell division and cell death events relative to Control cells (Figure 4a and b, Figure 4—figure supplement 1b c). This revealed that, even though Control and p53 RNAi cells showed similar cell population expansion curves (Figure 2i), the cell population sizes (total cell numbers) of the p53 RNAi and Control cell populations resulted from different processes. Increased multipolar cell division and cell death events following p53 silencing were reduced by MNNG treatment (Figure 4a and b, Figure 4—figure supplement 1b c), with the degree of suppression of multipolar cell division being more significant than that of cell death. Multipolar cell division and cell death occurred less frequently in Control cells, even after exposure to MNNG, except for cells exposed to 7 μM MNNG (Figure 4b). These results suggest that silencing of the low levels of p53 led to the induction of multipolar cell division and cell death.

We then determined the numbers of multipolar cell division and cell death events using single-cell-tracking-based cell-lineage analysis. Given that the cell-lineage database contains information on not only the events occurring in individual cells, but also their timing, it was possible to perform in-depth analysis of other events that occurred before and after the events in question, as well as sibling relationships. The areas selected for the analysis are indicated by black boxes in Figure 4—figure supplement 1b c. The results of analyses of multipolar cell division and cell death by single-cell-tracking analysis were consistent with the counting approach (Figure 4a and b [counting] vs. Figure 4c d [single-cell tracking]), suggesting that the number of events determined by tracking the 335 progenitors and their progeny was sufficient to represent the occurrence of these events in an entire field of view in the videos. In one case, that is, treatment of cells with 7 µM MNNG, the number of cell death events in Control cells determined by counting was higher than that determined by single-cell-tracking analysis. Given that such events tend to occur in a nonuniform manner within the field of view (Figure 4—figure supplement 1b c), there may be some variation between the counting and single-cell-tracking approaches. Although such variations should be taken into account when interpreting the single-cell-tracking results, this approach still has an advantage over the counting approach by detecting the cellular events encountered by a cell and their trajectories. Cell fusion, which required the fused cells to be followed for at least 30 time points (~5 hr), can thus be detected by single-cell-tracking analysis. Similar to multipolar cell division and cell death, p53 silencing increased the frequency of cell fusion, and this was counteracted by MNNG (Figure 4e). Taken together, these results suggest that silencing of the low levels of p53 induced multipolar cell division, cell death, and cell fusion, and these were reduced by exposure of the cells to MNNG.

Impact of cell death on cell population expansion of p53 RNAi cells using in silico generation of a cell-lineage database

The rate of cell population expansion was similar in Control and p53 RNAi cells (Figure 2c and i). However, detailed analysis revealed that silencing the low levels of p53 increased multipolar cell division, cell death, and cell fusion (Figure 4). The probabilities of detecting bipolar cell division, multipolar cell division, cell death, and cell fusion at a certain time point in an image were calculated as 0.54, 0.001, 0.004, and 0.004/100 lineages, respectively, for Control, and 0.54, 0.014, 0.037, and 0.023/100 lineages, respectively, for p53 RNAi cells. This implies that the more frequent occurrence of these events in p53 RNAi cells relative to Control cells did not reflect the overall rate of cell population expansion, even though the events, especially cell death, could counteract the expansion of the cell population. In this regard, given that the p53 RNAi cell population contained an increased number of cells with higher reproductive ability (e.g., group F cell lineages; Figure 3c) than Control cells, silencing p53 may have increased cells with higher reproductive ability than Control cells, but this increase may have been counteracted by the induction of cell death (Figure 4b and c), resulting in similar population expansion curves for p53 RNAi cells and Control cells. In this case, if no cell death occurred in p53 RNAi cells, they would show a faster rate of cell population expansion than Control cells.

To test the effects of cell death on the rate of population expansion, we generated a cell-lineage database in silico (Figure 5a) by assuming that cells that undergo cell death continue to proliferate.

Figure 5

Download asset Open asset

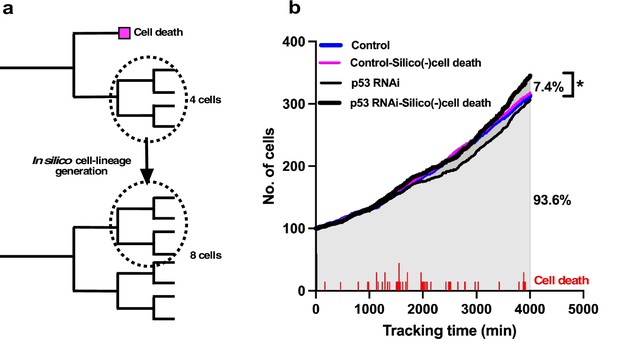
In silico generation of cell-lineage database to evaluate the impact of cell death on the cell population expansion.

(a) To evaluate the impact of cell death on population expansion, we created an in silico cell-lineage database, in which cells do not undergo cell death, to address the impact of cell death on the cell population expansion. In the example cell lineages, the number of survived cells was reduced by half as a result of cell death. If the siblings of the dead cell grew, the dead cell was assumed to continue to grow similar to its sibling, and a cell-lineage database was created in silico based on this assumption. (b) A cell population expansion curve was generated using the in silico-created cell-lineage database for Control and p53 RNAi cells (Control-Silico(-)cell death and p53 RNAi-Silico(-)cell death, respectively). At a tracking time of 4000 min, cell death resulted in a 7.4% reduction in the population size of p53 RNAi cells. The frequency of cell death (red lines) occurring during tracking is also shown. Statistical analysis was performed by ordinary one-way ANOVA (Tukey’s). *p<0.05.

Figure 5—source data 1 In silico generation of cell-lineage database to evaluate the impact of cell death on cell population expansion. Data used in Figure 5.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig5-data1-v3.xlsx
Download elife-72498-fig5-data1-v3.xlsx

To this end, we searched the data for siblings of cells that underwent cell death in a cell-lineage database. Given that their proliferation pattern was likely to be similar to their siblings, we replaced the data for cells that underwent cell death with those for their siblings (Figure 5a). The cell population expansion rate of the in silico-generated p53 RNAi cells without cell death (p53 RNAi-Silico(-)cell death) (Figure 5b) showed that the cell population size was 7.4% larger than that of the p53 RNAi cells at a tracking time of 4000 min (Figure 5b; p53 RNAi vs. p53 RNAi-Silico(-)cell death). The number of cell deaths that occurred in p53 RNAi cells is indicated in Figure 5b, and the p53 RNAi cell population expansion rate was reduced around 2000 min following cell death at 1000–2000 min of tracking. This reduction was less evident in p53 RNAi-Silico(-)cell death cells, suggesting that cell death in p53 RNAi cells did indeed counteract the expansion of this cell population. The cell population size of the p53 RNAi-Silico(-)cell death cells was also larger than those of the Control and in silico-generated Control cells (Control-Silico(-)cell death), where Control cells that underwent cell death were similarly replaced with their surviving siblings. These results suggest that p53 silencing promoted the reproductive ability of p53 RNAi cells, but this was counteracted by the induction of cell death, resulting in the formation of p53 RNAi cell populations that were similar to or smaller than Control cell populations (Figure 2i). This analysis also demonstrated that single-cell tracking provided more nuanced and detailed information about the effects of silencing p53 and the processes involved in determining the cell population size by taking account of the occurrences of multipolar cell division, cell death, and cell fusion, which are often difficult to put into spatiotemporal context in terms of the individual fate of cells when using methods that only reveal the status of cells at a certain moment in time.

Single-cell tracking revealed the most common event preceding multipolar cell division

While cell death counteracted the expansion of the cell population, multipolar cell division and cell fusion could have greater impacts than cell death in terms of creating diversity in the cell population by causing the formation of aneuploid cells (Boveri, 2008; Keryer et al., 1984; Holland and Cleveland, 2009; Gisselsson et al., 2008; Saunders, 2005; Emdad et al., 2005) if the progenies of these processes survive. We further examined how silencing the low levels of p53 altered the characteristics of cells by focusing on multipolar cell division and cell fusion and the relationships between these events. To this end, we used cell-lineage maps (Figure 1 and cell lineage maps deposited in Dryad) to identify cells that underwent multipolar cell division and traced back along the map to find an event that occurred prior to the division (Figure 6a). We identified two patterns: multipolar cell division occurring after cell fusion (Pattern 1a: cell fusion ➛ multipolar cell division) and multipolar cell division without cell fusion (Pattern 1b: multipolar cell division). Control and p53 RNAi cells demonstrated that 79.4 and 93.2% multipolar cell divisions, respectively, occurred following cell fusion (Pattern 1a). It is likely that cells with increased ploidy could have a higher chance of undergoing multipolar cell division and silencing of p53 increased the incidence of Pattern 1a (Figure 6a, Pattern 1a, Control vs. p53 RNAi). We then analyzed cells that fused by tracing further back along the cell-lineage maps (Figure 6b). Interestingly, cell fusion was more frequent between sibling cells (Pattern 2a). In this regard, a previous study reported that some persistent links remained after bipolar cell division leading to cell fusion (Shi and King, 2005). However, given that cell fusion also occurred between non-siblings (Pattern 2b), the cell fusion observed in this study was mediated by other processes. In summary, p53 silencing mainly promoted the sequence of events: bipolar cell division ➛ cell fusion between siblings ➛ multipolar cell division (Figure 6b, Pattern 2a).

Figure 6

Download asset Open asset

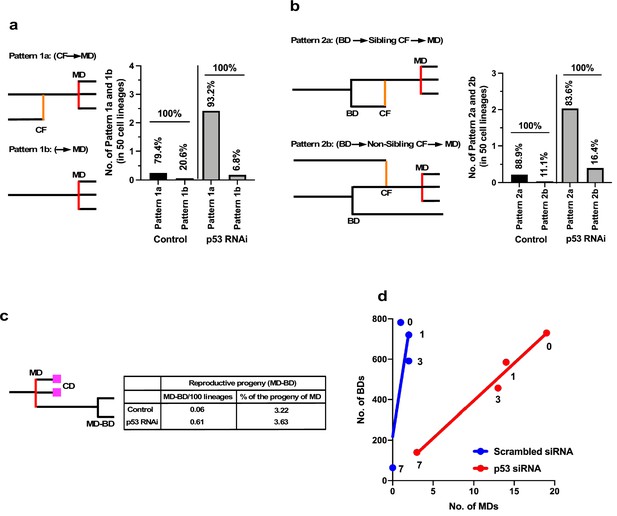
Events leading to the induction of multipolar cell division.

(a) Cellular events that occurred prior to multipolar cell division were analyzed by tracing the cell lineage backward. Pattern 1a (cell fusion [CF] ➛ multipolar cell division [MD]): cell fusion occurred prior to multipolar cell division. Pattern 1b (➛ MD): no cell fusion occurred. The numbers of each pattern occurring in 50 cell lineages are shown. Percentages of Patterns 1a and 1b in Control and p53 RNAi cells are also shown. (b) Cells that underwent multipolar cell division were identified. If the cells were generated by cell fusion, the origin of the fused cells was searched by tracing the cell lineage backward. Pattern 2a (BD ➛ sibling CF ➛ MD): bipolar cell division occurred, cells produced by division were fused, followed by multipolar cell division. Pattern 2b (BD ➛ non-sibling CF ➛ MD): one sibling produced by bipolar cell division was fused with another non-sibling cell, followed by multipolar cell division. The numbers of each pattern in 50 cell lineages are shown. Percentages of Patterns 2a and 2b in Control and p53 RNAi cells are also shown. (c) Progeny produced by multipolar cell division was tracked and the number of reproductive progeny that underwent bipolar cell division was determined. The numbers of reproductive progeny found in 100 cell lineages and the percentages of such progeny among the total number of progeny produced by multipolar cell divisions are shown. (d) The number of multipolar cell division events was plotted against the number of bipolar cell division events. Numbers in (d) indicate doses of MNNG. (**a–d**) Because the number of multipolar cell divisions in Control cells was low, we searched three videos to find multipolar cell divisions and then traced the cells back to their progenitors to determine the events preceding multipolar cell division. To normalize the values, we assumed that multipolar cell division occurred at a similar frequency to that recorded in the cell-lineage database. BD: bipolar cell division; MD: multipolar cell division, CD: cell death; and CF: cell fusion.

Figure 6—source data 1 Events leading to the induction of multipolar cell division. Data used in Figure 6.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig6-data1-v3.xlsx
Download elife-72498-fig6-data1-v3.xlsx

The progeny of multipolar cell division have been reported to be fragile, although some are capable of entering a proliferation cycle (Holland and Cleveland, 2009; Gisselsson et al., 2008). We, therefore, analyzed the survival of the progeny using cell-lineage maps. In terms of percentage survival, 3.2–3.6% of the total number of progeny produced by multipolar cell division survived in both Control and p53 RNAi cells (Figure 6c). On the other hand, given that silencing the low levels of p53 per se increased the number of multipolar cell divisions, the number of surviving progenies produced by division in the p53 RNAi cell population was increased 10.1-fold (0.61 progeny of multipolar cell division/100 cell lineages of p53 RNAi cells vs. 0.06 progeny of multipolar cell division/100 cell lineages of Control cells). These results suggest that p53 silencing mainly promoted the number of events with the sequence: bipolar cell division ➛ cell fusion between siblings ➛ multipolar cell division ➛ survival of aneuploid progeny, leading to the creation of genetic diversity in the p53 RNAi cell population.

We plotted the number of multipolar cell divisions against the number of bipolar cell divisions in Control and p53 RNAi cells and those treated with MNNG (Figure 6d). Although fewer multipolar cell divisions occurred in Control cells relative to p53 RNAi cells, MNNG exposure resulted in a dose-dependent linear reduction of bipolar vs. multipolar cell division, suggesting that the probability of inducing multipolar cell division was proportional to the number of bipolar cell divisions. These results also suggest that MNNG indirectly reduced the number of events in the sequence: bipolar cell division ➛ cell fusion between siblings ➛ multipolar cell division ➛ survival of aneuploid progeny. Although MNNG is a mutagen that induces G-T to A-T transversion mutations through the formation of O⁶-methylguanine (Lindahl et al., 1988), it could act to suppress the formation of aneuploid cells in some contexts, with possible relevance to the development of cancer (Rajagopalan and Lengauer, 2004).

Cell-fate simulation algorithm

The above data suggest that the fate of cell progeny following silencing of the low levels of p53 could alter the characteristics of the cells and their sensitivity to MNNG. However, characterization of the cells using a direct single-cell-tracking approach was limited by various factors. For example, there is a practical limit to the number of cells that can be analyzed by tracking and the duration that a cell culture can be maintained without cell passage, which makes it difficult to follow the fate of a cell beyond a certain duration. We, therefore, developed a cell-fate simulation algorithm to overcome this limitation and further analyzed the effects of p53 silencing on the fate of the cell population. For the simulation, we utilized the spatiotemporal information for each cell in the cell-lineage database records, which revealed the cell’s relationships with its parents, siblings, and offspring and events that occurred in that cell. In addition to overcoming the limitation, cell-fate simulations can provide powerful and flexible tools to model conditions that are not readily accessible by direct imaging, such as simulating the fate of a cell in a mixed culture population, evaluating the response of cells to drug treatment virtually, and testing existing models in silico.

The underlying concept of the cell-fate simulation algorithm is shown in Figure 7 (Figure 7—source code 1: overall scheme; and Figure 7—figure supplements 1–6: algorithms). We first decomposed a cell lineage into units sandwiched between two events, such as bipolar cell division, multipolar cell division, cell fusion, and cell death (Figure 7a). We referred to events that initiated and ended the unit as Start and End events, respectively, and each unit was thus defined by the nature of its Start and End events, and the length of time between the two events. An algorithm combining such units can thus be used to generate a virtual cell lineage with a similar pattern to an empirically determined lineage. Because each cell lineage in a cell population shows a variety of patterns, and the combination of these variations defines the characteristics of the cell population, the simulation algorithm thus needs to reflect this variation. To this end, we first produced a series of histograms of the distribution of the end events for each Start event (Figure 7b). For example, if the Start event was bipolar cell division, we created a histogram of the frequency of all possible End events; that is, bipolar cell division, multipolar cell division, cell death, and cell fusion. The histogram indicated the unique tendency of a cell population. For example, the Figure 7b histogram indicates that the most frequent End event in the cell population was bipolar division followed by multipolar division. The algorithm for the simulation thus utilized the frequency to generate virtual cell lineages (see Figure 7—figure supplement 2: 2 for the list of Start events). We referred to the histogram data as Operation data-Events, which is composed of a series of histograms corresponding to each Start event. The algorithm then reflected this distribution of the histograms to choose the End event. The selection of the End event was performed by converting the histogram data into an array by taking account of the frequency of the occurrence of each event to generate a random number to select an event type from the array. In this manner, an event type that occurred more frequently could have a higher chance of being selected, reflecting the unique characteristics of a cell population. Once the Start and End events were chosen, the algorithm referred to another set of histograms (Operation data-Time) that showed the distribution of the length of time for a given unit (Figure 7c). For example, for a unit with bipolar cell division as the Start event and cell fusion as the End event, the algorithm referred to the histogram data of time length distributions of the corresponding event combination (see the list of histograms for Figure 7—figure supplement 2: 1). The length of time was selected in a similar manner to the End event selection; that is, converting histogram data into an array and selecting an assigned length of time by generating a random number. These processes were repeated until the cell lineage reached the desired time point. In addition to the process of assigning event type and time length, the cell-doubling time of the parent cell was also taken into account. If both the Start and End events of a parent cell were bipolar cell division, our experimental results indicated that the length of time of its offspring was limited to ±10% of that of the parent cell. This restraint was determined by repeated stimulation with single-cell-tracking data generated using A549 cells. If a parent cell had a shorter length of time than others, its progeny could also have a shorter doubling time, creating an actively growing cell lineage. In this manner, the algorithm could generate lineages with different reproductive abilities, reflecting the characteristics of a cell population obtained by empirical live-cell imaging. This restraint for the duration between divisions was only applied to cells produced by bipolar cell division that underwent another bipolar division, given that cells produced by other types of events; for example, multipolar cell division and cell fusion, have less contribution to forming a cell population than those that undergo bipolar cell division.

Figure 7 with 7 supplements see all

Download asset Open asset

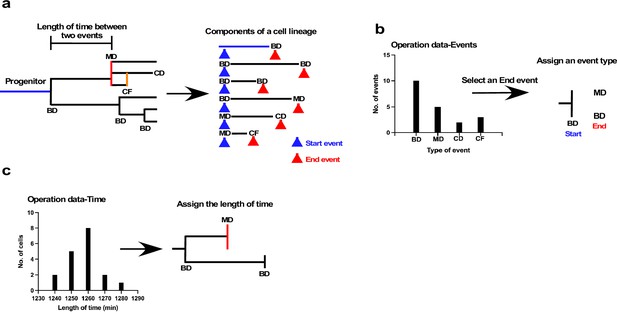
Schematic illustration of cell-fate simulation process.

(a) A cell lineage is composed of a progenitor and its progeny. Each of those cells is generated by a Start event (blue arrowhead), followed after a certain length of time by an End event (red arrowhead), such as bipolar cell division (BD), multipolar cell division (MD), cell death (CD), and cell fusion (CF). Cell-fate simulation was performed by combining these components, types of event, and length of time between the two events. To perform the simulation, cells were classified based on the combination of the Start and the End events; for example, BD-BD, and BD-MD (see Figure 7—figure supplement 2 for full list of classifications), and two sets of histogram data, referred to as Operation data-Events and Operation data-Time, were created. (b) The Operation data-Events holds the frequency of events that occurred following a Start event, such as BD, MD, or CF. In the case of the example shown in (b), if the Start event was BD, the histogram data indicated that the chances of the occurrence of each End event type, that is, BD, MD, CD, and CF, were 10, 5, 2, and 3, respectively. In the example, MD and BD were selected from the histogram to assign an End event type to daughter cells produced by BD. Selection was performed by generating a random value. (c) Operation data-Time was then used to assign the length of time between the Start and End events using histogram data (Operation data-Time) for BD-BD and BD-MD, which included the choices of length of time. The processes were repeated to generate cell-lineage data for virtual cells.

Figure 7—source code 1 Single-cell tracking and cell-fate simulation processes. (a) Overall scheme of single-cell tracking. (b) Processes of cell-fate simulation.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig7-code1-v3.docx
Download elife-72498-fig7-code1-v3.docx
Figure 7—source code 2 Cell-fate simulation.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig7-code2-v3.docx
Download elife-72498-fig7-code2-v3.docx
Figure 7—source code 3 Cell-fate simulation.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig7-code3-v3.docx
Download elife-72498-fig7-code3-v3.docx
Figure 7—source code 4 Cell-fate simulation.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig7-code4-v3.docx
Download elife-72498-fig7-code4-v3.docx
Figure 7—source code 5 Cell-fate simulation.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig7-code5-v3.docx
Download elife-72498-fig7-code5-v3.docx

We summarized the overall scheme of analysis with single-cell tracking and cell-fate simulation (Figure 7—source code 1a). After the generation of live-cell imaging videos, images were segmented and the segmented data was used for automatic single-cell tracking. Then, the database was used for cell-lineage map creation, data analysis, and generation of Operation data. Operation data was then used for the cell-fate simulation (Figure 7—source code 1b). After loading the cell-lineage data, Operation data-Time and -Events were created. The length of time for progenitors and a primary event type were assigned to each progenitor, followed by the generation of cell-lineage data by assigning an event type and length of time to a cell. Example cell-lineage maps generated by empirical single-cell tracking analysis and the algorithm are shown in Figure 7—figure supplement 2a and b, respectively (cell-lineage maps generated by the algorithm have been deposited in Dryad). Furthermore, because the simulation per se can be carried out using Operation data, various simulation options can be created by modifying the Operation data content.

Cell-fate simulation options with Operation data

We created five different modes of simulations (Figure 8): Standard, Dose simulation, Mix culture, Switch, and Mix culture-Switch (results shown in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 were generated by Standard, Dose simulation, Standard, Mix culture, and Mix culture-Switch modes, respectively). The Standard mode simulates the fate of one cell type using one Operation data (Figure 8a). We applied this mode to simulate the expansion of a cell population for an extended period of time, which cannot be achieved by in vitro cell culture (Figure 9 and Figure 11). The Dose simulation mode can be carried out by taking advantage of the fact that Operation data-Events and Operation data-Time are histogram data, in which values can be modified by applying a certain rule, for example, a linear relationship, to create new Operation data. For example, if histogram arrays of Operation data-Events A and B (in Figure 8) obtained from the single-cell analysis of cells treated with 2 and 5 μM of a drug, respectively, recorded 10 and 1 bipolar cell divisions following a Start event, the number of bipolar cell divisions of a cell population exposed to 3 μM was calculated to be 7. In the example (Figure 8b), we also calculated multipolar cell division, cell death, and cell fusion data stored in the histogram array. Similar calculations were made for other histogram data stored in Operation data-Events and Operation data-Time (Figure 7—figure supplement 2), generating new Operation data-Events and Operation data-Time. We applied this mode to simulate cellular responses to different doses of MNNG (Figure 10). For example, the fate of cells exposed to 5 μM MNNG can be simulated by creating Operation data for 5 μM MNNG from Operation data for 3 μM and 7 μM MNNG. The Mixed culture mode (Figure 8c) simulates a fate of a cell population composed of two or more types of cell populations using Operation data corresponding to each type of cell population. We applied this mode to simulate the expansion of cells under conditions in which 96% of cells were initially Control cells and 4% were p53 RNAi cells (Figure 12). The Switch mode per se was not used in this work, but this mode (Figure 8d) was used to perform virtual drug treatments. For example, simulation using the Operation data for Control cells was then switched to the second Operation data for cells treated with, for example, 3 μM MNNG, allowing simulation of the effect of 3 μM MNNG on Control cells. The Mixed culture with Switch mode (Figure 8e) allowed simulations to be started with a virtual cell population composed of two or more different types of cell populations with virtual drug treatment. Thus, if two types of cell population fates are to be simulated, two Operation data are used initially and then switched to Operation data for drug-treated cells of each type (Figure 13). If the cell types have different treatment sensitivities, the effects of this difference can be simulated by the Mixed culture with Switch mode. We applied this mode to simulate the impact of repeated MNNG treatments on the expansion of a cell population initially comprising 96% Control and 4% p53 RNAi cells at the start of the simulation (Figure 13h). In summary, cell-fate simulation using Operation data allows the creation of various simulation options and provides flexibility for designing virtual experiments that would otherwise be difficult to perform empirically.

Figure 8 with 1 supplement see all

Download asset Open asset

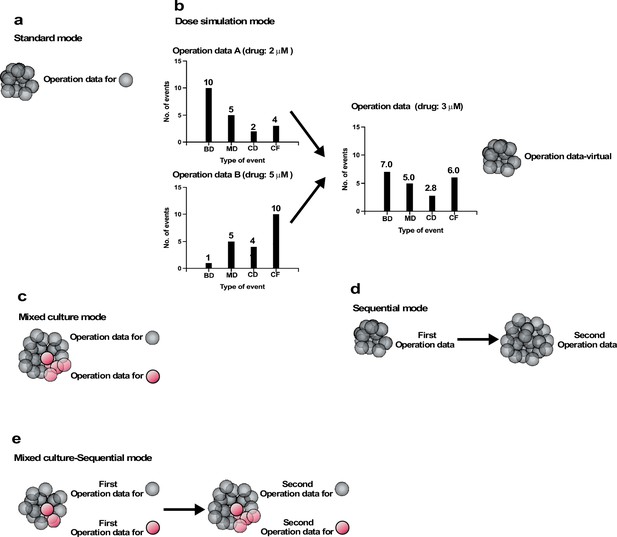
Operation modes.

(a) Standard mode: cell-fate simulation with one type of cell population performed with Operation data. (b) Dose simulation mode: Operation data created from other Operation data. The example in (b) represents an Operation data-Events, which holds information on the chance of the occurrence of subsequent events following an event, as outlined in Figure 7c. In the case of Operation data A, generated from a cell-lineage database created by tracking cells exposed to a dose of a drug (e.g., 2 µM MNNG), 10, 5, 2, and 4 bipolar cell division (BD), multipolar cell division (MD), cell death (CD), and cell fusion (CF) events, respectively, occurred following the event. On the other hand, Operation data B, generated from a cell-lineage database created by tracking cells in another cell population exposed to a different dose (e.g., 5 µM) of the drug, assumed that 1, 5, 4, and 10 BD, MD, CD, and CF events would occur following the same type of events referred to in Operation A. If a cell population was assumed to be exposed to the drug at 3 µM, Operation data for the exposed cells could be created by calculating; for example, BD (7) = BD for Operation data A (10) + [(Operation data B (1) − Operation data A (10)/(Dose 2 (×5) − Dose 1 (×2))) × (Intermediate dose (×3) − Dose 1 (×2))]. A similar calculation can be performed for all data stored in Operation data-Time and -Events to create new Operation data (Operation data-virtual). Using the Operation data, the cell fate could be simulated without the need for empirical analysis. (c) Mixed culture mode: assuming that multiple cell types coexist in a culture, simulation was performed using corresponding Operation data for each cell type. (d) Switch mode: cell-fate simulation is performed with Operation data and then switched to another Operation data. If the second Operation data is for cells treated with a drug, this simulation allow the effect of the drug treatment to be evaluated virtually. (e) Mixed culture-Switch mode: this mode is a combined Mixed culture (c) and Switch (d) mode.

Figure 9 with 2 supplements see all

Download asset Open asset

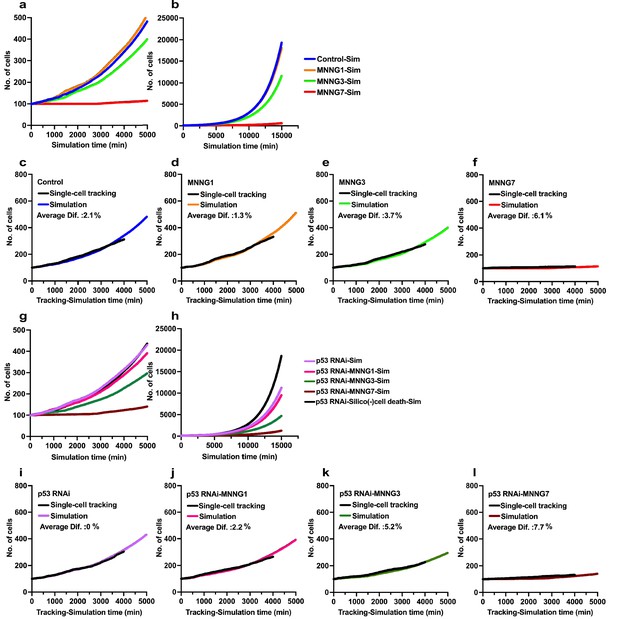
Simulations of effects of p53 silencing and MNNG exposure on cell population expansion.

Simulations were performed using Operation data generated from cell-lineage data with a total of 5000 virtual progenitors for a simulation time of 15,000 min. (**a, b**) Virtual cell population expansion curves of Control-Sim cells and cells exposed to various doses of MNNG (a) 0–4000 min and (b) whole scale (0–15,000 min). (**c–f**) Data obtained from the simulation were compared with cell population expansion curves determined by single-cell-tracking analysis; (c) Control, (d) MNNG1, (e) MNNG3, and (f) MNNG7. Difference (%) was determined by obtaining the sum of the number of cells (single-cell tracking)/the number of Simulated cells determined at each simulation time point divided by 1500 simulation time ×100. For example, a difference of 2.7% implied that the simulation generated 2.7% more cells compared with the single-cell-tracking data. (**g, h**) Virtual cell population expansion curves of p53 RNAi-Sim cells and cells exposed to various doses of MNNG (g) 0–4000 min and (h) whole scale (0–15,000 min). (**i–l**) These simulation data were compared with the cell population expansion curves determined by single-cell-tracking analysis; (i) p53 RNAi, (j) p53 RNAi-MNNG1, (k) p53 RNAi-MNNG3, and (l) p53 RNAi-MNNG7. Results of simulation obtained using Operation data-p53 RNAi-Silico(-)cell death are also included in (g) and (h).

Figure 9—source data 1 Simulations of effects of p53 silencing and MNNG exposure on cell population expansion. Data used in Figure 9.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig9-data1-v3.xlsx
Download elife-72498-fig9-data1-v3.xlsx

Figure 10

Download asset Open asset

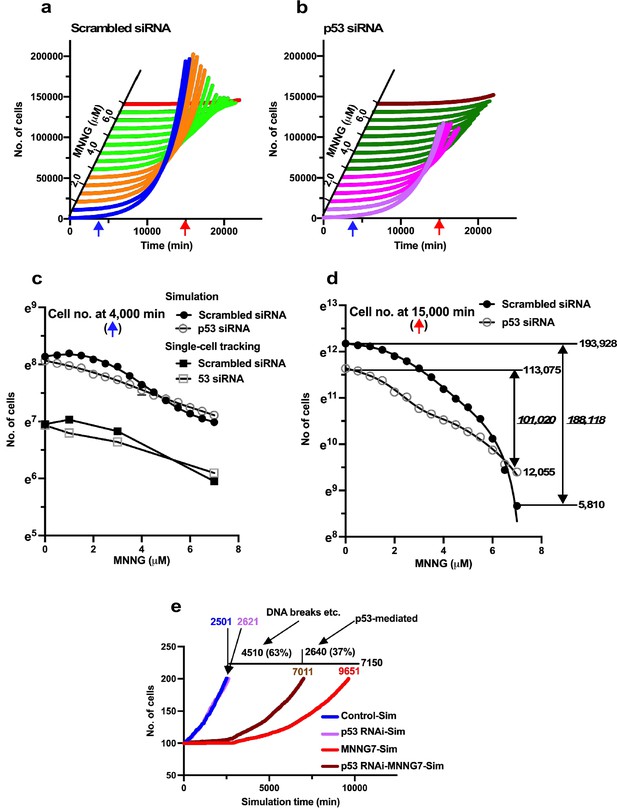
Virtual dose–response analysis.

Virtual Operation data corresponding to each 0.5 µM dose of MNNG was generated in Dose simulation mode. (**a, b**) Virtual MNNG-dose–response cell population expansion curves of Control and p53 RNAi cells generated by the simulation using Operation data-Control to MNNG 1.5 (purple), 2–3 (pink), 3.5–6.5 (dark green), and 7 (maroon) are shown. (c) The numbers of cells at simulation times of 4000 min (indicated by a blue arrow in a and b) are plotted. Results of single-cell-tracking analysis are also included. (d) The numbers of cells at simulation times of 15,000 min (indicated by a red arrow in a and b) are plotted. The difference of cell number between Control cells and the cells exposed to 7 μM MNNG, and p53 RNAi cells and the cells to the dose of MNNG is shown (italic). The number of cells at 0 and 15,000 min is also shown. (**c, d**) Standard deviations are shown. A natural log scale was used. (e) Time necessary to reach a cell population to be doubled (100–200 cells) was determined by using Operation data-Control, MNNG7, p53 RNAi, and p53 RNAi-MNNG7. The difference in time between MNNG7-Sim (9651 min) and Control-Sim (2501 min) was 7150 min. Similarly, the difference in doubling time between p53 RNAi-MNNG7-Sim and p53 RNAi-Sim was 4510 min. Assuming that the difference in doubling time between MNNG7-Sim and Control-Sim represents the effect of MNNG induced by, for example, DNA breaks and p53-mediated responses, while that between p53 RNAi-MNNG7-Sim and p53 RNAi-Sim only represents the effect of MNNG induced by, for example, DNA breaks, 63 and 37% of suppression of cell population expansion in MNNG7-Sim were likely to be due to the effect of MNNG caused by, for example, DNA breaks and responses induced by the stabilization of p53, respectively.

Figure 10—source data 1 Virtual dose–response analysis. Data used in Figure 10.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig10-data1-v3.xlsx
Download elife-72498-fig10-data1-v3.xlsx

Figure 11 with 2 supplements see all

Download asset Open asset

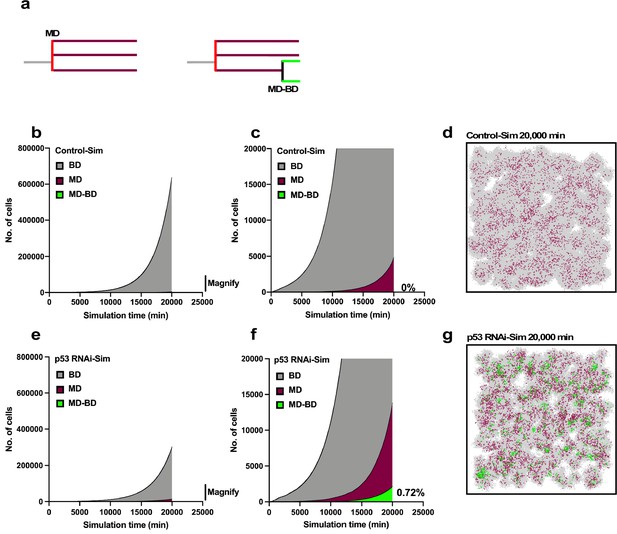
Simulation of proliferation of progeny of multipolar cell division.

The simulation was performed using Operation data-Control and p53 RNAi in Standard mode. (a) The numbers of progeny of bipolar cell division (gray), multipolar cell division (burgundy), and progeny cells that first underwent multipolar cell division followed by bipolar cell division (green) are plotted. The simulation was carried out for 2500 progeny, which generated 6.6 × 10⁶ cells during the 20,000 min of simulation. (**b, c**) Whole-scale and magnified images generated by the simulation using the Operation data-Control are shown in (b) and (c), respectively. (d) An animation was created to visualize the proliferation of Control-Sim cells (Figure 11—video 1), and an image at simulation time 20,000 min is shown. Gray, burgundy, and green dots represent cells that underwent bipolar division, multipolar division, and multipolar division followed by bipolar division, respectively. (**e, f**) Whole-scale and magnified images generated by the simulation using Operation data-p53 RNAi are shown in (e) and (f), respectively. (g) An animation was created to visualize the proliferation of p53 RNAi-Sim cells (Figure 11—video 2), and an image at simulation time 20,000 min is shown. Bipolar cell division (BD), multipolar cell division (MD), and multipolar cell division followed by bipolar cell division (MD-BD).

Figure 11—source data 1 Simulation of growth of the progeny of multipolar cell division. Data used in Figure 11.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig11-data1-v3.xlsx
Download elife-72498-fig11-data1-v3.xlsx

Figure 12 with 1 supplement see all

Download asset Open asset

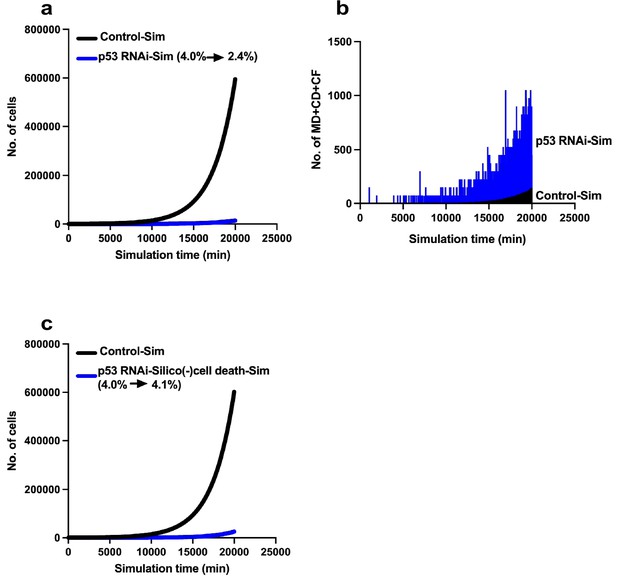
Limited expansion of p53 RNAi cells in a Control cell population.

We simulated the expansion of the p53 RNAi cell population (4% at the initial time point) in a Control cell population (96% at the initial time point) using Mixed culture mode with Operation data-Control and p53 RNAi for a simulation time of 20,000 min with 500 progenitors and repeating 10 simulations (total 5000 progenitors). (a) Simulation of 480 Control progenitors was carried out using Operation data-Control and 20 p53 RNAi progenitors with Operation data-p53 RNAi. The initial percentage of p53 RNAi cells was 4%, which was reduced to 2.4% at 20,000 min. (b) The sums of multipolar cell division, cell death, and cell fusion events (MD + CD + CF) are shown. (c) Simulation was performed using Operation data-p53 RNAi-Silico(-)cell death.

Figure 12—source data 1 Limiting expansion of p53 RNAi cells in a Control cell population. Data used in Figure 12.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig12-data1-v3.xlsx
Download elife-72498-fig12-data1-v3.xlsx

Figure 13 with 1 supplement see all

Download asset Open asset

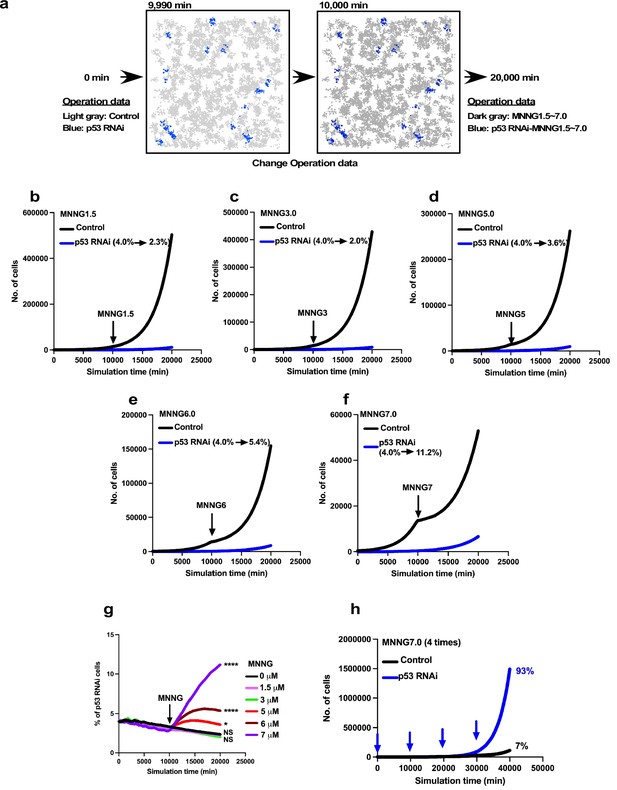
Expansion of p53 RNAi cells in a Control cell-dominant cell population subjected to virtual MNNG exposure.

We simulated the response of p53 RNAi cells in a Control cell-dominant cell population to MNNG exposure using Mixed culture- Switch mode. (a) The simulation was performed with 96% Control and 4% p53 RNAi cells, using Operation data-Control and p53 RNAi for 9900 min. The Operation data was then switched to, for example, MNNG7 and p53 RNAi-MNNG7 for virtual MNNG treatment, and the simulation was continued up to 20,000 min. In the animation (Figure 13—video 1), the pixel value of the image was reduced to indicate the virtual MNNG treatment. (**b–f**) In the simulation, Operation data corresponding to (b) 1.5, (c) 3, (d) 5, (e) 6, and (f) 7 µM MNNG were used to perform a virtual MNNG treatment. The numbers in the images indicate the percent of p53 RNAi cells at simulation times 0 and 20,000 min. (g) The percentages of p53 RNAi cells in the population are plotted. Statistical analysis (n = 10) was performed using data at simulation time 20,000 min by ordinary one-way ANOVA. NS, nonsignificant, *p<0.05, ^****p<0.0001. (h) Based on the simulation data for 7 µM MNNG, percentage of p53 RNAi cells following repeated 7 µM MNNG exposure every 10,000 min (~7 days) was calculated. Arrows indicate the time that the virtual exposure was performed.

Figure 13—source data 1 Expansion of p53 RNAi cells in a Control cell population subjected to virtual MNNG exposure. Data used in Figure 13.: https://cdn.elifesciences.org/articles/72498/elife-72498-fig13-data1-v3.xlsx
Download elife-72498-fig13-data1-v3.xlsx

Verification of number of progenitors used for simulation

We characterized the algorithm by performing a series of test simulations. To distinguish data produced by simulation from data produced by single-cell tracking, we referred to the cells as, for example, Control-Sim and MNNG7-Sim cells for the results produced by simulation (Figure 8—figure supplement 1). If the corresponding Operation data needed to be indicated, the cell populations were referred to as, for example, Operation data-Control and Operation data-MNNG7. We first performed simulations with 300, 500, 1000, 1500, and 2000 progenitors with a simulation time of 15,000 min, repeated five times to detect variations in the simulation. Cell population expansion curves of virtually created Control cells (Control-Sim cells) are shown in Figure 8—figure supplement 1a. Under these conditions, the variation was <2% of the average number of cells when the simulation was carried out with >1000 progenitors. The simulation performed using the Operation data-MNNG7 (Figure 8—figure supplement 1b) produced a larger variation, but this converged to about 6% when the simulation was carried out with >1000 progenitors. We therefore performed the simulation with 1000–2000 progenitors and repeated the simulation 5–10 times (total of 5000–10,000 progenitors).

Comparison between cell population expansion curves determined by simulation and single-cell tracking

We then evaluated the accuracy of the simulation by referencing the cell population expansion curves determined by single-cell tracking analysis (Figure 9). In the simulations, we used Standard mode with Operation data generated from the cell-lineage database and performed simulation with 5000 progenitors for 15,000 min. The number of progenitors was normalized to 100 to compare the results obtained by simulation with those obtained by single-cell-tracking analysis. During the simulation, a Control-Sim cell population size increased 193.5-fold (5000–967,281 cells), and about 2 × 10⁶ virtual cells were created in the simulation period of 15,000 min. The Control-Sim, MNNG1-Sim, MNNG3-Sim, and MNNG7-Sim cell population expansion curves (Figure 9a, 0–4000 min) were consistent with the curves determined using single-cell-tracking analysis (Figure 2g), although the Control-Sim cell curve intersected with the MNNG1-Sim cell curve at a simulation time of about 10,000 min (Figure 9b, 0–15,000 min). To evaluate the accuracy of the simulation, we calculated the average percent difference between the cell numbers determined by the simulation and by single-cell-tracking analysis (Figure 9c–f). When the number of cells determined by single-cell tracking was calculated as 100%, the average difference was 1–6%. We then performed a similar analysis with p53 RNAi cells and found that cell population expansion curves generated by the simulation showed consistent patterns (Figure 9g, 0–4000 min, and Figure 9h, 0–15,000 min) with those determined by single-cell-tracking analysis (Figure 2h). The percent differences were within 0–8% (Figure 9i–l). We thus concluded that the simulation could be performed within a variation of maximal 8% compared with the results of single-cell-tracking analysis.

Doubling time of cells generated by the simulation

We also analyzed the doubling time of individual cells generated by single-cell-tracking analysis and compared them with ones generated by simulation. The average cell doubling time was prolonged following the increased dose of MNNG (31.23–41.85 hr, Figure 9—figure supplement 1a–d). The doubling time of individual cells generated by the simulation (Figure 9—figure supplement 1e–h) was similarly prolonged following the increased dose of MNNG (29.36–39.43 hr), suggesting that the algorithm could simulate the effect of MNNG on cell doubling. Similarly, the effect of MNNG treatment on the cell doubling time of p53 RNAi cells (Figure 9—figure supplement 1i–l) could also be simulated, showing the consistent results with the analysis of single-cell-tracking analysis (Figure 9—figure supplement 1m–p compared with Figure 9—figure supplement 1i–l). On the other hand, the simulation tended to yield an average cell doubling time about 2 hr shorter than that determined by single-cell-tracking analysis. Given that the algorithm assigned a cell-doubling time to each cell by generating a random number with Operation data-Time (Figure 7), a long cell-doubling time, for example, 3,000 min, which occurred less frequently, may have a lower chance of being assigned, resulting in the generation of a simulated cell population with a cell-doubling time about 2 hr shorter than that of cells analyzed by single-cell tracking. Alternatively, the cell-doubling time distribution generated by the simulation would represent the actual cell-doubling time of a cell population, given that the quantity of data generated by the simulation was ~200 times larger than that by single-cell tracking. This shorter average cell-doubling time could translate into an increased rate of cell population expansion, and the maximal 8% variation in cell population expansion curves (Figure 9) could reflect the cell-doubling time of the simulated cell population.

Simulation of occurrence of multipolar cell division, cell death, and cell fusion

We examined how the algorithm simulated the occurrence of multipolar cell division, cell death, and cell fusion. Because these events were less frequent than bipolar cell division, simulations were performed 10 times with 1000 progenitors (total 10,000 progenitors). We compared the numbers of these events generated within 4000 min by the simulation with those obtained by single-cell-tracking analysis. These data were then shown as the percent of a total number of cells. The simulated results for multipolar cell division (Figure 9—figure supplement 2a), cell death (Figure 9—figure supplement 2b), and cell fusion (Figure 9—figure supplement 2c) showed similar tendencies to the single-cell-tracking results, and the differences between the tracking analysis and simulate results were within 1%. We, therefore, concluded that the cell-fate simulation algorithm could perform virtual cell experiments with similar accuracy to single-cell-tracking analysis.

Virtual dose–response analysis and damage response

To begin the study with the fate simulation, we reanalyzed the responses of cells transfected with Scrambled siRNA or p53 siRNA to MNNG. To this end, Operation data were created for every 0.5 µM of MNNG from 0 to 7 µM using Dose simulation mode to determine a more detailed dose–response curve. The virtual dose–response curves determined by the simulation are shown in Figure 10a and b, and the numbers of cells at simulation times of 4000 and 15,000 min (indicated by blue and red arrows, respectively, in Figure 10a and b) are shown as natural logarithm in Figure 10c and d, respectively. The dose–response curves of cells containing low levels of p53 (Control cells) and p53 RNAi cells determined at a simulation time of 4000 min showed similar patterns to those determined by single-cell tracking (Figure 10c), suggesting that the fate of cells exposed to 0.5 μM increments of MNNG can be simulated by the Dose simulation mode. We then analyzed the effects of MNNG exposure on Control and p53 RNAi cells at 15,000 min to determine the long-term impact of MNNG exposure. MNNG 7 µM reduced the cell population size of Control cells at 15,000 min from 193,928 to 5810 cells (Figure 10d, difference: 188,118 cells, 97%), while the number of p53 RNAi cells was reduced from 113,075 to 12,055 cells (difference: 101,020 cells, 89%), suggesting that Control cells showed a stronger inhibitory response to MNNG than p53 RNAi cells in terms of cell population expansion, possibly due to p53-induced responses (Figure 10d). These results suggest that the p53 RNAi cells were less sensitive to MNNG due to the removal of the low levels of p53, resulting in a low or absent p53-induced response triggered by MNNG.

MNNG induces its cytotoxic effects through the formation of DNA breaks and activation of the response caused by the accumulation of p53 (Wood, 1996; Jacobs and Schär, 2012; Lindahl, 1990; Satoh and Lindahl, 1992; Lindahl et al., 1995; Lindahl et al., 1988; Kim et al., 2005). It is therefore conceivable that responses induced in Control cells may be related to both DNA-break formation and the response induced by the DNA damage-initiated accumulation of p53, while responses in p53 RNAi cells are only related to DNA-break formation. To estimate the relative contributions of these two effects to the inhibition of cell population expansion, we plotted the population expansion curves of Control-Sim, MNNG7-Sim, p53 RNAi-Sim, and p53 RNAi-MNNG7-Sim cells and determined the population doubling time (Figure 10e). We hypothesized that the difference in times between Control-Sim and MNNG7-Sim (7150 min) was due to both effects, while the difference between p53 RNAi-Sim and p53 RNAi-MNNG7-Sim (4510 min) represented the effect caused by the break formation. Based on these data, we estimated that about 63 and 37% of inhibition of cell population expansion caused by 7 µΜ MNNG exposure were due to effects related to DNA-break formation and the accumulation of p53, respectively. Although these percentages could be affected by other factors, dissecting the cellular response based on the possible mechanism of cytotoxicity could provide a deeper understanding of how cells respond to cytotoxic drugs.

Survival of the progeny of multipolar cell division

Next, we asked how frequently the progeny of multipolar cell division can survive and grow by performing a simulation in Standard mode with 2500 progenitors for a simulation time of 20,000 min (13.8 days). Multipolar cell division-derived progeny, which lack reproductive ability (Figure 11a, left), and progeny that underwent multipolar cell division followed by bipolar cell division, thereby maintaining reproductive ability (Figure 11a, right), are shown in burgundy and green, respectively. When the simulation was performed using the Operation data-Control (Figure 11b and c), no reproductive progeny produced by multipolar cell division were found. To visually show such cells, we created a computer animation (Figure 11—video 1 and Figure 11d for still image at 20,000 min), which visualizes the population expansion of the virtual cells, showing only burgundy cells that eventually underwent cell death or remained as nongrowing cells. However, when the simulation was performed using Operation data-p53 RNAi (Figure 11e and f), some progeny of multipolar cell division underwent bipolar cell division, accounting for 0.72% of the cell population at a simulation time of 20,000 min. We showed the population expansion of the progeny of multipolar cell division visually by creating a computer animation (Figure 11—video 2 and Figure 11g for still image at 20,000 min), which showed the expansion of green cell populations (cells survived and expanded after multipolar cell division) in accordance with the suggestion (Holland and Cleveland, 2009; Gisselsson et al., 2008) that an aneuploid cell population, which could have distinct characteristics, could be generated by the survival of the progeny of multipolar cell division promoted by p53 silencing.

Limiting expansion of p53 RNAi cells in the presence of Control cells

We then investigated how the presence of Control cells influenced the population expansion of p53 RNAi cells, given that cells that lack p53 likely arise within a Control cell population during tumorigenesis. We performed a simulation based on the assumption that Control and p53 RNAi cells comprised 96 and 4% of the cell population, respectively, using Mixed culture mode with Operation data-Control and p53 RNAi. A total of 1.2 × 10⁷ virtual cells were generated after 20,000 min of simulation, and the percentage of p53 RNAi cell population was reduced from 4% to 2.4% (Figure 12a) because of the frequent occurrence of multipolar cell division, cell death, and cell fusion (Figure 12b, and Figure 12—video 1 for the animation; p53 RNAi cells shown as blue cells). These data suggested that, although p53 RNAi cells could generate characteristic diversity in their cell population through increased frequencies of multipolar cell division, cell death, and cell fusion compared with Control cells, this conferred a disadvantage in terms of p53 RNAi cell population expansion when both cell types co-existed in a population. We suggest that the occurrence of cell death in p53 RNAi cells may be the main factor limiting the expansion of these cells (Figure 5b). Indeed, a simulation using Operation data generated from p53 RNAi-Silico(-)cell death cells showed that the cell population expanded at a similar rate to Control-Sim cells (Figure 12c), again suggesting that cell death acted as a major factor limiting the population size of p53 RNAi cells.

Induction of damage response in Control cells and its impact on the expansion of p53 RNAi cell population

The relative population expansion rates of Control and p53 RNAi cells were altered by exposure to MNNG (Figure 10: Dose simulation mode). We, therefore, simulated the responses of a cell population comprising Control (96%) and p53 RNAi cells (4%) to virtual MNNG treatment using the Mixed culture-Switch mode. We used Operation data-Control and p53 RNAi up to a simulation time of 9900 min, and the Operation data was then switched to the one for relevant doses of MNNG and the simulation was continued for another 10,000 min (total 20,000 min simulation) (Figure 13a). We simulated the responses of cells to 1.5, 3, 5, 6, and 7 µM MNNG. p53 RNAi cells were still unable to expand their population relative to Control cells following exposure to 1.5 and 3 µM MNNG (Figure 13b and c). However, p53 RNAi cells started to gain an advantage in terms of population expansion over Control cells after exposure to 5 µM MNNG (Figure 13d) and started to expand their population at doses of 6 and 7 µM MNNG (Figure 13e and f, and Figure 13—video 1). These results suggested that the damage responses induced in Control cells reduced its expansion speed while the expansion of the p53 RNAi cells continued (Figure 13g). Indeed, when the exposure of cells to 7 µM MNNG was repeated four times, 93% of the cell population was replaced with p53 RNAi cells (Figure 13h). These results suggest that, although p53 could suppress the formation of aneuploid cells, which could have a role in tumorigenesis, it could also allow the expansion of cells lacking p53 expression under damage-response conditions. p53 may thus play a dual role in the suppression and promotion of malignant cell formation during tumorigenesis.

Discussion

Cell populations are known to be composed of cells with diverse phenotypic characteristics. Such diversity could be generated by the formation of a cell with distinct characteristics and the subsequent expansion of its progeny in the cell population. In this study, we revealed that silencing of the low levels of p53 generated cells with distinct characteristics from Control cells, and also affected the responses of cells to MNNG. These results suggest that a novel approach using single-cell tracking and cell-fate simulation can provide unique insights into the function of p53, thus deepening our understanding of its role in tumorigenesis.

Low levels of p53 and possible functions

p53 is required for cells to respond to stress, through regulation of its cellular content (Boutelle and Attardi, 2021; Kastenhuber and Lowe, 2017; Lavin and Gueven, 2006; Livingstone et al., 1992; Kastan et al., 1991; Clarke et al., 1993; Lowe et al., 1993; Campisi, 2005; Rufini et al., 2013; Haupt et al., 1997; Honda et al., 1997; Kubbutat et al., 1997). The equilibrium between p53 degradation (through ubiquitination mediated by Mdm2) and its synthesis can be changed, depending on the degree of stress (Boutelle and Attardi, 2021; Kastenhuber and Lowe, 2017; Lavin and Gueven, 2006; Haupt et al., 1997; Honda et al., 1997; Kubbutat et al., 1997). Stronger stress tends to shift the equilibrium towards increased p53 levels, leading to various responses, for example, metabolic regulation, DNA damage responses, autophagy, cell cycle regulation, and cell death (Kastenhuber and Lowe, 2017; Livingstone et al., 1992; Kastan et al., 1991; Clarke et al., 1993; Lowe et al., 1993; Campisi, 2005; Rufini et al., 2013). On the other hand, the functions of the low levels of p53 present in unstressed cells remain unclear, but they may have a housekeeping function. Indeed, several lines of evidence, including the promotion of induced pluripotent stem cells by silencing p53 (Guo et al., 2014), and the spontaneous formation of tetraploid cells, as proposed cancer precursor cells, in p53 knockout mice (Livingstone et al., 1992; Harvey et al., 1993), suggest that low levels of p53 are required for housekeeping and homeostasis functions in cells. In addition, Vousden and Lane pointed out that the low levels of p53 may play a role in responding to ‘daily levels of stress’ (Vousden and Lane, 2007), and Valente et al. recently demonstrated that p53 plays a role in responding to stress induced by physiological levels of oxygen tension (Valente et al., 2020). Furthermore, this study showed that low levels of p53 inhibited the induction of cell death and cell fusion, which could lead to the induction of multipolar cell division, suggesting that the low levels of p53 are involved in processes that ensure the accuracy of cell division.

Silencing of low levels of p53 and induction of cell death, cell fusion, and multipolar cell division

The different characteristics of Control and p53 RNAi cells are summarized in Figure 14a. Most Control cells underwent bipolar cell division, resulting in expansion of the cell population. Although cell death, cell fusion, and multipolar cell division occurred in Control cells, they had relatively little effect on the expansion of the cell population. In contrast, although p53 RNAi cells could expand their cell population through bipolar cell division, p53 silencing led to more frequent induction of cell death and cell fusion.

Figure 14

Download asset Open asset

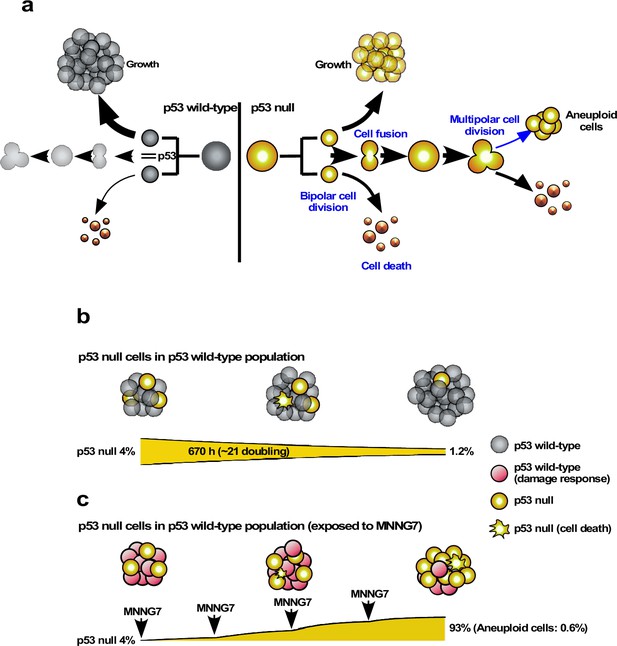
Role of the low levels of p53 in suppression of multipolar cell division, cell death, cell fusion, and damage response.

(a) Characteristics of Control and p53 RNAi cells. (b) The simulation of the fate of p53 RNAi cells in the Control cell population. (c) The simulation of the fate of p53 RNAi cells in the Control cell population, which were virtually exposed to 7 μM MNNG. The percentage of aneuploid cells is also shown.

The cell death events in p53 RNAi cells appeared to be induced by a p53-independent mechanism. Although the mechanism underlying the induction of cell death remains to be investigated, it may involve a natural defense mechanism to remove cells lacking p53 from a cell population. Indeed, we demonstrated that cell death caused a 7.4% reduction in the rate of p53 RNAi cell population expansion. Cell death thus conferred a disadvantage to p53 RNAi cells to expand their population relative to Control cells. Simulation of the fates of cells in a population containing 4% p53 RNAi and 96% Control cells showed that the proportion of p53 RNAi cells was reduced to 1.2% after 670 hr (28 days) of culture (Figure 14b). When such a simulation was initiated with 5000 cells, the cell number reached ~1 × 10⁹, with a mass equivalent to ~1 cm of cancer tissue, after 21 cell divisions. Within a cell tissue mass, p53 RNAi cells may occur as dormant cells, given that the percentage of p53 RNAi cells in the tissue would be reduced following the increase in tissue size. With regard to dormancy, many metastatic cells are known to become dormant (Hüsemann et al., 2008; Riethmüller and Klein, 2001), suggesting that their metastatic nature per se could confer a survival disadvantage on these cells relative to normal or non-metastatic cells, as indicated by the difference in expansion rates between p53 RNAi cells in a Control cell population.

Cell fusion was also increased following silencing of p53 (Figure 14a). Although the role of p53 in the suppression of cell fusion is unknown, previous reports have suggested a link between the loss of p53 and the induction of cell fusion. For example, fibroblasts derived from p53^−/− mice rapidly became tetraploid (Livingstone et al., 1992; Harvey et al., 1993). Increased cell fusion of p53 RNAi cells, mainly between sibling cells produced by bipolar cell division, could account for the formation of tetraploid cells (Figure 14a). Such fused cells may be formed by failure of cytokinesis, mitotic slippage, or the formation of a link between siblings (Shi and King, 2005; Eischen, 2016; Ganem et al., 2007; Storchova and Kuffer, 2008). However, low levels of p53 may block the process of fusion itself, given that we also observed cell fusion following abscission and between non-sibling cells. During development, such as myotube formation (Hernández and Podbilewicz, 2017; Shinn-Thomas and Mohler, 2011), a cell fusion mechanism is activated, implying that cells can acquire a fusion-prone status. In addition to the physiological process of cell fusion, if cells; for example, siblings produced by bipolar cell division, became fusion prone, it could lead to the formation of polyploid cells, which have been suggested to be precursors of cancer cells (Eischen, 2016; Deangelis et al., 1993; Dutertre et al., 2005; Galipeau et al., 1996; Ramel et al., 1995). The low levels of p53 may thus function to prevent cells from becoming fusion-prone, thereby reducing the risk of cells becoming cancer cells.

Loss of the low levels of p53 increased the induction of multipolar cell division following cell fusion (Figure 14a). The division of a cell into three and more cells generates progeny with different numbers of chromosomes. Although such aneuploid cells are generally fragile (Holland and Cleveland, 2009; Gisselsson et al., 2008), loss of p53 function has been suggested to contribute to the survival of aneuploid cells (Fujiwara et al., 2005; Thompson and Compton, 2008; Vitale et al., 2010). Indeed, we found that some such aneuploid cells underwent bipolar cell division and the progeny could propagate, creating an aneuploid cell population (Figure 14a). Even though gene mutation has been proposed as the main cause of cancer, aneuploidy is a near-universal feature of human cancers (Li and Zhu, 2022) and is also involved in the process of tumorigenesis (Boveri, 2008; Ganem et al., 2007). Furthermore, impaired p53 function is known to cause frequent alterations in cell ploidy (Eischen, 2016; Deangelis et al., 1993; Dutertre et al., 2005; Galipeau et al., 1996; Ramel et al., 1995). The proposed process could thus be involved in the process of tumorigenesis. In summary, the low levels of p53 found in unstressed cells could suppress cell fusion, which leads to multipolar cell division, and loss of this function could thus create conditions favoring the generation of cancer cells.

Response of p53-silenced cells to MNNG

The above-mentioned context reveals the potential roles of low levels of p53 under unstressed conditions. One of the best-established roles of p53 is related to cellular responses induced following its accumulation under stressed conditions, including its capacity to prevent the survival of damaged cells. This capacity is closely associated with cell growth arrest and cell death. On the other hand, induction of the damage response in Control cells may oppose the suppression of tumor formation. Exposure of a cell population composed of 4% p53 RNAi cells and 96% Control cells to 7 μM MNNG, which could lead to the accumulation of p53, was associated with growth suppression of the Control cell population due to induction of the damage response, conferring an opportunity for expansion of the p53 RNAi cell population, which lacks the p53-mediated damage response function. Indeed, our simulation results suggested that 4% of p53 RNAi cells present at the beginning expanded to 93% of the cell population (containing 0.6% aneuploid cells) after 40,000 min (27.78 days) if the population was exposed to 7 μM of MNNG every 10,000 min (Figure 14c). These results suggest that exposure of tumor tissue composed of p53-proficient and -deficient cells to a reagent that induces a damage response may lead to preferential expansion of the p53-deficient cell population that contains aneuploid cells with reproductive activity. If the deficient cells have a malignant nature, p53 could indirectly promote, rather than suppress the formation of a malignant tumor by suppressing the expansion of the p53-proficient cell population. Understanding the role of p53 in tumorigenesis thus requires the delineation of its role at both the cellular and population levels. Furthermore, because most cancer cells carrying p53 gene mutations express mutated p53 in the cytoplasm instead of the nucleus, cytoplasmic mutated p53 has been suggested to confer a cellular function, referred to as gain of function (Acin et al., 2011; Amelio and Melino, 2020; Bargonetti and Prives, 2019; Oren and Rotter, 2010; van Oijen and Slootweg, 2000; Yue et al., 2017). Such cells may have a combined phenotype of both loss of wild-type p53 and gain of function, or mutated p53 may alter the phenotype caused by the loss of the wild-type p53. Nevertheless, these need to be considered in the context of p53-related tumorigenesis, and the current approach may be used to gain clues to reveal the context.

Cell-fate simulation and its applications

Compared with other analytical methods, single-cell-tracking analysis has the ability to accurately detect various cellular events, regardless of the frequency of their occurrence, by creating spatiotemporal data for individual cells. However, because single-cell-tracking analysis is a morphological observation-based technique, we were unable to determine the silencing levels of p53 in individual cells. The availability of such information would allow deeper analysis, for example, to examine the relationship between p53-silencing levels and the chance of cell fusion. Although it is difficult to monitor expression levels of p53, or other proteins or genes, in individual live cells using existing methods, new technologies combining single-cell-tracking analysis with spatial transcriptomics (Hou et al., 2021; Joglekar et al., 2021), for example, could be developed to expand the applicability of this type of analysis. Such expansion could also provide additional flexibility for cell-fate simulations. We created a cell-fate simulation algorithm to allow the flexible design of various types of virtual experiments by creating Operation data, containing data generated by the categorization of event patterns. Such patterns could be further enriched by the addition of information on the expression levels of proteins or genes in individual cells, allowing the development of another new type of cell-fate simulation algorithm. Furthermore, given that each type of cell population tends to show a specific cell population expansion profile and response to treatment, the accumulation of public Operation data resources could be made accessible to various research projects to simulate the fate of cells of interest, predict the responses of cells to treatments, build models based on the simulations, and develop a theory-based model for cell behaviors. Because single-cell-tracking data contains information on the motility of each cell, it may also be possible to simulate cell behaviors that could be influenced by cell-to-cell contact. This simulation-based biology could thus help to overcome some of the limitations associated with empirical cell biological studies and provide greater flexibility in research with mammalian cells.

Conclusions

p53 may affect cell population dynamics, and loss of p53 could lead to the formation of an aneuploid cell population. In addition, the dynamics of cell populations containing both p53-null cells and wild-type cells may be affected by the status of the wild-type cells. Our results suggest that wild-type cells could gain a growth advantage over p53-null cells in low-stress environments, while the growth balance between the p53-null and wild-type cells may change under stress conditions, allowing p53-null cells to gain a growth advantage. The role of p53 in the process of tumorigenesis may thus depend on the environment surrounding the cell population, as well as the p53 status of individual cells within the population. Revealing the status of individual cells by single-cell tracking, cell-lineage analysis, and cell-fate simulation can thus further our understanding of the process of tumorigenesis.

Materials and methods

Key resources table

Reagent type (species) or resource	Designation	Source or reference	Identifiers	Additional information
Antibody	Mouse anti-p53 (DO-1, mouse monoclonal)	Invitrogen	AHO0152	1 µg/mL
Antibody	Horseradish peroxidase conjugated goat anti-mouse antibody (goat polyclonal)	Abcam	Ab205719	1:25,000
Chemical compound, drug	N-methyl-N′-nitroso-N-nitrosoguanidine	Sigma-Aldrich	129941
Cell line (human)	A549-luc-C8	Xenogen Corporation	N/A
Sequence- based reagent	p53 siRNA I	Cell Signaling Technology	6231
Sequence- based reagent	Control siRNA	Cell Signaling Technology	6568
Software, algorithm	MetaMorph (Quorum WaveFX, v7.8.12.0)	Quorum Technology	N/A
Software, algorithm	ImageJ	Schneider et al., 2012	https://imagej.nih.ggov/ij/
Software, algorithm	Computerized single-cell lineage tracking analysis system software	Rancourt, Sato, and Satoh	BioRxiv. doi: https://doi.org/10.1101/508705
Software, algorithm	Cell fate simulation algorithm	This paper		Results: ‘Cell-fate simulation algorithm’; Materials and methods: ‘Overall flow of cell-fate simulation algorithm’; Figure 7—source code 1
Other	Cell lineage data	This paper		Deposited in Dryad

Cells and cell culture

Request a detailed protocol

A549-luc-C8 cells were purchased from Xenogen Corporation and cultured in RPMI containing 10% fetal bovine serum (RPMI medium) in a humidified atmosphere with 5% CO₂. Cells were confirmed to be mycoplasma negative. Cells were plated in the center of each well of a cover glass Lab-Tek II 8-well chamber in 50 μL of cell suspension containing 3500 cells and left to attach to the cover glass surface. Culture was continued for 24 hr to allow more than 99% of cells attached to other cells, and culture medium (0.75 mL) was then added to each well and the chamber was viewed under a microscope (Olympus IX81) after 24 hr of plating.

Concurrent long-term live-cell imaging, siRNA transfection, and MNNG treatment

Request a detailed protocol

Concurrent long-term live-cell imaging was performed as described previously (Sato et al., 2018; Sato et al., 2016). Briefly, images were acquired under a microscope using near infrared DIC imaging with a ×20 dry objective (UPlanSApo, ×20/0.75 NA, α/0.17/FN2G.5) and a ×1.5 coupler (Quorum Technologies) to generate a ×30-equivalent image. Images were acquired by area scanning (5 × 5 dimension, 512 × 512 pixels each, 1.77 mm²) using multidimensional acquisition mode in MetaMorph (Quorum Technology Inc, WaveFX, v7.8.12.0) with 34 ms exposure and XY piezo stage. The selected area was close to the center of the cell population, given that the behavior of cells at the periphery may differ from those at the center, mainly due to differences in cell density and the chance of intercellular attachments. Typically, 30 z-planes were acquired every 1 µm, and 512 × 512 pixel multilayered .tiff files were created. Cells were maintained on the microscope stage in an environmental chamber (Live Cell Instrument, Korea) in a humidified atmosphere with 7.5% CO₂ and images were acquired every 10 min. Lipofection with scrambled siRNA and p53si RNA (Cell Signaling Technology) was performed approximately 24 hr after cell plating using Effectene Transfection Reagent (QIAGEN) with 1 µg siRNA in 742 µL transfection mixture, according to the supplier’s instructions. Image acquisition was started immediately after siRNA transfection. At 24 hr after siRNA treatment, cells were exposed to various doses of MNNG (Sigma-Aldrich) for 30 min in serum-free RPMI, and the medium was then replaced with fresh RPMI medium. The evaporation rate of the medium was about 10 μL per 24 hr, and each well of a cover glass Lab-Tek II 8-well chamber thus contained 800 μL of RPMI medium to minimize the impact of evaporation on cell growth. The RPMI medium contained phenol red to monitor the pH of the medium, and 7.5% CO₂ was typically required to maintain an optimal pH.

Image files corresponding to each field of view were saved using MetaMorph on the hard drive of a Windows computer. The files were then transferred automatically to a Macintosh computer (OS15) using in-house software (Sato et al., 2018). Unique file names were assigned to each file for archiving, followed by the creation of an all-in-focus image using in-house software (Sato et al., 2018). The focused images were positioned and the contrast was adjusted to create stitched images (25 images covering 5 × 5 dimension, approximately 2500 × 2500 pixels). The images were then saved in chronological order for display. File transferring, focused image creation, image positioning, and contrast adjustment were performed automatically, and eight stitched images that corresponding to each Lab-Tek II 8-well chamber well were typically created concurrently in an automatic manner (Sato et al., 2018). The files were displayed using an in-house movie player to monitor the progress of live-cell imaging (Sato et al., 2018).

DIC image segmentation

Request a detailed protocol

Image segmentation was performed using our image segmentation software (for details, see Sato et al., 2018). Image segmentation can be performed by various methods, such as the region growing, by setting an optimal parameter for an image. However, the optimal parameter for a time point of the image may be difficult to use for other time points, given that the optimal parameter is affected by the cell density and size, the relative location of a cell to other cells, the formation of cell debris, and image quality variations caused by the microscope system. We typically processed >8000 images, and our segmentation software was therefore developed to perform DIC image segmentation automatically, regardless of image quality (Sato et al., 2018). Briefly, in a DIC image, cells appear as illuminated objects associated with a shadow, and this rule can be applied to any cells in an image. For example, if a flat cell is located behind a bulky cell, the flat cell appears as a darker cell, but the cell itself is brighter than its shadow. Our segmentation software used these characteristics of the DIC images. The mean pixel value of a DIC image (256 grayscale images) was first adjusted to a grayscale value of 100, and four images were then created by applying four different pixel threshold values: for example, >200, >180, >160, and >150. The image with the highest threshold value was used first, and connected pixels, representing an area, were identified by connectivity analysis. The connected pixels were then overlaid on an original DIC image and the area of connected pixels was extended. The connected pixels were likely to represent the illuminated cells in the image, and expansion was carried out to identify the possible borders of the cells. The connected areas were then overlaid on the image created with the second highest grayscale threshold value. Connectivity analysis was performed, except for the areas where a connected area had already been set in the previous step. This process allowed us to identify darker cells in a DIC image than those identified previously. Connected areas identified in the second step were overlaid on the original DIC image and the area was expanded to find a border of darker cells. The same process was repeated for the images created by the third and fourth thresholds to identify cells in an image. By this approach, DIC images of various qualities could be segmented.

Single-cell tracking

Request a detailed protocol

Single-cell-tracking analysis was performed using in-house software that tracked cells automatically, detected cellular events, and allowed verification of the tracking results (Sato et al., 2018). Single-cell tracking was started by selecting a connected area (Area) that corresponded to a progenitor. Because the segmentation pattern of the next image was often changed, automatic cell tracking was performed by identifying the best-matched segmented area in the next image. Briefly, Area was overlaid on the connected areas in the next time point image. If Area overlapped with one area in the next image and the size of the area was within the twofold of Area, the area in the next image was determined as the area that corresponded to the cell that was being tracked. If Area overlapped with one area in the next image, but the size of the area was larger than twice Area , the area was likely divided into multiple areas and one area that overlapped with Area was determined as the area corresponding to the tracked cell. If multiple areas in the next image overlapped with Area , the multiple areas were likely merged and the merged area was determined as the area corresponding to the tracked cell. This process was carried out for all selected progenitors and repeated until the predetermined time point. When the tracking reached the target time point, manual data verification was performed to correct tracking errors. Detected errors were corrected manually, and automatic single-cell tracking was restarted. Typically, verification was performed every 100 time points to create error-free cell-lineage data. The required time for verification was ~48 hr for the tracking of 400 Control progenitors and their progeny for 400 time points. Concerning event detection, different approaches were used for cell division, cell fusion, and cell death. Bipolar and multipolar cell division were detected by first identifying a mitotic round cell. Typically, such cells appeared as bright round objects in DIC images. The in-house cell-tracking software thus built a data library of the shapes of mitotic cells and determined if a tracked cell underwent mitosis. During the manual verification step, if an error, such as the detection of a non-mitotic cell as a mitotic one or failure to detect a mitotic cell, was found, the failed or missed pattern was incorporated into the software to improve the subsequent detection accuracy. Following the detection of mitotic cells, if a connected area overlapped with two, three, and four connected areas in the next image, the software determined that bipolar, tripolar, and tetrapolar cell division, respectively, had occurred. Concerning cell fusion, if two connected areas corresponding to two different cells overlapped with the same connected area in the next image, and the area did not divide into multiple areas in the next 10–20-time points, the software determined that two cells were fused. In the case of cell death, dead cells typically formed remnants that appeared as bright, irregularly shaped objects. If a connected area overlapped with an area corresponding to such an object, and the object was also found in the next 10–20 time point images, the software determined that cell death had occurred.

Automated cell tracking and manual verification can be used to generate an error-free cell-lineage database. Furthermore, to ensure complete cell-lineage data, if any progeny of a cell lineage moved outside of the field of view, all the data corresponding to that lineage were excluded from the analyses. During single-cell tracking, information on cell-lineage number, cell number, the coordinates of the cells, the types of an events occurring in the cell, the relationship of a cell to its parent cell, and information related to fused cells were recorded in the cell-lineage database (Sato et al., 2018).

Western blotting

Request a detailed protocol

Cells were transfected with scrambled siRNA and p53 siRNA and treated with various doses of MNNG after 24 hr. At 48 hr after treatment, the cells were harvested and proteins (15 µg) were separated by 10% sodium dodecyl sulfate-polyacrylamide gel electrophoresis. Western blotting was performed using anti-p53 antibody (1 µg/mL, DO-1; Invitrogen) and horseradish peroxidase-conjugated goat anti-mouse antibody (25,000-fold dilution; Abcam). Proteins were visualized using an ECL reagent (Pierce). Quantitation of p53 was performed using ImageJ.

Generation of density maps

Request a detailed protocol

To create a cell density map, we assigned a value of 1 to a pixel within the 20-pixel diameter area for cell density and 100-pixel diameter area for multipolar cell division and cell death density from the position of the cell or position where multipolar cell division or cell death occurred. If an area overlapped with other areas, a pixel was assigned the sum of the number of overlapped areas. These values were used to generate heat maps.

Overall flow of the cell-fate simulation algorithm

Request a detailed protocol

The flow of the cell-fate simulation algorithm is shown in Figure 7—figure supplement 1. The simulation mode was selected from the available five modes; Standard, Dose simulation, Mix culture, Switch, and Mix culture-Switch (Figure 7—figure supplement 1: 1 and Figure 8). Standard mode performed a simulation by setting a simulation time (Sim. Time end) and an initial number of cells (Init. No. of cells; progenitors) followed by Operation data creation (Figure 7—figure supplement 1: 2, and Figure 7—figure supplement 2) or uploading, and generation of simulation arrays (Figure 7—figure supplement 1: 3, and Figure 7—figure supplement 2). Operation data held the categorized information of events, and Simulation arrays (Figure 7—figure supplement 1: 3) were used to assign the length of time between two events (Ltime) and event type. Dose–response mode was carried out by setting a simulation time, the initial number of cells, and an intermediate dose. Two sets of Operation data were then generated or uploaded and virtual Operation data corresponding to the intermediate dose were created using those Operation data. For example, if the intermediate dose was 5 µM MNNG, virtual Operation data were generated from Operation data for 3 µM and 7 µM MNNG. Mixed culture mode performed a simulation for a virtual cell population composed of two cell types. A simulation time and initial numbers of the first and second cell populations were set. Two sets of Operation data were used to simulate the proliferation of the first and second cell populations individually. Two sets of simulation arrays were also created. This mode could be used to simulate the proliferation of a cell population surrounded by another cell population. Switch mode was used to perform virtual drug treatment. The simulation times before and after treatment, and the initial number of cells were set. Two sets of Operation data for the first and second doses were used, and simulation arrays corresponding to each dose were created. Mixed culture-Switch mode was a combined version of Mixed culture and Switch. This mode used four sets of Operation data and generated four sets of simulation arrays. Initial processing was then performed by creating a cell data information array (CDI) that included the Ltime and event type assigned to each cell (, Figure 7—figure supplement 1: 4, and Figure 7—figure supplement 4a). Based on the information in the CDI, a virtual cell-lineage database was created (Figure 7—figure supplement 1, Figure 7—figure supplement 1: 5, and Figure 7—figure supplement 4b). After these initial processes, a repeated cycle of assigning Ltime and event type (Figure 7—figure supplement 5), reassigning Ltime and event type to adjust for the effect of cell fusion on Ltime (Figure 7—figure supplement 6a), and creating a virtual cell-lineage database (Figure 7—figure supplement 6b) were carried out until the simulation time was reached (Figure 7—figure supplement 1: 6). If Switch or Mixed culture-Switch mode was used, the cell-lineage database end was trimmed (Figure 7—figure supplement 6c), Operation data was switched to corresponding Operation data, and the process proceeded to the second round of the repeated cycle (Figure 7—figure supplement 1: 7). When processing reached the simulation time, the simulation was terminated and the results were displayed.

Cell-fate simulation algorithm: Operation data

Request a detailed protocol

Processing related to Operation data, which comprised three types of data, is outlined in Figure 7—figure supplement 2. Operation data were either uploaded or generated from a cell-lineage database. When the Operation data were generated, information held in the cell-lineage database was converted into an Operation data-Time (Figure 7—figure supplement 2: 1), Operation data-Event (Figure 7—figure supplement 2: 2), and Recovery data (Figure 7—figure supplement 2: 3). The Operation data-Time held categorized Ltime by event type; for example, Ltime between bipolar cell division and cell death (BD-CD data type) and Ltime from time 0 min to the time that an event occurred in a progenitor (First event data type) (Figure 7—figure supplement 2: 1). The Operation data-Event contained the frequency of events occurred following, for example, bipolar cell division (BD data type), or multipolar cell division (MD data type) (Figure 7—figure supplement 2: 2). Recovery data were used to simulate the rate of recovery of a cell population following treatment with MNNG. Most cells adopted a static status following treatment with MNNG; however, some cells regained their reproductive ability, as shown at the end of the imaging procedure. Typically, such cells underwent bipolar cell division to produce two offspring. However, live-cell imaging would be terminated before the offspring underwent cell division, as a culture of reference, nontreated cells become confluent. In this case, it was not possible to determine the cell-doubling time of the offspring. Recovery thus determined the percentage of cells that underwent bipolar cell division over a certain period from the end of the tracking time. For example, if the tracking time was 4000 min, the percentage of cells was calculated by the number of bipolar cell divisions that occurred within; for example, 3200–4000 min, and the number was converted into a percentage by dividing the total number of bipolar cell divisions that occurred during the tracking time and then multiplying by 100 (Figure 7—figure supplement 2; 3). Thus, if 10 bipolar cell divisions were found between 3200 and 4000 min out of a total of 300 bipolar cell divisions (entire time), the result was 3.3%. The simulation algorithm assigned bipolar cell division to 3.3% of nondividing cells at around 4000 min. Ltime, which was >80% of tracking time, was then assigned to cells produced by bipolar cell division. Using Dose–response mode, virtual Operation data were created from two sets of Operation data using the formula: virtual Operation data = Operation data 1 + [(Operation data 2 − Operation data 1)/(Dose 2 −Dose 1)] × (Intermediate dose − Dose 1) (Figure 7—figure supplement 2: 4).

Cell-fate simulation algorithm: Simulation arrays

Request a detailed protocol

The dataset stored in Operation data was then converted into Simulation arrays that were used to assign Ltime and event types (Figure 7—figure supplement 3). In the Operation data, each categorized Operation data-Time was stored in the format, that is, Ltime, and the number of Ltime that was found. For example, 20 min of Ltime found four times was written as 20:4. In the Simulation arrays corresponding to the Operation data-Time, this was converted to 20, 20, 20, 20, for example. If no corresponding type of event occurred, the array for the event held no data. To generate a simulation array from the Operation data-Event, the percentage of each event relative to the total number of cell divisions (total of bipolar cell division and multipolar cell division) was calculated. The maximum number of entries per array was 100. The total percentage of events could thus exceed 100, for example, first event list (bipolar cell division, cell death, multipolar cell division, and the number of cells with no cell division [nonDiv]). In this case, the percentage of each event was adjusted to make a total of 100. If the percentage of the event was <100, 0 was filled to make the total entry for the array 100. If no corresponding type of event occurred, an array for the event held no data. The Recovery percentage was calculated as described above.

Cell-fate simulation algorithm: Initial Ltime and event-type assignment

Request a detailed protocol

In the first event assignment (Figure 7—figure supplement 4a), the CDI that held the status of each cell throughout a simulation was created. In this step, the cell-lineage number was generated following the initial number of cells set previously, and the cell number 0 was assigned to each progenitor. Using the FirstEvent array, Ltime was then assigned to each cell. If the array was empty, the average time that bipolar cell division occurred was calculated and −25% to +25% of the time selected by random number (C++ rand ()) was assigned as Ltime, and bipolar cell division was then assigned to the cell. If the FirstEvent array held data, Ltime was assigned by creating a random number, but if Ltime was equal to the length of single-cell tracking, −30% to +30% of the length of the time of single-cell tracking was assigned as Ltime and the event type was selected using the FirstEvent list array. If there was no entry in the array, NonDiv was assigned; otherwise, bipolar cell division, multipolar cell division, or cell death was assigned. If cell death was assigned, Ltime was reassigned using the NonDivCD time data array.

Cell-fate simulation algorithm: Initial cell-lineage database creation

Request a detailed protocol

The cell-lineage database was created using information held by the CDI (Figure 7—figure supplement 4b). This array contained information regarding Ltime and event type as a blueprint of the virtual cells (Figure 7—figure supplement 4b). If Ltime exceeded the simulation time set previously, Ltime was adjusted to a time equal to the simulation time; otherwise, a cell-lineage database was generated composed of an X position, Y position, time point, event type, cell-lineage number, cell number, parent cell information, cell number, and the cell-lineage number of the cell that was fused in the event of cell fusion. If the event type was bipolar cell division or multipolar cell division, information related to the progeny created by bipolar cell division or multipolar cell division was entered into the CDI following the generation of corresponding cell numbers for each progeny.

Cell-fate simulation algorithm: Ltime and event-type assignment

Request a detailed protocol

In the repeated assignment cycle (Figure 7—figure supplement 1: 6), the next Ltime and event type was determined based on the current event type. If the current event in a cell was NonDiv (Figure 7—figure supplement 5), a randomized number between 0 and 100 was generated, and if the number was lower than the Recovery %, bipolar cell division was assigned to the cell. In the next cycle, this cell was entered into a growing cycle. If the Ltime was 80–100% of the length of the single-cell-tracking time, the Ltime was determined by generating random numbers between 80 and 100. Assignment of bipolar cell division in this manner only occurred once in the first cycle of the assignment. If the random value was higher than the Recovery %, either NonDiv or cell death was assigned, in which case the % of cell death of total cell division was calculated and, if the random number between 0 and 100 was lower than the cell death %, a cell death was assigned. In this case, Ltime was assigned using the NonDivCD time array. If the random number between 0 and 100 was higher than the cell death %, NonDiv was assigned, and the length of single-cell-tracking time was assigned as Ltime.

Next, if the current event was bipolar cell division, information related to its sibling was searched for. If a sibling was found, either bipolar cell division, multipolar cell division, or cell death was assigned using the Bipolar cell division list array; otherwise, bipolar cell division, multipolar cell division, cell fusion, or cell death was assigned. If the event assigned by the Bipolar cell division list array was cell fusion, then its sibling was again searched. If no sibling was found, Ltime was assigned by the BDCF time array. If the array was empty, the event type was changed to cell death and the average time that cell death occurred was set as Ltime. If a sibling was found, Ltime was assigned using the BDCF time array. If the array was empty, cell fusion was changed to cell death and the average cell death time was set as Ltime. If Ltime was set, but it was longer than the Ltime of its sibling, Ltime was made shorter than the sibling’s Ltime. If the event assigned using the Bipolar cell division list array was bipolar cell division, Ltime was assigned by the BDBD time array. If the array was empty, the average bipolar cell division time was set as Ltime. If Ltime was set by the BDBD time array but the Ltime was not within −10% to +10% of Ltime of its parent cell, Ltime was reselected until the Ltime fell within this range. If Ltime assigned by the Bipolar cell division list array was multipolar division, Ltime was assigned by the BDBD time array. If the array was empty, the average bipolar cell division time was set as Ltime. If the event assigned by the Bipolar cell division list array was cell death, Ltime was assigned the BDCD time array. If the array was empty, the average cell death time was set as Ltime.

If the current event was multipolar cell division, information related to its siblings was searched for. If siblings were found and cell fusion was assigned to two siblings, either bipolar cell division, multipolar cell division, or cell death was assigned by the Multipolar cell division list array, otherwise bipolar cell division, multipolar cell division, cell fusion, or cell death was assigned. If the event assigned by the Multipolar cell division list array was cell fusion, then, event type of its sibling was again searched. If no sibling was found, Ltime was assigned by the MDCF time array. If the array was empty, the event type was changed to cell death, and the average time that cell death occurred was set as Ltime. If only one sibling was found, Ltime was assigned by the MDCF time array. If the array was empty, cell fusion was changed to cell death and the average cell death time was set as Ltime. If two siblings were found and cell fusion was assigned to one of the siblings, Ltime was assigned by the MDCF time array. If the array was empty, cell fusion was changed to cell death and the average cell death time was set as Ltime. If Ltime was longer than the Ltime of its siblings, Ltime was made shorter than its siblings. If cell fusion was not assigned to any of its siblings, Ltime was assigned by the MDCF time array. If the array was empty, cell fusion was changed to cell death and the average cell death time was set as Ltime. If the event assigned by the Multipolar cell division list array was bipolar cell division, Ltime was assigned by the MDMD time array. If the array was empty, the average bipolar cell division time was set as Ltime. If Ltime assigned by the Multipolar cell division list array was multipolar cell division, Ltime was assigned by the MDMD time array. If the array was empty, the average bipolar cell division time was set as Ltime. If the event assigned by the Multipolar cell division list array was cell death, Ltime was assigned by the MDCD time array. If the array was empty, the average cell death time was set as Ltime.

Cell-fate simulation algorithm: Readjustment of Ltime in cells that underwent cell fusion

Request a detailed protocol

If cell fusion occurred in a cell, the Ltime of the cell being fused was often affected and the Ltime was readjusted (Figure 7—figure supplement 6a). Fusion between non-siblings was not simulated by this algorithm. If the current event was bipolar cell division, the next event was assigned by the BDCF lists. If the next event was bipolar cell division or multipolar cell division, Ltime was assigned by the DivCFDiv time array, and if the next event was cell death, Ltime was assigned by the BDCFCD array. If the current event was multipolar cell division, the next event was assigned by the MDCF lists. If the next event was bipolar cell division or multipolar cell division, Ltime was assigned by the DivCFDiv time array, and if the next event was cell death, Ltime was assigned by the MDCFCD array.

Cell-fate simulation algorithm: Cell-lineage database creation

Request a detailed protocol

The cell-lineage database was created using information held by the CDI (Figure 7—figure supplement 6b). If Ltime exceeded the simulation time set previously, Ltime was adjusted to a time equal to the simulation time. If the event type was bipolar cell division or multipolar cell division, information related to the progeny created by bipolar cell division or multipolar cell division was entered into the CDI following the generation of corresponding cell numbers for each progeny. If the event type was cell fusion, cells to be fused were searched and relevant information regarding cell-lineage number and cell number was recorded for the cell.

Cell-fate simulation algorithm: Trimming the end of the cell-lineage database

Request a detailed protocol

In Switch and Mixed culture-Switch modes, the end of the cell-lineage data was trimmed to the nearest cell division event (Figure 7—figure supplement 6c) before entering the second repeated cycle of assignment.

Statistical analysis

Request a detailed protocol

Statistical analyses were performed using Prism 8.

Naming rule for cells and Operation data

Request a detailed protocol

A549 cells treated with scrambled siRNA and p53 siRNA are referred to as Control and p53 RNAi cells, respectively. Those cells treated with MNNG are named by adding, for example, Control-MNNG1 (cells treated with 1 μM of MNNG). If a cell population that is generated by cell fate simulation is referred, -Sim was added, for example, Control-Sim and Control-MNNG1-Sim. In the case that cells generated in silico to remove cell death are referred, cells are named, for example, Control-Silico(-)cell death. If an Operation data-Time or Operation data-Events are required to be specified, the name of cells was added following Operation data, for example, Operation data-Control.

Data availability

All data generated or analyzed during this study are included in the paper and supporting file; Source Data files have been provided for Figure 1-figure supplements 2—4, Figures 2, Figures 3, Figures 4, Figure 4—figure supplement 1, Figures 5, Figures 6, Figure 7—figure supplements 1–7, Figure 8—figure supplement 1, Figure 9, Figure 9—figure supplement 1 and 2, and Figures 10–13. Source code has been provided for Figure 7. Figure 1—videos (cellular events), Figure 2—figure supplements (cell-lineage maps), Figure 2—videos (single-cell tracking), Figure 2—source data (cell-lineage database), and Figure 7—figure supplement 7 (cell-lineage maps) have been deposited in Dryad (https://doi.org/10.5061/dryad.pk0p2ngp5).

The following data sets were generated

1. Rancourt A
(2022) Dryad Digital Repository
Empirical single-cell tracking and cell-fate simulation reveal dual roles of p53 in tumor suppression.
https://doi.org/10.5061/dryad.pk0p2ngp5

References

1. Acin S
2. Li Z
3. Mejia O
4. Roop DR
5. El-Naggar AK
6. Caulin C
(2011) Gain-Of-Function mutant p53 but not p53 deletion promotes head and neck cancer progression in response to oncogenic K-ras
The Journal of Pathology 225:479–489.
https://doi.org/10.1002/path.2971
- PubMed
- Google Scholar
1. Amelio I
2. Melino G
(2020) Context is everything: extrinsic signalling and gain-of-function p53 mutants
Cell Death Discovery 6:16.
https://doi.org/10.1038/s41420-020-0251-x
- PubMed
- Google Scholar
1. Bargonetti J
2. Prives C
(2019) Gain-Of-Function mutant p53: history and speculation
Journal of Molecular Cell Biology 11:605–609.
https://doi.org/10.1093/jmcb/mjz067
- PubMed
- Google Scholar
1. Boutelle AM
2. Attardi LD
(2021) P53 and tumor suppression: it takes a network
Trends in Cell Biology 31:298–310.
https://doi.org/10.1016/j.tcb.2020.12.011
- PubMed
- Google Scholar
1. Boveri T
(2008) Concerning the origin of malignant tumours by Theodor Boveri. Translated and annotated by Henry Harris
Journal of Cell Science 121 Suppl 1:1–84.
https://doi.org/10.1242/jcs.025742
- PubMed
- Google Scholar
1. Campisi J
(2005) Senescent cells, tumor suppression, and organismal aging: good citizens, bad neighbors
Cell 120:513–522.
https://doi.org/10.1016/j.cell.2005.02.003
- PubMed
- Google Scholar
1. Chapal-Ilani N
2. Maruvka YE
3. Spiro A
4. Reizel Y
5. Adar R
6. Shlush LI
7. Shapiro E
(2013) Comparing algorithms that reconstruct cell lineage trees utilizing information on microsatellite mutations
PLOS Computational Biology 9:e1003297.
https://doi.org/10.1371/journal.pcbi.1003297
- PubMed
- Google Scholar
1. Chow K-HK
2. Budde MW
3. Granados AA
4. Cabrera M
5. Yoon S
6. Cho S
7. Huang T-H
8. Koulena N
9. Frieda KL
10. Cai L
11. Lois C
12. Elowitz MB
(2021) Imaging cell lineage with a synthetic digital recording system
Science 372:eabb3099.
https://doi.org/10.1126/science.abb3099
- PubMed
- Google Scholar
1. Clarke AR
2. Purdie CA
3. Harrison DJ
4. Morris RG
5. Bird CC
6. Hooper ML
7. Wyllie AH
(1993) Thymocyte apoptosis induced by p53-dependent and independent pathways
Nature 362:849–852.
https://doi.org/10.1038/362849a0
- PubMed
- Google Scholar
1. Deangelis P
2. Stokke T
3. Smedshammer L
4. Lothe R
5. Meling G
6. Rofstad M
7. Chen Y
8. Clausen O
(1993) P53 expression is associated with a high-degree of tumor DNA aneuploidy and incidence of p53 gene mutation, and is localized to the aneuploid component in colorectal carcinomas
International Journal of Oncology 3:305–312.
https://doi.org/10.3892/ijo.3.2.305
- PubMed
- Google Scholar
(2005) The absence of p53 aggravates polyploidy and centrosome number abnormality induced by aurora-C overexpression
Cell Cycle 4:1783–1787.
https://doi.org/10.4161/cc.4.12.2172
- PubMed
- Google Scholar
1. Eischen CM
(2016) Genome stability requires p53
Cold Spring Harbor Perspectives in Medicine 6:a026096.
https://doi.org/10.1101/cshperspect.a026096
- PubMed
- Google Scholar
1. Emdad L
2. Sarkar D
3. Su ZZ
4. Fisher PB
(2005) Emerging roles of centrosomal amplification and genomic instability in cancer
Frontiers in Bioscience 10:728–742.
https://doi.org/10.2741/1567
- PubMed
- Google Scholar
1. Fujiwara T
2. Bandi M
3. Nitta M
4. Ivanova EV
5. Bronson RT
6. Pellman D
(2005) Cytokinesis failure generating tetraploids promotes tumorigenesis in p53-null cells
Nature 437:1043–1047.
https://doi.org/10.1038/nature04217
- PubMed
- Google Scholar
1. Galipeau PC
2. Cowan DS
3. Sanchez CA
4. Barrett MT
5. Emond MJ
6. Levine DS
7. Rabinovitch PS
8. Reid BJ
(1996) 17P (p53) allelic losses, 4N (G2/tetraploid) populations, and progression to aneuploidy in Barrett ’ S esophagus
PNAS 93:7081–7084.
https://doi.org/10.1073/pnas.93.14.7081
- PubMed
- Google Scholar
(2007) Tetraploidy, aneuploidy and cancer
Current Opinion in Genetics & Development 17:157–162.
https://doi.org/10.1016/j.gde.2007.02.011
- PubMed
- Google Scholar
(2009) A mechanism linking extra centrosomes to chromosomal instability
Nature 460:278–282.
https://doi.org/10.1038/nature08136
- PubMed
- Google Scholar
1. Gisselsson D
2. Håkanson U
3. Stoller P
4. Marti D
5. Jin Y
6. Rosengren AH
7. Stewénius Y
8. Kahl F
9. Panagopoulos I
(2008) When the genome plays dice: circumvention of the spindle assembly checkpoint and near-random chromosome segregation in multipolar cancer cell mitoses
PLOS ONE 3:e1871.
https://doi.org/10.1371/journal.pone.0001871
- PubMed
- Google Scholar
1. Guo S
2. Zi X
3. Schulz VP
4. Cheng J
5. Zhong M
6. Koochaki SHJ
7. Megyola CM
8. Pan X
9. Heydari K
10. Weissman SM
11. Gallagher PG
12. Krause DS
13. Fan R
14. Lu J
(2014) Nonstochastic reprogramming from a privileged somatic cell state
Cell 156:649–662.
https://doi.org/10.1016/j.cell.2014.01.020
- PubMed
- Google Scholar
1. Hafner A
2. Bulyk ML
3. Jambhekar A
4. Lahav G
(2019) The multiple mechanisms that regulate p53 activity and cell fate
Nature Reviews. Molecular Cell Biology 20:199–210.
https://doi.org/10.1038/s41580-019-0110-x
- PubMed
- Google Scholar
1. Harvey M
2. Sands AT
3. Weiss RS
4. Hegi ME
5. Wiseman RW
6. Pantazis P
7. Giovanella BC
8. Tainsky MA
9. Bradley A
10. Donehower LA
(1993)
In vitro growth characteristics of embryo fibroblasts isolated from p53-deficient mice

Oncogene 8:2457–2467.
- PubMed
- Google Scholar
1. Haupt Y
2. Maya R
3. Kazaz A
4. Oren M
(1997) Mdm2 promotes the rapid degradation of p53
Nature 387:296–299.
https://doi.org/10.1038/387296a0
- PubMed
- Google Scholar
1. Hernández JM
2. Podbilewicz B
(2017) The hallmarks of cell-cell fusion
Development 144:4481–4495.
https://doi.org/10.1242/dev.155523
- PubMed
- Google Scholar
1. Holland AJ
2. Cleveland DW
(2009) Boveri revisited: chromosomal instability, aneuploidy and tumorigenesis
Nature Reviews. Molecular Cell Biology 10:478–487.
https://doi.org/10.1038/nrm2718
- PubMed
- Google Scholar
(1991) P53 mutations in human cancers
Science 253:49–53.
https://doi.org/10.1126/science.1905840
- PubMed
- Google Scholar
(1997) Oncoprotein MDM2 is a ubiquitin ligase E3 for tumor suppressor p53
FEBS Letters 420:25–27.
https://doi.org/10.1016/s0014-5793(97)01480-4
- PubMed
- Google Scholar
1. Hou X
2. Yang Y
3. Li P
4. Zeng Z
5. Hu W
6. Zhe R
7. Liu X
8. Tang D
9. Ou M
10. Dai Y
(2021) Integrating spatial transcriptomics and single-cell RNA-seq reveals the gene expression profling of the human embryonic liver
Frontiers in Cell and Developmental Biology 9:652408.
https://doi.org/10.3389/fcell.2021.652408
- PubMed
- Google Scholar
1. Hüsemann Y
2. Geigl JB
3. Schubert F
4. Musiani P
5. Meyer M
6. Burghart E
7. Forni G
8. Eils R
9. Fehm T
10. Riethmüller G
11. Klein CA
(2008) Systemic spread is an early step in breast cancer
Cancer Cell 13:58–68.
https://doi.org/10.1016/j.ccr.2007.12.003
- PubMed
- Google Scholar
1. Jacobs AL
2. Schär P
(2012) Dna glycosylases: in DNA repair and beyond
Chromosoma 121:1–20.
https://doi.org/10.1007/s00412-011-0347-4
- PubMed
- Google Scholar
1. Joglekar A
2. Prjibelski A
3. Mahfouz A
4. Collier P
5. Lin S
6. Schlusche AK
7. Marrocco J
8. Williams SR
9. Haase B
10. Hayes A
11. Chew JG
12. Weisenfeld NI
13. Wong MY
14. Stein AN
15. Hardwick SA
16. Hunt T
17. Wang Q
18. Dieterich C
19. Bent Z
20. Fedrigo O
21. Sloan SA
22. Risso D
23. Jarvis ED
24. Flicek P
25. Luo W
26. Pitt GS
27. Frankish A
28. Smit AB
29. Ross ME
30. Tilgner HU
(2021) A spatially resolved brain region- and cell type-specific isoform atlas of the postnatal mouse brain
Nature Communications 12:463.
https://doi.org/10.1038/s41467-020-20343-5
- PubMed
- Google Scholar
1. Kandoth C
2. McLellan MD
3. Vandin F
4. Ye K
5. Niu B
6. Lu C
7. Xie M
8. Zhang Q
9. McMichael JF
10. Wyczalkowski MA
11. Leiserson MDM
12. Miller CA
13. Welch JS
14. Walter MJ
15. Wendl MC
16. Ley TJ
17. Wilson RK
18. Raphael BJ
19. Ding L
(2013) Mutational landscape and significance across 12 major cancer types
Nature 502:333–339.
https://doi.org/10.1038/nature12634
- PubMed
- Google Scholar
1. Kastan MB
2. Radin AI
3. Kuerbitz SJ
4. Onyekwere O
5. Wolkow CA
6. Civin CI
7. Stone KD
8. Woo T
9. Ravindranath Y
10. Craig RW
(1991)
Levels of p53 protein increase with maturation in human hematopoietic cells

Cancer Research 51:4279–4286.
- PubMed
- Google Scholar
1. Kastenhuber ER
2. Lowe SW
(2017) Putting p53 in context
Cell 170:1062–1078.
https://doi.org/10.1016/j.cell.2017.08.028
- PubMed
- Google Scholar
1. Keryer G
2. Ris H
3. Borisy GG
(1984) Centriole distribution during tripolar mitosis in Chinese hamster ovary cells
The Journal of Cell Biology 98:2222–2229.
https://doi.org/10.1083/jcb.98.6.2222
- PubMed
- Google Scholar
(2005) The monofunctional alkylating agent N-methyl-N ’ -nitro-N-nitrosoguanidine triggers apoptosis through p53-dependent and -independent pathways
Toxicology and Applied Pharmacology 202:84–98.
https://doi.org/10.1016/j.taap.2004.06.009
- PubMed
- Google Scholar
(2015) P53 in survival, death and metabolic health: a lifeguard with a licence to kill
Nature Reviews. Molecular Cell Biology 16:393–405.
https://doi.org/10.1038/nrm4007
- PubMed
- Google Scholar
(1997) Regulation of p53 stability by MDM2
Nature 387:299–303.
https://doi.org/10.1038/387299a0
- PubMed
- Google Scholar
1. Lassus P
2. Ferlin M
3. Piette J
4. Hibner U
(1996) Anti-Apoptotic activity of low levels of wild-type p53
The EMBO Journal 15:4566–4573.
https://doi.org/10.1002/j.1460-2075.1996.tb00834.x
- PubMed
- Google Scholar
1. Lavin MF
2. Gueven N
(2006) The complexity of p53 stabilization and activation
Cell Death and Differentiation 13:941–950.
https://doi.org/10.1038/sj.cdd.4401925
- PubMed
- Google Scholar
1. Levine AJ
(2019) The many faces of p53: something for everyone
Journal of Molecular Cell Biology 11:524–530.
https://doi.org/10.1093/jmcb/mjz026
- PubMed
- Google Scholar
1. Li R
2. Zhu J
(2022) Effects of aneuploidy on cell behaviour and function
Nature Reviews. Molecular Cell Biology 23:250–265.
https://doi.org/10.1038/s41580-021-00436-9
- PubMed
- Google Scholar
(1988) Regulation and expression of the adaptive response to alkylating agents
Annual Review of Biochemistry 57:133–157.
https://doi.org/10.1146/annurev.bi.57.070188.001025
- PubMed
- Google Scholar
1. Lindahl T
(1990) Repair of intrinsic DNA lesions
Mutation Research 238:305–311.
https://doi.org/10.1016/0165-1110(90)90022-4
- PubMed
- Google Scholar
(1995) Post-Translational modification of poly (ADP-ribose) polymerase induced by DNA strand breaks
Trends in Biochemical Sciences 20:405–411.
https://doi.org/10.1016/s0968-0004(00)89089-1
- PubMed
- Google Scholar
1. Livingstone LR
2. White A
3. Sprouse J
4. Livanos E
5. Jacks T
6. Tlsty TD
(1992) Altered cell cycle arrest and gene amplification potential accompany loss of wild-type p53
Cell 70:923–935.
https://doi.org/10.1016/0092-8674(92)90243-6
- PubMed
- Google Scholar
1. Lowe SW
2. Schmitt EM
3. Smith SW
4. Osborne BA
5. Jacks T
(1993) P53 is required for radiation-induced apoptosis in mouse thymocytes
Nature 362:847–849.
https://doi.org/10.1038/362847a0
- PubMed
- Google Scholar
1. Oren M
2. Rotter V
(2010) Mutant p53 gain-of-function in cancer
Cold Spring Harbor Perspectives in Biology 2:a001107.
https://doi.org/10.1101/cshperspect.a001107
- PubMed
- Google Scholar
1. Petitjean A
2. Mathe E
3. Kato S
4. Ishioka C
5. Tavtigian SV
6. Hainaut P
7. Olivier M
(2007) Impact of mutant p53 functional properties on TP53 mutation patterns and tumor phenotype: lessons from recent developments in the IARC TP53 database
Human Mutation 28:622–629.
https://doi.org/10.1002/humu.20495
- PubMed
- Google Scholar
(1956) Clonal growth of mammalian cells in vitro; growth characteristics of colonies from single HeLa cells with and without a feeder layer
The Journal of Experimental Medicine 103:273–283.
https://doi.org/10.1084/jem.103.2.273
- PubMed
- Google Scholar
1. Rajagopalan H
2. Lengauer C
(2004) Aneuploidy and cancer
Nature 432:338–341.
https://doi.org/10.1038/nature03099
- PubMed
- Google Scholar
1. Ramel S
2. Sanchez CA
3. Schimke MK
4. Neshat K
5. Cross SM
6. Raskind WH
7. Reid BJ
(1995) Inactivation of p53 and the development of tetraploidy in the elastase-SV40 T antigen transgenic mouse pancreas
Pancreas 11:213–222.
https://doi.org/10.1097/00006676-199510000-00001
- PubMed
- Google Scholar
1. Riethmüller G
2. Klein CA
(2001) Early cancer cell dissemination and late metastatic relapse: clinical reflections and biological approaches to the dormancy problem in patients
Seminars in Cancer Biology 11:307–311.
https://doi.org/10.1006/scbi.2001.0386
- PubMed
- Google Scholar
1. Rufini A
2. Tucci P
3. Celardo I
4. Melino G
(2013) Senescence and aging: the critical roles of p53
Oncogene 32:5129–5143.
https://doi.org/10.1038/onc.2012.640
- PubMed
- Google Scholar
1. Sato S
2. Rancourt A
3. Sato Y
4. Satoh MS
(2016) Single-Cell lineage tracking analysis reveals that an established cell line comprises putative cancer stem cells and their heterogeneous progeny
Scientific Reports 6:23328.
https://doi.org/10.1038/srep23328
- PubMed
- Google Scholar
Preprint
(2018) Identification of SNA-I-Positive Cells as Stem-like Cells in an Established Cell Line Using Computerized Single-Cell Lineage Tracking
bioRxiv.
https://doi.org/10.1101/508705
- Google Scholar
1. Satoh MS
2. Lindahl T
(1992) Role of poly (ADP-ribose) formation in DNA repair
Nature 356:356–358.
https://doi.org/10.1038/356356a0
- PubMed
- Google Scholar
1. Saunders W
(2005) Centrosomal amplification and spindle multipolarity in cancer cells
Seminars in Cancer Biology 15:25–32.
https://doi.org/10.1016/j.semcancer.2004.09.003
- PubMed
- Google Scholar
(2012) NIH image to imagej: 25 years of image analysis
Nature Methods 9:671–675.
https://doi.org/10.1038/nmeth.2089
- PubMed
- Google Scholar
1. Shi Q
2. King RW
(2005) Chromosome nondisjunction yields tetraploid rather than aneuploid cells in human cell lines
Nature 437:1038–1042.
https://doi.org/10.1038/nature03958
- PubMed
- Google Scholar
1. Shinn-Thomas JH
2. Mohler WA
(2011) New insights into the mechanisms and roles of cell-cell fusion
International Review of Cell and Molecular Biology 289:149–209.
https://doi.org/10.1016/B978-0-12-386039-2.00005-5
- PubMed
- Google Scholar
1. Storchova Z
2. Kuffer C
(2008) The consequences of tetraploidy and aneuploidy
Journal of Cell Science 121:3859–3866.
https://doi.org/10.1242/jcs.039537
- PubMed
- Google Scholar
1. Thompson SL
2. Compton DA
(2008) Examining the link between chromosomal instability and aneuploidy in human cells
The Journal of Cell Biology 180:665–672.
https://doi.org/10.1083/jcb.200712029
- PubMed
- Google Scholar
1. Valente LJ
2. Tarangelo A
3. Li AM
4. Naciri M
5. Raj N
6. Boutelle AM
7. Li Y
8. Mello SS
9. Bieging-Rolett K
10. DeBerardinis RJ
11. Ye J
12. Dixon SJ
13. Attardi LD
(2020) P53 deficiency triggers dysregulation of diverse cellular processes in physiological oxygen
The Journal of Cell Biology 219:e201908212.
https://doi.org/10.1083/jcb.201908212
- PubMed
- Google Scholar
1. van Oijen MG
2. Slootweg PJ
(2000)
Gain-Of-Function mutations in the tumor suppressor gene p53

Clinical Cancer Research 6:2138–2145.
- PubMed
- Google Scholar
1. Vitale I
2. Senovilla L
3. Jemaà M
4. Michaud M
5. Galluzzi L
6. Kepp O
7. Nanty L
8. Criollo A
9. Rello-Varona S
10. Manic G
11. Métivier D
12. Vivet S
13. Tajeddine N
14. Joza N
15. Valent A
16. Castedo M
17. Kroemer G
(2010) Multipolar mitosis of tetraploid cells: inhibition by p53 and dependency on Mos
The EMBO Journal 29:1272–1284.
https://doi.org/10.1038/emboj.2010.11
- PubMed
- Google Scholar
(2000) Surfing the p53 network
Nature 408:307–310.
https://doi.org/10.1038/35042675
- PubMed
- Google Scholar
1. Vousden KH
2. Lane DP
(2007) P53 in health and disease
Nature Reviews. Molecular Cell Biology 8:275–283.
https://doi.org/10.1038/nrm2147
- PubMed
- Google Scholar
1. Wood RD
(1996) Dna repair in eukaryotes
Annual Review of Biochemistry 65:135–167.
https://doi.org/10.1146/annurev.bi.65.070196.001031
- PubMed
- Google Scholar
1. Yue X
2. Zhao Y
3. Xu Y
4. Zheng M
5. Feng Z
6. Hu W
(2017) Mutant p53 in cancer: accumulation, gain-of-function, and therapy
Journal of Molecular Biology 429:1595–1606.
https://doi.org/10.1016/j.jmb.2017.03.030
- PubMed
- Google Scholar
(2020) Single-Cell lineage tracing by integrating CRISPR-Cas9 mutations with transcriptomic data
Nature Communications 11:3055.
https://doi.org/10.1038/s41467-020-16821-5
- PubMed
- Google Scholar

Decision letter

Chunling Yi

Reviewing Editor; Georgetown University, United States
Aleksandra M Walczak

Senior Editor; CNRS LPENS, France
Jeroen S van Zon

Reviewer; AMOLF, Netherlands
Brian E Chen

Reviewer; McGill University, Canada
Pina Colarusso

Reviewer; University of Calgary, Canada

Our editorial process produces two outputs: i) public reviews designed to be posted alongside the preprint for the benefit of readers; ii) feedback on the manuscript for the authors, including requests for revisions, shown below. We also include an acceptance summary that explains what the editors found interesting or important about the work.

Decision letter after peer review:

Thank you for submitting your article "Empirical single-cell tracking and cell-fate simulation reveal dual roles of p53 in tumor suppression" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and Aleksandra Walczak as the Senior Editor. The following individuals involved in review of your submission have agreed to reveal their identity: Jeroen S van Zon (Reviewer #1); Brian E Chen (Reviewer #2); Colarusso Pina (Reviewer #3).

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission.

Essential revisions:

1) The manuscript needs major rewriting to make it more comprehensible to a general audience. Please rewrite the manuscript according to the specific recommendations from the three peer reviewers.

2) Please provide better explanation of the simulation algorithm and the assumptions behind it in plain language.

3) Please revise the figures according to the specific recommendations from the reviewers.

4) Please better discuss the general impact of this study in the Discussion section.

Reviewer #1 (Recommendations for the authors):

1) Limited lineage analysis.

In general, the combination of cell tracking and manual annotation of events in general is powerful and I think the analysis of cell fusion in Figure 6 is a nice example of this power. However, I think it is under utilised in the paper. Figures 2 and 4 could have been constructed without cell tracking and lineage analysis, but only by analysing total cell number (Figure 2) or by counting events without lineage information (Figure 4). In Figure 3, lineage structures are analysed (but in a way I don't understand, see further below) but apart from changes with increasing MNNG it doesn't provide much insight: it seems that cell proliferation/death is decreased/increased with stress (as expected) leading to fewer large lineages, with no compelling difference between p53 siRNA or control. There is a sentence ('For example, suppression … generate 10-12 progeny (Figure 3b)’) that suggests there is a difference, but I can't see it in the figure.

It also seems that for a single condition, not all lineages have the same number of progeny (e.g 1-3 vs 13-15). Why is it that for the same imaging time lineages have such different offspring? Is it because some cells die? Is it impacted by limits to cell tracking, e.g. if a cell moves out of the field of view it gives rise to a short lineage because the offspring cannot be followed? In the latter case, that would rather represent a technical limitation rather than biological insight.

2) Insight in simulation lacking.

The section 'Cell-fate simulation algorithm' gives information on highest-level procedure of simulating, but it lacks any discussion of assumptions: does each cell choose 'fate' (MD, CD, CF, etc.) independently, or are correlation between sisters, cousins, etc. taken into account? How is experimental data used to constrain parameters of the simulation? The explanation in the supplementary information was not understandable for me. The presentation of the simulation algorithm in Figure S7a-h seems too detailed (e.g. dealing with the choice to load a file or not at the top of Figure S7b), while some of the diagrams (e.g. Figure S7F) are so complex that it appears to me as if a coherent underlying model is lacking. At the very least, it made it impossible for me to check the validity of the underlying assumptions.

3) In silico data generation.

in Figure 5, in silico data is generated based on experimental data, to asses the role of cell death. However, the explanation raises questions. It says that for any cell that dies its lineage was replaced by that of its sibling. But this only works if lineages without any cell death are always symmetric between siblings. Is this indeed the case? Or can you find cases where one sister generates 4 daughter but the other only 2? In that case, it is not clear what the in silico data represent. This is not discussed anywhere

4) Space in simulations.

In the simulations in Figure 9-11, space is taken into account, but I could not find how this is incorporated in the simulations. Also, it is not clear why space is relevant to begin with. It seems the cells are not directly interacting, e.g. by signalling, so could these results not have been obtained by simulations without space? Or is there competition for space? And if cells fuse, do they fuse with a neighbor? This should be explicitly discussed in the paper.

5) Writing and terms unclear.

In many places, explanations are not clear (see below for examples). The authors use a lot of acronyms, which I partly understand, but some sentences become very hard to understand (e.g. p.33 'we asked how progeny of MD that undergo BD survive by performing a simulation in Std mode'). Captions are strangely formatted and seem to sometimes miss panels (e.g. (b) lacking in caption Figure 3, (c) + (d) lacking in Figure 8).

Reviewer #2 (Recommendations for the authors):

Overall the study is very well done. There are several areas that can be better clarified.

The sentence, "However, the function of maintaining low levels of p53 in unstressed cells remains unclear." Is not a great introduction to the rationale of the paper; in that maintaining low levels is not what is being investigated, nor the function of the low levels, nor really the differences between low and high levels.

It is not clear throughout the text what "cell-lineage datasets" means. This could mean many things to many different readers. A sentence as to how the authors will define it is very important. Datasets can mean anything.

Similarly, the quantification of lineage is also ambiguous. How is this defined/quantified? This is never stated in the Methods, and again can mean different things.

The entire section on "Minimum number of cell-lineage datasets required to build a cell-lineage database" is unclear. Is this a random subsampling analysis that is being performed? Are these from experimental triplicates in Supplementary Figure 3, or just a randomly subsampling, as is implied in the statement, "The analysis was repeated three times (green, orange, and red lines) to show variations at a tracking time," so only the analysis was repeated three times, but not the experiments? What is the relationship between all of the datasets starting at 100 cells in the y-axis, but having different numbers of cell lineages?

Quantification of the cell lineage categories was unclear. What does "7-9 progeny" mean? The "number of cells/lineage" (text within the figure) vs "number of progeny/lineage" (main text) doesn't make sense. This is further confused by the Figure 3 legend stating "Values shown in (a) are number of lineages". So if the bar graph is read, then 136 cell lineages had around 350 cells, and 127 cell lineages had 900 cells. This is extremely confusing.

Why are cell densities in control and p53 RNAi in Figure 2 always the same, if MD, CD, and CF are all highly induced after RNAi knockdown?

The normalization factor, "/300 lineages" is not clear. This makes it difficult to compare the rates of the MD, CD, and CF between experiments across the paper. For the numbers "0.0475, 0.125, and 0.0775 events per 10 min/300 lineages" to mean anything substantial to any reader, it should be in a metric that is meaningful.

It is not clear what the numbers in Figure 6a mean. Here, again it is difficult to compare what a low frequency of occurrence of "3.5 to 3.8% of progeny", or "0.7 progeny of MD/100 cell lineage of p53si cells vs. 0.05 progeny of MD/100 cell lineages of Control cells" means when they are normalized to /100 cell lineage.

In the extensive simulations sections, it is not clear that many of them are necessary as main figures (e.g., Figure 8-11). For example, is a simulation necessary to show that extremely high levels in vitro of 7uM MNNG severely sickens the cells? "we estimated that 63.1% and 36.9% of cell growth inhibition … were due to the direct effect of MNNG and damage response, respectively" is very precise for a simulation, but is confounded by biology: off target effects of RNAi, imprecise knockdown of p53 (as the western blot shows), etc.

Overexpression of p53 protein causes senescence, and the paper shows very nicely that p53 is involved in both cell proliferation and cell death. However, it is not clear what the implications are from this and why this is important.

On pg. 35 the use of the word suppressed/suppression and in the rest of the paper implies an active cellular mechanism. Here, it is simply that they are outgrowing or reproducing faster to represent a larger proportion of the population. In the methods on the algorithm, there is nothing that has the two populations interacting, and the two arrays can be "physically" separate in a visualized image and still see the same results. Thus, to state that "p53-silenced cells started to expand their population over that of the p53-expressing cells, " and "allowed the expansion of the p53-silenced cells," and "the cell population was replaced with p53-silenced cells," are all implying physical interactions that are all not really occurring and just two population rates that are simulated and then normalized to 100%. Other statements like, "However, the suppression became less prominent … and p53-silenced cells started to expand their population over that of the p53-expressing cells" are problematic and imply an active biological simulation of physically and chemically interacting cells that is not the case.

There is substantial use of jargon and unnecessary abbreviations in the paper. This is not a minor point and severely affects comprehension and readability. In silico experiments are all simulated by computer. Why the need to keep track of p53Si-Sil(-CD)-Sim? Of BD, CD, MD, and CF; the terms BD, CD, and MD are not related, CD means cell death, CF is also not related to CD, but rather the opposite of BD. On pg. 22, the abbreviations are completely unnecessary, and the information of the abbreviations to be memorized by the reader do not come up until much later in the paper. Event is abbreviated Evt, why is this necessary to get rid of 2 letters, "en"? The abbreviation Evt is never again used until the Methods, thus it is only a methodological importance. I understand as a programmer Event and event type are coded as separate variables containing different data, but for the reader this is irrelevant and superfluous. Similarly, "Among the five simulation modes, Standard mode (Std) …" all of these abbreviations Std, Ind, MX, SS, MCS, in a search function of the PDF, are used only 2-3 times in the main text of the paper.

Reviewer #3 (Recommendations for the authors):

Recommendations for improvement

The paper illustrates the advantages and pitfalls of interdisciplinary work, here cell biology and computational approaches. A more pedagogical approach would have made the paper's rationale clearer because some of the approaches, including the DIC image tracking and the cell simulation modelling are not part of the standard biologist's toolkit.

The paper would be greatly strengthened if the authors could summarize the tracking and simulations through pseudocode or a plain language description of the algorithm used for simulation. That way, the average biologist with or without computational expertise would have a sense of the underlying algorithmic thinking, which is separate from the technical details of the computational implementation. Taking the time to explain the algorithm accessibly yet rigorously, allows a reader new to cell lineage tracking and/or simulations to come away with a better sense of the power of these approaches in cell biology.

The paper also needs more transitions to guide the reader. Unless a reader has a background in this area, it can be hard to keep track of the different testing conditions and visualization of results as they represent a formidable number of combinations. At times reading the paper felt like trying to parse a logical puzzle rather than reading experimental results. In addition, the data sets are rich and varied, additional guidance is required in explaining results as in providing transition sentences that explicitly state the reasoning with a bit more detail.

In terms of the biological question, a statement about the novelty and impact of this work would be useful as it is not clear that the model is indeed testing the effect of homeostatic p53 levels. Tumour cells without p53 are able to avoid cell death and proliferate. It is unclear how having less of a wild-type protein in a cell represents a homeostatic model, distinct from having mutated forms within a cell. Also presenting a general result about homeostatic p53 using one cell line, also derived from a tumour, is questionable.

Additional comments for authors:

1. How is the DIC segmentation and object tracking implemented? Is the code developed by the group and is it available on Github or another public repository? Or is it available commercially? It would be good to document the version of the code. Also Cell Profiler apparently can segment DIC cells, so it would be good to know if the approach used by the authors is novel and/or available through open source, collaboration, purchase etc.

On page 69, this is hard to decipher:

Cell density map created by assigning value 1 to a pixel within the 20-pixel diameter area from the position of a cell (blue); if an area overlapped with other areas, the pixel was assigned the sum of the number of overlapped areas (light green).

Can the authors clarify here as this may also help explain communicate the DIC segmentation/tracking approach better?

2. Although the Figures, including Supplemental Figure 7, describe the simulation steps, a high-level description, such as pseudo-code, is missing. That is, a guide that helps the reader understand the logic and implementation of the simulation and help with the interpretation of the detailed steps given in Supplemental Figure 7.

For example, my interpretation of the algorithm is below. It is highly likely my interpretation in incorrect, yet this gives an indication of how and why pseudo-code would be useful and may point out the parts of the explanation that need more detail.

– All these simulations are based on the empirical tracking data. [Note I am not sure how the authors extrapolated past the time length of the experiment, which means I am missing something important]

– Data sets inputted into the simulation include the location, cell division (BP or MP), cell fusion, or cell death, as well as technical notes that affected the tracking.

– Algorithm starts by loading in cell lineages obtained from experiments randomly and automated tracking/manual correction data.

– Simulations progress by filling in the cell areas based on the cell lineage diagrams, and cells and events are encoded for ready visualization when needed.

– Cells were considered to be the same size throughout[?].

– I am not sure how the lineages are extrapolated past the 4000 min experimental time.

– Also I would explain the reason the simulation is so useful. Here is an example where it may seem so obvious to the authors it needs no mention. Yet sometimes it is better to be explicit. It can seem you are talking down but it is helpful!

With this simulation approach, we test whether the simulation matches the experimental results, and also uncouple the combined effect of cell division, cell death and cell fusion on cell proliferation, which would be difficult to do in an experiment with live cells.

3. Tumour cells without p53 can avoid cell death and proliferate. It is unclear how having less of a wild-type protein in a cell is different from having mutated forms within the cells.

– That is, how does the function differ here compared to a mutation in p53?

– How does reduction in p53 followed by inducing cell damage test the need for basal p53 as a unique pathway in cancer progression?

– In addition, more justification of the choice of A549 cells chosen as the model is required, in light of the statement in the Introduction: Here, we investigated the effects of low levels of p53 on the behavior of cells using empirical single-cell tracking.

What is their endogenous expression of p53 in A549 compared to other p53 proficient cells? How do these levels compare to normal cells, such as those derived from primary culture?

– How does inducing DNA damage test the function of low levels of p53 in unstressed cells? Wouldn't a better model be to compare different cell lines with different endogenous levels of p53 and see how they respond? Or this could be used as a second method to back up the conclusions when you damage silenced cells, it seems that the model is not delineated precisely for studying low levels of p53 on cells. Rather the test is studying the effects of DNA damage on p53 null cells which has been done many times? It would be good to hear more about the rationale here, as it is not clear from reading the paper's arguments.

Detailed questions:

4. Why were the cells monitored at such a high density? Was this choice governed by the biological question and/image analysis algorithm limitations, or some other reason(s)? (to follow the fate of individual cells by monitoring live cells, because the culture eventually became over-confluent).

5. Why were the concentrations of CO2 different in the incubator and experiment? Is it due to maintenance of pH, and if so, it would be good to mention this as not everyone monitors pH when carrying out long-term imaging?

6. The authors mention maintaining the integrity of the cell population in multiple sections, including the summary. How is integrity defined? Is it metabolic, genomic, structural?

[Editors’ note: further revisions were suggested prior to acceptance, as described below.]

Thank you for resubmitting your work entitled "Empirical single-cell tracking and cell-fate simulation reveal dual roles of p53 in tumor suppression" for further consideration by eLife. Your revised article has been evaluated by Aleksandra Walczak (Senior Editor) and a Reviewing Editor.

The manuscript has been improved but there are some remaining issues that need to be addressed, as outlined below:

Main issues:

– l. 316-318. The authors suggest that P53 RNAi cells proliferate faster, but have more cell death. Can this not be quantified directly from the data, rather than in the indirect manner pursued here? For instance, one could measure the probability that a cell will divide again, if it doesn't undergo cell death. The prediction would be that this probability is higher for P53 RNAi cells compared to Control.

– l. 391-396: This section is still unclear to me. Why not follow the same approach as shown in Figure 7c for time to MD? Is it because there is a correlation in cell cycle time between generations, i.e. a rapidly-dividing mother has rapidly dividing offspring? This should be explained more clearly.

– l. 418-421. I now understand conceptually what the others do, but from the text and Figure 8 I don't understand how this works in practice. Do the authors linearly interpolate between two Operation data sets? If so, then write that down explicitly. Some things in the text here still make no sense to me. "A start event of 10 and 1", what does this refer to, what sort of event? "The chance of a cell population exposed" A chance of what? Is there some probabilistic process that underlies this?

– l. 489-494. I am not sure I properly understand the origin of shorter doubling time. Is the problem that the cell cycle time is not drawn from a measured distribution (as in Figure 7b) and therefore misses rare but very long cell cycle times?

– l. 523-526. This seems a rather counterintuitive effect: removing the P53 stress response leads to higher cell proliferation when higher stress is applied. I do think it should be emphasized more that this is counterintuitive and perhaps also a possible explanation for this effect should be given.

– l 532-535. It is not clear what the simulations can add here. Is it not possible to use experimental data to measure this directly? After all, the simulations are driven by experimental data, so in principle, there cannot really be anything new from the simulations in that regard.

– l 535. "we assumed" I don't understand what the assumption is based on. Measurements in this paper? Existing biological knowledge?

– l. 550-551. The low frequency of multipolar division is put into the simulations directly from the experimental measurements. So why is this simulation result, which makes exactly the same conclusion, surprising or interesting?

– l. 552. "growth of virtual cells" It is not explained in the main text how the spatial cell dynamics is implemented in the simulations. It is also not explained why space is even important and what novel insights it will bring to incorporate it.

– l. 555-559. It is not clear why showing spatial expansion of MD progeny is important. Couldn't the same insights be gained from purely looking at images? This just means that you get clones of cells that are MD cell progeny, why is it important where they sit in space?

– l. 578. What novel insight does this section bring? The stress-shift experiments show the same conclusion of P53 RNAi outcompeting Control cells as Figure 10. Also, what does the inclusion of space bring to Figure 13a? Would the results in Figure 13b-h be different if space was not included? If not, then I would remove the spatial analysis.

– l. 636. "cancer tissue mass". I don't understand why this result is compared to cancer: most cells are Control (=wild-type?) cells with few P53- cells interspersed, and most of the growth is due to proliferation of Control cells, not P53- cells.

Reviewer #3:

Comment 1:

The experimental data and single-cell lineage analysis are important contributions to the field. Although the authors have included more detailed explanations, the additional insights offered by single cell tracking need to be described more clearly and emphasized throughout the text.

For example, when the authors move from reporting on the population level counting to the single cell tracking results (lines 197 -198), the authors should guide the reader by providing a transition between both approaches. Currently, the authors launch right from the population counting results to validation of single cell tracking without building up the need for single cell tracking.

To quote: We then compared the results obtained by cell counting with those obtained by computer-assisted single-cell tracking analysis to verify whether this analysis indeed yields results consistent with the classical counting method.

Before comparing the results, a transition highlighting the need for single-cell analysis is missing as well as the need for comparing both methods is needed. Suggestion: "Thus far, we have described how the different treatments affect cell numbers at the population level. We then analyzed the data sets using single cell tracking. This powerful approach can reveal how the events occurring at the individual cellular level contribute to what is observed at the population level."

Only then move on to the comparative results such as by stating: To test the accuracy and self-consistency between our standard cell counting and single cell tracking, we compared the results obtained with each approach.

Similarly, when the results obtained from single cell tracking add new information, additional context should be provided for the reader. This paper is cognitively challenging to read and interpret, and more explanation is needed to help the reader navigate and appreciate the significance of the results.

Comment 2:

Similar clear emphasis is needed when describing the simulation approaches and their significance. To illustrate: In the section introducing the cell-fate simulation algorithm (lines 363-372), confluency is mentioned as are "limitations of empirical approaches." Rather than stating confluency and the vague term "limitations," the justification needs to be clear from the start. My suggestion is move the explanation found later in the text to this introductory section.

For example, lines 440-442 state: "cell-fate simulation using Operation data allows the creation of various simulation options and provides flexibility for designing virtual experiments that would be difficult to perform empirically."

Rather than letting the reader wait for this statement, I recommend leading in with a similar statement (and dropping the technical reference to Operation data). Suggestion:" Cell-fate simulations are powerful and flexible tools help us model conditions that are not readily accessible by direct imaging, such as mixed cultures and mixed dosages. "

Other comments:

3. Ensure that cell growth is used when referring to cell size not to cell division within the text. The term "grow" is used colloquially in the lab but here should be reserved for area/volume not cell division. For example, see how "growth" is used in Line 125. Here it is confusing as the passage is describing cell area decreasing and then grow is used to mean cell proliferation.

4. What random number generator was used?

5. Figure 1—figure supplement 3. Y axis in last graph has the label "Variation" but the units are missing.

6. When discussing Figure 5, explain how the results

highlight the need for single-cell tracking studies and how this approach complements and enriches the population level studies. Suggestion: "The cell numbers over time are roughly equivalent for both the scr siRNA and the p53 siRNA treated cells, as shown in Figures 2c and 2i. The single cell tracking data, however, reveal differences that are not directly accessible through standard cell counting. Figure 4 reveals that although the overall cell death is higher in the p53 siRNA cells, it is compensated by increased multipolar cell division. Further, the simulations can help unravel the relative rates of multi-polar cell division compared to cell death. As shown in Figure 5, we see that the relative proliferation curves can be simulated in the presence or absence of cell death. By analyzing the individual cellular fates under well-defined conditions, we can then simulate scenarios that are not accessible through our direct imaging, such as analyzing how a population of mixed cells and/or heterogenous treatments will evolve over time. "

7. Line 226. Quote: To this end, we sorted each cell lineage into groups (Figure 3a).

The division into groups introduces a layer of complexity and seems arbitrary considering the small number of possible bins. Why is reporting the binned data through groups better than reporting the numerical value?

8. Lines 282-286. Quote: …the number of cell death events in Control cells determined by counting was higher than that determined by single-cell tracking analysis. This was because the area of single-cell tracking was slightly outside the area where cell death frequently occurred (Figure 4—figure supplement 1c). However, given that such events do not occur with the same probability throughout the field of view, some variation may occur with both the counting and single-cell tracking approaches.

Was this because cells that die move more than cells that do not or is it something specific about the cell imaging chamber with death occurring near the edges more than the centre?

9. I am confused by the reference to the "accuracy of a detecting a low frequency event." Quote: In general, the accuracy of detecting a low-frequency event is lower than that for frequently occurring events, e.g. bipolar cell division…

Are the authors referring to the probability of the event being captured by the imaging system rather than the detection of the event by their software and/or visual scorer? Or do they have evidence that the detection by the software and/or visual scorer is lower for these events compared to bipolar cell division?

10. The authors state in line 260 "We therefore determined if single-cell tracking could detect multipolar cell division, cell death, and cell fusion with adequate accuracy for statistical analysis. To this end, we determined the number of multipolar cell division and cell death events visually by manual counting in videos, and compared the results with those obtained using single-cell tracking analysis (Figure 4). Notably, cell fusion was not included in the counting analysis because it was difficult to detect without single-cell tracking."

Yet when review Figure 4, I am having trouble deciphering how the authors concluded that the single-cell tracking was accurate as the results are not directly compared to visual scoring. Please clarify.

11. Lines 316-318: These results suggest that p53 silencing promoted the reproductive ability of p53 RNAi cells, but this was counteracted by the induction of cell death, resulting in the formation of p53 RNAi cell populations that were smaller than Control cell populations (Figure 2i).

I see a small dip in the p53 RNAi curve compared to the Control curve in Figure 2i, but otherwise they look similar. Please clarify.

12. Line 318 Analysis also shows that the effect of silencing the low levels of p53 cannot be detected without access to the spatiotemporal information on individual cells provided by single-cell tracking.

Although this statement is likely, the counter-example can not be ruled out. Just to list possible alternative approaches that could reveal similarly nuanced effects of silencing p53. One can imagine a scenario where the number of live and dead cells are measured over time, without any single cell tracking. Or it may be possible to model the number of cells over time using an analytical expression that embeds cell division (bipolar, multipolar) as an exponential and cell death (say as a linear function of time). Suggestion-qualify statement: "This analysis also demonstrates single cell tracking provides more nuanced and detailed information about the effects of silencing p53. Here the single cell analysis revealed clear differences in the rates of cell proliferation and cell death among the scr siRNA and p53 siRNA conditions, differences would be obscured and/or missed if limiting the analysis to cell counts at the population level."

13. Line 331: Following cell fusion, Control and p53 RNAi cells demonstrated 79.4% and 93.2% multipolar cell divisions.

Please define the % values-how are they calculated? Also the numbers are listed on the bar graphs in Figure 6- the relative percentages of listed over the bar graphs is confusing in light of the numbers being relative to another 100, the 100 cell lineages. Also it would be helpful to see the spread of the data points illustrated by the bar graph.

14. Staring on line 385, the authors state: The algorithm then reflected this distribution to choose the End event.

– How is the weighted random assignment implemented? Specify the method or methods and justify why the choice is appropriate.

– Similarly, for LT and other random assignments, is the implementation always the same as for the Event assignment?

– Is the additional +/- 10% in ET imposed for BP events based on experimental data obtained here and/or reported elsewhere or there some other reason for constraining the ET for BP events in this way? Further, could this constraint have led to the observation summarized in lines 489-494: On the other hand, the simulation tended to yield an average cell doubling time about 2 h shorter than that determined by single-cell tracking analysis. Given that the algorithm assigned a cell doubling time to each cell by generating a random number with Operation data-Time (Figure 7), a long cell doubling time, e.g. 3,000 min, which occurred less frequently, may be less likely to be assigned, resulting in the generation of a simulated cell population

– When CF occurs, do these events also reflect the frequency of sibling vs non-sibling under the different conditions studied?

15. I have trouble understanding why calculating Recovery is important to the simulation and why it is listed before the other steps. Line 894 states: Recovery data was used to simulate the rate of recovery a cell population from the treatment of MNNG. When cells were treated with MNNG, the majority of cells may be killed. However, small number of cells gained reproductive ability, which could be found at the end of imaging.

I am confused here as I don't see evidence of the majority of cells being killed in the population expansion data and don't understand why they need to be tracked.

Lines 903-907: For example, if any of the progeny derived from a progenitor underwent bipolar cell division at last within 20% of the single-cell tracking period, e.g. 320 to 400 min when tracking was performed for 400 min, this cell lineage was counted as one upon the calculation of the percentage. Thus, if 10 such cell lineages were found out of a total of 300, the recovery percent was 3.3%.

I don't understand this statement-what does percentage refer to? Why is only BP considered and not MP, for example? Any why is calculating this value important to the simulations as illustrated in Figure 7, supplement 1c, Step 3?

16. Line 918-920: To generate a simulation array for the Operation data-Event, the percentage of each event relative to the total number of cell divisions (total of bipolar cell division and multipolar cell division) was calculated.

As shown in Figure In Figure 7, supplement 1 c, in the "Event" sequence I don't understand why calculating the "% event of total cell division" is possible before the simulation arrays are created?

17. Lines 931-933: the array was empty, the average time that bipolar cell division occurred was calculated and −25% to +25% of the time selected by random 933 number was assigned as LT, and bipolar cell division was then assigned to the cell.

Is this based on experimental data and/or another reason?

18. I appreciate the care and effort that went into detailing the algorithmic approach used for the simulations. The logical flow now is much clearer and moves away from being a "black box" to now being reproducible.

Recommendations and questions:

– Figure 7 supplement 2. Recommend placing this before supplement 1 as it presents the overall logic.

– In Figure 8, supplement 1a, (page 94). Change "Uze" to "Use" in Step 6.

– In Figure 7, supplement 1b (page 95), Step 3 defines the nBD but the description is confusing. Clarify the "last time point of cell tracking" – is this simply the LT associated with the event? Also what is the offset and what is its purpose?

– In Figure 7, supplement 2, there is a typo in "Select an e-vv-ent type"

19. Consider revising sub-headings to guide the reader. Revise to express purpose, result, significance etc. These could serve as signposts throughout the paper would improve the paper's accessibility.

20. In future work, consider graphical representations that are not limited to colour as in "burgundy" plot as 8-11% of the male sex is R/G colour blind. Consider using different plots styles as well as colour. I am not asking the figures to be revised for this publication, but ask that the authors consider visually accessible graphics / figure in future publications.

21. Similarly, consider box plots rather than bar graphs for future work.

https://doi.org/10.7554/eLife.72498.sa1

Author response

Essential revisions:

1) The manuscript needs major rewriting to make it more comprehensible to a general audience. Please rewrite the manuscript according to the specific recommendations from the three peer reviewers.

We have revised the entire manuscript to make it more understandable to a wider audience. We have revised the last part of the Introduction, added explanations between the paragraphs to smooth the transitions, and have rewritten the Discussion. We have also included methods related to image segmentation and single-cell tracking. We greatly appreciate the reviewers’ suggestions, which have allowed us to improve the manuscript.

2) Please provide better explanation of the simulation algorithm and the assumptions behind it in plain language.

We have created two sections related to the algorithms and added three figures. We hope that this revision will help the audience to follow the concept behind the development of the algorithm. We have retained details of the algorithms and code from the previous version in the current version.

3) Please revise the figures according to the specific recommendations from the reviewers.

We have revised the figures, following the reviewers’ recommendations.

4) Please better discuss the general impact of this study in the Discussion section.

We have added a general discussion regarding p53, single-cell tracking, and cell-fate simulation. We have also added a discussion regarding the prospective use of cell-fate simulations.

We have revised the manuscript extensively and have therefore assigned consecutive numbers to each comment, and indicated the numbers in the relevant parts of the revised manuscript, in addition to including line (L) and page (P) numbers.

Reviewer #1 (Recommendations for the authors):

1) Limited lineage analysis.

In general, the combination of cell tracking and manual annotation of events in general is powerful and I think the analysis of cell fusion in Figure 6 is a nice example of this power. However, I think it is under utilised in the paper.

We characterized the events that occurred before multipolar cell division using single-cell tracking data, and consider that the results were important for our conclusion. We have revised the related section “Events leading to multipolar cell division” in the Results (P14, L322).

Figures 2 and 4 could have been constructed without cell tracking and lineage analysis, but only by analysing total cell number (Figure 2) or by counting events without lineage information (Figure 4).

We made these figures to compare the results of counting and single-cell tracking data, given that no such verification experiments have been performed previously. We therefore think that both methods should be included in the same figure, to demonstrate the accuracy of single-cell tracking. We have rewritten the following sections in the Results to clarify the objective of the analyses:

“Effect of silencing the low levels of p53 on cell population expansion, P8, L169” and “Impact of p53-silencing and MNNG treatment on cell death, multipolar cell division, and cell fusion, P12, L255”.

In Figure 3, lineage structures are analysed (but in a way I don't understand, see further below) but apart from changes with increasing MNNG it doesn't provide much insight: it seems that cell proliferation/death is decreased/increased with stress (as expected) leading to fewer large lineages, with no compelling difference between p53 siRNA or control. There is a sentence ('For example, suppression … generate 10-12 progeny (Figure 3b)’) that suggests there is a difference, but I can't see it in the figure.

We agree that the section related to Figure 3 was difficult to follow. We have therefore rewritten this section and reorganized the figure. In this section, we intended to show that a cell population is composed of cells with different reproductive abilities, by analyzing the number of progeny produced from a progenitor. We also wanted to explain that cell expansion or growth curves may not represent the actual situation of the cell population. For example, if a cell population treated with a drug shows a similar expansion curve to a non-treated cell population, it may be concluded that the treatment had no effect. However, the drug may promote cell growth but also induce cell death, resulting in an overall similar cell population expansion curve to a non-treated population. Without analyzing the fates of individual cells, it is difficult to reveal the processes involved in building up a cell population. We believe that the relationship between Control and p53 RNAi cells provides an interesting example highlighting this matter: i.e. both Control and p53 RNAi cells showed similar cell population size, but p53 RNAi cells underwent more frequent cell death. We have rewritten the Results section “Analysis of a cell population at the level of cell-lineage” to clarify our intention (P10, L219).

It also seems that for a single condition, not all lineages have the same number of progeny (e.g 1-3 vs 13-15). Why is it that for the same imaging time lineages have such different offspring? Is it because some cells die? Is it impacted by limits to cell tracking, e.g. if a cell moves out of the field of view it gives rise to a short lineage because the offspring cannot be followed? In the latter case, that would rather represent a technical limitation rather than biological insight.

Regarding the first question: “It also seems that for a single condition, not all lineages have the same number of progeny (e.g 1-3 vs 13-15). Why is it that for the same imaging time lineages have such different offspring?”, cell populations are generally composed of cells with different reproductive abilities. Such differences will become evident during growth of the population, and these differences will be reflected in the number of progeny produced by a progenitor. We have reminded this in the first paragraph of the “Analysis of a cell population at the level of celllineage” in the Results (P10, L219).

Regarding the second question, “Is it because some cells die?”, the answer is yes, in some cases. This issue has been addressed in the section related to Figure 5 (P13, L296 and P55, L1255).

The third question was “Is it impacted by limits to cell tracking, e.g. if a cell moves out of the field of view it gives rise to a short lineage because the offspring cannot be followed? In the latter case, that would rather represent a technical limitation rather than biological insight”. This is not the case. We tracked all progeny until the end of tracking time, and the single-cell tracking data thus contained information on the progenitors and all their progeny. We have mentioned this in “System to investigate the functional implications of maintaining the low levels of p53 in unstressed cells, P5, L101” in the Results, and the technical matter related to single-cell tracking is mentioned in “Single-cell tracking” in the Methods (P38, L832).

2) Insight in simulation lacking.

The section 'Cell-fate simulation algorithm' gives information on highest-level procedure of simulating, but it lacks any discussion of assumptions: does each cell choose 'fate' (MD, CD, CF, etc.) independently, or are correlation between sisters, cousins, etc. taken into account?

As noted in our response to Comment 1, we have revised the sections and prepared three additional figures. “Cell-fate simulation algorithm, P16, L363” and “Cell-fate simulation options with Operation data, P18, L413”, as well as Figure 7 (P57, L1289), Figure 8 (P58, L1306), and Figure 7—figure supplement 2 (P65, L1471).

How is experimental data used to constrain parameters of the simulation? The explanation in the supplementary information was not understandable for me. The presentation of the simulation algorithm in Figure S7a-h seems too detailed (e.g. dealing with the choice to load a file or not at the top of Figure S7b), while some of the diagrams (e.g. Figure S7F) are so complex that it appears to me as if a coherent underlying model is lacking. At the very least, it made it impossible for me to check the validity of the underlying assumptions.

This comment is also related to Comment 1, and Dr. Colarusso also raised similar comments related to the algorithms. Figure 7 summarizes how our simulation works and Figure 7—figure supplement 2 includes an outline of the simulation processes. We hope those revisions will make it easier for the audience to follow the processes of the cell-fate simulation. “Cell-fate simulation algorithm, P16, L363” and “Cell-fate simulation options with Operation data, P18, L413”, as well as Figure 7 (P57, L1289), Figure 8 (P58, L1306), and Figure 7—figure supplement 2 (P65, L1471).

3) In silico data generation.

in Figure 5, in silico data is generated based on experimental data, to asses the role of cell death. However, the explanation raises questions. It says that for any cell that dies its lineage was replaced by that of its sibling. But this only works if lineages without any cell death are always symmetric between siblings. Is this indeed the case? Or can you find cases where one sister generates 4 daughter but the other only 2? In that case, it is not clear what the in silico data represent. This is not discussed anywhere

Regarding the growth patterns of sibling cells, it is rare for both to show exactly symmetric growth patterns. In response to the question “Or can you find cases where one sister generates 4 daughters but the other only 2?”, this could happen. However, in many cases, a cell shows the closest growth pattern to its sibling cell, as both inherit similar characteristics from their parent cell. Thus, if a cell only produces two siblings, its sibling also produces a similar number of offspring. Of course, there are many variations in growth patterns, but we believe that this assumption largely reflects the actual growth pattern of sibling cells, and the assumption was also confirmed using cell-fate simulation (Figure 12). We have emphasized some of these points in “In silico generation of a cell-lineage database of p53 RNAip53si cells” in the Results (P13, L296).

4) Space in simulations.

In the simulations in Figure 9-11, space is taken into account, but I could not find how this is incorporated in the simulations. Also, it is not clear why space is relevant to begin with. It seems the cells are not directly interacting, e.g. by signalling, so could these results not have been obtained by simulations without space? Or is there competition for space? And if cells fuse, do they fuse with a neighbor? This should be explicitly discussed in the paper.

Dr. Chen made similar comments. The primary purpose of the animation was to analyze a cell of interest. As shown in Figure 7—figure supplement 3, the cell-lineage map created by the simulation was very crowded, and we were therefore unable to detect any unique patterns by simply examining the maps (we usually examined cell-lineage maps to find unique growth patterns). We therefore used software to display the cell of interest. We have explained this in “Survival of the progeny of multipolar cell division” in the Results (P24, L550).

As Dr. van Zon has pointed out, we are also interested in simulating cell-to-cell interactions in the future. Using empirical data for e.g. activation of neutrophils by primarily activated neutrophils, the chain reaction of the activation could be animated by adding a code to the software. This animation could provide a useful research tool (P30, L711).

5) Writing and terms unclear.

In many places, explanations are not clear (see below for examples). The authors use a lot of acronyms, which I partly understand, but some sentences become very hard to understand (e.g. p.33 'we asked how progeny of MD that undergo BD survive by performing a simulation in Std mode').

Dr. Chen made similar comments regarding abbreviations. We have reduced the use of abbreviations in the revised version, e.g. BD, MD, CF and CD were spelled out (e.g. P5, L94).

Captions are strangely formatted and seem to sometimes miss panels (e.g. (b) lacking in caption Figure 3, (c) + (d) lacking in Figure 8).

We have revised the Legends for Figures 3 (P55, L1237) and 8 (now Figure 10, P59, L1344).

Reviewer #2 (Recommendations for the authors):

Overall the study is very well done. There are several areas that can be better clarified.

The sentence, "However, the function of maintaining low levels of p53 in unstressed cells remains unclear." Is not a great introduction to the rationale of the paper; in that maintaining low levels is not what is being investigated, nor the function of the low levels, nor really the differences between low and high levels.

We appreciate this comment and have revised the sentence accordingly (P3, L55).

It is not clear throughout the text what "cell-lineage datasets" means. This could mean many things to many different readers. A sentence as to how the authors will define it is very important. Datasets can mean anything.

We used the term “dataset” to distinguish between the cell-lineage database and a group of data for each cell lineage. However, these terms may be confusing. In the case of the DNA database, each gene is categorized by e.g. gene ID. We have therefore rephrased “dataset” as “cell lineage No”, and have included an explanation in “System to investigate the functional implications of maintaining low levels of p53 in unstressed cells” in the Results (P5, L103).

Similarly, the quantification of lineage is also ambiguous. How is this defined/quantified? This is never stated in the Methods, and again can mean different things.

We appreciate this comment. We agree that the phrase “quantitation of cell lineage” could be difficult to understand. In empirical studies e.g. with western blotting or enzyme assays, the analysis is designed to obtain information on a focus of interest, e.g. expression level of proteins. On the other hand, imaging data contains multidimensional information, e.g. cell shape and position, and events occurring in a cell, and cell-lineage data thus also contains some of this information. We therefore aimed to quantitate specific aspects of the cell lineage, e.g. the number of progeny produced from a progenitor, or time between events. We have added a paragraph, “System to investigate the functional implications of maintaining low levels of p53 in unstressed cells” to the Results to clarify this (P6, L108).

The entire section on "Minimum number of cell-lineage datasets required to build a cell-lineage database" is unclear. Is this a random subsampling analysis that is being performed? Are these from experimental triplicates in Supplementary Figure 3, or just a randomly subsampling, as is implied in the statement, "The analysis was repeated three times (green, orange, and red lines) to show variations at a tracking time," so only the analysis was repeated three times, but not the experiments?

We generated 485 cell lineage data, and selected 50-240 cells lineages randomly from the 485 cell lineages. Each repeated selection was performed such that the same lineage was not selected, except for the selection of 240 lineages. We have mentioned this in the related paragraphs (P7, L134) and in the legend for Supplementary Figure 3 (now Figure 1—figure supplement 3) (P63, L1428).

This analysis aimed to determine the number of cell lineages that needed to be used for singlecell tracking analysis. We therefore repeated the process three times using the cell-lineage database created for the purpose. Regarding variations between experiments or imaging, we have addressed this in the section related to Figure 2.

What is the relationship between all of the datasets starting at 100 cells in the y-axis, but having different numbers of cell lineages?

Because the initial number of cell lineages differed, we normalized the value to 100. We have mentioned this in Supplementary Figure 3 (now Figure 1—figure supplement 3) (P63, L1428).

Quantification of the cell lineage categories was unclear. What does "7-9 progeny" mean? The "number of cells/lineage" (text within the figure) vs "number of progeny/lineage" (main text) doesn't make sense. This is further confused by the Figure 3 legend stating "Values shown in (a) are number of lineages". So if the bar graph is read, then 136 cell lineages had around 350 cells, and 127 cell lineages had 900 cells. This is extremely confusing.

Dr. van Zon also commented on this section. We have therefore rewritten this section and reorganized the figures (P10, L219 and P55, L1237).

Why are cell densities in control and p53 RNAi in Figure 2 always the same, if MD, CD, and CF are all highly induced after RNAi knockdown?

We would like to emphasize this point in this manuscript. Cell population expansion curves or growth curves are often used in cell biological studies to assess the effects e.g. of drugs. However, such curves do not provide any information on the composition of the cell population. For example, if a drug promotes cell growth but also induces cell death, the size of the drugtreated population may appear to be similar to that of a non-treated population. However, singlecell tracking allows the growth profiles of each cell lineage to be analyzed, and can thus reveal the composition of the cell population. We consider that Control and p53 RNAi cells provide an interesting example to explain this matter. We have considered this in the “Analysis of a cell population at the level of cell-lineage, P10, L219” and “In silico generation of a cell-lineage database of p53 RNAi cells, P13, L296” sections in the Results.

The normalization factor, "/300 lineages" is not clear. This makes it difficult to compare the rates of the MD, CD, and CF between experiments across the paper. For the numbers "0.0475, 0.125, and 0.0775 events per 10 min/300 lineages" to mean anything substantial to any reader, it should be in a metric that is meaningful.

We realized that we normalized the number of cell-lineages to 100 or 300. We now consistently used 100 cell lineages for normalization (P13, L291).

It is not clear what the numbers in Figure 6a mean. Here, again it is difficult to compare what a low frequency of occurrence of "3.5 to 3.8% of progeny", or "0.7 progeny of MD/100 cell lineage of p53si cells vs. 0.05 progeny of MD/100 cell lineages of Control cells" means when they are normalized to /100 cell lineage.

We have reworked Figure 6 and the related sections. We previously used the terms e.g. CF > MD, etc., but have changed these to Pattern 1 and Pattern 2 in the revised version. Regarding the number in 100 cell lineages, we have included additional explanations in the figure legend. Because the number of multipolar cell divisions in Control cells was low, we searched all the videos (entire image of triplicated videos) to find multipolar cell divisions and then tracked the cells back to their progenitors to determine the events preceding multipolar cell division. To normalize the values, we therefore assumed that multipolar cell division occurred at a similar frequency to that recorded in the cell-lineage database. We have verified the numbers and revised the related sections. We hope that these changes make the manuscript easier to follow. Concerning 0.7 vs 0.05 progeny, this indicates the number of progeny produced by multipolar cell division that can undergo bipolar cell division, normalized to 100 cell lineages as described. The percentage is the percentage of such cells in the total number of progeny produced by multipolar cell division. We have revised “Events leading to multipolar cell division, P14, L322” in the Results, and have also revised the legend for Figure 6 (P56, L1267).

In the extensive simulations sections, it is not clear that many of them are necessary as main figures (e.g., Figure 8-11). For example, is a simulation necessary to show that extremely high levels in vitro of 7uM MNNG severely sickens the cells? "we estimated that 63.1% and 36.9% of cell growth inhibition … were due to the direct effect of MNNG and damage response, respectively" is very precise for a simulation, but is confounded by biology: off target effects of RNAi, imprecise knockdown of p53 (as the western blot shows), etc.

Regarding the comment, “In the extensive simulations sections, it is not clear that many of them are necessary as main figures (e.g., Figure 8-11, Now 10-12)”, we have changed the display items. We have removed the still images of the animations from Figures 12 and 13 (but kept the animations).

Regarding Figure 10e, we agree that the p53-mediated and non-mediated responses (e.g. by DNA-break formation) may not be distinguished. However, if a response is induced by exposure of cells to a drug following the accumulation of p53, it is often assumed that such a response is only related to p53, while it is likely to be due to the combined effect of p53 with other processes.

We also understand the point that Dr. Chen raised, as there would be a variation in the degree of silencing between cells, and p53 silencing may induce an effect that cannot be detected by single-cell tracking. However, conclusions that are drawn based on e.g. western blotting, and enzymatic assay (average-based analyses) may also contains ambiguities. As Dr. van Zon also raised similar comments, we responded to this matter in Comment 5.

We would therefore like to keep Figure 10e to make this point. Because the values may include an off-target effect, as mentioned by Dr. Chen, we made a statement about this matter in the text (P23, L539).

Overexpression of p53 protein causes senescence, and the paper shows very nicely that p53 is involved in both cell proliferation and cell death. However, it is not clear what the implications are from this and why this is important.

We have revised the entire Discussion to emphasize the implications of our work. We have included three sections to discuss the function of low levels of p53, the induction of multipolar cell division, cell death, and cell fusion, and the responses of Control and p53 RNAi cells to MNNG, respectively. We hope that these revisions have addressed Dr. Chen’s point (P26, L595).

On pg. 35 the use of the word suppressed/suppression and in the rest of the paper implies an active cellular mechanism. Here, it is simply that they are outgrowing or reproducing faster to represent a larger proportion of the population.

We agree that the mechanism was not “suppression”, because Control cells did not directly suppress the expansion of p53 RNAi cells. The current analysis was based on the relative growth abilities of Control and p53 RNAi cells. We have therefore rephrased this in “Limiting expansion of p53 RNAi p53-silenced cells by Control p53-expressing cells” in the Results (P24, L561).

In the methods on the algorithm, there is nothing that has the two populations interacting, and the two arrays can be "physically" separate in a visualized image and still see the same results. Thus, to state that "p53-silenced cells started to expand their population over that of the p53-expressing cells, " and "allowed the expansion of the p53-silenced cells," and "the cell population was replaced with p53-silenced cells," are all implying physical interactions that are all not really occurring and just two population rates that are simulated and then normalized to 100%. Other statements like, "However, the suppression became less prominent … and p53-silenced cells started to expand their population over that of the p53-expressing cells" are problematic and imply an active biological simulation of physically and chemically interacting cells that is not the case.

As noted in our response to Dr. van Zon (Comment 13), the primary purpose of the animation was to analyze the cell of interest. Because the simulation generates a large number of virtual cells, it is impossible to evaluate the events that occurred in the simulated cells. We therefore made animations to visually show the cells of interest. In the simulation mode with Control and p53 RNAi cells, the results reflected the relative growth abilities of both cell types. We therefore agree that our statement suggesting that the cell types interacted with each other was misleading, and we have rephrased such statements throughout the manuscript.

However, we would like to mention that cell-to-cell interactions could be simulated by adding some code and visualized by animations. However, this will be considered for future research (P30, L711).

There is substantial use of jargon and unnecessary abbreviations in the paper. This is not a minor point and severely affects comprehension and readability. In silico experiments are all simulated by computer. Why the need to keep track of p53Si-Sil(-CD)-Sim? Of BD, CD, MD, and CF; the terms BD, CD, and MD are not related, CD means cell death, CF is also not related to CD, but rather the opposite of BD. On pg. 22, the abbreviations are completely unnecessary, and the information of the abbreviations to be memorized by the reader do not come up until much later in the paper. Event is abbreviated Evt, why is this necessary to get rid of 2 letters, "en"? The abbreviation Evt is never again used until the Methods, thus it is only a methodological importance. I understand as a programmer Event and event type are coded as separate variables containing different data, but for the reader this is irrelevant and superfluous. Similarly, "Among the five simulation modes, Standard mode (Std) …" all of these abbreviations Std, Ind, MX, SS, MCS, in a search function of the PDF, are used only 2-3 times in the main text of the paper.

We have removed many of the abbreviations and jargon in the manuscript (e.g. BD, MD, CD, CF, Std, Ind, MX, SS, and MCS). For example, BD, MD, CD and CF were spelled out (P5, L94). Regarding p53 Si-sil(-CD)-Sim, etc., we have changed p53si to p53 RNAi, following the suggestion of Dr. Chen (Comment 40). Regarding “Sil”, we have changed the name of this cell population to p53 RNAi-Silico(-)cell death. We have also added the suffix “-Sim” where it was necessary to refer to cell populations generated by the simulation. We have revised the “Number of progenitors used for simulation (P19, L445)” section in the Results. We have removed the abbreviation “Evt” from the main text, and changed it to length of time (LT) in the Methods (P39, L862).

Reviewer #3 (Recommendations for the authors):

Recommendations for improvement

The paper illustrates the advantages and pitfalls of interdisciplinary work, here cell biology and computational approaches. A more pedagogical approach would have made the paper's rationale clearer because some of the approaches, including the DIC image tracking and the cell simulation modelling are not part of the standard biologist's toolkit.

The paper would be greatly strengthened if the authors could summarize the tracking and simulations through pseudocode or a plain language description of the algorithm used for simulation. That way, the average biologist with or without computational expertise would have a sense of the underlying algorithmic thinking, which is separate from the technical details of the computational implementation. Taking the time to explain the algorithm accessibly yet rigorously, allows a reader new to cell lineage tracking and/or simulations to come away with a better sense of the power of these approaches in cell biology.

We appreciate the encouraging comments. We have revised the Results section to improve the description of the algorithm. We have therefore included two sections, “Cell-fate simulation algorithm, P16, L363” and “Cell-fate simulation options with Operation data, P18, L413”, as well as Figure 7 (P57, L1289), Figure 8 (P58, L1306), and Figure 7—figure supplement 2 (P65, L1471).

Regarding the software for DIC segmentation and single-cell tracking, we described some details in our preprint (BioRxiv 508705; doi: https://doi.org/10.1101/508705 (2018)), and are planning to update and submit this for peer-review. We are currently cleaning up codes written during the past 10 years to allow third parties to perform code maintenance, and will include the pseudocode suggested by Dr. Colarusso in the preprint. We would like to make all the codes and software available to the public as soon as possible. In the current manuscript, we have included two sections regarding DIC segmentation (P35, L772) and single-cell tracking (P36, L798) in the Methods.

The paper also needs more transitions to guide the reader. Unless a reader has a background in this area, it can be hard to keep track of the different testing conditions and visualization of results as they represent a formidable number of combinations. At times reading the paper felt like trying to parse a logical puzzle rather than reading experimental results. In addition, the data sets are rich and varied, additional guidance is required in explaining results as in providing transition sentences that explicitly state the reasoning with a bit more detail.

As noted above, we have revised the section related to the algorithms and included a pseudocode (outlines, Figure 7—figure supplement 2). We have also revised the entire manuscript to try to make it more comprehensible to the readers.

In our previous version of the manuscript, we named the data used for the simulation as “Source data”. However, we realize that this journal uses this term for other purposes. We have therefore changed “Source data” to “Operation data” to avoid confusion.

In terms of the biological question, a statement about the novelty and impact of this work would be useful as it is not clear that the model is indeed testing the effect of homeostatic p53 levels. Tumour cells without p53 are able to avoid cell death and proliferate. It is unclear how having less of a wild-type protein in a cell represents a homeostatic model, distinct from having mutated forms within a cell. Also presenting a general result about homeostatic p53 using one cell line, also derived from a tumour, is questionable.

Please see our response to the use of one cell line and mutant p53 (Comment 44). With regard to mutant p53, we have included this in the Discussion section (P29, L686).

Additional comments for authors:

1. How is the DIC segmentation and object tracking implemented?

Regarding the first question, “How is the DIC segmentation and object tracking implemented?”, please see our response to Comment 47.

Is the code developed by the group and is it available on Github or another public repository?

As noted in our response to Comment 47, we aim to make all the codes available upon submission of BioRxiv 508705; doi: https://doi.org/10.1101/508705 (2018).

"Is the code developed by the group and is it available on Github or another public repository? "

As noted in our response to Comment 47, we aim to make all the codes available upon submission of BioRxiv 508705; doi: https://doi.org/10.1101/508705 (2018).

Or is it available commercially?

Because code maintenance and technical writing (manual) requires a large amount of work, we have been looking for a partner, but have so far been unable to find a commercial partner that appreciates the need for a single-cell tracking system in the field of cell biology research.

It would be good to document the version of the code.

Our system includes 20 software items (BioRxiv 508705; doi: https://doi.org/10.1101/508705 (2018)), which were written by the last author of the manuscript. We are planning to release all these codes upon the submission of the preprint.

Also Cell Profiler apparently can segment DIC cells, so it would be good to know if the approach used by the authors is novel and/or available through open source, collaboration, purchase etc.

We did not mention commercially available or freeware resources because these did not meet our needs. In our early stage of developing the segmentation software, we tested thresholding, clustering, histograms, edge extraction, and region-growing methods by writing the code ourselves. These could work for certain types of images using certain parameters, but not for other images. Because we carried out long-term live-cell imaging for more than 7 days, the image quality changed over time due to cell growth and the formation of cell debris, etc. A total of ~200,000 image files (515 × 515 pixels) recording the different cell statuses were thus created, and we had to develop our own strategy to segment those DIC images, because existing approaches did not have the ability to process images with diverse qualities automatically, within a reasonable processing time. Most of our software was thus written using low-level computer languages, such as C and C++, which allowed memory allocation to be controlled manually. Cell Profiler etc. are designed for general purposes, but did not meet our specific needs. We have therefore not compared our segmentation method with others. From the point of view of system development, the entire process needed to be designed in a coordinating manner, e.g. file name assignment, data archiving, video viewing, segmentation, single-cell tracking, and data analysis. We have therefore focused on developing our own system rather than using existing systems.

However, we appreciate the point raised by Dr. Colarusso and have mentioned the main characteristics of our segmentation approach in the Methods (P35, L772).

With regard to availability, we are happy to make the process available to allow other research groups to carry out spatiotemporal analysis of individual cells.

On page 69, this is hard to decipher:

Cell density map created by assigning value 1 to a pixel within the 20-pixel diameter area from the position of a cell (blue); if an area overlapped with other areas, the pixel was assigned the sum of the number of overlapped areas (light green).

Can the authors clarify here as this may also help explain communicate the DIC segmentation/tracking approach better?

We generated a cell-density map using the cell positions determined by single-cell tracking. We then drew a circle from the position. If the circle overlapped with other circles, a value of 1 was added. Values were increased in areas of high cell density, according to the number of overlaps. We have added an explanation in the legend of Supplementary Figure 2 (now Figure 1—figure supplement 2) (P63, L1418).

2. Although the Figures, including Supplemental Figure 7, describe the simulation steps, a high-level description, such as pseudo-code, is missing. That is, a guide that helps the reader understand the logic and implementation of the simulation and help with the interpretation of the detailed steps given in Supplemental Figure 7.

For example, my interpretation of the algorithm is below. It is highly likely my interpretation in incorrect, yet this gives an indication of how and why pseudo-code would be useful and may point out the parts of the explanation that need more detail.

We appreciate these comments. We have outlined the entire processing scheme of single-cell tracking (P17, L397) and cell-fate simulation in Figure 7—figure supplement 2 (P65, L1471).

– All these simulations are based on the empirical tracking data. [Note I am not sure how the authors extrapolated past the time length of the experiment, which means I am missing something important]

Simulations can be performed using both Operation data generated from empirically created single-cell tracking data and virtually created Operation data. We have described these in the sections related to the algorithms (P18, L413).

– Data sets inputted into the simulation include the location, cell division (BP or MP), cell fusion, or cell death, as well as technical notes that affected the tracking.

The current work did not take account of the location, and focused on other parameters, e.g. event patterns, for the simulation.

– Algorithm starts by loading in cell lineages obtained from experiments randomly and automated tracking/manual correction data.

We are unsure what you mean by “randomly”, but we hope that this is addressed in our revised explanations of the cell simulation in the sections related to the algorithm. In Figure 7—figure supplement 1, we wrote “randomize”, but it should be “generate random value”. This may be the cause of confusion. Thus, we revised Figure 7—figure supplement 1.

– Simulations progress by filling in the cell areas based on the cell lineage diagrams, and cells and events are encoded for ready visualization when needed.

Simulation per se is carried out based on event patterns (Figure 7), and the area is not a factor for the simulation. Regarding the cell area, this can be affected by the height of the cells (volume). We therefore considered that this did not provide useful information for the simulation. The animation was created to visualize the results of the simulation, given that the cell-lineage map created from the simulation data was too crowded to evaluate. We have mentioned this in the sections “Survival of the progeny of multipolar cell division“ in the Results, P24, L550.

– Cells were considered to be the same size throughout[?].

As for cell area, cell size was not taken into account for the simulation.

– I am not sure how the lineages are extrapolated past the 4000 min experimental time.

We have described how the simulation was performed in the section related to the algorithm (P16, L363).

– Also I would explain the reason the simulation is so useful. Here is an example where it may seem so obvious to the authors it needs no mention. Yet sometimes it is better to be explicit. It can seem you are talking down but it is helpful!

Thank you for your suggestion. We have added a section in the Discussion to emphasize how the single-cell tracking and simulation might be used (P30, L693).

With this simulation approach, we test whether the simulation matches the experimental results, and also uncouple the combined effect of cell division, cell death and cell fusion on cell proliferation, which would be difficult to do in an experiment with live cells.

We developed the simulation algorithm to follow the fates of cells beyond the time possible in empirical studies. We subsequently realized that this could be used to study the fates of cells in a population with other types of cells. In the typical setting of cell biological studies, comparisons are often made between e.g. cancer and control cells. Although such studies can provide information on mechanistic differences, it is difficult to evaluate how such differences affect the fate of e.g. cancer cells in the mixed cell population. Simulation can thus be used to investigate the fates of cells in a mixed population with other types of cells. We made a note in “Limiting expansion of p53 RNAi cells in the presence of Control cells” in the Results (P24, L561).

3. Tumour cells without p53 can avoid cell death and proliferate. It is unclear how having less of a wild-type protein in a cell is different from having mutated forms within the cells.

With regard to cells carrying mutant p53, we are interested in investigating if such cells have a p53 null+phenotype conferred by mutated p53, or if mutated p53 overrides the null phenotype. We have mentioned this in the Discussion section (P29, L686), and would like to investigate it further using our techniques.

– That is, how does the function differ here compared to a mutation in p53?

As noted above, this is an interesting question to pursue, given that most cancer cells carrying p53 mutations involve missense mutations.

– How does reduction in p53 followed by inducing cell damage test the need for basal p53 as a unique pathway in cancer progression?

This is an interesting question. In order to study the effect of lowering p53 levels on the cellular response to damage induced by physiological levels of a damaging agent, the damage is often undetectable using existing assays. However, a higher dose of the damaging agent could cause the cells to adopt a more homogeneous status, e.g. by inducing cell death, which may be not be relevant to the process of cancer progression.

If we use physiological levels of the damaging agent, we also need a technique able to deal with the heterogeneity of the cells. On the other hand, if the status of the cells is homogenized by exposing cells to e.g. a lethal dose of damaging agent, an average-based assay, e.g. cell death assay, can be used, although the status would not reflect the status of the cells under physiological conditions.

A similar paradox also exists for the studies using p53-proficient cells.

– In addition, more justification of the choice of A549 cells chosen as the model is required, in light of the statement in the Introduction: Here, we investigated the effects of low levels of p53 on the behavior of cells using empirical single-cell tracking.

In addition to the fact that A549 cells are p53-proficient cells, we also used these cells because their growth pattern is relatively linear. Some cell types, e.g. MCF10a (non-transformed breast epithelial) cells, are highly motile, but such motility is reduced by attaching cells together (a kind of contact inhibition, but not like primary fibroblasts). This reduced motility initially occurs locally and then spreads to the entire population as the cell density increases. These would be interesting cells for modeling, but it would be necessary to characterize their cell behaviors. We therefore considered that A549 cells were easier to handle. We have mentioned this in “Culture of A549 cells” in the Results (P6, L118).

What is their endogenous expression of p53 in A549 compared to other p53 proficient cells?

In the early stages of this study, we searched for studies regarding endogenous levels of p53 in unstressed cells, but were unable to find any specific papers dealing with the low levels of p53 itself. Some studies showed used cells with low levels as controls compared with accumulated levels, but the focus of these studies was on the function of the accumulated p53. In order to investigate the relationship between endogenous levels of p53 and induced cellular events, it is necessary to establish a technique to quantify the levels of p53 (or other proteins or genes) in individual tracked cells, and, as noted above, no such technique is currently available. However, it is possible that a technique could be developed by combining single-cell tracking analysis with e.g. spatial transcriptomics. We have mentioned this in the Discussion (P30, L693).

How do these levels compare to normal cells, such as those derived from primary culture?

Please see the above response. In addition, in order to make meaningful comparisons between cells with different levels of p53, it will be necessary to develop a method combining single-cell tracking analysis with e.g. spatial transcriptomics. Concerning primary cells, Guo et al. (Cell 156, 649-662 (2014)) found that the efficiency of iPS cell formation was increased by silencing the low levels of p53 (ref 19), and we are certainly interested in extending our study to other cell types.

– How does inducing DNA damage test the function of low levels of p53 in unstressed cells?

This is related to Comment 53, and as noted above, it involves the paradox of detection of damage vs. the status of the cells. If unstressed cells are exposed to a DNA-damaging agent that can induce detectable levels of damage, it could cause the accumulation of p53. On the other hand, if unstressed cells are exposed to physiological levels of a DNA-damaging agent, it may be difficult to detect the damage. We therefore consider that it is difficult to address this question without resolving this paradox.

Wouldn't a better model be to compare different cell lines with different endogenous levels of p53 and see how they respond?

The inclusion of more different cell lines would introduce new contexts. We agree that this type of study would be interesting, but at least six cell lines may be needed to allow a meaningful statistical analysis, and if a new context was found, more cell lines would need to be analyzed. If the behaviors of cells in a cell population differ (e.g. MCF10a vs A549), it may be necessary to develop a new algorithm to take account of the differences. There are thus many interesting possibilities, but these would involve too much work to be tackled by our group alone. We would therefore by happy to share our methods with other groups interested in performing similar studies.

Or this could be used as a second method to back up the conclusions when you damage silenced cells, it seems that the model is not delineated precisely for studying low levels of p53 on cells. Rather the test is studying the effects of DNA damage on p53 null cells which has been done many times? It would be good to hear more about the rationale here, as it is not clear from reading the paper's arguments.

With regard to the silencing of low levels of p53, we believe that our study provides a conclusion. Although it would be possible to prepare a manuscript focusing on this aspect, we chose to include the responses of cells to DNA-damaging agents, given that p53 is often referred to in the context of DNA damage.

As mentioned by Dr. Colarusso, previous studies have compared the responses of p53-null and Control cells exposed to DNA-damaging agents. However, the characteristics of the cells change over time, and there is no guarantee that the observed difference reflects the presence or absence of p53. In addition, cell status can be affected by the dose of DNA-damaging agent, with high doses potentially killing any growing cells, while intercellular heterogeneity becomes an issue at lower doses. Many factors may thus affect comparisons among cell types, or among cells treated with different doses. We therefore limited our study to a single cell type and transient silencing to minimize the influence of such factors on the interpretation of the results. We have emphasized this point in “System to investigate the functional implications of maintaining low levels of p53 in unstressed cells” in the Results (P5, L88).

Detailed questions:

4. Why were the cells monitored at such a high density?

Although A549 cells are less motile than e.g. MCF10a cells, they still move around at low densities, when the cells are isolated from each other. In contrast, the cells are less motile at higher densities. Because we wanted to minimize motility, we carried out imaging at a density at which most cells were attached. We have mentioned this in the Results (P6, L118).

Was this choice governed by the biological question and/image analysis algorithm limitations, or some other reason(s)? (to follow the fate of individual cells by monitoring live cells, because the culture eventually became over-confluent).

From a technical point of view in relation to image segmentation and single-cell tracking, lowdensity cultured cells are easier to track than confluent ones. As noted above, we chose the conditions to reduce the motility of A549 cells.

5. Why were the concentrations of CO2 different in the incubator and experiment? Is it due to maintenance of pH, and if so, it would be good to mention this as not everyone monitors pH when carrying out long-term imaging?

Some textbooks recommend using a colorless medium for long-term live-cell imaging. However, this does not allow the pH of the medium to be monitored, and several groups have failed to maintain cell cultures in an environmental chamber for long periods, particularly using multiwell chambers. We therefore used 7.5% CO₂ to maintain the pH of the medium. We have mentioned this in the Methods (P34, L755).

6. The authors mention maintaining the integrity of the cell population in multiple sections, including the summary. How is integrity defined? Is it metabolic, genomic, structural?

We have removed the term “integrity”, because this over-interprets our model.

[Editors’ note: further revisions were suggested prior to acceptance, as described below.]

Main issues:

– l. 316-318. The authors suggest that P53 RNAi cells proliferate faster, but have more cell death. Can this not be quantified directly from the data, rather than in the indirect manner pursued here? For instance, one could measure the probability that a cell will divide again, if it doesn't undergo cell death. The prediction would be that this probability is higher for P53 RNAi cells compared to Control.

This comment is related to the in silico generation of cell lineages. In this analysis, we evaluated the impact of the occurrence of cell death on the cell population expansion rate of p53 RNAi cells.

Concerning the quantitation of the number of cell deaths in the Control and p53 RNAi cells, this can indeed be carried out by analyzing the cell-lineage database or from live-cell imaging videos, as shown in Figure 4 and Figure 4—figure supplement 1, and the results accordingly show more cell death in p53 RNAi cells compared with Control cells. We had mentioned this in the previous version of the manuscript.

The main issue we wished to address was the impact of cell death on the cell population expansion rate, given that frequent cell death would counteract the expansion of the cell population. Both Control and p53 RNAi cells showed similar rates of cell population expansion (Figure 2c and i), but there was more cell death in p53 RNAi cells (Figure 4). These data thus suggest that some other factor(s) is/are altered in p53 RNAi cells, resulting in similar cell expansion rates in p53 RNAi and Control cells. The important question is what other factor(s) was altered?

We think that considering the “probability” per se does not address this issue, while analysis of cell-lineage data may provide a clue. By examining cell-lineage maps, we noted that some of the p53 RNAi cell lineages had higher reproductive abilities than Control cells. Thus, the promotion of reproductive ability may counteract the increased cell death in p53 RNAi cells, resulting in a similar cell population curve to Control cells. However, examining the cell-lineage map cannot prove this, and we therefore developed the in silico approach to examine this hypothesis. To clarify this matter, we have revised the first paragraph of this section (L335-371).

“The authors suggest that P53 RNAi cells proliferate faster, but have more cell death.”:

Notably, we did not specifically say that p53 cells proliferated faster, but rather that their reproductive ability (the number of progeny produced from a progenitor) was increased by the silencing of p53.

– l. 391-396: This section is still unclear to me. Why not follow the same approach as shown in Figure 7c for time to MD? Is it because there is a correlation in cell cycle time between generations, i.e. a rapidly-dividing mother has rapidly dividing offspring? This should be explained more clearly.

Compared with bipolar cell division, multipolar cell division contributes less to determine the population size, given that most progeny produced by multipolar cell division undergo cell death. We have added an explanation in the related section (L467–470).

– l. 418-421. I now understand conceptually what the others do, but from the text and Figure 8 I don't understand how this works in practice. Do the authors linearly interpolate between two Operation data sets? If so, then write that down explicitly. Some things in the text here still make no sense to me. "A start event of 10 and 1", what does this refer to, what sort of event? "The chance of a cell population exposed" A chance of what? Is there some probabilistic process that underlies this?

This comment is related to the Dose simulation mode. We have added an example to explain how the calculation was made and have revised the related section to clarify our meaning (L488-498).

– l. 489-494. I am not sure I properly understand the origin of shorter doubling time. Is the problem that the cell cycle time is not drawn from a measured distribution (as in Figure 7b) and therefore misses rare but very long cell cycle times?

In the related section, we intended to explain the possible reasons for some differences between cell-doubling time data obtained by single-cell tracking and simulation.

First, the difference may be related to the method used to assign the length of time between events; i.e., selecting a time from histogram data. In this case, less frequently occurring time lengths may have less chance of being assigned.

Second, as Dr. Colarusso pointed out, if the restraining range is > ±10%, the simulation of average cell-doubling time would change.

Third, the simulation data represent the actual distribution of cell-doubling time, while the distribution determined by single-cell tracking is biased because of fewer data compared with the simulation (e.g., ~2,000 v.s. ~9,000,000).

However, given that the difference was constant among cells, we did not make any adjustment, though this could be done by adding a certain bias upon assigning a doubling time. We have included the above explanations in the revised manuscript (L567-573).

Typically, cell-doubling time distribution tails towards longer doubling times, implying that cells with longer doubling times are generated from those with a shorter doubling time. Notably, a balance between the proliferation of cells with shorter cell-doubling times and the generation of longer ones may be critical to maintaining cell populations. The simulation of this process warrants further studies to clarify how the cell population is maintained.

– l. 523-526. This seems a rather counterintuitive effect: removing the P53 stress response leads to higher cell proliferation when higher stress is applied. I do think it should be emphasized more that this is counterintuitive and perhaps also a possible explanation for this effect should be given.

We have revised the related sections (L606-608). We have tried to clarify the relationship indicating that Control cells show a stronger response to MNNG than p53 RNAi because of the p53 response.

With regard to the statement, “removing the P53 stress response leads to higher cell proliferation when higher stress”, we would like to make a clarification, as the statement contains some ambiguity.

p53-induced stress responses, in general, lead to suppression of proliferation of cells by the induction of damage (stress) response (Introduction); not cause higher proliferation. This occurs through the elevation of the level of p53 in cells.

When the low level of p53 found in the non-stressed cells is removed, the reproductive ability of cells is increased, but cell death is also induced (our finding).

– l 532-535. It is not clear what the simulations can add here. Is it not possible to use experimental data to measure this directly?

Experimental data can be used directly but is limited by the scale of the practical analysis. For example, in the case of dose-response curve determination using classical colony-formation assays for two cell types, 3 dishes/dose and 10 doses can be done with 60 dishes; however, it would become more difficult to carry out these assays for more doses or cell lines. This limit can be significantly expanded by employing the simulation approach.

After all, the simulations are driven by experimental data, so in principle, there cannot really be anything new from the simulations in that regard.

As noted above, there are limitations to using an experimental approach. Considering the experiment shown in Figure 10 (a, b, and d): using a conventional approach, the cell culture has to be maintained for ~25 days, the number of doses is 15, and the cells are counted every day for 25 days, thus requiring at least 2250 dishes (15 doses × 25 counting × 3 (triplicate) × 2 cell types). Based on our experience, this is not realistic. We therefore consider that the results shown in Figure 10a, b, and d would be difficult to produce without using simulation.

With regard to “anything new”, we would like to make a clarification.

As single-cell tracking has never been used to investigate the function of p53, we think that data generated by single-cell tracking is “new”.

Thus, simulation data per se is also “new” relative to other data published by others. Relative to single-cell tracking data, simulation data shown in Figure 10c could provide a more detailed dose-response curve. However, the data shown in Figure 10d cannot be generated by single-cell tracking because of the limitations of real experiments.

In the manuscript, we add a statement that “to determine a more detailed dose-response curve” (L592–594).

– l 535. "we assumed" I don't understand what the assumption is based on. Measurements in this paper? Existing biological knowledge?

We used the word “assume” (as explained below), but agree that this word may be misleading, and have changed it to “hypothesized” (L616) in the revised text.

Many studies of p53-mediated damage response use, for example, > 10 Gy of ionizing radiation, and the induced responses tend to be interpreted as related to p53. Although this dosage has been used because of a lack of sensitivity in many classical approaches, it is an extremely high dose that could kill most cells within a day. Indeed, ionizing radiation induces various types of damage, and cellular responses induced by radiation are also caused by non-p53-related mechanisms. However, such distinctions are often not made in many reports. Although this seemed obvious (hence the word “assume”), we appreciate that it cannot be considered as “Existing biological knowledge”.

– l. 550-551. The low frequency of multipolar division is put into the simulations directly from the experimental measurements. So why is this simulation result, which makes exactly the same conclusion, surprising or interesting?

We would consider that, in a sense, the result to be confirmatory, rather than surprising or interesting. The hypothesis that the growth of progeny of multipolar cell division causes cancer (aneuploidy) was proposed in 1914 by T. Boveri (English translated version; ref 37). Gene mutations (chemical carcinogenesis) have subsequently become a central dogma of cancer development while it has been common knowledge that cancer tissues contain a high level of aneuploidy cells. Although our current work is not related to the cause of cancer, our results confirm Boveri’s hypothesis, as mentioned in our previous version (L748-750). We think it is often important to “confirm” a hypothesis that has been put aside for so many years.

Our single-cell tracking analyses allowed us to detect the progeny of multipolar cell division that undergo bipolar cell division, but the data did not demonstrate that the progeny could form a population, in generic words, a cell colony (it is not possible to extend single-cell tracking beyond cell confluence). However, the simulation results suggest that the progeny could indeed form a cell population. We think it is important to confirm that such progeny could form a cell population.

We have emphasized this in the revised version (L638-643).

– l. 552. "growth of virtual cells" It is not explained in the main text how the spatial cell dynamics is implemented in the simulations. It is also not explained why space is even important and what novel insights it will bring to incorporate it.

In our previous responses, we mentioned that the animation was created to visually show cells of interest, rather than to analyze the spatial dynamics. Notably, we did not specifically say that we analyze spatial dynamics in our original and previous revised manuscript.

We evaluated the results generated by single-cell tracking by examining cell-lineage maps. However, the simulation generated cell-lineage data with many cells, which were difficult to evaluate by examining the cell-lineage maps. We therefore created the animation as a tool to allow us to find a cell of interest in the simulation data. This placed the progenitor within a 2D space and showed the proliferation of progeny by coloring the cells of interest. We did not use the animation to analyze cell dynamics in 2D, and we apologize for the expression we used if the reviewer misunderstood this. Similar comments were raised in the review of our original manuscript, and, in our previous version of manuscript, we have already responded accordingly.

Notably, however, our simulation algorithm has the potential to include simulating 2D dynamics, and we have discussed this in our previous revision (L801-803).

We have emphasized the purpose of the animations in the revised text (L638-643).

– l. 555-559. It is not clear why showing spatial expansion of MD progeny is important.

When distinct cells start making a population, they expand themselves in a space (e.g. generation of iPS cell colonies); thus, if a cell is expanding spatially, it is generally considered that a new cell population is being created. Similarly, expansion of the progeny produced by multipolar cell division implies the formation of a new cell population. We considered that it was important to show, using simulation, that a progeny derived from multipolar division could form a cell population, given that these progenies are generally considered to be fragile and may not be able to form a population. We have emphasized this in the revised text (L638-643).

Couldn't the same insights be gained from purely looking at images?

Of course, the same insights could be gained from images. However, the imaging data contain various types of information, and the aim of the study was to convert the imaging data into numeric values to characterize specific aspects of the cells, using image segmentation and cell-tracking algorithms. Thus although some ideas can be obtained by looking at images, publishable and analyzable data cannot be produced by simply “looking at images”.

This just means that you get clones of cells that are MD cell progeny, why is it important where they sit in space?

As noted above, the animation was created to visually show cells of interest, rather than to analyze the spatial dynamics.

– l. 578. What novel insight does this section bring?

We have revised the end of the paragraph to summarise the implications (L678-682). The implications of the analysis have been explained in the Discussion.

The stress-shift experiments show the same conclusion of P53 RNAi outcompeting Control cells as Figure 10.

We used a different simulation approach in this section from that used for Figure 10 (L665-666).

Also, what does the inclusion of space bring to Figure 13a? Would the results in Figure 13b-h be different if space was not included? If not, then I would remove the spatial analysis.

As noted above, the animation was created to visually show cells of interest, rather than to analyze the spatial dynamics.

– l. 636. "cancer tissue mass". I don't understand why this result is compared to cancer: most cells are Control (=wild-type?) cells with few P53- cells interspersed, and most of the growth is due to proliferation of Control cells, not P53- cells.

We have rephrased this sentence (L724-725). We have provided the number as a reference.

Reviewer #3:

Comment 1:

The experimental data and single-cell lineage analysis are important contributions to the field. Although the authors have included more detailed explanations, the additional insights offered by single cell tracking need to be described more clearly and emphasized throughout the text.

For example, when the authors move from reporting on the population level counting to the single cell tracking results (lines 197 -198), the authors should guide the reader by providing a transition between both approaches. Currently, the authors launch right from the population counting results to validation of single cell tracking without building up the need for single cell tracking.

To quote: We then compared the results obtained by cell counting with those obtained by computer-assisted single-cell tracking analysis to verify whether this analysis indeed yields results consistent with the classical counting method.

Before comparing the results, a transition highlighting the need for single-cell analysis is missing as well as the need for comparing both methods is needed. Suggestion: "Thus far, we have described how the different treatments affect cell numbers at the population level. We then analyzed the data sets using single cell tracking. This powerful approach can reveal how the events occurring at the individual cellular level contribute to what is observed at the population level."

Only then move on to the comparative results such as by stating: To test the accuracy and self-consistency between our standard cell counting and single cell tracking, we compared the results obtained with each approach.

Similarly, when the results obtained from single cell tracking add new information, additional context should be provided for the reader. This paper is cognitively challenging to read and interpret, and more explanation is needed to help the reader navigate and appreciate the significance of the results.

Comment 2:

Similar clear emphasis is needed when describing the simulation approaches and their significance. To illustrate: In the section introducing the cell-fate simulation algorithm (lines 363-372), confluency is mentioned as are "limitations of empirical approaches." Rather than stating confluency and the vague term "limitations," the justification needs to be clear from the start. My suggestion is move the explanation found later in the text to this introductory section.

For example, lines 440-442 state: "cell-fate simulation using Operation data allows the creation of various simulation options and provides flexibility for designing virtual experiments that would be difficult to perform empirically."

Rather than letting the reader wait for this statement, I recommend leading in with a similar statement (and dropping the technical reference to Operation data). Suggestion:" Cell-fate simulations are powerful and flexible tools help us model conditions that are not readily accessible by direct imaging, such as mixed cultures and mixed dosages. "

We appreciate these suggestions. We have included more emphasis on the advantage of using the simulation (L417–429), and have also made revisions based on the other issues raised.

Other comments:

3. Ensure that cell growth is used when referring to cell size not to cell division within the text. The term "grow" is used colloquially in the lab but here should be reserved for area/volume not cell division. For example, see how "growth" is used in Line 125. Here it is confusing as the passage is describing cell area decreasing and then grow is used to mean cell proliferation.

We have checked the manuscript and used the terms “proliferate” or “cell population expansion” accordingly.

4. What random number generator was used?

We generated the random numbers using the C++ rand () % value. We have mentioned this in the Materials and methods (L1032).

5. Figure 1—figure supplement 3. Y axis in last graph has the label "Variation" but the units are missing.

We have added the units (no. of cells).

6. When discussing Figure 5, explain how the results

highlight the need for single-cell tracking studies and how this approach complements and enriches the population level studies. Suggestion: "The cell numbers over time are roughly equivalent for both the scr siRNA and the p53 siRNA treated cells, as shown in Figures 2c and 2i. The single cell tracking data, however, reveal differences that are not directly accessible through standard cell counting. Figure 4 reveals that although the overall cell death is higher in the p53 siRNA cells, it is compensated by increased multipolar cell division. Further, the simulations can help unravel the relative rates of multi-polar cell division compared to cell death. As shown in Figure 5, we see that the relative proliferation curves can be simulated in the presence or absence of cell death. By analyzing the individual cellular fates under well-defined conditions, we can then simulate scenarios that are not accessible through our direct imaging, such as analyzing how a population of mixed cells and/or heterogenous treatments will evolve over time. "

We appreciate the suggestions and have used some of the suggested phrases. We have added some sentences to the section related to the in silico analysis to emphasize the points raised (L366–371).

7. Line 226. Quote: To this end, we sorted each cell lineage into groups (Figure 3a).

The division into groups introduces a layer of complexity and seems arbitrary considering the small number of possible bins. Why is reporting the binned data through groups better than reporting the numerical value?

This section is related to the analysis of the reproductive ability of cells comprising a cell population. Dr van Zon and Dr Chen pointed out (in their comments on the original version of our manuscript) that this section was difficult to follow. We extensively revised the section, and detected an error.

Regarding the error, we used two approaches to evaluate the reproductive ability of cells comprising a cell population; i.e., we determined the number of cells comprising a cell lineage, and the number of progeny found at a certain point in time. Both yielded similar results, but the former included cells that undergo; e.g., cell death. In our original version of the manuscript, we showed the data obtained using the former approach, and the same data was shown in the previous revision of our manuscript. However, when we added an explanation regarding how reproductive ability was analyzed, we used Figures for the latter approach (Figure 3a). We have corrected this error in the current version.

Regarding the “bin”, we combined, for example, cell lineages comprising 1 and 2 cells to generate the data, because the number of cells comprising a cell population tends to be an odd number (progenitor: 1, after the first division: 3, after the second division: 7 etc.), and odd numbers are thus more frequent than even numbers. A numerical graph would thus show ups and downs between consecutive numbers. We therefore “binned” the data. However, we agree that binning; e.g., 1–3, is subjective. We have therefore binned the odd and even numbers; e.g., cell lineages comprising 1 and 2, 3 and 4, etc., in the revised version. The results using this method were similar to the previous results, but some calculated numbers were changed (% of a cell in the total number of cells). We have revised the relevant paragraphs (L242–280), figure legend, and source data.

In the annotated pdf, the reviewer asked why we did not use an average. We considered that the average value would not provide useful information regarding the reproductive ability of cells comprising a cell population. The average would be obtained by first categorizing each cell lineage based on the number of cells comprising the lineage, and then calculating the total number of cells belonging to the category. For example, if 10 cell lineages were categorized as lineages comprising 5 cells, the numbers would be “Cell lineage: 10, total number of cells: 50”. In this case, the average (number of cells/category) would be 5 (same as the number of cells per lineage). However, we wanted to show how many cells were produced from a progenitor, and we therefore think that the total number of cells/category could better represent the reproductive ability of cells comprising a cell population.

8. Lines 282-286. Quote: …the number of cell death events in Control cells determined by counting was higher than that determined by single-cell tracking analysis. This was because the area of single-cell tracking was slightly outside the area where cell death frequently occurred (Figure 4—figure supplement 1c). However, given that such events do not occur with the same probability throughout the field of view, some variation may occur with both the counting and single-cell tracking approaches.

Was this because cells that die move more than cells that do not or is it something specific about the cell imaging chamber with death occurring near the edges more than the centre?

We took an image of cells located close to the center of the cell population, given that the behaviors of cells located at the periphery were different from those at the center. We have emphasized this in the revised Materials and methods (L838–840).

In this sentence, we intended to indicate that cellular events do not occur with uniform probability throughout the field of view, and this variation may thus affect the results obtained by counting and single-cell tracking. Based on our experience, such variation occurs regardless of the type of dish or chamber. For example, in simple colony-formation analysis, larger colonies sometimes appeared more frequently in a certain area of a dish. Although using a larger number of dishes would normalize the results, the required number of dishes may become too large, making the experiment unrealistic to perform. In the case of single-cell tracking, increasing the area of imaging and the number of tracked cells would thus make the analysis per se unrealistic to perform. One aim of the current work was thus to find a realistic experimental scale for single-cell tracking. In the section related to Figure 1—figure supplement 3f, we mentioned that tracking ~240 cell lineages was sufficient to generate reproducible single-cell tracking data based on the rate of cell population expansion. We also evaluated the frequencies of multipolar cell division and cell death, and, after taking this into account, we selected 335 cell lineages. We have revised the manuscript to clarify the points raised by the reviewer (L322–326).

9. I am confused by the reference to the "accuracy of a detecting a low frequency event." Quote: In general, the accuracy of detecting a low-frequency event is lower than that for frequently occurring events, e.g. bipolar cell division…

Are the authors referring to the probability of the event being captured by the imaging system rather than the detection of the event by their software and/or visual scorer? Or do they have evidence that the detection by the software and/or visual scorer is lower for these events compared to bipolar cell division?

The authors state in line 260 "We therefore determined if single-cell tracking could detect multipolar cell division, cell death, and cell fusion with adequate accuracy for statistical analysis. To this end, we determined the number of multipolar cell division and cell death events visually by manual counting in videos, and compared the results with those obtained using single-cell tracking analysis (Figure 4). Notably, cell fusion was not included in the counting analysis because it was difficult to detect without single-cell tracking."

Yet when review Figure 4, I am having trouble deciphering how the authors concluded that the single-cell tracking was accurate as the results are not directly compared to visual scoring. Please clarify.

We realize that “detecting” is not an appropriate word, because it gives the impression that bipolar and multipolar cell divisions were determined using a device. However, these divisions, as well as cell death, and cell fusion, were found by following each cell. We have revised this section accordingly (L287–297).

10. Lines 316-318: These results suggest that p53 silencing promoted the reproductive ability of p53 RNAi cells, but this was counteracted by the induction of cell death, resulting in the formation of p53 RNAi cell populations that were smaller than Control cell populations (Figure 2i).

I see a small dip in the p53 RNAi curve compared to the Control curve in Figure 2i, but otherwise they look similar. Please clarify.

Single-cell tracking data for p53 RNAi cells showed that the rate of cell population expansion was reduced at ~2,000 min, and the population size then caught up with the Control. We have revised the text to clarify this (L356-359).

11. Line 318 Analysis also shows that the effect of silencing the low levels of p53 cannot be detected without access to the spatiotemporal information on individual cells provided by single-cell tracking.

Although this statement is likely, the counter-example can not be ruled out. Just to list possible alternative approaches that could reveal similarly nuanced effects of silencing p53. One can imagine a scenario where the number of live and dead cells are measured over time, without any single cell tracking. Or it may be possible to model the number of cells over time using an analytical expression that embeds cell division (bipolar, multipolar) as an exponential and cell death (say as a linear function of time). Suggestion-qualify statement: "This analysis also demonstrates single cell tracking provides more nuanced and detailed information about the effects of silencing p53. Here the single cell analysis revealed clear differences in the rates of cell proliferation and cell death among the scr siRNA and p53 siRNA conditions, differences would be obscured and/or missed if limiting the analysis to cell counts at the population level."

We appreciate these suggestions and have revised the end of the section using some of the suggested phrases (L366–371).

12. Line 331: Following cell fusion, Control and p53 RNAi cells demonstrated 79.4% and 93.2% multipolar cell divisions.

Please define the % values-how are they calculated? Also the numbers are listed on the bar graphs in Figure 6- the relative percentages of listed over the bar graphs is confusing in light of the numbers being relative to another 100, the 100 cell lineages. Also it would be helpful to see the spread of the data points illustrated by the bar graph.

Patterns 1 and 2 (now 1a and 1b) make 100%, and the value given refers to Pattern 1a. We have revised the text (L374-393) and mentioned 100% in the figure.

Regarding the 100 cell lineages and 100%, we have changed the number of cell lineages to 50 to avoid confusion and have revised the Figure and Source data accordingly.

Concerning the data points, we did not include these in the figure. To perform the analysis, we first searched for multipolar cell divisions and traced the cells that underwent this division back to determine the prior event. Totals of 34 and 59 multipolar cell divisions were found in the Control and p53 RNAi cells, respectively, and were used to produce data. Because different numbers of divisions were used, we showed the data as %. We have included the raw data related to the analysis in a Source data file in the current version of the manuscript.

13. Staring on line 385, the authors state: The algorithm then reflected this distribution to choose the End event.

– How is the weighted random assignment implemented? Specify the method or methods and justify why the choice is appropriate.

We generated the histogram arrays (for bipolar cell division, multipolar cell division, and combined events; e.g., multipolar cell division followed by cell fusion) for the Start events. Each array contained information regarding the event that occurred following the Start event. The internal data format was e.g. 0:BD (bipolar division), 1:BD, 2:BD, 3:MD (multipolar division)…100:MD. A random value of 0–100 was created, and a value of e.g. 1 picks up BD (L442-452).

– Similarly, for LT and other random assignments, is the implementation always the same as for the Event assignment?

Yes. The selection method per se was the same as that for Event. The only difference was the array that was used for the assignment (L456–458).

– Is the additional +/- 10% in ET imposed for BP events based on experimental data obtained here and/or reported elsewhere or there some other reason for constraining the ET for BP events in this way?

We performed a repeated simulation to find the optimal restraining value. We have indicated this in the revised text (L463).

Further, could this constraint have led to the observation summarized in lines 489-494: On the other hand, the simulation tended to yield an average cell doubling time about 2 h shorter than that determined by single-cell tracking analysis. Given that the algorithm assigned a cell doubling time to each cell by generating a random number with Operation data-Time (Figure 7), a long cell doubling time, e.g. 3,000 min, which occurred less frequently, may be less likely to be assigned, resulting in the generation of a simulated cell population

Reviewer #2 also commented on this section. As suggested, the restraining range (±10%) could also affect the simulating average cell-doubling time.

In addition, the simulation data may also represent the actual distribution of cell-doubling time, while the distribution determined by single-cell tracking may be biased because of fewer data compared with the simulation.

We have noted these possibilities in the revised manuscript (L567-573).

– When CF occurs, do these events also reflect the frequency of sibling vs non-sibling under the different conditions studied?

No. This algorithm does not assign cell fusion between non-siblings. Assignment of cell fusion between non-siblings was not complicated, but could create a problem when displaying cell-lineage data. When cell fusion occurred between non-siblings of, for example, Lineages 1, 10, and 20, we displayed all cell lineages in one window. To do this, the display order of each lineage has to be determined, which requires complicated coding. Because a cell lineage generated by the simulation contained a large number of cells, arranging the display order of multiple cell lineages was extremely difficult. Furthermore, cell fusion between non-siblings occurred less frequently, and we therefore did not include the simulation of fusion between non-siblings. We have noted that the algorithm generates fusion between siblings, but not non-siblings, in the revised text (L1106-1107).

14. I have trouble understanding why calculating Recovery is important to the simulation and why it is listed before the other steps. Line 894 states: Recovery data was used to simulate the rate of recovery a cell population from the treatment of MNNG. When cells were treated with MNNG, the majority of cells may be killed. However, small number of cells gained reproductive ability, which could be found at the end of imaging.

I am confused here as I don't see evidence of the majority of cells being killed in the population expansion data and don't understand why they need to be tracked.

Lines 903-907: For example, if any of the progeny derived from a progenitor underwent bipolar cell division at last within 20% of the single-cell tracking period, e.g. 320 to 400 min when tracking was performed for 400 min, this cell lineage was counted as one upon the calculation of the percentage. Thus, if 10 such cell lineages were found out of a total of 300, the recovery percent was 3.3%.

I don't understand this statement-what does percentage refer to? Why is only BP considered and not MP, for example? Any why is calculating this value important to the simulations as illustrated in Figure 7, supplement 1c, Step 3?

After pulse treatment of cells with a drug (e.g., high dose), most cells may become static or die, but some cells can regain reproductive ability. However, if a cell regains reproductive ability close to the end of the tracking time, no information regarding its doubling time can be found. Recovery thus calculates how many cells undergo bipolar division during a certain length of time (e.g., 3,600–4,000 min (end of tracking time)), and the algorithm then generates cells that are destined to gain reproductive ability. The algorithm assigned > 80% of the length of tracking time to the cell (3,200 min in the case of 4,000 min of tracking). We determined 3,600–4,000 min and > 80% as the value resulting in exponential cell population expansion for cells treated with MNNG7.

We have provided additional explanations in the revised version. Because A549 cells undergo non-dividing status following MNNG treatment, “killed” was not a correct term in relation to these cells.

We have revised the section related to Recovery (L991-1006).

15. Line 918-920: To generate a simulation array for the Operation data-Event, the percentage of each event relative to the total number of cell divisions (total of bipolar cell division and multipolar cell division) was calculated.

As shown in Figure In Figure 7, supplement 1 c, in the "Event" sequence I don't understand why calculating the "% event of total cell division" is possible before the simulation arrays are created?

There was an error in this sentence. Simulation array was generated “from” rather than “for” Operation data. We have corrected this error (L1016).

16. Lines 931-933: the array was empty, the average time that bipolar cell division occurred was calculated and −25% to +25% of the time selected by random 933 number was assigned as LT, and bipolar cell division was then assigned to the cell.

Is this based on experimental data and/or another reason?

If the FirstEvent array was empty, −25% to +25% was assigned. FirstEvent array holds the length of time to an event that occurred in the progenitors, implying that if the array was empty, it contained no cell-lineage data. Thus, if arrays containing data were used, processes related to the −25% to +25% would not be carried out. This step was included to prevent a software crash due to the processing of an empty data array, and −25% to +25% thus does not have any specific meaning.

17. I appreciate the care and effort that went into detailing the algorithmic approach used for the simulations. The logical flow now is much clearer and moves away from being a "black box" to now being reproducible.

We appreciate your help.

Recommendations and questions:

– Figure 7 supplement 2. Recommend placing this before supplement 1 as it presents the overall logic.

We have changed the figure numbers following this suggestion (L430).

– In Figure 8, supplement 1a, (page 94). Change "Uze" to "Use" in Step 6.

We have corrected this typo.

– In Figure 7, supplement 1b (page 95), Step 3 defines the nBD but the description is confusing. Clarify the "last time point of cell tracking" – is this simply the LT associated with the event? Also what is the offset and what is its purpose?

We have revised Figure 7, supplement 2b (Recovery). nBD is the number of bipolar cell divisions that occurred within a certain length of time from the time end. The default value to calculate the length was 20%, but this could depend on the cell type. We have therefore removed the number.

– In Figure 7, supplement 2, there is a typo in "Select an e-vv-ent type"

We have corrected this typo.

18. Consider revising sub-headings to guide the reader. Revise to express purpose, result, significance etc. These could serve as signposts throughout the paper would improve the paper's accessibility.

We have revised some of the subheadings to summarize the main point of each section.

19. In future work, consider graphical representations that are not limited to colour as in "burgundy" plot as 8-11% of the male sex is R/G colour blind. Consider using different plots styles as well as colour. I am not asking the figures to be revised for this publication, but ask that the authors consider visually accessible graphics / figure in future publications.

We appreciate this suggestion.

20. Similarly, consider box plots rather than bar graphs for future work.

We greatly appreciate the provision of the annotated pdf. We have incorporated your suggestions/corrections in the revised manuscript.

https://doi.org/10.7554/eLife.72498.sa2

Article and author information

Author details

Ann Rancourt
1. Glycobiology and Bioimaging Laboratory of Research Center for Infectious Diseases and Research Centre of CHU de Québec, Quebec, Canada
2. Laboratory of DNA Damage Responses and Bioimaging, Research Centre of CHU de Québec, Quebec, Canada
Contribution
Data curation, Formal analysis, Validation, Investigation, Visualization, Methodology, Writing – original draft

Competing interests
No competing interests declared
Sachiko Sato
1. Glycobiology and Bioimaging Laboratory of Research Center for Infectious Diseases and Research Centre of CHU de Québec, Quebec, Canada
2. Faculty of Medicine, Laval University, Quebec, Canada
Contribution
Conceptualization, Supervision, Funding acquisition, Validation, Investigation, Visualization, Methodology, Writing – original draft, Project administration, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-5960-1703
Masahiko S Satoh
1. Laboratory of DNA Damage Responses and Bioimaging, Research Centre of CHU de Québec, Quebec, Canada
2. Faculty of Medicine, Laval University, Quebec, Canada
Contribution
Conceptualization, Resources, Data curation, Software, Formal analysis, Supervision, Funding acquisition, Validation, Investigation, Visualization, Methodology, Writing – original draft, Project administration, Writing – review and editing

For correspondence
masahiko.sato@crchudequebec.ulaval.ca

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-0461-2296

Funding

Canadian Institutes of Health Research (Operating grant)

Masahiko S Satoh
Sachiko Sato

Canada Foundation for Innovation (Equipment Grant)

Sachiko Sato

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank Dr. Amélie Fradet-Turcotte for critical reading of the manuscript. We like to acknowledge the Bioimaging Platform of Research Centre for Infectious Diseases, CHU de Québec Research Centre for the technical support of microscopes. This work was supported by the Canadian Foundation for Innovation and Canadian Institutes for Health Research.

Senior Editor

Aleksandra M Walczak, CNRS LPENS, France

Reviewing Editor

Chunling Yi, Georgetown University, United States

Reviewers

Jeroen S van Zon, AMOLF, Netherlands
Brian E Chen, McGill University, Canada
Pina Colarusso, University of Calgary, Canada

Version history

Preprint posted: May 10, 2018 (view preprint)
Received: July 27, 2021
Accepted: September 13, 2022
Accepted Manuscript published: September 20, 2022 (version 1)
Accepted Manuscript updated: September 20, 2022 (version 2)
Version of Record published: October 13, 2022 (version 3)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.