1. Genetics and Genomics

Nomograms of human hippocampal volume shifted by polygenic scores

  1. Mohammed Janahi  Is a corresponding author
  2. Leon Aksman
  3. Jonathan M Schott
  4. Younes Mokrab
  5. Andre Altmann
  6. On behalf of for the Alzheimer’s Disease Neuroimaging Initiative
  1. Centre for Medical Image Computing (CMIC), Department of Medical Physics and Biomedical Engineering, University College London, United Kingdom
  2. Medical and Population Genomics Lab, Human Genetics Department, Research Branch, Sidra Medicine, Qatar
  3. Stevens Neuroimaging and Informatics Institute, Keck School of Medicine, University of Southern California, United States
  4. Dementia Research Centre (DRC), Queen Square Institute of Neurology, University College London, United Kingdom
  5. Department of Genetic Medicine, Weill Cornell Medicine-Qatar, Qatar
https://doi.org/10.7554/eLife.78232
Share this article
Cite this article
  1. Mohammed Janahi
  2. Leon Aksman
  3. Jonathan M Schott
  4. Younes Mokrab
  5. Andre Altmann
  6. On behalf of for the Alzheimer’s Disease Neuroimaging Initiative
(2022)
Nomograms of human hippocampal volume shifted by polygenic scores
eLife 11:e78232.
https://doi.org/10.7554/eLife.78232
  2. Download BibTeX
  3. Download .RIS

Abstract

Nomograms are important clinical tools applied widely in both developing and aging populations. They are generally constructed as normative models identifying cases as outliers to a distribution of healthy controls. Currently used normative models do not account for genetic heterogeneity. Hippocampal volume (HV) is a key endophenotype for many brain disorders. Here, we examine the impact of genetic adjustment on HV nomograms and the translational ability to detect dementia patients. Using imaging data from 35,686 healthy subjects aged 44–82 from the UK Biobank (UKB), we built HV nomograms using Gaussian process regression (GPR), which – compared to a previous method – extended the application age by 20 years, including dementia critical age ranges. Using HV polygenic scores (HV-PGS), we built genetically adjusted nomograms from participants stratified into the top and bottom 30% of HV-PGS. This shifted the nomograms in the expected directions by ~100 mm3 (2.3% of the average HV), which equates to 3 years of normal aging for a person aged ~65. Clinical impact of genetically adjusted nomograms was investigated by comparing 818 subjects from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database diagnosed as either cognitively normal (CN), having mild cognitive impairment (MCI) or Alzheimer’s disease (AD) patients. While no significant change in the survival analysis was found for MCI-to-AD conversion, an average of 68% relative decrease was found in intra-diagnostic-group variance, highlighting the importance of genetic adjustment in untangling phenotypic heterogeneity.

Editor's evaluation

This manuscript considers whether genetic information can improve the clinical utility of population norms derived from brain imaging data. The authors propose to incorporate polygenic scores into normative models of hippocampal volume to improve predictions of neurodegenerative disease. This approach is elegantly demonstrated in this manuscript and may be useful for clinical translation of population neuroimaging.

https://doi.org/10.7554/eLife.78232.sa0

Introduction

Brain imaging genetics is a rapidly evolving area of neuroscience combining imaging, genetic, and clinical data to gain insight into normal and diseased brain morphology and function (Shen and Thompson, 2020). Normative modelling is an emerging method in neuroscience, aiming to identify cases as outliers to a distribution of healthy controls and was shown to have potential to improve early diagnosis, progression models, and risk assessment (Marquand et al., 2016; Pinaya et al., 2020; Wolfers et al., 2020; Ziegler et al., 2014). Where conventional case-control studies generally require both cases and controls to be well clustered, normative models work well even when cases are not clustered or overlap with controls. Nomograms are a common implementation of normative models and have been used as growth charts of brain volumes across age in both developing and aging populations (Castellanos et al., 2002; Scahill et al., 2003; Peterson et al., 2018).

Normative modelling identifies cases by their deviation from normality, however, genetics shapes what is ‘normal’. Heritability studies have found that whole brain volume is 90 ± 4.8 heritable (Lukies et al., 2017), hippocampal volume (HV) is 75 ± 5 (Kremen et al., 2010; Thompson et al., 2020; Hibar et al., 2015), and other cortical brain areas between 34% and 80% (Rentería et al., 2014; Zhao et al., 2019). Genome-wide association studies (GWASs) have identified genome-wide significant variants that explain 13 ± 1.5 of the variation in HV (Hibar et al., 2017), 34 ± 3 in total cortical surface area, and 26±2% in average cortical thickness (Grasby et al., 2020). The gap between estimates from GWAS hits and formal heritability estimates (termed the ‘missing heritability’) (Manolio et al., 2009) implies that less significant variants also have an influence and that it may be captured through polygenic scores (PGSs) (Foo et al., 2021; Axelrud et al., 2018; Escott-Price et al., 2015). In this work we demonstrate the impact of accounting for polygenic effects in normative modelling of HV.

Damage to the hippocampus which is integral to memory processes (Bird and Burgess, 2008) has been associated with major depressive disorder (Bremner et al., 2000), schizophrenia (Nelson et al., 1998), epilepsy (Whelan et al., 2018), and Alzheimer’s disease (AD) (Pini et al., 2016). AD is a global health burden: 7% of people over 60 are diagnosed with dementia (van der Flier and Scheltens, 2005) of which AD accounts for 70% (Rabinovici, 2019). The pathophysiological processes underlying AD, namely amyloid and tau pathology accumulation, are thought to precede brain atrophy, which typically starts in the hippocampus and medial temporal lobe and then spreads throughout the neocortex (Rabinovici, 2019).

The normal variation of HV is of great clinical interest as the early and often prominent hippocampal atrophy seen in AD creates a need for early diagnosis and disease tracking. Many studies have examined HV across age (Schmidt et al., 2018; Fraser et al., 2015), for example, a recent study by Nobis et al., 2019, produced HV nomograms from UK biobank (UKB) for use in clinical settings. It is important to note that some of the variation in the normative models can be explained by the clear impact of genetics on HV (Hibar et al., 2017; Mather et al., 2015). Thus far, the few attempts at including genetics in the construction of HV nomograms have focussed on disease-related variants. For instance, two recent studies examined the impact of the AD-associated APOE gene (Ching et al., 2020; Veldsman et al., 2021), showing that APOE4/4 carriers had significantly lower HV trajectories. This effect is likely driven by AD-related disease processes since APOE4/4 carriers have a 10-fold risk of developing AD (Kim et al., 2009; Liu et al., 2013). However, the genetic impact on variation in HV in healthy population remains underexamined in the context of nomograms. In this work, we close this gap. We built HV nomograms using a GPR method (Figure 1A). We then computed a PGS of HV for subjects in our cohort and built genetically adjusted nomograms (Figure 1B). We found that genetic adjustment did in fact shift the nomograms and that, because the model requires no smoothing, our GPR nomograms provided an extended age range compared to previous methods.

Figure 1
Download asset Open asset
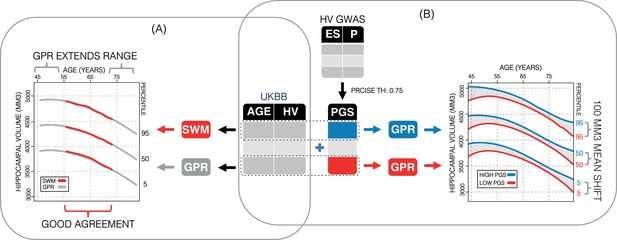
Study overview.

(A) Using 35,686 subjects from the UK Biobank, we generate nomograms using two methods: a previously reported sliding window method (SWM) and Gaussian process regression (GPR). We find that GPR is more data efficient than the SWM and can extend the nomogram into dementia critical age ranges. (B) Using a previously reported genome-wide association study, we generate polygenic scores (PGSs) for the subjects in our UK Biobank table. We then stratify the table by PGS and generate nomograms for the top and bottom 30% of samples separately. We find the genetic adjustment differentiates the nomograms by an average of 100 mm3, which is equivalent to about 3 years of normal aging for a 65-year-old.

Results

In the UKB sample, 453 subjects were excluded for various conditions, 3497 for genetic ancestry, and 28 subjects were outliers: leaving a total of 35,686 subjects. In the Alzheimer’s Disease Neuroimaging Initiative (ADNI) application dataset, 26 subjects were excluded for genetic ancestry, and 314 based on HV quality scores: leaving 818 subjects.

SWA vs. GPR for nomogram estimation

Nomograms of healthy subjects generated using the sliding window approach (SWA) and GPR method displayed similar trends (Figure 2; Figure 2—figure supplement 2). However, GPR nomograms spanned the entire training dataset age range (45–82 years) compared to the SWA (52–72 years). This is primarily because the SWA is a non-model-based approach that requires smoothing to avoid edge effects, and a Gaussian smoothing window of width 20 was used (Nobis et al., 2019). This extension allowed 86% of all diagnostic groups from the ADNI to be evaluated vs. 56% in the SWA nomograms (Figure 2; Figure 2—figure supplement 2). Furthermore, our GPR nomograms confirmed previously reported trends: Overall, the average 50th percentile in male nomograms (4162 ± 222) was higher than the female nomograms (3883 ± 170), and within each sex, right HV was larger than left HV (Figure 2; Figure 2—figure supplement 2). We also observed that along the 50th percentile, male HV declined faster (−20.3mm3/year) than female HV (−14.6mm3/year). Additionally, in GPR nomograms, HV peaks in women at age 53.5 years with a less pronounced peak in males at 50 years (Figure 2; Figure 2—figure supplement 2). Training the GPR model with 16,000 samples took ~1 hr on a consumer grade machine (2.3 GHz 8-Core Intel Core i9).

Figure 2 with 4 supplements see all
Download asset Open asset
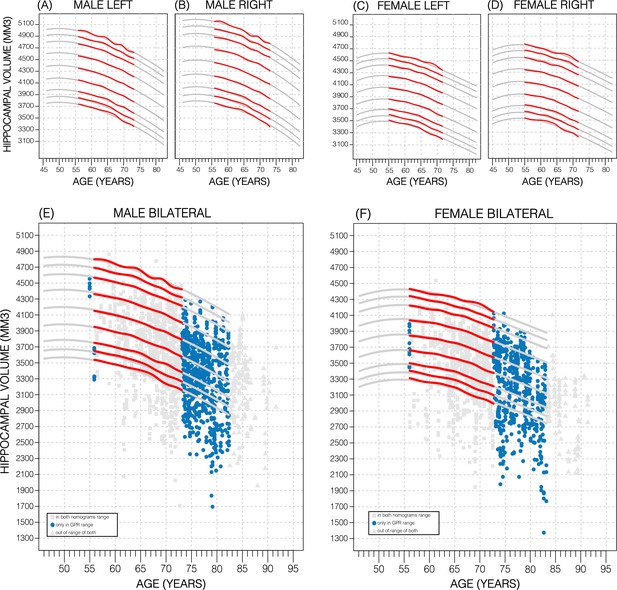
Comparing nomogram generation methods.

Nomograms produced from healthy UK Biobank (UKB) subjects using the sliding window approach (SWA) (red lines) and Gaussian process regression (GPR) method (grey lines) show similar trends. Both left hemisphere nomograms (A, C) are lower than their right counterparts (B, D). Male nomograms are higher than female nomograms (A vs. C) and (B vs. D). Female hippocampal volume (HV) shows a peak at 53.5 years of age, while male HV shows a less prominent peak at 50 years of age. SWA and GPR show good agreement, while GPR enables a 10-year nomogram extension in either direction. The benefits of this extension can be seen with scatter plots of Alzheimer’s Disease Neuroimaging Initiative (ADNI) subjects of all diagnoses overlayed (E, F). The extended age range of the GPR nomograms (45–82 years) enables the evaluation of an additional 43% of male data (E) and 34% of female data (F) (turquoise circles). A similar figure with only the cognitively normal ADNI subjects can be found in Figure 2—figure supplement 2.

PGS for HV

The calculated PGS, based on an earlier GWAS for average bilateral HV (Hibar et al., 2017), as expected, showed a strong correlation with HV in the UKB data. Overall, the PGSs showed a significant positive correlation with HV across all p-value thresholds and training sample subsets (p<2.7E-24; Table 1). PGSs explained more variance in males vs. females. Furthermore, PGSs did not show detectable differences in left vs. right HV; and explained the most variance in mean bilateral HV (Table 1, Figure 3—source data 1). In all tested settings, the explained variance (R2) by the PGS across p-value threshold was similar: with one peak at the 1E-7 threshold (capturing few but very significant SNPs), a higher peak at the 0.75 threshold (capturing many SNPs with mostly small effect sizes) (Figure 3). For the ADNI dataset, this distribution increased with the threshold. When investigating mean HV across percentile of PGS at the 0.75 threshold (highest R2), the top and bottom 20% of scores accounted for 41% of the variance in HV (Figure 3) with similar values observed across thresholds in both datasets (Figure 3—figure supplements 1 and 2).

Figure 3 with 2 supplements see all
Download asset Open asset
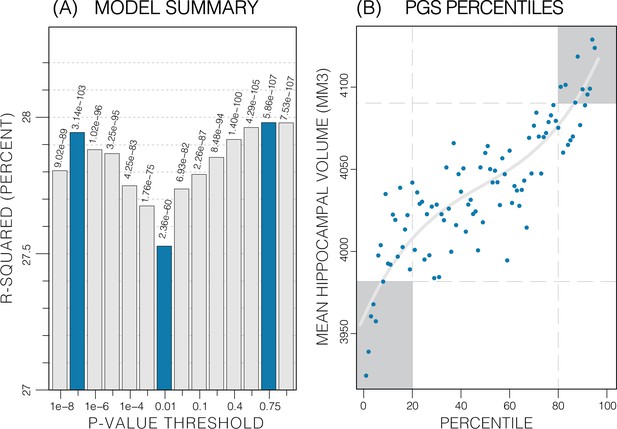
Summary of polygenic score (PGS) models.

Polygenic risk score in models of mean hippocampal volume (HV) across both sexes. (A) R2 of linear models across increasing p-value thresholds. All models are of bilateral HV and account for age, sex, and top 10 genetic principal components. The minimum R2 on the y-scale is the R2 of the models without any PGS. (B) Distribution of mean HV across percentiles of PGS. Excluding the top and bottom 20% of percentiles reduces the variance by 49% (darker grey areas). Fitting a cubic polynomial to the means produces the grey line.

Figure 3—source data 1

Summary of PGS vs HV regression models.

https://cdn.elifesciences.org/articles/78232/elife-78232-fig3-data1-v2.xlsx
Table 1
Association between polygenic scores (PGSs) and hippocampal volume (HV).

Linear models were built for HV (left; right; bilateral) using PGS across cohorts (male; female; both) at three representative p-value thresholds (1E-7; 0.01; 1). p-Values of the slope were significant across all categories, with the lowest being associated with the threshold value of 1 in all but a single case (both/right). Variance explained (R2) increased from left to right to bilateral volumes and increased from female to male to both.

GenderPGS thresholdLEFTRIGHTBILATERAL
Slope(×10–2)p-ValueR2Slope(×10–2)p-ValueR2Slope(×10–2)p-ValueR2
FEMALE1E-7101.8E-4613%9.42.4E-4514%111.4E-5115%
0.018.22.7E-2613%7.61.0E-2713%8.73.2E-3014%
1119.4E-5413%9.621.5E-4814%111.6E-5715%
MALE1E-78.21.4E-3518%7.52.6E-3518%9.24.1E-4020%
0.017.83.8E-2918%6.83.8E-2718%8.67.8E-3220%
19.43.2E-4818%8.04.7E-4318%109.1E-5220%
BOTH1E-78.48.1E-9025%7.96.4E-9326%9.33.1E-10328%
0.017.49.3E-5424%6.73.3E-5326%82.3E-6028%
19.62.1E-9925%8.31.8E-8926%107.5E-10728%

  1. Slope = beta coefficient for PGS in the linear mode; p-value for the slope; R2=variance explained by the linear model.

Genetics stratified nomograms

We will focus on the p-value threshold of 0.75 as it achieved best or close to best performance overall (Figure 3—source data 1). Genetics had a clear effect on the nomograms: the high PGS nomograms were shifted upwards while the low-PGS nomograms were shifted downwards; an effect which could be observed at both the model and data level (Figure 4; Figure 4—figure supplement 3), both by around 1.2% of the average HV (50 mm3). Thus, the difference between high and low PGS nomograms was ~2.3% of the average HV (100 mm3). An ANOVA test of the percentiles produced with the adjusted vs. unadjusted nomograms revealed that the groups were significantly different to each other (F>19; p<8.04E-6; Table 2). The HV peak previously observed at 50 years in males was less pronounced in the high PGS nomogram and more so in the low PGS nomogram (Figure 4, Figure 4—figure supplement 1). Adjusting nomograms using ICV and AD PGSs, instead of HV PGS, did not result in nomograms that were meaningfully different from the non-adjusted nomograms (Figure 4—figure supplement 2).

Figure 4 with 3 supplements see all
Download asset Open asset
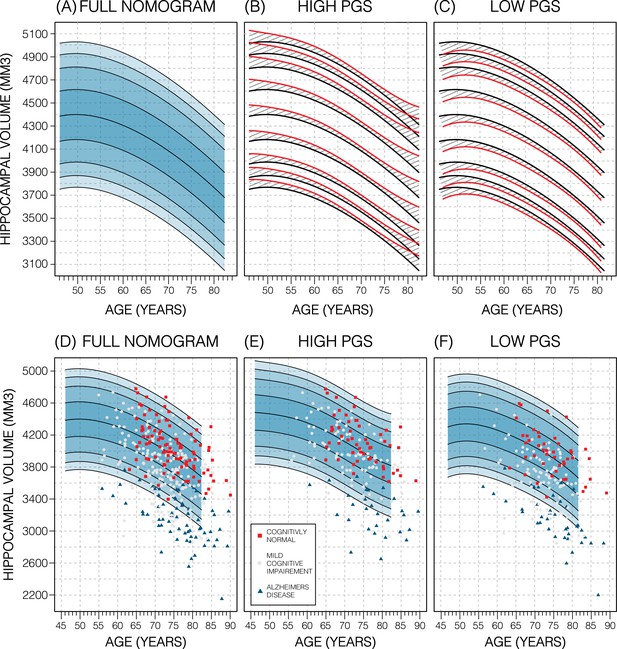
Genetically adjusted nomograms.

Results of genetic adjustment in bilateral male hippocampal volume (HV). (A, D) Nomograms of bilateral HV generated from all male UK Biobank (UKB) samples overlayed with male Alzheimer’s Disease Neuroimaging Initiative (ADNI) samples. Cognitively normal (CN) samples (red squares) centre around the 50th percentile, Alzheimer’s disease (AD) samples (turquoise triangles) lie mostly below the 2.5th percentile, and mild cognitive impairment (MCI) samples (grey circles) span both regions. (B, E) Nomograms generated using only high polygenic score (PGS) samples (top 30%) was shifted upwards (red lines) compared to the original (black lines) by an average of 50 mm3 (1.2% of mean HV). Plotting the high PGS ADNI samples (top 50%) slightly improves intra-group variance. (C, F) Similar results are seen in low PGS samples. Note, the black lines in panels (B, C) are the same as the nomogram in panel (A) and similarly the red lines in panel (B, C) are same as the nomogram in panels (E, F).

Table 2
Results of ANOVA tests of UK Biobank (UKB) hippocampal volume (HV) percentiles produced with genetically adjusted and unadjusted nomograms.
SEXSTRATADFSUM SQF-VALUEp-VALUE
MENHIGH118,78622.841.8E-06
LOW116,40719.968.04E-06
WOMENHIGH127,06832.929.97E-09
LOW130,10336.941.28E-09

External evaluation on ADNI data

In the ADNI dataset we investigated whether the shift in genetically adjusted nomograms could be leveraged for improved diagnosis. Using the non-adjusted nomogram, cognitively normal (CN) participants (n=225) had a median bilateral HV percentile of 61% (±25% SD), mild cognitive impairment (MCI) participants (n=391) had 25% (±26% SD), and AD participants (n=121) had 1% (±9% SD) (Figure 5). Visual inspection revealed that while CN participants were spread across the quantiles, AD participants lay mostly below the 2.5% quantile, and MCI participants spanned the range of both CN and AD participants (Figure 4). Bisecting the samples by PGS showed that high PGS CN samples had median percentiles of 65% (±27% SD) and low PGS had 54% (±26% SD). When comparing the same samples against the genetically adjusted nomograms instead, high PGS CN samples had 60% (±26% SD) and low PGS had 59% (±26% SD). Thus, reducing the gap between high and low PGS CN participants by 9% (from 10% to 1%, a 90% relative reduction). Similar analysis showed a reduction in MCI participants by 10% (60% relative reduction), and 0.5% (56% relative reduction) in AD participants. The above effects persisted across most strata (i.e., sex and hemisphere) (Figure 5; Figure 5—source data 1).

Figure 5
Download asset Open asset
Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset percentiles in genetically adjusted/non-adjusted nomograms.

Plotting the percentile distribution of the different diagnostic groups across adjusted and non-adjusted nomograms reveals that genetic adjustment increases group cohesiveness. (A) The percentile distributions of the different diagnostic groups against the non-adjusted nomograms. (B) In cognitively normal (CN) samples for example, when plotting against the non-adjusted nomogram (left adjoined boxplots), the median percentile of the top 30% of samples (darker turquoise) was 65%, while the median for the lower 30% of samples (lighter turquoise) was 54%. When using the genetically adjusted nomogram instead (right adjoined boxplots), those median percentiles become 60% and 59% respectively, a 90% relative reduction. Similar results can be seen with mild cognitive impairment (MCI) (C) and Alzheimer’s disease (AD) (D) samples, with 60% and 56% relative reduction, respectively.

Figure 5—source data 1

Summary of average percentiles across ADNI strata and UKB nomograms.

https://cdn.elifesciences.org/articles/78232/elife-78232-fig5-data1-v2.xlsx

Longitudinal evaluation

We also investigated whether genetically adjusted nomograms provided additional accuracy in distinguishing stable (n=299) from MCI-to-AD progressing subjects (n=83). With the non-adjusted nomogram, progressing MCI participants had a mean HV percentile of 11% and stable participants had 29% (Figure 6). Using the genetically adjusted nomograms, they had 10% and 28%, respectively. Cox proportional hazards models of percentiles obtained using both nomograms revealed little difference between the two in terms of clinical conversion: both models resulted in a hazard ratio of 0.97 for percentile in nomogram (beta of –0.03 at p-value<4.87E-08); confirming that participants within lower HV percentiles where more likely to convert earlier.

Figure 6
Download asset Open asset
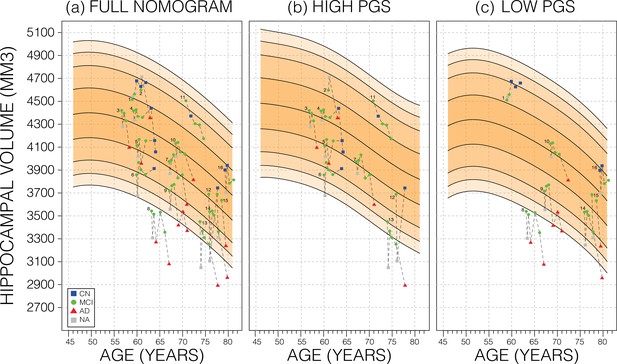
Longitudinal analysis.

A selection of mild cognitive impairment (MCI) samples longitudinal data plotted against nomograms of male mean hippocampal volume (HV). (a) All selected samples plotted against a non-adjusted nomogram. Lines connect visits of the same sample with diagnosis at each visit shown: cognitively normal (CN) as blue squares; MCI as green dots, Alzheimer’s disease (AD) as red triangles, and no diagnosis (NA) as grey squares. (b) Samples from (a) with high polygenic scores (PGS) plotted against a nomogram generated from high PGS CN samples in UK Biobank (UKB). (c) Equivalent result for low PGS samples from (a). For all sub-figures, the black lines – from top to bottom – represent the 2.5%, 5%, 10%, 25%, 50%, 75%, 90%, 95%, and 97.5% quantiles, respectively.

Discussion

We hypothesized that inclusion of genetic information associated with regional brain volume may substantially affect normative models. Indeed, the PGS for HV was significantly positively correlated with estimated HV from magnetic resonance imaging (MRI); translating into a shift of around 100 mm3 in nomograms based on PGS stratification (high vs. low PGS). Importantly, this magnitude corresponds to ~3 years’ worth of HV loss during normal aging for a 65-year-old. While previous studies have examined the impact of disease-associated variants, such as APOE status, on HV (Ching et al., 2020; Veldsman et al., 2021), our study relied on genetic variants influencing HV in healthy subjects. This is an important difference: the APOE genotype is associated with present or future AD status rather than having a direct influence on HV in healthy populations. Indeed, GWASs of the hippocampus that exclude dementia patients find little influence of AD-associated SNPs (Hibar et al., 2017). By design, nomograms are intended to model healthy progression and to simplify spotting disease-related outliers. Therefore, in theory, accounting for the genetics of healthy variation in HV should enable earlier detection of AD-related HV decline aging individuals. Conversely, stratifying by APOE-e4 status when creating HV nomograms charts the different HV trajectories among APOE genotypes, however, at the same time masks the pathological decline and thus will theoretically decrease the sensitivity to HV decline.

Subjects with extreme PGS account for significant amounts of the variance as indicated by the S-shape in the quantile plots (e.g., Figure 3). This has been observed in other PGS-trait combinations (Axelrud et al., 2018; Escott-Price et al., 2015; Ranlund et al., 2018). Furthermore, we found similar R2 values across all PGSs (±0.05 R2) with two peaks at thresholds of 1E-7 and 0.75. This reflects two types of genetic effects: the first is that few SNPs account for a substantial portion of the total variance in HV because of their high effect size (oligogenic effect) and the second is the combined effect of all common genetic variants on HV (polygenic effect). This type of effect has been reported in other studies of dementia (Bis et al., 2012).

In addition to demonstrating the clear effect of genetics on normative models, we have shown GPR to be effective for estimating nomograms. Using a model-based method allows us to generate accurate nomograms across the entire age range of the dataset. In fact, our GPR model can potentially be extended a few years beyond those limits (Figure 2—figure supplement 1). In comparison, the SWA nomograms age range is reduced by 20 years compared to the range of the training because of the required smoothing. Thus, compared to the SWA, we extended the age range forwards by 10 years, bringing it out to 82 years of age, which is relevant for AD where most patients display symptoms at around age 65–75 (Rabinovici, 2019; Mendez, 2017). While some methods like LOESS regression can be used to mitigate this need (Bethlehem et al., 2020), the GPR’s model-based approach does not need smoothing to begin with. However, there is a possibility that our results suffer from edge effects. For example, we suspect that the peak noted in the male nomogram is likely due to under-sampling in the younger participants. We found that building nomograms is data efficient: with the SWA, using around 17% (3000 samples) of training samples generated nomograms that were on average only 0.4% of average HV (19 mm3) different to those generated by the full training set. GPR nomograms achieved the same level of accuracy with only 5% (900 samples) of the dataset (Figure 2—figure supplement 3).

Using PGS improves the normative modelling in an independent dataset. In ADNI genetic adjustment reduced the percentile gap between similarly diagnosed subjects with genetically predicted high and low HV. The impact of the PGS adjusted model on CN samples was greater than on MCI or AD samples. Genetic adjustment centred the CN samples closer to the 50th percentile. As the effect of building separate nomograms was to mitigate the impact of genetic variability on HV it was not surprising that this effect did not carry over to MCI and AD subjects, likely because the pathological effect of AD on HV (~804 mm3 or 6.4% volume loss) far exceeds the shift in nomograms achieved with genetic adjustment (~100 mm3 or 0.8% of mean HV). Other studies have found that annual HV loss in CN subjects was between 0.38% and 1.73% (Scahill et al., 2003; Leong et al., 2017; Jack et al., 2000; Mori et al., 2002; Risacher et al., 2010). Using the nomograms from our work, genetic adjustment corresponds to ~3 years of normal aging for a 65-year-old. However, despite this sizable effect, genetically adjusted nomograms did not provide additional insight into distinguishing MCI subjects that remained stable or converted to AD. Nonetheless, the added precision may prove more useful in early detection of deviation among CN subjects, for instance in detecting subtle HV loss in individuals with presymptomatic neurodegeneration.

While this study has shown the significant impact of PGSs on HV nomograms, we have identified areas for improvement. Integrating the PGSs into the GP models would remove the need for stratification and allow for more adjustment precision, however, PGSs are prone to ‘site’ effects depending on the method and quality of genotyping and imputation. Consequently, using the ‘raw’ PGSs in predictive models presents its own challenges. Also, the PGSs used in this study were based on a GWAS of average bilateral HV in both male and female participants. Previous studies have shown a significant difference between these groups (Nobis et al., 2019), and nomograms estimated for these separate groups are distinct (Schmidt et al., 2018; Khlif et al., 2019; Pardoe et al., 2009; Figure 2). Therefore, using separate GWASs for each of these strata would potentially give the PGSs more accuracy. A second limitation of this study is the reliability of HV estimates. There is a significant difference between manual and automated segmentation of the hippocampus (Schmidt et al., 2018; Khlif et al., 2019; Pardoe et al., 2009) more so than other brain regions (Keller et al., 2012; Buser et al., 2020), and FreeSurfer is known to consistently overestimate HV (Perlaki et al., 2017). Therefore, other brain regions with higher SNP heritability like the cerebellum or whole brain volume (Zhao et al., 2019) may show more sensitivity on nomograms. Moreover, a recent study of PGS uncertainty revealed large variance in PGS estimates (Ding et al., 2020), which may undermine PGS-based stratification; hence a more sophisticated method of building PGS or stratification may improve results further. Finally, while NeuroCombat has been shown to remove most site effects, some may remain and still need to be adjusted for (Stamoulou et al., 2021).

In conclusion, our study demonstrated that PGS for HV was significantly positively correlated with HV, translating into a shift in the nomograms corresponding to ~3 years’ worth of normal aging HV loss for a 65-year-old. We have additionally shown that this effect can be observed in an independent dataset. And while more work in this direction is needed, successful integration of polygenic effects on multiple brain regions may help improve the sensitivity to detect early disease processes.

Materials and methods

Datasets

Request a detailed protocol

Data from a total of 39,664 subjects (18,718 female) aged 44–82 were obtained from the UKB (application number 65299) with available genotyping and imaging data. Imaging and genetic protocols are described in Bycroft et al., 2018, and Miller et al., 2016, respectively. Briefly, for this analysis we used HV estimated with FreeSurfer (Fischl, 2012) at the initial imaging visit. The dataset preparation followed the process described by Nobis et al., 2019. To ensure nomograms represent the spectrum of healthy aging, subjects were excluded based on history of neurological or psychiatric disorders, head trauma, substance abuse, or cardiovascular disorders. Furthermore, to control for population-level genetic heterogeneity, only subjects with ‘British’ ethnic backgrounds were considered. The dataset was then stratified by self-reported sex. HV outliers were excluded using mean absolute deviation with a threshold of 5.0. Subjects’ intracranial volume (ICV) was derived by using the volumetric scaling from T1 head image to standard space. Finally, ICV and scan date were linearly regressed out of the HVs.

For an application dataset, we used the ADNI database (http://adni.loni.usc.edu/) (Petersen et al., 2010). The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W Weiner, MD. The primary goal of ADNI has been to test whether serial MRI, positron emission tomography, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. A total of 1001 ADNI subjects (445 male) aged 55–95 were included in this analysis. Imaging and genetic protocols are described by Saykin et al., 2010, and by Jack et al., 2008, respectively. Briefly, we obtained HVs estimated with FreeSurfer v5.1. Subjects were excluded based on HV quality scores and based on genetic ancestry (i.e., restricted to self-reported white non-Hispanic ancestry). As with UKB, estimated volumes were stratified by sex, and ICV and scan date were regressed out of HV estimates. Finally, we used NeuroCombat (Fortin et al., 2018) to adjust across ADNI sites and harmonize the volumes with the UKB dataset. To do this we modelled 58 batches (UKB data as one batch and 57 ADNI sites as separate batches) and added ICV, sex, and diagnosis (assigning all UKB as healthy and using the diagnosis columns in ADNI) to retain biological variation. Demographics were obtained from the ADNIMERGE table (date accessed: 19 June 2020). Furthermore, we used genotyping data of ADNI subjects pre-processed as previously described by Scelsi et al., 2018.

Sliding window approach

Request a detailed protocol

As a baseline, we generated nomograms using the SWA described by Nobis et al., 2019. Briefly, we sorted UKB samples by age, and formed 100 quantile bins, each containing 10% of the samples. This means that neighbouring bins had a 90% overlap. For example, if we had 5000 samples, each bin contained 500 samples and consecutive bins were shifted by 50 samples. Thus, bin number 4 would start at index 151. Then, within each bin, the 2.5%, 5%, 10%, 25%, 50%, 75%, 90%, 95%, and 97.5% quantiles were calculated. The quantiles were then smoothed with a Gaussian kernel of width 20. The smoothing was needed because towards the ends of the data, the sliding windows approach becomes sensitive to noise.

Gaussian process regression

Request a detailed protocol

Our proposed approach uses GPR to build nomograms. Briefly, a GP is a probability distribution over possible functions that fit a set of points (Rasmussen and Williams, 2006; Wang, 2021). In our application it is a distribution of possible ‘HV trajectories across age’. The GPR models were trained with the laGP (Gramacy, 2016) R library, which implements a local approximation method that allows large datasets to be trained on consumer grade machines. We applied the commonly used squared exponential covariance kernel function:

Kx1,x2=σ2e-x1-x222L2,

where x1 and x2 are any two age values from the training set. The kernel function is hyper-parameterized by a vertical scale (σ) and a length scale (L), which, following initialization, are fitted using maximum likelihood estimation. The vertical scale is initialized to the mean HV of all samples, and the length scale is initialized to mean age difference between all samples. We trained models of left, right, and mean HV for each sex. Thanks to their probabilistic formulation, GP models naturally provide a standard deviation from which quantiles can be easily computed. After training, we generated models for ages 45–82 by increments of 0.25 years, and quantile curves at 2.5%, 5%, 10%, 25%, 50%, 75%, 90%, 95%, and 97.5%. The UKB dataset was used to train the models and the ADNI dataset was used to test them. For all GPR models, we only tested the ADNI samples that lay within the age range of each model respectively.

PGS for HV

Request a detailed protocol

A PGS is a sum of the impact of a selection of genetic variants on a trait, weighted by the allele count. That is:

PGS=∑∀i∈SNPsESi*Ci,

where (ESi) is the effect size (e.g., beta or log(odds) ratio from GWAS summary statistics), and (Ci) is the allele count of SNP i in the subject (either 0, 1, or 2). Thus, computing PGSs requires SNP-level genetic data. Using a previously reported GWAS of mean bilateral HV using 26,814 (European) subjects from the ENIGMA study (Hibar et al., 2017), we built a PGS for HV with PRSice v2 (Choi and O’Reilly, 2019). For both UKB and ADNI, we filter for minor allele frequency of 0.05, genotype missingness of 0.1, and clumping at 250 kb; after which we were left with 70,251 potential SNPS to include for UKB and 114,812 for ADNI. The most widely applied strategy for SNP selection is p-value thresholding. We generated PGSs at 14 p-value thresholds (1E-8, 1E-7, 1E-6, 1E-5, 1E-4, 1E-3, 0.01, 0.05, 0.1, 0.2, 0.4, 0.5, 0.75, 1). These thresholds produced a range of PGSs comprising as little as six SNPs (p-value cut-off at 1E-8) to all available SNPs (p-value cut-off at 1.0). Model fit is then checked by regressing HV against these PGSs while accounting for age, age2, sex, ICV, and 10 genetic principal components.

Genetically adjusted nomograms

Request a detailed protocol

Given the high heritability of HV we investigated whether nomograms can be genetically adjusted. Specifically, we used the top and bottom 30% samples by PGS (at p-value<0.75 threshold) separately to build genetically adjusted nomograms. We found that using a 30% cut-off provided a balance of training size and performance (Figure 2—figure supplement 4). Thus, PGS provided us with a way to place new samples in their ‘appropriate’ nomogram. For instance, within the ADNI dataset we generated PGSs and split the top and bottom (i.e., high and low expected HV, respectively) to test against genetically adjusted UKB nomograms. To evaluate the impact of genetic adjustment, we perform a series of ANOVA tests across adjusted nomograms. For example, we performed an ANOVA test of the HV percentiles of the top 30% UKB samples in the unadjusted than the adjusted nomograms. We did the same for bottom 30% and for men and women. To assess the specificity of the HV-based PGS, we performed this genetic adjustment using PGSs of ICV and AD based on previously reported GWASs (Adams et al., 2016; Lambert et al., 2013).

Longitudinal analysis

Request a detailed protocol

As nomograms are often used to track progression, we examined the impact of the genetically adjusted nomograms on prospective longitudinal data. To this end, we analysed patients from the ADNI cohort that were initially diagnosed as MCI and either converted to AD (progressor) or remained MCI (stable) within 5 years of follow-up. We tested whether the PGS-adjusted nomograms improved the separation between stable and progressor patients using Cox proportional hazards models while accounting for sex and age.

Code and data availability

Request a detailed protocol

The scripts and code used in this study have been made publicly available and can be found at: https://github.com/Mo-Janahi/NOMOGRAMS; Janahi, 2021. All underlying data, and derived quantities, are available by application from the UKB at http://www.ukbiobank.ac.uk, and by application from ADNI at http://adni.loni.usc.edu/data-samples/access-data/. Summary statistics from all GWAS described in this paper are available from the NHGRI-EBI GWAS catalog, study numbers: GCST003834, GCST002245, and GCST003961. URL: https://www.ebi.ac.uk/gwas/studies/.

Data availability

The scripts and code used in this study have been made publicly available and can be found at: https://github.com/Mo-Janahi/NOMOGRAMS, (copy archived at swh:1:rev:2522548b320b3a9859a539bd7b06768dffb38f7e).

The following previously published data sets were used
    1. Adams HH
    (2016) EMBL-EBI
    ID GCST003834. Novel genetic loci underlying human intracranial volume identified through genome-wide association.
    https://www.ebi.ac.uk/gwas/studies/GCST003834
    1. Lambert JC
    (2013) EMBL-EBI
    ID GCST002245. Meta-analysis of 74,046 individuals identifies 11 new susceptibility loci for Alzheimer's disease.
    https://www.ebi.ac.uk/gwas/studies/GCST002245
    1. Hibar DP
    (2017) EMBL-EBI
    ID GCST003961. Novel genetic loci associated with hippocampal volume.
    https://www.ebi.ac.uk/gwas/studies/GCST003961

References

    1. Adams HHH
    2. Hibar DP
    3. Chouraki V
    4. Stein JL
    5. Nyquist PA
    6. Rentería ME
    7. Trompet S
    8. Arias-Vasquez A
    9. Seshadri S
    10. Desrivières S
    11. Beecham AH
    12. Jahanshad N
    13. Wittfeld K
    14. Van der Lee SJ
    15. Abramovic L
    16. Alhusaini S
    17. Amin N
    18. Andersson M
    19. Arfanakis K
    20. Aribisala BS
    21. Armstrong NJ
    22. Athanasiu L
    23. Axelsson T
    24. Beiser A
    25. Bernard M
    26. Bis JC
    27. Blanken LME
    28. Blanton SH
    29. Bohlken MM
    30. Boks MP
    31. Bralten J
    32. Brickman AM
    33. Carmichael O
    34. Chakravarty MM
    35. Chauhan G
    36. Chen Q
    37. Ching CRK
    38. Cuellar-Partida G
    39. Braber AD
    40. Doan NT
    41. Ehrlich S
    42. Filippi I
    43. Ge T
    44. Giddaluru S
    45. Goldman AL
    46. Gottesman RF
    47. Greven CU
    48. Grimm O
    49. Griswold ME
    50. Guadalupe T
    51. Hass J
    52. Haukvik UK
    53. Hilal S
    54. Hofer E
    55. Hoehn D
    56. Holmes AJ
    57. Hoogman M
    58. Janowitz D
    59. Jia T
    60. Kasperaviciute D
    61. Kim S
    62. Klein M
    63. Kraemer B
    64. Lee PH
    65. Liao J
    66. Liewald DCM
    67. Lopez LM
    68. Luciano M
    69. Macare C
    70. Marquand A
    71. Matarin M
    72. Mather KA
    73. Mattheisen M
    74. Mazoyer B
    75. McKay DR
    76. McWhirter R
    77. Milaneschi Y
    78. Mirza-Schreiber N
    79. Muetzel RL
    80. Maniega SM
    81. Nho K
    82. Nugent AC
    83. Loohuis LMO
    84. Oosterlaan J
    85. Papmeyer M
    86. Pappa I
    87. Pirpamer L
    88. Pudas S
    89. Pütz B
    90. Rajan KB
    91. Ramasamy A
    92. Richards JS
    93. Risacher SL
    94. Roiz-Santiañez R
    95. Rommelse N
    96. Rose EJ
    97. Royle NA
    98. Rundek T
    99. Sämann PG
    100. Satizabal CL
    101. Schmaal L
    102. Schork AJ
    103. Shen L
    104. Shin J
    105. Shumskaya E
    106. Smith AV
    107. Sprooten E
    108. Strike LT
    109. Teumer A
    110. Thomson R
    111. Tordesillas-Gutierrez D
    112. Toro R
    113. Trabzuni D
    114. Vaidya D
    115. Van der Grond J
    116. Van der Meer D
    117. Van Donkelaar MMJ
    118. Van Eijk KR
    119. Van Erp TGM
    120. Van Rooij D
    121. Walton E
    122. Westlye LT
    123. Whelan CD
    124. Windham BG
    125. Winkler AM
    126. Woldehawariat G
    127. Wolf C
    128. Wolfers T
    129. Xu B
    130. Yanek LR
    131. Yang J
    132. Zijdenbos A
    133. Zwiers MP
    134. Agartz I
    135. Aggarwal NT
    136. Almasy L
    137. Ames D
    138. Amouyel P
    139. Andreassen OA
    140. Arepalli S
    141. Assareh AA
    142. Barral S
    143. Bastin ME
    144. Becker DM
    145. Becker JT
    146. Bennett DA
    147. Blangero J
    148. van Bokhoven H
    149. Boomsma DI
    150. Brodaty H
    151. Brouwer RM
    152. Brunner HG
    153. Buckner RL
    154. Buitelaar JK
    155. Bulayeva KB
    156. Cahn W
    157. Calhoun VD
    158. Cannon DM
    159. Cavalleri GL
    160. Chen C
    161. Cheng C-Y
    162. Cichon S
    163. Cookson MR
    164. Corvin A
    165. Crespo-Facorro B
    166. Curran JE
    167. Czisch M
    168. Dale AM
    169. Davies GE
    170. De Geus EJC
    171. De Jager PL
    172. de Zubicaray GI
    173. Delanty N
    174. Depondt C
    175. DeStefano AL
    176. Dillman A
    177. Djurovic S
    178. Donohoe G
    179. Drevets WC
    180. Duggirala R
    181. Dyer TD
    182. Erk S
    183. Espeseth T
    184. Evans DA
    185. Fedko IO
    186. Fernández G
    187. Ferrucci L
    188. Fisher SE
    189. Fleischman DA
    190. Ford I
    191. Foroud TM
    192. Fox PT
    193. Francks C
    194. Fukunaga M
    195. Gibbs JR
    196. Glahn DC
    197. Gollub RL
    198. Göring HHH
    199. Grabe HJ
    200. Green RC
    201. Gruber O
    202. Gudnason V
    203. Guelfi S
    204. Hansell NK
    205. Hardy J
    206. Hartman CA
    207. Hashimoto R
    208. Hegenscheid K
    209. Heinz A
    210. Le Hellard S
    211. Hernandez DG
    212. Heslenfeld DJ
    213. Ho B-C
    214. Hoekstra PJ
    215. Hoffmann W
    216. Hofman A
    217. Holsboer F
    218. Homuth G
    219. Hosten N
    220. Hottenga J-J
    221. Hulshoff Pol HE
    222. Ikeda M
    223. Ikram MK
    224. Jack CR Jr
    225. Jenkinson M
    226. Johnson R
    227. Jönsson EG
    228. Jukema JW
    229. Kahn RS
    230. Kanai R
    231. Kloszewska I
    232. Knopman DS
    233. Kochunov P
    234. Kwok JB
    235. Lawrie SM
    236. Lemaître H
    237. Liu X
    238. Longo DL
    239. Longstreth WT Jr
    240. Lopez OL
    241. Lovestone S
    242. Martinez O
    243. Martinot J-L
    244. Mattay VS
    245. McDonald C
    246. McIntosh AM
    247. McMahon KL
    248. McMahon FJ
    249. Mecocci P
    250. Melle I
    251. Meyer-Lindenberg A
    252. Mohnke S
    253. Montgomery GW
    254. Morris DW
    255. Mosley TH
    256. Mühleisen TW
    257. Müller-Myhsok B
    258. Nalls MA
    259. Nauck M
    260. Nichols TE
    261. Niessen WJ
    262. Nöthen MM
    263. Nyberg L
    264. Ohi K
    265. Olvera RL
    266. Ophoff RA
    267. Pandolfo M
    268. Paus T
    269. Pausova Z
    270. Penninx BWJH
    271. Pike GB
    272. Potkin SG
    273. Psaty BM
    274. Reppermund S
    275. Rietschel M
    276. Roffman JL
    277. Romanczuk-Seiferth N
    278. Rotter JI
    279. Ryten M
    280. Sacco RL
    281. Sachdev PS
    282. Saykin AJ
    283. Schmidt R
    284. Schofield PR
    285. Sigurdsson S
    286. Simmons A
    287. Singleton A
    288. Sisodiya SM
    289. Smith C
    290. Smoller JW
    291. Soininen H
    292. Srikanth V
    293. Steen VM
    294. Stott DJ
    295. Sussmann JE
    296. Thalamuthu A
    297. Tiemeier H
    298. Toga AW
    299. Traynor BJ
    300. Troncoso J
    301. Turner JA
    302. Tzourio C
    303. Uitterlinden AG
    304. Hernández MCV
    305. Van der Brug M
    306. Van der Lugt A
    307. Van der Wee NJA
    308. Van Duijn CM
    309. Van Haren NEM
    310. Van T Ent D
    311. Van Tol M-J
    312. Vardarajan BN
    313. Veltman DJ
    314. Vernooij MW
    315. Völzke H
    316. Walter H
    317. Wardlaw JM
    318. Wassink TH
    319. Weale ME
    320. Weinberger DR
    321. Weiner MW
    322. Wen W
    323. Westman E
    324. White T
    325. Wong TY
    326. Wright CB
    327. Zielke HR
    328. Zonderman AB
    329. Deary IJ
    330. DeCarli C
    331. Schmidt H
    332. Martin NG
    333. De Craen AJM
    334. Wright MJ
    335. Launer LJ
    336. Schumann G
    337. Fornage M
    338. Franke B
    339. Debette S
    340. Medland SE
    341. Ikram MA
    342. Thompson PM
    (2016) Novel genetic loci underlying human intracranial volume identified through genome-wide association
    Nature Neuroscience 19:1569–1582.
    https://doi.org/10.1038/nn.4398
  17. Book
    1. Fraser MA
    2. Shaw ME
    3. Cherbuin N
    (2015)
    A Systematic Review and Meta-Analysis of Longitudinal Hippocampal Atrophy in Healthy Human Ageing
    Academic Press Inc.
    1. Grasby KL
    2. Jahanshad N
    3. Painter JN
    4. Colodro-Conde L
    5. Bralten J
    6. Hibar DP
    7. Lind PA
    8. Pizzagalli F
    9. Ching CRK
    10. McMahon MAB
    11. Shatokhina N
    12. Zsembik LCP
    13. Thomopoulos SI
    14. Zhu AH
    15. Strike LT
    16. Agartz I
    17. Alhusaini S
    18. Almeida MAA
    19. Alnæs D
    20. Amlien IK
    21. Andersson M
    22. Ard T
    23. Armstrong NJ
    24. Ashley-Koch A
    25. Atkins JR
    26. Bernard M
    27. Brouwer RM
    28. Buimer EEL
    29. Bülow R
    30. Bürger C
    31. Cannon DM
    32. Chakravarty M
    33. Chen Q
    34. Cheung JW
    35. Couvy-Duchesne B
    36. Dale AM
    37. Dalvie S
    38. de Araujo TK
    39. de Zubicaray GI
    40. de Zwarte SMC
    41. den Braber A
    42. Doan NT
    43. Dohm K
    44. Ehrlich S
    45. Engelbrecht HR
    46. Erk S
    47. Fan CC
    48. Fedko IO
    49. Foley SF
    50. Ford JM
    51. Fukunaga M
    52. Garrett ME
    53. Ge T
    54. Giddaluru S
    55. Goldman AL
    56. Green MJ
    57. Groenewold NA
    58. Grotegerd D
    59. Gurholt TP
    60. Gutman BA
    61. Hansell NK
    62. Harris MA
    63. Harrison MB
    64. Haswell CC
    65. Hauser M
    66. Herms S
    67. Heslenfeld DJ
    68. Ho NF
    69. Hoehn D
    70. Hoffmann P
    71. Holleran L
    72. Hoogman M
    73. Hottenga JJ
    74. Ikeda M
    75. Janowitz D
    76. Jansen IE
    77. Jia T
    78. Jockwitz C
    79. Kanai R
    80. Karama S
    81. Kasperaviciute D
    82. Kaufmann T
    83. Kelly S
    84. Kikuchi M
    85. Klein M
    86. Knapp M
    87. Knodt AR
    88. Krämer B
    89. Lam M
    90. Lancaster TM
    91. Lee PH
    92. Lett TA
    93. Lewis LB
    94. Lopes-Cendes I
    95. Luciano M
    96. Macciardi F
    97. Marquand AF
    98. Mathias SR
    99. Melzer TR
    100. Milaneschi Y
    101. Mirza-Schreiber N
    102. Moreira JCV
    103. Mühleisen TW
    104. Müller-Myhsok B
    105. Najt P
    106. Nakahara S
    107. Nho K
    108. Olde Loohuis LM
    109. Orfanos DP
    110. Pearson JF
    111. Pitcher TL
    112. Pütz B
    113. Quidé Y
    114. Ragothaman A
    115. Rashid FM
    116. Reay WR
    117. Redlich R
    118. Reinbold CS
    119. Repple J
    120. Richard G
    121. Riedel BC
    122. Risacher SL
    123. Rocha CS
    124. Mota NR
    125. Salminen L
    126. Saremi A
    127. Saykin AJ
    128. Schlag F
    129. Schmaal L
    130. Schofield PR
    131. Secolin R
    132. Shapland CY
    133. Shen L
    134. Shin J
    135. Shumskaya E
    136. Sønderby IE
    137. Sprooten E
    138. Tansey KE
    139. Teumer A
    140. Thalamuthu A
    141. Tordesillas-Gutiérrez D
    142. Turner JA
    143. Uhlmann A
    144. Vallerga CL
    145. van der Meer D
    146. van Donkelaar MMJ
    147. van Eijk L
    148. van Erp TGM
    149. van Haren NEM
    150. van Rooij D
    151. van Tol MJ
    152. Veldink JH
    153. Verhoef E
    154. Walton E
    155. Wang M
    156. Wang Y
    157. Wardlaw JM
    158. Wen W
    159. Westlye LT
    160. Whelan CD
    161. Witt SH
    162. Wittfeld K
    163. Wolf C
    164. Wolfers T
    165. Wu JQ
    166. Yasuda CL
    167. Zaremba D
    168. Zhang Z
    169. Zwiers MP
    170. Artiges E
    171. Assareh AA
    172. Ayesa-Arriola R
    173. Belger A
    174. Brandt CL
    175. Brown GG
    176. Cichon S
    177. Curran JE
    178. Davies GE
    179. Degenhardt F
    180. Dennis MF
    181. Dietsche B
    182. Djurovic S
    183. Doherty CP
    184. Espiritu R
    185. Garijo D
    186. Gil Y
    187. Gowland PA
    188. Green RC
    189. Häusler AN
    190. Heindel W
    191. Ho BC
    192. Hoffmann WU
    193. Holsboer F
    194. Homuth G
    195. Hosten N
    196. Jack CR
    197. Jang M
    198. Jansen A
    199. Kimbrel NA
    200. Kolskår K
    201. Koops S
    202. Krug A
    203. Lim KO
    204. Luykx JJ
    205. Mathalon DH
    206. Mather KA
    207. Mattay VS
    208. Matthews S
    209. Mayoral Van Son J
    210. McEwen SC
    211. Melle I
    212. Morris DW
    213. Mueller BA
    214. Nauck M
    215. Nordvik JE
    216. Nöthen MM
    217. O’Leary DS
    218. Opel N
    219. Martinot MLP
    220. Pike GB
    221. Preda A
    222. Quinlan EB
    223. Rasser PE
    224. Ratnakar V
    225. Reppermund S
    226. Steen VM
    227. Tooney PA
    228. Torres FR
    229. Veltman DJ
    230. Voyvodic JT
    231. Whelan R
    232. White T
    233. Yamamori H
    234. Adams HHH
    235. Bis JC
    236. Debette S
    237. Decarli C
    238. Fornage M
    239. Gudnason V
    240. Hofer E
    241. Ikram MA
    242. Launer L
    243. Longstreth WT
    244. Lopez OL
    245. Mazoyer B
    246. Mosley TH
    247. Roshchupkin GV
    248. Satizabal CL
    249. Schmidt R
    250. Seshadri S
    251. Yang Q
    252. Alvim MKM
    253. Ames D
    254. Anderson TJ
    255. Andreassen OA
    256. Arias-Vasquez A
    257. Bastin ME
    258. Baune BT
    259. Beckham JC
    260. Blangero J
    261. Boomsma DI
    262. Brodaty H
    263. Brunner HG
    264. Buckner RL
    265. Buitelaar JK
    266. Bustillo JR
    267. Cahn W
    268. Cairns MJ
    269. Calhoun V
    270. Carr VJ
    271. Caseras X
    272. Caspers S
    273. Cavalleri GL
    274. Cendes F
    275. Corvin A
    276. Crespo-Facorro B
    277. Dalrymple-Alford JC
    278. Dannlowski U
    279. de Geus EJC
    280. Deary IJ
    281. Delanty N
    282. Depondt C
    283. Desrivières S
    284. Donohoe G
    285. Espeseth T
    286. Fernández G
    287. Fisher SE
    288. Flor H
    289. Forstner AJ
    290. Francks C
    291. Franke B
    292. Glahn DC
    293. Gollub RL
    294. Grabe HJ
    295. Gruber O
    296. Håberg AK
    297. Hariri AR
    298. Hartman CA
    299. Hashimoto R
    300. Heinz A
    301. Henskens FA
    302. Hillegers MHJ
    303. Hoekstra PJ
    304. Holmes AJ
    305. Hong LE
    306. Hopkins WD
    307. Hulshoff Pol HE
    308. Jernigan TL
    309. Jönsson EG
    310. Kahn RS
    311. Kennedy MA
    312. Kircher TTJ
    313. Kochunov P
    314. Kwok JBJ
    315. Le Hellard S
    316. Loughland CM
    317. Martin NG
    318. Martinot JL
    319. McDonald C
    320. McMahon KL
    321. Meyer-Lindenberg A
    322. Michie PT
    323. Morey RA
    324. Mowry B
    325. Nyberg L
    326. Oosterlaan J
    327. Ophoff RA
    328. Pantelis C
    329. Paus T
    330. Pausova Z
    331. Penninx B
    332. Polderman TJC
    333. Posthuma D
    334. Rietschel M
    335. Roffman JL
    336. Rowland LM
    337. Sachdev PS
    338. Sämann PG
    339. Schall U
    340. Schumann G
    341. Scott RJ
    342. Sim K
    343. Sisodiya SM
    344. Smoller JW
    345. Sommer IE
    346. St Pourcain B
    347. Stein DJ
    348. Toga AW
    349. Trollor JN
    350. Van der Wee NJA
    351. van ’t Ent D
    352. Völzke H
    353. Walter H
    354. Weber B
    355. Weinberger DR
    356. Wright MJ
    357. Zhou J
    358. Stein JL
    359. Thompson PM
    360. Medland SE
    361. Alzheimer’s Disease Neuroimaging Initiative
    362. CHARGE Consortium
    363. EPIGEN Consortium
    364. IMAGEN Consortium
    365. SYS Consortium
    366. Parkinson’s Progression Markers Initiative
    367. Enhancing NeuroImaging Genetics through Meta-Analysis Consortium —Genetics working group
    (2020) The genetic architecture of the human cerebral cortex
    Science 367:eaay6690.
    https://doi.org/10.1126/science.aay6690
    1. Hibar DP
    2. Stein JL
    3. Renteria ME
    4. Arias-Vasquez A
    5. Desrivières S
    6. Jahanshad N
    7. Toro R
    8. Wittfeld K
    9. Abramovic L
    10. Andersson M
    11. Aribisala BS
    12. Armstrong NJ
    13. Bernard M
    14. Bohlken MM
    15. Boks MP
    16. Bralten J
    17. Brown AA
    18. Chakravarty MM
    19. Chen Q
    20. Ching CRK
    21. Cuellar-Partida G
    22. den Braber A
    23. Giddaluru S
    24. Goldman AL
    25. Grimm O
    26. Guadalupe T
    27. Hass J
    28. Woldehawariat G
    29. Holmes AJ
    30. Hoogman M
    31. Janowitz D
    32. Jia T
    33. Kim S
    34. Klein M
    35. Kraemer B
    36. Lee PH
    37. Olde Loohuis LM
    38. Luciano M
    39. Macare C
    40. Mather KA
    41. Mattheisen M
    42. Milaneschi Y
    43. Nho K
    44. Papmeyer M
    45. Ramasamy A
    46. Risacher SL
    47. Roiz-Santiañez R
    48. Rose EJ
    49. Salami A
    50. Sämann PG
    51. Schmaal L
    52. Schork AJ
    53. Shin J
    54. Strike LT
    55. Teumer A
    56. van Donkelaar MMJ
    57. van Eijk KR
    58. Walters RK
    59. Westlye LT
    60. Whelan CD
    61. Winkler AM
    62. Zwiers MP
    63. Alhusaini S
    64. Athanasiu L
    65. Ehrlich S
    66. Hakobjan MMH
    67. Hartberg CB
    68. Haukvik UK
    69. Heister A
    70. Hoehn D
    71. Kasperaviciute D
    72. Liewald DCM
    73. Lopez LM
    74. Makkinje RRR
    75. Matarin M
    76. Naber MAM
    77. McKay DR
    78. Needham M
    79. Nugent AC
    80. Pütz B
    81. Royle NA
    82. Shen L
    83. Sprooten E
    84. Trabzuni D
    85. van der Marel SSL
    86. van Hulzen KJE
    87. Walton E
    88. Wolf C
    89. Almasy L
    90. Ames D
    91. Arepalli S
    92. Assareh AA
    93. Bastin ME
    94. Brodaty H
    95. Bulayeva KB
    96. Carless MA
    97. Cichon S
    98. Corvin A
    99. Curran JE
    100. Czisch M
    101. de Zubicaray GI
    102. Dillman A
    103. Duggirala R
    104. Dyer TD
    105. Erk S
    106. Fedko IO
    107. Ferrucci L
    108. Foroud TM
    109. Fox PT
    110. Fukunaga M
    111. Gibbs JR
    112. Göring HHH
    113. Green RC
    114. Guelfi S
    115. Hansell NK
    116. Hartman CA
    117. Hegenscheid K
    118. Heinz A
    119. Hernandez DG
    120. Heslenfeld DJ
    121. Hoekstra PJ
    122. Holsboer F
    123. Homuth G
    124. Hottenga JJ
    125. Ikeda M
    126. Jack CR
    127. Jenkinson M
    128. Johnson R
    129. Kanai R
    130. Keil M
    131. Kent JW
    132. Kochunov P
    133. Kwok JB
    134. Lawrie SM
    135. Liu X
    136. Longo DL
    137. McMahon KL
    138. Meisenzahl E
    139. Melle I
    140. Mohnke S
    141. Montgomery GW
    142. Mostert JC
    143. Mühleisen TW
    144. Nalls MA
    145. Nichols TE
    146. Nilsson LG
    147. Nöthen MM
    148. Ohi K
    149. Olvera RL
    150. Perez-Iglesias R
    151. Pike GB
    152. Potkin SG
    153. Reinvang I
    154. Reppermund S
    155. Rietschel M
    156. Romanczuk-Seiferth N
    157. Rosen GD
    158. Rujescu D
    159. Schnell K
    160. Schofield PR
    161. Smith C
    162. Steen VM
    163. Sussmann JE
    164. Thalamuthu A
    165. Toga AW
    166. Traynor BJ
    167. Troncoso J
    168. Turner JA
    169. Valdés Hernández MC
    170. van ’t Ent D
    171. van der Brug M
    172. van der Wee NJA
    173. van Tol MJ
    174. Veltman DJ
    175. Wassink TH
    176. Westman E
    177. Zielke RH
    178. Zonderman AB
    179. Ashbrook DG
    180. Hager R
    181. Lu L
    182. McMahon FJ
    183. Morris DW
    184. Williams RW
    185. Brunner HG
    186. Buckner RL
    187. Buitelaar JK
    188. Cahn W
    189. Calhoun VD
    190. Cavalleri GL
    191. Crespo-Facorro B
    192. Dale AM
    193. Davies GE
    194. Delanty N
    195. Depondt C
    196. Djurovic S
    197. Drevets WC
    198. Espeseth T
    199. Gollub RL
    200. Ho BC
    201. Hoffmann W
    202. Hosten N
    203. Kahn RS
    204. Le Hellard S
    205. Meyer-Lindenberg A
    206. Müller-Myhsok B
    207. Nauck M
    208. Nyberg L
    209. Pandolfo M
    210. Penninx B
    211. Roffman JL
    212. Sisodiya SM
    213. Smoller JW
    214. van Bokhoven H
    215. van Haren NEM
    216. Völzke H
    217. Walter H
    218. Weiner MW
    219. Wen W
    220. White T
    221. Agartz I
    222. Andreassen OA
    223. Blangero J
    224. Boomsma DI
    225. Brouwer RM
    226. Cannon DM
    227. Cookson MR
    228. de Geus EJC
    229. Deary IJ
    230. Donohoe G
    231. Fernández G
    232. Fisher SE
    233. Francks C
    234. Glahn DC
    235. Grabe HJ
    236. Gruber O
    237. Hardy J
    238. Hashimoto R
    239. Hulshoff Pol HE
    240. Jönsson EG
    241. Kloszewska I
    242. Lovestone S
    243. Mattay VS
    244. Mecocci P
    245. McDonald C
    246. McIntosh AM
    247. Ophoff RA
    248. Paus T
    249. Pausova Z
    250. Ryten M
    251. Sachdev PS
    252. Saykin AJ
    253. Simmons A
    254. Singleton A
    255. Soininen H
    256. Wardlaw JM
    257. Weale ME
    258. Weinberger DR
    259. Adams HHH
    260. Launer LJ
    261. Seiler S
    262. Schmidt R
    263. Chauhan G
    264. Satizabal CL
    265. Becker JT
    266. Yanek L
    267. van der Lee SJ
    268. Ebling M
    269. Fischl B
    270. Longstreth WT
    271. Greve D
    272. Schmidt H
    273. Nyquist P
    274. Vinke LN
    275. van Duijn CM
    276. Xue L
    277. Mazoyer B
    278. Bis JC
    279. Gudnason V
    280. Seshadri S
    281. Ikram MA
    282. Martin NG
    283. Wright MJ
    284. Schumann G
    285. Franke B
    286. Thompson PM
    287. Medland SE
    288. Alzheimer’s Disease Neuroimaging Initiative
    289. CHARGE Consortium
    290. EPIGEN
    291. IMAGEN
    292. SYS
    (2015) Common genetic variants influence human subcortical brain structures
    Nature 520:224–229.
    https://doi.org/10.1038/nature14101
    1. Hibar DP
    2. Adams HHH
    3. Jahanshad N
    4. Chauhan G
    5. Stein JL
    6. Hofer E
    7. Renteria ME
    8. Bis JC
    9. Arias-Vasquez A
    10. Ikram MK
    11. Desrivières S
    12. Vernooij MW
    13. Abramovic L
    14. Alhusaini S
    15. Amin N
    16. Andersson M
    17. Arfanakis K
    18. Aribisala BS
    19. Armstrong NJ
    20. Athanasiu L
    21. Axelsson T
    22. Beecham AH
    23. Beiser A
    24. Bernard M
    25. Blanton SH
    26. Bohlken MM
    27. Boks MP
    28. Bralten J
    29. Brickman AM
    30. Carmichael O
    31. Chakravarty MM
    32. Chen Q
    33. Ching CRK
    34. Chouraki V
    35. Cuellar-Partida G
    36. Crivello F
    37. Den Braber A
    38. Doan NT
    39. Ehrlich S
    40. Giddaluru S
    41. Goldman AL
    42. Gottesman RF
    43. Grimm O
    44. Griswold ME
    45. Guadalupe T
    46. Gutman BA
    47. Hass J
    48. Haukvik UK
    49. Hoehn D
    50. Holmes AJ
    51. Hoogman M
    52. Janowitz D
    53. Jia T
    54. Jørgensen KN
    55. Karbalai N
    56. Kasperaviciute D
    57. Kim S
    58. Klein M
    59. Kraemer B
    60. Lee PH
    61. Liewald DCM
    62. Lopez LM
    63. Luciano M
    64. Macare C
    65. Marquand AF
    66. Matarin M
    67. Mather KA
    68. Mattheisen M
    69. McKay DR
    70. Milaneschi Y
    71. Muñoz Maniega S
    72. Nho K
    73. Nugent AC
    74. Nyquist P
    75. Loohuis LMO
    76. Oosterlaan J
    77. Papmeyer M
    78. Pirpamer L
    79. Pütz B
    80. Ramasamy A
    81. Richards JS
    82. Risacher SL
    83. Roiz-Santiañez R
    84. Rommelse N
    85. Ropele S
    86. Rose EJ
    87. Royle NA
    88. Rundek T
    89. Sämann PG
    90. Saremi A
    91. Satizabal CL
    92. Schmaal L
    93. Schork AJ
    94. Shen L
    95. Shin J
    96. Shumskaya E
    97. Smith AV
    98. Sprooten E
    99. Strike LT
    100. Teumer A
    101. Tordesillas-Gutierrez D
    102. Toro R
    103. Trabzuni D
    104. Trompet S
    105. Vaidya D
    106. Van der Grond J
    107. Van der Lee SJ
    108. Van der Meer D
    109. Van Donkelaar MMJ
    110. Van Eijk KR
    111. Van Erp TGM
    112. Van Rooij D
    113. Walton E
    114. Westlye LT
    115. Whelan CD
    116. Windham BG
    117. Winkler AM
    118. Wittfeld K
    119. Woldehawariat G
    120. Wolf C
    121. Wolfers T
    122. Yanek LR
    123. Yang J
    124. Zijdenbos A
    125. Zwiers MP
    126. Agartz I
    127. Almasy L
    128. Ames D
    129. Amouyel P
    130. Andreassen OA
    131. Arepalli S
    132. Assareh AA
    133. Barral S
    134. Bastin ME
    135. Becker DM
    136. Becker JT
    137. Bennett DA
    138. Blangero J
    139. van Bokhoven H
    140. Boomsma DI
    141. Brodaty H
    142. Brouwer RM
    143. Brunner HG
    144. Buckner RL
    145. Buitelaar JK
    146. Bulayeva KB
    147. Cahn W
    148. Calhoun VD
    149. Cannon DM
    150. Cavalleri GL
    151. Cheng C-Y
    152. Cichon S
    153. Cookson MR
    154. Corvin A
    155. Crespo-Facorro B
    156. Curran JE
    157. Czisch M
    158. Dale AM
    159. Davies GE
    160. De Craen AJM
    161. De Geus EJC
    162. De Jager PL
    163. De Zubicaray GI
    164. Deary IJ
    165. Debette S
    166. DeCarli C
    167. Delanty N
    168. Depondt C
    169. DeStefano A
    170. Dillman A
    171. Djurovic S
    172. Donohoe G
    173. Drevets WC
    174. Duggirala R
    175. Dyer TD
    176. Enzinger C
    177. Erk S
    178. Espeseth T
    179. Fedko IO
    180. Fernández G
    181. Ferrucci L
    182. Fisher SE
    183. Fleischman DA
    184. Ford I
    185. Fornage M
    186. Foroud TM
    187. Fox PT
    188. Francks C
    189. Fukunaga M
    190. Gibbs JR
    191. Glahn DC
    192. Gollub RL
    193. Göring HHH
    194. Green RC
    195. Gruber O
    196. Gudnason V
    197. Guelfi S
    198. Håberg AK
    199. Hansell NK
    200. Hardy J
    201. Hartman CA
    202. Hashimoto R
    203. Hegenscheid K
    204. Heinz A
    205. Le Hellard S
    206. Hernandez DG
    207. Heslenfeld DJ
    208. Ho B-C
    209. Hoekstra PJ
    210. Hoffmann W
    211. Hofman A
    212. Holsboer F
    213. Homuth G
    214. Hosten N
    215. Hottenga J-J
    216. Huentelman M
    217. Hulshoff Pol HE
    218. Ikeda M
    219. Jack Jr CR
    220. Jenkinson M
    221. Johnson R
    222. Jönsson EG
    223. Jukema JW
    224. Kahn RS
    225. Kanai R
    226. Kloszewska I
    227. Knopman DS
    228. Kochunov P
    229. Kwok JB
    230. Lawrie SM
    231. Lemaître H
    232. Liu X
    233. Longo DL
    234. Lopez OL
    235. Lovestone S
    236. Martinez O
    237. Martinot J-L
    238. Mattay VS
    239. McDonald C
    240. McIntosh AM
    241. McMahon FJ
    242. McMahon KL
    243. Mecocci P
    244. Melle I
    245. Meyer-Lindenberg A
    246. Mohnke S
    247. Montgomery GW
    248. Morris DW
    249. Mosley TH
    250. Mühleisen TW
    251. Müller-Myhsok B
    252. Nalls MA
    253. Nauck M
    254. Nichols TE
    255. Niessen WJ
    256. Nöthen MM
    257. Nyberg L
    258. Ohi K
    259. Olvera RL
    260. Ophoff RA
    261. Pandolfo M
    262. Paus T
    263. Pausova Z
    264. Penninx BWJH
    265. Pike GB
    266. Potkin SG
    267. Psaty BM
    268. Reppermund S
    269. Rietschel M
    270. Roffman JL
    271. Romanczuk-Seiferth N
    272. Rotter JI
    273. Ryten M
    274. Sacco RL
    275. Sachdev PS
    276. Saykin AJ
    277. Schmidt R
    278. Schmidt H
    279. Schofield PR
    280. Sigursson S
    281. Simmons A
    282. Singleton A
    283. Sisodiya SM
    284. Smith C
    285. Smoller JW
    286. Soininen H
    287. Steen VM
    288. Stott DJ
    289. Sussmann JE
    290. Thalamuthu A
    291. Toga AW
    292. Traynor BJ
    293. Troncoso J
    294. Tsolaki M
    295. Tzourio C
    296. Uitterlinden AG
    297. Hernández MCV
    298. Van der Brug M
    299. van der Lugt A
    300. van der Wee NJA
    301. Van Haren NEM
    302. van ’t Ent D
    303. Van Tol M-J
    304. Vardarajan BN
    305. Vellas B
    306. Veltman DJ
    307. Völzke H
    308. Walter H
    309. Wardlaw JM
    310. Wassink TH
    311. Weale ME
    312. Weinberger DR
    313. Weiner MW
    314. Wen W
    315. Westman E
    316. White T
    317. Wong TY
    318. Wright CB
    319. Zielke RH
    320. Zonderman AB
    321. Martin NG
    322. Van Duijn CM
    323. Wright MJ
    324. Longstreth WT
    325. Schumann G
    326. Grabe HJ
    327. Franke B
    328. Launer LJ
    329. Medland SE
    330. Seshadri S
    331. Thompson PM
    332. Ikram MA
    (2017) Novel genetic loci associated with hippocampal volume
    Nature Communications 8:13624.
    https://doi.org/10.1038/ncomms13624
    1. Lambert JC
    2. Ibrahim-Verbaas CA
    3. Harold D
    4. Naj AC
    5. Sims R
    6. Bellenguez C
    7. DeStafano AL
    8. Bis JC
    9. Beecham GW
    10. Grenier-Boley B
    11. Russo G
    12. Thorton-Wells TA
    13. Jones N
    14. Smith AV
    15. Chouraki V
    16. Thomas C
    17. Ikram MA
    18. Zelenika D
    19. Vardarajan BN
    20. Kamatani Y
    21. Lin CF
    22. Gerrish A
    23. Schmidt H
    24. Kunkle B
    25. Dunstan ML
    26. Ruiz A
    27. Bihoreau MT
    28. Choi SH
    29. Reitz C
    30. Pasquier F
    31. Cruchaga C
    32. Craig D
    33. Amin N
    34. Berr C
    35. Lopez OL
    36. De Jager PL
    37. Deramecourt V
    38. Johnston JA
    39. Evans D
    40. Lovestone S
    41. Letenneur L
    42. Morón FJ
    43. Rubinsztein DC
    44. Eiriksdottir G
    45. Sleegers K
    46. Goate AM
    47. Fiévet N
    48. Huentelman MW
    49. Gill M
    50. Brown K
    51. Kamboh MI
    52. Keller L
    53. Barberger-Gateau P
    54. McGuiness B
    55. Larson EB
    56. Green R
    57. Myers AJ
    58. Dufouil C
    59. Todd S
    60. Wallon D
    61. Love S
    62. Rogaeva E
    63. Gallacher J
    64. St George-Hyslop P
    65. Clarimon J
    66. Lleo A
    67. Bayer A
    68. Tsuang DW
    69. Yu L
    70. Tsolaki M
    71. Bossù P
    72. Spalletta G
    73. Proitsi P
    74. Collinge J
    75. Sorbi S
    76. Sanchez-Garcia F
    77. Fox NC
    78. Hardy J
    79. Deniz Naranjo MC
    80. Bosco P
    81. Clarke R
    82. Brayne C
    83. Galimberti D
    84. Mancuso M
    85. Matthews F
    86. Moebus S
    87. Mecocci P
    88. Del Zompo M
    89. Maier W
    90. Hampel H
    91. Pilotto A
    92. Bullido M
    93. Panza F
    94. Caffarra P
    95. Nacmias B
    96. Gilbert JR
    97. Mayhaus M
    98. Lannefelt L
    99. Hakonarson H
    100. Pichler S
    101. Carrasquillo MM
    102. Ingelsson M
    103. Beekly D
    104. Alvarez V
    105. Zou F
    106. Valladares O
    107. Younkin SG
    108. Coto E
    109. Hamilton-Nelson KL
    110. Gu W
    111. Razquin C
    112. Pastor P
    113. Mateo I
    114. Owen MJ
    115. Faber KM
    116. Jonsson PV
    117. Combarros O
    118. O’Donovan MC
    119. Cantwell LB
    120. Soininen H
    121. Blacker D
    122. Mead S
    123. Mosley TH
    124. Bennett DA
    125. Harris TB
    126. Fratiglioni L
    127. Holmes C
    128. de Bruijn RF
    129. Passmore P
    130. Montine TJ
    131. Bettens K
    132. Rotter JI
    133. Brice A
    134. Morgan K
    135. Foroud TM
    136. Kukull WA
    137. Hannequin D
    138. Powell JF
    139. Nalls MA
    140. Ritchie K
    141. Lunetta KL
    142. Kauwe JS
    143. Boerwinkle E
    144. Riemenschneider M
    145. Boada M
    146. Hiltuenen M
    147. Martin ER
    148. Schmidt R
    149. Rujescu D
    150. Wang LS
    151. Dartigues JF
    152. Mayeux R
    153. Tzourio C
    154. Hofman A
    155. Nöthen MM
    156. Graff C
    157. Psaty BM
    158. Jones L
    159. Haines JL
    160. Holmans PA
    161. Lathrop M
    162. Pericak-Vance MA
    163. Launer LJ
    164. Farrer LA
    165. van Duijn CM
    166. Van Broeckhoven C
    167. Moskvina V
    168. Seshadri S
    169. Williams J
    170. Schellenberg GD
    171. Amouyel P
    172. European Alzheimer’s Disease Initiative
    173. Genetic and Environmental Risk in Alzheimer’s Disease
    174. Alzheimer’s Disease Genetic Consortium
    175. Cohorts for Heart and Aging Research in Genomic Epidemiology
    (2013) Meta-analysis of 74,046 individuals identifies 11 new susceptibility loci for alzheimer’s disease
    Nature Genetics 45:1452–1458.
    https://doi.org/10.1038/ng.2802
  49. Book
    1. Rasmussen CE
    2. Williams CKI
    (2006)
    Gaussian Processes for Machine Learning
    Gaussian.
    1. Shen L
    2. Thompson PM
    (2020) Brain imaging genomics: integrated analysis and machine learning
    Proceedings of the IEEE. Institute of Electrical and Electronics Engineers 108:125–162.
    https://doi.org/10.1109/JPROC.2019.2947272
  57. Conference
    1. Stamoulou E
    2. Manikis GC
    3. Tsiknakis M
    4. Marias K
    (2021)
    ComBat harmonization for multicenter MRI based radiomics features
    2021 IEEE International Conference on Imaging Systems and Techniques (IST.

Article and author information

Author details

  1. Mohammed Janahi

    1. Centre for Medical Image Computing (CMIC), Department of Medical Physics and Biomedical Engineering, University College London, London, United Kingdom
    2. Medical and Population Genomics Lab, Human Genetics Department, Research Branch, Sidra Medicine, Doha, Qatar
    Contribution
    Resources, Data curation, Software, Formal analysis, Investigation, Visualization, Methodology, Writing - original draft, Writing - review and editing
    For correspondence
    Rmapmja@ucl.ac.uk
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0001-7442-2298

  2. Leon Aksman

    Stevens Neuroimaging and Informatics Institute, Keck School of Medicine, University of Southern California, Los Angeles, United States
    Contribution
    Conceptualization, Writing - review and editing
    Competing interests
    No competing interests declared

  3. Jonathan M Schott

    Dementia Research Centre (DRC), Queen Square Institute of Neurology, University College London, London, United Kingdom
    Contribution
    Supervision, Writing - review and editing
    Competing interests
    No competing interests declared

  4. Younes Mokrab

    1. Medical and Population Genomics Lab, Human Genetics Department, Research Branch, Sidra Medicine, Doha, Qatar
    2. Department of Genetic Medicine, Weill Cornell Medicine-Qatar, Doha, Qatar
    Contribution
    Writing - review and editing
    Competing interests
    No competing interests declared

  5. Andre Altmann

    Centre for Medical Image Computing (CMIC), Department of Medical Physics and Biomedical Engineering, University College London, London, United Kingdom
    Contribution
    Conceptualization, Resources, Supervision, Project administration, Writing - review and editing
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-9265-2393

Funding

Medical Research Council (MR/L016311/1)

  • Andre Altmann

National Institute of Biomedical Imaging and Bioengineering (P41EB015922)

  • Leon Aksman

National Institute on Aging (P30AG066530)

  • Leon Aksman

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

AA holds an MRC eMedLab Medical Bioinformatics Career Development Fellowship. This work was supported by the Medical Research Council (grant number MR/L016311/1). This work was supported in part by Sidra Medicine, Qatar. LMA was supported by the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health under Award Number P41EB015922 and by the National Institute on Aging of the National Institutes of Health under Award Number P30AG066530. JMS acknowledges the support of the UCL/H NIHR Biomedical Research Centre. This work is supported by the EPSRC-funded UCL Centre for Doctoral Training in Intelligent, Integrated Imaging in Healthcare (i4health) (EP/S021930/1).

Data used in preparation of this article were obtained from the ADNI database (http://adni.loni.usc.edu/). Data collection and sharing for this project was funded by the ADNI (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc; Cogstate; Eisai Inc; Elan Pharmaceuticals, Inc; Eli Lilly and Company; EuroImmun; F Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (https://www.fnih.org/). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California. As such, the investigators within the ADNI contributed to the design and implementation of ADNI and/or provided data but did not participate in analysis or writing of this report. Data used in the preparation of this article were obtained from the ADNI database (http://adni.loni.usc.edu/). As such, the investigators within the ADNI contributed to the design and implementation of ADNI and/or provided data but did not participate in analysis or writing of this report. A complete listing of ADNI investigators can be found at: http://adni.loni.usc.edu/wp-content/uploads/how_to_apply/ADNI_Acknowledgement_List.pdf.

Copyright

© 2022, Janahi et al.

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

  • 862
    views
  • 139
    downloads
  • 7
    citations

Views, downloads and citations are aggregated across all versions of this paper published by eLife.

Citations by DOI

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Mohammed Janahi
  2. Leon Aksman
  3. Jonathan M Schott
  4. Younes Mokrab
  5. Andre Altmann
  6. On behalf of for the Alzheimer’s Disease Neuroimaging Initiative
(2022)
Nomograms of human hippocampal volume shifted by polygenic scores
eLife 11:e78232.
https://doi.org/10.7554/eLife.78232

Share this article

https://doi.org/10.7554/eLife.78232

Categories and tags

Research organism