Cortical magnification eliminates differences in contrast sensitivity across but not around the visual field

Abstract
Editor's evaluation
Introduction
Results
Discussion
Methods
Data availability
References
Article and author information
Metrics

Abstract

Human visual performance changes dramatically both across (eccentricity) and around (polar angle) the visual field. Performance is better at the fovea, decreases with eccentricity, and is better along the horizontal than vertical meridian and along the lower than the upper vertical meridian. However, all neurophysiological and virtually all behavioral studies of cortical magnification have investigated eccentricity effects without considering polar angle. Most performance differences due to eccentricity are eliminated when stimulus size is cortically magnified (M-scaled) to equate the size of its cortical representation in primary visual cortex (V1). But does cortical magnification underlie performance differences around the visual field? Here, to assess contrast sensitivity, human adult observers performed an orientation discrimination task with constant stimulus size at different locations as well as when stimulus size was M-scaled according to stimulus eccentricity and polar angle location. We found that although M-scaling stimulus size eliminates differences across eccentricity, it does not eliminate differences around the polar angle. This finding indicates that limits in contrast sensitivity across eccentricity and around polar angle of the visual field are mediated by different anatomical and computational constraints.

Editor's evaluation

This important study presents a thought-provoking challenge to the explanation of sensitivity around the visual field using cortical magnification factors. The evidence supporting this challenge is based on a combination of neuroimaging and psychophysics. The study will be of interest to both basic and medical vision researchers.

https://doi.org/10.7554/eLife.84205.sa0

Introduction

Human visual performance changes throughout the visual field for most visual tasks. Performance is typically best near the fovea and decreases with increasing eccentricity (for reviews, see Anton-Erxleben and Carrasco, 2013; Strasburger et al., 2011). Contrast sensitivity, a fundamental visual capability, is bandpass near the fovea, peaking at ~4 cycles per degree (cpd) (Campbell and Robson, 1968; Watson and Ahumada, 2005), and declines with eccentricity (Hilz and Cavonius, 1974; Robson and Graham, 1981; Wright and Johnston, 1983). Contrast sensitivity also varies around polar angle: it is higher along the horizontal than vertical meridian – horizontal-vertical anisotropy (HVA) – and along the lower than upper vertical meridian – vertical meridian asymmetry (VMA) (Abrams et al., 2012; Baldwin et al., 2012; Cameron et al., 2002; Carrasco et al., 2022; Carrasco et al., 2001; Hanning et al., 2022a; Hanning et al., 2022b; Himmelberg et al., 2022b; Himmelberg et al., 2020; Pointer and Hess, 1989; Rosén et al., 2014). These contrast asymmetries depend upon stimulus eccentricity (Carrasco et al., 2001; Hilz and Cavonius, 1974; Himmelberg et al., 2020; Robson and Graham, 1981; Wright and Johnston, 1983), spatial frequency (SF) (Baldwin et al., 2012; Cameron et al., 2002; Campbell and Robson, 1968; Carrasco et al., 2001; Himmelberg et al., 2020; Rovamo et al., 1992), and size (Himmelberg et al., 2020).

Perceptual polar angle asymmetries can be as pronounced as doubling stimulus eccentricity (Carrasco et al., 2001; Himmelberg et al., 2020) and are robust across stimulus content modulations. They persist across different stimulus orientations (Baldwin et al., 2012; Carrasco et al., 2001; Corbett and Carrasco, 2011), eccentricities and SFs (Barbot et al., 2021; Cameron et al., 2002; Carrasco et al., 2001; Himmelberg et al., 2020; Rijsdijk et al., 1980), luminance levels (Carrasco et al., 2001), head rotations (Corbett and Carrasco, 2011), and sizes (Himmelberg et al., 2020), in the presence of distractors (Carrasco et al., 2001; Purokayastha et al., 2021), across manipulations of covert attention (Cameron et al., 2002; Carrasco et al., 2001; Purokayastha et al., 2021; Roberts et al., 2018; Roberts et al., 2016; Talgar and Carrasco, 2002) and presaccadic attention (Hanning et al., 2022a; Hanning et al., 2022b), as well as under monocular and binocular viewing conditions (Barbot et al., 2021; Carrasco et al., 2001).

Importantly, the perceptual asymmetries are retinotopic rather than spatiotopic; when observers rotate their head, the asymmetries shift in line with the retinal location of the stimulus rather than their location in space (Corbett and Carrasco, 2011). These asymmetries have been related to optical (Kupers et al., 2019), retinal (Kupers et al., 2022), and cortical factors (Benson et al., 2021; Himmelberg et al., 2023a; Himmelberg et al., 2022b, Himmelberg et al., 2021; Silva et al., 2018). For a review, see Himmelberg et al., 2023b.

Cortical magnification –the amount of cortical surface area corresponding to one degree of visual angle (mm²/°) – declines with eccentricity (Benson et al., 2022; Engel et al., 1994; Himmelberg et al., 2021; Horton and Hoyt, 1991; Van Essen et al., 1984) and has been used to link perceptual performance to brain structure (Duncan and Boynton, 2003; Himmelberg et al., 2023a; Himmelberg et al., 2022b; Rovamo et al., 1978; Schwarzkopf et al., 2011; Schwarzkopf and Rees, 2013; Song et al., 2015). If performance differences as a function of stimulus location can be attributed to differences in cortical surface area, then performance should be equated when equating stimulus size to the amount of cortical area activated. This can be achieved by enlarging peripheral stimuli (i.e., cortically magnifying, or 'M-scaling') by an inverse proportion to a measure of cortical magnification in the periphery or at different polar angles in the visual field.

Indeed, for many visual tasks (e.g., contrast sensitivity, orientation and SF discrimination, grating acuity, temporal frequency sensitivity, and visual search), magnifying stimulus size such that the spatial extent of the cortical representation is equated eliminates performance differences at different eccentricities (Figure 1A; Anton-Erxleben and Carrasco, 2013; Carrasco et al., 1998; Carrasco and Frieder, 1997; Kitterle, 1986; Rovamo and Virsu, 1979; Strasburger et al., 2011). Particularly relevant to this study, grating contrast sensitivity as a function of SF successfully scales with eccentricity (Hilz and Cavonius, 1974; Koenderink et al., 1978; Rovamo et al., 1978; Virsu and Rovamo, 1979). These studies support a ‘quantitative’ hypothesis – the hypothesis that the decline in performance with eccentricity is due to decreasing neural count with eccentricity, given that the density, but not distribution, of V1 neurons is approximately uniform across cortex (and thus visual space) (Hubel and Wiesel, 1977; Rockel et al., 1980). This hypothesis then suggests that visual processing is invariant with location; neurons conduct the same computations, regardless of their receptive field position.

Figure 1

Download asset Open asset

Schematic predictions of contrast sensitivity functions (CSFs).

(A) CSFs decline between the parafovea (2°) and perifovea (6°) for fixed-sized gratings (top row), but differences at low and medium SFs diminish after M-scaling Virsu and Rovamo, 1979 (bottom row). (B) CSFs differ among the horizontal meridian (HM), lower vertical meridian (LVM), and upper vertical meridian (UVM) for fixed-sized stimuli (top row). If polar angle asymmetries derive from differences in neural count among locations, M-scaling will diminish them (‘quantitative’ hypothesis). Alternatively, if the asymmetries derive from qualitatively different neural image-processing capabilities among locations, then M-scaling will not eliminate them (‘qualitative’ hypothesis).

Alternatively, when performance cannot be matched by M-scaling stimulus size (Figure 1B), then a ‘qualitative hypothesis’ is supported, stating that performance differences are mediated both by the cortical representation – and thus neural count – but also by different computations within visual neurons that encode different visual field locations. Indeed, performance does not successfully scale for several visual tasks measuring higher-order dimensions (e.g., numerosity judgments, symmetry detection, and positional relation of image components; for review, see Strasburger et al., 2011).

So far, these hypotheses have been supported by different visual tasks. Here, we ask whether they are exclusive for a given task or whether some regions of the visual field might follow the quantitative hypothesis, whereas others might follow a qualitative hypothesis for the same task.

To investigate the effect of M-scaling on contrast sensitivity and acuity across locations, we measured the whole contrast sensitivity function (CSF, known as the ‘window of visibility’) and manipulated stimulus eccentricity and size to assess how CS-peak (contrast sensitivity), SF-peak, SF-cutoff (acuity), and the area under the log CSF curve (AULCSF) vary across conditions and locations. Our main interest was to assess whether M-scaling, and thus cortical magnification, eliminates polar angle asymmetries in contrast sensitivity (Figure 1B).

To do so, we magnified stimulus size to equate the cortical representation for stimuli at different visual field locations (Rovamo and Virsu, 1979). By measuring contrast sensitivity of sinusoidal gratings at different regions of the visual field, Rovamo and Virsu, 1979 derived a linear cortical magnification factor (CMF) that has been widely used. Linear cortical magnification (M) describes the distance along V1 corresponding to 1° of eccentricity and is expressed as millimeters of cortex per degree of visual angle. By applying this factor, one can equate the amount of cortex activated, regardless of retinal eccentricity, and achieve similar spatial and temporal CSFs. Rovamo and Virsu, 1979 provided a specific M-scaling equation for each principal half meridian: nasal, temporal, superior, and inferior. This M-scaling procedure eliminates the eccentricity effect on performance in contrast sensitivity along these four half meridians, and their calculations have been used in many other studies for which visual performance differences across locations are eliminated once stimuli have been magnified (Carrasco et al., 1998; Carrasco and Frieder, 1997; Goolkasian, 1994; Himmelberg and Wade, 2019; Prince and Rogers, 1998; Virsu et al., 1982).

Here, observers performed an orientation discrimination task, which is contingent upon contrast sensitivity (Nachmias, 1967; Olzak and Thomas, 2003; Pestilli et al., 2009), when gratings appeared along the horizontal and vertical meridians, at 2° and 6° eccentricity. For the M-scale condition, gratings appeared at 6° eccentricity along horizontal and vertical meridians and the grating sizes were scaled separately for each polar angle meridian, based on meridian-dependent M-scaling equations (Rovamo and Virsu, 1979).

Surprisingly, cortically magnifying the stimuli to account for different cortical representations at the polar angle meridians did not eliminate polar angle asymmetries in contrast sensitivity, supporting the qualitative hypothesis. In contrast, and as expected, contrast sensitivity differences for eccentricity were eliminated, supporting the quantitative hypothesis. These differential results indicate that limits in contrast sensitivity as a function of eccentricity and polar angle likely emerge from different anatomical and computational constraints.

Results

The CSF characterizes stimulus visibility. We measured human CSFs within the parafovea (2° eccentricity) and perifovea (6° eccentricity) at three polar angles: horizontal meridian (HM), lower vertical meridian (LVM), and upper vertical meridian (UVM). While maintaining fixation, observers reported the orientation of a target grating for which contrast and spatial frequency (SF) varied on each trial (Figure 2A). Using a parametric contrast sensitivity model, we characterized observers’ CSFs along the HM and VM, before and after M-scaling (Figure 2A and B, see ‘Methods’).

Figure 2

Download asset Open asset

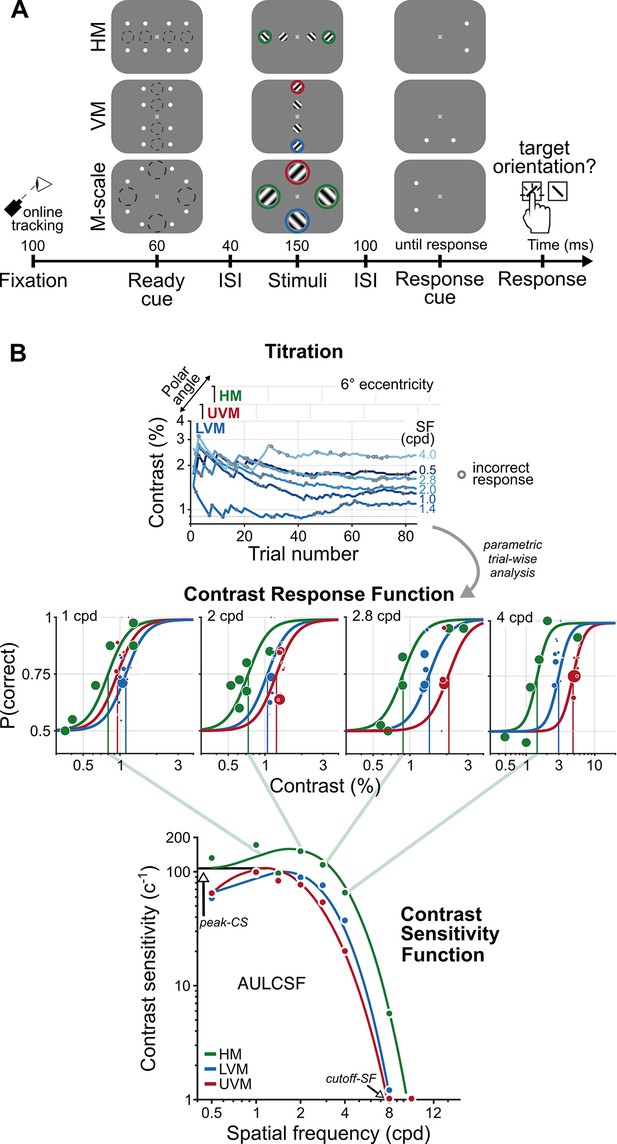
A psychophysical procedure to measure and a parametric model to characterize contrast sensitivity functions (CSFs).

(A) An example trial sequence for the orientation discrimination task. Each trial began with a fixation period, after which a cue indicated the onset of four gratings. The dashed circles illustrate the location and size of the grating stimuli; they did not appear during the experiment. Gratings appeared in the parafovea (2° eccentricity) and perifovea (6° eccentricity), separately along the horizontal (HM) or vertical meridian (VM) or were M-scaled, and presented simultaneously at each meridional location in the perifovea (M-scale). A response cue indicated which grating observers should report. The colored circles indicate the perifoveal locations we compared to assess the impact of M-scaling on polar angle asymmetries: Green, HM; blue, lower VM (LVM); red, upper VM (UVM). (B) Parametric contrast sensitivity model. Grating contrast varied throughout the experiment following independent titration procedures for each eccentricity and polar angle location. Gray circles indicate incorrect responses for a given trial (top row). A model composed of contrast response functions (CRF, middle row) and CSFs (bottom row) constrained the relation between trial-wise performance, SF, eccentricity, and polar angle. The diagonal green lines depict the connection between contrast thresholds from individual CRFs to contrast sensitivity on the CSF for the HM; contrast sensitivity is the inverse of contrast threshold. The colored dots in each CRF and CSF depict a representative observer’s task performance and contrast sensitivity, determined directly from the titration procedures. The colored lines depict the best-fitting model estimates. We derived key attributes of the CSF – peak contrast sensitivity (peak-CS), the acuity limit (cutoff-SF), and the area under the log contrast sensitivity function (AULCSF) – from the fitted parametric model.

We used model comparisons among nine CSF functional forms (Chung and Legge, 2016; Movshon and Kiorpes, 1988; Watson and Ahumada, 2005) to assess the differences across eccentricity and around polar angle for fixed-size gratings (Figure 3). The models were applied to group-level data. We extracted key CSF attributes – the peak contrast sensitivity (peak-CS), acuity limit (cutoff-SF), and area under the log contrast sensitivity function (AULCSF) – to characterize how contrast sensitivity changes with eccentricity, polar angle, and after M-scaling.

Figure 3

Download asset Open asset

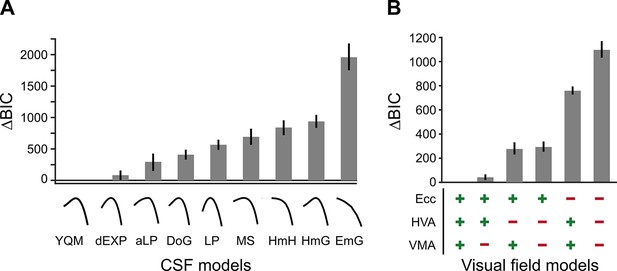
BIC model comparisons for contrast sensitivity function (CSF) and visual field models.

(A) CSF model comparisons for the nine candidate functional forms of the CSF applied to the group data (Table 1). Low ΔBIC values indicate superior model performance. Curves under each bar illustrate the best fit of each CSF model to a representative observer (n=10). (B) Visual field model comparisons (Table 2). ‘+’ and ‘-’ under each bar indicate the components included and excluded, respectively, in each model. For example, ‘+’ for ‘HVA’ indicates that CSFs could change between the horizontal and vertical meridians, whereas a ‘-’ indicates that CSFs for the horizontal meridian were identical to the lower vertical meridian.

Table 1

Candidate contrast sensitivity function (CSF) models.

The number of parameters included in each model (n) is denoted under the corresponding label, along with a brief description and the model equation. The bolded entry indicates the best-fitting model.

Label (n)	Description	Equation
YQM (4)	Derived from a model of contrast sensitivity Chung and Legge, 2016	$c_{t}^{- 1} (f, r, θ; α, β, γ, δ) = δ [\frac{e x p (- f / α)}{1 + \frac{γ}{1 + (f / β)}}]$
dEXP (3)	Double exponential function Chakravarthi et al., 2022	$c_{t}^{- 1} (f, r, θ; α, β, γ, δ) = δ f^{α} e x p (- f / β)$
aLP (4)	Asymmetric log parabola Corbett and Carrasco, 2011	$c_{t}^{- 1} (f, r, θ; α, β, γ, δ) = {δ - {(f - a)}^{2} β^{2} if f < α$ $c_{t}^{- 1} (f, r, θ; α, β, γ, δ) = {δ - {(f - a)}^{2} γ^{2} i f f \geq α$
DoG (4)	Difference of Gaussians Chung and Legge, 2016	$c_{t}^{- 1} (f, r, θ; α, β, γ, δ) = δ (e x p [- {(f / α)}^{2}] - γ e x p [- {(f / β)}^{2}])$
LP (3)	Log parabola Chung and Legge, 2016	$c_{t}^{- 1} (f, r, θ; α, β, γ, δ) = δ e x p [- {(\frac{l o g_{2} (\frac{f}{α})}{β})}^{2}]$
MS (4)	Generalized Gaussian with linear function of SF Chung and Legge, 2016	$c_{t}^{- 1} (f, r, θ; α, β, γ, δ) = δ (1 - β + \frac{f}{α}) e x p [- {(f / α)}^{γ}]$
HmH (4)	Difference of hyperbolic secants Chung and Legge, 2016	$c_{t}^{- 1} (f, r, θ; α, β, γ, δ) = δ (s e c h [f / α] - γ s e c h [f / β])$
HmG (4)	Hyperbolic secant minus a Gaussian Chung and Legge, 2016	$c_{t}^{- 1} (f, r, θ; α, β, γ, δ) = δ (s e c h [f / α] - γ e x p [- {(f / β)}^{2}])$
EmG (4)	Exponential minus a Gaussian Chung and Legge, 2016	$c_{t}^{- 1} (f, r, θ; α, β, γ, δ) = δ (e x p [- f / α] - γ e x p [- {(f / β)}^{2}])$

Table 2

Models of contrast sensitivity across eccentricity and polar angle.

The bolded entry indicates the best-fitting model.

Model label	Description	Max number of parameters
Ecc + HVA + VMA	CSFs vary across eccentricity and polar angle	24
Ecc +HVA - VMA	CSFs do not vary along the VM	16
Ecc - HVA + VMA	CSFs do not vary along the HM	16
-Ecc + HVA + VMA	CSFs do not vary across eccentricity	12
Ecc - HVA - VMA	CSFs do not vary along the VM and HM	8
-Ecc - HVA - VMA	CSFs are identical at all visual field locations	4

CSF: contrast sensitivity function; VM: vertical meridian; HM: horizontal meridian; HVA: horizontal-vertical anisotropy; VMA: vertical meridian asymmetry.

We magnified perifoveal gratings (6° eccentricity) following anisotropic M-scaling (Rovamo and Virsu, 1979) to equate their cortical representation with parafoveal (2° eccentricity) gratings (HM: 7.08°; LVM: 7.68°; UVM: 7.70°) and compared how this M-scaling changes CSFs attributes.

Contrast sensitivity peaked at a given SF and declined more rapidly for higher than lower SFs. We averaged CSFs across polar angle to isolate the eccentricity effect at 2°, 6°, and after M-scaling perifoveal CSFs (6°_M-scale; Figure 4A). CSFs decreased with eccentricity but less so after M-scaling. The eccentricity effect for fixed-size gratings, quantified as the percent change in contrast sensitivity for 2°, 6°, and 6°_M-scale, increased from ~30% to 120% across SF (Figure 4B).

Figure 4 with 1 supplement see all

Download asset Open asset

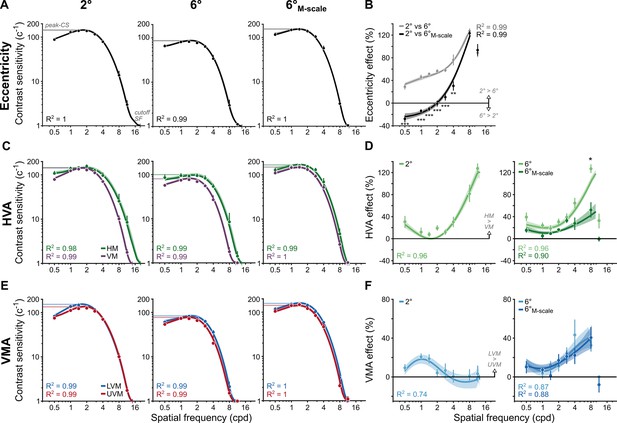
M-scaling diminishes the eccentricity effect, but neither the horizontal-vertical anisotropy (HVA) nor the vertical meridian asymmetry (VMA) (n=10).

(A) Contrast sensitivity functions (CSFs) averaged across polar angles for fixed-size gratings at 2° and 6°, as well as for M-scaled gratings at 6°. (B) Eccentricity effects are quantified as the percent change in contrast sensitivity between 2°and 6° as well as between 2° and 6°_M-scale. Positive values indicate higher contrast sensitivity at 2° than 6°. Negative values indicate a reversal: higher contrast sensitivity at 6° than 2°. (C) CSFs for the horizontal meridian (HM) compared to the average CSF across the lower vertical meridian (LVM) and upper vertical meridian (UVM). (D) The percent change between horizontal and vertical meridians at 2° (left) and the percentage change between meridians for 6° and 6°_M-scale (right). Values above 0% indicate higher sensitivity for the HM than VM. (E) CSFs for the LVM and UVM. (F) The percent change between LVM and UVM following the conventions in (D) (with a truncated y-axis); positive values indicate higher sensitivity for the LVM than UVM. All dots correspond to the group-average (n=10) contrast sensitivity and percent change in contrast sensitivity, as estimated from the titration procedures. Lines in panels (**A, C, E**) correspond to the group-average fit of the parametric contrast sensitivity model. Lines in panels (**B, D, F**) correspond to group average location percent differences as calculated in Equation 9 (see ‘Methods’). Note that the line does not reach the highest SF in these panels for the 6° and 6°_M-scale comparison, as observers performed at chance, consistent with the fact that SF is harder to discriminate in the periphery. Error bars and shaded areas denote bootstrapped 68% confidence intervals. Repeated-measures ANOVA; *p<0.05, **p<0.01, ***p<0.001.

After M-scaling, the eccentricity effect became negative for SFs <2 cpd, with higher contrast sensitivity at 6°_M-scale than 2° (Figure 4B). A repeated-measures ANOVA (SF: 0.5–11 cpd; stimulus size: fixed vs. M-scaled) showed that M-scaling diminished the eccentricity effect differentially across SF (interaction: F(7,63) = 61.13, p<0.001, η_G² = 0.872). Post hoc t-tests revealed significant reductions in contrast sensitivity for all SFs (0.5, 1, 1.4, 2, and 2.8 cpd, p<0.001; 4, cpd, p<0.01) except the two highest SFs (8 and 11 cpd, p>0.1), which reached the acuity limit. Thus, consistent with previous results (Rovamo et al., 1978; Rovamo and Virsu, 1979), M-scaling slightly reversed typical eccentricity effects for low SFs and reduced them for medium SFs (Figure 4—figure supplement 1).

Contrast sensitivity across SFs was greater for the HM than VM at 2°, 6°, and 6°_M-scale (Figure 4C). We quantified the HVA extent as the percent change in contrast sensitivity between the HM and VM (averaged LVM and UVM); positive values indicate higher sensitivity for the HM than VM. At 2° and 6°, the HVA extent increased from 20% to 120% across SF (Figure 4D). Remarkably, this HVA extent matched the eccentricity effect at high SFs (Figure 4B). Thus, differences in contrast sensitivity between the HM and VM at a fixed eccentricity were as pronounced as tripling stimulus eccentricity from 2° to 6°.

The HVA remained after M-scaling. A two-way ANOVA compared its extent at the perifovea (6° eccentricity) before and after M-scaling. M-scaling the stimulus reduced the HVA extent as a function of SF (interaction: F(7,63) = 7.32, p=0.0035, η_G² = 0.449). For all but one SF (8 cpd: p=0.021, 95% CI = [1.26 57.37], d = 0.75), M-scaling did not affect the HVA (p>0.05). This finding supports the ‘qualitative’ hypothesis – unlike eccentricity, the HVA must be mediated by factors beyond cortical magnification, such as qualitatively different image-processing capabilities and/or neural computations around polar angle (Figure 1B).

Contrast sensitivity across SFs was higher along the LVM than UVM for 2°, 6°, and 6°_M-scale (Figure 4E). We quantified the VMA extent as the percent change in contrast sensitivity between the LVM and UVM (Figure 4F). For fixed-size and M-scaled gratings, the VMA extent reached a maximum of 40% at 1 cpd in the parafovea and 8 cpd in the perifovea. The VMA has only been characterized at eccentricities > 2° (Abrams et al., 2012; Cameron et al., 2002; Carrasco et al., 2001; Himmelberg et al., 2020). This near-foveal location reveals that the SF at which the VMA peaks depends on eccentricity.

The VMA also remained after M-scaling (Figure 4F). A two-way ANOVA found a main effect of SF (F(7,63) = 10.16, p<0.001, η_G² = 0.53) due to an increasing perifoveal VMA extent across SF. We found neither a main effect of stimulus size nor an interaction effect (p>0.1), indicating no difference in VMA extent before and after M-scaling stimulus size. This finding further supports the ‘qualitative’ hypothesis – unlike eccentricity, the VMA must be mediated by factors beyond cortical magnification, such distinct neural computations and image-processing capabilities at the UVM and LVM (Figure 1B).

Key CSF attributes – peak-CS, cutoff-SF, and AULCSF – displayed changes consonant with eccentricity effects and polar angle asymmetries (Figure 5), but peak-SF and SF-bandwidth did not (Figure 5—figure supplement 1). We assessed each attribute with separate repeated-measures ANOVAs for the HVA and VMA across eccentricity and polar angle.

Figure 5 with 1 supplement see all

Download asset Open asset

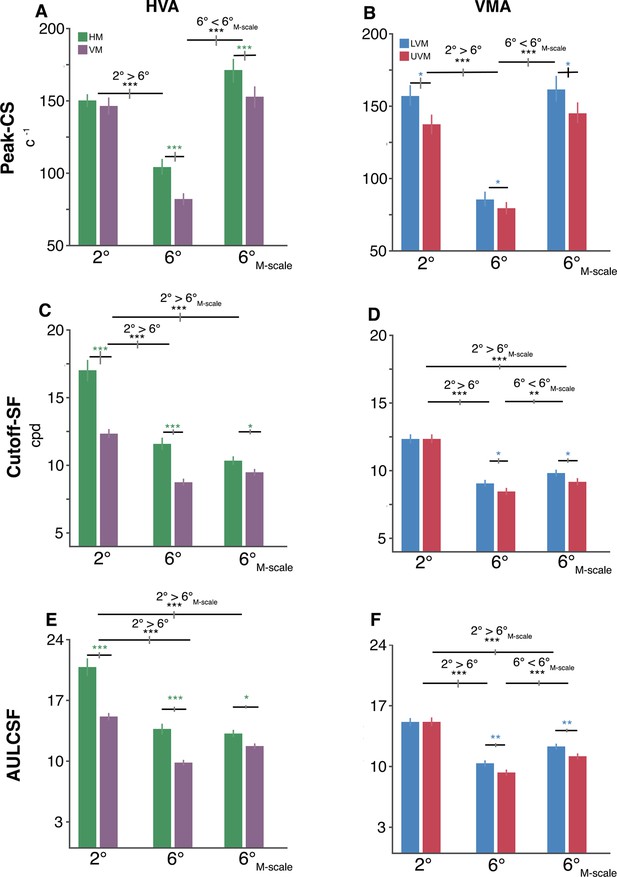
Polar angle asymmetries emerge in key contrast sensitivity function (CSF) attributes.

(**A, B**) Peak contrast sensitivity for the horizontal-vertical anisotropy (HVA) and vertical meridian asymmetry (VMA), respectively. (**C, D**) Cutoff-SF for the HVA and VMA, respectively. (**E, F**) Area under the log contrast sensitivity function (AULCSF) for the HVA and VMA, respectively. Each bar depicts the group-average (n=10) attribute at a given location, and error bars depict bootstrapped 68% confidence intervals. Horizontal gray lines denote significant comparisons of an ANOVA and of post hoc comparisons. The vertical lines displayed on the gray bars depict the 68% confidence interval for the differences between eccentricities or locations. Repeated-measures ANOVA; *p<0.05, **p<0.01, ***p<0.001.

The HVA emerged in the peak-CS only in the perifovea (interaction: F(2,18) = 18.33, p<0.001, η_G² = 0.671; Figure 5A). Peak-CS fell between 2° and 6° (HVA: p<0.001, 95% CI = [0.404 0.555], d = 4.52; VMA: p<0.001, 95% CI = [0.513 0.651], d = 6.039), increased in the perifovea after M-scaling (HVA: p<0.001, 95% CI = [-0.639–0.483], d = −5.14; VMA: p<0.001, 95% CI = [-0.681–0.562], d = −7.50), and did not differ between 2° and 6°_M-scale (p>0.1). Importantly, differences between HM and VM only emerged at 6° (p<0.001, 95% CI = [0.153 0.318], d = 2.04) and 6°_M-scale (p<0.01, 95% CI = [0.054 0.175], d = 1.35). In contrast, the VMA emerged at 2°, 6°, and 6°_M-scale (polar angle main effect: F(1,9) = 8.65, p<0.02, η_G² = 0.490; Figure 5B). These findings show that the HVA and VMA emerged in peak-CS, but the HVA only in the perifovea, whereas the VMA emerged at both eccentricities. Moreover, although M-scaling matched the peak-CS between the parafovea and perifovea, it did not equate contrast sensitivity around polar angle.

The HVA and VMA also emerged in the cutoff-SF, consistent with previous studies (Barbot et al., 2021; Wilkinson et al., 2016). M-scaling reduced the HVA extent (interaction: F(2,18) = 19.20, p<0.001, η_G² = 0.681; Figure 5C). The cutoff-SF decreased between HM and VM at 2° (p<0.001, 95% CI = [0.227 0.403], d = 2.56), 6° (p<0.001, 95% CI = [0.231 0.324], d = 4.24), and slightly less so at 6°_M-scale (p=0.0326, 95% CI = [0.0251 0.146], d = 1.01). Thus, M-scaling did not eliminate either the HVA or the eccentricity effect in the cutoff-SF; it was smaller at 6° (p<0.001, 95% CI = [0.318 0.409], d = 5.73) and 6°_M-scale (p<0.001, 95% CI = [0.324 0.431], d = 5.07) than at 2°.

The VMA extent in cutoff-SF only emerged in the perifovea (interaction: F(2,18) = 5.26, p=0.029, η_G² = 0.369; Figure 5D). It decreased between the LVM and UVM at 6° (p=0.0397, 95% CI = [0.0185 0.121], d = 0.972) and 6°_M-scale (p=0.0481, 95% CI = [0.0163 0.123], d = 0.935). Therefore, M-scaling did not eliminate either the VMA or the eccentricity effect in cutoff-SF (2° > 6°: p<0.001, 95% CI = [0.297 0.391], d = 5.25; 2° > 6°_M-scale: p<0.001, 95% CI = [0.235 0.291], d = 6.73). However, it increased the perifoveal cutoff-SF along the VM (6°_M-scale > 6°: p<0.005, 95% CI = [-0.119 –0.0437], d = −1.54). In short, the HVA in cutoff-SF occurred at both eccentricities but only in the perifovea for the VMA. Critically, M-scaling did not equate cutoff-SF among polar angles.

Similar to cut-off SF, the HVA in AULCSF was evident in both the peri- and parafovea (interaction: F(2,18) = 17.98, p<0.001, η_G² = 0.667; Figure 5E). AULCSF was greater for the HM than VM (HVA) for 2° (p<0.001, 95% CI = [3.866 7.540], d = 2.22), 6° (p<0.001, 95% CI = [2.956 4.792], d = 3.02), and 6°_M-scale (p<0.05, 95% CI = [0.569 2.314], d = 1.18). The AULCSF for HVA decreased between 2° and 6° (HVA: p<0.001, 95% CI = [5.440 6.988], d = 5.71) and between 2° and 6°_M-scale (p<0.001, 95% CI = [4.249 6.803], d = 3.096). M-scaling did not eliminate the AULCSF HVA (p=0.397, 95% CI = [–1.630 0.252], d = −0.523).

The VMA in AULCSF was only evident in the perifovea (interaction: F(2,18) = 7.27, p<0.005, η_G² = 0.447; Figure 5F). AULCSF was greater for the LVM than UVM at 6° (p=0.007, 95% CI = [0.479 1.634], d = 1.309) and at 6°_M-scale (p=0.010, 95% CI = [0.481 1.772], d = 1.248), but not at 2° (p=2.926, 95% CI = [–0.747 0.727], d = −0.01). The VMA extent decreased from 2° to 6° (p<0.001, 95% CI = [4.658 5.942], d = 5.91), from 2° to 6°_M-scale (p<0.001, 95% CI = [2.942 3.849], d = 5.36), and between 6° and 6°_M-scale (p<0.001, 95% CI = [-2.351–1.459], d = −3.05). Thus, M-scaling did not eliminate the VMA for AULCSF.

Next, we quantified the magnitude of the HVA and VMA for the 2°, 6°_M-scale peak-CS, cutoff-SF, and AULCSF measurements. The HVA magnitude was calculated as the percent increase from the VM to HM, whereas the VMA magnitude was calculated as the percent increase from the LVM to UVM. We ran a series of one-way ANOVAs, and when appropriate, used post hoc t-tests to assess how the HVA and VMA magnitudes changed between 2° and 6°, and 6° and 6°_M-scale conditions.

For peak-CS, the HVA magnitude (ANOVA: F(2,27) = 13.76, p<0.005) increased between 2° and 6° (p<0.001, CI = [-24.120 –11.691]). M-scaling the stimulus reduced, but did not eliminate the HVA magnitude (p=0.016, CI = [2.343 17.407]; Figure 6A). The VMA magnitude (ANOVA: F(2,27) = 0.51, p=0.6047) did not change between 2° and 6°, nor after M-scaling (Figure 6B).

Figure 6

Download asset Open asset

Horizontal-vertical anisotropy (HVA) and vertical meridian asymmetry (VMA) magnitudes for peak contrast sensitivity, spatial frequency cutoff, and area under the log contrast sensitivity function curve (AULCSF).

(**A, B**) Peak contrast sensitivity for the HVA and VMA, respectively, at 2°, 6°, and 6°_M-scale. (**C, D**) Cutoff-SF for the HVA and VMA, respectively, at 2°, 6°, and 6°_M-scale. (**E, F**) AULCSF for the HVA and VMA, respectively, at 2°, 6°, and 6° M-scaled. n=10. Error bars representing ±1 standard error of the mean (SEM) and horizontal gray lines denote significant comparisons of an ANOVA and post hoc comparisons. Vertical lines displayed on the gray bars denote the standard error of the difference (SED). *p<0.05, **p<0.01, ***p<0.001.

For cutoff-SF, the HVA magnitude (ANOVA: F(2,27) = 17.44, p<0.001) did not change between 2° and 6° (p=0.230, CI = [–1.904 6.927]), and although M-scaling reduced the HVA magnitude (p<0.001, CI = [8.661 23.721]), the HVA was still evident in the 6°_M-scale condition. The VMA magnitude (ANOVA: F(2,27) = 3.93, p=0.031) increased between 2° and 6° (p=0.028, CI = [-12.472 –0.902]), and M-scaling did not alter the VMA magnitude at 6° (p=0.985, CI = [–5.844 5.948]).

For AULCSF, the HVA magnitude (ANOVA: F(2,27) = 12.82, p<0.001) did not change between 2° and 6° (p=0.443, CI = [–5.605 2.671]), and although M-scaling reduced the HVA magnitude (p<0.001, CI = [9.181 25.393]), the HVA was still evident in the 6°_M-scale condition. The VMA magnitude (ANOVA: F(2,27) = 6.25, p=0.0177) increased between 2° and 6° (p=0.009, CI = [-18.323 –2.257]), but M-scaling did not alter the VMA magnitude at 6° (p=0.682, CI = [–4.615 6.732]).

These data show that M-scaling stimulus size based on its cortical representation eliminates differences in contrast sensitivity as a function of eccentricity, but not polar angle. fMRI work shows that there is an HVA and VMA in V1 surface area (Benson et al., 2021; Himmelberg et al., 2023a; Himmelberg et al., 2022b, Himmelberg et al., 2021; Silva et al., 2018), and that individual differences in these cortical asymmetries correlate with contrast sensitivity measurements (Himmelberg et al., 2022b). Here, we measured the distribution of V1 surface area at the polar angle meridians and confirmed that individual measurements of V1 surface area correlate with contrast sensitivity across our observers. We correlated the amount of V1 surface area representing ±15° wedge-ROIs (1–8° of eccentricity) centered along the HM, UVM, and LVM of the visual field with the respective peak-CS measurement at 2°, 6°, and 6°_M-scale for 7 of our 10 observers for whom we could obtain fMRI-derived retinotopic maps.

First, and in line with previous work, at the group level, there was more V1 surface area representing the HM than VM (p=0.001), and the LVM than UVM of the visual field (p=0.031) (Figure 7A). Next, we found that, across observers, V1 surface area measurements taken from a meridian correlated (one-tailed Spearman’s correlations) with the contrast sensitivity measurements from the corresponding meridian for the 6° (r = 0.40, p=0.036; Figure 7C) and 6°_M-scale (r = 0.39, p=0.040; Figure 7D) stimulus conditions, but not 2° (r = 0.16, p=0.400; Figure 7B). These positive correlations indicate that, for our observers, V1 surface area is linked to contrast sensitivity measurements, thus M-scaling should correct for polar angle differences in the cortical representation. However, correlating the difference in contrast sensitivity at each meridian, after M-scaling the stimulus size, against V1 surface area at the corresponding meridian yield a nonsignificant correlation (two-tailed Spearman’s correlation; r = 0.20, p=0.393).The finding that M-scaling does not correct for the cortical representation at the HM, LVM, and UVM supports the 'qualitative hypothesis' – that there are additional underlying neural and computational factors beyond V1 cortical magnification that contribute to perceptual polar angle asymmetries.

Figure 7

Download asset Open asset

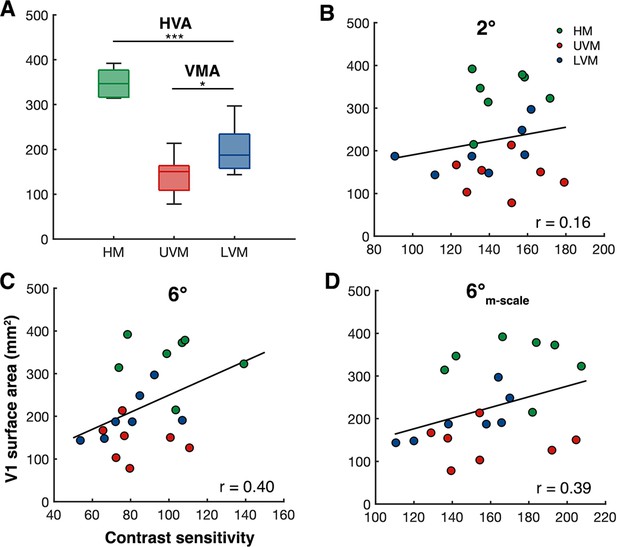
Individualized V1 surface area measurements at the cardinal meridians correlate with peak contrast sensitivity measurements.

(A) Group-level V1 surface area measurements (n=7) taken from the cortical representation of the horizontal meridian (HM) (mean of left and right HM), the upper vertical meridian (UVM), and lower vertical meridian (LVM). *p<0.05, ***p<0.001. (**B–, C**) Between-subject Spearman’s correlations of V1 surface area (±15° of angle, 1–8° eccentricity) at each meridian with peak contrast sensitivity measurements (n = 7, 3 measurements per observer) at the same meridian for (B) 2°, (C) 6°, and (D) 6°-_M-scale stimulus conditions.

Discussion

We investigated whether the quantitative or qualitative hypothesis can explain the differences in contrast sensitivity and acuity across eccentricity and around polar angle in the visual field. We found that M-scaling stimulus size, to equate for the differences of cortical representation as function of eccentricity and polar angle, eliminated the differences in contrast sensitivity as a function of eccentricity, in line with the quantitative hypothesis, but not polar angle, in line with the qualitative hypothesis.

M-scaling eliminates differences in contrast sensitivity as a function of eccentricity

Converging neural evidence demonstrates that cortical magnification limits peripheral vision. V1 surface area across eccentricity correlates with various perceptual measures, including acuity (Duncan and Boynton, 2003; Song et al., 2015), perceived angular size (Murray et al., 2006), and perceived object size (Schwarzkopf et al., 2011; Schwarzkopf and Rees, 2013). These perceptual differences across eccentricity arise from quantitative differences in the number of neurons for foveal and peripheral eccentricities. Consequently, accounting for cortical magnification via M-scaling diminishes or eliminates eccentricity effects. Our present results support these findings; M-scaling stimulus size diminished the difference in contrast sensitivity and acuity between 2° and 6°, indicating that cortical magnification predominantly underlies performance differences as a function of eccentricity.

M-scaling does not eliminate differences in contrast sensitivity as a function of polar angle

In contrast to the effect on eccentricity, M-scaling stimulus size did not eliminate differences in contrast sensitivity as a function of polar angle. After M-scaling stimulus size based on the meridian-dependent functions provided by Rovamo and Virsu, 1979, the HVA and VMA remained.

The finding that M-scaling does not eliminate polar angle asymmetries for contrast sensitivity and acuity is surprising as perceptual polar angle asymmetries have been linked to V1 cortical magnification. First, psychophysical measures of the HVA and VMA magnitude for contrast sensitivity (Abrams et al., 2012; Himmelberg et al., 2022b; Himmelberg et al., 2020) and acuity (Barbot et al., 2021; Benson et al., 2021) provide a close match with the cortical HVA and VMA; there is ~60% more V1 tissue representing the HM than VM, and ~25% more representing the LVM than UVM (Benson et al., 2021; Himmelberg et al., 2021; Himmelberg et al., 2023a; Himmelberg et al., 2022b). Thus, there are asymmetries in the distribution of V1 neurons that parallel behavior. Second, individual differences in contrast sensitivity at each of the cardinal meridians correlate with localized measures of the amount of V1 surface representing the same meridians (Himmelberg et al., 2022b). We found the same correlation for the contrast sensitivity measurements here, albeit with a reduced number of observers – which speaks to the high-level of reproducibility of location-specific brain–behavior correlations using retinotopic data (Himmelberg et al., 2022a). Thus, M-scaling stimulus size to compensate for cortical magnification around the polar angle should, in principle, equate contrast sensitivity. But here, we found it does not.

Our data showed that the magnitude of the HVA was larger than the VMA, consistent with prior work (Himmelberg et al., 2020). The magnitude of the HVA and VMA differed among the three stimulus conditions (2°, 6°, and 6°_M-scale) for the key CSF properties: (1) peak-CS, (2) SF-cutoff, and (3) AULCSF. (1) For peak-CS, there was a relatively weak HVA at 2°. The HVA magnitude increased at 6° eccentricity, consistent with previous studies (Baldwin et al., 2012; Carrasco et al., 2001; Fuller et al., 2008; Greenwood et al., 2017), and was still evident after the M-scaling stimulus size. On the other hand, the VMA magnitude was consistent across at 2°, 6°, and after M-scaling. Thus, both the HVA and VMA remained after M-scaling for peak-CS. (2) For cutoff-SF, the data showed a large HVA at 2° and 6°. M-scaling stimulus size decreased the magnitude of the HVA, but nonetheless the HVA remained. Likewise, the VMA for cutoff-SF remained after M-scaling stimulus size. (3) The HVA and VMA magnitude for AULCSF mimicked the results found for cutoff-SF; the HVA magnitude was large for 2° and 6°, and was reduced – but still clear – after M-scaling. The VMA was evident at 6° and persisted after M-scaling. Overall, across our three key CSF parameters, M-scaling stimulus size decreased the magnitude of the HVA and VMA, but did not eliminate the perceptual asymmetries. Thus, the asymmetries persisted after equating for their cortical representation.

There was an apparent reduction in the HVA extent at a high SF (8 cpd, Figure 4D). This may have resulted from the fact that M-scaling the stimulus slightly increased cutoff-SF for the VM, consistent with the notion that it should reduce the effect of eccentricity, but slightly decreased the cutoff-SF for the HM, which was unexpected (Figure 5C). Indeed, we found that individual scores for these differences were marginally correlated (r = 0.54, p=0.056), suggesting that for the same observers for whom M-scaling reduced the detrimental effect of eccentricity more along the VM, surprisingly it had the opposite effect for the HM. We do not know the source of this effect.

Might M-scaling eliminate polar angle asymmetries for visual dimensions other than contrast sensitivity? Polar angle asymmetries have been identified for fundamental basic visual properties (e.g., contrast sensitivity; Abrams et al., 2012; Baldwin et al., 2012; Cameron et al., 2002; Himmelberg et al., 2020; Pointer and Hess, 1989; Silva et al., 2008; acuity; Barbot et al., 2021; Greenwood et al., 2017; Kwak et al., 2023; Schwarzkopf, 2019; Wang et al., 2020), for mid-level properties (e.g., crowding; Greenwood et al., 2017; Petrov and Meleshkevich, 2011) and texture segmentation (Barbot et al., 2021; Greenwood et al., 2017; Kwak et al., 2023; Talgar and Carrasco, 2002; Wang et al., 2020), and for higher-order properties (e.g., speed of information accrual; Carrasco et al., 2004; numerosity processing; Chakravarthi et al., 2022; face perception; Afraz et al., 2010; Peterson and Eckstein, 2013; and perceived object size; Schwarzkopf, 2019). However, contrast sensitivity is the currency of the visual system, which most – if not all – visual dimensions depend upon in some capacity. Thus, if M-scaling does not eliminate the polar angle asymmetries at the most fundamental level, then it is unlikely to eliminate asymmetries for higher-order dimensions – although this has yet to be empirically tested.

Together, these novel findings support the ‘qualitative’ hypothesis. M-scaling stimulus size based on the cortical representation as a function of polar angle diminished – but did not eliminate – the HVA, and had no effect on the VMA. These findings suggest that performance differences as a function of polar angle are likely to be mediated by both the cortical representation and by differential computations or image-processing capabilities of these neurons (i.e., differently tuned spatial filters).

We note that observers’ viewing distance changed when the stimuli were presented at the HM and the VM for the non-scaled stimulus size. This change in distance changed monitor luminance (23 cd/m² and 19 cd/m², respectively). However, this change in luminance is not large enough to significantly affect contrast measurements (Rahimi-Nasrabadi et al., 2021). Moreover, these asymmetries in contrast sensitivity have been reported in many studies for which the viewing distance has been constant (Abrams et al., 2012; Baldwin et al., 2012; Barbot et al., 2021; Cameron et al., 2002; Carrasco et al., 2022; Carrasco et al., 2001; Hanning et al., 2022a; Himmelberg et al., 2022b; Himmelberg et al., 2020; Pointer and Hess, 1989; Regan and Beverley, 1983; Rijsdijk et al., 1980; Robson and Graham, 1981; Rosén et al., 2014; Silva et al., 2008).

What mechanism might underlie perceptual polar angle asymmetries?

If M-scaling stimulus size does not eliminate the polar angle asymmetries for contrast sensitivity, then what might be their underlying substrate? Perceptual asymmetries have been linked to the V1 properties (surface area, population receptive field [pRF] size, and BOLD amplitude) at the group- (Benson et al., 2021; Himmelberg et al., 2021; Liu et al., 2006; Moutsiana et al., 2016; O’Connell et al., 2016; Silva et al., 2018) and individual level (Himmelberg et al., 2022b). Further, here we show that individual differences in contrast sensitivity in our own data correlate with individual differences in V1 surface area along the polar angle meridians. Thus, the asymmetries must be explained by cortical magnification to some extent. What factors beyond neural count could contribute to the perceptual asymmetries, for which M-scaling cannot account for? To answer this, we are currently using reverse correlation to investigate whether and how eccentricity (Xue et al., 2022) and polar angle (Xue and Carrasco, 2023) alter orientation and SF tuning functions.

M-scaling has been shown to work for fundamental visual dimensions (Cowey and Rolls, 1974; Di Russo et al., 2005; Himmelberg and Wade, 2019; Levi et al., 1999; Ludvigh, 1941; Rovamo et al., 1978; Virsu et al., 1982; Virsu and Rovamo, 1979; Wertheim, 1894) – and fail for others, typically (but not always) more complex dimensions (Hilz et al., 1981; Levi and Klein, 1986; Solomon and Sperling, 1995; Strasburger et al., 1994; Strasburger et al., 1991; Tyler, 1999). Critically, here we found that for the same visual task and dimension, M-scaling stimulus size works for certain locations – eccentricity – but fails for others – cardinal polar angles. One possibility is that between-subject variability in the V1 polar angle representation underlies the inability of M-scaling to extinguish perceptual polar angle asymmetries. There is substantial variability in the size of V1 (Benson et al., 2022; Dougherty et al., 2003; Himmelberg et al., 2022b; Moutsiana et al., 2016) and how V1 tissue is distributed throughout the visual field (Benson et al., 2022; Himmelberg et al., 2023a; Himmelberg et al., 2022b). Another possibility is that there is greater variability in the cortical representation of polar angle compared to eccentricity that is not accounted for by the M-scaling equations that were derived from group-level data (Rovamo and Virsu, 1979). Finally, although we found a significant correlation between V1 surface area and contrast sensitivity at each meridian, we did not find a correlation between V1 surface area and the change in contrast sensitivity after M-scaling at each meridian. This suggests that even if stimulus size were adjusted via M-scaling equations based on individualized V1 surface measures, the perceptual asymmetries would likely remain.

Conclusions

We used psychophysics to probe the neural substrates of contrast sensitivity across and around the visual field. We found striking polar angle asymmetries in contrast sensitivity, which were as pronounced as tripling eccentricity. The asymmetries were still present after M-scaling stimulus size. The M-scaling estimate provided by Rovamo and Virsu, 1979 at the group level eliminated the decline in contrast sensitivity with eccentricity, but only diminished the HVA, and did not alter the VMA. These findings reveal that limits in contrast sensitivity across eccentricity and around polar angle likely emerge from different anatomical and computational constraints, and challenge the generalizability of the established view that cortical magnification limits basic visual perception throughout the visual field (Duncan and Boynton, 2003; Rovamo and Virsu, 1979; Schwarzkopf et al., 2011; Schwarzkopf and Rees, 2013; Song et al., 2015; Virsu and Rovamo, 1979). Although differences in contrast sensitivity at different eccentricities are predominantly mediated by cortical magnification, differences as a function of polar angle must be constrained by additional computational and neural image-processing capabilities. Models of spatial vision linking brain and behavior should account for what constrains basic visual perception not only across – but also around – the visual field.

Methods

Observers

We based our sample size on research on the impact of eccentricity (Jigo and Carrasco, 2020) and polar angle asymmetries on contrast sensitivity (Cameron et al., 2002) and acuity (Barbot et al., 2021). Ten observers with normal or corrected-to-normal vision participated in three conditions (eight females, aged 21–32 y, two authors: MJ and DT). All observers provided written informed consent under the University Committee’s protocol on Activities Involving Human Subjects at New York University agreeing to participate in the study and the public release of their data. All experimental procedures were approved by the Ethics Committee at the NYU Department of Psychology (IRB: FY2016-466) and in agreement with the Declaration of Helsinki. All observers, except the authors, were naïve to the purpose of the study and were paid $12/hr. Data and code pertaining to the experiment are available on the OSF repository (https://osf.io/gvkdh/; Jigo et al., 2023).

Stimuli

Gratings

Sinusoidal gratings with an SF of 0.5, 1, 1.4, 2, 2.8, 4, 8, or 11.3 cpd served as targets. For the HM condition, stimuli appeared along the left and right HM at 2° and 6° eccentricity. Similarly, stimuli appeared at the same eccentricities but along the upper and LVM for the VM condition. During the HM and VM conditions, a two-dimensional cosine function (4° wide, centered on the grating’s peak luminance) windowed each grating at 2° and 6° eccentricity. For the M-scale condition, gratings appeared at 6° eccentricity along HM and VM. We scaled grating sizes separately for each polar angle, based on meridian-dependent M-scaling equations (Rovamo and Virsu, 1979), resulting in gratings that subtended 7.68° for the LVM, 7.70° for the UVM, and 7.08° for the HM.

Specifically, we computed M-scaled sizes as

S_{X b} = \frac{S_{X a} \times M_{X a}}{M_{X b}}

where $S_{X b}$ corresponds to the magnified size in degrees of visual angle along meridian $X$ at eccentricity $b$ . This M-scaled size equates the cortical representation with that of a grating of size $S_{X a}$ , which equaled 4°, positioned along the same meridian but at a different eccentricity $a$ . $M_{X a}$ and $M_{X b}$ correspond to cortical magnification in mm/° along a given meridian $X$ at eccentricity $a$ and $b$ , respectively.

Cortical magnification differed among meridians. For the LVM:

M_{L V M} = M_{0} (1 + 0.42 E + 0.000055 E^{3})^{- 1}

where $M_{0}$ corresponds to cortical magnification at the central fovea, which was set to 7.99 mm/° and $E$ corresponds to the eccentricity of the stimulus.

Similarly, for the UVM:

M_{U V M} = M_{0} (1 + 0.42 E + 0.00012 E^{3})^{- 1}

For the HM, we used the cortical magnification equations for both the nasal ( $N$ ) and temporal ( $T$ ) meridians:

M_{N} = M_{0} (1 + 0.33 E + 0.00007 E^{3})^{- 1}

M_{T} = M_{0} (1 + 0.29 E + 0.000012 E^{3})^{- 1}

and computed the M-scaled size at eccentricity $b$ for the HM ( $S_{H M_{b}}$ ) using the average among M-scaled sizes for nasal ( $S_{N b}$ ) and temporal meridians ( $S_{T b}$ ):

S_{H M_{b}} = 0.5 ({S_{N b} + S_{T b})}_{}

Cues

‘Ready cues’ prepared observers for the onset of the grating stimuli and ‘response cues’ indicated which gratingto respond to. Response cues comprised a pair of white dots displaced 3.75° from the VM or HM for target gratings that appeared at those respective locations. Ready cues comprised the same white dots that appeared at all possible target locations for the HM (i.e., LHM and RHM) and VM (i.e., UVM and LVM) conditions.

Fixation and background

Observers maintained their gaze on a gray fixation cross (17 cd/m²) that subtended 0.35° and remained on the screen throughout the entire experiment. All stimuli appeared on a medium gray display background (26 cd/m²).

Apparatus

We generated visual stimuli on an Apple iMac using MGL (Gardner et al., 2018), a set of OpenGL libraries running in MATLAB (MathWorks, Natick, MA). Stimuli were displayed on a cathode ray tube (CRT) monitor (1280 × 960; 100 Hz). We gamma-corrected the monitor at a central location using a Konica Minolta LS-100 (Tokyo, Japan) with 8-bit accuracy. Observers sat in a dark and sound-proofed room and viewed the display binocularly with their heads stabilized by a chin-and-head rest positioned either 57 cm (VM and M-scale conditions) or 115 cm (HM condition, to display the highest SF tested, 16 cpd). The mean luminance of the display (from retina to monitor) was 23 cd/m² at 57 cm and 19 cd/m² at 115 cm. This difference in luminance does not significantly affect pupil size (<0.5 mm) or contrast sensitivity (Rahimi-Nasrabadi et al., 2021; Rovamo et al., 1992). An Eyelink 1000 eye tracker (S.R. Research, Ottawa, Ontario, Canada) monitored monocular eye position at 500 Hz (Cornelissen et al., 2002).

Behavioral protocol

We instructed observers to maintain fixation. Stimulus presentation was contingent upon fixation on a central cross for 100 ms, after which the ready cue appeared (60 ms for the dots, 300 ms for the ‘N’). The cue informed observers of the temporal onset of the target grating but provided no information about its location. Following an interstimulus interval (ISI; 40 ms for the dots, 100 ms for the ‘N’), four gratings with the same SF appeared for 150 ms. Grating contrast varied for each trial, determined by independent adaptive titration procedures for each grating (see ‘Titration’). A 100 ms ISI and the response cue followed the grating presentation. The response cue indicated which grating observers should report on each trial. Observers performed an orientation discrimination task. They used the right or left arrow keys on a keyboard to report whether the cued grating was tilted left or right of vertical. If the eye blinked or deviated >1° from fixation, the trial was immediately aborted and rerun at the end of the block.

Observers were instructed to be as accurate as possible,without time stress. They received auditory feedback for incorrect responses on a trial-by-trial basis. Once observers finished a block, the monitor displayed their overall accuracy (percent correct) as feedback.

Procedure

Observers performed three conditions: HM, VM, and M-scale. For the HM condition, they completed 1080 trials per location (left and right HM; 160 trials per SF), for the VM condition 1344 per location (UVM and LVM; 140 trials per SF), and for the M-scale condition 1008 per location (84 trials per SF). On each trial, we randomly interleaved the target’s orientation, SF, eccentricity, and/or polar angle (either left and right HM, or UVM and LVM), and adjusted grating contrast based on task performance (see ‘Titration’). Before the main experimental sessions, observers completed a single practice block of trials to familiarize themselves with the stimuli and task.

Titration

For VM and M-scale conditions, we titrated contrast separately for each combination of SF, eccentricity, and polar angle with best PEST, a maximum likelihood adaptive procedure, using custom code (https://github.com/michaeljigo/palamedes_wrapper; Jigo, 2021) that ran subroutines implemented in the Palamedes toolbox (Prins and Kingdom, 2018). For HM, we used a 3-down, 1-up weighted staircase (García-Pérez, 1998). Both titration procedures targeted 75% task performance.

Parametric contrast sensitivity model

We fit a parametric model that linked contrast response functions (CRFs) and CSFs to observers’ binary decisions (CW vs. CCW) on individual trials. Our model includes (1) a logistic function for the CRF, with slope fixed across SF (Jigo and Carrasco, 2020) and asymptotes matched to the specifications of the adaptive titration procedure; (2) nine candidate models of the CSF; and (3) six visual field models that specify how contrast sensitivity changes with eccentricity and polar angle.

CRF

We characterized the CRF – performance as a function of log₁₀-transformed contrast – using a logistic function (Equation 7) with lower and upper asymptotes ( $p_{l} = 0.5$ , $p_{u} = 0.99$ ) and slope ( $κ = 11.8$ ) matching the specifications of the adaptive titration procedure, as well as a log₁₀-transformed contrast threshold ( $c_{t} (f, r, θ)$ , Equation 8) that targets 75% discrimination accuracy ( $p_{t}$ =0.75) at each SF ( $f$ ), eccentricity ( $r$ ) and polar angle ( $θ$ ):

p (c, f, r, θ) = s (\frac{1}{1 + e x p (- κ (c - t))}) + p_{l}

where $s = 1 - (1 - p_{u}) - p_{l}$ , which scales the dynamic range of the function. Because contrast was log₁₀-transformed, adjusting the contrast threshold in Equation 7 yields rigid shifts in logarithmic contrast.

In Equation 7, $t$ corresponds to a transformation of contrast threshold, which ensures $p_{t}$ is accurately targeted given the constraints of the logistic function’s slope, upper and lower asymptotes:

t (c_{t} (f, r, θ), p_{r}) = c_{t} (f, r, θ) - κ^{- 1} l o g (\frac{p_{r}}{1 - p_{r}})

where $p_{r}$ denotes the ratio between the targeted performance level and the dynamic range of the CRF: $p_{r} = \frac{p_{t} - p_{l}}{s}$ .

CSF

Contrast sensitivity typically peaks at a given SF and declines precipitously for higher SFs and gradually for lower SFs (Chakravarthi et al., 2022; Chung and Legge, 2016; Kelly, 1977; Corbett and Carrasco, 2011). We implemented this pattern by constraining the contrast threshold ( $c_{t} (f, r, θ)$ in Equation 8) across SF to adhere to a functional form of the CSF. We implemented nine candidate CSF models that each determined contrast sensitivity ( $c_{t}^{- 1}$ ) as a function of SF ( $f$ ) at each eccentricity ( $r$ ) and polar angle ( $θ$ ) using three or four parameters (Table 1).

Visual field models

We implemented six models at the group level, specifying how CSFs change across eccentricity and polar angle. For each model, we iteratively fixed the CSF’s parameters to permit or restrict the impact of eccentricity, HVA, and/or VMA on contrast sensitivity (Figure 3). For example, the most permissive model (‘Ecc + HVA + VMA,’ Table 2) allowed CSFs to vary freely across eccentricity and polar angle, which yielded 24 parameters for CSF models with four parameters (e.g., YQM model, Table 1; 4 parameters × 2 eccentricities × 3 polar angles = 24 parameters, Table 2). In contrast, the most restrictive model (‘-Ecc – HVA – VMA,’ Table 2) enforced a single CSF at all visual field locations, yielding only four parameters. A detailed breakdown of the model alternatives is presented in Table 2. We additionally assessed whether CSFs depended on the pre-cue presented to observers in the fixed-size conditions and found that they did not.

Model fitting

Our parametric contrast sensitivity model generates the probability that an observer will correctly judge a grating’s orientation as a function of contrast, SF, and visual field location (Equation 7). We optimized the model’s parameters via maximum likelihood estimation. We considered performance at each contrast, SF, eccentricity, and polar angle as independent Bernoulli random variables and minimized the negative log-likelihood for an observer’s responses using fmincon in the MATLAB Optimization Toolbox. This procedure maximized the power of our analyses by leveraging each data point (i.e., trial).

We performed model fitting at the group level and in two stages to (1) identify the best-fitting CSF model and (2) determine the appropriate visual field model. To identify the best CSF model, we fit each CSF model (Table 1) to the group-level behavioral responses across all three conditions (HM, VM, and M-scale). For these fits, the CSFs followed the most permissive visual field model (Ecc + HVA + VMA, Table 2). Model comparisons determined the best-fitting CSF model (see ‘Model comparisons’).

After identifying the best CSF model, we determined which visual field model corresponded best to the observers’ contrast sensitivity across eccentricity and polar angle. To this end, we fit each visual field model (Table 2) to the group-level responses to fixed-size grating stimuli (HM and VM conditions) because these stimuli yield robust variations in contrast sensitivity across eccentricity and polar angle (Abrams et al., 2012; Cameron et al., 2002; Carrasco et al., 2001; Himmelberg et al., 2020; Jigo and Carrasco, 2020). For these fits, we used the best-fitting CSF model identified in stage 1.

Model comparisons

We compared CSF models (Table 1) and visual field models (Table 2). The difference in BIC values between model variants indexed model performance, with lower values corresponding to better performance. We calculated BIC values as $B I C = - 2 k l o g (n) L$ , where $k$ denotes the number of model parameters, $n$ denotes the number of trials, and $L$ corresponds to a model’s maximized log-likelihood.

Quantifying the extent of eccentricity effects and polar angle asymmetries

We quantified the impact of changing visual field location (e.g., 2° to 6°) as the percent change in contrast sensitivity ( $Δ c_{t}^{- 1}$ ) between one location ( $l_{1}$ ) and the other ( $l_{2}$ ), normalized by the average contrast sensitivity among locations (Equation 9):

Δ c_{t}^{- 1} = 100 \frac{l_{1} - l_{2}}{0.5 (l_{1} + l_{2})}

CSF attributes

For each observer, we extracted key CSF attributes from the best-fitting CSF model: peak-CS, peak-SF, cutoff-SF, AULCSF, and SF bandwidth. Because not all CSF models in Table 1 have parameters that map onto these attributes, we evaluated the CSF between 0.25 cpd and 24 cpd. We defined the peak-CS as the maximum contrast sensitivity of the CSF, the peak-SF as the SF at which peak-CS occurred, the cutoff-SF as the SF at which contrast sensitivity reached its minimum value of 1, and the SF bandwidth as the number of octaves spanned at the CSF’s full-width-at-half-maximum.

fMRI analysis

We were able to obtain seven observers population receptive field (pRF) (Dumoulin and Wandell, 2008) and anatomical data from the NYU Retinotopy Database (Himmelberg et al., 2021). These retinotopy data were used to calculate the amount of V1 surface area representing the HM, LVM, and UVM in each observer’s V1 map. The pRF stimulus, MRI and fMRI acquisition parameters, MRI and fMRI preprocessing (Esteban et al., 2019), the implementation of the pRF model, and the computation of the amount of V1 surface area represented by wedge-ROIs centered on the cardinal meridians of the visual field, were identical to the methods described in our prior work (Himmelberg et al., 2022b; Himmelberg et al., 2021). In brief, we calculated the amount of V1 surface area representing the HM (mean of left and right HM), the UVM, and the LVM by defining ±15° wedge-ROIs in the visual field that were centered along the four polar angle meridians. Each wedge-ROI extended from 1 to 8° of eccentricity. The amount of V1 surface area encapsulated by these wedge-ROIs was calculated by summing the surface (mm²) of the vertices that had pRF centers within these wedge-ROIs. The output of this analysis is the amount of V1 surface area (mm²) representing the wedge-ROIs at each meridian. Any differences in V1 surface area derived from these wedge-ROIs can be considered to index differences in cortical magnification – either among meridians or among observers.

Statistical analyses

We used repeated-measures ANOVAs followed by paired t-tests for post hoc comparisons. All post hoc comparisons were Bonferroni-corrected for multiple comparisons. All p-values for repeated-measures ANOVAs in which the assumption of sphericity was not met were Greenhouse–Geisser corrected. Each ANOVA assessed how M-scaling affected the extent of eccentricity effects and polar angle asymmetries. We used separate ANOVAs to assess how M-scaling affected the perifoveal HVA and VMA. We report effect sizes in terms of generalized eta squared (η_G²) for ANOVAs and Cohen’s d for t-tests.

Data availability

Data and code pertaining to the experiment are available on the OSF repository (https://osf.io/gvkdh/; Jigo et al., 2023).

The following data sets were generated

(2023) Open Science Framework
Mscaling eliminates contrast sensitivity across not around.

https://doi.org/10.17605/OSF.IO/GVKDH

References

(2012) Isoeccentric locations are not equivalent: the extent of the vertical meridian asymmetry
Vision Research 52:70–78.

https://doi.org/10.1016/j.visres.2011.10.016
- PubMed
- Google Scholar
(2010) Spatial heterogeneity in the perception of face and form attributes
Current Biology 20:2112–2116.

https://doi.org/10.1016/j.cub.2010.11.017
- PubMed
- Google Scholar
1. Anton-Erxleben K
2. Carrasco M
(2013) Attentional enhancement of spatial resolution: linking behavioural and neurophysiological evidence
Nature Reviews. Neuroscience 14:188–200.

https://doi.org/10.1038/nrn3443
- PubMed
- Google Scholar
(2012) The attenuation surface for contrast sensitivity has the form of a witch’s HAT within the central visual field
Journal of Vision 12:23.

https://doi.org/10.1167/12.11.23
- PubMed
- Google Scholar
(2021) Asymmetries in visual acuity around the visual field
Journal of Vision 21:2.

https://doi.org/10.1167/jov.21.1.2
- PubMed
- Google Scholar
1. Benson NC
2. Kupers ER
3. Barbot A
4. Carrasco M
5. Winawer J
(2021) Cortical magnification in human visual cortex parallels task performance around the visual field
eLife 10:e67685.

https://doi.org/10.7554/eLife.67685
- PubMed
- Google Scholar
1. Benson NC
2. Yoon JMD
3. Forenzo D
4. Engel SA
5. Kay KN
6. Winawer J
(2022) Variability of the surface area of the V1, V2, and V3 maps in a large sample of human observers
The Journal of Neuroscience 42:8629–8646.

https://doi.org/10.1523/JNEUROSCI.0690-21.2022
- PubMed
- Google Scholar
(2002) Covert attention affects the psychometric function of contrast sensitivity
Vision Research 42:949–967.

https://doi.org/10.1016/s0042-6989(02)00039-1
- PubMed
- Google Scholar
1. Campbell FW
2. Robson JG
(1968) Application of Fourier analysis to the visibility of gratings
The Journal of Physiology 197:551–566.

https://doi.org/10.1113/jphysiol.1968.sp008574
- PubMed
- Google Scholar
1. Carrasco M
2. Frieder KS
(1997) Cortical magnification neutralizes the eccentricity effect in visual search
Vision Research 37:63–82.

https://doi.org/10.1016/s0042-6989(96)00102-2
- PubMed
- Google Scholar
(1998) Feature asymmetries in visual search: effects of display duration, target eccentricity, orientation and spatial frequency
Vision Research 38:347–374.

https://doi.org/10.1016/s0042-6989(97)00152-1
- PubMed
- Google Scholar
(2001) Characterizing visual performance fields: effects of transient covert attention, spatial frequency, eccentricity, task and set size
Spatial Vision 15:61–75.

https://doi.org/10.1163/15685680152692015
- PubMed
- Google Scholar
(2004) Temporal performance fields: visual and attentional factors
Vision Research 44:1351–1365.

https://doi.org/10.1016/j.visres.2003.11.026
- PubMed
- Google Scholar
1. Carrasco M
2. Roberts M
3. Myers C
4. Shukla L
(2022) Visual field asymmetries vary between children and adults
Current Biology 32:R509–R510.

https://doi.org/10.1016/j.cub.2022.04.052
- PubMed
- Google Scholar
(2022) Visual field asymmetries in numerosity processing
Attention, Perception & Psychophysics 84:2607–2622.

https://doi.org/10.3758/s13414-022-02585-1
- PubMed
- Google Scholar
1. Chung STL
2. Legge GE
(2016) Comparing the shape of contrast sensitivity functions for normal and low vision
Investigative Ophthalmology & Visual Science 57:198–207.

https://doi.org/10.1167/iovs.15-18084
- PubMed
- Google Scholar
1. Corbett JE
2. Carrasco M
(2011) Visual performance fields: frames of reference
PLOS ONE 6:e24470.

https://doi.org/10.1371/journal.pone.0024470
- PubMed
- Google Scholar
(2002) The eyelink toolbox: eye tracking with Matlab and the psychophysics toolbox
Behavior Research Methods, Instruments, & Computers 34:613–617.

https://doi.org/10.3758/bf03195489
- PubMed
- Google Scholar
1. Cowey A
2. Rolls ET
(1974) Human cortical magnification factor and its relation to visual acuity
Experimental Brain Research 21:447–454.

https://doi.org/10.1007/BF00237163
- PubMed
- Google Scholar
1. Di Russo F
2. Pitzalis S
3. Spitoni G
4. Aprile T
5. Patria F
6. Spinelli D
7. Hillyard SA
(2005) Identification of the neural sources of the pattern-reversal VEP
NeuroImage 24:874–886.

https://doi.org/10.1016/j.neuroimage.2004.09.029
- PubMed
- Google Scholar
(2003) Visual field representations and locations of visual areas v1/2/3 in human visual cortex
Journal of Vision 3:586–598.

https://doi.org/10.1167/3.10.1
- PubMed
- Google Scholar
1. Dumoulin SO
2. Wandell BA
(2008) Population receptive field estimates in human visual cortex
NeuroImage 39:647–660.

https://doi.org/10.1016/j.neuroimage.2007.09.034
- PubMed
- Google Scholar
1. Duncan RO
2. Boynton GM
(2003) Cortical magnification within human primary visual cortex correlates with acuity thresholds
Neuron 38:659–671.

https://doi.org/10.1016/s0896-6273(03)00265-4
- PubMed
- Google Scholar
(1994) FMRI of human visual cortex
Nature 369:525.

https://doi.org/10.1038/369525a0
- PubMed
- Google Scholar
1. Esteban O
2. Markiewicz CJ
3. Blair RW
4. Moodie CA
5. Isik AI
6. Erramuzpe A
7. Kent JD
8. Goncalves M
9. DuPre E
10. Snyder M
11. Oya H
12. Ghosh SS
13. Wright J
14. Durnez J
15. Poldrack RA
16. Gorgolewski KJ
(2019) FMRIPrep: a robust preprocessing pipeline for functional MRI
Nature Methods 16:111–116.

https://doi.org/10.1038/s41592-018-0235-4
- PubMed
- Google Scholar
(2008) Apparent contrast differs across the vertical meridian: visual and attentional factors
Journal of Vision 8:16.

https://doi.org/10.1167/8.1.16
- PubMed
- Google Scholar
1. García-Pérez MA
(1998) Forced-choice staircases with fixed step sizes: asymptotic and small-sample properties
Vision Research 38:1861–1881.

https://doi.org/10.1016/s0042-6989(97)00340-4
- PubMed
- Google Scholar
Software
(2018) MGL: visual psychophysics stimuli and experimental design package, version 2.0
Zenodo.

https://doi.org/10.5281/zenodo.1299497
1. Goolkasian P
(1994) Size scaling and its effect on letter detection
Perception & Psychophysics 56:681–690.

https://doi.org/10.3758/bf03208361
- PubMed
- Google Scholar
(2017) Variations in crowding, saccadic precision, and spatial localization reveal the shared topology of spatial vision
PNAS 114:E3573–E3582.

https://doi.org/10.1073/pnas.1615504114
- PubMed
- Google Scholar
Preprint
(2022a) Presaccadic Attention Depends on Eye Movement Direction
bioRxiv.

https://doi.org/10.1101/2022.12.15.520489
- Google Scholar
(2022b) Presaccadic attention enhances contrast sensitivity, but not at the upper vertical meridian
IScience 25:103851.

https://doi.org/10.1016/j.isci.2022.103851
- PubMed
- Google Scholar
1. Hilz R
2. Cavonius CR
(1974) Functional organization of the peripheral retina: sensitivity to periodic stimuli
Vision Research 14:1333–1337.

https://doi.org/10.1016/0042-6989(74)90006-6
- PubMed
- Google Scholar
(1981) Insensitivity of peripheral vision to spatial phase
Experimental Brain Research 43:111–114.

https://doi.org/10.1007/BF00238818
- PubMed
- Google Scholar
1. Himmelberg MM
2. Wade AR
(2019) Eccentricity-dependent temporal contrast tuning in human visual cortex measured with fmri
NeuroImage 184:462–474.

https://doi.org/10.1016/j.neuroimage.2018.09.049
- PubMed
- Google Scholar
(2020) Stimulus-Dependent contrast sensitivity asymmetries around the visual field
Journal of Vision 20:18.

https://doi.org/10.1167/jov.20.9.18
- PubMed
- Google Scholar
(2021) Cross-dataset reproducibility of human retinotopic maps
NeuroImage 244:118609.

https://doi.org/10.1016/j.neuroimage.2021.118609
- PubMed
- Google Scholar
(2022a) What has vision science taught us about functional MRI?
NeuroImage 261:119536.

https://doi.org/10.1016/j.neuroimage.2022.119536
- PubMed
- Google Scholar
(2022b) Linking individual differences in human primary visual cortex to contrast sensitivity around the visual field
Nature Communications 13:3309.

https://doi.org/10.1038/s41467-022-31041-9
- PubMed
- Google Scholar
(2023a) Comparing retinotopic maps of children and adults reveals a late-stage change in how V1 samples the visual field
Nature Communications 14:1561.

https://doi.org/10.1038/s41467-023-37280-8
- PubMed
- Google Scholar
(2023b)
Polar angle asymmetries in visual perception and neural architecture

Trends in Neurosciences In press.
- Google Scholar
1. Horton JC
2. Hoyt WF
(1991) The representation of the visual field in human striate cortex: A revision of the classic Holmes MAP
Archives of Ophthalmology 109:816–824.

https://doi.org/10.1001/archopht.1991.01080060080030
- PubMed
- Google Scholar
1. Hubel DH
2. Wiesel TN
(1977) Ferrier lecture-functional architecture of macaque monkey visual cortex
Proceedings of the Royal Society of London. Series B. Biological Sciences 198:1–59.

https://doi.org/10.1098/rspb.1977.0085
- Google Scholar
1. Jigo M
2. Carrasco M
(2020) Differential impact of exogenous and endogenous attention on the contrast sensitivity function across eccentricity
Journal of Vision 20:11.

https://doi.org/10.1167/jov.20.6.11
- PubMed
- Google Scholar
Software
1. Jigo M
(2021) Palamedes wrapper, version version 1
Github.

https://github.com/michaeljigo/palamedes_wrapper
Software
(2023) Mscaling eliminates contrast sensitivity across not around, version version 1
OSF Storage.

https://osf.io/gvkdh/
1. Kelly DH
(1977) Visual contrast sensitivity
Optica Acta 24:107–129.

https://doi.org/10.1080/713819495
- Google Scholar
1. Kitterle FL
(1986) Psychophysics of lateral tachistoscopic presentation
Brain and Cognition 5:131–162.

https://doi.org/10.1016/0278-2626(86)90052-7
- PubMed
- Google Scholar
(1978) Perimetry of contrast detection thresholds of moving spatial sine wave patterns. I. the near peripheral visual field (eccentricity 0 degrees-8 degrees)
Journal of the Optical Society of America 68:845–849.

https://doi.org/10.1364/josa.68.000845
- PubMed
- Google Scholar
(2019) Modeling visual performance differences “around” the visual field: a computational observer approach
PLOS Computational Biology 15:e1007063.

https://doi.org/10.1371/journal.pcbi.1007063
- PubMed
- Google Scholar
(2022) Asymmetries around the visual field: from retina to cortex to behavior
PLOS Computational Biology 18:e1009771.

https://doi.org/10.1371/journal.pcbi.1009771
- PubMed
- Google Scholar
(2023) Presaccadic attention sharpens visual acuity
Scientific Reports 13:2981.

https://doi.org/10.1038/s41598-023-29990-2
- PubMed
- Google Scholar
1. Levi DM
2. Klein SA
(1986) Sampling in spatial vision
Nature 320:360–362.

https://doi.org/10.1038/320360a0
- PubMed
- Google Scholar
(1999) Position jitter and undersampling in pattern perception
Vision Research 39:445–465.

https://doi.org/10.1016/s0042-6989(98)00125-4
- PubMed
- Google Scholar
(2006) Neural correlates of the visual vertical meridian asymmetry
Journal of Vision 6:1294–1306.

https://doi.org/10.1167/6.11.12
- PubMed
- Google Scholar
1. Ludvigh E
(1941) Extrafoveal visual acuity as measured with Snellen test-letters*
American Journal of Ophthalmology 24:303–310.

https://doi.org/10.1016/S0002-9394(41)90648-7
- Google Scholar
(2016) Cortical idiosyncrasies predict the perception of object size
Nature Communications 7:12110.

https://doi.org/10.1038/ncomms12110
- PubMed
- Google Scholar
1. Movshon JA
2. Kiorpes L
(1988) Analysis of the development of spatial contrast sensitivity in monkey and human infants
Journal of the Optical Society of America. A, Optics and Image Science 5:2166–2172.

https://doi.org/10.1364/josaa.5.002166
- PubMed
- Google Scholar
(2006) The representation of perceived angular size in human primary visual cortex
Nature Neuroscience 9:429–434.

https://doi.org/10.1038/nn1641
- PubMed
- Google Scholar
1. Nachmias J
(1967) Effect of exposure duration on visual contrast sensitivity with square-wave gratings
Journal of the Optical Society of America 57:421.

https://doi.org/10.1364/JOSA.57.000421
- Google Scholar
1. O’Connell C
2. Ho LC
3. Murphy MC
4. Conner IP
5. Wollstein G
6. Cham R
7. Chan KC
(2016) Structural and functional correlates of visual field asymmetry in the human brain by diffusion kurtosis MRI and functional MRI
Neuroreport 27:1225–1231.

https://doi.org/10.1097/WNR.0000000000000682
- PubMed
- Google Scholar
1. Olzak LA
2. Thomas JP
(2003) Dual nonlinearities regulate contrast sensitivity in pattern discrimination tasks
Vision Research 43:1433–1442.

https://doi.org/10.1016/s0042-6989(03)00175-5
- PubMed
- Google Scholar
(2009) A population-coding model of attention’s influence on contrast response: estimating neural effects from psychophysical data
Vision Research 49:1144–1153.

https://doi.org/10.1016/j.visres.2008.09.018
- PubMed
- Google Scholar
1. Peterson MF
2. Eckstein MP
(2013) Individual differences in eye movements during face identification reflect observer-specific optimal points of fixation
Psychological Science 24:1216–1225.

https://doi.org/10.1177/0956797612471684
- PubMed
- Google Scholar
1. Petrov Y
2. Meleshkevich O
(2011) Asymmetries and idiosyncratic hot spots in crowding
Vision Research 51:1117–1123.

https://doi.org/10.1016/j.visres.2011.03.001
- PubMed
- Google Scholar
1. Pointer JS
2. Hess RF
(1989) The contrast sensitivity gradient across the human visual field: with emphasis on the low spatial frequency range
Vision Research 29:1133–1151.

https://doi.org/10.1016/0042-6989(89)90061-8
- PubMed
- Google Scholar
1. Prince SJ
2. Rogers BJ
(1998) Sensitivity to disparity corrugations in peripheral vision
Vision Research 38:2533–2537.

https://doi.org/10.1016/s0042-6989(98)00118-7
- PubMed
- Google Scholar
1. Prins N
2. Kingdom FAA
(2018) Applying the model-comparison approach to test specific research hypotheses in psychophysical research using the palamedes toolbox
Frontiers in Psychology 9:1250.

https://doi.org/10.3389/fpsyg.2018.01250
- PubMed
- Google Scholar
(2021) Voluntary attention improves performance similarly around the visual field
Attention, Perception & Psychophysics 83:2784–2794.

https://doi.org/10.3758/s13414-021-02316-y
- PubMed
- Google Scholar
1. Rahimi-Nasrabadi H
2. Jin J
3. Mazade R
4. Pons C
5. Najafian S
6. Alonso JM
(2021) Image luminance changes contrast sensitivity in visual cortex
Cell Reports 34:108692.

https://doi.org/10.1016/j.celrep.2021.108692
- PubMed
- Google Scholar
1. Regan D
2. Beverley KI
(1983)
Visual fields described by contrast sensitivity, by acuity, and by relative sensitivity to different orientations

Investigative Ophthalmology & Visual Science 24:753–759.
- Google Scholar
(1980) Contrast sensitivity as a function of position on the retina
Vision Res 20:235–241.

https://doi.org/10.1016/0042-6989(80)90108-X
- Google Scholar
(2016) Covert spatial attention is functionally intact in amblyopic human adults
J Vis 16:30.

https://doi.org/10.1167/16.15.30
- Google Scholar
(2018) When attention is intact in adults with ADHD
Psychonomic Bulletin & Review 25:1423–1434.

https://doi.org/10.3758/s13423-017-1407-4
- PubMed
- Google Scholar
1. Robson JG
2. Graham N
(1981) Probability summation and regional variation in contrast sensitivity across the visual field
Vision Research 21:409–418.

https://doi.org/10.1016/0042-6989(81)90169-3
- PubMed
- Google Scholar
(1980) The basic uniformity in structure of the neocortex
Brain 103:221–244.

https://doi.org/10.1093/brain/103.2.221
- PubMed
- Google Scholar
(2014) Quick contrast sensitivity measurements in the periphery
Journal of Vision 14:3.

https://doi.org/10.1167/14.8.3
- PubMed
- Google Scholar
(1978) Cortical magnification factor predicts the photopic contrast sensitivity of peripheral vision
Nature 271:54–56.

https://doi.org/10.1038/271054a0
- Google Scholar
1. Rovamo J
2. Virsu V
(1979) An estimation and application of the human cortical magnification factor
Exp Brain Re 37:495–510.

https://doi.org/10.1007/BF00236819
- Google Scholar
(1992) Contrast sensitivity as a function of spatial frequency, viewing distance and eccentricity with and without spatial noise
Vision Research 32:631–637.

https://doi.org/10.1016/0042-6989(92)90179-m
- PubMed
- Google Scholar
(2011) The surface area of human V1 predicts the subjective experience of object size
Nature Neuroscience 14:28–30.

https://doi.org/10.1038/nn.2706
- PubMed
- Google Scholar
1. Schwarzkopf DS
2. Rees G
(2013) Subjective size perception depends on central visual cortical magnification in human V1
PLOS ONE 8:e60550.

https://doi.org/10.1371/journal.pone.0060550
- PubMed
- Google Scholar
1. Schwarzkopf DS
(2019) Size perception biases are temporally stable and vary consistently between visual field meridians
I-Perception 10:2041669519878722.

https://doi.org/10.1177/2041669519878722
- PubMed
- Google Scholar
(2008) Retinal and cortical patterns of spatial anisotropy in contrast sensitivity tasks
Vision Research 48:127–135.

https://doi.org/10.1016/j.visres.2007.10.018
- PubMed
- Google Scholar
(2018) Radial asymmetries in population receptive field size and cortical magnification factor in early visual cortex
NeuroImage 167:41–52.

https://doi.org/10.1016/j.neuroimage.2017.11.021
- PubMed
- Google Scholar
1. Solomon JA
2. Sperling G
(1995) 1st- and 2nd-order motion and texture resolution in central and peripheral vision
Vision Research 35:59–64.

https://doi.org/10.1016/0042-6989(94)e0077-x
- PubMed
- Google Scholar
1. Song C
2. Schwarzkopf DS
3. Kanai R
4. Rees G
(2015) Neural population tuning links visual cortical anatomy to human visual perception
Neuron 85:641–656.

https://doi.org/10.1016/j.neuron.2014.12.041
- PubMed
- Google Scholar
(1991) Contrast thresholds for identification of numeric characters in direct and eccentric view
Perception & Psychophysics 49:495–508.

https://doi.org/10.3758/bf03212183
- PubMed
- Google Scholar
(1994) Cortical magnification theory fails to predict visual recognition
The European Journal of Neuroscience 6:1583–1587.

https://doi.org/10.1111/j.1460-9568.1994.tb00548.x
- PubMed
- Google Scholar
(2011) Peripheral vision and pattern recognition: a review
Journal of Vision 11:1–82.

https://doi.org/10.1167/11.5.13
- PubMed
- Google Scholar
1. Talgar CP
2. Carrasco M
(2002) Vertical meridian asymmetry in spatial resolution: visual and attentional factors
Psychonomic Bulletin & Review 9:714–722.

https://doi.org/10.3758/bf03196326
- PubMed
- Google Scholar
1. Tyler CW
(1999) Human symmetry detection exhibits reverse eccentricity scaling
Visual Neuroscience 16:919–922.

https://doi.org/10.1017/s0952523899165118
- PubMed
- Google Scholar
(1984) The visual field representation in striate cortex of the macaque monkey: asymmetries, anisotropies, and individual variability
Vision Research 24:429–448.

https://doi.org/10.1016/0042-6989(84)90041-5
- PubMed
- Google Scholar
1. Virsu V
2. Rovamo J
(1979) Visual resolution, contrast sensitivity, and the cortical magnification factor
Experimental Brain Research 37:475–494.

https://doi.org/10.1007/BF00236818
- PubMed
- Google Scholar
(1982) Temporal contrast sensitivity and cortical magnification
Vision Research 22:1211–1217.

https://doi.org/10.1016/0042-6989(82)90087-6
- PubMed
- Google Scholar
1. Wang Z
2. Murai Y
3. Whitney D
(2020) Idiosyncratic perception: a link between acuity, perceived position and apparent size
Proceedings. Biological Sciences 287:20200825.

https://doi.org/10.1098/rspb.2020.0825
- PubMed
- Google Scholar
1. Watson AB
2. Ahumada AJ
(2005) A standard model for foveal detection of spatial contrast
Journal of Vision 5:717–740.

https://doi.org/10.1167/5.9.6
- PubMed
- Google Scholar
1. Wertheim T
(1894)
Über die indirekte sehschärfe

Zeitschrift Für Psychologie Und Physiologie Der Sinnesorgane 7:172–187.
- Google Scholar
(2016) Neural bandwidth of veridical perception across the visual field
Journal of Vision 16:1.

https://doi.org/10.1167/16.2.1
- PubMed
- Google Scholar
1. Wright MJ
2. Johnston A
(1983) Spatiotemporal contrast sensitivity and visual field locus
Vision Research 23:983–989.

https://doi.org/10.1016/0042-6989(83)90008-1
- PubMed
- Google Scholar
(2022) Do sensory tuning functions differ between the fovea and periphery?
Journal of Vision 22:4418.

https://doi.org/10.1167/jov.22.14.4418
- Google Scholar
Report
1. Xue S
2. Carrasco M
(2023)
Featural representation underlies performance differences around the visual field

Vision Sciences Society.
- Google Scholar

Article and author information

Author details

Michael Jigo

Department of Psychology, New York University, New York, United States

Contribution
Conceptualization, Investigation, Visualization, Methodology, Writing - original draft, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-9742-4576
Daniel Tavdy

Department of Psychology, New York University, New York, United States

Contribution
Investigation, Methodology, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0009-0003-0431-1308
Marc M Himmelberg
1. Department of Psychology, New York University, New York, United States
2. Center for Neural Science, New York University, New York, United States
Contribution
Formal analysis, Investigation, Visualization, Methodology, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-9133-7984
Marisa Carrasco
1. Department of Psychology, New York University, New York, United States
2. Center for Neural Science, New York University, New York, United States
Contribution
Conceptualization, Supervision, Funding acquisition, Investigation, Methodology, Writing - original draft, Project administration, Writing – review and editing

For correspondence
marisa.carrasco@nyu.edu

Competing interests
Reviewing editor, eLife

"This ORCID iD identifies the author of this article:" 0000-0002-1002-9056

Funding

National Eye Institute (R01-EY027401)

Marisa Carrasco

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

The authors thank Antoine Barbot, Antonio Fernández, Nina Hanning, Shutian Xue, and other members of the Carrasco lab, as well as Michael Landy, for their helpful comments and discussion. This work was supported by the National Institutes of Health R01-EY027401 to MC.

Ethics

Human subjects: All observers provided written informed consent under the University Committee's protocol on Activities Involving Human Subjects at New York University agreeing to participate in the study and the public release of their data. All experimental procedures were approved by the Ethics Committee at the NYU Department of Psychology (IRB: FY2016-466) and were in agreement with the Declaration of Helsinki.

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

1,109

views
158

downloads
17

citations

Views, downloads and citations are aggregated across all versions of this paper published by eLife.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Michael Jigo
Daniel Tavdy
Marc M Himmelberg
Marisa Carrasco

(2023)

Cortical magnification eliminates differences in contrast sensitivity across but not around the visual field

eLife 12:e84205.

https://doi.org/10.7554/eLife.84205

Categories and tags

Research organism

Human

Share this article

Cite this article

Schematic predictions of contrast sensitivity functions (CSFs).

A psychophysical procedure to measure and a parametric model to characterize contrast sensitivity functions (CSFs).

BIC model comparisons for contrast sensitivity function (CSF) and visual field models.

Candidate contrast sensitivity function (CSF) models.

Models of contrast sensitivity across eccentricity and polar angle.

M-scaling diminishes the eccentricity effect, but neither the horizontal-vertical anisotropy (HVA) nor the vertical meridian asymmetry (VMA) (n=10).

Polar angle asymmetries emerge in key contrast sensitivity function (CSF) attributes.

Horizontal-vertical anisotropy (HVA) and vertical meridian asymmetry (VMA) magnitudes for peak contrast sensitivity, spatial frequency cutoff, and area under the log contrast sensitivity function curve (AULCSF).

Individualized V1 surface area measurements at the cardinal meridians correlate with peak contrast sensitivity measurements.

Author details

Michael Jigo

Contribution

Competing interests

Daniel Tavdy

Contribution

Competing interests

Marc M Himmelberg

Contribution

Competing interests

Marisa Carrasco

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Research organism

Further reading