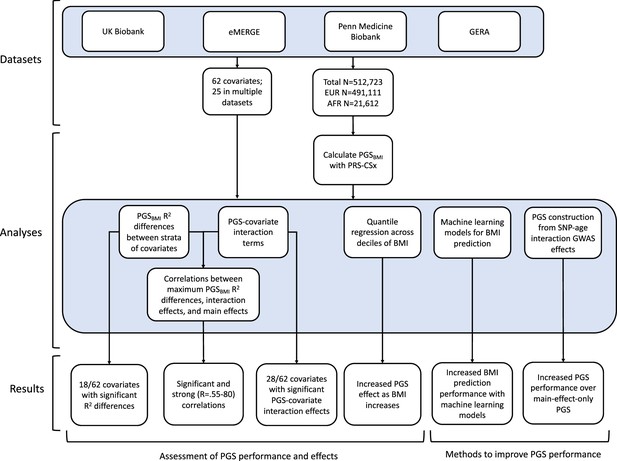
Risk factors affecting polygenic score performance across diverse cohorts
eLife assessment
This study presents a convincing analysis of the effects of covariates, such as age, sex, socioeconomic status, or biomarker levels, on the predictive accuracy of polygenic scores for body mass index; the work is further supported by important approaches for improving prediction accuracy by accounting for such covariates across a variety of association studies. The authors did a commendable job addressing reviewer suggestions and comments. The work will be of interest to colleagues using and developing methods for phenotypic prediction based on polygenic scores.
https://doi.org/10.7554/eLife.88149.3.sa0Important: Findings that have theoretical or practical implications beyond a single subfield
- Landmark
- Fundamental
- Important
- Valuable
- Useful
Convincing: Appropriate and validated methodology in line with current state-of-the-art
- Exceptional
- Compelling
- Convincing
- Solid
- Incomplete
- Inadequate
During the peer-review process the editor and reviewers write an eLife Assessment that summarises the significance of the findings reported in the article (on a scale ranging from landmark to useful) and the strength of the evidence (on a scale ranging from exceptional to inadequate). Learn more about eLife Assessments
Abstract
Apart from ancestry, personal or environmental covariates may contribute to differences in polygenic score (PGS) performance. We analyzed the effects of covariate stratification and interaction on body mass index (BMI) PGS (PGSBMI) across four cohorts of European (N = 491,111) and African (N = 21,612) ancestry. Stratifying on binary covariates and quintiles for continuous covariates, 18/62 covariates had significant and replicable R2 differences among strata. Covariates with the largest differences included age, sex, blood lipids, physical activity, and alcohol consumption, with R2 being nearly double between best- and worst-performing quintiles for certain covariates. Twenty-eight covariates had significant PGSBMI–covariate interaction effects, modifying PGSBMI effects by nearly 20% per standard deviation change. We observed overlap between covariates that had significant R2 differences among strata and interaction effects – across all covariates, their main effects on BMI were correlated with their maximum R2 differences and interaction effects (0.56 and 0.58, respectively), suggesting high-PGSBMI individuals have highest R2 and increase in PGS effect. Using quantile regression, we show the effect of PGSBMI increases as BMI itself increases, and that these differences in effects are directly related to differences in R2 when stratifying by different covariates. Given significant and replicable evidence for context-specific PGSBMI performance and effects, we investigated ways to increase model performance taking into account nonlinear effects. Machine learning models (neural networks) increased relative model R2 (mean 23%) across datasets. Finally, creating PGSBMI directly from GxAge genome-wide association studies effects increased relative R2 by 7.8%. These results demonstrate that certain covariates, especially those most associated with BMI, significantly affect both PGSBMI performance and effects across diverse cohorts and ancestries, and we provide avenues to improve model performance that consider these effects.
Introduction
Polygenic scores (PGS) provide individualized genetic predictors of a phenotype by aggregating genetic effects across hundreds or thousands of loci, typically estimated from genome-wide association studies (GWAS). In recent years, it has become increasingly apparent that the transferability of PGS performance across different cohorts is poor (Martin et al., 2019). Most analyses to date have focused on ancestry differences as the main driver of this lack of portability (Wang et al., 2020; Galinsky et al., 2019; Shi et al., 2021). However, a growing body of evidence has demonstrated that PGS performance and effect estimates are influenced by differences in certain contexts, that is, environmental (classically termed ‘gene–environment’ effects or interactions) or personal-level covariates – different phenotypes seem to be differently affected by these covariates, with adiposity traits such as body mass index (BMI) having substantial evidence for these effects (Rask-Andersen et al., 2017; Robinson et al., 2017; Sulc et al., 2020; Justice et al., 2017; Helgeland et al., 2019; Vogelezang et al., 2020; Couto Alves et al., 2019; Choh et al., 2014; Mostafavi et al., 2020; Elks et al., 2012). In one previous study, they showed that GWAS stratified by sample characteristics had better PGS performance in cohorts that matched the sample characteristics of the stratified GWAS, and that differences in heritability between the stratified cohorts partially explained this observation (Mostafavi et al., 2020).
There are several gaps in current knowledge about these covariate-specific effects. Many analyses have assessed only a handful of these covariates due to the myriad of choices possible in typical large-scale biobanks. Little investigation has been done to systematically understand why certain covariates affect PGS performance, with such knowledge being useful to reduce the potential search for variables that impart context-specific effects. Furthermore, most studies investigating PGS–covariate interactions have been in European ancestry individuals; notably, comparing differences in PGS performance and prediction while controlling for differences in ancestry versus differences in context has not been assessed in previous studies. Moreover, covariate-specific effects are notorious for replicating poorly in human genetics studies, and previous studies of PGS–covariate interactions have been predominantly performed in the UK Biobank (UKBB) (Bycroft et al., 2018), where the majority of individuals are aged 40–69 (i.e., excluding young adults), are overall healthier than those from other, for example, hospital-based cohorts, and are predominantly European ancestry. Additionally, PGS performance is often assessed using linear models and in isolation of clinical covariates, which in practice would often be available. Machine learning models can have increased performance over linear models and are capable of modeling complex relationships and interactions between variables, which may serve to increase predictive performance, especially given evidence for PGS–covariate-specific effects. Finally, given evidence for context-specific effects, it should be possible to directly incorporate SNP–covariate interaction effects from a GWAS directly to improve prediction performance, instead of relying on post hoc interactions from a typical PGS calculated from main GWAS effects.
Using genetic data with linked-phenotypic information from electronic health records, we estimated the effects of covariate stratification and interaction on performance and effect estimates of PGS for BMI (PGSBMI) – a flowchart summarizing our analyses is presented in Figure 1. These analyses were done across four datasets (Supplementary file 1a): UKBB, Penn Medicine BioBank (PMBB) (Verma et al., 2022), Electronic Medical Records and Genomics (eMERGE) network dataset (Stanaway et al., 2019), and Genetic Epidemiology Research on Adult Health and Aging (GERA) (Banda et al., 2015). These datasets include participants from two ancestry groups (N = 491,111 European ancestry [EUR], N = 21,612 African ancestry [AFR]), and 62 covariates (25 present in multiple datasets) representing laboratory, survey, and biometric data types typically associated with cardiometabolic health and adiposity. After constructing PGSBMI using out-of-sample multi-ancestry BMI GWAS, we assessed the effects of covariate stratification on PGSBMI R2, the significance of PGSBMI–covariate interaction terms and their increases to model R2 over models only using main effects, as well as correlation of main effect, interaction effect, and R2 differences. We then assessed ways to increase model performance through using machine learning models, and creating PGSBMI using GxAge GWAS effects. This study addresses a plethora of open issues considering performance and effects of PGS on individuals from diverse backgrounds.
Results
Effect of covariate stratification on PGSBMI performance
We assessed 62 covariates for PGSBMI R2 differences (25 present, or suitable proxies, in multiple datasets Supplementary file 1b) after stratifying on binary covariates and quintiles for continuous covariates. With UKBB EUR as discovery (N = 376,729), 18 covariates had significant differences (Bonferroni p<0.05/62) in R2 among groups (Figure 2a), including age, sex, alcohol consumption, different physical activity measurements, Townsend deprivation index, different dietary measurements, lipids, blood pressure, and HbA1c, with 40 covariates having suggestive (p<0.05) evidence of R2 differences. From an original PGSBMI R2 of 0.076, R2 increased to 0.094–0.088 for those in the bottom physical activity, alcohol intake, and high-density lipoprotein (HDL) cholesterol quintiles, and decreased to 0.067–0.049 for those in the top quintile, respectively, comparable to differences observed between ancestries (Martin et al., 2019). We note that the differences in R2 due to alcohol intake and HDL were larger than those of any physical activity phenotype, despite physical activity having one of the oldest and most replicable evidence of interaction with genetic effects of BMI (Kilpeläinen et al., 2011; Rampersaud et al., 2008). Despite considerable published evidence suggesting covariate-specific genetic effects between BMI and smoking behaviors (Robinson et al., 2017; Justice et al., 2017), we were only able to find suggestive evidence for R2 differences when stratifying individuals across several smoking phenotypes (minimum p=0.016, for smoking pack years). R2 differences due to educational attainment were also only suggestive (p=0.015), with published evidence on this association being conflicting (Amin et al., 2018; Li et al., 2021; Frank et al., 2019).
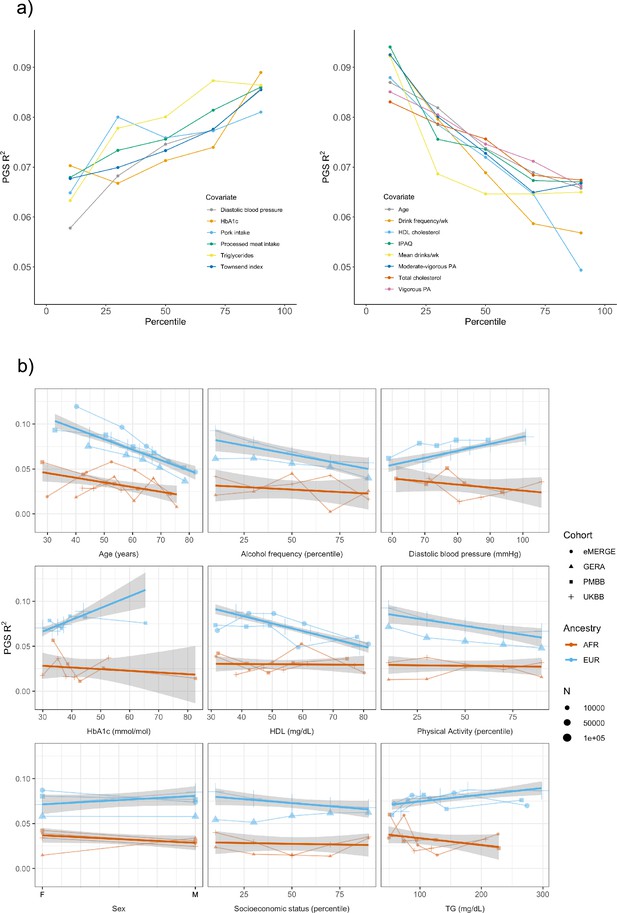
Polygenic score (PGS) R2 stratified by quintiles for quantitative variables and by binary variables.
(a) Continuous covariates with significant (p<8.1 × 10–4) R2 differences across quintiles in UK Biobank (UKBB) European ancestry (EUR). Pork and processed meat consumption per week were excluded from this plot in favor of pork and processed meat intake. (b) Covariates with significant differences that were available in multiple cohorts. When traits had the same or directly comparable units between cohorts we show the actual trait values (and show percentiles for physical activity, alcohol intake frequency, and socioeconomic status, which had slightly differing phenotype definitions across cohorts) plotted on x-axis. Townsend index and income were used as variables for socioeconomic status in UKBB and Genetic Epidemiology Research on Adult Health and Aging (GERA), respectively. Note that the sign for Townsend index was reversed, since increasing Townsend index is lower socioeconomic status, while increasing income is higher socioeconomic status. PA, physical activity (PA); IPAQ, International Physical Activity Questionnaire.
We replicated these analyses in three additional large-scale cohorts of European and African ancestry individuals (Figure 2b, Supplementary file 1c), as well as in African ancestry UKBB individuals. Among covariates with significant performance differences in the discovery analysis, we were able to replicate significant (p<0.05) R2 differences for age, HDL cholesterol, alcohol intake frequency, physical activity, and HbA1c, despite much smaller sample sizes. We again observed mostly insignificant differences across cohorts and ancestries when stratifying due to different smoking phenotypes and educational attainment. For each covariate and ancestry combination, we combined data across cohorts and conducted a linear regression weighted by sample size, regressing R2 values on covariate values across groupings. Slopes of the regressions across cohorts had different signs between ancestries for the same covariate (triglyceride levels, HbA1c, diastolic blood pressure, and sex), although larger sample sizes may be needed to confirm these differences are statistically significant.
Several observations related to age-specific effects on PGSBMI we considered noteworthy. First, in the weighted linear regression of all R2 values across ancestries, expected R2 for African ancestry individuals can become greater than that of European ancestry individuals among individuals within bottom and top age quintiles observed in these data. For instance, the predicted R2 of 0.048 for 80-year-old European ancestry individuals would be lower than that of African ancestry individuals aged 24.7 and lower, indicating that differences in covariates can affect PGSBMI performance more than differences due to ancestry. Second, we obtained these results despite the average age of GWAS individuals being 57.8, which should increase PGSBMI R2 for individuals closest to this age (Mostafavi et al., 2020). This result suggests that PGS performance due to decreased heritability with age cannot be fully reconciled using GWAS from individuals of similar age being used to create PGSBMI (as heritability is an upper bound on PGS performance). Finally, we observed that PGSBMI R2 increases as age decreases, consistent with published evidence suggesting that the heritability of BMI decreases with age (Ge et al., 2017; Min et al., 2013).
PGS–covariate interaction effects
Next, we estimated the differences in PGS effects due to interactions with covariates by modeling interaction terms between PGSBMI and the covariate for each covariate in our list (described in ‘Materials and methods’). We implemented a correction for shared heritability between covariates of interest and outcome (which can inflate test statistics Aschard et al., 2015) to better measure the environmental component of each covariate, and show that this correction successfully reduces significance of interaction estimates (Figure 3—figure supplement 1). Again, using UKBB EUR as the discovery cohort, we observed 28 covariates with significant (Bonferroni p<0.05/62) PGS–covariate interactions (Table 1), with 38 having suggestive (p<0.05) evidence (Supplementary file 1d). We observed the largest effect of PGS–covariate interaction with alcohol drinking frequency (20.0% decrease in PGS effect per 1 standard deviation [SD] increase, p=2.62 × 10–55), with large effects for different physical activity measures (9.4–12.5% decrease/SD, minimum p=3.11 × 10–66), HDL cholesterol (15.3% decrease/SD, p=1.71 × 10–96), and total cholesterol (12.7% decrease/SD, p=1.64 × 10–71). We observed significant interactions with diastolic blood pressure (10.8% increase/SD, p=6.06 × 10–60), but interactions with systolic blood pressure were much smaller (1.17% increase/SD, p=4.41 × 10–3). Significant interactions with HbA1c (4.63% increase/SD, p=5.37 × 10–14) and type 2 diabetes (27.2% PGS effect increase in cases, p=1.83 × 10–7) were also observed. Other significant PGS–covariate interactions included lung function, age, sex, and LDL cholesterol – various dietary measurements also had significant interactions, albeit with smaller effects than other significant covariates. We were able to find significant interaction effects for smoking pack years (4.78% increase/SD, p=3.68 × 10–7), but other smoking phenotypes had insignificant interaction effects after correcting for multiple tests (minimum p=2.7 × 10–3); interactions with educational attainment were also insignificant (p=4.54 × 10–2).
Model descriptive statistics on 28 of 62 covariates, which have significant (p<0.05/62) polygenic score (PGS)–covariate interaction terms, in UK Biobank (UKBB) European ancestry (EUR).
The third column is the percentage change in PGS effect per unit change (standard deviations for continuous variables, binary variables encoded as 0 or 1) in covariate. The fifth column is the increase in model R2 with a PGS–covariate interaction term versus a main effects only model.
| Variable type | Covariate | % change in βPGS per covariate unit change | Interaction p | R2 increase with interaction term | N | |
|---|---|---|---|---|---|---|
| Continuous | HDL cholesterol | –15.29 | 1.71 × 10–96 | 0.0012 | 328,719 | |
| Total cholesterol | –12.70 | 1.64 × 10–71 | 0.00082 | 359,221 | ||
| IPAQ | –12.50 | 3.11 × 10–66 | 0.001 | 304,951 | ||
| Moderate-vigorous PA | –11.41 | 8.92 × 10–65 | 0.001 | 304,951 | ||
| Diastolic BP | 10.84 | 6.06 × 10–60 | 0.0007 | 352,804 | ||
| Townsend Index | 6.78 | 2.86 × 10–58 | 0.00089 | 376,283 | ||
| Age | –9.02 | 3.60 × 10–57 | 0.00061 | 376,729 | ||
| FVC | –9.66 | 4.69 × 10–56 | 0.0008 | 343,467 | ||
| Drink frequency/week | –19.96 | 2.62 × 10–55 | 0.0024 | 122,281 | ||
| LDL cholesterol | –9.86 | 2.63 × 10–51 | 0.00058 | 358,556 | ||
| N days vigorous PA/week | –9.37 | 2.42 × 10–35 | 0.0007 | 299,963 | ||
| FEV1 | –7.38 | 7.15 × 10–35 | 0.0005 | 343,544 | ||
| Mean alcohol consumption | –7.38 | 7.65 × 10–22 | 0.00113 | 126,756 | ||
| HbA1c | 4.63 | 5.37 × 10–14 | 0.0002 | 358,798 | ||
| Mean drinks/week | –7.66 | 1.01 × 10–13 | 0.0008 | 112,204 | ||
| Water intake | 4.60 | 2.97 × 10–13 | 0.00014 | 347,472 | ||
| Processed meat intake | 3.70 | 2.38 × 10–7 | 0.0002 | 376,205 | ||
| Starch mean | 5.51 | 3.15 × 10–7 | 0.00018 | 128,346 | ||
| Smoking pack years | 4.78 | 3.68 × 10–7 | 0.0002 | 114,135 | ||
| Protein mean | 4.82 | 6.52 × 10–7 | 0.00018 | 128,181 | ||
| Saturated fat mean | 4.92 | 1.23 × 10–6 | 0.00017 | 127,899 | ||
| Fat mean | 4.40 | 1.64 × 10–5 | 0.00013 | 128,092 | ||
| Saturated fat grams/week | 2.46 | 1.79 × 10–5 | 4.00 × 10-5 | 364,629 | ||
| Retinol mean | 3.77 | 3.54 × 10–4 | 9.00 × 10-5 | 126,029 | ||
| Binary | IPAQ | –12.68 | 5.30 × 10–62 | 0.0009 | 304,951 | |
| Vigorous PA/week | –20.55 | 9.07 × 10–54 | 0.0009 | 304,951 | ||
| Sex | –11.02 | 1.41 × 10–24 | 0.00025 | 376,729 | ||
| Diabetes | 27.19 | 1.83 × 10–7 | 0.0004 | 375,903 | ||
-
BP = blood pressure, PA = physical activity, FVC = forced vital capacity, FEV1 = forced expiratory volume in 1 s, HDL = high-density lipoprotein, LDL = high-density lipoprotein, IPAQ = International Physical Activity Questionnaire.
We replicated these analyses across ancestries and the other non-UKBB EUR cohorts (Figure 3, Supplementary file 1d). For age and sex, which were available for all cohorts, interactions were significant (p<0.05) and directionally consistent across cohorts and ancestries (except for GERA AFR, which had small sample size [N = 1,789]). We were able to test interactions with alcohol intake frequency and physical activity in GERA, and replicated significant and directionally consistent associations. We observed poor replication for LDL cholesterol, HbA1c, and smoking pack years, with insignificant and directionally inconsistent interaction effects across cohorts. Educational attainment was available in GERA, and interactions were once again insignificant. We observed significant and directionally consistent interaction effects for TG in eMERGE EUR and PMBB EUR, while the effect was inconsistent in UKBB EUR despite much larger sample size.
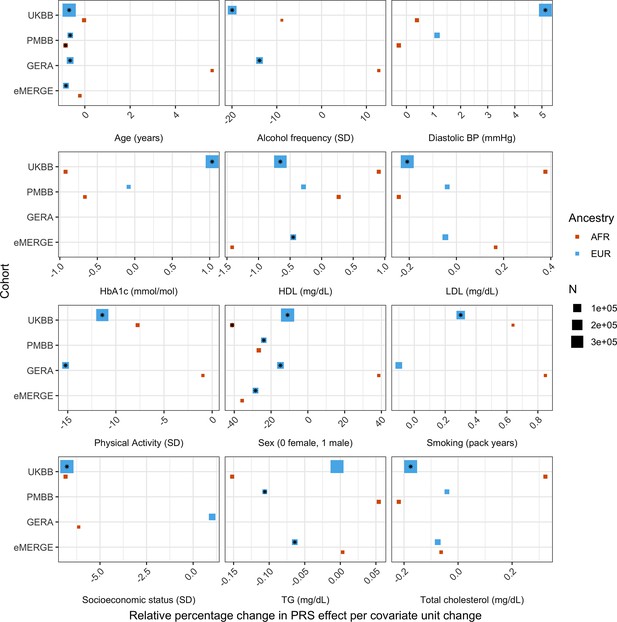
Relative percentage changes in polygenic score (PGS) effect per unit change in covariate, for covariates that significantly changed PGS effect (i.e., significant interaction beta at Bonferroni p<8.1 × 10–4 – denoted by asterisks) and were present in multiple cohorts and ancestries.
Same covariate groupings and transformations were performed as in Figure 1. Similarly, actual values were used when variables had comparable units across cohorts, and standard deviations (SD) used otherwise.
However, despite significance of interaction terms, increases in model R2 when including PGS–covariate interaction terms were small. For instance, the maximum increase among all covariates in UKBB EUR was only 0.0024 from a base R2 of 0.1049 (2.1% relative increase), for alcoholic drinks per week. Across all cohorts and ancestries, the maximum increase in R2 was only 0.0058 from a base R2 of 0.09454 (6.1% relative increase), when adding a PGS–age interaction term for eMERGE EUR (p=5.40 × 10–46) – this was also the largest relative increase among models with significant interaction terms. This result suggests that, while interaction effects can significantly modify PGSBMI effect, their overall impact on model performance is relatively small, despite large differences in R2 when stratifying by covariates.
Correlations between R2 differences, interaction effects, and main effects
We next investigated the relationship between interaction effects, maximum R2 differences across quintiles, and main effects of covariates on BMI. We first estimated the main effects of each covariate on BMI (‘Materials and methods’, Supplementary file 1e), and then calculated the correlation weighted by sample size between main effects, maximum PGSBMI R2 across quintiles, and PGS–covariate interaction effects (Figure 4) across all cohorts and ancestries – GERA data were excluded from these analyses due to slightly different phenotype definition (Supplementary file 1f), as were binary variables. Interaction effects and maximum R2 differences had a 0.80 correlation (p=2.1 × 10–27), indicating that variables with larger interaction effects also had larger effects on PGSBMI performance across quintiles, and that covariates that increase PGSBMI effect also have the largest effect on PGSBMI performance, that is, individuals most at risk for obesity will have both disproportionately larger PGSBMI effect and R2. Main effects and maximum R2 differences had a 0.56 correlation (p=1.3 × 10–11), while main effects and interaction effects had a 0.58 correlation (p=7.6 × 10–12), again suggesting that PGSBMI are more predictive in individuals with higher values of BMI-associated covariates, although less predictive than estimating the interaction effects themselves directly. However, this result demonstrates that covariates that influence both PGSBMI effect and performance can be predicted just using main effects of covariates, which are often known for certain phenotypes and easier to calculate, as genetic data and PGS construction would not be required.
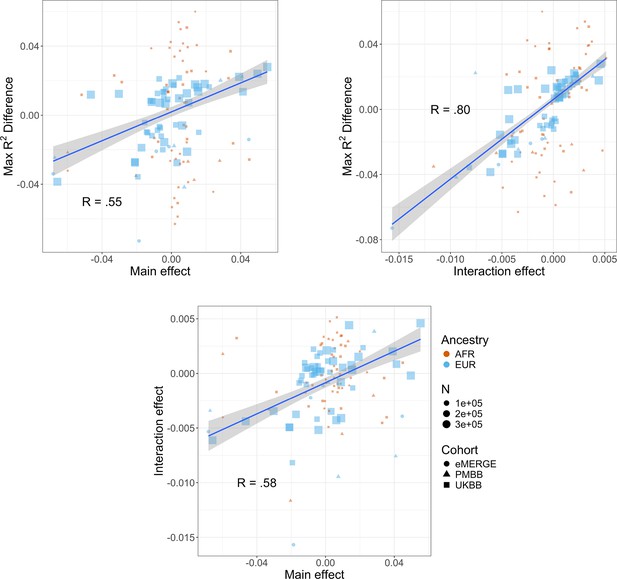
Relationships (Pearson correlations weighted by sample size) between maximum R2 differences across strata, main effects of covariate on log(BMI), and polygenic score (PGS)–covariate interaction effects on log(BMI).
Main effect units are in standard deviations, interaction effect units are in PGS standard deviations multiplied by covariate standard deviations. Only continuous variables are plotted and modeled. Genetic Epidemiology Research on Adult Health and Aging (GERA) was excluded due to slightly different phenotype definitions. BMI, body mass index.
Increase in PGS effect for increasing percentiles of BMI itself, and its relation to R2 differences when stratifying by covariates
Given large and replicable correlations between main effects, interaction effects, and maximum R2 differences for individual covariates, it seemed these differences may be due to the differences in BMI itself, rather than any individual or combination of covariates. To assess this, we used quantile regression to evaluate the effect of PGSBMI on BMI at different deciles of BMI itself. We observed that the effect of PGSBMI consistently increases from lower deciles to higher deciles across all cohorts and ancestries (Figure 5) – for instance, in European ancestry UKBB individuals, the effect of PGSBMI (in units of log(BMI)) when predicting the bottom decile of log(BMI) was 0.716 (95% CI: 0.701–0.732), and increased to 1.31 (95% CI: 1.29–1.33) in the top decile. Across all cohorts and ancestries, the effect of PGSBMI between lowest and highest effect decile ranged from 1.43 to 2.06 times larger, with all cohorts and ancestries having nonoverlapping 95% confidence intervals between their effects (except for African ancestry eMERGE individuals, which had much smaller sample size).
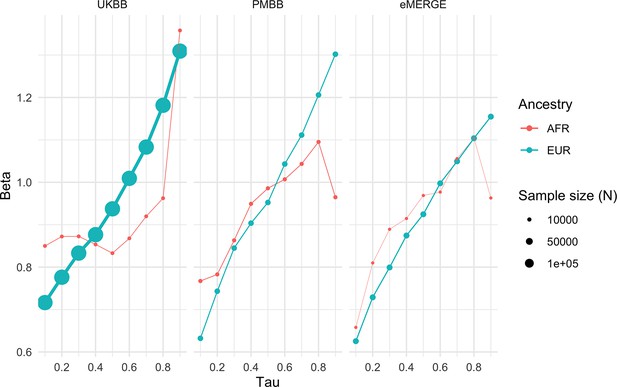
Quantile regression effects of PGSBMI (in units of log(BMI)) on log(BMI) at each decile of BMI in each cohort and ancestry.
Tau is an input parameter for quantile regression corresponding to the percentile of the BMI distribution being modeled, with lower tau values representing the lower deciles (e.g., tau = 0.1 for the 10th percentile) and higher tau values representing the upper deciles (e.g., tau = 0.9 for the 90th percentile). The effect of PGSBMI increases as BMI itself increases, suggesting that no individual covariate–PGS interaction is responsible for the nonlinear effect of PGSBMI. PGS, polygenic score; BMI, body mass index.
While this analysis showed that the effect of PGSBMI increases as BMI itself increases, which may help explain significant interaction effects between PGSBMI and different covariates, it does not directly explain differences in R2 when stratifying by different covariates – we describe several points that help explain this result and suggest they may actually be closely related. Essentially, as the magnitude of the slope of a regression line increases while the mean squared residual does not increase, model R2 will increase – we demonstrate this using simulated data (Figure 5—figure supplement 1). As the magnitude of the regression line’s slope decreases, the regression line becomes a comparatively worse predictor compared to just using the mean, which decreases R2 despite the mean error being the same across models. To demonstrate this in real data, we compared simple univariable models of log(BMI)~PGSBMI (in units of log(BMI)) between the bottom and top age quintiles in the European ancestry UKBB (Figure 5—figure supplement 2). As shown in previous sections, R2 and PGSBMI beta are higher in younger individuals (R2 = 0.088 versus R2 = 0.066, and beta = 1.12 and 0.87, respectively), which seem to be a direct consequence of one another, as the mean squared error in younger individuals is actually higher (0.027 versus 0.022, respectively). This description suggests that the use of R2 as the sole performance metric for evaluation of PGS may not always be appropriate, despite its overwhelming usage. Furthermore, this explanation helps explain the seemingly paradoxical results of significant interaction terms yet small increases in overall model R2 and comparably much larger differences in R2 in the stratified analyses.
Effects of machine learning approaches on predictive performance
Given evidence of PGS–covariate dependence, we aimed to assess increases in R2 when using machine learning models (neural networks), which can inherently model interactions and other nonlinearities, over linear models even with interaction terms. We first included age and sex as the only covariates (along with genotype PCs and PGSBMI), as age and sex were present in all datasets and had significant and replicable evidence for PGS-dependence across our analyses. Three models were assessed – L1-regularized (i.e., LASSO) linear regression without any interaction terms, LASSO including a PGS–age and PGS–sex interaction term, and neural networks (without interaction terms). When comparing neural networks to LASSO with interaction terms, the relative tenfold cross-validated R2 increased up to 67% (mean 23%) across cohorts and ancestries (Figure 6, Supplementary file 1g). The inclusion of interaction terms increased cross-validated R2 up to 12% (mean 3.9%) when comparing LASSO including interaction terms to LASSO with main effects only.
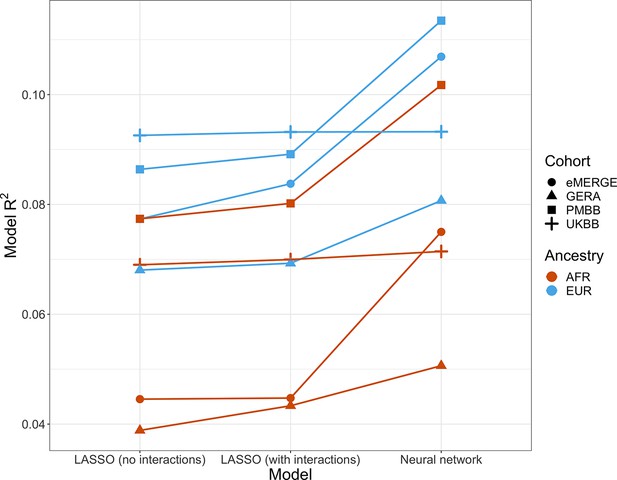
Model R2 from different machine learning models across cohorts and ancestries using age and gender as covariates (along with PGSBMI and PCs 1–5).
Across all cohorts and ancestries, LASSO with PGS–age and PGS–gender interaction terms had better average tenfold cross-validation R2 than LASSO without interaction terms, while neural networks outperformed LASSO models. PGS, polygenic score; BMI, body mass index.
We then modeled all available covariates and their interactions with PGS for each cohort and did similar comparisons. Cross-validated R2 increased by up to 17.6% (mean 9.5%) when using neural networks versus LASSO with interaction terms, and up to 7.0% (mean 2.0%) when comparing LASSO with interaction terms to LASSO with main effects only. Increases in model performance using neural networks were smaller in UKBB, perhaps due to the age range being smaller than other cohorts (all participants aged 39–73). This result suggests that additional variance explained through nonlinear effects with age and sex are explained by other variables present in the remainder of the datasets. Our findings show machine learning methods can improve model R2 that include PGSBMI as variables beyond including interaction terms in linear models, even when variable selection is performed using LASSO, demonstrating that model performance can be increased beyond modeling nonlinearities through linear interaction terms and a feature selection procedure.
Calculating PGS directly from GxAge GWAS effects
Previous studies Mostafavi et al., 2020 have created PGS using GWAS stratified by different personal-level covariates, but for practical purposes this leads to a large loss of power as the full size of the GWAS is not utilized for each strata and continuous variables are forced into bins. We developed a novel strategy where PGS are instead created from a full-size GWAS that includes SNP–covariate interaction terms (‘Materials and methods’). We focused on age interactions, given their large and replicable effects based on our results – similar to a previous study (Mostafavi et al., 2020), we conducted these analyses in the European UKBB. We used a 60% random split of study individuals to conduct three sets of PGS using GWAS of the following designs: main effects only, main effects also with an SNP–age interaction term, and main effects but stratified into quartiles by age. Twenty percent of the remaining data were used for training and the final 20% were held out as a test set. The best-performing PGS created from SNP–age interaction terms (PGSGxAge) increased test R2 to 0.0771 (95% bootstrap CI: 0.0770–0.0772) from 0.0715 (95% bootstrap CI: 0.0714–0.0716), a 7.8% relative increase compared to the best-performing main effect PGS (Figure 7, Supplementary file 1h) – age-stratified PGS had much lower performance than both other strategies (unsurprising given reasons previously mentioned). Including a PGSGxAge–age interaction term only marginally increased R2 (0.0001 increase), with similar increases for the other two sets of PGS, further demonstrating that post hoc modeling of interactions cannot reconcile performance gained through directly incorporating interaction effects from the original GWAS. The strategy of creating PGS directly from full-sized SNP–covariate interactions is potentially quite useful as it increases PGS performance without the need for additional data – there are almost certainly a variety of points of improvement (described more in ‘Discussion’), but we consider their investigation outside the scope of this study.
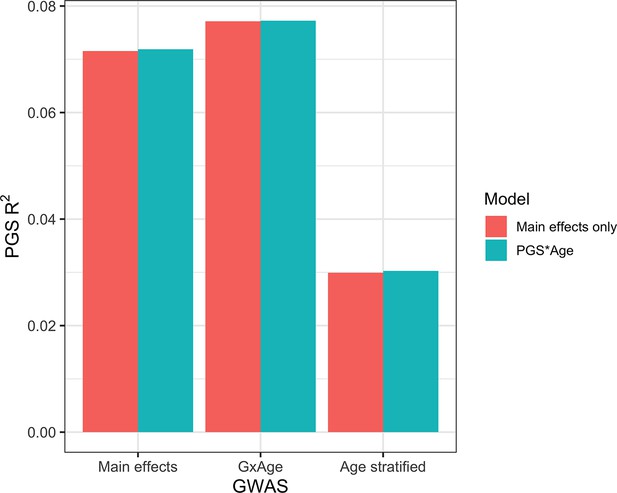
Polygenic score (PGS) R2 based on three sets of genome-wide association studies (GWAS) setups.
‘Main effects’ were from a typical main effect GWAS, ‘GxAge’ effects were from a GWAS with an SNP–age interaction term, and ‘Age stratified’ GWAS had main effects only but were conducted in four age quartiles. PGS R2 was evaluated using two models: one with main effects only and one with an additional PGS * Age interaction term.
Discussion
We uncovered replicable effects of covariates across four large-scale cohorts of diverse ancestry on both performance and effects of PGSBMI. When stratifying by quintiles of different covariates, certain covariates had significant and replicable evidence for differences in PGSBMI R2, with R2 being nearly double between top- and bottom-performing quintiles for covariates with the largest differences. When testing PGS–covariate interaction effects, we also found covariates with significant interaction effects, where, for the largest effect covariates, each standard deviation change affected PGSBMI effect by nearly 20%. Across analyses, we found age and sex had the most replicable interaction effects, with levels of serum cholesterol, physical activity, and alcohol consumption having the largest effects across cohorts. Interaction effects and R2 differences were strongly correlated, with main effects also being correlated with interaction effects and R2 differences, suggesting that covariates with the largest interaction effects also contribute to the largest R2 differences, with simple main effects also being predictive of expected differences in R2 and interaction effects. Relatedly, we observed the effect of PGSBMI increases as BMI itself increases, and reason that differences in R2 when stratifying by covariates are largely a consequence of difference in PGSBMI effects. Next, we employed machine learning methods for prediction of BMI with models that include PGSBMI and demonstrate that these methods outperform regularized linear regression models that include interaction effects. Finally, we employed a novel strategy that directly incorporates SNP interaction effects into PGS construction and demonstrate that this strategy improves PGS performance when modeling SNP–age interactions compared to PGS created only from main effects.
These observations are relevant to current research and clinical use of PGS, as individuals above a percentile cutoff are designated high risk (Ge et al., 2019), implying that individuals most at risk for obesity have both disproportionately higher predicted BMI and increased BMI prediction performance compared to the general population. More broadly, these results may likely extend to single variant effects instead of those aggregated into a PGS, which may inform the cause of previous GxE discoveries – for instance, variants near FTO that interact with physical activity discovered through GWAS of BMI are robust and well-documented. However, individuals engaging in physical activity will generally have lower BMI than those that are sedentary, and these results suggest it may not be the difference in physical activity that is driving the interaction, rather the difference in BMI itself. This concept may also apply to other traits – for instance, sex-specific analyses are commonly performed, and variants with differing effects between male and female GWAS may largely be explained by phenotypic differences, rather than any combination of biological or lifestyle differences.
Future work may include replicating these analyses across additional traits, and trying to understand why these differences occur, as well as further exploring machine learning and deep learning methods on other phenotypes to determine if this trend of inclusion of PGS, along with covariate interaction effects, outperforms linear models for risk prediction. Additionally, inclusion of a PGS for the covariate to better measure its environmental effect is potentially worth exploring further and should improve in the future as PGS performance continues to increase. A slight limitation of this method in our study is that for the UKBB analyses the GWAS used for PGS construction were also from UKBB, thus not out-of-sample, although many of the covariates only have GWAS available through UKBB individuals. Furthermore, a variety of improvements are likely possible when creating PGS directly from SNP–covariate interaction terms. First, we used the same SNPs that were selected by pruning and thresholding based on their main effect p-values, but selection of SNPs based on their interaction p-values should also be possible and would likely improve performance. Additionally, performance of pruning and thresholding-based strategies has largely been overtaken by methods that first adjust all SNP effects for LD and do not require exclusion of SNPs, and a method that could do a similar adjustment for interaction effects would likely outperform most current methods for traits with significant context-specific effects. Next, incorporating additional SNP–covariate interactions (e.g., SNP–sex) would also likely further improve prediction performance, although any SNP selection/adjustment procedures may be further complicated by additional interaction terms. Finally, if SNP effects do truly differ according to differences in phenotype, then SNP effects would differ depending on the alleles one has, implying epistatic interactions are occurring at these SNPs.
While difference in phenotype itself may be able to explain the difference in genetic effects, it still may be that specific environmental or lifestyle characteristics are driving the differences. We propose several ideas about why BMI-associated covariates have larger interaction effects and impact on R2 for PGSBMI. First, age may be a proxy for accumulated gene–environment interactions as younger individuals have less exposure to environmental influences on weight compared to older individuals; therefore, one may expect that in younger individuals their phenotype could be better explained by genetics compared to environment. Second, PGS may more readily explain high phenotype values especially for positively skewed phenotypes, as large effect variants (e.g., associated with very high weight or height; Robinson et al., 2006) may be more responsible for extremely high phenotypic values. For example, the distribution of BMI is often positively skewed, and effects in trait-increasing alleles may have a larger potential to explain trait variation compared to trait-reducing variants. This explanation would likely be better suited to positively skewed traits and is not fully satisfactory as first log-transforming or rank-normal transforming the phenotype, as was done in this study, may invalidate this explanation.
PGS is a promising technique to stratify individuals for their risk of common, complex disease. To achieve more accurate predictions as well as promote equity, further research is required regarding PGS methods and assessments. This research provides firm evidence supporting the context-specific nature of PGS and the impact of nonlinear covariate effects for improving polygenic prediction of BMI, promoting equitable use of PGS across ancestries and cohorts.
Materials and methods
Study datasets
Request a detailed protocolIndividual inclusion criteria and sample sizes per cohort are described below – additional information is available in Supplementary file 1a.
UKBB
Request a detailed protocolIndividual-level quality control (QC) and filtering have been described elsewhere (Zhang et al., 2022) for European ancestry individuals. Briefly, individuals were split by ancestry according to both genetically inferred ancestry and self-reported ethnicity (Bycroft et al., 2018). Individuals with low genotyping quality and sex mismatch were removed, only unrelated individuals (Plink pi-hat < 0.250) were retained, and variants were filtered at INFO > 0.30 and minor allele frequency > 0.01. For African ancestry, individuals were first selected based on self-reported ethnicity ‘Black or Black British’, ‘Caribbean’, ‘African’, or ‘Any other Black background’. Individuals who were low quality, that is, ‘Outliers for heterozygosity or missing rate’, and who were Caucasian from ‘Genetic ethnic grouping’ were removed. Of these individuals, those who were ±6 standard deviations from the mean of the first five genetic principal components provided by UKBB were excluded. Finally, only unrelated individuals were retained up to the second degree using plink2 (Chang et al., 2015) ‘-king-cutoff 0.125’. After QC and consideration of phenotype, a total of 7,046 individuals in the UKBB AFR data who also had BMI available were used for downstream analyses. In total, 383,775 individuals were used for analysis (NEUR = 376,729, NAFR = 7,046).
eMERGE
Request a detailed protocolAncestry and relatedness inference have been described elsewhere (Stanaway et al., 2019). Individuals were split into European and African ancestry cohorts, and related individuals were removed (Plink pi-hat > 0.250) such that all were unrelated. In total, 35,064 individuals (NEUR = 31,961, NAFR = 3,103) were used for analysis.
GERA
Request a detailed protocolAncestry inference has been described elsewhere (Banda et al., 2015), and study individuals were divided into European and African ancestry cohorts. Related individuals were removed using plink2 ‘-king-cutoff 0.125’. In total, 57,838 individuals (NEUR = 56,049, NAFR = 1,789) were used for analysis.
PMBB
Request a detailed protocolAncestry inference and relatedness inference have been described elsewhere (Penn Medicine BioBank, 2022). Individuals were split into European and African ancestry cohorts, and related individuals were removed at pi-hat > 0.250. In total, 36,046 individuals (NEUR = 26,372, NAFR = 9,674) were used for analysis.
Choice of covariates
Request a detailed protocolA total of 62 covariates were included in the analyses, 25 of which were present (or similar proxies) in multiple datasets. These covariates were selected based on relevance to cardiometabolic health and obesity, and previous evidence of context-specific effects with BMI (Rask-Andersen et al., 2017; Robinson et al., 2017; Justice et al., 2017; Tyrrell et al., 2017; Young et al., 2016; Winkler et al., 2015). For UKBB, phenotype values were used from the collection that was closest to recruitment, and for PMBB the median values were used – for GERA and eMERGE, only one value was available. Additional details on covariate constructions, transformations, filtering, and cohort availability are provided in Supplementary file 1b.
PGS construction
Request a detailed protocolPGS for BMI (PGSBMI) were constructed using PRS-CSx (Ruan et al., 2022), using GWAS summary statistics for individuals of European (Locke et al., 2015), African (Ng et al., 2017), and East Asian (Sakaue et al., 2021) ancestry that were out-of-sample of study participants. A set of 1.29 million HapMap3 SNPs provided by PRS-CSx was used for PGS calculation, which are generally well-imputed and variable frequency across global populations. Default settings for PRS-CSx (downloaded November 22, 2021) were used, which have been demonstrated to perform well for highly polygenic traits such as BMI (list of parameters is provided in Supplementary file 1i). The final PGSBMI per ancestry and cohort was calculated by regressing log(BMI) on the PGSBMI per ancestry without covariates – the combined, predicted value was used as a single PGSBMI in downstream analyses.
For GERA, BMI was not transformed as it was already binned into a categorical variable with five levels (18≤, 19–25, 26–29, 30–39, >40). Additionally, for GERA the uncombined ancestry-specific PGSBMI was used in the final models as it had higher R2 than using the combined PGSBMI (data not shown).
PGSBMI performance after covariate stratification
Request a detailed protocolAnalyses were performed separately for each cohort and ancestry. For each covariate, individuals were binned by binary covariates or quintiles for continuous covariates. Incremental PGSBMI R2 was calculated by taking the difference in R2 between:
We performed 5,000 bootstrap replications to obtain a bootstrapped distribution of R2. p-Values for differences in R2 were calculated between groups by calculating the proportion of overlap between two normal distributions of the R2 value using the standard deviations of the bootstrap distributions. Again for GERA, BMI was not transformed.
PGSBMI interaction modeling
Request a detailed protocolEvidence for interaction with each covariate with the PGSBMI was evaluated using linear regression. It has been reported that the inclusion of covariates that are genetically correlated with the outcome can inflate test statistic estimates (Aschard et al., 2015; Kerin and Marchini, 2020; Vanderweele et al., 2013). To assuage these concerns, we introduced a novel correction, where we first calculated a PGS for the covariate (PGSCovariate) and included it in the model, as well as an interaction term between PGSBMI and PGSCovariate. The PGSCovariate terms were calculated using the European ancestry Neale Lab summary statistics (URLs) and PRS-CS (Ge et al., 2019). To standardize effect sizes across analyses, PGSBMI and Covariate were first converted to mean zero and standard deviation of 1 (binary covariates were not standardized). We demonstrate inclusion of PGSCovariate terms successfully reduced significance of the PGSBMI * Covariate term (Figure 3—figure supplement 1). The final model used to evaluate PGSBMI and Covariate interactions was
We report the effect estimates of the PGSBMI * Covariate term, and differences in model R2 with and without the PGSBMI * Covariate term. Again for GERA, BMI was not transformed.
Correlation between R2 differences, interaction effects, and main effects
Request a detailed protocolWe estimated the main effects of each covariate on BMI with the following model:
Note that we ran new models with main effects only, instead of using the main effect from the interaction models (as the main effects in the interaction models depend on the interaction terms, and main effects used to create interaction terms are sensitive to centering of variables despite the scale invariance of linear regression itself; Afshartous and Preston, 2011). We then estimated the correlation between main effects, interaction effects, and maximum R2 differences across all cohorts and ancestries weighting by sample size, analyzing quantitative and binary variables separately.
Quantile regression to measure PGS effect across percentiles of BMI
Request a detailed protocolThe effect of PGSBMI on BMI at different deciles of BMI was assessed using quantile regression. Tau – the parameter that sets which percentile to be predicted – was set to 0.10,0.20, …,0.90. Models included age, sex, and the top 5 genetic PCs as covariates. Analyses were stratified by ancestry and cohort, and BMI was first log transformed. GERA was excluded from these analyses as a portion of the models failed to run (as BMI values from GERA were already binned, some deciles all had the same BMI value – additionally, difference in effects between bins would be harder to evaluate as BMI within each decile would be more homogeneous).
Machine learning models
Request a detailed protocolUKBB EUR and GERA EUR models were restricted to 30,000 random individuals for computational reasons – BMI distributions did not differ from the full-sized datasets (Kolmogorov–Smirnov p-values of 0.29 and 0.57, respectively). PGSBMI and top 5 genetic principal components were included as features in all models. Two sets of models were evaluated for each cohort and ancestry: including age and sex as features, and including all available covariates in each cohort as features. Interaction terms between PGS and each covariate were included for models using interaction terms. ‘Ever Smoker’ status was used in favor of ‘Never’ versus ‘Current smoking’ status (if present) as individuals with ‘Never’ versus ‘Current’ status are a subset of those with ‘Ever Smoker’ status. UKBB AFR with all covariates was excluded due to small sample size (N = 53).
Neural networks were used as the model of choice, given their inherent ability to model interactions and other nonlinear dependencies. Prior to modeling, all features were scaled to be between 0 and 1. We used average tenfold cross-validation R2 to evaluate model performance. Separate models were trained using untransformed and log(BMI). L1-regularized linear regression was used with 18 values of lambda (1.0, 5.0 × 10–1, 2.0 × 10–1, 1.0 × 10–1, 5.0 × 10–2, 2.0 × 10–2, …, 1.0 × 10–5, 5.0 × 10–6, 2.0 × 10–6). Models were trained without inclusion of interaction terms (which neural networks can implicitly model) using 1,000 iterations of random search with the following hyperparameter ranges: size of hidden layers [10, 200], learning rate [0.01, 0.0001], type of learning rate [constant, inverse scaling], power t [0.4, 0.6], momentum [0.80, 1.0], batch size [32, 256], and number of hidden layers [1, 2].
GxAge PGSBMI creation and assessment
Request a detailed protocolAnalyses were conducted in the European UKBB (N = 376,629), as was done in a study on a similar topic (Mostafavi et al., 2020). Three sets of analyses were performed using GWAS conducted in a 60% random split of individuals using the following models (BMI was rank-normal transformed before GWAS):
Using the model in (1) but stratified into quartiles by age. BMI was rank-normal transformed within each quartile.
Using each set of GWAS, PGS was first calculated in a 20% randomly selected training set of the dataset using pruning and thresholding using 10 p-value thresholds (0.50, 0.10, …, 5.0 × 10–5, 1.0 × 10–5) and remaining settings as default in Plink 1.9. For (2), GxAge PGSBMI was calculated using SNPs clumped by their main effect p-values from (1), and additionally incorporating the GxAge interaction effects per SNP. In other words, instead of typical PGS construction as
For an individual i’s PGS calculation, with main SNP effect β, and n SNPs, PGS incorporating GxAge effects (PGSGxAge) was calculated as
where βGxAge is the GxAge effect for each SNP n and Agei is the age for individual i.
For each of the three analyses, the parameters and models resulting in the best-performing PGS (highest incremental R2, using same main effect covariates as in the three GWAS) from the training set were evaluated in the remaining 20% of the study individuals. For (3), models were first trained within each quartile separately. To maintain sense of scale across quartiles (after rank-normal transformation), R2 between all predicted values and true values was calculated together. For R2 confidence intervals, the training set was bootstrapped and evaluated on the test set 5,000 times.
URLs
Neale Lab UKBB summary statistics: http://www.nealelab.is/uk-biobank.
Select analysis code and data are available at https://github.com/RitchieLab/BMI_PGS_eLife (copy archived at Ritchie Lab, 2024).
Appendix 1
RGC management and leadership team
Goncalo Abecasis, PhD, Aris Baras, M.D., Michael Cantor, M.D., Giovanni Coppola, M.D., Andrew Deubler, Aris Economides, Ph.D., Luca A. Lotta, M.D., Ph.D., John D. Overton, Ph.D., Jeffrey G. Reid, Ph.D., Katherine Siminovitch, M.D., Alan Shuldiner, M.D.
Sequencing and lab operations
Christina Beechert, Caitlin Forsythe, M.S., Erin D. Fuller, Zhenhua Gu, M.S., Michael Lattari, Alexander Lopez, M.S., John D. Overton, Ph.D., Maria Sotiropoulos Padilla, M.S., Manasi Pradhan, M.S., Kia Manoochehri, B.S., Thomas D. Schleicher, M.S., Louis Widom, Sarah E. Wolf, M.S., Ricardo H. Ulloa, B.S.
Clinical informatics
Amelia Averitt, Ph.D., Nilanjana Banerjee, Ph.D., Michael Cantor, M.D., Dadong Li, Ph.D., Sameer Malhotra, M.D., Deepika Sharma, MHI, Jeffrey Staples, Ph.D.
Genome informatics
Xiaodong Bai, Ph.D., Suganthi Balasubramanian, Ph.D., Suying Bao, Ph.D., Boris Boutkov, Ph.D., Siying Chen, Ph.D., Gisu Eom, B.S., Lukas Habegger, Ph.D., Alicia Hawes, B.S., Shareef Khalid, Olga Krasheninina, M.S., Rouel Lanche, B.S., Adam J. Mansfield, B.A., Evan K. Maxwell, Ph.D., George Mitra, B.A., Mona Nafde, M.S., Sean O’Keeffe, Ph.D., Max Orelus, B.B.A., Razvan Panea, Ph.D., Tommy Polanco, B.A., Ayesha Rasool, M.S., Jeffrey G. Reid, Ph.D., William Salerno, Ph.D., Jeffrey C. Staples, Ph.D., Kathie Sun, Ph.D.
Analytical genomics and data science
Goncalo Abecasis, D.Phil., Joshua Backman, Ph.D., Amy Damask, Ph.D., Lee Dobbyn, Ph.D., Manuel Allen Revez Ferreira, Ph.D., Arkopravo Ghosh, M.S., Christopher Gillies, Ph.D., Lauren Gurski, B.S., Eric Jorgenson, Ph.D., Hyun Min Kang, Ph.D., Michael Kessler, Ph.D., Jack Kosmicki, Ph.D., Alexander Li, Ph.D., Nan Lin, Ph.D., Daren Liu, M.S., Adam Locke, Ph.D., Jonathan Marchini, Ph.D., Anthony Marcketta, M.S., Joelle Mbatchou, Ph.D., Arden Moscati, Ph.D., Charles Paulding, Ph.D., Carlo Sidore, Ph.D., Eli Stahl, Ph.D., Kyoko Watanabe, Ph.D., Bin Ye, Ph.D., Blair Zhang, Ph.D., Andrey Ziyatdinov, Ph.D.
Therapeutic area genetics
Ariane Ayer, B.S., Aysegul Guvenek, Ph.D., George Hindy, Ph.D., Giovanni Coppola, M.D., Jan Freudenberg, M.D., Jonas Bovijn M.D., Katherine Siminovitch, M.D., Kavita Praveen, Ph.D., Luca A. Lotta, M.D., Manav Kapoor, Ph.D., Mary Haas, Ph.D., Moeen Riaz, Ph.D., Niek Verweij, Ph.D., Olukayode Sosina, Ph.D., Parsa Akbari, Ph.D., Priyanka Nakka, Ph.D., Sahar Gelfman, Ph.D., Sujit Gokhale, B.E., Tanima De, Ph.D., Veera Rajagopal, Ph.D., Alan Shuldiner, M.D., Bin Ye, Ph.D., Gannie Tzoneva, Ph.D., Juan Rodriguez-Flores, Ph.D.
Research program management and strategic initiatives
Esteban Chen, M.S., Marcus B. Jones, Ph.D., Michelle G. LeBlanc, Ph.D., Jason Mighty, Ph.D., Lyndon J. Mitnaul, Ph.D., Nirupama Nishtala, Ph.D., Nadia Rana, Ph.D., Jaimee Hernandez
Penn Medicine BioBank Banner Author List and Contribution Statements
PMBB Leadership Team
Daniel J. Rader, M.D., Marylyn D. Ritchie, Ph.D.
Contribution: All authors contributed to securing funding, study design and oversight. All authors reviewed the final version of the manuscript.
Patient Recruitment and Regulatory Oversight
JoEllen Weaver, Nawar Naseer, Ph.D., M.P.H., Giorgio Sirugo, M.D., P.h.D., Afiya Poindexter, Yi-An Ko, Ph.D., Kyle P. Nerz
Contributions: JW manages patient recruitment and regulatory oversight of study. NN manages participant engagement, assists with regulatory oversight, and researcher access. GS assists with researcher access. AP, YK, KPN perform recruitment and enrollment of study participants.
Lab Operations
JoEllen Weaver, Meghan Livingstone, Fred Vadivieso, Stephanie DerOhannessian, Teo Tran, Julia Stephanowski, Salma Santos, Ned Haubein, P.h.D., Joseph Dunn
Contribution: JW, ML, FV, SD conduct oversight of lab operations. ML, FV, AK, SD, TT,JS, SS perform sample processing. NH, JD are responsible for sample tracking and the laboratory information management system.
Clinical Informatics
Anurag Verma, Ph.D., Colleen Morse Kripke, M.S. DPT, MSA, Marjorie Risman, M.S., Renae Judy, B.S., Colin Wollack, M.S.
Contribution: All authors contributed to the development and validation of clinical phenotypes used to identify study subjects and (when applicable) controls.
Genome Informatics
Anurag Verma Ph.D., Shefali S. Verma, Ph.D., Scott Damrauer, M.D., Yuki Bradford, M.S., Scott Dudek, M.S., Theodore Drivas, M.D., Ph.D.
Contribution: AV, SSV, and SD are responsible for the analysis, design, and infrastructure needed to quality control genotype and exome data. YB performs the analysis. TD and AV provides variant and gene annotations and their functional interpretation of variants.
For PMBB, please use: biobank@pennmedicine.upenn.edu
For Regeneron, please use: RGCcollaborations@regeneron.com
Data availability
UK Biobank data was accessed under project #32133. eMERGE data is available at dbGaP in phs001584.v2.p2. GERA data is available at dbGaP in phs000674.v3.p3. PMBB individual level genotype and phenotype data can be accessed through a research collaboration with a Penn investigator, as long as the requestor is from a not-for-profit organization. The PMBB genetic data used in this study were generated in collaboration with Regeneron Genetics Center; as such, we are unable to share the data with for-profit organizations without a three-way research collaboration agreement. Data sharing will require a PMBB project proposal and IRB approval. Collaboration requests can be sent to biobank@upenn.edu. Select analysis code and data are available at https://github.com/RitchieLab/BMI_PGS_eLife (copy archived at Ritchie Lab, 2024).
References
-
Key results of interaction models with centeringJournal of Statistics Education 19:11889620.https://doi.org/10.1080/10691898.2011.11889620
-
Does education attenuate the genetic risk of obesity? Evidence from U.K. TwinsEconomics and Human Biology 31:200–208.https://doi.org/10.1016/j.ehb.2018.08.011
-
Adjusting for heritable covariates can bias effect estimates in genome-wide association studiesAmerican Journal of Human Genetics 96:329–339.https://doi.org/10.1016/j.ajhg.2014.12.021
-
Estimating cross-population genetic correlations of causal effect sizesGenetic Epidemiology 43:180–188.https://doi.org/10.1002/gepi.22173
-
Phenome-wide heritability analysis of the UK BiobankPLOS Genetics 13:e1006711.https://doi.org/10.1371/journal.pgen.1006711
-
Inferring Gene-by-Environment Interactions with a Bayesian Whole-Genome Regression ModelAmerican Journal of Human Genetics 107:698–713.https://doi.org/10.1016/j.ajhg.2020.08.009
-
Achieved educational attainment, inherited genetic endowment for education, and obesityBiodemography and Social Biology 66:132–144.https://doi.org/10.1080/19485565.2020.1869919
-
Physical activity and the association of common FTO gene variants with body mass index and obesityArchives of Internal Medicine 168:1791–1797.https://doi.org/10.1001/archinte.168.16.1791
-
SoftwareBMI_PGS_eLife, version swh:1:rev:58046f2f88349bfea043f97b0b2aac29b6f83004Software Heritage.
-
The molecular genetics of Marfan syndrome and related disordersJournal of Medical Genetics 43:769–787.https://doi.org/10.1136/jmg.2005.039669
-
Gene-obesogenic environment interactions in the UK Biobank studyInternational Journal of Epidemiology 46:559–575.https://doi.org/10.1093/ije/dyw337
-
Environmental confounding in gene-environment interaction studiesAmerican Journal of Epidemiology 178:144–152.https://doi.org/10.1093/aje/kws439
Article and author information
Author details
Funding
National Institutes of Health (AI077505)
- Daniel Hui
- Scott Dudek
- Marylyn D Ritchie
National Institutes of Health (HL169458)
- Daniel Hui
- Scott Dudek
- Marylyn D Ritchie
National Institute of Diabetes and Digestive and Kidney Diseases (DK52431)
- Wendy K Chung
National Institutes of Health (U01 HG011166)
- Josh F Peterson
National Institutes of Health (U01 HG008680)
- Chunhua Weng
Group Health Cooperative/University of Washington (U01HG008657)
- Gail P Jarvik
Brigham and Women's Hospital (U01HG008685)
- Elizabeth W Karlson
Vanderbilt University Medical Center (U01HG008672)
- Wei-Qi Wei
- Josh F Peterson
- Qiping Feng
Cincinnati Children’s Hospital Medical Center (U01HG008666)
- Leah C Kottyan
Mayo Clinic (U01HG006379)
- Iftikhar J Kullo
- Johanna L Smith
Columbia University Health Sciences (U01HG008680)
- Krzysztof Kiryluk
- Atlas Khan
- Chunhua Weng
- Wendy K Chung
Northwestern University (U01HG008673)
- Theresa L Walunas
- Megan J Puckelwartz
Vanderbilt University Medical Center serving as the Coordinating Center (U01HG008701)
- Josh F Peterson
- Wei-Qi Wei
The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.
Acknowledgements
For UK Biobank: This research has been conducted using the UK Biobank Resource under Application Number 32133. This work uses data provided by patients and collected by the NHS as part of their care and support.
For GERA: Data came from a grant, the Resource for Genetic Epidemiology Research in Adult Health and Aging (RC2 AG033067; Schaefer and Risch, PIs) awarded to the Kaiser Permanente Research Program on Genes, Environment, and Health (RPGEH) and the UCSF Institute for Human Genetics. The RPGEH was supported by grants from the Robert Wood Johnson Foundation, the Wayne and Gladys Valley Foundation, the Ellison Medical Foundation, Kaiser Permanente Northern California, and the Kaiser Permanente National and Northern California Community Benefit Programs. The RPGEH and the Resource for Genetic Epidemiology Research in Adult Health and Aging are described in the following publication, Schaefer C, et al., The Kaiser Permanente Research Program on Genes, Environment and Health: Development of a Research Resource in a Multi-Ethnic Health Plan with Electronic Medical Records, In preparation, 2013.
For eMERGE: We acknowledge David Crosslin for helping clean the eMERGE data. Please see funding section for eMERGE funding acknowledgments.
For PMBB: We acknowledge the Penn Medicine BioBank (PMBB) for providing data and thank the patient- participants of Penn Medicine who consented to participate in this research program. We would also like to thank the Penn Medicine BioBank team and Regeneron Genetics Center for providing genetic variant data for analysis. The PMBB is approved under IRB protocol# 813913 and supported by Perelman School of Medicine at University of Pennsylvania, a gift from the Smilow family, and the National Center for Advancing Translational Sciences of the National Institutes of Health under CTSA award number UL1TR001878.
Version history
- Sent for peer review:
- Preprint posted:
- Reviewed Preprint version 1:
- Reviewed Preprint version 2:
- Version of Record published:
Cite all versions
You can cite all versions using the DOI https://doi.org/10.7554/eLife.88149. This DOI represents all versions, and will always resolve to the latest one.
Copyright
© 2023, Hui et al.
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.
Metrics
-
- 1,522
- views
-
- 74
- downloads
-
- 5
- citations
Views, downloads and citations are aggregated across all versions of this paper published by eLife.
Citations by DOI
-
- 1
- citation for umbrella DOI https://doi.org/10.7554/eLife.88149
-
- 3
- citations for Reviewed Preprint v1 https://doi.org/10.7554/eLife.88149.1
-
- 1
- citation for Reviewed Preprint v2 https://doi.org/10.7554/eLife.88149.2