1. Structural Biology and Molecular Biophysics

Sequence co-evolution gives 3D contacts and structures of protein complexes

  1. Thomas A Hopf
  2. Charlotta P I Schärfe
  3. João P G L M Rodrigues
  4. Anna G Green
  5. Oliver Kohlbacher
  6. Chris Sander  Is a corresponding author
  7. Alexandre M J J Bonvin  Is a corresponding author
  8. Debora S Marks  Is a corresponding author
  1. Harvard University, United States
  2. Technische Universität München, Germany
  3. University of Tübingen, Germany
  4. Bijvoet Center for Biomolecular Research, Utrecht University, Netherlands
  5. Memorial Sloan Kettering Cancer Center, United States
https://doi.org/10.7554/eLife.03430
Share this article
Cite this article
  1. Thomas A Hopf
  2. Charlotta P I Schärfe
  3. João P G L M Rodrigues
  4. Anna G Green
  5. Oliver Kohlbacher
  6. Chris Sander
  7. Alexandre M J J Bonvin
  8. Debora S Marks
(2014)
Sequence co-evolution gives 3D contacts and structures of protein complexes
eLife 3:e03430.
https://doi.org/10.7554/eLife.03430
  2. Download BibTeX
  3. Download .RIS

Abstract

Protein–protein interactions are fundamental to many biological processes. Experimental screens have identified tens of thousands of interactions, and structural biology has provided detailed functional insight for select 3D protein complexes. An alternative rich source of information about protein interactions is the evolutionary sequence record. Building on earlier work, we show that analysis of correlated evolutionary sequence changes across proteins identifies residues that are close in space with sufficient accuracy to determine the three-dimensional structure of the protein complexes. We evaluate prediction performance in blinded tests on 76 complexes of known 3D structure, predict protein–protein contacts in 32 complexes of unknown structure, and demonstrate how evolutionary couplings can be used to distinguish between interacting and non-interacting protein pairs in a large complex. With the current growth of sequences, we expect that the method can be generalized to genome-wide elucidation of protein–protein interaction networks and used for interaction predictions at residue resolution.

https://doi.org/10.7554/eLife.03430.001

eLife digest

DNA is often referred to as the ‘blueprint of life’, as this molecule contains the instructions that are required to build a living organism from a single cell. But these instructions largely play out through the proteins that DNA encodes; and most proteins do not work alone. Instead they come together in different combinations, or complexes, and a single protein may participate in many complexes with different activities.

Proteins are so small that it is difficult to get clear information about what they look like. Visualizing protein complexes is even harder. Most protein–protein interactions remain poorly understood, even in the best-studied organisms such as humans, yeast, and bacteria.

Proteins are made from smaller molecules, called amino acids, strung together one after the other. The order in which different amino acids are arranged in a protein determines the protein’s shape and ultimately its function. Like DNA, protein sequences can change over time. Sometimes, the sequence of one protein changes in a way that prevents it binding to another protein. If these two proteins must work together for an organism to survive, the second protein will often develop a compensating change that allows the protein–protein complex to reform.

Identifying pairs of changes in the sequences of pairs of proteins suggests that the two proteins interact and gives some information about how the proteins fit together. Different species can have copies of the same proteins that have slightly different sequences. Since the DNA sequences from many different organisms are already known, there are now many opportunities to find sites in pairs of proteins that have evolved together, or co-evolved, over time.

To find sites that seem to have co-evolved, Hopf et al. used a computer program based on an approach from statistical physics to look at pairs of proteins that were already known to form complexes. Co-evolving sites were found in over 300 pairs of proteins; including 76 where the structure of the complex was already known. When sites that were predicted to be co-evolving were then mapped to these known complex structures, the co-evolving sites were remarkably close to the true protein–protein contacts. This indicates that the information from the co-evolved sequences is sufficient to show how two proteins fit together.

Hopf et al. then turned their attention to 82 pairs of proteins that were thought to interact, but where a structure was unavailable. For 32 of these pairs, structures of the entire complex could be predicted, showing how the two proteins might interact. Furthermore, when other researchers subsequently worked out the structure of one of these complexes, the prediction was a good match to the solved complex structure.

The machinery of life is largely made up of proteins, which must interact in ever-changing but precise ways. The new methods developed by Hopf et al. provide a new way to discover and investigate the details of these interactions.

https://doi.org/10.7554/eLife.03430.002

Introduction

A large part of biological research is concerned with the identity, dynamics, and specificity of protein interactions. There have been impressive advances in the three-dimensional (3D) structure determination of protein complexes which has been significantly extended by homology-inferred 3D models (Mosca et al., 2012; Webb et al., 2014) (Hart et al., 2006; Zhang et al., 2012). However, there is still little, or no, 3D information for ∼80% of the currently known protein interactions in bacteria, yeast, or human, amounting to at least ∼30,000/∼6000 incompletely characterized interactions in human and Escherichia coli, respectively (Mosca et al., 2012; Rajagopala et al., 2014). With the rapid rise in our knowledge of genetic variation at the sequence level, there is an increased interest in linking sequence changes to changes in molecular interactions, but current experimental methods cannot match the increase in the demand for residue-level information of these interactions. One way to address the knowledge gap of protein interactions has been the use of hybrid, computational–experimental approaches that typically combine 3D structural information at varying resolutions, homology models, and other methods (de Juan et al., 2013), with force field-based approaches such as RosettaDock, residue cross-linking, and data-driven approaches that incorporate various sources of biological information (Kortemme and Baker, 2002; Dominguez et al., 2003; Kortemme and Baker, 2004; Kortemme et al., 2004; Svensson et al., 2004; Chaudhury et al., 2011; Schneidman-Duhovny et al., 2012; Velazquez-Muriel et al., 2012; Karaca and Bonvin, 2013; Rodrigues et al., 2013; Webb et al., 2014). However, most of these approaches depend on the availability of prior knowledge and many biologically relevant systems remain out of reach, as additional experimental information is sparse (e.g., membrane proteins, transient interactions, and large complexes). One promising computational approach is to use evolutionary analysis of amino acid co-variation to identify close residue contacts across protein interactions, which was first used 20 years ago (Gobel et al., 1994; Pazos and Valencia, 2001), and subsequently used also to identify protein interactions (Pazos et al., 1997; Pazos and Valencia, 2002). Others have used some evolutionary information to improve a machine learning approach to developing docking potentials (Faure et al., 2012; Andreani et al., 2013; Andreani and Guerois, 2014). These previous approaches relied on a local model of co-evolution that is less likely to disentangle indirect and therefore incorrect correlations from the direct co-evolution, as has been described in work on residue–residue interactions in single proteins (Marks et al., 2012). More recently, reports using a global model have been successful in identifying residue interactions from evolutionary co-variation, for instance between histidine kinases and response regulators (Burger & van Nimwegen, 2008; Skerker et al., 2008; Weigt et al., 2009), and this approach has only recently been generalized and used to predict contacts between proteins in complexes of unknown structure, in an independent effort parallel to this work (Ovchinnikov et al., 2014). In principle, just a small number of key residue–residue contacts across a protein interface would allow computation of 3D models and provide a powerful, orthogonal approach to experiments.

Since the recent demonstration of the use of evolutionary couplings (ECs) between residues to determine the 3D structure of individual proteins (Marks et al., 2011; Morcos et al., 2011; Aurell and Ekeberg, 2012; Jones et al., 2012; Kamisetty et al., 2013), including integral membrane proteins (Hopf et al., 2012; Nugent and Jones, 2012), we reason that an evolutionary statistical approach such as EVcouplings (Marks et al., 2011) could be used to determine co-evolved residues between proteins. To assess this hypothesis, we built an evaluation set based on all known binary protein interactions in E. coli that have 3D structures of the complex as recently summarized (Rajagopala et al., 2014). We develop a score for every predicted inter-protein residue pair based on the overall inter-protein EC score distributions resulting in accurate predictions for the majority of top ranked inter-protein EC pairs (inter-ECs) and sufficient to calculate accurate 3D models of the complexes in the docked subset (Figure 1A). This approach was then used to predict evolutionary couplings for 32 complexes of unknown 3D structures that have a sufficient number of sequences. Predictions include the structurally unsolved interactions between the a-, b-, and c-subunits of ATP synthase, which are supported by previously published experimental results.

Figure 1 with 1 supplement see all
Download asset Open asset
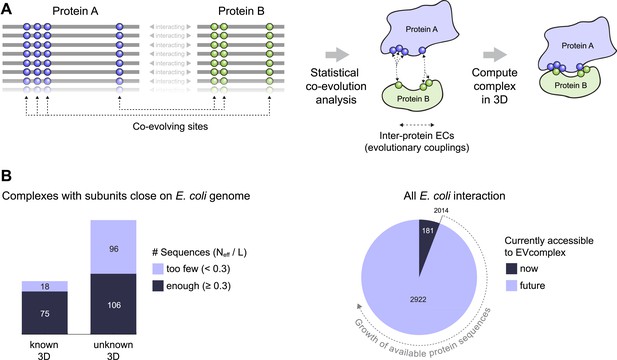
Co-evolution of residues across protein complexes from the evolutionary sequence record.

(A) Evolutionary pressure to maintain protein–protein interactions leads to the co-evolution of residues between interacting proteins in a complex. By analyzing patterns of amino acid co-variation in an alignment of putatively interacting homologous proteins (left), evolutionary couplings between co-evolving inter-protein residue pairs can be identified (middle). By defining distance restraints on these pairs, the 3D structure of the protein complex can be inferred using docking software (right). (B) Distribution of E. coli protein complexes of known and unknown 3D structure where both subunits are close on the bacterial genome (left), allowing sequence pair matching by genomic distance. For a subset of these complexes, sufficient sequence information is available for evolutionary couplings analysis (dark blue bars). As more genomic information is created through on-going sequencing efforts, larger fractions of the E. coli interactome become accessible for EVcomplex (right). A detailed version of the workflow used to calculate all E. coli complexes currently for which there is currently enough sequence information is shown in Figure1—figure supplement 1.

https://doi.org/10.7554/eLife.03430.003

Results

We first investigated whether co-evolving residues between proteins are close in three dimensions by assessing blinded predictions of residue co-evolution against experimentally determined 3D complex structures. We follow this evaluation by then predicting co-evolved residue pairs of interacting proteins that have no known complex structure.

Extension of the evolutionary couplings method to protein complexes

To compute co-evolution across proteins, individual protein sequences must be paired up with each other that are presumed to interact, or being tested to see if they interact. Without this condition, proteins could be paired together that do not in fact interact with each other and therefore detection of co-evolution would be compromised. Given that the evolutionary couplings method depends on large numbers of diverse sequences (Hopf et al., 2012), some assumption must be made about which proteins interact with each other in homologous sequences in other species. Since it is challenging to know a priori whether particular interactions are conserved across many millions of years in thousands of different organisms, we use proximity of the two interacting partners on the genome as a proxy for this, with the goal of reducing incorrect pairings.

To assemble the broadest possible data sets to test the approach and make predictions, we take all known interacting proteins assembled in a published data set that contains ∼3500 high-confidence protein interactions in E. coli (Rajagopala et al., 2014). After removing redundancy and requiring close genome distance between the pairs of proteins this results in 326 interactions, see ‘Materials and methods’ (Figure 1B, Figure 1—figure supplement 1, Supplementary file 1 and 2),

The paired sequences are concatenated and statistical co-evolution analysis is performed using EVcouplings (Marks et al., 2011; Morcos et al., 2011; Aurell and Ekeberg, 2012), that applies a pseudolikelihood maximization (PLM) approximation to determine the interaction parameters in the underlying maximum entropy probability model (Balakrishnan et al., 2011; Ekeberg et al., 2013; Kamisetty et al., 2013), simultaneously generating both intra- and inter-EC scores for all pairs of residues within and across the protein pairs (Figure 1A). Evolutionary coupling calculations in previous work have indicated that this global probability model approach requires a minimum number of sequences in the alignment with at least 1 non-redundant sequence per residue (Marks et al., 2011; Morcos et al., 2011; Hopf et al., 2012; Jones et al., 2012; Kamisetty et al., 2013). Our current approach allows complexes with fewer available sequences to be assessed (minimum at 0.3 non-redundant sequences per residue) by using a new quality assessment score to assess the likelihood of the predicted contacts to be correct. The EVcomplex score is based on the knowledge that most pairs of residues are not coupled and true pair couplings are outliers in the high-scoring tail of the distribution (See ‘Materials and methods’, Figure 2A,B, Figure 2—figure supplement 1 and 2). The score can intuitively be understood as the distance from the noisy background of non-significant pair scores, normalized by the number of non-redundant sequences and the length of the protein (‘Materials and methods’, equations 1 and 2). If the number of sequences per residue is not controlled for, there is a large bias in the results, overestimating performance with low numbers of sequences (Figure 2B,C). The precise functional form of the correction for low numbers of sequences was chosen non-blindly after observing the dependencies in the test set.

Figure 2 with 8 supplements see all
Download asset Open asset
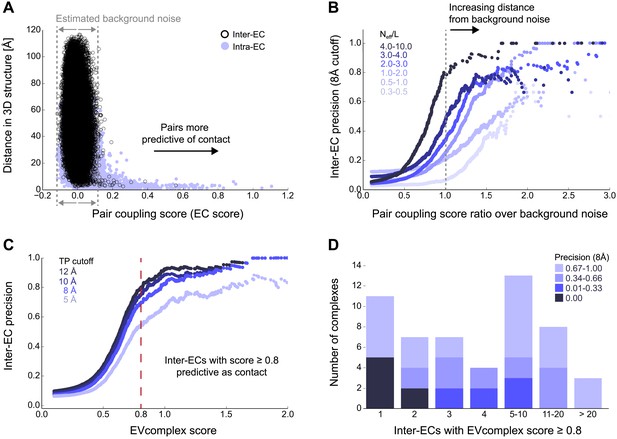
Evolutionary couplings capture interacting residues in protein complexes.

(A) Inter- and Intra-EC pairs with high coupling scores largely correspond to proximal pairs in 3D, but only if they lie above the background level of the coupling score distribution. To estimate this background noise a symmetric range around 0 is considered with the width being defined by the minimum inter-EC score. For the protein complexes in the evaluation set, this distribution is compared to the distance in the known 3D structure of the complex that is shown here for the methionine transporter complex, MetNI. (Plots for all complexes in the evaluation set are shown in Figure 2—figure supplement 1 and 2.) (B) A larger distance from the background noise (ratio of EC score over background noise line) gives more accurate contacts. Additionally, the higher the number of sequences in the alignment the more reliable the inferred coupling pairs are which then reduces the required distance from noise (different shades of blue). Residue pairs with an 8 Å minimum atom distance between the residues are defined as true positive contacts, and precision = TP/(TP + FP). The plot is limited to range (0,3) which excludes the histidine kinase—response regulator complex (HK–RR)—a single outlier with extremely high number of sequences. (C) To allow the comparison across protein complexes and to estimate the average inter-EC precision for a given score threshold independent of sequence numbers, the raw couplings score is normalized for the number of sequences in the alignment, resulting in the EVcomplex score. In this work, inter-ECs with an EVcomplex score ≥0.8 are used. Note: the shown plot is cut off at a score of 2 in order to zoom in on the phase change region and the high sequence coverage outlier HK-RR is excluded. (D) For complexes in the benchmark set, inter-EC pairs with EVcomplex score ≥0.8 give predictions of interacting residue pairs between the complex subunits to varying accuracy (8 Å TP distance cutoff). All predicted interacting residues for complexes in the benchmark set that had at least one inter-EC above 0.8 are shown as contact maps in Figure 2—figure supplement 3–8.

https://doi.org/10.7554/eLife.03430.005

Blinded prediction of known complexes

Evolutionary covariation reveals inter-protein contacts

Of the 329 interactions identified that are close on the E. coli genome, 76 have a sufficient number of alignable homologous sequences and known 3D structures either in E. coli or in other species. This set was used to test the inter-protein evolutionary coupling predictions (Supplementary file 1). The relationship between the EVcomplex score and the precision of the corresponding inter-protein ECs suggests that on average 74% (69%) of the predicted pairs with EVcomplex score greater than 0.8 will be accurate to within 10 Å (8 Å) of an experimental structure of the complex (Figure 2C). Most complexes have at least one inter-protein predicted contact above the selected score threshold of 0.8 (53/76 complexes). Three complexes have more than 20 predicted inter-protein residue contacts which are over 80% accurate, namely the histidine kinase and response regulator system (78 residue pairs), t-RNA synthetase (32 residue pairs), and the vitamin B importer complex (21 residue pairs), with precision over 80% (complex numbers 330, 019, 130 respectively, Figure 2D, Figure 2—figure supplements 3–8, Supplementary file 1).

We suggest that users of EVcomplex consider predicted contacts that lie below the threshold of 0.8 in the context of other biological knowledge, where available, or in comparison to other higher scoring contacts for the same complex. In this way additional true positive inter-residue contacts can be distinguished from false positives. For instance, the ethanolamine ammonia-lyase complex (complex 065) has only 3 predicted inter-protein residue pairs above the score threshold, but in fact has 5 additional correct pairs with EVcomplex scores slightly below the threshold of 0.8 which cluster with the 3 high-scoring contacts on the monomers, indicating that they are also correct.

Some of the high confidence inter-protein ECs in the test set are not close in 3D space when compared to their known 3D structures. These false positives may be a result of assumptions in the method that are not always correct. This includes (1) the assumption that the interaction between paired proteins is conserved across species and across paralogs, and (2) that truly co-evolved residues across proteins are indeed always close in 3D, which is not always the case. In addition, the complexes may also exist in alternative conformations that have not necessarily all been captured yet by crystal or NMR structures, for instance in the case of the large conformational changes of the BtuCDF complex (Hvorup et al., 2007).

Docking is accurate with few pairs of predicted contacts

To test whether the computed inter-protein ECs are sufficient for obtaining accurate 3D structures of the whole complex, we selected 15 diverse examples (with 5 or more inter-protein residue contacts) for docking (Table 1, Figure 3, Figure 3—figure supplement 1, Supplementary file 3) with HADDOCK (Dominguez et al., 2003; de Vries et al., 2007). The docking procedure is fast and generates 100 3D models of each complex using all residue pairs with EVcomplex scores above the selection threshold. We additionally dock negative controls to assess the amount of information added to the docking protocol by evolutionary couplings (500 models per run, no constraints other than center of mass, see ‘Materials and methods’). The best models for all 15 complexes docked with evolutionary couplings have interface RMSDs under 6 Å, 12/15 have the best scoring model under 4 Å and the top ranked models for 11/15 are under 5 Å backbone interface RMSD compared to a crystal or NMR structure interface. Over 70% of the generated models are close to the experimental structures of the complexes (<4 Å backbone iRMSD), compared to less than 0.5% in the controls (and these were not high–ranked) (Figure 3—figure supplement 1, Supplementary file 3, ‘Supplementary data’). Not surprisingly complexes that have the largest numbers of true positive predicted contacts perform the best when docking. For example, the ribosomal proteins RS3 and RS14 have 11 true positive inter-protein ECs and result in a top ranked model only 1.1 Å iRMSD from the reference structure. More surprisingly, other complexes with a lower proportion of true positive inter-protein contacts, such as Ubiquinol oxidase (6 out of 11) or the epsilon and gamma subunits of ATP synthase (8 out of 15) also produced accurate predicted complexes, with an iRMSD of 1.8 and 1.4 Å respectively. The docking experiments therefore demonstrate that inter-protein ECs, even in the presence of incorrect predictions, can be sufficient to give accurate 3D models of protein complexes, but more work will be needed to quantify the likelihood of successful docking from the predicted contacts.

Table 1

EVcomplex predictions and docking results for 15 protein complexes

https://doi.org/10.7554/eLife.03430.014
EVcomplex contactsDocking quality (iRMSD)
Complex nameSubunitsSeqs†ECs‡TP rate§Top ranked model#Best model
Carbamoyl-phosphate synthaseCarB:CarA2.3170.881.91.9
Aminomethyltransferase/Glycine cleavage system H proteinGcsH:GcsT2.950.25.45.4
Histidine kinase/response regulatorKdpD:CheY (T. maritima)95.4780.722.12.0
Ubiquinol oxidaseCyoB:CyoA1.0110.551.81.2
Outer membrane usher protein/Chaperone proteinFimD:FimC3.660.833.23.0
Molybdopterin synthaseMoaD:MoaE3.681.04.44.1
Methionine transporter complexMetN:MetI1.9140.861.51.2
Dihydroxyacetone kinaseDhaL:DhaK1.4120.426.72.4
Vitamin B12 uptake systemBtuC:BtuF3.250.62.82.8
Vitamin B12 uptake systemBtuC:BtuD9.8210.881.10.9
ATP synthase γ and ε subunitsAtpE:AtpG2.9150.531.41.4
IIA-IIB complex of the N,N'-diacetylchitobiose (Chb) transporterPtqA:PtqB3.150.27.25.5
30 S Ribosomal proteinsRS3:RS141.4110.911.11.1
Succinatequinone oxido-reductase flavoprotein/iron-sulfur subunitsSdhB:SdhA3.080.621.41.4
30 S Ribosomal proteinsRS10:RS141.261.05.32.5
  1. †

    Number of non-redundant sequences in concatenated alignment normalized by alignment length.

  2. ‡

    Inter-ECs with EVcomplex score ≥0.8.

  3. §

    True Positive rate for inter-ECs above score threshold.

  4. #

    iRMSD positional deviation of model from known structure, for docked model with best HADDOCK score.

  5. Lowest iRMSD observed across all models.

Figure 3 with 1 supplement see all
Download asset Open asset
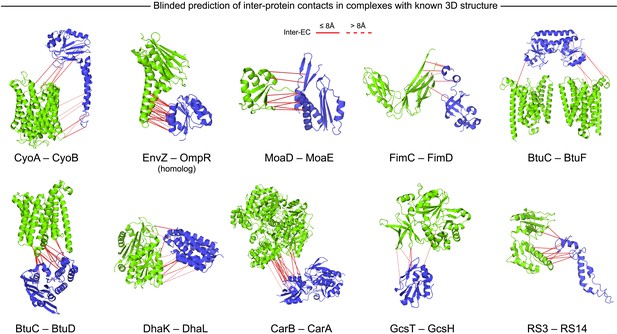
Blinded prediction of evolutionary couplings between complex subunits with known 3D structure.

Inter-ECs with EVcomplex score ≥0.8 on a selection of benchmark complexes (monomer subunits in green and blue, inter-ECs in red, pairs closer than 8 Å by solid red lines, dashed otherwise). The predicted inter-ECs for these ten complexes were then used to create full 3D models of the complex using protein–protein docking. For the fifteen complexes for which 3D structures were predicted using docking, energy funnels are shown in Figure 3—figure supplement 1.

https://doi.org/10.7554/eLife.03430.015

Conserved residue networks provide evidence of functional constraints

The top 10 inter-EC pairs between MetI and MetN are accurate to within 8 Å in the MetNI complex (PDB: 3tui [Johnson et al., 2012]), resulting in an average 1.4 Å iRMSD from the crystal structure for all 100 computed 3D models (Table 1, Supplementary file 3 and ‘Supplementary data’). The top 3 inter-EC residue pairs (K136-E108, A128-L105, and E74-R124, MetI-MetN respectively) constitute a residue network coupling the ATP-binding pocket of MetN to the membrane transporter MetI. This network calculated from the sequence alignment corresponds to residues identified experimentally that couple ATP hydrolysis to the open and closed conformations of the MetI dimer (Johnson et al., 2012) (Figure 4A). The vitamin B12 transporter (BtuC) belongs to a different structural class of ABC transporters, but also uses ATP hydrolysis via an interacting ATPase (BtuD). The top 5 inter-ECs co-locate the L-loop of BtuC close to the Q-loop ATP-binding domain of the ATPase, hence coupling the transporter with the ATP hydrolysis state in an analogous way to MetI-MetN. The identification of these coupled residues across the different subunits suggests that EVcomplex identifies not only residues close in space, but also particular pairs that are constrained by the transporter function of these complexes (Kadaba et al., 2008; Johnson et al., 2012).

Figure 4
Download asset Open asset
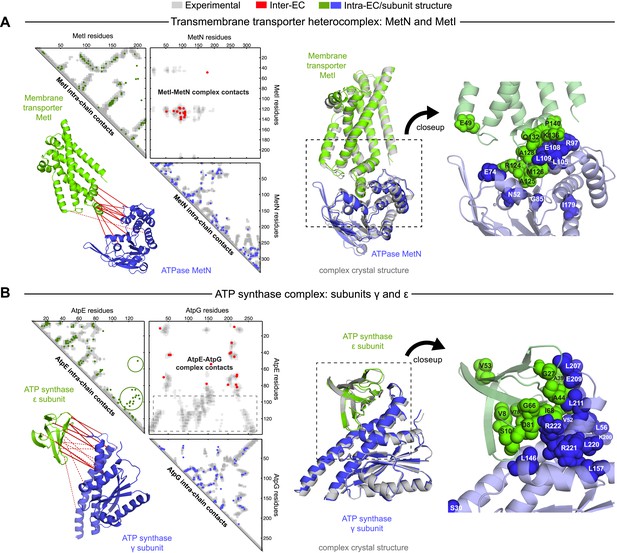
Evolutionary couplings give accurate 3D structures of complexes.

EVcomplex predictions and comparison to crystal structure for (A) the methionine-importing transmembrane transporter heterocomplex MetNI from E. coli (PDB: 3tui) and (B) the gamma/epsilon subunit interaction of E. coli ATP synthase (PDB: 1fs0). Left panels: complex contact map comparing predicted inter-ECs with EVcomplex score ≥0.8 (red dots, upper right quadrant) and intra-ECs (up to the last chosen inter-EC rank; green and blue dots, top left and lower right triangles) to close pairs in the complex crystal (dark/mid/light gray points for minimum atom distance cutoffs of 5/8/12 Å for inter-subunit contacts and dark/mid gray for 5/8 Å within the subunits). Inter-ECs with an EVcomplex score ≥0.8 are also displayed on the spatially separated subunits of the complex (red lines on green and blue cartoons, couplings closer than 8 Å in solid red lines, dashed otherwise, lower left). Right panels: superimposition of the top ranked model from 3D docking (green/blue cartoon, left) onto the complex crystal structure (gray cartoon) and close-up of the interface region with highly coupled residues (green/blue spheres).

https://doi.org/10.7554/eLife.03430.017

The ATP synthase ε and γ subunit complex provides a challenge to our approach, since the ε subunit can take different positions relative to the γ subunit, executing the auto-inhibition of the enzyme by dramatic conformational changes (Cingolani and Duncan, 2011). In a real-world scenario, where we might not know this a priori, there may be conflicting constraints in the evolutionary record corresponding to the different positions of the flexible portion of ε subunit. EVcomplex accurately predicts 6 of the top 10 inter-EC pairs (within 8 Å in the crystal structure 1fs0 (Rodgers and Wilce, 2000) or 3oaa (Cingolani and Duncan, 2011)), with the top 2 inter-ECs εA45-γL215 and εA40-γL207 providing contact between the subunits along an inter-protein beta sheet. The location of the C-terminal helices of the ε subunit is significantly different across 3 crystal structures (PDB IDs: 1fs0 [Rodgers and Wilce, 2000], 1aqt [Uhlin et al., 1997], 3oaa [Cingolani and Duncan, 2011]). The top ranked intra-ECs support the conformation seen in 1aqt, with the C-terminal helices packed in an antiparallel manner and tucked against the N-terminal beta barrel (Figure 4B, green circles) and do not contain a high ranked evolutionary trace for the extended helical contact to the γ subunit seen in 1fs0 or 3oaa (Figure 4B, gray box). Docking with the top inter-ECs results in models with 1.4 Å backbone iRMSDs to the crystal structure for the interface between the N-terminal domain of the ε subunit and the γ subunit (Table 1, Supplementary file 3). εD82 and γR222 connect the ε-subunit via a network of 3 high-scoring intra-ECs between the N- and C-terminal helices to the core of the F1 ATP synthase. In summary, these examples suggest that inter-protein evolutionary couplings can provide residue relationships across the proteins that could aid identification of functional coupling pathways, in addition to obtaining 3D models of the complex.

De novo prediction of unknown complexes

Prediction of interactions for 32 protein pairs with high-scoring evolutionary couplings

A total of 82 protein complexes with unknown 3D structure of the interaction that satisfy the conditions for the current approach, i.e., have sufficient sequences and are close in all genomes, were predicted using EVcomplex (all residue–residue inter-protein evolutionary couplings scores are available in ‘Supplementary data’). 32 of these have high EVcomplex scores with at least one predicted contact (Figure 5, Figure 5—figure supplement 1 and 2, and Supplementary file 4). Analysis of the inter-EC predictions for known 3D complex structures shows that protein pairs with more high-scoring ECs (EVcomplex score ≥0.8) have a higher proportion of true positives (Figure 2D). Hence, the protein complexes in the set of unknown structures with more high-scoring inter-ECs are most likely to have predicted ECs that indicate residue pairs close in 3D (column Q, Supplementary file 2, the exact pairs can be found in Supplementary file 4). Three examples of predictions with multiple high-scoring inter-ECs include MetQ-MetI, UmuD-UmuC, and DinJ–YafQ. The top 15 inter-ECs between MetQ and MetI are from one interface of MetQ to the MetI periplasmic loops, or the periplasmic end of the helices, consistent with the known binding of MetQ to MetI in the periplasm.

Figure 5 with 3 supplements see all
Download asset Open asset
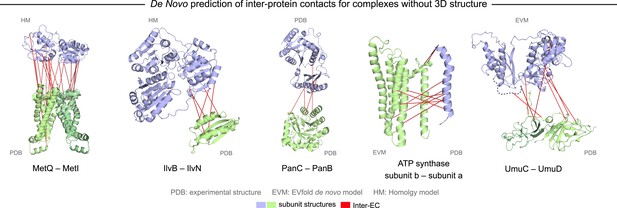
Evolutionary couplings in complexes of unknown 3D structure.

Inter-ECs for five de novo prediction candidates without E. coli or interaction homolog complex 3D structure (Subunits: blue/green cartoons; inter-ECs with EVcomplex score ≥0.8: red lines). For complex subunits which homomultimerize (light/dark green cartoon), inter-ECs are placed arbitrarily on either of the monomers to enable the identification of multiple interaction sites. Contact maps for all complexes with unsolved structures are provided in Figure 5—figure supplement 1 and 2. Left to right: (1) the membrane subunit of methionine-importing transporter heterocomplex MetI (PDB: 3tui) together with its periplasmic binding protein MetQ (Swissmodel: P28635); (2) the large and small subunits of acetolactate synthase IlvB (Swissmodel: P08142) and IlvN (PDB: 2lvw); (3) panthotenate synthase PanC (PDB: 1iho) together with ketopantoate hydroxymethyltransferase PanB (PDB: 1m3v); (4) subunits a and b of ATP synthase (model for a subunit a predict with EVfold-membrane, PDB: 1b9u for b subunit), for detailed information see Figure 6; and (5) the complex of UmuC (model created with EVfold) with one possible conformation of UmuD (PDB: 1i4v) involved in DNA repair and SOS mutagenesis. For alternative UmuD conformation, see Figure 5—figure supplement 3.

https://doi.org/10.7554/eLife.03430.018

The UmuD and UmuC complex is induced in the stress/SOS response facilitating the cleavage of UmuD to UmuD’ (between C24 and G25) to form UmuD’2 which then interacts with UmuC (DNA polymerase V) in order to copy damaged DNA (Beuning et al., 2006). The truncated dimer form (UmuD’2) has at least two contrasting conformations where the N-terminal arm is placed on opposite sides of the dimer in one conformation or in close proximity in the alternative (Figure 5—figure supplement 3). For 6/7 ECs above the score threshold, residues in UmuD predicted to interface with UmuC are co-located on one face of the dimer. Two residues (Y33, I38) are located in the N-terminal arm of UmuD that, after cleavage of the 24 N-terminal amino acids, may become available for binding UmuC. Since UmuD switches functions after this cleavage and can then bind UmuC, these inter-ECs may identify the critical residues for translesion synthesis function (Beuning et al., 2006). Although the ECs from this UmuD arm to UmuC involve residues in two separate domains of UmuC (S 415 and Y 74), intra-monomer evolutionary couplings predict that these residues are close in UmuC (Figure 5—figure supplement 3A, black rectangles). The relative positions of the contacting residues within each monomer therefore support the plausibility of the accuracy of the interaction interface.

Whilst this manuscript was in review, the 3D structure of the previously unsolved biofilm toxin/antitoxin DinJ–YafQ complex was published (PDB: 3mlo (Liang et al., 2014)), showing the intertwining of subunits in a heterotetrameric complex. 17/19 predicted EC residue pairs are within 8 Å in this 3D structure (Supplementary file 4 and ‘Supplementary data’). In general, the agreement between our de novo predicted inter-protein ECs and available experimental data serves as a measure of confidence for the predicted residue pair interactions and suggests that EVcomplex can be used to reveal 3D structural details of yet unsolved protein complexes given sufficient evolutionary information.

EVcomplex predicts interacting protein pairs in a large complex

To investigate whether the EVcomplex score can also distinguish between interacting and non-interacting pairs of proteins, we use the E. coli ATP synthase complex as a test case. The ATP synthase structure is of wide biological interest (reviewed in Walker, 2013) with a remarkable 3D structural arrangement, but completion of all aspects of the 3D structure has remained experimentally challenging (Baker et al., 2012) (Figure 6A). As a demonstration exercise, we calculated evolutionary couplings for all 28 possible pair combinations of different ATP synthase subunits (centered around the E. coli ATP synthase) and transformed the ECs into EVcomplex scores for all inter-protein residue pairs (experimentally determined stoichiometry: α3β3γδεab2c10, Supplementary file 5 and ‘Supplementary data’). Using the default EVcomplex score threshold of 0.8 to discriminate between interacting and non-interacting pairs of subunits, 24 of the 28 possible interactions between the subunits are correctly classified as interacting or non-interacting. The four incorrect predictions (namely: ε and c, γ and c, ε and β, b and β, for which there is some experimental evidence) are not identified as interacting using the 0.8 EVcomplex threshold. Choosing a threshold lower than 0.8 does identify 2 of these as interacting but also introduces new false positives. The ε and β interaction in the crystal structure 3oaa (Cingolani and Duncan, 2011) is a special case in that it involves a highly extended conformation of the last two helices of the ε subunit that reach up into the enzyme making contacts with the β subunit. The false negative EVcomplex score for this pair could be a result of the transience of their interaction or reflect a more general problem of lack of conservation of this interaction across the aligned proteins from different species. In total 80% of the interacting residue pairs in the known 3D structure parts of the synthase complex (7 pairs of subunits) are correctly predicted (threshold: 10 Å minimum atom distance between two residues). This exercise of predicting the presence or absence of interaction between any two proteins indicates the potential of the EVcomplex method in helping to elucidate protein–protein interaction networks from evolutionary sequence co-variation and identify interacting subunits of large macromolecular complexes.

Figure 6 with 1 supplement see all
Download asset Open asset
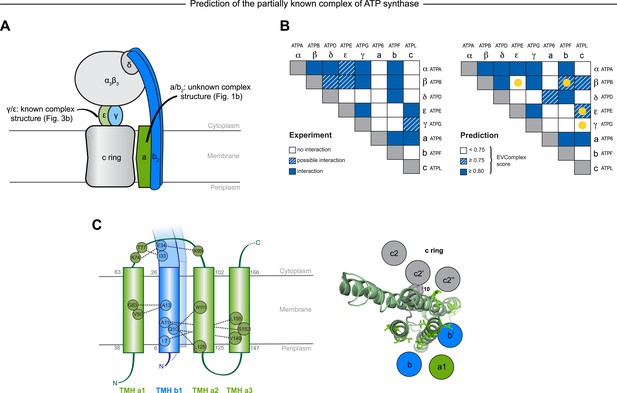
Predicted interactions between the a-, b-, and c-subunits of ATP synthase.

(A) The a- and b- subunits of E. coli ATP synthase are known to interact, but the monomer structure of subunits a and b and the structure of their interaction in the complex are unknown. (B) EVcomplex prediction (right matrix) for ATP synthase subunit interactions compared to experimental evidence (left matrix), which is either strong (left, solid blue squares) or indicative (left, crosshatched squares). Interactions that have experimental evidence, but are not predicted at the 0.8 threshold are indicated as yellow dots. (C) Left panel: residue detail of predicted residue–residue interactions (dotted lines) between subunit a and b (residue numbers at the boundaries of transmembrane helices in gray). Right panel: proposed helix–helix interactions between ATP synthase subunits a (green), b (blue, homodimer), and the c ring (gray). The proposed structural arrangement is based on analysis of the full map of inter-subunit ECs with EVcomplex score ≥0.8 (Figure 6—figure supplement 1).

https://doi.org/10.7554/eLife.03430.022

EVcomplex predicts details of subunit interactions in ATP synthase

While much of the 3D structure of ATP synthase is known (Walker, 2013), the details of interactions between the a-, b-, and c-subunits have not yet been determined by crystallography. We analyse the details in these interactions, as the EVcomplex scores between these subunits are substantial (Figure 6B). We are fortunately able to provide a missing piece for this analysis, the unknown structure of the membrane-integral penta-helical a-subunit, using our previously described method for de novo 3D structure prediction of alpha-helical transmembrane proteins (Hopf et al., 2012). To our knowledge, there are no experimentally determined atomic resolution structures of the a-subunit of ATP synthase. A 3D model of the a-subunit is from 1999 (1c17(Rastogi and Girvin, 1999)) and was computed using five helical–helical interactions that were inferred from second suppressor mutation experiments, and then imposed as distance restraints for TMH2-5, revealing a four helical bundle (with no information for TMH1). Later, cross-linking experiments (Schwem and Fillingame, 2006) identified contacting residues from all pairs of helical combinations of TM2-TM5 (6 pairs), supporting the earlier 4 helical bundle topology. 7 of the 8 cross-linked pairs are either exactly the same pair (L120-I246) or adjacent to many pairs in the top L intra a-subunit evolutionary couplings (ECs).

In fact, the helix packing arrangement in the predicted structure of the a-subunit is consistent with the topology suggested on the basis of crosslinking studies (Long et al., 2002; DeLeon-Rangel et al., 2003; Fillingame and Steed, 2014), including the lack of contacts for transmembrane helix 1 with the other 4 helices (‘Supplementary data’).

The top inter-protein EC pair between subunits a and b, aK74–bE34, coincides with experimental crosslinking evidence of the interaction of aK74 with the b-subunit and the position of E34 of the b subunit emerging from the membrane on the cytoplasmic side (Long et al., 2002; DeLeon-Rangel et al., 2003). Indeed, 6 of the 13 high score ECs are in the same region as the experimental crosslinks, for instance between the cytoplasmic loop between the first two helices of the a-subunit and the b-subunit helix as it emerges from the membrane bilayer (DeLeon-Rangel et al., 2013), or between a239V in TM helix 5 and bL16 (Figure 6C, Figure 6—figure supplement 1, Supplementary file 6). Additionally, the top EC between the a- and c-subunits (aG213 – cM65) lies close to the functionally critical aR210–cD61 interaction (Dmitriev et al., 1999) on the same helical faces of the respective subunits (Figure 6C). This prediction of missing aspects of subunit interactions may help in the design of targeted experiments to complete the understanding of the intricate molecular mechanism of the ATP synthase complex.

Discussion

A primary limitation of our current approach is its dependence on the availability of a large number of evolutionarily related sequences. If a protein interaction is conserved across enough sequenced genomes, using a single pair per genome can give accurate predictions of the interacting residues. However, if the protein pair is present in limited taxonomic branches, there may be insufficient sequences at any given time to make confident predictions. A solution to this could be to include multiple paralogs of the interacting proteins from each genome, but this requires correct pairing of the interaction partners, which is in general hard to ascertain. In addition, details of interactions may have diverged for paralogous pairs. Hence, in this current version of the method, we have imposed a genome distance requirement across all genomes for all homolog pairs in order to be less sensitive to these complications.

As the need to use genome proximity to pair sequences becomes less important with the increasing availability of genome sequences, there will be a dramatic increase in the number of interactions that can be inferred from evolutionary couplings, including those unique to eukaryotes. With currently available sequences (May 2014 release of the UniProt database), EVcomplex is able to provide information for about 1/10th of the known 3000 protein interactions in the E. coli genome. Once there are ∼10,000 bacterial genome sequences of sufficient diversity, one would have enough information to test each potentially interacting pair of homologs for evidence of interaction and, given sufficiently strong evolutionary couplings, infer the 3D structure of each protein–protein pair, as well as of complexes with more than two proteins. For any set of species, e.g., vertebrates or mammals, one can imagine guiding sequencing efforts to optimize species diversity to facilitate the extraction of evolutionary couplings. This can open the doors for more comprehensive and more rapid determination of approximate 3D structures of proteins and protein complexes, as well as for the elucidation in molecular detail of the most strongly evolutionarily constrained interactions, pointing to functional interactions.

Determining the three-dimensional models of complexes from the predicted contacts was successful in many of the tested instances. Using minimal computing resources and a small number of inter-EC-derived contacts, low interface positional RMSDs relative to experimental structures can be achieved. However, a significant number of proteins exist as homomultimers within larger complexes. To determine models of these complexes one must deconvolute homomultimeric inter-ECs from the intra-protein signal, which is an important technical challenge for future work.

The analysis of subunit interactions in ATP synthase in this work is a ‘proof of principle’ study showing that methods such as EVcomplex can determine which proteins interact with each other at the same time as specific residue pair couplings across the proteins (as also shown in the work by the Baker lab on ribosomal protein interactions (Ovchinnikov et al., 2014)). Understanding the networks of protein interactions is of critical interest in eukaryotic systems, such as networks of protein kinases, GPCRs, or PDZ domain proteins. An understanding of the distributions of interaction specificities is of high interest to many fields. Although we do not know how well our evolutionary coupling approach will handle less obligate interactions, results on the two-component signaling system (histidine kinase/response regulator) both here and in other work (Skerker et al., 2008; Weigt et al., 2009) suggest optimism.

The approximately scale-free EVcomplex score is a heuristic based on the distribution of raw EC scores from the statistical model, their dependence on sequence alignment depth and the length of the concatenated sequences. The score provides a simple way of accounting for these dependencies such that a uniform threshold, say 0.8, can be used for any protein pair with the expectation of reasonably accurate predictions. Since cutoff thresholds can be useful but overly sharp, we recommend investigating predicted contacts below the threshold used in this work, especially where there is independent biological knowledge to validate the predictions.

The work presented here is in anticipation of a genome-wide exploration and, as a proof of principle, shows the accurate prediction of inter-protein contacts in many cases and their utility for the computation of 3D structures across diverse complex interfaces. As with single protein (intra-EC) predictions, evolutionarily conserved conformational flexibility and oligomerization can result in more than one set of contacts that must be de-convoluted. Can evolutionary information help to predict the details and extent for each complex? A key challenge will be the development of algorithms that can disentangle evolutionary signals caused by alternative conformations of single complexes, alternative conformations of homologous complexes, and effectively deal with false positive signals. Taken together, these issues highlight fruitful areas for future development of evolutionary coupling methods.

Despite conditions for the successful de novo calculation of co-evolved residues, the method described here may accelerate the exploration of the protein–protein interaction world and the determination of protein complexes on a genome-wide scale at residue level resolution. The use of co-evolutionary analysis in computational models to determine protein specificity and promiscuity, co-evolutionary dynamics and functional drift will open up exciting future research questions.

Materials and methods

Selection of interacting protein pairs for co-evolution calculation

Request a detailed protocol

The candidate set of complexes for testing and de novo prediction was derived starting from a data set of binary protein–protein interactions in E. coli including yeast two-hybrid experiments, literature-curated interactions and 3D complex structures in the PDB (Rajagopala et al., 2014). Three complexes not contained in the list were added based on our analysis of other subunits in the same complex, namely BtuC/BtuF, MetI/MetQ, and the interaction between ATP synthase subunits a and b. Since our algorithm for concatenating multiple sequence pairs per species assumes the proximity of the interacting proteins on the respective genomes of each species (See below), we excluded any complex with a gene distance >20 from further analysis. The gene distance is calculated as the number of genes between the interacting partners based on an ordered list of genes in the E. coli genome obtained from the UniProt database. The resulting list of pairs (∼350) was then filtered for pseudo-homomultimeric complexes based on the identification of Pfam domains in the interacting proteins (330). All remaining complexes with a known 3D structure (as summarized in Rajagopala et al., 2014) or a homologous interacting 3D structure (93) (identified by intersecting the results of HMMER searches against the PDB for both monomers) were used for evaluating the method, while complexes without known structure (236) were assigned to the de novo prediction set (Figure 1—figure supplement 1). The set with protein complexes of known 3D structure was further filtered for structures that only cover fragments (<30 amino acids) of one or both of the monomers and structures with very low resolution (>5 Å), which led to the re-assignment of Ribonucleoside-diphosphate reductase 1 (complex_002), Type I restriction-modification enzyme EcoKI (complex_012), RpoC/RpoB (complex_041), RL11/Rl7 (complex_165), the ribosome with SecY (complex_226, complex_250, and complex_255), and RS3/RS (complex_254) to the set of unknown complexes. Large proteins were run with the specific interacting domains informed by the known 3D structure, when the full sequence was too large for the number of retrieved sequences (for domain annotation see ‘Supplementary data’).

This set could serve as a benchmark set for future development efforts in the community.

Multiple sequence alignments

Request a detailed protocol

Each protein from all pairs in our data set was used to generate a multiple sequence alignment (MSA) using jackhmmer (Johnson et al., 2010) to search the UniProt database (UniProt Consortium, 2014) with 5 iterations. To obtain alignments of consistent evolutionary depths across all the proteins, a bit score threshold of 0.5 * monomer sequence length was chosen as homolog inclusion criterion (-incdomT parameter), rather than a fixed E-value threshold which selects for different degrees of evolutionary divergence based on the length of the input sequence.

In order to calculate co-evolved residues across different proteins, the interacting pairs of sequences in each species need to be matched. Here, we assume that proteins in close proximity on the genome, e.g., on the same operon, are more likely to interact, as in the methods used previously matching histidine kinase and response regulator interacting pairs (Skerker et al., 2008; Weigt et al., 2009) (‘Supplementary data’). We retrieved the genomic locations of proteins in the alignments and concatenated pairs following 2 rules: (i) the CDS of each concatenated protein pair must be located on the same genomic contig (using ENA (Pakseresht et al., 2014) for mapping) and (ii) each pair must be the closest to one another on the genome, when compared to all other possible pairings in the same species. The concatenated sequence pairs were filtered based on the distribution of genomic distances to exclude outlier pairs with high genomic distances of more than 10k nucleotides (‘Supplementary data’). Alignment members were clustered together and reweighted if 80% or more of their residues were identical (thus implicitly removing duplicate sequences from the alignment). Supplementary file 1 and 2 report the total number of concatenated sequences, the lengths, and the effective number of sequences remaining after down-weighting in the evaluation and de novo prediction set, respectively.

Computation of evolutionary couplings

View detailed protocol

Inter- and intra-ECs were calculated on the alignment of concatenated sequences using a global probability model of sequence co-evolution, adapted from the method for single proteins (Marks et al., 2011; Morcos et al., 2011; Hopf et al., 2012) using a pseudo-likelihood maximization (PLM) (Balakrishnan et al., 2011; Ekeberg et al., 2013) rather than mean field approximation to calculate the coupling parameters. Columns in the alignment that contain more than 80% gaps were excluded and the weight of each sequence was adjusted to represent its cluster size in the alignment thus reducing the influence of identical or near-identical sequences in the calculation. For the evaluation set, we can then compare the predicted ECs for both within and between the proteins/domains to the crystal structures of the complexes (for contact maps and all EC scores, see ‘Supplementary data’).

Definition of a scale-free score for the assessment of interactions

Request a detailed protocol

In order to estimate the accuracy of the EC prediction, we evaluate the calculated inter-ECs based on the following observations: (1) most pairs of positions in an alignment are not coupled, i.e., have an EC score close to zero, and tend to be distant in the 3D structure; (2) the background distribution of EC scores between non-coupled positions is approximately symmetric around a zero mean; and (3) higher-scoring positive score outliers capture 3D proximity more accurately than lower-scoring outliers (See also Figure 2). The width of the (symmetric) background EC score distribution can be approximated using the absolute value of the minimal inter-EC score. The more a positive EC score exceeds the noise level of background coupling, the more likely it is to reflect true co-evolution between the coupled sites. For each inter-protein pair of sites i and j with pair coupling strength ECinter(i, j), we therefore calculate a raw reliability score ('pair coupling score ratio', Figure 2B) defined by

(1) Qinterraw(i,j)=ECinter(i,j)|mini,j(ECinter(i,j))|

Since the accuracy of evolutionary couplings critically depends both on the number and diversity of sequences in the input alignment and the size of the statistical inference problem (Marks et al., 2011; Morcos et al., 2011; Jones et al., 2012), we incorporate a normalization factor to make the raw reliability score comparable across different protein pairs. The normalized EVcomplex score is defined as

(2) EVcomplex−Score(i,j)=Qinterraw(i,j)1+(NeffL)−12

where Neff is the effective number of sequences in the alignment after redundancy reduction, and L (total number of residues) is the length of the concatenated alignment. Previous work on single proteins has shown that the method requires a sufficient number of sequences in the alignment to be statistically meaningful. We thus filter for sequence sufficiency requiring Neff/L > 0.3 (Table 1, Supplementary files 1 and 2). Predictions of coupled residues in the evaluation set were evaluated against their residue distances in known structures of protein pairs (Rajagopala et al., 2014) (See Supplementary file 7) in order to determine the precision of the method.

To interpret the EVcomplex prediction of interaction between subunits a and b of the ATP synthase as well as UmuC and UmuD, individual monomer models were built de novo for the structurally unsolved a-subunit of ATP synthase and UmuC using the EVfold pipeline as previously published (Marks et al., 2011; Hopf et al., 2012). In both cases coupling parameters were calculated using PLM (Balakrishnan et al., 2011; Ekeberg et al., 2013) and sequences were clustered and weighted at 90% sequence identity (the resulting models are provided in ‘Supplementary data’).

Prediction of interactions in a set of subunits

Request a detailed protocol

Following this same protocol EVcomplex scores were calculated for all possible 28 combinations of the 8 E. coli ATP synthase F0 and F1 subunits. Since we want to compare the computational predictions to some ‘ground truth’, as with the complexes for the rest of the manuscript, we used known 3D structures of the ATP synthase complex to assign whether or not the subunits interact (PDB: 3oaa, 1fs0, 2a7u; Supplementary file 7). Since we are also determining whether the subunits interact, not necessarily knowing full atomic detail residue interactions, we included subunit interactions that have been inferred from cryo-EM, crosslinking or other experiments, but do not necessarily have a crystal structure. These are represented as solid blue boxes, if the interaction is well established (DeLeon-Rangel et al., 2013; Schulenberg et al., 1999; Brandt et al., 2013; McLachlin and Dunn, 2000), or crosshatched blue if there is a lack of consensus in the community (Figure 6B, left panel).

For each possible interaction the EVcomplex score of the highest ranked inter-EC was considered as a proxy for the likelihood of interaction. Pairs with scores above 0.8 are considered likely to interact, between 0.75 and 0.8 weakly predicted, while interactions with scores below 0.75 are rejected as possible complexes (blue boxes, blue crosshatched, and white respectively in right panel of Figure 6B, and ‘Supplementary data’).

Computation of 3D structure of complexes

Request a detailed protocol

A diverse set of 15 complexes was chosen from the 22 in the evaluation set that had at least 5 couplings above a complex score of 0.8 and was subsequently docked (Supplementary file 3). Proteins that have been crystallized together in a complex could bias the results of the docking, as they have complementary positions of the surface side chains. Therefore, where possible we used complexes that had a solved 3D structure of the unbound monomer, namely GcsH/GcsT, CyoA, FimC, DhaL, AtpE, PtqA/PtqB, RS10, and HK/RR, and in all other cases the side chains of the monomers were randomized either by using SCWRL4 (Krivov et al., 2009) or restrained minimization with Schrodinger Protein Preparation Wizard (Sastry et al., 2013) before docking. For ubiquinol oxidase (complex_054) the unbound structure of subunit 2 (CyoA) only covers the COX2 domain. In this case docking was performed using this unbound structure plus an additional run using the bound complex structure with perturbed side chains.

We used HADDOCK (Dominguez et al., 2003), a widely used docking program based on ARIA (Linge et al., 2003) and the CNS software (Brunger, 2007) (Crystallography and NMR System), to dock the monomers for each protein pair with all inter-ECs with an EVcomplex score of 0.8 or above implemented as distance restraints on the α-carbon atoms of the backbone.

Each docking calculation starts with a rigid-body energy minimization, followed by semi-flexible refinement in torsion angle space, and ends with further refinement of the models in explicit solvent (water). 500/100/100 models generated for each of the 3 steps, respectively. All other parameters were left as the default values in the HADDOCK protocol. Each protein complex was run using predicted ECs as unambiguous distance restraints on the Cα atoms (deff 5 Å, upper bound 2 Å, lower bound 2 Å; input files available in ‘Supplementary data’). As a negative control, each protein complex was also docked using center of mass restraints alone (ab initio docking mode of HADDOCK) (de Vries et al., 2007) and in this case generating 10,000/500/500 models.

Each of the generated models is scored using a weighted sum of electrostatic (Eelec) and van der Waals (Evdw) energies complemented by an empirical desolvation energy term (Edesolv) (Fernandez-Recio et al., 2004). The distance restraint energy term was explicitly removed from the equation in the last iteration (Edist3 = 0.0) to enable comparison of the scores between the runs that used a different number of ECs as distance restraints.

Comparison of predicted to experimental structures

Request a detailed protocol

All computed models in the docked set were compared to the cognate crystal structures by the RMSD of all backbone atoms at the interface of the complex using ProFit v.3.1 (http://www.bioinf.org.uk/software/profit/). The interface is defined as the set of all residues that contain any atom <6 Å away from any atom of the complex partner. For the AtpE–AtpG complex, we excluded the 2 C-terminal helices of AtpE as these helices are mobile and take many different positions relative to other ATP synthase subunits (Cingolani and Duncan, 2011). Similarly, since the DHp domain of histidine kinases can take different positions relative to the CA domain, the HK-RR complex was compared over the interface between the DHp domain alone and the response regulator partner. In the case of the unbound ubiquinol oxidase docking results, only the interface between COX2 in subunit 2 and subunit 1 was considered. Accuracy of the computed models with EC restraints was compared with computed models with center of mass restraints alone (negative controls) (Figure 3—figure supplement 1, Supplementary file 3).

Data analysis was conducted primarily using IPython notebooks (Perez and Granger, 2007). A webserver and all data are available at EVcomplex.org and the Dryad Digital Repository (Hopf et al., 2014).

Supplementary Data

Request a detailed protocol

(Available at http://doi.org/10.5061/dryad.6t7b8 [Hopf et al., 2014])

Supplementary data 1: Concatenated alignments for complexes predicted in this work

Supplementary data 2: Genome distance distribution of concatenated sequences per alignment

Supplementary data 3: EVcomplex predictions for evaluation and de novo set

Supplementary data 4: Docking input files and top 10 predicted models for evaluation set

Supplementary data 5: ATP synthase predictions, ATP synthase subunit a model

Supplementary data 6: UmuC model

Data availability

The following data sets were generated
The following previously published data sets were used
    1. Schumacher MA
    (2008) MDT Protein
    ID 3DNV. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb3DNV/pdb
    1. Chaudhry C
    2. Horwich AL
    3. Brunger AT
    4. Adams PD
    (2004) GroEL-GroES-ADP7
    ID s1SX4. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb1SX4/pdb
    1. Hung CS
    2. Bouckaert J
    (2001) FIMH adhesin-FIMC chaperone complex with D-mannose
    ID 1KLF. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb1KLF/pdb
    1. Daniels J.N
    2. Schindelin H
    (2007) Crystal Structure of Activated MPT Synthase
    ID 3BII. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb3BII/pdb
    1. Jormakka M
    2. Richardson D
    3. Byrne B
    4. Iwata S
    (2003) Crystal Structure of NarGH complex
    ID 1R27. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb1R27/pdb
    1. Xia D
    2. Maurizi M.R
    3. Guo F
    4. Singh S.K
    5. Esser L
    (2003) ClpNS with fragments
    ID 1R6Q. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb1R6Q/pdb
    1. Schumacher M.A
    (2009) Structure of mdt protein
    ID 3HZI. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb3HZI/pdb
    1. Ha Y
    2. Allewell N.M
    (1998) ATCASE Y165F MUTANT
    ID 9ATC. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb9ATC/pdb
    1. Suh M.K
    2. Ku B
    3. Ha N.C
    4. Woo J.S
    5. Oh B.H
    (2008) Crystal Structure of the MukE-MukF Complex
    ID 3EUH. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb3EUH/pdb
    1. Rastogi V.K
    2. Girvin M.E
    (1999) A1C12 SUBCOMPLEX OF F1FO ATP SYNTHASE
    ID 1C17. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb1C17/pdb
    1. Okamura-Ikeda K
    2. Hosaka H
    (2009) Crystal Structure of ET-EHred complex
    ID 3A8J. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb3A8J/pdb
    1. Okamura-Ikeda K
    2. Hosaka H
    (2009) Crystal Structure of ETD97N-EHred complex
    ID 3A8K. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb3A8K/pdb
    1. Jormakka M
    2. Tornroth S
    3. Byrne B
    4. Iwata S
    (2002) FORMATE DEHYDROGENASE N FROM E. COLI
    ID 1KQG. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb1KQG/pdb
    1. Jormakka M
    2. Tornroth S
    3. Byrne B
    4. Iwata S
    (2002) FORMATE DEHYDROGENASE N FROM E. COLI
    ID 1KQF. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb1KQF/pdb
    1. Shomura Y
    2. Higuchi Y
    (2012) Crystal structure of HypE-HypF complex
    ID 3VTI. Publicly available at the RCSB Protein Data Bank.
    http://dx.doi.org/10.2210/pdb3VTI/pdb

References

    1. Ekeberg M
    2. Lovkvist C
    3. Lan Y
    4. Weigt M
    5. Aurell E
    (2013)
    Improved contact prediction in proteins: using pseudolikelihoods to infer Potts models
    Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics 87:012707.

Decision letter

  1. John Kuriyan
    Reviewing Editor; Howard Hughes Medical Institute, University of California, Berkeley, United States

eLife posts the editorial decision letter and author response on a selection of the published articles (subject to the approval of the authors). An edited version of the letter sent to the authors after peer review is shown, indicating the substantive concerns or comments; minor concerns are not usually shown. Reviewers have the opportunity to discuss the decision before the letter is sent (see review process). Similarly, the author response typically shows only responses to the major concerns raised by the reviewers.

Thank you for sending your work entitled “Sequence co-evolution gives 3D contacts and structures of protein complexes”““ for consideration at eLife. Your article has been favorably evaluated by John Kuriyan (Senior editor), working with a member of our Board of Reviewing Editors, and 3 reviewers.

The editors and the other reviewers discussed their comments before we reached this decision, and the Reviewing editor has assembled the following comments to help you prepare a revised submission.

This manuscript describes an approach to predict 3D residue-residue contacts at protein interfaces from an analysis of multiple sequence alignments. The described computational approach (using sequence co-evolution to predict contacts between interacting proteins and to generate three-dimensional models of complex structures) appears to be quite successful and is an important contribution that is of interest to a broad audience. The analyses, results, and conclusions are similar to work conducted during the same period by Baker & coworkers, published recently in eLife. Nevertheless, it is the consensus opinion of the reviewers that the present manuscript is potentially suitable for publication in eLife as well, provided that all of the comments raised by the reviewers can be addressed satisfactorily.

We have appended the comments from the three reviewers below. Although many individual points are raised, you will see that the principal concern of the reviewers is that the manuscript falls short of providing the reader with sufficient analysis to judge the validity of the conclusions. It should be possible for you to revise the manuscript to address these concerns without much in the way of new calculations, so we hope that it should be relatively straightforward to deal with these issues.

In addition, since the Baker paper came out recently, it should be given appropriate credit in a revised version. We recommend removing the word “new” from the manuscript for this reason, and instead simply state what was done.

Reviewer 1:

1) The Abstract claims that the authors' approach can discriminate between interacting and non-interacting proteins. However, as far as I can see, the rest of the paper concerns only calculating the interface residues of proteins which are known to interact. No evidence is presented to support the claim to be able to calculate non-interactors. The authors' claim should be corrected accordingly.

2) The authors claim that the co-evolutionary approach has not previously been applied to prediction of protein-protein interfaces. This is incorrect, as the authors seem to be unaware of the previous work of Raphael Guerois' group, which seems rather surprising. The authors should acknowledge the prior work of Faure et al (2012) and Andreani et al. (2013), and they should modify their claim to novelty accordingly. It would also be appropriate to cite properly the prior work of the Baker group (Ovchinnikov et al., 2014) in the same paragraph (the authors currently mention this work only as a “note added during submission”), and the recent review by Andreani and Guerois (2014).

3) In several places the authors say that their approach exploits the fact that interacting proteins are often coded close to each other in a genome. Why is this assumption necessary? According to the description given in Methods, any pair of sequences which are presumed to interact could be concatenated and then used in the authors method. Please clarify.

4) If I understand the authors’ method correctly, they first concatenate the multiple sequences of the presumed interactors, and they then use their previous approach for detecting interacting pairs of columns in the multiple alignment. In this case, when concatenating the alignments for protein “A” with those of protein “B”, the “intra-EC” pairs would appear as A-A and B-B pairs, while the “inter-EC” pairs would come from A-B or B-A interactions. My question is then, are there any observable differences in the inter and intra scores? One might expect that the conservation scores would be lower for inter interactions than intra interactions, as an interface might show more “plasticity” than the core of a domain. It would be very interesting if the authors could comment on this, preferably supported by numerical results.

5) It is incorrect for the authors to refer to their own data set as a “benchmark”. Suggestion: remove all references to the term “benchmark”. However, if the authors make all their data available in a convenient way on-line, it could be proposed as a new “benchmark”.

6) It is wrong to claim that “Experimental evidence... agrees with EVcomplex predictions” (!). Please rewrite this to say that your predictions agree with the experimental evidence. But, if this is your claim, please also support it in some way. What is the experimental evidence? How to you calculate and quantify “agrees with”?

7) Same point in the main text. “The resulting model is consistent with the topologies from cross-linking”. How do you quantify consistent? RMSD from the earlier models? Please provide supporting details.

Reviewer 2:

My main comments concern the way the data in the current manuscript are analyzed and presented. While the main Figures / Table 1 currently illustrate useful examples, they should also show overall analyses of the results over all cases in the benchmark datasets. In several cases this is essential to support the stated conclusions. It does not seem that this would require a substantial amount of new work or lengthy simulations, as most of the relevant data are in the Supplementary Materials (most data are in raw table format or with a separate Figure for each example, which makes it hard for the reader to gauge overall performance – this could be presented in a more easily digestible format in the main text). Specifically, I feel the paper could be substantially improved if the following points were addressed:

1) Please support the statement “Benchmark calculations here ... indicate that the number of sequences in the alignment is critical...” with a Figure showing overall performance versus # of sequences (Figure 3 shows dependency of accuracy on relative rank for only two examples).

2) Show a main Figure comparing predicted contacts against residue distances in the 30 known crystal structures of complexes that had a sufficient number of sequences (Figure 2 only shows contact plots for two examples, and structural pictures for several more, but no overall quantification). This type of analysis could also help to support the statement “For the top ranked benchmark complexes, the majority of the top 5 ECs is correct to within 8A...” with a more quantitative analysis (Table 1 only shows 7 of the 30 complexes in the dataset; Supplementary file 3 shows all individual contact maps, but no overall quantification).

3) “... these benchmarks show ... and demonstrate the criteria needed for successful prediction of unknown interactions”. To support this statement, it would be useful to have a main Figure / Table for each important criterion, analyzed over an entire benchmark set (as for the number of sequences in point 1).

4) Please add metrics to support statements that ECs are “completely consistent” with crosslinking data, or that a coupling “coincides with experimental evidence”. The comparison Table in Supplementary Figure 6 could be presented in more quantitative terms in the main text (for example, what does “crosslinking neighborhood” mean?).

5) What are the possible reasons for false-positive co-variation that does not correspond to contact?

6) The manuscript deals entirely with pairwise co-evolution, and seems to neglect the possibility of higher-order complexity in the sequence pattern.

Reviewer 3:

The manuscript presents an upbeat and optimistic view of the success of the method, with a relatively small amount of critical discussion and little if any investigation of what one can learn from cases in which it does not perform as expected. (For example, a list of possible reasons for false-positive co-variation that does not correspond to contact is given, but an analysis of actual instances is not.) Likewise, a set of methods is presented that is relatively particular, and the reason why these specific methods were chosen over other possibilities is not provided. Moreover, the manuscript deals entirely with pairwise co-evolution, and seems to neglect the possibility of higher-order complexity in the sequence pattern. The manuscript could be substantially strengthened by adding analyses and insights in these issues.

https://doi.org/10.7554/eLife.03430.031

Author response

Thank you for your comments and forwarded reviews of our paper. The revised paper addresses the questions from the reviewers. As you point out, the principal request of the reviewers was to see more quantitative analysis to judge the validity of the conclusions. This is addressed by detailed additions to the paper including:

1) A quantitative analysis of the accuracy with summary statistics (Figure 2A,B & C, with Supplementary figures, tables and data for each individual complex).

2) The use of the EVcomplex scores for inter-protein ECs that allow comparison across proteins (Figure 2A, Materials and methods, Supplementary files).

3) A fuller analysis and clearer explanation of how the scores are used to distinguish interactions from non-interactions with a proof of principle exercise of all ATP synthase subunits against all others (a total of 28 interactions), resulting in 86% accuracy.

4) Detailed analysis of agreement of cross-linking experiments and predictions for a –subunit ECs and a- to b- subunit inter-ECs, Supplementary file 6 and Author response image 1.

Author response image 1
Download asset Open asset

The results are essentially the same as in the original submission and we have now provided the reader with comprehensive access to the numerical results, including sequence alignments, list of all contact predictions, precision of predicted contacts with respect to known 3D structures for all complexes, docked models for 15 complexes,

Reviewer 1:

1) The Abstract claims that the authors' approach can discriminate between interacting and non-interacting proteins. However, as far as I can see, the rest of the paper concerns only calculating the interface residues of proteins which are known to interact. No evidence is presented to support the claim to be able to calculate non-interactors. The authors' claim should be corrected accordingly.

We have updated the manuscript to clarify the way in which the method addresses discrimination between interacting and non-interacting proteins, and give the specific example of all against all in the ATP synthase complex. We suggest that the correct identification of interacting and non-interacting protein subunits of the ATP synthase complex could serve as a 'proof of principle' that scores derived from evolutionary couplings can identify interactions (in addition to the identification of the interacting residues between protein pairs). Since identification of the interactions of the 8 subunits of ATP synthase is the only example we report, we have been careful to talk about this as a proof of principle that may be generalized with further work (changes in Abstract, Figure 5, Materials and Methods, Supplementary file 5, Supplementary data). [The EV complex score identifies 24/28 of the interactions as correctly interacting or not.]

2) The authors claim that the co-evolutionary approach has not previously been applied to prediction of protein-protein interfaces. This is incorrect, as the authors seem to be unaware of the previous work of Raphael Guerois' group, which seems rather surprising. The authors should acknowledge the prior work of Faure et al (2012) and Andreani et al. (2013), and they should modify their claim to novelty accordingly.

It would also be appropriate to cite properly the prior work of the Baker group (Ovchinnikov et al., 2014) in the same paragraph (the authors currently mention this work only as a “note added during submission”), and the recent review by Andreani and Guerois (2014).

We have now referred to the body of work by the Guerois group in the Introduction. We apologize for the oversight of this very interesting work. We also added more complete referencing to the work of the Valencia group; see response to reviewer 3. The Guerois group has used evolutionary information to improve their machine learnt statistical potentials. Our goal is to ask if we can we identify co-evolving residues (from sequence information alone) across proteins in order to ask whether these co-evolving pairs identify close residues, (1) whether they can be used to determine complexes in 3D and (2) whether we can use this to say if two proteins interact. Hence the approaches we present and those of the Guerois group are nicely synergistic and we hope to work with them to bring these methods together in the future.

3) In several places the authors say that their approach exploits the fact that interacting proteins are often coded close to each other in a genome. Why is this assumption necessary? According to the description given in Methods, any pair of sequences which are presumed to interact could be concatenated and then used in the authors method. Please clarify.

Thanks for making it clear that we did not explain this sufficiently well. We have now clarified this in Results, Discussion, and in the Materials and methods.

To summarize: The accuracy of the co-evolutionary analysis relies on the concatenation of the protein pair representing a true interaction. This means that the contact prediction across proteins will only be as good as the input alignment pairs. When there is only one protein family member of both interacting partners in each species, one is guaranteed to get the correct alignment, assuming that it is a real complex in all organisms. Hence, subunits of ATP synthase that have only one copy in the genome, would not require this condition, and one could have simply concatenated the one pair per genome. However, for most protein interactions in E. coli, there are not yet enough sequences available to allow the use of just one pair per genome, as the complex may not necessarily occur in all bacteria. In these cases, for the time-being, our approach relies on using paralogous interactions to get sufficient sequences for instance histidine kinase; response regulators, transporters and their ATPases. Since we therefore use several paralogous interactions per complex in each genome, the algorithm requires that the partner needs to be correctly paired, something that we do not necessarily know a priori, and for which we use genome proximity as a proxy (as others have done in references 22-25). Clearly this problem will secede for many interactions in the next few years as many thousand more bacterial genomes are sequenced, but the problem is an interesting one that we think will have to be thought about in relation to eukaryotic complexes, too.

4) If I understand the authors’ method correctly, they first concatenate the multiple sequences of the presumed interactors, and they then use their previous approach for detecting interacting pairs of columns in the multiple alignment. In this case, when concatenating the alignments for protein “A” with those of protein “B”, the “intra-EC” pairs would appear as A-A and B-B pairs, while the “inter-EC” pairs would come from A-B or B-A interactions. My question is then, are there any observable differences in the inter and intra scores? One might expect that the conservation scores would be lower for inter interactions than intra interactions, as an interface might show more “plasticity” than the core of a domain. It would be very interesting if the authors could comment on this, preferably supported by numerical results.

The reviewer makes a good point and one that we have now highlighted more clearly in the text. The inter-EC scores within each complex are almost universally lower than the intra–EC scores as would be expected, Figure 2 and Figure 2–figure supplement 1.

In general we observe that the accuracy of the intra-contacts up to the rank of the first inter contact, is a good indication of how accurate the predicted inter-contacts are likely to be. This means we could have used a measure of the accuracy of the intra-protein scores to assess the predicted inter-contacts. We chose to develop a scoring method independent that did not rely on the existence of experimentally determined 3D structures of the monomers. The EV complex score implicitly considers where the inter-EC scores lie in the whole distribution instead, hence excluding those inter-ECs that lie within the noise of the whole distribution, see Materials and Methods (equations 1 and 2), Figure 2A, Figure 2–figure supplement 1, Figure 2–figure supplement 2, and Supplementary data 3 “EVcomplex predictions”.

5) It is incorrect for the authors to refer to their own data set as a "benchmark". Suggestion: remove all references to the term "benchmark". However, if the authors make all their data available in a convenient way on-line, it could be proposed as a new "benchmark".

We have removed the references to the set of known 3D interactions as ‘benchmark’ and proposed this as a set the community could use in the future, as the reviewer suggests (Materials and methods).

6) It is wrong to claim that "Experimental evidence... agrees with EVcomplex predictions" (!). Please rewrite this to say that your predictions agree with the experimental evidence. But, if this is your claim, please also support it in some way. What is the experimental evidence? How to you calculate and quantify "agrees with"?

We have removed this sentence, and reworded this to reflect the fact we are using the experimental data to support the EC predictions and not the other way around.

7) Same point in the main text. "The resulting model is consistent with the topologies from cross-linking". How do you quantify consistent? RMSD from the earlier models? Please provide supporting details.

To our knowledge there are no experimentally determined atomic resolution structures of the a-subunit of ATP synthase. A 3D model of the a-subunit is from 1999 (PDB ID: 1c17) and was computed using five helical–helical interactions that were inferred from second suppressor mutation experiments, and then imposed as distance restraints for TMH2-5 [1], revealing a four helical bundle (with no information for TMH1). Later, zero-length cross-linking experiments by the Fillingame group [2] identified contacting residues from all pairs of helical combinations of TM2-TM5 (6), supporting the earlier 4 helical bundle topology. 7 of the 8 cross-linked pairs from Schwem et al., are either exactly the same pair (L120-I246) or adjacent to many pairs in the top L intra a-subunit evolutionary couplings (ECs)*, see Author response image 1. (Adjacent is defined as neighboring residues (±3) on chain or one helical turn.) * of ∼ L2 total, see previous work and work of others for why this number is chosen.

Information from the cross-linking was not used to construct the model and no presumed membrane topology was used as input. The consistency we report is based on the correspondence between the helical-helical contacts from the experiments and evolutionary couplings together with the resulting contacts in the computed model. These can be examined in detail in the supplementary material. We have clarified this part of the analysis and provided more detail.

Reviewer 2:

[…] I feel the paper could be substantially improved if the following points were addressed:

1) Please support the statement "Benchmark calculations here ... indicate that the number of sequences in the alignment is critical..." with a Figure showing overall performance versus # of sequences (Figure 3 shows dependency of accuracy on relative rank for only two examples).

2) Show a main Figure comparing predicted contacts against residue distances in the 30 known crystal structures of complexes that had a sufficient number of sequences (Figure 2 only shows contact plots for two examples, and structural pictures for several more, but no overall quantification). This type of analysis could also help to support the statement "For the top ranked benchmark complexes, the majority of the top 5 ECs is correct to within 8A..." with a more quantitative analysis (Table 1 only shows 7 of the 30 complexes in the dataset; Supplementary file 3 shows all individual contact maps, but no overall quantification).

3) "... these benchmarks show ... and demonstrate the criteria needed for successful prediction of unknown interactions". To support this statement, it would be useful to have a main Figure / Table for each important criterion, analyzed over an entire benchmark set (as for the number of sequences in point 1).

The claims in the paper are now supported by more explicit quantitative analysis, reported in the main figures, the text and supplementary material. Specifically we show a score that normalizes the ECs for the number of sequences and length of protein. This score allows a clear comparison of EC pairs across complexes so that one threshold can be applied across all complexes and precision can be measured for each complex and summarized overall. This material is provided in Figure 2 and Figure 2–figure supplements 1 & 2 (all EVcomplex scores, plots of raw scores showing length and number of sequences dependence, plots of EVcomplex scores versus accuracy), Supplementary data and Materials and methods.

4) Please add metrics to support statements that ECs are "completely consistent" with crosslinking data, or that a coupling "coincides with experimental evidence". The comparison Table in Supplementary Figure 6 could be presented in more quantitative terms in the main text (for example, what does "crosslinking neighborhood" mean?).

In summary, 77%/67% of the above threshold (13) predicted inter-protein contacts between subunit-a and subunit-b are in the neighborhood of residues identified in cross-linking studies, where neighborhood is defined as within 6/3 residues on the chain of the cross-linked residue (Supplementary file 6). The a239V- b16L cross-link is exactly one of the ECs. For 3/13 with no evidence, the proposed residue – residue contact between the subunits is consistent with the other cross-links: two are between midway on aTMH1 with midway of the membrane part of the b-subunit (aV50, aG53 with b13A), one is between aTMH3 and the N terminal end of the b-subunit (a155L, b7I) (these regions have not been tested to our knowledge). The 4th predicted EC with no cross-link support is between a66K and b68a. This EC is most likely a false positive as residue 68 in the b-subunit may be too far from the membrane surface to be plausible. Taking the body of work together from the experimental side [3-8], there are a number of specific regions of the a-subunit that are in contact with one or both of the b-monomers, and all of these regions are represented in the top evolutionary couplings; namely the first cytoplasmic loop, aTMH2, upper portion, aTMH3 and the periplasmic end of aTMH5, all of which are represented in the EVcomplex pairs (Supplementary file 6).

These clarifications are reflected in the main text and Supplementary file 6.

See reply to Reviewer 1 and Author response image 1 for more detail on the ECs and crosslink studies within the a-subunit.

5) What are the possible reasons for false-positive co-variation that does not correspond to contact?

There are two categories of false positives:

1) There is co-evolution between residues that are not close in a 3D structure.

i) This could be functional coupling – e.g. cases of information transmission through membrane proteins, allosteric signaling and indeed we have seen this anecdotally in a number of very interesting cases. The challenge is to distinguish this from other false positives.

ii) The current crystal structures do not capture all the conformations of the protein(s). This is very clear in examples such as alternating-access membrane transporters that alter their conformations substantially

2) The assumptions used for the input sequence alignments are wrong

i) The interactions in the alignments are not homologous despite sequence similarity of the component parts.

ii) The sequence diversity is insufficient to capture realistic parameters in the global model.

Deconvolution of these different causes of false positives is a critical part of future work. We have made these points clearer in the Results and the Discussion.

6) The manuscript deals entirely with pairwise co-evolution, and seems to neglect the possibility of higher-order complexity in the sequence pattern.

There could well be higher order correlations that the current method is unable to determine at this stage. The number of sequences needed for a global model such as this to determine accurate higher order covariation would be at least an order of magnitude higher than the requirement for the current method. Indeed there are insufficient sequences for many of the currently known E. coli interactions (Discussion) and see response to Reviewer 1 – comment 3. It will be interesting to see what the extent of this higher order dependence might be when enough sequences become available.

Reviewer 3:

The manuscript presents an upbeat and optimistic view of the success of the method, with a relatively small amount of critical discussion and little if any investigation of what one can learn from cases in which it does not perform as expected.

We have updated the manuscript to include far more quantitative analysis, see replies to Reviewer 2 comments 1-4 above. We have also balanced the enthusiasm with a more specific description of the current limitations, that include sequence availability but also some that require algorithmic development (see Discussion). Critical discussion on the classification of false positives is now more clearly organized in the manuscript; see response to Reviewer 2, comment 5.

(For example, a list of possible reasons for false-positive co-variation that does not correspond to contact is given, but an analysis of actual instances is not.) Likewise, a set of methods is presented that is relatively particular, and the reason why these specific methods were chosen over other possibilities is not provided.

There is a large body of work that has implemented other methods, both force field–based docking and other sequence based methods to explore co-variation e.g. mutual information and phylogeny to detect co-variation of residues across proteins. We have now added more discussion and references to this oeuvre in the Introduction, including new references to the body of work by the Valencia group that used correlations in multiple sequence alignments [9-10], and those suggested by Reviewer 1. Many other methods have addressed somewhat different issues, for instance, identification of interacting proteins (not residue level information), identification of residue patches rather than specific interactions, concentration on docking with hybrid approaches for known interactions or were relatively less successful (e.g. older work). For this reason it is hard to make direct comparisons. The unique aspect to this work is that it can resolve the question of interacting partners together with residue level information if the sequence diversity and space is sufficient. The EVcomplex approach, along with that of the recent work by the Baker group [11] also does this from sequences alone. Since experimentally determined structures may be a somewhat biased set of all protein interactions, our method has the advantage of not learning on known complex structures.

We look forward to the combination of the co-evolution approach together with existing computational and experimental approaches to accelerate the field.

Moreover, the manuscript deals entirely with pairwise co-evolution, and seems to neglect the possibility of higher-order complexity in the sequence pattern. The manuscript could be substantially strengthened by adding analyses and insights in these issues.

See response to Reviewer 2, comment 6.

References

1 Rastogi, V. K. & Girvin, M. E. Structural changes linked to proton translocation by subunit c of the ATP synthase. Nature 402, 263-268, doi:10.1038/46224 (1999).

2 Schwem, B. E. & Fillingame, R. H. Cross-linking between helices within subunit a of Escherichia coli ATP synthase defines the transmembrane packing of a four-helix bundle. The Journal of biological chemistry 281, 37861-37867, doi:10.1074/jbc.M607453200 (2006).

3 Long, J. C., DeLeon-Rangel, J. & Vik, S. B. Characterization of the first cytoplasmic loop of subunit a of the Escherichia coli ATP synthase by surface labeling, cross-linking, and mutagenesis. J Biol Chem 277, 27288-27293, doi:10.1074/jbc.M202118200 (2002).

4 Fillingame, R. H. & Steed, P. R. Half channels mediating H transport and the mechanism of gating in the F sector of Escherichia coli FF ATP synthase. Biochimica et biophysica acta, doi:10.1016/j.bbabio.2014.03.005 (2014).

5 DeLeon-Rangel, J., Ishmukhametov, R. R., Jiang, W., Fillingame, R. H. & Vik, S. B. Interactions between subunits a and b in the rotary ATP synthase as determined by cross-linking. FEBS Lett 587, 892-897, doi:10.1016/j.febslet.2013.02.012 (2013).

6 Fillingame, R. H., Angevine, C. M. & Dmitriev, O. Y. Mechanics of coupling proton movements to c-ring rotation in ATP synthase. FEBS Lett 555, 29-34 (2003).

7 Brandt, K. et al. Individual interactions of the b subunits within the stator of the Escherichia coli ATP synthase. The Journal of biological chemistry 288, 24465-24479, doi:10.1074/jbc.M113.465633 (2013).

8 McLachlin, D. T. & Dunn, S. D. Disulfide linkage of the b and delta subunits does not affect the function of the Escherichia coli ATP synthase. Biochemistry 39, 3486-3490 (2000).

9 Pazos, F., Helmer-Citterich, M., Ausiello, G. & Valencia, A. Correlated mutations contain information about protein-protein interaction. Journal of molecular biology 271, 511-523, doi:10.1006/jmbi.1997.1198 (1997).

10 Pazos, F. & Valencia, A. In silico two-hybrid system for the selection of physically interacting protein pairs. Proteins 47, 219-227 (2002).

11 Ovchinnikov, S., Kamisetty, H. & Baker, D. Robust and accurate prediction of residue-residue interactions across protein interfaces using evolutionary information. eLife 3, e02030, doi:10.7554/eLife.02030 (2014).

https://doi.org/10.7554/eLife.03430.032

Article and author information

Author details

  1. Thomas A Hopf

    1. Department of Systems Biology, Harvard University, Boston, United States
    2. Bioinformatics and Computational Biology, Department of Informatics, Technische Universität München, Garching, Germany
    Contribution
    TAH, Conception and design, Acquisition of data, Analysis and interpretation of data, Drafting or revising the article
    Contributed equally with
    Charlotta P I Schärfe and João P G L M Rodrigues
    Competing interests
    The authors declare that no competing interests exist.
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-7476-9539

  2. Charlotta P I Schärfe

    1. Department of Systems Biology, Harvard University, Boston, United States
    2. Applied Bioinformatics, Quantitative Biology Center, University of Tübingen, Tübingen, Germany
    3. Department of Computer Science, University of Tübingen, Tübingen, Germany
    Contribution
    CPIS, Conception and design, Acquisition of data, Analysis and interpretation of data, Drafting or revising the article
    Contributed equally with
    Thomas A Hopf and João P G L M Rodrigues
    Competing interests
    The authors declare that no competing interests exist.
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-6689-6423

  3. João P G L M Rodrigues

    Computational Structural Biology Group, Bijvoet Center for Biomolecular Research, Utrecht University, Utrecht, Netherlands
    Contribution
    JPGLMR, Assisted docking in Haddock
    Contributed equally with
    Thomas A Hopf and Charlotta P I Schärfe
    Competing interests
    The authors declare that no competing interests exist.

  4. Anna G Green

    Department of Systems Biology, Harvard University, Boston, United States
    Contribution
    AGG, Conducted comparison of ATP synthase subunit interactions
    Competing interests
    The authors declare that no competing interests exist.

  5. Oliver Kohlbacher

    1. Applied Bioinformatics, Quantitative Biology Center, University of Tübingen, Tübingen, Germany
    2. Department of Computer Science, University of Tübingen, Tübingen, Germany
    Contribution
    OK, Acquisition of data, Analysis and interpretation of data
    Competing interests
    The authors declare that no competing interests exist.

  6. Chris Sander

    Computational Biology Center, Memorial Sloan Kettering Cancer Center, New York, United States
    Contribution
    CS, Conception and design, Drafting or revising the article
    For correspondence
    sander@cbio.mskcc.org
    Competing interests
    The authors declare that no competing interests exist.

  7. Alexandre M J J Bonvin

    Computational Structural Biology Group, Bijvoet Center for Biomolecular Research, Utrecht University, Utrecht, Netherlands
    Contribution
    AMJJB, Provided expertise on Haddock docking protocols, Drafting or revising the article
    For correspondence
    a.m.j.j.bonvin@uu.nl
    Competing interests
    The authors declare that no competing interests exist.
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0001-7369-1322

  8. Debora S Marks

    Department of Systems Biology, Harvard University, Boston, United States
    Contribution
    DSM, Conception and design, Acquisition of data, Analysis and interpretation of data, Drafting or revising the article
    For correspondence
    debbie@hms.harvard.edu
    Competing interests
    The authors declare that no competing interests exist.
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0001-9388-2281

Funding

National Institute of General Medical Sciences (R01 GM106303)

  • Thomas A Hopf
  • Debora S Marks
  • Chris Sander

Fulbright Commission

  • Charlotta P I Schärfe

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Reviewing Editor

  1. John Kuriyan, Howard Hughes Medical Institute, University of California, Berkeley, United States

Publication history

  1. Received: May 21, 2014
  2. Accepted: September 23, 2014
  3. Accepted Manuscript published: September 25, 2014 (version 1)
  4. Version of Record published: November 3, 2014 (version 2)

Copyright

© 2014, Hopf et al.

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

  • 15,560
    Page views
  • 2,641
    Downloads
  • 327
    Citations

Article citation count generated by polling the highest count across the following sources: Scopus, Crossref, PubMed Central.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Thomas A Hopf
  2. Charlotta P I Schärfe
  3. João P G L M Rodrigues
  4. Anna G Green
  5. Oliver Kohlbacher
  6. Chris Sander
  7. Alexandre M J J Bonvin
  8. Debora S Marks
(2014)
Sequence co-evolution gives 3D contacts and structures of protein complexes
eLife 3:e03430.
https://doi.org/10.7554/eLife.03430

Categories and tags

Research organism

Further reading

    1. Biochemistry and Chemical Biology
    2. Structural Biology and Molecular Biophysics

    Drug Discovery: Decoding the mechanisms of allostery

    Saif Khan, Cornelius Gati
    Insight

    A complex interplay between structure, conformational dynamics and pharmacology defines distant regulation of G protein-coupled receptors.

    1. Structural Biology and Molecular Biophysics

    Biological condensates form percolated networks with molecular motion properties distinctly different from dilute solutions

    Zeyu Shen, Bowen Jia ... Mingjie Zhang
    Research Article

    Formation of membraneless organelles or biological condensates via phase separation and related processes hugely expands the cellular organelle repertoire. Biological condensates are dense and viscoelastic soft matters instead of canonical dilute solutions. To date, numerous different biological condensates have been discovered; but mechanistic understanding of biological condensates remains scarce. In this study, we developed an adaptive single molecule imaging method that allows simultaneous tracking of individual molecules and their motion trajectories in both condensed and dilute phases of various biological condensates. The method enables quantitative measurements of concentrations, phase boundary, motion behavior and speed of molecules in both condensed and dilute phases as well as the scale and speed of molecular exchanges between the two phases. Notably, molecules in the condensed phase do not undergo uniform Brownian motion, but instead constantly switch between a (class of) confined state(s) and a random diffusion-like motion state. Transient confinement is consistent with strong interactions associated with large molecular networks (i.e., percolation) in the condensed phase. In this way, molecules in biological condensates behave distinctly different from those in dilute solutions. The methods and findings described herein should be generally applicable for deciphering the molecular mechanisms underlying the assembly, dynamics and consequently functional implications of biological condensates.

    1. Structural Biology and Molecular Biophysics

    Robust membrane protein tweezers reveal the folding speed limit of helical membrane proteins

    Seoyoon Kim, Daehyo Lee ... Duyoung Min
    Tools and Resources

    Single-molecule tweezers, such as magnetic tweezers, are powerful tools for probing nm-scale structural changes in single membrane proteins under force. However, the weak molecular tethers used for the membrane protein studies have limited the observation of long-time, repetitive molecular transitions due to force-induced bond breakage. The prolonged observation of numerous transitions is critical in reliable characterizations of structural states, kinetics, and energy barrier properties. Here, we present a robust single-molecule tweezer method that uses dibenzocyclooctyne (DBCO) cycloaddition and traptavidin binding, enabling the estimation of the folding 'speed limit' of helical membrane proteins. This method is >100 times more stable than a conventional linkage system regarding the lifetime, allowing for the survival for ~12 h at 50 pN and ~1000 pulling cycle experiments. By using this method, we were able to observe numerous structural transitions of a designer single-chained transmembrane (TM) homodimer for 9 h at 12 pN, and reveal its folding pathway including the hidden dynamics of helix-coil transitions. We characterized the energy barrier heights and folding times for the transitions using a model-independent deconvolution method and the hidden Markov modeling (HMM) analysis, respectively. The Kramers rate framework yields a considerably low speed limit of 21 ms for a helical hairpin formation in lipid bilayers, compared to μs scale for soluble protein folding. This large discrepancy is likely due to the highly viscous nature of lipid membranes, retarding the helix-helix interactions. Our results offer a more valid guideline for relating the kinetics and free energies of membrane protein folding.