1. Biochemistry and Chemical Biology
  2. Structural Biology and Molecular Biophysics

Structure of catalase determined by MicroED

  1. Brent L Nannenga
  2. Dan Shi
  3. Johan Hattne
  4. Francis E Reyes
  5. Tamir Gonen  Is a corresponding author
  1. Janelia Research Campus, Howard Hughes Medical Institute, United States
https://doi.org/10.7554/eLife.03600
Share this article
Cite this article
  1. Brent L Nannenga
  2. Dan Shi
  3. Johan Hattne
  4. Francis E Reyes
  5. Tamir Gonen
(2014)
Structure of catalase determined by MicroED
eLife 3:e03600.
https://doi.org/10.7554/eLife.03600
  2. Download BibTeX
  3. Download .RIS

Abstract

MicroED is a recently developed method that uses electron diffraction for structure determination from very small three-dimensional crystals of biological material. Previously we used a series of still diffraction patterns to determine the structure of lysozyme at 2.9 Å resolution with MicroED (Shi et al., 2013). Here we present the structure of bovine liver catalase determined from a single crystal at 3.2 Å resolution by MicroED. The data were collected by continuous rotation of the sample under constant exposure and were processed and refined using standard programs for X-ray crystallography. The ability of MicroED to determine the structure of bovine liver catalase, a protein that has long resisted atomic analysis by traditional electron crystallography, demonstrates the potential of this method for structure determination.

https://doi.org/10.7554/eLife.03600.001

Introduction

MicroED is an emerging method, which uses electron diffraction to obtain structural information from extremely small three-dimensional (3D) crystals of biological material. In the original MicroED proof of concept paper (Shi et al., 2013), electron diffraction data were collected from stationary lysozyme microcrystals and the structure was determined to 2.9 Å resolution from a series of still diffraction patterns. The method was substantially improved by employing ‘continuous rotation’ where data were recorded as the crystals were continuously rotated, resulting in higher quality data and allowing simple integration with existing processing programs used for X-ray crystallography (Nannenga et al., 2014). This led to the structure of lysozyme being determined to 2.5 Å resolution with improved statistics and data quality relative to the original lysozyme MicroED study.

In this work, we used thin bovine liver catalase 3D microcrystals for structure determination by MicroED. Catalase is a more difficult target than lysozyme, because it has a much larger unit cell, lower symmetry, and four molecules in the asymmetric unit. Moreover, each catalase monomer contains one heme group as well as a bound NADP molecule (Fita and Rossmann, 1985). Catalase is one of the earliest samples studied by EM, but despite extensive efforts spanning decades, the 3D structure of catalase has not been solved using electron diffraction. This is because the crystals have variable thicknesses (6–10 protein layers have been reported [Dorset and Parsons, 1975b]), and therefore these crystals were not suitable for 3D structure determination by traditional electron crystallography procedures (Longley, 1967; Matricardi et al., 1972; Unwin, 1975; Unwin and Henderson, 1975; Dorset and Parsons, 1975a). Here we report the 3.2 Å structure of catalase determined by MicroED. This is an important next step for the MicroED method as the analysis was rapid, taking a total of 3 weeks from crystal growth to final structural refinement, and used data from only a single catalase microcrystal.

Results and discussion

Sample preparation and data collection

Catalase was chosen for this study as it readily forms thin 3D microcrystals, which can be analyzed by transmission electron microscopy (TEM) (Sumner and Dounce, 1937; Dorset and Parsons, 1975a; Baker et al., 2010). Well-ordered catalase microcrystals were grown by solubilizing crystalline catalase from an aqueous suspension followed by overnight dialysis in 0.05 M Sodium phosphate, pH 6.3. Following crystal formation, crystals were deposited on holey carbon grids and the sample was blotted and vitrified in liquid ethane prior to TEM analysis. The grids were screened in over-focused diffraction mode for the presence of thin 3D crystals (Figure 1, inset). The average crystal dimensions were found to be on the order of 8 µm by 4 µm in length and width and approximately 150 nm thick, in good agreement with previous crystallization results (Dorset and Parsons, 1975b). Suitable crystals were assessed by collecting a single still diffraction pattern at a total dose of 0.05 e−/Å2, where well-ordered crystals showed sharp reflections extending to approximately 3.0 Å for untilted crystals (Figure 1). When high-quality diffraction was observed for an untilted crystal, the crystal was then tilted to 60° to check the diffraction quality at higher tilt angles as crystal flatness and embedding could affect the diffraction quality at higher tilt (Gonen, 2013). Typically, well-embedded and relatively flat crystals yielded data to ∼2.8 Å resolution untilted but only ∼3.2 Å at high tilt. Data sets were then collected as a sequence of 6 s exposures per frame. An example data set is shown in Video 1 and was recorded as the stage was continuously rotated as described previously (Nannenga et al., 2014).

Figure 1
Download asset Open asset
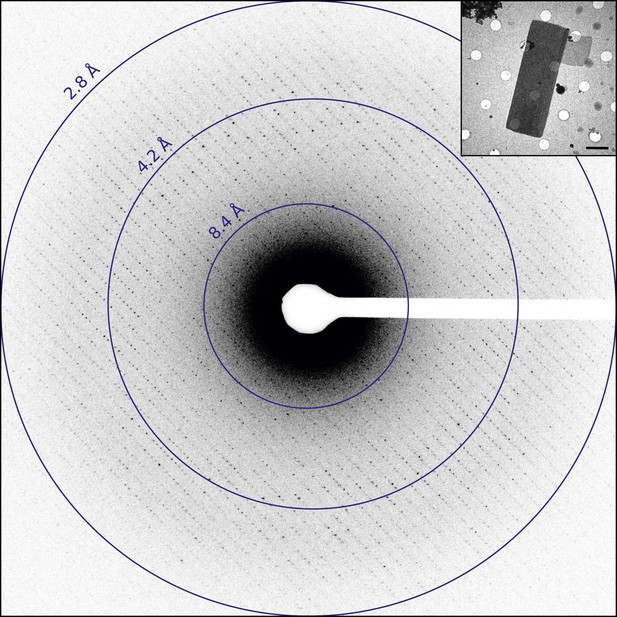
Diffraction from catalase microcrystals.

Representative untilted still diffraction pattern of a catalase microcrystal that shows sharp reflections extending to approximately 3.0 Å. Crystals of this quality were used to collect a data set by continuous rotation. Inset shows an example catalase microcrystal as seen in over-focused diffraction mode. Scale bar is 2 µm. The dimensions of most microcrystals varied between 6 and 20 µm in length, 2 and 8 µm in width, and the thickness was approximately 100–200 nm, in agreement with previous catalase crystal sizes (Dorset and Parsons, 1975b).

https://doi.org/10.7554/eLife.03600.002
Video 1
Download asset
Catalase diffraction data set collected by continuous rotation.

Diffraction data was recorded at an exposure time of 6 s per frame from a single crystal as the stage was continuously rotating at ∼0.09° s−1.

https://doi.org/10.7554/eLife.03600.003

Data analysis, processing, and structure refinement

We sought to analyze the levels of dynamic scattering in our catalase data in order to validate whether kinematical scattering could be assumed. We quantified the dynamic scattering of the catalase crystals using the ratio of the strongest diffracted intensity to the unscattered incident beam (Unwin and Henderson, 1975), as well as the ratio of the sum of all diffracted intensities on an image to the incident beam intensity as described by Dorset and Parsons (1975a). For the kinematical theory to apply, these ratios must be low. A representative crystal, which was approximately 200 nm thick, showed a ratio of 8.4 × 10−3 for the maximum intensity and 0.18 for the sum of all intensities, which are close to the previously reported values (Unwin and Henderson, 1975; Dorset and Parsons, 1975a), indicating that kinematical assumption is valid for these diffraction data.

Data sets from five microcrystals were each integrated with MOSFLM (Leslie and Powell, 2007) followed by merging and scaling with POINTLESS (Evans, 2011) and AIMLESS (Evans and Murshudov, 2013). All crystals yielded comparable resolution but varied in data completeness (Table 1). We combined all five data sets in an effort to increase completeness, multiplicity and to improve the quality of the data and in parallel we processed the data from crystal 4 separately for comparison. Crystal 4 was chosen for processing separately because it had a good compromise between resolution and completeness. The data sets were processed to a range of resolutions (Table 2) and phases were determined by molecular replacement (MR) as implemented in MOLREP (Vagin and Teplyakov, 1997) with PDB ID: 3NWL (Foroughi et al., 2011) as a search model. Following MR, refinement using PHENIX and REFMAC (Murshudov et al., 1997; Adams et al., 2010) with electron scattering factors was performed. Merging data from multiple crystals did not have a significant effect on data completeness, because the catalase crystals all orient on the grid with the c-axis parallel to the electron beam (Table 2). When comparing the statistics presented in Table 2, it was clear that merging multiple crystals had a negative impact on the final refinement statistics, most likely due to non-isomorphism between crystals, and therefore the multiple crystal data sets were disregarded. Crystals 1, 2, 3, and 5 were relatively isomorphous and their diffraction data merged well, but the completeness of this data set was low (∼62%), and we chose not to use it.

Table 1

Resolution and completeness for catalase data sets

https://doi.org/10.7554/eLife.03600.004
Crystal 1Crystal 2Crystal 3Crystal 4*Crystal 5
Resolution (Å)27.9–2.821.1–2.916.4–2.921.2–3.020.8–3.5
(3.0–2.8)(3.0–2.9)(3.0–2.9)(3.1–3.0)(3.9–3.5)
Unit cell dimensions
 a (Å)68.768.567.867.867.9
 b (Å)170.4170.1171.1172.1171.3
 c (Å)205.0203.6204.5182.1202.3
 α = β = γ (°)9090909090
Completeness (%)30.228.151.776.561.6
(37.1)(24.0)(42.2)(62.4)(56.9)

  1. Values in parentheses reflect the highest resolution shell.

  2. *

    Data set used for final structure.

Table 2

Comparison of merging and refinement statistics for catalase data sets

https://doi.org/10.7554/eLife.03600.005
Multi-2.8 ÅMulti-3.0 ÅMulti-3.2 ÅSingle-3.0 ÅSingle-3.2 Å*
Total crystals55511
Resolution (Å)27.8–2.827.8–3.027.8–3.221.2–3.021.2–3.2
(2.9–2.8)(3.1–3.0)(3.4–3.2)(3.1–3.0)(3.4–3.2)
Rmerge (%)25.825.524.818.717.5
(42.0)(41.2)(38.2)(38.8)(32.7)
CC1/20.9060.9200.9330.8860.891
(0.231)(0.348)(0.574)(0.426)(0.555)
Multiplicity4.85.25.62.42.4
(2.0)(3.1)(3.6)(2.2)(2.3)
Completeness (%)71.878.180.176.579.4
(35.2)(61.8)(72.2)(62.4)(75.5)
Mean (I/σ(I))3.23.43.53.23.4
(2.5)(2.2)(2.1)(1.7)(2.0)
Rwork/Rfree36.1/39.237.1/38.434.6/37.327.3/31.926.2/30.8

  1. Values in parentheses reflect the highest resolution shell.

  2. *

    Data set used for final structure.

The single crystal 4 dataset was used for the remainder of the study. Close analysis indicated that the information content in the 3–3.2 Å resolution shell was too low for inclusion, which was not surprising as the crystals did not diffract well beyond 3.2 Å at high tilt angles. We therefore truncated the resolution to 3.2 Å yielding a final model with acceptable refinement statistics (Rwork/Rfree = 26.2%/30.8%) and geometry (Table 3, Figure 2A, Video 2). The final 2mFobs-DFcalc density map shows well-defined density surrounding the final refined model (overall map CC = 92.3%), both around the backbone and the side-chains (Figure 2B, Video 2), without significant peaks in the mFobs-DFcalc difference density map (Figure 2C). Additionally, the solvent channels between the tetramers in the crystal lattice show very little density (Figure 2D), further evidence of the quality of the model and data. The final structure of catalase at 3.2 Å resolution determined by MicroED agrees well with previously solved X-ray structures, with an RMSD of 0.358 Å and 0.440 Å between the MicroED structure and PDB ID: 3NWL (Foroughi et al., 2011) and PDB ID: 4BLC (Ko et al., 1999), respectively.

Table 3

Data collection and refinement statistics

https://doi.org/10.7554/eLife.03600.006
Data Collection
 Excitation voltage200 kV
 Electron sourceField emission gun
 Wavelength (Å)0.025
 Total dose per crystal (e−/Å2)∼6.8
 Frame rate (frame/s)1/6
 Rotation rate (°/s)0.09
 Angular range per frame (°/s)0.54
 No. crystals used1
 Total angular range collected (°)∼61
Merging Statistics*
 Space groupP212121
 Unit cell dimensions
 a, b, c (Å)67.8, 172.1, 182.1
 α = β = γ (°)90
 Resolution (Å)21.2–3.2 (3.4–3.2)
 Total reflections67,064 (9873)
 Rmerge (%)17.5 (32.7)
 Total unique reflections28,143 (4278)
 Multiplicity2.4 (2.3)
 Completeness (%)79.4 (75.5)
 Mean (I/σ(I))3.4 (2.0)
 CC1/20.891 (0.555)
Data Refinement
 Reflections in working set26,732
 Reflections in test set1369
 Rwork/Rfree (%)26.2/30.8
 RMSD bonds (Å)0.006
 RMSD angles (°)1.05
 Ramachandran (%)†
 (Favored, allowed, outlier)96.6; 3.3; 0.1
  1. *

    Values in parentheses reflect the highest resolution shell.

  2. †

    Statistics given by MolProbity (Chen et al., 2010).

Figure 2 with 1 supplement see all
Download asset Open asset
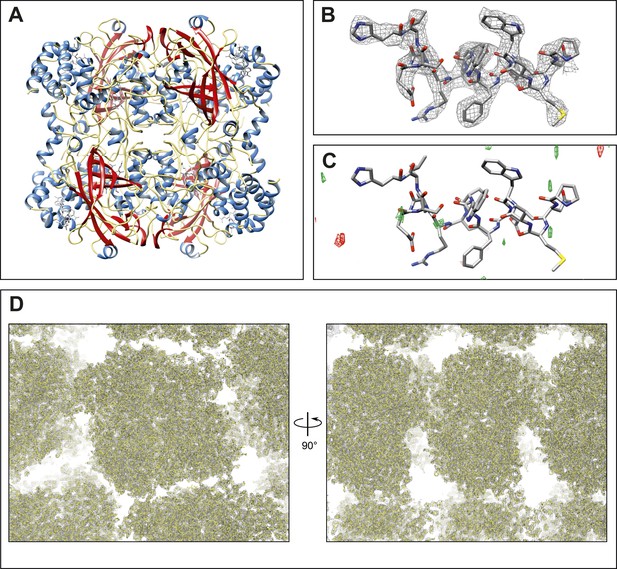
Final structure of catalase at 3.2 Å resolution determined by MircoED.

(A) The complete refined catalase structure shown as ribbons. The corresponding 2mFobs-DFcalc density map around the complete structure can be seen in Video 2. (B) The density map, contoured at 1.5 σ, around a representative region of the structure (residues 178–193 of chain A) shows well-defined density around the model. (C) The mFobs-DFcalc difference map, contoured at +2.5 σ (green) and −2.5 σ (red), around the same region shows no interpretable densities near the model indicating no obvious differences between the observed data and the calculated model. (D) Views of the density map (contoured at 1.0 σ) around a large region of the crystal lattice shows there is no significant density in the in the solvent channels of the catalase crystal.

https://doi.org/10.7554/eLife.03600.007
Video 2
Download asset
Final density map and model of catalase at 3.2 Å.

The 2mFobs-DFcalc density map contoured at 1.5 σ shows good agreement with the final refined model.

https://doi.org/10.7554/eLife.03600.009

Model validation

The orientation of our crystals prevented the full sampling of reciprocal space leading to systematic incompleteness (missing wedge or missing cone). While the incompleteness of data is significant, the resulting maps are still expected to be good enough for proper interpretation (Glaeser et al., 1989). To test the quality of the data and the resulting maps, and to identify any significant model bias or negative effects of the data incompleteness, the data were put through several validation tests. First, the robustness of the MR solution was tested by repeating the MR with a single monomeric chain of PDB ID: 3NWL (Foroughi et al., 2011) instead of the complete tetramer that was used originally. Even with a single chain, a strong solution was found with all four molecules successfully placed to recreate the complete tetramer (Figure 2—figure supplement 1; top MOLREP contrast score = 35.8, where a score of >3.0 is considered a strong solution. An identical test with synchrotron X-ray data yielded a top score of 23.7). We also phased the data with a poly-alanine model derived from PDB ID: 3NWL, and the resulting maps show clear density beyond the model where the correct side-chains could be rebuilt (Figure 2—figure supplement 1B,C).

In order to test the quality of the resulting maps following MR, autobuilding with Buccaneer (Cowtan, 2006) was performed and yielded 2120 residues in 160 fragments (Figure 2—figure supplement 1D). Out of the built residues, 1280 traced the correct backbone and 467 side-chains were correctly assigned. Manual curation in Coot (Emsley et al., 2010), exploiting the fourfold non-crystallographic symmetry, resulted in a nearly complete model indicating the maps initially produced from our data were of good quality.

The next validation test performed involved removing sections of the model and analyzing the effect this had on the resulting refined density maps. This was done in order to examine the strength of the data and to find any potential model bias introduced by the MR search model. For this test, two validation models were used, in which the same sections of all four monomers of the final tetrameric structure were removed. The first model had residues 181 to 185 removed (∆181–185) and the second model lacked the four heme groups (∆heme) that are normally found in catalase. Following refinement and simulated annealing, the resulting difference maps from the ∆181–185 model (Figure 3A) and ∆heme model (Figure 3C) both showed significant positive difference density corresponding to the deleted regions of the model. Additionally, automated ligand identification was performed on the ∆heme maps using phenix.ligand_identification (Terwilliger et al., 2006, 2007), and the program was able to correctly place two of the four heme groups present in the structure. The results of these tests indicate that the data do not suffer from bias introduced by the MR search model.

Figure 3
Download asset Open asset
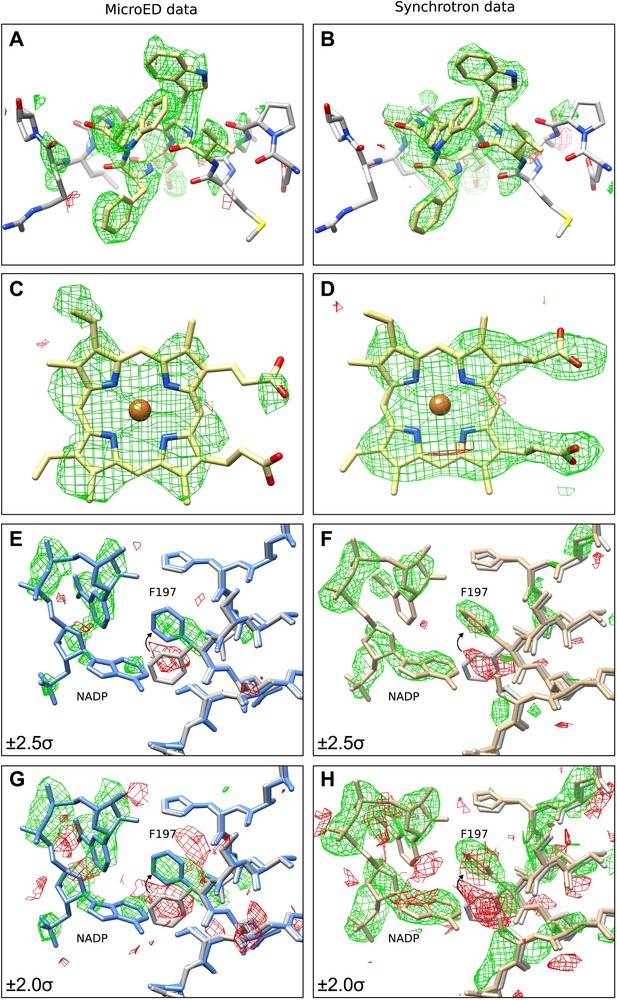
Final Model validation tests.

(A–D) To check for model bias in the final MicroED data (A and C), and to compare with data obtained from synchrotron X-ray diffraction (B and D), residues 181–185 (A–B) or the heme groups (C–D) from all four chains were removed prior to simulated annealing and re-refinement. In all cases, significant positive mFobs-DFcalc difference density (contoured at ±2.0 σ) can be seen for the missing regions, which are displayed in yellow for clarity, indicating no significant model bias in the final structure. (E–H) When a model (PDB ID: 3RGP; gray) lacking NADP was used to phase the MicroED data or the synchrotron x-ray data, both of which contained NADP, significant density in the mFobs-DFcalc difference map was observed although it appeared fragmented even at a lower contour level. This density could be fit with the NADP and the conformational change of residue F197 present in our final refined model is apparent. Maps presented in panels (E–H) are all unrefined, following MR.

https://doi.org/10.7554/eLife.03600.010

Next, we sought to determine whether data from MicroED was of sufficient accuracy to locate small molecule ligands and corresponding protein conformational changes in the ligand-binding pocket. Bovine catalase binds four NADP cofactors, one per monomer through several side-chain interactions including F197 (Kirkman and Gaetani, 1984; Fita and Rossmann, 1985). Recently, the structure of bovine catalase was solved lacking the NADP cofactor (PDB ID: 3RGP) (Purwar et al., 2011), and in the NADP-free structure F197 underwent a conformational change as it no longer interacted with NADP. The crystals used for our MicroED analysis do contain NADP. Therefore, we used PDB ID: 3RGP (NADP-free structure) as a molecular replacement model against the MicroED data to determine whether NADP could be visualized in our catalase crystals using difference maps. When analyzing the difference maps, positive density was observed in the location expected for NADP although it appeared fragmented even at lower contour levels (Figure 3E,G). For visual comparison, structure factors from PDB ID: 3NWL, which was solved by X-ray crystallography, were truncated to 3.2 Å, and difference maps were calculated for ∆181–185, ∆heme and NADP-free model (Figure 3B,D,F,H). Maps from both MicroED and synchrotron X-ray diffraction appear fragmented around the NADP even at lower contour levels (Figure 3G,H). The difference maps for both the MicroED and X-ray synchrotron data suggest that F197 should change its orientation to assume its correct position for NADP binding.

These results demonstrate the MicroED data is of sufficient quality to detect subtle differences among structures at atomic resolution. At the current level of methodology with samples that suffer from missing data like catalase, MicroED produces lower quality maps than synchrotron X-ray diffraction. However, the catalase crystals used for MicroED were approximately 1000 times smaller in volume than those used at the synchrotron (Foroughi et al., 2011), and the resulting maps are still of high enough quality to determine the structure.

Concluding Remarks

We present here the second protein structure determined by the emerging MicroED method. Bovine liver catalase resisted structural determination by traditional electron crystallography for decades, but the structure was readily determined by MicroED in 3 weeks from crystal formation to final structure determination using a single crystal. This is the second example where a single crystal was sufficient for structure determination by MicroED (Nannenga et al., 2014). Moreover, the continuous rotation method yields data similar in quality to X-ray diffraction allowing simple processing with existing X-ray data reduction software and further accelerating structure analysis by MicroED (Nannenga et al., 2014). The resulting maps allow us to distinguish between subtly different protein conformations and to identify of small-molecule ligands such as NADP. This study shows that MicroED can be used as an alternative to X-ray crystallography using extremely small crystals for both mechanistic studies as well as structure-based drug design studies where small ligands are assayed.

Materials and methods

Catalase crystallization and sample preparation

Request a detailed protocol

Catalase was recrystallized from a commercial aqueous suspension of catalase (C100; Sigma–Aldrich, St. Louis, MO) by first centrifuging the crystalline suspension and dissolving the pellet in 1.7 M NaCl. The solubilized catalase was then centrifuged and the supernatant was dialyzed against 50 mM sodium phosphate pH 6.3 overnight at 4°C. Crystals were removed from dialysis, stored in an Eppendorf tube, and incubated an additional 24 hr at 4°C. Catalase crystals were stored at 4°C and were washed with water prior to sample preparation. To prepare samples for the TEM, crystals were resuspended and the undiluted catalase crystal suspension was applied, blotted and vitrified in liquid ethane as described previously (Shi et al., 2013).

Collection of electron diffraction data

Request a detailed protocol

All electron diffraction was performed on a FEI Tecnai F20 TEM operated at 200 kV with a selected area aperture (6 μm in diameter at the specimen) and data were collected with 4k × 4k TVIPS F416 CMOS cameras (15.6 μm pixel size). Diffraction data were collected with a frame rate of 1 frame per 6 s as the sample was continuously rotated from high to low tilt angle at ∼0.09° s−1 (0.54°/frame) as described previously (Nannenga et al., 2014). A data set of approximately 61° was collected from a single crystal. Crystal thickness was estimated by measuring the intensity of the crystal (I) relative to the intensity of a hole in the carbon film (I0) from an image and using Beer's law:

lnII0=−εct

where ε is the molar absorptivity, c is the molar concentration, and t is the crystal thickness. As an approximation, the value of εc for catalase was assumed to be the same as those for calculated for lysozyme. The lysozyme coefficients were determined using images of lysozyme microcrystals with a known thickness as described previously (Nannenga et al., 2014).

Data processing and structure refinement

Request a detailed protocol

Raw TEM diffraction data were converted and processed using MOSFLM v7.1.0 (Leslie and Powell, 2007) and it's graphical interface iMOSFLM v1.0.7 (Battye et al., 2011), POINTLESS (Evans, 2006), and AIMLESS (Evans and Murshudov, 2013) as described in previous work (Nannenga et al., 2014). MOLREP (Vagin and Teplyakov, 1997) was used to perform molecular replacement using catalase PDB ID: 3NWL (Foroughi et al., 2011) as a search model (MOLREP contrast score = 40.8), and the molecular replacement solution was refined in PHENIX (Adams et al., 2010) and REFMAC (Murshudov et al., 1997) using a 5% free data set. Maps in Figure 3E,F,G and H were calculated using BUSTER-TNT (Blanc et al., 2004). Maps and models were displayed using the UCSF Chimera package (Pettersen et al., 2004).

Data availability

The following previously published data sets were used

References

    1. Emsley P
    2. Lohkamp B
    3. Scott WG
    4. Cowtan K
    (2010) Features and development of Coot
    Acta Crystallographica Section D, Biological Crystallography 66:486–501.
    https://doi.org/10.1107/S0907444910007493
    1. Evans P
    (2006) Scaling and assessment of data quality
    Acta Crystallographica Section D, Biological Crystallography 62:72–82.
    https://doi.org/10.1107/S0907444905036693
    1. Evans PR
    2. Murshudov GN
    (2013) How good are my data and what is the resolution?
    Acta Crystallographica Section D, Biological Crystallography 69:1204–1214.
    https://doi.org/10.1107/S0907444913000061
    1. Fita I
    2. Rossmann MG
    (1985) The NADPH binding site on beef liver catalase
    Proceedings of the National Academy of Sciences of USA 82:1604–1608.
    https://doi.org/10.1073/pnas.82.6.1604
    1. Leslie AGW
    2. Powell HR
    (2007) Processing diffraction data with MOSFLM
    NATO Science Series II: Mathematics, Physics and Chemistry 245:41–51.
    https://doi.org/10.1007/978-1-4020-6316-9_4
    1. Sumner JB
    2. Dounce AL
    (1937)
    Crystalline catalase
    The Journal of Biological Chemistry 121:417–424.

Decision letter

  1. Stephen C Harrison
    Reviewing Editor; Harvard Medical School, United States

eLife posts the editorial decision letter and author response on a selection of the published articles (subject to the approval of the authors). An edited version of the letter sent to the authors after peer review is shown, indicating the substantive concerns or comments; minor concerns are not usually shown. Reviewers have the opportunity to discuss the decision before the letter is sent (see review process). Similarly, the author response typically shows only responses to the major concerns raised by the reviewers.

Thank you for sending your work entitled “Structure of catalase solved by MicroED” for consideration at eLife. Your Research advance has been favorably evaluated by John Kuriyan (Senior editor) and 3 reviewers, one of whom is a member of our Board of Reviewing Editors.

The following individuals responsible for the peer review of your submission have agreed to reveal their identity: Richard Henderson (one of the peer reviewers).

The Reviewing editor and the other reviewers discussed their comments before we reached this decision and the Reviewing editor has assembled the following comments to help you prepare a revised submission.

This submission, a Research advance to the earlier Shi et al. paper, shows that electron diffraction can be used to determine the structure of catalase by molecular replacement from the known structure from x-ray crystallography. Does it add anything to the earlier paper on MicroED of lysozyme? Catalase is a much larger protein than lysozyme with much weaker diffraction, and it is a crystal form with a long track record for use as a test specimen for magnification calibration. The paper therefore does move the method forward, and it is in principle suitable to publish as an “advance”.

The reviewers were disappointed that the analysis was not very thorough. In particular:

1) The diffraction image (Figure 1) shows spots well past 2.8 A, but the structure was refined only to 3.2 A. Why was it not processed and refined to the diffraction limit of the crystal? A similar concern was raised by the reviewers of the original paper on lysozyme. It should be noted that the deposited crystal structures of catalase obtained by conventional X-ray crystallography were refined to substantially higher resolution.

2) The diffraction data are rather incomplete (∼80%), in a systematic way that by itself diminishes accuracy (missing wedge).

3) The omit maps (Figure 3B,C, D, E) are poor, even considering a refinement-diffraction limit of 3.2 A. The authors need to determine why these maps are so poor. Is it related to data quality? They may wish to use the X-ray diffraction data of catalase (PDB IDs 3NWL or 4BLC), truncated to 3.2 A, and then perform similar validation tests, as a benchmark. It certainly would have been nearly impossible to identify the NADP molecule in such a poor map (Figure 3D,E), and the heme group would have been a stretch, even knowing the identity of the ligand.

4) Only a single data set was analyzed, Redundancy could have improved the quality of the data, and it would have allowed the authors to assess the limitations imposed by data accuracy.

Reviewers also raised some more specific technical questions:

1) In the legend to Figure 1, the crystal shown is not the crystal (size roughly 12x4 um) used for data collection. The electron diffraction pattern is not the one used to collect the data used in the structure determination. The legend and the text state that the crystals were 8x4 um on average, yet the crystal used for the data collection was one of the larger ones at 15x7 um, and at 0.18um thick was also one of the thicker ones. In a sense, this rather undermines the unique selling point of MicroED. This observation does not invalidate the paper, but does reduce its potential impact. On the other hand, the work presented does demonstrate that there are no other serious problems (such as dynamical scattering); if it works on a big crystal, then it should also work on a smaller crystal, although it will be more work to collect the data because more crystals would be needed.

2) It is stated that an average crystal shows a maximum intensity for the strongest spot of 8.4 x 10**-3 of the direct beam. This is about 1% so the amplitude of that diffracted beam would be about 10% of the direct beam. This would produce some dynamical scattering. Since the crystal they actually used for the data collection was bigger than the average, it would presumably have a larger contribution from dynamical scattering. It would be useful if the authors had tried to further refine the structure using a protocol such as used by Grigorieff & Henderson in Ultramicroscopy, 1996. This would show how much the R-factor had been affected by dynamical scattering (i.e. increased by how much).

There was some discussion among the reviewers about whether these weaknesses eliminated the submission from further consideration, but we ultimately concurred that with careful attention to the points above, this work would meet the criteria of the new eLife category of “advance”. We would thus be willing to review a revised version that met the following criteria:

1) Analysis at full resolution. In the current version, the authors write that they cut off the data at 3.2 A because of merging statistics (text,Table 1). But an Rmerge of 32.7% and I/sigma(I) of 2 in the highest resolution bin is too strict. The authors should go at least to I/sigma(I) ∼ 1 and Rmerge in the last bin of 50% or even higher.

2) Efforts to reduce the substantial missing wedge (incompleteness).

3) Explicit evaluation of data quality and the effect of data quality on the clarity of the omit maps.

4) Evaluation of data from multiple crystals (this could be part of the response to criteria 2 and 3).

Additional analyses that the authors might wish to carry out (but not required for review) include use of several smaller and thinner crystals for data collection and a quantitative effort to get a lower R-factor by an explicit attempt to model the dynamical scattering quantitatively.

[Editors' note: further revisions were requested prior to acceptance, as described below.]

Thank you for resubmitting your Research advance entitled “Structure of catalase solved by MicroED” for further consideration at eLife. Your revised article has been favorably evaluated by John Kuriyan (Senior editor), a Reviewing editor, and two reviewers (Axel T Brunger and Richard Henderson). The manuscript has been improved but there are some remaining issues that need to be addressed before acceptance, as outlined below:

The reviewers agreed that many of their questions were answered by the revisions, although at least one of them felt that the paper would have been better had the authors collected more data from more crystals. Despite some mild disappointment, the consensus was to recommend publication, if the authors comply with the requests that follow.

1) The section that describes how the authors collected diffraction data from five different crystals is useful, since it shows how merging the data did not result in any improvement. They ascribe this outcome to lack of isomorphism, presumably due to slight cell dimension changes during the freezing. The authors should include in Figure 1A what the cell dimensions were for each of the five crystals, to show whether the non-isomorphism is apparent as cell dimension variability.

2) A useful addition is comparison of the molecular replacement solution and Fo-Fc difference maps with those from a set of X-ray data truncated to the same (3.2 Å) resolution. A “MOLREP contrast score” of 35.8 and 40.8 for the electron diffraction and equivalent truncated X-ray data will not be understood by most readers, however, as few of them will have used MOLREP. The authors should give a reference to an earlier paper or to a review by Vagin & Teplyakov in which the significance of 35.8 or 40.8 is discussed.

3) The reasons for data truncation at 3.2 Å should be stated clearly again (i.e., that the tilted crystals did not yield data beyond that limit).

4) Figure 4–figure supplement 2. This entire supplemental figure is an important validation of the method, so it must be included in the main part of the manuscript. Moreover, two different contour levels must be provided in panels C and D – it appears that the synchrotron map is better connected, whereas the microED map shows a false connection for the NADP. These differences will become probably become even clearer at a lower contour level.

5) In connection with the omit map results, currently in Figure 4–figure supplement 2 (to be moved to main part of the manuscript), it should be stated clearly in the main text that at the current level of the microED methodology, the maps obtained by microED are not of the same quality as those obtained by x-ray diffraction at synchrotrons. The microED maps are certainly not of “similar quality”, as stated (incorrectly) in the text.

https://doi.org/10.7554/eLife.03600.011

Author response

1) The diffraction image (Figure 1) shows spots well past 2.8 A, but the structure was refined only to 3.2 A. Why was it not processed and refined to the diffraction limit of the crystal? A similar concern was raised by the reviewers of the original paper on lysozyme. It should be noted that the deposited crystal structures of catalase obtained by conventional X-ray crystallography were refined to substantially higher resolution.

As presented in the revised manuscript, we have processed the data to 2.8 Å resolution. However, we note that such high resolution was obtained from untilted crystals. Once the crystals were tilted the resolution was typically lower. Therefore the data completeness at high resolution was rather low and we decided to truncate the resolution to a final 3.2 Å.

2) The diffraction data are rather incomplete (∼80%), in a systematic way that by itself diminishes accuracy (missing wedge).

The reviewers are correct in that this data does suffer from a missing wedge. Catalase crystals are long and wide but are thin and they always orient on the grid with their c-axis parallel to the electron beam. As the reviewers know, one can only tilt to a maximum angle of ∼70° in the EM before the beam is blocked by the holder. Therefore, crystals such as these will always have a missing wedge and are analogous to traditional 2D crystals in that respect.

We note that for different crystal forms, for example lysozyme, as crystals randomly orient on the grid the addition of multiple data sets from different crystals reduces and can eliminate the missing wedge. Therefore this problem is not universal but unfortunately does exist for catalase.

As we tilted the crystals up to 60° the expected missing wedge is ∼15% (Glaeser et al., 1989) while our data suggests ∼80% completeness. Therefore we have covered the reciprocal space as much as we could and additional data from multiple crystals did not increase the completeness. We present this data in the revised version.

Nevertheless, all of our map and model validations indicate that the final map is of good quality that does not suffer from major deformations (for example stretching of the maps as observed in some examples of density maps from 2D crystals).

3) The omit maps (Figure 3B,C, D, E) are poor, even considering a refinement-diffraction limit of 3.2 A. The authors need to determine why these maps are so poor. Is it related to data quality? They may wish to use the X-ray diffraction data of catalase (PDB IDs 3NWL or 4BLC), truncated to 3.2 A, and then perform similar validation tests, as a benchmark. It certainly would have been nearly impossible to identify the NADP molecule in such a poor map (Figure 3D,E), and the heme group would have been a stretch, even knowing the identity of the ligand.

We thank the reviewers for this suggestion. We have now generated maps using the published X-ray data (PDB ID: 3NWL) truncated to 3.2 Å and perform a comparison with our density maps for the NADP. The analysis suggests that at this resolution the density map from X-ray is equivalent in quality to the density map from MicroED. Moreover, we performed additional analyses that are presented in this revised manuscript. Phasing with a poly-alanine model indicated that the density “mutates” toward the correct residues (Supplementary Figure 1B and C). Finally, we subjected the initial resulting maps (prior to refinement) to auto ligand find and auto build. The first found strong match for 2 of the 4 heme groups and the latter was able to build ∼65% of the protein automatically. These results indicate that the catalase data are of high quality.

All of these tests have been included in the revised text.

4) Only a single data set was analyzed, Redundancy could have improved the quality of the data, and it would have allowed the authors to assess the limitations imposed by data accuracy.

Please see discussion above. We now include an analysis of 5 crystals and show that since all catalase crystals orient the same way on the grid with their c-axis parallel to the electron beam, we will always have a missing wedge of data in the catalase example. Therefore data from additional crystals did not increase the completeness. This discussion is now included in the revised text.

Reviewers also raised some more specific technical questions:

1) In the legend to Figure 1, the crystal shown is not the crystal (size roughly 12x4 um) used for data collection. The electron diffraction pattern is not the one used to collect the data used in the structure determination. The legend and the text state that the crystals were 8x4 um on average, yet the crystal used for the data collection was one of the larger ones at 15x7 um, and at 0.18um thick was also one of the thicker ones. In a sense, this rather undermines the unique selling point of MicroED. This observation does not invalidate the paper, but does reduce its potential impact. On the other hand, the work presented does demonstrate that there are no other serious problems (such as dynamical scattering); if it works on a big crystal, then it should also work on a smaller crystal, although it will be more work to collect the data because more crystals would be needed.

We believe that there is a misunderstanding. Even though the crystals are wide and long, they are still very thin at 100-200 nm. It is the thickness of the crystal, through which the electron beam must pass, that could be the limiting factor when considering dynamical scattering, not the width and length of the crystal. Please remember that we cannot tilt the crystals completely on their side so the beam never travels through a 15 micron or 7 micron thick crystal. Moreover, we use a selected area aperture (6 micron diameter at the specimen), therefore we disagree that this “undermines the unique selling point of MicroED” because crystals of 100-200 nm thickness cannot be studied by traditional x-ray crystallography but are studied here.

2) It is stated that an average crystal shows a maximum intensity for the strongest spot of 8.4 x 10**-3 of the direct beam. This is about 1% so the amplitude of that diffracted beam would be about 10% of the direct beam. This would produce some dynamical scattering. Since the crystal they actually used for the data collection was bigger than the average, it would presumably have a larger contribution from dynamical scattering. It would be useful if the authors had tried to further refine the structure using a protocol such as used by Grigorieff & Henderson in Ultramicroscopy, 1996. This would show how much the R-factor had been affected by dynamical scattering (i.e. increased by how much).

We thank the reviewers for this fine suggestion.

We have shown previously that an error of up to 35% in intensity values still yield acceptable data (Shi et al., 2013). Others have also shown that for catalase crystals of this thickness, kinematic scattering can be assumed (Unwin and Henderson, 1975; Dorset and Parsons, 1975a). Even though the crystal we chose to focus on is one of the thicker ones in our sample, it is still only ∼180 nm in thickness and kinematic scattering can still be assumed as we discussed.

We agree, however, with the reviewers that some dynamical scattering will be produced and we have not, as of yet, applied any corrections. We plan to do so in the future.

There was some discussion among the reviewers about whether these weaknesses eliminated the submission from further consideration, but we ultimately concurred that with careful attention to the points above, this work would meet the criteria of the new eLife category of “advance”. We would thus be willing to review a revised version that met the following criteria:

1) Analysis at full resolution. In the current version, the authors write that they cut off the data at 3.2 A because of merging statistics (text,Table 1). But an Rmerge of 32.7% and I/sigma(I) of 2 in the highest resolution bin is too strict. The authors should go at least to I/sigma(I) ∼ 1 and Rmerge in the last bin of 50% or even higher.

We now include analysis at full resolution and from multiple crystals. We have presented a more detailed analysis on how the final data set was chosen based on completeness, merging and the final refinement statistics. In short, the low information content in the higher resolution shells precludes their inclusion.

2) Efforts to reduce the substantial missing wedge (incompleteness).

As discussed above, the preferred orientation of the catalase crystals on the grid means that one will always suffer from a missing wedge with this sample. Nevertheless, we now present data from multiple crystals and explain that because of the preferred orientation of the crystals, merging multiple data sets together does not improve the data completeness over the completeness of crystal 4 dataset alone. Tilting the TEM stage beyond ∼60° for this sample (the angle used for the single crystal data set) did not provide useful data as the diffraction was generally quite poor at such high tilts.

3) Explicit evaluation of data quality and the effect of data quality on the clarity of the omit maps.

We have provided more detailed analysis in the Model validation section, specifically the results of autobuilding, automated ligand finding, and comparisons with X-ray data as suggested by the reviewers.

4) Evaluation of data from multiple crystals (this could be part of the response to criteria 2 and 3).

Done. As mentioned above we added our analysis on the effects of using multiple crystals.

[Editors' note: further revisions were requested prior to acceptance, as described below.]

1) The section that describes how the authors collected diffraction data from five different crystals is useful, since it shows how merging the data did not result in any improvement. They ascribe this outcome to lack of isomorphism, presumably due to slight cell dimension changes during the freezing. The authors should include in Figure 1A what the cell dimensions were for each of the five crystals, to show whether the non-isomorphism is apparent as cell dimension variability.

We have added the unit cell dimensions for the five crystals in Supplementary file 1. We also added text explaining that four of the crystals were relatively isomorphous; however, even when combined they yielded relatively incomplete data.

2) A useful addition is comparison of the molecular replacement solution and Fo-Fc difference maps with those from a set of X-ray data truncated to the same (3.2 Å) resolution. A “MOLREP contrast score” of 35.8 and 40.8 for the electron diffraction and equivalent truncated X-ray data will not be understood by most readers, however, as few of them will have used MOLREP. The authors should give a reference to an earlier paper or to a review by Vagin & Teplyakov in which the significance of 35.8 or 40.8 is discussed.

We thank the reviewers for this suggestion. We have provided a contrast score for an MR search with X-ray data and have provide what is considered a high quality score (>3.0) as defined in the official CCP4 documentation for MOLREP. We have also included omit maps generated from X-ray data truncated to 3.2 Å for comparison and added them to what is now called Figure 3.

3) The reasons for data truncation at 3.2 Å should be stated clearly again (i.e., that the tilted crystals did not yield data beyond that limit).

This has been added to the text.

4) Figure 4–figure supplement 2. This entire supplemental figure is an important validation of the method, so it must be included in the main part of the manuscript. Moreover, two different contour levels must be provided in panels C and D – it appears that the synchrotron map is better connected, whereas the microED map shows a false connection for the NADP. These differences will become probably become even clearer at a lower contour level.

Supplemental figure 2 has been moved back into the main manuscript and renamed Figure 3. Two different contour levels for the NADP have been added to this figure as requested.

5) In connection with the omit map results, currently in Figure 4–figure supplement 2 (to be moved to main part of the manuscript), it should be stated clearly in the main text that at the current level of the microED methodology, the maps obtained by microED are not of the same quality as those obtained by x-ray diffraction at synchrotrons. The microED maps are certainly not of “similar quality”, as stated (incorrectly) in the text.

It was never the focus of this work to directly compare the quality of maps obtained by MicroED with those obtained by X-ray diffraction. Regardless, we have added X-ray omit maps for comparison and have stated that the MicroED maps are not of the same quality. However, it needs to be noted that traditional X-ray crystallography could have never provided data, and subsequently density maps, from the crystals used in this study, as they are much too small.

https://doi.org/10.7554/eLife.03600.012

Article and author information

Author details

  1. Brent L Nannenga

    Janelia Research Campus, Howard Hughes Medical Institute, Ashburn, United States
    Contribution
    BLN, Conception and design, Acquisition of data, Analysis and interpretation of data, Drafting or revising the article
    Competing interests
    The authors declare that no competing interests exist.

  2. Dan Shi

    Janelia Research Campus, Howard Hughes Medical Institute, Ashburn, United States
    Contribution
    DS, Conception and design, Acquisition of data, Analysis and interpretation of data, Drafting or revising the article
    Competing interests
    The authors declare that no competing interests exist.

  3. Johan Hattne

    Janelia Research Campus, Howard Hughes Medical Institute, Ashburn, United States
    Contribution
    JH, Analysis and interpretation of data, Drafting or revising the article
    Competing interests
    The authors declare that no competing interests exist.
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-8936-0912

  4. Francis E Reyes

    Janelia Research Campus, Howard Hughes Medical Institute, Ashburn, United States
    Contribution
    FER, Analysis and interpretation of data, Drafting or revising the article
    Competing interests
    The authors declare that no competing interests exist.

  5. Tamir Gonen

    Janelia Research Campus, Howard Hughes Medical Institute, Ashburn, United States
    Contribution
    TG, Conception and design, Acquisition of data, Analysis and interpretation of data, Drafting or revising the article
    For correspondence
    gonent@janelia.hhmi.org
    Competing interests
    The authors declare that no competing interests exist.

Funding

Howard Hughes Medical Institute

  • Brent L Nannenga
  • Dan Shi
  • Johan Hattne
  • Francis E Reyes
  • Tamir Gonen

The funder had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

The authors wish to thank Garib Murshudov (MRC LMB) for providing a version of REFMAC with support for electron scattering factors and Andrew Leslie (MRC LMB) for data processing support and advice. We also would like to thank Steven Sawtelle (HHMI Janelia Research Campus) for technical support and Joanita Jakana (Baylor) for the protocol for catalase crystallization. Work in the Gonen lab is supported by the Howard Hughes Medical Institute.

Reviewing Editor

  1. Stephen C Harrison, Harvard Medical School, United States

Version history

  1. Received: June 6, 2014
  2. Accepted: September 28, 2014
  3. Version of Record published: October 10, 2014 (version 1)

Copyright

© 2014, Nannenga et al.

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

  • 4,907
    Page views
  • 590
    Downloads
  • 91
    Citations

Article citation count generated by polling the highest count across the following sources: Crossref, Scopus, PubMed Central.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Brent L Nannenga
  2. Dan Shi
  3. Johan Hattne
  4. Francis E Reyes
  5. Tamir Gonen
(2014)
Structure of catalase determined by MicroED
eLife 3:e03600.
https://doi.org/10.7554/eLife.03600

Categories and tags

Further reading

    1. Biochemistry and Chemical Biology
    2. Structural Biology and Molecular Biophysics

    Three-dimensional electron crystallography of protein microcrystals

    Dan Shi, Brent L Nannenga ... Tamir Gonen
    Research Article

    We demonstrate that it is feasible to determine high-resolution protein structures by electron crystallography of three-dimensional crystals in an electron cryo-microscope (CryoEM). Lysozyme microcrystals were frozen on an electron microscopy grid, and electron diffraction data collected to 1.7 Å resolution. We developed a data collection protocol to collect a full-tilt series in electron diffraction to atomic resolution. A single tilt series contains up to 90 individual diffraction patterns collected from a single crystal with tilt angle increment of 0.1–1° and a total accumulated electron dose less than 10 electrons per angstrom squared. We indexed the data from three crystals and used them for structure determination of lysozyme by molecular replacement followed by crystallographic refinement to 2.9 Å resolution. This proof of principle paves the way for the implementation of a new technique, which we name ‘MicroED’, that may have wide applicability in structural biology.

    1. Biochemistry and Chemical Biology
    2. Microbiology and Infectious Disease

    Indole produced during dysbiosis mediates host–microorganism chemical communication

    Rui-Qiu Yang, Yong-Hong Chen ... Cheng-Gang Zou
    Research Article Updated

    An imbalance of the gut microbiota, termed dysbiosis, has a substantial impact on host physiology. However, the mechanism by which host deals with gut dysbiosis to maintain fitness remains largely unknown. In Caenorhabditis elegans, Escherichia coli, which is its bacterial diet, proliferates in its intestinal lumen during aging. Here, we demonstrate that progressive intestinal proliferation of E. coli activates the transcription factor DAF-16, which is required for maintenance of longevity and organismal fitness in worms with age. DAF-16 up-regulates two lysozymes lys-7 and lys-8, thus limiting the bacterial accumulation in the gut of worms during aging. During dysbiosis, the levels of indole produced by E. coli are increased in worms. Indole is involved in the activation of DAF-16 by TRPA-1 in neurons of worms. Our finding demonstrates that indole functions as a microbial signal of gut dysbiosis to promote fitness of the host.

    1. Biochemistry and Chemical Biology
    2. Structural Biology and Molecular Biophysics

    The neuronal calcium sensor NCS-1 regulates the phosphorylation state and activity of the Ga chaperone and GEF Ric-8A

    Daniel Muñoz-Reyes, Levi J McClelland ... Maria Jose Sanchez-Barrena
    Research Article

    The Neuronal Calcium Sensor 1, an EF-hand Ca2+ binding protein, and Ric-8A coregulate synapse number and probability of neurotransmitter release. Recently, the structures of Ric-8A bound to Ga have revealed how Ric-8A phosphorylation promotes Ga recognition and activity as a chaperone and guanine nucleotide exchange factor. However, the molecular mechanism by which NCS-1 regulates Ric-8A activity and its interaction with Ga subunits is not well understood. Given the interest in the NCS-1/Ric-8A complex as a therapeutic target in nervous system disorders, it is necessary to shed light on this molecular mechanism of action at atomic level. We have reconstituted NCS-1/Ric-8A complexes to conduct a multimodal approach and determine the sequence of Ca2+ signals and phosphorylation events that promote the interaction of Ric-8A with Ga. Our data show that the binding of NCS-1 and Ga to Ric-8A are mutually exclusive. Importantly, NCS-1 induces a structural rearrangement in Ric-8A that traps the protein in a conformational state that is inaccessible to Casein Kinase II-mediated phosphorylation, demonstrating one aspect of its negative regulation of Ric-8A-mediated G-protein signaling. Functional experiments indicate a loss of Ric-8A GEF activity towards Ga when complexed with NCS-1, and restoration of nucleotide exchange activity upon increasing Ca2+ concentration. Finally, the high-resolution crystallographic data reported here define the NCS-1/Ric-8A interface and will allow the development of therapeutic synapse function regulators with improved activity and selectivity.