Phenotypic diversity and temporal variability in a bacterial signaling network revealed by single-cell FRET

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: February 12, 2018 (This version)
Accepted Manuscript updated: December 14, 2017 (Go to version)
Accepted Manuscript published: December 12, 2017 (Go to version)
Accepted: November 17, 2017
Received: April 4, 2017

1. Related to
Multiple sources of slow activity fluctuations in a bacterial chemosensory network

Remy Colin, Christelle Rosazza ... Victor Sourjik

Research Article Updated Feb 12, 2018
Further reading

Article
Figures and data
Abstract
eLife digest
Introduction
Results
Discussion
Materials and methods
References
Decision letter
Author response
Article and author information
Metrics

Abstract

We present in vivo single-cell FRET measurements in the Escherichia coli chemotaxis system that reveal pervasive signaling variability, both across cells in isogenic populations and within individual cells over time. We quantify cell-to-cell variability of adaptation, ligand response, as well as steady-state output level, and analyze the role of network design in shaping this diversity from gene expression noise. In the absence of changes in gene expression, we find that single cells demonstrate strong temporal fluctuations. We provide evidence that such signaling noise can arise from at least two sources: (i) stochastic activities of adaptation enzymes, and (ii) receptor-kinase dynamics in the absence of adaptation. We demonstrate that under certain conditions, (ii) can generate giant fluctuations that drive signaling activity of the entire cell into a stochastic two-state switching regime. Our findings underscore the importance of molecular noise, arising not only in gene expression but also in protein networks.

https://doi.org/10.7554/eLife.27455.001

eLife digest

Many sophisticated computer programs use random number generators to help solve challenging problems. These problems range from achieving secure communication across the Internet to deciding how best to invest in the stock market. Much research in recent years has found that randomness is also widespread in living cells, where it is often called “noise”. For example, the activity of some genes is so unpredictable to the extent that it appears random. Yet, relatively little is known about how such gene-expression noise propagates up to change how the cell behaves. Many open questions also remain about how cells might exploit these or other fluctuations to achieve complex tasks, like people use random number generators.

Bacteria perform a number of complex tasks. Some bacteria will swim toward chemicals that suggest a potential reward, such as food. Yet they swim away from chemicals that could lead them to harm. This ability is called chemotaxis and it relies on a network of interacting enzymes and other proteins that coordinates a bacterium’s movements with the input from its senses.

Keegstra et al. set out to find sources of noise that might act as random number generators and help the bacterium E. coli to best perform chemotaxis. An improved version of a technique called in vivo Förster resonance energy transfer (or in vivo FRET for short) was used to give a detectable signal when two proteins involved in the chemotaxis network interacted inside a single bacterium. The experiments showed that this protein network amplifies gene-expression noise for some genes while lessening it for others. In addition, the interactions between proteins encoded by genes acted as an extra source of noise, even when gene-expression noise was eliminated.

Keegstra et al. found that the amount of signaling within the chemotaxis network, as measured by in vivo FRET, varied wildly over time. This revealed two sources of noise at the level of protein signaling. One was due to randomness in the activity of the enzymes involved in tuning the cell’s sensitivity to changes in its environment. The other was due to protein interactions within a large complex that acts as the cell’s sensor. Unexpectedly, this second source of noise under some conditions could be so strong that it flipped the output of the cell’s signaling network back and forth between just two states: “on” and “off”.

Together these findings uncover how signaling networks can not only amplify or lessen gene-expression noise, but can themselves become a source of random events. The new knowledge of how such random events interact with a complex trait in a living cell – namely chemotaxis – could aid future antimicrobial strategies, because many bacteria use chemotaxis to help them establish infections. More generally, the new insights about noise in protein networks could help engineers seeking to build synthetic biochemical networks or produce useful compounds in living cells.

https://doi.org/10.7554/eLife.27455.002

Introduction

Cellular physiology is deeply shaped by molecular fluctuations, resulting in phenotypic diversity and temporal variability that can be both detrimental and beneficial (Rao et al., 2002; Kussell and Leibler, 2005; Lestas et al., 2010; Hilfinger et al., 2016). One of the most important and well-studied sources of intracellular fluctuations is stochastic gene expression (Elowitz et al., 2002; Eldar and Elowitz, 2010; Raj and van Oudenaarden, 2008), which can generate substantial cell-to-cell variability in protein levels within isogenic populations under invariant environmental conditions. Such heterogeneity in protein counts are readily measurable by fluorescent-protein reporters (Elowitz et al., 2002; Ozbudak et al., 2002) , but mechanistically tracing the consequences of such molecular noise to the level of complex cellular phenotypes such as signaling and motility remains a significant challenge, in part due to the multitude of interactions between gene products, but also because each of those interactions can, in principle, become an additional source of noise. In this paper, we study how multiple sources of molecular noise, arising in both gene expression and protein-protein interactions, affect performance of the E. coli chemotaxis network, a canonical signaling pathway.

In bacteria, gene-expression noise tends to manifest itself as stable cell-to-cell differences in phenotypes that persist over the cell’s generation time, because typical protein lifetimes are longer than the cell cycle (Li et al., 2014). The architecture of signaling networks can have a profound influence on their sensitivity to such noise-induced differences in protein levels, and it has been shown that the design of the E. coli chemotaxis network confers robustness of a number of signaling parameters, such as precision of adaptation, against variability in gene expression (Barkai and Leibler, 1997; Kollmann et al., 2005). On the other hand, cell-to-cell differences in behavior can also be advantageous for isogenic populations under uncertain and/or time-varying environments, and it has been argued that the manner in which the chemotaxis network filters gene expression noise to shape phenotype distributions could be under selective pressure (Frankel et al., 2014; Waite et al., 2016).

In principle, molecular noise arising in processes other than gene expression, such as protein-protein interactions within signaling pathways, can also contribute to cellular variability. However, such noise sources tend to be harder to study experimentally because, in contrast to gene-expression noise, which can be characterized by measuring fluorescent reporter levels (Elowitz et al., 2002; Raser et al., 2004), requirements for in vivo measurements of protein-protein interactions tend to be more demanding and no generically applicable strategies exist. The E. coli chemotaxis system provides a compelling experimental paradigm for addressing protein-signaling noise, because a powerful technique for in vivo measurements of protein signaling, based on Förster resonance energy transfer (FRET), has been successfully developed (Sourjik and Berg, 2002a; Sourjik et al., 2007).

The chemotaxis network controls the motile behavior of E. coli, a run-and-tumble random walk that is biased by the signaling network to achieve net migrations toward favorable directions. The molecular mechanisms underlying this pathway have been studied extensively (for recent reviews, see refs. (Wadhams and Armitage, 2004; Tu, 2013; Parkinson et al., 2015)). In brief, transmembrane chemoreceptors bind to ligand molecules, inhibiting the autophosphorylation of a central kinase, CheA. When active, CheA transfers its phosphate to CheY to form CheY-P. Meanwhile, the phosphatase CheZ dephosphorylates CheY-P to limit the signal lifetime. CheY-P binds to a flagellar motor, which in turn increases the chance of the motor to turn clockwise, leading to a tumble. An adaptation module consisting of the enzymes CheR and CheB implements negative integral feedback by tuning the sensitivity of the chemoreceptors via reversible covalent modifications that restore the kinase activity (and CheY-P level).

Despite its relative simplicity, this pathway exhibits many interesting network-level functionalities, such as cooperative signal amplification (Segall et al., 1986; Sourjik and Berg, 2002a; Bray et al., 1998), sensory adaptation (Barkai and Leibler, 1997; Alon et al., 1999), and Weber’s law and fold-change detection (Mesibov et al., 1973; Lazova et al., 2011; Clausznitzer et al., 2014), and FRET microscopy has proven extremely powerful in characterizing such signal processing of the chemotaxis pathway, especially in E. coli (Sourjik and Berg, 2002a; Sourjik and Berg, 2004; Shimizu et al., 2010; Oleksiuk et al., 2011), but also in Salmonella (Lazova et al., 2012; Rosier and Lazova, 2016) and B. subtilis (Yang et al., 2015). It has been implemented in various ways (Sourjik and Berg, 2002a; Sourjik and Berg, 2002b; Shimizu et al., 2006; Kentner and Sourjik, 2009; Neumann et al., 2012), but most commonly by using CFP and YFP as the FRET donor-acceptor pair, fused to CheY and CheZ, respectively. To date, however, nearly all applications of FRET in the bacterial chemotaxis system have been population-level measurements in which signals from hundreds to thousands of cells are integrated to achieve a high signal-to-noise ratio. A pioneering study applied FRET at the single-cell level to study spatial heterogeneities in CheY-CheZ interactions (Vaknin and Berg, 2004), but those measurements were limited to relatively short times due to phototoxicity and bleaching.

By exploring a range of fluorescent proteins as FRET pairs, and improving measurement protocols, we have developed a robust method for single-cell FRET measurements of chemotactic signaling dynamics in single bacteria over extended times. The data reveal extensive cell-to-cell variability, as well as temporal fluctuations that are masked in population-level FRET measurements. In contrast to previous single-cell experiments that relied on measurements of motor output or swimming behavior (Berg and Brown, 1972; Spudich and Koshland, 1976; Segall et al., 1986; Korobkova et al., 2004; Park et al., 2010; Masson et al., 2012), FRET alleviates the need to make indirect inferences about intracellular molecular interactions through the highly noisy 2-state switching of the flagellar motor, whose response function can vary over time due to adaptive remodeling (Yuan et al., 2012). In a typical experiment, we are able to obtain dozens of (up to $\sim$ 100) single-cell FRET time series simultaneously, to efficiently collect statistics of phenotypic diversity and temporal variability.

Results

Single-cell FRET reveals pervasive phenotypic diversity in intracellular signaling

To measure variability in intracellular signaling, we adapted a FRET assay for chemotaxis widely used for population-level measurements with fluorescent fusions to CheY and its phosphatase CheZ (Sourjik and Berg, 2002a). On timescales longer than the relaxation of CheY’s phosphorylation/dephosphorylation cycle, the FRET level reflects the phosphorylation rate of CheY by the CheA kinase, thus providing an efficient in vivo measurement of the network activity (Figure 1—figure supplement 1). Instead of the conventional CFP/YFP FRET pair we used the fluorophores YFP and mRFP1 to avoid excitation with blue light, which induces considerably stronger photoxicity and also perturbs the chemotaxis system as a repellent stimulus (Taylor and Koshland, 1975; Taylor et al., 1979; Wright et al., 2006). Fusions of these fluorophores to CheZ and CheY still yield a fully functional phenotype (Wolfe and Berg, 1989), when observing chemotaxis on soft agar (see Figure 1—figure supplement 1d).

A field of E. coli cells expressing this FRET pair were immobilized on a glass surface imaged in two fluorescence channels, and segmented offline to obtain fluorescence intensities of donor and acceptor. From the fluorescence ratio, FRET time series for each cell in the field of view (see Materials and methods) can be computed, after dividing out the decay (Figure 1—figure supplement 1) in each channel due to bleaching. Ratiometric FRET provides an anti-parallel response signature and confers robustness to parallel fluctuations that affect both fluorescent channels, such as differences in absolute fluorescence intensity due to inhomogeneous illumination and differences in cell size.

For wildtype cells (Figure 1a) we found that the ensemble mean of single-cell FRET responses, $⟨ FRET ⟩ (t)$ , agrees well with previous population-level measurements (Sourjik and Berg, 2002a). Upon prolonged stimulation with a saturating dose of attractant $α$ -methylaspartate (MeAsp), $⟨ FRET ⟩ (t)$ rapidly fell to zero before gradually returning to the pre-stimulus level due to adaptation. Upon removal of attractant, $⟨ FRET ⟩ (t)$ rapidly increased to a maximum before returning to the pre-stimulus baseline. Single-cell FRET time series, ${FRET}_{i} (t)$ , had qualitatively similar profiles, but the kinetics of adaptation and response amplitudes demonstrate differences from cell to cell. For each cell, ${FRET}_{i} (t)$ is limited by the autophosphorylation rate of CheA and hence is proportional to $a_{i}$ [CheA]_T,i(provided [CheY] and [CheZ] are sufficiently high, see Materials and methods), in which $a_{i}$ is the activity per kinase (0 ≤ $a_{i}$ ≤ 1) and [CheA]_T,i the total concentration of receptor-kinase complex of the $i$ -th cell. The FRET level of each cell is thus bounded at a value ${FRET}_{i, max}$ which occurs when its kinases are fully active ( $a_{i}$ =1), and can be measured by the removal of a sufficiently large stimulus after adaptation (as in the experiment of Figure 1). Hence from ${FRET}_{i} (t)$ the activity per kinase $a_{i} (t)$ can be readily determined by normalizing each FRET time series by its maximum response $a_{i} (t) = {FRET}_{i} (t) / {FRET}_{i, max}$ (Figure 1b). The steady-state activity $a_{0, i}$ , defined as the time-average of $a_{i} (t)$ before the addition of attractant, was found to vary from cell-to-cell with a coefficient of variation $C V (a_{0}) = 0.23$ (Figure 1c). The network activity controls the flagellar motor rotation, and hence this is consistent with the observation that cells in an isogenic population exhibit a broad range of steady-state tumble frequencies (Spudich and Koshland, 1976; Bai et al., 2013; Dufour et al., 2016).

Figure 1 with 3 supplements see all

Download asset Open asset

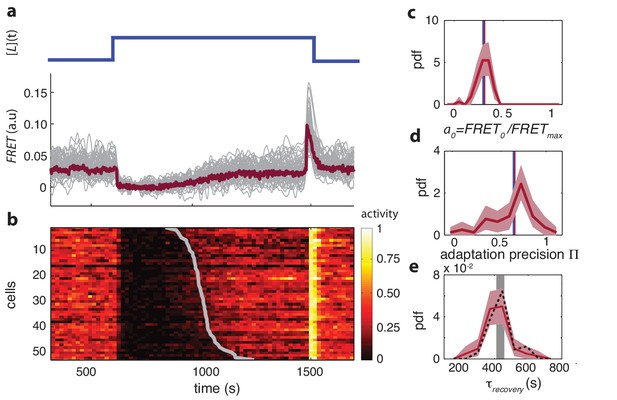
Single-cell FRET over extended times reveals cell-to-cell variability in signaling response.

(a) Step-response experiment on wildtype cells (CheRB+; VS115). (Top) The ligand time series $[L] (t)$ indicates the applied temporal protocol for addition and removal of 500 μM MeAsp. (Bottom) FRET response of 54 cells (grey) with the ensemble-averaged time series (dark red) overlaid from a representative single experiment. Single-cell time series were lowpass filtered with a 14 s moving-average filter. (b) Heatmap representation of the normalized FRET response time series, with each row representing a single cell, and successive columns representing the 10 s time bins in which the color-indicated activity was computed from the FRET time series. Activity was computed by normalizing FRET to the total response amplitude (Max-Min for each time series). Rows are sorted by the corresponding cell’s recovery time (grey curve), defined as the time at which the activity recovered to 50% of the activity level after adaptation (see panel e). Single-cell FRET assay schematic and image processing pipeline are shown in Figure 1—figure supplement 1. (c) Steady-state activity $a_{0}$ of the cells shown in panels (**a–b**). Also shown are the mean steady-state activity (red vertical line) and the steady-state activity of the population averaged time series (blue vertical line). (d) Adaptation precision $Π$ obtained from the FRET data. An adaptation precision of 1 denotes perfect adaptation. Also shown are the mean precision (red vertical line) and the precision of the population averaged time series (blue vertical line). The mean and std of the distribution is 0.79 $\pm$ 0.32. All colored shaded areas represent 95% confidence intervals obtained through bootstrap resampling. (e) Recovery time of cells defined as time to reach 50% of the post-adaptational activity level (red, 54 cells) or 50% of pre-stimulus activity (black dashed, 44 cells with precision >0.5) and simulated effect of experimental noise for a population with identical recovery times (grey). The latter was obtained from a simulated data set in which 55 time series were generated as described in Figure 1—figure supplement 3. The width of the bar is defined by the mean ± std of the simulated distribution. The mean ± std of the distributions for the experimental and simulated data sets are respectively 416 ± 83 and 420 ± 35 s.

https://doi.org/10.7554/eLife.27455.003

Figure 1—source data 1 Source data (.mat) file containing FRET data and analysis.: https://doi.org/10.7554/eLife.27455.007
Download elife-27455-fig1-data1-v3.zip

The adaptation precision is defined as its post-adaptational activity level divided by the pre-stimulus level ( $Π = a_{a d a p t e d, i} / a_{0, i}$ ), hence a precision of 1 refers to perfect adaptation. The adaptation kinetics are quantified by the recovery time $τ_{r e c o v e r y}$ , the time required for each cell to recover to 50% of its post-adaptation activity level ( $a_{a d a p t e d, i}$ ). When observing the distributions of these parameters we noted that the cell-to-cell variability is high in the precision $Π$ (Figure 1d, CV=0.40) but the average precision (0.79) agrees well with population measurements (Neumann et al., 2014). The variation is also substantial in $τ_{r e c o v e r y}$ (Figure 1e, CV=0.20) considering that the underlying kinetics of receptor methylation (catalyzed by CheR) involve thousands of events per cell, but falls within the range of ~20-50% from previous reports in which single-cell recovery times were estimated from motor-rotation or swimming-behavior measurements (Berg and Tedesco, 1975; Spudich and Koshland, 1976; Min et al., 2012). The time required to recover from a saturating amount of attractant is determined not only by the stimulus size, but also the methylation rate of receptor modification sites catalyzed by CheR and the number of such sites that need to be methylated. Variability in the recovery time is thus likely to reflect cell-to-cell variability in the ratio between the expression level of CheR and that of the chemoreceptor species responding to ligand (Tar for the experiment in Figure 1).

The diversity we observed here in adaptation precision, recovery time and steady-state activity was not explained by variation in salient experimental parameters (Figure 1—figure supplement 2a–f), are reproducible across experimental days (Figure 1—figure supplement 2g), and, on average, agree well with previous population-level FRET experiments and single-cell flagellar-based experiments. We thus conclude that single-cell FRET allows efficient measurement of signaling dynamics within individual bacteria to reveal variability in a wide variety of signaling parameters.

Diversity in the ligand response is modulated during population growth

The chemoreceptor clusters in E. coli are the central processing units and are responsible for signal integration and amplification. The sensory output of the cluster, the activity of the kinase CheA, is activated by a mixture of chemoreceptors. Cooperative interactions within the receptor-kinase complex leads to amplifications of small input stimuli and weighting different input signals. It has been shown that the composition of the receptor-kinase complexes can affect both the amplification as well as the weighting of different input signals (Ames et al., 2002; Sourjik and Berg, 2004; Kalinin et al., 2010), but how the amplification and integration varies across a population has not been characterized. To bridge the gap between collective behavior and its underlying single-cell motility it is essential to determine the variability of these important signaling parameters, as well as the origin of the variability. Also, current estimates of the apparent gain in the response (defined as the fractional change in output divided by fractional change in input) are based on population-averaged measurements which may or may not reflect single-cell cooperativity levels. In population averaged measurements, the largest gain is observed in adaptation-deficient (CheRB-) cells (Sourjik and Berg, 2004), in which the receptor population is homogeneous with respect to their adaptational modification state and hence in these cells variability in ligand sensing can be studied separately from variability induced by the adaptation enzymes.

We probed the ligand sensitivity of CheRB- cells (TSS58) at the single-cell level by FRET dose-response measurements in which step stimuli of successively larger amplitudes were applied over time (Figure 2). Considerable variability in the response to the attractant L-serine were observed across the population of immobilized cells simultaneously experiencing the same stimulus, with response magnitudes often ranging from virtually zero to full response (Figure 2a). The resulting dose-response data could be well described by a Hill curve of the form ${[1 + {([L] / K)}^{H}]}^{- 1}$ , where the parameters $(1 / K)$ and $H$ are defined as the sensitivity and steepness, respectively, of the response of each cell. The family of dose response curves constructed from this ensemble of fit parameters reveals considerable variability from cell to cell in the shape of the response curve (Figure 2b).

Figure 2 with 3 supplements see all

Download asset Open asset

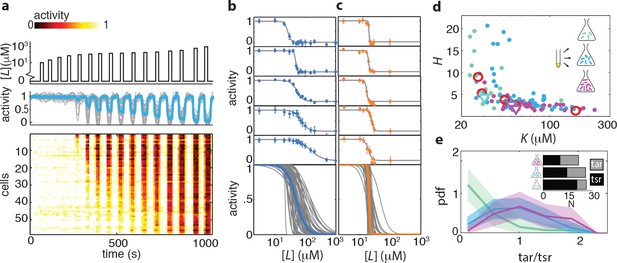
Ligand dose-response parameters vary strongly across cells in an isogenic population, even in the absence of adaptation, and depend on receptor-complex composition.

(a) Single-cell dose-response experiment on adaptation deficient (CheRB-; TSS58) cells with a wildtype complement of receptors. (Top) Temporal protocol of stimulation $[L] (t)$ by the attractant L-serine. (Middle) The ensemble-averaged FRET response of the population (blue) and single cells (gray) in signaling activity of 59 cells from a single experiment, normalized to the full-scale FRET response amplitude. (Bottom) Heatmap representation of the single-cell FRET timeseries, with the rows sorted by the sensitivity $K$ of the corresponding cell obtained from Hill-curve fits. (b) Ensemble of Hill-curve fits (gray) to single-cell dose-response data from a single experiment on CheRB- cells with a wildtype complement of receptors (TSS58). Fits for five example cells from the ensemble are shown above together with data points (error bars: $\pm$ 2 s.e.m. over 19 frames). The blue curve overlaid on the ensemble was obtained by applying the same analysis to the population-averaged time series shown in panel (a), yielding fit values $K$ =50 ± 3 $μ$ μM and $H$ =2.7 ± 0.5. (c) As in panel (b), but with CheRB- cells expressing only the serine receptor Tsr (UU2567/pPA114). The orange curve was obtained from fits to the population average, yielding $K$ =20.0 ± 0.3 $μ$ μM and $H$ =22 ± 8. (d) Cells from a single overnight culture were inoculated into three flasks harvested at different times during batch-culture growth to sample the state of the population at three points along the growth curve: at OD $_{600}$ = 0.31 (green), 0.45 (blue) and 0.59 (purple). Fits to the population-averaged time series are shown in Figure 2—figure supplement 2. Shown are Hill-curve sensitivity $(1 / K)$ and cooperativity $H$ obtained from fits to the single-cell dose-response data, at different harvesting OD’s (filled dots) together with the fit values for the population-averaged dose-response data (triangles). Also shown are population-FRET results from (Sourjik and Berg, 2004) in which the average Tar and Tsr levels were tuned using inducible promotors (red circles). Shown are 25 out of 28 cells harvested at OD = 0.31, 59 out of 64 cells at OD = 0.45, 34 out of 40 cells at OD = 0.59. The excluded cells had fits with a mean squared error higher then 0.05. The influence of experimental noise on the fit parameters is shown in Figure 2—figure supplement 3. (e) Histograms of Tar/Tsr ratio obtained by fitting the multi-species MWC model from (Mello and Tu, 2005) to single-cell FRET time series. The mean Tar/Tsr ratios (low to high OD) are 0.4, 0.9, and 1.2 with coefficients of variance of respectively 1.1, 0.5, and 0.4. Inset: average cluster size (MWC-model parameter N) of Tar (grey) and Tsr (black) at different harvesting OD’s obtained from the fit results in panel d.

https://doi.org/10.7554/eLife.27455.008

Figure 2—source data 1 Source data (.mat) file containing FRET data and analysis.: https://doi.org/10.7554/eLife.27455.012
Download elife-27455-fig2-data1-v3.zip

What could be the cause of the diversity in ligand response in the absence of adaptation-induced heterogeneity? We reasoned that expression-level variability of the five chemoreceptor species of E. coli, which are known to form mixed clusters with cooperative interactions (Ames et al., 2002; Sourjik and Berg, 2004), could endow isogenic populations with sensory diversity. In line with this idea, CheRB- cells expressing only a single chemoreceptor species (Tsr) demonstrated not only higher cooperativity, but also attenuated variability in the dose-response profile from cell to cell (Figure 2b–c), showing that the composition of the receptor population is important not only to tune the average ligand response of a population, but also in generating a wide range of sensory phenotypes within an isogenic population.

It has been shown that expression level of chemoreceptors changes during growth of E. coli batch cultures: concomitant with the slowing of growth upon the transition from the exponential phase towards early stationary phase, the relative expression level ratio Tar/Tsr, the two most abundant chemoreceptors, increases from majority Tsr (Tar/Tsr<1) to majority Tar (Tar/Tsr>1) (Salman and Libchaber, 2007; Kalinin et al., 2010). To probe the consequence of such changes for ligand-sensing diversity, we measured single-cell dose response curves in populations harvested at different cell densities during batch growth (Figure 2d). The resulting population-averaged responses show a dependence of dose-response parameters on the optical density (OD) of the culture, shifting from highly sensitive (low $K$ ) and highly cooperative (high $H$ ) at low cell densities (OD ≈ 0.3) to less sensitive (high $K$ ) and less cooperative (low $H$ ) at increased cell densities (OD ≈ 0.45, and OD ≈ 0.6) (Figure 2d, open triangles, and Figure 2—figure supplement 2). This trend is also visible at the level of single cells, but we found the responses to be highly variable under each condition (Figure 2d, filled points). Remarkably, both $K$ and $H$ varied by over an order of magnitude, far exceeding the uncertainty in parameter estimates due to experimental noise (Figure 2—figure supplement 3).

To further test the idea that ligand-response diversity is governed by differences in receptor expression levels, we considered the pattern of covariation between the fitted sensitivity $K$ and cooperativity $H$ in single cells (Figure 2b, blue). In contrast to cells expressing Tsr as the only chemoreceptor, in which the variability in $K$ is only ~0.15-20% (Figure 2c), single cells expressing a wildtype complement of chemoreceptors demonstrated strong variation in $K$ . This variation was negatively correlated with the cooperativity $H$ (Figure 2d). Noting that this overall pattern of covariation agrees well with dose response parameters obtained from population-level FRET experiments in which the Tar/Tsr ratio was experimentally manipulated via plasmid-based expression control (Figure 2d, red circles; data from (Sourjik and Berg, 2004)), we proceeded to quantitatively estimate the diversity in the Tar/Tsr ratio via fits of a multi-species MWC model (Mello and Tu, 2005; Keymer et al., 2006) to single-cell FRET data (see Materials and methods). The resulting distribution of single-cell Tar/Tsr estimates (Figure 2e) was dominated by Tsr in cells harvested early (OD ≈ 0.3) but the relative contribution of Tar increased in cells harvested at later stages of growth (OD ≈ 0.45) and OD ≈ 0.6). Interestingly, in addition to this increase in the mean of the Tar/Tsr distribution during batch growth, which confirms previous reports that found increased Tar/Tsr ratios at the population level (Salman and Libchaber, 2007; Kalinin et al., 2010), we find that the breadth of the distribution also increases at later stages of growth. Thus, modulation of receptor expression during growth provides a means of tuning not only response sensitivity and cooperativity, but also single-cell diversity in the response of cell populations experiencing identical changes in their common environment.

The large variability in the Tar/Tsr ratio (CV≈0.5 at OD=0.45) is somewhat surprising given that the mean expression level of both receptors are known to be high and of order 10³-10⁴ copies per cell (Li and Hazelbauer, 2004). At such high expression, intrinsic noise in expression levels (i.e. due to the production and degradation process of proteins, expected to scale as the square root of the mean) could be as low as a few percent of the mean, and gene-expression fluctuations are expected to be dominated by extrinsic noise components (i.e. those affecting regulation of gene expression, which do not scale with the mean). Quantitative measurements of gene expression reported in previous studies indicate a high degree of covariation among the expression level of chemotaxis genes, both at the population level under changes in growth conditions (Li and Hazelbauer, 2004) and at the single-cell level across isogenic cells sampled from the same growth culture (Kollmann et al., 2005). Correlated expression-level variation is also expected given the architecture of the flagellar regulon, in which all chemotaxis genes are under the control of a common master regulator (Chilcott and Hughes, 2000). These results indicate that the extrinsic (correlated) component of variation is greater than the intrinsic (uncorrelated) variability. Interestingly, however, a recent study (Yoney and Salman, 2015) found using single-cell flow-cytometry a high degree of variability in the ratio of Tar/Tsr promotor activities (CV≈0.45 at OD=0.51) comparable to the range of ratios extracted from our analysis of dose response data. Given that cell-to-cell variability in the Tar/Tsr ratio is much greater than achievable lower bounds of gene-expression noise in bacteria, it would be interesting to investigate the mechanistic sources of this variability, such as operon organization, promotor stochasticity, and translation-level regulatory structures (Frankel et al., 2014).

Variability in receptor expression could also explain the distribution of adaptation precision we observed in wildtype cells (Figure 1d). In a previous population-level study, it has been shown that adaptation precision depends strongly on the expression-level ratio between the multiple chemoreceptor species, with the highest adaptation precision being achieved when the ligand-binding receptor is a minority within the total receptor population (Neumann et al., 2014). Thus, the substantial heterogeneity in adaptation precision we observed (CV=0.40) upon a saturating MeAsp stimulus is consistent with strong variability in the Tar/Tsr ratio.

CheB phosphorylation feedback attenuates cell-to-cell variability

While bacteria can exploit molecular noise for beneficial diversification, variability can also limit reliable information transfer and degrade sensory performance. In the framework of E. coli’s run-and-tumble navigation strategy, chemotactic response to gradients requires that cells maintain a finite tumble bias, the fraction of time a bacterium spends tumbling, and avoids extreme values zero and one. The latter cases would correspond to unresponsive phenotypes that fail to switch between run and tumble states in response to the environmental inputs. One important mechanism that ensures responsiveness to stimuli over a broad range of input levels is sensory adaptation mediated by the methyltransferase/methylesterase pair CheR/CheB. These receptor-modifying enzymes provide negative feedback through the dependence of their catalytic activity on the receptor’s signaling state: the rate of methylation (demethylation) by CheR (CheB) is a decreasing (increasing) function of receptor-kinase activity (Borczuk et al., 1986; Amin and Hazelbauer, 2010). This dependence of enzyme activity on the substrate conformation provides negative integral feedback that ensures precise adaptation (Barkai and Leibler, 1997) toward the pre-stimulus steady-state activity $a_{0}$ .

Interestingly, one of the two adaptation enzymes, CheB, can be phosphorylated by CheA, the kinase whose activity CheB controls through its catalytic (demethylation) activity on receptors. Effectively, this adds an additional negative feedback loop to the network, but the role of this phosphorylation-dependent feedback has remained elusive since it has been shown to be dispensable for precise adaptation (Alon et al., 1999). Through theoretical analysis, it has been conjectured that this secondary feedback loop might play a role in attenuating effects of gene-expression noise (Kollmann et al., 2005), but experimental verification has been lacking. We therefore sought to investigate the influence of perturbations to this network topology on the variability of chemotactic signaling activity.

CheB consists of two domains connected by a flexible linker (Figure 3a). A regulatory domain, with structural similarity to CheY, can be phosphorylated at residue Asp $^{56}$ (Djordjevic et al., 1998; Stewart et al., 1990). A catalytic domain mediates binding to specific residues on chemoreceptor cytoplasmic domains and removes a methyl group added by the counterbalancing activity of CheR. Phosphorylation induces a conformational change and activates CheB (CheB*) (Djordjevic et al., 1998; Lupas and Stock, 1989). Several mutants of CheB lack phosphorylation feedback while retaining catalytic activity. Here, we focus on two specific mutants: CheB $^{D56E}$ , which bears a point mutation at the phosphorylation site, and CheB $_{c}$ , which expresses only the catalytic domain of CheB (Stewart et al., 1990; Alon et al., 1999). Cells expressing these mutants have an altered network topology (Figure 3b) which lacks CheB phosphorylation feedback.

Figure 3 with 5 supplements see all

Download asset Open asset

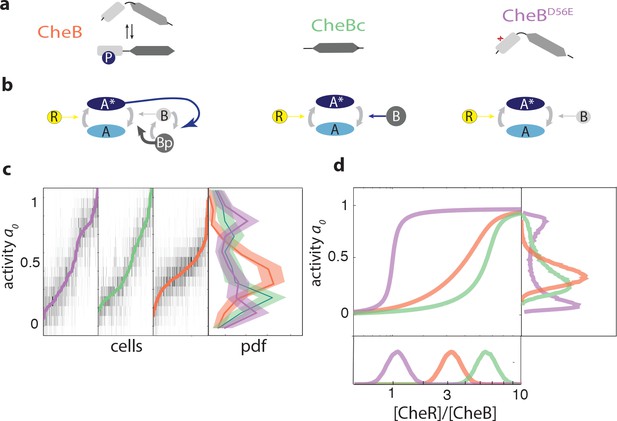
CheB phosphorylation feedback attenuates variability in steady-state kinase activity.

(a) Schematic depiction of CheB activation by phosphorylation. (Top) CheB consists of two domains connected by a flexible linker. The aspartate at residue 56 within the N-terminal receiver domain can be phosphorylated. (Middle) CheBc lacks the receiver domain with the phosphorylation site. (Bottom) CheB-D56E carries a point mutation at the phosphorylation site. (b) Effective network topology of cells expressing WT CheB (top), CheBc (middle) and CheB-D56E (bottom). All three topologies are capable of precise adaptation due to activity-dependent feedback (Barkai and Leibler, 1997). (c) Heatmap representation of histograms of the activity $a (t)$ about the unstimulated steady-state of single cells, from FRET experiments of the type shown in Figure 3—figure supplement 1. Each column represents a single cell, sorted by the steady-state activity $a_{0}$ (colored curves) for each CheB mutant expressed in a *cheB* background (VS124, colors as in panel (a)). (right) Normalized histograms (probability density function, pdf) of $a_{0}$ for each CheB mutant. Histograms contain results for cells with a signal-to-noise ratio greater than one from at least three independent FRET experiments, corresponding to 231 out of 280 cells (WT), 169 out of 210 cells (CheBc) and 156 out of 246 cells (D56E). Shaded regions represent bootstrapped 95% confidence intervals. We verified that the bimodality was not due to clipping from FRET-pair saturation, by mapping the dependence of FRET on donor/acceptor expression (Figure 3—figure supplement 2). (d) A simple kinetic model of the chemotaxis network illustrates the crucial role of CheB phosphorylation feedback in circumventing detrimental bimodality in $a_{0}$ . Due to sublinear enzyme kinetics in the adaptation system, the transfer function $a_{0}$ =ƒ([R]/[B]) mapping the P([R]/[B]) expression ratio to steady-state network output $a_{0}$ can be highly nonlinear (main panel). The shape of this transfer function determines the distribution P $(a_{0})$ of steady-state activity (right panel) by transforming the distribution P([R]/[B]) of adaptation-enzyme expression ratios (bottom panel). Three variations of the model are shown, corresponding to WT (orange, with phosphorylation feedback), CheB $^{D56E}$ (purple, no phosphorylation feedback and low catalytic rate), and CheBc (green, no phosphorylation feedback, high catalytic rate).

https://doi.org/10.7554/eLife.27455.013

Figure 3—source data 1 Source data (.mat) file containing FRET data and analysis.: https://doi.org/10.7554/eLife.27455.019
Download elife-27455-fig3-data1-v3.zip

To study the influence of network topology on cell-to-cell variability, we expressed different forms of CheB (CheB $^{WT}$ , CheB $^{D56E}$ , CheB $_{c}$ ) from an inducible promoter in a ΔcheB strain and measured the response to a saturating amount of attractant (500 μM MeAsp). The expression levels of each mutant are tuned such that they approximate the wildtype steady state activity level. The response of CheB $^{WT}$ was qualitatively very similar to cells in which CheB is expressed from its native chromosomal position (compare Figure 3—figure supplement 1a and Figure 1a) despite the fact that plasmid expression breaks the translational coupling with CheR (Løvdok et al., 2009). By contrast, cells expressing either of the two CheB mutants defective in phosphorylation demonstrated increased cell-to-cell variability in the steady-state activity compared to cells expressing CheB $^{WT}$ . The increased variability of the CheB phosphorylation-deficient mutants (CheB $^{D56E}$ and CheB $_{c}$ ) was manifested not only in a higher coefficient of variation in $a_{0}$ (1.07 and 1.10, respectively, and WT 0.7), but also a qualitatively different shape of the distribution of $a_{0}$ across the population (Figure 3c). Whereas the distribution demonstrated a single peak in CheB $^{WT}$ cells with phosphorylation feedback, the distribution for the phosphorylation-feedback mutants demonstrated a bimodal shape with peaks close to the extreme values $a_{0}$ ={0,1}.

We tested whether these strong differences in cell-to-cell variability might be the result of gene expression noise, by comparing expression-level distributions of the CheB mutants. We constructed fluorescent fusions of each cheB allele to the yellow fluorescent protein mVenus and quantified the distribution of single-cell fluorescence levels under the same induction conditions as in the FRET experiments (Figure 3—figure supplement 1). The ratio between the measured expression-levels (CheBc:WT:D56E≈0.7:1:2.5) was compatible with expectations from the hierarchy of reported in vitro catalytic rates of CheB ( $k_{b}^{D56E} < k_{b}^{W T} < k_{b}^{c}$ ) (Anand and Stock, 2002; Simms et al., 1985; Stewart, 1993), and expression-level variability was very similar between the three strains (CV’s of 0.87,0.90 and 0.82; we note that these rather high CV values likely include contributions from plasmid copy number variability). These findings suggest that the differences in cell-to-cell variability observed in FRET are not due to differences between the expression-level distributions of the three cheB alleles, but rather to the differences they impose on the signaling network topology.

What feature of the signaling network could generate such broad (and even bimodal) distributions of $a_{0}$ ? A general paradigm for models of adaptation that exhibit precise adaptation is activity-dependent (integral) feedback (Barkai and Leibler, 1997; Yi et al., 2000), which in bacterial chemotaxis can be implemented by the activity of the feedback enzymes CheR and CheB being dependent of the conformational state (i.e. activity) of their substrate chemoreceptors. This results in a steady-state activity $a_{0}$ that only depends on the [R]/[B] expression-level ratio and not on their absolute abundance. We can view this mapping as a transfer function ƒ between the ratio [R]/[B] and the steady-state activity,

a_{0} = f ([R] / [B])

Depending on the function ƒ, the input variance P_RB([R]/[B]) may lead to high or low variance in the distribution P( $a_{0}$ ). This is because the manner in which the transfer function ƒ filters the [R]/[B] distribution,

P (a_{0}) = \frac{P_{R B} (f^{- 1} (a_{0}))}{| f^{'} (f^{- 1} (a_{0})) |} .

Hence a steep function ƒ can impose bimodality in the methylation level, and thereby also in the activity of steady-state CheA activity, $a_{0}$ , even at quite modest input variances for distributions of the ratio [R]/[B].

Thus, even if expression-level noise for both CheR and CheB are modest, a sensitive transfer function ƒ can effectively amplify the variation in [R]/[B], and if the distribution of the latter ratio, P_RB([R]/[B]) extends below and above the narrow region over which ƒ is steep, the decreased slope of ƒ (i.e. lower ƒ'([R]/[B]) in those flanking regions will tend to increase the weight on both sides of the broad P $(a_{0})$ distribution to produce a bimodal profile. On the other hand, if the network topology effectively reduces the steepness of ƒ, the resulting P $(a_{0})$ will have a reduced variance for the same input P_RB([R]/[B]) (Figure 3d). Our results suggest that ƒ is much steeper in the absence of phosphorylation feedback than in its presence.

We find that models with linear or supra-linear dependence of the methylation rate on activity generate a function ƒ that is very shallow (Figure 3—figure supplement 3), making them unsuitable for explaining the observed bimodal behavior. However, if we assume CheR and CheB follow Michaelis-Menten kinetics in which the dependence of the methylation rates on receptor activity is sub-linear, the dependence of ƒ on [R]/[B] can become very steep. It has been conjectured (Barkai and Leibler, 1997; Emonet and Cluzel, 2008) that in vivo the enzymes CheR and CheB operate at or near saturation, an idea supported by population-level FRET measurements of adaptation kinetics (Shimizu et al., 2010). An important consequence of enzyme saturation in such reversible modification cycles is that the steady-state activity of the substrate can become highly sensitive to the expression level ratio of the two enzymes, a phenomenon known as zero-order ultrasensitivity ((Goldbeter and Koshland, 1981); see Materials and methods). Within the chemotaxis system, saturation of both CheR and CheB can thus render the receptor modification level, and in turn, the CheA activity $a_{0},$ ultrasensitive to the [R]/[B] concentration ratio (Emonet and Cluzel, 2008).

Could the known biochemical differences between the three forms of CheB (CheB $^{WT}$ , CheB $^{D56E}$ , CheB $_{c}$ ) explain the contrasting patterns of $a_{0}$ variability observed in our single-cell FRET experiments? In the absence of any feedback, the steepness of ƒ'([R]/[B]) is solely determined by the low Michaelis-Menten constants $K_{B, R}$ , which corresponds to saturated kinetics of the enzymatic activity of CheRB and hence ultransensitivity of the steady-state substrate activity. The expression ratio of CheR/CheB which determines the crossover point ( $a_{0}$ =0.5) is set by the ratio of catalytic rates of CheR and CheB ( $k_{r, b}$ ). Hence the phosphorylation deficient mutants CheB $^{D56E}$ and CheB $_{c}$ both have steep curves but are shifted along the R/B axis due to very different catalytic rates. However,in the case of phosphorylation feedback, CheB $^{WT}$ , the same enzyme can be in two states, each with equal $K_{r, b}$ but one low and one high $k_{r}$ . Whether CheB is in the one state or the other is determined by the activity-dependent phosphorylation feedback. As a result, the curve of CheB $^{WT}$ is activity dependent (ƒ(a,[R]/[B])) and changes with activity by shifting between the two curves corresponding to the extremes of all phosphorylated or all unphosphorylated. Effectively, this makes the resulting curve ƒ less steep (Emonet and Cluzel, 2008). The mean of the distributions P_RB are tuned such to get the same mean activity level $(⟨ a_{0} ⟩)$ , but the same variance in P_RB leads to very wide P $(a_{0})$ distributions in absence of phosphorylation, while phosphorylation feedback ensures a much smaller, single-peaked distribution.

It has also been conjectured that the CheB phosphorylation feedback is responsible for the highly nonlinear kinetics of recovery from repellent (or attractant removal) responses (Shimizu et al., 2010; Clausznitzer et al., 2010). Indeed, in cells expressing CheB $_{c}$ , the kinetics of recovery from the response to removal of 500 $μ$ μM MeAsp after adaptation appeared qualitatively different from that in cells expressing wildtype CheB, lacking the characteristic rapid recovery and instead appearing more symmetric with the CheR-mediated recovery upon addition of a saturating dose of attractant (Figure 3—figure supplement 4). By contrast, CheB $^{D56E}$ was found to still possesses a fast component, despite being defective in phosphorylation, albeit also with somewhat slower kinetics than wt. In summary, the clearest difference between wildtype and phosphorylation-defective CheB mutants is found in the variability of the steady-state signal output (i.e. kinase activity).

The bimodal distribution in kinase activity we observed in the phosphorylation-deficient CheB mutants implies that a large fraction of cells have a CheY-P concentration far below or far above the motor’s response threhold and hence will impair chemotactic responses to environmental gradients. Consistent with this idea, in motility-plate experiments (Supplementary Figure 3—figure supplement 5) we found that chemotactic migration on soft-agar plates was severely compromised for both CheB $^{D56E}$ and CheB $_{c}$ compared to CheB $^{WT}$ , indicating that the phosphorylation feedback is important for efficient collective motility.

Protein-signaling noise generates large temporal fluctuations in network output

The slow kinetics of the adaptation enzymes CheR and CheB have been hypothesized to play a role not only in determining the steady-state kinase activity $a_{0}$ , but also in generating temporal fluctuations of the intracellular signal (Korobkova et al., 2004; Emonet and Cluzel, 2008; Park et al., 2010; Celani and Vergassola, 2012). We found substantial differences between wildtype (CheRB+) and adaptation-deficient (CheRB-) cells in the variability of their FRET signals across time (Figure 4). The effect is clearly visible upon comparing long ( $\sim$ 1 hr) FRET time series obtained from cells of these two genotypes (Figure 4a). The FRET signal in wildtype cells demonstrated transient excursions from the mean level that were far greater in amplitude than those in CheRB- cells. To distinguish between variability across cells in a population (which we discuss in terms of coefficients of variation, CV) and that over time within a single cell, we denote the temporal noise amplitude as $η \equiv σ_{a} / a_{0}$ . This amplitude was quantified by computing the variance of each single-cell time series, low-pass filtered with a moving average filter of 10 s, and shows that the fluctuation amplitudes are much larger in wildtype cells compared to adaptation-deficient cells ( $⟨ η ⟩$ = 0.44 and 0.09 respectively, Figure 4b). Importantly, these experiments were carried out under conditions in which no protein synthesis can occur due to auxotrophic limiation (see Materials and methods), thus ruling out gene-expression processes as the source of these fluctuations.

Figure 4 with 3 supplements see all

Download asset Open asset

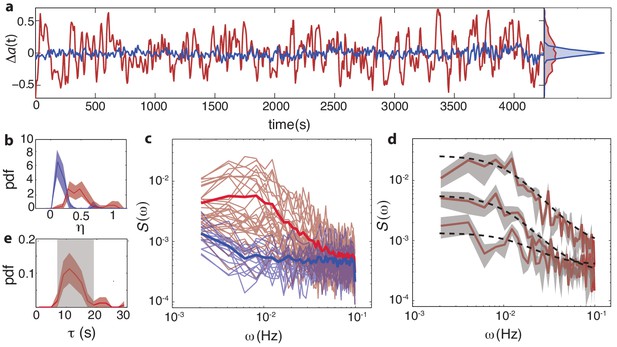
Temporal fluctuations in WT cells due to stochastic activity of adaptation enzymes CheR/CheB.

(a) Representative single-cell FRET time series of steady-state fluctuations Δa(t)=a(t)-a₀ in WT cells (VS115, red), together with analogous data from CheRB- cells (TSS58,blue) for comparison (low-pass filtered with a 10 s moving average filter). (b) Histogram of fluctuation amplitude $η$ ( $\equiv σ_{a} / a_{0}$ ) for both WT (89 cells, red, from three independent experiments) and CheRB- (33 cells, blue, from two independent experiments), extracted from calculating the standard deviation of a low-pass filtered FRET time series over a 10 s window divided by the mean FRET level of a single cell. Shaded areas represent 95% confidence intervals obtained from bootstrap resampling. (c) Power spectral density (PSD) computed from single-cell FRET time series of 31 WT cells (red, from single experiment) and 17 CheRB- cells (blue, from single experiment), each from a single experiment. Thin curves in the lighter shade of each color represent single-cell spectra, and their ensemble average is shown as thick curves in a darker shade. The increased power at low-frequencies in WT cells was lost when PSD was computed after ensemble-averaging the time series Figure 4—figure supplement 1, indicating that these slow fluctuations are uncorrelated across cells. (d) Representative single-cell PSDs and fits by an Ornstein-Uhlenbeck (O–U) process. Shown are O-U fits (Lorentzian with constant noise floor; dashed curves) to three single-cell PSDs (solid curves). Shaded areas represent standard errors of the mean for PSDs computed from nine non-overlapping segments of each single-cell time series. Fits to all cells from the same experiment are shown in (Figure 4—figure supplement 2). Noise amplitudes computed from the O-U fit parameters (Figure 4—figure supplement 3) demonstrate excellent agreement with those computed directly from the time series (panel b). (e) Histogram of fluctuation timescales $τ$ extracted from O-U fits to single-cell PSDs (red, 75 out of 89 cells). Cells without a clear noise plateau at low frequencies were excluded from the analysis (Figure 4—figure supplement 3). Red shaded region represents 95% confidence intervals obtained from bootstrap resampling. The gray shaded region indicates the variability (mean±std) that can be explained by experimental noise and a finite time window, obtained from simulated O-U time series (see Materials and methods).

https://doi.org/10.7554/eLife.27455.020

Figure 4—source data 1 Source data (.mat) file containing FRET data and analysis.: https://doi.org/10.7554/eLife.27455.024
Download elife-27455-fig4-data1-v3.zip

Power spectral density (PSD) estimates computed from such time series confirm a nearly flat noise spectrum for CheRB- cells, whereas CheRB+ cells demonstrated elevated noise at low frequencies (Figure 4c). The amplitude of these low-frequency noise components do clearly vary from cell to cell, as can be gleaned in the diversity of single-cell power spectra. To quantify this protein-level noise due to CheR/CheB activity, we describe the fluctuating signal as an Ornstein-Uhlenbeck (O-U) process of the single variable $a$ , with relaxation timescale τ and diffusion constant c, which can be interpreted as a linear-noise approximation (Van Kampen, 1981; Elf and Ehrenberg, 2004) to the multivariate stochastic kinetics of the underlying chemical network controlling the mean kinase activity $a$ (Tu and Grinstein, 2005; Emonet and Cluzel, 2008):

\frac{d a}{d t} = - \frac{1}{τ_{m}} a (t) + \sqrt{c} Γ (t)

where $Γ (t)$ is a Gaussian white noise process. The parameters τ_m $τ_{m}$ and c for each cell are readily extracted via the power-spectrum solution of the O-U process:

S_{a} (ω) = \frac{2 c τ^{2}}{1 + {(2 π ω τ_{m})}^{2}} + E

where we have added to the standard Lorentzian solution (Gillespie, 1996) a white-noise term $E$ that may vary from cell to cell to account for experimental shot noise in the photon-limited FRET signal. Single-cell PSD data were well fit by Equation 2 (Figure 4d), and the average of extracted single-cell fluctuation timescales ( $⟨ τ_{m} ⟩ = 12.6$ s) (Figure 4e) are in good agreement with previously reported correlation times of flagellar motor switching (Park et al., 2010; Korobkova et al., 2004), as well as the kinetics of CheRB-mediated changes in receptor modification from in vivo measurements using radioactively labeled methyl groups (Lupas and Stock, 1989; Terwilliger et al., 1986). The variance of the fluctuations obtained from the fits of the PSD, $σ_{a} = \sqrt{c τ_{m} / 2}$ yielded very similar noise amplitudes $η_{O U} \equiv σ_{a, O U} / a_{0}$ as calculated from the time series ( $⟨ η_{O U} ⟩ = 0.42$ , Figure 4—figure supplement 3). We note that these noise levels are larger than expected - in a considerable fraction of cells, the standard deviation of fluctuations is comparable to the mean level of activity, and the steady-state fluctuations span the full range of kinase activity (see e.g. that represented by the red curve in Figure 4a). Previous studies had predicted a value of ~10-20%, based either on reported fluctuation amplitudes of motor switching (Korobkova et al., 2004; Tu and Grinstein, 2005) or biochemical parameters of the intracellular signaling network (Emonet and Cluzel, 2008; Shimizu et al., 2010). The noise amplitudes are also highly variable (CV=0.55, σ_η=0.24) from cell to cell.

In summary, we confirmed the presence of strong temporal fluctuations in single-cell chemotaxis signaling attributable to the stochastic kinetics of the adaptation enzymes CheR/CheB, and further found that the amplitude of these fluctuations vary considerably across cells in an isogenic population.

Receptor-kinase fluctuations in the absence of adaptation reveal two-level switching

The fluctuation amplitude $η$ in CheRB+ cells (Figure 4b) is much greater than previous estimates from pathway-based models that considered sublinear kinetics in the enzymatic activities of CheR and CheB (Emonet and Cluzel, 2008) and receptor cooperativity (Shimizu et al., 2010) as possible mechanisms that amplify noise originating in the stochastic kinetics of receptor methylation/demethylation. A possible explanation for this discrepency is the presence of one or more additional noise source(s) independent of methylation/demethylation dynamics. Although we found that the noise amplitude $η$ was much lower than wildtype in unstimulated CheRB- cells (Figure 4), it is possible that the strong activity bias of these cells in the absence of chemoeffectors ( $a_{0}$ ≈1) masks noise contributions that would be observable if receptors were tuned to the more responsive regime of intermediate activity (e.g. as in wt cells, where $a_{0}$ ≈1/3). We reasoned that in CheRB- cells, tuning the activity to an intermediate level by adding and sustaining a sub-saturating dose of attractant could reveal additional noise sources. Hence we measured the temporal variability of CheRB- cells during prolonged stimulation with 50 μM L-serine, which elicits a half-maximal population-level response (Figure 5b). Although no large fluctuations were be observed in the population-averaged time series (Figure 5b), averaging the power spectra computed from all single-cell time series revealed a somewhat elevated noise level at low frequencies, compared to the case without ligand (Figure 5a), indicating the possibility of a noise source independent of receptor methylation.

Figure 5 with 3 supplements see all

Download asset Open asset

Temporal fluctuations in adaptation-deficient cells depend strongly on activity and composition of chemoreceptor population.

(a) Power spectral density (PSD) for temporal signal fluctuations during sub-saturating ligand stimulation of 18 cells with wild-type receptor complement (light blue, CheRB-, TSS58) and 58 cells expressing only chemoreceptor Tsr (orange, CheRB- Tsr+, TSS1964/pPA114). Also shown, for comparison, are PSDs from experiments without ligand stimulation for WT cells and CheRB- cells (red and dark blue, respectively; same data as in Figure 4). Error bars represent standard error of the mean. We note that the Tsr+ experiment had a larger FRET amplitude scaling factor ${FRET}_{max}$ (see Materials and methods) compared to the standard conditions under which the other strains were measured, and to account for this difference, the Tsr+ power spectrum has been scaled by a factor $ρ^{2} = 0.17$ , where $ρ \equiv {FRET}_{max, std} / {FRET}_{max, Tsr+}$ to account for this difference. (b) (Top) Stimulus protocol for modulation of the L-serine ligand concentration ([L](t)). Cells were incubated either in buffer ([L]=0, white) or a subsaturating stimulus ([L] = 50 μM, gray) for 1> hr. A saturating stimulus ([L] = 1 mM, black) is applied at the end of the experiment. (Bottom) Population- averaged time series for adaptation-deficient cells with wildtype receptor complement (CheRB-, TSS58) for experiments with (18 cells, light blue) and without (17 cells, dark blue) a sustained 50 μM L-serine stimulus during the time interval used to compute the PSDs in panel a (indicated by the red bar). (c) (Top) Stimulus protocol for L-serine concentration ([L](t)). At the start of the experiment, a saturating concentration ([L] = 1 mM, black) is applied for a short time. After flushing buffer ([L]=0, white), an intermediate concentration ([L] = 25 μM, gray) is sustained for 10 min. (Bottom) Population-averaged time series of 58 adaptation-deficient cells expressing Tsr as the sole chemoreceptor (RB-Tsr+; TSS1964/pPA114) under the stimulus protocol indicated above. (d) Selected single-cell time series of the population shown in panel (c), each normalized to its activity level before adding the first stimulus. To the unfiltered data (gray) a 7 s moving average filter is applied and superimposed (colored according to categories in panel (e)). All time series and corresponding activity histograms of the same experiment are shown in Figure 5 - Supplement 1 and 5. (e) Classification of RB-Tsr+ single cell fluctuation phenotypes by the number of stable activity levels observed during the sustained subsaturating stimulus. Many cells show only one stable activity level (yellow), corresponding to either full-amplitude response ( $a \to 0$ ) or no response ( $a \to a_{0}$ ). Some cells show two (red) or more (purple) apparently stable states. In other cells, fluctuations appeared chaotic with no discernibly stable state (black). (f) Definitions for analysis of two-state switching dynamics. The transition timescales $τ_{+}$ and $τ_{-}$ were determined by fits of a symmetric exponential function (see main text) to the upward (cyan) and downward (purple) switching transients, respectively. Residence times $Δ t_{up,down}$ were defined as the interval between two successive transitions, at 50 $%$ activity. (g) Histogram of transition timescales, $τ_{+}$ (4.2 ± 2.2 s, 26 events, cyan) and $τ_{-}$ (3.5 ± 3.2, 29 events, purple) from 10 two-state switching cells of a single experiment with 1 Hz acquisition frequency. (h) Mean residence times $τ_{up}$ and $τ_{down}$ for two-state switching cells as a function of the average activity bias $\ln [a_{1 / 2} / (1 - a_{1 / 2})]$ . The slopes are $γ_{d o w n} = - 0.4$ and $γ_{u p} = 0.6$ , and the crossover point at $τ_{up} = τ_{down} = 110 \pm 10$ s defines a characteristic switching timescale. Data of 17 cells from three independent experiments (one at 1 Hz acqusition, two at 0.2 Hz acquisition).

https://doi.org/10.7554/eLife.27455.025

Figure 5—source data 1 Source data (.mat) file containing FRET data and analysis.: https://doi.org/10.7554/eLife.27455.028
Download elife-27455-fig5-data1-v3.zip

To further test whether and how these methylation-independent fluctuations are affected by the composition of the chemoreceptor arrays, we also measured the response of CheRB- cells expressing Tsr as the sole chemoreceptor during a sustained stimulus of magnitude close to the population-level $K$ (Figure 5c). Surprisingly, the averaged single-cell power spectra (Figure 5a) indicated the presence of very large fluctuations, even surpassing the fluctuation magnitude in CheRB+ cells. The time series of single-cell responses demonstrated strong deviations from the population average (Figure 5d and - Video Supplement). Whereas all cells responded identically to the saturating dose of attractant, the behavior during the sub-saturating step was highly diverse. Some cells (11/141) showed no apparent response in kinase activity, whereas in others (32/141) complete inhibition was observed (Figure 5d, yellow curves). The majority of cells (98/141), however, had an intermediate level of activity when averaged over time, but demonstrated strong temporal fluctuations, often with magnitudes exceeding those observed in wildtype cells.

We further noted that within this subset of cells with large temporal fluctuations, a large fraction (54/98) demonstrated fluctuations that resemble rapid step-like transitions between discrete levels of relatively stable activity that could be identified as peaks in the distribution of activity values across time (Figure 5d, marginal histograms). Among these ‘stepper’ cells, the majority (37/54) appeared to transition between three or more discrete activity levels (Figure 5d, brown curve), whereas the remaining sizable minority of steppers (17/54) demonstrated binary switching between two discrete levels corresponding to the maximum ( $a$ ≈1) and minimum ( $a$ ≈0) receptor-kinase activity states (Figure 5d, red curve). The remaining fraction of cells (44/98) demonstrated fluctuations that were also often large but in which discrete levels could not be unambiguously assigned (Figure 5d, black curve). The numbers of cells corresponding to each of the categories described above are summarized in Figure 5e.

The observation of cells that demonstrate spontaneous two-level switching is particularly surprising, given the large number of molecules involved in receptor-kinase signaling. The expression level of each protein component of the chemoreceptor-CheW-CheA signaling complex in our background strain (RP437) and growth medium (TB) has been estimated (by quantitative Western Blots) to be of order $10^{4}$ copies/cell (Li and Hazelbauer, 2004). Considering that the core unit of signaling has a stoichiometric composition of receptor:W:A = 12:2:2 (monomers) (Li and Hazelbauer, 2011), the number of core units is likely limited by the number of receptors, leading to an estimate 10⁴/12~10³ core units for a typical wildtype cell. This estimate does not apply directly to the experiments of Figure 5 because receptors are expressed from a plasmid in a strain deleted for all receptors. But the FRET response amplitudes of these cells were similar to those of cells with a wildtype complement of receptors, and we thus expect the number of active core units per cell in the experiments of Figure 5 to be similar to or greater than that in wildtype cells.

We analyzed further the temporal statistics of the discrete transitions in the subset of cells exhibiting two-level switching (Figure 5g–h). We first quantified the duration of such transitions by fitting segments of the activity time series over which these switches occured (Figure 5d) by a symmetrized exponential decay function (see Materials and methods) to obtain switch durations $τ_{+}$ and $τ_{-}$ for upward and downward transitions, respectively. The fitted values for $τ_{+}$ and $τ_{-}$ correspond to the duration over which the activity trajectory traverses a fraction $1 - e^{- 1}$ of the transition’s full extent, and were found to be similar between switches in both directions: $⟨ τ_{+} ⟩ \pm σ_{τ_{+}} =$ 4.2 ± 2.2 s and $⟨ τ_{-} ⟩ \pm σ_{τ_{-}} =$ 3.5 ± 3.2 s (Figure 5e). We note that these transition times are significantly greater than, but close to, the data acquisition interval (1 s), and so the shape of the fitted function should be considered a first approximation to the true rise and decay dynamics.

We then considered the duration of time between switching events. We defined $Δ t_{u p, k}$ and $Δ t_{d o w n, k}$ as the duration of the $k$ -th time interval between transitions with high- and low-activities, respectively (Figure 5d), and computed the average over all $k$ of $Δ t_{u p / d o w n, k}$ for each individual cell to estimate its residence timescales $τ_{u p / d o w n}$ for states of high/low activity, respectively. From each cell’s set of intervals ${Δ t_{u p / d o w n, k}}$ we also computed a parameter $a_{1 / 2}$ , defined as the fraction of time the cell spent in the high activity level, as a measure of its time-averaged activity during the sub-saturating (20 $μ$ M) L-serine stimulus that yielded a population-averaged response $⟨ a ⟩ \approx 1 / 2$ (see Materials and methods).

We found that the logarithms of the mean residence times $τ_{u p}$ and $τ_{d o w n}$ scale approximately linearly with $\ln [a_{1 / 2} / (1 - a_{1 / 2})]$ (Figure 5f). The latter can be considered a free-energy difference $(- Δ G) = G_{d o w n} - G_{u p}$ between the inactive and active states of an equilibrium two-state switching process in which the time-averaged activity $a_{1 / 2}$ is given by the probability of being in the active state, $a_{1 / 2} = p (active) = {(1 + e^{Δ G})}^{- 1}$ . The residence time in each state can then be described by an Arrhenius-type relation with characteristic time for barrier crossing $τ_{r}$ and the height of the energy barrier dependent on $Δ G$ ,

\begin{aligned} τ_{d o w n} & = τ_{r} \exp [- γ_{d o w n} Δ G / k_{B} T] \\ τ_{u p} & = τ_{r} \exp [- γ_{u p} Δ G / k_{B} T] \end{aligned}

where the (dimensionless) constants $γ_{d o w n}$ and $γ_{u p}$ describe how the barrier heights of the down and up states, respectively, depend on the free-energy difference $Δ G = k_{B} T \ln [(1 - a_{1 / 2}) / a_{1 / 2}]$ . We find $γ_{d o w n} = - 0.4 \pm 0.1$ , $γ_{u p} = 0.6 \pm 0.1$ , and the characteristic timescale $τ_{r}$ , defined here as equivalent to $τ_{u p} = τ_{d o w n}$ when $Δ G = 0$ (and hence $a_{1 / 2} = 0.5$ ), was found to be 110 ± 10 s. The fact that the mean residence times ( $τ_{u p}, τ_{d o w n}$ ) scale exponentially with the apparent free energy difference ( $Δ G$ ) indicates that receptor-kinase switching can, to a first approximation, be treated as a barrier-crossing process.

In summary, these data demonstrate the existence of a signaling noise source that is independent of the adaptation enzymes CheR/CheB. The fluctuations they generate can be very strong in cells expressing Tsr as the sole chemoreceptor, leading to two-level switching in a subset of cells. The latter observation suggests that cooperativity among signaling units in homogeneous chemoreceptor arrays can reach extremely high values, with up to $\sim 10^{3}$ units switching in a cooperative fashion. The temporal statistics of these two-level switches are consistent with a barrier-crossing model in which the residence time of both states depend on the activity bias $\ln [a_{1 / 2} / (1 - a_{1 / 2})]$ in a nearly symmetric manner with opposing signs.

Discussion

The single-cell FRET measurements described here allowed us to quantify variability in a variety of signaling parameters of the bacterial chemotaxis system, both across cells in a population and within individual cells over time. The magnitude of variation was large across a wide variety of signaling parameters, as summarized in Table 1. By imaging many (typically ~50) cells simultaneously, we are able to record signaling in individual cells at high throughput, to build up single-cell statistics. Although single-cell experiments have a long history in studies of bacterial chemotaxis (Berg and Brown, 1972; Spudich and Koshland, 1976; Block et al., 1982; Korobkova et al., 2004; Dufour et al., 2016), nearly all examples to date have relied on measurements of flagellar motor output (in either tethered or swimming cells). A major advantage of the FRET approach is that it provides a direct measurement of intracelluar signaling that bypasses the noisy behavior of the flagellar motor (a stochastic two-state switch), thereby enabling accurate and efficient determination of signaling parameters. The anti-parallel response signature of ratiometric FRET provides a good way to discriminate genuine FRET changes from imaging artifacts. As in population-level FRET, single-cell FRET is most easily applied to study large and rapid changes in signaling (e.g. response to step stimuli), but we have shown that with careful correction of drifts in the signal level (primarily due to bleaching, but also including contributions from fluorophore maturation and/or recovery from long-lived dark states), it can be applied effectively to measure more subtle changes in signaling over extended times, including steady-state fluctuations. Care is required in these corrections of long-time fluorescence-intensity drifts because imperfect correction can distort dynamics on timescales comparable to that of the signal drift. We note that our analysis of chemotaxis signaling dynamics presented here is relatively insensitive to such artifacts, given that the longest timescales we observed ( $\sim$ 400 s for sensory adaptation, Figure 1) are well below the time constants of fluorescence intensity drift (>1 hr under hour experimental conditions), but caution is warranted for future applications to systems with slower dynamics. More generally, quantification of single-cell variability is a challenging task because any experimental noise source can potentially contribute to the observed variability. Although we have not undertaken here a comprehensive survey of experimental noise sources for single-cell FRET, our results demonstrate meaningful differences in variability across cells measured under identical experimental conditions. The experimental duration for single-cell FRET is photon-limited, meaning that optimal experimental strategies must carefully negotiate with a finite photon budget an inherent trade-off between measurement duration, temporal resolution, and signal-to noise ratio. Future improvements of donor/acceptor fluorophores (in parameters such as photostability, brightness, maturation, as well as FRET efficiency) could enhance the effective photon budget, and hence the power of the experiment.

Table 1

Variability in signaling parameters reported in this study with 95 $%$ CI obtained by bootstrap resampling.

N.D.: Not determined; N/A: Not applicable.

https://doi.org/10.7554/eLife.27455.030

Parameter	Genotype			Literature
CheR,CheB	CheRB+	CheRB-	CheRB-
Chemoreceptors	+ (all)	+ (all)	Tsr+
$C V (a_{0})$	0.23 $\pm$ 0.06	N/A	N/A
$C V (τ_{r e c o v e r y})$	0.20 $\pm$ 0.06	N/A	N/A	0.18–0.5^*
$C V (Π)$	0.40 $\pm$ 0.10	N/A	N/A
$C V (K)$	N.D.	0.49 $\pm$ 0.09	0.16 $\pm$ 0.07
$η$	0.44 $\pm$ 0.12	0.09 $\pm$ 0.04	0.49 $\pm$ 0.09	>0.2^†
$C V (η)$	0.52 $\pm$ 0.08	1.25 $\pm$ 0.60	0.64 $\pm$ 0.12

^*Berg and Tedesco, 1975; Min et al., 2012

^†Tu and Grinstein, 2005

From gene-expression noise to diversity in signaling phenotypes

A key feature of bacterial chemotaxis as an experimental system is that one can study in vivo signaling and behavior in a manner that is decoupled from gene expression and growth. Being an entirely protein-based signaling network, chemotaxis signaling responses do not require changes in gene expression, and the relatively short timescales of signaling reactions (subsecond to minutes) are well separated from those of changes in protein counts due to gene expression noise (minutes to hours). The ensemble of single-cell FRET time series measured in each of our experiments thus provide a snapshot of cell-to-cell variability due to stochastic gene expression in a variety of signaling parameters.

Our data revealed high variability in important signaling parameters connected to the adaptation system (Figure 1). In the case of the variability in recovery times (CV=0.20), this is likely due to variability in the CheR/receptor ratio from cell to cell. What consequences might such variability have on chemotactic behavior? A recent theoretical study has established that long (short) adaptation times are better suited for maximizing chemotactic migration rates in shallow (steep) gradients (Frankel et al., 2014). Thus, variability in adaptation times could partition the population into cells that will be more efficient in running up steep gradients, and others better suited to climbing shallow ones. Interestingly, it was also found that optimal performance at each gradient involves tuning not only the adaptation time, but also other parameters such as swimming speed or tumble bias, leading to the prediction that selective pressures act not only on the distribution of individual parameters, but also on the pattern of covariation among them (Frankel et al., 2014; Waite et al., 2016). Exploring such correlated variation of signaling parameters, both under changes in environmental conditions such as nutrient levels (Khursigara et al., 2011) and within identically grown populations, would be a fruitful avenue for future single-cell FRET studies.

In the ligand response of the network, we observed large cell-to-cell variability in the sensitivity $(1 / K)$ and steepness $(H)$ of dose-response relations, for cells with a wildtype receptor population (Figure 2). Using a mixed-species MWC model (Mello and Tu, 2005), we were able to estimate the Tar/Tsr ratio in single cells, which spans a broad range from nearly zero to more than two. This strong variability in the receptor-cluster composition has the potential to dramatically impact behavior. In their natural habitats, cells likely experience a variety chemoeffector gradients simultaneously, each associated with an unknown fitness payoff for chemotactic pursuit. Generating diversity in the chemoreceptor ratio, which has been shown to determine which gradient to climb when challenged with such conflicting possibilities (Kalinin et al., 2010), could allow the isogenic population to hedge its bets to maximize net fitness gains. The Tar/Tsr ratio has also been shown to play an important role in setting the preferred temperature for thermotaxis (Salman and Libchaber, 2007; Yoney and Salman, 2015; Paulick et al., 2017). Variability in Tar/Tsr would allow diversification of the preferred temperature across cells in the population, which will promote spreading of bacteria in environments with temperature gradients. Finally, when chemotactic bacteria colonize an initially nutrient-rich environment, they are known to successively exploit resources by emitting multiple traveling waves of chemotactic bacteria, each of which consumes and chases by chemotaxis a different nutrient component outward from the colony origin (Adler, 1966). Our observation that the population diversity in receptor ratios, and hence chemotactic preference, varies concomitantly with population growth could provide a means to tune the population fractions that engage in such excursions into virgin territory, and those that remain for subsequent exploitation of remaining resources. Thus, the diversity in ligand response and preference generated by variability in the Tar/Tsr ratio could have nontrivial consequences in a variety of behavioral contexts encountered by isogenic chemotactic (and thermotactic) populations.

Suppression of gene expression noise by CheB phosphorylation feedback

The role of phosphorylation feedback has been a long standing open question in the field of bacterial chemotaxis signaling, ever since its presumed role in providing precise adaptation was decisively ruled out by (Alon et al., 1999). In the ensuing years, a diverse set of hypotheses have been proposed to explain its purpose. Apart from precise adaptation, CheB phosphorylation has been suggested as possibly responsible for the non-linear response of CheB activity to changes in CheA kinase activity (Shimizu et al., 2010; Clausznitzer et al., 2010), ligand sensitivity of wildtype cells (Barkai et al., 2001), and has been implicated theoretically as a possible mechanism to buffer gene-expression noise to suppress detrimental variability in the steady-state kinase activity (Kollmann et al., 2005; Emonet and Cluzel, 2008; Pontius et al., 2013). Here, we tested the latter hypothesis, by severing the phosphorylation feedback loop as a possible noise-reduction mechanism. Our single-cell FRET data revealed that, not only does CheB phosphorylation feedback strongly attenuate the magnitude of variability in the steady-state kinase activity $a_{0}$ , it also qualitatively changes the shape of the distribution $P (a_{0})$ across cells to convert an otherwise bimodal distribution into a unimodal one (Figure 3d). The highly polarized bimodal distribution of steady-state activities in CheB phosphorylation mutants are likely detrimental, as they could drive $a_{0}$ of a large fraction of the population too far from the flagellar motor’s steep response threshold (Cluzel et al., 2000; Yuan and Berg, 2013) to effectively control swimming.

By analyzing simplified models of adaptation kinetics, we found that a bimodal $P (a_{0})$ could occur in the absence of phosphorylation feedback if the enzyme kinetics of CheR and CheB depend sublinearly on the activity $a$ of their receptor substrates. As a limiting case, when both enzymes work at or near saturation, this model leads to zero-order ultrasensitivity (Goldbeter and Koshland, 1981; Emonet and Cluzel, 2008), which could act as a strongly non-linear transfer function $f ([R]/[B])$ that converts a unimodal distribution $P ([R]/[B])$ into a bimodal $P (a_{0})$ . We note that ultrasensitivity due to sublinear (Michaelis-Menten) enzyme kinetics is by no means the only possible explanation for the observed bimodality in $P (a_{0})$ . Any mechanism that renders $f ([R]/[B])$ a strongly nonlinear (sigmoidal) function could lead to the same effect. The merit of the sublinear kinetic (ultrasensitivity) model is in its simplicity, but it is worth noting that reality is likely to be more complex due to, for example, effects of spatial organization. It is known that both CheR and CheB interact with chemoreceptors not only at their substrate modification residues, but also with a second binding site on a flexible tether at the receptor C-terminus. Such bivalent interactions with the receptor array could affect the movement of these enzymes across the receptor lattice (Levin et al., 2002), and such movements could shift the balance between processivity and distributivity of enzyme activity on their substrate receptors (Pontius et al., 2013), which could in turn attenuate or enhance the nonlinearity in the relationship $f ([R] / [B])$ between the enzyme expression ratio [R]/[B] and the steady-state activity $a_{0}$ of their substrate receptors (Takahashi et al., 2010).

Diversity in temporal variability: bet-hedging across exploration and exploitation strategies

In addition to cell-to-cell variability in signaling parameters, single-cell FRET allowed us to resolve temporal fluctuations in signaling about the steady-state output within individual cells. In wildtype cells, we found that the steady-state activity fluctuates slowly (Figure 4,correlation time $τ \approx$ 10s) with a large amplitude ( $η = σ_{a} / ⟨ a ⟩ \approx$ 40%), but this amplitude also varies significantly from cell to cell (CV ≈ 0.6). Fluctuations on this timescale were absent in CheRB- cells defective in receptor methylation/demethylation, indicating that these fluctuations are generated by stochastic processes in the activity of the adaptation enzymes CheR and CheB. Whereas the fluctuation correlation time $τ$ in our FRET experiments was in close agreement with those from previously reported flagellar motor switching experiments (Korobkova et al., 2004; Park et al., 2010), the fluctuation amplitude $⟨ η ⟩ \approx$ 40% was surprisingly large. Theoretical analysis of the motor-based noise measurements indicated that, in the frequency range of our experiments, stochastic methylation kinetics are indeed the dominant source of noise (Clausznitzer and Endres, 2011). Another theoretical study of the motor noise (Tu and Grinstein, 2005), had predicted a modest noise level of intracellular noise, with a lower bound of 20% of the mean. The discrepancy is likely due, at least in part, to the recently discovered adaptation at the level of the flagellar motor (Yuan et al., 2012), which must effectively act as a high-pass filter that attenuates frequencies near or below a cutoff frequency determined by its own characteristic timescale for adaptation. The fluctuation amplitude $η$ was also much greater than previous estimates from pathway-based models and we have shown that there is an additional noise source, independent from methylation, which contributes to the total noise amplitude in wildtype cells and not considered in previous modeling efforts.

The large temporal noise we observed in wildtype (CheRB+) cells may seem counterintuitive, given that the chemotaxis pathway is a transduction path for sensory information, and noise generally reduces information transmission capacity of communication channels (Shannon, 1949). However, the chemotaxis signaling pathway is not only a sensory system but also a control circuit for motile behavior, and recent studies have highlighted the importance of considering the behavioral context in understanding the design of this signaling pathway (Dufour et al., 2016; Wong-Ng et al., 2016; Long et al., 2017). The temporal noise we observed could have profound implications for E. coli’s random-walk motility strategy, because slow fluctuations in the intracellular signal can enhance the likelihood of long run events and stretch the tail of the run-length distribution to yield power-law-like switching-time distributions over a range of time scales (Korobkova et al., 2004; Tu and Grinstein, 2005). Such non-exponential statistics are known to yield superior foraging performance in environments where resource distribution is sparse (Viswanathan et al., 1999), and temporal fluctuations in run-tumble behavior has also been shown theoretically to enhance climbing of shallow gradients by generating runs that are long enough to integrate over the faint gradient a detectable difference in ligand input (Flores et al., 2012; Sneddon et al., 2012). Hence, the noise generated by the adaptation system can be advantageous in resource-poor environments (deserts) in which efficient exploration of space for sparsely distributed sources (oases) is of utmost importance. By contrast, strong temporal noise clearly degrades response fidelity in rich environments where the gradient signal is strong enough for detection with short runs, and might also complicate coordination of cells in collective behaviors such as the aforementioned traveling-wave exploitation of nutrients. Our finding that the noise amplitude varies strongly from cell to cell thus suggests that isogenic populations might be hedging their bets by partitioning themselves between specialists for local exploitation of identified resource patches and those for long-range exploration in search for new ones.

Giant fluctuations and digital switching in adaptation deficient cells with homogeneous chemoreceptor arrays

We found the most dramatic temporal fluctuations in adaptation-deficient (CheRB-) cells expressing Tsr as the sole chemoreceptor species (Figure 5). When brought close to their dose-response transition point ( $K$ ) by attractant stimulation, these cells demonstrated strong temporal fluctuations, revealing that there exist sources of signal fluctuations that are independent of CheR and CheB activity. The origin of these adaptation-independent fluctuations remain unknown, but in broad terms, one can envisage that they are due to either intrinsic sources (i.e. fluctuations arising within the components of the receptor-kinase complex), extrinsic sources (i.e. fluctuations in other cellular processes/environmental variables), or both. Possible intrinsic sources include coupled fluctuations in protein conformations (Duke and Bray, 1999; Shimizu et al., 2003; Mello et al., 2004; Skoge et al., 2011), the slow-timescale changes in receptor ‘packing’ that have been observed by fluorescence anisotropy measurements (Frank and Vaknin, 2013; Vaknin, 2014), and the stochastic assembly dynamics of receptor clusters (Greenfield et al., 2009). Possible extrinsic sources include fluctuations in metabolism, membrane potential, or active transport/consumption of ligand. Many of these possibilities could be tested by experiments of the type presented here with appropriate mutant strains and environmental controls, and present promising directions for future research.

The adaptation-independent fluctuations we observed were not only large in amplitude but often (though not always) took the form of discrete steps in activity, in some cases between only two levels. Two-state descriptions of receptor signaling are a common feature of nearly all mechanistic models of bacterial chemotaxis signaling addressing both cooperativity (Duke and Bray, 1999; Shimizu et al., 2003; Mello et al., 2004; Mello and Tu, 2005; Keymer et al., 2006) and adaptation (Asakura and Honda, 1984; Barkai and Leibler, 1997; Morton-Firth et al., 1999; Endres and Wingreen, 2006; Emonet and Cluzel, 2008; Tu et al., 2008), yet direct evidence for two-state switching by receptor-kinase complexes has been lacking. Although as noted above, it is yet possible that the two-level switching we observed (Figure 5d) is due to extrinsic noise sources (e.g. metabolism or transport), the temporal statistics (Figure 5e–h) are compatible with a simple model in which two stable signaling states are separated by an energy barrier sensitive to both environmental stimuli and internal cell variables. Regarding cells that exhibited step-like transitions among more than two stable states, a plausible interpretation is that the underlying transitions are actually two-level, but the majority of the receptor-kinase population is partitioned into two or more disjoint signaling arrays which fluctuate independently.

While two-state switching has been observed in small oligomers such as ion channels (Keller et al., 1986) and larger protein assemblies such as the bacterial flagellar motor (Silverman and Simon, 1974; Bai et al., 2010), controlled by up to a few dozen units, our findings suggest (as discussed in results) that at least many hundreds, if not thousands of receptor-kinase units can switch in a concerted fashion. The rather long timescale associated with intervals between switches (≈10²s) is clearly distinct from the methylation-dependent fluctuation timescale (≈10¹ s) observed in CheRB+ cells, and might reflect the large size of the cooperatively switching signaling array. The switching duration (≈4 s), is also much slower than the sub-second response to attractant stimuli (Segall et al., 1982; Sourjik and Berg, 2002b). These fluctuations of surprisingly large magnitude indicate the possibility that cooperativity between arrayed chemoreceptors are much stronger than suggested by previous population-averaged measurements, and represent a promising direction for future investigations.

Concluding remarks

We described a new single-cell FRET technique capable of resolving intracellular signaling dynamics in live bacteria over extended times. Our results highlight how a protein-based signaling network can either generate or attenuate variability, by amplifying or filtering molecular noise of different molecular origins. Gene expression noise is harnessed, on the one hand, to generate diversity in the ligand response of isogenic populations, or attenuated, on the other the hand, in the control of steady-state signal output. In addition, we showed that signaling noise generated at the level of interacting gene products can have a profound impact. Stochastic protein-protein interactions within the signaling network, as well as other ‘extrinsic’ fluctuations, can be amplified by the signaling network to generate strong temporal fluctuations in the network activity.

Materials and methods

Strains and plasmids

Request a detailed protocol

All strains used are descendants of E. coli K-12 HCB33 (RP437). Growth conditions were kept uniform by transforming all strains with two plasmids. All strains and plasmids are shown in Tables 2 and 3.

Table 2

Strains used in this study.

https://doi.org/10.7554/eLife.27455.031

Background			Plasmids
Strain	Source	Relevant genotype	Plasmid 1	Plasmid 2
VS115	V. Sourjik	$Δ$ YZ $Δ$ FliC	pSJAB106	pZR1
VS104	Sourjik and Berg, 2002a	$Δ$ CheYZ	pSJAB12	pBAD33
TSS58	this work	$Δ$ RBYZ $Δ$ FliC	pSJAB106	pZR1
VS149	Sourjik and Berg, 2004	$Δ$ RBYZ	pVS12	pVS33
VS124	Clausznitzer et al., 2010	$Δ$ CheBYZ	pSJAB12	pVS112
VS124		$Δ$ CheBYZ	pSJAB12	pVS97
VS124		$Δ$ CheBYZ	pSJAB12	pVS91
UU2567	Kitanovic et al., 2015	$Δ$ CheRBYZ, $Δ$ MCP^†	pSJAB106	pPA114 Tsr
TSS1964	this work	$Δ$ CheRBYZ, $Δ$ MCP FliC*	pSJAB106	pPA114 Tsr
UU2614	J.S. Parkinson	CheB $Δ$ (4-345)	pTrc99a	pVS91,97,112

All strains are descendants of E. coli K-12 HCB33 (RP437). In all FRET experiments, strains carry two plasmids and therefore confer resistance to chloramphenicol and ampicillin.

^†all five chemoreceptor genes tar tsr tap trg aer deleted.
*expresses sticky FliC filament (Scharf et al., 1998)

Table 3

Plasmids used in this study.

https://doi.org/10.7554/eLife.27455.032

Plasmid	Product	System	Ind	Res	Source
pVS52	CheZ-5G-YFP	pBAD33	ara	cam	Sourjik and Berg, 2002a
pVS149	CheY-5G-mRFP1	pTrc99a	IPTG	amp	Sourjik and Berg, 2002a
pSJAB12	CheZ-5G-YFP/CheY-5G-mRFP1	PTrc99a	IPTG	amp	This work
pSJAB106	CheZ-5G-YFP/CheY-5G-mRFP1^¶	PTrc99a	IPTG	amp	This work
pVS91	CheB^†	pTrc99a	ara	cam	Liberman et al., 2004
pVS97	CheB-D56E^‡	pBAD33	ara	cam	Clausznitzer et al., 2010
pVS112	CheBc^§	pBAD33	ara	cam	V. Sourjik
pSJAB 122	CheBc-GS4G-mVenus	pBAD33	ara	cam	This work
pSJAB 123	CheB(D56E)-GS4G-mVenus	pBAD33	ara	cam	This work
pSJAB 124	CheB-GS4G-mVenus	pBAD33	ara	cam	This work
pZR 1	FliC*	pKG116	NaSal	cam	This work
pPA114 Tsr	Tsr	pPA114	NaSal	cam	Ames et al., 2002

^¶Contains a A206K mutation to enforce monomerity..

^†expresses WT CheB.
^‡carries a point mutation D56E in CheB.

^§expresses only residues 147–349 of CheB, preceded by a start codon (Met).
*expresses sticky FliC filament (Scharf et al., 1998)

Table 4

List of global parameters used for model of Mello and Tu.

In these fits, $\tilde{K}$ is a free parameter while others are constrained ±5% by published values.

https://doi.org/10.7554/eLife.27455.033

Parameter	Start value (Mello and Tu, 2007)	Final value
$C$	0.314	0.29
$ϵ_{0}$	0.80	0.84
$ϵ_{A}$	1.23	1.29
$ϵ_{S}$	1.54	1.61
$\tilde{K}$	–	21.2 $μ$ μM

The FRET acceptor-donor pair (CheY-mRFP and CheZ-YFP) is expressed in tandem from a IPTG inducible pTrc99A plasmid, pSJAB12 or pSJAB106, with respective induction levels of 100 and 50 μM IPTG. The differences between pSJAB12 and pSJAB106 are (i) the presence of a noncoding spacer in pSJAB106 to modify the ribosome binding site of CheZ (Salis et al., 2009), such that CheZ is expressed approximately three fold less, and (ii) a A206K mutation in YFP to enforce monomerity. We also used pVS52 (CheZ-YFP) and pVS149 (CheY-mRFP1) to express the fusions from separate plasmids with induction levels of 50 μM IPTG and 0.01 % arabinose, respectively. We transformed the FRET plasmids in an adaptation-proficient strain (VS104) to yield CheRB+ and an adaptation-deficient strain (VS149) to get CheRB-. For attachment with sticky flagella from pZR1 we used the equivalent strains in fliC background (VS115 and TSS58).

Experiments with Tsr as the sole chemoreceptor were performed in UU2567 or TSS1964, in which the native FliC gene is changed to sticky FliC (FliC*). Tsr is expressed from pPA114 Tsr, a pKG116 derivative, at with an induction of 0.6 $μ$ μM NaSal.

For the experiments with the CheB mutants, pSJAB12 was transformed into VS124 together with plasmids expressing CheB $^{W T}$ , CheB $^{D 56 E}$ and truncated mutant CheB $_{c}$ (plasmids pVS91, pVS97 and pVS112, respectively, with induction levels of 1.5E-4, 6E-4 and 3E-4 % arabinose.

FRET microscopy

Request a detailed protocol

Föster Resonance Energy Transfer [FRET] microscopy was performed as previously reported (Sourjik et al., 2007; Vaknin and Berg, 2004). Cells were grown to OD = 0.45–0.5 in Tryptone Broth (TB) medium from a saturated overnight culture in TB, both with 100 $μ$ g/mL ampicillin and 34 $μ$ g/mL chloramphenicol and appropriate inducers in the day culture. For the FRET experiments we used Motility Media (MotM, (Shimizu et al., 2006)), in which cells do not grow and protein expression is absent. Cells were washed in 50 mL MotM, and then stored 0.5–6 hr before experiment. In the dose-response curve experiments and the temporal fluctuation measurements, cells were stored up to three hours at room temperature to allow for further red fluorescence maturation. A biological replicate or independent FRET experiment was defined as a measurement from separately grown cultures, each grown on a separate day.

Cells were attached by expressing sticky FliC (FliC*) from a pKG116 plasmid or the chromosome (TSS1964), induced with 2 $μ$ μM Sodium Salicylate (NaSal), or with Poly-L-Lysine (Sigma), or with anti-FliC antibodies column purified (Using Protein A sepharose beads, Amersham Biosciences) from rabbit blood serum and pre-absorbed to FliC- cells (HCB137, gifts from Howard Berg). We found FRET experiments with sticky FliC to have the highest signal-to-noise ratio.

Fluorescent images of the cells were obtained with a magnification of 40-100x (Nikon instruments). For excitation of YFP, we either used 514 nm laser excitation set to 30 mW for 2 ms or an LED system (CoolLED, UK) with an approximate exposure time of 40 ms to approximate the same illumination intensity per frame. The sample was illuminated stroboscopically with a frequency between 1 and 0.2 Hz. RPF excitation was performed by 2 ms exposure of 60 mW 568 nm laser or equivalent with LED to measure acceptor levels independently from FRET.

Excitation light was sent through a 519 nm dichroic mirror (Semrock, USA). Epifluorescent emission was led into an Optosplit (Cairn Research, UK) with a second dichroic mirror 580 nm and two emission filters (527/42 nm and 641/75 nm, Semrock, USA) to project the RFP and YFP emission side by side on an EM-CCD (Princeton Instruments, USA) with multiplication gain 100.

Image processing

Request a detailed protocol

Images were loaded and analyzed by means of in-house written scripts (Image segmentation script FRETimaging.py available online) in MATLAB and Python. For ratiometric FRET experiments, we segmented single cells using the donor emission with appropriate filter steps to remove clusters of cells or cells improperly attached to the coverslip. At the position of each cell a rectangular ROI is defined in which all fluorescence intensity is integrated.

For FRET experiments in which the concentration of donor molecules may influence the FRET signal, the experiments on the CheB mutants, segmentation was done separately for each frame to determine the cell shape and then linking these segmented images with a tracking algorithm (Crocker and Grier, 1996), afterwards, fluorescence intensities are normalized for the cell size (mask surface area) in segmentation, intensities were corrected for inhomogeneous illumination, and cells with low acceptor intensities were excluded from the analysis. The ROI for the donor intensity were subsequently used to obtain the acceptor intensity per cell, both in photon-count per pixel.

Fluorescence intensities were corrected for long-time drift (primarily due to bleaching, but also including contributions from fluorophore maturation and/or recovery from long-lived dark states) by fitting a linear, single exponential or double exponential function to the fluorescence decay, separately for both donor and acceptor channels. The net decay in the FRET signal was dominated by photobleaching of the donor (YFP) intensity (on average 25% over the course of a 30 min experiment; Figure 1—figure supplement 2). Red fluorescent proteins tend to have long maturation times, which under our experimental conditions (in which gene expression is halted upon harvesting via auxotrophic limitation) could result in a residual increase in red fluorescence intensity during experiments. In control experiments, we determined mRFP1’s maturation half time under our conditions to be ~2–3 hr, with a maximum increase in the FRET signal of ~25% at ~5–6 hr. Cells in which the intensity decay could not accurately be corrected were excluded from the analysis.

In non-ratiometic fluorescence experiments (CheB-mVenus) the fluorescence intensities obtained after segmentation were corrected for inhomogeneous illumination and divided by cell area.

FRET analysis

Request a detailed protocol

The FRET signal is calculated from fluorescent time series. We observe changes in the ratio $R = A / D$ , in which A and D are the fluorescence intensities of the acceptor and donor. In previous population-averaged FRET experiments the FRET per donor molecule ( $Δ D / D_{0}$ ) is calculated as (Sourjik and Berg, 2002a; Sourjik et al., 2007):

\frac{Δ D}{D_{0}} = \frac{Δ R}{α + R_{0} + Δ R}

in which $R_{0}$ is the ratio in absence of FRET, $α = | Δ A / Δ D |$ is a constant that depends on the experimental system (in our case α = 0.30) and the change in ratio as a result of energy transfer $Δ R$ and $R_{0}$ are obtained through observing the ratio just after adding and removing saturated attractant stimuli. This expression is convenient for population FRET since is invariant to attachment densities of a population. However, in single-cell FRET this expression may generate additional variability in FRET due to variable donor levels from cell to cell. Hence it is more convenient to define the FRET levels in terms of the absolute change in donor level $Δ D$ , since this reflects the number of resonance energy transfer pairs

FRET (t) = Δ D = D_{0} \frac{Δ R}{α + R_{0} + Δ R}

Since FRET occurs only when CheY-P and CheZ interact, the FRET level is proportional to the concentration of complex [Yp-Z]. If we assume the CheY-P dephosphorylation by CheZ follows Michaelis-Menten kinetics we can describe the [Yp-Z] concentration in terms of the activity of the kinase CheA. For this, we assume the system is in steady-state for timescales much larger than CheY phosphorylation-dephosphorylation cycle ( $\approx$ 100 ms). In that case, the destruction rate should equal the rate of CheA phosphorylation and hence the FRET signal is proportional to the activity per kinase $a$ and the amount of CheA in the receptor-kinase complex (Sourjik and Berg, 2002a; Oleksiuk et al., 2011):

FRET \propto [Yp-Z] = a \frac{k_{A}}{k_{Z}} [CheA] \approx a \frac{k_{A}}{k_{Z}} {[CheA]}_{T}

This last step is only valid if we further assume CheA autophosphorylation being the rate-limiting step. This is the case only if sufficient amounts of CheZ and CheY present in the cell. We have found that the FRET level initially increases with donor (CheZ) levels, but then saturates and remains constant for CheY and CheZ (see Figure 3—figure supplement 2).

In many cases the most relevant parameter is the normalized FRET response. The FRET level reaches maximum if all kinases are active ( $a \approx 1$ ). In case of CheRB+cells, this is the case when removing a saturating amount of attractant after adaptation (Sourjik and Berg, 2002a). For CheRB- cells the baseline activity is (Sourjik and Berg, 2002a; Shimizu et al., 2010) close to 1. Hence the normalized FRET $FRET (t) / {FRET}_{max}$ represents the activity per kinase $a (t)$ and is the relevant parameter for many quantitative models for chemoreceptor activity (Tu, 2013).

a (t) = \frac{FRET(t)}{{FRET}_{m a x}}

and from $a (t)$ the steady-state activity $a_{0}$ can be determined by averaging $a (t)$ over baseline values before adding attractant stimuli.

Analysis of power spectra

Request a detailed protocol

From FRET time series of length $T$ and acquisition frequency $f$ we calculated Power Spectral Density (PSD) estimates as

S_{FRET} (ω) = \frac{1}{T} {| ℱ (ω) |}^{2}

where $ℱ (ω)$ is the (discrete-time) Fourier transform of the FRET time series $FRET (t)$ . We only consider positive frequencies and multiply by two to conserve power.

To study the influence of experimental noise and the effect of estimating $τ$ and $c$ from a finite time window, we generated O-U time series using the update formula (Gillespie, 1996)

X (t + Δ t) = X (t) - τ^{- 1} Δ t + c^{1 / 2} n {(Δ (t))}^{1 / 2}

in which $n$ denotes a sample value from a normally distributed random variable ( $μ = 0, σ = 1$ ). To the generated time series Gaussian white noise was added to simulate experimental noise. The experimental noise amplitude was obtained from the average power at high frequencies.

Two-state switching analysis

Request a detailed protocol

Since the amplitude of two-state switches is much greater than the noise, switching events times $t_{0}$ could be easily read off by eye. We obtained switching durations by fitting the function

\begin{array}{ll} a (t) & = \frac{1}{2} \pm \frac{1}{2} \frac{t - t_{0}}{| t - t_{0} |} (1 - e^{- 2 | t - t_{0} | / τ_{\pm}}) \end{array}

to the normalized FRET time series in a 30 s time window, approximately ±15 s from $t_{0}$ . The residence times $Δ t_{u p, i, k}$ and $Δ t_{d o w n, i, k}$ of event $k$ in cell $i$ were defined by the time between transitions or the beginning/end of the 25 μM stimulus time window. The steady-state activity during activity was then calculated as

a_{1 / 2, i} = \frac{\sum_{k} Δ t_{u p, i, k}}{\sum_{k} Δ t_{d o w n, i, k} + \sum_{k} Δ t_{u p, i, k}}

and for the residence times we take the mean over $k$ to get $τ_{d o w n}$ and $τ_{u p}$ . If we treat the system as an equilibrium process we can use the Arrhenius equations that describe the residence times as a function of the distance to the energy barrier

\begin{array}{ll} τ_{d o w n} & = τ_{r} \exp [γ_{d o w n} \ln [a_{1 / 2} / (1 - a_{1 / 2})] / k_{B} T] \\ τ_{u p} & = τ_{r} \exp [γ_{u p} \ln [a_{1 / 2} / (1 - a_{1 / 2})] / k_{B} T] \end{array}

in which $γ_{d o w n}$ and $γ_{u p}$ are constants corresponding to the slopes of $\ln τ_{d o w n}$ and $\ln τ_{u p}$ against $\ln [a_{1 / 2} / (1 - a_{1 / 2})]$ , respectively. The fit parameters and standard error are obtained with the robustfit function in Matlab (statistics toolbox).

Dose response curve analysis

Request a detailed protocol

Normalized FRET responses to different levels of ligand are fit to a hill curve of the form

a = \frac{{[L]}^{H}}{{[L]}^{H} + {[K]}^{H}}

This can be connected to an MWC-type model (Monod et al., 1965) of receptor cluster activity (Tu et al., 2008) in the regime $K_{I} ≪ [L] ≪ K_{A}$ , resulting in the correspondence key

\begin{aligned} H & = N \\ K & = K_{I} e^{f_{m} (m)} \end{aligned}

which relates the Hill slope directly to the cluster size $N$ , and sensitivity $K$ to the methylation energy of the receptor. We plot $K$ on a logarithmic scale to scale linearly with energy.

The parameter estimate uncertainties of $K$ and $H$ are defined by the covariance matrix for each cell $i$

{COV}_{i} = {[\begin{matrix} σ_{K K} & σ_{H K} \\ σ_{K H} & σ_{H H} \end{matrix}]}_{i}

in which $σ$ denotes the standard error from the fit. For each covariance matrix the corresponding eigenvectors and eigenvalues are determined. The eigenvalues and vectors constitute an ellipsoid which represent error basins in $K - H$ space.

To obtain expression level estimates of different receptor species we use a different MWC model. Following (Mello and Tu, 2005), we use as an expression for the normalized response of cells to ligand $[L]$ serine

a = \frac{ϵ_{0} ϵ_{S}^{N_{S}} ϵ_{A}^{N_{A}} {(1 + C [L] / \tilde{K})}^{N_{s}}}{{(1 + [L] / \tilde{K})}^{N_{s}} + ϵ_{0} ϵ_{S}^{N_{S}} ϵ_{A}^{N_{A}} {(1 + C [L] / \tilde{K})}^{N_{s}}}

in which $N_{A}$ is the number of Tar receptors in the cluster and $N_{S}$ is the number of Tsr receptors. Parameters $ϵ_{A}$ , $ϵ_{S}$ , $ϵ_{0}$ are the energies corresponding to binding of ligand to Tar, Tsr and the other three receptors and are the same for each cell, like $C$ and $\tilde{K}$ which describe the disassociation constant for the active state as $K_{A} = \tilde{K} / C$ , while $N_{A}$ and $N_{T}$ may vary from cell to cell. This yields the minimization problem for all 128 cells

min \sum_{i}^{N_{c e l l s}} \sum_{j}^{N_{s t i m}} {(m_{i, j} - a_{i, j})}^{2}

in which $m_{i, j}$ the measured FRET response normalized to the response amplitude of cell $i$ to stimulus $L_{j}$ . This function was minimized using the matlab function fmincon (optimization toolbox). The total number $N_{T} = N_{A} + N_{S}$ is limited to 32. When fitting the model used the energy parameters $ϵ$ from reference (Mello and Tu, 2005) where used as initial guess with a maximum of $\pm 5 %$ deviation. This yielded an estimate of $N_{A}$ and $N_{S}$ for each cell. Under the assumption that receptor clusters are well-mixed, this yields a Tar/Tsr ratio of $N_{A} / N_{S}$ .

Sublinear model of adaptation kinetics with phoshorylation feedback

Request a detailed protocol

For our model, we consider CheR and CheB to perform opposite operations on the same substrate. For simplicity, we do not explicitly describe the methylation and demethylation of the receptors explicitly but instead assume that CheR (R) activates the receptor-kinase complex directly (A $^{*}$ ), and that CheB (B) deactivates it (A)

In general, the corresponding reaction equation is a function of the methylation of inactive kinases by CheR, and demethylation of active kinases by CheB, described by two functions $g$ and $h$

\frac{d a}{d t} = g (v_{r}, a) - h (v_{b}, a)

with $v_{r}$ and $v_{b}$ being the rates for CheR and CheB, respectively. We now assume that these reactions follow Michaelis-Menten kinetics, following (Goldbeter and Koshland, 1981) and (Emonet and Cluzel, 2008), and the total amount of kinase complexes is constant ( $A_{T} = A^{*} + A$ ). Hence the change in activity $a = A^{*} / A_{T}$ has a sublinear dependence on $a$ :

\frac{d a}{d t} = v_{r} \frac{1 - a}{K_{r} + 1 - a} - v_{b} \frac{a}{a + K_{b}}

The Michaelis-Menten constants $K_{b}$ and $K_{r}$ are in units of $A_{T}$ and are therefore dimensionless numbers. We are interested in the steady-state level $a_{0}$ and its dependence on the kinetic parameters in equation 18. This is described by the Goldbeter-Koshland function (Tyson et al., 2003), an exact solution to the system in case [R] and [B] are much smaller than [A] $_{T}$ .

a_{0} [v_{r}, v_{b}, K_{r}, K_{b}] = \frac{2 v_{r} K_{r}}{(v_{b} - v_{r} + v_{b} K_{b} + v_{r} K_{r} + \sqrt{{(v_{b} - v_{r} + v_{b} K_{b} + v_{r} K_{r})}^{2} - 4 (v_{b} - v_{r}) v_{r} K_{r}}}

The shape of this curve is sigmoidal if the Michaelis-Menten constants $K_{r}$ and $K_{b}$ are much smaller than one. For CheB phosphorylation, we assume the phosphorylation rate depends linearly on active CheA and write

\frac{d [Bp]}{d t} = k_{p} [B] a (v_{r}, v_{b}, K_{b}, K_{r}) - k_{d p} [Bp]

with the corresponding conservation law B $_{T}$ = B $_{P}$ + B. For the case for wild-type CheB, with phosphorylation feedback, the rates can be described in terms of catalytic rate times the enzyme (subspecies) concentration

\begin{aligned} v_{b} & = k_{b} ([B_{T}] - [Bp]) + M k_{b} [Bp] \\ v_{r} & = k_{r} [R] \end{aligned}

in which $M$ stands for the ratio of demethylation rates of unphosphorylated and phosphorylated CheB. The fraction of the phosphorylated CheB, [Bp]/ ${[B]}_{T}$ then determines the effective activity of CheB. Equation 20 is solved numerically using Mathematica (Mathematica model source code available online) for [Bp] and the result is substituted in equation 19. In the absence of feedback, the activity can be directly calculated from equation 19 with the rates being simply

\begin{array}{lrlrlrlr} v_{b} & = k_{b} [B] \\ v_{r} & = k_{r} [R] \end{array}

We only need to consider the ratio of rate constants $k_{r}$ and $k_{b}$ which determines at which expression ratio [CheR]/[CheB] the activity equals 1/2. We assume $k_{r} = k_{b}$ for simplicity, since the shape of the curve from Equation 19 is not affected by the values of $k_{r}$ and $k_{b}$ , changing their ratio only shifts the curve along the horizontal axis. Similarly, we only consider the ratio of phosphorylation and dephosphorylation rates. This leaves the system of equations above only has a few parameters: $K_{b, r}$ and M; and the ratios $k_{r} / b_{b}$ and $k_{p} / k_{d p}$ . In Table 5, the parameters used for the calculations are listed.

Table 5

List of parameters used for Goldbeter-Koshland description of CheB phosphorylation feedback.

https://doi.org/10.7554/eLife.27455.034

Parameter	Value	Literature	Source
$k_{r} / k_{p}$	1	0.75	Shimizu et al., 2010
$k_{d p} / k_{p}$	2	$k_{p} = 0.37$ $s^{- 1}$	Kentner and Sourjik, 2009
$K_{r}$	0.03	<<1	Emonet and Cluzel, 2008
$K_{b}$	0.03	<<1	Emonet and Cluzel, 2008
$K_{b} (C h e B c)$	0.2	<<1
M (WT)	15	100	Anand and Stock, 2002
M (CheBc)	7	15	Simms et al., 1985

We first fixed the phosphorylation rates $k_{p}$ = $1 / 2 k_{d p}$ . This means that the steady-state phosphorylated level of CheB [B $_{p}$ ]/[B $_{T}$ ] at activity $\approx 1 / 3$ is around 15 $%$ . This parameter is not constrained by any direct observation, but it is clear the system benefits from a relatively low fraction of phosphorylation, to be able to up and down regulate the levels effectively upon changes in activity.

Generally, we assume CheB-D56E to behave like unphosphorylated CheB. The gain in catalytic rate of activated CheB is estimated to be nearly a 100 fold, but this does not agree with the expression level differences between the different CheB mutants so we made a conservative estimate of 15 (the attenuating effect increases with the gain). CheBc behaves approximately like phosphorylated CheB (albeit with increase of only seven compared to D56E), qualitatively consistent with measured in vitro rates for CheBc and phosphorylated intact CheB (Anand and Stock, 2002). The difference between predicted rates and might be due to the fact that the rate experiments were performed in vitro. Michaelis Menten constants used in the model are lower than 1, but how low is not well constrained by data, and estimations do not take into account the possible attenuating effect of phosphorylation. Our experimental data on the distribution of $a_{0}$ implies the sigmodial curve is steep in the absence of phosphorylation and hence that $K_{b}$ and $K_{r}$ are quite small. The variability in $a_{0}$ for CheBc is lower than D56E, implying that the curve is less steep and hence we have chosen are $K_{r}$ which is not quite as low as D56E.

To simulate gene expression noise, we simulated [CheR]/[CheB] log-normal distributions with $σ = 0.18$ for all three strains. The mean of the distribution was chosen to yield an average steady-state network activity ( $a_{0}$ ) of 0.4. The resulting distribution of $a_{0}$ was calculated using the corresponding Goldbeter-Koshland function for each genotype.

Linear and supralinear models of adaptation kinetics

Request a detailed protocol

Instead of assuming a sub-linear (Michaelis-Menten) dependence of CheR- and CheB-catalyzed rates on the receptor-kinase activity $a$ , one may also assume linear, quadratic or cubic dependence of the methylation rates on the activity, as was for example done in (Clausznitzer et al., 2010). Here, CheR feedback is assumed to be linear ( $g = k_{r} [R] (1 - a)$ ), while CheB feedback can be linear ( $h = k_{b} [B] a$ ), quadratic ( $h = k_{b} [B] a^{2}$ ) or cubic ( $h = k_{b} [B] a^{3}$ ) in the receptor-kinase activity $a$ . The supralinear (quadratic and cubic) forms of dependence are intended to model the case with CheB phosphorylation, and the linear form the case without CheB phosphorylation. The steady-state activity $a_{0}$ can be found by solving $g (v_{r}, a) = h (v_{b}, a)$ and the dependence of $a_{0}$ to [R]/[B] ( $a_{0}$ =f([R]/[B])) for these linear and supralinear cases are shown in Figure 3—figure supplement 3.

References

1. Adler J
(1966) Chemotaxis in bacteria
Science 153:708–716.
https://doi.org/10.1126/science.153.3737.708
- PubMed
- Google Scholar
1. Alon U
2. Surette MG
3. Barkai N
4. Leibler S
(1999) Robustness in bacterial chemotaxis
Nature 397:168–171.
https://doi.org/10.1038/16483
- PubMed
- Google Scholar
(2002) Collaborative signaling by mixed chemoreceptor teams in Escherichia coli
PNAS 99:7060–7065.
https://doi.org/10.1073/pnas.092071899
- PubMed
- Google Scholar
1. Amin DN
2. Hazelbauer GL
(2010) Chemoreceptors in signalling complexes: shifted conformation and asymmetric coupling
Molecular Microbiology 78:1313–1323.
https://doi.org/10.1111/j.1365-2958.2010.07408.x
- PubMed
- Google Scholar
1. Anand GS
2. Stock AM
(2002) Kinetic basis for the stimulatory effect of phosphorylation on the methylesterase activity of CheB
Biochemistry 41:6752–6760.
https://doi.org/10.1021/bi012102n
- PubMed
- Google Scholar
1. Asakura S
2. Honda H
(1984) Two-state model for bacterial chemoreceptor proteins. The role of multiple methylation
Journal of Molecular Biology 176:349–369.
https://doi.org/10.1016/0022-2836(84)90494-7
- PubMed
- Google Scholar
1. Bai F
2. Branch RW
3. Nicolau DV
4. Pilizota T
5. Steel BC
6. Maini PK
7. Berry RM
(2010) Conformational spread as a mechanism for cooperativity in the bacterial flagellar switch
Science 327:685–689.
https://doi.org/10.1126/science.1182105
- PubMed
- Google Scholar
1. Bai F
2. Che YS
3. Kami-ike N
4. Ma Q
5. Minamino T
6. Sowa Y
7. Namba K
(2013) Populational heterogeneity vs. temporal fluctuation in Escherichia coli flagellar motor switching
Biophysical Journal 105:2123–2129.
https://doi.org/10.1016/j.bpj.2013.09.043
- PubMed
- Google Scholar
(2001) Robust amplification in adaptive signal transduction networks
Comptes Rendus De l'Académie Des Sciences - Series IV - Physics-Astrophysics 2:871–877.
https://doi.org/10.1016/S1296-2147(01)01230-6
- Google Scholar
1. Barkai N
2. Leibler S
(1997) Robustness in simple biochemical networks
Nature 387:913–917.
https://doi.org/10.1038/43199
- PubMed
- Google Scholar
1. Berg HC
2. Brown DA
(1972) Chemotaxis in Escherichia coli analysed by Three-dimensional Tracking
Nature 239:500–504.
https://doi.org/10.1038/239500a0
- Google Scholar
1. Berg HC
2. Tedesco PM
(1975) Transient response to chemotactic stimuli in Escherichia coli
PNAS 72:3235–3239.
https://doi.org/10.1073/pnas.72.8.3235
- PubMed
- Google Scholar
(1982) Impulse responses in bacterial chemotaxis
Cell 31:215–226.
https://doi.org/10.1016/0092-8674(82)90421-4
- PubMed
- Google Scholar
(1986) Demethylation of bacterial chemoreceptors is inhibited by attractant stimuli in the complete absence of the regulatory domain of the demethylating enzyme
Biochemical and Biophysical Research Communications 141:918–923.
https://doi.org/10.1016/S0006-291X(86)80130-9
- PubMed
- Google Scholar
(1998) Receptor clustering as a cellular mechanism to control sensitivity
Nature 393:85–88.
https://doi.org/10.1038/30018
- Google Scholar
1. Celani A
2. Vergassola M
(2012) Nonlinearity, fluctuations, and response in sensory systems
Physical Review Letters 108:258102.
https://doi.org/10.1103/PhysRevLett.108.258102
- PubMed
- Google Scholar
1. Chilcott GS
2. Hughes KT
(2000) Coupling of flagellar gene expression to flagellar assembly in Salmonella enterica serovar typhimurium and Escherichia coli
Microbiology and Molecular Biology Reviews 64:694–708.
https://doi.org/10.1128/MMBR.64.4.694-708.2000
- PubMed
- Google Scholar
1. Clausznitzer D
2. Endres RG
(2011) Noise characteristics of the Escherichia coli rotary motor
BMC Systems Biology 5:151.
https://doi.org/10.1186/1752-0509-5-151
- PubMed
- Google Scholar
(2014) Predicting chemical environments of bacteria from receptor signaling
PLoS Computational Biology 10:e1003870.
https://doi.org/10.1371/journal.pcbi.1003870
- PubMed
- Google Scholar
(2010) Chemotactic response and adaptation dynamics in Escherichia coli
PLoS Computational Biology 6:e1000784.
https://doi.org/10.1371/journal.pcbi.1000784
- PubMed
- Google Scholar
(2000) An ultrasensitive bacterial motor revealed by monitoring signaling proteins in single cells
Science 287:1652–1655.
https://doi.org/10.1126/science.287.5458.1652
- PubMed
- Google Scholar
1. Crocker JC
2. Grier DG
(1996) Methods of digital video microscopy for colloidal studies
Journal of Colloid and Interface Science 179:298–310.
https://doi.org/10.1006/jcis.1996.0217
- Google Scholar
1. Djordjevic S
2. Goudreau PN
3. Xu Q
4. Stock AM
5. West AH
(1998) Structural basis for methylesterase CheB regulation by a phosphorylation-activated domain
PNAS 95:1381–1386.
https://doi.org/10.1073/pnas.95.4.1381
- PubMed
- Google Scholar
1. Dufour YS
2. Gillet S
3. Frankel NW
4. Weibel DB
5. Emonet T
(2016) Direct correlation between motile behavior and protein abundance in single cells
PLOS Computational Biology 12:e1005041.
https://doi.org/10.1371/journal.pcbi.1005041
- PubMed
- Google Scholar
1. Duke TA
2. Bray D
(1999) Heightened sensitivity of a lattice of membrane receptors
PNAS 96:10104–10108.
https://doi.org/10.1073/pnas.96.18.10104
- PubMed
- Google Scholar
1. Eldar A
2. Elowitz MB
(2010) Functional roles for noise in genetic circuits
Nature 467:167–173.
https://doi.org/10.1038/nature09326
- PubMed
- Google Scholar
1. Elf J
2. Ehrenberg M
(2004) Spontaneous separation of bi-stable biochemical systems into spatial domains of opposite phases
Systems Biology 1:230–236.
https://doi.org/10.1049/sb:20045021
- PubMed
- Google Scholar
(2002) Stochastic Gene Expression in a Single Cell
Science 297:1183–1186.
https://doi.org/10.1126/science.1070919
- Google Scholar
1. Emonet T
2. Cluzel P
(2008) Relationship between cellular response and behavioral variability in bacterial chemotaxis
PNAS 105:3304–3309.
https://doi.org/10.1073/pnas.0705463105
- PubMed
- Google Scholar
1. Endres RG
2. Wingreen NS
(2006) Precise adaptation in bacterial chemotaxis through "assistance neighborhoods"
PNAS 103:13040–13044.
https://doi.org/10.1073/pnas.0603101103
- PubMed
- Google Scholar
(2012) Signaling noise enhances chemotactic drift of E. coli
Physical Review Letters 109:148101.
https://doi.org/10.1103/PhysRevLett.109.148101
- PubMed
- Google Scholar
1. Frank V
2. Vaknin A
(2013) Prolonged stimuli alter the bacterial chemosensory clusters
Molecular Microbiology 88:634–644.
https://doi.org/10.1111/mmi.12215
- PubMed
- Google Scholar
1. Frankel NW
2. Pontius W
3. Dufour YS
4. Long J
5. Hernandez-Nunez L
6. Emonet T
7. Marder E
(2014) Adaptability of non-genetic diversity in bacterial chemotaxis
eLife 3:e03526.
https://doi.org/10.7554/eLife.03526
- PubMed
- Google Scholar
1. Gillespie DT
(1996) The mathematics of Brownian motion and Johnson noise
American Journal of Physics 64:225–240.
https://doi.org/10.1119/1.18210
- Google Scholar
1. Goldbeter A
2. Koshland DE
(1981) An amplified sensitivity arising from covalent modification in biological systems
PNAS 78:6840–6844.
https://doi.org/10.1073/pnas.78.11.6840
- PubMed
- Google Scholar
1. Greenfield D
2. McEvoy AL
3. Shroff H
4. Crooks GE
5. Wingreen NS
6. Betzig E
7. Liphardt J
(2009) Self-organization of the Escherichia coli chemotaxis network imaged with super-resolution light microscopy
PLoS Biology 7:e1000137.
https://doi.org/10.1371/journal.pbio.1000137
- PubMed
- Google Scholar
(2016) Constraints on fluctuations in sparsely characterized biological systems
Physical Review Letters 116:058101.
https://doi.org/10.1103/PhysRevLett.116.058101
- PubMed
- Google Scholar
1. Kalinin Y
2. Neumann S
3. Sourjik V
4. Wu M
(2010) Responses of Escherichia coli bacteria to two opposing chemoattractant gradients depend on the chemoreceptor ratio
Journal of Bacteriology 192:1796–1800.
https://doi.org/10.1128/JB.01507-09
- PubMed
- Google Scholar
(1986) Sodium channels in planar lipid bilayers. Channel gating kinetics of purified sodium channels modified by batrachotoxin
The Journal of General Physiology 88:1–23.
https://doi.org/10.1085/jgp.88.1.1
- PubMed
- Google Scholar
1. Kentner D
2. Sourjik V
(2009) Dynamic map of protein interactions in the Escherichia coli chemotaxis pathway
Molecular Systems Biology 5:238.
https://doi.org/10.1038/msb.2008.77
- PubMed
- Google Scholar
1. Keymer JE
2. Endres RG
3. Skoge M
4. Meir Y
5. Wingreen NS
(2006) Chemosensing in Escherichia coli: Two regimes of two-state receptors
PNAS 103:1786–1791.
https://doi.org/10.1073/pnas.0507438103
- PubMed
- Google Scholar
1. Khursigara CM
2. Lan G
3. Neumann S
4. Wu X
5. Ravindran S
6. Borgnia MJ
7. Sourjik V
8. Milne J
9. Tu Y
10. Subramaniam S
(2011) Lateral density of receptor arrays in the membrane plane influences sensitivity of the E. coli chemotaxis response
The EMBO Journal 30:1719–1729.
https://doi.org/10.1038/emboj.2011.77
- PubMed
- Google Scholar
(2015) A Trigger Residue for Transmembrane Signaling in the Escherichia coli Serine Chemoreceptor
Journal of Bacteriology 197:2568–2579.
https://doi.org/10.1128/JB.00274-15
- PubMed
- Google Scholar
(2005) Design principles of a bacterial signalling network
Nature 438:504–507.
https://doi.org/10.1038/nature04228
- Google Scholar
(2004) From molecular noise to behavioural variability in a single bacterium
Nature 428:574–578.
https://doi.org/10.1038/nature02404
- Google Scholar
1. Kussell E
2. Leibler S
(2005) Phenotypic diversity, population growth, and information in fluctuating environments
Science 309:2075–2078.
https://doi.org/10.1126/science.1114383
- PubMed
- Google Scholar
1. Lazova MD
2. Ahmed T
3. Bellomo D
4. Stocker R
5. Shimizu TS
(2011) Response rescaling in bacterial chemotaxis
PNAS 108:13870–13875.
https://doi.org/10.1073/pnas.1108608108
- PubMed
- Google Scholar
(2012) Salmonella chemoreceptors McpB and McpC mediate a repellent response to L-cystine: a potential mechanism to avoid oxidative conditions
Molecular Microbiology 84:697–711.
https://doi.org/10.1111/j.1365-2958.2012.08051.x
- PubMed
- Google Scholar
(2010) Fundamental limits on the suppression of molecular fluctuations
Nature 467:174–178.
https://doi.org/10.1038/nature09333
- PubMed
- Google Scholar
(2002) Binding and diffusion of CheR molecules within a cluster of membrane receptors
Biophysical Journal 82:1809–1817.
https://doi.org/10.1016/S0006-3495(02)75531-8
- PubMed
- Google Scholar
1. Li GW
2. Burkhardt D
3. Gross C
4. Weissman JS
(2014) Quantifying absolute protein synthesis rates reveals principles underlying allocation of cellular resources
Cell 157:624–635.
https://doi.org/10.1016/j.cell.2014.02.033
- PubMed
- Google Scholar
1. Li M
2. Hazelbauer GL
(2004) Cellular stoichiometry of the components of the chemotaxis signaling complex
Journal of Bacteriology 186:3687–3694.
https://doi.org/10.1128/JB.186.12.3687-3694.2004
- PubMed
- Google Scholar
1. Li M
2. Hazelbauer GL
(2011) Core unit of chemotaxis signaling complexes
PNAS 108:9390–9395.
https://doi.org/10.1073/pnas.1104824108
- PubMed
- Google Scholar
(2004) Effect of Chemoreceptor Modification on Assembly and Activity of the Receptor-Kinase Complex in Escherichia coli
Journal of Bacteriology 186:6643–6646.
https://doi.org/10.1128/JB.186.19.6643-6646.2004
- Google Scholar
(2017) Feedback between motion and sensation provides nonlinear boost in run-and-tumble navigation
PLOS Computational Biology 13:e1005429.
https://doi.org/10.1371/journal.pcbi.1005429
- PubMed
- Google Scholar
1. Lupas A
2. Stock J
(1989)
Phosphorylation of an N-terminal regulatory domain activates the CheB methylesterase in bacterial chemotaxis

The Journal of Biological Chemistry 264:17337–17342.
- PubMed
- Google Scholar
1. Løvdok L
2. Bentele K
3. Vladimirov N
4. Müller A
5. Pop FS
6. Lebiedz D
7. Kollmann M
8. Sourjik V
(2009) Role of translational coupling in robustness of bacterial chemotaxis pathway
PLoS Biology 7:e1000171.
https://doi.org/10.1371/journal.pbio.1000171
- PubMed
- Google Scholar
(2012) Noninvasive inference of the molecular chemotactic response using bacterial trajectories
PNAS 109:1802–1807.
https://doi.org/10.1073/pnas.1116772109
- PubMed
- Google Scholar
1. Mello BA
2. Shaw L
3. Tu Y
(2004) Effects of receptor interaction in bacterial chemotaxis
Biophysical Journal 87:1578–1595.
https://doi.org/10.1529/biophysj.104.042739
- PubMed
- Google Scholar
1. Mello BA
2. Tu Y
(2005) An allosteric model for heterogeneous receptor complexes: understanding bacterial chemotaxis responses to multiple stimuli
PNAS 102:17354–17359.
https://doi.org/10.1073/pnas.0506961102
- PubMed
- Google Scholar
1. Mello BA
2. Tu Y
(2007) Effects of adaptation in maintaining high sensitivity over a wide range of backgrounds for Escherichia coli chemotaxis
Biophysical Journal 92:2329–2337.
https://doi.org/10.1529/biophysj.106.097808
- PubMed
- Google Scholar
(1973) The range of attractant concentrations for bacterial chemotaxis and the threshold and size of response over this range. Weber law and related phenomena
The Journal of General Physiology 62:203–223.
https://doi.org/10.1085/jgp.62.2.203
- PubMed
- Google Scholar
1. Min TL
2. Mears PJ
3. Golding I
4. Chemla YR
(2012) Chemotactic adaptation kinetics of individual Escherichia coli cells
PNAS 109:9869–9874.
https://doi.org/10.1073/pnas.1120218109
- PubMed
- Google Scholar
(1965) On the nature of allosteric transitions: A plausible model
Journal of Molecular Biology 12:88–118.
https://doi.org/10.1016/S0022-2836(65)80285-6
- Google Scholar
(1999) A free-energy-based stochastic simulation of the Tar receptor complex
Journal of Molecular Biology 286:1059–1074.
https://doi.org/10.1006/jmbi.1999.2535
- PubMed
- Google Scholar
(2012) Chemotactic signaling via carbohydrate phosphotransferase systems in Escherichia coli
PNAS 109:12159–12164.
https://doi.org/10.1073/pnas.1205307109
- PubMed
- Google Scholar
(2014) Imprecision of adaptation in Escherichia coli chemotaxis
PLoS One 9:e84904–84906.
https://doi.org/10.1371/journal.pone.0084904
- PubMed
- Google Scholar
1. Oleksiuk O
2. Jakovljevic V
3. Vladimirov N
4. Carvalho R
5. Paster E
6. Ryu WS
7. Meir Y
8. Wingreen NS
9. Kollmann M
10. Sourjik V
(2011) Thermal Robustness of Signaling in Bacterial Chemotaxis
Cell 145:312–321.
https://doi.org/10.1016/j.cell.2011.03.013
- Google Scholar
(2002) Regulation of noise in the expression of a single gene
Nature Genetics 31:69–73.
https://doi.org/10.1038/ng869
- Google Scholar
1. Park H
2. Pontius W
3. Guet CC
4. Marko JF
5. Emonet T
6. Cluzel P
(2010) Interdependence of behavioural variability and response to small stimuli in bacteria
Nature 468:819–823.
https://doi.org/10.1038/nature09551
- Google Scholar
(2015) Signaling and sensory adaptation in Escherichia coli chemoreceptors: 2015 update
Trends in Microbiology 23:257–266.
https://doi.org/10.1016/j.tim.2015.03.003
- PubMed
- Google Scholar
1. Paulick A
2. Jakovljevic V
3. Zhang S
4. Erickstad M
5. Groisman A
6. Meir Y
7. Ryu WS
8. Wingreen NS
9. Sourjik V
(2017) Mechanism of bidirectional thermotaxis in Escherichia coli
eLife 6:e26607.
https://doi.org/10.7554/eLife.26607
- PubMed
- Google Scholar
(2013) Adaptation dynamics in densely clustered chemoreceptors
PLoS Computational Biology 9:e1003230.
https://doi.org/10.1371/journal.pcbi.1003230
- PubMed
- Google Scholar
1. Raj A
2. van Oudenaarden A
(2008) Nature, nurture, or chance: stochastic gene expression and its consequences
Cell 135:216–226.
https://doi.org/10.1016/j.cell.2008.09.050
- PubMed
- Google Scholar
1. Rao CV
2. Wolf DM
3. Arkin AP
(2002) Control, exploitation and tolerance of intracellular noise
Nature 420:231–237.
https://doi.org/10.1038/nature01258
- PubMed
- Google Scholar
(2004) Control of stochasticity in eukaryotic gene expression
Science 304:1811–1814.
https://doi.org/10.1126/science.1098641
- PubMed
- Google Scholar
1. Rosier BT
2. Lazova MD
(2016) Dose-response analysis of chemotactic signaling response in salmonella typhimurium LT2 upon exposure to cysteine/cystine redox pair
Plos One 11:e0152815.
https://doi.org/10.1371/journal.pone.0152815
- PubMed
- Google Scholar
(2009) Automated design of synthetic ribosome binding sites to control protein expression
Nature Biotechnology 27:946–950.
https://doi.org/10.1038/nbt.1568
- PubMed
- Google Scholar
1. Salman H
2. Libchaber A
(2007) A concentration-dependent switch in the bacterial response to temperature
Nature Cell Biology 9:1098–1100.
https://doi.org/10.1038/ncb1632
- PubMed
- Google Scholar
1. Scharf BE
2. Fahrner KA
3. Turner L
4. Berg HC
(1998) Control of direction of flagellar rotation in bacterial chemotaxis
PNAS 95:201–206.
https://doi.org/10.1073/pnas.95.1.201
- PubMed
- Google Scholar
(1986) Temporal comparisons in bacterial chemotaxis
PNAS 83:8987–8991.
https://doi.org/10.1073/pnas.83.23.8987
- Google Scholar
(1982) Signal processing times in bacterial chemotaxis
Nature 296:855–857.
https://doi.org/10.1038/296855a0
- PubMed
- Google Scholar
1. Shannon CE
(1949) Communication in the Presence of Noise
Proceedings of the IRE 37:10–21.
https://doi.org/10.1109/JRPROC.1949.232969
- Google Scholar
(2003) A spatially extended stochastic model of the bacterial chemotaxis signalling pathway
Journal of Molecular Biology 329:291–309.
https://doi.org/10.1016/S0022-2836(03)00437-6
- PubMed
- Google Scholar
(2006) Monitoring bacterial chemotaxis by using bioluminescence resonance energy transfer: absence of feedback from the flagellar motors
PNAS 103:2093–2097.
https://doi.org/10.1073/pnas.0510958103
- PubMed
- Google Scholar
1. Shimizu TS
2. Tu Y
3. Berg HC
(2010) A modular gradient-sensing network for chemotaxis in Escherichia coli revealed by responses to time-varying stimuli
Molecular Systems Biology 6:382.
https://doi.org/10.1038/msb.2010.37
- PubMed
- Google Scholar
1. Silverman M
2. Simon M
(1974) Flagellar rotation and the mechanism of bacterial motility
Nature 249:73–74.
https://doi.org/10.1038/249073a0
- Google Scholar
(1985)
Multiple forms of the CheB methylesterase in bacterial chemosensing

The Journal of Biological Chemistry 260:10161–10168.
- PubMed
- Google Scholar
(2011) Dynamics of Cooperativity in Chemical Sensing among Cell-Surface Receptors
Physical Review Letters 107:178101.
https://doi.org/10.1103/PhysRevLett.107.178101
- Google Scholar
(2012) Stochastic coordination of multiple actuators reduces latency and improves chemotactic response in bacteria
PNAS 109:805–810.
https://doi.org/10.1073/pnas.1113706109
- PubMed
- Google Scholar
1. Sourjik V
2. Berg HC
(2002a) Receptor sensitivity in bacterial chemotaxis
PNAS 99:123–127.
https://doi.org/10.1073/pnas.011589998
- Google Scholar
1. Sourjik V
2. Berg HC
(2002b) Binding of the Escherichia coli response regulator CheY to its target measured in vivo by fluorescence resonance energy transfer
PNAS 99:12669–12674.
https://doi.org/10.1073/pnas.192463199
- Google Scholar
1. Sourjik V
2. Berg HC
(2004) Functional interactions between receptors in bacterial chemotaxis
Nature 428:437–441.
https://doi.org/10.1038/nature02406
- Google Scholar
1. Sourjik V
2. Vaknin A
3. Shimizu TS
4. Berg HC
(2007) In vivo measurement by FRET of pathway activity in bacterial chemotaxis
Methods in Enzymology 423:365–391.
https://doi.org/10.1016/S0076-6879(07)23017-4
- PubMed
- Google Scholar
1. Spudich JL
2. Koshland DE
(1976) Non-genetic individuality: chance in the single cell
Nature 262:467–471.
https://doi.org/10.1038/262467a0
- Google Scholar
(1990) Mutations that affect control of the methylesterase activity of CheB, a component of the chemotaxis adaptation system in Escherichia coli
Journal of Bacteriology 172:3388–3399.
https://doi.org/10.1128/jb.172.6.3388-3399.1990
- PubMed
- Google Scholar
1. Stewart RC
(1993)
Activating and inhibitory mutations in the regulatory domain of CheB, the methylesterase in bacterial chemotaxis

The Journal of Biological Chemistry 268:1921–1930.
- PubMed
- Google Scholar
(2010) Spatio-temporal correlations can drastically change the response of a MAPK pathway
PNAS 107:2473–2478.
https://doi.org/10.1073/pnas.0906885107
- PubMed
- Google Scholar
1. Taylor BL
2. Koshland DE
(1975)
Electron taxis and blue light effect on bacterial chemotaxis

Journal of Bacteriology 123:557–569.
- Google Scholar
(1979)
Electron acceptor taxis and blue light effect on bacterial chemotaxis

Journal of Bacteriology 140:567–573.
- PubMed
- Google Scholar
(1986)
Kinetics of receptor modification

Journal of Biol Chemistry 261:10814–10820.
- Google Scholar
1. Tu Y
2. Grinstein G
(2005) How white noise generates power-law switching in bacterial flagellar motors
Physical Review Letters 94:208101.
https://doi.org/10.1103/PhysRevLett.94.208101
- PubMed
- Google Scholar
1. Tu Y
2. Shimizu TS
3. Berg HC
(2008) Modeling the chemotactic response of Escherichia coli to time-varying stimuli
PNAS 105:14855–14860.
https://doi.org/10.1073/pnas.0807569105
- PubMed
- Google Scholar
1. Tu Y
(2013) Quantitative modeling of bacterial chemotaxis: signal amplification and accurate adaptation
Annual Review of Biophysics 42:337–359.
https://doi.org/10.1146/annurev-biophys-083012-130358
- PubMed
- Google Scholar
1. Tyson JJ
2. Chen KC
3. Novak B
(2003) Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell
Current Opinion in Cell Biology 15:221–231.
https://doi.org/10.1016/S0955-0674(03)00017-6
- PubMed
- Google Scholar
1. Vaknin A
2. Berg HC
(2004) Single-cell FRET imaging of phosphatase activity in the Escherichia coli chemotaxis system
PNAS 101:17072–17077.
https://doi.org/10.1073/pnas.0407812101
- Google Scholar
1. Vaknin A
(2014) The dynamics in the bacterial chemosensory arrays
AIP Conference Proceedings 1610:34–40.
https://doi.org/10.1063/1.4893507
- Google Scholar
Book
1. Van Kampen NG
(1981)
Stochastic Processes in Physics and Chemistry

Elsevier Science.
- Google Scholar
(1999) Optimizing the success of random searches
Nature 401:911–914.
https://doi.org/10.1038/44831
- PubMed
- Google Scholar
1. Wadhams GH
2. Armitage JP
(2004) Making sense of it all: bacterial chemotaxis
Nature Reviews Molecular Cell Biology 5:1024–1037.
https://doi.org/10.1038/nrm1524
- PubMed
- Google Scholar
1. Waite AJ
2. Frankel NW
3. Dufour YS
4. Johnston JF
5. Long J
6. Emonet T
(2016) Non-genetic diversity modulates population performance
Molecular Systems Biology 12:895.
https://doi.org/10.15252/msb.20167044
- PubMed
- Google Scholar
1. Wolfe AJ
2. Berg HC
(1989) Migration of bacteria in semisolid agar
PNAS 86:6973–6977.
https://doi.org/10.1073/pnas.86.18.6973
- Google Scholar
(2016) The Role of Adaptation in Bacterial Speed Races
PLOS Computational Biology 12:e1004974.
https://doi.org/10.1371/journal.pcbi.1004974
- PubMed
- Google Scholar
1. Wright S
2. Walia B
3. Parkinson JS
4. Khan S
(2006) Differential activation of Escherichia coli chemoreceptors by blue-light stimuli
Journal of Bacteriology 188:3962–3971.
https://doi.org/10.1128/JB.00149-06
- PubMed
- Google Scholar
1. Yang Y
2. M Pollard A
3. Höfler C
4. Poschet G
5. Wirtz M
6. Hell R
7. Sourjik V
(2015) Relation between chemotaxis and consumption of amino acids in bacteria
Molecular Microbiology 96:1272–1282.
https://doi.org/10.1111/mmi.13006
- PubMed
- Google Scholar
1. Yi TM
2. Huang Y
3. Simon MI
4. Doyle J
(2000) Robust perfect adaptation in bacterial chemotaxis through integral feedback control
PNAS 97:4649–4653.
https://doi.org/10.1073/pnas.97.9.4649
- PubMed
- Google Scholar
1. Yoney A
2. Salman H
(2015) Precision and variability in bacterial temperature sensing
Biophysical Journal 108:2427–2436.
https://doi.org/10.1016/j.bpj.2015.04.016
- PubMed
- Google Scholar
1. Yuan J
2. Berg HC
(2013) Ultrasensitivity of an adaptive bacterial motor
Journal of Molecular Biology 425:1760–1764.
https://doi.org/10.1016/j.jmb.2013.02.016
- PubMed
- Google Scholar
1. Yuan J
2. Branch RW
3. Hosu BG
4. Berg HC
(2012) Adaptation at the output of the chemotaxis signalling pathway
Nature 484:233–236.
https://doi.org/10.1038/nature10964
- PubMed
- Google Scholar

Decision letter

Naama Barkai

Reviewing Editor; Weizmann Institute of Science, Israel

In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.

Thank you for submitting your article "Generation and attenuation of variability in a bacterial signaling network revealed by single-cell FRET" for consideration by eLife. Your article has been reviewed by three peer reviewers, and the evaluation has been overseen by a Reviewing Editor and Naama Barkai as the Senior Editor. The reviewers have opted to remain anonymous.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Summary:

The authors setup an improved in vivo FRET assay which allowed them to measure intracellular responses at the single cell level. They then applied this unique single-cell technology for studying the cell-cell variability of signaling characteristics of the E. coli chemotaxis pathway. By this, they provided convincing evidence that CheB phosphorylation plays a role in suppressing fluctuations, as suggested in previous theoretical work. further, they show that in the absence of methylation-dependent feedback, the combined kinase activity of thousands of receptors follows that of a stochastic two-state switching behavior. This new observation will likely lead to new insights on how receptor clustering affects signaling.

As you can see below, all three reviewers supported the study and would like to see if published in eLife, provided that you address the main technical comments that were raised. This includes in particular:

1) Giant FRET activity fluctuations are extraordinary claim and so require more support, at least by providing controls. Why not provide fluorescence sample movies of some individual cells and their segmentation?

2) The interpretation in terms of zeroth-order sensitivity is largely based on the author's own previous modeling. It would therefore be informative to extend the discussion and perhaps include additional papers which might not fit the same framework

3) Fitting of Hill parameters H and K from noisy data might be difficult. please discuss this as requested below.

4) Large coefficients of variation need more explanation/discussion, following the comment below.

Reviewer #1:

The aim of this paper is the predominantly experimental investigation of the variability in signaling in the E. coli chemotaxis pathway using in vivo single-cell FRET experiments. Specifically, signaling in single cells is compared with signaling in isogenetic populations. Furthermore, different mutants are considered such as cells expressing only a single receptor type, cells with modified CheB demethylation enzyme, and cells without adaptation (no CheR and CheB enzymes). The latter allows the investigation of signaling noise in absence of gene expression noise, which can be considerable as adaptation enzymes are expressed at a low level. In cells without adaptation very interesting "giant fluctuations" are observed, when the applied ligand concentration is in the sensitive regime of the receptors. Here, apparently thousands of receptors switch in their activity state synchronously. Furthermore, the previously raised idea of zeroth-order sensitivity in adaptation is further promoted, believed to explain the interesting bistable activity profile when no adaptation enzymes are around. The paper is well and clearly written, and full of nice details, and it should be interesting to a broad readership in quantitative biology and systems/synthetic biology. While I do not always fully agree with the interpretation of the results, the questions investigated are certainly well motivated and conceptually well introduced, e.g. the difference in gene and signaling noise, and also why the latter is harder to investigate.

Subsection “Diversity in the ligand response is modulated during population growth”: The extracted Hill coefficients range from approximately 2 to 20 in Figure 2B–D. A Hill coefficient of 20 would be similar to recent data on the motor bias. However, the curves shown in panels B and C show no actual data points, just the fits. Based on Endres et al., (2008) the FRET data for populations expressing receptors from a plasmid varies dramatically from day to day, and in order to extract parameters like the Hill coefficient, a principal component analysis was used, and the uncertainties of the parameters calculated. Here, are the dose-response curves for single cells based on a single time course (a la Figure 2A) or is each single cell measured multiple times? If measured only once the curve might be very noisy, and even if measured multiple times, the activity may also vary drastically as shown in Figure 5B. How can one reliably estimate Hill coefficients? Certainly, the uncertainty of the parameters should also be estimated. In Figure 2—figure supplement 2 the experimental errors are estimated but I do not fully understand what this figure really shows (basically distributions of the data values are provided but that can already be seen by the scatter plots). Ideally something like the PCA or a Bayesian framework should be applied.

The paper demonstrates that without fully functional CheB phosphorylation feedback, the receptor activity can be bimodal (Figure 3 and text insubsection “CheB phosphorylation feedback attenuates cell-to-cell variability”). To interpret this, the authors reiterate the previous suggestion of zeroth-order sensitivity in adaptation, where enzymes CheR and CheB work at saturation and the activity is highly sensitive to an imbalance in the enzymes. This may lead to strongly fluctuating adaptation times, allowing cells to perform long runs (good in patchy environments, subsection “Diversity in temporal noise: bet-hedging across exploration and exploitation strategies”). Although this idea is quite neat, I have trouble with it. To me, adding noise into a sensory system seems to contradict what is known about other sensory systems. While the authors then say that the phosphorylation feedback turns the bistable activity distribution into a monostable activity distribution, I still have trouble buying the zeroth-order sensitivity argument. In particular, Figure 4 in Clausznitzer et al., (2010) specifically addressed this issue based on FRET data, and no evidence for zeroth-order sensitivity was found (even when CheB phosphorylation is added).

The paper further demonstrates that without adaptation, there can be giant fluctuations in the receptor activity (Figure 5 and text in subsection “Receptor-kinase fluctuations in the absence of adaptation reveal two-level switching”), potentially demonstrating the coordinated switching of thousands of receptors (subsection “Receptor-kinase fluctuations in the absence of adaptation reveal two-level switching”, and subsection “Giant fluctuations and digital switching in adaptation deficient cells”). This is fascinating and unexpected as individual receptor complexes might switch between inactive and active states, but not all complexes in the whole cell together. Can the authors rule out that cells without fully functional CheB and cells with Tsr(QEQE) without adaptation are not in a highly active state, and, while immobilized, tumble a lot, leading to errors in cell segmentation and activity determination?

Reviewer #2:

This manuscript by Keegstra et al. uses improved FRET measurements combined with standard microscopy to quantify various aspects of the chemotaxis systems in E. coli cells.

I am not an expert in chemotaxis and therefore defer to reviewers more familiar with that field to assess the novelty of the specific claims. Given the sheer number of results presented it was not possible for me to go back to previous works to judge that in any meaningful way. However, given the authors' great expertise in the area, and the impressive quantity of high-quality work presented, I strongly suspect the paper will be of great interest to that field. I do have some broader concerns but overall, I think the paper still makes a nice contribution and I would recommend it for publication in eLife.

My broader concern is unfortunately hard to address. To my taste the authors try to do way too much in one paper. I would have preferred to read a story that drilled down deeper into one or two of the many effects studied. To me the manuscript comes across as a survey of effects, with a somewhat meandering narrative. With a little more work this could likely have been three high-quality papers, each focused on a more specific question. However, it would be unreasonable to expect the authors to address that issue at this stage. They chose to produce a different type of paper, and though I believe that makes it harder for the general reader to take home a clear message (beyond the rather non-distinct message that there is noise in protein networks etc.), it will likely still be important. That said, if in the revisions the authors find that some parts are dispensible, I would encourage them to take those parts out and focus more on the core results. At the very least they may want to tighten the discussion.

Other concerns:

1) It seems the authors went through a substantial effort to optimize the FRET pair, but I wonder if they considered the artefactual effects that can come from the slow and distributed maturation of their mRFP? Even the half-way time of maturation for every red protein I have seen has been longer than 30 minutes. This could have many effects on the measurements. For example, only a fraction of FRET pairs will be active at any given time, that fraction will depend on the history of expression dynamics, and because maturation is distributed, the effect of extrinsic noises can be underestimated because the maturation step will serve as a time-averaging step, much like a low-pass filter. Though the authors obviously cannot be expected to repeat the results with a different FRET pair, this should be discussed.

2) Related to 1, I would like to see a more thorough discussion of potential experimental artefacts. The fact that the average of their single cell data agree with population measurements does not mean that the fluctuations around the average can be trusted. Because this is a novel method I would like to see at least one paragraph describing the controls made to ensure that the noise is due to the biology, and not to imaging (heterogeneity in the evenness of excitation, camera noise etc.), to cell handling (that conditions are uniform in space and time etc.) or to reporter artefacts (that the FRET pair does not affect the circuit's behavior). Only once these controls are completed would it make sense to consider the biology. I do not believe this is a great problem because so much of the data makes sense, but it should still be described for a novel method. On a minor note it should also be pointed out in the main text (my apologies if I just missed it) if the measurements are for total fluorescence or if the authors divide the intensity by the area or volume of the cell. In the former case much of the heterogeneity could come from the differences in cell sizes in a population, so I suspect the authors normalize by cell size.

3) It is striking that the noise is so high in general. The authors compare their results to the extrinsic noise floor of CV=30% in Taniguchi et al. This paragraph needs to be fixed or removed though. The Taniguchi paper considered fluctuations in a cloning strain of E. coli, under great starvation conditions, in an unestablished microfluidic device where cells grew twice as slowly as in batch culture with the same medium, and possibly displayed great heterogeneity in growth. When the same protein fusions are imaged under more uniform conditions without using the cloning strain, the total CV drops to <10% in many cases, and the extrinsic part seems to be less than 5%. This pattern has been observed across many labs, including the intrinsic/extrinsic paper by Elowitz and Leibler who reported extrinsic noise levels as low as 5%.

In particular I would like to see more of a discussion for the very high CV observed in the expression levels of CheB, with CVs of 80-90%. Can that be explained extremely weak transcription and strong translation, or do the authors suspect some other mechanism? Can the authors observe noise levels as low as 10% for other genes with the same set-up, to make sure this is not due to the imaging set-up somehow? I noticed the OD was mid-exponential, close to the diaxic shift where some cells start changing gene expression patterns. Could that be the explanation?

4). For the residence time distributions, I would like to see the authors spend more time to confirm that the way residence times are called does not affect the results. I would also make a bigger point of the fact that the residence times actually seem to fit exponential distributions, rather than merely using exponentials to get at the rate constant. For exponentials the

Slightly related to this issue, for other waiting time distributions they see a CV of 20% and call that broad, though the switching times at the end supposedly have CVs of 1, if they are exponential. Though the first waiting times are not from two-state models, it is quite difficult to reduce the heterogeneity in timing even in multi-state switching.

Reviewer #3:

It was a pleasure to read the manuscript by Keegstra el al. on "Generation and attenuation of.…". Indeed, there is nothing to dislike about this paper.

By improving an in vivo FRET assay, which was developed and used to measure the response of a population of cells to external stimuli, the Shimizu group has now for the first time (in my knowledge) been able to measure these intracellular responses at the single cell level. That's a significant achievement all by itself. This unique single-cell measurement, together with existing modeling approach, allows the authors to quantify the cell-cell variability of the intracellular dynamics (response and adaptation) as well as the key components (e.g., Tar/Tsr ratio) in the E. coli chemotaxis pathway during different stages (phases) of the population growth process from the response measurements of individual cells. The new technique, single cell FRET, has already shed some new lights onto an old problem/puzzle. In particular, it is shown quite convincingly here that the role of the CheB phosphorylation is to suppress fluctuations in the response regulator as suggested by previous theoretical work. Finally, what is most exciting about the present work is that it revealed something quite unexpected, namely, for at least some of the CheRB- cells (without adaptation) the kinase activity of the entire cell (with thousands of receptors) follows that of a stochastic two-state switching behavior. This new observation will likely lead to new insights on how receptor clustering affects signaling.

The paper is well written. It contains a lot of information, yet it is written in a way easy for the readers to get the main ideas. The paper should be published after the authors consider a few questions/comments that came up while reading the manuscript:

1) Different attractants are used in this paper, e.g. MeAsp for wt cells used in Figure 1 and L-Serine for CheRB- mutants shown in Figure 2. Any reason for doing that, i.e., not using both like what's done in Sourjik and Berg (2004)? From the response data to L-Serine and the model parameters inferred, the response to MeAsp may be predicted, which would be a test for the theoretical model used here.

2) The values of K and H for different individual cells, as shown in Figure 2D, are quite interesting. For different cells and cells in different growth phase, the cooperativity H and the inverse sensitivity K seem to collapse onto a single curve. Is there a reason for that? Furthermore, in a previous work ("Lateral density of receptor arrays in the membrane plane influences sensitivity of the E. coli chemotaxis response", C. M. Khursigara et al., 2011), it was found that while cooperativity H is higher for cells grown in H1 medium than that of cells grown in TB, its K value is also larger. How does the result shown here relate to that reported in this previous observation?

3) In Figure 4A, the blue line shows a very small fluctuation for the ChRB- mutant in comparison with the wt cell (red line). It is a bit confusing in light of the following Figure 5 which shows the giant fluctuation of the CheRB- mutants. The reason for this difference needs to be explained.

4) It needs to be pointed out that the Ornstein-Uhlenbeck equation for kinase activity (Eq. (1) in this manuscript) was first proposed in Tu & Grinstein, (2005), where a 20% fluctuation was given as a lower bound for observing 1-decade of power law CCW duration time distribution. This lower bound is certainly satisfied by the new observation presented in this paper.

https://doi.org/10.7554/eLife.27455.037

Author response

Summary:

The authors setup an improved in vivo FRET assay which allowed them to measure intracellular responses at the single cell level. They then applied this unique single-cell technology for studying the cell-cell variability of signaling characteristics of the E. coli chemotaxis pathway. By this, they provided convincing evidence that CheB phosphorylation plays a role in suppressing fluctuations, as suggested in previous theoretical work. further, they show that in the absence of methylation-dependent feedback, the combined kinase activity of thousands of receptors follows that of a stochastic two-state switching behavior. This new observation will likely lead to new insights on how receptor clustering affects signaling.

We thank reviewers #1-3 and the reviewing editor for their time and helpful comments to our manuscript. Before addressing each comment individually, we summarize here the main changes to our manuscript. In response to reviewers’ comments we have made substantial edits to the text (at locations specified within the point-by-point responses below), changes to two of the main figures (Figure 2 and Figure 5), added three new supplementary figures (Figure 1—figure supplement 3, Figure 2—figure supplement 1 and Figure 3—figure supplement 5) and added new panels to two existing supplementary figures (Figure 1—figure supplement 1 and Figure 4—figure supplement 3). Regarding, reviewer #2’s comment that the overall presentation / clarity of narrative could be improved, we have opted not to drastically modify the structure of the text, but have implemented a change in the title of the paper that we feel would help the reader in approaching the rather diverse body of results reported within this paper.

As you can see below, all three reviewers supported the study and would like to see if published in eLife, provided that you address the main technical comments that were raised. This includes in particular:

1) Giant FRET activity fluctuations are extraordinary claim and so require more support, at least by providing controls. Why not provide fluorescence sample movies of some individual cells and their segmentation?

We thank the editor for this suggestion. We have added Video 1 which shows fluorescence image sequences for segmented regions of three example cells demonstrating giant step-like fluctuations, together with a synchronously animated time series of the donor, acceptor and ratiometric FRET signal. The image sequences clearly demonstrate that the cells remain immobile during these fluctuations, directly addressing reviewer #1’s concern that the fluctuations might be due to cell movement. We note that within the image sequences, the fluorescence intensity changes appear rather subtle (which is expected for FRET, which typically accounts for a small fraction of total fluorescence intensity), but the time series plots clearly demonstrate that the step-like intensity changes far exceed shot noise levels and furthermore the changes in the donor and acceptor intensities are anti-parallel, which is characteristic of bona fide changes in FRET.

2) The interpretation in terms of zeroth-order sensitivity is largely based on the author's own previous modeling. It would therefore be informative to extend the discussion and perhaps include additional papers which might not fit the same framework

We agree that zero-order ultrasensitivity is not the only possible explanation for the observed bimodality in the steady-state kinase activity (a₀). But it is a particularly simple mechanism capable of generating the observed phenomenology, and thus deserves serious consideration, if as nothing more than a falsifiable hypothesis for more detailed future investigations. Nevertheless, we agree that our presentation could benefit from further clarification of this point, and we have implemented a number of improvements to this end. In the Results section, we have modified the narrative to more generically introduce the nonlinear mapping between the [R]/[B] ratio and the steady-state activity a₀, prior to introducing the possible models that could account for that mapping, including ultrasensitivity (subsection “CheB phosphorylation feedback attenuates cell-to-cell variability”). In the Discussion section, we have added a paragraph discussing the implications and assumptions of the zero-order model, together with other models of nonlinear adaptation kinetics in the literature. In addition, we have furnished a new supplementary figure (Figure 5—figure supplement 4) which demonstrates that models with linear or supralinear dependence of adaptation kinetics on kinase activity (a) that have been suggested in the literature cannot on their own provide an explanation for the bimodality in steady-state activity (a₀), while a model with sublinear dependence due to Michalis-Menten kinetics (which can lead to zero-order ultrasensitivity in appropriate parameter regimes) can explain such behavior without invoking any additional assumptions. We once again emphasize that our intention is not to claim that ultrasensitivity is the only possible explanation for the bimodality in a₀, but rather to provide a mechanistic perspective amenable to refinement in future studies.

3) Fitting of Hill parameters H and K from noisy data might be difficult. please discuss this as requested below.

We agree that the reader would benefit from a clearer view of the quality of dose-response data and fitting uncertainties, and thank the editor for this suggestion. We have added a more detailed analysis of Hill parameter estimation uncertainty (including parameter covariance) with a new Figure supplement to Figure 2 and have also modified Figure 2 itself to show representative example of fits to dose response curves.

4) Large coefficients of variation need more explanation/discussion, following the comment below.

We agree that the variability is very large over all, and that the reader would benefit from further comments on this point. To address this, we have added edits to the text (at locations indicated in point-by-point responses below), and in addition furnished a new table within the main text (Table 2), which summarizes the coefficients of variation (CV) of various signaling parameters measured in this work, as well as the temporal variability (η), in a manner that facilitates comparison across genotypes and (where available) also to previous estimates from the literature. We have listed each reported CV and show that we have always tried to contrast surprisingly high CV’s with alternative measurements or genotypes in which the CV in the parameter is lower.

Reviewer #1:

The aim of this paper is the predominantly experimental investigation of the variability in signaling in the E. coli chemotaxis pathway using in vivo single-cell FRET experiments. Specifically, signaling in single cells is compared with signaling in isogenetic populations. Furthermore, different mutants are considered such as cells expressing only a single receptor type, cells with modified CheB demethylation enzyme, and cells without adaptation (no CheR and CheB enzymes). The latter allows the investigation of signaling noise in absence of gene expression noise, which can be considerable as adaptation enzymes are expressed at a low level. In cells without adaptation very interesting "giant fluctuations" are observed, when the applied ligand concentration is in the sensitive regime of the receptors. Here, apparently thousands of receptors switch in their activity state synchronously. Furthermore, the previously raised idea of zeroth-order sensitivity in adaptation is further promoted, believed to explain the interesting bistable activity profile when no adaptation enzymes are around. The paper is well and clearly written, and full of nice details, and it should be interesting to a broad readership in quantitative biology and systems/synthetic biology. While I do not always fully agree with the interpretation of the results, the questions investigated are certainly well motivated and conceptually well introduced, e.g. the difference in gene and signaling noise, and also why the latter is harder to investigate.

Subsection “Diversity in the ligand response is modulated during population growth”: The extracted Hill coefficients range from approximately 2 to 20 in Figure 2B–D. A Hill coefficient of 20 would be similar to recent data on the motor bias. However, the curves shown in panels B and C show no actual data points, just the fits. Based on Endres et al., (2008) the FRET data for populations expressing receptors from a plasmid varies dramatically from day to day, and in order to extract parameters like the Hill coefficient, a principal component analysis was used, and the uncertainties of the parameters calculated. Here, are the dose-response curves for single cells based on a single time course (a la Figure 2A) or is each single cell measured multiple times? If measured only once the curve might be very noisy, and even if measured multiple times, the activity may also vary drastically as shown in Figure 5B. How can one reliably estimate Hill coefficients? Certainly, the uncertainty of the parameters should also be estimated. In Figure 2—figure supplement 2 the experimental errors are estimated but I do not fully understand what this figure really shows (basically distributions of the data values are provided but that can already be seen by the scatter plots). Ideally something like the PCA or a Bayesian framework should be applied.

We thank the referee for this constructive criticism. To make the best use of the stringent photon budget of single-cell FRET experiments, we are deliberately operating near the low signal-to-noise limit, and we couldn’t agree more that fits of nonlinear functions to noisy data need to be interpreted with care. The supplementary figure referred to by the reviewer (formerly Figure 2—figure supplement 2, now Figure 2—figure supplement 3) was indeed provided to address such concerns, and compares the variability in the fitted parameters for experimental data against the that for simulated data in which the only source of variability is added noise representing experimental (shot) noise. More specifically, the grey points in those scatter plots were obtained by adding to the population-averaged dose response curve Gaussian noise of the same magnitude of experimental shot noise and applying the same data fitting procedure applied to the experimental data. In general, the variability of fit parameters for the experimental data exceeds that of the simulated data. The sole exception is the parameter H in Tsr+ cells (Figure 2—figure supplement 3D), for which the simulations suggest the experimentally observed variability could be dominated by experimental noise.

To better convey the care we have taken in the interpretation of these single-cell dose-response data, and to provide the reader with a means of assessing the fit quality, we have implemented the following improvements:

We have modified Figure 2 to include example fits of the hill function to the single-cell dose response curves. The finite photon budget of single-cell FRET experiments renders multiple dose response measurements on the same set of cells challenging, but at each stimulus the response is averaged over 10-20 data points to average out shot noise. The example fits show that the fit quality is very high, and bad fits are excluded from the analysis.

We have added a supplementary figure (Figure 2—figure supplement 1) showing the parameter uncertainty by decomposing the covariance matrix of the fit of each individual curve into its eigenvectors, and used these to draw error basins in K-H space. In this figure, it is shown that indeed the exact value of H becomes less constrained when the number of points along the decaying part of the activity to [L] decreases, but the values of some cells definitely exceed 10.

Regarding how temporal fluctuations of the type depicted in Figure 5 might affect dose-response measurements of Tsr+ cells, we do not expect a very strong effect for two reasons. First, the timescale of fluctuations we observed in CheRB- cells are very slow (of order 100 s), whereas the ligand-exposure time in our donse-response measurements are relatively short (10-20 s). Temporal fluctuations within the ligand-exposure interval are thus very small. Second, the largest temporal fluctuations are observed in cells with the steepest dose-response curves (expressing Tsr as the sole chemoreceptor), but the large fluctuations are observed only within the very narrow range of ligand concentration corresponding to the dose-response transient (i.e. where activity is neither zero or one). This narrowness of the response regime dominates Hill fits for this genotype, and activity fluctuations within this narrow regime can only mildly affect the fit parameters.

The reviewer also raises a valid concern regarding day-to-day variation, but this is actually much less of an issue for our experiment and analysis. One important difference with the experiments performed in this work and Endres et al., (2008) is that the variability in Figure 2 does not include day-to-day variability because all cells are measured in the same experiment. Furthermore, much of the variability in Endres, 2008 is believed to originate from copy number variation of plasmids from which receptors were expressed, whereas the largest dose-response variability observed in our experiments was in cells with a WT receptor complement, which express receptors from their native chromosomal locus. In our experiments on Tsr+ cells, the receptors were expressed from a plasmid, but in those populations we found cell-to-cell variability to be much lower.

The paper demonstrates that without fully functional CheB phosphorylation feedback, the receptor activity can be bimodal (Figure 3 and text insubsection “CheB phosphorylation feedback attenuates cell-to-cell variability”). To interpret this, the authors reiterate the previous suggestion of zeroth-order sensitivity in adaptation, where enzymes CheR and CheB work at saturation and the activity is highly sensitive to an imbalance in the enzymes. This may lead to strongly fluctuating adaptation times, allowing cells to perform long runs (good in patchy environments, subsection “Diversity in temporal noise: bet-hedging across exploration and exploitation strategies”). Although this idea is quite neat, I have trouble with it. To me, adding noise into a sensory system seems to contradict what is known about other sensory systems.

We agree with the reviewer that generating noise in a sensory system is at first counterintuitive, given that noise in communication channels do generally degrade information transfer. However, while it is possible (and can be meaningful) to view the bacterial chemotaxis signaling pathway as a sensory communication channel, it clearly functions not only to transduce information, but also to modulate motile behavior. Thus, it functions not only as a sensory system but also a locomotor control circuit. This pleiotropy demands that we consider its design in a somewhat different light from the more dedicated sensory systems (typically from more complex organisms) on which we surmise the reviewer’s opinion might be founded.

Viewed as a control circuit implementing a random-walk search strategy, it is entirely natural to expect that selection acts on behavioral statistics, and by extension, also on the intracellular stochastic processes that generate those statistics. The idea that temporal noise in the intracellular CheY-P signal can transform E. coli’s run-and-tumble statistics from a Brownian walk into a Levy walk is now very well established with both experimental and theoretical support (Korobkova et al., 2004, Tu & Grinstein, 2005, Emonet & Cluzel, 2008, Matthäus et al., 2011, Zaburdaev et al., 2015), and in addition, it has also been shown theoretically that a finite amount of temporal noise can enhance chemotactic responses in shallow spatial gradients (Sneddon et al., 2012, Flores et al., 2012).

Yet, there must also be ecological contexts in which the reviewer’s opinion/intuition is correct, that is, noise is clearly not always beneficial. Indeed, the same studies cited above (Sneddon et al., 2012, Flores et al., 2012) demonstrated that in steeper gradients, chemotactic performance monotonically deteriorates with noise. Our finding in the present work that the amplitude of temporal noise (η) is highly variable from cell to cell in an isogenic population (CV(η)≈0.44) thus raises the compelling possibility that E. coli hedges its bets by phenotypically diversifying into subpopulations that excel at exploratory behavior (driven by large signal fluctuations) and those that excel in more exploitative behavior (with lower signal fluctuations).

To better convey to the reader these concepts, which can at first be counter-intuitive, we have added the following passage to the Discussion section:

While the authors then say that the phosphorylation feedback turns the bistable activity distribution into a monostable activity distribution, I still have trouble buying the zeroth-order sensitivity argument. In particular, Figure 4 in Clausznitzer et al., (2010) specifically addressed this issue based on FRET data, and no evidence for zeroth-order sensitivity was found (even when CheB phosphorylation is added).

While we agree with the reviewer that Figure 4 in Clausznitzer et al., (2010) shows no evidence for zeroth-order sensitivity, it shows no evidence against zero-order ultrasensitivity either. This is further substantiated in the supporting information of the same paper where the authors show that a model with ultrasensitivity and CheB-P feedback fits the data in Figure 4A nearly as well (χ2=0.0025) as a model without ultrasensitivity (χ2=0.0022). Clonal populations of E. coli exhibit substantial cell-to-cell variability in their chemotaxis system (e.g. Spudish and Koshland, 1976; Park et al., 2010; Dufour et al., 2016; and this manuscript). Given that ultrasensitivity manifests itself mostly in the nonlinear adaptation kinetics of single cells, it is not surprising that it is difficult to assess the presence of this effect from FRET measurements averaged over several hundred cells (Figure 4 in Clausznitzer et al.). Note however that even at the population level, temporal ramp-response data (Shimizu et al., 2010) were shown to fit well Michaelis-Menten adaptation kinetics, a functional form that tends to produce fluctuations when the enzymes work at or near saturation.

The main point of Figure 4 from Clausznitzer et al. is not about ultrasensitivity but about the nonlinear activation of CheB, which becomes suddenly very high at high level of fractional kinase activity (a > 0.7). Clausznitzer et al. proposed that even though there is no known molecular mechanism for this effect, one could model it by assuming that the demethylation rate exhibits a supralinear (cubic) dependency with respect to the fractional kinase activity rather than the quadratic dependency that comes from the CheB-P feedback. Following the reviewer’s suggestion we examined (new Figure 3—Figure supplement 5) how the steady-state activity (a₀) depends on the CheR/CheB ratio for both sublinear kinetic models (i.e. Michaelis-Menten (de)methylation rates, which can lead to ultrasensitivity) and for the supralinear kinetic models studied by Clausznitzer et al., where the enzyme kinetics are assumed to operate at kinetic order > 1. In both cases we consider what happens when the CheB phosphorylation feedback is present (quadratic or cubic dependencies of the demethylation rate on a) or not. In the presence of CheB feedback, the model with Michaelis-Menten rates the steady state activity a0 is more sensitive to cell-to-cell variations in [R]/[B], than the other models as expected. However, when the CheB feedback is removed, the ultrasensitive model shows an increased sensitivity of a₀ to [R]/[B], as seen in our data (CheB-D56E mutant), whereas the model with enzymes operating in the linear regime exhibit a reduced sensitivity of a0 to [R]/[B], independently of the parameter values chosen. To explain bimodality in activity levels due to loss of phosphorylation feedback, a much steeper dependence of a₀ to [R]/[B] is required.

This being said, we do acknowledge that the model with saturated Michaelis-Menten kinetics is a coarse-grained model that can be further refined, especially concerning the interaction of the methylation enzymes with the receptor tether. Also, we do not rule out alternative explanations for bimodality in a₀. Therefore, we have added the following paragraph in the Discussion section:

By analyzing simplified models of adaptation kinetics, we found that a bimodal 𝑃(a₀) could occur in the absence of phosphorylation feedback if the enzyme kinetics of CheR and CheB depend sublinearly on the activity 𝑎 of their receptor substrates. As a limiting case, when both enzymes work at or near saturation, this model leads to zero-order ultrasensitivity (Goldbeter and Koshland, 1981; Emonet and Cluzel, 2008), which could act as a strongly non-linear transfer function 𝑓([R]/[B]) that converts a unimodal distribution 𝑃([R]/[B]) into a bimodal 𝑃(𝑎0). We note that ultrasensitivity due to sublinear (Michaelis-Menten) enzyme kinetics is by no means the only possible explanation for the observed bimodality in 𝑃(a₀). Any mechanism that renders f([R]/[B]) a strongly nonlinear (sigmoidal) function could lead to the same effect. The merit of the sublinear kinetic (ultrasensitivity) model is in its simplicity, but it is worth noting that reality is likely to be more complex due to, for example, effects of spatial organization. It is known that both CheR and CheB interact with chemoreceptors not only at their substrate modification residues, but also with a second binding site on a flexible tether at the receptor C-terminus. Such bivalent interactions with the receptor array could affect the movement of these enzymes across the receptor lattice (Levin et al., 2002), and such movements could shift the balance between processivity and distributivity of enzyme activity on their substrate receptors (Pontius et al., 2013), which could in turn attenuate or enhance the nonlinearity in the relationship f([R]/[B]) be- tween the enzyme expression ratio [R]/[B] and the steady-state activity a₀ of their substrate receptors (Takahashi et al., 2010).

The paper further demonstrates that without adaptation, there can be giant fluctuations in the receptor activity (Figure 5 and text in subsection “Receptor-kinase fluctuations in the absence of adaptation reveal two-level switching”), potentially demonstrating the coordinated switching of thousands of receptors (subsection “Receptor-kinase fluctuations in the absence of adaptation reveal two-level switching”, and subsection “Giant fluctuations and digital switching in adaptation deficient cells”). This is fascinating and unexpected as individual receptor complexes might switch between inactive and active states, but not all complexes in the whole cell together. Can the authors rule out that cells without fully functional CheB and cells with Tsr(QEQE) without adaptation are not in a highly active state, and, while immobilized, tumble a lot, leading to errors in cell segmentation and activity determination?

We appreciate this concern, which seems to be shared by reviewer 2, and in the Results section we emphasize that ratiometric FRET measurements involve an anti-parallel response in the donor and acceptor channels, which can help to discriminate true changes in FRET from various artefacts that can cause changes in the donor/acceptor ratio. We have also added Video 1 which shows cells that do not move during image acquisition. Cells with small response amplitudes, which is a strong indication of low kinase activity but is only a small fraction of the population, are not included in the switching analysis. The response amplitudes of cells with CheB mutants is on average not different from WT CheB, and cells with a very low steady-state activity manifest themselves by barely responding to the addition of attractant, but with a large response to the removal of ligand.

Reviewer #2:

This manuscript by Keegstra et al. uses improved FRET measurements combined with standard microscopy to quantify various aspects of the chemotaxis systems in E. coli cells.

I am not an expert in chemotaxis and therefore defer to reviewers more familiar with that field to assess the novelty of the specific claims. Given the sheer number of results presented it was not possible for me to go back to previous works to judge that in any meaningful way. However, given the authors' great expertise in the area, and the impressive quantity of high-quality work presented, I strongly suspect the paper will be of great interest to that field. I do have some broader concerns but overall, I think the paper still makes a nice contribution and I would recommend it for publication in eLife.

My broader concern is unfortunately hard to address. To my taste the authors try to do way too much in one paper. I would have preferred to read a story that drilled down deeper into one or two of the many effects studied. To me the manuscript comes across as a survey of effects, with a somewhat meandering narrative. With a little more work this could likely have been three high-quality papers, each focused on a more specific question. However, it would be unreasonable to expect the authors to address that issue at this stage. They chose to produce a different type of paper, and though I believe that makes it harder for the general reader to take home a clear message (beyond the rather non-distinct message that there is noise in protein networks etc.), it will likely still be important. That said, if in the revisions the authors find that some parts are dispensible, I would encourage them to take those parts out and focus more on the core results. At the very least they may want to tighten the discussion.

We agree with the reviewer that this paper contains a lot of information. However, we feel that all the experimental results shown are necessary to convey the message that signaling variability in E. coli chemotaxis is large and pervasive and that a certain completeness in measured signaling parameters is of added value. However, we have also critically examined the paper text and have almost completely removed two paragraphs in the Discussion Section, which we considered interesting but optional speculation.

Also, to focus the reader on the core results of the paper we have changed the title from “Generation and attenuation of signaling variability in a bacterial signal network (…)” to “Phenotypic diversity and temporal variability in a bacterial signaling network (…)”. We feel that this change to the title goes some way in addressing the reviewer’s concern that the narrative is somewhat meandering, by clarifying from the outset that we have studied here multiple types of variability that fall into two broad classes: (i) ‘phenotypic diversity’, differences across cells in parameters that persist over the cells’ generation time, due largely to gene expression fluctuations, and (ii) temporal variability within each individual cell, due to factors other than gene expression such as protein-protein interactions.

1) It seems the authors went through a substantial effort to optimize the FRET pair, but I wonder if they considered the artefactual effects that can come from the slow and distributed maturation of their mRFP? Even the half-way time of maturation for every red protein I have seen has been longer than 30 minutes. This could have many effects on the measurements. For example, only a fraction of FRET pairs will be active at any given time, that fraction will depend on the history of expression dynamics, and because maturation is distributed, the effect of extrinsic noises can be underestimated because the maturation step will serve as a time-averaging step, much like a low-pass filter. Though the authors obviously cannot be expected to repeat the results with a different FRET pair, this should be discussed.

[We thank the reviewer for raising this issue and we believe confusion might arise from] intuitions from measurements of gene-regulatory circuit dynamics, on which most experimental studies on cellular noise and variability have focused. In such experiments, the dynamics of the circuit often play out on timescales comparable to the maturation time and the signal that provides the circuit dynamics are changes in protein abundance, measured by fluorescence intensity. The intrinsic response time of the signal in such an experiment is limited by the turnover kinetics of the fluorescent species, and a delay in maturation kinetics can influence the dynamics and distributions to be smeared out, as described by the reviewer. However, our FRET experiment on the bacterial chemotaxis system differs from those experiments in the sense that the ratiometric FRET signal measures protein interaction, not abundance, and is far less sensitive to changes in the copy number (due e.g. to maturation) of fluorophores.

More concretely, in our FRET analysis of the chemotaxis network, dynamic changes in intensity due to maturation cannot be strictly excluded, but its effects are negligible in our analysis for three reasons:

(a) Small amplitude: under our experimental conditions, its effects on the net fluorescence intensity drift (and hence also the FRET signal), are very small compared to that of photobleaching.

(b) Timescale separation: the timescales involved in the fluorescence intensity drifts (including both bleaching and maturation) are much longer (> 1hr) than the longest timescales (~400s) we have studied in this paper.

(c) Further attenuation in data analysis: the fluorescence-intensity drift correction we apply in our data analysis means that effects of processes contributing to drift (bleaching, maturation etc) on both the intensity and dynamics of signals are effectively canceled, up to the accuracy of the fits used in the correction.

2) Related to 1, I would like to see a more thorough discussion of potential experimental artefacts. The fact that the average of their single cell data agree with population measurements does not mean that the fluctuations around the average can be trusted. Because this is a novel method I would like to see at least one paragraph describing the controls made to ensure that the noise is due to the biology, and not to imaging (heterogeneity in the evenness of excitation, camera noise etc.), to cell handling (that conditions are uniform in space and time etc.) or to reporter artefacts (that the FRET pair does not affect the circuit's behavior). Only once these controls are completed would it make sense to consider the biology. I do not believe this is a great problem because so much of the data makes sense, but it should still be described for a novel method. On a minor note it should also be pointed out in the main text (my apologies if I just missed it) if the measurements are for total fluorescence or if the authors divide the intensity by the area or volume of the cell. In the former case much of the heterogeneity could come from the differences in cell sizes in a population, so I suspect the authors normalize by cell size.

We appreciate the reviewer’s rigor concerning this point. We agree that the reader benefits from a more elaborate discussion of potential artefacts. Hence to address these concerns we have changed a paragraph in the Results section to explain more clearly how the FRET experiment is performed, and in which we stress the anti-parallel response signature of the ratiometric FRET imaging:

“A field of E. coli cells expressing this FRET pair were immobilized on a glass surface imaged in two fluorescence channels, and segmented offline to obtain fluorescence intensities of donor and acceptor. From the fluorescence ratio FRET time series for each cell in the field of view (see Materials and methods section) can be computed, after dividing out the decay (Figure 1—figure supplement 1) in each channel due to bleaching. Ratiometric FRET provides an anti-parallel response signature and confers robustness to parallel fluctuations that affect both fluorescent channels, such as differences in absolute fluorescence intensity due to inhomogeneous illumination and differences in cell size.”

We have also changed and added the following figures to show that the cellular variability cannot be explained by experimental parameters and that the FRET protein fusions generate a fully functional genotype:

A supplementary figure to Figure 1 (Figure 1—figure supplement 3) which shows the correlations between the signaling parameters (parameters recovery time, steady-state activity and adaptation precision) and experimental parameters. It clearly shows the variability in signaling cannot be explained by imaging parameters such as illumination intensity or fluorophore emission. The only significant correlation we found between fluorophore intensity and recovery time is weak (-0.3) and the recovery time does not correlate significantly with the distance from the highest intensity on the sample plane.

An extra panel to Figure 1—figure supplement 1, which shows that cells expressing the FRET plasmid are fully functional in chemotaxis. The fact that their collective behavior agrees well with wild-type, provides also some evidence that not only the means of certain signaling parameters can be trusted, but also the distributions of those parameters from cell to cell. We do note that this functional phenotype is a sufficient but not necessary condition for ruling out fluorophore interference with the kinase activity, since downstream artefacts cannot disqualify the measurement of upstream pathway activity.

We have added panels to show how reproducible the signaling parameter distributions are, for Figure 1—figure supplement3, Figure 2—figure supplement 1 and Figure 4—figure supplement 3. Generally, they show very high agreement between independent experiments.

Finally, in the Discussion section we have added some more general statements regarding the strength and limitations of the method:

"The anti-parallel response signature of ratiometric FRET provides a good way to discriminate genuine FRET changes from imaging artifacts. As in population-level FRET, single-cell FRET is most easily applied to study large and rapid changes in signaling (e.g. response to step stimuli), but we have shown that with careful correction of drifts in the signal level (primarily due to bleaching), it can be applied effectively to measure more subtle changes in signaling over extended times, including steady-state fluctuations. Nevertheless, absolute quantification of single-cell variability remains challenging, since any experimental noise source can potentially contribute to the observed variability. Although we have not undertaken here a comprehensive survey of experimental noise sources for single-cell FRET, our results demonstrate meaningful differences in variability across cells measured under identical experimental conditions. The experimental duration for single-cell FRET is photon-limited, meaning that optimal experimental strategies must carefully negotiate with a finite photon budget an inherent trade-off between measurement duration, temporal resolution, and signal-to noise ratio. Future improvements of donor/acceptor fluorophores (in parameters such as photostability, brightness, maturation, as well as FRET efficiency) could enhance the effective photon budget, and hence the power of the experiment.

3) It is striking that the noise is so high in general. The authors compare their results to the extrinsic noise floor of CV=30% in Taniguchi et al. This paragraph needs to be fixed or removed though. The Taniguchi paper considered fluctuations in a cloning strain of E. coli, under great starvation conditions, in an unestablished microfluidic device where cells grew twice as slowly as in batch culture with the same medium, and possibly displayed great heterogeneity in growth. When the same protein fusions are imaged under more uniform conditions without using the cloning strain, the total CV drops to <10% in many cases, and the extrinsic part seems to be less than 5%. This pattern has been observed across many labs, including the intrinsic/extrinsic paper by Elowitz and Leibler who reported extrinsic noise levels as low as 5%.

We agree that the CV of many of the parameters we extract suggest that the underlying variability in the expression of chemotaxis genes is greater than the 5-10% lower limit. Relatively large variability in the expression of chemotaxis genes is consistent with published flow cytometry measurements of chemotaxis genes by Kollmann et al. (2005) who reported a CV of 0.67 for the cheY gene. For the cheA-cheY gene pair they reported η_int = 0.26 and η_ext = 0.35 for the intrinsic and extrinsic components of noise, respectively. Yoney and Salman, (2015) report a Tar/Tsr ratio distribution with a CV≈0.5 and a Pearson correlation coefficient between the tar and tsr genes of ≈0.65. These values from the published literature on expression variation of chemotaxis genes are compatible with our finding that strong cell-to-cell variability is pervasive in E. coli chemotaxis signaling parameters, and underscore our interpretation that the large CVs likely reflect that of the underlying variability in gene expression.

Regarding our reference to the work of Taniguchi et al., this was intended to support the idea that in general a considerable fraction of the CV can be attributed to extrinsic noise (correlated variation), which is relevant for considering effects on the chemotaxis system, where it has been shown (e.g. in Kollmann et al., 2005) that many properties of the system depend on the ratio between expression levels (e.g. CheR/CheB, Tar/Tsr, CheR/receptor), rather than the expression level of individual components. Observing a lower limit to the CV (which scales as the inverse square root of the mean at low expression levels where intrinsic noise dominates), Taniguchi et al. attributed that lower limit to a noise floor due to extrinsic noise. However, we do appreciate the reviewer’s reservations about this interpretation by Taniguchi et al., and have thus removed the reference to that work. Commenting on such genome-wide gene expression trends is in any case somewhat superfluous in this context, given that a high degree of covariation among the expression level of chemotaxis genes has been experimentally demonstrated both at the single-cell (Kollmann et al., 2005) and population levels (Li and Hazelbauer, 2004), and is also expected given the architecture of the flagellar regulon in which all chemotaxis genes are under the control of a common master regulator (Chilcott and Hughes, 2000). These observations underscore the significance of our finding that the uncorrelated component of variability in the Tar/Tsr ratio is much higher than expected. We have included these arguments above in the Results section.

More generally, we believe reviewer #2’s concern here is related to his/her point 2, namely that the high CVs we observe might reflect experimental artifacts rather than bona fide biological variability. We agree with reviewer #2 that experimental results with a lower level of variability would provide proof that the observed variability is not simply the result of hitting a lower bound arising from experimental limitations. In our case, we can contrast high levels of variability with experiments in which the variability is much lower. In case we cannot provide such an experiment, we compare the variability directly to the variability of relevant parameters reported in the literature. This is summarized below.

Adaptation time/precision:The CV for the recovery time is around 0.2. This quantity has been estimated in previous studies by measuring recovery times of motor switching bias after ligand stimulation. In one study, (Berg and Tedesco, 1975) found a large variability (CV≈0.48, 17 cells). Another study (Spudich and Koshland, 1976) reported a lower value (CV≈0.2), which is in agreement with a more recent study (Min et al., 2009, CV≈0.18, 496 pairs) that observed tumbles in optically trapped bacteria. While these results might not be directly comparable due to differences in experimental conditions and analysis, our estimate (CV≈0.2) certainly falls within the reported range. The CV we find for the imprecision of adaptation is relatively high (0.4). Adaptation imprecision has only started to receive attention fairly recently, and to our knowledge, no other study has quantified it at the single-cell level. However, a high CV for the adaptation precision can be rationalized by the hypothesis that this precision is mainly determined by the expression-level ratios among the multiple chemoreceptor species (Meir et al., 2010; Neumann et al., 2014), combined with our finding that the variability of those ratios are very high (see below).

Dose-response parameters:For ligand dose-response curves we find high variability in Hill-fit parameters (K and H). The inverse sensitivity (K) is in general better constrained by the data than the coopertivity (H), as illustrated in the newly furnished Figure 2 Supp. 1b, with the median of the uncertainty (defined as the 95% confidence interval width) divided by the fitted parameter value being 0.19. The variability in K for cells with all five chemoreceptors is quite high (CV=0.49), but a much lower variability for the same parameter is observed in cells expressing Tsr as the sole chemoreceptor species (CV=0.16).

Steady-state activity:In our experiments comparing different network topologies due to CheB phosphorylation feedback, we find very high CVs for the steady-state activity a₀ in cells deficient in phosphorylation feedback (1.10 and 1.07 for respectively CheBc and CheB-D56E) while the CV for cells expressing wild-type CheB is considerably lower (0.7). The latter variability for wild-type CheB is still quite large in absolute terms, but we note that in these cells CheB is expressed from a plasmid, which is expected to increase cell-to-cell variability due to plasmid copy number variation, and also by breaking the translational coupling between CheR and CheB (Løvdok et al., 2009). In the case of wild-type cells (which express both CheR and CheB from their native polycistronic operon) the variability in a₀ is much lower (CV=0.23) as shown in Figure 1 (although we note this comparison with the data of Figure 1 requires caution, as the overall noise-to-signal ratio was also lower in the latter experiment due to differences in experimental conditions).

Temporal fluctuations: The temporal noise amplitudes of the steady-state FRET signal in wild-type cells is much larger (0.44) than cells lacking genes for the adaptation enzymes CheR and CheB (0.09). The CV for the cell-to-cell variability in those noise magnitudes across wild-type cells is 0.6. To compare the variability in noise levels between CheRB+ and CheRB- we find 0.55 and 1.25, respectively. We not that the latter value is high because of a low mean noise amplitude. Without normalization, the variability (σ) of RB+ is 0.24 compared to 0.11 for RB-.

Gene expression variability:We measure a CV of 0.8-0.9 for the expression of CheB. The expression level of CheZ and CheY (Figure 3—figure supplement 2) is much less noisy (CV=0.3). We believe both have contributions from plasmid copy number variation. For these non-ratiometric measurements we do correct for cell size (segmentation surface area) and inhomogeneous illumination. We have added clarifying statements about these corrections to the figure captions in Figure 3—figure supplement 1C and Figure 3—figure supplement 2. We have not measured the gene expression variability of the Tar and Tsr proteins, but using a model on the FRET data, we extract a CV of 0.5 in the Tar/Tsr ratio, which is indeed surprisingly high given the high expression level of these proteins (>10³ copies per cell), but as noted in the manuscript text it is in good agreement with published dual reporter flow cytometry experiments (CV=0.45, Yoney and Salman, 2005).

While all of the above information is present in the main text and figures we agree that a brief summary of variability (both across cells within a population, over time within a single cell) would aid the reader in making these comparisons. Hence, we have furnished a new table (Table 2) to the paper in which our main findings are summarized which is referred to in the Discussion Section.

In particular I would like to see more of a discussion for the very high CV observed in the expression levels of CheB, with CVs of 80-90%. Can that be explained extremely weak transcription and strong translation, or do the authors suspect some other mechanism? Can the authors observe noise levels as low as 10% for other genes with the same set-up, to make sure this is not due to the imaging set-up somehow? I noticed the OD was mid-exponential, close to the diaxic shift where some cells start changing gene expression patterns. Could that be the explanation?

We agree with the reviewer that the variability in CheB expression is high. But this is not unexpected given that measured protein copy numbers for CheB (and also CheR) in wildtype cells are known to be very low (few hundred copies per cell; Li and Hazelbauer, 2004), unlike most other chemotaxis proteins which are expressed at much higher levels (thousands of copies per cell). It is certainly plausible that the high CVs we observe for CheB expression reflects weak transcription coupled with strong translation (which would enhance noise due to the resulting ‘burstiness’ in protein synthesis), but our data do not on their own argue for or against this particular mechanism. We note that CheB expression in these experiments are from plasmids and this may cause additional cell-to-cell variability due to plasmid copy number variation. Hence, we do not make any claims regarding the absolute level of CheB expression variability in wildtype cells, but have merely made the observation that the variability among the three CheB mutants is similar under our experimental conditions. To clarify this issue, we have added a short cautionary statement in the Results section that the CVs measured for CheB likely include a contribution from plasmid copy number variation (subsection “CheB phosphorylation feedback attenuates cell-to-cell variability”):

4). For the residence time distributions, I would like to see the authors spend more time to confirm that the way residence times are called does not affect the results. I would also make a bigger point of the fact that the residence times actually seem to fit exponential distributions, rather than merely using exponentials to get at the rate constant. For exponentials the

Although this comment seems to have been truncated prematurely (the last sentence is incomplete), the reviewer raises the important point that in considering residence-time statistics, not only the mean but also the shape of the distribution matters. We could not agree more with this point, but precisely determining the shape of the residence-time distribution is a significant experimental challenge, given that these time intervals are quite long (mean ~10² s) and a typical single-cell FRET experiment (the duration of which is limited by the finite photon budget to ~10³ s) yields at most a few dozen events per cell. We have thus chosen to focus here on an analysis of the mean residence time (and its dependence on each cell’s activity bias), deferring a more detailed investigation of residence time statistics to a future study.

We point out, however, that we have made no explicit assumptions about the shape of the residence-time distribution (exponential or otherwise) in our analysis. Rather, we have shown that, to a first approximation, the mean residence times (τ_up, t_down) scale exponentially (Eq. 3) with the apparent free-energy difference between active and inactive states (ΔG = k_BT ln[(1-a_1/2)/a_1/2]), with slopes (γ_up,down) of opposing sign. To clarify this point, we have added the following sentence in the Results section:

“The fact that the mean residence times (τ_up,τ_down) scale exponentially with the apparent free energy difference (ΔG) indicates that, to a first approximation, receptor-kinase switching can be treated as a barrier-crossing process.”

Regarding how residence times are called, because the number of switching events in each two-state time series is rather small (typically less than 10 transitions per cell) we chose here to read off transition time points by eye (with ≈ 2.5 s accuracy). Because the amplitude of such transitions far exceeds that of high-frequency (shot) noise, these events can be identified unambiguously by eye, but the gradual drift of the FRET signal baseline (due to bleaching etc.) renders automatic detection challenging. We are developing a more refined (and automated) analysis for a follow-up study that addresses residence-time statistics in more detail, but for our purpose here of analyzing mean residence times (on a logarithmic scale), small errors in residence time intervals have negligible effects.

Slightly related to this issue, for other waiting time distributions they see a CV of 20% and call that broad, though the switching times at the end supposedly have CVs of 1, if they are exponential. Though the first waiting times are not from two-state models, it is quite difficult to reduce the heterogeneity in timing even in multi-state switching.

We agree with the reviewer that whether a CV is large or small depends on the (assumed) distribution underlying the statistics. In the case of the residence times, since the number of events per cell is so small we have not been able to confirm that the underlying distribution is exponential. We have only shown that the average residence time for each cell scales exponentially with the activity-biasing free energy ΔG.

While for a passive (thermally driven) process waiting time distributions are expected to be exponential, for the two-level switching behavior we have observed in RB- cells, at this stage we cannot rule out the involvement of one or more active (dissipative) process(es), which can lead to peaked distributions (and hence lower CV’s). In our discussion text we refer to the case of allosteric switching events in flagellar motor rotation, for which recently peaked residence times were measured and interpreted using a non-equilibrium switching model (Wang et al., 2017).

We assume that the “other waiting time distributions” referred to by the reviewer is the recovery-time distribution upon adaptation to a large step stimulus (Figure 1E), as that is the only measured time interval for which we report a CV of ≈0.2. A CV of 0.2 is indeed small compared to that of an exponential distribution, but is much greater than mechanistically expected from the underlying stochastic chemical kinetics alone. This basic reason is that adaptational recovery from large step stimuli requires a large number of receptor-methylation events. From previous calibration measurements of an allosteric model of receptor signaling (Shimizu et al., 2010, Figure 7) we can estimate precisely that adaptation to the 500 μM MeAsp stimulus of Figure 1e requires ~1.5 methyl groups per receptor, and there are >10³ receptor molecules per cell. It is reasonable to assume that the waiting time for each individual methylation event obeys Poisson statistics (with CV=1), but the recovery time would then be the sum of thousands such independent random variables. So by the central limit theorem the CV would be reduced by the square-root of the number of events, i.e. given N_events>10³, the expected CV=(1/ N_events)^1/2<≈3%. We therefore maintain that the distribution of recovery times we observe upon adaptation to large attractant steps (Figure 1E) are substantially broader than expected from the underlying stochastic methylation kinetics alone. To clarify this issue, we have added the following passage to the Results section reporting this CV:

“The variation is also substantial in 𝜏_recovery (Figure 1e, 𝐶𝑉 =0.20), considering that the underlying kinetics of receptor methylation (catalyzed by CheR) involve thousands of events per cell, but falls within the range.”

Reviewer #3:

It was a pleasure to read the manuscript by Keegstra el al on "Generation and attenuation of.…". Indeed, there is nothing to dislike about this paper.

By improving an in vivo FRET assay, which was developed and used to measure the response of a population of cells to external stimuli, the Shimizu group has now for the first time (in my knowledge) been able to measure these intracellular responses at the single cell level. That's a significant achievement all by itself. This unique single-cell measurement, together with existing modeling approach, allows the authors to quantify the cell-cell variability of the intracellular dynamics (response and adaptation) as well as the key components (e.g., Tar/Tsr ratio) in the E. coli chemotaxis pathway during different stages (phases) of the population growth process from the response measurements of individual cells. The new technique, single cell FRET, has already shed some new lights onto an old problem/puzzle. In particular, it is shown quite convincingly here that the role of the CheB phosphorylation is to suppress fluctuations in the response regulator as suggested by previous theoretical work. Finally, what is most exciting about the present work is that it revealed something quite unexpected, namely, for at least some of the CheRB- cells (without adaptation) the kinase activity of the entire cell (with thousands of receptors) follows that of a stochastic two-state switching behavior. This new observation will likely lead to new insights on how receptor clustering affects signaling.

The paper is well written. It contains a lot of information, yet it is written in a way easy for the readers to get the main ideas. The paper should be published after the authors consider a few questions/comments that came up while reading the manuscript:

1) Different attractants are used in this paper, e.g., MeAsp for wt cells used in Figure 1 and L-Serine for CheRB- mutants shown in Figure 2. Any reason for doing that, i.e., not using both like what's done in Sourjik and Berg (2004)? From the response data to L-Serine and the model parameters inferred, the response to MeAsp may be predicted, which would be a test for the theoretical model used here.

In our single-cell FRET experiments, we were mainly concerned with ensuring response saturation for each individual cell. We know that the population averaged FRET signal of RB- cells can be shut down completely with L-serine, but not with MeAsp (Sourjik and Berg, 2002). Otherwise, we know that the response to MeAsp in RB+ shows near-perfect adaptation but to serine the system adapts much less precisely. Hence, we do think that these are nice suggestions for additional experiments and analysis but fall beyond the scope of this work.

2) The values of K and H for different individual cells, as shown in Figure 2D, are quite interesting. For different cells and cells in different growth phase, the cooperativity H and the inverse sensitivity K seem to collapse onto a single curve. Is there a reason for that?

We agree that the parameters K and H of different cells to first approximation seem to collapse on the same curve, while we also note that there is additional variability.

With the two-receptor-species MWC model of Mello and Tu, (2005) one can obtain a relation between K and H roughly similar to the trend between the K and H parameters by only changes the relative abundance of the two chemoreceptor species. Hence according to this model the dominant source of variability from cell to cell is the variability in the abundance ratio of the two chemoreceptors Tar and Tsr. The fact that cells from different harvesting OD’s preserve the relation between K and H also is consistent with our interpretation that the dominant source of variation caused by harvesting OD is the Tar/Tsr ratio.

However, we do note that the model does not provide a direct relation between the abundance of the chemoreceptor and the signaling team size of each chemoreceptor, only the notion that the ratio of the signaling team sizes should be determined by the ratio of expression levels, if one assumes the cluster is well-mixed. Hence inferring absolute abundances of chemoreceptors directly (instead of their ratio) is not possible unless further assumptions are made.

Furthermore, in a previous work ("Lateral density of receptor arrays in the membrane plane influences sensitivity of the E. coli chemotaxis response", C. M. Khursigara et al., 2011), it was found that while cooperativity H is higher for cells grown in H1 medium than that of cells grown in TB, its K value is also larger. How does the result shown here relate to that reported in this previous observation?

The study by Khursigara et al., (2011) mentioned by the reviewer is very interesting and we have added a reference to this work in the Discussion section. However, we have chosen not to include an in-depth comparison of the mentioned work with our results because of experimental differences.

The work of Khursigara et al., (2011) shows that chemoreceptor array structure is hard to predict from expression levels only. While it is known that cells grown in H1 express many more receptors compared to cells grown in TB, the cluster sizes are comparable between the two growth conditions, while the density of the chemoreceptor arrays does change, with H1 cells having more dense arrays. This roughly agrees with the idea that higher chemoreceptor expression increases the signaling team size and hence cooperativity of the response, but we lack the predictive power to relate the signaling team size to the expression level. Hence if there is significant additional variability beyond the Tar/Tsr expression level ratio it is not surprising that the observed anti-correlation between K and H no longer holds.

We do note that the results of the paper are mostly based on population-averaged measurements. Cell-to-cell variability may influence the apparent cooperativity of the population response (see the family of dose response curves in Figure 2B of our manuscript). Hence it is technically possible that the lower cooperativity of cells grown in TB is caused by larger variability. This is consistent with the fact that the referred manuscript shows lower variability in the receptor array density for cells grown in TB (Figure 3E), although the number of cells presented is small. We think performing single-cell FRET experiments to study the relation between growth condition and signalling parameters provides a good direction for further studies.

3) In Figure 4A, the blue line shows a very small fluctuation for the ChRB- mutant in comparison with the wt cell (red line). It is a bit confusing in light of the following Figure 5 which shows the giant fluctuation of the CheRB- mutants. The reason for this difference needs to be explained.

We agree with the reviewer that the transition from Figure 4 to Figure 5 could be improved. Therefore, we have added two panels to Figure 5, in which the result is shown of an experiment with CheRB- cells with the same genotype as Figure 4, but then with the addition of ligand to bring the CheRB- cells into a sensitive regime. The spectrum shows elevation at low frequencies compared to the case where no ligand is applied. We also included a power spectrum from experiments with CheRB- and only one chemoreceptor, which reveals even more temporal noise. We believe that this additional data will help the reader to see how the fluctuations presented in Figures 4 and 5 are connected.

4) It needs to be pointed out that the Ornstein-Uhlenbeck equation for kinase activity (Eq. (1) in this manuscript) was first proposed in Tu & Grinstein, (2005), where a 20% fluctuation was given as a lower bound for observing 1-decade of power law CCW duration time distribution. This lower bound is certainly satisfied by the new observation presented in this paper.

We have added this reference at Eqn 1 and we have changed another mention of this work in the Discussion section to (subsection “Diversity in temporal variability: bet-hedging across exploration and exploitation strategies”):

"Another theoretical study of the motor noise (Tu and Grinstein 2005), had predicted a more modest noise level of intracellular noise, with a lower bound of 20% of the mean."

https://doi.org/10.7554/eLife.27455.038

Article and author information

Author details

Johannes M Keegstra

AMOLF Institute, Amsterdam, The Netherlands

Contribution
Conceptualization, Resources, Data curation, Software, Formal analysis, Supervision, Investigation, Visualization, Methodology, Writing—original draft, Writing—review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-8877-4881
Keita Kamino

AMOLF Institute, Amsterdam, The Netherlands

Contribution
Formal analysis, Investigation, Methodology, Writing—review and editing

Competing interests
No competing interests declared
François Anquez

AMOLF Institute, Amsterdam, The Netherlands

Present address
Laboratoire de Physique des Lasers, Atomes et Molécules, UMR CNRS 8523, Universite Lille 1, France

Contribution
Data curation, Software, Methodology

Competing interests
No competing interests declared
Milena D Lazova

AMOLF Institute, Amsterdam, The Netherlands

Contribution
Investigation, Methodology, Writing—review and editing

Competing interests
No competing interests declared
Thierry Emonet
1. Department of Molecular, Cellular and Developmental Biology, Yale University, New Haven, United States
2. Department of Physics, Yale University, New Haven, United States
Contribution
Formal analysis, Funding acquisition, Methodology, Writing—review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-6746-6564
Thomas S Shimizu

AMOLF Institute, Amsterdam, The Netherlands

Contribution
Conceptualization, Formal analysis, Supervision, Funding acquisition, Investigation, Visualization, Methodology, Writing—original draft, Writing—review and editing

For correspondence
shimizu@amolf.nl

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-0040-7380

Funding

Paul G. Allen Family Foundation (11562)

Thierry Emonet
Thomas S Shimizu

National Institutes of Health (R01GM106189)

Thierry Emonet

Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO Vidi 680-47-515)

Thomas S Shimizu

Stichting voor Fundamenteel Onderzoek der Materie (FOM Projectruimte 11PR2958)

Thomas S Shimizu

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank Sandy Parkinson and Germán Piñas for strains, many useful discussions and critical reading of the manuscript, Istvan Kleijn, Yuki Esser, Iwan Vaandrager, Francesca van Tartwijk and Pieter de Haan for help with experiments at various phases of the project, William Pontius for useful discussions, Simone Boskamp and Zuzana Rychnavska for cell culture and cloning, Marco Kamp for microscopy assistance and Marco Konijnenburg, Brahim Ait Said, Luc Blom and Eric Clay for software and electronic support. This work was supported by NWO/FOM and the Paul G. Allen Family Foundation. Thierry Emonet acknowledges support from NIH grant R01GM106189.

Reviewing Editor

Naama Barkai, Weizmann Institute of Science, Israel

Publication history

Received: April 4, 2017
Accepted: November 17, 2017
Accepted Manuscript published: December 12, 2017 (version 1)
Accepted Manuscript updated: December 14, 2017 (version 2)
Version of Record published: February 12, 2018 (version 3)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

3,562

Page views
598

Downloads
43

Citations

Article citation count generated by polling the highest count across the following sources: Scopus, Crossref, PubMed Central.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Johannes M Keegstra
Keita Kamino
François Anquez
Milena D Lazova
Thierry Emonet
Thomas S Shimizu

(2017)

Phenotypic diversity and temporal variability in a bacterial signaling network revealed by single-cell FRET

eLife 6:e27455.

https://doi.org/10.7554/eLife.27455

Categories and tags

Research organism

E. coli

Share this article

Cite this article

Single-cell FRET over extended times reveals cell-to-cell variability in signaling response.

Figure 1—source data 1

Ligand dose-response parameters vary strongly across cells in an isogenic population, even in the absence of adaptation, and depend on receptor-complex composition.

Figure 2—source data 1

CheB phosphorylation feedback attenuates variability in steady-state kinase activity.

Figure 3—source data 1

Temporal fluctuations in WT cells due to stochastic activity of adaptation enzymes CheR/CheB.

Figure 4—source data 1

Temporal fluctuations in adaptation-deficient cells depend strongly on activity and composition of chemoreceptor population.

Figure 5—source data 1

Variability in signaling parameters reported in this study with 95 % CI obtained by bootstrap resampling.

Strains used in this study.

Plasmids used in this study.

List of global parameters used for model of Mello and Tu.

List of parameters used for Goldbeter-Koshland description of CheB phosphorylation feedback.

Author details

Johannes M Keegstra

Contribution

Competing interests

Keita Kamino

Contribution

Competing interests

François Anquez

Present address

Contribution

Competing interests

Milena D Lazova

Contribution

Competing interests

Thierry Emonet

Contribution

Competing interests

Thomas S Shimizu

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Research organism

Further reading

Variability in signaling parameters reported in this study with 95 $%$ CI obtained by bootstrap resampling.