Conjunction of factors triggering waves of seasonal influenza

Abstract
eLife digest
Introduction
Results
Discussion
Materials and methods
Appendix 1
References
Article and author information
Metrics

Abstract

Using several longitudinal datasets describing putative factors affecting influenza incidence and clinical data on the disease and health status of over 150 million human subjects observed over a decade, we investigated the source and the mechanistic triggers of influenza epidemics. We conclude that the initiation of a pan-continental influenza wave emerges from the simultaneous realization of a complex set of conditions. The strongest predictor groups are as follows, ranked by importance: (1) the host population’s socio- and ethno-demographic properties; (2) weather variables pertaining to specific humidity, temperature, and solar radiation; (3) the virus’ antigenic drift over time; (4) the host population’€™s land-based travel habits, and; (5) recent spatio-temporal dynamics, as reflected in the influenza wave auto-correlation. The models we infer are demonstrably predictive (area under the Receiver Operating Characteristic curve 80%) when tested with out-of-sample data, opening the door to the potential formulation of new population-level intervention and mitigation policies.

https://doi.org/10.7554/eLife.30756.001

eLife digest

Influenza – or ‘the flu’ – is a contagious disease which sweeps across the globe like clockwork, claiming tens of thousands of lives. This is known as ‘seasonal flu’.

Many scientists have tried to identify the factors that spark these yearly outbreaks. Some past studies have found that seasonal flu occurs when air that is normally humid turns dry, suggesting weather patterns play an important part. Other research has shown that air travel contributes to the flu spreading across the world. However, these studies typically focus on just one or two factors on their own. It is still not clear how exactly these factors combine to drive outbreaks, and then sustain the wave of infection.

To address this, Chattopadhyay et al. analyze the medical histories of 150 million American people over a decade, combining this information with large datasets about the different factors that trigger flu outbreaks. This includes detailed data about air travel and weather patterns, as well as census data that describe features of the population. Patterns of movement are also examined, for example by processing billions of Twitter messages “tagged” with a location. Chattopadhyay et al. used all of these datasets to model outbreaks of the flu in the United States, and see which factors play the biggest role.

It turns out that yearly outbreaks of seasonal flu are a result of a combination of elements. Some factors interact to help trigger the start of the wave, like humid weather in a highly populated area with nearby airports. Other factors, such how people move, encourage the spread of the infection. Finally, certain features of the population, for example how closely knitted a community is, make specific areas of the country more susceptible to the arrival of the disease. Overall, some of the most important elements of the model relate to the characteristics of the populations, the weather, the type of virus, and the number of short-distance journeys (rather than air travel).

Understanding how and why outbreaks occur can help policy-makers design strategies that reduce the spread and impact of seasonal flu, which could potentially save thousands of lives. Ultimately, the model developed by Chattopadhyay et al. could be used to test whether these policies would work before they are implemented in the real world.

https://doi.org/10.7554/eLife.30756.002

Introduction

Seasonal influenza is a serious threat to public health, claiming tens of thousands of lives every year. A large number of past studies have focused on identifying the likely factors responsible for initiating each seasonal disease wave. Typically, each such study focused on one or a few hypothetical factors. Our study aimed at an integrative, joint analysis of numerous suggested disease triggers, comparing their relative importance and possible cooperation in triggering pan-US waves of seasonal influenza infection. The goal of this study was to identify the most informative combinations of statistical predictors associated with the initiation of pan-US influenza infection waves.

Recent computational studies of influenza:

Computational study of the dynamics and factors influencing infectious disease spread began with compartmental models, such as the Susceptible-Infected-Resistant (SIR) model, which traces its origins to the beginning of the last century (Kermack and McKendrick, 1927). Initially a purely theoretical tool, these SIR-style models were subsequently enhanced with population and geographic data, allowing their application to specific cities and the distances between them (Keeling and Rohani, 2002). For instance, one approach, termed ‘gravity wave’ modeling, used geographic, short- and long-range, work-related human movement and demographic data to formulate gravity potentials between US counties in order to infer the dynamics of infection spread (Viboud et al., 2006).

Some studies have focused on one specific factor affecting infection, such as air travel, to simulate the spread of influenza (Colizza et al., 2006); other studies used SIR models, generalized for a collection of interconnected geographic areas, spatial-network or patch models, to model a number of common infections, including influenza, measles, and foot-and-mouth disease (Riley, 2007).

More ambitious network model approaches have simulated the global transmission of infectious disease using high-resolution, worldwide population data and the locations of International Air Transport Association (IATA)-indexed airports (Balcan et al., 2009). Similar to (Viboud et al., 2006), the authors of the study computed the global infection-pre-disposing ‘gravity field’ over the network of international airports. This network-based approach was subsequently developed further (Balcan and Vespignani, 2011) through the modeling of ‘phase transition’–that is the chain-reaction switch of geographic infection status–in complex networks, utilizing approaches introduced in theoretical physics.

Another layer of sophistication was achieved by incorporating rich historical records. For example, Eggo et al. (Eggo et al., 2011) modeled the Spanish influenza epidemic of 1918–1919, using mortality documents from both the UK and the US, explicitly accounting for the size and distances between cities. In the same spirit, Brockmann and Helbing (Brockmann and Helbing, 2013) represented infection as diffusion on a complex network, estimating arrival times for infection across the globe.

Following the formulation of the hypothesis that absolute humidity modulates influenza survival and transmission (Shaman and Kohn, 2009), researchers began incorporating climate variables into SIR-like models (Chowell et al., 2012). More recent dynamic models have incorporated a probabilistic description of influenza infection’s spatial transitions in space and time, accounting for selected demographic confounders (Gog et al., 2014) and (Charu et al., 2017).

In this study, rather than following the SIR-style modeling tradition, we used statistical epidemiology- and econometric-like approaches, in addition to a causality-network method presented here for the first time. There are some prior studies that are close to ours in spirit (but not in details). For example, (Barreca and Shimshack, 2012) used historical US influenza mortality data (1973–2002) in conjunction with collinear humidity and temperature records to establish county-level statistical associations between variables in the datasets. They concluded that absolute humidity was ‘an especially critical determinant of observed human influenza mortality, even after controlling for temperature.’ Another study, focusing on historical influenza records in the Netherlands, (te Beest et al., 2013) used the number of weekly influenza-like patient visits (transformed into an estimated rate of infection) as a response variable in a regression analysis of climate data. They concluded that the bulk of explained variation (57%) was attributed to the depletion of susceptible hosts during the disease season and non-weather-related ‘between-season effects,’ with only 3% explained by absolute humidity, represented as a continuous predictor variable. Additionally, this study observed that school holidays did not have a statistically significant effect on influenza transmission.

As all causality detection methods come with dissimilar limitations and are imperfect in unique ways, we designed our study intentionally to attack the same target problem using three different statistical approaches: Approach 1: A non-parametric Granger analysis (Granger, 1980) focusing on infection flows’ directionalities across the US and whether influenza propagates via long- vs. short-distance travel (we run analysis across all pairs of air- and land-travel county neighbors, respectively). Approach 2: A mixed-effect Poisson regression (Hedeker and Gibbons, 2006) explicitly accounting for the auto-correlation of infection waves in time and space, along with the full set of socioeconomic, climate, and geographic predictors. Approach 3: A county-matching, non-parametric analysis to identify the minimum predictive set of factors that distinguish those counties associated with the onset of the influenza season (Morgan and Winship, 2015).

Our study became possible through access to several, very large longitudinal datasets: (1) a nine-year collection of insurance records capturing the dynamics of influenza-like illnesses (ILIs) in the United States (Truven MarketScan database, see Materials and methods); (2) temporally collinear, high-resolution weather measurements over every US county; (3) detailed air travel (The United States Bureau of Transportation Statistics, 2010) and geographic proximity data (The United States Census, 2016) showing connectivity between US counties; (4) billions of geo-located Twitter messages reflecting long- and short-distance human movement patterns, and; (5) US census data accounting for US county and county-equivalent population distribution, demographic, and socioeconomic properties (HRSA, 2016). An explicit comparison of the ILI data in the insurance claims to the influenza records provided by the Center for Disease Control and Prevention (CDC, 2016) showed that the two sources agree well ( $ρ = 0.91, p = 3.5 \times 10^{- 201}$ ), with insurance claims providing higher data resolution, see Figure 1—figure supplement 1. Curiously, the relationship between the two sources of ILI observations is not linear: We attribute this to the lower resolution of the CDC data. These three types of analysis produce congruent–albeit not identical–results.

Results

The logical flow of our analysis is as follows: (1) We first show that our definition of ILIs corresponds well with CDC data, and that our causality coefficients, defined in Approach 1, have similar meanings to coefficients in the regression analysis; (2) We then explain the outcomes of the analysis according to Approach 1; (3) We then analyze the importance of putative casual factors, Figure 1, as applied to an initiation of influenza season, Figure 2; (4) In Approach 2, we pay special attention to the relative importance of short- and long-distance travel in influenza propagation, Figure 4; (5) We further test the best regression model in terms of predictive accuracy, Figure 5, using disjointed data parts for training and testing, and; (6) We culminate our analysis with a county-matching analysis, Figure 6.

Figure 1 with 6 supplements see all

Download asset Open asset

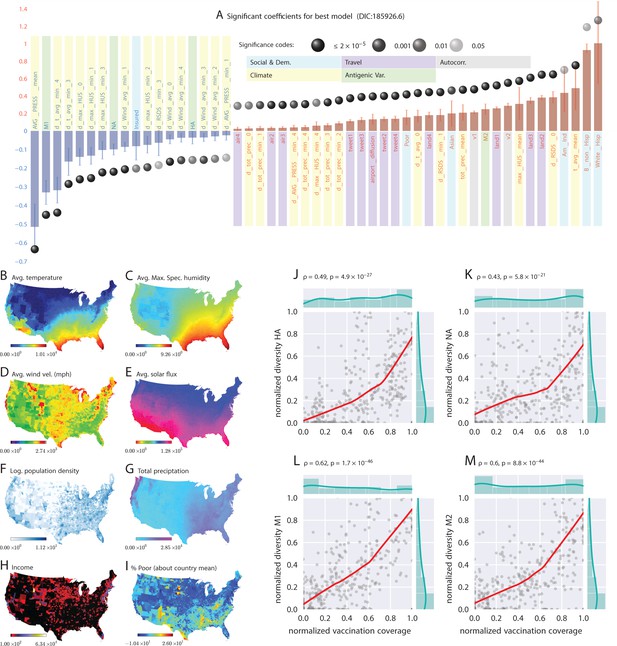
Putative determinants of seasonal influenza onset in the continental US and Poisson mixed-effect regression analysis (Approach 2).

Plate A shows the significant variables along with their computed influence coefficients from the mixed-effect Poisson regression analysis (the best model chosen from $126$ different regression equations with different variable combinations). The statistically significant estimates of fixed effects are grouped into several classes: climate variables, economic and demographic variables, auto-regression variables, variables related to travel, and those related to antigenic diversity (see the last entry in Table 5 for the detailed regression equation used. The complete list of all models considered is given in Table S-D7). The fixed-effect regression coefficients plotted in Plate A are shown on a logarithmic scale, meaning that the absolute magnitude of predictor-specific effect is obtained by exponentiating the parameter value. A negative coefficient for a predictor variable suggests that the influenza rate falls as this factor increases, while a positive coefficient predicts a growing rate of infection as the parameter value grows. The integrated influence of individual predictors, under this model, is additive with respect to the county-specific rate of infection. For example, a coefficient of $- 0.6$ for parameter AVG_PRESS_mean tells us that the average atmospheric pressure has a negative association with the influenza rate. As the mean atmospheric pressure for the county grows, the probability that the county would participate in an infection initiation wave falls. As $\exp (- 0.6) = 0.54$ , the rate of infection drops by $46 %$ when atmospheric pressure increases by one unit of zero-centered and standard-deviation-normalized atmospheric pressure. Similarly, an increase in the share of a white Hispanic population predicts an increase in influenza rate: A coefficient of 1.3 translates into a $\exp (1.3) \times 100 % - 100 % = 267 %$ rate increase, possibly, because of the higher social network connectivity associated with this segment of population. Plates B - I enumerate the average spatial distribution of a few key significant factors considered in Poisson regression: (B) average temperature; (C) average maximum specific humidity; (D) average wind velocity in miles per hour; (E) average solar flux; (F) logarithm of population density (people per square mile); (G) total precipitation; (H) income, and; (I) percent of poor as deviations about the country average. Plates J-M show the strong dependence between our estimated antigenic diversity (normalized, see Definition in text) corresponding to the HA, NA, M1, and M2 viral proteins, and the cumulative fraction of the inoculated population (normalized between 0 and 1), where both sets of variables are geo-spatially and temporally stratified. Pearson’s correlation tests shown in Plates J-M were performed under null hypothesis that there the two quantities (plotted along axes X and Y) are statistically independent ( $H_{0} : ρ = 0$ ).

https://doi.org/10.7554/eLife.30756.003

Figure 2 with 1 supplement see all

Download asset Open asset

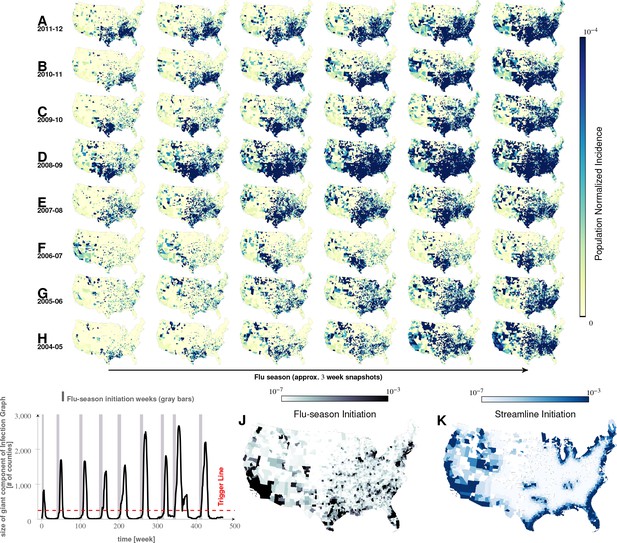
Characteristics of seasonal influenza in the continental US An analysis of county-specific, weekly reports on the number of influenza cases for a period of $471$ weeks spanning January 2003 to December 2013 (Plates A-H) for recurrent patterns of disease propagation.

In particular, the weeks leading up to that in which an epidemic season peaks (determined by significant infection reports from the maximum number of counties for that season) demonstrate an apparent flow of disease from south to north, which cannot be explained by population density alone (also see movie in Supplement). Plate I illustrates the near-perfect time table for a seasonal epidemic. Plates J and K compare the county-specific initiation probabilities of an influenza season, and the causality streamlines.

https://doi.org/10.7554/eLife.30756.010

Table 1

Social connectivity: The US Southern region appears to have an unusually high level of social connectivity.

(In GSS survey results, the number of close friends, close friends who are neighbors, and number of friends who all or mostly know each other is higher in the South, especially in the East/South/Central census region, than in the country at large.)

https://doi.org/10.7554/eLife.30756.011

	WSC (TX, OK, AR, LA)	ESC (MS, AL, TN, KY)	SA (FL, GA, SC, NC, VA, WV, MD, DC)	Country-at-large	WNC (ND, SD, NE, KS, MO, IA, MN) (not in South/Southeast) this is the second most social region following ESC (MS, AL, TN, KY)
Close friends	7.22	12.76	8.20	7.57	10.56
Close friends who are neighbors	1.02	3.40	1.32	1.45	3.15
% of friends who all or mostly know each other	All:20% Mostly: 43%	All:18% Mostly: 58%	All: 11% Mostly: 52%	All: 12 Mostly: 50%	All: 16% Mostly: 58%
How often visit closest friends*	107	151	126	122	129

*Survey options are: lives in household, daily, several times a week, once a week, once a month, several times a year, and less often. These are converted to approximate number of visits per year (see Supplement for more information about the GSS analysis).

Table 2

Fisher’s exact test results on matched treatment combinations

https://doi.org/10.7554/eLife.30756.012

YR	dh ${}_{0}^{⋆}$	dh ${}_{1}^{⋆}$	dt ${}_{0}^{⋆}$	h $^{⋆}$	t $^{⋆}$	u $^{⋆}$	M1 $^{⋆}$	M2 $^{⋆}$	V ${}_{0}^{⋆}$	V ${}_{1}^{⋆}$	a $^{⋆}$	p-value	Odds ratio	Lower 99% cnf. bnds.	Upper 99% cnf. bnds.
2003	X	X	Y	Y	Y	Y	X	X	X	X	X	$1.9 \times 10^{- 8}$	2.83	1.73	4.66
2004	X	X	Y	Y	Y	Y	X	X	Y	X	X	$6.5 \times 10^{- 3}$	6.22	1.08	132.03
2005	X	X	Y	Y	Y	Y	X	Y	X	X	X	$3.4 \times 10^{- 6}$	8.31	2.16	54.93
2006	X	X	Y	Y	Y	Y	X	Y	X	X	X	$5.3 \times 10^{- 7}$	4.56	1.96	12.0
2007	Y	Y	X	Y	Y	Y	X	Y	X	X	X	$2.1 \times 10^{- 2}$	3.85	0.82	28.16
2008	Y	Y	Y	Y	Y	X	X	X	X	X	X	$1.9 \times 10^{- 3}$	5.26	1.23	50.2
2009	Y	Y	X	Y	Y	Y	X	X	X	X	X	$3.1 \times 10^{- 10}$	4.78	2.38	10.34
2010	X	X	Y	Y	Y	Y	X	X	X	Y	X	$1.4 \times 10^{- 2}$	3.64	0.93	24.27
2011	X	X	Y	Y	Y	Y	X	X	Y	X	X	$4.9 \times 10^{- 11}$	4.91	2.51	10.05
All Years	Y	Y	Y	Y	Y	Y	Y	Y	Y	Y	X	$7.2 \times 10^{- 9}$	3.88	2.10	7.89
All Years	Y	Y	Y	Y	Y	Y	Y	Y	Y	Y	Y	$1.0$	1.0	0.48	2.15

Table 3

Fisher’s exact test results on matched treatment combinations

https://doi.org/10.7554/eLife.30756.013

(a)
YR p	-value 99%	Conf. Bnd.
max hus avg
2003	0.003603	1.0, 4.21
2004	0.6919	0.16, 17.63
2005 0.	1948	0.61, 7.89
2006 0.	6525 0.28, 3.06
2007 0.	3574 0.49, 18.85
2008 0.	103	0.55, 1.23
2009 0	.1067	0.68, 8.77
2010	0.5318	0.27, 41.03
2011	0.09054	0.74, 5.17
ALL YRS	1[1]10-4	1.12, 1.88
t avg mean
2003	0.06439	0.81, 3.65
2004	1	0.27, 10.62
2005	0.003339	1.17, 123.0
2006	0.8172	0.29, 4.0
2007	0.537	0.47, 7.42
2008	0.05985	0.59, Inf
2009	0.0006337	1.37, 51.68
2010	0.2853	0.50, 9.28
2011	0.05729	0.85, 3.49
ALL YRS 5.87	[1]10-9	1.36, 2.23
d hus 0
2003	0.5374	0.55, 3.41
2004	1	0.27, 11.01
2005	0.04401	0.81, 7.13
2006	0.001708	1.31, Inf
2007	0.009199	1.0, 37.34
2008	0.3051	0.60, 5.92
2009	0.02726	0.82, 90.16
2010	1	0.41, 2.78
2011	0.577	0.57, 2.77
ALL YRS	1.48[1]10-5	1.12, 1.64
d t avg mean 0
2003	0.004956	1.0, 24.12
2004	0.445	0.14, 6.0
2005	0.001164	1.23, 12.03
2006	0.01198	0.97, 11.08
2007	0.01147	0.96, 11.05
2008	0.08552	0.74, 11.18
2009	0.06847	0.73, 17.69
2010	0.08251	0.15, 1.63
2011	0.6031	0.47, 3.55
ALL	YRS 4.98[1]10-11	1.35, 2.06

(b)
YR p-	value	99% Conf. Bnd.
hus 1
2003	0.1652	0.10, 2.43
2004	1	0.22, 24.42
2005	0.002004	0.09, 0.87
2006	1	0.32, 7.65
2007	0.389	0.33, 1.90
2008	0.02142	0.9, 8.48
2009	0.1822	0.67, 6.06
2010	0.6005	0.23, 4.22
2011	0.9166	0.6, 1.88
ALL YRS	0.07	0.72, 1.06
d hus 2
2003	0.0083	1.01, 5.77
2004	0.79	0.36, 13.33
2005	0.275	0.71, 2.54
2006	0.24	0.66, 4.36
2007	0.19	0.62, 9.33
2008	0.18	0.65, 7.52
2009	0.53	0.44, 6.25
2010	0.08	0.21, 1.51
2011	0.59	0.69, 1.87
ALL YRS	0.13	0.78, 1.07
urbanity
2003	0.0083	1.01, 5.77
2004	0.79	0.36, 13.33
2005	0.275	0.71, 2.54
2006	0.24	0.66, 4.36
2007	0.19	0.62, 9.33
2008	0.18	0.65, 7.52
2009	0.53	0.44, 6.25
2010	0.08	0.21, 1.51
2011	0.59	0.69, 1.87
ALL YRS	2.2_10-16	3.67, 5.06
airport proximity
2003	0.004956	1.0, 24.12
2004	0.445	0.14, 6.0
2005	0.001164	1.23, 12.03
2006	0.01198	0.97, 11.08
2007	0.01147	0.96, 11.05
2008	0.08552	0.74, 11.18
2009	0.06847	0.73, 17.69
2010	0.08251	0.15, 1.63
2011	0.6031	0.47, 3.55
ALL YRS	1_10-16	1.73, 2.93

Approach 1: Causality streamlines from non-parametric granger analysis

Our analysis of health insurance claims covers nine years of influenza cycles ( $2003$ to $2011$ , inclusively), see Figure 2. We visualized weekly, county-level prevalence as a movie (see Supplement); Figure 2A–H show a few relevant weekly snapshots from different years. The plates in Figure 2A–H, and especially the movie, clearly show that seasonal influenza cycles initiate in the South/Southeastern US and sweep the country from south to north. This pattern is repeated, with some variation, each season.

Figure 3G shows the country-wide propagation dynamics as represented by our computed causality streamlines. The alignment of causality flow vectors into long, continuous streamlines suggests a stable propagation mechanism across the country; the probability of a long sequence of summary movement vectors accidentally matching in the direction by mere chance is vanishingly small ( $p < 10^{- 16}$ for longer streamlines).

Figure 3

Download asset Open asset

Computation of causality field, Approach 1 Plates A and B: Incidence data from neighboring counties in Alabama, US.

Plates C and D: Transformation to difference-series, $i . e .$ , change in the number of reported cases between weeks. We imposed a binary quantization, with positive changes mapping to ‘1,’ and negative changes mapping to ‘0.’ From a pair of such symbol streams, we computed the direction-specific coefficients of Granger causality (see Supplement). For each county, we obtained a coefficient for each of its neighbors, which captured the degree of influence flowing outward to its respective neighbors (Plate L). We computed the expected outgoing influence by considering these coefficients as representative of the vector lengths from the centroid of the originating county to centroids of its neighbors. Viewed across the continental US, we then observed the emergence of clearly discernible paths outlining the ‘causality field’ (Plate G). The long streamlines shown are highly significant, with the probability of chance occurrence due to accidental alignment of component stitched vectors less than $10^{- 185}$ ; while each individual relationship has a chance occurrence probability of $\sim 6 %$ (Plates E and F). Plate H: Spatially-averaged travel patterns (see text in Materials and methods) and the sink distribution between expected travel patterns. These patterns (Plate H), along with the inferred causality field (Plate I), match up closely, with sinks showing up largely in the Southern US, explaining the central role played there. In Plate H, the size of the blue circles indicate the percentage of movement streamlines (computed by interpreting the locally averaged movement directions as a vector field) that sink to those locations. In Plate I, the size of the red circles indicate the percentage of causality streamlines that sink to the indicated locations. We note that $\sim 75 %$ of the movement streamlines sink in counties belonging to the Southern states, which matches up well with the sinks of the causality streamlines. In Plates J and K show spatial analysis results for two different infections (HIV and *E. coli*, respectively) and which exhibit very different causality fields, negating the possibility of boundary effects.

https://doi.org/10.7554/eLife.30756.015

Do epidemics originate from the same counties season after season? To answer this question, we follow ‘causality streamlines’ back to their source county. Informally, influenza onset in these source counties has little or no causal dependency on their neighbors. That is, their epidemic states are seemingly caused by factors outside of disease prevalence in other counties. Figure 2K presents the county-specific likelihood of streamline initiation across our nine years of data. To verify the near-shores position of these source counties is not a mere manifestation of a boundary effect of shore counties (no neighbors at the side of large water body), we carried out identical causality analyses with two different infections, specifically choosing diseases less likely to share etiologies with influenza: HIV and Escherichia coli. The results for both HIV and Escherichia coli infections are shown in Figure 3J and K, which exhibit flow patterns very different from those obtained for influenza. These streamlines almost never originate from the coasts, thus reducing the likelihood that the pattern observed for influenza is a geo-spatial boundary effect. Combined with the exceedingly low probability ( $\sim 10^{- 185}$ ) of chance inference for the streamlines, this strongly supports our conclusion that the epidemics are of coastal origin.

We directly validated our conclusion that influenza waves tend to start in the South by identifying counties which seem to trigger the epidemic. We computed a ‘trigger period’ of five to six weeks for each season, defined as the period immediately preceding an exponential increase in influenza dispersion. To calculate this weekly dispersion, we treated each county as a node in an undirected graph, each with an edge connecting two geographically adjacent counties–only if they had both reported at least one influenza case in the specified week. We defined dispersion as the size of the largest, connected component in this undirected graph. Thus, a trigger period describes the period in which the size of the giant component of the infection graph rises above $250$ counties from being under $100$ as shown in Figure 2I, and then proceeds to the seasonal peak. Figure 2J presents the likelihood of a county being part of this largest, connected component during the trigger period. In the second approach, we followed causality streamlines back to their source county. Figure 2K presents the county-specific likelihood of streamline initiation across nine years.

These approaches produced qualitatively similar results (Figure 2J and K). While epidemics seem to start in many places around the country (see the origins of streamlines in Figure 3J and I), they successfully gain traction near large bodies of water (as evidenced by the most likely places of epidemic onset, see Figure 2J and K)). Otherwise, they fizzle out before triggering an actual epidemic cycle (see Figure 2J). Seasonal initiation is neither spatially uniform nor simply a reflection of county-specific population density.

Our analysis of the Twitter movement matrix indicates that people most frequently travel between neighboring counties, preferentially towards higher-population-density areas, which shows that the maximum-probability movement patterns follow the local gradient of increasing population density (see Figure 4—figure supplement 1). In contrast, the geo-spatially-averaged movement vectors for each county reveal global flows in the movement patterns (see Figure 3H, along with Methods for the calculation of spatial averages).

Figure 3H–I suggest that average movement patterns largely agree with the influenza streamlines: Both patterns, especially in the South/Southeast of the country, are associated with flow pointing away from large bodies of water.

In addition to looking at the direction of short-range travel, we used our non-parametric Granger analysis to investigate the comparative strength of short- vs. long-range influenza propagation. In the first case, we considered the neighborhood map shown in Figure 4A (for a detailed definition of ”neighbors,’ see Materials and methods), and the in the second case, we considered associations between major, airport-bearing counties (see Figure 4B). We then plotted the distribution of the maximum pairwise coefficient of causality, where the maximization is carried out by fixing the source and the target and varying the delay in weeks, after which we attempt to predict the target stream.

Figure 4 with 1 supplement see all

Download asset Open asset

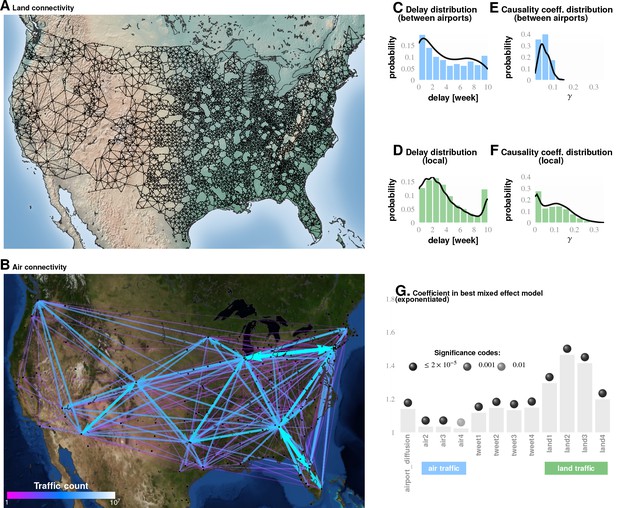
Comparing influence of short- and long-distance travel on infection propagation Plate A shows land connectivity visualized as a graph with edges between neighboring counties.

Plate B shows air connectivity as links between airports, with edge thickness proportional to traffic volume. Plate C shows the delay in weeks for the propagation of Granger-causal influence between counties in which major airports are located, and Plate E shows the distribution of the inferred causality coefficient between those same counties. Plates D and F show the delay and the causality coefficient distribution respectively, which we computed by considering spatially neighboring counties. The results show that local connectivity is more important. We reached a similar conclusion using mixed-effect Poisson regression, as shown in Plate G: The inferred coefficients for land connectivity are significantly larger than those for air connectivity, tweet-based connectivity, or exponential diffusion from the top $30$ largest airports. The coefficients shown in Plate G are exponentiated, allowing us to visualize probability magnitudes (see ‘Model Definition’).

https://doi.org/10.7554/eLife.30756.016

Conclusions associated with Approach 1: The inferred causality streamlines computed from the infection time series in all counties (Figure 3) show that epidemics are mostly triggered near large water bodies and flow inland and away. They also illustrate that the US continental Southern states act as ‘sinks’ to a large proportion of these streamlines. (‘Sinks,’ in our definition here, are geographic areas that multiple streamlines converge towards; sinks are especially obvious when we look at the vector representation of causality direction. The opposite of a ‘sink’ is a ‘source,’ defined as an area at which at least one streamline starts.) This might explain the increased prevalence in the designated region. Additionally, the analysis shows that human travel is a very important driver of emergent epidemiological patterns, and that short-range, land-based travel is more important than air-travel. This result is cross-corroborated by our Poisson regression analysis (described next in Approach 2).

Approaches 2 and 3 are motivated by the ‘why’ questions: (1) Why do epidemics initiate where and when they do? and; (2) Why do some disease initiations become epidemics while others do not?

Approach 2: Importance of factors from poisson regression

We focused on a subset of weeks associated with the initial rise of influenza waves (indicated by the gray bars in Figure 2I, and calculated as discussed earlier). The results from our best-fit model are illustrated in Figure 1A. We selected this particular model out of a total of $126$ compared in the Bayesian analysis, a few of which we list in Table 5, ranked by their decreasing goodness-of-fit, measured with the Deviance Information Criterion, DIC (see Supplement). From the values of the inferred coefficients corresponding to the different factors, and taking into account their significance levels and credible intervals, we concluded that the roles played by weather variables, particularly humidity, appear to be substantially more complicated compared to what has been suggested in the literature.

The surprisingly unimportant factors

School schedule was not predictive of influenza onset in our analysis: We ended up with a $p$ -value of $0.84$ and an odds ratio of $0.8403$ , strongly suggesting that school opening dates are not a significant factor in triggering the seasonal epidemic.

We are not claiming here that closing down schools during the seasonal peak, or during an initial phase of a seasonal epidemic, would not have a beneficial effect on maximum incidence. Rather, the observed epidemiological patterns over the time period we analyzed (2003–2011) do not seem to name ‘school opening times’ as a significant predictive factor–at least in the continental US.

We factored in the effect of vaccination coverage by estimating the cumulative fraction of the population that received the current influenza vaccine stratified by geo-spatial location and time of inoculation within each influenza season. Our analysis indicated that vaccination coverage is not a significant predictor of influenza onset/triggering period. It could be a reflection of overall vaccine ineffectiveness, or the choice of outcome predicted (i.e. vaccination might effect overall infection numbers over the entire outbreak, but not the timing of the trigger). It could also reflect the fact that different influenza type/subtypes have different virulence–so a vaccine against H3N2 during an H3N2 year, may be more effective, but due to that fact that H3N2 is more virulent, more people still wind up seeking medical care.

Vaccination coverage failed to reach predictive significance. The variables corresponding to spatio-temporal indicators of the cumulative fraction of the inoculated population are included in our best model (see the last entry in Table 5), but their effect fails to be significant. However, if we drop those variables from the model, the DIC increases. We suggest that the strong dependence between antigenic diversity and vaccination coverage (see Figure 1J–M) is responsible for this effect: Vaccination coverage is important, but its influence is captured by the antigenic variation.

The most important factors

The strongest predictor groups (ranked by importance) are the population’s socio-demographic properties, weather, antigenic drift of the virus, land-based travel, and auto-correlation of influenza waves.

Weather As far as weather effects are concerned, epidemics tend to originate in places with high mean, maximum specific humidity, high average temperature, and low average air pressure, namely, in counties at the Southern, and, to a lesser extent, Eastern and Western US coastlines. Additionally, the spread of an epidemic is significantly influenced by a drop in specific humidity up to four weeks before its onset. However, this effect is weaker than the mean maximum specific humidity effect. Drop in average temperature that dips one to three weeks prior to the epidemic onset is also significantly important (this is consistent with earlier experiments [Lowen et al., 2008]), especially when the temperature drop is accompanied by a decrease in specific humidity, average wind speed, and solar flux. However, high levels of solar flux in the week of onset are also important. This complicated set of weather conditions, a signature of the cold air front (Shaman et al., 2010), is validated by our out-of sample predictions to increase the risk of triggering the seasonal epidemic. Total precipitation also plays a positive role.

The weather/humidity paradox

How can colder weather and lower humidity be a predictor of influenza, if influenza epidemic waves tend to start in the South with warmer climates and higher humidity? Our resolution of this seeming controversy is as follows: The stress is on the drop in both humidity and temperature in those areas with high average annual values of these measurements. A blast of colder, lower-humidity weather in these warm-climate areas has two effects: (1) The influenza virus can stay viable in water droplets longer than in hot, sunny weather, and; (2) Humans tend to interact indoors, in more crowded conditions. Both of these factors are favorable for transmission of the virus to the population at large.

Antigenic variation Antigenic diversity for HA, NA, M1, and M2 are important predictors. While HA, NA, and M1 inhibit the trigger, M2 diversity enhances it. This peculiar difference in the direction of influence might be a manifestation of the roles played by the individual viral proteins in its life-cycle.

The first three proteins are directly involved in the viral binding to host cell surface receptors, while M2 activity is needed only during HA biosynthesis. Additionally, proteolysis experiments indicated that M2 proton channel activity helped to protect (H1N1)pdm09 HA from premature conformational changes as it traversed low-pH compartments during transport to the cell surface (Alvarado-Facundo et al., 2015).

We found that antigenic diversity is a significant predictor in all four of the viral proteins we considered. Interestingly, while the increasing diversity found in HA, NA, and M1 inhibits the epidemic trigger, the higher diversity in M2 enhances it (see Discussion).

Travel Land travel intensity one to three weeks before epidemic onset is a strong predictor. Air travel is also predictive, but its strength is an order of magnitude weaker than that of land travel.

Autocorrelation The increase in an influenza outbreak’s infection weekly rate one and two weeks before an epidemic onset (in the epidemic source county itself) is predictive of epidemic wave origin.

We have used substantially richer datasets than those used by earlier studies (Shaman et al., 2010; Tamerius et al., 2013), which lends strong statistical support to our conclusions. It also allowed us to disentangle and make precise the contributions from different factors, $e . g .$ , mean county humidity vs. drops in humidity before an infection. While we found the former effect to be clearly stronger (in accordance to previously reported results [Shaman et al., 2010]), the other diverse set of factors were also found to be significant.

Validation of predictive capability

The robustness of our results is established in a number of ways:

In mixed-effect regression (Approach 2), we compared over $120$ chosen model variations (see Table 5 for an abridged list, and Supplementary file 3for the complete enumeration of considered models); the results appear to be qualitatively stable, though the quantitative performance of the models vary somewhat as measured by DIC for different configurations of regression equations.
We carried out a direct validation of predictive performance by estimating model parameters using the first six seasons and predicting the epidemic trigger locations using the last three (see Figure 5 and Materials and methods). The out-of-sample predictions of influenza incidence are always positively correlated with observed incidence (Plate A). Perhaps more importantly, we obtained good predictability as measured by the area under the curve (AUC $\approx 80 %$ ) for the receiver operating characteristics (ROC, See Plates B-D). Plates E-G show that our out-of-sample predictions correctly identified epidemic initiation in the Southern and Southeastern counties of the continental US.
As we discuss in the next section, in Approach 3, we conducted a corroborating matched effect analysis on the counties, using combinations of county-specific factors as a ‘treatment,’ not unlike clinical trials in which patients on a drug regimen are matched to patients receiving a placebo (Morgan and Winship, 2015).

Figure 5

Download asset Open asset

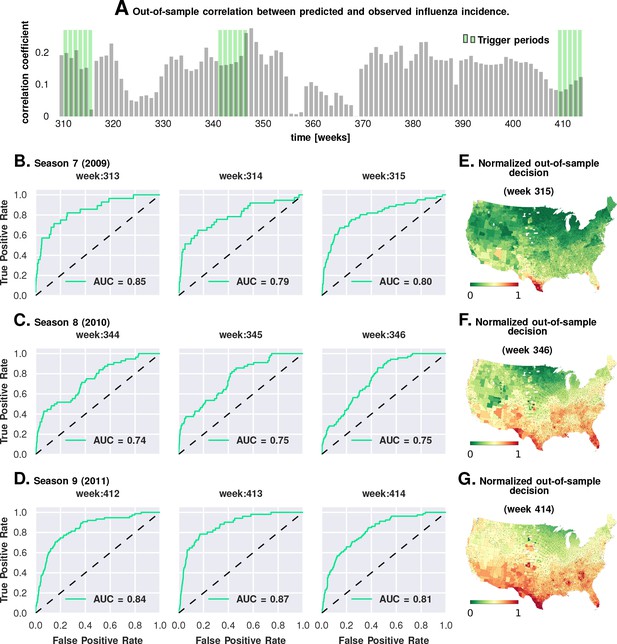
Prediction performance with training data from the first six seasons and validation on the last three.

Plate A shows the correlation between the observed incidence and the model-predicted response. We show significant positive correlation, particularly within the trigger periods, between the model predictions and the actual held-out data. This gives us confidence to construct ROC curves for each week. Plates B-D show the ROC curves for the last three weeks of each of the three seasons in the out-of-sample period (potentially, these computations can be repeated for all possible partitions of study weeks into training and test samples). Plates E-G illustrate that the normalized decision variable, which is the normalized response from the model, identifies the South and Southeastern counties as the trigger zones.

https://doi.org/10.7554/eLife.30756.018

Approach 3: Matching counties and factor combinations

In Approach 3, we investigated combinations of factors presented as ‘treatment’ via a non-parametric, exact-matching analysis of US counties during the weeks of epidemic onset on a season-by-season basis.

First, we collected the list of all counties with a drop in maximum specific humidity during the weeks leading up to an influenza season in a particular year. This is the ‘treated set’: the set of counties that may be thought of as subjected to the positive ‘treatment’ of a drop in specific humidity. We split this set into two, considering counties that also experience increased influenza prevalence during the epidemic onset, and ones that do not (counties with two different values of the outcome variable). The number of counties in these two sets define the first row of a $2 \times 2$ contingency table. In the second row (the ‘control set’), we focused on counties that do not experience a drop in the maximum specific humidity. However, we only considered counties that have a matching counterpart in the treated set in the following sense: For each county in the control set, we found at least one in the treated set such that the rest of the significant variables (other than specific humidity) had similar variation patterns in both counties. Once we defined the control set, we split it in the manner described for the treated set: We counted the number of control counties that experienced an increased influenza prevalence during epidemic onset, and those which did not. This defined the second row of the contingency table. Finally, we used Fisher’s exact test to compute an odds ratio (the odds of realizing these numbers by chance), along with the test-derived significance of the association between the ‘treatment’ and epidemic wave initiation (p-value). Furthermore, we defined our treatment to consist of multiple factors simultaneously, $e . g .$ specific humidity and its change in the preceding week, along with average temperature and degree of urbanity, see Figure 6.

Figure 6

Download asset Open asset

Results for our analysis involving county-matching (Approach 3).

Plate A illustrates the factor combinations that turn out to be significant over the nine seasons. Notably, for each season, we have multiple, distinct factor sets that turn out to be significant ( $p < 0.05$ ) and yield a greater-than-unity odd ratio. Plotting the probability with which different factors are selected when we look at season-specific county matchings (the top panel in Plate A), we see a corroboration of the conclusions drawn in Approach 2. We find that specific humidity and average temperature, along with their variations, are almost always included. We do see some new factors that fail to be significant in the regression analysis, $e . g .$ , degree of urbanity and vaccination coverage. While vaccination coverage is indeed included as a factor in our best performing model, in Approach two it failed to achieve significance, perhaps due to its strong dependence on antigenic variation (see Figure 1J–M). Degree of urbanity is indeed significant for some of the regression models we considered (see Supplementary Information), but was not significant for the model with the smallest DIC. Note that ‘Treatment’ here is defined as a logical combination of weather factors. A treatment is typically a conjunction of several weather variables. For example, the treatment shown in top left panel of Plate B involves a conjunction of: (1) a drop in average temperature during the week of infection; (2) a drop in temperature during the week of infection; (3) a higher-than-average specific humidity; (4) a higher-than-average temperature, and; (5) a high degree of urbanity. With respect to the ‘treatment,’ we can divide counties into three groups: (1) ‘treated counties,’ shown in green; (2) at least one matching county for each of the treated counties (matching counties are very close to the treated counties in all aspects but in treatment, which we called ‘control’ counties), shown in black, and; (3) other counties, shown in grey. The counties in the ‘treatment’ and ‘control’ groups are further subdivided into those counties that initiated an influenza wave and those that have not, resulting in four counts arranged into a two-by-two contingency table. We then used the Fisher exact test to test for association between treatment and influenza onset. Panels in Plate B show both the treated and control sets for the $9$ seasons for a subset of chosen factors. The results are significant, as shown in Tables 2 and 3. The variable definitions are given in Table 4. Notably, some of the variables found significant in the regression analysis are not included above, and some which are not found to be significant in the best regression model show up here. This is not to imply that they are not predictive or lack causal influence. The matched treatment approach, as described above, is not very effective if we use more than $\sim 10 - 15$ factors simultaneously to define the treated set (for the amount of data we have); this results in a contingency table populated with zero entries.

https://doi.org/10.7554/eLife.30756.019

Note that geographic clustering of ‘treated’ and ‘untreated’ counties arose automatically as a result of similar weather patterns being imposed via the constraint of multiple climate variables.

Table 4

Variables in mixed-effect Poisson regression analysis (Approach 2)

https://doi.org/10.7554/eLife.30756.020

Variable name	physical effect

N	Total number of patient visits given week and county (the offset)
max_HUS_mean	Mean county-specific maximum specific humidity over nine years
d_max_HUS_i	Normalized and zero-centered deviations of maximum humidity, i = 0–4 weeks before
t_avg_mean	Mean county-specific temperature over nine years
d_t_avg_i	Normalized and zero-centered deviations of mean temperature, i = 0–4 weeks before
RSDS_mean	Mean county-specific solar insolation over nine years
d_RSDS_i	Normalized and zero-centered deviations of mean solar insolation, i = 0–4 weeks before
AVG_PRESS mean	Mean county-specific solar insolation over nine years
d_AVG_PRESS_i	Normalized and zero-centered deviations of mean surface pressure, i = 0–4 weeks before
tot_prec_mean	Mean county-specific total precipitation over nine years
d_tot_prec_i	Normalized and zero-centered deviations of mean total precipitation, i = 0–4 weeks before
Wind_avg_mean	Mean county-specific average wind speed over nine years
d_Wind_avg_i	Normalized and zero-centered deviations of average wind speed, i = 0–4 weeks before
Income	County-specific mean income
airport_diffusion	Influence from proximity to airports, modeled as human traffic-weighted exponential diffusion from the 30 largest US airports
Am_Ind	% of American Indians in the county
Asian	% of Asians
White_Hisp	% of Caucasian/Hispanics
W_non_Hisp	% of Caucasian/Non-Hispanics
Black_Hisp	% of Black/Hispanics
B_non_Hisp	% of Black/Non-Hispanics
Pacific	% of Pacific Islanders
Insured	% of county population insured
Poor	% of county population under poverty line
Urban	% of county population classified as urban
land_i	influenza velocity change in the land neighbors of the county $i$ weeks before the current week
tweet_i	influenza velocity change in the Twitter neighbors of the county $i$ weeks before the current week
air_i	influenza velocity change in airport neighbors of the county $i$ weeks before the current week
v_i	change in rate of infection in the county itself $i$ weeks from the current
M1	Diversity in M1 protein primary structure
M2	Diversity in M2 protein primary structure
NA	Diversity in NA protein primary structure
HA	Diversity in HA protein primary structure
Cum_vac_per_N_i	vaccination coverage in the county cumulated over past 20 weeks $i$ weeks from the current

(a) Definition of variables

Unlike the mixed-effect regression approach (Approach 2), this matching analysis is non-parametric, and intended to reveal whether multiple factors are, indeed, simultaneously necessary.

The results of Approach 3’s analysis are presented in Figure 6 and Tables 2 and 3. We found that no single variable was able to consistently yield a statistically significant odds ratio greater than one; multiple factors interacted to shape an epidemic trigger (see Table 3 for a few examples). With a total of $47$ significant variables in our best mixed-effect model, an exhaustive search for all combinations was not feasible. Instead, we performed a standard evolutionary search, looking for combinations that yielded a significant odds ratio for individual seasons. Additionally, we considered all seasons together (by simply adding the contingency tables, element-wise) in order to increase the test’s statistical power.

We isolated ten variables (as shown in Figure 6, Plate B) in this manner which included maximum specific humidity and average temperature along with their variations, the degree of urbanity, antigenic variation, and vaccination coverage.

The factors that appeared most often in our analysis are illustrated in Plate A: It appears that maximum specific humidity and average temperature, along with their variations, and the degree of urbanity have the most frequent contribution, followed by antigenic variation and vaccination coverage.

We did see some new factors here that failed to be of significance in the regression analysis (Approach 2), $e . g .$ , degree of urbanity and vaccination coverage. While vaccination coverage was included as a factor in our best performing model in Approach 2, it failed to achieve significance, perhaps due to its strong dependence on antigenic variation (see Figure 1J–M). Degree of urbanity was indeed significant for some of the regression models we considered (see Supplementary Information), but failed to be so for the model with the least DIC.

Thus, Approach three corroborates and strengthens key claims of Approach 2.

The exact set of factors varied somewhat over the seasons; nevertheless, together, they yield significant results when all seasons are considered together. The matching analysis corroborates our results from both the mixed-effect regression and the geographic streamline analyses: The sets of counties initiating the wave are near coasts on the Southern region of the continental US (see Plates A - I in Figure 6).

Local travel vs. long-distance travel and influenza

Our conclusion that local travel is predominantly responsible for disease wave propagation is supported by several lines of analysis.

First, continuous land-movement infection waves are visible in the weekly influenza rate movie; we computed this movie from insurance claim data and made it available with results of this study.

Second, because our all-weeks-included dataset was too large for the R MCMCglmm package to handle, we performed mixed-effect Poisson regression calculations using a 50 percent random sample of all the weeks for which data were available. In this computation, the airport-proximity, fixed-effect coefficient turned out to be statistically significantly negative (see Supplement A, as well as the editable output file ‘flu-50-percent-weeks.txt’).

Third, the results from our Granger-causality inference showed that:

Local county-to-county movements were much more predictive of influenza wave change than airport movements. In comparing Plates E and F in Figure 4, we see that the local movement causality coefficient ( $γ$ ) is, on average, twice as large as that for long-range movement (Figure 4E). Figure 4E shows that the mean long-range causality coefficient is approximately 0.05, whereas it is just over 0.1 in the local propagation. As the causality coefficient quantifies the amount of predictability (measured as information in bits) communicated about the target data stream per observed bit in the source data stream, it follows that, on average, every ten bits of sequential incidence data from an influencing location tells us one bit about the unfolding incidence dynamics in the target location. Therefore, in case of the long-range movement, informativeness is twice as low, so we need on average 20 bits to infer one bit about the state of infection. These calculations strongly suggest that local movement is predictively stronger with regards to influenza infection propagation.
While the most frequent value of the computed time delay in influence propagation between counties with large airports is zero weeks, this distribution is significantly flatter compared to that for local, county-to-county influence propagation.

Discussion

A summary of the complex relationship between the driving factors that contribute to the trigger and subsequent development of a seasonal epidemic can be clarified with a forest fire metaphor.

The maturation of a forest fire requires the collusion of multiple factors—namely the presence of flammable media, an initiating spark, and a wind current to help spread the fire. Our conceived mapping of this analogy to influenza infection is as follows:

Flammable Media: The Southern US appears to have an unusually high level of social connectivity; it is at least one order of magnitude higher than that in the north of the country (see GSS survey results (Smith et al., 1972) and Table 1). The number of close friends, close friends who are neighbors, and communities of people who all, or mostly, know each other is much higher in the South than in the country at large. Our conjecture is that a manifestation of this high-connectivity is the highest apparent percentage of people infected with influenza ( $20 %$ as opposed to $4 %$ in other parts of the country).
Initiation Spark: An initial spark for the infection wave is generated by a combination of weather and demographic factors. Specifically, warm, humid places are conducive to influenza wave initiation - particularly in weeks where specific humidity drops. Airport proximity is important, as well as demographic and economic makeup and also the degree of urbanization. Note that the first static condition (warm humid places) is highly correlated with areas in the South with greater social connectivity. It is possible that static meteorological variables (warm mean temperature and high mean humidity) serve as proxies for high social connectivity or other correlated socioeconomic factors.
Wind: The ‘wind’ in this analogy is the collective movement of a large number of people, integrated over time, revealing persistent ‘currents.’ These currents reproducibly point from coastlines and move inwards towards the center of the continent, making them perfect vehicles to transmit the infection inland from the shores.

Each of our three types of computational approaches has their strengths and weaknesses: (1) The Poisson mixed-effect regression allows for the direct comparison of the predictive strength of numerous predictor variables and accounts for spatial and temporal autocorrelation, but relies on strong modeling assumptions; (2) The non-parametric Granger analysis is not limited by restrictive modeling assumptions in our implementation, though it focuses only on trends of infection propagation between counties, and; (3) The county-matching analysis is also model-free, but this freedom comes at the expense of lesser statistical power.

What is new in this study?

The following aspects make our study of influenza triggers new in the influenza literature: (1) Instead of simulating the plausibility of one particular epidemic trigger model with a dynamic disease transmission model, we used formal model selection tools to compare the goodness of fit of hundreds of plausible models; (2) We explicitly attempted to systematically cross-compare the importance of numerous individual factors typically hypothesized to contribute to epidemic onset; (3) To accomplish this, we collected an unprecedented volume of temporal and spatial data on disease dynamics and the dynamics of putative predisposing factors; (4) We used several orthogonal, computational causality-inference techniques (one of which was developed specifically for this study) to probe associations between disease onset and putative epidemic triggers; (5) We tested our best models for their predictive potential and demonstrated that they are, indeed, suitable for forecasting disease waves, and; (6) We combined, for the first time, numerous candidate factors in a single, integrative study.

Convergent conclusions, culled from these radically different techniques, strengthen our claims and make it statistically unlikely that we are observing analysis artifacts. First, the Granger causality analysis results (Approach 1) provide insights into the details of influenza’s epidemiological dynamics. Figure 3G traces out the paths most likely followed by the infection, on average, across the continental US. We note that $\sim 75 %$ of the streamlines sink in counties belonging to the Southern states, which matches up well with the streamline-encoded dynamics of weekly disease incidence over nine years (see Figure 3I). What drives this particular causality field’s geometry? While we cannot definitively answer this question, a comparison of the global patterns emerges from the local mobility data culled from the aforementioned Twitter database and offers a tentative explanation (see Figure 3H). Second, contrary to reported human travel pattern influence on seasonal epidemics (Viboud et al., 2006) (but consistent with [Gog et al., 2014]), we find that short-distance travel contributes more significantly to disease spread (see Figure 4). In particular, we find that long-range air travel is important as an epidemic trigger, but once infection waves are triggered, air travel patterns (or proximity to major airports) become less important. Short-range mobility, on the other hand, is apparently important for sustaining infection transmission over each season. Thus, we find short-range travel to be more important for defining the emergent spatio-temporal geometry of infection waves, while proximity to airports is more important for actually triggering an influenza season; the latter loses positive influence once an infection is under way. This conclusion is justified as follows: (1) When we performed regression calculations using all weeks for which data were available (as opposed to wave initiation weeks only) the airport proximity predictor coefficient turned out to be statistically significantly negative (see Supplement). (2) Results from our Granger-causal inference indicate that, on average, the local, putatively causal connections are far stronger compared to the putatively causal connections between counties within which the major airports are located (see Figure 4C and F). Additionally, from our best mixed-effect regression model (Figure 1A), we find that land connectivity effects are significantly stronger than air connectivity effects. The predictive value of Twitter connectivity, which intuitively captures both local and long-distance travel, lies in-between land and air connectivity coefficients. Note that Twitter connectivity is represented as a directed graph, where for each pair of counties, $i$ and $j$ , the $(i, j)$ edge weight represents the conditional probability of ending at county $j$ , given that a traveler/Twitter user started her journey in county $i$ . Transition probabilities from $i$ to $j$ sum to one over all $j$ . Therefore, intuitively, the Twitter connectivity graph should have the features of both a land-connectivity and an air travel graph; which indeed appears to be close to reality. 3) While airport diffusion is a significant factor in our best Poisson model (using data from the initiation period), the causal streamlines (constructed with the complete, all-year incidence data) do not seem to originate from airport-bearing counties.

The role of short-distance travel is particularly crucial in explaining influenza’s time-averaged, geo-spatial prevalence. While the mixed-effect regression analysis explains seasonal initiation in the vicinity of the continental US Southern shores, it might not, by itself, adequately explain its average prevalence patterns across the country.

Also not explained solely by our regression models is the occurrence of relatively high infection prevalence in the central parts of the country. These differences cannot be attributed to long-distance air travel, as discussed before. However, the routes taken by the causality streamlines (as computed by the non-parametric Granger analysis), interpreted as paths followed by an infection on average, suggest an explanation: The close match between the Granger-causal flow and the short-range mobility patterns (derived from Twitter analysis) strongly suggest that average disease prevalence is modulated by short-range mobility.

Rationale for observational analysis

The traditional empirical approach of testing a causal link between a factor and an outcome of an experiment was to vary one factor at a time, while keeping the other factors (experimental conditions) constant. This ‘all the rest of the conditions are equal’ assumption is often referred to by its Latin form as ceteris paribus. R.A. Fisher ([Fisher, 1935], p. 18) noted that, in real-life experiments, perfect ceteris paribus is not achievable ‘because uncontrollable causes which may influence the results are always … innumerable.’ Fisher’s proposed solution to this problem is to design experiments to involve random assignment of treatment (the putative causal factorâ€™s states) to individual trials and then use regression analysis to estimate the value and significance of the putative causal effect.

Likewise, hypothesis-driven science, wherein investigators formulate a single, testable hypothesis and design specific experiments to test it, is a core element of the scientific method, and works well in most scientific fields. However, a new challenge emerges in data-rich scientific fields, such as genomics, epidemiology, economics, climate modeling, and astronomy: How do we choose the most promising hypotheses among millions of eligible candidates that potentially fit data? One solution to this challenge is the many-hypotheses approach, a method of automated hypothesis generation in which many hypotheses are systematically produced and simultaneously tested against all available data. This approach is currently used, for example, in whole-genome association or genetic linkage studies, and often enables truly unexpected discoveries. In contrast to the single-hypothesis approach, the many-hypotheses approach explicitly accounts for the large universe of possible hypotheses through calibrated statistical tests, effectively reducing the likelihood of accidentally accepting a mediocre hypothesis as a proxy for the truth (Nuzzo, 2014).

The many-hypotheses approach provides a complement to carefully controlled and highly focused wet laboratory experiments. Running controlled experiments to test a single hypothesis necessarily ignores many of the complexities of a real-world phenomenon; these complexities are necessarily present in large, longitudinal datasets. Of course, the data-driven ‘many-hypotheses’ approach is only one aspect of the broader scientific process progressing toward the development of verifiable general theories.

Agreement and disagreement between methods

Intuitively, we expected that all three approaches would produce similar, if not identical results. In practice, while the three approaches agreed in most cases, this agreement was not perfect. For example, the highlighted areas (greater incidence) in the first influenza season snapshot for Figure 2A–H each should match relatively well to the maps in Figure 6B (or at least some unspecified subset of ‘high incidence treatment counties’). While the county-matching results point to initiation at coasts, in Figure 2, 2006-2007 initiation seems to spread from the West Coast and, in , 2010 has a scattered pattern across the middle of the US.

The intuitive explanation of perceived discrepancy is that the matching method agrees with other analysis types predominantly, but not in all cases. Each analysis has limitations. In the case of the matching analysis, we have less statistical power than in, for example, Poisson regression; matching by numerous parameters reduces the initial set of thousands of counties to a handful of matching ‘treated’ counties (which meet a particular combination of weather and sociodemographic conditions) and ‘untreated’ counties (very similar to ‘treated’ ones in all respects but treatment). The difficult-to-match, ‘weeded out’ counties may happen to be in the coastal areas indicated as the most likely places of influenza wave origin by other analyses.

In the case of the 2007 and 2010 results, the matching analyses pick patterns that are different from those produced by the causality streamline analysis and mixed-effect Poisson regression models.

Figure 6’s Plate B shows the distribution of the treatment counties and matched-non-treatment counties. Note that here, we are not directly predicting initiation, so while the patterns in Figure 2 and Figure 6 should indeed show some similarity, they are not required to match up perfectly. The most similar treated counties do indeed show up in the Southern shores.

Generalizability

Our analysis uses no prior knowledge specific to influenza epidemiology. As such, these methods are not limited by either the pathogen under consideration (influenza), or the geospatial context (United States). The tools developed here are expected to be equally applicable to analyzing general epidemiological dynamics for pathogens other than influenza, unfolding in arbitrary geographical regions. The specific conclusions we draw about the initiation and propagation of the seasonal influenza in US might not hold true for influenza epidemiology in a different geographical context. However, the analysis tools are still applicable. More broadly, our tools delineate a general approach to modeling complex spatio-temporal dynamics, with applications beyond solely disease epidemiology.

We conclude by highlighting the structure of overlapping conclusions delivered by our three approaches. Approach 1: Granger-causality analysis suggests that an epidemic tends to begin in the South, near water bodies and that short-range, land-based travel is more influential compared to air-travel for infection propagation, providing a map of mean infection flow across the continental US. Approach 2: Poisson regression identifies significant predictive factors, ranks these factors by importance, suggests that Southern shores are where the epidemic begins, and corroborates Approach 1’s result on short-range vs. long-range travel. Approach 3 (county-matching): This approach drills down further to the epidemic onset source to the Southeastern shores of continental US, and identifies a smaller validated subset of predictive factors.

Materials and methods

The methods and putative predictors identified in our study should be directly applicable to data outside the US. While the balance (relative importance) of putative triggers of influenza waves may vary, the factors themselves should be universal globally, because the virus and host biology are universal.

Candidate factors in influenza initiation

To investigate county-specific variability, we grouped candidate factors into several categories: demographic, relation to human movement, infection state of county neighbors, and county’s own recent state, and climatic.

Major hypotheses regarding putative causal factors affecting infection dynamics can be traced to a handful of earlier publications:

Short- and long-range, work-related human movement (Viboud et al., 2006), including air travel (Colizza et al., 2006; Balcan et al., 2009; Viboud et al., 2006)
Demographic confounders (Gog et al., 2014; Charu et al., 2017)
Social contact among children in schools, or the ‘Return-to-school effect’ (Gog et al., 2014)
Absolute humidity (Shaman and Kohn, 2009)
Other climate variables (Chowell et al., 2012; te Beest et al., 2013)
Host immunity, as affected by vaccination coverage, previous infections, and antigenic variation (Centers for Disease Control and Prevention et al., 2009).

Equation used in Poisson regression	DIC
flu $\sim$ LOGN + 1 + max_HUS_mean + d_max_HUS_0 + d_max_HUS_min_1 + d_max_HUS_min_2 + d_max_HUS_min_3 + t_avg_mean + d_t_avg_0 + d_t_avg_min_1 + d_t_avg_min_2 + d_t_avg_min_3 + max_HUS_mean * t_avg_mean + d_max_HUS_0 * d_t_avg_0 + d_max_HUS_min_1 * d_t_avg_min_1 + d_max_HUS_min_2 * d_t_avg_min_2 + d_max_HUS_min_3 * d_t_avg_min_3 + RSDS_mean + d_RSDS_0 + d_RSDS_min_1 + d_RSDS_min_2 + d_RSDS_min_3 + AVG_PRESS_mean + d_AVG_PRESS_0 + d_AVG_PRESS_min_1 + d_AVG_PRESS_min_2 + d_AVG_PRESS_min_3 + Income + airport_diffusion + Am_Ind + Asian + White_Hisp + W_non_Hisp + Black_Hisp + B_non_Hisp + Pacific + Insured+Poor + Urban+v1+v2+land1+land2+land3+land4+tweet1+tweet2+tweet3+tweet4+air1+air2+air3+air4+HA + M1+M2+NA.	185942
flu $\sim$ LOGN + 1 + max_HUS_mean + d_max_HUS_0 + d_max_HUS_min_1 + d_max_HUS_min_2 + d_max_HUS_min_3 + d_max_HUS_min_4 + t_avg_mean + d_t_avg_0 + d_t_avg_min_1 + d_t_avg_min_2 + d_t_avg_min_3 + d_t_avg_min_4 + RSDS_mean + d_RSDS_0 + d_RSDS_min_1 + d_RSDS_min_2 + d_RSDS_min_3 + d_RSDS_min_4 + AVG_PRESS_mean + d_AVG_PRESS_0 + d_AVG_PRESS_min_1 + d_AVG_PRESS_min_2 + d_AVG_PRESS_min_3 + d_AVG_PRESS_min_4 + tot_prec_mean + d_tot_prec_0 + d_tot_prec_min_1 + d_tot_prec_min_2 + d_tot_prec_min_3 + d_tot_prec_min_4 + Wind_avg_mean + d_Wind_avg_0 + d_Wind_avg_min_1 + d_Wind_avg_min_2 + d_Wind_avg_min_3 + d_Wind_avg_min_4 + Income + airport_diffusion + Am_Ind + Asian + White_Hisp + W_non_Hisp + Black_Hisp + B_non_Hisp + Pacific + Insured+Poor + Urban+v1+v2+land1+land2+land3+land4+tweet1+tweet2+tweet3+tweet4+air1+air2+air3+air4+HA + M1+M2+NA.+HA * NA.	185940.6
flu $\sim$ LOGN + 1 + max_HUS_mean + d_max_HUS_0 + d_max_HUS_min_1 + d_max_HUS_min_2 + d_max_HUS_min_3 + t_avg_mean + d_t_avg_0 + d_t_avg_min_1 + d_t_avg_min_2 + d_t_avg_min_3 + max_HUS_mean * t_avg_mean + d_max_HUS_0 * d_t_avg_0 + d_max_HUS_min_1 * d_t_avg_min_1 + d_max_HUS_min_2 * d_t_avg_min_2 + d_max_HUS_min_3 * d_t_avg_min_3 + RSDS_mean + d_RSDS_0 + d_RSDS_min_1 + d_RSDS_min_2 + d_RSDS_min_3 + AVG_PRESS_mean + d_AVG_PRESS_0 + d_AVG_PRESS_min_1 + d_AVG_PRESS_min_2 + d_AVG_PRESS_min_3 + Income + airport_diffusion + Am_Ind + Asian + White_Hisp + W_non_Hisp + Black_Hisp + B_non_Hisp + Pacific + Insured+Poor + Urban+v1+v2+land1+land2+land3+land4+tweet1+tweet2+tweet3+tweet4air1+air2+air3+air4+HA + M1+M2+NA.+Cum_vac_per_N_0	185938.1
flu $\sim$ LOGN + 1 + max_HUS_mean + d_max_HUS_0 + d_max_HUS_min_1 + d_max_HUS_min_2 + d_max_HUS_min_3 + d_max_HUS_min_4 + t_avg_mean + d_t_avg_0 + d_t_avg_min_1 + d_t_avg_min_2 + d_t_avg_min_3 + d_t_avg_min_4 + RSDS_mean + d_RSDS_0 + d_RSDS_min_1 + d_RSDS_min_2 + d_RSDS_min_3 + d_RSDS_min_4 + AVG_PRESS_mean + d_AVG_PRESS_0 + d_AVG_PRESS_min_1 + d_AVG_PRESS_min_2 + d_AVG_PRESS_min_3 + d_AVG_PRESS_min_4 + tot_prec_mean + d_tot_prec_0 + d_tot_prec_min_1 + d_tot_prec_min_2 + d_tot_prec_min_3 + d_tot_prec_min_4 + Wind_avg_mean + d_Wind_avg_0 + d_Wind_avg_min_1 + d_Wind_avg_min_2 + d_Wind_avg_min_3 + d_Wind_avg_min_4 + Income + airport_diffusion + Am_Ind + Asian + White_Hisp + W_non_Hisp + Black_Hisp + B_non_Hisp + Pacific + Insured+Poor + Urban+v1+v2+land1+land2+land3+land4+tweet1+tweet2+tweet3+tweet4+air1+air2+air3+air4+HA + M1+M2+NA.+Cum_vac_per_N_diff_1 + Cum_vac_per_N_diff_2 + Cum_vac_per_N_diff_3 + Cum_vac_per_N_diff_4	185935.9
flu $\sim$ LOGN + 1 + max_HUS_mean + d_max_HUS_0 + d_max_HUS_min_1 + d_max_HUS_min_2 + d_max_HUS_min_3 + d_max_HUS_min_4 + t_avg_mean + d_t_avg_0 + d_t_avg_min_1 + d_t_avg_min_2 + d_t_avg_min_3 + d_t_avg_min_4 + RSDS_mean + d_RSDS_0 + d_RSDS_min_1 + d_RSDS_min_2 + d_RSDS_min_3 + d_RSDS_min_4 + AVG_PRESS_mean + d_AVG_PRESS_0 + d_AVG_PRESS_min_1 + d_AVG_PRESS_min_2 + d_AVG_PRESS_min_3 + d_AVG_PRESS_min_4 + tot_prec_mean + d_tot_prec_0 + d_tot_prec_min_1 + d_tot_prec_min_2 + d_tot_prec_min_3 + d_tot_prec_min_4 + Wind_avg_mean + d_Wind_avg_0 + d_Wind_avg_min_1 + d_Wind_avg_min_2 + d_Wind_avg_min_3 + d_Wind_avg_min_4 + Income + airport_diffusion + Am_Ind + Asian + White_Hisp + W_non_Hisp + Black_Hisp + B_non_Hisp + Pacific + Insured+Poor + Urban+v1+v2+land1+land2+land3+land4+tweet1+tweet2+tweet3+tweet4+air1+air2+air3+air4+HA + M1+M2+NA.	185933.7
flu $\sim$ LOGN + 1 + max_HUS_mean + d_max_HUS_0 + d_max_HUS_min_1 + d_max_HUS_min_2 + d_max_HUS_min_3 + d_max_HUS_min_4 + t_avg_mean + d_t_avg_0 + d_t_avg_min_1 + d_t_avg_min_2 + d_t_avg_min_3 + d_t_avg_min_4 + RSDS_mean + d_RSDS_0 + d_RSDS_min_1 + d_RSDS_min_2 + d_RSDS_min_3 + d_RSDS_min_4 + AVG_PRESS_mean + d_AVG_PRESS_0 + d_AVG_PRESS_min_1 + d_AVG_PRESS_min_2 + d_AVG_PRESS_min_3 + d_AVG_PRESS_min_4 + tot_prec_mean + d_tot_prec_0 + d_tot_prec_min_1 + d_tot_prec_min_2 + d_tot_prec_min_3 + d_tot_prec_min_4 + Wind_avg_mean + d_Wind_avg_0 + d_Wind_avg_min_1 + d_Wind_avg_min_2 + d_Wind_avg_min_3 + d_Wind_avg_min_4 + Income + airport_diffusion + Am_Ind + Asian + White_Hisp + W_non_Hisp + Black_Hisp + B_non_Hisp + Pacific + Insured+Poor + Urban+v1+v2+land1+land2+land3+land4+tweet1+tweet2+tweet3+tweet4+air1+air2+air3+air4+HA + M1+M2+NA.+Cum_vac_per_N_0	185932.3
flu $\sim$ LOGN + 1 + max_HUS_mean + d_max_HUS_0 + d_max_HUS_min_1 + d_max_HUS_min_2 + d_max_HUS_min_3 + d_max_HUS_min_4 + t_avg_mean + d_t_avg_0 + d_t_avg_min_1 + d_t_avg_min_2 + d_t_avg_min_3 + d_t_avg_min_4 + RSDS_mean + d_RSDS_0 + d_RSDS_min_1 + d_RSDS_min_2 + d_RSDS_min_3 + d_RSDS_min_4 + AVG_PRESS_mean + d_AVG_PRESS_0 + d_AVG_PRESS_min_1 + d_AVG_PRESS_min_2 + d_AVG_PRESS_min_3 + d_AVG_PRESS_min_4 + tot_prec_mean + d_tot_prec_0 + d_tot_prec_min_1 + d_tot_prec_min_2 + d_tot_prec_min_3 + d_tot_prec_min_4 + Wind_avg_mean + d_Wind_avg_0 + d_Wind_avg_min_1 + d_Wind_avg_min_2 + d_Wind_avg_min_3 + d_Wind_avg_min_4 + Income + airport_diffusion + Am_Ind + Asian + White_Hisp + W_non_Hisp + Black_Hisp + B_non_Hisp + Pacific + Insured+Poor + Urban+v1+v2+land1+land2+land3+land4+tweet1+tweet2+tweet3+tweet4+air1+air2+air3+air4+HA + M1+M2+NA.+Cum_vac_per_N_0 + Cum_vac_per_N_1 + Cum_vac_per_N_2 + Cum_vac_per_N_3	185926.6

Share this article

Cite this article

Putative determinants of seasonal influenza onset in the continental US and Poisson mixed-effect regression analysis (Approach 2).

Characteristics of seasonal influenza in the continental US An analysis of county-specific, weekly reports on the number of influenza cases for a period of 471 weeks spanning January 2003 to December 2013 (Plates A-H) for recurrent patterns of disease propagation.

Social connectivity: The US Southern region appears to have an unusually high level of social connectivity.

Fisher’s exact test results on matched treatment combinations

Fisher’s exact test results on matched treatment combinations

Computation of causality field, Approach 1 Plates A and B: Incidence data from neighboring counties in Alabama, US.

Comparing influence of short- and long-distance travel on infection propagation Plate A shows land connectivity visualized as a graph with edges between neighboring counties.

Prediction performance with training data from the first six seasons and validation on the last three.

Results for our analysis involving county-matching (Approach 3).

Variables in mixed-effect Poisson regression analysis (Approach 2)

Different Models Considered and DIC Ranking

Intuitive Description of Self and Cross Models.

Author details

Ishanu Chattopadhyay

Contribution

Competing interests

Emre Kiciman

Contribution

Competing interests

Joshua W Elliott

Contribution

Competing interests

Jeffrey L Shaman

Contribution

Competing interests

Andrey Rzhetsky

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Research organisms

Further reading

Characteristics of seasonal influenza in the continental US An analysis of county-specific, weekly reports on the number of influenza cases for a period of $471$ weeks spanning January 2003 to December 2013 (Plates A-H) for recurrent patterns of disease propagation.