Research Article

Cell lineage-dependent chiral actomyosin flows drive cellular rearrangements in early Caenorhabditis elegans development

Max Planck Institute of Molecular Cell Biology and Genetics, Germany
Biotechnology Center, TU Dresden, Germany
Cluster of Excellence Physics of Life, TU Dresden, Germany
Max Planck Institute for the Physics of Complex Systems, Germany
Chair of Scientific Computing for Systems Biology, Faculty of Computer Science, TU Dresden, Germany
Center for Systems Biology Dresden, Germany
Department of Mathematics, Massachusetts Institute of Technology, United States

Jul 9, 2020

https://doi.org/10.7554/eLife.54930

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: July 31, 2020 (This version)
Accepted Manuscript published: July 9, 2020 (Go to version)
Accepted: July 5, 2020
Received: January 6, 2020

1. Of interest
Single-cell RNA sequencing reveals cellular and molecular heterogeneity in fibrocartilaginous enthesis formation

Tao Zhang, Liyang Wan ... Hongbin Lu

Research Article Sep 21, 2023
Further reading

Abstract
Introduction
Results
Discussion
Materials and methods
Appendix 1
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Proper positioning of cells is essential for many aspects of development. Daughter cell positions can be specified via orienting the cell division axis during cytokinesis. Rotatory actomyosin flows during division have been implied in specifying and reorienting the cell division axis, but how general such reorientation events are, and how they are controlled, remains unclear. We followed the first nine divisions of Caenorhabditis elegans embryo development and demonstrate that chiral counter-rotating flows arise systematically in early AB lineage, but not in early P/EMS lineage cell divisions. Combining our experiments with thin film active chiral fluid theory we identify a mechanism by which chiral counter-rotating actomyosin flows arise in the AB lineage only, and show that they drive lineage-specific spindle skew and cell reorientation events. In conclusion, our work sheds light on the physical processes that underlie chiral morphogenesis in early development.

Introduction

Proper positioning of cells is instrumental for many aspects of early embryonic development (Wong et al., 2010; Bronner, 2012; Buchsbaum and Cappello, 2019). One way to achieve proper cell positioning is via migration (Scarpa and Mayor, 2016; De Pascalis and Etienne-Manneville, 2017). Another way by which cell positions can be specified is via the orientation of the cell division axis (Fishkind and Wang, 1995; Glotzer, 1997; Field et al., 1999). Since the orientation of the mitotic spindle dictates the cell division axis, the orientation of the mitotic spindle at cleavage plays a key role in determining daughter cell positions (Haydar et al., 2003; Egger et al., 2007; Kulukian and Fuchs, 2013; Howard and Garzon-Coral, 2017). This axis can be set at the beginning of cytokinesis, by assembling the mitotic spindle in the correct orientation from the start, or during cytokinesis by reorientation of the mitotic spindle (Wilson, 1925; Meshcheryakov and Beloussov, 1975; Kaltschmidt et al., 2000; Matsumura et al., 2012; Sugioka and Bowerman, 2018; Galli and van den Heuvel, 2008). While several studies highlight the mechanisms that determine the initial orientation of the mitotic spindle at the onset of cytokinesis (Sugioka and Bowerman, 2018; Matsumura et al., 2012; Kaltschmidt et al., 2000; Grill et al., 2001; Knoblich, 2010) the mechanisms controlling reorientation remain not very well understood. In this work, we investigate cell repositioning during cytokinesis in the early development of the Caenorhabditis elegans nematode. The fully grown hermaphrodite worm consists of exactly 959 somatic cells that are essentially invariant both in terms of position and lineage (Sulston and Horvitz, 1977; Sulston et al., 1983; Schnabel et al., 2006; Li et al., 2019). Development is deterministic from the start: the one-cell embryo undergoes an asymmetric cell division that gives rise to the AB (somatic) lineage and the P lineage (Sulston et al., 1983; Bruce et al., 2002). While the anterior daughter cell, AB, undergoes a symmetric cell division into ABa and ABp, the posterior daughter cell, P₁, divides asymmetrically into EMS forming the endoderm and mesoderm, and P₂ forming the germ line (Sulston et al., 1983). Appropriate cell-cell contacts are instrumental for development as they can determine cell identity (Priess, 2005; Artavanis-Tsakonas et al., 1999; Mango et al., 1994; Mello et al., 1994; Moskowitz et al., 1994). For example, reorientation of the ABa and ABp cells via pushing with a micro needle leads to an altered cell-cell contact pattern and an altered body plan with an inverted L/R body axis (Wood, 1991). Consequently, proper cell positioning, perhaps mediated via repositioning of the mitotic spindle during cytokinesis, is crucial (Hennig et al., 1992). Here, we set out to investigate which of the cells of the early embryo undergo reorientations during cytokinesis, and by which mechanism they do so.

Recently, a role for the actomyosin cell cortex in determining the cell division axis of early C. elegans blastomeres was identified (Naganathan et al., 2014; Sugioka and Bowerman, 2018). The actomyosin cortex is a thin layer below the plasma membrane that consists mainly of actin filaments, actin binding proteins and myosin motor proteins (Pollard and Cooper, 1986). Collectively, these molecules generate contractile forces that can shape the cell, drive cortical flows during polarization and orchestrate other active processes such as cell division (Mayer et al., 2010; Pollard, 2017). Cell-cell contacts can impact on the activity of myosin and the generation of contractile stresses, and the resultant pattern of cortical flows can determine the orientation of the mitotic spindle at the onset of cytokinesis (Sugioka and Bowerman, 2018). From a physical point of view, the actomyosin cortex can be thought of as a thin layer of a mechanically active fluid (Jülicher et al., 2007; Ramaswamy and Simha, 2006; Salbreux et al., 2009; Mayer et al., 2010) with myosin-driven active stress gradients generating cortical flows (Mayer et al., 2010). Interestingly, actomyosin can also exhibit rotatory flows driven by active torque generation. These chiral rotatory cortical flows reorient the ABa cell and the ABp cell during cytokinesis, driving a cell skew of ∼20° during division (Naganathan et al., 2014). This skew results in a L/R asymmetric cell-cell contact pattern (Pohl and Bao, 2010), thus executing left-right (L/R) symmetry breaking in the entire organism. However, how general such reorientation events are, and how they are controlled, remains unclear. Furthermore, it remains poorly understood whether chiral flows are prevalent in other cell divisions as well, and if they play a prominent role in cell repositioning during early embryogenesis of the C. elegans nematode.

Results

Early cell divisions of the AB lineage, but not of the P/EMS lineage, undergo chiral counter-rotating actomyosin flows

We set out to quantify chiral rotatory flows in the actomyosin cell cortex of the first nine cell divisions in early C. elegans development. In order to image C. elegans embryogenesis, various mounting techniques have been described that either mildly compress the embryo or mount the embryo uncompressed. We first compared the degree of embryo compression using two common mounting methods (Figure 1—figure supplement 1): (1) Attaching the embryos to an agarose pad (Bargmann and Avery, 1995) and (2) embedding the embryos in low-melt agarose (Naganathan et al., 2014). As reported before (Walston and Hardin, 2010), we found that the first method indeed compressed the embryos and leads to an aspect ratio of 1.29 ± 0.14. Embedding embryos in low-melt agarose resulted in an aspect ratio of 1.02 ± 0.3 and hence a reduced compression. Measurements of early embryos in the adult uterus revealed an aspect ratio of 1.16 ± 0.7. (Figure 1—figure supplement 1), indicating that in-utero embryo compression strength is intermediate. Throughout this study, we used the classic mounting method using an agarose pad, unless stated otherwise.

We started with investigating the first two divisions, the divisions of the P₀ zygote and the AB cell, and quantified flows from embryos containing endogenously tagged non-muscle myosin-II (NMY-2)::GFP using spinning disc microscopy (Videos 1 and 2). We used particle image velocimetry (PIV) to determine cortical flow velocities in two rectangular regions of interest (ROIs) placed on opposite sides of the cytokinetic ring (Figure 1A, Figure 1—figure supplement 2). In particular, we were interested in chiral cortical flows that yield velocity contributions parallel to the cytokinetic ring, referred to as ‘y-direction flows’ (Figure 1—figure supplement 2). Beginning at the onset of furrow ingression, y-direction flows were averaged in each ROI over a time period of 21 s. This narrow time window provides a characterization of cortical flows restricted to mid-cytokinesis, and it ensures that shape changes of the dividing cell are minor and do not affect the velocity measurements. Note that, over the full time course from early to late cytokinesis, cortical flow velocities vary (Figure 1—figure supplement 2), while we did not observe major differences in the myosin distribution (Figure 1—figure supplement 3).

Figure 1 with 10 supplements see all

Download asset Open asset

Chiral counter-rotating flows are cell-lineage specific.

(A) Representative images of cortical myosin (grey, NMY-2::GFP) for the first (P₀, yellow) and the second (AB, blue) cell division of *C. elegans* embryos. Arrows indicate the cortical flow field as measured by PIV and time-averaged over 21 s and over the onset of cytokinesis. Arrow colors indicate the y-direction velocity (parallel to the cytokinesis furrow, coordinate systems are indicated). Dotted lines indicate cell boundaries, black boxes represent the regions of interest used for calculating velocities. Scale bar, 10 µm. (B) Histograms of the instantaneous chiral counter-rotating flow velocity $v_{c}$ (see Materials and methods for definition). Solid lines indicate the best-fit gaussian probability density function. Dotted vertical colored lines represent the mean $v_{c}$ , grey boxes represent the error of the mean. Thin black solid lines indicate a chiral flow velocity of zero. Inset, colored cells indicate the cell analyzed; AB lineage in blue, P/EMS lineage in yellow. (C) Dotted lines with shaded error region indicate the average myosin concentration profile along the long axis of the AB (blue) and P₁ (orange) dividing cell, solid lines represent a best fit with a combined step and gaussian function (see Materials and methods) Inset, colored cells indicate the cell analyzed; grey stripe indicates the region used for averaging. (D) Average relative position of the cytokinetic ring along the long axis of the dividing cell for the first 6 cell divisions. Black thin lines in (C) and (D) indicate the center of the cell (n = 8 for all cell divisions). (E) Myosin asymmetry ratio (Anterior [NMY-2::GFP]/Posterior [NMY-2::GFP]) (see Materials and methods) for the first six-cell divisions along the long axis of the dividing cell (n = 8 for all cell divisions). Errors indicate the error of the mean at 95% confidence.

Video 1

Download asset

posterframe for video — Movie of the actomyosin cortex during the first cell division.

The cortex is marked by NMY-2::GFP. The P₀ cell does not exhibit chiral counter-rotating flows during its division. Cortical flows in the two dividing halves of the P₀ cell flow in the same y-direction. Scale bar 10 µm.

Video 2

Download asset

Strikingly, while y-direction flows in both ROIs of the P₀ cell occur with the same orientation (Figure 1A, left), they have opposite orientations in AB cells (Figure 1A, right), such that the two dividing cell halves of the AB cell effectively spin in opposite directions. We refer to such flows as chiral counter-rotating flows (Figure 1—figure supplement 2, Videos 1 and 2). To quantify the speed and the handedness of counter-rotating flows more generally, we use the measured velocities in each ROI, denoted as $\underline{v_{1}}$ and $\underline{v_{2}}$ , and define a chiral counter-rotation flow velocity $v_{c} = \underline{e_{z}} \cdot (\underline{e_{x}} \times \underline{v_{2}} - \underline{e_{x}} \times \underline{v_{1}})$ , where $\underline{e_{x}}$ is a unit length base vector pointing from the cytokinetic ring toward the pole, $\underline{e_{y}}$ is an orthogonal unit length vector parallel to the cytokinetic plane (Figure 1A), and $\underline{e_{z}} = \underline{e_{x}} \times \underline{e_{y}}$ . With this definition, $| v_{c} |$ quantifies the speed of counter-rotating flows and the sign of $v_{c}$ denotes their handedness (see Materials and methods and Figure 1—figure supplement 2). For the AB cell division, we then find $v_{c}$ = −7.01 ± 0.34 µm/min (mean ± error of the mean at 95% confidence, unless otherwise stated), indeed indicating the presence of counter-rotating flows with consistent handedness. Furthermore, for the division of the P₀ cell, we find that counter-rotating flows are essentially absent ( $v_{c}$ = 0.01 ± 0.51 µm/min). Instead, the cortical flows of dividing P₀ cells, where both cell halves move in the same direction, correspond to net-rotating flows that resemble whole embryo rotations (Schonegg et al., 2014). We conclude that out of the first two cell divisions in the developing nematode, only one is accompanied by chiral counter-rotating actomyosin flows.

This raises the question which of the later cell divisions display chiral counter-rotating flows, and which do not. To answer this, we quantified chiral counter-rotating flows for the next seven cell divisions as described above. We found that cells of the AB lineage (ABa, ABp, ABar and ABpr) exhibit chiral counter-rotating flows with $v_{c}$ = −3.46 ± 0.33 µm/min, −3.68 ± 0.41 µm/min, −1.24 ± 0.19 µm/min and −1.16 ± 0.22 µm/min respectively (Figure 1B). In contrast, average chiral counter-rotating flow velocities of cells of the P/EMS lineage (P₁, EMS and P₂) are small: 0.15 ±0.38 µm/min, 0.03 ± 0.14 µm/min and 0.25 ± 0.19 µm/min, respectively (Figure 1B). Like P₀, cells of the P/EMS lineage, instead exhibit net-rotating flows, where the y-direction flows have the same orientation in both cell halves (Figure 1—figure supplement 4, Videos 1–5). To conclude, early cell divisions of the AB lineage, but not of the P/EMS lineage, undergo chiral counter-rotating flows. We note that due to a decrease in the overall cortical flow speed, also the chiral counter-rotating flow velocity $v_{c}$ in the AB lineage decreases as development progresses and cells become smaller (Figure 2B, Figure 1—figure supplement 5). This is accompanied by a decrease in the myosin concentration in the cytokinetic ring (Figure 1—figure supplement 5) and is consistent with overall contractility being reduced when development progresses. Together, these findings show that both the presence and the strength of chiral counter-rotating flows are related to the fate of the dividing cell.

Figure 2

Download asset Open asset

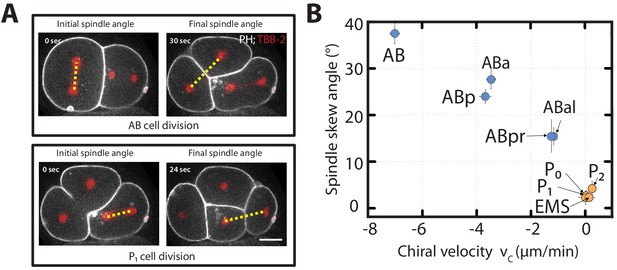
Chiral counter-rotating flow velocity and spindle skew decreases as development progresses.

(A) Representative images show the angle of the mitotic spindle (yellow dotted line) before the onset (left) and at the end (right) of the second (AB, top) and the third (P₁, bottom) cell division. White, cell membrane imaged by PH::GFP; red, spindle poles as imaged by TBB-2::mCherry. (B) Spindle skew angle (final minus initial spindle angle) vs. chiral velocity for the first nine cell divisions (N = 8 for all cell diviisons).

Video 3

Download asset

Video 4

Download asset

Video 5

Download asset

We have shown previously that chiral counter-rotating cortical flows are driven by active torque generation that depends on the myosin distribution (Naganathan et al., 2014). Given that chiral counter-rotating flows arise only during AB and not P/EMS cell divisions, we hypothesize that myosin distributions during division of the AB and the P/EMS-lineage cells differ in specific features. To investigate this, we determined the NMY-2 distribution along the long axis of dividing cells for the first six cell divisions (Figure 1C), and extracted two features (see Materials and methods): (1) a myosin ratio that characterizes the difference in myosin intensity between the two cell halves (Figure 1D, Figure 1—figure supplement 6) and (2) the relative myosin peak position along the long axis, which characterizes the cytokinetic ring position and the degree of asymmetry in the cell division (Figure 1E). We note that these quantities could be coupled, either mechanically (Sedzinski et al., 2011) or via par polarity complexes that facilitate cellular myosin asymmetry (Munro et al., 2004; Gross et al., 2019) and asymmetric positioning of the cleavage plane (Galli and van den Heuvel, 2008; Colombo et al., 2003). We find that myosin ratios in dividing AB, ABa and ABp cells are 1.0 ± 0.13, 0.92 ± 0.29, and 1.00 ± 0.24, respectively, indicating that there is no significant difference in cortical myosin concentration between the two halves of dividing cells from the AP lineage. In contrast, the myosin ratios in P₀, P₁ and EMS are 1.67 ± 0.3, 2.07 ± 0.61, 1.68 ± 0.33, respectively (Figure 1E). Furthermore, we find that the relative position of myosin peaks along the long axis of dividing AB, ABa and ABp cells are 0.49 ± 0.01, 0.49 ± 0.01 and 0.51 ± 0.02, respectively. In contrast, myosin peaks in dividing P₀, P₁ and EMS cells are positioned at 0.58 ± 0.01, 0.57 ± 0.02 and 0.59 ± 0.01 relative to cell length, respectively (Figure 1D). To conclude, the early cell divisions of the AB lineage are symmetric in terms of myosin intensity ratio and cytokinetic ring position, while early cell divisions of the P/EMS lineage are asymmetric in these two features.

We next asked if the presence and absence of chiral counter-rotating flows in AB and P/EMS cells can be accounted for by the observed difference in myosin ratio and cytokinetic ring position. To this end, we utilized a thin film active chiral fluid theory (Fürthauer et al., 2013; Naganathan et al., 2014) that describes active chiral processes in a fluid-like material and the flows these processes are expected to give rise to. We then considered a minimal model that allows to compute $y$ -direction flows, and hence chiral counter-rotating flow velocities $v_{c}$ , from a given myosin ratio and cytokinetic ring position (Appendix, Videos 6–8). We find that a symmetric myosin distribution and cytokinetic ring position (myosin ratio $\approx 1$ , relative myosin peak position $\approx 0.5$ ) result in a maximum value of $v_{c}$ . Accordingly, myosin ratios different from one and an asymmetric ring position result in smaller values of $v_{c}$ , where the model suggests that $v_{c}$ is more sensitive to changes in the myosin ratio than to changes in the ring position (Figure 1—figure supplement 7).

Video 6

Download asset

Video 7

Download asset

Video 8

Download asset

Our results indicate that the switch between chiral and non-chiral flows between the two lineages could in principle be attributed to the observed difference in myosin ratio, cytokinetic ring position or both (Appendix 1—table 1). We note, however, that while the thin film active chiral fluid theory can quantitatively relate y-direction flows of dividing AB, ABa, and ABp cells with the myosin profiles along their long axis (Figure 1—figure supplement 8, Appendix 1—table 1), this is not possible for the P/EMS lineage. We suspect that this is due to specific features of the overall dynamics that are not included in our theoretical description, such as movements of the midbody remnant particular to the P/EMS linage (Singh and Pohl, 2014), as well as more general aspects that we have neglected for simplicity, such as the shape dynamics of the dividing cell (Mietke et al., 2019) and possible inhomogeneities in friction forces due to mechanical interactions with the surrounding. This indicates that our understanding of the mechanisms that lead to the cortical flows in P/EMS linage divisions is still incomplete. Taken together, our analysis implies a mechanism whereby the occurrence of chiral counter-rotating actomyosin flows depends on the amount of cortical myosin in the cell halves and the position of the cytokinetic ring.

Next, we asked whether symmetric cell division is indeed required for chiral counter-rotating flows to emerge. The first cell division in wild-type embryos is asymmetric and does not display chiral counter-rotating flows. The asymmetry of the P₀ division is controlled by Par polarity complexes (Kemphues et al., 1988) and depletion of the posterior Par protein, PAR-2, led to a symmetric myosin distribution with a myosin ratio of one and centered ring position (Figure 1—figure supplement 9). Strikingly, par-2 depletion also triggered the emergence of chiral counter-rotating flow during P₀ cytokinesis ( $v_{c}$ = −5.71 ± 0.89 µm/min; Figure 1—figure supplement 9) demonstrating that inducing symmetric cell division via par-2 (RNAi) is sufficient to trigger chiral counter-rotating flows in P₀. Moreover, our hydrodynamic theory predicts that a centered ring position should result in chiral counter-rotating flows regardless of myosin asymmetry (Figure 1—figure supplement 7). To test this, we performed lin-5 (RNAi) treatment and analyzed cortical actomyosin flows. LIN-5 is involved in generating asymmetric pulling forces that displace the spindle from the center (Galli and van den Heuvel, 2008; Lorson et al., 2000). We first confirmed that indeed the myosin distribution in P₀ is still asymmetric in these embryos (albeit reduced when compared with control), while the ring position is at the center (Figure 1—figure supplement 10). Quantifying cortical actomyosin flows revealed that lin-5 (RNAi) triggered the emergence of chiral counter-rotating flows ( $v_{c}$ = −1.73 ± 0.74 µm/min; Figure 1—figure supplement 10). Given that cortical myosin levels upon lin-5 (RNAi) are comparable to those observed in control, the emergence of chiral counter-rotating flows is unlikely to be the result of higher overall actomyosin activity (Figure 1—figure supplement 10). Although we cannot fully uncouple the effect of myosin asymmetry and ring position, these experimental results are qualitatively consistent with our theoretical predictions and thus suggest that both, asymmetries in myosin distribution and ring position, counteract the emergence of chiral counter-rotating flows. We conclude that symmetric cell division is required for chiral counter-rotating actomyosin flows to emerge during cytokinesis.

Cells exhibiting chiral counter-rotating actomyosin flows also undergo spindle skews

We next focus our attention on the mechanism by which dividing cells assume their correct position inside the developing embryo. Specific rotations of the spindle (termed spindle skews) are thought to be a key mechanism by which dividing cells reposition themselves in the embryo (Naganathan et al., 2014; Singh and Pohl, 2014; Liro and Rose, 2016; Bergmann et al., 2003). One hypothesis is that spindle skews are driven by spindle elongation (Hennig et al., 1992). In this scenario, spindle elongation causes a skew because the spindle rearranges within an asymmetric cell shape, thus responding to the constraints provided by neighboring cells and the eggshell (Figure 3A). An alternative hypothesis is that spindle skews are driven by chiral counter-rotating flows of the dividing cell halves (Naganathan et al., 2014). In this case, the mechanism is akin to a bulldozer rotating on the spot by spinning its chains in opposite directions. If the cortical surface experiences a spatially inhomogeneous friction, e.g. when the friction with the eggshell is different from the friction with a neighboring cell, chiral counter-rotating cortical flows of the two cell halves will lead to a torque that acts on the cell and can lead to a cell skew (Figure 3A). In this scenario, the cell orientation changes over time, and the spindle simply aligns accordingly.

Figure 3 with 2 supplements see all

Download asset Open asset

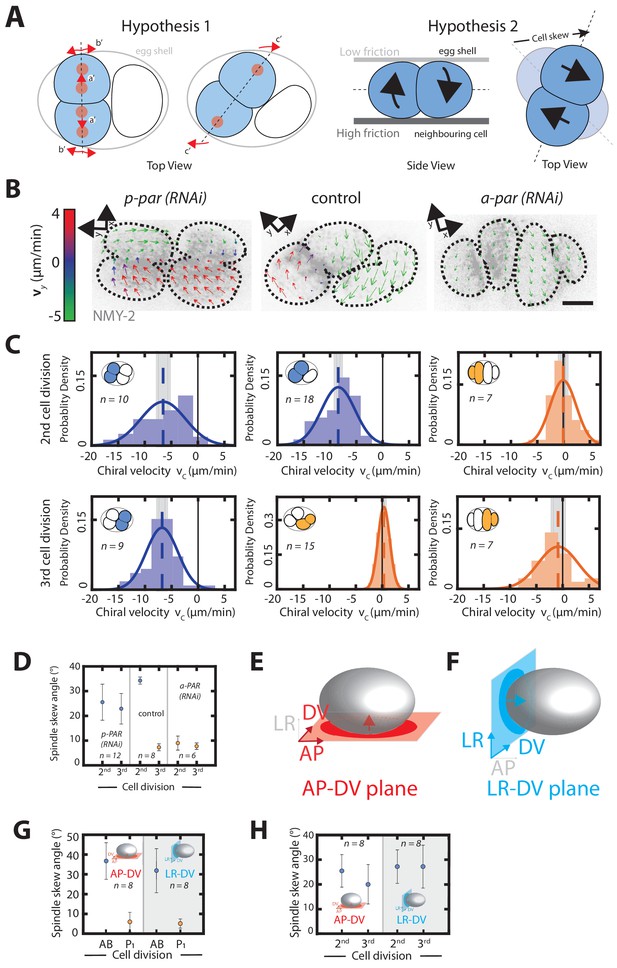
Chiral counter-rotating flows are cell-lineage dependent.

(A) Possible mechanisms of spindle skew and cell rearrangement. Hypothesis one: spindle skews are driven by spindle elongation. The mitotic spindle initially elongates along the dorsoventral axis (a’ and b’), but then skews (c’) because there is not enough space given the physical constraints imposed by the eggshell. Dashed line depicts the cell division axis, red dots depict spindle poles, arrows indicate spindle pole movements. Hypothesis two: spindle skews are driven by counter-rotating flows of the dividing cell halves. Left: top view, right: side view. Chiral counter-rotation of the two halves of a dividing cell gives rise to a cell skew if the dividing cell experiences non-uniform friction with its surroundings, e.g. a lower friction with the eggshell above and a higher friction with the cell below. (B) Representative images of cortical myosin (grey, NMY-2::GFP) for the second and the third cell division of *C. elegans* embryos. Arrows indicate the cortical flow field as measured by PIV and time-averaged over 21 s and over the onset of cytokinesis. Arrow colors indicate the y-direction velocity (parallel to the cytokinesis furrow, coordinate systems are indicated). (C) Histograms of the instantaneous chiral counter-rotating flow velocity $v_{c}$ for *par* perturbations (see Materials and methods for definition). Solid lines indicate the best-fit gaussian probability density function. Dotted vertical colored lines represent the mean $v_{c}$ , grey boxes represent the error of the mean. Thin black solid lines indicate a chiral flow velocity of zero. Inset, colored cells indicate the cell analyzed; AB lineage in blue, P/EMS lineage in orange. (D) Spindle skew angle for control (L4440), *par-2; chin-1; lgl-1 (RNAi)* and *par-6 (RNAi)* embryos. (**E, F**) Schematic of a *C. elegans* embryo. 3-D recordings capturing spindle pole movements and corresponding spindle skews were projected on either the (E) anteroposterior-dorsoventral (AP-DV) plane (red) or the (F) left-right-dorsoventral (LR-DV) plane (blue). (**G, H**) Spindle skew angles during the second and third cell division in control (G) and upon *par-2 (RNAi)* (H) projected onto the anteroposterior-dorsoventral plane (termed AP-DV plane, left) or onto the dorsoventral-left-right plane (termed LR-DV plane, right). The embryo schematic denotes the plane of projection (rectangle) and the direction of view (arrow) as described above. Scale bars, 10 µm. Errors indicate the error of the mean at 95% confidence.

To discriminate between these two hypotheses, we first asked if those cells that undergo spindle skews also exhibit chiral counter-rotating flows. We quantified spindle skews by determining the positions of spindle poles at the beginning and at the end of cytokinesis in embryos expressing TBB-2::mCherry for the first 11 cell divisions (Video 9). The angle between the lines that join the two spindle poles at the onset and after cell division defines the spindle skew angle (Figure 2A). We find that cells of the early AB lineage undergo an average skew angle of 21.17 ± 3.22° (AB: 37.51 ± 2.51°, ABa: 27.64 ± 2.29°, ABp: 23.98 ± 1.19°, ABal: 17.73 ± 1.98°, ABar: 15.51 ± 3.51°, ABpl: 10.43 ± 1.92° and ABpr: 15.42 ± 2.11°). In comparison, P/EMS lineage cells undergo significantly reduced spindle skews with an average skew angle of of 2.32 ± 0.43° (P₀: 2.31 ± 1.67°, P₁: 2.25 ± 0.66°, EMS: 2.66 ± 1.25°, P₂: 4.36 ± 1.67°). Note also, that spindle skew angles in the AB lineage decrease as development progresses, while the P/EMS lineage spindle skew angles remain small and approximately constant (Figure 2B). Given that AB lineage cells, but not P/EMS lineage cells, undergo chiral counter-rotating flows, we conclude that cells that exhibit significant chiral counter-rotating flows also undergo significant spindle skews during early development (Figure 2B).

Video 9

Download asset

In our earlier work, we showed that the skew of the ABa and ABp cells is in fact a three-dimensional process, tilting the spindle in both the anteroposterior-left-right (AP-LR) plane and in the orthogonal left-right-dorsoventral (LR-DV) plane (Naganathan et al., 2014). Therefore, in addition to the well known skew of the AB cell in the anteroposterior-dorsoventral (AP-DV) plane that sets up the dorsoventral axis, we hypothesized that there might be an additional skew in the orthogonal LR-DV plane (Figure 3E, Figure 3—figure supplement 1). In order to test this hypothesis, we examined spindle orientation throughout AB cell cytokinesis from an anterior view down the anteroposterior axis, but did initially not observe any obvious skews in the orthogonal LR-DV plane (Figure 3—figure supplement 1). However, as discussed above, the embryo mounting method used in this study slightly compresses the embryos along their left-right axis, which could constrain spindle movements along this direction. In order to determine whether the spindle skew in the LR-DV plane is concealed by embryo compression, embryos were embedded in low-melt agarose to prevent compression and subsequently analyzed. Chiral counter-rotating flows in the AB cell could still be observed and the spindle skew in the AP-DV plane was similar in compressed and uncompressed conditions (37.51 ± 2.51° and 36.67 ± 9.24°, respectively). However, the absence of embryo compression revealed a significant clockwise skew in the LR-DV plane (when viewed from the anterior) with a skew angle of 31.85 ± 11.11° (Figure 3G, Figure 3—figure supplement 1, Video 10). We did not observe any significant skew in the P₁ cell in the LR-DV plane (Figure 3—figure supplement 1). These findings show that skews of the AB cell division axis are in fact also a three-dimensional process, where the skew occurs in both the AP-DV and LR-DV planes. Note that, under the assumption that the friction forces at the interface between AB and P₁ cell are high compared to those between AB cell and the surrounding vitelline layer and egg shell, the handedness of the chiral counter-rotating flows is consistent with the observed orientation of the spindle skew in the LR-DV plane. Using the same argument, the skew in the AP-DV plane could in principle result from friction forces between the AB cell and the egg shell that are different on the left and on the right side (see section 'Left-right asymmetric friction forces can account for the skew of the AB cell’ for a further analysis of this hypothesis).

Video 10

Download asset

The results obtained so far are consistent with a scenario in which cell fate determines the presence of chiral counter-rotating flows, and these chiral counter-rotating flows then drive spindle skews. We test for these two causal relationships separately. We first asked if cell fate determines the presence of chiral counter-rotating flows. In this case, we expect that on the one hand, anteriorizing the worm leads to equal and significant chiral counter-rotating flows for the second and third division. On the other hand, we expect that posteriorizing the worm would lead to an absence of chiral counter-rotating flows. Consistent with the first expectation, anteriorizing the embryo via par-2; chin-1; lgl-1 (RNAi) (Beatty et al., 2013) results in the second and the third cell division exhibiting chiral counter-rotating flows with $v_{c}$ values that are not significantly different from one another (−6.53 ± 1.13 µm/min and −6.67 ± 0.8 µm/min, respectively; Wilcoxon rank sum test at 95% confidence; Figure 3B,C). Consistent with the second expectation, posteriorizing the embryo via par-6 (RNAi) (Hung and Kemphues, 1999) results in both the second and the third cell division not exhibiting counter-rotating flows ( $v_{c}$ = 0.07 ± 0.71 µm/min and −0.85 ± 1.13 µm/min, respectively; Figure 3B,C, Videos 11–13). Hence, cell fate determines the presence or absence of chiral counter-rotating flows. Furthermore, switching the cell fate results in concomitant changes in the spindle skew angle in the AP-DV plane for both the second and third cell division in compressed as well as non-compressed embryos (Figure 3D,H). Strikingly, we observed that spindles of the two AB-like cells in uncompressed anteriorized embryos undergo clockwise skew in the LR-DV plane when viewed from the closest pole (skew angles of each AB-like cell = 26.93 ± 6.78° and 27.44 ± 8.66°) (Figure 3H, Figure 3—figure supplement 2, Videos 14–16). Again, assuming that the friction forces at the cell-cell contact surface are high, the orientation of these skews is consistent with the handedness of the observed chiral counter-rotating flows (Figure 3—figure supplement 1). We conclude that cell fate determines both the presence of chiral counter-rotating flows and the degree as well as the direction of spindle skew.

Video 11

Download asset

Video 12

Download asset

Video 13

Download asset

Video 14

Download asset

Video 15

Download asset

Video 16

Download asset

Chiral counter-rotating flows drive spindle skews

We next tested the second causal relationship, and asked if chiral counter-rotating flows in the cortex drive spindle skews. Borrowing from the analogy of a bulldozer, for which the speed of the chiral counter-rotating chains sets the speed at which the entire bulldozer rotates, we investigated if increasing or decreasing the chiral counter-rotating flow velocities results in corresponding changes of the spindle skew rate. We first evaluated if we can increase and decrease chiral counter-rotating flow velocities in the AB cell, by RNAi of RhoA regulators. Weak perturbation RNAi of ect-2 results in $v_{c}$ = −3.57 ± 0.57 µm/min, which is reduced in comparison to the unperturbed embryo ( $v_{c}$ = −6.6 ± 0.37 µm/min, Wilcoxon rank sum test at 95% confidence, Figure 4A,B). Conversely, weak perturbation RNAi of rga-3 increases the chiral counter-rotating flow velocity to $v_{c}$ = −8.71 ± 0.58 µm/min (Figure 4A,B). Note that these perturbations impact only chiral counter-rotating flows, and do not significantly change overall contractility, as illustrated by the on-axis flow into the contractile ring, which is not significantly altered (Wilcoxon rank sum test at 95% confidence, Figure 4C). We now use these perturbations to test whether chiral counter-rotating flows determine the rate of spindle skew. We indeed find that decreasing the chiral counter-rotating flow velocity by mild ect-2 (RNAi) leads to concomitant reduction of the rate of spindle skew (average peak rate: 0.59 ± 0.05°/min, Video 17) as compared to 1.01 ± 0.1°/min in control embryos (Figure 4D, Video 18). Conversely, increasing RhoA signaling by mild rga-3 (RNAi) treatment leads to an increase of both the chiral counter-rotating flow velocity and the rate of spindle skew (average peak rate: 1.29 ± 0.12°/min (Video 19, Figure 4D). Note that the peak rates of spindle elongation remain unchanged as compared to the control for both perturbations (Figure 4D, Figure 4—figure supplement 1). We conclude that changing chiral counter-rotating flow velocities results in concomitant changes of the rates of spindle skews without impacting on the dynamics of spindle elongation. In addition, given that the contractility-driven flows remain unaltered upon rga-3 (RNAi) and ect-2 (RNAi), overall actomyosin contractility is unlikely to contribute significantly to cell division skews. These results instead support our second hypothesis, that chiral counter-rotating flows mechanically drive cell skews and consequently also spindle skews.

Figure 4 with 2 supplements see all

Download asset Open asset

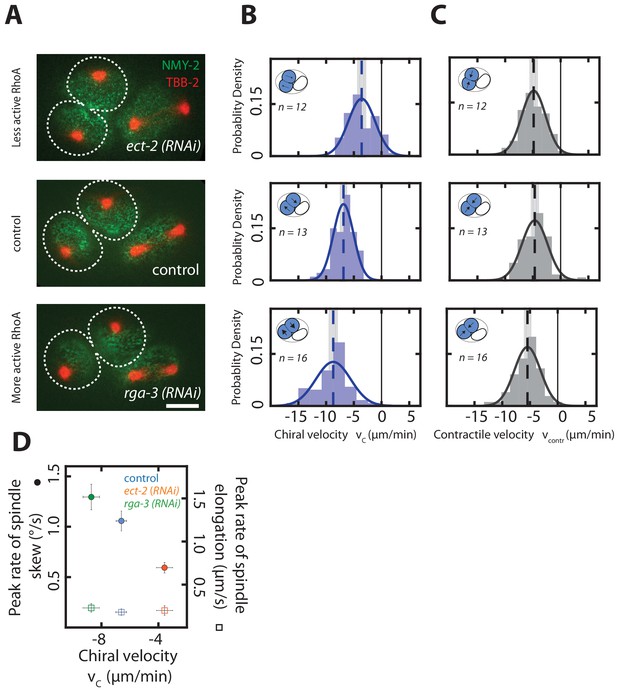
Chiral counter-rotating flow velocity determines the rate of spindle skew in the AB cell.

(A) Fluorescence images of two-cell embryos during cytokinesis upon *ect-2 (RNAi)* and *rga-3 (RNAi)*. Spindle poles are marked by TBB-2::mCherry (red), the cortex is marked by NMY-2::GFP (green). Dotted white lines indicate boundaries of the dividing AB cells. Scale bar, 10 µm. (**B, C**) Histograms of (B) the instantaneous chiral counter-rotating flow velocity $v_{c}$ (see Materials and methods for definition) and (C) the instantaneous contractile flow velocity $v_{c o n t r}$ , representing the flow velocity along the long axis of the dividing cell (see Materials and methods for definition). Dotted vertical colored lines represent the mean $v_{c}$ or mean $v_{c o n t r}$ , grey boxes represent the error of the mean. Thin black solid lines indicate zero velocities. Inset, blue shading indicates the AB cell analyzed, arrows indicate rotatory cortical flow. (D) Peak rate of spindle skew (filled circles) and peak rate of spindle elongation (open squares) with the RNAi feeding control (control, *n = 10; ect-2 (RNAi), n = 12; rga-3 (RNAi), n = 9*). The full time series is given in Figure 4—figure supplement 1. Errors indicate the error of the mean at 95% confidence.

Video 17

Download asset

Video 18

Download asset

Video 19

Download asset

The position of the mitotic spindle is determined by an evolutionary conserved protein complex, containing GPR-1/2 and its interacting partner LIN-5/NuMa, that facilitates pulling forces on astral microtubules at the cell cortex (Srinivasan et al., 2003; Galli et al., 2011; Colombo et al., 2003). Therefore, we next asked whether spindle skews during anaphase of dividing AB lineage cells are dependent on this known spindle orientation pathway. To address this, we analyzed actomyosin flows and the cell division skew of AB upon depletion of lin-5 and gpr-1/2. Both perturbations resulted in defects that have been previously described, including symmetric cell division of P₀ (Figure 1—figure supplement 10 and data not shown) and misaligned spindles in the P₁ and AB cells (Figure 4—figure supplement 2) indicating that RNAi treatment was effective. Moreover, the AB cell exhibited chiral counter-rotating flows during division ( $v_{c}$ = −5.05 ± 1.12 µm/min) and, although the AB spindle was often misaligned, it skewed substantially during anaphase (spindle skew angle = 23.14 ± 7.46°, Figure 4—figure supplement 2). These results argue against an important role for the known spindle orientation pathway in driving spindle skews. Alternatively, given that the LIN-5-dependent spindle orientation pathway is known to reorient the metaphase spindle in the P₁ cell, this pathway might inhibit actomyosin dependent spindle skews in the P/EMS lineage during anaphase. Analyzing spindle skews in P₁ upon lin-5 (RNAi) and gpr-1/2 (RNAi) revealed no significant difference when compared to control embryos, which suggests that the spindle orientation pathway does not overrule actomyosin-dependent spindle skews (Figure 4—figure supplement 2). Altogether, we conclude that the LIN-5/GPR-1/2-dependent spindle orientation pathway determines the initial spindle orientation, while chiral actomyosin flows drive the spindle skews observed during anaphase.

If chiral counter-rotating flows indeed drive spindle skews, we predict that a complete absence of chiral flows leads to a complete absence of spindle skews. We test this prediction in the AB cell, by inactivating cortical flows entirely through a fast acting temperature sensitive nmy-2(ts) mutant (Liu et al., 2010). Worms were dissected to obtain one-cell embryos and mounted at the permissive temperature at 15°C that allows them to develop normally. Approximately 60 s after the completion of the first (P₀) cell division, the temperature was rapidly shifted to the restrictive temperature of 25°C using a CherryTemp system. Imaging was started as soon as the AB cell entered anaphase. In all nmy-2(ts) mutant embryos (12 out of 12), an ingressing cytokinetic ring was absent and cytokinesis failed after temperature shifting, indicating that NMY-2 was effectively inactivated (Davies et al., 2014; Videos 20 and 21). Interestingly, while the dynamics of spindle elongation, including the peak rate of spindle elongation and the final spindle length, are essentially unchanged as compared to control embryos at restrictive temperature, the average peak rate of spindle skew was significantly reduced (0.33 ± 0.09°/min as compared to 1.43 ± 0.13°/min in control embryos, Wilcoxon rank sum test at 95% confidence, Figure 5A,B, Figure 5—figure supplement 1, Videos 20 and 21). This demonstrates that a functional actomyosin cortex with chiral cortical flows is required for spindle skews of the AB cell. In light of our experiments above, we conclude that spindle skews in the AB cell are independent of spindle elongation, but are instead a consequence of the cell skews that are driven by chiral counter-rotating flows. Finally, we performed temperature shift experiments for the first 11 divisions in the nematode, and found that all cells belonging to the AB cell lineage show a significantly reduced skew in the nmy-2(ts) embryos at restrictive temperatures as compared to the control (Figure 5C). We conclude that a functional actomyosin cortex with chiral cortical flows is required for spindle skews of early AB lineage cell divisions during worm development.

Figure 5 with 3 supplements see all

Download asset Open asset

Spindle skews in early development are driven by chiral actomyosin flows.

(A) Fluorescence images of control and myosin temperature-sensitive (ts) mutants (*nmy-2(ts)* ,permissive at 15°C, restrictive at 25°C) two-cell embryos with TBB-2::mCherry labelled for visualizing spindle poles (red). All embryos were shifted from 15°C to 25°C at the end of the first division. Dotted white lines indicate boundaries of the dividing AB cells. Time t = 60 s indicates the onset of cytokinesis. Scale bar, 10 µm. (B) Corresponding peak rate of spindle skew (circles) and spindle elongation (squares) for the AB cell in control and *nmy-2(ts)* embryos. The full time series is given in Figure 5—figure supplement 1. (C) Spindle skew angle in control embryos (blue circles) and *nmy-2(ts)* embryos (red squares) during the first 11 cell divisions at temperature of 25°C. Errors indicate the error of the mean at 95% confidence.

Video 20

Download asset

Video 21

Download asset

Left-right asymmetric friction forces can account for the skew of the AB cell

We propose that chiral counter-rotating flows, together with inhomogeneous friction forces with the surroundings, drive cell division skews in a manner similar to a bulldozer rotating on the spot by rotating its chains in opposite directions. Following this analogy, the direction of the cell division skew is determined by (1) the handedness of the chiral counter-rotating flow and (2) the distribution of friction forces across the cellular surface. As described above, the AB cell simultaneously skews in two orthogonal planes, AP-DV and LR-DV. Assuming that there are high friction forces at the AB-P₁ interface, the clockwise skew (when viewed from the anterior down the anteroposterior axis) in the LR-DV plane is consistent with the handedness of the chiral counter-rotating cortical flows (Figure 3—figure supplement 1). Similarly, for the observed clockwise skew in the AP-DV plane (when viewed from the left down the left-right axis) to be consistent with the handedness of chiral counter-rotating flows of AB, we expect that the total friction forces between the AB cell and vitelline layer and/or the egg shell are elevated on the right side of the embryo, as compared to the left side (Figure 5—figure supplement 3).

In order to test this hypothesis, we first set out to identify signatures of left-right asymmetric friction forces. Because such forces are expected to reduce cortical flow speed, we argued that cortical flow speeds may be different on the future left and right sides of the dividing AB cell. Note that in our analysis, we have so far only reported values of the chiral counter-rotating flow velocity $v_{c}$ for flows measured on the right side of the embryo. Measuring the chiral counter-rotating flow velocities of the AB cell also on the left side, we indeed find that y-direction flows in each cell half, and consequently $v_{c}$ , are significantly increased on the left side, as compared to the right side (Figure 5—figure supplement 3, velocity values are given in Appendix 1—table 3). This observation is consistent with the hypothesis that the friction forces experienced by the AB cell are higher on the right side than on the left side.

Based on these qualitative insights, we investigated if the observed spindle skew rates can be quantitatively predicted from measured chiral counter-rotating flow velocities and basic geometric features of the dividing AB cell. This was done in two steps: First, we tested if the cortical flow velocities are consistent with the geometric predictions that follow from the bulldozer analogy. In the second step, we investigated if physical interactions with the egg shell are sufficient to explain the skewing rate and direction.

For the first step, we note that the velocities of the bulldozer chains on top and bottom (corresponding to the left and right side of the embryo) can be measured (A) while standing next to the spinning bulldozer (measurement in the ’lab frame’) or (B) while sitting in the co-rotating drivers cab, from which one always expects to observe two perfectly counter-rotating chains. The differences in the velocities measured in A) and B) are due to the overall rotation of the system, that is, the spinning of the bulldozer or, in our case, the skewing of the dividing AB cell in the AP-DV plane. Formalizing this geometric description, we derived a parameter-free relation between the skew rate of the dividing AB cell and the cortical y-direction flows on the left and right side (see Appendix). We measured y-direction flows (measurement in the 'lab frame') in wild type, ect-2 (RNAi) and rga-3 (RNAi) on the left and right side of the embryo and found for all three conditions that the calculated angular skew velocities agree well with the experimentally measured average AP-DV spindle skew rates of the dividing AB cell (Appendix 1—table 3). This provides a first, direct quantitative relationship between chiral actomyosin flows and cell division skews. Additionally, it shows that the skewing motion and chiral flows across the AB cell cortex are compatible with a simplified geometry that is analogous to a spinning bulldozer.

In the second step, we used the geometric model to derive the torque balance that connects the AB cell skews to the mechanical interactions with the surrounding. For the skew in the AP-DV plane, we consider a scenario where the relevant torques arise from friction forces between the counter-rotating cell halves and the egg-shell on the left and right side, and then tested, if this is sufficient to explain the observed amplitude and handedness of the spindle skews. Neglecting contributions from the $A B$ - $P_{1}$ cell contact and extra-embryonic fluid that may counteract the AP-DV skew, the torque balance of the system implies an angular skew velocity given by (see Appendix)

ω = \frac{γ_{L} A_{L} - γ_{R} A_{R}}{γ_{L} A_{L} + γ_{R} A_{R}} \frac{v}{R} .

In this expression, $γ_{L}$ and $γ_{R}$ denote local friction coefficients, and $A_{L}$ and $A_{R}$ denote the corresponding contact surface areas between the AB cell and the egg shell on the left and right side. The velocity $v$ , which is positive for all conditions, is related to the measured chiral counter-rotating flow velocity $v_{c}$ , and $R$ is the distance between the cytokinetic ring and the ROIs where y-direction flows are measured (see Appendix). $ω < 0$ corresponds to a clockwise skew when the embryo is viewed from the left side. Equation 1 implies that, if chiral counter-rotating flows are present ( $v \neq 0$ ), any left-right asymmetry in total friction forces $γ_{L} A_{L} v$ and $γ_{R} A_{R} v$ leads to an angular skew in the AP-DV plane, while their relative amplitude defines the skew handedness. In order to test this minimal physical model, we estimated the contact surface areas on the left and right side by measuring the area of the cortex that is in focus in our confocal movies ( $A_{R} / A_{L} \approx 1.3 \pm 0.2$ , Figure 5—figure supplement 3, Appendix 1—table 4). The local friction coefficients were estimated by fitting the thin film active chiral fluid theory to measured flow profiles on the left and right side, where we assumed that the cortical viscosity does not significantly vary across the cell surface and hence that differences in the hydrodynamic length arise from differences in friction coefficients ( $γ_{R} / γ_{L} \approx 1.7$ , Figure 5—figure supplement 3, see Appendix). Together with $R = 4.5 μ m$ and $v$ determined from the measured y-direction flows (see Appendix), Equation 1 allows for each condition to estimate the angular skew velocity that is expected from the torque balance of the system. The resulting angular skew velocities $ω = - 0.42 \pm 0.15^{\circ}$ /min; $- 0.28 \pm 0.04^{\circ}$ /min; $- 0.49 \pm 0.19^{\circ}$ /min (wt; ect-2 (RNAi); rga-3 (RNAi)) correctly predict the experimentally observed skew handedness and faithfully recapitulate the behavior of the average spindle skew rates in all three conditions (see Appendix). Together, these results lend credence to our conclusion that chiral actomyosin flows drive the three-dimensional cell division skew of the AB cell. Furthermore, they suggest that inhomogeneous mechanical interactions with the surrounding are sufficient to explain the handedness and amplitude of these skews.

Discussion

In this work, we have shown that lineage-specific chiral flows of the actomyosin cortex drive lineage-specific cell rearrangements in early C. elegans development. Recently, it was demonstrated that actomyosin flows are required for determining the initial orientation of the mitotic spindle (Sugioka and Bowerman, 2018). Here, we have shown that the actomyosin cortex drives an active counter-rotation of the two halves of dividing early AB lineage cells, leading to cellular repositioning of these cells during anaphase. We propose that chiral counter-rotating flows represent a general mechanism by which dividing cells can reorient themselves in order to allow their daughters to achieve their appropriate positions.

During early C. elegans development cell lineage specifications are mainly driven by short-range intercellular signaling cascades (Priess, 2005; Eisenmann, 2005) and therefore, correct positioning of blastomeres is instrumental for normal development. For example, the cell division skew of the AB blastomere puts the ABp daughter cell in close contact with the posterior P₂ cell. In turn, this results in Notch signaling activation in the ABp cell but not in the ABa cell, triggering the distinct development of the ABa and ABp lineages (Hutter and Schnabel, 1994). The subsequent spindle skew of ABa and ABp lies at the heart of left-right patterning and is essential for proper left-right asymmetric inductions, again driven by short-range signaling cascades (Pohl and Bao, 2010; Hardin and King, 2008; Walston and Hardin, 2006; Priess, 2005). We propose that the chiral flow-driven spindle skews described here, allow cells in the AB lineage to acquire their precise position and thereby permit normal cell fate inductions.

How does the cell lineage determine the presence or absence of chiral cortical flows? We know that AB lineage cells divide symmetrically, while the early P/EMS lineage cell divisions are asymmetric (Rose and Gönczy, 2014). We have shown here that the occurrence of chiral counter-rotating actomyosin flows depends on the amount of cortical myosin in each cell half and on the position of the cytokinetic ring. Accordingly, AB lineage cell divisions are symmetric in terms of cytokinetic ring positioning and myosin distribution and display chiral counter-rotating flows, while divisions in the P/EMS lineage are asymmetric in these measures and chiral counter-rotating flows are absent (Figure 1B–E, Figure 1—figure supplement 4). Cell lineage determinants like PAR proteins, instrumental for cell polarity, therefore likely act to control chiral flows by modulating the distribution of molecular motors along the cell division axis (Gross et al., 2019; Munro et al., 2004) .

By which mechanism are the active torques generated that drive chiral counter-rotating cortical flows? We showed previously that chiral active fluid theory can be used to describe the chiral counter-rotating flows during zygote polarization. In this coarse-grained hydrodynamic description, the cortex is treated as a two-dimensional gel that has liquid-like properties and generates active torques. In turn, these torques tend to locally rotate the cortex clockwise (when viewed from the outside) and thereby determine flow handedness. Assuming that the local torque density is proportional to the measured NMY-2 levels, we have shown here that this theory can quantitatively recapitulate the observed chiral flow behavior in the dividing AB blastomeres (Figure 1—figure supplement 8). However, the molecular underpinnings that determine the observed flow handedness remain elusive. Additionally, given that many actin-binding proteins localize in a pattern similar to myosin (Tse et al., 2012; Maddox et al., 2005; Motegi and Sugimoto, 2006; Davies et al., 2018), and many of these affect the chirality of actomyosin flows in the polarizing one-cell embryo (Naganathan et al., 2018), we cannot exclude that other force generators provide the active torque needed for chiral counter-rotating flows. Due to the helical nature of actin, both myosins (Lebreton et al., 2018) and formins (Mizuno et al., 2011; Jégou et al., 2013) can twist actin filaments while they respectively pull or polymerize them, and therefore both are potential sources of molecular torques. Interestingly, myosins as well as formins are also required for numerous cellular and organismal chiral processes (Tee et al., 2015; Davison et al., 2016; Kuroda et al., 2016; Hozumi et al., 2006; Maderspacher, 2016; Spéder et al., 2006; Chougule et al., 2020). Future work will be required to identify the molecular source of torque generation in the actomyosin layer, as well as its organization principles that ensure a consistent handedness of the emerging torques and chiral cortical flows.

Our work shows that the handedness of chiral counter-rotating actomyosin flows, together with asymmetries in the effective friction forces between cells and the surrounding determine the direction of cell division skews (Figure 3A right panel). In general, such friction forces can vary arbitrarily across the cell surface. Therefore, chiral flow-driven cell division skews represent a three-dimensional process in which skews occur simultaneously in different planes (Figure 3G, Figure 3—figure supplement 1). Obvious sources of an effective friction force between cell-cell contacts are provided by adhesions. Moreover, our results suggest that differences in friction forces also exist between the AB blastomere and the egg shell on the left and right side. This friction force difference, together with the handedness of the chiral counter-rotating flow will cause the AB cell to skew clockwise in the AP-DV plane (when viewed from the left side down the left-right axis), thereby establishing the dorsoventral axis. The origin of this difference in friction force may be twofold: A first possibility is that there could be an, as of yet unidentified, adhesion receptor that binds to the vitelline layer and/or to the egg shell in an inhomogeneous fashion. Although a role for integrins has not been reported during early C. elegans development, integrin complexes have been shown to anchor the Tribolium blastoderm to the vitelline envelope (Münster et al., 2019). Future work will be required to determine whether integrins could play a similar role in C. elegans. A second possibility we favor is that the AB cell surface area that is in contact with the egg shell is different on the left and ride side of the embryo, thus contributing to an asymmetry in the corresponding friction forces. Interestingly, an earlier report showed that the cytokinetic ring of the AB cell ingresses in a left-right asymmetric fashion and pinches off toward the embryo’s right side (Schonegg et al., 2014). Left/right asymmetric ring ingression likely reduces the AB cell surface area that contacts the egg shell, and – given that ring ingression begins on the left side – this could lead to a left-right asymmetry in contact surface area and thus also an asymmetry in the resulting frictional forces. From our confocal imaging of the actomyosin cortex on left and right sides, we indeed measured a reduced surface area on the left side of the AB cell (Figure 5—figure supplement 3, Appendix 1—table 4, see Appendix). While these measurements, as well as the fits to approximate the local friction coefficients, only provide coarse approximations, a physical model that incorporates the measured values yields agreement with experimentally measured cell division skews. Hence, our results show that large-scale cellular rearrangements can be accounted for at a quantitative level from the interplay between chiral surface flows and spatial patterns of effective friction forces.

To conclude, our work shows that chiral rotatory movements of the actomyosin cortex are more prevalent in development than one might have suspected. We report on an intricate pattern of chiral flows during early C. elegans development, which, together with patterned frictional forces leads to dedicated cell skew and cell reorientation patterns. This is interesting from a physical perspective, since together the cells of the early embryo represent a new class of active chiral material that requires an explicit treatment of angular momentum conservation (Fürthauer et al., 2013; Naganathan et al., 2014). This is interesting from a biological perspective, since cell skews driven by actomyosin torque generation represent a novel class of lineage-specific morphogenetic rearrangements. Together, our work provides new insights into chiral active matter and the mechanisms by which chiral processes contribute to animal development.

Materials and methods

Worm strains and handling

Request a detailed protocol

C. elegans worms were cultured on NGM agar plates seeded with OP50 as previously described (Brenner, 1974). The following C. elegans strains were used in this study: LP133 : nmy-2(cp8[nmy-2::GFP + unc-119(+)]) I; unc-119(ed3) III for imaging cortical flows (Dickinson et al., 2013). SWG063 : nmy-2(cp8[nmy-2::GFP + LoxP])I; unc-119(ed3)III; weIs21[Ppie-1::mCherry::beta-tubulin::pie-1 3’UTR] (cross between (LP133 and JA1559 (Gift from J. Ahringer lab)) for measuring spindle skews in the AB cell. SWG204 : nmy-2(ne3409ts) I; unc-119(ed3)III; weIs21[pJA138(Ppie-1::mCherry::beta-tubulin::pie-1 3’UTR)] (cross between WM179 and JA1559) for temperature-sensitive experiments. TH155 : unc-119(ed3)III; weIs21[pJA138(Ppie-1::mCherry::beta-tubulin::pie-1 3’UTR)]; PH::GFP (cross between JA1559 and OD70 [Kachur and Pilgrim, 2008]) for measuring spindle skews with the membrane marker and to measure relative cytokinetic ring position along the cell division axis.

RNA interference

Request a detailed protocol

All RNAi experiments in this study were performed at 20°C (Sijen et al., 2001). For performing weak perturbation RNAi experiments, L4 staged worms were first incubated overnight on OP50 plates. Young adults were then transferred to respective RNAi feeding plates (NGM agar containing 1 mM isopropyl- $β$ -D-thiogalactoside and 50 µg ml-1 ampicillin seeded with RNAi bacteria). Feeding times for RNAi experiments were 4–5 hr for ect-2 (RNAi) and 6–8 hr for rga-3 (RNAi). For par-2, chin-1, lgl-1 (RNAi), par-6 (RNAi), par-2 (RNAi), lin-5 (RNAi) and gpr-1/2 (RNAi) conditions, young L4 were transferred to feeding plates 24 hr before imaging. Embryos used as controls for all RNAi experiments were grown on plates seeded with bacteria containing a L4440 empty vector, and exposed for the same number of hrs as the corresponding experimental RNAi perturbed worms.

The indicated hours of RNAi treatment reflects the time that worm spent on the feeding plate. All dissections were done in M9 buffer to obtain early embryos. Embryos were mounted on 2% agarose pads for image acquisition for the all cell divisions except 4–6 cell stage (Bargmann and Avery, 1995). Four cell embryos and uncompressed embryos were mounted using low-melt agarose (Naganathan et al., 2014). The rga-3 feeding clone was obtained from the Ahringer lab (Gurdon institute, Cambridge, United Kingdom) and the ect-2 feeding clone from the Hyman lab (MPI-CBG, Dresden, Germany). RNAi feeding clones for par-2, par-6, chin-1 and lgl-1 were obtained from Source Bioscience (Nottingham, United Kingdom).

Image acquisition

Request a detailed protocol

All the imagining done in this study was performed at room temperature (22–23°C) with a spinning disk confocal microscope. Two different spinning disk microscope systems were used for the study. System 1: Axio Observer Z1 - ZEISS spinning disk confocal microscope; Apochromat 63X/1.2 NA objective lens; Yokogawa CSU-X1 scan head; Andor iXon EMCCD camera (512 by 512 pixels) , Andor iQ software. System 2: Axio Observer Z1 - ZEISS spinning disk confocal microscope; Apochromat 63X/1.2 NA objective lens; Yokogawa CSU-X1 scan head ; Hamamatsu ORCA-flash 4.0 camera (2048 by 2048 pixels); micromanager software (Edelstein et al., 2014).

Confocal videos of cortical NMY-2::GFP for the first three cell divisions for control and RNAi conditions were acquired using system (1) A stack was acquired using 488 nm laser and an exposure of 150 ms was acquired at an interval of 3 s between image acquisition consisting of three z-planes (0.5 µm apart). The maximum intensity projection of the stack at each time point was then used for further analysis. 21 s of time frames were analyzed for each embryo starting from the time frame when the cytokinetic ring has ingressed ~10%. Time intervals between consecutive frames were increased at later cell stage to avoid photo-toxicity and bleaching. From the 4–6 cell stage onwards, imaging was performed using system (2) A time period of 20 s was analyzed for measuring chiral counter-rotation flow velocity. Image stacks with a spacing of 0.5 µm for 20 z-slices from the bottom surface toward the inside of the embryo were taken with 488 nm laser with exposure of 150 ms at an interval of 5 s during the time of cytokinetic ring ingression and projected with maximum intensity projection.

Imaging of the spindle poles (TBB-2::mCherry) was done using SWG63 (Figures 2A–B, 3D, G, H, 4A and 5A–C). TH155 strain was used to image TBB-2::mCherry together with PH::GFP to determine cytokinetic ring position and spindle skew angle in Figure 2B for 11-cell stages. SWG204 strain was used for temperature-sensitive experiments (Figure 4A–C). Spindle pole imaging for AB cell (TBB-2::mCherry) was performed by acquiring nine-z-planes (1 µm apart) with a 594 nm laser and exposure of 150 ms on the second system at an interval of 3 s. For long-term imaging using TH155 strain (Figure 2B), TBB-2::mCherry together with PH::GFP was imaged in 24 z-slices (1 µm apart) with 594 nm laser and exposure of 150 ms at an interval of 30 s (Video 9). For uncompressed embryos, 21 and 25–31 µm z-stacks with z-spacing of 0.5 and 1 µm apart were recorded at time interval between 5 and 10 s using system two for measuring cortical flows and spindle poles during division, respectively. For a faster temporal resolution, we restricted to imaging either spindle skews or cortical flows for individual embryos for all perturbations.

Image analysis

Request a detailed protocol

Cortical flow velocity fields in the 2D $x y$ -plane were obtained using a MATLAB code based on the freely available Particle Image Velocimetry (PIVlab) MATLAB algorithm (Raffel, 2007). Throughout the study, we used the three-step multi-pass with linear window deformation, a step size of 8 pixels and a final interrogation area of 16 pixels.

To determine the average flow fields that were fitted by the chiral thin film theory (Figure 1—figure supplement 8), we first tiled the flow field determined by PIV into nine sections along the long-axis of cells. Within each section, we averaged the flow field over the entire duration during which flows occur. Since we were only interested in flows that are generated by the cytokinetic ring, we excluded embryos in which we could not differentiate whole body rotation from cytokinesis (Schonegg et al., 2014). Note that cortical flow velocities change over the duration of cytokinesis and are likely to be influenced by changes in the AB cell geometry due to asymmetric ring ingression (Schonegg et al., 2014). Hence, for quantitative comparisons, we restricted the analysis of flows on the future right side (except for Par polarity perturbations where axis establishment was perturbed) and to the narrow time frame as described in the main text. Flow velocities observed from the future left side have been reported in Figure 5—figure supplement 3 and in Appendix 1—table 3. From all the imaged cell divisions, a small subset of measurements, in which the optical focus on the cortical plane was lost during imaging, was discarded.

From the measured cortical flows, we extracted properties that are later used to quantify their chiral counter-rotating nature in the following way. First, we identified the cleavage plane or the cytokinetic ring by eye. We then defined a region of interest (ROI) on each side of the cytokinetic ring (Figure 1A). In order to ensure that PIV measurements were not affected by the saturating fluorescence signal from the cytokinetic ring, we placed the inner boundary of each ROI at a distance of 1 µm from the ring. The position of the outer boundary of each ROI (along the long axis) was scaled with the size of the analyzed cells (10 µm, 8.5 µm, 6 µm, 6.5 µm, 6.5 µm, 6.5 µm for P₀, AB, P₁, ABa, ABp and EMS, respectively, measured from the position of the cytokinetic ring). For P₂, ABal and ABpr cells the distance of the outer ROI boundary to the cytokinetic ring varied around 4 µm, depending on the cell surface area visible in the imaging focal plane. For every cell, the width of ROIs was set equal to the length of the cytokinetic ring visible in the focal plane. In each ROI, we averaged the observed flow field over a period of 21 s. Consistent with earlier findings, we observed a whole cell rotation prior to P₀ cytokinesis (Schonegg et al., 2014; Singh et al., 2019). We discarded a small subset of embryos (4 out of 17), where this whole cell rotation coincided with the time frames in which we performed the flow analysis.

In order to quantify chiral flows, we defined a chiral counter-rotating flow velocity $v_{c}$ together with a handedness as follows. First, we introduce a unit vector that is orthogonal to the contractile ring and points toward the cell pole that is in the direction of the anteroposterior-axis of the overall embryo ( $\underline{e_{x}}$ , see Figure 1—figure supplement 2). A second unit vector $\underline{e_{y}}$ is used, which is parallel to the cytokinetic ring and orthogonal to $\underline{e_{x}}$ . We denote the average velocities determined in the two halves of the cell (measured within the ROIs described above) as $\underline{v_{1}}$ and $\underline{v_{2}}$ . With this, we define the chiral counter-rotating flow velocity $v_{c}$ by

v_{c} = \underline{e_{z}} \cdot (\underline{e_{x}} \times \underline{v_{2}} - \underline{e_{x}} \times \underline{v_{1}}),

where $\underline{e_{z}} = \underline{e_{x}} \times \underline{e_{y}}$ is the third base vector of a right-handed orthonormal coordinate system. With this definition, $| v_{c} |$ represents the speed of chiral counter-rotating flows, while the sign of $v_{c}$ determines the flow’s handedness: If cortical flows appear clockwise when viewed from the cytokinetic plane toward each pole, one has $v_{c} > 0$ and the counter-rotating flows are left-handed. If cortical flows appear counter-clockwise, one has $v_{c} < 0$ and counter-rotating flows are right-handed. In order to quantify mean chiral counter-rotating velocity, we averaged $v_{c}$ over multiple embryos for every timepoint that was analyzed. From the analysis of the first nine cell divisions, we found that intensities in the P/EMS lineage are lower and hence the PIV flow analysis is less coherent in the P/EMS lineage as compared to the AB lineage, leading to increased uncertainty in PIV measurements.

To characterize net-rotating flows in a similar fashion, we use the net-rotating flow velocity $v_{r}$ defined by (Figure 1—figure supplement 4)

v_{r} = \underline{e_{z}} \cdot (\underline{e_{x}} \times \underline{v_{1}} + \underline{e_{x}} \times \underline{v_{2}}) .

If average flows in both cell halves are equal and in the same direction, that is, $\underline{v_{1}} = \underline{v_{2}}$ , there are no counter-rotating flows ( $v_{c} = 0$ ) and the corresponding net-rotating flow is quantified by $v_{r}$ .

Finally, in order to determine a flow measure that captures cortical flows along the cell’s long axis and into the contractile ring, we define the contractile flow velocity ( $v_{contr}$ ) depicted in Figure 3B by

v_{contr} = \underline{e_{x}} \cdot (\underline{v_{2}} - \underline{v_{1}}) .

For contractile cortical flows into the cytokinetic ring, we have $\underline{e_{x}} \cdot {\underline{v}}_{1} > 0$ and $\underline{e_{x}} \cdot {\underline{v}}_{2} < 0$ , and therefore $v_{contr} < 0$ .

Flow speed during cell division was calculated by adding the magnitude of mean absolute values of flow vectors in the two boxes from either side of the cytokinetic ring in the dividing cells.

Spindle skew and elongation analysis

Request a detailed protocol

In order to measure spindle skew angles, z-stacks (nine planes, each 1 µm apart recorded in 3 s time intervals) of the spindle poles were first projected on the plane perpendicular to the cytokinetic ring. For uncompressed embryos mounted using low-melt agarose method, z-stacks (25–31 z-planes; 1 µm apart with maximum possible temporal resolution between 5 and 10 seconds time intervals) were captured. For P₀, AB and P₁ the imaging plane was already perpendicular to the plane of cytokinesis while for the remaining cell divisions the embryos were rotated accordingly using the clear volume plugin (Royer et al., 2015) in FIJI. Subsequently, the spindle skew angle was defined as the angle between the line that joins the spindle poles at the onset of spindle elongation (anaphase-B) (initial spindle angle) and at completion of cytokinesis (final spindle angle) (Figure 2A). Spindle elongation length was defined as the distance between the two spindle poles during the same time-frames. To measure the dynamics of spindle elongation and skew angle in the AB cell (Figure 4—figure supplement 1, Figure 5—figure supplement 1) the spindle poles were automatically tracked and the spindle skew angle was plotted using custom-written MATLAB code (refer to spindle skew analysis MATLAB code). In order to compare the dynamics of spindle elongation and spindle skew, we first synchronized all the AB cells in each condition at the onset of anaphase-B and, subsequently, averaged over multiple embryos. The difference beween the spindle angle at each timepoint and the spindle angle at anaphase-B onset timepoint was measured and plotted over time. The maximum value of the slope for spindle elongation and spindle skew angle curves for each embryo between time window of 60–120 s (Figure 4—figure supplement 1, Figure 5—figure supplement 1) was identified as peak rate of spindle elongation and peak rate of spindle skew. In order to reduce noise in calculating slope, a moving average was performed to smooth the spindle skew angle and elongation profiles using moving slope function in MATLAB. Average peak rates were calculated by averaging the maximum values over multiple embryos for each condition.

Determining myosin ratio, cytokinetic ring position and fitting myosin profiles

Request a detailed protocol

In order to obtain cortical myosin distributions (Figure 1C, Source data 1), we normalized the axis of cell division and calculated the mean myosin intensity in a 20 pixel-wide stripe along this axis for the same timepoints when $v_{c}$ was calculated. The myosin ratio (Figure 1E) was determined by dividing the mean intensity at the anterior (0–20% of the normalized cell division axis) by the mean intensity at the posterior (80–100% of the normalized cell division axis) for P₀, AB, P₁ and EMS. For ABa and ABp the myosin intensity was calculated similarly but along the L/R axis. We have restricted myosin intensity measurements to the 20% outer segments of the cell division axis in order to prevent the strong fluorescent signal from the cytokinetic ring from affecting this analysis (Figure 1—figure supplement 6). Similar to myosin ratio, myosin concentration at the anterior was normalized with mean posterior myosin concentration for multiple embryos and plotted (Figure 1—figure supplements 9 and 10). To determine the position of the cytokinetic ring, we performed midplane imaging using a strain expressing a membrane marker (PH::GFP) and a tubulin marker to label spindle poles (TBB-2::mCherry). The cell division axis was defined as the line through the two opposing spindle poles and was normalized between cell boundaries. The relative cytokinetic ring position was defined as the position where the ingressing ring intersects the normalized cell division axis.

For visualization purposes (Figure 1C), we fitted the myosin distributions using the fitting function

I (x) = \frac{1}{2} (I_{P} - I_{A}) (erf [\frac{x - x_{r}}{w}] - 1) + I_{P} + \frac{I_{R}}{\sqrt{2 π w^{2}}} exp [- \frac{{(x - x_{r})}^{2}}{2 * w^{2}}] .

The errorfunction erf and the Gaussian represent contributions from the anteroposterior myosin asymmetry and from the contractile ring, respectively. The fitting parameters $I_{P}$ , $I_{A}$ , $I_{R}$ , $w$ and $x_{r}$ , respectively, describe myosin intensities at the posterior pole, the anterior pole and in the cytokinetic ring, as well as the width and position of the ring.

Temperature-sensitive experiments

Request a detailed protocol

We used the cherry temp temperature control stage from Cherry Biotech for all temperature sensitive experiments in the study. L4 worms carrying tbb-2::mCherry (SWG63, control) and nmy-2(ts); tbb-2::mCherry (SWG204) were grown at 15°C (permissive temperature for nmy-2(ts) mutants) overnight. During image acquisition, embryos were mounted using agar pad mounting method and temperature was maintained using the cherry temp temperature control stage from Cherry Biotech. For imaging the dynamics of spindle elongation and skew angle in the AB cell for nmy-2(ts) and control embryos, 60 s after the successful completion of the first cell division (P₀ cell division), temperature was raised to 25°C. Embryos were imaged approximately 5 min after the temperature shift to minimize photo toxicity. Similarly, for later cell stages, the temperature shift was carried out right after completion of cytokinesis of the mother cell. A small subset of embryos in which spindle poles of daughter cells could not be visualized were discarded.

Determining embryo thickness

Request a detailed protocol

In order to determine embryo thickness, we collected an ensemble of up to nine two-cell embryos from SWG59, SWG70, OD70 strains mounted using the agar pad method or low-melt agarose method. To measure embryo thickness in utero, young adult worms (24 hrs post L4) were paralyzed in 0.1% tretramisole (Sigma-Aldrich T1512) for 3 min on a cover slip and mounted on 2% agarose pads. The AB cell in the two-cell embryos was projected on a view down the anterior end along the anteroposterior axis. Thickness of the embryo was determined by measuring the end to end distance between the opposing membrane signal (denoted by arrows in Figure 1—figure supplement 1). For each embryo, aspect ratio was calculated as the ratio of thickness values of the AB cell when projected along the AP-DV plane and the LR-DV plane as shown in Figure 1—figure supplement 1. All embryo rotations for post-processing and time-lapse along various axis were captured using clearvolume as described in the spindle skew analysis section.

Appendix 1

Thin film active chiral fluid theory

Cortical flows in Caenorhabditis elegans embryos have been successfully described using the thin film theory of active chiral fluids (Naganathan et al., 2014; Naganathan et al., 2016). We use the fact that cells are approximately axisymmetric, and we assume that the active forces during cell division vary mostly along their symmetry axis, in the following referred to as long axis. In this case, the hydrodynamic equations of a chiral thin film can be formulated as an effectively one-dimensional system of equations, capturing flows parallel ( $v_{x}$ ) and orthogonal ( $v_{y}$ ) to the long axis:

η \partial_{x}^{2} v_{x} + \partial_{x} T = γ v_{x}

\frac{η}{2} \partial_{x}^{2} v_{y} + \partial_{x} τ = γ v_{y} .

Here, $η$ is the viscosity of the cortex and $γ$ is the friction with surrounding material. Note that the assumption of a homogeneous friction $γ$ is a strong simplification, where we neglect details of the potentially inhomogeneous mechanical interactions between cells, as well as with the extra-embryonic fluid and the egg shell. Gradients of active tension $T$ and active torques $τ$ lead to contractile and chiral flows, respectively. It has been demonstrated previously that active tension and active torques both dependent on the local myosin concentration in the cortex (Mayer et al., 2010; Naganathan et al., 2014; Naganathan et al., 2016). Using the fluorescent myosin intensity $I (x)$ as a proxy for the myosin concentration, we can write in the simplest case $T = T_{0} I (x)$ and $T = τ_{0} I (x)$ .

Denoting the length of the measurement domain by $L$ (approximately the length of the cell’s long axis), we can identify three independent parameters in the model Equations S1 and S2: The characteristic contractile and chiral velocities $v_{T} = L T_{0} / η$ and $v_{τ} = L τ_{0} / η$ , respectively, as well as the hydrodynamic length $ℓ = \sqrt{η / γ}$ .

Fitting cortical flows

For the fitting of cortical flows for given myosin profiles, we closely follow our previous work (Naganathan et al., 2014). Briefly, we use experimentally determined myosin profiles $I (x)$ in Equations S1 and S2 to calculate flows $v_{x}$ and $v_{y}$ . We then determine the parameters $v_{T}$ , $v_{τ}$ and $ℓ$ for which the predicted flows best match the experimental data. To extract unique solutions from Equations S1 and S2, we use the experimentally measured flow velocities at the boundaries of the measurement domain as boundary conditions. Note that due to imaging limitations for smaller cells (after the eight-cell stage) as development progresses, it was not possible to extract spatially resolved velocity line profiles and fits for the cortical flows in ABal cell and ABpr cell. The final best fit parameters for AB, ABa and ABp cells are shown in Appendix 1—table 1. The corresponding contractile flow profiles $v_{x}$ and chiral flow profiles $v_{y}$ are shown in Figure 1—figure supplement 8.

Appendix 1—table 1

Best fit parameters.

The average domain lengths (approximately the size of the cell’s long axis) on which the myosin profiles were given were $L_{A B} = 27.4 μ m$ , $L_{A B a} = 19.5 μ m$ and $L_{A B p} = 17.9 μ m$ . The corresponding fits are shown in Figure 1—figure supplement 8.

Cell type	$ℓ$ [µm]	$v_{T}$ [µm/min]	$v_{τ}$ [µm/min]
AB	18.7	0.15	0.25
ABa	10.4	0.19	0.15
ABp	8.2	0.4	0.4

We also considered asymmetrically dividing cells (P₀, P₁, EMS) in which, instead of counter-rotating flows ( $| v_{c} | > 0$ , $v_{r} \approx 0$ ), mainly net-rotating flows occur ( $v_{c} \approx 0$ , $| v_{r} | > 0$ ) (Figure 1—figure supplement 4). Following the same fitting procedure as described in the previous section, we noticed that the chiral thin film theory Equations S1 and S2 generally could not account quantitatively for the observed cortical flow profiles. However, using the theory it is still possible to rationalize qualitative properties of the observed cortical flows, as we discuss in the following.

Qualitative properties of myosin distributions and chiral flows

While the chiral thin film theory does not recapitulate all of the experimentally observed flows quantitatively, the theory allows linking qualitative predictions to key properties of observed myosin distributions and chiral flows. In particular, we noticed that the myosin profiles in asymmetrically diving cells consistently featured a rather asymmetrically positioned contractile ring (Figure 1D). Furthermore, the myosin profiles of asymmetrically dividing cells are asymmetric with respect to the cytokinetic ring and exhibit plateaus toward the anterior cell poles (Figure 1C and Figure 1E). An overview of these qualitative properties for the P/EMS lineage and the AB-lineage is given in Appendix 1—table 2.

Appendix 1—table 2

Qualitative properties of myosin distributions and chiral flows consistently observed in P/EMS lineage (P₀, P₁, EMS, P₂) and AB-lineage (AB, ABa, ABp, ABal, ABar) cells.

	Myosin peak position	Anterior-posterior myosin	Chiral flow properties
AB-lineage	Centered	Symmetric	$v_{r} \approx 0$ , $\| v_{c} \| > 0$
P/EMS lineage	Off-center	Asymmetric	$\| v_{r} \| > 0$ , $v_{c} \approx 0$

To establish how a contractile ring and an overall myosin asymmetry generally affect flows predicted by the chiral thin film theory, we generalize the chiral thin film equations (Naganathan et al., 2014) to curved surfaces and solve them on an ellipsoid using corresponding synthetic torque profiles (Figure 1—figure supplement 7). We find that a symmetrically placed ring pattern yields perfectly counter-rotating flows ( $v_{r} = 0$ , $| v_{c} | > 0$ , Figure 1—figure supplement 7, left), while anterior-posterior myosin asymmetry ratio results in net-rotating flow ( $| v_{r} | > 0$ , $v_{c} = 0$ , Figure 1—figure supplement 7, middle) while an anterior-posterior myosin asymmetry along with a symmetrically placed ring pattern yields net-rotating flows such as observed in P/EMS cells (Figure 1—figure supplement 7, right). To study the combined effect of a varying position of the contractile ring and a myosin asymmetry, we develop in the following section a simple minimalistic model of the system.

Chiral flow minimal model

In the following, we develop a minimal description of the occurrence of counter- and net-rotating flows based on key characteristics of the myosin profiles discussed in the previous section. We consider a simplified myosin profile in the form

I (x) = I_{r} (x) + I_{a p} (x)

with

I_{r} (x) = I_{R} w δ (x - x_{r})

I_{a p} (x) = (I_{P} - I_{A}) Θ (x - x_{r}) + I_{A} .

Here, $δ (x)$ is the delta function, $Θ (x)$ the Heaviside step function and $x_{r}$ is the position of an idealized cytokinetic ring. The intensity profile $I_{r} (x)$ captures the presence of a myosin peak (the later contractile ring) of width $w$ and average intensity $I_{R}$ at $x_{r}$ . The profile $I_{a p} (x)$ represents the large-scale asymmetry in myosin between anterior pole ( $I_{A}$ ) and posterior pole ( $I_{P}$ ). We solve Equation S2 on a domain of length $L$ and for boundary conditions $v_{y} (0) = v_{y} (L) = 0$ using the simplified myosin intensities given in Equations S4 and S5, which yields

\frac{v_{y}^{(i)}}{v_{τ}} = {\begin{matrix} A_{(i)} \sinh (α x / L) & f o r 0 \leq x \leq x_{r} \\ B_{(i)} \sinh [α (x - L) / L] & f o r x_{r} \leq x \leq L \end{matrix} .

Here, $α = \sqrt{2 γ L^{2} / η}$ is an inverse dimensionless hydrodynamic length and $v_{τ} = L τ_{0} / η$ the characteristic velocity associated with active torques. The coefficients in Equation S6 are given by

A_{r} = I_{R} \frac{w}{L} \frac{\cosh [α (1 - x_{r} / L)]}{\sinh α} A_{a p} = \frac{I_{P} - I_{A}}{α} \frac{\sinh [α (1 - x_{r} / L)]}{\sinh α}

B_{r} = I_{R} \frac{w}{L} \frac{\cosh (α x_{r} / L)}{\sinh α} B_{a p} = - \frac{I_{P} - I_{A}}{α} \frac{\sinh (α x_{r} / L)}{\sinh α} .

With these coefficients, Equation S6 describes flows $v_{y}^{r}$ resulting from the contractile ring given in Equation S4 and flows $v_{y}^{a p}$ resulting from the asymmetric myosin profile given in Equation S5. Note that, as expected, flows due to the presence of the contractile ring vanish for $I_{R} = 0$ and flows due to the presence of a myosin asymmetry vanish if $I_{A} = I_{P}$ . General flow profiles are given as superposition of the two contributions: $v_{y} = v_{y}^{r} + v_{y}^{a p}$ .

Finally, to evaluate these solutions, we define a dimensionless counter-rotating velocity ${\tilde{v}}_{c}$ and the net-rotating velocity ${\tilde{v}}_{r}$ in analogy to the quantities introduced in the main text and methods, Equations 2 and 3, as

{\tilde{v}}_{c} = \frac{1}{L} (\int_{x_{r}}^{x_{r} + Δ} {\tilde{v}}_{y} d x - \int_{x_{r} - Δ}^{x_{r}} {\tilde{v}}_{y} d x)

{\tilde{v}}_{r} = \frac{1}{L} \int_{x_{r} - Δ}^{x_{r} + Δ} {\tilde{v}}_{y} d x .

Here, ${\tilde{v}}_{y} = v_{y} / v_{τ}$ and we consider a window of 15 % ( $Δ / L = 0.15$ ) of the total length toward either side of the idealized contractile ring over which the mean flow velocity is determined (Figure 1A, Figure 1—figure supplements 2 and 4). Using this minimal model, we can now investigate how the combined contributions of a large-scale myosin asymmetry ( $I_{a p}$ ) and a varying contractile ring position $(I_{r})$ affect the counter-rotating velocity ${\tilde{v}}_{c}$ and net-rotating velocity ${\tilde{v}}_{r}$ . In particular, we fix for the discussion $α = 1$ and $w / L = 0.1$ , as well as $I_{R} / I_{P} = 2$ . In this case, the counter-rotating flow velocity ${\tilde{v}}_{c}$ and the net-rotating flow velocity ${\tilde{v}}_{r}$ are only functions of the relative ring position $x_{r} / L$ and the anterior-posterior myosin ratio $I_{A} / I_{P}$ with properties shown in Figure 1—figure supplement 7 and described in the following.

For an anterior-posterior symmetric myosin profile, counter-rotating flows $| {\tilde{v}}_{c} |$ have a weak maximum in their amplitude if the contractile ring is at a centered position $x_{r} / L = 0.5$ (Figure 1—figure supplement 7). Furthermore, a centered contractile ring has no effect on the counter-rotating flow measure ${\tilde{v}}_{c}$ if a large-scale myosin asymmetry $I_{A} / I_{P} > 1$ is introduced (Figure 1—figure supplement 7). However, for an off-centered ring $x_{r} / L > 0.5$ the presence of a myosin asymmetry will contribute flows that reduce ${\tilde{v}}_{c}$ and can even lead to vanishing counter-rotating flows ${\tilde{v}}_{c} = 0$ if $I_{A} / I_{P}$ is sufficiently large. While this matches the qualitative experimental observations listed in Appendix 1—table 2, the required asymmetry predicted by the theory is significantly larger than the experimentally measured one.

Also, the behavior of ${\tilde{v}}_{r}$ in our minimal model is compatible with the qualitative properties listed in Appendix 1—table 2. In particular, for a large-scale myosin asymmetry $I_{A} / I_{P} > 1$ , the net-rotation velocity ${\tilde{v}}_{r}$ is negative for any ring position, while it can becomes positive for $x_{r} / L > 0.5$ if $I_{A} = I_{P}$ (Figure 1—figure supplement 7). Furthermore, net-rotating flows vanish for a symmetric myosin profile $I_{A} = I_{P}$ and a centered contractile ring $x_{r} / L = 0.5$ (Figure 1—figure supplement 7), which corresponds to the observations made in AB-lineage cells. Finally, the presence of large-scale myosin asymmetries $I_{A} / I_{P} \neq 1$ is generally expected to contribute to net rotating flows (Figure 1—figure supplement 7). This holds true for essentially arbitrary positions of the contractile ring and indicates that such asymmetries could play an important role for developing a better understanding of net-rotating flows in the P/EMS lineage cells in the future.

Theoretical descriptions of AB cells skews

In the following, we introduce a minimal model that can quantitatively link cell skews to the chiral cortical flows and mechanical interactions with the surrounding. Note that while the model describes the general scenario of two confined, counter-rotating surfaces, we focus its application to the case of the dividing AB cell and its skew in the AP-DV plane, for which all the required experimental information is available to make quantitative predictions.

We consider an idealized configuration of two connected incompressible surfaces that represent the cortices of the future ABa and ABp cell during AB cell division and reorientation-skew. Chiral counter-rotating cortical flows correspond to rotations of these surfaces in opposite directions around a common axis. For simplicity, we neglect more complex aspects of the surface deformations that occur during the cell division and skewing inside the constraining egg shell. This system is analogous to the two chains under a bulldozer, where the motion of the chains represent chiral cortical actomyosin flows and the operators cab, with a fixed orientation relative to the two chains, indicates the orientation of the dividing AB cell. The two connected surfaces are additionally confined by two opposing rigid surfaces that are parallel to the AP-DV-midplane and represent the egg shell (Figure 5—figure supplement 3).

Geometric description of counter-rotating and skewing surfaces

We first describe the surface motion in a reference frame that is co-rotating with the angular skew occurring in the AP-DV-plane. We assume that active chirality leads to a counter-rotating surface motion, and the local velocities of the ABa and ABp cell on the the embryo’s future left side at a distance $R$ from the cytokinetic ring are given by $- v_{a}$ and $v_{p}$ , respectively. Observing the two counter-rotating surfaces in a common co-rotating reference frame, the local velocities of each cell on the future right side are then given by $v_{a}$ and $- v_{p}$ , respectively (Figure 5—figure supplement 3). In experiments, cortical flows ( $v_{L}^{(a)}$ , $v_{L}^{(p)}$ , $v_{R}^{(a)}$ , $v_{R}^{(p)}$ ) of the ABa and ABp cell on each surface are measured in the lab frame, which is defined as the reference frame in which the egg shell is at rest. These measurements are related to the parameters of the simplified geometric model by

= - v_{a} + ω_{g} (R - δ)

= v_{p} - ω_{g} (R + δ)

= v_{a} + ω_{g} (R - δ)

= - v_{p} - ω_{g} (R + δ) .

Here, $ω_{g}$ is the angular skew velocity around an axis that is orthogonal to the AP-DV plane and $δ$ describes a possible displacement of the rotation axis from the center (Figure 5—figure supplement 3). If $δ > 0$ ( $δ < 0$ ) the axis of rotation is shifted toward the ABa (ABp) cell. The sign in front of $ω_{g}$ is chosen such that $ω_{g} > 0$ ( $ω_{g} < 0$ ) corresponds to anti-clockwise (clockwise) skews when viewed from the left side down the left-right axis (Figure 5—figure supplement 3). From Equations S9–S12, we then find

= \frac{1}{2 R} (α - β)

= R \frac{α + β}{β - α}

= \frac{1}{2} (v_{R}^{(a)} - v_{L}^{(a)})

= \frac{1}{2} (v_{L}^{(p)} - v_{R}^{(p)}),

where $α = (v_{L}^{(a)} + v_{R}^{(a)}) / 2$ and $β = (v_{L}^{(p)} + v_{R}^{(p)}) / 2$ . Note that Equations S9–S16 essentially represent the transformation of velocities between two reference frames that rotate relative to each other.

To test if this simplified geometric representation of two counter-rotating and skewing surfaces is consistent with experiments, we measured $v_{L}^{(a)}$ , $v_{L}^{(p)}$ , $v_{R}^{(a)}$ and $v_{R}^{(p)}$ during the late state of the AB cell skew and computed the cell skew parameters using Equations S13–S16 for the wt, ect-2 and rga-3 conditions (Appendix 1—table 3). For all three conditions, the calculated angular skew velocities $ω_{g}$ agree well with the average angular skewing velocities of the spindle measured in experiments (Appendix 1—table 4, right column). This strongly suggests that chiral cortical flows across the cortex are not only qualitatively, but even quantitatively linked to the corresponding skewing motion of the spindle. Furthermore, we find for all three conditions $δ / R \approx 1$ (Appendix 1—table 3), which implies that the axis around which the AB cell skews is shifted toward the ABa cell. During later stages of the skew, the time point at which the velocities $v_{L}^{(a)}$ , $v_{L}^{(p)}$ , $v_{R}^{(a)}$ and $v_{R}^{(p)}$ given in Appendix 1—table 3 were measured, this can indeed be observed as a feature of the spindle skew (Figure 5—figure supplement 3): Both spindle poles of the AB cell move nearly parallel to the AP axis, but the ABp cell’s spindle pole does so faster. As a result, the rotation axis is located closer to the ABa spindle pole than to the ABp spindle pole.

Appendix 1—table 3

Chiral counter-rotations in experiments and in a minimal geometric model.

Left: Experimentally measured chiral cortical flows (± error at 95 % confidence interval) of the ABa and ABp cell at late stages of the spindle skew for different conditions. Flows on both cells are measured on the future left ( $v_{L}^{(a)}$ , $v_{L}^{(p)}$ ) and right side ( $v_{R}^{(a)}$ , $v_{R}^{(p)}$ ). Right: Assuming two rigid, counter-rotating and skewing surfaces, the velocities measured in the lab frame (left) can be mapped via Equations S13–S16 to the skewing properties ( $ω_{g}$ , $δ$ ) and surface velocities ( $v_{a}$ , $v_{p}$ ) in the co-rotating frame (± propagated uncertainty). Distance between cytokinetic ring and points of velocity measurements: $R = 4.5 μ m$ .

Measured vel.	wt	ect-2	rga-3	Equations S13–S16	wt	ect-2	rga-3
$v_{L}^{(a)}$ [µm/min]	$- 4.6 \pm 0.8$	$- 3.0 \pm 0.7$	$- 5.9 \pm 0.7$	$ω_{g}$ [°/s]	$- 0.31 \pm 0.14$	$- 0.19 \pm 0.18$	$- 0.38 \pm 0.15$
$v_{R}^{(a)}$ [µm/min]	$5.0 \pm 0.7$	$2.6 \pm 1.0$	$5.3 \pm 0.9$	$δ / R$	$1.14 \pm 0.13$	$0.80 \pm 0.42$	$0.83 \pm 0.13$
$v_{L}^{(p)}$ [µm/min]	$8.6 \pm 0.7$	$5.7 \pm 0.7$	$9.8 \pm 0.6$	$v_{a}$ [µm/min]	$4.8 \pm 0.8$	$2.8 \pm 0.85$	$5.6 \pm 0.8$
$v_{R}^{(p)}$ [µm/min]	$- 2.4 \pm 0.5$	$- 2.5 \pm 1.0$	$- 3.2 \pm 0.6$	$v_{p}$ [µm/min]	$5.5 \pm 0.6$	$4.1 \pm 0.85$	$6.5 \pm 0.6$

Appendix 1—table 4

Comparison of the angular velocity $ω$ determined from the physical skew model with experimentally measured average spindle skew rates.

The angular velocity $ω$ is calculated for each condition using Equations S21 with $R = 4.5 μ m$ and $v = (v_{a} + v_{p}) / 2$ (see Appendix 1—table 3). $Γ$ is given by Equation S23, with the hydrodynamic lengths $ℓ_{L} = 24.8 μ m$ and $ℓ_{R} = 18.7 μ m$ (Figure 5—figure supplement 3), and the measured contact surface areas on the future left and right side given by $A_{L} = 166.13 \pm 22.63 μ m^{2}$ and $A_{R} = 210.49 \pm 39.9 μ m^{2}$ , respectively. Theory error: ± propagated uncertainty, Measurement error: ± 95 % confidence interval

Condition	Angular skew velocity $ω$ [°/s] from theory	Measured average spindle skew rate [°/s]
wt	$- 0.42 \pm 0.15$	$- 0.32 \pm 0.04$
ect-2	$- 0.28 \pm 0.04$	$- 0.29 \pm 0.04$
rga-3	$- 0.49 \pm 0.19$	$- 0.36 \pm 0.16$

Derivation of a physical skew model

Chiral surface flows and the motion of the AB cell relative to the surrounding material can in general give rise to friction forces and external torques that act on the cell. For the angular cell skew in the AP-DV-plane, the relevant frictions forces would have to occur dominantly through interactions with the egg shell on the future left and right side of the embryo (Figure 5—figure supplement 3). The corresponding flows are described by the velocities $v_{L}^{(a)}$ , $v_{L}^{(p)}$ , $v_{R}^{(a)}$ and $v_{R}^{(p)}$ measured in the lab frame, such that the external torques on future left and right side are given, respectively, by

\begin{array}{ll} τ_{L} & = R (F_{L}^{(a)} - F_{L}^{(p)}) \\ \approx - R γ_{L} (A_{L}^{(a)} v_{L}^{(a)} - A_{L}^{(p)} v_{L}^{(p)}) \\ = R γ_{L} [A_{L} (v - ω R) + ω δ (A_{L}^{(a)} - A_{L}^{(p)})] \end{array}

\begin{array}{ll} τ_{R} & = R (F_{R}^{(a)} - F_{R}^{(p)}) \\ \approx - R γ_{R} (A_{R}^{(a)} v_{R}^{(a)} - A_{R}^{(p)} v_{R}^{(p)}) \\ = - R γ_{R} [A_{R} (v + ω R) + ω δ (A_{R}^{(p)} - A_{R}^{(a)})] . \end{array}

Here, $F_{L}^{(a)} = - γ_{L} A_{L}^{(a)} v_{L}^{(a)}$ depicts the total external friction force on the future left side of the ABa cell (similarly for the other forces), $A_{L} = A_{L}^{(a)} + A_{L}^{(p)}$ and $A_{R} = A_{R}^{(a)} + A_{R}^{(p)}$ are the total contact surface areas between the AB cell and egg shell on the left and right side (Figure 5—figure supplement 3), respectively, and we have used Equations S9–S12 for simplicity with $v_{a} = v_{p} = v$ . The external torques in Equation S17 and S18 transfer a total torque

τ_{c} = τ_{L} + τ_{R}

onto the AB cell. This total torque on the other hand is balanced by a dissipative torque $τ_{ω}$ that arises through the angular skew of the dividing AB cell inside the egg shell, that is,

τ_{ω} + τ_{c} = 0 .

For simplicity, we consider $τ_{ω} = - \bar{η} R^{3} ω$ , where $\bar{η}$ denotes an effective rotational viscosity that captures interactions of the skewing AB cell with the extra-embryonic fluid inside the egg shell and potentially also interactions with the $P_{1}$ cell. Combining Equations S17–S20, we find

ω = Γ \frac{v}{R},

with

Γ = \frac{A_{L} γ_{L} - A_{R} γ_{R}}{\bar{η} R + γ_{L} (A_{L} + \frac{δ}{R} Δ A_{L}) + γ_{R} (A_{R} + \frac{δ}{R} Δ A_{R})},

where $Δ A_{L} = A_{L}^{(p)} - A_{L}^{(a)}$ , $Δ A_{R} = A_{R}^{(p)} - A_{R}^{(a)}$ . Equation S21 with $Γ$ given in Equation S22 provides a minimal model that can be used to estimate the expected angular cell skew velocity $ω$ from the measured cortical velocities ( $v_{L}^{(a)}, v_{L}^{(p)}, v_{R}^{(a)}, v_{R}^{(p)}$ ) that define $v$ , basic known measures of the cell geometry ( $A_{L}, A_{R}, R$ ) and the friction parameters ( $γ_{L}$ , $γ_{R}$ , $\bar{η}$ ).

Quantitative comparison of the physical skew model with experiments

In the following, we want to use Equation S21 together with the experimentally measured parameters listed in Appendix 1—table 3 to calculate the expected angular skew frequency $ω$ . Note that the agreement of $ω_{g}$ calculated from Equation S13 with the experimental values validates the simplifying geometric assumptions of our model, while Equation S21) indicates how specific mechanical interactions with the surrounding can lead to the handedness and amplitude of the angular skew.

To compute the required coefficient $Γ$ given in Equation S22, we use that $δ / R \approx 1$ (Appendix 1—table 3) for all conditions, and we consider approximately similar contact surface areas of the ABa and ABp cell halves on each side ( $A_{L}^{(a)} \approx A_{L}^{(p)}$ , $A_{R}^{(a)} \approx A_{R}^{(p)}$ ). In this case, $Γ$ only depends on the total contact surface areas $A_{L}$ and $A_{R}$ that we estimate from confocal images ( $A_{R} / A_{L} \approx 1.3$ , Figure 5—figure supplement 3). Furthermore, we can express the friction coefficients in Equation S22 as $γ_{L} = η_{L} / ℓ_{L}^{2}$ and $γ_{R} = η_{R} / ℓ_{R}^{2}$ , where $ℓ_{L}$ and $ℓ_{R}$ are the hydrodynamic lengths. The latter are determined by fitting the chiral thin film theory Equations S1 and S2 to measured flow profiles on the left and right side of dividing AB cells (Figure 5—figure supplement 3), from which we find ${(ℓ_{L} / ℓ_{R})}^{2} = η_{L} γ_{R} / (η_{R} γ_{L}) \approx 1.7$ . Note, that we can in general not exclude spatial variations of the cortical viscosity that would lead to $η_{L} \neq η_{R}$ and accordingly affect the estimated local friction parameters. However, even if viscosity variations would fully account for the observed difference in hydrodynamic length such that $γ_{L} = γ_{R}$ , the contact area asymmetry with $A_{R} > A_{L}$ would still be sufficient to explain the handedness of the observed skews. Finally, to allow for quantitative predictions, we make the simplifying assumption $η_{L} \approx η_{R} = η$ , such that Equation S22 is for all three conditions given by

\begin{array}{ll} Γ & = \frac{A_{L} / ℓ_{L}^{2} - A_{R} / ℓ_{R}^{2}}{\bar{η} R / η + A_{L} / ℓ_{L}^{2} + A_{R} / ℓ_{R}^{2}} \\ \approx \frac{A_{L} ℓ_{R}^{2} - A_{R} ℓ_{L}^{2}}{A_{L} ℓ_{R}^{2} + A_{R} ℓ_{L}^{2}} . \end{array}

In the second step, we have assumed that the cortical viscosity $η$ is large compared to the effective viscosity $\bar{η}$ that describes interactions with the extra-embryonic fluid ( $\bar{η} R / η \approx 0$ ). Equation S21 with $Γ$ given in Equation S23 is equivalent to Equation 1 and shows that contributions to the hydrodynamic length and to the contact surface area that are different on the future left and right side can generate an angular cell skew, where their relative values define the handedness of the skew. With Equation S23, the angular skew velocity $ω$ given in Equation S21 is fully determined by parameters known from experiments and the corresponding values for all three conditions are shown in Appendix 1—table 4. Despite the geometric simplifications, our minimal model can predict the experimentally measured cell skew velocities for all three conditions within a relative error margin of approximately 5–25%.

Data availability

We have provided all data in the manuscript and supporting files. Due to the large size of the movies, the source movies are available upon request.

References

(1999) Notch signaling: cell fate control and signal integration in development
Science 284:770–776.
https://doi.org/10.1126/science.284.5415.770
- PubMed
- Google Scholar
1. Bargmann CI
2. Avery L
(1995) Laser killing of cells in Caenorhabditis elegans
Methods in Cell Biology 48:225–250.
https://doi.org/10.1016/s0091-679x(08)61390-4
- PubMed
- Google Scholar
(2013) PAR-2, LGL-1 and the CDC-42 GAP CHIN-1 act in distinct pathways to maintain polarity in the C. elegans embryo
Development 140:2005–2014.
https://doi.org/10.1242/dev.088310
- PubMed
- Google Scholar
1. Bergmann DC
2. Lee M
3. Robertson B
4. Tsou MF
5. Rose LS
6. Wood WB
(2003) Embryonic handedness choice in C. elegans involves the galpha protein GPA-16
Development 130:5731–5740.
https://doi.org/10.1242/dev.00839
- PubMed
- Google Scholar
1. Brenner S
(1974)
The genetics of Caenorhabditis elegans

Genetics 77:71–94.
- PubMed
- Google Scholar
1. Bronner ME
(2012) Formation and migration of neural crest cells in the vertebrate embryo
Histochemistry and Cell Biology 138:179–186.
https://doi.org/10.1007/s00418-012-0999-z
- PubMed
- Google Scholar
Book
1. Bruce A
2. Julian L
3. Martin R
4. Keith R
5. Peter W
6. Johnson A
(2002)
Molecular Biology of the Cell

W. W. Norton & Company.
- Google Scholar
1. Buchsbaum IY
2. Cappello S
(2019) Neuronal migration in the CNS during development and disease: insights from in vivo and in vitro models
Development 146:dev163766.
https://doi.org/10.1242/dev.163766
- PubMed
- Google Scholar
1. Chougule A
2. Lapraz F
3. Földi I
4. Cerezo D
5. Mihály J
6. Noselli S
(2020) The Drosophila actin nucleator DAAM is essential for left-right asymmetry
PLOS Genetics 16:e1008758.
https://doi.org/10.1371/journal.pgen.1008758
- PubMed
- Google Scholar
(2003) Translation of polarity cues into asymmetric spindle positioning in Caenorhabditis elegans embryos
Science 300:1957–1961.
https://doi.org/10.1126/science.1084146
- PubMed
- Google Scholar
1. Davies T
2. Jordan SN
3. Chand V
4. Sees JA
5. Laband K
6. Carvalho AX
7. Shirasu-Hiza M
8. Kovar DR
9. Dumont J
10. Canman JC
(2014) High-resolution temporal analysis reveals a functional timeline for the molecular regulation of cytokinesis
Developmental Cell 30:209–223.
https://doi.org/10.1016/j.devcel.2014.05.009
- PubMed
- Google Scholar
(2018) Cell-intrinsic and -extrinsic mechanisms promote cell-type-specific cytokinetic diversity
eLife 7:e36204.
https://doi.org/10.7554/eLife.36204
- PubMed
- Google Scholar
1. Davison A
2. McDowell GS
3. Holden JM
4. Johnson HF
5. Koutsovoulos GD
6. Liu MM
7. Hulpiau P
8. Van Roy F
9. Wade CM
10. Banerjee R
11. Yang F
12. Chiba S
13. Davey JW
14. Jackson DJ
15. Levin M
16. Blaxter ML
(2016) Formin is associated with Left-Right asymmetry in the pond snail and the frog
Current Biology 26:654–660.
https://doi.org/10.1016/j.cub.2015.12.071
- PubMed
- Google Scholar
1. De Pascalis C
2. Etienne-Manneville S
(2017) Single and collective cell migration: the mechanics of adhesions
Molecular Biology of the Cell 28:1833–1846.
https://doi.org/10.1091/mbc.e17-03-0134
- PubMed
- Google Scholar
(2013) Engineering the Caenorhabditis elegans genome using Cas9-triggered homologous recombination
Nature Methods 10:1028–1034.
https://doi.org/10.1038/nmeth.2641
- PubMed
- Google Scholar
(2014) Advanced methods of microscope control using μmanager software
Journal of Biological Methods 1:10.
https://doi.org/10.14440/jbm.2014.36
- PubMed
- Google Scholar
1. Egger B
2. Boone JQ
3. Stevens NR
4. Brand AH
5. Doe CQ
(2007) Regulation of spindle orientation and neural stem cell fate in the Drosophila optic lobe
Neural Development 2:1.
https://doi.org/10.1186/1749-8104-2-1
- PubMed
- Google Scholar
Book
1. Eisenmann DM
(2005)
WormBook : The Online Review of C. elegans Biology

WormBook.
- Google Scholar
1. Field C
2. Li R
3. Oegema K
(1999) Cytokinesis in eukaryotes: a mechanistic comparison
Current Opinion in Cell Biology 11:68–80.
https://doi.org/10.1016/S0955-0674(99)80009-X
- PubMed
- Google Scholar
1. Fishkind DJ
2. Wang YL
(1995) New horizons for cytokinesis
Current Opinion in Cell Biology 7:23–31.
https://doi.org/10.1016/0955-0674(95)80041-7
- PubMed
- Google Scholar
(2013) Active chiral processes in thin films
Physical Review Letters 110:048103.
https://doi.org/10.1103/PhysRevLett.110.048103
- PubMed
- Google Scholar
1. Galli M
2. Muñoz J
3. Portegijs V
4. Boxem M
5. Grill SW
6. Heck AJ
7. van den Heuvel S
(2011) aPKC phosphorylates NuMA-related LIN-5 to position the mitotic spindle during asymmetric division
Nature Cell Biology 13:1132–1138.
https://doi.org/10.1038/ncb2315
- PubMed
- Google Scholar
1. Galli M
2. van den Heuvel S
(2008) Determination of the cleavage plane in early C. elegans embryos
Annual Review of Genetics 42:389–411.
https://doi.org/10.1146/annurev.genet.40.110405.090523
- Google Scholar
1. Glotzer M
(1997) The mechanism and control of cytokinesis
Current Opinion in Cell Biology 9:815–823.
https://doi.org/10.1016/S0955-0674(97)80082-8
- PubMed
- Google Scholar
(2001) Polarity controls forces governing asymmetric spindle positioning in the Caenorhabditis elegans embryo
Nature 409:630–633.
https://doi.org/10.1038/35054572
- PubMed
- Google Scholar
1. Gross P
2. Kumar KV
3. Goehring NW
4. Bois JS
5. Hoege C
6. Jülicher F
7. Grill SW
(2019) Guiding self-organized pattern formation in cell polarity establishment
Nature Physics 15:293–300.
https://doi.org/10.1038/s41567-018-0358-7
- PubMed
- Google Scholar
1. Hardin J
2. King RS
(2008) The long and the short of wnt signaling in C. elegans
Current Opinion in Genetics & Development 18:362–367.
https://doi.org/10.1016/j.gde.2008.06.006
- PubMed
- Google Scholar
1. Haydar TF
2. Ang E
3. Rakic P
(2003) Mitotic spindle rotation and mode of cell division in the developing telencephalon
PNAS 100:2890–2895.
https://doi.org/10.1073/pnas.0437969100
- PubMed
- Google Scholar
Book
(1992) Early Embryonic Development of Animals
Springer-Verlag.
https://doi.org/10.1007/978-3-540-47191-2
- Google Scholar
1. Howard J
2. Garzon-Coral C
(2017) Physical limits on the precision of mitotic spindle positioning by microtubule pushing forces: mechanics of mitotic spindle positioning
BioEssays : News and Reviews in Molecular, Cellular and Developmental Biology 39:201700122.
https://doi.org/10.1002/bies.201700122
- Google Scholar
1. Hozumi S
2. Maeda R
3. Taniguchi K
4. Kanai M
5. Shirakabe S
6. Sasamura T
7. Spéder P
8. Noselli S
9. Aigaki T
10. Murakami R
11. Matsuno K
(2006) An unconventional myosin in Drosophila reverses the default handedness in visceral organs
Nature 440:798–802.
https://doi.org/10.1038/nature04625
- PubMed
- Google Scholar
1. Hung TJ
2. Kemphues KJ
(1999)
PAR-6 is a conserved PDZ domain-containing protein that colocalizes with PAR-3 in Caenorhabditis elegans embryos

Development 126:127–135.
- PubMed
- Google Scholar
1. Hutter H
2. Schnabel R
(1994)
glp-1 and inductions establishing embryonic axes in C. elegans

Development 120:2051–2064.
- PubMed
- Google Scholar
(2013) Formin mDia1 senses and generates mechanical forces on actin filaments
Nature Communications 4:1883.
https://doi.org/10.1038/ncomms2888
- PubMed
- Google Scholar
1. Jülicher F
2. Kruse K
3. Prost J
4. Joanny J
(2007) Active behavior of the cytoskeleton
Physics Reports 449:3–28.
https://doi.org/10.1016/j.physrep.2007.02.018
- Google Scholar
1. Kachur TM
2. Pilgrim DB
(2008) Myosin assembly, maintenance and degradation in muscle: role of the chaperone UNC-45 in myosin thick filament dynamics
International Journal of Molecular Sciences 9:1863–1875.
https://doi.org/10.3390/ijms9091863
- PubMed
- Google Scholar
(2000) Rotation and asymmetry of the mitotic spindle direct asymmetric cell division in the developing central nervous system
Nature Cell Biology 2:7–12.
https://doi.org/10.1038/71323
- PubMed
- Google Scholar
(1988) Identification of genes required for cytoplasmic localization in early C. elegans embryos
Cell 52:311–320.
https://doi.org/10.1016/S0092-8674(88)80024-2
- PubMed
- Google Scholar
1. Knoblich JA
(2010) Asymmetric cell division: recent developments and their implications for tumour biology
Nature Reviews Molecular Cell Biology 11:849–860.
https://doi.org/10.1038/nrm3010
- PubMed
- Google Scholar
1. Kulukian A
2. Fuchs E
(2013) Spindle orientation and epidermal morphogenesis
Philosophical Transactions of the Royal Society B: Biological Sciences 368:20130016.
https://doi.org/10.1098/rstb.2013.0016
- Google Scholar
1. Kuroda R
2. Fujikura K
3. Abe M
4. Hosoiri Y
5. Asakawa S
6. Shimizu M
7. Umeda S
8. Ichikawa F
9. Takahashi H
(2016) Diaphanous gene mutation affects spiral cleavage and chirality in snails
Scientific Reports 6:34809.
https://doi.org/10.1038/srep34809
- PubMed
- Google Scholar
1. Lebreton G
2. Géminard C
3. Lapraz F
4. Pyrpassopoulos S
5. Cerezo D
6. Spéder P
7. Ostap EM
8. Noselli S
(2018) Molecular to organismal chirality is induced by the conserved myosin 1D
Science 362:949–952.
https://doi.org/10.1126/science.aat8642
- PubMed
- Google Scholar
1. Li X
2. Zhao Z
3. Xu W
4. Fan R
5. Xiao L
6. Ma X
7. Du Z
(2019) Systems properties and spatiotemporal regulation of cell position variability during embryogenesis
Cell Reports 26:313–321.
https://doi.org/10.1016/j.celrep.2018.12.052
- PubMed
- Google Scholar
1. Liro MJ
2. Rose LS
(2016) Mitotic spindle positioning in the EMS cell of Caenorhabditis elegans Requires LET-99 and LIN-5/NuMA
Genetics 204:1177–1189.
https://doi.org/10.1534/genetics.116.192831
- PubMed
- Google Scholar
1. Liu J
2. Maduzia LL
3. Shirayama M
4. Mello CC
(2010) NMY-2 maintains cellular asymmetry and cell boundaries, and promotes a SRC-dependent asymmetric cell division
Developmental Biology 339:366–373.
https://doi.org/10.1016/j.ydbio.2009.12.041
- PubMed
- Google Scholar
(2000) LIN-5 is a novel component of the spindle apparatus required for chromosome segregation and cleavage plane specification in Caenorhabditis elegans
The Journal of Cell Biology 148:73–86.
https://doi.org/10.1083/jcb.148.1.73
- PubMed
- Google Scholar
(2005) Distinct roles for two C. elegans anillins in the gonad and early embryo
Development 132:2837–2848.
https://doi.org/10.1242/dev.01828
- PubMed
- Google Scholar
1. Maderspacher F
(2016) Snail chirality: the unwinding
Current Biology 26:R215–R217.
https://doi.org/10.1016/j.cub.2016.02.008
- PubMed
- Google Scholar
(1994)
Two maternal genes, apx-1 and pie-1, are required to distinguish the fates of equivalent blastomeres in the early Caenorhabditis elegans embryo

Development 120:2305–2315.
- PubMed
- Google Scholar
1. Matsumura S
2. Hamasaki M
3. Yamamoto T
4. Ebisuya M
5. Sato M
6. Nishida E
7. Toyoshima F
(2012) ABL1 regulates spindle orientation in adherent cells and mammalian skin
Nature Communications 3:626.
https://doi.org/10.1038/ncomms1634
- PubMed
- Google Scholar
1. Mayer M
2. Depken M
3. Bois JS
4. Jülicher F
5. Grill SW
(2010) Anisotropies in cortical tension reveal the physical basis of polarizing cortical flows
Nature 467:617–621.
https://doi.org/10.1038/nature09376
- PubMed
- Google Scholar
(1994) The maternal genes apx-1 and glp-1 and establishment of dorsal-ventral polarity in the early C. elegans embryo
Cell 77:95–106.
https://doi.org/10.1016/0092-8674(94)90238-0
- PubMed
- Google Scholar
1. Meshcheryakov VN
2. Beloussov LV
(1975) Asymmetrical rotations of blastomeres in early cleavage of gastropoda
Wilhelm Roux's Archives of Developmental Biology 177:193–203.
https://doi.org/10.1007/BF00848080
- PubMed
- Google Scholar
(2019) Self-organized shape dynamics of active surfaces
PNAS 116:29–34.
https://doi.org/10.1073/pnas.1810896115
- PubMed
- Google Scholar
1. Mizuno H
2. Higashida C
3. Yuan Y
4. Ishizaki T
5. Narumiya S
6. Watanabe N
(2011) Rotational movement of the formin mDia1 along the double helical strand of an actin filament
Science 331:80–83.
https://doi.org/10.1126/science.1197692
- PubMed
- Google Scholar
(1994)
Combinatorial specification of blastomere identity by Glp-1-Dependent cellular interactions in the nematode Caenorhabditis-Elegans

Development 120:3325–3338.
- PubMed
- Google Scholar
1. Motegi F
2. Sugimoto A
(2006) Sequential functioning of the ECT-2 RhoGEF, RHO-1 and CDC-42 establishes cell polarity in Caenorhabditis elegans embryos
Nature Cell Biology 8:978–985.
https://doi.org/10.1038/ncb1459
- PubMed
- Google Scholar
(2004) Cortical flows powered by asymmetrical contraction transport PAR proteins to establish and maintain anterior-posterior polarity in the early C. elegans embryo
Developmental Cell 7:413–424.
https://doi.org/10.1016/j.devcel.2004.08.001
- PubMed
- Google Scholar
1. Münster S
2. Jain A
3. Mietke A
4. Pavlopoulos A
5. Grill SW
6. Tomancak P
(2019) Attachment of the blastoderm to the vitelline envelope affects gastrulation of insects
Nature 568:395–399.
https://doi.org/10.1038/s41586-019-1044-3
- PubMed
- Google Scholar
(2014) Active torque generation by the actomyosin cell cortex drives left-right symmetry breaking
eLife 3:e04165.
https://doi.org/10.7554/eLife.04165
- PubMed
- Google Scholar
(2016) Actomyosin-driven left-right asymmetry: from molecular torques to chiral self organization
Current Opinion in Cell Biology 38:24–30.
https://doi.org/10.1016/j.ceb.2016.01.004
- PubMed
- Google Scholar
(2018) Morphogenetic degeneracies in the actomyosin cortex
eLife 7:e37677.
https://doi.org/10.7554/eLife.37677
- PubMed
- Google Scholar
1. Pohl C
2. Bao Z
(2010) Chiral forces organize left-right patterning in C. elegans by uncoupling midline and anteroposterior Axis
Developmental Cell 19:402–412.
https://doi.org/10.1016/j.devcel.2010.08.014
- PubMed
- Google Scholar
1. Pollard TD
(2017) Nine unanswered questions about cytokinesis
Journal of Cell Biology 216:3007–3016.
https://doi.org/10.1083/jcb.201612068
- PubMed
- Google Scholar
1. Pollard TD
2. Cooper JA
(1986) Actin and actin-binding proteins A critical evaluation of mechanisms and functions
Annual Review of Biochemistry 55:987–1035.
https://doi.org/10.1146/annurev.bi.55.070186.005011
- PubMed
- Google Scholar
1. Priess JR
(2005) Notch signaling in the C. elegans embryo
WormBook 5:1.
https://doi.org/10.1895/wormbook.1.4.1
- Google Scholar
Book
1. Raffel M
(2007) Particle Image Velocimetry : A Practical Guide
Heidelberg, New York: Springer.
https://doi.org/10.1007/978-3-319-68852-7
- Google Scholar
1. Ramaswamy S
2. Simha RA
(2006) The mechanics of active matter: broken-symmetry hydrodynamics of motile particles and granular layers
Solid State Communications 139:617–622.
https://doi.org/10.1016/j.ssc.2006.05.042
- Google Scholar
1. Rose L
2. Gönczy P
(2014) Polarity establishment, asymmetric division and segregation of fate determinants in early C. elegans embryos
WormBook 2:1–43.
https://doi.org/10.1895/wormbook.1.30.2
- Google Scholar
1. Royer LA
2. Weigert M
3. Günther U
4. Maghelli N
5. Jug F
6. Sbalzarini IF
7. Myers EW
(2015) ClearVolume: open-source live 3D visualization for light-sheet microscopy
Nature Methods 12:480–481.
https://doi.org/10.1038/nmeth.3372
- PubMed
- Google Scholar
(2009) Hydrodynamics of cellular cortical flows and the formation of contractile rings
Physical Review Letters 103:058102.
https://doi.org/10.1103/PhysRevLett.103.058102
- PubMed
- Google Scholar
1. Scarpa E
2. Mayor R
(2016) Collective cell migration in development
Journal of Cell Biology 212:143–155.
https://doi.org/10.1083/jcb.201508047
- PubMed
- Google Scholar
1. Schnabel R
2. Bischoff M
3. Hintze A
4. Schulz AK
5. Hejnol A
6. Meinhardt H
7. Hutter H
(2006) Global cell sorting in the C. elegans embryo defines a new mechanism for pattern formation
Developmental Biology 294:418–431.
https://doi.org/10.1016/j.ydbio.2006.03.004
- PubMed
- Google Scholar
(2014) Timing and mechanism of the initial cue establishing handed left–right asymmetry in Caenorhabditis elegans embryos
Genesis 52:572–580.
https://doi.org/10.1002/dvg.22749
- PubMed
- Google Scholar
1. Sedzinski J
2. Biro M
3. Oswald A
4. Tinevez JY
5. Salbreux G
6. Paluch E
(2011) Polar actomyosin contractility destabilizes the position of the cytokinetic furrow
Nature 476:462–466.
https://doi.org/10.1038/nature10286
- PubMed
- Google Scholar
1. Sijen T
2. Fleenor J
3. Simmer F
4. Thijssen KL
5. Parrish S
6. Timmons L
7. Plasterk RH
8. Fire A
(2001) On the role of RNA amplification in dsRNA-triggered gene silencing
Cell 107:465–476.
https://doi.org/10.1016/S0092-8674(01)00576-1
- PubMed
- Google Scholar
1. Singh D
2. Odedra D
3. Dutta P
4. Pohl C
(2019) Mechanical stress induces a scalable switch in cortical flow polarization during cytokinesis
Journal of Cell Science 132:jcs231357.
https://doi.org/10.1242/jcs.231357
- Google Scholar
1. Singh D
2. Pohl C
(2014) Coupling of rotational cortical flow, asymmetric midbody positioning, and spindle rotation mediates dorsoventral Axis formation in C. elegans
Developmental Cell 28:253–267.
https://doi.org/10.1016/j.devcel.2014.01.002
- PubMed
- Google Scholar
(2006) Type ID unconventional myosin controls left-right asymmetry in Drosophila
Nature 440:803–807.
https://doi.org/10.1038/nature04623
- PubMed
- Google Scholar
(2003) A complex of LIN-5 and GPR proteins regulates G protein signaling and spindle function in C elegans
Genes & Development 17:1225–1239.
https://doi.org/10.1101/gad.1081203
- PubMed
- Google Scholar
1. Sugioka K
2. Bowerman B
(2018) Combinatorial contact cues specify cell division orientation by directing cortical myosin flows
Developmental Cell 46:257–270.
https://doi.org/10.1016/j.devcel.2018.06.020
- PubMed
- Google Scholar
(1983) The embryonic cell lineage of the nematode Caenorhabditis elegans
Developmental Biology 100:64–119.
https://doi.org/10.1016/0012-1606(83)90201-4
- PubMed
- Google Scholar
1. Sulston JE
2. Horvitz HR
(1977) Post-embryonic cell lineages of the nematode, Caenorhabditis elegans
Developmental Biology 56:110–156.
https://doi.org/10.1016/0012-1606(77)90158-0
- PubMed
- Google Scholar
1. Tee YH
2. Shemesh T
3. Thiagarajan V
4. Hariadi RF
5. Anderson KL
6. Page C
7. Volkmann N
8. Hanein D
9. Sivaramakrishnan S
10. Kozlov MM
11. Bershadsky AD
(2015) Cellular chirality arising from the self-organization of the actin cytoskeleton
Nature Cell Biology 17:445–457.
https://doi.org/10.1038/ncb3137
- PubMed
- Google Scholar
1. Tse YC
2. Werner M
3. Longhini KM
4. Labbe J-C
5. Goldstein B
6. Glotzer M
(2012) RhoA activation during polarization and cytokinesis of the early Caenorhabditis elegans embryo is differentially dependent on NOP-1 and CYK-4
Molecular Biology of the Cell 23:4020–4031.
https://doi.org/10.1091/mbc.e12-04-0268
- Google Scholar
1. Walston TD
2. Hardin J
(2006) Wnt-dependent spindle polarization in the early C. elegans embryo
Seminars in Cell & Developmental Biology 17:204–213.
https://doi.org/10.1016/j.semcdb.2006.04.005
- PubMed
- Google Scholar
1. Walston T
2. Hardin J
(2010) An agar mount for observation of Caenorhabditis elegans embryos
Cold Spring Harbor Protocols 2010:pdb.prot5540.
https://doi.org/10.1101/pdb.prot5540
- PubMed
- Google Scholar
Book
1. Wilson EB
(1925)
The Cell in Development and Heredity

New York: The MacMillan Company.
- Google Scholar
1. Wong CC
2. Loewke KE
3. Bossert NL
4. Behr B
5. De Jonge CJ
6. Baer TM
7. Reijo Pera RA
(2010) Non-invasive imaging of human embryos before embryonic genome activation predicts development to the blastocyst stage
Nature Biotechnology 28:1115–1121.
https://doi.org/10.1038/nbt.1686
- PubMed
- Google Scholar
1. Wood WB
(1991) Evidence from reversal of handedness in C. elegans embryos for early cell interactions determining cell fates
Nature 349:536–538.
https://doi.org/10.1038/349536a0
- PubMed
- Google Scholar

Decision letter

Thomas Surrey

Reviewing Editor; Centre for Genomic Regulation (CRG), Spain
Aleksandra M Walczak

Senior Editor; École Normale Supérieure, France

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

This study demonstrates that acto-myosin driven intracellular flows are lineage specific during C. elegans development and that they re-orient mitotic spindles during the division of cells. Using theory, the authors are able to explain the quantitative observations made in their experiments. This work supports the notion that developmentally controlled intracellular flows play an important role for determining cell fate.

Decision letter after peer review:

Thank you for submitting your work entitled "Cell lineage-dependent chiral actomyosin flows drive cellular rearrangements in early development" for consideration by eLife. Your article has been reviewed by two peer reviewers, and the evaluation has been overseen by a Reviewing Editor and a Senior Editor. The reviewers have opted to remain anonymous.

Our decision has been reached after consultation between the reviewers. Based on these discussions and the individual reviews below, it was concluded that in order to satisfy the reviewers' concerns, additional experiments will be required that are expected to take more than 2 months, i.e. the maximum period envisaged by eLife for a revision. We therefore regret to inform you that your work will not be considered further for publication in eLife at this stage.

While the reviewers found that your study was interesting and well written, they were not convinced that this manuscript represents a sufficient advance over your previous work published in eLife in 2014 (Naganathan et al). The specific major points of criticism that were identified in the discussion between the reviewers were:

1) Technical concern:

The reviewers were not convinced that the measured spindle skew was due to torque-driven spindle rotation. If true rotation is observed, it was considered important to clarify that it is not due to compression of the embryo. The reviewers considered control experiments essential. For example, "hanging drop" imaging may resolve this.

2) Concerns over the proposed mechanism:

The reviewers criticized that the mechanism of how actin-myosin counter-flows induce spindle tilt/skew remains unclear. More importantly, they were not convinced that the study demonstrates that counter-flows were necessarily the cause of spindle skew/tilt, as they saw several other possibilities that were not considered in the manuscript:

i) The known active spindle orientation pathway in P1 cells might remove spindle skew. This could be tested by disrupting spindle orientation pathways.

ii) Cell length extension, overall cortical contractility in combination with geometrical confinement instead of cortical flows may cause spindle skew. This could be tested for example by using embryos without eggshell.

iii) The reviewers saw also the possibility that cortical flows change cell shape/positioning (by frictional coupling of flow to the neighboring cells/egg shell) instead of cell-internal frictional coupling of the spindle to the cortex. Analysis of cell shape changes under normal or perturbation conditions could give indications.

Please find below the original comments of the reviewers. We hope that they will be useful for your next steps with this manuscript.

Reviewer #1:

Pimpale et al. report on the quantitative description of rotary actomyosin flows during early cell divisions in C.elegans development and their role in spindle skew and cell positioning.

This study builds on previous work, especially the article by Naganathan et al., 2014, in which the presence of chiral flows and a theoretical model description based on thin film active chiral fluid theory have been introduced. The authors now continue to employ elegant quantitative live cell imaging and theoretical modelling to show that chiral counter-rotating flows are present in the following nine cell divisions of C.elegans development. Lineage specific analysis revealed that chiral counter-rotating flows are restricted to the AB lineage (versus P/EMS lineage) and a minimal theoretical model is presented to qualitatively describe the appearance of chiral counter-rotating versus net rotating-flows observed in different cell lineages. The authors use various complementary perturbation approaches to show that rotary cortical flows correlate with the positioning of the cell division axis. These observations suggest that rotary cortical flows generate active forces to drive cell re-positioning in multicellular tissues, establishing an interesting concept with potential relevance in various developmental and dynamic tissue remodeling processes.

The presented article is very well written, provides high-quality data and analysis methods and includes a relevant discussion of obtained results.

General concerns and questions are related to the following points:

The authors describe that chiral counter-rotating flow velocities in the AB lineage decrease as development progresses. Does this decrease in vc occur because cortical flow is reduced in the e_y direction or absolute flow velocities are reduced?

Is decreasing rotary flow also associated with a change in absolute myosin density levels in dividing cells?

Why was the myosin ratio (Figure 1E) determined only from intensity values within the first 20% outer segments along the cell division axis?

The authors show that rotary cortical flows are correlated with spindle skew and cell positioning but the underlying mechanism remains to be addressed. Can the authors dissect if cortical flows induce cellular turning by flow-friction with the environment (neighboring cells/egg shell) followed by spindle skew, or is spindle positioning primarily mediated by cell internal friction between the rotating cortex and the spindle and subsequent reorientation of the cell division axis? Interfering with cell-cell/cell-matrix adhesion or cortex-spindle coupling could allow to distinguish these scenarios.

A minimal theoretical model is presented how rotary cortex flows depend on cleavage furrow position and myosin density asymmetries in dividing cell halves. How far can these parameters be considered as independent variables considering possible feedback between the cell cortex dynamics and furrow positioning? (see also Sedzinski et al., 2011).

The authors provide a discussion on how active torques are generated on a molecular level. It would be interesting to further comment on how the handedness of chiral flow could be generated in first instance.

Supplementary figure 1C shows a pronounced dependence of chiral velocity vc over time in the AB cell. Does this velocity profile correlate with changes in myosin ratios or cleavage furrow positioning according to model predictions?

Supplementary figure 3C provides 2 exemplary modelling results for rotary flows on an ellipsoid surface. As the authors are studying rotary flows during division it would be interesting to provide additional examples with settings such as asymmetric myosin densities in the presence of high myosin levels in the cleavage furrow. Also, an animation video showing how rotary flows change depending on cleavage furrow positioning and varying myosin density levels in dividing cells would be very instructive to illustrate changes in cortical flow dynamics under varying parameters of furrow position and myosin density asymmetries.

Reviewer #2:

The manuscript by Pimpale et al. investigates the mechanisms by which actomyosin chiral flows drive spindle skew and consequently the positioning of cells within the early C. elegans embryo.

In Naganathan et al., 2014, the authors demonstrated (1) that the acto-myosin cortex generates active torque, (2) that this torque can result in counter rotation of AB daughter cells (ABa, ABp) during cytokinesis, and (3) that the resulting spindle skew breaks left-right symmetry resulting in a relative shift in the position of blastomeres on the right and left sides of the embryo.

This new work is largely an extension of the previous paper, adding two key findings that are well supported by the experimental data: First, that chiral counter-rotating flows are not restricted to the ABa/p cells analysed previously, and second, that counter-rotating flows are restricted to symmetrically-dividing AB lineage cells and absent in the asymmetrically dividing P/EMS lineage cells, pointing to lineage-specific regulation. The authors then use a combination of theory and experiment to understand the origin of this lineage specific behaviour, suggesting the key determinants are furrow position and myosin asymmetry. However, in my opinion, these latter aspects of the manuscript are not sufficiently explored to support their conclusions, particularly with respect to analysis division of AB and P1 which constitute the majority of Figures 2-4.

Major Concerns:

1) While their 2014 work nicely illustrates the importance of counter-rotation in left-right symmetry-breaking and presents a model for understanding the emergence of chiral flows, this manuscript primarily documents that counter-rotations are not confined to the previously studied ABa/p cells. The relevance of counter-rotations for later divisions is unclear. Notably the degree of counter-rotation and resultant skew declines after ABa/p, suggesting it may simply be an echo of processes required in Aba/p. Is it clear whether the embryo cares about counter rotations beyond ABa/p? Similarly, rotation of AB relative to P around the AP axis, while interesting in defining the physical mechanism, would seem to be irrelevant to the embryo given that the left-right/DV axes are not yet defined.

2) One major issue is that the manuscript uses the division of AB (not the well characterized ABa/p from their prior work) to validate many of their conclusions regarding the link between counter-rotation and spindle skew (e.g. Figures 2-4). However, in all cases, spindle skew in AB is analysed in the X-Y plane (see Figure 2), whereas counter-rotation of the dividing AB cell relative to P ought to primarily induce skew in the Y-Z plane (e.g. rotation around the AP axis), which would only be evident in an end-on view down the A-P axis. How counter-rotation around the cleavage furrow would lead to the observed tilting of the division axis towards the P cell in X-Y is not obvious, unless I am misunderstanding the geometry.

3) Have the authors considered potential issues of embryo compression? Prior works have shown that embryo compression by agarose pads can influence developmental processes. Most critical for this work, the spindle in AB invariably comes to lie in the X-Y plane in agarose compressed embryos, even if initially oriented along z-axis, presumably due to geometric constraints. This may limit the ability of the authors to reliably detect the contribution of counter-rotating flows to spindle skew by fixing the plane of cell division. Presumably, if there was a counter-rotation in AB and the division plane was fixed by eggshell geometry, one might expect to see rotation of P1 relative to AB. Other groups have used so-called hanging drops to avoid this issue and facilitate end on analysis. I wonder if this geometry would be more useful if one wants to properly analyse spindle skew in AB.

4) The authors use par mutants to assess the link between fate, chiral rotations, and spindle skew. As predicted, in par mutants that yield two AB like cells, both cells undergo counter-rotating flows and high levels of spindle skew, while mutants yielding two P1 like cells show no chiral rotations and reduced spindle skew. However, P1 cells have an active spindle orientation pathway which may dominate the system, preventing analysis of actomyosin generated spindle skew. I also worry about this analysis due to concerns in point 2 above – tilt in X-Y seems very different from spindle skew that would be driven by counter-rotation. Finally, it is unclear to me what kind of skew to expect when one obtains two adjacent cells with similar counter-rotations (e.g. Figure 2D), which I would have expected might just cancel out if divisions are all symmetric.

5) The authors nicely show how counter-rotation depends on myosin activity (though this is known from their prior work and already explored extensively for Aba/p cells). Notably, at low levels of myosin, counter-rotation declines, which they then explore in Figure 3 and 4. However, the link to spindle skew is tenuous for the AB cell. Could one not explain the data more simply by imagining that cell length extension and the contractility of the cortex during cytokinesis combined with eggshell geometry drives tilt? A more compliant / soft cortex might simply deform during division and hence tilt less, while a stiff/contractile cortex would require the dividing cell to tilt as cell poles encounter the eggshell. This would also be compatible with the coordinated tilting of the two identical AB like cells produced by par mutants, which seems hard to explain from the balance of chiral flows alone.

6) The proposed model suggests that furrow position and myosin asymmetry are the key differentiating features of P lineage cells that prevent counter-rotating flow. However, the other obvious difference is that the two lineages show dramatic differences in actomyosin contractility and as the authors show myosin activity is directly related to the magnitude of counter-rotation. Can the authors exclude that reduced myosin activity in P lineage cells, rather than ring position and myosin asymmetry, is the key difference? The model makes two key predictions that the authors do not test: First, a symmetrically-positioned cleavage furrow should lead to counter-rotating flow independent of myosin asymmetry – hence P₀ cells with spindle positioning defects should exhibit counter-rotating flow. Second, polarized, asymmetrically dividing cells such as P₀ should never show chiral counter-rotation regardless of actomyosin levels. What happens in P₀ if actomyosin activity is enhanced, e.g. with a strong rga-3/4 (RNAi), which the authors showed in 2014 enhances chiral flows in the one cell embryo?

7) The authors make a strong point that given symmetric myosin, there is nevertheless a weak influence of furrow position. However, this plot (Sup Figure 3E) is somewhat misleading as the maximal effect on rotation is ~1% if myosin is symmetric – one could as easily argue that there is an insignificant contribution of furrow position relative to other factors.

[Editors’ note: further revisions were suggested prior to acceptance, as described below.]

Thank you for submitting your article "Cell lineage-dependent chiral actomyosin flows drive cellular rearrangements in early development" for consideration by eLife. Your revised manuscript has been seen by the two original reviewers of your manuscript, an additional reviewer who is a senior expert in the field with relevant expertise, a Reviewing Editor and Aleksandra Walczak as the Senior Editor. While all reviewers see potential for an excellent paper, the majority opinion still sees major deficits as outlined below.

The Reviewing Editor has drafted this decision to help you prepare a revised submission.

As the editors have judged that your manuscript is of interest, but as described below that additional experiments/analysis/modelling/theory are required before it is published, we would like to draw your attention to changes in our revision policy that we have made in response to COVID-19 (https://elifesciences.org/articles/57162). First, because many researchers have temporarily lost access to the labs, we will give authors as much time as they need to submit revised manuscripts. We are also offering, if you choose, to post the manuscript to bioRxiv (if it is not already there) along with this decision letter and a formal designation that the manuscript is "in revision at eLife". Please let us know if you would like to pursue this option. (If your work is more suitable for medRxiv, you will need to post the preprint yourself, as the mechanisms for us to do so are still in development.)

Summary:

All reviewers appreciate that the analysis of the P₀ cell has been improved and new data using spindle positioning mutants have been added that are consistent with the model. The reviewers agree also that the data generally support the idea that chiral flows can induce spindle rotation (which was known from previous work) and that this study shows that this operates also in other cells, making it a more general phenomenon. It is also appreciated that the manuscript presents a theory that can explain chiral flows.

It remained however unclear to the reviewers how chiral flow around the long axis of the cell produces the tilt in X-Y. Given that so much of the analysis rests on this tilt phenomenon, as indeed does the claim to relevance for development, because the manuscript suggests that this tilt allows ABp-P2 contact, the absence of an attempt to provide a physical explanation for the tilt was considered a critical weakness. The reviewers expect at least some attempt to understand theoretically how the observed tilt can be obtained from the patterns of flow that is observed.

Essential revisions:

The reviewers note that the motion of an elongated objects in a rotational flow is one of the best-studied problems in viscous fluid mechanics and conclude that even with the obvious complexities in the present setup (geometry, non-Newtonian fluids, etc.) it should be possible to make some sensible estimates.

In this context, a particular statement that the reviewers struggled with was "Strikingly, when viewed from either embryo pole, the closest AB-like cell skews clockwise, meaning that the two juxtaposed cells counter- rotate (new, Figure 2—figure supplement 2) and new Video 14–16." The reviewers argued that the direction of rotation of both cells in this particular case can be explained by the cell-cell contact area having an increased friction coefficient when compared to the cell- vitelline membrane and/or cell-eggshell contact. Given this topology, the handedness of the chiral flow indeed would be expected to give rise to clockwise rotation of both cells when viewed from the closest pole." This raises the question of whether the cells counter-rotate or both rotate clockwise. The reviewers also note that the observed X-Y tilt of the cells in the same direction has not been addressed here.

Finally, the notion emerged that the manuscript is not particularly reader-friendly, a concern that should be addressed. It is recommended to add a clear schematic early on that explains the geometry more clearly than Figure 1 (or the supplements). Moreover, the terminology "no chiral counter-rotating flows" was found to be confusing. Does that mean that there are chiral flows but they are not counter-rotating, or there are counter-rotating flows but they are not chiral? Indeed, chiral in this sense is not well-explained geometrically (here a schematic could help), especially since the experiments appear to only look at planar projections of the flows.

We would also like to encourage you to include the species studied in the title.

In conclusion, we regret to inform you that your manuscript cannot be accepted in its present form. Because the reviewers see however potential for a manuscript that can be accepted at eLife, they encourage you to address the concerns raised above. In that case, we would be prepared to consider a re-revised version of your manuscript.

https://doi.org/10.7554/eLife.54930.sa1

Author response

[Editors’ note: The authors appealed the original decision. What follows is the authors’ response to the first round of review.]

We do want to point out that in comparison to the first series of papers published on chiral actomyosin movements, we here report on the discoveries that chiral flows in the

actomyosin cortex are much more prevalent that perhaps envisioned, that they arise in

approximately half of the early divisions of the nematode, and that they do so in a lineage-specific manner. Hence, chiral flows are part of normal development, and they are under specific control. What are these flows utilized for? Through an elegant combination of RNAi experiments as well as utilizing rapid-switching temperature-sensitive mutants, and together with physical theory, we show that chiral flows of actomyosin drive cell rearrangements and cause cell shifts, a morphogenetic activity that in C. elegans had previously been attributed to the mitotic spindle. We think that this changes to a significant degree our understanding of early C. elegans development, and casts actomyosin cellular function in the context of development into a new perspective.

Again, we acknowledge the points that have been raised by the reviewers. We have

amongst the authors carefully discussed the major concerns and have in the meantime also already carried out and analyzed a number of additional experiments that have been requested by the reviewers. For example, by imaging uncompressed embryos (using a method equivalent to the hanging drop method) we have now confirmed that embryo compression does not affect counter rotating flows or overall spindle skew movements, addressing a key technical concern. We also already have the data ready in which we perturbed components of the known spindle orientation pathway (lin-5 and gpr-1/2). The results argue against a role for known spindle orientation pathways in driving chiral skews. Importantly, the known spindle reorientation pathway in the P₁ cell acts early during mitosis (prophase) while the spindle skew events that we report here act much later, during anaphase (Rose & Kemphues, Development, 1998). To rule out an inhibitory role of the spindle reorientation pathway in P₁ we will in the coming weeks perform RNAi treatment against let-99 and quantify the cell division skew during anaphase B. The results will be added in the revised manuscript. Together, we are now confident that we can address and answer all but one of the reviewer concerns within the two month period, and within the next six weeks.

With respect to the experiment that we cannot do within the two months, we will not be

able to rule out the possibility that cell length extension, combined with contractility and geometric confinement, drives cell division skew (reviewer 2, concern 5). However, we do show that subtle reduction of the RhoA regulators ect-2 and rga-3 specifically alters the chiral counter rotation velocity and cell division skew (fig 4b), while leaving the non-chiral component of the cortical flow unaffected (fig 4c). This strongly suggest that contractility and cortical stiffness are not significantly affected upon mild depletion of RhoA regulators. This argues that actomyosin contractility per se does not play a major role in driving cell division skews, and lends credence to the statement that active torques and chiral flows do. However, it is not possible to completely decouple the effects, but we hope that you agree with us that this does not matter that much, as we do provide significant evidence that chiral flows play an essential role here.

Reviewer #1:

Pimpale et al. report on the quantitative description of rotary actomyosin flows during early cell divisions in C.elegans development and their role in spindle skew and cell positioning.

This study builds on previous work, especially the article by Naganathan et al., 2014, in which the presence of chiral flows and a theoretical model description based on thin film active chiral fluid theory have been introduced. The authors now continue to employ elegant quantitative live cell imaging and theoretical modelling to show that chiral counter-rotating flows are present in the following nine cell divisions of C.elegans development. Lineage specific analysis revealed that chiral counter-rotating flows are restricted to the AB lineage (versus P/EMS lineage) and a minimal theoretical model is presented to qualitatively describe the appearance of chiral counter-rotating versus net rotating-flows observed in different cell lineages. The authors use various complementary perturbation approaches to show that rotary cortical flows correlate with the positioning of the cell division axis. These observations suggest that rotary cortical flows generate active forces to drive cell re-positioning in multicellular tissues, establishing an interesting concept with potential relevance in various developmental and dynamic tissue remodeling processes.

The presented article is very well written, provides high-quality data and analysis methods and includes a relevant discussion of obtained results.

General concerns and questions are related to the following points:

The authors describe that chiral counter-rotating flow velocities in the AB lineage decrease as development progresses. Does this decrease in vc occur because cortical flow is reduced in the e_y direction or absolute flow velocities are reduced?

Is decreasing rotary flow also associated with a change in absolute myosin density levels in dividing cells?

To address question, we have now performed additional quantifications of flow velocities and myosin intensities in AB, ABa and ABp cells. We indeed found that both, 1) the absolute flow velocity and 2) the overall myosin intensities, are smaller in ABa/ABp than in AB cells. This suggests that an overall reduction in myosin density during the developmental progress also contributes to the reduction in the observed chiral flows.

We have added these results in three new supplementary figure panels (Figure 1—figure supplement 5 A-C) and complemented the Results section in the main text accordingly (paragraph three).

Why was the myosin ratio (Figure 1E) determined only from intensity values within the first 20% outer segments along the cell division axis?

This choice was made in order to prevent the strong fluorescent signal from the cytokinetic furrow to affect the measurements of the myosin ratio. During the onset of cytokinesis, the time point at which we measure the myosin ratio, the cytokinetic furrow often covers up to 60% of the cortical surface that is in the focal plane and consequently, we used only myosin intensities from the outer 20% of the AP-axis.

In order to better clarify this point, we have now added a new supplemental figure panel with a new schematic (Figure 1—figure supplement 6) and we have added a clarification in the Materials and methods section (subsection “Determining myosin ratio, cytokinetic ring position and fitting myosin profiles:”).

The authors show that rotary cortical flows are correlated with spindle skew and cell positioning but the underlying mechanism remains to be addressed. Can the authors dissect if cortical flows induce cellular turning by flow-friction with the environment (neighboring cells/egg shell) followed by spindle skew, or is spindle positioning primarily mediated by cell internal friction between the rotating cortex and the spindle and subsequent reorientation of the cell division axis? Interfering with cell-cell/cell-matrix adhesion or cortex-spindle coupling could allow to distinguish these scenarios.

We thank the reviewer raising this important point. We propose that the cell division skew is due to chiral cortical flows in combination with an inhomogeneous friction of the rotating cell with its surrounding. In our work, we have used the orientation of the spindle only as a quantitative measure for the orientation of the dividing cell and our results suggest that neither a force generation within the spindle nor the interaction between the spindle and the cortex, are the main drivers of the skew.

To exclude a role of spindle-cortex interactions in guiding the spindle orientation, we quantified both the cortical flow profile and the cell division skew of AB cells upon RNAi perturbation of lin-5, which is known to affect cortex spindle interactions (Srinivasan et al., 2003; Galli et al., 2011). Upon perturbation of lin-5, we observed spindle defects that have been previously described, including a misaligned metaphase spindle in the P₁ cell (new, Figure 3—figure supplement 2C). However, chiral actomyosin flows were still present in in the AB cell (new, Figure 3—figure supplement 2B). Although the orientation of the AB spindle was often aberrant, a pronounced cell axis rotation (new, Figure 3—figure supplement 2A) along with the spindle skews could still be observed (new, Figure 3—figure supplement 2F). These results argue against direct spindle-cortex interactions, but suggest that the spindle simply follows the cell axis rotation and that the main driver of these rotations are the chiral cortical flows.

We have compiled the aforementioned lin-5 (RNAi) results in the new, Figure 3—figure supplement 2 and complemented the main text accordingly (subsection “Cells exhibiting chiral counter-rotating actomyosin flows also undergo spindle skews” and “ Chiral counter-rotating flows drive spindle skews”).

A minimal theoretical model is presented how rotary cortex flows depend on cleavage furrow position and myosin density asymmetries in dividing cell halves. How far can these parameters be considered as independent variables considering possible feedback between the cell cortex dynamics and furrow positioning? (see also Sedzinski et al., 2011)

We thank the reviewer for pointing this out. Indeed, several biological mechanisms exist that could couple the cleavage furrow position to myosin asymmetries. These include, for example, polar relaxation (Sedzinski et al., 2011) PAR polarity that drives polar myosin asymmetry (Gross et al., 2018, Nat. Physics) or signaling between an asymmetrically positioned mitotic spindle and the cortex (Grill et al., 2001).

While these phenomena may constrain the parameter-space of a fully quantitative description, we used our minimal model only to gain qualitative insights into the relative effects of contractile ring position and myosin asymmetry. Furthermore, a possible coupling between ring position and myosin asymmetry would not change the quantitative part of the theoretical analysis. To predict cortical flows, we directly use the observed myosin profiles which already contain the information about ring position and myosin asymmetry – as given inputs. Therefore, the quantitative flow predictions are independent of the more complex processes that set up the global myosin profile.

We have adjusted the text in the Results (paragraph three) to clarify these points.

The authors provide a discussion on how active torques are generated on a molecular level. It would be interesting to further comment on how the handedness of chiral flow could be generated in first instance.

We thank the reviewer for raising this interesting point. While this is in fact a matter of currently ongoing research in our lab, we have now complemented the discussion and included our current conceptual view on how the handedness of the flow could arise on a molecular level. Briefly, we argue that chiral flow handedness originates from 1) the action of molecular torque generator and 2) the orientation of this torque generator to generate in plane torque density.

We have added a part in the Discussion to further elaborate on this matter (paragraph four).

Suppl. Figure 1C shows a pronounced dependence of chiral velocity vc over time in the AB cell. Does this velocity profile correlate with changes in myosin ratios or cleavage furrow positioning according to model predictions?

We thank the reviewer for this interesting question. To test this, we have now quantified myosin profiles over time and did in fact not observe changes in the myosin ratio or the furrow position during early (t=1s), mid (t=24s) or late cytokinesis (t=45s) (new, Figure 1—figure supplement 3). During cytokinesis progression, the myosin gradient sharpens strongly along the contractile ring, and the ring starts ingressing. Ingression makes it move out of the focal plane, which prevents a more quantitative and spatially resolved flow analyses after t = 30 seconds (new Figure 1—figure supplement 2D, right). However, during this additional analysis, we noted that the total flow speed changes over time in a similar fashion as vc, which explains a large part of the temporal changes of counter-rotating flows. Moreover, we expect measurements of vc to be affected by the changes in the overall AB cell geometry and by the furrow ingression, which are both very dynamic in this time window.

In light of this, we have now added a new panel to supplementary figure (new, Figure 1—figure supplement 3) and discuss these aspects in the manuscript in (Results paragraph two)

Supplementary figure 3C provides 2 exemplary modelling results for rotary flows on an ellipsoid surface. As the authors are studying rotary flows during division it would be interesting to provide additional examples with settings such as asymmetric myosin densities in the presence of high myosin levels in the cleavage furrow. Also, an animation video showing how rotary flows change depending on cleavage furrow positioning and varying myosin density levels in dividing cells would be very instructive to illustrate changes in cortical flow dynamics under varying parameters of furrow position and myosin density asymmetries.

We agree with the reviewer that these additional examples would be insightful to add.

We have now added a new sub panel in Figure 1—figure supplement 7A; right, to depict the rotatory flow pattern that emerges when a contractile ring and a myosin asymmetry are simultaneously present. As suggested by the reviewer, we have also attached several animations that illustrate the effects of different myosin profiles on the chiral flow fields:

1) Increasing myosin asymmetry in the presence of a centered contractile ring (Video 6)

2) Varying position of the contractile ring in the presence of symmetric myosin. (Video 7)

3) Varying position of the contractile ring in the presence of asymmetric myosin. (Video 8)

We have also included discussed these results in the Results section (paragraph five). We also further elaborate on this point in Results section with new experiments (paragraph seven).

Reviewer #2:

[…] Major Concerns:

1) While their 2014 work nicely illustrates the importance of counter-rotation in left-right symmetry-breaking and presents a model for understanding the emergence of chiral flows, this manuscript primarily documents that counter-rotations are not confined to the previously studied ABa/p cells. The relevance of counter-rotations for later divisions is unclear. Notably the degree of counter-rotation and resultant skew declines after ABa/p, suggesting it may simply be an echo of processes required in Aba/p. Is it clear whether the embryo cares about counter rotations beyond ABa/p? Similarly, rotation of AB relative to P around the AP axis, while interesting in defining the physical mechanism, would seem to be irrelevant to the embryo given that the left-right/DV axes are not yet defined.

The reviewer raises the important point that spindle skew events of the AB cell or the daughter cells of ABa/ABp may not be functionally relevant for embryonic development. However, early work from the Schnabel lab (Hutter and Schnabel, 1994) has shown that the skew of the dividing AB cell puts the ABp daughter cell in close contact with the posterior P₂ cell. In turn, this results in Notch signaling activation in the ABp cell but not in the ABa cell, which is essential for normal development of the ABp and ABa lineages. Given that most intercellular signaling cascades during early development are short range (Hardin and King, 2008; Priess, 2005, Wormbook; Walston and Hardin, 2006), we propose that subtle changes in daughter cell positioning, and thereby intercellular contact areas, can be instrumental for cell lineage determination, also beyond the 6-cell stage.

We have added a discussion on this topic to the Discussion section (paragraph two).

2) One major issue is that the manuscript uses the division of AB (not the well characterized ABa/p from their prior work) to validate many of their conclusions regarding the link between counter-rotation and spindle skew (e.g. Figures 2-4). However, in all cases, spindle skew in AB is analysed in the X-Y plane (see Figure 2), whereas counter-rotation of the dividing AB cell relative to P ought to primarily induce skew in the Y-Z plane (e.g. rotation around the AP axis), which would only be evident in an end-on view down the A-P axis. How counter-rotation around the cleavage furrow would lead to the observed tilting of the division axis towards the P cell in X-Y is not obvious, unless I am misunderstanding the geometry.

We thank the reviewer for raising this point. We agree with the reviewer that one would expect the AB cell to skew in the YZ-plane and that tilting towards the P cell in the XY-plane seems not obvious. When analyzing the cell division skew in an end-on view down the A-P axis, we did not observe obvious skew in the YZ-plane (new, Figure 3—figure supplement 1). However, as the reviewer correctly points out in his next comment (3), we used an embryo mounting method that slightly compresses the embryo (referred to as mildly squeezed embryos; new, Figure 1—figure supplement 1) and this likely prevents cell division skew in the YZ-plane. Therefore, in order to address this comment, as well as comment 3, we mounted embryos by embedding them in low-melt agarose to prevent embryo compression.

We first confirmed that this method indeed resulted in embryos being uncompressed by measuring the aspect ratio. The aspect ratio was 1.02 ± 0.3 under these conditions, while the aspect ratio was 1.29 ± 0.14 when using the classic agar pad method (new, Figure 1—figure supplement 1). Subsequently, we analyzed spindle skews in the AB cell in both the XY- and YZ-plane. We found that the spindle skew in the XY-plane was comparable in compressed and uncompressed embryos and therefore our key results are not affected by embryo compression (new Figure 2B and 2G). Moreover, as was predicted by the reviewer, we did observe an additional clockwise skew in the YZ-plane, when viewed end-on down the AP axis, only in uncompressed embryos (new Figure 2G and new, Figure 2—figure supplement 1). Similarly, in our previous work (Naganathan et al., 2014) we had shown that, the skew of the ABa and ABp cells also occurs in 2 perpendicular planes: the well-known skew is in the AP-LR plane, but we have also reported a substantial skew in the DV-LR plane, perpendicular plane.

Together, these findings show that chiral flow-driven skew of the cell division axis is a complex process that occurs in 3 dimensions. We propose here that, in addition to chiral surface flows, an inhomogeneous friction of the cell surface with its surroundings will determine the direction of the skew. Therefore, predicting the skew in 3 dimensions would involve quantitative mapping of both the cortical flow as well as friction coefficients along the entire surface of the dividing cell. While such an analysis is beyond the scope of this study, it indeed provides an interesting challenge for future research.

We now have added these additional findings in the main text (Resutls section) along with a new sub panel in main figure 3 (Figure 3G) and added two new supplementary figures (new, Figure 1—figure supplement 1 and new, Figure 3—figure supplement 1) along with new, Video 10. In addition, we added a part in the Discussion to elaborate more on the cell division skews in three dimensions (see Discussion paragraph five).

3) Have the authors considered potential issues of embryo compression? Prior works have shown that embryo compression by agarose pads can influence developmental processes. Most critical for this work, the spindle in AB invariably comes to lie in the X-Y plane in agarose compressed embryos, even if initially oriented along z-axis, presumably due to geometric constraints. This may limit the ability of the authors to reliably detect the contribution of counter-rotating flows to spindle skew by fixing the plane of cell division. Presumably, if there was a counter-rotation in AB and the division plane was fixed by eggshell geometry, one might expect to see rotation of P₁ relative to AB. Other groups have used so-called hanging drops to avoid this issue and facilitate end on analysis. I wonder if this geometry would be more useful if one wants to properly analyse spindle skew in AB.

We thank the reviewer for these suggestions. As discussed in detail in our response to point 2, above, we have performed an analysis on uncompressed embryos and found that the skew in the XY plane is similar in compressed and uncompressed conditions. Therefore, our conclusions are not affected by embryo compression. Furthermore, we have found an additional skew in the YZ plane that was masked by the embryo compression (new, Figure 2—figure supplement 1).

We have added these new quantified results as a new figure panel (Figure 2G) and a new supplementary figure (new, Figure 1—figure supplement 1 and new, Figure 3—figure supplement 1) and complemented the main text accordingly (paragraph three subsection “Cells exhibiting chiral counter-rotating actomyosin flows also undergo spindle skews”). Also refer to reviewer 2, point 2.

4) The authors use par mutants to assess the link between fate, chiral rotations, and spindle skew. As predicted, in par mutants that yield two AB like cells, both cells undergo counter-rotating flows and high levels of spindle skew, while mutants yielding two P₁ like cells show no chiral rotations and reduced spindle skew. However, P₁ cells have an active spindle orientation pathway which may dominate the system, preventing analysis of actomyosin generated spindle skew.

We thank the reviewer for bringing up the argument that the known spindle orientation pathway in the P₁ cell might prevent an analysis of actomyosin generated spindle skew. Before we address this concern, we first want to point out that the mentioned spindle reorientation pathway in the P₁ cell acts during early during mitosis (prophase) (Rose and Kemphues, 1998, Development), while the spindle skew events that we report occur much later, during anaphase. We have now modified the text to clarify this point results (subsection “Chiral counter-rotating ows drive spindle skews”).

In order to determine whether the spindle orientation pathway might prevent actomyosin generated spindle skew, we have perturbed the spindle orientation pathway in P₁ by performing lin-5 and gpr-1/2(RNAi) (Srinivasan et al., 2003). Upon knock-down of lin-5, we observed spindle defects that have been previously described, including a misaligned metaphase spindle in the P₁ cell (new, Figure 3—figure supplement 2C, E) and confirming that the spindle orientation pathway was attenuated. Although the spindle was often misaligned, during anaphase we did not observe any spindle skew in P₁ (new, Figure 3—figure supplement 2I), while spindle skews were still observed in AB cells (new, Figure 3—figure supplement 2B). Therefore, we conclude that the spindle orientation pathway in P₁ does not mask actomyosin driven cell division skew.

We have added these results in a new supplementary figure (new, Figure 3—figure supplement 2) and adjusted the main text accordingly (subsection “Chiral counter-rotating ows drive spindle skews”).

I also worry about this analysis due to concerns in point 2 above – tilt in X-Y seems very different from spindle skew that would be driven by counter-rotation. Finally, it is unclear to me what kind of skew to expect when one obtains two adjacent cells with similar counter-rotations (e.g. Figure 2D), which I would have expected might just cancel out if divisions are all symmetric.

We thank the reviewer for bringing up this important point related to the direction of the spindle skew in 3 dimensions, and related to concern 2. Again, we agree with the notion that chiral flows are expected to tilt the division in the YZ-plane and that it seems not obvious how they could result in skew in the XY-plane. Similar to our reply to point 2, we have addressed this point by performing the posterior par RNAi perturbation in uncompressed embryos by embedding the embryo’s in low melt agarose. We first confirmed that the skew in the XY-plane is similar in compressed and uncompressed embryo’s (new Figure 2F and 2H) showing that our key results are not affected by embryo compression. In addition, we observed a clockwise skew in the YZ direction, similar to the AB cell in uncompressed wild type embryos (see response to point 2). Strikingly, when viewed from either embryo pole, the closest AB-like cell skews clockwise, meaning that the two juxtaposed cells counterrotate (new, Figure 3—figure supplement 2) and new Video 14–16.

Notably, the direction of rotation of both cells in this particular case can be explained by the cell-cell contact area having an increased friction coefficient when compared to the cellvitelline membrane and/or cell-eggshell contact. Given this topology, the handedness of the chiral flow indeed would give rise to clockwise rotation of both cells when viewed from the closest pole. These findings further substantiate our model in which chiral flows together with inhomogeneous friction drive cell skews.

As mentioned in our response to point 2, the exact direction of cell division skew in 3 dimensions would involve an in-depth analysis of surface flows and friction coefficients along the cell surface and is beyond the scope of this study.

To clarify these issues, we now provide a new supplementary figure (new, Figure 3—figure supplement 2) and three new Videos 11–13, we have adjusted the Results section accordingly and we have added a part to the Discussion.

5) The authors nicely show how counter-rotation depends on myosin activity (though this is known from their prior work and already explored extensively for Aba/p cells). Notably, at low levels of myosin, counter-rotation declines, which they then explore in Figure 3 and 4. However, the link to spindle skew is tenuous for the AB cell. Could one not explain the data more simply by imagining that cell length extension and the contractility of the cortex during cytokinesis combined with eggshell geometry drives tilt? A more compliant / soft cortex might simply deform during division and hence tilt less, while a stiff/contractile cortex would require the dividing cell to tilt as cell poles encounter the eggshell. This would also be compatible with the coordinated tilting of the two identical AB like cells produced by par mutants, which seems hard to explain from the balance of chiral flows alone.

We agree with the reviewer that we cannot fully exclude that cell length extension together with overall contractility of the cortex and eggshell geometry drives tilt. However, there are two observations that we believe argue against this hypothesis:

1) The force driving cell length extension is likely to be provided by the elongation of the mitotic spindle apparatus during anaphase. We have quantified spindle elongation in control conditions and upon ect-2(RNAi) (reduced chirality) and rga-3(RNAi) (increased chirality) and, although cell skews correlated with the chiral flow velocity, elongation of the mitotic spindle was similar in all three conditions (Supplement Figure 4A). These results rule out the possibility that spindle elongation, together with egg shell geometry drives the observed skew.

2) In order to determine the role of chirality in AB cell skews, our RNAi treatments of ect-2 and rga-3(RNAi) were subtle and did not lead to a full knock-down of either gene product. Given that cytokinesis occurred normally under these conditions, we infer that overall contractility is not strongly affected. Corroborating this statement is our finding that the nonchiral component of the flow (the x-velocity, or contractile velocity) is not significantly affected in either RNAi (Figure 4C). In contrast, the chiral velocity is significantly affected and this correlates strongly with the skew extent (Figure 4B).

Although we cannot formally rule out the possibility that overall contractility, together with cell length extension and egg shell geometry is driving the AB skew, the tight correlation between chirality and cell division skew upon several different genetic perturbations strongly suggests that chirality, rather than overall contractility, drives the AB cell skew.

In order to clarify these issues, we have changed our wording in the main text.

6) The proposed model suggests that furrow position and myosin asymmetry are the key differentiating features of P lineage cells that prevent counter-rotating flow. However, the other obvious difference is that the two lineages show dramatic differences in actomyosin contractility and as the authors show myosin activity is directly related to the magnitude of counter-rotation. Can the authors exclude that reduced myosin activity in P lineage cells, rather than ring position and myosin asymmetry, is the key difference?

We thank the reviewer for this question and apologize if this point was not clear in the manuscript. While overall actomyosin contractility in the P₁ lineage is lower than in the AB lineage, the actomyosin contractility during division of the P₀ cell is not (new, Figure 1—figure supplement 5G). Still, this first cell division is asymmetric in terms of the ring position and myosin ratio, and it does not display any counter-rotating flows. This suggest that indeed the contractile ring position and myosin ratio, rather than the overall actomyosin contractility, are key determinants of counter-rotating flows.

We have adjusted the text for this concern and concern 7 in the Results and added a new Supplementary panel (new, Figure 1—figure supplement 5G) to improve clarity on this point (see also response to question 7b, from reviewer 2).

The model makes two key predictions that the authors do not test: First, a symmetrically-positioned cleavage furrow should lead to counter-rotating flow independent of myosin asymmetry – hence P₀ cells with spindle positioning defects should exhibit counter-rotating flow.

We agree with the reviewer that a symmetrically positioned cleavage furrow would be expected to lead to counter-rotating flow independent of myosin asymmetry. In order to test this hypothesis, we performed a lin-5 (RNAi) treatment and analyzed cortical flows during the division of P₀ cells. LIN-5 is involved in generating asymmetric pulling forces that displace the spindle from the center (Galli et al., 2011). We first confirmed that the myosin ratio in these P₀ cells is still significantly different from one in these embryos (albeit reduced when compared with the control), while the ring position is centered (new, Figure 1—figure supplement 10A). Moreover, as the reviewer predicts, quantifying cortical flows revealed that counter-rotating actomyosin flows do emerge upon lin-5 (RNAi) treatment (new, Figure 1—figure supplement 10C). These results confirm our theoretical predictions and further substantiate our conclusions. However, we note that the myosin asymmetry is much less profound than in wild type cells. Therefore, it is difficult to fully decouple the effects of ring position and myosin asymmetry experimentally (see also response to question 4. from reviewer 1).

We have added these results in the new supplementary figure (new, Figure 1—figure supplement 10) and added the findings to the Results section.

Second, polarized, asymmetrically dividing cells such as P₀ should never show chiral counter-rotation regardless of actomyosin levels. What happens in P₀ if actomyosin activity is enhanced, e.g. with a strong rga-3/4 (RNAi), which the authors showed in 2014 enhances chiral flows in the one cell embryo?

We thank the reviewer for this suggestion and we agree with the statement that polarized, asymmetrically dividing cells, such as P₀, should never show chiral counter rotation regardless of actomyosin levels. To test this, we first analyzed cortical flows upon an increase of RhoA signaling levels. Instead of using rga-3(RNAi), we used an ect-2 gain of function allele; (ect-2 (gof)) (Canevascini et al., EMBO rep 2005). While the myosin concentration increased when compared to control, we observed no chiral counter rotation in this gain of function allele (see Author response image 1). In addition, we also performed par-2 RNAi to make the ring position and the myosin ratio symmetric during the first cell division. In this condition, we do observe chiral counter rotating flows (new, Figure 1—figure supplement 9 C, D). Finally, these chiral counter rotating flows were dramatically enhanced in the ect-2 gain of function background (see Author response image 1). Taken together, increasing RhoA signaling levels alone in asymmetrically dividing cells is not sufficient to induce chiral counter-rotating flows. These results are consistent with the model predictions and corroborate our finding that chiral counter-rotating flows can only emerge in symmetrically dividing cells.

We have added the analysis of the P₀ division upon par-2(RNAi) as new, Figure 1—figure supplement 9 and added the findings to the Results section.

Our findings using the ect-2 gain of function allele, we would prefer not to publish because this allele is central to an ongoing project in the lab. We have therefore added this data as a separate figure (see ) for the editors and the reviewers to consult. However, if the reviewers insist, we could include these results as a supplementary figure.

Author response image 1

Download asset Open asset

Enhancing actomyosin activity is not sufficient to generate chiral counterrotating flows during cytokinesis.

A, B: Histogram of instantaneous chiral counter-rotating velocity vc for the first, P₀ cell division in, control (A) and *ect-2 (gof)* embryos (B). C, D: Mean myosin concentration profile along the cell division axis of the P₀ cell in control and *ect-2 (gof)* embryos. Vertical black line indicate centre of the cell. E, F: Histogram of instantaneous chiral counter-rotating velocity vc for the first cell division in par-2 (RNAi) embryos in control (E) and *ect-2 (gof)* embryos (F). Solid lines in A, B, E and F indicate the best fit Gaussian probability density function. Dotted vertical lines indicate mean vc; grey boxes represent the error of the mean at 95% confidence interval. G: Mean myosin concentration profile along the cell division axis of the first cell division in control, *par-2 (RNAi)* embryos. Vertical black line indicate centre of the cell. Right, normalized myosin concentration levels in the 20% anterior end of the cell compared to 20% of posterior end of the dividing cell. Shaded region indicates error at 95% confidence interval.

7) The authors make a strong point that given symmetric myosin, there is nevertheless a weak influence of furrow position. However, this plot (Figure1-Supplementary figure 3E) is somewhat misleading as the maximal effect on rotation is ~1% if myosin is symmetric – one could as easily argue that there is an insignificant contribution of furrow position relative to other factors.

The reviewer is correct that the amplitude of this effect as predicted by our minimal model is small, which can also be seen in Figure 1—figure supplement 7B. We believe that this is consistent with the experimental data, as it would effectively contribute the robustness of dominating counter-rotations during symmetric divisions, even if the furrow position is not perfectly symmetric. As mentioned in our response to question 4. from the first reviewer and in the first part of our response to the previous question 7, experimentally we could only partially decouple the role of contractile ring position and myosin asymmetry to confirm this hypothesis. However, our new results using lin-5(RNAi) (see response to reviewer 2 comment 7A) are in line with our theoretical predictions on the effect of ring position on chiral flows.

We clarified this point in the main text and adjusted our wording accordingly and as stated above have added our results using lin-5(RNAi) in new, Figure 1—figure supplement 10 and new, Figure 3—figure supplement 2.

[Editors’ note: what follows is the authors’ response to the second round of review.]

Essential revisions:

The reviewers note that the motion of an elongated objects in a rotational flow is one of the best-studied problems in viscous fluid mechanics and conclude that even with the obvious complexities in the present setup (geometry, non-Newtonian fluids, etc.) it should be possible to make some sensible estimates.

We agree with the reviewers that it was not obvious how the tilt of the AB cell in the X-Y plane (or AP-DV plane) could be controlled by chiral counter-rotating flows, and we also agree that a lack of explanation for this particular skew was a weakness of the manuscript. Therefore, we have analyzed this particular skew event, and the accompanying chiral counter-rotating flows, in more detail, and found experimental as well as theoretical evidence that indeed strengthens our proposed hypothesis.

In our manuscript we propose that chiral counter-rotating flows, together with inhomogeneities in friction with the surroundings, will determine the direction of cell division skews. When viewed from the left side, the skew of the AB cell in the X-Y (AP-DV) plane is always clockwise. Given the handedness of the chiral counter-rotating flow, for this to occur, the friction forces experienced by the dividing AB cell must be higher on the right side than on the left side of the embryo. Given that friction forces act opposite to the direction of cortical flow, we measured cortical flow velocities in the AB cell on the future left and future right side. Note that previously, we have only presented data measured in the AB cell at the future right side (we only reported velocities on both sides for the PAR-perturbation experiments, Figure 3 B, C). We found that the velocities, and thus the v_c, on the future left side, are significantly higher than on the future right side (new Figure 5—figure supplement 2). This is indeed consistent with the friction forces, being higher on the right side. Moreover, we have estimated the friction coefficient by fitting our active chiral fluid theory to the measured velocity distributions on the left and right sides. This yielded a friction coefficient that was higher on the right side than on the left side, again consistent with friction forces being higher on the right side of the AB cell. Finally, we estimated the cell-egg shell contact surface area from our confocal videos and found the right side of the AB cell having a slightly increased surface area that touches the egg shell. Again, this is consistent with the right side experiencing higher friction forces than the left side of the AB cell.

To further elaborate on these findings, we first derived a parameter-free geometric description that relates measured chiral flow velocities on the left and right sides of the AB cell to the cell division skew. In this model we discriminate between the cortical flow velocities in the lab frame (as measured directly from our videos) and the flow velocities in the frame that is co-rotating with the skewing cell. Here, the difference in cortical flow velocity in the lab frame and the co-rotating frame is due to the rotation of the system as a whole, e.g. the skew of the dividing AB cell. Using this simplified parameter-free geometric model the AB cell skew direction as well as its speed can be computed from the measured chiral flow velocities on the left and right sides. Indeed, predictions using this model correlate well with the experimentally measured cell division skew direction in the AP-DV plane, as well as its magnitude for wild type, and upon RhoA perturbations (ect-2(RNAi) and rga-3(RNAi)). We think that this is a large step forward and a big improvement to the manuscript which has come about by this comment, and we thank the reviewer for it.

In addition, we built a physical model that considers the torque balance of the AB cell with the eggshell. For this we explicitly considered friction forces with the eggshell on the left and right sides, by considering the areas of contact on the two sides and the respective frictional coefficients. Using the estimated friction coefficients as well the measured egg shell contact surface areas on the left and right side as input parameters, this physical model correctly predicts the direction of the AB cell skew in the AP-DV plane and qualitatively recapitulates the skew speed observed in wild type, and upon RhoA perturbations (ect-2(RNAi) and rga-3(RNAi)). Together, these findings underline quantitatively our proposed mechanism, indicating that the AB cell division skew in the X-Y (AP-DV) plane is the result of chiral counter-rotating actomyosin flows together with a left-right asymmetry of friction forces.

Altogether, our results are consistent with the right side of the AB cell experiencing higher friction forces with the egg shell than the left side. We also found indications that this is due to both an increased friction coefficient as well as an increased contact area. We note, that a previous study has shown that the cytokinetic ring of the AB cell ingresses in a left-right asymmetric fashion (Schonegg et al., 2014). Given that ring ingression likely decreases the contact area with the egg shell, these results are consistent with our new findings. We have modified the discussion of the paper where we further elaborate on these findings.

We are very thankful to the reviewers for pointing out this important issue. It has motivated us to look in more detail at the cell division skew in the AB cell. We feel that our additional experimental and theoretical analysis has substantially improved the manuscript.

We now provide two new theory predictions in Results section, two new supplementary figures and an appendix section (new Figure 5—figure supplement 2 and 3). Moreover, we have changed one paragraph in the Discussion to further elaborate on our new findings.

In this context, a particular statement that the reviewers struggled with was "Strikingly, when viewed from either embryo pole, the closest AB-like cell skews clockwise, meaning that the two juxtaposed cells counter- rotate (new, Figure 2—figure supplement 2) and new Video 14–16." The reviewers argued that the direction of rotation of both cells in this particular case can be explained by the cell-cell contact area having an increased friction coefficient when compared to the cell- vitelline membrane and/or cell-eggshell contact. Given this topology, the handedness of the chiral flow indeed would be expected to give rise to clockwise rotation of both cells when viewed from the closest pole." This raises the question of whether the cells counter-rotate or both rotate clockwise. The reviewers also note that the observed X-Y tilt of the cells in the same direction has not been addressed here.

We thank the reviewers for bringing it to our notice that this was not clear, and we agree that the term “counter-rotate” is confusing in this context. Moreover, we fully agree with the reviewer that the direction of the skew can be explained by flow handedness together with the cell-cell contact area having an increased friction coefficient when compared to the cell-vitelline layer and/or egg shell. The handedness of the flow is indeed predicted to lead to clockwise rotation of either cell when viewed from the closest pole. In addition, the reviewers correctly point out that the skew of both AB-like cells in the AP-DV plane in compressed embryos is occurring in the same direction. This is not immediately obvious from the handedness of the flow together with inhomogeneous friction forces. However, one of the two AB-like cells started skewing before the other one. Therefore, we argue that the AB-like cell that skews first results in geometry changes of the embryo that may push the neighboring cell, thereby biasing its cell division skew direction.

In order to clarify these points we have now changed the text in the Results section.

Finally, the notion emerged that the manuscript is not particularly reader-friendly, a concern that should be addressed. It is recommended to add a clear schematic early on that explains the geometry more clearly than Figure 1 (or the supplements).

We thank the reviewers for these comments and have added new clarifying illustrations in main Figure 3E and Figure 3F, that explain the geometry and the projection planes more clearly. In order to add these illustrations without decreasing figure panel sizes, we subdivided Figure 2 over two figures. Moreover, we have modified the text to make it more reader-friendly, especially when addressing the results using different projection planes. For example, we have changed our terminology and are now using the embryo body axes to describe projection planes. Hence, instead of the “X-Y plane” and “Y-Z plane” we now used “AP-DV (anteroposterior-dorsoventral) plane” and “LR-DV (left-right-dorsoventral) plane” consistently throughout the manuscript.

To clarify these issues, we have changed and rephrased many sections in the main results.

Moreover, the terminology "no chiral counter-rotating flows" was found to be confusing. Does that mean that there are chiral flows but they are not counter-rotating, or there are counter-rotating flows but they are not chiral? Indeed, chiral in this sense is not well-explained geometrically (here a schematic could help), especially since the experiments appear to only look at planar projections of the flows.

Our results show that there are chiral, counter-rotating flows in the AB lineage. In the P lineage, we observed flows that undergo net rotations, where both halves of the dividing cell move in the same direction. These net-rotating flows are therefore chiral, but are not counter-rotating. We have now explained these results more explicitly in the Results section. In addition, we have added a new illustration that clarifies the difference between chiral counter-rotating flows and chiral, net-rotating flows (new Figure 1—figure supplement 2 panels A and B), and we have now used the term “chiral counter-rotating flows” (instead of “chiral flows”) consistently throughout the manuscript.

To clarify these issues, we now provide two new subpanels in supplementary figure (new, Figure 1—figure supplement 2A – B)

We would also like to encourage you to include the species studied in the title.

We have added the species in the title of the study.

https://doi.org/10.7554/eLife.54930.sa2

Article and author information

Author details

Lokesh G Pimpale
1. Max Planck Institute of Molecular Cell Biology and Genetics, Dresden, Germany
2. Biotechnology Center, TU Dresden, Dresden, Germany
3. Cluster of Excellence Physics of Life, TU Dresden, Dresden, Germany
Contribution
performed all experiments, conceptualized the work, analyzed the data and wrote the manuscript

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-6145-1516
Teije C Middelkoop
1. Max Planck Institute of Molecular Cell Biology and Genetics, Dresden, Germany
2. Biotechnology Center, TU Dresden, Dresden, Germany
3. Cluster of Excellence Physics of Life, TU Dresden, Dresden, Germany
Contribution
assisted with experimental design, conceptualized the work, analyzed the data and wrote the manuscript

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-0346-6143
Alexander Mietke
1. Max Planck Institute of Molecular Cell Biology and Genetics, Dresden, Germany
2. Max Planck Institute for the Physics of Complex Systems, Dresden, Germany
3. Chair of Scientific Computing for Systems Biology, Faculty of Computer Science, TU Dresden, Dresden, Germany
4. Center for Systems Biology Dresden, Dresden, Germany
5. Department of Mathematics, Massachusetts Institute of Technology, Cambridge, United States
Contribution
developed the theory, conceptualized the work, analyzed the data and wrote the manuscript

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-1170-2406
Stephan W Grill
1. Max Planck Institute of Molecular Cell Biology and Genetics, Dresden, Germany
2. Biotechnology Center, TU Dresden, Dresden, Germany
3. Cluster of Excellence Physics of Life, TU Dresden, Dresden, Germany
Contribution
S.W.G conceptualized the work, analyzed the data and wrote the manuscript

For correspondence
grill@mpi-cbg.de

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-2290-5826

Funding

European Union's Horizon 2020 research and innovation program - Marie Sklodowska-Curie Grant (641639)

Lokesh G Pimpale

EMBO long-term fellowship (ALTF 1033-2015)

Teije C Middelkoop

Dutch Research Council (NWO) Rubicon fellowship (825.15.010)

Teije C Middelkoop

DFG (SPP 1782)

Stephan W Grill

DFG (GSC 97)

Stephan W Grill

DFG (GR 3271/2)

Stephan W Grill

DFG (GR 624 3271/3)

Stephan W Grill

DFG (GR 3271/4)

Stephan W Grill

European Research Council (281903)

Stephan W Grill

European Research Council (742712)

Stephan W Grill

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank Masatoshi Nishikawa for critical inputs on the theory, A Honigmann and P Gönczy for critical reading of the manuscript. We also thank T Hyman and B Bowerman for sharing C. elegans strains. We thank T Hyman, Kwabena Badu-Nkansah and all the members of Grill lab for critical input and discussions. We thank Julia Hubatsch for providing movies of C. elegans gonads. Some strains were provided by the CGC, which is funded by NIH Office of Research Infrastructure Programs (P40 OD010440). Furthermore, we thank the light microscopy facility of CMCB of TU Dresden, and the light microscopy facility of MPI-CBG for their support. We would like to acknowledge a long standing collaboration with Frank Jülicher on active chiral matter, and thank him for many discussions that were essential for the work here. LP acknowledges funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No 641639. TCM was supported by the European Molecular Biology Organization (EMBO) long-term fellowship ALTF 1033–2015, and by the Dutch Research Council (NWO) Rubicon fellowship 825.15.010. AM thanks the ELBE Phd fellowship from the Center for Systems Biology, Dresden. SWG was supported by the DFG (SPP 1782, GSC 97, GR 3271/2, GR 3271/3, GR 3271/4), the European Research Council (grants 281903 and 742712).

Senior Editor

Aleksandra M Walczak, École Normale Supérieure, France

Reviewing Editor

Thomas Surrey, Centre for Genomic Regulation (CRG), Spain

Version history

Received: January 6, 2020
Accepted: July 5, 2020
Accepted Manuscript published: July 9, 2020 (version 1)
Version of Record published: July 31, 2020 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

2,801

Page views
396

Downloads
17

Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Lokesh G Pimpale
Teije C Middelkoop
Alexander Mietke
Stephan W Grill

(2020)

Cell lineage-dependent chiral actomyosin flows drive cellular rearrangements in early Caenorhabditis elegans development

eLife 9:e54930.

https://doi.org/10.7554/eLife.54930

Categories and tags

Research organism

C. elegans

Share this article

Cite this article

Chiral counter-rotating flows are cell-lineage specific.

Movie of the actomyosin cortex during the first cell division.

Movie of the actomyosin cortex during the second cell division.

Chiral counter-rotating flow velocity and spindle skew decreases as development progresses.

Movie of the actomyosin cortex during the third cell division (left) and with PIV flow fields (right).

Movie of the actomyosin cortex during the ABa and the ABp cell divisions (left) and with PIV flowfield (right).

Movie of the actomyosin cortex during the EMS division (left) and with PIV flowfield (right).

Chiral surface flows on an ellipsoidal surface for a centered contractile ring, xr/L=0.5, and varying myosin asymmetries.

Chiral surface flows on an ellipsoidal surface for a symmetric myosin profile, IA/IP=1 and varying positions of the contractile ring.

Chiral surface flows on an ellipsoidal surface for an asymmetric myosin profile, IA/IP=1.5 and varying positions of the contractile ring.

Chiral counter-rotating flows are cell-lineage dependent.

Movie of maximum intensity projection of dividing embryo from one-cell stage to 24-cell stage.

Spindle skew in the AB cell imaged in uncompressed wild type embryos (SWG63) projected along the (left) LR-DV plane and (right) AP-DV plane by visualizing TBB-2::mCherry.

Chiral counter-rotating cortical flows during the second and third cell division in par-2; chin-1; lgl-1(RNAi) embryos.

Cortical flows during the second and third cell division in control embryos.

Cortical flows during the second and third cell division in par-6 (RNAi) embryos.

Spindle skew in uncompressed par-2 (RNAi) anteriorized embryos during third and fourth cell division projected in the AP-DV plane by visualizing TBB-2::mCherry.

Spindle skew in uncompressed par-2 (RNAi) anteriorized embryos during (left) third and (right) fourth cell division projected along the (left) LR-DV plane viewed from anterior end and (right) LR-DV plane viewed from posterior end by visualizing TBB-2::mCherry.

Spindle skew in uncompressed par-2 (RNAi) anteriorized embryos in two juxtaposed AB-like cells when projected along LR-DV plane and viewed from anterior end.

Chiral counter-rotating flow velocity determines the rate of spindle skew in the AB cell.

Cortical flows during the second cell division in ect-2 (RNAi) embryos. 4 hr of ect-2 (RNAi) leads to reduction in chiral counter-rotating flow velocity (NMY-2::GFP, cortex marked in green and TBB-2::mCherry, spindle poles marked in red) Scale bar 10 µm.

Cortical flows during the second cell division in L4440 embryos (feeding control) (NMY-2::GFP, cortex marked in green and TBB-2::mCherry, spindle poles marked in red) Scale bar 10 µm.

Cortical flows during the second cell division in rga-3 (RNAi) embryos.

Spindle skews in early development are driven by chiral actomyosin flows.

Spindle skew in the AB cell imaged in control embryos (SWG63) by visualizing TBB-2::mCherry at restrictive temperature of 25°C.

Spindle skew in the AB cell imaged in the mutant nmy-2(ts) embryos (SWG204) by visualizing TBB-2::mCherry at restrictive temperature of 25°C.

Best fit parameters.

Qualitative properties of myosin distributions and chiral flows consistently observed in P/EMS lineage (P0, P1, EMS, P2) and AB-lineage (AB, ABa, ABp, ABal, ABar) cells.

Chiral counter-rotations in experiments and in a minimal geometric model.

Comparison of the angular velocity ω determined from the physical skew model with experimentally measured average spindle skew rates.

Enhancing actomyosin activity is not sufficient to generate chiral counterrotating flows during cytokinesis.

Author details

Lokesh G Pimpale

Contribution

Competing interests

Teije C Middelkoop

Contribution

Competing interests

Alexander Mietke

Contribution

Competing interests

Stephan W Grill

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Research organism

Further reading

Chiral surface flows on an ellipsoidal surface for a centered contractile ring, $x_{r} / L = 0.5$ , and varying myosin asymmetries.

Chiral surface flows on an ellipsoidal surface for a symmetric myosin profile, $I_{A} / I_{P} = 1$ and varying positions of the contractile ring.

Chiral surface flows on an ellipsoidal surface for an asymmetric myosin profile, $I_{A} / I_{P} = 1.5$ and varying positions of the contractile ring.

Qualitative properties of myosin distributions and chiral flows consistently observed in P/EMS lineage (P₀, P₁, EMS, P₂) and AB-lineage (AB, ABa, ABp, ABal, ABar) cells.

Comparison of the angular velocity $ω$ determined from the physical skew model with experimentally measured average spindle skew rates.