1. Epidemiology and Global Health
  2. Medicine

Epidemiological transition to mortality and refracture following an initial fracture

  1. Thao Phuong Ho-Le  Is a corresponding author
  2. Thach S Tran
  3. Dana Bliuc
  4. Hanh M Pham
  5. Steven A Frost
  6. Jacqueline R Center
  7. John A Eisman
  8. Tuan V Nguyen  Is a corresponding author
  1. Healthy Ageing Theme, Garvan Institute of Medical Research, Australia
  2. Swinburne University of Technology, Australia
  3. Faculty of Engineering and Information Technology, Hatinh University, Viet Nam
  4. St Vincent Clinical School, UNSW Sydney, Australia
  5. Fertility Department, Andrology and Fertility Hospital of Hanoi, Viet Nam
  6. School of Medicine Sydney, University of Notre Dame Australia, Australia
  7. School of Biomedical Engineering, University of Technology, Australia
https://doi.org/10.7554/eLife.61142
Share this article
Cite this article
  1. Thao Phuong Ho-Le
  2. Thach S Tran
  3. Dana Bliuc
  4. Hanh M Pham
  5. Steven A Frost
  6. Jacqueline R Center
  7. John A Eisman
  8. Tuan V Nguyen
(2021)
Epidemiological transition to mortality and refracture following an initial fracture
eLife 10:e61142.
https://doi.org/10.7554/eLife.61142
  2. Download BibTeX
  3. Download .RIS

Abstract

This study sought to redefine the concept of fracture risk that includes refracture and mortality, and to transform the risk into "skeletal age". We analysed data obtained from 3521 women and men aged 60 years and older, whose fracture incidence, mortality, and bone mineral density (BMD) have been monitored since 1989. During the 20-year follow-up period, among 632 women and 184 men with a first incident fracture, the risk of sustaining a second fracture was higher in women (36%) than in men (22%), but mortality risk was higher in men (41%) than in women (25%). The increased risk of mortality was not only present with an initial fracture, but was accelerated with refractures. Key predictors of post-fracture mortality were male gender (hazard ratio [HR] 2.4; 95% CI, 1.79–3.21), advancing age (HR 1.67; 1.53–1.83), and lower femoral neck BMD (HR 1.16; 1.01–1.33). A 70-year-old man with a fracture is predicted to have a skeletal age of 75. These results were incorporated into a prediction model to aid patient-doctor discussion about fracture vulnerability and treatment decisions.

Introduction

Fracture due to osteoporosis imposes a significant health care burden to the society. From the age of 50, the residual lifetime risk of fracture is ~50% in women and ~30% in men (Nguyen et al., 2007a). In women, the lifetime risk of hip fracture is actually equivalent to or higher than the risk of invasive breast cancer (Nguyen et al., 2007a; Cummings et al., 1989). In men, the lifetime risk of hip and vertebral fractures (17%) is comparable to the lifetime risk of being diagnosed with prostate cancer (Cummings et al., 1989; Shortt and Robinson, 2005). In the United States alone, the cost attributable to osteoporosis and fracture was estimated to be $22 billion (2008), higher than the cost attributable to breast cancer (Blume and Curtis, 2011). With the rapid aging of the population, the burden of osteoporosis and fracture will become much more pronounced worldwide.

Various studies have found that an existing fracture signals an increased risk of subsequent fracture and/or mortality (Shortt and Robinson, 2005; Center et al., 2007; Bliuc et al., 2009). However, the sequential consequences of fracture, recurrent fracture, and mortality are highly heterogeneous among individuals, and it is not clear why some individuals do well after an initial fracture, but others go on to sustain a refracture and mortality. Existing fracture risk assessment tools focus on predicting the risk of an initial fracture (Kanis et al., 2008; Nguyen et al., 2007b; Nguyen et al., 2008; Hippisley-Cox and Coupland, 2012), but ignore the risks of refracture or mortality following an initial fracture.

We hypothesize that the three events—fracture, refracture, and mortality—are correlated and that the correlation is underlined by advancing age and low bone mineral density (BMD). The present study sought to test that hypothesis by pursuing two specific aims: (i) to quantify the risk of fracture-related consequences, including refracture and post-fracture mortality; and (ii) to define the contributions of age and low bone BMD to the transition between fracture, refracture, and mortality for an individual. Addressing the aims will advance the risk assessment and help identify individuals who do badly after an initial fracture for appropriate intervention and reduce mortality burden in the general population.

Results

Baseline characteristics of participants

The study included 2046 women and 1205 men, all aged 60 years and older at baseline. Mean age at baseline was 70 (SD 7) in women and 70 (SD 6) in men. At baseline, approximately 22% (n = 458) women and 9% (n = 111) men were having osteoporosis (femoral neck BMD T-score ≤ –2.5) (Table 1). Prior fracture (those occurring prior to study entry) was reported in 17.5% of women and 11.5% of men. More women (38%, n = 776) than men (26%, n = 317) self-reported a fall over the previous 12 months. Men were more susceptible than women to cardiovascular disease and type 2 diabetes.

Table 1
Baseline characteristics and incident illnesses of 2046 women and 1205 men in the Dubbo Osteoporosis Epidemiology Study.
WomenMenP-value
Number of participants20461205
BMI (kg/m2)26.5 (5.1)26.8 (3.9)0.035
FNBMD (g/cm2)0.81 (0.14)0.92 (0.15)<0.001
FNBMD T-score−1.62 (–1.15)−0.99 (–1.22)<0.001
Osteoporosis (n; %)458 (22.4)111 (9.2)<0.001
History of falls (n; %)776 (37.9)317 (26.3)<0.001
Prior fracture since age 50 (n; %)357 (17.5)139 (11.5)<0.001
Cardiovascular disease (n; %)632 (30.9)470 (39.0)<0.001
Bone-unrelated cancer (n; %)174 (8.5)108 (9.0)0.654
Neurological disease (n; %)142 (6.9)69 (5.7)0.175
Rheumatoid arthritis (n; %)84 (4.1)25 (2.1)0.002
Respiratory disease (n; %)221 (10.8)141 (11.7)0.431
Type 2 diabetes (n; %)219 (10.7)158 (13.1)0.038

  1. Notes: Values shown are mean and standard deviation (in brackets), unless otherwise specified. P-values were derived from t-test for continuous variables and from chi-squared test for binary variables. FNBMD, femoral neck bone mineral density.

On average, the first fracture occurred at age 79 (SD 8), followed by the second fracture at age 82 (SD 7) and the third fracture at age 83 (SD 7; Supplementary file 1). Age at death, including death following a fracture and death without a fracture, was 83 (SD 8). Comparison between men and women reveals that despite the age at entry and at initial fracture was not substantially different, age at subsequent events, that is, second and third fracture and death, was younger in men than in women, suggesting that once a fracture occurred, men transitioned more quickly to adverse stages than women did (Supplementary file 1).

Incidence of fracture and mortality

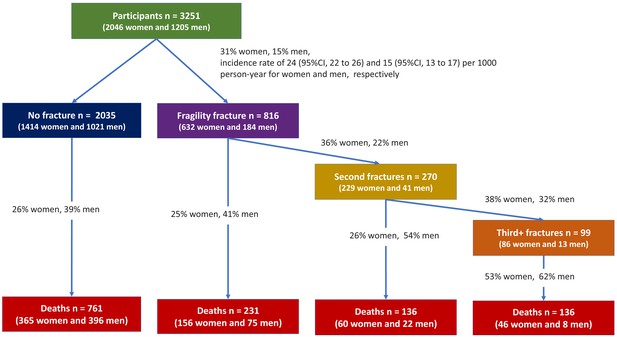
During the follow-up period, 632 (31%) women and 184 (15%) men who had sustained at least one fracture over 21,723 and 11,968 person-years were at risk, yielding a fracture incidence rate of 24 (95% CI, 22–26) and 15 (95% CI, 13–17) per 1000 person-years for women and men, respectively (Figure 1). Among the 816 individuals with fracture, 270 went on to have another fracture, with 99 having more than two fractures.

Figure 1
Download asset Open asset
Flowchart of recruitment and follow-up.

Overall, 627 (31%) women and 501 (42%) men had died over the same period, yielding a mortality rate of 33 (95% CI, 31–35) and 42 (95% CI, 38–46) per 1000 person-years for women and men, respectively. Among the deceased, 262 (42%) women and 105 (57%) men died following a fragility fracture (Figure 1, Supplementary file 2). A more detailed description of transition between health states during the follow-up period is shown in Supplementary file 2.

Risk of transition between health states

The instantaneous risk of transition to next heath states is shown in Table 2. In fracture-free women, the instantaneous risk of having the first fracture was 2.7% (95% CI, 2.4–3.0%). Once the initial fracture occurred, the risk of sustaining another fracture was almost doubled (4.8%; 95% CI, 3.8–6.3%). This second fracture kept signaling an increased risk of further fractures. This trend was also observed for mortality: while women with no fracture had the lowest risk of mortality (1.8%; 95% CI, 1.5–2.0%), those with one, two, and three or more fractures had an increased risk of mortality from 2.1% to 12.9%.

Table 2
Instantaneous risk of transition between states of bone health for women and men.
Transitional stateWomen: risk (95% CI)Men: risk (95% CI)Hazard ratio for men vs women
(95% CI)
 No Fx → Initial Fx2.7 (2.4–3.0)1.7 (1.4–2.0)0.63 (0.53–0.75)
 Initial Fx → Second Fx4.8 (3.8–6.3)4.1 (2.8–5.9)0.85 (0.61–1.19)
 Second Fx → Third+ Fx6.3 (3.7–10.9)13.3 (6.7–26.1)2.11 (1.13–3.95)
 No Fx → Death1.8 (1.5–2.0)3.2 (2.8–3.7)1.81 (1.55–2.10)
 Initial Fx → Death2.1 (1.5–2.9)5.0 (3.5–7.4)2.40 (1.79–3.21)
 Second Fx → Death2.2 (1.1–4.4)16.5 (8.8–32.9)7.52 (4.33–13.07)
 Third+ Fx → Death12.9 (5.8–28.9)33.9 (11.8–86.2)2.62 (1.17–5.87)

  1. Note: ‘Fx’, fracture. CI, confidence interval. BMD, bone mineral density. BMI, body mass index. See Data Analysis for the definition of ‘instantaneous risk’ (hazard). Risk was estimated for a ‘typical’ man or woman having average BMD, characterized by mean values of predictors as follows: age at event = 70 years, femoral neck bone mineral density T-score = −1.5 (equal to mean), BMI = 26.6 kg/m2 (equal to mean), no history of falls, no prior fracture, no comorbidities. Hazard ratio and 95% confidence interval were derived from the multistate model, adjusting for age, femoral neck BMD, BMI, history of a fall within 12 months, prior fracture, and other comorbidities (cardiovascular disease, cancer, type 2 diabetes, neuromuscular, rheumatoid arthritis, and chronic obstructive pulmonary disease). Bold-face values indicate a statistically significant difference between men and women. In each cell, values are percentage of risk and 95% confident interval (in the brackets).

The risk of first incident fracture was lower in men than in women (HR 0.63; 95% CI, 0.53–0.75). However, there was no significant difference in the risk of second fracture between genders. More interestingly, the risk of third fracture in men was 2.1-fold higher than that in women (HR 2.11; 95% CI, 1.13–3.95). Moreover, the risk of death, regardless of fracture status, was consistently higher in men than in women (Table 2).

Risk factors for transition between states

Risk factors for the transition from no fracture to an initial fracture, no fracture to death, first fracture to second fracture, and first fracture to death are shown in Figure 2A. As previously known, men were less likely than women to suffer an initial fracture (HR 0.63; 95% CI, 0.53–0.75), but after a fracture men were more likely than women to die (HR 2.40; 95% CI, 1.79–3.21) (Figure 2B). In either men or women, advancing age was associated with an increased risk of initial fracture, second fracture, and mortality. For a given age and gender, individuals with lower femoral neck BMD were associated with increased risks of initial fracture, second fracture, and mortality. A personal history of fracture was a risk factor for subsequent fracture, but was not associated with the transition between fracture and mortality. In both women and men, those having rheumatoid arthritis were more likely to have an increased risk of initial fracture and second fracture (Figure 2A).

Figure 2
Download asset Open asset
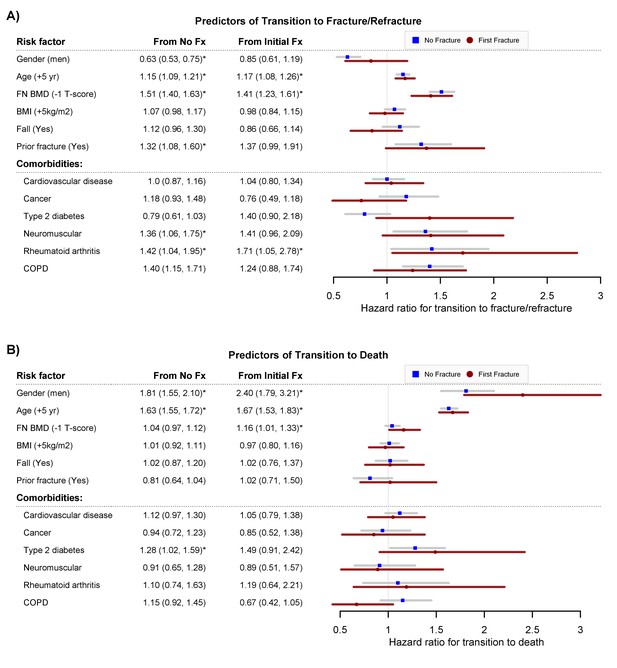
Predictors of transition to fracture/refracture (Panel A) and predictors of transition to death (Panel B): hazard ratio and 95% confidence interval from the multistate model, adjusting for age, femoral neck BMD, BMI, history of fall within 12 months, prior fracture, and other comorbidities (cardiovascular disease, cancer, type 2 diabetes, neuromuscular, rheumatoid arthritis, and chronic obstructive pulmonary disease).

Fx, fracture. FNBMD, femoral neck bone mineral density. COPD, chronic obstructive pulmonary disease. Symbol * indicates statistical significance at level of 5% (p<0.05).

The 'sojourn time' for each transitional status is shown in Table 3. Women tended to stay at each health state longer than men. The predicted sojourn time in state 1 (fracture free) of a 'typical' woman with osteopenic BMD (T-score = −1.5) was 22.4 years, 5.5 years longer than that of an osteoporotic woman (T-score = −2.5). Once the initial fracture occurred, the difference in sojourn time between a person with low BMD and a person with normal BMD was not as much as in those who have not yet sustained a fracture, especially for men.

Table 3
Sojourn time (in years) of women/men with different bone health*.
TransitionT-score = 0T-score = −1.5T-score = −2.5
Women
 No Fx.32.1 (28.2–36.6)22.4 (20.4–24.6)16.9 (15.2–18.7)
 Initial Fx.21.9 (16.7–28.8)14.5 (11.8–17.7)10.1 (8.8–13.4)
 Second Fx.18.5 (10.1–34.0)11.8 (7.6–18.1)8.7 (5.7–13.1)
 Third+ Fx.5.2 (1.7–15.9)7.7 (3.4–17.7)10.0 (4.7–21.5)
Men
 No Fx.25.5 (22.5–28.9)20.4 (18.3–22.8)16.9 (14.8–19.3)
 Initial Fx.15.5 (11.5–20.9)11.0 (8.5–14.3)08.7 (6.6–11.4)
 Second Fx.5.4 (3.0–9.9)3.3 (2.2–5.4)2.4 (1.5–3.9)
 Third+ Fx.2.0 (0.6–7.2)3.0 (1.1–8.2)3.8 (1.5–9.9)

  1. *Time was estimated for women or men with different BMD profiles (i.e., 0, –1.5 vs −2.5), at the age of 70, with BMI of 26.6 kg/m2 (equal to mean), with no history of falls, no prior fracture and no comorbidities. Sojourn time is defined as the predicted time an individual stays in one state before moving to the next state. Fx, fracture. In each cell, values are number of years and 95% confident interval (in the brackets).

Individualization of risk

Using the risk factors and instantaneous risk, we estimated the 5-year probability of transition between health states for a 'typical' individual based on the individual's risk profile (Table 4). For a woman aged 70 years, with a BMD T-score = −1.5 and BMI being 26.6 kg/m2, no history of fall, no prior fracture, no comorbidities, the probability of transition from no fracture to fracture (10.1%) was not much different from the risk of mortality (8.6%). However, once a fracture has occurred, her risk of next fracture increased by almost 1.7-fold (16.5%), which was greater than the risk of mortality (10.4%). In the same state, a woman with low BMD would have a higher risk of progressing to fracture or death than a woman with normal BMD (Supplementary file 3).

Table 4
Five-year probability of transition between states of bone health for women and men.
Women
FromTo
No fracture1st fracture2nd fracture3rd fractureDeath
No fracture80.0
(78.2–81.4)		10.1
(9.1–11.3)		1.2
(0.9–1.5)		0.1
(0.1–0.2)		8.6
(7.6–9.7)
1st fracture70.8
(65.3–75.4)		16.5
(12.9–20.6)		2.4
(1.4–3.9)		10.4
(7.9–14.0)
2nd fracture65.3
(51.4–75.5)		18.5
(10.2–28.9)		16.2
(10.0–26.4)
3rd fracture52.4
(22.9–75.0)		47.6
(25.0–77.1)
Men
FromTo
No fracture1st fracture2nd fracture3rd fractureDeath
No fracture78.3
(76.1–80.3)		6.0
(5.0–7.0)		0.4
(0.3–0.6)		0.1
(0.0–0.2)		15.3
(13.6–17.2)
1st fracture63.5
(54.9–70.2)		8.1
(4.9–12.1)		2.1
(0.8–4.3)		26.3
(20.0–34.3)
2nd fracture22.4
(8.4–38.4)		13.6
(3.7–29.7)		64.0
(44.5–82.5)
3rd fracture18.4
(0.8–53.8)		81.6
(46.2–99.2)

  1. Note: Risk was estimated for a ‘typical’ man or woman having a risk profile characterized by mean values of predictors as follows: age at event = 70 years, femoral neck bone mineral density T-score of −1.5, BMI = 26.6 kg/m2, no history of falls, no prior fracture, no comorbidities. In each cell, values are percentage of risk and 95% confident interval (in the brackets).

For a man with a similar profile as a woman, the risk of an initial fracture (6.0%) was lower than the risk of mortality (15.3%). If the man has sustained a fracture, then his risk of mortality is predicted to increase to 26.3%.

For both men and women, the risk of mortality was associated with a lower BMD T-score and advancing age (Figure 3). Importantly, the mortality risk increased with the increasing number of fractures; however, the increase was more pronounced in men than in women. Less than 50% of men who sustained a refracture survived longer than 5 years. Figure 3—figure supplement 1 further illustrates the effect of BMD on the compound risk of mortality associated with the number of fractures.

Figure 3 with 2 supplements see all
Download asset Open asset
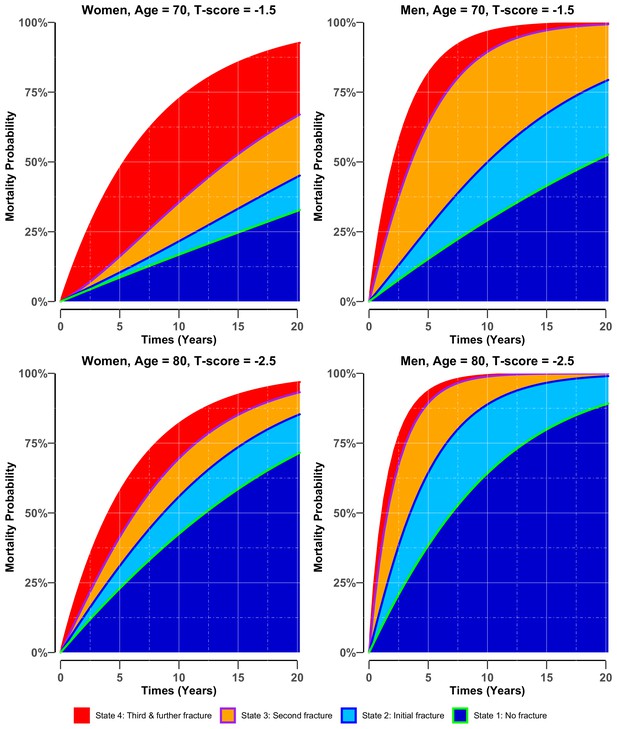
Adjusted cumulative probability of mortality in women (left panel) and men (right panel) who had stayed in different states of bone health.

There were four potential bone heath states before transiting to state 5 (i.e., mortality): state 1: no fracture (green blue colour area) if the individual entered the study without any osteoporotic fracture; state 2: initial fracture (light blue area) if an individual had sustained a fracture after study entry; state 3: second fracture (purple-orange area) if an individual had suffered a second fracture; and state 4: third and further fractures (red area) if an individual had suffered two or more subsequent fractures during the follow-up period. Risk was estimated for women and men with different BMD profiles (i.e., −1.5 vs −2.5), at the event age of 70 and 80, having all other factors set to the population mean, that is, body mass index = 26.6 kg/m2, no history of fall at baseline, no prior fracture and no comorbidities.

Figure 3—source data 1

Adjusted cumulative probability of mortality in women and men, who had stayed in different states of bone health.

Risk was estimated for women and men with different BMD profiles (i.e.,−1.5 vs −2.5), at the event age of 70 and 80, having all other factors set to the population mean, that is, body massindex = 26.6 kg/m2, no history of fall at baseline, no prior fracture and no comorbidities.

https://cdn.elifesciences.org/articles/61142/elife-61142-fig3-data1-v2.xlsx

The prediction model has good calibration as there was a close agreement between the observed and predicted incidence of fracture and mortality (Figure 3—figure supplement 2).

Discussion

In many individuals, fracture, refracture, and death were sequentially linked events: individuals with an initial fracture have an increased risk of subsequent fracture and mortality. Previous studies investigated risk factors for each pair of consecutive states at a time (Bliuc et al., 2009; Bliuc et al., 2013). This study took a systemic approach to examine these linked events in its flow in each individual, and then modeled the transition between health states. The novel outcome of this study is an individualized predictive model to predict not only the probability but also the time of an incident fracture. Moreover, the model at the same time provides these estimates for consequences of fracture, that is, recurrent fracture and premature death. More importantly, by timing the duration that people on a specific state occupy this state, for the first time, we can quantify the number of healthy years lost (in the view of bone health) due to osteoporotic fracture and recurrent fracture.

This is, to our knowledge, the first investigation into the transition between fracture and fracture-associated events. However, for each event our findings were similar to those from previous studies, in that women have a higher risk of fracture than men (Johnell and Kanis, 2005) and once men sustain the first fracture, risk of the second fracture is similar to that in women (Center et al., 2007). Moreover, in contrast to risk of fracture, risk of death, regardless of fracture status, is greater in men than in women (Bliuc and Center, 2016; Kannegaard et al., 2010). However, the difference in risk estimation in our study and previous studies is that whereas many other studies reported lifetime risk (Johnell and Kanis, 2005), our model estimated instantaneous risk, beside with the estimation of 5-year risk. The estimation of lifetime risk for fracture can be misleading as once an incident fracture, an event with several consequences, occurs, this event shifts the remaining lifetime risk of the individual.

The progression to premature mortality following a fragility fracture has been described in many studies, but the underlying mechanism is still unclear. Mortality following a hip fracture is best studied due to its severity. Adverse events related to surgery to repair a fractured hip have been also implicated in the increased mortality observed among the older people (Nikkel et al., 2015). However, the specific cause for long-term increase in mortality following hip fracture and other types of fracture is largely unknown. The role of comorbidities has been reported but with inconsistent findings across studies (Cenzer et al., 2016; Cree et al., 2000; Liem et al., 2013). Risk factors for fracture such as low bone mineral density, bone loss, and low muscle strength have recently been linked to mortality risk in the general population as well as post-fracture mortality (Nguyen et al., 2007c; Van Der Klift et al., 2002; Kado et al., 2000; Rantanen et al., 2000; Pham et al., 2017).

We found that once the initial fracture occurred, the difference in sojourn time between a person with low BMD and a person with normal BMD was not as much as in those who have not yet sustained a fracture, especially for men. This suggests that after an initial fracture, factors other than BMD might play a more important role than BMD in the progression to subsequent fractures and premature death. Therefore, further studies to investigate which factors are dominant of the progression after an initial fracture are required. The shorter transition time after an initial fracture also suggests that any intervention strategy which focuses on improving BMD would be more beneficial if implemented at early stage than at later stages.

Current tools for fracture prediction suffer from a number of major weaknesses (Nguyen and Eisman, 2018): lack of mortality data and no contextualised estimate of risk. All existing prediction models such as the Garvan Fracture Risk Calculator (Nguyen et al., 2008) and FRAX (Kanis et al., 2008) provide only an estimate of fracture risk, with no estimate of mortality risk. This is a weakness because mortality is clearly strongly associated with fracture (Cree et al., 2000; Bliuc et al., 2009; Nguyen et al., 2007c) and treatment can reduce fracture-associated mortality risk (Lyles et al., 2007; Reid et al., 2018). Moreover, the risk estimate produced by these prediction models are not put into context. They do not provide the benefit in terms of fracture reduction and increased survival (and potential risk) if a high-risk patient opts for treatment; limiting the communication of risk and clinically useful discussions between patients and their physicians.

Thus, our results have important implications for fracture risk prediction and risk communication. Unlike other chronic diseases where the deterioration of the functional organs is associated with clinical signs, the deterioration of bone health is mainly silent until the first fracture occurs. However, the lack of adverse events estimation in the existing fracture risk prediction tools can be an obstacle for both patients and doctors to be fully aware of the significance of the patients’ bone health condition, which would lead to under-management of the conditions. By providing the estimate of fracture risk and the estimate of mortality risk, our unified model will enable patients and doctors to fully appreciate the serious nature of fragility fracture. Patients do not always appreciate the serious consequence of fracture (e.g., subsequent fractures and mortality), and as a result, they usually underestimate their risk of adverse outcomes. Patients are however concerned about quality of life and mortality, and providing the estimated risk of mortality can motivate them to take preventive measures.

One way to convey the new compound risks of fracture and mortality is to transform the risks into 'skeletal age'. Based on the idea of 'lung age' (Morris and Temple, 1985) and 'effective age' (Spiegelhalter, 2016), skeletal age can be defined as the age of an individual's skeleton as a result of the individual's risk factors for fracture. In the normal circumstance, skeletal age is the same as chronological age, but in high-risk individuals, skeletal age is greater than chronological age. The number of years lost or gained in effective age for a risk factor with mortality hazard ratio of H is log(H)/log(h), where h represents the annual risk of mortality which is approximately 1.1 (Spiegelhalter, 2020). For instance, for a 70-year-old man who has sustained a fracture, the hazard ratio of 1.67 (Figure 2B) is equivalent to a loss of ~ 5.4 years of life (log(1.67)/log(1.1)). In other words, for the 70-year-old man, the hazard ratio of 1.67 corresponds to a skeletal age of 75.4years. In other words, if an individual is 70 years old (chronological age) but skeletal age is 75.4, then this means that the individual is the same risk profile as a 75.4-year-old individual with a 'healthy profile.' Moreover, for an individual who has sustained a fracture, each standard deviation lower in femoral neck BMD on average take around 1.5 years of life of the individual.

Evidence from randomized controlled trials suggest that in patients with osteoporosis and/or a pre-existing fracture, bisphosphonate treatment reduces fracture risk and mortality risk. In a placebo-controlled trial, Lyles and colleagues found that among elderly hip fracture patients, intravenous zoledronic acid reduced the risk of subsequent fracture by 35% and reduced mortality risk by 28%, regardless of bone mineral density (Lyles et al., 2007). A recent placebo-controlled trial further showed that in osteopenic patients with a fracture, zoledronic acid also reduced mortality risk with an odds ratio of 0.65 (95% CI, 0.40–1.05) (Reid et al., 2018). A review of all clinical trials reported that treatment of osteoporotic patients with medications with proven fracture efficacy reduced mortality risk by approximately 10% (Bolland et al., 2010). However, a recent meta-analysis found that the effect of bisphosphonate treatment on mortality was less certain (Cummings et al., 2019). Taken together, these results suggest that in osteoporotic or osteopenic patients with a fracture, bisphosphonate treatment may reduce mortality risk. The beneficial effect of treatment can also be expressed in terms of 'skeletal age'.

Our results clearly show that the risk of fracture and subsequent events should be individualized. This is true, because there is no ‘average person’ in the population. Two women having the same BMD and age but different fracture history could have different risk estimates, and this difference must be taken into account in the assessment of risk. Our new model provides a tool and a framework for including other risk factors such as genetic profile (Ho-Le et al., 2017; Ho-Le et al., 2021; Nielson et al., 2016) and bone microarchitecture (Karasik et al., 2017; Pepe et al., 2016) to be included in the personalized assessment of fracture and fracture-related outcomes. An important advantage of using genomic data in fracture risk assessment is that genotypes do not change with time, and as a result, the risk of fracture for the individual can be predicted at younger ages, well before the conventional risk factors become apparent. Although there is no 'genetic therapy' for individuals at high risk of fracture, the use of an osteogenomic profile could help segregate individuals at high risk from those with low risk of fracture, and facilitate educational aspects of prevention and counseling services.

These findings should be interpreted within the context of strengths and weaknesses. The strength of the study is its prospective design and the long follow-up of 21 years allowing us to identify a large number of multiple subsequent fractures and death, therefore, making it possible for the transition analysis. However, the cause of death was not available, and it was not possible to conduct an in-depth analysis of mortality-attributable risk. Because this cohort included mainly Caucasians (98.6%) (Nguyen et al., 2008), the present findings might not be generalizable to other ethnicities. Despite the relative large sample size in general, the number of men who sustained three and more fractures was not sufficiently enough for the statistical analysis to produce a stable result for this group. In the present study, the transition between states of bone health following specific fracture types has not been investigated due to the modest number of events in each group of type of fracture. Comorbidities occurring during the follow-up time were not ascertained and could not be treated as time-variant covariates in the analysis.

In summary, we have developed a multistate model that provides the general community with not just fracture risk estimate but also the likelihood of refracture and survival. This information can encourage at-risk people to proactively make changes in lifestyle to mitigate their elevated risk. Our model also provides a personalized window of opportunity for intervention to reduce the burden of fracture-associated outcomes in at-risk individuals.

Materials and methods

Key resources table
Reagent type (species) or resourceDesignationSource or referenceIdentifiersAdditional information
Software, algorithmR Project for Statistical ComputingR Project for Statistical ComputingRRID:SCR_001905
Software, algorithmAlgorithm SAS programStatistical Analysis SystemRRID:SCR_008567

Participants and setting

Request a detailed protocol

This study was part of the ongoing Dubbo Osteoporosis Epidemiology Study (DOES) which was designed as a population-based prospective investigation, with the setting being Dubbo and surrounding districts. The study was commenced in 1989, and is still ongoing. Dubbo was selected for the study site because it has a relatively stable population whose age structure resembled that of the Australian population at large. Moreover, because Dubbo city has only two radiological services that can cover the totality of fracture ascertainment for local residents. In 1989, approximately 2100 women and 1600 men aged 60 years or over were living in the city of Dubbo (Jones et al., 1994), and at the time of commencement (1989), DOES involved over 60% of this population, with 98.6% of them being Caucasian origin (Bliuc et al., 2015). The median follow-up time for the cohort was 9 years (interquartile range 5–18 years). The study was approved by the Ethics Committee of St Vincent’s Hospital (Sydney) (HREC reference number 13/254) and carried out according to the Australian National Health and Medical Research Council (NHMRC) Guidelines, consistent with the Declaration of Helsinki (established in 1964 and revised in 1989) and US Food and Drug Administration guidelines. All participants have provided written informed consent.

At the time of conception (mid-1989), DOES had hypothesized that the risk of fracture could be predicted by about 10 risk factors, and under the presumption that (i) each factor needs at least 10 events, (ii) the incidence rate is about 1% per year, then a sample of 2000 individuals would be required to follow for 5 years. Ultimately, the study has recruited more than 3200 individuals of both genders, and over the past 20 years, the number of fractures was 632 in women and 184 in men. In other words, the number of events is adequate for developing a reproducible prediction model.

Fracture ascertainment

Request a detailed protocol

Fractures occurring during the study period were identified through radiologists’ reports from the only two radiology centers providing x-ray services within the Dubbo region as previously described (Nguyen et al., 2007d). Circumstances surrounding the fracture were also confirmed with participants on the next visit that was close to the fracture. In this study, we included only fractures having definite reports and resulting from low-energy trauma such as falls from standing height or less in this analysis. Fractures due to malignant diseases or high-impact trauma (e.g., motor vehicle accident, sport injury, or fall from above standing height) were excluded from the analysis. No systematic x-ray screening for asymptomatic vertebral fracture was conducted; therefore, vertebral fractures were incidental findings in x-ray reports or were x-rayed due to the presence of back pain. Fractures of the skull, fingers, and toes were not included in the analysis.

The incidence of death was ascertained by the NSW Registry of Births, Deaths and Marriages. Deaths were also monitored by systematically searching funeral director lists, local newspapers, and on radio, or by word of mouth with a confirmation or biannual telephone contact.

Bone measurements and risk factor assessment

Request a detailed protocol

Bone mineral density (BMD) was measured at the femoral neck and lumbar spine by dual energy x-ray absorptiometry (DXA), using GE LUNAR DPX-L and later PRODIGY densitometer (GE LUNAR, Madison, WI). The radiation dose used is less than 0.1 µGy and the coefficient of variation of BMD at our laboratory is 0.98% for lumbar spine and 0.96% for femoral neck (Nguyen et al., 1997; Ho-Le et al., 2021). The femoral neck BMD was converted into T-score using our own young population reference values of mean and standard deviation; mean of 1.00 (SD 0.12) is for women and 1.04 (SD 0.12) is for men. Approximately 1.5% of participants had no femoral neck BMD measurement at baseline; and those missing values were imputed based on age, height, weight, and lumbar spine BMD at baseline, using the multivariate imputation by chained equations algorithm (van Buuren and Groothuis-Oudshoorn, 2011).

Body weight (kg) was measured in light clothing and without shoes using an electronic scale. Height (cm) was measured without shoes by a wall-mounted stadiometer. Body mass index (BMI, kg/m2) was calculated based on the weight and height measured at baseline. History of falls was obtained via a structured questionnaire administered by a trained nurse during the interviews at baseline and biennial follow-up visits.

Data analysis

Request a detailed protocol

A multistate model was used to describe the transition between a series of states in continuous time for an individual. We considered five states: (1) an individual at state 1 if the individual entered the study without any fracture; (2) state 2 if an individual had sustained a fracture (after study entry); (3) state 3 if an individual had suffered a second fracture; (4) state 4 if an individual had suffered two or more subsequent fractures during the follow-up period; and (5) state 5 if an individual had died during the follow-up period. Any individual at state 1, 2, 3, or 4 could transit to state 5 (i.e., death). Once individuals entered state 5 (i.e., they could no longer move to any other state); therefore, death is called ‘absorbing state’ (Figure 4).

Figure 4
Download asset Open asset
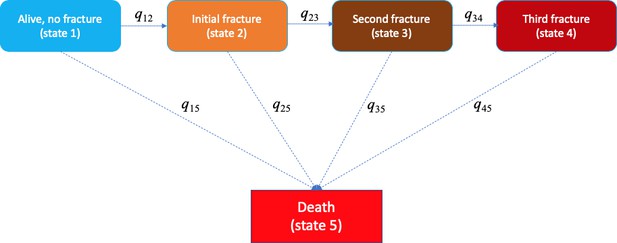
Markovian model of transition between five heath states (e.g., alive without a fracture, initial fracture, second fracture, third and further fractures, and death).

The transition between state r to state s is 'governed' by the instantaneous risk of transition (i.e., intensity) qrs, where r and s represent each of the five health states. At a given time point, for example, a fracture-free individual (state 1) had an instantaneous risk of staying at that state 1 (q11), an instantaneous risks of suffering an initial fracture (q12), and an instantaneous risk of death (q15).

In the multistate model, the transition from state r to s is governed by transition intensities (qrs) which are estimated from the observed data using the maximum likelihood method. These transition intensities represent the instantaneous risk of moving from current state (state r) to the next state (state s). Instantaneous risk (also referred to as 'hazard') is the probability that an individual would experience an event at a particular given point in time. This risk is very small over a very short time period, but can accumulate over time. Thus, the incidence of an event is the instantaneous risk multiplied by the length of time. In our study, except for the absorbing state, for states 1 to 4, at any time point, individuals who stay in one of these states have an instantaneous risk of staying in that state (qrr) and an instantaneous risk of moving to the next states (–qrs) (Figure 4). At a given time point, for example, a fracture-free individual (state 1) had an instantaneous risk of staying at that state 1 (q11), an instantaneous risk of suffering an initial fracture (q12), and an instantaneous risk of death (q15). These instantaneous risks were estimated for an individual based on the individual’s risk profile and adjusted for age. From these instantaneous risks, we can quantify the individualised risk of fracture, refracture, and mortality for an individual. Besides transition intensities, we also estimated the sojourn time which is defined as the predicted time an individual stays in one state before moving to the next state.

The effect of each potential risk factor on transition intensities was estimated as relative risk. Our model considered six specific risk factors: age, bone mineral density, body mass index, a history of falls, prior fracture, and common diseases. Age was included in the model as a time-variant factor, and for simplicity, age henceforth is referred to as age at event. Age at event is the age of an individual at the beginning of each state. The reason to adjust for age at event rather than age at baseline is to avoid the problem of immortal time bias. Immortal time bias could occur in groups where individuals transitioned through several states as they had to survive long enough to be able to make these transitions. Other covariates were treated as time-invariant factors. All data analysis and modeling were conducted with SAS software version 9.4 (SAS Institute, Inc Cary, NC, USA) and R Statistical Environment (R Development Core Team, 2008). The multistate model was fitted with the R package msm (Jackson, 2011).

Data availability

All data generated or analysed during this study are included in the manuscript and supporting files. Source data files have been provided for Figures 3, Figure 3 - figure supplement 1, and Figure 3 - figure supplement 2.

References

Decision letter

  1. Clifford J Rosen
    Senior Editor; Maine Medical Center Research Institute, United States
  2. Dolores Shoback
    Reviewing Editor; University of California, San Francisco, United States
  3. Gina Woods
    Reviewer

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

Your studies emphasize the greater risk of death with initial and subsequent fractures in an individual with low bone mass or osteoporosis. That greater risk of death not only is present with the initial fracture in individuals, but is accelerated by repeat fracture events. You also advance the concept of skeletal age, underscoring the fact that once a fracture has occurred, the condition of bone tissue has deteriorated as a composite of the risk factors for fracture represented in the individual patient.

Decision letter after peer review:

Thank you for submitting your article "Predicting mortality and refracture following an initial fracture" for consideration by eLife. Your article has been reviewed by three peer reviewers, one of whom is a member of our Board of Reviewing Editors, and the evaluation has been overseen by Clifford Rosen as the Senior Editor. The following individual involved in review of your submission has agreed to reveal their identity: Gina Woods (Reviewer #3).

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

We would like to draw your attention to changes in our revision policy that we have made in response to COVID-19 (https://elifesciences.org/articles/57162). Specifically, when editors judge that a submitted work as a whole belongs in eLife but that some conclusions require a modest amount of additional new data, as they do with your paper, we are asking that the manuscript be revised to either limit claims to those supported by data in hand, or to explicitly state that the relevant conclusions require additional supporting data.

Our expectation is that the authors will eventually carry out the additional analyses and report on how they affect the relevant conclusions either in a preprint on bioRxiv or medRxiv, or if appropriate, as a Research Advance in eLife, either of which would be linked to the original paper.

Summary:

This interesting paper aligns quantitatively the recurrence of fractures in a well-known cohort of aging men and women in Australia with mortality over time. The key goal of the paper is to demonstrate that men and women who fracture have greater mortality than non-fracturing individuals. While this message has noted before, the quantitative handling of the data from the cohort is the new and welcome addition to the literature. The authors look at transitions from different states of fracture and estimate instantaneous risks. Mortality has not heretofore been a component in patient-physician joint decision-making about undertaking therapy for osteoporosis.

Please address the reviewers’ comments and questions below.

Title: Please see the suggestions of reviewer 3 below for possible revision of the title itself for the paper.

Reviewer #1:

This is an interesting further analysis of the Dubbo osteoporosis study. Its headline conclusions are easily understood, though the methodology involves esoteric mathematics that will not be readily accessible to clinicians. However, it will be of interest to epidemiologists. My specific questions are as follows:

1) The concept of instantaneous risk will be unfamiliar to many readers. It needs to be explained in more detail to make these sections of the manuscript understandable.

2) Subsection “Instantaneous risk of transition between health states”, where instantaneous risks are being presented, have these calculations been adjusted for age? Those who have already had one, two or three fractures will on average be older than those with fewer fractures and so this will impact on their risk of the next fracture or of death.

3) The discussions of "typical 70 year olds" are problematic where risk at a T-score of 0 is contrasted with a risk of a T-score of -2.5. T=0 is certainly not typical of a 70 year old, where the average value is closer to -2.0.

Reviewer #2:

The manuscript "Predicting mortality and refracture following an initial fracture" by Ho-Le and colleagues reports on data from the Dubbo cohort that examines first fracture, subsequent fracture and mortality in 2046 women and 1205 men followed for 20 years. The authors report that 31% of the women and 15% of the men sustain a first fracture. The risk of the second fracture is 36% in the women and 22% of the men with a mortality that is higher in the men (41%) than in the women (25%). The key predictors of mortality are being male (HR 2.4), old (HR 1.67), and having fem neck BMD (1.16) – all with acceptable confidence intervals. The authors make a prediction model in an effort to provide an evidence-based treatment decision support. The authors feel the impact of their work will be to "change the perception of osteoporosis" because their work is pointing out the "mortality risk".

1) Abstract:

a) The authors are working on an important area in osteoporosis care – the impact of initial fractures in the elderly and of subsequent fractures on mortality. There is no question mortality is key, but many of the observations that are made and noted in the Abstract of the paper are not new. Male gender and age and BMD – all are known to correlate with poorer outcomes and recurrent fractures in osteoporosis. All the data supporting FRAX and other calculators use these variables. This is not new.

b) Please re-write or revise the sentences in your Abstract as it is not crystal clear what you mean. Is the 31% meaning 31% of the women (634 women)? Did 634 women have a fracture and over what period of time? I think you will need to state the period of observation. Was it the full 20 years? Similarly, with the men (~181 men), when did this 15% have their fractures? Was it 20 years into the collection of data or earlier? Please state this.

c) When you say the patients sustained a second fracture, what does 36% (women) and 22% (men) refer to? Is this referring back to the original group of women – i.e., 36% of the 634, and for men 22% of the 181 men? Please sharpen up the numbers and clarify the detail. The numbers may be in one of the tables, but it should be clear from the Abstract what you are talking about.

d) eTable 1 and 2: the numbers are all different from what you are presenting in the Abstract. Your Abstract needs to be understandable on its own, since most readers only read the Abstract (and then cite or not a paper).

2) When you refer to “eTable 2”, where are the numbers for death following a fragility fracture – 262 women, 105 men. Or are you saying that of the patients who died overall – 627 women, 501 men – these are the %'s of women and men (262 and 105). And the numbers mentioned are "data not shown" in the Tables?

3) eTable 3: what is "instantaneous risk" of transition? Please consider including this definition in the legend to this table. Also please explain what is in the legend. This reviewer does not believe that a general reader will understand (reading the "Note" at the bottom of the table) what was done to generate the numbers in this table. It seems like it will not be clear to the general reader why this set of assumptions were selected. How do the instantaneous risks lead to the Hazard Ratio's in the final column of Table 3 or are they unrelated variables?

4) In the presentation of the results in Figure 2A, if the reviewer is reading the data correctly you are seeing an increased risk of transition to fracture/refracture with history of RA for both men and women, which could be highlighted in the paper. The other factors do include age, FN BMD, and prior fracture which you have mentioned in the Abstract and in the subsection “Risk factors for transition between states”. Of interest, neuromuscular disease and COPD are important predictors of fracture/refracture in men and not in women. Was the statistical power (# of events in this modest sized cohort) sufficient to be definitive about the predictive value of the specific clinical risks and disorder (i.e., enough cases, etc)? This question is for Figure 2A and B.

5) What does the sentence "The predicted probability of mortality (e.g., fracture, refracture or mortality) for women and men…." Do you mean morbidity and mortality, because when you say "mortality" and then say for example – fracture, refracture or mortality – it is not clear what you mean.

6) Figure 3: this is a very important figure in your paper. It is not clear to the reviewer why you chose to do the hypothetical T score of 0 and -2.5 in the text and then chose to do T scores of +0.5 and -2.5 in the Figure 3. Please explain. Also the figure legend describes 5 bone health states but there seem to be only 4 states in the boxes (state 1,2,3,4). In the legend there is no mention of orange, there is mention of green, and there is no green apparent in the figure and there are two different blue's. There needs to be some attention given to clarifying the boxes, the legend and the figure itself and harmonizing it all. What does "event age" mean? Please define it. When you label these "age 60" vs. "age 80", do you mean this is the probability for the next 20 year for mortality (i.e., age 60-80, and ages 80-100)? If all subjects had to be 60 years old + to get into the study, there would be relatively few who were age 60 when their event (fracture) occurred from which to generate these curves. Could you provide insight into what data you had that went into the “age 60” as well as age 80? It is appreciated that these are estimates but what could you be estimating from at age 60 when you are talking about State 3 or 4? It is expected that it would take some years to get that 2nd, 3rd or 4th fracture.

7) Discussion:

a) The progression to premature mortality after a fracture could be due to the acquisition over time of other co-morbid conditions that occur in aging. Are you sure that strokes, infarct, cancer, infections/sepsis/COVID-19 etc did not occur in the years post a fracture? After reading the Materials and methods it is not clear that once a subject is enrolled that he or she would be removed from analysis if terminal cancer developed. Granted you have presumably the same rates of cancer across the board, for example, but some of these groups may not be so large – 2, 3, 4 fractures. There would be no reason to anticipate that terminal events tracked with fractures especially if the fracture was years before or tracked with the fractures. There has been some attention to this issue with hip fractures because of the sarcopenia and disability that they cause – perhaps mortality is related to that attendant frailty. However, here you are counting all fragility fractures and it is hard to see that they would have the same impact as hip fracture on the overall health.

b) In the sixth paragraph of the Discussion you are discussing estimating fracture risk and mortality risk, but you then say that patients "usually underestimate their overall health". Do you mean overestimate their health or underestimate their risk of death?

c) While you have provided models of risk of death, you have not established causality between the fractures and mortality to my review of the paper. Therefore it seems an over-strong statement to say – "…providing the estimated risk of mortality can motivate them to take preventive measures." In an non-interventional, observational study, you cannot assume that fracture prevention will significantly change the mortality risks, curves.

d) Were patients in this cohort ever given any treatments and how did you handle concomitant medications such as estrogen, bisphosphonates, SERM, testosterone and so forth? If the cohort was started in 1989 (21 years would be through 2009), and repeated fractures were occurring in hundreds of these patients, were they treated, if so with what and how was that handled in the data analysis? Were individuals specifically not treated, which would be an ethical issue? You also state (subsection “Participants and Setting”) that the study is ongoing. Surely by now subjects in the cohort have been receiving treatments for osteoporosis.

e) It would be of interest to the reader to know the breakdown of fractures that you counted. How many were clinical vertebral, hip, humerus, rib, tibia, fibula, wrist etc. What kinds of fractures are these models resting on? What are the causes of death in the cohort?

8) The reports were reviewed, but were the fractures adjudicated? Were all deaths confirmed? (Subsection “Fracture ascertainment”).

9) One wonders if Figure 1 is needed and whether the figures mainly containing the dots are needed. Please consider another shorter way to convey this information.

10) Please read the legend to eTable 4. Please revise "the person who ages of 70". There is a misspelling in the legend to Supplementary eFigure 1.

Reviewer #3:

The authors used data from the Dubbo Osteoporosis Epidemiology Study to analyze risk for initial fracture, subsequent fractures and mortality in older men and women followed for 20 years. They found that fractures were common, occurred earlier in women than in men, and were associated with earlier mortality. Mortality risk following a fracture was higher in men compared to women. The authors presented a detailed analysis of refracture and mortality rates in men and women following fracture at age 60 and age 80, to create a prediction model.

1) The major findings of this study are not new. We already know that fractures occur at an earlier age in women compared to men, and that mortality following fracture is higher in men than women. We also know that advancing age and lower BMD are associated with higher risk for fracture. This study presents a more detailed analysis of risk for subsequent fracture and mortality following a fracture than previous studies have done.

2) The author claim to have developed a prediction model to help patients and doctors make evidence-based treatment decisions. I did not find this study to offer a clinically useful risk prediction model, nor does this study address osteoporosis treatment. It does offer new information about mortality following fracture. Life expectancy is not commonly discussed in osteoporosis care, in the way it may be discussed in cancer treatment, for example. Given the average age of participants in this study, and without presenting evidence that osteoporosis treatment can influence mortality rates, I am not sure that these data will be readily incorporated into osteoporosis treatment discussions.

3) Impact Statement: "Our results will change the perception of osteoporosis because it increases mortality risk. The personalized risk prediction model presented here will change the assessment of fracture risk in the future."

Many patients are diagnosed with osteoporosis based on T-score criteria (no prior fracture). Figure 2B shows that in those without prior fracture, BMD is not associated with mortality. Perhaps this impact statement should read "osteoporotic fracture increases mortality risk".

https://doi.org/10.7554/eLife.61142.sa1

Author response

Summary:

This interesting paper aligns quantitatively the recurrence of fractures in a well-known cohort of aging men and women in Australia with mortality over time. The key goal of the paper is to demonstrate that men and women who fracture have greater mortality than non-fracturing individuals. While this message has noted before, the quantitative handling of the data from the cohort is the new and welcome addition to the literature. The authors look at transitions from different states of fracture and estimate instantaneous risks. Mortality has not heretofore been a component in patient-physician joint decision-making about undertaking therapy for osteoporosis.

Thank you for the summary which captures the key idea of the paper. Although the association between fracture and mortality has previously been observed by us and others, many doctors still do not necessarily appreciate that mortality is a consequence of fracture. The current crisis of undertreatment in osteoporosis is thought partly due to the lack of appreciation of mortality risk associated with a fracture.

We think that it is time to change the way fracture risk is communicated. Traditionally, the risk of fracture is conveyed as the probability of sustaining a fracture over a period of time, usually 5 or 10 years. However, given that a fracture is the key risk factor for subsequent fractures and mortality, the new compound risk of fracture should be a combination of the risk that someone will sustain a fracture, and the risk that, once they have sustained a fracture, they will sustain further fractures and die.

That thinking guides this study, in which we developed a Markovian model that helps doctors quantify the risk of subsequent fractures and mortality following a fracture for an individual patient.

Please address the reviewers’ comments and questions below.

Title: Please see the suggestions of reviewer 3 below for possible revision of the title itself for the paper.

We have modified the short title to read as follows: "Predicting mortality and fracture in patients with osteoporosis." We have also changed the title to read "Epidemiological transition to mortality and refracture following an initial fracture".

Reviewer #1:

This is an interesting further analysis of the Dubbo osteoporosis study. Its headline conclusions are easily understood, though the methodology involves esoteric mathematics that will not be readily accessible to clinicians. However, it will be of interest to epidemiologists. My specific questions are as follows:

1) The concept of instantaneous risk will be unfamiliar to many readers. It needs to be explained in more detail to make these sections of the manuscript understandable.

As the reviewer notes, the concept of instantaneous risk is not quite accessible to most readers, but it is the basic concept in survival analysis that has been applied in virtually all scientific disciplines. The concept of instantaneous risk was defined in the “Data Analysis” subsection as follows:

“In the multistate model, the transition from state r to s is governed by transition intensities (qrs) which are estimated from the observed data using the maximum likelihood method. These transition intensities represent the instantaneous risk of moving from current state (state r) to the next state (state s).”

We have added an explanation in the “Data Analysis” subsection:

"Instantaneous risk (also referred to as “hazard”) is the probability that an individual would experience an event at a particular given point in time. This risk is very small over a very short time period, but can accumulate over time. Thus, the incidence of an event is the product of instantaneous risk and length of time."

An example was now added for more details as follows:

“At a given time point, for example, a fracture-free individual (state 1) had an instantaneous risk of staying at that state 1 (q11), an instantaneous risks of suffering initial fracture (q12), and an instantaneous risk of death (q15). These instantaneous risks were estimated for an individual based on the individual’s risk profile and adjusted for age. From these instantaneous risks, we can quantify the individualised risk of fracture, refracture, and mortality for an individual”.

2) Subsection “Instantaneous risk of transition between health states”, where instantaneous risks are being presented, have these calculations been adjusted for age? Those who have already had one, two or three fractures will on average be older than those with fewer fractures and so this will impact on their risk of the next fracture or of death.

The reviewer raises an important point. The instantaneous risk has been adjusted for age. This is now clarified in the manuscript in the “Data Analysis” subsection as follows:

"These instantaneous risks were estimated for individuals based on the individual’s risk profile and adjusted for age."

3) The discussions of "typical 70 year olds" are problematic where risk at a T-score of 0 is contrasted with a risk of a T-score of -2.5. T=0 is certainly not typical of a 70 year old, where the average value is closer to -2.0.

We agree with the reviewer's suggestion, and have re-estimated the risk for T-score = -1.5 (Table 2 and Table 4).

Reviewer #2:

The manuscript "Predicting mortality and refracture following an initial fracture" by Ho-Le and colleagues reports on data from the Dubbo cohort that examines first fracture, subsequent fracture and mortality in 2046 women and 1205 men followed for 20 years. The authors report that 31% of the women and 15% of the men sustain a first fracture. The risk of the second fracture is 36% in the women and 22% of the men with a mortality that is higher in the men (41%) than in the women (25%). The key predictors of mortality are being male (HR 2.4), old (HR 1.67), and having fem neck BMD (1.16) – all with acceptable confidence intervals. The authors make a prediction model in an effort to provide an evidence-based treatment decision support. The authors feel the impact of their work will be to "change the perception of osteoporosis" because their work is pointing out the "mortality risk".

The link between mortality and osteoporosis is not widely appreciated. In this study we provide evidence from a well characterized cohort to show that fracture does increase the risk of mortality, and that risk should be part of the fracture risk assessment.

We consider that the communication of fracture risk should incorporate mortality risk. Until now, the risk of fracture has been conveyed to patients as the probability of having a fracture over period of time. However, we think that this is inadequate, because the risk should encompass the risks of subsequent fractures and mortality. The new compound risk of fracture should therefore be a combination of the risk that someone will sustain a fracture, and the risk that, once they have sustained a fracture, they will sustain further fractures and die. This work contributes to that research direction.

1) Abstract:

a) The authors are working on an important area in osteoporosis care – the impact of initial fractures in the elderly and of subsequent fractures on mortality. There is no question mortality is key, but many of the observations that are made and noted in the Abstract of the paper are not new. Male gender and age and BMD – all are known to correlate with poorer outcomes and recurrent fractures in osteoporosis. All the data supporting FRAX and other calculators use these variables. This is not new.

Our focus is not on risk factors for fracture (which is not new); this work focuses on the risk factors for transition between health states (e.g. no fracture to fracture, fracture to refracture, fracture to death, etc). Both Garvan Fracture Risk Calculator and FRAX at present estimate the risk of fracture, not the risk of refractures or mortality. Thus, as mentioned above, we consider that our work is unique and will pave way for a new generation of models for fracture risk assessment.

b) Please re-write or revise the sentences in your Abstract as it is not crystal clear what you mean. Is the 31% meaning 31% of the women (634 women)? Did 634 women have a fracture and over what period of time? I think you will need to state the period of observation. Was it the full 20 years? Similarly, with the men (~181 men), when did this 15% have their fractures? Was it 20 years into the collection of data or earlier? Please state this.

We have rewritten the Abstract, including the mentioned sentence: "During the 20-year follow-up period, among 632 women and 184 men those with a first incident fracture, the risk of sustaining a second fracture was higher in women (36%) than men (22%), but mortality risk was higher in men (41%) than women (25%).” This is shown in the paper's new diagram (Figure 1) and the updated Supplementary file 2.

c) When you say the patients sustained a second fracture, what does 36% (women) and 22% (men) refer to? Is this referring back to the original group of women – i.e., 36% of the 634, and for men 22% of the 181 men? Please sharpen up the numbers and clarify the detail. The numbers may be in one of the tables, but it should be clear from the Abstract what you are talking about.

The figures of 36% (in women) and 22% (in men) refer to the incidence of second fracture among 632 women and 184 men with an initial incident fracture. This is now clarified in the revised Abstract and the new diagram (Figure 1).

d) eTable 1 and 2: the numbers are all different from what you are presenting in the Abstract. Your Abstract needs to be understandable on its own, since most readers only read the Abstract (and then cite or not a paper).

We thank the reviewer for this comment. The data mentioned in the Abstract are consistent with eTable 2. However, eTable 2 gives more specific data than the text mentioned. We have rewritten the Abstract, updated the eTable 2 (now mentioned as Supplementary file 2), and added a data flow (Figure 1) to demonstrate the number of each state.

2) When you refer to “eTable 2”, where are the numbers for death following a fragility fracture – 262 women, 105 men. Or are you saying that of the patients who died overall – 627 women, 501 men – these are the %'s of women and men (262 and 105). And the numbers mentioned are "data not shown" in the tables?

The numbers (262 women and 105 men) were derived as the total numbers of women and men who died after an initial fracture + second fracture + subsequent fractures, which were 156+60+46 = 262 for women and 75+22+8 = 105 for men. We have updated eTable 2 (now mentioned as Supplementary file 2) and added a flowchart (Figure 1) to clarify the numbers.

3) eTable 3: what is "instantaneous risk" of transition? Please consider including this definition in the legend to this table. Also please explain what is in the legend. This reviewer does not believe that a general reader will understand (reading the "Note" at the bottom of the table) what was done to generate the numbers in this table. It seems like it will not be clear to the general reader why this set of assumptions were selected. How do the instantaneous risks lead to the Hazard Ratio's in the final column of Table 3 or are they unrelated variables?

We thank the reviewer for this comment. We have moved eTable 3 to the main text (Table 2). We have added an explanation of the concept of instantaneous risk in the “Data Analysis” subsection, which are shown in reviewer 1, comment 1. We have updated the legend of Table 2 to read as follows:

“"Fx", fracture. CI, Confidence interval. […] In each cell, values are percentage of risk and 95% confident interval (in the brackets).”

The hazard ratios in the final column of the table show the ratios of the risks between men and women at each transition, adjusted for age, BMD, history of fall, prior fracture, and comorbidities. This has been clarified in the legend of Table 2.

4) In the presentation of the results in Figure 2A, if the reviewer is reading the data correctly you are seeing an increased risk of transition to fracture/refracture with history of RA for both men and women, which could be highlighted in the paper. The other factors do include age, FN BMD, and prior fracture which you have mentioned in the Abstract and in the subsection “Risk factors for transition between states”. Of interest, neuromuscular disease and COPD are important predictors of fracture/refracture in men and not in women. Was the statistical power (# of events in this modest sized cohort) sufficient to be definitive about the predictive value of the specific clinical risks and disorder (i.e., enough cases, etc)? This question is for Figure 2A and 2B.

The reviewer is correct that women and men with RA had higher risk of transition to fracture/refracture. We have highlighted this finding in the Results section to read as follows:

“In both women and men, having rheumatoid arthritis were more likely to have increased risk of initial fracture and second fracture”.

However, the main purpose of this study was to investigate the impact of advancing age and BMD on the risk of fracture/refracture/mortality. Because all of the concomitant diseases were based on self-report, we were not quite confident in the estimates of association.

5) What does the sentence "The predicted probability of mortality (e.g., fracture, refracture or mortality) for women and men…." Do you mean morbidity and mortality, because when you say "mortality" and then say for example – fracture, refracture or mortality – it is not clear what you mean.

We thank the reviewer for his/her comment. The sentence "The predicted probability of mortality.…" refers to the adjusted cumulative probability of mortality by fracture status. We have removed the sentence because it is confusing.

6) Figure 3: this is a very important figure in your paper. It is not clear to the reviewer why you chose to do the hypothetical T score of 0 and -2.5 in the text and then chose to do T scores of +0.5 and -2.5 in the Figure 3. Please explain.

The original choice of T-scores was for the purpose of risk contrasting between an individual with normal BMD (T-score = 0) and an osteoporotic individual (T-score = -2.5). However, we think the reviewer 3's point is valid, and we have set the T-score at -1.5 which is the average BMD T-score value for the 70-year old women and men. Thus, Figure 3 has now been modified to show the contrast between T-score of -1.5 and -2.5.

Also the figure legend describes 5 bone health states but there seem to be only 4 states in the boxes (state 1,2,3,4).

Thank you. State 5 is death which is shown in Figure 3. We have corrected the legend of Figure 3 and Figure 3—figure supplement 1 to read as follows:

“There were 4 potential bone heath states an individual could stay before transiting to state 5 (mortality): state 1: No fracture (blue area) if the individual entered the study without any osteoporotic fracture; state 2: initial fracture (light blue area) if an individual had sustained a fracture after study entry; state 3: Second fracture (orange area) if an individual had suffered a second fracture; and state 4: Third and further fractures (red area) if an individual had suffered two or more subsequent fractures during the follow-up period.”

In the legend there is no mention of orange, there is mention of green, and there is no green apparent in the figure and there are two different blue's. There needs to be some attention given to clarifying the boxes, the legend and the figure itself and harmonizing it all.

The legend has now been corrected as above. Thank you.

What does "event age" mean? Please define it.

Event age is the age of an individual at the beginning of each state. We have added this definition to the “Data Analysis” subsection to read as follows:

“Age was included in the model as a time-variant factor, and for simplicity, age henceforth is referred to as age at event. […] Immortal time bias could occur in groups where individuals transitioned through several states as they had to survive long enough to be able to make these transitions.”

When you label these "age 60" vs. "age 80", do you mean this is the probability for the next 20 year for mortality (i.e., age 60-80, and ages 80-100)?

That “age 60” or “age 80” is the age of an individual at the beginning of each heath state. We estimated the risk that an individual may die at any time within t years from the current state, t ranges from 0 to 20 as shown in the X axis of Figure 3. For example, t = 5 means 5-year probability of mortality for women and men at the age of 60 (i.e. from age 60 to 65) or for women and men at the age of 80 (i.e. from age 80 to 85).

If all subjects had to be 60 years old + to get into the study, there would be relatively few who were age 60 when their event (fracture) occurred from which to generate these curves. Could you provide insight into what data you had that went into the “age 60” as well as age 80? It is appreciated that these are estimates but what could you be estimating from at age 60 when you are talking about State 3 or 4? It is expected that it would take some years to get that 2nd, 3rd or 4th fracture.

The reviewer is correct that it takes some years to move from one state to another (eg fracture to mortality). As explained above, we used the “event age” at the begining of each health state as an input variable. We have provided in Author response table 1 data on fracture incidence stratified by age groups for your perusal.

Author response table 1
Event age (years)
60-6970-79≥80Total
Baseline age (years)60-6915820968435
70-79-115171286
≥80--9595
Total158324334816

7) Discussion:a) The progression to premature mortality after a fracture could be due to the acquisition over time of other co-morbid conditions that occur in aging. Are you sure that strokes, infarct, cancer, infections/sepsis/COVID-19 etc did not occur in the years post a fracture? After reading the Materials and methods it is not clear that once a subject is enrolled that he or she would be removed from analysis if terminal cancer developed.

We thank the reviewer for his/her comment. We only adjusted for baseline comorbidities, because we have not ascertained the incidence of comorbidities over time. We have discussed this as a potientalweakness of study:

“Comorbidities occurred during the follow-up time were not ascertained, and could not treat as time-variant covariates in the analysis.”

Granted you have presumably the same rates of cancer across the board, for example, but some of these groups may not be so large – 2, 3, 4 fractures. There would be no reason to anticipate that terminal events tracked with fractures especially if the fracture was years before or tracked with the fractures. There has been some attention to this issue with hip fractures because of the sarcopenia and disability that they cause – perhaps mortality is related to that attendant frailty. However, here you are counting all fragility fractures and it is hard to see that they would have the same impact as hip fracture on the overall health.

We agree that the increased mortality risk after a hip fracture could be attributed to frailty and comorbidities. However, a number of previous studies have shown that even after accounting for frailty and comorbidities, patients with a hip fracture still have excess mortality risk.

b) In the sixth paragraph of the Discussion you are discussing estimating fracture risk and mortality risk, but you then say that patients "usually underestimate their overall health". Do you mean overestimate their health or underestimate their risk of death?

The reviewer is correct. We have rewritten the text under the Discussion section as follows:

"Patients do not always appreciate the serious consequence of fracture (e.g. subsequent fractures and mortality), and as a result, they usually underestimate their risk of adverse outcomes".

c) While you have provided models of risk of death, you have not established causality between the fractures and mortality to my review of the paper. Therefore it seems an over-strong statement to say – "…providing the estimated risk of mortality can motivate them to take preventive measures." In an non-interventional, observational study, you cannot assume that fracture prevention will significantly change the mortality risks, curves.

Although we could monitor the movement between health states, we could not make any causal inference from the data, because this is an observational study. However, there are several lines of evidence (from randomized controlled trials [RCT]) that treating patients with osteoporosis and/or fracture reduces their risk of fracture by approximately 50%. We also have RCT evidence that treating patients with a hip fracture reduces their risk of mortality by between 28 and 35%. Thus, these evidence into context, we consider that our statement is not that strong. We have mentioned these studies in the Discussion section as follows:

“Evidence from randomized controlled trials suggest that in patients with osteoporosis and/or a pre-existing fracture, bisphosphonate treatment reduces fracture risk and mortality risk. […] However, a recent meta-analysis found that the effect of bisphosphonate treatment on mortality was less certain (Cummings et al., 2019).”

d) Were patients in this cohort ever given any treatments and how did you handle concomitant medications such as estrogen, bisphosphonates, SERM, testosterone and so forth? If the cohort was started in 1989 (21 years would be through 2009), and repeated fractures were occurring in hundreds of these patients, were they treated, if so with what and how was that handled in the data analysis? Were individuals specifically not treated, which would be an ethical issue? You also state (subsection “Participants and Setting”) that the study is ongoing. Surely by now subjects in the cohort have been receiving treatments for osteoporosis.

A small proportion (<2% of participants) has been on any anti-osteoporosis treatment. Due to the small sample size of treated individuals, we did not consider treatment in the model of analysis.

e) It would be of interest to the reader to know the breakdown of fractures that you counted. How many were clinical vertebral, hip, humerus, rib, tibia, fibula, wrist etc. What kinds of fractures are these models resting on? What are the causes of death in the cohort?

The incidence of fractures stratified by gender is shown in Author response table 2:

Author response table 2
Fracture typeWomenMenTotal
Hip fracture8729116
Vertebral fracture24080320
Non-hip non-vertebral fracture30575380
Total632184816

We could not ascertain the cause of death in the study, and this is a weakness that we have mentioned in the Discussion section to read as follows:

“However, the cause of death was not available, and it was not possible to conduct an in-depth analysis of mortality attributable risk.”

8) The reports were reviewed, but were the fractures adjudicated? Were all deaths confirmed? (Subsection “Fracture ascertainment”).

Yes, all deaths were confirmed and all fractures were adjudicated. These information have been clarified in the subsection “Fracture ascertainment”, as follows:

"Fractures occurring during the study period were identified through radiologists’ reports from the only two radiology centers providing X-ray services within the Dubbo region as previously described. […] In this study, we included only fractures having definite reports and resulting from low-energy trauma such as falls from standing height or less in this analysis."

“The incidence of death was ascertained by the NSW Registry of Births, Death and Marriages. Deaths were also monitored by systematically searching funeral director lists, local newspapers and on radio or by word of mouth with a confirmation or bi-annual telephone contact.”

9) One wonders if Figure 1 is needed and whether the figures mainly containing the dots are needed. Please consider another shorter way to convey this information.

Thank you for the suggestion. The dot figures visualize the data shown in Table 2. However, we agree with the reviewer that Figure 1 is no longer required.

10) Please read the legend to eTable 4. Please revise "the person who ages of 70". There is a misspelling in the legend to Supplementary eFigure 1.

Thank you. We have moved the eTable 4 to the main text (Table 3) and the legend is now rewritten as follows: "at the age of 70". The eFigure 1 has been moved to the main text (Figure 4) and the legend has now been corrected to read as follows:

“Figure 4: Markovian model of transition between 5 heath states (e.g. alive without a fracture, initial fracture, second fracture, third and further fracture, and death). […] At a given time point, for example, a fracture-free individual (state 1) had an instantaneous risk of staying at that state 1 (q11), an instantaneous risks of suffering initial fracture (q12), and an instantaneous risk of death (q15)”.

Reviewer #3:

The authors used data from the Dubbo Osteoporosis Epidemiology Study to analyze risk for initial fracture, subsequent fractures and mortality in older men and women followed for 20 years. They found that fractures were common, occurred earlier in women than in men, and were associated with earlier mortality. Mortality risk following a fracture was higher in men compared to women. The authors presented a detailed analysis of refracture and mortality rates in men and women following fracture at age 60 and age 80, to create a prediction model.

Thank you for taking time to consider our manuscript. We think that mortality should be part of the doctor – patient communication. The "risk of fracture" should encompass the probability of sustaining a future fracture, and one a fracture has occurred, the probability of mortality. That thinking underlies the model developed here.

1) The major findings of this study are not new. We already know that fractures occur at an earlier age in women compared to men, and that mortality following fracture is higher in men than women. We also know that advancing age and lower BMD are associated with higher risk for fracture. This study presents a more detailed analysis of risk for subsequent fracture and mortality following a fracture than previous studies have done.

We thank the reviewer for his/her comment. The focus of this study is not on the association between fracture and mortality which we and others have previously shown. Our focus is on the development of a new prediction model for quantifying the risks of transition between health states (e.g. fracture to refracture, fracture to death, refracture to death, etc). This Markovian model is first introduced in the field of osteoporosis research. In the Discussion, we also introduce the idea of “skeletal age” for fracture and mortality risk communication.

2) The author claim to have developed a prediction model to help patients and doctors make evidence-based treatment decisions. I did not find this study to offer a clinically useful risk prediction model, nor does this study address osteoporosis treatment. It does offer new information about mortality following fracture. Life expectancy is not commonly discussed in osteoporosis care, in the way it may be discussed in cancer treatment, for example. Given the average age of participants in this study, and without presenting evidence that osteoporosis treatment can influence mortality rates, I am not sure that these data will be readily incorporated into osteoporosis treatment discussions.

The prediction model is shown in Table 2, Table 4, Figures 2A and B, and illustrated by Figure 4. In the revised manuscript, we further provide an example of interpretation in terms of what we call “skeletal age” (Discussion section). For example, for a 70 years old man who has sustained a fracture, the hazard ratio of 1.67 is equivalent to a loss of 5.4 years of life. In other words, for the 70 years old man, the hazard ratio of 1.67 corresponds to a skeletal age of 75.4 years.

Several lines of evidence suggest that bisphosphonate (the first line pharmacologic treatment for osteoporosis) is associated with reduced mortality risk. For instance, data from randomized controlled clinical trial show that in osteoporotic patients with a preexisting fracture, zoledronic acid reduces fracture risk and mortality risk (Lyles et al., 2007; Reid et al., 2018). The beneficial effect of treatment (relative risk reduction of mortality) can also be expressed in terms of “skeletal age”. We have discussed this point in the manuscript (Discussion section) as follows:

“Evidence from randomized controlled trials suggest that in patients with osteoporosis and/or a pre-existing fracture, bisphosphonate treatment reduces fracture risk and mortality risk. […] Taken together, these results suggest that in osteoporotic or osteopenic patients with a fracture, bisphosphonate treatment may reduce mortality risk. The beneficial effect of treatment can also be expressed in terms of “skeletal age”.”

We also revised the conclusion of the Abstract to read as follows:

"These results were incorporated into a prediction model to aid patient-doctor discussion about fracture vulnerability and treatment decisions."

In the future, we will also implement a web based risk calculator that incorporates life expectancy into fracture risk assessment.

3) Impact Statement: "Our results will change the perception of osteoporosis because it increases mortality risk. The personalized risk prediction model presented here will change the assessment of fracture risk in the future."

Many patients are diagnosed with osteoporosis based on T-score criteria (no prior fracture). Figure 2B shows that in those without prior fracture, BMD is not associated with mortality. Perhaps this impact statement should read "osteoporotic fracture increases mortality risk".

We have modified the Impact Statement as follows:

"The concept of compound fracture risk is redefined to combine the risk that an individual will sustain a fracture, and the risk of mortality once a fracture has occurred."

https://doi.org/10.7554/eLife.61142.sa2

Article and author information

Author details

  1. Thao Phuong Ho-Le

    1. Healthy Ageing Theme, Garvan Institute of Medical Research, Darlinghurst, Australia
    2. Swinburne University of Technology, Melbourne, Australia
    3. Faculty of Engineering and Information Technology, Hatinh University, Hatinh, Viet Nam
    Contribution
    Conceptualization, Data curation, Software, Formal analysis, Validation, Visualization, Methodology, Writing - original draft, Writing -review and editing
    For correspondence
    t.ho-le@garvan.org.au
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-8387-1893

  2. Thach S Tran

    1. Healthy Ageing Theme, Garvan Institute of Medical Research, Darlinghurst, Australia
    2. St Vincent Clinical School, UNSW Sydney, Sydney, Australia
    Contribution
    Data curation, Formal analysis, Methodology, Writing - original draft, Writing - review and editing
    Competing interests
    No competing interests declared

  3. Dana Bliuc

    1. Healthy Ageing Theme, Garvan Institute of Medical Research, Darlinghurst, Australia
    2. St Vincent Clinical School, UNSW Sydney, Sydney, Australia
    Contribution
    Conceptualization, Data curation, Writing - review and editing
    Competing interests
    No competing interests declared

  4. Hanh M Pham

    1. Healthy Ageing Theme, Garvan Institute of Medical Research, Darlinghurst, Australia
    2. Fertility Department, Andrology and Fertility Hospital of Hanoi, Hanoi, Viet Nam
    Contribution
    Data curation, Formal analysis, Methodology, Writing - original draft, Writing - review and editing
    Competing interests
    No competing interests declared

  5. Steven A Frost

    Healthy Ageing Theme, Garvan Institute of Medical Research, Darlinghurst, Australia
    Contribution
    Formal analysis, Investigation, Writing - review and editing
    Competing interests
    No competing interests declared

  6. Jacqueline R Center

    1. Healthy Ageing Theme, Garvan Institute of Medical Research, Darlinghurst, Australia
    2. St Vincent Clinical School, UNSW Sydney, Sydney, Australia
    Contribution
    Resources, Data curation, Investigation, Writing - review and editing
    Competing interests
    has given educational talks for and received travel expenses from Amgen, Merck Sharp & Dohme, Novartis, Sanofi-Aventis. She has received travel expenses from Merck Sharp & Dohme, Amgen and Aspen.

  7. John A Eisman

    1. Healthy Ageing Theme, Garvan Institute of Medical Research, Darlinghurst, Australia
    2. St Vincent Clinical School, UNSW Sydney, Sydney, Australia
    3. School of Medicine Sydney, University of Notre Dame Australia, Sydney, Australia
    Contribution
    Conceptualization, Resources, Investigation, Project administration, Writing - review and editing
    Competing interests
    has served as consultant on Scientific Advisory Boards for Amgen, 35 Eli Lilly, Merck Sharp & Dohme, Novartis, Sanofi-Aventis, Servier and deCode.

  8. Tuan V Nguyen

    1. Healthy Ageing Theme, Garvan Institute of Medical Research, Darlinghurst, Australia
    2. St Vincent Clinical School, UNSW Sydney, Sydney, Australia
    3. School of Medicine Sydney, University of Notre Dame Australia, Sydney, Australia
    4. School of Biomedical Engineering, University of Technology, Sydney, Australia
    Contribution
    Conceptualization, Resources, Data curation, Formal analysis, Supervision, Funding acquisition, Validation, Investigation, Methodology, Writing - original draft, Project administration, Writing - review and editing
    For correspondence
    t.nguyen@garvan.org.au
    Competing interests
    has received honoraria for consulting or speaking in symposia sponsored by Merck Sharp & Dohme, Roche, Sanofi-Aventis, Novartis, Amgen, and Bridge Healthcare Pty Ltd (Vietnam).

Funding

National Health and Medical Research Council (NHMRC APP1195305)

  • Tuan V Nguyen

Amgen (Competitive Grant Program (2019))

  • Tuan V Nguyen

Amgen (Christine & T. Jack Martin Research travel grant)

  • Thao Phuong Ho-Le

Australian and New Zealand Bone and Mineral Society (Christine & T. Jack Martin Research travel grant)

  • Thao Phuong Ho-Le

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

The authors gratefully acknowledge the expert assistance of Janet Watters, Donna Reeves, Shaye Field, and Jodie Rattey in the interview, data collection, and measurement of bone densitometry, and the invaluable help of the Dubbo Base Hospital radiology staff, PRP Radiology and Orana radiology. We thank the IT group of the Garvan Institute of Medical Research for help in managing the data. This work is supported by NHMRC and in part by a grant from the Amgen Competitive Grant Program (2019).

Ethics

Human subjects: The study was approved by the Ethics Committee of St Vincent's Hospital (Sydney) (HREC reference number: 13/254) and carried out according to the Australian National Health and Medical Research Council (NHMRC) Guidelines, consistent with the Declaration of Helsinki (established in 1964 and revised in 1989) (US Food and Drug Administration). All participants have provided written informed consent.

Senior Editor

  1. Clifford J Rosen, Maine Medical Center Research Institute, United States

Reviewing Editor

  1. Dolores Shoback, University of California, San Francisco, United States

Reviewer

  1. Gina Woods

Publication history

  1. Received: July 16, 2020
  2. Accepted: January 25, 2021
  3. Accepted Manuscript published: February 9, 2021 (version 1)
  4. Version of Record published: March 2, 2021 (version 2)

Copyright

© 2021, Ho-Le et al.

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

  • 1,572
    Page views
  • 176
    Downloads
  • 8
    Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Thao Phuong Ho-Le
  2. Thach S Tran
  3. Dana Bliuc
  4. Hanh M Pham
  5. Steven A Frost
  6. Jacqueline R Center
  7. John A Eisman
  8. Tuan V Nguyen
(2021)
Epidemiological transition to mortality and refracture following an initial fracture
eLife 10:e61142.
https://doi.org/10.7554/eLife.61142

Categories and tags

Research organism

    1. Related to

    Osteoporotic Fracture: Bone age is not just for kids

    Jane A Cauley, Dolores M Shoback
  2. Further reading

Further reading

    1. Epidemiology and Global Health
    2. Medicine

    Osteoporotic Fracture: Bone age is not just for kids

    Jane A Cauley, Dolores M Shoback
    Insight

    More informed discussions between physicians and older adults about the consequences of an initial osteoporotic fracture could encourage more patients to consider treatments that protect against future fracture.

    1. Epidemiology and Global Health

    Nation-wide participation in FIT-based colorectal cancer screening in Denmark during the COVID-19 pandemic: An observational study

    Tina Bech Olesen, Henry Jensen ... Morten Rasmussen
    Research Article

    Background: Worldwide, most colorectal cancer screening programmes were paused at the start of the COVID-19 pandemic, whilst the Danish faecal immunochemical test (FIT)-based programme continued without pausing. We examined colorectal cancer screening participation and compliance with subsequent colonoscopy in Denmark throughout the pandemic.

    Methods: We used data from the Danish Colorectal Cancer Screening Database among individuals aged 50-74 years old invited to participate in colorectal cancer screening from 2018-2021 combined with population-wide registries. Using a generalised linear model, we estimated prevalence ratios (PR) and 95% confidence intervals (CI) of colorectal cancer screening participation within 90 days since invitation and compliance with colonoscopy within 60 days since a positive FIT test during the pandemic in comparison with the previous years adjusting for age, month and year of invitation.

    Results: Altogether, 3,133,947 invitations were sent out to 1,928,725 individuals and there were 94,373 positive FIT tests (in 92,848 individuals) during the study period. Before the pandemic, 60.7% participated in screening within 90 days. A minor reduction in participation was observed at the start of the pandemic (PR=0.95; 95% CI: 0.94-0.96 in pre-lockdown and PR=0.85; 95% CI: 0.85-0.86 in 1st lockdown) corresponding to a participation rate of 54.9% during pre-lockdown and 53.0% during 1st lockdown. This was followed by a 5-10% increased participation in screening corresponding to a participation rate of up to 64.9%. The largest increase in participation was observed among 55-59 year olds and among immigrants. The compliance with colonoscopy within 60 days was 89.9% before the pandemic. A slight reduction was observed during 1st lockdown (PR=0.96; 95% CI: 0.93-0.98), where after it resumed to normal levels.

    Conclusions: Participation in the Danish FIT-based colorectal cancer screening programme and subsequent compliance to colonoscopy after a positive FIT result was only slightly affected by the COVID-19 pandemic.

    Funding: The study was funded by the Danish Cancer Society Scientific Committee (grant number R321-A17417) and the Danish regions.

    1. Epidemiology and Global Health
    2. Medicine

    Antibody levels following vaccination against SARS-CoV-2: associations with post-vaccination infection and risk factors in two UK longitudinal studies

    Nathan J Cheetham, Milla Kibble ... Claire J Steves
    Research Article

    Background: SARS-CoV-2 antibody levels can be used to assess humoral immune responses following SARS-CoV-2 infection or vaccination, and may predict risk of future infection. Higher levels of SARS-CoV-2 anti-Spike antibodies are known to be associated with increased protection against future SARS-CoV-2 infection. However, variation in antibody levels and risk factors for lower antibody levels following each round of SARS-CoV-2 vaccination have not been explored across a wide range of socio-demographic, SARS-CoV-2 infection and vaccination, and health factors within population-based cohorts.

    Methods: Samples were collected from 9,361 individuals from TwinsUK and ALSPAC UK population-based longitudinal studies and tested for SARS-CoV-2 antibodies. Cross-sectional sampling was undertaken jointly in April-May 2021 (TwinsUK, N = 4,256; ALSPAC, N = 4,622), and in TwinsUK only in November 2021-January 2022 (N = 3,575). Variation in antibody levels after first, second, and third SARS-CoV-2 vaccination with health, socio-demographic, SARS-CoV-2 infection and SARS-CoV-2 vaccination variables were analysed. Using multivariable logistic regression models, we tested associations between antibody levels following vaccination and: (1) SARS-CoV-2 infection following vaccination(s); (2) health, socio-demographic, SARS-CoV-2 infection and SARS-CoV-2 vaccination variables.

    Results: Within TwinsUK, single-vaccinated individuals with the lowest 20% of anti-Spike antibody levels at initial testing had 3-fold greater odds of SARS-CoV-2 infection over the next six to nine months (OR = 2.9, 95% CI: 1.4, 6.0), compared to the top 20%. In TwinsUK and ALSPAC, individuals identified as at increased risk of COVID-19 complication through the UK 'Shielded Patient List' had consistently greater odds (2- to 4-fold) of having antibody levels in the lowest 10%. Third vaccination increased absolute antibody levels for almost all individuals, and reduced relative disparities compared with earlier vaccinations.

    Conclusions: These findings quantify the association between antibody level and risk of subsequent infection, and support a policy of triple vaccination for the generation of protective antibodies.

    Funding: Antibody testing was funded by UK Health Security Agency. The National Core Studies program is funded by COVID-19 Longitudinal Health and Wellbeing - National Core Study (LHW-NCS) HMT/UKRI/MRC (MC_PC_20030 & MC_PC_20059). Related funding was also provided by the NIHR 606 (CONVALESCENCE grant COV-LT-0009). TwinsUK is funded by the Wellcome Trust, Medical Research Council, Versus Arthritis, European Union Horizon 2020, Chronic Disease Research Foundation (CDRF), Zoe Ltd and the National Institute for Health Research (NIHR) Clinical Research Network (CRN) and Biomedical Research Centre based at Guy's and St Thomas' NHS Foundation Trust in partnership with King's College London. The UK Medical Research Council and Wellcome (Grant ref: 217065/Z/19/Z) and the University of Bristol provide core support for ALSPAC.