Research Article

Neuroscience

Learning to stand with unexpected sensorimotor delays

School of Physical Education, Sport, and Exercise Sciences, University of Otago, New Zealand
Department of Neuroscience, Erasmus MC, University Medical Center Rotterdam, Netherlands
School of Kinesiology, University of British Columbia, Canada
Faculty of Kinesiology, University of Calgary, Canada
Hotchkiss Brain Institute, Canada
Faculty of Kinesiology, University of New Brunswick, Canada
Djavad Mowafaghian Centre for Brain Health, University of British Columbia, Canada
Institute for Computing, Information and Cognitive Systems, University of British Columbia, Canada

Aug 10, 2021

https://doi.org/10.7554/eLife.65085

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record updated: October 5, 2021 (This version)
Version of Record published: September 29, 2021 (Go to version)
Accepted Manuscript published: August 10, 2021 (Go to version)
Accepted: August 4, 2021
Received: November 22, 2020

1. Of interest
Translation of dipeptide repeat proteins in C9ORF72 ALS/FTD through unique and redundant AUG initiation codons

Yoshifumi Sonobe, Soojin Lee ... Paschalis Kratsios

Research Article Sep 29, 2023
Further reading

Abstract
eLife digest
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Human standing balance relies on self-motion estimates that are used by the nervous system to detect unexpected movements and enable corrective responses and adaptations in control. These estimates must accommodate for inherent delays in sensory and motor pathways. Here, we used a robotic system to simulate human standing about the ankles in the anteroposterior direction and impose sensorimotor delays into the control of balance. Imposed delays destabilized standing, but through training, participants adapted and re-learned to balance with the delays. Before training, imposed delays attenuated vestibular contributions to balance and triggered perceptions of unexpected standing motion, suggesting increased uncertainty in the internal self-motion estimates. After training, vestibular contributions partially returned to baseline levels and larger delays were needed to evoke perceptions of unexpected standing motion. Through learning, the nervous system accommodates balance sensorimotor delays by causally linking whole-body sensory feedback (initially interpreted as imposed motion) to self-generated balance motor commands.

eLife digest

When standing, neurons in the brain send signals to skeletal muscles so we can adjust our movements to stay upright based on the requirements from the surrounding environment. The long nerves needed to connect our brain, muscles and sensors lead to considerable time delays (up to 160 milliseconds) between sensing the environment and the generation of balance-correcting motor signals. Such delays must be accounted for by the brain so it can adjust how it regulates balance and compensates for unexpected movements.

Aging and neurological disorders can lead to lengthened neural delays, which may result in poorer balance. Computer modeling suggests that we cannot maintain upright balance if delays are longer than 300-340 milliseconds. Directly assessing the destabilizing effects of increased delays in human volunteers can reveal how capable the brain is at adapting to this neurological change.

Using a custom-designed robotic balance simulator, Rasman et al. tested whether healthy volunteers could learn to balance with delays longer than the predicted 300-340 millisecond limit. In a series of experiments, 46 healthy participants stood on the balance simulator which recreates the physical sensations and neural signals for balancing upright based on a computer-driven virtual reality. This unique device enabled Rasman et al. to artificially impose delays by increasing the time between the generation of motor signals and resulting whole-body motion.

The experiments showed that lengthening the delay between motor signals and whole-body motion destabilized upright standing, decreased sensory contributions to balance and led to perceptions of unexpected movements. Over five days of training on the robotic balance simulator, participants regained their ability to balance, which was accompanied by recovered sensory contributions and perceptions of expected standing, despite the imposed delays. When a subset of participants was tested three months later, they were still able to compensate for the increased delay.

The experiments show that the human brain can learn to overcome delays up to 560 milliseconds in the control of balance. This discovery may have important implications for people who develop balance problems because of older age or neurologic diseases like multiple sclerosis. It is possible that robot-assisted training therapies, like the one in this study, could help people overcome their balance impairments.

Introduction

The nervous system learns and maintains motor skills by forming probabilistic estimates of self-motion. The resulting inferred relationships between sensory and motor signals form a representation of the world and self that allows the brain to identify unexpected behavior and adapt motor control (Friston, 2010; Krakauer and Mazzoni, 2011; Wolpert et al., 2011). Due to neural conduction delays, these estimates of self-motion rely on the expected timing between motor commands and resulting sensory feedback. As such, errors associated with self-generated movement increase with larger feedback delays (Gifford and Lyman, 1967; Miall et al., 1985; Smith et al., 1960). Through repeated exposure to an imposed delay, the brain can learn to expect the delayed feedback associated with self-motion, leading to improvements in movement control with delays up to 430 ms (Cunningham et al., 2001; Miall and Jackson, 2006). When balancing upright, sensory feedback associated with lower-limb motor commands is delayed by up to ~100–160 ms (Forbes et al., 2018; Kuo, 2005; van der Kooij et al., 1999). As a consequence of these relatively long delays, computational feedback models of upright standing predict that balance controllers cannot adjust their sensorimotor gains and stabilize balance in the anteroposterior (AP) direction with imposed delays larger than ~300–340 ms (Milton and Insperger, 2019; van der Kooij and Peterka, 2011). These predictions contrast the reported upper-limb sensorimotor adaptation to imposed delays (Cunningham et al., 2001; Miall and Jackson, 2006). The present study aims to directly quantify the destabilizing effects of imposed delays between ankle torque and whole-body motion during standing balance, and to determine the underlying mechanisms responsible for any subsequent adaptation and learning.

Imposed delays inserted within the balance control task are expected to increase postural oscillations and, past a critical delay, lead to falls (Bingham et al., 2011; Milton and Insperger, 2019; van der Kooij and Peterka, 2011). The sensorimotor mechanisms underlying these predicted effects, however, are unknown. Of particular interest is the vestibular control of balance due to its task-dependent modulations (Fitzpatrick and McCloskey, 1994; Forbes et al., 2016; Luu et al., 2012; Mian and Day, 2014), which rely on predictable associations between self-generated motor and resulting sensory signals. For example, participants exposed to novel vestibular feedback of balance motion initially exhibit increased postural oscillations but decreased muscle responses to a vestibular error signal (Héroux et al., 2015). With practice, participants improve their balance and vestibular-evoked muscle responses return to baseline amplitudes, suggesting that the brain updated its vestibular estimates of self-motion. Based on these observations, we hypothesized that increasing balance delays would initially increase whole-body motion and attenuate vestibular-evoked responses but these effects would diminish following a learning period. Another critical feature of probabilistic associations between motor and sensory cues is our ability to perceptually distinguish between self-generated or externally imposed motions. Imposed sensorimotor delays during self-generated movements evoke a sensation interpreted to arise from external causes rather than oneself (Blakemore et al., 1999; Farrer et al., 2008; Wen, 2019). Repeated exposures to delayed self-generated touch can re-align the perceived timing of the contact with the imposed delay (Kilteni et al., 2019; Stetson et al., 2006). Therefore, we further hypothesized that balance behavior under imposed delays would be inferred as externally imposed motion but this likelihood would decrease through repeated exposure to the delay.

To test these hypotheses, we performed three experiments where participants balanced in a robotic simulator (Figure 1) in the AP direction with imposed delays ranging from 20 to 500 ms. These delays were in addition to the physiological delays (~100–160 ms) inherent to standing balance. In Experiment 1, we characterized standing behavior across this range of delays. Generally, whole-body sway variability increased with larger imposed delays and participants repeatedly fell into virtual limits of the balance simulation (i.e., 6° anterior and 3° posterior) for added delays larger than ~200–300 ms. In Experiment 2, participants trained to balance upright with a 400 ms added delay (testing beyond the critical delay previously proposed) for 100 min over five consecutive days. We probed the vestibular-evoked muscle responses and the perception of body motion before, after and 3 months following training to assess how the brain adapted to and processed the delayed sensory feedback. Initially, participants exhibited increased postural oscillations while the vestibular contributions to balance decreased and their perception of unexpected balance motion increased. After training, participants’ balance behavior improved, their vestibular-evoked responses increased, and larger imposed delays were needed to elicit perceptions of unexpected balance motion. To further evaluate the effect of imposed delays on the vestibular control and perception of balance, we exposed participants to transient delays (Experiment 3). Within a few seconds of transitioning to a 200 ms delay, whole-body sway variability increased, vestibular responses attenuated (~70–90% decline) and participants perceived unexpected balancing motion. Collectively, our findings demonstrate how novel sensorimotor delays disrupt standing balance and suggest that the nervous system can learn to maintain standing balance with imposed delays by associating delayed whole-body motion with self-generated balancing motor commands.

Figure 1

Download asset Open asset

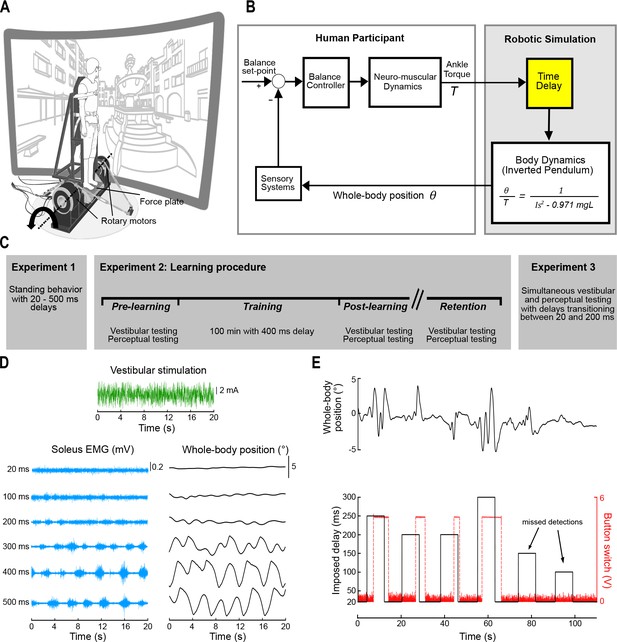
Experimental setup and block diagram of robotic simulation.

(A) The participant stood on a force plate mounted to an ankle-tilt platform and was securely strapped to a rigid backboard. The ankle-tilt platform and backboard were independently controlled by rotary motors. In all experiments, the ankle-tilt platform was held at horizontal (earth-fixed reference) while the backboard rotated the participant in the anteroposterior plane. Motion of the backboard was controlled by ankle torques exerted on the force plate based on the mechanics of an inverted pendulum. The backboard rotated about an axis that passed through the participant’s ankles (dashed line). Participants wore 3D goggles and viewed a virtual scene of a courtyard. (B) Participants balanced the robotic simulator as it operated with a 20–500 ms delay. Torque signals (T) from the force plate were buffered in the robotic simulation computer model such that angular rotation of the whole body (θ) about the ankle joint could be delayed. (C) Experimental design. Experiment 1 involved testing standing balance when naïve participants (n = 13) were first exposed to delays. Experiment 2 involved learning to balance with delays and was performed in two groups: vestibular testing and perceptual testing (*see Experiment 2 methods*). All participants who performed the learning experiments (vestibular testing group, n = 8; perceptual testing group, n = 8) completed an identical training protocol. The vestibular and perceptual tests were completed before, immediately after, and ~3 months following training. Training was completed over 5 days, in which the participant balanced the robotic simulator with a 400 ms delay (20 min per day). Experiment 3 tested a new group of participants (n = 7) and evaluated the time-dependent attenuation in vestibular-evoked responses together with changes in sway behavior and perception of unexpected balance motion. Trials in Experiment 3 were of similar design to perceptual testing in Experiment 2 (see panel E), except that the robot only transitioned between baseline (20 ms) and 200 ms delays. (D) Raw data of a sample participant from Experiment 2 vestibular testing. The participant was exposed to electrical vestibular stimulation while balancing the robotic simulator as it operated at fixed delays. Raw traces of the vestibular stimulus (green), soleus muscle EMG (blue), and whole-body position (black) are shown for a single trial at each delay condition. (E) During perceptual testing (Experiments 2 and 3), the participant balanced the robotic balance simulator and held a button switch. Delays were manipulated in the robotic balance simulation and the participant was required to press and hold the button when unexpected balance motion was detected. Raw data traces of whole-body position (black, upper trace), imposed simulation delay (black, lower trace), and the button switch (red) are shown during a perceptual trial from Experiment 2. Black arrows indicate examples of imposed delays that did not elicit a perceptual detection. Figure 1A was adapted from Shepherd, 2014.

Results

Experiment 1: imposed sensorimotor delays increase postural oscillations

Thirteen healthy participants were instructed to stand quietly on a robotic balance simulator for 60 s trials (Materials and methods) while experiencing fixed imposed delays (20, 100, 200, 300, 400, 500 ms) between the torques generated at their feet and resulting whole-body motion. These delays were in addition to the ~100–160 ms sensorimotor feedback delays inherent to standing balance. Whole-body sway was recorded throughout these trials to quantify the effect of the additional delay on standing balance. The robot was programmed to rotate the whole body in the AP direction about the participant’s ankles. Angular position limits of 6° anterior and 3° posterior from vertical were imposed into the simulation to represent the physical limits of sway during standing balance, whereby the robot constrained the angular rotation when these virtual limits were exceeded (see Materials and methods).

While balancing on the robotic simulator at the 20 ms delay (baseline condition), all participants maintained standing balance with small postural oscillations around their preferred upright posture (sway velocity variance: 0.07 ± 0.07 [°/s]² [mean ± standard deviation]). Whole-body oscillations increased with the imposed delays, leading to marked difficulties in maintaining a stable posture when a 400 ms delay was imposed. Representative data (Figure 2A) illustrate a participant exceeding the virtual balance limits (i.e., whole-body position traces exceeding dashed lines) 20 times within a 60 s period. This observation was confirmed in the group data. No participant exceeded these virtual balance limits at the 20 ms condition (only one participant reached the limit during the 100 ms condition) whereas every participant exceeded the virtual limits at least once within the 60 s balance period when delays were ≥200 ms. There was a main effect of delay on sway velocity variance (extracted over 2 s windows of continuous balance; Materials and methods), such that sway velocity variance was smallest for the 20 ms condition (0.07 ± 0.07 [°/s]²) and increased with the magnitude of the imposed delay and reached a maximum at 400 ms (21.08 ± 15.41 [°/s]²; p<0.001; Table 1 and Figure 2B). We also quantified the percent time participants balanced within the virtual limits. There was a main effect of delay on the percent time within the balance limits (p<0.001; Table 1 and Figure 2B), which decreased from 100% ± 0% during the 20 ms condition to 54% ± 9% during the 500 ms condition. Decomposition of the main effects revealed that participants exhibited greater sway velocity variance and lower percentage of trial duration within the virtual limits compared to the 20 ms condition when imposed delays were ≥200 ms (all p-values <0.05).

Figure 2

Download asset Open asset

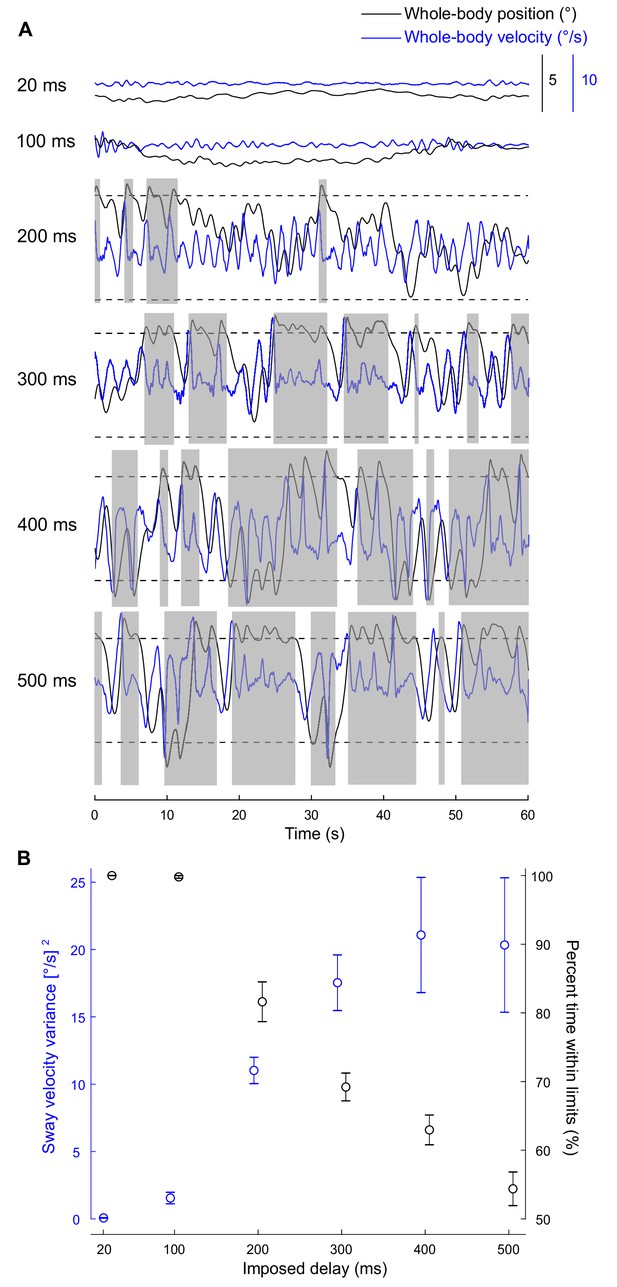
Standing balance behavior with delays.

(A) Experiment 1: raw traces of body position (black) and velocity (blue) for a single participant balancing on the robotic simulator for 60 s at different imposed delay conditions. Dashed lines represent the virtual position limits (6° anterior, 3° posterior). Sway velocity variance was calculated over 2 s windows (extracted by taking segments when sway was within balance limits for at least two continuous seconds) and the resulting data were averaged to provide a single estimate per participant and delay (see Materials and methods). Data that are not grayed out represent periods where there is at least two continuous seconds of balance within the virtual position limits. The percentage of trial time participant’s whole-body position remained within the limits was also quantified. (B) Group (n = 13) averages of sway velocity variance (blue) and percent time within balance limits (black). Error bars represent ± s.e.m.

Table 1

Summary of statistical results.

	Delay		Learning		Delay × learning interaction
Variable	F	p	F	p	F	p
Sway velocity variance
Exp 1: standing balance trials	F_(5,59.15) = 14.98	< 0.001	N/A	N/A	N/A	N/A
Exp 2: vestibular testing	F_(5,111.26) = 33.89	< 0.001	F_(2,113.19) = 46.65	< 0.001	F_(10,111.25) = 5.72	< 0.001
Exp 2: perceptual testing	F_(6,118.83) = 31.00	< 0.001	F_(2,121.47) = 25.82	< 0.001	F_(12,118.83) = 2.08	= 0.023
Other variables
Exp 1: percent within limits	F_(5,60) = 127.48	< 0.001	N/A	N/A	N/A	N/A
Exp 2: cross-covariance	W₍₅₎ = 1158.86	< 0.001	W₍₂₎ = 70.57	< 0.001	W₍₇₎ = 90.89	< 0.001
Exp 2: perceptual threshold	N/A	N/A	F_(2,11.84) = 7.52	= 0.008	N/A	N/A

For Exp 2, vestibular cross-covariance responses (peak-to-peak amplitudes) were analyzed using an ordinal logistic regression after rank transforming the data.

Experiment 2: learning to stand upright with a 400 ms delay

In a second set of experiments, we tested whether humans can adapt and learn to stand with imposed sensorimotor delays. Participants (n = 16) performed a training protocol over five consecutive days (two 10 min trials per day) where they balanced on the robot with a 400 ms delay. To explore the neural processes involved in balancing with novel sensorimotor delays, we characterized the participants’ vestibular control of balance (vestibular testing, see below) or their perceptual detection of unexpected motion (perceptual testing, see below) before and after training. Twelve participants also returned ~3 months later to examine whether any learning was retained.

Within the first minute of training with the 400 ms delay, no participant could remain upright: on average, they reached the forward or backward virtual balancing limits 18 ± 5 times (see representative participant in Figure 3A) and could only remain within the balancing limits for 64% ± 9 % of the time (or 38.5 s). This unstable balancing behavior was characterized by large whole-body sway velocity variance (12.62 ± 9.03 [°/s]²). During training, participants progressively reduced the variance of their sway velocity and increased the percentage of time they balanced within the virtual limits. The first minute of each day (i.e., start of every 20 min interval) was characterized by an increase of sway velocity variance and a decrease of percentage of time within the limits relative to the last min of the previous day (see filled circles, Figure 3B). By the end of training (100 min), participants exhibited an ~80% decrease in sway velocity variance and a 51% increase in percent time within the virtual limits. First-order exponential fits estimated the changes in sway velocity variance and percent time within the limits. The time constant for the decrease in sway velocity variance (i.e., 63.2% attenuation) was 27.9 min (corresponding to a value of 6.44 [°/s]²), and the time constant for the increase in percent time within limits (i.e., 63.2% increase) was 32.5 min (corresponding to a value of 85% within the balance limits). By the last 60 s of training, participants could balance the robot within the simulation limits on average for 97% ± 3% of the time (or 59.2 s), with four participants capable of balancing for the final 60 s interval without reaching a limit. However, the smallest sway velocity variance observed with a 400 ms imposed delay remained ~38× greater than the baseline condition (400 ms at 93rd min vs. 20 ms variance: 1.91 ± 1.12 [°/s]² vs. 0.05 ± 0.05 [°/s]²; t₍₁₅₎ = 6.74: p<0.001).

Figure 3

Download asset Open asset

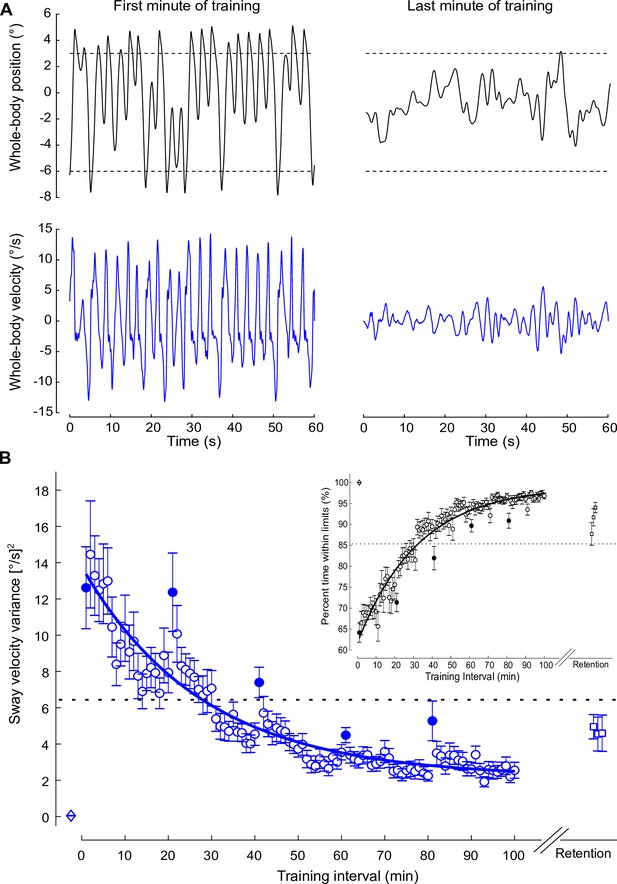
Standing balance behavior during the training protocol.

(A) Whole-body position (°; black) and velocity (°/s; blue) traces of a representative participant when balancing in the first (left) and last (right) minute of training. During training trials, the robotic simulator operated with a 400 ms delay. (B) Average sway velocity variance and percentage of time spent within the virtual balance limits (inset) estimated over 1 min intervals during the 400 ms delay training (open circles) from all participants who completed the training protocol (n = 16). The first interval for each training session is represented by filled circles. Data from vestibular testing and perceptual testing groups were combined because both groups performed the same training protocol. Sway velocity variance progressively decreased and percentage of the interval time within the virtual limits progressively increased with each session of training (one session = 20 intervals). The solid lines show the fitting of sway velocity variance and percentage within virtual balance limits to a first-order exponential function using a least-square method: $f (x) = a * \exp (- \frac{x}{b}) + c$ . For sway velocity variance, a = 11.61, b = 27.86, and c = 2.17; for percentage time within balance limits, a = –37.38, b = 32.45, and c = 99.12. The dashed horizontal lines represent the values at the estimated time constants. Data for the first minute of standing at 20 ms (open diamond) and the three minutes at 3 months after training (retention) at the 400 ms delay (open squares) are also presented. Error bars represent the s.e.m. for all data.

When participants (n = 12) returned for retention testing ~3 months later, these balance improvements were partially maintained. Sway velocity variance in the first minute of retention testing was ~60.8% lower than the sway velocity variance from the first minute of training (4.95 ± 2.32 [°/s]² vs. 12.62 ± 9.03 [°/s]²; independent samples t-test: t₍₂₆₎ = –2.86, p<0.01). Sway velocity variance at the first minute of retention testing, however, remained greater than the last minute of training (4.95 ± 2.32 [°/s]² vs. 2.55 ± 1.76 [°/s]²; independent samples t-test: t₍₂₆₎ = 3.11, p<0.01). Similarly, the first minute of retention was associated with a greater percentage of time within the balancing limits compared to the first minute of training (88% ± 9% vs. 64% ± 9%; independent samples t-test: t₍₂₆₎ = 6.67, p<0.001), but less than the last minute of training (88% ± 9% vs. 97% ± 3%; independent samples t-test: t₍₂₆₎ = –3.68, p<0.01). When using only data from participants who performed the retention session (n = 12; paired t-tests with df = 11), sway velocity variance and percent time within the balance limits revealed identical results (all p-values < 0.01). Overall, these results indicate that while standing with an imposed 400 ms delay is initially difficult (if not impossible), participants learn to balance with the delay with sufficient training (i.e., >30 min) and this ability is partially retained 3 months later.

Vestibular testing: sensorimotor delays decrease vestibular contributions to balance

During vestibular testing, we probed the vestibular contribution to soleus muscle activity by exposing participants (n = 8) to a non-painful electrical vestibular stimulus (EVS) while they balanced on the robot at different delays (20–500 ms; Materials and methods) before, after, and 3 months following training. Vestibular-evoked muscle responses are known to attenuate when actual sensory feedback does not align with expected estimates from balancing motor commands (Héroux et al., 2015; Luu et al., 2012). Therefore, we hypothesized that increasing the delay between ankle torques and body motion would progressively diminish the vestibular response. We further hypothesized that learning to control balance with imposed delays would allow the brain to update its sensorimotor estimates of balance motion and consequently increase the vestibular-evoked muscle responses. Frequency domain measures (coherence and gain; see Materials and Methods) were evaluated qualitatively using the pooled participant estimates because with delays ≥ 200 ms, single-participant coherence only exceeded significance at sporadic frequencies and significant coherence is needed to obtain a reliable gain estimate. Our time-domain measure (cross-covariance; see Materials and methods), which estimates the net vestibular contribution to muscle activity at all stimulated frequencies, was extracted on a participant-by-participant basis and used for statistical analysis. Participants exhibited the largest vestibular-evoked muscle responses (coherence, gain,and cross-covariance) for the 20 and 100 ms delay conditions, where significant coherence was observed at frequencies between 0 and 25 Hz and cross-covariance responses were characterized by short (~60 ms) and medium (~100 ms) latency peaks exceeding the 95% confidence interval (see Figure 4A). Prior to learning, pooled coherence and gain decreased with imposed delays ≥ 200 ms, and coherence fell below the significance threshold at most frequencies for delays ≥ 300 ms. Similarly, cross-covariance amplitudes decreased with increasing delay (≥200 ms), with only five out of eight participants showing significant biphasic muscle responses (cross-covariance) for the 400 ms delay condition (and six out of eight participants at 500 ms).Across training conditions (pre, post, retention), increasing the delay reduced the cross-covariance peak-to-peak amplitudes (main effect of delay, p<0.001; Figure 4A and B, Table 1).

Figure 4

Download asset Open asset

Experiment 2 vestibular-evoked muscle responses.

Data are from pre-learning (n = 8), post-learning (n = 8), and retention (n = 7) conditions. (A) Coherence, gain, and cross-covariance between vestibular stimuli and rectified soleus EMG activity were calculated from the data concatenated from all participants. Estimates are presented from all six delay conditions (see legend). Horizontal dashed lines represent 95% confidence limits for coherence and the 95% confidence intervals for cross-covariance. Note that gain estimates are only reliable at frequencies with significant coherence; therefore, at delays ≥ 300 ms, where coherence falls below significance at most frequency points, the corresponding gain in the pre-learning condition was plotted using light lines. EMG was scaled by baseline EMG from each testing session (see Materials and methods), resulting in units for gain and cross-covariance of %EMG/mA and %EMG mA, respectively. (B) Group cross-covariance amplitudes (peak-to-peak) plotted relative to imposed delay. Across pooled estimates and group data, vestibular responses attenuated with increasing imposed delays and their amplitudes partially recovered after training. (C) Average sway velocity variance during vestibular stimulation trials. Non-normally distributed group data (vestibular response amplitudes) are plotted as medians (horizontal lines in boxes), 25 and 75 percentiles (boxes) and extreme data points (error bars). Normally distributed data (sway velocity variance) are presented as means with s.e.m (error bars).

Following training, pooled vestibular-evoked muscle responses (coherence, gain, cross-covariance) partially recovered in both the post-learning and retention phases. Every participant exhibited biphasic muscle responses that exceeded significance thresholds for every delay after training. A significant interaction between delay and learning was observed for the cross-covariance (p<0.001, Table 1), suggesting that the recovery of vestibular responses was dependent on the delay magnitude. Planned comparisons (Wilcoxon sign-rank test, Bonferroni corrected) revealed that cross-covariance response amplitudes were larger during post-learning relative to pre-learning for delays ≥ 200 ms (all p-values <0.05) and were larger during retention relative to pre-learning for 300 and 400 ms (p<0.05). Similar to Experiment 1, sway velocity variance generally increased with increasing delays (Figure 4C, Table 1, Table 2; p<0.001), while learning decreased sway velocity variance at almost all imposed delays (Figure 4C, Table 1; p<0.001), resulting in a significant delay × learning interaction (Figure 4C, Table 1; p<0.001). Planned comparisons (paired t-tests, Bonferroni corrected) revealed that sway velocity variance decreased during post-learning relative to pre-learning for delays between 20 and 400 ms (all p-values <0.05) and decreased during retention relative to pre-learning for delays between 100 and 400 ms (all p-values <0.05). Because training was only performed with the 400 ms delay, these training-related changes in vestibular responses (cross-covariance) and sway behavior across delays indicate that learning generalized to different sensorimotor delays.

Table 2

Vestibular response magnitude and sway behavior from vestibular stimulation trials in Experiment 2 vestibular testing.

Delay (ms)	20	100	200	300	400	500
Pre-learning (n = 8)
Cross-cov. (%EMG·mA)	17.7/16.0	20.7/18.8	14.0/11.0	8.10/12.4	5.54/10.9	4.35/5.50
Sway velocity variance [°/s]²	0.18 ± 0.17	0.93 ± 0.58	6.52 ± 4.40	11.35 ± 5.10	16.79 ± 8.51	11.80 ± 6.53
Post-learning (n = 8)
Cross-cov. (%EMG·mA)	20.4/23.2	20.4/26.7	21.5/19.6	19.1/20.5	15.7/16.0	14.1/21.4
Sway velocity variance [°/s]²	0.05 ± 0.05	0.13 ± 0.09	0.54 ± 0.32	1.58 ± 0.74	4.20 ± 1.05	6.99 ± 2.61
Retention (n = 7)
Cross-cov. (%EMG·mA)	18.8/20.0	15.3/17.6	19.3/20.1	16.4/12.5	11.8/9.16	10.6/13.3
Sway velocity variance [°/s]²	0.09 ± 0.11	0.20 ± 0.12	0.90 ± 0.48	2.91 ± 1.25	5.51 ± 0.98	6.48 ± 3.51

Perceptual testing: sensorimotor delays induce a perception of unexpected balance motion

During perceptual testing, we assessed whether participants (n = 18) perceived unexpected balance motion when transient delays (20–350 ms applied for 8 s periods; see Materials and methods) were imposed while balancing on the robot. Behavioral studies in humans suggest that delayed self-motion is perceived as unexpected (or externally imposed) because it does not align with prior expectations of the intended movement (Blakemore et al., 1999; Farrer et al., 2008; Wen, 2019). Therefore, we hypothesized that increasing the delay in the control of standing balance would evoke motion that is increasingly perceived as unexpected. We further hypothesized that learning to control balance with imposed delays would allow the brain to update its estimates of balance motion and consequently greater delays would be needed to elicit a perception of unexpected balance movements. When delays were transiently imposed during balance, whole-body sway became more variable and, as delays increased, participants perceived unexpected balance motion more often. Data from a representative participant (see Figure 1E) show missed detections of the 100 and 150 ms imposed delays, and this participant had a resulting 70% correct detection threshold occurring at a delay of 136 ms. Across participants, the probability of perceiving unexpected postural motion increased with delays: from 4% detection for the 50 ms delay up to 100% for the 350 ms delay (Table 3). We found no significant difference in the 70% correct detection thresholds for participants who did not participate in training (i.e., the no-learning group) and those who did during the pre-learning phase (156 ± 33 ms vs. 147 ± 21 ms; independent samples t-test: t₍₁₆₎ = 0.706, p=0.49). On average, when unexpected balance motion was correctly detected, participants pressed the button at least ~2 s after the delay was imposed across all delays and learning conditions (Table 3).

Table 3

Perceptual detection rates and sway behavior from perceptual testing in Experiment 2.

Delay (ms)	50	100	150	200	250	300	350
No learning (n = 10)^*
Used trials (out of 200)	197	194	195	196	195	198	N/A
Detections (% detected)	8 (4%)	60 (31%)	128 (66%)	172 (88%)	186 (95%)	198 (100%)	N/A
Sway velocity variance [°/s]²	0.12 ± 0.05	0.57 ± 0.48	1.69 ± 1.21	3.71 ± 2.52	4.87 ± 2.62	6.32 ± 1.95	N/A
Detection time (s)	3.8 ± 2.0	4.7 ± 2.0	4.0 ± 1.9	3.5 ± 1.8	2.9 ± 1.5	2.6 ± 1.2	N/A
Pre-learning (n = 8)
Used trials (out of 160)	148	151	147	147	150	151	152
Detections (% detected)	20 (14%)	46 (30%)	111 (76%)	132 (90%)	146 (97%)	151 (100%)	152 (100%)
Sway velocity variance [°/s]²	0.24 ± 0.27	0.45 ± 0.33	1.84 ± 1.36	4.01 ± 2.33	4.18 ± 1.38	5.09 ± 1.46	4.70 ± 1.64
Detection time (s)	4.1 ± 2.1	3.7 ± 1.9	3.6 ± 1.8	3.2 ± 1.6	2.9 ± 1.6	2.4 ± 1.2	2.3 ± 1.1
Post-learning (n = 8)
Used trials (out of 160)	157	156	157	156	157	157	151
Detections (% detected)	16 (10%)	23 (15%)	52 (33%)	101 (65%)	136 (87%)	153 (97%)	151 (100%)
Sway velocity variance [°/s]²	0.11 ± 0.10	0.16 ± 0.13	0.40 ± 0.26	1.34 ± 1.09	2.20 ± 1.61	3.02 ± 2.33	3.70 ± 2.37
Detection time (s)	4.2 ± 2.0	3.8 ± 2.4	4.1 ± 1.7	3.9 ± 1.7	3.4 ± 1.8	2.7 ± 1.3	2.2 ± 1.1
Retention (n = 5)
Used trials (out of 100)	96	93	98	98	96	98	92
Detections (% detected)	8 (8%)	21 (23%)	40 (41%)	50 (51%)	71 (74%)	84 (86%)	92 (100%)
Sway velocity variance [°/s]²	0.05 ± 0.03	0.13 ± 0.06	0.27 ± 0.15	0.84 ± 0.51	1.51 ± 0.76	1.89 ± 1.09	2.60 ± 1.05
Detection time (s)	5.0 ± 1.7	4.2 ± 2.0	4.2 ± 2.2	3.8 ± 2.0	3.4 ± 1.8	3.1 ± 1.8	3.1 ± 1.4

Sway velocity variance and detection time are presented as mean ± SD.
*No learning group is an independent sample of participants that were not exposed to a 350 ms delay.

After participants (n = 8) completed training with the 400 ms delay, psychometric functions shifted to the right, resulting in increased thresholds for detecting unexpected balance movements (Figure 5A and B, Table 1; p=0.008, Bonferroni corrected). Thresholds were larger during post-learning relative to pre-learning (Figure 5B; 192 ± 40 ms vs. 147 ± 21 ms; p=0.032, Bonferroni corrected) and were larger for retention relative to pre-learning (209 ± 82 ms vs. 147 ± 21 ms; p=0.014, Bonferroni corrected). For the whole-body oscillations (sway velocity variance extracted over the 8 s periods when delays were imposed, see Table 1), we again confirmed significant main effects of delay (p<0.001) and learning (p<0.001) as well as a delay × learning interaction (p=0.023). Planned comparisons (paired t-tests, Bonferroni corrected) revealed that sway velocity variance decreased during post-learning relative to pre-learning for delays ranging from 150 to 250 ms (all p-values <0.05) and decreased during retention relative to pre-learning for the 150, 200, 300, and 350 delays (all p-values <0.05).

Figure 5

Download asset Open asset

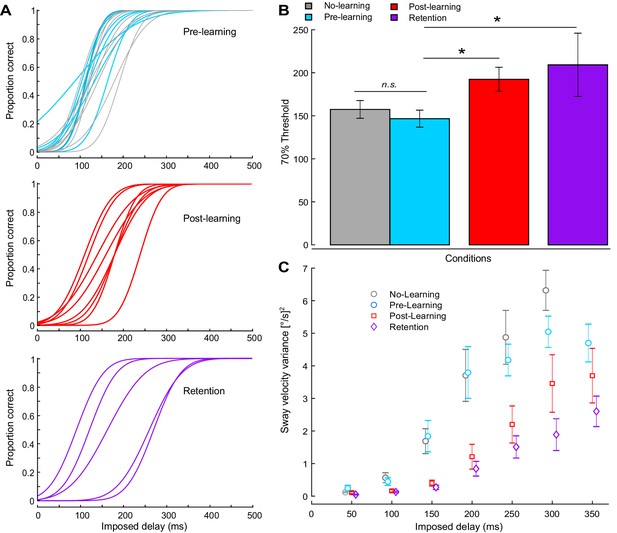
Experiment 2 perceptual testing and standing behavior results.

(A) A Bayesian estimation procedure was used to fit sigmoidal functions to perceptual responses. The proportion of correct responses (i.e., button pressed during delay period) was calculated for each participant at each delay level. Individual psychometric functions are shown for all participants. The top panel shows participants tested before training (n = 18), with 10 participants who did not participate in the learning procedure shown in gray. The middle panel shows post-learning (n = 8), and the bottom panel shows retention results (n = 5). (B) Average 70% interpolated threshold for pre, post, and retention conditions. Perceptual thresholds increased following training, such that larger imposed delays were needed to elicit perceptual detections. (C) Average velocity variance for different delays. Error bars indicate s.e.m.

Experiment 3: rapid attenuation of vestibular responses accompanies balance variability and perceptual detection of unexpected balance motion

Our results from the vestibular and perceptual testing of Experiment 2 indicate that reduced vestibular responses (Figure 4) and a higher probability of perceiving unexpected balance behavior (Figure 5) were accompanied by increased sway velocity variance. These two experiments, however, involved different methodologies (trials with constant delays vs. transient changes in delay), making it difficult to compare sway behavior between data sets or determine if vestibular modulations coincided with perceptual changes. Therefore, in Experiment 3 we tracked the time course of vestibular responses and the occurrence of perceptual detections together with whole-body oscillations when delays were transiently imposed. Here, participants (n = 7) were exposed to a transient delay of 200 ms because Experiment 2 revealed that this delay increases sway variability, attenuates vestibular responses, and elicits frequent perceptions of unexpected standing motion. To quantify balance variability throughout the transitions, sway velocity variance was estimated across a 2 s sliding window on a point-by-point basis (Figure 6A). Furthermore, to link changes in vestibular responses and perception, we compared vestibular response attenuation – estimated with a time-frequency analysis of coherence and gain (see Materials and methods) – at the time of perceptual detection of unexpected balance motion.

Figure 6

Download asset Open asset

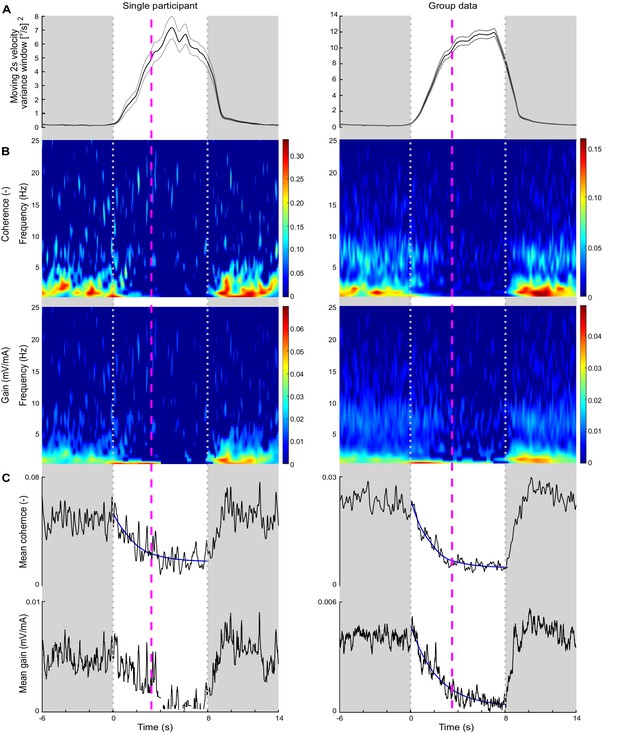
Experiment 3 sway velocity variance, time-varying electrical vestibular stimulus-electromyography (EVS-EMG) coherence and gain, and perceptual detection time during delay transitions.

Data are presented across transition periods where time zero represents the transition point from baseline (20 ms) to 200 ms delayed balance control, which lasted for 8 s (between grayed out areas) and returned to baseline. Data are presented for a representative participant (left) and the group data (right; n = 7) using only data from transitions that were perceived as unexpected and the button was pressed after the delay was introduced (single participant: 77, group: 489). (A) Average (black line) 2 s sliding window of velocity variance over transitions with ±s.e.m. (gray lines). Time-varying variance was calculated using the *movvar* MATLAB function, which calculated variance over 2 s segments using a sliding window. The velocity variance trace begins to decline prior to the end of the delay period because the sliding window starts estimating variances from data points both during and after the delay. (B) Time-frequency plots of EVS-EMG coherence and gain (i.e., vestibular-evoked muscle responses) during the delay transition. For illustrative purposes, and because gain values are not reliable when coherence is below the significance threshold, we set coherence and gain data points where coherence was non-significant (i.e., below 99% confidence limit) to zero (dark blue). (C) Mean time-dependent EVS-EMG coherence and gain across the 0.5–25 Hz frequency range. For each participant and group data, an exponential decay function: $f (x) = a * \exp (- \frac{x}{b}) + c$ was fit to the average coherence over the 8 s period during which the 200 ms delay was present. For gain, we removed values corresponding to non-significant coherence (see single participant trace) and only fit an exponential function to the group mean gain estimate. The average perceptual detection times for the representative participant (3.2 s) and group data (3.4 s) are indicated by the dashed magenta lines, and at these times, vestibulomuscular coherence had attenuated by 83% and 90%, respectively. Group mean gain attenuated by 73% at the group average perceptual detection time.

Out of the 588 total transitions, 489 were perceived as eliciting unexpected balance motion and used for all analyses. During periods of standing preceding the imposed delays, participants swayed with low-velocity variance (Figure 6A) and with consistent vestibular control of balance as shown by coherence and gain estimates between the vestibular stimulus and soleus EMG activity (Figure 6B and C). Transitions between baseline and delayed balance control increased whole-body sway velocity variance throughout most of the delay period (see Figure 6A). Over the same period, coherence and gain between EVS and EMG decreased. To characterize the time course of the decrease in this vestibular contribution to balance, we fit an exponential decay function to the mean coherence (i.e., coherence averaged over 0.5–25 Hz at each time point) from each participant. The 63.2% attenuation (i.e., the time constant) for coherence occurred at 1.5 ± 0.6 s following delay onset while the 95% attenuation (i.e., 3× time constant) occurred at 4.4 ± 2.6 s following delay onset. For gain, we fit an exponential decay only to the mean gain estimated from the pooled data because for some participants coherence decreased below significance at all frequencies for some periods of the delay exposure (see Figure 6C, left-lower panel). The 63.2% attenuation from this mean gain estimate occurred at 2.3 s while the 95% attenuation occurred at 6.8 s. Perceptual detection times occurred over a similar time period, with the group averaged (489 detections) detection occurring at 3.4 ± 1.8 s after delay onset (see magenta line in Figure 6, right panel) and the 95th percentile for detection time occurring at 6.9 ± 0.8 s. Comparing the perceptual detection timing with the exponential decrease in coherence estimated from each participant, we found that the average time to detect the imposed delay (3.4 ± 1.8 s) corresponded to a 90% ± 7% average reduction in mean coherence. For the mean gain estimate (from all participants), this average perceptual time aligned with a 73% reduction in gain. The peak velocity variance leading up to a perceptual detection was also extracted for each perceived transition and resulted in an average peak velocity variance of 8.42 ± 8.62 [°/s]². Overall, these results indicate that the perception of unexpected motion and increased sway variability arising from an imposed delay are accompanied by an ~70–90% attenuation of vestibular contributions to balance.

Discussion

The primary aims of this study were to (1) characterize the destabilizing effects of imposed delays between ankle torque and whole-body motion during standing balance and (2) determine the underlying mechanisms responsible for adaptation and learning to these imposed delays. When delays were first imposed, the variance of whole-body sway velocity during balance increased with larger delays and all participants exceeded the virtual balance limits (6° anterior, 3° posterior) when delays were ≥200 ms. Balancing with imposed delays also attenuated vestibular-evoked muscle responses and led to perceptions of unexpected movement during standing balance, supporting the interpretation that imposing delays increased uncertainty in the internal estimate of balancing self-motion. Importantly, participants learned to balance with an imposed sensorimotor delay of 400 ms over 5 days (100 min of training), showing decreased sway velocity variance and increased percent time balancing within the virtual limits, partially restored vestibular control of balance, and fewer unexpected movement detections while balancing with the delay. These effects were generalized across delays despite training to balance only at the 400 ms delay. Our findings reveal that, while there may be a critical delay for the balance system, the brain can find a solution to overcome this limitation, learning to maintain standing balance with imposed delays by causally linking delayed whole-body sensory feedback that was initially interpreted as imposed motion to self-generated balance motor commands.

Learning to stand with novel sensorimotor delays

When delays were first inserted in the control of standing balance, sway velocity variance increased with larger delays to the point that upright balance could not be maintained for at least 60 s at imposed delays ≥ 200 ms (i.e., total sensorimotor delay ≥300–360 ms). These results support predictions from computational models that upright standing is destabilized with added delays and that balance is impossible passed a critical delay of ~300–340 ms (Milton and Insperger, 2019; van der Kooij and Peterka, 2011). This critical delay was previously estimated by varying the parameters of a proportional-derivative (PD) feedback control model of standing balance, and suggests that even with training, the balance controller is incapable of adjusting the gain of its feedback to maintain upright stance with delays beyond this upper limit. Our results, in contrast, clearly demonstrate that participants improved their balance behavior (i.e., reduced sway velocity variance) when given the opportunity to train with a 400 ms delay (~63% by 28–33 min), and that this improvement was retained, at least partially, 3 months later. Therefore, the nervous system can learn to control standing balance (although with more variability) with a net delay of up to 500–560 ms. The notable learning observed after training may have been partly due to participants being passively supported past the virtual balance limits because it prevented certain nonlinear behaviors that disrupt continuous balance control such as taking steps or falls.

This remarkable ability for humans to adapt and maintain upright stance with delays raises questions regarding the principles underlying the neural control of balance. Compared to feedback controllers (i.e., PD and proportional-integral-derivative), which are not optimal in the presence of delays, optimal controllers can model the control of human standing (Kiemel et al., 2002; Kuo, 1995; Kuo, 2005; van der Kooij et al., 1999; van der Kooij et al., 2001) and theoretically stabilize human standing with large (>500 ms) delays (Kuo, 1995). This ability, however, rapidly declines with increasing center of mass accelerations (Kuo, 1995), including those driven by external disturbances (Zhou and Wang, 2014). Although feedback and optimal controllers assume that the nervous system linearly and continuously modulates the balancing torques to stand (Fitzpatrick et al., 1996; Masani et al., 2006; van der Kooij and de Vlugt, 2007; Vette et al., 2007), intermittent corrective balance actions (Asai et al., 2009; Bottaro et al., 2005; Gawthrop et al., 2011; Loram et al., 2011; Loram et al., 2005) may represent a solution when time delays rule out continuous control (Gawthrop and Wang, 2006; Arsan et al., 1999). Intermittent muscle activations are also sufficient to stabilize the upright body during a robotic standing balance task similar to the one used in the present study (Huryn et al., 2014). The nervous system may use a combination of the controllers during standing (Elias et al., 2014; Insperger et al., 2015), but our study did not explicitly test for evidence of these different controllers or their ability to stabilize upright stance with large delays.

Learning to expect novel sway behavior caused by imposed sensorimotor delays

Increasing the imposed delay between balancing motor commands and the whole-body motion associated with those actions progressively attenuated vestibular-evoked muscle responses and led to more frequent perceptual detections of unexpected movement. The attenuation of vestibular-evoked responses to increased sensorimotor delays could be explained through processes of sensory reweighting (Cenciarini and Peterka, 2006; Peterka, 2002), where the decreasing reliability in sensory cues when balancing with additional delays decreases feedback gains. Indeed, feedback control models of standing predict that sensorimotor gains should decrease with increasing sensorimotor delays (Bingham et al., 2011; Le Mouel and Brette, 2019; van der Kooij and Peterka, 2011). However, our results show the partial return of vestibular response amplitude and shifted perceptual responses after training at a delay of 400 ms, indicating the involvement of alternative processes of sensorimotor recalibration. Both the vestibular and perceptual measures are influenced by whether the brain interprets sensory feedback as self-generated (expected) or externally imposed (unexpected), and their adaptation indicates that the nervous system learned to expect the delayed balancing-related feedback associated with self-generated balancing motor commands. Similar recalibration of the vestibular control of balance has been observed when humans stand with manipulated vestibular feedback gains (Héroux et al., 2015). When first standing with altered vestibular feedback (via a head-coupled EVS), variability in balance behavior increased and the amplitude of vestibular-evoked muscle responses (probed with an independent EVS signal) decreased. After a short (240 s) calibration period with the novel head-coupled vestibular stimulus, postural sway and vestibular responses returned to baseline levels (Héroux et al., 2015), suggesting that the brain learned to expect the modified vestibular feedback. Notably, this could not be explained by sensory reweighting mechanisms since adaptation did not occur when applying matching levels of EVS that were uncoupled from head motion. Perceptually, there is similar evidence of recalibration to new sensorimotor delays. Following repeated exposure to imposed sensorimotor delays, the perceived timing between motor actions and sensory feedback can be shifted according to the magnitude of the delay (Stetson et al., 2006) and the perceived intensity (i.e., force, tickle sensation) of delayed touch returns to baseline (i.e., no delay) levels (Kilteni et al., 2019). Our results suggest that these forms of recalibration are possible for the vestibular control of standing balance and the perception of standing balance. Because we naturally experience changing neural delays during growth and aging (Eyre et al., 1991), it is crucial that the nervous system adapts and recalibrates to unexpected temporal relationships between sensory and motor signals to maintain stable balance control and perception of standing movement.

What neural substrates could be responsible for the brain learning to expect standing balance feedback that is initially unexpected? When faced with a new sensorimotor relationship, deep cerebellar neurons (rostral fastigial nucleus) initially increase their activity to vestibular signals because the motor commands result in unexpected sensory feedback (Brooks et al., 2015; Brooks and Cullen, 2013). Learning this new sensorimotor relationship results in a gradual increase in the probability that this unexpected feedback arises from desired motor commands, leading to a gradual return of the normal firing patterns of the deep cerebellar neurons (Brooks et al., 2015). These neuronal recordings further indicate that the nervous system scales responses (i.e., not a switch-like mechanism) to sensory inputs based on the relative probability that sensory feedback is caused by motor actions. Our vestibular experiment results reflect a similar mechanism – vestibular response amplitudes gradually decreased with the magnitude of the delay – extending this framework to a standing balance control context. Additionally, training led to modified vestibular and perceptual responses as well as decreased sway velocity variance that transferred to different imposed delays, indicating a generalized effect of learning. This suggests that the nervous system did not specifically recalibrate sensorimotor cues to the 400 ms delay but estimated the source of the unexpected balance motion (i.e., distorted motor command – whole-body motion relationship) and broadly updated its control (Berniker and Kording, 2008; Braun et al., 2010; Krakauer and Mazzoni, 2011) to accommodate for imposed delays.

Rapid attenuation of vestibular responses accompanies perception and postural instability

Our third experiment showed that within a few seconds of balancing with a 200 ms delay, an ~70–90% attenuation of vestibular responses accompanied increased sway velocity variance and the perception of unexpected standing motion. Part of the variability in whole-body sway caused by sensory manipulations is considered to represent errors in balance estimates (Kiemel et al., 2002). Because imposed delays should evoke unexpected feedback errors (Blakemore et al., 1999; Farrer et al., 2008; Haering and Kiesel, 2015; Wen, 2019), the changes in vestibular-evoked muscle responses and perception with sway velocity variance may reflect that the two behavioral responses are linked to balance errors. However, it is not explicitly clear from our data what specific component of the standing behavior can be attributed to discrepancies between actual and expected feedback. Therefore, changes in standing behavior following adaptation to a delay could also be attributed to other factors induced by the imposed delays, such as a change in control policy or increased volitional control to balance (Elias et al., 2014; Ozdemir et al., 2018; Peterson and Ferris, 2019). When accounting for this limitation, it is also plausible that the observed changes in vestibular and perceptual responses were partially driven by whole-body motion (i.e., magnitude and variability) and not solely prediction errors. For instance, vestibular responses are known to be modulated by standing kinematics (Day et al., 1997; Rasman et al., 2018; Son et al., 2008) and perceiving balance motion is related to whether the experienced motion exceeds sensory detection thresholds (Fitzpatrick and McCloskey, 1994). The important questions regarding whether movement variability is attributed to control errors and their resulting influence on balance control, perception, and adaptation are inherently challenging for standing balance because the task is continuous and does not have an effective end-point target (thus no computable end-point error). Future studies using carefully designed sensorimotor manipulations of balance control (Rasman et al., 2018) with differing effects (perhaps directional) on unexpected errors and whole-body sway behavior may resolve these critical issues.

Clinical implications

During aging and certain diseases (e.g., diabetic neuropathy or multiple sclerosis), the sensory and/or motor conduction times increase and may affect an individual’s ability to maintain their body center of mass position within their base of support. According to our results, the standing balance system can be trained to accommodate a larger range of sensorimotor delays than previously predicted, which may be valuable for clinical populations who are thought to experience instability and an increased risk of falls as a result of increased neural delays. Adaptation to increased neural delays with aging, for example, is thought to occur through decreased sensorimotor gains and increased ankle stiffness (Le Mouel and Brette, 2019). Because our results show that training with an additional 400 ms delay can restore vestibular contributions of balance across a broad range of imposed delays (and are retained over a 3 month period), it may be possible to explore targeted rehabilitation of aging-related balance impairments by training with delays to restore and sustain sensory contributions to standing balance.

Limitations and other considerations

We manipulated the delay between ankle-produced torques (measured from the force plate) and the resulting whole-body motion (angular rotation about the ankle joints). This manipulation altered the timing between the net output of self-generated balance motor commands (i.e., ankle torques) and resulting sensory cues (visual, vestibular, and somatosensory) encoding whole-body and ankle motion. However, the timing between motor commands and part of the somatosensory signals from muscles (muscle spindles and Golgi tendon organs) and/or skin (cutaneous receptors under the feet) that are sensitive to muscle force (and related ankle torque) or movements and pressure distribution under the feet were unaltered by the imposed delays to whole-body motion. This may have led to potential conflicts in the sensory coding of balance motion and may have influenced the ability to control and learn to stand with imposed delays. As methodologies to probe and manipulate the sensorimotor dynamics of standing improve, future experiments can be envisioned to replicate and modify specific aspects (i.e., specific sensory afferents) of the physiological code underlying standing balance. Such endeavors are needed to unravel the sensorimotor principles governing balance control.

Conclusion

We observed that increasing the imposed sensorimotor delays in standing balance results in unstable standing balance, attenuated vestibular control of balance, and perceptual detections of unexpected motion. The nervous system, however, can adapt to novel sensorimotor delays and learn to maintain upright standing despite their initially disruptive influence. This learning is accompanied by vestibular contributions to balance partially returning and standing motion more likely to be perceived as self-generated. Thus, our results suggest that the nervous system can learn to control standing balance with added sensorimotor delays by causally relating delayed whole-body sensory feedback (initially deemed unexpected) with self-generated balancing motor commands.

Materials and methods

Participants

A total of 46 healthy adult participants (32 males, age: 24.0 ± 3.9 years [mean ± SD]; range 19–34 years) with no known history of neurological deficits participated in this study. The experimental protocol was verbally explained before the experiment and written informed consent was obtained. The experiments were approved by the University of British Columbia Human Research Ethics Committee and conformed to the Declaration of Helsinki, with the exception of registration to a database.

Experimental setup

Request a detailed protocol

Three experiments were conducted to investigate how imposed sensorimotor delays affect standing balance. We first performed an experiment evaluating standing balance behavior when participants balanced upright with different imposed sensorimotor delays. We then conducted a second experiment to determine (1) whether participants could learn to maintain standing balance with a 400 ms delay and (2) whether learning to control balance would lead to changes in the vestibular control of balance (Experiment 2 – vestibular testing) and perception of postural behavior (Experiment 2 – perceptual testing). To probe the vestibular control of balance, we delivered EVS while participants balanced upright with different delays. To assess perception, we applied transient delays during ongoing standing balance and asked participants to report when they consciously perceived unexpected postural motion. Finally, we performed a third experiment to track the time course of modulations in vestibular contributions to balance caused by imposed delays and how it follows changes in sway behavior variability and perception of unexpected balance motion.

For all experiments, participants stood on a custom-designed robotic balance simulator programmed with the mechanics of an inverted pendulum to replicate the load of the body during standing (Figure 1A). Specifically, the simulator used a continuous transfer function that was converted to a discrete-time equivalent for real-time implementation using the zero-order hold method

I \ddot{θ} - m_{m} g L θ = T \frac{θ}{T} = \frac{1}{I s^{2} - 0.971 m g L}

as described by Luu et al., 2011, where $θ$ is the angular position of the body’s center of mass relative to the ankle joint from vertical and is positive for a plantar-flexed ankle position, $T$ is the ankle torque applied to the body, $m_{m}$ is the participant’s effective moving mass, $L$ is the distance from the body’s center of mass to the ankle joint, $g$ is gravitational acceleration (9.81 m/s²), and $I$ is mass moment of inertia of the body measured about the ankles ( $m_{m} L^{2}$ ). The body weight above the ankles was simulated by removing the approximate weight of the feet from the participant’s total body weight so that the effective mass was calculated as $0.971 m$ , where $m$ is the participant’s total mass. The balance simulator was controlled by a real-time system (PXI-8119; National Instruments, TX, USA) running at 2000 Hz and consisted of an ankle-tilt platform and rigid backboard independently controlled by two rotary motors (resolution of 0.00034°; SCMCS-2ZN3A-YA21, Yaskawa, Japan). The backboard was lined with a layer of medium-density foam and memory foam. Participants were secured to the backboard through seat belts at the waist and shoulders, and the backboard orientation was adjusted relative to the frame to account for the participant’s natural standing posture. Participants stood on a force plate (OR6-7-1000; AMTI, MA, USA) secured to the ankle-tilt platform. In all experiments, the ankle-tilt platform was held horizontal (earth-fixed reference) while the backboard moved the upright body in the AP direction in response to ankle plantar- and dorsiflexion torques, thus replicating whole-body AP movements associated with standing (Luu et al., 2011). The delay between a position command and the measured position of the motor was estimated to be 20 ms (Shepherd, 2014). A visual projection screen was located to the left of the robotic device on which a 3D scene of a city courtyard with a water fountain was presented (Vizard 2013 software; WorldViz, CA, USA). Rendering and projection of the visual scene took approximately 70 ms; therefore, a linear least-squares predictor algorithm was used to synchronize the visual motion (i.e., predict visual motion occurring 50 ms later) together with the motors at a delay of 20 ms (Shepherd, 2014). The linear prediction model used six data points, and the coefficients were selected by fitting data of participant sway to the corresponding data shifted by the appropriate delay using a linear least-squares method. Participants wore active 3D glasses (DLP Link 3D Glasses; BenQ, Taipei, Taiwan), modified to block out peripheral vision and limit the participant’s field of view to approximately ±45° horizontally and ±30° vertically. Participants also wore earplugs and noise canceling headphones (Bose Soundlink Around, Bose Corporation, MA, USA) with audio of a water fountain to minimize acoustic cues of motion produced by the motors as well as other extraneous sounds. To represent the physical limits of sway during standing balance, the backboard rotated in the AP direction about the participant’s ankles with virtual angular position limits of 6° anterior and 3° posterior (Luu et al., 2011; Shepherd, 2014). When the backboard position exceeded these position limits, the program gradually increased the simulated stiffness such that the participants could not rotate further in that direction regardless of the ankle torques they produced. This was implemented by linearly increasing a passive supportive torque to a threshold equivalent to the participant’s body load over a rotation range of 1° beyond the balance limits (i.e., passively maintaining the body at that angle). Any active torque applied by participants in the opposite direction would enable them to get out of the limits. Finally, to avoid a hard stop at these secondary limits (i.e., 7° anterior and 4° posterior), the supportive torque was decreased according to an additional damping term that was chosen to ensure a smooth attenuation of motion.

The balance simulation was modified to add a delay between the measured ankle torque (i.e., motor command) and whole-body sway (i.e., sensory feedback). Delays were programmed by buffering ankle torque recordings such that the signals driving motor position commands, and therefore whole-body sway, could be delivered based on the torque participants performed up to 500 ms in the past. The natural sensorimotor delays within the standing balance controller are estimated to be ~100–160 ms (Forbes et al., 2018; Kuo, 2005; van der Kooij et al., 1999). Here, as our delays are in the robotic system, they need to be added to the internal delays to estimate the overall standing balance delays. Throughout this study, we refer to the delays added to the robotic simulator (20–500 ms), but the total sensorimotor delays for the standing balance task are ~100–160 ms larger. All participants were naïve to the delay protocols and were simply told that ‘at times during the balance simulation, control may change such that your body movement may seem unexpected or abnormal, and standing balance may become more difficult.’ In all experiments, participants were instructed to stand upright normally at their preferred standing angle (typically ~1–2° anterior). In trials with delays ≥ 200 ms, participants had difficulty maintaining a stable upright posture and would often reach the virtual balancing limits (i.e., 6° anterior or 3° posterior). When this happened, participants were immediately instructed by the experimenter to get out of the limits and continue to balance upright. Despite these efforts, trials with larger imposed delays were often characterized by brief periods (~2–5 s) of active balancing before crossing the virtual balancing limits (i.e., angular whole-body position exceeding the angular position limits). After a trial was completed, the robot was returned to a neutral position (0°) at a fixed velocity (0.5°/s) in preparation for the next trial.

Data recordings

Request a detailed protocol

Signals used to control the robotic simulation in real time were processed via a multifunction reconfigurable module (PXI-7853R; National Instruments, Austin, TX, USA). The backboard motor encoder provided backboard angular position data regarding the participant’s whole-body position during the task. The delay (ms) used during the simulation was recorded for all experiments. Force plate signals (forces and torques) were amplified ×4000 (MSA-6; AMTI, Watertown, MA, USA) prior to being digitized. Vestibular stimuli (see Experiment 2 – vestibular testing and Experiment 3) and button switch signals (see Experiment 2 – perceptual testing and Experiment 3) were also recorded. For Experiment 2 – vestibular testing and Experiment 3, surface electromyography (EMG) was collected from the right soleus to measure the vestibular-evoked responses. We measured activity from this muscle for two reasons: (1) the head was turned left during all experiments and this orientation aligns the vestibular-evoked error with soleus muscle’s line of action (see Vestibular stimulation) and (2) the soleus was shown to have the most consistent activity during pilot testing at the manipulated delay conditions, which is a prerequisite to estimate a vestibular-evoked response in lower-limb muscles (Dakin et al., 2007; Forbes et al., 2013). The skin over the muscle was cleaned with an alcohol swab and abraded with gel (Nu-Prep, Weaver and Company, Aurora, CO, USA). Self-adhesive Ag-AgCl surface electrodes (Blue Sensor M, Ambu A/S, Ballerup, Denmark) were positioned over the belly of the muscle in a bipolar configuration, with an inter-electrode distance of 2 cm center-to-center. For each participant, we noted the electrode placement on the soleus (by measuring the distance from the electrodes to the heel) during the first experimental session and used the same placement for consistency across experimental sessions (pre-learning, post-learning, retention). To reduce electrical noise from the motors, two ground electrodes were used: a nickel-plated disc electrode coated with electrode gel (Spectra 360 Parker Laboratories, NJ, USA) secured to the right medial malleolus, and a Velcro strap electrode secured around the right lower leg overlaying the tibial tuberosity and head of the fibula. Surface EMG signals were amplified (×5000, Neurolog, Digitimer Ltd., Hertfordshire, UK) and band-pass filtered (10–1000 Hz) prior to digitization. Force plate, vestibular stimuli, EMG, and button switch signals were recorded via a data acquisition board (PXI-6289; National Instruments). All signals were digitized at 2000 Hz.

Familiarization

Request a detailed protocol

For all experiments, a balance session was first completed to familiarize the participant with the control of the robot. Instructions were given on the nature of movement control; that is, similar to standing, applying torque to the support surface (force plate) will control the motion of the upright body (backboard). In a forward leaning position, plantar-flexor torque is required to stabilize the body and an increase in plantar-flexor torque greater than the gravitational torque will cause the body to accelerate backward. Similarly, a dorsiflexor torque is required when standing in a backward leaning position and an increase in dorsiflexor torque will accelerate the body forward. Participants were instructed to sway back and forth and allow the robot to reach its limits (6° anterior, 3° posterior), which occurs if the magnitude of the generated ankle torque is not large enough to resist the toppling torque of gravity. After becoming familiar with the control of the robot, participants were then asked to stand quietly and maintain an upright posture (normal standing). Participants were also instructed to focus on the sensation of balance control and told that this setting was the ‘normal’ condition, which was of particular importance for perception experiments (Experiment 2 – perceptual testing and Experiment 3). Participants performed this familiarization period until they were accustomed to the sensation of standing balance on the robot. This ensured that participants could confidently discern between normal and novel (i.e., unexpected) standing balance behavior caused by manipulating delays. They completed the entire familiarization session within 5–7 min.

Vestibular stimulation

Request a detailed protocol

In Experiment 2 – vestibular testing and Experiment 3, we used transmastoid EVS to probe vestibular-evoked muscle responses. Vestibular stimulation was delivered in a binaural bipolar configuration to modulate the firing rates of all vestibular afferents (Goldberg et al., 1984; Kim and Curthoys, 2004; Kwan et al., 2019) and provide an isolated vestibular error signal that evoked a virtual sensation of head motion about an axis-oriented posteriorly and superiorly by ~17–19° above Reid’s plane (Fitzpatrick and Day, 2004; Peters et al., 2015). The head was pitched up such that Reid’s plane was oriented ~17–19° up from horizontal. In this head position, EVS evokes a net signal of angular head rotation orthogonal to gravity (Chen et al., 2020; Fitzpatrick and Day, 2004; Schneider et al., 2002) and, through integration with an internal estimate of gravity, an inferred interaural linear acceleration signal (Khosravi-Hashemi et al., 2019). While standing, this imposed vestibular error evokes stereotypical compensatory muscle and whole-body responses (Dakin et al., 2007; Day et al., 1997; Fitzpatrick and Day, 2004; Forbes et al., 2014). The head was also turned ~90° to the left, which aligns the vestibular-evoked error signal with the AP direction of balance and line of action for the soleus, maximizing the muscle response (Dakin et al., 2007; Forbes et al., 2016). We chose stochastic vestibular stimuli (a white noise signal low-pass filtered to contain a set bandwidth of frequencies) rather than square-wave stimuli as it improves signal-to-noise ratio and reduces testing time (Dakin et al., 2007; Reynolds, 2011). EVS signals with a 0–25 Hz frequency bandwidth were generated offline using custom-designed computer code (LabVIEW 2013, National Instruments). The stimuli were delivered to participants through carbon rubber electrodes (9 cm²) coated with Spectra 360 electrode gel and secured over the mastoid processes in a binaural bipolar configuration. The stimuli were sent as analog signals via a data acquisition board (PXI-6289, National Instruments) to an isolated constant current stimulator (DS5, Digitimer, Hertfordshire, England). Throughout the trials, head position was monitored and maintained using a head-mounted laser and verbal feedback, respectively.

Experiment 1

Request a detailed protocol

Computational models indicate that adding sensorimotor delays will destabilize balance control (Insperger et al., 2015; Milton and Insperger, 2019; van der Kooij et al., 1999) and that upright standing cannot be maintained past a critical delay of ~340 ms (Milton and Insperger, 2019; van der Kooij and Peterka, 2011). To determine how imposed balance delays destabilize and limit balance control, 13 participants balanced the robotic system for 60 s with different imposed delays (20, 100, 200, 300, 400, and 500 ms). Trial order was the same for each participant, with delays presented in ascending order to avoid crossover effects from larger delays to smaller delays. Participants were not given any information regarding the different delay conditions or strategies on how to best control the robot.

Experiment 2

Request a detailed protocol

Based on observations from Experiment 1, we designed a training protocol (Experiment 2) to determine if participants could learn to stand when the robotic balance control simulation operated with 400 ms delay (i.e., a total feedback delay of 500–560 ms). This delay was chosen because it is larger than the ~300–340 ms critical feedback delay of standing balance proposed previously (Milton and Insperger, 2019; van der Kooij and Peterka, 2011). To investigate the underlying physiological mechanisms of this learning process, we conducted Experiment 2 to evaluate how imposed delays influenced the vestibular-evoked balance responses and perception of standing motion, respectively, before and after training as well as 3 months later.

Training procedure and timeline

Request a detailed protocol

Sixteen participants (vestibular testing, n = 8; perceptual testing, n = 8) performed the training protocol over five consecutive days (see Figure 1C). On the first day, prior to any training, participants completed pre-learning session (vestibular or perceptual testing; see below). Each training session then started with a 60 s standing balance trial with the 20 ms delay. This was followed by two 10 min training trials at the 400 ms delay. To minimize fatigue, participants rested for 2–3 min between these two trials. Participants were not given any specific instruction on how to improve their balance. On each day, the training trials were followed by a final 60 s trial at the 20 ms delay. In total, participants performed 100 min of training over 5 days at the 400 ms delay condition. After finishing the training session on the fifth day, participants completed the post-learning session (vestibular or perceptual testing). Finally, 12 of the 16 participants (seven vestibular, five perceptual) returned ~3 months later (range: 81–110 days) to perform a retention session. The retention testing session began with a short familiarization period (<60 s) of balancing the robot with the 20 ms delay. Participants then completed vestibular or perceptual testing followed by two 3 min standing balance trials: one with the 20 ms delay and one with the 400 ms delay (order randomized between participants).

Vestibular testing

Request a detailed protocol

Eight of the 16 training participants in Experiment 2 completed vestibular testing (Figure 1C). Here, we probed the vestibular-evoked responses in the soleus muscle while participants maintained standing balance at six imposed delays (see below). Vestibular testing was conducted for pre-learning, post-learning, and retention sessions. Seven participants returned ~3 months after the post-learning session to complete the retention session. Because vestibular-evoked responses are attenuated when actual sensory feedback does not align with estimates from balancing motor commands (Héroux et al., 2015; Luu et al., 2012), we hypothesized that increasing the delay between ankle torques and body motion would progressively attenuate the vestibular response. We further hypothesized that learning to control balance with imposed delays would allow the brain to update its sensorimotor estimates of balance motion and consequently increase the vestibular-evoked muscle responses.

For all vestibular response testing, participants stood on the robotic balance simulator with different delays while being exposed to EVS (Figure 1D). Six delay conditions were tested: 20, 100, 200, 300, 400, and 500 ms. Each trial began with a short period of data collection (~3–5 s) while the participants stood quietly on top of the robotic balance simulator, after which the electrical stimulus was delivered. For each delay condition, EVS was delivered in four 20 s trials, resulting in a total of 80 s of data (24 total trials). We performed short trials to minimize potential adaptation during a trial. Four different EVS signals (0–25 Hz bandwidth) were generated offline with root-mean-square (RMS) ranging from 1.47 to 1.61 mA (due to stochastic variation in signal generation) and each EVS stimulus was delivered once per delay condition (24 trials). We presented the trials in four subgroups, each containing the six delay conditions ordered randomly.

Perceptual testing

Request a detailed protocol

A total of 18 participants, 8 of which participated in the training protocol of Experiment 2, completed perceptual testing (Figure 1C). Here, we examined if participants perceived unexpected postural behavior while being exposed to intervals of imposed sensorimotor delays (see below). All participants completed the pre-learning session, eight then completed the training protocol and were tested in the post-learning session and five of those eight returned ~3 months later for the retention session. If adding balance delays reduces the probability that sensory feedback is associated with motor commands, we hypothesized that participants would perceive self-generated balance oscillations as unexpected motion under delayed balance conditions. If training to stand with the imposed delay allows the brain to update its sensorimotor estimates of balance motion, we hypothesized that after training participants would be less prone to detecting unexpected standing motion when balancing with experimental delays (i.e., psychometric functions would shift rightward).

During the perception trials, the delay imposed by the robotic simulator transitioned while participants were actively balancing (see Figure 1E). Participants were instructed to indicate by pressing and holding a hand-held button switch when they perceived unexpected balance movements and release the button when balance felt normal. Delays were manipulated using a variation of the method of constant stimuli. We used seven different delays in the trials. For the 10 participants who did not participate in the training protocol (no-learning group), the delays were 20 (catch trial), 50, 100, 150, 200, 250, and 300 ms. We limited the delay to a maximum of 300 ms because preliminary testing showed that participants always perceived unexpected balance at the 300 ms delay. Participants that partook in the training protocol were presented with 50, 100, 150, 200, 250, 300, and 350 ms delays. We expected that after training some 300 ms delay periods would not elicit perceptions of unexpected motion (see Results), and therefore increased the experimental delay to a maximum of 350 ms. Participants balanced themselves in the robotic simulator for ~260 s in 10 separate trials. While participants actively balanced, we randomly inserted delays in the balance control for 8 s. During each trial, the robot transitioned instantaneously from the baseline 20 ms balance delay to one of the experimental delays (20–350 ms) before returning to 20 ms. The inter-transition interval varied randomly between 7 and 10 s. In this manner, 14 delay periods (two of each delay level) were presented in a random order for each trial, resulting in a total of 20 delay periods for each experimental delay (yielding a 5% resolution). The catch delay period (20 ms) from the no-learning group did not reveal any different performance from the existing inter-delay intervals and both the no-learning and pre-learning participants had 100% success at detecting the 300 ms delay. Therefore, we present the psychometric functions (see Psychometric functions) of these two groups together.

Experiment 3

Request a detailed protocol

Our results from the vestibular and perceptual testing in Experiment 2 showed that with added delays, (1) vestibular-evoked muscle responses are attenuated and participants perceive unexpected behavior, and (2) both vestibular and perceptual response modulations occur together with increases in sway variability (i.e., sway velocity variance) (see Results). Vestibular stimulation trials in Experiment 2 – vestibular testing had single, fixed delays (no transition between delays within the trial); consequently, we could not assess the time course of vestibular response attenuation. In Experiment 3, we tracked the time course of the vestibular, balance, and perceptual responses to imposed delays by repeatedly exposing participants (n = 7) to transient periods (8 s) of a 200 ms delay period while delivering EVS and instructing them to report perceptions of unexpected balance. Specifically, we determined (1) vestibular response attenuation in relation to when participants perceive unexpected standing behavior, and (2) the sway velocity variance associated with modulations in the vestibular and perceptual responses. Participants balanced on the robotic balance system for six separate trials lasting ~260 s each and were instructed to indicate perceived changes in balance control via button press. To probe the vestibular-evoked muscle responses, right soleus EMG was recorded and stochastic EVS was delivered (RMS: 1.38 mA) throughout each trial. The trials were similar to those of Experiment 2 – perceptual testing, except that only the 200 ms experimental delay was presented. We chose 200 ms based on our results from Experiments 1 and 2 (see Results). This specific delay increases sway velocity variance, attenuates vestibular-evoked balance responses, and elicits frequent perceptual detections (~80%) of unexpected standing motion. During each trial, the robot transitioned from the baseline balance condition (20 ms delay) to a 200 ms delay before returning to baseline. Transition to the delayed period occurred randomly over an inter-transition interval of 8–9 s and each delay period lasted exactly 8 s. Each trial consisted of 14 delay periods and a total of six trials were performed, providing 84 delay periods.

Data reduction and signal analysis

Request a detailed protocol

All non-statistical processing and analyses were performed using custom-designed routines in MATLAB (2018b version, MathWorks, Natick, MA, USA) and LabVIEW software (LabVIEW 2013, National Instruments).

Balance behavior

Request a detailed protocol

To quantify how balance behavior was affected by imposed delays in Experiments 1 and 2, we estimated the variance of whole-body sway velocity within each trial. Sway velocity variance was estimated only from data in which whole-body angular position was within the virtual balance limits (6° anterior and 3° posterior). Specifically, data were extracted in non-overlapping 2 s windows, when there was at least one period of two continuous seconds of balance within the virtual limits. Data windows were only extracted in multiples of 2 s. For instance, if there was an 11 s segment of continuous balance, we only extracted five 2 s windows (i.e., first 10 s of the segment). Sway velocity variance was estimated over these 2 s windows (see Figure 2A) because (1) participants could only balance within the balance limits for periods of ~2–5 s during some trials with delays ≥ 200 ms and (2) the transient delays in perceptual testing lasted only 8 s. Although too short to evaluate low-frequency postural sway position, this analysis window was considered appropriate to evaluate the variance of sway velocity because the velocity signal primarily consists of frequencies > 0.5 Hz (van der Kooij et al., 2011). On a participant-by-participant basis, we then averaged the sway velocity variance from the 2 s windows to provide an estimate of sway velocity variance for each participant in each balance condition (e.g., Experiment 1, 200 ms delay). For Experiments 1 and 2 (training trials), we also computed the percentage of time (over 60 s intervals) that whole-body sway position was within the virtual balance limits. For the training trials in Experiment 2, sway velocity variance was estimated from non-overlapping 2 s windows taken across 1 min intervals (thus a maximum of 30 available windows per minute) throughout the training and retention phases, as well as during standing balance prior to training. These sway velocity variances were then averaged for every minute across all participants, providing a minute-by-minute representation of sway velocity variance in the training trials. For perceptual testing, where delays transitioned during perception trials, we evaluated the variance of sway velocity from 2 s windows over the period during which a delay was imposed. Since each delay was presented 20 times, this provided 160 s of data for each delay.

For Experiment 3, we identified peak sway velocity variance leading up to a perceptual detection. We therefore used a 2 s sliding window to extract the time course of sway velocity variance. Time-varying variance was calculated using the movvar MATLAB function, which calculated variance over 2 s segments while repeatedly moving over the data on a point-by-point basis. On a participant-by-participant basis, all delay periods (84 total) were classified as detected (button pressed during delay) or missed (button not pressed during delay). Using only perceptually detected trials (499 out of 588), we then extracted peak sway velocity variance over a period starting at the onset of the delay and ending at the perceptual detection from each perceived trial. Transitions where a button press occurred before delay onset were removed from the analysis (group data: 10 out of 499 transitions), providing 489 transitions in total.

Vestibular-evoked muscle responses

Request a detailed protocol

To estimate the presence and magnitude of vestibular-evoked muscle responses in Experiment 2 - vestibular testing, we used a Fourier analysis to estimate the relationship between vestibular stimuli and muscle activity in the frequency and time domains. Specifically, we computed the coherence, gain, and cross-covariance functions between the electrical stimulus and soleus EMG for each participant (Dakin et al., 2007). Because vestibular stimulation trials were performed on three separate days (pre-learning, post-learning, retention sessions), we scaled soleus EMG to each session’s baseline EMG measure. Specifically, for each testing session (e.g., pre-learning), we estimated the mean soleus EMG amplitude from a baseline quiet standing trial. We calculated the mean EMG amplitude recorded while participants maintained standing balance within ±0.25° around their preferred standing posture. We then scaled soleus EMG recorded during the vestibular stimulation trials by dividing it by the calculated mean EMG amplitude. In this manner, each participant’s EMG during vestibular trials from a given session was scaled to the baseline EMG measured during that session. EMG data were high-pass filtered (30 Hz, zero lag, sixth-order Butterworth) and full-wave rectified. Data were cut into segments of 2048 data points (~1 s) providing a frequency resolution of ~0.98 Hz. For each participant and condition (e.g., pre-learning 100 ms delay), data were concatenated over the four balance trials providing 76 segments equating to 77.82 s of data. Over each segment (no overlap between segments), the autospectra for EVS and soleus EMG as well as the cross-spectra between EVS and EMG were calculated. The spectra were then averaged in the frequency domain to estimate coherence, gain, and cross-covariance. Coherence is a measure of the linear relationship between two signals in the frequency domain and is given by $C (f) = {{| P}_{s r} (f) |}^{2} / (P_{s s} (f) P_{r r} (f))$ where $P_{s r} (f)$ is the stimulus-response cross spectrum, $P_{s s} (f)$ is the autospectrum of the EVS stimulus, and $P_{r r} (f)$ is the autospectrum of the rectified EMG. At each frequency point, coherence ranges from 0 (no linear relationship) to 1 (noise-free linear relationship). We interpreted coherence at each frequency point as significant if it exceeded the 95% confidence limit derived from the number of disjoint segments (Halliday et al., 1995). Gain was computed by dividing the EVS-EMG cross spectrum by the EVS autospectrum and represents the ratio of the output signal to the input signal. Gain must be assessed alongside coherence because its estimate is unreliable at frequency points where coherence is below the significance threshold.

In the time domain, we estimated the non-normalized cross-covariance, which provides a time-domain measure of EVS-EMG association. We estimated cross-covariance for individual participants and group pooled data by taking the inverse Fourier transform of the EVS-EMG cross spectra (Halliday et al., 1995). Cross-covariance (sometimes referred to as cumulant density) estimates are used in neurophysiological and motor control studies to characterize the correlation between two signals (Brown et al., 1999; Brown et al., 2001; Halliday et al., 1995; Halliday et al., 2006; Hansen et al., 2005; Nielsen et al., 2005; Tijssen et al., 2000). These measures have been widely used to estimate time domain vestibulo-motor responses to EVS during postural control activities (Dakin et al., 2010; Dakin et al., 2007; Mackenzie and Reynolds, 2018; Mian and Day, 2009; Mian and Day, 2014; Reynolds, 2011). During standing balance, lower-limb EVS-EMG cross-covariance responses exhibit a biphasic pattern with opposite peaks, defined as short- (50–70 ms) and medium-latency (100–120 ms) responses that match the responses elicited by square wave stimuli (Dakin et al., 2010; Dakin et al., 2007). For statistical analysis in Experiment 2- vestibular testing, the peak-to-peak amplitude of the cross-covariance estimates was extracted from each participant’s response and used as a measure of response magnitude. When either of the short- or medium-latency cross-covariance peaks did not surpass the 95% confidence interval, the value of that peak was set to zero (Dakin et al., 2007; Forbes et al., 2016). Therefore, if both short- and medium-latency peaks did not exceed the confidence intervals, the cross-covariance vestibular response amplitude was zero and considered absent.

For Experiment 3, we tracked time-varying changes in the vestibular-evoked muscle responses during transitions to 200 ms delayed balance control by estimating the time-varying coherence and gain between EVS and rectified EMG activity. Segments of 24 s of data, including 8 s prior to and after the imposed delay, from each trial were used for analysis. Because estimates of vestibulomuscular coherence and gain required multiple repetitions of the imposed delay, we did not evaluate vestibular responses on a trial-by-trial basis. Time–frequency vestibulomuscular coherence and gain were calculated by convolving the input EVS and output EMG with a set of complex Morlet wavelets (Blouin et al., 2011; Zhan et al., 2006), defined as complex sine waves tapered by a Gaussian (Cohen, 2014; Cohen, 2019). The peak frequencies of the wavelets were linearly spaced from 0.5 to 25 Hz in 40 steps, and the number of cycles used for each wavelet was logarithmically spaced from 3 to 12 with increasing wavelet peak frequency. This corresponds to a full-width at half maximum (FWHM) ranging from 168 ms to 2249 ms and a spectral FWHM range of 0.39–5.25 Hz (Cohen, 2019). For each participant, the wavelet analysis was performed on a data set consisting of all segments of data (each 24 s in length) and averaged across the number of transitions. To compare vestibular responses with the reported perception of unexpected balance, we only included transitions that were perceived by the participants (group data: 489 out of 584). A pooled wavelet analysis was also performed on a concatenated data set of all 489 participant data segments. Time–frequency contour plots of coherence and gain are presented with the first and last 2 s of data removed due to the distortion by window edge effects when applying wavelet analysis. For illustrative purposes, and because gain is only reliable when coherence is significant, we plotted non-significant coherence points and their gain counterparts as zero in the time-frequency contour plots (Figure 6B). To compare the overall strength of the EVS-EMG relationship during the period of baseline balance control vs. delayed balance control, we computed mean coherence and mean gain (Luu et al., 2012). Mean coherence and mean gain were calculated by averaging values across the 0.5–25 Hz bandwidth at each time point. For the mean gain estimate, only gain values for which coherence was significant at each corresponding time and frequency points were used (which was primarily across the 0–10 Hz bandwidth). To characterize the time course of vestibular response attenuation induced by the imposed delay, we fit exponential decay functions to each participant’s average coherence and during the 8 s period of 200 ms delay. For gain, we fit an exponential only to the group mean gain because for some participants coherence decreased below significance at all frequencies for some periods of the delay exposure (see Figure 6C, left-lower panel).

Psychometric functions

Request a detailed protocol

For perception trials, psychometric functions were generated using the participant button switch responses during the experimental delay periods. The following criteria were used to classify a participant’s response: (1) detected, identified if the button was pressed at any time during an 8 s delay period; and (2) missed, identified if the button was not pressed during an 8 s delay period. If the button was pressed prior to the onset of the delay and held until the 8 s delay period started, the trial was removed from analysis (see Table 3). Mean detection rates for each delay were computed by dividing the number of detected balance control transitions (delay trial presented with button switch on) by the total number of used delay trials (see Table 3). Detection time was computed as the time between the onset of the delay and the button press. Psychometric functions were generated by relating the participant’s proportion of detected responses to the magnitude of the delay (ms) to estimate a delay threshold level of detected unexpected balance behavior induced by the simulation delays. Using custom software (LabVIEW 2013, National Instruments; Rasman et al., 2021; available at https://doi.org/10.5683/SP2/IKX9ML), a sigmoidal cumulative normal function was fit to each participant’s response data across the different delays using a robust Bayesian curve fitting procedure (Peters et al., 2016; Peters et al., 2015). Briefly, we parameterized each participant’s psychometric function using the following mixture model:

p (d a t a| μ, σ, δ) = \frac{δ}{2} + (1 - δ) (\int_{- \infty}^{x} \frac{1}{\sqrt{2 π} σ^{2}} e^{- \frac{{(u - μ)}^{2}}{2 σ^{2}}})

where µ is the position of the sigmoidal curve along the x-axis, σ is the slope of the sigmoidal curve, and δ is the realistic probability of a lapse in performance (e.g., loss of concentration, accidental button pushes, etc.) on some small proportion of trials (Goldreich et al., 2009; Kontsevich and Tyler, 1999). We set the range of possible µ values from 0 to 0.5 (seconds) in steps of 0.005, σ (standard deviation) values from 0.01 to 5 in steps of 0.01, and δ (lapse rate) values from 0.01 to 0.05 (%) in steps of 0.01. We began with a uniform prior distribution over this parameter space. We marginalized over the δ, a nuisance parameter in this case, to obtain a joint posterior probability distribution over µ and σ. The best-fitting curve was taken as the mode of this joint posterior probability distribution. Participants’ perceptual threshold was calculated by averaging the interpolated 70% correct threshold value across the joint posterior probability distribution.

For Experiment 3, we used only a 200 ms experimental delay because we were primarily interested in comparing perceptual detection times with vestibular response attenuation and relating those latencies to standing behavior (sway velocity variance). Because only one stimulus level (200 ms) was presented, we were unable to use psychometric functions to estimate a perceptual threshold and instead we simply report the proportion of 200 ms transitions that were detected.

Statistical analysis

All statistical analyses were performed using SPSS22 software (IBM) and the significance level was set at 0.05. Group data in text, tables, and figures are presented as mean ± standard deviations unless otherwise specified.

Experiment 1

Request a detailed protocol

To test our hypothesis that novel delays would influence standing balance behavior, we assessed changes in whole-body sway across delays using linear mixed models (fixed effect: delay level; random effect: participant ID). This analysis was run using the extracted sway velocity variance (from 2 s windows) and the percentage of the trial within the balance limits as dependent variables.

Experiment 2

Request a detailed protocol

To establish how balance behavior changed during the 400 ms delay training session, we fit a first-order exponential function to the velocity variance data (2 s windows) obtained from all participants over the 100 min of training. We further compared differences in behavior at different time points using t-tests. Specifically, we assessed (1) whether balancing with the 400 ms delay after training was different than baseline balance by comparing the last minute of training to baseline standing, (2) adaptation during training by comparing the last minute of training to the first minute of training, and (3) whether the improvements in balance behavior were maintained after 3 months by comparing the first minute of retention to the first minute of training and the first minute of retention to the last minute of training. We performed identical analyses using the percentage of the trial within the balance limits as the dependent variable.

To evaluate how imposed delays influenced the vestibular-evoked balance responses (vestibular testing) and perception of standing motion (perceptual testing), we emphasized mainly on interactions (delay × learning) and main effects (delay, learning). Specifically, if there was an interaction, we quantified how the training protocol influenced the vestibular-evoked responses and perception of balance at each delay. Therefore, we decomposed any detected interaction effects by comparing pre-learning to post-learning and pre-learning to retention across delays. Accordingly, we performed planned comparisons with either paired t-tests (for parametric tests) or Wilcoxon signed-rank tests (non-parametric tests), which were Bonferroni corrected for multiple comparisons.

Vestibular testing trials

Request a detailed protocol

To test our hypotheses that vestibular-evoked responses would first attenuate with imposed delays and then increase following the training protocol, we evaluated EVS-EMG cross-covariance responses across conditions. As there were missing data (only seven retention participants) and the responses were not normally distributed (Shapiro–Wilk test), we assessed the effects of delay and learning on the amplitude of vestibular-evoked cross-covariance (peak-to-peak) responses using a non-parametric analysis. We rank transformed the data and ran an ordinal logistic regression through the generalized estimated equations in SPSS (within-subject variables: delay and learning; participant variable: participant ID), which is a nonparametric test that accounts for repeated measures and missing data. We then decomposed the main effects and interaction effects using Bonferroni corrected Wilcoxon signed-rank tests. Because standing balance variability is partially linked to balance control errors (Kiemel et al., 2002) that may be evoked by the imposed delays, we also compared sway velocity variance using a linear mixed model (fixed effects: delay level and learning condition; random effect: participant ID) and decomposed the main and interaction effects using Bonferroni corrected pairwise comparisons.

Perceptual testing trials

Request a detailed protocol

To test our hypothesis that sensorimotor adaptation to delayed balance control would reduce perceptual sensitivity to manipulated delays (i.e., shift psychometric functions to the right), we compared 70% detection thresholds using a linear mixed model (fixed effect: learning condition; random effect: participant ID). Significant main effects of learning were decomposed using Bonferroni corrected pairwise comparisons. Additionally, to determine how balance control errors (see above) varied across conditions, we compared sway velocity variance during the delay period for perception trials using linear mixed models (fixed effects: delay level and learning condition; random effect: participant ID). We decomposed detected main and interaction effects using Bonferroni corrected pairwise comparisons.

Experiment 3: vestibular and perception modulation

Request a detailed protocol

Experiment 3 was designed to track time-dependent modulations in the vestibular control of balance together with changes in sway velocity variance and perceptual detections. For these results, we report only descriptive statistics. For vestibular responses, we report the time when the vestibular-evoked muscle responses (coherence and gain) were attenuated by 63.2% and 95% (extracted from exponential decay functions) during the delay period. For perception, we report the group average perceptual detection time and 95th percentile. Finally, to link the vestibular and perceptual responses, we report the amount of vestibular attenuation that aligned with the average perceptual detection time.

Data availability

We have created a Dataverse link for the source files needed to generate the group result figures. This can be found at https://doi.org/10.5683/SP2/IKX9ML.

The following data sets were generated

1. Rasman BG
2. Forbes PA
3. Peters RM
4. Ortiz O
5. Franks IM
6. Inglis JT
7. Chua R
8. Blouin JS
(2021) Scholars Portal Dataverse
Data and code for Learning to stand with unexpected sensorimotor delays.
https://doi.org/10.5683/SP2/IKX9ML

References

(1999) Open-loop intermittent feedback control: Practical continuous-time GPC
IEE Proceedings - Control Theory and Applications 146:426–434.
https://doi.org/10.1049/ip-cta:19990504
- Google Scholar
1. Asai Y
2. Tasaka Y
3. Nomura K
4. Nomura T
5. Casadio M
6. Morasso P
(2009) A model of postural control in quiet standing: robust compensation of delay-induced instability using intermittent activation of feedback control
PLOS ONE 4:e6169.
https://doi.org/10.1371/journal.pone.0006169
- PubMed
- Google Scholar
1. Berniker M
2. Kording K
(2008) Estimating the sources of motor errors for adaptation and generalization
Nature Neuroscience 11:1454–1461.
https://doi.org/10.1038/nn.2229
- PubMed
- Google Scholar
(2011) Stability in a frontal plane model of balance requires coupled changes to postural configuration and neural feedback control
Journal of Neurophysiology 106:437–448.
https://doi.org/10.1152/jn.00010.2011
- PubMed
- Google Scholar
(1999) Spatio-temporal prediction modulates the perception of self-produced stimuli
Journal of Cognitive Neuroscience 11:551–559.
https://doi.org/10.1162/089892999563607
- PubMed
- Google Scholar
(2011) Extracting phase-dependent human vestibular reflexes during locomotion using both time and frequency correlation approaches
Journal of Applied Physiology 111:1484–1490.
https://doi.org/10.1152/japplphysiol.00621.2011
- PubMed
- Google Scholar
(2005) Body sway during quiet standing: is it the residual chattering of an intermittent stabilization process
Human Movement Science 24:588–615.
https://doi.org/10.1016/j.humov.2005.07.006
- PubMed
- Google Scholar
(2010) Structure learning in action
Behavioural Brain Research 206:157–165.
https://doi.org/10.1016/j.bbr.2009.08.031
- PubMed
- Google Scholar
1. Brooks JX
2. Cullen KE
(2013) The primate cerebellum selectively encodes unexpected self-motion
Current Biology: CB 23:947–955.
https://doi.org/10.1016/j.cub.2013.04.029
- PubMed
- Google Scholar
(2015) Learning to expect the unexpected: rapid updating in primate cerebellum during voluntary self-motion
Nature Neuroscience 18:1310–1317.
https://doi.org/10.1038/nn.4077
- PubMed
- Google Scholar
(1999) Coherent cortical and muscle discharge in cortical myoclonus
Brain 122:461–472.
https://doi.org/10.1093/brain/122.3.461
- PubMed
- Google Scholar
1. Brown P
2. Oliviero A
3. Mazzone P
4. Insola A
5. Tonali P
6. Di Lazzaro V
(2001) Dopamine dependency of oscillations between subthalamic nucleus and pallidum in Parkinson’s disease
The Journal of Neuroscience 21:1033–1038.
https://doi.org/10.1523/JNEUROSCI.21-03-01033.2001
- PubMed
- Google Scholar
1. Cenciarini M
2. Peterka RJ
(2006) Stimulus-dependent changes in the vestibular contribution to human postural control
Journal of Neurophysiology 95:2733–2750.
https://doi.org/10.1152/jn.00856.2004
- PubMed
- Google Scholar
(2020) Development of a conversion model between mechanical and electrical vestibular stimuli
Journal of Neurophysiology 123:548–559.
https://doi.org/10.1152/jn.00276.2019
- PubMed
- Google Scholar
Book
1. Cohen MX
(2014)
Analyzing Neural Time Series Data: Theory and Practice

MIT press.
- Google Scholar
1. Cohen MX
(2019) A better way to define and describe Morlet wavelets for time-frequency analysis
Neuroimage 199:81–86.
https://doi.org/10.1016/j.neuroimage.2019.05.048
- PubMed
- Google Scholar
(2001) Driving in the future: temporal visuomotor adaptation and generalization
Journal of Vision 1:88–98.
https://doi.org/10.1167/1.2.3
- PubMed
- Google Scholar
1. Dakin CJ
2. Son GM
3. Inglis JT
4. Blouin JS
(2007) Frequency response of human vestibular reflexes characterized by stochastic stimuli
The Journal of Physiology 583:1117–1127.
https://doi.org/10.1113/jphysiol.2007.133264
- PubMed
- Google Scholar
(2010) Frequency-specific modulation of vestibular-evoked sway responses in humans
Journal of Neurophysiology 103:1048–1056.
https://doi.org/10.1152/jn.00881.2009
- PubMed
- Google Scholar
(1997) Human body-segment tilts induced by galvanic stimulation: a vestibularly driven balance protection mechanism
The Journal of Physiology 500:661–672.
https://doi.org/10.1113/jphysiol.1997.sp022051
- PubMed
- Google Scholar
(2014) Spinal mechanisms may provide a combination of intermittent and continuous control of human posture: predictions from a biologically based neuromusculoskeletal model
PLOS Computational Biology 10:e1003944.
https://doi.org/10.1371/journal.pcbi.1003944
- PubMed
- Google Scholar
(1991) Constancy of central conduction delays during development in man: investigation of motor and somatosensory pathways
The Journal of Physiology 434:441–452.
https://doi.org/10.1113/jphysiol.1991.sp018479
- PubMed
- Google Scholar
(2008) Effect of distorted visual feedback on the sense of agency
Behavioural Neurology 19:53–57.
https://doi.org/10.1155/2008/425267
- PubMed
- Google Scholar
1. Fitzpatrick R
2. McCloskey DI
(1994) Proprioceptive, visual and vestibular thresholds for the perception of sway during standing in humans
The Journal of Physiology 478:173–186.
https://doi.org/10.1113/jphysiol.1994.sp020240
- PubMed
- Google Scholar
(1996) Loop gain of reflexes controlling human standing measured with the use of postural and vestibular disturbances
Journal of Neurophysiology 76:3994–4008.
https://doi.org/10.1152/jn.1996.76.6.3994
- PubMed
- Google Scholar
1. Fitzpatrick RC
2. Day BL
(2004) Probing the human vestibular system with galvanic stimulation
Journal of Applied Physiology 96:2301–2316.
https://doi.org/10.1152/japplphysiol.00008.2004
- PubMed
- Google Scholar
1. Forbes PA
2. Dakin CJ
3. Vardy AN
4. Happee R
5. Siegmund GP
6. Schouten AC
7. Blouin JS
(2013) Frequency response of vestibular reflexes in neck, back, and lower limb muscles
Journal of Neurophysiology 110:1869–1881.
https://doi.org/10.1152/jn.00196.2013
- PubMed
- Google Scholar
(2014) Task, muscle and frequency dependent vestibular control of posture
Frontiers in Integrative Neuroscience 8:94.
https://doi.org/10.3389/fnint.2014.00094
- PubMed
- Google Scholar
1. Forbes PA
2. Luu BL
3. Van der Loos HF
4. Croft EA
5. Inglis JT
6. Blouin JS
(2016) Transformation of Vestibular Signals for the Control of Standing in Humans
The Journal of Neuroscience 36:11510–11520.
https://doi.org/10.1523/JNEUROSCI.1902-16.2016
- PubMed
- Google Scholar
Book
(2018)
Handbook of Clinical Neurology, Vol. 159

Sensorimotor control of standing balance.
- Google Scholar
1. Friston K
(2010) The free-energy principle: a unified brain theory
Nature Reviews Neuroscience 11:127–138.
https://doi.org/10.1038/nrn2787
- PubMed
- Google Scholar
1. Gawthrop PJ
2. Wang L
(2006) Intermittent predictive control of an inverted pendulum
Control Engineering Practice 14:1347–1356.
https://doi.org/10.1016/j.conengprac.2005.09.002
- Google Scholar
1. Gawthrop P
2. Loram I
3. Lakie M
4. Gollee H
(2011) Intermittent control: a computational theory of human control
Biological Cybernetics 104:31–51.
https://doi.org/10.1007/s00422-010-0416-4
- PubMed
- Google Scholar
1. Gifford RN
2. Lyman J
(1967) Tracking Performance with Advanced and Delayed Visual Displays
Human Factors 9:127–132.
https://doi.org/10.1177/001872086700900204
- Google Scholar
(1984) Relation between discharge regularity and responses to externally applied galvanic currents in vestibular nerve afferents of the squirrel monkey
Journal of Neurophysiology 51:1236–1256.
https://doi.org/10.1152/jn.1984.51.6.1236
- PubMed
- Google Scholar
(2009) A tactile automated passive-finger stimulator (taps
Journal of Visualized Experiments 1374.
https://doi.org/10.3791/1374
- PubMed
- Google Scholar
1. Haering C
2. Kiesel A
(2015) Was it me when it happened too early? Experience of delayed effects shapes sense of agency
Cognition 136:38–42.
https://doi.org/10.1016/j.cognition.2014.11.012
- PubMed
- Google Scholar
1. Halliday DM
2. Amjad AM
3. Breeze P
4. Conway BA
5. Farmer SF
(1995) A Framework for the Analysis of Mixed Time Series/Point Process Data--Theory and Application to the Study of Physiological Tremor, Single Motor Unit Discharges and Electromyograms
Progress in Biophysics and Molecular Biology 64:237–278.
https://doi.org/10.1016/s0079-6107(96)00009-0
- PubMed
- Google Scholar
(2006) Neural spike train synchronization indices: definitions, interpretations, and applications
IEEE Transactions on Bio-Medical Engineering 53:1056–1066.
https://doi.org/10.1109/TBME.2006.873392
- PubMed
- Google Scholar
(2005) Reduction of common synaptic drive to ankle dorsiflexor motoneurons during walking in patients with spinal cord lesion
Journal of Neurophysiology 94:934–942.
https://doi.org/10.1152/jn.00082.2005
- PubMed
- Google Scholar
(2015) Cross-modal calibration of vestibular afference for human balance
PLOS ONE 10:e0124532.
https://doi.org/10.1371/journal.pone.0124532
- PubMed
- Google Scholar
(2014) Experimental performance evaluation of human balance control models
IEEE Transactions on Neural Systems and Rehabilitation Engineering 22:1115–1127.
https://doi.org/10.1109/TNSRE.2014.2318351
- PubMed
- Google Scholar
(2015) Semidiscretization for Time-Delayed Neural Balance Control
SIAM Journal on Applied Dynamical Systems 14:1258–1277.
https://doi.org/10.1137/140975632
- Google Scholar
(2019) Virtual signals of head rotation induce gravity-dependent inferences of linear acceleration
The Journal of Physiology 597:5231–5246.
https://doi.org/10.1113/JP278642
- PubMed
- Google Scholar
1. Kiemel T
2. Oie KS
3. Jeka JJ
(2002) Multisensory fusion and the stochastic structure of postural sway
Biological Cybernetics 87:262–277.
https://doi.org/10.1007/s00422-002-0333-2
- PubMed
- Google Scholar
(2019) Rapid learning and unlearning of predicted sensory delays in self-generated touch
eLife 8:e42888.
https://doi.org/10.7554/eLife.42888
- PubMed
- Google Scholar
1. Kim J
2. Curthoys IS
(2004) Responses of primary vestibular neurons to galvanic vestibular stimulation (GVS) in the anaesthetised guinea pig
Brain Research Bulletin 64:265–271.
https://doi.org/10.1016/j.brainresbull.2004.07.008
- PubMed
- Google Scholar
1. Kontsevich LL
2. Tyler CW
(1999) Bayesian adaptive estimation of psychometric slope and threshold
Vision Research 39:2729–2737.
https://doi.org/10.1016/s0042-6989(98)00285-5
- PubMed
- Google Scholar
1. Krakauer JW
2. Mazzoni P
(2011) Human sensorimotor learning: adaptation, skill, and beyond
Current Opinion in Neurobiology 21:636–644.
https://doi.org/10.1016/j.conb.2011.06.012
- PubMed
- Google Scholar
1. Kuo AD
(1995) An optimal control model for analyzing human postural balance
IEEE Transactions on Bio-Medical Engineering 42:87–101.
https://doi.org/10.1109/10.362914
- PubMed
- Google Scholar
1. Kuo AD
(2005) An optimal state estimation model of sensory integration in human postural balance
Journal of Neural Engineering 2:S235–S249.
https://doi.org/10.1088/1741-2560/2/3/S07d
- Google Scholar
1. Kwan A
2. Forbes PA
3. Mitchell DE
4. Blouin JS
5. Cullen KE
(2019) Neural substrates, dynamics and thresholds of galvanic vestibular stimulation in the behaving primate
Nature Communications 10:1904.
https://doi.org/10.1038/s41467-019-09738-1
- PubMed
- Google Scholar
1. Le Mouel C
2. Brette R
(2019) Anticipatory coadaptation of ankle stiffness and sensorimotor gain for standing balance
PLOS Computational Biology 15:e1007463.
https://doi.org/10.1371/journal.pcbi.1007463
- PubMed
- Google Scholar
(2005) Human postural sway results from frequent, ballistic bias impulses by soleus and gastrocnemius
The Journal of Physiology 564:295–311.
https://doi.org/10.1113/jphysiol.2004.076307
- PubMed
- Google Scholar
1. Loram ID
2. Gollee H
3. Lakie M
4. Gawthrop PJ
(2011) Human control of an inverted pendulum: is continuous control necessary? Is intermittent control effective? Is intermittent control physiological
The Journal of Physiology 589:307–324.
https://doi.org/10.1113/jphysiol.2010.194712
- PubMed
- Google Scholar
(2011) Validation of a robotic balance system for investigations in the control of human standing balance
IEEE Transactions on Neural Systems and Rehabilitation Engineering 19:382–390.
https://doi.org/10.1109/TNSRE.2011.2140332
- PubMed
- Google Scholar
1. Luu BL
2. Inglis JT
3. Huryn TP
4. Van der Loos HF
5. Croft EA
6. Blouin JS
(2012) Human standing is modified by an unconscious integration of congruent sensory and motor signals
The Journal of Physiology 590:5783–5794.
https://doi.org/10.1113/jphysiol.2012.230334
- PubMed
- Google Scholar
1. Mackenzie SW
2. Reynolds RF
(2018) Differential effects of vision upon the accuracy and precision of vestibular-evoked balance responses
The Journal of Physiology 596:2173–2184.
https://doi.org/10.1113/JP275645
- PubMed
- Google Scholar
(2006) Controlling balance during quiet standing: Proportional and derivative controller generates preceding motor command to body sway position observed in experiments
Gait & Posture 23:164–172.
https://doi.org/10.1016/j.gaitpost.2005.01.006
- Google Scholar
(1985) Visuomotor tracking with delayed visual feedback
Neuroscience 16:511–520.
https://doi.org/10.1016/0306-4522(85)90189-7
- PubMed
- Google Scholar
1. Miall RC
2. Jackson JK
(2006) Adaptation to visual feedback delays in manual tracking: evidence against the Smith Predictor model of human visually guided action
Experimental Brain Research 172:77–84.
https://doi.org/10.1007/s00221-005-0306-5
- PubMed
- Google Scholar
1. Mian OS
2. Day BL
(2009) Determining the direction of vestibular-evoked balance responses using stochastic vestibular stimulation
The Journal of Physiology 587:2869–2873.
https://doi.org/10.1113/jphysiol.2009.171256
- PubMed
- Google Scholar
1. Mian OS
2. Day BL
(2014) Violation of the craniocentricity principle for vestibularly evoked balance responses under conditions of anisotropic stability
The Journal of Neuroscience 34:7696–7703.
https://doi.org/10.1523/JNEUROSCI.0733-14.2014
- PubMed
- Google Scholar
1. Milton J
2. Insperger T
(2019) Acting together, destabilizing influences can stabilize human balance
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 377:20180126.
https://doi.org/10.1098/rsta.2018.0126
- PubMed
- Google Scholar
(2005) Organization of common synaptic drive to motoneurones during fictive locomotion in the spinal cat
The Journal of Physiology 569:291–304.
https://doi.org/10.1113/jphysiol.2005.091744
- PubMed
- Google Scholar
(2018) Cortical control of upright stance in elderly
Mechanisms of Ageing and Development 169:19–31.
https://doi.org/10.1016/j.mad.2017.12.004
- PubMed
- Google Scholar
1. Peterka RJ
(2002) Sensorimotor integration in human postural control
Journal of Neurophysiology 88:1097–1118.
https://doi.org/10.1152/jn.2002.88.3.1097
- PubMed
- Google Scholar
(2015) Gain and phase of perceived virtual rotation evoked by electrical vestibular stimuli
Journal of Neurophysiology 114:264–273.
https://doi.org/10.1152/jn.00114.2015
- PubMed
- Google Scholar
(2016) Older adults demonstrate superior vestibular perception for virtual rotations
Experimental Gerontology 82:50–57.
https://doi.org/10.1016/j.exger.2016.05.014
- PubMed
- Google Scholar
1. Peterson SM
2. Ferris DP
(2019) Group-level cortical and muscular connectivity during perturbations to walking and standing balance
Neuroimage 198:93–103.
https://doi.org/10.1016/j.neuroimage.2019.05.038
- PubMed
- Google Scholar
(2018) Sensorimotor Manipulations of the Balance Control Loop-Beyond Imposed External Perturbations
Frontiers in Neurology 9:899.
https://doi.org/10.3389/fneur.2018.00899
- PubMed
- Google Scholar
Data
1. Rasman BG
2. Forbes PA
3. Peters RM
4. Ortiz O
5. Franks I
6. Inglis JT
7. Chua R
8. Blouin JS
(authors) (2021) Data and code for “Learning to stand with unexpected sensorimotor delays”
Scholars Portal Dataverse.
https://doi.org/10.5683/SP2/IKX9ML
1. Reynolds RF
(2011) Vertical torque responses to vestibular stimulation in standing humans
The Journal of Physiology 589:3943–3953.
https://doi.org/10.1113/jphysiol.2011.209163
- PubMed
- Google Scholar
(2002) Comparison of human ocular torsion patterns during natural and galvanic vestibular stimulation
Journal of Neurophysiology 87:2064–2073.
https://doi.org/10.1152/jn.00558.2001
- PubMed
- Google Scholar
Thesis
1. Shepherd M
(2014) Intersensory Vestibular Control of Standing Balance
University of British Columbia.

https://open.library.ubc.ca/cIRcle/collections/ubctheses/24/items/1.0167073
- Google Scholar
(1960) Delayed Visual Feedback and Behavior
Science 132:1013–1014.
https://doi.org/10.1126/science.132.3433.1013
- PubMed
- Google Scholar
(2008) Short-duration galvanic vestibular stimulation evokes prolonged balance responses
Journal of Applied Physiology 105:1210–1217.
https://doi.org/10.1152/japplphysiol.01398.2006
- PubMed
- Google Scholar
(2006) Motor-sensory recalibration leads to an illusory reversal of action and sensation
Neuron 51:651–659.
https://doi.org/10.1016/j.neuron.2006.08.006
- PubMed
- Google Scholar
(2000) Frequency analysis of EMG activity in patients with idiopathic torticollis
Brain 123:677–686.
https://doi.org/10.1093/brain/123.4.677
- PubMed
- Google Scholar
(1999) A multisensory integration model of human stance control
Biological Cybernetics 80:299–308.
https://doi.org/10.1007/s004220050527
- PubMed
- Google Scholar
(2001) An adaptive model of sensory integration in a dynamic environment applied to human stance control
Biological Cybernetics 84:103–115.
https://doi.org/10.1007/s004220000196
- PubMed
- Google Scholar
1. van der Kooij H
2. de Vlugt E
(2007) Postural responses evoked by platform pertubations are dominated by continuous feedback
Journal of Neurophysiology 98:730–743.
https://doi.org/10.1152/jn.00457.2006
- PubMed
- Google Scholar
(2011) Sampling duration effects on centre of pressure descriptive measures
Gait & Posture 34:19–24.
https://doi.org/10.1016/j.gaitpost.2011.02.025
- Google Scholar
1. van der Kooij H
2. Peterka RJ
(2011) Non-linear stimulus-response behavior of the human stance control system is predicted by optimization of a system with sensory and motor noise
Journal of Computational Neuroscience 30:759–778.
https://doi.org/10.1007/s10827-010-0291-y
- PubMed
- Google Scholar
(2007) Implementation of a physiologically identified PD feedback controller for regulating the active ankle torque during quiet stance
IEEE Transactions on Neural Systems and Rehabilitation Engineering 15:235–243.
https://doi.org/10.1109/TNSRE.2007.897016
- PubMed
- Google Scholar
1. Wen W
(2019) Does delay in feedback diminish sense of agency? A review
Consciousness and Cognition 73:102759.
https://doi.org/10.1016/j.concog.2019.05.007
- PubMed
- Google Scholar
(2011) Principles of sensorimotor learning
Nature Reviews Neuroscience 12:739–751.
https://doi.org/10.1038/nrn3112
- PubMed
- Google Scholar
1. Zhan Y
2. Halliday D
3. Jiang P
4. Liu X
5. Feng J
(2006) Detecting time-dependent coherence between non-stationary electrophysiological signals--a combined statistical and time-frequency approach
Journal of Neuroscience Methods 156:322–332.
https://doi.org/10.1016/j.jneumeth.2006.02.013
- PubMed
- Google Scholar
1. Zhou Y
2. Wang Z
(2014) Optimal Feedback Control for Linear Systems with Input Delays Revisited
Journal of Optimization Theory and Applications 163:989–1017.
https://doi.org/10.1007/s10957-014-0532-8
- Google Scholar

Decision letter

Noah J Cowan

Reviewing Editor; Johns Hopkins University, United States
Ronald L Calabrese

Senior Editor; Emory University, United States
Noah J Cowan

Reviewer; Johns Hopkins University, United States

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

This is an exciting paper and provides new insights into sensorimotor learning for delay, including its time course, limits, and sensory mechanisms.

Decision letter after peer review:

Thank you for submitting your article "Learning to stand with unexpected sensorimotor delays" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, including Noah J Cowan as Reviewer #1 and Reviewing Editor, and the evaluation has been overseen by Ronald Calabrese as the Senior Editor.

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission. All reviewers agree there is the potential for this paper to provide a significant contribution to the literature, but there was strong agreement across the reviewers that there are fundamental gaps in the analysis and, potentially as a result, the interpretation of the results. In addition, each reviewer has read each others' reviews, and all three reviewers agree with the technical points of the other reviewers, and so each of these should be addressed in a revision.

Summary:

This manuscript will be of interest to a wide range of readers interested in motor control, motor adaptation and motor learning. Using an innovative robotic system, artificial time delays from muscle forces to movement were imposed during standing balance. The results clearly show both the difficulties that the imposed delays have on stabilizing movements and the ability of individuals to adapt to the imposed delays to maintain balance. This provides insight into how the nervous system is able to use sensory information to control movements under normal conditions given the time delays inherent in sensory, motor and neural processes.

Essential Revisions:

1. To characterize how strongly soleus EMG (the output) responds to vestibular stimulation (the input), standard measures designed to characterize input-output mappings should be used. Gain in the frequency domain and the unnormalized impulse response function in the time domain are the standard choices. Both measures used do not distinguish between decreases in EMG variability and gain.

1a) Coherence (while important to report) does not provide even an indirect measure of gain: two systems with gains different by an order of magnitude both reach maximum coherence of 1, depending on the amount of noise in the system. In terms of this research result, if an imposed delay increases output variance but does not change gain, then coherence decreases. Presumably soleus EMG variance increases with sway variance, so the decrease in coherence and Figure 6, for example, may simply reflect an increase in soleus EMG variance, not a decrease in the magnitude of vestibular-evoked muscles EMG responses.

2a) The authors use normalized cumulant density in the time domain as a stand in for gain. In principle, an unnormalized version of this should work, as it is related to the impulse response function (but not quite). It would be better to just directly use the standard estimate based on cross spectrum divided by the power spectrum of the input, rather than the normalized IFT of the cross spectrum that the authors used. But, by normalizing by the EMG signal properties (also by electrical stim -- but that would be the same/similar for all subjects), if EMG variance is increased with increasing delay (a plausible result), the cumulant density function amplitude would decrease due to this normalization, even if the vestibular gain remained unchanged.

So, in your revision, we require the use of a standard measure, e.g. cross spectral density between the input and output (as now calculated) divided by the power spectral density of the input. This would give a frequency domain response function. Taking the inverse Fourier transform would put this in the time domain as an estimate of the impulse response function. Other standard measures are possible.

Critically, this change in analysis may provide a new result, and thus require new interpretation. E.g., it may be that the "scalar" gain estimate does not change, but rather there is a change in the variance that explained your previous analysis. In this case, the transfer function estimate could be examined for alternative interpretations. The reviewers all felt that while this would not necessarily be as striking a result, it would still be nevertheless an important paper, and so it is important when re-analyzing this data not to have the forgone conclusion of a change in gain, which is not yet supported by the analysis.

2. We emphasize one of the major concerns of reviewer #2: Rather than report mean-removed RMS sway (in other words, sway standard deviation) it would be better to report percentage of time within specified sway limits

3. The authors should address whether existing models can stabilize an inverted pendulum with long feedback time delays. Sway variance will increase with increasing time delay, so at some point standing balance is not possible due to one's finite base of support (a type of plant nonlinearity). Specifically, the manuscript should be improved with a more nuanced Discussion (near lines 401-421) to consider the other classes of control models (optimal or intermittent control) that possibly could be candidates for controlling a system with long time delays. For example, if optimal control rather than proportional-derivative control is used, then it is possible in principle (perhaps excluding special cases) to stabilize a linear plant with arbitrarily long delays (e.g., Zhou and Wang 2014, DOI 10.1007/s10957-014-0532-8), although for long time delays such control can be quite fragile with respect to disturbances or plant parameters.

4. Bootstrapping should be better justified or not used.

Reviewer #1:

This paper aims to understand how imposed delays between ankle torque and whole-body motion destabilize standing balance, and determine the mechanisms that the nervous system uses to learn to compensate for these imposed delays. Related studies have estimated the critical delay at which upright standing is destabilized, and shown that humans can learn to compensate for increased delay. This study supports these prior results in the literature and delves deeper into human's standing balance. Specifically, they demonstrate that, although initially vestibulomotor responses are attenuated during imposed delays before learning, eventually subjects learn to partially recover their reliance on vestibular feedback, while, at the same time, improving postural control in the face of delay. Furthermore, after learning, subjects' ability to perceive unexpected delays was reduced, leading the authors to speculate that subjects may learn to "internalize" the experimentally added delay, making it hard to identify said delay an external perturbation. So, this study would be of broad interests for researchers who are studying human control of standing balance as well as other models of sensorimotor control across taxa.

Strengths:

1) The manuscript provides a clear and cogent motivation, and the hypotheses are well grounded in the literature.

2) The data, including the tables and graphs in this manuscript, verify the authors' hypotheses in a generally convincing way.

Weaknesses:

1) Clarification of velocity variance with bootstrapping: The estimates of sway velocity variance using bootstrapping was not well described nor justified. In figure 2, it said 'Sway velocity variance ..., and the resulting data were bootstrapped to provide a single estimate per participant and delay'. 'estimate per participant' sounds like simply using bootstrapping to estimate the mean, which is not a standard use of bootstrapping. It can be used to estimate SEM etc, also in line 795-797, it said 'we bootstrapped the participant's data with replication 10,000 times and then averaged across participants for each delay and learning condition.' from which it seems that the authors are computing the SEM across subjects. In sum the statistics associated with variance estimation and bootstrapping is unclear.

2) The use of Cumulant Density: cumulant density as a gain measure is not a standard technique for gain estimation in the motor control literature, and needs further justification.

3) The use of 2s windows for variance estimation in Experiment 1 was unclear. When estimating sway velocity variance in Experiment 1, 2s non-overlapping windows were applied and "if fewer than five 2 s windows were present, the average was taken across the available data (denoted with filled circles in figures)". And in Figure 2A, "Data not included in the velocity variance analysis are grayed out." However, some non-grayed-out regions in Fig 2A are not to be multiples of 2s, which is confusing.

Although the experimental methods, data analysis and writing skills in this paper are detailed, some improvements are needed for figure illustrations and terminology.

For example, Figure 1B is confusing. There is a circle with δ t inside which represents the imposed delay but it is not good to put both the "Whole body sway" and "Delayed whole-body sway" out of that circle. This is a confusing (and nonstandard!) way of schematizing a closed-loop system such as this. See many examples from the literature, including but not limited to papers by Lena Ting, Michael Dickinson, Daniel Robinson, my lab, and many others for standard ways of writing control system block diagrams that would be more easiliy interpretable. Lena Ting's lab (Lockhart and Ting 2007, expressed in time domain) and Simon Sponberg's lab (https://science.sciencemag.org/content/348/6240/1245.abstract, expressed as a general block diagram) both have nice papers that explicitly include delay in the feedback loop. My lab has three review papers with numerous examples that can be found here: https://limbs.lcsr.jhu.edu/publications/#Reviews.

Some figures in this paper are not straightforward for the readers to understand. Especially in Figure 1, the descriptions are complete, but figures themselves are not informative enough. For instance, in Figure 1 C, the descriptions of the experiment 3 whose trials ("of similar design to Experiment 2B, except that the robot only transitioned between baseline (20 ms) and 200 ms delays (not illustrated)") is unclear. This figure is significant to the paper's results in order to show the procedure of three experiments. Thus, it should be better clarified, or supplemental figures should be used to further explicate such issues.

More details about the load in Figure 1B is needed. We can only learn from line 541 that "For all experiments, participants stood on a custom-designed robotic balance simulator programmed with the mechanics of an inverted pendulum to replicate the load of the body during standing (Figure 1A)". However, the authors need to show in specific equations that were simulated, and the parameters they set in their design, to enable reproducibility of the results.

Moreover, important data points should be marked on the figure. On Figure 1E, the y axis "imposed delay" has only 20 ms and 300 ms marked, but authors later mentioned that "Data from a representative participant (see Figure 1E) show missed 299 detections of the 100 and 150 ms imposed delays", so it would be clearer if they can also mark 150 ms and 100 ms on the graph, because those are critical points.

RE: Cumulant Density: It is indeed critical to have a gain estimate in the vestibulomotor analysis, since coherence alone does not indicate the strength of response to a stimulus: nonlinearities and noise can decrease coherence, even if the gain to stimulus remains unchanged. The authors perform such a gain analysis (see e.g. Figure 4A) using "Cumulant density". This is an interesting technique for identifying the sensorimotor gain but does not seem to be in widespread use, and I could not find a theoretical justification in the system ID textbooks I have. That said, it appears possible that under the right conditions, the appropriately normalized Inverse Fourier Transform of the cross spectral density (i.e. the so-called Cumulant Density) should amount to the impulse response function, but I'm not sure of this. It would be helpful if the authors could better justify this approach or use a more standard analysis, such as impulse response recovery.

The authors call the Vestibular-Evoked Muscle Responses assays an "Experiment" (Experiment 2A), but the experiment is actually much broader, and covers all everything in the gray box in Figure 1C. Likewise for the perception assay ("Experiment 2B"). This terminology is confusing and I recommend dropping that nomenclature and just saying "Vestibular Testing" and "Perceptual Testing". Also, Figure 1C is laid out to look like a table, with two rows, and the first "column" appears to be labeling the rows, but it is not. Please rework this panel to be less confusing.

Reviewer #2:

Using a robotic system, the manuscript demonstrates that imposing time delays from ankle torques to movement causes postural sway to increase, as one would expect based on stochastic models of postural control. What is more surprising is the extent to which participants can adapt to imposed delays and decrease postural sway over multiple days. The evidence of adaptation is exceptionally clear. Another strength of the manuscript is that it relates these decreases in postural sway to a decrease in how often participants perceive unexpected balance movements, suggesting that over time participants learn that their ankles torques are causing the movements even though the movements are artificially delayed. These perceptual measures were obtained in real time during standing balance and carefully characterized, sometime that is not typically done in postural adaptation experiments.

The manuscript also characterizes the relationship between vestibular stimulation and surface electromyography EMG signals from the soleus muscle, using coherence in the frequency domain and the normalized cumulant density function in the time domain. Often gain, which has units of (output units)/(input units), is used to measure how responses to a perturbation change. A common example is using gain to quantify sensory re-weighting during standing balance. (It would be helpful if the authors discussed whether their hypothesized changes in vestibular-evoked muscle responses can be thought of as sensory re-weighting.)

One concern is whether the measures used in this study conflate changes in output magnitude with changes in output variance. For example, if an imposed delay increases output variance but does not change gain, then coherence decreases. For this reason, gain seems a better choice than coherence given the questions the authors are addressing. Similarly, in the time domain, an unnormalized impulse response function seems a better choice than the normalized cumulant density function. Similar comments apply to the time-frequency analysis of Experiment 3, which the manuscript uses to track changes in the relationship between vestibular stimulation and soleus EMG.

One important implication of the reported results that is discussed is that models that predict the maximal sensorimotor delay that allows standing balance are probably underestimating the maximal delay because they assume proportional-derivative (PD) or proportional-integral-derivative (PID) controllers, which are not optimal controllers when there are time delays. The predictions are also based a linear analysis of stability. In reality, due to a person's limited base of support, the person may fall or take a step even though a linear analysis shows that they are stable. It might be helpful to discuss this in relation to the study's imposition of specified limits of body sway.

One other issue that would be helpful to discuss in more detail would the exact sensory consequences of the imposed delays used in this study. The researchers imposed delays from the forces participants produce (forces applied to the support surface) to body movements. This delays sensory feedback related to body movements, but other sensory feedback, such as proprioceptive feedback about muscle forces and cutaneous feedback about the center of pressure (COP) have normal sensory delays. The component of COP dependent on center-of-mass position is delayed but the component dependent on ankle torque is not. Even the way proprioceptive information about muscle length is altered is more complex than a simple time delay, since length changes in tendons allow changes in muscles lengths without joint rotations. It would be helpful to discuss whether the resulting sensory conflicts contribute to the difficulty of balancing with an imposed delay and the implications for adaptation.

Abstract: It would be helpful to mention that sway was restricted to rotation about the ankles.

Figure 1 caption: Why was it necessary to use 3D googles to provide a visual scene to participants? Since the participants are actually moving, would it not be easier just to have participants look at an actual fixed visual scene?

Lines 171-174: Does "both p < 0.001" refer to overall tests for dependence on imposed delay? If so, it would be helpful to indicate which statements in this sentence are supported by statistical tests.

Lines 212-217: The comparing the retention test to sway attenuation corresponding to the time constant seems arbitrary and apparently does not take into account uncertainty in the estimated time constant. To support the statment that "balance improvements were partially maintained" it seems more relevant to compare the retention test to sway variance at the beginning of training to test whether improvements are at least partially maintained and to sway variance at the end of training to test whether improvements are only partially maintained.

Line 521: What was the range of participant ages?

Line 554: The delay from specified to measured motor position was estimated to be 20 ms. Is this with the inertial load of the backboard and participant? Should this be thought of a pure time delay or some other type of frequency response function (transfer function)?

Line 558: The linear least squares predictor algorithm used to synchronize the visual motion with the motors is not described in sufficient detail in the cited reference (Shepherd 2014) to permit others to reproduce this aspect of the experimental setup. It would be helpful to do so here.

Line 569: It would be helpful to specify the functional form and parameters of the stiffness that "caught" the backboard when it exceeded the specified limits.

Line 590: Does "reaching a limit" mean crossing from outside to inside the specified limits?

Lines 674-754: The text describing the protocols for Experiments 2A and 2B refer to pre-learning and post-learning testing, consistent with Figure 1C, but I cannot find where the details of these testing procedures are described. It would be helpful to explicitly refer to pre- and post-learning testing when describing these testing procedures in this section of the manuscript.

Line 697: Please clarify what it means that "Participants then completed Experiment 2A or 2B testing" during the retention testing.

Line 718: Was the range of root-mean-square amplitudes of the electrical vestibular stimulation due to stochastic variation or was amplitude systematically varied?

Line 712: Were conditions tested in order from small to large delays, as in Experiment 1?

Line 719: Does "pseudo-random order" refer to the order of trials within each condition?

Line 746: Was the transition from the 20-ms delay to the experimental delay instantaneous?

Line 746-750: It would be clearer to only use the term "transition" to refer to a change in imposed delay and use a different term to refer to the period of time during which the experimental delay is imposed.

Line 750: Please explain the reason a "catch" 20-ms delay was included in the experimental protocol, since this seems to be the same as the baseline delay. Did anything actually change in how the robotic system was controlled when the "catch" 20-ms delay was imposed? In other words, was the failure to find an effect preordained?

Line 776: Does the term "window" here mean the same thing as term "inter-transition delay" on Line 747? If so, it would be helpful to use the same term in both places.

Line 785: It is implied that the 2-s windows excluded periods of time when body angle was outside the specified limits, but it would be helpful to explicity state this restriction up front.

Line 795: What was bootstrapping used to estimate, the average variance for that participant? Why not just use the actual average variance, as was done when there were fewer than five 2-s windows? Bootstrapping is typically done to test a null hypthosis or construct a confidence interval and assumes independent samples, which would not be the case for data from the same participant.

Line 812: Did the 2-s window have to start after the delay was imposed AND end before the button press?

Line 821: Does concatenating the trials mean that the jumps in signal values from the end of one trial to the beginning of the next are affecting the results?

Reviewer #3:

The study describes three experiments that investigated the influence of increased feedback time delay in the ability of human subjects to maintain stable upright balance and their ability to learn/adapt to control balance at time delays values that are greater than those predicted to be possible based on existing simple feedback control models of balance. The studies made use of a unique robot balance device that allowed the generation of continuous body motion as a function of a time-delayed version of the corrective ankle torque generated by the subject as they swayed.

The experiments quantified changes in body sway behaviors as a function of added time delay and characterized the time course of improvements in balance control as subjects learned to stand with a long delay value imposed by the robotic device. The learning was acquired over multiple training sessions and was demonstrated both by a reduction over time in sway measures and by changes in psychophysical measures that demonstrated a reduction in a subject's indication of the occurrence of unexpected body motions. Additionally, the learned ability to control balance with an added time delay was very well retained at 3 months post training.

A final experiment used electrical vestibular stimulation (EVS) to demonstrate the changing contribution of vestibular information to balance control following a transient increase in time delay. This experiment demonstrated a marked reduction in activity in the soleus muscle that was correlated with the EVS following the onset of an added feedback time delay indicating that the added delay caused a reduction in the vestibular contribution to balance.

In general, the experiments were appropriately designed and analyzed. Although the number of participants in each experiment were not large, they were sufficient given the rather robust effects observed when time delays were added to be feedback.

The robotic balance device not only permitted manipulation of the time delay, but also guarded against subjects actually falling when they swayed beyond the normal range of sways compatible with stable balance. This artificial stabilization of balance beyond the normal range permitted subjects to recover from what would otherwise have been a fall and to immediately continue their attempts to learn a balance strategy that was able to overcome the detrimental effects of increased feedback delay. Thus the training procedure was likely much more effective than if trials had been stopped when sway moved beyond the normal range. One imagines such a training device could have important uses in rehabilitation of balance deficits.

But this artificial stabilization also interfered with one of the balance measures used to quantify the influence of added time delay. Specifically, the RMS sway measure used by the authors did not distinguish between time periods when the subject was being artificially stabilized and the time periods when sway was within the normal sway range. Thus the results that were based on the RMS sway measure were not convincing. But fortunately a sway velocity variance measure was also used to quantify sway behavior as a function of time delay and this measure only used data that was within the normal range of sway.

Overall results are an important addition to knowledge related to how humans control standing balance and demonstrate an ability to learn, with training, to balance with unexpectedly long delays between control action and the resulting body motion.

Overall results are clearly presented but this reviewer has some suggestions for improvement.

1. Experiment 1 quantifies changes in balance control as a function of added time delay by measuring RMS sway amplitude and sway velocity variance. It seems incorrect to use the entire 60 seconds of data in the calculation of RMS sway when there are periods of sway beyond the 3 deg backward and 6 deg forward sway balance limits since the backboard motion is artificially stabilized in the region outside the balance limits. It is only with detailed reading of the methods that the reader understands that the backboard motion is artificially stabilized at extremes of sway so this makes a complete understanding of the RMS sway results presented in Figure 2 difficult. But the problem is not fixed by just making the artificial stabilization methods more evident when presenting the Figure 2 results. The problem is that this RMS sway calculation is not representative of the overall subject-controlled sway behavior when there are periods in the trails when the sway was not controlled by the subject (which occurred frequently with longer delays). This reviewer suggests that a much more useful measure would be to calculate and display the percentage of time that subjects were maintaining control within the balance limits. It would be similarly informative to see this type of percentage measure used to track the Experiment 2 learning results in addition to the velocity variance measures shown in Figure 3.

2. In Experiment 3, group data results show changes in muscle activation evoked by electrical vestibular stimulation based on the 489 of 588 trials on which subjects signaled that they detected an unexpected balance motion. But what about the other 99 trials when subjects did not signal unexpected balance motion? Since the authors suggest there is a possible linkage between the time course of vestibular decline and the detection of unexpected motion, it may be that there was a slower (longer time constant) or reduced amplitude of vestibular decline on the 99 trials where unexpected motion was not detected. Such a finding would strengthen the notion of a linkage between vestibular inhibition and motion detection. Alternatively, if the vestibular declines were indistinguishable between trials with and without unexpected motion this would suggest that the linkage was not tight and something else may be involved. In either case this comparison would be useful. Additionally, it seems that 99 trials should be enough data since Figure 6 shows good results from a single subject based on 77 trials.

3. The section on pages 23 and 24 discusses alternative models that might be able to explain how subjects can learn to tolerate long time delays. I believe that all of the references to alternative models are to models that would be classified as continuous control models as opposed to intermittent control schemes that have been proposed as an alternative (e.g. Ian Loram references such as Loram et al., J Physiol 589.2:307-324, 2011, Gawthrop, Loram, Lakie, Biol Cybern 101:131-146, 2009, and the Morasso reference in the authors manuscript). It seems that Loram's work has shown that it is possible to visually control an unstable load with properties similar to those of a human body using an intermittent control scheme. This intermittent control scheme should be referenced. But beyond just mentioning these alternative control structures as possibilities, do the authors know of actual simulations of these models that can demonstrate that an inverted pendulum system can be made stable with the extremely long time delays that the authors investigated?

4. Several places in the manuscript the authors refer to estimates of maximal time delays based on simpler feedback control models. Specifically, the Bingham et al. 2011 and the van der Kooij and Peterka, 2011 references are given. But the values of the maximal time delays are not consistent across the various mentions of these two references. Here is a listing of those mentions:

- Line 78: ~300 ms

- Line 406: 340-430 ms

- Line 667: ~400 ms

- Line 678: ~400 ms

This reviewer could find mention of 340 ms in the van der Kooij and Peterka paper, but it seems that the Bingham paper did not really investigate time delay in detail and that paper also was investigating body motion in the frontal plane that has considerably different lower body dynamics compared to a single segment inverted pendulum.

5. The authors indicated that analysis programs and data will be made publicly available upon acceptance for publication.

https://doi.org/10.7554/eLife.65085.sa1

Author response

Essential Revisions:

1. To characterize how strongly soleus EMG (the output) responds to vestibular stimulation (the input), standard measures designed to characterize input-output mappings should be used. Gain in the frequency domain and the unnormalized impulse response function in the time domain are the standard choices. Both measures used do not distinguish between decreases in EMG variability and gain.

1a) Coherence (while important to report) does not provide even an indirect measure of gain: two systems with gains different by an order of magnitude both reach maximum coherence of 1, depending on the amount of noise in the system. In terms of this research result, if an imposed delay increases output variance but does not change gain, then coherence decreases. Presumably soleus EMG variance increases with sway variance, so the decrease in coherence and Figure 6, for example, may simply reflect an increase in soleus EMG variance, not a decrease in the magnitude of vestibular-evoked muscles EMG responses.

2a) The authors use normalized cumulant density in the time domain as a stand in for gain. In principle, an unnormalized version of this should work, as it is related to the impulse response function (but not quite). It would be better to just directly use the standard estimate based on cross spectrum divided by the power spectrum of the input, rather than the normalized IFT of the cross spectrum that the authors used. But, by normalizing by the EMG signal properties (also by electrical stim -- but that would be the same/similar for all subjects), if EMG variance is increased with increasing delay (a plausible result), the cumulant density function amplitude would decrease due to this normalization, even if the vestibular gain remained unchanged.

So, in your revision, we require the use of a standard measure, e.g. cross spectral density between the input and output (as now calculated) divided by the power spectral density of the input. This would give a frequency domain response function. Taking the inverse Fourier transform would put this in the time domain as an estimate of the impulse response function. Other standard measures are possible.

Critically, this change in analysis may provide a new result, and thus require new interpretation. E.g., it may be that the "scalar" gain estimate does not change, but rather there is a change in the variance that explained your previous analysis. In this case, the transfer function estimate could be examined for alternative interpretations. The reviewers all felt that while this would not necessarily be as striking a result, it would still be nevertheless an important paper, and so it is important when re-analyzing this data not to have the forgone conclusion of a change in gain, which is not yet supported by the analysis.

We thank the reviewers for highlighting these points regarding the analyses of vestibular-evoked muscle responses. Below we have provided answers to the points raised above.

For clarity, we have now replaced the term “cumulant density” with its equivalent, “cross-covariance” in the revised manuscript and the response to the reviewers. Cumulant density estimates are the equivalent of cross-covariance estimates and provide an analogous interpretation as cross-correlations (Halliday et al., 1995; Halliday et al. 2006). These measures are used often in neurophysiology and motor control studies to characterize the correlation between two signals (Brown et al., 1999; Brown et al., 2001; Halliday et al., 2006; Hansen et al., 2005; Nielsen et al., 2005). We also note that in our original submission, we estimated normalized cross-covariance (cumulant density) responses in order to compare vestibular-evoked muscle responses across the different testing sessions (pre-learning, post-learning, retention), which were performed on different days. This was to account for any inter-session variability in the surface EMG measurements, which can occur for example, due to changes in electrode placement or skin conductance. While we took precautions to ensure consistent EMG recordings across testing sessions (noting the electrode placement for each participant), there is still potential for inter-session variability in EMG signals. Therefore, to account for any differences in EMG measurements across sessions when using the non-normalized measures (i.e. cross-covariance and gain, see below), we first scaled the EMG signals by a baseline EMG measurement from each session prior to estimating the time and frequency domain measures. We outline this scaling approach and its effects on the data after the description of our modified vestibulomotor analyses (see EMG scaling and Response Figure 4).

We agree with the reviewers that our assessment of changes in vestibulomotor contributions to balance across different time delays could be better suited with non-normalized impulse response functions in the time domain and gain in the frequency domain. A summary of the changes made to the revised manuscript for both time and frequency domain measures is provided below.

Time-domain responses

As noted by the reviewers, one approach to estimate the impulse response function is to take the IFFT of the gain. The difficulty with this approach, however, is that gain estimates above 25 Hz become unreliable (i.e. coherence falls below significance) because we only applied a stimulus with power at frequencies up to and including 25 Hz. In fact, gains at frequencies > 25 Hz become erratic and very large because the cross-spectrum is divided by a very small (i.e., low power) autospectrum. Because taking the IFFT of the gain is performed using all frequencies, the resultant impulse response function is dominated by frequencies > 25 Hz and the estimate is very noisy (Author response image 1). This example analysis was performed on the pre-learning data (without scaling EMG) after concatenating the data from all subjects.

Author response image 1

Download asset Open asset

Pooled non-normalized cross-covariance (left) and impulse response (right) estimates from pre-learning data set sampled at 2000 Hz.

Estimates were calculated by concatenating data from all eight participants.

An option to avoid these distortions is to first downsample the data to 50 Hz prior to estimating the impulse response functions. This approach eliminates the influence of these high frequencies but comes at the cost of resolution in the time domain. We performed this analysis (estimating both non-normalized cross-covariance and an impulse response function) on the pre-learning data after concatenating the data from all subjects. From these estimates (Author response image 2), we observed the typical biphasic response of the muscle to the electrical stimulation, as well as the delay-dependent decrease in the magnitude of the impulse response. This initial estimate suggests that the changes in the normalized cross-covariance from our original analysis were not simply dependent upon the variance of the measured EMG signals.

Author response image 2

Download asset Open asset

Pooled non-normalized cross-covariance (left) and impulse response (right) functions from pre-learning data, originally sampled at 2000Hz and then down-sampled offline to 50Hz.

Note that cross-covariance and impulse response functions now provide similar results after down-sampled to 50Hz. Both responses, however, have poor resolution when compared to the original cross-covariance (Response Figure 1; 2000Hz).

To address the substantial loss in time-resolution, we then tried increasing the sampling frequency to 100 Hz (see Author response image 3). Despite only a moderate increase in the sampling rate, frequencies > 25 Hz dominated the response and again produced a very noisy impulse response function. Given these issues, our preferred approach is to follow the reviewers’ alternative suggestion of estimating the vestibular contributions across the different delay conditions using non-normalized cross-covariance estimates in the time domain. For Experiment 2, the results of this new analysis on the individual subject data revealed that the changes in non-normalized cross-covariance responses matched those of the normalized cross-covariance both across delays and conditions, as well as their interaction. These new data (and statistics) are presented in Figure 4, Tables 1 and 2 and pages 9-11 in the Results section of our revised submission.

Author response image 3

Download asset Open asset

Frequency-domain responses

Estimating gain from our data was relatively straight-forward and these analyses have been added to the manuscript. Specifically, we now present both coherence and gain for estimating the vestibular-evoked muscle response in the frequency domain for Experiments 2 and 3. Gain must be assessed alongside coherence because its value is unreliable at frequency points where coherence is below the significance threshold. However, because coherence was below significance at delays ≥ 200 ms for the majority of frequencies, we limited the analysis of coherence and gain to qualitative assessments across delay using the pooled participant estimates of all subject (see Figure 4 in the revised manuscript). Overall, these pooled coherence and gain estimates followed the same trend as cross-covariance, decreasing as the time delay increased. These results provide additional evidence to support the conclusions drawn in our original submission.

EMG scaling

As noted above, to control for any inter-session variation in our EMG recordings, we first scaled the EMG signals by a baseline EMG measurement from each session. For each participant, soleus EMG from vestibular stimulation trials from a given session (e.g., pre-learning) was scaled using data from a baseline (20 ms delay on robot) quiet standing trial from the same day. In these baseline trials, participants stood quietly at their preferred posture (typically ~1 – 2° anterior). We estimated the mean EMG amplitude while participants maintained their preferred posture (± 0.25°). This baseline value was then used to scale EMG from vestibular stimulation trials performed on a given day. We then estimated vestibular-evoked muscle responses (coherence, gain, cross-covariance). We have added this information in the methods on pages 35-37.

To demonstrate the effects of this scaling here, we have estimated vestibular evoked muscle responses (cross-covariance) using three methods: normalized estimates (i.e., original submission), non-normalized estimates (without any scaling), and non-normalized estimates that were scaled by baseline EMG. Crucially, regardless of the approach, the main outcomes remain the same: vestibular-evoked responses attenuate with larger imposed delays (particularly in pre-learning) and partially return to normal amplitudes after training in post-learning and retention (see Author response image 4). Following the reviewers’ suggestion, in the revised manuscript we have presented the non-normalized responses (scaled to each session’s baseline EMG).

Author response image 4

Download asset Open asset

Pooled cross-covariance estimates of vestibular-evoked muscle responses.

Normalized responses (left), non-normalized responses (center) and scaled non-normalized responses (right). All three approaches produce a similar outcome: vestibular-evoked response amplitudes attenuate with increasing imposed delays (particularly in pre-learning) and partially return to baseline levels after training (observed in post-learning and retention). Dashed lines are 95% confidence intervals.

2. We emphasize one of the major concerns of reviewer #2: Rather than report mean-removed RMS sway (in other words, sway standard deviation) it would be better to report percentage of time within specified sway limits

We appreciate the reviewers’ perspective that mean-removed RMS of sway – calculated over periods in which the participant can be within or outside the robotic simulation sway position limits – may not only reflect processes of balance since they include time periods of artificial stabilization. It was for this reason that we only provided this measure in Experiment 1. Our original aim was to compare this more common measure (Day et al. 1993; Hsu et al., 2007; van der Kooij et al., 2011; Winter et al., 2001) of balance behaviour to the alternative – though more appropriate – measure of sway velocity variance extracted over periods of balance within the specified sway limits. To avoid further confusion on this matter we removed the mean-removed RMS of sway measure from the paper. We further agree that the percentage of time a participant is balancing within the sway limits is a more useful measure and have added this analysis to the Methods and Results section when assessing Experiments 1 and 2 (training data).

3. The authors should address whether existing models can stabilize an inverted pendulum with long feedback time delays. Sway variance will increase with increasing time delay, so at some point standing balance is not possible due to one's finite base of support (a type of plant nonlinearity). Specifically, the manuscript should be improved with a more nuanced Discussion (near lines 401-421) to consider the other classes of control models (optimal or intermittent control) that possibly could be candidates for controlling a system with long time delays. For example, if optimal control rather than proportional-derivative control is used, then it is possible in principle (perhaps excluding special cases) to stabilize a linear plant with arbitrarily long delays (e.g., Zhou and Wang 2014, DOI 10.1007/s10957-014-0532-8), although for long time delays such control can be quite fragile with respect to disturbances or plant parameters.

We thank the reviewers for their suggestions. Specifically, in the Discussion section, “learning to stand with novel sensorimotor delays” (Lines 358 – 375), we have now included a discussion of different balance control models that may or may not be capable of stabilizing standing balance with long feedback time delays. Here, we discuss how feedback (i.e., PID) and optimal controllers are expected to perform with large delays. We note that Kuo (1995) has described the robustness of an optimal controller for standing balance to control delays, showing that at very small center of mass accelerations, the system can be stabilized with large (> 500 ms) delays. However, this robustness rapidly declines with increasing external disturbances (Kuo 1995), as is also expected from the paper the reviewers provided (Zhou and Wang 2014). Additionally, we considered both continuous and intermittent controllers which have been proposed for standing balance and discussed their potential performance in the context of standing with large delays. The nervous system may use a combination of continuous and intermittent controllers, as proposed from previous models (Elias et al., 2014; Insperger et al., 2015). Since we did not explicitly explore or test the performance of different models with balance delays in our study, we refrain from making extensive conclusions on the model that would be best suited to replicate our data.

4. Bootstrapping should be better justified or not used.

For simplicity, we have removed all bootstrapping analyses that were used in our estimation of sway velocity variance (Experiments 1 and 2). Importantly, this has not changed the main outcomes, i.e., the effects of delay and training on sway velocity variance (see Table 1, Figure 2, Figure 3, Figure 4, Figure 5).

Reviewer #1:

This paper aims to understand how imposed delays between ankle torque and whole-body motion destabilize standing balance, and determine the mechanisms that the nervous system uses to learn to compensate for these imposed delays. Related studies have estimated the critical delay at which upright standing is destabilized, and shown that humans can learn to compensate for increased delay. This study supports these prior results in the literature and delves deeper into human's standing balance. Specifically, they demonstrate that, although initially vestibulomotor responses are attenuated during imposed delays before learning, eventually subjects learn to partially recover their reliance on vestibular feedback, while, at the same time, improving postural control in the face of delay. Furthermore, after learning, subjects' ability to perceive unexpected delays was reduced, leading the authors to speculate that subjects may learn to "internalize" the experimentally added delay, making it hard to identify said delay an external perturbation. So, this study would be of broad interests for researchers who are studying human control of standing balance as well as other models of sensorimotor control across taxa.

Strengths:

1) The manuscript provides a clear and cogent motivation, and the hypotheses are well grounded in the literature.

2) The data, including the tables and graphs in this manuscript, verify the authors' hypotheses in a generally convincing way.

Weaknesses:

1) Clarification of velocity variance with bootstrapping: The estimates of sway velocity variance using bootstrapping was not well described nor justified. In figure 2, it said 'Sway velocity variance ..., and the resulting data were bootstrapped to provide a single estimate per participant and delay'. 'estimate per participant' sounds like simply using bootstrapping to estimate the mean, which is not a standard use of bootstrapping. It can be used to estimate SEM etc, also in line 795-797, it said 'we bootstrapped the participant's data with replication 10,000 times and then averaged across participants for each delay and learning condition.' from which it seems that the authors are computing the SEM across subjects. In sum the statistics associated with variance estimation and bootstrapping is unclear.

We thank the reviewer for raising these concerns regarding the bootstrapping of the sway velocity variance data. As recommended from all reviewers, we have removed all bootstrapping of sway velocity variance from our analyses. For Experiments 1 and 2, on a participant-by-participant basis, we averaged the sway velocity variance from the extracted 2-s windows to provide an estimate of sway velocity variance for each participant at each condition (e.g., Experiment 1, 200 ms delay). The procedure was the same as in our original submission except we did not perform any bootstrapping. We then performed the same statistical tests on the group data. Importantly, re-performing our analysis without any bootstrapping did not influence the outcomes for sway velocity variance in Experiments 1 and 2. In addition, for Experiment 1 and 2, we have also added an outcome measure – the percent of time participants balanced within the sway position limits – as recommended by the reviewers.

2) The use of Cumulant Density: cumulant density as a gain measure is not a standard technique for gain estimation in the motor control literature, and needs further justification.

We thank the reviewer for raising these points, and refer to our main response above regarding the re-analysis of vestibular-evoked muscle responses. Briefly, cumulant density estimates are the equivalent of cross-covariance estimates (interchangeable in the literature), and provide an analogous interpretation as a cross-correlation (Halliday et al. 1995; Halliday et al. 2006). These measures are used regularly in neurophysiology and motor control studies to characterize the correlation between two signals (Brown et al. 1999; Brown et al. 2001; Halliday et al. 1995; Halliday et al. 2006; Hansen et al. 2005; Nielsen et al. 2005; Tijssen et al. 2000) and have been used extensively to estimate vestibular-evoked responses during standing balance (Dakin et al. 2010; Dakin et al. 2007; Mackenzie and Reynolds 2018; Mian and Day 2009; 2014; Reynolds 2011). For clarity, we have now replaced the “cumulant density” with its equivalent, “cross-covariance”, which is the more widely recognized terminology.

Briefly describing our revisions for vestibular-evoked muscle responses, we have re-analyzed our data using non-normalized cross-covariance estimates for an estimation of the response in the time domain. While we performed an impulse response function analysis, we do not believe this measure is appropriate for our data and demonstrate this point in our response above. This was primarily because useful impulse response functions could only be estimated by downsampling the original data from 2000Hz to 50Hz. Due to the loss in time-resolution, however, our preferred approach is to follow the reviewer’s alternative suggestion of estimating the vestibular contributions across the different delay conditions using non-normalized cross-covariance estimates in the time domain and gain estimates in the frequency domain (at frequencies where coherence is above significance).

We have also added text in the Materials and Methods section (lines 827 – 875) of our revised manuscript, explaining and rationalizing our use of coherence, gain and cross-covariance to estimate the vestibular-evoked muscle response. The revised text reads

“To estimate the presence and magnitude of vestibular-evoked muscle responses in Experiment 2 vestibular testing, we used a Fourier analysis to estimate the relationship between vestibular stimuli and muscle activity in the frequency and time domains. […] Therefore, if both short and medium latency peaks did not exceed the confidence intervals, the cross-covariance vestibular response amplitude was zero and considered absent.”

3) The use of 2s windows for variance estimation in Experiment 1 was unclear. When estimating sway velocity variance in Experiment 1, 2s non-overlapping windows were applied and "if fewer than five 2 s windows were present, the average was taken across the available data (denoted with filled circles in figures)". And in Figure 2A, "Data not included in the velocity variance analysis are grayed out." However, some non-grayed-out regions in Fig 2A are not to be multiples of 2s, which is confusing.

We acknowledge that the description of the 2s data windows used to estimate sway velocity variance should have been clearer. Figure 2A highlights the regions of the trial that were within or outside the balance simulation limits (i.e., unshaded or gray shaded regions respectively) but that does not mean that every data point in the unshaded regions was used for the analysis. To clarify, we have added the following text to the methods section (Lines 791 – 797),

“Sway velocity variance was estimated only from data in which whole-body angular position was within the virtual balance limits (6° anterior and 3° posterior). Specifically, data were extracted in non-overlapping 2 s windows, when there was at least one period of 2 continuous seconds of balance within the virtual limits. Data windows were only extracted in multiples of 2 s. For instance, if there was an 11 s segment of continuous balance, we only extracted five 2 s windows (i.e., first 10 s of the segment).”

We have also clarified the description of Figure 2, stating “Sway velocity variance was calculated over 2 s windows (extracted by taking segments when sway was within balance limits for at least 2 continuous seconds)” (Lines 1261-1263).

Although the experimental methods, data analysis and writing skills in this paper are detailed, some improvements are needed for figure illustrations and terminology.

For example, Figure 1B is confusing. There is a circle with δ t inside which represents the imposed delay but it is not good to put both the "Whole body sway" and "Delayed whole-body sway" out of that circle. This is a confusing (and nonstandard!) way of schematizing a closed-loop system such as this. See many examples from the literature, including but not limited to papers by Lena Ting, Michael Dickinson, Daniel Robinson, my lab, and many others for standard ways of writing control system block diagrams that would be more easiliy interpretable. Lena Ting's lab (Lockhart and Ting 2007, expressed in time domain) and Simon Sponberg's lab (https://science.sciencemag.org/content/348/6240/1245.abstract, expressed as a general block diagram) both have nice papers that explicitly include delay in the feedback loop. My lab has three review papers with numerous examples that can be found here: https://limbs.lcsr.jhu.edu/publications/#Reviews.

We agree with the reviewer and have modified the figure according to the reviewer’s suggestions. The original figure meant to depict that the participant was in control of the robot and that self-generated (participant) ankle torque could result in either normal robotic sway (20ms delay) or delayed robotic sway (> 20ms). The revised figure highlights that the participant is in the control loop and that the robotic simulation takes in measured ankle-produced torques and uses an inverted pendulum transfer function to output whole-body angular motion.

Some figures in this paper are not straightforward for the readers to understand. Especially in Figure 1, the descriptions are complete, but figures themselves are not informative enough. For instance, in Figure 1 C, the descriptions of the experiment 3 whose trials ("of similar design to Experiment 2B, except that the robot only transitioned between baseline (20 ms) and 200 ms delays (not illustrated)") is unclear. This figure is significant to the paper's results in order to show the procedure of three experiments. Thus, it should be better clarified, or supplemental figures should be used to further explicate such issues.

We thank the reviewer for raising this concern regarding Figure 1. We have made modifications to this figure, including changes to Figure 1B, 1C, and 1E. Figure 1B has now been updated to reflect a closed-loop feedback control and depicts the inverted pendulum transfer function used in the robotic simulation (see response to previous comment above). Figure 1C has been modified to reflect that Experiment 2 involved vestibular or perceptual testing in pre-learning, post-learning and retention sessions. Additionally, Figure 1C now states that Experiment 3 involved “simultaneous vestibular and perceptual testing with delays transitioning between 20 and 200 ms”. Figure 1E has been updated to mark the delays which were not perceived in this example trial (see response to comment below).

More details about the load in Figure 1B is needed. We can only learn from line 541 that "For all experiments, participants stood on a custom-designed robotic balance simulator programmed with the mechanics of an inverted pendulum to replicate the load of the body during standing (Figure 1A)". However, the authors need to show in specific equations that were simulated, and the parameters they set in their design, to enable reproducibility of the results.

We have now included more information regarding the equations used in the robotic balance simulation. This information has been added in the text (Lines 518-532). This text reads:

“For all experiments, participants stood on a custom-designed robotic balance simulator programmed with the mechanics of an inverted pendulum to replicate the load of the body during standing (Figure 1A). Specifically, the simulator used a continuous transfer function that was converted to a discrete-time equivalent for real-time implementation using the zero-order hold method

I \ddot{θ} + \dot{θ} - m_{m} g L θ = T

\frac{θ}{T} = \frac{1}{I s^{2} + s - 0.971 m g L}

as described by Luu et al., (2011), where $θ$ is the angular position of the body’s center of mass relative to the ankle joint from vertical and is positive for a plantar-flexed ankle position, $T$ is the ankle torque applied to the body, $m_{m}$ is the participant’s effective moving mass, $L$ is the distance from the body’s center of mass to the ankle joint, $g$ is gravitational acceleration (9.81 m/s²), and $I$ is mass moment of inertia of the body measured about the ankles $m_{m} L^{2}$ . The body weight above the ankles was simulated by removing the approximate weight of the feet from the participant’s total body weight so that the effective mass was calculated as $0.971 m$ , where $m$ is the participant’s total mass.”

As mentioned above, we have modified Figure 1B to depict the inverted pendulum equation used in the robotic simulation.

Moreover, important data points should be marked on the figure. On Figure 1E, the y axis "imposed delay" has only 20 ms and 300 ms marked, but authors later mentioned that "Data from a representative participant (see Figure 1E) show missed 299 detections of the 100 and 150 ms imposed delays", so it would be clearer if they can also mark 150 ms and 100 ms on the graph, because those are critical points.

We have added the reviewer’s suggestions to Figure 1E.

RE: Cumulant Density: It is indeed critical to have a gain estimate in the vestibulomotor analysis, since coherence alone does not indicate the strength of response to a stimulus: nonlinearities and noise can decrease coherence, even if the gain to stimulus remains unchanged. The authors perform such a gain analysis (see e.g. Figure 4A) using "Cumulant density". This is an interesting technique for identifying the sensorimotor gain but does not seem to be in widespread use, and I could not find a theoretical justification in the system ID textbooks I have. That said, it appears possible that under the right conditions, the appropriately normalized Inverse Fourier Transform of the cross spectral density (i.e. the so-called Cumulant Density) should amount to the impulse response function, but I'm not sure of this. It would be helpful if the authors could better justify this approach or use a more standard analysis, such as impulse response recovery.

We thank the reviewer for raising these points and refer the reviewer to our main response above regarding the vestibular-evoked muscle response analysis. Briefly, we have re-analyzed our data using non-normalized cross-covariance (cumulant density) functions for an estimation of the response in the time domain. While we performed an impulse response function analysis, we do not believe this measure is appropriate for our data and demonstrate this point in our response above. We have also added a standard measure of gain to be presented alongside coherence in the frequency domain, as recommended by the reviewers. For Experiment 2, frequency domain measures (coherence and gain) were evaluated qualitatively using the pooled participant estimates because with delays ≥ 200 ms, single-participant coherence only exceeded significance at sporadic frequencies, and gain values are unreliable when coherence is not significant. Importantly, our main outcomes are confirmed with this re-analysis: increasing the imposed delay attenuates the vestibular response and training to stand with a 400 ms delay leads to these responses partially increasing.

The authors call the Vestibular-Evoked Muscle Responses assays an "Experiment" (Experiment 2A), but the experiment is actually much broader, and covers all everything in the gray box in Figure 1C. Likewise for the perception assay ("Experiment 2B"). This terminology is confusing and I recommend dropping that nomenclature and just saying "Vestibular Testing" and "Perceptual Testing". Also, Figure 1C is laid out to look like a table, with two rows, and the first "column" appears to be labeling the rows, but it is not. Please rework this panel to be less confusing.

We have reworked this part of the figure. As suggested, we have removed the Experiment 2A and 2B nomenclature and now state “vestibular testing” and “perceptual testing” for Experiment 2. These changes are reflected in the figure and throughout the manuscript text.

Reviewer #2:

Using a robotic system, the manuscript demonstrates that imposing time delays from ankle torques to movement causes postural sway to increase, as one would expect based on stochastic models of postural control. What is more surprising is the extent to which participants can adapt to imposed delays and decrease postural sway over multiple days. The evidence of adaptation is exceptionally clear. Another strength of the manuscript is that it relates these decreases in postural sway to a decrease in how often participants perceive unexpected balance movements, suggesting that over time participants learn that their ankles torques are causing the movements even though the movements are artificially delayed. These perceptual measures were obtained in real time during standing balance and carefully characterized, sometime that is not typically done in postural adaptation experiments.

The manuscript also characterizes the relationship between vestibular stimulation and surface electromyography EMG signals from the soleus muscle, using coherence in the frequency domain and the normalized cumulant density function in the time domain. Often gain, which has units of (output units)/(input units), is used to measure how responses to a perturbation change. A common example is using gain to quantify sensory re-weighting during standing balance. (It would be helpful if the authors discussed whether their hypothesized changes in vestibular-evoked muscle responses can be thought of as sensory re-weighting.)

The reviewer notes that the estimation of a gain function (in the frequency domain) is a common method to quantify how responses to a sensory perturbation change. In our revision, we have added a gain analysis to Experiment 2 and 3. We further elaborate on the addition of gain in our response to the reviewer’s next comment (below) and the group review major comments.

In response to the reviewer’s final point above that imposing delays in the sensorimotor control loop should lead to sensory feedback becoming less reliable, and consequently the associated sensorimotor feedback gains could decrease. This is predicted from computational models of standing balance that consider increasing sensory delays (Bingham et al. 2011; Le Mouel and Brette 2019; van der Kooij and Peterka 2011). Because our delays are imposed between ankle-produced torques and whole-body motion, we expect that visual, vestibular, and somatosensory cues of body motion should be delayed, while acknowledging that muscle spindle, GTO and cutaneous cues regarding muscle contractions remain unaltered. Therefore, from a sensory re-weighting perspective: visual, vestibular and somatosensory gains should decline. Although our results show that vestibular-evoked muscle response decrease, our experiments were not designed to assess whether remaining sensory channels were also modified in a manner that follows the principles of sensory re-weighting. Instead, our results show the partial return of vestibular response amplitude after training at a delay of 400 ms. These results suggest the involvement of alternative processes of sensorimotor recalibration, where the brain learns to associate delayed whole-body motion with self-generated motor commands. This is further supported by the changes in perception after training.

We have added some sentences in the discussion acknowledge the sensory re-weighting hypothesis in regards to our data. This discussion section now reads:

“The attenuation of vestibular-evoked responses to increased sensorimotor delays could be explained through processes of sensory re-weighting (Cenciarini and Peterka 2006; Peterka 2002), where the decreasing reliability in sensory cues when balancing with additional delays decreases feedback gains. […] Our results suggest that these forms of recalibration are possible for the vestibular control of standing balance and the perception of standing balance” (Lines 379-407).

One concern is whether the measures used in this study conflate changes in output magnitude with changes in output variance. For example, if an imposed delay increases output variance but does not change gain, then coherence decreases. For this reason, gain seems a better choice than coherence given the questions the authors are addressing. Similarly, in the time domain, an unnormalized impulse response function seems a better choice than the normalized cumulant density function. Similar comments apply to the time-frequency analysis of Experiment 3, which the manuscript uses to track changes in the relationship between vestibular stimulation and soleus EMG.

We acknowledge the reviewer’s concerns that adding a gain estimate to the analysis would be beneficial. We have added this analysis, and refer the reviewer to our main response to the group review comments. Briefly, we now present both coherence and gain for estimating the vestibular-evoked muscle response in the frequency domain for Experiments 2 and 3. Because gain is unreliable when coherence is not significant, we always present coherence and gain together. For Experiment 2, coherence and gain were evaluated qualitatively using the pooled participant estimates because for delays ≥ 200 ms single-participant coherence only exceeded significance at sporadic frequencies, and gain is unreliable at non-significant frequencies.

For our time domain estimates, we acknowledge the reviewer’s comments about normalized cumulant density responses. Briefly, we have replaced this estimate of vestibulomotor responses with non-normalized cross-covariance responses. To account for any differences across sessions (please see main response for details), we first scaled the EMG data by baseline muscle activity measured from the same session. In our main response, we also assessed the pros and cons of using cross-covariance vs impulse responses, and have chosen to cross-covariance as our primary outcome measure. Importantly, our results using non-normalized responses show the same main outcomes as with our previous analysis (normalized responses). Therefore, our observations of biphasic vestibular response attenuation with increased imposed delays are not simply due to an increase in output variance.

One important implication of the reported results that is discussed is that models that predict the maximal sensorimotor delay that allows standing balance are probably underestimating the maximal delay because they assume proportional-derivative (PD) or proportional-integral-derivative (PID) controllers, which are not optimal controllers when there are time delays. The predictions are also based a linear analysis of stability. In reality, due to a person's limited base of support, the person may fall or take a step even though a linear analysis shows that they are stable. It might be helpful to discuss this in relation to the study's imposition of specified limits of body sway.

The reviewer raises valid points regarding feedback control models (PD, PID) not being optimal in the presence of time delays and basing their predictions on linear analysis of stability. In our revised discussion, we have included a discussion of different control models and have incorporated these points raised by the reviewer, as well as those made by the other reviewers. These additions are included on lines 358-375, and reads:

“This remarkable ability for humans to adapt and maintain upright stance with delays raises questions regarding the principles underlying the neural control of balance. Compared to feedback controllers (i.e. proportional-derivative and proportional-integral-derivative), which are not optimal in the presence of delays, optimal controllers can model the control of human standing (Kiemel et al. 2002; Kuo 1995; 2005; van der Kooij et al. 1999; van der Kooij et al. 2001) and theoretically stabilize human standing with large (> 500 ms) delays (Kuo 1995). This ability, however, rapidly declines with increasing center of mass accelerations (Kuo 1995), including those driven by external disturbances (Zhou and Wang 2014). Although feedback and optimal controllers assume that the nervous system linearly and continuously modulates the balancing torques to stand (Fitzpatrick et al. 1996; Masani et al. 2006; van der Kooij and de Vlugt 2007; Vette et al. 2007), intermittent corrective balance actions (Asai et al. 2009; Bottaro et al. 2005; Gawthrop et al. 2011; Loram et al. 2011; Loram et al. 2005) may represent a solution when time delays rule out continuous control (Gawthrop and Wang 2006; Ronco et al. 1999). Intermittent muscle activations are also sufficient to stabilize the upright body during a robotic standing balance task similar to the one used in the present study (Huryn et al. 2014). The nervous system may use a combination of the controllers during standing (Elias et al. 2014; Insperger et al. 2015) but our study did not explicitly test for evidence of these different controllers or their ability to stabilize upright stance with large delays.”

In agreement with Reviewer 3, we speculate that by allowing participants to continue balancing after hitting these limits, learning may have been more effective as compared to halting the simulation every time sway moved beyond the normal range.

“The notable learning observed after training may have been partly due to participants being passively supported past the virtual balance limits because it prevented certain non-linear behaviors that disrupt continuous balance control such as taking steps or falls.” (Lines 354-357)

One other issue that would be helpful to discuss in more detail would the exact sensory consequences of the imposed delays used in this study. The researchers imposed delays from the forces participants produce (forces applied to the support surface) to body movements. This delays sensory feedback related to body movements, but other sensory feedback, such as proprioceptive feedback about muscle forces and cutaneous feedback about the center of pressure (COP) have normal sensory delays. The component of COP dependent on center-of-mass position is delayed but the component dependent on ankle torque is not. Even the way proprioceptive information about muscle length is altered is more complex than a simple time delay, since length changes in tendons allow changes in muscles lengths without joint rotations. It would be helpful to discuss whether the resulting sensory conflicts contribute to the difficulty of balancing with an imposed delay and the implications for adaptation.

The reviewer raises an important consideration. Indeed, our experimental set-up only allows for the manipulation of delays between the torques participants produced (measured from the force plate they stood on) and body movements (AP rotations about the ankle joint axis). Other feedback loops (i.e., between motor commands and sensory information related to muscle contractions) had normal delays. This could have resulted in sensory conflicts and potentially influenced balance stability with delays as well as the ability to adapt. We have added a section in the discussion titled – Limitations and other considerations – that discuss these possible implications. This discussion is found on lines 472-485 of the revised manuscript and reads:

“We manipulated the delay between ankle-produced torques (measured from the force plate) and the resulting whole-body motion (angular rotation about the ankle joints). This manipulation altered the timing between the net output of self-generated balance motor commands (i.e., ankle torques) and resulting sensory cues (visual, vestibular and somatosensory) encoding whole-body and ankle motion. However, the timing between motor commands and part of the somatosensory signals from muscles (muscle spindles and golgi tendon organs) and/or skin (cutaneous receptors under the feet) that are sensitive to muscle force (and related ankle torque) or movements and pressure distribution under the feet, were unaltered by the imposed delays to whole-body motion. This may have led to potential conflicts in the sensory coding of balance motion and may have influenced the ability to control and learn to stand with imposed delays. As methodologies to probe and manipulate the sensorimotor dynamics of standing improve, future experiments can be envisioned to replicate and modify specific aspects (i.e., specific sensory afferents) of the physiological code underlying standing balance. Such endeavors are needed to unravel the sensorimotor principles governing balance control.”

Abstract: It would be helpful to mention that sway was restricted to rotation about the ankles.

We have specified that the sway was restricted to rotation about the ankle joints in the abstract. Lines 40-42.

Figure 1 caption: Why was it necessary to use 3D googles to provide a visual scene to participants? Since the participants are actually moving, would it not be easier just to have participants look at an actual fixed visual scene?

For this experiment, yes, we could technically have the participants view a normal (or real) scene since they are moving. However, we instead took advantage of the systems available within the laboratory setup. The visual display system, with the use of 3D goggles, provides the participant with an immersive visual scene during the experiments. Because the screen was fixed next to the participant (they looked left to view it), the only alternative would be to have participants view the screen without a visual field leaving only a vague uniform grey display screen. We believe the virtual reality setup provided a natural visual environment.

Lines 171-174: Does "both p < 0.001" refer to overall tests for dependence on imposed delay? If so, it would be helpful to indicate which statements in this sentence are supported by statistical tests.

Yes, in the original submission this line referred to that there was a main effect of imposed delay on sway velocity variance and mean-removed RMS of sway position. We have modified this sentence and other statements to clarify which statistical tests reveal main effects. (Lines 128-147).

Lines 212-217: The comparing the retention test to sway attenuation corresponding to the time constant seems arbitrary and apparently does not take into account uncertainty in the estimated time constant. To support the statment that "balance improvements were partially maintained" it seems more relevant to compare the retention test to sway variance at the beginning of training to test whether improvements are at least partially maintained and to sway variance at the end of training to test whether improvements are only partially maintained.

Thank you for this comment. As suggested, we have provided these statistical comparisons for our two dependent variables of balance behaviour: sway velocity variance and for percent time within limits. This information has been added to the Results section on lines 179-192. The text reads:

“Sway velocity variance in the first minute of retention testing was ~60.8% lower than the sway velocity variance from the first minute of training (4.95 ± 2.32 [°/s]² vs 12.62 ± 9.03 [°/s]²; independent samples t-test: t₍₂₆₎ = -2.86, p < 0.01). Sway velocity variance at the first minute of retention testing, however, remained greater than the last minute of training (4.95 ± 2.32 [°/s]² vs 2.55 ± 1.76 [°/s]²; independent samples t-test: t₍₂₆₎ = 3.11, p < 0.01). Similarly, the first minute of retention was associated with a greater percentage of time within the balancing limits compared to the first minute of training (88 ± 9% vs 64 ± 9%; independent samples t-test: t₍₂₆₎ = 6.67, p < 0.001), but less than the last minute of training (88 ± 9% vs 97 ± 3%; independent samples t-test: t₍₂₆₎ = -3.68, p < 0.01). When using only data from participants who performed the retention session (n = 12; paired t-tests with df = 11), sway velocity variance and percent time within the balance limits revealed identical results (all p values < 0.01). Overall, these results indicate that while standing with an imposed 400 ms delay is initially difficult (if not impossible), participants learn to balance with the delay with sufficient training (i.e., > 30 mins) and this ability is partially retained three months later.”

Line 521: What was the range of participant ages?

The participants were 19-34 years of age. We have added this information (Lines 498-499).

Line 554: The delay from specified to measured motor position was estimated to be 20 ms. Is this with the inertial load of the backboard and participant? Should this be thought of a pure time delay or some other type of frequency response function (transfer function)?

This is a pure delay and is estimated from the motion command delivered to the motors and the movement of the motors.

Line 558: The linear least squares predictor algorithm used to synchronize the visual motion with the motors is not described in sufficient detail in the cited reference (Shepherd 2014) to permit others to reproduce this aspect of the experimental setup. It would be helpful to do so here.

We have added this requested information to the revised text. The text now reads:

“Rendering and projection of the visual scene took approximately 70 ms; therefore, a linear least-squares predictor algorithm was used to synchronize the visual motion (i.e., predict visual motion occurring 50 ms later) together with the motors at a delay of 20 ms (Shepherd 2014). The linear prediction model used 6 data points, and the coefficients were selected by fitting data of participant sway to the corresponding data shifted by the appropriate delay using a linear least squares method.” Lines 546-551.

Line 569: It would be helpful to specify the functional form and parameters of the stiffness that "caught" the backboard when it exceeded the specified limits.

We have added the following text to the revised manuscript:

“To represent the physical limits of sway during standing balance, the backboard rotated in the AP direction about the participant’s ankles with virtual angular position limits of 6° anterior and 3° posterior (Luu et al., 2011; Shepherd 2014). When the backboard position exceeded these position limits, the program gradually increased the simulated stiffness such that the participants could not rotate further in that direction regardless of the ankle torques they produced. This was implemented by linearly increasing a passive supportive torque to a threshold equivalent to the participant’s body load over a rotation range of one degree beyond the balance limits (i.e., passively maintaining the body at that angle). Any active torque applied by participants in the opposite direction would enable them to get out of the limits. Finally, to avoid a hard stop at these secondary limits (i.e., 7° anterior and 4° posterior), the supportive torque was decreased according to an additional damping term that was chosen to ensure a smooth attenuation of motion.” Lines 556-567.

Line 590: Does "reaching a limit" mean crossing from outside to inside the specified limits?

Reaching or crossing a limit means the angular position of the backboard has exceeded the angular position limits (i.e. crossing from inside to outside the specified limits, and not outside to inside). We have clarified this on Lines: 586-587.

Lines 674-754: The text describing the protocols for Experiments 2A and 2B refer to pre-learning and post-learning testing, consistent with Figure 1C, but I cannot find where the details of these testing procedures are described. It would be helpful to explicitly refer to pre- and post-learning testing when describing these testing procedures in this section of the manuscript.

We have modified the text to provide clarity regarding Experiment 2 pre-learning and post-learning. Related to this, we have removed the nomenclature Experiments 2A and 2B (as suggested by Reviewer 1) and have replaced it with “vestibular testing” and “perceptual testing”. As the reviewer suggested, we have added text in this section of the manuscript to explain that the vestibular testing and perceptual testing procedures were performed in pre-learning, post-learning and retention sessions. This revised section also explains the testing procedures in details and can be found on lines 686–785.

Line 697: Please clarify what it means that "Participants then completed Experiment 2A or 2B testing" during the retention testing.

Participants for Experiment 2 either performed vestibular testing or perceptual testing. These testing sessions were performed prior to training (pre-learning), immediately after training (post-learning) or ~3 months after training (retention). We have removed nomenclature of Experiment 2A and 2B and replaced it with vestibular testing and perceptual testing, respectively. This is now explained in the Results and Materials and methods sections (193-264; 686–784). This has been updated in the manuscript text and figure descriptions.

Line 718: Was the range of root-mean-square amplitudes of the electrical vestibular stimulation due to stochastic variation or was amplitude systematically varied?

The range of RMS amplitudes of the electrical vestibular stimulation was indeed due to stochastic variation when generating the different stimulus profiles. We have included this additional information on lines 720-721.

Line 712: Were conditions tested in order from small to large delays, as in Experiment 1?

The delay conditions for Experiment 2 vestibular testing were randomly ordered (see lines 721-723).

Line 719: Does "pseudo-random order" refer to the order of trials within each condition?

For each testing session (pre-learning, post-learning, retention), participants performed 24 total trials (6 delay levels repeated 4 times each). The 24 total trials were completed in four subgroups, where each subgroup consisted of the six delay conditions which were randomly ordered. (Lines 721-723).

Line 746: Was the transition from the 20-ms delay to the experimental delay instantaneous?

Yes, the transition was instantaneous. We have added this information. (Line 751)

Line 746-750: It would be clearer to only use the term "transition" to refer to a change in imposed delay and use a different term to refer to the period of time during which the experimental delay is imposed.

We agree with the reviewer and have modified the text to refer to the change in the imposed delay value as the “transition” and the time the experimental delay is imposed as the “delay period.” These changes can be found on lines 747-784.

Line 750: Please explain the reason a "catch" 20-ms delay was included in the experimental protocol, since this seems to be the same as the baseline delay. Did anything actually change in how the robotic system was controlled when the "catch" 20-ms delay was imposed? In other words, was the failure to find an effect preordained?

During each trial, the robot transitioned instantaneously from baseline 20 ms balance delay to one of the experimental delays (20-350 ms) before returning to 20 ms. The inter-transition interval varied randomly between 7-10s. We included the catch 20ms delay to check whether participants were simply cueing off of an expectation of when unexpected behavior (i.e. standing with delays) would occur based on a prediction of the time period (i.e. the 7-10s inter-transition interval). Nothing changed in the robotic system control when the robot “transitioned” from baseline (20ms) to the catch 20ms delay. In other words, imposing of a catch trial amounted to: 7-10s of 20ms (inter-transition interval), followed by the 8s of 20ms catch, followed by another 7-10s of 20ms (inter-transition interval).

Line 776: Does the term "window" here mean the same thing as term "inter-transition delay" on Line 747? If so, it would be helpful to use the same term in both places.

We thank the reviewer for highlighting this confusion. We have changed the text to accurately describe these periods as inter-transition intervals, which is what was meant by the original term “window”. This change can be found on line 783.

Line 785: It is implied that the 2-s windows excluded periods of time when body angle was outside the specified limits, but it would be helpful to explicity state this restriction up front.

We have added text at the start of this section to explicitly state that we only extracted and analyzed data when whole-body angular position was within the simulated balance limits.

Specifically, the revised text reads:

Line 795: What was bootstrapping used to estimate, the average variance for that participant? Why not just use the actual average variance, as was done when there were fewer than five 2-s windows? Bootstrapping is typically done to test a null hypthosis or construct a confidence interval and assumes independent samples, which would not be the case for data from the same participant.

We have removed the bootstrapping analysis throughout the entire manuscript and instead, as suggested, use the actual velocity variance average.

Line 812: Did the 2-s window have to start after the delay was imposed AND end before the button press?

For Experiment 3, we identified peak sway velocity variance leading up to a perceptual detection. We used a 2-s sliding window to extract the time course of sway velocity variance. The 2-s sliding window of variance started 6s before the delay was imposed and ended 6s after the delay was imposed. We extracted the peak sway velocity variance between the start of the imposed delay and either the button press (for detections) or the end of the delay (for missed detections). (Lines 816-825; 1313-1316)

Line 821: Does concatenating the trials mean that the jumps in signal values from the end of one trial to the beginning of the next are affecting the results?

While concatenating the trials does result in jumps in the signal values (end of one trial to start of next trial), we avoided these jumps within the FFT analysis windows by segmenting the data carefully. Each of the vestibular trials was cut into 19 segments of 2048 data points (i.e., ~1 second segments), and the four vestibular trials with the same delay (i.e. pre-learning 100 ms) were then concatenated to provide 76 total segments. Auto and cross-spectra were then calculated from the individual segments and the spectra were averaged in the frequency domain. Therefore, there is no segment overlap in the FFT analysis for auto and cross-spectra. We provide details of this concatenation and state that there was no segment overlap in lines 840 – 846.

Reviewer #3:

The study describes three experiments that investigated the influence of increased feedback time delay in the ability of human subjects to maintain stable upright balance and their ability to learn/adapt to control balance at time delays values that are greater than those predicted to be possible based on existing simple feedback control models of balance. The studies made use of a unique robot balance device that allowed the generation of continuous body motion as a function of a time-delayed version of the corrective ankle torque generated by the subject as they swayed.

The experiments quantified changes in body sway behaviors as a function of added time delay and characterized the time course of improvements in balance control as subjects learned to stand with a long delay value imposed by the robotic device. The learning was acquired over multiple training sessions and was demonstrated both by a reduction over time in sway measures and by changes in psychophysical measures that demonstrated a reduction in a subject's indication of the occurrence of unexpected body motions. Additionally, the learned ability to control balance with an added time delay was very well retained at 3 months post training.

A final experiment used electrical vestibular stimulation (EVS) to demonstrate the changing contribution of vestibular information to balance control following a transient increase in time delay. This experiment demonstrated a marked reduction in activity in the soleus muscle that was correlated with the EVS following the onset of an added feedback time delay indicating that the added delay caused a reduction in the vestibular contribution to balance.

In general, the experiments were appropriately designed and analyzed. Although the number of participants in each experiment were not large, they were sufficient given the rather robust effects observed when time delays were added to be feedback.

The robotic balance device not only permitted manipulation of the time delay, but also guarded against subjects actually falling when they swayed beyond the normal range of sways compatible with stable balance. This artificial stabilization of balance beyond the normal range permitted subjects to recover from what would otherwise have been a fall and to immediately continue their attempts to learn a balance strategy that was able to overcome the detrimental effects of increased feedback delay. Thus the training procedure was likely much more effective than if trials had been stopped when sway moved beyond the normal range. One imagines such a training device could have important uses in rehabilitation of balance deficits.

But this artificial stabilization also interfered with one of the balance measures used to quantify the influence of added time delay. Specifically, the RMS sway measure used by the authors did not distinguish between time periods when the subject was being artificially stabilized and the time periods when sway was within the normal sway range. Thus the results that were based on the RMS sway measure were not convincing. But fortunately a sway velocity variance measure was also used to quantify sway behavior as a function of time delay and this measure only used data that was within the normal range of sway.

We agree with the reviewer’s point that interpreting mean-removed RMS of sway when the participant was beyond the simulation limits (and thus artificially stabilized by the robotic balance system) may not reflect processes of balance since they include time periods of artificial stabilization. It was for this reason that we provided this measure only in Experiment 1. Our original aim was to compare this more common measure of balance behaviour (Day et al. 1993; Hsu et al. 2007; Jeka et al. 2004; van der Kooij et al. 2011; Winter et al. 2001) to the alternative – though more appropriate – measure of sway velocity variance extracted over periods of balance within the specified sway limits. To avoid further confusion on this matter we removed the mean-removed RMS of sway measure from the paper. Furthermore, as the reviewer suggested, we have added the percent of time participants balanced within the position limits as an additional measure (see response to major comment below and manuscript revisions to Experiment 1 and 2 in the Methods and Materials and Results sections).

Overall results are an important addition to knowledge related to how humans control standing balance and demonstrate an ability to learn, with training, to balance with unexpectedly long delays between control action and the resulting body motion.

We thank the reviewer for the positive remarks about our study and its relevance.

Overall results are clearly presented but this reviewer has some suggestions for improvement.

1. Experiment 1 quantifies changes in balance control as a function of added time delay by measuring RMS sway amplitude and sway velocity variance. It seems incorrect to use the entire 60 seconds of data in the calculation of RMS sway when there are periods of sway beyond the 3 deg backward and 6 deg forward sway balance limits since the backboard motion is artificially stabilized in the region outside the balance limits. It is only with detailed reading of the methods that the reader understands that the backboard motion is artificially stabilized at extremes of sway so this makes a complete understanding of the RMS sway results presented in Figure 2 difficult. But the problem is not fixed by just making the artificial stabilization methods more evident when presenting the Figure 2 results. The problem is that this RMS sway calculation is not representative of the overall subject-controlled sway behavior when there are periods in the trails when the sway was not controlled by the subject (which occurred frequently with longer delays). This reviewer suggests that a much more useful measure would be to calculate and display the percentage of time that subjects were maintaining control within the balance limits. It would be similarly informative to see this type of percentage measure used to track the Experiment 2 learning results in addition to the velocity variance measures shown in Figure 3.

The reviewer is correct that the mean-removed RMS of sway over the entire trial should not be interpreted as exclusively subject-controlled sway because for periods of balance where the limits are exceeded, the participants are artificially supported by the robot. It was for this reason that we (a) grayed out these time periods in the example sway data shown in Figure 2, and (b) extracted sway velocity variance using only periods of balance where the participant was within the limits. Because this distinction in the different balance measures is not entirely explicit when examining our results, we have agreed to remove the RMS sway measure and adopt the reviewer’s suggested improvement. Specifically, we now report the percentage of time participants maintained balance control within the limits alongside the sway velocity variance results for both for Experiment 1 (see Figure 2B) and the Experiment 2 training protocol (Figure 3B inset) results (pages 7-9). Briefly, these data demonstrate that for Experiment 1, the percent time within limits declined at delays ≥ 200 ms. For the Experiment 2 training data (balancing with a 400 ms delay), participants gradually increased the percent time they balanced within the limits, reaching ~97% (of 60s) by the final minute of training.

2. In Experiment 3, group data results show changes in muscle activation evoked by electrical vestibular stimulation based on the 489 of 588 trials on which subjects signaled that they detected an unexpected balance motion. But what about the other 99 trials when subjects did not signal unexpected balance motion? Since the authors suggest there is a possible linkage between the time course of vestibular decline and the detection of unexpected motion, it may be that there was a slower (longer time constant) or reduced amplitude of vestibular decline on the 99 trials where unexpected motion was not detected. Such a finding would strengthen the notion of a linkage between vestibular inhibition and motion detection. Alternatively, if the vestibular declines were indistinguishable between trials with and without unexpected motion this would suggest that the linkage was not tight and something else may be involved. In either case this comparison would be useful. Additionally, it seems that 99 trials should be enough data since Figure 6 shows good results from a single subject based on 77 trials.

The reviewer raises an interesting question, and one that we had briefly explored in our original data analysis. To address this question, we first extracted all transitions that were missed from all subject data together with an equal number of randomly selected transitions that were detected. For instance, for a subject who missed 13 transitions, we randomly selected 13 transitions that were detected. Therefore, each subject contributed the same number of missed and detected transitions to our final estimate of coherence and gain. In total, this procedure provided 82 missed transitions and 82 detected transitions. We then computed time-frequency coherence and gain using this subset of data according to the same approach employed for the total dataset. From these time-frequency estimates, mean coherence and mean gain were calculated across the 0-25 Hz bandwidth throughout the trial (Author response image 5). Finally, we also tracked the sway velocity variance (2s sliding window, as in our original analysis) for the missed and detected trials to examine any changes in balance behaviour.

Author response image 5

Download asset Open asset

Experiment 3 time-varying EVS-EMG coherence, gain and sway velocity variability during detected (perceived) and missed (not perceived) delay transitions.

Data are presented across transition periods, where the simulation transitioned from baseline to 200 ms delayed balance control, which lasted for 8s (between dashed red vertical lines). Top panel, a comparison of 82 detected and missed transitions vestibular-evoked muscle coherence and gain. Dashed lines represent coherence and gain levels which are 2 standard deviations below the mean levels in the 6 seconds preceding the onset of the delay. Bottom panel, a comparison of sway velocity variance from 82 detected and 82 missed transitions. Thick lines represent the mean with lighter lines representing the s.e.m. For both panels, blue and red traces represent detected and missed transitions, respectively.

During the detected transitions, both coherence and gain decreased following the onset of the 200 msec delay and returned to normal levels when the delay was removed. Although limited attenuation of the mean coherence and gain was observed in the missed transitions, the variability in both missed and detected trials was large such that the difference between detected and missed transitions was not substantial. We also observed that sway velocity variance during the 82 missed transitions was smaller (reaching a peak ~3x lower) than the 82 detected transitions. As a result, we cannot be certain that the (limited) difference in coherence and gain between detected and missed transitions is related entirely to the perceptual motion detection, because the whole-body sway behavior (i.e., sway velocity variance) is clearly different. As mentioned in our original submission, and revised manuscript, our results from Experiment 2 and 3 suggest that whole-body sway behavior influences both vestibular muscle responses and perception of unexpected balance motion. Currently, we have only presented this analysis in the response to the reviewer’s document. If the reviewer feels strongly about including this in the manuscript, we would be happy to include it as a supplementary figure.

3. The section on pages 23 and 24 discusses alternative models that might be able to explain how subjects can learn to tolerate long time delays. I believe that all of the references to alternative models are to models that would be classified as continuous control models as opposed to intermittent control schemes that have been proposed as an alternative (e.g. Ian Loram references such as Loram et al., J Physiol 589.2:307-324, 2011, Gawthrop, Loram, Lakie, Biol Cybern 101:131-146, 2009, and the Morasso reference in the authors manuscript). It seems that Loram's work has shown that it is possible to visually control an unstable load with properties similar to those of a human body using an intermittent control scheme. This intermittent control scheme should be referenced. But beyond just mentioning these alternative control structures as possibilities, do the authors know of actual simulations of these models that can demonstrate that an inverted pendulum system can be made stable with the extremely long time delays that the authors investigated?

We thank the reviewer for raising these points regarding the discussion of balance control models that may or may not be able to stabilize upright stance with long delays. We refer to our response to all the reviewers (at the start of this document) for how we addressed these points. Briefly, we have now added a discussion of the different control models for standing balance and how they may (or may not) be capable of replicating our results of stabilizing human standing with large delays. This discussion can be found on lines 358-375.

To answer the reviewer’s question of model simulations that can stabilize with long delays, we note that Kuo (1995) has described the robustness of an optimal controller for standing balance to control delays, showing that at very small center of mass accelerations, the system can be stabilized with large (> 500 ms) delays. However, this robustness rapidly declines with increasing external disturbances (Kuo 1995) as is also expected from the paper the reviewers provided (Zhou and Wang 2014). We include these points in our discussion on lines 358-375.

4. Several places in the manuscript the authors refer to estimates of maximal time delays based on simpler feedback control models. Specifically, the Bingham et al. 2011 and the van der Kooij and Peterka, 2011 references are given. But the values of the maximal time delays are not consistent across the various mentions of these two references. Here is a listing of those mentions:

- Line 78: ~300 ms

- Line 406: 340-430 ms

- Line 667: ~400 ms

- Line 678: ~400 ms

We agree with the reviewer that this inconsistency should be rectified. Considering the reviewer’s next comment (that the Bingham et al., 2011 study focused on frontal plane standing control), we are removing the Bingham et al., (2011) study when referring to critical delays (although we include the study to discuss balance delays in general). Computational models of standing suggest that upright posture cannot be maintained with delays ~300-340 ms (Milton and Insperger 2019; van der Kooij and Peterka 2011). Considering that inherent sensorimotor loop delays in human stance can vary (~100-160ms), we consider that any imposed delay (via robotic simulation) above 200ms would therefore surpass the low end of the critical delay range. For consistency, we now refer to previously proposed critical delays to be in the range of ~300-340ms.

This reviewer could find mention of 340 ms in the van der Kooij and Peterka paper, but it seems that the Bingham paper did not really investigate time delay in detail and that paper also was investigating body motion in the frontal plane that has considerably different lower body dynamics compared to a single segment inverted pendulum.

The Bingham paper mentions a critical delay of 429 ms on page 441 of their manuscript and describes its calculation in the appendix section. That being said, we agree with the reviewer that because Bingham et al., (2011) were assessing frontal plane (ML) control dynamics, this critical delay may not be the same for sagittal plane (AP) control. Therefore, we have removed explicitly referencing Bingham’s estimated ~430 ms critical delay for this paper. Nevertheless, we still refer to the Bingham paper when discussing delays in balance control in general.

5. The authors indicated that analysis programs and data will be made publicly available upon acceptance for publication.

We have created a dataverse link for the source files and code needed to generate the group result figures. This can be found at https://doi.org/10.5683/SP2/IKX9ML.

https://doi.org/10.7554/eLife.65085.sa2

Article and author information

Author details

Brandon G Rasman
1. School of Physical Education, Sport, and Exercise Sciences, University of Otago, Dunedin, New Zealand
2. Department of Neuroscience, Erasmus MC, University Medical Center Rotterdam, Rotterdam, Netherlands
3. School of Kinesiology, University of British Columbia, Vancouver, Canada
Contribution
Conceptualization, Formal analysis, Investigation, Methodology, Project administration, Software, Validation, Writing – original draft, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-8031-8320
Patrick A Forbes

Department of Neuroscience, Erasmus MC, University Medical Center Rotterdam, Rotterdam, Netherlands

Contribution
Conceptualization, Formal analysis, Methodology, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-0230-9971
Ryan M Peters
1. School of Kinesiology, University of British Columbia, Vancouver, Canada
2. Faculty of Kinesiology, University of Calgary, Calgary, Canada
3. Hotchkiss Brain Institute, Calgary, Canada
Contribution
Conceptualization, Formal analysis, Methodology, Writing – review and editing

Competing interests
No competing interests declared
Oscar Ortiz
1. School of Kinesiology, University of British Columbia, Vancouver, Canada
2. Faculty of Kinesiology, University of New Brunswick, Fredericton, Canada
Contribution
Investigation, Writing – review and editing

Competing interests
No competing interests declared
Ian Franks

School of Kinesiology, University of British Columbia, Vancouver, Canada

Contribution
Conceptualization, Writing – review and editing

Competing interests
No competing interests declared
J Timothy Inglis
1. School of Kinesiology, University of British Columbia, Vancouver, Canada
2. Djavad Mowafaghian Centre for Brain Health, University of British Columbia, Vancouver, Canada
Contribution
Conceptualization, Methodology, Writing – review and editing

Competing interests
No competing interests declared
Romeo Chua

School of Kinesiology, University of British Columbia, Vancouver, Canada

Contribution
Conceptualization, Methodology, Writing – review and editing

Competing interests
No competing interests declared
Jean-Sébastien Blouin
1. School of Kinesiology, University of British Columbia, Vancouver, Canada
2. Djavad Mowafaghian Centre for Brain Health, University of British Columbia, Vancouver, Canada
3. Institute for Computing, Information and Cognitive Systems, University of British Columbia, Vancouver, Canada
Contribution
Conceptualization, Formal analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Writing – review and editing

For correspondence
jsblouin@mail.ubc.ca

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-0046-4051

Funding

Natural Sciences and Engineering Research Council of Canada (Graduate Student Scholarship)

Brandon G Rasman

Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO #016. Veni. 188.049)

Patrick A Forbes

Natural Sciences and Engineering Research Council of Canada (RGPIN-2020-05438)

Jean-Sébastien Blouin

University of Otago (Post-graduate Research Scholarship)

Brandon G Rasman

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank Hasrit Sidhu for his help with data collection and all the participants who participated in this research. This study was funded by the Natural Sciences and Engineering Research Council of Canada, grant number RGPIN-2020-05438, awarded to J-SB. BGR received graduate student funding from the Natural Sciences and Engineering Research Council of Canada and The University of Otago (Post-graduate Research Scholarship). PAF received funding from the Netherlands Organization for Scientific Research (NWO #016. Veni. 188.049). RMP was funded by a Natural Sciences and Engineering Research Council Grant to JTI.

Ethics

Human subjects: The experimental protocol was verbally explained before the experiment and written informed consent was obtained. The experiments were approved by the University of British Columbia Human Research Ethics Committee and conformed to the Declaration of Helsinki, with the exception of registration to a database.

Senior Editor

Ronald L Calabrese, Emory University, United States

Reviewing Editor

Noah J Cowan, Johns Hopkins University, United States

Reviewer

Noah J Cowan, Johns Hopkins University, United States

Version history

Received: November 22, 2020
Accepted: August 4, 2021
Accepted Manuscript published: August 10, 2021 (version 1)
Version of Record published: September 29, 2021 (version 2)
Version of Record updated: October 5, 2021 (version 3)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.