Focal seizures are organized by feedback between neural activity and ion concentration changes

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: August 15, 2022 (This version)
Accepted Manuscript published: August 2, 2022 (Go to version)
Accepted: July 12, 2022
Preprint posted: March 19, 2021 (Go to version)
Received: March 18, 2021

1. Of interest
ProteInfer, deep neural networks for protein functional inference

Theo Sanderson, Maxwell L Bileschi ... Lucy J Colwell

Tools and Resources Updated Mar 30, 2023
Further reading

Article
Figures and data
Abstract
Editor's evaluation
Introduction
Results
Discussion
Materials and methods
Appendix 1
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Human and animal EEG data demonstrate that focal seizures start with low-voltage fast activity, evolve into rhythmic burst discharges and are followed by a period of suppressed background activity. This suggests that processes with dynamics in the range of tens of seconds govern focal seizure evolution. We investigate the processes associated with seizure dynamics by complementing the Hodgkin-Huxley mathematical model with the physical laws that dictate ion movement and maintain ionic gradients. Our biophysically realistic computational model closely replicates the electrographic pattern of a typical human focal seizure characterized by low voltage fast activity onset, tonic phase, clonic phase and postictal suppression. Our study demonstrates, for the first time in silico, the potential mechanism of seizure initiation by inhibitory interneurons via the initial build-up of extracellular K⁺ due to intense interneuronal spiking. The model also identifies ionic mechanisms that may underlie a key feature in seizure dynamics, that is, progressive slowing down of ictal discharges towards the end of seizure. Our model prediction of specific scaling of inter-burst intervals is confirmed by seizure data recorded in the whole guinea pig brain in vitro and in humans, suggesting that the observed termination pattern may hold across different species. Our results emphasize ionic dynamics as elementary processes behind seizure generation and indicate targets for new therapeutic strategies.

Editor's evaluation

In this manuscript the authors build a small-scale biophysically realistic network model to study seizure dynamics which incorporates Hodgkin Huxley mechanisms and ion dynamics. The model enhances our understanding of the mechanisms underlying the evolution and termination of focal seizures. In particular it demonstrates that intense activation of inhibitory interneurons, by driving changes in transmembrane ion dynamics are a possible mechanism for driving the initiation and prolongation of seizures.

https://doi.org/10.7554/eLife.68541.sa0

Introduction

Focal seizure patterns recorded with intracranial and intracerebral electrodes in patients submitted to presurgical evaluation often consist of distinct phases (Franaszczuk et al., 1998; Spencer et al., 1992; Velascol et al., 2000). A frequently observed onset pattern in patients with temporal lobe epilepsy (TLE) is characterized by low-voltage fast (LVF) activity in the gamma range (30–80 Hz) (Avoli et al., 2016; de Curtis and Gnatkovsky, 2009; Lagarde et al., 2019; Perucca et al., 2014). LVF seizure onset is followed by the recruitment of irregular spiking behavior which evolves into periodic burst discharges that gradually decrease in frequency and suddenly cease. Seizures are often followed by a period of reduced EEG amplitude known as postictal EEG suppression. The traditional view on epileptic seizures is that they result from an imbalance of synaptic excitation and inhibition (Bradford, 1995; Bragin et al., 2009). It is unclear how this concept may account for the electroencephalographic complexity of TLE seizures and their characteristic progression from one phase to the next. The findings of several studies have not confirmed the role of synaptic interaction in seizure generation or progression. It has been shown that blocking synaptic transmission via a low Ca²⁺ solution led to the development of synchronized seizure-like events (SLE) in hippocampal CA1 slices (Jefferys and Haas, 1982; Yaari et al., 1983) and in the intact hippocampus (Feng and Durand, 2003). Moreover, the synchronized epileptiform activity can be recorded across two hippocampal regions separated by a mechanical lesion, without the involvement of electrochemical synaptic communication (Lian et al., 2001). Finally, in photosensitive baboons, light-induced neocortical seizure discharges were accompanied by depletion of extracellular Ca²⁺ to levels incompatible with the chemical synaptic transmission (Pumain et al., 1985). Additionally, a paradoxical increase in inhibitory cell firing and a decrease in pyramidal cell activity at seizure onset was documented in in vitro rodent slices (Derchansky et al., 2008; Fujiwara-Tsukamoto et al., 2007; Lévesque et al., 2016; Lillis et al., 2012; Ziburkus et al., 2006), in the in vitro whole guinea pig brain (Gnatkovsky et al., 2008; Uva et al., 2015), and in human and animal in vivo recordings (Elahian et al., 2018; Grasse et al., 2013; Miri et al., 2018; Toyoda et al., 2015; Truccolo et al., 2011). The above-mentioned studies suggest that processes at the network level related to changes in synaptic gains cannot be the sole mechanisms that control seizure generation and progression, and that other factors must be involved in the process of ictogenesis.

Although several non-synaptic mechanisms have been proposed to influence abnormal synchronization (Blauwblomme et al., 2014; de Curtis et al., 2018; Jefferys et al., 2012; Raimondo et al., 2015), the specific mechanisms responsible for seizure induction, evolution and termination remain unclear. Specifically, the relative contribution of raised extracellular potassium (Avoli et al., 1996; Gnatkovsky et al., 2008) vs. increased intracellular chloride leading to depolarizing GABA responses (Alfonsa et al., 2015; Lillis et al., 2012) remains to be established. In the present study, we investigated the possible mechanisms of the LVF seizure pattern using a realistic computational model of the hippocampal network that included activity-dependent ion concentration changes. We based our simulations on the data recorded in the in vitro isolated guinea pig brain preparation because SLE in this model closely resemble human temporal lobe seizures (de Curtis et al., 2006; de Curtis and Gnatkovsky, 2009) and are initiated by enhanced firing of inhibitory interneurons (Gnatkovsky et al., 2008). We used these experimental recordings to guide our in silico study due to the availability of data at the network, cellular, and ionic levels. A computer model showed that simulated seizures initiated via increased interneuron discharges, evolved and terminated autonomously due to activity-dependent ion concentration shifts and homeostatic mechanisms that worked continuously to restore physiological transmembrane ion levels. Our modelling results suggest a link between the seizure termination mechanism and postictal suppression state and predict a specific scaling law of inter-bursting intervals observed at the end of seizures, which was validated experimentally.

Results

The model consisted of five cells, four pyramidal neurons (PY) and a fast-spiking inhibitory interneuron (IN), arranged as a chain structure (Figure 1). The ionic dynamics of K⁺, Na⁺, Ca²⁺, and Cl⁻ were incorporated and activity-dependent changes in their concentrations were computed. Concentration changes in each extracellular or intracellular compartment were dependent on several mechanisms such as active and passive membrane currents, inhibitory synaptic GABAa currents, Na⁺/K⁺-pump, KCC2 cotransporter, glial K⁺ buffer, Ca²⁺ pump and buffer, radial diffusion, longitudinal diffusion and volume changes. Additionally, we included impermeant anions (A^-) with concentration-dependent volume changes and bicarbonate ions (HCO₃^-) that contributed to GABAa currents.

Figure 1

Download asset Open asset

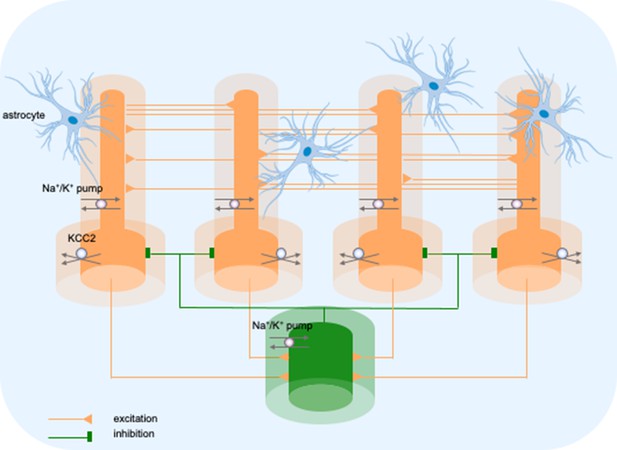
Model diagram.

The model consisted of four pyramidal cells (orange) and an interneuron (green) linked by excitatory (AMPA) and inhibitory (GABAa) synaptic connections. Each cellular compartment was surrounded by an interstitial compartment. The interstitial space was enclosed in a common bath (blue) which represented the surrounding tissue and vasculature not included in the model. The model included variable intracellular and extracellular ion concentrations computed according to ionic currents flowing across neuronal membranes, longitudinal diffusion between the dendritic and somatic compartments, radial diffusion between neighboring interstitial compartments and diffusion to/from the bath. Additionally, the model included ionic regulation mechanisms: a Na⁺/K⁺-pump, a KCC2 cotransporter and K⁺ buffering by astrocytes.

Three phases of an LVF onset SLE

Brief perfusion (3 min) of 50 microM bicuculline in the isolated guinea pig brain transiently reduces GABAergic inhibition to 60–70% and leads to strong interneuron bursting in the absence of principal cells activity (Gnatkovsky et al., 2008; Uva et al., 2015). Therefore, to initiate a SLE in the model we choose to selectively and transiently enhance discharge of the inhibitory interneuron. In this way, we made our model more general and applicable to other experimental data in which paradoxical increase in GABAergic cell firing is observed at seizure onset.

A simulated seizure emerging from normal background activity is shown in Figure 2. The SLE was triggered by depolarizing current applied to the IN at second 60 (Figure 2C, yellow trace). Strong firing (initial rate of 150 Hz) of the IN (Figure 2C) led to small amplitude fast activity in the LFP signal (Figure 2A between the 60 and 68 s timestamps) associated with the onset of the simulated SLE. After approximately 10 s, the PY cells began to generate a strong tonic discharge, resulting in an irregular LFP spiking signal with increased amplitude typically associated with the SLE tonic phase (Figure 2B; 65–80 s). Approximately 20 s after the onset of the SLE, the cellular firing pattern of PY cells switched from tonic to bursting discharge, leading to LFP oscillations which corresponded to the bursting phase (Figure 2A, after 80 s). The three types of PY cell activity are shown in an extended time scale in Appendix 1—figure 1A. As the SLE progressed, the burst rate gradually decreased and ictal discharges spontaneously terminated. Postictally, the SLE was followed by a period of silence for approximately 90 s which was visible in the LFP signal and in the PY and IN traces (Figure 2A–C). After the postictal depression, the background firing reappeared and gradually returned to a baseline level. The SLE discharges were accompanied by significant changes in the intracellular and extracellular ionic concentrations. At the onset of the seizure, extracellular potassium concentration ([K⁺]_o) increased sharply in the somatic compartment, remained elevated throughout the SLE and slightly decreased toward the end of the episode (Figure 2D). Intracellular sodium concentration ([Na⁺]_i) steadily increased during the bursting phase in both somatic and dendritic compartments and reached a plateau around the offset of the SLE (Figure 2E). Intracellular chloride concentration ([Cl^-]_i) exhibited a gradual increase from the beginning of the SLE and was highest at the end of the paroxysmal firing (Figure 2F).

Figure 2

Download asset Open asset

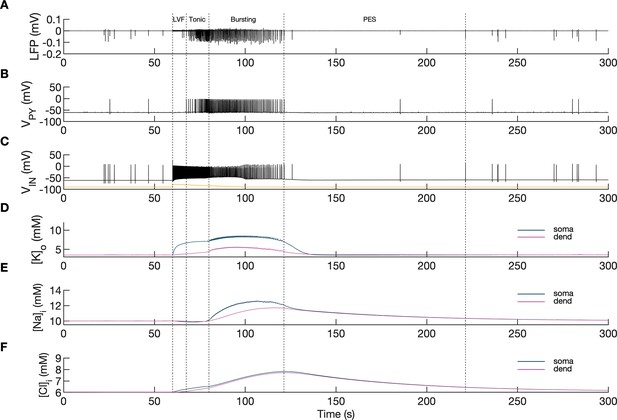
Model behavior during an SLE.

(A) Local field potential (LFP) signal. (B) Pyramidal cell (PY) membrane potential. (C) Interneuron (IN) membrane potential. (D) Extracellular potassium concentration. (E) Intracellular sodium concentration. (F) Intracellular chloride concentration. In the interictal phase (0–60 s), the model generated irregular background firing and the ion concentrations were at their resting values (**A–F**). The current injected into the interneuron at second 60 (C) yellow triggered fast IN spiking (C), black which also manifested as low voltage fast (LVF) activity in the LFP signal (A) Approximately 10 s after the initiation of the SLE, PY cells initiated tonic firing that subsequently shifted to bursting (B) The behavior of the PY cells was reflected in the LFP trace which showed irregular activity and synchronized bursting (A) The SLE terminated at approximately second 120 and was followed by postictal EEG suppression (PES) (**A–C**). The cellular activity was accompanied by significant ion concentration shifts. Extracellular potassium in the somatic compartment increased sharply and remained elevated throughout the SLE (D) dark blue. The [K⁺]_o increase in the dendritic compartment was slower and less pronounced (D) violet. The intracellular sodium increased gradually toward a plateau (E) The intracellular chloride accumulated steadily throughout the SLE (F).

Figure 2—source data 1 Main simulation results.: https://cdn.elifesciences.org/articles/68541/elife-68541-fig2-data1-v2.zip
Download elife-68541-fig2-data1-v2.zip

A comparison of the simulation results with the available experimental data is shown in Figure 3. In the isolated guinea pig brain, the SLE activity with an LVF onset pattern (Figure 3A, top trace) was induced by 3 min arterial application of bicuculine. The transition from preictal to ictal state which occurred at approximately second 10 was associated with a strong discharge of fast-spiking interneurons (Figure 3A, third trace) and transient silencing of the PY cells (Figure 3A, second trace). Within a few seconds from the initiation of the sustained interneuron discharge, the principal PY cells were recruited first into tonic firing and subsequently into bursting discharges which were visible in the PY membrane potential and LFP signals. [K⁺]_o sharply increased at the onset of the SLE and remained elevated afterward (Figure 3A, bottom trace). The in silico results (shown for comparison in the same timescale in Figure 3B) replicated the experimental data in many respects including LFP signal characteristics, cellular firing pattern and [K⁺]_o time course.

Figure 3

Download asset Open asset

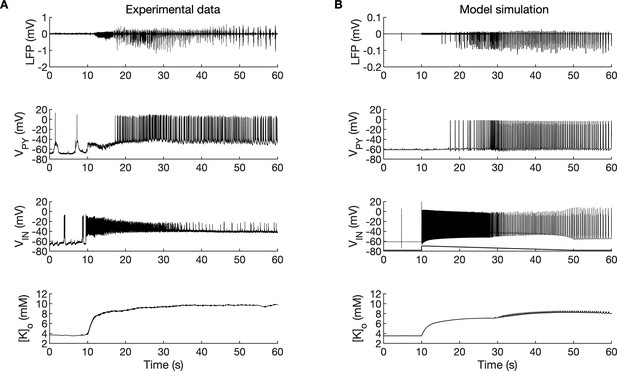
A comparison between the experimental data and the model simulation.

(A) Experimental recordings of a seizure-like event (SLE) in the in vitro isolated whole guinea pig brain preparation (de Curtis et al., 2006; Gnatkovsky et al., 2008; Uva et al., 2015). From top to bottom: LFP signal, intracellular recording of pyramidal cell (PY) and interneuron (IN), extracellular potassium. The onset of the SLE was associated with increased IN firing, silencing PY and low-voltage fast (LVF) activity in the LFP signal. Approximately 10 s after the onset of the SLE, the PY exhibited a tonic and then burst firing behavior. The extracellular potassium increased up to approximately 10 mM at the onset of the SLE and remained elevated afterward. (B) The activity patterns in the LFP signal, pyramidal cells, interneuron and [K⁺]_o were reproduced accurately by the model. Signals presented in (A) were recorded in different experiments. LFP and interneuron data have been published previously (Gentiletti et al., 2017; Gnatkovsky et al., 2008) while pyramidal cell and [K⁺]_o data have never been published before.

Figure 3—source data 1 Source files for an SLE recordings in the in vitro isolated whole guinea pig brain. This zip archive contains experimental data shown in Figure 3. Seizure-like events were induced by 3 min arterial perfusion of 50 microM bicuculline and were recorded in the entorhinal cortex of the in vitro isolated whole guinea pig brain. The data are in the Matlab format (.mat). Matlab script (.m) loads the data from the file and creates the plot.: https://cdn.elifesciences.org/articles/68541/elife-68541-fig3-data1-v2.zip
Download elife-68541-fig3-data1-v2.zip

In the simulations, the excitatory and inhibitory synaptic conductances were ‘clamped’ throughout the entire simulation period, hence, they could not contribute to the progression from one phase to another. Conversely, variations in ion concentrations were expected to affect neuronal excitability. For example, an increase in [K⁺]_o reduces the driving force of K⁺ currents responsible for hyperpolarized resting membrane potential and spike repolarization. [Cl^-]_i accumulation causes depolarizing shift in E_GABAa reducing the efficacy of GABAa inhibition. [Na⁺]_i and [K⁺]_o affect the rate of the Na⁺/K⁺-pump that transports three Na⁺ ions out of the cell for every two K⁺ ions pumped into the cell, thus producing an outward current. Accumulation of [K⁺]_o and [Na⁺]_i increases the pump rate and enhances the hyperpolarizing pump current. Hence, to determine the intrinsic mechanism that modulates excitability, we first investigated the behavior of the model in response to variations in extracellular potassium and intracellular sodium concentrations and next we considered the role of chloride dynamics.

The effects of [K⁺]_o and [Na⁺]_i on the network model

Activity-dependent changes in ion concentrations are slow compared to neuronal dynamics, which are relatively fast. To analyze such a system, with slow and fast timescales, it is possible to decouple the fast variables (e.g. membrane potential) from the slow variables (e.g. ionic concentrations). Accordingly, to analyze the role of [K⁺]_o and [Na⁺]_i in shaping single-cell and network dynamics, we disabled all mechanisms controlling ionic concentrations and analyzed the behavior of the model for different values of [K⁺]_o and [Na⁺]_i. The values of these variables were modified externally and treated as control parameters. To obtain improved affinity with the reference simulation (Figure 2), the chloride concentration in the somatic and dendritic compartments of the PY cells was set to 7 mM, which corresponded to its mean value during the SLE (Figure 2F). In the single-cell analysis, all synaptic connections were removed. In the network analysis, all synaptic connections were intact except afferent excitatory input, which was removed from PY cells to eliminate the stochastic component from the analysis; depolarizing current injection was removed from the interneuron. The behavior of a single PY cell was analyzed for different values of extracellular potassium concentration in the dendritic ([K⁺]_o,dend) and somatic compartments ([K⁺]_o,soma). During the analysis, for each fixed value of [K⁺]_o,dend, we performed simulations when sweeping the [K⁺]_o,soma value from 3 mM to 12 mM (in steps of 0.25 mM) in the forward and backward direction. The initial conditions for each [K⁺]_o,soma value corresponded to the final states in the previous step. For each [K⁺]_o,soma step, we simulated 5 s of activity. After a full sweep with all [K⁺]_o,soma steps in both directions, the [K⁺]_o,dend was increased and the analysis was repeated. The analysis was performed for the [K⁺]_o,dend values in the range of 3–6 mM, in steps of 0.5 mM (or 0.25 mM and 0.125 mM if a better resolution was required). We found that the behavior of the single cell and network models was the same for increasing and decreasing steps of [K⁺]_o,soma with small domains of bistability not larger than one step (0.25 mM) between the activity phases. Analysis of the dynamics of a single isolated cell for a reference value of [Na⁺]_i at 10 mM can be found in Appendix 1—figure 1. In the network analysis, a full sweep with all [K⁺]_o,soma and [K⁺]_o,dend steps (as described above) was performed for three different values of [Na⁺]_i,soma namely, 10 mM, 11 mM and 12 mM. Following Figure 2E we assumed, that corresponding values of [Na⁺]_i,dend were lower and were 10 mM, 10.5 mM and 11 mM, respectively. The analysis results are shown in Figure 4A, in which the various activity patterns, i.e., rest, tonic firing and bursting are color-coded (as shown on the right). A comparison of the network activities for different values of [Na⁺]_i in the three graphs in Figure 4A demonstrates that the main effect of an increase in [Na⁺]_i was a shrinking of the tonic and bursting domains and an expansion of the resting domain due to upregulation of the hyperpolarizing effect of increased [Na⁺]_i on the pump current.

Figure 4

Download asset Open asset

Analysis of the model.

In the bifurcation analysis extracellular potassium and intracellular sodium concentrations in the PY and IN cells were control parameters. Concentrations of all other ions were fixed at their reference values (except chloride: [Cl^-]_i,soma, [Cl^-]_i,dend equal to 7 mM), all ion accumulation mechanisms were blocked and background input was removed. (A) Bifurcation diagrams showing the dependence of the behavior of the model on [K⁺]_o,dend and [K⁺]_o,soma for varying values of [Na⁺]_i,soma, [Na⁺]_i,dend. The diagram colors correspond to types of activity shown on the right: rest (yellow), tonic firing (violet) and bursting (dark blue). An increase in [Na⁺]_i progressively decreased the domains of tonic firing and bursting and increased the resting domain indicating a general decrease in network excitability. The black and gray arrows correspond to the evolution of [K⁺]_o,soma, [K⁺]_o,dend during different phases of the SLE, shown in part B. (B) A simulation of the model with [K⁺]_o,soma, [K⁺]_o,dend and [Na⁺]_i,soma, [Na⁺]_i,dend as the external control parameters, that illustrated the occurrence of transitions between different types of activity during the SLE. The top two panels show the time course of [K⁺]_o,soma, [K⁺]_o,dend and [Na⁺]_i,soma, [Na⁺]_i,dend and approximate their evolution during the SLE (Figure 2). The third panel shows the resulting PY cell behavior. The parameter evolution is divided into four phases indicated by the arrows denoted as I–IV in part (A) and (B). Phase I corresponds to a sharp increase in [K⁺]_o,soma which led to a transition from rest to tonic firing (marked as a black arrow ‘I’ in the first panel in A). Phase II corresponds to a slow increase in [K⁺]_o,dend which led to a transition from tonic firing to bursting (marked as a black arrow ‘II’ in the first and second panels in A). Phase III represents a period of increased [Na⁺]_i,soma, [Na⁺]_i,dend and decreasing [K⁺]_o,soma and [K⁺]_o,dend which led to the termination of the SLE represented by a black arrow ‘III’ with its tip in the yellow domain in the third panel in (A). Phase IV corresponds to the postictal period with elevated [Na⁺]_i and a return of [K⁺]_o,soma, [K⁺]_o,dend to their baseline values marked as a black arrow ‘IV’ in the third panel in (A).

The evolution of the SLE mediated by [K⁺]_o and [Na⁺]_i

In the previous section, the influence of [K⁺]_o and [Na]_i on network behavior was examined without accounting for the time factor. Here, we present a fast-slow system analysis approach that considers the time evolution of ionic concentrations, as shown in Figure 2. Hence, we assessed the dependence of the evolution of an SLE on externally manipulated changes in [K⁺]_o and [Na]_i with fixed concentrations of all other ions. As in Figure 4A, the chloride concentration in the somatic and dendritic compartments of the PY cells was set to 7 mM. To schematically describe the extracellular potassium concentration time course from preictal to postictal state (as shown in Figure 2D), we identified four distinct stages (as shown in Figure 4B top panel): (I) a sharp increase in [K⁺]_o,soma, (II) elevated [K⁺]_o,soma, a slow increase in [K⁺]_o,dend, (III) a slow decrease in [K⁺]_o,soma and [K⁺]_o,dend, (IV) a decrease in [K⁺]_o,soma and [K⁺]_o,dend back to their resting values. Variations in potassium concentrations were accompanied by changes in [Na⁺]_i (Figure 2E). In the preictal period and during the SLE tonic firing phase, [Na⁺]_i in the soma and dendrite was stable, while it increased during the burst firing phase and reached a plateau toward the end of the episode. In the postictal period, [Na⁺]_i in both compartments slowly returned to the initial value. The time course of [Na⁺]_i approximating intracellular somatic and dendritic sodium evolution is shown in Figure 4B (middle panel). The corresponding representative PY cell activity is shown in Figure 4B (bottom trace). To distinguish different SLE phases, the PY cell activity pattern was marked using a color-code, as in Figure 4A. As [K⁺]_o and [Na⁺]_i followed their predefined time course, PY cells exhibited transition from rest to tonic firing, progressed into bursting with a slowing-down pattern and eventually returned to the resting state. In the postictal period (after stage IV), the [Na⁺]_i remained elevated for more than 40 s (Figure 4B middle panel) giving rise to an enhanced hyperpolarizing Na⁺/K⁺-pump current that reduced the excitability of the network and contributed to postictal depression, as described in the last paragraph. To further observe the time evolution of the SLE in the [K⁺]_o,soma, [K⁺]_o,dend parameter space, we superimposed potassium changes on the bifurcation diagrams in Figure 4A. The distinct stages of the potassium time course are marked by arrows. The crossing of a color border by an arrow corresponds to a transition between different firing regimes. The initial increase of somatic [K⁺]_o (stage I) led to a transition from the resting state to tonic firing (Figure 4A, first panel), while a subsequent increase in dendritic [K⁺]_o (stage II) led to a transition from tonic firing to bursting (Figure 4A, middle panel). A subsequent decrease in somatic and dendritic [K⁺]_o (stage III) led to the termination of the SLE, as the cell activity reentered the resting state region (Figure 4A, last panel). After termination of the SLE, [K⁺]_o,soma and [K⁺]_o,dend returned to their resting values (stage IV in Figure 4A, last panel).

The role of [Cl^-]_i

Chloride accumulation depends on Cl^- influx through chloride leak and GABAa receptor channels, but it is also affected by variations in potassium concentrations mediated via KCC2 cotransport. Hence, chloride and potassium could not be considered as independent control parameters in the fast-slow system analysis approach. Furthermore, visualization of the results with five control parameters ([K⁺]_o,soma, [K⁺]_o,dend, [Na⁺]_i,soma, [Na⁺]_i,dend and [Cl^-]_i) is challenging. Therefore, to evaluate the role of chloride accumulation, we compared the reference model with the model in which chloride dynamics was excluded (Figure 5). When considering the role of chloride homeostasis mediated via KCC2, the direction of K–Cl cotransport depends on the E_Cl vs E_K or the ratio [K⁺]_i[Cl^-]_i/[K⁺]_o[Cl^-]_o (Payne et al., 2003). If the ratio is greater than 1, KCC2 extrudes Cl^- and K⁺. If E_K is greater than E_Cl, the KCC2 flow is reversed and Cl^- and K⁺ ions are transported into the cell. When chloride accumulation was removed (Figure 5A), the reversal potentials of the Cl^- and GABAa currents (E_Cl and E_GABAa) were fixed (blue and light blue lines in Figure 5A, second panel). Under such conditions, the firing of the interneuron (Figure 5A, third panel) exerted a steady inhibitory influence on the PY cells. Additionally, it increased [K⁺]_o above fixed [Cl^-]_i level (Figure 5A, fourth panel). As a result, E_K exceeded E_Cl and the KCC2 transported K⁺ and Cl^- into the cells (Figure 5A, fifth panel) and reduced the external K⁺ concentration. All these effects transiently increased the PY cells tonic firing but the bursting SLE phase was not manifested (Figure 5A, first and second panel). Conversely, activation of the IN in the reference model, with chloride dynamics intact, led to a typical SLE (Figure 5B, top panel). The [Cl^-]_i accumulation was dominated by Cl^- influx through GABAa receptors and to lesser degree by KCC2 cotransport (Figure 5B, fifth and bottom panel). It led to enhanced excitability in two ways: (i) by increasing the chloride reversal potential (blue line in Figure 5B, second panel) toward the PY membrane potential, reducing the hyperpolarizing chloride leak current; (ii) by increasing the GABAa reversal potential (Figure 5B, second panel, light blue) that approached the PY cell membrane potential, reducing the postsynaptic inhibitory current. These changes led to the stronger tonic firing of the PY cells, which contributed to enhanced [K⁺]_o accumulation (Figure 5B, third panel) leading to the transition into the SLE bursting phase.

Figure 5

Download asset Open asset

A comparison of the model without and with chloride accumulation.

The six panels in each column show respectively (from top to bottom): the LFP signal, the PY cell membrane potential, the IN membrane potential, the extracellular potassium concentration and intracellular chloride concentration, the chloride and potassium KCC2 currents in the somatic compartments and the GABAa synaptic currents (Cl^- and HCO₃-) together with the leak chloride current. Additionally, the equilibrium potential of chloride and GABAa are shown in the second panel from the top. (A) When the [Cl^-]_i accumulation mechanism was blocked, the chloride concentration was fixed at the reference value (fourth panel, blue). Without chloride accumulation, the PY cell (second panel) fired tonic train of spikes due to transient rise in [K⁺]_o (fourth panel, red) mediated by the IN discharge triggered by the current injection (yellow, third panel). Elevated [K⁺]_o and fixed [Cl^-]_i promoted K⁺ influx via KCC2 (fifth panel, red), thus lowering [K⁺]_o and further preventing the generation of the full SLE. (B) With chloride accumulation, the IN discharge led to an increase in *E_Cl* and *E_GABAa* (second panel, blue and light blue) which reduced the hyperpolarizing *I_Cl,leak* and *I_GABAa* currents and enhanced excitability. The increase in firing rate of the PY cells led to prolonged [K⁺]_o accumulation (fourth panel, red) leading to the full SLE.

Model predictions

The computer model generated predictions about features that were not explicitly implemented but were consequences of the elementary neurobiological mechanisms used to create the model. These phenomena are described below. The experimental confirmation of features predicted by a model is an essential step in model validation.

The evolution of the inter-burst interval duration

It is well known that muscle jerking during the clonic phase of a tonic-clonic seizure slows down before ceasing when seizure ends (Bromfield et al., 2006). Frequency slowing has also been observed in video sequences (Kalitzin et al., 2016) and electrographic counterparts of a seizure revealed by either EEG (Franaszczuk et al., 1998; Schiff et al., 2000) or EMG (Conradsen et al., 2013). In the model, a gradual increase in the interval between ictal bursts (IBI) was visible (Figures 2A and 3B). To observe the evolution of the IBI more precisely and identify the scaling pattern, the background noise was removed from the simulation. The absence of excitatory dendritic synaptic input was compensated with a steady depolarizing DC current of 1.85 pA injected into the dendrites of all PY cells. Current intensity was adjusted to preserve the original duration of the SLE as observed in the model with the background noise present. A simulated SLE trace and the detected ictal bursts (short bars) are shown in Figure 6A (top panel). The evolution of the IBI is shown below with either a linear (Figure 6A, middle panel) or a logarithmic (Figure 6A, bottom panel) y-axis. The IBI on the semi-log graph laid on a straight line suggesting an exponential relationship. The evolution of the IBI during an SLE in a whole-brain in vitro preparation (Figure 6B) and a human TLE seizure (Figure 6C) exhibited the same characteristics. Based on literature, we considered four different scenarios of IBI evolution: linear, exponential, square root, and logarithmic. The fits were evaluated by the root mean square error (RMSE). Exact RMSE values depended on the duration of the analyzed IBI sequence. In the model, RMSE values for logarithmic and exponential fits were often comparable. In the experimental data the exponential fit always had the lowest RMSE. Next, we used the fast-slow system analysis approach, as in Figure 4, to demonstrate how separate variations in [K⁺]_o, [Na⁺]_i and [Cl^-]_i affect IBI slowing towards the end of an SLE. Linear decrease in [K⁺]_o led to exponential IBI evolution, while linear increase in [Na⁺]_i or decrease in [Cl^-]_i led to SLE termination with logarithmic scaling of IBI as determined by RMSE (Figure 6—figure supplement 1). Note, that in this figure we simulated a decrease in [Cl^-]_i unlike increasing trend in [Cl^-]_i seen in Figure 2F. We observed that a linear increase in [Cl^-]_i didn’t lead to IBI slowing and SLE termination, when simulated for up to 20 min (not shown). These results suggest that in the model, slowing of inter-burst interval towards the end of an SLE is mediated by simultaneous changes in [K⁺]_o and [Na⁺]_i.

Figure 6 with 1 supplement see all

Download asset Open asset

The evolution of inter-burst intervals (IBI) in the model and experimental data.

(A) In the simulation, the background input was removed and compensated with a small depolarizing current injected into the PY cells to preserve the duration of the SLE. A decreasing rate of bursting is visible in the LPF signal and in the detected bursts marked above the trace (top panel). The evolution of the IBI is shown with the y-axis on a linear scale (middle panel) and a log scale (bottom). On a linear y-axis plot, the data appear curved while on a semi-log plot they lay on a straight line, suggesting exponential scaling of the IBI with time. The red line in each plot represents the best fit for the detected IBI; linear function (middle panel) and exponential function providing a linear relationship on a semi-log plot (bottom panel). The root mean square error (RMSE) between the data points and fitted function is shown in each window. The exponential function fit yielded a smaller RMSE compared to the linear, logarithmic or square root fits (see Materials and methods), providing quantitative confirmation that at the end of the simulated SLE, the IBI duration increased exponentially with time. (B) The evolution of the IBI during the SLE induced by application of bicuculline in the whole-brain in vitro preparation (Boido et al., 2014; Gnatkovsky et al., 2008). (C) IBI evolution during a seizure recorded with intracerebral electrodes positioned in the temporal lobe in a patient submitted to presurgical evaluation (courtesy of Laura Tassi, Epilepsy Surgery Center, Niguarda Hospital, Milano, Italy). In (B) and (C), the detected IBI lay on a straight line on the semi-log plot and the exponential fit resulted in a smaller RMSE compared to the linear, logarithmic or square root fits, validating the model prediction of an exponential increase in the IBI at the end of a seizure. Only linear and exponential fits are shown. The results for all considered fits are provided in Figure 6—source data 1.

Figure 6—source data 1 Source files for seizure data used in the analysis of inter-burst interval slowing. This zip archive contains simulated and experimental data shown in Figure 6. The source data are in the Matlab format (.mat). Separate Matlab scripts (.m) are provided for the analysis of inter-burst interval distribution at the end of a seizure in the Model, Whole guinea pig brain and TLE patient. Each script loads the data, calculates linear, exponential, logarithmic and square root fits with root mean square error and creates the plots for each fit.: https://cdn.elifesciences.org/articles/68541/elife-68541-fig6-data1-v2.zip
Download elife-68541-fig6-data1-v2.zip

The postictal period

An additional model prediction concerned the postictal period which is characterized by reduced excitability and firing. As shown in Figure 2A–C, after the termination of an SLE there was an approximate 90-s period during which firing was either absent or reduced with respect to the interictal period. The exact duration of the postictal period was difficult to assess, as the gap in firing after the SLE was dependent on background fluctuations. To directly investigate the network excitability, we analyzed the responsiveness of the model to external periodic stimulation (see Boido et al., 2014). The background noise was removed and was compensated with a steady depolarizing current, as in Figure 6. Stimulation was delivered by activating the excitatory synapses every 5 s at each PY soma (arrows in Figure 7B). The amplitude of the excitatory postsynaptic current was set at just above the threshold for triggering the spike in the interictal period (before the timestamp at 60 s). The external stimulation triggered a burst and two single spike responses after the SLE termination (Figure 7, vertical broken line) and failed to trigger a suprathreshold response for approximately 90 s afterwards. In line with the PY response pattern, no response to the simulated stimulation was observed in the LFP signal during the postictal suppression period (Figure 7A). The high excitability immediately after termination of the SLE (timestamps between seconds 110 and 125) was correlated with elevated [K⁺]_o which was present shortly after the SLE (Figure 7C). The subsequent postictal reduction of excitability was associated with decay of [K⁺]_o and an increased hyperpolarizing Na⁺/K⁺-pump current in somatic and dendritic compartments. The pump current decayed with a slower time constant associated with a gradual clearance of [Na⁺]_i by the pump (Figure 7DE).

Figure 7

Download asset Open asset

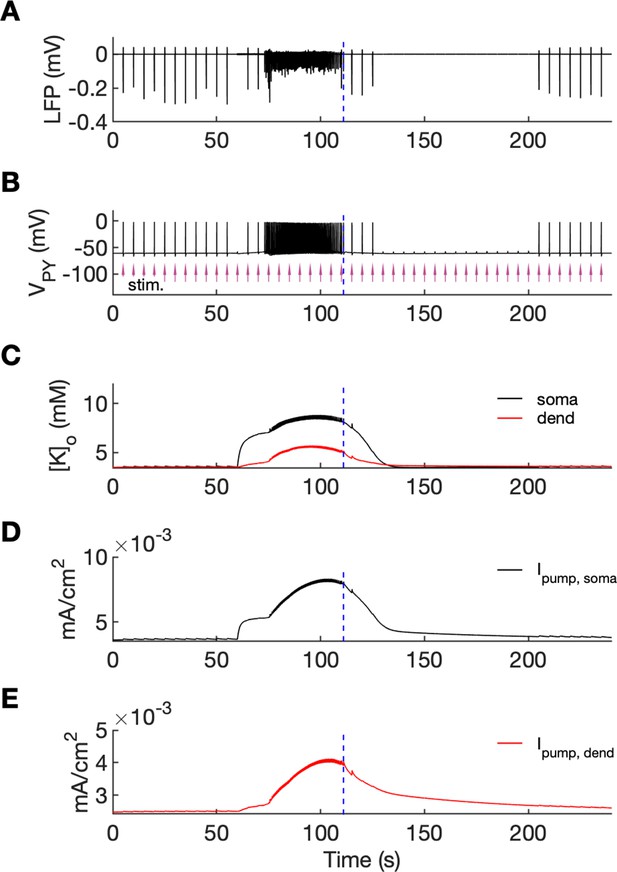
An analysis of network excitability in the postictal period.

In this figure, the background input was removed from the simulation and compensated with a small depolarizing current injected into the PY cells, as in Figure 6. (A) The LFP signal. (B) The PY cell membrane potential with external periodic stimulation delivered every 5 s, marked by the arrows (violet, stim.). The amplitude of the stimulation was set at just above the threshold for triggering a spike in the interictal period. (C) The extracellular potassium in the somatic and dendritic compartments. (**D and E**) The net Na⁺/K⁺-pump current in the somatic and dendritic compartment, respectively. The vertical broken line (blue) in all panels marks the SLE offset time without periodic stimulation. Immediately after termination of the SLE, the network was still excitable due to increased [K⁺]_o. Shortly afterward, the excitability decreased due to an increased Na⁺/K⁺-pump current that outlasted the increase in [K⁺]_o. Increased *I_pump* and decreased [K⁺]_o which occurred shortly after the termination of the SLE, led to a postictal period during which the network did not respond to external stimulation for approximately 90 s.

Discussion

The present study aimed to better define the mechanisms underlying focal seizures. The ictal pattern most frequently observed in human and experimental TLE, that is, the LVF onset pattern, exhibits a stereotypical sequence of fast activity, irregular spiking and periodic bursting (as shown in Figure 3A, first panel) (Avoli et al., 2016; de Curtis and Avoli, 2016; Devinsky et al., 2018; Velascol et al., 2000). We successfully reproduced this pattern in the computer model by transiently increasing the firing of the IN. After this trigger, the simulated SLE phases evolved autonomously. Our study suggests that the various seizure phases and transitions from one phase to another are mediated by feedback mechanisms between neuronal activities, ion concentration changes and ion homeostasis processes. The distinct mechanisms that shape the activities at various seizure stages are discussed below.

Seizure initiation

There is increasing evidence showing that seizures with LVF onset are initiated by discharges of fast-spiking GABAergic interneurons (de Curtis and Avoli, 2016; de Curtis and Gnatkovsky, 2009; Devinsky et al., 2018). Increased interneuron discharges and decreased PY activity around the time of seizure onset were first evidenced in in vitro and in vivo animal models (Gnatkovsky et al., 2008; Grasse et al., 2013; Lévesque et al., 2016; Lopantsev and Avoli, 1998; Miri et al., 2018; Toyoda et al., 2015; Ziburkus et al., 2006). A similar scenario was observed with single-unit recordings performed during intracerebral presurgical monitoring in neocortical and temporal lobe epilepsy patients (Elahian et al., 2018; Truccolo et al., 2011). Causal relationship between increased interneuron firing and ictogenesis may include intracellular chloride accumulation resulting in a shift in E_GABAa and/or the elevation of [K⁺]_o, which leads to subsequent depolarization of PY cells and seizure development (Magloire et al., 2019b). The hypothesis suggested by Jensen and Yaari, 1997 that seizure initiation is related to an elevation in [K⁺]_o caused by a strong initial discharge has been tested in computational models with ion concentration changes. In these simulations, seizure-like activity has been induced by DC stimulation of the PY cells alone (Bazhenov et al., 2004; Buchin et al., 2016; Kager et al., 2002), by a brief increase in [K⁺]_o (Fröhlich et al., 2006), by stimulation of the IN and PY cells (Y Ho and Truccolo, 2016) or by varying the extracellular concentration of K⁺ and O₂ (Wei et al., 2014b). However, as mentioned above, transitions to spontaneous seizures that begin with LFV pattern were not associated with increased excitatory activity, but with increased firing of inhibitory interneurons. Pyramidal cell – interneuron interplay during SLE was first investigated in the computational model of Wei et al., 2014a which mimicked 4-aminopyridine (4-AP) and decreased magnesium in vitro conditions (Ziburkus et al., 2006). They showed that when potassium diffusion rate around the IN was lower than around the PY cell, the IN depolarized and increased its activity and eventually entered depolarization block giving way to the strong firing of the PY cell during an SLE. The following in silico tests on seizure initiation by selective involvement of fast-spiking interneurons were conducted by us (Gentiletti et al., 2017) and others (González et al., 2018). We demonstrated that an increase in interneuron firing triggered a transition to a self-sustained SLE during which both IN and PY cells were active simultaneously. González et al., 2018 showed that interneuron stimulation by current pulses led to the development of an SLE via a gradual increase in [K⁺]_o mediated by the KCC2 cotransporter. Activation of the KCC2 pump was [Cl^-]_i dependent, while [K⁺]_o influenced cotransporter time constant.

In the current study, an SLE was initiated by increased IN firing rate in response to depolarizing current injection. We didn’t attempt to demonstrate the mechanism leading to increase in IN activity following bicuculline application in the isolated guinea pig brain, as the mechanisms underlying this phenomenon are not fully understood. A decrease in GABAa conductance by bicuculline likely affects interneuron-interneuron inhibition more than interneuron-principal cell inhibition (Gnatkovsky et al., 2008). Accordingly, reciprocal release of inhibition between the IN cells (i.e. disinhibition) may lead to preictal interneuronal spikes contributing to increase in extracellular potassium. It would further depolarize interneuronal network and initiate SLE (de Curtis and Avoli, 2016; Figure 4). In an alternative scenario, increased excitability of interneurons could lead to a transition in a bistable IN network, from asynchronous low firing mode to synchronous high firing rate mode due to small perturbation (Rich et al., 2020). In order to fully investigate these effects using a model, one should consider extended interneuronal network with mutual inhibitory interactions. In the current study, we focused on SLE initiation mediated by increased discharge of interneurons, without simulating the underlying processes. It makes the model more general and corresponding to commonly observed paradoxical increase in GABAergic cell firing at the LVF seizure onset. In our present model, the IN was activated by a depolarizing, decreasing current ramp of 40 s. The IN discharge initially led to the silencing of the PY cells, which was correlated with low amplitude fast activity in the LFP signal. The sustained interneuron activity caused a gradual increase in [Cl^-]_i and [K⁺]_o in the PY cells. The increase in [K⁺]_o produced a positive shift in the K⁺ reversal potential which led to a reduction in the K⁺ leak current and membrane depolarization. The accumulation of [Cl^-]_i increased the Cl^- reversal potential and decreased the driving force of the Cl^- ions, which led to a reduction in GABAa IPSC and the Cl^- leak current. An increase in the E_K, E_Cl and E_GABAa, and a weakening of the associated hyperpolarizing currents resulted in a gradual depolarization of the PY cells and sustained firing, which was correlated with the tonic SLE phase.

To address the role of potassium and chloride accumulation in seizure initiation, we considered the elevation of [K⁺]_o and [Cl^-]_i separately. As shown in Figure 5, a selective increase in [K⁺]_o with a fixed concentration of Cl^- did not trigger full SLE. When [Cl^-]_i was increased and the concentration of K⁺ remained fixed at the reference level the PY cells exhibited normal background firing (not shown). This suggests that in our model a change in both [K⁺]_o and [Cl^-]_i act in synergy to mediate full SLE. These findings corroborate the results of a study by Alfonsa et al., 2015 which demonstrated that optogenetic chloride loading of PY cells did not trigger ictal events, while the addition of a subictal dose of 4-AP led to full ictal activity. Our results do not contradict in vitro experimental observations that elevated [K⁺]_o alone is sufficient to induce epileptiform activity (Jensen and Yaari, 1997; Traynelis and Dingledine, 1988). As shown by a bifurcation diagram (Figure 4A and Appendix 1—figure 1) an increase in [K⁺]_o may lead to a transition from a silent state to tonic and burst firing.

Although in our model chloride accumulation increased E_GABAa and lowered synaptic inhibition contributing to full-blown SLE, we didn’t observe depolarizing GABA responses as seen in some in vitro studies (Cossart et al., 2005; Miles et al., 2012; Ellender et al., 2014). It should be kept in mind that depolarizing GABA responses were found mainly in immature neurons, which have more depolarized Cl^- gradient (Cherubini et al., 1991). Another possible explanation of the limited shift in E_GABAa in the model may be related to somatic localisation of inhibitory input from the IN. Following the observation that activation of parvalbumin-positive (PV) interneurons was implicated in spontaneous seizures (Toyoda et al., 2015), we simulated soma-targeting, PV interneurons but not dendrite-targeting, somatostatin-expressing (SST) interneurons. To see if a more pronounced shift in E_GABAa could be observed in SST interneuron mediated dendritic responses, we reduced the size of all model compartments to account for distal dendrites. Under these conditions, strong activation of inhibitory interneuron as in Kaila et al., 1997 led to biphasic, hyperpolarizing-depolarizing GABAa response shown in Appendix 1—figure 3. These results are in agreement with other studies suggesting that [Cl^-]_i can change rapidly and contribute to depolarizing GABAa responses especially in the structures with low volume to GABAa receptor density ratio (Staley et al., 1995; Staley and Proctor, 1999).

The observation that the development of seizures may be related to an increase in [K⁺]_o beyond the physiological values suggests that the modulation of [K⁺]_o by the use of K⁺ chelators is a potential strategy for the control of seizures. In our previous work, we demonstrated that an artificial potassium buffer, which mimicked the function of astrocytes by balancing neuronal K⁺ release, could reduce neuronal excitability and prevent an SLE (Suffczynski et al., 2017).

The mechanisms of [K⁺]_o accumulation

A question arises: what causes [K⁺]_o accumulation? The buildup of Cl^- inside the PY neurons during interneuron-induced GABA release results in the activation of the KCC2 cotransporter, which extrudes Cl^- and K⁺ into the extracellular space. This hypothesis is supported by in vitro experiments which showed that activation of GABAa receptors led to an increase in [K⁺]_o and cell depolarization, which were eliminated by the KCC2 inhibitor, furosemide (Viitanen et al., 2010). The above-mentioned hypothesis is also consistent with the findings that the application of the KCC2 blockers VU0240551 and bumetanide prevented SLEs during 4-AP application in rat brain slices (Hamidi and Avoli, 2015). However, it is not clear whether the ictal activity is consistently based on K⁺ efflux through KCC2. In the pilocarpine model, the enhancement of KCC2 in principal cortical neurons is associated with a reduction in seizure duration (Magloire et al., 2019a). Based on these results, the authors suggested that KCC2 activity does not affect seizure initiation, but influences seizure maintenance during a prolonged period of Cl^- accumulation. The antiepileptic role of enhanced KCC2 activity has also been suggested by Moore et al., 2018, who showed that KCC2 potentiation delayed the onset of an SLE after 4-AP application in vitro and reduced the severity of kainate-induced seizures in vivo. When considering the role of KCC2 in [K⁺]_o and [Cl^-]_i accumulation, it is necessary to note that the direction and magnitude of KCC2 transport depend on the concentration gradients of Cl^- and K⁺ (Kaila et al., 2014). Under normal conditions, when [K⁺]_o is sufficiently controlled by homeostatic mechanisms, GABAergic activity leads to the extrusion of Cl^- and K⁺ by KCC2. However, an increase in [K⁺]_o may reverse the K⁺–Cl^- cotransport, thus contributing to [K⁺]_o buffering rather than accumulation (Payne, 1997; Thompson and Gahwiler, 1989) The activation of IN in our model led to a rapid increase in [K⁺]_o in the narrow extracellular interstitial compartments, while intracellular Cl^- accumulation was more gradual (Figure 2). This generated an influx of K⁺ and Cl^- via KCC2 (Figure 5B), which led to [K⁺]_o buffering and [Cl^-]_i accumulation. The exclusion of KCC2 involvement in the increase in [K⁺]_o suggests that the primary mechanism of [K⁺]_o accumulation in our model was due to other processes, such as the outward K⁺ current that repolarizes action potentials in activated IN and PY cells. This observation is consistent with in vivo experimental evidence that showed a significant local [K⁺]_o rise due to increased spiking activity following electrical stimulation of the cat cerebral cortex (Heinemann and Lux, 1975).

It is worth noting that in our model KCC2 resumes extruding Cl^- shortly after SLE termination (Figure 5B). Accordingly, [Cl^-]_i build up is observed over the whole SLE. Intracellular chloride imaging during SLE induced in vitro by Mg²⁺-free solution showed that [Cl^-]_i started to decline before the end of SLE (Raimondo et al., 2013), while during SLE induced in vivo by 4-AP [Cl^-]_i recovery begun instantly after SLE offset (Sulis Sato et al., 2017). These dissimilar observations might be related to distinct firing patterns of inhibitory and excitatory neurons in 4-AP and low Mg²⁺ seizure models (Codadu et al., 2019), which in turn could lead to different Cl^- and K⁺ and accumulation patterns.

The tonic-to-bursting transition

Potassium ions released by interneuron discharges initially diffused to the somatic extracellular compartments of the PY cells and contributed to PY soma depolarization and tonic firing, as described above. The initial fast rise of [K⁺]_o in the somatic compartment and slower rise in dendritic segment (Figure 2D) was related to the localisation of inhibitory neuron near the PY soma. Subsequently, K⁺ diffusion from the somatic to dendritic compartments promoted regenerative dendritic spikes in PY cells. In the model, the dendritic conductance of voltage-gated K⁺ currents associated with spiking was about 10% of the somatic conductance (Fransen et al., 2002) hence release of K⁺ ions into the dendritic interstitial space was smaller than in the somatic compartment. On the other hand, radial diffusion and glial buffering processes had the same efficiency in both compartments maintaining lower dendritic [K⁺]_o. This model prediction appears to agree with experimental data of simultaneous recordings of [K⁺]_o in somatic and dendritic layers during hippocampal seizures in anesthetized rats. During paroxysmal firing induced by electrical stimulation, [K⁺]_o in dentate gyrus reached significantly higher levels in cell body layers than in the layers containing dendrites (Somjen and Giacchino, 1985). High [K⁺]_o in the soma and moderately increased [K⁺]_o in dendrites favored burst firing (Figure 4A and Appendix 1—figure 1) through the reduction of repolarizing K⁺ currents, the activation of a Na⁺ persistent current, and a shift from spike after-hyperpolarization toward depolarizing after-potentials. Prolonged depolarization led to the activation of slow M-type K⁺ conductance (Appendix 1—figure 2), which hyperpolarized the PY cells after a series of fast spikes. The bursting mechanism in our model originated from currents used in the original entorhinal cortex cells model (Fransen et al., 2002) and was similar to the mechanism in CA1 neurons (Golomb et al., 2006).

We note that in our model a transition from resting to tonic and then to bursting activity in PY cells was not critically dependent on perisomatic inhibition and would be also observed if we simulated dendrite-targeting, SST interneurons. As shown by the bifurcation diagram in Figure 4A (first panel) an increase in either somatic or dendritic [K⁺]_o may lead to a transition from rest to tonic spiking and then bursting. This observation is in agreement with the study showing that optogenetic activation of either PV or SST inhibitory interneurons can trigger SLE (Yekhlef et al., 2015).

Seizure termination

Various mechanisms underlying seizure termination have been suggested (Lado and Moshé, 2008; Zubler et al., 2014), however, researchers have not yet reached a consensus regarding which one plays a dominant role. In our model, the SLE terminated spontaneously. Following the fast-slow analysis approach (Fröhlich et al., 2006), we created a simplified model in which [K⁺]_o,soma, [K⁺]_o,dend together with [Na⁺]_{i, soma} and [Na⁺]_{i, dend} were treated as control parameters. Hence, the influence of neuronal activity on ionic variations was removed and the dependence of network activity on K⁺ and Na⁺ concentrations was analyzed (Figure 4A). When the time course of the concentration changes of these two ions were tuned to reproduce the decrease in [K⁺]_o and maintained increased level of [Na⁺]_i observed in the late SLE phase, the ictal activity spontaneously terminated (Figure 4B). This indicates that SLE cessation in the model can be explained by two coincident factors, namely the decrease in [K⁺]_o during stable levels of increased [Na⁺]_i. An increase in [Na⁺]_i led to an increased hyperpolarizing Na⁺/K⁺-pump current, which increased the firing threshold in the neurons. The increased pump activity also contributed to a progressive decrease in [K⁺]_o. Potassium repolarization currents increased after each burst and eventually prevented the initiation of a new cycle of the oscillation. The idea that negative feedback between [Na⁺]_i accumulation and neuronal firing is responsible for seizure termination was first formulated by Jensen and Yaari, 1997. Even though it has not been tested experimentally, this hypothesis is consistent with the observation that the inhibition of Na⁺/K⁺-pump activity occurring during hypoxia prolongs SLE discharges and shortens post-SLE period in hippocampal slices with blocked synaptic transmission (Haas and Jefferys, 1984). It was also observed that a decrease in Na⁺ channel conductance via the antiepileptic drug phenytoin, increased the seizure threshold but prolonged the afterdischarges and seizure durations in the rat kindling model of epilepsy (Ebert et al., 1997). In the computational model developed by the Bazhenov team (Krishnan et al., 2015; Krishnan and Bazhenov, 2011) and Chizhov et al., 2018, a progressive increase in [Na⁺]_i and activation of the electrogenic Na⁺/K⁺-pump were identified as the primary factor of SLE termination. The seizure termination mechanism in the above-mentioned studies is similar to the mechanism observed in the present study, even though different specifications of neuronal mechanisms, network characteristics and seizure morphologies were used.

It should be also noted that activation of the Na⁺/K⁺-pump by [Na⁺]_i is not the only proposed mechanism of seizure termination. An alternative mechanism, also linked to an increase in [Na⁺]_i, is dependent on the Na⁺-activated K⁺ channels (Igelström, 2013). Moreover, many other mechanisms such as acidosis (Ziemann et al., 2008), the upregulation of inhibitory neurons (Wen et al., 2015), glutamate depletion (Lado and Moshé, 2008), the depolarization block of neurons mediated by K⁺ release from astrocytes (Bragin et al., 1997), after-hyperpolarization due to K⁺ channels (Bazhenov et al., 2004; Timofeev and Steriade, 2004), postburst depression (Boido et al., 2014), increased synchrony (Schindler et al., 2007) and the release of adenosine During and Spencer, 1992; Uva and de Curtis, 2020 have been suggested to play a role in seizure termination.

The abrupt termination of a seizure across the entire brain (Salami et al., 2022) requires long-range communication which may involve thalamocortical interactions (Aracri et al., 2018; Evangelista et al., 2015), travelling waves (Martinet et al., 2017; Proix et al., 2018) and ephaptic interactions (Jefferys, 1995; Shivacharan et al., 2019). Multiple neuromodulatory, ionic, synaptic and neuronal components likely cooperate to terminate a seizure. Further insight into these mechanisms may be obtained by their selective blockage (Uva and de Curtis, 2020), the tracking of EEG signal changes as seizure offset approaches (Boido et al., 2014; Saggio et al., 2020) and from analysis of the duration of postictal suppression (Payne et al., 2018).

Frequency Slowing

The approach of seizure termination is often (but not always) accompanied by an increase in the intervals between successive bursts that form the late seizure phase. Saggio et al., 2020 analyzed frequency slowing in human focal onset seizures and estimated that approximately 40% exhibited unequivocal discharge slowing down toward the end. Burst frequency slowing was confirmed in a study on the entorhinal cortex of the isolated brain preparation during bicuculline- and 4AP-induced SLE (Boido et al., 2014). Our model prediction of the exponential increase in the IBI toward the SLE offset (Figure 6A) was confirmed with experimental data (Figure 6BC). These findings are also consistent with those of Bauer et al., 2017, which demonstrated that inter-burst intervals in focal epilepsy patients were predominantly described by the exponential scaling law. Conversely, it has been suggested that depending on the bifurcation which leads to seizure termination, the burst oscillation frequency can be constant or decrease according to the logarithmic or square root relationship (Izhikevich, 2000; Jirsa et al., 2014). This theory has not been confirmed by our model and experimental seizure data (Figure 6). On the other hand, when specific ion types were varied linearly and led to linearly decreasing membrane current (not shown), logarithmic increase in IBI was observed (Figure 6—figure supplement 1B,C). It shows that when the assumption of slow linear membrane current dynamics was satisfied, the IBI evolved according to the bifurcation theory. However, when various processes influenced seizure termination and the current changed non linearly, the IBI slowing deviated from the predicted scaling laws.

In our model, progressive decrease in neuronal excitability related to simultaneous decrease in [K⁺]_o and increase in [Na⁺]_i, was responsible for the IBI slowing toward an SLE end. Alternative explanations for the increasing inter-burst intervals have been proposed. Bauer et al., 2017 included a plasticity parameter that progressively decoupled spatially distributed neural mass units based on the synchrony level. This mechanism accounted for seizure termination, exponential IBI increase and the presence of a transient postictal state. In the model of Liou et al., 2020 the IBI was constant during seizure expansion and only when the spatial propagation of ictal discharge ceased, the seizure entered the pre-termination stage with a slowing-down trend. An increase in the IBI in this phase was related to the recovery of inhibition and restoration of the Cl^- concentration gradient. These studies indicate that spatial properties related to seizure propagation and synchrony are other factors that may affect the evolution of the IBI.

The postictal period

Seizures are followed by the suppression of physiological rhythms known as postictal EEG suppression (PES) that lasts for seconds or minutes (Pottkämper et al., 2020). Using the stimulation protocol, we investigated the duration of PES in the model. Our results showed that shortly after termination of the SLE, burst responses were still triggered, however, after few seconds, the excitability decreased and remained reduced for approximately 90 s (Figure 7B). The PES duration in our model is consistent with a typical ‘seconds to minutes’ timescale although available estimates depend on the PES duration assessment method. In single-unit recordings in epileptic patients with neocortical seizures neuronal spiking was fully suppressed for 5–30 s after seizure termination (Truccolo et al., 2011). Average duration of postictal suppression based on EEG features in focal seizure patients was estimated at 17 s (Grigorovsky et al., 2020; Table 1), 120 s (Payne et al., 2018; Table 1) and around 50–100 s (Bauer et al., 2017; Figure 5). Our in silico-derived prediction that postictal ‘silence’ depends on the increased rate of hyperpolarizing Na⁺/K⁺-pump has been previously suggested (Fisher and Schachter, 2000) and simulated (Krishnan et al., 2015; Krishnan and Bazhenov, 2011). In these models, postictal state was generated via both, reduced [K⁺]_o to below baseline level and increased [Na⁺]_i after termination of an SLE. [K⁺]_o decrease below baseline resulted in a negative shift in E_K and membrane hyperpolarization, while elevated [Na⁺]_i increased Na⁺/K⁺-pump hyperpolarizing current. A below-reference value of [K⁺]_o was indeed observed after seizure termination (Heinemann et al., 1977). On the other hand, in other studies, [K⁺]_o decayed to baseline level after an SLE offset (Fisher et al., 1976; Futamachi et al., 1974) and couldn’t contribute to the postictal state. Also in our model [K⁺]_o undershoot was not observed (Figure 7C), suggesting that the main cause of postictal reduction in excitability was hyperpolarizing effect of the Na⁺/K⁺-pump current, which remained elevated above baseline for about 100 s after SLE termination (Figure 7DE). The findings generated by our computational model suggest that ion homeostatic processes activated and sustained by the excessive seizure discharges provide a negative feedback mechanism, eventually leading to the cessation of the seizure itself and to the restoration of the normal state after a transitional period of postictal silence.

Table 1

Gating variables of the ionic currents in pyramidal cell model.

Current	Kinetics/time constant (ms)
I_Na,soma	$α_{m} = \frac{0.8 (- V - 39.8)}{e x p (\frac{- V - 39.8}{4}) - 1}$	$β_{m} = \frac{0.7 (V + 14.8)}{e x p (\frac{V + 14.8}{5}) - 1}$
I_Na,soma	$α_{h} = 0.32 e x p (\frac{- V - 15}{18})$	$β_{h} = \frac{10}{e x p (\frac{- V - 15}{5}) + 1}$
I_Na,dendrite	$α_{m} = \frac{0.32 (- V - 48.9)}{e x p (\frac{- V - 48.9}{4}) - 1}$	$β_{m} = \frac{0.28 (V + 21.9)}{e x p (\frac{V + 21.9}{5}) - 1}$
I_Na,dendrite	$α_{h} = 0.128 e x p (\frac{- V - 44}{18})$	$β_{h} = \frac{4}{e x p (\frac{- V - 21}{5})}$
I_NaP	$m_{\infty} = \frac{1}{1 + e x p (\frac{- 48.7 - V}{4.4})}$	$τ_{m} = \frac{1}{\frac{0.091 (V + 38)}{1 - e x p (\frac{- V - 38}{5})} - \frac{0.062 (V + 38)}{1 - e x p (\frac{V + 38}{5})}}$
I_NaP	$h_{\infty} = \frac{1}{1 + e x p (\frac{48.8 + V}{9.98})}$	if $V_{m} \leq - 60$ : $τ_{h} = 3700 + \frac{2000}{\frac{0.091 (V + 60)}{1 - e x p (\frac{- V - 60}{5})} - \frac{0.062 (V + 60)}{1 - e x p (\frac{V + 60}{5})}}$ if $V_{m} > - 60$ : $τ_{h} = 1200 + \frac{8000}{\frac{0.091 (V + 74)}{1 - e x p (\frac{- V - 74}{5})} - \frac{0.062 (V + 74)}{1 - e x p (\frac{V + 74}{5})}}$
I_Kdr,soma	$n_{\infty} = \frac{1}{1 + e x p (\frac{- 22.8 - V}{13.6})}$	$τ_{m} = \frac{1.6 (C + e x p (\frac{V}{5}))}{D exp (\frac{- V}{40}) (C + e x p (\frac{V}{5})) + 0.016 e x p (\frac{V}{5}) (64.9 + V)}$ $C = - 0.00000230599; D = 0.0338338$
I_Kdr,dend	$n_{\infty} = \frac{1}{1 + e x p (\frac{- 14.8 - V}{13.6})}$	$τ_{m} = \frac{1.6 (C + e x p (\frac{V}{5}))}{D exp (\frac{- V}{40}) (C + e x p (\frac{V}{5})) + 0.016 e x p (\frac{V}{5}) (64.9 + V)}$ $C = - 0.00000230599; D = 0.0338338$
I_CaL	$α_{m} = \frac{1.6}{1 + e x p (- 0.072 (V - 5))}$	$β_{m} = \frac{0.02 (V + 8.9)}{exp (\frac{V + 8.9}{5}) - 1}$
I_KAHP	$α_{m} = 2000 ({[C a]}_{i} - {[C a]}_{i, r e s t})$	$β_{m} = 0.01$
I_KC_, if $V_{m} \leq - 10$	$α_{m} = \frac{e x p (\frac{V + 50}{11} - \frac{V + 53.5}{27})}{18.975}$	$β_{m} = 2 e x p (\frac{- V - 53.5}{27})$
I_KC_, if $V_{m} > - 10$	$α_{m} = 2 e x p (\frac{- V - 53.5}{27})$	$β_{m} = 0$
I_KM	$m_{\infty} = \frac{1}{1 + e x p (\frac{- V + 33}{5})}$	$τ_{m} = \frac{1000}{3.3 [e x p (\frac{V + 35}{40})] + [e x p (\frac{- V - 35}{20})]}$

Materials and methods

Geometry

Request a detailed protocol

The cell morphology was based on entorhinal cortex PY cells and an interneuron model (Fransen et al., 2002), further reduced to equivalent cylinder models. The PY cell consisted of two compartments: a soma with a length of 20 μm and a diameter of 15 μm, and a dendrite with a length of 450 μm and a diameter of 6.88 μm. The interneuron only had a somatic compartment with a length of 20 μm and a diameter of 15 μm. Each compartment was surrounded by its own extracellular space (ECS). The extracellular compartments were embedded in a common bathing medium which represented the surrounding neural tissue and vasculature. The size of the ECS was estimated by the extracellular volume fraction, α defined as the ratio volume of extracellular space/volume of tissue. We used α=0.131 which corresponded to the CA1 st. pyramidale and a K⁺ concentration of 3.5 mM (McBain et al., 1990).

Biophysics

Request a detailed protocol

The active membrane currents in the PY cell were the fast Na⁺ and K⁺ currents (I_Na and I_Kdr, respectively) in both compartments and were responsible for action potential generation; a persistent Na⁺ current, I_NaP in the soma; a high-threshold Ca²⁺ current, I_CaL in both compartments; a calcium-dependent after-hyperpolarization K⁺ current, I_KAHP in both compartments; a fast calcium- and voltage-dependent K⁺ current, I_KC in both compartments; and a noninactivating muscarinic K⁺ current, I_KM in the soma. The IN included only the I_Na and I_Kdr currents responsible for spike generation. All the equations for the active currents were initially based on those described by Fransen et al., 2002, however, an additional modification of the parameters described below was required to account for ionic regulation mechanisms. Simulations were performed using the NEURON simulator with a fixed integration step of 0.05ms.

Passive properties

Request a detailed protocol

The reversal potentials were obtained via the Nernst equation:

E_{X} = 2.3 \frac{R T}{z F} l o g (\frac{{[X]}_{o}}{{[X]}_{i}})

where [X]_i and [X]_o are intra- and extracellular concentrations, respectively, of the ions. X = {Na⁺, K⁺, Ca²⁺, Cl^-, HCO₃^-}, F is the Faraday constant, R is the gas constant, z is the valence of the ions and T=273,16 + 32 is the absolute temperature (Gnatkovsky et al., 2008). A leak current, I_leak, was present in all compartments of both cells and was a sum of the leak currents of Na⁺, K⁺, and Cl^-, modeled as:

I_{i, l e a k} = g_{i, l e a k} (V - E_{i})

where g_i,leak is the leak current conductance of the ion of interest i = {Na⁺, K⁺, Cl^-}. The resting membrane potential was –61 mV in the pyramidal cell and in the interneuron. The specific axial resistance in both cells was set to R_a = 100 Ohm*cm and the specific membrane capacitance was set to C_m = 1 μF/cm², as in Fransen et al., 2002. Based on the R_a and PY cell geometry, the somato-dendritic coupling conductance, g_c, was calculated as 1.5 mS.

Active currents

Request a detailed protocol

The original equations used time constant units in seconds (s) and voltage units in volts (V), with 0 V corresponding to the resting membrane potential. All equations were modified to account for the millivolt (mV) and millisecond (ms) units used in our model and the voltage was shifted by –60 mV to correspond to the membrane potential relative to the extracellular space, which was assumed to be 0 mV. Additional modifications of the parameters were required to account for the ionic regulation mechanisms that were not present in the original model. I_NaP: the activation gate exponent was 2 and the inactivation gate time constant, τ_h, was estimated by fitting the activation function form described by Fransen et al., 2002 to the experimental data (Magistretti and Alonso, 1999). I_Kdr: the steady-state activation function, n_inf, and the activation gate time constant, τ_n, were estimated by empirical fit to the experimental data (Sah et al., 1988). To increase the firing threshold, the activation curve was shifted toward positive potentials by 18 mV in the soma and 10 mV in the dendrites. The model generated spontaneous fast spiking otherwise. I_KAHP, I_KC: these Ca²⁺-dependent currents were modelled according to the model described by Traub et al., 2003 and were implemented in ModelDB (https://senselab.med.yale.edu/ModelDB/), accession number 20,756. Due to the arbitrary units for Ca²⁺ concentration in Traub’s model, we modified the current formula to correspond to mM units and resting level of [Ca²⁺]_i used in our model. In pyramidal cells, the soma and dendrite membrane potentials, V_s and V_d, respectively, were governed by the following Hodgkin-Huxley equations:

\begin{array}{ll} C \frac{d V_{s}}{d t} = - I_{N a, s o m a} - I_{N a P} - I_{K d r, s o m a} - I_{C a L} - I_{K A H P} - I_{K C} - I_{K M} \\ - I_{l e a k} - I_{N a K p u m p} - I_{C a P u m p} - g_{c} (V_{s} - V_{d}) - I_{s y n} \end{array}

C \frac{d V_{d}}{d t} = - I_{N a, d e n d} - I_{K d r, d e n d} - I_{C a L} - I_{K A H P} - I_{K C} - I_{N a K p u m p} {- I}_{C a P u m p} - g_{c} (V_{d} - V_{s}) - I_{s y n}

Transient sodium current

I_{N a, s o m a} = g_{N a, P Y s o m a} m^{3} h (V - E_{N a})

I_{N a, d e n d} = g_{N a, P Y d e n d} m^{2} h (V - E_{N a})

Persistent sodium current:

I_{N a P} = g_{N a P} m^{2} h (V - E_{N a})

Delayed rectifier:

I_{K d r, s o m a} = g_{K d r, P Y s o m a} n^{4} (V - E_{K})

I_{K d r, d e n d} = g_{K d r, P Y d e n d} n^{2} (V - E_{K})

High-threshold Ca²⁺ current:

I_{C a L} = g_{C a L} m^{2} (V - E_{C a})

Ca²⁺-dependent K⁺ (afterhyperpolarization) current:

I_{K A H P} = g_{K A H P} m (V - E_{K})

Fast Ca²⁺- and voltage-dependent K⁺ current:

I_{K C} = g_{K C} m i n ([C a^{2 +}]_{i} / 250, 1) m (V - E_{K})

Muscarinic current:

I_{K M} = g_{K M} m (V - E_{K})

Equations of gating variables are given in Table 1. Conductance values are given in Table 2.

Table 2

Conductances used in the model.

Current conductance	Description	Values (S/cm²)
g_{Na,leak,PYsoma}	I_Na,leak conductance in PY soma	1.5*10^–5
g_{Na,leak,PYdend}	I_Na,leak conductance in PY dendrite	1.1*10^–5
g_K,leak,PY	I_K,leak conductance in PY soma and dendrite	3*10^–5
g_Cl,leak,PY	I_Cl,leak conductance in PY soma and dendrite	1*10^–5
g_Na,PYsoma	I_Na conductance in PY soma	0.014
g_Na,PYdend	I_Na conductance in PY dendrite	0.0014
g_Kdr,PYsoma	I_Kdr conductance in PY soma	0.032
g_Kdr,PYdend	I_Kdr conductance in PY dendrite	0.0032
g_NaP	I_NaP conductance in PY soma	60*10^–5
g_CaL	I_CaL conductance in PY soma and dendrite	15*10^–5
g_KAHP	I_KAHP conductance in PY soma and dendrite	5*10^–5
g_KC	I_KC conductance in PY soma and dendrite	0.196*1e3
g_KM	I_KM conductance in PY soma	0.006
g_Na,leak,IN	I_Na,leak conductance in IN	2.9*10^–5
g_K,leak,IN	I_K,leak conductance in IN	6*10^–5
g_Cl,leak,IN	I_Cl,leak conductance in IN	1*10^–5
g_Na,IN	I_Na conductance in IN	0.013
g_Kdr,IN	I_Kdr conductance in IN	0.027

Membrane potential of the interneuron was governed by the following Hodgkin-Huxley equations:

C \frac{d V}{d t} = - I_{N a} - I_{K d r} - {I_{l e a k} - I}_{N a K p u m p} - I_{s y n} - I_{s t i m}

Current equations, kinetics and time constants of these currents were the same as in pyramidal cell soma. To prevent depolarization block of the IN during current stimulation, activation curve of I_Na was shifted 3 mV toward more negative potential values, while activation curve of I_Kdr was shifted by 19 mV toward more negative potential values.

Ionic dynamics

Request a detailed protocol

The model included six types of ions (K⁺, Na⁺, Cl^-, Ca²⁺, A^-, and HCO₃^-) with variable intra- and extracellular concentrations, except for HCO₃^-, for which equilibrium is rapidly attained (Theparambil et al., 2020). The evolution of the ion concentrations was based on the following equations:

\frac{d [K^{+}]_{i}}{d t} = J_{K}^{i} + J_{K, l o n g i t u d i n a l}^{i} + J_{K, K C C 2}^{i} + J_{K, P u m p}^{i} + J_{K, v o l}^{i}

\frac{d [K^{+}]_{o}}{d t} = J_{K}^{o} + J_{K, r a d i a l} + J_{K, l o n g i t u d i n a l}^{o} + J_{K, b a t h} + J_{K, K C C 2}^{o} + J_{K, P u m p}^{o} + J_{g l i a} + J_{K, v o l}^{o}

\frac{d [N a^{+}]_{i}}{d t} = J_{N a}^{i} + J_{N a, l o n g i t u d i n a l}^{i} + J_{N a, P u m p}^{i} + J_{v o l}^{i}

\frac{d [N a^{+}]_{o}}{d t} = J_{N a}^{o} + J_{N a, r a d i a l} + J_{N a, l o n g i t u d i n a l}^{o} + J_{N a, b a t h} + J_{N a, P u m p}^{i} + J_{N a, v o l}^{o}

\frac{d [C l^{-}]_{i}}{d t} = J_{C l}^{i} + J_{C l, G A B A a}^{i} + J_{C l, l o n g i t u d i n a l}^{i} + J_{C l, K C C 2}^{i} + J_{C l, v o l}^{i}

\frac{d [C l^{-}]_{o}}{d t} = J_{C l}^{o} + J_{C l, G A B A a}^{o} + J_{C l, l o n g i t u d i n a l}^{o} + J_{C l, b a t h} + J_{C l, K C C 2}^{o} + J_{C l, v o l}^{o}

\frac{d [C a^{2 +}]_{i, t o t}}{d t} = J_{C a}^{i} + J_{C a, l o n g i t u d i n a l}^{i} + J_{C a P u m p}^{i} + J_{C a, v o l}^{i}

\frac{d [C a^{+}]_{o}}{d t} = J_{C a}^{o} + J_{C a, l o n g i t u d i n a l}^{o} + J_{C a P u m p}^{o} + J_{C a, v o l}^{o}

\frac{d [A^{-}]_{i}}{d t} = J_{A, v o l}^{i}

where [Ca²⁺]_i,tot is the total intracellular calcium concentration (see calcium buffer below). All fluxes (mM/ms) are specified below.

Membrane currents

Request a detailed protocol

The contribution of transmembrane currents to variations in intra- and extracellular ion concentrations was obtained via the following equations:

J_{X}^{i} = \frac{- \sum I_{X} S}{z F V_{i}}

J_{X}^{o} = \frac{\sum I_{X} S}{z F V_{o}}

where the sum of I_X is a net membrane current carrying ion X, S is the surface area of the compartment, z is the valence of the ions, F is the Faraday constant and V_i and V_o are the volumes of the intra- and extracellular compartments.

Longitudinal diffusion

Request a detailed protocol

Longitudinal diffusion of K⁺, Na⁺, Ca²⁺ and Cl⁻ was implemented between the somatic and dendritic compartments in the intracellular and extracellular space of the same cell. It was described by Fick’s first law:

J_{X, l o n g i t u d i n a l}^{i o} = D_{x} \frac{({[X]}_{i o, a} - {[X]}_{i o}) S}{L V_{i o}}

where D_x is the diffusion coefficient for the ion X, [X]_io is the ion concentration in a given intra- or extracellular compartment, [X]_oi,_a is the ion concentration in the adjacent compartment, S is the cross-sectional area between the compartments, V_io is the compartment volume, L is the distance between the centers of the compartments. The diffusion coefficients were (in um²/ms): D_Na = 1.33, D_K = 1.96, D_Ca = 0.6, D_Cl = 2.03 (as in Somjen et al., 2008).

Radial diffusion

Request a detailed protocol

Na⁺ and K⁺ ions diffused radially between adjacent extracellular compartments modeled as concentric shells around the neurons. The radial exchange of ions between adjacent shells was described by Fick’s first law:

J_{X, r a d i a l} = D_{x} \frac{\sum ({[X]}_{o, a} - {[X]}_{o}) S}{d r V}

where [X]_o is the ion concentration in a given shell and the sum goes over all adjacent shells having concentrations [X]_o,_a, V is a given shell volume, dr is the distance between the centers of the shells and S is the surface contact area between the shells calculated at 16% of the total outer shell surface. The electrostatic drift of ions was neglected as the ion movement due to the electrical potential gradient in the extracellular space was small compared to the diffusion.

Diffusion to/from the bath

Request a detailed protocol

Radial diffusion of K⁺, Na⁺ and Cl⁻ between the ECS and the bath was described by Fick’s first law:

J_{X, b a t h} = \frac{1}{s} D_{x} \frac{({[X]}_{b a t h} - {[X]}_{o}) S}{d r V}

where D_x is the diffusion coefficient for the ion X, s is the scaling constant, S is the outer surface of the shell, [X]_bath is the bath concentration of the ion X, [X]_o is the ion concentration in a given shell, V is the shell volume, dr is the distance between the extracellular space and the bath (assumed to be half of the shell thickness). Flux J_bath represents various processes such as diffusion to more distant areas of the brain and cerebrospinal fluid, active transport of potassium into capillaries and potassium spatial buffering by astrocytes. The effective time constant of these joint processes is likely to be much slower than that of radial and longitudinal diffusion and is described by the scaling constant s=4.4*10⁴.

The Na⁺/K⁺ pump

Request a detailed protocol

The Na⁺/K⁺ pump was modeled as the sodium and potassium transmembrane currents (Kager et al., 2000):

I_{N a, P u m p} = 3 I_{m a x} f l u x ([N a^{+}]_{i}, [K^{+}]_{o})

I_{K, P u m p} = - 2 I_{m a x} f l u x ([N a^{+}]_{i}, [K^{+}]_{o})

f l u x ([N a^{+}]_{i}, [K^{+}]_{o}) = {(1 + \frac{K m_{K}}{[K^{+}]_{o}})}^{- 2} {(1 + \frac{K m_{N a}}{[N a^{+}]_{i}})}^{- 3}

with Km_K = 2 mM and Km_Na = 10 mM. I_max values were computed for each cell and compartment to balance Na⁺ and K⁺ membrane currents at rest and were as follows (in mA/cm²): 0.014 (PY soma), 0.009 (PY dendrite), 0.025 (IN).

KCC2 cotransport

Request a detailed protocol

The KCC2 cotransporter currents were modeled according to Wei et al., 2014a:

I_{K, K C C 2} = U_{K C C 2} l o g (\frac{[K^{+}]_{i} [C l^{-}]_{i}}{[K^{+}]_{o} [C l^{-}]_{o}})

I_{C l, K C C 2} = - I_{K, K C C 2}

with cotransporter strength adjusted to balance chloride leak current at rest, U_KCC2=0.002 mA/cm².

Glial uptake

Potassium uptake by the glia was modeled as a set of differential equations (Kager et al., 2000):

J_{g l i a} = - k_{2} [K^{+}]_{o} [B] + k_{1} [K B]

\frac{d [B]}{d t} = - k_{2} [K^{+}]_{o} [B] + k_{1} [K B]

\frac{d [K B]}{d t} = k_{2} [K^{+}]_{o} [B] - k_{1} [K B]

where [B] is the free buffer, [KB] is the bound buffer (= [B]_max–[B]), B_max = 1100 mM. k₁=0.0008 ms^–1 and $k_{2} = \frac{k_{1}}{1 + e x p (\frac{{[K]}_{o} - 16}{- 1.25})}$ are backward and forward rate constants, respectively.

The calcium pump and buffer

Request a detailed protocol

The calcium pump and buffer which altered the intracellular Ca²⁺ were modeled according to the model implementation of Somjen et al., 2008 in ModelDB, accession number 113,446. The calcium pump which extruded Ca²⁺ from the cells was modeled as a Ca²⁺ transmembrane current:

I_{C a P u m p} = \frac{I_{m a x}}{1 + \frac{K_{p u m p}}{[C a^{2 +}]_{i}}}

with I_max = 2.55 mA/cm² and K_pump = 0.0069 mM. Intracellular Ca²⁺ was buffered by first-order chemical Ca²⁺ buffer with a total concentration of [B]_i and an equilibrium constant of K_d. Calcium buffering was fast and under the assumption of equilibrium conditions, the relationship between the total and free intracellular calcium concentrations, [Ca²⁺]_i,tot and [Ca²⁺]_i, was given by Borgdorff, 2002, pg. 27:

[C a^{2 +}]_{i, t o t} = [C a^{2 +}]_{i} \frac{[B]_{i} + K_{d} + [C a^{2 +}]_{i}}{K_{d} + [C a^{2 +}]_{i}}

where [B]_i = 1.562 mM*(V_i⁰/V_i), V_i is the intracellular compartment volume, V_i⁰ is the intracellular compartment volume at rest and K_d = 0.008 mM.

Volume changes

Request a detailed protocol

Volume changes were modeled according to Somjen et al., 2008. The rates of intra- and extracellular volume changes were proportional to the difference in osmotic pressure between the intra- and extracellular compartments and fulfilled the conservation of total volume.

\frac{d V_{i}}{d t} = Δ

\frac{{d V}_{o}}{d t} = - Δ

where

Δ = \frac{c (π_{i} - π_{o})}{τ}

π_{i} = [N a^{+}]_{i} + [K^{+}]_{i} + [C l^{-}]_{i} + [C a^{2 +}]_{i} + [H C O_{3}^{-}]_{i} + [A^{-}]_{i}

π_{o} = [N a^{+}]_{o} + [K^{+}]_{o} + [C l^{-}]_{o} + [C a^{2 +}]_{o} + [H C O_{3}^{-}]_{o} + [A^{-}]_{o}

V_i and V_o are the volumes of the intra- and extracellular compartments and τ=250ms. The constant c is introduced for unit conversion and is equal to 1 µm³/mM, hence units of Δ are µm³/ms. The extracellular volume was initially 15% of the cellular volume and was allowed to shrink maximally down to 4%. Volume changes affected concentrations but not the total mass of each ion within a compartment. The conservation of mass required additional fluxes:

Intracellular

J_{X, v o l}^{i} = \frac{- Δ}{V_{i}} {[X]}_{i}

Extracellular

J_{X, v o l}^{o} = \frac{Δ}{V_{o}} {[X]}_{o}

Extracellular space (ES) volume shrinks maximally by about 27%, comparable to average reduction of 30% during self-sustained epileptiform discharges (Dietzel et al., 1980). Intracellular space (IS) volume expands about 4%, being a consequence of constant total volume (ES +IS = const). Volume changes and resulting shifts in representative ion concentrations are shown in Appendix 1—figure 4. We note that volume changes in our model didn’t have big impact on the observed model dynamics. Shifts in ionic gradients contributed by slow volume changes were efficiently compensated by other homeostatic mechanisms, which acted on a faster time scale. In the real tissue astrocyte swelling may be significant and may reduce flow of ions and oxygen (affecting Na⁺/K⁺-pump activity) contributing to seizures and spreading depression (Hübel and Ullah, 2016). In our model, glial cell swelling was not included and its effects on diffusion and the Na⁺/K⁺-pump were not simulated which is one of the model limitations.

Initial ion concentrations

Request a detailed protocol

The initial concentrations were based on existing literature: [Na⁺]_i, [Ca²⁺]_i, [Na⁺]_o, [K⁺]_o, [Ca²⁺]_o and [A^-]_o (Somjen et al., 2008); [Cl^-]_i, [HCO₃^-]_i, [HCO₃^-]_o (Doyon et al., 2011); [K⁺]_i [Cl^-]_o (Payne et al., 2003). In setting chloride and potassium concentrations, we additionally aimed to fulfill E_K <E_Cl and E_GABAa ~ –70 mV (Andersen et al., 1980). The [A^-]_i concentration was set to fulfill osmotic equilibrium condition. Hence, the initial concentrations were as follows (in mM): [Na⁺]_i = 10, [Na⁺]_o = 140, [K⁺]_i = 87, [K⁺]_o = 3.5, [Cl^-]_o = 135, [Cl^-]_i = 6, [Ca²⁺]_i = 5e-5, [Ca²⁺]_o = 2, [A^-]_i = 187.5, [A^-]_o = 0, [HCO₃^-]_i = 15, [HCO₃^-]_o = 25. These values gave the following Nernst potentials (in mV): E_Na = 69.4, E_K = –84.5, E_Cl = –81.8, E_Ca = 139.3, E_HCO3 = –13.4, E_GABAa = –69.5.

Resting state

Request a detailed protocol

Steady-state conditions at rest were characterized by no net flux of the ions at the resting potential (–61 mV). These conditions were determined separately for each cell and compartment. For chloride, KCC2 cotransport strength U_KCC2 was adjusted to balance Cl^- leak current at rest, that is:

{I_{C l, l e a k} = - I}_{C l, K C C 2}

For sodium and potassium, first, Na⁺ leak current conductance g_Na,leak was adjusted to ensure that at rest all passive and voltage-gated membrane currents I_Na and I_K are in the ratio –3/2, that is,:

I_{N a} = \frac{- 3}{2} I_{K}

Next, the Na⁺/K⁺-pump strength I_max was adjusted such that I_Na and I_K currents were balanced by equal and opposite pump currents:

{- I}_{N a} = I_{N a, p u m p}

{{- I}_{K} = I}_{K, P u m p}

Synaptic connections and model inputs

Request a detailed protocol

The pyramidal cells created excitatory AMPA synaptic connections with the interneuron and all other pyramidal cells. The interneuron created an inhibitory GABAa synaptic connection with each pyramidal cell. Excitatory synapses were placed in the middle of the PY dendrite and the middle of the IN soma. Inhibitory synapses were placed in the middle of the PY soma. The time course of synaptic conductance was modeled with a built-in NEURON mechanism Exp2Syn, implementing a dual exponential function:

g = g_{m a x} [e x p (\frac{- t}{τ_{2}}) - e x p (\frac{- t}{τ_{1}})]

where the rise and decay time constants, τ₁ and τ₂, were 2ms and 6ms, respectively, for all synapses. g_max = weight*factor, where the factor was defined so that the normalized peak was 1. The weights for the synapses between the PY and from the PY to the IN were w_ee = 0.0002 μS and w_ei = 0.0017 μS, respectively. The inhibitory synaptic weight, w_ie, was 0.0005 μS. All pyramidal cells received background input modeled as a Poisson spike train, which was different in each cell, activated an excitatory synapse at a rate of 5 Hz and had a synaptic weight w_input = 0.0004 μS. To initiate the SLE, a depolarizing ramp current, I_inj, was injected into the interneuron, with the initial amplitude of 0.35 nA linearly decreasing toward 0 over 40 s.

The inhibitory GABA_a postsynaptic currents were carried by Cl⁻ and HCO₃⁻ ions (Jedlicka et al., 2010):

I_{G A B A a} = I_{C l G A B A a} + I_{H C O 3 G A B A a}

I_{C l G A B A a} = (1 - P) g (V - E_{C l})

I_{H C O 3 G A B A a} = P g (V - E_{H C O 3})

E_{G A B A a} = (1 - P) E_{C l} + P E_{H C O 3}

where relative permeability P was 0.18.

Calculation of the LFP

Request a detailed protocol

The local field potentials were calculated based on all transmembrane currents in all cells using the following equation (Nunez and Srinivasan, 2006):

ϕ (r, t) = \frac{1}{4 π σ} \sum_{n = 1}^{N} \frac{I_{n} (t)}{|r - r_{n}|}

where I_n is a point current source at position r_n (taken as the position of a mid-point of a compartment) and r is the position of the electrode. σ=0.3 S/m is the extracellular conductivity (Lindén et al., 2014). The electrode was located in the middle of the somatic layer of the PY and IN cells, approximately 16 µm from the centers of the somas of two neighbouring PY cells. The currents from the interneuron were taken with a weight of 0.2 to decrease their contribution. Also, the influence of the injected current on the LFP was removed. The amplitude of the simulated LFP signal was an order of magnitude smaller than the experimental data. This was due to current point-source approximation and the small number of cells in the modeled network.

Inter-burst interval fitting

Request a detailed protocol

Inter-burst intervals were fitted in Matlab with linear, exponential, logarithmic and square root relationships. The linear function, IBI(t)=A + Bt, was fitted using the polyfit procedure. The exponential function, IBI(t)=A + Bexp(Ct), was fitted using the fminsearch procedure. The logarithmic and square root fits were based on the bifurcation theory, which suggests that close to bifurcation, the oscillation frequency may be constant or decay as square root or inverse of a logarithm of the distance to the bifurcation (Izhikevich, 2000). Accordingly, we fitted IBI (i.e. inverse of frequency) with logarithmic and inverse square root functions IBI(λ)=A + Blog(λ), where log() denotes the natural logarithm function, and IBI(λ)=A + B/sqrt(λ), where sqrt() denotes the square root function. Both functions were fitted using the polyfit procedure with log(λ) and 1/sqrt(λ) treated as a predictor variable. The distance to the bifurcation point was computed as λ=t_end – t+1, where t_end denotes bifurcation point, that is, time of an SLE end while t is time since the beginning of an SLE. One second offset in λ was necessary to avoid infinity in the predictor variables when t=t_end. The goodness of fit was evaluated by Root Mean Square Error (RMSE).

Software accessibility

Request a detailed protocol

The model is publicly available in the ModelDB (http://modeldb.yale.edu/267499).

Appendix 1

Appendix 1—figure 1

Download asset Open asset

A bifurcation diagram of a single PY cell.

The 2D bifurcation diagram demonstrates the behavior of a single PY cell as a function of extracellular potassium concentration in the dendritic ([K⁺]_o,dend) and somatic compartments ([K⁺]_o,soma) used as control parameters. Concentrations of all other ions were fixed at their reference values (except chloride: [Cl^-]_i,soma, [Cl^-]_i,dend equal to 7 mM), all ion accumulation mechanisms were blocked and all synaptic connections were removed. (A) The three graphs show the PY cell activity traces for different values of the control parameters: resting (yellow, [K⁺]_o,soma = 3.5 mM, [K⁺]_o,dend = 3.5 mM), tonic firing (violet, [K⁺]_o,soma = 4.5 mM, [K⁺]_o,dend = 4 mM) and bursting (dark blue, [K⁺]_o,soma = 6.5 mM, [K⁺]_o,dend = 4 mM). In each panel, 2 seconds of activity is shown. (B) The colors of the 2D diagram correspond to the types of activity shown above in (A). For low [K⁺]_o,dend and [K⁺]_o,soma the cell was at rest. A moderate increase in either [K⁺]_o,dend or [K⁺]_o,soma, or both, led to tonic firing. Subsequent increases in these parameters led to bursting.

Appendix 1—figure 2

Download asset Open asset

A comparison of tonic firing (A) and bursting (B) of a PY cell.

In each column, the membrane potential of a cell (top) and the activation gate of *I_KM* (bottom) is shown. During tonic firing, the activation gate of the M-type potassium current was closed. The prolonged depolarization of the cell during bursting led to the opening of the activation gate m and activation of the *I_KM* current, which eventually terminated the burst. The simulation was performed using an isolated PY cell model with the concentrations of all ions fixed at their reference values, except [Cl^-]_i,soma = 7, [Cl^-]_i,dend = 7 mM and (A): [K⁺]_o,soma = 3.5 mM, [K⁺]_o,dend = 4.5 mM, (B): [K⁺]_o,soma = 5.25 mM and [K⁺]_o,dend = 4.5 mM.

Appendix 1—figure 3

Download asset Open asset

A simulation of biphasic GABAa response.

In this simulation size of both PY compartments was scaled down by factor 10, to represent small dendritic compartments. Single GABAa synapse was located in a segment having diameter 1.5 um and length 2 um (i.e., having volume 1,000 times smaller and GABAa conductance density 100 times larger than soma in the original model). (A) High frequency IN firing (shown schematically by *V_IN*, yellow; not to scale) was induced by IN current stimulation of 100ms duration. GABAa receptor-mediated postsynaptic potential response consisted of the initial hyperpolarization followed by a long-lasting depolarization (*V_PY*, black). Chloride accumulation ((B), blue) was mediated by large Cl^- influx via GABAa receptor as compared to Cl^- extrusion via KCC2 ((C) vs. (D)). Accordingly, the biphasic potential resulted from positive shift in *E_Cl* ((A), blue) and relatively high *E_HCO3* ((A), violet) leading to depolarizing shift in *E_GABAa* ((A), light blue). During GABAa receptor activation *V_PY* was clamped to *E_GABAa* due to large GABAa conductance density.

Appendix 1—figure 4

Download asset Open asset

Volume changes during an SLE in the model.

The panels show from top to bottom: LFP, relative volume changes and representative changes in intracellular A^- ion and extracellular Cl^- concentration in the PY somatic compartment during an SLE. [A^-]_i was affected only by volume changes while [Cl^-]_o was additionally affected by inward chloride leak and GABAa currents, KCC2 and Cl^- diffusion to the bath. It can be seen that an increase in intracellular space (IS) volume (second panel, dark blue) is exactly mirrored by a decrease in [A^-]_i. A decrease in extracellular space (ES) volume (third panel, violet) gives rise to an increase in [Cl^-]_o above baseline despite Cl^- influx into the cells, in agreement with the experimental data (Dietzel et al., 1982).

Data availability

All experimental data and analysis code is provided. Source data and analysis code (Matlab) is provided for Figure 2. Source data is provided for Figure 3A Source data and analysis code (Matlab) is provided separately for Figure 6A, 6B, 6C. Source data and analysis code (Matlab) is provided for Figure 6 - figure supplement 1. The model NEURON files with a code reproducing Figure 2 (main simulation results) is publicly available at Model DB database (http://modeldb.yale.edu/267499).

The following data sets were generated

1. Suffczynski P
2. Gentiletti D
(2022) ModelDB
ID 267499. A focal seizure model with ion concentration changes.

http://modeldb.yale.edu/267499

References

(2015) The contribution of raised intraneuronal chloride to epileptic network activity
The Journal of Neuroscience 35:7715–7726.
https://doi.org/10.1523/JNEUROSCI.4105-14.2015
- PubMed
- Google Scholar
(1980) Two different responses of hippocampal pyramidal cells to application of gamma-amino butyric acid
The Journal of Physiology 305:279–296.
https://doi.org/10.1113/jphysiol.1980.sp013363
- PubMed
- Google Scholar
1. Aracri P
2. de Curtis M
3. Forcaia G
4. Uva L
(2018) Enhanced thalamo-hippocampal synchronization during focal limbic seizures
Epilepsia 59:1774–1784.
https://doi.org/10.1111/epi.14521
- PubMed
- Google Scholar
1. Avoli M
2. Barbarosie M
3. Lücke A
4. Nagao T
5. Lopantsev V
6. Köhling R
(1996) Synchronous GABA-mediated potentials and epileptiform discharges in the rat limbic system in vitro
The Journal of Neuroscience 16:3912–3924.
https://doi.org/10.1523/JNEUROSCI.16-12-03912.1996
- PubMed
- Google Scholar
1. Avoli M
2. de Curtis M
3. Gnatkovsky V
4. Gotman J
5. Köhling R
6. Lévesque M
7. Manseau F
8. Shiri Z
9. Williams S
(2016) Specific imbalance of excitatory/inhibitory signaling establishes seizure onset pattern in temporal lobe epilepsy
Journal of Neurophysiology 115:3229–3237.
https://doi.org/10.1152/jn.01128.2015
- PubMed
- Google Scholar
1. Bauer PR
2. Thijs RD
3. Lamberts RJ
4. Velis DN
5. Visser GH
6. Tolner EA
7. Sander JW
8. Lopes da Silva FH
9. Kalitzin SN
(2017) Dynamics of convulsive seizure termination and postictal generalized EEG suppression
Brain : A Journal of Neurology 140:655–668.
https://doi.org/10.1093/brain/aww322
- PubMed
- Google Scholar
(2004) Potassium model for slow (2-3 Hz) in vivo neocortical paroxysmal oscillations
Journal of Neurophysiology 92:1116–1132.
https://doi.org/10.1152/jn.00529.2003
- PubMed
- Google Scholar
(2014) Mechanisms of ictogenesis
International Review of Neurobiology 114:155–185.
https://doi.org/10.1016/B978-0-12-418693-4.00007-8
- PubMed
- Google Scholar
(2014) Simultaneous enhancement of excitation and postburst inhibition at the end of focal seizures
Annals of Neurology 76:826–836.
https://doi.org/10.1002/ana.24193
- Google Scholar
Book
1. Borgdorff JA
(2002)
Calcium Dynamics in Hippocampal Neurones

University of Amsterdam.
- Google Scholar
1. Bradford HF
(1995) Glutamate, GABA and epilepsy
Progress in Neurobiology 47:477–511.
https://doi.org/10.1016/0301-0082(95)00030-5
- PubMed
- Google Scholar
(1997)
Termination of epileptic afterdischarge in the hippocampus

The Journal of Neuroscience 17:2567–2579.
- PubMed
- Google Scholar
1. Bragin A
2. Azizyan A
3. Almajano J
4. Engel J
(2009) The cause of the imbalance in the neuronal network leading to seizure activity can be predicted by the electrographic pattern of the seizure onset
The Journal of Neuroscience 29:3660–3671.
https://doi.org/10.1523/JNEUROSCI.5309-08.2009
- PubMed
- Google Scholar
Book
(editors) (2006)
An Introduction to Epilepsy

American Epilepsy Society.
- Google Scholar
1. Buchin A
2. Chizhov A
3. Huberfeld G
4. Miles R
5. Gutkin BS
(2016) Reduced efficacy of the kcc2 cotransporter promotes epileptic oscillations in a subiculum network model
The Journal of Neuroscience 36:11619–11633.
https://doi.org/10.1523/JNEUROSCI.4228-15.2016
- PubMed
- Google Scholar
(1991) GABA: an excitatory transmitter in early postnatal life
Trends in Neurosciences 14:515–519.
https://doi.org/10.1016/0166-2236(91)90003-d
- PubMed
- Google Scholar
(2018) Minimal model of interictal and ictal discharges “Epileptor-2.”
PLOS Computational Biology 14:1006186.
https://doi.org/10.1371/journal.pcbi.1006186
- PubMed
- Google Scholar
(2019) Divergent paths to seizure-like events
Physiological Reports 7:e14226.
https://doi.org/10.14814/phy2.14226
- PubMed
- Google Scholar
1. Conradsen I
2. Moldovan M
3. Jennum P
4. Wolf P
5. Farina D
6. Beniczky S
(2013) Dynamics of muscle activation during tonic-clonic seizures
Epilepsy Research 104:84–93.
https://doi.org/10.1016/j.eplepsyres.2012.09.004
- PubMed
- Google Scholar
(2005) Multiple facets of GABAergic neurons and synapses: multiple fates of GABA signalling in epilepsies
Trends in Neurosciences 28:108–115.
https://doi.org/10.1016/j.tins.2004.11.011
- PubMed
- Google Scholar
Book
(2006) In Vitro Isolated Guinea Pig Brain
In: Pitkänen A, Schwartzkroin PA, Moshé SL, editors. Models of Seizures and Epilepsy. Academic Press Inc. pp. 103–109.
https://doi.org/10.1016/B978-012088554-1/50011-6
- Google Scholar
1. de Curtis M
2. Gnatkovsky V
(2009) Reevaluating the mechanisms of focal ictogenesis: The role of low-voltage fast activity
Epilepsia 50:2514–2525.
https://doi.org/10.1111/j.1528-1167.2009.02249.x
- PubMed
- Google Scholar
1. de Curtis M
2. Avoli M
(2016) GABAergic networks jump-start focal seizures
Epilepsia 57:679–687.
https://doi.org/10.1111/epi.13370
- PubMed
- Google Scholar
(2018) Potassium dynamics and seizures: Why is potassium ictogenic?
Epilepsy Research 143:50–59.
https://doi.org/10.1016/j.eplepsyres.2018.04.005
- PubMed
- Google Scholar
1. Derchansky M
2. Jahromi SS
3. Mamani M
4. Shin DS
5. Sik A
6. Carlen PL
(2008) Transition to seizures in the isolated immature mouse hippocampus: a switch from dominant phasic inhibition to dominant phasic excitation
The Journal of Physiology 586:477–494.
https://doi.org/10.1113/jphysiol.2007.143065
- PubMed
- Google Scholar
(2018) Epilepsy
Nature Reviews. Disease Primers 4:18024.
https://doi.org/10.1038/nrdp.2018.24
- PubMed
- Google Scholar
(1980) Transient changes in the size of the extracellular space in the sensorimotor cortex of cats in relation to stimulus-induced changes in potassium concentration
Experimental Brain Research 40:432–439.
https://doi.org/10.1007/BF00236151
- PubMed
- Google Scholar
(1982) Stimulus-induced changes in extracellular Na+ and Cl- concentration in relation to changes in the size of the extracellular space
Experimental Brain Research 46:73–84.
https://doi.org/10.1007/BF00238100
- PubMed
- Google Scholar
(2011) Efficacy of synaptic inhibition depends on multiple, dynamically interacting mechanisms implicated in chloride homeostasis
PLOS Computational Biology 7:e1002149.
https://doi.org/10.1371/journal.pcbi.1002149
- PubMed
- Google Scholar
1. During MJ
2. Spencer DD
(1992) Adenosine: A potential mediator of seizure arrest and postictal refractoriness
Annals of Neurology 32:618–624.
https://doi.org/10.1002/ana.410320504
- PubMed
- Google Scholar
(1997) Phenytoin’s effect on the spread of seizure activity in the amygdala kindling model
Naunyn-Schmiedeberg’s Archives of Pharmacology 356:341–347.
https://doi.org/10.1007/PL00005060
- PubMed
- Google Scholar
1. Elahian B
2. Lado NE
3. Mankin E
4. Vangala S
5. Misra A
6. Moxon K
7. Fried I
8. Sharan A
9. Yeasin M
10. Staba R
11. Bragin A
12. Avoli M
13. Sperling MR
14. Engel J
15. Weiss SA
(2018) Low-voltage fast seizures in humans begin with increased interneuron firing
Annals of Neurology 84:588–600.
https://doi.org/10.1002/ana.25325
- PubMed
- Google Scholar
(2014) Excitatory effects of parvalbumin-expressing interneurons maintain hippocampal epileptiform activity via synchronous afterdischarges
The Journal of Neuroscience 34:15208–15222.
https://doi.org/10.1523/JNEUROSCI.1747-14.2014
- PubMed
- Google Scholar
1. Evangelista E
2. Bénar C
3. Bonini F
4. Carron R
5. Colombet B
6. Régis J
7. Bartolomei F
(2015) Does the thalamo-cortical synchrony play a role in seizure termination?
Frontiers in Neurology 6:192.
https://doi.org/10.3389/fneur.2015.00192
- PubMed
- Google Scholar
1. Feng Z
2. Durand DM
(2003) Low-calcium epileptiform activity in the hippocampus in vivo
Journal of Neurophysiology 90:2253–2260.
https://doi.org/10.1152/jn.00241.2003
- PubMed
- Google Scholar
(1976) The role of extracellular potassium in hippocampal epilepsy
Archives of Neurology 33:76–83.
https://doi.org/10.1001/archneur.1976.00500020004002
- PubMed
- Google Scholar
1. Fisher RS
2. Schachter SC
(2000) The postictal state: A neglected entity in the management of epilepsy
Epilepsy & Behavior 1:52–59.
https://doi.org/10.1006/ebeh.2000.0023
- PubMed
- Google Scholar
(1998) Time-frequency analysis using the matching pursuit algorithm applied to seizures originating from the mesial temporal lobe
Electroencephalography and Clinical Neurophysiology 106:513–521.
https://doi.org/10.1016/s0013-4694(98)00024-8
- PubMed
- Google Scholar
(2002) Simulations of the role of the muscarinic-activated calcium-sensitive nonspecific cation current INCM in entorhinal neuronal activity during delayed matching tasks
The Journal of Neuroscience 22:1081–1097.
https://doi.org/10.1523/JNEUROSCI.22-03-01081.2002
- PubMed
- Google Scholar
(2006) Slow state transitions of sustained neural oscillations by activity-dependent modulation of intrinsic excitability
The Journal of Neuroscience 26:6153–6162.
https://doi.org/10.1523/JNEUROSCI.5509-05.2006
- PubMed
- Google Scholar
(2007) Distinct types of ionic modulation of GABA actions in pyramidal cells and interneurons during electrical induction of hippocampal seizure-like network activity
The European Journal of Neuroscience 25:2713–2725.
https://doi.org/10.1111/j.1460-9568.2007.05543.x
- PubMed
- Google Scholar
(1974) Potassium activity in rabbit cortex
Brain Research 75:5–25.
https://doi.org/10.1016/0006-8993(74)90767-7
- PubMed
- Google Scholar
(2017) Changes of ionic concentrations during seizure transitions - a modeling study
International Journal of Neural Systems 27:1–16.
https://doi.org/10.1142/S0129065717500046
- PubMed
- Google Scholar
(2008) Fast activity at seizure onset is mediated by inhibitory circuits in the entorhinal cortex in vitro
Annals of Neurology 64:674–686.
https://doi.org/10.1002/ana.21519
- PubMed
- Google Scholar
1. Golomb D
2. Yue C
3. Yaari Y
(2006) Contribution of persistent Na+ current and M-type K+ current to somatic bursting in CA1 pyramidal cells: combined experimental and modeling study
Journal of Neurophysiology 96:1912–1926.
https://doi.org/10.1152/jn.00205.2006
- PubMed
- Google Scholar
1. González OC
2. Shiri Z
3. Krishnan GP
4. Myers TL
5. Williams S
6. Avoli M
7. Bazhenov M
(2018) Role of KCC2-dependent potassium efflux in 4-Aminopyridine-induced Epileptiform synchronization
Neurobiology of Disease 109:137–147.
https://doi.org/10.1016/j.nbd.2017.10.011
- PubMed
- Google Scholar
(2013) Neuronal synchrony and the transition to spontaneous seizures
Experimental Neurology 248:72–84.
https://doi.org/10.1016/j.expneurol.2013.05.004
- PubMed
- Google Scholar
1. Grigorovsky V
2. Jacobs D
3. Breton VL
4. Tufa U
5. Lucasius C
6. Del Campo JM
7. Chinvarun Y
8. Carlen PL
9. Wennberg R
10. Bardakjian BL
(2020) Delta-gamma phase-amplitude coupling as a biomarker of postictal generalized EEG suppression
Brain Communications 2:fcaa182.
https://doi.org/10.1093/braincomms/fcaa182
- PubMed
- Google Scholar
1. Haas HL
2. Jefferys JG
(1984) Low-calcium field burst discharges of CA1 pyramidal neurones in rat hippocampal slices
The Journal of Physiology 354:185–201.
https://doi.org/10.1113/jphysiol.1984.sp015371
- PubMed
- Google Scholar
1. Hamidi S
2. Avoli M
(2015) KCC2 function modulates in vitro ictogenesis
Neurobiology of Disease 79:51–58.
https://doi.org/10.1016/j.nbd.2015.04.006
- PubMed
- Google Scholar
1. Heinemann U
2. Lux HD
(1975) Undershoots following stimulus-induced rises of extracellular potassium concentration in cerebral cortex of cat
Brain Research 93:63–76.
https://doi.org/10.1016/0006-8993(75)90286-3
- PubMed
- Google Scholar
(1977) Extracellular free calcium and potassium during paroxsmal activity in the cerebral cortex of the cat
Experimental Brain Research 27:237–243.
https://doi.org/10.1007/BF00235500
- PubMed
- Google Scholar
1. Hübel N
2. Ullah G
(2016) Anions govern cell volume: a case study of relative astrocytic and neuronal swelling in spreading depolarization
PLOS ONE 11:e0147060.
https://doi.org/10.1371/journal.pone.0147060
- PubMed
- Google Scholar
1. Igelström KM
(2013) Is slack an intrinsic seizure terminator?
The Neuroscientist 19:248–254.
https://doi.org/10.1177/1073858412446311
- PubMed
- Google Scholar
1. Izhikevich EM
(2000) Neural excitability, spiking and bursting
International Journal of Bifurcation and Chaos 10:1171–1266.
https://doi.org/10.1142/S0218127400000840
- Google Scholar
(2010) Activity-dependent intracellular chloride accumulation and diffusion controls GABA(A) receptor-mediated synaptic transmission
Hippocampus 21:885–898.
https://doi.org/10.1002/hipo.20804
- PubMed
- Google Scholar
1. Jefferys JGR
2. Haas HL
(1982) Synchronized bursting of CA1 hippocampal pyramidal cells in the absence of synaptic transmission
Nature 300:448–450.
https://doi.org/10.1038/300448a0
- PubMed
- Google Scholar
1. Jefferys JG
(1995) Nonsynaptic modulation of neuronal activity in the brain: electric currents and extracellular ions
Physiological Reviews 75:689–723.
https://doi.org/10.1152/physrev.1995.75.4.689
- PubMed
- Google Scholar
1. Jefferys J
2. Jiruska P
3. de Curtis M
4. Avoli M
5. Noebels J
6. Avoli M
7. Rogawski M
8. Olsen R
9. Delgado-Escueta A
(2012)
Jasper’s Basic Mechanisms of the Epilepsies

1–18, Limbic network synchronization and temporal lobe epilepsy, Jasper’s Basic Mechanisms of the Epilepsies, Bethesda, National Center for Biotechnology Information, 10.1093/med/9780199746545.001.0001.
- Google Scholar
1. Jensen MS
2. Yaari Y
(1997) Role of intrinsic burst firing, potassium accumulation, and electrical coupling in the elevated potassium model of hippocampal epilepsy
Journal of Neurophysiology 77:1224–1233.
https://doi.org/10.1152/jn.1997.77.3.1224
- PubMed
- Google Scholar
(2014) On the nature of seizure dynamics
Brain : A Journal of Neurology 137:2210–2230.
https://doi.org/10.1093/brain/awu133
- PubMed
- Google Scholar
(2000) Simulated seizures and spreading depression in a neuron model incorporating interstitial space and ion concentrations
Journal of Neurophysiology 84:495–512.
https://doi.org/10.1152/jn.2000.84.1.495
- PubMed
- Google Scholar
(2002) Conditions for the triggering of spreading depression studied with computer simulations
Journal of Neurophysiology 88:2700–2712.
https://doi.org/10.1152/jn.00237.2002
- PubMed
- Google Scholar
1. Kaila K
2. Lamsa K
3. Smirnov S
4. Taira T
5. Voipio J
(1997) Long-lasting GABA-mediated depolarization evoked by high-frequency stimulation in pyramidal neurons of rat hippocampal slice is attributable to a network-driven, bicarbonate-dependent K+ transient
The Journal of Neuroscience 17:7662–7672.
https://doi.org/10.1523/jneurosci.17-20-07662.1997
- PubMed
- Google Scholar
1. Kaila K
2. Price TJ
3. Payne JA
4. Puskarjov M
5. Voipio J
(2014) Cation-chloride cotransporters in neuronal development, plasticity and disease
Nature Reviews. Neuroscience 15:637–654.
https://doi.org/10.1038/nrn3819
- PubMed
- Google Scholar
(2016) Automated video detection of epileptic convulsion slowing as a precursor for post-seizure neuronal collapse
International Journal of Neural Systems 26:100–104.
https://doi.org/10.1142/S0129065716500271
- PubMed
- Google Scholar
1. Krishnan GP
2. Bazhenov M
(2011) Ionic dynamics mediate spontaneous termination of seizures and postictal depression state
The Journal of Neuroscience 31:8870–8882.
https://doi.org/10.1523/JNEUROSCI.6200-10.2011
- PubMed
- Google Scholar
(2015) Electrogenic properties of the Na
Journal of Neurophysiology 113:3356–3374.
https://doi.org/10.1152/jn.00460.2014
- PubMed
- Google Scholar
1. Lado FA
2. Moshé SL
(2008) How do seizures stop?
Epilepsia 49:1651–1664.
https://doi.org/10.1111/j.1528-1167.2008.01669.x
- PubMed
- Google Scholar
1. Lagarde S
2. Buzori S
3. Trebuchon A
4. Carron R
5. Scavarda D
6. Milh M
7. McGonigal A
8. Bartolomei F
(2019) The repertoire of seizure onset patterns in human focal epilepsies: Determinants and prognostic values
Epilepsia 60:85–95.
https://doi.org/10.1111/epi.14604
- PubMed
- Google Scholar
(2016) Interneurons spark seizure-like activity in the entorhinal cortex
Neurobiology of Disease 87:91–101.
https://doi.org/10.1016/j.nbd.2015.12.011
- PubMed
- Google Scholar
1. Lian J
2. Bikson M
3. Shuai J
4. Durand DM
(2001) Propagation of non-synaptic epileptiform activity across a lesion in rat hippocampal slices
The Journal of Physiology 537:191–199.
https://doi.org/10.1111/j.1469-7793.2001.0191k.x
- PubMed
- Google Scholar
1. Lillis KP
2. Kramer MA
3. Mertz J
4. Staley KJ
5. White JA
(2012) Pyramidal cells accumulate chloride at seizure onset
Neurobiology of Disease 47:358–366.
https://doi.org/10.1016/j.nbd.2012.05.016
- PubMed
- Google Scholar
(2014) LFPy: a tool for biophysical simulation of extracellular potentials generated by detailed model neurons
Frontiers in Neuroinformatics 7:1–15.
https://doi.org/10.3389/fninf.2013.00041
- PubMed
- Google Scholar
1. Liou J-Y
2. Smith EH
3. Bateman LM
4. Bruce SL
5. McKhann GM
6. Goodman RR
7. Emerson RG
8. Schevon CA
9. Abbott LF
(2020) A model for focal seizure onset, propagation, evolution, and progression
eLife 9:e50927.
https://doi.org/10.7554/eLife.50927
- PubMed
- Google Scholar
1. Lopantsev V
2. Avoli M
(1998) Participation of GABA _A -mediated inhibition in ictallike discharges in the rat entorhinal cortex
Journal of Neurophysiology 79:352–360.
https://doi.org/10.1152/jn.1998.79.1.352
- PubMed
- Google Scholar
1. Magistretti J
2. Alonso A
(1999) Biophysical properties and slow voltage-dependent inactivation of a sustained sodium current in entorhinal cortex layer-ii principal neurons
Journal of General Physiology 114:491–509.
https://doi.org/10.1085/jgp.114.4.491
- PubMed
- Google Scholar
1. Magloire V
2. Cornford J
3. Lieb A
4. Kullmann DM
5. Pavlov I
(2019a) KCC2 overexpression prevents the paradoxical seizure-promoting action of somatic inhibition
Nature Communications 10:1–13.
https://doi.org/10.1038/s41467-019-08933-4
- PubMed
- Google Scholar
(2019b) GABAergic Interneurons in seizures: investigating causality with optogenetics
The Neuroscientist 25:344–358.
https://doi.org/10.1177/1073858418805002
- PubMed
- Google Scholar
1. Martinet LE
2. Fiddyment G
3. Madsen JR
4. Eskandar EN
5. Truccolo W
6. Eden UT
7. Cash SS
8. Kramer MA
(2017) Human seizures couple across spatial scales through travelling wave dynamics
Nature Communications 8:14896.
https://doi.org/10.1038/ncomms14896
- PubMed
- Google Scholar
(1990) Regional variation of extracellular space in the hippocampus
Science 249:674–677.
https://doi.org/10.1126/science.2382142
- PubMed
- Google Scholar
Book
1. Miles R
2. Blaesse P
3. Huberfeld G
4. Wittner L
5. Kaila K
(2012)
Jasper’s Basic Mechanisms of the Epilepsies

National Center for Biotechnology Information.
- Google Scholar
1. Miri ML
2. Vinck M
3. Pant R
4. Cardin JA
(2018) Altered hippocampal interneuron activity precedes ictal onset
eLife 7:e40750.
https://doi.org/10.7554/eLife.40750
- PubMed
- Google Scholar
1. Moore YE
2. Deeb TZ
3. Chadchankar H
4. Brandon NJ
5. Moss SJ
(2018) Potentiating KCC2 activity is sufficient to limit the onset and severity of seizures
PNAS 115:10166–10171.
https://doi.org/10.1073/pnas.1810134115
- PubMed
- Google Scholar
Book
1. Nunez PL
2. Srinivasan R
(2006)
Electric Fields of the Brain

Oxford University Press.
- Google Scholar
1. Payne JA
(1997) Functional characterization of the neuronal-specific K-Cl cotransporter: implications for [K ⁺ ] _o regulation
American Journal of Physiology-Cell Physiology 273:C1516–C1525.
https://doi.org/10.1152/ajpcell.1997.273.5.C1516
- Google Scholar
1. Payne JA
2. Rivera C
3. Voipio J
4. Kaila K
(2003) Cation–chloride co-transporters in neuronal communication, development and trauma
Trends in Neurosciences 26:199–206.
https://doi.org/10.1016/S0166-2236(03)00068-7
- PubMed
- Google Scholar
1. Payne DE
2. Karoly PJ
3. Freestone DR
4. Boston R
5. D’Souza W
6. Nurse E
7. Kuhlmann L
8. Cook MJ
9. Grayden DB
(2018) Postictal suppression and seizure durations: A patient-specific, long-term iEEG analysis
Epilepsia 59:1027–1036.
https://doi.org/10.1111/epi.14065
- PubMed
- Google Scholar
(2014) Intracranial electroencephalographic seizure-onset patterns: effect of underlying pathology
Brain: A Journal of Neurology 137:183–196.
https://doi.org/10.1093/brain/awt299
- PubMed
- Google Scholar
(2020) The postictal state — What do we know?
Epilepsia 61:1045–1061.
https://doi.org/10.1111/epi.16519
- PubMed
- Google Scholar
1. Proix T
2. Jirsa VK
3. Bartolomei F
4. Guye M
5. Truccolo W
(2018) Predicting the spatiotemporal diversity of seizure propagation and termination in human focal epilepsy
Nature Communications 9:1088.
https://doi.org/10.1038/s41467-018-02973-y
- PubMed
- Google Scholar
(1985) Chemical synaptic transmission is not necessary for epileptic seizures to persist in the baboon Papio papio
Experimental Neurology 89:250–258.
https://doi.org/10.1016/0014-4886(85)90280-8
- PubMed
- Google Scholar
1. Raimondo JV
2. Joyce B
3. Kay L
4. Schlagheck T
5. Newey SE
6. Srinivas S
7. Akerman CJ
(2013) A genetically-encoded chloride and pH sensor for dissociating ion dynamics in the nervous system
Frontiers in Cellular Neuroscience 7:202.
https://doi.org/10.3389/fncel.2013.00202
- PubMed
- Google Scholar
(2015) Ion dynamics during seizures
Frontiers in Cellular Neuroscience 9:1–14.
https://doi.org/10.3389/fncel.2015.00419
- PubMed
- Google Scholar
1. Rich S
2. Chameh HM
3. Rafiee M
4. Ferguson K
5. Skinner FK
6. Valiante TA
(2020) Inhibitory network bistability explains increased interneuronal activity prior to seizure onset
Frontiers in Neural Circuits 13:81.
https://doi.org/10.3389/fncir.2019.00081
- PubMed
- Google Scholar
1. Saggio ML
2. Crisp D
3. Scott JM
4. Karoly P
5. Kuhlmann L
6. Nakatani M
7. Murai T
8. Dümpelmann M
9. Schulze-Bonhage A
10. Ikeda A
11. Cook M
12. Gliske SV
13. Lin J
14. Bernard C
15. Jirsa V
16. Stacey WC
(2020) A taxonomy of seizure dynamotypes
eLife 9:e55632.
https://doi.org/10.7554/eLife.55632
- PubMed
- Google Scholar
1. Sah P
2. Gibb AJ
3. Gage PW
(1988) Potassium current activated by depolarization of dissociated neurons from adult guinea pig hippocampus
The Journal of General Physiology 92:263–278.
https://doi.org/10.1085/jgp.92.2.263
- PubMed
- Google Scholar
1. Salami P
2. Borzello M
3. Kramer MA
4. Westover MB
5. Cash SS
(2022) Quantifying seizure termination patterns reveals limited pathways to seizure end
Neurobiology of Disease 165:105645.
https://doi.org/10.1016/j.nbd.2022.105645
- PubMed
- Google Scholar
1. Schiff SJ
2. Colella D
3. Jacyna GM
4. Hughes E
5. Creekmore JW
6. Marshall A
7. Bozek-Kuzmicki M
8. Benke G
9. Gaillard WD
10. Conry J
11. Weinstein SR
(2000) Brain chirps: spectrographic signatures of epileptic seizures
Clinical Neurophysiology 111:953–958.
https://doi.org/10.1016/s1388-2457(00)00259-5
- PubMed
- Google Scholar
(2007) Assessing seizure dynamics by analysing the correlation structure of multichannel intracranial EEG
Brain: A Journal of Neurology 130:65–77.
https://doi.org/10.1093/brain/awl304
- PubMed
- Google Scholar
(2019) Self-propagating, non-synaptic epileptiform activity recruits neurons by endogenous electric fields
Experimental Neurology 317:119–128.
https://doi.org/10.1016/j.expneurol.2019.02.005
- PubMed
- Google Scholar
1. Somjen GG
2. Giacchino JL
(1985) Potassium and calcium concentrations in interstitial fluid of hippocampal formation during paroxysmal responses
Journal of Neurophysiology 53:1098–1108.
https://doi.org/10.1152/jn.1985.53.4.1098
- PubMed
- Google Scholar
(2008) Computer simulations of neuron-glia interactions mediated by ion flux
Journal of Computational Neuroscience 25:349–365.
https://doi.org/10.1007/s10827-008-0083-9
- PubMed
- Google Scholar
1. Spencer SS
2. Guimaraes P
3. Katz A
4. Kim J
5. Spencer D
(1992) Morphological patterns of seizures recorded intracranially
Epilepsia 33:537–545.
https://doi.org/10.1111/j.1528-1157.1992.tb01706.x
- PubMed
- Google Scholar
(1995) Ionic mechanisms of neuronal excitation by inhibitory GABAA receptors
Science 269:977–981.
https://doi.org/10.1126/science.7638623
- PubMed
- Google Scholar
1. Staley KJ
2. Proctor WR
(1999) Modulation of mammalian dendritic GABA(A) receptor function by the kinetics of Cl- and HCO3- transport
The Journal of Physiology 519 Pt 3:693–712.
https://doi.org/10.1111/j.1469-7793.1999.0693n.x
- PubMed
- Google Scholar
Book
(2017) Extracellular Potassium and Focal Seizures—Insight from In Silico Study
In: Érdi P, Bhattacharya B Sen, Cochran A, editors. Computational Neurology and Psychiatry. Springer Series in Bio-/Neuroinformatics. Cham: Springer. pp. 49–72.
https://doi.org/10.1007/978-3-319-49959-8
- Google Scholar
1. Sulis Sato S
2. Artoni P
3. Landi S
4. Cozzolino O
5. Parra R
6. Pracucci E
7. Trovato F
8. Szczurkowska J
9. Luin S
10. Arosio D
11. Beltram F
12. Cancedda L
13. Kaila K
14. Ratto GM
(2017) Simultaneous two-photon imaging of intracellular chloride concentration and pH in mouse pyramidal neurons in vivo
PNAS 114:E8770–E8779.
https://doi.org/10.1073/pnas.1702861114
- PubMed
- Google Scholar
(2020) Astrocytes regulate brain extracellular pH via a neuronal activity-dependent bicarbonate shuttle
Nature Communications 11:5073.
https://doi.org/10.1038/s41467-020-18756-3
- PubMed
- Google Scholar
1. Thompson SM
2. Gahwiler BH
(1989) Activity-dependent disinhibition. II. Effects of extracellular potassium, furosemide, and membrane potential on ECl- in hippocampal CA3 neurons
Journal of Neurophysiology 61:512–523.
https://doi.org/10.1152/jn.1989.61.3.512
- PubMed
- Google Scholar
1. Timofeev I
2. Steriade M
(2004) Neocortical seizures: initiation, development and cessation
Neuroscience 123:299–336.
https://doi.org/10.1016/j.neuroscience.2003.08.051
- PubMed
- Google Scholar
(2015) Unit activity of hippocampal interneurons before spontaneous seizures in an animal model of temporal lobe epilepsy
The Journal of Neuroscience 35:6600–6618.
https://doi.org/10.1523/JNEUROSCI.4786-14.2015
- PubMed
- Google Scholar
(2003) Fast rhythmic bursting can be induced in layer 2/3 cortical neurons by enhancing persistent Na+ conductance or by blocking BK channels
Journal of Neurophysiology 89:909–921.
https://doi.org/10.1152/jn.00573.2002
- PubMed
- Google Scholar
1. Traynelis SF
2. Dingledine R
(1988) Potassium-induced spontaneous electrographic seizures in the rat hippocampal slice
Journal of Neurophysiology 59:259–276.
https://doi.org/10.1152/jn.1988.59.1.259
- PubMed
- Google Scholar
1. Truccolo W
2. Donoghue JA
3. Hochberg LR
4. Eskandar EN
5. Madsen JR
6. Anderson WS
7. Brown EN
8. Halgren E
9. Cash SS
(2011) Single-neuron dynamics in human focal epilepsy
Nature Neuroscience 14:635–641.
https://doi.org/10.1038/nn.2782
- PubMed
- Google Scholar
(2015) Synchronous inhibitory potentials precede seizure-like events in acute models of focal limbic seizures
The Journal of Neuroscience 35:3048–3055.
https://doi.org/10.1523/JNEUROSCI.3692-14.2015
- PubMed
- Google Scholar
1. Uva L
2. de Curtis M
(2020) Activity- and pH-dependent adenosine shifts at the end of a focal seizure in the entorhinal cortex
Epilepsy Research 165:106401.
https://doi.org/10.1016/j.eplepsyres.2020.106401
- PubMed
- Google Scholar
(2000) Functional and anatomic correlates of two frequently observed temporal lobe seizure-onset patterns
Neural Plasticity 7:49–63.
https://doi.org/10.1155/NP.2000.49
- PubMed
- Google Scholar
(2010) The K+-Cl cotransporter KCC2 promotes GABAergic excitation in the mature rat hippocampus
The Journal of Physiology 588:1527–1540.
https://doi.org/10.1113/jphysiol.2009.181826
- PubMed
- Google Scholar
1. Wei Y
2. Ullah G
3. Ingram J
4. Schiff SJ
(2014a) Oxygen and seizure dynamics: II. Computational modeling
Journal of Neurophysiology 112:213–223.
https://doi.org/10.1152/jn.00541.2013
- PubMed
- Google Scholar
1. Wei Y
2. Ullah G
3. Schiff SJ
(2014b) Unification of neuronal spikes, seizures, and spreading depression
Journal of Neuroscience 34:11733–11743.
https://doi.org/10.1523/JNEUROSCI.0516-14.2014
- PubMed
- Google Scholar
1. Wen B
2. Qian H
3. Feng J
4. Ge RJ
5. Xu X
6. Cui ZQ
7. Zhu RY
8. Pan LS
9. Lin ZP
10. Wang JH
(2015) A portion of inhibitory neurons in human temporal lobe epilepsy are functionally upregulated: an endogenous mechanism for seizure termination
CNS Neuroscience & Therapeutics 21:204–214.
https://doi.org/10.1111/cns.12336
- PubMed
- Google Scholar
1. Y Ho EC
2. Truccolo W
(2016) Interaction between synaptic inhibition and glial-potassium dynamics leads to diverse seizure transition modes in biophysical models of human focal seizures
Journal of Computational Neuroscience 41:225–244.
https://doi.org/10.1007/s10827-016-0615-7
- PubMed
- Google Scholar
(1983) Spontaneous epileptiform activity of CA1 hippocampal neurons in low extracellular calcium solutions
Experimental Brain Research 51:153–156.
https://doi.org/10.1007/BF00236813
- PubMed
- Google Scholar
(2015) Selective activation of parvalbumin- or somatostatin-expressing interneurons triggers epileptic seizurelike activity in mouse medial entorhinal cortex
Journal of Neurophysiology 113:1616–1630.
https://doi.org/10.1152/jn.00841.2014
- PubMed
- Google Scholar
(2006) Interneuron and pyramidal cell interplay during in vitro seizure-like events
Journal of Neurophysiology 95:3948–3954.
https://doi.org/10.1152/jn.01378.2005
- PubMed
- Google Scholar
1. Ziemann AE
2. Schnizler MK
3. Albert GW
4. Severson MA
5. Howard MA
6. Welsh MJ
7. Wemmie JA
(2008) Seizure termination by acidosis depends on ASIC1a
Nature Neuroscience 11:816–822.
https://doi.org/10.1038/nn.2132
- PubMed
- Google Scholar
(2014) Seizure termination
International Review of Neurobiology 114:187–207.
https://doi.org/10.1016/B978-0-12-418693-4.00008-X
- PubMed
- Google Scholar

Decision letter

Joseph V Raimondo

Reviewing Editor; University of Cape Town, South Africa
Ronald L Calabrese

Senior Editor; Emory University, United States
Joseph V Raimondo

Reviewer; University of Cape Town, South Africa
Maxim Bazhenov

Reviewer; University of California, San Diego, United States

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Decision letter after peer review:

[Editors’ note: the authors submitted for reconsideration following the decision after peer review. What follows is the decision letter after the first round of review.]

Thank you for submitting your work entitled "Focal seizures are organized by feedback between neural activity and ion concentration changes" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and a Senior Editor. The following individuals involved in review of your submission have agreed to reveal their identity: Joseph V Raimondo (Reviewer #1); Maxim Bazhenov (Reviewer #2).

Comments to the Authors:

We are sorry to say that, after consultation with the reviewers, we have decided that your work will not be considered further for publication by eLife.

Although there was certainly enthusiasm about the model, which was found to be generally thorough and broadly satisfying in its behaviour and predictions, there was ultimately collective concern from all 3 reviewers about whether there was the requisite level of novelty and advance over prior work to justify publication in eLife.

Please find the reviews below.

Reviewer #1 (Recommendations for the authors):

The model uses the NEURON framework and is well put together. On the whole its behaviour is both satisfying and reassuring. The model recapitulates the electrographic behaviour of animal model and human EEG recordings in particular the low-voltage fast activity preceding the tonic phase of a seizure, which transitions into bursting. The bursts then slow in frequency before postictal suppression of activity is observed. These dynamics emerge out of the model due to its inclusion of ion dynamics of K⁺, Na⁺ and Cl^- and multiple cellular mechanisms including accounting for excitatory and inhibitory cell populations, dendritic and somatic compartments, diffusion, glial buffering, ion channels and ion transporters.

Whilst the work is very much worthy of publication, I am not convinced that it generates sufficiently novel findings and advances over previous work in the field (e.g. Krishnan 2011 and Krishnan 2015 and others) to be of sufficient interest to warrant publication in eLife. In my opinion the importance of K⁺, Cl^- and Na⁺ dynamics for seizure evolution have been demonstrated before. (e.g. increases in K⁺ driving SLE initiation, transition between tonic and bursting activity and seizure cessation occurring due to enhanced Na+/K⁺ ATPase activity).

(1) I am concerned as to the applicability of the experimental data to this model. SLEs in the whole guinea pig brain were elicited using bicuculline, which blocks GABAaR transmission yet current from the IN to PYs via activated GABAaRs is presumably an important component of the computational model?

(2) Understandably the model cannot recapitulate all biological detail but there are some aspects about the model which seem odd and would need justification:

a. e.g. Intracellular HCO₃^- is higher than intracellular bicarbonate (15 mM) being higher than extracellular bicarbonate (11 mM). This suggests that intracellular pH is more alkaline than extracellular pH which is not the case. In addition, this would make the bicarb reversal +8 mV which is high and unrealistic.

b. In the neurons the Na⁺ leak conductance is 40% of the K⁺ leak conductance, this seems very high and not a typical ratio of permeabilities for neurons.

c. It wasn't clear whether the leak conductances for the various ions were actually contributing to the ion dynamics, e.g. was Cl^- flux through the baseline Cl^- leak conductance in neurons contributing to changes in [Cl^-]i?

d. Ek = Ecl at rest, this is also not physiological, I understand why this was done so that KCC2 was at equilibrium at baseline, but this is not ideal. Rather there should be a tonic Cl^- leak influx ensuring that "at baseline" Ecl>Ek as observed experimentally.

(3) Modelling of Cl^- changes especially Cl^- flux through GABAaRs. I am also not entirely sure that Cl^- flux through GABAaRs was modelled correctly to capture the potential for biphasic/ depolarizing responses via intensely activated GABAaRs (the authors should note amongst others Ruusuvuori 2004). The calculation of Egaba included HCO₃^- (line 833) but how was Icl (Cl^- flux) via activated GABAaRs calculated? Ie in the model if Vm is at the GABAaR reversal potential (Egaba) would Cl^- ion flux into the cell via GABAaRs (Icl) be zero? Ie in the model if Icl calculated as 4/5 of Igaba and Igaba = Ggaba(Vm – Egaba), then when Vm = Egaba, Igaba and consequently Icl is 0. This shouldn't be the case. Rather Igaba = Icl + Ihco3 where Icl = gcl(Vm – Ecl) and Ihco3 = ghco3(Vm – Ehco3) and ggaba = 4/5xgcl +1/5xghco3. Seeing as Cl^- accumulation is a fundamental part of the model this should have been made more clear. E.g. in Figure 5, could Icl via GABAaRs also be plotted? I worry as the Cl^- influx in the model seemed to be coming predominantly via KCC2 (due to the raised extracellular K⁺) whereas experimentally this is likely also coming predominantly through GABAaRs. This is reflected in the time course of [Cl^-]i changes in the model which are slower than [K⁺]o and continue increasing until the end of the SLE which is not typically what is observed experimentally (see intracellular Cl^- recordings e.g. Raimondo 2013).

(4) Perhaps the authors could make it more clear that the exact same experimental data was also presented in Gentilleti 2017.

Reviewer #2 (Recommendations for the authors):

Gentiletti et al. investigated potential role of non-synaptic mechanisms driving seizure-like event (SLE) generation. Using a detailed computational model of a small network of neurons, the authors demonstrate that the complex interaction between specific ion species may give rise to SLE. The detailed analysis of the computational model provides an interesting approach to developing a unifying framework for neural dynamics. The strength of this manuscript is in the direct validation of key aspects of the computational model using in vitro electrophysiology. Additionally, predictions made by the model such as the slowing of inter-burst intervals are subsequently validated in both human and mouse data. The conclusions made by the authors of this manuscript are supported by their results and are in line with previous work in the field. Finally, the manuscript does a good job relating the novel results of this new manuscript with established results in the field.

1. A strength of this manuscript is the direct validation of the computational model with experimental results. Given the multitude of methods available for inducing seizure-like events (SLE) in vitro, it is a bit surprising that the authors chose to use an arterial application of bicuculline (Figure 3). Bicuculline is a competitive antagonist of the GABA-A receptor resulting in the reduction of inhibitory GABAergic signaling. However, the SLE induced in the model is caused by an increase in inhibitory activity, through direct depolarization, rather than a decrease in GABAergic signaling. At first glance these methods for inducing SLE seem to be at odds with one another. Given the observed increase in extracellular K⁺ at SLE onset, this mismatch in the method for SLE generation in vitro and in silico may further highlight one of the primary claims of the manuscript specifically that disruption of ionic homeostasis rather than solely synaptic excitatory/inhibitory imbalance is a mechanism for SLE generation. Additional discussion of this observation and similar phenomena in other methods for SLE generation in vitro would further strengthen this interesting point.

2. Bifurcation analysis in figure 4A produces interesting results that are in line with and supported by previous work. As stated in the text, an assumption made by the authors is that the intracellular dendritic and somatic Na⁺ is equal. The authors further mention that this assumption may result in an overestimation of dendritic Na⁺ and Na/K pump activity but do not discuss how this might impact the results presented in the bifurcation diagrams. Please include.

3. It is striking that the time course of the extracellular dendritic K⁺ concentration is much slower than for the soma. It is not clear if the delayed increase in dendritic K⁺ is a prediction of the computational model or if it has been experimentally observed and incorporated into the model as such. Some discussion clarifying this point is needed. To that point, are the authors suggesting that the longitudinal diffusion of K⁺ from soma to dendrite is driving the delayed increase? If so, how might the observed dynamics change if the direction was reversed? The computational model contains an inhibitory neuron which seems to target specifically the soma. For this reason, it is not surprising that the somatic K⁺ increases first. However, peri-somatic inhibition is a characteristic of PV-inhibitory interneurons. Somatostatin (SOM) expressing inhibitory interneurons predominantly target dendrites. Given recent studies showing that stimulation of either SOM or PV interneurons can trigger seizure onset, how might this impact the bifurcation dynamics presented here?

4. The results pertaining to Cl concentration are interesting and extend a large number of recent studies examining the role of Cl in seizure dynamics. With regards to the KCC2 co-transporter this story becomes more interesting as it may have an impact on febrile seizures and seizures in children as the levels of KCC2 are lower and so the Cl concentration dynamics are not regulated in the same manner as in the adult brain. This may lead to age-related differences in seizure susceptibility between children and adults. Given the results presented in this manuscript some brief discussion on this topic may help highlight the impact of this finding.

5. Given the amount of detail in the computational model there remains a number of network parameters that would be interesting to explore. Of specific interest would be the volume dynamics as there is ample experimental data demonstrating substantial changes in interstitial volume prior to seizure onset.

1. In its current form, the schematic in figure 1 gives the impression that vasculature and astrocytic interactions are included in the model. I believe it is not. It might be useful to drop those cartoons from the schematic to prevent confusion regarding what is specifically being modeled.

2. Please show specific examples of each activity type (resting state, tonic spiking, and bursting), in figure 2 when they are first described.

3. The stimulation of IN was said to result in a firing rate of 270Hz. It does not seem to be very realistic. Is there experimental evidence to justify such an increase in firing rate of IN neuron prior to SLE? If the model would be changed to get a lower firing rate would this affect the results?

4. Does blocking or reducing GABA-A conductance in the model without additional IN stimulation result in SLE? It is not clear if that is the case. If it does, this would be an interesting result to show or reference as it is a more one-to-one comparison with the experimental model of SLE.

5. In figure 3, a better comparison might be to apply the same or similar depolarization to the model PY as was done in the experiment. This could better highlight the match between the experimental and modelling results.

6. When discussing the bifurcation diagrams, it might be beneficial to discuss the types of bifurcations that occur at the specific transitions between activity regimes.

7. Did the authors consider the effects of HCO₃^- in GABAergic currents? Since it was included as part of the GABA current and the fact the HCO₃^- concentrations are crucial for maintaining GABA-A receptor reversal potentials some discussion on the role of HCO₃^- in this regard would be needed.

8. Volume dynamics were included in this model and have been previously explored in other models (e.g., Schiff lab). How did volume change during the course of the simulation? How does volume impact the bifurcation diagrams for dendritic vs somatic K concentration?

Reviewer #3 (Recommendations for the authors):

Gentiletti et al. uses a computational model to investigate the mechanism underlying focal seizures. The small-network model consists of one interneuron and four pyramidal cells with various active and passive currents, and detailed ion concentration dynamics. The main focus of the study is to validate the hypothesis and previous results about the interneuronal origin of focal seizures. Specifically, in the model seizures are induced by stimulating the interneuron, which then raises the extracellular potassium ([K]o) levels, leading to high-frequency spiking in pyramidal cells. Detailed analysis of the pre-ictal, ictal, and post-ictal periods during seizures is also offered.

While technically sound, the study does not offer any major new innovations to warrant publication in eLife. I believe that the analysis presented is similar, in many ways, to previous modeling studies, but with a slightly different view. As detailed below, in some places it feels that the model parameters are selected so that a desired result is produced. The idea that interneurons can cause seizures by itself is not entirely new. There is extensive experimental (some cited by authors) and some modeling data supporting this hypothesis. Thus, I feel that the paper is more suitable for a specialized journal in computational neuroscience.

Following are some specific concerns about the study.

Figure 2 and related text: The experimental data shown for comparison is confusing. It is not clear if these are new experiments done for this study or data from three different previous studies are combined for comparison with the model. Another confusion about the experimental data is that in the beginning, it is mentioned that seizures are induced by bicuculine in the isolated guinea pig brain (Figure 3A), but later it is mentioned that "The strong preictal firing of the PY cells was artificially triggered by the injection of a steady depolarizing current via the intracellular recording electrode to analyze the intracellular firing correlates during the SLE (Gnatkovsky et al., 2008)." This gives the impression that the experimental traces shown for comparison are from three different experiments where the seizures are induced by different mechanisms, and are selected because they match what the model does.

Figure 6. In some places, it seems that the model is made to behave like the experiment. For example, in Figure 6, no reason is given for why the pyramidal cells are stimulated with 6 pA current. What would be the circumstances in the tissue or intact brain where the pyramidal cells would receive such input?

Lines 413 – 419: The paper claims that the previous modeling studies induced seizures by either stimulating pyramidal cells or increasing [K]o, whereas in this study, seizure is induced in the model by stimulating the interneuron. On the surface, this is true. But in reality, the approach adopted by this study is an indirect method of raising extracellular potassium of pyramidal cells. Stimulating interneurons leads to higher [K]o and hence seizures. This is also acknowledged by the authors. However, what is not clear is that why in the network only interneurons would receive strong depolarizing stimulus but not pyramidal cells. It should also be noted that the interplay between interneurons and pyramidal cells during seizures under normal [K]o in a modeling study was first reported by Wei et al. (2014) (PMID: 24671540).

Line 437-439: "This suggests that in our model, a change in the concentrations of either [K⁺]o or [Cl^-]i was not sufficient to initiate an SLE and that an increase in both is necessary." This seems to be a model-specific effect because several modeling studies have shown that raising [K]o alone can cause the network to enter seizure-like state.

Line 250: [Na+]I should be [Na+]i.

[Editors’ note: further revisions were suggested prior to acceptance, as described below.]

Thank you for resubmitting your article "Focal seizures are organized by feedback between neural activity and ion concentration changes" for consideration by eLife. We apologise for the delay in assessing your revised manuscript, this was caused by our inability to secure one of the original reviewers which required finding an additional reviewer. This version of your article has now been reviewed by 3 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and Ronald Calabrese as the Senior Editor. The following individual involved in the review of your submission has agreed to reveal their identity: Joseph V Raimondo (Reviewer #1).

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission.

In general, the reviewers were positive about the manuscript and the changes made.

Essential revisions:

We ask that you focus specifically on addressing the following

1. Clarify the specific novel contributions of this work in the abstract. The role of Na+, Na+/K⁺ pump on termination and Cl^- on seizure initiation have been previously shown.

2. The bifurcation analysis that suggests soma and dendrite differences for K⁺ concentration resulting in different regimes is interesting. Could you add to the discussion whether there is any experimental evidence for such significant differences in the concentrations for soma and dendrite?

3. With reference to the bicuculline model, could you add to the discussion in order to explain your mechanistic reasoning for how this “recruits the interneuronal network”

4. As the slowing of the interburst interval is one of the novel aspects of this work, it would be helpful to show that ion changes influence the inter-burst interval variations observed during the course of the seizure. Specifically, could you identify the bursting frequencies from the bifurcation analysis and confirm the role of Na⁺ accumulation in the slowing of burst interval.

Please find the full reviews below:

Reviewer #1 (Recommendations for the authors):

In this much revised manuscript the authors have improved several features of how ion dynamics were modelled enhancing the validity of their findings. The authors have gone to great lengths to address my concerns. In my opinion the manuscript enhances our understanding of the mechanisms underlying seizure dynamics.

Novelty

[Interneurons driving seizure onset] The authors have generated a thorough model of how intense activity of interneurons can drive K⁺ build-up and the initiation of seizures. This is certainly the most thorough and biophysically realistic model which recapitulates the electrographic feature of human seizures in a satisfying manner.

[Increased Na+/K⁺-pump driving the SLE termination and the post-ictal state]. The authors state that “We show for the first time that seizure termination and postictal state may be generated by the same mechanism mediated by increased activity of the Na+/K⁺-pump. It is an alternative mechanism of the postictal state, which previously has been suggested to depend on potassium undershoot (Krishnan and Bazhenov, 2011).” I disagree with the authors’ interpretation and insistence that this is novel. In Krishnan and Bazhenov, they explicitly describe essentially the same mechanism. Their potassium undershoot is caused by increased activity of the Na+/K⁺-pump (the show and state this explicitly).

“In our model extracellular potassium decays to baseline after an SLE offset, hence it cannot account for the postictal state.” This is also what (Krishnan and Bazhenov, 2011) show (see their Figure 8). I can’t see any fundamental difference between your interpretation and theirs, which is certainly satisfying, but not new as far as I can tell.

[Exponential IBI distribution]. I agree that the model satisfyingly shows how accounting for ion concentration changes can generate an exponential IBI distribution toward the end of the seizure.

Other responses:

I thank the authors for clarifying that in their model bicuculline does not block all of GABAergic inhibition, but is likely a transient perturbation which somewhat counterintuitively recruits the interneuronal network.

The authors have gone to great lengths to improve how Cl^- flux through GABAaRs and the Cl^- leak conductance was modelled. Figure 5 is a wonderful figure (along with Appendix – Figure 3). I am now satisfied that the ion dynamics were modelled in a suitable way which gives me much increased confidence in the authors’ findings.

Reviewer #4 (Recommendations for the authors):

In this work, the authors use a computational model to examine the role of ion dynamics in inhibition-mediated TLE seizures. Of significance, the seizure activity precisely matched the experimental data, specifically the time course of the inter-burst interval. The study also replicates previous experimental and computational observations on the role of K⁺ on seizure initiation, Na+, Na+/K⁺ pump on seizure termination. Further, the findings from this work suggest additional contributions of Na+/K⁺ pump to post-ictal depression and K⁺ influence on KCC2 pump promote seizure initiation.

While the paper’s findings are a significant contribution that emphasizes the importance of ion dynamics on seizure, the novel contribution highlighted by authors seems only as slight variations of previously proposed mechanisms. Nevertheless, the manuscript is definitely worthy of publication, perhaps in a more specialized journal.

Few suggestions that could improve the manuscript:

1. Bicuculline, a GABA antagonist induced the seizure in the experimental condition, but in the computational model, seizure was induced by increasing the inhibitory neurons’ activity. While the increase in inhibitory neuron’s activity is observed following bicuculline in the experiment, there is a missing network mechanism that results in this increase of inhibitory neurons activity following the application of bicuculline. It would be more compelling if the authors could identify this mechanism and demonstrate the onset of a seizure by bicuculline in the computational model.

2. It would be very helpful to clarify the specific novel contributions of this work in the abstract. The role of Na+, Na+/K⁺ pump on termination and Cl^- on seizure initiation have been previously shown. Also, it would be helpful ’or authors to note that K⁺ influenced the KCC2 pump time constant in Gonzalez et al., 2018.

3. The bifurcation analysis that suggests soma and dendrite differences for K⁺ concentration resulting in different regimes is interesting. It would be helpful to expand on this finding, and the report is one of the novel contributions. Is there any experimental evidence for such significant differences in the concentrations for soma and dendrite?

4. It would be helpful to show that ion changes influence the inter-burst interval variations observed during the course of the seizure. Specifically, the authors could identify the bursting frequencies from the bifurcation analysis and confirm the role of Na⁺ accumulation in the slowing of burst interval.

https://doi.org/10.7554/eLife.68541.sa1

Author response

[Editors’ note: The authors appealed the original decision. What follows is the authors’ response to the first round of review.]

Comments to the Authors:

We are sorry to say that, after consultation with the reviewers, we have decided that your work will not be considered further for publication by eLife.

Although there was certainly enthusiasm about the model, which was found to be generally thorough and broadly satisfying in its behaviour and predictions, there was ultimately collective concern from all 3 reviewers about whether there was the requisite level of novelty and advance over prior work to justify publication in eLife.

Please find the reviews below.

Reviewer #1 (Recommendations for the authors):

The model uses the NEURON framework and is well put together. On the whole its behaviour is both satisfying and reassuring. The model recapitulates the electrographic behaviour of animal model and human EEG recordings in particular the low-voltage fast activity preceding the tonic phase of a seizure, which transitions into bursting. The bursts then slow in frequency before postictal suppression of activity is observed. These dynamics emerge out of the model due to its inclusion of ion dynamics of K⁺, Na⁺ and Cl^- and multiple cellular mechanisms including accounting for excitatory and inhibitory cell populations, dendritic and somatic compartments, diffusion, glial buffering, ion channels and ion transporters.

Whilst the work is very much worthy of publication, I am not convinced that it generates sufficiently novel findings and advances over previous work in the field (e.g. Krishnan 2011 and Krishnan 2015 and others) to be of sufficient interest to warrant publication in eLife. In my opinion the importance of K⁺, Cl^- and Na⁺ dynamics for seizure evolution have been demonstrated before. (e.g. increases in K⁺ driving SLE initiation, transition between tonic and bursting activity and seizure cessation occurring due to enhanced Na+/K⁺ ATPase activity).

We thank for overall positive judgment of our model. In our opinion our simulation data are novel and do advance mechanistic insight obtained from previous models as we demonstrate at least three important novel features/mechanisms that were not captured by any realistic computational seizure model so far.

Bazhenov’s team developed a model of neocortical seizures (Krishnan and Bazhenov 2011; Krishnan et al., 2015) which exhibit multiple transitions between tonic and bursting phases. Differently, our model considered for the first time a typical focal seizure pattern observed in human temporal lobe epilepsy (TLE) consisting of distinct phases, i.e., low voltage fast activity onset, tonic phase, clonic phase and postictal suppression phase. Human TLE seizures were shown to begin with increased firing of inhibitory interneurons (Elahian et al., 2018). Hence, the leading question behind our model was the mechanism by which interneuronal discharges initiate seizures. While this mechanism was investigated by others only once before (Gonzalez et al., 2018), we find these results not fully conclusive. In that model the direction of current flow through KCC2 was explicitly assumed to be outward and the influence of K⁺ concentration on flux direction was not considered. We note that in Gonzalez et al. (2018) rise in [K⁺]_o was larger than rise in [Cl^-]_I (their Figure 4A) suggesting that in their model the direction of KCC2 transport would presumably be reversed. Therefore, the conclusion provided by the model, that SLE can be induced by K⁺ accumulation via outward K-Cl cotransport is still open for discussion. Our present model suggests an alternative scenario in which initial build-up of extracellular K⁺ occurs via voltage-gated K⁺ channels activated by intense interneuronal spiking. Our preliminary study showed seizure initiation by interneurons (Gentiletti et al., 2017) in a simple two-cell model, and the underlying mechanism was not investigated.

We show for the first time that seizure termination and postictal state may be generated by the same mechanism mediated by increased activity of the Na⁺/K⁺-pump. It is an alternative mechanism of postictal state, which previously has been suggested to depend on potassium undershoot (Krishnan and Bazhenov, 2011). In our model extracellular potassium decays to baseline after an SLE offset, hence it cannot account for the postictal state. It is important to mention that both patterns of postictal potassium time course were observed experimentally (with undershoot, e.g., Dreier and Heinemann (1991) and with slow decay e.g., Fisher et al., 1976). Our novel hypothesis, which is consistent with the experimental evidence that inhibition of Na⁺/K⁺-pump prolongs SLE and reduces post-SLE period (Haas and Jefferys, 1984), has never been demonstrated by any computational model so farThe model predicts for a first time that ion concentration changes at the end of seizures lead to exponential inter-burst interval (IBI) distribution as indeed observed experimentally. Recently, there is increased interest in the IBI pattern due to seizure taxonomy developed by Victor Jirsa’s group (Jirsa et al., 2014, Saggio et al., 2020). His generic epileptor model predicts logarithmic relationship of IBI which is in contrast to human seizure data analyzed by us in the manuscript and others (Bauer et al., 2017).

(1) I am concerned as to the applicability of the experimental data to this model. SLEs in the whole guinea pig brain were elicited using bicuculline, which blocks GABAaR transmission yet current from the IN to pYs via activated GABAaRs is presumably an important component of the computational model?

We thank the Reviewer for raising this point as it allows us to better clarify this issue. We tend to maintain our opinion that choice of experimental model was appropriate. On the other hand, we recognize that our original presentation needed further explanation. We used experimental data from SLEs induced by brief perfusions of convulsive drugs in the whole guinea pig brain in vitro model (Gnatkovsky et al. 2008; Uva et al. 2009; Uva et al. 2015). In the whole brain in vitro model, transient (3 minute) arterial perfusion of 50 microM bicuculline reduces GABAergic inhibition only transiently to 60-70% (Gnatkovsky et al., 2008, Figure 1). This treatment does not block GABAergic transmission, but reduces it. As discussed in Gnatkovsky et al. (2008), this brief bicuculline application likely affects interneuron-interneuron inhibition more than interneuron-principal cell inhibition and recruits the interneuronal network. With this treatment (and also with 5-minute perfusion with 100 µM 4 aminopyridine) SLE onset correlates with interneuron bursting and with no activity in principal cells (Uva et al., 2015). The same phenomena have been observed in spontaneous seizures in patients with mesial-temporal epilepsy (Elahian et al., 2018). Hence we choose bicuculline model to guide our modeling work because: (i) SLEs in this model are initiated by enhanced firing of inhibitory interneurons, (ii) SLE pattern in this model closely resemble human temporal lobe seizure (iii) LFP, single unit and ionic data are available. We explain the choice of this model in the Introduction (ln. 64-69) and we describe it more thoroughly in the Results (ln. 98-103).

(2) Understandably the model cannot recapitulate all biological detail but there are some aspects about the model which seem odd and would need justification:

a. e.g. Intracellular HCO₃^- is higher than intracellular bicarbonate (15 mM) being higher than extracellular bicarbonate (11 mM). This suggests that intracellular pH is more alkaline than extracellular pH which is not the case. In addition, this would make the bicarb reversal +8 mV which is high and unrealistic.

In the original model the [HCO3]_o was calculated based on electric and osmotic equilibrium but we admit that its value was not optimal. In the revised version of the model we modified some ionic concentrations and we set [HCO3]_o = 25 mM, [HCO3]_i = 15 mM (Doyon et al., 2011) giving the HCO₃^- reversal potential, E_HCO3 = -13.4 mV. It is described in the Initial ion concentrations subsection of the revised manuscript starting at ln. 878.

b. In the neurons the Na⁺ leak conductance is 40% of the K⁺ leak conductance, this seems very high and not a typical ratio of permeabilities for neurons.

In the revised model, Na⁺ leak current conductance was determined by a condition that at rest all Na⁺ and K⁺ currents are in ratio -3/2 and are counterbalanced by a Na⁺/K⁺-pump. Accordingly, there is no net flux of Na⁺ and K⁺ ions at rest. E.g, in the PY soma it led to the following values: g_K,leak = 3*10^-5 S/cm², g_Na,leak = 1.5*10^-5 S/cm². These values are comparable to g_Na,leak/g_K,leak ratio used in other realistic models e.g., 45% (Krishnan et al., 2015), 49 % (Wei et al., 2014b). We note that leak currents in our manuscript are calculated using ohmic model with conductance values expressed in unit of S/cm², while permeability values are typically expressed in units of m/s and are used in Goldman-Hodgkin-Katz model. Therefore, leak conductance values and permeability values are difficult to compare directly. In order to validate our setting of leak conductances we calculated resting membrane potential in two ways. First, we used classical Goldman-Hodgkin-Katz voltage equation and second, we calculated resting membrane voltage derived from the ohmic model i.e., Vrest = (g_KE_K + g_KE_K + g_ClE_Cl)/(g_K + g_Na + g_Cl). For PY somatic compartment, the leak conductances used in our model were: g_K,leak = 3*10^-5 S/cm², g_Na,leak = 1.5*10^-5 S/cm², g_Cl,leak = 1*10^-5 S/cm². For these values we obtained an agreement with the Goldman-Hodgkin-Katz model having permeabilities P_K : P_Na : P_Cl = 1 : 0.075 : 0.1. These permeabilities are comparable to experimental data (e.g., in the squid giant axon the ratio is 1: 0.03: 0.1) what gave us confidence that the leak current conductances used in the model are in physiological range.

c. It wasn't clear whether the leak conductances for the various ions were actually contributing to the ion dynamics, e.g. was Cl^- flux through the baseline Cl^- leak conductance in neurons contributing to changes in [Cl^-]i?

In the revised model we increased g_Cl,leak and we set E_Cl > E_k at rest, hence the KCC2 was not in equilibrium. In this way all leak conductances were contributing to the ion dynamics, including baseline Cl^- flux, which at rest was compensated by Cl^- extrusion by KCC2.

d. Ek = Ecl at rest, this is also not physiological, I understand why this was done so that KCC2 was at equilibrium at baseline, but this is not ideal. Rather there should be a tonic Cl^- leak influx ensuring that "at baseline" Ecl>Ek as observed experimentally.

We thank the Reviewer for this suggestion. We modified the model accordingly.

(3) Modelling of Cl^- changes especially Cl^- flux through GABAaRs. I am also not entirely sure that Cl^- flux through GABAaRs was modelled correctly to capture the potential for biphasic/ depolarizing responses via intensely activated GABAaRs (the authors should note amongst others Ruusuvuori 2004). The calculation of Egaba included HCO₃^- (line 833) but how was Icl (Cl^- flux) via activated GABAaRs calculated? Ie in the model if Vm is at the GABAaR reversal potential (Egaba) would Cl^- ion flux into the cell via GABAaRs (Icl) be zero? Ie in the model if Icl calculated as 4/5 of Igaba and Igaba = Ggaba(Vm – Egaba), then when Vm = Egaba, Igaba and consequently Icl is 0. This shouldn't be the case. Rather Igaba = Icl + Ihco3 where Icl = gcl(Vm – Ecl) and Ihco3 = ghco3(Vm – Ehco3) and ggaba = 4/5xgcl +1/5xghco3. Seeing as Cl^- accumulation is a fundamental part of the model this should have been made more clear. E.g. in Figure 5, could Icl via GABAaRs also be plotted? I worry as the Cl^- influx in the model seemed to be coming predominantly via KCC2 (due to the raised extracellular K⁺) whereas experimentally this is likely also coming predominantly through GABAaRs. This is reflected in the time course of [Cl^-]i changes in the model which are slower than [K⁺]o and continue increasing until the end of the SLE which is not typically what is observed experimentally (see intracellular Cl^- recordings e.g. Raimondo 2013).

These are very relevant points and we recognize that we used simplified formula for Icl flux through GABAaR in the original manuscript. In the revised manuscript we carefully addressed this issue and corrected our approach. We divide our answer into separate sections.

Modelling of Cl^- flux through GABAaRs

Indeed, in the original manuscript we considered HCO₃^- influence on the I_Cl GABAA current via E_GABAa, which depended on both Cl^- and HCO₃^- concentrations but we didn’t model I_HCO3 flux separately. Following Reviewer’s suggestion, we used extended formula of Igaba as described by the Reviewer and also used by Jedlicka et al., (2011):

Igaba = Icl + Ihco3

Icl = (1-P)*g*(v-Ecl)

Ihco3 = P*g*(v-Ehco3)

Egaba = P*Ehco3 + (1-P)*Ecl

P = 0.18 (relative permeability)

HCO3i = 15 mM

HCO3o = 25 mM

With the modified formula for Igaba we obtained model behavior that was qualitatively the same as in the original model. It shows that our conclusions were not affected by a simplified formula for Igaba or by imprecise setting of [HCO₃^-]_o. However, we agree that the recommended changes were appropriate, and we thank the Reviewer for this suggestion.

Cl^- influx through GABAaR and KCC2

In the revised manuscript we plot Cl^- currents flowing via GABAaR and KCC2 (Figure 5B, two bottom panels). It can be seen that during an SLE chloride accumulation is dominated by Cl^- influx via GABAaR with smaller flux via KCC2 transporter and only small contribution from I_Cl,leak.

Continuous increase of [Cl^-]_i during an SLE

Indeed, in our model, the [Cl^-]_i continues to increase due to both GABAaR and KCC2 mediated currents until the end of an SLE. In other realistic models (Krishnan and Bazhenov, 2011; Krishnan et al., 2015), which mimic neocortical electrographic seizures, [Cl^-]_i also builds up over the course of the whole SLE and the [Cl^-]_i increase was proposed to contribute to seizure termination by changing the minimal [K⁺]_o level required to initiate next tonic spiking episode (Krishnan and Bazhenov, 2011). These modeling results showing continuous [Cl^-]_i increase during SLE agree with [Cl^-]_i recordings during SLE induced in vivo by 4-AP (Sato et al., 2017; Figure 8). On the other hand, they differ from experimental data showing decline of [Cl^-]_i during SLE induced by bath application of Mg²⁺-free solutions in rat organotypic hippocampal slice cultures or acute mice cortical slices (Raimondo et al., 2013; Figure 3 and 4). These findings might suggest that there is no single scenario of [Cl^-]_i time course during SLE and that different seizure models could exhibit different [Cl^-]_i evolution patterns, which depend on simultaneously changing [K⁺]_o among other mechanisms. E.g., it has been shown that there is differential involvement of inhibitory interneurons in 4AP and low Mg²⁺ models (Codadu et al., 2019), which, in turn, could lead to different K⁺ and Cl^- accumulation patterns. We discuss this issue in the revised manuscript (ln. 518 – 525).

Biphasic/ depolarizing responses following GABAaR activation

The model has a potential to generate biphasic/ depolarizing responses via intensely activated GABAaRs (Kaila et al., 1997; Ruusuvuori et al., 2004; Viitanen et al., 2010). These responses could be elicited in the model only if GABAergic inputs were located in small compartments representing distal dendrites (i.e., having smaller volume and higher GABAA receptor density than soma in the reference model). An example of hyperpolarizing-depolarizing GABAA response in a small dendritic compartment is shown in Appendix I – figure 3. The depolarizing component is related to strong Cl^- accumulation and depolarizing shift in E_GABAa. We hypothesize that depolarizing responses following GABAaR activation might be more readily observed due to activation of dendrite-targeting somatostatin-expressing (SST) interneruons rather than soma-targeting parvalbumin-positive (PV) interneurons. In our reference model GABAA synapses are located in the soma, which is based on the observation that activation of PV interneurons was implicated in spontaneous seizures (Toyoda et al., 2015). Due to large size of somatic compartment, GABAaR activation leads to moderate Cl^- accumulation giving rise to limited shift in E_GABAa (Figure 5B)_. Our hypothesis is in agreement with other studies suggesting that [Cl^-]_i can change rapidly and contribute to depolarizing GABAA responses especially in the structures with low volume to GABAA receptor density ratio (Staley et al., 1995; Staley and Proctor, 1999).

(4) Perhaps the authors could make it more clear that the exact same experimental data was also presented in Gentilleti 2017.

We thank the Reviewer for pointing this out. We added appropriate references to the experimental data.

Reviewer #2 (Recommendations for the authors):

Gentiletti et al. investigated potential role of non-synaptic mechanisms driving seizure-like event (SLE) generation. Using a detailed computational model of a small network of neurons, the authors demonstrate that the complex interaction between specific ion species may give rise to SLE. The detailed analysis of the computational model provides an interesting approach to developing a unifying framework for neural dynamics. The strength of this manuscript is in the direct validation of key aspects of the computational model using in vitro electrophysiology. Additionally, predictions made by the model such as the slowing of inter-burst intervals are subsequently validated in both human and mouse data. The conclusions made by the authors of this manuscript are supported by their results and are in line with previous work in the field. Finally, the manuscript does a good job relating the novel results of this new manuscript with established results in the field.

We thank for overall positive judgment of our model and our results.

1. A strength of this manuscript is the direct validation of the computational model with experimental results. Given the multitude of methods available for inducing seizure-like events (SLE) in vitro, it is a bit surprising that the authors chose to use an arterial application of bicuculline (Figure 3). Bicuculline is a competitive antagonist of the GABA-A receptor resulting in the reduction of inhibitory GABAergic signaling. However, the SLE induced in the model is caused by an increase in inhibitory activity, through direct depolarization, rather than a decrease in GABAergic signaling. At first glance these methods for inducing SLE seem to be at odds with one another. Given the observed increase in extracellular K⁺ at SLE onset, this mismatch in the method for SLE generation in vitro and in silico may further highlight one of the primary claims of the manuscript specifically that disruption of ionic homeostasis rather than solely synaptic excitatory/inhibitory imbalance is a mechanism for SLE generation. Additional discussion of this observation and similar phenomena in other methods for SLE generation in vitro would further strengthen this interesting point.

We thank the Reviewer for this relevant comment. We agree that the rationale for using direct depolarization of the interneuron to initiate an SLE and the use bicuculline model data could seem inconsistent and needed further explanation. Increased interneuron discharges and decreased PY activity around the time of seizure onset have been shown in SLE induced in vitro by 4-AP (Ziburkus et al., 2006; Lévesque et al., 2016; Uva et al., 2015) and brief bicuculline applications (Gnatkovsky et al., 2008), in acute and chronic seizure models in vivo (Grasse et al., 2013; Miri et al., 2018; Toyoda et al., 2015) and temporal lobe of epilepsy patients (Elahian et al., 2018). Motivated by this general observation obtained under different experimental conditions, we aimed to test whether fast intraneuronal discharges can indeed trigger an SLE in silico and if so, what would be the underlying mechanism.

We used data obtained during transient bicuculline perfusion in the isolated guinea pig brain because SLE in this model closely resemble human TLE seizures (de Curtis and Gnatkovsky 2009) and are initiated by increased interneuron discharges (Gnatkovsky et al., 2008). Brief bicuculline application likely affects interneuron-interneuron inhibition more than interneuron-principal cell inhibition (Gnatkovsky et al., 2008). With this treatment SLE onset correlates with interneuron bursting and with no activity in principal cells (Uva et al., 2015), suggesting that interneuron-principal cell GABAergic signaling is still functional at the beginning of an SLE. On the other hand, reduced inhibition among IN cells could possibly produce interictal spikes generated by interneurons leading to increase in extracellular potassium, that in turn would further depolarize interneuronal network and initiate SLE (de Curtis and Avoli, 2016, Figure 4). In alternative scenario reduced inhibition among interneurons could lead to abrupt switch from low firing to high firing rate mode of IN network (Rich et al., 2020). Hence, to initiate an SLE we decided to simulate only the ‘effect’ of reduced interneuron-interneuron inhibition manifested by their increased discharge. In this way we made our model more general and applicable to numerous experimental data in which paradoxical increase of GABAergic cell firing is observed at seizure onset. We explain choice of bicuculline model in the Introduction (ln. 64-69) and we describe bicuculline action more thoroughly in the Results (ln. 98-103).

2. Bifurcation analysis in figure 4A produces interesting results that are in line with and supported by previous work. As stated in the text, an assumption made by the authors is that the intracellular dendritic and somatic Na⁺ is equal. The authors further mention that this assumption may result in an overestimation of dendritic Na⁺ and Na/K pump activity but do not discuss how this might impact the results presented in the bifurcation diagrams. Please include.

Following Reviewer’s suggestion, in Figure 4A we present more detailed bifurcation analysis with separate values for dendritic and somatic [Na⁺]_i in the revised version of the manuscript.

3. It is striking that the time course of the extracellular dendritic K⁺ concentration is much slower than for the soma. It is not clear if the delayed increase in dendritic K⁺ is a prediction of the computational model or if it has been experimentally observed and incorporated into the model as such. Some discussion clarifying this point is needed. To that point, are the authors suggesting that the longitudinal diffusion of K⁺ from soma to dendrite is driving the delayed increase? If so, how might the observed dynamics change if the direction was reversed? The computational model contains an inhibitory neuron which seems to target specifically the soma. For this reason, it is not surprising that the somatic K⁺ increases first. However, peri-somatic inhibition is a characteristic of PV-inhibitory interneurons. Somatostatin (SOM) expressing inhibitory interneurons predominantly target dendrites. Given recent studies showing that stimulation of either SOM or PV interneurons can trigger seizure onset, how might this impact the bifurcation dynamics presented here?

We thank the Reviewer for pointing out this important issue and we agree that it was not properly discussed. Indeed, the time course of [K⁺]_o rise is slower and its magnitude is diminished in dendritic vs. somatic compartment. We are not aware of any experimental data showing such effect; hence it can be considered a model prediction.

The Reviewer is correct that initial fast rise of [K⁺]_o in somatic compartment and slower rise in dendritic segment is related to inhibitory neuron, which targets specifically the soma and also to small longitudinal diffusion between extracellular compartments. During the course of the SLE, as interneuron activity decreases, the additional contribution to [K⁺]_o comes from pyramidal cell firing, The dendritic conductance of voltage-gated K⁺ currents associated with spiking is about 10% of the somatic conductance (Fransen et al., 2002) hence release of K⁺ ions into the dendritic interstitial space is smaller than in somatic compartment. On the other hand, radial diffusion (to the bath) and glial buffering processes have the same efficiency in both compartments maintaining higher K⁺ near the soma.

As the Reviewer points out, indeed, activation of either PV or SOM inhibitory interneurons can trigger SLE (Yekhlef et al., 2015). In our model, we predict that if the interneuron was targeting the dendrite, it could still trigger an SLE. As shown by the bifurcation diagram in Figure 4A (first panel) an increase in either somatic or dendritic [K⁺]_o leads to transition from rest to tonic spiking and then bursting. Given these two possible scenarios, our choice to include soma-targeting fast spiking interneuron was motivated by the fact that PV interneurons were more often selected as target for optogenetic stimulation (Ellender et al., 2014; Sessolo et al., 2015) and were supposed to be implicated in spontaneous seizures (Toyoda et al., 2015). We addressed this relevant issue in ln. 527-535 and ln. 543-548 of the revised manuscript.

4. The results pertaining to Cl concentration are interesting and extend a large number of recent studies examining the role of Cl in seizure dynamics. With regards to the KCC2 co-transporter this story becomes more interesting as it may have an impact on febrile seizures and seizures in children as the levels of KCC2 are lower and so the Cl concentration dynamics are not regulated in the same manner as in the adult brain. This may lead to age-related differences in seizure susceptibility between children and adults. Given the results presented in this manuscript some brief discussion on this topic may help highlight the impact of this finding.

Indeed, KCC2-dependent chloride and potassium homeostasis may depend on age. E.g., it has been shown in rats that KCC2 shows little expression in neonates and increases with neuronal maturation but there is also high heterogeneity of KCC2 expression in pyramidal cells at birth, with some neurons having efficient KCC2 activity and low [Cl^-]_i (Ben Ari, 2002). With regard to febrile seizures, it has been shown that they may be related to reduced Cl^- extrusion through KCC2 (Puskarjov et al., 2014) what in turn could lead to decreased formation of dendritic spines. During an SLE generated in our model, E_K is higher than E_Cl and KCC2 operates in reverse direction (Figure 5). Despite KCC2 activity leads to Cl^- and K⁺ transport into the cells during an SLE and contributes to positive E_Cl shift, depolarizing GABAA responses are not observed in the model. In the revised manuscript we discuss that limited shift in EGABAa in the model may be related to large size of the somatic compartment, which is targeted by inhibitory input from the IN (ln. 465-680 and Appendix I – figure 3). At the same time, we would prefer not to relate our model findings to neonatal seizures, as the current model may be too limited (e.g., lack of NKCC1 cotransporter) to mechanistically account for these phenomena.

5. Given the amount of detail in the computational model there remains a number of network parameters that would be interesting to explore. Of specific interest would be the volume dynamics as there is ample experimental data demonstrating substantial changes in interstitial volume prior to seizure onset.

This is relevant point and indeed we recognize that we didn’t discuss this topic sufficiently in our original presentation. In the revised manuscript we added Appendix I – figure 4 showing volume changes. It can be seen that extracellular space (ES) volume shrinks maximally by about 27%, which is comparable to Dietzel et al. (1980) who reported average reduction of the ES by about 30%. Intracellular space (IS) volume expands about 4%, which comes from the fact that the total volume is constant (ES+IS = const). Volume changes affect all ion concentrations as demonstrated using the time course of the intracellular A^- and extracellular Cl^- ion concentrations in Appendix I – figure 4. We selected these ions as an example because [A^-]_i concentration doesn’t depend on any other mechanism while [Cl^-]_o is not regulated by the efficient Na⁺/K⁺ pump and glial buffering. Despite extracellular volume changes in our model are significant, counterintuitively, these changes don’t have big impact on the observed model dynamics. We notice that due to slow time course of the volume changes, extracellular concentrations of all ions are efficiently compensated by other mechanisms e.g., radial diffusion to the bath, which act on a faster time scale. Additionally, extracellular potassium is under efficient and relatively fast control of the glial buffering and Na⁺/K⁺ pump which dominate the effect of extracellular volume changes in both somatic and dendritic compartments. However, it should be noted that in our model glial cell swelling was not included and diffusion to the bath was not affected by the volume changes. In the revised manuscript we mention it as one of the model limitations. In the real tissue astrocyte swelling may be significant and flow of ions and oxygen (affecting Na⁺/K⁺-pump activity) may be reduced contributing to seizures and spreading depression (Hubel and Ullah, 2016) (ln. 865-875).

Regarding preictal volume changes indeed, constriction of blood vessels (Patel et al., 2013), lowering extracellular ca²⁺ concentration was observed. The exact mechanism linking these changes to spontaneous seizure generation is still unclear but might be investigated with computational models. As discussed in Somjen (2004; p. 84), lowered concentration of [ca²⁺]_o might decrease surface charge screening effect and depolarize cells leading to network hyperexcitability. However, the effect of surface charge on membrane potential was not included in the current model hence it is not well-suited to explore this question.

6. In its current form, the schematic in figure 1 gives the impression that vasculature and astrocytic interactions are included in the model. I believe it is not. It might be useful to drop those cartoons from the schematic to prevent confusion regarding what is specifically being modeled.

Indeed, vasculature is included in the model only indirectly by fluxes to/from the bath medium, which represents various processes such as diffusion to more distant areas of the brain and cerebrospinal fluid, active transport of potassium into capillaries and potassium spatial buffering by astrocytes. Glial cell interactions are not included explicitly but the process of spatial potassium buffering by astrocytes is accounted for by the glial buffer included in each extracellular compartment. We agree that as the vasculature was not explicitly modeled, the blood vessel drawing might create confusion and should be removed. On the other hand, we would prefer to keep astrocyte cells in the model diagram to emphasize that potassium regulation by glial cells is essential part of the model.

7. Please show specific examples of each activity type (resting state, tonic spiking, and bursting), in figure 2 when they are first described.

We agree that the details of membrane potential traces are not well visible in Figure 2, but showing them as insets in that figure is also not optimal due small panel size. In the revised manuscript we clarify (ln. 113-114) that the three types of activity are shown in an extended time scale in Appendix I – figure 3.

8. The stimulation of IN was said to result in a firing rate of 270Hz. It does not seem to be very realistic. Is there experimental evidence to justify such an increase in firing rate of IN neuron prior to SLE? If the model would be changed to get a lower firing rate would this affect the results?

As mentioned in Gnatkovsky et al. (2008), putative interneurons in the entorhinal cortex generated fast discharges above 150 Hz before or at the onset of an SLE. Although some interneurons were indeed able to generate very fast (e.g., 270 Hz) discharges, the mean firing rate was around 166 Hz (Uva et al., 2015). Therefore, in the revised manuscript the initial firing rate of the interneuron was 150 Hz in order to match these experimental data.

9. Does blocking or reducing GABA-A conductance in the model without additional IN stimulation result in SLE? It is not clear if that is the case. If it does, this would be an interesting result to show or reference as it is a more one-to-one comparison with the experimental model of SLE.

Blocking GABA-A conductance in the model doesn’t lead to SLE by itself. It might sound counterintuitive as in general blockade of inhibition was shown to lead to synchronized paroxysmal activity (Connors, 1984). Several studies demonstrated that prolonged perfusion of brain slices with bicuculine generates large interictal spikes and afterdischarges lasting max 1 second (see de Curtis and Avanzini 2001), but never leads to true focal SLEs. As discussed in the answer to Reviewer #2 point 1 above, the mechanism leading to SLE after transient reduction of GABAergic inhibition is not entirely clear, but it may not be primarily related to a reduction of IN to PY inhibition but rather to IN disinhibition. We might hypothesize that in order to fully investigate this effect using a model one should include more extended interneuronal network with mutual inhibitory interactions. Blocking or decreasing GABA-A conductance in such a network could disinhibit IN cells and produce interictal spikes generated by interneurons contributing to increase of extracellular potassium. It would further depolarize interneuronal network and initiate SLE (de Curtis and Avoli, Figure 4). In an alternative scenario, reduction of GABA-A conductance in IN cells could lead to abrupt switch from low firing to high firing rate mode of the intraneuronal network (Rich et al., 2020) and trigger SLE via [K⁺]_o and [Cl^-]_i accumulation.

10. In figure 3, a better comparison might be to apply the same or similar depolarization to the model PY as was done in the experiment. This could better highlight the match between the experimental and modelling results.

Thank you for your remark. We agree that indeed PY cell membrane potential trace was misleading. We use alternative pyramidal cell data in Figure 3 of the revised manuscript.

11. When discussing the bifurcation diagrams, it might be beneficial to discuss the types of bifurcations that occur at the specific transitions between activity regimes.

Indeed, to get a better theoretical insight into transitions between different firing regimes it would be useful to analyze types of bifurcations associated with these transitions. Firstly, we note that in a model as complex as ours (each 2-compartment cell is described by about 60 differential equations) it would require a separate project to be carried out using Content or XPP Auto software package. Secondly, we used Neuron simulator, in which some differential equations are built-in in the simulator and while their general form is known, obtaining all necessary details is not straightforward. Finally, we prepared our manuscript for a wide audience of physiologists or clinicians working in the field of epilepsy. To increase clarity, we decided to avoid concepts from other disciplines e.g., dynamical system theory. Nevertheless, we appreciate your suggestion as it may motivate us to complement our current work with the future study directed to more theoretically oriented audience.

12. Did the authors consider the effects of HCO₃^- in GABAergic currents? Since it was included as part of the GABA current and the fact the HCO₃^- concentrations are crucial for maintaining GABA-A receptor reversal potentials some discussion on the role of HCO₃^- in this regard would be needed.

In the original model we included HCO₃^- only in the calculation of the GABAA reversal potential. Following Reviewers suggestion in the revised manuscript we used an extended formula of Igaba with explicitly modeled HCO₃^- currents (Jedlicka et al., 2011):

Igaba = Icl + Ihco3

Icl = (1-P)*g*(v-Ecl)

Ihco3 = P*g*(v-Ehco3)

Egaba = P*Ehco3 + (1-P)*Ecl

P = 0.18 (relative permeability)

HCO3i = 15 mM

HCO3o = 25 mM

In our reference model, GABAA receptors are located in the relatively large somatic compartments, what limits [Cl^-]_i accumulation and prevents depolarizing GABAA responses even when HCO₃^- currents are included explicitly. However, the role of HCO₃^- ions becomes especially evident in the simulation of GABAA responses in small dendritic compartments, in which [Cl^-]_i accumulation together with depolarized E_HCO3 leads to depolarizing shift in E_GABAa as shown in Appendix I – figure 3.

13. Volume dynamics were included in this model and have been previously explored in other models (e.g., Schiff lab). How did volume change during the course of the simulation? How does volume impact the bifurcation diagrams for dendritic vs somatic K concentration?

As discussed in the answer to Reviewer #2 point 5 above, volume changes were of realistic magnitude but didn’t have big impact on the observed model dynamics. Changes related to shrinkage of extracellular space had slower dynamics than other homeostatic processes and were efficiently compensated by various mechanisms (diffusion, glial buffering and transmembrane ion transporters). On the other hand, as shown by Hubel and Ullah (2016) astrocyte swelling may play a significant role leading to reduced flow of ions and oxygen (affecting Na⁺/K⁺-pump activity) in the tissue and contributing to seizures and spreading depression. These effects (reduced diffusion and reduced Na⁺/K⁺-pump rate) were not included in our model what is described as one of the model limitations (ln. 865-875).

Reviewer #3 (Recommendations for the authors):

Gentiletti et al. uses a computational model to investigate the mechanism underlying focal seizures. The small-network model consists of one interneuron and four pyramidal cells with various active and passive currents, and detailed ion concentration dynamics. The main focus of the study is to validate the hypothesis and previous results about the interneuronal origin of focal seizures. Specifically, in the model seizures are induced by stimulating the interneuron, which then raises the extracellular potassium ([K]o) levels, leading to high-frequency spiking in pyramidal cells. Detailed analysis of the pre-ictal, ictal, and post-ictal periods during seizures is also offered.

While technically sound, the study does not offer any major new innovations to warrant publication in eLife. I believe that the analysis presented is similar, in many ways, to previous modeling studies, but with a slightly different view. As detailed below, in some places it feels that the model parameters are selected so that a desired result is produced. The idea that interneurons can cause seizures by itself is not entirely new. There is extensive experimental (some cited by authors) and some modeling data supporting this hypothesis. Thus, I feel that the paper is more suitable for a specialized journal in computational neuroscience.

We thank the Reviewer for careful reading of our manuscript and his/her pertinent remarks. We fully agree that the idea that interneurons can cause seizures is not new but to the best of our knowledge the underlying mechanism is still a matter of debate. Specifically, the relative contribution of raised extracellular potassium (Avoli et al., 1996; Gnatkovsky et al., 2008) vs. increased intracellular chloride leading to depolarizing GABA responses (Lillis et al., 2012; Alfonsa et al., 2012) remains to be established. Furthermore, the question regarding the main source of extracellular potassium rise (voltage-gated K⁺ currents associated with interneuronal spiking vs. K⁺ extrusion via KCC2) is still open. We address and provide answers to these questions in our in silico study. We are convinced that such theoretical explanations contribute to better understanding of these complex mechanisms, which are currently not fully understood.

As also argued in response to Reviewer #1 our model exhibits at least three novel features/mechanisms that were not captured by any realistic computational seizure model so far. (i) The model reproduces all four phases of focal seizures (low voltage fast activity onset, tonic phase, clonic phase and postictal suppression phase) as observed in human focal epilepsy. (ii) It suggests a novel, Na⁺/K⁺-pump-based link between the seizure termination mechanism and postictal suppression state. (iii) It shows that ion accumulation-related mechanism may lead to specific scaling law of inter-bursting intervals (IBI) observed at the end of seizures. The exponential scaling law predicted by the model has been verified experimentally. We note that the recognized epileptor model developed by Victor Jirsa’s group (Jirsa et al., 2014, Saggio et al., 2020) predicted logarithmic relationship of IBI which is in contrast to our model and human seizure data. Therefore, we hope that our work provides satisfactory amount of novel contribution and offers new and advanced mechanistic insight into unsettled or unexplored seizure generation processes to warrant publication in eLife.

Following are some specific concerns about the study.

Figure 2 and related text: The experimental data shown for comparison is confusing. It is not clear if these are new experiments done for this study or data from three different previous studies are combined for comparison with the model. Another confusion about the experimental data is that in the beginning, it is mentioned that seizures are induced by bicuculine in the isolated guinea pig brain (Figure 3A), but later it is mentioned that "The strong preictal firing of the PY cells was artificially triggered by the injection of a steady depolarizing current via the intracellular recording electrode to analyze the intracellular firing correlates during the SLE (Gnatkovsky et al., 2008)." This gives the impression that the experimental traces shown for comparison are from three different experiments where the seizures are induced by different mechanisms, and are selected because they match what the model does.

We thank the Reviewer for pointing not sufficient information on experimental data used in Figure 3a and we recognize that our original description needed more clarity. Some experimental recordings used for comparison with model simulation were published previously, specifically, LFP and interneuron data were published in Gnatkovsky et al., 2008 (Figure 3A and 6B) and Gentiletti et al., 2017 (Figure 3). The PY cell and [K⁺]_o data have never been published before. It is challenging to carry out simultaneous intracellular recording from pyramidal cell and interneuron together with extracellular potassium recording in the in vitro isolated whole brain. Hence, the four signals presented in Figure 3a were recorded in different experiments during SLE in the entorhinal cortex of the isolated guinea pig brain, induced by a brief and transient 3-min perfusion of 50 microM bicuculline (that reduces GABAergic transmission by about 40%).

We would also like to clarify that the experimental traces shown for comparison were not selected to match the model simulations. Rather these experimental data were used as guidelines to create and evaluate the computational model.

Finally, we thank the Reviewer for the comment regarding the confusion created by preictal firing of the PY cell. We agree that indeed the PY cell membrane potential trace was misleading. We use alternative pyramidal cell data in Figure 3 of the revised manuscript.

Figure 6. In some places, it seems that the model is made to behave like the experiment. For example, in Figure 6, no reason is given for why the pyramidal cells are stimulated with 6 pA current. What would be the circumstances in the tissue or intact brain where the pyramidal cells would receive such input?

The main reason for pyramidal cell stimulation is given in the manuscript text and legend to Figure 6 (“The absence of excitatory dendritic synaptic input was compensated with a steady depolarizing DC current […] adjusted to preserve the original duration of the SLE”) but we are glad to use this opportunity to further explain why such manipulation was necessary. In order to observe inter-burst intervals (IBI) evolution and find best fit of a mathematical function we removed the stochastic component, i.e., background input noise, from the model. Without this excitatory dendritic synaptic input, the SLE were shorter and there were less data for fitting. To restore SLE duration as was seen in reference simulation (Figure 2) we compensated the absence of excitatory noise input by a small depolarizing current. In the tissue or intact brain, the pyramidal cells could receive such steady input by means of optogenetic manipulation. On the other hand, it is not possible to remove stochastic component in the real tissue. Hence ‘noise-free’ experiments with compensative steady current injection can indeed be carried out only in silico.

Lines 413 – 419: The paper claims that the previous modeling studies induced seizures by either stimulating pyramidal cells or increasing [K]o, whereas in this study, seizure is induced in the model by stimulating the interneuron. On the surface, this is true. But in reality, the approach adopted by this study is an indirect method of raising extracellular potassium of pyramidal cells. Stimulating interneurons leads to higher [K]o and hence seizures. This is also acknowledged by the authors. However, what is not clear is that why in the network only interneurons would receive strong depolarizing stimulus but not pyramidal cells. It should also be noted that the interplay between interneurons and pyramidal cells during seizures under normal [K]o in a modeling study was first reported by Wei et al. (2014) (PMID: 24671540).

We agree with the Reviewer that the reason for using direct depolarization of the interneuron to initiate SLE could seem unjustified and needed further explanation. Please, see also our answer to Reviewer #2 point 1.

Increased interneuron discharges and decreased PY activity around the time of seizure onset have been shown in SLE induced in vitro by 4-AP (Ziburkus et al., 2006; Lévesque et al., 2016) and bicuculline (Gnatkovsky et al., 2008), in acute and chronic seizure models in vivo (Grasse et al., 2013; Miri et al., 2018; Toyoda et al., 2015) and temporal lobe of epilepsy patients (Elahian et al., 2018). Motivated by this general observation obtained under different experimental conditions, we aimed to test whether fast intraneuronal discharges can indeed trigger SLE in silico and if so, what would be the underlying mechanism. We didn’t aim to rise extracellular potassium of pyramidal cells or increase their discharges by depolarizing stimulus at SLE onset because, as noted above, the transitions to spontaneous seizures that begin with LFV pattern were not associated with increased excitatory activity, but with increased firing of inhibitory interneurons. In the revised manuscript it is explained in ln. 428-430 and the pioneer modeling work by Wei et al., 2014a, which considered an interplay between interneurons and pyramidal cells during seizures, based on the experimental data of Ziburkus et al. (2006) is now quoted in ln. 431-436.

Line 437-439: "This suggests that in our model, a change in the concentrations of either [K⁺]o or [Cl^-]i was not sufficient to initiate an SLE and that an increase in both is necessary." This seems to be a model-specific effect because several modeling studies have shown that raising [K]o alone can cause the network to enter seizure-like state.

This is a relevant point, and we recognize that our statement was imprecise and should be clarified. In the revised manuscript we modified the sentence mentioned above (ln. 455-457) and we add that our results don’t contradict in vitro experimental observations that elevated [K⁺]_o alone is sufficient to induce epileptiform activity (Jensen and Yaari, 1997; Traynelis and Dingledine, 1988). As shown by a bifurcation diagram (Figure 4A and Appendix I – figure 1) an increase in [K⁺]_o alone may lead to a transition from a silent state to tonic and burst firing (ln. 460-464).

Line 250: [Na+]I should be [Na+]i.

Thank you, the typo has been corrected.

[Editors’ note: what follows is the authors’ response to the second round of review.]

Essential revisions:

We ask that you focus specifically on addressing the following

1. Clarify the specific novel contributions of this work in the abstract. The role of Na+, Na+/K⁺ pump on termination and Cl^- on seizure initiation have been previously shown.

We clarified the following novel contributions of our work in the abstract:

– We describe the most accurate biophysical model to date replicating electrographic pattern of a typical human focal seizure characterized by low voltage fast activity onset, tonic phase, clonic phase and postictal suppression.

– We report the first in silico demonstration of seizure initiation by inhibitory cells via the initial build-up of extracellular K⁺ due to intense interneuronal firing.

– We identify the ionic mechanisms that may underlie a key feature in seizure dynamics, i.e., progressive slowing down of ictal discharges.

– We predict the exponential scaling of inter-burst intervals, confirmed in the whole guinea pig brain in vitro and human seizure data.

2. The bifurcation analysis that suggests soma and dendrite differences for K⁺ concentration resulting in different regimes is interesting. Could you add to the discussion whether there is any experimental evidence for such significant differences in the concentrations for soma and dendrite?

We appreciate the suggestion to check the existing literature on this subject. Our modeling predictions of different K⁺ concentrations around soma and dendrite during seizures are confirmed by experimental data of simultaneous [K⁺]o recordings in somatic and dendritic layers during hippocampal seizures induced in vivo in anesthetized rats (Somjen and Giacchino, (1985); presented also in Somjen (2004), Figure 8-2). We added this information to the manuscript (ln. 568-572).

3. With reference to the bicuculline model, could you add to the discussion in order to explain your mechanistic reasoning for how this "recruits the interneuronal network"

In the revised manuscript we describe hypotheses regarding the mechanism leading to an increase in interneuronal network activity following a decrease in GABA-A conductance by brief bicuculline application (ln 460-475)

4. As the slowing of the interburst interval is one of the novel aspects of this work, it would be helpful to show that ion changes influence the inter-burst interval variations observed during the course of the seizure. Specifically, could you identify the bursting frequencies from the bifurcation analysis and confirm the role of Na⁺ accumulation in the slowing of burst interval.

We performed further simulations and analyses to demonstrate how a change of different ion types affects seizure termination and inter-burst interval variations (Figure 6 – supplementary figure 1). We conclude that in the model simultaneous changes in [K⁺]_o and [Na⁺]_i contribute to the slowing of inter-burst interval towards the end of an SLE. Additionally, we consider slowing down scenarios predicted by the bifurcation theory of Izhikevich (2000) and observed in the phenomenological epileptor model of Jirsa et al. (2014). We observe that inter-burst intervals in our biophysical model and in the experimental data don’t follow these predictions and we suggested the reason for this discrepancy (ln. 345-357 and 648-654).

Reviewer #1 (Recommendations for the authors):

In this much revised manuscript the authors have improved several features of how ion dynamics were modelled enhancing the validity of their findings. The authors have gone to great lengths to address my concerns. In my opinion the manuscript enhances our understanding of the mechanisms underlying seizure dynamics.

We truly appreciate your positive statements about improvements of the model and the significance of our manuscript.

Novelty

[Interneurons driving seizure onset] The authors have generated a thorough model of how intense activity of interneurons can drive K⁺ build-up and the initiation of seizures. This is certainly the most thorough and biophysically realistic model which recapitulates the electrographic feature of human seizures in a satisfying manner.

Thank you for the overall positive evaluation of our manuscript. In the Abstract we emphasized novelty of our study, which shows for the first time in silico that interneuronal firing may initiate seizures via build-up of extracellular potassium.

[Increased Na+/K⁺-pump driving the SLE termination and the post-ictal state]. The authors state that "We show for the first time that seizure termination and postictal state may be generated by the same mechanism mediated by increased activity of the Na+/K⁺-pump. It is an alternative mechanism of the postictal state, which previously has been suggested to depend on potassium undershoot (Krishnan and Bazhenov, 2011)." I disagree with the authors' interpretation and insistence that this is novel. In Krishnan and Bazhenov, they explicitly describe essentially the same mechanism. Their potassium undershoot is caused by increased activity of the Na+/K⁺-pump (the show and state this explicitly).

"In our model extracellular potassium decays to baseline after an SLE offset, hence it cannot account for the postictal state." This is also what (Krishnan and Bazhenov, 2011) show (see their Figure 8). I can't see any fundamental difference between your interpretation and theirs, which is certainly satisfying, but not new as far as I can tell.

We thank the Reviewer for the thorough discussion and comments on this topic. We agree that in Krishnan and Bazhenov (2011) postictal state was due to [Na]_i accumulation during seizure leading to increased activity of the Na+/K⁺-pump. However, the specific mechanism of reduced postictal excitability is not clear from the paper. In the Abstract, the authors say, “After seizure termination, the extracellular potassium was reduced below baseline, resulting in postictal depression.”. Also, in the Results, a subsection title is: “Below baseline reduction of the extracellular potassium mediates postictal depression state”. On the other hand, at the end of the Introduction they say: “We found that progressive increase in [Na+]i over the course of seizure leads to the changes in the balance of excitatory and inhibitory currents that mediate spontaneous seizure termination and may explain postictal depression state.”. In the Discussion they also say that the reduced postictal excitability was related to both lower than baseline [K⁺]o and increased over baseline [Na+]i (pg. 8880). This view is also presented in their later paper (Krishnan et al., 2015), where they explicitly state that the main cause for termination of seizure and postictal depression state was outward Na/K-pump current. Accordingly, we rephrased the respective paragraph and did not claim the novelty for our finding. Instead, we emphasized that postictal reduction of excitability might be observed both with and without [K⁺]_o undershoot and that in our model, reduction in excitability was established through the hyperpolarizing Na/K-pump current (ln. 679-694).

[Exponential IBI distribution]. I agree that the model satisfyingly shows how accounting for ion concentration changes can generate an exponential IBI distribution toward the end of the seizure.

We appreciate your comment. We further extended this part of analysis to demonstrate how individual ion concentration changes influence IBI distribution toward the end of the seizure (Figure 6 —figure supplement 1).

Other responses:

I thank the authors for clarifying that in their model bicuculline does not block all of GABAergic inhibition, but is likely a transient perturbation which somewhat counterintuitively recruits the interneuronal network.

The authors have gone to great lengths to improve how Cl^- flux through GABAaRs and the Cl^- leak conductance was modelled. Figure 5 is a wonderful figure (along with Appendix – Figure 3). I am now satisfied that the ion dynamics were modelled in a suitable way which gives me much increased confidence in the authors' findings.

We sincerely appreciate the above comments on the early version of our study as they significantly contributed to improvement of the manuscript.

Reviewer #4 (Recommendations for the authors):

In this work, the authors use a computational model to examine the role of ion dynamics in inhibition-mediated TLE seizures. Of significance, the seizure activity precisely matched the experimental data, specifically the time course of the inter-burst interval. The study also replicates previous experimental and computational observations on the role of K⁺ on seizure initiation, Na+, Na+/K⁺ pump on seizure termination. Further, the findings from this work suggest additional contributions of Na+/K⁺ pump to post-ictal depression and K⁺ influence on KCC2 pump promote seizure initiation.

While the paper's findings are a significant contribution that emphasizes the importance of ion dynamics on seizure, the novel contribution highlighted by authors seems only as slight variations of previously proposed mechanisms. Nevertheless, the manuscript is definitely worthy of publication, perhaps in a more specialized journal.

Few suggestions that could improve the manuscript:

1. Bicuculline, a GABA antagonist induced the seizure in the experimental condition, but in the computational model, seizure was induced by increasing the inhibitory neurons' activity. While the increase in inhibitory neuron's activity is observed following bicuculline in the experiment, there is a missing network mechanism that results in this increase of inhibitory neurons activity following the application of bicuculline. It would be more compelling if the authors could identify this mechanism and demonstrate the onset of a seizure by bicuculline in the computational model.

We thank the Reviewer for this relevant comment. Indeed, brief bicuculline application in the isolated guinea pig brain leads to an increase of inhibitory neurons (IN) activity, but the mechanism of this phenomenon is not fully understood. We might hypothesize that in order to fully investigate this effect using a model one should focus on simulating extended interneuronal network with mutual inhibitory interactions, which is unfeasible in the current model. However, in the revised manuscript we describe hypotheses regarding the mechanism leading to an increase in interneuronal network activity following a decrease in GABA-A conductance. Brief bicuculline application likely affects interneuron-interneuron inhibition more than interneuron-principal cell inhibition (Gnatkovsky et al., 2008). Accordingly, reciprocal release of inhibition between IN cells (i.e., disinhibition) could lead to the increased and synchronous firing of inhibitory interneurons and produce preictal spikes generated by interneurons contributing to an increase in extracellular potassium. It would further depolarize the interneuronal network and initiate SLE (de Curtis and Avoli, 2016; Figure 4). In an alternative scenario increased excitability of interneurons could lead to a transition in a bistable IN network, from asynchronous low firing rate mode to synchronous high firing rate mode due to small perturbation (Rich et al. 2020). These hypotheses were added to the Discussion, ln 460-475.

2. It would be very helpful to clarify the specific novel contributions of this work in the abstract. The role of Na+, Na+/K⁺ pump on termination and Cl^- on seizure initiation have been previously shown. Also, it would be helpful for authors to note that K⁺ influenced the KCC2 pump time constant in Gonzalez et al., 2018.

We thank the Reviewer for pointing this out. We clarified the novel contributions of our work in the Abstract. Our model generates for the first time an electrographic pattern of a typical human focal seizures consisting of distinct phases, i.e., low voltage fast activity onset, tonic phase, clonic phase and postictal suppression. Our study suggests that interneurons can initiate seizures via an initial build-up of extracellular K⁺ due to intense interneuronal spiking. The model also explains mechanisms that may underlie a key feature in seizure dynamics, i.e., progressive slowing down of ictal discharges. Our model predictions of exponential scaling of inter-burst intervals are confirmed in the whole guinea pig brain in vitro and human seizure data, suggesting that these mechanisms may be preserved across different models and species. We also clarified that in Gonzalez et al., 2018 the KCC2 pump time constant was potassium-dependent (ln 458-459).

3. The bifurcation analysis that suggests soma and dendrite differences for K⁺ concentration resulting in different regimes is interesting. It would be helpful to expand on this finding, and the report is one of the novel contributions. Is there any experimental evidence for such significant differences in the concentrations for soma and dendrite?

We appreciate the suggestion to check existing literature on this subject as we agree that it was not properly discussed. Indeed, during an SLE in the model the increase of [K⁺]_o is faster and more pronounced in the somatic vs. dendritic compartment. It is related to activity of the inhibitory neuron, which is located near the soma and also to small longitudinal diffusion between extracellular compartments. As interneuron activity decreases during the course of SLE, the additional contribution to [K⁺]_o comes from pyramidal cell firing, The dendritic conductance of voltage-gated K⁺ currents associated with spiking is about 10% of the somatic conductance (Fransen et al., 2002), hence release of K⁺ ions into the dendritic interstitial space is smaller than into somatic interstitial compartment. On the other hand, radial diffusion and glial buffering processes have the same efficiency in both compartments maintaining higher K⁺ near the soma. Our modeling predictions agree with experimental data of simultaneous recordings of [K⁺]o in somatic and dendritic layers during hippocampal seizures induced in vivo in anesthetized rats. During paroxysmal firing induced by electrical stimulation, [K⁺]o in dentate gyrus reached significantly higher levels in cell body layers than in the layers containing dendrites (Somjen and Giacchino, (1985); results reproduced in Somjen (2004), Figure 8-2) We addressed this issue in ln 568-572 of the revised manuscript.

4. It would be helpful to show that ion changes influence the inter-burst interval variations observed during the course of the seizure. Specifically, the authors could identify the bursting frequencies from the bifurcation analysis and confirm the role of Na⁺ accumulation in the slowing of burst interval.

We thank the Reviewer for this comment as it motivated us to perform additional analyses and investigate how a concentration change of K⁺, Na⁺ and Cl^- affects inter-burst intervals (IBI). Using slow fast analysis approach as in Figure 4 we varied the concentration of one ion type at a time while holding constant concentrations of the other ions. From the obtained membrane potential traces, we analyzed IBI slowing pattern mediated by changes of each ion type separately. In the analyses, in addition to linear and exponential slowing scenarios, we considered IBI slowing predicted by the bifurcation theory of Izhikevich (2000), who showed that termination of firing may be described by square root or logarithmic relationship of inter-spike intervals. In our analysis, a linear decrease in [K⁺]_o led to IBI evolution with exponential characteristics, while a linear increase in [Na⁺]_i or decrease in [Cl^-]_i led to SLE termination with logarithmic scaling of IBI as determined by Root Mean Square Error calculated for all four fitted functions (Figure 6 – supplementary figure 1). Yet, the full model, with simultaneously changing K⁺, Na⁺ and Cl^- led to exponential slowing. The discrepancy between the results obtained for varying concentration of one ion type at a time and for full SLE in our model and real seizure data suggests that when different factors simultaneously influence seizure termination and the overall slow current change is not necessarily linear, the IBI may not follow slowing predicted by the bifurcation mechanism. We expanded on this finding in the revised manuscript (ln. 345-357 and 648-654).

References:

de Curtis, M., and Avoli, M. (2016). GABAergic networks jump-start focal seizures. Epilepsia, 57(5), 679–687. https://doi.org/10.1111/epi.13370

Gnatkovsky, V., Librizzi, L., Trombin, F., and De Curtis, M. (2008). Fast activity at seizure onset is mediated by inhibitory circuits in the entorhinal cortex in vitro. Annals of Neurology, 64(6), 674–686. https://doi.org/10.1002/ana.21519

Krishnan, G. P., and Bazhenov, M. (2011). Ionic dynamics mediate spontaneous termination of seizures and postictal depression state. Journal of Neuroscience, 31(24), 8870–8882. https://doi.org/10.1523/JNEUROSCI.6200-10.2011

Krishnan, G. P., Filatov, G., Shilnikov, A., and Bazhenov, M. (2015). Electrogenic properties of the Na+/K⁺ ATPase control transitions between normal and pathological brain states. Journal of Neurophysiology, 113(9), 3356–3374. https://doi.org/10.1152/jn.00460.2014

E.M. Izhikevich, Neural excitability, spiking and bursting. International Journal of Bifurcation and Chaos 10(6):1171-1266 (2000)

Jirsa, V. K., Stacey, W. C., Quilichini, P. P., Ivanov, A. I., and Bernard, C. (2014). On the nature of seizure dynamics. Brain, 137(8), 2210–2230. https://doi.org/10.1093/brain/awu133

Rich S, Chameh HM, Rafiee M, Ferguson K, Skinner FK, Valiante TA. Inhibitory Network Bistability Explains Increased Interneuronal Activity Prior to Seizure Onset. Front Neural Circuits. 2020;13:81

Somjen GG, Giacchino JL. Potassium and calcium concentrations in interstitial fluid of hippocampal formation during paroxysmal responses. J Neurophysiol. 1985 Apr;53(4):1098-108. doi: 10.1152/jn.1985.53.4.1098. PMID: 3998794.

G.G Somjen, Ions in the Brain: Normal Function, Seizures, and Stroke (Oxford University Press, USA, 2004).

https://doi.org/10.7554/eLife.68541.sa2

Article and author information

Author details

Damiano Gentiletti

Department of Biomedical Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland

Contribution
Software, Investigation, Visualization, Methodology

Competing interests
No competing interests declared
Marco de Curtis

Epilepsy Unit, Istituto Neurologico Carlo Besta, Milan, Italy

Contribution
Conceptualization, Resources, Data curation, Validation, Writing – original draft, Writing – review and editing

Competing interests
No competing interests declared
Vadym Gnatkovsky
1. Epilepsy Unit, Istituto Neurologico Carlo Besta, Milan, Italy
2. Department of Epileptology, University Hospital Bonn, Bonn, Germany
Contribution
Resources, Data curation, Validation, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-4543-0464
Piotr Suffczynski

Department of Biomedical Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland

Contribution
Conceptualization, Formal analysis, Supervision, Validation, Investigation, Visualization, Methodology, Writing – original draft, Writing – review and editing

For correspondence
suffa@fuw.edu.pl

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-2300-1415

Funding

Associazione Paolo Zorzi for the Neuroscience (EPICARE)

Marco de Curtis
Vadym Gnatkovsky

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We are grateful to Laura Uva and Laura Librizzi for helpful discussions throughout the preparation of this work and for providing the SLE data from the in vitro isolated whole guinea pig brain. We thank Laura Tassi from the Claudio Munari Epilepsy Surgery Center of the Niguarda Hospital in Milano, Italy, for providing the intracerebral data on human seizures. The work of MdC and VG was supported by the EPICARE grant of the Associazione Paolo Zorzi for the Neuroscience.

Senior Editor

Ronald L Calabrese, Emory University, United States

Reviewing Editor

Joseph V Raimondo, University of Cape Town, South Africa

Reviewers

Joseph V Raimondo, University of Cape Town, South Africa
Maxim Bazhenov, University of California, San Diego, United States

Publication history

Received: March 18, 2021
Preprint posted: March 19, 2021 (view preprint)
Accepted: July 12, 2022
Accepted Manuscript published: August 2, 2022 (version 1)
Version of Record published: August 15, 2022 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.