Research Article

Physics of Living Systems

3D single cell migration driven by temporal correlation between oscillating force dipoles

Laboratory of Cell Physics, ISIS/IGBMC, UMR 7104, Inserm, and University of Strasbourg, France
Institut Curie, Université PSL, Sorbonne Université, CNRS UMR168, Laboratoire Physico Chimie Curie, France
Université Paris-Saclay, CNRS, Laboratoire de l’accélérateur linéaire, France
Univ. Lyon, Université Claude Bernard Lyon 1, CNRS, France
Saarland University, Center for Biophysics, Biologische Experimentalphysik, Germany
Tumor Biomechanics, INSERM UMR S1109, Institut d’Hématologie et d’Immunologie, France

Jul 28, 2022

https://doi.org/10.7554/eLife.71032

Open access
Copyright information

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: August 18, 2022 (This version)
Accepted: July 28, 2022
Accepted Manuscript published: July 28, 2022 (Go to version)
Received: June 6, 2021
Preprint posted: May 8, 2020 (Go to version)

1. Of interest
A unified approach to dissecting biphasic responses in cell signalling

Vaidhiswaran Ramesh, J Krishnan

Research Article Dec 6, 2023
Further reading

Abstract
Editor's evaluation
Introduction
Results
Discussion
Materials and methods
Appendix 1
Appendix 2
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Directional cell locomotion requires symmetry breaking between the front and rear of the cell. In some cells, symmetry breaking manifests itself in a directional flow of actin from the front to the rear of the cell. Many cells, especially in physiological 3D matrices, do not show such coherent actin dynamics and present seemingly competing protrusion/retraction dynamics at their front and back. How symmetry breaking manifests itself for such cells is therefore elusive. We take inspiration from the scallop theorem proposed by Purcell for micro-swimmers in Newtonian fluids: self-propelled objects undergoing persistent motion at low Reynolds number must follow a cycle of shape changes that breaks temporal symmetry. We report similar observations for cells crawling in 3D. We quantified cell motion using a combination of 3D live cell imaging, visualization of the matrix displacement, and a minimal model with multipolar expansion. We show that our cells embedded in a 3D matrix form myosin-driven force dipoles at both sides of the nucleus, that locally and periodically pinch the matrix. The existence of a phase shift between the two dipoles is required for directed cell motion which manifests itself as cycles with finite area in the dipole-quadrupole diagram, a formal equivalence to the Purcell cycle. We confirm this mechanism by triggering local dipolar contractions with a laser. This leads to directed motion. Our study reveals that these cells control their motility by synchronizing dipolar forces distributed at front and back. This result opens new strategies to externally control cell motion as well as for the design of micro-crawlers.

Editor's evaluation

This manuscript suggests a novel mechanism by which an animal cell can move through a three-dimensional extracellular matrix, namely by synchronized oscillations in contraction at the front and at the back of the cell. It should be of great interest to a variety of researchers in cellular biophysics.

https://doi.org/10.7554/eLife.71032.sa0

Introduction

Cell motility is essential in a variety of biological phenomena (Yamada and Sixt, 2019). Cells move during development in the presence or in the absence of chemical gradients. Their relevant localizations at the right moment is essential to secure completion of viable developing embryos. Also, defects in migrations are known to be involved in cancer progression with the increased motility of cells during invasion (Stuelten et al., 2018). Understanding cell motion in physiological environment is therefore recognized as a central question in basic and in applied sciences.

In this context, the determination of genetic and proteins networks has been instrumental in identifying the central pathways at play for motility (Jia et al., 2022). These steps in outlining specific partners are important in localizing defects and they open potential perspectives for testing new strategies to act on these situations where cell migration is impaired in vivo and in vitro. However, cell motion calls also for physical principles because motion at this scale is not intuitive (Tanimoto and Sano, 2014). This requires alternative approaches in synergy between experiments and theory.

Cells motion in 2D flat surfaces has been documented in details (Alberts, 2002). The classical image of extension of lamellipodia and retraction of the back of the cells is known. Cells crawl and protrusions grow and retract around the cell. New dynamics are also associated with the motion of confined cells in microfabricated channels where retrograde flow of actin at the scale of the entire cell was reported to play central roles in motility (Liu et al., 2015; Reversat et al., 2020). However, both approaches – cells crawling on 2D flat surfaces and in channels – call for tests in actual 3D situations where cells interact with an environment similar to physiological 3D situations. This experimental challenge of mimicking in vivo environments goes together with theoretical basic questions.

At cellular scales inertia is negligible which puts some particular constraints on self-propelled microscopic objects (Purcell, 1977; Tanimoto and Sano, 2014). Low Reynolds number micro-swimmers in Newtonian fluids must obey the scallop theorem, stating that the cyclic sequence of shape changes they perform to swim cannot be symmetrical in time (Purcell, 1977; Najafi and Golestanian, 2004; Golestanian and Ajdari, 2008; Barry and Bretscher, 2010; Leoni and Sens, 2015). In his seminal work, Purcell illustrated such behavior as closed trajectories encompassing a finite area in some properly chosen phase space (Purcell, 1977).

Crawling cells are not strictly bound to obey the scallop theorem, which stems from the time reversibility of the Stokes equation. Cells moving in 2D or in micro-channels often display clear spatial polarization, characterized by F-actin flowing from the front to the back of the cell (Barnhart et al., 2011; Liu et al., 2015). For such fast moving cells, the lack of time reversal symmetry – the fact that the system looks different when the movie is played backward – clearly manifests itself by the existence of a coherent actin flow at the scale of the entire cell and the cell velocity is directly related to the dynamics of the actin flow. This mode of motility has been studied in detail theoretically, in particular to understand how the positive feedback between actin flow and the distribution of contractile units (myosin motors) may lead to spontaneous symmetry breaking (Blanch-Mercader and Casademunt, 2013; Recho et al., 2013; Recho et al., 2014; Maiuri et al., 2015). Many cells, especially mesenchymal cells, do not show such polarized actin flow at the scale of the entire cell, but instead display cycles of protrusion/retraction at both ends of the cell. The actin dynamics within protrusions is comparable to that of fast-moving cells, but the existence of multiple competing protrusion leads to slow cell translocation (see for example Caballero et al., 2014; Lo Vecchio et al., 2020). Slow moving cells in complex environments such as the extracellular matrix (ECM) could leverage the visco-elastic nature of the environment (Qiu et al., 2014; Datt et al., 2018) or the complex dynamics of adhesion and detachment (Wagner and Lauga, 2013; Leoni and Sens, 2017). This makes the search for unifying principles underlying 3D cell movement challenging.

In this article, we report the experimental design of a 3D physiological matrix which single cells deform while moving. We label fluorescently the important cellular proteins involved in cell motility. Deformation of the matrix correlated with motility/adhesion proteins localizations allow us to show that two forces dipoles mediated by acto-myosin at each side of the nucleus are correlated with a phase shift when cells move directionally. We propose a model which is consistent with this explanation and test this mechanism by inducing force dipoles. Our results shed light on generic physical mechanisms at play in cell migration.

Results

Fibroblasts in CDMs generate contractile-extensile regions on either side of the nucleus

To search for generic readouts for 3D cell migration, we designed an assay where cell migration and the spatial distribution of cell-matrix interactions could be tracked simultaneously and quantified over time. In our experiment, NIH 3T3 fibroblasts moved inside a fluorescently labelled cell derived matrix (CDM) (Figure 1a, left panels and Video 1), obtained using a protocol adapted from (Cukierman et al., 2001). Briefly, a confluent monolayer of NIH3T3 cells expressing fluorescently labeled fibronectin was triggered to synthesize ECM proteins for 8 days. Then, cells were removed by lysis, generating a 3D protein meshwork (Figure 1—figure supplement 1a). The resulting CDM had large pores inside, but it was covered by a dense crust, as shown by electron microscopy (EM) (Figure 1—figure supplement 1b). Despite this, 3T3 fibroblasts seeded on top of the CDM passed through and spread within the matrix, which was significantly thicker than cells themselves (Figure 1—figure supplement 1c and d). We then determined by micromanipulation of embedded beads the mechanical properties of these cell derived matrices (Figure 1—figure supplement 1e, Video 2, and Appendix 1). Optical tweezer experiments showed no hysteresis in the displacement curves, suggesting that the matrix behaved as an elastic material within the amplitudes and timescales explored (Figure 1—figure supplement 1f and g), which is in agreement with previous reports (Petrie et al., 2012). Moreover, the relationship between force and displacement was linear (Figure 1—figure supplement 1h) and we could determine the CDM’s elastic modulus to be ≈50 Pa (Figure 1—figure supplement 1h and i) and no modification of the meshwork was observed after 24 hr of cell migration inside (Figure 1—figure supplement 1j). Altogether, these physiological 3D porous matrices were thick enough to host 3D cell migration and were sufficiently soft and elastic to relate cell dynamics to matrix deformation.

Figure 1 with 3 supplements see all

Download asset Open asset

Figure 1—source data 1 CDM characterization. (i) Values for the height and the thickness of the cell derived matrix (CDM). (ii) Raw values of the CDM’s Young’s modulus. (iii) Values for the cytoplasts’ period of oscillation.: https://cdn.elifesciences.org/articles/71032/elife-71032-fig1-data1-v2.xlsx
Download elife-71032-fig1-data1-v2.xlsx

Video 1

Download asset

posterframe for video — NIH3T3 fibroblast transfected with mCherry-LifeAct deforms the fibronectin network in yellow while moving, scale bar 20 μm, time in hh:mm.

Video 2

Download asset

For migration experiments, 3T3 fibroblasts were plated at low density, spontaneously penetrated the matrix and could be followed individually. Cells displayed an elongated morphology (Figure 1—figure supplement 2), typical of fibroblasts in these soft and elastic matrices (Cukierman et al., 2001; Petrie et al., 2012; Caballero et al., 2017). We observed (i) a cortical distribution of acto-myosin (Figure 1a), (ii) the presence of focal adhesions distributed all over the cell membrane and mediating its adhesion to the surrounding matrix (Figure 1—figure supplement 2 and Video 3), and (iii) the microtubule cytoskeleton expanding from the centrosome to the periphery of the cell (Figure 1d and Video 4). Strikingly, the CDM was easily deformed by cells as they moved through (Figure 1a, right panels and Video 5). This enabled us to quantify the associated matrix deformation (Delanoë-Ayari et al., 2008) via the Kanade-Lucas-Tomasi (KLT) tracker method (Lucas and Kanade, 1981; Figure 1b). These deformations were present at the front and at the back of the nucleus of polarized cells, where phases with both contractile and extensile patterns were observed. Similar patterns were also observed in other cell types migrating in CDMs. Both mouse embryonic fibroblasts (MEFs) and rat embryo Fbroblasts 52 (REF52) exhibited phases of contraction and extension patterns at the front and the back of the nucleus (Figure 1—figure supplement 3). Moreover, the matrix deformation could be imaged concomitantly with the cellular machinery responsible for force generation. We could observe a transient densification of the myosin signal forming clusters of myosin associated with the contraction observed in the matrix displacement (Figure 1c and Video 6). This force transmission between the cell and the CDM was also observed at the focal contact level: enlargement of pores of the fibronectin meshwork suggested a local pulling force by the cells (Figure 1—figure supplement 2). Therefore, cells embedded in CDMs generate forces which translate into contractile and extensile deformations in the surrounding matrix.

Video 3

Download asset

Video 4

Download asset

Video 5

Download asset

Video 6

Download asset

Dynamics of matrix deformation for migrating and non-migrating cells

During migration experiments, some cells showed persistent motion (Video 7) while others moved back and forth along a constant central position. Hereafter, we denote as migrating cells the first type and as non-migrating cells the second type. Interestingly, both migrating and non-migrating cells exhibited local zones of contraction-extension along time (Figure 2a). Such regions can be seen on both sides of the nucleus (Figure 1b). To characterize the behavior of these contraction-extension regions over time, we defined the cell axis along the direction of polarization (defined by a more protrusive cell end) for non-migrating cells and along the direction of migration for migrating cells (Figure 2b and c). Then, we projected the divergence of the matrix across the x-y plane on the cell axis for every timepoint and plotted the corresponding kymographs (Figure 2d and e). For non-migrating cells, we could observe sequences of positive and negative divergence along time (alternating blue and yellow area) on still regions (black lines in Figure 2d) at both sides of the nucleus. For migrating cells, sequences alternating positive and negative divergence were present as well (Figure 2e). However, these contraction-extension patterns were not still, but moved along with the cell (blue and red lines in Figure 2e correspond to the back and front of the nucleus, respectively). Thus, we suggest that these contraction-extension regions are equivalent to two force dipoles on either side of the nucleus.

Figure 2 with 2 supplements see all

Download asset Open asset

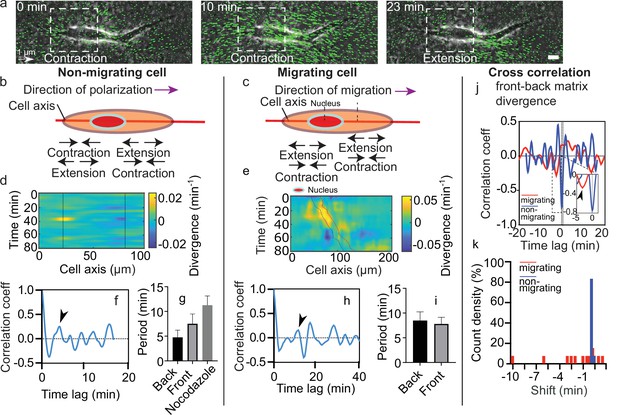
Dynamics of matrix deformation for migrating and non-migrating cells.

(a) Snapshots overlaying phase contrast images and Kanade-Lucas-Tomasi (KLT) calculation of matrix rate of deformation (green arrows indicate displacement between two consecutive frames, Δt=1 min) showing a contraction/extension center, scale bar 10 µm, time in minutes. (**b–c**) Schematics of the alternating phases of contraction and extension for a non-migrating cell (b) and a migrating cell (c). (**d–e**) Heatmap of the divergence of the corresponding matrix displacement. Contractile and extensile force dipoles correspond to blue and yellow spots, respectively. Non-migrating cells (d) show two oscillating dipoles (their centers are approximately indicated by the solid black lines), while migrating cells (e) show a different spatio-temporal pattern with sequences of alternating positive and negative divergence. The blue and red solid lines in (e) indicate the two sides of the nucleus. (f) Correlation function of the contraction-extension time series at the back of a non-migrating cell, with a first peak at ≈5 min. Time trace 36 min. (g) Average periods of contraction-extension cycles: 4.8±1.5 min for the front, 7.5±2.0 min for the back, and 11.0±1.9 min for nocodazole-treated cells. Error bars represent standard error of the mean (SEM). (h) Correlation function of the divergence at the back of a migrating cell, with a first peak at ≈10 min. Time trace 100 min. (i) Average period of the contraction-extension cycles for migrating cells of 8.5±1.8 min for the front and 7.8±1.4 min for the back. (j) Typical cross-correlation function between back and front divergence for a migrating cell and a non-migrating cell. Time trace non-migrating cell 36 min and migrating cell 100 min. (k) Distribution of the values of the time lag for migrating and non-migrating cells. Distribution of time lag for migrating cells is statistically significant to the time lag for non-migrating cells (p=0.0246, Kruskal-Wallis test). Error bars represent SEM. t-Tests show differences in oscillation periods between motile, non-motile, and nocodazole-treated cells are not statistically significant (with n_mot = 13 motile cells, n_nomot = 6 non-motile cells, n_Noco = 6, and N>3 biological repeats).

Figure 2—source data 1 Matrix contraction. (i) Raw values for the periods of non-migrating and nocodazole-treated cells. (ii) Raw values for the periods of migrating cells. (iii) Front-back phase shift for migrating and non-migrating cells. (iv) Raw values for the amplitude of the divergence peaks.: https://cdn.elifesciences.org/articles/71032/elife-71032-fig2-data1-v2.xlsx
Download elife-71032-fig2-data1-v2.xlsx

Video 7

Download asset

As it can be seen from the kymographs, these deformations were cyclic. To determine their period of contraction, we extracted temporal profiles of the divergence of the matrix displacement by averaging over the regions at the front and the back of the nucleus (Figure 2—figure supplement 1a-d). By doing so, we obtained the traces of the contractions at the front and the back over time for single cells (Figure 2—figure supplement 1e). Measurements of the magnitude of the peaks observed in the divergence traces showed no difference between front and back in migrating cells (Figure 2—figure supplement 2). The same behavior was observed for non-migrating cells, which were also similar in magnitude to the ones observed in migrating cells (Figure 2—figure supplement 2). We then performed the autocorrelation of these traces to obtain the period of the contractile and extensile patterns (Figure 2—figure supplement 1f). Autocorrelation of the divergence profile for individual non-migrating cells (Figure 2f – representative example for one cell) resulted in periods of oscillation similar at the front and back of the cell (≈6 min) (Figure 2g) (see Materials and methods section for quantification of the oscillations). For individual migrating cells, autocorrelation of divergence profiles (Figure 2h – representative example for one cell) gave oscillation periods of ≈8 min, similar at the front and the back as well (Figure 2i). These contraction relaxation cycles with periods of ≈8 min and amplitudes of typically 2.5 µm are reminiscent of previous reports of cell autonomous contractile oscillations (Kruse and Riveline, 2011). Periods of oscillations were comparable for motile and non-motile cells (Figure 2g and i). The phases of contraction seemed to correlate with the formation of local myosin clusters as described above (Figure 1c), which is consistent with the observation of distinct myosin-driven contraction centers in the migration of neurons on 2D surfaces (Jiang et al., 2015).

We observed more protrusive activity at one of the two ends of elongated cells, in both motile and non-motile cells. Since this apparent spatial polarization was not sufficient to elicit directed motion, we looked for other sources of symmetry breaking. We measured the temporal cross-correlation function of the contraction-extension cycles at the two cell ends (Figure 2—figure supplement 1g and Figure 2j). This revealed significant differences between migrating and non-migrating cells. While non-migrating cells systematically showed no phase shift between the two ends, with cross-correlation peaks localized at a time shift t=0, migrating cells showed cross-correlation peaks at non-zero time lags (Figure 2k), suggesting a phase shift between the front and back contraction-extension cycles (differences of phase shift in migrating and non-migrating cells were statistically significant with p=0.0246). A system undergoing directed motion must exhibit time reversal asymmetry. In our case, this asymmetry manifests itself through a time lag between the contraction-extension cycles of the two force dipoles.

Multipole analysis of the matrix deformation

The most intuitive way to visualize time reversal symmetry breaking is through the existence of cycles in a properly chosen phase space. This phase space may be based on a multipole expansion of the traction force exerted by the cell on its surrounding. This approach was pioneered by Tanimoto and Sano for Dictyostelium discoideum crawling on deformable 2D substrate (Tanimoto and Sano, 2014). In particular, they showed that crawling D. discoideum exhibits cycles of finite area in the dipole-quadrupole phase space. In the present work, the traction forces exerted by the cell are analyzed indirectly through the deformation of the matrix. Indeed, our characterization of the mechanical properties of the CDM showed that it locally behaves as a linear elastic material with a well-defined elastic modulus (Figure 1—figure supplement 1f-j). This supports the approximation of a linear relationship between the moments of the force distribution and the moments of the resulting matrix displacement distribution. Note however that the relationship could be more complex due to matrix heterogeneities.

We analyzed the 2D projection of the 3D deformation field of the CDM and computed the dipolar and quadrupolar moments of the rate of matrix deformation (see Appendix 2 and Figure 3—figure supplement 1 for details). Briefly, we extracted the 2D projected velocity vector field $u_{i}^{(n)}$ for the component $i$ of the change of substrate deformation between two consecutive frames at position $n$ of the mesh. The dipole is a tensor defined as $S_{i j} = \frac{D_{i j} + D_{j i}}{2}$ with $D_{i j} = \sum_{n} ∆_{i}^{(n)} u_{j}^{(n)}$ , where $Δ_{i}^{(n)}$ is the i th component of the vector joining the cell center and the point $n$ on the mesh. Similarly, the quadrupole tensor is defined as $Q_{i j k} = \sum_{n} ∆_{i}^{(n)} ∆_{j}^{(n)} u_{k}^{(n)}$ . The largest eigenvalues of the dipole and quadrupole tensors are defined as the main dipole, $D$ , and the main quadrupole, $Q$ , and the corresponding eigenvectors are defined as the main dipole and quadrupole axes. Figure 3a shows an example of the orientation of the main dipole, and Figure 3b shows a sketch of the physical/geometrical meaning of these quantities. The main dipole axis was aligned with the direction of motion – within experimental noise (see Figure 3—figure supplement 2 for a quantification) – as was reported for 2D motion (Tanimoto and Sano, 2014).

Figure 3 with 3 supplements see all

Download asset Open asset

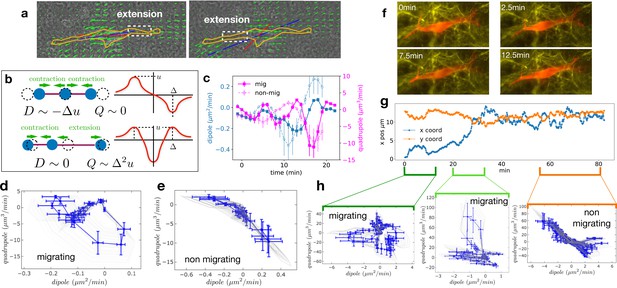
Multipole analysis of the matrix deformation rate.

(a) Snapshots of a cell with: matrix rate of deformation, green arrows, the main dipole axis, blue, the axis of the cell motion, red. (b) Schematic representation of dipoles (D) and quadrupoles (Q) of the 1D matrix displacement (rate) distributions. The distribution on top has non-zero dipole but vanishing quadrupole, and that on the bottom has vanishing dipole and non-zero quadrupole. (c) Time series of the main dipole, blue, and quadrupole, magenta – projected on the cell axis – for a migrating cell (squares) and a non-migrating cell (circles), sampling approximately 1/10 of the duration of the entire experiment. (**d–e**) Cell trajectory in the dipole/quadrupole phase space for a migrating cell (d) and a non-migrating cell (e). The migrating cell follows a cycle with a finite area and the non-migrating cell does not. The error bars are obtained following the procedure described in Appendix 2. The individual cycles for different radii are shown in light gray. (f) Snapshots of a cell which in the course of the same experiment displays a transition from migrating to non-migrating behavior (LifeAct in red and fibronectin in yellow), scale bar 10 µm. (g) Cell positions in the x-y plane (blue and orange curves) showing a transition from migrating to non-migrating phase. (h) Trajectories in the dipole/quadrupole phase space for three different time intervals showing cycles with finite area in the migrating phase and with vanishing area in the non-migrating phase (see also Video 8).

Figure 3—source data 1 Dipole and quadrupole moments. (i) Raw data for the dipole and quadrupole moments in panel Figure 3d. (ii) Raw data for the dipole and quadrupole moments in panel Figure 3e. (iii) Raw data for the angular distribution.: https://cdn.elifesciences.org/articles/71032/elife-71032-fig3-data1-v2.xlsx
Download elife-71032-fig3-data1-v2.xlsx

We then determined the time variation of the main dipole and quadrupole. The level of traction exerted by the cell on the matrix observed for non-migrating cells is comparable in magnitude to those of migrating cells (Figure 3—figure supplement 3b, differences between migrating and non-migrating cells are not statistically significant with p=0.2766). This shows that the absence of migration is not due to the lack of traction forces (see also Figure 3—figure supplement 1). Identifying time reversal symmetry breaking phenomena is not straightforward in the temporal representation of Figure 3c. Therefore, we instead represent the cell trajectory in the dipole/quadrupole phase space, in which non-reversible periodic trajectories appear as closed cycles of finite area (Tanimoto and Sano, 2014). We indeed observe that trajectories showed a cycle enclosing a finite area for migrating cells, but a negligible area for non-migrating cells (Figure 3d and e, and more examples in Figure 3—figure supplement 3). To further test the relationship between finite cycle area and motility of individual cells, we analyzed the migration of a cell that underwent motion and then stopped (Figure 3f–h and Video 8). Strikingly, we observed that the cycles switched from a finite area while the cell was moving to a vanishing area when the cell stopped (Figure 3h). The finite area is a direct illustration of the fact that the phase shift between the contraction-extension cycles at the two ends of migrating cells observed in Figure 2 also manifests itself in the pattern of matrix displacement. This is a clear signature of time reversal symmetry breaking. The quantification of the area enclosed by the trajectories in the D-Q plane of migrating and non-migrating cells is detailed in Appendix 2 and shown in Figure 3—figure supplement 3c. Both absolute areas (in µm⁵/min²) and normalized areas (in percent of the area of the rectangle fitting the trajectory) were substantially larger for migrating cells than for non-migrating cells (differences were statistically significant with p=0.0177 and p=0.0431, respectively). This supports our claim that the relevant difference between the two behaviors is the existence of a phase shift rather than a difference in the level of traction forces.

Video 8

Download asset

To test whether we could correlate the oscillations at the two cell ends with molecular actors, we tracked cell motion in the presence of the microtubule depolymerizing agent, nocodazole. Upon addition of the drug, cell migration stopped (Figure 4—figure supplement 1h). Some cells then underwent a forward backward movement in the matrix (Video 9), which hinted at an oscillation driven by local force dipoles. We observed a similar behavior in nucleus-free cells, generated when protrusions rupture from the cell. The resulting cytoplast underwent a forward backward movement in the CDM (Figure 1—figure supplement 3c, Video 10). They switched polarization over time, with a frequency of one direction reversal every ≈36 min. Although the nocodazole-treated cells did not maintain a fixed cell polarization either, we extracted matrix displacement which showed a typical period as for non-treated cells of ≈11 min (Figure 2g). Due to the lack or switch in polarity we could not define a back and a front. However, oscillations at different cell ends were in phase and cells did not show directed motion. This suggests that the coupling between oscillators needed to promote directed motion could involve microtubules. Indeed, the microtubular network spans the entirety of the cell body (Figure 1d and Video 4), and is thus a natural candidate to transfer information between the two ends of the cell. This suggestion is consistent with the notion that the microtubular network regulates the polarity axis of migrating cells (Etienne-Manneville, 2004; Kaverina and Straube, 2011).

Video 9

Download asset

Video 10

Download asset

Persistent speed is related to the period of oscillations

The geometry and dynamics of the distribution of matrix displacement call for a direct comparison with models of self-propelled objects made of discrete moving beads (Najafi and Golestanian, 2004; Golestanian and Ajdari, 2008; Wagner and Lauga, 2013; Leoni and Sens, 2015; Leoni and Sens, 2017; Datt et al., 2018). Figure 4a and b displays an idealized cell with two oscillating pairs of beads exerting time-shifted oscillatory force dipoles at its two ends. Here, the contractions at either ends of the cell are chosen to have the same magnitude for simplicity and in agreement with our observations (Figure 2—figure supplements 1 and 2), but this is not required to elicit net cell translocation. The cell activity is characterized by the amplitude $d$ and period $T$ of the oscillations and a phase shift $ψ = 2 π Δ T / T$ between oscillations at the two ends. The simplest self-propelled object is a micro-swimmer embedded in a Newtonian fluid and migrating due to hydrodynamic interactions (Najafi and Golestanian, 2004; Golestanian and Ajdari, 2008; Leoni and Sens, 2015). In this case, the period of oscillation is the only timescale in the problem, and the swimming velocity must scale inversely with the period. In the limit of small oscillation amplitudes and weak hydrodynamic interactions, that is if $d ≪ a ≪ D ≪ r$ (where $d$ is the oscillation amplitude, $a$ the bead size, $D$ the dipole size, and $r$ the cell size, Figure 4a), the net cell velocity over a cycle follows the scaling (Leoni and Sens, 2015)

V_{s w i m} = \frac{d^{2}}{L_{s} T} f_{s} (ψ)

where $f_{s} (ψ)$ is a periodic function of the phase shift satisfying $f_{s} (ψ = 0) = 0$ , that is, no velocity without phase shift, as required by the scallop theorem, and $L_{s} \sim r^{4} / (a D^{2})$ is a length scale set by the cell geometry. Examples of theoretically computed cell trajectories in the dipole/quadrupole phase space for non-migrating and migrating cells are shown in Figure 4—figure supplement 2.

Figure 4 with 2 supplements see all

Download asset Open asset

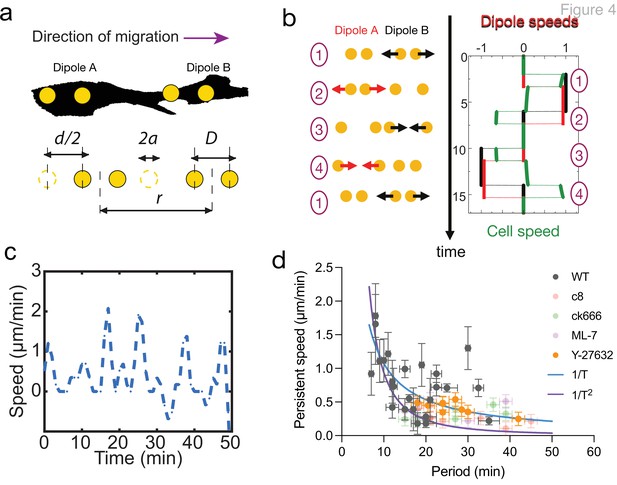
Persistent speed is related to the period of oscillations.

(a) Schematics of dipoles distribution highlighting quantities used in the theoretical model: two dipolar units (‘A’ and ‘B’) made up of disks of radius a, through which cells exert traction forces on the extracellular environment. The dipoles, at distance r apart, oscillate with period T, with minimum amplitude D and a maximum amplitude D+d. (b) Model dynamics. Left: Alternate phases of extension/contraction are imposed to the two dipoles, defining a cycle (‘1, 2, 3, 4, 1...’) that is not time-reversible. Right: The extension/contraction rates of dipole ‘A’ and ‘B’ are shown in red and black, respectively, in unit d/T. The cell velocity, calculated using the model discussed in Leoni and Sens, 2015, is shown in green in the same units. It oscillates between positive and negative values – with a non-vanishing mean – with a period equal to that of individual dipoles. (c) Typical plot of the experimentally measured instantaneous speed of a migrating cell over time, showing oscillation with a non-vanishing mean. (d) Persistent speed as a function of speed period for control cells and cells treated with specific inhibitors: 10 µM ROCK inhibitor Y-27632; 10 µM MLCK inhibitor ML-7; 100 µM lamellipodia growth promoter C8-BPA, and 50 µM Arp2/3 inhibitor CK666. Error bars derived from acquisition time in x and pixel resolution in y, both divided by two. Each data point corresponds to one cell (see Figure 4—figure supplement 1 for the number of cells). The plot displays a decay consistent with a power law. The continuous lines show the fits for V~1/T (dark blue) and V~1/T 2 (magenta), following Equations 1 and 2 for WT cells.

Figure 4—source data 1 Persistent speed and period of cell migration trajectories. (i) Data shown in the panel Figure 4d, persistent speed vs. period. (ii) Persistent speed for WT cells, C8-BPA-treated cells, CK666-treated cells, ML-7-treated cells and Y27632-treated cells. (iii) Period of WT cells, C8-BPA-treated cells, CK666-treated cells, ML-7-treated cells, and Y27632-treated cells. (iv) Dipole and quadrupole moments of simulated cells (migrating and non-migrating).: https://cdn.elifesciences.org/articles/71032/elife-71032-fig4-data1-v2.xlsx
Download elife-71032-fig4-data1-v2.xlsx

A key aspect of cell crawling, which is absent for micro-swimmers, is the dynamics of cell attachment and detachment from the surrounding matrix. Our observations suggest that dipole contraction is associated with an active contraction of acto-myosin clusters and that dipole extension corresponds to the elastic relaxation of the CDM following local cell detachment, that is, the loss of focal contacts (Video 3 and Godeau et al., 2020). The kinetics of cell binding/unbinding to the ECM defines additional dynamic parameters, so that the scaling relationship between cell velocity and the oscillation period is less universal than Equation 1 for the swimmer’s case. An important factor is how the rate of unbinding of adhesion bonds depends on the force applied on them. At the simplest level – in the limit of fast binding kinetics and small applied force – this can be captured by a velocity scale $v_{a d h} = δ_{o f f} k_{o f f}$ , where $k_{o f f}$ is the unbinding rate under no force and $δ_{o f f}$ is a matrix deformation amplitude characterizing bond mechano-sensitivity (Leoni and Sens, 2017). In this case, the net velocity of the idealized cell sketched in Figure 4a for small oscillation amplitude reads (Leoni and Sens, 2017):

V_{c r a w l} = \frac{d^{3}}{{v_{a d h} L}_{c} T^{2}} f_{c} (ψ)

where $f_{c} (ψ = 0) = 0$ as for swimmers, and the length scale $L_{c} \sim r^{2} / a$ also includes additional dimensionless factors related to substrate dissipations (see Leoni and Sens, 2017, for more details).

These simple models predict how the velocity should vary with the period of oscillation $T$ . The result depends on whether the amplitude of oscillations $d$ is fixed or is a function of $T$ . For oscillations of constant amplitude, the net velocity of both swimmers and crawlers decreases if the period of oscillation increases. On the contrary, the velocity is expected to increase with the period if the amplitude increases linearly with the period: $d \sim T$ , as can be expected if the self-propelled object operates under constant force – or equivalently constant contraction/extension rate.

The temporal oscillations of the instantaneous cell velocity are a good readout for the dynamics of internal force generation. For such self-propelled objects, the instantaneous velocity oscillates around the average values given by Equations 1 and 2, with a time dependence that reflects the dynamics of the underlying force dipoles. An example of such (theoretical) velocity oscillations can be seen in Figure 4b. Experimental observations indeed report strong oscillations of the instantaneous cell velocity (Figure 4c).

To test how the period of oscillation of migrating cells influenced their velocity, we took advantage of the inherent variability of cells and plotted the velocity vs. period for WT cells and observed a clear anticorrelation (Figure 4d). Although the large cellular noise prevented us from quantitatively comparing the scaling relations given by Equations 1 and 2, this is consistent with locomotion being driven by controlling cell deformation instead of cell traction forces. Similar conclusions have been reached in the different context of adherent epithelial cells (Saez et al., 2005). To extend the range of variation of the different cellular parameters, we treated cells with a collection of specific inhibitors that impact cell migration in CDMs (Caballero et al., 2017). We tracked cell trajectories for control cells (Figure 4—figure supplement 1a), cells treated with myosin ATPase activity inhibitor Blebbistatin (Figure 4—figure supplement 1b and Video 11), ROCK inhibitor Y27632 (Figure 4—figure supplement 1c), myosin light chain kinase inhibitor ML7 (Figure 4—figure supplement 1d), actin polymerization inhibitor latrunculin A (Figure 4—figure supplement 1e), lamellipodia growth promoter C8-BPA (Figure 4—figure supplement 1f), Arp2/3 complex inhibitor CK666 (Figure 4—figure supplement 1g), and nocodazole (Figure 4—figure supplement 1h). As expected, all pharmacological treatments altered cell migration. Latrunculin A (Video 12) and nocodazole (Video 9) stalled migration completely. Among the others, we observed speed oscillations for cells treated with Y-27632, ML-7, C8-BPA, and CK666. Those treatments reduced persistent cell speed (Figure 4—figure supplement 1i) and increased the period of speed oscillations (Figure 4—figure supplement 1j), showing that we could indeed alter cell migration behavior. We then plotted the velocity as a function of the oscillation period, for individual cells of drug treatments with speed oscillations aggregated (Y-27632, ML-7, C8-BPA, and CK666) together with control cells (WT). We could observe an inverse correlation between period and velocity overall for these cells (Figure 4d, Pearson’s correlation coefficient –0.4978 with p<0.0001). However, when looking at each condition separately, persistent speed was still significantly anticorrelated with oscillation period for WT cells and Y-27632-treated cells (Pearson’s correlation coefficient –0.4119 with p=0.0455 and –0.7435 with p=0.0217, respectively), but it was not in the case of ML-7, C8-BPA, and CK666. This may be caused by variability among individual cells, nevertheless on average cell speed decreased and oscillation period increased upon treatment with these compounds as well (Figure 4—figure supplement 1i and j). Therefore, an inverse correlation between period and velocity is evident at the population level, both for WT cells and when those are aggregated to pharmacologically treated cells.

Video 11

Download asset

Video 12

Download asset

Externally triggered contractions by means of laser ablation induce cell translocation

Altogether, these results suggest that the temporal coupling between spatially distributed force dipoles along the cell promotes cell motion. To verify this, we designed an experiment to externally trigger localized cellular force dipoles. We observed that localized laser ablation within the cortex of a cell (Figure 5a and b before ablation) triggered the relaxation of the cell and the surrounding matrix, as marked by the displacement of the matrix away from the cut region (Figure 5b ablation). This process was then followed by a contraction of the cell along with the surrounding matrix (Figure 5b after ablation). Remarkably, laser ablation led to the transient recruitment of actin and myosin (Figure 5c bottom left and Figure 5—figure supplement 1a), which co-localized with cell contraction (Figure 5c bottom right and Video 13). For a polarized cell the laser-induced contraction triggered the translocation of the cell (Figure 5b), whereas for a cell with no clear polarization and multiple attachment points no cell body translocation was observed (Figure 5c). Therefore, by laser ablation we could induce matrix pinching that could lead to a cell translocation given certain cell morphology.

Figure 5 with 1 supplement see all

Download asset Open asset

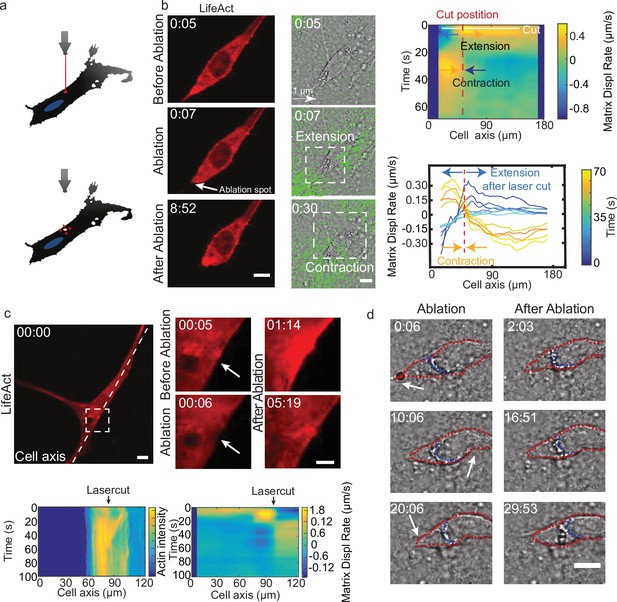
Cell motion is triggered by means of laser-induced force dipoles.

(a) Schematic of laser ablation experiment. (b) (Left panel: LifeAct, middle panel: phase contrast and KLT, arrows indicate displacement between two consecutive frames, Δt=10 s). Ablation at the back of the cell (white arrow) immediately followed by an extension, and later by a contraction of the matrix (both highlighted using white square window). Scale bar LifeAct: 10 µm KLT: 20 µm. Right panel. Bottom: Plot of the displacement rate along the cell axis at different timepoints (color coded) showing extension and contraction. Top: Heatmap of displacement rates indicating the initial extension and the subsequent contraction. (c) Top: Sequence of snapshots during laser ablation on a cell expressing mCherry-LifeAct. Intensity drops locally immediately after the cut, followed by a local recruitment of actin, scale bar 20 µm, scale bar in zoom 5 µm. Bottom: The intensity heatmap reveals a focused actin flow (see also Video 13). As shown in the deformation map, the contraction precedes this flow. (d) Consecutive ablations (indicated with white arrows) mimic contraction-extension cycles at the front and back of the cell. Ablation is performed in the following order: at the cell back, at the front and then at the back again. In all panels, scale bar 10 µm and time in mm:ss. Note cell motion to the right (see also Video 14), scale bar 10 µm. The cell is outlined in red and the back of the nucleus with a blue dashed line.

Figure 5—source data 1 Cell migration induced by laser ablation. (i) Migration trajectories of cells which are exposed to laser ablation-induced contractions.: https://cdn.elifesciences.org/articles/71032/elife-71032-fig5-data1-v2.xlsx
Download elife-71032-fig5-data1-v2.xlsx

Video 13

Download asset

Mimicking the periodic alternation of contractile and extensile dipoles at both ends of the cell, a second contraction at the opposite side of the cell should lead to forward displacement. So, we then used this method to repeatedly locally impose cellular force dipoles, by triggering local contractions alternatively at the front and the back of a polarized cell (see schematics in Figure 5—figure supplement 1b). We imposed correlated contractions by selecting a constant time interval between consecutive laser ablations: this triggered reiterated translocation and led to a net movement of the cell (Figure 5—figure supplement 1b and Video 14). This externally induced cell displacement was achieved when laser ablation of equal power was applied sequentially at the front and the back of the nucleus, both with about 6 and 10 min intervals between cuts (Figure 5—figure supplement 1b). In contrast, when this sequential ablation was applied repeatedly only at one side of a polarized cell (front), net displacement was either absent or smaller than when alternating front and back, both with about 5 and 10 min intervals between cuts (Figure 5—figure supplement 1c). This shows that externally induced force dipoles are sufficient to promote directed cell motion and illustrates that by alternating induced force dipoles at front and back of the nucleus leads to net cell motion. Altogether, this supports the principle of a phase shift between local dipoles as a trigger for cell motility.

Video 14

Download asset

Discussion

Acto-myosin complexes are likely to be the functional elements that control the dynamics of the individual contractile units. The cycles of protrusion/retraction at both ends of the cell likely involves transient retrograde actin flow whose periodic nature could be linked to a stick-slip phenomenon (Sens, 2020). Therefore, although the local actin dynamics within protrusions could be comparable to that fast moving cells in 2D or under confinement (Barnhart et al., 2011; Liu et al., 2015), the absence of a coherent actin flow at the scale of the entire cell and the existence of multiple competing protrusions considerably slows down cell motion. Our results show that for cells moving in 3D CDMs, the lack of time reversal symmetry required for cell motion is associated with a time shift between the oscillating dynamics of the two cell ends. Remarkably, the dynamics of individual dipoles appear similar in migrating and non-migrating cells, suggesting that the same force generation machinery is equally active in both types of cells, and that it is the synchronization between individual units that makes movement possible. Altering the dynamics of individual units can affect motion, in particular, faster oscillations can lead to faster motion, but the coordination between units is key in enabling cell translocation.

Acto-myosin networks commonly show oscillatory dynamics in vitro and in vivo in a variety of systems and over a large range of length scales (Kruse and Riveline, 2011): single filaments in motility assays (Riveline et al., 1998; Gillo et al., 2009; Plaçais et al., 2009), cells (Negrete et al., 2016) and cell fragments (Paluch et al., 2005), and even entire organisms (Martin et al., 2009). The biological function of these generic dynamics is often unclear. However, in our case, they appear to be essential. We conjecture that cellular systems could adapt their velocity by modulating the oscillation period. In this context, it would be interesting to test this proposal by combining tracking of single moving cells and local matrix deformations in vivo. If confirmed, this would provide an outstanding example of a physiological relevance for such oscillations. The phase shift between contractile units encodes cell polarity. Its maintenance in the course of time requires the existence of a polarity memory. If this type of phase locking can be expected in non-linear systems (Pikovsky et al., 2002), it is more demanding in the cellular context, where it is challenged by strong fluctuations in protein concentrations and activities. Our results suggest that the microtubular network is involved. However, other cytoskeletal elements and their interplay with adhesion dynamics are likely to play a role as well. Disentangling the interplay between mechanics and biochemical regulation in this process remains an important open question.

Our results show that for several cell types moving in CDMs, there exist two contractile units exerting force dipoles at both ends of the cell, and the lack of time reversal symmetry required for motion is associated with a time shift between the oscillating dynamics of the two cell ends. It is interesting to note that in other reports of cell motions in 3D gels (Steinwachs et al., 2016), cell appears to behave as fluctuating single contractile units, with no mention of coexistence of contraction at one end and extension at the other as we report here (for instance in Figure 1b). This type of motion is physically possible (see for instance Wagner and Lauga, 2013, or Datt et al., 2018). It thus appears that different cell types may undergo distinct dynamics to promote directed cell motion. Single force dipoles would be related with correlation of the contractile machinery across the cell whereas two dipoles could be associated with autonomous acto-myosin contractile units on each side of the cell. It would be interesting to relate this principle of length scale of mesoscopic unit dynamics with cytoskeletal structures and compositions in different cell lines.

We have explained the mechanisms of our directed cell motion with the concept of synchronized force dipoles and our results are consistent with the associated model. However, many assumptions were made. The CDMs are not continuous media, they are hydrogels of porous nature which may halt the motion when the pore size blocks the nucleus, for example. This may contribute to phases where cells are trapped and do not move at all. This situation would not challenge our model, since the directed motion phases presumably bypass this potential blockage. Also, growth and detachments of cell adhesion at both cell ends could be involved in the migratory phases along our observations of focal contacts dynamics (Video 3). Again, this would not challenge the main result of our rule for finite area when cells move directionally. It may however contribute to alternative mechanisms in the model where mechanosensing at focal contacts rather than force dipoles or in synergy with force dipoles mediated by acto-myosin would contribute to the basic synchronization mechanism. These potential contributions could be disentangled by future experiments tracking both acto-myosin and focal contact proteins over time together with matrix deformations.

We propose that temporal correlations between distinct contraction-extension units along the cell body is a general principle used by mesenchymal cells to achieve directional motility in 3D. This suggests new strategies to control the motion of cells by externally modulating their local contractile activity, for which we give a proof-of-principle using a standard laser setup. This concept could also be used to design synthetic micro-crawlers. Whereas there exist many examples of artificial micro-swimmers (see Elgeti et al., 2015, for a review), there is to our knowledge no realization of micro-crawler in regimes where inertia is negligible.

Materials and methods

Cell lines

Request a detailed protocol

NIH3T3 MEF cell line was obtained from ATCC. REF52 and primary MEFs were obtained from the IGBMC cell culture facility. Cells lines tested negative for mycoplasma.

Preparation of CDMs

Request a detailed protocol

For the CDM preparation (see Figure 1—figure supplement 1a and Godeau et al., 2020), a glass coverslip (CS) was incubated with 1% gelatin (gelatin from cold water fish skin, Sigma) and put at 37°C in the incubator for 1 hr. After two washing steps with PBS, the CS with the gelatin solution was incubated for 20 min at room temperature with 1% glutaraldehyde (Sigma). The CS was rinsed again twice with PBS before incubation for 20–30 min with 1 M glycine (Sigma). Subsequently the CS was washed twice with PBS before plating of the NIH3T3 fibroblasts. Cells were plated at high density in order to produce CDMs. For NIH3T3, this corresponded to a cell density of 10⁵ cells/mm² in the Petri dish. The culture medium was supplemented with 50 μg/mL L-ascorbic acid and changed every 2 days. The culture was maintained for 8–9 days. Cells were removed by a lysis medium consisting of 20 mM NH₄OH and 0.5% Triton (both from Sigma) in PBS after two washing steps with PBS. The pre-warmed lysis medium was carefully pipetted on the CS and incubated for up to 10 min at 37°C in the incubator. PBS solution was added and the CDM stored at 4°C. The day after, the PBS solution was carefully changed three times to remove residues of Triton. The matrices were covered with PBS and stored for up to 1 month at 4°C. For alignment purposes after image acquisition, beads (200 nm, BioSpheres) were spin-coated on the CS before incubation with gelatin. Beads for optical tweezers measurements (L4530, Sigma) were inserted when seeding the cells. For visualization of fibronectin inside the CDM, two methods were used with no apparent differences: we prepared a stable cell line expressing fluorescent fibronectin (construct kindly provided by Erickson laboratory, Duke University), alternatively, fluorescently labelled fibronectin (Cytoskeleton Inc) was added to the culture.

Cell culture, transfection, and inhibitors

Request a detailed protocol

Cells were cultured at 37°C under 5% CO₂ with a culture medium, high glucose D-MEM with 1% penstrep (penicillin-streptomycin, Thermo Fisher Scientific) supplemented with 10% bovine calf serum (Sigma). Transfections were performed with Lipofectamin 2000 (Invitrogen) using a standard protocol, and the following constructs were used: mCherry-Lifeact, GFP-NMHC2A (nonmuscle myosin heavy chain 2A, kindly provided by Ewa Paluch lab, UCL), RFP-zyxin (kindly provided by Anna Huttenlocher lab, University of Wisconsin-Madison), or mCherry-MRLC2A (Addgene). For experiments with inhibitors, ROCK inhibitor Y-27632 was used at a concentration of 10 μM, microtubule de-polymerizing agent nocodazole at 10 μM, myosin-II inhibitor blebbistatin at 25 μM, MLCK inhibitor ML-7 at 10 μM, F-actin depolymerizing agent latrunculin A at 1 μM, Arp2/3 inhibitor CK666 at 50 μM (all from Sigma), and lamellipodia growth promoter C8-BPA at 100 μM (Nedeva et al., 2013). Before drug addition, we performed a control acquisition of at least 1 hr. To prevent flows, defocusing or potential damage of the CDM during manipulation, medium with drugs was added to the running experiment without removing the medium to reach the target concentration.

Time-lapse imaging and laser ablation, optical setups, EM

Request a detailed protocol

We used a Nikon Ti Eclipse inverted microscope equipped with a Lambda DG-4 (Shutter Instruments Company), a charge coupled device (CCD) camera CoolSNAP HQ2 (Photometrics), a temperature control system (Life Imaging Services) and, if needed, CO₂ control. The objectives were the following: PhLL 20× (air, 0.95 NA, phase contrast, Nikon), a Plan Apo 60× objective (oil, 1.40 NA, DIC, Nikon) and a 40× (air, 0.95 NA, Olympus) objective with a home-made adapter to fit the Nikon microscope. Images were acquired with the NIS Elements software (v3.10, SP3, Nikon) and then exported for further processing. We also used a CKX41 inverted phase contrast microscope (Olympus) with a cooled CCD camera (Hamamatsu). The system was equipped with a temperature control (Cube box system) and 4×, 10×, 20×, and 40× phase contrast air objectives. For confocal imaging, we used a Leica TCS SP5-MP inverted microscope equipped with a Leica Application Suite Advanced Fluorescence LAS AF 2.6.3.8173/LASAF 3.1.2.8785 acquisition system with hybrid detectors (HyD), photomultiplier tube (PMT), and a heating system (Cube box system); with a HCX PL APO 63× oil objective (1.4 NA, Leica). Additionally, a Leica DMI6000 inverted microscope was used as a spinning disk, equipped with a Andor iQ 1.9.1 acquisition system, Yokogawa CSU22 spinning disk unit, and a heating system (Tokai Hit Stage Top Incubator, INU incubation system for microscopes). A HCX PLAPO 40× oil objective (1.25 NA, Leica) was used. The time between two frames ranged from 10 s to 5 min and typical exposure time was 100–200 ms. The software Imaris was used for reconstructing and animating 3D datasets. For laser ablation, a Leica TCS SP8-MP based on a Leica DM6000 CFS upright microscope was used, equipped with a Leica Application Suite Advanced Fluorescence LAS AF 2.6.3.8173/LAS AF 3.1.2.8785 acquisition system with PMT and HyD and an environmental chamber for temperature control (Cube box system). A 25× HCX IRAPO L water objective (0.95 NA, Leica) was used and ablation performed with infrared pulsed laser (Coherent Vision II with pre-compensation). FRAP module was used with point ablation with a wavelength set at 800 nm and an exposition time of 100–200 ms. During experiments, parameters such as laser power and gain were set to minimum to have the smallest cut possible while maintaining cell and CDM integrity. ‘Exploding’ cells were discarded and analysis performed as described in the section referring to Image analysis.

Native CDMs with integrated cells were imaged by EM. To obtain cross-sections of the CDM, they were grown on Polystyrene sheets. The CDMs were fixed by immersion in 2.5% glutaraldehyde and 2.5% paraformaldehyde in cacodylate buffer (0.1 M, pH 7.4), and post-fixed in 1% osmium tetroxide in 0.1 M cacodylate buffer for 1 hr at 4°C. The samples were dehydrated through graded alcohol (50%, 70%, 90%, 100%), and critical point dried with hexamethyldisilazane. After mounting on stubs with conductive carbon adhesive tabs, the CDMs were coated with gold-palladium in a sputter coater (BAL-TEC SCD 005). For imaging along the z-axis, CDMs were cut and mounted upright with conductive carbon tape. Then they were examined by XL SIRION 200 FEG SEM (FEI Company, Eindhoven, The Netherlands).

Image analysis

Request a detailed protocol

For quantification, the myosin intensity profiles were obtained on the raw images of the selected time frames. ImageJ was used to obtain the intensity values along a 6 µm long line, with a line width of 20 pixels to average the intensity values. Data was further normalized by the maximum value of intensity among all the frames analyzed. For visual representation, images of myosin clusters were filtered with a median filter and the background signal subtracted. To enhance the contrast of the clusters, a contrast-limited adaptative histogram equalization was applied. For KLT analysis, images were pretreated. In the case of a z-stack, images were projected with average or maximal projection and outliers were removed with Remove Outlier function of ImageJ. Then, deformation was tracked in 2D. A ‘pyramidal implementation’ of KLT tracker method was used to detect deformation in the mesh (Godeau et al., 2020). This method is based on KLT algorithm and follows bright features from one image to another. Therefore, a textured patch with high intensity variation in x and y is required. A multi-resolution pyramid of the image intensity and its gradients are computed before tracking is performed. Then, the KLT algorithm is first applied to lower resolution image, where it detects coarse movement before a higher resolution image is taken for fine movement detection. After having reached the maximum iteration steps for all pyramid levels, the displacement of the feature is extracted (between two frames). The Computer Vision Toolbox for MatLab was used with a customary written code with number of features varying between 5000 and 10,000 and a minimum distance from 8 to 14 px depending on image size and resolution, making sure that features were sufficiently spaced. Parameter window interrogation size was set to 40 px and maximal iteration to 20 px. The number of pyramids was two for all calculations. For each image an overlay of displacement vectors and phase contrast or fluorescent image of the cell was generated. Drift calculation was performed with a maximum of 40 px features with a minimum distance of 8 px with a window size of 20 px and one pyramid. The displacement due to drift was subtracted from the cell-induced displacement of the mesh.

Analysis of the contractile and extensile patterns over time

Request a detailed protocol

The displacement of the meshwork calculated via the KLT feature tracker was projected onto a line going through the cell axis in order to observe 1D matrix displacement and the heatmap of displacement plotted. The matrix displacement amplitude is color coded in the heatmap. To highlight the cell position in the heatmap, cell features such as nuclear front, back, and cell tail were tracked and plotted in the heatmap. To investigate recurring contractile and extensile patterns, the divergence of matrix displacement along the cell axis was obtained. The divergence was averaged over a region of 2–5 μm wide either at the cell back or the cell front, resulting in traces for the front and the back of at least 30 min in duration with points every 30 s. Average divergence was subtracted to reduce background and autocorrelation performed via Matlab using the xcorr function with coefficient normalization so that the autocorrelation at zero lag equals 1. To determine the period, the first peak next to zero with amplitude larger than 1 standard deviation was selected. Graphs where no peak could be identified were discarded. To compare matrix displacement at two distinct positions along cell axis, cross-correlation analysis was performed with the same parameters as for the autocorrelation. In this case the largest peak (either positive or negative) was extracted. Graphs where no peak could be identified were discarded. To obtain the period of cell speed, cell movement was tracked with the nucleus as reference point using ImageJ Manual Tracking Plugin. The trajectory was projected on the axis of migration and autocorrelation performed via Matlab. The xcorr function with coefficient normalization was used so that the autocorrelation at zero lag equals 1. The highest peak next to 0 with amplitude larger than 1 standard deviation was extracted. Graphs where no peak could be identified were discarded.

Elasticity CDM measurements by optical tweezers

Request a detailed protocol

CDM with fluorescent beads were mounted on a holder and placed on an inverted microscope (Olympus IX71). A Spectra Physics YAG laser (1064 nm) was used and focused through a high numerical oil immersion objective (Zeiss achromat 100× 1.25 NA). We acquired the movies with a second objective (Olympus X40 0.6 NA associated with a CCD camera (DCC3240C, Thorlabs)). The setup was controlled by LabView 9 (National Instruments). Beads were centered in the optical trap (Figure 1—figure supplement 1e). The position of the CS (bottom of CDM) was registered to obtain the z position of the measured beads in the CDM. Stage was moved in 0.2 μm/s, covering a distance of 2–4 μm in x/-x and y/-y directions (Video 2). The laser power was calibrated with beads in solution. Subsequent data processing was performed with ImageJ bead Tracker Plugin and further post-processed with IgorPro Wavemetrics.

Statistical analysis

Request a detailed protocol

No statistical methods were used to predetermine sample size. The number of experiments (N) and the number of cells (n) included in every experiment can be found at the corresponding figure caption. Individual data points are shown when possible, accompanied by the mean value and error bars corresponding to the standard error of the mean. The statistical analysis was done with GraphPad Prism, pairwise t-tests, Kruskal-Wallis tests, and one-way ANOVA for multiple comparisons were performed, and the outcomes are shown in the corresponding panels as well as indicated in the figure captions.

Appendix 1

Optical tweezers

The optical tweezers setup has been described in Drobczynski, 2009. The calibration of the stiffness as a function of the laser power was performed in PBS buffer. Two μm beads were diluted in PBS buffer and trapped. We, then, acquired a power spectrum (Helfer et al., 2000; Harlepp et al., 2017) on the quadrant photodiode and we extracted the trap stiffness. We checked the linear dependence between the stiffness and the laser power. The elastic modulus of the ECM is obtained by mixing 2 µm polystyrene beads in the matrix formation process. We follow two beads in the same field of view (Figure 1—figure supplement 1f). One bead is trapped in the optical tweezers whereas the second is used as a reference. Then, the piezoelectrical stage is moved and the two beads displacement is recorded on the CCD camera. A post-acquisition treatment with ImageJ allows us to extract the displacement expressed in nm of the two beads. These displacements are different one from the other due to the optical restoring force. We haven’t detected any hysteresis between back and forth displacement on the same bead. This observation led us to think that the ECM in the ranges (frequency and amplitude) we were looking at was totally elastic with no viscous behavior. The knowledge of the trap stiffness allows us to determine the forces exerted on the trapped bead. The force curves obtained are linear in the regime we are exploring. We show a linear relation between the applied force and the indentation allowing us to adjust these curves with the linear model and extract the elastic modulus E. We performed 37 measurements at different positions in the ECM and plotted the elastic modulus obtained over the experiments. The average value of the elastic modulus that we found is around 50 Pa. We assume that the average refraction index of the ECM is close to the refraction index found in PBS. We, therefore, use the trap stiffness found in PBS to extract the forces in the ECM. We move the sample with a piezoelectrical stage at a speed rate of 200 nm/s. The displacement of the beads was recorded on the CCD camera at a framerate of 10 fps. The position of the reference bead and the trapped bead were extracted using ImageJ and the particle analysis plugin. We extracted the subpixel resolution of the center of mass positions of the beads over time and calculated the beads displacement $r = \sqrt{{(x - x_{0})}^{2} + {(y - y_{0})}^{2}}$ . The displacement of the bead in the trap was linked to the force applied to the ECM, and the difference between the total displacement (reference bead) and the trapped bead was related to the ECM compression (indentation). We used several models to extract the Young’s modulus from the experiments. The Hertz model described in Nawaz et al., 2012, and Yousafzai et al., 2016, were used to understand how to link the indentation to the displacement. Nevertheless, the models described in these papers were linked to single cells and not to the fibers present in the medium. We, thus, used the model described by Laurent et al., 2002, in the case the bead is totally immersed in an infinite 3D medium. We modified the model to introduce the indentation instead of the bead displacement in the trap that would have given a linear relation between the stiffness and the elastic modulus. Therefore, the linear relationship between the elastic modulus and the force is: $F = 2 π R E d$ with $R$ the bead radius, $E$ the elastic modulus, d the indentation, and $F$ the measured force. The indentation $d$ is given by $d = d_{T} - d_{B}$ , where $d_{T}$ is the reference bead displacement and $d_{B}$ the displacement of the bead in the trap.

Appendix 2

Multipolar expansion

As discussed in the main text, we quantify the cell-matrix interaction via the distribution of matrix displacement rate ax`round the cell, calling $u_{i}^{(n)}$ the component $i$ at position $n$ of the meshwork. We then calculate the monopole vector $M_{i} = \sum_{n} u_{j}^{(n)}$ , the dipole matrix $S_{i j} = \frac{D_{i j} + D_{j i}}{2}$ , where $D_{i j} = \sum_{n} ∆_{i}^{(n)} u_{j}^{(n)}$ and the quadrupole matrix $Q_{i j k} = \sum_{n} ∆_{i}^{(n)} ∆_{j}^{(n)} u_{k}^{(n)}$ , with $Δ_{i}^{(n)}$ the $i$ th component of the vector joining the cell center (defined below) and the point $n$ on the mesh. We also compute the characteristic scale of matrix displacement rate defined as $\sum_{n} |u^{(n)}| .$ The largest component of the monopole vector is called the main monopole, $M$ , and the largest eigenvalues of the dipole and quadrupole tensors are defined as the main dipole, $D$ , and the main quadrupole, $Q$ . The corresponding eigenvectors are defined as the main dipole and quadrupole axes.

A cell that migrates spontaneously (i.e. in absence of external forces) can be viewed as a force-free body, hence in the absence of inertia the sum of all the traction forces add up to zero (Tanimoto and Sano, 2014). Thus, for a homogeneous material under linear elasticity, the monopole of displacement rate should be zero. In our experiments, 3D imaging is challenged by a limited and asymmetric field of view which leads to a non-zero value of the monopole. To reduce these imaging asymmetries, the traction, monopole, dipole, and quadrupole are computed and averaged over disks (Figure 3—figure supplement 1) of increasing radius $R_{k}, k = 0, 1, . . . M$ starting from a minimum radius $R_{0} ≃ 20 μ m$ and up to a maximum radius $R_{M}$ defined as the largest radius such that the circular region is fully contained within the boundaries of the experimental images. To minimize the spurious monopole, the center of the disk is varied around the apparent cell center (obtained from cell tracking) and the location for which the monopole is minimum is adopted as the center of the disks on which the dipoles and quadrupoles are computed. This is done at every time step. Note that matrix heterogeneities could also possibly contribute to a non-zero monopole. Figure 3—figure supplement 2 shows histograms for difference of orientation between the main dipole axis and the direction of motion for three examples of migrating cells, showing a clear peak near zero angle difference. In addition to cellular noise, the rather large spread of these data is also explained by the fact that the major dipole is a fluctuating quantity which frequently crosses zero, at which point the largest dipole is the minor dipole, which is typically oriented perpendicular to the direction of motion.

Additional examples of cycles for migrating and non-migrating cells are shown in Figure 3—figure supplement 3a. As in the main text, the cycles shown for migrating cells are obtained by first identifying intervals of time with clear oscillating behavior in the speed and focusing on that time interval when we compute the multipolar expansion. For cells which are non-migrating, we cannot apply this scheme as we have no notion of oscillating speed, thus the choice in Figure 3—figure supplement 3a is somehow arbitrary. Nonetheless, we find that the areas of cycles for non-migrating cells are systematically smaller when compared to the areas of migrating cells. Importantly, the comparison between the absolute values of the multipoles of displacement rates between different cells is not straightforward, as these measures depend on the spatial and temporal resolution of the movies, which may vary from cell to cell. To support our claim that the main difference between migrating and non-migrating cells is the existence of a phase shift and not the cell’s ability to exert traction forces, we show in Figure 3—figure supplement 3b the average of the absolute value of the rate of deformation field for migrating and non-migrating cells. This quantity is obtained for each cell by computing the sum of the displacement rate amplitude within a disk, divided by the number of measurement points within the disk, averaged over disk radii spanning the accessible range for each cell, and averaged over time. Although this quantity varies from cell to cell, there is no significant difference (p=0.2766) between migrating and non-migrating cells. On the other hand, the area enclosed by the cycle in the dipole/quadrupole phase space is systematically higher for migrating than non-migrating cells. Figure 3—figure supplement 3c shows the cycle area, defined as the area $A (n_{1}, n_{s}) = \sum_{i = n_{1}}^{n_{2} - 1} I_{i + 1, i} + I_{n_{1}, n_{2}}$ with $I_{i + 1, i} = \int_{i}^{i + 1} Q (D) d D = \frac{1}{2} (Q_{i + 1} + Q_{i}) (D_{i + 1} - D_{i})$ , where $D_{i}$ and $Q_{i}$ are the dipole and quadrupole values at the ith time frame and $n_{1}$ and $n_{2}$ are the starting and ending time frames. Both the absolute value of this quantity in physical units and the fraction (in %) of normalized the area of the rectangle tightly enclosing the cycle are shown.

Data availability

All data generated or analysed during this study are included in the manuscript and supporting file; Source Data files have been provided for Figures 1, 2, 3, 4 and 5.

References

Book
1. Alberts B
(2002)
Molecular Biology of the Cell

Garland Science.
- Google Scholar
1. Barnhart EL
2. Lee KC
3. Keren K
4. Mogilner A
5. Theriot JA
(2011) An adhesion-dependent switch between mechanisms that determine motile cell shape
PLOS Biology 9:e1001059.
https://doi.org/10.1371/journal.pbio.1001059
- PubMed
- Google Scholar
1. Barry NP
2. Bretscher MS
(2010) Dictyostelium amoebae and neutrophils can swim
PNAS 107:11376–11380.
https://doi.org/10.1073/pnas.1006327107
- PubMed
- Google Scholar
1. Blanch-Mercader C
2. Casademunt J
(2013) Spontaneous motility of actin lamellar fragments
Physical Review Letters 110:1–5.
https://doi.org/10.1103/PhysRevLett.110.078102
- PubMed
- Google Scholar
(2014) Protrusion fluctuations direct cell motion
Biophysical Journal 107:34–42.
https://doi.org/10.1016/j.bpj.2014.05.002
- PubMed
- Google Scholar
(2017) An interplay between matrix anisotropy and actomyosin contractility regulates 3D-directed cell migration
Advanced Functional Materials 27:1702322.
https://doi.org/10.1002/adfm.201702322
- Google Scholar
(2001) Taking cell-matrix adhesions to the third dimension
Science 294:1708–1712.
https://doi.org/10.1126/science.1064829
- PubMed
- Google Scholar
(2018) Two-sphere swimmers in viscoelastic fluids
Physical Review Fluids 3:123301.
https://doi.org/10.1103/PhysRevFluids.3.123301
- Google Scholar
1. Delanoë-Ayari H
2. Iwaya S
3. Maeda YT
4. Inose J
5. Rivière C
6. Sano M
7. Rieu J-P
(2008) Changes in the magnitude and distribution of forces at different Dictyostelium developmental stages
Cell Motility and the Cytoskeleton 65:314–331.
https://doi.org/10.1002/cm.20262
- PubMed
- Google Scholar
1. Drobczynski S
(2009) Design and realization of a high-stability optical tweezer
Optical Engineering 48:1–5.
https://doi.org/10.1117/1.3257269
- Google Scholar
(2015) Physics of microswimmers--single particle motion and collective behavior: A review
Reports on Progress in Physics. Physical Society 78:056601.
https://doi.org/10.1088/0034-4885/78/5/056601
- PubMed
- Google Scholar
1. Etienne-Manneville S
(2004) Actin and microtubules in cell motility: which one is in control?
Traffic 5:470–477.
https://doi.org/10.1111/j.1600-0854.2004.00196.x
- PubMed
- Google Scholar
(2009) The fusion of actin bundles driven by interacting motor proteins
Physical Biology 6:036003.
https://doi.org/10.1088/1478-3975/6/3/036003
- PubMed
- Google Scholar
(2020) Generation of fluorescent cell-derived-matrix to study 3D cell migration
Methods in Cell Biology 156:185–203.
https://doi.org/10.1016/bs.mcb.2019.11.013
- PubMed
- Google Scholar
1. Golestanian R
2. Ajdari A
(2008) Analytic results for the three-sphere swimmer at low Reynolds number
Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics 77:036308.
https://doi.org/10.1103/PhysRevE.77.036308
- PubMed
- Google Scholar
(2017) Hemodynamic forces can be accurately measured in vivo with optical tweezers
Molecular Biology of the Cell 28:3252–3260.
https://doi.org/10.1091/mbc.E17-06-0382
- PubMed
- Google Scholar
(2000) Microrheology of biopolymer-membrane complexes
Physical Review Letters 85:457–460.
https://doi.org/10.1103/PhysRevLett.85.457
- PubMed
- Google Scholar
1. Jia Q
2. Chu H
3. Jin Z
4. Long H
5. Zhu B
(2022) High-throughput single-сell sequencing in cancer research
Signal Transduction and Targeted Therapy 7:145.
https://doi.org/10.1038/s41392-022-00990-4
- PubMed
- Google Scholar
1. Jiang J
2. Zhang Z
3. Yuan X
4. Poo M
(2015) Spatiotemporal dynamics of traction forces show three contraction centers in migratory neurons
The Journal of Cell Biology 209:759–774.
https://doi.org/10.1083/jcb.201410068
- PubMed
- Google Scholar
1. Kaverina I
2. Straube A
(2011) Regulation of cell migration by dynamic microtubules
Seminars in Cell & Developmental Biology 22:968–974.
https://doi.org/10.1016/j.semcdb.2011.09.017
- PubMed
- Google Scholar
1. Kruse K
2. Riveline D
(2011) Spontaneous mechanical oscillations: implications for developing organisms
Current Topics in Developmental Biology 95:67–91.
https://doi.org/10.1016/B978-0-12-385065-2.00003-7
- PubMed
- Google Scholar
1. Laurent VM
2. Hénon S
3. Planus E
4. Fodil R
5. Balland M
6. Isabey D
7. Gallet F
(2002) Assessment of mechanical properties of adherent living cells by bead micromanipulation: comparison of magnetic twisting cytometry vs optical tweezers
Journal of Biomechanical Engineering 124:408–421.
https://doi.org/10.1115/1.1485285
- PubMed
- Google Scholar
1. Leoni M
2. Sens P
(2015) Polarization of cells and soft objects driven by mechanical interactions: consequences for migration and chemotaxis
Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics 91:022720.
https://doi.org/10.1103/PhysRevE.91.022720
- PubMed
- Google Scholar
1. Leoni M
2. Sens P
(2017) Model of cell crawling controlled by mechanosensitive adhesion
Physical Review Letters 118:228101.
https://doi.org/10.1103/PhysRevLett.118.228101
- PubMed
- Google Scholar
1. Liu Y-J
2. Le Berre M
3. Lautenschlaeger F
4. Maiuri P
5. Callan-Jones A
6. Heuzé M
7. Takaki T
8. Voituriez R
9. Piel M
(2015) Confinement and low adhesion induce fast amoeboid migration of slow mesenchymal cells
Cell 160:659–672.
https://doi.org/10.1016/j.cell.2015.01.007
- PubMed
- Google Scholar
(2020) Collective dynamics of focal adhesions regulate direction of cell motion
Cell Systems 10:535–542.
https://doi.org/10.1016/j.cels.2020.05.005
- PubMed
- Google Scholar
Conference
1. Lucas BD
2. Kanade T
(1981)
An iterative image registration technique with an application to stereo vision

Proceedings of the 7th international joint conference on Artificial intelligence. pp. 674–679.
- Google Scholar
1. Maiuri P
2. Rupprecht J-F
3. Wieser S
4. Ruprecht V
5. Bénichou O
6. Carpi N
7. Coppey M
8. De Beco S
9. Gov N
10. Heisenberg C-P
11. Lage Crespo C
12. Lautenschlaeger F
13. Le Berre M
14. Lennon-Dumenil A-M
15. Raab M
16. Thiam H-R
17. Piel M
18. Sixt M
19. Voituriez R
(2015) Actin flows mediate a universal coupling between cell speed and cell persistence
Cell 161:374–386.
https://doi.org/10.1016/j.cell.2015.01.056
- PubMed
- Google Scholar
(2009) Pulsed contractions of an actin-myosin network drive apical constriction
Nature 457:495–499.
https://doi.org/10.1038/nature07522
- PubMed
- Google Scholar
1. Najafi A
2. Golestanian R
(2004) Simple swimmer at low Reynolds number: three linked spheres
Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics 69:062901.
https://doi.org/10.1103/PhysRevE.69.062901
- PubMed
- Google Scholar
1. Nawaz S
2. Sánchez P
3. Bodensiek K
4. Li S
5. Simons M
6. Schaap IAT
(2012) Cell visco-elasticity measured with AFM and optical trapping at sub-micrometer deformations
PLOS ONE 7:e45297.
https://doi.org/10.1371/journal.pone.0045297
- PubMed
- Google Scholar
1. Nedeva I
2. Koripelly G
3. Caballero D
4. Chièze L
5. Guichard B
6. Romain B
7. Pencreach E
8. Lehn J-M
9. Carlier M-F
10. Riveline D
(2013) Synthetic polyamines promote rapid lamellipodial growth by regulating actin dynamics
Nature Communications 4:2165.
https://doi.org/10.1038/ncomms3165
- PubMed
- Google Scholar
1. Negrete J
2. Pumir A
3. Hsu H-F
4. Westendorf C
5. Tarantola M
6. Beta C
7. Bodenschatz E
(2016) Noisy oscillations in the actin cytoskeleton of chemotactic amoeba
Physical Review Letters 117:148102.
https://doi.org/10.1103/PhysRevLett.117.148102
- PubMed
- Google Scholar
1. Paluch E
2. Piel M
3. Prost J
4. Bornens M
5. Sykes C
(2005) Cortical actomyosin breakage triggers shape oscillations in cells and cell fragments
Biophysical Journal 89:724–733.
https://doi.org/10.1529/biophysj.105.060590
- PubMed
- Google Scholar
(2012) Nonpolarized signaling reveals two distinct modes of 3D cell migration
The Journal of Cell Biology 197:439–455.
https://doi.org/10.1083/jcb.201201124
- PubMed
- Google Scholar
Book
(2002) Synchronization: A Universal Concept in Nonlinear Science
Cambridge University Press.
https://doi.org/10.1017/CBO9780511755743
- Google Scholar
(2009) Spontaneous oscillations of a minimal actomyosin system under elastic loading
Physical Review Letters 103:158102.
https://doi.org/10.1103/PhysRevLett.103.158102
- PubMed
- Google Scholar
1. Purcell EM
(1977) Life at low Reynolds number
American Journal of Physics 45:3–11.
https://doi.org/10.1119/1.10903
- Google Scholar
1. Qiu T
2. Lee T-C
3. Mark AG
4. Morozov KI
5. Münster R
6. Mierka O
7. Turek S
8. Leshansky AM
9. Fischer P
(2014) Swimming by reciprocal motion at low Reynolds number
Nature Communications 5:5119.
https://doi.org/10.1038/ncomms6119
- PubMed
- Google Scholar
(2013) Contraction-driven cell motility
Physical Review Letters 111:2–6.
https://doi.org/10.1103/PhysRevLett.111.108102
- PubMed
- Google Scholar
(2014) Optimality of Contraction-Driven Crawling
Physical Review Letters 112:1–5.
https://doi.org/10.1103/PhysRevLett.112.218101
- Google Scholar
1. Reversat A
2. Gaertner F
3. Merrin J
4. Stopp J
5. Tasciyan S
6. Aguilera J
7. de Vries I
8. Hauschild R
9. Hons M
10. Piel M
11. Callan-Jones A
12. Voituriez R
13. Sixt M
(2020) Cellular locomotion using environmental topography
Nature 582:582–585.
https://doi.org/10.1038/s41586-020-2283-z
- PubMed
- Google Scholar
(1998) Acting on actin: the electric motility assay
European Biophysics Journal 27:403–408.
https://doi.org/10.1007/s002490050147
- PubMed
- Google Scholar
1. Saez A
2. Buguin A
3. Silberzan P
4. Ladoux B
(2005) Is the mechanical activity of epithelial cells controlled by deformations or forces?
Biophysical Journal 89:L52–L54.
https://doi.org/10.1529/biophysj.105.071217
- PubMed
- Google Scholar
1. Sens P
(2020) Stick-slip model for actin-driven cell protrusions, cell polarization, and crawling
PNAS 117:24670–24678.
https://doi.org/10.1073/pnas.2011785117
- PubMed
- Google Scholar
1. Steinwachs J
2. Metzner C
3. Skodzek K
4. Lang N
5. Thievessen I
6. Mark C
7. Münster S
8. Aifantis KE
9. Fabry B
(2016) Three-dimensional force microscopy of cells in biopolymer networks
Nature Methods 13:171–176.
https://doi.org/10.1038/nmeth.3685
- PubMed
- Google Scholar
(2018) Cell motility in cancer invasion and metastasis: insights from simple model organisms
Nature Reviews. Cancer 18:296–312.
https://doi.org/10.1038/nrc.2018.15
- PubMed
- Google Scholar
1. Tanimoto H
2. Sano M
(2014) A simple force-motion relation for migrating cells revealed by multipole analysis of traction stress
Biophysical Journal 106:16–25.
https://doi.org/10.1016/j.bpj.2013.10.041
- PubMed
- Google Scholar
1. Wagner GL
2. Lauga E
(2013) Crawling scallop: friction-based locomotion with one degree of freedom
Journal of Theoretical Biology 324:42–51.
https://doi.org/10.1016/j.jtbi.2013.01.021
- PubMed
- Google Scholar
1. Yamada KM
2. Sixt M
(2019) Mechanisms of 3D cell migration
Nature Reviews. Molecular Cell Biology 20:738–752.
https://doi.org/10.1038/s41580-019-0172-9
- PubMed
- Google Scholar
1. Yousafzai MS
2. Coceano G
3. Mariutti A
4. Ndoye F
5. Amin L
6. Niemela J
7. Bonin S
8. Scoles G
9. Cojoc D
(2016) Effect of neighboring cells on cell stiffness measured by optical tweezers indentation
Journal of Biomedical Optics 21:57004.
https://doi.org/10.1117/1.JBO.21.5.057004
- PubMed
- Google Scholar

Decision letter

Raymond E Goldstein

Reviewing Editor; University of Cambridge, United Kingdom
Aleksandra M Walczak

Senior Editor; CNRS LPENS, France

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Decision letter after peer review:

Thank you for sending your article entitled "Temporal correlation between oscillating force dipoles drives 3D single cell migration" for peer review at eLife. Your article is being evaluated by 2 peer reviewers, and the evaluation is being overseen by a Reviewing Editor and Aleksandra Walczak as the Senior Editor. We apologize for the delay in furnishing this report.

Given the list of essential revisions, including new experiments, the editors and reviewers invite you to respond as soon as you can with an action plan for the completion of the additional work. We expect a revision plan that under normal circumstances can be accomplished within two months, although we understand that in reality revisions will take longer at the moment. We plan to share your responses with the reviewers and then advise further with a formal decision.

While both reviewers are very supportive of the work, it was clearly felt that the experimental data was not sufficiently convincing. This suggests additional experiments may be warranted, or at the very least more analysis of the data is called for, especially in light of the fact that the underlying theory has already been published elsewhere.Reviewer #2 (Recommendations for the authors):

The manuscript proposes a model of cell motion in which the cell front and back are performing the same kind of contraction-extension cycles. When these two cycles are in antiphase, this results in back-and-forth motion while a phase difference between the two cycles not equal to zero or π results in cell migration i.e. a non-zero average velocity. This is an interesting model which differs from the usual views of cell motion coming from the treadmilling of actin in a lamellipod or by extension of pseudopods at the cell front. However, I am not fully convinced that the presented evidence supports this model rather than alternative ones.

The main results of the manuscript are obtained by observing and comparing the matrix deformations for migrating fibroblasts and for non-migrating ones that undergo back and forth motion. These observations as well as theoretical arguments led the authors to conclude that cell migration is associated to periodic localized contractions at the front and back of the cell with a finite phase difference. I find it difficult to assert from these data only that the contraction processes are similar at the front and back of the cells. For instance, the data seem similar in many respects, to those of Tanimoto and Sano (2014) obtained for 2D amoeboid motion on a substrate.

I list below more specific concerns with the presented data.

The assay which uses extracellular matrix deposited by confluent cells seems adequate and the quantification of matrix deformation soundly performed. I am less convinced by the presented quantification of the data in Figure 2 and 3.

Figure 2. The autocorrelations of the deformations in Figure 2d and 2e clearly show their periodic character. I guess these are representative curves for a single cell but this is not clearly stated. No details are given on how it was decided that an autocorrelation was periodic and how the period was extracted. The duration of the time traces that were used to compute these auto correlations is not stated either. The number of cells/observations used for the quantitations of the periods are not provided. The crucial panels j and k are even less clear for me. I clearly see from Figure 1j that matrix deformations at the front and back are in antiphase for the non-migrating cells. I also see that the cross-correlation is non symmetric in time for the migrating cell but I am unable to see how a phase lag was extracted for the presented example (there clearly seem to be a negative peak at zero). All this would need to be precisely explained to assess these results.

Figure 3. In (c) for the non-migrating cell the presented time trace for the dipolar and quadrupolar deformation are clearly in antiphase which nicely agree with Figure 1j.

However, for the migrating cell I again do not see a definite phase lag for the two traces. It rather seems for this particular trace, that the dipolar and quadrupolar deformations do not oscillate at the same frequency.

Figure 3d-h illustrate the cycle with a finite area in the dipole-quadrupole plane but appear as anecdotal examples. However, this should be quantified (average area, perhaps correlated with some characteristic of the motion since I guess cell may change direction).

Figure 4. I am not sure to understand the logic behind this experiment nor exactly what to conclude from it. First, when one considers separately each category of cells (untreated, treated with a given compound) it seems that there is no correlation between the period and the speed (is this the case?). This indicates that the variability between individual cells is large. Then, it would seem better to compare the effect of each treatment at the level of individual cells i.e. for given cell how the treatment change its period of contractions and its speed. Is this compatible with (VT^n)_(before treatment) = (VT^n)_(after treatment). If this equality is not obtained, this would indicate that other parameters are affected by the treatment and the need to determine them before concluding anything (in the framework of the authors, it would for instance be useful to assess whether the dephasing psi is modified by the treatment).

Figure 5. Artificially-induced contractions produced by laser ablation are taken as further evidence in favor of the model. This is obviously very different from physiological motion but in addition, I am not sure how this really fits with the proposed model. As far as I can see, in the example provided in Figure 5h, the ablation at the back and front were in antiphase, which should produce back and forth motion rather than directed migration. Again here, one would like convincing quantification (distance travelled given number of cycles of front/back ablations) and the dependence on important parameters like the dephasing between cycles of ablation at the cell back and front.

I do not have specific suggestions beyond those made in the public review but I like to add one additional point. The dipolar deformation is a 3X3 matrix. The authors computed its 2D projection but made use only of its projection on the direction of average cell velocity. I would welcome a discussion of the respective directions of the cell velocity and the main axis of the projected 2D dipolar deformation matrix.Reviewer #3 (Recommendations for the authors):

The authors have studied fibroblasts migrating in cell-derived matrix (CDM), which is a fibrous three-dimensional ECM with fluorescently labeled fibronectin and large pores. Cell were divided into two classes, non-migrating and migrating ones. In both cases, phases of contraction and extension were observed at the front and at the back (separated by the nucleus), with a typical oscillation period of 10 min, but the migrating cells showed a time lag, while the non-migrating ones did not. The authors argued that this phase shift (or phase locking) is the hallmark of migration, because it breaks the time-reversal symmetry in the phase space defined by deformation dipole and quadrupole (because the matrix is shown to be elastic by laser optical tweezer experiments, this should correspond to a cycle in force dipole and quadrupole space). In analogy to the scallop theory for microswimmers (equation 1, from Leoni and Sens 2015), the authors argue that only a non-vanishing phase shift leads to a finite crawling velocity (equation 2, from Leoni and Sens 2017). The have performed two experiments to validate this concept. With a large range of pharmacological inhibitions, they show that crawling speed is inversely proportional to oscillation period, as predicted by the theory. By using laser ablation to generate force contraction dipoles, they show that cell motion can be induced by alternating dipoles.

The big strength of this work is the elegance of the theoretical concept and the creativity in analyzing a well-known system from a new and quantitative angle. The weakness of this work is that the experimental data is not entirely convincing and that open questions remain regarding the generality of this concept.

I first note that three-dimensional traction force microscopy in collagen gels (as done e.g. by the group of Ben Fabry, often for cancer cells similar to the ones studied here) usually shows a clear dipole. Here the authors suggest that if one looks closely, there are actually two dipoles, separated by the nuclear region. I wonder if this observation depends on the matrix used (CDM with large holes) and the cell type used.

Next the authors describe that the two dipoles show oscillations which are phase-shifted in the migratory case. It is not entirely clear what causes these oscillations. Figure 1c and d suggest a relation to myosin and microtubules, but here the image quality is very bad and no quantification is being given. Figure 4d seems to suggest that oscillations and migration persist even under severe perturbations. Therefore it remains unclear what causes these oscillations and if they are really needed for productive cell migration.

The phase plane plot with dipoles and quadrupoles in Figure 3 is very interesting and similar to earlier work on Dictyostelium migrating on a two-dimensional substrate (Tanimoto and Sano BPJ 2014). I wonder why the same plot is not being shown for the theory part of Figure 4, because if it agreed, it would strengthen the relation between theory and experiment. Moreover the work by Tanimoto and Sano raises the question why the authors do not apply their concept to two dimensions. They argue in the discussion that in two dimensions, actin flow breaks the front-back symmetry and thus another mechanism is needed in three dimensions. This brings up two questions. First is the approach by Tanimoto and Sano for two dimensions not valid and second what is the proof that there is no retrograde flow in three dimensions.

Finally, it is really hard to assess if the laser ablation experiments do support the concept that oscillating dipoles leads to cell migration. Obviously, they not only cause relaxation and reformation of contractile structures, but they also interfere with adhesion and one effect might be to simply cause recoil in an elastic matrix.

In summary, the theoretical concept is very appealing and the experiments conducted are creative and interesting, but the relation between theory and experiment is not entirely convincing. Therefore, impact in the wider community of quantitative life sciences might remain limited for the current form of this manuscript.

In order to improve the relation between the general concept and the supporting experimental data, it would be very informative to conduct these experiment with different matrices and different cells types (ideally even with ghosts without nucleus), to see how general this observation is. How much does pore size of CDM matters, both for the oscillations and the laser ablation experiments? Is it important that the nucleus separates these two regions of the cell? Why cannot the same experiment be one in two dimensions, where the nucleus is out of the way? It would also be interesting to consider if less perturbative experiments might be feasible (e.g. optogenetics to locally induce contractility).

For the theory part, it would be interesting to give more background on the calculations behind Equation 2 and to explain if it also generates an open loop in the D-Q-plane as shown here for the experimental data.

Finally, I note that the discussions of the scallop theorem for swimming, although interesting, are not directly relevant to this work, because as the authors comment themselves, the situation is very different for crawling. Of course, this is an interesting analogy, but it also might be distracting or confusing to the general readers of eLife; it would be more interesting in the context of a physics journal. It is somehow odd that there are more references on the theory of swimming than on the theory of crawling. I note that there is actually a literature on the scallop theorem for crawling cells not cited here, most prominently the work by Pierre Recho, compare Recho, P., J-F. Joanny, and L. Truskinovsky. "Optimality of contraction-driven crawling." Physical Review Letters 112.21 (2014): 218101. I also miss references to earlier use of force multipoles in the cellular context (here mainly the work of Tanimoto and Sano is cited), and to traction force microscopy (including the work by Ben Fabry), which can be used to measure them.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

Thank you for resubmitting your work entitled "Temporal correlation between oscillating force dipoles drives 3D single cell migration" for further consideration by eLife. Your revised article has been evaluated by Aleksandra Walczak (Senior Editor) and a Reviewing Editor.

The manuscript has been improved but there are some remaining issues that need to be addressed, as outlined below:

1) The revised submission is strongly improved over the initial submission. The authors have conducted new experiments (other matrix, other cell types, laser ablation), added more theory results (in particular the D-Q plots), improved image quality and analysis, and made the main text more accessible. In my view, however, there still remains some doubt about the general validity of these results. As the authors write themselves, cell migration in 3D matrices can also occur through coherent actin flows or with single rather than double dipoles, so the title "Temporal correlation between oscillating force dipoles drives 3D single cell migration" and the corresponding abstract still sound too general. Interestingly, there now seem to be at least two scallop theorems for crawling, one for actin flow by Recho and coworkers and one for the contractile oscillations described here. We suggest that it is erroneous to now only citie Recho PRL 2013, because it is really the PRL 2014 that discusses the scallop theorem.

2) The manuscript has improved with more quantification available to assess the results and more precise explanations of how the results were obtained. The quantified data appear to support the interesting finding that there are two extension/contraction dipoles at the front and back of the cell. The dipole/quadupole cycle differences (Figure 3) also appear convincing, in agreement with the previous work of Tanimoto and Sano.

Yet, there remain several further points that are not fully convincing. The first main one is the dephasing between the two dipoles which is based on a single peak in the cross correlation and appears very noisy (the statistical significance of the count statistics Figure 2k should at least be provided).

Second, we are uneasy with the conclusions drawn for the laser ablations (Figure 5) and still do not see how they support (or not) the model. For instance, repeated ablations in the front of the cell would not lead to cell translocation given the model advocated by the authors (if we understand correctly). But this control has not been performed. Moreover, given the authors' model one would expect some dependence on the relative phase of ablations in the front and the back. But this is not attempted. We are thus unsure if one can conclude something very definite from these ablation experiments.

3) Overall, the reviewers are of the option that the study is strongly theory-driven and that the authors could do better in describing the experimental evidence. The whole design of the manuscript is such that the idea is put first and then some experimental evidence is provided. An alternative approach would be to start with the general status of the field of cell migration, then introduce the experimental results for this specific and certainly interesting system, and then the theory explanation as one way to explain these observations. Please consider this possible revision.

https://doi.org/10.7554/eLife.71032.sa1

Author response

Reviewer #2 (Recommendations for the authors):

The manuscript proposes a model of cell motion in which the cell front and back are performing the same kind of contraction-extension cycles. When these two cycles are in antiphase, this results in back-and-forth motion while a phase difference between the two cycles not equal to zero or π results in cell migration i.e. a non-zero average velocity. This is an interesting model which differs from the usual views of cell motion coming from the treadmilling of actin in a lamellipod or by extension of pseudopods at the cell front. However, I am not fully convinced that the presented evidence supports this model rather than alternative ones.

We thank the reviewer for acknowledging the interest and originality of our model and hope that the improvement to the manuscript detailed below will convince the referee.

The main results of the manuscript are obtained by observing and comparing the matrix deformations for migrating fibroblasts and for non-migrating ones that undergo back and forth motion. These observations as well as theoretical arguments led the authors to conclude that cell migration is associated to periodic localized contractions at the front and back of the cell with a finite phase difference. I find it difficult to assert from these data only that the contraction processes are similar at the front and back of the cells. For instance, the data seem similar in many respects, to those of Tanimoto and Sano (2014) obtained for 2D amoeboid motion on a substrate.

We thank the reviewer for raising this point. We provide more quantification of the oscillations at the back and front of the cell, which happen to show no significant differences between the two sides (Figure 2 Supplementary Figure 1 and Figure 2 Suppl. Figure 2 and Results section p. 4). It is worth noting that from the theoretical perspective, front and back ‘contractions’ do not need to be similar to elicit net cell translocation. Indeed, we did not include analysis of the magnitude of the contractions since phase difference is sufficient to break symmetry. This is now discussed explicitly in the text (p. 6).

Regarding the novelty compared to Tanimoto and Sano 201 : their paper on Dictyostelium discoideum crawling on deformable 2D substrate (Tanimoto and Sano, 2014) was important regarding the use of multipole analysis to identify the existence of a finite cycle in a well chosen phase space. Here, in addition to the 3D nature of motion in a physiological environment (the CDM), we substantiate the lack of time reversal symmetry as originating from: (i) the existence of (at least) two contractile units in the cell, and (ii) the appearance of a phase shift between their dynamics. Furthermore, we make the connection between the force dipoles and cellular readouts, i.e. myosin cluster formation and contraction.

I list below more specific concerns with the presented data.

The assay which uses extracellular matrix deposited by confluent cells seems adequate and the quantification of matrix deformation soundly performed. I am less convinced by the presented quantification of the data in Figure 2 and 3.

Figure 2. The autocorrelations of the deformations in Figure 2d and 2e clearly show their periodic character. I guess these are representative curves for a single cell but this is not clearly stated. No details are given on how it was decided that an autocorrelation was periodic and how the period was extracted. The duration of the time traces that were used to compute these auto correlations is not stated either. The number of cells/observations used for the quantitations of the periods are not provided.

The reviewer is correct that these curves are for single cells and are statistically representative. This is now stated in the revised version (p. 4) when the panels are quoted in the text. We agree that the process followed to determine periodicity in autocorrelation functions needed clarification. We now detail how the correlation functions were obtained and analyzed including the specific points raised by the reviewer. The process is now fully explained in the methods section “Analysis of the contractile and extensile patterns over time”, p. 13. Moreover, we added a new supplementary figure (Figure 2 – supplementary figure 1) that shows the analysis pipeline. The duration of the traces was at least 30 minutes with time points every 30 seconds. When traces are shown, their duration is stated in the Figure caption. The number of cells used is also provided in captions. The criteria for determining the period was the existence of a peak larger than 1 standard deviation. Finally, we added a section for the statistics (p. 14).

The crucial panels j and k are even less clear for me. I clearly see from Figure 1j that matrix deformations at the front and back are in antiphase for the non-migrating cells. I also see that the cross-correlation is non symmetric in time for the migrating cell but I am unable to see how a phase lag was extracted for the presented example (there clearly seem to be a negative peak at zero). All this would need to be precisely explained to assess these results.

The Phase lag in panel j, which is an example, is obtained from the position of the peak of largest amplitude. We agree with the referee that these panels are of key importance, and we now clarify this analysis better. To do so, we clarified the panels 2f, j and h indicating the peaks considered in these clearer examples. Moreover, the criteria followed have been further clarified in the methods section (Analysis of the contractile and extensile patterns over time). Also, another example of individual correlation functions that leads to the distribution of Figure 2k is shown in the new Figure 2 —figure supplement 1, that acts as guide for the analysis pipeline as well.

Figure 3. In (c) for the non-migrating cell the presented time trace for the dipolar and quadrupolar deformation are clearly in antiphase which nicely agree with Figure 1j.

However, for the migrating cell I again do not see a definite phase lag for the two traces. It rather seems for this particular trace, that the dipolar and quadrupolar deformations do not oscillate at the same frequency.

We thank the reviewer for raising this point. The cellular system is noisy, and it is indeed not straightforward to extract an average phase lag for migrating cells in (c). To address this, we used the phase space representation of panel (d), (e), (h), and in the other examples shown in Figure 3 —figure supplement 3. This representation is more appropriate to reveal the mean phase lag through the existence of a cycle with finite area unlike what is seen for non-migrating cells. As the referee pointed out, this is an important element that is now discussed in the new version (p. 5).

Figure 3d-h illustrate the cycle with a finite area in the dipole-quadrupole plane but appear as anecdotal examples. However, this should be quantified (average area, perhaps correlated with some characteristic of the motion since I guess cell may change direction).

As the referee indicates, we provided several examples of the dipole-quadrupole analysis. We agree that further quantification was needed. In the revised version of the manuscript, we show the quantification of areas enclosed by the trajectories of migrating and non-migrating cells in the D-Q plane. The results are shown in Figure 3 —figure supplement 3 (with technical explanations in Appendix 2) and discussed in the main text (p.6). The area is systematically larger for migrating cells. In order to compensate for possible variation of dipole and quadrupole intensity between migrating and non-migrating cells, we also show a normalized area independent of the absolute values of the multipoles (explained in Appendix 2), which also show a systematic difference between the two cellular behaviors.

Figure 4. I am not sure to understand the logic behind this experiment nor exactly what to conclude from it. First, when one considers separately each category of cells (untreated, treated with a given compound) it seems that there is no correlation between the period

and the speed (is this the case?). This indicates that the variability between individual cells is large. Then, it would seem better to compare the effect of each treatment at the level of individual cells i.e. for given cell how the treatment change its period of contractions and its speed. Is this compatible with (VT^n)_(before treatment) = (VT^n)_(after treatment). If this equality is not obtained, this would indicate that other parameters are affected by the treatment and the need to determine them before concluding anything (in the framework of the authors, it would for instance be useful to assess whether the dephasing psi is modified by the treatment).

As the referee points out, the drug experiments that we performed did not intend to identify a molecular actor involved in the migration process. On the contrary, we used the different drug treatments as a tool to perturb cell speed and relate it to changes in period as the model suggests. We have studied the correlations between persistence speed and period for wild type and for different drug treatments, both as a whole and separately. An inverse correlation between period and speed can be statistically demonstrated when cells for all conditions are aggregated (Pearson’s coeff -0.4978 with significance p < 0.0001). When this anticorrelation was analyzed individually for each condition, we found that it still held for WT cells (Pearson’s coeff -0.4119 with significance p = 0.0455). Among the different drugs we tried, only Y27632 showed a significant anticorrelation at the population level (Pearson’s coefficient -0,7435 with p = 0.0217). The other drugs tested (C8, CK666 and ML-7) did show correlations but were not statistically significant (C8) or showed no correlation (CK666 and ML7). We therefore fitted the expected power-law relationship between period and velocity only using WT treatment (modified Figure 4d). Nonetheless, on average all treatments showed a reduction of speed and an increment of oscillation period, suggesting that there is indeed a high variability among individual cells as indicated by the referee. We therefore tested the single cell analysis suggested by the reviewer before and after treatment. Due to the low number of cells that were migrating both before and after the treatment, the results were affected by the inherent variability of the experimental system and results were not conclusive.

However, this does not challenge our main conclusions that the 3D motility of our cells is based on phase shifted oscillating force dipoles. This claim is substantiated by the systematic existence of a phase shift and a cycle of finite area for motile cells and its systematic absence for non-motile cells (Figure 2k and the new quantification of cycle area in Figure 3 Suppl. Figure 3 b). The results of Figure 4 attempt to deepen our understanding of the motility strategy by analyzing correlations between speed and oscillation period and comparing our results with theoretical models. A clear anticorrelation exists for WT cell which allows us to conclude that locomotion being driven by controlling cell deformation instead of cell traction forces.

We thank the reviewer for pointing out that the use of drugs does not merely allow to travel in the parameter space proposed by the theoretical model but can have complex effects which are clearly beyond the scope of the present paper. These points are now discussed in the new version of the text p. 8.

Figure 5. Artificially-induced contractions produced by laser ablation are taken as further evidence in favor of the model. This is obviously very different from physiological motion but in addition, I am not sure how this really fits with the proposed model. As far as I can see, in the example provided in Figure 5h, the ablation at the back and front were in antiphase, which should produce back and forth motion rather than directed migration. Again here, one would like convincing quantification (distance travelled given number of cycles of front/back ablations) and the dependence on important parameters like the dephasing between cycles of ablation at the cell back and front.

We agree that further quantification of the effect that the artificially-induced contractions have in migration will help in strengthening the model. We added new laser ablation experiments (see new Figure 5 —figure supplement 1). In particular, we performed multiple ablations: the second ablation occurs while the first ablation and myosin enrichment has not yet relaxed, and we expected the two induced contractions to interact and help motion. This was specifically observed and this result is now reported. We quantified and analyzed cell migration with these artificially-induced contractions (see new Figure 5 —figure supplement 1) and we now discuss this within the framework of the model p. 9.

I do not have specific suggestions beyond those made in the public review but I like to add one additional point. The dipolar deformation is a 3X3 matrix. The authors computed its 2D projection but made use only of its projection on the direction of average cell velocity. I would welcome a discussion of the respective directions of the cell velocity and the main axis of the projected 2D dipolar deformation matrix.

These two axes tend to be aligned although not exactly because of noise. We now discuss in p. 5 this point in the new version with added data on the distribution of the angle between the two axes (Figure 3 —figure supplement 2).

Reviewer #3 (Recommendations for the authors):

The authors have studied fibroblasts migrating in cell-derived matrix (CDM), which is a fibrous three-dimensional ECM with fluorescently labeled fibronectin and large pores. Cell were divided into two classes, non-migrating and migrating ones. In both cases, phases of contraction and extension were observed at the front and at the back (separated by the nucleus), with a typical oscillation period of 10 min, but the migrating cells showed a time lag, while the non-migrating ones did not. The authors argued that this phase shift (or phase locking) is the hallmark of migration, because it breaks the time-reversal symmetry in the phase space defined by deformation dipole and quadrupole (because the matrix is shown to be elastic by laser optical tweezer experiments, this should correspond to a cycle in force dipole and quadrupole space). In analogy to the scallop theory for microswimmers (equation 1, from Leoni and Sens 2015), the authors argue that only a non-vanishing phase shift leads to a finite crawling velocity (equation 2, from Leoni and Sens 2017). The have performed two experiments to validate this concept. With a large range of pharmacological inhibitions, they show that crawling speed is inversely proportional to oscillation period, as predicted by the theory. By using laser ablation to generate force contraction dipoles, they show that cell motion can be induced by alternating dipoles.

The big strength of this work is the elegance of the theoretical concept and the creativity in analyzing a well-known system from a new and quantitative angle. The weakness of this work is that the experimental data is not entirely convincing and that open questions remain regarding the generality of this concept.

I first note that three-dimensional traction force microscopy in collagen gels (as done e.g. by the group of Ben Fabry, often for cancer cells similar to the ones studied here) usually shows a clear dipole. Here the authors suggest that if one looks closely, there are actually two dipoles, separated by the nuclear region. I wonder if this observation depends on the matrix used (CDM with large holes) and the cell type used.

We thank the reviewer for acknowledging the originality of our work. We agree that further data and analysis do now strengthen our manuscript. As requested by the reviewer #2, we show in more detail the existence of the two dipoles with further quantification of their magnitude (Figure 2 —figure supplement 2). As the referee points out, the existence of two dipoles differs from previous work on collagen gels. We now discuss this further in the revised version of the manuscript. Moreover, we show how other cell types and cytoplasts (cell fragments lacking nucleus) migrate in our set-up (Figure 1 —figure supplement 3 and Video 10).

We also elaborate further in the discussion about the two dipoles we report and its potential difference with the single dipole per cell reported by Ben Fabry in articles. For example, in Steinwachs et al., Nature Methods 13:171 (2016) https://doi.org/10.1038/nmeth.3685, single dipoles are visible throughout the paper and for different matrices (collagen, fibrin, Matrigel) and for different collagen concentrations. Pore sizes are similar to our work. So, the cell type could be involved in the phenomena. It is worth noting that we also now show measurements of these two dipoles for two more cell types (primary mouse embryonic fibroblasts and REF52 cell line). We agree with the reviewer that the two dipole features could depend on the cell lines and their inherent ability to contract autonomously on each side of the nucleus. This point is now reported in the revised version p.11.

Next the authors describe that the two dipoles show oscillations which are phase-shifted in the migratory case. It is not entirely clear what causes these oscillations. Figure 1c and d suggest a relation to myosin and microtubules, but here the image quality is very bad and no quantification is being given.

We agree with the referee. We increased the quality of images in Figure 1c-d accordingly. We treated the images in order to facilitate the visualization. Microtubule cytoskeleton is shown now in a clearer manner. Clarity of myosin clusters during the contraction process has been improved as well. Moreover, we added a new vidoe (Video 6) to show how the myosin signal densifies over time and vanishes afterwards. This new vidoe goes along with new quantification of the process, which is given in new Figure 1c.

Figure 4d seems to suggest that oscillations and migration persist even under severe perturbations. Therefore, it remains unclear what causes these oscillations and if they are really needed for productive cell migration.

As we wrote for reviewer 2, the drug experiments that we performed did not intend to identify a molecular actor involved in the migration process. We used the different drug treatments as a tool to perturb cell speed and relate it to changes in period as the model suggests. We now clarify this point further in the Results section. Moreover, correlation coefficients between velocity and oscillation period along with their statistical significance are now reported as well (on p. 8). Please refer to our answer to reviewer 2 on this point for a detailed explanation. Briefly, the sustained motion in the presence of the drug does not challenge the main mechanism: it suggests that cells adopt alternative strategies to keep the generic oscillatory patterns and perform persistent motion.

The phase plane plot with dipoles and quadrupoles in Figure 3 is very interesting and similar to earlier work on Dictyostelium migrating on a two-dimensional substrate (Tanimoto and Sano BPJ 2014). I wonder why the same plot is not being shown for the theory part of Figure 4, because if it agreed, it would strengthen the relation between theory and experiment.

We thank the referee for the suggestion. We now add the phase plane plot for the theory (Figure 4 —figure supplement 2), which indeed strengthens the relation between theory and experiments by showing a cycle with finite area for migrating cells and a vanishing area for non-migrating cells.

Moreover, the work by Tanimoto and Sano raises the question why the authors do not apply their concept to two dimensions. They argue in the discussion that in two dimensions, actin flow breaks the front-back symmetry and thus another mechanism is needed in three dimensions. This brings up two questions. First is the approach by Tanimoto and Sano for two dimensions not valid and second what is the proof that there is no retrograde flow in three dimensions.

The point raised by the referee is very important. We are not saying that the motility strategies in 2D and 3D are different, one consisting of retrograde flow and the other not. We propose that these two strategies can exist in any dimension. Therefore, we certainly believe that Tanimoto and Sano approach is valid.

We do not claim there is no retrograde flow at all for cells moving in our CDM: cells form protrusions and this process should involve some local retrograde flow. We claim that there is no retrograde flow from the front to the back of the cell as reported in former studies quoted in the article but instead growing and shrinking protrusions can be seen at the front and at the back of cells. This is further discussed in the revision (p. 9).

Finally, it is really hard to assess if the laser ablation experiments do support the concept that oscillating dipoles leads to cell migration. Obviously, they not only cause relaxation and reformation of contractile structures, but they also interfere with adhesion and one effect might be to simply cause recoil in an elastic matrix.

We added more experiments of laser ablation along with the quantification of the induced migration (see new Figure 5 —figure supplement 1 and Results section p. 9). The matrix recoil does occur immediately following laser ablation and lasts a few seconds, but it is followed by myosin recruitment and active contraction at a longer time scale of about a minute (Figure 5b). This substantiates that local dipoles are induced within cells. In addition, we show the subsequent motion of cells when induced dipoles are applied on both sides of the nucleus, thereby mimicking the two phase-shifted dipoles that we report in the text and in the model. These data further support our general mechanism.

In summary, the theoretical concept is very appealing and the experiments conducted are creative and interesting, but the relation between theory and experiment is not entirely convincing. Therefore, impact in the wider community of quantitative life sciences might remain limited for the current form of this manuscript.

We thank the referee for the positive evaluation. As we detail, we provided more experimental data and analysis to substantiate the relation between theory and experiments.

In order to improve the relation between the general concept and the supporting experimental data, it would be very informative to conduct these experiment with different matrices and different cells types (ideally even with ghosts without nucleus), to see how general this observation is. How much does pore size of CDM matters, both for the oscillations and the laser ablation experiments? Is it important that the nucleus separates these two regions of the cell? Why cannot the same experiment be one in two dimensions, where the nucleus is out of the way? It would also be interesting to consider if less perturbative experiments might be feasible (e.g. optogenetics to locally induce contractility).

We performed and now report some of the experiments suggested by the reviewer – which involved experiments within the plan of action. We had performed experiments with collagen and these conditions did not significantly modify the motion of cells, which is consistent with the report of Ben Fabry et al., Nature Methods 2015 now quoted. In addition, and as suggested by the referee, we added new experiments with two other cell types: one fibroblast cell line and primary fibroblasts. These two cell lines also display similar patterns of contraction and extension at the front and the back of the nucleus. These results are added in a new supplementary figure (Figure 1 —figure supplement 3), video and in the Results section (p. 3). In addition, we now show that cytoplasts (cell fragments without nuclei or ‘ghosts without nucleus’ asked by the reviewer) perform oscillatory motions similar to the ones observed for nocodazole treated cells. These new experiments are shown in Figure 1 – supplementary figure 3 and in Video 10, and discussed in the Results section (p. 6). Altogether, our results suggest that the oscillatory pattern is generic and does not necessarily require the nucleus.

For the theory part, it would be interesting to give more background on the calculations behind Equation 2 and to explain if it also generates an open loop in the D-Q-plane as shown here for the experimental data.

We now give more background on the calculations on p. 7. We also show the trajectories in the D-Q plane generated by the theoretical model in the new Figure 4 —figure supplement 2 and refer to this figure on p. 7.

Finally, I note that the discussions of the scallop theorem for swimming, although interesting, are not directly relevant to this work, because as the authors comment themselves, the situation is very different for crawling. Of course, this is an interesting analogy, but it also might be distracting or confusing to the general readers of eLife; it would be more interesting in the context of a physics journal. It is somehow odd that there are more references on the theory of swimming than on the theory of crawling. I note that there is actually a literature on the scallop theorem for crawling cells not cited here, most prominently the work by Pierre Recho, compare Recho, P., J-F. Joanny, and L. Truskinovsky. "Optimality of contraction-driven crawling." Physical Review Letters 112.21 (2014): 218101. I also miss references to earlier use of force multipoles in the cellular context (here mainly the work of Tanimoto and Sano is cited), and to traction force microscopy (including the work by Ben Fabry), which can be used to measure them.

We now better acknowledge the theoretical literature on crawling cells in the introduction. Instead of the proposed reference, we now cite and discuss in the introduction (p. 2) P. Recho, T. Putelat, and L. Truskinovsky: Contraction-Driven Cell Motility PRL 111, 108102 (2013), which seems more appropriate to the current context, together with other references (Blanch-Mercader and Casademunt, 2013, Maiuri et al., 2015). However, we would like to stress that these models focus on steady crawling, where there exists a permanent spatial asymmetry between the cell front and back leading to a cell-scale cytoskeletal flow. As such, these correspond to the classical “keratocyte type of motility” for which the scallop theorem is naturally satisfied. Such models do not reproduce our observations which rather support a model based on phase shifted contractile units, which is very similar to toy models initially developed for micro-swimmers. We therefore find it useful to introduce our model in this context.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

The manuscript has been improved but there are some remaining issues that need to be addressed, as outlined below:

1) The revised submission is strongly improved over the initial submission. The authors have conducted new experiments (other matrix, other cell types, laser ablation), added more theory results (in particular the D-Q plots), improved image quality and analysis, and made the main text more accessible. In my view, however, there still remains some doubt about the general validity of these results. As the authors write themselves, cell migration in 3D matrices can also occur through coherent actin flows or with single rather than double dipoles, so the title "Temporal correlation between oscillating force dipoles drives 3D single cell migration" and the corresponding abstract still sound too general. Interestingly, there now seem to be at least two scallop theorems for crawling, one for actin flow by Recho and coworkers and one for the contractile oscillations described here. We suggest that it is erroneous to now only citie Recho PRL 2013, because it is really the PRL 2014 that discusses the scallop theorem.

We thank the reviewer for acknowledging the improvements made to the paper. We certainly agree with the referee that cells may use different motility strategies, especially in 3D matrices. As the referee found the title of the article too general, we changed it for "3D single cell migration driven by temporal correlation between oscillating force dipoles".

The abstract was also modified along the lines suggested by the referee.

Regarding the reference from Recho et al., the PRL 2014 does make explicit mention of the “scallop theorem” (after Equation 3), and the PRL 2013 refers to “Purcell’s theorem” (after Equation 2), so we now cite both papers p. 3 l. 6.

2) The manuscript has improved with more quantification available to assess the results and more precise explanations of how the results were obtained. The quantified data appear to support the interesting finding that there are two extension/contraction dipoles at the front and back of the cell. The dipole/quadupole cycle differences (Figure 3) also appear convincing, in agreement with the previous work of Tanimoto and Sano.

Yet, there remain several further points that are not fully convincing. The first main one is the dephasing between the two dipoles which is based on a single peak in the cross correlation and appears very noisy (the statistical significance of the count statistics Figure 2k should at least be provided).

We agree with the referee that assessing the statistical significance of the differences between phase-shifts distributions for non-migrating and migrating cells will strengthen the result. We performed ANOVA test on the data and found that distributions are indeed statistically different with p = 0.0246. This analysis has been added to the figure caption (Figure 2k) as well as in the Results section p. 5 l. 35.

Second, we are uneasy with the conclusions drawn for the laser ablations (Figure 5) and still do not see how they support (or not) the model. For instance, repeated ablations in the front of the cell would not lead to cell translocation given the model advocated by the authors (if we understand correctly). But this control has not been performed. Moreover, given the authors' model one would expect some dependence on the relative phase of ablations in the front and the back. But this is not attempted. We are thus unsure if one can conclude something very definite from these ablation experiments.

We agree with the referees that adding the suggested control would add clarity to the conclusions from the laser ablation experiments. Therefore, we performed these experiments and results are now reported in the Results section and Figure 5 —figure supplement 1. Briefly, we performed laser ablation repeatedly at the front of a polarized cell using two different time lags (5 minutes and 10 minutes). In both cases (repeated cuts at the front every 5 minutes and repeated cuts at the front every 10 minutes), net motion was non-existent or smaller than the one observed when cuts were performed by alternating back and front of the cell. The results are shown in Figure 5 —figure supplement 1. This control indeed strengthens our result about the coupling between front and back dipoles for directed motion. The text is modified accordingly p. 10 l. 10. As for the systematic changes of phases of ablation in the front and the back, this requires a dedicated new study in its own right and we leave study the complete characterizations for another article.

3) Overall, the reviewers are of the option that the study is strongly theory-driven and that the authors could do better in describing the experimental evidence. The whole design of the manuscript is such that the idea is put first and then some experimental evidence is provided. An alternative approach would be to start with the general status of the field of cell migration, then introduce the experimental results for this specific and certainly interesting system, and then the theory explanation as one way to explain these observations. Please consider this possible revision.

We agree with the suggestions and we modified the article accordingly. We now start the article by general status of cell migration and the strategy for the design of the experiments before outlining the need for physical approaches to explain how cell move with zero force. We also discuss that this theory is a potential way of explaining the dynamics and measurements in the discussion with a dedicated new paragraph.

https://doi.org/10.7554/eLife.71032.sa2

Article and author information

Author details

Amélie Luise Godeau

Laboratory of Cell Physics, ISIS/IGBMC, UMR 7104, Inserm, and University of Strasbourg, Strasbourg, France

Contribution
Data curation, Formal analysis, Validation, Investigation, Visualization, Methodology, Writing - original draft, Writing – review and editing

Contributed equally with
Marco Leoni

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-8778-0120
Marco Leoni
1. Institut Curie, Université PSL, Sorbonne Université, CNRS UMR168, Laboratoire Physico Chimie Curie, Paris, France
2. Université Paris-Saclay, CNRS, Laboratoire de l’accélérateur linéaire, Orsay, France
Contribution
Data curation, Software, Formal analysis, Validation, Visualization, Methodology, Writing - original draft, Writing – review and editing

Contributed equally with
Amélie Luise Godeau

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-3965-0575
Jordi Comelles

Laboratory of Cell Physics, ISIS/IGBMC, UMR 7104, Inserm, and University of Strasbourg, Strasbourg, France

Contribution
Data curation, Visualization, Methodology, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-9297-830X
Tristan Guyomar

Laboratory of Cell Physics, ISIS/IGBMC, UMR 7104, Inserm, and University of Strasbourg, Strasbourg, France

Contribution
Investigation

Competing interests
No competing interests declared
Michele Lieb

Laboratory of Cell Physics, ISIS/IGBMC, UMR 7104, Inserm, and University of Strasbourg, Strasbourg, France

Contribution
Investigation

Competing interests
No competing interests declared
Hélène Delanoë-Ayari

Univ. Lyon, Université Claude Bernard Lyon 1, CNRS, Villeurbanne, France

Contribution
Data curation, Software, Formal analysis, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-8658-3942
Albrecht Ott

Saarland University, Center for Biophysics, Biologische Experimentalphysik, Saarbrücken, Germany

Contribution
Funding acquisition, Investigation, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-0481-2658
Sebastien Harlepp

Tumor Biomechanics, INSERM UMR S1109, Institut d’Hématologie et d’Immunologie, Strasbourg, France

Contribution
Data curation, Validation, Visualization, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-8891-7953
Pierre Sens

Institut Curie, Université PSL, Sorbonne Université, CNRS UMR168, Laboratoire Physico Chimie Curie, Paris, France

Contribution
Conceptualization, Formal analysis, Supervision, Funding acquisition, Validation, Visualization, Methodology, Writing - original draft, Writing – review and editing

For correspondence
pierre.sens@curie.fr

Competing interests
Reviewing editor, eLife

"This ORCID iD identifies the author of this article:" 0000-0003-4523-3791
Daniel Riveline

Laboratory of Cell Physics, ISIS/IGBMC, UMR 7104, Inserm, and University of Strasbourg, Strasbourg, France

Contribution
Conceptualization, Formal analysis, Supervision, Funding acquisition, Validation, Investigation, Visualization, Methodology, Writing - original draft, Writing – review and editing

For correspondence
riveline@unistra.fr

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-4632-011X

Funding

Deutsch-Französische Hochschule (CDFA-01-13)

Albrecht Ott
Daniel Riveline

Deutsche Forschungsgemeinschaft (SFB 1027)

Albrecht Ott

Centre National de la Recherche Scientifique

Daniel Riveline

ciFRC Strasbourg

Daniel Riveline

University of Strasbourg

Daniel Riveline

Labex IGBMC

Daniel Riveline

Fondation Simone et Cino Del Duca

Daniel Riveline

Region Alsace

Daniel Riveline

Saarland University

Daniel Riveline

Agence Nationale de la Recherche (ANR-10-IDEX-0002-02)

Daniel Riveline

ICAM Branch Contributions

Marco Leoni
Pierre Sens

Agence Nationale de la Recherche (ANR-10-LBX-0038)

Marco Leoni
Pierre Sens

Agence Nationale de la Recherche (ANR-10-IDEX-0001-02)

Marco Leoni
Pierre Sens

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank the Riveline Lab for discussions and help, M Maaloum, the Imaging and Microscopy Platform of IGBMC, and HP Erickson, A Huttenlocher, E Paluch for constructs, J Goetz for the former CDM protocol and M Piel for critical reading of the manuscript. DR acknowledges support from CNRS (ATIP), ciFRC Strasbourg, the University of Strasbourg, Labex IGBMC, Foundation Cino del Duca, Région Alsace, Saarland University. A Ott and D Riveline acknowledge support from DFH-UFA through the Collège Doctoral Franco-Allemand CDFA-01-13. This study with the reference ANR-10-LABX-0030-INRT has been supported by a French state fund through the Agence Nationale de la Recherche under the frame programme Investissements d’Avenir labelled ANR-10-IDEX-0002–02. ML acknowledges financial support from the ICAM Branch Contributions and Labex CelTisPhyBio No ANR-10-LBX-0038 part of the IDEX PSL No ANR-10-IDEX-0001-02 PSL. A Ott acknowledges support by DFG within the collaborative research center SFB 1027.

Senior Editor

Aleksandra M Walczak, CNRS LPENS, France

Reviewing Editor

Raymond E Goldstein, University of Cambridge, United Kingdom

Version history

Preprint posted: May 8, 2020 (view preprint)
Received: June 6, 2021
Accepted: July 28, 2022
Accepted Manuscript published: July 28, 2022 (version 1)
Version of Record published: August 18, 2022 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

3,089

Page views
471

Downloads
3

Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Amélie Luise Godeau
Marco Leoni
Jordi Comelles
Tristan Guyomar
Michele Lieb
Hélène Delanoë-Ayari
Albrecht Ott
Sebastien Harlepp
Pierre Sens
Daniel Riveline

(2022)

3D single cell migration driven by temporal correlation between oscillating force dipoles

eLife 11:e71032.

https://doi.org/10.7554/eLife.71032

Share this article

Cite this article

Key players in cell motility.

Figure 1—source data 1

NIH3T3 fibroblast transfected with mCherry-LifeAct deforms the fibronectin network in yellow while moving, scale bar 20 μm, time in hh:mm.

Cell derived matrix (CDM) is elastic, as shown by optical tweezer characterization, time in mm:ss.

Cells motion in 3D with cell derived matrix (CDM) and the associated focal contacts dynamics fibronectin in yellow and zyxin in red, time in hh:mm:ss.

Microtubule asymmetric distribution (left) is associated with cell polarity during motion, time in hh:mm.

Cell deforms the cell derived matrix (CDM), time in hh:mm.

Formation of myosin clusters simultaneously to contraction, time in mm:ss.

Dynamics of matrix deformation for migrating and non-migrating cells.

Figure 2—source data 1

Another example of cell motion in cell derived matrix (CDM), scale bar 25 μm, time in hh:mm.

Multipole analysis of the matrix deformation rate.

Figure 3—source data 1

Phase shift between local dipoles is associated with cell motion; cell motion (left, LifeAct red), fibronectin network deformation (center yellow), merge, time in hh:mm:ss.

Cell motility in the presence of nocodazole added at time 0, time in hh:mm, scale bar 25 μm.

Nucleus-free cell forms and shows oscillatory motion in cell derived matrix (CDM).

Persistent speed is related to the period of oscillations.

Figure 4—source data 1

Cell motility in the presence of blebbistatin added at time 0, time in hh:mm, scale bar 25 μm.

Cell motility in the presence of latrunculin A added at time 0, time in hh:mm, scale bar 25 μm.

Cell motion is triggered by means of laser-induced force dipoles.

Figure 5—source data 1

Local laser ablation triggers the local recruitment of actin and local contraction, time in mm:ss.

Induced dipoles by local laser ablations (indicated by arrows) trigger cell motion, time in mm:ss.

Author details

Amélie Luise Godeau

Contribution

Contributed equally with

Competing interests

Marco Leoni

Contribution

Contributed equally with

Competing interests

Jordi Comelles

Contribution

Competing interests

Tristan Guyomar

Contribution

Competing interests

Michele Lieb

Contribution

Competing interests

Hélène Delanoë-Ayari

Contribution

Competing interests

Albrecht Ott

Contribution

Competing interests

Sebastien Harlepp

Contribution

Competing interests

Pierre Sens

Contribution

For correspondence

Competing interests

Daniel Riveline

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Further reading