Research Article

Genetics and Genomics

Quantifying concordant genetic effects of de novo mutations on multiple disorders

Center for Statistical Science, Tsinghua University, China
Department of Industrial Engineering, Tsinghua University, China
MOE Key Laboratory of Bioinformatics, School of Life Sciences, Tsinghua University, China
Yale School of Management, Yale University, United States
Department of Genetics, Washington University in St. Louis, United States
Department of Genetics, Yale University, United States
Laboratory of Human Genetics and Genomics, Rockefeller University, United States
Department of Biostatistics, Yale School of Public Health, United States
Department of Pediatrics, Yale University, United States
Program of Computational Biology and Bioinformatics, Yale University, United States
Department of Biostatistics and Medical Informatics, University of Wisconsin-Madison, United States

Jun 6, 2022

Open access
Copyright information

Abstract
Editor's evaluation
Introduction
Results
Discussion
Materials and methods
Data availability
References
Article and author information
Metrics

Abstract

Exome sequencing on tens of thousands of parent-proband trios has identified numerous deleterious de novo mutations (DNMs) and implicated risk genes for many disorders. Recent studies have suggested shared genes and pathways are enriched for DNMs across multiple disorders. However, existing analytic strategies only focus on genes that reach statistical significance for multiple disorders and require large trio samples in each study. As a result, these methods are not able to characterize the full landscape of genetic sharing due to polygenicity and incomplete penetrance. In this work, we introduce EncoreDNM, a novel statistical framework to quantify shared genetic effects between two disorders characterized by concordant enrichment of DNMs in the exome. EncoreDNM makes use of exome-wide, summary-level DNM data, including genes that do not reach statistical significance in single-disorder analysis, to evaluate the overall and annotation-partitioned genetic sharing between two disorders. Applying EncoreDNM to DNM data of nine disorders, we identified abundant pairwise enrichment correlations, especially in genes intolerant to pathogenic mutations and genes highly expressed in fetal tissues. These results suggest that EncoreDNM improves current analytic approaches and may have broad applications in DNM studies.

Editor's evaluation

Lu et al. provide a powerful statistical method that measures excess sharing of de novo mutations between pairs of disorders. This method extends the concept of 'genetic correlation' to disorders caused by de-novo mutations, measuring the correlation in excess de-novo mutations in genome-wide genes for different classes of mutations. The authors apply the method to nine disorders including a developmental disorder, autism spectrum disorder, congenital heart disease, schizophrenia, and intellectual disability, finding a statistically significant overlap between 12 pairs of disorders in de novo mutations that cause a loss of gene function. This method will be of interest to researchers working on disorders caused by de-novo mutations.

https://doi.org/10.7554/eLife.75551.sa0

Introduction

De novo mutations (DNMs) can be highly deleterious and provide important insights into the genetic cause for disease (Veltman and Brunner, 2012). As the cost of sequencing continues to drop, whole-exome sequencing (WES) studies conducted on tens of thousands of family trios have pinpointed numerous risk genes for a variety of disorders (Lelieveld et al., 2016; Kaplanis et al., 2020; Satterstrom et al., 2020). In addition, accumulating evidence suggests that risk genes enriched for pathogenic DNMs may be shared by multiple disorders (Hoischen et al., 2014; Fromer et al., 2014; Homsy et al., 2015; Li et al., 2016; Nguyen et al., 2020). These shared genes could reveal biological pathways that play prominent roles in disease etiology and shed light on clinically heterogeneous yet genetically related diseases (Homsy et al., 2015; Li et al., 2016; Nguyen et al., 2020).

Most efforts to identify shared risk genes directly compare genes that are significantly associated with each disorder (Nguyen et al., 2017; Willsey et al., 2018). There have been some successes with this approach in identifying shared genes and pathways (e.g. chromatin modifiers) underlying developmental disorder (DD), autism spectrum disorder (ASD), and congenital heart disease (CHD), thanks to the large trio samples in these studies (Kaplanis et al., 2020; Satterstrom et al., 2020; Jin et al., 2017), whereas findings in smaller studies remain suggestive (Allen et al., 2013; Jin et al., 2020b). Even in the largest studies to date, statistical power remains moderate for risk genes with weaker effects (Kaplanis et al., 2020; Howrigan et al., 2020). It is estimated that more than 1000 haploinsufficient genes contributing to developmental disorder risk have not yet achieved statistical significance in large WES studies (Kaplanis et al., 2020). Therefore, analytic approaches that only account for top significant genes cannot capture the full landscape of genetic sharing in multiple disorders. Recently, a Bayesian framework named mTADA was proposed to jointly analyze DNM data of two diseases and improve risk gene mapping (Nguyen et al., 2020). Although mTADA produces estimates for the proportion of shared risk genes, the statistical property of these parameter estimates has not been studied. There is a pressing need for powerful, robust, and interpretable methods that quantify concordant DNM association patterns for multiple disorders using exome-wide DNM counts.

Recent advances in estimating genetic correlations using summary data from genome-wide association studies (GWAS) may provide a blueprint for approaching this problem in DNM research (Zhang et al., 2021a). Modeling ‘omnigenic’ associations as independent random effects, linear mixed-effects models leverage genome-wide association profiles to quantify the correlation between additive genetic components of multiple complex traits (Lee et al., 2012; Bulik-Sullivan et al., 2015; Lu et al., 2017; Ning et al., 2020). These methods have identified ubiquitous genetic correlations across many human traits and revealed significant and robust genetic correlations that could not be inferred from significant GWAS associations alone (Shi et al., 2017; Brainstorm, 2018; Guo et al., 2021; Zhang et al., 2021b).

Here, we introduce EncoreDNM (Enrichment correlation estimator for De Novo Mutations), a novel statistical framework that leverages exome-wide DNM counts, including genes that do not reach exome-wide statistical significance in single-disorder analysis, to estimate concordant DNM associations between disorders. EncoreDNM uses a generalized linear mixed-effects model to quantify the occurrence of DNMs while accounting for de novo mutability of each gene and technical inconsistencies between studies. We demonstrate the performance of EncoreDNM through extensive simulations and analyses of DNM data of nine disorders.

Results

Method overview

DNM counts in the exome deviate from the null (i.e. expected counts based on de novo mutability) when mutations play a role in disease etiology. Disease risk genes will show enrichment for deleterious DNMs in probands and non-risk genes may be slightly depleted for DNM counts. Our goal is to estimate the correlation of such deviation between two disorders, which we refer to as the DNM enrichment correlation. More specifically, we use a pair of mixed-effects Poisson regression models (Munkin and Trivedi, 1999) to quantify the occurrence of DNMs in two studies.

[\begin{matrix} Y_{i 1} \\ Y_{i 2} \end{matrix}] \sim P o i s s o n ([\begin{matrix} λ_{i 1} \\ λ_{i 2} \end{matrix}]),

\log ([\begin{matrix} λ_{i 1} \\ λ_{i 2} \end{matrix}]) = [\begin{matrix} β_{1} \\ β_{2} \end{matrix}] + \log ([\begin{matrix} 2 N_{1} m_{i} \\ 2 N_{2} m_{i} \end{matrix}]) + [\begin{matrix} ϕ_{i 1} \\ ϕ_{i 2} \end{matrix}],

[\begin{matrix} ϕ_{i 1} \\ ϕ_{i 2} \end{matrix}] \sim M V N ([\begin{matrix} 0 \\ 0 \end{matrix}], [\begin{matrix} σ_{1}^{2} & ρ σ_{1} σ_{2} \\ ρ σ_{1} σ_{2} & σ_{2}^{2} \end{matrix}]) .

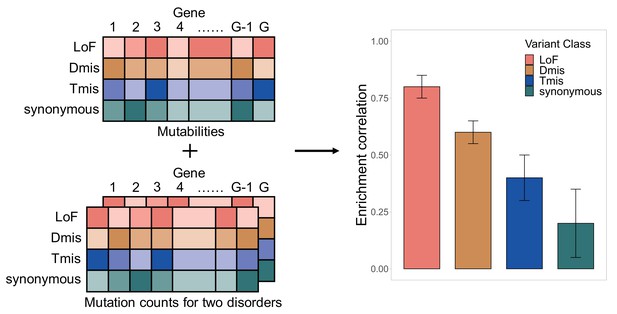
Here, $Y_{i 1}, Y_{i 2}$ are the DNM counts for the i-th gene and $N_{1}, N_{2}$ are the number of parent-proband trios in two studies, respectively. The log Poisson rates of DNM occurrence are decomposed into three components: the elevation component, the background component, and the deviation component. The elevation component $β_{k}$ ( $k = 1,2$ ) is a fixed effect term adjusting for systematic, exome-wide bias in DNM counts. One example of such bias is the batch effect caused by different sequencing and variant calling pipelines in two studies. The elevation parameter $β_{k}$ tends to be positive when DNMs are over-called with higher sensitivity and negative when DNMs are under-called with higher specificity (Wei et al., 2015). The background component $l o g (2 N_{k} m_{i})$ is a gene-specific fixed effect that reflects the expected mutation counts determined by the genomic sequence context under the null (Samocha et al., 2014). $m_{i}$ is the de novo mutability for the i-th gene, and $2 N_{1} m_{i}$ and $2 N_{2} m_{i}$ are the expected DNM counts in the i-th gene under the null in two studies. The deviation component $ϕ_{i k}$ is a gene-specific random effect that quantifies the deviation of DNM profile from what is expected under the null (i.e. no risk genes for the disorder). $ϕ_{i 1}$ and $ϕ_{i 2}$ follow a multivariate normal distribution with dispersion parameters $σ_{1}$ and $σ_{2}$ and a correlation $ρ$ . A larger value of the dispersion parameter $σ_{k}$ indicates a more substantial deviation from the null. That is, DNM counts show strong enrichment in some genes and depletion in other genes compared to the expectation based on de novo mutability. A smaller value of $σ_{k}$ suggests that the DNM count data is well in line with what is expected based on the null model. DNM enrichment correlation is denoted by $ρ$ and is our main parameter of interest. It quantifies the concordance of DNM burden in two disorders.

Parameters in this model can be estimated using a Monte Carlo maximum likelihood estimation (MLE) procedure. Standard errors of the estimates are obtained through inversion of the observed Fisher information matrix. In practice, we use annotated DNM data as input and fit mixed-effects Poisson models for each variant class separately: loss of function (LoF), deleterious missense (Dmis, defined as MetaSVM-deleterious), tolerable missense (Tmis, defined as MetaSVM-tolerable), and synonymous (Figure 1). More details about model setup and parameter estimation are discussed in Materials and methods.

Figure 1

Download asset Open asset

EncoreDNM workflow.

The inputs of EncoreDNM are de novo mutability of each gene and exome-wide, annotated DNM counts from two studies. We fit a mixed-effects Poisson model to estimate the DNM enrichment correlation between two disorders for each variant class.

Simulation results

We conducted simulations to assess the parameter estimation performance of EncoreDNM in various settings. We focused on two variant classes, that is, Tmis and LoF variants, since they have the highest and lowest median mutabilities in the exome. We used EncoreDNM to estimate the elevation parameter $β$ , dispersion parameter $σ$ , and enrichment correlation $ρ$ (Materials and methods). Under various parameter settings, EncoreDNM always provided unbiased estimation of the parameters (Figure 2 and Figure 2—figure supplements 1–2). Furthermore, the 95% Wald confidence intervals achieved coverage rates close to 95% under all simulation settings, demonstrating the effectiveness of EncoreDNM to provide accurate statistical inference.

Figure 2 with 2 supplements see all

Download asset Open asset

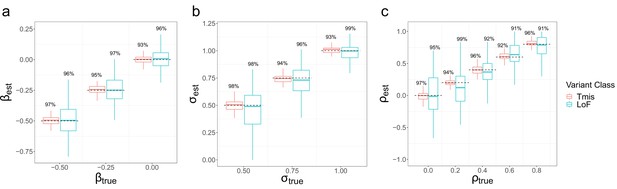
Parameter estimation results of EncoreDNM.

(a) Boxplot of $β$ estimates in single-trait analysis with $σ$ fixed at 0.75. (b) Boxplot of $σ$ estimates in single-trait analysis with $β$ fixed at –0.25. (c) Boxplot of $ρ$ estimates in cross-trait analysis with $β$ and $σ$ fixed at –0.25 and 0.75. True parameter values are marked by dashed lines. The number above each box represents the coverage rate of 95% Wald confidence intervals. Each simulation setting was repeated 100 times.

Next, we compared the performance of EncoreDNM with mTADA (Nguyen et al., 2020), a Bayesian framework that estimates the proportion of shared risk genes for two disorders. First, we simulated DNM data under the mixed-effects Poisson model. We evaluated two methods across a range of combinations of elevation parameter, dispersion parameter, and sample size for two disorders. The false positive rates for our method were well-calibrated in all parameter settings, but mTADA produced false positive findings when the observed DNM counts were relatively small (e.g. due to reduced elevation or dispersion parameters or a lower sample size; Figure 3a). We also assessed the statistical power of two approaches under a baseline setting where false positives for both methods were controlled. As enrichment correlation increased, EncoreDNM achieved universally greater statistical power compared to mTADA (Figure 3b).

Figure 3

Download asset Open asset

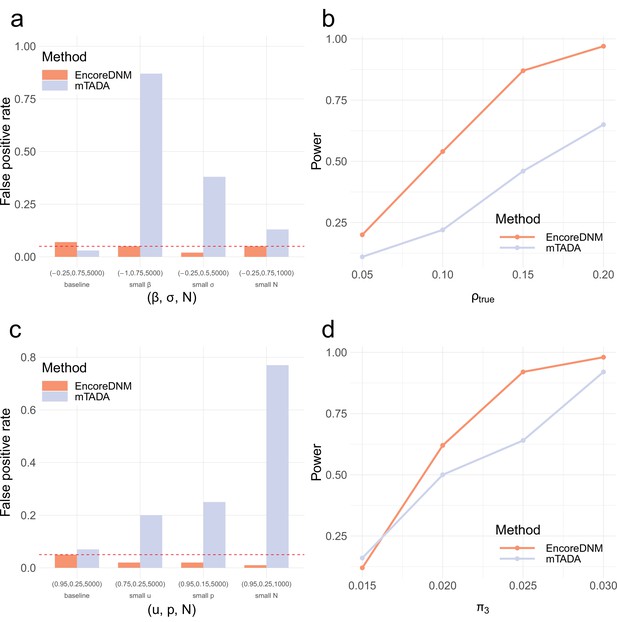
Comparison of EncoreDNM and mTADA.

(a) False positive rates under a mixed-effects Poisson regression model. (b) Statistical power of two methods under a mixed-effects Poisson regression model as the enrichment correlation increases. Parameters ( $β, σ, N$ ) were fixed at (–0.25, 0.75, 5000) for both disorders. (c) False positive rates under a multinomial model. (d) Statistical power under a multinomial model with varying proportion of shared causal genes. Parameters ( $u, p, N$ ) were fixed at (0.95, 0.25, 5000) for both disorders. Each simulation setting was repeated 100 times.

To ensure a fair comparison, we also considered a mis-specified model setting where we randomly distributed the total DNM counts for each disorder into all genes with an enrichment in causal genes (Materials and methods). EncoreDNM showed well-controlled false positive rate across all simulation settings, whereas severe inflation of false positives arose for mTADA when the total mutation count, the proportion of probands that can be explained by DNMs, or the sample size were small (Figure 3c). Furthermore, we compared the statistical power of two methods under this model in a baseline setting where false positive rate was controlled. EncoreDNM showed higher statistical power compared to mTADA as the fraction of shared causal genes increased (Figure 3d).

Pervasive enrichment correlation of damaging DNMs among developmental disorders

We applied EncoreDNM to DNM data of nine disorders (Supplementary file 1-STable 1; Materials and methods): developmental disorder (n=31,058; number of trios; Kaplanis et al., 2020), autism spectrum disorder (n=6430; Satterstrom et al., 2020), schizophrenia (SCZ; n=2772; Howrigan et al., 2020), congenital heart disease (n=2645; Jin et al., 2017), intellectual disability (ID; n=820; Lelieveld et al., 2016), Tourette disorder (TD; n=484) Willsey et al., 2017, epileptic encephalopathies (EP; n=264; Allen et al., 2013), cerebral palsy (CP; n=250; Jin et al., 2020b), and congenital hydrocephalus (CH; n=232; Jin et al., 2020a). In addition, we also included 1789 trios comprising healthy parents and unaffected siblings of autism probands as controls (Krumm et al., 2015).

We first performed single-trait analysis under the mixed-effects Poisson model for each disorder. The estimated elevation parameters (i.e. $β$ ) were negative for almost all disorders and variant classes (Figure 4a), with LoF variants showing particularly lower parameter estimates. This may be explained by more stringent quality control in LoF variant calling (Jin et al., 2017) and potential survival bias (Lek et al., 2016). It is also consistent with a depletion of LoF DNMs in healthy control trios (Homsy et al., 2015). The dispersion parameter estimates (i.e. $σ$ ) were higher for LoF variants than other variant classes (Figure 4b), which is consistent with our expectation that LoF variants have stronger effects on disease risk and should show a larger deviation from the null mutation rate in disease probands. We also compared the goodness of fit of our proposed mixed-effects Poisson model to a simpler fixed-effects model without the deviation component (Materials and methods). The expected distribution of recurrent DNM counts showed substantial and statistically significant improvement under the mixed-effects Poisson model (Figure 4c–f, Figure 4—figure supplement 1, and Supplementary file 1-STable 2).

Figure 4 with 1 supplement see all

Download asset Open asset

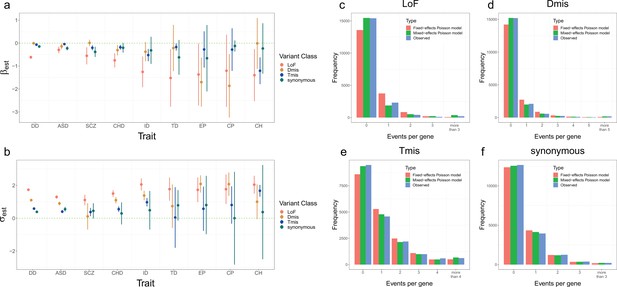
Model fitting results for nine disorders.

(**a, b**) Estimation results of $β$ and $σ$ for nine disorders and four variant classes. Error bars represent 1.96*standard errors. Sample sizes of DNM datasets for each disorder are provided in Supplementary file 1-STable 1. (**c–f**) Distribution of DNM events per gene in four variant classes for developmental disorder. Red and green bars represent the expected frequency of genes under the fixed-effects and mixed-effects Poisson regression models, respectively. Blue bars represent the observed frequency of genes.

Next, we estimated pairwise DNM enrichment correlations for 9 disorders. In total, we identified 25 pairs of disorders with significant correlations at a false discovery rate (FDR) cutoff of 0.05 (Figure 5 and Figure 5—figure supplement 1), including 12 significant correlations for LoF variants, 7 for Dmis variants, 5 for Tmis variants, and only 1 significant correlation for synonymous variants. Notably, all significant correlations are positive (Supplementary file 1-STable 3). No significant correlation was identified between any disorder and healthy controls (Figure 5—figure supplement 2). This is consistent with our expectation, since DNMs in the control groups will distribute proportionally according to the de novo mutability without showing enrichment in certain genes. The number of identified significant correlations for each disorder was proportional to the sample size in each study (Spearman correlation = 0.70) with controls being a notable outlier (Figure 5—figure supplement 3).

Figure 5 with 9 supplements see all

Download asset Open asset

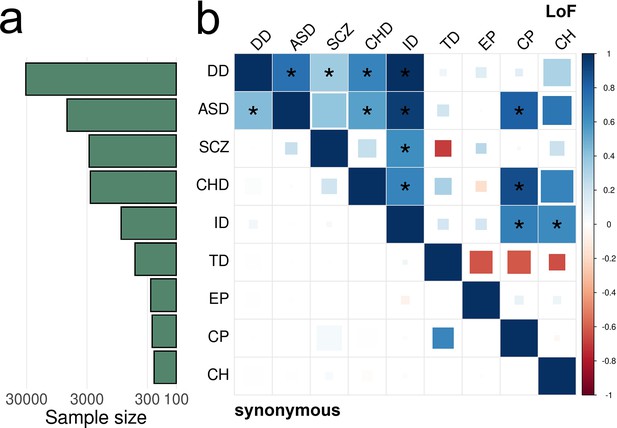
EncoreDNM identifies pervasive enrichment correlations of damaging DNMs among nine disorders.

(a) Shows sample size (for example, number of trios) for each disease. X-axis denotes sample size on the log scale. (b) Heatmap of enrichment correlations for LoF (upper triangle) and synonymous (lower triangle) DNMs among nine disorders. Larger squares represent more significant p-values, and deeper color represents stronger correlations. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.

We identified highly concordant and significant LoF DNM enrichment among developmental disorder, autism, intellectual disability, and congenital heart disease, which is consistent with previous reports (Li et al., 2016; Nguyen et al., 2020; Nguyen et al., 2017; Hormozdiari et al., 2015). Schizophrenia shows highly significant LoF correlations with developmental disorder (p=2.0e-3) and intellectual disability (3.7e-5). The positive enrichment correlation between autism and cerebral palsy in LoF variants ( $ρ$ =0.81, p=3.3e-3) is consistent with their co-occurrence (Christensen et al., 2014). The high enrichment correlation between intellectual disability and cerebral palsy in LoF variants ( $ρ$ =0.68, p=1.0e-4) is consistent with the associations between intellectual disability and motor or non-motor abnormalities caused by cerebral palsy (Reid et al., 2018). A previous study also suggested significant genetic sharing of intellectual disability and cerebral palsy by overlapping genes harboring rare damaging variants (Jin et al., 2020b). Here, we obtained consistent results after accounting for de novo mutabilities and potential confounding bias.

Some significant correlations identified in our analysis are consistent with phenotypic associations in epidemiological studies, but have not been reported using genetic data to the extent of our knowledge. For example, the LoF enrichment correlation between congenital heart disease and cerebral palsy ( $ρ$ =0.88, p=1.7e-3) is consistent with findings that reduced supply of oxygenated blood in fetal brain due to cardiac malformations may be a risk factor for cerebral palsy (Garne et al., 2008). The enrichment correlation between intellectual disability and congenital hydrocephalus in LoF variants ( $ρ$ =0.63, p=2.4e-3) is consistent with lower intellectual performance in a proportion of children with congenital hydrocephalus (Lumenta and Skotarczak, 1995).

Genes showing pathogenic DNMs in multiple disorders may shed light on the mechanisms underlying enrichment correlations (Supplementary file 1-STable 4). We identified five genes (CTNNB1, NBEA, POGZ, SPRED2, and KMT2C) with LoF DNMs in five different disorders and 21 genes had LoF DNMs in four disorders (Supplementary file 1-STable 5). These 26 genes with LoF variants in at least four disorders were significantly enriched for 63 gene ontology (GO) terms with FDR <0.05 (Supplementary file 1-STable 6). Chromatin organization (p=7.8e-11), nucleoplasm (p=2.8e-10), chromosome organization (p=6.8e-10), histone methyltransferase complex (p=1.4e-9), and positive regulation of gene expression (p=2.2e-9) were the most significantly enriched GO terms. One notable example consistently included in these gene sets is CTNNB1 (Figure 5—figure supplement 4). It encodes $β$ -catenin, is one of the only two genes reaching genome-wide significance in a recent WES study for cerebral palsy (Jin et al., 2020b), and also harbors multiple LoF variants in developmental disorder, intellectual disability, autism, and congenital heart disease. It is a fundamental component of the canonical Wnt signaling pathway which is known to confer genetic risk for autism (O’Roak et al., 2012). Genes with recurrent damaging DNMs in multiple disorders also revealed shared biological function across these disorders (Rees et al., 2021). We identified 30 recurrent cross-disorder LoF mutations that were not recurrent in developmental disorder alone (Supplementary file 1). FBXO11, encoding the F-box only protein 31, shows two recurrent p.Ser831fs LoF variants in autism and congenital hydrocephalus (Figure 5—figure supplement 5; p=1.9e-3; Materials and methods). The F-box protein constitutes a substrate-recognition component of the SCF (SKP1-cullin-F-box) complex, an E3-ubiquitin ligase complex responsible for ubiquitination and proteasomal degradation (Cardozo and Pagano, 2004). DNMs in FBXO11 have been previously implicated in severe intellectual disability individuals with autistic behavior problem (Jansen et al., 2019) and neurodevelopmental disorder (Gregor et al., 2018).

For comparison, we also applied mTADA to the same nine disorders and control trios. In total, mTADA identified 117 disorder pairs with significant genetic sharings at an FDR cutoff of 0.05 (Supplementary file 1-STable 8 and Figure 5—figure supplement 6). Notably, we identified significant synonymous DNM correlations for all 36 disorder pairs and between all disorders and healthy controls (Figure 5—figure supplement 7). These results are consistent with the simulation results and suggest a substantially inflated false positive rate in mTADA.

Partitioning DNM enrichment correlation by gene set

To gain biological insights into the shared genetic architecture of nine disorders, we repeated EncoreDNM correlation analysis in several gene sets. First, we defined genes with high/low probability of intolerance to LoF variants using pLI scores (Karczewski et al., 2020), and identified genes with high/low brain expression (HBE/LBE) (Werling et al., 2020; Materials and methods; Supplementary file 1-STable 9). We identified 11 and 12 disorder pairs showing significant enrichment correlations for LoF DNMs in high-pLI genes and HBE genes, respectively (Figure 6a–b). We observed fewer significant correlations for Dmis and Tmis variants in these gene sets (Figure 6—figure supplements 1–2). All identified significant correlations were positive (Supplementary file 1-STables 10 -11). No significant correlations were identified for synonymous variants (Figure 6—figure supplements 1–2) or between disorders and controls (Figure 6—figure supplements 3–4).

Figure 6 with 8 supplements see all

Download asset Open asset

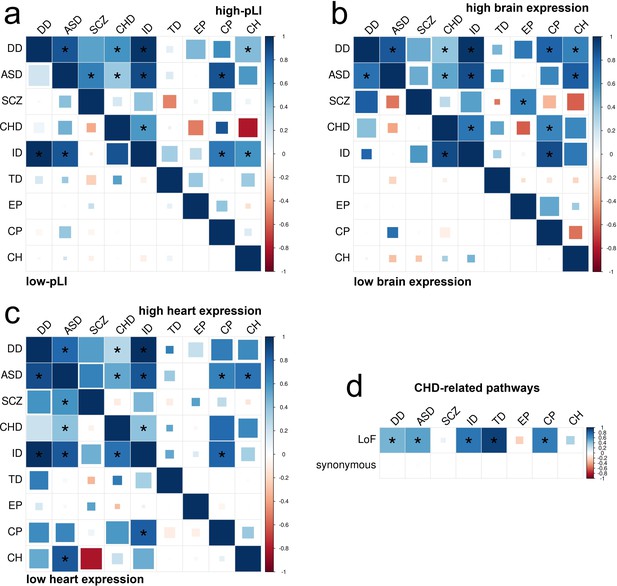
DNM enrichment correlations in disease-relevant gene sets.

(a) Enrichment correlations in high-pLI genes (upper triangle) and low-pLI genes (lower triangle) for LoF variants. Here, pLI is the probability of being loss-of-function intolerant (see Materials and methods). (b) Enrichment correlations in HBE genes (upper triangle) and LBE genes (lower triangle) for LoF variants. (c) Enrichment correlations in HHE genes (upper triangle) and LHE genes (lower triangle) for LoF variants. (d) Enrichment correlations in CHD-related pathways for LoF and synonymous variants. Larger squares represent more significant p-values, and deeper color represents stronger correlations. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.

We observed a clear enrichment of significant correlations in disease-relevant gene sets. Overall, high-pLI genes showed substantially stronger correlations across disorders than genes with low pLI (one-sided Kolmogorov-Smirnov test; p=2.3e-6). Similarly, enrichment correlations were stronger in HBE genes than in LBE genes (p=8.8e-7). Among the 11 disorder pairs showing significant enrichment correlations in high-pLI genes, two pairs, that is, autism-schizophrenia ( $ρ$ =0.68, p=2.4e-3) and developmental disorder-congenital hydrocephalus ( $ρ$ =0.43, p=1.5e-3), were not identified in the exome-wide analysis. We also identified four novel disorder pairs with significant correlations in HBE genes, including developmental disorder-cerebral palsy ( $ρ$ =0.80, p=9.5e-5), developmental disorder-congenital hydrocephalus ( $ρ$ =0.67, p=1.4e-3), autism-congenital hydrocephalus ( $ρ$ =0.82, p=4.7e-4), and schizophrenia-epileptic encephalopathies ( $ρ$ =0.66, p=2.0e-3). These novel enrichment correlations are consistent with known comorbidities between these disorders (Kielinen et al., 2004; Kilincaslan and Mukaddes, 2009) and findings based on significant risk genes (Li et al., 2016; Jin et al., 2020a; Kume et al., 1998; Cao and Wu, 2015).

Furthermore, we estimated DNM enrichment correlations in genes with high/low expression in mouse developing heart (HHE/LHE) (Homsy et al., 2015; Materials and methods; Supplementary file 1-STable 9). We identified 9 significant enrichment correlations for LoF variants in HHE genes (Figure 6c). Strength of enrichment correlations did not show a significant difference between HHE and LHE genes (p=0.846), possibly due to a lack of cardiac disorders in our analysis. Finally, we estimated enrichment correlations between congenital heart disease and other disorders in known pathways for congenital heart disease (Zaidi and Brueckner, 2017; Materials and methods; Supplementary file 1-STable 9). We identified five significant correlations for LoF variants (Figure 6d), including a novel correlation between congenital heart disease and Tourette disorder ( $ρ$ =0.93, p=3.3e-9). Of note, arrhythmia caused by congenital heart disease is a known risk factor for Tourette disorder (Gulisano et al., 2011). In these analyses, all significant enrichment correlations were positive (Supplementary file 1) and other variant classes showed generally weaker correlations than LoF variants (Figure 6—figure supplements 5–6). We did not observe significant correlations in these gene sets between disorders and controls (Figure 6—figure supplements 7–8).

Discussion

In this paper, we introduced EncoreDNM, a novel statistical framework to quantify correlated DNM enrichment between two disorders. Through extensive simulations and analyses of DNM data for nine disorders, we demonstrated that our proposed mixed-effects Poisson regression model provides unbiased parameter estimates, shows well-controlled false positive rate, and is robust to exome-wide technical biases. Leveraging exome-wide DNM counts and genomic context-based mutability data, EncoreDNM achieves superior fit for real DNM datasets compared to simpler models and provides statistically powerful and computationally efficient estimation of DNM enrichment correlation. Further, EncoreDNM can quantify concordant genetic effects for user-defined variant classes within pre-specified gene sets, thus is suitable for exploring diverse types of hypotheses and can provide crucial biological insights into the shared genetic etiology in multiple disorders. In comparison, the Bayesian approach implemented in mTADA can produce false positives findings, especially when the DNM count is low, possibility due to the overestimated proportion of risk genes. We still observed inflation in false positive rates under a more stringent significance cutoff or using posterior probability threshold strategy (Supplementary file 1-STables 14-17).

Multi-trait analyses of GWAS data have revealed shared genetic architecture among many neuropsychiatric traits (Brainstorm, 2018; Lee et al., 2013; Gratten et al., 2014; Abdellaoui and Verweij, 2021). These findings have led to the identification of pleiotropic variants, genes, and hub genomic regions underlying many traits and have revealed multiple psychopathological factors jointly affecting human neurological phenotypes (Lee, 2019; Wang et al., 2015). Although emerging evidence suggests that causal DNMs underlying several disorders with well-powered studies (e.g. congenital heart disease and neurodevelopmental disorders; Homsy et al., 2015) may be shared, our understanding of the extent and the mechanism underlying such sharing remains incomplete. Applied to DNM data for nine disorders, EncoreDNM identified pervasive enrichment correlations of DNMs. We observed particularly strong correlations in pathogenic variant classes (e.g. LoF and Dmis variants) and disease-relevant genes (e.g. genes with high pLI and genes highly expressed in relevant tissues). Genes underlying these correlations were significantly enriched in pathways involved in chromatin organization and modification and gene expression regulation. The DNM correlations were substantially attenuated in genes with lower expression and genes with frequent occurrences of LoF variants in the population. A similar attenuation was observed in less pathogenic variant classes (e.g., synonymous variants). Further, no significant correlations were identified between any disorder and healthy controls. We also compared DNM enrichment correlations of five disorders with genetic correlations estimated from GWAS summary statistics (Supplementary file 1-STable 18). We had consistent findings from GWAS and DNM data (Spearman correlation = 0.70; Figure 5—figure supplement 8 and Supplementary file 1-STable 19). These results lay the groundwork for future investigations of pleiotropic mechanisms of DNMs.

Our study has some limitations. First, EncoreDNM assumes probands from different input studies to be independent. In rare cases when two studies have overlapping proband samples, enrichment correlation estimates may be inflated and must be interpreted with caution. Second, genetic correlation methods based on GWAS summary data provided key motivations for the mixed-effects Poisson regression model in our study. Built upon genetic correlations, a plethora of methods have been developed in the GWAS literature to jointly model more than two GWAS (Turley et al., 2018), identify and quantify common factors underlying multiple traits (Grotzinger et al., 2019; Grotzinger et al., 2020), estimate causal effects among different traits (Pickrell et al., 2016), and identify pleiotropic genomic regions through hypothesis-free scans (Guo et al., 2021). Future directions of EncoreDNM include using enrichment correlation to improve gene discovery, learning the directional effects and the causal structure underlying multiple disorders, and dynamically searching for gene sets and annotation classes with shared genetic effects without pre-specifying the hypothesis.

Taken together, we provide a new analytic approach to an important problem in DNM studies. We believe EncoreDNM improves the statistical rigor in multi-disorder DNM modeling and opens up many interesting future directions in both method development and follow-up analyses in WES studies. As trio sample size in WES studies continues to grow, EncoreDNM will have broad applications and can greatly benefit DNM research.

Materials and methods

Statistical model

Request a detailed protocol

For a single study, we assume that DNM counts in a given variant class (for example, synonymous variants) follow a mixed-effects Poisson model:

Y_{i} \sim P o i s s o n (λ_{i}),

\log (λ_{i}) = β + \log (2 N m_{i}) + ϕ_{i},

ϕ_{i} \sim N (0, σ^{2}), f o r i = 1, \dots, G,

where $Y_{i}$ is the DNM count in the i-th gene, $N$ is the number of trios, $m_{i}$ is the de novo mutability for the i-th gene (for example, mutation rate per chromosome per generation) which is known a priori (Samocha et al., 2014), and $G$ is the total number of genes in the study. The elevation parameter $β$ quantifies the global elevation of mutation rate compared to mutability estimates based on genomic sequence alone. Gene-specific deviation from expected DNM rate is quantified by random effect $ϕ_{i}$ with a dispersion parameter $σ$ . Here, the $ϕ_{i}$ are assumed to be independent across different genes, in which case the observed DNM counts of different genes are independent. There is no constraint on the value of $β$ , and the dispersion parameter $σ$ can be any positive value.

Next, we describe how we expand this model to quantify the shared genetics of two disorders. We adopt a flexible Poisson-lognormal mixture framework that can accommodate both overdispersion and correlation (Munkin and Trivedi, 1999). We assume DNM counts in a given variant class for two diseases follow:

[\begin{matrix} Y_{i 1} \\ Y_{i 2} \end{matrix}] \sim P o i s s o n ([\begin{matrix} λ_{i 1} \\ λ_{i 2} \end{matrix}]),

\log ([\begin{matrix} λ_{i 1} \\ λ_{i 2} \end{matrix}]) = [\begin{matrix} β_{1} \\ β_{2} \end{matrix}] + \log ([\begin{matrix} 2 N_{1} m_{i} \\ 2 N_{2} m_{i} \end{matrix}]) + [\begin{matrix} ϕ_{i 1} \\ ϕ_{i 2} \end{matrix}],

[\begin{matrix} ϕ_{i 1} \\ ϕ_{i 2} \end{matrix}] \sim M V N ([\begin{matrix} 0 \\ 0 \end{matrix}], [\begin{matrix} σ_{1}^{2} & ρ σ_{1} σ_{2} \\ ρ σ_{1} σ_{2} & σ_{2}^{2} \end{matrix}]),

where $Y_{i 1}, Y_{i 2}$ are the DNM counts for the i-th gene and $N_{1}, N_{2}$ are the trio sizes in two studies, respectively. Similar to the single-trait model, $m_{i}$ is the mutability for the i-th gene. $β_{1}, β_{2}$ are the elevation parameters, and $ϕ_{i 1}, ϕ_{i 2}$ are the gene-specific random effects with dispersion parameters $σ_{1}, σ_{2}$ , for two disorders respectively. $ρ$ is the enrichment correlation which quantifies the concordance of the gene-specific DNM burden between two disorders. Here, $β_{1}, β_{2}, σ_{1}, σ_{2}, ρ$ are unknown parameters. The gene specific effects for two disorders are assumed to be independent for different genes. We also assume that there is no shared sample for two disorders, in which case $Y_{i 1}$ is independent with $Y_{i 2}$ given $[\begin{matrix} λ_{i 1} \\ λ_{i 2} \end{matrix}]$ .

Parameter estimation

Request a detailed protocol

We implement an MLE procedure to estimate unknown parameters. For single-trait analysis, the log-likelihood function can be expressed as follows:

l (β, σ| Y) = \sum_{i = 1}^{G} \log [\int \exp (- λ_{i}) λ_{i}^{Y_{i}} * f (ϕ_{i}) d ϕ_{i}] + C,

where $Y = {[Y_{1}, \dots, Y_{G}]}^{T}$ , $λ_{i} = 2 N m_{i} \exp (β + ϕ_{i})$ , $C = - \sum_{i = 1}^{G} \log (Y_{i}!)$ , and $f (ϕ_{i}) = \frac{1}{\sqrt{2 π} σ} \exp (- \frac{ϕ_{i}^{2}}{2 σ^{2}})$ . Note that there is no closed form for the integral in the log-likelihood function. Therefore, we use Monte Carlo integration to evaluate the log-likelihood function. Let $ϕ_{i j} = σ ξ_{i j}$ , where the $ξ_{i j}$ are independently and identically distributed random variables following a standard normal distribution. We have

l (β, σ| Y) \approx l ` (β, σ| Y) = \sum_{i = 1}^{G} \log [\sum_{j = 1}^{M} \exp (- λ_{i j}) λ_{i j}^{Y_{i}}] + C,

where $λ_{i j} = 2 N m_{i} \exp (β + σ ξ_{i j})$ , and $M$ is the Monte Carlo sample size which is set to be 1,000. Then, we could obtain the MLE of $β, σ$ through maximization of $l^{'} (β, σ | Y)$ . We obtain the standard error of the MLE through inversion of the observed Fisher information matrix. However, when the DNM count is small, the Fisher information may be non-invertible and the parameter vector is not numerically identifiable. In this case, we employ group-wise jackknife using 100 randomly partitioned gene groups to obtain standard errors for parameter estimates. This approach produces consistent standard errors compared to the Fisher information approach (Figure 5—figure supplement 9).

The estimation procedure can be generalized to multi-trait analysis. Log-likelihood function can be expressed as follows:

l (β_{1}, β_{2}, σ_{1}, σ_{2}, ρ| Y_{1}, Y_{2}) = \sum_{i = 1}^{G} \log [\int \exp (- λ_{i 1} - λ_{i 2}) λ_{i 1}^{Y_{i 1}} λ_{i 2}^{Y_{i 2}} * f (ϕ_{i 1}, ϕ_{i 2}) d ϕ_{i 1} d ϕ_{i 2}] + C,

where $Y_{1} = {[Y_{11}, \dots, Y_{G 1}]}^{T}$ , $Y_{2} = {[Y_{12}, \dots, Y_{G 2}]}^{T}$ , $λ_{i 1} = 2 N_{1} m_{i} \exp (β_{1} + ϕ_{i 1})$ , $λ_{i 2} = 2 N_{2} m_{i} \exp (β_{2} + ϕ_{i 2})$ , $C = - \sum_{i = 1}^{G} [\log (Y_{i 1}!) + \log (Y_{i 2}!)]$ , and $f (ϕ_{i 1}, ϕ_{i 2}) = \frac{1}{2 π σ_{1} σ_{2} \sqrt{1 - ρ^{2}}} \exp [- \frac{1}{2 \sqrt{1 - ρ^{2}}} (\frac{ϕ_{i 1}^{2}}{σ_{1}^{2}} + \frac{ϕ_{i 2}^{2}}{σ_{2}^{2}} - \frac{2 ρ ϕ_{i 1} ϕ_{i 2}}{σ_{1} σ_{2}})]$ . We use Monte Carlo integration to evaluate the log-likelihood function. Let $ϕ_{i 1 j} = σ_{1} ξ_{i 1 j}$ and $ϕ_{i 2 j} = σ_{2} (ρ ξ_{i 1 j} + \sqrt{1 - ρ^{2}} ξ_{i 2 j})$ , where the $ξ_{i 1 j}$ and $ξ_{i 2 j}$ are independently and identically distributed random variables following a standard normal distribution. We have

l (β_{1}, β_{2}, σ_{1}, σ_{2}, ρ| Y_{1}, Y_{2}) \approx l ` (β_{1}, β_{2}, σ_{1}, σ_{2}, ρ| Y_{1}, Y_{2}) = \sum_{i = 1}^{G} \log [\sum_{j = 1}^{M} \exp (- λ_{i 1 j} - λ_{i 2 j}) λ_{i 1 j}^{Y_{i 1}} λ_{i 2 j}^{Y_{i 2}}] + C,

where $λ_{i 1 j} = 2 N_{1} m_{i} \exp (β_{1} + σ_{1} ξ_{i 1 j})$ and $λ_{i 2 j} = 2 N_{2} m_{i} \exp [β_{2} + σ_{2} (ρ ξ_{i 1 j} + \sqrt{1 - ρ^{2}} ξ_{i 2 j})]$ . Then, we obtain the MLE of $β_{1}, β_{2}, σ_{1}, σ_{2}, ρ$ through maximization of $l ` (β_{1}, β_{2}, σ_{1}, σ_{2}, ρ| Y_{1}, Y_{2})$ . Standard error of MLE can be obtained either through inversion of the observed Fisher information matrix or group-wise jackknife if non-invertibility issue occurs.

Computation time

Request a detailed protocol

Analysis of a typical pair of disorders with 18,000 genes takes about 10 min on a 2.5 GHz cluster with 1 core.

DNM data and variant annotation

Request a detailed protocol

We obtained DNM data from published studies (Supplementary file 1-STable 1). DNM data for epileptic encephalopathies from the original release (Allen et al., 2013) were not in an editable format and were instead collected from denovo-db (Turner et al., 2017). We used ANNOVAR (Wang et al., 2010) to annotate all DNMs. Synonymous variants were determined based on the ‘synonymous SNV’ annotation in ANNOVAR; Variants with ‘startloss’, ‘stopgain’, ‘stoploss’, ‘splicing’, ‘frameshift insertion’, ‘frameshift deletion’, or ‘frameshift substitution’ annotations were classified as LoF; Dmis variants were defined as nonsynonymous SNVs predicted to be deleterious by MetaSVM Dong et al., 2015; nonsynonymous SNVs predicted to be tolerable by MetaSVM were classified as Tmis. Other DNMs which did not fall into these categories were removed from the analysis. For each variant class, we estimated the mutability of each gene using a sequence-based mutation model (Samocha et al., 2014) while adjusting for the sequencing coverage factor based on control trios as previously described (Jin et al., 2017; Supplementary file 1-STable 20). We included 18,454 autosomal protein-coding genes in our analysis. TTN was removed due to its substantially larger size.

Description and implementation of mTADA

Request a detailed protocol

The method mTADA employs a Bayesian framework and estimates the proportion of shared risk genes. Specifically, mTADA assigns all genes into four groups: genes that are not relevant for either disorder, risk genes for the first disorder alone, risk genes for the second disorder alone, and risk genes shared by both disorders. The proportion of these groups are parametrized as $π_{0}, π_{1}, π_{2}, π_{3}$ , respectively. In particular, parameter $π_{3}$ quantifies the extent of genetic sharing between two disorders, with a larger value indicating stronger genetic overlap (Nguyen et al., 2020). The 95% credible interval constructed through MCMC is used to measure the uncertainty in $π_{3}$ estimates.

The software mTADA requires the following parameters as inputs: proportion of risk genes ( $π_{1}^{S}, π_{2}^{S}$ ), mean relative risks ( ${\bar{γ}}_{1}^{S}, {\bar{γ}}_{2}^{S}$ ), and dispersion parameters ( ${\bar{β}}_{1}^{S}, {\bar{β}}_{2}^{S}$ ) for both disorders. We used extTADA (Nguyen et al., 2017 )to estimate these parameters as suggested by the mTADA paper (Nguyen et al., 2020). mTADA reported the estimated proportion of shared risk genes $π_{3}$ (posterior mode of $π_{3}$ ) and its corresponding 95% credible interval $[L B, U B]$ . We considered $π_{1}^{S} * π_{2}^{S}$ as the expected proportion of shared risk genes, and there is significant genetic sharing between two disorders when $L B > π_{1}^{S} * π_{2}^{S}$ . We quantify statistical evidence for genetic sharing by comparing the posterior distribution of $π_{3}$ with $π_{1}^{S} * π_{2}^{S}$ ,

p = 2 * \frac{\sum_{i = 1}^{N_{M C M C}} I (π_{3}^{i} < π_{1}^{S} * π_{2}^{S})}{N_{M C M C}},

where $π_{3}^{i}$ is the i-th MCMC iteration sample, $N_{M C M C}$ is the number of iterations, and $I ()$ is the indicator function. This is also equivalent to performing two-sided inference using posterior probability P $(π_{3} > π_{1}^{S} * π_{2}^{S})$ . Number of MCMC chain was set as 2 and number of iterations was set as 10,000.

Simulation settings

Request a detailed protocol

We assessed the performance of EncoreDNM under the mixed-effects Poisson model. We performed simulations for two variant classes: Tmis and LoF variants, which have the largest and the smallest median mutability values across all genes. First, we performed single-trait simulations to assess estimation precision of elevation parameter $β$ and dispersion parameter $σ$ . We set the true values of $β$ to be −0.5,–0.25, and 0, and the true values of $σ$ to be 0.5, 0.75, and 1. These values were chosen based on the estimated parameters in real DNM data analyses and ensured simulation settings to be realistic. Next, we performed simulations for cross-trait analysis to assess estimation precision of enrichment correlation $ρ$ , whose true values were set to be 0, 0.2, 0.4, 0.6, and 0.8. Sample size for each disorder was set to be 5000. Coverage rate was calculated as the percentage of simulations that the 95% Wald confidence interval covered the true parameter value. Each parameter setting was repeated 100 times.

We also carried out simulations to compare the performance of EncoreDNM and mTADA. False positive rate and statistical power for EncoreDNM were calculated as the proportion of simulation repeats that p-value for enrichment correlation $ρ$ was smaller than 0.05. and the proportion of simulation repeats that p-value for estimated proportion of shared risk genes $π_{3}$ was smaller than 0.05 was used for mTADA. We aggregated all variant classes together, so mutability for each gene was determined as the sum of mutabilities across four variant classes (i.e. LoF, Dmis, Tmis, and synonymous).

First, we simulated DNM data under the mixed-effects Poisson model. To see whether two methods would produce false positive findings, we performed simulations under the null hypothesis that the enrichment correlation $ρ$ is zero. We compared two methods under a range of parameter combinations of ( $β, σ, N$ ) for both disorders: (–0.25, 0.75, 5000) for the baseline setting, (–1, 0.75, 5000) for a setting with small $β$ , (–0.25, 0.5, 5000) for a setting with small $σ$ , and (–0.25, 0.75, 1000) for a setting with small sample size. We also assessed the statistical power of two methods under the alternative hypothesis. True value of enrichment correlation $ρ$ was set to be 0.05, 0.1, 0.15, and 0.2. In the power analysis, parameters ( $β, σ, N$ ) were fixed at (–0.25, 0.75, 5000) as in the baseline setting when both methods had well-controlled false positive rate.

To ensure a fair comparison, we also compared EncoreDNM and mTADA under a multinomial model, which is different from the data generation processes for the two approaches. For each disorder ( $k = 1,2$ ), we randomly selected causal genes of proportion $π_{k}^{S}$ . A proportion (i.e. $π_{3}$ ) of causal genes overlap between two disorders. We assumed that the total DNM count to follow a Poisson distribution: $C_{k} ~ P o i s s o n (u_{k} * 2 N_{k} \sum_{i = 1}^{G} m_{i})$ , where $u_{k}$ represents an elevation factor to represent systematic bias in the data. Let $Y_{k}$ denote the vector of DNMs counts in the exome, $m$ denote the vector of mutability values for all genes, and $m_{c a u s a l, k}$ denote the vector of mutability with values set to be 0 for non-causal genes of disorder $k$ . We assumed that a proportion $p_{k}$ of the probands could be attributed to DNMs burden in causal genes, and $1 - p_{k}$ of the probands obtained DNMs by chance:

Y_{k} = Y_{c a u s a l, k} + Y_{b a c k g r o u n d, k},

Y_{c a u s a l, k} ~ M u l t i n o m i a l (p_{k} C_{k}, m_{c a u s a l, k}),

Y_{b a c k g r o u n d, k} ~ M u l t i n o m i a l ((1 - p_{k}) C_{k}, m) .

To check whether false positive findings could arise, we performed simulations under the null hypothesis that $π_{3} = π_{1}^{S} * π_{2}^{S}$ across a range of parameter combinations of ( $u, p, N$ ) for both disorders: (0.95, 0.25, 5000) for the baseline setting, (0.75, 0.25, 5000) for a setting with small $u$ (i.e., reduced total mutation count), (0.95, 0.15, 5000) for a setting with small $p$ (fewer probands explained by DNMs), and (0.95, 0.25, 1000) for a setting with smaller sample size. $π_{1}^{S}$ and $π_{2}^{S}$ were set as 0.1. We also assessed the statistical power of two methods under the alternative hypothesis that $π_{3} > π_{1}^{S} * π_{2}^{S}$ . In power analysis, ( $u, p, N$ ) were fixed at (0.95, 0.25, 5000) as in the baseline setting when false positive rate for both methods were well-calibrated.

Comparison to the fixed-effects Poisson model

Request a detailed protocol

For single-trait analysis, the fixed-effects Poisson model assumes that

Y_{i} \sim P o i s s o n (λ_{i}),

\log (λ_{i}) = β + \log (2 N m_{i}), f o r i = 1, \dots, G .

Note that the fixed-effects Poisson model is a special case of our proposed mixed-effects Poisson model when $σ = 0$ . We compared the two models using likelihood ratio test. Under the null hypothesis that $σ = 0$ , $2 (l_{a l t} - l_{n u l l}) \sim \frac{1}{2} χ_{1}^{2}$ asymptotically, where $l_{a l t}$ and $l_{n u l l}$ represent the log likelihood of the fitted mixed-effects and fixed-effects Poisson models respectively.

Recurrent genes and DNMs

Request a detailed protocol

We used FUMA (Watanabe et al., 2017) to perform GO enrichment analysis for genes harboring LoF DNMs in multiple disorders. Due to potential sample overlap between the studies of developmental disorder (Kaplanis et al., 2020) and intellectual disability (Lelieveld et al., 2016), we excluded intellectual disability from the analysis of recurrent DNMs. We calculated the probability of observing two identical DNMs in two disorders using a Monte Carlo simulation method. For each disorder, we simulated exome-wide DNMs profile from a multinomial distribution, where the size was fixed at the observed DNM count and the per-base mutation probability was determined by the tri-nucleotide base context. We repeated the simulation procedure 100,000 times to evaluate the significance of recurrent DNMs. Lollipop plots for recurrent mutations were generated using MutationMapper on the cBio Cancer Genomics Portal (Cerami et al., 2012).

Implementation of cross-trait LD score regression

Request a detailed protocol

We used cross-trait LDSC (Bulik-Sullivan et al., 2015) to estimate genetic correlations between disorders. LD scores were computed using European samples from the 1000 Genomes Project Phase 3 data (Auton et al., 2015). Only HapMap 3 SNPs were used as observations in the explanatory variable with the --merge-alleles flag. Intercepts were not constrained in the analyses.

Estimating enrichment correlation in gene sets

Request a detailed protocol

Genes with a high/low probability of intolerance to LoF variants (high-pLI/low-pLI) were defined as the 4,614 genes in the upper/lower quartiles of pLI scores (Karczewski et al., 2020). Genes with high/low brain expression (HBE/LBE) were defined as the 4,614 genes in the upper/lower quartiles of expression in the human fetal brain (Werling et al., 2020). Genes with high/low heart expression (HHE/LHE) were defined as the 4,614 genes in the upper/lower quartiles of expression in the developing heart of embryonic mouse (Zaidi et al., 2013). Five biological pathways have been reported to be involved in congenital heart disease: chromatin remodeling, Notch signaling, cilia function, sarcomere structure and function, and RAS signaling (Zaidi and Brueckner, 2017). We extracted 1730 unique genes that belong to these five pathways from the gene ontology database (Ashburner et al., 2000) and referred to the union set as CHD-related genes. We repeated EncoreDNM enrichment correlation analysis in these gene sets. One-sided Kolmogorov-Smirnov test was used to assess the statistical difference between enrichment correlation signal strength in different gene sets.

URLs

GWAS summary statistics data of autism spectrum disorder, schizophrenia, and Tourette disorder were downloaded on the PGC website, https://www.med.unc.edu/pgc/download-results/; Summary statistics of cognitive performance were downloaded on the SSGAC website, https://thessgac.com/; Summary statistics of epilepsy were downloaded on the epiGAD website, https://www.epigad.org/; pLI scores were downloaded from gnomAD v3.1 repository https://gnomad.broadinstitute.org/downloads; mTADA, https://github.com/hoangtn/mTADA, Nguyen et al., 2021; denovo-db, https://denovo-db.gs.washington.edu/denovo-db/; MutationMapper on cBioPortal, https://www.cbioportal.org/mutation_mapper; LDSC, https://github.com/bulik/ldsc; Schorsch, 2020.

Code availability

Request a detailed protocol

EncoreDNM software is available at https://github.com/ghm17/EncoreDNM; Guo, 2022.

Data availability

The current manuscript is a computational study, so no data have been generated for this manuscript.

References

1. Abdellaoui A
2. Verweij KJH
(2021) Dissecting polygenic signals from genome-wide association studies on human behaviour
Nature Human Behaviour 5:686–694.

https://doi.org/10.1038/s41562-021-01110-y
- PubMed
- Google Scholar
1. Allen AS
2. Berkovic SF
3. Cossette P
4. Delanty N
5. Dlugos D
6. Eichler EE
7. Epstein MP
8. Glauser T
9. Goldstein DB
10. Han Y
11. Heinzen EL
12. Hitomi Y
13. Howell KB
14. Johnson MR
15. Kuzniecky R
16. Lowenstein DH
17. Lu Y-F
18. Madou MRZ
19. Marson AG
20. Mefford HC
21. Esmaeeli Nieh S
22. O’Brien TJ
23. Ottman R
24. Petrovski S
25. Poduri A
26. Ruzzo EK
27. Scheffer IE
28. Sherr EH
29. Yuskaitis CJ
30. Abou-Khalil B
31. Alldredge BK
32. Bautista JF
33. Berkovic SF
34. Boro A
35. Cascino GD
36. Consalvo D
37. Crumrine P
38. Devinsky O
39. Dlugos D
40. Epstein MP
41. Fiol M
42. Fountain NB
43. French J
44. Friedman D
45. Geller EB
46. Glauser T
47. Glynn S
48. Haut SR
49. Hayward J
50. Helmers SL
51. Joshi S
52. Kanner A
53. Kirsch HE
54. Knowlton RC
55. Kossoff EH
56. Kuperman R
57. Kuzniecky R
58. Lowenstein DH
59. McGuire SM
60. Motika PV
61. Novotny EJ
62. Ottman R
63. Paolicchi JM
64. Parent JM
65. Park K
66. Poduri A
67. Scheffer IE
68. Shellhaas RA
69. Sherr EH
70. Shih JJ
71. Singh R
72. Sirven J
73. Smith MC
74. Sullivan J
75. Lin Thio L
76. Venkat A
77. Vining EPG
78. Von Allmen GK
79. Weisenberg JL
80. Widdess-Walsh P
81. Winawer MR
82. Epi4K Consortium
83. Epilepsy Phenome/Genome Project
(2013) De novo mutations in epileptic encephalopathies
Nature 501:217–221.

https://doi.org/10.1038/nature12439
- PubMed
- Google Scholar
1. Ashburner M
2. Ball CA
3. Blake JA
4. Botstein D
5. Butler H
6. Cherry JM
7. Davis AP
8. Dolinski K
9. Dwight SS
10. Eppig JT
11. Harris MA
12. Hill DP
13. Issel-Tarver L
14. Kasarskis A
15. Lewis S
16. Matese JC
17. Richardson JE
18. Ringwald M
19. Rubin GM
20. Sherlock G
(2000) Gene Ontology: tool for the unification of biology
Nature Genetics 25:25–29.

https://doi.org/10.1038/75556
- Google Scholar
(2015) A global reference for human genetic variation
Nature 526:68–74.

https://doi.org/10.1038/nature15393
- PubMed
- Google Scholar
1. Brainstorm C
(2018) Analysis of shared heritability in common disorders of the brain
Science (New York, N.Y.) 360:aap875.

https://doi.org/10.1126/science.aap875
- Google Scholar
(2015) An atlas of genetic correlations across human diseases and traits
Nature Genetics 47:1236–1241.

https://doi.org/10.1038/ng.3406
- PubMed
- Google Scholar
1. Cao M
2. Wu JI
(2015) Camk2a-Cre-mediated conditional deletion of chromatin remodeler Brg1 causes perinatal hydrocephalus
Neuroscience Letters 597:71–76.

https://doi.org/10.1016/j.neulet.2015.04.041
- PubMed
- Google Scholar
1. Cardozo T
2. Pagano M
(2004) The SCF ubiquitin ligase: insights into a molecular machine
Nature Reviews. Molecular Cell Biology 5:739–751.

https://doi.org/10.1038/nrm1471
- PubMed
- Google Scholar
1. Cerami E
2. Gao J
3. Dogrusoz U
4. Gross BE
5. Sumer SO
6. Aksoy BA
7. Jacobsen A
8. Byrne CJ
9. Heuer ML
10. Larsson E
11. Antipin Y
12. Reva B
13. Goldberg AP
14. Sander C
15. Schultz N
(2012) The cBio cancer genomics portal: an open platform for exploring multidimensional cancer genomics data
Cancer Discovery 2:401–404.

https://doi.org/10.1158/2159-8290.CD-12-0095
- PubMed
- Google Scholar
(2014) Prevalence of cerebral palsy, co-occurring autism spectrum disorders, and motor functioning - Autism and Developmental Disabilities Monitoring Network, USA, 2008
Developmental Medicine and Child Neurology 56:59–65.

https://doi.org/10.1111/dmcn.12268
- PubMed
- Google Scholar
1. Dong C
2. Wei P
3. Jian X
4. Gibbs R
5. Boerwinkle E
6. Wang K
7. Liu X
(2015) Comparison and integration of deleteriousness prediction methods for nonsynonymous SNVs in whole exome sequencing studies
Human Molecular Genetics 24:2125–2137.

https://doi.org/10.1093/hmg/ddu733
- PubMed
- Google Scholar
1. Fromer M
2. Pocklington AJ
3. Kavanagh DH
4. Williams HJ
5. Dwyer S
6. Gormley P
7. Georgieva L
8. Rees E
9. Palta P
10. Ruderfer DM
11. Carrera N
12. Humphreys I
13. Johnson JS
14. Roussos P
15. Barker DD
16. Banks E
17. Milanova V
18. Grant SG
19. Hannon E
20. Rose SA
21. Chambert K
22. Mahajan M
23. Scolnick EM
24. Moran JL
25. Kirov G
26. Palotie A
27. McCarroll SA
28. Holmans P
29. Sklar P
30. Owen MJ
31. Purcell SM
32. O’Donovan MC
(2014) De novo mutations in schizophrenia implicate synaptic networks
Nature 506:179–184.

https://doi.org/10.1038/nature12929
- PubMed
- Google Scholar
(2008) Cerebral palsy and congenital malformations
European Journal of Paediatric Neurology 12:82–88.

https://doi.org/10.1016/j.ejpn.2007.07.001
- PubMed
- Google Scholar
(2014) Large-scale genomics unveils the genetic architecture of psychiatric disorders
Nature Neuroscience 17:782–790.

https://doi.org/10.1038/nn.3708
- PubMed
- Google Scholar
1. Gregor A
2. Sadleir LG
3. Asadollahi R
4. Azzarello-Burri S
5. Battaglia A
6. Ousager LB
7. Boonsawat P
8. Bruel A-L
9. Buchert R
10. Calpena E
11. Cogné B
12. Dallapiccola B
13. Distelmaier F
14. Elmslie F
15. Faivre L
16. Haack TB
17. Harrison V
18. Henderson A
19. Hunt D
20. Isidor B
21. Joset P
22. Kumada S
23. Lachmeijer AMA
24. Lees M
25. Lynch SA
26. Martinez F
27. Matsumoto N
28. McDougall C
29. Mefford HC
30. Miyake N
31. Myers CT
32. Moutton S
33. Nesbitt A
34. Novelli A
35. Orellana C
36. Rauch A
37. Rosello M
38. Saida K
39. Santani AB
40. Sarkar A
41. Scheffer IE
42. Shinawi M
43. Steindl K
44. Symonds JD
45. Zackai EH
46. University of Washington Center for Mendelian Genomics
47. DDD Study
48. Reis A
49. Sticht H
50. Zweier C
(2018) De Novo Variants in the F-Box Protein FBXO11 in 20 Individuals with a Variable Neurodevelopmental Disorder
American Journal of Human Genetics 103:305–316.

https://doi.org/10.1016/j.ajhg.2018.07.003
- PubMed
- Google Scholar
1. Grotzinger AD
2. Rhemtulla M
3. de Vlaming R
4. Ritchie SJ
5. Mallard TT
6. Hill WD
7. Ip HF
8. Marioni RE
9. McIntosh AM
10. Deary IJ
11. Koellinger PD
12. Harden KP
13. Nivard MG
14. Tucker-Drob EM
(2019) Genomic structural equation modelling provides insights into the multivariate genetic architecture of complex traits
Nature Human Behaviour 3:513–525.

https://doi.org/10.1038/s41562-019-0566-x
- PubMed
- Google Scholar
Preprint
(2020) Genetic Architecture of 11 Major Psychiatric Disorders at Biobehavioral, Functional Genomic, and Molecular Genetic Levels of Analysis
medRxiv.

https://doi.org/10.1101/2020.09.22.20196089
- Google Scholar
1. Gulisano M
2. Calì PV
3. Cavanna AE
4. Eddy C
5. Rickards H
6. Rizzo R
(2011) Cardiovascular safety of aripiprazole and pimozide in young patients with Tourette syndrome
Neurological Sciences 32:1213–1217.

https://doi.org/10.1007/s10072-011-0678-1
- PubMed
- Google Scholar
1. Guo H
2. Li JJ
3. Lu Q
4. Hou L
(2021) Detecting local genetic correlations with scan statistics
Nature Communications 12:2033.

https://doi.org/10.1038/s41467-021-22334-6
- PubMed
- Google Scholar
Software
1. Guo H
(2022) EncoreDNM, version swh:1:rev:44ec5903b4c34e7b73ed7791f30d0b3544bafcd1
GitHub.

https://github.com/ghm17/EncoreDNM
(2014) Prioritization of neurodevelopmental disease genes by discovery of new mutations
Nature Neuroscience 17:764–772.

https://doi.org/10.1038/nn.3703
- PubMed
- Google Scholar
1. Homsy J
2. Zaidi S
3. Shen Y
4. Ware JS
5. Samocha KE
6. Karczewski KJ
7. DePalma SR
8. McKean D
9. Wakimoto H
10. Gorham J
11. Jin SC
12. Deanfield J
13. Giardini A
14. Porter GA Jr
15. Kim R
16. Bilguvar K
17. López-Giráldez F
18. Tikhonova I
19. Mane S
20. Romano-Adesman A
21. Qi H
22. Vardarajan B
23. Ma L
24. Daly M
25. Roberts AE
26. Russell MW
27. Mital S
28. Newburger JW
29. Gaynor JW
30. Breitbart RE
31. Iossifov I
32. Ronemus M
33. Sanders SJ
34. Kaltman JR
35. Seidman JG
36. Brueckner M
37. Gelb BD
38. Goldmuntz E
39. Lifton RP
40. Seidman CE
41. Chung WK
(2015) De novo mutations in congenital heart disease with neurodevelopmental and other congenital anomalies
Science (New York, N.Y.) 350:1262–1266.

https://doi.org/10.1126/science.aac9396
- PubMed
- Google Scholar
(2015) The discovery of integrated gene networks for autism and related disorders
Genome Research 25:142–154.

https://doi.org/10.1101/gr.178855.114
- PubMed
- Google Scholar
1. Howrigan DP
2. Rose SA
3. Samocha KE
4. Fromer M
5. Cerrato F
6. Chen WJ
7. Churchhouse C
8. Chambert K
9. Chandler SD
10. Daly MJ
11. Dumont A
12. Genovese G
13. Hwu H-G
14. Laird N
15. Kosmicki JA
16. Moran JL
17. Roe C
18. Singh T
19. Wang S-H
20. Faraone SV
21. Glatt SJ
22. McCarroll SA
23. Tsuang M
24. Neale BM
(2020) Exome sequencing in schizophrenia-affected parent-offspring trios reveals risk conferred by protein-coding de novo mutations
Nature Neuroscience 23:185–193.

https://doi.org/10.1038/s41593-019-0564-3
- PubMed
- Google Scholar
1. Jansen S
2. van der Werf IM
3. Innes AM
4. Afenjar A
5. Agrawal PB
6. Anderson IJ
7. Atwal PS
8. van Binsbergen E
9. van den Boogaard M-J
10. Castiglia L
11. Coban-Akdemir ZH
12. van Dijck A
13. Doummar D
14. van Eerde AM
15. van Essen AJ
16. van Gassen KL
17. Guillen Sacoto MJ
18. van Haelst MM
19. Iossifov I
20. Jackson JL
21. Judd E
22. Kaiwar C
23. Keren B
24. Klee EW
25. Klein Wassink-Ruiter JS
26. Meuwissen ME
27. Monaghan KG
28. de Munnik SA
29. Nava C
30. Ockeloen CW
31. Pettinato R
32. Racher H
33. Rinne T
34. Romano C
35. Sanders VR
36. Schnur RE
37. Smeets EJ
38. Stegmann APA
39. Stray-Pedersen A
40. Sweetser DA
41. Terhal PA
42. Tveten K
43. VanNoy GE
44. de Vries PF
45. Waxler JL
46. Willing M
47. Pfundt R
48. Veltman JA
49. Kooy RF
50. Vissers LELM
51. de Vries BBA
(2019) De novo variants in FBXO11 cause a syndromic form of intellectual disability with behavioral problems and dysmorphisms
European Journal of Human Genetics 27:738–746.

https://doi.org/10.1038/s41431-018-0292-2
- PubMed
- Google Scholar
1. Jin SC
2. Homsy J
3. Zaidi S
4. Lu Q
5. Morton S
6. DePalma SR
7. Zeng X
8. Qi H
9. Chang W
10. Sierant MC
11. Hung W-C
12. Haider S
13. Zhang J
14. Knight J
15. Bjornson RD
16. Castaldi C
17. Tikhonoa IR
18. Bilguvar K
19. Mane SM
20. Sanders SJ
21. Mital S
22. Russell MW
23. Gaynor JW
24. Deanfield J
25. Giardini A
26. Porter GA Jr
27. Srivastava D
28. Lo CW
29. Shen Y
30. Watkins WS
31. Yandell M
32. Yost HJ
33. Tristani-Firouzi M
34. Newburger JW
35. Roberts AE
36. Kim R
37. Zhao H
38. Kaltman JR
39. Goldmuntz E
40. Chung WK
41. Seidman JG
42. Gelb BD
43. Seidman CE
44. Lifton RP
45. Brueckner M
(2017) Contribution of rare inherited and de novo variants in 2,871 congenital heart disease probands
Nature Genetics 49:1593–1601.

https://doi.org/10.1038/ng.3970
- PubMed
- Google Scholar
1. Jin SC
2. Dong W
3. Kundishora AJ
4. Panchagnula S
5. Moreno-De-Luca A
6. Furey CG
7. Allocco AA
8. Walker RL
9. Nelson-Williams C
10. Smith H
11. Dunbar A
12. Conine S
13. Lu Q
14. Zeng X
15. Sierant MC
16. Knight JR
17. Sullivan W
18. Duy PQ
19. DeSpenza T
20. Reeves BC
21. Karimy JK
22. Marlier A
23. Castaldi C
24. Tikhonova IR
25. Li B
26. Peña HP
27. Broach JR
28. Kabachelor EM
29. Ssenyonga P
30. Hehnly C
31. Ge L
32. Keren B
33. Timberlake AT
34. Goto J
35. Mangano FT
36. Johnston JM
37. Butler WE
38. Warf BC
39. Smith ER
40. Schiff SJ
41. Limbrick DD
42. Heuer G
43. Jackson EM
44. Iskandar BJ
45. Mane S
46. Haider S
47. Guclu B
48. Bayri Y
49. Sahin Y
50. Duncan CC
51. Apuzzo MLJ
52. DiLuna ML
53. Hoffman EJ
54. Sestan N
55. Ment LR
56. Alper SL
57. Bilguvar K
58. Geschwind DH
59. Günel M
60. Lifton RP
61. Kahle KT
(2020a) Exome sequencing implicates genetic disruption of prenatal neuro-gliogenesis in sporadic congenital hydrocephalus
Nature Medicine 26:1754–1765.

https://doi.org/10.1038/s41591-020-1090-2
- PubMed
- Google Scholar
1. Jin SC
2. Lewis SA
3. Bakhtiari S
4. Zeng X
5. Sierant MC
6. Shetty S
7. Nordlie SM
8. Elie A
9. Corbett MA
10. Norton BY
11. van Eyk CL
12. Haider S
13. Guida BS
14. Magee H
15. Liu J
16. Pastore S
17. Vincent JB
18. Brunstrom-Hernandez J
19. Papavasileiou A
20. Fahey MC
21. Berry JG
22. Harper K
23. Zhou C
24. Zhang J
25. Li B
26. Zhao H
27. Heim J
28. Webber DL
29. Frank MSB
30. Xia L
31. Xu Y
32. Zhu D
33. Zhang B
34. Sheth AH
35. Knight JR
36. Castaldi C
37. Tikhonova IR
38. López-Giráldez F
39. Keren B
40. Whalen S
41. Buratti J
42. Doummar D
43. Cho M
44. Retterer K
45. Millan F
46. Wang Y
47. Waugh JL
48. Rodan L
49. Cohen JS
50. Fatemi A
51. Lin AE
52. Phillips JP
53. Feyma T
54. MacLennan SC
55. Vaughan S
56. Crompton KE
57. Reid SM
58. Reddihough DS
59. Shang Q
60. Gao C
61. Novak I
62. Badawi N
63. Wilson YA
64. McIntyre SJ
65. Mane SM
66. Wang X
67. Amor DJ
68. Zarnescu DC
69. Lu Q
70. Xing Q
71. Zhu C
72. Bilguvar K
73. Padilla-Lopez S
74. Lifton RP
75. Gecz J
76. MacLennan AH
77. Kruer MC
(2020b) Mutations disrupting neuritogenesis genes confer risk for cerebral palsy
Nature Genetics 52:1046–1056.

https://doi.org/10.1038/s41588-020-0695-1
- PubMed
- Google Scholar
1. Kaplanis J
2. Samocha KE
3. Wiel L
4. Zhang Z
5. Arvai KJ
6. Eberhardt RY
7. Gallone G
8. Lelieveld SH
9. Martin HC
10. McRae JF
11. Short PJ
12. Torene RI
13. de Boer E
14. Danecek P
15. Gardner EJ
16. Huang N
17. Lord J
18. Martincorena I
19. Pfundt R
20. Reijnders MRF
21. Yeung A
22. Yntema HG
23. Deciphering Developmental Disorders Study
24. Vissers LELM
25. Juusola J
26. Wright CF
27. Brunner HG
28. Firth HV
29. FitzPatrick DR
30. Barrett JC
31. Hurles ME
32. Gilissen C
33. Retterer K
(2020) Evidence for 28 genetic disorders discovered by combining healthcare and research data
Nature 586:757–762.

https://doi.org/10.1038/s41586-020-2832-5
- PubMed
- Google Scholar
1. Karczewski KJ
2. Francioli LC
3. Tiao G
4. Cummings BB
5. Alföldi J
6. Wang Q
7. Collins RL
8. Laricchia KM
9. Ganna A
10. Birnbaum DP
11. Gauthier LD
12. Brand H
13. Solomonson M
14. Watts NA
15. Rhodes D
16. Singer-Berk M
17. England EM
18. Seaby EG
19. Kosmicki JA
20. Walters RK
21. Tashman K
22. Farjoun Y
23. Banks E
24. Poterba T
25. Wang A
26. Seed C
27. Whiffin N
28. Chong JX
29. Samocha KE
30. Pierce-Hoffman E
31. Zappala Z
32. O’Donnell-Luria AH
33. Minikel EV
34. Weisburd B
35. Lek M
36. Ware JS
37. Vittal C
38. Armean IM
39. Bergelson L
40. Cibulskis K
41. Connolly KM
42. Covarrubias M
43. Donnelly S
44. Ferriera S
45. Gabriel S
46. Gentry J
47. Gupta N
48. Jeandet T
49. Kaplan D
50. Llanwarne C
51. Munshi R
52. Novod S
53. Petrillo N
54. Roazen D
55. Ruano-Rubio V
56. Saltzman A
57. Schleicher M
58. Soto J
59. Tibbetts K
60. Tolonen C
61. Wade G
62. Talkowski ME
63. Genome Aggregation Database Consortium
64. Neale BM
65. Daly MJ
66. MacArthur DG
(2020) The mutational constraint spectrum quantified from variation in 141,456 humans
Nature 581:434–443.

https://doi.org/10.1038/s41586-020-2308-7
- PubMed
- Google Scholar
(2004) Associated medical disorders and disabilities in children with autistic disorder: a population-based study
Autism 8:49–60.

https://doi.org/10.1177/1362361304040638
- PubMed
- Google Scholar
1. Kilincaslan A
2. Mukaddes NM
(2009) Pervasive developmental disorders in individuals with cerebral palsy
Developmental Medicine and Child Neurology 51:289–294.

https://doi.org/10.1111/j.1469-8749.2008.03171.x
- PubMed
- Google Scholar
1. Krumm N
2. Turner TN
3. Baker C
4. Vives L
5. Mohajeri K
6. Witherspoon K
7. Raja A
8. Coe BP
9. Stessman HA
10. He Z-X
11. Leal SM
12. Bernier R
13. Eichler EE
(2015) Excess of rare, inherited truncating mutations in autism
Nature Genetics 47:582–588.

https://doi.org/10.1038/ng.3303
- PubMed
- Google Scholar
1. Kume T
2. Deng KY
3. Winfrey V
4. Gould DB
5. Walter MA
6. Hogan BL
(1998) The forkhead/winged helix gene Mf1 is disrupted in the pleiotropic mouse mutation congenital hydrocephalus
Cell 93:985–996.

https://doi.org/10.1016/s0092-8674(00)81204-0
- PubMed
- Google Scholar
1. Lee SH
2. Yang J
3. Goddard ME
4. Visscher PM
5. Wray NR
(2012) Estimation of pleiotropy between complex diseases using single-nucleotide polymorphism-derived genomic relationships and restricted maximum likelihood
Bioinformatics (Oxford, England) 28:2540–2542.

https://doi.org/10.1093/bioinformatics/bts474
- PubMed
- Google Scholar
1. Lee SH
2. Ripke S
3. Neale BM
4. Faraone SV
5. Purcell SM
6. Perlis RH
7. Mowry BJ
8. Thapar A
9. Goddard ME
10. Witte JS
11. Absher D
12. Agartz I
13. Akil H
14. Amin F
15. Andreassen OA
16. Anjorin A
17. Anney R
18. Anttila V
19. Arking DE
20. Asherson P
21. Azevedo MH
22. Backlund L
23. Badner JA
24. Bailey AJ
25. Banaschewski T
26. Barchas JD
27. Barnes MR
28. Barrett TB
29. Bass N
30. Battaglia A
31. Bauer M
32. Bayés M
33. Bellivier F
34. Bergen SE
35. Berrettini W
36. Betancur C
37. Bettecken T
38. Biederman J
39. Binder EB
40. Black DW
41. Blackwood DHR
42. Bloss CS
43. Boehnke M
44. Boomsma DI
45. Breen G
46. Breuer R
47. Bruggeman R
48. Cormican P
49. Buccola NG
50. Buitelaar JK
51. Bunney WE
52. Buxbaum JD
53. Byerley WF
54. Byrne EM
55. Caesar S
56. Cahn W
57. Cantor RM
58. Casas M
59. Chakravarti A
60. Chambert K
61. Choudhury K
62. Cichon S
63. Cloninger CR
64. Collier DA
65. Cook EH
66. Coon H
67. Cormand B
68. Corvin A
69. Coryell WH
70. Craig DW
71. Craig IW
72. Crosbie J
73. Cuccaro ML
74. Curtis D
75. Czamara D
76. Datta S
77. Dawson G
78. Day R
79. De Geus EJ
80. Degenhardt F
81. Djurovic S
82. Donohoe GJ
83. Doyle AE
84. Duan J
85. Dudbridge F
86. Duketis E
87. Ebstein RP
88. Edenberg HJ
89. Elia J
90. Ennis S
91. Etain B
92. Fanous A
93. Farmer AE
94. Ferrier IN
95. Flickinger M
96. Fombonne E
97. Foroud T
98. Frank J
99. Franke B
100. Fraser C
101. Freedman R
102. Freimer NB
103. Freitag CM
104. Friedl M
105. Frisén L
106. Gallagher L
107. Gejman PV
108. Georgieva L
109. Gershon ES
110. Geschwind DH
111. Giegling I
112. Gill M
113. Gordon SD
114. Gordon-Smith K
115. Green EK
116. Greenwood TA
117. Grice DE
118. Gross M
119. Grozeva D
120. Guan W
121. Gurling H
122. De Haan L
123. Haines JL
124. Hakonarson H
125. Hallmayer J
126. Hamilton SP
127. Hamshere ML
128. Hansen TF
129. Hartmann AM
130. Hautzinger M
131. Heath AC
132. Henders AK
133. Herms S
134. Hickie IB
135. Hipolito M
136. Hoefels S
137. Holmans PA
138. Holsboer F
139. Hoogendijk WJ
140. Hottenga J-J
141. Hultman CM
142. Hus V
143. Ingason A
144. Ising M
145. Jamain S
146. Jones EG
147. Jones I
148. Jones L
149. Tzeng J-Y
150. Kähler AK
151. Kahn RS
152. Kandaswamy R
153. Keller MC
154. Kennedy JL
155. Kenny E
156. Kent L
157. Kim Y
158. Kirov GK
159. Klauck SM
160. Klei L
161. Knowles JA
162. Kohli MA
163. Koller DL
164. Konte B
165. Korszun A
166. Krabbendam L
167. Krasucki R
168. Kuntsi J
169. Kwan P
170. Landén M
171. Långström N
172. Lathrop M
173. Lawrence J
174. Lawson WB
175. Leboyer M
176. Ledbetter DH
177. Lee PH
178. Lencz T
179. Lesch K-P
180. Levinson DF
181. Lewis CM
182. Li J
183. Lichtenstein P
184. Lieberman JA
185. Lin D-Y
186. Linszen DH
187. Liu C
188. Lohoff FW
189. Loo SK
190. Lord C
191. Lowe JK
192. Lucae S
193. MacIntyre DJ
194. Madden PAF
195. Maestrini E
196. Magnusson PKE
197. Mahon PB
198. Maier W
199. Malhotra AK
200. Mane SM
201. Martin CL
202. Martin NG
203. Mattheisen M
204. Matthews K
205. Mattingsdal M
206. McCarroll SA
207. McGhee KA
208. McGough JJ
209. McGrath PJ
210. McGuffin P
211. McInnis MG
212. McIntosh A
213. McKinney R
214. McLean AW
215. McMahon FJ
216. McMahon WM
217. McQuillin A
218. Medeiros H
219. Medland SE
220. Meier S
221. Melle I
222. Meng F
223. Meyer J
224. Middeldorp CM
225. Middleton L
226. Milanova V
227. Miranda A
228. Monaco AP
229. Montgomery GW
230. Moran JL
231. Moreno-De-Luca D
232. Morken G
233. Morris DW
234. Morrow EM
235. Moskvina V
236. Muglia P
237. Mühleisen TW
238. Muir WJ
239. Müller-Myhsok B
240. Murtha M
241. Myers RM
242. Myin-Germeys I
243. Neale MC
244. Nelson SF
245. Nievergelt CM
246. Nikolov I
247. Nimgaonkar V
248. Nolen WA
249. Nöthen MM
250. Nurnberger JI
251. Nwulia EA
252. Nyholt DR
253. O’Dushlaine C
254. Oades RD
255. Olincy A
256. Oliveira G
257. Olsen L
258. Ophoff RA
259. Osby U
260. Owen MJ
261. Palotie A
262. Parr JR
263. Paterson AD
264. Pato CN
265. Pato MT
266. Penninx BW
267. Pergadia ML
268. Pericak-Vance MA
269. Pickard BS
270. Pimm J
271. Piven J
272. Posthuma D
273. Potash JB
274. Poustka F
275. Propping P
276. Puri V
277. Quested DJ
278. Quinn EM
279. Ramos-Quiroga JA
280. Rasmussen HB
281. Raychaudhuri S
282. Rehnström K
283. Reif A
284. Ribasés M
285. Rice JP
286. Rietschel M
287. Roeder K
288. Roeyers H
289. Rossin L
290. Rothenberger A
291. Rouleau G
292. Ruderfer D
293. Rujescu D
294. Sanders AR
295. Sanders SJ
296. Santangelo SL
297. Sergeant JA
298. Schachar R
299. Schalling M
300. Schatzberg AF
301. Scheftner WA
302. Schellenberg GD
303. Scherer SW
304. Schork NJ
305. Schulze TG
306. Schumacher J
307. Schwarz M
308. Scolnick E
309. Scott LJ
310. Shi J
311. Shilling PD
312. Shyn SI
313. Silverman JM
314. Slager SL
315. Smalley SL
316. Smit JH
317. Smith EN
318. Sonuga-Barke EJS
319. St Clair D
320. State M
321. Steffens M
322. Steinhausen H-C
323. Strauss JS
324. Strohmaier J
325. Stroup TS
326. Sutcliffe JS
327. Szatmari P
328. Szelinger S
329. Thirumalai S
330. Thompson RC
331. Todorov AA
332. Tozzi F
333. Treutlein J
334. Uhr M
335. van den Oord EJCG
336. Van Grootheest G
337. Van Os J
338. Vicente AM
339. Vieland VJ
340. Vincent JB
341. Visscher PM
342. Walsh CA
343. Wassink TH
344. Watson SJ
345. Weissman MM
346. Werge T
347. Wienker TF
348. Wijsman EM
349. Willemsen G
350. Williams N
351. Willsey AJ
352. Witt SH
353. Xu W
354. Young AH
355. Yu TW
356. Zammit S
357. Zandi PP
358. Zhang P
359. Zitman FG
360. Zöllner S
361. Devlin B
362. Kelsoe JR
363. Sklar P
364. Daly MJ
365. O’Donovan MC
366. Craddock N
367. Sullivan PF
368. Smoller JW
369. Kendler KS
370. Wray NR
371. Cross-Disorder Group of the Psychiatric Genomics Consortium
372. International Inflammatory Bowel Disease Genetics Consortium (IIBDGC)
(2013) Genetic relationship between five psychiatric disorders estimated from genome-wide SNPs
Nature Genetics 45:984–994.

https://doi.org/10.1038/ng.2711
- PubMed
- Google Scholar
1. Lee PH
(2019) Genomic relationships, novel loci, and pleiotropic mechanisms across eight psychiatric disorders
Cell 179:1469–1482.

https://doi.org/10.1016/j.cell.2019.11.020
- Google Scholar
1. Lek M
2. Karczewski KJ
3. Minikel EV
4. Samocha KE
5. Banks E
6. Fennell T
7. O’Donnell-Luria AH
8. Ware JS
9. Hill AJ
10. Cummings BB
11. Tukiainen T
12. Birnbaum DP
13. Kosmicki JA
14. Duncan LE
15. Estrada K
16. Zhao F
17. Zou J
18. Pierce-Hoffman E
19. Berghout J
20. Cooper DN
21. Deflaux N
22. DePristo M
23. Do R
24. Flannick J
25. Fromer M
26. Gauthier L
27. Goldstein J
28. Gupta N
29. Howrigan D
30. Kiezun A
31. Kurki MI
32. Moonshine AL
33. Natarajan P
34. Orozco L
35. Peloso GM
36. Poplin R
37. Rivas MA
38. Ruano-Rubio V
39. Rose SA
40. Ruderfer DM
41. Shakir K
42. Stenson PD
43. Stevens C
44. Thomas BP
45. Tiao G
46. Tusie-Luna MT
47. Weisburd B
48. Won H-H
49. Yu D
50. Altshuler DM
51. Ardissino D
52. Boehnke M
53. Danesh J
54. Donnelly S
55. Elosua R
56. Florez JC
57. Gabriel SB
58. Getz G
59. Glatt SJ
60. Hultman CM
61. Kathiresan S
62. Laakso M
63. McCarroll S
64. McCarthy MI
65. McGovern D
66. McPherson R
67. Neale BM
68. Palotie A
69. Purcell SM
70. Saleheen D
71. Scharf JM
72. Sklar P
73. Sullivan PF
74. Tuomilehto J
75. Tsuang MT
76. Watkins HC
77. Wilson JG
78. Daly MJ
79. MacArthur DG
80. Exome Aggregation Consortium
(2016) Analysis of protein-coding genetic variation in 60,706 humans
Nature 536:285–291.

https://doi.org/10.1038/nature19057
- PubMed
- Google Scholar
1. Lelieveld SH
2. Reijnders MRF
3. Pfundt R
4. Yntema HG
5. Kamsteeg E-J
6. de Vries P
7. de Vries BBA
8. Willemsen MH
9. Kleefstra T
10. Löhner K
11. Vreeburg M
12. Stevens SJC
13. van der Burgt I
14. Bongers EMHF
15. Stegmann APA
16. Rump P
17. Rinne T
18. Nelen MR
19. Veltman JA
20. Vissers LELM
21. Brunner HG
22. Gilissen C
(2016) Meta-analysis of 2,104 trios provides support for 10 new genes for intellectual disability
Nature Neuroscience 19:1194–1196.

https://doi.org/10.1038/nn.4352
- PubMed
- Google Scholar
1. Li J
2. Cai T
3. Jiang Y
4. Chen H
5. He X
6. Chen C
7. Li X
8. Shao Q
9. Ran X
10. Li Z
11. Xia K
12. Liu C
13. Sun ZS
14. Wu J
(2016) Genes with de novo mutations are shared by four neuropsychiatric disorders discovered from NPdenovo database
Molecular Psychiatry 21:290–297.

https://doi.org/10.1038/mp.2015.40
- PubMed
- Google Scholar
1. Lu Q
2. Li B
3. Ou D
4. Erlendsdottir M
5. Powles RL
6. Jiang T
7. Hu Y
8. Chang D
9. Jin C
10. Dai W
11. He Q
12. Liu Z
13. Mukherjee S
14. Crane PK
15. Zhao H
(2017) A Powerful Approach to Estimating Annotation-Stratified Genetic Covariance via GWAS Summary Statistics
American Journal of Human Genetics 101:939–964.

https://doi.org/10.1016/j.ajhg.2017.11.001
- PubMed
- Google Scholar
1. Lumenta CB
2. Skotarczak U
(1995) Long-term follow-up in 233 patients with congenital hydrocephalus
Child’s Nervous System 11:173–175.

https://doi.org/10.1007/BF00570260
- PubMed
- Google Scholar
1. Munkin MK
2. Trivedi PK
(1999) Simulated maximum likelihood estimation of multivariate mixed‐Poisson regression models, with application
The Econometrics Journal 2:29–48.

https://doi.org/10.1111/1368-423X.00019
- Google Scholar
1. Nguyen HT
2. Bryois J
3. Kim A
4. Dobbyn A
5. Huckins LM
6. Munoz-Manchado AB
7. Ruderfer DM
8. Genovese G
9. Fromer M
10. Xu X
11. Pinto D
12. Linnarsson S
13. Verhage M
14. Smit AB
15. Hjerling-Leffler J
16. Buxbaum JD
17. Hultman C
18. Sklar P
19. Purcell SM
20. Lage K
21. He X
22. Sullivan PF
23. Stahl EA
(2017) Integrated Bayesian analysis of rare exonic variants to identify risk genes for schizophrenia and neurodevelopmental disorders
Genome Medicine 9:114.

https://doi.org/10.1186/s13073-017-0497-y
- PubMed
- Google Scholar
1. Nguyen T-H
2. Dobbyn A
3. Brown RC
4. Riley BP
5. Buxbaum JD
6. Pinto D
7. Purcell SM
8. Sullivan PF
9. He X
10. Stahl EA
(2020) mTADA is a framework for identifying risk genes from de novo mutations in multiple traits
Nature Communications 11:2929.

https://doi.org/10.1038/s41467-020-16487-z
- PubMed
- Google Scholar
Software
1. Nguyen TH
2. Dobbyn A
3. Brown RC
4. Riley BP
5. Buxbaum J
6. Pinto D
7. Purcell SM
8. Sullivan PF
9. He X
10. Eli A
(2021) mTADA is a framework for identifying risk genes from de novo mutations in multiple traits, version 7630c4b
GitHub.

https://github.com/hoangtn/mTADA
1. Ning Z
2. Pawitan Y
3. Shen X
(2020) High-definition likelihood inference of genetic correlations across human complex traits
Nature Genetics 52:859–864.

https://doi.org/10.1038/s41588-020-0653-y
- PubMed
- Google Scholar
1. O’Roak BJ
2. Vives L
3. Girirajan S
4. Karakoc E
5. Krumm N
6. Coe BP
7. Levy R
8. Ko A
9. Lee C
10. Smith JD
11. Turner EH
12. Stanaway IB
13. Vernot B
14. Malig M
15. Baker C
16. Reilly B
17. Akey JM
18. Borenstein E
19. Rieder MJ
20. Nickerson DA
21. Bernier R
22. Shendure J
23. Eichler EE
(2012) Sporadic autism exomes reveal a highly interconnected protein network of de novo mutations
Nature 485:246–250.

https://doi.org/10.1038/nature10989
- PubMed
- Google Scholar
1. Pickrell JK
2. Berisa T
3. Liu JZ
4. Ségurel L
5. Tung JY
6. Hinds DA
(2016) Detection and interpretation of shared genetic influences on 42 human traits
Nature Genetics 48:709–717.

https://doi.org/10.1038/ng.3570
- PubMed
- Google Scholar
1. Rees E
2. Creeth HDJ
3. Hwu H-G
4. Chen WJ
5. Tsuang M
6. Glatt SJ
7. Rey R
8. Kirov G
9. Walters JTR
10. Holmans P
11. Owen MJ
12. O’Donovan MC
(2021) Schizophrenia, autism spectrum disorders and developmental disorders share specific disruptive coding mutations
Nature Communications 12:5353.

https://doi.org/10.1038/s41467-021-25532-4
- PubMed
- Google Scholar
(2018) Intellectual disability in cerebral palsy: a population-based retrospective study
Developmental Medicine and Child Neurology 60:687–694.

https://doi.org/10.1111/dmcn.13773
- PubMed
- Google Scholar
1. Samocha KE
2. Robinson EB
3. Sanders SJ
4. Stevens C
5. Sabo A
6. McGrath LM
7. Kosmicki JA
8. Rehnström K
9. Mallick S
10. Kirby A
11. Wall DP
12. MacArthur DG
13. Gabriel SB
14. DePristo M
15. Purcell SM
16. Palotie A
17. Boerwinkle E
18. Buxbaum JD
19. Cook EH Jr
20. Gibbs RA
21. Schellenberg GD
22. Sutcliffe JS
23. Devlin B
24. Roeder K
25. Neale BM
26. Daly MJ
(2014) A framework for the interpretation of de novo mutation in human disease
Nature Genetics 46:944–950.

https://doi.org/10.1038/ng.3050
- PubMed
- Google Scholar
1. Satterstrom FK
2. Kosmicki JA
3. Wang J
4. Breen MS
5. De Rubeis S
6. An J-Y
7. Peng M
8. Collins R
9. Grove J
10. Klei L
11. Stevens C
12. Reichert J
13. Mulhern MS
14. Artomov M
15. Gerges S
16. Sheppard B
17. Xu X
18. Bhaduri A
19. Norman U
20. Brand H
21. Schwartz G
22. Nguyen R
23. Guerrero EE
24. Dias C
25. Autism Sequencing Consortium
26. iPSYCH-Broad Consortium
27. Betancur C
28. Cook EH
29. Gallagher L
30. Gill M
31. Sutcliffe JS
32. Thurm A
33. Zwick ME
34. Børglum AD
35. State MW
36. Cicek AE
37. Talkowski ME
38. Cutler DJ
39. Devlin B
40. Sanders SJ
41. Roeder K
42. Daly MJ
43. Buxbaum JD
(2020) Large-Scale Exome Sequencing Study Implicates Both Developmental and Functional Changes in the Neurobiology of Autism
Cell 180:568–584.

https://doi.org/10.1016/j.cell.2019.12.036
- PubMed
- Google Scholar
Software
1. Schorsch E
(2020) LDSC (LD SCore) v1.0.1, version aa33296
GitHub.

https://github.com/bulik/ldsc
(2017) Local Genetic Correlation Gives Insights into the Shared Genetic Architecture of Complex Traits
American Journal of Human Genetics 101:737–751.

https://doi.org/10.1016/j.ajhg.2017.09.022
- PubMed
- Google Scholar
(2018) Multi-trait analysis of genome-wide association summary statistics using MTAG
Nature Genetics 50:229–237.

https://doi.org/10.1038/s41588-017-0009-4
- PubMed
- Google Scholar
1. Turner TN
2. Yi Q
3. Krumm N
4. Huddleston J
5. Hoekzema K
6. F Stessman HA
7. Doebley A-L
8. Bernier RA
9. Nickerson DA
10. Eichler EE
(2017) denovo-db: A compendium of human de novo variants
Nucleic Acids Research 45:D804–D811.

https://doi.org/10.1093/nar/gkw865
- PubMed
- Google Scholar
1. Veltman JA
2. Brunner HG
(2012) De novo mutations in human genetic disease
Nature Reviews. Genetics 13:565–575.

https://doi.org/10.1038/nrg3241
- PubMed
- Google Scholar
1. Wang K
2. Li M
3. Hakonarson H
(2010) ANNOVAR: functional annotation of genetic variants from high-throughput sequencing data
Nucleic Acids Research 38:e164.

https://doi.org/10.1093/nar/gkq603
- PubMed
- Google Scholar
1. Wang Q
2. Yang C
3. Gelernter J
4. Zhao H
(2015) Pervasive pleiotropy between psychiatric disorders and immune disorders revealed by integrative analysis of multiple GWAS
Human Genetics 134:1195–1209.

https://doi.org/10.1007/s00439-015-1596-8
- PubMed
- Google Scholar
(2017) Functional mapping and annotation of genetic associations with FUMA
Nature Communications 8:1–11.

https://doi.org/10.1038/s41467-017-01261-5
- PubMed
- Google Scholar
1. Wei Q
2. Zhan X
3. Zhong X
4. Liu Y
5. Han Y
6. Chen W
7. Li B
(2015) A Bayesian framework for de novo mutation calling in parents-offspring trios
Bioinformatics (Oxford, England) 31:1375–1381.

https://doi.org/10.1093/bioinformatics/btu839
- PubMed
- Google Scholar
1. Werling DM
2. Pochareddy S
3. Choi J
4. An JY
5. Sheppard B
6. Peng M
7. Li Z
8. Dastmalchi C
9. Santpere G
10. Sousa AMM
11. Tebbenkamp ATN
12. Kaur N
13. Gulden FO
14. Breen MS
15. Liang L
16. Gilson MC
17. Zhao X
18. Dong S
19. Klei L
20. Cicek AE
21. Buxbaum JD
22. Adle-Biassette H
23. Thomas JL
24. Aldinger KA
25. O’Day DR
26. Glass IA
27. Zaitlen NA
28. Talkowski ME
29. Roeder K
30. State MW
31. Devlin B
32. Sanders SJ
33. Sestan N
(2020) Whole-Genome and RNA Sequencing Reveal Variation and Transcriptomic Coordination in the Developing Human Prefrontal Cortex
Cell Reports 31:e107489.

https://doi.org/10.1016/j.celrep.2020.03.053
- PubMed
- Google Scholar
(2017) De Novo Coding Variants Are Strongly Associated with Tourette Disorder
Neuron 94:486–499.

https://doi.org/10.1016/j.neuron.2017.04.024
- PubMed
- Google Scholar
1. Willsey AJ
2. Morris MT
3. Wang S
4. Willsey HR
5. Sun N
6. Teerikorpi N
7. Baum TB
8. Cagney G
9. Bender KJ
10. Desai TA
11. Srivastava D
12. Davis GW
13. Doudna J
14. Chang E
15. Sohal V
16. Lowenstein DH
17. Li H
18. Agard D
19. Keiser MJ
20. Shoichet B
21. von Zastrow M
22. Mucke L
23. Finkbeiner S
24. Gan L
25. Sestan N
26. Ward ME
27. Huttenhain R
28. Nowakowski TJ
29. Bellen HJ
30. Frank LM
31. Khokha MK
32. Lifton RP
33. Kampmann M
34. Ideker T
35. State MW
36. Krogan NJ
(2018) The Psychiatric Cell Map Initiative: A Convergent Systems Biological Approach to Illuminating Key Molecular Pathways in Neuropsychiatric Disorders
Cell 174:505–520.

https://doi.org/10.1016/j.cell.2018.06.016
- PubMed
- Google Scholar
1. Zaidi S
2. Choi M
3. Wakimoto H
4. Ma L
5. Jiang J
6. Overton JD
7. Romano-Adesman A
8. Bjornson RD
9. Breitbart RE
10. Brown KK
11. Carriero NJ
12. Cheung YH
13. Deanfield J
14. DePalma S
15. Fakhro KA
16. Glessner J
17. Hakonarson H
18. Italia MJ
19. Kaltman JR
20. Kaski J
21. Kim R
22. Kline JK
23. Lee T
24. Leipzig J
25. Lopez A
26. Mane SM
27. Mitchell LE
28. Newburger JW
29. Parfenov M
30. Pe’er I
31. Porter G
32. Roberts AE
33. Sachidanandam R
34. Sanders SJ
35. Seiden HS
36. State MW
37. Subramanian S
38. Tikhonova IR
39. Wang W
40. Warburton D
41. White PS
42. Williams IA
43. Zhao H
44. Seidman JG
45. Brueckner M
46. Chung WK
47. Gelb BD
48. Goldmuntz E
49. Seidman CE
50. Lifton RP
(2013) De novo mutations in histone-modifying genes in congenital heart disease
Nature 498:220–223.

https://doi.org/10.1038/nature12141
- PubMed
- Google Scholar
1. Zaidi S
2. Brueckner M
(2017) Genetics and Genomics of Congenital Heart Disease
Circulation Research 120:923–940.

https://doi.org/10.1161/CIRCRESAHA.116.309140
- PubMed
- Google Scholar
1. Zhang Y
2. Cheng Y
3. Jiang W
4. Ye Y
5. Lu Q
6. Zhao H
(2021a) Comparison of methods for estimating genetic correlation between complex traits using GWAS summary statistics
Briefings in Bioinformatics 22:bbaa442.

https://doi.org/10.1093/bib/bbaa442
- Google Scholar
1. Zhang Y
2. Lu Q
3. Ye Y
4. Huang K
5. Liu W
6. Wu Y
7. Zhong X
8. Li B
9. Yu Z
10. Travers BG
11. Werling DM
12. Li JJ
13. Zhao H
(2021b) SUPERGNOVA: local genetic correlation analysis reveals heterogeneous etiologic sharing of complex traits
Genome Biology 22:1–30.

https://doi.org/10.1186/s13059-021-02478-w
- PubMed
- Google Scholar

Article and author information

Author details

Hanmin Guo
1. Center for Statistical Science, Tsinghua University, Beijing, China
2. Department of Industrial Engineering, Tsinghua University, Beijing, China
Contribution
Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing - original draft, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-9022-5307
Lin Hou
1. Center for Statistical Science, Tsinghua University, Beijing, China
2. Department of Industrial Engineering, Tsinghua University, Beijing, China
3. MOE Key Laboratory of Bioinformatics, School of Life Sciences, Tsinghua University, Beijing, China
Contribution
Conceptualization, Methodology, Project administration, Supervision, Writing - original draft, Writing - review and editing

Competing interests
No competing interests declared
Yu Shi

Yale School of Management, Yale University, New Haven, United States

Contribution
Formal analysis

Competing interests
No competing interests declared
Sheng Chih Jin

Department of Genetics, Washington University in St. Louis, St. Louis, United States

Contribution
Data curation, Writing - review and editing

Competing interests
No competing interests declared
Xue Zeng
1. Department of Genetics, Yale University, New Haven, United States
2. Laboratory of Human Genetics and Genomics, Rockefeller University, New York, United States
Contribution
Data curation

Competing interests
No competing interests declared
Boyang Li

Department of Biostatistics, Yale School of Public Health, New Haven, United States

Contribution
Data curation

Competing interests
No competing interests declared
Richard P Lifton
1. Department of Genetics, Yale University, New Haven, United States
2. Laboratory of Human Genetics and Genomics, Rockefeller University, New York, United States
Contribution
Validation

Competing interests
No competing interests declared
Martina Brueckner
1. Department of Genetics, Yale University, New Haven, United States
2. Department of Pediatrics, Yale University, New Haven, United States
Contribution
Validation

Competing interests
No competing interests declared
Hongyu Zhao
1. Department of Genetics, Yale University, New Haven, United States
2. Department of Biostatistics, Yale School of Public Health, New Haven, United States
3. Program of Computational Biology and Bioinformatics, Yale University, New Haven, United States
Contribution
Methodology, Validation, Writing - review and editing

For correspondence
Hongyu.Zhao@yale.edu

Competing interests
No competing interests declared
Qiongshi Lu

Department of Biostatistics and Medical Informatics, University of Wisconsin-Madison, Madison, United States

Contribution
Conceptualization, Methodology, Project administration, Supervision, Writing - original draft, Writing - review and editing

For correspondence
qlu@biostat.wisc.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-4514-0969

Funding

National Science Foundation of China (No. 12071243)

Lin Hou

Shanghai Municipal Science and Technology Major Project (No. 2017SHZDZX01)

Lin Hou

Wisconsin Alumni Research Foundation

Qiongshi Lu

Waisman Center pilot grant program at University of Wisconsin-Madison

Qiongshi Lu

National Institutes of Health (No. R03HD100883 and R01GM134005)

Hongyu Zhao

National Science Foundation (DMS 1902903)

Hongyu Zhao

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

LH acknowledges research support from the National Science Foundation of China (Grant No. 12071243) and Shanghai Municipal Science and Technology Major Project (Grant No. 2017SHZDZX01). QL acknowledges research support from the University of Wisconsin-Madison Office of the Chancellor and the Vice Chancellor for Research and Graduate Education with funding from the Wisconsin Alumni Research Foundation and the Waisman Center pilot grant program at University of Wisconsin-Madison. HZ acknowledges research support from the National Institutes of Health (Grant No. R03HD100883 and R01GM134005) and the National Science Foundation (DMS 1902903).

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.