Neural assemblies uncovered by generative modeling explain whole-brain activity statistics and reflect structural connectivity
- Computational Neuroscience Lab, Department of Neurophysiology, Donders Center for Neuroscience, Radboud University, Netherlands
- Sorbonne Université, CNRS, Institut de Biologie Paris-Seine (IBPS), Laboratoire Jean Perrin (LJP), France
- Department of Physiology, Anatomy and Genetics, University of Oxford, United Kingdom
- Blavatnik School of Computer Science, Tel Aviv University, Israel
- Department Genes – Circuits – Behavior, Max Planck Institute for Biological Intelligence, Germany
- Allen Institute for Brain Science, United States
Abstract
Patterns of endogenous activity in the brain reflect a stochastic exploration of the neuronal state space that is constrained by the underlying assembly organization of neurons. Yet, it remains to be shown that this interplay between neurons and their assembly dynamics indeed suffices to generate whole-brain data statistics. Here, we recorded the activity from ∼40,000 neurons simultaneously in zebrafish larvae, and show that a data-driven generative model of neuron-assembly interactions can accurately reproduce the mean activity and pairwise correlation statistics of their spontaneous activity. This model, the compositional Restricted Boltzmann Machine (cRBM), unveils ∼200 neural assemblies, which compose neurophysiological circuits and whose various combinations form successive brain states. We then performed in silico perturbation experiments to determine the interregional functional connectivity, which is conserved across individual animals and correlates well with structural connectivity. Our results showcase how cRBMs can capture the coarse-grained organization of the zebrafish brain. Notably, this generative model can readily be deployed to parse neural data obtained by other large-scale recording techniques.
Editor's evaluation
Large scale recordings, sometimes involving 10s of thousands of neurons, are becoming increasingly common. Making sense of these recordings, however, is not easy. This paper introduces a new method, the compositional Restricted Boltzmann Machine, that overcomes this problem -- it can find structure in data, including both "cell assemblies" and structural connectivity, without inordinate computing resources (data from 40,000 neurons recorded from zebrafish can be analyzed in less than a day). This is a valuable contribution, both to those interested in data analysis, and to those interested in zebrafish.
https://doi.org/10.7554/eLife.83139.sa0Introduction
The brain is a highly connected network, organized across multiple scales, from local circuits involving just a few neurons to extended networks spanning multiple brain regions (White et al., 1986; Song et al., 2005; Kunst et al., 2019). Concurrent with this spatial organization, brain activity exhibits correlated firing among large groups of neurons, often referred to as neural assemblies (Harris, 2005). This assembly organization of brain dynamics has been observed in, for example, auditory cortex (Bathellier et al., 2012), motor cortex (Narayanan et al., 2005), prefrontal cortex (Tavoni et al., 2017), hippocampus (Lin et al., 2005), retina (Shlens et al., 2009), and zebrafish optic tectum (Romano et al., 2015; Mölter et al., 2018; Diana et al., 2019; Triplett et al., 2020). These neural assemblies are thought to form elementary computational units and subserve essential cognitive functions such as short-term memory, sensorimotor computation or decision-making (Hebb, 1949; Gerstein et al., 1989; Harris, 2005; Buzsáki, 2010; Harris, 2012; Palm et al., 2014; Eichenbaum, 2018). Despite the prevalence of these assemblies across the nervous system and their role in neural computation, it remains an open challenge to extract the assembly organization of a full brain and to show that the assembly activity state, derived from that of the neurons, is sufficient to account for the collective neural dynamics.
The need to address this challenge is catalyzed by technological advances in light-sheet microscopy, enabling the simultaneous recording of the majority of neurons in the zebrafish brain at single-cell resolution in vivo (Panier et al., 2013; Ahrens et al., 2013; Wolf et al., 2015; Wolf et al., 2017; Migault et al., 2018; Vanwalleghem et al., 2018). This neural recording technique opens up new avenues for constructing near-complete models of neural activity, and in particular its assembly organization. Recent attempts have been made to identify assemblies using either clustering (Panier et al., 2013; Triplett et al., 2018; Chen et al., 2018; Mölter et al., 2018; Bartoszek et al., 2021), dimensionality reduction approaches (Lopes-dos-Santos et al., 2013; Romano et al., 2015; Mu et al., 2019) or latent variable models (Diana et al., 2019; Triplett et al., 2020), albeit often limited to single brain regions. However, these methods do not explicitly assess to what extent the inferred assemblies could give rise to the observed neural data statistics, which is a crucial property of physiologically meaningful assemblies (Harris, 2005). Here, we address this challenge by developing a generative model of neural activity that is explicitly constrained by the assembly organization, thereby quantifying if assemblies indeed suffice to produce the observed neural data statistics.
Specifically, we formalize neural assemblies using a bipartite network of two connected layers representing the neuronal and the assembly activity, respectively. Together with the maximum entropy principle (Jaynes, 1957; Bialek, 2012), this architecture defines the Restrictive Boltzmann Machine (RBM) model (Hinton and Salakhutdinov, 2006). Here, we use an extension to the classical RBM definition termed compositional RBM (cRBM) that we have recently introduced (Tubiana and Monasson, 2017; Tubiana et al., 2019a) and which brings multiple advances to assembly-based network modeling: (1) The maximum entropy principle ensures that neural assemblies are inferred solely from the data statistics. (2) The generative nature of the model, through alternate data sampling of the neuronal and assembly layers, can be leveraged to evaluate its capacity to replicate the empirical data statistics, such as the pairwise co-activation probabilities of all neuron pairs. (3) The cRBM steers the assembly organization to the so-called compositional phase where a small number of assemblies are active at any point in time, making the resulting model highly interpretable as we have shown previously for protein sequence analysis (Tubiana et al., 2019b).
Here, we have successfully trained cRBMs to brain-scale, neuron-level recordings of spontaneous activity in larval zebrafish containing 41,000 neurons on average (Panier et al., 2013; Wolf et al., 2017; Migault et al., 2018). This represents an increase of ∼2 orders of magnitude in number of neurons with respect to previously reported RBM implementations (Köster et al., 2014; Gardella et al et al., 2017; Volpi et al., 2020), attained through significant algorithmic and computational enhancements. We found that all cells could be grouped into 100–200 partially overlapping assemblies, which are anatomically localized and together span the entire brain, and accurately replicate the first and second order statistics of the neural activity. These assemblies were found to carry more predictive power than a fully connected model which has orders of magnitude more parameters, validating that assemblies underpin collective neural dynamics. Further, the probabilistic nature of our model allowed us to compute a functional connectivity matrix by quantifying the effect of activity perturbations in silico. This assembly-based functional connectivity is well-conserved across individual fish and consistent with anatomical connectivity at the mesoscale (Kunst et al., 2019).
In summary, we present an assembly decomposition spanning the zebrafish brain, which accurately accounts for its activity statistics. Our cRBM model provides a widely applicable tool to the community to construct low-dimensional data representations that are defined by the statistics of the data, in particular for very high-dimensional systems. Its generative capability further allows to produce new (synthetic) activity patterns that are amenable to direct in silico perturbation and ablation studies.
Results
Compositional RBMs construct Hidden Units by grouping neurons into assemblies
Spontaneous neural activity was recorded from eight zebrafish larvae aged 5–7 days post fertilization expressing the GCaMP6s or GCaMP6f calcium reporters using light-sheet microscopy (Panier et al., 2013; Wolf et al., 2017; Migault et al., 2018). Each data set contained the activity of a large fraction of the neurons in the brain (; mean ± standard deviation), which, after cell segmentation, were registered onto the ZBrain atlas (Randlett et al., 2015) and mapzebrain atlas (Kunst et al., 2019). Individual neuronal fluorescence traces were deconvolved to binarized spike trains using blind sparse deconvolution (Tubiana et al., 2020). This data acquisition process is depicted in Figure 1A.
Figure 1
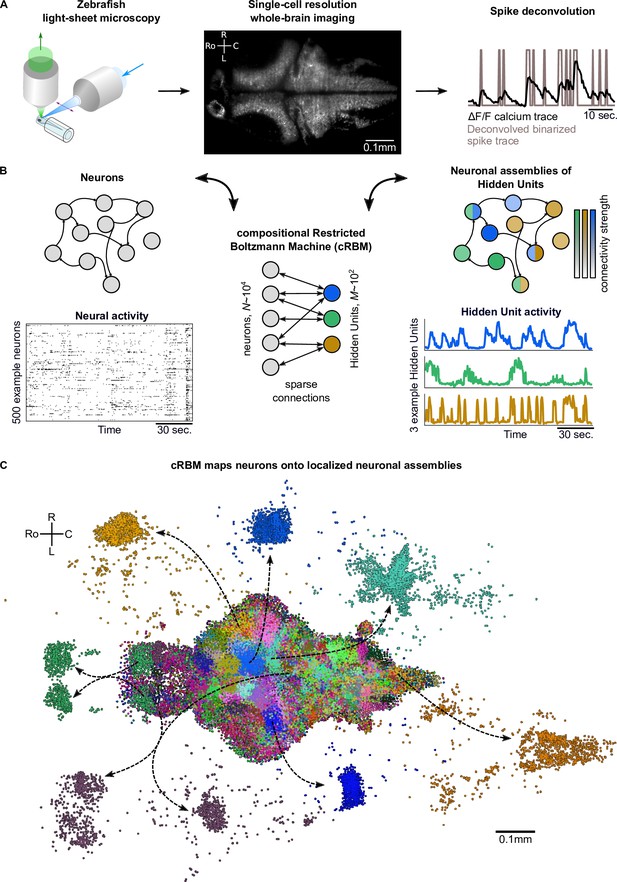
cRBMs construct Hidden Units by grouping neurons into assemblies.
(A) The neural activity of zebrafish larvae was imaged using light-sheet microscopy (left), which resulted in brain-scale, single-cell resolution data sets (middle, microscopy image of a single plane shown for fish #1). Calcium activity was deconvolved to binarized spike traces for each segmented cell (right, example neuron). (B) cRBM sparsely connects neurons (left) to Hidden Units (HUs, right). The neurons that connect to a given HU (and thus belong to the associated assembly), are depicted by the corresponding color labeling (right panel). Data sets typically consist of neurons and HUs. The activity of 500 randomly chosen example neurons (raster plot, left) and HUs 99, 26, 115 (activity traces, right) of the same time excerpt is shown. HU activity is continuous and is determined by transforming the neural activity of its assembly. (C) The neural assemblies of an example data set (fish #3) are shown by coloring each neuron according to its strongest-connecting HU. 7 assemblies are highlighted (starting rostrally at the green forebrain assembly, going clockwise: HU 177, 187, 7, 156, 124, 64, 178), by showing their neurons with a connection . See Figure 3 for more anatomical details of assemblies. R: Right, L: Left, Ro: Rostral, C: Caudal.
We trained compositional Restricted Boltzmann Machine (cRBM) models to capture the activity statistics of these neural recordings. cRBMs are maximum entropy models, that is, the maximally unconstrained solution that fits model-specific data statistics (Hinton and Salakhutdinov, 2006; Tubiana and Monasson, 2017; Gardella et al., 2019), and critically extend the classical RBM formulation. Its architecture consists of a bipartite graph where the high-dimensional layer of neurons (named ‘visible units’ in RBM terminology) is connected to the low-dimensional layer of latent components, termed Hidden Units (HUs) . Their interaction is characterized by a weight matrix that is regularized to be sparse. The collection of neurons that have non-zero interactions with a particular HU, noted (i.e. with ), define its corresponding neural assembly μ (Figure 1B). This weight matrix, together with the neuron weight vector and HU potential , defines the transformation from the binarized neural activity to the continuous HU activity (Figure 1B). Figure 1C shows all recorded neurons of a zebrafish brain, color-labeled according to their strongest-connecting HU, illustrating that cRBM-inferred assemblies (hereafter, neural assemblies for conciseness) are typically densely localized in space and together span the entire brain.
Beyond its architecture (Figure 2A), the model is defined by the probability function of any data configuration (see Materials and methods ‘Restricted Boltzmann Machines’ and ‘Compositional Restricted Boltzmann Machine’ for details):
(1)
where is the partition function that normalizes Equation 1 and is the following energy function:
(2)
HU activity h is obtained by sampling from the conditional probability function :
(3)
Conversely, neural activity is obtained from HU activity through:
(4)
Equations 3 and 4 mathematically reflect the dual relationship between neural and assembly states: the Hidden Units drive ‘visible’ neural activity , expressed as , while the stochastic assembly activity itself is defined as a function of the activity of the neurons: . Importantly, the model does not include direct connections between neurons, hence neural correlations can arise solely from shared assemblies. Moreover, this bipartite architecture ensures that the conditional distributions factorize, leading to a sampling procedure where all neurons or all HUs can be sampled in parallel. The cRBM leverages this property to efficiently generate new data by Monte Carlo sampling alternately from and (Figure 2B).
Figure 2 with 7 supplements see all
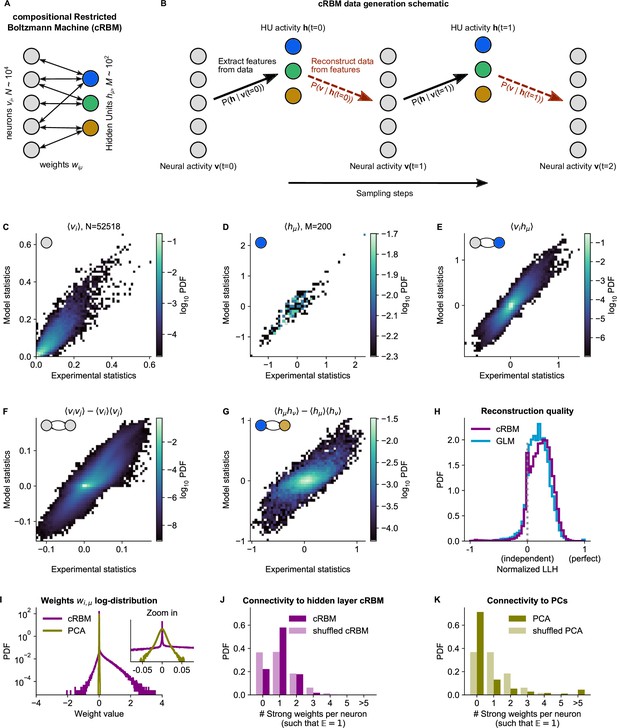
cRBM is optimized to accurately replicate data statistics.
(A) Schematic of the cRBM architecture, with neurons on the left, HUs on the right, connected by weights . (B) Schematic depicting how cRBMs generate new data. The HU activity is sampled from the visible unit (i.e. neuron) configuration , after which the new visible unit configuration is sampled and so forth. (C) cRBM-predicted and experimental mean neural activity were highly correlated (Pearson correlation , ) and had low error (, normalized Root Mean Square Error, see Materials and methods - ‘Calculating the normalized Root Mean Square Error’ ). Data displayed as 2D probability density function (PDF), scaled logarithmically (base 10). (D) cRBM-predicted and experimental mean Hidden Unit (HU) activity also correlated very strongly (, ) and had low (other details as in C) (E) cRBM-predicted and experimental average pairwise neuron-HU interactions correlated strongly (, ) and had a low error (). (F) cRBM-predicted and experimental average pairwise neuron-neuron interactions correlated well (, ) and had a low error (, where the negative nRMSE value means that cRBM-predictions match the test data slightly better than the train data). Pairwise interactions were corrected for naive correlations due to their mean activity by subtracting . (G) cRBM-predicted and experimental average pairwise HU-HU interactions correlated strongly (, ) and had a low error (). (H) The low-dimensional cRBM bottleneck reconstructs most neurons above chance level (purple), quantified by the normalized log-likelihood (nLLH) between neural test data vi and the reconstruction after being transformed to HU activity (see Materials and methods - ‘Reconstruction quality’). Median normalized = 0.24. Reconstruction quality was also determined for a fully connected Generalized Linear Model (GLM) that attempted to reconstruct the activity of a neuron vi using all other neurons (see Materials and methods - ‘Generalized Linear Model’). The distribution of 5000 randomly chosen neurons is shown (blue), with median . The cRBM distribution is stochastically greater than the GLM distribution (one-sided Mann Whitney U test, ). (I) cRBM (purple) had a sparse weight distribution, but exhibited a greater proportion of large weights than PCA (yellow), both for positive and negative weights, displayed in log-probability. (J) Distribution of above-threshold absolute weights per neuron vi (dark purple), indicating that more neurons strongly connect to the cRBM hidden layer than expected by shuffling the weight matrix of the same cRBM (light purple). The threshold was set such that the expected number of above-threshold weights per neuron . (K) Corresponding distribution as in (J) for PCA (dark yellow) and its shuffled weight matrix (light yellow), indicating a predominance of small weights in PCA for most neurons vi. All panels of this figure show the data statistics of the cRBM with parameters and (best choice after cross-validation, see Figure 2—figure supplement 1) of example fish #3, comparing the experimental test data test and model-generated data after cRBM training converged.
The cRBM differs from the classical RBM formulation (Hinton and Salakhutdinov, 2006) through the introduction of double Rectified Linear Unit (dReLU) potentials , weight sparsity regularization and normalized HU activity (further detailed in Methods). We have previously demonstrated in theory and application (Tubiana and Monasson, 2017; Tubiana et al., 2019a; Tubiana et al., 2019b) that this new formulation steers the model into the so-called compositional phase, which makes the latent representation highly interpretable. This phase occurs when a limited number of HUs co-activate such that where is the total number of HUs. Thus, each visible configuration is mapped to a specific combination of activated HUs. This contrasts with the ferromagnetic phase () where each HU encodes one specific activity pattern, thus severely limiting the possible number of encoded patterns, or the spin-glass phase () where all HUs activate simultaneously, yielding a very complex assembly patchwork (Tubiana and Monasson, 2017). Therefore, the compositional phase can provide the right level of granularity for a meaningful interpretation of the cRBM neural assemblies by decomposing the overall activity as a time-dependent co-activation of different assemblies of interpretable size and extent.
Trained cRBMs accurately replicate data statistics
cRBM models are trained to maximize the log-likelihood of the zebrafish data recordings, which is achieved by matching the model-generated statistics , and (the mean neuronal activity, mean HU activity and their correlations, respectively) to the empirical data statistics (Equation 14). In order to optimize the two free parameters of the cRBM model – the sparsity regularization parameter and the total number of HUs – we assessed the cRBM performance for a grid of -values for one data set (fish #3). This analysis yielded an optimum for and (Figure 2—figure supplement 1). These values were subsequently used for all recordings, where was scaled with the number of neurons .
We trained cRBMs on 70% of the recording length, and compared the statistics of model-generated data to the withheld test data set (the remaining 30% of recording, see Materials and methods ‘Train / test data split’ and ‘Assessment of data statistics’ for details). After convergence, the cRBM generated data that replicated the training statistics accurately, with normalized Root Mean Square Error (nRMSE) values of , and (Figure 2C-E). Here, nRMSE is normalized such that 1 corresponds to shuffled data statistics and 0 corresponds to the best possible RMSE, i.e., between train and test data.
We further evaluated cRBM performance to assess its ability to capture data statistics that the cRBM was not explicitly trained to replicate: the pairwise correlations between neurons and the pairwise correlations between HUs . We found that these statistics were also accurately replicated by model-generated data, with (meaning that the model slightly outperformed the train-test data difference) and (Figure 2F, G). The fact that cRBM also accurately replicated neural correlations (Figure 2F) is of particular relevance, since this indicates that (1) the assumption that neural correlations can be explained by their shared assemblies is justified and (2) cRBMs may provide an efficient mean to model neural interactions of such large systems () where directly modeling all interactions would be computationally infeasible or not sufficiently constrained by the available data.
Next, we assessed the reconstruction quality after neural data was compressed by the cRBM low-dimensional bottleneck. The reconstruction quality is defined as the log-likelihood of reconstructed neural data (i.e. that is first transformed to the low-dimensional , and then back again to the high-dimensional , see Materials and methods - ‘Reconstruction quality’). This is important to prevent trivial, undesired solutions like which would directly lead to (potentially because of strong sparsity regularization). Figure 2H shows the distribution of cRBM reconstruction quality of all neurons (in purple), quantified by the normalized log-likelihood (nLLH) such that 0 corresponds to an independent model and 1 corresponds to perfect reconstruction (non-normalized ). For comparison, we also reconstructed the neural activity using a fully connected Generalized Linear Model (GLM, see Materials and methods - ‘Generalized Linear Model’ and Figure 2, Figure 2—figure supplement 2H, blue). The cRBM nLLH distribution is significantly greater than the GLM nLLH distribution (one-sided Mann Whitney U test, ), with medians and . Hence, projecting the neural data onto the low-dimensional representation of the HUs does not compromise the ability to explain the neural activity. In fact, reconstruction quality of the cRBM slightly outperforms the GLM, possibly due to the suppression of noise in the cRBM estimate. The optimal choice of free parameters was selected by cross-validating the median of the cRBM reconstruction quality, together with the normalized RMSE of the five previously described statistics (Figure 2—figure supplement 1).
Lastly, we confirmed that the cRBM indeed resides in the compositional phase, characterized by where is the number of HUs active at time point (Figure 2—figure supplement 3A). This property is a consequence of the sparse weight matrix , indicated by its heavy-tail log-distribution (Figure 2I, purple). The compositional phase is the norm for the presently estimated cRBMs, evidenced by the distribution of median values for all recordings (average is 0.26, see Figure 2—figure supplement 3B). Importantly, the sparse weight matrix does not automatically imply that only a small subset of neurons is connected to the cRBM hidden layer. We validated this by observing that more neurons strongly connect to the hidden layer than expected by shuffling the weight matrix (Figure 2J). Further, we quantified the number of assemblies that each neuron was embedded in, which showed that increasing the embedding threshold did not notably affect the fraction of neurons embedded in at least 1 assembly (93–94%, see Figure 2—figure supplement 4). To assess the influence of and on the inferred assemblies, we computed, for all cRBM models trained during the optimization of and , the distribution of assembly sizes (Figure 2—figure supplement 5A-F). We found that and controlled the distribution of assembly sizes in a consistent manner: assembly size was a gradually decreasing function of both and (two-way ANOVA, both ). Furthermore, for and values close to the optimal parameter-setting (, ), the changes in assembly size were very small and gradual. This showcases the robustness of the cRBM to slight changes in parameter choice.
Sparsity facilitated that each assembly only connects to a handful of anatomical regions, as we quantified by calculating the overlap between cRBM assemblies and anatomical regions (Figure 2—figure supplement 6). We found that cRBM assemblies connect to a median of three regions (interquartile range: 2–6 regions). Importantly, the cRBM has no information about the locations of neurons during training, so the localization to a limited set of anatomical areas that we observe is extracted from the neural co-activation properties alone. For comparison, Principal Component Analysis (PCA), a commonly used non-sparse dimensionality reduction method that shares the cRBM architecture, naturally converged to a non-sparse weight matrix (Figure 2I, yellow), with fewer connected neurons than expected by shuffling its weight matrix (Figure 2K). This led to unspecific assemblies that are difficult to interpret by anatomy (Figure 2—figure supplement 6). As a result, sparsity, a cRBM property shared with some other dimensionality reduction techniques, is crucial to interpret the assemblies by anatomy as we demonstrate in the next section.
We next asked whether sparsity alone was sufficient for a generative model to accurately recapitulate the neural recording statistics. To address this question, we trained sparse linear Variational Autoencoders (VAEs) using the same parameter-optimization protocol (Figure 2—figure supplement 7A). Like cRBMs, linear VAEs are generative models that learn a latent representation of a dataset (Tubiana et al., 2019a). We observed that VAEs were not able to replicate the second-order statistics, and therefore were not able to reconstruct neural activity from latent representation (Figure 2—figure supplement 7B-D), even though they also obtained sparse representations (Figure 2—figure supplement 7E, F). Other clustering or dimensionality reduction methods, such as k-means, PCA and non-negative matrix factorization, have been used previously to cluster neurons in the zebrafish brain (Chen et al., 2018; Mu et al., 2019; Marques et al., 2020). However, because these methods cannot generate artificial neural data using their inferred assemblies, their quality cannot be quantitatively assessed as we have done for the cRBM (but see Tubiana et al., 2019a for other comparisons).
cRBM assemblies compose functional circuits and anatomical structures
Above, we have shown that cRBMs converge to sparse weight matrix solutions. This property enables us to visualize the cRBM-inferred neural assemblies as the collection of significantly connected neurons to an HU. Neurons from a given neural assembly display concerted dynamics, and so one may expect their spatial organization to reflect the neuroanatomy and functional organization of the brain. We here highlight a selection of salient examples of neural assemblies, illustrating that assemblies match well with anatomical structures and functional circuits, while the complete set of neural assemblies is presented in Video 1. In particular, we identified assemblies that together compose a neural circuit, are neurotransmitter-specific, encompass a long-range pathway, or can be identified by anatomy. The examples shown here are from a single fish (#3), but results from other fish were comparable.
Video 1
All neural assemblies of one example fish All 200 inferred assemblies of the example fish #2 of Figure 3 are shown in sequence.
Top: neural assembly. Bottom: HU activity of test data.
First, we identified six assemblies that together span the hindbrain circuit that drives eye and tail movements (Dunn et al., 2016; Wolf et al., 2017; Chen et al., 2018). We find two neural assemblies in rhombomere 2 which align with the anterior rhombencephalic turning region (ARTR, Ahrens et al., 2013; Dunn et al., 2016; Wolf et al., 2017, Figure 3A, B). Each assembly primarily comprises neurons of either the left or right side of the ARTR, but also includes a small subset of contralateral neurons with weights of opposite sign in line with the established mutual inhibition between both subpopulations. Two other symmetric assemblies (Figure 3C, D) together encompass the oculomotor nucleus (nIII) and the contralateral abducens nucleus (nVI, in rhombomere 6), two regions engaged in ocular saccades (Ma et al., 2014) and under the control of the ARTR (Wolf et al., 2017). Additionally, we observed two symmetric assemblies (Figure 3E, F) in the posterior hindbrain (in rhombomere 7), in a region known to drive unilateral tail movements (Chen et al., 2018; Marques et al., 2020) and whose antiphasic activation is also controlled by the ARTR activity (Dunn et al., 2016).
Figure 3
cRBM assemblies compose functional circuits and anatomical structures.
(A–I) Individual example assemblies μ are shown by coloring each neuron with its connectivity weight value (see color bar at the right hand side). The assembly index μ is stated at the bottom of each panel. The orientation and scale are given in panel A (Ro: rostral, C: caudal, R: right, L: left, D: dorsal, V: ventral). Anatomical regions of interest, defined by the ZBrain Atlas (Randlett et al., 2015), are shown in each panel (Rh: rhombomere, nMLF: nucleus of the medial longitudinal fascicle; nIII: oculomotor nucleus nIII, Cl: cluster; Str: stripe, P. nV TG: Posterior cluster of nV trigeminal motorneurons; Pa: pallium; Hb: habenula; IPN: interpeduncular nucleus). (J–L) Groups of example assemblies that lie in the same anatomical region are shown for cerebellum (Cb), torus semicircularis (TSC), and optic tectum (OT). Neurons i were defined to be in an assembly μ when , and colored accordingly. If neurons were in multiple assemblies shown, they were colored according to their strongest-connecting assembly.
Next, we observed assemblies that correspond to particular neurotransmitter expressions in the ZBrain atlas (Randlett et al., 2015), such as the excitatory Vglut2 (Figure 3G) and inhibitory Gad1b (Figure 3H) neurotransmitters. These assemblies consist of multiple dense loci that sparsely populate the entire brain, confirming that cRBMs are able to capture a large morphological diversity of neural assemblies. Figure 3I depicts another sparse, brain-wide assembly that encompasses the pallium, habenula (Hb) and interpeduncular nucleus (IPN), and thus captures the Hb-IPN pathway that connects to other regions such as the pallium (Beretta et al., 2012; Bartoszek et al., 2021).
Larger nuclei or circuits were often composed of a small number of distinct neural assemblies with some overlap. For example, the cerebellum was decomposed into multiple, bilateral assemblies (Figure 3J) whereas neurons in the torus semicircularis were grouped per brain hemisphere (Figure 3K). As a last example, the optic tectum was composed of a larger set of approximately 18 neural assemblies, which spatially tiled the volume of the optic tectum (Figure 3L). This particular organization is suggestive of spatially localized interactions within the optic tectum, and aligns with the morphology of previously inferred assemblies in this specific region (Romano et al., 2015; Diana et al., 2019; Triplett et al., 2020). However, Figure 3 altogether demonstrates that the typical assembly morphology of the optic tectum identified by our and these previous analyses does not readily generalize to other brain regions, where a large range of different assembly morphologies compose neural circuits.
Overall, the clear alignment of cRBM-based neural assemblies with anatomical regions and circuits suggests that cRBMs are able to identify anatomical structures from dynamical activity alone, which enables them to break down the overall activity into parts that are interpretable by physiologists in the context of previous, more local studies.
HU dynamics cluster into groups and display slower dynamics than neurons
HU activity, defined as the expected value of (Equation 9), exhibits a rich variety of dynamical patterns (Figure 4A). HUs can activate very transiently, slowly modulate their activity, or display periods of active and inactive states of comparable duration. Figure 4B highlights a few HU activity traces that illustrate this diversity of HU dynamics. The top three panels of Figure 4B show the dynamics of the assemblies of Figure 3A-F which encompass the ARTR hindbrain circuit that controls saccadic eye movements and directional tail flips. HUs 99 and 161 drive the left and right ARTR and display antiphasic activity with long dwell times of ∼15s, in accordance with previous studies (Ahrens et al., 2013; Dunn et al., 2016; Wolf et al., 2017). HU 102 and 163 correspond to the oculomotor neurons in the nuclei nIII and nVI that together drive the horizontal saccades. Their temporal dynamics are locked to that of the ARTR units in line with the previously identified role of ARTR as a pacemaker for the eye saccades (Wolf et al., 2017). HUs 95 and 135, which drive directional tail flips, display transient activations that only occur when the ipsilateral ARTR-associated HU is active. This is consistent with the previous finding that the ARTR alternating activation pattern sets the orientation of successive tail flips accordingly (Dunn et al., 2016). The fourth panel shows the traces of the brain-wide assemblies of Figure 3G, I, displaying slow tonic modulation of their activity. Finally, the bottom panel, which corresponds to the collective dynamics of assembly 122 (Figure 3H), comprises short transient activity that likely corresponds to fictive swimming events.
Figure 4
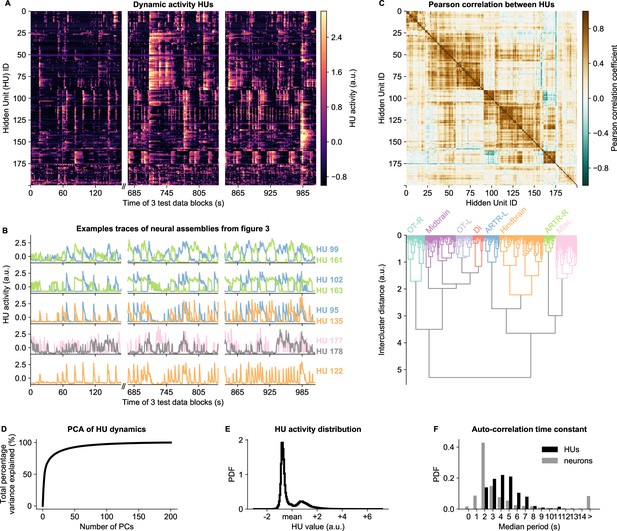
HU dynamics are bimodal and activate slower than neurons.
(A) HU dynamics are diverse and are partially shared across HUs. The bimodality transition point of each HU was determined and subtracted individually, such that positive values correspond to HU activation (see Materials and methods - ‘Time constant calculation’6.12). The test data consisted of three blocks, with a discontinuity in time between the first and second block (Materials and methods). (B) Highlighted example traces from panel A. HU indices are denoted on the right of each trace, colored according to their cluster from panel D. The corresponding cellular assemblies of these HU are shown in Figure 3A-I. (C) Top: Pearson correlation matrix of the dynamic activity of panel A. Bottom: Hierarchical clustering of the Pearson correlation matrix. Clusters (as defined by the colors) were annotated manually. This sorting of HUs is maintained throughout the manuscript. OT: Optic Tectum, Di: Diencephalon, ARTR: ARTR-related, Misc.: Miscellaneous, L: Left, R: Right. (D) A Principal Component Analysis (PCA) of the HU dynamics of panel A shows that much of the HU dynamics variance can be captured with a few PCs. The first 3 PCs captured 52%, the first 10 PCs captured 73% and the first 25 PCs captured 85% of the explained variance. (E) The distribution of all HU activity values of panel A shows that HU activity is bimodal and sparsely activated (because the positive peak is smaller than the negative peak). PDF: Probability Density Function. (F) Distribution of the time constants of HUs (black) and neurons (grey). Time constants are defined as the median oscillation period, for both HUs and neurons. An HU oscillation is defined as a consecutive negative and positive activity interval. A neuron oscillation is defined as a consecutive interspike-interval and spike-interval (which can last for multiple time steps, for example see Figure 1A). The time constant distribution of HUs is greater than the neuron distribution (Mann Whitney U test, ).
Some HUs regularly co-activate, leading to strong correlations between different HUs. This is quantified by their Pearson correlation matrix shown in Figure 4C (top), which reveals clusters of correlated HUs. These were grouped using hierarchical clustering (Figure 4C, bottom), and we then manually identified their main anatomical location (top labels). These clusters of HUs with strongly correlated activity suggest that much of the HU variance could be captured using only a small number of variables. We quantified this by performing PCA on the HU dynamics, finding that indeed 52% of the variance was captured by the first three PCs, and 85% by the first 20 PCs (Figure 4D). We further observed that HU activity is bimodal, as evidenced by the distribution of all HU activity traces in Figure 4E. This bimodality can emerge because the dReLU potentials (Equation 13) can learn to take different shapes, including a double-well potential that leads to bimodal dynamics (see Materials and methods - ‘Choice of HU potential’). This allows us to effectively describe HU activity as a two-state system, where increases the probability to spike () for its positively connected neurons, and decreases their probability to spike. The binarized neuron activity is also a two-state system (spiking or not spiking), which enabled us to compare the time constants of neuron and HU state changes, quantified by the median time between successive onsets of activity. We find that HUs, which represent the concerted dynamics of neuronal assemblies, operate on a slower time scale than individual neurons (Figure 4F, Figure 2—figure supplement 5G-L). This observation aligns with the expected difference between cellular and circuit-level time scales.
cRBM embodies functional connectivity that is strongly correlated across individuals
The probabilistic nature of cRBMs uniquely enables in silico perturbation experiments to estimate the functional connection between pairs of neurons, where is quantified by directly perturbing the activity of neuron and observing the change in probability to spike of neuron . We first defined the generic, symmetric functional connection using (Equation 15) and then used (Equation 12) to derive the cRBM-specific (Equation 17, see Materials and methods - ‘Effective connectivity matrix’). Using this definition of , we constructed a full neuron-to-neuron effective connectivity matrix for each zebrafish recording. We then asked whether this cRBM-inferred connectivity matrix was robust across individuals. For this purpose, we calculated the functional connections between anatomical regions, given by the assemblies that occupy each region, because neuronal identities can vary across individual specimen. We aggregated neurons using the L1 norm for each pair of anatomical regions to determine the functional connection between regions (see Materials and methods - ‘From inter-neuron to inter-region connectivity’). For this purpose, we considered anatomical regions as defined by the mapzebrain atlas (Kunst et al., 2019) for which a regional-scale structural connectivity matrix exists to which we will compare our functional connectivity matrix.
This led to a symmetrical functional connectivity matrix for each animal, three of which are shown in Figure 5A-C (where non-imaged regions are left blank, and all eight animals are shown in Figure 5—figure supplement 1). The strength of functional connections is distributed approximately log-normal (Figure 5D), similar to the distribution of structural region-to-region connections (Kunst et al., 2019). To quantify the similarity between individual fish, we computed the Pearson correlation between each pair of fish. Functional connectivity matrices correlate strongly across individuals, with an average Pearson correlation of 0.69 (Figure 5E and F).
Figure 5 with 1 supplement see all
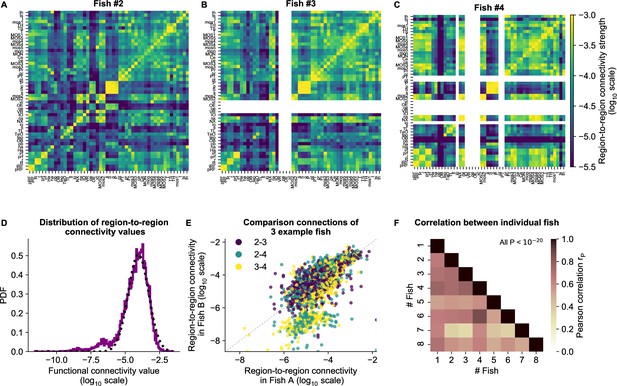
cRBM gives rise to functional connectivity that is strongly correlated across individuals.
(A) The functional connectivity matrix between anatomical regions of the mapzebrain atlas (Kunst et al., 2019) of example fish #2 is shown. Functional connections between two anatomical regions were determined by the similarity of the HUs to which neurons from both regions connect to (Materials and methods). Mapzebrain atlas regions with less than five imaged neurons were excluded, yielding regions in total. See Supplementary file 1 for region name abbreviations. The matrix is shown in log10 scale, because functional connections are distributed approximately log-normal (see panel D). (B) Equivalent figure for example fish #3 (example fish of prior figures). (C) Equivalent figure for example fish #4. Panels A-C share the same log10 color scale (right). (D) Functional connections are distributed approximately log-normal. (Mutual information with a log-normal fit (black dashed line) is 3.83, while the mutual information with a normal fit is 0.13). All connections of all eight fish are shown, in log10 scale (purple). (E) Functional connections of different fish correlate well, exemplified by the three example fish of panels A-C. All non-zero functional connections (x-axis and y-axis) are shown, in log10 scale. Pearson correlation between pairs: , , . All correlation p values (two-sided t-test). (F) Pearson correlations of region-to-region functional connections between all pairs of 8 fish. For each pair, regions with less than five neurons in either fish were excluded. All p values (two-sided t-test), and average correlation value is 0.69.
We conclude that similar functional circuits spontaneously activate across individuals, despite the limited duration of neural recordings (∼25 minutes), which can be identified across fish using independently estimated cRBMs. In the next section, we aggregate these individual matrices to a general functional connectivity matrix for comparison with the zebrafish structural connectivity matrix.
cRBM-inferred functional connectivity reflects structural connectivity
In the previous section we have determined the functional connections between anatomical regions using the cRBM assembly organization. Although functional connectivity stems from the structural (i.e. biophysical) connections between neurons, it can reflect correlations that arise through indirect network interactions (Bassett and Sporns, 2017; Das and Fiete, 2020). Using recently published structural connectivity data of the zebrafish brain (Kunst et al., 2019), we are now able to quantify the overlap between a structurally defined connectivity matrix and our functional connectivity matrix estimated through neural dynamics. Kunst et al., 2019 determined a zebrafish structural connectivity matrix between 72 anatomical regions using structural imaging data from thousands of individually Green Fluorescent Protein (GFP)-labeled neurons from multiple animals. We slightly extended this matrix by using the most recent data, filtering indirect connections and accounting for the resulting sampling bias (Figure 6A, regions that were not imaged in our light-sheet microscopy experiments were excluded). Next, we aggregated the functional connectivity matrices of all our calcium imaging recordings to one grand average functional connectivity matrix (Figure 6B).
Figure 6 with 1 supplement see all
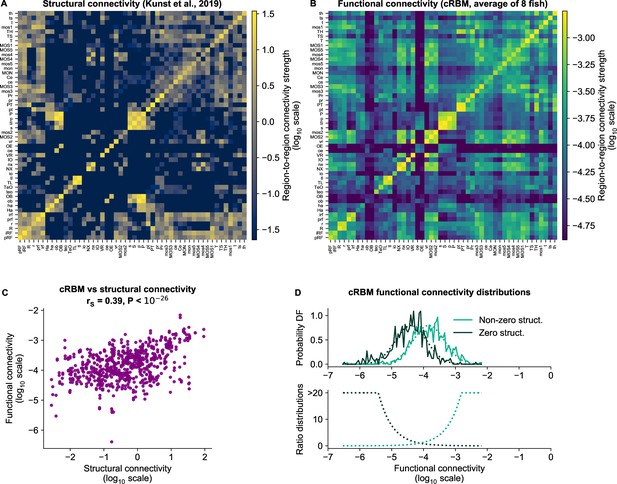
cRBM-inferred functional connectivity reflects structural connectivity.
(A) Structural connectivity matrix is shown in log10 scale, updated from Figure 8C of Kunst et al., 2019. Regions that were not imaged in our experiments were excluded (such that out of 72 regions remain). Regions (x-axis and y-axis) were sorted according to Kunst et al., 2019. Compared to Figure 8C of Kunst et al., 2019 additional structural data was added and the normalization procedure was updated to include within-region connectivity (see Materials and methods - ‘Extensions of the structural connectivity matrix’). See Supplementary file 1 for region name abbreviations. (B) Average functional connectivity matrix is shown in log10 scale, as determined by averaging the cRBM functional connectivity matrices of all 8 fish (see Materials and methods - ‘Specimen averaging of connectivity matrices’). The same regions (x-axis and y-axis) are shown as in panel A. (C) The average functional and structural connectivity of panels A and B correlate well, with Spearman correlation (, two-sided t-test). Each data point corresponds to one region-to-region pair. Data points for which the structural connection was exactly 0 were excluded (see panel D for their analysis). (D) The distribution of average functional connections of region pairs with non-zero structural connections is greater than functional connections corresponding to region pairs without structural connections (, two-sided Kolmogorov-Smirnov test). The bottom panel shows the evidence for inferring either non-zero or zero structural connections, defined as the fraction between the PDFs of the top panel (fitted Gaussian distributions were used for denoising).
For comparison, we also calculated the connectivity matrices defined by either covariance or Pearson correlation (Figure 6—figure supplement 1). The cRBM functional connectivity spans a larger range of values than either of these methods, leading to a more fine-grained connectivity matrix akin to the structural connectivity map (Figure 6B). This greater visual resemblance was statistically confirmed by calculating the Spearman correlation between structural and functional connectivity, which is greater for cRBM (, Figure 6C), than for covariance-based connectivity (, Figure 6—figure supplement 1 left) or correlation-based connectivity (, Figure 6—figure supplement 1 right). Hence, using recordings of ∼25 min on average, cRBMs were able to identify functional connections that resemble the anatomical connectivity between brain regions. Strong or weak functional connections are predictive of present or absent structural connections respectively (Figure 6D), and could thus potentially be used for inference in systems where the structural connectivity pattern is unknown.
Discussion
We have developed a cRBM model that accurately replicated the data statistics of brain-scale zebrafish recordings, thereby forming neural assemblies that spanned the entire brain. The objective of our study was threefold: first, to show that the cRBM model can be applied to high-dimensional data, such as whole-brain recordings, second, to prove that an assembly-based model is sufficient to generate whole-brain neural data statistics, and third, to describe the physiological properties of the assembly organization in the zebrafish brain and use it to create a functional connectivity map. We have shown that, after convergence, the cRBM-generated data not only replicated the data statistics that it was constrained to fit, but also extrapolated to fit the pairwise correlation statistics of neurons and HUs, leading to a better reconstruction of neural data than a fully connected GLM (Figure 2). These results thereby quantify how neural assemblies play a major role in determining the collective dynamics of the brain. To achieve this, cRBMs formed sparsely localized assemblies that spanned the entire brain, facilitating their biological interpretation (Figures 3 and 4, Figure 2—figure supplement 6). Further, the probabilistic nature of the cRBM model allowed us to create a mesoscale functional connectivity map that was largely conserved across individual fish and correlated well with structural connectivity (Figures 5 and 6).
The maximum entropy principle underlying the cRBM definition has been a popular method for inferring pairwise effective connections between neurons or assemblies of co-activating cells (Schneidman et al., 2006; Tavoni et al., 2017; Ferrari et al., 2017; Meshulam et al., 2017; Posani et al., 2018; Chen et al., 2019). However, its computational cost has limited this pairwise connectivity analysis to typically neurons. The two-layer cRBM model that we used here alleviates this burden, because the large number of neuron-to-neuron connections are no longer explicitly optimized, which enables a fast data sampling procedure (Figure 2B). However, we have shown that these connections are still estimated indirectly with high accuracy via the assemblies they connect to (Figure 2F). We have thus shown that the cRBM is able to infer the (symmetric) pairwise connections through its assembly structure, a feat that is computationally infeasible for many other methods. By implementing various algorithmic optimizations (Materials and methods - ‘Algorithmic Implementation’), cRBM models converged in approximately 8–12 hr on high-end desktop computers (also see Materials and methods - ‘Computational limitations’).
Previously, we have extensively compared cRBM performance to other dimensionality reduction techniques, including Principal Component Analysis (PCA), Independent Component Analysis (ICA), Variational Autoencoders (VAEs) and their sparse variants, using protein sequence data as a benchmark (Tubiana et al., 2019a). Briefly put, we showed that PCA and ICA could not accurately model the system due to their deterministic nature, putting too much emphasis on low-probability high-variance states, while VAEs were unable to capture all features of data due to the unrealistic assumption of independent, Gaussian-distributed latent variables. In this study, we repeated this comparison with sparse linear VAEs, and reached similar conclusions: VAEs trained using the same protocol as cRBMs failed to reproduce second-order data statistics and to reconstruct neural activity via the latent layer, while the learnt assemblies were of substantially lower quality (indicated by a large fraction of disconnected HUs, as well as a highly variable assembly size; Figure 2—figure supplement 7). Additionally, while PCA has previously been successful in describing zebrafish neural dynamics in terms of their main covariances modes (Ahrens et al., 2012; Marques et al., 2020), we show here that it is not appropriate for assembly extraction due to the absence of both a compositional and stochastic nature (Figure 2, Figure 2—figure supplement 6). Furthermore, we have shown that the generative component of cRBM models is essential for quantitatively assessing that the assembly organization is sufficient for reproducing neural statistics (Figure 2), moving beyond deterministic clustering analyses such as k-means (Panier et al., 2013; Chen et al., 2018), similarity graph clustering (Mölter et al., 2018) or non-negative matrix factorization (Mu et al., 2019) (see Supplementary file 2).
After having quantitatively validated the resultant assemblies, we moved to discussing the biological implications of our findings. Previous studies of the zebrafish optic tectum have identified neural assemblies that were spatially organized into single dense clusters of cells (Romano et al., 2015; Diana et al., 2019; Triplett et al., 2020). We have replicated these findings by observing the distinct organization of ball-shaped assemblies in the optic tectum (Figure 3L). However, our data extends to many other anatomical regions in the brain, where we found that assemblies can be much more dispersed, albeit still locally dense, consisting of multiple clusters of neurons (Figure 3). In sum, cRBM-inferred cell assemblies display many properties that one expects from physiological cell assemblies: they are anatomically localized, can overlap, encompass functionally identified neuronal circuits and underpin the collective neural dynamics (Harris, 2005; Harris, 2012; Eichenbaum, 2018). Yet, the cRBM bipartite architecture lacks many of the traits of neurophysiological circuits. In particular, cRBMs lack direct neuron-to-neuron connections, asymmetry in the connectivity weights and a hierarchical organization of functional dependencies beyond one hidden layer. Therefore, to what extent cRBM-inferred assemblies identify to neurophysiological cell assemblies, as postulated by Hebb, 1949 and others, remains an open question.
cRBM allowed us to compute the effective, functional connections between each pair of neurons, aggregated to functional connections between each pair of regions, by perturbing neural activity in silico. Importantly, we found that this region-scale connectivity is well-conserved across specimen. This observation is non-trivial because each recording only lasted ∼25 min, which represents a short trajectory across accessible brain states. It suggests that, although each individual brain may be unique at the neuronal scale, the functional organization could be highly stereotyped at a sufficiently coarse-grained level.
It would be naive to assume that these functional connections equate biophysical, structural connections (Das and Fiete, 2020). Both represent different, yet interdependent aspects of the brain organization. Indeed, we found that structural connectivity is well-correlated to functional connectivity, confirming that functional links are tied to the structural blueprint of brain connectivity (Figure 6). Furthermore, strong (weak) functional connections are predictive of present (absent) structural connections between brain regions, although intermediate values are ambiguous.
It will be crucial to synergistically merge structural and dynamic information of the brain to truly comprehend brain-wide functioning (Bargmann and Marder, 2013; Kopell et al., 2014). Small brain organisms are becoming an essential means to this end, providing access to a relatively large fraction of cells (Ahrens and Engert, 2015). To generate new scientific insights it is thus essential to develop analytical methods that can scale with the rapidly growing size of both structural and dynamic data (Helmstaedter, 2015; Ahrens, 2019). In this study, we have established that the cRBM can model high-dimensional data accurately, and that its application to zebrafish recordings was crucial to unveil their brain-scale assembly organization. In future studies, cRBMs could be used to generate artificial data whose statistics replicate those of the zebrafish brain. This could be used for further in silico ablation and perturbation studies with strong physiological footing, crucial for developing hypotheses for future experimental work (Jazayeri and Afraz, 2017; Das and Fiete, 2020). Lastly, the application of cRBMs is not specific to calcium imaging data, and can therefore be readily applied to high-dimensional neural data obtained by other recording techniques.
Materials and methods
Key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Software, algorithm | cRBM algorithm | This paper and Tubiana and Monasson, 2017 | github.com/jertubiana/PGM | Materials and methods - ‘Restricted Boltzmann Machines’ , ‘Compositional Restricted Boltzmann Machine’ and Algorithmic Implementation |
| Software, algorithm | Fishualizer | Migault et al., 2018 | bitbucket.org/benglitz/fishualizer_public | |
| Software, algorithm | Blind Sparse Deconvolution | Tubiana et al., 2020 | github.com/jertubiana/BSD | |
| Software, algorithm | ZBrain Atlas | Randlett et al., 2015 | engertlab.fas.harvard.edu/Z-Brain | |
| Software, algorithm | mapzebrain atlas | Kunst et al., 2019 | fishatlas.neuro.mpg.de | |
| Software, algorithm | MATLAB (data preprocessing) | MathWorks | mathworks.com/products/matlab.html | |
| Software, algorithm | Computational Morphometry Toolkit (CMTK) | NITRC | nitrc.org/projects/cmtk | |
| Software, algorithm | Python | Python Software Foundation | python.org | |
| Strain, strain background (Danio rerio, nacre mutant) | Tg(elavl3:H2B-GCaMP6f) | Quirin et al., 2016 | ||
| Strain, strain background (Danio rerio, nacre mutant) | Tg(elavl3:H2B-GCaMP6s) | Vladimirov et al., 2014 |
Data and code availability
Request a detailed protocolThe cRBM model has been developed in Python 3.7 and is available at: https://github.com/jertubiana/PGM, (copy archived at swh:1:rev:caf1d9fc545120f7f1bc1420135f980d5fd6c1fe; Tubiana and van der Plas, 2023). An extensive example notebook that implements this model is provided here.
Calcium imaging data pre-processing was performed in MATLAB (Mathworks) using previously published protocols and software (Panier et al., 2013; Wolf et al., 2017; Migault et al., 2018; Tubiana et al., 2020). The functional data recordings, the trained cRBM models and the structural and functional connectivity matrix are available at https://gin.g-node.org/vdplasthijs/cRBM_zebrafish_spontaneous_data.
Figures of neural assemblies or neurons (Figures 1 and 3) were made using the Fishualizer, which is a 4D (space +time) data visualization software package that we have previously published (Migault et al., 2018), available at https://bitbucket.org/benglitz/fishualizer_public. Minor updates were implemented to tailor the Fishualizer for viewing assemblies, which can be found at https://bitbucket.org/benglitz/fishualizer_public/src/assembly_viewer.
All other data analysis and visualization was performed in Python 3.7 using standard packages (numpy Harris et al., 2020), scipy (Virtanen et al., 2020), scikit-learn (Pedregosa, 2011), matplotlib (Hunter, 2007), pandas (McKinney, 2010), seaborn (Waskom, 2021), h5py. The corresponding code is available at https://github.com/vdplasthijs/zf-rbm (copy archived at swh:1:rev:b5df4e37434c0b18120485b8d856596db0b92444; van der Plas, 2023).
Zebrafish larvae
Request a detailed protocolExperiments were conducted on nacre mutants, aged 5–7 days post-fertilization (dpf). Larvae were reared in Petri dishes at 28 °C in embryo medium (E3) on a 14/10 hr light/dark cycle, and were fed powdered nursery food every day from 6 dpf. They were expressing either the calcium reporter GCaMP6s (fish 1–4, 6, and 8) or GCaMP6f (fish 5 and 7) under the control of the nearly pan-neuronal promoter elavl3 expressed in the nucleus Tg(elavl3:H2B-GCaMP6). Both lines were provided by Misha Ahrens and published by Vladimirov et al., 2014 (H2B-GCaMP6s) and Quirin et al., 2016 (H2B-GCaMP6f). Experiments were approved by Le Comité d’Éthique pour l’Experimentation Animale Charles Darwin C2EA-05 (02601.01).
Light-sheet microscopy of zebrafish larvae
Request a detailed protocolSpontaneous neural activity (i.e. in the absence of sensory stimulation) was recorded in larval zebrafish using light-sheet microscopy, which acquires brain-scale scans by imaging multiple -planes sequentially (Panier et al., 2013; Wolf et al., 2017; Migault et al., 2018). Larvae were placed in 2% low melting point agarose (Sigma-Aldrich), drawn tail-first into a glass capillary tube with 1 mm inner diameter via a piston and placed in chamber filled with E3 in the microscope. Recordings were of length 1514 ± 238 seconds (mean ± standard deviation), with a brain volume imaging frequency of 3.9 ± 0.8 Hz.
The following imaging pre-processing steps were performed offline using MATLAB, in line with previously reported protocols (Panier et al., 2013; Migault et al., 2018). Automated cell segmentation was performed using a watershed algorithm (Panier et al., 2013; Migault et al., 2018) and fluorescence values of pixels belonging to the same neuron was averaged to obtain cell measurements. The fluorescence intensity values were normalized to where is the baseline signal per neuron and F0 is the overall background intensity (Migault et al., 2018). The activity of different imaging planes was subsequently temporally aligned using interpolation (because of the time delay between imaging planes; Migault et al., 2018) and deconvolved to binarized spike traces using Blind Sparse Deconvolution (BSD) (Tubiana et al., 2020). BSD estimates the most likely binary spike trace by minimizing the L2 norm of the difference between the estimated spike trace convolved with an exponential kernel and the ground-truth calcium data, using L1 sparsity regularization and online hyperparameter optimization. Calcium kernel time constants used for deconvolution were inferred using BSD on the spontaneous activity of three different fish (approximately 5000 neurons per fish, recorded at 10 Hz, previously reported by Migault et al., 2018). For the GCaMP6s line, we used a rise time of 0.2 s and a decay time of 3.55 s; for the GCaMP6f line, we used 0.15 s and 1.6 s, respectively.
Brain activity was recorded of 15 animals in total. Of these recordings, 1 was discarded because of poor image quality and 6 were discarded because neurons were inactive (defined by less than 0.02 spikes/(neurons × time points)), hence leaving 8 data sets for further analysis. The recorded brains were then registered onto the ZBrain Atlas (Randlett et al., 2015) and the mapzebrain atlas (Kunst et al., 2019) for anatomical labeling of neurons (Migault et al., 2018). The ZBrain Atlas was used in Figures 1—4 because of its detailed region descriptions (outlining 294 regions in total). However, we also registered our data to the mapzebrain atlas (72 regions in total) in order to compare our results with the structural connectivity matrix which was defined for this atlas only (Kunst et al., 2019). Only neurons that were registered to at least 1 ZBrain region were used for analysis (to filter imaging artefacts). This resulted in neurons per recording (mean ± standard deviation, minimum = 23446, maximum = 65517).
Maximum entropy principle
Here, we provide in brief the general derivation of the class of maximum entropy probabilistic models. Restricted Boltzmann Machines are an instance of this model, which is detailed in the following sections. The maximum entropy principle is used to create probabilistic models (where denotes one data configuration sample) that replicate particular data statistics fk, but are otherwise most random, and therefore least assumptive, by maximizing their entropy (Gardella et al., 2019). The goal of the model is to match its model statistics to the empirical data statistics . This is done using Lagrange multipliers :
(5)
which yields, when is maximized with respect to , the Boltzmann distribution (see, e.g., Bialek, 2012 for a full derivation):
(6)
where is defined as the resulting energy function. Importantly, the data dependency () disappears when going from Equation 5 to Equation 6. Hence, the maximum entropy principle only defines the shape of the distribution , but not its specific parameters (Bialek, 2012). In the case of RBM, these are then optimized using maximum likelihood estimation, as detailed in the sections below.
Motivation for choice of statistics
Request a detailed protocolThe derivation above describes the general maximum entropy model for a set of statistics . The objective of this study is to extract the assembly structure from neural data, therefore creating two layers: a visible (neural data) layer and a hidden (latent) layer . The model should capture the mean activity of each neuron , their pairwise correlations , the neuron-HU interactions and a function of . The latter is determined by the potential , which we set to be a double Rectified Linear Unit (dReLU), as motivated in the following sections. Fitting all pairwise interactions is computationally infeasible, but under the cell assembly hypothesis we assume that this should not be necessary because collective neural behavior is expected to be explained by membership to similar assemblies via , and can therefore be excluded. We later show that pairwise correlations are indeed optimized implicitly (Figure 2). All other statistics are included and therefore explicitly optimized, also see Equation 14.
Restricted Boltzmann machines
A Restricted Boltzmann Machine (RBM) is an undirected graphical model defined on a bipartite graph (Smolensky, 1986; Hinton, 2002; Hinton and Salakhutdinov, 2006), see Figure 2A. RBMs are constituted by two layers of random variables, neurons and Hidden Units (HUs) , which are coupled by a weight matrix . There are no direct couplings between pairs of units within the same layer. Here, each visible unit vi corresponds to a single recorded neuron with binary (spike-deconvolved) activity (). Each Hidden Unit (HU) corresponds to the (weighted) activity of its neural assembly and is chosen to be real-valued. The joint probability distribution writes (Hinton and Salakhutdinov, 2006; Tubiana and Monasson, 2017):
(7)
where is the energy function and is the partition function. The weights gi and potentials control the activity level of the visible units and the marginal distributions of the HUs respectively, and the weights couple the two layers. Note that while is directly observed from the neural recordings, is by definition unobserved (i.e. hidden) and is sampled from the observed values instead.
From data to features
Request a detailed protocolGiven a visible layer configuration , a HU receives the input and, owing to the bipartite architecture, the conditional distribution factorizes as:
(8)
where is the cumulant generating function associated to the potential that normalizes Equation 8 (Tubiana et al., 2019b). The average activity of HU associated to a visible configuration is given by a linear-nonlinear transformation (as defined by the properties of the cumulant generating function):
(9)
Throughout the manuscript, we use this definition to compute HU activity (e.g., in Figure 4).
From features to data
Request a detailed protocolConversely, given a hidden layer configuration , a visible unit vi receives the input and the conditional distribution factorizes as:
(10)
and the average sampled vi activity is given by:
(11)
where is the logistic function. Hence, a sampled visible layer configuration is obtained by a weighted combination of the HU activity followed by Bernoulli sampling. RBMs are generative models, in the sense that they can generate new, artificial data using Equations 8 and 10. Figure 2B illustrates this Markov Chain Monte Carlo (MCMC) process, by recursively sampling from and , which converges at equilibrium to .
Marginal distributions
Request a detailed protocolThe marginal distribution has a closed-form expression because of the factorized conditional distribution of Equation 9 (Tubiana et al., 2019a; Tubiana et al., 2019b):
(12)
For a quadratic potential , the cumulant generating function would also be quadratic and would reduce to a Hopfield model, that is, a pairwise model with an interaction matrix (Tubiana et al., 2019a). Otherwise, is not quadratic, yielding high-order effective interaction terms between visible units and allowing RBMs to express more complex distributions. Importantly, the number of parameters remains limited, controlled by and does not scale as (unlike pairwise models).
Choice of HU potential
Request a detailed protocolThe choice of HU potential determines three related properties: the HU conditional distribution , the transfer function of the HUs and the parametric form of the marginal distribution . Hereafter we use the double-Rectified Linear Unit (dReLU) potential:
(13)
Varying the parameters allows the potential to take a variety of shapes, including quadratic potentials (, ), ReLU potentials and double-well potentials (Tubiana et al., 2019b). The associated cumulant generating function is non-quadratic in general, and depending on the parameters, the transfer function can be linear, ReLU-like (asymmetric slope and thresholding) or logistic-like (strong local slopes for binarizing inputs). Closed-form expressions of are detailed in Tubiana et al., 2019a; Tubiana et al., 2019b, and its derivatives are also detailed in Tubiana, 2018, p49-50. Note that the dReLU potential and distribution are invariant to the sign swap transformation and (leading to ). For visual clarity, we perform this sign swap transformation after training on all HUs with predominantly negative weights (defined by ). Subsequently all HUs are positively activated if the group of neurons to which it connects is strongly active.
RBM training
Request a detailed protocolThe RBM is trained by maximizing the average log-likelihood of the empirical data configurations , using stochastic gradient descent methods. The gradient update steps are derived by calculating the derivative of , using Equation 12, with respect to the model parameters (Tubiana et al., 2019a):
(14)
Each gradient of is thus the difference between a data statistic and a model statistic . Hence the model learns to match these statistics to the training data. Importantly, model statistics cannot be evaluated exactly due to the exponentially large number of data configurations (e.g. visible configurations). Therefore they are approximated by computing the statistics of model-generated data using the MCMC sampling scheme defined with Equations 8 and 10 (see Materials and methods - ‘Matching data statistics to model statistics’ for more detail). MCMC sampling of a Boltzmann distribution in such high-dimensional space is in general very challenging owing to the exponentially long time to reach equilibrium. We use the persistent contrastive divergence approximation (Tieleman, 2008) and discuss its validity below.
Compositional restricted boltzmann machine
Request a detailed protocolIn the previous sections, we have described the general properties of RBMs. We now motivate the specific RBM model choices that we have implemented, such as the dReLU potential and sparsity regularization, by discussing their impact on the properties of RBM-generated data.
Directed graphical models, for example, PCA, ICA, sparse dictionaries or variational autoencoders, prescribe a priori statistical constraints for their data representations, such as orthogonality/independence or specific marginal distributions such as Gaussian/sparse distributions. In contrast, the statistical properties of the representation of the data learned by RBMs are unknown a priori by construction (because of the maximum entropy principle). Instead, they emerge from the structure of the weight matrix, the potentials and the recursive back-and-forth sampling procedure described above. We have therefore previously studied the properties of typical samples of RBM with random weights as a function of the visible and hidden unit potentials and properties of the weight matrix using statistical mechanics tools (Tubiana and Monasson, 2017; Tubiana et al., 2019a). We have identified the three following typical behaviors, or phases.
In the ferromagnetic phase, a typical sample from has a single strongly activated HU (, where is the number of activated HUs at time ), whereas the others are not or merely weakly activated. The corresponding active visible units vi are defined by the weight vector associated to the active HU (see Equation 10).
In the spin-glass phase, a typical sample does not have any relatively strongly activated HUs, but instead many moderately activated ones (). They interfere in a complex fashion to produce different visible unit configurations and there is no clear correspondence between the weight matrix and a typical data configuration.
Finally, in the compositional phase, a typical sample from has a small number of strongly activated HUs () whereas the others are weak or silent. Their weights are linearly combined through Equation 10 to produce the corresponding visible layer configuration. The compositional phase is desirable because, firstly, there exists a simple link between the weight matrix and typical data configurations (they are obtained by combining a few weights), which facilitates interpretation of biological systems (Tubiana et al., 2019b). Secondly, the corresponding neural activity distribution is rich, as different choices of HU subsets yield a combinatorial diversity of visible layer configurations. Moreover, the modular nature of the compositional phase facilitates the assembly organization of neural dynamics, as motivated in the Introduction.
A set of sufficient conditions for the emergence of the compositional phase are (Tubiana and Monasson, 2017):
The HUs are unbounded and real-valued with a non-linear, ReLU-like transfer function.
The weight matrix is sparse.
The columns of the weight matrix have similar norm. (If a weight column associated to one HU is much larger than the others, visible configurations are solely aligned to it according to Equation 10.)
The first condition is satisfied by the dReLU potential (but not by quadratic potentials or binary-valued HUs). The second condition is enforced in practice by adding a L1 sparse penalty term to the log-likelihood cost function. In our experiments, the optimal sparsity parameter was determined to be by cross-validation (Figure 2—figure supplement 1). The final condition is achieved by enforcing that and . This is done by an appropriate reparameterization of the HU potential of Equation 13 and a batch-norm–like procedure, described in detail in Tubiana, 2018. This normalization promotes homogeneity among HU importance, preventing some units from being disconnected or others from dominating. In addition, ensuring that irrespective of the visible layer size (as opposed to e.g., which yields ) avoids the problem of ill-conditioned Hessians that was previously described by Hinton, 2012.
To emphasise the departure from the classic RBM formulation in this study, we name our model compositional RBM (cRBM).
Algorithmic implementation
In the previous sections, we have described the cRBM model in full mathematical detail. The corresponding algorithmic implementation was adapted from Tubiana et al., 2019b. In addition, we have made several major implementation and algorithmic changes to accommodate the large data size of the zebrafish neural recordings. We provide the code open-source, and describe the code improvements and hyperparameter settings in this section. The following improvements were made, leading to a substantial reduction of computation time:
Python 3 and numba (Lam et al., 2015) were used to compile custom functions, enabling SIMD vectorization and multicore parallelism.
The sampling of and evaluating its cumulant generating function and various moments requires repeated and costly evaluation of error functions erf and related functions (Tubiana, 2018, p49-50). Fast numerical approximations of these functions were implemented based on Abramowitz et al., 1988 (p299).
The number of memory allocation operations was minimized.
The optimization algorithm was changed from stochastic gradient ascent to RMSprop (i.e. ADAM without momentum) with learning rate to , , , , see Kingma and Ba, 2014 for a definition of the parameters. Compared to the original stochastic gradient ascent, the adaptive learning rates of RMSprop/ADAM yield larger updates for the weights attached to neurons with very sparse activity, resulting in substantially faster convergence.
Hyperparameter settings
Request a detailed protocolThe following hyperparameters were used in the experiments of this manuscript:
Number of hidden unit : 200. This value was determined by cross-validation (Figure 2—figure supplement 1) on one data set (example fish #3). Because this cross-validation procedure was computationally expensive, the same value was used for all other data sets, except for 3 data sets which used because their .
Sparse regularization penalty : 0.02 (determined by cross-validation).
Batch size: 100, 200, or 400. Larger batch sizes yield longer training time but more stable training; batch size was increased if training failed to converge.
Number of Monte Carlo chains: 100.
Number of gradient updates: .
Number of Monte Carlo steps between each gradient update: 15.
Initial learning rate : between and . We used by default and if weight divergence was observed, the learning was reinitialized with a reduced learning rate. This occurred notably for high- and low- models during the cross-validation procedure of Figure 2—figure supplement 1.
Learning rate annealing scheme: the learning rate geometrically decayed during training, starting after 25% of the gradient update steps, from its initial value to a final value of .
Number of training data samples: 70% of frames of each recording (=4086 training data samples on average), see section ‘Train / test data split’ for details.
Computational limitations
Request a detailed protocolWe found that 57.5% () of cRBMs with optimal settings successfully converged. cRBM models of these zebrafish data sets could be estimated in approximately 8–12 hr using 16 CPU threads (Intel Xeon Phi processor). The -cross-validation was therefore completed in three weeks using two desktop computers. Previously, we observed that this model requires a fixed number of gradient updates to converge, rather than a fixed number of epochs (Tubiana et al., 2019a; Tubiana et al., 2019b; Bravi et al., 2021). Hence, in principle, runtime does not strictly depend on the recording length, as the number of epochs can be reduced for longer recordings (assuming that the data distribution remains statistically stationary).
Validity of the persistent contrastive divergence algorithm
Request a detailed protocolTraining RBM requires extensive MCMC sampling which is notoriously difficult for high-dimensional data sets. We resolve this by using Persistent Contrastive Divergence (PCD) to approximate the gradients (Tieleman, 2008). In this section, we discuss why this worked to successfully converge, despite the very large data size.
The typical number of Monte Carlo steps required to transition from one energy minimum to another through an energy barrier follows the Arrhenius law, scaling as . In the thermodynamic limit (), scales as the system size multiplied by the typical energy required to flip a single visible unit, corresponding here to the inputs received from the hidden layer . In contrast, for PCD only a limited number of MC steps (here, 15) are applied between each gradient update. Three factors explain why reasonably successful convergence was achieved in the trainings presented here.
Firstly, the use of the L1 regularization limits the magnitude of the weights and therefore limits the input scale . Secondly, in the compositional phase, the energy barriers do not scale as the full system size but rather as the size of one assembly where is the fraction of non-zero weights (Tubiana and Monasson, 2017). Indeed, transitioning from one energy minimum, characterized by a subset of strongly activated HUs, to another minimum, characterized by another set of strongly activated HUs, is done by gradually morphing the first set into the second (Roussel et al., 2021). Compared to a direct transition, such a path is favored because the intermediate states are thermodynamically stable and energy barriers are smaller as each HU flip has an energy cost . Lastly, throughout PCD training, MCMC sampling is not performed at thermal equilibrium and the model updates of the parameters of the distribution promote mixing (Tieleman and Hinton, 2009). This is seen from Equation 14: the log-likelihood gradient is the difference between the gradient of the energy averaged over the empirical data and the energy averaged over MCMC samples. Ascending the gradient amounts to pushing down the energy of data configurations and pushing up the energy of MCMC samples, thereby promoting mixing of the Markov chains.
Overall, combining small learning rates (and large number of gradient updates), large regularization, large number of Markov Chains and Monte Carlo steps has allowed convergence to be reached for the majority of cRBM training sessions.
Functional connectivity inference
Effective connectivity matrix
Request a detailed protocolIn this section, we present a derivation of the effective coupling matrix between neurons from the marginal distribution using cRBMs. This is achieved by perturbing the activity of each neuron individually and quantifying the effect on other neurons. We first define the local coupling between two neurons vi and vj for a generic probability distribution , given a data configuration :
(15)
In other words, is defined as the impact of the state of neuron on neuron in the context of activity pattern . Hence, the effective connectivity matrix mathematically defines the functional connections, which can only be done using a probabilistic model . A positive (negative) coupling indicates correlated (anti-correlated) collective behavior of neurons . This effective coupling value is symmetric (because of Bayes’ rule): . For context, note that is uniformly zero for an independent model of the form , and that for a maximum entropy pairwise (Ising) model, with , the matrix exactly identifies with the coupling matrix , and does not depend on the data configuration (so ).
However, in general, and for RBMs in particular, depends on the data set , and an overall coupling matrix can be derived by taking its average over all data configurations:
(16)
Although Equation 16 has a closed-form solution for RBMs (by inserting Equation 12), a naive evaluation requires operations where is the number of data samples. However, a fast and intuitive approximation can be derived by performing a second-order Taylor expansion of :
(17)
Equation 17 is exact for quadratic potential and in general justified as the contribution of neurons is small compared to the scale of variation of , where is the fraction of non-zero couplings. In conclusion, we have mathematically derived the effective coupling between any two neurons and . Intuitively, two neurons are effectively connected if they are connected to the same HUs (Equation 17).
From inter-neuron to inter-region connectivity
Request a detailed protocolIn the above section, we have derived the inter-neuronal connectivity matrix . This matrix is then aggregated to an inter-regional connectivity matrix by taking the normalised L1-norm of the corresponding matrix block elements (i.e., , where is the set of neurons in region ).
Next, to derive the average connectivity matrix across multiple recordings, we used a weighted average of the individual recordings, with a region-pair specific weight equal to the length of the recording multiplied by the sum of the number of neurons in both regions (also see Section - ‘Specimen averaging of connectivity matrices’). Compared to a naive average, this weighted average accounts for the variable number of neurons per region between recordings.
Training cRBM models for connectivity estimates
Request a detailed protocolConstructing the functional connectivity matrix of a cRBM does not require test data, but just the estimated weight matrix (as explained above). Therefore we trained new cRBMs using the entire recordings (100% of data) to fully use the information available. cRBM training is stochastic, and to mitigate the possible variability that could arise we trained five cRBMs for each recording. Then, to assess convergence, we selected all cRBMs with , where std denotes standard deviation, for further functional connectivity analysis (yielding 23 cRBMs for 8 data sets in total). Connectivity estimates of multiple cRBM models per data sets were averaged.
Connectivity inference baselines
Request a detailed protocolWe considered four additional connectivity inference baseline methods:
The covariance matrix.
The Pearson correlation matrix.
The sparse inverse covariance matrix inferred by graphical LASSO (Friedman et al., 2008) (as implemented in scikit-learn with default settings Pedregosa, 2011). Graphical LASSO is an efficient method for inference of large scale connectivity. Unfortunately, the implementation available failed to converge in reasonable time due to the high dimensionality of the data.
The Ising model with pseudo-likelihood maximization (PLM) inference (Ravikumar et al., 2010).
Results obtained with the covariance and correlation matrices are presented in Figure 6—figure supplement 1. The connectivity matrices obtained by the PLM Ising model (not shown) correctly identified the diagonal entries of the region-region matrix, but not the off-diagonal coefficients and had a weaker correlation with the structural connectivity matrix than the covariance and correlation matrices ( using 4 fish).
Optimizing the free parameters of cRBM
We set the free parameters (sparsity regularization parameter) and (number of HUs) by cross-validating a large range of values for one data set (fish #3). This was done by training cRBMs on 70% of the data, and evaluating model performance on the remaining test data, as detailed below. The resulting optimal values could then be used for all data sets (where was scaled with the number of neurons ). Importantly, the parameters implicitly tune the average assembly size. Increasing the number of HUs and/or increasing the regularization strength decreases the average number of neurons per assembly (Tubiana et al., 2019a). Intuitively, assemblies that are too small do not have the capacity to capture high-order correlations, while assemblies that are too large would fail to account for local co-activations. Hence, the -cross-validation effectively identifies the optimal assembly sizes that fit the data statistics.
Train / test data split
Request a detailed protocolWe split up one recording (fish #3) into training data (70% of recording) and withheld test data (30% of recording) for the free parameter () optimization procedure. This enabled us to assess whether the cRBMs learned to model the data statistics (as described in the main text, Figure 2, Figure 2—figure supplement 1), while ensuring that the cRBMs are not overfitted to the specific training data configurations. Importantly, this assumes that the test data comes from the same statistical distribution as the training data (while consisting of different data configurations). To ensure this, we split up the recording of example fish #3 (used for parameter optimization) in training and test splits as follows (before training the cRBMs): We divided the recording of length in 10 chronological segments of equal length (so that segment 1 has time points et cetera), with the rationale that by maintaining temporal order within each segment we would later be able to conduct dynamic activity analysis. This yielded possible training/test splits of the neural data. We then evaluated the statistical similarity between the training and test split of each combination, by assessing the mean neural activity and pairwise neural correlations statistics. We quantified the similarity between training and test statistics by calculating the Root Mean Square Error (). The most similar split is defined by the lowest RMSE, but to show that cRBM are not dependent on picking the best possible split, but rather on avoiding the bad splits, we then chose to use the split with the -percentile ranking RMSE. We hope that this aids future studies, where a potentially high number of possible splits prevents researchers from evaluating all possible splits, but a good split may nevertheless be found efficiently.
Assessment of data statistics
Request a detailed protocolPlease note that the loss function, the log-likelihood, is computationally intractable and therefore cannot be readily used to monitor convergence or goodness-of-fit after training (Fischer & Igel and Igel, 2012). Moreover, approximations of the log-likelihood based on annealed importance sampling were found to be unreliable due to the large system size. However, because (c)RBM learn to match data statistics to model statistics (see Materials and methods–RBM training), we can directly compare these to assess model performance. Therefore, we assessed the following quantities.
Matching data statistics to model statistics
Request a detailed protocolFirstly, we evaluated three statistics that cRBMs are trained to optimize: the mean activity of neurons , the mean activity of HUs and their pairwise interactions . Additionally, second order statistics of pairwise neuron-neuron interactions , HU-HU interactions and the reconstruction quality were evaluated, which the cRBM was not constrained to fit. Monitoring HU single and pairwise statistics and served two purposes: (i) validation of model convergence and (ii) assessing whether correlations between assemblies can be captured by this bipartite model (i.e., without direct couplings between hidden units or an additional hidden layer). For each statistic , we computed its value based on empirical data and on the model , which we then quantitatively compared to assess model performance.
Data statistics were calculated on withheld test data (30% of recording). Naturally, the neural recordings consisted only of neural data and not of HU data . We therefore computed the expected value of at each time point conditioned on the empirical data , as further detailed in Methods - ‘From data to features’.
Model statistics cannot be calculated exactly, because that would require one to sample all possible states , and were therefore approximated by evaluating cRBM-generated data. Here, 300 Monte Carlo chains were each initiated on random training data configurations and 50 configurations were sampled consecutively for each chain, with 20 sampling steps between saved configurations, after a burn-in period of 100 effective sampling configurations.
The statistic (Figure 2C) was corrected for the sparsity regularization, by adding the sparsity regularization parameter to . Furthermore, pairs with exactly were excluded from analysis (5% of total for optimal cRBM in Figure 2C).
The pairwise neuron-neuron and HU-HU statistics (, ) were corrected for their (trivially) expected correlation due to their mean activities (by subtraction of and respectively), so that only true correlations were assessed.
Calculating the normalized Root Mean Square Error
Request a detailed protocolGoodness of fit was quantified by computing the normalized Root Mean Square Error (nRMSE) for each statistic (shown in Figure 2—figure supplement 1). The RMSE between two vectors of length is defined as . Ordinary RMSE was normalized so that different statistics could be compared, where 1 corresponds to , where both data and model statistics were randomly shuffled, and 0 corresponds to which is the RMSE between the training data and test data (by ).
Reconstruction quality
Request a detailed protocolAdditionally, we assessed the reconstruction quality of the test data. Here, the log-likelihood (LLH) between the test data and its reconstruction was computed. Because , the LLH is defined as
(18)
The resulting LLH was normalized (nLLH) such that 0 corresponds to an independent model (i.e., fitting neural activity with ) and 1 to optimal performance (which is ), by .
Generalized Linear Model
Request a detailed protocolWe used logistic regression, a Generalized Linear Model (GLM), to quantify the reconstruction quality of a fully connected model (i.e., with neuron-to-neuron connections, see Figure 2—figure supplement 2A). Logistic regression makes a probabilistic binary prediction (Bishop, 2006), hence allowing direct comparison to the probabilistic estimates of neural activity by the cRBM. In logistic regression, for a neuron at time , the activity of all other neurons at time was used to predict where is the estimated weight vector. This was implemented with scikit-learn (Pedregosa, 2011), using L2 regularization. L2 regularization was favored over L1 as it typically yields higher reconstruction performance; in the related context of protein contact map prediction, L2-regularized GLMs also better reconstructed contacts than L1-regularized GLMs (Morcos et al., 2011). The parameter was optimized to using cross-validation (Figure 2—figure supplement 2B). This is a computationally intensive model to compute because of the large number of regressor neurons : only matrix rows could be inferred in 1 day on a 16-thread CPU desktop computer. Therefore, we performed the cross-validation of Figure 2—figure supplement 2B on 2% of all neurons (=1050 neurons) and computed the final distribution of Figure 2H on 10% of all neurons (=5252 neurons). GLMs were trained on the same train data as cRBMs, and evaluated on the same withheld test data as cRBMs (as described above).
Variational Autoencoders
Request a detailed protocolVariational Autoencoders (VAEs) were implemented in Tensorflow (2.1.10) using Keras (Chollet, 2015). For the encoder, we used a two-layer perceptron with intermediate layer size equal to the dimension of the latent space, a ReLU non-linearity for the intermediate layer and no non-linearity for the conditional mean and log-variance outputs. Batch normalization was used after each dense layer of the encoder. For the decoder, we used a dense layer with a sigmoid non-linearity (no batch normalization). To obtain sparse assemblies, a L1 penalty on the weights of the decoder was added, such that the latent variables correspond to sparse neural assemblies at generation time. Models were trained by ELBO maximization using a very similar protocol as cRBMs: 200 K updates using the Adam optimizer (initial learning rate , , batch size: 100), with geometric decay schedule of learning rate after 50% of the training to a final learning rate of . We tested the same hyperparameter range as for cRBMs, and selected the optimal model based on the held-out ELBO values (10 Gaussian samples per data configuration were used to compute the ELBO). The optimal hyperparameters were , , but several values were very close to optimal (Figure 2—figure supplement 7A), including the value used for cRBMs (, ). We chose the latter for comparison to cRBM for the sake of simplicity, although we also included performance metrics of the VAE model (Figure 2—figure supplement 7B-H).
Regional occupancy
Request a detailed protocolWe determined the anatomical region labels of each neuron by registering our recordings to the ZBrain Atlas (as described previously). This yields a matrix of size , which elements are if neuron is embedded in region and 0 if it is not. A cRBM neural assembly of HU μ is defined by its weight vector (of size ). Because cRBMs converge to sparse solutions, most of the weight elements will be very close to 0. To determine which anatomical regions are occupied by the assembly neurons with significantly nonzero weights, we computed the dot product between the weight vector and matrix , leading to a weighted region label vector (of size ) for each HU. The matrix of all weighted region label vectors is shown in Figure 2—figure supplement 6A for cRBM and Figure 2—figure supplement 6B for PCA.
The effective number of anatomical regions that one cRBM/PCA assembly is embedded in was then calculated using the Participation Ratio (PR) of each HU/Principal Axis. PRs are used to estimate the effective number of nonzero elements in a vector, without using a threshold (Tubiana and Monasson, 2017). The PR of a vector is defined by:
(19)
PR varies from when only 1 element of is nonzero and when all elements are equal. We therefore estimated the effective number of regions by multiplying PR of the weighted region label vectors with the total number of regions in Figure 2—figure supplement 6C.
Time constant calculation
Request a detailed protocolThe dReLU potential of Equation 13 can learn to take a variety of shapes, including a double-well potential (Tubiana et al., 2019a). HUs generally converged to this shape, giving rise to bimodal HU activity distributions (Figure 4). We determined the positions of the two peaks per HU using Gaussian Mixture Models fitted with two Gaussians. The bimodality transition point was then defined as the average between the two peaks (which was approximately 0 for most HUs). To calculate the time constant of state changes between the two activity modes, we subtracted the bimodality transition point from each HU activity individually. For clarity, all dynamic activity traces shown (e.g. Figure 4) are thus bimodality transition point subtracted. The time constant of an activity trace was then defined as the period of a (two-state) oscillation. A HU oscillation is defined as a consecutive negative and positive activity interval (because the bimodality now occurs at 0). A neuron oscillation is defined as a consecutive interspike-interval and spike-interval (which can last for multiple time steps, for example see Figure 1A, right panel).
Sorting of HUs
Request a detailed protocolHUs were sorted by hierarchical clustering of the Pearson correlation matrix of their dynamic activity (Figure 2B). Hierarchical clustering was performed using the Ward variance minimization algorithm that defines the distance between clusters (Virtanen et al., 2020). This sorting of HUs (and thus assemblies) is maintained throughout the manuscript for the sake of consistency.
Validating that the cRBM is in the compositional phase
Request a detailed protocolTo validate that the cRBMs converged to the compositional phase (see section - ‘Compositional restricted boltzmann machine’, compositional RBM formulation), we calculated the effective number of active HUs per data configuration (i.e., time step) where PR is the participation ratio (Equation 19), the number of HUs and , where is the inactive peak as calculated with the Gaussian Mixture Models (see section - ‘Time constant calculation’), because PR assumes that inactive elements are approximately zero (Tubiana et al., 2019a). A cRBM is said to be in the compositional phase if , which is true for all cRBMs (Figure 2—figure supplement 3).
Extensions of the structural connectivity matrix
Request a detailed protocolThe inter-region structural connectivity matrix was derived from the single cell zebrafish brain atlas (Kunst et al., 2019). We used the post-publication updated data set from Kunst et al., 2019 (timestamp: 28 October 2019). The data set consists of neurons, each characterized by the 3D coordinates of the soma center and of its neurites; there is no distinction between dendrites and axons. The brain is subdivided into regions and each neuron is duplicated by left/right hemisphere symmetry. We aim to estimate , the average strength of the connection between two neurons belonging to regions . For each neuron , we determine, using region masks, the region where its soma is located and the cumulative length of the intersection between all its neurites and each region . Under the assumptions that (i) the linear density of dendritic spines / axon presynaptic boutons is constant and (ii) the volumetric density of neurons is identical throughout regions, is proportional to the volume of region times the average (bidirectional) connection strength between neuron and any neuron of region . Aggregating over all neurons and symmetrizing, we obtain the following estimator for :
(20)
where if neuron has its soma in region and 0 if not. Using the same notations, the formula previously used in Kunst et al., 2019 is:
(21)
Equation 20 differs from Equation 21 in three aspects:
It discriminates between direct and indirect connections. Previously, a structural connection between region and region was established if a neuron had neurites with either tips or its soma within both regions. This may however result in indirect connections between and , in cases where the neuron soma resides in another region . Here, we only account for direct connections, resulting in an overall slightly sparser connectivity matrix.
It is well-defined along the diagonal, i.e., for intra-region connections, whereas in Equation 21, each neurite would be counted as a self-connection.
The denominator corrects for non-uniform sampling of the traced neurons throughout regions. Note that this issue only arose in the post-publication data set as non-uniform sampling was used to fill missing entries of the matrix.
Specimen averaging of connectivity matrices
Request a detailed protocolThe number of neurons in a particular brain region can vary across recordings from different specimen. Since the entries of the connectivity matrix are expected to be more accurate for well-sampled regions, we computed the weighted average of region-to-region connections as follows:
(22)
Where is the recording length and is the number of neurons in region of fish that were recorded.
Correlation analysis of connectivity matrices
Request a detailed protocolPearson correlation was used to assess the similarity between cRBM functional connectivity matrices of different individual animals (Figure 5). Spearman correlation was used to compare structural connectivity versus functional connectivity (Figure 6), because these two metrics do not necessarily scale linearly. All correlation analyses, and the Kilmogorov-Smirnov test of Figure 6—figure supplement 1C, performed on symmetric matrices excluded one off-diagonal triangle (of symmetrical values) to avoid duplicates.
Data availability
The cRBM model has been developed in Python 3.7 and is available at: https://github.com/jertubiana/PGM (copy archived at swh:1:rev:caf1d9fc545120f7f1bc1420135f980d5fd6c1fe). An extensive example notebook that implements this model is also provided. Calcium imaging data pre-processing was performed in MATLAB (Mathworks) using previously published protocols and software (Panier et al., 2013; Wolf et al., 2017; Migault et al., 2018; Tubiana et al., 2020). The functional data recordings, the trained cRBM models and the structural and functional connectivity matrix are available at https://gin.g-node.org/vdplasthijs/cRBM_zebrafish_spontaneous_data. Figures of neural assemblies or neurons (Figure 1, 3) were made using the Fishualizer, which is a 4D (space + time) data visualization software package that we have previously published (Migault et al., 2018), available at https://bitbucket.org/benglitz/fishualizer_public . Minor updates were implemented to tailor the Fishualizer for viewing assemblies, which can be found at https://bitbucket.org/benglitz/fishualizer_public/src/assembly_viewer/. All other data analysis and visualization was performed in Python 3.7 using standard packages (numpy [Harris et al., 2020], scipy [Virtanen et al., 2020], scikit-learn [Pedregosa, 2011], matplotlib [Hunter, 2007], pandas [McKinney, 2010], seaborn [Waskom, 2021], h5py). The corresponding code is available at https://github.com/vdplasthijs/zf-rbm (copy archived at swh:1:rev:b5df4e37434c0b18120485b8d856596db0b92444).
-
GINID cRBM_zebrafish_spontaneous_data. Data from: Neural assemblies uncovered by generative modeling explain whole-brain activity statistics and reflect structural connectivity.
References
-
Handbook of mathematical functions with formulas, graphs, and mathematical tablesAmerican Journal of Physics 56:958.https://doi.org/10.1119/1.15378
-
Large-scale imaging in small brainsCurrent Opinion in Neurobiology 32:78–86.https://doi.org/10.1016/j.conb.2015.01.007
-
Habenula circuit development: past, present, and futureFrontiers in Neuroscience 6:51.https://doi.org/10.3389/fnins.2012.00051
-
Searching for collective behavior in a small brainPhysical Review. E 99:052418.https://doi.org/10.1103/PhysRevE.99.052418
-
Systematic errors in connectivity inferred from activity in strongly recurrent networksNature Neuroscience 23:1286–1296.https://doi.org/10.1038/s41593-020-0699-2
-
Bayesian inference of neuronal assembliesPLOS Computational Biology 15:e1007481.https://doi.org/10.1371/journal.pcbi.1007481
-
Random versus maximum entropy models of neural population activityPhysical Review. E 95:042321.https://doi.org/10.1103/PhysRevE.95.042321
-
Modeling the correlated activity of neural populations: a reviewNeural Computation 31:233–269.https://doi.org/10.1162/neco_a_01154
-
ConferenceRestricted boltzmann machines provide an accurate metric for retinal responses to visual stimuli5th International Conference on Learning Representations, ICLR 2017. pp. 24–26.
-
Neuronal assembliesIEEE Transactions on Bio-Medical Engineering 36:4–14.https://doi.org/10.1109/10.16444
-
Neural signatures of cell assembly organizationNature Reviews. Neuroscience 6:399–407.https://doi.org/10.1038/nrn1669
-
Training products of experts by minimizing contrastive divergenceNeural Computation 14:1771–1800.https://doi.org/10.1162/089976602760128018
-
Matplotlib: a 2D graphics environmentComputing in Science & Engineering 9:90–95.https://doi.org/10.1109/MCSE.2007.55
-
Information theory and statistical mechanicsPhysical Review 106:620–630.https://doi.org/10.1103/PhysRev.106.620
-
Modeling higher-order correlations within cortical microcolumnsPLOS Computational Biology 10:e1003684.https://doi.org/10.1371/journal.pcbi.1003684
-
ConferenceNumba: A llvm-based python jit compilerProceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC. pp. 1–6.
-
Detecting cell assemblies in large neuronal populationsJournal of Neuroscience Methods 220:149–166.https://doi.org/10.1016/j.jneumeth.2013.04.010
-
Development of oculomotor circuitry independent of hox3 genesNature Communications 5:1–12.https://doi.org/10.1038/ncomms5221
-
ConferenceData Structures for Statistical Computing in PythonPython in Science Conference. pp. 51–56.https://doi.org/10.25080/Majora-92bf1922-00a
-
Redundancy and synergy of neuronal ensembles in motor cortexThe Journal of Neuroscience 25:4207–4216.https://doi.org/10.1523/JNEUROSCI.4697-04.2005
-
Cell assemblies in the cerebral cortexBiol Cybern 108:559–572.https://doi.org/10.1007/s00422-014-0596-4
-
Scikit-learn: machine learning in pythonThe Journal of Machine Learning Research 12:2825–2830.
-
Integration and multiplexing of positional and contextual information by the hippocampal networkPLOS Computational Biology 14:e1006320.https://doi.org/10.1371/journal.pcbi.1006320
-
Whole-Brain activity mapping onto a zebrafish brain atlasNature Methods 12:1039–1046.https://doi.org/10.1038/nmeth.3581
-
High-dimensional ising model selection using ℓ1-regularized logistic regressionThe Annals of Statistics 38:1287–1319.https://doi.org/10.1214/09-AOS691
-
The structure of large-scale synchronized firing in primate retinaThe Journal of Neuroscience 29:5022–5031.https://doi.org/10.1523/JNEUROSCI.5187-08.2009
-
BookInformation processing in dynamical systems: foundations of harmony theoryIn: Rumelhart DE, McClellan JL, editors. Parallel Distributed Processing Chapter 6. Cambridge: MIT Press. pp. 194–281.
-
ConferenceTraining restricted Boltzmann machines using approximations to the likelihood gradient25th international conference. pp. 1064–1071.https://doi.org/10.1145/1390156.1390290
-
ConferenceUsing fast weights to improve persistent contrastive divergenceProceedings of the 26th annual international conference on machine learning. pp. 1033–1040.
-
Emergence of spontaneous assembly activity in developing neural networks without afferent inputPLOS Computational Biology 14:e1006421.https://doi.org/10.1371/journal.pcbi.1006421
-
Model-based decoupling of evoked and spontaneous neural activity in calcium imaging dataPLOS Computational Biology 16:e1008330.https://doi.org/10.1371/journal.pcbi.1008330
-
Emergence of compositional representations in restricted Boltzmann machinesPhysical Review Letters 118:138301.https://doi.org/10.1103/PhysRevLett.118.138301
-
BookRestricted Boltzmann Machines: From Compositional Representations to Protein Sequence AnalysisParis, France: PSL Research University.
-
Blind deconvolution for spike inference from fluorescence recordingsJournal of Neuroscience Methods 342:108763.https://doi.org/10.1016/j.jneumeth.2020.108763
-
SoftwareProbabilistic graphical models (PGM, version swh:1:rev:caf1d9fc545120f7f1bc1420135f980d5fd6c1feSoftware Heritage.
-
Integrative whole-brain neuroscience in larval zebrafishCurrent Opinion in Neurobiology 50:136–145.https://doi.org/10.1016/j.conb.2018.02.004
-
Light-Sheet functional imaging in fictively behaving zebrafishNature Methods 11:883–884.https://doi.org/10.1038/nmeth.3040
-
Seaborn: statistical data visualizationJournal of Open Source Software 6:3021.https://doi.org/10.21105/joss.03021
-
The structure of the nervous system of the nematode Caenorhabditis elegansPhilosophical Transactions of the Royal Society of London. Series B, Biological Sciences 314:1–340.https://doi.org/10.1098/rstb.1986.0056
-
Sensorimotor computation underlying phototaxis in zebrafishNature Communications 8:651.https://doi.org/10.1038/s41467-017-00310-3
Decision letter
-
Peter LathamReviewing Editor; University College London, United Kingdom
-
Laura L ColginSenior Editor; University of Texas at Austin, United States
In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.
[Editors' note: this paper was reviewed by Review Commons.]
https://doi.org/10.7554/eLife.83139.sa1Author response
Reviewer #1 (Evidence, reproducibility and clarity (Required)):
Summary:
In the present manuscript, van der Plas et al. compellingly illustrated a novel technique for engendering a wholebrain functional connectivity map from single-unit activities sampled through a large-scale neuroimaging technique. With some clever tweaks to the restricted Boltzmann Machine, the cRBM network is able to learn a low-dimensional representation of population activities, without relying on constrained priors found in some traditional methods. Notably, using some 200 hidden layer neurons, the employed model was able to capture the dynamics of over 40,000 simultaneously imaged neurons with a high degree of accuracy. The extracted features both illustrate the anatomical topography/connectivities and capture the temporal dynamics in the evolution of brain states. The illustrated technique has the potential for wide-spread applications spanning diverse recording techniques and animal species. Furthermore, the prospectives of modeling whole-brain network dynamics in 'neural trajectory' space and of generating artificial data in silico make for very enticing reasons to adopt cRBM.
Major comments:
1. Line 164. The authors claim that conventional methods "such as k-means, PCA and non-negative matrix factorization" cannot be quantitatively assessed for quality on the basis that they are unable to generate new artificial data. Though partly true, in most neuroscience applications, this is hardly cause for concern. Most dimensionality reduction methods (with few exceptions such as t-sne) allow new data points to be embedded into the reduced space. As such, quality of encoding can be assessed by cross-validation much in the same way as the authors described, and quantified using traditional metrics such as percentage explained variance. The authors should directly compare the performance of their proposed model against that of NNMF and variational auto-encoders. Doing so would offer a more compelling argument for the advantage of their proposed method over more widely-used methods in neuroscience applications. Furthermore, a direct comparison with rastermap, developed by Stringer lab at Janelia (https://github.com/MouseLand/rastermap), would be a nice addition. This method presents itself as a direct competitor to cRBM. Additionally, the use of GLM doesn't do complete justice to the comparison point used, since a smaller fraction of data were used for calculating performance using GLM, understandably due to its computationally intensive nature.
We thank the reviewer for the comment, and certainly agree that there are multiple methods for unsupervised feature extraction from data and that they can be validated for encoding quality by cross-validation. Below, we follow the reviewers suggestion to directly compare with VAEs, but argue first that a comparison with NNMF and rastermap is not appropriate. Specifically, we would like to stress that reconstructing through a low-dimensional, continuous bottleneck is a different (and arguably, easier) task, than generating whole distributions as the cRBM does. Reconstruction delineates the manifold of possible configurations, whereas generative modeling must weigh such configurations adequately. Moreover, none of the methodologies mentioned can perform the same tasks as cRBMs. For instance, NNMF learns localized assemblies, but cannot faithfully model inhibitory connections since, by definition, only nonnegative weights are learnt. Also, the connection between the learnt assemblies and the underlying connectivity is unclear. Similarly, rastermap is an algorithm for robustly i) sorting neurons along a set number of dimensions (typically 1 or 2) such that neighboring neurons are highly correlated, and ii) performing dimensionality reduction by clustering along these dimensions. Because Rastermap uses kmeans as the basis for grouping together neurons, it does not quantify connections between neurons and assemblies, nor assign neurons to multiple assemblies. Moreover, it is not a generative model, and thus cannot predict perturbation experiments, infer connectivities or assign probabilities to configurations. Therefore, we do not believe that NNMF or Rastermap would be a suitable alternative for cRBM in our study. We nonetheless appreciate the reviewer’s suggestions and agree that we should motivate more clearly why these methods are not applicable for our purposes. Therefore, to emphasize the relative merit of cRBM with respect to other unsupervised algorithms, we now provide a table (Supplementary Table 2) that lists their specific characteristics. We stress that we do not claim that cRBM are consistently better than these classical tools for dimensionality reduction, but focus only on the properties relevant to our study.
Regarding VAEs, we agree that these are close competitors of cRBMs, as they also jointly learn a representation and distribution of the data,. In Tubiana et al. Neural Computation 2019, we previously compared sparse VAEs with cRBMs for protein sequence modeling, and found that RBMs consistently outperformed VAEs. In the revised manuscript, we repeated the comparison with VAEs for Zebrafish neural recordings, and reached similar conclusions. Specifically, we found that for sparse linear VAEs trained using a similar protocol as cRBMs (ELBO loss minimization using ADAM optimizer, sparsity regularization, hyperparameter search using held-out validation set): i) the generated samples failed to replicate the second-order statistics of the data ii) the VAE could not reconstruct accurately neural spikes from the latent representation and iii) the majority (~60%) of the latent variables were completely disconnected from the neurons, and the remaining ones had highly variable size. This analysis shows that cRBMs consistently outperform VAE in terms of both interpretability and performance. The comparison between cRBM and VAE performance is now provided in the Manuscript (Section 7.10.4), and illustrated in Supplementary Figure S7 (shown below).
Results 2.2, last paragraph:
“We next asked whether sparsity alone was sufficient for a generative model to accurately recapitulate the neural recording statistics. To address this question, we trained sparse linear Variational Autoencoders (VAEs) using the same parameter-optimization protocol (Figure S7A). Like cRBMs, linear VAEs are generative models that learn a latent representation of a dataset (Tubiana et al., 2019a). We observed that VAEs were not able to replicate the second-order statistics, and therefore were not able to reconstruct neural activity from latent representation (Figure S7B-D), even though they also obtained sparse representations (Figure S7E, F).”
Discussion, 3rd paragraph
“In this study we repeated this comparison with sparse linear VAEs, and reached similar conclusions: VAEs trained using the same protocol as cRBMs failed to reproduce second-order data statistics and to reconstruct neural activity via the latent layer, while the learnt assemblies were of substantially lower quality (indicated by a large fraction of disconnected HUs, as well as a highly variable assembly size) (Figure S7).”
As for GLM, it is true that the comparison involved subsampling of the neurons (10%, i.e. 5252 neurons, due to the very high computational cost of GLM, where we could estimate the connectivity of ~1000 neurons per day). This was already denoted in the relevant figure caption, as the reviewer has seen, but we have now also clarified this point in Methods 7.10.3.
We think that, because this is a large and randomly selected sample of neurons, these 5252 neurons represent the full data set, and the GLM distribution of reconstruction likelihood (Figure 2H) will not change qualitatively if a larger sample would be used.
In contrast to GLM, optimized cRBM models converged learning of the entire data set in half a day, emphasizing their ability to handle very large datasets, such as the presently used zebrafish whole-brain recordings, which is crucial for any model to be applied in practice.
2. Line 26. The authors describe their model architecture as a formalization of cell assemblies. Cell assemblies, as originally formulated by Hebb, pertains to a set of neurons whose connectivity matrix is neither necessarily complete nor symmetric. Critically, in the physiological brain, the interactions between the individual neurons that are part of an assembly would occur over multiple orders of dependencies. In a restricted Boltzmann machine, neurons are not connected within the same layer. Instead, visible layer neurons are grouped into "assemblies" indirectly via a shared connection with a hidden layer neuron. Furthermore, a symmetrical weight matrix connects the bipartite graph, where no recurrent connectivities are made. As such, the proposed model still only elaborates symmetric connections pertaining to first-order interactions (as illustrated in Figure 4C). Such a network may not be likened with the concept of cell assemblies. The authors should refrain from detailing this analogy (of which there are multiple instances of throughout the text). It is true that many authors today refer to cell assemblies as any set of temporally-correlated neurons. However, saying "something could be a cell assembly" is not the same as saying "something is a cell assembly". How about sticking with cRBM-based cell assemblies (as used in section 2.3) and defining it beforehand?
We thank the reviewer for this excellent question. We agree that there is, in general, a discrepancy between computationally-defined assemblies and conceptual/neurophysiological definition of cell assemblies. We have added a clarification in Results 2.1 to clarify the use of this term when it first occurs in Results. However, we still believe that our work contributes to narrowing the gap. Indeed, our RBM-defined assemblies are i) localized, ii) overlapping, iii) rooted in connectivity patterns (both excitatory and inhibitory), and iv) cannot be reduced to a simple partitioning of the brain with full and uniform connectivity within and between partitions. This is unlike previous work based on clustering (no overlaps or heterogeneous weights), NNMF (no inhibition) or correlation network analysis (no low-dimensional representation).
Regarding the specific comments pointed here, we stress that:
– Effective interactions between neurons are not purely pairwise (“First order”), due to the usage of the non-quadratic potential. (see Equation 12-13). If the reviewer means by “First-order” interactions the lack of hierarchical organization, we agree, to some extent: in the current formulation, correlations between assemblies are mediated by overlaps between their weights. Fully hierarchical organization, e.g. by using Deep Boltzmann Machines or pairwise connections within the hidden layer is an interesting future direction, but on the other hand may make it hard to clearly identify assemblies as they might be spread out over multiple layers
– Neurons that participate in a given assembly (as defined by a specific hidden unit) are not all connected with one another with equal strength. Indeed, these neurons may participate in other assemblies, resulting in heterogeneity of connections (see Equation. 15-17) and interactions between assemblies.
– We acknowledge that the constraint of symmetrical connections is a core limitation of our method. Arguably, asymmetric connections are critical for predicting temporal evolution but less important for inferring a steady-state distribution from data, as we do here.
In the revised submission, we added a new paragraph in the Discussion section (lines 350-356) in which these limitations are discussed, including the imposed symmetry of the connections and the lack of hierarchical structures, copied below. We trust that this addresses the reviewer’s criticism:
In sum, cRBM-inferred cell assemblies display many properties that one expects from physiological cell assemblies: they are anatomically localized, can overlap, encompass functionally identified neuronal circuits and underpin the collective neural dynamics (Harris, 2005, 2012; Eichenbaum, 2018). Yet, the cRBM bipartite architecture lacks many of the traits of neurophysiological circuits. In particular, cRBMs lack direct neuron-to-neuron connections, asymmetry in the connectivity weights and a hierarchical organization of functional dependencies beyond one hidden layer. Therefore, to what extent cRBM-inferred assemblies identify to neurophysiological cell assemblies, as postulated by Hebb (1949) and others, remains an open question.
3. I would strongly recommend adding a paragraph discussing the limitation of using the cRBM, things future researchers need to keep in mind before using this method. One such recommendation is moving the runtimerelated discussion for cRBM, i.e. 8-12 hrs using 16 CPU from Methods to Discussion, since it's relevant for an algorithm like this. Additionally, a statement mentioning how this runtime will increase with the length of recordings and/or with the number of neurons might be helpful. What if the recordings were an hour-long rather than 25mins. This would help readers decide if they can easily use a method like this.
We thank the reviewer for the suggestion, and agree that it is important to cover the computational cost in the main text. Regarding the runtime for longer recordings, the general rule of thumb is that the model requires a fixed number of gradient updates to converge (20-80k depending on the data dimensionality) rather than a fixed number of epochs. Thus, runtime should not depend on recording length, as the number of epochs can be reduced for longer recordings. While we did not verify this rule for neural recordings, this is what we previously observed when modeling protein/DNA sequence data sets, whose size range from few hundreds to hundreds of thousands of samples (Tubiana et al., 2019, eLife; Tubiana et al. 2019, Neural Computation; Bravi et al. Cell Systems 2021; Bravi et al. PLOS CB 2021; Fernandez de Cossio Diaz et al. Arxiv 2022 Di Gioacchino et al. BiorXiv 2022). We have now added a summary of these points in Methods 7.7.2, also refer to this with explicit mention of the runtime in the Discussion, end of 2nd paragraph:
By implementing various algorithmic optimizations (Methods 7.7), cRBM models converged in approximately 812 hours on high-end desktop computers (also see Methods 7.7.2).
4. Line 515. A core feature of the proposed compositional RBM is the addition of a soft sparsity penalty over the weight matrix in the likelihood function. The authors claim that "directed graphical models" are limited by the a priori constraints that they impose on the data structure. Meanwhile, a more accurate statistical solution can be obtained using a RBM-based model, as outlined by the maximum entropy principle. The problem with this argument is that the maximum entropy principle no longer applies to the proposed model with the addition of the penalty term. In fact, the λ regularization term, which was estimated from a set of data statistics motivated by the experimenter's research goals (Figure S1), serves to constrict the prior probability. Moreover, in Figure S1F, we clearly see that reconstruction quality suffers with a higher penalty, suggesting that the principle had indeed been violated. That being said, RBMs are notoriously hard to train, possibly due to the unconstrained nature of the optimization. I believe that cRBM can help bring RBM into wider practical applications. The authors could test their model on a few values of the free parameter and report this as a supplementary. I believe that different parameters of λ could elaborate on different anatomical clusters and temporal dynamics. Readers who would like to implement this method for their own analysis would also benefit tremendously from an understanding of the effects of λ on the interpretation of their data. Item (1) on line 35 (and other instances throughout the text) should be corrected to reflect that cRBM replaces the hard constraints found in many popular methods with a soft penalty term, which allows for more accurate statistical models to be obtained.
We thank the reviewer for their analysis and suggestion. Indeed, adding the regularization term – not present in the classical formulation of the RBM (Hinton and Salakhutdinov, 2006, Science) – was critical for significantly enhancing its performance, which allowed us to implement this model on our large scale datasets (~50K visible units). We agree that providing more information on the effect of the regularization term will benefit readers who would like to use this method. We have now included an extensive analysis of the effects of λ in the revised manuscript, which is detailed in our answer to a similar question from reviewer 2. We therefore refer to our answer in response to the first question of reviewer 2.
The reviewer’s comment on the Maximum Entropy issue calls for some clarification. The maximum entropy principle is a recipe for finding the least constrained model that reproduces specified data-dependent moments. However, it cannot determine which moments are statistically meaningful in a finite-sized data set. A general practice is to only include low-order moments (1st and 2nd), but this is sometimes already too much for biological data. Regularization provides a practical means to select stable moments to be fitted and others to be ignored. This can be seen from the optimality condition, which writes, e.g., for the weights wi,mu:
| < vi h,mu>data – < vi h,mu>model | < λ if wi,mu = 0.
< vi h,mu>data – < vi h,mu>model | = λ(wi,mu) if |wi,mu| > 0.
Essentially, this lets the training decide which subset of the constraints should actually be used. Thus, regularized models are closer to the uniform distribution (g=w=0), and actually have higher entropy than unregularized one (see, e.g., Fanthomme et al. Journal of Statistical Mechanics, 2022). Therefore, we believe that a regularized maximum entropy model can still be considered a bona fide MaxEnt model. This formulation should not be confused with another formulation (that perhaps the reviewer has in mind) where a weighted sum of the entropy and the regularization term is maximized under the same moment-matching constraints. In this case, we agree that maximum entropy principle (MaxEnt) would be violated.
The choice of regularization value should be dictated by bias-variance trade-off considerations. Ideally, we would use the same criterion as for training, i.e., maximization of log-likelihood for the held-out test set, but it is intractable. Thus, we used a consensus between several tractable performance metrics as a surrogate; we believe this consensus to be principally independent of the research goal. While the reconstruction error indeed increases for large regularization values, this is simply because too few constraints are retained at high regularizations.
Essentially, the parameters selected by likelihood maximization find the finest assembly scale that can be accommodated by the data presented. Thus, the number and size of the assemblies are not specified by the complexity of the data set alone. Rather, the temporal resolution and length of the recordings play a key role; higher resolution recordings will allow the inference of a larger number of smaller assemblies, and enable the study of their hierarchical organization.
That being said, we fully agree that the regularization strength and number of hidden units have a strong impact on the nature of the representation learnt. In the revised manuscript, we follow the reviewer’s suggestion and provide additional insights on the effect of these parameters on the representation learnt (please see p9-10).
Minor comments:
5. From a neuroscience point of view, it might be interesting to show what results are achieved using different values of M (say 100 or 300), rather than M=200, while still maintaining the compositional phase. Is there any similarity between the cRBM-based cell assemblies generated at different values of M? Is there a higher chance of capturing certain dynamics either functional or structural using cRBM? For example, did certain cRBM-based cell assemblies pop up more frequently than others at all values of M (100,200,300)?
Please find the answer p9-10, in response to a similar question raised by Reviewer #2, Q1.
6. The authors have mentioned that this approach can be readily applied to data obtained in other animal models and using different recording techniques. It might be nice to see a demonstration of that.
We agree that showing additional data analysis would be interesting, but we feel that it would overburden the supplementary section of the manuscript, which is already lengthy. In previous works, we and collaborators have used cRBMs for analyzing MNIST data (Tubiana and Monasson, 2017, PRL; Roussel et al. 2022 PRE), protein sequence data (Tubiana et al., 2019, eLife; Tubiana et al. 2019, Neural Computation; Bravi et al. Cell Systems 2021; Bravi et al. PLOS CB 2021; Fernandez de Cossio Diaz et al. Arxiv 2022), DNA sequences (Di Gioacchino et al. BiorXiv 2022), spin systems (Harsh et al. J. Phys. A 2020), etc. Many are included as example notebooks – next to the zebrafish data – in the linked code repository. For neural data, we have recently shared our code with another research group working on mice auditory cortex (2-photon, few thousands of neurons, Léger and Bourdieu). Preliminary results are encouraging, but not ready for publication yet.
7. Line 237. The justification for employing a dReLU transfer function as opposed to ReLU is unclear, at least within the context of neurobiology. Given that this gives rise to a bimodal distribution for the activity of HUs, the rationale should be clearly outlined to facilitate interpretability.
We thank the reviewer for the question. As we detail in the manuscript (Methods), the dReLU potential is one of the sufficient requirements for the RBM to achieve the compositional phase. The compositional phase is characterized by localized assemblies that co-activate to generate the whole-brain neural dynamics. This property reflects neurobiological systems (Harris, 2005, Neuron), which is one of the reasons why we employed compositional RBMs for this study.
As the reviewer points out, the HUs that we infer exhibit bimodal activity (Figure 4). Importantly, the HU activity is not constrained by the model to take this shape, as dReLU potentials allow for several activity distributions (see Methods 7.5.4; “Choice of HU potential”). In fact, ReLU potentials are a special case of dReLU (by ), so our model allows HU potentials to behave like ReLUs, but in practice they converge to a double-well potential for almost all HUs, leading to bimodal activity distributions.
Following the suggestion of the reviewer, we have now added this detail for clarity in Methods 7.5.4 and referenced this Methods section at line 237.
Reviewer #1 (Significance (Required)):
van der Plas et al. highlighted a novel dimensionality reduction technique that can be used with success for discerning functional connectivities in large-scale single-unit recordings. The proposed model belongs to a large collection of dimensionality reduction techniques (for review, Cunningham, J., Yu, B. Dimensionality reduction for large-scale neural recordings. Nat Neurosci 17, 1500-1509 (2014). https://doi.org/10.1038/nn.3776; Paninski, L., and Cunningham, J. P. (2018). Neural data science: accelerating the experiment-analysis-theory cycle in largescale neuroscience. Current opinion in neurobiology, 50, 232-241.). The authors themselves highlighted some of the key methods, such as PCA, ICA, NNMF, variational auto-encoders, etc. The proposed cRBM model has also been published a few times by the same authors in previous works, although specifically pertaining to protein sequences. The use of RBM-like methods in uncovering functional connectivities is not novel either (see Hjelm RD, Calhoun VD, Salakhutdinov R, Allen EA, Adali T, Plis SM. Restricted Boltzmann machines for neuroimaging: an application in identifying intrinsic networks. Neuroimage. 2014 Aug 1;96:245-60. doi: 10.1016/j.neuroimage.2014.03.048.). However, given that the authors make a substantial improvement on the RBM network and have demonstrated the value of their model using physiological data, I believe that this paper would present itself as an attractive alternative to all readers who are seeking better solutions to interpret their data. However, as I mentioned in my comments, I would like to see more definitive evidence that the proposed solution has a serious advantage over other equivalent methods.
Reviewer's expertise:
This review was conducted jointly by three researchers whose combined expertise includes single-unit electrophysiology and two-photon calcium imaging, using which our lab studies the neurobiology of learning and memory and spatial navigation. We also have extensive experience in computational neuroscience, artificial neural network models, and machine learning methods for the analysis of neurobiological data. We are however limited in our knowledge of mathematics and engineering principles. Therefore, our combined expertise is insufficient to evaluate the correctness of the mathematical developments.
Reviewer #2 (Evidence, reproducibility and clarity (Required)):
In their manuscript, van der Plas et al. present a generative model of neuron-assembly interaction. The model is a restricted Boltzmann machine with its visible units corresponding to neurons and hidden units to neural assemblies. After fitting their model to whole-brain neural activity data from larval zebrafish, the authors demonstrate that their model is able to replicate several data statistics. In particular, it was able to replicate the pairwise correlations between neurons as well as assemblies that it was not trained on. Moreover, the model allows the authors to extract neural assemblies that govern the population activity and compose functional circuits and can be assigned to anatomical structures. Finally, the authors construct functional connectivity maps from their model that are then shown to correlate with established structural connectivity maps.
Overall, the authors present convincing evidence for their claims. Furthermore, the authors state that their code to train their restricted Boltzmann machine models is already available on GitHub and that the data underlying the results presented in this manuscript will be made publicly available upon publication, which will allow people to reproduce the results and apply the methods to their data.
One thing the authors could maybe discuss a bit more is the "right" parameter value M, especially since they used the optimal value of 200 found for one sample also for all the others. More specifically, how sensitive are the results to this value?
In the following we jointly address three of the reviewers’ questions (2 from reviewer 1, and 1 from reviewer 2).
Shortly summarized, the cRBM model has 2 free parameters; the number of hidden units M and the regularization parameter λ. In figures 2 and S1 we optimize their values through cross-validation, and then perform the subsequent analyses on models with these optimal values. The reviewers ask us to examine the outcome of the model for slightly different values of both parameters, in particular in relation to the sensitivity of the cRBM results to selecting the optimal parameters and the change in inferred assemblies and their dynamics.
We thank the reviewers for these questions and appreciate their curiosity to understand the effects of changing either of these two free parameters.
To assess the influence of both the number of hidden units M and the sparsity regularization parameter λ, we computed, for all cRBMs models trained in the hyperparameter search procedure, two metrics: the distribution of assembly sizes, and the distribution of HU dynamics time scales (as in Figure 4). We have now added a supplementary Figure S5 that shows these two distributions for the grid of M, λ values of Supplementary Figure S1, and have performed two-way ANOVA tests to determine the significance of M and λ on these two metrics. We found that M and λ controlled the distribution of assembly sizes in a consistent manner: assembly size was a gradually decreasing function of both M and λ (Figure S5A-F). Further, M, but not λ, similarly controlled the distribution of time scales (Figure S5G-L). However, for M and λ values close to the optimal parameter-setting (M=200, λ=0.01, determined by model selection), the changes in assembly size and time scale distributions were very gradual and minimal. This showcases the robustness of the cRBM to slight changes in parameter choice.
For illustration purposes, we also added panels M-O of the median-sized assemblies of 3 very different models (M=5, M=20, M=200).
Results 2.2:
To assess the influence of M and λ on the inferred assemblies, we computed, for all cRBM models trained during the optimization of M and λ, the distribution of assembly sizes (Figure S5 A-F). We found that M and λ controlled the distribution of assembly sizes in a consistent manner: assembly size was a gradually decreasing function of both M and λ(twoway ANOVA, both P < 10-3). Furthermore, for M and λ values close to the optimal parameter-setting (M=200, λ=0.02), the changes in assembly size were very small and gradual. This showcases the robustness of the cRBM to slight changes in parameter choice.
And, what happens if one would successively increase that number, would the number of assemblies (in the sense of hidden units that strongly couple to some of the visible units) eventually saturate?
This point will be addressed by inspecting models at different M values (see #1). We would like to further answer this question by referring to past work. In Tubiana et al., 2019, eLife (Appendix 1) we have done this analysis, and the result is consistent with the reviewer’s intuition. Because of the sparsity regularization, if M becomes larger than its optimum, the assemblies further sparsify without benefiting model performance, and eventually new assemblies duplicate previous assemblies or become totally sparse (i.e., all weights = 0) to not further induce a sparsity penalty in the loss function. So the ‘effective’ number of assemblies indeed saturates for high M.
Moreover, regarding the presentation, I have a few minor suggestions and comments that the authors also might want to consider:
– In Figure 6C, instead of logarithmic axes, it might be better to put the logarithmic connectivity on a linear axis. This way the axes can be directly related to the colour bars in Figures 6A and B.
We agree and thank you for the suggestion. We have changed this accordingly (and also in the equivalent plots in figure S6).
– In Equation (8), instead of \it should be
Done, thank you.
– In Section 7.0.5, it might make sense to have the subsection about the marginal distributions before the ones about the conditional distributions. The reason would be that if one wants to confirm Equation (8) one necessarily has to compute the marginal distribution in Equation (12) first.
We thank the reviewer for the suggestion, but respectfully propose to leave the section ordering as is. We understand what the reviewer means, but Equation (8) can also be obtained by factorizing P(v,h) Equation (7) and removing the v_i dependency. In Equation (8), \Γ can then be obtained by normalization. We believe this flow aligns better with the main text (where conditionals come first, when used for sampling, followed by the marginal of P(v) used for the functional connectivity inference).
– In Line 647f, the operation the authors are referring to is strictly speaking not an L1-norm of the matrix block. It might be better to refer to that e.g. as a normalised L1-norm of the matrix block elements.
Done, thank you.
– In Line 22, when mentioning dimensionality reduction methods to identify assemblies, it might make sense to also reference the work by Lopes-dos-Santos et al. (2013, J. Neurosci. Methods 220).
Done, thank you for the suggestion.
Reviewer #2 (Significance (Required)):
The work presented in this manuscript is very interesting for two reasons. First, it has long been suggested that assemblies are a fundamental part of neural activity and this work seems to support that by showing that one can generate realistic whole-brain population activity imposing underlying assembly dynamics. Second, in recent years much work has been devoted to developing methods to find and extract neural assemblies from data and this work and the modelling approach can also be seen as a new method to achieve that. As such, I believe this work is relevant for anyone interested in neural population activity and specifically neural assemblies and certainly merits publication.
Regarding my field of expertise, I used to work on data analysis of neural population activity and in particular on the question of how one can extract neural assemblies from data. I have to say that I have not much experience with fitting statistical models to data, so I can't provide any in-depth comments on that part of the work, although what has been done seems plausible.
Reviewer #3 (Evidence, reproducibility and clarity (Required)):
Summary: Understanding the organization of neural population activities in the brain is one of the most important questions in neuroscience. Recent technique advance has enabled researchers to record a large number of neurons and some times the whole brain. Interpreting and extracting meaningful insights from such data sets are challenging. van der Plas et al applied a generative model called compositional Restricted Boltzmann Machine (cRBM) to discover neuron assemblies from spontaneous activities of zebra fish brain. They found that neurons can be grouped into around 200 assemblies. Many of them have clear neurophysiological meaning, for example, they are anatomically localized and overlapped with known neural circuits. The authors also inferred a coarse-grained functional connectivity which is similar to known structural connectivity.
The structure of the paper is well organized, the conclusion seems well supported by their numerical results. While this study provides a compelling demonstration that cRBM can be used to uncover meaningful structures from large neural recordings, the following issues limit my enthusiasm.
Major:
1) The overall implication is not clear to me. Although the authors mentioned this briefly in the discussion. It is not clear what else do we learn from discovered assemblies beyond stating that they are consist with previous study. For example, the author could have more analysis of the assembly dynamics, such as whether there are low dimensional structure etc.
First, we will comment on our analysis of the assemblies, before we continue to discuss the main implications of our work, which we believe are the inferred generative model of the zebrafish brain and the perturbation-based connectivity matrix that we discovered. Further, we have implemented the reviewer’s suggestion of analyzing the low-dimensional structure of the hidden unit activity, as further detailed in Question 7.
Indeed, the example assemblies that we show in Figure 3 have been thoroughly characterized in previous studies, which is why we chose to showcase these examples. Previous studies (including our own) typically focused on particular behaviors or sensory modalities, and aimed at identifying the involved neural circuit. Here, we demonstrate that by using cRBM on spontaneous activity recordings, one can simultaneously identify many of those circuits. In other words, these functional circuits/assemblies activate spontaneously, but in many different combinations and perhaps infrequently, so that it is very difficult to infer them from the full neural dynamics that they generate. cRBM has been able to do so, and Figure 3 (and supplementary video 1) serve to illustrate the variety of (known) circuits and assemblies that it inferred, some of which may represent true but not yet characterized circuits, which thus provide hypotheses for subsequent studies.
Further, we believe that the implication of our study goes beyond the properties of the assemblies we’ve identified, in several ways.
We demonstrate the power of cRBM’s generative capacity for inferring low-dimensional representations in neuroscience. Unlike standard dimensional reductionality methods, generative models can be assessed by comparing the statistics of experimental vs in-silico generated data. This is a powerful approach to validate a model, rarely used in neuroscience because of the scarcity of generative models compatible with large-scale data, and we hope that our study will inspire the use of this method in the field. We have made our cRBM code available, including notebook tutorials, to facilitate this.
The generative aspect of our model allowed us to predict the effect of single-neuron perturbations between all ~ 109 pairs of neurons per fish, resulting in a functional connectivity matrix. We believe that the functional connectivity matrix is a major result for the field, similar to the structural connectivity matrix from Kunst et al., 2019, Neuron. The relation between functional and structural connectivity is unknown and of strong interest to the community (e.g., Das and Fiete, 2020, Nature Neuroscience). Our results allowed for a direct comparison of whole-brain region-by-region structural and functional connectivity. We were thus able to quantify the similarity between these two maps, and to identify specific region-pair matches and non-matches of functional and structural connectivity – which will be of particular interest to the zebrafish neuroscience community for developing future research questions.
Further, using these trained models – that will be made public upon publication – anyone can perform any type of in silico perturbation experiments, or generate endless artificial data with matching data statistics to the in vivo neural recordings.
We hope that this may convince the reviewer of the multiple directions of impact of our study. We will further address their comment on analysis of assembly dynamics below (question 7).
2) The learning algorithm of cRBM can be interpreted as matching certain statistics between the model and the experiment. For a general audience, it is not easy to understand . Since these are not directly calculated from experimental observed activities vi, but rather the average is conditioned on the empirical distribution of p(vi). For example, the meaning of means , where S is the set of all observed neural activities: . The authors should explain this in the main text or method, since they are heavily loaded in figure 2.
We thank the reviewer for their suggestion, and have now implemented this. Their mathematics are correct; and we agree that it is not easy to understand without going through the full derivation of the (c)RBM. At the same time, we have tried not to alienate readers who might be more interested in the neuroscience findings than in understanding the computational method used. Therefore, we have kept mathematical details in the main text to a minimum (and have used schematics to indicate the statistics in Figures 2C-G), while explaining it in detail in Methods.
Accordingly, we have now extended section 7.10.2 (“Assessment of data statistics”) that explains how the data statistics were computed in Methods (and have referenced this in Results and in Methods 7.5.5), using the fact that we already explain the process of conditioning on v in Methods 7.5.1. The following sentences were added:
“[...]However, because (c)RBM learn to match data statistics to model statistics (see Methods 7.5.5), we can directly compare these to assess model performance. […]”
[..]
“For each statistic ⟨fk⟩ we computed its value based on empirical data ⟨fk⟩data and on the model ⟨fk⟩model, which we then quantitatively compared to assess model performance. Data statistics ⟨fk⟩data were calculated on withheld test data (30% of recording). Naturally, the neural recordings consisted only of neural data v and not of HU data h. We therefore computed the expected value of ht at each time point t conditioned on the empirical data vt, as further detailed in Methods 7.5.1.”
[...]
3) As a modeling paper, it would be great to have some testable predictions.
We thank the reviewer for the enthusiasm and suggestion. We agree, and that is why we have included this in the form of functional connectivity matrices in Figures 5 and 6. To achieve this, we leveraged the generative aspect of the cRBM to perform in silico single-neuron perturbation experiments, which we aggregated to connectivity matrices. In other words, we have used our model to predict the functional connectivity between brain regions using the influence of single-neuron perturbations.
Obtaining a measure of functional connectivity/influence using single-neuron perturbations is also possible using state-of-the-art neuro-imaging experiments (e.g., Chettih and Harvey, 2019, Nature), though not at the scale of our in silico experiments. We therefore verify our predictions using structural data from Kunst et al., 2019, which we have extended substantially. We provide our functional connectivity result in full, and hope that this can inspire future zebrafish research by predicting which regions are functionally connected, which includes many pairs of regions that have not yet directly been studied in vivo.
Minor:
1) The assembly is defined by the neurons that are strongly connected with a given hidden unit. Thus, some neurons may enter different assemblies. A statistics of such overlap would be helpful. For example, a Venn diagram in figure 1 that shows how many of them assigned to 1, 2, etc assemblies.
We thank the reviewer for this excellent suggestion. Indeed, neurons can be embedded in multiple assemblies. This is an important property of cRBMs, which deserves to be quantified in the manuscript. We have now added this analysis as a new supplementary figure 4. Neurons are embedded in an assembly if their connecting weight is ‘significantly’ non-zero, depending on what threshold one uses. We have therefore shown this statistic for 3 values of the threshold (0.001, 0.01 and 0.1) – demonstrating that most neurons are strongly embedded in at least 1 assembly and that many neurons connect to more than 1 assembly.
Updated text in Results:
“Further, we quantified the number of assemblies that each neuron was embedded in, which showed that increasing the embedding threshold did not notably affect the fraction of neurons embedded in at least 1 assembly (93% to 94%, see Figure S4).”
2) What does the link between hidden units in Figure 1B right panel mean?
Thank you for the question, and we apologize for the confusion: if we understand the question right, the reviewer asks why the colored circles under the title ‘Neuronal assemblies of Hidden Units’ are linked. This schematic shows the same network of neurons as shown in gray at the left side of Figure 1B, but now colored by the assembly ‘membership’ of each neuron. Hence, the circles shown are still neurons (and not HUs), and their links still represent synaptic connections between neurons. We apologize for the confusion, and have updated the caption of Figure 1B to explain this better:
“[..] The neurons that connect to a given HU (and thus belong to the associated assembly), are depicted by the corresponding color labeling (right panel).[..]”.
3) A side-by-side comparison of neural activity predicted by model and the experimentally recorded activities would help the readers to appreciate the performance of the model. Such comparison can be done at both single neuron level or assembly level.
We thank the reviewer for this suggestion. The cRBM model is a statistical model, meaning that it fits the statistics of the data, and not the dynamics. The data that it generates therefore (should) adhere to the statistics of the training data, but does not reflect their dynamics. We believe that showing generated activity side-by-side of empirical activity is therefore not a meaningful example of generated data, as this would exemplify the dynamics, which this model is not designed to capture. Instead, in Figure 2, we show the statistics of the generated data versus the statistics of the empirical data (e.g., Figure 2C for the mean activity of all neurons). We believe that this is a better example representation of the generative performance of the model.
4) Definition of reconstruction quality in line 130.
We thank the reviewer for the suggestion, and have added the following sentence after line 130:
“The reconstruction quality is defined as the log-likelihood of reconstructed neural data vrecon (i.e., v that is first transformed to the low-dimensional h, and then back again to the high-dimensional vrecon, see Methods 7.10.2).”
Further, please note that Methods describes the definition in detail (Eq 18 of the submitted manuscript), although we agree with the reviewer that more detail was required in the Results section at line 130.
5) Line 165. If PCA is compared with cRBM, why other dimensionality reduction methods, such as k-means and non-negative matrix factorization, can not be compared in terms of the sparsity?
Please see answer to question 1 from Reviewer 1.
6) Line 260, please provide minimum information about how the functional connectivity is defined based on assemblies discovered by cRBM.
We apologize if this was not clear. The first paragraph of this section (lines 248-259) of the submitted manuscript, provides the detail that the reviewer asks for, and we realize that the sentence of line 260 is better placed in the first paragraph, as it has come across as a very minimal explanation of how functional connectivity is defined.
We have now moved this sentence to the preceding paragraph, as well as specified the Method references (as suggested by this reviewer below), for additional clarity. We thank the reviewer for pointing out this sentence.
7) Some analysis of the hidden units population activities. Such as whether or not there are interesting low dimensional structure from figure 4A.
We thank the reviewer for their suggestion. In our manuscript we have used the cRBM model to create a lowdimensional (M=200) representation of zebrafish neural recordings (N=50,000). The richness of this model owes to possible overlaps between HUs/assemblies that can result in significant correlation in their activities. The latter is illustrated in Figure 4A-C: the activity of some HUs can be strongly correlated.
The reviewer’s suggestion is similar; to perform some form of dimensionality reduction on the low-dimensional HU activity shown in Figure 4. We have now added a PCA analysis to Figure 4 to quantify the degree of lowdimensional structure in the HU dynamics, and show the results in a new panel Figure 4D.
The following text has been added to the Results section:
These clusters of HUs with strongly correlated activity suggest that much of the HU variance could be captured using only a small number of variables. We quantified this by performing PCA on the HU dynamics, finding that indeed 52% of the variance was captured by the first 3 PCs, and 85% by the first 20 PCs (Figure 4D).
We believe that further visualization of these results, such as plotting the PC trajectories, would not further benefit the manuscript. The manuscript focuses on cRBM, and the assemblies/HUs it infers. Unlike PCA, these are not ranked/quantified by how much variance they explain individually, but rather they together ‘compose’ the entire system and explain its (co)variance (Figure 2). Breaking up a dominant activity mode (as found by PCA), such as the ARTR dynamics, into multiple HUs/assemblies, allows for some variation in activity of individual parts of the ARTR circuit (such as tail movement and eye movement generation), even though at most times the activity of these HUs is coordinated. We hope the reviewer agrees with our motivation to keep the manuscript focused on the nature of cRBM-inferred HUs.
8) Figure 4B right panel, how did the authors annotate the cluster manually? As certain assembly may overlap with several different brain regions, for example, figure 4D.
We thank the reviewer for this question, and we presume they meant to reference figure 3D as an example? For figure 4, as well as Figure 3, we used the ZBrain Atlas (Randlett et al., 2015) for definition of brain regions. This atlas presents a hierarchy of brain regions: for example, many brain regions are part of the rhombencephalon/hindbrain. This is what we used for midbrain/hindbrain/diencephalon. Further, many assemblies are solely confined to Optic Tectum (see Figure 3L), which we therefore used (split by hemisphere). Then, many brain regions are (partly) connected to the ARTR circuit, such as the example assembly of Figure 3D that the reviewer mentions. These we have all labeled as ARTR (left or right), though technically only part of their assembly is the ARTR. These two clusters therefore rather mean ‘ARTR-related’, in particular because their activity is locked to the rhythm of the ARTR (see Figure 4A). The final category is ‘miscellaneous’ (like Figure 3G).
However we agree that this wasn’t clear from the manuscript text, so we have changed the figure 4C caption to mention that ‘ARTR’ stands for ARTR-related assemblies, which we hope clarifies that ARTR-clustered assemblies can exist of multiple, disjoint groups of neurons, which relate to the ARTR circuit.
9) Better reference of the methods cited in the main text. The method part is quite long, it would be helpful to cite the section number when referring it in the main text.
We thank the reviewer for this helpful suggestion, we agree that it would benefit the manuscript to reference specific sections of the Methods. We have now changed all references to Methods to incorporate this.
10) Some discussion about the limitation of cRBM would be great.
We thank the reviewer for this suggestion, and have now included this. As Reviewer 1 had the same suggestion, we refer our answer to questions 2 and 3 from Reviewer 1 for more detail.
Reviewer #3 (Significance (Required)):
This work provides a timely new technique to extract meaningful neural assemblies from large scale recordings. This study should be interested to both researchers doing either experiments and computation/theory. I am a computational neuroscientist.
Description of analyses that authors prefer not to carry out.
Please include a point-by-point response explaining why some of the requested data or additional analyses might not be necessary or cannot be provided within the scope of a revision. This can be due to time or resource limitations or in case of disagreement about the necessity of such additional data given the scope of the study. Please leave empty if not applicable.
We propose to limit the comparison to other assembly inference techniques to generative models.
https://doi.org/10.7554/eLife.83139.sa2Article and author information
Author details
Thijs L van der Plas
Funding
Biotechnology and Biological Sciences Research Council (BB/M011224/1)
- Thijs L van der Plas
Edmond J. Safra Center for Bioinformatics at Tel Aviv University
- Jérôme Tubiana
Human Frontier Science Program (LT001058/2019-C)
- Jérôme Tubiana
European Research Council (715980)
- Volker Bormuth
Human Frontier Science Program (RGP0060/2017)
- Georges Debrégeas
Nederlandse Organisatie voor Wetenschappelijk Onderzoek (016.VIDI.189.052)
- Bernhard Englitz
- Thijs L van der Plas
The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.
Acknowledgements
TLvdP had an Erasmus +fellowship (European Union) and acknowledges support from the Biotechnology and Biological Sciences Research Council (BBSRC, grant No. BB/M011224/1). JT acknowledges support from the Edmond J Safra Center for Bioinformatics at Tel Aviv University and from the Human Frontier Science Program (cross-disciplinary postdoctoral fellowship LT001058/2019 C). GM was funded by a PhD fellowship from the Doctoral School in Physics, Ile de France (EDPIF). GLG had a PhD fellowship from the Systems Biology Network of Sorbonne Université. BE and TLvdP. were supported by an NWO-VIDI Grant. Funding sources: European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program grant agreement number 715980. Human Frontier Science Program (RGP0060/2017). The French Research National Agency under grant No. ANR-16-CE16-0017. Dutch Institute for Scientific Research NWO (Nederlandse Organisatie voor Wetenschappelijk Onderzoek) grant No. 016.VIDI.189.052. We thank the IBPS fish facility staff for the fish maintenance, in particular Stéphane Tronche and Alex Bois. We are grateful to Carounagarane Dore for his contribution to the design of the experimental setup. We thank Misha Ahrens for providing the GCaMP lines. We are also grateful to Rémi Monasson for very fruitful discussions and his comments on the manuscript.
Ethics
Experiments were approved by Le Comité d’Éthique pour l’Experimentation Animale Charles Darwin C2EA-05 (02601.01).
Senior Editor
- Laura L Colgin, University of Texas at Austin, United States
Reviewing Editor
- Peter Latham, University College London, United Kingdom
Publication history
- Preprint posted: November 11, 2021 (view preprint)
- Received: September 21, 2022
- Accepted: January 15, 2023
- Accepted Manuscript published: January 17, 2023 (version 1)
- Version of Record published: February 20, 2023 (version 2)
Copyright
© 2023, van der Plas, Tubiana et al.
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.
Metrics
-
- 1,049
- Page views
-
- 169
- Downloads
-
- 2
- Citations
Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Neural assemblies uncovered by generative modeling explain whole-brain activity statistics and reflect structural connectivity
eLife 12:e83139.
https://doi.org/10.7554/eLife.83139
Further reading
-
- Medicine
- Neuroscience
The cell bodies of postganglionic sympathetic neurons innervating the heart primarily reside in the stellate ganglion (SG), alongside neurons innervating other organs and tissues. Whether cardiac-innervating stellate ganglionic neurons (SGNs) exhibit diversity and distinction from those innervating other tissues is not known. To identify and resolve the transcriptomic profiles of SGNs innervating the heart, we leveraged retrograde tracing techniques using adeno-associated virus (AAV) expressing fluorescent proteins (GFP or Td-tomato) with single cell RNA sequencing. We investigated electrophysiologic, morphologic, and physiologic roles for subsets of cardiac-specific neurons and found that three of five adrenergic SGN subtypes innervate the heart. These three subtypes stratify into two subpopulations; high (NA1a) and low (NA1b and NA1c) neuropeptide-Y (NPY) -expressing cells, exhibit distinct morphological, neurochemical, and electrophysiologic characteristics. In physiologic studies in transgenic mouse models modulating NPY signaling, we identified differential control of cardiac responses by these two subpopulations to high and low stress states. These findings provide novel insights into the unique properties of neurons responsible for cardiac sympathetic regulation, with implications for novel strategies to target specific neuronal subtypes for sympathetic blockade in cardiac disease.
-
- Neuroscience
Oscillations of extracellular voltage, reflecting synchronous, rhythmic activity in large populations of neurons, are a ubiquitous feature in the mammalian brain, and are thought to subserve important, if not fully understood roles in normal and abnormal brain function. Oscillations at different frequency bands are hallmarks of specific brain and behavioral states. At the higher end of the spectrum, 150-200 Hz ripples occur in the hippocampus during slow-wave sleep, and ultrafast (400-600 Hz) oscillations arise in the somatosensory cortices of humans and several other mammalian species in response to peripheral nerve stimulation or punctate sensory stimuli. Here we report that brief optogenetic activation of thalamocortical axons, in brain slices from mouse somatosensory (barrel) cortex, elicited in the thalamorecipient layer local field potential (LFP) oscillations which we dubbed “ripplets”. Ripplets originated in the postsynaptic cortical network and consisted of a precisely repeating sequence of 2‑5 negative transients, closely resembling hippocampal ripples but, at ~400 Hz, over twice as fast. Fast-spiking (FS) inhibitory interneurons fired highly synchronous 400 Hz spike bursts entrained to the LFP oscillation, while regular-spiking (RS), excitatory neurons typically fired only 1-2 spikes per ripplet, in antiphase to FS spikes, and received synchronous sequences of alternating excitatory and inhibitory inputs. We suggest that ripplets are an intrinsically generated cortical response to a strong, synchronous thalamocortical volley, and could provide increased bandwidth for encoding and transmitting sensory information. Importantly, optogenetically induced ripplets are a uniquely accessible model system for studying synaptic mechanisms of fast and ultrafast cortical and hippocampal oscillations.
