Evolutionary and functional insights into the mechanism underlying body-size-related adaptation of mammalian hemoglobin

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: October 24, 2019 (This version)
Accepted: September 19, 2019
Received: April 11, 2019

1. Of interest
Indole produced during dysbiosis mediates host–microorganism chemical communication

Rui-Qiu Yang, Yong-Hong Chen ... Cheng-Gang Zou

Research Article Dec 1, 2023
Further reading

Abstract
eLife digest
Introduction
Results
Discussion
Materials and methods
Appendix 1
Appendix 2
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Hemoglobin (Hb) represents a model protein to study molecular adaptation in vertebrates. Although both affinity and cooperativity of oxygen binding to Hb affect tissue oxygen delivery, only the former was thought to determine molecular adaptations of Hb. Here, we suggest that Hb affinity and cooperativity reflect evolutionary and physiological adaptions that optimized tissue oxygen delivery. To test this hypothesis, we derived the relationship between the Hill coefficient and the relative affinity and conformational changes parameters of the Monod-Wymann-Changeux allosteric model and graphed the ‘biophysical Hill landscape’ describing this relation. We found that mammalian Hb cooperativity values all reside on a ridge of maximum cooperativity along this landscape that allows for both gross- and fine-tuning of tissue oxygen unloading to meet the distinct metabolic requirements of mammalian tissues for oxygen. Our findings reveal the mechanism underlying body size-related adaptation of mammalian Hb. The generality and implications of our findings are discussed.

https://doi.org/10.7554/eLife.47640.001

eLife digest

In humans and other mammals, a protein in the blood called hemoglobin carries oxygen from the lungs to other parts of the body. This protein contains four subunits that can each bind to one molecule of oxygen, so a single hemoglobin can carry up to four oxygen molecules at the same time. Previous studies have found that, although each subunit can potentially bind oxygen on its own, the subunits actually work together to help each other bind to oxygen in the body.

Two biochemical properties of hemoglobin affect how it carries oxygen molecules. First, oxygen-binding affinity, or how tightly the protein can bind to oxygen; and secondly cooperativity, or the degree to which the subunits interact with each other to bind oxygen more tightly. Mammals of different shapes and sizes have different requirements for transporting oxygen from the lungs to organ tissues, which have shaped their hemoglobin proteins over evolutionary timescales. While the contribution of affinity to hemoglobin evolution in animals of different sizes has been addressed in the past, the role of cooperativity in hemoglobin adapting to body size has remained unclear.

Here, Rapp and Yifrach used a mathematical approach to analyze existing data from 14 different mammals – including mice, sheep, humans and elephants – on how oxygen binds to hemoglobin. Using this approach, they were able to explain why different mammalian hemoglobins present different oxygen-binding affinity and cooperativity values. Furthermore, they demonstrated that the cooperativity values were very close to the maximum they could be for each version of hemoglobin.

These findings suggest that, as mammals evolved, genetic mutations that altered the oxygen-binding affinity or the ability of hemoglobin subunits to cooperate may have allowed hemoglobin proteins to adapt to meet the oxygen needs of mammals of different sizes and shapes. In the future, the approach used by Rapp and Yifrach could be adapted to study how other proteins that bind molecules in a cooperative manner have evolved.

https://doi.org/10.7554/eLife.47640.002

Introduction

Two major obstacles hamper understanding the evolutionary origins of properties seen in modern-day proteins. One stems from the fact that mutation and selection are separated by several levels of biological organization such that it is difficult to elucidate the complex relationships between protein sequence and organismal/population fitness. Second, even in those cases where the molecular properties of a protein (e.g. affinity or cooperativity) have adaptive value with respect to organismal fitness, we often lack an understanding of the molecular mechanism underlying changes in the values of these properties. Given these challenges, we currently understand the mechanisms underlying adaptive behavior for only a very limited number of proteins (e.g. Mello and Tu, 2005; Keymer et al., 2006; Swem et al., 2008; Storz et al., 2009).

Hb represents an excellent model protein to study molecular adaptation in vertebrates (Perutz, 1983; Poyart et al., 1992; Hourdez and Weber, 2005; Storz and Moriyama, 2008). Hb is a tetrameric allosteric protein responsible for tissue oxygen delivery in a manner controlled by the midpoint and slope of its oxygen saturation curve. These macroscopic parameters reflect the effective affinity (p₅₀) and cooperativity (n_H) of oxygen binding by Hb, respectively and are traditionally evaluated using the Hill equation, derived assuming an all-or-none mode of binding (Hill, 1910). Over the years, many studies have indicated that Hb oxygen affinity (p₅₀) is an adaptive trait, that is its value has been tuned during evolution so as to tailor tissue oxygen delivery to the particular metabolic requirements of vertebrates due to variations in body size, lifestyle and/or environmental conditions. For example, vertebrates native to mountain habitats where low ambient oxygen pressures prevail usually possess Hb that exhibits higher affinity for oxygen than does the Hb of lowland dwellers (Lenfant, 1973; Bunn, 1980; Weber, 2007; Storz and Moriyama, 2008; Storz, 2016). Likewise, Hb in small-sized animals that display high metabolic rates presents lower affinity for oxygen than does the same protein in large-sized animals, again reflecting the adaptive adjustment of tissue oxygen unloading by Hb (Schmidt-Neilsen and Larimer, 1958; Schmidt-Nielsen, 1970). Accordingly, early respiratory system physiologists assigned great significance to the p₅₀ parameter, terming it ‘oxygen unloading tension’, and proposed that Hb function could be explained in terms of adaptive evolution of this value (Schmidt-Neilsen and Larimer, 1958; Schmidt-Nielsen, 1970). At the same time, such studies ignored the adaptive potential of cooperativity (n_H) with respect to Hb function. This is surprising, given that n_H also affects Hb tissue oxygen delivery. Moreover, mechanisms underlying changes in p₅₀, such as changes in oxygen affinity of the oxy- or deoxy-states of Hb, changes in the ratio between these states or changes in their sensitivity to allosteric effectors, are all also expected to affect n_H. Indeed, the finding by Milo et al. (2007) that mammalian Hbs exhibit variations in the Hill cooperativity value hints at the adaptive potential of the n_H trait.

The need to also consider n_H in addressing adaptation of Hb function becomes evident when we examine the implications of accepting the notion that molecular adaptation of Hb function in vertebrates relies primarily on its p₅₀ affinity property. Given the inherent tradeoff between arterial O₂ loading and peripheral O₂ unloading, it is not clear whether improved tissue oxygen delivery is achieved by increased oxygen affinity to improve Hb loading or by decreased affinity to favor unloading (Storz, 2016). Either very high or very low oxygen affinity would result in a low fraction of tissue oxygen delivery unless cooperativity (n_H) between Hb subunits is introduced as a means to switch between low- and high-affinity Hb states. It would thus seem that the values of both p₅₀ and n_H of Hb should reflect physiological optimization of the tradeoff between O₂ loading in the lungs and O₂ unloading in tissues, so as to optimize tissue oxygen delivery. Although this is a seemingly obvious claim, it has yet to be tested experimentally.

Here, we tested whether the values of both p₅₀ and n_H of Hb are indeed optimized in the case of body size-related adaptation of mammalian Hb, relying on extensive evolutionary and physiological oxygen saturation datasets available for mammalian Hb proteins. The former comprises a set of oxygen binding curves of homologous Hb proteins from different mammalian species, all measured under similar physiological conditions (Milo et al., 2007; Rapp and Yifrach, 2017). The latter comprises a set of binding curves of human Hb measured under a variety of different physiological conditions, that is, in the presence of different concentrations of H⁺, CO₂ and organophosphate, all inhibitory allosteric ligands of Hb (Rapp and Yifrach, 2017). For all data sets curves, reliable estimates for p₅₀ and n_H Hill parameters and for the elementary relative affinity (c) and conformational changes (L) parameters of the MWC concerted allosteric model (Monod et al., 1965; Rubin and Changeux, 1966) are available. By deriving the explicit mathematical dependence of both p₅₀ and n_H on the MWC parameters of a tetrameric protein, we were able to draw the theoretical ‘biophysical Hill cooperativity landscape’ at half-saturation that graphically describes how n_H varies with changes in the values of the MWC parameters. The mapping of experimentally derived Hill and MWC parameters of all evolutionary and physiological dataset curves on this landscape provided insight into the mechanism underlying the adaptive behavior of p₅₀ and n_H with respect to tissue oxygen delivery by mammalian Hb and their relation to organism fitness. The principles underlying the ‘biophysical Hill landscape’-mapping strategy are general and offer mechanistic-level understanding of how physiological and evolutionary variations operate to shape the molecular property of a protein.

Results

Hemoglobin evolutionary and physiology datasets

The evolutionary and physiological datasets for Hb used in the current study were respectively compiled in the meta-analysis of Hb function by Milo et al. (2007) and by Rapp and Yifrach (2017). Specifically, the Hb evolutionary dataset comprises 14 different mammalian Hb oxygen saturation curves obtained under similar physiological conditions (Materials and methods and Supplementary file 1). The Hb physiological dataset comprises 26 different human Hb saturation curves collected under a variety of different physiological conditions, including those involving changes in H⁺(Di Cera et al., 1988; Imai, 1983), CO₂(Doyle et al., 1987) and 2,3-BPG (bis-phosphoglycerate) (Benesch et al., 1971) concentrations.

For each dataset curve, the magnitude of cooperativity in oxygen binding was evaluated using either the Hill (Figure 1a) or MWC model (Figure 1b). In the former, the sigmoidal saturation curve is fitted to the Hill equation (Equation 1) (Hill, 1910):

\bar{Y} = \frac{{[S]}_{}^{n_{H}}}{{[S]}_{}^{n_{H}} + K_{0.5}^{n_{H}}}

where $\bar{Y}$ represents the fraction of bound sites and p₅₀ (~K_0.5) and n_H correspond to the midpoint and slope parameters of the curve. The Hill all-or-none binding mode corresponds to a simplification that is far from what occurs in reality. Instead, Hb oxygen binding generally involves intermediate ligation and conformational species, as delineated by the MWC allosteric model (Marzen et al., 2013; Monod et al., 1965; Rubin and Changeux, 1966) (Figure 1b) (see Appendix 1 for a detailed discussion on why we think the classical MWC allosteric model adequately describes hemoglobin oxygen ligation in the presence or absence of its allosteric ligands; see also Henry et al., 1997; Milo et al., 2007; Rapp and Yifrach, 2017; Storz, 2016). According to the MWC model, tetrameric Hb is assumed to be in equilibrium between the un-liganded low-affinity T (tense or deoxy) and the high-affinity R (relaxed or oxy) states, as described by the L allosteric constant (L=[T]/[R]). In the presence of oxygen, this equilibrium is shifted toward the R state in a manner determined by the ligation number and by the ratio of dissociation constants of oxygen from the two states, c (c=K_R/K_T). These aspects of the MWC model are quantitatively described by Equation 2 (Monod et al., 1965):

{\bar{Y}}_{M W C} = \frac{\frac{[S]}{K_{R}} {(1 + \frac{[S]}{K_{R}})}^{3} + L \frac{[S]}{K_{T}} {(1 + \frac{[S]}{K_{T}})}^{3}}{{(1 + \frac{[S]}{K_{R}})}^{4} + L {(1 + \frac{[S]}{K_{T}})}^{4}} = \frac{a {(1 + a)}^{3} + L c a {(1 + c a)}^{3}}{{(1 + a)}^{4} + L {(1 + c a)}^{4}}

where α in the non-dimensional form of the MWC equation denotes substrate (S) concentration in K_R units (α=[S]/K_R). In the classical MWC model, cooperativity in substrate binding (homotropic interactions) is determined by both L and c (Monod et al., 1965). Heterotropic interactions, on the other hand, describing the effects of allosteric ligands on substrate binding, only affect the L parameter. Hb conformational equilibrium can thus be further shifted toward the T state upon binding of allosteric inhibitors. Such dependence is described by Equation 3 assuming non-exclusive binding of the inhibitor (I) to both the T and R MWC conformations exhibiting $K_{I}^{T}$ and $K_{I}^{R}$ affinities, respectively (Rubin and Changeux, 1966):

L_{a p p} = L (\frac{(1 + [I] / K_{I}^{T})}{(1 + [I] / K_{I}^{R})})^{4}

Figure 1

Download asset Open asset

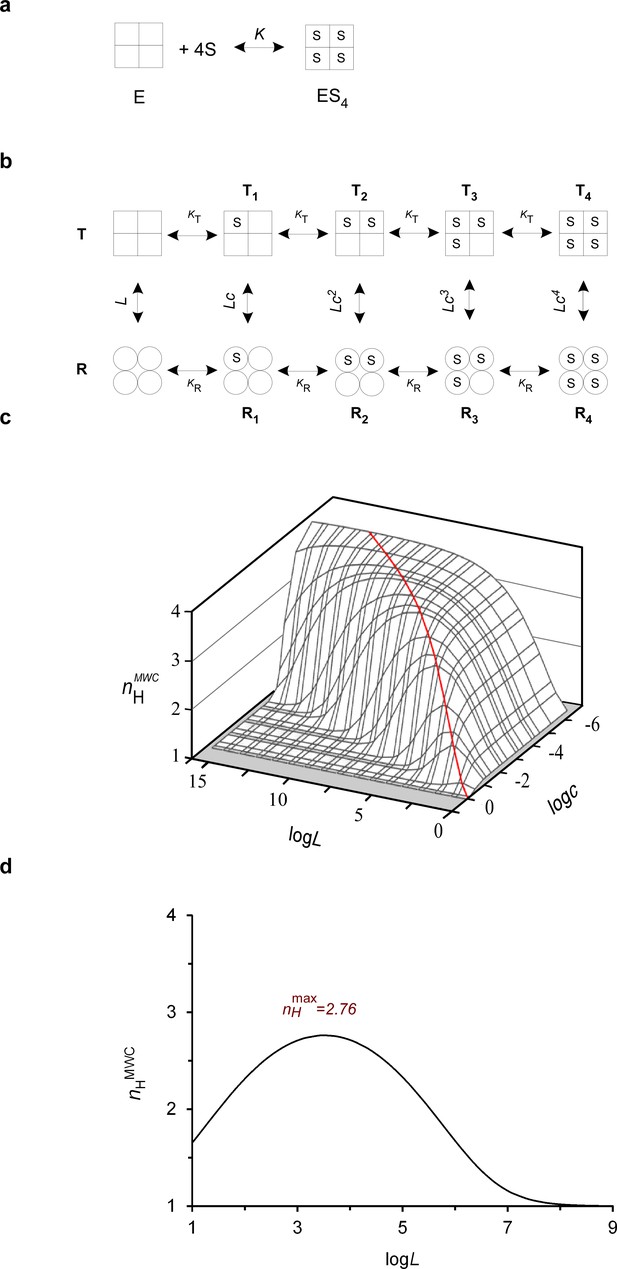
The biophysical Hill landscape of a tetrameric MWC protein.

(a) Schematic representation of the all-or-none Hill binding mode by a tetrameric protein (E), with K referring to the substrate (S) dissociation equilibrium constant. (b) Schematic representation of the MWC model applied to a tetrameric allosteric protein. Square and round symbols represent the tense (T) and relaxed (R) subunit conformations, respectively. L, K_T and K_R denote the T to R transition equilibrium constant in the absence of substrate and substrate affinity to the T and R conformations, respectively. The parameter c corresponds to the ratio of substrate affinity to the R and T conformations (=K_R/K_T). (c) The theoretical three-dimensional Hill landscape describing the dependence of n_H^MWC at half-saturation on both the L and c parameters (calculated based on Equation 5). The red ridge line trajectory corresponds to parameter value pairs giving rise to maximum cooperativity. (d) Dependence of the Hill coefficient at half-saturation (n_H^MWC) on the allosteric constant L, as determined according to Equation 5. The curve was plotted assuming a c value of ~ 0.01, typical for the ratio of oxygen affinity to the R and T conformations of human Hb. The saddle point of the bell-shaped curve corresponds to a Hill value of ~ 2.8 (as observed for human Hb), fulfilling the L = *c^-*² criterion giving rise to maximum cooperativity.

https://doi.org/10.7554/eLife.47640.003

Reliable values for the L and c MWC parameters of all evolutionary dataset Hb saturation curves and for the apparent L values of all physiological dataset human Hb saturation curves were recently reported (Rapp and Yifrach, 2017) and are given in Supplementary files 1 and 2, respectively. Values for n_H and p₅₀ for the same dataset curves were previously reported (Milo et al., 2007; Rapp and Yifrach, 2017).

The biophysical Hill landscape of a tetrameric MWC allosteric protein

To describe the driving force(s) that shape Hb affinity and cooperativity oxygen binding properties, one must first derive the exact relationship between p₅₀ and n_H and the parameters of the MWC model. Accordingly, to bridge between the non-realistic Hill analysis and the MWC ligation pathway, we followed others (Levitzki, 1978; Yifrach, 2004) and employed Equation 4 (Wyman, 1964) on the MWC model equation under conditions of half-saturation:

n_{H}^{} = \frac{\partial l o g (\frac{\bar{Y}}{1 - \bar{Y}})}{\partial (\log [S])} = \frac{[S] \partial (\bar{Y}) / \partial ([S])}{(\bar{Y}) (1 - \bar{Y})}

Plugging the explicit mathematical expressions for ${\bar{Y}}_{M W C}$ , $1 - {\bar{Y}}_{M W C}$ and $\partial ({\bar{Y}}_{M W C}) / \partial ([S])$ into Equation 4 yields the explicit mathematical dependence of n_H on the L, K_R and K_T biophysical parameters of the MWC model. Earlier studies (Levitzki, 1978; Yifrach, 2004) employed this analysis for assessing variations of a dimeric MWC protein to obtain analytic solutions for the dependence of n_H on model parameters. Here, we solved for the tetrameric MWC protein case, yielding Equation 5:

\begin{array}{ll} n_{H}^{M W C} = \frac{\partial (\frac{{\bar{Y}}_{M W C}}{1 - {\bar{Y}}_{M W C}})}{\partial (\log [S])} = (4 [S] (\frac{\partial ({\bar{Y}}_{M W C})}{\partial ([S])})) |_{[S] = {[S]}_{0.5}} = \\ (4 [S] (\frac{\frac{3 [S] {(1 + \frac{[S]}{K_{R}})}^{2}}{K_{R}^{2}} + \frac{{(1 + \frac{[S]}{K_{R}})}^{3}}{K_{R}} + \frac{3 L [S] {(1 + \frac{[S]}{K_{T}})}^{2}}{K_{T}^{2}} + \frac{L {(1 + \frac{[S]}{K_{T}})}^{3}}{K_{T}}}{{(1 + \frac{[S]}{K_{R}})}^{4} + L {(1 + \frac{[S]}{K_{T}})}^{4}} \frac{- (\frac{4 {(1 + \frac{[S]}{K_{R}})}^{3}}{K_{R}} + \frac{4 L {(1 + \frac{[S]}{K_{T}})}^{3}}{K_{T}}) (\frac{[S] {(1 + \frac{[S]}{K_{R}})}^{3}}{K_{R}} + \frac{L [S] {(1 + \frac{[S]}{K_{T}})}^{3}}{K_{T}})}{{({(1 + \frac{[S]}{K_{R}})}^{4} + L {(1 + \frac{[S]}{K_{T}})}^{4})}^{2}})) |_{[S] = {[S]}_{0.5}} \end{array}

The expression for [S]_0.5 can be obtained by setting ${\bar{Y}}_{M W C}$ (Equation 2) to a value of 0.5. Given that [S] is raised to a power of up to 4, the exact analytic expression for [S]₀.₅(L, K_R, K_T) is not manually solvable and was obtained using Mathematica software (Wolfram Research Inc; see Materials and methods). Substituting the solution for [S]₀.₅(L, K_R, K_T) in Equation 5 then allows obtaining the explicit expression for $n_{H}^{M W C}$ in terms of the MWC model parameters. The long and complex expressions of both [S]₀.₅ and $n_{H}^{M W C}$ can be found at the GitHub repository under the following address: https://github.com/OlgaRL/MWC_Parameters (Rapp, 2019; copy archived at https://github.com/elifesciences-publications/MWC_Parameters). Thus, for any L, K_R and K_T values, $n_{H}^{M W C}$ is unequivocally determined (Equation 5). A good approximation for n_H (based on the [S]_0.5 expression of the $\bar{R}$ conformational state function; Gruber et al., 2019) that is over 98% accurate across most of the range of L and c values is presented in Appendix 2.

Plotting the three-dimensional surface of the Hill slope at half-saturation (now referred to as n_H^MWC) as a function of both logL and logc (based on equation 5) generates what we refer to as the theoretical ‘biophysical Hill landscape’ for a tetrameric MWC protein (Figure 1c). This landscape graphically describes the parameter space available for such a MWC protein and summarizes many of the known cooperativity-related aspects of the MWC model documented in classical papers (Monod et al., 1965; Rubin and Changeux, 1966; Edelstein, 1975; Perutz, 1989) and textbooks. In the Hill landscape, n_H^MWC values between one to four are obtained as a function of the L and c values chosen. The n_H^MWC surface presents a topology that resembles an upward-running ridge, with the maximum points obtained by introducing various L and c values (as indicated by the trajectory drawn in red). Such mapping is better appreciated in the bell-shaped dependence of n_H^MWC on logL at a given logc value (c = 0.01, a value typical for human Hb), seen in a cross-section of such a surface (Figure 1d) (Rubin and Changeux, 1966; Edelstein, 1971). Inspecting the landscape cross-sections reveals that systematically higher maximum Hill points are obtained when higher L and lower c values are simultaneously chosen. Furthermore, as indicated by Rubin and Changeux (1966), the different L and c value pairs underlying the maximum n_H^MWC points must all fulfill a particular dependence expressed by L = c ^-n/2, as obtained by setting ∂n_H/∂logL equals zero. Another important aspect of the maximum Hill points is that they reside at the apex of rather wide hilltops. This can be seen in the bell-shaped cross-sections of n_H^MWC as a function of logL at any particular logc value (Figure 1c,d), suggesting that around the maximum cooperativity points, only minor changes in n_H are to be expected upon changes in L brought about by binding of allosteric inhibitors or activators (Equation 3). This relative insensitivity of n_H^MWC to changes in physiological conditions was referred to as a ‘buffering of cooperativity’ phenomenon by the MWC model founders (Rubin and Changeux, 1966; Edelstein, 1971). Using the biophysical Hill landscape described here, we can now examine where evolutionary and physiological considerations have affected Hb behavior.

The characteristic n_H value of hemoglobin is a maximum cooperativity point

Where along the three-dimensional n_H^MWC landscape can one find the (L, c, n_H) points of the different binding curves of the evolutionary and physiological Hb datasets? We first considered the 14 mammalian oxygen saturation curves comprising the evolutionary dataset. As can be seen in Supplementary file 1, the different mammal Hbs exhibit variations in both L and c values, thus giving rise to different Hill values (calculated based on the MWC model using Equation 5). These values resemble the observed ‘Hill model’-derived coefficients (Milo et al., 2007), as indicated by the linear correlation between the observed and calculated Hill values reported by Rapp and Yifrach (2017) (Figure 1 therein; see also Supplementary file 1). When mapped onto the theoretical Hill landscape, the calculated Hill values of all mammalian Hbs reside close to the maximum points of the bell-shaped contours of the three-dimensional Hill landscape (Figure 2a). Furthermore, the logarithms of the values for L and c of the different Hbs are linearly correlated (Figure 2b) with a slope value of −2.7 (±0.3), close to a value of −2 that would be expected for proteins that evolved to present maximum cooperativity in ligand binding (L = c ^-n/2). The observation that the logL-logc correlation crosses very close to the (0,0) axis origin point further supports this assertion. Given that L and c are independent parameters of the MWC model, the logarithms of their values for a given protein set are not expected to be linearly-dependent. This is, in particular, true if one considers that these values were derived using reliable data fitting strategies that prevent potential parameter dependence artifacts (Rapp and Yifrach, 2017) and that changes in either c or L (or in both) were reported for native or mutant Hb variants over many years of Hb research. We thus suggest that the observed linearity between mammalian logL and logc values does not imply causation or is an artifact but rather points to co-evolution of the two MWC parameters so as to shape Hb cooperativity close to the maximum value. Deviation between the observed and expected slope values of the logL-logc correlation can be explained by differences in the techniques and experimental protocols used to evaluate the Hb saturation data from the different organisms and inaccuracies in data collection and analysis (for detailed discussion, see Milo et al., 2007). Nevertheless, even with such limitations, the results derived from the evolutionary dataset support the hypothesis that changes in mammalian Hb binding and conformation have been tuned during evolution, giving rise to close to maximum cooperativity in oxygen binding, albeit yielding a different maximum n_H value in each case. To further examine whether this indeed is the case, we considered the human Hb physiological dataset.

Figure 2

Download asset Open asset

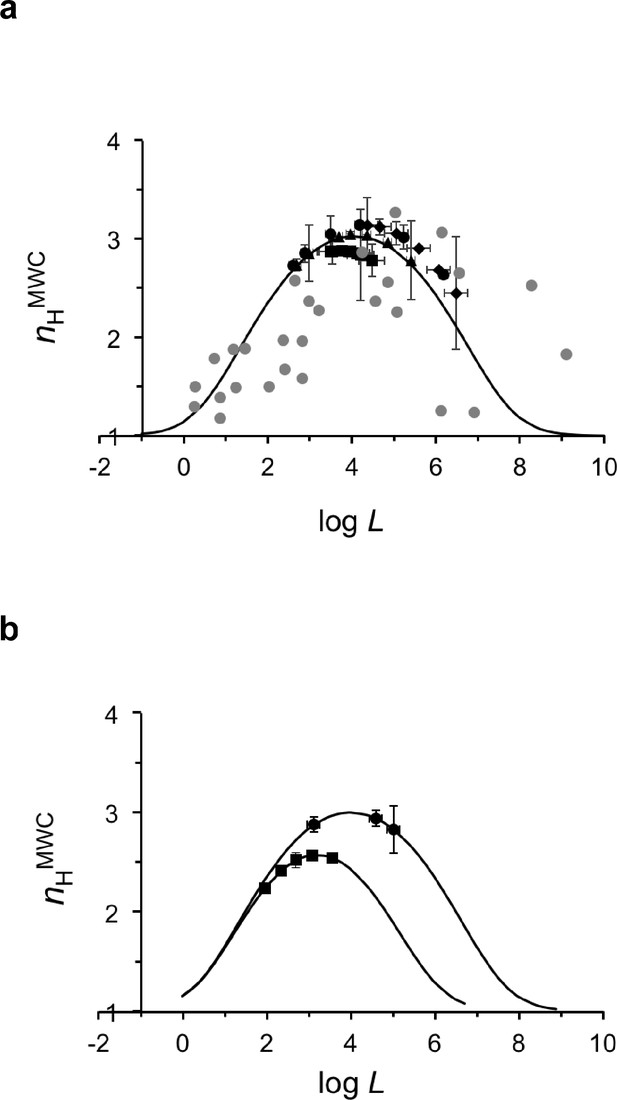
Mammalian hemoglobins exhibit maximum cooperativity *n_H* values.

(a) $n_{H}^{M W C}$ values of the different mammal Hbs from the evolutionary dataset, calculated based on derived values for the L, K_T and K_R elementary MWC parameters, reside close to the ridge line of the three-dimensional biophysical Hill landscape. (b) Correlation plot relating the logarithms of the relative affinity (c) and conformational ratio (L) of the T and R quaternary MWC states of different mammalian Hbs comprising the evolutionary dataset (Supplementary file 1). The solid curve corresponds to a linear regression with a R² correlation coefficient of 0.93, a slope of -2.7 (± 0.3) and an intercept at logL of -0.2, very close to the 0 value expected based on the Lc²=1 criterion. In both panels, the red data point corresponds to the values for human Hb.

https://doi.org/10.7554/eLife.47640.004

As highlighted above, a buffering of cooperativity regime is observed around a maximum cooperativity Hill point. As such, minor changes in n_H are to be expected upon changes in L brought about by the binding of allosteric inhibitors or activators. Reliable estimates for the apparent L values of all of 26 different concentration-related saturation curves of the H⁺, CO₂ and 2,3-BPG physiological datasets were recently obtained (Rapp and Yifrach, 2017), assuming a constant c value in each case, as predicted by the MWC model (Supplementary file 2). The different L_app values obtained for each effector dataset saturation curve scales with effector concentration in a manner predicted by the MWC model (Rapp and Yifrach, 2017; Appendix 1), confirming the reliability of the values derived.

For the physiological Hb dataset, a cross-section of the biophysical Hill landscape at the characteristic c value of human Hb should be considered. We thus examined where along the bell-shaped human Hb n_H-logL curve do the characteristic pairs of logL-n_H values of the 26 physiological dataset curves reside. As can be seen in Figure 3a, logL-n_H data points of the physiological dataset (black symbols) cluster around the maximum point of the bell-shaped curve. This pattern is in sharp contrast to the scattered pattern of the pairs of logL-n_H values for Hb mutants reported in the literature (gray circles) (Baldwin, 1976) and assumed by Baldwin (1976) (and later by Fersht, 1985) to have the same c value. Significant deviations from the maximum cooperativity value of wild-type human Hb were also observed for naturally occurring Hb mutants, such as the Kansas and Chesapeake variants (Edelstein, 1971). A clustering pattern similar to that shown for human Hb is also seen for bovine and dog Hbs, despite being based on the limited physiological datasets available for these species (Figure 3b) (Jensen, 2004; Breepoel et al., 1981).

Figure 3

Download asset Open asset

A buffering of cooperativity physiological regime is observed for human hemoglobin around its maximum cooperativity value.

(a) Mapping of the Hill coefficient and the logarithm of the apparent allosteric constant (L) values for all human oxygen saturation curves of the pH, CO₂ and BPG physiological datasets (Supplementary file 2) onto the theoretical n_H-*logL* curve of human Hb. The n_H values for all physiological dataset curves were calculated using the derived apparent L value for each curve and assuming a common c value. The theoretical n_H-*logL* curve was calculated assuming a c value of 0.007 (±0.001), corresponding to the averaged c value of all human physiological datasets (Supplementary file 2). Black circles, squares and diamonds correspond to pH, CO₂ and BPG data points, respectively. Gray symbols represent pairs of *logL-n*_H values for Hb mutantS reported in the literature and assuming no change in c upon mutation (Baldwin, 1976). (b) Dependence of the Hill coefficient at half-saturation on the apparent allosteric constant for all oxygen saturation curves of the dog and bovine physiological datasets (squares and circles, respectively). For each species, the appropriate c value (Supplementary file 1) was used to calculate the theoretical curve, onto which the actual *logL-n*_H data points were mapped.

https://doi.org/10.7554/eLife.47640.005

The clustering of all logL-n_H experimental data points of the H⁺, CO₂ and 2,3-BPG datasets around the maximum point reveals that the Hill value for human Hb is relatively insensitive to changes in physiological conditions. Such n_H-insensitive behavior was noted for the pH-related Bohr effect of Hb (Wyman, 1964; Di Cera et al., 1988) and later extended to other allosteric effectors of Hb (Milo et al., 2007). Our results showing the invariance of n_H with respect to logL thus provide a mechanistic explanation, based on the MWC model parameters, for the ‘buffering of cooperativity’ property of Hb. Such behavior should only appear if human Hb had evolved to present maximum cooperativity in oxygen binding (Figure 1c,d). As site-directed point mutants of Hb are not subjected to the selection pressure that leads to maximum cooperativity, the values of logL-n_H pairs for such mutants fall off the extremum point of the logL-n_H cross-section (Baldwin, 1976).

The maximum Hill point of a MWC-type protein allows for gross- and fine-tuning of substrate unbinding sensitivity

We next explored the potential evolutionary and physiological advantages of setting Hb cooperativity around the maximum n_H point. We asked the following questions: Does the value of the maximum Hill point determine the sensitivity of Hb to tissue oxygen unloading? Does the value of the maximum n_H point affect the dynamic range of the buffering of cooperativity phenomenon? How is Hb protein unbinding sensitivity changes within the buffering of cooperativity range? To answer these questions, we turned to Equation 2 and the biophysical Hill landscape (Figure 1c).

Using the MWC equation, we generated ligand saturation binding curves exhibiting increasing maximum Hill cooperativity values (Figure 4a). This was achieved by appropriate selection of L and c values (indicated in Table 1), all fulfilling the L=c^-² parameter criterion. To allow direct comparison, the saturation curves were plotted as a function of the scaled concentration α (=[S]/K_R), as is commonly done (Monod et al., 1965; Rubin and Changeux, 1966). Under such conditions, the affinity and maximum Hill point are correlated (Figure 4a). The higher the value of the maximum Hill point of the appropriate binding curve, the more it is displaced to the right along the scaled concentration axis. This is reflected in Figure 4b, showing monotonic correlation between the maximum Hill value and logα_1/2 (α_1/2=[S]_1/2/K_R). It thus seems that under the maximum cooperativity parameter condition, a tradeoff exist between the cooperativity and affinity properties of a MWC-type protein. We next examined if and how this tradeoff affects the sensitivity of the protein for substrate unbinding upon chemical potential change. For each of the curves presented in Figure 4a, we considered the chemical potential difference (Δlogα) needed to achieve a constant reduction in the fractional saturation from 100 to 40%, as typically observed for mammalian Hb saturation under physiological lung and tissue oxygen pressures (100 and 40 mmHg, respectively). The Δ ${\bar{Y}}_{100 \to 40 %}$ /Δlogα parameter depends on both the affinity and cooperativity attributes of the binding curve and reflects the sensitivity of the MWC protein to substrate unloading. The narrower the difference in chemical potential that results in a 60% reduction in fractional saturation, the higher is the sensitivity of the protein to substrate unbinding. As can be seen in Figure 4c (filled black symbols), the value for this parameter increases monotonically in a power law manner with increases in the value of the maximum Hill point. Similar results were obtained when other Δ $\bar{Y}$ ranges were considered (e.g. Δ ${\bar{Y}}_{100 \to 20 %}$ ; not shown). Higher maximum Hill points thus ensure higher sensitivity for substrate unbinding by the MWC protein.

We next addressed the dynamic range implicated in physiology adaptation. The maximum n_H points of the different curves shown in Figure 4a reside precisely at the apex of the appropriate bell-shaped n_H-logL curve, calculated using the appropriate c value (Figure 4d and Table 1). As mentioned earlier, around this maximum n_H point cooperativity is invariant to changes in L brought about by binding of allosteric modulators. To assess the broadness of the buffering of cooperativity regime around each maximum cooperativity point, we next generated a set of physiological dataset curves by systematically changing the value of L by several orders of magnitude, such that the resulting saturation curves exhibited essentially the same Hill value for ligand binding as did the original maximum Hill value (less than a 1% change). This ensured that our analysis remained within the ‘buffering of cooperativity’ region, characteristic of each maximum Hill value (see the yellow-marked logL range highlighted in each of the curves in Figure 4d). One such physiological dataset generated around the maximum point of human Hb (n_H = ~2.8) is shown in Figure 4e. For curves based on other maximum cooperativity points, see Figure 4—figure supplement 1. For each of the different datasets, we calculated the logL range between the two extreme binding curves and defined this value (ΔlogL) as the broadness of the buffering of cooperativity regime, or the dynamic range for physiological adaptation where only affinity (p₅₀) matters. Plotting the dependence of ΔlogL on the maximum cooperativity Hill value (Figure 4f) reveals that higher maximum Hill values give rise to broader L ranges, where ‘buffering of cooperativity’ is observed. The maximum Hill point thus further controls the dynamic range of physiological adaptation.

Figure 4 with 1 supplement see all

Download asset Open asset

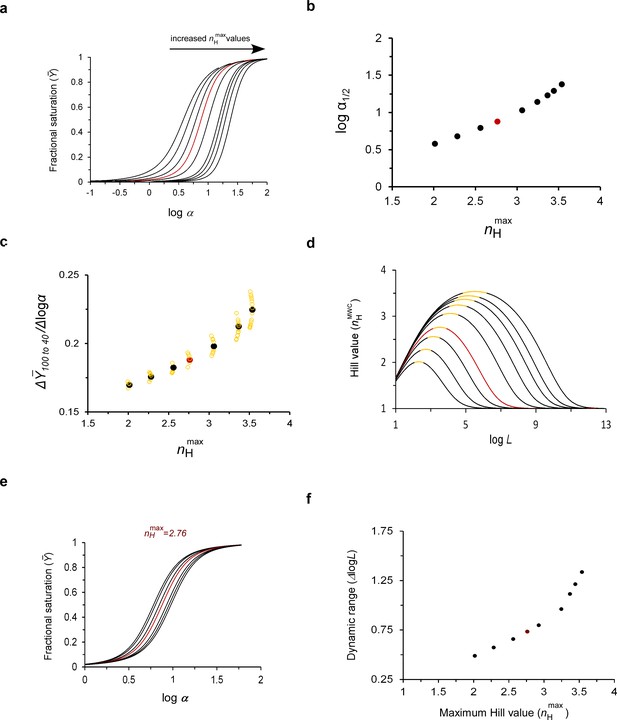
The maximum cooperativity point determines MWC protein substrate unbinding sensitivity and the dynamic range of physiological adaptation.

(a) Fractional saturation binding curves of a MWC protein as a function of the logarithm of the scaled concentration α, with parameter values that give rise to systematically higher maximum cooperativity n_H values. The pairs of L and c values for all curves obey the maximum cooperativity criterion and are listed in Table 1. (b) Dependence of the logarithm of the scaled affinity (logα_1/2) of the curves presented in (a) on the maximum cooperativity Hill value (n_H^max). (c) Dependence of the substrate unbinding sensitivity (Δ ${\bar{Y}}_{100 \to 40 %}$ /Δlogα) of a tetrameric MWC protein on n_H^max (filled black symbols). The array of open yellow symbols decorating each maximum cooperativity point corresponds to changes in the Y axis values due to changes in L that reside within the correspondingly encoded buffering of cooperativity regime (see text) (d) Dependence of $n_{H}^{M W C}$ on the logarithm of the allosteric constant L around the different maximum cooperativity points indicated in (a) and Table 1 (and assuming their different c values). For each curve, the portion highlighted in yellow corresponds to the logL range fulfilling the ‘buffering of cooperativity’ regime, that is the L range around the maximum Hill point that gives rise to fractional saturation curves all exhibiting less than 1% change in the maximum Hill coefficient value. Such a physiological dataset is observed for the maximum point of ~2.8, characteristic of human Hb in panel (e) (calculated using its appropriate c value; see Supplementary file 1). Similar data for different maximum cooperativity values are presented in Figure 4—figure supplement 1. In each physiological dataset, the curve indicated in red corresponds to the maximum cooperativity curve (f) Dependence of the broadness of the ‘buffering of cooperativity’ regime (the dynamic range), as defined above, on the maximum cooperativity Hill value. In all figure panels, the curves indicated in red were calculated using the experimental values for human Hb reported in the literature. The red data points in several of the panels represent approximated values of human Hb.

https://doi.org/10.7554/eLife.47640.006

Table 1

Values for the L and c MWC parameters giving rise to systematically higher maximum cooperativity Hill values^a

https://doi.org/10.7554/eLife.47640.008

c	L	Maximum Hill value (n_H^max)
0.07071	200	2.02
0.04472	500	2.28
0.02582	1500	2.56
0.01741	3300	2.76
0.01222	6700	3.06
0.00524	36400	3.24
0.0035	81800	3.37
0.00262	145400	3.44
0.00175	327200	3.54

^aValues for the c and L parameters giving rise to the maximum Hill slopes (indicated in the right-most column), characteristic of the binding saturation curves analyzed in Figure 4a. All parameter sets meet the Lc² = 1 criterion. The parameter set giving rise to the maximum cooperativity of human Hb, as reported in the literature and in Supplementary file 1, is indicated in bold. The different c values indicated were obtained by varying the K_R affinity parameter while assuming a constant K_T value of 143 (see Supplementary file 1).

Lastly, we considered how protein sensitivity to substrate unbinding, as defined above, varied within the yellow marked buffering of cooperativity regime (Figure 4d). Thus, for each set of fractional saturation curves calculated around the different maximum cooperativity points and residing within this regime (Figure 4e and Figure 4—figure supplement 1), we calculated Δ ${\bar{Y}}_{100 \to 40 %}$ /Δlogα. Variations in this parameter are plotted as open yellow symbols around each of the maximum cooperativity points presented in Figure 4c, with the lower and upper data points, respectively, corresponding to the lower and upper logL values defining the boundaries of this range. As can be seen, within this range, changes of up to 6% are observed in the value of protein unbinding sensitivity in response to changes in physiological conditions brought about by changes in L alone yet reflected in changes in p₅₀ alone.

The maximum cooperativity point of hemoglobin is related to organismal fitness

The fact that different mammalian Hbs exhibit different maximum n_H values (Figure 2a), combined with the observation made above whereby systematically higher maximum Hill value gives rise to higher sensitivities to substrate unloading by MWC proteins (Figure 4c), led us to hypothesize that the maximum cooperativity point of Hb has been tuned during evolution to satisfy the particular physiological requirements of different tissues for oxygen supply. We thus returned to the datasets comparing oxygen saturation of different mammalian Hbs (all measured using similar methodology) that revealed the linear correlation between animal metabolic rate and logp₅₀ (Schmidt-Neilsen and Larimer, 1958; Schmidt-Nielsen, 1970). We are aware that these data may not necessarily reflect functional effects on a single Hb form. Still, in cases where adult mammalian Hb expresses more than one variant, both usually present similar sequences and functional properties (Storz, 2016). Rather than taking the affinity-centric approach employed in the earlier studies, we instead adopted a complementary cooperativity-centric mindset and re-fitted all of the saturation curves to the Hill equation to derive both n_H and p₅₀ values for Hb of each animal (Figure 5a and Table 2). The derived n_H values, although obtained under the slightly different physiological conditions typical of the blood of each animal, nevertheless correspond to maximum cooperativity values, as n_H is relatively invariant to physiological changes around the maximum point (Figures 2 and 3). This assertion is further strengthened by the results shown in Figure 5b describing the linear relation between affinity (logp₅₀) and cooperativity (n_H), as expected for parameter values underlying maximum cooperativity (Figure 4b). Finally, plotting either the affinity (~log(1/p₅₀)) or cooperativity properties of Hb as a function of the logarithm of metabolic rate of an animal yielded linear correlations in both cases (Figure 5c). Specifically, the greater an animal’s metabolic rate, the higher was the observed maximum Hill cooperativity value of oxygen binding by Hb. Furthermore, as previously shown (Schmidt-Neilsen and Larimer, 1958; Schmidt-Nielsen, 1970), an inverse linear correlation was found between the metabolic rate and Hb affinity. These empirical observations directly relate the maximum cooperativity and affinity properties of Hb to an organismal-level trait that is related to fitness (Dykhuizen et al., 1987; Kacser and Burns, 1981; Bershtein et al., 2017).

Figure 5

Download asset Open asset

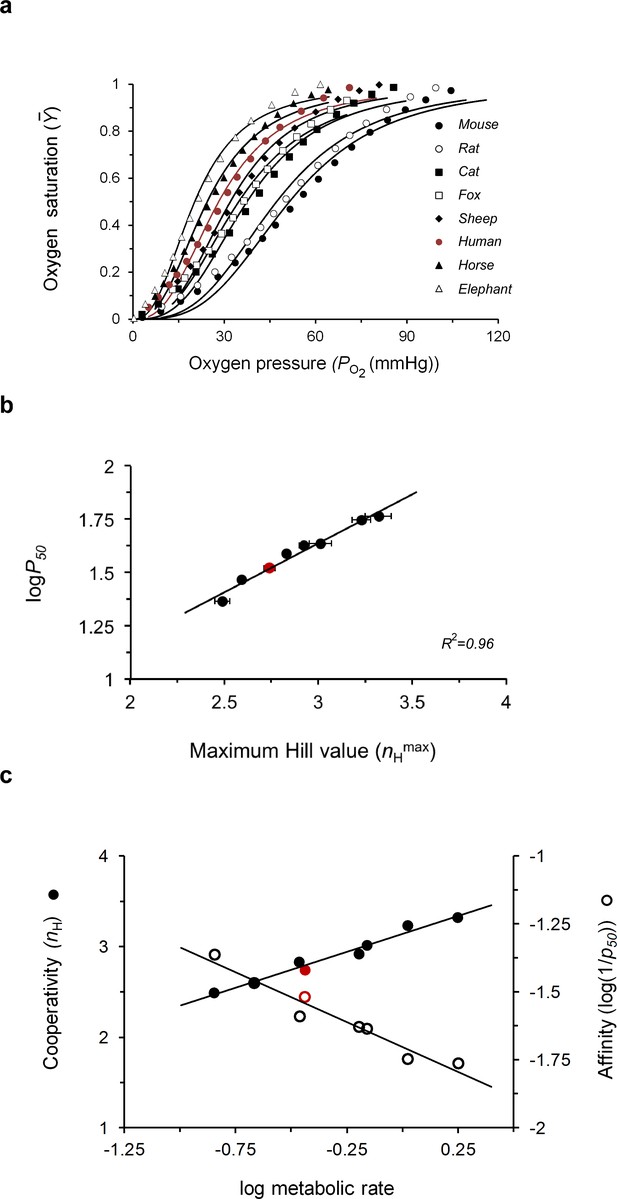
Evolutionary tuning of the maximum cooperativity and affinity points of mammalian hemoglobins underlies physiological adaptation.

(a) Dependence of the fractional oxygen saturation of animal blood sample Hbs on partial oxygen pressure, as reported by Schmidt-Neilsen and Larimer (1958), Schmidt-Nielsen (1970). Solid curves represent data fitting to the Hill equation (Equation 1). p₅₀ and n_H values for oxygen binding to the different mammalian Hb datasets are reported in Table 2. (b) Correlation plot relating the maximum n_H and *logp*₅₀ values of the curves shown in a. (c) Dependence of the values for both cooperativity (filled symbols) and affinity (open symbols) properties of different animal Hbs on normalized metabolic rates in that animal (relative to body weight). A linear trend is observed in both cases, with R² values of 0.97 and 0.9 for the cooperativity and affinity correlations, respectively. Values for animal metabolic rates were taken from Schmidt-Neilsen and Larimer (1958). The red curve or data points presented in panels **5a-c** correspond to the values for human Hb.

https://doi.org/10.7554/eLife.47640.009

Table 2

Values for the affinity and cooperativity parameters of animal blood hemoglobin binding curves^a

https://doi.org/10.7554/eLife.47640.010

Animal	P₅₀ (mmHg)	n_H
Elephant	23.03 ± 0.32	2.49 ± 0.04
Horse	29.26 ± 0.16	2.59 ± 0.01
*Human*	33.02 ± 0.29	2.74 ± 0.03
Sheep	38.82 ± 0.11	2.83 ± 0.01
Fox	42.36 ± 0.22	2.92 ± 0.02
Cat	43.22 ± 0.62	3.01 ± 0.06
Rat	55.63 ± 0.57	3.23 ± 0.05
Mouse	57.86 ± 0.76	3.32 ± 0.07

^aValues for the point of half-saturation (P₅₀) and the Hill coefficient at half-saturation (n_H) were derived by fitting blood sample animal Hb oxygen saturation curves (Schmidt-Neilsen and Larimer, 1958; Schmidt-Nielsen, 1970) to the Hill equation.

Discussion

In the current study, we emphasized the need to consider the property of Hb cooperativity (n_H), along with p₅₀, in addressing molecular adaptation of Hb in mammals. We formulated the explicit mathematical dependences of the n_H and p₅₀ macroscopic Hb parameters on the elementary microscopic parameters of the MWC model, thus providing a quantitative framework to understand the mechanism underlying the adaptive behavior of these two parameters with respect to tissue oxygen delivery. Indeed, relying on the biophysical Hill landscape, we were able to rationalize mammalian Hb n_H and p₅₀ diversity among large and small body-sized animals. The biophysical Hill landscape mapping strategy may further serve to define the mechanism underlying other molecular adaptation modes involving Hb of organisms living at high altitudes or presenting burrowing or diving lifestyles, for example.

Mammalian Hb diversity resides on the ridge of maximum cooperativity

Our findings revealed that mammalian Hb cooperativity values have been tuned during evolution to reside on a ridge of the theoretical biophysical Hill cooperativity landscape describing a MWC protein (Figures 2 and 3). These ridge-located Hill values all correspond to maximum cooperativity extremum points and were achieved by tuning of the relative affinity (c) and conformational ratio (L) of the T and R quaternary states of the protein (Figure 2). These maximum points are thus unique points along the Hill cooperativity scale continuum. There is no a priori reason to expect that physiological and evolutionary diversity in Hb would be reflected by this low dimensional ridge feature of the Hill landscape. As can be seen in the three dimensional Hill landscape, many combinations of L and c values can give rise to the same Hill value. Yet, only one of these combinations obeys the L = c⁻² maximum cooperativity criterion. The observed variations in maximum cooperativity Hill values among mammalian Hb proteins thus reflect co-evolution of binding and conformational changes of Hb. Such tuning gives rise to a buffering of cooperativity effect, suggesting that the degree of cooperativity is robust to changes in physiological conditions brought about by tuning L alone (Figure 3). Our results thus reveal the evolutionary strategy underlying the observed variations in Hb behavior.

Evolutionary and physiological adaptations of hemoglobin serve to optimize tissue oxygen delivery

The functional advantages of the balance between the relative affinity and conformational ratio of Hb quaternary states underlying the maximum Hill point become clear when considering that both the affinity and cooperativity parameters of Hb saturation curves affect tissue oxygen unloading. First, the c-L tradeoff gives rise to the highest possible Hill value for any given c value, thereby ensuring maximal oxygen unloading upon Hb transfer from the lungs to other tissues (Figure 1cd). Either very high or very low L values would give rise to hyperbolic oxygen saturation curves with an n_H value of one (Figure 1c), which would ensure poor and unregulated tissue oxygen unloading by Hb. The same is true when c is assigned the value of one. Second, tuning the Hb maximum Hill point to higher values further leads to greater sensitivity to tissue oxygen unloading (Figure 4c filled, symbols). Third, parameter adjustments that lead to higher maximum n_H values also give rise to reduced Hb oxygen affinity (p₅₀) (Figures 4b and 5b), thus reinforcing oxygen unloading upon Hb transfer from the lungs to other tissues. Indeed, the affinity-cooperativity tradeoff typical of the ridge of maximum cooperativity suggests that cooperativity can compensate for changes in affinity, with respect to tissue oxygen unloading, as usually described in any Biochemistry textbook. Fourth, the balanced parameter values give rise to the ‘buffering of cooperativity’ regime, thus ensuring that the n_H-related oxygen unloading effect is not compromised in response to physiological changes brought about by variations in L and reflected as changes in p₅₀. Indeed, under such a regime, relatively minor changes in Hb sensitivity for oxygen release are expected in response to changes in allosteric effector binding (Figure 4c, open symbols). Finally, the co-varied c and L values underlying maximum cooperativity allow for control of the broadness of the ‘buffering of cooperativity’ regime (Figure 4d,f).

Taken together, these points support the assertion that mammalian Hb n_H and p₅₀ values reflect evolutionary and physiological adaptations that serve to optimize the tradeoff between O₂ loading in pulmonary capillaries and O₂ unloading in tissue capillaries, so as to optimize tissue oxygen delivery. Based on experimental (Figures 2 and 3) and theoretical (Figure 4) results, we suggest that evolutionary (i.e., across species) variations allow for gross changes in Hb oxygen unloading sensitivity. Such changes are controlled by the maximum cooperativity and affinity values of Hb, in turn determined by changes in both L and c (Figure 4c, filled symbols). Fine-tuning changes in Hb oxygen unloading sensitivity may further be brought about by physiological variations within the buffering of cooperativity regime, this time, however, reflected in changes in L and p₅₀ alone (Figure 4c, open symbols).

The biophysical Hill landscape as a low dimensional biophysical fitness landscape

The linear dependence between the metabolic rate of an animal and the maximum Hill value for Hb (Figure 5c), combined with the results presented in Figure 4c, indicates that n_H, like p₅₀, carries adaptive value with respect to mammalian Hb tissue oxygen unloading. As such, small body-sized animals presenting high metabolic rates require high oxygen supplies that can be more efficiently delivered by Hb presenting higher maximum Hill values. Considering that an animal’s metabolic rate is a trait related to organism fitness, we suggest that both the affinity and cooperativity traits of Hb represent low dimensional components of the fitness landscape, independent of other components. In this respect, the biophysical n_H landscape of Hb can be regarded as a biophysical fitness landscape that serves to bridge the genotype-phenotype gap in assessing the relation between sequence variations in Hb (that affect its affinity and cooperativity properties) and their ensuing fitness effects (Bershtein et al., 2017). Evolutionary tuning of mammalian Hb maximum cooperativity and affinity points, achieved by co-varying the relative affinity and conformational ratio of its quaternary states, thus regulates tissue oxygen delivery by Hb and serves as one mean to meet the distinct needs of different animal tissues for oxygen (Figures 4 and 5). Clearly, other mechanisms related to cardiac output and to convective and diffusive steps in the oxygen transport pathway are as well contribute to modulation of tissue oxygen transport (reviewed in Schmidt-Nielsen, 1975). For example, it has been shown that the capillary density of a mammal is also inversely correlated to body size (Schmidt-Nielsen, 1975).

How general are our findings regarding maximum cooperativity in ligand binding?

The buffering of cooperativity regime in Hb reflects the case where the fractional saturation curves of the protein seem parallel in shape and are only displaced along the substrate concentration axis in response to changes in effector ligand concentrations (see Figure 4e). As revealed by Olsman and Goentoro (2016), it is exactly this behavior the qualifies a MWC protein as a logarithmic sensor, reflecting the capacity of the protein to respond identically over a broad range of changes in chemical potential. Such behavior is in contrast to the case where the protein sensor responds to the absolute value of the signal intensity. Upon surveying the literature, Olsman and Goentoro (2016) found that many MWC allosteric proteins, including phosphofructokinase, Hb, cyclic nucleotide-gated ion channels, Tar receptors, G-protein coupled receptors and EGF receptors exhibit a buffering of cooperativity or logarithmic sensing regime in response to changes in the concentration (or magnitude) of the modulatory allosteric signal. The dynamic range for this behavior can vary from 10-fold (Hb) to 10,000-fold (GPCR). These findings suggest that all these MWC proteins evolved to present maximum cooperativity values in ligand binding and operate under the L = c ^-n/2 parameter regime that gives rise to the buffering of cooperativity phenomenon. However, other than Hb, the significance of this finding to organismal fitness is known only in the case of a single protein (Keymer et al., 2006). Realizing the physiological advantage(s) of attaining the maximum cooperativity point of any protein and its relation to organismal fitness, is, of course, case-specific.

The relation between physiological and evolutionary adaptations in shaping a protein molecular property

Finally, the roadmap that underlies the ‘biophysical Hill landscape’-mapping strategy is general and can be applied to reveal the relation between evolutionary (i.e. sequence) and physiological (e.g. changes in metabolite concentrations) variations in shaping any molecular property of a protein. Although operating on different time scales and through different mechanisms, these traits are linked through the biophysical model describing the function of the protein. Elucidating this linkage requires extensive physiological and evolutionary datasets of the protein and that the steady-state biophysical model describing the function of the protein is known so that the explicit mathematical dependence of the molecular property under study on biophysical model parameters can be elucidated. This allows for constructing a ‘biophysical molecular property landscape’ onto which experimentally derived values of the macroscopic and microscopic parameters of all physiological and evolutionary dataset measurements can be mapped. Rationalizing the pattern of such mapping in terms of the relation between model parameters reflecting particular protein processes, such as catalysis, binding or conformational changes, might then reveal the driving forces that shape the molecular property under study.

Materials and methods

Datasets

Request a detailed protocol

The functional data analyzed here considered the evolutionary and physiology Hb datasets respectively complied in Milo et al. (2007) and Rapp and Yifrach (2017). The evolutionary dataset comprised oxygen saturation curves of Hb from 14 different mammal samples obtained under similar physiological conditions. Using a three-equation system strategy (Rapp and Yifrach, 2017), the values for the L and c MWC allosteric parameters of all dataset curves were recently reported (Supplementary file 1). The physiological dataset comprised four independent human Hb sub-datasets, obtained from three different labs, with two reporting pH modulation, one considering CO₂ modulation and the last addressing 2,3-BPG modulation, as discussed in the meta analyses by Rapp and Yifrach (2017). These sub-datasets each include between 5 and 7 oxygen saturation curves obtained at different effector concentrations. Using global fitting analysis, we recently reported reliable estimates for the apparent L values for the different concentration-related physiological datasets curves (see Rapp and Yifrach, 2017 and Supplementary file 2).

The biophysical Hill landscape

Request a detailed protocol

Cooperativity in oxygen binding by Hb was assessed using the Hill or MWC models, as quantitatively described by Equation 1 and 2. The dependence of n_H at half-saturation ( $n_{H}^{M W C}$ ) on the MWC elementary parameters was obtained by applying Equation 4 to the MWC equation, assuming ${\bar{Y}}_{M W C}$ equals ½. Explicit solving for [S]_1/2 in terms of K_R, K_T and L was obtained using the Mathematica 11.2 software package (Wolfram research Inc). Substituting this expression in Equation 5 using the same software yields the explicit expression for $n_{H}^{M W C}$ (at half-saturation) in terms of the MWC model parameters. It should be noted that $n_{H}^{M W C}$ (at half-saturation) is an approximate measure of $n_{H, m a x}^{M W C}$ , the more natural Hill value for specifying homotropic cooperativity in the framework of the MWC model (Rubin and Changuex, 1966). In our analysis, we used $n_{H}^{M W C}$ rather than the $n_{H, m a x}^{M W C}$ as the former is the actual parameter that is usually evaluated when fitting experimental data to the Hill equation (Equation 1). As for $n_{H, m a x}^{M W C}$ , the expression for $n_{H}^{M W C}$ at half-saturation also exhibits a bell-shaped dependence on L, thereby also describing the characteristic ‘buffering of cooperativity’ effect. Furthermore, $n_{H, m a x}^{M W C}$ is equal to $n_{H}^{M W C}$ exactly at the maximum cooperativity point (Rubin and Changeux, 1966). It should be emphasized that the $n_{H}^{M W C}$ expression derived here relates to cooperativity in ligand binding (as it is calculated based on $\bar{Y}$ ) and is different than the expressions for n_H derived in other studies based on the active state function ( $\bar{R}$ in the case of an enzyme or ${\bar{P}}_{o p e n}$ in case of an ion channel) and which relates to cooperativity of conformational switching (Einav and Phillips, 2017; Martins and Swain, 2011; Marzen et al., 2013). For plotting the three-dimensional Hill landscape ( $n_{H}^{M W C}$ ) as a function of both logL and logc, a constant K_T (=143 mmHg, the average value for K_T in the evolutionary dataset (See Supplementary file 1) and varying K_R parameters were used. The Hill biophysical landscape shape, however, is invariant to other choices made for changing the relative affinity c parameter.

MWC model simulations

View detailed protocol

Simulated MWC-based $\bar{Y}$ data were generated using Equation 2 by changing the appropriate biophysical parameters (K_T, K_R or L), as described in the text and in figure legends. For evaluating the sensitivity of oxygen unloading, simulated MWC-based $\bar{Y}$ curves were first generated around several maximum cooperativity values by systematically changing c and adjusting L so as to fulfill the Lc²=1 maximum cooperativity criterion. Nevertheless, since scaled $\bar{Y}$ curves are presented, the analysis is invariant to parameter choice. Around each maximum cooperativity graph, the dependence of $n_{H}^{M W C}$ on the allosteric constant L was plotted assuming the appropriate constant c value in each case.

Data extraction and fitting

Request a detailed protocol

To extract $\bar{Y}$ data from previously published graphs, the WebPlotDigitizer net-based program was used. Only experimental data points were sampled unless the reported graph presented the experimental trend by a continuous line rather than scattered data points, as is typical of saturation data presented in older manuscripts. In such cases, the curves were evenly sampled by taking systematic steps along the x-axis. $\bar{Y}$ data were fitted using either the Hill or MWC equations (Equation 1 and 2, respectively). The adequacy of fit was judged based on attaining a R² coefficient greater than 0.97.

Appendix 1

Hb oxygen ligation is reasonably described by the MWC allosteric model

Does indeed the MWC model adequately describe Hb function? It is clear and long accepted that the MWC model sufficiently describes the cooperative binding of oxygen to Hb (Eaton et al., 1999). However, rationalizing the effects of modulatory ligands on Hb function using the MWC model, remained long controversial (Imai, 1973). This was a result of the fact that fitting saturation curves of Hb in the presence of its various inhibitors to the MWC equation, assuming L-only effects, consistently failed. Rather, successful fits were obtained only when both L and the c parameters were allowed to change (Imai, 1973; Yonetani et al., 2002). In recent years, however, it became clear that data fitting analysis using the traditional MWC model equation may not provide reliable estimates for L and c (Milo et al., 2007; Rapp and Yifrach, 2017) thus calling for a re-examination of previous data using alternative fitting strategies.

Recently, we reported on two simple fitting strategies that allowed obtaining reliable estimates for the L and c parameters of Hb saturation curves in cases of both evolutionary and physiological variations (Rapp and Yifrach, 2017). In particular, we showed that Hb effector dataset saturation curves may be globally fitted successfully using the MWC equation assuming varying L values for the different curves and a constant c value for all curves. Furthermore, we showed that the derived L values of all curve scaled with effector concentration, exactly as predicted by the MWC theory. These results, thus suggested that the simple MWC model provides a reasonable description that can also account for heterotropic interactions in Hb. The tertiary two-state model (TTS) (Viappiani et al., 2014) is a natural extension of the MWC model, and no doubt, performs better. Still, even with this more accurate description, the traditional MWC model provides a reasonable approximation to explain steady-state physiological effects on Hb saturation. Such approximation can provide initial estimates of the ‘quaternary contribution’ (L’) of allosteric effectors within the framework of the TTS model, not previously possible, due to data fitting difficulties.

To summarize, in the analysis here we treat Hb as a pure MWC protein and make use of the values for the L and c MWC parameters of all evolutionary and physiological dataset saturation curves obtained using reliable data fitting strategies (Supplementary files 1 and 2, respectively) (Rapp and Yifrach, 2017), thus allowing us to address the driving forces that shaped Hb affinity and cooperativity in oxygen binding and its implications with respect to the molecular basis for body size related adaptation of Hb.

https://doi.org/10.7554/eLife.47640.014

Appendix 2

A good approximation for the dependence of the Hill coefficient at half saturation on the MWC model parameters

Equation A2.1 below corresponds to Equation 5 in the main text. As can be seen in $\bar{Y}$ MWC Equation 2 of the main text, under half- saturation condition (where $\bar{Y} = 1 / 2$ ), [S]_0.5 is raised to a power of up to four and its explicit expression (obtained using the Mathematica software package) is long and complex. An approximation for [S]_0.5 may be obtained using the [S]_0.5 of the $\bar{R}$ conformational state function (the fraction of R state as a function of substrate concentration), as described in Equation A2.2 below (Gruber et al., 2019). Plugging this expression into Equation A2.1 results in an explicit expression for $n_{H}^{M W C}$ that depends on the MWC model parameters, as described by the long Equation A2.3, below. The biophysical Hill landscape obtained using this equation is very similar to that calculated directly based on Equation A2.1 over most of the range of L and c values (less than 2% difference in n_H values) and is identical under the parameter regime of maximum cooperativity.

\begin{array}{ll} n_{H}^{M W C} = \frac{\partial (\frac{{\bar{Y}}_{M W C}}{1 - {\bar{Y}}_{M W C}})}{\partial (\log [S])} = (4 [S] (\frac{\partial ({\bar{Y}}_{M W C})}{\partial ([S])})) |_{[S] = {[S]}_{50}} = \\ (4 [S] (\frac{\frac{3 [S] {(1 + \frac{[S]}{K_{R}})}^{2}}{K_{R}^{2}} + \frac{{(1 + \frac{[S]}{K_{R}})}^{3}}{K_{R}} + \frac{3 L [S] {(1 + \frac{[S]}{K_{T}})}^{2}}{K_{T}^{2}} + \frac{L {(1 + \frac{[S]}{K_{T}})}^{3}}{K_{T}}}{{(1 + \frac{[S]}{K_{R}})}^{4} + L {(1 + \frac{[S]}{K_{T}})}^{4}} \frac{- (\frac{4 {(1 + \frac{[S]}{K_{R}})}^{3}}{K_{R}} + \frac{4 L {(1 + \frac{[S]}{K_{T}})}^{3}}{K_{T}}) (\frac{[S] {(1 + \frac{[S]}{K_{R}})}^{3}}{K_{R}} + \frac{L [S] {(1 + \frac{[S]}{K_{T}})}^{3}}{K_{T}})}{{({(1 + \frac{[S]}{K_{R}})}^{4} + L {(1 + \frac{[S]}{K_{T}})}^{4})}^{2}})) \\ |_{[S] = {[S]}_{50}} \end{array}

{[S]}_{0.5} = \frac{(\sqrt[4]{L - 1})}{\frac{1}{K_{R}} + \frac{\sqrt[4]{L}}{K_{T}}}

\begin{array}{lll} n_{H}^{M W C} = & \frac{\begin{matrix} 4 (K_{т} + \sqrt[4]{L} K_{R})^{4} ({\sqrt[4]{L}}^{3} K_{R}^{4} (K_{R} + K_{т})^{3} + K_{т}^{4} (2 \sqrt[4]{L} K_{R} + K_{т} - K_{R})^{3}) \\ ({\sqrt[4]{L}}^{3} K_{R}^{4} (K_{R} + K_{т})^{3} + K_{т}^{4} L (2 \sqrt[4]{L} K_{R} + K_{т} - K_{R})^{3}) \end{matrix}}{K_{R}^{9} K_{т}^{9} (\sqrt[4]{L} - 1 (K_{т} + \sqrt[4]{L} K_{R}) (\frac{L (K_{R} + K_{т})^{4}}{K_{т}^{4}} + \frac{(2 \sqrt[4]{L} K_{R} + K_{т} - K_{R})^{4}}{K_{R}^{4}})^{2}} - \\ \frac{\begin{matrix} 4 \sqrt[4]{L} K_{R} K_{т} (K_{т} + \sqrt[4]{L} K_{R})^{2} ({\sqrt[4]{L}}^{3} K_{R}^{4} (K_{R} + K_{т})^{3} + 3 K_{R}^{4} \\ (K_{R} + K_{т})^{2} (K_{т} + \sqrt[4]{L} K_{R}) - 3 K_{т}^{4} L (K_{т} + K_{R}) \\ (2 K_{R} \sqrt[4]{L} + K_{т} - K_{R})^{2} + \sqrt[4]{L} K_{т}^{4} L (2 \sqrt[4]{L} K_{R} + K_{т} - K_{R})^{3}) \\ (L K_{R}^{4} (K_{R} + K_{т})^{4} + K_{т}^{4} (2 \sqrt[4]{L} K_{R} + K_{т} - K_{R})^{4}) \end{matrix}}{K_{R}^{9} K_{т}^{9} (\sqrt[4]{L} - 1) (K_{т} + \sqrt[4]{L} K_{R}) (\frac{L (K_{R} + K_{т})^{4}}{K_{т}^{4}} + \frac{(2 \sqrt[4]{L} K_{R} + K_{т} - K_{R})^{4}}{K_{R}^{4}})^{2}} \end{array}

https://doi.org/10.7554/eLife.47640.015

Data availability

All data generated or analysed in the current study are included in the manuscript and supporting files. Supporting Files 1 and 2 delineate the principal data analyzed in the current study and were adopted from Rapp and Yifrach (2017).

References

1. Baldwin JM
(1976) Structure and function of haemoglobin
Progress in Biophysics and Molecular Biology 29:225–320.
https://doi.org/10.1016/0079-6107(76)90024-9
- Google Scholar
(1971) Cofactor binding and oxygen equilibria in haemoglobin
Nature New Biology 234:174–176.
https://doi.org/10.1038/newbio234174a0
- PubMed
- Google Scholar
(2017) Bridging the physical scales in evolutionary biology: from protein sequence space to fitness of organisms and populations
Current Opinion in Structural Biology 42:31–40.
https://doi.org/10.1016/j.sbi.2016.10.013
- PubMed
- Google Scholar
(1981) Interaction of organic phosphates with bovine hemoglobin. II. oxygen binding equilibria of newborn and adult hemoglobin
Pflugers Archiv : European Journal of Physiology 389:227–235.
https://doi.org/10.1007/bf00584783
- PubMed
- Google Scholar
1. Bunn H-F
(1980) Regulation of hemoglobin function in mammals
American Zoologist 20:199–211.
https://doi.org/10.1093/icb/20.1.199
- Google Scholar
(1988) Alkaline bohr effect of human hemoglobin ao
Journal of Molecular Biology 200:593–599.
https://doi.org/10.1016/0022-2836(88)90545-1
- PubMed
- Google Scholar
1. Doyle ML
2. Di Cera E
3. Robert CH
4. Gill SJ
(1987) Carbon dioxide and oxygen linkage in human hemoglobin tetramers
Journal of Molecular Biology 196:927–934.
https://doi.org/10.1016/0022-2836(87)90414-1
- PubMed
- Google Scholar
(1987)
Metabolic flux and fitness

Genetics 115:25–31.
- PubMed
- Google Scholar
(1999) Is cooperative oxygen binding by hemoglobin really understood?
Nature Structural Biology 6:351–358.
https://doi.org/10.1038/7586
- PubMed
- Google Scholar
1. Edelstein SJ
(1971) Extensions of the allosteric model for haemoglobin
Nature 230:224–227.
https://doi.org/10.1038/230224a0
- PubMed
- Google Scholar
1. Edelstein SJ
(1975) Cooperative interactions of hemoglobin
Annual Review of Biochemistry 44:209–232.
https://doi.org/10.1146/annurev.bi.44.070175.001233
- PubMed
- Google Scholar
1. Einav T
2. Phillips R
(2017) Monod-Wyman-Changeux analysis of Ligand-Gated ion channel mutants
The Journal of Physical Chemistry B 121:3813–3824.
https://doi.org/10.1021/acs.jpcb.6b12672
- PubMed
- Google Scholar
Book
1. Fersht A-R
(1985)
Enzyme Structure and Mechanism

New York: WH Freeman.
- Google Scholar
(2019) GroEL allostery illuminated by a relationship between the hill coefficient and the MWC model
Biophysical Journal.
https://doi.org/10.1016/j.bpj.2019.10.013
- Google Scholar
(1997) Can a two-state MWC allosteric model explain hemoglobin kinetics?
Biochemistry 36:6511–6528.
https://doi.org/10.1021/bi9619177
- PubMed
- Google Scholar
1. Hill A-V
(1910)
The possible effects of the aggregation of the molecules of haemoglobin on its oxygen dissociation curve

The Journal of Physiology 40:4–7.
- Google Scholar
1. Hourdez S
2. Weber RE
(2005) Molecular and functional adaptations in deep-sea hemoglobins
Journal of Inorganic Biochemistry 99:130–141.
https://doi.org/10.1016/j.jinorgbio.2004.09.017
- PubMed
- Google Scholar
1. Imai K
(1973) Analyses of oxygen equilibria of native and chemically modified human adult hemoglobins on the basis of Adair's stepwise oxygenation theory and the allosteric model of Monod, Wyman, and Changeux
Biochemistry 12:798–808.
https://doi.org/10.1021/bi00729a003
- PubMed
- Google Scholar
1. Imai K
(1983) The Monod-Wyman-Changeux allosteric model describes haemoglobin oxygenation with only one adjustable parameter
Journal of Molecular Biology 167:741–749.
https://doi.org/10.1016/S0022-2836(83)80107-7
- PubMed
- Google Scholar
1. Jensen FB
(2004) Red blood cell pH, the bohr effect, and other oxygenation-linked phenomena in blood O₂ and CO₂ transport
Acta Physiologica Scandinavica 182:215–227.
https://doi.org/10.1111/j.1365-201X.2004.01361.x
- PubMed
- Google Scholar
1. Kacser H
2. Burns JA
(1981)
The molecular basis of dominance

Genetics 97:639–666.
- PubMed
- Google Scholar
1. Keymer JE
2. Endres RG
3. Skoge M
4. Meir Y
5. Wingreen NS
(2006) Chemosensing in Escherichia coli: two regimes of two-state receptors
PNAS 103:1786–1791.
https://doi.org/10.1073/pnas.0507438103
- PubMed
- Google Scholar
1. Lenfant C
(1973) High altitude adaptation in mammals
American Zoologist 13:447–456.
https://doi.org/10.1093/icb/13.2.447
- Google Scholar
Book
1. Levitzki A
(1978) Quantitative Aspects of Allosteric Mechanisms
Springer-Verlag, Berlin.
https://doi.org/10.1007/978-3-642-81231-6
- Google Scholar
1. Martins BM
2. Swain PS
(2011) Trade-offs and constraints in allosteric sensing
PLOS Computational Biology 7:e1002261.
https://doi.org/10.1371/journal.pcbi.1002261
- PubMed
- Google Scholar
(2013) Statistical mechanics of Monod-Wyman-Changeux (MWC) models
Journal of Molecular Biology 425:1433–1460.
https://doi.org/10.1016/j.jmb.2013.03.013
- PubMed
- Google Scholar
1. Mello BA
2. Tu Y
(2005) An allosteric model for heterogeneous receptor complexes: understanding bacterial chemotaxis responses to multiple stimuli
PNAS 102:17354–17359.
https://doi.org/10.1073/pnas.0506961102
- PubMed
- Google Scholar
1. Milo R
2. Hou JH
3. Springer M
4. Brenner MP
5. Kirschner MW
(2007) The relationship between evolutionary and physiological variation in hemoglobin
PNAS 104:16998–17003.
https://doi.org/10.1073/pnas.0707673104
- PubMed
- Google Scholar
(1965) On the nature of allosteric transitions: a plausible model
Journal of Molecular Biology 12:88–118.
https://doi.org/10.1016/S0022-2836(65)80285-6
- PubMed
- Google Scholar
1. Olsman N
2. Goentoro L
(2016) Allosteric proteins as logarithmic sensors
PNAS 113:E4423–E4430.
https://doi.org/10.1073/pnas.1601791113
- PubMed
- Google Scholar
1. Perutz MF
(1983) Species adaptation in a protein molecule
Molecular Biology and Evolution 1:1–28.
https://doi.org/10.1093/oxfordjournals.molbev.a040299
- PubMed
- Google Scholar
1. Perutz MF
(1989) Mechanisms of cooperativity and allosteric regulation in proteins
Quarterly Reviews of Biophysics 22:139–237.
https://doi.org/10.1017/S0033583500003826
- PubMed
- Google Scholar
(1992) Molecular adaptation of hemoglobin function in mammals
Respiration Physiology 90:3–17.
https://doi.org/10.1016/0034-5687(92)90130-O
- PubMed
- Google Scholar
Software
1. Rapp O
(2019) MWC_Parameter, version 92160fe
Github.

https://github.com/OlgaRL/MWC_Parameters
1. Rapp O
2. Yifrach O
(2017) Using the MWC model to describe heterotropic interactions in hemoglobin
PLOS ONE 12:e0182871.
https://doi.org/10.1371/journal.pone.0182871
- PubMed
- Google Scholar
1. Rubin MM
2. Changeux JP
(1966) On the nature of allosteric transitions: implications of non-exclusive ligand binding
Journal of Molecular Biology 21:265–274.
https://doi.org/10.1016/0022-2836(66)90097-0
- PubMed
- Google Scholar
1. Schmidt-Neilsen K
2. Larimer JL
(1958) Oxygen dissociation curves of mammalian blood in relation to body size
American Journal of Physiology-Legacy Content 195:424–428.
https://doi.org/10.1152/ajplegacy.1958.195.2.424
- Google Scholar
1. Schmidt-Nielsen K
(1970)
Energy metabolism, body size, and problems of scaling

Federation Proceedings 29:1524–1532.
- PubMed
- Google Scholar
Book
1. Schmidt-Nielsen K
(1975)
Animal Physiology

London: Cambridge University Press.
- Google Scholar
1. Storz JF
2. Runck AM
3. Sabatino SJ
4. Kelly JK
5. Ferrand N
6. Moriyama H
7. Weber RE
8. Fago A
(2009) Evolutionary and functional insights into the mechanism underlying high-altitude adaptation of deer mouse hemoglobin
PNAS 106:14450–14455.
https://doi.org/10.1073/pnas.0905224106
- PubMed
- Google Scholar
1. Storz JF
(2016) Hemoglobin-oxygen affinity in high-altitude vertebrates: is there evidence for an adaptive trend?
The Journal of Experimental Biology 219:3190–3203.
https://doi.org/10.1242/jeb.127134
- PubMed
- Google Scholar
1. Storz JF
2. Moriyama H
(2008) Mechanisms of hemoglobin adaptation to high altitude hypoxia
High Altitude Medicine & Biology 9:148–157.
https://doi.org/10.1089/ham.2007.1079
- PubMed
- Google Scholar
(2008) Deducing receptor signaling parameters from in vivo analysis: luxn/AI-1 quorum sensing in Vibrio harveyi
Cell 134:461–473.
https://doi.org/10.1016/j.cell.2008.06.023
- PubMed
- Google Scholar
1. Viappiani C
2. Abbruzzetti S
3. Ronda L
4. Bettati S
5. Henry ER
6. Mozzarelli A
7. Eaton WA
(2014) Experimental basis for a new allosteric model for multisubunit proteins
PNAS 111:12758–12763.
https://doi.org/10.1073/pnas.1413566111
- PubMed
- Google Scholar
1. Weber RE
(2007) High-altitude adaptations in vertebrate hemoglobins
Respiratory Physiology & Neurobiology 158:132–142.
https://doi.org/10.1016/j.resp.2007.05.001
- PubMed
- Google Scholar
1. Wyman J
(1964)
Linked functions and reciprocal effects in hemoglobin: a second look

Advances in Protein Chemistry 19:223–286.
- PubMed
- Google Scholar
1. Yifrach O
(2004) Hill coefficient for estimating the magnitude of cooperativity in gating transitions of voltage-dependent ion channels
Biophysical Journal 87:822–830.
https://doi.org/10.1529/biophysj.104.040410
- PubMed
- Google Scholar
1. Yonetani T
2. Park SI
3. Tsuneshige A
4. Imai K
5. Kanaori K
(2002) Global allostery model of hemoglobin. Modulation of O₍₂) affinity, cooperativity, and bohr effect by heterotropic allosteric effectors
The Journal of Biological Chemistry 277:34508–34520.
https://doi.org/10.1074/jbc.M203135200
- PubMed
- Google Scholar

Decision letter

John Kuriyan

Senior and Reviewing Editor; University of California, Berkeley, United States
Rama Ranganathan

Reviewer; University of Chicago, United States

In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.

Thank you for submitting your article "On the driving forces that shape the characteristic Hill cooperativity value of an allosteric protein" for consideration by eLife. Your article has been reviewed by a Senior Editor, John Kuriyan as the Reviewing Editor, and three reviewers. The following individuals involved in review of your submission have agreed to reveal their identity: Rama Ranganathan (Reviewer #2).

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Summary:

This paper concerns the relationship between the Hill coefficient for an allosteric system (as defined by the MWC model), and the physical parameters of the model (the equilibrium constant between states and the ligand affinities). As noted by Reviewer 1, this interesting paper is a follow up to an earlier excellent article recently published in PLOS One by the same authors in which they showed that the model of Monod-Wyman-Changeux can self-consistently describe the extant data on hemoglobin, including in the presence of a variety of effectors. The current article goes much farther now by providing an interpretative framework in terms of the "Hill landscape". The argument made is that there is a surface of n_H,the effective Hill coefficient, as a function of the MWC parameters L and c and that hemoglobins have been tuned in evolution so as to live on a ridge on this surface.

The reviewers have raised a number of issues that should be addressed in a revised version of the manuscript. Note that no additional calculations or new work is called for. But it should be clear from the reviewer comments that a careful revision of the manuscript, with inclusion of explanatory points as well as the complete set of equations in the main text, will help make this paper more effective.

Note that one of the reviewers (Reviewer 3) questions some of the fundamental assumptions underlying this work. Please respond to these concerns as well as possible.

Reviewer 1:

Essential revisions:

1) The lack of equations in the main text. For a paper that is performing a theoretical analysis couched in the language of mathematics, the relevant equations should not be relegated to the Supplementary information. Further, there are far more equations to be included (in my opinion) than the several presented there. For example, there is an equation in Figure 3 of their PLOS One paper that gives the effective L parameter that is very important and I think most people are not aware of that is the fundamental basis of interpreting how the "bare" MWC model can be used in the context of effector molecules and why the dissociation constants K_A and K_I are immune to the effector.

2) Overarching concept – I find it is a missed opportunity that the authors do so little to talk about the generic truths they are making as opposed to the very specific comments relative to hemoglobin. Further, I challenge comments such as "Hemoglobin is the only allosteric protein with a known mechanism of action". I object to this comment on several grounds – first, these authors over and over again use the word "mechanism" without once attempting to define it (at least that I can find after reading the paper carefully twice) and second, I think this is false. People have done beautiful, deep work on ion channels, on transcription factors such as LacI, on chemotaxis receptors, etc.

3) On a related point: I find the citations of the literature quite inconsistent with my own take on the literature on the field. For example, how can the amazing paper of Martins and Swain not be cited? They carried out deep analysis on the nature of allosteric molecules. Similarly, the work of – Keymer et al., 2006, Swem et al., 2009, the first on chemotaxis receptors, the latter on quorum sensing receptors. This work would benefit from embracing some of research that these people and others (Mirny, 2010; Tu et al., 2019, Marzen et al., 2015) have been doing.

4) Abstract and beyond: I found the generally evolutionary tone of this paper to be not wholly scientific. In the abstract we have "found it evolved", "showed that" and "evolutionary tuning", all indicating that the authors are convinced that hemoglobin evolved in order to achieve some optimality. There is never any discussion of the fact that correlation does not imply causation – nor any discussion of the null hypothesis of neutrality, nor any discussion of the possible fitness landscape that would produce such optimality.

5) Introduction: – "the characteristic n_H values of almost all allosteric proteins rarely approaches the maximal value n". In some ways I completely disagree with this perspective. My take is that this is true for only one reason and that is because the model of the Hill function is the wrong model for those molecules. If you write the MWC model, the equation (which should be front and center in the paper – their equation 2 sort of) the "4" in the partition function in the denominator is perfectly well aligned with the fact that there are 4 binding sites for hemoglobin. If you do this same thing for cyclic nucleotide gated ion channels and fit a Hill function, you don't get the correct number of binding sites. If you use MWC, you do.

6) Though the authors are constantly talking about c and L,, shouldn't we think of the MWC model as a three-parameter model? I just don't follow their thinking on this point.

7) "the molecular phenotype of a protein" – to me, the molecular phenotype is much broader than this. IT includes the leakiness 1/(1+L), the EC50, the dynamic range as well as the Hill parameter.

8) Subsection “The biophysical Hill landscape of a tetrameric MWC allosteric protein”: "summarizes all known aspects" – As mentioned above, the known aspects of the model include Leakiness, EC50, saturation, dynamic range, effective Hill parameter, but there are other deep things such as the way Wingreen and coworkers have repeatedly shown the data collapse achieved in these models. See the Keymer et al., papers where the data collapse in chemotaxis is demonstrated

9) I am not sure what they are talking about, but I think that there are mutants of MWC proteins that do something other than change L. See the work of Daber and Lewis for an example.

10) Subsection /2The characteristic n_H value of hemoglobin is a maximum cooperativity point”: "very close to a value of…" given that in physics people argue about exponents of 1/3 vs. 1/2 in the context of different scaling relations, it is hard to see how 2.7 and 2 are "very close".

11) "results imply that evolutionary tuning of.…" It would be very interesting to understand more about the multi-dimensional fitness landscape that a living organism faces and how a particular piece of that ends up as a low dimensional fitness landscape that only cares about n_H. My point is that the organism as a whole faces the battle for existence. This depends upon all of its physiology, not just oxygen binding. Do all the separate pieces of physiology each optimize separately? Are some unique and privileged? The authors could attempt to address these kinds of issues rather than just giving the usual arguments about evolutionary tuning and optimization.

12) Subsection “Datasets”, "considered part" some discussion of the logic of which parts are included would be great.

13) Supplementary file 1. One thing I wondered about both here and in the PLOS paper (which I have also read many times) is about the "sloppy" nature of the parameters. I am not sure if these authors have encountered the work of Jim Sethna (Cornell, Physics), but they have done very interesting things about parameter nonuniqueness. I am not sure how that plays out here but in our own experience using MWC in many contexts, the nonuniqueness of parameters comes up again and again.

Reviewer 2:

This paper focuses on developing a general model that explains the mechanistic origin of the cooperativity displayed by allosteric proteins, and presents this model in the context of hemoglobin, a classic model system with the kind of diverse datasets required for this analysis. The authors claim (1) that they have rich datasets regarding oxygen saturation curves for 14 different mammalian hemoglobins in a similar physiological condition (the evolutionary dataset) and for human hemoglobin in 26 different physiological conditions (the physiological dataset), (2) that from these datasets they can derive half maximal saturation and the Hill coefficient (n_H), and can derive the key parameters of the MWC model (L, the equilibrium constant of the T to R conformational change, and c, the ratio of binding affinity to the T and R states), (3) that using the so-called "Hill transformation" they can create an analytic relationship that shows by n_H depends on the mechanistic parameters L and c (a "biophysical landscape"), (4) that slices through this landscape qualitatively account for many prior reports on the literature, (5) that despite considerable variation in the actual value, the characterstic n_H of all the mammalian hemoglobins occur near to the maximum value possible given their mechanistic parameters, (6) that for physiological variations of human hemoglobin where c is fixed, all the data cluster around the maximum n_H, indicating that the degree of cooperativity is rather robust to physiological changes, a property previously described as "buffering of cooperativity", (7) that adopting the maximum n_H possible facilitates the delivery of oxygen to tissues, with the buffering property ensuring that the delivery is robust to changes in physiological conditions, (8) that animals with lower body weight and higher oxygen consumption also linearly show higher maximum cooperativities, a finding that suggests evolutionarily selection of n_H for optimal organismal fitness and physiological robustness. From all this the authors conclude that they have a new global understanding of the mechanistic features that control the physiological and evolutionary dynamics of hemoglobin. By extension, there is the idea that this same framework might be useful for the study of multisubunit allosteric proteins in general (e.g. GroEL or K⁺ ion channels).

In general, this is a great paper. The logic is clear, the specific analyses and data presented do support the claims, and the general conclusions are of great interest. From this reviewer's point of view, the real value here lies in two findings: (1) that there is a low-dimensional feature (the ridge of maximum cooperativity) in the biophysical landscape in which the physiological and evolutionary diversity of hemoglobin lives, and (2) that using this landscape it is possible to argue for a logical evolutionary strategy that underlies the observed variation. These are non-trivial achievements; there are probably 10's of thousands of papers relating the various details of hemoglobin mechanism n various conditions but few that present a unifying picture. This work will be of great value to both mechanistic biochemists and evolutionary biologists.

Reviewer 3:

The manuscript by Rapp and Yifrach attempts to understand the mechanistic forces that guide evolutionary and physiological adaptations which determine the value of Hill coefficients in cooperative systems. Assuming a MWC model of four identical oxygen-binding sites, the authors plot n_H as a function of L and c, assuming a homogeneous tetramer. They then map published hemoglobin measurements of n_H, L and c. They argue that the published n_H values lie along the maximal possible theoretical values. They also observe a linear correlation between log(L) and log[c] and suggest that this reflects some co-evolution. They further argue that their slope of the log(L)/log[c] correlation, 2.7, is very close to the maximum value allowed (2) and therefore hemoglobins have evolved to display maximal cooperativity.

I am personally not convinced regarding the validity of the claims of maximal cooperativity in hemoglobin evolution. First of all, the authors do not define maximal cooperativity. Is the value of the slope of the Hill plot at 50% saturation necessarily synonymous with (degree of) cooperativity? Second, L, c and n_H are mechanistically correlated by theory, and the correlation observed need not be taken as evidence of evolutionary cause and effect.

Essential revisions:

1) Hemoglobin is not a good model for a classical MWC-type cooperative tetramer. Many models will reproduce cooperative binding isotherms faithfully, even if they are physically implausible. A case in point is the original Hill plot itself. MWC-type cooperative binding assumes N indistinguishable binding sites, and hemoglobin has physically distinct α and β subunits whose oxygen binding sites are known to have different binding constants. The implication of two distinguishable classes of binding sites is that the maximal n_H is- a priori- lower than 4. The fact that the authors do not take this into account is problematic, as they are focusing on understanding the reasons for n_H not achieving its maximal value of 4.

2) Subsection “The characteristic nH value of hemoglobin is a maximum cooperativity point” and onward. The authors regenerate n_H from calculated L and c values of different hemoglobins. However, the original datasets show significantly diverging empirical n_H values. How good is the correspondence between the calculated and empirical n_H values? Does this indicate a problem with the applicability of the model?

3) Subsection “The characteristic n_H value of hemoglobin is a maximum cooperativity point” and Figure 2B. L and c are not linearly correlated. logL and log[c] are linearly correlated. I am also not sure why this indicates co-evolution, because the two parameters are linked by theory.

4) Subsection “The characteristic n_H value of hemoglobin is a maximum cooperativity point” and Figure 2B: The original formula for the relationship between L and c (from Rubin and Changeux) is L=c⋀-(n/2), where for the case of hemoglobin n=4. The authors find n/2=2.7 (Figure2B). Does this imply n=5.4? What does this imply in terms of the physical reality? The authors state that this is very close to the maximal value of 2. I am not sure that I agree, since the scale is logarithmic, base 10. Finally, does the regression line in Figure 2B cross the origin? This is not evident from the graph.

5) Figure 3A and related text. It is unclear where the authors derive their justification for invariant c values. I can see perhaps how this could, perhaps, be valid for WT hemoglobins but I cannot see any justification for constant c in the mutants.

6) The authors fail to relate the physical significance of the slope of the Hill plot to the 'degree of cooperativity' and fail to cite literature on this subject.

7) The Title is misleading and needs to explicitly state that the analysis is limited to MWC type cooperativity

8) In some cases, the citation of Levitzki, (1978) is misapplied. For example, Wyman, (1963,1964) should be cited for the modern equation defining the slope of the Hill plot (which the authors incorrectly term "Hill transformation").

https://doi.org/10.7554/eLife.47640.017

Author response

Reviewer 1:

Essential revisions:

1) The lack of equations in the main text. For a paper that is performing a theoretical analysis couched in the language of mathematics, the relevant equations should not be relegated to the Supplementary information. Further, there are far more equations to be included (in my opinion) than the several presented there. For example, there is an equation in Figure 3 of their PLOS One paper that gives the effective L parameter that is very important and I think most people are not aware of that is the fundamental basis of interpreting how the "bare" MWC model can be used in the context of effector molecules and why the dissociation constants K_A and K_I are immune to the effector.

The reviewer is right. All equations are now indicated in the main text body (Results section), including the specific equation mentioned by the reviewer (now Equation 3).

2) Overarching concept – I find it is a missed opportunity that the authors do so little to talk about the generic truths they are making as opposed to the very specific comments relative to hemoglobin. Further, I challenge comments such as "Hemoglobin is the only allosteric protein with a known mechanism of action". I object to this comment on several grounds – first, these authors over and over again use the word "mechanism" without once attempting to define it (at least that I can find after reading the paper carefully twice) and second, I think this is false. People have done beautiful, deep work on ion channels, on transcription factors such as LacI, on chemotaxis receptors, etc.

We now discuss the implications and generality of our findings for understanding the molecular evolution of protein properties in subsection “How general are our findings regarding maximum cooperativity in ligand

binding?” and subsection “The relation between physiological and evolutionary adaptations in shaping a protein molecular property”. Hemoglobin as a rare protein with a known mechanism: Of course, the reviewer is right. Hb is definitely not the only protein with a known mechanism of action. In our original submission, we wrote that “Hb is the only allosteric protein with a known mechanism and for which extensive physiological and evolutionary datasets are available”. The references are given after the first half of the sentence to separate the two parts of the sentence, which is the source for the misunderstanding. Mechanism: In using the term ‘mechanism’ in the original submission, we were referring to the biophysical allosteric model that describes the ligation pathway of the protein. This was not properly explained in the original submission and is explicitly defined in the Introduction of the new submission.

3) On a related point: I find the citations of the literature quite inconsistent with my own take on the literature on the field. For example, how can the amazing paper of Martins and Swain not be cited? They carried out deep analysis on the nature of allosteric molecules. Similarly, the work of – Keymer et al., 2006, Swem et al., 2009, the first on chemotaxis receptors, the latter on quorum sensing receptors. This work would benefit from embracing some of research that these people and others (Mirny, 2010; Tu et al., 2019, Marzen et al., 2015) have been doing.

We thank the reviewer for referring us to the indicated papers. We now cite the Keymer et al., (2006), Swem et al., (2008) and Mello and Tu, (2005) papers on the introduction section as examples where the mechanism underlying protein molecular adaptation is understood. The Marzen et al., (2013) and Martins and Swain, (2011) excellent papers are also cited in the appropriate place at the main text. It should be emphasized that in these two latter papers, the expressions derived for nHMWC relate not to cooperativity in ligand binding (as derived here based onY-) but rather to cooperativity in conformational switching as it is based on the R state function (R-). This is now indicated in the subsection “Datasets”.

4) Abstract and beyond: I found the generally evolutionary tone of this paper to be not wholly scientific. In the abstract we have "found it evolved", "showed that" and "evolutionary tuning", all indicating that the authors are convinced that hemoglobin evolved in order to achieve some optimality. There is never any discussion of the fact that correlation does not imply causation – nor any discussion of the null hypothesis of neutrality, nor any discussion of the possible fitness landscape that would produce such optimality.

We concur with the reviewer. Throughout the new version, we have attempted to put forward evolutionary hypotheses, to provide evidence to substantiate them and to draw immediate conclusions and interpretations based on the data.

5) Introduction: – "the characteristic n_H values of almost all allosteric proteins rarely approaches the maximal value n". In some ways I completely disagree with this perspective. My take is that this is true for only one reason and that is because the model of the Hill function is the wrong model for those molecules. If you write the MWC model, the equation (which should be front and center in the paper – their equation 2 sort of) the "4" in the partition function in the denominator is perfectly well aligned with the fact that there are 4 binding sites for hemoglobin. If you do this same thing for cyclic nucleotide gated ion channels and fit a Hill function, you don't get the correct number of binding sites. If you use MWC, you do.

In our original submission, we did not assign the n_H index to mean a number of subunits but rather a measure for the degree of coupling/cooperativity between subunits. Apparently, we were not clear about this. In any case, in light of the changes made in the revised version, such clarification is no longer relevant.

6) Though the authors are constantly talking about c and L,, shouldn't we think of the MWC model as a three-parameter model? I just don't follow their thinking on this point.

We only considered the c and L parameters for several reasons: First, according to the MWC model, cooperativity in ligand binding (n_H) is determined by the c and L dimensionless parameters. n_H value is sensitive to the ratio of affinities (c) and not for the absolute K_R or K_T values giving rise to this ratio. Second, the dimensionless form of the MWC equation, where substrate concentration is expressed in K_R units, allows for better comparison of differences in Y-shape due to parameter choice. Three, our choice pays tribute to the original 1965 and 1966 MWC papers and other classical publications, all of which were based on use of the dimensionless form of the MWC equation. Last, it is more simple to graph and comprehend a 3- rather that a 4-dimensional surface. All but the last of these arguments are discussed at the appropriate place in the text (particularly in the subsection “The biophysical Hill landscape of a tetrameric MWC allosteric protein”) and subsection “The maximum Hill point of a MWC-type protein allows for gross- and fine-tuning of substrate unbinding sensitivity”.

7) "the molecular phenotype of a protein" – to me, the molecular phenotype is much broader than this. IT includes the leakiness 1/(1+L), the EC50, the dynamic range as well as the Hill parameter.

We concur with the reviewer regarding the broad definition of ‘phenotype’. In our manuscript we emphasized the need to consider n_H, along with p₅₀, in addressing molecular adaptation of Hb in mammals. These are two principal attributes of Hb function that control tissue oxygen delivery. It is indeed possible that other protein traits, not addressed in the current manuscript, might as well contribute to tissue oxygen unloading.

8) Subsection “The biophysical Hill landscape of a tetrameric MWC allosteric protein”: "summarizes all known aspects" – As mentioned above, the known aspects of the model include Leakiness, EC50, saturation, dynamic range, effective Hill parameter, but there are other deep things such as the way Wingreen and coworkers have repeatedly shown the data collapse achieved in these models. See the Keymer et al., papers where the data collapse in chemotaxis is demonstrated.

We are sorry for our apparent haughtiness. We meant that the landscape summarizes all cooperativity-related aspects of the MWC model. This is now corrected in the new version.

9) I am not sure what they are talking about, but I think that there are mutants of MWC proteins that do something other than change L. See the work of Daber and Lewis for an example.

The lines of the original submission referred to by the reviewerdid not address Hb mutants but rather the effect of allosteric modulators on the L allosteric constant, in the framework of the MWC model. In any case, with respect to mutation affecting both L and c, see our comment to point # 5 of reviewer 3.

10) Subsection /2The characteristic n_H value of hemoglobin is a maximum cooperativity point”: "very close to a value of…" given that in physics people argue about exponents of 1/3 vs. 1/2 in the context of different scaling relations, it is hard to see how 2.7 and 2 are "very close".

The reviewer is right. We now correct the term ‘very close’ to ‘close’, and provide the reasons for the apparent deviation of the observed value from that expected and allow the reader to judge the validity of our argument. Furthermore, as advised by reviewer 3, we now also point out that the logc-logL correlation crosses the (0,0) axis origin, as expected for the maximum cooperativity parameter criterion.

11) "results imply that evolutionary tuning of.…" It would be very interesting to understand more about the multi-dimensional fitness landscape that a living organism faces and how a particular piece of that ends up as a low dimensional fitness landscape that only cares about n_H. My point is that the organism as a whole faces the battle for existence. This depends upon all of its physiology, not just oxygen binding. Do all the separate pieces of physiology each optimize separately? Are some unique and privileged? The authors could attempt to address these kinds of issues rather than just giving the usual arguments about evolutionary tuning and optimization.

Indeed, in the original version, we over-stressed the cooperativity mindset and collapsed the entire fitness landscape on the n_H parameter. This, of course, is simple-minded. We now address and elaborate on the multidimensional aspects of the fitness landscape in subsection “The biophysical Hill surface as a low dimensional biophysical fitness landscape”.

12) Subsection “Datasets”, "considered part" some discussion of the logic of which parts are included would be great.

In the current analysis we used only the subset of Milo et al., data for which we managed to obtain reliable (and physiological) estimates for L and c, as we report in our PLOS One paper. As we elaborated in this paper, our three equation system strategy applied for Milo et al. evolutionary dataset revealed non-physiological L and c values for 10 out of the 24 mammals (L values close to 1 and c values at the order of 0.2). This sub dataset was not further addressed in the PLOS one paper nor in here.

13) Supplementary file 1. One thing I wondered about both here and in the PLOS paper (which I have also read many times) is about the "sloppy" nature of the parameters. I am not sure if these authors have encountered the work of Jim Sethna (Cornell, Physics), but they have done very interesting things about parameter nonuniqueness. I am not sure how that plays out here but in our own experience using MWC in many contexts, the nonuniqueness of parameters comes up again and again.

The issue of MWC parameter dependence indeed comes up repeatedly. This was dealt, at least in part, in Milo et al. using the modified form of the MWC equation, on which our analysis is based. In any case, thanks for the reference to Jim Sethna’s work. We weren’t aware of it.

Reviewer 3:

I am personally not convinced regarding the validity of the claims of maximal cooperativity in hemoglobin evolution. First of all, the authors do not define maximal cooperativity. Is the value of the slope of the Hill plot at 50% saturation necessarily synonymous with (degree of) cooperativity? Second, L, c and n_Hare mechanistically correlated by theory, and the correlation observed need not be taken as evidence of evolutionary cause and effect.

Lack of definition for the maximum cooperativity: In our original submission, we explicitly defined the maximum cooperativity point as the extremum point of the bell-shaped n_H-logL curves at any given c value (see Materials and methods section). This extremum point is obtained by setting ∂n_H/∂logL as equal to zero, which gives rise to the L=c^-² parameter criterion underlying the maximum cooperativity point. This is now better explained in the main text body (subsection “The biophysical Hill landscape of a tetrameric MWC allosteric protein”). The slope value of the Hill plot is indeed a scaled slope of the actual ∂Y-/∂[S] relation and is considered as a cooperativity index to evaluate site-site coupling. We purposely derived the dependence of the Hill value at half-saturation on MWC model parameters because this is what we usually assess experimentally using the Hill equation (see also our remark in the Materials and methods section).

Inherent dependence of L and c: The L and c parameters of the MWC model are independent parameters. The logarithms of the values obtained for a series of proteins are not necessarily expected to be linearly dependent. Given that the experimentally derived values for L and c are reliable and were obtained using data fitting strategies preventing potential parameter dependence artifacts, we interpreted this correlation as reflecting co-evolution or evolutionary tradeoff between binding and conformational changes transitions of Hb giving rise to the maximum cooperativity point. We now stress these points better in subsection “e characteristic n_H value of hemoglobin is a maximum cooperativity point” of the new submission.

Essential revisions:

1) Hemoglobin is not a good model for a classical MWC-type cooperative tetramer. Many models will reproduce cooperative binding isotherms faithfully, even if they are physically implausible. A case in point is the original Hill plot itself. MWC-type cooperative binding assumes N indistinguishable binding sites, and hemoglobin has physically distinct α and β subunits whose oxygen binding sites are known to have different binding constants. The implication of two distinguishable classes of binding sites is that the maximal n_His- a priori- lower than 4. The fact that the authors do not take this into account is problematic, as they are focusing on understanding the reasons for n_Hnot achieving its maximal value of 4.

The MWC model is thought to adequately describe Hb function, to a first approximation, and is still widely used by many researchers (see, for example, JF Storz’s papers on Hb molecular adaptations published throughout recent years). Indeed, a model is not a proof of a mechanism and several other models can account for the data. However, the simple MWC can explain many observations made with Hb and provides a quantitative framework to interpret these data. Furthermore, by using reliable data fitting strategies, we recently presented data arguing that the pure classical MWC model can explain both homotropic and heterotropic interactions in Hb. Supplementary file 1 of our submission addresses exactly this point and summarizes our arguments regarding why we think the MWC model adequately describe Hb function. Deviations and extensions from the simple two-state model are sometimes needed to account for detailed transient kinetics data (see the Eaton's group Tertiary Two States model, for instance (Viappiani etal., (2014)). With respect to the second issue raised in this comment, as we wrote in our response to comment 5 of reviewer 1, we wanted to rationalize the n_H value not as a measure of the number of subunits but rather as a parameter for evaluating the extent of cooperativity among subunits.

2) Subsection “The characteristic n_Hvalue of hemoglobin is a maximum cooperativity point” and onward. The authors regenerate n_Hfrom calculated L and c values of different hemoglobins. However, the original datasets show significantly diverging empirical n_Hvalues! How good is the correspondence between the calculated and empirical n_Hvalues? Does this indicate a problem with the applicability of the model?

The Hill values calculated based on the MWC model are linearly correlated to those observed with a slope of almost one (0.97) and R² coefficient of 0.92 (see Figure 1A in Rapp and Yifrach, 2017 and Supplementary file 1 (compare the two right-most columns)). Also, for the physiological data, the calculated n_H values fit those observed reasonably well (see Figure 2A in Rapp and Yifrach, 2017). In any case, our analysis assuming L-alone effects performs much better than those calculated by others who assumed that allosteric effectors affect both L and c (Yonetani et al., 2002). In this case, strong dependence is observed between parameters (see Figure 2B in Rapp and Yifrach, 2017).

3) Subsection “The characteristic n_Hvalue of hemoglobin is a maximum cooperativity point” and Figure 2B. L and c are not linearly correlated. logL and log[c] are linearly correlated. I am also not sure why this indicates co-evolution, because the two parameters are linked by theory.

As for the comment on parameter dependence, see our response above.

4) Subsection “The characteristic n_Hvalue of hemoglobin is a maximum cooperativity point” and Figure 2B: The original formula for the relationship between L and c (from Rubin and Changeux) is L=c⋀-(n/2), where for the case of hemoglobin n=4. The authors find n/2=2.7 (Figure2B). Does this imply n=5.4? What does this imply in terms of the physical reality? The authors state that this is very close to the maximal value of 2. I am not sure that I agree, since the scale is logarithmic, base 10…Finally, does the regression line in Figure 2B cross the origin? This is not evident from the graph.

See also our response to reviewer 1, point 18. Given the error in the slope measurement and inaccuracies steaming from data compilations (typical for meta analyses), we believe that the observed 2.7 value is close to that expected (i.e., 2). Of course, there is no physical meaning for n=5.4. In the ideal case, we should obtain n=4. We specify these arguments in the main text for the readers' judgement. As for the Y intercept of the correlation in Figure 2b, indeed it crosses very close to the axis (0,0) origin point, thus further supporting the validity of our findings. This is now reported in the main text with a new version of Figure 2B where the linear regression is extrapolated towards the 0,0 axis origin point. We thank the reviewer for raising this point.

5) Figure 3A and related text. It is unclear where the authors derive their justification for invariant c values. I can see perhaps how this could, perhaps, be valid for WT hemoglobins but I cannot see any justification for constant c in the mutants.

Hb mutations can affect either L or c or both MWC parameters. The assumption for a constant c value for the reported Hb mutants used in the current analysis was made by Baldwin in his original paper (1975) and further adopted by Fersht, (1985). We only follow their lead. This is now indicated in subsection “The characteristic n_Hvalue of hemoglobin is a maximum cooperativity point”).

6) The authors fail to relate the physical significance of the slope of the Hill plot to the 'degree of cooperativity' and fail to cite literature on this subject.

In the Introduction of the original submission, we explicitly wrote that the slope of the saturation curve, as evaluated by the Hill equation, is a cooperativity index to evaluate coupling between the multiple ligand binding sites. We further cited Hill’s 1910 paper.

7) The Title is misleading and needs to explicitly state that the analysis is limited to MWC type cooperativity

The Title has been changed in the revised version.

8) In some cases, the citation of Levitzki, (1978) is misapplied. For example, Wyman, (1963,1964) should be cited for the modern equation defining the slope of the Hill plot (which the authors incorrectly term "Hill transformation").

Indeed, the reviewer is right. We have added the appropriate 1964 paper of Wyman.

https://doi.org/10.7554/eLife.47640.018

Article and author information

Author details

Olga Rapp

Department of Life Sciences, Zlotowski Center for Neuroscience, Ben-Gurion University of the Negev, Beer Sheva, Israel

Contribution
Resources, Data curation, Software, Formal analysis, Validation, Investigation

Competing interests
No competing interests declared
Ofer Yifrach

Department of Life Sciences, Zlotowski Center for Neuroscience, Ben-Gurion University of the Negev, Beer Sheva, Israel

Contribution
Conceptualization, Formal analysis, Supervision, Funding acquisition, Validation, Investigation, Project administration, Writing—review and editing

For correspondence
ofery@bgu.ac.il

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-9020-9745

Funding

Israel Science Foundation (488/12)

Ofer Yifrach

Israel Science Foundation (296/16)

Ofer Yifrach

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank Dr. Amnon Horovitz for insightful comments and to Drs. Eyal Gur, Shimon Bershtein and Jerry Eichler for critical reading of the manuscript. This work was supported by the Israel Science Foundation (grants 488/12 and 296/16 to OY).

Senior and Reviewing Editor

John Kuriyan, University of California, Berkeley, United States

Reviewer

Rama Ranganathan, University of Chicago, United States

Version history

Received: April 11, 2019
Accepted: September 19, 2019
Version of Record published: October 24, 2019 (version 1)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

1,800

Page views
172

Downloads
1

Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Olga Rapp
Ofer Yifrach

(2019)

Evolutionary and functional insights into the mechanism underlying body-size-related adaptation of mammalian hemoglobin

eLife 8:e47640.

https://doi.org/10.7554/eLife.47640

Share this article

Cite this article

The biophysical Hill landscape of a tetrameric MWC protein.

Mammalian hemoglobins exhibit maximum cooperativity nH values.

A buffering of cooperativity physiological regime is observed for human hemoglobin around its maximum cooperativity value.

The maximum cooperativity point determines MWC protein substrate unbinding sensitivity and the dynamic range of physiological adaptation.

Values for the L and c MWC parameters giving rise to systematically higher maximum cooperativity Hill valuesa

Evolutionary tuning of the maximum cooperativity and affinity points of mammalian hemoglobins underlies physiological adaptation.

Values for the affinity and cooperativity parameters of animal blood hemoglobin binding curvesa

Author details

Olga Rapp

Contribution

Competing interests

Ofer Yifrach

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Further reading

Mammalian hemoglobins exhibit maximum cooperativity n_H values.

Values for the L and c MWC parameters giving rise to systematically higher maximum cooperativity Hill values^a

Values for the affinity and cooperativity parameters of animal blood hemoglobin binding curves^a