1. Neuroscience

Neural variability determines coding strategies for natural self-motion in macaque monkeys

  1. Isabelle Mackrous
  2. Jérome Carriot
  3. Kathleen E Cullen
  4. Maurice J Chacron  Is a corresponding author
  1. Department of Physiology, McGill University, Canada
  2. The Department of Otolaryngology- Head and Neck Surgery, Johns Hopkins University School of Medicine, United States
  3. The Department of Biomedical Engineering, Johns Hopkins University School of Medicine, United States
  4. The Department of Neuroscience, Johns Hopkins University School of Medicine, United States
  5. Kavli Neuroscience Discovery Institute, Johns Hopkins University, United States
https://doi.org/10.7554/eLife.57484
Share this article
Cite this article
  1. Isabelle Mackrous
  2. Jérome Carriot
  3. Kathleen E Cullen
  4. Maurice J Chacron
(2020)
Neural variability determines coding strategies for natural self-motion in macaque monkeys
eLife 9:e57484.
https://doi.org/10.7554/eLife.57484
  2. Download BibTeX
  3. Download .RIS

Abstract

We have previously reported that central neurons mediating vestibulo-spinal reflexes and self-motion perception optimally encode natural self-motion (Mitchell et al., 2018). Importantly however, the vestibular nuclei also comprise other neuronal classes that mediate essential functions such as the vestibulo-ocular reflex (VOR) and its adaptation. Here we show that heterogeneities in resting discharge variability mediate a trade-off between faithful encoding and optimal coding via temporal whitening. Specifically, neurons displaying lower variability did not whiten naturalistic self-motion but instead faithfully represented the stimulus’ detailed time course, while neurons displaying higher variability displayed temporal whitening. Using a well-established model of VOR pathways, we demonstrate that faithful stimulus encoding is necessary to generate the compensatory eye movements found experimentally during naturalistic self-motion. Our findings suggest a novel functional role for variability toward establishing different coding strategies: (1) faithful stimulus encoding for generating the VOR; (2) optimized coding via temporal whitening for other vestibular functions.

Introduction

Our previous study was the first to investigate how neurons within the first central stage of vestibular processing in macaque monkeys respond to natural self-motion (Mitchell et al., 2018). Specifically, we focused on a class of neurons within the vestibular nuclei, vestibular-only (VO) neurons, that mediate vestibulo-spinal reflexes as well as self-motion perception (Abzug et al., 1974; Shinoda et al., 1988; Gdowski and McCrea, 1999; Meng et al., 2007; Marlinski and McCrea, 2009). Our results revealed that VO neurons optimally encoded naturalistic self-motion stimuli through temporal whitening (i.e., the spike train power spectrum is independent of temporal frequency and thus "white") because both neuronal variability and tuning were matched to effectively complement natural stimulus statistics (Carriot et al., 2014; Carriot et al., 2017; Mitchell et al., 2018). Our previous study was however limited since we only considered a single class of neurons within the vestibular nuclei and further did not take into account the effects of neural heterogeneities.

Importantly, while VO neurons mediate vestibulo-spinal reflexes as well as self-motion perception as mentioned above, two other distinct neuronal classes instead mediate the vestibulo-ocular reflex (VOR) and its adaptation. Specifically, position-vestibular-pause (PVP) neurons make the primary contribution to the VOR, whereas eye-head (EH) neurons receive cerebellar input and are required for VOR adaptation and motor learning (see Cullen, 2012 for review) (Lisberger, 1984; Lisberger, 1994; Lisberger et al., 1994; Ramachandran and Lisberger, 2008). The VOR generates robust compensatory eye movements in response to head movements encountered during everyday life in order to stabilize gaze (Goldberg et al., 2012) and is an attractive model for understanding how information transmitted by sensory neurons is actually decoded downstream to generate behavior. Importantly, the VOR requires that information as to the detailed timecourse of head movements be contained in the spiking activities of sensory neurons and transmitted to motor areas. However, to date, the effects of neural heterogeneities, particularly in terms of variability, within and across all three vestibular neuronal classes (i.e., PVP, EH, and VO) on coding of naturalistic self-motion remains unknown.

Accordingly, here we investigated how differences in variability within and across distinct central vestibular neuronal classes impact coding strategy during naturalistic self-motion. We first establish that, in the absence of stimulation, all three neural classes displayed a similar wide range of variability as quantified by the coefficient of variation (CV) of the resting discharge. To next determine whether neurons optimally encoded naturalistic self-motion stimuli, we computed their response power spectra as well as the mutual information. Specifically, we tested whether the response power spectrum was independent of frequency or, equivalently, whether the mutual information was close to its maximum possible value for a given level of variability as predicted by theory (Shannon, 1948; Rieke et al., 1996). We found that, within each class, neurons displaying high resting discharge variability displayed temporal whitening. In contrast, neurons displaying lower resting discharge variability did not display temporal whitening but instead faithfully encoded the stimulus’s detailed timecourse as assessed by linear stimulus reconstruction. Interestingly, our results show that faithful encoding was greatest for PVP neurons, suggesting that this coding strategy is necessary to generate the compensatory VOR eye movements observed during naturalistic self-motion stimulation. Using a well-established model of VOR pathways, we validated this prediction. Our findings suggest a novel functional role for variability toward establishing different coding strategies as required for different vestibular functions.

Results

In order to investigate the effects of differences in variability on coding strategy for naturalistic self-motion by central vestibular neurons, single-unit recordings were made from PVP (N = 20), EH (N = 15), and VO (N = 17) neurons within the vestibular nuclei of macaque monkeys (Figure 1A, top). PVP, EH, and VO neurons were identified using standard methodology (reviewed in Cullen, 2012) that characterized a given neuron’s responses to rotational vestibular stimulation in the yaw axis (1 Hz, 40°/s peak velocity) and eye movements (Figure 1—figure supplement 1; see Materials and methods). Specifically, each neuron’s sensitivity to sinusoidal vestibular stimulation was recorded in the dark and while monkeys cancelled their VOR by fixating a target that moved with the vestibular turntable (VOR cancellation). Neuronal sensitivity to eye movements was assessed during steady fixation, saccades, and smooth pursuit (see Materials and methods). The vestibular and eye movement sensitivities of PVP, EH, and VO neurons in our dataset are shown in Figure 1—figure supplement 2 and agreed with previously published values (Roy and Cullen, 2002; Roy and Cullen, 2003; Massot et al., 2011; Mitchell et al., 2018). In particular, we note that PVP and EH neurons can be distinguished based on their differential sensitivities to eye and head movements during smooth pursuit and VOR cancellation, respectively (Figure 1—figure supplement 1).

Figure 1 with 2 supplements see all
Download asset Open asset
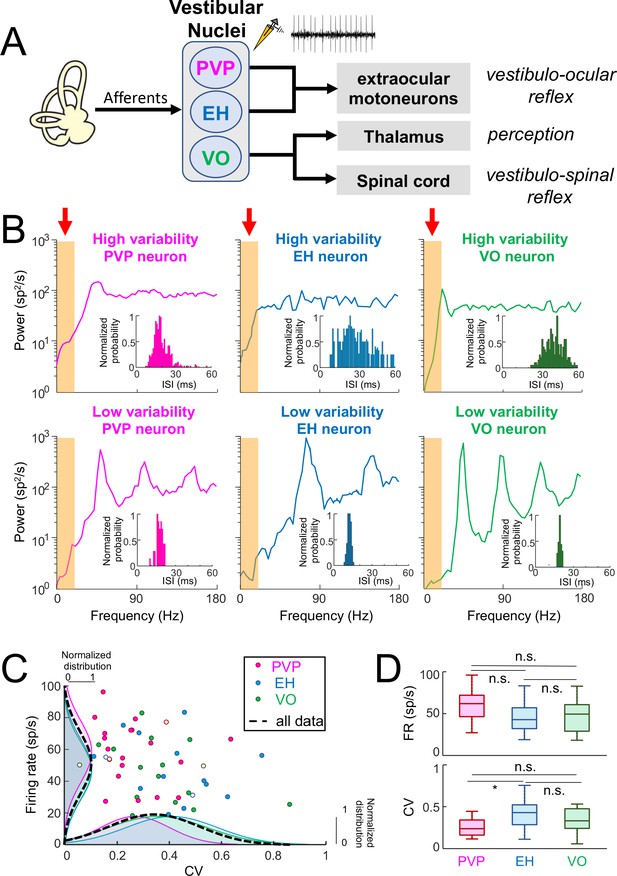
Central vestibular neurons display a wide range of variability in the absence of stimulation.

(A) Afferents from the vestibular periphery project to three classes of neurons found in the vestibular nuclei. Position-vestibular-pause (PVP, magenta) and eye-head (EH, blue) neurons project to extraocular motoneurons within the abducens nucleus and mediate reflexive behaviors such as the vestibulo-ocular reflex (VOR). Vestibular-only (VO, green) neurons project to the ventral posterolateral (VPL) nucleus of the Thalamus, thereby mediating self-motion perception, as well as to the spinal cord, mediating vestibulo-spinal reflexes. Recordings were made from PVP, EH and VO neurons. (B) Top: Spike train power spectra of example PVP (left), EH (middle), and VO (right) neurons that display high variability. Bottom: Spike train power spectra of example PVP (left), EH (middle), and VO (right) neurons that display low variability. The orange bands indicated by the red arrows show the frequency range of naturalistic head motion stimuli (0–20 Hz). The insets show the interspike interval (ISI) distribution for each example neuron. (C) Firing rate as a function of the ISI coefficient of variation (CV). In all three cases, there was no significant correlation (PVP: R = −0.08, p=0.71; EH: R = −0.29, p=0.29; VO: R = −0.38, p=0.13). The dashed black curves show the distributions for all data. The six example neurons shown in panel B are represented by open symbols. (D) Top: Population-averaged firing rates for PVP, EH, and VO neurons did not differ significantly from one another (one-way ANOVA, F(2,51) = 2.31, p=0.11). Bottom: Population-averaged CV values for PVP, EH, and VO neurons. The CV of VO neurons was more broadly distributed than that of PVP and EH neurons (Levene’s test F = 7.2, p=0.001) while the distribution of the firing rate was similar for all classes of neuron (Levene’s test F = 0.87, p=0.43). PVP neurons displayed lower CV values than VO and EH neurons on average (one-way ANOVA, F(2,51) = 3.58, p=0.03).

During stimulation, there is a component of the variability in the neural response that can be explained by the stimulus and a component that cannot (Stein et al., 2005). The latter component contributes to what is known as trial-to-trial variability in the neural response to repeated presentations of a given stimulus. Such trial-to-trial variability is largely determined by the variability of the resting discharge for vestibular neurons (Sadeghi et al., 2007; Massot et al., 2011; Jamali et al., 2013; Mitchell et al., 2018). This is because, in order to be detected, head movements must sufficiently perturb the resting discharge. As such, it is much easier to detect stimulation when the resting discharge is more regular (i.e., less variability) than when it is more irregular (i.e., more variability) (reviewed in Cullen, 2012).

Central vestibular neurons display large heterogeneity in their resting discharges

We quantified the resting discharges of central vestibular neurons using both the mean firing rate as well as the CV of the interspike interval (ISI) distribution (see Materials and methods). The latter measure was used to quantify the resting discharge variability. Our results show that central vestibular neurons displayed resting discharges that were quite variable (PVP: 58 ± 19 sp/s, CV = 0.26 ± 0.13; EH: 47 ± 19 sp/s, CV = 0.40 ± 0.17; VO: 50 ± 18 sp/s, CV = 0.35 ± 0.18). Interestingly, for all three classes, some neurons displayed resting discharges that were more regular as quantified by low CV values, while other neurons instead displayed resting discharges that were more irregular as quantified by higher CV values (Figure 1B, insets).

We also quantified the resting discharge of central vestibular neurons by computing the spike train power spectrum (see Materials and methods). There were large differences between the power spectra of neurons displaying low and high resting discharge variability. Indeed, for neurons with low variability, the spike train power spectrum varied strongly as a function of frequency. Notably, spectral power displayed local maxima at the neuron’s firing frequency (i.e., the fundamental; Figure 1B) as well as higher harmonics (i.e., integer multiples of the fundamental). Spectral power was low within the frequency range of natural self-motion (i.e., 0–20 Hz; see orange bands in bottom panels of Figure 1B), which is expected as theory predicts spectral power at low frequencies is proportional to CV2 (Holden, 1976). In contrast, the spike train power spectrum of more irregular neurons was more independent of frequency as evidenced from lack of local maxima at higher harmonics (Figure 1B, top panels). Spectral power within the frequency range of natural self-motion (see orange bands in bottom panels of Figure 1B) was higher than for neurons with low variability. We note that this is again expected based on theory (Holden, 1976). It is important to note that the CV distribution was unimodal for all neuron classes (Figure 1C, bottom) which suggests that variability is distributed along a continuum for central neurons. We emphasize that we looked at example neurons whose CV was within the lower and higher range of the distribution. For simplicity, we will henceforth refer to these neurons as having "low resting discharge variability" and "high resting discharge variability", respectively.

To assess whether differences in resting discharge variability displayed by central vestibular neurons were related to other discharge properties, we first compared the mean firing rate to CV across our dataset (Figure 1C). We found that the mean firing rate was not significantly correlated with CV for all central vestibular neuronal classes (PVP: R = −0.08, p=0.71; EH: R = −0.29, p=0.29; VO: R = −0.38, p=0.13). Further, we did not observe any significant differences between the resting firing rates of PVP, EH, and VO neurons (p≥0.11, one-way ANOVA with Bonferroni correction; Figure 1D, top panel) in general, except that PVP neurons displayed significantly lower CV values than EH neurons (p<0.03, one-way ANOVA with Bonferroni correction; Figure 1D, bottom panel). Thus, while central vestibular neurons displayed a wide range of resting discharge firing rate and variability within each class, both quantities were similarly distributed for all three classes.

Effects of variability on central vestibular neuronal coding of naturalistic self-motion

We next investigated the effects of variability on coding strategy during naturalistic self-motion stimulation. To do so, we recorded each neuron’s activity during the application of yaw rotations whose time course closely mimicked those experienced during natural conditions (i.e., the naturalistic self-motion stimulus; Figure 2A,B, see Materials and methods). The time-dependent firing rates in response to naturalistic self-motion stimulation of two example PVP neurons displaying high (left panel) and low (right panel) variability are shown in Figure 2C. Similar graphs for both high and low variability EH and VO example neurons are shown in Figure 2—figure supplement 1. These examples were typical in that all neurons responded to the head motion stimulus, although EH neurons typically responded with less modulation in firing rate than PVP and VO neurons (compare Figure 2—figure supplement 1 to Figure 2C). To quantify optimized coding via temporal whitening, we computed the spike train power spectrum during naturalistic stimulation (see Materials and methods). Our analysis revealed that the power spectra of PVP, EH, and VO neurons displaying high variability were independent of frequency (Figure 2D, solid curves) as they did not deviate from the Poisson confidence interval with the exception of low (<1 Hz) frequencies for the example EH neuron (Figure 2D, gray bands). As mentioned above, the fact that the spectral power was independent of frequency is indicative of temporal whitening. In contrast, spectral power for PVP, EH, and VO neurons displaying low variability decayed similarly to the stimulus power spectrum with increasing frequency and was thus not independent of frequency (Figure 2D, compare dashed curves to solid black). As such, these power spectra strongly deviated from the Poisson confidence interval (Figure 2D, gray bands), indicating that these neurons did not display temporal whitening.

Figure 2 with 7 supplements see all
Download asset Open asset
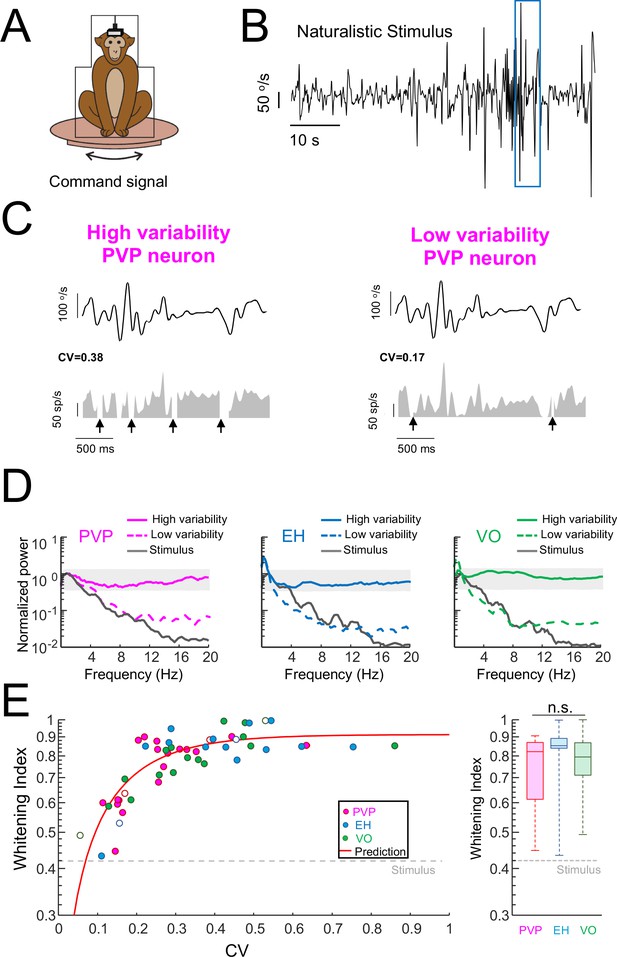
Variability strongly influences optimized coding via temporal whitening.

(A) The animal was head fixed within a chair that was mounted on top of a turn table whose command signal was adjusted to give rise to head movements that closely matched those seen under natural conditions. (B) Time series showing the entire time course of the naturalistic stimulus. (C) Segment of the naturalistic stimulus (top) corresponding to the blue rectangle in panel B together with time-dependent firing rate responses from the same example PVP neurons shown in Figure 1 with high (left) and low (right) variability. Black arrows indicate times at which vestibular quick phases occurred and during which the neurons paused. (D) Response power spectra of PVP (left), EH (middle), and VO (right) neurons with high (solid) and low (dashed) variability. The gray bands show the Poisson confidence interval. It is seen that, while the power spectra of neurons with high variability were always well within the confidence interval and were thus independent of frequency, this was not the case for neurons with low variability whose power spectra decayed as a function of increasing frequency similarly to that of the stimulus (black). (E) Left: Whitening index increases as a function of CV. Our model (red line) accurately fits experimental data (all data: R2 = 0.63; PVP: R2 = 0.53; EH: R2 = 0.63; VO: R2 = 0.78). The six example neurons shown in panel B are represented by open symbols. Right: Population-averaged whitening index values were similar for PVP, EH, and VO neurons (Kruskal-Wallis, H(2) = 2.63, p=0.26). The gray-dashed lines show the whitening index value computed when using the stimulus’ power spectrum.

To quantify differences in temporal whitening, we computed the same whitening index measure that was used in our previous study (Mitchell et al., 2018). Overall, we found that the whitening index similarly depended on CV for all neuronal classes (Figure 2E, left panel). Further, we found that the whitening index was independent of resting discharge firing rate (Figure 2—figure supplement 2A) and the whitening index computed from neurons whose resting discharge firing rates were within a narrow range (45–55 sp/s) strongly depended on CV (Figure 2—figure supplement 2B). These results, together with the fact that neural sensitivity was independent of variability (Figure 2—figure supplement 3), suggest that the differences in whitening are primarily due to differences in variability and, as such, are universal for central vestibular neurons. To test that changes in whitening index were primarily due to changes in CV, we first built a simple model (see Materials and methods) in which changes in variability were explored systematically. Overall, this model correctly fits data from PVP, EH, and VO neurons across all levels of resting discharge variability (Figure 2E, left panel, red curve). Second, to further test our hypothesis, we built a linear-nonlinear cascade model (see Materials and methods and Figure 2—figure supplement 4A) that included the effects of variability in order to predict the spike train power spectrum during naturalistic stimulation for individual neurons. Overall, this model accurately predicted the response power spectra of the same six example neurons (Figure 2—figure supplement 4B). As such, there was excellent agreement between predicted and actual whitening index values for our dataset (Figure 2—figure supplement 4C; Student’s t-test, PVP: F(19) = 0.44, p=0.66; EH: F(14) = 0.98, p=0.34; VO = F(16)=0.96, p=0.35). We note that the power spectrum of the resting discharge variability was not different from that of the trial-to-trial variability during stimulation for our dataset (Figure 2—figure supplement 5). Thus, it is reasonable to model the noise/variability during stimulation by adding the variability from the resting discharge. On average, whitening index values for PVP and EH neurons were comparable to those obtained for VO neurons (Figure 2E, right panel). While consistent with our previous finding that, at the population level, VO neurons tend to optimally encode the stimulus via temporal whitening, our current findings emphasize that there are important differences in optimal coding at the individual neuron level both within and across neuronal classes. Specifically, central neurons with low variability tend to not display temporal whitening.

We note that, unlike VO neurons, PVP and EH neurons are sensitive to eye as well as head movements. Thus, we next tested that our results for PVP and EH neurons were not due to patterning of quick phases and/or systematic changes in eye position that occurred throughout vestibular stimulation. To do so, we first compared results obtained on data where spiking activity during vestibular quick phases was removed and the remaining slow phase epochs concatenated (i.e., was is shown in Figure 2) to the entire dataset. Overall, no differences were observed (data not shown). Next, we compared results obtained by restricting our analysis to epochs during which the eye position was relatively constant (i.e., within + / - 5°; see Materials and methods) to those obtained using the full dataset (i.e., when eye position was not restricted). No significant differences were observed (Figure 2—figure supplement 6; Student’s t-test, F(34) = 1.3, p=0.2). Thus, our analysis indicates that differences in whitening observed for PVP and EH neurons are not due to differences in quick phase generation and/or changes in eye position during stimulation.

Finally, we investigated the relative contributions of variability vs. tuning toward determining temporal whitening for all central vestibular neural classes. Our previous results have shown that variability within the VO neuron population was essential toward determining temporal whitening (Mitchell et al., 2018). Here we extended this analysis to all three central vestibular neuron classes and investigated the effects of different levels of resting discharge variability within each class (Figure 2—figure supplement 7). Overall, central neurons with lower variability as quantified by the CV of the resting discharge displayed lower noise power than their counterparts with higher variability. However, there were no significant differences in the amount of signal power transmitted. As such, the signal-to-noise ratio (SNR) decreased with increasing variability. This latter result is important as it suggests that central vestibular neurons with lower variability actually transmit more information than those with higher variability. To test this, we computed the mutual information rate (see Materials and methods) for our dataset and found a significant decrease with increasing CV, thereby confirming our hypothesis (Figure 2—figure supplement 7). Finally, we quantified optimality of coding (i.e., the mutual information divided by its maximum possible value for a given level of variability) and found a significant increase with increasing CV (Figure 2—figure supplement 7), thereby confirming results obtained using the whitening index. Thus, while central vestibular neurons with high variability transmit less information in absolute terms than their counterparts with low variability, they are more optimal in the sense that the mutual information is closer to the maximum possible value.

Neurons with lower variability faithfully encode the detailed time course of naturalistic self-motion stimuli

Our results so far have shown that central vestibular neurons with low variability did not optimally encode naturalistic self-motion stimuli via temporal whitening but transmitted more information than their counterparts with high variability. This raises the question as to what is the functional role of such neurons? Our results showing that the spike train power spectrum of these neurons decayed with increasing frequency like that of the naturalistic self-motion stimulus, together with higher mutual information rates, suggest that these neurons faithfully relay information about the detailed time course of self-motion signals. Indeed, inspection of their time-dependent firing rate responses to naturalistic self-motion stimulation suggests a strong linear relationship between their responses and the stimulus (Figure 2C and Figure 2—figure supplement 1, bottom panels). To test this hypothesis, we quantified the fraction of variance in the stimulus that could be correctly reconstructed from the spiking activity by using a linear decoder that minimizes the mean-squared error between the original and reconstructed stimulus waveforms. Specifically, the reconstructed stimulus was obtained by convolving the spiking activity with a filter whose shape was chosen such as to minimize the mean-squared error between the reconstructed and original stimulus waveforms (see Materials and methods and Figure 3A). The left panel of Figure 3B shows the original naturalistic self-motion stimulus (black) together with the reconstructed stimulus (red) for an example PVP neurons with high variability. The right panel of Figure 3B shows the same but for an example PVP neuron with low variability. These examples were typical in that there was a much better match between the original and reconstructed stimuli for the PVP neuron with low variability (Figure 3B, compare left and right panels). Qualitatively similar results were obtained for EH and VO neurons (Figure 3—figure supplement 1). We quantified these results by computing the coding fraction (CF), which is the fraction of variance in the stimulus that is correctly reconstructed (see Materials and methods). Overall, we found a strong negative correlation between CF and variability as quantified by CV (Figure 3C; All data: R = −0.53, p=10−4; PVP: R = −0.51; p=0.02; EH: R = −0.07, p=0.8; VO: R = −0.65,p=4.5×10−3). Further, we found that CF was independent of the resting discharge firing rate (Figure 3—figure supplement 2A: All data: R = 0.13, p=0.34; PVP: R = 0.05, p=0.82; EH: R = 0.01, p=0.96; VO: R = −0.06, p=0.81). Moreover, CF computed from neurons whose firing rates were within a narrow range (45–55 sp/s) also strongly depended on CV (Figure 3—figure supplement 2B: All data: R = −0.54, p=0.03; PVP: R = −0.96, p=0.03; EH: R = −0.20, p=0.7; VO: R = −0.87, p=0.02). These results strongly suggest that changes in CF were primarily due to changes in the resting discharge CV.

Figure 3 with 2 supplements see all
Download asset Open asset
Central vestibular neurons with low variability faithfully encode the detailed time course of naturalistic self-motion stimuli.

(A) Schematic showing the stimulus reconstruction technique. The head velocity stimulus (left) is presented while neural activity (middle) is recorded and the neuron (middle left) is treated as a "black box". The neural activity is then convolved with an optimal filter (middle right) in order to obtain the reconstructed stimulus (right). This filter is chosen such as to minimize the mean square error between the original and reconstructed stimuli (see Materials and methods). (B) Head velocity (black) and reconstructed (red) stimuli from the same example PVP neurons as in Figure 1 with high (left) and low (right) variability. The quality of the reconstruction was quantified using the coding fraction (CF), which ranges between 0 and 1 and represents the fraction of variance in the stimulus that is correctly reconstructed (see Materials and methods). The insets show the optimal kernel for each example neuron. The gaps in the reconstructed stimulus traces indicate segments during vestibular quick phases. (C) CF decreases as a function of increasing CV (all data: R = −0.53, p=1.0×10−4; PVP: R = −0.51; p=0.02; EH: R = −0.07, p=0.8; VO: R = −0.65, p=4.5×10−3; R values were computed on log-transformed data). The six example neurons shown in panel B are represented by open symbols. (D) Top: Neural sensitivity did not decrease with increasing CV (all data: R = −0.24, p=0.09; PVP: R = −0.22; p=0.35; EH: R = 0.35, p=0.20; VO: R = −0.25, p=0.34). The legend is the same as in panel C. Bottom: Population-averaged values of CF were highest for PVP and lowest for EH neurons (one-way ANOVA, F(2,51) = 9.1, p=4.5×10−4).

Importantly, the fact that low values of CF were obtained for neurons with high variability was not trivially due to a lack of response. This is because, as mentioned above, there was no significant correlation between neural sensitivity and variability (Figure 3D). Moreover, as noted above, there was no significant correlation between neural sensitivity to sinusoidal stimulation at different frequencies and variability (Figure 2—figure supplement 2). Overall, PVP neurons displayed the largest coding fraction, followed by VO neurons, and EH neurons displayed the lowest coding fractions overall (Figure 3E). These results demonstrate that neurons with low variability more faithfully represented the stimulus’ detailed time course in their spiking activities than their counterparts with high variability. Thus, together with our results above showing that neurons with low variability do not display temporal whitening, we conclude that variability establishes a trade-off between faithful stimulus encoding and temporal whitening.

Faithful encoding of the time course of naturalistic self-motion stimuli by neurons with low variability is best matched to the known decoding properties of VOR pathways in order to generate the VOR.

Our results show that, across all classes, PVP neurons most faithfully represented the stimulus’ detailed time course in their firing activities. Nevertheless, a significant fraction of PVP neurons displayed temporal whitening. Importantly, information is only useful to the organism if it is decoded by downstream brain areas. As mentioned above, VOR pathways are an attractive model for understanding how information transmitted by sensory neurons is actually decoded downstream to generate behavior because of their relatively simple and well-understood neural circuitry. We first tested whether the VOR evoked in response to naturalistic self-motion stimulation was in fact compensatory. We found that indeed both animals generated robust compensatory eye movements characterized by gains approaching unity, such that the eye velocity was essentially the opposite of head velocity (Figure 4A). This brings the important question as to how these compensatory eye movements are generated. Specifically, which of faithful encoding or temporal whitening by PVP neurons is most appropriate to generate compensatory VOR eye movements during naturalistic self-motion stimulation.

Figure 4 with 3 supplements see all
Download asset Open asset
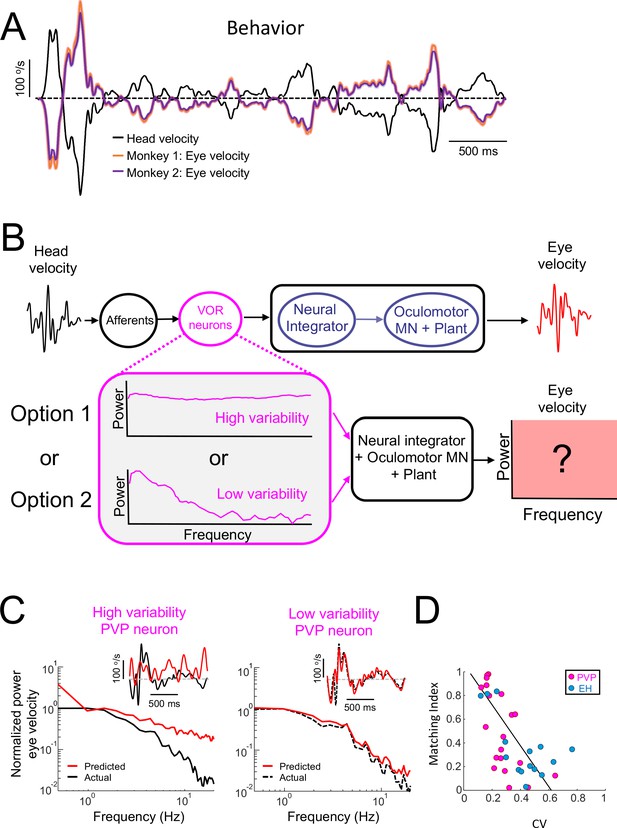
Central VOR neurons (i.e., PVP and EH) with low variability are necessary to properly generate compensatory VOR eye movements.

(A) Head (black) and trial-averaged eye (orange and purple) velocity traces during naturalistic self-motion stimulation for the two animals used in this study. Activity during saccades were not included in the averaging. VOR gain values for both animals were close to unity (VOR gain for monkey 1 = 0.95 ± 0.14; VOR gain for monkey 2 = 0.90 ± 0.12). (B) Top: schematic showing VOR pathways. VOR neurons receive input from peripheral afferents that respond to head movement input and project to the neural integrator as well as extraocular motoneurons ("MN") and the oculomotor plant which generates compensatory eye movements. Bottom: We used the spiking activities from both high ("option 1") and low ("option 2") variability VOR neurons as inputs to the neural integrator and oculomotor plant in order to generate predicted eye movements (red box) that were compared with actual eye movement. (C) Predicted (red) and actual (black) power spectra of eye velocity when the input is from a neuron with high (left) and low (right) variability. The insets show the corresponding time series where the dashed gray lines indicate zero velocity. (D) The matching index was negatively correlated with CV (all data: R = −0.65, p=2.9×10−5; PVP: R = −0.64, p=2.4×10−3; EH: R = −0.64, p=0.01).

To answer this question, we used well-established models of VOR pathways in which the head velocity input elicits responses from peripheral vestibular afferents that project to VOR neurons. The output of VOR neurons is in turn decoded by the neural integrator as well as by extraocular motoneurons and the oculomotor plant in order to generate compensatory eye movements (Figure 4B, top; see Materials and methods). Our simulations show that, when the naturalistic head velocity stimulus was used as input, the model generated a robust VOR consistent with that observed experimentally (Figure 4—figure supplement 1). Next, we used the spiking activities of PVP neurons during naturalistic stimulation as input to downstream decoders (i.e., the neural integrator, extraocular motoneurons, and the oculomotor plant) in order to predict compensatory VOR eye movements (Figure 4B, bottom). The predicted eye velocity was then compared to the actual eye velocity (i.e., that computed from measured eye movements) for each PVP neuron in our dataset. Figure 4C shows the predicted (red) and actual (black) eye velocity time series (inset) and power spectra (main panels) when the spiking activities from example PVP neurons with low (left) and high (right) variability were used as input. We found that there was much better agreement between the predicted and actual eye velocity signals when the input from an example PVP neuron with low variability was used (compare right and left panels in Figure 4C). The agreement between predicted and actual eye velocity signals was quantified using a matching index that ranged between 0 (no agreement) and 1 (perfect agreement; see Materials and methods). There was a strong negative correlation between the matching index and variability (R = −0.64, p=2.4×10−3; Figure 4D, magenta), suggesting that PVP neurons with lower variability that faithfully represent the detailed time course of head movements make the primary contribution to generate compensatory VOR eye movements. To further test this proposal, we compared the performance at stimulus reconstruction from neuron pairs with varying levels of variability. Overall, we found that the performance of neuron pairs with low variability was overall greater than that obtained when considering pairs with low and high variability (Figure 4—figure supplement 2), which confirms our proposal. For completeness, we also tested which of faithful encoding or temporal whitening by EH neurons, which are required for VOR adaptation and motor learning, is most appropriate to generate compensatory VOR eye movements. Overall, results for EH neurons were qualitatively similar to those obtained for PVP neurons (Figure 4—figure supplement 3 and Figure 4D, blue; R = −0.64, p=0.01). Thus, taken together, our results point to an important functional role for VOR neurons with low variability that faithfully represent the detailed time course of head movements. Specifically, the activities of these neurons are best matched to the known dynamics of downstream decoders in order to generate compensatory VOR eye movements.

Discussion

Summary of results

We investigated the effects of variability on the responses of three different central vestibular neuronal classes: neurons that mediate vestibulo-spinal pathways and project to the vestibular thalamus (i.e., VO), neurons that make the primary contribution to the VOR (i.e., PVP), and neurons that mediate VOR adaptation (i.e., EH). Overall, we found that heterogeneities in resting discharge variability within each class strongly influenced coding strategies. Specifically, neurons with lower resting discharge variability transmitted the highest amounts of information and thus most faithfully encoded the stimulus’ detailed timecourse. In contrast, neurons with higher resting discharge variability most optimally encoded the stimulus via temporal whitening, as their mutual information rates were closer to the maximum possible value. These latter neurons displayed lower information rates and thus did not faithfully encode the stimulus. We emphasize that both temporal whitening and faithful encoding were distributed along a continuum for our dataset. Interestingly, we found that PVP neurons, on average, more faithfully encoded the stimulus’ detailed time course as compared to the two other classes, as quantified by their higher coding fraction values. Using well-established models of VOR pathways, we showed that faithful stimulus encoding, rather than temporal whitening, is required to generate the compensatory VOR eye movements measured in our experiments during naturalistic self-motion stimulation.

Faithful encoding vs. temporal whitening by VOR neurons, implications for decoding

Here we show for the first time that the detailed time course of head motion can be best recovered from the spiking activities of PVP neurons during naturalistic stimulation. This finding has important implications for understanding the sensory-motor transformations that underlie the generation of the VOR. Indeed, in this context, VOR pathways must account for the dynamics of the oculomotor plant, which are dominated by the visco-elastic properties of the extraocular muscles and passive tissues in the orbit (Robinson, 1964; Enderle and Wolfe, 1988). Because the properties of the oculomotor plant effectively make it a low-pass filter, the relationship between extraocular motoneuron activity and eye movement must have compensatory frequency dependent dynamics (reviewed in Robinson, 1981). More recent studies have shown that the properties of extraocular motoneurons indeed complement those of the oculomotor plant (reviewed in Cullen, 2012) during the VOR (Sylvestre and Cullen, 1999; Ramachandran and Lisberger, 2006). This raises the question as to what the output of PVP neurons should be in order to generate the VOR during naturalistic head movements. Because PVP neurons receive afferent input from the periphery and in turn project directly to extraocular motoneurons to generate compensatory VOR eye movements within 5 ms (Huterer and Cullen, 2002), information must be decoded with little or no integration time as achieved by a coding strategy based on faithful stimulus encoding. In contrast, we argue that temporal whitening, which requires filtering of the input and thus more complex decoding strategies with larger integration times, are not suitable for feedforward control of direct VOR pathways.

An open question for understanding the sensory-motor pathways that mediate the VOR is to reconcile how the known nonlinearities displayed by PVP neurons mediate such a linear behavior. Specifically, the VOR shows remarkable linearity in that the resulting eye movements effectively compensate for head movements over a wide range of frequencies and amplitudes (Huterer and Cullen, 2002; Ramachandran and Lisberger, 2006; Sadeghi et al., 2006). In contrast, PVP neurons demonstrate substantial nonlinearities: their spiking activity is silenced for off-direction rotations and demonstrates saturation for on-direction rotations for velocities greater than 200 °/s (Roy and Cullen, 2004; Ramachandran and Lisberger, 2006). In this context, it is important to note that previous studies have shown that extraocular motoneurons display substantial nonlinearities (Sylvestre and Cullen, 1999). It is further conceivable that, for higher amplitude stimuli than the ones considered in the present study, PVP neurons that perform temporal whitening contribute to compensating the nonlinear properties of extraocular motoneurons to ensure a robust VOR.

Interestingly, our results from EH neurons, which mediate VOR adaptation and motor learning (Lisberger, 1984; Lisberger, 1994; Lisberger et al., 1994; Ramachandran and Lisberger, 2008), contrast those described above for PVP neurons. Specifically, EH neurons least faithfully followed the naturalistic stimulus’ detailed time course as compared to other central vestibular neuronal classes (Figure 3D,E). This result is consistent with previous observations that EH neurons displayed weak sensitivities to artificial vestibular sinusoidal stimuli and are more strongly driven by pursuit signals (Roy and Cullen, 2003). Our results show that EH neurons responded to naturalistic head motion such that their spiking activities were temporally whitened. This observation raises the question as to why such an encoding scheme has been adopted in a pathway that was previously shown to be specifically responsible for VOR adaptation and motor learning. We hypothesize that the larger integration time windows needed to properly decode information transmitted via temporal whitening by EH neurons are beneficial for VOR adaptation and motor learning. Further studies are required to test this hypothesis.

Faithful encoding vs. temporal whitening by VO neurons, implications for decoding

The vestibular system is not only necessary for generating the VOR, but also has multiple other important functions such as self-motion perception and vestibulo-spinal reflexes that control posture. These functions are mediated by a distinct class of neurons within the vestibular nuclei (i.e., VO neurons) that project to the thalamus (Meng et al., 2007; Marlinski and McCrea, 2009) as well as to the spinal cord (Abzug et al., 1974; Shinoda et al., 1988; Gdowski and McCrea, 1999). Our previous study showed that VO neurons optimally encoded naturalistic self-motion via temporal whitening (Mitchell et al., 2018). The present study provides an important addition to this by investigating the effects of variability on coding strategy. Specifically, our new findings reveal that, while the majority of VO neurons displayed high variability and optimally encoded naturalistic head motion stimuli via temporal whitening, a minority of VO neurons displayed low variability and instead faithfully followed the stimulus’ detailed time course. This raises the question: why are there differences in coding strategies across the VO neuron population?

We speculate that temporal whitening by VO neurons with high variability is functionally advantageous for the control of vestibulo-spinal reflexes. Notably, the inertia of the head-neck system is higher than that of the oculomotor plant, which has implications for motor control requirements. To date, studies have shown that central vestibular nuclei neurons within vestibulo-spinal pathways are more likely to receive input from afferents with more irregular resting discharges (i.e., irregular afferents), while those within vestibulo-ocular pathways are instead more likely to receive input from afferents with more regular resting discharges (i.e., regular afferents) (Goldberg et al., 1987; Sato and Sasaki, 1993). Further, the response dynamics of irregular versus regular afferents are best matched to the mechanical demands of the vestibulo-spinal reflex versus the VOR, respectively (Fernandez and Goldberg, 1971; Bilotto et al., 1982). Recent studies have further shown that irregular but not regular afferents display spike timing precision/phase locking (Jamali et al., 2016; Jamali et al., 2019). Interestingly, spike timing precision/phase locking was also observed at the next level (Jamali et al., 2016). We hypothesize that this single neuron property induces greater synchrony at the VO population level that in turn better compensates for the inertia of the head-neck system (reviewed in Cullen, 2019). As such, we propose that temporal whitening by VO neurons with high variability that preferentially receive input from irregular afferents provides enhanced information at the population level, as seen in other systems (Doi et al., 2012; Kastner et al., 2015). Further studies using multi-unit recordings from VO neurons are needed to test this hypothesis.

While most VO neurons optimally encoded the naturalistic head motion stimulus via temporal whitening, a subset of VO neurons instead faithfully encoded the stimulus. This raises the question: what is the functional role of this subset of neurons? To answer this question, it is useful to consider that VO neurons also project to the thalamus and thus are thought to play a role in self-motion perception and spatial orientation computation (Meng et al., 2007; Marlinski and McCrea, 2009). One possibility is that the subset of VO neurons that faithfully follows the stimulus’ detailed timecourse preferentially projects to thalamus in order to provide information as to the detailed timecourse of head movements. Additional neurophysiological experiments focusing on how neurons within the vestibular thalamus respond to naturalistic head motion stimulation, as well as anatomical studies in which the post-synaptic targets of individual VO neurons are identified, are needed to understand how information transmitted by the VO neuron population is ultimately decoded.

Finally, we note that, throughout this study and our previous publication (Mitchell et al., 2018), we assumed that optimality of coding is achieved via temporal whitening. Theoretical studies have shown that temporal whitening gives rise to maximal information if the input SNR is high (van Hateren, 1992a; Rieke et al., 1996). In the case where the input noise for a given frequency is high (i.e., a low input SNR), optimal coding is instead achieved by filtering out the neural output at that frequency due to noise contamination (van Hateren, 1992a), which has been observed in the retina for weak stimulus intensities (van Hateren, 1992b). As such, it is theoretically conceivable that the lack of temporal whitening observed for central vestibular neurons with low variability could be a form of optimized coding that is based on a different constraint than temporal whitening. However, this is unlikely to be the case here since both regular and irregular vestibular afferents that provide input to central neurons display low trial-to-trial variability during naturalistic self-motion stimulation (Sadeghi et al., 2007; Jamali et al., 2016; Mitchell et al., 2018). As such, the input SNRto central vestibular neurons is very likely to be high, such that optimized coding is achieved via temporal whitening according to theory. Moreover, as mentioned above, central neurons within VOR pathways receive input primarily from regular afferents (Goldberg et al., 1987; Sato and Sasaki, 1993) which display the least trial-to-trial variability during stimulation and thus the highest input SNR (Sadeghi et al., 2007; Jamali et al., 2016; Mitchell et al., 2018). Thus, our results showing that these neurons display the most faithful encoding and the least temporal whitening further support the hypothesis that optimized coding is achieved via temporal whitening for central vestibular neurons.

Mechanisms underlying differences in variability in central vestibular pathways

Here, we have established that differences in resting discharge variability strongly influence coding strategies by central vestibular neuron populations. This finding then leads to the important question as to what mechanism(s) underlie the different levels of variability observed across all three classes of central vestibular neurons. Notably, our results show that variability is distributed along a continuum for all central neural classes. This is different than for vestibular afferents in which variability displays a bimodal distribution with two distinct classes: regular and irregular (Goldberg, 2000). As mentioned above, VOR neurons are more likely to receive input from regular afferents, whereas neurons within vestibulo-spinal pathways are instead more likely to receive input from irregular afferents (Goldberg et al., 1987; Sato and Sasaki, 1993). Thus, one possibility is that differences in variability across central neurons are due to different amounts of feedforward input from regular and irregular afferents. Another possibility, which is not mutually exclusive, is that differences in the intrinsic properties of central neurons contribute to differences in variability (Babalian and Vidal, 2000; Ris et al., 2001; Sekirnjak and du Lac, 2002; Kodama et al., 2020). Finally, it is important to note that central vestibular neurons also receive direct input from central structures including cortical, cerebellar, as well as numerous brain stem nuclei (Akbarian et al., 1994; Voogd et al., 1996; McCrea and Horn, 2006) (see (Angelaki and Cullen, 2008) for review). These central inputs also likely contribute to shaping neuronal variability. For example, extracellular recordings in the cerebellar flocculus reveal irregularities in the spontaneous simple spike firing rate of Purkinje cells (Hoebeek et al., 2005), which provides a clear source of variability to EH neurons. Further studies are needed to understand how these different sources of input, together with differences in intrinsic properties, contribute to generating the different levels of variability seen experimentally in central vestibular neurons.

Materials and methods

Surgical procedures and data acquisition

Request a detailed protocol

All experimental protocols were approved by the McGill University Animal Care Committee and complied with the guidelines of the Canadian Council on Animal Care. Two rhesus macaque monkeys (Macaca mulatta) were prepared for chronic extracellular recording using aseptic surgical techniques as previously described (Mitchell et al., 2018). Briefly, animals were pre-anesthetized with ketamine hydrochloride (15 mg/kg im) and injected with buprenorphine (0.01 mg/kg im) and diazepam (1 mg/kg im) to provide analgesia and muscle relaxation, respectively. Loading doses of dexamethasone (1 mg/kg im) and cefazolin (50 mg/kg iv) were administered to minimize swelling and prevent infection, respectively. Anticholinergic glycopyrrolate (0.005 mg/kg im) was also preoperatively injected to stabilize heart rate and to reduce salivation, and then every 2.5–3 hr during surgery. During surgery, anesthesia was maintained using isoflurane gas (0.8–1.5%), combined with a minimum 3 l/min (dose adjusted to effect) of 100% oxygen. Heart rate, blood pressure, respiration, and body temperature were monitored throughout the procedure. During the surgical procedure, a titanium post for head immobilization and a titanium recording chambers that allowed access to the vestibular nucleus (VN) were fastened to each animal's skull with titanium screws and dental acrylic. Craniotomy was performed within the recording chamber to allow electrode access to the brain stem. An 18-mm-diameter eye coil (three loops of Teflon-coated stainless-steel wire) was implanted in one eye behind the conjunctiva (Fuchs and Robinson, 1966). Following surgery, we continued dexamethasone (0.5 mg/kg im; for 4 days), anafen (2 mg/kg day one, 1 mg/kg on subsequent days), and buprenorphine (0.01 mg/kg im; every 12 hr for 2–5 days). In addition, cefazolin (25 mg/kg) was injected twice daily for 10 days. Animals recovered in 2 weeks before any experimenting began.

During experiments, monkeys were head-restrained and seated in a primate chair mounted on a motion platform rotating about the vertical axis (i.e., yaw rotation). We recorded the single-unit activities of three classes of vestibular neurons within the vestibular nuclei (PVP, EH and VO neurons) using enamel-insulated tungsten microelectrodes. Extracellular activity of the vestibular neurons was initially recorded during standard head-restrained paradigms to characterize their sensitivity to eye movements and head velocity. To quantify the neuronal sensitivity to eye movements, monkeys were trained to visually track a target light. Gaze position was measured using the magnetic search-coil technique. Eye sensitivity was then characterized during saccadic and smooth pursuit eye movements. Both PVP and EH responses were proportional to eye position following saccade and were responsive during smooth pursuit. Characteristic to the PVP, they paused during saccades (Figure 1—figure supplement 1). VO neurons were unresponsive to eye movements. Neuronal sensitivities to head velocity were assessed during VOR and vestibulo-ocular reflex cancellation (VORc) paradigms while the monkeys were passively rotated about the vertical axis. During naturalistic yaw rotation, all neuronal classes responded to stimulation in a manner consistent with their classification (Cullen et al., 1993; Cullen and McCrea, 1993). Sinusoidal head motion stimuli with frequencies 0.5, 1, 2, 3, 4, 5, 8, 17 Hz and amplitudes of 20 deg/s were then applied to characterize head motion sensitivity. We then recorded neural activity during naturalistic head yaw rotation that mimicked the head velocity of a freely moving monkey (Carriot et al., 2017), as previously described (Mitchell et al., 2018). We note that the probability distribution of the naturalistic head motion stimulus was well-fit by a Gaussian (see Figure 1—figure supplement 1B of Mitchell et al., 2018). We note that the distribution of head velocities was symmetric around zero (p=0.33, triples test) (Randles et al., 1980). Motion platform velocity was measured using a one-dimensional angular gyroscope (Watson Inc). Data were collected through the Cerebus Neural Signal Processor (Blackrock Microsystems). Action potentials were discriminated from extracellular recordings offline by using a custom-written algorithm (Matlab).

Analysis of neuronal discharges

Data were imported into Matlab for analysis using custom-written algorithms. Head velocity signals were sampled at 1 kHz and digitally low-pass filtered at 125 Hz. For each neuron, we generated a binary spike train R(t) with a sampling rate of 1 kHz. Eye position sensitivities were determined from saccadic as well as smooth pursuit eye movements using standard methodologies (Roy and Cullen, 2002). Head velocity sensitivities were then determined during sinusoidal stimulation using standard models (Roy and Cullen, 1998). Neuron response spectra during naturalistic stimulation were computed from digitized spike trains using the Matlab function "pwelch" in which epochs during vestibular quick phases were removed. Quick phases were detected using standard methodology (Roy and Cullen, 2002). To test whether the neuron’s response power spectra was constant across frequencies, we calculated the whitening index as the integral of the spike train power spectrum from 0 to 20 Hz divided by the integral of a simulated white response at maximum neuron power across frequency range (i.e., 0–20 Hz). The stimulus power spectrum and whitening index were computed from the head velocity signal using the same method as for the neuron’s response. Periods of spontaneous activity were used to calculate the resting discharge power spectra using the Matlab function "pwelch". For EH and PVP neurons, we concatenated epochs during fixation at 0 deg. Variability was quantified using the CV, which is the standard deviation to mean ratio of the interspike interval (i.e., the times between consecutive action potential firing) distribution.

Response dynamics for naturalistic stimuli

Request a detailed protocol

The response tuning function was computed from the transfer function H(f) using:

Gf= H(f)
Hf=PRS(f)PSS(f)

Where PRS(f) is the cross-spectrum between the stimulus St and the binary spike train R(t), and PSSf is the power spectrum of the stimulus St. We used Gf=1 Hz to quantify sensitivity for plotting as a function of variability. Spectral quantities (i.e., power spectra, cross-spectra) were estimated using multitaper estimation techniques (Jamali et al., 2016; Jamali et al., 2019; Jarvis and Mitra, 2001; Schneider et al., 2015). We used the stimulus reconstruction method to quantify faithful encoding of the stimulus’ detailed time course by neural activity (Gabbiani and Koch, 1998; Marre et al., 2015; Massot et al., 2011; Rieke et al., 1996). Specifically, the reconstructed stimulus for N neurons is given by:

Sreconstructedt=∑i=1N(Ki*Ri)(t)

where, for neuron i, Rit is the binary sequence and Ki is the optimal kernel. When N=1, the Fourier transform of the kernel K1t is given by the following equation:

K~1f=PR1S(-f)PR1R1(f)

where, for neuron i, PRiRi(f) is the power spectrum of the binary spike train Ri(t), and PRiS(f) is the cross-spectrum between the binary spike train Ri(t) and the stimulus S(t). When N = 2, the Fourier transforms of the kernels are given by:

K~1fK~2f=PR1R1(f)PR1R2(f)PR2R1(f)PR2R2(f)-1PR1S(-f)PR2S(-f)

where, for neurons i and j, PRiRj(f) is the cross-spectrum between the binary spike trains Ri(t) and Rj(t). We assessed the quality of the reconstruction by computing the coding fraction CF:

CF=1-ε2σ

where ε2=St-Sreconstructedt2 is the mean square error, <…> denotes an average over time, and σ is the standard deviation of the stimulus S(t). CF ranges between 0 and 1 and represents the fraction of variance in the stimulus that is correctly reconstructed. The stimulus reconstruction was applied to single neurons (i.e., N=1) as well as for PVP neuron pairs (i.e., N=2). For PVP neuron pairs, neurons were grouped into those with “low resting discharge variability” and those with “high resting discharge variability”. Specifically, we took the 5 PVP neurons having the lowest resting discharge variability and the 5 PVP neurons with the highest resting discharge variability, as quantified by CV.

We computed the trial-to-trial variability as done previously (Mitchell et al., 2018). Briefly, the residuals ΔRi were computed as:

∆Ri= Ri-1N∑i=1NRi

and the variability power spectrum was computed as the average power spectrum of the residuals. Here Ri is the binary spike train obtained for the ith presentation of the stimulus. Our results show that this power spectrum was similar to that of the resting discharge obtained in the absence of stimulation (Figure 2—figure supplement 3).

To predict the response power spectrum PRR,predicted(f) to the naturalistic stimulus, we fit a linear-nonlinear cascade model to our data (Chichilnisky, 2001), where the predicted firing rate is given by:

FRpredictedt=G(H~*S)(t)

where S(t) is the stimulus, H~(t) is the Fourier transform of the transfer function H(f), "*" denotes the convolution, and G is a nonlinear function that is determined by plotting the actual firing rate as a function of the linear prediction (H~*S)(t) (Schneider et al., 2015). The predicted response power spectrum Pr(f) is then given by:

PRR,predictedf= P0f+PFR,predicted(f)

where PFR,predicted(f) is the power spectrum of FRpredictedt and P0f is the power spectrum of the binary sequence obtained in the absence of stimulation (i.e., resting discharge). We note that the above mentioned fact that the head velocity stimulus probability distribution is symmetric with respect to zero (i.e., P(s)=P(-s)) implies that there will not be any inconsistencies or biases in our transfer function and LN model estimates (Meyer et al., 2016; Paninski, 2003; Chichilnisky, 2001).

To test whether the response power is independent of frequency f, we simulated 1000 Poisson processes with the same number of spikes as contained in each neuron’s spike train and computed the power spectra obtained for each Poisson spike train. We found that the distributions at every frequency were Gaussian (Shapiro-Wilk test, all p-values>0.05) as expected from the central limit theorem and obtained a 95% confidence interval that is shown in the figures.

Contribution of the neuron’s eye sensitivity to response power spectrum

Request a detailed protocol

PVP and EH neurons are responsive to changes in eye position that occur during naturalistic head motion during the VOR or during quick phases. To test whether the transmitted power is influenced by the neuronal sensitivity to eye position, we computed the response power for concatenated segments of the naturalistic stimulus for which the eye position was confined between ± 5o.

VOR

Request a detailed protocol

VOR gain was computed as the opposite of the slope of the best-fit linear regression between head velocity and eye velocity. Epochs during which the monkeys performed saccades were not included in the regression.

Model of ocular motoneuron responses to naturalistic self-motion

Request a detailed protocol

We used the following model (Robinson, 2011) in which the eye velocity is related to the head velocity by the following:

EV~f=Tafferentsf TVNf TNIf TPlantf HV~f

Where EV~f is the Fourier transform of the eye velocity, HV~f  is the Fourier transform of the head velocity, and we have:

Tafferents(f)=s (s T1+1)(s T2+1)(s Tc+1)TVN(f)=−gVORTVOR(s TVOR+1)(s Tc+1)Tc TNI(f)=Te1+1sTPlant(f)=s e−sτ(s Te1+1)(s Te2+1)

where s=2πif, i=-1, T1= 0.0175 s, T2 = 0.0027 s, Tc=5.7 s are time constants representing the dynamics of sensory transduction and afferent filtering properties (Hullar et al., 2005; Schneider et al., 2015). gVOR is the VOR gain, TVOR=16 s is the VOR time constant. “NI” is the neural integrator. Te1= 1 s and Te2= 0.016 s are time constants describing the neural integrator and plant dynamics, while τ = 0.008 s is the delay (Robinson, 2011). The output of VOR neurons is given by:

R~VORf=Tafferentsf TVNf HV~f

where R~VORf is the Fourier transform of the spiking activity of VOR neurons. As such, the predicted eye velocity is given by:

EV~predicted(f)= TNI(f) TPlant(f) R∼VOR(f)

where EV~predictedf= TNIf TPlantf R~VORf is the Fourier transform of the predicted eye velocity. Multiplying both sides by the complex conjugate gives us the power spectrum of the predicted eye velocity:

EV~predictedf

which was then compared with the power spectrum of the eye velocity signal recorded during experiments. The matching index was computed as:

PEV,predictedf= TNIf TPlantf2PVOR(f)

where MI=1-logPEV,predicted(f)-logPEV,actual(f)2σEP,actual is the power spectrum of the actual eye velocity, PEP,actualf is the standard deviation of σEV,actual and “log” denotes the natural logarithm.

Statistics

Our sample size was comparable to those employed in the field (Massot et al., 2011; Mitchell et al., 2018). Before statistical analysis, normality of distribution was evaluated using a Shapiro-Wilk’s test. Parametric analysis was used (two-tailed t-test or ANOVA) when data were normally distributed. When the data deviated from a normal distribution, non-parametric statistic was performed on the data. All significant effects are reported at p<0.05. The data are available on figshare (http://doi.org/10.6084/m9.figshare.12594803).

Data availability

The data is available on figshare http://doi.org/10.6084/m9.figshare.12594803.

The following data sets were generated
    1. Mackrous I
    2. Carriot J
    3. Cullen KE
    4. Chacron MJ
    (2020) figshare
    Data from neural variability determines coding strategies for natural self-motion in macaque monkeys.
    https://doi.org/10.6084/m9.figshare.12594803

References

  17. Book
    1. Gabbiani F
    2. Koch C
    (1998)
    Principles of spike train analysis
    In: Koch C, Segev I, editors. Methods in Neuronal Modeling: From Ions to Networks. Cambridge: MIT Press. pp. 313–360.
  46. Book
    1. Rieke F
    2. Warland D
    3. de Ruyter van Steveninck RR
    4. Bialek W
    (1996)
    Spikes: Exploring the Neural Code
    Cambridge, MA: MIT.
  50. Book
    1. Robinson DA
    (2011) Control of Eye Movements
    In: Prakash Y. S, editors. Comprehensive Physiology. Wiley. pp. 1275–1320.
    https://doi.org/10.1002/cphy.cp010228

Decision letter

  1. Fred Rieke
    Reviewing Editor; University of Washington, United States
  2. Joshua I Gold
    Senior Editor; University of Pennsylvania, United States

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Thank you for submitting your article "Neural variability determines coding strategies for natural self-motion: implications for perception and behavior" for consideration by eLife. Your article has been reviewed by three peer reviewers, one of whom is a member of our Board of Reviewing Editors, and the evaluation has been overseen by Joshua Gold as the Senior Editor. The reviewers have opted to remain anonymous.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

As the editors have judged that your manuscript is of interest, but as described below that substantial additional analyses and clarifications are required before it is published, we would like to draw your attention to changes in our revision policy that we have made in response to COVID-19 (https://elifesciences.org/articles/57162). First, because many researchers have temporarily lost access to the labs, we will give authors as much time as they need to submit revised manuscripts. We are also offering, if you choose, to post the manuscript to bioRxiv (if it is not already there) along with this decision letter and a formal designation that the manuscript is "in revision at eLife". Please let us know if you would like to pursue this option. (If your work is more suitable for medRxiv, you will need to post the preprint yourself, as the mechanisms for us to do so are still in development.)

The dichotomy between faithful and efficient coding neurons received a good deal of attention in the consultation among the reviewers. All of the reviewers felt that more needed to be done to clarify and to test this distinction. For example, it is not clear how the decoding errors could be larger for the efficient coding neurons if they really are efficient. Related to this point is whether the efficient coding neurons are simply noisier, and if the whitening comes at the expense of higher noise. Several additional specific points raised in the individual reviews are related to this point. I should emphasize that in consultation the reviewers felt more strongly about this point than is reflected in the individual reviews, and whether you are able to deal with it clearly and effectively will be critical to a re-evaluation of the paper.

Reviewer #1:

This paper follows a previous paper from some of the same authors exploring coding of naturalistic inputs in the vestibular system. The previous paper showed that the combination of stimulus power spectrum, neural filtering and noise led to spectrally-flat ("whitened") responses in one class of vestibular neuron. The present paper extends this analysis to two other types of vestibular neurons, concluding that they show considerable heterogeneity in the degree of whitening. I had several concerns about the analysis/presentation:

Filter calculations and non-Gaussian stimuli:

The paper relies on naturalistic head movement stimuli and uses these for the coding analyses. Some of the calculations presented, however, are valid only for gaussian stimuli. This is particularly true of the linear-nonlinear model and more broadly the construction of the transfer functions. Thus, it seems that the filters extracted could be impacted by the correlation structure of the stimulus. This is a key issue for interpretation of the paper.

Adding noise and optimality:

Neurons that whiten the stimulus are referred to as optimal, while other neurons that encode the stimulus faithfully are referred to as non-optimal. If much of the whitening comes from noise in the resting discharge, however, it does not seem that the "optimal" neurons are really optimal – i.e. they would encode better with non-white responses and less noise. This issue recurs throughout the paper and bears on the tradeoff of optimal vs faithful coding.

How does coding in low and high noise neurons differ:

It would be very useful to see a separation of differences in encoded signal and noise to differences in response power spectra. For example, in Figure 2D, how much of the power spectrum in the high variability neurons is due to noise and how much is due to signal? Related, is the spectrum of the encoded signal similar in high and low variability neurons?

Related to this point, in subsection “Neurons with lower variability faithfully encode the detailed time course of naturalistic self-motion stimuli”: the observation that neurons with low variability encode the stimulus more faithfully than those with high variability is not too surprising. It would help to analyze the nature of the coding – e.g. are there systematic errors or bias in encoding in the case of the high variability neurons? Or are both low and high variability neurons encoding the same temporal frequencies, just with different signal to noise ratios?

Reviewer #2:

This is a very nice extension of previous work, now including more classes of vestibular neurons (PVP/EH/VO), whereas only VO were published on in the earlier work. Some excellent hypotheses are outlined about how different types of signals (faithful stimulus encoders versus efficient whitened outputs) are used in different behaviors. This work nicely connects input statistics to encoding with an eye on behavior.

I have just a few main points that I think would enhance the presentation of these results in the manuscript:

1) A main claim of the paper relies on the dissection of neurons in to high and low CV cells, but it really doesn't seem like the data support a statistical distinction between classes, Figure 1D. Specific questions and comments are:

a) Something else needs to be shown here in Figure 1, like the overall histogram of CV, and the accompanying text should not state that there were significant differences amongst these classes of neurons, then point to a figure in which almost all group comparisons are not significant. This just needs to be made crystal clear throughout: this is a hard-fought-and-won dataset that shows some differences amongst neurons, but there aren't enough data to make claims about broad differences between PVP/EH/VO classes, except for the CF result for PVP vs. EH/VO. The result that the PVP class has a lower CV than EH seems like a very small effect size.

b) This appears to be mostly a paper about high versus low baseline variability (though it would be nice to make rate-matched comparisons, next comment), not about differences in response classes. Put another way, it seems like all classes contain neurons that follow the stimulus and some that perform temporal whitening. The first figure could be reformatted to highlight that more clearly.

c) What is the main claim about subtypes, if the above true? Is it that each type needs a "faithful encoder" channel and a "whitened" channel? It seems that this is exactly what is presented in the Discussion, but then the claims about differences in the EH population and a longer discussion about the VO subtype seems out of place, if that's true. Perhaps PVP can be separated by CF, but the distinction between VO and EH neurons in these data seem more tenuous.

2) Do these results hold if high/low variability neurons are compared in pairs that have similar firing rates?

Reviewer #3:

The authors record from three classes of central vestibular neurons (PVP, EH, VO), which project to different areas. They show that functionally, neurons in each of the classes can be divided into "high variability" (HV) and "low variability" (LV) neurons based on characteristics such as CV of the ISI. HV neurons perform decorrelation (=whitening) consistent with efficient coding, while LV neurons perform "faithful encoding", i.e., permit a precise linear reconstruction of the stimulus. The suggested implication is that this division makes sense in the light of downstream computations: e.g., control of eye velocity in VOR favors LV type encoding, as they show computationally.

I find the paper well-written and well-argued, and would support publication after revisions. I do not see any major technical flaws, but recommend one extra analysis as detailed below.

1) I was confused in how precisely the authors define "High variability" and "Low variability" classes. They look at the FR and CV statistics, and also at the power in the natural frequency band, and all these statistics can be done on natural stim or in the resting state. I presume the classification is based only on the CV in the resting state. If that is true, this should be said explicitly (and if you use any thresholds to decide what is "high" and what "low", please specify). Please clarify.

But if the variability is "continuously distributed", then the HV and LV neurons (used as the examples) are only at the extreme ends of that CV distribution. Can you mark where the example neurons of 1B are in Figure 1C (and perhaps in other relevant figures)? For how many of all your neurons do you then see such clear differences between two encoding schemes, what are the neurons in the middle of the CV distribution doing and what is your functional expectation for them? Figures 2E and 3C show the "interpolation" as a function of CV in terms of whitening and CF, showing this continuum of behaviors, but the story seems to tend to much towards a black and white dichotomy between the two extreme behaviors. I would suggest rewording to make clearer that this is not a dichotomy.

2) Figure 2E and 3C show a pretty strong dependence of WI and CF on CV. If the baseline firing rate (that the authors also quantified in Figure 1) is included as an additional explanatory variable for CF in addition to CV, do you see a much better prediction of CF or WI? For example, are low-CV neurons that have a high CF in Figure 3C the ones that have higher firing rates?

3) When the authors interpret the function of HV / LV neurons in Figure 3 and 4, suggesting that LV neurons are better for VOR, they imply that the system is choosing to use one or the other class. But I imagine the population, which is mixed and has a full CV spectrum, is input to the neural integrator. In fact, it would make lots of sense if I look at Figure 3A, to interpret LV neurons as tracking the slower changes in the stimulus well, whereas HV neurons emphasize faster modulation. A system that reads out both types of neurons (or the full heterogenous population) is thus expected to perform much better in reconstructing the stimulus and controlling the eyes.

I suggest that the authors test this hypothesis by linearly decoding from two or more neurons. In the easiest scenario, they could take one LV and one HV neuron (maybe examples in Figure 3B) and jointly linearly decode the stimulus. This could be compared with the decoding based on two LV and two HV neurons, to see if the major benefit comes from combination of the two classes. One could reconstruct from even more neurons if that is feasible, to see how the reconstruction depends on the number / type of neurons (cf. Marre et al., 2015), but I don't consider necessary for resubmission. If, however, it turns out that the authors discover a large benefit to decoding really from two classes (LV + HV) jointly, I think the interpretation and discussion needs to be modified: heterogeneity is beneficial since it permits precise full stimulus reconstruction, and so VOR control should not only be done with low variability neurons.

An additional discussion point that the authors may want to consider is that LV neurons can be decoded with more instantaneous filters, whereas decoding from neurons (like HV) that decorrelate requires decoding filters that are extended in time; this may cause delays in the reconstruction and is possibly detrimental if the sensory-motor loop in VOR needs to be fast?

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

Thank you for resubmitting your work entitled "Neural variability determines coding strategies for natural self-motion in macaque monkeys" for further consideration by eLife. Your revised article has been evaluated by Joshua Gold (Senior Editor) and Fred Rieke (Reviewing Editor).

The manuscript has been improved but there are some remaining issues that need to be addressed before we can make a final decision, as outlined below:

As you will see below, reviewer #3 has some remaining substantial concerns. In consultation, both reviewers and the Reviewing Editor agreed that these points are quite important and dealing with them fully will be essential if we are to proceed with the paper.

Reviewer #2:

I feel that the paper is much improved after revision. Many of my claims were addressed, as were several of the other reviewers. The Gaussian shape of the naturalistic inputs to this system were clearly a point that needed more emphasis and explanation. I'm glad that's been addressed fully.

The distinction amongst classes of neurons is now much clearer, as is, I believe the Abstract and Results section.

Reviewer #3:

The authors have addressed many of my concerns and their additional analyses have clarified the situation. Especially important are the new quantifications that make it clear that low-CV neurons actually transmit more information (thus better stimulus reconstruction) but do not whiten, whereas high-CV neurons transmit less information due to higher noise power, but their output spectra are white.

I have a two outstanding comments:

1) The authors respond that the self-motion marginal PDF is ~Gaussian with low skew. Even small skew can cause distortions in RF estimates (Meyer et al., 2016); more importantly, the necessary condition for the consistency of RF estimates is spherical symmetry, i.e., P(s) = P(-s) where s is the full stimulus waveform, not just a single marginal value (which is what they report). I understand the authors are faced with the empirical issue of a naturalistic stimulus, so I just ask to clarify precisely the conditions for consistent estimation.

2) Perhaps most importantly, although it may appear nitpicking, I would like the authors to go through the text and be very careful about the interchangeable use of "optimal coding" and "whitening", for their high-CV class neurons. I agree that these neurons produce, to a good approximation, a whitened output. I also agree that there is a regime of efficient coding theory, but by no means the only operating regime, where the theory predicts as optimal a match between stim statistics, noise, and the neural filter that generates white outputs (van Hateren, 1992a): specifically, this happens at high SNR, where the "input noise" Np (in van Hateren paper) is vanishing (Equation 25). But this is not the only regime of optimality. When input noise is high, filters are proportional to (sqrt of) signal spectrum (Equation 30), in this case neurons would not whiten but still be optimal.

In your analysis, you have access to channel noise (Nc in van Hateren notation) which you empirically equate by resting discharge spectrum. But I am not sure if you have direct access to the input noise, Np (I am not familiar enough with the system to know what this would constitute). While the traditional regime of application of efficient coding theory is the regime where channel noise dominates over input noise and thus the optimal prediction is whitening, there are cases where the system is not in this regime (retina at low light, or processing of higher order spatial textures beyond V1).

As a consequence, it could be that low-CV neurons are or are not optimal even in the sense of efficient coding, depending on noise constraints we do not know; but they for sure don't whiten.

I would thus recommend being very precise about the claims, e.g., in the Abstract, instead of saying that the neurons did not optimally encode…, I would say they do not whiten. I think it is fair to point out in the paper that the typical regime of efficient coding predicts whitening (van Hateren et al.), but it may be going beyond what you can demonstrate to claim that absence of whitening means non-optimal coding in low-CV neurons. I think that these world-level corrections, to focus on non-whitening vs whitening rather than optimal vs. non-optimal encoding, should not detract from the main message of the paper, and provide an interesting discussion point about optimality.

https://doi.org/10.7554/eLife.57484.sa1

Author response

The dichotomy between faithful and efficient coding neurons received a good deal of attention in the consultation among the reviewers. All of the reviewers felt that more needed to be done to clarify and to test this distinction. For example, it is not clear how the decoding errors could be larger for the efficient coding neurons if they really are efficient. Related to this point is whether the efficient coding neurons are simply noisier, and if the whitening comes at the expense of higher noise. Several additional specific points raised in the individual reviews are related to this point. I should emphasize that in consultation the reviewers felt more strongly about this point than is reflected in the individual reviews, and whether you are able to deal with it clearly and effectively will be critical to a re-evaluation of the paper.

We understand and appreciate your and the reviewers’ comments regarding optimality vs. faithfulness and agree that this is an important point. To directly address this point in the current manuscript, we have first defined our terms (i.e., optimal vs. faithful coding) in the Introduction. Specifically, optimal coding refers to the fact that the mutual information is at its maximum possible value for a given level of variability or, equivalently, that the output power spectrum is independent of frequency (Shannon, 1946; Rieke et al., 1996). Further, we defined faithful encoding as the spike train containing information as to the detailed timecourse of the stimulus and quantified it by comparing the reconstructed stimulus to the original through the coding fraction (i.e., the relative variance of the stimulus that is correctly reconstructed).

Second, in order to directly address the relationship between faithful encoding and optimal coding in our current dataset, we have performed additional analysis which is shown in Figure 2—figure supplement 7. Specifically, we have separated the response power spectra into their noise and transmitted signal power components and now show these as requested by reviewer 1 in panel A. Further, as requested, we have computed the signal-to-noise ratio and show a strong decrease with increasing variability. As such, the high variability neurons are in fact “noisier” than their low variability counterparts. Further, to clarify what is meant by optimal coding, we computed the mutual information between the stimulus and the spike train and compared it to its maximum possible value for a given level of variability. Our results show that, while the absolute mutual information decreases with increasing CV (Panel B, middle), the relative mutual information (i.e., the ratio of the mutual information to its maximum possible value) actually increases (Panel B, right). Thus, neurons with higher CV, while transmitting less information in absolute terms, are more optimal because the mutual information is closer to its maximum possible value for that level of variability. In contrast, neurons with lower CV transmit more information as to the stimulus’ detailed timecourse (i.e., faithful encoding). These new results are now described and discussed in the revised manuscript. In addition, we address the specific reviewers’ comments below.

Reviewer #1:

This paper follows a previous paper from some of the same authors exploring coding of naturalistic inputs in the vestibular system. The previous paper showed that the combination of stimulus power spectrum, neural filtering and noise led to spectrally-flat ("whitened") responses in one class of vestibular neuron. The present paper extends this analysis to two other types of vestibular neurons, concluding that they show considerable heterogeneity in the degree of whitening. I had several concerns about the analysis/presentation:

Filter calculations and non-Gaussian stimuli:

The paper relies on naturalistic head movement stimuli and uses these for the coding analyses. Some of the calculations presented, however, are valid only for gaussian stimuli. This is particularly true of the linear-nonlinear model and more broadly the construction of the transfer functions. Thus, it seems that the filters extracted could be impacted by the correlation structure of the stimulus. This is a key issue for interpretation of the paper.

We understand the reviewer’s comment and had previously directly addressed this important issue in the original paper (Mitchell et al., 2018 ). Specifically, we have shown that the naturalistic self-motion probability distribution is well-fit by a Gaussian (see Figure 1—figure supplement 1B of Mitchell et al., 2018). We further note that the stimulus probability distribution is symmetric with respect to zero, as evidenced by a low skewness of 0.24. As such, there are no inconsistencies or biases in our transfer function and LN model estimates (Chichilnisky, 2001; Paninski, 2003; see Meyer et al., 2016 for review). This is now mentioned in the Materials and methods.

Adding noise and optimality:

Neurons that whiten the stimulus are referred to as optimal, while other neurons that encode the stimulus faithfully are referred to as non-optimal. If much of the whitening comes from noise in the resting discharge, however, it does not seem that the "optimal" neurons are really optimal – i.e. they would encode better with non-white responses and less noise. This issue recurs throughout the paper and bears on the tradeoff of optimal vs. faithful coding.

We understand and appreciate the reviewer’s comment regarding optimality and faithfulness. We agree that this is a major point as mentioned above in our response to the editor’s comments. To directly address this point, we have first clearly defined our terms (i.e., optimal vs. faithful coding) in the revised Introduction. Specifically, optimal coding refers to the fact that the mutual information is close to its maximum possible value for a given level of variability, while faithful encoding refers to the fact the neuron transmits high levels of information about the stimulus, such that the stimulus’ detailed timecourse can be recovered from its spiking activity. Second, we have performed additional analysis of our data to directly demonstrate that neurons with high variability (i.e., HV neurons) are more optimal than neurons with low variability (i.e., LV neurons; see Figure 2—figure supplement 7B, right panel). Indeed, our new results show that the mutual information is closer to its maximum possible value when variability increases. However, the absolute mutual information decreased with increasing variability (Figure 2—figure supplement 7B, middle panel), implying that LV neurons more faithfully encode the stimulus than their HV counterparts. We have revised the text to include description of these new results.

How does coding in low and high noise neurons differ:

It would be very useful to see a separation of differences in encoded signal and noise to differences in response power spectra. For example, in Figure 2D, how much of the power spectrum in the high variability neurons is due to noise and how much is due to signal? Related, is the spectrum of the encoded signal similar in high and low variability neurons?

We now show both signal and noise power in Figure 2—figure supplement 7A. The noise power was higher for high variability neurons than for low variability neurons, thereby leading to a signal-to-noise ratio that decreases with increasing variability (Figure 2—figure supplement 7B, left panel). However, both low and high variability neurons displayed similar signal power (Figure 2—figure supplement 7A).

Related to this point, in subsection “Neurons with lower variability faithfully encode the detailed time course of naturalistic self-motion stimuli”: the observation that neurons with low variability encode the stimulus more faithfully than those with high variability is not too surprising. It would help to analyze the nature of the coding – e.g. are there systematic errors or bias in encoding in the case of the high variability neurons? Or are both low and high variability neurons encoding the same temporal frequencies, just with different signal to noise ratios?

As mentioned above, the fact that the stimulus probability distribution is symmetric implies that there are no systematic biases or errors in our estimates. Moreover, as mentioned for the previous comment, our new analysis shows that low and high variability neurons encode the same range of temporal frequencies with similar tuning functions, but that the signal-to-noise ratio is lower for the latter (Figure 2—figure supplement 7B, left panel).

Reviewer #2:

This is a very nice extension of previous work, now including more classes of vestibular neurons (PVP/EH/VO), whereas only VO were published on in the earlier work. Some excellent hypotheses are outlined about how different types of signals (faithful stimulus encoders versus efficient whitened outputs) are used in different behaviors. This work nicely connects input statistics to encoding with an eye on behavior.

I have just a few main points that I think would enhance the presentation of these results in the manuscript:

1) A main claim of the paper relies on the dissection of neurons in to high and low CV cells, but it really doesn't seem like the data support a statistical distinction between classes, Figure 1D. Specific questions and comments are:

a) Something else needs to be shown here in Figure 1, like the overall histogram of CV, and the accompanying text should not state that there were significant differences amongst these classes of neurons, then point to a figure in which almost all group comparisons are not significant. This just needs to be made crystal clear throughout: this is a hard-fought-and-won dataset that shows some differences amongst neurons, but there aren't enough data to make claims about broad differences between PVP/EH/VO classes, except for the CF result for PVP vs. EH/VO. The result that the PVP class has a lower CV than EH seems like a very small effect size.

We now plot the firing rate and CV distribution for all three classes pooled in Figure 1 as requested. We have furthermore rewritten the Results to emphasize that the distributions of resting discharge variability and firing rate were similar for all neural classes. Finally, we agree with the reviewer and we now emphasize throughout that variability is distributed along a continuum for our dataset, and that we are showing examples within the lower and higher parts of the range of variability displayed by each class.

b) This appears to be mostly a paper about high versus low baseline variability (though it would be nice to make rate-matched comparisons, next comment), not about differences in response classes. Put another way, it seems like all classes contain neurons that follow the stimulus and some that perform temporal whitening. The first figure could be reformatted to highlight that more clearly.

We agree with the reviewer and we have rewritten this sentence to state that: “Thus, while central vestibular neurons displayed a wide range of resting discharge firing rate and variability within each class, both quantities were similarly distributed for all three classes.”. Thus, while there are strong differences in resting discharge variability within each cell class, there are no major differences across cell classes. Further, we now make rate-matched comparisons as described below in answer to comment 2.

c) What is the main claim about subtypes, if the above true? Is it that each type needs a "faithful encoder" channel and a "whitened" channel? It seems that this is exactly what is presented in the Discussion, but then the claims about differences in the EH population and a longer discussion about the VO subtype seems out of place, if that's true. Perhaps PVP can be separated by CF, but the distinction between VO and EH neurons in these data seem more tenuous.

The reviewer raises an interesting point. Based on our dataset, we show that faithful encoding by PVP neurons is necessary to generate compensatory VOR eye movements as it is best matched to the oculo-motor plant requirements. In contrast, we speculate that the larger integration time window needed to decode temporally whitened information is better suited for VOR adaptation, as seen for EH neurons which displayed poor faithful encoding as compared to the other two classes. For VO neurons, we speculate that temporal whitening is better suited to the mechanical demands of the head-neck system (i.e., head inertia) for vestibulo-spinal reflexes. Further, we propose that faithful encoding by a subset of VO neurons serves to improve perception. To make these points clearer in the revised manuscript, we have rewritten the discussion about PVP/EH neurons. Further, we have shortened the discussion about VO neurons as requested.

2) Do these results hold if high/low variability neurons are compared in pairs that have similar firing rates?

We thank the reviewer for raising this important point. To address it, we have added 2 supplementary figures (Figure 2—figure supplement 2 and Figure 3—figure supplement 2). Our new analysis shows that there is no significant correlation between either of whitening index (Figure 2—figure supplement 2A) or coding fraction (Figure 3—figure supplement 2A) and firing rate. Next, we show that, if we only take neurons whose firing rates are within a restricted range (i.e., 45 to 55 sp/s), there is still a positive correlation between the whitening index and CV (Figure 2—figure supplement 2B), and a significant negative correlation between the coding fraction and CV (Figure 3—figure supplement 2B).

Reviewer #3:

The authors record from three classes of central vestibular neurons (PVP, EH, VO), which project to different areas. They show that functionally, neurons in each of the classes can be divided into "high variability" (HV) and "low variability" (LV) neurons based on characteristics such as CV of the ISI. HV neurons perform decorrelation (=whitening) consistent with efficient coding, while LV neurons perform "faithful encoding", i.e., permit a precise linear reconstruction of the stimulus. The suggested implication is that this division makes sense in the light of downstream computations: e.g., control of eye velocity in VOR favors LV type encoding, as they show computationally.

I find the paper well-written and well-argued, and would support publication after revisions. I do not see any major technical flaws, but recommend one extra analysis as detailed below.

1) I was confused in how precisely the authors define "High variability" and "Low variability" classes. They look at the FR and CV statistics, and also at the power in the natural frequency band, and all these statistics can be done on natural stim or in the resting state. I presume the classification is based only on the CV in the resting state. If that is true, this should be said explicitly (and if you use any thresholds to decide what is "high" and what "low", please specify). Please clarify.

We understand the reviewer’s comment. The quantification of variability is based solely on the CV of the resting discharge activity and this is now clearly mentioned in the results. Further, to avoid confusion, we now refer to “resting discharge variability” throughout the manuscript. We have also emphasized that the distribution of CV is continuous and that we are looking at exemplar neurons whose CV values were within the lower and higher range of this distribution.

But if the variability is "continuously distributed", then the HV and LV neurons (used as the examples) are only at the extreme ends of that CV distribution. Can you mark where the example neurons of 1B are in Figure 1C (and perhaps in other relevant figures)? For how many of all your neurons do you then see such clear differences between two encoding schemes, what are the neurons in the middle of the CV distribution doing and what is your functional expectation for them? Figures 2E and 3C show the "interpolation" as a function of CV in terms of whitening and CF, showing this continuum of behaviors, but the story seems to tend to much towards a black and white dichotomy between the two extreme behaviors. I would suggest rewording to make clearer that this is not a dichotomy.

We understand the reviewer’s comment. First, we now mark the example neurons in Figures 1C, 2E, 3C using open symbols as requested. Further, we have emphasized throughout the results that the variability is distributed continuously and that we are looking at example neurons within the lower and higher range of variability throughout. We also now emphasize that both faithful encoding and optimal coding are distributed continuously in our dataset in the discussion in order to stress that this is not a dichotomy, as requested.

2) Figure 2E and 3C show a pretty strong dependence of WI and CF on CV. If the baseline firing rate (that the authors also quantified in Figure 1) is included as an additional explanatory variable for CF in addition to CV, do you see a much better prediction of CF or WI? For example, are low-CV neurons that have a high CF in Figure 3C the ones that have higher firing rates?

We thank the reviewer for raising this important point. To address it, we have added 2 supplementary figures where we show that there is no significant correlation between either of whitening index (Figure 2—figure supplement 2A) or coding fraction (Figure 3—figure supplement 2A) and baseline firing rate. Next, we show that, if we only take neurons whose baseline firing rates are within a restricted range (i.e., 45 to 55 sp/s), there is still a positive correlation between whitening index and CV (Figure 2—figure supplement 2B), and a significant negative correlation between coding fraction and CV (Figure 3—figure supplement 2B).

3) When the authors interpret the function of HV / LV neurons in Figure 3 and 4, suggesting that LV neurons are better for VOR, they imply that the system is choosing to use one or the other class. But I imagine the population, which is mixed and has a full CV spectrum, is input to the neural integrator. In fact, it would make lots of sense if I look at Figure 3A, to interpret LV neurons as tracking the slower changes in the stimulus well, whereas HV neurons emphasize faster modulation. A system that reads out both types of neurons (or the full heterogenous population) is thus expected to perform much better in reconstructing the stimulus and controlling the eyes.

I suggest that the authors test this hypothesis by linearly decoding from two or more neurons. In the easiest scenario, they could take one LV and one HV neuron (maybe examples in Figure 3B) and jointly linearly decode the stimulus. This could be compared with the decoding based on two LV and two HV neurons, to see if the major benefit comes from combination of the two classes. One could reconstruct from even more neurons if that is feasible, to see how the reconstruction depends on the number / type of neurons (cf. Marre et al., 2015), but I don't consider necessary for resubmission. If, however, it turns out that the authors discover a large benefit to decoding really from two classes (LV + HV) jointly, I think the interpretation and discussion needs to be modified: heterogeneity is beneficial since it permits precise full stimulus reconstruction, and so VOR control should not only be done with low variability neurons.

We thank the reviewer for raising this important point. To address, we have split our PVP dataset into neurons with “low variability” and “high variability” as suggested, keeping in mind that variability is actually distributed along a continuum. Specifically, we took the 5 neurons with the lowest values of CV as the “low variability” group and the 5 neurons with the highest values of CV as the “high variability” group. Next, we compared the coding fraction values from all possible pairings between low variability neurons (LVLV), high variability neurons (HVHV), and all possible pairings between low and high variability neurons (HVLV). Overall, the pair-averaged coding fraction for LVHV was significantly lower than that obtained from LVLV pairs (Figure 4—figure supplement 2A). Moreover, the pair-averaged change in coding fraction (i.e., the coding fraction computed from the pair minus the maximum value obtained for individual neurons within that pair) for HVLV was significantly lower than that obtained for LVLV pairs (Figure 4—figure supplement 2B). These results suggest that there is no net advantage in considering mixed neural populations as opposed to populations consisting only of LV neurons for reconstructing the stimulus.

An additional discussion point that the authors may want to consider is that LV neurons can be decoded with more instantaneous filters, whereas decoding from neurons (like HV) that decorrelate requires decoding filters that are extended in time; this may cause delays in the reconstruction and is possibly detrimental if the sensory-motor loop in VOR needs to be fast?

We thank the reviewer for raising this important point and have revised the Discussion accordingly.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

As you will see below, reviewer #3 has some remaining substantial concerns. In consultation, both reviewers and the Reviewing Editor agreed that these points are quite important and dealing with them fully will be essential if we are to proceed with the paper.

Reviewer #3:

The authors have addressed many of my concerns and their additional analyses have clarified the situation. Especially important are the new quantifications that make it clear that low-CV neurons actually transmit more information (thus better stimulus reconstruction) but do not whiten, whereas high-CV neurons transmit less information due to higher noise power, but their output spectra are white.

I have a two outstanding comments:

1) The authors respond that the self-motion marginal PDF is ~Gaussian with low skew. Even small skew can cause distortions in RF estimates (Meyer et al., 2016); more importantly, the necessary condition for the consistency of RF estimates is spherical symmetry, i.e., P(s) = P(-s) where s is the FULL stimulus waveform, not just a single marginal value (which is what they report). I understand the authors are faced with the empirical issue of a naturalistic stimulus, so I just ask to clarify precisely the conditions for consistent estimation.

We understand the reviewer’s comment and agree that the necessary condition for the consistency of RF estimates is spherical symmetry. Our original intent in providing the skewness value was to illustrate that, while non-Gaussian, the distribution of natural head velocities was symmetric with respect to zero. In this revised version, we now explicitly test symmetry by performing a triples test (Randles et al., 1980) and found that we could not reject the null hypothesis (p=0.33). This is now reported in the Materials and methods.

2) Perhaps most importantly, although it may appear nitpicking, I would like the authors to go through the text and be very careful about the interchangeable use of "optimal coding" and "whitening", for their high-CV class neurons. I agree that these neurons produce, to a good approximation, a whitened output. I also agree that there is a regime of efficient coding theory, but by no means the only operating regime, where the theory predicts as optimal a match between stim statistics, noise, and the neural filter that generates white outputs (van Hateren, 1992a): specifically, this happens at high SNR, where the "input noise" Np (in van Hateren paper) is vanishing (Equation 25). But this is not the only regime of optimality. When input noise is high, filters are proportional to (sqrt of) signal spectrum (Equation 30), in this case neurons would not whiten but still be optimal.

In your analysis, you have access to channel noise (Nc in van Hateren notation) which you empirically equate by resting discharge spectrum. But I am not sure if you have direct access to the input noise, Np (I am not familiar enough with the system to know what this would constitute). While the traditional regime of application of efficient coding theory is the regime where channel noise dominates over input noise and thus the optimal prediction is whitening, there are cases where the system is not in this regime (retina at low light, or processing of higher order spatial textures beyond V1).

As a consequence, it could be that low-CV neurons are or are not optimal even in the sense of efficient coding, depending on noise constraints we do not know; but they for sure don't whiten.

I would thus recommend being very precise about the claims, e.g., in the Abstract, instead of saying that the neurons did not optimally encode…, I would say they do not whiten. I think it is fair to point out in the paper that the typical regime of efficient coding predicts whitening (van Hateren et al.), but it may be going beyond what you can demonstrate to claim that absence of whitening means non-optimal coding in low-CV neurons. I think that these world-level corrections, to focus on non-whitening vs whitening rather than optimal vs. non-optimal encoding, should not detract from the main message of the paper, and provide an interesting discussion point about optimality.

We agree that this is an important point. To address it, we have made the requested word changes throughout: specifically, we now make it clear that, when we refer to optimal coding, we mean temporal whitening explicitly. We have furthermore added a new paragraph to the discussion to address the case mentioned by the reviewer for which the input signal-to-noise ratio is low. Specifically, in the vestibular system, input noise to central neurons would come from vestibular afferents. Our previous studies have shown that the trial-to-trial variability displayed by these afferents is low during naturalistic stimulation, as their responses can be predicted solely by considering their tuning (Figure 4—figure supplement 3 of Mitchell et al., 2018), which implies that the input signal-to-noise ratio is high. As such, it is unlikely that the deviation from whitening observed is a signature of optimized coding based on a low input signal-to-noise ratio as seen elsewhere. This argument is made in the Discussion.

https://doi.org/10.7554/eLife.57484.sa2

Article and author information

Author details

  1. Isabelle Mackrous

    Department of Physiology, McGill University, Montreal, Canada
    Contribution
    Data curation, Formal analysis, Validation, Investigation, Visualization, Methodology, Writing - original draft, Writing - review and editing
    Competing interests
    No competing interests declared

  2. Jérome Carriot

    Department of Physiology, McGill University, Montreal, Canada
    Contribution
    Formal analysis, Validation, Investigation, Visualization, Writing - original draft, Writing - review and editing
    Competing interests
    No competing interests declared

  3. Kathleen E Cullen

    1. The Department of Otolaryngology- Head and Neck Surgery, Johns Hopkins University School of Medicine, Baltimore, United States
    2. The Department of Biomedical Engineering, Johns Hopkins University School of Medicine, Baltimore, United States
    3. The Department of Neuroscience, Johns Hopkins University School of Medicine, Baltimore, United States
    4. Kavli Neuroscience Discovery Institute, Johns Hopkins University, Baltimore, United States
    Contribution
    Conceptualization, Supervision, Funding acquisition, Validation, Methodology, Writing - original draft, Writing - review and editing
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-9348-0933

  4. Maurice J Chacron

    Department of Physiology, McGill University, Montreal, Canada
    Contribution
    Conceptualization, Resources, Software, Supervision, Funding acquisition, Validation, Methodology, Writing - original draft, Project administration, Writing - review and editing
    For correspondence
    maurice.chacron@mcgill.ca
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-3032-452X

Funding

Canadian Institutes of Health Research (162285)

  • Jérome Carriot
  • Kathleen E Cullen
  • Maurice J Chacron

National Institutes of Health (R01-DC002390)

  • Kathleen E Cullen

National Institutes of Health (R01-DC018061)

  • Kathleen E Cullen

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

This research was supported by the Canadian Institutes of Health Research (JC, KEC, MJC) as well as grants R01-DC002390 and R01-DC018061 from the National Institutes of Health (KEC).

Ethics

Animal experimentation: All experimental protocols were approved by the McGill University Animal Care Committee (#4096) and complied with the guidelines of the Canadian Council on Animal Care.

Senior Editor

  1. Joshua I Gold, University of Pennsylvania, United States

Reviewing Editor

  1. Fred Rieke, University of Washington, United States

Publication history

  1. Received: April 2, 2020
  2. Accepted: September 10, 2020
  3. Accepted Manuscript published: September 11, 2020 (version 1)
  4. Version of Record published: September 28, 2020 (version 2)

Copyright

© 2020, Mackrous et al.

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

  • 931
    Page views
  • 128
    Downloads
  • 5
    Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Isabelle Mackrous
  2. Jérome Carriot
  3. Kathleen E Cullen
  4. Maurice J Chacron
(2020)
Neural variability determines coding strategies for natural self-motion in macaque monkeys
eLife 9:e57484.
https://doi.org/10.7554/eLife.57484

Categories and tags

Research organism

Further reading

    1. Neuroscience

    Neuronal variability and tuning are balanced to optimize naturalistic self-motion coding in primate vestibular pathways

    Diana E Mitchell, Annie Kwan ... Kathleen E Cullen
    Research Article Updated

    It is commonly assumed that the brain’s neural coding strategies are adapted to the statistics of natural stimuli. Specifically, to maximize information transmission, a sensory neuron’s tuning function should effectively oppose the decaying stimulus spectral power, such that the neural response is temporally decorrelated (i.e. ‘whitened’). However, theory predicts that the structure of neuronal variability also plays an essential role in determining how coding is optimized. Here, we provide experimental evidence supporting this view by recording from neurons in early vestibular pathways during naturalistic self-motion. We found that central vestibular neurons displayed temporally whitened responses that could not be explained by their tuning alone. Rather, computational modeling and analysis revealed that neuronal variability and tuning were matched to effectively complement natural stimulus statistics, thereby achieving temporal decorrelation and optimizing information transmission. Taken together, our findings reveal a novel strategy by which neural variability contributes to optimized processing of naturalistic stimuli.

    1. Neuroscience

    Cholinergic and noradrenergic axonal activity contains a behavioral-state signal that is coordinated across the dorsal cortex

    Lindsay Collins, John Francis ... David A McCormick
    Research Article Updated

    Fluctuations in brain and behavioral state are supported by broadly projecting neuromodulatory systems. In this study, we use mesoscale two-photon calcium imaging to examine spontaneous activity of cholinergic and noradrenergic axons in awake mice in order to determine the interaction between arousal/movement state transitions and neuromodulatory activity across the dorsal cortex at distances separated by up to 4 mm. We confirm that GCaMP6s activity within axonal projections of both basal forebrain cholinergic and locus coeruleus noradrenergic neurons track arousal, indexed as pupil diameter, and changes in behavioral engagement, as reflected by bouts of whisker movement and/or locomotion. The broad coordination in activity between even distant axonal segments indicates that both of these systems can communicate, in part, through a global signal, especially in relation to changes in behavioral state. In addition to this broadly coordinated activity, we also find evidence that a subpopulation of both cholinergic and noradrenergic axons may exhibit heterogeneity in activity that appears to be independent of our measures of behavioral state. By monitoring the activity of cholinergic interneurons in the cortex, we found that a subpopulation of these cells also exhibit state-dependent (arousal/movement) activity. These results demonstrate that cholinergic and noradrenergic systems provide a prominent and broadly synchronized signal related to behavioral state, and therefore may contribute to state-dependent cortical activity and excitability.

    1. Neuroscience

    Early language exposure affects neural mechanisms of semantic representations

    Xiaosha Wang, Bijun Wang, Yanchao Bi
    Research Article Updated

    One signature of the human brain is its ability to derive knowledge from language inputs, in addition to nonlinguistic sensory channels such as vision and touch. How does human language experience modulate the mechanism by which semantic knowledge is stored in the human brain? We investigated this question using a unique human model with varying amounts and qualities of early language exposure: early deaf adults who were born to hearing parents and had reduced early exposure and delayed acquisition of any natural human language (speech or sign), with early deaf adults who acquired sign language from birth as the control group that matches on nonlinguistic sensory experiences. Neural responses in a semantic judgment task with 90 written words that were familiar to both groups were measured using fMRI. The deaf group with reduced early language exposure, compared with the deaf control group, showed reduced semantic sensitivity, in both multivariate pattern (semantic structure encoding) and univariate (abstractness effect) analyses, in the left dorsal anterior temporal lobe (dATL). These results provide positive, causal evidence that language experience drives the neural semantic representation in the dATL, highlighting the roles of language in forming human neural semantic structures beyond nonverbal sensory experiences.