Spatial modulation of individual behaviors enables an ordered structure of diverse phenotypes during bacterial group migration

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record updated: November 8, 2021 (This version)
Version of Record published: November 2, 2021 (Go to version)
Accepted: September 16, 2021
Preprint posted: February 18, 2021 (Go to version)
Received: February 7, 2021

1. Of interest
Candida albicans exhibits heterogeneous and adaptive cytoprotective responses to antifungal compounds

Vanessa Dumeaux, Samira Massahi ... Michael T Hallett

Research Article Dec 6, 2023
Further reading

Abstract
eLife digest
Introduction
Results
Discussion
Materials and methods
Appendix 1
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Coordination of diverse individuals often requires sophisticated communications and high-order computational abilities. Microbial populations can exhibit diverse individualistic behaviors, and yet can engage in collective migratory patterns with a spatially sorted arrangement of phenotypes. However, it is unclear how such spatially sorted patterns emerge from diverse individuals without complex computational abilities. Here, by investigating the single-cell trajectories during group migration, we discovered that, despite the constant migrating speed of a group, the drift velocities of individual bacteria decrease from the back to the front. With a Langevin-type modeling framework, we showed that this decreasing profile of drift velocities implies the spatial modulation of individual run-and-tumble random motions, and enables the bacterial population to migrate as a pushed wave front. Theoretical analysis and stochastic simulations further predicted that the pushed wave front can help a diverse population to stay in a tight group, while diverse individuals perform the same type of mean reverting processes around centers orderly aligned by their chemotactic abilities. This mechanism about the emergence of orderly collective migration from diverse individuals is experimentally demonstrated by titration of bacterial chemoreceptor abundance. These results reveal a simple computational principle for emergent ordered behaviors from heterogeneous individuals.

eLife digest

Organisms living in large groups often have to move together in order to navigate, forage for food, and increase their roaming range. Such groups are often made up of distinct individuals that must integrate their different behaviors in order to migrate in the same direction at a similar pace. For instance, for the bacteria Escherichia coli to travel as a condensed group, they must coordinate their response to a set of chemical signals called chemoattractants that tell them where to go.

The chemoattractants surrounding the bacteria are unequally distributed so that there is more of them at the front than the back of the group. During migration, each bacterium moves towards this concentration gradient in a distinct way, spontaneously rotating its direction in a ‘run-and-tumble’ motion that guides it towards areas where there are high levels of these chemical signals. In addition to this variability, how well individual bacteria are able to swim up the gradient also differs within the population. Bacteria that are better at sensing the chemoattractant gradient are placed at the front of the group, while those that are worst are shifted towards the back. This spatial arrangement is thought to help the bacteria migrate together. But how E. coli organize themselves in to this pattern is unclear, especially as they cannot communicate directly with one another and display such diverse, randomized behaviors.

To help answer this question, Bai, He et al. discovered a general principle that describes how single bacterial cells move within a group. The results showed that E. coli alter their run-and-tumble motion depending on where they reside within the population: individuals at the rear drift faster so they can catch up with the group, while those leading the group drift slower to draw themselves back. This ‘reversion behavior’ allows the migrating bacteria to travel at a constant speed around a mean position relative to the group.

A cell’s drifting speed is determined by how well it moves towards the chemoattractant and its response to the concentration gradient. As a result, the mean position around which the bacterium accelerates or deaccelerates will vary depending on how sensitive it is to the chemoattractant gradient. The E. coli therefore spatially arrange themselves so that the more sensitive bacteria are located at the front of the group where the gradient is shallower; and cells that are less sensitive are located towards the back where the gradient is steeper.

These findings suggest a general principle for how bacteria form ordered patterns whilst migrating as a collective group. This behavior could also apply to other populations of distinct individuals, such as ants following a trail or flocks of birds migrating in between seasons.

Introduction

Collective group migration, as an important class of coordinated behaviors, is ubiquitous in living systems, such as navigation, foraging, and range expansion (Krause et al., 2002; Partridge, 1982; Sumpter, 2010). In the presence of individual heterogeneity, the migrating group often exhibits spatially ordered arrangements of phenotypes (Krause et al., 2002; Parrish and Edelstein-Keshet, 1999; Partridge, 1982; Sumpter, 2010). In animal group migration, individual behavioral abilities (e.g., directional sensitivity) would result in social hierarchy, which further drives the spatial arrangement in a coordinated group (Couzin et al., 2005). At the same time, spatial arrangements can lead to different costs and benefits for the individuals participating in the group migration (Krause, 1994; Parrish and Edelstein-Keshet, 1999; Partridge, 1982). Participating individuals must follow disciplinary rules to organize themselves into coordinated patterns while on the move, which requires complex computational abilities to interact with the group and the environment (Couzin and Krause, 2003; Couzin et al., 2002; Vicsek and Zafeiris, 2012). Therefore, understanding how individuals of different phenotypes determine their location in the group is an essential prerequisite to uncover the organization principles of collective populations.

The chemotactic microbe, Escherichia coli, provides a simple model to address the emergence of collective decision-making among diverse population, as it can exhibit both individualistic behaviors (Dufour et al., 2016; Frankel et al., 2014; Kussell and Leibler, 2005; Waite et al., 2016; Waite et al., 2018) and collective migratory patterns (Adler, 1966a; Fu et al., 2018; Keller and Segel, 1971a, Wolfe and Berg, 1989). Individual cells perform run-and-tumble random motions by spontaneously switching the rotating direction of flagella (Berg, 2004; Berg and Brown, 1972). These cells can facilitate the chemotaxis pathway to control the switching frequency to bias their motions toward their favorable direction along the chemoattractant gradient, where the efficiency to climb the gradient is defined as the chemotactic ability ( $χ$ ) (Celani and Vergassola, 2010; Dufour et al., 2014; de Gennes, 2004; Si et al., 2012). In addition, the chemotactic abilities of individual cells exhibit substantial phenotypic heterogeneity even for the clonal bacterial population, which diversifies the chemotactic response to identical signals (Spudich and Koshland, 1976; Waite et al., 2016; Waite et al., 2018). Despite the stochastic solitary behavior and variations in phenotypic ability, the E. coli population can migrate as a coherent group by following a self-generated attractant gradient, via consumption of the whole population (Adler, 1966a; Saragosti et al., 2011; Wolfe and Berg, 1989). The migratory group form a stable pattern of phenotypes sorted by their chemotactic abilities (Figure 1A), which is believed to maintain phenotypic diversity in the group (Fu et al., 2018; Waite et al., 2018). Although a previous study showed that behavior modulation helps migrating bacteria to maintain a consistent group (Saragosti et al., 2011), how individuals with phenotypic variations manage to determine their relative positions in the group remains to be determined.

Figure 1

Download asset Open asset

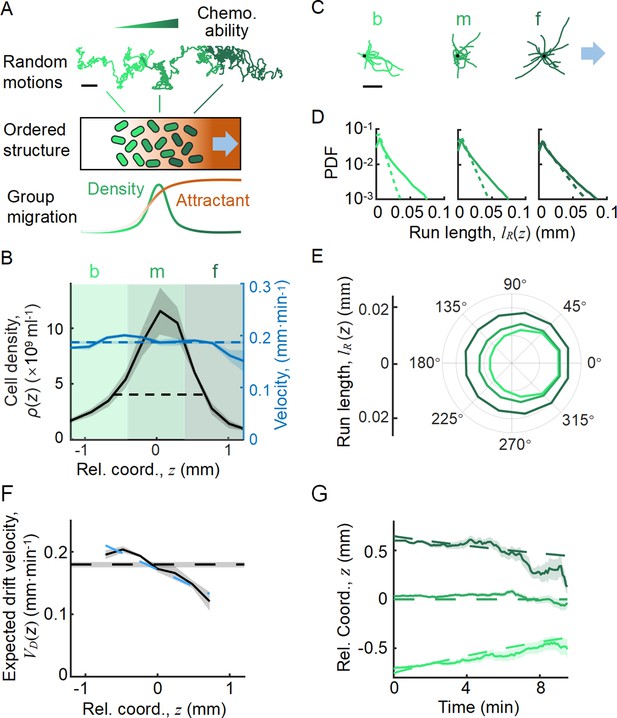
Statistics of single-cell behavior during collective group migration.

(A) Bacterial population of diverse phenotypes sorted according to their chemotactic abilities (increasing from light green to dark green) during collective migration following the self-generated attractant gradient (brown color). Meanwhile, individual cells perform run-and-tumble random motions biased toward the migration direction. Scale bar reflects 0.1 mm. (B) Bacterial density profile $ρ (z)$ is stable (black solid line) in the moving coordinate $z = x - V_{G} t$ . Where the width, represented by the black dashed-dotted line, is defined by two times the standard deviation of the bacterial relative position ( $2 σ,$ black dashed line). The instantaneous velocity ( $V_{I} (z)$ ) (blue solid line) is uniform and is equal to the average group velocity $V_{G}$ (blue dashed line). This observation was independent of the sampling time interval (Appendix 1—figure 2). (C) Sample runs of bacteria aligned by their initial positions (black dots) from the three regions (defined by colored regions in B) showed that cells at the back of the group tended to run forward, compared with cells in other regions. b, m, and f stand for the back, middle, and front of the migration group, respectively. Scale bar reflects 5 µm. (D) The exponential distributions of forward runs (solid lines) and backward runs (dashed lines) suggested the increasing efficiency of runs from the back to the front. (E) The mean run length in different directions confirmed the increasing efficiency of runs. (F) The expected drift velocity $V_{D} (z) = \frac{⟨ l_{R} (z) \cdot \cos θ_{R} (z) ⟩}{⟨ τ_{R} (z) + τ_{T} (z) ⟩}$ (black solid line) decreased from the back to the front, and is linearly fitted by $V_{D} (z) \approx - r z + V_{D 0}$ , with $r = 0.05 m i n^{- 1}$ and $V_{D 0} = 0.17 m m \cdot m i n^{- 1}$ . $V_{D}$ (z) crossing with the average group velocity $V_{G}$ (black dashed line), implied that bacteria perform mean reversion motions. The $V_{D} (z)$ profile was cut to present the majority of cells (~90%) ( $\pm 1.65 σ$ ). (G) The time evolution of the average position ( $z$ , solid lines) of cells starting from the back, middle, and front of the migration group (color code was defined in B) confirmed the reversion behavior. Shaded area represents the s.e.m. of more than 450 cells (see Materials and methods). Analytically, the OU-type model predicted that $z = C_{0} e^{- r t} - (V_{D 0} - V_{G}) / r$ (dashed lines), where $C_{0}$ can be fitted by the starting position (see supplementary text). In panels B, F, and G, the shaded area represents the s.e.m. of three biological replicates. The spatial bin size was 240 µm .

Here, we analyzed single-cell trajectories of bacterial run-and-tumble motions in the chemotactic migration group (see Materials and methods). We found that the expected drift velocity of individual cells decreased from the back to the front. Such a spatial profile modulates cells to behave as mean reverting processes relative to the entire group, that is, cells effectively tend to revert their direction of runs toward the mean position of the group. Using an Ornstein-Uhlenbeck (OU)-type model, we demonstrated that the mean reversion behavior is a result of a pushed wave, where the driving force decreases from the back to the front of the group. Cells of different phenotypes are imposed to the same type of driving force, of which the strength is coupled with their chemotactic abilities. As a result, the pushed wave front, driven by the spatially structured force, can maintain more diverse individuals in the migratory group. By theoretical analysis and stochastic simulations, we also discovered that the balanced locations of diverse phenotypes are spatially ordered by their chemotaxis abilities. Further simulations and experiments with cells of titrated chemoreceptor abundance demonstrated that this spatial modulation of individual behavior enables the ordering of bacteria with diverse chemotaxis abilities. Therefore, although the high-order computational abilities are not available to simple organisms, the spatial modulation of stochastic behaviors at the individual level reveals novel decision-making capabilities at the population level.

Results

The drift velocity of individual cells during group migration exhibits a spatially structured profile

To directly investigate the ordering mechanism in a coherent migration group, we quantified the stochastic behaviors of bacterial run-and-tumble motions relative to the stable migrating group. To achieve this, we employed a microfluidic device that generated a stable propagating band of bacteria, as previously reported (Fu et al., 2018; Saragosti et al., 2011). Using aspartate (Asp) as the only chemoattractant to drive the migration of E. coli, we tracked a small fraction of fluorescent bacteria (JCY1) as representatives of the non-fluorescent wild-type cells (RP437) (see Materials and methods, Appendix 1—figure 1, Video 1). Because the group velocity $V_{G} = 〈 Δ x_{i} (t) / Δ t 〉$ was constant over time, $V_{G} \sim 3.0 μ m / s$ (Appendix 1—figure 2), we were able to map the tracks to a moving coordinate $z = x - V_{G} t$ .

Video 1

Download asset

posterframe for video — Bacterial tracking in the migration group.

Each dot represents a bacterium captured under microscope. Lines represent typical tracks. The colors of tracks from light green to dark green represent the mean positions of the tracks from the back to the front of the migrating group.

With the shifted tracks, we calculated the key statistics of the single-cell behaviors. We first checked that the average instantaneous velocity, $V_{I} (z) = ⟨ Δ x_{i} (z) / Δ t ⟩$ , was constant along the density profile $ρ (z)$ (Figure 1B). This result confirmed that the group migrates coherently. Then, we identified all the run states and tumble states of individual trajectories using a previously described computer assistant program (Dufour et al., 2016; Waite et al., 2016), to ensure that the tracks are separated into successive tumble-and-run events (see Materials and methods). Comparing the sample events initiated from the back (b), middle (m), and front (f) of the migration group, we observed that the runs in the front were longer but distributed more uniformly in terms of the directionality, whereas the runs in the back were shorter but more oriented toward the group migration direction (Figure 1C, Appendix 1—figure 3A, B). Quantitatively, the statistics of run length (and duration) displayed exponential distributions with the means for the direction of group migration longer than those for the opposite direction (Figure 1D, Appendix 1—figure 3C). The angular distribution of the run length confirmed the difference in directionality between cells in different spatial locations (Figure 1E, Appendix 1—figure 3D). We also confirmed that cells in the back showed greater directional persistence toward the migration direction (Appendix 1—figure 4A–C), as (Saragosti et al., 2011) reported previously. All these results suggested that the bacteria in the back run more effectively toward the direction of group migration than those in the front.

To quantify the spatial extent of the drift efficiency, we defined the expected drift velocity $V_{D} \equiv \frac{⟨ l_{R} \cdot \cos θ_{R} ⟩}{⟨ τ_{R} + τ_{T} ⟩}$ , by the projection of the average run length along the migration direction over the average duration of runs and tumbles (Dufour et al., 2014). This quantity reflects the effective run speed of run-and-tumble events that start running on a given location relative to the group. The drift velocity was found to decrease from the back to the front, crossing the group velocity $V_{G}$ in the middle of the group (Figure 1F). This particular trend of $V_{D} (z)$ suggests a mean reverting behavior of bacteria in the group: the cells at the back drift faster than the group ( $V_{D} > V_{G}$ ), enabling the cells to catch up with the group; at the same time, the cells in the front drift slower than the group ( $V_{D} < V_{G}$ ), causing them to slow down and fall back (Figure 1G). Such mean reverting process also results in sub-diffusion of individuals relative to the group (Appendix 1—figure 3F), for which the mean square displacement (MSD) is constrained over time (Appendix 1—figure 3G). The slope of the spatial extent of $V_{D} (z)$ , $- r = - 0.05 m i n^{- 1}$ , quantifies the speed at which individuals revert to its center.

We noted that the spatial profile of the expected drift velocity $V_{D} (z)$ was different from the instantaneous velocity $V_{I} (z)$ . This is because the instantaneous velocity $V_{I} (z)$ defines the average speed of cells in a given time interval $d t$ , which reflects the positional shift of a group of cells at a given position. However, the expected drift velocity $V_{D} (z)$ defines the average speed of run-and-tumble events that start tumbling at a given position. Since the run duration is explicitly modulated by the gradient of chemoattractant $g (z)$ and is dependent on the chemotactic ability $χ$ , $V_{D} (z) = χ g (z)$ represents the drift velocity driven by the external stimuli (Celani and Vergassola, 2010; de Gennes, 2004; Dufour et al., 2014; Si et al., 2012).

The decreasing drift velocity implies a pushed wave front of group migration

To understand how the spatially structured profile of the drift velocity $V_{D}$ impacts on the group migration, we first adopted a Langevin-type model that describes bacterial motions as an active Brownian particle driven by the expected drift velocity $V_{D}$ and a random force: $d x = V_{D} d t + ϵ d W$ (Berg, 2004). In this model, the run-and-tumble random motions are considered as a Gaussian random force $ϵ d W$ , while the cell motions are imposed to a deterministic force $V_{D}$ (Rosen, 1973; Rosen, 1974). The strength of Gaussian noise can be estimated by the effective diffusion coefficient $ϵ = \sqrt{2 D}$ , while the drift velocity is determined by the product of the perceived gradient $g (z)$ and the chemotactic ability $χ$ , $V_{D} = χ g (z)$ . Such a stochastic description of bacterial motions has been proven equivalent to the classic Keller-Segel (KS) model that described the population dynamics of bacterial chemotactic group migration (Keller and Segel, 1971a, Rosen, 1973). In the moving coordinate, $z = x - V_{G} t$ , this Langevin-type model specifies that $d z = V_{D} (z) d t - V_{G} d t + ϵ d W$ . Thereby, the cell motions relative to the migrating group are modulated by two effective forces: one generated by $V_{D} (z)$ , which pushes the cells to catch up with the wave; and another generated by $- V_{G}$ , which drags the cells to fall behind the wave. These two ‘forces’ constrain the random motions of individuals in an effective potential well $U (z)$ (Figure 2A).

Figure 2

Download asset Open asset

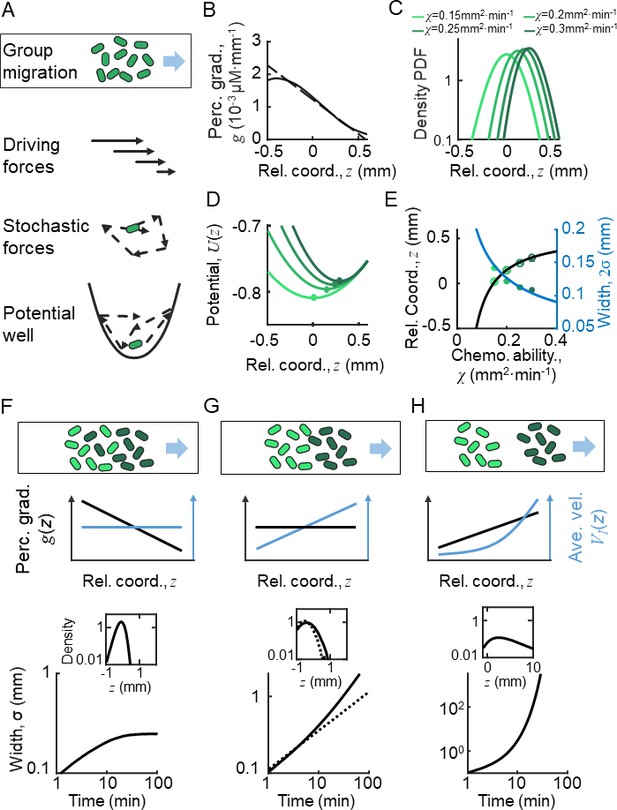
Ordered location of phenotypes of active particles in a moving gradient as a result of a pushed wave.

(A) Illustration of the Langevin-type model where the migrating bacteria are modeled by active particles under a deterministic decreasing driving force and a stochastic force. These forces allow the particles to form collective migration. On the moving coordinate of the migration group, active particles are bounded in a potential well generated by the driving force and the motion relative to the moving group ( $- V_{G}$ ). (B) The perceived gradient $g (z)$ (blue line) is deduced from $S (z)$ , which is further calculated from the experimentally measured density profile (Appendix 1—figure 4D). This gradient profile was then transformed to a moving gradient $g (x, t) = g (z) + V_{G} t$ , and applied in the simulations of different active particles following Langevin dynamics. A linear fit of $g (z)$ around $z = 0$ is plotted (dashed blue line) and is applied to the Ornstein-Uhlenbeck (OU)-type model. (C) Particles migrate collectively with a moving gradient, while they are located in ordered locations according to their phenotype $χ_{i}$ (green lines). Colors from light to dark represent increasing $χ$ . (D) The effective potential wells generated by the effective force ( $χ g (z)$ ) are spatially ordered. Circles present the minimum of the potential wells. (E) The peak positions (cross) and the mean positions (circles) increase with $χ$ . These were predicted by the OU-type model (Equation S15) (black line). The width of the density profile is defined by two times the standard deviation of all cells ( $2 σ$ ), which decreases with $χ$ , which was consistent with the prediction of Equation S18 (blue line). (**F–H**) Group migration of mixed phenotypes under decreasing, invariant, and increasing gradient. Simulations were performed in one dimension (1D) with the chemotaxis ability of the group following a Gaussian distribution with a mean of 0.11 mm² min⁻¹ and a variation of 0.02 mm² min⁻¹ (Appendix 1—figure 5C). The force field used in the simulation followed the linearized force field, as in Equation 1, while $g_{1} > 0$ in F, $g_{1} = 0$ in G, and $g_{1} < 0$ in H. All force fields were set as moving with velocity $V_{G}$ . The dashed line in G represents a group with a single phenotype of $χ = 0.11 m m^{2} m i n^{- 1}$ . Insert plots represent the wave front in the moving coordinate after 10 min of simulation. The width of the moving group, defined by the standard deviation of all particles, converges under decreasing gradient (F) while it diverges in cases of G and H.

To estimate the spatial profile of the effective driven force $V_{D} (z)$ , we analyzed the KS model with moving ansatz (supplementary text). Assuming the density profile $ρ (z)$ directly measured from experiments (Figure 1B), we can deduce the chemoattractant concentration profile $S (z)$ (Appendix 1—figure 4D), as well as the perceived gradient $g (z)$ (Figure 2B). Since the perceived gradient $g (z)$ is almost linear in the main part of the wave profile, we approximated it by $g (z) \approx g_{0} + g_{1} z$ (Figure 2B, dashed line), which allows us to transform the stochastic model to an OU-type equation:

d z = χ g_{1} z d t + (χ g_{0} - V_{G}) d t + ϵ d W

By this simplified model, we obtained a clear picture how individual behaviors are regulated relative to the group: cells are imposed to a driving force linearly dependent on their relative positions in the group, $F (z) = χ g_{1} z + (χ g_{0} - V_{G})$ . This suggests that the random motions of bacteria are constrained in a parabolic moving potential well, $U (z) = \frac{1}{2} χ |g_{1}| z^{2} + (χ g_{0} - V_{G}) z + U_{0}$ (Figure 2A), where $U_{0}$ is set by $U (\infty) = 0$ . The position that minimizes $U (z)$ is also the balanced position, $z_{0} = - \frac{g_{0}}{g_{1}} - \frac{V_{G}}{χ |g_{1}|}$ , where the driving force is null $F (z_{0}) = 0$ . Behind the balanced position, cells experience a pushed force to catch up the group. Cells would start to fall back once they exceed the balanced position, where the driving force becomes negative. Therefore, the decreasing profile of the driving force enable cells to perform mean reverting behaviors around the balanced position. In addition, the expected rate that cells tend to revert back to the balanced position is defined by the slope of the spatially dependent driving force, $r = χ |g_{1}|$ (Figure 2B).

Given the knowledge of individual behaviors, we studied the spatial distribution of population on the group migration. The OU model (Equation 1) which describes the single-cell stochastic motions has an equivalent form, known as the Fokker-Planck equation (Equation S19) which describes the spatial-temporal dynamics of cell density distribution. This population model provides a traveling wave solution with the mean position around $z_{0}$ and standard deviation $σ = \frac{ϵ}{\sqrt{2 χ |g_{1}|}}$ .

From the solution, we noted that the effective driving force, as well as the drift velocity, has a negative slope ( $g_{1} < 0$ ). The decreasing profile of the drift velocity suggests that the leading front of the group migrates as a pushed wave front (Gandhi et al., 2016; van Saarloos, 2003). As a key feature of the pushed wave, the leading front of the group drops parabolically, which is much faster than that of diffusion front. This further leads to a tight density profile of group migration for a single phenotype population.

The pushed wave front results ordered pattern of phenotypes

To address whether this pushed wave front still holds in presence of phenotypic diversity, we further examined the above analysis with cells of diverse chemotactic abilities $χ_{i}$ imposed to the same moving perceived gradient $g (z)$ (Figure 2B). Given a monotonically decreasing profile of perceived gradient $g (z)$ , the driving force that each phenotypic individual experiences exhibits the same spatial dependency with the slopes depend on the intrinsic phenotypic properties of each phenotype $r_{i} = χ_{i} |g_{1}|$ . This monotonic dependency means that the balanced positions $z_{0}$ of the diverse phenotypes are orderly arranged. By the stochastic Langevin-type model with phenotypic diversity in chemotactic ability, we first confirmed that each phenotypic population migrates at a constant speed $V_{G}$ , following the moving gradient $g (z)$ (see supplementary text). The density profiles of cells with different $χ_{i}$ follow the same shape but are spatially orderly aligned (Figure 2C). Under the same moving gradient $g (z)$ , the driving force $χ_{i} g (z)$ is phenotype-dependent, so that the bottom position of the potential well, $z_{0, i} = - \frac{g_{0}}{g_{1}} - \frac{V_{G}}{χ_{i} |g_{1}|}$ , is also spatially arranged according to $χ_{i}$ (Figure 2D). As predicted by the OU model, the balanced positions $z_{0, i}$ of different phenotypes increase with their chemotactic abilities $χ_{i}$ (Figure 2E, black line), while the standard deviation ( $σ_{i}$ ) of the density profiles decreases with $χ_{i}$ (Figure 2E, blue line). We also confirmed the ordered structure of phenotypes by a particle-based model of the Langevin-type dynamics coupled with chemoattractant consumption (Appendix 1—figure 5). Therefore, under the spatially decreasing driving force, cells with phenotypic diversity perform the same type of mean reverting processes with spatially ordered mean positions.

The spatial order of phenotypes does not directly promise a compact group migration with phenotypic diversity. By close examination of the density profile, we found that each phenotypic subpopulation propagates as a pushed wave front. We further calculated the total density profile of the entire migratory group with Gaussian distribution of chemotactic abilities under a decreasing linear gradient. Simulation reveals a pushed wave front for the combination of these subpopulations with different chemotactic abilities (Figure 2F, insert). In addition, we checked that the width of the entire group maintains in a converged width over long time, suggesting that the pushed wave profile enables the migratory population with diversity to keep in a tight shape (Figure 2F).

We examined the migration profiles under other forms of perceived gradient $g (z)$ : a constant perceived gradient and a spatially increasing perceived gradient. In the first case, individual bacteria of identical phenotype follow the diffusion process relative to the group, where the standard deviation of the population increasing with time by $σ = 2 \sqrt{D t}$ (Figure 2G, dashed line). Each phenotype subpopulation is expected to have a constant drift velocity over space. However, as the drift velocity would vary by the chemotactic ability, each subpopulation migrates in different group speeds, suggesting a compact group migration of diverse population cannot be maintained in a constant perceived gradient (Figure 2G). In the latter case, when imposed to a spatially increasing driving force (a pulled wave, by definition), individual cells display super-diffusion processes. The density profile easily diverges in this case (Figure 2H). Therefore, we concluded that the pushed wave front, driven by a decreasing shape of driving force, enables a spatially ordered and compact pattern of phenotypes while on the move.

Spatially ordered individual behaviors predicted by agent-based simulation

Although the simplified OU-type model (Equation1) represents a key aspect of the ordering mechanism of phenotypes, it does not detail the signaling processes of bacterial chemotaxis, such as receptor amplification, adaptation, and motor responses (Sumpter, 2010), and it cannot predict bacterial run-and-tumble behavior. To consolidate the proposed mechanism underlying the emergence of spatial orders from the individual random motions, we further performed agent-based simulations integrated with the chemotactic pathway, multi-flagella competition, and boundary effect in three dimensions (3D) (Dufour et al., 2014; Jiang et al., 2010; Sneddon et al., 2012). In the agent-based model, the attractant dynamics governed by diffusion and bacterial consumption is described by a reaction-diffusion equation (Equation S2) as previous multiscale models (Erban and Othmer, 2005; Xue and Othmer, 2009). We constructed a population with multiple phenotypes defined by different chemotactic abilities $χ_{i}$ , where $χ_{i}$ was varied by changing the receptor gain $N$ (for details, see supplementary text). Since the receptor gain $N$ only affects the amplification factor by which a cell responds to the gradient, the variation in bacterial motility $ϵ$ is unchanged. As a result, a dense band of migrating cells that follow a self-generated moving chemoattractant gradient via consumption were recaptured as experiments (Appendix 1—figure 6A). The phenotypes were spatially ordered as $χ$ varies (Appendix 1—figure 6B), and the velocity profile of each phenotype decreases from the back to front (Appendix 1—figure 6C) as predicted by the OU-type model.

To better analyze the simulations, we simplified the simulation with a non-consumable attractant profile $S (z)$ moving with constant speed $V_{G}$ (Appendix 1—figure 4D). Using this simplified model, we first checked that the mean positions of the density profiles of cells with different receptor gains $N$ , as well as their peaks, were orderly aligned with respect to chemotactic ability $χ_{i}$ .

As an important advantage of the agent-based simulations, the model allowed us to analyze single-cell behavior during the ordered group migrations. For each phenotype $i$ , the expected drift velocity $V_{D, i} (z)$ decreased along the density profile (Figure 3A). Consistent with the ordered structure of the density profiles, the intersection between $V_{D, i} (z)$ and $V_{G}$ exhibited the same order of chemotactic ability $χ_{i}$ (Appendix 1—figure 7). As the reversion rate $r_{i} = |\frac{d V_{D, i} (z)}{d z}|$ showed a positive correlation to $χ_{i}$ , cells with lower receptor gain $N$ (resulting in a smaller $χ$ ) experienced a weaker reverting force toward the center (Figure 3A insert). Thus, the effective moving potential, $U_{i} (z)$ , which constrains the cells around the mean positions sorted by their chemotactic abilities, becomes flat for cells with lower chemotaxis ability $χ$ (Figure 3B; Long, 2019). As a result, cells of each phenotype perform sub-diffusion, whereby the MSD along the migration coordinate relative to the group was bound at a level negatively correlated to $χ$ (Figure 3C). The width of the density distribution, as an effect of the reversion force, decreased with the reversion rate, as an approximate linear function. Using this agent-based model, we further obtained similar results for populations of different $χ_{i}$ through adaptation time $τ$ , or basal CheY protein level $Y_{p 0}$ , which determined the basic tumble bias $T B_{0}$ (Dufour et al., 2014; Jiang et al., 2010; Sneddon et al., 2012; Appendix 1—figure 8).

Figure 3

Download asset Open asset

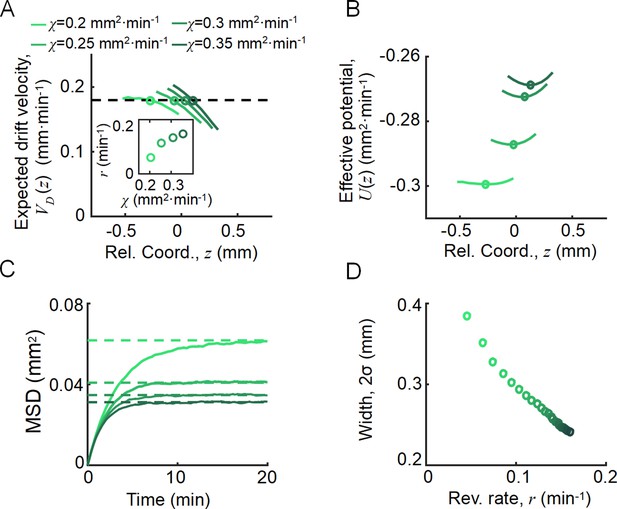
Agent-based simulations recapture the ordered behavior of individuals.

(A) The expected drift velocity $V_{D} (z)$ of simulated bacteria decreased from the back to the front of the migration group, where the chemotactic ability $χ$ ranged from 0.2 to 0.35 mm²min^-1 , which was consistent with the experimental results shown in Figure 1F. The intersections between the $V_{D}$ curves with the preset group velocity $V_{G}$ (black dashed line) shifted toward the back of the migration group as $χ$ decreased (circles). The different colors of the lines and circles correspond to different chemotactic abilities $χ$ , as shown in the legend. The same color coding also applies to (B–D). (B) The reversion rate $r_{i} = | d V_{D, i} (z) / d z |$ increased with chemotactic ability. (C) The effective potential well calculated by $U_{i} (z) = \int_{z}^{+ \infty} V_{d, i} (z) d z$ . Positions of the potential minimum $z_{m i n}$ are marked as circles. As illustrated, for a lower chemotaxis ability $χ$ , the potential well is shallower and $z_{m i n}$ shifts toward the back of the migration group. (D) The width of the density profile (measured by $2 σ$ , see Figure 1B) decreases with the reversion rate $r_{i}$ as well as the chemotaxis ability $χ_{i}$ . The mean square displacement (MSD) of bacteria (insert, solid lines) is bound to $2 σ_{i}^{2}$ (insert, dashed lines) (see supplementary text). In panel (**A, C**), curves were cut to present the majority of cells (90%) ( $z_{m i n} \pm 1.65 σ_{i}$ ). More details on the results of this simulation are presented in Appendix 1—figure 7.

Experiments with titrated phenotypes confirm ordered behavior modulation

To verify the model predictions on the individual behaviors of different phenotypes, we experimentally measured the trajectories of cells with different chemotactic abilities during the group migration. Specifically, we altered the chemotaxis abilities of cells by titrating the expression level of Tar, which is under the control of a small molecule inducer aTc (Sourjik and Berg, 2004; Zheng et al., 2016) (see Materials and methods and Figure 4A). The variations in the expression of Tar would lead to different receptor gains in response to the Asp gradient (Adler, 1966b; Adler, 1969; Sumpter, 2010), but the tumble bias and growth rate would not change. Using the migration speed of the bacterial range expansion to quantify the chemotaxis ability of the titrated strains, we found that the chemotaxis ability increases with aTc concentration (see Materials and methods and Appendix 1—figure 9).

Figure 4

Download asset Open asset

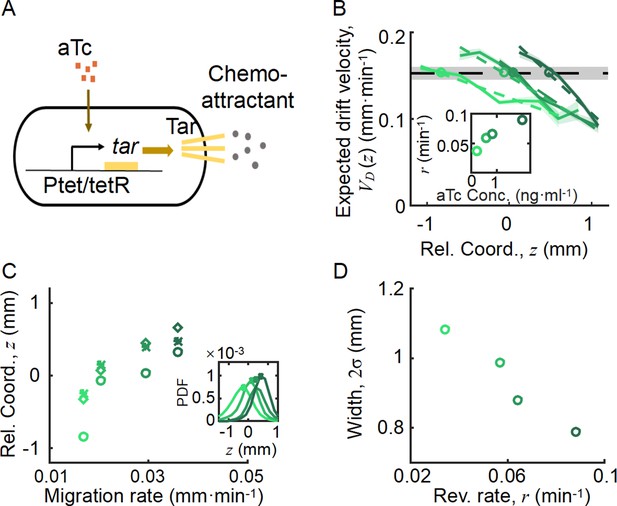
Spatial ordered structure emerged from the behavioral modulation of cells with different chemoreceptors.

(A) Genetic circuit of the Tar-titratable strain. In the experiments, the expression level of Tar (a chemoattractant receptor protein) was titrated by the concentration of external inducer (aTc). The chemotactic ability $χ$ of bacteria was then determined by the expression level of Tar (Adler, 1969). (B) The expected drift velocity $V_{D, i} (z)$ of the Tar-titratable strain JCY20 (colored solid line) was spatially modulated and decreased from the back to the front of the migration group and intersected with a group migration velocity $V_{G} \approx 0.15 m m / m i n$ (black dashed line). The linear fit of $V_{D, i} (z)$ (colored dashed lines) intersected with $V_{G}$ at positions (circles) determined by the corresponding Tar expression level. Colors from dark to light green corresponded to inducer (aTc) concentrations of $[1, 3, 6, 20] n g / m L$ . The black shaded area of $V_{G}$ represents the s.d. of four experiments, while the colored shaded area of the $V_{D}$ curves presents the s.e.m. of the counted runs. (C) In the experiment, the positions of the $V_{D, i} (z) - V_{G}$ intersections (circles, illustrated in B), together with the peaks (stars, illustrated in the insert figure), and the average positions (diamond) of the bacterial density profiles, all shifted toward the front of the migration group for strains with higher Tar expression levels, which had higher chemotactic abilities and migrated faster on agar plates (x-axis, see Materials and methods; Appendix 1—figure 9). The related density profiles (PDF) were shown in the insert plot and the color coding of lines/symbols in both panels C and D was the same as that in B. (D) The width of density profiles ( $2 σ$ ) of Tar-titrated bacteria decreased with the reversion rate $r$ .

The Tar-titrated cells labeled with yellow fluorescent protein (YFP; strain JCY20) were added to the wild-type population at a ratio of 1 in 400. Within the wild-type population, 1 in 50 cells was labeled with red fluorescent protein (RFP) (strain JCY2). As the Tar-titrated strain constituted a small portion of the pre-mixed population, we considered that the density profile of the population would be invariant to different levels of induction of Tar. The premixed population could generate collective group migration, similar to the wild-type population (Appendix 1—figure 9). The trajectories of the YFP-labeled cells were tracked to represent the behavior of cells with different chemotactic abilities, while the profile of wild-type cells with RFP was also measured to characterize the density distribution of the entire migratory population.

By comparing the statistics of cells with different Tar expression levels, we found that the expected drift velocity $V_{D, i} (z)$ followed the same decreasing pattern from back to front (Figure 4B). More importantly, as the Tar expression level (chemotactic ability) increased, the slope of the decreasing pattern increased, which was consistent with the model prediction shown in Figure 3A. The intersections between $V_{D, i} (z)$ and $V_{G}$ , as well as the peak positions and mean positions of each Tar-titrated density profile (Figure 4C), shifted toward the front as the chemotactic ability increased (as measured by the migration rate on agar plates; Cremer et al., 2019; Liu et al., 2019). The $V_{D}$ cross point was always behind the peak position and the mean position (Figure 4C), suggesting that cells were leaking behind. Moreover, the width of each Tar-titrated density profile (defined by $2 σ_{i}$ ) decreased as the reversion rate $r_{i}$ increased (Figure 4D), consistent with the model results in Figure 3C. Thus, as the OU-type model predicts, the width of the density profile is controlled by the reversion rate determined by the chemotactic ability $χ_{i}$ .

Discussion

In summary, coordinated behaviors with ordered spatial arrangements of phenotypes are abundant in a wide range of biological and human-engineered systems, and are believed to involve elaborate control mechanisms. For animal migrations, it is challenging to characterize simultaneously the computational strategy and behavior at the individual level so as to avoid averaging out phenotypic diversity, and the emergent behavior at the population level (Couzin et al., 2005; Couzin et al., 2002; Vicsek and Zafeiris, 2012). For bacterial chemotactic migration, cells with different phenotypes are spatially aligned based on their chemotactic abilities. This observation was explained as a self-consistent result with the decreasing profile of attractant predicted by KS model (Fu et al., 2018). In this study, we demonstrated that the collective consumption of attractant by bacterial group generates a spatial structure of individual drift velocity along the migrating group profile. Such a spatial profile of drift velocity results a pushed wave front on population level, and maintains diverse phenotypes in a compact migration group. Moreover, this pushed wave front enables spatial modulation of individuals to perform mean reverting random motions around centers sequentially aligned by their chemotactic abilities, thereby giving rise to a spatially ordered pattern. Therefore, we demonstrated that the population order could emerge among diverse individuals that following the same rule of behavioral modulation.

This strategy of self-organization does not require sophisticated communications (Curatolo et al., 2020; Karig et al., 2018; Liu et al., 2011; Payne et al., 2013) nor other hydrodynamic interactions (Chen et al., 2017; Drescher et al., 2011; Zhang et al., 2010) among individuals. Our observation of the decreasing drift velocity can imply the effective perceived gradient that cells experience. We believe that this spatial profile is mainly contributed by the consumption of the chemoattractant. By using a Tar-only strain (UU1624) (Gosink et al., 2006), we demonstrated that the mutant could also generate a stable group migration in our experimental condition similar to the wild-type strain (Appendix 1—figure 9G). This further suggests that the secretion of self-attractants is unlikely a necessary condition of collective group migration (Cremer et al., 2019; Fu et al., 2018; Keller and Segel, 1971a), although there are doubts about the existence of self-attractants in high density (Budrene and Berg, 1995).

The spatially dependent drift velocity provides a structured driving force of a migration group, resulting a pushed wave front. Pushed and pulled waves are determined by the spatial distribution of the spreading velocity of a propagation front (van Saarloos, 2003; Figure 2F–H). The properties of pushed and pulled waves have been discussed in growth-driven range expansion (Birzu et al., 2018; Erm and Phillips, 2020; Gandhi et al., 2016), where the wave type is determined by density-dependent growth rates. A prominent example of pulled wave is known as the Fisher wave (Fisher, 1937), where the population expansion is driven by constant diffusion and logistic growth of individuals. However, in such biological systems, the spatial dependence of front speeds is hardly quantified in experiments. Here, by direct measurement of drift velocity on single-cell level, we identified the chemotactic migration group of bacteria as a pushed wave. This chemotaxis system would provide a unique multi-scale model to study further details of pushed wave.

The spatially decreasing profile of driving force does not only cause an ordered pattern of phenotypes, but also results a pushed wave front that enables a negative feedback control on the propagating speed. This further allows a compact density profile for heterogenous population to migrate at the collective level. The advantageous to keep diversity in the pushed wave front was also reported in the growth-driven range expansion system (Birzu et al., 2018). Our study revealed that, other than spatial regulation of fitness, the direct modulation of individual drift velocity in space could also maintain diversity in range expansion.

Detailed analysis of the spatial structured driving force could also provide the limits of phenotype that is allowed in the group. In the migratory group, the same rule of behavioral modulation applied to cells with different phenotypes, such that the random motions of cells were bound by moving potential wells whose basins were sequentially aligned. However, it is noteworthy that cells could skip the potential wells from the back because the ‘driving force’ decreased again at the far back of the group (Long, 2019). This results in leakage of cells in the migratory group (Holz and Chen, 1978; Novickcohen and Segel, 1984; Scribner et al., 1974). Phenotypes with weaker chemotactic abilities were located at the back of the group, where the effective potential well was shallower (Figure 3C), allowing for more chances to skip. Thus, such collective migration selects bacteria with higher chemotactic abilities (Liu et al., 2021; Liu et al., 2019).

The simple computational principle of behavioral modulation to allocate different phenotypes in the collective group is likely not limited to sensing the self-generated signal by consumption of attractant. A prominent example of trail-following migration (Couzin and Krause, 2003; Helbing et al., 1997) and a typical class of collective behavior is represented by a modified Langevin-type model, where individuals tracing the accumulated signal secreted by all participants (Equation S20) can reproduce similar spatial-temporal dynamics of behavioral modulation, as well as ordered arrangements of phenotypes in the migratory group (Appendix 1—figure 10). Thus, this mechanism of matching individual abilities by the signal strength might provide an explanation of how other higher organisms organize ordered structures during group migration.

Materials and methods

Strains

The wild-type strain E. coli (RP437) and its mutants were used in this study, where all plasmids were kindly provided by Dr Chenli Liu. Specifically, the Tar-titratable strain was constructed by recombineering according to previous research (Zheng et al., 2016). Specifically, the DNA cassette of the Ptet-tetR-tar feedback loop was amplified and inserted into the chromosomal attB site by recombineering with the aid of plasmid pSim5. The tar gene at the native locus was seamlessly replaced with the aph gene by using the same recombineering protocol. To color-code the strains, we use plasmids with chloramphenicol-resistant gene carrying yfp under constitutive promoter (for JCY1 strain) and pLambda-driven mRFP1 plasmids maintained by kanamycin (for JCY2). To color-code Tar-titratable strain (JCY20), a plasmid carrying yfp chloramphenicol-resistant gene was transformed into constructed Tar-titratable strain. The tar-only strain (UU1624) was modified from RP734 and was kindly provided by Prof. Johan Sandy Parkinson.

Media and growth conditions

Request a detailed protocol

For bacterial culture, the M9 supplemented medium was used. The preparation of the M9 supplemented medium follows the recipe in previous study (Fu et al., 2018): 1×M9 salts, supplemented with 0.4% (v/v) glycerol, 0.1% (w/v) casamino acids, 1.0 mM magnesium sulfate, and 0.05% (w/v) polyvinylpyrrolidone-40. 1×M9 salts were prepared to be 5×M9 salts stock solution: 33.9 g/L Na₂HPO₄, 15 g/L KH₂PO₄, 2.5 g/L NaCl, 5.0 g/L NH₄Cl.

For migration experiments in the micro-channel, the M9 motility buffer was used. The recipe was:1×M9 salts, supplemented with 0.4% (v/v) glycerol, 1.0 mM magnesium sulfate, and 0.05% (w/v) polyvinylpyrrolidone-40, 0.1 mM EDTA, 0.01 mM methionine, and supplemented with 200 µM aspartic acid.

For the migration rate measurements, the M9 amino acid medium with 0.2% (w/v) agar was used to prepare swim plate (Liu et al., 2019). The recipe was: 1× M9 salts, supplemented with 0.4% (v/v) glycerol, 1× amino acid, 200 µM aspartic acid, 1.0 mM magnesium sulfate, and 0.05% (w/v) polyvinylpyrrolidone-40. 1× amino acid were prepared to be 5× amino acid stock solution: 4 mM alanine, 26 mM arginine (HCl), 0.5 mM cysteine (HCl·H₂O), 3.3 mM glutamic acid (K salt), 3 mM glutamine, 4 mM glycine, 1 mM histidine (HCl·H₂O), 2 mM isoleucine, 4 mM leucine, lysine, 1 mM methionine, 2 mM phenylalanine, 2 mM proline, threonine, 0.5 mM tryptophane, 1 mM tyrosine, 3 mM valine. All experiments were carried out at 30°C. Plasmids were maintained by 50 µg/mL kanamycin or 25 µg/mL chloramphenicol.

Sample preparation

Request a detailed protocol

The bacteria from frozen stock were streaked onto the standard Luria-Bertani agar plate with 2% (w/v) agar and cultured at 37°C overnight. Three to five separate colonies were picked and inoculated in 2 mL M9 supplemented medium for overnight culture with corresponding antibiotics to maintain plasmids. The overnight culture was diluted by 1:100 into 2 mL M9 supplemented medium the next morning. For Tar titration strains, related aTc were added in this step. When the culture OD600 reaches 0.2–0.25, it was then diluted into pre-warmed 15 mL M9 supplemented medium so that the final OD600 was about 0.05 (Liu et al., 2019; Zheng et al., 2020; Zheng et al., 2016).

Bacteria were washed with the M9 motility buffer and were re-suspended in fresh M9 motility buffer to concentrate cell density at OD600 about 1.0. Then, the wild-type strain and fluorescent strain were mixed with ratio of 400:1 before loaded in the microfluidic chamber (Fu et al., 2018; Saragosti et al., 2011). For Tar titration experiments, the wild-type strain (RP437) was mixed with two fluorescent strains (JCY2 and JCY20) by 400:8:1.

Microfabrication

Request a detailed protocol

The microfluidic devices were fabricated with the same protocol and the same design as previous research (Bai et al., 2018; Fu et al., 2018), except that the capillary channel was designed longer than that of previous ones. The size of the main channel was 20 mm×0.6 mm× 0.02 mm and only one gate at the end of the channel was kept (Appendix 1—figure 1A).

Band formation

Request a detailed protocol

Fluorescent cells were mixed with non-fluorescent cells by 1:400 for cell tracking in the dense band. Sample of mixed cells with density OD600 ≈1.0 was gently loaded into the microfluidic device and then the device was spun for 15 min at 3000 rpm in a 30°C environmental room so that almost 100,000-150,000 cells were placed to the end of the channel. After spinning, the microfluidic device was placed on an inverted microscope (Nikon Ti-E) equipped with a custom environmental chamber set to 50% humidity and 30°C.

Imaging

Request a detailed protocol

The microscope and its automated stage were controlled by a custom MATLAB script via the μManager interface (Edelstein et al., 2014; Fu et al., 2018). About 30 min after the sample loading, a 4× objective (Nikon CFI Plan Fluor DL4X F, NA 0.13, WD 16.4 mm , PhL) was placed in the wave front for imaging. The fluorescent bacteria, seen as randomly picked samples of the migrating group, were captured continuously with frame rate of 9 fps in 10 min until they leave the view. Typical tracks are longer than 300 s. Time-lapsed images were acquired by a ZYLA 4.2MP Plus CL10 camera (2048 × 2048 arrays of 6.5 µm×6.5 µm pixels) at 9 frames/s (fps) . An LED illuminator (0034R-X-Cite 110LED) and an EYFP block (Chroma 49003; Ex: ET500/X 20, Em: ET535/30 m) compose the lightening system.

For the Tar titration experiments, the channel was first scanned with 10× objective (CFI Plan Fluor DL 10× A, NA 0.30, WD 15.2 mm, PH-1) enlighten by an LED illuminator (0034R-X-Cite 110LED) through the RFP block (Chroma 49005, Ex: ET545/X 30, Em: ET620/60 m) and EYFP block channels for seven neighbored views around the migration group. These images were further combined to two large pictures of the RFP strains and YFP strains. The channel was scanned twice, respectively before and after the 10 min tracking of fluorescent Tar-titrated cells.

Track extraction and state assignment

Request a detailed protocol

The acquired movie was first analyzed with the U-track software package to identify bacteria and to get their trajectories (Jaqaman et al., 2008). Then the tracks were labeled by run state and tumble state by a custom MATLAB package (Waite et al., 2016) using a previously described clustering algorithm (Dufour et al., 2016).

Track analysis

Request a detailed protocol

The group velocity $V_{G}$ was calculated by averaging the frame-to-frame velocity ( $d t \approx 0.11 s$ ) over all tracks and all time. The cell number for the first frame over a spatial bin of $Δ x = 60 μ m$ and a channel section a=12,000 µm² were calculated to get the density profile $ρ (x, t = 0) = \frac{\sum i (x, t)}{a \cdot d x}$ . The peak position of the first frame ( $x_{p e a k} (t = 0)$ ) was then determined by the maximum of $ρ (x, t = 0)$ . The position of each bacterium ( $x_{i} (t)$ ) was transformed to moving coordinate position $z_{i}$ by the group velocity $V_{G}$ and origin of the axis on the density peak by $z_{i} = x_{i} (t) - V_{G} t - x_{p e a k} (t = 0)$ . Given the relative position of each cell, we recalculated the density profile in moving coordinate $ρ (z) = \frac{\sum i (z)}{a \cdot d x}$ . The width of the density profile was defined by two times the standard deviation of relative positions $2 σ = 2 \sqrt{\frac{1}{n - 1} \sum_{i = 1}^{n} {(z_{i} - 〈 z 〉)}^{2}}$ . The spatial distribution of the instantaneous velocities $〈 V_{I} (z) 〉$ was calculated by averaging the velocity in spatial bin of $Δ z = 240 μ m$ .

A tumble-run event is the minimal element of bacterial behavior. The typical spatial scale of a tumble-run event is about 20 μm, which is much smaller than the spatial bin size chosen in this study (240 µm). The spatial distributions of run time $〈 τ_{R} (z) 〉$ , tumble time $〈 τ_{T} (z) 〉$ , and run length $〈 l_{R} (z) 〉$ were calculated by averaging the related values of all the events with tumbling position ( $z_{T}$ ) located in each spatial bin ( $z$ ). As the displacement of tumble is small, the tumbling position is approximately the starting position of runs. For each tumble-run event, we have the vector linking starting position and end position of the run. The running angle $θ_{R}$ is then defined by the angle between run direction and the group migration direction. One can easily deduce all the other quantities with the formulations in Table 1.

Table 1

Summary of quantities.

Quantities	Definition	Formulations
$V_{G}$	Group velocity	$V_{G} = 〈 \frac{d x}{d t} 〉$
$z$	Moving coordinate	$z = x - V_{G} t$
$V_{I} (z)$	Instantaneous velocity	$V_{I} (z) = 〈 \frac{d x (z)}{d t} 〉$
$V_{D} (z)$	Expected drift velocity	$V_{D} (z) = \frac{⟨ L_{R} (z) \cdot \cos θ_{R} (z) ⟩}{⟨ τ_{R} (z) + τ_{T} (z) ⟩}$
$ρ (z)$	Cell density	$ρ (z) = \frac{\sum i (z)}{a \cdot Δ z}$
$S (z)$	Chemoattractant concentration	$- V_{G} \frac{d S}{d z} = D_{s} \frac{\partial^{2} S}{\partial z^{2}} - k ρ$
$g (z)$	Perceived gradient	$g (z) = \frac{d l n (\frac{1 + S (z) / K_{o f f}}{1 + S (z) / K_{o n}})}{d z}$

Growth rate and migration rate measurement

Request a detailed protocol

Growth rates of Tar-titrated strains were calculated from exponential fitting ( $R^{2} > 0.99$ ) over measured curves of cell density (OD600) with respect to time. A 250 mL flask with 20 mL M9 supplement medium were used. All measurements were performed in a vibrator of rotation rate of 150 rpm at 30 °C. OD600 was measured by a spectrophotometer reader every 25 min. Each strain has been measured for at least three times.

The semi-solid agar plate was illuminated from bottom by a circular white LED array with a light box as described previously (Liu et al., 2011; Liu et al., 2019; Wolfe and Berg, 1989) and was imaged at each 2 hr by a camera located on the top. As bacteria swimming in the plate forms ‘Adler ring’, we used the first maximal cell density from the edge to define the moving edge of bacterial chemotaxis. The migration rate was then calculated from a linear fit over the data of edge positions in respect to time ( $R^{2} > 0.99$ ).

Models and simulations

Request a detailed protocol

Details of the theoretical models and numerical simulations were presented in the appendix notes. In which, the Langevin equation was deduced and solved numerically with a particle-based simulation; the approximated OU-type equation and its traveling wave solution were deduced; an agent-based simulation of bacterial with chemotaxis pathway was performed following previous works (Dufour et al., 2014; Jiang et al., 2010; Sneddon et al., 2012).

Appendix 1

Theory and numerical simulations

Summary

In this note, we first deduced the Langevin-type equation from the classic KS model that describes bacteria group migration in a capillary. The Langevin-type equation describes the dynamics of single-cell particle motion as active particles (Section 1). Together with the chemoattractant consumption equation, we investigated the Langevin-type equation through particle-based simulations for a group of particles of single phenotype or multi-phenotypes (Section 2). Then, we transformed the equations into moving coordinate, so that the stable density profiles as well as the chemoattractant profiles were observed (Section 3). In this moving coordinate, the chemoattractant consumption can be decoupled from particle dynamics, which allows us to simulate particle motions over a non-consumable field of chemoattractant on the move (Section 4). Furthermore, the Langevin dynamics describes that the particle motion was simplified to an OU-type process, of which the particle dynamics can be solved analytically (Section 5). To gain more insights of the chemotactic response, we described an agent-based model which integrated the bacterial chemotaxis pathway in Section 6. And specifically, we deduced the chemotactic ability $χ$ from the pathway parameters (Section 7). The agent-based simulations were performed under a moving gradient, from which ordered structures of phenotypes were recaptured (Section 8). The model was further extended to system with signal secretion and shows similar results (Section 9).

1. The Langevin equation with chemoattractant consumption

The bacterial chemotactic migration in a capillary was first modeled by Keller and Segel in 1971 (Keller and Segel, 1971a). In this model, the bacterial cell division was neglected as the nutrition in the capillary was poor. In 1D, the dynamics of cell density $ρ (x, t)$ is a combination of diffusion and chemotaxis:

\frac{\partial ρ (x, t)}{\partial t} = D \frac{\partial^{2} ρ (x, t)}{\partial x^{2}} + χ \frac{\partial}{\partial x} (ρ (x, t) g (x, t))

where $D$ and $χ$ respectively represent the diffusion coefficient and chemotactic ability of bacteria, and $g (x, t)$ represents the perceived gradient of chemoattractant.

The dynamics of the chemoattractant $S (x, t)$ follows a reaction-diffusion-type equation with a diffusion coefficient $D_{s}$ and consumption with a constant rate $k$ :

\frac{\partial S (x, t)}{\partial t} = D_{s} \frac{\partial^{2} S (x, t)}{\partial x^{2}} - k ρ (x, t)

From the chemoattractant profile $S (x, t)$ , we can get $g (x, t)$ by:

g (x, t) = \frac{\partial l n (\frac{1 + S (x, t) / K_{o f f}}{1 + S (x, t) / K_{o n}})}{\partial x}

with $K_{o n}, K_{o f f}$ were dissociation constants for active and inactive conformation of the receptor, respectively.

Following Rosen, 1973, one can deduce the Fokker-Planck equation associated to the KS model that describes the probability $P = P (x, y; t)$ to observe of a cell which initiates from position $y$ at position $x$ and time $t$ . The related equation writes:

\frac{\partial P}{\partial t} = D \frac{\partial^{2} P}{\partial x^{2}} + χ \frac{\partial (P g (x, t))}{\partial x}

Equation S4 is equivalent to the Langevin dynamics as:

d x_{i} = χ g (x_{i}, t) d t + ϵ d W

where $x_{i}$ represents the position of the i-th bacteria and $g (x_{i}, t)$ is the perceived gradient of each bacteria at time $t$ . $d W$ is a Wiener process that describes a random walk with noise level $ϵ = \sqrt{2 D}$ .

As previously proofed, the expected drift velocity equals the production of chemotactic ability $χ$ and the perceived gradient $g$ , $V_{D} = χ g$ (Waite et al., 2016). So that, the Langevin-type Equation S5 can be reformed to:

d x_{i} = V_{D, i} d t + ϵ d W

The initial condition of the chemoattractant was $S (x, 0) = S_{0} = 200 μ M$ . In the stochastic model, the density profile $ρ (x, t)$ was calculated by the sum of cell number ( $\sum i (x, t)$ ) in certain location $[x, x + Δ x]$ and time $t$ over volume $a \cdot Δ x$ , where $a$ is the capillary section area and $d x$ is the spatial bin size:

ρ (x, t) = \frac{\sum i (x, t)}{a \cdot Δ x}

2. Particle-based simulation with consumption

The Langevin-type model in the absolute coordinate $x$ (Equation S5) was simulated with a customized code using MATLAB. In each case, 100,000 particles were simulated in a 1D space where $x \in [0, 20] m m$ . The absorption boundaries were applied for $x = 0 m m$ and $x = 20 m m$ , so that particles stay at the boundary until they leave them actively ( $x (x > 0 m m) = 0$ and $x (x > 20 m m) = 20 m m$ ). Initially all particles were placed at $x = 0 m m$ and their positions were calculated according to Equation S7 at each time step of $Δ t = 0.05 s$ for 60 min. The random noise follows a Gaussian distribution generated by MATLAB function ‘randn.m’ with amplitude multiplied by $\sqrt{2} ϵ \sqrt{Δ t}$ .

Unlike the particles that change their position continuously, the spatial profile of cell density $ρ (x, t)$ was first calculated on a space mesh of grid $Δ x = 10 μ m$ , and then linearly interpolated to a finer mesh of grid $Δ x = 0.1 μ m$ . The chemoattractant $S (x, t)$ and perceived gradient $g (x, t)$ were deduced accordingly. At each time point, following Equation S7, cells located on grid $[x, x + Δ x]$ were summed and were divided over $a Δ x$ to get the density profile. In order to avoid fast consumption near $S = 0$ , a saturation effect of consumption rate was added to Equation S3 using $S / (S + K_{s})$ .

\frac{\partial S (x, t)}{\partial t} = D_{s} \frac{\partial^{2} S (x, t)}{\partial x^{2}} - k ρ (x, t) \frac{S (x, t)}{S (x, t) + K_{s}}

where $K_{s} = 0.1 μ M$ , of which the value was small and does not affect the linear relation in most range of $S > K_{s}$ .

Then the chemoattractant profile $S (x, t)$ was calculated from $ρ (x, t)$ according to Equation S8, using a fourth-order Runge-Kutta method from an initial condition of $S (x, 0) = S_{0}$ . The perceived gradient $g (x, t)$ was further calculated from $S (x, t)$ on Equation S3. Having the discrete $g (x, t)$ over grid of $Δ x = 0.1 μ m$ , the perceived gradient of each particle $g (x_{i})$ was assigned by detecting the particle position over the spatial mesh grid.

Following the above instructions, density profile and peak positions with bacteria of $χ = 0.11 m m^{2} m i n^{- 1}$ and $D = χ / 22$ were plotted in Appendix 1—figure 5A. The group migration reached steady state after 20 min simulation. The peak velocity was then defined by linear fitting of peak positions for $t \in [20, 60] m i n$ , which was found to be $V_{p} = 3.03 μ m / s$ .

To simulate a bacterial group of multiple phenotypes, we constructed 100,000 cells with their chemotactic ability $χ$ follows a Gaussian distribution with the average chemotactic ability $⟨ χ ⟩ = 0.11 m m^{2} m i n^{- 1}$ and s.d. of 0.03 mm²min^-1 (Appendix 1—figure 5B) while the diffusion coefficient $D$ was fixed to $〈 χ 〉 / 22$ for all cells. The consumption rate of each bacterium was also set constant of $4.6 \cdot 10^{- 9} μ M / c e l l / s$ . The group of multi-phenotypes migrates slower than single phenotype with peak velocity $V_{p} = 2.90 μ m / s$ (Appendix 1—figure 5A). The bacterial positions after 20 min simulation were further transformed to the moving coordinate $z_{i} = x_{i} - V_{p} t$ . They were subgrouped according to their chemotactic ability $χ$ to six subgroups. And the corresponding average density profiles of each subgroups were plotted in Appendix 1—figure 5D with colors defined in Appendix 1—figure 5C. The density profile of subgroups was found ordered according to their average chemotactic ability $χ$ . The time-shifted profiles, $S (z)$ and $g (z)$ , were shown in Appendix 1—figure 5E,F.

The simulations of bacteria with consumption confirmed that coherent group migration and ordered spatial structures can emerge from a system of active particles modulated by gradient of consumable chemoattractant.

3. Traveling wave solution

As the density profile was found stable during the experimental time scale (30 min), we are allowed to use a moving coordinate $z = x - V_{G} t$ in searching for a traveling wave solution. Equation S2, Equation S5, Equation S7 become:

d z_{i} + V_{G} d t = χ g (z_{i}) d t + ϵ d W

- V_{G} \frac{d S (z)}{d z} = D_{s} \frac{d^{2} S (z)}{d z^{2}} - k ρ (z)

ρ (z) = \frac{\sum i (z)}{a \cdot Δ z}

Given a stable density profile measured experimentally, we can integrate Equation S10 to get a stable profile of chemoattractant $S (z)$ . As the chemoattractant was unconsumed at $z = \infty$ and it is completely consumed as the wave passes $z = - \infty$ , the boundary condition of $S (z)$ can be written as $S (\infty) = S_{0}$ and $S (- \infty) = 0$ . We get:

S (z) = S_{0} - \frac{k}{D_{s}} e^{- \frac{V_{G}}{D_{s}} z} \int_{z}^{\infty} M (z) e^{\frac{V_{G}}{D_{s}} z} d z

where $M (z) = \int_{z}^{\infty} ρ (z) d z$ is the accumulated number of cells up to position $z$ . We then used the experimentally measured cell density profile together with the group speed $V_{G}$ to calculate the moving attractant profile $S (z)$ (Appendix 1—figure 5A). The perceived gradient $g (z)$ in the moving coordinate was then calculated by:

g (z) = d l n (\frac{1 + S (z) / K_{o f f}}{1 + S (z) / K_{o n}}) / d z

In a stable migration group, the $g (z)$ deceases from back to front over the density profile. Suppose the gradient does not steepen toward the back, then cells with lower chemotactic abilities will fall behind and see shallower gradient, drifting even slower and causing the wave to spread out. Since the gradient is formed by local consumption, the front of the wave will have less cells and become shallower, while the back of the wave will accumulate more cells and become steeper. This will automatically readjust the gradient steepness until the back becomes steep enough to allow cells will lower chemotactic abilities to catch up, stabilizing the gradient and the traveling wave.

4. Particle-based model with preset moving gradient

The chemoattractant profile $S (z)$ can be deduced by an experimentally measured stable density profile $ρ (z)$ in the moving coordinate. With the experimental mesh grid $Δ x = 240 μ m$ , we plot the average $S (z)$ over three biological replicates in Appendix 1—figure 4D (circles). In order to apply this profile into the particle-based simulation, we first expanded the space range of $S (z)$ to $x \in [- 4800, 4800] μ m$ by setting $S (z < - 2400 μ m) = 0$ and $S (z > 2400 μ m) = S_{0}$ . Next, we used a cubic spline data interpolation to construct a profile of $S (z)$ with much finer spatial mesh grid $Δ x = 0.001 μ m$ (Appendix 1—figure 4D, line). Therefore, a $g (z)$ profile on finer meshes was calculated accordingly (Figure 2A). The $g (z)$ profile was then translated to an absolute coordinate by $g (x, t) = g (z) + V_{G} t$ , with $V_{G} = 3.0 μ m / s$ .

Using the preset moving gradient $g (x, t)$ , we can simulate the particle motions without calculation of $ρ (x, t)$ and $S (x, t)$ . We used the same method as described in Section 2 to simulate particle motions, and at each time point $t$ , we assigned $g (x_{i})$ by indexing bacterial position on $g (x, t)$ , with spatial precision of $Δ x = 0.001 μ m$ .

For bacteria of four different $χ$ ranging from 0.15 to 0.3 mm²min^-1 , we simulated 10,000 particles for each phenotype with the same noise level $ϵ = 15 m m \cdot m i n^{- 0.5}$ . During simulation of 60 min, bacteria of all phenotypes move as a group with peak positions linearly increasing with time. The fitted slope of all peaks equals the preset velocity of the moving gradient $V_{G}$ . In the moving coordinate $z$ , the density profiles of all phenotypes were ordered (Figure 2A), and they were clearly ordered by $χ$ . The peak positions and mean positions of the density profile increase with $χ$ (Figure 2C), while the width (defined by $σ$ ) decreases with $χ$ (Figure 2D).

5. The type model

The perceived gradient $g (z)$ deduced from experimental data shows linear decreasing trend in the major range of density profile $- 0.4 m m < z < 0.4 m m$ . It can be then linearly fitted by $g (z) \approx g_{1} z + g_{0}$ with $g_{1} \approx - 2.1 m m^{- 2}$ and $g_{0} \approx 1.2 m m^{- 1}$ . Subscribe this linear approximation in Equation S7, we get:

d z_{i} = χ g_{1} z_{i} d t + (χ g_{0} - V_{G}) d t + ϵ d W

Now, we compare Equation S10 to the standard OU model given by $d x = - λ x d t + ϵ d W$ . Equation S9 can be taken as an OU-type process with $- χ g_{1}$ as the reversion rate $λ$ and the mean position deviated from origin to $z_{0}$ :

z_{0} = \frac{χ g_{0} - V_{G}}{χ g_{1}}

where the mean position $z_{0}$ is the steady-state position of its ensemble average $〈 z 〉$ :

d 〈 z 〉 = χ g_{1} 〈 z 〉 d t + (χ g_{0} - V_{G}) d t

The original OU model describes an active particle motion under a linear force field around $x = 0$ . Since Equation S10 can be taken as a generalized OU model, we can thus consider our bacteria in the migration group as an active particle under an effective force field of $χ g_{1} z + (χ g_{0} - V_{G})$ . Integrating this force field over $z$ , we get an effective potential well $U (z)$ :

U (z) = \int (χ |g_{1}| z + (χ g_{0} - V_{G})) d z = \frac{1}{2} χ |g_{1}| z^{2} + (χ g_{0} - V_{G}) z + U_{0}

The $U_{0}$ is an integral constant controlled by boundary condition, which was set by $U (\infty) = 0$ in this article. The effective potential well $U (z)$ generated by $U (z) = \int (χ g (z) - V_{G}) d z$ from the particle-based simulation and Equation S17 are compared in Figure 2B.

Using a variable substitution of $\tilde{x} = z - (χ g_{0} - V_{G}) / g_{1}$ , and applying the general solution of the standard OU model of $\tilde{x} (t) = {\tilde{x}}_{0} e^{- λ t} + \int_{0}^{t} ϵ d W \cdot e^{- λ (t - t^{`})} d t^{`}$ (Cherstvy et al., 2018), we get the mean square displacement: $M S D \equiv 〈 {(z (t) - z_{0})}^{2} 〉 = {〈 z_{0} 〉}^{2} {(1 - e^{- χ g_{1} t})}^{2} + \frac{ϵ^{2}}{2 χ g_{1}} (1 - e^{- 2 χ g_{1} t})$ . The standard distribution $σ$ of the density distribution is the limit of MSD:

σ = {〈 z_{0} 〉}^{2} + \frac{ϵ^{2}}{2 χ g_{1}}

The trend of both mean positions (Figure 2C) and width (Figure 2D) was successfully predicted by analytical solutions of the OU-type model Equation S15 and Equation S18.

Moreover, the OU-type model Equation S14 has an equivalent Fokker-Planck equation that describes the probability density function of particles on $z$ , $P (z, t)$ :

\frac{\partial P (z, t)}{\partial t} = \frac{\partial}{\partial z} ((χ g_{1} z + (χ g_{0} - V_{G})) P (z, t)) + D \frac{\partial^{2} P (z, t)}{\partial z^{2}}

At $t \to \infty$ , the probability density function reaches the steady stat $P (z)$ , where the density profile follows $0 = \frac{d}{d z} ((χ g_{1} z_{i} + (χ g_{0} - V_{G})) P (z)) + D \frac{d^{2} P (z)}{d z^{2}}$ . Solving this equation with boundary conditions of $P (z = \pm \infty) = 0$ and $\frac{\partial P (z = \pm \infty)}{\partial z} = 0$ , we get the steady stat density profile $P (z) = e^{- \frac{1}{D} (\frac{1}{2} χ g_{1} z^{2} + (χ g_{0} - V_{G}) z + C_{0})}$ with $C_{0}$ is the integral constant that allows $\int_{- \infty}^{\infty} P (z) d z = 1$ . The exponent of this density profile is position-dependent that drops in parabolic form as $z \to \infty$ . Compare to the front of Fisher wave, where the exponent of the density profile decreases linearly with $z$ ( $P (z) = e^{- C z}$ ), we know that the density profile of a chemotaxis migration wave is more compact than a Fisher wave.

6. Agent-based simulation with chemotaxis pathway

In order to simulate more details of bacterial group migration in a capillary, we use a previously established chemotactic pathway integrated agent-based simulation. This model integrated bacterial chemotactic signaling pathway to determine the switch rate of motors, the conformation changes of flagella, as well as the competition of multiple flagella.

We first simulated 80,000 cells evenly distributed in four phenotypes of different receptor gain $N$ with consumption of chemoattractant. The cells were simulated as described in a previous paper (Saragosti et al., 2011), while the chemoattractant field S was calculated at each time step ( $Δ t = 0.01 s$ ) according to Equation S8. In a 3D channel of 0.2 mm×0.01 mm× 10 mm, space was discretized to grid of 2.5 µm×2.5 µm× 2.5 µm . The evolution of the attractant during each time step was calculated by the sum of the consumption of every cell in the neighbor grids weighted by their effective diffusion distance. The consumption rate was fitted for reasonable migration speed. Detailed methods were described in a previous paper (Xue and Othmer, 2009). The perceived attractant of each cell was then linearly interpolated from the closest grids of the attractant field.

Simulation starts by setting all cells in one end of the channel ( $x = 0$ ), randomized in y and z directions and setting uniform chemoattractant concentration $S_{0} = 200 μ M$ within the channel. Flip boundary condition was used for all three directions. After 20 min simulation, the bacterial population from stable migration groups (Appendix 1—figure 6A) tracks with cellular run-tumble stat was recorded from 30 to 32 min with time step of 0.1 s. Using the group velocity $V_{G}$ of this period as the speed of moving coordinate $z = x - V_{G} t$ , density distribution of subgroups of different receptor gain $N$ was plotted to show spatial ordering of subgroups (Appendix 1—figure 6B). The tracks were analyzed with exactly the same method as the experimental tracks (see Materials and methods). The expected drift velocity $V_{D} (z)$ of all subgroups decreases from back to front and was also spatially ordered (Appendix 1—figure 6C).

The particle-based simulations (Section 4) have already shown that the chemoattractant consumption can be decoupled from bacterial motions. To simplify the analysis, we used the same non-consumable moving gradient $g (x, t)$ described in Figure 2A. Using the preset gradient, we simulated 100,000 bacteria of four evenly distribution phenotypes of different receptor gain $N$ or adaptation time $τ$ or basal CheY-p level $Y_{p 0}$ . The simulation was performed in 3D with reflection boundary on $x = 0 m m & x = 20 m m$ and with free boundaries in the other two directions ( $y, z$ ). Initially all cells were placed on $x = 2 m m, y = z = 0 m m$ . In each time point with step $Δ t = 0.01 s$ , the internal states of every bacterium were updated according to their perceived gradient indexed by $g (x_{i})$ with spatial precision $Δ x = 0.001 μ m$ . And then the bacterial moving stat (run or tumble) was updated accordingly, which results in movement to the next time point. Most parameters used in the simulation follow previous paper (Saragosti et al., 2011), while the changed parameters were the upper limit of chemoattractant sensing $K_{o n} = 1000 μ M$ (Fu et al., 2018); the lower limit of chemoattractant sensing $K_{o f f} = 1 μ M$ (Si et al., 2012); the diffusion coefficient of chemoattractant $D_{s} = 1000 μ m^{2} / s$ (Fu et al., 2018); the run speed of bacteria $v_{0} = 30 μ m / s$ (Keller and Segel, 1971b); the adaptation time $τ_{M} = 1 s$ (Waite et al., 2016); the motor number was set 5 as in Sneddon et al., 2012; while the basic CheY-P level $Y p_{0}$ = $2.77 μ M$ , which corresponds to $T B_{0} \approx 0.27$ . After 40 min of simulation, bacterial tracks were recorded with 10 fps for 20 min.

7. Estimation of $χ$ from chemotaxis pathway

In order to compare the agent-based simulation results to the analytical OU-type model, we need to estimate the chemotactic ability $χ$ from the parameters of chemotaxis pathway. Considering an simple case where perceived gradient of chemoattractant $g$ is a fixed value, the averaged drift velocity of a group of bacteria $V_{D}$ can be estimated by the parameters of bacterial chemotaxis pathway (Dufour et al., 2014): $V_{D} \approx \frac{τ_{R 0}^{`}}{1 + τ_{R 0} / τ_{M}} \frac{(1 - T B_{0}) v_{0}^{2} N g}{d}$ . In this equation, $τ_{R 0}$ is the run time in homogenous environment, $τ_{R 0}^{`} = d τ_{R 0} / d f$ with $f$ is the free energy of the receptor, $τ_{M}$ is the adaptation time, $d$ is the dimension (e.g. d is 3 in this case), $T B_{0}$ is the tumble bias in homogenous environment, and $N$ is the receptor gain.

On the other hand, given the expression of $V_{D}$ , comparing the two expressions of expected drift velocity in fixed gradient, we can deduce:

χ \approx \frac{τ_{R 0}^{`}}{1 + τ_{R 0} / τ_{M}} \frac{(1 - T B_{0}) v_{0}^{2} N}{d}

Using the expression Equation S20, we can deduce the required receptor gain $N$ from $χ$ , which is the case shown in the main text in Figure 3.

8. Agent-based simulation for different parameters

To investigate the bacterial behavior in moving gradient, we have simulated bacteria with $χ$ ranging from 0.15 to 0.30 corresponding to receptor gain $N$ ranging from 14.5 to 25.4. Related results were shown in Figure 3 and discussed in the main text.

Receptor gain is not the only parameter that affects the chemotactic ability. We have also varied the adaptation time $τ_{M}$ and basal CheY-p level $Y_{p 0}$ to investigate the effect of these parameters on bacterial behaviors with a moving chemoattractant profile of larger slope of perceived gradient, $g_{1} = - 2.5 m m^{- 2}$ . For both cases, the density profile $ρ (z)$ spatially ordered according to the variant parameter, and the expected velocities for call parameters $V_{d} (z)$ decrease from back to front. These results show that bacteria perform mean reversion flow for all these parameters and were spatially ordered according to phenotypes.

For the case of basic CheY-p level $Y_{p 0}$ ranging from 2.70 µM to 2.85 µM, the basic tumble bias $T B_{0}$ varies from 0.07–0.19, and the chemotactic ability $χ$ decreases with $Y_{p 0}$ from 0.16 to 0.25 mm²min^-1 . The mean positions of subgroups increase with $χ$ so that it decreases with $Y_{p 0}$ . Unlike the receptor gain $N$ , the basic tumble bias also increases the diffusion coefficient $D$ . Analogized to the OU-type model, varying $Y_{p 0}$ changes the reversion rate $χ g$ and the noise level $ϵ = \sqrt{2 D}$ at the same time. Thus, the reversion rate decreases with $Y_{p 0}$ and the width of the density profile $σ$ increases with the reversion rate $r$ (Appendix 1—figure 8A–D).

For the case of adaptation time $τ_{M}$ ranging from 1 to 10 s, mean positions and width of the density profile show non-monotonic dependence on $τ_{M}$ . This phenomenon shows that adaptation time has a trade-off effect on bacterial chemotaxis. As Frankel et al., 2014 have discussed, the increasing adaptation time enforces chemotactic ability, while it weakens the sensitivity of bacteria to the chemoattractant gradient changes. Such dual effect was also reflected on the reversion rate defined by the slope of $V_{D}$ (Appendix 1—figure 8E–H).

9. Modified Langevin-type model for accumulated signals

As discussed in the main text, the reversion flow of individuals in the migrating group relies on a decreasing driving force from back to front. In the case of bacterial chemotaxis, such decreasing force comes from the gradient of perceived signal of chemoattractant, which is consumed by all the agents. Such mechanism can be generalized to the systems of trail-following migration (e.g. ants), where the signal is secreted by agents instead of being consumed. In this case, the signal concentration $S_{s} (x, t)$ decreases from back to front, because more agents have passed the back than front, thus have secreted more signal on the back. Such dynamics can be modeled by similar Langevin equations and signal accumulations as discussed in Section 1:

{d x}_{i} = χ_{i} S d t + ϵ d W

\frac{\partial S_{s}}{\partial t} = \frac{D_{s} \partial^{2} S_{s}}{\partial x^{2}} + γ ρ - β S_{s}

ρ (x, t) = \frac{\sum i (x, t)}{a \cdot Δ x}

where $γ = 3 * 10^{- 13} μ M \cdot s^{- 1} \cdot c e l l^{- 1}$ is the secretion rate of the signal $S_{s}$ and $β = 0.001 s^{- 1}$ is the decay rate of it. Other terms and parameters are identical to equations in Section 1.

Then, we solve Equation S21 numerically by applying 10⁶ particles with normally distributed response ability $χ_{i}$ of mean value of 1 and s.d. of 0.3 (Appendix 1—figure 10C). Results show that a coherent migrating group is formed spontaneously with constant migration speed ∼6.7 µm/s (Appendix 1—figure 10B). In the moving coordinate, the ‘effective global force’ $S_{s} (z)$ decreases from the back to front as predicted. The particles with different response ability $χ_{i}$ are ordered arranged (Appendix 1—figure 10D), while particles with larger χ locate more in the front.

Appendix 1—figure 1

Download asset Open asset

Experiment protocol, sample tracks, and fluorescent labeled cells.

(A) The microfluidic chip used in this study is consisted of a long channel (20 mm×0.6 mm×0.02 mm) and a large chamber (3 mm× 3 mm). Prepared bacteria are first loaded in the chip through inlets with M9 motility buffer (see Materials and methods). Next, the chip is spun at 3000 rpm for 15 min so that the bacteria are concentrated to one end of the channel. Bacteria consume aspartate (Asp) as the single chemoattractant to form a moving gradient that attracts the group migration. Finally, the bacterial motions are tracked under microscope of 4× objective by frame rate of 9 fps. (B) Cells expressing fluorescent protein (strain JCY2) are premixed into strain RP437 by 1:400 and counted each frame. Cell counts in nine successive frames ( $1 s$ ) were plotted within bin size of $Δ x = 100 μ m$ . Colors from light to dark red represent time from 1 to 10 min. (C) Sample tracks of bacteria (colored lines) and bacterial signal (black dots) on the last captured frame. (D) Fluorescent labeled cells (strain JCY1 and JCY2) and the wild-type strain (RP437) were tracked separately on growth medium. All three strains show the same distribution of tumble bias (left), mean speed (middle), and mean run speed (right) of each track. All these quantities are average of more than 9000 tracks, weighted by their trajectory time. Each curve show data of one experiment.

Appendix 1—figure 2

Download asset Open asset

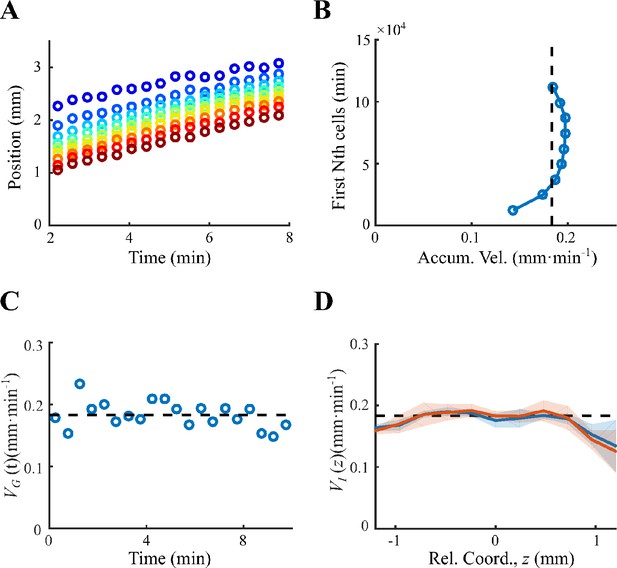
Determination of coherent migration group.

(A) Positions of first n-th cell (counted from the front, from blue to red $n = [1.24 2.48 3.72 4.96 6.2 7.44 8.68 9.92 1.16] \times 10^{4}$ ) increase linearly with time, of which the slope gives the traveling speeds. (B) The traveling speeds of the first n-th cells are close to the group velocity $V_{G}$ (black dashed line), representing a coherent migration group. (C). The instantaneous group velocity $V_{G} (t)$ was constant over time. $V_{G} (t)$ was averaged for all tracks over 30 s (blue dots). Black dashed line represents the average group velocity for all tracks on all times $V_{G}$ . (D). The constant instantaneous velocity $V_{I} (z) = 〈 Δ x (z) / Δ t 〉$ for sampling time $Δ t = 1 s$ (blue solid line) and $Δ t = 10 s$ (red solid line), where shaded area was s.e.m. of three replicates. Both curves equal to the group velocity $V_{G}$ , indicating the migration group is coherent. Data in (**A–C**) was extracted from one experiment.

Appendix 1—figure 3

Download asset Open asset

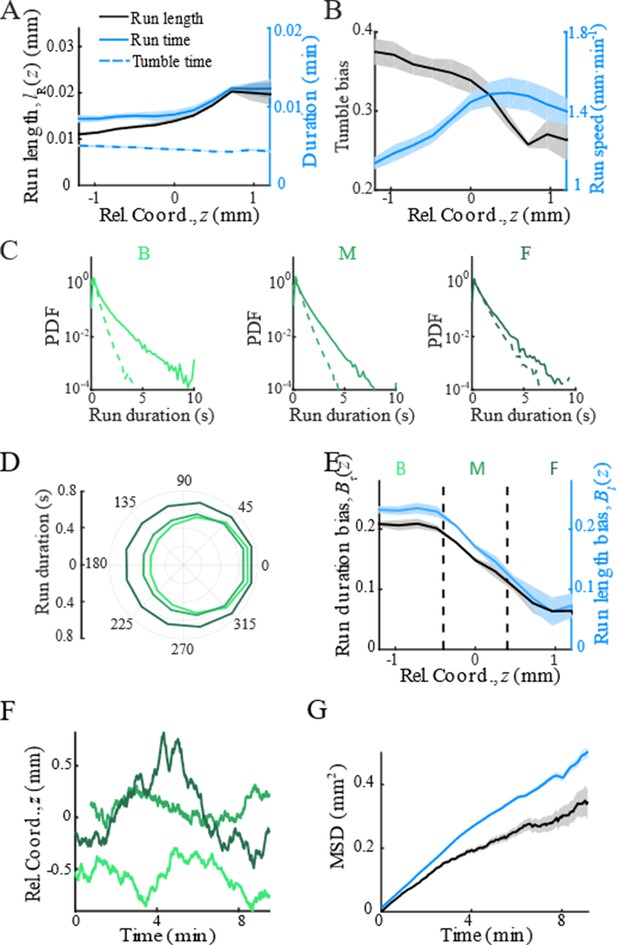
Modulation of bacterial behaviors.

(A) Distribution of forward run duration (solid line) and backward run duration (dash line) in three regions defined in Figure 1D and Appendix 1—figure 3E. (B) Mean run duration in different directions of bacteria in three regions. s.e.m. of four replicates is smaller than thickness of lines. Angular bin size is 15°. (C) Spatial structure of adapted tumbled bias (blue) and run speed (red). (D) The mean run length in different directions, with the angular bin size of 15°, also shows that cells in the back were better skewed to run forward. (E) The run length bias $B_{l} (z) = \frac{⟨ l_{R} (z) \cdot \cos θ_{R} (z) ⟩}{⟨ l_{R} (z) ⟩}$ (black solid line) and the run time bias $B_{τ} (z) = \frac{⟨ τ_{R} (z) \cdot \cos θ_{R} (z) ⟩}{⟨ τ_{R} (z) ⟩}$ (blue solid line) both decreased from the back to the front of the migration group. In panels C–E, shaded area represents s.e.m. of three biological replicates. The spatial bin size is 240 µm. (F) Representative examples of single-cell trajectories (three colors represent three different tracks) showed the reversion behavior of bacteria around their mean positions. (G) The mean reversion behavior results in limited diffusion of bacteria in the moving frame. So that the mean square displacement (MSD) in the direction of migration (black curve) was lower than the pure diffusion of bacteria measured on free liquid with M9 motility buffer (blue curve). The shaded area on black curve represents the s.e.m. of more than 2900 tracks, while the shaded area on blue curve represents the s.e.m. of more than 1900 tracks.

Appendix 1—figure 4

Download asset Open asset

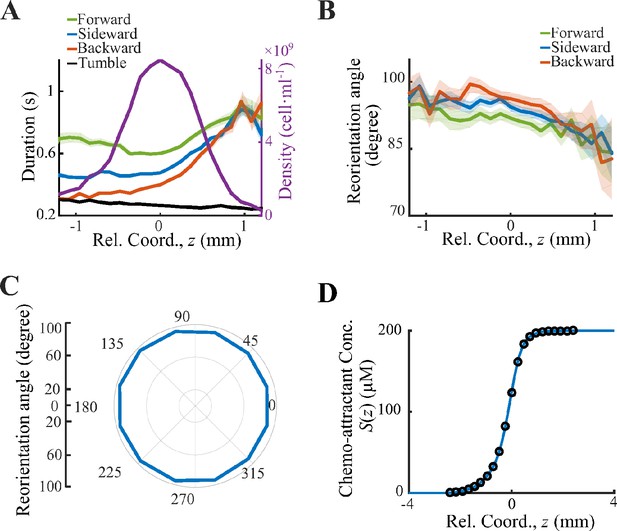
Behavior analysis and deduction of the chemoattractant profile.

(A) All cell tracks are divided into three sectors: forward ( $| θ | \leq 45^{\circ}$ ) (green line), sideward ( $45^{\circ} < | θ | < 135^{\circ}$ ) (blue line), backward ( $| θ | \geq 135^{\circ}$ ) (red line). The run durations in all three sectors increase form back to front. (B) Spatial distribution of reorientation angle. (C) Reorientation angles defined in Saragosti et al., 2011 are plotted over the direction of previous runs. Such angles are biased to the back, indicating that bacteria running down the gradient reorient more in the next tumble. Shaded area shows s.e.m. of 14,892 tracks. The s.e.m. in panel C is smaller than the thickness of the curve. (D) The chemoattractant profile $S (z)$ used for the simulation is interpolated by $Δ z = 0.001 m m$ (blue line) from the experimental $S (z)$ (black circles). While the experimental chemoattractant is deduced from the averaged density profile $ρ (z)$ (Figure 1B).

Appendix 1—figure 5

Download asset Open asset

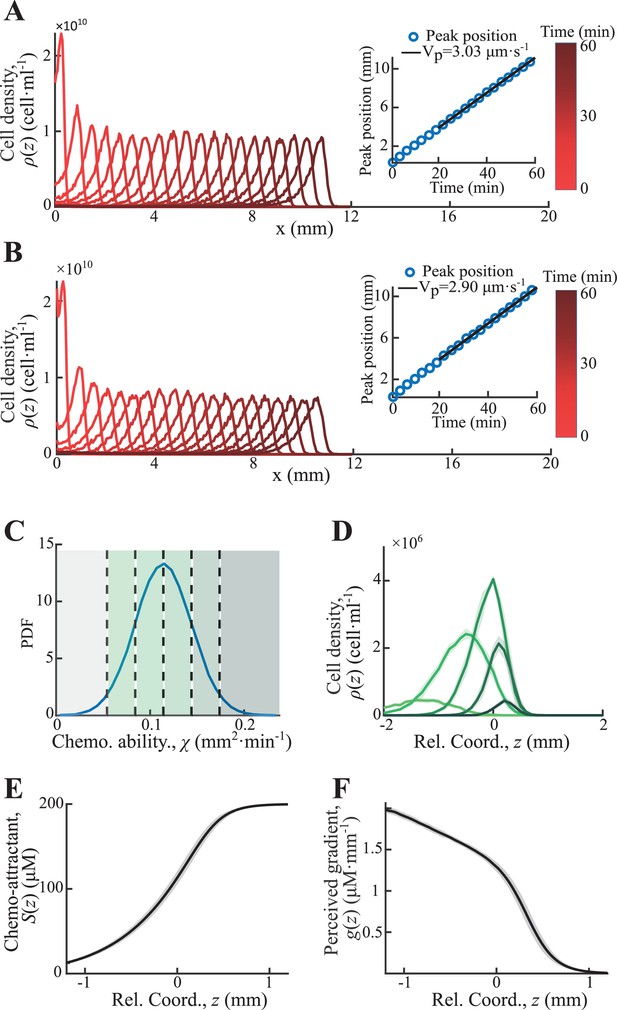
Particle-based simulation with chemoattractants consumption.

(A) Simulated density profiles of active particles of single phenotype of $χ = 0.11 m m^{2} / m i n$ . $V_{G} = 3.0 μ m / s$ over time. The peak positions increase linearly with time (insert plot). (B) Simulated density profiles of active particles of heterogenous phenotypes distributed in (C). The peak positions follow a stable speed of $V_{G} = 2.9 μ m / s$ (insert plot). (D) Time-shifted density profiles of different phenotypes exhibit spatially ordered in moving coordinate. Cells in the gray area drop the group during migration. Time-shifted chemoattractant profile increases from back to front (E) while the perceived gradient decreases with a quasi-linear region around 0. (F) Shaded area in D, E, F represents s.d. of 40 profiles recorded at stable region (from 21 to 60 min) with time step of 1 min.

Appendix 1—figure 6

Download asset Open asset

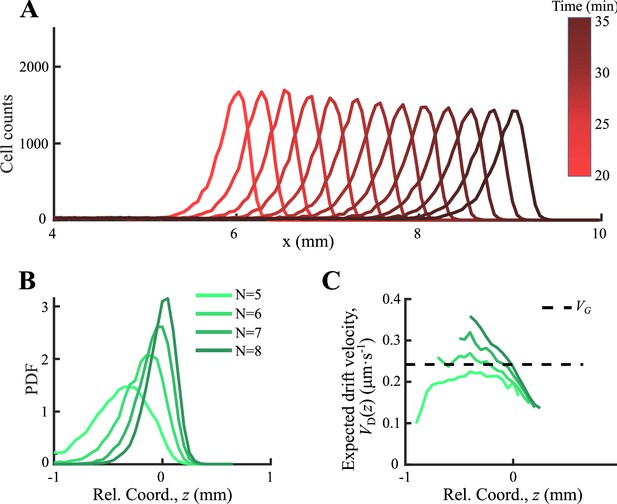
Agent-based simulations with consumption of chemoattractant.

(A) Simulated density profiles of bacteria integrated with chemotactic pathway show stable migration after 20 min simulation. Tracks were obtained in from 30 to 32 min, and were calibrated into a moving coordinate through group migration speed. (B) Four subgroups of different receptor gain N were orderly distributed. (C) The expected drift velocity $V_{D} (z)$ is decreasing and is spatially ordered.

Appendix 1—figure 7

Download asset Open asset

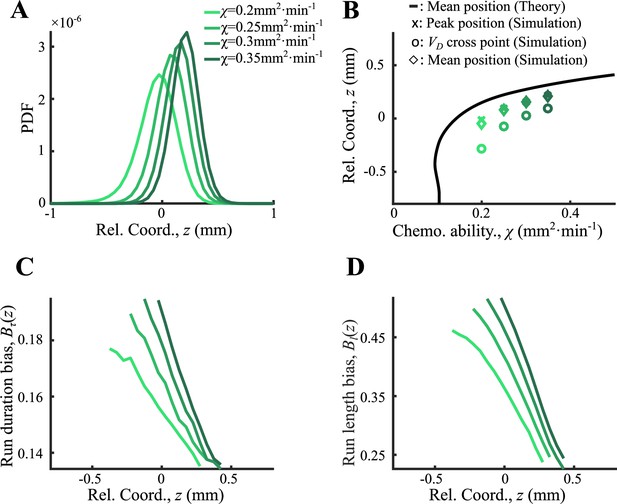
Agent-based simulations of cells with different receptor gains.

(A) Bacteria of different chemotatic ability ( $χ$ ) form ordered structure in a moving chemoattractant field as in Appendix 1—figure 4D with fixed velocity $V_{G} = 3.0 μ m / s$ . (B) The average positions of each phenotype (diamonds), the peak positions (crosses), and the cross positions between their $V_{D}$ curves and the group velocity $V_{G}$ (circles) increase with $χ$ . These positions follow the same trend as predicted by Ornstein-Uhlenbeck (OU) model (black line). (**C, D**) Run duration bias $B_{τ}$ and run length bias $B_{l}$ of different subgroups decrease from back to front. Both curves were also spatially ordered by $χ$ (color from light to dark green).

Appendix 1—figure 8

Download asset Open asset

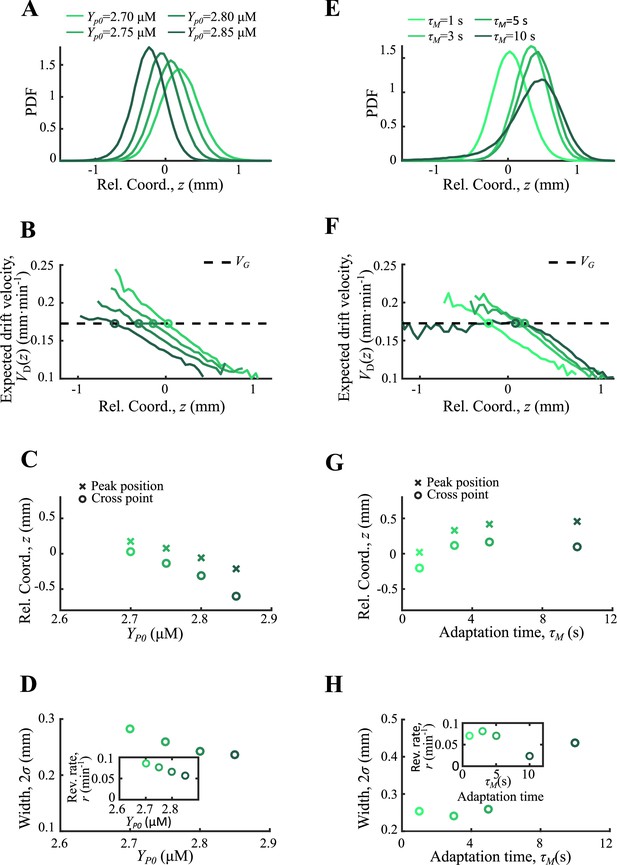
Agent-based simulations of cells with different CheY-P levels and adaptation times.

Simulations results for CheY-P concentration $Y_{p 0}$ ranging from 2.70 to 2.85 µM (A–D) and for adaptation time $τ_{M}$ ranging from 1 to 10 s (E,H) are presented. In both cases the cell density $ρ (z)$ (A, E) and the expected drift velocity $V_{D} (z)$ (B, F) are spatially ordered according to the varying parameter. The mean position (crossed) together with the cross position between $V_{D} (z)$ and $V_{G}$ (circles) increase with $Y_{p 0}$ (C) while they show non-monotonic trend to $τ_{M}$ (G). The width of the density profile (defined by s.d. of all cells) and the reversion rate decrease with $Y_{p 0}$ (D). And they showed a non-monotonic dependence on $τ_{M}$ . The receptor gain $N$ is set to 24 in both cases, while $Y_{p 0}$ is set to 2.77 µM for the $τ_{M}$ varying case and $τ_{M}$ is 1 s for the $Y_{p 0}$ varying case. Simulations are performed under a steeper moving chemoattractant gradient of $g_{1} = - 2.5 m m^{- 2}$ .

Appendix 1—figure 9

Download asset Open asset

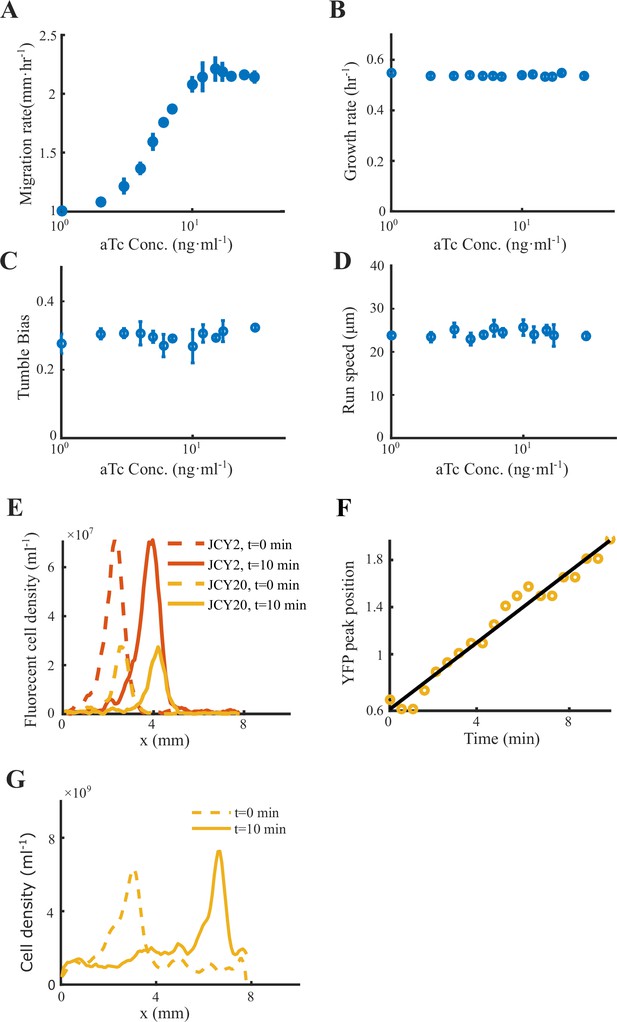
Migration rates, growth rates, motilities and coherent migration of the Tar-titratable strain.

(A) Tar-titratable strain (JCY20) allows us to change its chemotaxis ability (measured by its migration rate on agar plate) by adding inducer ([aTc]) of different concentrations. (B) This strain has constant growth rates measured in liquid batch culture. (**C–D**) Motility statistics were extracted from bacterial tracks in free liquid. The growth rate, tumble bias, and mean run speed were found constant with all tested aTc concentrations. Error bar represents s.d. of three biological replicates. (E) The density profile of the wild-type (WT) strain with red fluorescent protein (RFP) (strain JCY2) (red lines) and Tar-titratable strain with yellow fluorescent protein (YFP) (strain JCY20) (yellow lines) are plotted over space at time before (dashed lines) and after tracking (solid lines). Because the density profiles of both strains before and after tracking are considered to be identical, the migration group is stable during the tracking period (10 min ). The fluorescent strains (JCY2 and JCY20) are mixed with WT non-fluorescent strain (RP437) by ratio of 8:1:400. (F) During the 10 min tracking period, only the Tar-titratable strain (JCY20) is recorded. For each half a minute, we plotted the density profiles and find their peak positions (yellow circles). Such peak positions increase linearly with time (fitted by the black line). Data were extracted from one experiment. (G) The density profile of the Tar-only strain with YFP (strain UU1624 from Prof. Parkinson) are plotted over space at time before (dashed lines) and after 10 min (solid lines).

Appendix 1—figure 10

Download asset Open asset

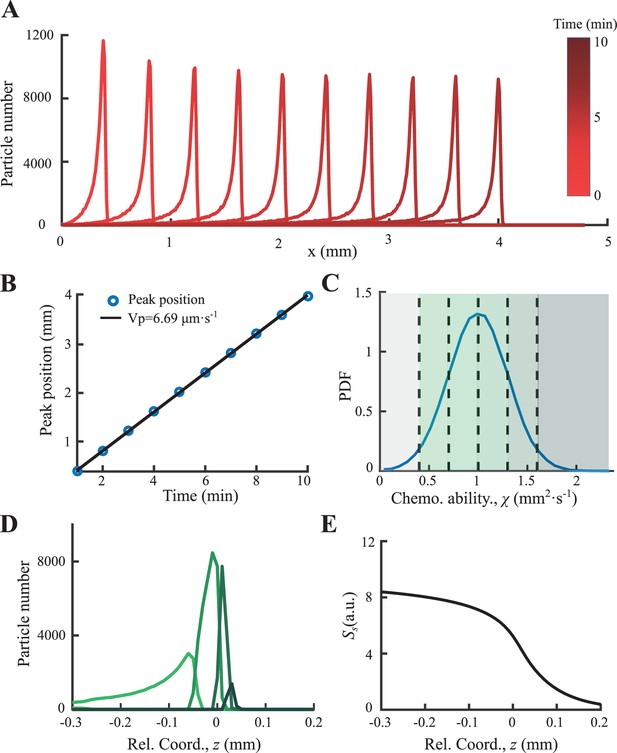
Particle based simulation of the signal secretion model.

(A) Simulated density profiles of heterogenous phenotypes distributed in C show (B) stable group migration with its peak positions following a constant speed of $V_{p} = 6.69 μ m / s$ . (C) The phenotypic diversity was set by a Gaussian distribution on $χ$ , with mean value of 1 and s.d. of 0.3. (D) Time-shifted density profiles of different phenotypes exhibit spatially ordered in moving coordinate. Color code follows C, while cells in the gray area drop from the group. (E) Time-shifted signal profile $S_{s}$ , which plays the role of ‘global driving force’, decreases from back to front.

Appendix 1—table 1

Strains and plasmids used in this study.

Strains	Description	Source
RP437	Wild-type strain for chemotaxis	Fu et al., 2018
JCY1	RP437+ a Cm^r plasmid with YFP	This study
JCY2	RP437+ a Kan^r plasmid with mRFP1	This study
JCY20	Construction based on RP437, tar<> loxp, bla:P_tet-tetR-tar at attB site,+ a Cm^r plasmid with YFP	This study
UU1624	Δaer-1 Δtsr-7028 Δtap-3654 Δtrg-100	Gosink et al., 2006

Appendix 1—table 2

Summary of parameters in agent-based simulation.

Symbol	Definition	Value	Source
$χ$	Chemotaxis ability	Defined in context	This study
$k$	Consumption rate of chemoattractant	Fitted parameter for migration speed	This study
$K_{o n}$	Upper limit of chemoattractant sensing	1 mM	Fu et al., 2018
$K_{o f f}$	Lower limit of chemoattractant sensing	1 µM	Si et al., 2012
$D_{s}$	Diffusion coefficient of chemoattractant	1000 µm²/s	Fu et al., 2018
$v_{0}$	Run speed of bacteria	30 µm/s	Keller and Segel, 1971b
$τ_{M}$	Adaptation time	1 s	Waite et al., 2016
$N$	Receptor gain	Deduced from chemotactic ability	SI notes in Section 7
$M$	Motor number	5	Sneddon et al., 2012
$Y p_{0}$	Basic CheY-P level	2.77 µM	Correspond to $T B_{0} \approx 0.27$

Data availability

All data generated or analysed during this study are included in the manuscript and supporting files.

References

1. Adler J
(1966a) Chemotaxis in Bacteria
Science 153:708–716.
https://doi.org/10.1126/science.153.3737.708
- Google Scholar
1. Adler J
(1966b) Effect of Amino Acids and Oxygen on Chemotaxis in Escherichia Coli
Journal of Bacteriology 92:121–129.
https://doi.org/10.1128/jb.92.1.121-129.1966
- Google Scholar
1. Adler J
(1969) Chemoreceptors in bacteria
Science 166:1588–1597.
https://doi.org/10.1126/science.166.3913.1588
- PubMed
- Google Scholar
1. Bai Y
2. Gao M
3. Wen L
4. He C
5. Chen Y
6. Liu C
7. Fu X
8. Huang S
(2018) Applications of Microfluidics in Quantitative Biology
Biotechnology Journal 13:e1700170.
https://doi.org/10.1002/biot.201700170
- PubMed
- Google Scholar
1. Berg HC
2. Brown DA
(1972) Chemotaxis in Escherichia coli analysed by three-dimensional tracking
Nature 239:500–504.
https://doi.org/10.1038/239500a0
- PubMed
- Google Scholar
Book
1. Berg HC
(2004) E. Coli in Motion
Springer-Verlag.
https://doi.org/10.1007/b97370
- Google Scholar
(2018) Fluctuations uncover a distinct class of traveling waves
PNAS 115:E3645–E3654.
https://doi.org/10.1073/pnas.1715737115
- Google Scholar
1. Budrene EO
2. Berg HC
(1995) Dynamics of Formation of Symmetrical Patterns by Chemotactic Bacteria
Nature 376:49–53.
https://doi.org/10.1038/376049a0
- PubMed
- Google Scholar
1. Celani A
2. Vergassola M
(2010) Bacterial strategies for chemotaxis response
PNAS 107:1391–1396.
https://doi.org/10.1073/pnas.0909673107
- PubMed
- Google Scholar
1. Chen C
2. Liu S
3. Shi XQ
4. Chate H
5. Yl W
(2017) Weak synchronization and large-scale collective oscillation in dense bacterial suspensions
Nature 542:210–214.
https://doi.org/10.1038/nature20817
- PubMed
- Google Scholar
(2018) Time averages and their statistical variation for the Ornstein-Uhlenbeck process: Role of initial particle distributions and relaxation to stationarity
Physical Review. E 98:022134.
https://doi.org/10.1103/PhysRevE.98.022134
- PubMed
- Google Scholar
1. Couzin ID
2. Krause J
3. James R
4. Ruxton GD
5. Franks NR
(2002) Collective Memory and Spatial Sorting in Animal Groups
Journal of Theoretical Biology 218:1–11.
https://doi.org/10.1006/jtbi.2002.3065
- PubMed
- Google Scholar
1. Couzin ID
2. Krause J
(2003) Self-organization and collective behavior in vertebrates
Advances in the Study of Behavior 32:1–75.
https://doi.org/10.1016/S0065-3454(03)01001-5
- Google Scholar
1. Couzin ID
2. Krause J
3. Franks NR
4. Levin SA
(2005) Effective leadership and decision-making in animal groups on the move
Nature 433:513–516.
https://doi.org/10.1038/nature03236
- PubMed
- Google Scholar
1. Cremer J
2. Honda T
3. Tang Y
4. Wong-Ng J
5. Vergassola M
6. Hwa T
(2019) Chemotaxis as a navigation strategy to boost range expansion
Nature 575:658–663.
https://doi.org/10.1038/s41586-019-1733-y
- PubMed
- Google Scholar
1. Curatolo AI
2. Zhou N
3. Zhao Y
4. Liu C
5. Daerr A
6. Tailleur J
7. Huang J
(2020) Cooperative pattern formation in multi-component bacterial systems through reciprocal motility regulation
Nature Physics 16:1152–1157.
https://doi.org/10.1038/s41567-020-0964-z
- Google Scholar
1. de Gennes PG
(2004) Chemotaxis: the role of internal delays
European Biophysics Journal 33:691–693.
https://doi.org/10.1007/s00249-004-0426-z
- PubMed
- Google Scholar
(2011) Fluid dynamics and noise in bacterial cell-cell and cell-surface scattering
PNAS 108:10940–10945.
https://doi.org/10.1073/pnas.1019079108
- PubMed
- Google Scholar
(2014) Limits of Feedback Control in Bacterial Chemotaxis
PLOS Computational Biology 10:e1003694.
https://doi.org/10.1371/journal.pcbi.1003694
- PubMed
- Google Scholar
1. Dufour YS
2. Gillet S
3. Frankel NW
4. Weibel DB
5. Emonet T
(2016) Direct Correlation between Motile Behavior and Protein Abundance in Single Cells
PLOS Computational Biology 12:e1005041.
https://doi.org/10.1371/journal.pcbi.1005041
- PubMed
- Google Scholar
(2014) Advanced methods of microscope control using muManager software
Journal of Biological Methods 1:e10.
https://doi.org/10.14440/jbm.2014.36
- PubMed
- Google Scholar
1. Erban R
2. Othmer HG
(2005) From individual to collective behavior in bacterial chemotaxis
SIAM Journal on Applied Mathematics 65:361–391.
https://doi.org/10.1137/S0036139903433232
- Google Scholar
1. Erm P
2. Phillips BL
(2020) Evolution Transforms Pushed Waves into Pulled Waves
The American Naturalist 195:E87–E99.
https://doi.org/10.1086/707324
- PubMed
- Google Scholar
1. Fisher RA
(1937) The wave of advance of advantageous genes
Ann Eugenic 7:355–369.
https://doi.org/10.1111/j.1469-1809.1937.tb02153.x
- Google Scholar
(2014) Adaptability of non-genetic diversity in bacterial chemotaxis
eLife 3:e03526.
https://doi.org/10.7554/eLife.03526
- PubMed
- Google Scholar
1. Fu X
2. Kato S
3. Long J
4. Mattingly HH
5. He C
6. Vural DC
7. Zucker SW
8. Emonet T
(2018) Spatial self-organization resolves conflicts between individuality and collective migration
Nature Communications 9:1–12.
https://doi.org/10.1038/s41467-018-04539-4
- Google Scholar
(2016) Range expansions transition from pulled to pushed waves as growth becomes more cooperative in an experimental microbial population
PNAS 113:6922–6927.
https://doi.org/10.1073/pnas.1521056113
- Google Scholar
(2006) Signaling Interactions between the Aerotaxis Transducer Aer and Heterologous Chemoreceptors in Escherichia coli
Journal of Bacteriology 188:3487–3493.
https://doi.org/10.1128/JB.188.10.3487-3493.2006
- PubMed
- Google Scholar
(1997) Modelling the evolution of human trail systems
Nature 388:47–50.
https://doi.org/10.1038/40353
- PubMed
- Google Scholar
1. Holz M
2. Chen SH
(1978) Quasi-Elastic Light-Scattering from Migrating Chemotactic Bands of Escherichia-Coli
Biophysical Journal 23:15–31.
https://doi.org/10.1016/S0006-3495(78)85429-0
- PubMed
- Google Scholar
1. Jaqaman K
2. Loerke D
3. Mettlen M
4. Kuwata H
5. Grinstein S
6. Schmid SL
7. Danuser G
(2008) Robust single-particle tracking in live-cell time-lapse sequences
Nature Methods 5:695–702.
https://doi.org/10.1038/nmeth.1237
- PubMed
- Google Scholar
1. Jiang LL
2. Oy Q
3. Yh T
(2010) Quantitative Modeling of Escherichia coli Chemotactic Motion in Environments Varying in Space and Time
PLOS ONE 6:1000735.
https://doi.org/10.1371/journal.pcbi.1000735
- Google Scholar
1. Karig D
2. Martini KM
3. Lu T
4. DeLateur NA
5. Goldenfeld N
6. Weiss R
(2018) Stochastic Turing patterns in a synthetic bacterial population
PNAS 115:6572–6577.
https://doi.org/10.1073/pnas.1720770115
- PubMed
- Google Scholar
1. Keller EF
2. Segel LA
(1971a) Model for chemotaxis
Journal of Theoretical Biology 30:225–234.
https://doi.org/10.1016/0022-5193(71)90050-6
- PubMed
- Google Scholar
1. Keller EF
2. Segel LA
(1971b) Traveling bands of chemotactic bacteria: A theoretical analysis
Journal of Theoretical Biology 30:235–248.
https://doi.org/10.1016/0022-5193(71)90051-8
- Google Scholar
1. Krause J
(1994) Differential fitness returns in relation to spatial position in groups
Biological Reviews of the Cambridge Philosophical Society 69:187–206.
https://doi.org/10.1111/j.1469-185x.1994.tb01505.x
- PubMed
- Google Scholar
Book
1. Krause J
2. Ruxton GD
3. Ruxton G
4. Ruxton IG
(2002)
Living in Groups

Oxford University Press.
- Google Scholar
1. Kussell E
2. Leibler S
(2005) Phenotypic diversity, population growth, and information in fluctuating environments
Science 309:2075–2078.
https://doi.org/10.1126/science.1114383
- PubMed
- Google Scholar
1. Liu C
2. Fu X
3. Liu L
4. Ren X
5. Chau CK
6. Li S
7. Xiang L
8. Zeng H
9. Chen G
10. Tang LH
11. Lenz P
12. Cui X
13. Huang W
14. Hwa T
15. Huang JD
(2011) Sequential establishment of stripe patterns in an expanding cell population
Science 334:238–241.
https://doi.org/10.1126/science.1209042
- PubMed
- Google Scholar
1. Liu WR
2. Cremer J
3. Dj L
4. Hwa T
5. Liu CL
(2019) An evolutionarily stable strategy to colonize spatially extended habitats
Nature 575:664–668.
https://doi.org/10.1038/s41586-019-1734-x
- PubMed
- Google Scholar
1. Liu W
2. Tokuyasu TA
3. Fu X
4. Liu C
(2021) The spatial organization of microbial communities during range expansion
Current Opinion in Microbiology 63:109–116.
https://doi.org/10.1016/j.mib.2021.07.005
- PubMed
- Google Scholar
Book
1. Long J
(2019)
From Individual to Collective Behavior: The Role of Memory and Diversity in Bacterial Navigation

Yale University.
- Google Scholar
1. Novickcohen A
2. Segel LA
(1984) A Gradually Slowing Traveling Band of Chemotactic Bacteria
Journal of Mathematical Biology 19:125–132.
https://doi.org/10.1007/BF00275935
- PubMed
- Google Scholar
1. Parrish JK
2. Edelstein-Keshet L
(1999) Complexity, pattern, and evolutionary trade-offs in animal aggregation
Science 284:99–101.
https://doi.org/10.1126/science.284.5411.99
- PubMed
- Google Scholar
1. Partridge BL
(1982) The structure and function of fish schools
Scientific American 246:114–123.
https://doi.org/10.1038/scientificamerican0682-114
- PubMed
- Google Scholar
1. Payne S
2. Li B
3. Cao Y
4. Schaeffer D
5. Ryser MD
6. You L
(2013) Temporal control of self-organized pattern formation without morphogen gradients in bacteria
Molecular Systems Biology 9:697.
https://doi.org/10.1038/msb.2013.55
- PubMed
- Google Scholar
1. Rosen G
(1973) Fundamental theoretical aspects of bacterial chemotaxis
Journal of Theoretical Biology 41:201–208.
https://doi.org/10.1016/0022-5193(73)90113-6
- PubMed
- Google Scholar
1. Rosen G
(1974) On the propagation theory for bands of chemotactic bacteria
Mathematical Biosciences 20:185–189.
https://doi.org/10.1016/0025-5564(74)90078-9
- Google Scholar
(2011) Directional persistence of chemotactic bacteria in a traveling concentration wave
PNAS 108:16235–16240.
https://doi.org/10.1073/pnas.1101996108
- PubMed
- Google Scholar
(1974) Numerical Study of Formation and Propagation of Travelling Bands of Chemotactic Bacteria
Journal of Theoretical Biology 46:189–219.
https://doi.org/10.1016/0022-5193(74)90147-7
- PubMed
- Google Scholar
1. Si G
2. Wu T
3. Ouyang Q
4. Tu Y
(2012) Pathway-based mean-field model for Escherichia coli chemotaxis
Physical Review Letters 109:0–4.
https://doi.org/10.1103/PhysRevLett.109.048101
- Google Scholar
(2012) Stochastic coordination of multiple actuators reduces latency and improves chemotactic response in bacteria
PNAS 109:805–810.
https://doi.org/10.1073/pnas.1113706109
- PubMed
- Google Scholar
1. Sourjik V
2. Berg HC
(2004) Functional interactions between receptors in bacterial chemotaxis
Nature 428:437–441.
https://doi.org/10.1038/nature02406
- PubMed
- Google Scholar
1. Spudich JL
2. Koshland DE
(1976) Non-genetic individuality: Chance in the single cell
Nature 262:467–471.
https://doi.org/10.1038/262467a0
- PubMed
- Google Scholar
Book
1. Sumpter DJT
(2010)
Collective Animal Behavior

Princeton University Press.
- Google Scholar
1. van Saarloos W
(2003) Front propagation into unstable states
Physics Reports 386:29–222.
https://doi.org/10.1016/j.physrep.2003.08.001
- Google Scholar
1. Vicsek T
2. Zafeiris A
(2012) Collective motion
Physics Reports 517:71–140.
https://doi.org/10.1016/j.physrep.2012.03.004
- Google Scholar
1. Waite AJ
2. Frankel NW
3. Dufour YS
4. Johnston JF
5. Long J
6. Emonet T
(2016) Non‐genetic diversity modulates population performance
Molecular Systems Biology 12:895.
https://doi.org/10.15252/msb.20167044
- PubMed
- Google Scholar
(2018) Behavioral Variability and Phenotypic Diversity in Bacterial Chemotaxis
Annual Review of Biophysics 47:595–616.
https://doi.org/10.1146/annurev-biophys-062215-010954
- Google Scholar
1. Wolfe AJ
2. Berg HC
(1989) Migration of Bacteria in Semisolid Agar
PNAS 86:6973–6977.
https://doi.org/10.1073/pnas.86.18.6973
- PubMed
- Google Scholar
1. Xue C
2. Othmer HG
(2009) Multiscale Models of Taxis-Driven Patterning in Bacterial Populations
SIAM Journal on Applied Mathematics 70:133–169.
https://doi.org/10.1137/070711505
- PubMed
- Google Scholar
(2010) Collective motion and density fluctuations in bacterial colonies
PNAS 107:13626–13630.
https://doi.org/10.1073/pnas.1001651107
- PubMed
- Google Scholar
1. Zheng H
2. Py H
3. Jiang M
4. Tang B
5. Liu W
6. Li D
7. Yu X
8. Kleckner NE
9. Amir A
10. Liu C
(2016) Interrogating the Escherichia coli cell cycle by cell dimension perturbations
PNAS 113:15000–15005.
https://doi.org/10.1073/pnas.1617932114
- PubMed
- Google Scholar
1. Zheng H
2. Bai Y
3. Jiang M
4. Tokuyasu TA
5. Huang X
6. Zhong F
7. Wu Y
8. Fu X
9. Kleckner N
10. Hwa T
11. Liu C
(2020) General quantitative relations linking cell growth and the cell cycle in Escherichia coli
Nature Microbiology 5:995–1001.
https://doi.org/10.1038/s41564-020-0717-x
- PubMed
- Google Scholar

Decision letter

Agnese Seminara

Reviewing Editor; University of Genoa, Italy
Aleksandra M Walczak

Senior Editor; École Normale Supérieure, France

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

The authors present a study on the cohesion maintenance of E. coli during collective migration in a self-generated gradient. They performed experiments and complemented the study with a predictive model and simulation to understand how bacteria with different phenotype are able to move as a cohesive group and how the individual bacterium defines its own position within the group. Particularly interesting aspects of the study are the use of titration of behavior with chemoreceptor abundance and the use of potential wells to model the attraction of bacteria to the center of their cohesive group. This approach will be of interest to physicists and biologists interested in collective motility and migration.

Decision letter after peer review:

[Editors’ note: the authors submitted for reconsideration following the decision after peer review. What follows is the decision letter after the first round of review.]

Thank you for submitting your work entitled "Spatial modulation of individual behaviors enables collective decision-making during bacterial group migration" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and a Senior Editor. The reviewers have opted to remain anonymous.

We are sorry to say that, after consultation with the reviewers, we have decided that your work will not be considered further for publication by eLife.

In this paper, Bai et al. investigate through experiments and agent-based modelling how cohesion is maintained in bacterial waves on chemotactic landscapes created by nutrient consumption. The manuscript confirms that the behavior of individuals is modulated in such a way that makes cells converge towards the center of the group. Behavioral modulation in different phenotypes ensures an ordered spatial arrangement of the phenotypes. All reviewers appreciate the careful experiments and data analysis as well as the introduction of a number of technical advancements (e.g. the titration of behavior with the chemo receptor abundance, and the formalization of bacterial attraction as a potential well). However, the main results appear to confirm previous findings (Saragosti et al. 2011, Fu et al. 2018). Thus, the level of insight provided by the analysis is not sufficient to grant publication in eLife.

Reviewer #1:

In this paper, Bai et al. investigate in experiments and simulations how cohesion is maintained in chemotactic travelling waves of bacteria. These waves emerge from the bacterial population consuming an attractant, thus carving a gradient which they follow chemotactically. This paper builds up on previous work of some of the authors (Fu et al., Nat Commun 2018), which found that in these waves bacteria with varying degree of chemotactic sensitivity organize spatially in the band, which allows for its cohesiveness despite varying phenotypes. The authors investigate here an additional element for the cohesiveness of the wave: because the sharpness of the gradient increases from the front to the back of the wave, 'late' cells catch up via a stronger chemotactic response, and front cells slow down via a weaker one. This had been already postulated in earlier work on the phenomenon (Saragosti et al. PNAS 2011), but here the authors investigate how this applies to cells with varying chemotactic sensitivity. They also performed agent-based simulations of the cells behavior in the gradient and developed a model of the motion in the gradient. The latter maps the spatial dependence of the gradient steepness onto an effective travelling potential which keeps the cells together in a group as the gradient and the wave propagate. Importantly, the effective potential is predicted to be tighter for cells with higher chemotactic sensitivity, in agreement with the cell behavior they observe in experiments where the chemotactic sensitivity is artificially modulated. This suggests that weakly chemotactic cells are more weakly bound to the group and have a higher chance of being left behind. This last part is interesting in the context of range extension in semi-solid agar, where bacteria are known to be spatially organized and selected according to their chemotactic motility (Ni et al., Cell reports 2017, Liu et al. Nature 2019).

This paper builds its strengths on the extensive experimental characterization of the system and a variety of modeling approaches and makes a fairly convincing case for the way of understanding the mechanism of cohesion maintenance they propose.

From a methodological perspective, only a few points need to be addressed:

Control experiments need to quantify the cell-to-cell variability of the induction level of Tar by tetracycline.

Chemical attraction to cues released by other cells is a well-documented way to create cohesive large scale structures in E. coli (Budrene and Berg Nature 1995, Park et al. PNAS 2003, Jani et al. Microbiology 2017, Laganenka et al. Nat commun 2016). The cohesion of the wave have never been analyzed in this optic, despite being a possible alternative explanation to the gradient shape. Since the authors main claim is about the wave cohesion, they should provide evidence that such an explanation can be ruled out or considered secondary.

Possible effects of physical interactions between cells on the chemotactic response are not accounted for. The consequences should be better discussed, because they are known to influence chemotactic motility at the densities encountered in the present experiments (Colin et al. Nat commun 2019).

Additionally, the paper could better emphasize the new results and separate them from the confirmations of previous results.

1. I would highly recommend a thorough correction of the English language. Although some parts are quite fine and require only minor fix, others can be very hard to read and understand. Even when the English is fine, streamlining the presentation of the results could also improve the read considerably.

2. The discussion and the abstract are the places to better separate between confirmation of previous results and new finding, to emphasize the new findings.

3. For the possible effect of chemical cues, simulations or experiments in a Tar-only strain could be good tests.

4. The maximal density in the peak seems to be about 1% volume fraction (10^10 cells/mL, Figure 1) in the experiments. At these densities, chemotaxis is known to be affected by physical interaction between cells (Colin et al. Nat commun 2019). I would suggest additional simulation were \chi is modulated according to local density following (Colin et al. Nat commun 2019) to test whether an effect is present.

5. I would suggest to explain why agent based simulations are necessary (memory effects, etc) after the particle based simulation.

6. L216 it would be a good idea to explain the conceptual difference between VD(z) and VI(z)(=VG), and why they differ, since this is central to the analysis, and might not be obvious to all readers.

Reviewer #2:

The manuscript by Bai et al. explores the single-cell motility dynamics within a chemotactic soliton wave in E. coli. They tracked individual cells and measured their trajectory speed and orientation distributions behind and ahead of the wave. They showed cells behind the wave were moving in a more directed fashion towards the center of the wave compared to cells ahead of the wave. This behavior explains the stability of group migration, as confirmed by numerical simulations.

I do not recommend this manuscript for publication in eLife since it basically reproduces and deepens previous published works. In particular, Saragosti et al. (2011) already provided exactly what the authors claim to do here : "How individuals with phenotypic and behavioral variations manage to maintain the consistent group performance and determine their relative positions in the group is still a mystery." (Line 75-77) (See the last sentences from Saragosti et al. : "This modulation of the reorientations significantly improves the efficiency of the collective migration. Moreover, these two quantities are spatially modulated along the concentration profile. We recover quantitatively these microscopic and macroscopic observations with a dedicated kinetic model.")

What is novel here is the titration of the behavior with chemo-receptor abundance, but I believe the scope is not wide enough for publication in eLife. I suggest the authors to submit in a more specialized journal.

The authors should make more explicit what is really new in their work, compared to what is already known. In the present form, it is hard to pinpoint exactly the novelty of this research.

Reviewer #3:

The authors present a study on the collective behaviour of E. coli during migration in a self-generated gradient. Taking into account phenotypic variation within a biological population, they performed experiments and complemented the study with a predictive model used for simulation to understand how bacteria can move as a group and how the individual bacterium defines its own position within the group.

They observed experimentally that phenotype variation within the bacterial population causes a spatial distribution within the chemotactic band that is not continuous but formed by subpopulations with specific properties such as run length, run duration, angular distribution of trajectories, drift velocity. They attribute this behaviour to the chemotaxis ability, which varies between phenotypes and defines a potential well that anchors each bacterium in its own group. This was proven by the subdiffusive dynamics of the bacteria in each subgroup. Many cases were studied in the experiments and the authors present many controls to clearly demonstrate their hypothesis.

These are interesting results that prove how a discretised distribution can produce continuous collective behaviour. It presents also an interesting example in the field of active matter about collective behaviour on a large scale that is generated by a different behaviour of individuals on a much smaller scale. However, it is not clear how the subpopulations can be held together in the group. Moreover, a link between bacterial dynamics and the biological necessary mechanism is not clear.

They formulate a theoretical description based on the classical Keller-Segel model. Langevin dynamics was used to describe bacterial activity in terms of drift velocity for simulation, which agrees very well with experimental observations.

One can appreciate the interesting results of the study describing Ecoli chemotaxis as a mean-reversion process with an associated potential, but it is not clear to what extent the results can be generalised to all bacteria or rather relate to the strain the authors investigated.

1) In the Results section, lines 93-181, the authors show the results of their experiments, which essentially confirm the results of previous studies in terms of the average speed of the group and the distribution of running length and running duration from back to front within the group, as well as the angular distribution of running length. I have difficulty seeing the differences between this work and the previous studies. In fact, other studies already showed the persistence of the cell migration pathway from the back to the front as well as cells migrating faster in the back and slower in the front.

The manuscript would benefit greatly from a clear comparison between the authors' results and the previous studies.

2) However, they noted that the tumble bias is constant and not spatially modulated. This is the first difference compared to the previous studies cited, and it would be useful to have a guess or speculation about the physiological significance of this. Is the tumble bias related to the bacterial strain? Shouldn't the tumble bias be a strategy of the organism to scan the environment? Do the authors believe that tumble bias is intrinsic to the system and cannot be influenced by physiological priorities such as receptor occupancy and foraging? In the previous study, tumble bias caused faster migration in the posterior region and slower migration in the anterior region. The authors observed that in their case, the faster migration in the back and slower migration in the front was due to drift speed. How do they explain this difference in these observations?

Such aspects should be clarified if the authors intend to claim that their outcomes advance the knowledge in the field of bacterial migration otherwise they are rather considering a subcase, a special Ecoli bacteria strain.

3) The authors propose a discretisation of the chemotactic band into subgroups whose dimension is defined by the chemotactic ability with an inverse relationship to the SD γ of the bacterial distribution. Based on this idea, they suggest that each group represents a potential well. Although the idea is very interesting, it is not entirely clear to me how the bacteria can reverse to the mean of the group just because they rely on the molecular migration pathway. How is the attraction to each group generated? Would it make sense to think about the mechanism of quorum sensing, which Ecoli bacteria are known to use for population sensing? This would also explain how the exit of each group is avoided: the chemotactic ability pulls the bacteria towards the gradient, but the quorum sensing, e.g. a population sensing, drives the mechanism towards the group. This means that the driving force that causes the group to move together is the sum of at least two contributions.

4) Linked to the previous question: How are the different subpopulations kept together? Is a difference in drift velocity within a range between the back and the front sufficient to prevent the entire chemotactic group from disintegrated? Have the authors tested other drift velocity ranges to see if there is a threshold for these group dynamics? What about accounting for a molecular response?

5) In line 360, the authors claim to obtain the same subdiffusive behaviour of the bacteria when the migratory ability is influenced by the adaptation time or the basal CheY protein level. From the supplementary material, one can understand that this was the result of the simulation. For this reason, the authors should be very careful when claiming that they have observed how different proteins influence the modulation of behaviour. It is not clear from the simulation how this result can be clearly attributed to the specific protein CheY. One can choose a different protein and simulate the behaviour and get the same result without having any connection to the biological real state. I suggest that the authors explain more about this point or remove it from the text and just leave it in the supplementary material with a clear explanation about the missing connection with the biology and clarify that this is a speculation.

6) In line 104, the authors explain that the band forms after centrifugation. Their simulation shows that this happens after 20 min. What about the experiments? Is there consistency between simulation and experiments?

[Editors’ note: further revisions were suggested prior to acceptance, as described below.]

Thank you for submitting your article "Spatial modulation of individual behaviors enables an ordered structure of diverse phenotypes during bacterial group migration" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and Aleksandra Walczak as the Senior Editor. The reviewers have opted to remain anonymous.

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission.

The revised manuscript addresses more clearly the novelty of the work. However, some concerns remain over novelty and new concepts introduced within the revision.

Essential revisions:

1) One main novelty the authors claim with respect to Fu et al. is they propose a mechanism for the ordering. Please clarify whether this is different from the mechanism proposed by Fu et al.

2) Explain that the wave travels because of attractant consumption. Verify with numerical simulations that the ordering persists even when the gradient is continuously modified by consumption.

3) Clarify what a pushed wave precisely is.

Please address all other points raised by the individual referees as you see fit.

Reviewer #1:

In their appeal, the authors have rewritten the text to make it significantly clearer and put the work better in context with previous publications. They also addressed my technical concerns. The main reason for rejection was however the lack of sufficient novelty. The two main points of the paper are:

1) Bringing evidence of a mechanism of wave coherence at fixed chemotactic sensitivity by an increased drift of the late cells and a reduced drift for the early ones thanks to the shape of the gradient, which the authors called mean-reversion or now pushed wave-front. This mechanism was already heavily suggested by the results of Saragosti et al. 2011 and proposed as a mechanism in that paper. On this point, I acknowledge that the presentation and analysis of the cell behavior in this paper does a better and more thorough job at demonstrating the phenomenon than the previous one, and the authors do show that this coherence holds for different values of the chemotactic sensitivity. It however remains that the results simply confirm the previously inferred mechanism, using the same experimental technique.

2) Explaining how spatial ordering allows the reconciliation of phenotypic variability and a coherent wave-front. On this point, I do not think the authors bring any new information compared to Fu et al. (2018). For instance, the mechanism for spatial ordering of the mean position of the various spatial phenotypes is already very well illustrated by Figure 3a of that paper.

The authors also reemphasized the importance of the gradient shape in maintaining the coherence of the wave. Here, and contrary to Fu 2018, they however systematically took the gradient shape as a given during simulations and did not investigate its emergence from consumption by the heterogeneous population. This diminishes the interest of the paper by this much.

All in all, I maintain my appreciation that this is technically a work of quality but its findings still remain fairly incremental, and I think it could be best suited for a more specialist journal.

Reviewer #2:

In the revised version of the manuscript, the authors satisfactorily added significant pieces of data to the whole story. They explained why their work differs from previously published data (Saragosti at all, 2011).

They improved the logical flow of the text (presentation of tracking data, stochastic modeling, agent-based modeling, titration), which now better pinpoints what is novel. They added a stochastic model to better understand the mechanisms underlying group migration.

Therefore, I recommend this manuscript for publication in eLife, provided that the authors can answer the following point.

Could the authors explain what a pushed wave is? Pushed wave/pulled wave have a clear meaning in the context of traveling waves (FKPP reaction and variants). Briefly, a pulled wave is when the per capita growth rate is the highest at the edge of the front. A pushed wave is when the per capita growth rate is the highest behind the front. Here, cells move but do not divide. This should be clarified.

Reviewer #3:

In this new version of the manuscript, authors Bai et al. offer a rewording of the text that greatly improves the understanding of their study.

They provide a new abstract that helps to explain the innovation of their results and their relevance to the biological event of cell migration.

They expand the text by adding details about their experiments, how they confirm the theoretical model and how these can improve our knowledge on collective motion of bacteria. They explain why their results are able to answer the open questions left by the studies of Saragosti 2011 and Fu 2018. In this way they discuss the differences between their study and the previous ones.

Overall, the text and the improved figures allow one to appreciate the originality of her study. Specially on the following points:

1) The analysis at the level of the individual cell and how individual behaviour can lead to collective migratory behaviour;

2) The importance of decreasing drift velocity within the chemotactic band for the collective migration of bacteria as a group;

3) The coexistence of phenotypic variability within the same migratory population and the formulation of the potential well hypothesis to explain group cohesion;

5) The adequacy of the titrated phenotype control experiment, which may also suggest a possible molecular pathway involved in the process.

The new version is able to convey the importance of the study, which is robust from an experimental point of view, with several control experiments that leave no doubt about the hypothesis that the authors draw from their observations and that are used to confirm their theoretical model. All the concerns I expressed were satisfactorily addressed.

I would suggest improving the text further so that some repetitions and mistakes are removed to make it more easy to read, and then I would suggest the manuscript for publication.

https://doi.org/10.7554/eLife.67316.sa1

Author response

[Editors’ note: The authors appealed the original decision. What follows is the authors’ response to the first round of review.]

Reviewer #1:

In this paper, Bai et al. investigate in experiments and simulations how cohesion is maintained in chemotactic travelling waves of bacteria. These waves emerge from the bacterial population consuming an attractant, thus carving a gradient which they follow chemotactically. This paper builds up on previous work of some of the authors (Fu et al., Nat Commun 2018), which found that in these waves bacteria with varying degree of chemotactic sensitivity organize spatially in the band, which allows for its cohesiveness despite varying phenotypes. The authors investigate here an additional element for the cohesiveness of the wave: because the sharpness of the gradient increases from the front to the back of the wave, 'late' cells catch up via a stronger chemotactic response, and front cells slow down via a weaker one. This had been already postulated in earlier work on the phenomenon (Saragosti et al. PNAS 2011), but here the authors investigate how this applies to cells with varying chemotactic sensitivity. They also performed agent-based simulations of the cells behavior in the gradient and developed a model of the motion in the gradient. The latter maps the spatial dependence of the gradient steepness onto an effective travelling potential which keeps the cells together in a group as the gradient and the wave propagate. Importantly, the effective potential is predicted to be tighter for cells with higher chemotactic sensitivity, in agreement with the cell behavior they observe in experiments where the chemotactic sensitivity is artificially modulated. This suggests that weakly chemotactic cells are more weakly bound to the group and have a higher chance of being left behind. This last part is interesting in the context of range extension in semi-solid agar, where bacteria are known to be spatially organized and selected according to their chemotactic motility (Ni et al., Cell reports 2017, Liu et al. Nature 2019)

This paper builds its strengths on the extensive experimental characterization of the system and a variety of modeling approaches and makes a fairly convincing case for the way of understanding the mechanism of cohesion maintenance they propose.

In fact, we have addressed both the mechanism to maintain a coherent group and also the mechanism to form ordered pattern of diverse phenotypes. Thanks to the reviewer, we noticed that the second point was not clearly showed out in our previous version. So that we have largely rewritten the texts and reorganized the results to prominent both mechanism.

From a methodological perspective, only a few points need to be addressed:

Control experiments need to quantify the cell-to-cell variability of the induction level of Tar by tetracycline.

The distributions of the titrate cells are presented by a ptet-Tar-GFP strain, where the GFP is used as a reporter of the expressed Tar protein. The results are shown in Author response image 1.

Author response image 1

Download asset Open asset

Chemical attraction to cues released by other cells is a well-documented way to create cohesive large scale structures in E. coli (Budrene and Berg Nature 1995, Park et al. PNAS 2003, Jani et al. Microbiology 2017, Laganenka et al. Nat commun 2016). The cohesion of the wave has never been analyzed in this optic, despite being a possible alternative explanation to the gradient shape. Since the authors main claim is about the wave cohesion, they should provide evidence that such an explanation can be ruled out or considered secondary.

We thank the reviewer to point out the self-attractant secretion as a possible mechanism to maintain coherent group. We argue that this mechanism is not necessary for the chemotactic group to maintain coherency, because the migration group keeps without considering these effects in our agent based simulations.

Moreover, as suggested by the reviewer, we Used a Tar only strain, which do not sense any chemo-attractant other than aspartate, to show that the migration group maintained coherent (see Figure S9). This experiment showed that the secretion of self-attractant is not essential for the coherent group migration.

Possible effects of physical interactions between cells on the chemotactic response are not accounted for. The consequences should be better discussed, because they are known to influence chemotactic motility at the densities encountered in the present experiments (Colin et al. Nat commun 2019).

As being reported by Colin et al., the effective drift velocity and the chemotactic ability deceases when cells are condensed (volume fraction >0.01). However, the cell density is smaller than this critical value (volume fraction<0.01).

Additionally, the paper could better emphasize the new results and separate them from the confirmations of previous results.

In the revised version, we addressed 2 new findings:

1. The individual drift velocity decreases from back to front of the bacterial migration group, which makes the chemotactic migration wave a pushed wave.

Cells of diversed phenotypes follows the same reversion behavior, ie. drift faster in the back and slower in the front, but with ordered mean positions, to achieve the ordered pattern in the migration group.

1. I would highly recommend a thorough correction of the English language. Although some parts are quite fine and require only minor fix, others can be very hard to read and understand. Even when the English is fine, streamlining the presentation of the results could also improve the read considerably.

The texts are largely rewritten and the English language is edited by a professional English editor.

2. The discussion and the abstract are the places to better separate between confirmation of previous results and new finding, to emphasize the new findings.

Abstract and discussion are rewritten to emphasize the new findings:

1. The drift velocities of individual bacteria decrease from the back to the front.
2. The individual run-and-tumble random motions are spatially modulated, and enables the bacterial population to migrate as a pushed wave.
3. The pushed wave can help a diverse population to stay in a tight group.
4. Diverse individuals perform the same type of mean reverting processes around centers orderly aligned by their chemotactic abilities.

3. For the possible effect of chemical cues, simulations or experiments in a Tar-only strain could be good tests.

Our agent-based simulation was based on an single chemical cue and uses Tar receptor only. New experiments is performed with a Tar-only strain provide by Prof. Johan Sandy Parkinson. Coherent group migration was observed, related results were added in the Figure S9.

4. The maximal density in the peak seems to be about 1% volume fraction (10^10 cells/mL, Figure 1) in the experiments. At these densities, chemotaxis is known to be affected by physical interaction between cells (Colin et al. Nat commun 2019). I would suggest additional simulation were \chi is modulated according to local density following (Colin et al. Nat commun 2019) to test whether an effect is present.

The effect of interaction between cells can be neglected. According to Colin et al. Nat commun 2019, the chemotactic drift velocity and the chemotaxis coefficient of bacterial are almost constant for volume fraction <0.01. Since the volume fraction in our case maximize in 0.01, the cell density in the migrating band can be considered as a constant.

5. I would suggest to explain why agent based simulations are necessary (memory effects, etc) after the particle based simulation.

Addressed in the main text, see Line 326-330.

6. L216 it would be a good idea to explain the conceptual difference between VD(z) and VI(z)(=VG), and why they differ, since this is central to the analysis, and might not be obvious to all readers.

Addressed in the main text, see Line 148-156.

Reviewer #2:

The manuscript by Bai et al. explores the single-cell motility dynamics within a chemotactic soliton wave in E. coli. They tracked individual cells and measured their trajectory speed and orientation distributions behind and ahead of the wave. They showed cells behind the wave were moving in a more directed fashion towards the center of the wave compared to cells ahead of the wave. This behavior explains the stability of group migration, as confirmed by numerical simulations.

I do not recommend this manuscript for publication in eLife since it basically reproduces and deepens previous published works. In particular, Saragosti et al. (2011) already provided exactly what the authors claim to do here : "How individuals with phenotypic and behavioral variations manage to maintain the consistent group performance and determine their relative positions in the group is still a mystery." (Line 75-77) (See the last sentences from Saragosti et al. : "This modulation of the reorientations significantly improves the efficiency of the collective migration. Moreover, these two quantities are spatially modulated along the concentration profile. We recover quantitatively these microscopic and macroscopic observations with a dedicated kinetic model.")

Saragosti et al. talks about the modulation of reorientation angle of bacteria along directions. It is not equal to the spatial modulation of drift velocities along space. They claim that cells moving along the gradient direction reorient less during a tumble than cells moving against the gradient. This phenomenon increases the migration efficiency of the group. Here, in our paper, we claim that the drift velocity of bacteria is spatially modulated, where cells on the back drifts faster while the cells in the front drift slower. This phenomenon is important because it makes the chemotactic migration front a pushed wave, that helps the group to keep diversed phenotypes.

Although Saragosti et al. Have also suggested spatial modulation of bias in run length to explain the coherency of the migration group. But they did not quantify such bias nor did they explain the causes and consequences of the spatial modulation. Moreover, Their model consisting their proposed mechanism of directional persistence, cannot explain their observed phenomenon of the decreasing bias of run length (see figure 4A and C).In this circumstance, we can’t agree that they already proofed how cells with diversed phenotype to maintain coherent group.

Moreover, they did not talk about diversities in the group.

Saragosti et al. Figure 4 shows that the theoretical predictions (green and red lines in C) do not match the experiment measurement (green and red lines in A).

What is novel here is the titration of the behavior with chemo-receptor abundance, but I believe the scope is not wide enough for publication in eLife. I suggest the authors to submit in a more specialized journal.

The titration of the chemo-receptor abundance of bacteria serves as a tool to explain how diverse individuals manage to form the ordered patterns in a group. This question worth several discussion because diversity is known as an important feature to keep a group to survive. The ordered pattern was found the key for a migrating group to keep the diversity while performing consistent migration speed. In this paper we successfully explained how individuals performing biased random walk are able to form ordered structure.

The authors should make more explicit what is really new in their work, compared to what is already known. In the present form, it is hard to pinpoint exactly the novelty of this research.

We notice that our previous layout of the results didn’t highlight the novelty of this paper. So that we have reorganized the results and have largely revised the texts to address the new findings.

Reviewer #3:

The authors present a study on the collective behaviour of E. coli during migration in a self-generated gradient. Taking into account phenotypic variation within a biological population, they performed experiments and complemented the study with a predictive model used for simulation to understand how bacteria can move as a group and how the individual bacterium defines its own position within the group.

They observed experimentally that phenotype variation within the bacterial population causes a spatial distribution within the chemotactic band that is not continuous but formed by subpopulations with specific properties such as run length, run duration, angular distribution of trajectories, drift velocity. They attribute this behaviour to the chemotaxis ability, which varies between phenotypes and defines a potential well that anchors each bacterium in its own group. This was proven by the subdiffusive dynamics of the bacteria in each subgroup. Many cases were studied in the experiments and the authors present many controls to clearly demonstrate their hypothesis.

These are interesting results that prove how a discretised distribution can produce continuous collective behaviour. It presents also an interesting example in the field of active matter about collective behaviour on a large scale that is generated by a different behaviour of individuals on a much smaller scale. However, it is not clear how the subpopulations can be held together in the group.

The decreasing chemo-attractant gradient makes the migration wavefront a pushed wavefront. So that the balanced position of the subpopulation with larger chemotactic ability is located in the front where the gradient is small. So that diverse phenotypes form ordered pattern to achieve identical migration speed on their balanced positions. This discussion was added in the revised text (see line 268-277).

Moreover, a link between bacterial dynamics and the biological necessary mechanism is not clear.

The bacterial individual dynamics is controlled by the bacterial chemotaxis pathway, which is clear according to previous studies. Basically, the biased random motion was controlled by alternating expected run length through a temporal comparison mechanism between received chemo-attractant concentrations.(Jiang et al. 2010 Plos Comp. Biol.)

They formulate a theoretical description based on the classical Keller-Segel model. Langevin dynamics was used to describe bacterial activity in terms of drift velocity for simulation, which agrees very well with experimental observations.

One can appreciate the interesting results of the study describing Ecoli chemotaxis as a mean-reversion process with an associated potential, but it is not clear to what extent the results can be generalised to all bacteria or rather relate to the strain the authors investigated.

The mean reversion process is a result of decreasing drift velocity (or a pushed wave). Although our study focuses on bacterail chemotaxis migration, but the ordering mechanism of diversed phenotypes follows a OU type model, which is not limited to bacterial chemotaxis. In this case, we argue that the ordering mechanism that we proposed is universal to all active particles that generate signals as a global cue of collective motion.

1) In the Results section, lines 93-181, the authors show the results of their experiments, which essentially confirm the results of previous studies in terms of the average speed of the group and the distribution of running length and running duration from back to front within the group, as well as the angular distribution of running length. I have difficulty seeing the differences between this work and the previous studies. In fact, other studies already showed the persistence of the cell migration pathway from the back to the front as well as cells migrating faster in the back and slower in the front.

The manuscript would benefit greatly from a clear comparison between the authors' results and the previous studies.

Thank for the valuable suggestion. We realized that our previous layout of the results buries our key idea and mislead the reader to confuse our results with previous studies (especially the study of Saragosti et al.). So that we have largely reorganized our results to highlight the ordering mechanism of diversed phenotypes, that none of the previous studies have proposed before.

In fact, although Saragosti et al. have proposed the scenario of reversion behavior in bacterial chemotaxis group migration, they did not prove it through experimental quantification nor numerical simulations. The have proposed the dynamics of directional persistence that bacterial reorient less during a tumble event if they are migrating to the gradient direction. However, this dynamic is insufficient to explain the spatial distribution of run lengths nor the bias of it

2) However, they noted that the tumble bias is constant and not spatially modulated. This is the first difference compared to the previous studies cited, and it would be useful to have a guess or speculation about the physiological significance of this. Is the tumble bias related to the bacterial strain? Shouldn't the tumble bias be a strategy of the organism to scan the environment? Do the authors believe that tumble bias is intrinsic to the system and cannot be influenced by physiological priorities such as receptor occupancy and foraging? In the previous study, tumble bias caused faster migration in the posterior region and slower migration in the anterior region. The authors observed that in their case, the faster migration in the back and slower migration in the front was due to drift speed. How do they explain this difference in these observations?

We didn’t observe different tumble bias profile compared to previous studies. It has a decreasing profile from back to front, indicating that cells of better motility are located in the front. This phenomenon is also consistent with our agent-based simulations (Figure S8).

Such aspects should be clarified if the authors intend to claim that their outcomes advance the knowledge in the field of bacterial migration otherwise they are rather considering a subcase, a special Ecoli bacteria strain.

The tumble bais is not constant over space, since the run time increase form back to front while the tumble time keeps constant. Our experiment supports the fact that tumble bias decrease from back to front. This phenomenon is a result of both phenotypic ordering and the spatial modulation, and the spatial profile of tumble bias depends on the distribution of phenotypes in the group. The tumble bias is intrinsic however, it is also affected by the environment through the adaptation process. (Fu et al. 2018).

3) The authors propose a discretisation of the chemotactic band into subgroups whose dimension is defined by the chemotactic ability with an inverse relationship to the SD γ of the bacterial distribution. Based on this idea, they suggest that each group represents a potential well. Although the idea is very interesting, it is not entirely clear to me how the bacteria can reverse to the mean of the group just because they rely on the molecular migration pathway. How is the attraction to each group generated?

The potential well is generated by two opposite forces, the decreasing gradient of chemo-attractant that pushes the cells to catch up the group and relative motion of the group itself that lefts cells to fall behind.

Would it make sense to think about the mechanism of quorum sensing, which Ecoli bacteria are known to use for population sensing? This would also explain how the exit of each group is avoided: the chemotactic ability pulls the bacteria towards the gradient, but the quorum sensing, e.g. a population sensing, drives the mechanism towards the group. This means that the driving force that causes the group to move together is the sum of at least two contributions.

As you may know, previous studies have shown that bacterial may secret self-attractant or auto-inducer to modify their motions. However, the collective migration doesn’t rely on this effect because theories (Keller et al. 1973) and simulations may easily repeat the collective migration without considering these effects.

Moreover, we used a Tar only strain which senses only aspatate as chemo-attractant, may form the same coherent collective migration as the wild type strain. New results were added in Figure S9, and it further confirms the effect of self-attractant and quorum sensing can be neglected. This discussion was added in the main text, see line 473-476.

4) Linked to the previous question: How are the different subpopulations kept together? Is a difference in drift velocity within a range between the back and the front sufficient to prevent the entire chemotactic group from disintegrated? Have the authors tested other drift velocity ranges to see if there is a threshold for these group dynamics? What about accounting for a molecular response?

The decreasing profiles of the drift velocity makes sure that the driving force of the migration wave has a decreasing form (also known as a pushed wave), In a pushed wave, subpopulations are able to keep moving coherently. To Proof this, we simulated sub populations migration from pushed wave to pulled waves, corresponding to the diving force from decreasing form to increasing form. The results confirmed that pushed wave maintains diversity, these results were added to figure 2.

However, in the real system, the decreasing drift velocity has an upper bound on the back of the wave, so that the height of the potential well that pushes bacteria to move forward is limited. So that cells are continuously left behind. See discussions in line 500-511

5) In line 360, the authors claim to obtain the same subdiffusive behaviour of the bacteria when the migratory ability is influenced by the adaptation time or the basal CheY protein level. From the supplementary material, one can understand that this was the result of the simulation. For this reason, the authors should be very careful when claiming that they have observed how different proteins influence the modulation of behaviour.

Good suggestion, we have clarified it in the new version (see line 363)

It is not clear from the simulation how this result can be clearly attributed to the specific protein CheY. One can choose a different protein and simulate the behaviour and get the same result without having any connection to the biological real state. I suggest that the authors explain more about this point or remove it from the text and just leave it in the supplementary material with a clear explanation about the missing connection with the biology and clarify that this is a speculation.

The agent based simulation is constructed based on knowledge of bacterial chemotaxis signaling pathway. Thanks to the previous studies (Jiang, Qi et al. 2010, Sneddon, Pontius et al. 2012), the molecular mechanism is quantitatively established. The agent based model we use in this text is modified from previous models that has been well demonstrated (Dufour, Fu et al. 2014, Long 2019). So that we have the confidence to say that the parameters in the simulation is related to specific proteins of clear biological meaning.

6) In line 104, the authors explain that the band forms after centrifugation. Their simulation shows that this happens after 20 min. What about the experiments? Is there consistency between simulation and experiments?

The experiments were performed in half an hour after sample loading, which is comparable to our simulations. This information is added in the protocol part. (see line 599).

[Editors’ note: what follows is the authors’ response to the second round of review.]

Essential revisions:

1) One main novelty the authors claim with respect to Fu et al. is they propose a mechanism for the ordering. Please clarify whether this is different from the mechanism proposed by Fu et al.

We thank for this advice. To clarify the novelty of this study, we revised the discussion in Line459-470, and specifically discussed our new findings in respect to Fu et al.

Fu et al. first discovered the ordered structure of cells with different phenotypes during group migration. By classic Keller-Segel model, Fu et al. has proposed a phenomenological explanation that the maintenance of group speed over different phenotypes is self-consistent with the constant product of chemotactic ability and perceived gradient. The KS model predicts that perceived gradient is high in the back and low in the front, which suggests the cells maintain an opposite order in terms of chemotactic abilities. However, Fu et al. did not provide a direct measurement of gradient shape, nor explain how individual bacteria (as small as micrometer scales) behave so as to determine their relative positions in the migration group (in millimeter scales).

In this study, our study bridges from single-cell behaviors to population coherent performance, and separate the contributions of phenotypic diversity and dynamic behavioral modulation to group structure, further clarifying the explanation proposed by Fu et al. By analyzing single cell trajectories during group migration, we discovered the spatially structured profile of drift velocity. This finding is a direct evidence how individual behaviors are modulated when imposed to the perceived gradient during the group migration. The decreasing profile of drift velocity plays a role of driving force, which enables the migratory population to propagate as a pushed wavefront. We further demonstrated that the pushed wave can maintain cells with diversity in a compact group, and individuals behave as mean reversion relative to the group. Moreover, cells with phenotypic diversity exhibit the same shape of drift velocities, but perform mean reverting processes around centers spatially aligned based on their chemotactic abilities. Therefore, we demonstrated that population order can emerge from diverse individuals following the same rule of behavioral modulation.

2) Explain that the wave travels because of attractant consumption. Verify with numerical simulations that the ordering persists even when the gradient is continuously modified by consumption.

Thanks for the advice. We added an explanation that the attractant consumption was the cause of the traveling wave in the revised introduction text line 72.

The agent-based simulation with attractant consumption was already presented in FigS6, showing that the ordering remains. However, this was not emphasized in the previous version. In the revised version, we addressed both the numerical methods to solve the attractant consumption equation and relating results in the revised text line 334-345.

Moreover, the numerical simulation based on the Langevin-type model with attractant consumption may also confirm that the ordering effect is independent to the source of the decreasing moving gradient (see Figure S5 and main text line 263-265).

3) Clarify what a pushed wave precisely is.

A pushed wave or pulled wave is originally defined by the driving force profile across a front of a traveling wave. As their names have inferred a ‘pushed’ wave has its maximal driving force in the back while a ‘pulled’ wave has its maximal driving force in the front [van Saarloos, 2003]. In the context of the diffusion-growth system, the traveling wave known as the Fisher wave or F-KPP wave, the criterion of pushed or pulled wave is translated into the profile of per capita growth rate because the driving force of such traveling wave is the population growth, so that a decreasing or increasing profile of the growth rate is used as the criterion of pushed or pulled wave. The definition of the pushed wave is given in the revised text line 237-240. And a discussion of the pulled wave in the F-KPP case is added in the revised text line 489-493.

Reviewer #1:

In their appeal, the authors have rewritten the text to make it significantly clearer and put the work better in context with previous publications. They also addressed my technical concerns. The main reason for rejection was however the lack of sufficient novelty. The two main points of the paper are:

1) Bringing evidence of a mechanism of wave coherence at fixed chemotactic sensitivity by an increased drift of the late cells and a reduced drift for the early ones thanks to the shape of the gradient, which the authors called mean-reversion or now pushed wave-front. This mechanism was already heavily suggested by the results of Saragosti et al. 2011 and proposed as a mechanism in that paper. On this point, I acknowledge that the presentation and analysis of the cell behavior in this paper does a better and more thorough job at demonstrating the phenomenon than the previous one, and the authors do show that this coherence holds for different values of the chemotactic sensitivity. It however remains that the results simply confirm the previously inferred mechanism, using the same experimental technique.

We thank the reviewer for the appreciation of the quality of our work. In this study, we improved our single cell tracking technique, enabling us to obtain long trajectories. This improvement helps us to get the spatial profile of the drift velocity which is not reported previously. Based on this observation, we further established a pushed wavefront picture of population propagation emerging from behavioral modulation of individual cells. This further allowed us to explain the mechanism of the ordering phenomenon from the single cell perspective. Although Saragosti et al. 2011 has suggested a similar picture (the mean-reversion), we don’t think their proposed model (e.g. the directional persistence) has explained the reversion behavior.

2) Explaining how spatial ordering allows the reconciliation of phenotypic variability and a coherent wave-front. On this point, I do not think the authors bring any new information compared to Fu et al. (2018). For instance, the mechanism for spatial ordering of the mean position of the various spatial phenotypes is already very well illustrated by Figure 3a of that paper.

Fu et al. first discovered the ordered structure of cells with different phenotypes during group migration. They have proposed a phenomenological explanation that the maintenance of group speed over different phenotypes is self-consistent with the constant product of chemotactic ability and perceived gradient (Figure 3a). However, this phenomenological explanation did not provide a direct measurement of gradient shape, nor how individual bacteria (as small as micrometer scales) behave so as to determine their relative positions in the migration group (in millimeter scales).

In this study, we provided a clear mechanism how this population order arises from individual random motions. The measured single cell behavior and the drift velocity profile is a direct evidence how individual behavior are modulated when imposed to the perceived gradient during the group migration. And the decreasing profile of drift velocity plays a role of driving force, which enables the migratory population to propagate as a pushed wavefront. We further demonstrated that the pushed wave can maintain cells with diversity in a compact group, and individuals behave as mean reversion relative to the group. Moreover, cells with phenotypic diversity exhibit the same shape of drift velocities, but perform mean reverting processes around centers spatially aligned based on their chemotactic abilities. Therefore, our study further clarifies the explanation proposed by Fu et al., and proposed a novel mechanism of population order emerging from diverse individuals with stochastic behaviors.

The authors also reemphasized the importance of the gradient shape in maintaining the coherence of the wave. Here, and contrary to Fu 2018, they however systematically took the gradient shape as a given during simulations and did not investigate its emergence from consumption by the heterogeneous population. This diminishes the interest of the paper by this much.

We have taken the measured gradient shape to simplify the analysis of the OU-type model, and to emphasize that our proposed ordering mechanism are extendable to all the pushed waves. But we did investigate the emergence of the gradient from population consumption by both the Langevin type model (Figure S5), and the simulation of the agent-based model (Figure S6). Moreover, we have extended the emergence of a decreasing global force from population consumption to population secretion (Figure S10) to generalize our proposed ordering mechanism.

Reviewer #2:

In the revised version of the manuscript, the authors satisfactorily added significant pieces of data to the whole story. They explained why their work differs from previously published data (Saragosti at all, 2011).

They improved the logical flow of the text (presentation of tracking data, stochastic modeling, agent-based modeling, titration), which now better pinpoints what is novel. They added a stochastic model to better understand the mechanisms underlying group migration.

Therefore, I recommend this manuscript for publication in eLife, provided that the authors can answer the following point.

We thank the reviewer for the recommendation.

Could the authors explain what a pushed wave is? Pushed wave/pulled wave have a clear meaning in the context of traveling waves (FKPP reaction and variants). Briefly, a pulled wave is when the per capita growth rate is the highest at the edge of the front. A pushed wave is when the per capita growth rate is the highest behind the front. Here, cells move but do not divide. This should be clarified.

Yes, the cells in our case does divide, but we can still define a pushed wave in its original definition: a ‘pushed’ wave has its maximal driving force in the back while a ‘pulled’ wave has its maximal driving force in the front of a traveling wave [van Saarloos, 2003]. In the context of the diffusion-growth system, known as the Fisher wave or F-KPP wave, the original criterion of pushed or pulled wave was translated into the position of the per capita growth rate. This is because the driving force of such traveling wave is the population growth, so that a decreasing or increasing profile of the growth rate is used as the criterion of pushed or pulled wave.

Reviewer #3:

In this new version of the manuscript, authors Bai et al. offer a rewording of the text that greatly improves the understanding of their study.

They provide a new abstract that helps to explain the innovation of their results and their relevance to the biological event of cell migration.

They expand the text by adding details about their experiments, how they confirm the theoretical model and how these can improve our knowledge on collective motion of bacteria. They explain why their results are able to answer the open questions left by the studies of Saragosti 2011 and Fu 2018. In this way they discuss the differences between their study and the previous ones.

Overall, the text and the improved figures allow one to appreciate the originality of her study. Specially on the following points:

1) The analysis at the level of the individual cell and how individual behaviour can lead to collective migratory behaviour;

2) The importance of decreasing drift velocity within the chemotactic band for the collective migration of bacteria as a group;

3) The coexistence of phenotypic variability within the same migratory population and the formulation of the potential well hypothesis to explain group cohesion;

5) The adequacy of the titrated phenotype control experiment, which may also suggest a possible molecular pathway involved in the process.

The new version is able to convey the importance of the study, which is robust from an experimental point of view, with several control experiments that leave no doubt about the hypothesis that the authors draw from their observations and that are used to confirm their theoretical model. All the concerns I expressed were satisfactorily addressed.

I would suggest improving the text further so that some repetitions and mistakes are removed to make it more easy to read, and then I would suggest the manuscript for publication.

Thanks for the appreciation and the advice. In the revised version, the typos are corrected and phrases are revised. Main figures are reformatted to be clear.

https://doi.org/10.7554/eLife.67316.sa2

Article and author information

Author details

Yang Bai

CAS Key Laboratory for Quantitative Engineering Biology, Guangdong Provincial Key Laboratory of Synthetic Genomics, Shenzhen Institute of Synthetic Biology, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China

Contribution
Data curation, Formal analysis, Funding acquisition, Investigation, Writing - original draft

Contributed equally with
Caiyun He

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-9976-2686
Caiyun He
1. CAS Key Laboratory for Quantitative Engineering Biology, Guangdong Provincial Key Laboratory of Synthetic Genomics, Shenzhen Institute of Synthetic Biology, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China
2. University of Chinese Academy of Sciences, Beijing, China
Contribution
Data curation, Investigation, Methodology, Writing - original draft

Contributed equally with
Yang Bai

Competing interests
No competing interests declared
Pan Chu
1. CAS Key Laboratory for Quantitative Engineering Biology, Guangdong Provincial Key Laboratory of Synthetic Genomics, Shenzhen Institute of Synthetic Biology, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China
2. University of Chinese Academy of Sciences, Beijing, China
Contribution
Methodology

Competing interests
No competing interests declared
Junjiajia Long

Yale University, Department of Physics, New Haven, United States

Contribution
Writing - review and editing

Competing interests
No competing interests declared
Xuefei Li
1. CAS Key Laboratory for Quantitative Engineering Biology, Guangdong Provincial Key Laboratory of Synthetic Genomics, Shenzhen Institute of Synthetic Biology, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China
2. University of Chinese Academy of Sciences, Beijing, China
Contribution
Formal analysis, Writing - review and editing

Competing interests
No competing interests declared
Xiongfei Fu
1. CAS Key Laboratory for Quantitative Engineering Biology, Guangdong Provincial Key Laboratory of Synthetic Genomics, Shenzhen Institute of Synthetic Biology, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China
2. University of Chinese Academy of Sciences, Beijing, China
Contribution
Conceptualization, Formal analysis, Funding acquisition, Project administration, Resources, Supervision, Writing - review and editing

For correspondence
xiongfei.fu@siat.ac.cn

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-3657-8296

Funding

National Key Research and Development Program of China (2018YFA0903400)

Xiongfei Fu

National Natural Science Foundation of China (32071417)

Xiongfei Fu

CAS Interdisciplinary Innovation Team (JCTD-2019-16)

Xiongfei Fu

Guangdong Provincial Key Laboratory of Synthetic Genomics (2019B030301006)

Xiongfei Fu

Strategic Priority Research Program of Chinese Academy of Sciences (XDPB1803)

Xiongfei Fu

National Natural Science Foundation of China (11804355)

Yang Bai

National Natural Science Foundation of China (31770111)

Yang Bai

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

The authors acknowledge C Liu, for sharing E. coli strains and plasmids; S Huang for help with the microfluidics; T Emonet for help with single-cell tracking and agent-based simulations; T Hwa, F Jin, L Luo, J Long for insightful discussions. This work was financially supported by the National Key R&D Program of China (Grant No. 2018YFA0903400), National Natural Science Foundation of China (Grant No. 32071417), CAS Interdisciplinary Innovation Team (Grant No. JCTD-2019-16), Guangdong Provincial Key Laboratory of Synthetic Genomics (Grant No. 2019B030301006), Strategic Priority Research Program of Chinese Academy of Sciences (XDPB1803) to XF, National Natural Science Foundation of China (Grant Nos. 11804355 and 31770111) to YB.

Senior Editor

Aleksandra M Walczak, École Normale Supérieure, France

Reviewing Editor

Agnese Seminara, University of Genoa, Italy

Version history

Received: February 7, 2021
Preprint posted: February 18, 2021 (view preprint)
Accepted: September 16, 2021
Version of Record published: November 2, 2021 (version 1)
Version of Record updated: November 8, 2021 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.