A Brownian ratchet model for DNA loop extrusion by the cohesin complex

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: July 26, 2021 (This version)
Accepted: June 10, 2021
Received: February 14, 2021

1. Related to
Genome Organization: The loopy world of cohesin

Kazuhiro Maeshima, Shiori Iida

Insight Jul 26, 2021
Further reading

Abstract
eLife digest
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

The cohesin complex topologically encircles DNA to promote sister chromatid cohesion. Alternatively, cohesin extrudes DNA loops, thought to reflect chromatin domain formation. Here, we propose a structure-based model explaining both activities. ATP and DNA binding promote cohesin conformational changes that guide DNA through a kleisin N-gate into a DNA gripping state. Two HEAT-repeat DNA binding modules, associated with cohesin’s heads and hinge, are now juxtaposed. Gripping state disassembly, following ATP hydrolysis, triggers unidirectional hinge module movement, which completes topological DNA entry by directing DNA through the ATPase head gate. If head gate passage fails, hinge module motion creates a Brownian ratchet that, instead, drives loop extrusion. Molecular-mechanical simulations of gripping state formation and resolution cycles recapitulate experimentally observed DNA loop extrusion characteristics. Our model extends to asymmetric and symmetric loop extrusion, as well as z-loop formation. Loop extrusion by biased Brownian motion has important implications for chromosomal cohesin function.

eLife digest

When a cell divides, it has to ensure that each of its daughter cells inherits one copy of its genetic information. It does this by duplicating its chromosomes (the DNA molecules that encode the genome) and distributing one copy of each to its daughter cells. Once a cell duplicates a chromosome, the two identical chromosomes must be held together until the cell is ready to divide in two. A ring-shaped protein complex called cohesin does this by encircling the two chromosomes. Cohesin embraces both chromosome copies, as they emerge from the DNA replicating machinery. The complex is formed of several proteins that bind to a small molecule called ATP, whose arrival and subsequent breakdown release energy.

Cohesin also interacts with DNA in a different way: it can create loops of chromatin (the complex formed by DNA and its packaging proteins) that help regulate the activity of genes. Experiments performed on single molecules isolated in the laboratory show that cohesin can form a small loop of DNA that is then enlarged through a process called DNA loop extrusion. However, it is not known whether loop extrusion occurs in the cell.

Although both of cohesin’s roles have to do with how DNA is organised in the cell, it remains unclear how a single protein complex can engage in two such different activities. To answer this question, Higashi et al. used a structure of cohesin from yeast cells gripping onto DNA to build a model that simulates how the complex interacts with chromosomes and chromatin. This model suggested that when ATP is broken down, the cohesin structure shifts and DNA enters the ring, allowing DNA to be entrapped and chromosomes to be bound together. However, a small change in how DNA is gripped initially could prevent it from entering the ring, creating a ratchet mechanism that forms and enlarges a DNA loop.

This molecular model helps explain how cohesin can either encircle DNA or create loops. However, Higashi et al.’s findings also raise the question of whether loop extrusion is possible inside cells, where DNA is densely packed and bound to proteins which could be obstacles to loop extrusion. Further research to engineer cohesin that can only perform one of these roles would help to clarify their individual contributions in the cell.

Introduction

Cohesin is a member of the Structural Maintenance of Chromosomes (SMC) family of ring-shaped chromosomal protein complexes that are central to higher order chromosome organization (Hirano, 2016; Uhlmann, 2016; Yatskevich et al., 2019). Cohesin holds together replicated sister chromatids from the time of their synthesis in S phase, until mitosis, to ensure their faithful segregation during cell divisions (Guacci et al., 1997; Michaelis et al., 1997). In addition, budding yeast cohesin participates in mitotic chromosome condensation, while higher eukaryotic cohesin impacts gene regulation by defining boundary elements during interphase chromatin domain formation (Parelho et al., 2008; Wendt et al., 2008). Cohesin is also recruited to sites of double-stranded DNA breaks to promote DNA repair by homologous recombination and to stalled DNA replication forks to aid restart of DNA synthesis (Ström et al., 2004; Unal et al., 2004; Tittel-Elmer et al., 2012). Understanding how cohesin carries out all these biological functions requires the elucidation of the molecular mechanisms by which cohesin interacts with DNA, as well as how cohesin establishes interactions between more than one DNA.

Cohesin’s DNA binding activity is contained within its unique ring architecture (Gligoris et al., 2014; Huis in 't Veld et al., 2014). Two SMC subunits, Smc1^Psm1 and Smc3^Psm3, form long flexible coiled coils that are connected at one end by a dimerization interface known as the hinge (generic gene names are accompanied by fission yeast subunit names in superscript; fission yeast cohesin was used for the experiments and structural analyses in this study, see Figure 1A). At the other end lie ABC transporter-type ATPase head domains whose dimerization is regulated by ATP binding. The two SMC heads are further connected by a kleisin subunit, Scc1^Rad21. The kleisin N-terminus reversibly engages with Smc3^Psm3 coiled coil next to the ATPase head, forming the kleisin N-gate through which DNA enters the cohesin ring (Figure 1A; Higashi et al., 2020). The kleisin C-terminus in turn binds to the Smc1 head domain. These kleisin terminal domains are connected via a long unstructured region, to which two HEAT repeat subunits bind that promote topological cohesin loading onto DNA. Scc3^Psc3 interacts with the middle of the kleisin unstructured region. Scc2^Mis4, together with its binding partner Scc4^Ssl3, transiently associates with the kleisin between the kleisin N-gate and Scc3^Psc3. Once cohesin loading onto DNA is complete, Scc2^Mis4 is replaced by a related HEAT repeat subunit, Pds5 (Murayama and Uhlmann, 2015; Petela et al., 2018). Because of its transient role, Scc2^Mis4-Scc4^Ssl3 is often thought of as a cofactor, termed ‘cohesin loader’ (Ciosk et al., 2000; Murayama and Uhlmann, 2014). Following topological loading, cohesin is free to linearly diffuse along DNA in vitro (Davidson et al., 2016; Kanke et al., 2016; Stigler et al., 2016), while RNA polymerases push cohesin along chromosomes toward sites of transcriptional termination in vivo (Lengronne et al., 2004; Ocampo-Hafalla et al., 2016; Busslinger et al., 2017). Cohesin promotes sister chromatid cohesion following DNA replication by topologically entrapping two sister DNAs (Haering et al., 2008; Murayama et al., 2018).

Figure 1 with 1 supplement see all

Download asset Open asset

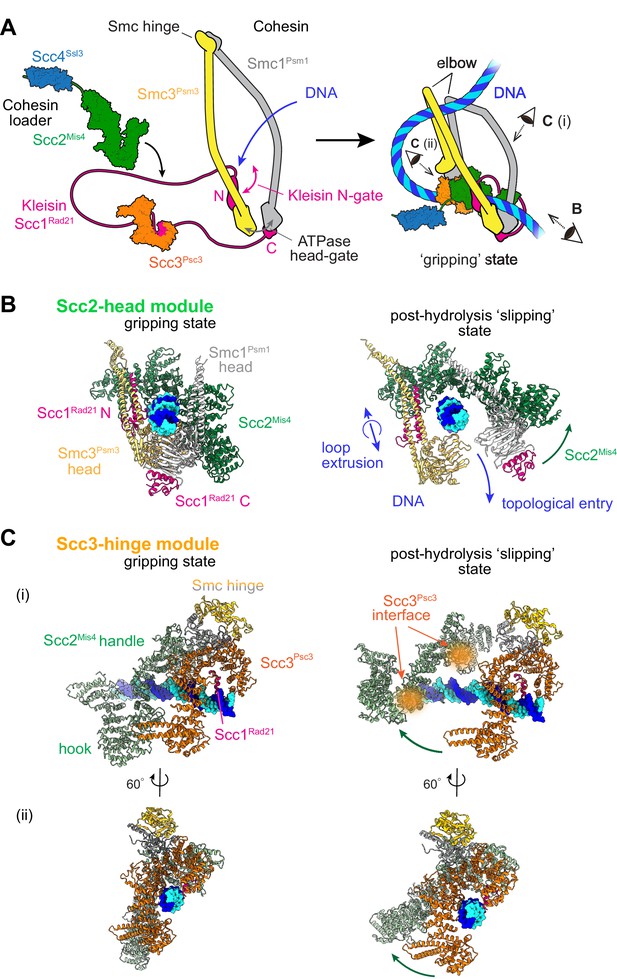
Two cohesin DNA binding modules in the gripping state and in their projected post-hydrolysis states.

(A) Structural overview of the cohesin complex components and assembly of the DNA gripping state. Viewpoints of the structures shown in (B and C) are indicated. (B) The Scc2-head module in the gripping state and its predicted conformation following ATP hydrolysis. ATPase head disengagement and return of Scc2^Mis4 from the gripping state conformation to its extended crystal structure form results in loss of DNA interactions, turning the module into its ‘slipping state’. (C) The Scc3-hinge module. The DNA binding surface of this module remains unaltered by ATP hydrolysis. However, the Scc2^Mis4 conformational change leads to uncoupling of the Scc3-hinge from the Scc2-head module.

In addition to topologically entrapping DNA, in vitro experiments have revealed the ability of human cohesin to translocate along DNA in a directed motion, as well as its ability to extrude DNA loops (Davidson et al., 2019; Kim et al., 2019). These activities are reminiscent of those previously observed with a related SMC complex, condensin, a central mediator of mitotic chromosome condensation (Terakawa et al., 2017; Ganji et al., 2018). Like topological loading onto DNA, loop extrusion by cohesin depends on its ATPase, as well as on the human Scc3^Psc3 homolog SA1 and the cohesin loader (NIPBL-MAU2). In contrast to topological loading, cohesin is able to extrude DNA loops if all three cohesin ring interfaces are covalently closed (Davidson et al., 2019). This suggests that loop extrusion does not involve topological DNA entry into the cohesin ring.

Several models have been proposed as to how SMC complexes extrude DNA loops. These include a tethered-inchworm model in which a scissoring motion of the ATPase heads translates into movement along DNA (Nichols and Corces, 2018). The DNA-segment-capture model instead suggests that a pumping motion between open and closed configurations of the SMC coiled coils constrains DNA loops (Marko et al., 2019). Finally, a scrunching model proposes that the SMC hinge reaches out to capture and reel in DNA loops (Ryu et al., 2020a). A characteristic of experimentally observed loop extrusion is that very small counterforces (<1 pN) stall loop growth (Ganji et al., 2018; Golfier et al., 2020). Both the DNA-segment-capture and the scrunching models therefore suggest that diffusive DNA motion contributes to loop growth. However, molecular details how SMC complexes enact these loop extrusion mechanisms remain elusive. Another important open question remains whether SMC complexes can move along and extrude physiological chromatin substrates, densely decorated by histones and other DNA binding proteins and folded into higher order structures (Nozaki et al., 2017; Xu et al., 2018).

We recently solved a cryo-EM structure of fission yeast cohesin with its loader in a nucleotide-bound DNA gripping state (Higashi et al., 2020). Together with DNA-protein crosslinking and biophysical experiments, this allowed us to trace the DNA trajectory into the cohesin ring by sequential passage through a kleisin N-gate and an ATPase head gate. We noticed, however, that kleisin N-gate passage might not be a strict prerequisite for DNA to reach the gripping state. We speculated that an alternative gripping state arises in which DNA has not passed the kleisin N-gate. While topological DNA entry is barred, this state might constitute an intermediate during loop extrusion. Here, we show how two DNA binding modules of the cohesin complex, formed by its HEAT repeat subunits (Murayama and Uhlmann, 2014; Li et al., 2018; Collier et al., 2020; Kurokawa and Murayama, 2020), are juxtaposed in the gripping state but swing apart following ATP hydrolysis. We illustrate how this swinging motion promotes completion of topological DNA entry, or alternatively generates DNA movements. Computational simulations of the latter scenario demonstrate how a Brownian ratchet forms that can drive loop extrusion. Our study provides a molecular proposal for both topological entry into the cohesin ring as well as for DNA loop extrusion.

Results

Two DNA binding modules in the cohesin-DNA gripping state

Two cryo-EM structures of fission yeast and human cohesin in the presence of non-hydrolyzable ATP analogs Higashi et al., 2020; Shi et al., 2020 have revealed how the cohesin complex components come together during topological loading onto DNA (Figure 1A). ATP binding to the ATPase heads opens up a kleisin N-gate, allowing DNA to enter and reach the top of the engaged ATPase heads. The Scc2^Mis4 cohesin loader subunit then embraces the DNA, thereby closing the kleisin N-gate again and forming the DNA ‘gripping state’ that is captured by the cryo-EM structures (Figure 1B, left). The DNA is held in place by numerous positively charged surface residues, contributed by both the SMC heads and Scc2^Mis4. The cohesin loader has undergone a marked conformational change, compared to its crystallographically observed ‘extended’ form. Its N-terminal handle embraces the DNA in the gripping state, thereby adopting a ‘bent’ conformation. We refer to the composite DNA interaction site, consisting of Scc2^Mis4 and the SMC ATPase heads, as the ‘Scc2-head module’.

A second DNA contact in the gripping state, situated behind the cohesin loader, is made by Scc3^Psc3 in conjunction with the kleisin middle region (Figure 1A and Figure 1C, left). The SMC hinge touches down to bridge cohesin loader and Scc3^Psc3, enabled by SMC coiled coil inflection at their elbows. Scc3^Psc3 and the kleisin middle region bind DNA in a fashion similar to that previously seen in a crystal structure of budding yeast Scc3, with an Scc1 peptide, bound to DNA (Li et al., 2018). The DNA interaction is again provided by an array of positively charged amino acids that line the combined Scc3^Psc3 and kleisin surface. We refer to this second DNA binding site as the ‘Scc3-hinge module’ (see Figure 1—figure supplement 1A for details of the structural model).

Predicted conformational changes following ATP hydrolysis

We now consider the consequences of ATP hydrolysis on the two DNA binding modules outlined above. Upon ATP hydrolysis, the ATPase heads disengage, leading to loss of at least some of the DNA contacts within the Scc2-head module. If we assume that Scc2^Mis4 returns to its extended crystal structure form, further DNA contacts are lost as the gripping state opens up (Figure 1B, right). We can see how, in this state, DNA is free to leave the Scc2-head module during topological DNA entry (a structural model for the full DNA trajectory during topological entry is provided in Figure 3).

During loop extrusion, we propose that DNA fails to exit the Scc2-head module through the ATPase head gate following ATP hydrolysis. This could be because an alternative kleisin path obstructs the head gate, or due to persisting electrostatic interactions between Scc2^Mis4 and the DNA (discussed below in Figure 3). DNA movements are instead limited to transverse DNA sliding, that is in and out of the image plane in Figure 1B, akin to experimentally observed cohesin loader sliding along DNA (Stigler et al., 2016). Because of the moveable nature of the DNA interaction, we refer to this shape of the Scc2-head module as its ‘slipping state’.

A bent Scc2^Mis4 conformation that embraces DNA, compared to its extended crystal structure form, is shared between the fission yeast, human and budding yeast gripping states (Figure 1—figure supplement 1B; Collier et al., 2020; Higashi et al., 2020; Shi et al., 2020). This commonality opens up the possibility that the gripping to slipping state conformational transition is a conserved feature of the Scc2-head module.

In contrast to the Scc2-head module, the Scc3-hinge module and its DNA binding site do not undergo an obvious conformational change when comparing its gripping state and free crystal structure forms. Human Scc3^SA1 in the gripping state shows an almost perfect overlap with the crystal structure conformation of free Scc3^SA2 (RMSD = 2.4 Å, Figure 1—figure supplement 1C; Hara et al., 2014; Shi et al., 2020). In the gripping state, Scc3^Psc3 interacts with the cohesin loader both along the N-terminal Scc2^Mis4 handle, as well as the central Scc2^Mis4 hook. Scc2^Mis4 rearrangement into its extended form disrupts at least some of these contacts, thereby terminating Scc3^Psc3 - Scc2^Mis4 juxtaposition (Figure 1C, right). A conformational change within the Scc2^Mis4 handle is furthermore likely to weaken its interaction with the SMC hinge. We therefore hypothesize that, as a consequence of Scc2^Mis4 structural rearrangements following ATP hydrolysis, the interaction between the Scc2-head and Scc3-hinge modules resolves. While the Scc2-head module turns from the DNA gripping to the slipping state, the DNA binding characteristics of the Scc3-hinge module remain unaltered.

Measured positional changes between the Scc3-hinge and Scc2-head modules

Above, we predicted positional changes of the Scc3-hinge module relative to the Scc2-head module, when comparing the gripping and ATP post-hydrolysis states. To experimentally observe the positions of module components, we designed FRET reporters inserted at the hinge within Smc1^Psm1, at the C-terminus of Scc3^Psc3 and at the N-terminus of Scc2^Mis4(N191) (Figure 2A). Scc2^Mis4(N191) is an N-terminally truncated Scc2^Mis4 variant missing the first 191 amino acids. The truncation abrogates Scc4^Ssl3 interaction, a factor important for in vivo cohesin loading onto chromatin. In vitro, using naked DNA as a substrate, Scc2^Mis4(N191) retains full biochemical capacity to promote gripping state formation, topological cohesin loading, as well as loop extrusion (Chao et al., 2015; Higashi et al., 2020; Shi et al., 2020). Based on our structural model, these locations are within distances that should allow FRET signal detection in the gripping state. CLIP or SNAP tags, inserted at these positions, served as fluorophore receptors. We labeled these tags during protein purification with Dy547 and Alexa 647 dyes as donor and acceptor fluorophores, respectively (Figure 2B and Figure 2—figure supplement 1A). The tagged and labeled proteins retained the ability to topologically load onto DNA in vitro, albeit at slightly reduced efficiencies (Figure 2—figure supplement 1B). We then mixed labeled cohesin, cohesin loader, a 3 kb circular double stranded plasmid DNA and ATP in the indicated combinations. To create the gripping state, we included all components but substituted ATP for the non-hydrolyzable nucleotide ground state mimetic ADP · BeF₃^-. Following Dy547 excitation, we measured the relative FRET efficiency, defined as the Alexa 647 emission divided by the sum of Dy547 and Alexa 647 emissions.

Figure 2 with 2 supplements see all

Download asset Open asset

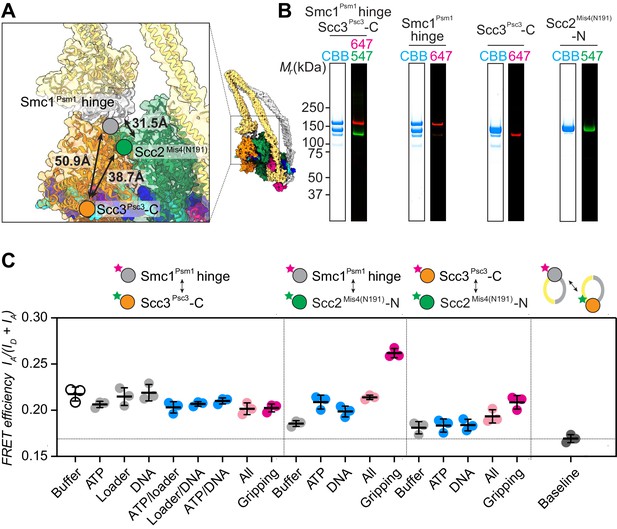
FRET-based conformational analyses of the Scc3-hinge and Scc2-head modules.

(A) FRET reporter positions on the fission yeast cohesin structural model in the DNA gripping state. The silver, orange, and green circles mark the positions of the Smc1^Psm1 hinge residue R593, the Scc3^Psc3 C-terminal residue E959 and Scc2^Mis4 residue P209, respectively. The Euclidean distances between the C_α atoms of these residues are indicated. (B) The purified and labeled cohesin complexes and Scc2^Mis4(N191) cohesin loader were analyzed by SDS-PAGE followed by Coomassie blue staining (CBB) or in gel fluorescence detection of the Cy547 (547) and Alexa 647 (647) dyes. (C) Relative FRET efficiencies I_A/(I_D + I_A) between the respective elements were recorded under the indicated conditions, where I_D is the donor and I_A the acceptor emission intensity resulting from donor excitation. The apparent FRET value observed using a mixture of single-labeled cohesins is indicated as a baseline. Results from three independent repeats of the experiments, their means and standard deviations are shown.

We first recorded FRET between the fluorophore pair at the Smc1^Psm1 hinge and the Scc3^Psc3 C-terminus. The FRET efficiency measured with the cohesin complex alone was 0.22 and displayed only negligible changes following the addition of one or more of the different cofactors. Even under conditions of gripping state formation, the FRET efficiency remained unchanged (Figure 2C). As a control, we prepared a mixture of singly Smc1^Psm1 hinge and singly Scc3^Psc3 C-terminus labeled cohesin complexes. This mixture provides a baseline for the apparent background FRET value due to spectral overlap. At 0.17 the measurement remained substantially below the FRET values observed when both fluorophores were incorporated within the same cohesin complex. This observation supports the idea that the SMC hinge and Scc3^Psc3 lie in proximity of each other to form an Scc3-hinge module, consistent with biochemically observed Scc3^Psc3-hinge binding (Murayama and Uhlmann, 2015). Module formation was observed under all tested conditions, irrespective of the stage during cohesin’s ATP binding and hydrolysis cycle.

Next, we investigated the positioning of the Scc3-hinge module relative to the Scc2-head module. We first measured FRET between a donor fluorophore at the Scc2^Mis4(N191) N-terminus and an acceptor fluorophore at the Smc1^Psm1 hinge. We observed FRET at relatively low values under most conditions. Strikingly, the FRET efficiency markedly increased under conditions of gripping state formation (Figure 2C). This observation confirms that the Scc3-hinge and Scc2-head modules come into proximity in the ATP-bound gripping state, as seen in the cryo-EM structures. We also measured FRET between the Scc2^Mis4(N191) N-terminus and an acceptor fluorophore at the Scc3^Psc3 C-terminus. Again, FRET showed a relative increase under conditions of gripping state formation. The absolute FRET efficiency at this fluorophore pair remained lower when compared with the acceptor fluorophore at the Smc1^Psm1 hinge. This is expected from a longer predicted Euclidean distance between Scc2^Mis4(N191) and the Scc3^Psc3 C-terminus in the gripping state, compared to Scc2^Mis4(N191) and the Smc1^Psm1 hinge (Figure 2A). Together, these observations suggest that the Scc3-hinge and Scc2-head modules come close to each other in the gripping state but separate from each other in other conditions.

When using Scc2^Mis4(N191) as the FRET donor, its transitory interaction with cohesin becomes a confounding factor. Higher FRET efficiency in the gripping state could have been due to increased cohesin-Scc2^Mis4(N191) complex formation, rather than a conformational change. To examine this possibility, we monitored the cohesin-Scc2^Mis4(N191) interaction by co-immunoprecipitation. This revealed equal interaction efficiencies under all of our incubation conditions (Figure 2—figure supplement 2). Therefore, the observed FRET differences cannot be explained by different cohesin-Scc2^Mis4(N191) complex stabilities. Rather, the FRET changes indeed point to conformational transitions within the cohesin complex.

The role of the Scc3-hinge module during topological DNA entry

What are the consequences of the Scc3-hinge module, and its movement relative to the Scc2-head module, for the DNA trajectory during topological DNA entry? Our earlier results suggested that DNA arrives from the top of the ATPase heads and usually passes the kleisin N-gate before reaching the gripping state (Figure 3A, panel a) (Higashi et al., 2020). The kleisin N-gate initially opens as the consequence of ATP-dependent SMC head engagement (Muir et al., 2020). A positively charged kleisin N-tail then guides DNA through this gate en route to the gripping state. In the gripping state, the DNA together with the Scc2^Mis4 cohesin loader shut the gate, while the Scc3-hinge module docks onto the Scc2-head module. The straight DNA path through both DNA binding modules in turn requires that the DNA bends where it arrives between the Smc1^Psm1 and Smc3^Psm3 coiled coils. The DNA path shown in Figure 3A, panel a, highlights the position of the bend, based on our DNA-protein crosslink mass spectrometry data (Higashi et al., 2020). The notion of DNA bending in the gripping state finds further support from magnetic tweezer experiments, in which condensin introduced a discrete DNA shortening step under gripping state conditions (Ryu et al., 2020b).

Figure 3 with 1 supplement see all

Download asset Open asset

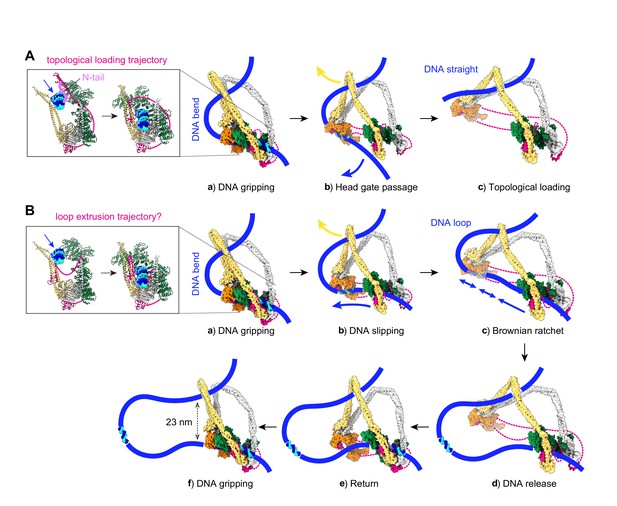
Molecular models for topological DNA entry into the cohesin ring and for loop extrusion.

(A) Topological DNA entry into the cohesin ring. (a) DNA enters through the open kleisin-N gate. DNA binding by both the Scc2-head and Scc3-hinge modules introduces a DNA bend. (b) ATP hydrolysis opens the SMC head gate. The swinging motion of the Scc3-hinge module (indicated by a yellow arrow) steers the DNA through the head gate to complete topological entry. (c) DNA is topologically entrapped in the Scc3-Smc3-kleisin-N chamber. (B) Loop extrusion. (a) DNA arrives in the gripping state without passing the kleisin N-gate. (b) ATP hydrolysis leads to SMC head gate opening, but the kleisin path prevents DNA passage. The swinging motion of the Scc3-hinge module instead turns the DNA bend into a loop, while DNA slips along the Scc2-head module. (c) Loop growth depends on the stochastic Brownian motion of the Scc3-hinge module. (d) The low DNA affinity of the Scc3-hinge module results in DNA release. (e) The Scc3-hinge module returns to form a new DNA gripping state upon nucleotide binding. (f) The next loop extrusion cycle begins. The in- and outbound DNAs are constrained by cohesin at a distance of ~23 nm, in line with recent measurements of the condensin neck size when engaged in loop extrusion (Ryu et al., 2020a).

A stable DNA gripping state forms only in the presence of non-hydrolyzable ATP. Usually, gripping state formation triggers ATP hydrolysis, resulting in ATPase head gate opening and Scc3-hinge and Scc2-head module uncoupling. This uncoupling allows a swinging motion of the Scc3-hinge module and proximal coiled coil, with a pivot point at the elbow (Figure 3A, panel b). No force needs to be transmitted along the SMC coiled coil for this swinging motion to initiate. Rather, following release, Brownian motion can take the Scc3-hinge module only in one direction, away from the Scc2-head module. When we consider the consequence of the Scc3-hinge swinging motion on the DNA path, we make two observations. Firstly, the bent DNA straightens, an effect that might favor the swinging motion. Secondly, the movement effectively steers the DNA through the ATPase head gate to complete topological entry into the cohesin ring.

Following head gate passage, we expect that DNA retains Scc3-hinge module association only for a limited time. DNA affinity to Scc3^Psc3 and the kleisin middle region in isolation has been measured at around 2 μM (Li et al., 2018), a relatively low affinity that implies a fast off-rate once Scc3^Psc3 has left the gripping state. DNA consequently finds itself in a cohesin chamber delineated by Scc3^Psc3, the Smc3^Psm3 coiled coil, as well as the unstructured part of the kleisin between the kleisin N-gate and the kleisin middle region (Figure 3A, panel c). We refer to this space as cohesin’s Scc3-Smc3-kleisin-N chamber. Two separase recognition sites in Scc1^Rad21, whose cleavage liberates DNA from the cohesin ring to trigger anaphase (Tomonaga et al., 2000; Uhlmann et al., 2000), are situated within this part of the kleisin unstructured region (Figure 3—figure supplement 1A).

Single molecule imaging of cohesin, topologically loaded onto DNA, showed that its diffusion is blocked by obstacles smaller than those expected to be accommodated by cohesin’s SMC compartment (Davidson et al., 2016; Kanke et al., 2016; Stigler et al., 2016). This observation is consistent with the possibility that DNA resides in a sub-chamber of the cohesin ring following topological loading. How durable the Scc3^Psc3-SMC hinge association is, whether DNA permanently resides inside the Scc3-Smc3-kleisin-N chamber, or whether subunit rearrangements take place following successful topological loading, for example when the cohesin loader is replaced by Pds5, remains to be further ascertained.

An alternative gripping state that initiates loop extrusion

The structured components of the gripping state do not by themselves contain information about whether DNA has in fact passed the kleisin N-gate. While mechanisms are in place to ensure kleisin N-gate passage, for example the kleisin N-tail, DNA might under certain conditions reach the gripping state without having passed this gate (Figure 3B, panel a). What will be the consequence of ATP hydrolysis in such an alternative gripping state? The Scc2-head module turns into its DNA slipping state, but the kleisin path prevents DNA from passing between the ATPase heads. The Scc3-hinge module again uncouples from the Scc2-head module, but now its diffusion-driven swinging motion cannot steer DNA through the head gate. The only way for the Scc3-hinge module to launch its swinging motion is to further bend the DNA, turning it into a loop, while DNA slips through the Scc2-head module (Figure 3B, panel b). The directed diffusive motion of the Scc3-hinge module has created a Brownian ratchet, allowing DNA motion only in one direction (Figure 3B, panel c). The entropy gain from gripping state disassembly in turn helps to offset the energetic cost of DNA loop formation.

Once a DNA loop is initiated, the extent of loop growth per reaction cycle is limited by how far the Scc3-hinge and Scc2-head modules separate from each other. The maximum separation is likely dictated by the kleisin unstructured regions that link Scc3^Psc3 to the Scc2-head module. Their lengths of 135 amino acids (between the Scc2^Mis4 and Scc3^Psc3 binding sites) and 109 amino acids (between the Scc3^Psc3 binding site and the kleisin C-terminal domain) gives a conservative estimate of ~40 nm (Figure 3—figure supplement 1B; Ainavarapu et al., 2007). This distance allows considerable, but perhaps not complete, extension of the ~47 nm long SMC proteins. As we will see below, the actual amount of loop growth is likely less and depends on the SMC elbow angle reached by stochastic diffusive motion at the time when DNA dissociates (Figure 3B, panel d).

After DNA dissociation from the Scc3-hinge module, there is a time when there is only loose cohesin-DNA contact with the Scc2-head module. Thermal fluctuations now lead to random loop size changes, depending on the probability of diffusion and on external forces that might apply. As long as the Scc2^Mis4 cohesin loader remains part of the Scc2-head module, the local proximity of all components means that a return of the Scc3-hinge module (Figure 3B, panel e) and the establishment of a new DNA gripping state following nucleotide binding (Figure 3B, panel f) are very likely events. The next loop extrusion cycle begins.

Variants of the molecular DNA loop extrusion model

The above model makes a specific molecular proposal for DNA loop extrusion by the cohesin complex. At its core lies a Brownian ratchet built from the Scc3-hinge and Scc2-head modules, juxtaposed during gripping state formation but allowing unidirectional DNA diffusion following ATP hydrolysis. This robust core of a loop extrusion mechanism tolerates variations in its surrounding features.

One point of uncertainty regards the Scc3^Psc3 interaction with the SMC hinge. While our FRET observations suggest proximity of Scc3^Psc3 and the SMC hinge under all tested solution conditions, others have observed Scc3^Psc3 close to the ATPase heads and distant from the hinge (Anderson et al., 2002; Huis in 't Veld et al., 2014). It is possible that the Scc3^Psc3-hinge interaction has a limited lifetime following gripping state disassembly. As long as Scc3^Psc3 retains hinge association during initial SMC coiled coil unfolding, the Brownian ratchet has served its purpose. Scc3^Psc3 might then dissociate from both the DNA and the hinge without impacting on loop extrusion efficiency (Figure 3—figure supplement 1C), as long as all subunits rejoin during gripping state reassembly.

Another open question in our molecular proposal is whether DNA indeed fails to pass the kleisin N-gate before the initiation of loop extrusion. The finding that loop extrusion is not prevented by covalent fusions between cohesin ring subunits (Davidson et al., 2019) does not strictly answer the question whether or not DNA passes the kleisin N-gate, which lies at a distinct distance from the kleisin N-terminus. If DNA did pass the kleisin N-gate, as it would during topological entry into the cohesin ring, the kleisin path would not obstruct DNA exit from the Scc2-head module. Instead, under the low-salt conditions typical for loop extrusion experiments, DNA might retain electrostatic contact with the positive charges of the Scc2-head module in the slipping state (Figure 3—figure supplement 1D). Whether or not such interactions are sufficient to sequester DNA within the Scc2-head module during loop extrusion remains to be learned.

Loop extrusion by the fission yeast cohesin complex

The above molecular model for loop extrusion is based on experiments using the fission yeast cohesin complex and its loader. To date, loop extrusion by cohesin has only been observed using human proteins, while attempts to observe loop extrusion by budding yeast cohesin have remained unsuccessful (Ryu et al., 2021). We therefore asked whether fission yeast cohesin is able to extrude DNA loops. We employed a single-molecule assay similar to those previously used to observe DNA loop extrusion by budding yeast condensin and human cohesin (Ganji et al., 2018; Davidson et al., 2019). Individual molecules of λ-phage DNA were tethered via both ends to a cover glass surface of a microfluidic flow cell, stained with Sytox Orange and stretched by continuous buffer flow while being imaged using total internal reflection (TIRF) microscopy. In the presence of 5 nM fission yeast cohesin, the cohesin loader and ATP, over 40% of the DNA molecules were seen to display active DNA loop extrusion (Figure 4A, Video 1). Loop extrusion proceeded in a symmetrical manner at a mean rate of ~1 kbp s⁻¹ (maximal rate 2.4 kbp s⁻¹, Figure 4B) resembling DNA loop extrusion by human cohesin (Davidson et al., 2019; Kim et al., 2019). This confirms that fission yeast cohesin can both, topologically load onto DNA and extrude DNA loops.

Figure 4

Download asset Open asset

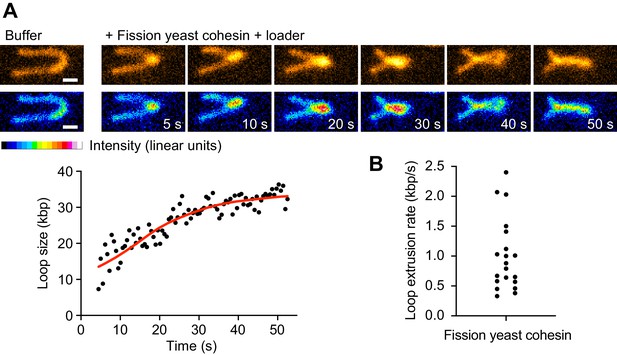
Loop extrusion by the fission yeast cohesin complex.

(A) Time course of DNA loop extrusion. Scale bar 1 μm. A doubly tethered DNA molecule (48.5 kbp) is stained with Sytox Orange and stretched using buffer flow at 15 μl/min. Upon addition of cohesin and cohesin loader in the presence of ATP, a loop formed at the tip of the DNA and dynamically extended toward the DNA ends. The corresponding loop size change over time is plotted. (B) Mean DNA loop extrusion rates from n = 21 DNA molecules analyzed.

Video 1

Download asset

posterframe for video — Movie showing formation and extension of a loop on doubly tethered DNA in the presence of cohesin, the cohesin loader and ATP.

Scale bar 1 μm. A DNA molecule (48.5 kbp) is stained with Sytox Orange and stretched at 15 μL/min buffer flow.

A computational model for Brownian ratchet-driven DNA loop extrusion

In our proposed model of loop extrusion, two DNA binding modules within the cohesin complex generate a Brownian ratchet. The ratchet is operated by repeated cycles of ATP-dependent DNA gripping state formation and its unidirectional dissolution following ATP hydrolysis. To evaluate whether such a mechanism is physically plausible, we constructed a structure-based molecular-mechanical model of the cohesin-DNA interaction and carried out computational simulations to explore its behavior. We modeled DNA as a discrete stretchable, shearable wormlike chain (dssWLC), which describes DNA with persistence length as the only parameter (Figure 5A; Koslover and Spakowitz, 2014). We assumed the persistence length to be L_p = 50 nm (Wang et al., 1997; Bustamante et al., 2000). The cohesin coiled coil segments as well as the linkage between the two SMC heads were modeled using the same approach. Each coiled coil was represented as three beads that interact via a dssWLC (Figure 5B). This again leaves persistence length as the sole parameter that we chose such that it leads to a head-to-hinge distance distribution that matches experimentally measured head-to-hinge distances in a freely diffusing eukaryotic SMC complex (Ryu et al., 2020a).

Figure 5

Download asset Open asset

3D Metropolis Monte-Carlo simulation of cohesin-DNA interactions.

(A) Representation of DNA as a dssWLC model. DNA is split into 5 nm long segments. Each segment is described by its radius vector ${\vec{r}}_{i}$ and a unit vector ${\vec{u}}_{i}$ that defines segment orientation. (B) Cohesin is described by five beads corresponding to Smc1 and Smc3 heads and elbows as well as the hinge. The bead positions are defined by the corresponding vector radii (not shown) and their orientation by unit vectors. (C) The two equilibrium conformations of the model, corresponding to the gripping and slipping states. (D) Snapshots from a simulation, started in a gripping state. The system was sampled 2.5·10⁶ times and then the equilibrium state was changed to the slipping state. It was sampled for another 8·10⁶ iterations, which led to cohesin unfolding and loop extension. At iteration 1·10⁷, the equilibrium conformation was returned to gripping state. (E) Loop length increase shown as function of Metropolis Monte-Carlo (MMC) iterations following the gripping to the slipping state transition. Before iteration zero, the system was equilibrated for 2·10⁶ rounds in the gripping state. The black line represents the average and the gray area the standard deviation across 10 independent simulation replicates. (F) Schematic to show time progression of the DNA interaction with the Scc3-hinge module. Time intervals show indicative ranges of model parameters.

Based on our structural and biochemical observations, we define two states of the cohesin complex. In the gripping state, the Scc3-hinge and Scc2-head modules are engaged and the coiled coil elbows are folded. Both modules make stable contact with DNA (Figure 5C, Gripping state). In the second state, the slipping state, the Scc3-hinge and Scc2-head modules do not interact, allowing an unfolded cohesin conformation. In this state, the Scc2-head module permits free transverse DNA motion. DNA association with the Scc3-hinge module, defined by its equilibrium dissociation constant, is manually controlled in our model (Figure 5C, Slipping state).

First, we explored the dynamics of the transition between cohesin’s gripping and slipping states. As a starting point we assume that a small DNA loop is inserted into the cohesin ring in the gripping state. The first panel in Figure 5D shows a snapshot of this initial state after equilibration by the Metropolis Monte-Carlo algorithm (see Materials and methods). Our 3D model has no explicit chemical kinetics, and to simulate transitions between chemical states we prescribed parameter changes corresponding to a new state, then sampled a sufficient number of iterations to reach a new equilibrium. To simulate transition to the slipping state, we impose parameter changes that disconnect the Scc3-hinge from the Scc2-head module and switch the Scc2-head module to its slipping state, while the Scc3-hinge module remains bound to DNA. We then sampled conformations with the new parameters until a new equilibrium was reached. As cohesin unfolds, DNA binding to the Scc3-hinge module limits DNA movement at the Scc2-head module to only one direction, toward an increased loop size (Figure 5D). The average increase in loop size during multiple repeats of this transition is ~30 nm (Figure 5E). When we then prescribe DNA detachment from the Scc3-hinge module and switch cohesin back to the gripping state, the system readily resets and primes itself for the next cycle (Figure 5D). Our simulations reveal that repeated rounds of the states: ‘gripping - > slipping - > DNA detachment from the Scc3-hinge module - > gripping’ results in continuous extrusion of DNA with an average loop size increase of ~30 nm per cycle (Video 2).

Video 2

Download asset

DNA affinity of the Scc3-hinge module controls loop extrusion

In the above computational model, all state transitions were manually prescribed to obtain cycles of DNA loop extrusion. In the following, we consider requirements for such cycles to arise based on the chemical kinetics of the cohesin complex. We assume, based on the structural data, that both the Scc2-head and Scc3-hinge modules bind DNA in the ATP-bound gripping state. Following ATP hydrolysis, the Scc2-head module switches to its slipping state, while DNA remains bound to the Scc3-hinge module. To achieve processive cycles of loop extrusion, DNA binding must persist for long enough to ensure biased DNA diffusion toward loop growth while cohesin unfolds (Figure 5F). An upper limit for the time it takes cohesin to unfold is given by the time of a diffusive process that separates the Scc3-hinge and Scc2-head modules. Assuming molecular masses of both modules in the 200 kDa range, it takes ~0.1 ms for them to diffuse ~50 nm apart (see Materials and methods). This time is an upper estimate. If cohesin opening was driven not merely by diffusion, but assisted by internal stiffnesses of the coiled coils, this could speed up opening. Based on this estimate, our model predicts that the DNA off-rate at the Scc3-hinge module should be lower than 1/0.1 ms = 10,000 s⁻¹ in order for DNA to maintain Scc3-hinge module association until cohesin fully unfolds.

After cohesin has opened, two further scenarios are possible. Firstly, DNA could dissociate from the Scc3-hinge module before cohesin transitions back into the next gripping state. In this case a loop length gain is made and the ensuing gripping state primes cohesin for the next round of loop extrusion (Figure 5F). Alternatively, cohesin could switch back to the gripping state before DNA is released from the Scc3-hinge module. In this situation, DNA ends up in the same position as before and there is no net loop size gain, resulting in an unproductive cycle. Based on these considerations, loop extrusion in our model is most effective when the DNA lifetime at the Scc3-hinge module is longer than the time required for diffusion-driven cohesin unfolding, but shorter than it takes cohesin to transition back into the next gripping state. Such a lifetime would ensure that most reaction cycles result in net loop growth.

The ATP-bound DNA gripping state is an unstable state, so we can expect cohesin to spend the majority of its time in the post-hydrolysis slipping state. We can then approximate the lifetime of the slipping state based on cohesin’s ATP hydrolysis rate. This rate has been measured with a lower limit of ~ 2 s⁻¹ (Davidson et al., 2019; Ganji et al., 2018; Murayama and Uhlmann, 2014). As two ATPs are coordinately hydrolyzed by the two ATPase heads, this equates to a cycle rate of ~ 1 s⁻¹. Thus, our model predicts that efficient loop extrusion is achieved when the DNA off-rate from the Scc3-hinge module is in the range of 1 – 10,000 s⁻¹. While we do not know the actual off-rate, the equilibrium dissociation constant $K_{d}$ between DNA and Scc3 has been measured at ~ 2 μM (Li et al., 2018). Assuming an association rate $k_{o n}$ typical for biomolecular interactions of ~ 10⁷ M⁻¹ s⁻¹ (Howard, 2001), we arrive at a corresponding off-rate $k_{o f f} = K_{d} \times k_{o n}$ of ~ 20 s⁻¹. This value sits well within the range predicted to support processive loop extrusion. The number ensures processivity even if cohesins that are actively engaged in loop extrusion undergo conformational cycles and hydrolyze ATP up to twenty times faster than measured in bulk solution experiments.

Loop extrusion by biased DNA diffusion

Having established that transitions between cohesin’s gripping and slipping states can drive directional DNA movements, we explored how this mechanism compares to available experimental observations of loop extrusion at realistic time scales. To do this, we constructed a simplified model of loop development. We assume that both DNAs that enter cohesin at the Scc2-head module and exit cohesin at the Smc3^Psm3 elbow can randomly diffuse in and out of the ring with rates depending on a DNA diffusion coefficient $D$ . We then use a Monte-Carlo algorithm to simulate DNA loop dynamics as a function of time.

If we adopt a diffusion coefficient of ~1 μm²/s, as measured for cohesin movements on DNA following topological loading (Davidson et al., 2016; Kanke et al., 2016; Stigler et al., 2016), we see that both strands randomly diffuse back and forth, leading to stochastic loop size changes (Figure 6A). Within a few minutes, a typical time frame used to microscopically observe DNA loop extrusion, the loop size changes over a range of several kilobases. However, these random movements do not show a preferred direction and cannot drive loop extrusion.

Figure 6 with 1 supplement see all

Download asset Open asset

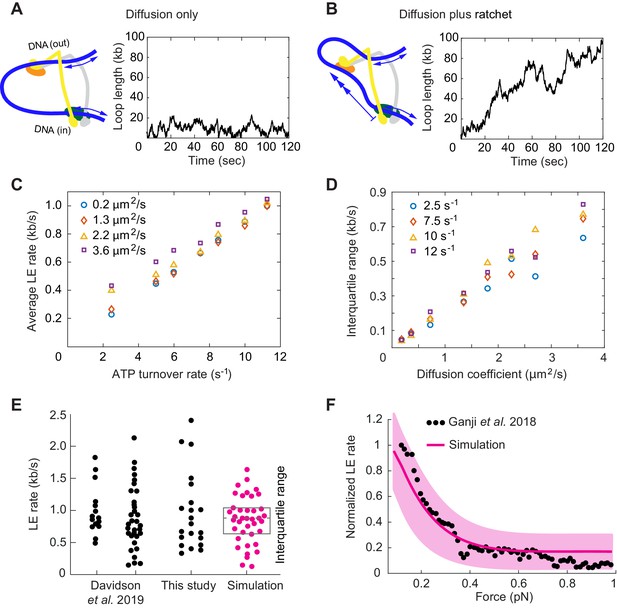
Loop extrusion by cohesin as a Brownian ratchet.

(A) DNA loop size changes due to diffusion only of both DNAs. (B) DNA loop size changes due to random diffusion plus directed diffusion generated by cohesin’s gripping to slipping state transition at a rate of 9 s⁻¹. (C) Simulated average loop extrusion (LE) rates as a function of the cohesin cycle (ATP turnover) rate. Symbol colors represent simulations with the indicated diffusion coefficients. (D) Scatter in the loop extrusion rates, generated during 3 min simulations and quantified as the interquartile range, shown as a function of the outbound DNA diffusion coefficient. The diffusion coefficient for the inbound strand was 0.05 μm²/s. Symbol colors indicate simulations with different cohesin cycle rates. (E) Comparison of experimentally observed LE rate distributions of HeLa cell and recombinant human cohesin (left and right, Davidson et al., 2019), fission yeast cohesin from Figure 4, and an example of simulated data over the same time interval. (F) Comparison of the experimentally observed force dependence of condensin LE rates (Ganji et al., 2018) with the simulated outcome. The pink line shows the median across 35 simulations performed with discrete force values at 0.1 pN increments. The light pink area shows the corresponding interquartile range. Parameters for the simulations in (E) and (F) were: cohesin cycle rate = 9 s⁻¹, DNA diffusion coefficient = 1.5 μm²/s, simulation time = 3 min.

This situation changes when the Scc3-hinge module engages with DNA in the gripping state and disengages predominantly in the slipping state. The Scc3-hinge module restricts DNA diffusion at the Scc2-head module to only one direction – toward loop growth. This effect applies only to the DNA that enters the loop at the Scc2-head module, but not to the DNA that exits cohesin. We assume that the latter DNA continues to diffuse randomly in both directions irrespective of the cohesin state. If we simulate directed DNA motion at the Scc2-head module of 30 nm per cohesin turnover cycle, we see how, overlaid over stochastic diffusive loop size fluctuations, the loop length steadily increases over time (Figure 6B).

We next explored how the variables in this model affect the outcome of loop extrusion. There are three independent variables: the two diffusion coefficients that describe the two DNAs that enter and exit cohesin, as well as the ATPase turnover rate, that is the lifetime of each slipping state. We simulated multiple 10 min intervals of cohesin-DNA dynamics and compared loop extrusion rates extracted from these simulations to those determined in our and in published experiments (Davidson et al., 2019).

The simulations revealed that the average loop extrusion rate is unaffected by the DNA diffusion coefficients (Figure 6C). Indeed, thermal movement of DNA has no net direction and therefore should not contribute to directed loop growth. Instead, the average loop extrusion rate $v$ is simply a product of the step size during cohesin’s state transitions $L$ and the frequency $γ$ of these events:

v = γ * L

Using the value of $L$ = 30 nm = 0.088 kb, we find that there must be around 10 successful cohesin state transitions per second to reach experimentally observed average loop extrusion speeds of ~ 1 kb s⁻¹. The required rate of cohesin state transitions necessitates an equal rate of ATPase cycles. This means that a cohesin complex that is actively engaged in loop extrusion hydrolyzes ATP ~ 10 times faster than average bulk solution ATP hydrolysis rates suggested.

A striking feature of experimentally observed loop extrusion is a high variation in loop growth rates (Figure 4B; Ganji et al., 2018; Davidson et al., 2019). To obtain insight into the origin of these variations, we compared scatter in our modeled traces with experimental data. We quantified the scatter as the interquartile range, that is the range that contains 50% of datapoints around the median. This analysis revealed that extrusion rate variations strongly correlated with the DNA diffusion coefficient. The bigger the diffusion coefficient, the greater is the variation (Figure 6D).

Of the two DNAs that enter and exit cohesin, additional simulations showed that only the DNA with the higher diffusion coefficient determines the amount of scatter in extrusion speed (Figure 6—figure supplement 1). A diffusion coefficient of ~1.5 µm²/s resulted in a good match to the experimentally observed variation (Figure 6E), matching the upper range of experimentally measured values (Davidson et al., 2016; Kanke et al., 2016; Stigler et al., 2016). We imagine that the outward pointing DNA, which is not constrained by the Scc2-head module, might not interact strongly with cohesin and show the greater diffusion coefficient amongst the two DNAs. In addition to the high variations of loop extrusion rates, the low friction of the outward pointing DNA could also explain why DNA can be readily pulled from a condensin complex undergoing loop extrusion (Kim et al., 2020).

Finally, we explored how Brownian ratchet-driven loop extrusion in our model is affected by external force. If cohesin unfolding in the slipping state is driven by thermal motion, its rate $k$ in response to external force is given by:

k = k_{o} e^{- \frac{δ ∙ F}{k_{B} T}}

where $k_{0}$ is the rate in the absence of external force, $F$ is the external force and $δ$ = 30 nm from our simulations (Howard, 2001). Introducing this dependency into our model, we find good agreement between simulations in the presence of a range of applied external forces and the experimentally observed decay of the force-velocity relationship (Figure 6F; Ganji et al., 2018). Both the similarity between the simulated and experimentally observed responses to external force, as well as the high variation of experimentally observed loop extrusion rates, support the idea of a largely diffusion-driven molecular mechanism of loop extrusion.

Symmetric loop extrusion as a special case of asymmetric loop extrusion

In our molecular model of DNA loop extrusion, the Brownian ratchet acts only on the DNA that enters the cohesin ring through the Scc2-head module. No directional effect is exerted on the DNA that exits cohesin. This results in asymmetric loop extrusion (Figure 7A, Asymmetric loop extrusion), a scenario that is seen in the case of the condensin complex (Ganji et al., 2018; Golfier et al., 2020). In contrast, both our and the published experimental observations (Davidson et al., 2019; Kim et al., 2019) suggest that the cohesin complex symmetrically extrudes DNA loops. How could this difference be explained?

Figure 7

Download asset Open asset

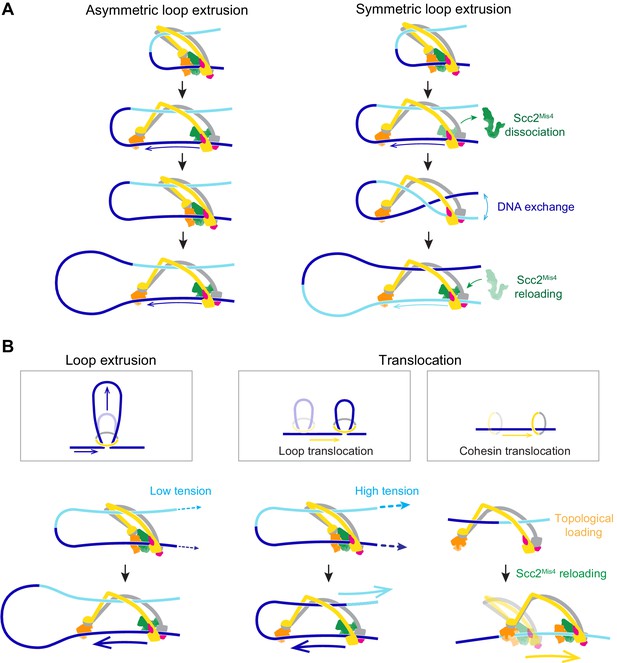
A model for asymmetric and symmetric loop extrusion, as well as possible mechanisms for cohesin translocation along stretched DNA.

(A) A model for symmetric loop extrusion as a special case of asymmetric loop extrusion. Continued action of the Brownian ratchet on the DNA that enters the cohesin ring results in *Asymmetric loop extrusion*. If the cohesin loader dissociates, reassembly of the Brownian ratchet following Scc2^Mis4 reloading gives both DNAs an equal chance to become part of the ratchet. Over time, alternating asymmetric extrusion of both DNAs results in apparent *Symmetric loop extrusion*. (B) Two possible mechanisms for cohesin translocation along DNA under tension. *Loop extrusion* is possible only against very weak DNA counterforces. If loop growth stalls due to DNA tension, the continued operation of the Brownian ratchet leads to *Loop translocation*. Alternatively, cohesin might at first topologically load onto DNA. Recurring gripping state formation and resolution following topological loading results in Brownian ratchet driven *Cohesin translocation*.

In our model, the cohesin loader is a stable part of the cohesin complex. However, Scc2^Mis4 only weakly binds to the cohesin complex. Suggestive of subunit turnover, the continuous presence of cohesin loader in the incubation buffer is a requirement for processive loop extrusion by human cohesin (Davidson et al., 2019). If we picture a situation in which Scc2^Mis4 dissociates from the cohesin complex, DNA will be released from the Scc2-head module (Figure 7A, Symmetric loop extrusion). The DNAs that enter and exit the cohesin ring are now indistinguishable and, once Scc2^Mis4 rebinds, both DNAs have an equal chance to associate with the Scc2-head module during gripping state formation. Every round of cohesin loader dissociation and reloading thereby results in a one-in-two chance that the extruded DNA strand switches. Averaged over time, this takes the appearance of symmetric loop extrusion.

Loop extrusion versus directional cohesin translocation

In addition to loop extrusion, single-molecule studies have reported ATP-dependent unidirectional cohesin and condensin translocation along DNA (Terakawa et al., 2017; Davidson et al., 2019). The experimental conditions under which both complexes move along DNA, or extrude DNA loops, are largely similar. A difference lies in the DNA substrates on which translocation was observed. These substrates were stretched, either by liquid flow or by being double tethered to a flow cell surface. We have seen above that a Brownian ratchet is able to extrude DNA loops only against very small externally applied forces (Figure 7B, Loop extrusion). If DNA is longitudinally stretched, loop extrusion will thus be limited to a small loop size. As the Brownian ratchet continues to deliver DNA to enlarge the loop, the stretching force begins to extract the DNA from the opposite side. This will especially be the case if, as suggested above, the diffusion coefficient of the outward pointing DNA is higher than that of the inward moving DNA (Figure 7B, Loop translocation). Instead of promoting loop growth, the Brownian ratchet now fuels a motor that moves along the DNA. Consistent with this scenario, a small DNA loop was observed to precede initiation of condensin translocation along stretched DNA (Ganji et al., 2018).

We can imagine an alternative scenario by which cohesin could turn into a Brownian ratchet-driven motor. Following successful topological loading onto DNA, cohesin might be able to return to a gripping state, for example if Scc2^Mis4 is not replaced by Pds5. This scenario finds support from the observation that the cohesin loader retains the ability to stimulate cohesin’s ATPase following completion of topological loading (Çamdere et al., 2015). Repeated gripping to slipping state transitions could then result in cohesin translocation along DNA (Figure 7B, Cohesin translocation). This second model for directed cohesin movement is not mutually exclusive with the ‘loop translocation’ model. Both models make the prediction that, similar to what is observed during loop extrusion, cohesin is a weak translocating motor that can be stalled by very small forces.

Possible outcomes of cohesin collisions with DNA-bound obstacles

DNA loop extrusion by cohesin and condensin has so far only been observed in vitro and only using naked DNA substrates. In vivo, DNA is densely decorated by histones and other DNA binding proteins related to transcription, DNA replication and other forms of DNA metabolism. If we portray a loop extruding cohesin complex in its slipping state next to a nucleosome (Figure 8A, left), it becomes apparent that a nucleosome is too big to pass through the channel formed between Scc2^Mis4 and the SMC ATPase heads.

Figure 8 with 2 supplements see all

Download asset Open asset

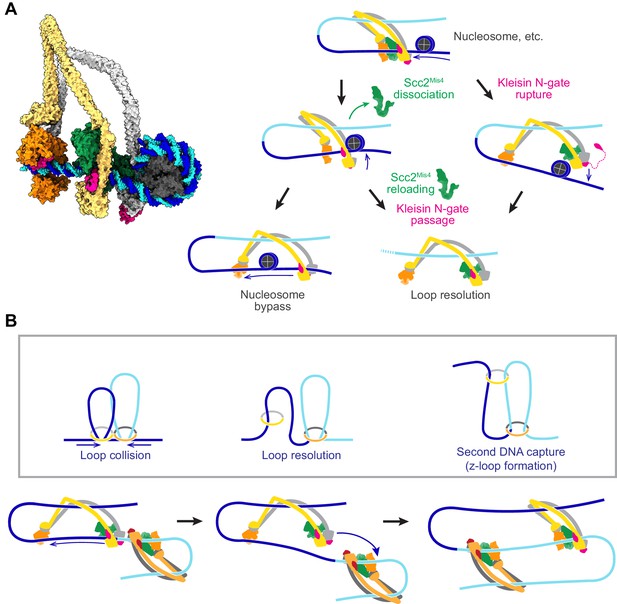
Possible outcomes of obstacle encounters.

(A) Structural model of cohesin in the slipping state encountering a nucleosome (left). Three possible outcomes are shown on the right. If the cohesin loader dissociates, an Scc3-hinge module stroke can achieve *Nucleosome bypass* before the next gripping state forms. Alternatively, cohesin loader dissociation and reloading opens a renewed opportunity for *Kleisin N-gate passage* by DNA, resulting in *Loop resolution*. The impact of a nucleosome collision might alternatively cause *Kleisin N-gate rupture*, which again results in *Loop resolution*. (B) A model for z-loop formation following head-on *Loop collision* of two loop extruding condensin complexes. One of the two condensins undergoes *Loop resolution*, by either kleisin N-gate passage or N-gate rupture. The now topologically bound condensin complex diffuses in search for a substrate for *Second DNA capture*, resulting in *z-loop formation*. During two-sided z-loop growth, depicted here, both in and outward pointing DNAs move through both condensin complexes. One is moved by each condensin’s Brownian ratchet, the other by the motion of the opposite condensin.

A possible path for nucleosome bypass opens up when the Scc2^Mis4 cohesin loader transiently dissociates. DNA now passes in and out of cohesin through the Scc3-Smc3-kleisin-N chamber (Figure 8A, Nucleosome bypass, and Figure 8—figure supplement 1A). If Scc3^Psc3 disengages from the SMC hinge in the slipping state, the clearance available for obstacle bypass further increases (Figure 8—figure supplement 1B). In the case of topologically loaded cohesin, the same channel is in principle wide enough to allow nucleosome bypass, albeit denser nucleosome arrays block purely diffusive cohesin sliding (Stigler et al., 2016). During loop extrusion, on one hand, Brownian ratchet-driven directional cohesin movement will facilitate nucleosome bypass. On the other hand, only one DNA lies in the Scc3-Smc3-kleisin-N chamber following topological loading, but both in and outward pointing DNAs must be accommodated during loop extrusion. If both DNAs are histone-bound, especially if these histones form part of higher order structures, considerable steric constraints will be encountered that likely slow down or stop loop extrusion.

An alternative outcome of cohesin-nucleosome collisions is therefore that loop extrusion at least temporarily stalls. As the cohesin loader dissociates, DNA is released from the Scc2-head module and free to move within the Scc3-Smc3-kleisin-N chamber. As Scc2^Mis4 rejoins the complex, there is a new chance for kleisin N-gate passage during gripping state formation, as originally foreseen during topological loading (Figure 8A, Kleisin N-gate passage). If this occurs, the DNA loop resolves following ATP hydrolysis, resulting in cohesin topologically embracing one DNA.

There might be yet another possible outcome of cohesin-nucleosome encounters. Given the thrust of a diffusion-mediated collision between cohesin and an obstacle, the closed kleisin N-gate might rupture (Figure 8A, Kleisin N-gate rupture). If this happens, the extruded DNA loop will again resolve, resulting in cohesin topologically embracing one DNA. One can imagine that frequent stalling on a nucleosome-dense chromatin template prevents processive loop extrusion. The encountered obstacles could be seen as triggering a ‘proofreading’ mechanism, prompting recurring attempts at kleisin-N gate passage, eventually resulting in successful topological cohesin loading.

Z-loop formation by SMC ring complexes

Chromosomal cohesin loading sites lie at considerable distances from each other (Schmidt et al., 2009). Nevertheless, we cannot outright dismiss the possibility that loop extruding cohesin complexes might collide in head-on encounters. In vitro observations of colliding, loop-extruding condensins have revealed that these complexes are able to traverse each other to form distinctive z-loop structures (Kim et al., 2020). Can this behavior be explained by our molecular model of SMC complex function? Upon encounter, condensins have been observed to pause for a period of time. This is consistent with the behavior of two Brownian ratchets that collide (Figure 8B, Loop collision). A way out of this conflict is provided by one of the above-mentioned loop resolution pathways, kleisin N-gate passage or N-gate rupture. Both allow one of the colliding condensins to resolve their loop and turn into a topologically loaded condensin (Figure 8B, Loop resolution). The newly gained freedom of movement of the now singly tethered condensin allows it to diffuse. If, akin to how cohesin entraps a second single-stranded DNA (Murayama et al., 2018), condensin engages with a second double-stranded DNA that lies beyond the colliding condensin complex, a z-loop is formed (Figure 8B, second DNA capture). Various outcomes have been observed during z-loop formation in vitro, including one- and two-sided z-loop growth. It is possible to explain both behaviors if we assume that second DNA capture during z-loop formation results in either topological capture of the second DNA or results in the second DNA entering loop extrusion mode.

Discussion

Here, we use structures of a nucleotide-bound DNA gripping state (Higashi et al., 2020; Shi et al., 2020) as the starting point to develop a molecular framework for DNA entry into the cohesin ring, as well as to show how a subtle but important difference in the starting topology turns this gripping state into a Brownian ratchet that can fuel loop extrusion. The resulting model of cohesin function is able to explain numerous experimentally observed features of both topological loading and loop extrusion and makes a number of testable predictions.

Use of the energy from ATP binding and hydrolysis during topological entry

Any model of cohesin function must explain how the energy from ATP binding and hydrolysis is used to fuel or regulate its activities. ATP binding leads to SMC head engagement and to a conformational change at the Smc3^Psm3 neck that favors kleisin N-gate opening (Higashi et al., 2020; Muir et al., 2020). However, kleisin N-gate opening might not be hard-wired and it is possible that head engagement occurs sometimes without kleisin N-gate opening (see below). Head engagement creates a composite DNA binding surface on top of the ATPase heads. The next steps in cohesin’s reaction cycle are now likely driven by the binding energy of DNA itself. First, DNA establishes contact with the extensive positively charged surface on the ATPase heads. Next, the DNA engages Scc2^Mis4, which turns into its gripping state conformation as its own positive charges embrace the DNA. Together, the DNA and cohesin loader also establish contact with and close the kleisin N-gate.

The DNA-induced Scc2^Mis4 conformational change creates a docking interface for Scc3^Psc3. The latter subunit joins the complex by concurrently binding the DNA, as well as by recruiting the SMC hinge. The binding energy released from these additional interactions compensates for the energetic cost of introducing a DNA bend, required to reach this configuration. Assembly of the energy-loaded gripping state is now complete; DNA has entered the cohesin ring through the kleisin N-gate. ATP hydrolysis now ensues, which dissolves the gripping state. However, dissolution equates to more than mere dispersal of the components. The geometric arrangement of the Scc3-hinge and Scc2-head modules means that diffusion-driven gripping state dissolution generates a swinging motion of the Scc3-hinge module that guides DNA through the head gate to complete topological entry into the cohesin ring.

Use of the energy from ATP binding and hydrolysis during loop extrusion

If DNA did not pass the kleisin N-gate, all other considerations for gripping state assembly remain unchanged. Again, gripping state dissolution initiates Brownian Scc3-hinge swinging motion. However, the kleisin prevents head gate passage, instead resulting in DNA slippage along the Scc2-head module and the initiation of a DNA loop. Based on the observed DNA path, DNA binding to the Scc3-hinge and Scc2-head modules has already introduced a roughly 120° DNA bend in the gripping state. This bend must mature into a 180° turn that fits through the approximately 23 nm clearance of the Scc3-Smc3-kleisin-N chamber. DNA spontaneously adopts narrow bends (Vafabakhsh and Ha, 2012) and DNA thermal fluctuations might suffice for loop extrusion to commence, possibly after a certain delay. We cannot exclude that additional mechanisms or DNA-protein contacts contribute to loop initiation, a process that remains to be experimentally examined. Once a DNA loop is formed, its extension is energetically favorable as the loop radius increases. The energetic cost of reducing the loop radius again decreases the chance that a DNA loop slips back, once formed.

A key feature that determines the processivity of the Brownian ratchet is the half-life of the Scc3-hinge module interaction with DNA following the gripping to slipping state transition. This interaction should last long enough to guide directed diffusion but short enough so that DNA is released before the next gripping state forms. Given the stochastic nature of Scc3-hinge module dissociation from, and possible re-association with the DNA, we expect that not all loop extrusion cycles result in productive loop size gain, a fact that might contribute to the wide spread of observed loop extrusion rates. The corresponding component of the Scc3-hinge module in the condensin complex is its putative Ycg1-hinge module. Experiments with condensin harboring a DNA binding site mutation in the Ycg1-hinge module revealed greatly compromised loop extrusion (Ganji et al., 2018), consistent with an important role of this element.

Biological motors typically couple ATP-dependent conformational changes to their motion, allowing for robust movements in the presence of counteracting forces (Howard, 2001). We cannot exclude the possibility that cohesin also uses an ATP-dependent mechanism to control the relative positions of the Scc3-hinge and Scc2-head modules. For example SMC coiled coil stiffness could store torsional energy during gripping state formation that is released following ATP hydrolysis to add a power stroke to loop extrusion. However, SMC coiled coils appear very flexible (Eeftens et al., 2016; Ryu et al., 2020a) and as yet there is no evidence for energy coupling between the ATPase heads and hinge. Our computational simulations suggest that a purely diffusion-driven Brownian ratchet recapitulates experimental observations well. In this scenario, the energy from ATP binding and hydrolysis operates a Brownian ratchet, while thermal energy moves the DNA.

Bulk solution measurements suggested that cohesin undergoes on average approximately one ATP hydrolysis cycle per second in the presence of the cohesin loader and DNA. In contrast, our simulations predict that ATP hydrolysis cycles must happen an order of magnitude faster for the Brownian ratchet to reach experimentally observed loop extrusion speeds. These observations are not necessarily incompatible if complex formation between cohesin, the cohesin loader and DNA is a rate-limiting step. In a typical bulk cohesin loading reaction, approximately 20% of DNA is captured by cohesin within an hour of incubation (Murayama and Uhlmann, 2014). This illustrates that gripping state formation is likely a slow process in solution. ATP hydrolysis rates might well be substantially greater than average, once a protein-DNA assembly has formed.

The importance of kleisin N-gate passage

A conserved kleisin N-tail interacts with DNA to ensure kleisin N-gate passage during gripping state formation (Higashi et al., 2020). Why then might kleisin N-gate passage sometimes fail, resulting in loop extrusion? A potentially relevant observation is that the biochemical reconstitution of both topological cohesin loading onto DNA (Murayama and Uhlmann, 2014), as well as DNA loop extrusion (Ganji et al., 2018), are helped by unphysiologically low-salt concentrations. Electrostatic interactions between DNA and cohesin, which characterize the gripping state, are stronger when less salt competes with them in the incubation buffer. While enhanced DNA-protein contacts likely promote the biochemical reactions, the low ionic strength will also affect protein-protein interactions. For instance, electrostatic interactions contribute to keeping the kleisin N-gate shut, which are augmented in a low salt buffer and could impede N-gate opening. The boosted efficiency of gripping state formation at low-salt concentrations might thus come at the cost of an increased fraction of failed topological entry events.

Even if kleisin N-gate passage is disfavored in a low-salt environment, recurrent cohesin loader dissociation and reassociation events during loop extrusion might eventually permit successful N-gate passage. This outcome would result in topological cohesin loading onto DNA and loop resolution, similar to what we envision might happen when loop extrusion meets an obstacle. How easily the fate of DNA with respect to the kleisin N-gate changes once loop extrusion has started will be important to explore.

Alternative molecular models of DNA loop extrusion

How does our Brownian ratchet model compare to previously proposed models for DNA loop extrusion? The first proposed, tethered inchworm model (Nichols and Corces, 2018), also features the two HEAT repeat subunits as DNA binding elements that perform a scissoring motion while remaining connected by a flexible kleisin linker. Instead of forming head and hinge modules, the HEAT subunits associate with one of the two ATPase heads, each. The HEAT subunit DNA affinity is postulated to change during the ATP hydrolysis cycle such that force from ATP head engagement and resolution is transferred to move DNA. The SMC hinge in turn is tacitly assumed to act as a second DNA anchor, thereby achieving asymmetric DNA loop extrusion. The authors suggest that obstacle bypass is possible in a stepping motion, as the HEAT subunits alternatingly reduce their DNA affinity. In retrospect, the tethered inchworm model shares several components of our Brownian ratchet. A main difference is that its deterministic nature should achieve a defined loop extrusion speed, even against small counteracting forces.

The DNA segment capture model makes use of one major DNA binding site at the ATPase heads (Marko et al., 2019), not too dissimilar to the Scc2-head module of our Brownian ratchet. A key difference is that the head module in the segment capture model exerts a power stroke that alters the angle at which the DNA intersects with the SMC complex, thereby initiating DNA looping or promoting loop growth. After the power stroke, DNA affinity at the head module changes following ATP hydrolysis, again not too dissimilar to our Brownian ratchet. Evidence for the proposed power stroke, as well as for the required mechanism by which DNAs change place between hinge and heads between cycles, remains to be sought.

Finally, the scrunching model is similar to our Brownian ratchet in that thermal fluctuations between DNA binding sites at the head and hinge form the basis for loop formation and loop growth (Ryu et al., 2020a). However, the DNA trajectories in the two models show opposite polarity. The scrunching model foresees DNA capture by the SMC hinge in the unfolded state and DNA release in the folded state. This requires at least two regulated DNA binding sites, in addition to which the HEAT repeat subunits are thought to form a static DNA anchor. This contrasts with our proposed ratchet where DNA is caught in the folded state and released after unfolding, and where the HEAT subunits are the two dynamic components that control DNA motion.

Molecular models of topological DNA entry into the cohesin ring

Our model for cohesin function also makes a molecular proposal for how DNA topologically enters the cohesin ring by sequential passage through the kleisin N-gate and then the ATPase head gate in a top-down direction (Figure 8—figure supplement 2). DNA arrival from the top is experimentally supported by DNA-protein crosslink mass spectrometry data and by the fact that covalent closure of the ATPase head gate does not block gripping state formation (Higashi et al., 2020). Despite this, an alternative model for DNA entry into the cohesin ring was proposed, in which DNA entry starts by bottom-up passage through the ATPase head gate (Collier et al., 2020; Shi et al., 2020). While this latter model left open the question how topological entry might be completed, an apparent argument for bottom-up DNA passage through the head gate came from experiments to locate the DNA using chemical crosslinkers. Immediately upon cohesin addition to DNA, before topological loading becomes detectable, the DNA takes up a position in which crosslinkers can trap it within what have been termed engaged-SMC and engaged-kleisin compartments (Figure 8—figure supplement 2; Collier et al., 2020), a position that can be reached by bottom-up passage through the ATPase head gate. Our model offers an alternative explanation for this positioning. If we imagine DNA approaching from the top, between the SMC coiled coils, it might frequently pass the disengaged ATPase heads, top-down, before the relatively infrequent ATP-dependent series of head engagement and kleisin N-gate opening commences. This approach results in an equivalent DNA topology following crosslinking.

On the origin of loop extrusion

Could SMC complexes have evolved to be loop extruding Brownian ratchets? If the primordial function of SMC complexes was that of loop extruders, we should expect the loop extrusion mechanism to be conserved in evolutionary ancient SMC complexes. Our model of loop extrusion suggests that cohesin’s DNA-interacting HEAT repeat subunits are key components of the Brownian ratchet. These HEAT repeat subunits are relatively modern additions to SMC complexes. Evolutionarily older SMC complexes that are reflected in today’s prokaryotic SMC complexes, as well as in the Smc5-Smc6 complex, contain in place of HEAT subunits two smaller kleisin interacting tandem winged helix elements (Kite) (Palecek and Gruber, 2015). While Kite subunits interact with DNA (Zabrady et al., 2016), they show important differences from how HEAT subunits are incorporated into SMC complexes. Kite subunits bind in close proximity to each other to a relatively short kleisin unstructured region (Woo et al., 2009; Bürmann et al., 2013; Jo et al., 2021). This observation makes it hard to imagine that a similar ratchet mechanism, which requires the DNA binding modules to separate from each other, operates in SMC-kite complexes. In vitro DNA loop extrusion by SMC-kite complexes has not yet been observed, while the molecular basis for SMC-dependent chromatin proximities in B. subtilis, attributed to loop extrusion (Wang et al., 2018), remains to be fully understood. Further biochemical investigations of SMC-Kite complexes (Kanno et al., 2015; Niki and Yano, 2016) will provide necessary insight into the question whether these complexes act by topologically loading onto DNA or by DNA loop extrusion.

Implications for in vivo loop extrusion

Cohesin topologically entraps DNA to promote sister chromatid cohesion (Haering et al., 2008). It is possible that kleisin N-gate passage is an error-prone event and that accidental failure of kleisin N-gate passage during a topological DNA loading attempt initiates DNA looping. A close-by obstacle would soon stall loop extrusion and allow proofreading in the form of kleisin N-gate passage or N-gate rupture to reinstate topological loading. This scenario portrays loop extrusion as an unwanted, and possibly rare, side effect of topological cohesin loading. Alternatively, was it a cunning evolutionary twist that allowed cohesin to add loop extrusion to its repertoire of DNA acrobatics?

An obvious challenge to DNA loop extrusion in vivo is the presence of histones and other DNA binding proteins. Our model predicts that obstacle bypass by loop extruding SMC complexes is possible, but also that obstacles reduce the speed and processivity of extrusion, especially when present at a high density on both the in- and outward pointing DNAs. Recent studies reported DNA compaction of histone-bound DNA by cohesin and condensin, but whether SMC complexes indeed bypassed histones in these experiments is not yet known (Kim et al., 2019; Kong et al., 2020). DNA loop extrusion was also observed in Xenopus egg extracts, but loop extrusion was detectable only following histone depletion (Golfier et al., 2020). Obstacle encounters during in vitro loop extrusion are an obvious and important area for experimental investigation.

Many cellular DNA transactions make use of histone chaperones and chromatin remodellers to navigate the nucleosome landscape. Indeed, in vitro reconstituted chromosome assembly using purified histones and condensin depends on the histone chaperone FACT (Shintomi et al., 2015). While FACT loosens histone-DNA interaction, this chaperone does not possess catalytic activity. FACT typically acts together with much slower-moving RNA or DNA polymerases. Whether FACT can facilitate nucleosome eviction by a Brownian ratchet remains to be explored. Other than FACT, ATP-dependent chromatin remodelers could aid in vivo loop extrusion. When studying the contribution of histone chaperones and chromatin remodelers, we have to keep in mind that topological cohesin and condensin loading onto chromosomes also requires free DNA access that these enzymes provide (Toselli-Mollereau et al., 2016; Garcia-Luis et al., 2019; Muñoz et al., 2019).

DNA loop extrusion by SMC complexes is a captivating molecular event that provides an at first sight intuitive explanation for chromosome loop formation. However, DNA extrusion is not the only explanation for loop formation. Cohesin and condensin could alternatively generate loops simply by sequential topological capture of two DNAs that come into proximity by Brownian motion, a mechanism that we refer to as diffusion capture (Cheng et al., 2015; Gerguri et al., 2021). When cohesin is depleted and re-supplied to human cells, small and large loops form with similar kinetics (Rao et al., 2017), a behavior that is more readily explained by a diffusion-mediated process than by gradual loop growth.

In addition to cohesin and condensin, weak diffusion-driven motors, chromosomes harbor abundant, strong DNA translocases in the form of RNA polymerases. These are known to push SMC complexes as they move along chromosomes during gene transcription (Lengronne et al., 2004; Davidson et al., 2016; Ocampo-Hafalla et al., 2016; Busslinger et al., 2017). We have suggested that, following loop formation by diffusion capture, RNA polymerases provide extrinsic motor activity that promotes loop expansion (Uhlmann, 2016). Such transcription-dependent extrinsic loop growth could explain chromatin domain features in an analogous fashion to cohesin moving on its own accord (Bailey et al., 2020). The role of RNA polymerase-dependent SMC complex movements in chromosome architecture deserves further attention.

Outlook

Our molecular proposal for SMC complex function informs the evaluation how topological loading onto DNA and loop extrusion by SMC complexes contribute to chromosome function. While topological loading and loop extrusion share many reaction steps, the two mechanisms also differ. The next challenge will be to exploit these differences to engineer SMC complexes that can topologically load onto DNA but not loop extrude, and vice versa. This will eventually enable genetic experiments that clarify the respective physiological contributions of topological loading and loop extrusion by SMC complexes.

Materials and methods

Key resources table

Reagent type (species) or resource	Designation	Source or reference	Identifiers	Additional information
Strain, strain background (S. cerevisiae)	MATa URA3::pGAL1-psm3-3Pk-7his/pGAL10-psm1, LEU2::pGAL1-rad21-HA-pps-protein A/pGAL10-7his-psc3, pep4Δ::HIS3	Murayama and Uhlmann, 2014	Y4443	Wild type cohesin purification
Strain, strain background (S. pombe)	pMis4-pps-protein A (LEU2), pSsl3(ura4+), h-, lue1-32, ura4-D18	Murayama and Uhlmann, 2014	Y4483	Mis4-Ssl3 purification
Strain, strain background (S. cerevisiae)	MATa URA3::pGAL1-psm3-3Pk-7his/pGAL10-psm1(R593-SNAP-P594), LEU2::pGAL1-rad21-HA-pps-protein A/pGAL10-7his-psc3-CLIP, pep4Δ::HIS3	This study		Smc1^Psm1hinge/Scc3^Psc3-C FRET construct purification
Strain, strain background (S. cerevisiae)	MATa URA3::pGAL1-psm3-3Pk-7his/pGAL10-psm1,LEU2::pGAL1-rad21-HA-pps-protein A/pGAL10-7his-psc3-CLIP, pep4Δ::HIS3	This study		Scc3^Psc3-C(CLIP) FRET construct purification
Strain, strain background (S. cerevisiae)	MATa URA3::pGAL1-psm3-3Pk-7his/pGAL10-psm1,LEU2::pGAL1-rad21-HA-pps-protein A/pGAL10-7his-psc3-SNAP, pep4Δ::HIS3	This study		Scc3^Psc3-C(SNAP) FRET construct purification
Strain, strain background (S. pombe)	pCLIP-Mis4 N191-pps-protein A (LEU2), h-, lue1-32, ura4-D18	This study		Scc2^Mis4(N191)-N FRET construct purification
Antibody	anti-V5(Pk) (Mouse monoclonal)	Bio-Rad	Cat# MCA1360	(1:20,000)
Antibody	anti-HA (Mouse monoclonal)	Sigma-Aldrich	Cat# 11583816001	(1:20,000)
Antibody	Anti-mouse IgG-HRP (Sheep polyclonal)	GE Healthcare	Cat# NXA931	(1:20,000)
Antibody	Anti-Digoxigenin-AP, Fab fragments (Sheep polyclonal)	Roche	Cat# 11093274910	(1:30)
Recombinant DNA reagent	Lambda DNA	New England BioLabs	Cat# N3013L
Chemical compound, drug	SNAP-Surface Alexa Fluor 647	New England BioLabs	Cat# S9136S
Chemical compound, drug	CLIP-Surface 547	New England BioLabs	Cat# S9233S
Chemical compound, drug	SYBR Gold Nucleic Acid Gel Stain	ThermoFisher	Cat# S11494
Chemical compound, drug	ATP	Sigma-Aldrich	Cat# A2383
Chemical compound, drug	ADP	Sigma-Aldrich	Cat# A2754
Chemical compound, drug	Beryllium sulfate tetrahydrate	VWR international LTD	Cat# 16104.14
Chemical compound, drug	Sodium fluoride 0.5 M Solution	Sigma-Aldrich	Cat# 67414–1 ML-F
Chemical compound, drug	Dynabeads Protein A	ThermoFisher	Cat#10002D
Chemical compound, drug	Protease K	TaKaRa	Cat# 9034
Chemical compound, drug	Pluronic F127	Sigma-Aldrich	Cat# P2443
Chemical compound, drug	β-Casein from bovine milk	Sigma-Aldrich	Cat# C6905
Chemical compound, drug	DIG-11-dUTP	Jena Bioscience	NU-803-DIGXS
Chemical compound, drug	SYTOX Orange Nucleic Acid Stain	Invitrogen	Cat# S11368
Software, algorithm	UCSF ChimeraX	https://www.cgl.ucsf.edu/chimerax/
Software, algorithm	PyMOL	https://pymol.org/2/
Software, algorithm	SWISS-MODEL	https://swissmodel.expasy.org
Software, algorithm	CCBuilder 2.0	http://coiledcoils.chm.bris.ac.uk/ccbuilder2/builder
Software, algorithm	Fiji Image J	https://imagej.net/Fiji

Molecular model of the cohesin complex

Request a detailed protocol

The molecular model of cohesin in this study is based on our cryo-EM structure of the fission yeast cohesin complex together with its loader in the nucleotide-bound DNA gripping state (PDB: 6YUF) (Higashi et al., 2020). A molecular model of the fission yeast SMC hinge domain was obtained based on a mouse cohesin hinge crystal structure as a template (PDB:2WD5) (Kurze et al., 2011) using SWISS-MODEL (Waterhouse et al., 2018). Scc3^Psc3 with the kleisin middle region, bound to DNA, was modeled based on a crystal structure of the corresponding budding yeast components (PDB: 6H8Q) (Li et al., 2018). The hinge and Scc3^Psc3 were manually placed so that they align with the respective positions of the SMC hinge and Scc3^SA1 in the cryo-EM structure of human cohesin in the gripping state (PDB: 6WG3) (Shi et al., 2020). The indicative position of Scc3^Psc3 in the fission yeast structure, shown for comparison, was estimated based on distance constraints from a protein crosslink mass spectrometry dataset and guided by the negative staining EM density (Higashi et al., 2020). The coiled coils emanating from the ATPase heads were extended toward the SMC hinge using modeled Smc1^Psm1 and Smc3^Psm3 coiled coil segments, built based on their amino acid sequence using CCbuilder2.0 (Wood and Woolfson, 2018). The elbow positions in Smc1^Psm1 and Smc3^Psm3 were previously identified (Higashi et al., 2020).

To build a molecular model of cohesin in the post-hydrolysis slipping state, Scc2^Mis4 and the Smc3^Psm3 head domain were replaced with models of the same elements in new conformational forms, corresponding to previously observed free crystal structure states, as described (Gligoris et al., 2014; Kikuchi et al., 2016; Higashi et al., 2020). To model Brownian motion of the Scc3-hinge module relative to the Scc2-head module, Scc3^Psc3 with the kleisin middle region and DNA together with the SMC hinge were considered to be one rigid body. The position of this Scc3-hinge module was then developed using a swinging motion of the SMC coiled coils with the inflection point at their elbows.

The molecular model of a nucleosome is based on the crystal structure of a human nucleosome (PDB: 3AFA) (Tachiwana et al., 2010). All structural figures were prepared using Pymol (Schrödinger) and ChimeraX (Goddard et al., 2018).

Protein purification and labeling

Request a detailed protocol

For the construction of cohesin complexes harboring FRET reporters, SNAP- and CLIP-tag sequences were introduced into the YIplac211-Psm1-Psm3 and YIplac128-Rad21-Psc3 budding yeast expression vectors, as well as the pMis4(N191)-PA fission yeast expression vector that were previously described (Murayama and Uhlmann, 2014; Chao et al., 2015; Higashi et al., 2020). For labeling the Psm1 hinge, the SNAP tag sequence was inserted between Psm1 amino acids R593 and P594. Psc3 was fused to the SNAP or CLIP tag sequence at its C-terminus. For labeling Mis4, the CLIP tag sequence preceded the Mis4(N191) N-terminus. All proteins were purified and labeled with BG-surface Alexa 647 and BC-surface Dy547 dyes (New England Biolabs) as previously described (Murayama and Uhlmann, 2014; Higashi et al., 2020). The absorbance spectra of the labeled proteins were recorded between 220–800 nm in 1 nm increments using a V-550 Spectrophotometer (Jasco). The concentrations of protein, Dy547 and Alexa 647 were determined from the absorbance at 280, 550, and 650 nm, respectively, and the labeling efficiencies calculated (assuming molar extinction coefficient (ε) for Dy547 and Alexa 647 of 150,000 M⁻¹ cm⁻¹ and 270,000 M⁻¹ cm⁻¹, respectively). Topological DNA loading assays to confirm the biochemical activity of the cohesin fluorophore fusions were performed as previously described (Higashi et al., 2020).

Bulk FRET measurements

Request a detailed protocol

Bulk FRET measurement were performed as previously described (Higashi et al., 2020), with minor modifications. All fluorescence measurements were carried out in reaction buffer (35 mM Tris-HCl pH 7.5, 0.5 mM TCEP, 25 mM NaCl, 1 mM MgCl₂, 15% (w/v) glycerol and 0.003% (w/v) Tween 20). Forty μl of reaction mixtures containing 37.5 nM of the respective labeled cohesin, 100 nM Mis4-Ssl3 or 12.5 nM Dy547-labeled Mis4(N191) and 10 nM pBluescript KSII(+) as the DNA substrate were mixed and the reaction was started by addition of 0.5 mM ATP. Alternatively, 0.5 mM ADP and 0.5 mM BeSO₄ +10 mM NaF were included to generate the DNA gripping state. The reactions were incubated at 32°C for 20 min. The samples were then applied to a 384-well plate and fluorescence spectra were recorded at 25°C on a CLARIOstar Microplate Reader (BMG LABTECH). Samples were excited at 525 nm and emitted light was recorded between 560–700 nm in 0.5 nm increments. To evaluate FRET changes caused by cohesin’s conformational changes across different experimental conditions, we report relative FRET efficiency, I_A/(I_D + I_A), where I_D is the donor emission signal intensity at 565 nm resulting from donor excitation at 525 nm and I_A is the acceptor emission signal intensity at 665 nm resulting from donor excitation. To obtain a baseline of apparent FRET due to spectral overlap, we mixed singly Dy547 and Alexa 647-labeled cohesin at concentrations of 12.5 nM and 37.5 nM, respectively, to reflect the fluorophore stoichiometry of the double labeled complex.

Co-immunoprecipitation

Request a detailed protocol

100 nM cohesin labeled at the Psm1 hinge with Alexa 647, 100 nM Mis4∆N191 labeled at the N-terminus with Dy547, 10 nM pBluescript KSII (+) DNA and 0.5 mM ATP or 0.5 mM ADP/0.5 mM BeSO₄/10 mM NaF were incubated in 15 μl of reaction buffer at 32°C for 20 min, then diluted with 100 μl of reaction buffer. 5 μl of anti-Pk antibody (Bio-Rad, MCA1360)-bound Protein A conjugated magnetic beads were added to the reactions and rotated at 25°C for 10 min. The beads were washed twice with 500 μl of reaction buffer and the recovered proteins were analyzed by SDS-PAGE followed by in gel fluorescence detection, as well as immunoblotting with the indicated antibodies.

DNA loop extrusion by the fission yeast cohesin complex

Request a detailed protocol

Flow cells were assembled using a piece of parafilm in which a microfluidic channel (1.5 × 40 mm) was pre-cut, sandwiched between a glass slide and a salinized cover slip (Marienfeld, High-precision, 24 × 60 mm). Two holes were drilled in a glass slide and a metal tubing (New England Small Tube Corp) was glued using an epoxy glue (Devcon) to form an inlet and an outlet of the flow cell. Slides were cleaned by sequential 5 min sonication in ethanol, 1 M NaOH and purified water, then baked at 100°C for 10 min on a heating plate and finally plasma cleaned for 5 min. Cover slips were first cleaned by sequential sonication in acetone, ethanol, 0.1 M NaOH and purified water (5 min for each step), then blow-dried using compressed air and plasma cleaned for 5 min. Subsequently the cover slip surface was silanized by incubating for 1 hr in 5% dichlorodimethylsilane (Sigma-Aldrich) dissolved in heptane. Finally, cover slips were washed by 10 min sonication in chloroform followed by 10 min sonication in purified water and blow-dried using compressed air.

Flow cells were incubated with anti-Digoxigenin antibodies (Roche, 150U) diluted 30 times in PBS for 20 min and washed with 400 µl PBS. To prevent non-specific binding of DNA and proteins, the surface of the flow cell was passivated by incubating with Pluronic F127 (Sigma-Aldrich, 1% solution in PBS) for 10 min followed by PBS wash and incubating with β-Casein (Sigma-Aldrich, 10 mg/ml in PBS) for at least 1 hr. Subsequently the flow cell was washed with PBS and equilibrated with 50 µl of buffer W (0.1 mg/ml β-Casein in PBS). Forty µl of 10 pM of Digoxigenin-labeled λ-phage DNA in buffer W were introduced into the flow cell, incubated for 15 min and washed with 60 µl of buffer W at 4 µl/min using a syringe pump (Harvard Apparatus, Pico Plus Elite 11). The flow cell was further equilibrated with 150 µl of buffer R (40 mM Tris-HCl pH 7.5, 50 mM NaCl, 2 mM MgCl₂, 5 mM ATP, 10 mM DTT, 250 nM Sytox Orange, 0.2 mg/ml glucose oxidase, 35 µg/ml catalase and 4.5 mg/ml dextrose) at 15 µl/min. Fission yeast cohesin and cohesin loader were introduced at 5 nM and 10 nM concentration, respectively, in buffer R at 15 µl/min. Individual DNA molecules stained with Sytox Orange were imaged at two frames per second using a Nikon Eclipse Ti2 commercial TIRF microscope. Flow cells were illuminated with a 561 nm laser through a Nikon SR HP Apo TIRF 100x/1.49 oil immersion objective. Images were collected using a sCMOS camera (Photometrics, Prime 95B) and saved as TIFF files without compression for further analysis using FIJI ImageJ. All experiments were performed at room temperature.

λ-phage DNA was terminally labelled with Digoxigenin in a 50 µl reaction containing 0.25 mg/ml λ-phage DNA (NEB), DNA Taq polymerase (NEB), dATP, dCTP, dGTP (Promega), dUTP-Digoxigenin (Jena Bioscience) and 1X Standard Taq buffer (NEB). The mixture was incubated at 72°C for 30 min and cleaned up to remove unincorporated nucleotides using a spin-column (Bio-Rad, Micro Bio-Spin P30). The concentration of the final product was assessed by measuring absorbance at 260 nm using a Nanodrop ND1000 spectrophotometer. Digoxigenin-labelled λ-phage DNA was aliquoted and stored at −20°C.

Loop extrusion rates were determined using FIJI ImageJ software as described (Davidson et al., 2019). The length of each DNA molecule was manually measured before loop extrusion to convert distance in pixels into kbp. During loop extrusion the length of DNA not contained inside the loop was measured manually, converted into kbp and subtracted from the full length of Lambda DNA (48.5 kbp) to calculate the size of the DNA loop. The loop extrusion rate was determined as the slope of a linear fit to the experimental loop growth data.

Mathematical modeling of loop extrusion

DNA model

Request a detailed protocol

We based modeling of our DNA on a dssWLC model, as described in Koslover and Spakowitz, 2014. The DNA is defined by a sequence of beads with positions ${\vec{r}}_{i}$ and an orientation unit vector ${\vec{u}}_{i}$ attached to each bead. The energy for a particular chain configuration is given by:

E ({{\vec{r}}_{i}, {\vec{u}}_{i}}) = \sum_{i = 1}^{N} [\frac{ϵ_{b}}{2 ∆} {|{\vec{u}}_{i} - {\vec{u}}_{i - 1} - η {\vec{R}}_{i}^{⊥}|}^{2} + \frac{ϵ_{∥}}{2 ∆} {({\vec{R}}_{i} ∙ {\vec{u}}_{i - 1} - ∆ γ)}^{2} + \frac{ϵ_{⊥}}{2 ∆} {|{\vec{R}}_{i}^{⊥}|}^{2}]

where ${\vec{R}}_{i} = {\vec{r}}_{i} - {\vec{r}}_{i - 1}$ and ${\vec{R}}_{i}^{⊥} = {\vec{R}}_{i} - ({\vec{R}}_{i} ∙ {\vec{u}}_{i - 1}) {\vec{u}}_{i - 1}$ .

The DNA in this model is split into segments with contour length Δ. The model parameters $ϵ_{b}$ , $ϵ_{∥}$ , $ϵ_{⊥}$ , $γ$ and $η$ are unambiguous functions of Δ and polymer persistence length $l_{P}$ taken from Koslover and Spakowitz, 2013. For all our simulations we use Δ = 5 nm and $l_{P}$ = 50 nm.

Cohesin model

Request a detailed protocol

We generated a simplified model of cohesin using five beads representing the Smc1 and Smc3 heads, the Smc1 and Smc3 elbows as well as the hinge. Similar to DNA, each bead is defined by its position and orientation vectors (e.g. ${\vec{r}}_{S m c 3 h}$ , ${\vec{u}}_{S m c 3 h}$ for the Smc3 head, etc). We describe the interaction between hinge, elbow and the corresponding head beads via dssWLCs and the corresponding energy term is given by Equation (3). Based on the experimentally determined elbow position (Higashi et al., 2020; Bürmann et al., 2019), we choose contour length between the head and elbow to be 30 nm, while the contour length between the elbow and hinge is 20 nm. In order to determine the persistence length of the connecting coiled coil for our simulations, we sampled conformational states of cohesin alone as it transitions multiple times between slipping and gripping states. We found that at the persistence length $l_{C C} =$ 50 nm our simulations match the experimentally observed head-to-hinge distance distribution available for the condensin complex (Ryu et al., 2020b). A smaller persistence length for condensin’s coiled coil of $l_{C C} =$ 4 nm was previously reported (Eeftens et al., 2016), which included the flexible elbow region that is considered separately in our simulations.

The interaction between the Smc1 and Smc3 heads is treated differently because of their geometry. We describe their interaction with the same dssWLC approach, corrected for their positions and orientations. Interaction energy between the head domains is given by:

E_{H H} = \frac{{ξ ϵ}_{b}}{2 ∆} {|{\vec{u}}_{S m c 3 h} - {\vec{u}}_{S m c 1 h} - η {\vec{R}}_{i}^{∥}|}^{2} + \frac{ξ ϵ_{∥}}{2 ∆} {(|{\vec{R}}_{i}^{⊥}| - ∆)}^{2} + \frac{{ξ ϵ}_{⊥}}{2 ∆} {|{\vec{R}}_{i}^{∥}|}^{2}

where ${\vec{R}}_{i} = {\vec{r}}_{i} - {\vec{r}}_{i - 1}$ ; ${\vec{R}}_{i}^{∥} = ({\vec{R}}_{i} ∙ \vec{u}_{S m c 1 h}) {\vec{u}}_{S m c 1 h}$ and ${\vec{R}}_{i}^{⊥} = {\vec{R}}_{i} - {\vec{R}}_{i}^{∥}$ .

In Equation (4), we use the same set of parameters $ϵ_{b}$ , $ϵ_{∥}$ , $ϵ_{⊥}$ , $γ$ and $η$ as in Equation (3) for the SMC coiled coils. However, SMC heads are connected by the cohesin loader subunit, which provides unknown additional stiffness to this connection. To take this into account, we introduce an additional parameter $ξ$ . We find that as long as $ξ > 5$ , it does not noticeably affect our simulations. Therefore, for most simulations we used a value of $ξ = 10$ .

Interaction between cohesin and DNA

Request a detailed protocol

We introduce two separate energy terms describing interactions between DNA and the Smc3 head as well as DNA and the hinge:

E_{S m c 3 - D N A} = \frac{α}{2} {|{\vec{R}}_{⊥}|}^{2} + \frac{β}{2} {|\vec{n}|}^{2} + \frac{γ}{2} {|{\vec{r}}_{S m c 3 h} - {\vec{r}}_{i}|}^{2}

where ${\vec{R}}_{⊥}$ is the shortest distance between Smc3 and the center of the closest DNA bead,

\vec{n} = {\vec{u}}_{S m c 3 h} \times ({\vec{r}}_{S m c 1 h} - {\vec{r}}_{S m c 3 h}) / |{\vec{r}}_{S m c 1 h} - {\vec{r}}_{S m c 3 h}| - {\vec{u}}_{i}

where $i$ is the index of the DNA bead currently interacting with Smc3.

In Equation (5), the first two terms describe the slipping interaction between DNA and Smc3 which allows diffusion of DNA along the Smc3 head. The second term is introduced to take into account the orientation of DNA with respect to the orientation of cohesin. The third term describes a point-to-point gripping interaction. We assume $γ = 0$ in the slipping state.

The interaction between the DNA and the hinge is:

E_{H i n g e - D N A} = \frac{δ}{2} {|{\vec{r}}_{H i n g e} - {\vec{r}}_{j}|}^{2}

where $j$ is the index of the DNA bead currently interacting with the hinge.

Equation (5) and Equation (7) describe physical bonds between DNA and cohesin. Because these terms grow indefinitely with the relative distance between the two, they do not describe the dynamics of the bond breakage. In order to account for cohesin changes between gripping and slipping states, parameter $γ$ was changed to zero for the slipping state. The exact values of parameters $α, β, γ$ and $δ$ are inconsequential as they only affect the extent to which the relative distance between cohesin and the DNA fluctuate. We have chosen values of these parameters as a trade-off between minimizing fluctuations to within one spatial discretization step (5 nm) and improving algorithm convergence. A table with all model parameters and their changes between the computational gripping and slipping states can be found in Supplementary file 1.

3D Monte-Carlo simulations

Request a detailed protocol

Numerical calculations were carried out with the Metropolis method for Monte-Carlo simulation (Heermann, 1990). Briefly, random beads representing a DNA segment or a part of cohesin is chosen at each step and its position or orientation vectors are randomly modified. Position vectors are modified by adding a random 3D vector with each coordinate distributed evenly on a [-0.75:0.75] nm interval. Orientation vectors are rotated in random direction in 3D by an angle randomly distributed on [-0.8:0.8]. The new full energy of the system $E_{n e w}$ is calculated. If the new energy is lower than the previous value $E_{n e w}$ , the new state is accepted. If it is larger, the new state Boltzmann factor is calculated: $r = e^{- \frac{E_{n e w} - E_{o l d}}{k_{B} T}}$ and the new state is accepted if $r > p$ , where $p$ is drawn from a standard uniform distribution on the interval (0,1).

Simplified model of diffusion-based loop extrusion

Request a detailed protocol

In the simplified model for DNA loop extrusion, a DNA loop inside a cohesin molecule consists of N segments, each 5 nm in length. On each iteration of the algorithm, we consider all possible events that can happen to the system consisting of cohesin and a DNA loop inside. There are five types of events: 1. Random thermal movement of the inbound DNA at the Smc3 head (only possible in the slipping state), 2. Random thermal movement of the outbound DNA, 3. If the hinge is bound to DNA, DNA can move with the hinge if cohesin changes its state from the folded gripping to the unfolded slipping state, or the other way around, 4. The hinge can bind/unbind DNA, 5. Cohesin can change state, from gripping to slipping state, or vice versa.

At each iteration, rate constants are calculated for all possible events. The rate constant of DNA diffusion is the rate at which one DNA segment moves one step forward or backward. It is given by:

k_{\pm} = \frac{D}{a^{2}}

where $D$ is the diffusion coefficient and $a = 5 n m$ length of the DNA segment.

Off-rate of hinge DNA unbinding:

k_{H i n g e} = \frac{1}{t_{D N A - h i n g e}}

where $t_{D N A - h i n g e}$ is the lifetime of DNA-hinge interaction defined in the main text.

We assume that the rates of slipping - > gripping and gripping - > slipping state conversion are the same:

k_{C o h e s i n} = \frac{1}{t_{e x t e n d e d}}

where $t_{e x t e n d e d}$ is the lifetime of the slipping state defined in the main text.

At a given iteration of the Monte Carlo simulation, we calculate a set of times at which each possible event stochastically occurs:

t_{i}^{(j)} = - l n (1 - r_{i}) / k_{i}

where $j$ is the current iteration, $i$ is the given event. $r_{i}$ is a uniformly distributed number on the interval (0,1), and $k_{i}$ the rate for event $i$ . Then we implement the event which has the smallest $t_{i}^{(j)}$ and modify the system based on which event occurred. The total time of the simulation is extended by $t_{i}^{(j)}$ .

Estimation of the diffusion-driven rate of cohesin unfolding

Request a detailed protocol

The simplest assumption about the nature of the cohesin transition from the folded gripping to the unfolded slipping state is that it is driven by diffusion only. The diffusion coefficient can be estimated as:

D = \frac{k_{B} T}{6 π η r}

where $η$ = 10⁻³ Pa·s is the viscosity of water and $r$ is the effective radius of the diffusing protein. The estimate of the time it takes to diffuse distance $x$ is:

t = \frac{< x^{2} >}{2 D}

The size of the protein is related to its molecular weight. Given cohesin’s irregular shape, the diffusion can be better estimated based on the actual size of the protein. Using a size of ~ 20 nm for the Scc3-hinge and Scc2-head modules, we get a conservative estimate of ~ 0.1 ms for the time it will take the modules to separate by diffusion ~ 50 nm.

Data and software availability

Request a detailed protocol

All data generated in this study are included in the manuscript. Materials and resources described in this manuscript will be made available by the authors upon reasonable request. The code used for the molecular-mechanical simulation of behavior and DNA loop extrusion is available in the GitHub repository (https://github.com/FrancisCrickInstitute/CohesinModel, copy archived at swh:1:rev:62d9088238066810feb6a98e56cc0940fd4943d1, Higashi, 2021).

Data availability

The code used for the computational simulations of the cohesin-DNA complex is available in the github repository (https://github.com/FrancisCrickInstitute/CohesinModel (copy archived at https://archive.softwareheritage.org/swh:1:rev:62d9088238066810feb6a98e56cc0940fd4943d1)).

References

1. Ainavarapu SR
2. Brujic J
3. Huang HH
4. Wiita AP
5. Lu H
6. Li L
7. Walther KA
8. Carrion-Vazquez M
9. Li H
10. Fernandez JM
(2007) Contour length and refolding rate of a small protein controlled by engineered disulfide bonds
Biophysical Journal 92:225–233.
https://doi.org/10.1529/biophysj.106.091561
- PubMed
- Google Scholar
(2002) Condensin and cohesin display different arm conformations with characteristic hinge angles
Journal of Cell Biology 156:419–424.
https://doi.org/10.1083/jcb.200111002
- Google Scholar
Preprint
1. Bailey MLP
2. Surovtsev I
3. Williams JF
4. Yan H
5. Mochrie SGJ
6. King MC
(2020) Nucleosome-constrained loop extrusion model for the origin of topologically associating domains
bioRxiv.
https://doi.org/10.1101/2020.02.29.969683
- Google Scholar
1. Bürmann F
2. Shin HC
3. Basquin J
4. Soh YM
5. Giménez-Oya V
6. Kim YG
7. Oh BH
8. Gruber S
(2013) An asymmetric SMC-kleisin bridge in prokaryotic condensin
Nature Structural & Molecular Biology 20:371–379.
https://doi.org/10.1038/nsmb.2488
- PubMed
- Google Scholar
1. Bürmann F
2. Lee BG
3. Than T
4. Sinn L
5. O'Reilly FJ
6. Yatskevich S
7. Rappsilber J
8. Hu B
9. Nasmyth K
10. Löwe J
(2019) A folded conformation of MukBEF and cohesin
Nature Structural & Molecular Biology 26:227–236.
https://doi.org/10.1038/s41594-019-0196-z
- PubMed
- Google Scholar
(2017) Cohesin is positioned in mammalian genomes by transcription, CTCF and wapl
Nature 544:503–507.
https://doi.org/10.1038/nature22063
- PubMed
- Google Scholar
(2000) Single-molecule studies of DNA mechanics
Current Opinion in Structural Biology 10:279–285.
https://doi.org/10.1016/S0959-440X(00)00085-3
- PubMed
- Google Scholar
(2015) The ATPases of cohesin interface with regulators to modulate cohesin-mediated DNA tethering
eLife 4:e11315.
https://doi.org/10.7554/eLife.11315
- PubMed
- Google Scholar
1. Chao WC
2. Murayama Y
3. Muñoz S
4. Costa A
5. Uhlmann F
6. Singleton MR
(2015) Structural studies reveal the functional modularity of the Scc2-Scc4 cohesin loader
Cell Reports 12:719–725.
https://doi.org/10.1016/j.celrep.2015.06.071
- PubMed
- Google Scholar
1. Cheng TM
2. Heeger S
3. Chaleil RA
4. Matthews N
5. Stewart A
6. Wright J
7. Lim C
8. Bates PA
9. Uhlmann F
(2015) A simple biophysical model emulates budding yeast chromosome condensation
eLife 4:e05565.
https://doi.org/10.7554/eLife.05565
- PubMed
- Google Scholar
1. Ciosk R
2. Shirayama M
3. Shevchenko A
4. Tanaka T
5. Toth A
6. Shevchenko A
7. Nasmyth K
(2000) Cohesin's binding to chromosomes depends on a separate complex consisting of Scc2 and Scc4 proteins
Molecular Cell 5:243–254.
https://doi.org/10.1016/S1097-2765(00)80420-7
- PubMed
- Google Scholar
1. Collier JE
2. Lee B-G
3. Roig MB
4. Yatskevich S
5. Petela NJ
6. Metson J
7. Voulgaris M
8. Gonzalez Llamazares A
9. Löwe J
10. Nasmyth KA
(2020) Transport of DNA within cohesin involves clamping on top of engaged heads by Scc2 and entrapment within the ring by Scc3
eLife 9:e59560.
https://doi.org/10.7554/eLife.59560
- Google Scholar
(2016) Rapid movement and transcriptional re-localization of human cohesin on DNA
The EMBO Journal 35:2671–2685.
https://doi.org/10.15252/embj.201695402
- PubMed
- Google Scholar
1. Davidson IF
2. Bauer B
3. Goetz D
4. Tang W
5. Wutz G
6. Peters JM
(2019) DNA loop extrusion by human cohesin
Science 366:1338–1345.
https://doi.org/10.1126/science.aaz3418
- PubMed
- Google Scholar
1. Eeftens JM
2. Katan AJ
3. Kschonsak M
4. Hassler M
5. de Wilde L
6. Dief EM
7. Haering CH
8. Dekker C
(2016) Condensin Smc2-Smc4 dimers are flexible and dynamic
Cell Reports 14:1813–1818.
https://doi.org/10.1016/j.celrep.2016.01.063
- PubMed
- Google Scholar
1. Ganji M
2. Shaltiel IA
3. Bisht S
4. Kim E
5. Kalichava A
6. Haering CH
7. Dekker C
(2018) Real-time imaging of DNA loop extrusion by condensin
Science 360:102–105.
https://doi.org/10.1126/science.aar7831
- PubMed
- Google Scholar
1. Garcia-Luis J
2. Lazar-Stefanita L
3. Gutierrez-Escribano P
4. Thierry A
5. Cournac A
6. García A
7. González S
8. Sánchez M
9. Jarmuz A
10. Montoya A
11. Dore M
12. Kramer H
13. Karimi MM
14. Antequera F
15. Koszul R
16. Aragon L
(2019) FACT mediates cohesin function on chromatin
Nature Structural & Molecular Biology 26:970–979.
https://doi.org/10.1038/s41594-019-0307-x
- PubMed
- Google Scholar
1. Gerguri T
2. Fu X
3. Kakui Y
4. Khatri BS
5. Barrington C
6. Bates PA
7. Uhlmann F
(2021) Comparison of loop extrusion and diffusion capture as mitotic chromosome formation pathways in fission yeast
Nucleic Acids Research 49:1294–1312.
https://doi.org/10.1093/nar/gkaa1270
- PubMed
- Google Scholar
1. Gligoris TG
2. Scheinost JC
3. Bürmann F
4. Petela N
5. Chan KL
6. Uluocak P
7. Beckouët F
8. Gruber S
9. Nasmyth K
10. Löwe J
(2014) Closing the cohesin ring: structure and function of its Smc3-kleisin interface
Science 346:963–967.
https://doi.org/10.1126/science.1256917
- PubMed
- Google Scholar
1. Goddard TD
2. Huang CC
3. Meng EC
4. Pettersen EF
5. Couch GS
6. Morris JH
7. Ferrin TE
(2018) UCSF ChimeraX: meeting modern challenges in visualization and analysis
Protein Science 27:14–25.
https://doi.org/10.1002/pro.3235
- PubMed
- Google Scholar
1. Golfier S
2. Quail T
3. Kimura H
4. Brugués J
(2020) Cohesin and condensin extrude DNA loops in a cell cycle-dependent manner
eLife 9:e53885.
https://doi.org/10.7554/eLife.53885
- PubMed
- Google Scholar
(1997) A direct link between sister chromatid cohesion and chromosome condensation revealed through the analysis of MCD1 in S. cerevisiae
Cell 91:47–57.
https://doi.org/10.1016/S0092-8674(01)80008-8
- PubMed
- Google Scholar
(2008) The cohesin ring concatenates sister DNA molecules
Nature 454:297–301.
https://doi.org/10.1038/nature07098
- PubMed
- Google Scholar
1. Hara K
2. Zheng G
3. Qu Q
4. Liu H
5. Ouyang Z
6. Chen Z
7. Tomchick DR
8. Yu H
(2014) Structure of cohesin subcomplex pinpoints direct shugoshin-Wapl antagonism in centromeric cohesion
Nature Structural & Molecular Biology 21:864–870.
https://doi.org/10.1038/nsmb.2880
- PubMed
- Google Scholar
Book
1. Heermann DW
(1990) Computer-simulation methods
In: Heermann D. W, editors. Computer Simulation Methods in Theoretical Physics. Springer. pp. 8–12.
https://doi.org/10.1007/978-3-642-75448-7
- Google Scholar
1. Higashi TL
2. Eickhoff P
3. Sousa JS
4. Locke J
5. Nans A
6. Flynn HR
7. Snijders AP
8. Papageorgiou G
9. O'Reilly N
10. Chen ZA
11. O'Reilly FJ
12. Rappsilber J
13. Costa A
14. Uhlmann F
(2020) A Structure-Based mechanism for DNA entry into the cohesin ring
Molecular Cell 79:917–933.
https://doi.org/10.1016/j.molcel.2020.07.013
- PubMed
- Google Scholar
Software
1. Higashi TL
(2021) CohesinModel, version swh:1:rev:62d9088238066810feb6a98e56cc0940fd4943d1
Software Heritage.

https://archive.softwareheritage.org/swh:1:rev:62d9088238066810feb6a98e56cc0940fd4943d1
1. Hirano T
(2016) Condensin-Based chromosome organization from Bacteria to vertebrates
Cell 164:847–857.
https://doi.org/10.1016/j.cell.2016.01.033
- PubMed
- Google Scholar
Book
1. Howard J
(2001)
Mechanics of Motor Proteins and the Cytoskeleton

Sinauer Associates.
- Google Scholar
(2014) Characterization of a DNA exit gate in the human cohesin ring
Science 346:968–972.
https://doi.org/10.1126/science.1256904
- PubMed
- Google Scholar
1. Jo A
2. Li S
3. Shin JW
4. Zhao X
5. Cho Y
(2021) Structure basis for shaping the Nse4 protein by the Nse1 and Nse3 dimer within the Smc5/6 complex
Journal of Molecular Biology 433:166910.
https://doi.org/10.1016/j.jmb.2021.166910
- PubMed
- Google Scholar
(2016) Cohesin acetylation and Wapl-Pds5 oppositely regulate translocation of cohesin along DNA
The EMBO Journal 35:2686–2698.
https://doi.org/10.15252/embj.201695756
- PubMed
- Google Scholar
(2015) The Smc5/6 complex is an ATP-Dependent intermolecular DNA linker
Cell Reports 12:1471–1482.
https://doi.org/10.1016/j.celrep.2015.07.048
- PubMed
- Google Scholar
1. Kikuchi S
2. Borek DM
3. Otwinowski Z
4. Tomchick DR
5. Yu H
(2016) Crystal structure of the cohesin loader Scc2 and insight into cohesinopathy
PNAS 113:12444–12449.
https://doi.org/10.1073/pnas.1611333113
- PubMed
- Google Scholar
1. Kim Y
2. Shi Z
3. Zhang H
4. Finkelstein IJ
5. Yu H
(2019) Human cohesin compacts DNA by loop extrusion
Science 366:1345–1349.
https://doi.org/10.1126/science.aaz4475
- PubMed
- Google Scholar
(2020) DNA-loop extruding condensin complexes can traverse one another
Nature 579:438–442.
https://doi.org/10.1038/s41586-020-2067-5
- PubMed
- Google Scholar
1. Kong M
2. Cutts EE
3. Pan D
4. Beuron F
5. Kaliyappan T
6. Xue C
7. Morris EP
8. Musacchio A
9. Vannini A
10. Greene EC
(2020) Human condensin I and II drive extensive ATP-Dependent compaction of Nucleosome-Bound DNA
Molecular Cell 79:99–114.
https://doi.org/10.1016/j.molcel.2020.04.026
- PubMed
- Google Scholar
1. Koslover EF
2. Spakowitz AJ
(2013) Discretizing elastic chains for coarse-grained polymer models
Soft Matter 9:7016–7027.
https://doi.org/10.1039/c3sm50311a
- Google Scholar
1. Koslover EF
2. Spakowitz AJ
(2014) Multiscale dynamics of semiflexible polymers from a universal coarse-graining procedure
Physical Review E 90:013304.
https://doi.org/10.1103/PhysRevE.90.013304
- Google Scholar
1. Kurokawa Y
2. Murayama Y
(2020) DNA binding by the Mis4^Scc2loader promotes topological DNA entrapment by the cohesin ring
Cell Reports 33:108357.
https://doi.org/10.1016/j.celrep.2020.108357
- PubMed
- Google Scholar
1. Kurze A
2. Michie KA
3. Dixon SE
4. Mishra A
5. Itoh T
6. Khalid S
7. Strmecki L
8. Shirahige K
9. Haering CH
10. Löwe J
11. Nasmyth K
(2011) A positively charged channel within the Smc1/Smc3 hinge required for sister chromatid cohesion
The EMBO Journal 30:364–378.
https://doi.org/10.1038/emboj.2010.315
- PubMed
- Google Scholar
1. Lengronne A
2. Katou Y
3. Mori S
4. Yokobayashi S
5. Kelly GP
6. Itoh T
7. Watanabe Y
8. Shirahige K
9. Uhlmann F
(2004) Cohesin relocation from sites of chromosomal loading to places of convergent transcription
Nature 430:573–578.
https://doi.org/10.1038/nature02742
- PubMed
- Google Scholar
1. Li Y
2. Muir KW
3. Bowler MW
4. Metz J
5. Haering CH
6. Panne D
(2018) Structural basis for Scc3-dependent cohesin recruitment to chromatin
eLife 7:e38356.
https://doi.org/10.7554/eLife.38356
- PubMed
- Google Scholar
(2019) DNA-segment-capture model for loop extrusion by structural maintenance of chromosome (SMC) protein complexes
Nucleic Acids Research 47:6956–6972.
https://doi.org/10.1093/nar/gkz497
- PubMed
- Google Scholar
(1997) Cohesins: chromosomal proteins that prevent premature separation of sister chromatids
Cell 91:35–45.
https://doi.org/10.1016/S0092-8674(01)80007-6
- PubMed
- Google Scholar
1. Muir KW
2. Li Y
3. Weis F
4. Panne D
(2020) The structure of the cohesin ATPase elucidates the mechanism of SMC-kleisin ring opening
Nature Structural & Molecular Biology 27:233–239.
https://doi.org/10.1038/s41594-020-0379-7
- PubMed
- Google Scholar
(2019) A role for chromatin remodeling in cohesin loading onto chromosomes
Molecular Cell 74:664–673.
https://doi.org/10.1016/j.molcel.2019.02.027
- PubMed
- Google Scholar
(2018) Establishment of DNA-DNA interactions by the cohesin ring
Cell 172:465–477.
https://doi.org/10.1016/j.cell.2017.12.021
- PubMed
- Google Scholar
1. Murayama Y
2. Uhlmann F
(2014) Biochemical reconstitution of topological DNA binding by the cohesin ring
Nature 505:367–371.
https://doi.org/10.1038/nature12867
- PubMed
- Google Scholar
1. Murayama Y
2. Uhlmann F
(2015) DNA entry into and exit out of the cohesin ring by an interlocking gate mechanism
Cell 163:1628–1640.
https://doi.org/10.1016/j.cell.2015.11.030
- PubMed
- Google Scholar
1. Nichols MH
2. Corces VG
(2018) A tethered-inchworm model of SMC DNA translocation
Nature Structural & Molecular Biology 25:906–910.
https://doi.org/10.1038/s41594-018-0135-4
- PubMed
- Google Scholar
1. Niki H
2. Yano K
(2016) In vitro topological loading of bacterial condensin MukB on DNA, preferentially single-stranded DNA rather than double-stranded DNA
Scientific Reports 6:29469.
https://doi.org/10.1038/srep29469
- PubMed
- Google Scholar
1. Nozaki T
2. Imai R
3. Tanbo M
4. Nagashima R
5. Tamura S
6. Tani T
7. Joti Y
8. Tomita M
9. Hibino K
10. Kanemaki MT
11. Wendt KS
12. Okada Y
13. Nagai T
14. Maeshima K
(2017) Dynamic organization of chromatin domains revealed by Super-Resolution Live-Cell imaging
Molecular Cell 67:282–293.
https://doi.org/10.1016/j.molcel.2017.06.018
- PubMed
- Google Scholar
(2016) Evidence for cohesin sliding along budding yeast chromosomes
Open Biology 6:150178.
https://doi.org/10.1098/rsob.150178
- PubMed
- Google Scholar
1. Palecek JJ
2. Gruber S
(2015) Kite proteins: a superfamily of SMC/Kleisin partners conserved across Bacteria, archaea, and eukaryotes
Structure 23:2183–2190.
https://doi.org/10.1016/j.str.2015.10.004
- PubMed
- Google Scholar
1. Parelho V
2. Hadjur S
3. Spivakov M
4. Leleu M
5. Sauer S
6. Gregson HC
7. Jarmuz A
8. Canzonetta C
9. Webster Z
10. Nesterova T
11. Cobb BS
12. Yokomori K
13. Dillon N
14. Aragon L
15. Fisher AG
16. Merkenschlager M
(2008) Cohesins functionally associate with CTCF on mammalian chromosome arms
Cell 132:422–433.
https://doi.org/10.1016/j.cell.2008.01.011
- PubMed
- Google Scholar
1. Petela NJ
2. Gligoris TG
3. Metson J
4. Lee B-G
5. Voulgaris M
6. Hu B
7. Kikuchi S
8. Chapard C
9. Chen W
10. Rajendra E
11. Srinivisan M
12. Yu H
13. Löwe J
14. Nasmyth KA
(2018) Scc2 Is a Potent Activator of Cohesin’s ATPase that Promotes Loading by Binding Scc1 without Pds5
Molecular Cell 70:1134–1148.
https://doi.org/10.1016/j.molcel.2018.05.022
- Google Scholar
1. Rao SSP
2. Huang SC
3. Glenn St Hilaire B
4. Engreitz JM
5. Perez EM
6. Kieffer-Kwon KR
7. Sanborn AL
8. Johnstone SE
9. Bascom GD
10. Bochkov ID
11. Huang X
12. Shamim MS
13. Shin J
14. Turner D
15. Ye Z
16. Omer AD
17. Robinson JT
18. Schlick T
19. Bernstein BE
20. Casellas R
21. Lander ES
22. Aiden EL
(2017) Cohesin loss eliminates all loop domains
Cell 171:305–320.
https://doi.org/10.1016/j.cell.2017.09.026
- PubMed
- Google Scholar
1. Ryu JK
2. Katan AJ
3. van der Sluis EO
4. Wisse T
5. de Groot R
6. Haering CH
7. Dekker C
(2020a) The condensin holocomplex cycles dynamically between open and collapsed states
Nature Structural & Molecular Biology 27:1134–1141.
https://doi.org/10.1038/s41594-020-0508-3
- PubMed
- Google Scholar
Preprint
(2020b) Resolving the step size in condensin‐driven DNA loop extrusion identifies ATP binding as the step‐generating process
bioRxiv.
https://doi.org/10.1101/2020.11.04.368506
- Google Scholar
1. Ryu J-K
2. Bouchoux C
3. Liu HW
4. Kim E
5. Minamino M
6. de Groot R
7. Katan AJ
8. Bonato A
9. Marenduzzo D
10. Michieletto D
11. Uhlmann F
12. Dekker C
(2021) Bridging-induced phase separation induced by cohesin SMC protein complexes
Science Advances 7:eabe5905.
https://doi.org/10.1126/sciadv.abe5905
- Google Scholar
(2009) Conserved features of cohesin binding along fission yeast chromosomes
Genome Biology 10:R52.
https://doi.org/10.1186/gb-2009-10-5-r52
- PubMed
- Google Scholar
1. Shi Z
2. Gao H
3. Bai XC
4. Yu H
(2020) Cryo-EM structure of the human cohesin-NIPBL-DNA complex
Science 368:1454–1459.
https://doi.org/10.1126/science.abb0981
- PubMed
- Google Scholar
(2015) Reconstitution of mitotic chromatids with a minimum set of purified factors
Nature Cell Biology 17:1014–1023.
https://doi.org/10.1038/ncb3187
- PubMed
- Google Scholar
(2016) Single-Molecule imaging reveals a collapsed conformational state for DNA-Bound cohesin
Cell Reports 15:988–998.
https://doi.org/10.1016/j.celrep.2016.04.003
- PubMed
- Google Scholar
(2004) Postreplicative recruitment of cohesin to double-strand breaks is required for DNA repair
Molecular Cell 16:1003–1015.
https://doi.org/10.1016/j.molcel.2004.11.026
- PubMed
- Google Scholar
(2010) Structural basis of instability of the nucleosome containing a testis-specific histone variant, human H3T
PNAS 107:10454–10459.
https://doi.org/10.1073/pnas.1003064107
- PubMed
- Google Scholar
1. Terakawa T
2. Bisht S
3. Eeftens JM
4. Dekker C
5. Haering CH
6. Greene EC
(2017) The condensin complex is a mechanochemical motor that translocates along DNA
Science 358:672–676.
https://doi.org/10.1126/science.aan6516
- PubMed
- Google Scholar
1. Tittel-Elmer M
2. Lengronne A
3. Davidson MB
4. Bacal J
5. François P
6. Hohl M
7. Petrini JHJ
8. Pasero P
9. Cobb JA
(2012) Cohesin association to replication sites depends on rad50 and promotes fork restart
Molecular Cell 48:98–108.
https://doi.org/10.1016/j.molcel.2012.07.004
- PubMed
- Google Scholar
1. Tomonaga T
2. Nagao K
3. Kawasaki Y
4. Furuya K
5. Murakami A
6. Morishita J
7. Yuasa T
8. Sutani T
9. Kearsey SE
10. Uhlmann F
11. Nasmyth K
12. Yanagida M
(2000) Characterization of fission yeast cohesin: essential anaphase proteolysis of Rad21 phosphorylated in the S phase
Genes & Development 14:2757–2770.
https://doi.org/10.1101/gad.832000
- PubMed
- Google Scholar
1. Toselli-Mollereau E
2. Robellet X
3. Fauque L
4. Lemaire S
5. Schiklenk C
6. Klein C
7. Hocquet C
8. Legros P
9. N'Guyen L
10. Mouillard L
11. Chautard E
12. Auboeuf D
13. Haering CH
14. Bernard P
(2016) Nucleosome eviction in mitosis assists condensin loading and chromosome condensation
The EMBO Journal 35:1565–1581.
https://doi.org/10.15252/embj.201592849
- PubMed
- Google Scholar
1. Uhlmann F
2. Wernic D
3. Poupart MA
4. Koonin EV
5. Nasmyth K
(2000) Cleavage of cohesin by the CD clan protease separin triggers anaphase in yeast
Cell 103:375–386.
https://doi.org/10.1016/S0092-8674(00)00130-6
- PubMed
- Google Scholar
1. Uhlmann F
(2016) SMC complexes: from DNA to chromosomes
Nature Reviews Molecular Cell Biology 17:399–412.
https://doi.org/10.1038/nrm.2016.30
- PubMed
- Google Scholar
1. Unal E
2. Arbel-Eden A
3. Sattler U
4. Shroff R
5. Lichten M
6. Haber JE
7. Koshland D
(2004) DNA damage response pathway uses histone modification to assemble a double-strand break-specific cohesin domain
Molecular Cell 16:991–1002.
https://doi.org/10.1016/j.molcel.2004.11.027
- PubMed
- Google Scholar
1. Vafabakhsh R
2. Ha T
(2012) Extreme bendability of DNA less than 100 base pairs long revealed by single-molecule cyclization
Science 337:1097–1101.
https://doi.org/10.1126/science.1224139
- PubMed
- Google Scholar
1. Wang MD
2. Yin H
3. Landick R
4. Gelles J
5. Block SM
(1997) Stretching DNA with optical tweezers
Biophysical Journal 72:1335–1346.
https://doi.org/10.1016/S0006-3495(97)78780-0
- PubMed
- Google Scholar
1. Wang X
2. Hughes AC
3. Brandão HB
4. Walker B
5. Lierz C
6. Cochran JC
7. Oakley MG
8. Kruse AC
9. Rudner DZ
(2018) In Vivo Evidence for ATPase-Dependent DNA Translocation by the Bacillus subtilis SMC condensin complex
Molecular Cell 71:841–847.
https://doi.org/10.1016/j.molcel.2018.07.006
- PubMed
- Google Scholar
1. Waterhouse A
2. Bertoni M
3. Bienert S
4. Studer G
5. Tauriello G
6. Gumienny R
7. Heer FT
8. de Beer TAP
9. Rempfer C
10. Bordoli L
11. Lepore R
12. Schwede T
(2018) SWISS-MODEL: homology modelling of protein structures and complexes
Nucleic Acids Research 46:W296–W303.
https://doi.org/10.1093/nar/gky427
- PubMed
- Google Scholar
1. Wendt KS
2. Yoshida K
3. Itoh T
4. Bando M
5. Koch B
6. Schirghuber E
7. Tsutsumi S
8. Nagae G
9. Ishihara K
10. Mishiro T
11. Yahata K
12. Imamoto F
13. Aburatani H
14. Nakao M
15. Imamoto N
16. Maeshima K
17. Shirahige K
18. Peters JM
(2008) Cohesin mediates transcriptional insulation by CCCTC-binding factor
Nature 451:796–801.
https://doi.org/10.1038/nature06634
- PubMed
- Google Scholar
1. Woo JS
2. Lim JH
3. Shin HC
4. Suh MK
5. Ku B
6. Lee KH
7. Joo K
8. Robinson H
9. Lee J
10. Park SY
11. Ha NC
12. Oh BH
(2009) Structural studies of a bacterial condensin complex reveal ATP-dependent disruption of intersubunit interactions
Cell 136:85–96.
https://doi.org/10.1016/j.cell.2008.10.050
- PubMed
- Google Scholar
1. Wood CW
2. Woolfson DN
(2018) CCBuilder 2.0: powerful and accessible coiled-coil modeling
Protein Science 27:103–111.
https://doi.org/10.1002/pro.3279
- PubMed
- Google Scholar
1. Xu J
2. Ma H
3. Jin J
4. Uttam S
5. Fu R
6. Huang Y
7. Liu Y
(2018) Super-Resolution imaging of Higher-Order chromatin structures at different epigenomic states in single mammalian cells
Cell Reports 24:873–882.
https://doi.org/10.1016/j.celrep.2018.06.085
- PubMed
- Google Scholar
(2019) Organization of chromosomal DNA by SMC complexes
Annual Review of Genetics 53:445–482.
https://doi.org/10.1146/annurev-genet-112618-043633
- Google Scholar
1. Zabrady K
2. Adamus M
3. Vondrova L
4. Liao C
5. Skoupilova H
6. Novakova M
7. Jurcisinova L
8. Alt A
9. Oliver AW
10. Lehmann AR
11. Palecek JJ
(2016) Chromatin association of the SMC5/6 complex is dependent on binding of its NSE3 subunit to DNA
Nucleic Acids Research 44:1064–1079.
https://doi.org/10.1093/nar/gkv1021
- PubMed
- Google Scholar

Decision letter

Aleksandra M Walczak

Senior Editor; École Normale Supérieure, France
Megan C King

Reviewing Editor; Yale School of Medicine, United States

Our editorial process produces two outputs: i) public reviews designed to be posted alongside the preprint for the benefit of readers; ii) feedback on the manuscript for the authors, including requests for revisions, shown below. We also include an acceptance summary that explains what the editors found interesting or important about the work.

Acceptance summary:

This work combines experiments and simulations together with previously reported biophysical and structural observations to develop a structure-based model that provides mechanistic insight into the two functions of cohesin: cohesion and loop extrusion. This intriguing and informative manuscript will be of broad interest to those working in the fields of chromatin structure, chromosome biology and molecular machines.

Decision letter after peer review:

Thank you for submitting your article "A Brownian ratchet model for DNA loop extrusion by the cohesin complex" for consideration by eLife. Your article has been reviewed by 4 peer reviewers, one of whom is a member of our Board of Reviewing Editors, and the evaluation has been overseen by Aleksandra Walczak as the Senior Editor. The reviewers have opted to remain anonymous.

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission.

Essential revisions:

1) There was a consensus that the manuscript needs to be extensively edited to better introduce the reader to the structures described in the prior work from the group published in 2020. One approach suggested by the reviewers would be to present a series of increasingly complex representations that would help to position the reader to better understand the work, starting with a global structural view of the cohesin complex first that introduces the key elements: hinge, ATPase domains, kleisin and loading factors. From this point representations akin to the current Figure 1—figure supplement 1 will position the reader to fully understand Figure 1. Similarly, introduction of the key terms (e.g. "N gate", the geometry of "entering/exiting the cohesin ring") at the start and ensuring that the helpful general/fission nomenclature is used throughout the text and all Figures would be helpful. Last, clear articulation of what structures arise from high-resolution data versus structural modeling should be clarified.

2) Please clarify what assumptions are made and/or are implicitly defined in the modeling. Specifically, is the sequence of changes between DNA binding and cohesin conformation prescribed and are there any assumptions on whether DNA binding to the hinge domain is dependent (i.e. temporally linked) to the ATPase cycle? How are chemical kinetics combined with the bead dynamic simulation?

3) A common thread in the reviews relates to questions regarding the position, bending, binding and release of the DNA, which need to be addressed. DNA bending is mentioned in the text but it is not discussed quantitatively (and in the context of to the persistence length) particularly with regards to the initiation of loop extrusion. DNA conformation is also not communicated well in the Figures. Further clarification is needed to address what occurs upon DNA release – whether there are concerns about tangling – and discussing what prevents the DNA loop from sliding outwards from the cohesin ring to release the bending strain. Last, the authors should address what rules out the random binding of the DNA to the hinge module in the unfolded cohesin state, which upon locking the hinge and head together could result in a "backward" sliding with DNA being pushed back through the head domain.

4) The authors should discuss how their model impinges on (or is influenced by) the discrepancy between the rates of loop extrusion and measured ATPase activity.

5) The authors should include further discussion of how their work informs on other models for cohesin and loop extrusion. There is value in evaluating these other models more critically based on the findings reported in the manuscript.

6) The authors should address two issues related to the FRET measurements, namely 1) concerns over the sensitivity of the proximity of Scc3-C and Scc2-N and how this impinges on the modeling and 2) the functionality of the SNAP/CLIP-tagged proteins.

Reviewer #1 (Recommendations for the authors):

1. The manuscript will benefit from a clearer articulation of what information arises from previously described structures (for example conformation in the "gripping state") and what is structural modeling based on the available separated structural data. These details could be deduced from the description in the Materials and methods but it will help the reader appreciate the authors' arguments if it is stated in the main text.

2. Regarding the mechanism of the loop extrusion, there are some aspects that remain unclear. First, are there any assumptions on whether DNA binding to the hinge domain is dependent (i.e. temporally linked) to the ATPase cycle steps happening at the head domain? This question is relevant, as one might think that absolutely random independent binding of the DNA to the hinge module could also result in DNA binding to the hinge domain in the unfolded cohesin state, in which case locking the hinge and head together may result in a "backward" sliding with DNA being pushed back through the head domain.

3. Related to Point 2, what, if any, assumptions were made about the sequence of changes between DNA binding and cohesin conformation in the Monte-Carlo simulations? In the text, it is stated (ln 384-389) "When we then allow DNA to detach from the Scc3-hinge module and switch cohesin back to the gripping state, the system readily resets and primes itself for the next cycle (Figure 4D). Our simulations reveal that repeated rounds of the states: "gripping → slipping → DNA detachment from the Scc3-hinge module → gripping" results in continuous extrusion of DNA with an average loop size increase of ~ 30 nm per cycle". It is crucial to clarify whether the sequence of events described here was explicitly imposed or whether independent stochastic "gripping-slipping" and "DNA binding/detachment" were also considered in some simulations. In the latter case, what prevents the DNA thread from sliding back? Perhaps a discussion on what sets the directionality of the DNA translocation would help: is it DNA bending, timing of DNA binding at the hinge module, etc?

4. While the authors provide detailed descriptions of the simulations there are some aspects that would benefit from further clarification. For the Monte Carlo simulations, it is not clear how chemical kinetics was combined with the bead dynamic simulation: (1) DNA binding – what determines/switches which D bead is "currently interacting" with hinge or with head beads, (2) ATPase cycle – what determines the timing of switching from gripping to slipping state, (3) do the head beads change their interaction with the hinge bead, and if so what determines the switch? If not, some explanation for how random folding-unfolding results in directed translocation would be very helpful. Regarding the Monte Carlo steps, it is not clear what were allowed as random moves, i.e. from a given state how a new state was generated. For the diffusion-based model, a more detailed description (and perhaps a cartoon of the simulation model) would be helpful. Would it be correct to say that this model has two spatially fixed points through which a DNA polymer can perform a 1D random walk for "diffusion only", with a constant directed polymer translocation through one of the points was added in "diffusion plus ratchet"?

5. The authors suggest that their mechanism generally results in an asymmetric loop extrusion (Figure 6A left). Once DNA unbinds from the hinge module, what prevents the DNA loop from sliding outwards from the cohesin ring to release the bending strain?

6. In the introduction, the authors described three proposed models for loop extrusion; in the discussion it would be helpful to "circle" back and compare the presented model with these prior considerations to highlight commonalities and incompatibilities.

7. The authors describe the role of kleisin position relative to the DNA much later in the text rather than introducing the concept with the slipping state. Explaining it earlier will help in better understanding the terminology and the key difference between the "topological entry" and "loop extrusion" modes.

8. Bars in Figure 2 might be somewhat misleading as their height does not represent values. I would suggest using a scatter plot instead.

9. A few points on terminology: 1) "Loop extrusion by biased Brownian fluctuations" (l.41) – it seems that fluctuations are not biased, but instead repeatedly get caught in one "loaded" conformation, relaxation of which drives the directed translocation. I would consider more precise wording to highlight the beauty of the mechanism. 2) 'kleisin path' (l.318) – perhaps, 'kleisin chain' as path is used to refer to temporal changes in conformations throughout the paper.

Reviewer #2 (Recommendations for the authors):

1. In higher eukaryotes, chromatin seems to have clusters of nucleosomes (e.g., PMID: 32967822; PMID: 28712725; PMID: 30044984), but not stretched nucleosome fiber. It might be better to discuss that this nucleosome clustering can be a more severe issue for cohesin's loop extrusion activity.

2. Page 11. "Maturation of the bent DNA in the gripping state.… Brownian motion will have.…" These sentences are unclear to me and should be rephrased.

3. The reference (Suhas et al., 2017) should be Rao et al., 2017 (PMID: 28985562 ).

Reviewer #3 (Recommendations for the authors):

1. Please provide a global structural view of the cohesin complex first. It is provided in figure supplement 1 but it has its own problem (see below), and I could not understand Figure 1 until I spent a long time staring at figure supplement 1. For those who are not up to date on cohesin structures (such as me), cohesin is a ring that can open and close at the hinge and at the ATPase domain and DNA passage through the gap in ATPase domain is modulated by kleisin and cohesin loader, and I could not understand figure 1 description and figure 1 because I could not place different parts in the cohesin complex in my imagination.

2. Figure 1 supplement is probably still too complex. Colors are confusing because Rad21 is shown in pink and its color coding is shown above the figure but Psc3 is shown in a similar color and its color coding is missing in the color guide above the figure. Also, fission yeast names are used here instead of the helpful generic^fission naming scheme used elsewhere in the paper so it is very challenging to connect figure 1 to figure 1 supplement. The authors should try to reduce mental gymnastics on the part of the readers!

3. Line 272. "The DNA path shown in Figure 3A, panel a, highlights the position of such a bend, based on our DNA-protein crosslink mass spectrometry data (Higashi et al., 2020)."

– Bending of DNA is mentioned but the figures do not make DNA bending obvious. It is not clear where the bend is, looking at the figure. Some quantification is needed to aid the reader in their assessment of this statement, whether there is a significant degree of bending as the authors claim.

4. Line 280. "ATP hydrolysis, resulting in ATPase head gate opening and Scc3-hinge and Scc2-head module uncoupling. This will initiate a swinging motion of the Scc3-hinge module and proximal coiled coil, with a pivot point at the elbow"

– There appears to be a logical jump here. Why would this cause a swinging motion? In addition, a subsequent sentence refers to this movement as Brownian motion, which is even more confusing. Statement such as 'energizing the swinging motion' is not helpful because it is not precise enough.

5. Line 293. 'fast DNA off-rate'. Rate is high or low, not fast or slow, because it is a quantity.

6. I found some of the terminologies confusing. I suspect the readers will have difficult in understanding what an N gate is, for example.

7. Figure 3 description should make it explicit that DNA loop is inserted into the cohesin channel.

8. Figure 3Aa, it appears to me here that DNA is behind both of the yellow protein segments, going up and down, and panel Ab shows a yellow arrow that suggest that something happens so that now one of the yellow segments is not behind the DNA. However, their model, after considering staring at the figures on my part, seems to assume that DNA is simply bent to form a loop and this loop is inserted so that there is no DNA segment behind the yellow protein segments. Figure 3Aa should be redrawn to avoid misleading the readers. Also, what the yellow arrow means needs to be explained.

9. They need to confirm that SNAP/CLIP tags and labeling do not perturb proteins' function. They may have done this in their 2020 Mol Cell paper that introduced the tagged constructs for FRET analysis and if they have done so, it should be mentioned in this manuscript still.

10. Other models for loop extrusion are mentioned in Introduction but it is difficult to tell how they are different among themselves and from the model proposed here just from reading the text. In addition, the authors do not attempt to evaluate other models based on the findings reported here, and that seems to be a missed opportunity for the discussion sect

Reviewer #4 (Recommendations for the authors):

The wording "Enter/Exit cohesin ring" is unclear. The authors should explain which side is "enter" and "exit" in the text and/or corresponding figure.

https://doi.org/10.7554/eLife.67530.sa1

Author response

Essential revisions:

1) There was a consensus that the manuscript needs to be extensively edited to better introduce the reader to the structures described in the prior work from the group published in 2020. One approach suggested by the reviewers would be to present a series of increasingly complex representations that would help to position the reader to better understand the work, starting with a global structural view of the cohesin complex first that introduces the key elements: hinge, ATPase domains, kleisin and loading factors. From this point representations akin to the current Figure 1—figure supplement 1 will position the reader to fully understand Figure 1. Similarly, introduction of the key terms (e.g. "N gate", the geometry of "entering/exiting the cohesin ring") at the start and ensuring that the helpful general/fission nomenclature is used throughout the text and all Figures would be helpful. Last, clear articulation of what structures arise from high-resolution data versus structural modeling should be clarified.

We apologise that our introduction was based on too much prior knowledge and that our figures were restricted to only new information. We now provide an introductory structural summary figure (the new Figure 1A). It portrays the different parts of the cohesin complex and how they come together during assembly of the DNA gripping state. The Figure also introduces key terms (kleisin N-gate, hinge, elbow, etc.). The definition of what we mean by DNAs that ‘enter’ or ‘exit’ the cohesin ring during loop extrusion is now also made explicit at the start of their description following from line 491. We have also ensured that generic nomenclature (with fission yeast names in superscript) is used throughout the manuscript and figures. Lastly, we clarify the origin of the different parts of our hybrid cohesin structural model in the rewritten legend to Figure 1—figure supplement 1.

2) Please clarify what assumptions are made and/or are implicitly defined in the modeling. Specifically, is the sequence of changes between DNA binding and cohesin conformation prescribed and are there any assumptions on whether DNA binding to the hinge domain is dependent (i.e. temporally linked) to the ATPase cycle? How are chemical kinetics combined with the bead dynamic simulation?

We thank the reviewers for the opportunity to make our model assumption clearer. We have expanded the description of the model in the methods section as well as revised the main text. Briefly, we used our three-dimensional model to explore how the transition from gripping to slipping state leads to directional DNA loop growth. This model contains no explicit chemical kinetics, and all transitions were prescribed. The system was allowed to equilibrate in each state and then state changes were manually introduced. This is now made clear in the relevant text starting in line 418. We also supply a new Supplementary table 1 that contains all parameters and their values that describe the cohesin-DNA interaction in the gripping and slipping states.

Thus, supplementary video 2 illustrates a “gripping → slipping → DNA detachment from the Scc3-hinge module → gripping” sequence of events that was imposed on our simulations. To simulate this sequence, we initiated the switch from the gripping to slipping state by imposing the change in parameters that describe the equilibrium conformations of these states. Simulations were then continued until the system reached a new equilibrium. After 2 x 10⁷ iterations, sufficient to reach equilibrium, we imposed DNA detachment from the Scc3-hinge module. At this time, we changed the equilibrium parameters back to those of the gripping state and performed simulations further. Once complete, the cycle was repeated. This is clarified in the Supplementary video 2 legend.

In agreement with the prescribed state transition in our simulations, we think it is reasonable to expect that the hinge-DNA interaction is formed as soon as the hinge contacts the ATPase heads in the gripping state and persists for as long as cohesin remains in the gripping state. This assumption is based on the structural observation of aligned Scc2-head and Scc3-hinge modules in the gripping state. Once this ordered state dissolves following ATP hydrolysis (the gripping to slipping state transition), the Scc3-hinge likely continues to interact with DNA for a random amount of time characterized by its in-solution off rate. This behaviour is analysed in Figure 5F, but it differs from our simulations, where we manually impose Scc3-hinge module dissociation from the DNA. These differences are made clear in the rewritten section that discusses Figure 5F in lines 440 and following. We also discuss that, in the unlikely event that the Scc3-hinge module does not detach from the DNA, or reattaches outside the gripping state, the results will be a non-productive loop extrusion cycle. See lines 463, 727 – 737.

3) A common thread in the reviews relates to questions regarding the position, bending, binding and release of the DNA, which need to be addressed. DNA bending is mentioned in the text but it is not discussed quantitatively (and in the context of to the persistence length) particularly with regards to the initiation of loop extrusion. DNA conformation is also not communicated well in the Figures. Further clarification is needed to address what occurs upon DNA release – whether there are concerns about tangling – and discussing what prevents the DNA loop from sliding outwards from the cohesin ring to release the bending strain. Last, the authors should address what rules out the random binding of the DNA to the hinge module in the unfolded cohesin state, which upon locking the hinge and head together could result in a "backward" sliding with DNA being pushed back through the head domain.

The reviewers bring up an important topic for consideration that we have ourselves given much thought. How likely is it that, by mere thermal fluctuation, DNA reaches a 180° bend, small enough to fit through the 23 nm clearance of the Scc3-Smc3-kleisin-N chamber to initiate loop extrusion? We have taken various semi-quantitative approaches, e.g. considering the angle distribution of a polymer with a persistence length l_P = 50 nm and estimating the time it takes to reach the required conformation based on a probable friction coefficient. While many assumptions go into such estimates, they suggest that the required bends do form in relevant timescales. Additionally, empirical observations agree that DNA readily adopts sharp turns (e.g. Vafabakhsh and Ha, Science, 2012). Another relevant consideration is that the highly ordered gripping state presents an entropy minimum and that the entropy gain from its disassembly should at least in part compensate for the energetic cost of loop formation. However, it remains hard to quantitatively translate these estimates to the specific context of the cohesin-DNA complex, incubated in a non-physiologically low ionic strength environment. This is discussed in the revised manuscript, lines 316 – 322 and 712 – 723.

Once a loop is formed, its extension is energetically favorable as the loop radius increases. The energetic cost of reducing the DNA loop radius again decreases the chance that the DNA loop slips back, once formed. This is explained in lines 723 – 726. We do not foresee tangling between DNA and the cohesin ring, as this would require much sharper bending of DNA and protein, compared to the bends discussed above.

To better communicate the issue of DNA bending, we have highlighted the DNA bend in the gripping state in Figure 3, as well as straightening of the bend during topological DNA entry (Figure 3A) or its development into a DNA loop during the initiation of loop extrusion (Figure 3B).

Lastly, we cannot exclude that the Scc3-hinge module sometimes fails to detach from DNA before cohesin returns to its next gripping state. We also cannot exclude that the Scc3-hinge module detaches and then re-attaches, though the latter scenario is less likely, as the correct geometry for reestablishment of the Scc3-hinge module interaction with DNA will be hard to find outside the gripping state. Nevertheless, both possible scenarios suggest that unproductive loop extrusion steps occasionally occur and might contribute to the wide spread of observed loop extrusion rates. This is discussed in lines 727 – 737.

4) The authors should discuss how their model impinges on (or is influenced by) the discrepancy between the rates of loop extrusion and measured ATPase activity.

There is indeed an apparent discrepancy between the low cohesin ATP hydrolysis rates measured in bulk solution experiments and our simulations. The latter predict that ATP hydrolysis cycles must happen an order of magnitude faster for the Brownian ratchet to reach experimentally observed loop extrusion speeds. These observations are not necessarily incompatible. If complex formation between cohesin, the cohesin loader and DNA is a rate limiting step, then the ATP hydrolysis rate of the assembled complex might well be substantially faster than bulk measurements suggest. In a typical bulk topological cohesin loading reaction, approximately 20% of DNA is captured by cohesin within one hour of incubation (Murayama and Uhlmann, 2014). This illustrates that gripping state formation is indeed likely to be a slow process in solution. The ATP hydrolysis rate once a protein-DNA assembly is formed could be substantially higher. This is explained in lines 750 – 760 of the revised manuscript.

5) The authors should include further discussion of how their work informs on other models for cohesin and loop extrusion. There is value in evaluating these other models more critically based on the findings reported in the manuscript.

We are grateful for the opportunity to discuss how our new insight relates to alternative models for topological DNA entry into the cohesin ring and for DNA loop extrusion. There are interesting parallels, but also important differences, between the previous models and our new structure-based model. We contrast and explore these similarities and differences in an added section of our Discussion between lines 785 and 841.

6) The authors should address two issues related to the FRET measurements, namely 1) concerns over the sensitivity of the proximity of Scc3-C and Scc2-N and how this impinges on the modeling and 2) the functionality of the SNAP/CLIP-tagged proteins.

1) It is true that the absolute FRET efficiency reached by the Scc3-C and Scc2-N fluorophore pair is lower than that reached by our other FRET pairs. This is not unexpected, based on our structural modelling, given the predicted larger Euclidean distance between the Scc3-C and Scc2-N fluorophores. Despite the lower absolute values, the relative FRET efficiency of the Scc3-C and Scc2-N fluorophore pair does increase in the DNA gripping state, consistent with the operation of our proposed Brownian ratchet. This is better explained in the revised manuscript, lines 230 – 245.

2) Following the reviewers’ pertinent suggestion, we now show control experiments that confirm the biochemical activity of each of our fluorophore-tagged cohesin and cohesin loader variants. All the tagged and labelled variants retained the ability to promote topological cohesin loading onto DNA in an ATP and cohesin loader-dependent manner, albeit some of them at a slightly reduced efficiency. This is shown in a new Figure 2—figure supplement 1B.

Reviewer #1 (Recommendations for the authors):

1. The manuscript will benefit from a clearer articulation of what information arises from previously described structures (for example conformation in the "gripping state") and what is structural modeling based on the available separated structural data. These details could be deduced from the description in the Materials and methods but it will help the reader appreciate the authors' arguments if it is stated in the main text.

Please confer Essential Revisions, point 1.

2. Regarding the mechanism of the loop extrusion, there are some aspects that remain unclear. First, are there any assumptions on whether DNA binding to the hinge domain is dependent (i.e. temporally linked) to the ATPase cycle steps happening at the head domain? This question is relevant, as one might think that absolutely random independent binding of the DNA to the hinge module could also result in DNA binding to the hinge domain in the unfolded cohesin state, in which case locking the hinge and head together may result in a "backward" sliding with DNA being pushed back through the head domain.

Please confer Essential Revisions, point 2.

3. Related to Point 2, what, if any, assumptions were made about the sequence of changes between DNA binding and cohesin conformation in the Monte-Carlo simulations? In the text, it is stated (ln 384-389) "When we then allow DNA to detach from the Scc3-hinge module and switch cohesin back to the gripping state, the system readily resets and primes itself for the next cycle (Figure 4D). Our simulations reveal that repeated rounds of the states: "gripping → slipping → DNA detachment from the Scc3-hinge module → gripping" results in continuous extrusion of DNA with an average loop size increase of ~ 30 nm per cycle". It is crucial to clarify whether the sequence of events described here was explicitly imposed or whether independent stochastic "gripping-slipping" and "DNA binding/detachment" were also considered in some simulations. In the latter case, what prevents the DNA thread from sliding back? Perhaps a discussion on what sets the directionality of the DNA translocation would help: is it DNA bending, timing of DNA binding at the hinge module, etc?

Please confer Essential Revisions, point 2.

4. While the authors provide detailed descriptions of the simulations there are some aspects that would benefit from further clarification. For the Monte Carlo simulations, it is not clear how chemical kinetics was combined with the bead dynamic simulation: (1) DNA binding – what determines/switches which D bead is "currently interacting" with hinge or with head beads, (2) ATPase cycle – what determines the timing of switching from gripping to slipping state, (3) do the head beads change their interaction with the hinge bead, and if so what determines the switch? If not, some explanation for how random folding-unfolding results in directed translocation would be very helpful. Regarding the Monte Carlo steps, it is not clear what were allowed as random moves, i.e. from a given state how a new state was generated. For the diffusion-based model, a more detailed description (and perhaps a cartoon of the simulation model) would be helpful. Would it be correct to say that this model has two spatially fixed points through which a DNA polymer can perform a 1D random walk for "diffusion only", with a constant directed polymer translocation through one of the points was added in "diffusion plus ratchet"?

Please confer Essential Revisions, point 2.

5. The authors suggest that their mechanism generally results in an asymmetric loop extrusion (Figure 6A left). Once DNA unbinds from the hinge module, what prevents the DNA loop from sliding outwards from the cohesin ring to release the bending strain?

Please confer Essential Revisions, point 3.

6. In the introduction, the authors described three proposed models for loop extrusion; in the discussion it would be helpful to "circle" back and compare the presented model with these prior considerations to highlight commonalities and incompatibilities.

Please confer Essential Revisions, point 5.

7. The authors describe the role of kleisin position relative to the DNA much later in the text rather than introducing the concept with the slipping state. Explaining it earlier will help in better understanding the terminology and the key difference between the "topological entry" and "loop extrusion" modes.

Please confer Essential Revisions, point 1.

8. Bars in Figure 2 might be somewhat misleading as their height does not represent values. I would suggest using a scatter plot instead.

A scatter plot is now used instead of bar graph in Figure 2C.

9. A few points on terminology: 1) "Loop extrusion by biased Brownian fluctuations" (l.41) – it seems that fluctuations are not biased, but instead repeatedly get caught in one "loaded" conformation, relaxation of which drives the directed translocation. I would consider more precise wording to highlight the beauty of the mechanism. 2) 'kleisin path' (l.318) – perhaps, 'kleisin chain' as path is used to refer to temporal changes in conformations throughout the paper.

We thank reviewer 1 overall for the numerous insightful and helpful suggestions, including these comments on terminology. ‘Biased fluctuations’ is indeed an oxymoron and incorrect. This was replaced with ‘biased Brownian motion’. We have also applied a consistent terminology to describe the temporal movement of DNA through space as its ‘trajectory’ while the spatial positioning of DNA or of the kleisin unstructured regions is referred to as their ‘path’.

Reviewer #2 (Recommendations for the authors):

1. In higher eukaryotes, chromatin seems to have clusters of nucleosomes (e.g., PMID: 32967822; PMID: 28712725; PMID: 30044984), but not stretched nucleosome fiber. It might be better to discuss that this nucleosome clustering can be a more severe issue for cohesin's loop extrusion activity.

The reviewer brings up an excellent point. We now state that higher order nucleosome assemblies can be expected to cause even greater impediment to loop extrusion than histones by themselves, referring to the key references by Nozaki et al. 2017 and Xu et al. 2018 in our introduction, lines 107 – 108.

2. Page 11. "Maturation of the bent DNA in the gripping state.… Brownian motion will have.…" These sentences are unclear to me and should be rephrased.

3. The reference (Suhas et al., 2017) should be Rao et al., 2017 (PMID: 28985562).

We thank the reviewer for pointing out these shortcomings, which have been rectified.

Reviewer #3 (Recommendations for the authors):

1. Please provide a global structural view of the cohesin complex first. It is provided in figure supplement 1 but it has its own problem (see below), and I could not understand Figure 1 until I spent a long time staring at figure supplement 1. For those who are not up to date on cohesin structures (such as me), cohesin is a ring that can open and close at the hinge and at the ATPase domain and DNA passage through the gap in ATPase domain is modulated by kleisin and cohesin loader, and I could not understand figure 1 description and figure 1 because I could not place different parts in the cohesin complex in my imagination.

Please confer Essential Revisions, point 1.

2. Figure 1 supplement is probably still too complex. Colors are confusing because Rad21 is shown in pink and its color coding is shown above the figure but Psc3 is shown in a similar color and its color coding is missing in the color guide above the figure. Also, fission yeast names are used here instead of the helpful generic^fission naming scheme used elsewhere in the paper so it is very challenging to connect figure 1 to figure 1 supplement. The authors should try to reduce mental gymnastics on the part of the readers!

Please confer Essential Revisions, point 1.

3. Line 272. "The DNA path shown in Figure 3A, panel a, highlights the position of such a bend, based on our DNA-protein crosslink mass spectrometry data (Higashi et al., 2020)."

– Bending of DNA is mentioned but the figures do not make DNA bending obvious. It is not clear where the bend is, looking at the figure. Some quantification is needed to aid the reader in their assessment of this statement, whether there is a significant degree of bending as the authors claim.

The DNA bend is now highlighted in Figure 3, as well as its straightening following topological loading or its alternative development into a loop during loop extrusion.

4. Line 280. "ATP hydrolysis, resulting in ATPase head gate opening and Scc3-hinge and Scc2-head module uncoupling. This will initiate a swinging motion of the Scc3-hinge module and proximal coiled coil, with a pivot point at the elbow"

– There appears to be a logical jump here. Why would this cause a swinging motion? In addition, a subsequent sentence refers to this movement as Brownian motion, which is even more confusing. Statement such as 'energizing the swinging motion' is not helpful because it is not precise enough.

5. Line 293. 'fast DNA off-rate'. Rate is high or low, not fast or slow, because it is a quantity.

6. I found some of the terminologies confusing. I suspect the readers will have difficult in understanding what an N gate is, for example.

7. Figure 3 description should make it explicit that DNA loop is inserted into the cohesin channel.

8. Figure 3Aa, it appears to me here that DNA is behind both of the yellow protein segments, going up and down, and panel Ab shows a yellow arrow that suggest that something happens so that now one of the yellow segments is not behind the DNA. However, their model, after considering staring at the figures on my part, seems to assume that DNA is simply bent to form a loop and this loop is inserted so that there is no DNA segment behind the yellow protein segments. Figure 3Aa should be redrawn to avoid misleading the readers. Also, what the yellow arrow means needs to be explained.

We thank the reviewer for pointing out shortcomings in the text and figures, which have been rectified.

9. They need to confirm that SNAP/CLIP tags and labeling do not perturb proteins' function. They may have done this in their 2020 Mol Cell paper that introduced the tagged constructs for FRET analysis and if they have done so, it should be mentioned in this manuscript still.

Please confer Essential Revisions, point 6.

10. Other models for loop extrusion are mentioned in Introduction but it is difficult to tell how they are different among themselves and from the model proposed here just from reading the text. In addition, the authors do not attempt to evaluate other models based on the findings reported here, and that seems to be a missed opportunity for the Discussion section.

Please confer Essential Revisions, point 5.

Reviewer #4 (Recommendations for the authors):

The wording "Enter/Exit cohesin ring" is unclear. The authors should explain which side is "enter" and "exit" in the text and/or corresponding figure.

Please confer Essential Revisions, point 1.

https://doi.org/10.7554/eLife.67530.sa2

Article and author information

Author details

Torahiko L Higashi

Chromosome Segregation Laboratory, The Francis Crick Institute, London, United Kingdom

Contribution
conceived the study, performed the biochemical and FRET experiments and drew the structural figures, wrote the manuscript with input from all coauthors

Competing interests
No competing interests declared
Georgii Pobegalov
1. Mechanobiology and Biophysics Laboratory, The Francis Crick Institute, London, United Kingdom
2. Department of Physics and Astronomy, University College London, London, United Kingdom
Contribution
performed the loop extrusion experiments, designed the mathematical model and performed the computational simulations

Competing interests
No competing interests declared
Minzhe Tang

Chromosome Segregation Laboratory, The Francis Crick Institute, London, United Kingdom

Contribution
contributed the concept of second DNA capture by condensin

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-2645-8880
Maxim I Molodtsov
1. Mechanobiology and Biophysics Laboratory, The Francis Crick Institute, London, United Kingdom
2. Department of Physics and Astronomy, University College London, London, United Kingdom
Contribution
conceived the study, wrote the manuscript with input from all coauthors

For correspondence
m.molodtsov@ucl.ac.uk

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-3066-0515
Frank Uhlmann

Chromosome Segregation Laboratory, The Francis Crick Institute, London, United Kingdom

Contribution
conceived the study, wrote the manuscript with input from all coauthors

For correspondence
frank.uhlmann@crick.ac.uk

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-3527-6619

Funding

European Research Council (AdG 670412)

Frank Uhlmann

Boehringer Ingelheim Fonds (PhD Fellowship)

Minzhe Tang

Medical Research Council (FC001198)

Frank Uhlmann

Medical Research Council (FC001750)

Maxim Molodtsov

Wellcome Trust (FC001198)

Frank Uhlmann

Wellcome Trust (FC001750)

Maxim Molodtsov

Cancer Research UK (FC001198)

Frank Uhlmann

Cancer Research UK (FC001750)

Maxim Molodtsov

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank A Costa and S Henrikus for their collaboration on cohesin structural biology and for their advice, B Khatri for discussions, S Kunzelmann and S Mouilleron from the Crick Structural Biology Science Technology Platform for instrument access and advice, and all our laboratory members for discussions and critical reading of the manuscript. Funder Grant reference number Author European Research Council AdG 670412 Frank Uhlmann Boehringer Ingelheim Fonds PhD Fellowship Minzhe Tang The Francis Crick Institute Frank Uhlmann UK Medical Research Council FC001198 Wellcome Trust FC001198 Cancer Research UK FC001198 The Francis Crick Institute Maxim Molodtsov UK Medical Research Council FC001750 Wellcome Trust FC001750 Cancer Research UK FC001750 The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Senior Editor

Aleksandra M Walczak, École Normale Supérieure, France

Reviewing Editor

Megan C King, Yale School of Medicine, United States

Version history

Received: February 14, 2021
Accepted: June 10, 2021
Version of Record published: July 26, 2021 (version 1)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.