Most cancers carry a substantial deleterious load due to Hill-Robertson interference

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: September 22, 2022 (This version)
Accepted Manuscript published: September 1, 2022 (Go to version)
Accepted: August 31, 2022
Received: February 23, 2021
Preprint posted: September 14, 2019 (Go to version)

1. Of interest
A timeline of bacterial and archaeal diversification in the ocean

Carolina A Martinez-Gutierrez, Josef C Uyeda, Frank O Aylward

Research Article Dec 7, 2023
Further reading

Abstract
Editor's evaluation
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Cancer genomes exhibit surprisingly weak signatures of negative selection (Martincorena et al., 2017; Weghorn, 2017). This may be because selective pressures are relaxed or because genome-wide linkage prevents deleterious mutations from being removed (Hill-Robertson interference; Hill and Robertson, 1966). By stratifying tumors by their genome-wide mutational burden, we observe negative selection (dN/dS ~ 0.56) in low mutational burden tumors, while remaining cancers exhibit dN/dS ratios ~1. This suggests that most tumors do not remove deleterious passengers. To buffer against deleterious passengers, tumors upregulate heat shock pathways as their mutational burden increases. Finally, evolutionary modeling finds that Hill-Robertson interference alone can reproduce patterns of attenuated selection and estimates the total fitness cost of passengers to be 46% per cell on average. Collectively, our findings suggest that the lack of observed negative selection in most tumors is not due to relaxed selective pressures, but rather the inability of selection to remove deleterious mutations in the presence of genome-wide linkage.

Editor's evaluation

This is an important paper that shows most cancers unavoidably accumulate damaging mutations. Whilst the majority of claims are convincingly supported by the data, evidence that damaging changes are buffered by heat shock pathways is currently incomplete. The insights into selection efficiency are important for the understanding of cancer growth and response to therapy. A broader implication is that high mutation load tumors may use common strategies to tolerate accumulated deleterious mutations, providing a therapeutic target.

https://doi.org/10.7554/eLife.67790.sa0

Introduction

Tumor progression is an evolutionary process acting on somatic cells within the body. These cells acquire mutations over time that can alter cellular fitness by either increasing or decreasing the rates of cell division and/or cell death. Mutations which increase cellular fitness (drivers) are observed in cancer genomes more frequently because natural selection enriches their prevalence within the tumor population (Martincorena et al., 2017; Weghorn and Sunyaev, 2017). This increased prevalence of mutations across patients within specific genes is used to identify driver genes. Conversely, mutations that decrease cellular fitness (deleterious passengers) are expected to be observed less frequently. This enrichment or depletion is often measured by comparing the expected rate of nonsynonymous mutations (dN) accruing within a region of the genome to the expected rate of synonymous mutations (dS), which are presumed to be neutral. This ratio, dN/dS, is expected to be below 1 when the majority of nonsynonymous mutations are deleterious and removed by natural selection, be ~1 when all nonsynonymous mutations are neutral, and can be >1 when a substantial proportion of nonsynonymous mutations are advantageous.

Two recent analyses of dN/dS patterns in cancer genomes found that for most nondriver genes dN/dS is ~1 and that only 0.1–0.4% of genes exhibit detectable negative selection (dN/dS < 1) (Martincorena et al., 2017; Weghorn and Sunyaev, 2017).This differs substantially from patterns in human germline evolution where most genes show signatures of negative selection (dN/dS ~ 0.4) (Martincorena et al., 2017). Two explanations for this difference have been posited. First, the vast majority of nonsynonymous mutations may not be deleterious in somatic cellular evolution despite their deleterious effects on the organism. While most genes may be critical for proper organismal development and multicellular functioning, they may not be essential for clonal tumor growth. In this hypothesis, negative selection (dN/dS < 1) should be observed only within essential genes and absent elsewhere (dN/dS ~ 1). While appealing in principle, most germline selection against nonsynonymous variants appears to be driven by protein misfolding toxicity (Drummond and Wilke, 2008; Lobkovsky et al., 2010), in addition to gene essentiality. These damaging folding effects ought to persist in somatic evolution.

A second hypothesis is that even though many nonsynonymous mutations are deleterious in somatic cells, natural selection fails to remove them. One possible reason for this inefficiency is the unique challenge of evolving without recombination. Unlike sexually recombining germline evolution, tumors must evolve under genome-wide linkage that creates interference between mutations, known as Hill-Robertson interference, which reduces the efficiency of natural selection (Hill and Robertson, 1966). Without recombination to link and unlink combinations of mutations, natural selection must act on entire genomes – not individual mutations – and select for clones with combinations of mutations of better aggregate fitness. Thus, advantageous drivers may not fix in the population, if they arise on an unfit background, and conversely, deleterious passengers can fix, if they arise on fit backgrounds.

The inability of asexuals to eliminate deleterious passengers is driven by two Hill-Robertson interference processes: hitchhiking and Muller’s ratchet (Figure 1A). Hitchhiking occurs when a strong driver arises within a clone already harboring several passengers. Because these passengers cannot be unlinked from the driver under selection, they are carried with the driver to a greater frequency in the population. Muller’s ratchet is a process where deleterious mutations continually accrue within different clones in the population until natural selection is overwhelmed. Whenever the fittest clone in an asexual population is lost through genetic drift, the maximum fitness of the population declines to the next most fit clone (Figure 1B). The rate of hitchhiking and Muller’s ratchet both increase with the genome-wide mutation rate (Johnson, 1999; Neher and Shraiman, 2012). Therefore, the second hypothesis predicts that selection against deleterious passengers should be more efficient (dN/dS < 1) in tumors with lower mutational burdens.

Figure 1

Download asset Open asset

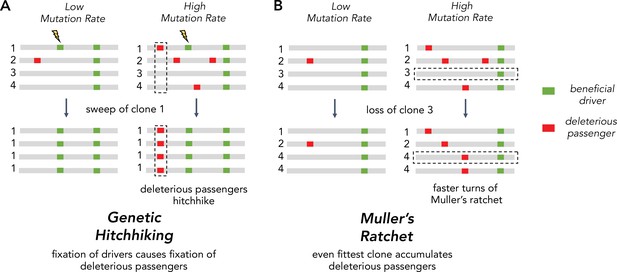
Two Hill-Robertson interference processes that accumulate deleterious mutations at high mutation rates.

(A) Genetic hitchhiking. Each number identifies a different segment of a clone genome within a tumor. De novo beneficial driver mutations that arise in a clone can drive other mutations (passengers) in the clone to high frequencies (black dotted column). If the passenger is deleterious, both beneficial drivers and deleterious passengers can accumulate. (B) Muller’s ratchet. As the mutation rate within a tumor increases, deleterious passengers accumulate on more clones. If the fittest clone within the tumor is lost through genetic drift (black dotted row), the overall fitness of the population will decline.

Here, we leverage the 10,000-fold variation in tumor mutational burden across 33 cancer types to quantify the extent that selection attenuates, and thus becomes more inefficient, as the mutational burden increases. Using dN/dS, we find that selection against deleterious passengers and in favor of advantageous drivers is most efficient in low mutational burden cancers. Furthermore, low mutational burden cancers exhibit efficient selection across cancer subtypes, as well as within subclonal mutations, homozygous mutations, somatic copy number alterations (CNAs), and essential genes. Additionally, high mutational burden tumors appear to mitigate this deleterious load by upregulating protein folding and degradation machinery. Finally, using evolutionary modeling, we find that Hill-Robertson interference alone can in principle explain these observed patterns of selection. Modeling predicts that most cancers carry a substantial deleterious burden (~46%) that necessitates the acquisition of multiple strong drivers (~5) in malignancies that together provide a benefit of ~119%. Collectively, these results explain why signatures of selection are largely absent in cancers with elevated mutational burdens and indicate that the vast majority of tumors harbor a large mutational load.

Results

Null models of mutagenesis in cancer

Mutational processes in cancer are heterogeneous, which can bias dN/dS estimates of selective pressures. dN/dS overcomes this issue by dividing observed mutation counts by what is expected under neutral evolution using null models. These null models must account for mutational biases that are often specific to cancer types and genomic regions.

To ensure our dN/dS calculations are robust and reproducible, we applied two different methods to account for mutational biases. The first approach uses a previously established parametric mutational model (dNdScv) that explicitly estimates the background mutational bias of each gene in its calculation of dN/dS (Martincorena et al., 2017). The second approach uses a permutation-based, non-parametric (parameter-free) estimation of dN/dS. In this approach, every observed mutation is permuted while preserving the gene, patient samples, specific base change (e.g. A>T) and its tri-nucleotide context. Note that permutations do not preserve the codon position of a mutation and thus can change its protein coding effect (nonsynonymous vs. synonymous). The permutations are then tallied for both nonsynonymous d_N^(permuted) and synonymous d_S^(permuted) substitutions (Figure 2—figure supplement 1) and used as expected proportional values for the observed number of nonsynonymous d_N^(observed) (or simply d_N) and synonymous d_S^(observed) (d_S) mutations in the absence of selection. The unbiased effects of selection on a gene, dN/dS, is then:

\frac{d N}{d S} = \frac{d_{N}^{(o b s e r v e d)} / d_{N}^{(p e r m u t e d)}}{d_{S}^{(o b s e r v e d)} / d_{S}^{(p e r m u t e d)}}

For all cancer types and patient samples, p-values and confidence intervals are determined by bootstrapping patient samples. Note that this permutation procedure will account for gene and tumor-level mutational biases (e.g. neighboring bases [Alexandrov and Stratton, 2014], transcription-coupled repair, S phase timing [Haradhvala et al., 2016], mutator phenotypes) and their covariation. We confirmed that this approach accurately measures selection even in the presence of simulated mutational biases (Materials and methods, Figure 2—figure supplement 2A). In addition, this approach also reliably measures the absence of selection (dN/dS = 1) in weakly expressed genes (Figure 2—figure supplement 2C).

We find that both the parametric and non-parametric approaches identify similar patterns of selection (Figure 2A). Since parametric mutational models can become very complex in cancer (exceeding 5000 parameters in some cases; Martincorena et al., 2017; Zapata et al., 2018), we elected to use the non-parametric approach, which makes fewer assumptions about underlying mutational processes, in subsequent calculations of dN/dS.

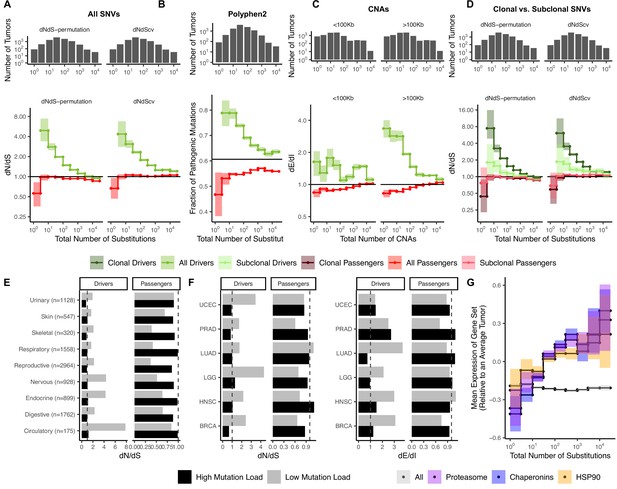
Figure 2 with 16 supplements see all

Download asset Open asset

Attenuation of selection and increased protein folding stress in high mutation load tumors.

(A) dN/dS of passenger (red) and driver (green) gene sets within 10,288 tumors in TCGA stratified by total number of substitutions present in the tumor (d_N^(observed)+d_S^(observed)). dN/dS is calculated with error bars using a permutation-based null model (left) and *dNdScv* (right). A dN/dS of 1 (solid black line) is expected under neutrality. Solid gray line denotes pan-cancer genome-wide dN/dS. (B) Fraction of pathogenic missense mutations, annotated by PolyPhen2, in the same driver and passenger gene sets also stratified by total number of substitutions. Black line denotes the pathogenic fraction of missense mutations across the entire human genome. (C) Breakpoint frequency of copy number alterations (CNAs) that reside within exonic (dE) to intergenic (dI) regions within putative driver and passenger gene sets (identified by GISTIC 2.0, Materials and methods) in tumors stratified by the total number of CNAs present in each tumor and separated by CNA length. Solid black line of 1 denotes values expected under neutrality. (D) dN/dS of clonal (variant allele frequency [VAF] > 0.2; darker colors) and subclonal (VAF < 0.2; lighter colors) passenger and driver gene sets in tumors stratified by the total number of substitutions. A dN/dS of 1 (solid black line) is expected under neutrality. (**A–D**) Histogram counts of tumors within mutational burden bins are shown in the top panels. (E) Driver and passenger dN/dS values of the highest and lowest defined mutational burden bin in broad anatomical sub-categories. (F) Same as (E), except for all specific cancer subtypes with ≥500 samples. (G) Z-scores of median gene expression within all genes, HSP90, Chaperonin, and Proteasome gene sets averaged across patients (relative to an average tumor) stratified by the total number of substitutions. All shaded error bars are 95% confidence intervals determined by bootstrap sampling.

Attenuation of selection in drivers and passengers for elevated mutational burden tumors

We estimated dN/dS patterns in both driver and passenger gene sets across 10,288 tumors from TCGA aggregated over 33 cancer types (Ellrott et al., 2018) (Materials and methods). Since TCGA is composed of whole-exome data, which limits our ability to assess mutations in non-coding regions, we elected to use the total number of protein-coding mutations as our proxy for the mutational burden of tumors. To quantify the extent that selection attenuates as the mutational burden increases, we stratified tumors into bins based on their total number of substitutions on a log-scale. For each bin of tumors, we pooled all of the variants together and estimated dN/dS jointly. Consistent with the inefficient selection model, whereby selection fails to eliminate deleterious mutations in high mutational burden tumors, we observe pervasive selection against passengers exclusively in tumors with low mutational burdens (dN/dS ~ 0.56 in tumors with ≤3 substitutions, while dN/dS ~ 0.93 in tumors with >10 substitutions, Figure 2A). We observed little negative selection in passenger genes when aggregating tumors across all mutational burdens (dN/dS ~ 0.93), which is broadly similar to previous estimates (Martincorena et al., 2017; Weghorn and Sunyaev, 2017; Zapata et al., 2018; Ostrow et al., 2014).

We confirmed that negative selection on passengers is specific to low mutational burden tumors and not biased by small sample sizes (Figure 2—figure supplement 2B). We randomly sampled passengers from high mutational burden tumors (>10 substitutions) 1000 times using the same bin sizes in Figure 2A and calculated dN/dS. Within the smallest bin size (N=168 somatic nucleotide variant [SNVs]), negative selection on passengers sampled from high mutational burden tumors was absent (average dN/dS ~ 0.96) compared to observed dN/dS in low mutational burden tumors (dN/dS ~ 0.56; p<2.2^–16). In fact, only 1.7% of randomly sampled sets of sites had similar signals of negative selection (dN/dS < 0.56).

Also consistent with the inefficient selection model, drivers exhibit a similar but opposing trend of attenuated selection at elevated mutational burdens (dN/dS ~ 2.7 when in tumors with ≤3 substitutions and dN/dS gradually declines to ~1.16 in tumors with >100 substitutions). This pattern is not specific to drivers that are oncogenes or tumor suppressors (Figure 2—figure supplement 3). While the attenuation of selection against passengers in higher mutational burden tumors is a novel discovery, this pattern among drivers has been reported previously (Martincorena et al., 2017). Furthermore, we confirmed that these patterns are robust to the choices that we made in our analysis pipeline. These include the: (i) effects of germline SNP contamination (Figure 2—figure supplement 4), (ii) choice of driver gene set (Bailey et al., 2018, IntOGen Gonzalez-Perez et al., 2013, and COSMIC Tate et al., 2019; Forbes et al., 2008, Figure 2—figure supplement 5), (iii) differences in tumor purity and thresholding (Figure 2—figure supplement 6), and (iv) null model of mutagenesis (dNdScv, Figure 2A and Figure 2—figure supplement 7; Martincorena et al., 2017) (Materials and methods).

If negative selection is more pronounced in low mutational burden tumors, then the nonsynonymous mutations observed should also be less functionally consequential. By annotating the functional effect of all missense mutations using PolyPhen2 (Adzhubei et al., 2010; Figure 2B), we indeed find that observed nonsynonymous passengers are less damaging in low mutational burden cancers. Similarly, driver mutations become less functionally consequential as mutational burden increases, as expected for mutations experiencing inefficient positive selection (Figure 2B). Together these two trends provide additional and orthogonal evidence that selective forces on nonsynonymous mutations are more efficient in low mutational burden cancers.

Since all mutational types experience Hill-Robertson interference, attenuated selection should also persist in CNAs. We used two previously published statistics to quantify selection in CNAs: breakpoint frequency (Korbel et al., 2007) and fractional overlap (Zack et al., 2013). For both measures, we compare the number of CNAs that either terminate (breakpoint frequency) within or partially overlap (fractional overlap) Exonic regions of the genome relative to non-coding (Intergenic and Intronic) regions (dE/dI, see Materials and methods). Like dN/dS, dE/dI is expected to be <1 in genomic regions experiencing negative selection, >1 in regions experiencing positive selection (e.g. driver genes), and ~1 when selection is absent or inefficient (Figure 2—figure supplement 8). Using dE/dI, we observe attenuating selection in both driver and passenger CNAs as the total number of CNAs increases for both breakpoint frequency (Figure 2C) and fractional overlap (Figure 2—figure supplement 9). While CNAs of all lengths experience attenuated selection, CNAs longer than the average gene length (>100 KB) experience greater selective pressures in drivers. Collectively, these results strongly support the inefficient selection model and argue that the observed patterns must be due to a universal force in tumor evolution. We find that selection consistently attenuates in both drivers and passengers across all cancers as mutational burden increases.

Strong selection in low mutational burden tumors cannot be explained by mutational timing, gene function, or tumor type

We next tested alternative hypotheses to the inefficient selection model. We considered the possibility that selection is strong only during normal tissue development, but absent after cells have transformed to malignancy. This would disproportionately affect low mutational burden tumors, as a greater proportion of their mutations arise prior to tumor transformation. If true, then attenuated selection should be absent in subclonal mutations, which must arise during tumor growth. However, selection clearly attenuates with increasing mutational burden for the subset of likely subclonal mutations with variant allele frequency (VAF) below 20% (Figure 2D and Figure 2—figure supplement 10). Although selection attenuates in drivers and passengers in both subclonal and clonal mutations, selection is weaker in both drivers and passengers with lower VAFs. Weaker efficiency of selection among less frequent variants is expected under a range of population genetic models (Messer, 2009) and especially so in rapidly expanding, spatially constrained cancers (Sottoriva et al., 2015). In addition, heterozygous mutations, to the extent they are only partially dominant (López et al., 2020), are also expected to exhibit lower VAFs and experience weaker selection.

Next, we considered and rejected the possibility that attenuated selection is limited to particular types of genes. We first annotated our observed mutations by different functional categories and Gene Ontology (GO) terms (Harris et al., 2004) and find that negative selection is not specific to any particular gene functional category expected to be under constraint, and specifically not limited to essential or housekeeping genes – a key prediction of the ‘weak selection’ model (Martincorena et al., 2017; Figure 2—figure supplement 11, p<0.05, Wilcoxon signed-rank test).

Finally, we found that these patterns of attenuated selection persist across cancer subtypes for both SNVs and CNAs. We calculated dN/dS in tumors grouped by nine broad anatomical sub-categories (e.g. neuronal) and 33 subtype classifications (Grossman et al., 2016; Figure 2E–F). We find that patterns of attenuated selection in SNVs persists in the broad and specific (drivers p=3.8 × 10^–5, passengers p=1.7 × 10^–2, Wilcoxon signed-rank test; Figure 2—figure supplement 12) classification schemes. Furthermore, dE/dI measurements of CNAs exhibit similar patterns of selection in broad (Figure 2—figure supplement 13) and specific subtypes (Figure 2F; drivers p<0.05 and passengers p<0.05).

Collectively, these results suggest that tumors with elevated mutational burdens carry a substantial deleterious load. Since nonsynonymous mutations are thought to be primarily deleterious by inducing protein misfolding (Drummond and Wilke, 2008; Lobkovsky et al., 2010), we tested whether an increase in the number of passenger mutations in tumors would lead to elevated protein folding stress, and, in turn, drive the upregulation of heat shock and protein degradation (McGrail et al., 2020) pathways in cancer (Santagata et al., 2011). Indeed, gene expression of HSP90, Chaperonins, and the Proteasome does increase across the whole range of SNV (weighted R² of 0.84, 0.78, and 0.78, respectively) and CNA burdens (weighted R² of 0.83, 0.88, and 0.85, respectively) (Figure 2G and Figure 2—figure supplement 14A). This trend persists across cancer types for SNVs and CNAs (Figure 2—figure supplement 14D-E). Importantly, expression of these gene sets increases across the whole range of mutational burdens, even after the dN/dS of passengers approaches 1. This result presents additional evidence that passengers continue to impart a substantial cost to cancer cells, even in high mutational burden tumors.

Evolutionary modeling estimates the fitness effects of drivers and passengers, and rate of Hill-Robertson interference processes

We next tested whether Hill-Robertson interference – a process where selection becomes inefficient due to interference between linked mutations with competing fitness effects – alone can generate these patterns of attenuated selection. Specifically, we modeled tumor progression as a simple evolutionary process with advantageous drivers and deleterious passengers. We then used approximate Bayesian computation (ABC) to compare these simulations to observed data and infer the mean fitness effects of drivers and passengers.

Our previously developed evolutionary simulations model a well-mixed population of tumor cells that can randomly acquire advantageous drivers and deleterious passengers during cell division (McFarland et al., 2013). The product of the individual fitness effects of these mutations determines the relative birth and death rate of each cell, which in turn dictates the population size N of the tumor. If the population size of a tumor progresses to malignancy (N>1,000,000) within a human lifetime (≤100 years), the accrued mutations and patient age are recorded. The mutation rate of each simulated tumor is randomly sampled from a broad range (10^–12–10^–7 mutations · nucleotide^–1 · generation^–1, Materials and methods). Although this model ignores a great deal of known tumor biology, we believe it constitutes the simplest evolutionary model that could possibly recapitulate observed selection for drivers and against passengers. Our question is not whether this model is correct in all details but rather whether even such a simple model can generate quantitatively similar patterns as observed in the data with sensible values of mutation rates and selection coefficients.

Figure 3A illustrates the ABC procedure. To compare our model to observed data, we simulated an exponential distribution of fitness effects (DFEs) with mean fitness values that spanned a broad range (10^–2–10⁰ for driver and 10^–4–10^–2 for passengers, Materials and methods). We summarized observed and simulated data using statistics that capture three relationships: (i) the dependence of driver and passenger dN/dS rates on mutational burden, (ii) the rate of cancer age incidence (SEERs database National Cancer Institute, 2007), and (iii) the distribution of mutational burdens (summary statistics of (ii) and (iii) were based on theoretical parametric models Frank, 2007, Materials and methods, Figure 3—figure supplements 1–2). We then inferred the posterior probability distribution of mean driver fitness benefit and mean passenger fitness cost using a rejection algorithm that we validated using leave-one-out cross validation (CV) (Materials and methods, Figure 3—figure supplement 3).

Figure 3 with 6 supplements see all

Download asset Open asset

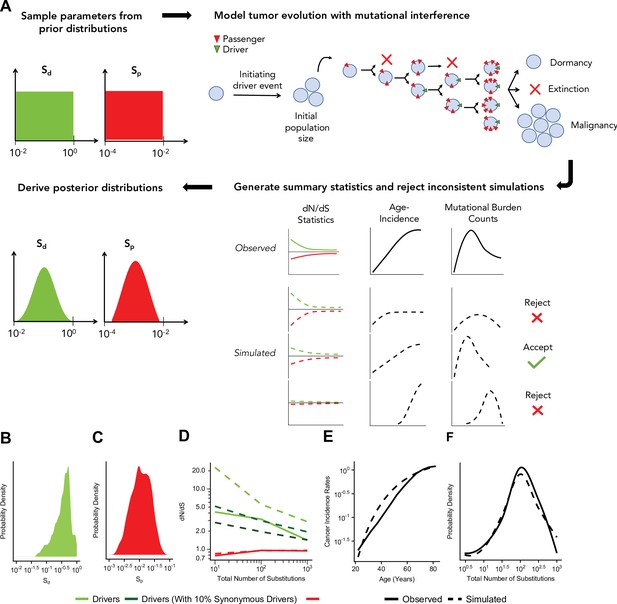
Approximate Bayesian computation (ABC) procedure estimates the strength of selection in passengers and drivers.

(A) Schematic overview of the ABC procedure used. A model of tumor evolution with genome-wide linkage contains two parameters – s_drivers (mean fitness benefit of drivers) and s_passengers (mean fitness cost of passengers) – sampled over broad prior distributions of values. Simulations begin with an initiating driver event that establishes the initial population size of the tumor. The birth rate of each individual cell within the tumor is determined by the total accumulated fitness effects of drivers and passengers. If the final population size of the tumor exceeds 1 million cells within a human lifetime (100 years), patient age and accrued mutations are recorded. Summary statistics of four relationships are used to compare simulations to observed data: (i) dN/dS rates of drivers and (ii) passengers across mutational burden, (iii) rates of cancer incidence vs. age, and (iv) the distribution of mutational burdens. Simulations that excessively deviate from observed data are rejected (Materials and methods). (**B–C**) Inferred posterior probability distributions of s_drivers and s_passengers. The maximum likelihood estimate (MLE) of s_drivers is 53.0% (green, 95% CI [16.0, 111.4]), and the MLE of s_passengers is 1.03% (green, 95% CI [0.40, 3.98%]). (**D–F**) Comparison of the summary statistics of the best-fitting simulations (MLE parameters, dashed lines) to observed data (solid lines). (D) dN/dS rates of passengers (red) and drivers (light green) for simulated and observed data vs. mutational burden. A model where 6% of synonymous mutations within drivers experience positive selection (dark green) was also considered. (E) Cancer incidence rates for patients above 20 years of age. (F) Distribution of the mutational burdens of tumors.

Using this approach, the maximum likelihood estimate (MLE) of mean driver fitness benefit is 53% (Figure 3B), while the MLE of passenger mean fitness cost is 1.03% (Figure 3C). Simulations with these MLE values agree well with all observed data (Figure 3D–F, Pearson’s r=0.988 for combined driver/passenger dN/dS).

While Hill-Robertson interference alone explains dN/dS rates in the passengers well, the simulations most consistent with observed data still exhibited consistently higher dN/dS rates in drivers (Figure 3D). We tested whether positive selection on synonymous mutations within driver genes could explain this discrepancy. Indeed, we find that a model incorporating synonymous drivers agrees modestly better with observed statistics (3.5-fold relative likelihood, ABC posterior probability). The best-fitting model predicts that ~6% of synonymous mutations within driver genes experience positive selection, which is consistent with previous estimates for human oncogenes (Supek et al., 2014) (Materials and methods, Figure 3D and Figure 3—figure supplement 4). Furthermore, we observe additional evidence of selection and codon bias in synonymous drivers exclusive to low mutational burdens (TCGA samples, Materials and methods, Figure 3—figure supplement 4).

We note that although deleterious passengers are necessary to explain attenuation of negative selection with mutational burden in passengers, alternative explanations could also contribute to attenuation of positive selection in drivers. Specifically, high mutational burden tumors are more likely to contain mutations in pan-cancer driver gene sets which might not directly contribute to tumorigenesis in specific tumors, and thus might not be under direct positive selection in all tumors. Similarly, additional driver mutations might not directly contribute to tumor fitness beyond a certain number of driver mutations (e.g. 5-hit model). Nonetheless, it’s important to note that Hill-Robertson interference is capable of reproducing all the features of the data (steep attenuation of negative selection in passengers and gradual attenuation of positive selection in drivers).

Overall, our results indicate that rapid adaptation through natural selection – acting on entire genomes, rather than individual mutations – is pervasive in all tumors, including those with elevated mutational burdens. Given the quantity of drivers and passengers observed in a typical cancer (TCGA), our model implies that cancer cells are in total ~90% fitter than normal tissues (119% total benefit of drivers, 46% total cost of passengers). A median of five drivers each of which has a mean benefit of ~19% accumulate per tumor in these simulations – also consistent with estimates from age incidence curves (National Cancer Institute, 2007), known hallmarks of cancer (Hanahan and Weinberg, 2000), and estimates of the selective benefit of individual drivers (Dai et al., 2007). Lastly, the mutation rates of tumors that could progress to cancer in our model also recapitulate observed mutation rates in human cancer (Camps et al., 2007) (median 3.7×10^–9, 95% interval 1.1×10^–10–8.2×10^–8, Figure 3—figure supplement 5).

Most notably, under our modeling assumptions, all passengers together confer a fitness cost of ~46% per tumor. While this collective burden appears large, the individual fitness effects of accumulated passengers in these simulations (mean 0.8%) are similar to observed fitness costs in cancer cell lines (1–3%) (Williams et al., 2008) and the human germline (0.5%) (Cassa et al., 2017). Note that in our model, these passengers accumulated primarily via Muller’s ratchet, while only ~5% accumulated via hitchhiking inferred using population genetics theory (McFarland et al., 2013) and MLE fitness effects, Materials and methods, Figure 3—figure supplement 6. These results suggest that Hill-Robertson interference is a plausible model for the empirical patterns of attenuated selection with mutational burden observed in the data.

Discussion

Here, we argue that signals of selection are largely absent in cancer because of the inefficiency of selection and not because of weakened selective pressures. In low mutational burden tumors (≤3 total substitutions per tumor), increased selection for drivers and against passengers is observed and ubiquitous: in SNVs and CNAs; in heterozygous, homozygous, clonal, and subclonal mutations; and in mutations predicted to be functionally consequential. These trends are not specific to essential or housekeeping genes. Importantly, these patterns persist across broad and specific tumor subtypes. Collectively, these results suggest that inefficient selection is generic to tumor evolution and that deleterious load is a nearly universal hallmark of cancer.

Importantly, these patterns of selection are missed when dN/dS rates are not stratified by mutational burden. Since <0.1% of mutations in TCGA reside within low mutational burden tumors (~1% of all tumors, N=83), dN/dS in passengers at low mutational burdens (~0.56) does not appreciably alter pan-cancer dN/dS of passengers (0.97 in our study, 0.82–0.98 in Martincorena et al., 2017; Weghorn and Sunyaev, 2017; Zapata et al., 2018; Ostrow et al., 2014). In fact, the power to detect negative selection on passengers at low mutational burdens is only possible by aggregating all mutations within these tumors and estimating dN/dS jointly. Thus, we believe that low mutational burden tumors are uniquely valuable for identifying genes and pathways under positive and negative selection. While only ~1% of tumors exhibit substantial negative selection, selection in drivers, selection on CNAs, and expression patterns of chaperones and proteasome components all show a continuous response to deleterious passenger load across a broad range of mutational burdens. Collectively, this suggests that passengers continue to be deleterious even in high mutational burden tumors.

Using a simple evolutionary model, we show that Hill-Robertson interference alone can explain this ubiquitous trend of attenuated selection in both drivers and passengers. dN/dS rates attenuate in drivers because the background fitness of a clone becomes more important than the fitness effects of an additional driver at elevated mutation rates. Furthermore, these simulations indicate that, despite dN/dS patterns approaching 1 in tumors with elevated mutational burdens, passengers are not effectively neutral (Ns > 1). Instead, passengers confer an individually weak, but collectively substantial fitness cost of ~46% that measurably impacts tumor progression. Because this simple evolutionary model does not explicitly incorporate many known aspects of tumor biology (e.g. haploinsufficiency, see Supplementary file 1), these fitness estimates are highly provisional. Nonetheless, we note that selection’s efficiency in cancer is further reduced when spatial constraints are considered (Sottoriva et al., 2015).

The functional explanation for why passengers in cancer are deleterious is unknown. In germline evolution, mutations are believed to be primarily deleterious because of protein misfolding (Drummond and Wilke, 2008; Lobkovsky et al., 2010). Deleterious passengers in somatic cells should confer similar effects. Indeed, we find that elevated mutational burden tumors may buffer the cost of deleterious mutations by upregulating multiple heat shock pathways. However, deleterious passengers may carry other costs to cancers or be buffered by additional mechanisms. Understanding and identifying how tumors manage this deleterious burden should identify new cancer vulnerabilities that enable new therapies and better target existing ones (Gorgoulis et al., 2018; Dai et al., 2007; Glaire and Church, 2017).

Materials and methods

Defining mutational burden in SNVs and binning tumors

Request a detailed protocol

Since TCGA is composed of whole-exome data, which limits our ability to accurately assess mutations in non-coding regions, we elected to use the total number of protein-coding mutations (i.e. missense, nonsense, and synonymous mutations) as our proxy for the mutational burden of tumors. This allows us to focus on the highest quality set of mutations that we have, which can impact the power to detect selection (Figure 2—figure supplement 15). We note that this high-quality set mutations does not have evidence of germline contamination by common SNPs (MAF > 5%) from 1000 Genomes Project (1000 Genomes Project Consortium et al., 2015) (v2015 Aug) using ANNOVAR (Wang et al., 2010) to annotate mutations in TCGA (Figure 2—figure supplement 4). For all analyses calculating dN/dS in tumors stratified by their mutational burden, all variants within each bin of tumors were pooled together and dN/dS was calculated jointly on each bin of tumors. Counts of the number of mutations use to estimate dN/dS in each mutational burden can be found in Figure 2—figure supplement 16.

A non-parametric null model of mutagenesis to calculate dN/dS

Request a detailed protocol

We assume that for any particular tumor, mutation rates are constant across a gene for a particular tri-nucleotide context and base change (e.g. C>G). Our procedure is inspired by constrained marginal models (or ‘edge switching’ in network analysis), whereby the marginal distributions of observations aggregated over known confounding variables are preserved under permutation to create a null distribution. In our application of this strategy, the marginal distributions of mutations (across tri-nucleotide context, base change, gene, and tumor) remain preserved – as they would be in a constrained marginal model; however, we exhaustively consider every acceptable permutation of the data. Because our approach is highly constrained, these permutations are exhaustively computable (median 36 alternatives per mutation). Thus, resampling is unnecessary.

Our null model presumes that all mutations of type i, defined by a tri-nucleotide context and base change, arise with probability M_igt within each gene g and tumor t. For each gene, we tally the total quantity of nonsynonymous mutations N_ig and synonymous mutations S_ig. Suppose selection enriches or depletes nonsynonymous mutations within a gene and tumor by a rate ω_gt. The expected number of nonsynonymous and synonymous mutations within a particular tumor and gene are $E [d_{N}] = ω_{} \sum_{i} M_{i g t} N_{i g}$ and $E [d_{S}] = \sum_{i} M_{i g t} S_{i g}$ in the absence of selective pressures on synonymous mutations. As with the main text, d_N and d_N^(observed) are used interchangeably. Although M_igt is unknown, dN/dS statistics attempt to infer selection nonetheless by noting that:

\frac{E [d_{N}]}{E [d_{S}]} = \frac{ω_{g t} \sum_{i} M_{i g t} N_{i g}}{\sum_{i} M_{i g t} S_{i g}} = ω_{g t} \frac{< M_{i g t}, N_{i g t} >}{< M_{i g t}, S_{i g t} >} = ω_{g t} \frac{ρ_{M N} | | M_{g t} | | | | N_{g t} | |}{ρ_{M S} | | M_{g t} | | | | S_{g t} | |} = ω_{g t} \frac{ρ_{M N} | | N_{g t} | |}{ρ_{M S} | | S_{g t} | |}

Note that $ρ_{A B} = A, B > (‖ A ‖ ‖ B ‖)$ , where $\begin{matrix} ‖ A ‖ = \sqrt{< A, A >} \end{matrix}$ is the Pearson product-moment correlation coefficient. When ρ_MN ≈ ρ_MS,

\frac{E [d_{N}] / {‖N‖}_{i}}{E [d_{S}] / {‖S‖}_{i}} {\approx ω}_{}

That is, dN/dS is approximately equal to the selective pressures on nonsynonymous mutations when the accessible nonsynonymous and synonymous loci are properly accounted and when the correlation between mutational processes and nonsynonymous loci are roughly equivalent to the correlation between mutational processes and synonymous loci. Traditionally, this assumption was used to calculate dN/dS. To improve resolution of dN/dS, researchers have attempted to account for these correlations using sophisticated parametric models of M_igt. An alternative statistical approach, however, is to treat these correlations as nuisance parameters.

Constrained marginal models permute observed data in all possible manners that preserve the underlying covariance structure of the data (e.g. ρ_MN, ρ_MS). In our particular case of this method, we note that by definition, $d_{N}^{p e r m u t e d} = \sum_{i} ({d_{N}^{o b s e r v e d}}_{i} N_{i} + {d_{S}^{o b s e r v e d}}_{i} N_{i})$ . Thus:

\begin{array}{ll} \frac{E [d_{N}^{p e r m u t e d}]}{E [d_{S}^{p e r m u t e d}]} & = \frac{\sum_{i} (ω_{} M_{i g t} N_{i g t}^{2} + M_{i g t} N_{i g t} S_{i g t})}{\sum_{i} (ω_{} M_{i g t} N_{i g t} S_{i g t} + M_{i g t} S_{i g t}^{2})} \\ = \frac{ω_{} ρ_{M N} ‖ M_{} ‖ {‖ N_{} ‖}^{2} + ρ_{M N} ‖ M_{} ‖ ‖ N_{} ‖ ‖ S_{} ‖}{ω_{} ρ_{M S} ‖ M_{} ‖ ‖ S_{} ‖ ‖ N_{} ‖ + ρ_{M S} ‖ M_{} ‖ {‖ S_{} ‖}^{2}} \\ = \frac{ρ_{M N} ‖ N_{} ‖}{ρ_{M S} ‖ S_{} ‖} \end{array}

Hence, by dividing the observed mutations by all permutations, we eliminate the covariance of mutational processes with available loci and, thus, measure ω_gt directly for any particular gene-tumor combination without mutational bias.

Unfortunately, because of the log-sum inequality, mutational bias can arise once cohorts of genes and cohorts of tumor samples are binned. This problem is common to all dN/dS measures and is a consequence of the correlation of mutational biases with selection (i.e. $M_{i g t}, ω_{} >$ ) – not the correlation of mutational biases with one another, as these covariances are already accounted for in a constrained marginal model. For example, if tri-nucleotide biases covary linearly with gene-level biases, and are independent of tumor-level biases, then a parametric estimate of M_igt may deconstruct M_igt into $M_{i g t} = f (i, g, t, ρ_{i g})$ , where $ρ_{i g}$ is the covariation of tri-nucleotide mutational biases with gene-level biases. Nonetheless, $M_{i g t}, ω_{} >\propto< ρ_{i g}, ω_{} >$ will still be ignored. Indeed, this covariation of mutational processes with selective forces is the focus of our current study: selection and genome-wide mutation rate are correlated (i.e. $\sum_{t} M_{i g t} ω_{} \neq 0$ ) because of Hill-Robertson interference. Hence, the level at which observed d_N values d_S are binned necessarily ignores covariation between mutational processes and selection (in addition to any variation of ω_gt within the bin). Another example of this binning challenge arises when positive and negative selection act on different regions of the same gene, which gene-level dN/dS binning can misinterpret as neutral evolution.

Validation of non-parametric null model

Request a detailed protocol

To confirm that our null model can accurately estimate dN/dS even in the presence of extreme tri-nucleotide mutational biases, we simulated artificial data where different COSMIC signatures (Tate et al., 2019 Forbes et al., 2008; Forbes et al., 2008) (SBS Signatures 1–9, v3) contribute to all of the mutations. Permuted d_N and d_S tallies for each mutational context were simulated by randomly sampling 1000 genes with the same mutational context. The fraction of permuted d_N and d_S tallies for each mutational context was used as weighted probabilities to derive observed d_N and d_S tallies. To simulate negative selection, d_N counts were randomly removed from each context at a rate 1 − ω_gt (e.g. a simulated ‘true’ dN/dS of 0.8 in a cohort of samples indicates a 20% chance of nonsynonymous mutations being removed in the samples). These simulated (true) rates were then compared to observed and permuted d_N and d_S tallies according to the dN/dS metric that we used throughout this study:

\frac{d N}{d S} = \frac{d_{N}^{(observed)} / d_{N}^{(permuted)}}{d_{S}^{(observed)} / d_{S}^{(permuted)}}

We confirmed that this approach accurately measures selection in the presence of simulated mutational biases (Figure 2—figure supplement 2).

Lastly, we note that binning nonsynonymous and synonymous mutations at the genome-wide level (e.g. drivers and passengers) provided the most robust estimates of dN/dS when bootstrapping observed tumor samples. Statistical power is insufficient when binning at the individual gene level. Bootstrapping also demonstrated that log-transformation of dN/dS values increases statistical power, and thus was generally applied to dN/dS analyses in this study.

A parametric null model of mutagenesis

Request a detailed protocol

For comparison, we also calculated dN/dS using dNdScv (Campbell and Martincorena, 2017) – a previously published parametric null model of mutagenesis in cancer (Martincorena et al., 2017). To compare both methods, dNdScv ran globally and separately on samples stratified by the total number of substitutions using the following parameters: max_coding_muts_per_sample = Inf max_muts_per_gene_per_sample = Inf.

Global dN/dS values of all nonsynonymous mutations (w_all, reported by dNdScv) were used. This model reproduced our non-parametric dN/dS trends (Figure 2A) and was used to infer patterns of selection in synonymous mutations (Figure 3—figure supplement 4). We note that stratifying tumors in TCGA into 20 bins of equal sample size (as was done in Martincorena et al., 2017), rather than evenly spaced bins, averages out a significant proportion of the negative selection observed in passengers, since low mutation burden tumors reside within the tail-end of the distribution (Figure 2—figure supplement 7).

Identification of driver genes in cancer

Request a detailed protocol

For all analysis using SNVs, unless explicitly stated, a comprehensive list of 299 pan-cancer driver genes derived from 26 computational tools was used to catalog driver genes (Bailey et al., 2018). Other pan-cancer driver gene sets tested were derived from COSMIC’s Driver Gene Census (Tate et al., 2019; Forbes et al., 2008) (downloaded on October 2016) and IntOGen’s Cancer Drivers Database (Gonzalez-Perez et al., 2013) (v2014.12) which contained 602 and 459 number of driver genes, respectively.

Many driver genes are associated with only particular tumor subtypes. To compare patterns of selection across cancer subtypes without increasing or decreasing the size of the list for each subtype, we chose to use a single set of driver genes for most analyses. This may understate the degree of positive selection in driver genes as mutations in these genes may be passengers in some tumor subtypes. In Figure 2—figure supplement 5, we investigate patterns of selection using the top 100 driver genes identified for each tumor type and observe decreased signatures of positive selection overall in driver genes. Nevertheless, the patterns of attenuated selection in drivers and passengers remain. While tissue-type specific driver genes certainly exist, our results suggest that our statistical power to detect drivers still remains too limited to justify subdividing analyses by tumor type in many cases.

For all CNA analysis, GISTIC 2.0 Mermel et al., 2011 was used to identify a set of genomic regions enriched for copy number gains and copy number losses using recommended settings with a confidence threshold of 0.9. CNAs used to identify these peaks were downloaded from the NIH Genomic Data Commons (GDC) (Grossman et al., 2016) in the TCGA cohort. For each amplification peak, the closest gene was annotated as a putative oncogene, and similarly the closest gene to each deletion peak was annotated as a putative tumor suppressor. The top 100 amplification peaks (oncogenes) and deletion peaks (tumor suppressors) were classified as drivers for each of the 32 tumor types. Thirty-four percent of identified driver genes appear in more than one tumor type, while 2.6% of identified driver genes appear in more than five tumor types.

For both SNV and CNA analysis, passengers were defined as mutations that did not reside within driver genes. The vast majority of mutations are passengers, and their relative totals for both SNVs and CNAs are depicted in Figure 2—figure supplement 16.

Annotation of clonal and subclonal mutations

Request a detailed protocol

VAFs were calculated per site as the number of mutant read counts divided by the total number of read counts. VAFs were adjusted for purity using calls made by ABSOLUTE (Grossman et al., 2016; Carter et al., 2012), collected from GDC. A VAF threshold of 0.2 was used to define ‘subclonal’ (<0.2) vs. ‘clonal’ (>0.2) SNVs. Different VAF thresholds were considered (Figure 2—figure supplement 10) and the choice of ‘clonal’ thresholding did not impact the conclusions of this study.

PolyPhen2 analysis

Request a detailed protocol

PolyPhen2 annotations in the MC3 SNP calls were used (Adzhubei et al., 2010). Only missense mutations that were categorized as either ‘benign’, ‘probably damaging’, or ‘possibly damaging’ were used. The fraction of pathogenic missense mutations was calculated as the number of pathogenic mutations categorized as either ‘probably damaging’ or ‘possibly damaging’ divided by the total number of categorized mutations.

Classification of genes by functional category

Request a detailed protocol

To test for patterns of selection in functionally related genes, we annotated all mutations by different functional categories and GO terms (Harris et al., 2004). Oncogenes and tumor suppressors were annotated from a curated set of 99 high confidence cancer genes (Kumar et al., 2015). Essential genes were collected from a genome-wide CRISPR screen that identified genes required for proliferation and survival in a human cancer cell line (Wang et al., 2015). Housekeeping genes were defined as genes with an exon that is expressed in all tissues at any non-zero level, and exhibits a uniform expression level across tissues (Eisenberg and Levanon, 2015). Interacting proteins were downloaded from the mentha database in April 2019 (Calderone and Cesareni, 2012).

To identify highly expressed genes, median transcripts per million (TPM) in 54 tissue types (v7 release) were downloaded from the Genotype-Tissue Expression (GTEx) project (GTEx Consortium, 2020; Carithers and Moore, 2015). Tissues that contained high expression in most genes, specifically testes, were removed. Only genes that had TPM counts above zero in any of the 53 remaining tissues were used. TPM counts were averaged across all tissues. Highly expressed genes were defined as the top 1000 genes expressed across all tissues.

To test for signals of negative selection in other functional groups, we annotated mutations by candidate GO terms according to biological processes: Transcription Regulation (GO Term ID: 0140110), Translation Regulation (GO Term ID: 0045182), and Chromosome Segregation (GO Term ID: 0007059).

Somatic CNAs

Request a detailed protocol

All CNAs were downloaded from the COSMIC database on June 2015 (Tate et al., 2019; Forbes et al., 2008). Mitochondrial CNAs were discarded from analysis, as copy number changes are difficult to infer. Gene annotations and the locations of telomeres and centromeres were downloaded from the UCSC Genome Browser (hg19). Telomeric and centromeric regions were masked from all measurements of dE/dI. Because the selection patterns of non-focal CNAs – alterations with at least one terminus in a telomere or centromeric region – were not noticeably different from long (>100 kb) focal CNAs, these two alteration classes were aggregated for analysis. Notably, we observed positive selection for both amplifications and deletions within oncogenes, and for both deletions and amplifications within tumor suppressors. For this reason, we did not distinguish between gains and losses, nor oncogenes and tumor suppressors in published analyses: any CNA that overlapped an oncogene or tumor suppressor in any region (for any fraction of the CNA) was classified as a driver. Mutational burden was defined simply as the total number of CNAs within a sample. Pan-cancer CNAs from cBioPortal (August 2018) were also analyzed, however consistent purity and ploidy estimates could not be obtained by using either ABSOLUTE (Carter et al., 2012) or TITAN (Ha et al., 2015), so this data was not used for published analyses of CNAs.

Measurements of selection on CNAs

Request a detailed protocol

dE/dI was calculated using a ‘breakpoint frequency’ metric and a ‘fractional overlap’ metric. For both metrics, the dE/dI of a particular gene set i (e.g. driver or passenger genes) is defined by a genomic track T_i,g, which is one for every annotated region g of the track and zero elsewhere. Only non-centromeric and non-telomeric regions are considered in the mappable human genome G. Each CNA C_g,m is defined by its position on the genome g and the mutational burden m of the tumor harboring the mutation. For ‘breakpoint frequency’ C_m,i is one at the position of both termini of the CNA and zero elsewhere. For ‘fractional overlap’ C_m,i is 1/L, where L is the length of the CNA, for every region of the genome spanned by the CNA and zero elsewhere. For a particular range of mutational burdens M, dE/dI was defined as:

{\frac{d E}{d I}}_{i, M} = \frac{\sum_{m}^{M} \sum_{g}^{G} T_{i, g} C_{m, g}}{\sum_{g}^{G} T_{i, g}}

We note that calculation is accelerated by >×100 by commuting T_i,g with the outer summation (Σ_m^M). Lastly, we randomly permuted the start and stop positions of each CNA, while preserving its length, to derive a set of neutral CNAs not experiencing selection. This permutation analysis finds that dE/dI for both breakpoint frequency and fractional overlap is ~1 in the absence of selection (Figure 2—figure supplement 8).

Tumor purity analysis in TCGA samples

Request a detailed protocol

Tumor purity estimates from the ABSOLUTE algorithm (Carter et al., 2012) were downloaded from the GDC on May 2020. To evaluate the effects of tumor purity on patterns of selection, tumors below increasing thresholds of tumor purity were removed from the analysis, and dN/dS was calculated on tumors stratified by mutational burden bins (as described above.)

Expression analysis

Request a detailed protocol

Gene expression data was downloaded from the COSMIC database on September 2019. Genes used to identify different protein folding pathways were downloaded from Kampinga et al., 2009, genes involved in protein degradation pathways were identified from Tanaka, 2009. The median gene expression of all genes in each protein folding pathway was used. Patients were binned by the total number of substitutions (using MC3 SNP calls from TCGA) and CNAs, and the average gene expression of each bin was calculated.

Cancer subtype analysis

Request a detailed protocol

All tumor subtypes in were grouped into nine sub-categories, based on broad, predominantly anatomical features. Anatomical features (i.e. organ and systems of organs), rather than histological features or inferred cell-of-origin, were used as groupings because we believe that the fitness effects of mutations should be predominantly defined by the environment of the tumor. Nevertheless, we observed attenuated selection in both drivers and passengers in many broad histologically defined classifications (e.g. adenocarcinomas and sarcomas). For all cancer grouping analysis (broad and subtype), tumors were stratified into bins by the total number of substitutions (d_N+d_S) on a log-scale. Since tumor subtypes vary in their range of mutational burdens, (e.g. KIRC cancer subtypes only have tumors with <100 substitutions), dN/dS values in the lowest and highest mutational burden bin for each cancer subtype are shown.

Specific cancer subtype categories were taken directly from the NCI GDC (Grossman et al., 2016). Because CNAs were downloaded from COSMIC, CNA datasets were not classified with this same ontology. Supplementary file 2 details how CNA classifications were mapped on GDC categories (and sometimes more broadly defined groups). All subtypes with >200 samples were used in our CNA subtype analyses (Figure 2—figure supplement 13).

An evolutionary model with Hill-Robertson interference

Request a detailed protocol

Somatic cells in our populations are modeled as individual cells that can stochastically divide and die in a first-order (memoryless) Gillespie algorithm. This model was developed and described previously (McFarland et al., 2014). During division, cells can acquire advantageous drivers with rate µT_drivers and deleterious passengers with rate µT_passengers – these values specify the mean of Poisson-distributed pseudo-random number (PRN) generators that prescribe the number of drivers and passengers conferred during division (e.g. the number of drivers per division n_d = Poisson[n_d = k; λ = µT_drivers] = λ^k e^−k/k!). The DFEs conferred by each driver and each passenger are exponentially distributed PRNs with probability densities P(s_i = x; s_drivers)=Exp[−x/s_drivers]/s_drivers and P(s_i = x; s_passengers) = −Exp[−x/s_passengers]/s_passengers, respectively. Simulations with other exponential-family DFEs do not qualitatively differ from these exponential distributions (McFarland et al., 2013). The aggregate absolute cellular fitness is $f = \prod_{i}^{a l l m u t a t i o n s} (1 + s_{i})$ in our multiplicative epistasis model and $Δ f = s_{i} / (1 + ν f)$ with ν=1 in our diminishing-returns epistasis model, where Δf is the change in cellular fitness with each mutation (Arjan et al., 1999). The rate of cell birth is inversely proportional to cellular fitness, while the rate of cell death $D (N; N^{0}) = Log [1 + \frac{N}{(e - 1) N^{0}}]$ increases with the population size of the tumor N. With these birth and death processes, mean population size abides by a Gompertzian growth law in the absence of additional mutations, which is scaled by the mean cellular fitness E[N(<f > )]=log[1 +<f >/ N ⁰] (derived from master equation McFarland et al., 2013). While, programmatically, mutations exclusively affect the birth rate and the constraints on growth exclusively affect the death rate, we previously demonstrated that birth and death rates are generally nearly balanced such that dynamics are not affected by this design choice.

Because somatic cells do not recombine during cell division, dominance coefficients were not explicitly modeled. Thus in diploid cancers, our selection coefficients estimate the mean heterozygous effect of drivers and passenger (i.e. hs). Similarly, loss of heterozygosity (LOH) events (gene losses, gene conversions, mitotic recombination, etc.) are not explicitly modeled either; however, these events can be viewed as additional mutations that may be either adaptive drivers or deleterious passengers in the model. As sequencing data improves, we believe that it will be informative to explicitly model dominance coefficients, tumor ploidy, and LOH events.

Simulations progressed until tumor extinction (N=0 cells), malignant transformation (N=10⁶ cells), or until ~100 years had passed (18,500 generations). Only fixed mutations (present in the most recent common ancestor) within clinically detectable growths were analyzed in our ABC pipeline. The behavior of this model has been described previously (McFarland et al., 2013; McFarland et al., 2014) and the most relevant assumptions of this model and their effects on the conclusions of this study are described in Supplementary file 1.

Cells in our populations are fully described by their accrued mutations, and birth and death times. Birth and death events were modeled using an implementation of the next reaction (Gibson and Bruck, 2000), a Gillespie algorithm that orders events using a heap queue. Generation time in our model was defined as the inverse of the mean birth rate of the population: 1/<B(d, p)>. While all mutation events occurred during cell division, if mutations were to occur per unit of time (rather than per generation), rapidly growing tumors would acquire drivers at a slightly slower rate as generation times decline over time. This effect, however, is negligible compared to the variation in waiting times conferred by the variation in mutation rates (division times merely double, while mutation rates vary by 100,000-fold).

This simple evolutionary model is defined by five parameters µT_drivers, µT_passengers, s_drivers, s_passengers, and N⁰. The target size of drivers is defined as the approximate number of nonsynonymous mutations in the Bailey driver screen T_drivers = (# of driver genes)·(mean driver length)·(fraction of SNVs that are nonsynonymous)=300 genes · 1298 loci/gene · 0.737 nonsynonymous loci/ loci = 286,886 nonsynonymous loci. The target size of passengers was simply the remaining loci in the protein coding genome, T_passengers = 20,451,136 nonsynonymous loci. The mutation rate was constant throughout each tumor simulation and randomly sampled from a uniform distribution in log-space that ranged from 10^–12 to 10^–7 mutations·loci^–1·generation^–1. While tumors were initiated from this broad range, malignancies (N>10⁶ cells) were almost always restricted to mutation rates between 10^–10 and 10^–8 (Figure 3—figure supplement 5), as tumors with mutation rates drawn below this range almost never progressed to cancer within 100 years and tumors with mutation rates drawn above this range went extinct through natural selection.

The likelihood that tumors progress to cancer in the presence of deleterious passengers depends heavily on the initial population size N⁰ of the tumor. This dependence was studied previously (McFarland et al., 2014), where it was demonstrated that reasonable evolutionary simulations (those that progress to cancer >10% of the time, but <90% of the time) are restricted to a four-dimensional manifold N* within the five-dimensional phase space of parameters. For this reason, N⁰=N*(s_drivers, s_passengers, µT_drivers, µT_passengers) was determined by the other four parameters. To first order, this manifold is T_passengerss_paassengers/ (T_drivers s_drivers) (Weghorn and Sunyaev, 2017), however a more precise estimate (Equation S8 of McFarland et al., 2014) incorporating more precise estimates of Muller’s ratchet and the effects of hitchhiking on both driver and passenger accumulation rates, which does not exist in closed form was used. Additionally, at very low values of s_drivers, progression to cancer is limited by time, not by the accumulation of deleterious passengers. Hence, we assigned N⁰ such that:

N^{0} = M a x_{N^{0} [P_{c a n c e r} (N^{0} / N^{*}) = 0.5, \bar{t_{c a n c e r}} (N^{0} / N^{*}) = 18, 500 g e n e r a t i o n s]}

Here, P_cancer and t_cancer – the likelihood and waiting time to cancer – are defined byEquation S8 and S12 respectively in McFarland et al., 2014. N⁰ was determined from these equations using Brent’s method. Figure 3—figure supplement 2 depicts the values of N⁰, which ranged from 1 to 100 for all simulations.

In tumors that progress to malignancy (N=10⁶), only fixed nonsynonymous mutations (present in all simulated cells) were recorded. We also recorded (i) the fitness effect of these mutations, (ii) the mean population fitness, (iii) the number of generations until malignancy, and (iv) the mutation rate. These two values were used to generate the number of synonymous drivers and passengers, where P(d_s = k)=Poisson[k; λ = µT_{drivers/passengers}/r t_MRCA] defines the number of synonymous drivers/passengers conferred, t_MRCA represents the number of division until the most recent common ancestor arose in the simulation, r=2.795 represents the ratio of nonsynonymous to synonymous loci within the genome, weighted by the genome-wide tri-nucleotide somatic mutation rate, and the Poisson PRN generator was defined above. In simulations where synonymous drivers could arise, a fraction of the recorded nonsynonymous mutations (ranging from 0% to 20%) were simply re-labeled as synonymous drivers (as opposed to nonsynonymous drivers). This was done, again, by Poisson sampling in proportion to the desired fraction for each cancer simulation.

20×20 combinations of s_drivers and s_passengers parameters were simulated (Figure 3—figure supplements 1–2). Simulations were repeated until 10,000 cancers at each parameter combination were obtained or until 10 million tumor populations were simulated. While we attempted to initiate tumors at a population size where the probability of progression to cancer was 50%, some parameter combinations still did not yield 10,000 cancers after 10 million attempts (i.e. P_cancer < 0.1%). These combinations were predominately at low values of s_drivers, which were far from the MLE estimate of s_drivers and represent unrealistic evolutionary scenarios: drivers cannot be weakly beneficial, relegated to only 300 genes, and still overcome deleterious passengers within 100 years. These simulations are annotated as ‘progression impossible’. Simulation parameter sweeps were performed for both the multiplicative and diminishing returns epistasis models. Twenty fractions of synonymous drivers were also generated (ranging from 0% to 20%). These fractions were generated by simply re-labeling the driver mutations which conferred fitness (generated during the simulation) as synonymous, instead of nonsynonymous.

Summary statistics of simulated and observed tumors

Request a detailed protocol

For both simulated and observed data, we summarized dN/dS rates vs. mutational burden for drivers and for passengers by decade-sized bins: (0, 10], (10, 100], (100, 1,000]. Mutational burden for simulations was defined as the total number of substitutions (d_N+d_S) – exactly as it was defined for observed data. For simulated data, dN/dS = d_N/(d_S · r). Like observed data, dN/dS rates attenuated toward 1 for both drivers and passengers for all values of s_drivers and s_passengers.

Mutational burdens (MB) for simulated and observed data were summarized with the parameters of a negative binomial distribution, where $P (MB = k; n, p) = (\begin{matrix} k + n - 1 \\ n - 1 \end{matrix}) p^{n} {(1 - p)}^{k}$ . This distribution has been used previously to summarize the MB of human tumors (Turajlic et al., 2012) and exactly defines the expected number of mutations at transformation in a multi-stage model of tumorigenesis (Frank, 2007) when n drivers are needed for transformation and the probability that any mutation be a driver is 1 – p (Michor et al., 2005). Both n and p were used to summarize MB. These quantities were determined by maximum likelihood optimization of the probability mass function above over the support of mutational burdens of [1, 1,000] substitutions. The Han-Powell quasi-Newton least-squares method was used for optimization.

Age-dependent cancer incidence rates (CI) were summarized with the parameters of a gamma distribution, where $P (C I \leq t; k, θ) = \frac{1}{Γ (k)} γ (k, \frac{t}{θ})$ . Here, $γ (s, x) = \int_{0}^{x} t^{s - 1} e^{- t} d t$ is the lower incomplete gamma function and Γ(k) = γ(k, ∞) is the regular gamma function. Similar to our summarization of mutational burdens, this distribution is a generalization of the exact waiting time to transformation expected from a multi-stage model of tumorigenesis when tumors arise at a uniform rate over time, require k drivers for transformation, and wait an average time of θ between drivers (Michor et al., 2005). This cumulative distribution function was fit to observed incidence rates for all patients above 20 years of age using the least squares numerical optimization defined above (all cancer sites combined, both sexes, all races, 2012–2016; Howlader, 2013). Patients under 20 years of age were excluded because cancers in these patients generally arise from germline predispositions to cancer, which are (i) not directly modeled by our simulations, (ii) not detected as somatic mutations, and (iii) result in age incidence curves that do not agree with a gamma distribution (Frank, 2007). Because all cancer simulations are initiated at t=0 (instead of uniformly in time, as is presumed in the multi-stage model), the simulated data was fit using the probability density function of this distribution (instantaneous derivative) using maximum likelihood and the optimization algorithm described above. The cumulative distribution, then, represents the expected age incidence cancer incidence rate when simulations begin at uniformly distributed moments in time and, thus, was used to generate Figure 3D. Only the shape parameter k was used in ABC (and θ was ignored), as this parameter only specifies the dimensionality of time (simulation time was measured in cellular generations, not years) and all values of θ in our simulations are equivalent under a gauge transformation. Additionally, we do not expect the exact times of incidence to be particularly informative as the time of transformation is generally somewhat earlier than the time of detection.

Use of ABC for model selection and parameter inference

Request a detailed protocol

Like many Bayesian analyses, the main steps of an ABC analysis scheme are: (i) formulating a model, (ii) fitting the model to data (parameter estimation), and (iii) improving the model by checking its fit (posterior-predictive checks), and (iv) comparing this model to other models (Csilléry et al., 2012; Gelman, 2004).

The nine summary statistics described above were used to compare simulations to observed data. Agreement was summarized with a log-Euclidean distance, as all summary statistics resided on the domain [0, ∞) and log-transformation of the summary statistics minimized heteroscedasticity of the simulated data relative to a square-root or no transformation. Variance of the summary statistics was not normalized. ABC was performed using the ‘abc’ R package (Csilléry et al., 2012).

The rejection method (feedforward neural net) and tolerance (0.5) were chosen based on their capacity to minimize prediction error of the simulated data using leave-one-out CV (Figure 3—figure supplement 3). Ten-thousand instances of the neural network, which was restricted to a single layer, were initiated and the median prediction of these networks were used. These parameters were used for both model comparison and parameter inference. For parameter inferencing, the s_drivers and s_passengers prior values were log-transformed.

For the synonymous driver model, the base model (without synonymous drivers) was simply the lowest quantity of synonymous drivers (0%) in the parameter sweep of synonymous driver quantities (Figure 3—figure supplement 3B). The posterior probability mass of this value 0.017 was used as the one-sided p-value for the null hypothesis that these two models are equally predictive. Although the synonymous driver model agreed with the observed data slightly better, s_drivers and s_passengers parameters could not be inferred from the data because the potential for synonymous drivers destroys the utility of a dN/dS statistics, which is predicated on the notion that synonymous mutations are neutral. Virtually any value of dN/dS is attainable when the right combinations of selective pressures on nonsynonymous and synonymous are paired (Figure 3—figure supplement 3C).

Code availability

Request a detailed protocol

All code for empirical analysis and generation of summary statistics are publicly available under the open-source MIT License at https://github.com/petrov-lab/cancer-HRI. (Tilk, 2022a copy archived at swh:1:rev:5d67f4a946e2d80efdc71c2ef689266678d8ff75). Code for simulations of tumor growth with advantageous drivers and deleterious passengers is also available at https://github.com/mirnylab/pdSim, (Tilk, 2022b copy archived at swh:1:rev:f08bd75aabf7213e253baf26d219c374a745c8d4).

Data availability

Exonic, open-access SNV calls (WES) of 10,486 cancer patients in (The Cancer Genome Atlas) TCGA were downloaded from the Multi-Center Mutation Calling in Multiple Cancers (MC3) project. This repository uses a consensus of seven mutation-calling algorithms. Expression data of SNVs were downloaded from the Genotype-Tissue Expression (GTEx) project (v7 release). All CNAs were downloaded from the COSMIC database on June 2015.Gene expression data compared to CNAs was downloaded from the COSMIC database on 14 September 2019.

The following previously published data sets were used

(2018) Genomic Data Commons
ID mc3-2017. TCGA - MC3 mutation calls.

https://gdc.cancer.gov/about-data/publications/mc3-2017
1. Tate JG
(2018) COSMIC
ID nar/gky1015. COSMIC - gene expression data.

https://cancer.sanger.ac.uk/cosmic/download
1. GTEX Consortium
(2020) GTEX
ID phs000424.v8. GTEX - expression data.

https://www.gtexportal.org/home/datasets

References

(2015) A global reference for human genetic variation
Nature 526:68–74.
https://doi.org/10.1038/nature15393
- PubMed
- Google Scholar
(2010) A method and server for predicting damaging missense mutations
Nature Methods 7:248–249.
https://doi.org/10.1038/nmeth0410-248
- PubMed
- Google Scholar
1. Alexandrov LB
2. Stratton MR
(2014) Mutational signatures: the patterns of somatic mutations hidden in cancer genomes
Current Opinion in Genetics & Development 24:52–60.
https://doi.org/10.1016/j.gde.2013.11.014
- PubMed
- Google Scholar
1. Arjan JA
2. Visser M
3. Zeyl CW
4. Gerrish PJ
5. Blanchard JL
6. Lenski RE
(1999) Diminishing returns from mutation supply rate in asexual populations
Science 283:404–406.
https://doi.org/10.1126/science.283.5400.404
- PubMed
- Google Scholar
1. Bachtrog D
2. Gordo I
(2004) Adaptive evolution of asexual populations under muller’s ratchet
Evolution; International Journal of Organic Evolution 58:1403–1413.
https://doi.org/10.1111/j.0014-3820.2004.tb01722.x
- PubMed
- Google Scholar
1. Bailey MH
2. Tokheim C
3. Porta-Pardo E
4. Sengupta S
5. Bertrand D
6. Weerasinghe A
7. Colaprico A
8. Wendl MC
9. Kim J
10. Reardon B
11. Ng PK-S
12. Jeong KJ
13. Cao S
14. Wang Z
15. Gao J
16. Gao Q
17. Wang F
18. Liu EM
19. Mularoni L
20. Rubio-Perez C
21. Nagarajan N
22. Cortés-Ciriano I
23. Zhou DC
24. Liang W-W
25. Hess JM
26. Yellapantula VD
27. Tamborero D
28. Gonzalez-Perez A
29. Suphavilai C
30. Ko JY
31. Khurana E
32. Park PJ
33. Van Allen EM
34. Liang H
35. Lawrence MS
36. Godzik A
37. Lopez-Bigas N
38. Stuart J
39. Wheeler D
40. Getz G
41. Chen K
42. Lazar AJ
43. Mills GB
44. Karchin R
45. Ding L
46. MC3 Working Group
47. Cancer Genome Atlas Research Network
(2018) Comprehensive characterization of cancer driver genes and mutations
Cell 173:371–385.
https://doi.org/10.1016/j.cell.2018.02.060
- PubMed
- Google Scholar
1. Calderone A
2. Cesareni G
(2012) Mentha: the interactome browser
EMBnet.Journal 18:128.
https://doi.org/10.14806/ej.18.A.455
- Google Scholar
Book
1. Campbell P
2. Martincorena I
(2017)
DNdScv

Welcome sanger institute.
- Google Scholar
1. Camps M
2. Herman A
3. Loh E
4. Loeb LA
(2007) Genetic constraints on protein evolution
Critical Reviews in Biochemistry and Molecular Biology 42:313–326.
https://doi.org/10.1080/10409230701597642
- PubMed
- Google Scholar
1. Carithers LJ
2. Moore HM
(2015) The genotype-tissue expression (gtex) project
Biopreservation and Biobanking 13:307–308.
https://doi.org/10.1089/bio.2015.29031.hmm
- PubMed
- Google Scholar
1. Carter SL
2. Cibulskis K
3. Helman E
4. McKenna A
5. Shen H
6. Zack T
7. Laird PW
8. Onofrio RC
9. Winckler W
10. Weir BA
11. Beroukhim R
12. Pellman D
13. Levine DA
14. Lander ES
15. Meyerson M
16. Getz G
(2012) Absolute quantification of somatic DNA alterations in human cancer
Nature Biotechnology 30:413–421.
https://doi.org/10.1038/nbt.2203
- PubMed
- Google Scholar
1. Cassa CA
2. Weghorn D
3. Balick DJ
4. Jordan DM
5. Nusinow D
6. Samocha KE
7. O’Donnell-Luria A
8. MacArthur DG
9. Daly MJ
10. Beier DR
11. Sunyaev SR
(2017) Estimating the selective effects of heterozygous protein-truncating variants from human exome data
Nature Genetics 49:806–810.
https://doi.org/10.1038/ng.3831
- PubMed
- Google Scholar
(2012) ABC: an R package for approximate bayesian computation (ABC)
Methods in Ecology and Evolution 3:475–479.
https://doi.org/10.1111/j.2041-210X.2011.00179.x
- Google Scholar
(2007) Heat shock factor 1 is a powerful multifaceted modifier of carcinogenesis
Cell 130:1005–1018.
https://doi.org/10.1016/j.cell.2007.07.020
- PubMed
- Google Scholar
1. Drummond DA
2. Wilke CO
(2008) Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution
Cell 134:341–352.
https://doi.org/10.1016/j.cell.2008.05.042
- PubMed
- Google Scholar
1. Drummond DA
2. Wilke CO
(2009) The evolutionary consequences of erroneous protein synthesis
Nature Reviews. Genetics 10:715–724.
https://doi.org/10.1038/nrg2662
- PubMed
- Google Scholar
1. Eisenberg E
2. Levanon EY
(2015) Human housekeeping genes, revisited
Trends in Genetics 29:569–574.
https://doi.org/10.1016/j.tig.2013.05.010
- PubMed
- Google Scholar
1. Ellrott K
2. Bailey MH
3. Saksena G
4. Covington KR
5. Kandoth C
6. Stewart C
7. Hess J
8. Ma S
9. Chiotti KE
10. McLellan M
11. Sofia HJ
12. Hutter C
13. Getz G
14. Wheeler D
15. Ding L
16. MC3 Working Group
17. Cancer Genome Atlas Research Network
(2018) Scalable open science approach for mutation calling of tumor exomes using multiple genomic pipelines
Cell Systems 6:271–281.
https://doi.org/10.1016/j.cels.2018.03.002
- PubMed
- Google Scholar
1. Forbes SA
2. Bhamra G
3. Bamford S
4. Dawson E
5. Kok C
6. Clements J
7. Menzies A
8. Teague JW
9. Futreal PA
10. Stratton MR
(2008) The catalogue of somatic mutations in cancer (COSMIC)
Current Protocols in Human Genetics Chapter 10:Unit.
https://doi.org/10.1002/0471142905.hg1011s57
- PubMed
- Google Scholar
Book
1. Frank SA
(2007)
Dynamics of Cancer: Incidence, Inheritance, and Evolution

Princeton University.
- Google Scholar
1. Futreal PA
2. Coin L
3. Marshall M
4. Down T
5. Hubbard T
6. Wooster R
7. Rahman N
8. Stratton MR
(2004) A census of human cancer genes
Nature Reviews. Cancer 4:177–183.
https://doi.org/10.1038/nrc1299
- PubMed
- Google Scholar
1. Gelman A
(2004) Parameterization and bayesian modeling
Journal of the American Statistical Association 99:537–545.
https://doi.org/10.1198/016214504000000458
- Google Scholar
1. Gibson MA
2. Bruck J
(2000) Efficient exact stochastic simulation of chemical systems with many species and many channels
The Journal of Physical Chemistry A 104:1876–1889.
https://doi.org/10.1021/jp993732q
- Google Scholar
Book
1. Glaire MA
2. Church DN
(2017) Hypermutated colorectal cancer and neoantigen load
In: David K, Rebecca J, editors. Immunotherapy for Gastrointestinal Cancer. Springer. pp. 187–215.
https://doi.org/10.1007/978-3-319-43063-8_8
- Google Scholar
(2013) IntOGen-mutations identifies cancer drivers across tumor types
Nature Methods 10:1081–1082.
https://doi.org/10.1038/nmeth.2642
- PubMed
- Google Scholar
(2018) Integrating the DNA damage and protein stress responses during cancer development and treatment
The Journal of Pathology 246:12–40.
https://doi.org/10.1002/path.5097
- PubMed
- Google Scholar
1. Grossman RL
2. Heath AP
3. Ferretti V
4. Varmus HE
5. Lowy DR
6. Kibbe WA
7. Staudt LM
(2016) Toward a shared vision for cancer genomic data
The New England Journal of Medicine 375:1109–1112.
https://doi.org/10.1056/NEJMp1607591
- PubMed
- Google Scholar
1. GTEx Consortium
(2020) The gtex Consortium atlas of genetic regulatory effects across human tissues
Science 369:1318–1330.
https://doi.org/10.1126/science.aaz1776
- PubMed
- Google Scholar
1. Ha G
2. Roth A
3. Khattra J
4. Ho J
5. Yap D
6. Prentice LM
7. Melnyk N
8. McPherson A
9. Bashashati A
10. Laks E
11. Biele J
12. Ding J
13. Le A
14. Rosner J
15. Shumansky K
16. Marra MA
17. Gilks CB
18. Huntsman DG
19. McAlpine JN
20. Aparicio S
21. Shah SP
(2015) TITAN: inference of copy number architectures in clonal cell populations from tumor whole-genome sequence data
Genome Research 24:1881–1893.
https://doi.org/10.1101/gr.180281.114
- PubMed
- Google Scholar
1. Hanahan D
2. Weinberg RA
(2000) The hallmarks of cancer
Cell 100:57–70.
https://doi.org/10.1016/s0092-8674(00)81683-9
- PubMed
- Google Scholar
1. Haradhvala NJ
2. Polak P
3. Stojanov P
4. Covington KR
5. Shinbrot E
6. Hess JM
7. Rheinbay E
8. Kim J
9. Maruvka YE
10. Braunstein LZ
11. Kamburov A
12. Hanawalt PC
13. Wheeler DA
14. Koren A
15. Lawrence MS
16. Getz G
(2016) Mutational strand asymmetries in cancer genomes reveal mechanisms of DNA damage and repair
Cell 164:538–549.
https://doi.org/10.1016/j.cell.2015.12.050
- PubMed
- Google Scholar
1. Harris MA
2. Clark J
3. Ireland A
4. Lomax J
5. Ashburner M
6. Foulger R
7. Eilbeck K
8. Lewis S
9. Marshall B
10. Mungall C
11. Richter J
12. Rubin GM
13. Blake JA
14. Bult C
15. Dolan M
16. Drabkin H
17. Eppig JT
18. Hill DP
19. Ni L
20. Ringwald M
21. Balakrishnan R
22. Cherry JM
23. Christie KR
24. Costanzo MC
25. Dwight SS
26. Engel S
27. Fisk DG
28. Hirschman JE
29. Hong EL
30. Nash RS
31. Sethuraman A
32. Theesfeld CL
33. Botstein D
34. Dolinski K
35. Feierbach B
36. Berardini T
37. Mundodi S
38. Rhee SY
39. Apweiler R
40. Barrell D
41. Camon E
42. Dimmer E
43. Lee V
44. Chisholm R
45. Gaudet P
46. Kibbe W
47. Kishore R
48. Schwarz EM
49. Sternberg P
50. Gwinn M
51. Hannick L
52. Wortman J
53. Berriman M
54. Wood V
55. de la Cruz N
56. Tonellato P
57. Jaiswal P
58. Seigfried T
59. White R
60. Gene Ontology Consortium
(2004) The gene ontology (GO) database and informatics resource
Nucleic Acids Research 32:D258–D261.
https://doi.org/10.1093/nar/gkh036
- PubMed
- Google Scholar
1. Hill WG
2. Robertson A
(1966) The effect of linkage on limits to artificial selection
Genetical Research 8:269–294.
https://doi.org/10.1017/S001667230800949X
- PubMed
- Google Scholar
Book
1. Howlader N
(2013)
SEER Cancer Stastistics Review 1975-2010

National Cancer Institute.
- Google Scholar
1. Johnson T
(1999) Beneficial mutations, hitchhiking and the evolution of mutation rates in sexual populations
Genetics 151:1621–1631.
https://doi.org/10.1093/genetics/151.4.1621
- PubMed
- Google Scholar
1. Kampinga HH
2. Hageman J
3. Vos MJ
4. Kubota H
5. Tanguay RM
6. Bruford EA
7. Cheetham ME
8. Chen B
9. Hightower LE
(2009) Guidelines for the nomenclature of the human heat shock proteins
Cell Stress & Chaperones 14:105–111.
https://doi.org/10.1007/s12192-008-0068-7
- PubMed
- Google Scholar
1. Korbel JO
2. Urban AE
3. Grubert F
4. Du J
5. Royce TE
6. Starr P
7. Zhong G
8. Emanuel BS
9. Weissman SM
10. Snyder M
11. Gerstein MB
(2007) Systematic prediction and validation of breakpoints associated with copy-number variants in the human genome
PNAS 104:10110–10115.
https://doi.org/10.1073/pnas.0703834104
- PubMed
- Google Scholar
(2015) Statistically identifying tumor suppressors and oncogenes from pan-cancer genome-sequencing data
Bioinformatics 31:3561–3568.
https://doi.org/10.1093/bioinformatics/btv430
- PubMed
- Google Scholar
(2010) Universal distribution of protein evolution rates as a consequence of protein folding physics
PNAS 107:2983–2988.
https://doi.org/10.1073/pnas.0910445107
- PubMed
- Google Scholar
1. López S
2. Lim EL
3. Horswell S
4. Haase K
5. Huebner A
6. Dietzen M
7. Mourikis TP
8. Watkins TBK
9. Rowan A
10. Dewhurst SM
11. Birkbak NJ
12. Wilson GA
13. Van Loo P
14. Jamal-Hanjani M
15. TRACERx Consortium
16. Swanton C
17. McGranahan N
(2020) Interplay between whole-genome doubling and the accumulation of deleterious alterations in cancer evolution
Nature Genetics 52:283–293.
https://doi.org/10.1038/s41588-020-0584-7
- PubMed
- Google Scholar
1. Martincorena I
2. Raine KM
3. Gerstung M
4. Dawson KJ
5. Haase K
6. Van Loo P
7. Davies H
8. Stratton MR
9. Campbell PJ
(2017) Universal patterns of selection in cancer and somatic tissues
Cell 171:1029–1041.
https://doi.org/10.1016/j.cell.2017.09.042
- PubMed
- Google Scholar
(2013) Impact of deleterious passenger mutations on cancer progression
PNAS 110:2910–2915.
https://doi.org/10.1073/pnas.1213968110
- PubMed
- Google Scholar
(2014) Tug-of-war between driver and passenger mutations in cancer and other adaptive processes
PNAS 111:15138–15143.
https://doi.org/10.1073/pnas.1404341111
- PubMed
- Google Scholar
1. McGrail DJ
2. Garnett J
3. Yin J
4. Dai H
5. Shih DJH
6. Lam TNA
7. Li Y
8. Sun C
9. Li Y
10. Schmandt R
11. Wu JY
12. Hu L
13. Liang Y
14. Peng G
15. Jonasch E
16. Menter D
17. Yates MS
18. Kopetz S
19. Lu KH
20. Broaddus R
21. Mills GB
22. Sahni N
23. Lin S-Y
(2020) Proteome instability is a therapeutic vulnerability in mismatch repair-deficient cancer
Cancer Cell 37:371–386.
https://doi.org/10.1016/j.ccell.2020.01.011
- PubMed
- Google Scholar
1. Mermel CH
2. Schumacher SE
3. Hill B
4. Meyerson ML
5. Beroukhim R
6. Getz G
(2011) GISTIC2.0 facilitates sensitive and confident localization of the targets of focal somatic copy-number alteration in human cancers
Genome Biology 12:R41.
https://doi.org/10.1186/gb-2011-12-4-r41
- PubMed
- Google Scholar
1. Messer PW
(2009) Measuring the rates of spontaneous mutation from deep and large-scale polymorphism data
Genetics 182:1219–1232.
https://doi.org/10.1534/genetics.109.105692
- PubMed
- Google Scholar
1. Michor F
2. Iwasa Y
3. Lengauer C
4. Nowak MA
(2005) Dynamics of colorectal cancer
Seminars in Cancer Biology 15:484–493.
https://doi.org/10.1016/j.semcancer.2005.06.005
- PubMed
- Google Scholar
Website
1. National Cancer Institute
(2007) Cancer incidence – surveillance, epidemiology, and end results (SEER) registries research data
Accessed July 30, 2019.

http://www.seer.cancer.gov
1. Neher RA
2. Shraiman BI
(2012) Fluctuations of fitness distributions and the rate of muller’s ratchet
Genetics 191:1283–1293.
https://doi.org/10.1534/genetics.112.141325
- PubMed
- Google Scholar
(2014) Cancer evolution is associated with pervasive positive selection on globally expressed genes
PLOS Genetics 10:1004239.
https://doi.org/10.1371/journal.pgen.1004239
- PubMed
- Google Scholar
1. Potapova T
2. Gorbsky GJ
(2017) The consequences of chromosome segregation errors in mitosis and meiosis
Biology 6:E12.
https://doi.org/10.3390/biology6010012
- PubMed
- Google Scholar
1. Santagata S
2. Hu R
3. Lin NU
4. Mendillo ML
5. Collins LC
6. Hankinson SE
7. Schnitt SJ
8. Whitesell L
9. Tamimi RM
10. Lindquist S
11. Ince TA
(2011) High levels of nuclear heat-shock factor 1 (HSF1) are associated with poor prognosis in breast cancer
PNAS 108:18378–18383.
https://doi.org/10.1073/pnas.1115031108
- PubMed
- Google Scholar
1. Sottoriva A
2. Kang H
3. Ma Z
4. Graham TA
5. Salomon MP
6. Zhao J
7. Marjoram P
8. Siegmund K
9. Press MF
10. Shibata D
11. Curtis C
(2015) A big bang model of human colorectal tumor growth
Nature Genetics 47:209–216.
https://doi.org/10.1038/ng.3214
- PubMed
- Google Scholar
(2014) Synonymous mutations frequently act as driver mutations in human cancers
Cell 156:1324–1335.
https://doi.org/10.1016/j.cell.2014.01.051
- PubMed
- Google Scholar
1. Tanaka K
(2009) The proteasome: overview of structure and functions
Proceedings of the Japan Academy. Series B, Physical and Biological Sciences 85:12–36.
https://doi.org/10.2183/pjab.85.12
- PubMed
- Google Scholar
1. Tate JG
2. Bamford S
3. Jubb HC
4. Sondka Z
5. Beare DM
6. Bindal N
7. Boutselakis H
8. Cole CG
9. Creatore C
10. Dawson E
11. Fish P
12. Harsha B
13. Hathaway C
14. Jupe SC
15. Kok CY
16. Noble K
17. Ponting L
18. Ramshaw CC
19. Rye CE
20. Speedy HE
21. Stefancsik R
22. Thompson SL
23. Wang S
24. Ward S
25. Campbell PJ
26. Forbes SA
(2019) Cosmic: the Catalogue of somatic mutations in cancer
Nucleic Acids Research 47:D941–D947.
https://doi.org/10.1093/nar/gky1015
- PubMed
- Google Scholar
Software
1. Tilk S
(2022a) Hill-Robertson interference (HRI) in cancer paper, version swh:1:rev:5d67f4a946e2d80efdc71c2ef689266678d8ff75
SoftwarevHeritage.

https://archive.softwareheritage.org/swh:1:dir:e4a6f9d73932cdce98d9de0cc1394b45d41252ec;origin=https://github.com/petrov-lab/cancer-HRI;visit=swh:1:snp:2996ca9f1c1709095fb538f591d3ede58d5eac3a;anchor=swh:1:rev:5d67f4a946e2d80efdc71c2ef689266678d8ff75
Software
1. Tilk S
(2022b) PdSim, version swh:1:rev:f08bd75aabf7213e253baf26d219c374a745c8d4
SoftwarevHeritage.

https://archive.softwareheritage.org/swh:1:dir:2837cecedb2ca8992d5afa9ee54102a1e8fa61b6;origin=https://github.com/mirnylab/pdSim;visit=swh:1:snp:9023cfe7eac951feac42e3bd4133ce866a0fe0f0;anchor=swh:1:rev:f08bd75aabf7213e253baf26d219c374a745c8d4
1. Turajlic S
2. Furney SJ
3. Lambros MB
4. Mitsopoulos C
5. Kozarewa I
6. Geyer FC
7. Mackay A
8. Hakas J
9. Zvelebil M
10. Lord CJ
11. Ashworth A
12. Thomas M
13. Stamp G
14. Larkin J
15. Reis-Filho JS
16. Marais R
(2012) Whole genome sequencing of matched primary and metastatic acral melanomas
Genome Research 22:196–207.
https://doi.org/10.1101/gr.125591.111
- PubMed
- Google Scholar
1. Wang K
2. Li M
3. Hakonarson H
(2010) ANNOVAR: functional annotation of genetic variants from high-throughput sequencing data
Nucleic Acids Research 38:e164.
https://doi.org/10.1093/nar/gkq603
- PubMed
- Google Scholar
1. Wang T
2. Birsoy K
3. Hughes NW
4. Krupczak KM
5. Post Y
6. Wei JJ
7. Lander ES
8. Sabatini DM
(2015) Identification and characterization of essential genes in the human genome
Science 350:1096–1101.
https://doi.org/10.1126/science.aac7041
- PubMed
- Google Scholar
1. Weghorn D
2. Sunyaev S
(2017) Bayesian inference of negative and positive selection in human cancers
Nature Genetics 49:1785–1788.
https://doi.org/10.1038/ng.3987
- PubMed
- Google Scholar
1. Williams BR
2. Prabhu VR
3. Hunter KE
4. Glazier CM
5. Whittaker CA
6. Housman DE
7. Amon A
(2008) Aneuploidy affects proliferation and spontaneous immortalization in mammalian cells
Science 322:703–709.
https://doi.org/10.1126/science.1160058
- PubMed
- Google Scholar
1. Zack TI
2. Schumacher SE
3. Carter SL
4. Cherniack AD
5. Saksena G
6. Tabak B
7. Lawrence MS
8. Zhsng C-Z
9. Wala J
10. Mermel CH
11. Sougnez C
12. Gabriel SB
13. Hernandez B
14. Shen H
15. Laird PW
16. Getz G
17. Meyerson M
18. Beroukhim R
(2013) Pan-cancer patterns of somatic copy number alteration
Nature Genetics 45:1134–1140.
https://doi.org/10.1038/ng.2760
- PubMed
- Google Scholar
(2018) Negative selection in tumor genome evolution acts on essential cellular functions and the immunopeptidome
Genome Biology 19:67.
https://doi.org/10.1186/s13059-018-1434-0
- PubMed
- Google Scholar
1. Zhang L
2. Li WH
(2004) Mammalian housekeeping genes evolve more slowly than tissue-specific genes
Molecular Biology and Evolution 21:236–239.
https://doi.org/10.1093/molbev/msh010
- PubMed
- Google Scholar

Decision letter

Martin Taylor

Reviewing Editor; University of Edinburgh, United Kingdom
Molly Przeworski

Senior Editor; Columbia University, United States
Elena Kuzmin

Reviewer; Concordia University, Canada
Martin Taylor

Reviewer; University of Edinburgh, United Kingdom

Our editorial process produces two outputs: (i) public reviews designed to be posted alongside the preprint for the benefit of readers; (ii) feedback on the manuscript for the authors, including requests for revisions, shown below. We also include an acceptance summary that explains what the editors found interesting or important about the work.

Decision letter after peer review:

Thank you for submitting your article "Most cancers carry a substantial deleterious load due to Hill-Robertson interference" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, including Martin Taylor as the Reviewing Editor and Reviewer #3, and the evaluation has been overseen by Molly Przeworski as the Senior Editor. The following individual involved in review of your submission has agreed to reveal their identity: Elena Kuzmin (Reviewer #1).

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission.

Essential revisions:

(1) The authors state that they are excluding tumors with either nonsynonymous(n)=0 or synonymous(s)=0 mutations. Since nonsynonymous and synonymous variants occur in a ratio of about 3:1, this exclusion of tumors would seem to lead to an inflation of the signal of selection in the first (lowest mutation) bins. Additional demonstration is required to show if this distorts the estimate of selection for low mutation burden tumours. For example, by adding pseudo-counts of mutations or by aggregation over tumours in the same mutation load "bin" as was performed for some analyses.

(2) The decline of dN/dS on driver genes is the subject of the supplementary text and we note the efforts taken to disentangle Hill-Robertson interference effects from other possible explanations for dN/dS decay in drivers with increasing tumor mutation burden (TMB). Driver genes can be quite tissue-specific (and thus mus-identified for a tumor) and number of drivers per tumour estimated to span approximately 1 to 10 (Martincorena et al., 2017). Consequently, the fitting of a single set of model parameters and showing they do not match well the observed data (Supplementary note figure) is insufficient to exclude the misidentification of driver genes, or presence of nonsynonymous-neutral mutations in annotated driver genes, as an explanation for the decline in dN/dS with increased TMB. We think it important that a range of justifiable parameters are applied in this modelling, to test if the observed data is robustly outside reasonable parametrisation of the model.

(3) In many figures that show dN/dS as a function of n+s (starting with Figure 2A and extending to Figures S2, 3, 9, 10, 12, 22 and 25), there are no error bars indicated, as opposed to the statement in the figure caption. The error bars/shading should be shown. In Figure 2A, is the observed depletion in the second bin still significant?

Reviewer #1 (Recommendations for the authors):

1. Figure panels should be called out sequentially. For example, Figure 2G is called out before Figure 2D. This happens throughout the text, including main and supplementary figures, and should be corrected.

2. Figure 2G shows that mean gene expression of genes encoding chaperones and the proteasome increases with increasing mutational burden. What about protein abundance? Is this in agreement with gene expression?

3. Figure 2 mentions error bars in the figure legend, but no panel displays error bars. This is also true for Figure S13 and other figures. Authors should display the error bars to which they are referring to make their analysis more convincing.

4. Pg. 9 line 295 describes results of the analysis across genes belonging to different GO terms. However, Figure S13 only shows 3 categories: chromosome segregation, transcription and translation. How were these categories chosen? What about other categories? Such cherry picking doesn't convincingly support the conclusions that no specific GO functions are enriched. Also, translational regulation shows higher dN/dS in low mutation tumors suggesting that there is positive selection for passengers in this category. Authors should discuss in their manuscript why this is the case.

5. Figure S15 shows the attenuation in selection of CNAs across cancer subtypes and broad cancer groups. However, HNSC and kidney cancer appear to be the exceptions. Authors should provide an explanation for these observations in the main text.

6. Generally, copy number variations are considered to be > 50 bp. Is there a rationale as to why authors chose 100 kb to be their cut-off in Figure 2C? If the size of CNA is an important parameter, then authors should explain why that is.

7. Non-allelic recombination and non-homologous recombination mechanisms involving replication accidents that lead to chromosome breakage occur with some frequency in somatic cells. How does the frequency of these events impact the selection efficiency in cancer as it relates to drivers and passengers? Can this also be incorporated in their evolutionary model?

8. Authors mentioned that haploinsufficiency was not used in the model. What about loss of heterozygosity which is extensive in cancer genomes? Can this parameter be included in the evolutionary model and how would it impact the results?

Reviewer #2 (Recommendations for the authors):

1. The authors have taken great care to study single-nucleotide variants and large CNAs. It would be great if they could confirm their findings by also showing the effect on small insertions and deletions.

2. Figure S5 is showing a bias in the determination of dN/dS from simulation results and the correlation between mutation rate and n+s. I am not sure I understand why dN/dS under a neutral simulation would be biased. Also, the low median correlation between n+s and the mutation rate (<0.4) is quite surprising. I would have expected these to be almost perfectly correlated. Likewise, I do not understand the formula after l. 631. It states that this is the joint density of the two Poisson random variables that denote nonsynonymous and synonymous mutation count, yet there is an additional unexplained factor in the denominator, which corresponds to the probability of s>0. If the simulation that underlies Figure S5 was also used in the ABC-based parameter inference, this would raise a serious cause for concern.

3. The simulation starts when the first mutation with positive selective effect initiates population growth, which can be very late in a patient's life. How does the assumption that up to 100 years can pass after this affect the parameter estimates?

4. To which extent does the inferred distribution of selection effects depend on the allowable parameter range? For example, s_passengers extends beyond the initially allowable range after the fit (Figure 3C).

5. It is not entirely clear to me how the partitioning of the likelihood between Muller's ratchet and hitchhiking vs other effects can be made and how robust these inferences are with respect to variation of the modeling assumptions (e.g. about initial population size or mode of selection). Is the necessity of inclusion of selected synonymous variants on driver genes a robust result or not, taking into account the discussion on p. 26f.?

6. In Figure S4, the authors report the correlation of n+s with other measures of tumor mutation load. Given the relative sizes of the different regions that are displayed, i.e. whole genome:intergenic:intronic:exonic:protein-coding, of roughly 100:60:40:2:1, the displayed numbers do not make sense, as their ratios are 100:100:100:1:0.001.

7. I am not sure I understood well how CNAs were analyzed. Based on the description in l. 669ff., it appears that putative cancer driver genes were identified from the CNA data based on recurrence. Were the same data then analyzed for CNAs falling into said putative cancer driver gene regions to infer selection? This would appear a bit circular.

8. I do not understand the formula shown after li. 738. It appears it is showing the fraction of genes that intersect a CNA boundary, summed over all tumors in a given n+s bin. Each CNA can be counted twice if both of its boundaries fall into a gene. Why is the mean value of this 1?

9. In all figures that show dN/dS as a function of n+s (starting with Figure 2A and extending to Figures S2, 3, 9, 10, 12, 22 and 25), there are no error bars indicated, as opposed to the statement in the figure caption. In Figure 2A, is the observed depletion in the second bin still significant?

10. In l. 290, I understand that the authors argue that differential dominance effects between heterozygous early- and late-arising mutations could be affecting the efficacy of selection on subclonal variants compared to clonal variants. I do not see this claim well motivated or corroborated.

11. In Figure 2D, the caption states that mutations have been separated into two groups by their clonality, yet the figure shows three curves. What do they correspond to? Are the results still significant given the partitioning of the mutation data into smaller subsets?

12. Figure 3 does not have a panel G.

Reviewer #3 (Recommendations for the authors):

I enjoyed reading the manuscript, it was well written, generally clear figures and very through provoking.

Only a small number of specific points to address:

Line 60.- The description of dN and dS here along with the interpretation of dN/dS=1 as neutral implies that you are just counting non-synonymous and synonymous mutations and dividing one by the other. This of course is not the case. Perhaps dN and dS could be described as rates or dN/dS as the dN:dS odds ratio which is how it's calculated for your permutation metric.

Line 112 – 40% of what, benefit of ~130% of what. This becomes apparent later into the manuscript but not clear how to interpret when reading at this point for the first time.

Line 188 – Mutational burden <= 3 (what units).

Line 189 – "We observed little negative selection in passengers" be clear what passengers (previous identified passenger genes).

Line 252 – Panel G, y-axis, what units? Why are "all" genes uniformly at approximately -0.2? Assuming this is fold-change or log-fold-change I'd expect 1 or zero respectively.

Line 275 – Figure 2G, shaded error bars are not visible.

https://doi.org/10.7554/eLife.67790.sa1

Author response

Essential revisions:

(1) The authors state that they are excluding tumors with either nonsynonymous(n)=0 or synonymous(s)=0 mutations. Since nonsynonymous and synonymous variants occur in a ratio of about 3:1, this exclusion of tumors would seem to lead to an inflation of the signal of selection in the first (lowest mutation) bins. Additional demonstration is required to show if this distorts the estimate of selection for low mutation burden tumours. For example, by adding pseudo-counts of mutations or by aggregation over tumours in the same mutation load "bin" as was performed for some analyses.

We thank the reviewers for bringing up this important point. Our original reasoning for applying this filtering procedure was the concern that false positive random mutations, which would push dN/dS to 1, would dominate the signal in tumors with very few true mutations. Nonetheless, we agree with the reviewers that this filtering procedure can introduce potential biases into dN/dS estimates and thus, we have now re-analyzed all the main and supplemental figures in the re-submission without this filtering step.

Overall, we find that although negative selection on passengers is still present in low TMB tumors after removing this filtering procedure, signals of negative selection are diminished (from dN/dS ~0.4 to ~0.7 when combining all tumors in TCGA and ICGC and using both null models of dN/dS).

Author response image 1

Download asset Open asset

Since we are no longer applying any quality control filters, we need to be particularly stringent about the mutational calls we use to ensure we don’t lose all signal to potential false positives. Indeed, we empirically observe that the power to detect selection is strongly dependent on the quality of mutation calls in the sample. We find that even within the same dataset (TCGA), signals of negative selection on passengers in low TMB tumors disappears (dN/dS ~ 1) when just one mutation caller is used (‘Mutect 2 SNP Calls’) but can still be detected (dN/dS ~ 0.5) when we use a consensus set of mutation calls (‘MC3 SNP Calls’; which uses 7 different mutation callers). This is true when using either null model of dN/dS (dNdScv and dNdS-permutation). Similarly, signals of positive selection on drivers in low TMB tumors also diminishes (from dN/dS ~5 to ~4) when low quality mutation calls are used. The figure is now included in the re-submission as Figure 2—figure supplement 15Since coverage in protein-coding regions in whole-genome data is much lower than in the whole-exome data and combining datasets can potentially introduce further bias, we elected to only use TCGA whole-exome data – which contains the most stringent consensus mutation calls (MC3 SNP Calls) – in the re-submission to focus on patterns of selection in the highest quality set of mutations available. We also note that others have similarly raised concerns about difficulties combining whole-genome sequencing and whole-exome tumors even using the same cancer samples, which produce only 75% of concordant mutations when comparing mutation calls in protein-coding regions (Bailey et al., 2020, Nature Communications). As expected, we find stronger signals of selection in drivers (from dN/dS ~5.5 to ~4) and passengers (from dN/dS in ~0.7 to ~0.6) in low TMB tumors (< 3 protein-coding mutations) in TCGA (‘MC3 SNP Calls’) when compared to the combining both TCGA and ICGC using both null models of mutagenesis.

(2) The decline of dN/dS on driver genes is the subject of the supplementary text and we note the efforts taken to disentangle Hill-Robertson interference effects from other possible explanations for dN/dS decay in drivers with increasing tumor mutation burden (TMB). Driver genes can be quite tissue-specific (and thus mus-identified for a tumor) and number of drivers per tumour estimated to span approximately 1 to 10 (Martincorena et al., 2017). Consequently, the fitting of a single set of model parameters and showing they do not match well the observed data (Supplementary note figure) is insufficient to exclude the misidentification of driver genes, or presence of nonsynonymous-neutral mutations in annotated driver genes, as an explanation for the decline in dN/dS with increased TMB. We think it important that a range of justifiable parameters are applied in this modelling, to test if the observed data is robustly outside reasonable parametrisation of the model.

Our goal for the modeling section was to investigate whether a simple evolutionary model of linkage with damaging passengers and advantageous drivers could reproduce similar patterns of selection observed in the empirical data. We agree with the reviewers that attenuation of dN/dS in drivers can be explained by processes other than Hill-Robertson interference. As the reviewers pointed out, we focus on alternative explanations for attenuation in the drivers within the supplemental portion of the text. In the previous submission, we explored a similar scenario that the reviewers suggest (i.e. 50% of neutral mutations accumulating in driver genes). However, we agree with the reviewers that this does not conclusively allow us to reject or make claims about the contribution of alternative models in drivers. To correct this, we have now included these potential alternative explanations suggested by the reviewers into the main text (Page. 11, Lines 16-26) and removed the supplemental note.

We would like to emphasize, however, that the focus of our paper is on negative selection on passengers. In all of the alternative models of dN/dS in drivers, passenger mutations are required to impose a fitness cost to be able to observe attenuation of negative selection in passengers.

(3) In many figures that show dN/dS as a function of n+s (starting with Figure 2A and extending to Figures S2, 3, 9, 10, 12, 22 and 25), there are no error bars indicated, as opposed to the statement in the figure caption. The error bars/shading should be shown. In Figure 2A, is the observed depletion in the second bin still significant?

To clarify, error bars were already displayed in all of the figures mentioned, but are currently visualized as shading (rather than traditional error bars). We recognize that the light opacity of this shading might make it difficult to visualize for some readers, especially in print. To correct this, we have now increased the opacity of the shading in all of the figures throughout the text so that this is clearer. We thank the reviewers for bringing up this concern.

After removing this filtering step in our analysis, we find that tumors in the second bin are no longer significant within Figure 2A.

Reviewer #1 (Recommendations for the authors):

1. Figure panels should be called out sequentially. For example, Figure 2G is called out before Figure 2D. This happens throughout the text, including main and supplementary figures, and should be corrected.

We thank the reviewer for bringing up this point and have now corrected the text.

2. Figure 2G shows that mean gene expression of genes encoding chaperones and the proteasome increases with increasing mutational burden. What about protein abundance? Is this in agreement with gene expression?

We agree with the reviewer that this would be an interesting avenue to explore further. Unfortunately, the only proteomics data that currently exists within TCGA is RPPA, which is very limited (only ~100 genes have been profiled across tumors), and these particular gene sets of interest have not yet been assayed across tumors.

3. Figure 2 mentions error bars in the figure legend, but no panel displays error bars. This is also true for Figure S13 and other figures. Authors should display the error bars to which they are referring to make their analysis more convincing.

As mentioned above, error bars are already displayed in all of the figures the reviewer has mentioned but are currently visualized as shading (rather than error bars). We recognize that the light opacity of this shading might make it difficult to visualize for some readers, especially in print. To correct this, we have now increased the opacity of the shading in the figures so that this is clearer throughout the text. We thank the reviewer for bringing up this concern.

4. Pg. 9 line 295 describes results of the analysis across genes belonging to different GO terms. However, Figure S13 only shows 3 categories: chromosome segregation, transcription and translation. How were these categories chosen? What about other categories? Such cherry picking doesn't convincingly support the conclusions that no specific GO functions are enriched. Also, translational regulation shows higher dN/dS in low mutation tumors suggesting that there is positive selection for passengers in this category. Authors should discuss in their manuscript why this is the case.

We appreciate the reviewer’s concern that there was little justification for why these gene sets were chosen for analysis. These were chosen based on previous literature that has supported these groups of genes being relevant to protein misfolding, and thus we hypothesized they might be under constraint. We have now extended the figure captions to include this.

5. Figure S15 shows the attenuation in selection of CNAs across cancer subtypes and broad cancer groups. However, HNSC and kidney cancer appear to be the exceptions. Authors should provide an explanation for these observations in the main text.

There are many potential reasons for why this signal might be missing in certain tumor types or broad tumor groups. For example, tumors that are not copy number driven or tend to be on the low-spectrum of CNAs overall, might simply not have enough CNAs across all tumors to generate a strong enough signal.

6. Generally, copy number variations are considered to be > 50 bp. Is there a rationale as to why authors chose 100 kb to be their cut-off in Figure 2C? If the size of CNA is an important parameter, then authors should explain why that is.

100kb was used to partition copy number variation into ‘small’ and ‘large’ categories. Copy number variation <100kb was still considered in our study. As mentioned in the text, the reason we chose this cut-off is that the average length of a gene is ~100kb. Thus, we would expect the selective effects of CNAs that are sufficiently large to disrupt genes or multiple genes to be stronger.

7. Non-allelic recombination and non-homologous recombination mechanisms involving replication accidents that lead to chromosome breakage occur with some frequency in somatic cells. How does the frequency of these events impact the selection efficiency in cancer as it relates to drivers and passengers? Can this also be incorporated in their evolutionary model?

We agree that this would be an interesting phenomenon to model. However, it’s hard to make inferences on how this would impact the efficacy of selection overall in drivers and passengers. More empirical information about how frequently these events occur on average per generation in a cell is needed before one can accurately model these scenarios. Thus, we believe this is beyond the scope of the paper.

8. Authors mentioned that haploinsufficiency was not used in the model. What about loss of heterozygosity which is extensive in cancer genomes? Can this parameter be included in the evolutionary model and how would it impact the results?

Our goal for the modeling section was to present a simple model of Hill-Robertson interference to examine if it's plausible that this could explain patterns of attenuated selection with mutational burden as observed in the data. There are many attributes of cancer biology that were not considered and how the relaxation of certain assumptions might impact the results has already been documented in Supplementary File 1. In addition, this particular point about haploinsufficiency has already been explored by others (Lopez et.al 2020 Nature Genetics) and thus, was not considered here.

Reviewer #2 (Recommendations for the authors):

1. The authors have taken great care to study single-nucleotide variants and large CNAs. It would be great if they could confirm their findings by also showing the effect on small insertions and deletions.

We agree with the reviewer that this would be an interesting direction to explore. However, we are not currently aware of any null models that take into account the expected behavior of neutral insertions/deletions. Thus, this is not something that we could explore in this manuscript.

2. Figure S5 is showing a bias in the determination of dN/dS from simulation results and the correlation between mutation rate and n+s. I am not sure I understand why dN/dS under a neutral simulation would be biased. Also, the low median correlation between n+s and the mutation rate (<0.4) is quite surprising. I would have expected these to be almost perfectly correlated. Likewise, I do not understand the formula after l. 631. It states that this is the joint density of the two Poisson random variables that denote nonsynonymous and synonymous mutation count, yet there is an additional unexplained factor in the denominator, which corresponds to the probability of s>0. If the simulation that underlies Figure S5 was also used in the ABC-based parameter inference, this would raise a serious cause for concern.

dN/dS in a neutral simulation could be biased because the probability of a nonsynonymous mutation is larger than the probability of a synonymous mutation (because of constraints of the genetic code). For low mutation counts, there are only certain integer totals possible (e.g. 2 nonsynonymous & 1 synonymous) which might subtly bias results. In the previous submission, Figure S5 showed that this bias is very subtle. For clarity, however, we have elected to remove this figure in the resubmission.

The equation on line 631 was not used in the ABC-based parameter inference, and it also does not explicitly consider any selection coefficient. The denominator of this equation depends on three variables dN dS and λS, which are the observed nonsynonymous and synonymous mutation counts, and the mean number of synonymous mutations. The subscript S in these equations represents ‘synonymous’ mutations and not ‘selection coefficient’; we apologize for this overloaded use of nomenclature – these nomenclature choices predate our study. In the resubmission, this equation now explicitly states its parameters.

3. The simulation starts when the first mutation with positive selective effect initiates population growth, which can be very late in a patient's life. How does the assumption that up to 100 years can pass after this affect the parameter estimates?

To clarify, the model assumes that a tumor has equal probability of arising (via an initating driver or 1^st mutation with positive effect) at any point between 0 and 100 years of life. Thus, if a late-stage tumor arises (e.g. at age 70), the tumor doesn’t have 100 years from initiation (it has 30 years to become a successful tumor). This assumption has also been previously described in detail in (McFarland et al. 2014) and is common in mathematical models of cancer age-incidence rates. 4. To which extent does the inferred distribution of selection effects depend on the allowable parameter range? For example, s_passengers extends beyond the initially allowable range after the fit (Figure 3C).

The reviewed version of the manuscript had this figure reflecting ABC simulations extrapolating beyond the simulated range of parameters, which was needed to model the tail of the S_passenger probability distribution. This extrapolation may create unforeseen issues, so in the revised manuscript, we now simulate s_passengers from 10^-4 to 10^-1, and the new figures are updated accordingly. The posterior distribution of s_passengers did not change substantially; our estimate is now that S_passengers is 1.03% 95% CI [0.39%, 4.0%].

5. It is not entirely clear to me how the partitioning of the likelihood between Muller's ratchet and hitchhiking vs other effects can be made and how robust these inferences are with respect to variation of the modeling assumptions (e.g. about initial population size or mode of selection). Is the necessity of inclusion of selected synonymous variants on driver genes a robust result or not, taking into account the discussion on p. 26f.?

In the revised manuscript, we now indicate that the rates of Muller’s Ratchet and hitchhiking are derived from analytical theory in the Figure Legend and cite this theory. The robustness of these results are well-discussed in the papers that derive these formulae.

Reviewer #1 also raised concerned about explanations for the dN/dS attenuation of drivers, so we have removed the Supplementary Note discussing this topic.

6. In Figure S4, the authors report the correlation of n+s with other measures of tumor mutation load. Given the relative sizes of the different regions that are displayed, i.e. whole genome:intergenic:intronic:exonic:protein-coding, of roughly 100:60:40:2:1, the displayed numbers do not make sense, as their ratios are 100:100:100:1:0.001.

This figure has now been removed in the re-submission.7. I am not sure I understood well how CNAs were analyzed. Based on the description in l. 669ff., it appears that putative cancer driver genes were identified from the CNA data based on recurrence. Were the same data then analyzed for CNAs falling into said putative cancer driver gene regions to infer selection? This would appear a bit circular.

The copy number specific drivers were called using GISTIC 2.0, which are indeed based on recurrence across cancer types. We appreciate the reviewer’s point that the some of the data used to identify drivers was also used to infer selection on these genes. However, the metric used to infer selection (dE/dI) is a different method/static from the one GISTIC uses. Furthermore, this is a problem that generally applies to all methods that are currently used to infer drivers, even for point mutation-specific drivers.

8. I do not understand the formula shown after li. 738. It appears it is showing the fraction of genes that intersect a CNA boundary, summed over all tumors in a given n+s bin. Each CNA can be counted twice if both of its boundaries fall into a gene. Why is the mean value of this 1?

Within the methods section, we reference Figure 2—figure supplement 8 where we show that dEdI of random CNAs (where the start and stop locations are randomly permuted across the genome) recapitulates expected neutral values of 1.9. In all figures that show dN/dS as a function of n+s (starting with Figure 2A and extending to Figures S2, 3, 9, 10, 12, 22 and 25), there are no error bars indicated, as opposed to the statement in the figure caption. In Figure 2A, is the observed depletion in the second bin still significant?

As mentioned above, error bars are already displayed in all of the figures the reviewer has mentioned but are currently visualized as shading (rather than error bars). We recognize that the light opacity of this shading might make it difficult to visualize for some readers and have corrected the figures by increasing the opacity. The observed depletion of the second bin in passengers is no longer significant.

10. In l. 290, I understand that the authors argue that differential dominance effects between heterozygous early- and late-arising mutations could be affecting the efficacy of selection on subclonal variants compared to clonal variants. I do not see this claim well motivated or corroborated.

To clarify, we don’t claim that dominance affects the efficacy of selection. We were stating that early-arising mutations, which tend to be low frequency variants that are likely to be heterozygous, are expected to experience weaker selection overall.

11. In Figure 2D, the caption states that mutations have been separated into two groups by their clonality, yet the figure shows three curves. What do they correspond to? Are the results still significant given the partitioning of the mutation data into smaller subsets?

The three curves were meant for the reader to visualize and compare how selection in drivers and passengers changes when all variants are included (variants of all VAF values), only subclonal variants are included (VAF < 0.2) or only clonal variants are included (VAF > 0.2). In the resubmission, we have now removed variants of all VAF values to make it simpler to compare selection on clonal vs subclonal variants. The revised results in the resubmission are significant for clonal mutations, but not subclonal mutations.12. Figure 3 does not have a panel G.

This has now been corrected, thank you.

Reviewer #3 (Recommendations for the authors):

I enjoyed reading the manuscript, it was well written, generally clear figures and very through provoking.

We thank the reviewer for these kind words.Only a small number of specific points to address:

Line 60.- The description of dN and dS here along with the interpretation of dN/dS=1 as neutral implies that you are just counting non-synonymous and synonymous mutations and dividing one by the other. This of course is not the case. Perhaps dN and dS could be described as rates or dN/dS as the dN:dS odds ratio which is how it's calculated for your permutation metric.

We appreciate the reviewer’s concern that the dN/dS calculations presented here are not simply counts of nonsynonymous and synonymous mutations. In the resubmission, we have now added the word rate in the main text to refer to our dN/dS calculations more accurately. However, we worry that adding additional terms to the metric ‘dN/dS’ can potentially add to more confusion – especially since others that calculate dN/dS with null models of mutagenesis simply use ‘dN/dS’ when referring to this statistic (Martincorena et al. 2017).

Line 112 – 40% of what, benefit of ~130% of what. This becomes apparent later into the manuscript but not clear how to interpret when reading at this point for the first time.

Thank you, we have now corrected this.

Line 188 – Mutational burden <= 3 (what units).

Thank you, we have corrected the text.Line 189 – "We observed little negative selection in passengers" be clear what passengers (previous identified passenger genes).

We have changed the text to clarify this.

Line 252 – Panel G, y-axis, what units? Why are "all" genes uniformly at approximately -0.2? Assuming this is fold-change or log-fold-change I'd expect 1 or zero respectively.

These values are z-scale normalized and this normalization was already performed by COSMIC when the data was downloaded.

Line 275 – Figure 2G, shaded error bars are not visible.

Thank you, this has been fixed.

https://doi.org/10.7554/eLife.67790.sa2

Article and author information

Author details

Susanne Tilk

Department of Biology, Stanford University, Stanford, United States

Contribution
Conceptualization, Data curation, Software, Formal analysis, Funding acquisition, Validation, Investigation, Visualization, Methodology, Writing - original draft, Writing - review and editing

For correspondence
tilk@stanford.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-9156-9360
Svyatoslav Tkachenko

Department of Genetics and Genome Sciences, Case Western Reserve University, Cleveland, United States

Contribution
Validation

Competing interests
No competing interests declared
Christina Curtis
1. Department of Medicine, Division of Oncology, Stanford University School of Medicine, Stanford, United States
2. Department of Genetics, Stanford University School of Medicine, Stanford, United States
3. Stanford Cancer Institute, Stanford University School of Medicine, Stanford, United States
Contribution
Supervision, Funding acquisition, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-0166-3802
Dmitri A Petrov

Department of Biology, Stanford University, Stanford, United States

Contribution
Conceptualization, Supervision, Funding acquisition, Validation, Methodology, Writing - original draft, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-3664-9130
Christopher D McFarland

Department of Genetics and Genome Sciences, Case Western Reserve University, Cleveland, United States

Contribution
Conceptualization, Software, Formal analysis, Supervision, Investigation, Visualization, Methodology, Writing - original draft, Writing - review and editing

For correspondence
cdm113@case.edu

Competing interests
No competing interests declared

Funding

National Human Genome Research Institute (T32-HG000044-21)

Christopher D McFarland

National Institutes of Health (E25-CA180993)

Christopher D McFarland

National Institutes of Health (DP1-CA238296)

Christina Curtis

National Cancer Institute (R01-CA207133)

Dmitri A Petrov

National Institute of General Medical Sciences (R35-GM118165)

Dmitri A Petrov

National Institutes of Health (R01-CA231253)

Dmitri A Petrov

National Cancer Institute (K99-CA226506)

Christopher D McFarland

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank Judith Frydman for her contribution on the heat shock response analysis, Monte Winslow for his contribution on cancer subtype analysis, Donate Weghorn for her contribution on the interdependence of dN/dS and mutational burden, Leonid Mirny, Grant Kinsler, Gabor Boross, Chuan Li, Alison Feder, Eliot Cowan, and other members of the Petrov and Curtis labs for helpful comments and discussions. This work is supported by NIH grants T32-HG000044-21, E25-CA180993; the Director’s Pioneer Award DP1-CA238296 to CC; R01-CA207133, R35-GM118165, and R01-CA231253 to DAP; and K99-CA226506 to CDM.

Senior Editor

Molly Przeworski, Columbia University, United States

Reviewing Editor

Martin Taylor, University of Edinburgh, United Kingdom

Reviewers

Elena Kuzmin, Concordia University, Canada
Martin Taylor, University of Edinburgh, United Kingdom

Version history

Preprint posted: September 14, 2019 (view preprint)
Received: February 23, 2021
Accepted: August 31, 2022
Accepted Manuscript published: September 1, 2022 (version 1)
Version of Record published: September 22, 2022 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.