Mother cells control daughter cell proliferation in intestinal organoids to minimize proliferation fluctuations

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: November 29, 2022 (This version)
Accepted: October 20, 2022
Received: May 31, 2022
Preprint posted: March 17, 2022 (Go to version)

1. Of interest
A comprehensive model of Drosophila epithelium reveals the role of embryo geometry and cell topology in mechanical responses

Mohamad Ibrahim Cheikh, Joel Tchoufag ... Konstantin Doubrovinski

Research Article Oct 2, 2023
Further reading

Abstract
Editor's evaluation
eLife digest
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

During renewal of the intestine, cells are continuously generated by proliferation. Proliferation and differentiation must be tightly balanced, as any bias toward proliferation results in uncontrolled exponential growth. Yet, the inherently stochastic nature of cells raises the question how such fluctuations are limited. We used time-lapse microscopy to track all cells in crypts of growing mouse intestinal organoids for multiple generations, allowing full reconstruction of the underlying lineage dynamics in space and time. Proliferative behavior was highly symmetric between sister cells, with both sisters either jointly ceasing or continuing proliferation. Simulations revealed that such symmetric proliferative behavior minimizes cell number fluctuations, explaining our observation that proliferating cell number remained constant even as crypts increased in size considerably. Proliferative symmetry did not reflect positional symmetry but rather lineage control through the mother cell. Our results indicate a concrete mechanism to balance proliferation and differentiation with minimal fluctuations that may be broadly relevant for other tissues.

Editor's evaluation

This paper is a fundamental work in developmental biology that supports its findings with compelling evidence drawn from both theoretical and experiment insights. It provides a potentially general mechanism for the control of a proliferative cell population. This work will be of interest to researchers in the fields of developmental and stem cell biology.

https://doi.org/10.7554/eLife.80682.sa0

eLife digest

The vast majority of cells lining our intestine die within three to five days. They are replaced by a small group of stem cells which divide to produce either more stem cells, or cells that stop dividing and transform, or ‘differentiate’, in to mature cells in the intestine. Stem cells must generate the same number of dividing and differentiated cells. If there is even a slight bias and too many stem cells are produced, this can lead to uncontrolled growth, which is the root cause of cancer.

In principal, the best way to achieve this balance is for stem cells to always asymmetrically divide in to two distinct cells: one that will continue to divide, and another that will mature in to an adult cell. However, recent research suggests that this process is much more random, with stem cells also dividing symmetrically, either in to two stem cells or two differentiated cells. So, how does the random nature of stem cell divisions not cause the number of dividing cells to fluctuate unpredictably in the intestine?

To investigate, Huelsz-Prince et al. studied stem cells in a miniature model of the mouse intestine, known as an organoid, which can be grown outside of the body in a laboratory. All stem cells and their progeny were tracked for over 65 hours using a microscope to see how many dividing and differentiated cells they formed. This revealed that almost all stem cells in the organoid split symmetrically rather than asymmetrically.

Huelsz-Prince et al. then developed a computer model of stem cells in the model intestine and tested the impact of changing the proportion of symmetric and asymmetric divisions. The results showed that having more symmetric divisions reduced fluctuations in the number of dividing cells better than high levels of asymmetric divisions.

Other organs rely on a similar system to the intestine to replenish their mature cells. Consequently, the finding that symmetric divisions control fluctuations in the number of stem cells may be applicable to other parts of the body. Further testing with human disease samples, such as cells from cancer patients, using the organoid model system may also shed light on how division is disrupted in these conditions.

Introduction

Most adult organs and tissues constantly renew themselves by replacing old and damaged cells, while retaining their structure (Simons and Clevers, 2011). Theory indicates that this homeostasis requires a precise balance between proliferating and non-proliferating cells, as even a slight systematic bias toward producing proliferating cells yields uncontrolled exponential cell growth (Lander et al., 2009; Clayton et al., 2007; Klein et al., 2007; Klein and Simons, 2011; Lopez-Garcia et al., 2010; Rué and Martinez Arias, 2015). Moreover, the exponential nature of proliferation also readily amplifies fluctuations in the number of proliferating cells, which can lead to stochastic cell overgrowth or depletion in the absence of additional control mechanisms (Feller, 1939; Sun and Komarova, 2012). How cell proliferation is balanced despite fluctuations has remained challenging to test in direct experiments, given the difficulties of following this process in time.

The mammalian intestine has become an important model system to study the mechanisms of tissue renewal and homeostasis (Simons and Clevers, 2011; Gehart and Clevers, 2019). The proliferating stem cells that sit at the base of intestinal crypts generate rapidly dividing transit-amplifying (TA) cells that in turn replenish the absorptive and secretory cells populating the lining of intestinal villi. Paneth cells positioned at the crypt bottom provide short-range signals that affect the proliferative and undifferentiated state of intestinal stem cells (Farin et al., 2012; Sato et al., 2011; Shoshkes-Carmel et al., 2018). Originally, it was proposed that one or a few stem cells generated all differentiated cells by strictly asymmetric cell divisions (Scoville et al., 2008; Winton and Ponder, 1990), thus directly ensuring a constant stem cell pool. Subsequent studies rather suggested that individual cells stochastically and independently cease to divide or not (Lopez-Garcia et al., 2010; Snippert et al., 2010; Ritsma et al., 2014). In this ‘population asymmetry’ model, in principle, one stem cell daughter could remain proliferative by staying adjacent to a Paneth cell, while the other daughter exits the stem cell niche, differentiates, and stops proliferating. However, such asymmetric outcome is no longer guaranteed. Instead, proliferation and differentiation are balanced more indirectly, by averaging these stochastic events across the total stem cell population.

Observations of neutral drift, in which the offspring of a single cell randomly takes over the stem cell population of intestinal crypts (Lopez-Garcia et al., 2010; Snippert et al., 2010; Ritsma et al., 2014) established the stochastic nature of stem cell proliferation that distinguishes the population asymmetry model from the earlier division asymmetry model. However, approaches used thus far do not follow the underlying cell divisions and lineages in time. Proliferation symmetry between sister cells and its role in homeostasis of the intestinal epithelium has so far only been inferred indirectly, typically by quantifying the clone size distributions at a certain time point. Hence, we also lack insight into the fluctuations in the number of proliferating cells and the mechanisms that control them.

Here, we developed an alternative approach: we employed time-lapse microscopy and single-cell tracking of all cells in crypts of mouse intestinal organoids (Sato et al., 2009), thus providing complete lineage trees, division dynamics, and cell movement, and combine it with mathematical modeling and intravital imaging of the mouse intestine. Surprisingly, we found that most cell divisions (>90%) were symmetric in proliferative outcome, producing daughter cells that either both continued to proliferate or both ceased proliferating. Proliferation was symmetric even when one daughter neighbored a Paneth cell, the source of proliferative signals in the crypt, while the other did not. Hence, proliferation was not independent between sisters but rather controlled through the lineage by the mother. Our data and simulations explained not only how this behavior achieves homeostasis, but moreover, that it constitutes a near-optimal strategy to minimize fluctuations in the number of proliferating cells. Consistently, despite their large size increases over multiple generations in crypts of various sizes, the number of proliferating cells was notably constant in time and exhibited sub-Poissonian fluctuations, indicating a precise balance between proliferative and non-proliferative sister pairs. Finally, by measuring clone size distributions in mice, we showed that stem cell divisions in vivo reproduced the strong symmetry in proliferative behavior between sister cells seen in organoids. As cell proliferation in many tissues follows inherently stochastic ‘population asymmetry’ mechanisms (Clayton et al., 2007; Snippert et al., 2010; Doupé et al., 2012; Klein et al., 2010; Teixeira et al., 2013), we conjecture that high symmetry in proliferative behavior, controlled through the lineage, may be a more general mechanism to limit proliferation fluctuations.

Results

Single-cell tracking of complete crypts in growing intestinal organoids

To examine the dynamics of individual cells within crypts during growth, we used organoids with a H2B-mCherry nuclear reporter (Figure 1A) and performed confocal three-dimensional (3D) time-lapse microscopy for up to 65 hours at a time resolution of 12 minutes. Cell division events were distinguished by the apical displacement of the mother cell nucleus, followed by chromosome condensation and separation, and finally, basal migration of the daughter cell nuclei (Figure 1B), consistent with epithelial divisions (Ragkousi and Gibson, 2014). Custom-written software (Kok and van Zon, 2016) was used to track every cell within organoid crypts by recording their nuclei positions in 3D space and time (Figure 1C, Figure 1—video 1) and reconstruct lineage trees containing up to six generations (Figure 1F, Figure 1—figure supplement 1).

Figure 1 with 2 supplements see all

Download asset Open asset

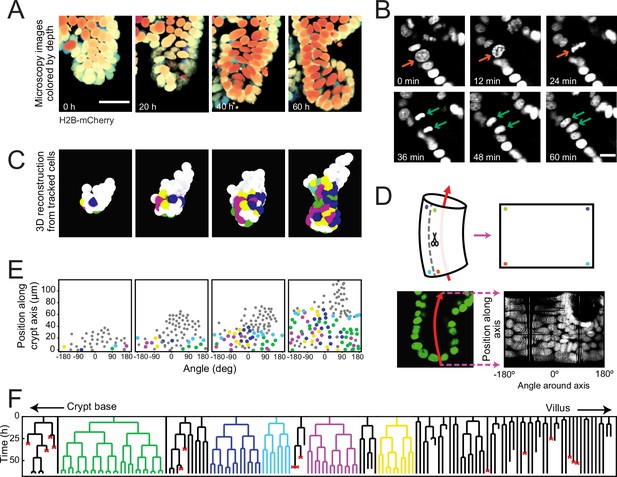
Time-lapse imaging and single-cell tracking of intestinal organoid crypts.

(A) Three-dimensional (3D) reconstruction of an organoid expressing an H2B-mCherry reporter to visualize individual nuclei. Shown here is the crypt region, with nuclei colored by their depth along the optical axis. Scale bar is 25 μm. (B) Snapshots of a cell division event in a crypt. Cell divisions are distinguished by the apical migration of the nucleus followed by chromosome condensation (red arrows). After mitosis, the nuclei of the two newly born cells are displaced basally (green arrows). Scale bar is 10 μm. (C) 3D reconstruction of a crypt growing in time using the positions of tracked nuclei. Colors represent cells that belong to the same lineage. (D) Illustration of crypt unwrapping. After the crypt-villus axis is annotated (red arrow), tracked cell positions are projected onto the surface of a bent cylinder. The cylinder is then unfolded, and its surface is mapped onto a two-dimensional plane defined by the distance along the axis and the angle around the axis. (E) Unwrapped representation of the crypt in (C), where colors represent the same lineages. (F) Lineage trees of cells within the crypt in (C) and colored accordingly. Cells in the initial time point are ordered according to their distance to the crypt base. Red crosses indicate cell deaths, and incomplete lines indicate cells that could not be accurately traced further due to insufficient fluorescence intensity or movement outside of the field of view.

To study the cell lineages along the crypt surface, we ‘unwrapped’ the crypts: first, we annotated the crypt axes at every time point, then projected every cell position onto the surface of a corresponding cylinder, which we then unfolded (Figure 1D and E). This allowed us to visualize the cellular dynamics in a two-dimensional plane defined by two coordinates: the position along the axis and the angle around the axis. We found that lineages starting close to the crypt bottom typically continued to proliferate and expand in cell number, while those further up in the crypt contained cells that no longer divided during the experiment, consistent with stem cells being located at the crypt bottom and terminal differentiation occurring higher up along the crypt axis (Figure 1F). Lineages were also terminated by the death of cells, as observed by their extrusion into the lumen. This fate occurred more often in some lineages compared to others, and the frequency did not depend strongly on position along the crypt-villus axis. At the crypt bottom we also observed a small number of non-dividing cells, suggestive of terminally differentiated Paneth cells. Indeed, these cells typically exhibited the larger cell size and granules typical of Paneth cells. Finally, a small fraction of cells could not be tracked during the experiment, as they moved outside of the field of view, or their fluorescence signal was degraded due to scattering in the tissue.

Control of cell proliferation in organoid crypts

To systematically study proliferation control, we classified cells as proliferating when they divided during the experiment. Cells were classified as non-proliferating when they did not divide for >30 hr or were born >60 μm away from the crypt bottom, as such cells rarely divided in our experiments (see Materials and methods for details). A smaller fraction of cells could not be classified. Some cells were lost from tracking (7%, N=2880 cells). These cells were typically located in the villus region (Figure 1F) and therefore likely non-proliferating. For other cells, the experiment ended before a division could be observed or excluded based on the criteria above (27%). Such cases were particularly prominent in the last 15 hr of each time-lapse data set (22%). To analyze proliferation control, we therefore excluded all cells born <15 hr before the end of each experiment, thereby reducing the fraction of unclassified cells to 10%.

Using this classification procedure, we then quantified the total number of cells born in the tracked cell lineages for nine crypts and found a strong (~fourfold) increase in time (Figure 2A). In contrast, the number of proliferating cells remained approximately constant in time for most crypts (Figure 2B). Two crypts (crypts 3 and 4 in Figure 2) formed an exception with ~twofold increase in the number of proliferating cells, an observation that we discuss further below. We then estimated the exponential growth rate $α$ for each crypt, by fitting the dynamics of total number of cells born and proliferating cell number to a simple model of cell proliferation (discussed further below as the Uniform model), where proliferating cells divide randomly into proliferating and non-proliferating cells. In this model, the number of proliferating and non-proliferating cells increases on average by $α$ and $1 - α$ per cell division, respectively (Materials and methods). Apart from crypts 3 and 4, that displayed growth ( $α ≈ 0.3$ ), the remaining crypts showed a low growth rate, $α = 0.05 ± 0.07$ (Figure 2—figure supplement 1A–C), indicating that birth of proliferating and non-proliferating cells was balanced on average. We then quantified the magnitude of fluctuations in the number of proliferating cells, $N$ . Calculations of birth-death models of cell proliferation show that, without any control, the standard deviation of the proliferating cell number grows in time without bounds as $σ_{D} \sqrt{N t}$ (Feller, 1939). In models without exponential growth, with proliferating cells born at constant rate, fluctuations are reduced: they are constant in time and Poissonian, $σ_{D} \sqrt{N}$ (Swain, 2016). In models where exponential growth was controlled by homeostatic feedback loops, fluctuations were further reduced to sub-Poissonian: $σ_{D} < \sqrt{N}$ (Sun and Komarova, 2012). Using the same measures, we found here that most crypts exhibited sub-Poissonian fluctuations (Figure 2—figure supplement 1D), implying the presence of a mechanism to limit fluctuations in proliferating cell number. Finally, we quantified the frequency of cell divisions along the crypt axis. Notably, divisions occurred in a region below 60 μm from the crypt base throughout the experiment, even as the crypts grew significantly (Figure 2C), indicating that the size of the proliferative region was constant in time. Moreover, the proliferative region was found to have a similar size in all analyzed crypts (Figure 2D), even though crypts varied both in size, as measured by diameter (30–50 μm, Figure 2—figure supplement 1E), and number of proliferating cells (Figure 2B). Overall, these results show that crypts by themselves are already capable of a specific form of homeostasis, namely, maintaining a stationary number of proliferating cells that occupy a region of the crypt of constant size.

Figure 2 with 1 supplement see all

Download asset Open asset

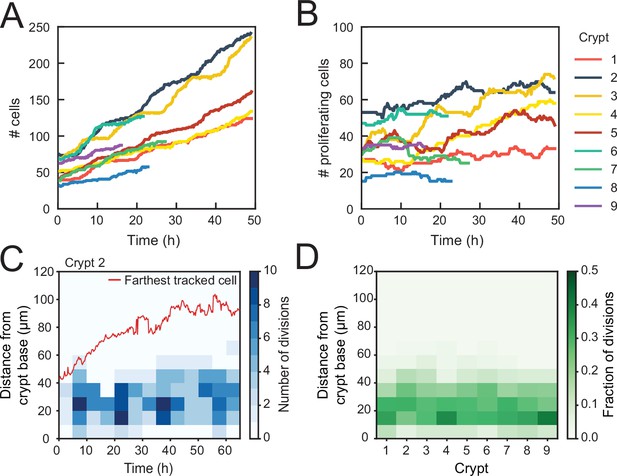
Control of cell divisions in intestinal organoids.

(A) Total number of cells born and (B) number of proliferating cells as a function of time for all cell lineages followed in nine tracked crypts. Cells that died were classified as non-proliferating. Note the different scales along the y-axis. Whereas total cell number increases, the number of proliferating cells remains approximately constant. The strongest increase in number of proliferating cells (~twofold) was seen in crypts 3 and 4. (C) Number of divisions that occurred at different positions along the crypt axis as a function of time in a single-tracked crypt. Red line corresponds to the position of the farthest tracked cell from the crypt base at every time point. Divisions occur in a compartment close to the crypt base, whose size remains constant over time. Apical displacement of the nuclei during mitosis results in few divisions occurring at less than 10 μm from the crypt base. (D) Fraction of divisions that occurred at different positions along the crypt axis for all tracked crypts, averaged over the full-time course. The size of the proliferative region is similar between crypts, despite differences in the total number of divisions.

Symmetry of proliferative behavior between sister cells

To examine the origin of the observed balance between the birth of proliferating and non-proliferating cells, we first examined whether cell proliferation or cell death was correlated between sisters, for all observed sister pairs S₁ and S₂ (Figure 3A). Strikingly, we found that the decision to divide or not was highly symmetrical between sisters. In particular, occurrences where one sister divided but the other not were rare (2%) compared to cases where both divided or stopped dividing (74%). This correlation was also apparent by visual inspection of individual lineages, as sisters showed the same division behavior (Figure 3B, top). Indeed, if we ignore cell death, the fraction of pairs with symmetric proliferative outcome was high (97%) and could not be explained by sister cells making an independent decision to proliferate or not [(p<10⁻⁵, bootstrap simulation, Materials and methods]. We also compared lineage dynamics between all cousin pairs C₁ and C₂ (Figure 3A). While we indeed found a significantly increased fraction (9%) of cousin pairs with asymmetrical division outcome, i.e., C₂ dividing and C₁ not, compared to sister pairs (2%), this fraction was still low, indicating that symmetric outcomes also dominated for cousins.

Figure 3 with 2 supplements see all

Download asset Open asset

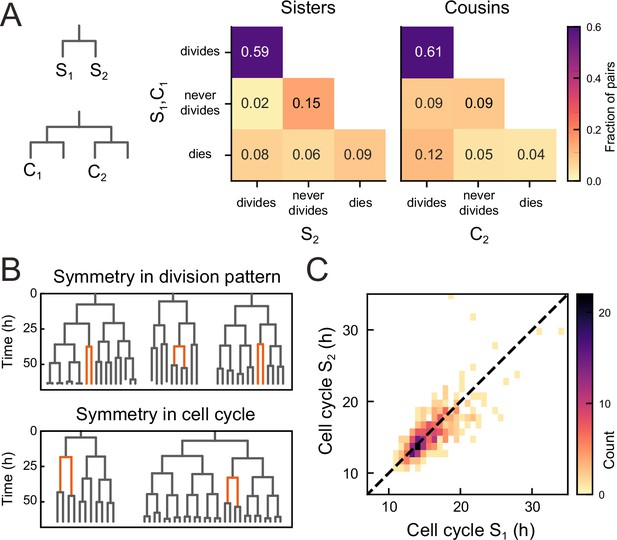
Symmetry of lineage dynamics between sister cells.

(A) Correlations in division patterns between sister (**S₁,S₂**) and cousin cells (**C₁,C₂**) (n=1004 and 1304 sister and cousin cell pairs). Most sister pairs show symmetrical outcomes, with most pairs consisting of sisters that either both divide or both cease dividing. Cell death occurs at low frequency and impacts sister cells asymmetrically. Symmetrical outcomes are still dominant for cousins, but the fraction of pairs that exhibited asymmetric proliferative outcomes (C₁ never divides, C₂ divides) was significantly increased in cousins compared to sisters (p=2.4∙10⁻⁷, Pearson’s Chi Square test). (B) Representative examples of measured lineages highlighting pairs of sister cells (orange) that differ in lineage dynamics from their more distant relatives (black), either in terms of proliferative behavior (top) or cell cycle duration (bottom). (C) Duration of sister cell cycles plotted against each other for pairs in which both sisters divided. Cell cycle duration is strongly correlated between sisters (R=0.80).

We found that symmetry between sisters did not only impact proliferation arrest, but also cell cycle duration: when a cell exhibited a longer-than-average cell cycle, this was typically mirrored by a similar lengthening of the cell cycle of its sister (Figure 3B, bottom). Indeed, cell cycle duration was strongly correlated between sisters (R=0.8, Figure 3C), even as cell cycle duration showed a broad distribution among tracked cells (Figure 3—figure supplement 1). In contrast, cell death was not symmetric between sisters, as the fraction of pairs where both cells died (9%) was smaller than the fraction of pairs where only a single sister died (14%, Figure 3A).

When examining all sister pairs in our data set, pairs of dividing sisters (59%) outnumber pairs of non-dividing sisters (15%), which appeared at odds with the observation that in most crypts the number of proliferating cells remains approximately constant (Figure 2B). This apparent mismatch was due to the exclusion of sister pairs where the proliferative state could not be classified in one sister or both (Figure 3—figure supplement 2), as the majority of these unclassified cells were likely non-proliferating. Indeed, when we restricted our sister pair analysis to the cells of crypts with α≈0 in Figure 2A and B (crypts 1, 2, 5, 7–9), and furthermore, assumed that all unclassified cells were non-proliferating, we found that now proliferating sister pairs (43%) are approximately balanced by non-proliferating sisters (40%, Figure 3—figure supplement 2).

Symmetry between sisters minimizes fluctuations in a cell proliferation model

In principle, any combination of (a)symmetric divisions would yield a constant number of proliferating cells on average, as long as the birth of proliferating and non-proliferating cells is balanced. We therefore hypothesized that the observed dominance of symmetric divisions might have a function specifically in controlling fluctuations in the number of proliferating cells. To test this hypothesis, we used mathematical modeling. Mathematical models of intestinal cell proliferation have been used to explain observed clone size statistics of stem cells (Lopez-Garcia et al., 2010; Snippert et al., 2010; Ritsma et al., 2014; Corominas-Murtra et al., 2020) but so far not to examine the impact of division (a)symmetry on cell number fluctuations. We therefore examined simple stem cell models in which the degree of symmetry of sister cell proliferation could be tuned as an external parameter.

We first examined this in context of the canonical stochastic stem cell model (Clayton et al., 2007), that we here refer to as the Uniform model. This model only considers cells as ‘proliferating’ or ‘non-proliferating’ (approximating stem and differentiated cells), and tissues that are unbounded in size, while ignoring spatial cell distributions. The parameter $ϕ$ describes the division symmetry, with $ϕ = 1$ corresponding to purely symmetric divisions and $ϕ = 0$ to purely asymmetric divisions. The growth rate $α$ describes the proliferation bias, with $α > 0$ indicating more proliferating daughters, and $α < 0$ more non-proliferating daughters on average. In our simulations, cells either divide symmetrically to produce two proliferating cells with probability $\frac{1}{2} (ϕ + α)$ or two non-proliferating cells with probability $\frac{1}{2} (ϕ - α)$ , while the probability to divide asymmetrically is $1 - ϕ$ (Figure 4A). The number of proliferating cells increases exponentially for $α > 0$ or decreases exponentially for $α < 0$ while homeostasis requires $α = 0$ (Lander et al., 2009; Clayton et al., 2007; Figure 4B).

Figure 4 with 2 supplements see all

Download asset Open asset

Cell number fluctuations in stem cell models.

(A) ‘Uniform’ stem cell model. The probability of each division pattern depends on $α$ , the average increase in the number of proliferating cells per division, and, $ϕ$ , the fraction of divisions with symmetric outcome, while the total cell number is unconstrained. (B) Number of proliferating cells, $N$ as function of time for different values of $α$ (top) and $ϕ$ (bottom). For, $a = 0$ , $N$ remains constant on average, yet in this case, fluctuations can cause stochastic depletion or overgrowth of proliferating cells, as shown for $ϕ = 0.9$ (bottom). (C) Coefficient of variation (standard deviation divided by mean) of $N$ as a function of $ϕ$ (top panel) and the probability of depletion ( $N = 0$ , blue) or overgrowth ( $N ≥$ 150, pink) events (bottom panel), for the ‘Uniform’ model with $a = 0$ . Frequency of overgrowth depends strongly on the threshold value used. Fluctuations are minimal for $ϕ = 0$ , i.e., only asymmetric divisions. (D) ‘Compartment’ model. Cells divide according to (A), but now the tissue is divided in a niche compartment $n$ , with $α_{n} > 0$ , and a differentiation compartment $d$ , where $α_{d} < 0$ . Both compartments have the same $ϕ$ . In the niche compartment, the total number of cells cannot exceed $S$ , so that upon cell division the distalmost cell (dashed square) moves into the differentiation compartment. Cells in the niche compartment switch positions at rate $r$ . (E) Number of proliferating cells as a function of time in the niche (green) and differentiation compartment (blue). The total number of proliferating cells (black) fluctuates around the dashed line corresponding to $⟨N⟩$ . Each panel’s number refers to the parameter sets shown in (F). The parameter set with lowest fluctuations is outlined in red. (F) Coefficient of variation of $N$ . Left panel shows the effects of varying the growth rates of both compartments when all divisions are symmetric ( $ϕ = 1$ ), and right panel of varying the degree of symmetry when both compartments have opposite growth rates ( $α_{n} = - α_{d}$ , dashed line in top panel). The gray region in bottom panel is inaccessible parameter space. Simulations ran with $⟨ N ⟩ = 30$ , corresponding to our experimental observations, and rearrangements occurring approximately once per cell cycle. Fluctuations are minimized for $α_{n}, - α_{d} = 1$ and $ϕ = 1$ , i.e., only symmetric divisions.

When varying the division symmetry Φ while maintaining α=0, we found that fluctuations in the number of proliferating cells $N$ were minimized for Φ=0 (Figure 4B and C), i.e., every division was asymmetric. In this scenario, the number of proliferating cells remains constant throughout each individual division by definition. Adding only a small fraction of symmetric divisions strongly increased the fluctuations in $N$ . These fluctuations increased the risk of stochastic depletion, where all proliferating cells are lost, or uncontrolled increase in cell number, as previously observed in simulations (Sun and Komarova, 2012), with the probability of such events occurring increasing with Φ (Figure 4B and C). These trends are inconsistent with the symmetry between sisters we observed experimentally.

Hence, we extended the model by explicitly incorporating the observed subdivision of the crypt in a stem cell niche region, corresponding roughly to the stem cell niche, and a differentiation region, corresponding to the villus domain (Figure 4D). In the niche compartment, which has fixed size $S$ , most divisions generate two proliferating daughter cells (α_n > 0), while in the differentiation compartment, which has no size constraints, most divisions yield two non-proliferative daughters (α_d < 0). Cell divisions in the niche compartment result in expulsion of the distalmost cell into the differentiation compartment, while neighboring cells swap positions in the niche compartment with rate $r$ to include cell rearrangements. In contrast to the uniform model, where homeostasis only occurred for $α = 0$ , the compartment model shows homeostasis with α_{n, d} in either compartment. Specifically, we found that the average number of proliferating cells in the two compartments, $N_{n}$ and $N_{d}$ , is given by $D_{n} = α_{n} S$ and $N_{d} = S l n (1 + α_{n}) \frac{α_{d} - α_{n}}{α_{d}} - α_{n} S$ , independent of the division symmetry Φ (Kok et al., 2022). We simulated the proliferation dynamics for different values of α_n , α_d, and Φ (Figure 4E and F), where for simplicity we assumed the same Φ in both compartments. For each combination of parameters, we varied the compartment size $S$ so that $⟨N⟩$ = $N_{n} + N_{d}$ = 30, comparable to the number of proliferating cells per crypt in our experiments (Materials and methods, Figure 4—figure supplement 1A). For cell rearrangements, we used $r ⋅ T = 1$ , where $T$ is the average cell cycle time, meaning that cells rearrange approximately once per cell cycle. For this $r$ , our simulations reproduced the correlations in division outcome that we observed experimentally for cousins (Figure 4—figure supplement 2A–C), although we found that the dependence of the dynamics of $N$ on the parameters $ϕ, α_{n}$ , and $α_{d}$ did not depend strongly on $r$ (Figure 4—figure supplement 2D).

By fixing $⟨N⟩$ , all simulations maintained the same number of proliferating cells on average but potentially differed in the magnitude of fluctuations. Indeed, we found parameter combinations that generated strong fluctuations (Figure 4E and F, scenario 1) and stochastic depletion of all proliferating cells (scenario 2). Stochastic depletion occurred at significant rate (>1 event per 10³ hr) when $α_{n} ≲ 0.5$ ≲0.5 (Figure 4—figure supplement 1B) and implies that the existence of a stem cell niche, defined as a compartment with α > 0, by itself does not guarantee homeostasis, unless its bias toward proliferation is high, α≈1. For fixed $α_{d}$ and $α_{n}$ , we observed that fluctuations in $N$ always decreased with more asymmetric divisions (Φ→0) (Figure 4E and F, scenarios 2,3), similar to the uniform model. However, the global fluctuation minimum was strikingly different (Figure 4E and F, scenario 4). Here, symmetric divisions dominated (Φ=1), with all divisions generating two proliferative daughters in the niche compartment ( $α_{n} = 1$ ) and two non-proliferating daughters in the differentiation compartment (α_d=–1). Similar low fluctuations were found for a broader range of $α_{d}$ , provided that α_n≈1. When we quantified the magnitude of fluctuations versus the average number of proliferating cells, we found that fluctuations for the suboptimal scenarios 1–3 were larger than those expected for a Poisson birth-death process (Figure 2—figure supplement 1D). In contrast, fluctuations in the optimal scenario 4 were similar to the low fluctuations we observed experimentally.

Our simulations also provided an intuitive explanation for this global minimum. A bias α_n = 1 is only reached when the birth of non-proliferating cells in the niche compartment, by symmetric or asymmetric divisions, is fully avoided. In this limit, all cells in this compartment are proliferating, meaning that fluctuations in the niche compartment are entirely absent, with the only remaining fluctuations due to cells ejected from the niche compartment that subsequently divide in the differentiation compartment. Consistent with this explanation, we found that fluctuations in $N$ increased when more symmetric divisions in the niche compartment generated non-proliferating daughters (scenarios 1 and 2). Finally, we note that the well-established neutral drift model of symmetrically dividing stem cells in a niche of fixed size (Lopez-Garcia et al., 2010; Snippert et al., 2010) fails to reproduce the high symmetry in proliferation we experimentally observe between sister cells (Figure 4—figure supplement 2E), indicating that the size constraint of a niche is by itself not sufficient to generate this symmetry. In conclusion, our simulations show that the dominance of symmetric divisions we observed experimentally might function to minimize fluctuations in cell proliferation.

Symmetry of proliferation is independent of Paneth cell distance

Our results raised the question how the strong symmetry in proliferative behavior between sister cells is generated. Stem cell maintenance and cell proliferation are controlled by signals such as Wnt and EGF, that in organoids are locally produced by Paneth cells (Sato et al., 2011; Farin et al., 2016). The symmetry between sister cells could therefore be explained by these sisters having a similar position relative to Paneth cells, leading them to experience a near identical environment in terms of proliferative signals. Alternatively, the proliferative behavior of sister cells could be controlled through the lineage, by their mother. In this case, symmetric proliferative behavior would even be seen in sisters that differ in position relative to Paneth cells. To differentiate between these two scenarios, we performed lysozyme staining after time-lapse imaging to retrospectively identify Paneth cells in our tracking data. Using crypt ‘unwrapping’ (Figure 1D and E), we calculated for each cell and each time point the link distance δ to the closest Paneth cell (Materials and methods, Figure 5—figure supplement 1A and B, Figure 5—video 1), i.e., the number of cells between the cell of interest and its closest Paneth cell, allowing us to examine proliferative behavior as function of distance to Paneth cells.

Paneth cell-derived Wnt ligands form gradients that only penetrate 1–2 cells into the surrounding tissue (Farin et al., 2016), suggesting that the steepest gradient in proliferative signals is found in close proximity to the Paneth cell. We therefore selected all dividing mother cells directly adjacent to a Paneth cell (δ_M = 0) and examined their daughters. These sister pairs varied in Paneth cell distance (δ_{1, 2} ≈ 0–2, Figure 5A, Figure 5—figure supplement 1C), with differences between sisters (δ₁) seen in 42% of pairs. We classified each sister pair as asymmetric in outcome, when only one sister continued proliferating, or symmetric (Figure 5B). In the latter case, we distinguished between symmetric pairs where both sisters divided and those were both stopped proliferating. We found that most daughters cells divided again, even though a small fraction ceased division even in close proximity to Paneth cells (Figure 5B, Figure 5—figure supplement 1D). However, whether cells divided or not was fully symmetric between sister pairs, even when one cell remained adjacent to a Paneth cell (δ₁ = 0) while the other lost contact (δ₂ >0). This also held for the few pairs where Paneth cell distance differed most between sisters (δ₁ = 0, δ₂ = 2).

Figure 5 with 2 supplements see all

Download asset Open asset

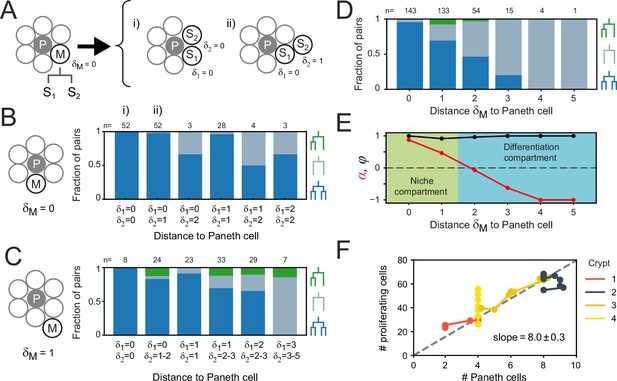
Impact of Paneth cell distance on proliferation.

(A) Dependence of proliferation on contact with Paneth cells. We examined cases where a mother cell (M) that touched a Paneth cell (P) divided into sister cells, S₁ and S₂, that either retained or lost Paneth cell contact. Here, the link distances $δ_{1}$ and $δ_{2}$ represent the number of cells between each sister and its closest Paneth cell. (B) Probability that both cells divide (blue), neither cell divides (orange) nor only a single cell divides (green) for all sister pairs S₁ and S₂ of which the mother touched a Paneth cell ( $δ_{M}$ = 0). Sister pairs exhibited full symmetry in proliferative behavior, even when distance to the Paneth cell differed between sisters ( $δ_{1} ≠ δ_{2}$ ). (C) Same as (B) but for a mother cell positioned one cell away from the Paneth cell ( $δ_{M}$ = 1). More daughter cells cease proliferation. While the fraction of pairs where only one sister divides increases, most sisters exhibit symmetric behavior. (D) Probability of each division pattern as a function of Paneth cell distance of the mother cell. (E) Proliferative bias α and degree of symmetry Φ as a function of Paneth cell distance. The observed values of α define a proliferative niche (green, $α \approx 1$ ) and non-proliferative differentiation (blue, $α < 0$ ) compartment, with the former corresponding approximately to the first two ‘rings’ of cells surrounding the Paneth cell. (F) Number of proliferating cells as a function of Paneth cell number. Time courses for individual crypts were divided into 5-hr intervals (markers), for which average cell numbers were calculated. Apart from crypt 4, Paneth cell number correlated well with number of proliferating cells, even when Paneth cell number increased in time due to divisions. Dashed line is a linear fit to the data.

When we instead examined mother cells that just lost contact with a Paneth cell ( $δ_{M}$ = 1), we found that their offspring stopped proliferating more frequently (Figure 5C). While here we did find a substantial fraction of sister pairs with asymmetric outcome, for most pairs the outcome was still symmetric (92% of pairs), even for pairs that differed considerably in relative distance to the Paneth cell. Sister pairs with asymmetric outcome occurred more frequently for pairs with different Paneth cell distances (δ₁≠δ₂). For these pairs, however, the non-proliferating cell was the sister closest to the Paneth cell about as often as it was the more distant (five and three pairs, respectively), indicating that position relative to the Paneth cell had little impact on each sister’s proliferative behavior. Overall, these results show that the symmetry of proliferative behavior between sisters did not reflect an underlying symmetry in distance to Paneth cells, thus favoring a model where this symmetry is controlled by the mother cell.

Paneth cells control proliferative bias

Even though the proliferative behavior of sisters was not explained by their relative Paneth cell distance, we found that the bias toward proliferating daughters was clearly reduced when the Paneth cell distance of the mother increased (Figure 5B and C). Our simulations showed that both division symmetry and proliferative bias are important parameters in controlling fluctuations in the number of proliferating cells, with fluctuations minimized when most divisions are symmetric (Φ≈1), biased strongly toward producing two proliferating daughters in one compartment (α≈1) and two non-proliferating daughters in the other (α≈-1). To compare our experiments against the model, we therefore measured the frequency of each division class as a function of the mother’s Paneth cell distance, averaging over all positions of the daughter cells (Figure 5D). Overall, cells had a broad range of Paneth cell distances (δ=0–10). Close to Paneth cells (δ≤1), most divisions generated two proliferating daughters, while further away (δ>1), the majority yielded two non-proliferating cells. Asymmetry was rare and only occurred for δ=1–2. No divisions were seen for δ>5. When we used these measured frequencies to calculate α and Φ as a function of Paneth cell distance (Figure 5E), we found good agreement with the parameter values that minimized fluctuations in the model, with a niche compartment of strong proliferation close to Paneth cells (α=0.67, δ≤1) and a non-proliferative compartment beyond (α=−0.67), while almost all divisions were symmetric ( $ϕ$ =0.98).

The compartment model also predicted that the number of proliferating cells increases linearly with size $S$ of the niche compartment. Above, we observed that the number of proliferating cells differed between crypts (Figure 2B). We therefore examined whether variation in number of proliferating cells between crypts could be explained by differences in Paneth cell number, in those crypts where we identified Paneth cells by lysozyme staining (crypts 1–4). For the crypts that maintained a constant number of proliferating cells in time (crypts 1–2), we found that differences in number of proliferating cells were well explained by differences in Paneth cell number. Moreover, in crypts with increasing number of proliferating cells (crypts 3–4), we found that for crypt 3, this change could be explained by an increase of Paneth cell number, due to cell divisions that generated Paneth cell sisters. In crypt 4, however, proliferating cells increased in number without apparent Paneth cell proliferation. This crypt appeared to undergo crypt fission (Langlands et al., 2016) at the end of the experiment, suggesting that during fission cell proliferation is altered without concomitant changes in Paneth cell number. For crypts 1–3, the relationship between number of proliferating and Paneth cells was well fitted by a linear function (Figure 5F), consistent with the compartment model. The fitted slope of this line indicates that one Paneth cell maintains approximately eight proliferating cells. This agrees with the observation in Figure 5D that divisions are strongly biased toward proliferation only for cells within the first and second ring of cells around each Paneth cell. Taken together, these results show that Paneth cells control proliferation by tuning the proliferative bias of divisions that are otherwise symmetric in proliferative outcome.

In vivo lineage tracing confirms symmetric proliferative behavior of sister cells

Finally, we asked whether the symmetry of proliferative behavior between sister cells was also observed in intestinal (stem) cells in vivo. Studying lineage dynamics with the high spatial and temporal resolution we employed here is currently impossible in vivo. However, we found that clone size distributions, which can be measured in vivo, exhibited a clear signature consistent with symmetric divisions. Specifically, clone size distributions of lineages generated by the compartment model showed that enrichment of even-sized clones depended strongly on a high frequency of symmetric divisions (Figure 6A). When we quantified clone size distributions for our organoid lineage data, by counting the number of progeny of each cell at the end of a 40-hr time window, while sliding that window through our ~60-hr data set, we indeed found that even clone sizes were strongly enriched compared to odd clone sizes (Figure 6B). Both for organoid and model data, we still observed odd clone sizes even when virtually all divisions were symmetric in proliferative behavior. This reflected variability in the cell cycle duration, with odd clone sizes typically resulting from symmetric divisions where one daughter had divided, but the other not yet.

Figure 6

Download asset Open asset

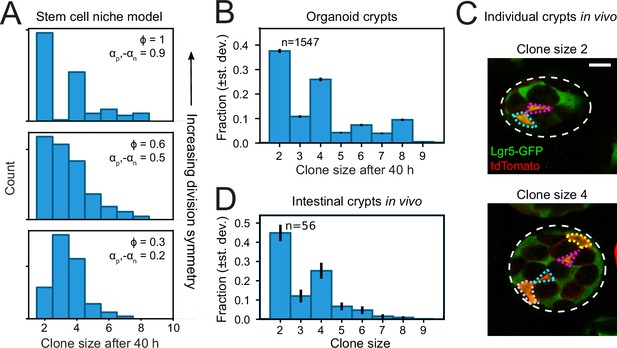
Clone size distributions reveal symmetry of proliferative behavior.

(A) Clone size distributions calculated for the Compartment model, for different degrees of division symmetry Φ. Top panel corresponds to parameters that minimize fluctuations in number of proliferating cells. For high division symmetry, Φ, even clone sizes are enriched compared to odd clone sizes. (B) Clone size distributions calculated for the lineage data obtained in organoids, for a sliding window of 40 hr. Even clone sizes are enriched, consistent with the observed dominance of divisions with symmetric proliferative outcome. Error bars indicate standard deviation calculated using a bootstrapping approach (Materials and methods). (C) Examples of individual crypts found in vivo, displaying clone size 2 (top) and 4 (bottom). Crypts are viewed from the bottom, with individual cells belonging to a tdTomato+ clone (red) outlined. Scale bar is 10 µm. (D) Clone size distributions measured in vivo 60 hr after induction of Cre-mediated recombination in small intestinal crypts of *Lgr*5^{EGFP-ires-CreERT2};R26_LSL-tdTomato mice (n=160 crypts). Even clone sizes 2 and 4 are enriched compared to odd clone sizes 3 and 5. Error bars indicate standard deviations calculated using a bootstrapping approach.

To measure clone size distributions in the small intestine in vivo, we stochastically induced heritable tdTomato expression in Lgr5 + stem cells using Lgr5^{EGFP-ires-CreERT2};R26_LSL-tdTomato mice. We activated Cre-mediated recombination by tamoxifen and examined tdTomato expression after 60 hr, similar to the timescale of our organoid experiments, and imaged crypts with 3D confocal microscopy. Cre-activation occurred in one cell per ~10 crypts, indicating that all labeled cells within a crypt comprised a single clone. Indeed, we typically found a small number of tdTomato + cells per crypt, of which most also expressed Lgr5-GFP (Figure 6C). We then counted the number of tdTomato + cells per crypt to determine the clone size distribution and found a clear enrichment of even clone sizes (Figure 6D), with the overall shape of the distribution similar to that measured in organoids. Overall, these results indicated a dominant contribution of divisions with symmetric proliferative outcome also in the lineage dynamics of Lgr5 + stem cells in vivo.

Discussion

Self-renewing tissues exhibit homeostasis at multiple levels, such as overall tissue morphology, total cell number, and the relative frequency of different cell types. To prevent exponential growth or tissue atrophy, the birth of each proliferating cell must be balanced by the loss of another through terminal differentiation. Experiments in a range of systems indicate that this is achieved through ‘population asymmetry’, with each cell making the decision to proliferate or not in a stochastic manner and this balance only achieved averaged over the entire population (Simons and Clevers, 2011; Clayton et al., 2007; Snippert et al., 2010; Klein et al., 2010). However, our simulations showed that even though ‘population asymmetry’ ensures a constant pool of proliferating cells on average, its inherently stochastic nature can cause strong fluctuations in proliferating cell number, even resulting in their full depletion (Figure 4). This raises the question how these fluctuations are controlled.

We addressed this by a combined experimental and theoretical approach. We tracked all cell movements and divisions in the crypts of growing intestinal organoids, to reconstruct the full lineage of these crypts up to six generations (Figure 1). These data showed that the number of proliferating cells in most organoid crypts was approximately stationary, with small, i.e., sub-Poissonian fluctuations in their number, while non-proliferating cells were born at a constant rate (Figure 2, Figure 2—figure supplement 1), an indication of homeostatic control of cell proliferation that also limits fluctuations. That intestinal organoids exhibited homeostasis is notable, as organoid culture completely lacks surrounding tissue, such as the mesenchyme, that provides key signals regulating stem cell fate and proliferation (Farin et al., 2012; Shoshkes-Carmel et al., 2018), and shows that this form of homeostasis is inherent to the epithelium itself.

Our simulations showed that the fluctuations in proliferating cell number depended strongly on the relative proportion of divisions with symmetric proliferative outcome (either two proliferating or two non-proliferating daughters) and asymmetric outcome (one proliferating and one non-proliferating daughter), with small, sub-Poissonian cell number fluctuations only seen when most divisions had symmetric outcome (Figure 4, Figure 2—figure supplement 1). So far, the relative contribution of these three divisions patterns in the intestine could only be inferred indirectly from static measurements, leading to conflicting results (Lopez-Garcia et al., 2010; Snippert et al., 2010; Itzkovitz et al., 2012; Sei et al., 2019). Here, we used direct measurements of cell dynamics in time to unambiguously identify the proliferative state of successive generations of cells. These measurements show that virtually all cell divisions (>90%) showed symmetric proliferative behavior, generating either two proliferating or two non-proliferating sisters (Figure 3). Clone size distributions calculated based on our measured lineage data in organoids showed that this symmetry in proliferative behavior between sister cells gave rise to an enrichment of even clone sizes (Figure 6). Using short-term lineage tracing experiments in the mouse small intestine, we found that single Lgr5 + stem cells also gave rise to more even-sized than odd-sized clones, indicating that divisions that are symmetric in proliferative behavior indeed also dominate stem cell proliferation in vivo.

The symmetry in proliferative behavior we observe between sister cells could arise because both cells experience a highly similar environment, in terms of proliferative signals, or rather indicate control of cell proliferation through the lineage, by the mother cell. The current models of stem cell dynamics in the intestinal crypt favor a strong role for position relative to the stem cell niche, formed in organoids by Paneth cells, and a minor role, if any, for control of cell proliferation through the lineage (Lopez-Garcia et al., 2010; Snippert et al., 2010; Ritsma et al., 2014). We found that sister cells exhibited symmetric proliferative behavior, even when sisters differed in distance to Paneth cells (Figure 5), the sole source of proliferative Wnt signals in intestinal organoids (Sato et al., 2011). This result implies control of proliferation by the mother cell rather than by each daughter’s position in the stem cell niche. Our simulations provided a potential function for the predominance of divisions with symmetric proliferative outcome. When the tissue was subdivided into compartments of low and high cell proliferation, with the latter resembling the stem cell niche, we found that fluctuations in the number of proliferating cells were virtually eliminated, provided that cell divisions were symmetric, with all divisions generating two proliferating daughters in the niche compartment and two non-proliferating daughters outside (Figure 4). Consistently, in our experiment we found that frequency of mother cells generating two proliferating rather than two non-proliferating daughters decreased with the mother’s distance to the closest Paneth cell (Figure 5). Taken together, our results suggest a model where differences in proliferative behavior emerge in the cell lineage over at least two generations: while a mother cell division generates two daughters with the same proliferative behavior, these daughters might subsequently generate grand-daughters that differ in proliferative behavior, depending on each daughter’s position relative to the Paneth cells. This is consistent with our observation that the symmetry of proliferative behavior between cousins is reduced significantly compared to sisters (Figure 3).

We used mathematical modeling to explore the dependence of fluctuations in cell proliferation on the degree of symmetry in cell division outcome, arriving at a two-compartment model that matched key features of our experiments (Figure 4D–F). It reproduced the observed low, sub-Poissonian fluctuations in number of proliferating cells (Figure 2—figure supplement 1D), but only when division symmetry was high, as we also observed experimentally. In contrast, high symmetry increased fluctuations in a spatially uniform stem cell model (Figure 4B and C), while a standard neutral drift model of a stem cell niche (Lopez-Garcia et al., 2010; Snippert et al., 2010) failed to reproduce the observed symmetry in outcome (Figure 4—figure supplement 2). Our model also reproduced the observed correlation in proliferative state between cousin cells (Figure 4—figure supplement 2), explaining it as arising from closely related cells having similar location in the tissue and therefore similar probability of leaving the stem cell niche. Finally, it predicted the observed division of the tissue in a compartment where most divisions generated proliferating cells (close to Paneth cells) and one where divisions mostly generated non-proliferating daughters (away from Paneth cells) (Figure 5). However, the simplified nature of our model also poses limits. First, the observed transition from proliferating to non-proliferating daughter cells was more gradual than predicted by the model, indicating that each divisions proliferative outcome depended on space in a more complex manner than captured by the model. Second, the existence of compartments and the degree of symmetry in division outcome are imposed externally by the model rules. It will be interesting to examine whether simple mathematical models can explain how these properties emerge from the internal cellular states, long-range signaling pathways, and local cell-cell interactions involved in intestinal homeostasis (Simons and Clevers, 2011; Gehart and Clevers, 2019).

Precise control of cell proliferation is key to homeostasis. It has been proposed that cells may sense cell density, either by chemical signals or mechanical cues, and decrease cell proliferation (known as contact inhibition) if the cell number is too high (Lander et al., 2009; Sun and Komarova, 2012; Eisenhoffer and Rosenblatt, 2013), thereby ensuring homeostasis of and minimize fluctuations in the number of proliferating cells. Here, we provide a mechanism that achieves this without explicit sensing of cell density. Instead, it relies on the dominance of divisions symmetric in proliferative behavior of the daughter cells, coupled with the organization of a tissue in a proliferative niche (stem and TA cell) compartment, and a non-proliferative differentiation compartment. Such an organization is found widely, e.g., in the skin, hair follicles, testis, among others (Li and Xie, 2005). In all these tissues, homeostasis of and minimizing fluctuations in the number of proliferating and differentiated cells must be essential. Hence, we speculate that the model we propose here, which exploits proliferative symmetry between sister cells to minimize fluctuations, is conserved more broadly and relevant to diverse tissue systems.

Materials and methods

Key resources table

Reagent type (species) or resource	Designation	Source or reference	Identifiers	Additional information
Biological sample (Mus musculus)	H2B-mCherry (intestinal organoids)	Other	-	Gift from Hubrecht Institute, Clevers group
Antibody	anti-lysozyme (polyclonal rabbit)	Dako	RRID:AB_2341230; Cat# A0099	IF(1:800)
Antibody	anti-rabbit IgG H&L (Alexa Fluor 405) (polyclonal donkey)	Abcam	RRID:AB_2715515; Cat# ab175649	IF(1:1000)
Chemical compound, drug	Advanced DMEM/F-12 medium	Life Technologies	Cat# 12634010	-
Other	Wheat Germ Agglutinin (WGA), CF488 A Conjugate	Biotium	Cat# 29022	5 μg/ml
Other	RedDot1 Far-Red Nuclear Stain	Biotium	Cat# 40060	1:200

Organoid culture

Request a detailed protocol

H2B-mCherry murine intestinal organoids were a gift from Norman Sachs and Joep Beumer (Hubrecht Institute, The Netherlands). Organoids were cultured in basement membrane extract (BME, Trevingen) and overlaid with growth medium consisting of murine recombinant epidermal growth factor (EGF 50 ng/ml, Life Technologies), murine recombinant Noggin (100 ng/ml, Peprotech), human recombinant R-spondin 1 (500 ng/ml, Peprotech), n-acetylcysteine (1 mM, Sigma-Aldrich), N2 supplement (1×, Life Technologies) and B27 supplement (1×, Life Technologies), Glutamax (2 mM, Life Technologies), HEPES (10 mM, Life Technologies), and Penicilin/Streptomycin (100 U/ml 100 μg/ml, Life Technologies) in Advanced DMEM/F-12 (Life Technologies). Organoid passaging was performed by mechanically dissociating crypts using a narrowed glass pipette.

Time-lapse imaging

Request a detailed protocol

Mechanically dissociated organoids were seeded in imaging chambers 1 day before the start of the time-lapse experiments. Imaging was performed using a scanning confocal microscope (Nikon A1R MP) with a ×40 oil immersion objective (NA = 1.30). 30 z-slices with 2-μm step size were taken per organoid every 12 min. Experiments were performed at 37°C and 5% CO₂. Small but already formed crypts that were budding perpendicularly to the objective were selected for imaging. Imaging data was collected for three independent experiments.

Fluorescent staining

Request a detailed protocol

After time-lapse imaging, organoids were fixed with 4% formaldehyde (Sigma) at room temperature for 30 min. Next, they were permeabilized with 0.2% Triton-X-100 (Sigma) for 1 hr at 4°C and blocked with 5% skim milk in Tris-Buffered Saline (TBS) at room temperature for 1 hr. Subsequently, organoids were incubated in blocking buffer containing primary antibody (rabbit anti-lysozyme 1:800, Dako #A0099) overnight at 4°C and then incubated with secondary antibody (anti-rabbit conjugated to Alexa Fluor405 1:1,000, Abcam #ab175649) at room temperature for 1 hr. Afterward, they were incubated with wheat germ agglutinin (WGA) conjugated to CF488 A (5 μg/ml Biotium) at room temperature for 2 hr, followed by incubation with RedDot1 Far-Red Nuclear Stain (1:200, Biotium) at room temperature for 20 min. Finally, organoids were overlaid with mounting medium (Electron Microscopy Sciences). The procedure was performed in the same imaging chambers used for time-lapse imaging in order to maintain organoids in the same position. Imaging was performed with the same microscope as previously described. Note that WGA stains both Paneth and Goblet cells, but the lysozyme staining allowed the unequivocal distinction between them.

Single-cell tracking

Request a detailed protocol

Cells were manually tracked by following the center of mass of their nuclei in 3D space and time using custom-written image analysis software. Each cell was assigned a unique label at the start of the track. For every cell division, we noted the cell labels of the mother and two daughter cells, allowing us to reconstruct lineage trees. We started by tracking cells that were at the crypt bottom in the initial time point and progressively tracked cells positioned toward the villus region until we had covered all cells within the crypt that divided during the time-lapse recording. We then tracked at least one additional row of non-dividing cells positioned toward the villus region. Cell deaths were identified either by the extrusion of whole nuclei into the organoid lumen or by the disintegration of nuclei within the epithelial sheet. Only crypts that grew approximately perpendicular to the imaging objective and that did not undergo crypt fission were tracked. During imaging, a fraction of cells could not be followed as they moved out of the microscope’s field of view or moved so deep into the tissue that their fluorescence signal was no longer trackable. Because these cells were predominantly located in the villus region, where cells cease division, this likely resulted in the underestimation of non-proliferating cells. Data was discarded when a large fraction (>25%) of the cells in the crypt move out of the imaged volume.

Classifying cell state

Request a detailed protocol

To classify cells as either proliferating or non-proliferating, we followed the following procedure. Defining proliferating cells was straightforward, as their division could be directly observed. As for non-proliferating cells, we applied two criteria. First, cells were assigned as non-proliferating when they were tracked for at least 30 hr without dividing. This was based on our observation that cell cycle times longer than 30 hr were highly unlikely (p=7.1∙10^–7, from fit of skew normal distribution, Figure 3—figure supplement 1). However, we were not able to track all cells for at least 30 hr, as cells moved out of the field of view during the experiment or, more frequently, because they were born less than 30 hr before the end of the experiment. In this case, we defined a cell as non-proliferating if its last recorded position along the crypt axis was higher than 60 μm, as almost no divisions were observed beyond this distance (Figure 2). Finally, cells were assigned as dying based on their ejection from the epithelium, while the remaining unassigned cells were classified as undetermined and not included in the analysis.

We tested the accuracy of this approach as follows. In data sets of >60 hr in length, we selected the subset of all cells for which we could with certainty determine proliferative state, either because they divided or because they did not divide for at least 40 hr. We then truncated these data sets to the first 40 hr, which reduced the number of cells whose proliferative state we could identify with certainty, and instead determined each cells proliferative state based on the above two criteria. When we compared this result with the ground truth obtained from the >60-hr data sets, we found that out of 619 cells, we correctly assigned 141 cells as non-proliferative and 474 as proliferative. Only four cells were incorrectly assigned as non-dividing, whereas they were seen to divide in the >60-hr data sets.

Estimation of significance of symmetric divisions

Request a detailed protocol

To estimate whether the experimentally observed fraction of sisters with symmetric division outcome could be explained by sister deciding independently to proliferate further or not, we used a bootstrapping approach. In our experimental data, we identified n=499 sister pairs, where the proliferative state of each cell was known and excluding pairs where one or both sisters died. In this subset of sisters, the probability of a cell dividing was found to be p=0.79. For N=10⁵ iterations, we randomly drew n sister pairs, which each cell having probability p to be proliferative and 1 p to cease proliferation. For each iteration, we then calculated the resulting symmetry fraction Φ. This resulted in a narrow distribution of Φ with average ± tandard deviation of 0.67±0.02, well separated from the experimentally observed value of Φ=0.97. In particular, none of 10⁵ iterations resulted in a value Φ ≥ 0.97, leading to our estimated p-value of p<10^–5. Overall, this means that the high fraction of sisters with symmetric division outcome reflects correlations in sister cell fate.

Estimation of crypt growth rate

Request a detailed protocol

To estimate an effective growth rate from the time dynamics of the total cell number and number of proliferating cells $N$ for each individual crypt, we used the ‘Uniform’ model as defined in the main text. Here, each generation the number of proliferating cells increases by $α N$ , and the number of non-proliferating cells, $M$ , changes by $(1 - α) N$ , where α is the growth rate with $- 1 \leq α \leq 1$ . For α sufficiently close to zero, the resulting dynamics of the number of proliferating and non-proliferating cells, $N$ and $M$ , is given by $\frac{d N}{d t} = \frac{α}{T} N$ and $\frac{d M}{d t} = \frac{1 - α}{T} N$ , where $T$ is the average cell cycle duration. Solving these differential equations yields $N (t) = N (0) e x p (\frac{α t}{T})$ and $U (t) = M (0) - \frac{1 - α}{α} D (0) + \frac{D (0)}{α} e x p (\frac{α t}{T})$ for the total number of cells, where $U = N + M$ . We then fitted $U (t)$ and $N (t)$ to the experimental data in Figure 2A and B, using a single value of the fitting parameter $α$ for each crypt and the experimentally determined value of T=16.2 hr.

Crypt unwrapping

Request a detailed protocol

At every time point, the crypt axis was manually annotated in the $x y$ plane at the $z$ position corresponding to the center of the crypt, since tracked crypts grew perpendicularly to the objective. Three to six points were marked along the axis, through which a spline curve $s (r)$ was interpolated. Then, for each tracked cell $i$ , we determined its position along the spline by finding the value of $r$ that minimized the distance $d$ between the cell position $x_{i}$ and the spline, i.e., $d (r_{i}) = m i n_{r} | s (r) - x_{i} |$ . At each time point, the bottom-most cell of the crypt, i.e., that with the lowest value of $r_{i}$ , was defined as position zero. Thus, the position along the axis $p_{i}$ for cell $i$ was defined as $p_{i} = r_{i} - {m i n}_{i} (r_{i})$ . To determine the angle around the axis $θ_{i}$ for cell $i$ , we considered a reference vector $u$ pointing in the direction of the imaging objective, given by $u = (0,0, - 1)$ , and the vector $v_{i} = x_{i} - s (r_{i})$ defined by the position of the cell $x_{i}$ and the position of minimum distance along the spline $s (r_{i})$ . Then, the angle is given by $θ_{i} = a c o s (u \cdot v_{i} / u v)$ .

Distance to Paneth cells

Request a detailed protocol

To estimate the distance between cells we used the following approach. For each cell at each time point we found the five closest cells within a 15-μm radius, which became the edges in a graph representation of the crypt (Figure 5—figure supplement 1). These values were chosen because a visual inspection revealed an average nucleus size of 10 μm and an average of five neighbors per cell. This graph was then used to define the edge distance of a cell to the nearest Paneth cell. At every time point during the lifetime of that cell, the minimum number of edges required to reach the nearest Paneth cell was recorded. The edge distance is then defined as the number of edges minus one. For example, a neighbor cell of a Paneth cell (1 edge) has a distance of zero. When the edge distance of a cell to a Paneth cell varied in time, we used the mode of its distance distribution, i.e., the most frequently occuring value, as recorded during its lifetime.

In vivo clonal tracing

Request a detailed protocol

All experiments were carried out in accordance with the guidelines of the animal welfare committee of the Netherlands Cancer Institute. Lgr5^{EGFP-ires-CreERT2};R26_LSL-tdTomato double heterozygous male and female mice (Bl6 background) were housed under standard laboratory conditions and received standard laboratory chow and water ad libitum prior to start of the experiment. 60 hr before sacrifice, mice received an intraperitoneal injection with 0.05 mg tamoxifen (Sigma, T5648; dissolved in oil) resulting in maximally 1 labeled cell per ~10 crypts. After sacrifice, the distal small intestine was isolated, cleaned, and flushed with ice cold phosphate-buffered saline (PBSO), pinned flat and fixed for 1.5 hr in 4% paraformaldehyde (PFA) (7.4 pH) at 4°C. The intestine was washed in Phosphate Buffered Solution/1% Tween-20 (1% PBT) for 10 min at 4°C after which it was cut into pieces of ~2 cm and transferred to a 12-well plate for staining. The pieces were permeabilized for 5 hr in 3% BSA and 0.8% Triton X-100 in PBSO and stained overnight at 4°C using anti-RFP (Rockland, 600-401-379) and anti-GFP (Abcam, ab6673) antibodies. After 3 times 30 min washes at 4°C in 0.1% Triton X-100 and 0.2% BSA in PBSO, the pieces were incubated with Alexa fluor Donkey anti rabbit 568 (Invitrogen, A10042) and Alexa fluor Donkey anti goat 488 (Invitrogen, A11055) secondary antibodies overnight at 4°C. After an overnight wash in PBT, the pieces were incubated with DAPI (Thermo Fisher Scientific, D1306) for 2 hr and subsequently washed in PBS for 1 hr at 4°C. Next, the intestinal pieces were cleared using ‘fast light-microscopic analysis of antibody-stained whole organs’ described in Messal et al. (Sato et al., 2011) In short, samples were moved to an embedding cassette and dehydrated in 30, 75, 2×100% MetOH for 30 min each at RT. Subsequently, samples were put into MetOH in a glass dish and immersed in methyl salicylate diluted in MetOH: 25, 75, 2×100% methyl salicylate (Sigma-Aldrich) 30 min each at RT protected from light. Samples were mounted in methyl salicylate in between two glass coverslips, and images were recorded using an inverted Leica TCS SP8 confocal microscope. All images were collected in 12 bit with ×25 water immersion objective (HC FLUOTAR L N.A. 0.95 W VISIR 0.17 FWD 2.4 mm). Image analysis was carried out independently by two persons. Afterward, all discrepancies between both datasets were inspected, resulting in a single dataset. Each biologically stained cell was annotated once in the 3D image. Different cells in the same crypt were marked as belonging to the same crypt, which is necessary to calculate the clone size for that crypt. Only crypts that were fully visible within the microscopy images were analyzed.

Uncertainty estimation in clone size distributions

Request a detailed protocol

In organoids, the clone sizes are measured by calculating the number of offspring the cell will have 40 hr later. This calculation is performed for every hour of the time lapse, up to 40 hr before the end. In vivo, clone sizes are measured once per crypt, as we cannot view the dynamics over time. To estimate the uncertainty in our clone size distribution, both in organoids and in vivo, we use a bootstrapping approach. We denote the total number of clones observed as N. We then used random resampling with replacement, by drawing N times a random clone from the data set of observed clones, to construct a new clone size distribution. We ran this procedure 100 times, each run storing the measured fraction of clones sizes. As a result, for every clone size we obtained a distribution of fractions, which we used to calculate the standard deviation of the fraction, as a measure of sampling error.

Computational model

Request a detailed protocol

Simulations were initialized by generating a collection of proliferating cells, each belonging to either the niche or differentiation compartment. For each parameter combination, the initial number of proliferating cells assigned to each compartment was obtained by rounding to the closest integer the values given by the equations for $N_{n}$ and $N_{d}$ in the main text. When the initial number of proliferating cells in the niche compartment was lower than the compartment size $S$ , they were randomly distributed over the compartment, with the remaining positions taken up by non-proliferating cells in order to fill the compartment. Each proliferating cell $c$ that was generated was assigned a current age $A_{c}$ and a cell cycle time $C_{c}$ , i.e., the age at which the cell will eventually divide. The current age was obtained by randomly drawing a number from an interval ranging from 0 hr to the mean cell cycle time obtained from experimental data, while the cell cycle was obtained by drawing a random number from a skew normal distribution, which was fitted to the experimental distribution of cell cycle times as shown in Figure 3—figure supplement 1.

Simulations were performed by iterating the following routine over time, until a total simulation time $T_{} = 10^{6}$ hr was reached. At each iteration $i$ , we found the cell $c_{i}$ that was due to divide next, and a time step $Δ t_{i}$ was defined by the time remaining for this cell to divide, i.e., $Δ t_{i} = {m i n}_{c} (C_{c} - A_{c})$ . Then, the ages of all proliferating cells were updated, and the division of cell $c_{i}$ was executed. This was done by randomly choosing one of the three division modes defined in Figure 4C, according to the probabilities determined by the parameters $α$ and $ϕ$ of the compartment to which the cell belonged. Any proliferating daughters that were born were initialized with age zero and a random cell cycle time drawn. For the two-compartment model, if the proliferating cell belonged to the niche compartment, the distalmost cell within this compartment was transferred to the differentiation compartment, without changes to its proliferative state. This means that a proliferating cell that is transferred to the differentiation compartment will still divide, with the symmetry only determined by $ϕ$ , even if α_d =−1, i.e., all divisions in the differentiation compartment generate non-proliferating daughters. This corresponds to the assumption that the decision to proliferate or not, as well as the symmetry between the resulting daughters, is set by the external environment (niche or differentiation compartments) the cell experiences at birth and cannot be reversed at a later point. Finally, the number of proliferating and non-proliferating cells in each compartment was updated accordingly. Cell rearrangements were implemented as follows. For each iteration $i$ , with time step $Δ t_{i}$ , we drew the number of cell rearrangements from a Poisson distribution with mean $(r \cdot S) Δ t_{i}$ , where $r$ is the rearrangement rate per cell. We then implemented each individual rearrangement by randomly selecting a cell at position $j \in (0, S - 1)$ and swapping it with the cell at position $j + 1$ .

The model had six parameters, of which three ( $α_{n}, α_{d}, ϕ$ ) were systematically varied in our simulations. The remaining parameters were constrained by the experiments. We picked the niche size $S$ so that the total number of proliferating cells was 30, corresponding to the typical number of dividing cells observed in the experiments, through a procedure outlined in the main text. We obtained the average cell cycle duration $T$ , as well as its distribution, from the data in Figure 3—figure supplement 1. Finally, we obtained the rearrangement rate $r$ from the observed (a)symmetry in proliferative fate observed between cousin cells. For a ‘well-mixed’ niche compartment, cousin pairs showed asymmetric outcome as often as symmetric outcome (Figure 4—figure supplement 2), in contrast to our experimental observations (Figure 3A). In contrast, for infrequent cell rearrangement, $r ⋅ T = 1$ , cells expeled from this compartment close together in time are also closely related by lineage, leading to correlations in division outcome between cousins that reproduced those observed experimentally (Figure 4—figure supplement 2, Figure 3A).

For some parameter values, simulations were ended earlier than the total time $T_{}$ . This occurred when no proliferating cells were left in either compartment (defined as a depletion event), or when the number of proliferating cells reached an arbitrarily set maximum limit of five times its initial value (defined as an overgrowth event, occurring only in the one-compartment model). In these cases, simulations were restarted until a total simulation time $T_{}$ was reached, and the total number of events was recorded. Thus, the rate of depletion or overgrowth refers to the number of times simulations had to be restarted for each value of $ϕ$ divided by the total simulation time.

To obtain statistics regarding fluctuations on the number of proliferating cells $N$ through time, at each iteration $i$ we kept track of the number of proliferating cells in the niche compartment $d_{i}^{p}$ and in the differentiation compartment $d_{i}^{n}$ . With these quantities, we could compute the standard deviation $σ$ of $N$ according to $σ^{2} = ⟨N^{2}⟩ - {⟨N⟩}^{2}$ . Given that $N = N_{n} + N_{d}$ , where $N_{n}$ and $N_{d}$ are the number of proliferating cells in the niche and differentiation compartments, $σ$ can be expressed as $σ^{2} = ⟨N_{n}^{2}⟩ - {⟨N_{n}⟩}^{2} + ⟨N_{d}^{2}⟩ - {⟨N_{d}⟩}^{2} + 2 〈 N_{n} N_{d} 〉 - 2 〈 N_{n} 〉 〈 N_{d} 〉$ , where $⟨N_{n, d}⟩ = \sum_{i} \frac{d_{i}^{n, d} Δ t_{i}}{T}$ , $⟨N_{n, d}^{2}⟩ = \sum_{i} \frac{{(d_{i}^{n, d})}^{2} Δ t_{i}}{T}$ and $⟨N_{n} N_{d}⟩ = \sum_{i} \frac{d_{i}^{n} d_{i}^{d} Δ t_{i}}{T}$ .

Data availability

All cell lineage data, simulation code and data analysis scripts used to generate the figures have been deposited in Zenodo under accession codes https://doi.org/10.5281/zenodo.7197573.

The following data sets were generated

(2022) Zenodo
Code and data from "Mother cells control daughter cell proliferation in intestinal organoids to minimize proliferation fluctuations".
https://doi.org/10.5281/zenodo.7197573

References

1. Clayton E
2. Doupé DP
3. Klein AM
4. Winton DJ
5. Simons BD
6. Jones PH
(2007) A single type of progenitor cell maintains normal epidermis
Nature 446:185–189.
https://doi.org/10.1038/nature05574
- PubMed
- Google Scholar
(2020) Stem cell lineage survival as a noisy competition for niche access
PNAS 117:16969–16975.
https://doi.org/10.1073/pnas.1921205117
- PubMed
- Google Scholar
1. Doupé DP
2. Alcolea MP
3. Roshan A
4. Zhang G
5. Klein AM
6. Simons BD
7. Jones PH
(2012) A single progenitor population switches behavior to maintain and repair esophageal epithelium
Science 337:1091–1093.
https://doi.org/10.1126/science.1218835
- PubMed
- Google Scholar
1. Eisenhoffer GT
2. Rosenblatt J
(2013) Bringing balance by force: live cell extrusion controls epithelial cell numbers
Trends in Cell Biology 23:185–192.
https://doi.org/10.1016/j.tcb.2012.11.006
- PubMed
- Google Scholar
(2012) Redundant sources of Wnt regulate intestinal stem cells and promote formation of Paneth cells
Gastroenterology 143:1518–1529.
https://doi.org/10.1053/j.gastro.2012.08.031
- PubMed
- Google Scholar
1. Farin HF
2. Jordens I
3. Mosa MH
4. Basak O
5. Korving J
6. Tauriello DVF
7. de Punder K
8. Angers S
9. Peters PJ
10. Maurice MM
11. Clevers H
(2016) Visualization of a short-range Wnt gradient in the intestinal stem-cell niche
Nature 530:340–343.
https://doi.org/10.1038/nature16937
- PubMed
- Google Scholar
1. Feller W
(1939) Die grundlagen Der volterraschen theorie des kampfes ums dasein in wahrscheinlichkeitstheoretischer behandlung
Acta Biotheoretica 5:11–40.
https://doi.org/10.1007/BF01602932
- Google Scholar
1. Gehart H
2. Clevers H
(2019) Tales from the crypt: new insights into intestinal stem cells
Nature Reviews. Gastroenterology & Hepatology 16:19–34.
https://doi.org/10.1038/s41575-018-0081-y
- PubMed
- Google Scholar
(2012) Optimality in the development of intestinal crypts
Cell 148:608–619.
https://doi.org/10.1016/j.cell.2011.12.025
- PubMed
- Google Scholar
1. Klein AM
2. Doupé DP
3. Jones PH
4. Simons BD
(2007) Kinetics of cell division in epidermal maintenance
Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics 76:021910.
https://doi.org/10.1103/PhysRevE.76.021910
- PubMed
- Google Scholar
(2010) Mouse germ line stem cells undergo rapid and stochastic turnover
Cell Stem Cell 7:214–224.
https://doi.org/10.1016/j.stem.2010.05.017
- PubMed
- Google Scholar
1. Klein AM
2. Simons BD
(2011) Universal patterns of stem cell fate in cycling adult tissues
Development 138:3103–3111.
https://doi.org/10.1242/dev.060103
- PubMed
- Google Scholar
Software
1. Kok RNU
2. van Zon JS
(2016) OrganoidTracker, version c97816d
Github.

https://github.com/jvzonlab/OrganoidTracker/tree/v1
Preprint
(2022) Minimizing Cell Number Fluctuations in Self-Renewing Tissues with a Stem Cell Niche
bioRxiv.
https://doi.org/10.1101/2022.03.10.483777
- Google Scholar
1. Lander AD
2. Gokoffski KK
3. Wan FYM
4. Nie Q
5. Calof AL
(2009) Cell lineages and the logic of proliferative control
PLOS Biology 7:e15.
https://doi.org/10.1371/journal.pbio.1000015
- PubMed
- Google Scholar
(2016) Paneth cell-rich regions separated by a cluster of lgr5+ cells initiate crypt fission in the intestinal stem cell niche
PLOS Biology 14:e1002491.
https://doi.org/10.1371/journal.pbio.1002491
- PubMed
- Google Scholar
1. Li L
2. Xie T
(2005) Stem cell niche: structure and function
Annual Review of Cell and Developmental Biology 21:605–631.
https://doi.org/10.1146/annurev.cellbio.21.012704.131525
- PubMed
- Google Scholar
(2010) Intestinal stem cell replacement follows a pattern of neutral drift
Science 330:822–825.
https://doi.org/10.1126/science.1196236
- PubMed
- Google Scholar
1. Ragkousi K
2. Gibson MC
(2014) Cell division and the maintenance of epithelial order
The Journal of Cell Biology 207:181–188.
https://doi.org/10.1083/jcb.201408044
- PubMed
- Google Scholar
(2014) Intestinal crypt homeostasis revealed at single-stem-cell level by in vivo live imaging
Nature 507:362–365.
https://doi.org/10.1038/nature12972
- PubMed
- Google Scholar
1. Rué P
2. Martinez Arias A
(2015) Cell dynamics and gene expression control in tissue homeostasis and development
Molecular Systems Biology 11:792.
https://doi.org/10.15252/msb.20145549
- PubMed
- Google Scholar
1. Sato T
2. Vries RG
3. Snippert HJ
4. van de Wetering M
5. Barker N
6. Stange DE
7. van Es JH
8. Abo A
9. Kujala P
10. Peters PJ
11. Clevers H
(2009) Single LGR5 stem cells build crypt-villus structures in vitro without a mesenchymal niche
Nature 459:262–265.
https://doi.org/10.1038/nature07935
- PubMed
- Google Scholar
1. Sato T
2. van Es JH
3. Snippert HJ
4. Stange DE
5. Vries RG
6. van den Born M
7. Barker N
8. Shroyer NF
9. van de Wetering M
10. Clevers H
(2011) Paneth cells constitute the niche for LGR5 stem cells in intestinal crypts
Nature 469:415–418.
https://doi.org/10.1038/nature09637
- PubMed
- Google Scholar
1. Scoville DH
2. Sato T
3. He XC
4. Li L
(2008) Current view: intestinal stem cells and signaling
Gastroenterology 134:849–864.
https://doi.org/10.1053/j.gastro.2008.01.079
- PubMed
- Google Scholar
1. Sei Y
2. Feng J
3. Chow CC
4. Wank SA
(2019) Asymmetric cell division-dominant neutral drift model for normal intestinal stem cell homeostasis
American Journal of Physiology. Gastrointestinal and Liver Physiology 316:G64–G74.
https://doi.org/10.1152/ajpgi.00242.2018
- PubMed
- Google Scholar
(2018) Subepithelial telocytes are an important source of Wnts that supports intestinal crypts
Nature 557:242–246.
https://doi.org/10.1038/s41586-018-0084-4
- PubMed
- Google Scholar
1. Simons BD
2. Clevers H
(2011) Strategies for homeostatic stem cell self-renewal in adult tissues
Cell 145:851–862.
https://doi.org/10.1016/j.cell.2011.05.033
- PubMed
- Google Scholar
(2010) Intestinal crypt homeostasis results from neutral competition between symmetrically dividing LGR5 stem cells
Cell 143:134–144.
https://doi.org/10.1016/j.cell.2010.09.016
- PubMed
- Google Scholar
1. Sun Z
2. Komarova NL
(2012) Stochastic modeling of stem-cell dynamics with control
Mathematical Biosciences 240:231–240.
https://doi.org/10.1016/j.mbs.2012.08.004
- PubMed
- Google Scholar
Preprint
1. Swain PS
(2016) Lecture Notes on Stochastic Models in Systems Biology
arXiv.
https://doi.org/10.48550/arXiv.1607.07806
- Google Scholar
1. Teixeira VH
2. Nadarajan P
3. Graham TA
4. Pipinikas CP
5. Brown JM
6. Falzon M
7. Nye E
8. Poulsom R
9. Lawrence D
10. Wright NA
11. McDonald S
12. Giangreco A
13. Simons BD
14. Janes SM
(2013) Stochastic homeostasis in human airway epithelium is achieved by neutral competition of basal cell progenitors
eLife 2:e00966.
https://doi.org/10.7554/eLife.00966
- PubMed
- Google Scholar
1. Winton DJ
2. Ponder BA
(1990) Stem-Cell organization in mouse small intestine
Proceedings. Biological Sciences 241:13–18.
https://doi.org/10.1098/rspb.1990.0059
- PubMed
- Google Scholar

Decision letter

Steffen Rulands

Reviewing Editor; Max Planck Institute for the Physics of Complex Systems, Germany
Didier YR Stainier

Senior Editor; Max Planck Institute for Heart and Lung Research, Germany
Philip Greulich

Reviewer; University of Southampton, United Kingdom

Our editorial process produces two outputs: i) public reviews designed to be posted alongside the preprint for the benefit of readers; ii) feedback on the manuscript for the authors, including requests for revisions, shown below. We also include an acceptance summary that explains what the editors found interesting or important about the work.

Decision letter after peer review:

Thank you for submitting your article "Mother cells control daughter cell proliferation in intestinal organoids to minimize proliferation fluctuations" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, one of whom is a member of our Board of Reviewing Editors, and the evaluation has been overseen by Didier Stainier as the Senior Editor. The following individual involved in the review of your submission has agreed to reveal their identity: Philip Greulich (Reviewer #3).

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission.

Essential revisions:

1) Please clarify the model definition such that there is no ambiguity regarding whether the compartments pertain to fate or proliferation (Reviewer 2).

2) Please clearly line out in the text how this model is to be interpreted by a readership that might not be familiar with mathematical modelling and in particular the way "simple" models as the one presented here relate to potentially more complex biology. Specifically, as Reviewers 1 and 3 point out, it needs to be discussed whether the compartment model should be interpreted at face value or whether it is a simplified mathematical description for potentially diverse biological scenarios.

Reviewer #1 (Recommendations for the authors):

The manuscript would benefit from a discussion of the scope of the findings, in particular the modelling results. The authors propose a compartmentalized model, which is to be understood as a coarse-grained mathematical description of a potentially diverse set of biological realities. The authors should be clearer in the discussion about what is the precise biological scope of the mathematical model.

L53: The final sentence of this paragraph is not clear. Presumably, the authors mean "fluctuations in the number of proliferating cells".

L97: The definition of proliferating cells of course strongly depends on the ratio of the typical cell cycle time and the time of duration of the experiment. Can the authors give a statistical estimate on the percentage of cells being misclassified as "non-proliferating" due to the finite length of the observation interval?

L104: It would help the readers if the authors briefly stated the basic assumptions underlying the "simple model of cell proliferation" in the main text.

L108: I was at first very confused about the naming of the variable D describing the number of proliferating cells. I would usually associate "D" with a diffusion coefficient with units m²/s while the number of cells is dimensionless. The authors might consider renaming this variable to "N".

Figure 2A, B: To my eyes, there are oscillations in the number of cells and partially the number of proliferating cells. Is this evidence for temporal synchronization of cell divisions?

Figure 2B: This figure would benefit from a statistical analysis of the slopes as it is not evident to me whether the majority of lines have a vanishing slope or positive slope.

Figure 2B, D: Could the enrichment of even clone sizes have arisen by chance (p-value)?

Reviewer #2 (Recommendations for the authors):

I have a few comments though on a few additional analyses/theoretical controls that might help the paper even more readable – especially as model-data comparisons are sometimes not the most straightforward in presentation, making me unsure I fully follow the reasoning in places.

Point A/ Figure 4: the text is in general well-written, although I had to re-read this a few times this part to make sure I fully understood the model. I feel like calling the two domains "proliferative compartments" vs "non-proliferative compartments" is a bit confusing, because in fact the compartments are not implemented through changing proliferation, but instead changing fate.

On the first read, I thought the model would be that the authors would simply turn on proliferation in the bottom compartment, and turn it off in the other. In fact, I wonder – given the fact that Figure 2 identifies each compartment by proliferation rate, whether it would be pedagogical for the reader to go through this model first (it can be in SI obviously). I guess the point of the author is that this model would fail vs data. But it would be interesting to see exactly how, to set the stage for their model (because as the best-fit requires anyways \α_p close to 1, this might give rise to similar predictions?). Plotting the model output in the same way as the previous data from Figure 2C-D might also be nice for comparison.

The last thing where I got confused by the model is that it implements compartments in a spatial way – if I understand correctly (line 637 of the SI). But the point of the authors, based on data, is that fate of daughters is dependent on lineage rather than position (although they say in lines 646-647 that the two are highly correlated in the model for the rT they choose – see also point below). It would be good to clarify this.

Point B: Also in Figure 4, it is not very clear how the authors pick their rearrangement rate rT (lines 188-191). They say that they pick rT=1 to reproduce well the correlation between cousins, but that they find similar findings for larger rT. Would this mean then that this parameter is not necessary for the model, and that this leads to over-fitting? (But then I got a bit confused as in the Supp part, they say large rT do no work? (Line 644-646). As the authors have done high-quality tracking, I would have thought that maybe they could "just" infer this parameter from the x,y,z, and t coordinates of neighboring cells. This would help distinguish model fitting and model prediction in a better way in the manuscript. In general, maybe the authors could use the modelling section on the SI to summarise a bit the fitting and prediction strategy (and maybe provide in Figure S5 a more systematic fitting/sensitivity analysis rather than showing two extreme values only of rT?).

Point C: Figure 6: Maybe the authors could define an "asymmetry index" (eg. the cumulative probability "missing" from the odd clones assuming some smooth gaussian from neutral drift without lineage correlations). I also wonder whether the authors could recapitulate their findings in a toy model of stochastic fate choices with correlation time T in outcome (to connect it more directly to previous models of neutral drift on a 1D ring). This type of model making correlation time in fates an explicit variable would go well with the discussion on the number of generations at which correlations in fate are lost (line 360-370). It would also be nice to mention the consequence that this would have on longer-term clonal conversion dynamics that have been extensively studied in the past.

Reviewer #3 (Recommendations for the authors):

As said in the public review, my concern is to take the two-compartment model too literally. I do agree that the presented analysis is fine, and the two-compartment model works as a valid simplification to capture the qualitative features of the mechanism, but I am worried that the reader takes this at face value. Instead, given the measurements in Figure 5E, it is more likely that the proliferative potential decreases continuously with distance from Paneth cells. So while the two-compartment model works as a simplification of the numerical analysis (being a representative of a larger class of models where proliferative potential decreases with distance), it does not work well as a description of reality.

Further suggestions, questions, and corrections:

– When saying that fractions of asymmetric divisions are "low" (e.g. line 135), then this should be compared with the case to be expected when sister cell fate is unrelated: namely in that case, asymmetric divisions would be at 50%.

– For α=0 one wouldn't expect uncontrolled exponential growth as stated in line 170. Stochastic fluctuations can be very large for α=0, even exceeding the set threshold of 5-fold, but this is still not exponential growth. It should also be mentioned that this may depend strongly on the arbitrarily set threshold.

– In line 195 it is said that "stochastic depletion occurred when α_p <~ 0.5". However, the scale in the referred figure is set arbitrarily. Since there the depletion rate is always non-zero, depletion will always occur after sufficiently large times. So when saying "stochastic depletion occurred when α_p <~ 0.5", then it should be said over which time scale of observation this is meant.

– In the caption of Figure 1 the part for panel G should refer to panel F instead.

– Figure 5: the colours are difficult to distinguish for a red-green colour impaired reader (roughly 10% of the male population): orange vs. green is difficult to distinguish and the thin black font colour vs. thin red font colour of vertical axis labels in Figure 5E are difficult to distinguish.

– The value of phi reported in Figure 5E (phi=0.98) is significantly higher than that reported in Figure 3A (adding the symmetric events when both sisters go on dividing, never dividing, or dying, gives phi = 0.81). Where does this discrepancy come from?

– Figure 6D: It would be helpful to have an interpolation curve to see the enrichment at n=6 (currently this is not visible). Alternatively, plotting on a logarithmic scale could make this more visible.

https://doi.org/10.7554/eLife.80682.sa1

Author response

Essential revisions:

1) Please clarify the model definition such that there is no ambiguity regarding whether the compartments pertain to fate or proliferation (Reviewer 2).

We now refer to ‘niche’ and ‘differentiation’ compartment, to emphasize that cells indeed change fate, from stem cell to differentiated cell, upon transitioning from one compartment to the next. For more details, see our response to Reviewer 2.

2) Please clearly line out in the text how this model is to be interpreted by a readership that might not be familiar with mathematical modelling and in particular the way "simple" models as the one presented here relate to potentially more complex biology. Specifically, as Reviewers 1 and 3 point out, it needs to be discussed whether the compartment model should be interpreted at face value or whether it is a simplified mathematical description for potentially diverse biological scenarios.

We addressed this now in the Discussion. For more details, see our response to Reviewer 3.

Reviewer #1 (Recommendations for the authors):

The manuscript would benefit from a discussion of the scope of the findings, in particular the modelling results. The authors propose a compartmentalized model, which is to be understood as a coarse-grained mathematical description of a potentially diverse set of biological realities. The authors should be clearer in the discussion about what is the precise biological scope of the mathematical model.

We addressed this now in the Discussion. For more details, see our response to Reviewer 3, who raised similar issues.

L53: The final sentence of this paragraph is not clear. Presumably, the authors mean "fluctuations in the number of proliferating cells".

The Reviewer is correct, we changed this in the text.

L97: The definition of proliferating cells of course strongly depends on the ratio of the typical cell cycle time and the time of duration of the experiment. Can the authors give a statistical estimate on the percentage of cells being misclassified as "non-proliferating" due to the finite length of the observation interval?

Based on the measured distribution of cell cycle times, we can estimate that within 30 hours, 99.93% of all proliferating cells will have divided (Figure 3 —figure supplement 1B). For that reason, we classify cells for which we have not seen a division, and that we could track for at least 30 hours, as non-dividing. However, particularly towards the end of the experiment, cells cannot be followed for 30 hours, precluding assignment of non-proliferative fate based on that single criterium. We therefore employed a further criterium: any cell that is located at least 60 μm above the bottom of the crypt, is considered non-proliferating (as detailed in the Methods section ‘Classifying cell state’).

This leaves a fraction of cells that cannot be classified as (non)-proliferating (34%), either because they could not be tracked or because they were born to close to the end of the experiment to observe a division or exclude division based on the criteria above. The latter category is (by definition) particularly prominent towards the end of the experiment. By truncating our data set to cells born at least 15 hours before the end of the experiment we reduce the fraction of unclassified cells to 10%.

We had so far not explicitly tested the accuracy of our classification criteria. To do so we performed the following test: in >60 hour data sets, we selected all cells whose proliferative state we could determine with certainty, i.e. they either divided or did not divide after 40 hours, thereby representing a ground truth proliferation data set. We then truncated our >60 hour data sets to the first 40 hours, so that lineages of many of the cells in the ground truth data set were truncated as well. We then used the two above criteria (including position along the crypt-villus axis) to identify (non-)proliferative cells, and found that only 4/619 cells were misidentified compared to the ground truth data, being assigned as non-proliferative even though they were observed to divide in the ground truth data. Overall, this indicates that our procedure correctly assigns proliferative fate to the majority of cells.

Changes to the manuscript:

– We added a new panel (Figure 3 —figure supplement 1B) that shows the estimated probability of a proliferating cell having not yet divided after time T.

– We modified the text “To systematically study … cells to 10%” in the section “Control of cell proliferation in organoid crypts” in the Results to explain the criteria for classification of proliferation state and add information on the fraction of cells that cannot be classified based on these criteria.

– We edited the section ‘Classifying cell state’ in the Methods to more clearly explain the assignment procedure outlined above, and added the text “we tested the accuracy… data sets.” to describe the new analysis of the procedure’s accuracy.

L104: It would help the readers if the authors briefly stated the basic assumptions underlying the "simple model of cell proliferation" in the main text.

Changes to the manuscript:

– We edited the text “We then estimated … by α and 1-α per division, respectively” in the section “Control of cell proliferation in organoid crypts’ to clarify the underlying model assumptions.

– We edited the section ‘Estimation of crypt growth rate’ in the Methods to clarify the underlying model assumptions.

L108: I was at first very confused about the naming of the variable D describing the number of proliferating cells. I would usually associate "D" with a diffusion coefficient with units m²/s while the number of cells is dimensionless. The authors might consider renaming this variable to "N".

Originally, D stood for dividing cells, but we agree that in the current version this is not clear. We have therefore changed it to N, as suggested by the Reviewer. In the Methods section (“Estimation of crypt growth rate”), we previously used N for the total number of cells, which we now changed to U.

Figure 2A, B: To my eyes, there are oscillations in the number of cells and partially the number of proliferating cells. Is this evidence for temporal synchronization of cell divisions?

The observation is correct, but not seen in all organoids. We currently don’t think this synchronization is somehow regulated, but rather reflects the strong correlation we observe in the cell cycle times between mother and daughter cells (this data is not shown in the manuscript). Indeed, cells that divide at the same time are typically closely related. We speculate that in organoids where many cells divide at the same time, these might all have been generated from a single stem cell formed at the budding stage of the organoid, when only a small number of stem cells are present. Because of the correlation in cell cycle time, this stem cell’s daughters, granddaughters, etc. will still divide at similar times. Because the degree of synchrony varied strongly between organoids, we chose not to discuss it in the manuscript.

Figure 2B: This figure would benefit from a statistical analysis of the slopes as it is not evident to me whether the majority of lines have a vanishing slope or positive slope.

We have added error bars to the fitted values of α in Figure 2 —figure supplement 1C. These error bars indicate that for the majority of crypts α significantly deviates from zero, with most crypts showing a positive growth rate. We note that in the main text we do not claim that crypts show no growth (α=0), but rather that the growth rate is low, i.e. the change in number of dividing cells is small on the timescale of the average cell cycle duration.

Changes to the manuscript:

– We added error bars to Figure 2 —figure supplement 1C.

– We added the sentence “For most … was low” to the caption of Figure 2 —figure supplement 1, to emphasize that the growth rate deviates from zero for most crypts, even though the deviation is small.

– We added the sentence “Error bars are the standard deviation in the fit of α” to the caption of Figure 2 – supplementary figure 1.

Figure 2B, D: Could the enrichment of even clone sizes have arisen by chance (p-value)?

We used bootstrapping to calculate the standard deviations of the fraction of clones of size 2, 3, etc. The resulting error bars show that both for organoids (Figure 5B) and in vivo crypts (Figure 5D) the differences between even and odd-size clones are significant, apart from the difference between clone size 5 and 6 for in vivo crypts.

Changes to the manuscript:

– We changed Figure 5B,D, to display the histogram with fraction of clones rather than number of clones on the y-axis, and add error bars indicating standard deviation. We edited the caption to explain how the standard deviation was calculated.

– We added a section ‘Uncertainty estimation in clone size distributions’ to the Methods to explain the procedure we followed.

Reviewer #2 (Recommendations for the authors):

I have a few comments though on a few additional analyses/theoretical controls that might help the paper even more readable – especially as model-data comparisons are sometimes not the most straightforward in presentation, making me unsure I fully follow the reasoning in places.

Point A/ Figure 4: the text is in general well-written, although I had to re-read this a few times this part to make sure I fully understood the model. I feel like calling the two domains "proliferative compartments" vs "non-proliferative compartments" is a bit confusing, because in fact the compartments are not implemented through changing proliferation, but instead changing fate.

Our original reasoning for the compartment labels, is that for α_p>0 (‘proliferative compartment’) most divisions generate proliferating cells, while for α_n<0 (‘non-proliferative compartment’) most divisions generate non-proliferating cells. However, because of the nature of our simulation rules, for all values of -1<α<0 individual dividing cells can still be found in the non-proliferative compartment, which we agree is confusing.

We agree with the Reviewer that in our model cells do not always change from proliferating to non-proliferating upon changing compartment, but rather from one cell fate/type to another: from proliferating stem cells to non-proliferating differentiated cells. We therefore changed our wording to ‘stem cell niche’ or ‘niche’ compartment (α>0) and ‘differentiation compartment’ (α<0) throughout the paper.

Changes to the manuscript:

– We now used ‘(stem cell) niche’ or ‘differentiation’ compartment throughout the paper.

– We use the subscripts _n and _d to refer to these two compartments, e.g. α_n>0 and α_d<0.

On the first read, I thought the model would be that the authors would simply turn on proliferation in the bottom compartment, and turn it off in the other. In fact, I wonder – given the fact that Figure 2 identifies each compartment by proliferation rate, whether it would be pedagogical for the reader to go through this model first (it can be in SI obviously). I guess the point of the author is that this model would fail vs data. But it would be interesting to see exactly how, to set the stage for their model (because as the best-fit requires anyways \α_p close to 1, this might give rise to similar predictions?).

We have implemented the suggested model (which is equivalent to the ‘neutral drift on a 1D ring’ models mentioned by the Reviewer further below) as follows: we assumed a niche compartment of fixed size S. Every cell in the niche compartment will proliferate. However, after every division, a single randomly selected cell is removed from the niche compartment and thus halts proliferation. We find that this model fails to reproduce the experimental data in a number of ways (Figure 4 – supplementary figure 2E). Most prominently, asymmetric sister fate is as likely as symmetric fate (phi=0.5), independent of niche size (the only model parameter), in contrast to the high symmetry (phi=0.97, Figure 3A) observed experimentally.

It might be possible to extend this model, e.g. by introducing correlations between sister cells through spatial organization (as in Figure 4 – supplementary figure 2C,D) or by introducing a correlation time in fate transitions (as suggested by the Reviewer below), in such a way that it matches the experimental data more closely. However, we want to point out that the aim of our model was not to construct the simplest model that reproduces our experimental data (including the value of phi), but rather to construct the simplest realistic model in which we can vary phi explicitly, to systematically study the impact of changing division symmetry on the key properties of the model.

Changes made to the manuscript:

– We added the sentence “Finally, we note … generate this symmetry” to the section “Symmetry between sisters minimizes fluctuations in a cell proliferation model” in the Results, that mentions the mismatch between the neutral drift model and the experiments.

– We added the panel Figure 4 – supplementary figure 2E showing the results of the neutral drift model and added a caption that explains the model and interprets its results in more detail.

Plotting the model output in the same way as the previous data from Figure 2C-D might also be nice for comparison.

We use Figure 2C,D to show that in the experiments the proliferating region has fixed size in time (Figure 2C) and similar size between crypts (Figure 2D). However, in simulations the size of the proliferative/niche region is fixed, and has a very different (1D) geometry compared to the more complex (2/3D) geometry in organoids. Moreover, in our simulations we don’t take space into account for the non-proliferative/differentiation region (which is show in Figures 2C,D). Overall, this means we cannot plot simulation data as in Figure 2C,D and compare it to that figure in a meaningful way.

The last thing where I got confused by the model is that it implements compartments in a spatial way – if I understand correctly (line 637 of the SI). But the point of the authors, based on data, is that fate of daughters is dependent on lineage rather than position (although they say in lines 646-647 that the two are highly correlated in the model for the rT they choose – see also point below). It would be good to clarify this.

The experiments indeed show that sister cells typically share the same fate (Figure 3A), consistent with their fate being dependent more on lineage. In the model this is purely determined by the parameter phi. For phi=0.95 (high symmetry), the model reproduces this correlation in fate of sisters by definition, independent of the value of rT.

The reason for incorporating space within the proliferative/niche compartment (rather than having rT -> infinity, corresponding to selecting a random cell for transferal to the differentiation compartment) is the experimentally observed correlation between the fate of cousins, with most cousins showing the same fate (Figure 3A). If we randomly select a stem cell for transferal to the differentiation compartment (well approximated by rT=100), we find that the fate of cousins lacks correlation (Figure 4 – supplementary figure 2B,C), with most cousins showing different fate. This is because cousin fate is not hard-wired by an external parameter, like for sisters, but depends on the statistics by which each cell of a sister pair ends up being eject from the niche compartment. When cell mixing is decreased (e.g. rT=1), the probability of moving to the differentiation compartment depends strongly on the cell’s spatial position within the niche compartment, with sister cells typically being located at similar position. As a result, when one sister is ejected, typically the other sister is ejected soon after. In that case, their offspring will both have ‘differentiated’ fate. Indeed, for rT=1 the correlation between cousins is similar to what is seen experimentally (Figure 4 – supplementary figure 2B).

Changes to the manuscript:

– We edited the text “For the two-compartment … at a later point” in the section “Computational model” in the Methods, to clarify how lineage and space control the decision to proliferate or not.

Point B: Also in Figure 4, it is not very clear how the authors pick their rearrangement rate rT (lines 188-191). They say that they pick rT=1 to reproduce well the correlation between cousins, but that they find similar findings for larger rT. Would this mean then that this parameter is not necessary for the model, and that this leads to over-fitting? (But then I got a bit confused as in the Supp part, they say large rT do no work? (Line 644-646). As the authors have done high-quality tracking, I would have thought that maybe they could "just" infer this parameter from the x,y,z, and t coordinates of neighboring cells. This would help distinguish model fitting and model prediction in a better way in the manuscript.

This was indeed unclear. Only for sufficiently low rT can our simulation reproduce the observed correlation in fate between cousins (as outlined in the point above), see Figure 4 – supplementary figure 2B. This means that here our experimental observations properly constrain the rT parameter. However, the original sentence “…although we found similar results for higher r…” was incomplete. We meant to say that the magnitude of the fluctuations in cell number and their dependence on phi, α_n and α_d did not depend on the magnitude of r.

Because of the differences in geometry between simulation (1D) and experiments (2/3D) it is not straightforward to obtain a value for r directly from the experiments. However, rT=1 corresponds to one cell pair rearrangement per cell division. This is consistent with our observation that rearrangements tend to occur almost always when a (nearby) cell divides.

Changes to manuscript:

– We changed the sentence “although we found… strongly on r” in the section “Symmetry between sisters minimizes fluctuations in a cell proliferation model” in the Results, to explain that our conclusions on fluctuations do not depend on the value of rT.

In general, maybe the authors could use the modelling section on the SI to summarise a bit the fitting and prediction strategy (and maybe provide in Figure S5 a more systematic fitting/sensitivity analysis rather than showing two extreme values only of rT?).

As we explained above, we believe that the simulation data in Figure S5B (now Figure 4 – supplementary figure 2B) is sufficient for fitting rT=1.

We have added the text “The model had…those observed experimentally (Figure 4—figure supplement 2, Figure 3A)” to the section “Computational model” in the Methods, that summarizes together how we varied or constrained all model parameters.

Point C: Figure 6: Maybe the authors could define an "asymmetry index" (eg. the cumulative probability "missing" from the odd clones assuming some smooth gaussian from neutral drift without lineage correlations).

In principle, it is an interesting idea to compare an “asymmetry index” between experiments and models. However, as our model results in Figure 6A show, the exact value of such an index would depend in a complex manner on the exact model parameters. Comparing with a Gaussian function based on a neutral drift model is also challenging, in terms of interpretation. In our understanding, such Gaussians emerge in the limit of large clone size N as scaling functions (e.g. in Snippert, Cell 2010) of the form F(x), where x=N/<N>, which because of the dependence on <N> explicitly makes no statement on the relative contribution of even and odd clones.

Based on the comments of Reviewer #1, we have now added a statistical analysis of the measured clone size distributions, that shows that the enrichment of even clones is statistically significant.

I also wonder whether the authors could recapitulate their findings in a toy model of stochastic fate choices with correlation time T in outcome (to connect it more directly to previous models of neutral drift on a 1D ring). This type of model making correlation time in fates an explicit variable would go well with the discussion on the number of generations at which correlations in fate are lost (line 360-370). It would also be nice to mention the consequence that this would have on longer-term clonal conversion dynamics that have been extensively studied in the past.

It is an interesting question whether the experimentally observed correlations in fate/behavior of sister and cousin cells could be explained by an even simpler model than in Figure 4, by considering a ‘standard’ neutral drift model (i.e. a single compartment of fixed size) but with the decision to change fate (and thus leave the compartment) occurring with some correlation time. However, there appear to us to be many ways to implement such a type of model, with the details of implementation likely having major impact on the observed statistics. We therefore think that examining the behavior of such a different class of models would be an entire project in itself.

Reviewer #3 (Recommendations for the authors):

As said in the public review, my concern is to take the two-compartment model too literally. I do agree that the presented analysis is fine, and the two-compartment model works as a valid simplification to capture the qualitative features of the mechanism, but I am worried that the reader takes this at face value. Instead, given the measurements in Figure 5E, it is more likely that the proliferative potential decreases continuously with distance from Paneth cells. So while the two-compartment model works as a simplification of the numerical analysis (being a representative of a larger class of models where proliferative potential decreases with distance), it does not work well as a description of reality.

We agree with the Reviewer that the function of the mathematical model is not described sufficiently clearly. The model’s main aim was to systematically examine the impact of changing the symmetry of fate (proliferative or not) between sister cells, as described by the parameter phi, on fluctuations in the number of proliferating cells. This was of course inspired by our experimental observation of strong symmetry between sisters, and allowed us to propose a potential function for this observed symmetry: minimization of fluctuations. Given the poor performance of the simplest, spatially uniform model (Figure 4B,C), we turned to the two-compartment model as the most basic extension of the uniform model.

Our aim was thus not to construct the ‘most realistic’ model and we did not explore models that would reproduce the experimentally observed symmetry without explicitly including a symmetry parameter like phi. Indeed, our experimental observations suggested a more continuous transition in proliferation, as the Reviewer points out. It is also possible that ‘simpler’ models, like the model with correlation time suggested by Reviewer #2, exist that can reproduce our experimental findings without explicitly including division symmetry as a parameter. We have now added a paragraph to the discussion that outlines the limits of our model, both in terms of fitting to the data and in explaining the origin of the division symmetry.

We want to point out that, in response to a point raised by Reviewer #2, we added simulation results of a simple ‘standard’ neutral drift model of symmetrically dividing stem cells with niche crowding control, i.e. for every cell division one cell is randomly selected to differentiate. This model fails to reproduce the observed symmetry between sisters cells (Figure 4 —figure supplement 2E). Hence, it is to us a priori not obvious that the class of models with negative feedback control, that Reviewer #3 refers to in the public review, can easily reproduce these results: it would be an interesting future direction for theoretical study.

Changes made to the manuscript:

– We added a paragraph “We used mathematical … intestinal homeostasis[1, 10]” to the Discussion, explaining key features of the experiments captured by the two-compartment model, as well as limits of our model.

– We added the sentence “We therefore examined … an external parameter” to the section “Symmetry between sisters minimizes fluctuations in a cell proliferation model” to explain more explicitly aim of the model.

– We added the sentence “Finally, we note … generate this symmetry” to the section “Symmetry between sisters minimizes fluctuations in a cell proliferation model” in the Results, to explain that the neutral drift models cannot explain the observed symmetry.

– We added the panel Figure 4 —figure supplement 2E showing the results of the neutral drift model and added a caption that explains the model and interprets its results in more detail.

Further suggestions, questions, and corrections:

– When saying that fractions of asymmetric divisions are "low" (e.g. line 135), then this should be compared with the case to be expected when sister cell fate is unrelated: namely in that case, asymmetric divisions would be at 50%.

The Reviewer is correct that this is the number the fraction should be compared to. We have added the sentence “Indeed, if we … or not independently” to the section “Symmetry of proliferative behavior between sister cells” in the Results, to compare this fraction to what would be expected if the decision was uncorrelated between sisters.

– For α=0 one wouldn't expect uncontrolled exponential growth as stated in line 170. Stochastic fluctuations can be very large for α=0, even exceeding the set threshold of 5-fold, but this is still not exponential growth. It should also be mentioned that this may depend strongly on the arbitrarily set threshold.

We agree with both points the Reviewer raises here and made the following changes in response:

– We changed ‘uncontrolled exponential growth’ to ‘uncontrolled growth’.

– We added the sentence “Frequency of overgrowth depends strongly on the threshold value used” to the caption of Figure 4.

– In line 195 it is said that "stochastic depletion occurred when α_p <~ 0.5". However, the scale in the referred figure is set arbitrarily. Since there the depletion rate is always non-zero, depletion will always occur after sufficiently large times. So when saying "stochastic depletion occurred when α_p <~ 0.5", then it should be said over which time scale of observation this is meant.

We agree with the Reviewer that the depletion rate is always non-zero. We changed this sentence to “Stochastic depletion occurred at significant rate (>1 event per 10³ hours)” to make clear that this is an observation about the probability that this occurs.

– In the caption of Figure 1 the part for panel G should refer to panel F instead.

We corrected this.

– Figure 5: the colours are difficult to distinguish for a red-green colour impaired reader (roughly 10% of the male population): orange vs. green is difficult to distinguish and the thin black font colour vs. thin red font colour of vertical axis labels in Figure 5E are difficult to distinguish.

We changed the orange color to grey in Figure 5B-D and changed text color and size in Figure 5E.

– The value of phi reported in Figure 5E (phi=0.98) is significantly higher than that reported in Figure 3A (adding the symmetric events when both sisters go on dividing, never dividing, or dying, gives phi = 0.81). Where does this discrepancy come from?

We thank the reader for pointing out this discrepancy, which in the end took us more effort to fully resolve than we anticipated at first glance.

The first part of the explanation is that the number of phi = 0.81 quoted by the Reviewer is due to the inclusion of cell death. While we report the prevalence of cell death in Figure 3A, its occurrence seems highly complex. As can be seen in Figure 1F, it can be highly prevalent in specific, rapidly dividing lineages in the crypt, but not in other crypt lineages, suggesting the presence of heritable chromosomal defects. In addition, it is seen to occur, at much lower frequency, in non-proliferating cells in the villus, in a process that appears similar to cell extrusion as seen in vivo. Overall, this suggests to us that cell death is a process that is controlled rather independently from the decision to proliferate or not. For that reason, when calculating the experimentally observed value of phi, we ignore sister pairs in which one or two cells die. This led to a higher value for phi (0.92) than the one calculated by the Reviewer. This is also consistent with our simulations, that don’t include cell death, corresponding to the implicit assumption that if a cell wouldn’t have died, it would have likely adopted the same fate (proliferating or ceasing proliferation) as its sister.

However, this was still lower than the value of phi=0.98 reported for Figure 5E. Tracking down this difference eventually led us to uncover an error in calculating the fractions in Figure 3A. Specifically, we used a misplaced position of the crypt bottom. Combined with the rule that cells more than 60 μm from the crypt bottom are considered non-proliferative (see “Classifying cell state” in the Methods), this resulted in an erroneously high number of non-proliferative cells in the villus region. This error was only present in the analysis for Figure 3A and Figure 4 —figure supplement 2A and didn’t impact the other figures.

Correcting these numbers changed the fractions both for sisters and cousins in Figure 3A and Figure 4 —figure supplement 2A. Calculating phi based on the numbers in Figure 3A now gives phi=(0.59+0.15)/(0.59+0.15+0.02)=0.97, close to the number in Figure 5E. The remaining discrepancy is explained by the fact that in Figure 5E we use a smaller subset of organoids, in which Paneth cells were stained by lysozyme. That small difference between these different sets of organoids in itself indicates that this fraction is remarkably invariant between different organoids.

However, one consequence of correcting this error is that the fraction of non-proliferating sisters and cousins in Figure 3A and Figure 4 —figure supplement 2A has decreased substantially, from 0.4 to 0.15 for sisters. This also means that the reported ratio between symmetrically proliferating and non-proliferating sisters has decreased, from 0.38:0.4 to 0.59:0.15. At first sight, this now appears inconsistent with our observation in Figure 2A,B that the number of proliferating cells remains approximately constant in most crypts, as this would imply that this ratio should be close to 50:50.

However, we performed new analysis (Figure 3—figure supplement 2) that indicates that this apparent mismatch is likely an artefact of analysis choices made in constructing Figure 3A. As this figure focuses on the high symmetry of proliferative outcome between sisters, we included all sister pairs for which the proliferative state could be unambiguously classified, for all crypts. This includes crypts 3 and 4 that showed considerably growth in number of proliferating cells. Indeed, including only crypts with low growth rate already reduces this mismatch (Figure 3—figure supplement 2), even though it doesn’t fully resolve it. The second reason for this mismatch is that we excluded sister pairs where one or two cells were unclassified. As our experiments suggest that these unclassified cells are in majority non-dividing cells, Figure 3A thus likely undercounts non-proliferating sister pairs.

As we explain in more detail in the current version of the section ‘Control of cell proliferation in organoid crypts’, unclassified cells are either ‘untracked’, i.e. impossible to track due to imaging issues, or ‘undetermined’, meaning that they were born too close to the end of the experiment to be unambiguously identified as proliferating (division observed) or non-proliferating (no division observed for >30 h). Untracked cells, as can be seen for instance in Figure 1F, are typically found in the villus, in lineages that are unlikely to produce many proliferating cells. Undetermined cells are particularly prevalent in the final ~15 h of each time-lapse experiment, as many cells are born that will not be able to execute their cell division before the end of the imaging time window. However, if we constrain our analysis to cells that are born >15 h before the end of imaging (as we did in Figure 2A,B and now do in Figure 3—figure supplement 2), most cells that are undetermined are likely non-proliferating based on the measured cell cycle distribution (Figure 3—figure supplement 1). As a test, we calculated the ratio between proliferative and non-proliferative sisters under the most extreme assumption that all unclassified cells are non-proliferating. In this case, we indeed find a balanced ratio for proliferative and non-proliferative sisters in crypts with low growth rate (Figure 3—figure supplement 2B).

In response to our discovery of the analysis error in Figure 3A, we made two further changes:

First, in the previous version of the manuscript, we concluded, based on the incorrect fractions, that cells ceasing proliferation were more important for homeostasis than cell death. We still believe this is the case, but because of our likely underestimation of non-proliferating cells, as described above, we feel this conclusion is no longer supported by the data in Figure 3A, and we have therefore removed it.

Second, we examined whether the reduced fraction of non-diving cells in the new Figure 3A impact the statistical validity of our conclusion that sisters with symmetric outcome are overrepresented. We have now added analysis that the observed fraction of symmetric sisters cannot be explained by each sister making the independent decision to proliferate or not, and thus our conclusion that sister cell behavior is strongly correlated still firmly stands.

As an overall conclusion, the different values for the fractions in Figure 3A are still consistent with our observation of homeostasis in the number of proliferating cells in Figure 2, assuming that unclassified cells are predominantly non-proliferating as our experiments suggest. Moreover, the changes to Figure 3A do not impact in any way our paper’s main conclusion regarding the prevalence and potential function of high symmetry in division outcome between sisters.

Changes to the figures:

– We changed Figures 3A and 4 —figure supplement 2A to incorporate the correct fractions of sister and cousin pairs.

– We added the new Figure 3-supplement 2, that explains that the apparent mismatch between proliferating and non-proliferating sisters is likely due to the exclusion of sister pairs with unclassified cells, as these were probably in majority non-proliferating.

Changes to the Result section “Single-cell tracking of complete crypts in growing intestinal organoids”:

– We added the sentence “Finally, a small … scattering in the tissue” to point out more explicitly that we cannot track some cells, predominantly in the villus region.

Changes to the Results section “Control of cell proliferation in organoid crypts”:

– We edited the text “To systematically … cells to 10%” to explain the criteria for classification of proliferation state and add information on the fraction of cells that cannot be classified based on these criteria.

– We edited the sentence “Using this classification … for nine crypts”. In particular, we changed ‘number of cells’ to ‘number of cells born’, to emphasize that we are not tracking total cell number, but rather number of proliferating and non-proliferating cells. The birth of a cell that dies is therefore counted as an increase in number of non-proliferating cells rather than an decrease in total cell number. This is clarified also in the caption of Figure 2A.

Changes to Results section “Symmetry of proliferative behavior between sister cells”:

– We edited the sentence “To examine … S1 and S2” to clarify that Figure 3A focuses on correlations in proliferative behavior between sisters, not on the balance between proliferation and non-proliferation.

– We removed the sentence “We found that sister pairs showed cell death more rarely than division arrest in at least one of the sisters (16% vs. 54%), indicating that cell death played a minor role in balancing cell proliferation.”

– We changed the percentages to match the corrected values of the fractions in Figure 3A.

– We have added the sentence “Indeed, if we … was high (97%)” that discusses the 97% fraction when cell death is excluded.

– We added the sentence "and could not … bootstrap simulation, Materials and methods)" to describe the statistical test of the observed symmetry.

– We added the section “When examining all sister pairs … sisters (40%, Figure 3—figure supplement 2)” to describe the apparent mismatch between proliferating and non-proliferating sisters in Figure 3A and our explanation that this likely reflects that sisters with unclassified cells, which are excluded from Figure 3A, are predominantly non-proliferating sisters.

Changes to the Methods:

– We have added the sentence “During imaging … of non-proliferating cells.” to the section “Single cell tracking” to explain the likely origin of the discrepancy between proliferating and non-proliferating cells born.

– We added the section “Estimation of significance of symmetric divisions” to explain our bootstrapping approach.

– Figure 6D: It would be helpful to have an interpolation curve to see the enrichment at n=6 (currently this is not visible). Alternatively, plotting on a logarithmic scale could make this more visible.

We added a statistical analysis of the measured clone size distribution in Figure 6D (See response to Reviewer #1 for more details). This showed that the difference between n=5 and n=6 is not significant (i.e. error bars overlap), indicating that we have too few data points for n=6 to establish whether there is a significant enrichment compared to n=5 and n=7.

Other changes to the manuscript:

– We changed the references to SI figures to adhere to eLife conventions

– We made changes to adhere to eLife conventions for reporting statistical analysis.

https://doi.org/10.7554/eLife.80682.sa2

Article and author information

Author details

Guizela Huelsz-Prince

AMOLF, Science Park, Amsterdam, Netherlands

Contribution
Data curation, Software, Formal analysis, Investigation, Visualization, Methodology, Writing - original draft

Competing interests
No competing interests declared
Rutger Nico Ulbe Kok

AMOLF, Science Park, Amsterdam, Netherlands

Contribution
Data curation, Software, Formal analysis, Visualization, Writing - original draft

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-6214-681X
Yvonne Goos

AMOLF, Science Park, Amsterdam, Netherlands

Contribution
Data curation, Investigation, Methodology

Competing interests
No competing interests declared
Lotte Bruens

Department of Molecular Pathology, Oncode Institute, Netherlands Cancer Institute, Amterdam, Netherlands

Contribution
Resources, Investigation, Methodology, Writing - original draft

Competing interests
No competing interests declared
Xuan Zheng

AMOLF, Science Park, Amsterdam, Netherlands

Contribution
Data curation, Software, Visualization, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-1700-9082
Saskia Ellenbroek

Department of Molecular Pathology, Oncode Institute, Netherlands Cancer Institute, Amterdam, Netherlands

Contribution
Resources, Investigation, Methodology, Writing - original draft

Competing interests
No competing interests declared
Jacco Van Rheenen

Department of Molecular Pathology, Oncode Institute, Netherlands Cancer Institute, Amterdam, Netherlands

Contribution
Conceptualization, Supervision, Funding acquisition, Writing - review and editing

Competing interests
No competing interests declared
Sander Tans

AMOLF, Science Park, Amsterdam, Netherlands

Contribution
Conceptualization, Supervision, Funding acquisition, Writing - review and editing

Competing interests
No competing interests declared
Jeroen S van Zon

AMOLF, Science Park, Amsterdam, Netherlands

Contribution
Conceptualization, Formal analysis, Supervision, Funding acquisition, Writing - original draft, Writing - review and editing

For correspondence
j.v.zon@amolf.nl

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-6021-2924

Funding

Nederlandse Organisatie voor Wetenschappelijk Onderzoek (VIDI)

Guizela Huelsz-Prince
Yvonne Goos
Jeroen S van Zon

Nederlandse Organisatie voor Wetenschappelijk Onderzoek (Building blocks of Life)

Rutger Nico Ulbe Kok
Xuan Zheng
Sander Tans
Jeroen S van Zon

Nederlandse Organisatie voor Wetenschappelijk Onderzoek (680-47-529)

Guizela Huelsz-Prince
Yvonne Goos
Jeroen S van Zon

Nederlandse Organisatie voor Wetenschappelijk Onderzoek (737.016.009)

Rutger Nico Ulbe Kok
Xuan Zheng
Sander Tans
Jeroen S van Zon

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Ethics

All experiments were carried out in accordance with the guidelines of the animal welfare committee of the Netherlands Cancer Institute.

Senior Editor

Didier YR Stainier, Max Planck Institute for Heart and Lung Research, Germany

Reviewing Editor

Steffen Rulands, Max Planck Institute for the Physics of Complex Systems, Germany

Reviewer

Philip Greulich, University of Southampton, United Kingdom

Version history

Preprint posted: March 17, 2022 (view preprint)
Received: May 31, 2022
Accepted: October 20, 2022
Version of Record published: November 29, 2022 (version 1)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.