1. Neuroscience

Schema-based predictive eye movements support sequential memory encoding

  1. Jiawen Huang  Is a corresponding author
  2. Isabel Velarde
  3. Wei Ji Ma
  4. Christopher Baldassano
  1. Department of Psychology, Columbia University, United States
  2. Center for Neural Science and Department of Psychology, New York University, United States
https://doi.org/10.7554/eLife.82599
Share this article
Cite this article
  1. Jiawen Huang
  2. Isabel Velarde
  3. Wei Ji Ma
  4. Christopher Baldassano
(2023)
Schema-based predictive eye movements support sequential memory encoding
eLife 12:e82599.
https://doi.org/10.7554/eLife.82599
  2. Download BibTeX
  3. Download .RIS

Abstract

When forming a memory of an experience that is unfolding over time, we can use our schematic knowledge about the world (constructed based on many prior episodes) to predict what will transpire. We developed a novel paradigm to study how the development of a complex schema influences predictive processes during perception and impacts sequential memory. Participants learned to play a novel board game (‘four-in-a-row’) across six training sessions and repeatedly performed a memory test in which they watched and recalled sequences of moves from the game. We found that participants gradually became better at remembering sequences from the game as their schema developed, driven by improved accuracy for schema-consistent moves. Eye tracking revealed that increased predictive eye movements during encoding, which were most prevalent in expert players, were associated with better memory. Our results identify prediction as a mechanism by which schematic knowledge can improve episodic memory.

Editor's evaluation

This work designed a novel board game paradigm (4-in-a-row, a sort of tic-tack-toe expansion) in combination with eye movement recordings to examine how schemas gradually learned in the game influence memory. They provide impressive evidence that, in both behavior and eye movements, schema indeed guides the encoding of sequential events and facilitates memory performance. This paper would be of great interest to many fields, such as memory, learning, and decision-making.

https://doi.org/10.7554/eLife.82599.sa0

Introduction

A key benefit of having a memory system is that it enables us to use the past to make predictions about the future, which is adaptive for survival (Cowan et al., 2021). Prediction can be defined as a top-down process in which people generate expectations about what they will experience next, based on their previous experiences and the current context. A particularly important source of prediction is schemas, which are adaptable knowledge structures reflecting generalized information abstracted from multiple episodic experiences (Ghosh and Gilboa, 2014). For example, we may have schemas about the kinds of objects that tend to occur at a beach, the social norms for ordering food at different kinds of restaurants, or the typical stages of a chess game.

Previous research has shown that having a detailed and robust schema yields improvements in memory (Alba and Hasher, 1983). This memory improvement has been attributed in part to processes during recall since schemas provide cues that can be used to retrieve episodic details that would otherwise be forgotten (Anderson and Pichert, 1978; Watkins and Gardiner, 1979). Additionally, schemas could play a role during memory encoding, by helping people represent information more meaningfully (Bransford and Johnson, 1972; Chase and Simon, 1973).

One question that has been relatively unexplored in this literature is whether schemas improve episodic memory by enabling sophisticated predictions during encoding. In the past 20 years, there has been a growing recognition of the importance of prediction on how we perceive, understand, and interact with the world (Bar, 2009; Clark, 2013; Friston, 2010; Rao and Ballard, 1999). There is evidence that domain experts (i.e. people with a strong schema in a specific field) automatically engage these predictive processes; for example, basketball experts shown a clip from a game tended to remember the final positions of the players as being ahead of their actual positions (Gorman et al., 2012). These predictive processes are only possible with a pre-existing schema and might partially explain the large literature showing selective memory improvement for schema-consistent (i.e. predictable) information (Anderson, 1981) and highly unexpected information (i.e. prediction errors, Bonasia et al., 2018; Quent et al., 2021).

Previous prediction research has typically used two types of approaches. The first approach uses people’s pre-existing real-world knowledge, such as the regularity of language structure (Goldstein et al., 2022; Shain et al., 2020) or event sequences in a familiar setting (Baldassano et al., 2018). Due to their complexity, however, it is difficult to build a ground-truth model for these schemas. These types of knowledge are also learned slowly, making it difficult to study their development in a lab setting. The second paradigm, commonly used in memory research, teaches participants simple and novel sequences of discrete stimuli like abstract shapes and pictures (e.g. Schapiro et al., 2012; Sherman and Turk-Browne, 2020). Due to their simplicity, it is possible for participants to learn these sequences in a short period of time and they are easy to model. However, the predictive processes examined in these studies might not engage the same mechanisms as when predictions are based on more complex schemas that generalize to new stimuli.

In this study, we investigate prediction as a potential mechanism for schema-related memory improvement, in a domain that avoids the issues with overly simplistic or poorly defined schemas. Specifically, we have participants remember sequences from a simple board game recently developed by van Opheusden et al., 2021 called four-in-a-row. In this two-player game, a generalization of tic-tac-toe, players compete to be the first to connect four pieces in a row on a 4 × 9 board. The schema of the game encompasses not just this rule (which is easily learned), but an understanding of what kinds of move sequences are typical, an emergent property of the game rules that requires playing experience to learn. Expertise in four-in-a-row has been shown to change how individual game boards are remembered, with experts better representing arrangements of pieces that are strategically important (van Opheusden et al., 2021). The game has a complexity far exceeding typical tasks in previous schema and prediction research, yet it is possible to capture near-optimal play with a linear model. The novelty and simplicity of the game ensure that participants start the experiment without a schema but can acquire the schema over several hours of practice, allowing us to tractably study how schema development is related to changes in prediction and memory longitudinally in a lab setting. The fact that possible moves correspond to different spatial locations allows us to use eye movements as an indication of people’s predictive processes, as in previous paradigms with spatial actions (e.g. Tal et al., 2021).

Based on findings in previous schema research, we hypothesized that people’s memory for move sequences would improve over training sessions, alongside improvements in a schema, operationalized as improved gameplay ability. Although previous research has sometimes found novelty-driven memory improvements for schema-inconsistent information (reviewed in Frank and Kafkas, 2021), studies of memory for complex memoranda such as chess boards have shown an advantage for schema-consistent stimuli (e.g. board positions from actual chess games) (Gobet and Waters, 2003). Thus, we hypothesized that the memory improvement resulting from the development of schema in four-in-a-row should similarly be specific to moves that are schema-consistent. People’s schema quality should also be related to their memory performance, such that people with stronger gameplay abilities will have better sequence memory. If the prediction is indeed a potential mechanism for schema-related improvement, we would expect people’s eye movements to become more anticipatory as they gain more experience playing the game and can rely more on internal predictive models. The extent of predictive eye movements should also mediate the relationship between schema quality and memory performance, providing a mechanism through which schematic knowledge can impact episodic memory. Here, we find support for all these hypotheses.

Results

Memory and gameplay improvement

Over six sessions (each separated by 2.15 days on average), participants performed two separate tasks (Figure 1). In the memory task, participants were presented with a novel gameplay sequence and asked to remember it. After a distractor task, they were shown the first board of the sequence and they were given an unlimited amount of time to reconstruct the rest of the sequence from memory. In the first session, participants were not told that these stimuli came from a game, and were only instructed to remember circles appearing on a grid. The first session therefore provided a no-schema baseline, since participants could not use a game model to make predictions about upcoming moves. In a post-task questionnaire, we confirmed that in session 1 most participants did not suspect that the stimuli were from a game or guess the rules of the game (14 out of 19 in the online study, and 13 out of 16 in the in-person study). In a separate gameplay task (occurring after the memory task on all but the last day), they were provided with the rules of the game and played the four-in-a-row game against an AI opponent, staircase to match the skill level of the player.

Figure 1
Download asset Open asset
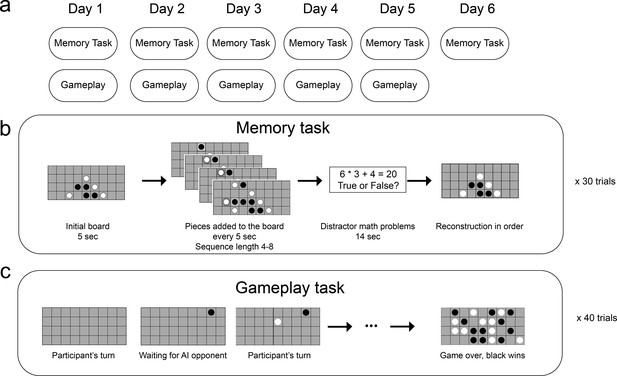
A schematic of the experimental method.

(a) Task structure across six (non-consecutive) days. (b) Memory task. In each of the 30 trials, participants saw an initial board for 5 s, and then a move was added to the board every 5 s. After viewing a sequence of 4four to eight moves and completing a distractor task, participants were shown the initial board and asked to reconstruct the sequence by placing the pieces on the board. (c) Gameplay task. Participants played 40 games against an adaptive-difficulty AI agent.

Participants recall accuracy (combined across the online and in-lab data), calculated as the percent of moves they recalled at the right location in the right order, improved across training sessions, improving from 61.6% (SD = 18.1%) in session 1 to 69.5% (SD = 20.6%) in session 6 (Figure 2a). At the same time, participants’ playing strength, measured with an Elo rating (Elo, 1978), increased (Figure 2b). Elo ratings are computed based on how often people win against opponents of varying skill levels, and we use Elo as a measure of schema quality – the better a player is, the better knowledge they have about the move probabilities during near-optimal gameplay. We fit mixed-effect models with a fixed effect of the session and a random slope for the participant to predict recall accuracy and Elo. The fixed effect of the session was significant in both models (for memory, β=0.015, t=3.215, p=0.003; for Elo, β=24.92, t=5.102, p<0.001), demonstrating improvement in both recall accuracy and gameplay over time. We also found that Elo’s rating in a session was correlated with memory performance in the following session, Pearson r=0.298, p<0.001 (Figure 2c), showing that having a better schema for the game was associated with better episodic memory for move sequences. To understand whether this relationship was present within individual participants, we fit a linear mixed-effect model to predict memory performance from Elo with per-participant intercepts and slopes as random effects. We found that the relationship between Elo and memory accuracy was not significant in this model (β=0.012, t=1.196, p=0.242), suggesting that this effect was primarily driven by individual differences (people with better schema tend to have better memory) rather than across-session improvements in Elo.

Figure 2
Download asset Open asset
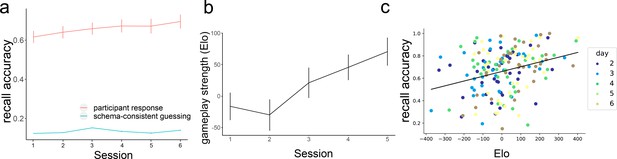
Participants’ performance in memory and gameplay.

(a) On average, Participants become better at remembering sequences over the course of the training (red line, N = 35). In each session, memory accuracy is much higher than the performance that would be achieved if people were simply guessing according to the gameplay model (green line, simulated, N = 100). (b) On average, participants become better at playing the game across sessions. Error bars represent the standard error of the mean. (c) There is a positive correlation between people’s playing strength and their recall accuracy (each dot corresponds to one session of one participant).

Out of the 30 sequences shown to participants in each session, 10 of them ended with one player successfully getting four pieces in a row (more details in Methods). After learning the rules of the game, the presence of such a win could be a salient event for the participant and could lead to changes in the memory performance. Indeed, we found that in sessions 2–6, memory for sequences that ended in a win state was significantly better (t=6.67, p<0.001). We did not observe this pattern in the first session (before participants were taught the game rules) and actually found a marginally significant effect in the opposite direction, with worse memory for winning sequences (t=–2.01, p=0.052). This result provides additional evidence that schema-related features of a sequence play a role in the memory performance.

Modeling schema-related memory improvement

To investigate how schema consistency is related to memory for individual moves and how this relationship evolves, we trained a model of the schema for the game on moves played by a near-optimal AI agent. The model identifies the features each move forms (such as three-in-a-row, a line of three pieces of the same color) and assigns a value to each feature based on the training data (described in more detail in the Method section). Given a current board position, the model outputs a probability distribution over the next move that would likely be played by a very strong player (Figure 3a). Using this model, we can measure the extent to which each move shown to participants is likely (schema-consistent) vs unlikely (schema-inconsistent), and how this is linked to recall accuracy. Here, schema consistency is used as an objective, the subject-independent measure of how good a move is. Each subject will exhibit different degrees of alignment to this ‘ground-truth’ schema.

Figure 3
Download asset Open asset
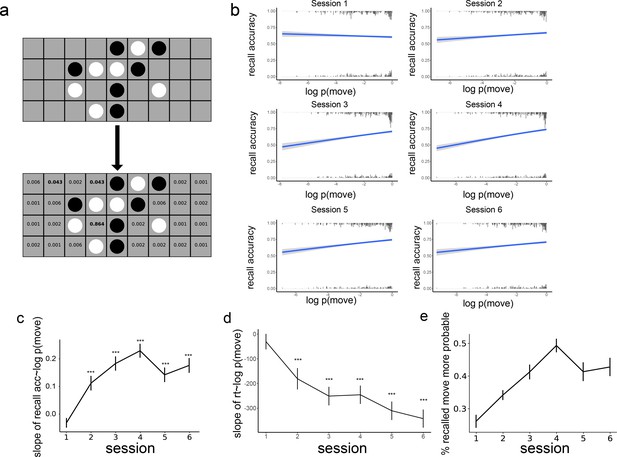
The effect of schema consistency on memory and its development across training sessions.

(a) An example of the model’s evaluation of a board where the next player is black. Based on features that would be generated by each possible next move (e.g. creating three-in-a-row), the model generates a probability distribution over potential next moves. We apply this model to the stimuli in the memory task to estimate the probability of each move. (b) The effect of schema consistency of a move on the recall accuracy for the move. The x-axis is the log probability of a move, which reflects schema consistency. The y-axis is the probability that a participant will remember the move. In session 1, there is no relationship between the probability of moves and subsequent memory. In sessions 2–6, people are more likely to remember schema-consistent moves. The histogram at the top and bottom of the figure is the frequency of moves with certain log probabilities that are remembered and forgotten, respectively (c) The relationship between move probability and recall accuracy over the 6 sessions. (*** denotes p<0.001). (d) The relationship between move probability and reaction time at recall for correctly remembered moves. (*** denotes p<0001). (e) The proportion of times the first mistake in a sequence is a more probable move than the actual move that was observed. Error bars represent the standard error of the mean, and the sample size is 35 participants.

Separately for each session, we ran a mixed-effects logistic regression with subsequent memory (right or wrong) as the outcome variable, with the probability of the move as the fixed effect, and with a participant random intercept. As shown in Figure 3b, there was initially no relationship between the probability of a move and the probability that the move will be remembered in session 1 (β=–0.031, z=–1.813, p=0.07), but in sessions 2 through 6, schema-consistent moves were more likely to be remembered (all p<0.001). This effect emerged over the first four sessions of learning (Figure 3c) and then dropped slightly in sessions 5 and 6.

To see whether this increase in the relationship between move probability and recall accuracy over time is significant, we aggregated the data from all the sessions and ran a mixed-effects logistic regression with subsequent memory as the outcome variable, with the probability of the move, the session the move was in, and their interactions as fixed effects, and with a participant random slope of the session and move probability. We found a main effect of session on memory (β=0.164, z=5.763, p<0.001) but no main effect of move probability (β=–0.0046, z=–0.249, p=0.804). However, there was a significant interaction between move probability and session on memory (β=0.035, z=7.561, p<0.001), indicating that participants became better at remembering schema-consistent moves over the time.

In addition to recall accuracy, we looked at reaction time for placing moves at recall. We only looked at moves that were correctly recalled in each session and removed outliers with reaction times longer than 30 s (0.6% of all the correct moves were removed this way). Similar to accuracy, we found that reaction time during retrieval was initially not related to the probability of the move (β=–30.5, t=0.975, p=0.329) but consistently faster for more schema-consistent moves in sessions 2 through 6 (all p<0.001, Figure 3d). Running a mixed-effects model as for the accuracy (using linear rather than logistic regression), we found a main effect of session on reaction time (β=–156.3, t=–2.39, p=0.017), such that participants were faster in later training sessions. There was no main effect of move probability (β=- 46.1, t=−0.440, p=0.660) but a significant interaction between move probability and the session on reaction time (β=−71.06, t=–2.593, p=0.010), with faster responses when remembering more schema-consistent moves.

If participants are using a schema as part of their recall process, we would expect a bias toward schema-consistent moves when participants make mistakes during sequence reconstruction. To test whether this is the case, we looked at the mistakes participants made in each sequence reconstruction, measuring the fraction of the time that their answer was more schema-consistent than the correct answer, indicating a bias toward schema-consistent moves during recall. We only considered the first mistake, since after that mistake, the encoding and retrieval boards are different, and therefore the likely moves are no longer comparable. As can be seen in Figure 3e, the proportion of schema-consistent mistakes increased over the first 4 training sessions. After that, there is a drop similar to the drop in accuracy in sessions 5 and 6. We ran a mixed-effects model with a participant random slope, the proportion of schema-consistent mistakes as the outcome variable, and session as a fixed-effect predictor, and found a significant effect of the session (β=0.032, t=5.413, p<0.001).

Although an overall increase across sessions was observed in both schema-consistent mistakes and the relationship between recall accuracy and move probability, these effects were significantly weaker at session 5 (for schema-consistent mistakes, t=–2.51, p=0.02; for the relationship between recall accuracy and move probability, t=–3.24, p=0.001), and numerically weaker at session 6 (for schema consistent mistakes, t=–1.70, p=0.099; for the relationship between recall accuracy and move probability, t=–1.93, p=0.053). One potential explanation for this drop is that people developed new strategies in later sessions to remember schema-inconsistent moves. As can be seen in Figure 3b, the modeled recall accuracy for highly schema-inconsistent moves (low x values) increased from session 4–5 while the recall accuracy for schema-consistent moves remained relatively stable. This is consistent with the highest overall accuracy that occurred in session 6 (Figure 2a), suggesting that this decrease in slope does not come at a cost for memory accuracy. Note that reaction time did not show this weakening relationship with move probability in sessions 5 and 6, as its slope continues to decrease.

The results demonstrate that the memory benefit from gameplay training is driven in part by enhanced memory for schema-consistent moves. A possible alternative explanation of this effect is that rather than using generalized schematic knowledge, participants are in fact using episodic memories of specific move sequences that they have seen in past gameplay sessions. To test this possibility, we examined all the boards that participants saw during gameplay and the moves played on these boards, and found the repetition of exact move sequences to be very rare; out of over 1000 moves across 6 sessions there were on average 1.0 repeats (SD = 1.67) that participants experienced during gameplay and were later part of a memory sequence. Thus, the mere repetition of schema-consistent moves could not be driving the observed differences in memory. Another potential explanation could be a change in the participants’ strategy. In the beginning, participants can only use their episodic memory, but over time participants could start to use a purely schema-based strategy in which they simply place moves as if they are playing the game from this board position. We simulated this strategy by drawing moves probabilistically from the gameplay (schema) model for each initial board that participants saw during the memory task in each session. We found that purely schema-based guessing can only achieve an average accuracy of 13.39% across the ix sessions (Figure 2a), which is much lower than participants’ average recall accuracy of 65.91%. This low accuracy is due to the fact that, for most of the sequences, there are multiple plausible moves that could be played and it is therefore difficult to guess the sequence without episodic knowledge. Therefore, the improvement in performance after learning the schema is unlikely due to mere guessing of the boards.

Eye movements became more predictive over training

A potential driver of memory improvements could be a change in encoding strategy. In particular, schemas allow people to make online predictions, which allows additional encoding time if moves are successfully predicted or generate prediction errors otherwise, both of which have been shown to be beneficial for memory (e.g. Quent et al., 2021). We used eye-tracking data to understand how participants’ encoding strategies were related to schemas and later memory. We modeled fixations as a linear combination of six different possible strategies (Figure 4), including a ‘prediction’ strategy (regressor 3) in which fixation durations are related to the model-derived probabilities for the next move. The coefficient for each fitted regressor reflects the extent to which the strategy is used during encoding.

Figure 4
Download asset Open asset
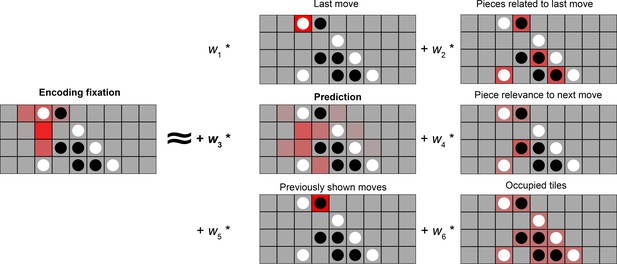
Using eye movements to reveal encoding strategies.

Left: A participant’s fixation heatmaps over a 5 s encoding period. right: the 6 regressors that we consider as potential encoding strategies. 1: Participants could look at the last (most recent) move, which is what they need to remember. 2: Participants could look at occupied tiles that might be relevant to the most recent move, to try to see what features the move forms. 3: Participants could be anticipating the upcoming move, meaning they will look at the empty squares on the board that are likely to be the next move. 4: Participants could also look at current pieces that are relevant for predicting the next move, i.e., pieces related to empty squares that are likely to be the next moves. 5: Participants could be looking at moves that previously appeared, in order to rehearse the observed move sequence. 6: Participants might have an overall tendency to look at occupied or unoccupied tiles.

To look at whether the eye movements become more predictive over time, we first ran a linear mixed-effects model with prediction coefficient as the outcome variable, session as the predictor variable, and a participant random slope, to see if eye movements became more predictive over time. There was a significant fixed effect of session, β=0.009, t=4.261, p<0.001, providing evidence that people’s eye movements became more predictive over training (Figure 5a).

Figure 5
Download asset Open asset
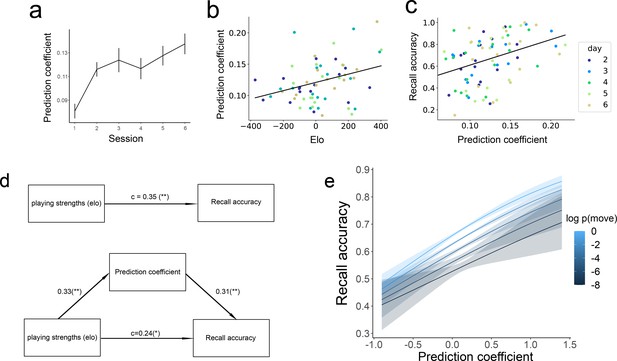
The relationship between prediction, playing strengths, and recall accuracy.

(a) The extent to which eye movements on empty squares align with the gameplay model (prediction coefficient; see Figure 4) increases over training sessions. (b) Correlation between Elo (playing strength) and prediction coefficient in the 35 participants. (c) Correlation between prediction coefficient and recall accuracy. (d) Mediation analysis: the effect of playing strength on recall accuracy is mediated by the amount of prediction participants made during encoding. The values on the arrows represent regression coefficients for standardized measures of Elo, prediction coefficient, and recall accuracy (* denotes p<0.05, ** denotes p<0.01). (e) Move-level analysis on the effect of schema consistency on memory, predicting whether a move will be remembered based on the probability of the move (brighter colors are more schema-consistent) and prediction coefficient in the previous move. Error bars represent the standard error of the mean.

Better performance in better players is mediated by more schema-based predictions

We next sought to test whether this increase in predictive eye movements could serve as a mechanism through which expertise improves memory performance. We found that, on a session-by-session basis, more sophisticated gameplay (higher Elo) was associated with more prediction in the next memory session (Pearson r=0.33, p=0.002), demonstrating that better players predict more during encoding (Figure 5b). Memory sessions in which a player exhibited high levels of predictive eye movements also showed better reconstruction accuracy (Pearson r=0.40, p<0.001), despite there being no explicit demand to generate predictions during encoding (Figure 5c). A mediation analysis was performed to assess the mediating role of the prediction coefficient on the link between Elo and recall accuracy (Figure 5d). The total effect of Elo on recall accuracy was significant (β=0.35, t=3.26, p=0.002). The effect of Elo on the prediction coefficient was also significant, (β=0.33, t=3.13. p=0.002). The bootstrapped indirect effect was 0.10, 95% CI = [0.03, 0.19], p=0.006, suggesting that improved memory for better players is partially mediated by improved predictions during encoding. Significant mediation was not found for any of the other regressors (all p>0.3, except previously shown moves, p=0.056), suggesting that better prediction is uniquely important for driving the memory benefit from better gameplay. With the inclusion of the prediction coefficient, the impact of Elo on recall accuracy was reduced but remained significant (β=0.24, t=2.26, p=0.03), indicating that expertise also improves memory accuracy through additional mechanisms (at encoding and/or retrieval). We again tested whether these effects were present at the individual-participant level by running a linear mixed-effect model with participant random intercepts and slopes. Due to model convergence issues, we employed a Bayesian version of this model to regularize the coefficient estimates (see Methods). We found that the 95% credibility interval for the fixed effect of Elo on the prediction coefficient overlapped with 0 (β=0.007, 95% CI = [–0.003, 0.016]). The 95% credibility interval for the fixed effect of the prediction coefficient on recall accuracy also overlapped with 0 (β=0.164, 95% CI = [–0.54, 0.87]). Together with previous findings, these results suggest that the observed mediation effect is primarily driven by individual differences rather than within-subject development over time.

The above analysis demonstrated that making more schema-consistent predictions is correlated with better memory at the level of experimental sessions. We next constructed a logistic regression model to predict subsequent memory at the scale of individual moves, as a function of the move’s probability and the prediction coefficient during the 5 s window before the move appeared with a subject random slope for the prediction coefficient (Figure 5e). There was a main effect of log probability of the move (β=0.083, z=5.882, p<0.001), consistent with our session-level results demonstrating a memory benefit for more likely moves. We also found a significant effect on the prediction coefficient (β=0.508, z=3.187, p=0.001). There is no interaction between the move probability and prediction coefficient (β=0.024, z=0.395, p=0.693). This result shows that making schema-consistent predictions before a move appears is correlated with better memory for the move, independent of the schema-consistency of the move.

Model-free measures of prediction confidence and surprise

In addition to the prediction coefficient, which measured the extent to which eye movements are consistent with next-move predictions from our gameplay model, we considered two model-free aspects of eye movements on empty squares (Figure 6a). The first is prediction confidence, measuring the extent to which a participant was attending to a specific empty square (vs. looking evenly at many empty squares or at occupied squares). We use this as a measure of whether participants have a specific expectation about the next move position. The second measure is surprise, which is the negative log of the proportion of fixation time spent looking at the correct next move position. A high level of surprise indicates that a participant spent very little time looking at the square where the next move ended up appearing, which indicates low prediction accuracy. We then conducted a move-level logistic regression similar to the one described above, to predict whether a move will be remembered or not based on both prediction confidence and surprise while looking at the previous board (Figure 6b), with the subject random slope for both prediction confidence and surprise. We found the main effects of both factors, indicating that (a) making confident predictions before a move is related to better memory for that move (β=0.375, z=4.372, p<0.001) and (b) unexpected (surprising) moves are more poorly remembered (β=–0.015, z=–2.448, p=0.014).

Figure 6
Download asset Open asset
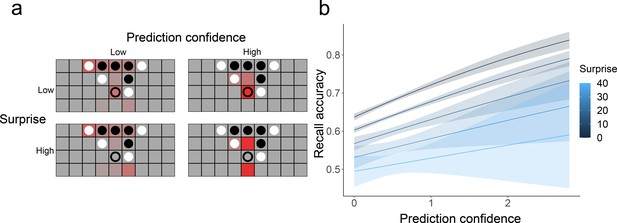
Model-free measure of prediction and their relationship with memory.

(a) Example fixation heatmaps (in red) of high and low prediction confidence and surprise. Confidence measures the extent to which fixations were focused on a small number of unoccupied squares, while surprise measures how well these fixations aligned with the actual next move (indicated with an empty circle). (b) Recall accuracy was best when prediction confidence was high and surprise was low. Error bars represent the standard error of the mean.

Discussion

The main goal of the current study was to look at how schema-based predictive processes support sequential memory encoding. Participants learned a novel schema (likely move sequences and board configurations in our-in-a-row) with much higher complexity than most artificial schemas learned in the lab. Developing a schema for moves in the game requires a significant amount of playing experience (reflected in the slow improvement in Elo ratings we observed across sessions), but can still be accomplished within a single experiment, unlike games like chess. We observed schema-related effects on sequence memory and found that these effects emerge over time as the schema develops. We also investigated the role predictions during encoding played in the relationship between schema and memory, finding that making schema-consistent predictions, making confident predictions, and making accurate predictions were all related to successful recall at the level of individual moves.

Schema-related memory effects and how they develop

Our behavioral findings showed that previously-studied schema effects from previous studies extend to this more complex experimental paradigm, and demonstrated how these effects developed over time. First, memory gradually improved as people’s schemas gradually improved. People with a better schema had better memory, consistent with the literature on how expertise influences memory (Chase and Simon, 1973; Gobet and Waters, 2003). Second, the memory benefit over the training session was driven by the improved recall for schema-consistent information, consistent with schema literature (e.g. Anderson, 1981). Previous work has also shown that in some situations, schema-inconsistent information is better remembered (Frank and Kafkas, 2021), which we did not observe in this study. All the sequences we used were generated by a gameplay agent, so highly schema-inconsistent moves were rare, and none of our stimuli exhibited the extreme kind of ‘contextual novelty’ (Ranganath and Rainer, 2003; Stark et al., 2018) that often drives these effects; for example, we never showed a move that broke the rules of the game or played an expected sound. Future work could test whether highly schema-inconsistent items exhibit memory benefits equal to or greater than highly schema-consistent items. Third, participants’ mistakes became more schema-consistent across sessions. These errors could reflect false memories for schema-consistent sequences that never occurred, similar to false memories generated by naturalistic videos or stories conforming to schematic scripts (Lampinen et al., 2000; Neuschatz et al., 2002). Alternatively, participants may be guessing schema-consistent moves when they failed to encode or retrieve the sequence; in future work, confidence responses could be used to distinguish between these possibilities. Note that some of the overall accuracy increase in the memory task across sessions could be attributable to a practice effect, but general practice-related improvement does not explain the schema-related effects that we observed on individual trials.

Interestingly, the relationship between recall accuracy and memory is attenuated in the last two sessions, driven by improved memory for schema-inconsistent moves. Expertise effects that partially extend to non-schematic situations have been previously observed; although chess experts’ memory advantage was primarily driven by very high accuracy for schema-consistent (legitimate) boards in Gobet and Waters, 2003, experts also exhibited memory for random boards that was better than that of weaker players. One possibility is that experts may be able to devote fewer attentional resources to schematic moves, freeing up additional resources to handle more unusual moves. Participants in our study may have also developed an effortful strategy to remember schema-inconsistent moves (such as switching to a shape-based encoding for these moves), consistent with the longer reaction times observed for low-probability moves in later sessions.

There are other potential mechanisms for the schema-related memory improvement that were not explored in the current study. For example, the ways in which moves are represented in the brain may shift with schema learning, moving from a purely spatial system (e.g. remembering that a move occurred at row three, column two) to a more feature-based representation (e.g. remembered a move as ‘blocking opponent’s three-in-a-row’), which makes remembering easier and more robust. Future neuroimaging work can use techniques such as representational similarity analysis (Kriegeskorte et al., 2008) to model the representational geometry of remembered board positions and track how it changes over sessions.

The development of predictions and their influences on memory

The eye-tracking study showed that participants spontaneously exhibited predictive eye movements consistent with the game schema, without any explicit prediction demands. This is consistent with earlier work showing automatic predictive representations in basketball experts (Didierjean and Marmèche, 2005). We also found that schema-based predictions were associated with improved memory (at the level of participants and the level of individual moves) and that these encoding-time predictions provide a mechanism for the impact of schema quality on memory performance. There are several reasons why within-participant increases in Elo across sessions were not predictive of improvements in prediction and memory. First, our estimate of Elo during each memory task was based on gameplay performance on the prior day, which may not be a precise measure of the participant’s current schema. Second, the biggest increase in prediction occurred between sessions one and two, but the session one memory-task data cannot be included in this prediction model since participants have not yet played the game (and we therefore cannot estimate their Elo). Third, we may simply be underpowered to detect within-participant effects, since we only collected data from six sessions for each subject. Despite the lack of within-subject effect, the session-level analysis provided the novel insight that the memory advantage for more-expert players may be driven by superior predictive processes during encoding.

Despite the numerous studies looking at how item novelty impacts memory (Greve et al., 2017; Quent et al., 2021; van Kesteren et al., 2012), relatively few studies have looked at the impact of temporal schematic prediction on memory for upcoming items. In a recent study, Sherman and Turk-Browne, 2020 showed that making predictions does not benefit memory for the upcoming item and impairs the encoding of the current item, which is inconsistent with our findings. One possibility is that their study (in which participants implicitly learned arbitrary statistical dependencies between image categories presented in a continuous stream) engages a predictive process that relies on the hippocampus (Schapiro et al., 2017), creating interference between prediction and encoding processes. On the other hand, the explicit schematic predictions in our study that are based on rules and progression toward goal states might rely on a different network such as the medial prefrontal cortex (Bonasia et al., 2018; Robin and Moscovitch, 2017; van Kesteren et al., 2012).

Our eye movement data suggest that making high-confidence predictions is related to better memory, even when that prediction is inaccurate. This is in line with the generation effect (e.g. Potts and Shanks, 2014; Slamecka and Graf, 1978), which showed that people better remember unfamiliar study materials (meaning of foreign words) if they make a guess before seeing the correct answer. Potts and Shanks, 2014 demonstrated a benefit even for minimal predictions when predictions are based on random guessing and are wrong almost all the time. In our study, although participants never made explicit predictions, high-confidence fixations (even to the wrong square) could benefit memory through a similar predictive process.

Memory is also best when predictions are most accurate (the observed move is the least surprising, coming exactly where participants anticipated it to be). Surprise or atypicality has sometimes been shown to improve memory since it attracts attention and can result in stronger encoding (Frank and Kafkas, 2021; Neuschatz et al., 2002; Quent et al., 2021). On the other hand, unexpected events can sometimes be difficult to retrieve at recall, since they are less connected to the schema (Bower et al., 1979; Frankenstein et al., 2020). It is possible that the degree of surprise makes a difference; as discussed above, we never presented invalid moves or unexpected categories of stimuli, which could have strongly driven attention. The type of task used might also matter, as it has been previously shown that schema-inconsistent object-location pairs are better recognized, but not better recalled when given only location as a cue (Lew and Howe, 2017).

Previous research has found a relationship between pupil dilation and surprise (Antony et al., 2021; Lavín et al., 2014; Preuschoff et al., 2011), but our study was not well-suited to measure subtle changes in pupil diameter. Studies of pupil dilation generally require tight control over the experimental stimuli, using either purely non-visual stimuli (Preuschoff et al., 2011), or by presenting luminance-controlled stimuli at fixation (Lavín et al., 2014). In our study, the luminance at fixation is highly variable since eye movements are not controlled and squares can be unoccupied (gray) or occupied by white or black pieces. Future work could attempt to study pupil dilation in this paradigm using models to control for local and global luminance (Antony et al., 2021) or by modifying the stimuli to ensure that all board spaces are isoluminant.

To conclude, we showed that people spontaneously engage in more sophisticated predictive processes as their schemas develop, which are beneficial for memory. The current study adds to the literature showing the adaptive values of making predictions for perception and action, and extends its benefit into the memory domain. It also provides a novel mechanism for the benefit of schemas on memory. Our paradigm uses a complex temporal schema that is much more complicated than most artificial schemas (e.g. Tompary et al., 2020; van Buuren et al., 2014) but does not take years to develop, like a chess schema (e.g. Chase and Simon, 1973; Gobet and Waters, 2003). This makes four-in-a-row an exciting testbed for future studies of the cognitive and neural mechanisms of schema development and its impact on episodic memory.

Methods

The study used a longitudinal design, in which participants completed six sessions over a period of about one to two weeks (Figure 1a). The mean interval between sessions was 2.15 days. In sessions 1–5, participants completed 2 (practice) + 30 (formal) trials of the memory task, followed by playing 40 games against an AI opponent. The gameplay task was designed to both develop participants’ schema and measure their playing strength in each session. On day six, participants completed 30 trials of the memory task only. Both the memory task and the gameplay were built on Psiturk (Gureckis et al., 2016) and hosted on Heroku (https://www.heroku.com/).

Participants

The first set of 19 participants (12 female, six male, and two non-binary) completed the task online on their home computers (and were instructed to maximize their browser windows during the task). The online study participants had a mean age of 20.95 years (SD = 2.84). Participants were paid $70 upon completion of the study. A second set of 16 participants (nine female, six male, and one declined to answer) performed an identical task in the lab while eye-tracking data was collected. The eye-tracking study participants had a mean age of 21.81 years (SD = 3.21). Participants were paid $100, plus up to $20 performance-based bonus. For both versions of the study, we recruited participants via online ads and personal contacts. All participants were over 18 years of age with normal or corrected-to-normal vision and gave informed consent for the study. The experimental protocol was approved by the Institutional Review Board of Columbia University (AAAS0252). One participant from the online study did not complete the last session of the study, and we have included their data for the first five sessions. All the other participants completed all six sessions of the study. Two in-person participants experienced technical issues in one of their sessions, resulting in the loss of data from one game for one participant and 15 games for the other participant. The same technical issues during the eye-tracking study resulted in a small number of trials being shown more than once to several participants; we included only data from the first presentation of each trial in the dataset.

Experimental design

The memory task (Figure 1b) required participants to watch a sequence of moves and then recall the moves from memory. In each trial, participants saw an initial board for 5 s. Then one move was added to the board every 5 s. After all moves in the sequence had been added, participants completed 14 s of simple distractor math problems asking them to judge whether an equation is true or false. They had 6 s to respond to each question. After the distractor, they were shown the initial board and instructed to reconstruct the sequence in the right locations and in the right order. To account for motor mistakes, they could undo the most recent move they placed.

The first two memory trials on each day were always practice trials that had four-move sequences, and participants were given feedback on whether a move they just placed was correct or not during retrieval. Participants needed to get all moves correct in the practice trials to proceed to the formal study. The practice trials made sure participants understood the task and followed the instruction. No one was excluded from the study for failing to follow the instructions. Participants then completed 30 trials of the main memory task where they did not receive feedback during the retrieval.

The sequences of moves were generated using an AI agent from van Opheusden et al., 2021 with an relatively weak Elo rating similar to participants’ average playing strengths during their first session. We sampled from 180 unique games, each longer than 16 moves and shorter than 36 moves (i.e. the game did not end with a draw). For each session, 30 game segments with lengths ranging from four to eight moves were extracted from unique games. To ensure that meaningful schematic predictions were always possible, the first move of the sequence was always after the fifth move of the game. For example, if a game was 30 moves long and the sequence length was four, the beginning of the sequence could be anywhere between the 5th move and the 26th move of the game. Of the 30 sequences in each session, 10 sequences (two of each length) ended with one player winning (i.e. the last move created a four-in-a-row). This single set of 30 sequences for this session was shown to all participants in a randomized order (with a different set for each session). The whole memory task takes about 50 min.

At the beginning of day one, the participants were told that the stimuli were ‘circles appearing on a grid.’ After the memory tasks, they were told that the stimuli were actually drawn from a game that they were about to play. They were then shown the rules of the game and played 40 games against an AI agent (Figure 1c), which takes about 40 min. We used a staircasing procedure, such that the agent became stronger if the participant won and weaker if the participant lost. We used the Elo rating to measure participants’ playing strength (Elo, 1978). The ratings were computed using BayesElo (Hunter, 2004) to measure participants’ playing strength in each session based on their performance against the AI agents. After they finished playing the games, they were asked whether they had guessed the stimuli in the memory tasks were from a game, and if so, whether they guessed the rules of the game. We did not include a control group that completed six memory sessions without being told the rules of the game or playing against the AI agent. Ensuring that participants never develop a game schema would be difficult since even without explicit instruction they could still learn the schema through implicit statistical learning or by guessing the (simple) rules of the game. Due to these challenges, we instead used the first-session performance of each participant as our no-schema control.

From Day two onwards, they were reminded of the rules of the four-in-a-row game at the beginning of the memory task. On Day six, after completing the memory task, participants completed a questionnaire asking them what strategies they used for the memory and whether their strategies changed over the course of the training.

Gameplay model

The original model in van Opheusden et al., 2021 used a tree search model. However, obtaining accurate move probabilities from this model would require extensive sampling. Instead, we used a feature-based myopic model of gameplay. We first defined features relevant for gameplay, which represent the relationship between the potential next move and the current board state:

  1. Distance of the move from the horizontal center

  2. Distance of the move from the vertical center

  3. How many four-in-a-rows the move forms?

  4. How many three-in-a-rows the move forms? There are three sub-categories based on the type of three-in-a-row formed: connected, disconnected, and horizontally connected that were not blocked on either side (force a win after the opponent’s move, so it might have a higher value).

  5. How many two-in-a-rows the move forms? There are two sub-categories based on the type of two-in-a-row formed: connected, disconnected.

  6. How many opponent’s three-in-a-rows the move blocks?

  7. How many opponent’s two-in-a-rows the move blocks? There are two sub-categories based on the type of two-in-a-row blocked: horizontally connected two-in-a-row that was not blocked in either direction (if not blocked, the opponent can force a win, so it might have a higher value), or other situations.

We then used a very strong AI agent to generate 800 games. This agent has an Elo of 365, a level similar to the best players in our study, so its move decisions can be considered an approximation of the schema of a very strong player. To fit the model, for each board state in the 800 games, we represented every possible move xi as a feature vector F based on the features described above. Each move was assigned a value V that is a weighted combination of the features it forms, with weights defined by a vector w:

V(xi)=w⋅F(xi)

We then applied a softmax function to get the probability distribution over possible moves, pxi=eVxi/∑ieVxi . We used Pytorch (Paszke et al., 2019) backpropagation to learn the feature weights w that minimized the cross-entropy loss of the moves actually made by the agent. We trained eight models using the data from 100 of the 800 games for each model and averaged the weight vectors across models to obtain a final weight vector w.

We use the model’s evaluation of each move as a measure of the schema consistency of a move, assuming that stronger and weaker players have qualitatively the same schema for what makes a good move. An alternative possibility is that individuals develop schemas that are qualitatively distinct from the gameplay model, which will be reflected in some people playing moves that have a very low probability in our gameplay model. We did not find evidence for this possibility in our dataset; during the gameplay sessions, all participants tended to play moves with relatively high probability under the gameplay model (M=0.213, range=0.143–0.297, compared to a random-move baseline of 0.040). We also observed a strong correlation between Elo and this move probability measure (r=0.40, p<0.001), showing that stronger players are more aligned with our model. Future work (with more extensive gameplay sessions) could attempt to model unique feature weights for each specific individual.

We evaluated each move in the stimulus set with this model to determine the probability of each move under a very good strategy. Note that the stimuli were generated by a non-optimal AI agent, and, therefore, move quality varies over a wide range; the moves participants observe are often not the optimal move for a given board configuration. We also used this model to measure the probability of the move participants recalled during retrieval when they made a mistake.

Eye-tracking

For the in-lab subset of participants, eye-tracking data was collected during the memory task on each day. The design was otherwise identical to the online experiment. Participants were seated 100 centimeters in front of a monitor and placed their heads in a chin rest 45 centimeters away from the eye-tracker. They were instructed to remain as still as possible while the eye-tracker was running and were told that they could take breaks during the experiment in between trials. Before beginning the experiment and when the participants returned from their breaks, the eye-tracker calibration and subsequent validation were done using a nine-point grid. We recorded binocular eye movement using EyeLink 1000 plus at 1000 Hz recording frequency. Light levels remained constant for the duration of the 50 min memory portion of the study. The stimuli were displayed on a 24-inch LED monitor, with a resolution of 1920 by 1080 pixels and a refresh rate of 60 Hz. The outputted EDF files were converted to asc files and parsed with PyGaze (Dalmaijer et al., 2014).

Fixation maps were created for each 5 s period during which an initial board was shown or a move was shown. To handle uncertainty in assigning gaze to squares, we performed a soft assignment to board locations based on distance. For a fixation at the position xF with duration tF the square with center coordinate xi was assigned a fixation weight of

tF⋅e−‖xF−xi‖2/25∑je−‖xF−xj‖2/25

Here, distance is in the unit of pixels. Since the length of the square is 136 pixels, the smoothing temperature of 25 is approximately 1/5 the length of a square and, therefore, is only relevant for fixations close to square boundaries. The weights for all fixations during the 5 s window were summed to obtain a final map of fixation weights for all board squares.

Eye movement regression model

We modeled fixation maps as a linear combination of six potential strategies that could be used during memory encoding. For each board, the regressors, described below, are length-36 vectors that correspond to the 36 tiles in the game.

  1. The most recent move: has a value of one in the square that corresponds to the most recent move, and 0 s elsewhere (all 0 s at the initial board). This regressor captures the extent to which participants are looking at the move that just appeared on the board.

  2. Pieces related to the most recent move: has a value of one in occupied squares that are related to the most recent move (within three tiles from the most recent move in any direction), and 0 s elsewhere. This regressor captures the behavior of looking at how a move relates to previously-placed pieces (e.g. to detect whether it adds onto a line of same-color pieces).

  3. Anticipation of the upcoming move (prediction): for the unoccupied squares, is equal to the probabilities of that square being the location of the next move, as calculated by the near-optimal gameplay model. For occupied squares, has a constant value equal to the mean value of the unoccupied squares. This regressor measures how well participants’ eye movements predict likely positions for the next move.

  4. Piece relevance to the next move: for each occupied square, is the sum of the next-move probabilities for all empty squares that are related to it (within three squares). For unoccupied squares, its value is equal to the mean value of the occupied squares. This regressor reflects the tendency to focus on squares that are likely to be related to the next move.

  5. Observed previous moves: has a value of one for the moves seen earlier in the sequence (excluding the most recent move), 0 s elsewhere. This reflects a strategy of reviewing previous moves during memory encoding.

  6. Occupied tiles: has values of 1 s on occupied tiles and 0 s on unoccupied tiles. This measures the preference for looking at occupied squares versus empty squares.

Each regressor and the eye movement fixation maps were z-scored within each board. We concatenated each of these across all the boards that each participant saw during a session and ran a multiple linear regression (with the fixation maps as the outcome variable, and the six regressors as the predictor variables). The coefficient for each regressor reflects the extent to which this participant used this eye movement strategy when encoding boards in this session. We also ran this regression separately for each individual board (for each move shown during encoding) to obtain trial-level estimates of eye movement strategy.

Regression models

For each model, we started with the most complex frequentist model, including a subject slope for all of the predictors. In case they did not converge, we used simpler models with either fewer random slopes or just a random intercept. If this happens, we also checked whether the effect holds with a more complex model using a Bayesian model. The reported effects with more simpler frequentist models have been shown to hold with a more complex Bayesian model. If a different result was obtained, we report the results of the more complex Bayesian model. For frequentist models, we use lme4 pacakge (Bates et al., 2015). For the Bayesian models, we used the default settings of rstanarm package (Goodrich et al., 2022).

Mediation analysis

The total effect was calculated by running a linear regression predicting recall accuracy from Elo. Next, we calculated the effect of Elo on the prediction coefficient and the effect of Elo and the prediction coefficient on recall accuracy. The significance of the mediation was computed with the package mediation (Tingley et al., 2014) that used a bootstrapping procedure. Standardized indirect effects were computed for each of the 10,000 bootstrapped samples, and the 95% CI was computed by determining the indirect effects at the 2.5th and 97.5th percentiles.

Estimating trial-level prediction confidence and surprise

We constructed two trial-level measures of fixation statistics which allowed us to describe eye movement strategies at a finer scale and in a model-free way (without assuming that participants were making predictions according to our schema model). The first is prediction confidence, which measured the extent to which a participant spent time focused on specific empty squares. High values of confidence indicate that a participant spent a large fraction of the trial looking at only a small number of empty squares, indicating a strong prediction about the upcoming move. We compute this as the expected information gain between a uniform distribution over all empty squares and the fixation distribution. Given the fixation time Txi for each square xi , we define Pempty as the fraction of the 5 s window spent fixating on empty squares, and Pxi=Txi/Pempty as the normalized fixation distribution over empty squares. The information gained from a fixation is 0 for fixations on occupied squares, and for fixations on empty squares reflects the entropy difference between a uniform distribution and the fixation distribution. Therefore, we define:

Predictionconfidence=P(empty)⋅(log(Nempty)−∑iNP(xi)logP(xi))

The second is prediction surprise, indicating the extent to which a participant failed to look at the location where the next move was going to appear. High values of surprise indicate that the move appeared in a location that the participant spent very little time looking at. This is defined as the negative log of the percentage of time participants looked at the correct upcoming move position xnext :

Predictionsurprise=−log(P(xnext))

Data availability

All the data is openly available through https://osf.io/29cpg/.

The following data sets were generated
    1. Jiawen H
    2. Isabel V
    3. Wei JM
    4. Christopher B
    (2022) Open Science Framework
    Schema-based predictive eye movements support sequential memory encoding.
    https://doi.org/10.17605/OSF.IO/29CPG

References

    1. Bar M
    (2009) The proactive brain: memory for predictions
    Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 364:1235–1243.
    https://doi.org/10.1098/rstb.2008.0310
  16. Book
    1. Elo AE
    (1978)
    The Rating of Chessplayers, Past and Present
    New York: Arco Pub.
    1. Gobet F
    2. Waters AJ
    (2003) The role of constraints in expert memory
    Journal of Experimental Psychology. Learning, Memory, and Cognition 29:1082–1094.
    https://doi.org/10.1037/0278-7393.29.6.1082
  33. Book
    1. Paszke A
    2. Gross S
    3. Massa F
    4. Lerer A
    5. Bradbury J
    6. Chanan G
    7. Killeen T
    8. Lin Z
    9. Gimelshein N
    10. Antiga L
    11. Desmaison A
    (2019)
    Pytorch: an imperative style, high-performance deep learning library
    In: Jordan MI, editors. Advances in Neural Information Processing Systems. MIT Press. pp. 8026–8037.

Decision letter

  1. Huan Luo
    Reviewing Editor; Peking University, China
  2. Timothy E Behrens
    Senior Editor; University of Oxford, United Kingdom
  3. Zachariah M Reagh
    Reviewer

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Decision letter after peer review:

Thank you for submitting your article "Schema-based predictive eye movements support sequential memory encoding" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, one of whom is a member of our Board of Reviewing Editors, and the evaluation has been overseen by Timothy Behrens as the Senior Editor. The following individual involved in review of your submission has agreed to reveal their identity: Zachariah M. Reagh (Reviewer #2).

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission. All the reviewers agree that it is an impressive and well-done study to explore a very important question, i.e., the nature and origins of schema-based effect on memory. The clever experimental paradigm strikes a nice balance between complexity in capturing elements of naturalistic human behavior and simplicity in terms of analyses. Meanwhile, the reviewers also raised several critical concerns that need further control experiments and analyses to support the conclusion.

Essential revisions:

1) Instead of memorizing the board positions, subjects might simply consider how they play from that position, a strategy that could account for all the observations. To decouple the schema-based and purely-memory-based influences, a further control study needs to be conducted (see details in Reviewer 3's comments);

2) There lacks a control group who neither knows the rule nor play the game before. The prediction is that the control group will show (1) worse memory; (2) their error patterns are different and unrelated to p (move);

3) Reanalyzing the data to address the potential mixture of session-level and participant-level variability (see Reviewer 1's 2nd concern)；

4) Further clarifications are needed, such as the drop-off in late sessions, reasons for not looking at pupil dilation, the rationale for schema-based memory facilitation hypothesis, and presentation of RT data (see Reviewer 2's comments)

Reviewer #1 (Recommendations for the authors):

This paper develops an interesting and new experimental paradigm to investigate how schema participates in memory and helps to generate predictions, using behavioral measurements, eye movement recordings, and computational modeling. The results show the correlation between memory accuracy, game performance, and predictive eye movements, supporting that schema significantly boosts memory and guide prediction. This paper would be of potential interest to many fields, such as memory, learning, and decision-making.

We see two major strengths in the paper. First, although schema-based memory is crucial, it is very hard to study it in a natural and also controllable way in the lab. This work develops a complex game paradigm with proper difficulty levels, enabling the examination of the characteristics of the process. Second, the combination of memory behavior, eye movement, and game playing provides a comprehensive framework to tackle the question.

The major weakness of the work mainly lies in its lack of a control group, that is, subjects who neither know the rule nor play the game before. This would be important evidence to support the advantage of schema-based memory boosting. Moreover, the source of the effects needs to be further clarified using additional analyses.

Concerns:

1. Schema-based boost in memory and predictive eye movement lacks a control group who neither know the rule nor play the game before. The prediction is that the control group will show (1) worse memory; (2) their error patterns are different and unrelated to p (move).

2. Most of the correlation analyses mixed the variability levels and thus confused the source of the memory boosting effects. For example, when calculating the correlation results (Figure 2C), each data point represents a session of a participant. In this case, the source of the effect could come from either session-level variability that is due to training or participant-level variability. In fact, all the linear mixed-effect models have the same problem and need to be fixed. I would not suggest excluding the random effect for slopes since that would increase the probability of Type I error and as a consequence, the observed effect might arise from individual differences rather than experimental manipulation (see Brauer and Curtin, Psychol Methods, 2018 and Bates, arXiv, 2018 for guides). It is important to include individual-level random effects in the analysis.

Reviewer #2 (Recommendations for the authors):

This paper by Huang and colleagues uses a simple board game, "4-in-a-row," to test the relationship between schemas and episodic memory. Specifically, the goal here was to examine the way schemas can guide encoding of sequential events as the game unfolded. In sum, the authors report that memory for move sequences in the game improved with player skill, and that memory was particularly improved for schema-consistent sequences. Further, eye movements during encoding were associated with stronger memory for move sequences, which was most prevalent in expert players.

We think this study does a fine job of answering how the development of schema aid in prediction and thereby memory through use of a stimulus that is at once naturalistic but learnable by participants in laboratory time. This is a difficult set of boxes to check. While 4-in-a-row is certainly a simplistic way of testing encoding and retrieval of "events," it nonetheless tests memory in a fairly rich and meaningful way compared to much existing research, especially with regard to sequential order. The approach itself strikes a really nice balance between complexity in capturing elements of naturalistic human behavior, and simplicity in terms of analyses. Overall we think this experiment is sound, and the paper is well-written.

We have some requests for expansion/clarification and a few suggestions for strengthening the paper.

1. Looking at Figure 3c and 3d, it struck us that the slope of recall accuracy increases linearly across sessions 1-4, but then drops pretty markedly to sessions 5 and 6. If things simply leveled-off or dropped slightly, it would seem less important or interesting, but the drop-off is quite stark. What could be happening here? What do the authors make of this?

2. It was actually a bit surprising to us that the authors didn't use pupillometry when evaluating surprise. Pupil dilation has been strongly linked to the constructs of surprise and prediction error, more so than gaze. We are not necessarily suggesting that the authors rerun their model using pupillometry, but some rationale for why gaze rather than pupil dilation was optimal for testing surprise in this context would help. As it stands, we felt that this disconnect left the reasoning behind the surprise model feeling unclear, and we think a more explicit discussion of this would be helpful.

3. As the authors themselves flesh out in the Discussion, there is a fair amount of inconsistency in the literature as to whether schema-consistent (or "congruent," as others often say) or schema-inconsistent information provides relative a boost to episodic memory. And although we think their points related to this in the Discussion are fine, we think it would be worth laying out the reasoning for the prediction that schema-consistency should benefit memory in the Introduction. Our reasoning here is that, from our point of view, it could have easily gone either way. And we think that the field can benefit at this point from clear logic laying out predictions related to schema and memory.

4. Did the authors analyze reaction time data at all? To be clear, we are not making a strong suggestion to do so, but given links between surprise and response time variability, and the logical relationship between increasing experience and time taken to do something, it seems a logical thing to do in characterizing performance.

Reviewer #3 (Recommendations for the authors):

This paper presents a series of analyses of the relationship between predictive schemas – representations that allow people to form predictions about events in their environment – and performance in a memory task. Participants in the experiments learned to play a novel board game over a period of several days, and also performed a memory task in which they had to recall sequences of board positions. The first time they performed the memory task they had no experience with the game, so these just looked like random configurations of black and white circles. As players became more familiar with the game, the memory performance also improved.

Several analyses dig deeper into this phenomenon, examining how participants' memory for specific board positions are related to the probability of the corresponding moves in the game, as estimated by an AI agent. This analysis shows that people have better memory for higher probability moves. By bringing another group of participants into the laboratory and performing eye tracking, it was shown that people's eyes movements also seem to be influenced by the probability of moves. Further analyses that express confidence and surprise in terms of these eye movements – how focused people seem to be on a specific position and how long they spend looking at the correct position – show that these quantities are also related to memory.

Overall, I think this is an impressive piece of work that does a nice job of exploring several questions about the nature and origins of schema-based effects on memory performance through the clever use of a novel task. However, I do think there is one substantial potential confound. As people are getting better at playing the game, it seems like one potential strategy they might use is to worry less about memorizing the board positions and instead to simply consider how they would play from that position. People following this strategy would seem to account for all of the results that are presented: it would result in a higher probability of being correct on higher probability moves, and potentially produce the associated effects involving eye-movements since those eye-movements tend to be concentrated on the high probability moves as well.

This kind of confound is likely to arise in studies looking at schema effects on memory, because if people have a schema they can use that schema to make informed guesses that are more likely to be right for schema-consistent items. However, in this setting it seems like there is actually an opportunity to address this confound directly. I think this could be done by conducting a further study in which people play from the same board positions that are used to initiate the memory recall sequences – perhaps doing so on different days so as to remove concerns about interference. By measuring the actual play sequences that people generate, it would be possible to focus the analyses on cases where the memory sequences differ from these play sequences. In fact, if the play sequences are generated the day before the memory test, the memory test could include two kinds of trials: one set where the memory sequence corresponds to that produced by the participant on the previous day, and one where it diverges. If the reported effects are observed in both of these conditions, that helps to decouple simulated play from generic schema use (that is, if a move in a memory sequence that has high probability but wasn't played by the participant the previous day is still remembered well, it provides strong support for a schema effect rather than a play-based strategy).

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

Thank you for resubmitting your work entitled "Schema-based predictive eye movements support sequential memory encoding" for further consideration by eLife. Your revised article has been evaluated by Timothy Behrens (Senior Editor) and a Reviewing Editor.

Since the original two reviewers were not available to review the revised version, we have invited Reviewer 4 to evaluate the revision.

The manuscript has been improved but there are some remaining issues that need to be addressed, as outlined below:

1) Providing the learning curve of the control group (first session here) instead of the averaged results;

2) Please see detailed comments by Reviewer 4.

Reviewer #1 (Recommendations for the authors):

About the two major comments or experiments I raised, the authors have done a fine job addressing them. They have performed a simulation analysis to exclude the alternative explanation raised in the first question. They chose to use the first session of the data as the control group to answer the second question.

Their answers are fine but I would like to clarify my original point that may have been unclear. That is, showing the learning curve rather than a single point of the control group's performance, i.e., the first session, as a control.

Reviewer #4 (Recommendations for the authors):

Huang et al. examined the influence of schemas on prediction and sequence memory for a novel board game. Participants' memory for sequences of moves was tested across several sessions as they learned the game and improved. Over the sessions, and accompanied by a skill increase, participants' memory for the sequences improved. This learning was also related to eye-movements during encoding which were predictive of memory for the sequences.

This study does an excellent job of linking schema development to prediction/attention and memory.

Comments:

In the first paragraph of the Results section, it was unclear whether during the game play task participants were provided instructions or whether they had to learn the game through some kind of trial and error. It should be specified that they were provided with rules since early in the paragraph it notes that the participants were naive to the fact that a game was being shown in the initial memory test phase.

"Modeling schema-related memory improvement" In this section a model is trained based on moves from a near optimal AI. A probability distribution is made for upcoming moves based on the likelihood a move would be made by a near optimal AI. This probability is interpreted to be related to the schema consistency of a move. This may be true for an expert player. However, a near optimal move may not be schema-consistent for a new player or maybe even an average player. The participant's internal schema when they are beginners and progress may not map on to the near optimal AI moves. This is an interesting analysis, but calling the near optimal AI move schema consistent just slightly seems like a miswording for me.

Discussion "One possibility is that their study (in which participants implicitly learned statistical dependencies between image categories presented in a continuous stream) engages a predictive process that relies on the hippocampus (Schapiro et al., 2017), creating interference between prediction and encoding processes, while the explicit schematic predictions in our study could rely on a different network such as the medial prefrontal cortex " While this is a compelling assertion, can you describe anything that psychologically varies between these tasks? For example, Shapiro et al. had participants learn arbitrary statistical sequences, but here the sequences could be understood in the context of rules, goals, and progression towards goal states.

Methods: During the memory task, 10 out of the 30 sequences ended in a win state. Since a win-state caps off a sequence this could be thought of as an event boundary. Was there any effect of these 10 sequences that differed from the other 20 or interacted with other effects? For example, if a win-state is an event boundary, is particularly salient, and is better remembered, then a participant merely has to reconstruct the sequence from probe to win-state, rather than remembering each move.

Modeling schema-related memory improvement" In this section the authors missed a period in "near- optimal AI agent The model identifies".

https://doi.org/10.7554/eLife.82599.sa1

Author response

Essential revisions:

1) Instead of memorizing the board positions, subjects might simply consider how they play from that position, a strategy that could account for all the observations. To decouple the schema-based and purely-memory-based influences, a further control study needs to be conducted (see details in Reviewer 3's comments);

We have now conducted an additional analysis, in which we simulate schema-consistent guessing on the memory task using our AI game-playing model. Because this model was trained on gameplay distribution similar to those used in the memory task, this provides an upper bound on the best-possible performance achievable without using any episodic memory. We included a discussion of this simulation in the result section:

“Another potential explanation could be a change in participants’ strategy. In the beginning, participants can only use their episodic memory, but over time participants could start to use a purely schema-based strategy in which they simply place moves as if they are playing the game from this board position. We simulated this strategy by drawing moves probabilistically from the gameplay (schema) model for each initial board that participants saw during the memory task in each session. We found that purely schema-based guessing can only achieve an average accuracy of 13.39% across the 6 sessions (Figure 2a), which is much lower than participants’ average recall accuracy of 65.91%. This low accuracy is due to the fact that, for most of the sequences, there are multiple plausible moves that could be played and it is therefore difficult to guess the sequence without episodic knowledge. Therefore, the improvement in performance after learning the schema is unlikely due to mere guessing of the boards.” (line 268-280)

This simulation demonstrates that, even under optimal guessing, it is not possible for a non-episodic strategy to produce our observed results. We therefore do not believe it is necessary to run the proposed behavioral experiment with human participants, since selecting moves based on how the participant would play the game cannot yield performance higher than 13.39%.

Additionally, if participants were no longer attempting to memorize the specific moves being played, the time spent looking at the most recent move on the board would drop sharply after participants developed a schema. We therefore looked at the change across sessions for the last-move coefficient in our eye-movement analysis, which describes the extent to which participants look at the most recently-placed move. Although the last move coefficient did reduce numerically over time, this reduction is small and not significant (p = .114).

Author response image 1
Download asset Open asset

Based on the analyses presented above, we believe that a purely schema-based strategy is unlikely to explain the effects we observed in the study.

2) There lacks a control group who neither knows the rule nor play the game before. The prediction is that the control group will show (1) worse memory; (2) their error patterns are different and unrelated to p (move);

The first session for each participant did serve as exactly this control group, which we have now emphasized in the beginning of the result section.

“In the first session, participants were not told that these stimuli came from a game, and were only instructed to remember circles appearing on a grid. The first session therefore provided a no-schema baseline, since participants could not use a game model to make predictions about upcoming moves. In a post-task questionnaire, we confirmed that in session 1 most participants did not suspect that the stimuli were from a game or guess the rule of the game (14 out of 19 in the online study, and 13 out of 16 in the in-person study).” (line 111-114)

We found that subjects indeed had worse memory in this first session (figure 1) and that their recall accuracy was not related to the probability of the move (figure 3b, top left figure).

3) Reanalyzing the data to address the potential mixture of session-level and participant-level variability (see Reviewer 1's 2nd concern);

We now include random participant intercepts and slopes for all our regression models in the study, following the approach of Brauer and Curtin, Psychol Methods, 2018 (as recommended by Reviewer #1). In cases where this model failed to converge, we simplify the model, and used Bayesian priors to stabilize the coefficient estimates. This approach yielded conclusions largely similar to our previous (random-intercept-only) models for almost all analyses (lines 126-128, 171, 180-181, 197, 223, 295-296, 352-356, 372-377).

We described our approach for using frequentist and Bayesian models in the Methods:

“Regression Models

For each model, we started with the most complex frequentist model, including a subject slope and intercept for all the predictors. In cases where this model did not converge, we took two parallel approaches. First, we simplified the frequentist model by removing random slopes for some or all of the effects until the model converged. We also fit a Bayesian version of the complex model (with all random slopes). If these two approaches yielded the same result (with the same coefficients statistically different from zero), we reported the simpler frequentist model; if the results differed, we reported the result for the full Bayesian model. For frequentist models, we use lme4 pacakge (Bates et al., 2015). For the Bayesian models, we used the default settings of rstanarm package (Goodrich et al., 2022).” (line 719-727)

Accounting for across-subject variability did yield a different outcome for our analyses examining the relationship between Elo, prediction coefficient, and memory accuracy:

“To understand whether this relationship was present within individual participants, we fit a linear mixed effect model to predict memory performance from Elo with per-participant intercepts and slopes as random effects. We found that the relationship between Elo and memory accuracy was not significant in this model (β = 0.012, t = 1.196, p = .242), suggesting that this effect was primarily driven by individual differences (people with better schema tend to have better memory) rather than across-session improvements in Elo.” (line 143-148)

“We again tested whether these effects were present at the individual-participant level by running a linear mixed effect model with participant random intercepts and slopes. Due to model convergence issues, we employed a Bayesian version of this model to regularize the coefficient estimates (see Methods). We found that the 95% credibility interval for the fixed effect of Elo on prediction coefficient overlapped with 0 (β = 0.007, 95% CI = [-0.003, 0.016]). The 95% credibility interval for the fixed effect of prediction coefficient on recall accuracy also overlapped with 0 (β = 0.164, 95% CI = [-0.54, 0.87]). Together with previous findings, these results suggest that the observed mediation effect is primarily driven by individual differences rather than within-subject development over time.” (line 317-328)

We included in the discussion some interpretation of this results.

“There are several reasons why within-participant increases in Elo across sessions were not predictive of improvements in prediction and memory. First, our estimate of Elo during each memory task was based on gameplay performance on the prior day, which may not be a precise measure of the participant’s current schema. Second, the biggest increase in prediction occurred between sessions one and two, but the session one memory-task data cannot be included in this prediction model since participants have not yet played the game (and we therefore cannot estimate their Elo). Third, we may simply be underpowered to detect within-participant effects, since we only collected data from six sessions for each subject. Despite the lack of within-subject effect, the session-level analysis provided the novel insight that the memory advantage for more-expert players may be driven by superior predictive processes during encoding.” (line 419-429)

4) Further clarifications are needed, such as the drop-off in late sessions, reasons for not looking at pupil dilation, the rationale for schema-based memory facilitation hypothesis, and presentation of RT data (see Reviewer 2's comments)

Presentation of RT data

Thank you for the suggestion to include the RT data. It indeed showed a similar pattern to what we observed in accuracy data, further strengthening our conclusions about the relationship between schema-consistency and memory. We’ve included a discussion about this in the results:

“In addition to recall accuracy, we looked at reaction time for placing moves at recall. We only looked at moves that were correctly recalled in each session and removed outliers with reaction times longer than 30 sec (0.6% of all the correct moves were removed this way). Similar to accuracy, we found that reaction time during retrieval was initially not related to the probability of the move (β = -30.5, t = 0.975, p = .329) but consistently faster for more schema-consistent moves in session 2 through 6 (all p <.001, figure 3d). Running a mixed-effects model as for the accuracy (using linear rather than logistic regression), we found a main effect of session on reaction time (β = -156.3, t = -2.39, p = .017), such that participants were faster in later training sessions. There was no main effect of move probability (β = – 46.1, t = -0.440, p = .660) but a significant interaction between move probability and session on reaction time (β = – 71.06, t = -2.593, p = .010), with faster responses when remembering more schema-consistent moves.” (line 200-210)

We also modified figure 3 to include the figure showing the change in slope.

Drop-off in late sessions:

The reviewers are correct that, in the late sessions, move probability is less strongly related to memory accuracy and memory errors. We now statistically quantify this drop-off and discuss how participants may be changing their memory strategies in the final sessions of the experiment in order to further improve their accuracy:

“Although an overall increase across sessions was observed in both schema-consistent mistakes and the relationship between recall accuracy and move probability, these effects were significantly weaker at session 5 (for schema-consistent mistakes, t = -2.51, p = .02; for the relationship between recall accuracy and move probability, t = -3.24, p = .001), and numerically weaker at session 6 (for schema consistent mistakes, t = -1.70, p = 0.099; for the relationship between recall accuracy and move probability, t = -1.93, p = .053). One potential explanation for this drop is that people developed new strategies in later sessions to remember schema-inconsistent moves. As can be seen in figure 3b, the modeled recall accuracy for highly schema-inconsistent moves (low x values) increased from session 4 to 5 while the recall accuracy for schema-consistent moves remained relatively stable. This is consistent with the highest overall accuracy occurred in session 6 (figure 2a), suggesting that this decrease in slope does not come at a cost for memory accuracy. Note that reaction time did not show this weakening relationship with move probability in session 5 and 6, as its slope continues to decrease.” (line 225-237)

We also included a paragraph in the discussion about possible explanations for the observed effects.

“Interestingly, the relationship between recall accuracy and memory is attenuated in the last 2 sessions, driven by improved memory for schema-inconsistent moves. Expertise effects that partially extend to non-schematic situations have been previously observed; although chess experts’ memory advantage was primarily driven by very high accuracy for schema-consistent (legitimate) boards in Gobet and Waters (2003), experts also exhibited memory for random boards that was better than that of weaker players. One possibility is that experts may be able to devote fewer attentional resources to schematic moves, freeing up additional resources to handle more unusual moves. Participants in our study may have also developed an effortful strategy to remember schema-inconsistent moves (such as switching to a shape-based encoding for these moves), consistent with the longer reaction times observed for low-probability moves in later sessions.” (line 435-445)

The rationale for schema-based memory facilitation hypothesis

We modified the introduction to provide more justification for the hypothesis of schema-consistent memory benefits.

“Although previous research has sometimes found novelty-driven memory improvements for schema-inconsistent information (reviewed in Frank and Kafkas, 2021), studies of expert memory for complex memoranda such as chess boards have shown an advantage for schema-consistent stimuli (e.g., board positions from actual chess games) (Gobet and Waters, 2003). Thus, we hypothesized that the memory improvement resulting from the development of schema in 4-in-a-row should similarly be specific to moves that are schema-consistent.” (line 82-88)

Reasons for not looking at pupil dilation

The study was not designed to measure subtle changes in pupil diameter, and we have now added a paragraph about this limitation to the Discussion:

“Previous research has found a relationship between pupil dilation and surprise (e.g., Antony et al., 2021; Lavín et al., 2014; Preuschoff et al., 2011), but our study was not well-suited to measure subtle changes in pupil diameter. Studies of pupil dilation generally require tight control over the experimental stimuli, using either purely non-visual stimuli (Preuschoff et al., 2011), or by presenting luminance-controlled stimuli at fixation (Lavín et al., 2014). In our study the luminance at fixation is highly variable, since eye movements are not controlled and squares can be unoccupied (grey) or occupied by white or black pieces. Future work could attempt to study pupil dilation in this paradigm using models to control for local and global luminance (Antony et al. 2021) or by modifying the stimuli to ensure that all board spaces are isoluminant.” (Line 508-516)

That said, we did look at the time course of pupil size over time (5 sec before a move shows up and 5 sec after, downsampled to 100 Hz) when surprise (as defined by the extent to which pre-move fixations were in the incorrect location) is high (top 25%), low (bottom 25%), and medium (50% in the middle). We found that there was a consistent pattern of pupil size across trials, a ramp in size during each trial peaking about 300 ms after the presentation of the next move, and followed by a sharp constriction. This kind of decrease at event switches has also been observed at event boundaries in movies, and is hypothesized to be due to a drop in cognitive load at boundaries (Smith et al., 2006). As shown in Author response image 2, high-surprise moves did indeed have larger pupil sizes just after the move (at 300ms) and after the constriction (at 500-800ms). However, this effect is present even before the move is shown (starting at -4000ms), suggesting that surprise may be related to pre-move attentional state or may be more likely to occur on certain kinds of boards (e.g. boards with many pieces). Although this is an interesting result, we believe that it is out of the scope for the current paper. We are conducting a follow-up study in which the move participants see is independently manipulated to have different levels of surprise, and hope to more comprehensively explore the question about pupil size and surprise in this paradigm.

Author response image 2
Download asset Open asset

Reviewer #1 (Recommendations for the authors):

This paper develops an interesting and new experimental paradigm to investigate how schema participates in memory and helps to generate predictions, using behavioral measurements, eye movement recordings, and computational modeling. The results show the correlation between memory accuracy, game performance, and predictive eye movements, supporting that schema significantly boosts memory and guide prediction. This paper would be of potential interest to many fields, such as memory, learning, and decision-making.

We see two major strengths in the paper. First, although schema-based memory is crucial, it is very hard to study it in a natural and also controllable way in the lab. This work develops a complex game paradigm with proper difficulty levels, enabling the examination of the characteristics of the process. Second, the combination of memory behavior, eye movement, and game playing provides a comprehensive framework to tackle the question.

The major weakness of the work mainly lies in its lack of a control group, that is, subjects who neither know the rule nor play the game before. This would be important evidence to support the advantage of schema-based memory boosting. Moreover, the source of the effects needs to be further clarified using additional analyses.

Concerns:

1. Schema-based boost in memory and predictive eye movement lacks a control group who neither know the rule nor play the game before. The prediction is that the control group will show (1) worse memory; (2) their error patterns are different and unrelated to p (move).

Please see our response to Essential revisions comment #2.

2. Most of the correlation analyses mixed the variability levels and thus confused the source of the memory boosting effects. For example, when calculating the correlation results (Figure 2C), each data point represents a session of a participant. In this case, the source of the effect could come from either session-level variability that is due to training or participant-level variability. In fact, all the linear mixed-effect models have the same problem and need to be fixed. I would not suggest excluding the random effect for slopes since that would increase the probability of Type I error and as a consequence, the observed effect might arise from individual differences rather than experimental manipulation (see Brauer and Curtin, Psychol Methods, 2018 and Bates, arXiv, 2018 for guides). It is important to include individual-level random effects in the analysis.

Please see our response to Essential revisions comment #3.

Reviewer #2 (Recommendations for the authors):

This paper by Huang and colleagues uses a simple board game, "4-in-a-row," to test the relationship between schemas and episodic memory. Specifically, the goal here was to examine the way schemas can guide encoding of sequential events as the game unfolded. In sum, the authors report that memory for move sequences in the game improved with player skill, and that memory was particularly improved for schema-consistent sequences. Further, eye movements during encoding were associated with stronger memory for move sequences, which was most prevalent in expert players.

We think this study does a fine job of answering how the development of schema aid in prediction and thereby memory through use of a stimulus that is at once naturalistic but learnable by participants in laboratory time. This is a difficult set of boxes to check. While 4-in-a-row is certainly a simplistic way of testing encoding and retrieval of "events," it nonetheless tests memory in a fairly rich and meaningful way compared to much existing research, especially with regard to sequential order. The approach itself strikes a really nice balance between complexity in capturing elements of naturalistic human behavior, and simplicity in terms of analyses. Overall we think this experiment is sound, and the paper is well-written.

We have some requests for expansion/clarification and a few suggestions for strengthening the paper.

1. Looking at Figure 3c and 3d, it struck us that the slope of recall accuracy increases linearly across sessions 1-4, but then drops pretty markedly to sessions 5 and 6. If things simply leveled-off or dropped slightly, it would seem less important or interesting, but the drop-off is quite stark. What could be happening here? What do the authors make of this?

Please see our response to Essential revisions comment #4.

2. It was actually a bit surprising to us that the authors didn't use pupillometry when evaluating surprise. Pupil dilation has been strongly linked to the constructs of surprise and prediction error, more so than gaze. We are not necessarily suggesting that the authors rerun their model using pupillometry, but some rationale for why gaze rather than pupil dilation was optimal for testing surprise in this context would help. As it stands, we felt that this disconnect left the reasoning behind the surprise model feeling unclear, and we think a more explicit discussion of this would be helpful.

Here, we sought to operationalize surprise in terms of prediction accuracy. High surprise means that the specific move prediction made by the participant (as measured via gaze position) was not confirmed. We have now clarified our definition of surprise in the Results:

“The second measure is surprise, which is the negative log of the proportion of fixation time spent looking at the correct next move position. A high level of surprise indicates that a participant spent very little time looking at the square where the next move ended up appearing, which indicates low prediction accuracy.” (line 366-370)

For a discussion of pupil dilation effects in the study, please see our response to Essential revisions comment #4.

3. As the authors themselves flesh out in the Discussion, there is a fair amount of inconsistency in the literature as to whether schema-consistent (or "congruent," as others often say) or schema-inconsistent information provides relative a boost to episodic memory. And although we think their points related to this in the Discussion are fine, we think it would be worth laying out the reasoning for the prediction that schema-consistency should benefit memory in the Introduction. Our reasoning here is that, from our point of view, it could have easily gone either way. And we think that the field can benefit at this point from clear logic laying out predictions related to schema and memory.

Please see our response to Essential revisions comment #4.

4. Did the authors analyze reaction time data at all? To be clear, we are not making a strong suggestion to do so, but given links between surprise and response time variability, and the logical relationship between increasing experience and time taken to do something, it seems a logical thing to do in characterizing performance.

Please see our response to Essential revisions comment #4.

Reviewer #3 (Recommendations for the authors):

This paper presents a series of analyses of the relationship between predictive schemas – representations that allow people to form predictions about events in their environment – and performance in a memory task. Participants in the experiments learned to play a novel board game over a period of several days, and also performed a memory task in which they had to recall sequences of board positions. The first time they performed the memory task they had no experience with the game, so these just looked like random configurations of black and white circles. As players became more familiar with the game, the memory performance also improved.

Several analyses dig deeper into this phenomenon, examining how participants' memory for specific board positions are related to the probability of the corresponding moves in the game, as estimated by an AI agent. This analysis shows that people have better memory for higher probability moves. By bringing another group of participants into the laboratory and performing eye tracking, it was shown that people's eyes movements also seem to be influenced by the probability of moves. Further analyses that express confidence and surprise in terms of these eye movements – how focused people seem to be on a specific position and how long they spend looking at the correct position – show that these quantities are also related to memory.

Overall, I think this is an impressive piece of work that does a nice job of exploring several questions about the nature and origins of schema-based effects on memory performance through the clever use of a novel task. However, I do think there is one substantial potential confound. As people are getting better at playing the game, it seems like one potential strategy they might use is to worry less about memorizing the board positions and instead to simply consider how they would play from that position. People following this strategy would seem to account for all of the results that are presented: it would result in a higher probability of being correct on higher probability moves, and potentially produce the associated effects involving eye-movements since those eye-movements tend to be concentrated on the high probability moves as well.

This kind of confound is likely to arise in studies looking at schema effects on memory, because if people have a schema they can use that schema to make informed guesses that are more likely to be right for schema-consistent items. However, in this setting it seems like there is actually an opportunity to address this confound directly. I think this could be done by conducting a further study in which people play from the same board positions that are used to initiate the memory recall sequences – perhaps doing so on different days so as to remove concerns about interference. By measuring the actual play sequences that people generate, it would be possible to focus the analyses on cases where the memory sequences differ from these play sequences. In fact, if the play sequences are generated the day before the memory test, the memory test could include two kinds of trials: one set where the memory sequence corresponds to that produced by the participant on the previous day, and one where it diverges. If the reported effects are observed in both of these conditions, that helps to decouple simulated play from generic schema use (that is, if a move in a memory sequence that has high probability but wasn't played by the participant the previous day is still remembered well, it provides strong support for a schema effect rather than a play-based strategy).

Please see our response to Essential revisions comment #1.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

Reviewer #1 (Recommendations for the authors):

About the two major comments or experiments I raised, the authors have done a fine job addressing them. They have performed a simulation analysis to exclude the alternative explanation raised in the first question. They chose to use the first session of the data as the control group to answer the second question.

Their answers are fine but I would like to clarify my original point that may have been unclear. That is, showing the learning curve rather than a single point of the control group's performance, i.e., the first session, as a control.

Also, in response to our request for additional clarification, an editor wrote:

(1) providing the learning curve of a control group who are naïve to game rules, instead of using only the first session of the old data as a control. The authors chose to use the first session of data as a control group to answer the second question raised by Reviewer 1. Meanwhile, to demonstrate that the memory improvement after the first gameplay task is due to schema as claimed by the authors rather than training practice, it would be helpful to show the learning curve of a control group who are naïve to game rules throughout the whole experiment, rather than only the first-day memory performance.

Our response: Providing a full learning curve for a control group presents some logistical challenges, since this would require at least three months of new data collection using our department’s shared eye-tracking equipment. There is also a more fundamental challenge, in that participants are likely to eventually learn the rules of the game through pure exposure, even without explicit instruction. We now address these issues in the Methods:

“We did not include a control group that completed six memory sessions without being told the rules of the game or playing against the AI agent. Ensuring that participants never develop a game schema would be difficult, since even without explicit instruction they could still learn the schema through implicit statistical learning or by guessing the (simple) rules of the game. Due to these challenges, we instead used the first-session performance of each participant as our no-schema control.”

We also discuss the limitations of our one-session control in our Discussion:

“Note that some of the overall accuracy increase in the memory task across sessions could be attributable to a practice effect, but general practice-related improvement does not explain the schema-related effects that we observed on individual trials.”

Reviewer #4 (Recommendations for the authors):

Huang et al. examined the influence of schemas on prediction and sequence memory for a novel board game. Participants' memory for sequences of moves was tested across several sessions as they learned the game and improved. Over the sessions, and accompanied by a skill increase, participants' memory for the sequences improved. This learning was also related to eye-movements during encoding which were predictive of memory for the sequences.

This study does an excellent job of linking schema development to prediction/attention and memory.

Comments:

In the first paragraph of the Results section, it was unclear whether during the game play task participants were provided instructions or whether they had to learn the game through some kind of trial and error. It should be specified that they were provided with rules since early in the paragraph it notes that the participants were naive to the fact that a game was being shown in the initial memory test phase.

Thank you for your comments. We have now clarified this in the Results section.

“In a separate game play task (occurring after the memory task on all but the last day), the player was provided with the rules of the game and played the 4-in-a-row game against an AI opponent, staircased to match the skill level of the player.”

"Modeling schema-related memory improvement" In this section a model is trained based on moves from a near optimal AI. A probability distribution is made for upcoming moves based on the likelihood a move would be made by a near optimal AI. This probability is interpreted to be related to the schema consistency of a move. This may be true for an expert player. However, a near optimal move may not be schema-consistent for a new player or maybe even an average player. The participant's internal schema when they are beginners and progress may not map on to the near optimal AI moves. This is an interesting analysis, but calling the near optimal AI move schema consistent just slightly seems like a miswording for me.

Thank you for your comments on the use of the term "near-optimal AI" and its relation to schema consistency. Upon reflection, we realize that describing our gameplay model as "near-optimal" might be misleading. Our model was trained on near-optimal gameplay generated by near-optimal AI used in van Opheusden et al. (2021). However, our model is a simplified myopic model, which only captures some of the features of the near-optimal gameplay. We have removed the words “optimal” or “near-optimal” when they are used to describe our gameplay model.

We have clarified our use of “schema consistency” in the result section.

“Here, schema consistency is used as an objective, subject-independent measure of how good a move is. Each subject will exhibit different degrees of alignment to this “ground-truth” schema.”

We agree that individual participants’ schemas (especially those of the novices) will not always match exactly with our gameplay model. This difference in schema across people is one of the things that leads to the variability in our dependent measures (like how much schema-dependent prediction they exhibit). We would also like to note that although people have different degrees of alignment to the optimal AI schema, these schemas are qualitatively the same. We’ve included a discussion of this in Method section:

“We use the model’s evaluation of each move as a measure of the schema consistency of a move, assuming that stronger and weaker players have qualitatively the same schema for what makes a good move. An alternative possibility is that individuals develop schemas that are qualitatively distinct from the gameplay model, which will be reflected in some people playing moves that have very low probability in our gameplay model. We did not find evidence for this possibility in our dataset; during the gameplay sessions, all participants tended to play moves with relatively high probability under the gameplay model (M = 0.213, range = 0.143 – 0.297, compared to a random-move baseline of 0.040). We also observed a strong correlation between Elo and this move probability measure (r = .40, p <.001), showing that stronger players are more aligned with our model. Future work (with more extensive gameplay sessions) could attempt to model unique feature weights for each specific individual.”

Discussion "One possibility is that their study (in which participants implicitly learned statistical dependencies between image categories presented in a continuous stream) engages a predictive process that relies on the hippocampus (Schapiro et al., 2017), creating interference between prediction and encoding processes, while the explicit schematic predictions in our study could rely on a different network such as the medial prefrontal cortex " While this is a compelling assertion, can you describe anything that psychologically varies between these tasks? For example, Shapiro et al. had participants learn arbitrary statistical sequences, but here the sequences could be understood in the context of rules, goals, and progression towards goal states.

Thank you for your points about the cognitive difference between tasks. We have now incorporated these cognitive differences into our description of why they might rely on different neural mechanisms:

“One possibility is that their study (in which participants implicitly learned arbitrary statistical dependencies between image categories presented in a continuous stream) engages a predictive process that relies on the hippocampus (Schapiro et al., 2017), creating interference between prediction and encoding processes. On the other hand, the explicit schematic predictions in our study that are based on rules and progression towards goal states might rely on a different network such as the medial prefrontal cortex (Bonasia et al., 2018; Robin and Moscovitch, 2017; van Kesteren et al., 2012).”

Methods: During the memory task, 10 out of the 30 sequences ended in a win state. Since a win-state caps off a sequence this could be thought of as an event boundary. Was there any effect of these 10 sequences that differed from the other 20 or interacted with other effects? For example, if a win-state is an event boundary, is particularly salient, and is better remembered, then a participant merely has to reconstruct the sequence from probe to win-state, rather than remembering each move.

Thank you for your suggestions. We have now conducted additional analyses that indeed show that memory for sequences that ended in a win state differ from the rest of other sequences after people developed a schema. We discussed this finding in the Results:

“Out of the 30 sequences shown to participants in each session, ten of them ended with one player successfully getting four pieces in a row (more details in Methods). After learning the rules of the game, the presence of such a win could be a salient event for the participant and could lead to changes in memory performance. Indeed, we found that in sessions 2-6, memory for sequences that ended in a win state was significantly better (t = 6.67, p <.001). We did not observe this pattern in the first session (before participants were taught the game rules), and actually found a marginally significant effect in the opposite direction, with worse memory for winning sequences (t = -2.01, p = .052). This result provides additional evidence that schema-related features of a sequence play a role in memory performance.”

Modeling schema-related memory improvement" In this section the authors missed a period in "near- optimal AI agent The model identifies"

Fixed.

https://doi.org/10.7554/eLife.82599.sa2

Article and author information

Author details

  1. Jiawen Huang

    Department of Psychology, Columbia University, New York, United States
    Contribution
    Conceptualization, Data curation, Software, Formal analysis, Investigation, Visualization, Methodology, Writing - original draft, Project administration, Writing - review and editing
    For correspondence
    jh4290@columbia.edu
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0003-1362-0412

  2. Isabel Velarde

    Department of Psychology, Columbia University, New York, United States
    Contribution
    Data curation, Project administration, Writing - review and editing
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0001-5639-0907

  3. Wei Ji Ma

    Center for Neural Science and Department of Psychology, New York University, New York, United States
    Contribution
    Conceptualization, Resources, Software, Supervision, Methodology, Writing - review and editing
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-9835-9083

  4. Christopher Baldassano

    Department of Psychology, Columbia University, New York, United States
    Contribution
    Conceptualization, Resources, Software, Formal analysis, Supervision, Funding acquisition, Validation, Visualization, Methodology, Project administration, Writing - review and editing
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0003-3540-5019

Funding

Columbia University (Graduate Student Fellowship)

  • Jiawen Huang

Columbia University (start-up funding)

  • Christopher Baldassano

National Institutes of Health (R21MH126269)

  • Wei Ji Ma

National Institutes of Health (R01MH118925)

  • Wei Ji Ma

National Science Foundation (2008331)

  • Wei Ji Ma

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Ethics

The experimental protocol was approved by the Institutional Review Board of Columbia University. (AAAS0252) All participants were over 18 years of age with normal or corrected-to-normal vision, and gave informed consent.

Senior Editor

  1. Timothy E Behrens, University of Oxford, United Kingdom

Reviewing Editor

  1. Huan Luo, Peking University, China

Reviewer

  1. Zachariah M Reagh

Version history

  1. Preprint posted: July 20, 2022 (view preprint)
  2. Received: August 10, 2022
  3. Accepted: March 24, 2023
  4. Accepted Manuscript published: March 27, 2023 (version 1)
  5. Version of Record published: April 12, 2023 (version 2)

Copyright

© 2023, Huang et al.

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

  • 1,087
    Page views
  • 159
    Downloads
  • 2
    Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Jiawen Huang
  2. Isabel Velarde
  3. Wei Ji Ma
  4. Christopher Baldassano
(2023)
Schema-based predictive eye movements support sequential memory encoding
eLife 12:e82599.
https://doi.org/10.7554/eLife.82599

Categories and tags

Research organism

Further reading

    1. Neuroscience

    Associative memory neurons of encoding multi-modal signals are recruited by neuroligin-3-mediated new synapse formation

    Yang Xu, Tian-liang Cui ... Jin-Hui Wang
    Research Article

    The joint storage and reciprocal retrieval of learnt associated signals are presumably encoded by associative memory cells. In the accumulation and enrichment of memory contents in lifespan, a signal often becomes a core signal associatively shared for other signals. One specific group of associative memory neurons that encode this core signal likely interconnects multiple groups of associative memory neurons that encode these other signals for their joint storage and reciprocal retrieval. We have examined this hypothesis in a mouse model of associative learning by pairing the whisker tactile signal sequentially with the olfactory signal, the gustatory signal, and the tail-heating signal. Mice experienced this associative learning show the whisker fluctuation induced by olfactory, gustatory, and tail-heating signals, or the other way around, that is, memories to multi-modal associated signals featured by their reciprocal retrievals. Barrel cortical neurons in these mice become able to encode olfactory, gustatory, and tail-heating signals alongside the whisker signal. Barrel cortical neurons interconnect piriform, S1-Tr, and gustatory cortical neurons. With the barrel cortex as the hub, the indirect activation occurs among piriform, gustatory, and S1-Tr cortices for the second-order associative memory. These associative memory neurons recruited to encode multi-modal signals in the barrel cortex for associative memory are downregulated by neuroligin-3 knockdown. Thus, associative memory neurons can be recruited as the core cellular substrate to memorize multiple associated signals for the first-order and the second-order of associative memories by neuroligin-3-mediated synapse formation, which constitutes neuronal substrates of cognitive activities in the field of memoriology.

    1. Chromosomes and Gene Expression
    2. Neuroscience

    Avoiding false discoveries in single-cell RNA-seq by revisiting the first Alzheimer’s disease dataset

    Alan E Murphy, Nurun Fancy, Nathan Skene
    Research Article

    Mathys et al. conducted the first single-nucleus RNA-seq (snRNA-seq) study of Alzheimer’s disease (AD) (Mathys et al., 2019). With bulk RNA-seq, changes in gene expression across cell types can be lost, potentially masking the differentially expressed genes (DEGs) across different cell types. Through the use of single-cell techniques, the authors benefitted from increased resolution with the potential to uncover cell type-specific DEGs in AD for the first time. However, there were limitations in both their data processing and quality control and their differential expression analysis. Here, we correct these issues and use best-practice approaches to snRNA-seq differential expression, resulting in 549 times fewer DEGs at a false discovery rate of 0.05. Thus, this study highlights the impact of quality control and differential analysis methods on the discovery of disease-associated genes and aims to refocus the AD research field away from spuriously identified genes.

    1. Neuroscience

    Network-level changes in the brain underlie fear memory strength

    Josue Haubrich, Karim Nader
    Research Article

    The strength of a fear memory significantly influences whether it drives adaptive or maladaptive behavior in the future. Yet, how mild and strong fear memories differ in underlying biology is not well understood. We hypothesized that this distinction may not be exclusively the result of changes within specific brain regions, but rather the outcome of collective changes in connectivity across multiple regions within the neural network. To test this, rats were fear conditioned in protocols of varying intensities to generate mild or strong memories. Neuronal activation driven by recall was measured using c-fos immunohistochemistry in 12 brain regions implicated in fear learning and memory. The interregional coordinated brain activity was computed and graph-based functional networks were generated to compare how mild and strong fear memories differ at the systems level. Our results show that mild fear recall is supported by a well-connected brain network with small-world properties in which the amygdala is well-positioned to be modulated by other regions. In contrast, this connectivity is disrupted in strong fear memories and the amygdala is isolated from other regions. These findings indicate that the neural systems underlying mild and strong fear memories differ, with implications for understanding and treating disorders of fear dysregulation.