How cells determine the number of polarity sites

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: May 12, 2021 (This version)
Accepted Manuscript published: April 26, 2021 (Go to version)
Accepted: April 23, 2021
Received: May 10, 2020

1. Of interest
Insights into cargo sorting by SNX32 and its role in neurite outgrowth

Jini Sugatha, Amulya Priya ... Sunando Datta

Research Article Updated May 26, 2023
Further reading

Article
Figures and data
Abstract
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

The diversity of cell morphologies arises, in part, through regulation of cell polarity by Rho-family GTPases. A poorly understood but fundamental question concerns the regulatory mechanisms by which different cells generate different numbers of polarity sites. Mass-conserved activator-substrate (MCAS) models that describe polarity circuits develop multiple initial polarity sites, but then those sites engage in competition, leaving a single winner. Theoretical analyses predicted that competition would slow dramatically as GTPase concentrations at different polarity sites increase toward a ‘saturation point’, allowing polarity sites to coexist. Here, we test this prediction using budding yeast cells, and confirm that increasing the amount of key polarity proteins results in multiple polarity sites and simultaneous budding. Further, we elucidate a novel design principle whereby cells can switch from competition to equalization among polarity sites. These findings provide insight into how cells with diverse morphologies may determine the number of polarity sites.

Introduction

Eukaryotic cells display a very wide diversity of cell morphologies, which are often critical to carry out specialized cell functions. Different morphologies arise through specific arrangements and actions of the cytoskeleton. In turn, the cytoskeleton is regulated by the conserved Rho family of GTPases (Etienne-Manneville and Hall, 2002). A subset of these GTPases (Cdc42, Rac, Rop) regulates cell polarity by concentrating at one or more regions of the plasma membrane (Park and Bi, 2007; Wu and Lew, 2013). In many cell types (e.g. migrating cells, plant pollen tubes, and root hairs or diverse budding yeasts including Saccharomyces cerevisiae, Candida albicans, Cryptococcus neoformans, and Ustilago maydis), it is crucial to maintain one and only one polarity domain, establishing a single polarity axis (front) that leads to movement or growth in that direction (Chiou et al., 2017; Houk et al., 2012; Wu and Lew, 2013; Yang and Lavagi, 2012). In other cell types (e.g. neurons with many neurite tips, plant cells that form xylem, or filamentous fungal cells with branches), multiple active-GTPase polarity sites coexist in the same cell (Dotti et al., 1988; Knechtle et al., 2003; Oda and Fukuda, 2012). These differences raise the question of how Rho-GTPase polarity systems in specific cell types can be tuned to yield the desired number of polarized fronts.

It has long been appreciated that interacting biochemical networks that include positive feedback and differential diffusion of reactants can generate systems capable of spontaneous pattern formation (Meinhardt, 2008; Meinhardt and Gierer, 1974; Turing, 1952). Key properties of pattern formation by polarity GTPase systems can be captured by a subset of such systems that we refer to as Mass Conserved Activator Substrate (MCAS) models (Brauns et al., 2020b; Chiou et al., 2018; Goryachev and Pokhilko, 2008; Halatek et al., 2018; Jilkine and Edelstein-Keshet, 2011; Mori et al., 2008; Otsuji et al., 2007; Otsuji et al., 2010). These models consist of sets of partial differential equations (PDEs) that encode the interconversion of polarity factors between two forms: a membrane-bound (and hence slow-diffusing) ‘activator’ and a cytosolic (and hence rapidly diffusing) ‘substrate’ (Figure 1A). One critical feature of these systems is positive feedback, such that membrane regions with higher concentrations of activator can locally recruit and activate more substrate from the cytoplasm. A second critical feature is the difference in diffusivity between the activator and the substrate, allowing a localized accumulation of activator to recruit substrate from a much wider region of cytoplasm. A third critical feature is mass conservation: because the combined amount of activator and substrate is fixed, accumulation of activator at the membrane depletes substrate from the cytoplasm, limiting the size, activator concentration, and potentially the number of permissible activator-enriched regions.

Figure 1 with 1 supplement see all

Download asset Open asset

Competition in a mechanistic Rho-GTPase model.

(A) Rho-GTPase polarity circuits can be modeled as mass-conserved reaction-diffusion systems where membrane-bound Rho-GTP (red) is a slow-diffusing activator and cytosolic Rho-GDP (blue) is a fast-diffusing substrate. Such systems polarize Rho-GTPase to spatially confined polarity sites based on positive feedback (+) via local activation that recruits substrate from the cytoplasm, leading to global substrate depletion. (B) A starting condition with two unequal peaks of activator can evolve in three ways. Competition occurs if the larger peak recruits substrate better than the smaller; coexistence occurs if both peaks recruit substrate equally well; and equalization occurs if the smaller peak recruits substrates better than the larger. (C) Schematic of the minimalistic MCAS model with one Rho-GTPase converting between activator (u: Rho-GTP, red) and substrate (v: Rho-GDP, blue) forms. Arrows depict reactions. The positive feedback is highlighted in red (see text for details). (D) In the minimalistic model, as total protein amount in the system increases, peak u concentration (red) approaches a saturation point while basal v concentration (blue) declines to a limit. Basal here refers to the concentration at the edge of the peak. 1x protein amount equivalent to starting uniform v concentration of 2. (E) Snapshots of simulations starting from two single peak steady states placed next to each other in the same domain. With peaks far from saturation, the larger peak depletes more substrate than the smaller (Left panel, starting protein amounts 0.6x, 1x), leading to a net flux of substrate (arrow) that results in competition. With peaks close to saturation, substrate depletion is similar for both (Right panel, starting protein amounts 2x, 4x), leading to little flux and therefore coexistence. (F) Schematic of a mechanistic model of the yeast polarity circuit: arrows depict reactions assumed to occur with mass-action kinetics. The positive feedback is highlighted in red. (G) Increasing total protein amount saturates the peaks similarly to D. (H) Basal cytosolic level of the limiting species Bem1-GEF declines to a limit while that of Cdc42 increases with increased total protein amount. (I) Competition time increases as peaks saturate. Competition was started from two insulated 1-peak steady states each containing 60% and 40% of the total proteins. Competition time is defined by the time it takes to evolve from 70%:30% (relative Cdc42T amounts between two peaks) to 99%:1%.

MCAS models at the homogeneous steady state can develop inhomogeneous activator distributions either spontaneously through Turing instability, or in response to external cues. Once a local region becomes enriched for activator, it grows (acquires more activator) by recruiting more activator from the cytoplasm, eventually depleting cytoplasmic substrate levels until the system reaches a polarized steady state with a local peak in activator concentration. However, the fate of any given peak depends on the presence of other peaks, which can also deplete substrate from the cytoplasm. Peaks that differ in amount of activator would also differ in their ability to recruit cytoplasmic substrate (Chiou et al., 2018). A hypothetical case with two initial unequal peaks could evolve in three possible directions (Figure 1B): (1) Competition: If the peak with more activator grows more rapidly, then as cytoplasmic substrate levels become depleted, the smaller peak would be starved of the fuel it needs to survive, and begin to shrink, losing activator until there is only one peak at steady state. (2) Coexistence: If the two unequal peaks both grow at the same rate, they would persist indefinitely. (3) Equalization: If the peak with less activator grows more rapidly, then that would continue until the two are equal.

To capture essential behaviors of MCAS systems, previous research conducted in-depth mathematical analyses on minimalistic one-activator, one-substrate MCAS models. These analyses indicated that the mass conservation feature enforces the competition scenario, with the largest peak eventually becoming the only one (Brauns et al., 2020b; Chiou et al., 2018; Ishihara et al., 2007; Otsuji et al., 2007; Otsuji et al., 2010). However, recent modeling studies have shown that the growth rate of a peak ‘saturates’ as the activator in the peak exceeds a threshold. If more than one peak saturates, then the system switches to a coexistence scenario for biologically relevant timescales. This conclusion is general for minimalistic MCAS models, and the degree of saturation is the dominant factor determining uni- or multi-polar outcomes (Brauns et al., 2020a; Chiou et al., 2018). Equalization does not appear possible in minimalistic MCAS models, but has been observed in more complex models of some polarity circuits (Howell et al., 2012; Jacobs et al., 2019). The basis for equalization in such models is not well understood, and it has not yet been determined whether saturation or equalization occurs in cells.

One well-studied experimental system ideal for testing theoretical predictions of MCAS models is the budding yeast Saccharomyces cerevisiae. In yeast, the polarity GTPase Cdc42 cycles between a slow-diffusing GTP-bound form and a rapidly diffusing GDP-bound form. GTP-Cdc42 binds effector p21-activated kinases (PAKs)(Bose et al., 2001; Cvrcková et al., 1995; Lamson et al., 2002; Zhao et al., 1995), which bind the scaffold protein Bem1 (Bose et al., 2001; Leeuw et al., 1995), which binds the GEF Cdc24 that activates Cdc42 (Bose et al., 2001; Butty et al., 2002; Ito et al., 2001; Peterson et al., 1994; Rapali et al., 2017). These interactions allow GTP-Cdc42 to recruit its own GEF, activating neighboring Cdc42 to yield positive feedback (Johnson et al., 2011; Kozubowski et al., 2008). This mechanism of positive feedback has recently been powerfully supported by findings of optogenetic approaches in several fungi (Lamas et al., 2020; Silva et al., 2019; Witte et al., 2017). Competition between polarity peaks has been observed experimentally in yeast, leading to development of a single Cdc42-enriched cortical region that generates a single bud in every cell cycle (Howell et al., 2012; Witte et al., 2017; Wu et al., 2015).

Here, we show that consistent with MCAS model predictions, larger yeast cells can generate multiple buds, in a manner that depends on the dosage of polarity genes. Furthermore, we identify a key feature in mechanistic MCAS models that enables equalization, and elucidate the underlying theoretical basis. By imaging polarization in cells that make multiple buds, we find that coexistence is the predominant mechanism that yields multi-budded yeast cells.

Results

A mechanistic model for the yeast Cdc42 system exhibits saturation, and switches from competition to coexistence as protein levels increase

In minimalistic models, positive feedback ensures that peaks with more activator are better at recruiting substrate than peaks with less, and therefore that larger peaks deplete cytoplasmic substrate more effectively than smaller peaks. Thus, when peaks of unequal size are present, the larger peak more effectively depletes the substrate, creating a cytoplasmic substrate gradient toward the larger peak that drives competition. However, as the amount of activator in a peak increases, the ability to recruit substrate eventually saturates, yielding a plateau in basal cytoplasmic substrate level (Chiou et al., 2018; Figure 1D). Note that at steady state, there is a local dip in cytoplasmic substrate concentration that mirrors the local peak in activator at the membrane: here we refer to the ‘basal’ substrate level as the substrate concentration that is reached outside this dip (i.e. the substrate concentration just outside the peak). It is a difference in the basal substrate levels between two peaks that can drive a flux of substrate from one peak to the other. But, as peaks approach saturation, the cytoplasmic substrate gradient becomes negligible, resulting in apparent coexistence (Figure 1E). This general result applies to both 1D and 2D models, although timescales of competition may differ (Chiou et al., 2018). However, it was unclear whether more complex MCAS models with multiple species would similarly exhibit saturation.

We first asked whether a multi-species mechanistic 2D model of the budding yeast system (Goryachev and Pokhilko, 2008; Wu et al., 2015) behaved in a similar manner to the minimalistic models in terms of saturation. The mechanistic model explicitly considers two species analogous to ‘activators’ at the membrane (GTP-Cdc42 and the Bem1-GEF-Cdc42 complex), either of which can be considered as promoting positive feedback through the other. The model also considers two cytoplasmic species as their respective ‘substrates’ (GDP-Cdc42 and Bem1-GEF), as well as other intermediate species with different characteristics (GDP-Cdc42 and Bem1-GEF at the membrane) (Figure 1F). When the total amounts of both Cdc42 and Bem1-GEF were increased in parallel, the cytoplasmic substrate Bem1-GEF was depleted and quickly reached a plateau (Figure 1G,H), similar to substrate depletion in the minimalistic model. In contrast, levels of the cytoplasmic substrate Cdc42 increased, indicating that this substrate was in excess and failed to saturate (Figure 1H). Increasing the amount of Cdc42 or Bem1-GEF complex individually also resulted in substrate depletion, but the species exhibiting saturation changed depending on which protein was added (Figure 1—figure supplement 1). We conclude that similar to minimalistic models, the mechanistic model exhibits saturation. However, in a multi-component system saturation is only seen for the limiting species. We note that the limiting species may not be the less abundant one, as other parameters of the model also influence which species becomes limiting.

We next asked whether saturation leads to coexistence in the mechanistic model. When simulations were initiated with two unequal peaks, competition occurred rapidly with low protein amounts, but slowed in a non-linear manner as the total amount of protein in the system was increased (Figure 1I), generating competition times that would be long compared to the yeast bud emergence timescale. In summary, saturation is also evident in a mechanistic model with multiple species, and as in minimalistic models, the approach to saturation slows competition, driving the system toward coexistence.

Testing model predictions: multi-polar growth in large yeast cells

A simple prediction emerging from the polarity models discussed above is that cells should switch from competition to coexistence as the amount of polarity ‘activators’ in the peaks increase. However, raising total protein concentrations in MCAS models generally drives them into a regime where Cdc42 activation occurs over the entire surface, yielding a uniform (depolarized) steady state. Indeed, previous work indicated that extreme overexpression or global optogenetic activation of polarity proteins leads primarily to depolarization, with only occasional multi-polarity (Howell et al., 2012; Howell et al., 2009; Lamas et al., 2020; Silva et al., 2019; Witte et al., 2017; Ziman and Johnson, 1994). A more robust way to generate multiple polarity domains would be to increase the size of cell while keeping overall protein concentrations constant (Chiou et al., 2018; Ishihara et al., 2007): this should lead to multi-budded cells while avoiding depolarized outcomes. One way to increase cell size is to arrest the cell cycle, but in yeast this approach leads to cytoplasm dilution as biosynthesis fails to keep pace with volume growth (Neurohr et al., 2019). Instead, we utilized cytokinesis-defective yeast mutants to obtain large connected cells that continue cycling but retain a normal overall protein composition.

The temperature-sensitive septin mutant cdc12-6 is defective in cytokinesis at 37°C, generating chains of elongated, connected cells (Figure 2A, Video 1; Hartwell, 1971). Control experiments confirmed the continuity of the cytoplasm between the connected cells (Figure 2—figure supplement 1A), and showed that the concentration of polarity proteins remained constant as the cells grew larger (see below). In the first cell cycle after switching to 37°C, all cells generated a single bud, which remained connected to the mother. In the second cell cycle, most cells formed a single bud despite having two cell bodies and two nuclei. This is consistent with the idea that these larger cells retained an effective competition mechanism that yields only a single winning polarity site to produce the bud. However, a few cells generated two buds simultaneously. The fraction of multi-budded cells increased dramatically in the third and the fourth cell cycles (Figure 2B). Similar multi-budded outcomes were observed in a conditional cytokinesis-defective iqg1 strain (Figure 2—figure supplement 1B; Shannon and Li, 1999), indicating that the phenotype is not specific to septin mutants. These results are consistent with the hypothesis that larger cells with more polarity proteins (due to their larger volume) can trigger a transition from competition to coexistence.

Figure 2 with 2 supplements see all

Download asset Open asset

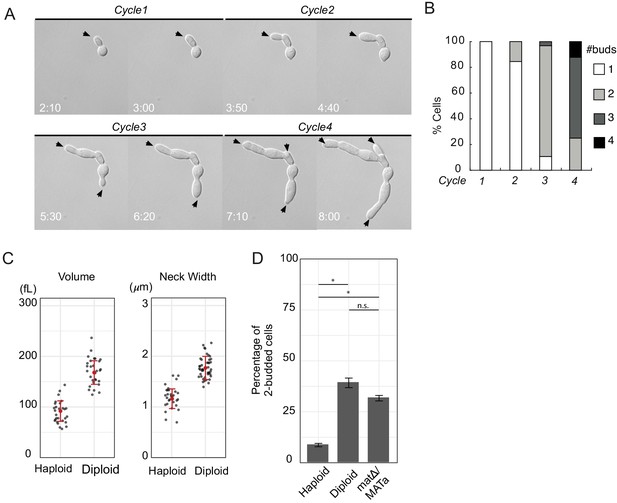
Large yeast cells can generate multiple buds simultaneously.

(A) DIC time lapse movie of a haploid cytokinesis-defective *cdc12-6* mutant (DLY20240) over four budding cycles at restrictive temperature (37°C). Black arrows indicate growing buds. Time in hr:min. (B) The number of buds generated in each cell cycle was scored for N = 35 cells. (C) Volume and neck width of diploid (DLY20569) and haploid (DLY9455) *cdc12-6* cells in the second cell cycle at restrictive temperature. Red dot and intervals indicate mean and standard deviation. (D) Percentage of two-budded cells observed in the second cell cycle at restrictive temperature for diploid (DLY20569) and haploid (DLY9455) *cdc12-6* cells (Fisher’s exact test p<10⁻⁵). *mat*Δ/MATa cells (DLY22887) are diploid but have a haploid mating type (Fisher’s exact test p=0.0431 compared to diploid; p<10⁻⁵ compared to haploid). Asterisks indicate p<10⁻⁵ and n.s. indicates p>0.01. Error bars indicate SEM.

Video 1

Download asset

posterframe for video — Large yeast cells can generate multiple buds simultaneously.

Time-lapse DIC images of a pair of *cdc12-6* cells (DLY20240) growing at restrictive temperature for four-cell cycles. The mother-daughter pair of cells were shifted to 37°C when the video begins. Time stamp indicates hr:min.

In MCAS models, the entire cell is diffusionally connected, allowing fluxes of polarity substrates in the cytoplasm. However, the geometry of septin-mutant cells raised the possibility that the undivided mother-bud neck might impose a diffusion barrier that suffices to yield multi-polarity. The narrowing at the neck is predicted to slow diffusional fluxes between cell bodies by about 20%, and this mild effect was indeed detected experimentally using photo-bleaching (Figure 2—figure supplement 2). To distinguish whether increased volume or slower diffusion from neck geometry is the dominant contributing factor for multipolar outcomes, we compared haploid and diploid mutant cells. Diploid cells have larger volume (and hence more polarity proteins) but also wider necks (which would provide a smaller impediment to diffusion) compared to haploids (Figure 2C). Despite having wider necks, the larger diploids generated significantly more two-budded cells than did the haploids (Figure 2D). This was due to cell size and not mating type, as MATΔ/MATa cells (cells that have the large size of a diploid but the mating type of a haploid) behaved similarly to normal diploids (Figure 2D). Taken together, our findings indicate that the large cells generated following failure of cytokinesis can yield multi-budded outcomes, and that such outcomes can be predominantly attributed to the larger cell size.

Competition in cytokinesis-defective cells can become ineffective

Larger cell size could lead to a multi-polar outcomes by affecting the number of polarity sites that initially form during polarity establishment, or the subsequent competition between sites, or both. To evaluate these features, we introduced the polarity probe Bem1-GFP (Howell et al., 2012), and employed a cdc12-6 rsr1Δ genetic background to avoid complexities associated with Rsr1-mediated bud-site-selection, which biases the location of polarity sites and slows competition by unknown mechanisms (Bi and Park, 2012; Wu et al., 2013). Control experiments indicated that cdc12-6 rsr1Δ mutants generated increasing numbers of multi-budded cells with increasing cell size, although fewer compared to the cdc12-6 RSR1 cells (Figure 3—figure supplement 1). In addition to polarity sites, Bem1 could localize to attempted cytokinesis sites, but these were easily distinguishable by cell cycle timing (Figure 3—figure supplement 2).

As cells entered the second cell cycle after switching to 37°C, Bem1 became concentrated at one or two initial polarity sites, but cells with two initial sites often made only one bud, presumably as a result of competition (Figure 3A). Competition was evident both within individual cell compartments and between cell compartments connected by necks. However, in some cases, the initial sites persisted and gave rise to two buds. As cells entered the third cell cycle, Bem1 sometimes localized to three initial sites. The outcome in these cases was variable, with competition leaving one or two sites that gave rise to buds (Figure 3B). Thus, unipolar versus multipolar outcomes depend both on the number of initial polarity sites that form and on whether they are subsequently eliminated by competition.

Figure 3 with 3 supplements see all

Download asset Open asset

Polarity sites in large *cdc12-6* cells.

(A) Cells that start with two polarity sites can show competition or coexistence. Example cells demonstrating typical Bem1 behaviors in *cdc12-6 rsr1* Δ diploids (DLY15376) in the second G1 phase after switching to restrictive temperature. Cartoons (left) depict the dynamics of polarity sites (red). Red bulges (right) indicate buds (note that buds can emerge in directions that are not within the focal plane). Cells i and ii: competition yields one bud. Cell iii: coexistence yields two buds. (B) Example cells from the third G1 phase after switching to restrictive temperature. These cells initially had three polarity sites but made only one (cell i) or two (cell ii) buds. Scale bar = 2 µm. White regions cover auto-fluorescent dead cells.

Increasing polarity protein abundance decreases the effectiveness of competition

To assess how cell size might affect the number of initial polarity sites, we compared cdc12-6 rsr1Δ cells in the second cell cycle versus the third cell cycle after switching to 37°C, as well as haploid and diploid mutant cells. As expected, third-cycle cells were larger than second-cycle cells, and diploids were larger than haploids (Figure 4A). The number of initial sites formed by each cell increased in a manner correlated with cell length (Figure 4B), suggesting that cell length can influence initial polarization. Variability in the number of initial sites that form is expected for a process that depends on inhomogeneities in the initial polarity protein distribution stemming from molecular noise to initiate polarization. However, the locations at which initial sites formed were non-random, with a preference for bud tips and mother cell locations (Figure 4C), suggesting that (even without Rsr1) polarity may not initiate purely from molecular noise, and that geometric factors may bias the process. When cells formed two initial sites, the distance between the sites was highly variable (Figure 4D). This is contrary to the expectation for classical Turing-type models, which tend to form peaks separated by a characteristic length scale (Meinhardt, 2008). However, it is consistent with predictions from MCAS models that have no preferred inter-peak length scale (Goryachev and Leda, 2020; Goryachev and Pokhilko, 2008; Halatek et al., 2018).

Figure 4 with 2 supplements see all

Download asset Open asset

Increasing abundance of polarity proteins enhances the frequency of multipolar outcomes.

(A) Cell volume and length in three populations of *cdc12-6 rsr1*Δ cells at restrictive temperature: diploids (DLY15376) in the second or third cell cycle and haploids (DLY9453) in the third cell cycle. Red dot and interval indicate mean and standard deviation. (B) The number of initial polarity sites in each population. (C) Initial sites form at non-random positions. N = 123 initial polarity sites in cycle three diploids were mapped onto a generic cell outline. (D) The distance between polarity sites is highly variable. (E) Percentage of two-budded cells (bipolar outcomes) among those that established two initial sites. Larger cells show more frequent multipolar outcomes (13.3%, 21.4%, 46.2%). Error bars indicate SEM from three experiments. (F) Diploid and haploid *cdc12-6 rsr1*Δ cells with normal (DLY15376, DLY9453) or double (DLY23308, DLY23302) the gene dosage of *CDC42*, *BEM1* and *CDC24* show that cell size is unaffected by polarity gene dosage. (G) The number of initial polarity sites does not vary systematically as a function of polarity gene dosage (strains as in F). (H) The percentage of two-budded cells within the subpopulation that established two initial polarity sites (strains as in F). Similar sized cells expressing more polarity proteins display more frequent multipolar outcomes (13.3% vs 29.4% in cycle two diploids, although not significant, Fisher's exact test p=0.25. 21.4% vs 68.4% in cycle three haploids, Fisher’s exact test p=0.0094). Error bars indicate SEM from three experiments.

To focus on the outcome of competition, we narrowed our analysis to the cells that established just two initial sites. Of these cells, the fraction that yielded two-budded outcomes increased with cell size (Figure 4E). Notably, similar-sized cells within the same population could differ their eventual outcomes (Figure 4E). Such variability may reflect the variability in protein concentrations between cells, or stochastic differences in the size of the initial peaks that formed (with similar peaks coexisting and unequal peaks competing). Overall, the probability of successful competition between polarity sites decreased as cells grew larger, consistent with a transition from competition to coexistence regimes.

In MCAS models, the main effect of larger size on system behavior is due to the increased total abundance of polarity proteins in the system, rather than the increased length or volume per se (Chiou et al., 2018). To ask whether this was also the case in yeast cells, we integrated additional copies of the CDC42, CDC24 (GEF), and BEM1 genes into our mutant cells. Doubling the gene copy number led to the expected increase in the concentration of the encoded proteins (Figure 4—figure supplement 1). An extra copy of any single gene did not greatly affect the frequency of multi-budded cells produced by cdc12-6 rsr1Δ mutants (Figure 4—figure supplement 2), consistent with previous overexpression reports in other strain backgrounds (Freisinger et al., 2013; Howell et al., 2012; Howell et al., 2009). We reasoned that by altering the stoichiometry of the polarity genes relative to each other, we might have changed the identity of the limiting species. To avoid that, we made a strain with double the gene copy number for each of the three genes. This did not affect the morphology, volume, or length of the cells (Figure 4F), and there was no systematic effect on the number of initial polarity sites formed (Figure 4G). However, among the cells that established two initial sites, the frequency of multi-polar outcomes was significantly increased (Figure 4H). We conclude that increasing the abundance of polarity proteins is sufficient to decrease the effectiveness of competition, yielding multi-polar outcomes.

Equalization is enabled by an indirect pathway from activator to substrate

The experimental results thus far are consistent with a switch from competition to coexistence, as predicted by the minimalistic MCAS model. However, multi-component MCAS models that incorporate negative feedback as well as positive feedback can yield a qualitatively different behavior, in which starting unequal peaks become equal. The first report to show equalization considered a mechanistic model of yeast polarity that incorporated a hypothesized negative feedback pathway (Howell et al., 2012). An intuitive explanation for such equalization is that larger peaks are penalized by generating more negative feedback, allowing smaller peaks to compete successfully (Jacobs et al., 2019). However, equalization behavior does not necessarily follow from the presence of negative feedback (Chiou et al., 2018; Jacobs et al., 2019), suggesting that this intuition is insufficient to account for equalization. Here, we sought to understand the features of polarity models that enable equalization.

Addition of a negative feedback loop to a minimalistic model (Figure 5Ai) did not enable equalization (Chiou et al., 2018). However, addition of a negative feedback via activation of a Cdc42 GAP (Figure 5Aii; Jacobs et al., 2019) did enable equalization. Addition of a negative feedback to our mechanistic model (Figure 1F) via inhibition of the GEF (simplified in Figure 5Aiii. Complete scheme in Figure 5—figure supplement 1F) also enabled equalization (Figure 5B). This mechanism was suggested by more recent experimental findings that Cdc42 promotes inhibitory phosphorylation of its GEF in yeast (Kuo et al., 2014). These findings suggested that some feature(s) absent from the first model (Figure 5Ai) but shared by the others (Figure 5Aii–iii) might explain equalization. One such feature is the addition of a new species (the GAP in model ii and the inhibited GEFi in model iii).

Figure 5 with 1 supplement see all

Download asset Open asset

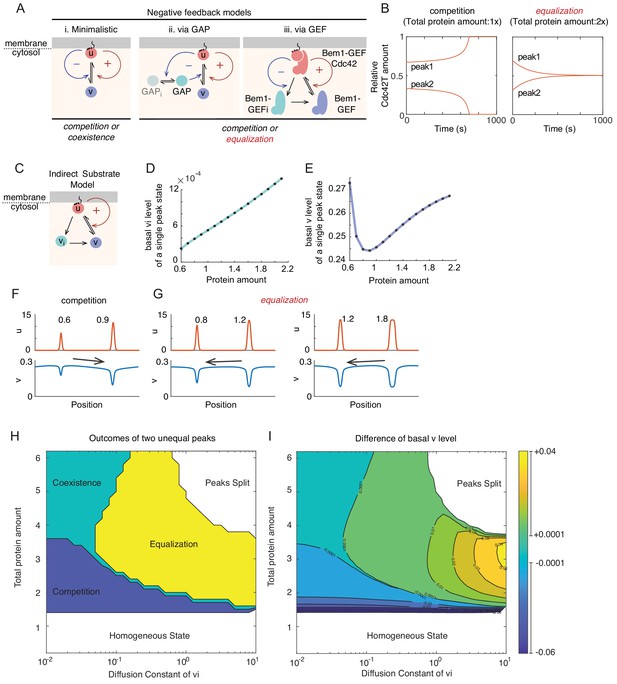
Basis for equalization in more complex models.

(A) Schematic of models incorporating negative feedback. (i) In the minimalistic model, negative feedback adds a term in which u promotes conversion of u to v in a non-linear manner. (ii) This model incorporates conversion of an inactive GAP (GAPi) to an active GAP in a manner stimulated by u. The GAP promotes conversion of u to v, providing negative feedback. (**iii**) Simplified scheme of a mechanistic model where positive feedback occurs via recruitment of a substrate (Bem1-GEF) to become an activator (Bem1-GEF-Cdc42). Negative feedback occurs because the activator promotes inhibitory phosphorylation of the Bem1-GEF, generating inactive Bem1-GEFi. For details of the full model see Figure 5—figure supplement 1F and Materials and methods. (B) With the GEF negative feedback model, two peaks can compete (protein amount 0.5x, 1x) or equalize (protein amount 1x, 2x). (C) Schematic of the indirect substrate model. In addition to the reactions from minimalistic MCAS model in Figure 1C,u (red) can be converted into the indirect cytoplasmic substrate *v_i* (teal), which itself can be converted to the substrate v (blue). (D) The basal level of indirect substrate (*v_i*) increases as the amount of total protein in the system goes up. (E) The basal substrate level (v) first decreases but then increases as the amount of total protein in the system goes up. (F) Competition occurs when the larger peak depletes cytoplasmic substrates more than the smaller. Protein amount 0.6x:0.9x. (G) Equalization occurs when the smaller peak depletes cytoplasmic substrates more than the larger. Protein amount 0.8x:1.2x and 1.2x:1.8x. (H) Outcomes vary depending on the diffusion constant of v_i and total protein amount. Simulations were initiated with two single peak steady states containing unequal total protein amounts 0.4:0.6. Outcomes were classified as follows: Competition, simulations evolve to a single peak steady state within t < 2000; Coexistence, unequal peaks remain unequal (±1%) within t < 2000; Equalization, simulations evolve to a two-equal-peak steady state within t < 2000; Peaks split, simulations evolve to split a starting peak into two smaller peaks; Homogeneous, simulations evolve to a homogeneous steady state. (I) Contour plot of the difference in basal v concentration between the two initial peaks (v_P0.6 - v_P0.4). Contour lines are at 0.01 intervals except when basal levels are very close, when we indicate ±0.0001 contours. The starting difference in basal substrate between the peaks predicts the outcome.

The GAP and the inhibited GEFi are neither substrates nor activators, and appear to play different roles in the polarity circuit. However, we noticed that they both provide a source of substrate: the GAP converts local GTP-Cdc42 into the substrate GDP-Cdc42, while the inhibited GEFi turns into the substrate GEF upon dephosphorylation. Thus, in both cases a new species produced by the activator is highly mobile and generates a substrate in the cytoplasm. We reasoned that a larger peak of activator would generate more of this new species (GAP or GEFi) in its vicinity, and by generating more substrate this new species might reverse the concentration gradient of substrate in the cytoplasm, driving a flux of substrate toward the smaller peak to yield equalization.

Interestingly, the key to equalization in the hypothesis proposed above is not negative feedback per se, but rather the existence of a new species created by an activator that can generate a substrate. To test our hypothesis, we modified the minimalistic model to include an ‘indirect substrate’ species (Figure 5C): In addition to direct conversion of the activator u to the substrate v, u can also be converted to the indirect substrate v_i, which can then be converted to v. We made the u→ v_i reaction linear with u, such that this model lacks the non-linear negative feedback present in the models discussed above, allowing us to probe whether equalization arises due to the presence of indirect substrate even without such negative feedback.

The new indirect substrate model recapitulated the switch from competition to equalization behavior as the total protein amount in the system was increased. Previously, at the single peak steady states of the minimalistic model (Figure 1D), basal levels of the cytoplasmic substrate v decreased until they reached a limit as the total protein amount in the system was increased. However, in the indirect substrate model, basal levels of v_i rose steadily as the total protein amount was increased (Figure 5D). The basal level of substrate v initially decreased, but then rose as total protein amount was increased (Figure 5E), presumably due to flux from v_i. When two unequal peaks were placed together, the system evolved either to a single peak (competition) or to two equal peaks (equalization), depending on the amount of protein in the system (Figure 5F,G). A key factor appeared to be the relative basal levels of cytoplasmic substrate associated with each peak: when the larger peak was associated with lower substrate levels, the system displayed competition; when the smaller peak was associated with lower substrate levels, the system displayed equalization.

The indirect substrate model is clarifying in its simplicity: lacking negative feedback, it demonstrates that the key to equalization is the presence of an indirect pathway to convert activator into substrate. As the minimalistic model already had a direct pathway to convert activator into substrate, this implies that it is important to introduce a delay in this conversion. Without this delay, the substrate generated from a peak is immediately available to be recruited back to the same peak. With a delay, the indirect substrate can migrate away from the center of the peak where it was generated before being converted to substrate, which can then feed a different peak. If this reasoning is correct, then the mobility of the indirect substrate should be critical for the model to yield equalization. To assess this, we examined how changing the diffusion constant of the indirect substrate would impact system behavior of a starting two-peak condition as the total amount of protein in the system was increased (Figure 5H,I). This analysis confirmed that the mobility of the indirect substrate must surpass a threshold in order to yield equalization, and showed that equalization became the favored outcome as that mobility increased (Figure 5H). Thus, equalization occurs when local production of a mobile indirect substrate by the larger peak drives a flux of substrate toward the smaller peak.

In addition, the analysis confirmed that the difference between the basal substrate level associated with each peak precisely predicted the outcome of the simulations (Figure 5I). When basal substrate was higher at the smaller peak, there was a flux of substrate toward the larger peak and the system displayed competition. When basal substrate was higher at the larger peak, there was a flux of substrate toward the smaller peak and the system displayed equalization. When basal substrate was very similar at the two peaks, the system displayed coexistence.

Our conclusions from analysis of the simple indirect substrate model can explain the outcomes from all of the models discussed above and in previous studies (Figure 5—figure supplement 1). All MCAS models can yield competition, but only models with indirect pathways to convert activator to substrate can yield equalization, and this occurs regardless of whether the models have negative feedback.

Are multi-polar outcomes a result of equalization or coexistence?

Returning to the switch from unipolar to multipolar outcomes that we observed when yeast cells grew larger, we now have two potential explanations for this phenomenon: a slowing of competition to yield coexistence, or a switch to equalization. As the original impetus for the analysis of equalization stemmed from models that contained a phosphorylated and inhibited GEF, we wondered whether GEF phosphorylation might contribute to the outcome. We constructed a mutant strain in which the wild-type Cdc24 (GEF) was replaced with a non-phosphorylatable version, Cdc24^38A. This did not diminish multipolar outcomes: in fact, this strain made two-budded cells at a higher frequency than size-matched Cdc24-wild-type controls (of the second-cycle cells that established two initial sites, 65% of the Cdc24^38A cells were two-budded compared to 12% of the Cdc24 cells).

Although phosphorylated Cdc24 is not required for multipolar outcomes, it remained possible that some other species (e.g. a mobile GAP or another species that acts as an indirect substrate) might be causing equalization. Equalization and competition are distinct behaviors in which initial polarity sites evolve in opposite directions. In contrast, coexistence is an intermediate behavior that could reflect either very slow competition or very slow equalization (Figure 5H,I). During equalization, two initially unequal peaks evolve toward two equal peaks. During coexistence, unequal peaks remain unequal. We asked which of these scenarios best accounts for the behavior of cytokinesis-defective yeast cells.

A difficulty in distinguishing equalization and competition behaviors in cells with wild-type Cdc24 is that negative feedback through Cdc24 phosphorylation can cause oscillation in the protein amount at each polarity peak, obscuring the underlying processes (Howell et al., 2012; Kuo et al., 2014). The CDC24^38A strain short-circuits this negative feedback and does not show oscillations, allowing us to circumvent this complexity. Focusing on CDC24^38A cells that had two starting polarity sites in the second cycle at 37°C, we tracked the total Bem1 fluorescence at each polarity site over time until the time of bud emergence. We quantified the fluorescence in each site as a fraction of the sum total in both sites, for each timepoint. Time-courses for 32 cells are shown in Figure 6 and Figure 6—figure supplement 1. These cells exhibited a continuum of behaviors that could almost all be classified as competition (15 cells: the larger peak grew and the smaller one shrank, Figure 6A) or coexistence (14 cells: the relative Bem1 amount in each peak stayed approximately constant, Figure 6C). There were three cells in which quantification indicated that the larger peak shrank and the smaller one grew, consistent with equalization (Figure 6D). However, these instances of possible equalization were rare, and their interpretation is dependent on quantification of a single timepoint (the last timepoint before budding), which leaves us uncertain as to whether they represent equalization or coexistence. Interestingly, five of the cells with the slowest competition did not complete competition by the time of bud emergence, and went on to grow two buds (Figure 6B). This phenotype, which we call ‘aborted competition’, appears to reflect slow competition curtailed by budding. In aggregate, these data suggest that coexistence is the dominant reason for multipolar outcomes in yeast.

Figure 6 with 1 supplement see all

Download asset Open asset

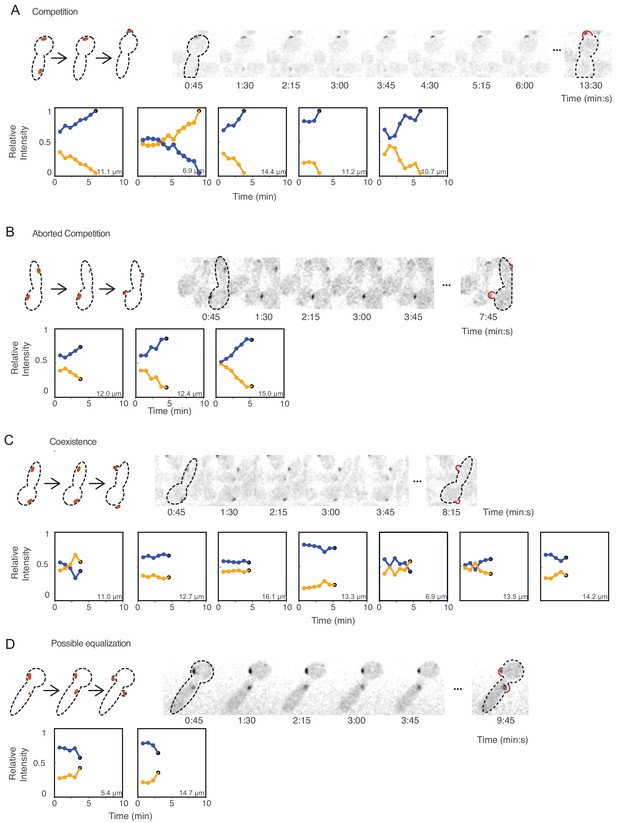
Competition, coexistence, and equalization in yeast.

Cells that exhibit (A) competition, (B) aborted competition, (C) coexistence, or (D) possible equalization. Cartoons depict the dynamics of polarity sites (red) in the accompanying montages. Red bulges (right) indicate buds, which sometimes emerge away from the focal plane (note that polarity sites in small buds were always at the bud tip, but the appearance in 2D maximum projections may not convey that when buds grow away from the focal plane). The amounts of Bem1 in each site were quantified from sum intensity traces from z-stacks of *cdc12-6 rsr1Δ CDC24^38A* cells (DLY21100) that had two initial polarity sites. We plotted the relative amounts of Bem1 at the two polarity sites from when both sites had grown until the time of budding, with blue and orange dots representing the initially more (blue) or less (orange) intense polarity sites. Polarity sites that eventually led to bud-emergence are indicated by black dots at the last time point. Inset numbers denote the distance between the two initial polarity sites. Timelapse montages show the first cell in each category. Additional traces are shown in Figure 6—figure supplement 1.

Discussion

Previous studies on MCAS models applicable to cell polarity indicated that competition between polarity sites would yield unipolar final states, but that the timescale of competition would slow as the amount of polarity proteins in the system increased, potentially yielding coexistence of polarity sites and hence multipolar outcomes (Brauns et al., 2020a; Chiou et al., 2018; Goryachev and Leda, 2020). Our findings expand on this work in three ways. First, we show experimentally that yeast cells behave as predicted by the models, producing multipolar outcomes as the amount of polarity proteins increases. Second, we provide an explanation for a phenomenon called equalization, seen in more complex MCAS models, which can also produce multipolar outcomes. And third, we documented the dynamics of polarity sites in yeast cells, supporting coexistence as the dominant mechanism for multi-polar outcomes.

Yeast cells switch from unipolar to multipolar outcomes as polarity protein abundance is increased

Using conditional cytokinesis-defective yeast mutants, we found that larger cells produced progressively higher numbers of buds. Increasing numbers of polarity sites with cell size is predicted by different classes of simple mathematical pattern-formation models relevant to polarity establishment. The models provide different explanations (intrinsic length scale, coexistence, and equalization) for the switch from unipolar to multipolar outcomes.

Classical (not mass-conserved) turing models exhibit a characteristic length scale, such that local peaks of an activator form spontaneously at spatial intervals corresponding to this length scale. Cells develop one or more peaks depending on how large the cell is compared to the characteristic length scale (Cornwall Scoones et al., 2020; Meinhardt, 2008).

Mass-conserved activator-substrate (MCAS) models can develop variable numbers of initial activator peaks, but as substrate is depleted from the cytoplasm the peaks compete with each other. Eventually, competition leads to a single-peak steady state, but the timescale of competition slows dramatically as the total abundance of activator/substrate in the system is increased (Brauns et al., 2020a; Chiou et al., 2018; Ishihara et al., 2007; Otsuji et al., 2010), yielding coexistence on biologically relevant timescales.

More complex MCAS models can switch from a regime exhibiting competition (where a larger peak grows faster than a smaller peak) to a regime exhibiting equalization (where a smaller peak grows faster than a larger peak) as parameters change (Howell et al., 2012). The basis for this behavior is discussed in more detail below. For now, we note that a switch from competition to equalization as cells become larger could also explain the observed switch from unipolar to multipolar outcomes.

The number of initial polarity sites in our cells increased with increasing cell length, reminiscent of classical Turing models. However, there was no obvious preferred length scale for the distance between sites, as would be expected from classical Turing systems. A potential explanation for the increase in initial sites stems from the observation that polarity locations were non-random, with a preference for cell tips. For the geometry of our cytokinesis-defective cells, the number of tips correlates with cell length, because longer cells arise from the formation of additional buds. Thus, the number of initial polarity sites may reflect the specifics of our experimental system rather than a feature of classical Turing systems.

Those cells that did form more than one initial polarity peak often exhibited competition between peaks. Competition emerges as a consequence of mass conservation, and suggests that MCAS models provide the explanation that best fits the behavior of the yeast system. Additional copies of genes encoding polarity proteins led to a marked increase in the frequency of multi-polar outcomes with no change in cell size. Tracking a polarity marker in time-lapse imaging, we found two predominant behaviors among large yeast cells that generated two initial polarity sites: one subset exhibited competition between sites to yield a single bud, while the other exhibited apparent coexistence between sites yielding two buds. These findings strongly support the idea that multipolar outcomes in this system arise due to a slowing in the timescale of competition.

Other features of competition in cytokinesis-defective cells

A subset of our cells exhibit aborted competition, which failed go to completion before budding and gave rise to two buds with stable polarity sites. This behavior is at odds with the predictions of MCAS models, in which competition accelerates as the amount of activator in the peaks becomes more uneven and always goes to completion. This discrepancy may indicate that some aspect of the polarity circuit changes at around the time of bud emergence, reducing the efficacy of competition. Cell cycle control by the cyclin/CDK system provides one plausible candidate regulator that could prompt such a change in polarity circuit behavior (Knaus et al., 2007; Moran et al., 2019; Sopko et al., 2007; Witte et al., 2017).

While competition could occur between peaks in the same or different lobes of cytokinesis-defective cells, all of the multibudded cells we observed had buds emanating from different cell lobes. This observation suggests that competition is more effective within a lobe than between lobes. A possible basis for this effect is that the geometrical narrowing at the neck of multi-lobed cells slightly retards diffusional communication between lobes.

Saturation in multi-component MCAS models

Analyses of minimalistic two-component MCAS models demonstrated that competition between activator peaks was inevitable, and that the timescale of competition was determined by a single dominant factor, which we refer to as saturation (Brauns et al., 2020a; Chiou et al., 2018; Jacobs et al., 2019; Otsuji et al., 2010). When activator concentration in two or more peaks approaches a saturation point set by system parameters, competition slows dramatically, allowing coexistence of the peaks on biologically relevant timescales. We show that these findings from minimalistic one-activator, one-substrate models hold in a more complex and realistic model of the yeast polarity circuit, with two activators, two substrates, and two intermediate species, with some additional complexity discussed below.

In minimalistic MCAS models, positive feedback ensures that addition of more substrate/activator to the system results in conversion of more substrate to activator. Due to positive feedback, the concentration of substrate is depleted below the level obtained with less substrate/activator in the system at steady state. In addition, the concentration profile of activator in the peak changes in a characteristic way as the local activator concentration approaches the saturation point, flattening from a sharp peak to a mesa. In the multi-component model, substrate depletion and the activator concentration profile can vary for different protein species. Depending on the relative amounts of the different species, different substrates may become limiting. For the limiting species, addition of more protein will generally lead to depletion of the cytoplasmic substrate, similar to saturation in the minimalistic models. However, other (non-limiting) species can display increasing cytoplasmic substrate concentration as more protein is added. Moreover, addition of one species can lead to a switch in the identity of the limiting species. As with minimalistic MCAS models, the timescale of competition in the mechanistic multi-component model slows as more protein is added to the system, in a manner consistent with saturation of the limiting species.

Equalization in multi-component MCAS models

Unlike minimalistic MCAS models, previous research has shown that more complex models incorporating negative feedback can yield equalization of polarity peaks in some parameter regimes (Howell et al., 2012; Jacobs et al., 2019). Local negative feedback provides an intuitive rationale for equalization: by penalizing a larger peak more than a smaller peak, a localized negative feedback loop could switch the competitive advantage toward the smaller peak. However, we found that negative feedback was neither necessary nor sufficient to produce equalization. Instead, the key to equalization is the existence of additional species that provide indirect pathways to convert an activator into a substrate.

The key features of an additional species that enable equalization are as follows. First, the new species is produced from (or by) an activator. Second, the new species produces substrate. Third, the new species must be more mobile than the activator. In combination, these features create a pathway whereby activator from a peak is converted to a new species that diffuses away from the peak before it generates substrate, which can then be used to ‘feed’ a different peak. A larger activator peak produces more of the new species than a smaller peak, yielding a flux of mobile species from the larger peak to the smaller peak that can produce equalization.

The simplest model containing an indirect pathway from activator to substrate is a three-species model with an activator, a substrate, and an indirect substrate. Using this model, we characterized the full spectrum of behaviors as a function of the mobility of the indirect substrate (Figure 5I). When the indirect substrate diffused slowly (comparable to the activator), the system exclusively displayed competition or coexistence, indicating that rapid mobility of the indirect substrate is essential for equalization. At the other extreme, when the indirect substrate diffused much faster than the substrate, the system exhibited classical (not mass conserved) Turing behavior, generating peaks separated by a characteristic wavelength. We note that in the limit of infinite diffusion of the indirect substrate, this mass-conserved system would resemble some models that do not assume mass conservation (Brauns et al., 2020a; Jacobs et al., 2019). In that limit, the indirect substrate concentration is uniform, so that its conversion into substrate becomes equivalent to a simple ‘substrate synthesis’ term. As indirect substrate is produced from activator, that process becomes equivalent to a simple ‘activator degradation’ term. Thus, in that limit the system behaves as if synthesis and degradation were allowed, so each peak’s activator concentration profile reflects a local steady state between synthesis and degradation. The peaks are equal because they share the same synthesis and degradation parameters. Finally, when the mobility of the indirect substrate was comparable to that of the substrate (i.e. in between the extremes considered above), the system exhibited competition or equalization depending on the total abundance of polarity proteins.

Do yeast cells contain indirect pathways from activator to substrate that could enable equalization? Past work suggests several candidates for such pathways. For example, GTP-Cdc42 promotes inhibitory phosphorylation of its GEF (Kuo et al., 2014), and a model in which GTP-Cdc42 promotes GEF phosphorylation to make GEFi (new species) that can then be dephosphorylated to make active GEF (substrate) can yield equalization (Figure 5B). Similarly, a Cdc42-directed GAP is locally concentrated/activated by proteins downstream of Cdc42 (Okada et al., 2013), and a model in which GTP-Cdc42 activates a GAP (new species) that can then convert GTP-Cdc42 to GDP-Cdc42 (substrate) can also yield equalization (Jacobs et al., 2019). Moreover, the yeast polarity circuit has several other species that could similarly provide indirect pathways from activator to substrate. For example, a multi-component complex containing GTP-Cdc42 and bound effector, scaffold, and GEF proteins (activator) can dissociate to yield individual components (GEFs, scaffolds, effectors) that are absent in minimalistic models. Only when these proteins re-associate to form cytoplasmic GEF-scaffold-effector complexes (substrate) can they be recruited back to bind GTP-Cdc42 at the polarity site. Thus, there are multiple plausible candidates that could enable equalization in the yeast polarity circuit. However, we detect very few cases of possible equalization in the cells we analyzed, suggesting that the physiological parameter space in which this circuit operates is not prone to equalization.

Implications for other systems

Turing-type systems have enormous and well-appreciated potential to generate biologically useful patterns (Meinhardt, 2008; Meinhardt and Gierer, 2000). However, they can also display chaotic outcomes that change dramatically with small differences in starting conditions or parameter values (Pearson, 1993). Thus, biological circuits that exploit such reaction-diffusion systems are likely to employ only a small subset of such circuits that robustly produce reliable outcomes. MCAS circuits are now recognized to produce desirable outcomes for morphogenetic biological systems, including polarization, in a robust manner (Goryachev and Leda, 2017). Moreover, recent advances have provided insight into how such systems can be tuned to produce unipolar or multipolar outcomes (Chiou et al., 2018; Goryachev and Leda, 2020; Halatek et al., 2018). One property that can effectively control the number of polarity sites that form is cell size (Cornwall Scoones et al., 2020). For example, there is a minimum size below which MCAS circuits are unable to polarize at all, and recent work indicates that the decrease in cell size that occurs during worm embryogenesis causes a switch from asymmetric cell division of polarized large cells to symmetric division of unpolarized small cells (Hubatsch et al., 2019).

Our findings show that yeast cells can switch from having a single polarity site to two or more polarity sites as cell size increases. The Saccharomyces polarity circuit has presumably been evolutionarily selected to produce uni-polar outcomes, which are beneficial during budding and mating in this genus. However, this polarity circuit is highly conserved among ascomycetes that display other growth modes (Bendezú et al., 2015; Lamas et al., 2020). Schizosaccharomyces pombe naturally switch from uni-polar to bi-polar growth during each cell cycle (Grallert et al., 2013; Martin and Chang, 2005). Ashbya gossypii, which evolved relatively recently from a common ancestor with S. cerevisiae, form branching hyphae that exhibit increasing number of polarity sites as each cell grows (Knechtle et al., 2003; Schmitz and Philippsen, 2011). The correlation between cell size and number of polarity sites in these systems suggests that, as proposed for MCAS models, cell size and the associated higher abundance of polarity factors may trigger the increase in number of polarity sites. Most remarkably, yeast cells of Aureobasidium sp. generate variable numbers of buds simultaneously (Mitchison-Field et al., 2019), a capacity shared with the much more distantly related zygomycete Mucor circinelloides (Lee et al., 2013). This phenotypic diversity may be enabled by a polarity circuit that allows a switch between competition, coexistence, and equalization behaviors in response to appropriate tuning of parameter values. Similar principles may apply to other systems where activator species produce robustly tunable numbers of polarity sites.

Materials and methods

Yeast strains

Request a detailed protocol

All yeast strains (Table 1) are in the YEF473 background (his3-Δ200; leu2-Δ1; lys2-801amber; trp1-Δ63; ura3-52)(Bi and Pringle, 1996). The cdc12-6 mutation in the YEF473 background was a gift from John Pringle (Stanford University). The rsr1 deletion (Schenkman et al., 2002), GAL4BD-hER-VP16 construct (Takahashi and Pryciak, 2008), and CDC24^38A mutation (Kuo et al., 2014; Wai et al., 2009) were described previously, as was tagging at the endogenous loci for the fluorescent probes BEM1-GFP (Kozubowski et al., 2008), BEM1-tdTomato (Howell et al., 2012), CDC3-mCherry (Howell et al., 2009), CLA4-GFP (Wild et al., 2004), HTB2-mCherry, and WHI5-GFP (Doncic et al., 2011). Standard yeast genetic procedures were used to generate all of the strains.

Table 1

Strains.

Strain	Relevant genotype	Source
DLY9453	a; cdc12-6; rsr1::HIS3; BEM1-GFP:LEU2	This study
DLY9455	a; cdc12-6; BEM1-GFP:LEU2	This study
DLY13030	a; cdc42::TRP1; rsr1::TRP1; URA3:GFP-CDC42	This study
DLY15376	a/α; cdc12-6/cdc12-6; rsr1::HIS3/rsr1::HIS3; BEM1-GFP:LEU2/BEM1-GFP:LEU2	This study
DLY16767	a; cdc12-6; rsr1::TRP1; BEM1-GFP:LEU2; CDC24^38A	This study
DLY20240	a; cdc12-6; BEM1-GFP:LEU2; HTB2-mCherry:nat^R	This study
DLY20569	a/α; cdc12-6/cdc12-6; BEM1-GFP:LEU2/BEM1-GFP:LEU2	This study
DLY21100	a/α; cdc12-6/cdc12-6; BEM1-GFP:LEU2/BEM1-GFP:LEU2; CDC24^38A/CDC2438^38A	This study
DLY22875	a; cdc12-6; WHI5-GFP:SpHIS5; BEM1-GFP:LEU2; pTEF1-PSR1-mCherry-tADH1:LEU2; rsr1::TRP1	This study
DLY22887	a/matαΔ::nat^R; cdc12-6/cdc12-6; BEM1-GFP:LEU2/BEM1-GFP:LEU2	This study
DLY22915	a/α; WHI5-GFP:SpHIS5/WHI5; rsr1::TRP1/RSR1; BEM1-tdTomato:HIS3/BEM1-tdTomato:HIS3; pGAL1-IQG1:LEU2/pGAL1-IQG1:LEU2; pTEF1-PSR1-GFP-tADH1:LEU2/leu2; Gal4BD-hER-VP16:URA3/Gal4BD-hER-VP16:URA3	This study
DLY22920	a/α; cdc12-6/cdc12-6; WHI5-GFP:SpHIS5/WHI5-GFP:SpHIS5; BEM1-tdTomato:HIS3/BEM1-tdTomato:HIS3	This study
DLY22957	a/α; cdc12-6/cdc12-6; BEM1-tdTomato::HIS3/BEM1; pTEF1-GFP:LEU2/pTEF1-GFP:LEU2	This study
DLY22980	α; rsr1::TRP1; BEM1-GFP:LEU2; CDC24-HA:kan^R	This study
DLY22993	α; cdc12-6; BEM1-GFP:LEU2; CDC24-HA:kan^R	This study
DLY23302	a; cdc12-6; CDC24-HA:kan^R; BEM1-GFP:TRP1:BEM1-GFP:LEU2; ura3::CDC24-HA:URA3; CDC42:TRP1:CDC42; rsr1::TRP1	This study
DLY23308	a/α; cdc12-6/cdc12-6; CDC24-HA:kan^R/CDC24-HA:kan^R; BEM1-GFP:TRP1:BEM1-GFP:LEU2/BEM1-GFP:TRP1:BEM1-GFP:LEU2; ura3::CDC24-HA:URA3/ura3::CDC24-HA:URA3; CDC42:TRP1:CDC42/CDC42:TRP1:CDC42; rsr1::TRP1/rsr1::TRP1	This study
DLY23359	a/α; cdc12-6/cdc12-6; CLA4-GFP::HIS3/CLA4; BEM1-tdTomato::HIS3/BEM1	This study
DLY23269	α; cdc12-6; rsr1::TRP1; BEM1-GFP:TRP1:BEM1-GFP:LEU2; CDC24-HA:kan^R; ura3::CDC24-HA:URA3; CDC42:TRP1:CDC42	This study
DLY23829	a; cdc12-6; rsr1::HIS3; BEM1-GFP:TRP1:BEM1-GFP:LEU2	This study
DLY23830	a; cdc12-6; rsr1::TRP1; BEM1-GFP:LEU2; CDC24-HA:kan^R; ura3::CDC24-HA:URA3	This study
DLY23831	a; cdc12-6; rsr1::HIS3; BEM1-GFP:LEU2; CDC42:TRP1:CDC42	This study
DLY23832	a; cdc12-6; rsr1::TRP1; BEM1-GFP:LEU2; ura3::CDC24-HA:URA3; CDC42:TRP1:CDC42	This study
DLY23833	α; cdc12-6; rsr1::HIS3; BEM1-GFP:TRP1:BEM1-GFP:LEU2; CDC24-HA:KAN; CDC42:TRP1:CDC42	This study
DLY23843	α; cdc12-6; rsr1::HIS3; BEM1-GFP:TRP1:BEM1-GFP:LEU2; CDC24-HA:KAN; ura3::CDC24-HA:URA3	This study

To generate a strain with regulatable expression of IQG1, the first 500 bp of the IQG1 open reading frame were amplified by PCR and cloned downstream of the GAL1 promoter in YIpG2 (Richardson et al., 1989) to generate DLB2126. Digestion at the unique NheI site targets integration of this construct at IQG1, making Iqg1 expression galactose-dependent and shut off on glucose media. To introduce a 3xHA epitope tag at the C-terminus of CDC24, we used a pFA6-series plasmid template and the PCR-based one-step replacement method (Longtine et al., 1998). To delete the MATα locus, we used a pFA6-series plasmid template and the PCR-based one-step replacement method (Longtine et al., 1998) to replace a part of the locus inactivating the divergent α1 and α2 genes while leaving the surrounding genes intact. In a haploid, this deletion converts an α mating type to an a mating type. In a diploid, this deletion converts the strain to a mating type.

To label the plasma membrane, we expressed a fusion between the N-terminal 28 residues of Psr1 and GFP. The Psr1 N-terminal fragment is myristoylated and doubly palmitoylated, targeting GFP to the plasma membrane (Siniossoglou et al., 2000). The construct was cloned between the TEF1 promoter and ADH1 terminator sequences in a pRS305 (Sikorski and Hieter, 1989) backbone, generating plasmid DLB4206. Digestion at the unique PpuMI targets integration at the LEU2 locus.

To express an extra copy of CDC42, the CDC42 gene (open-reading frame plus 500 bp upstream and 250 bp downstream) was cloned into the integrating plasmids pRS304 and pRS306 (Sikorski and Hieter, 1989), generating plasmids DLB3904 and DLB4115 respectively. Digestion of DLB3904 at the unique StyI site was used to target integration of the TRP1-marked plasmid at CDC42. To express an extra copy of CDC24, the CDC24-3HA gene (open reading frame plus upstream and downstream sequence) was cloned into the integrating plasmid pRS306 (Sikorski and Hieter, 1989), generating plasmid DLB4134. Digestion at the unique PstI site was used to target integration of the plasmid at URA3. To express an extra copy of BEM1-GFP, the BEM1-GFP gene (open reading frame plus upstream and downstream sequence) was cloned into the integrating plasmid pRS304 (Sikorski and Hieter, 1989), generating plasmid DLB2997. Digestion at the unique BamHI site was used to target integration of the plasmid at BEM1.

Cell growth, hydroxyurea treatment, and timelapse imaging conditions

Request a detailed protocol

Cells were grown in liquid complete synthetic media (CSM, MP Biomedicals) with 2% dextrose at 24°C overnight until they reached log phase (5 × 10⁶ cells/mL). cdc12-6 cultures were shifted to 37°C and treated with 200 mM hydroxyurea (Sigma) for 1 hr to protect cells from subsequent phototoxicity during imaging (Howell et al., 2012). Cells were pelleted, washed with and released into fresh media at 37°C for an additional 1 hr (for imaging of the second cell cycle) or 3 hr (for imaging of the third cell cycle). Cells were then harvested by centrifugation and mounted on a 37°C slab composed of CSM solidified with 2% agarose (Denville Scientific, Inc) prior to imaging.

For Figure 2A, the cells were imaged at 37°C on an Axio Observer.Z1 (Zeiss) with Pecon XL S1 incubator and control modules, a X-CITE 120XL metal halide fluorescence light source, and a 100x/1.46 (Oil) Plan Apochromat objective controlled by MetaMorph 7.8 (Universal Imaging). Images were captured with a Photometrics Evolve back-thinned EM-CCD camera. The fluorescence light source was set to 50% of the maximal output with a 2% ND filter. An EM-Gain of 750 and 200 ms exposure was set for the red channel (HTB2-mCherry, not shown), and an EM-Gain of 100 and 20 ms exposure was set for the Differential interference contrast (DIC) channel.

Other videos and images were acquired with an Andor XD revolution spinning disk confocal microscope (Olympus) with a Yokogawa CsuX-1 5000 rpm disk unit and a 100x/1.4 U PlanSApo oil-immersion objective controlled by MetaMorph 7.8. 20 Z-stacks of 0.5 µm z-step were captured at 45 s intervals with Andor Ixon3 897 512 EMCCD camera (Andor Technology).

The maximal power for the 488 nm laser varied between 1.60 mW and 3.26 mW, and the maximal power for the 561 nm laser varied between 1.19 mW and 1.68 mW. We adjusted the illumination to 6–8% for the 488 nm channel and 8–10% for the 561 nm channel to provide a more consistent sample illumination. An EM-Gain of 200 and exposures of 250 ms were used.

Fluorescent images were deconvolved with SVI Huygens Deconvolution (Scientific Volume Imaging) and analyzed using Fiji (Schindelin et al., 2012). For deconvolution, a signal to noise ratio of 3 was used for Confocal images. Only cells that were not connected to neighboring cells were used for quantification to avoid cell pairs that might be connected from the previous cell cycle.

Cell fixation and membrane staining

Request a detailed protocol

To score the number of buds at the second cell cycle in Figure 2D, cells were grown overnight at 24°C and log phase cultures (10⁷ cells/mL) were shifted to 37°C for 4 hr. One mL cell culture was then harvested, spun down, and resuspended in 100 µL ice cold 10 µM FM4-64fx in water (Thermofisher Scientific) on ice. After 1 min staining, 1 mL ice cold 4% paraformaldehyde was added and the mixture was incubated on ice for 10 min. The cells were then washed twice with phosphate-buffered saline (PBS) and stored at 4°C. Images were then taken, and only cells that were budding from two connected compartments were counted.

Photo-bleaching

Request a detailed protocol

Photo-bleaching experiments were conducted on a DeltaVision Elite Deconvolution Microscope (Applied Precision) with a 100x/1.40 oil UPLSAPO100 × 0 1-U2B836 WD objective controlled by SoftWoRx 6.1 (Softworx Inc). Images were captured with a Coolsnap HQ2 high resolution CCD camera. Photobleaching experiments were conducted on budded cycle two cdc12-6 cells expressing cytoplasmic GFP. The bleaching 488 nm laser was used for 5 ms at 20% of maximal intensity. Cells were imaged with 50 ms exposure time, and 2 × 2 binning for three images before bleach and 15 images after bleach. Imaging interval was set automatically by the software assuming 1 s half-time.

Images were analyzed using Fiji and MATLAB (Mathworks). Fluorescence signal was averaged within a 3 µm diameter circular area at the bleach site and at sites in the mother and daughter compartments equidistant to the bleach site, and normalized with an unbleached cell and the background fluorescence nearby using the formula:

I_{n o r m a l i z e d} = (I_{r a w} - I_{b a c k g r o u n d}) / (I_{u n b l e a c h e d} - I_{b a c k g r o u n d})

Normalized intensity at the mother site was fit to an exponential decay ae^-kt +c, normalized intensity at the bleach site was fit to an exponential recovery -ae^-kt+c, and normalized intensity at the daughter site was fit to a linear combination of the two ae^-kt +be^ct + d. The recovery half-time can then be calculated by T_1/2 = ln(2)/k.

Simulated Photo-bleaching in 3D cells

Request a detailed protocol

The three-dimensional geometry of a typical second-cycle cdc12-6 cell was modeled by the closest point method described in Ramirez et al., 2015. The cell shape was designated as the combination of a 6 µm diameter sphere and an ellipsoid with length 6 µm and width 2 µm, partially overlapped to create a neck of 2 µm diameter. The shape of the cell was modeled in Cartesian coordinates with the boundary of the cell interpolated with the closest grid points. The closest points were implemented with C++, and the main diffusion code was simulated by the implicit Euler method in MATLAB. The bleach was incorporated in the initial condition as a cylinder of 1 µm diameter and zero intensity. ‘Fluorescence intensities’ were the measured from the sum of z-stacks to mimic non-deconvolved microscopy images from the DeltaVision microscope.

Immunoblotting

Request a detailed protocol

Cells were grown overnight in YEPD at 24°C to mid-log phase. Where indicated, cultures were shifted to 37°C for 4 hr prior to TCA precipitation. For all samples,~10⁷ cells were collected via centrifugation. Pellets were resuspended in 225 μl of cold pronase buffer (25 mM Tris-HCl, pH 7.5, 1.4 M sorbitol, 20 mM NaN₃, 2 mM MgCl₂) and 48 μl of cold TCA (100% wt/vol; Sigma-Aldrich) before being frozen at −80°C. Samples were thawed on ice and cells were homogenized by vortexing with sterile acid-washed glass beads at 4°C for 10 min. Lysates were collected and the beads were washed with TCA (5% wt/vol) to collect remaining lysate. Precipitated proteins were pelleted by centrifugation at 4°C for 10 min. Pellets were resuspended in Thorner sample buffer (40 mM Tris-HCl, pH 6.8, 8 M urea, 5% SDS, 143 mM β-mercaptoethanol, 0.1 mM EDTA, 0.4 mg/ml bromophenol blue) and any remaining TCA was neutralized by adding 2 M Tris-HCl, pH 8.0.

Samples were heated at 95°C for 5 min prior to loading on 12.5% polyacrylamide gels. After electrophoresis, proteins were transferred to nitrocellulose membranes. Membranes were blocked with 3% nonfat dry milk in phosphate-buffered saline with 0.1% Tween-20 (PBST). Blots were incubated in blocking buffer with monoclonal mouse anti-GFP antibodies (Roche) at 1:1000 dilution, monoclonal mouse anti-HA antibodies (Roche) at 1:1000 dilution, or monoclonal mouse anti-Cdc42 antibodies (Wu and Brennwald, 2010) at 1:500 dilution. After multiple washes with PBST, blots were incubated in blocking buffer with 0.01% SDS and fluorophore-conjugated secondary anti-mouse antibodies (IRDye 800CW goat anti-mouse IgG, LI-COR) at 1:10,000 dilution. Following multiple washes with PBST plus 0.01% SDS, blots were visualized and quantified using the ODYSSEY imaging system (LI-COR). Two percent Ponceau S solution was used to detect total protein in each blot and ImageJ was used to quantify total protein in each lane. For a given blot, the signal for each detected band was scaled according to the total protein measured in its corresponding lane. These scaled intensities were then normalized to the wild-type signal for that blot.

Polarity models

Request a detailed protocol

We performed simulations with four polarity models in this study: a minimalistic mass-conserved activator-substrate (MCAS) model, two mechanistic models of the yeast polarity circuit with or without the negative feedback via GEF phosphorylation, and an extension of the minimalistic MCAS model that incorporates an indirect substrate.

The minimalistic MCAS model considers the concentrations of two interconvertible forms of a protein (activator and substrate: u, v) in one spatial dimension (Figure 1C; Chiou et al., 2018). The protein can diffuse and convert between the two forms but is not synthesized or degraded:

\frac{\partial u}{\partial t} = a u^{2} v - b u + D_{m} \frac{\partial^{2} u}{\partial x^{2}}

\frac{\partial u}{\partial t} = a u^{2} v - b u + D_{m} \frac{\partial^{2} u}{\partial x^{2}}

\frac{\partial v}{\partial t} = - a u^{2} v + b u + D_{v} \frac{\partial^{2} v}{\partial x^{2}}

u enhances the conversion of v into more u through an implicit positive feedback loop modeled by the quadratic term au²v. u converts back to v in a first order process. u diffuses slowly relative to v. The parameters are:

Description	Parameter	Value	Reference
u → v	a	1	Chiou et al., 2018
v → u	b	1	Chiou et al., 2018
Diffusion constant of u	D_m	0.01	Chiou et al., 2018
Diffusion constant of v	D_c	1	Chiou et al., 2018

The indirect-substrate model is similar to the minimalistic model except for the inclusion of a new species, the indirect-substrate v_i (Figure 5C). u converts to v_i in a first-order process, and v_i converts to v in a first-order process. The differences from the minimalistic MCAS model are highlighted in bold:

\frac{\partial u}{\partial t} = a u^{2} v - b u - c u + D_{m} \frac{\partial^{2} u}{\partial x^{2}}

\frac{\partial v}{\partial t} = - a u^{2} v + b u + d v_{i} + D_{v} \frac{\partial^{2} v}{\partial x^{2}}

\frac{\partial v_{i}}{\partial t} = c u - d v_{i} + D_{v i} \frac{\partial^{2} v_{i}}{\partial x^{2}}

Description	Parameter	Value	Reference
u → v	a	1	Chiou et al., 2018
v → u	b	1	Chiou et al., 2018
u → v_i	c	0.01	This study
v_i→ v	d	1	This study
Diffusion constant of u	D_m	0.01	Chiou et al., 2018
Diffusion constant of v	D_c	1	Chiou et al., 2018
Diffusion constant of v	D_vi	1	This study

The mechanistic positive feedback model (Wu et al., 2015) is based on reactions assumed to occur with first order kinetics that account for various interconversions of Cdc42 and PAK-Bem1-GEF complexes. Cdc42 can interconvert between active GTP-bound (Cdc42T) and inactive GDP-bound (Cdc42D) states. Activation is catalyzed by GEF at the membrane, while inactivation is catalyzed by an implicit GAP. GDP-Cdc42 can also exchange between membrane (Cdc42D_m) and cytoplasmic (Cdc42D_c) forms (in cells this is catalyzed by GDP-dissociation Inhibitor or GDI). The PAK-Bem1-GEF complex (here called BemGEF) is considered as a single species following the analysis of Goryachev and Pokhilko, 2008, who showed that separating the complex into distinct components did not affect the qualitative behavior of the system in the parameter ranges they considered (although we note that given the potential for separate PAK, Bem1, or GEF species to act as indirect substrates it is possible that considering the species separately would yield different outcomes in some parameter regimes). BemGEF can exchange between membrane (BemGEF_m) and cytoplasmic (BemGEF_c) forms, and in all cases membrane species diffuse much less than cytoplasmic species. Positive feedback occurs due to reversible binding of BemGEF to Cdc42T, generating the complex BemGEF42 at the membrane. This leads to accumulation of GEF at sites with elevated GTP-Cdc42, which promotes local activation of more Cdc42. These reactions are modeled as:

\frac{\partial}{\partial t} C d c 42 T = (k_{2 a} B e m G E F_{m} + k_{3} B e m G E F 42) \cdot C d c 42 D_{m} - (k_{2 b} + k_{4 a} B e m G E F_{m} + k_{7} B e m G E F_{c}) \cdot C d c 42 T + k_{4 b} B e m G E F 42 + D_{m} Δ C d c 42 T

\frac{\partial}{\partial t} C d c 42 D_{m} = k_{2 b} C d c 42 T - (k_{2 a} B e m G E F_{m} + k_{3} B e m G E F 42) \cdot C d c 42 D_{m} - k_{5 b} C d c 42 D_{m} + k_{5 a} C d c 42 D_{c} + D_{m} Δ C d c 42 D_{m}

\frac{\partial}{\partial t} B e m G E F 42 = (k_{4 a} B e m G E F_{m} + k_{7} B e m G E F_{c}) \cdot C d c 42 T - k_{4 b} B e m G E F 42 + D_{m} Δ B e m G E F 42

\frac{\partial}{\partial t} B e m G E F_{m} = k_{1 a} B e m G E F_{c} - k_{1 b} B e m G E F_{m} + k_{4 b} B e m G E F 42 - k_{4 a} B e m G E F_{m} \cdot C d c 42 T + D_{m} Δ B e m G E F_{m}

\frac{\partial}{\partial t} C d c 42 D_{c} = η (k_{5 b} C d c 42 D_{m} - k_{5 a} C d c 42 D_{c}) + D_{c} Δ C d c 42 D_{c}

\frac{\partial}{\partial t} B e m G E F_{c} = η (k_{1 b} B e m G E F_{m} - k_{1 a} B e m G E F_{c} - k_{7} B e m G E F c \cdot C d c 42 T) + D_{c} Δ B e m G E F_{c}

Description	Parameter	Value	Unit	Reference
BemGEF_c→ BemGEF_m	k_1a	10	s⁻¹	Goryachev and Pokhilko, 2008
BemGEF_m→ BemGEF_c	k_1b	10	s⁻¹	Goryachev and Pokhilko, 2008
Cdc42D_m + BemGEF_m→ Cdc42T_m + BemGEF_m	k_2a	0.16	µM⁻¹ s⁻¹	Howell et al., 2009
Cdc42T → Cdc42D_m	k_2b	1.75	s⁻¹	Wu et al., 2015
Cdc42D_m + BemGEF42 → Cdc42T + BemGEF42	k₃	0.35	µM⁻¹ s⁻¹	Howell et al., 2009
BemGEF + Cdc42T → BemGEF42	k_4a	10	µM⁻¹ s⁻¹	Goryachev and Pokhilko, 2008
BemGEF42 →BemGEF + Cdc42T	k_4b	10	s⁻¹	Goryachev and Pokhilko, 2008
Cdc42D_c→ Cdc42D_m	k_5a	36	s⁻¹	Kuo et al., 2014
Cdc42D_m→ Cdc42D_c	k_5b	0.65	s⁻¹	Kuo et al., 2014
BemGEF_c + Cdc42T → BemGEF42	k₇	10	µM⁻¹ s⁻¹	Goryachev and Pokhilko, 2008
Diffusion constant on the membrane	D_m	0.0025	µm² s⁻¹	Goryachev and Pokhilko, 2008
Diffusion constant in the cytoplasm	D_c	10	µm² s⁻¹	Goryachev and Pokhilko, 2008
Membrane to cytoplasm volume ratio	η	0.01		Goryachev and Pokhilko, 2008

In addition, the yeast polarity circuit contains a negative feedback loop due to multi-site phosphorylation of the GEF by the PAK, causing inactivation of the GEF (Kuo et al., 2014). Phosphorylation occurs when the PAK from one complex phosphorylates the GEF from another complex, which only happens when both complexes are bound to GTP-Cdc42. Dephosphorylation occurs only in the cytoplasm. The phosphorylated species, BemGEF*, can still exchange between cytoplasmic (BemGEF*_c) and membrane (BemGEF*_m) forms, and bind reversibly to Cdc42T (generating BemGEF*42). The addition of negative feedback leads to the differences highlighted in bold:

\frac{\partial}{\partial t} C d c 42 T = (k_{2 a} B e m G E F_{m} + k_{3} B e m G E F 42) \cdot C d c 42 D_{m} - (k_{2 b} + k_{4 a} B e m G E F_{m t} + k_{7} B e m G E F_{c t}) \cdot C d c 42 T + k_{4 b} B e m G E F 42_{t} + D_{m} Δ C d c 42 T

\frac{\partial}{\partial t} C d c 42 D_{m} = k_{2 b} C d c 42 T - (k_{2 a} B e m G E F_{m} + k_{3} B e m G E F 42) \cdot C d c 42 D_{m} - k_{5 b} C d c 42 D_{m} + k_{5 a} C d c 42 D_{c} + D_{m} Δ C d c 42 D_{m}

\frac{\partial}{\partial t} B e m G E F 42 = (k_{4 a} B e m G E F_{m} + k_{7} B e m G E F_{c}) \cdot C d c 42 T - (k_{4 b} + k_{8} B e m G E F 42) \cdot B e m G E F 42 + D_{m} Δ B e m G E F 42

\frac{\partial}{\partial t} B e m G E F_{m} = k_{1 a} B e m G E F_{c} - k_{1 b} B e m G E F_{m} + k_{4 b} B e m G E F 42 - k_{4 a} B e m G E F_{m} \cdot C d c 42 T + D_{m} Δ B e m G E F_{m}

\frac{\partial}{\partial t} C d c 42 D_{c} = η (k_{5 b} C d c 42 D_{m} - k_{5 a} C d c 42 D_{c}) + D_{c} Δ C d c 42 D_{c}

\frac{\partial}{\partial t} B e m G E F_{c} = η (k_{1 b} B e m G E F_{m} - k_{1 a} B e m G E F_{c} - k_{7} B e m G E F_{c} \cdot C d c 42 T) + k_{9} B e m G E F_{c}^{*} + D_{c} Δ B e m G E F_{c}

\frac{\partial}{\partial t} B e m G E F_{m}^{*} = k_{1 a} B e m G E F_{c}^{*} - k_{1 b} B e m G E F_{m}^{*} + k_{4 b} B e m G E F^{*} 42 - k_{4 a} B e m G E F_{m}^{*} \cdot C d c 42 T + D_{m} Δ B e m G E F_{m}^{*}

\frac{\partial}{\partial t} B e m G E F_{c}^{*} = η (k_{1 b} B e m G E F_{m}^{*} - k_{1 a} B e m G E F_{c}^{*} - k_{7} B e m G E F_{c}^{*} \cdot C d c 42 T) - k_{9} B e m G E F_{c}^{*} + D_{c} Δ B e m G E F_{c}^{*}

\frac{\partial}{\partial t} B e m G E F^{*} 42 = (k_{4 a} B e m G E F_{m}^{*} + k_{7} B e m G E F_{c}^{*}) \cdot C d c 42 T - k_{4 b} \cdot B e m G E F^{*} 42 + k_{8} B e m G E F 42_{t} \cdot B e m G E F 42 + D_{m} Δ B e m G E F^{*} 42

Note that the subscript ‘t’ is used to denote the sum of phosphorylated and unphosphorylated species, which can both undergo reversible binding to either membranes or GTP-Cdc42.

B e m G E F_{m t} = B e m G E F_{m} + B e m G E F_{m}^{*}

B e m G E F_{c t} = B e m G E F_{c} + B e m G E F_{c}^{*}

B e m G E F 42_{t} = B e m G E F 42 + B e m G E F^{*} 42

Also, although only unphosphorylated species can act as GEFs, both phosphorylated and unphosphorylated complexes can act as PAKs to phosphorylate other GEFs. Multi-site phosphorylation and dephosphorylation are assumed to occur in an ultrasensitive manner.

k_{8} = k_{8 m a x} \frac{B e m G E F_{m t}^{k_{8 n}}}{k_{8 h}^{k_{8 n}} + B e m G E F_{m t}^{k_{8 n}}}

k_{9} = k_{9 m a x} \frac{B e m G E F_{m t}^{* k_{9 n}}}{k_{9 h}^{k_{9 n}} + B e m G E F_{c}^{* k_{9 n}}}

Description	Parameter	Value	Unit	Reference
BemGEF_c→ BemGEF_m BemGEF^_c→ BemGEF^_m	k_1a	10	s⁻¹	Goryachev and Pokhilko, 2008
BemGEF_m→ BemGEF_c BemGEF^_m→ BemGEF^_c	k_1b	10	s⁻¹	Goryachev and Pokhilko, 2008
Cdc42D_m + BemGEF_m → Cdc42T_m + BemGEF_m	k_2a	0.16	µM⁻¹ s⁻¹	Howell et al., 2009
Cdc42T → Cdc42D_m	k_2b	0.35	s⁻¹	Wu et al., 2015
Cdc42D_m + BemGEF42 → Cdc42T + BemGEF42	k₃	0.35	µM⁻¹ s⁻¹	Howell et al., 2009
BemGEF_m + Cdc42 → BemGEF42 BemGEF^*_m + Cdc42 → BemGEF42	k_4a	10	µM⁻¹ s⁻¹	Goryachev and Pokhilko, 2008
BemGEF42 → BemGEF^_m + Cdc42T BemGEF^42 → BemGEF^*_m + Cdc42T	k_4b	10	s⁻¹	Goryachev and Pokhilko, 2008
Cdc42D_c→ Cdc42D_m	k_5a	36	s⁻¹	Kuo et al., 2014
Cdc42D_m→ Cdc42D_c	k_5b	0.65	s⁻¹	Kuo et al., 2014
BemGEF_c + Cdc42T → BemGEF42 BemGEF^_c + Cdc42T → BemGEF^42	k₇	10	µM⁻¹ s⁻¹	Goryachev and Pokhilko, 2008
BemGEF42 + BemGEF42 →BemGEF42 + BemGEF^42 BemGEF42 + BemGEF^42 → BemGEF^42 + BemGEF^42	k₈	k_8max = 0.0063 k_8n = 6 k_8h= 10	µM⁻¹ s⁻¹	Kuo et al., 2014
BemGEF^*_c → BemGEF_c	k₉	k_9max = 0.0044 k_8n = 6 k_8h= 0.003	s⁻¹	Kuo et al., 2014
Diffusion constant on the membrane	D_m	0.0025	µm² s⁻¹	Kuo et al., 2014
Diffusion constant in the cytoplasm	D_c	10	µm² s⁻¹	Goryachev and Pokhilko, 2008
Membrane to cytoplasm volume ratio	η	0.01		Goryachev and Pokhilko, 2008

Numerical simulations

Request a detailed protocol

Simulations of the MCAS models were done on MATLAB. Simulations of conceptual models were done on one-dimensional domains with spatial resolution of 500 grid points. Finite differences were used with the linear diffusion being treated implicitly and the nonlinear reaction term explicitly in the time stepping. Mechanistic models were simulated on two-dimensional domains with 100 × 100 grid points. All simulations proceeded with adaptive time stepping according to relative error in the reaction term. Initial conditions for simulations of two unequal peaks were standardized by simulating two insulated subsystems containing 60% and 40% of the total mass. After they reached steady state, the two subsystems were allowed to communicate by diffusion. The MATLAB code used for simulations is provided in Source Code Files.

Data availability

All data generated or analyses during this study are included in the manuscript and supporting files.

References

1. Atkins BD
2. Yoshida S
3. Saito K
4. Wu C-F
5. Lew DJ
6. Pellman D
(2013) Inhibition of Cdc42 during mitotic exit is required for cytokinesis
Journal of Cell Biology 202:231–240.
https://doi.org/10.1083/jcb.201301090
- Google Scholar
(2015) Spontaneous Cdc42 polarization independent of GDI-mediated extraction and actin-based trafficking
PLOS Biology 13:e1002097.
https://doi.org/10.1371/journal.pbio.1002097
- PubMed
- Google Scholar
1. Bi E
2. Park HO
(2012) Cell polarization and cytokinesis in budding yeast
Genetics 191:347–387.
https://doi.org/10.1534/genetics.111.132886
- PubMed
- Google Scholar
1. Bi E
2. Pringle JR
(1996) ZDS1 and ZDS2, genes whose products may regulate Cdc42p in Saccharomyces cerevisiae
Molecular and Cellular Biology 16:5264–5275.
https://doi.org/10.1128/MCB.16.10.5264
- PubMed
- Google Scholar
1. Bose I
2. Irazoqui JE
3. Moskow JJ
4. Bardes EG
5. Zyla TR
6. Lew DJ
(2001) Assembly of Scaffold-mediated complexes containing Cdc42p, the exchange factor Cdc24p, and the effector Cla4p required for cell Cycle-regulated phosphorylation of Cdc24p
Journal of Biological Chemistry 276:7176–7186.
https://doi.org/10.1074/jbc.M010546200
- Google Scholar
Preprint
1. Brauns F
2. Weyer H
3. Halatek J
4. Yoon J
5. Frey E
(2020a) Wavelength selection by interrupted coarsening in reaction-diffusion systems
arXiv.

https://arxiv.org/abs/2005.01495
- Google Scholar
(2020b) Phase-Space geometry of Mass-Conserving Reaction-Diffusion dynamics
Physical Review X 10:041036.
https://doi.org/10.1103/PhysRevX.10.041036
- Google Scholar
1. Butty AC
2. Perrinjaquet N
3. Petit A
4. Jaquenoud M
5. Segall JE
6. Hofmann K
7. Zwahlen C
8. Peter M
(2002) A positive feedback loop stabilizes the guanine-nucleotide exchange factor Cdc24 at sites of polarization
The EMBO Journal 21:1565–1576.
https://doi.org/10.1093/emboj/21.7.1565
- PubMed
- Google Scholar
(2017) Cell polarity in yeast
Annual Review of Cell and Developmental Biology 33:77–101.
https://doi.org/10.1146/annurev-cellbio-100616-060856
- PubMed
- Google Scholar
1. Chiou JG
2. Ramirez SA
3. Elston TC
4. Witelski TP
5. Schaeffer DG
6. Lew DJ
(2018) Principles that govern competition or co-existence in Rho-GTPase driven polarization
PLOS Computational Biology 14:e1006095.
https://doi.org/10.1371/journal.pcbi.1006095
- PubMed
- Google Scholar
(2020) Size-Regulated symmetry breaking in Reaction-Diffusion models of developmental transitions
Cells 9:1646.
https://doi.org/10.3390/cells9071646
- Google Scholar
1. Costanzo M
2. Nishikawa JL
3. Tang X
4. Millman JS
5. Schub O
6. Breitkreuz K
7. Dewar D
8. Rupes I
9. Andrews B
10. Tyers M
(2004) CDK activity antagonizes Whi5, an inhibitor of G1/S transcription in yeast
Cell 117:899–913.
https://doi.org/10.1016/j.cell.2004.05.024
- PubMed
- Google Scholar
(1995) Ste20-like protein kinases are required for normal localization of cell growth and for cytokinesis in budding yeast
Genes & Development 9:1817–1830.
https://doi.org/10.1101/gad.9.15.1817
- PubMed
- Google Scholar
(2004) Cln3 activates G1-specific transcription via phosphorylation of the SBF bound repressor Whi5
Cell 117:887–898.
https://doi.org/10.1016/j.cell.2004.05.025
- PubMed
- Google Scholar
(2011) Distinct interactions select and maintain a specific cell fate
Molecular Cell 43:528–539.
https://doi.org/10.1016/j.molcel.2011.06.025
- PubMed
- Google Scholar
(1988) The establishment of polarity by hippocampal neurons in culture
The Journal of Neuroscience 8:1454–1468.
https://doi.org/10.1523/JNEUROSCI.08-04-01454.1988
- PubMed
- Google Scholar
1. Etienne-Manneville S
2. Hall A
(2002) Rho GTPases in cell biology
Nature 420:629–635.
https://doi.org/10.1038/nature01148
- PubMed
- Google Scholar
1. Freisinger T
2. Klünder B
3. Johnson J
4. Müller N
5. Pichler G
6. Beck G
7. Costanzo M
8. Boone C
9. Cerione RA
10. Frey E
11. Wedlich-Söldner R
(2013) Establishment of a robust single Axis of cell polarity by coupling multiple positive feedback loops
Nature Communications 4:1807.
https://doi.org/10.1038/ncomms2795
- PubMed
- Google Scholar
1. Goryachev AB
2. Leda M
(2017) Many roads to symmetry breaking: molecular mechanisms and theoretical models of yeast cell polarity
Molecular Biology of the Cell 28:370–380.
https://doi.org/10.1091/mbc.e16-10-0739
- PubMed
- Google Scholar
1. Goryachev AB
2. Leda M
(2020) Compete or coexist? why the same mechanisms of symmetry breaking can yield distinct outcomes
Cells 9:2011.
https://doi.org/10.3390/cells9092011
- Google Scholar
1. Goryachev AB
2. Pokhilko AV
(2008) Dynamics of Cdc42 network embodies a Turing-type mechanism of yeast cell polarity
FEBS Letters 582:1437–1443.
https://doi.org/10.1016/j.febslet.2008.03.029
- PubMed
- Google Scholar
1. Grallert A
2. Patel A
3. Tallada VA
4. Chan KY
5. Bagley S
6. Krapp A
7. Simanis V
8. Hagan IM
(2013) Centrosomal MPF triggers the mitotic and morphogenetic switches of fission yeast
Nature Cell Biology 15:88–95.
https://doi.org/10.1038/ncb2633
- PubMed
- Google Scholar
(2018) Self-organization principles of intracellular pattern formation
Philosophical Transactions of the Royal Society B: Biological Sciences 373:20170107.
https://doi.org/10.1098/rstb.2017.0107
- Google Scholar
1. Hartwell LH
(1971) Genetic control of the cell division cycle in yeast. IV. genes controlling bud emergence and cytokinesis
Experimental Cell Research 69:265–276.
https://doi.org/10.1016/0014-4827(71)90223-0
- PubMed
- Google Scholar
1. Holly SP
2. Blumer KJ
(1999) Pak-Family kinases regulate cell and actin polarization throughout the cell cycle of Saccharomyces cerevisiae
Journal of Cell Biology 147:845–856.
https://doi.org/10.1083/jcb.147.4.845
- Google Scholar
1. Houk AR
2. Jilkine A
3. Mejean CO
4. Boltyanskiy R
5. Dufresne ER
6. Angenent SB
7. Altschuler SJ
8. Wu LF
9. Weiner OD
(2012) Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration
Cell 148:175–188.
https://doi.org/10.1016/j.cell.2011.10.050
- PubMed
- Google Scholar
1. Howell AS
2. Savage NS
3. Johnson SA
4. Bose I
5. Wagner AW
6. Zyla TR
7. Nijhout HF
8. Reed MC
9. Goryachev AB
10. Lew DJ
(2009) Singularity in polarization: rewiring yeast cells to make two buds
Cell 139:731–743.
https://doi.org/10.1016/j.cell.2009.10.024
- PubMed
- Google Scholar
1. Howell AS
2. Jin M
3. Wu CF
4. Zyla TR
5. Elston TC
6. Lew DJ
(2012) Negative feedback enhances robustness in the yeast polarity establishment circuit
Cell 149:322–333.
https://doi.org/10.1016/j.cell.2012.03.012
- PubMed
- Google Scholar
(2019) A cell-size threshold limits cell polarity and asymmetric division potential
Nature Physics 15:1078–1085.
https://doi.org/10.1038/s41567-019-0601-x
- Google Scholar
(2007) Transient and steady state of mass-conserved reaction-diffusion systems
Physical Review E 75:015203.
https://doi.org/10.1103/PhysRevE.75.015203
- Google Scholar
1. Ito T
2. Matsui Y
3. Ago T
4. Ota K
5. Sumimoto H
(2001) Novel modular domain PB1 recognizes PC motif to mediate functional protein-protein interactions
The EMBO Journal 20:3938–3946.
https://doi.org/10.1093/emboj/20.15.3938
- PubMed
- Google Scholar
(2019) Small GTPase patterning: how to stabilise cluster coexistence
PLOS ONE 14:e0213188.
https://doi.org/10.1371/journal.pone.0213188
- PubMed
- Google Scholar
1. Jilkine A
2. Edelstein-Keshet L
(2011) A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues
PLOS Computational Biology 7:e1001121.
https://doi.org/10.1371/journal.pcbi.1001121
- PubMed
- Google Scholar
1. Johnson JM
2. Jin M
3. Lew DJ
(2011) Symmetry breaking and the establishment of cell polarity in budding yeast
Current Opinion in Genetics & Development 21:740–746.
https://doi.org/10.1016/j.gde.2011.09.007
- PubMed
- Google Scholar
(2007) Phosphorylation of Bem2p and Bem3p may contribute to local activation of Cdc42p at bud emergence
The EMBO Journal 26:4501–4513.
https://doi.org/10.1038/sj.emboj.7601873
- PubMed
- Google Scholar
(2003) Maximal polar growth potential depends on the polarisome component AgSpa2 in the filamentous fungus Ashbya gossypii
Molecular Biology of the Cell 14:4140–4154.
https://doi.org/10.1091/mbc.e03-03-0167
- PubMed
- Google Scholar
1. Kozubowski L
2. Saito K
3. Johnson JM
4. Howell AS
5. Zyla TR
6. Lew DJ
(2008) Symmetry-breaking polarization driven by a Cdc42p GEF-PAK complex
Current Biology 18:1719–1726.
https://doi.org/10.1016/j.cub.2008.09.060
- PubMed
- Google Scholar
1. Kuo CC
2. Savage NS
3. Chen H
4. Wu CF
5. Zyla TR
6. Lew DJ
(2014) Inhibitory GEF phosphorylation provides negative feedback in the yeast polarity circuit
Current Biology 24:753–759.
https://doi.org/10.1016/j.cub.2014.02.024
- PubMed
- Google Scholar
1. Lai H
2. Chiou JG
3. Zhurikhina A
4. Zyla TR
5. Tsygankov D
6. Lew DJ
(2018) Temporal regulation of morphogenetic events in Saccharomyces cerevisiae
Molecular Biology of the Cell 29:2069–2083.
https://doi.org/10.1091/mbc.E18-03-0188
- PubMed
- Google Scholar
(2020) Optogenetics reveals Cdc42 local activation by scaffold-mediated positive feedback and ras GTPase
PLOS Biology 18:e3000600.
https://doi.org/10.1371/journal.pbio.3000600
- PubMed
- Google Scholar
(2002) Cdc42 regulation of kinase activity and signaling by the yeast p21-activated kinase Ste20
Molecular and Cellular Biology 22:2939–2951.
https://doi.org/10.1128/MCB.22.9.2939-2951.2002
- PubMed
- Google Scholar
1. Lee SC
2. Li A
3. Calo S
4. Heitman J
(2013) Calcineurin plays key roles in the dimorphic transition and virulence of the human pathogenic zygomycete Mucor circinelloides
PLOS Pathogens 9:e1003625.
https://doi.org/10.1371/journal.ppat.1003625
- PubMed
- Google Scholar
1. Leeuw T
2. Fourest-Lieuvin A
3. Wu C
4. Chenevert J
5. Clark K
6. Whiteway M
7. Thomas DY
8. Leberer E
(1995) Pheromone response in yeast: association of Bem1p with proteins of the MAP kinase cascade and actin
Science 270:1210–1213.
https://doi.org/10.1126/science.270.5239.1210
- PubMed
- Google Scholar
1. Longtine MS
2. McKenzie A
3. Demarini DJ
4. Shah NG
5. Wach A
6. Brachat A
7. Philippsen P
8. Pringle JR
(1998) Additional modules for versatile and economical PCR-based gene deletion and modification in Saccharomyces cerevisiae
Yeast 14:953–961.
https://doi.org/10.1002/(SICI)1097-0061(199807)14:10<953::AID-YEA293>3.0.CO;2-U
- PubMed
- Google Scholar
1. Martin SG
2. Chang F
(2005) New end take off: regulating cell polarity during the fission yeast cell cycle
Cell Cycle 4:4046–4049.
https://doi.org/10.4161/cc.4.8.1853
- PubMed
- Google Scholar
1. Meinhardt H
(2008) Models of biological pattern formation: from elementary steps to the organization of embryonic axes
Current Topics in Developmental Biology 81:1–63.
https://doi.org/10.1016/S0070-2153(07)81001-5
- PubMed
- Google Scholar
1. Meinhardt H
2. Gierer A
(1974) Applications of a theory of biological pattern formation based on lateral inhibition
Journal of Cell Science 15:321–346.
https://doi.org/10.1242/jcs.15.2.321
- PubMed
- Google Scholar
1. Meinhardt H
2. Gierer A
(2000) Pattern formation by local self-activation and lateral inhibition
BioEssays 22:753–760.
https://doi.org/10.1002/1521-1878(200008)22:8<753::AID-BIES9>3.0.CO;2-Z
- PubMed
- Google Scholar
(2019) Unconventional cell division cycles from Marine-Derived yeasts
Current Biology 29:3439–3456.
https://doi.org/10.1016/j.cub.2019.08.050
- PubMed
- Google Scholar
1. Moran KD
2. Kang H
3. Araujo AV
4. Zyla TR
5. Saito K
6. Tsygankov D
7. Lew DJ
(2019) Cell-cycle control of cell polarity in yeast
Journal of Cell Biology 218:171–189.
https://doi.org/10.1083/jcb.201806196
- PubMed
- Google Scholar
(2008) Wave-pinning and cell polarity from a bistable reaction-diffusion system
Biophysical Journal 94:3684–3697.
https://doi.org/10.1529/biophysj.107.120824
- PubMed
- Google Scholar
1. Neurohr GE
2. Terry RL
3. Lengefeld J
4. Bonney M
5. Brittingham GP
6. Moretto F
7. Miettinen TP
8. Vaites LP
9. Soares LM
10. Paulo JA
11. Harper JW
12. Buratowski S
13. Manalis S
14. van Werven FJ
15. Holt LJ
16. Amon A
(2019) Excessive cell growth causes cytoplasm dilution and contributes to senescence
Cell 176:1083–1097.
https://doi.org/10.1016/j.cell.2019.01.018
- PubMed
- Google Scholar
1. Oda Y
2. Fukuda H
(2012) Initiation of cell wall pattern by a rho- and microtubule-driven symmetry breaking
Science 337:1333–1336.
https://doi.org/10.1126/science.1222597
- PubMed
- Google Scholar
1. Okada S
2. Leda M
3. Hanna J
4. Savage NS
5. Bi E
6. Goryachev AB
(2013) Daughter cell identity emerges from the interplay of Cdc42, septins, and exocytosis
Developmental Cell 26:148–161.
https://doi.org/10.1016/j.devcel.2013.06.015
- PubMed
- Google Scholar
1. Otsuji M
2. Ishihara S
3. Co C
4. Kaibuchi K
5. Mochizuki A
6. Kuroda S
(2007) A mass conserved reaction-diffusion system captures properties of cell polarity
PLOS Computational Biology 3:e108.
https://doi.org/10.1371/journal.pcbi.0030108
- PubMed
- Google Scholar
(2010) A conceptual molecular network for chemotactic behaviors characterized by feedback of molecules cycling between the membrane and the cytosol
Science Signaling 3:ra89.
https://doi.org/10.1126/scisignal.2001056
- PubMed
- Google Scholar
1. Park HO
2. Bi E
(2007) Central roles of small GTPases in the development of cell polarity in yeast and beyond
Microbiology and Molecular Biology Reviews 71:48–96.
https://doi.org/10.1128/MMBR.00028-06
- PubMed
- Google Scholar
1. Pearson JE
(1993) Complex patterns in a simple system
Science 261:189–192.
https://doi.org/10.1126/science.261.5118.189
- PubMed
- Google Scholar
1. Peterson J
2. Zheng Y
3. Bender L
4. Myers A
5. Cerione R
6. Bender A
(1994) Interactions between the bud emergence proteins Bem1p and Bem2p and Rho-type GTPases in yeast
Journal of Cell Biology 127:1395–1406.
https://doi.org/10.1083/jcb.127.5.1395
- PubMed
- Google Scholar
(2015) Dendritic spine geometry can localize GTPase signaling in neurons
Molecular Biology of the Cell 26:4171–4181.
https://doi.org/10.1091/mbc.E15-06-0405
- PubMed
- Google Scholar
1. Rapali P
2. Mitteau R
3. Braun C
4. Massoni-Laporte A
5. Ünlü C
6. Bataille L
7. Arramon FS
8. Gygi SP
9. McCusker D
(2017) Scaffold-mediated gating of Cdc42 signalling flux
eLife 6:e25257.
https://doi.org/10.7554/eLife.25257
- PubMed
- Google Scholar
(1989) An essential G1 function for cyclin-like proteins in yeast
Cell 59:1127–1133.
https://doi.org/10.1016/0092-8674(89)90768-X
- PubMed
- Google Scholar
(2002) The role of cell cycle-regulated expression in the localization of spatial landmark proteins in yeast
Journal of Cell Biology 156:829–841.
https://doi.org/10.1083/jcb.200107041
- PubMed
- Google Scholar
1. Schindelin J
2. Arganda-Carreras I
3. Frise E
4. Kaynig V
5. Longair M
6. Pietzsch T
7. Preibisch S
8. Rueden C
9. Saalfeld S
10. Schmid B
11. Tinevez JY
12. White DJ
13. Hartenstein V
14. Eliceiri K
15. Tomancak P
16. Cardona A
(2012) Fiji: an open-source platform for biological-image analysis
Nature Methods 9:676–682.
https://doi.org/10.1038/nmeth.2019
- PubMed
- Google Scholar
1. Schmitz HP
2. Philippsen P
(2011) Evolution of multinucleated Ashbya gossypii hyphae from a budding yeast-like ancestor
Fungal Biology 115:557–568.
https://doi.org/10.1016/j.funbio.2011.02.015
- PubMed
- Google Scholar
1. Shannon KB
2. Li R
(1999) The multiple roles of Cyk1p in the assembly and function of the actomyosin ring in budding yeast
Molecular Biology of the Cell 10:283–296.
https://doi.org/10.1091/mbc.10.2.283
- PubMed
- Google Scholar
1. Sikorski RS
2. Hieter P
(1989) A system of shuttle vectors and yeast host strains designed for efficient manipulation of DNA in Saccharomyces cerevisiae
Genetics 122:19–27.
https://doi.org/10.1093/genetics/122.1.19
- PubMed
- Google Scholar
(2019) Secretory vesicle clustering in fungal filamentous cells does not require directional growth
Cell Reports 28:2231–2245.
https://doi.org/10.1016/j.celrep.2019.07.062
- Google Scholar
(2000) Psr1p/Psr2p, two plasma membrane phosphatases with an essential DXDX(T/V) motif required for sodium stress response in yeast
Journal of Biological Chemistry 275:19352–19360.
https://doi.org/10.1074/jbc.M001314200
- PubMed
- Google Scholar
(2008) Positive feedback of G1 cyclins ensures coherent cell cycle entry
Nature 454:291–296.
https://doi.org/10.1038/nature07118
- PubMed
- Google Scholar
1. Sopko R
2. Huang D
3. Smith JC
4. Figeys D
5. Andrews BJ
(2007) Activation of the Cdc42p GTPase by cyclin-dependent protein kinases in budding yeast
The EMBO Journal 26:4487–4500.
https://doi.org/10.1038/sj.emboj.7601847
- PubMed
- Google Scholar
1. Takahashi S
2. Pryciak PM
(2008) Membrane localization of scaffold proteins promotes graded signaling in the yeast MAP kinase cascade
Current Biology 18:1184–1191.
https://doi.org/10.1016/j.cub.2008.07.050
- Google Scholar
1. Turing AM
(1952) The chemical basis of morphogenesis
Philosophical Transactions of the Royal Society of London Series B-Biological Sciences 237:37–72.
https://doi.org/10.1007/BF02459572
- Google Scholar
1. Wai SC
2. Gerber SA
3. Li R
(2009) Multisite phosphorylation of the guanine nucleotide exchange factor Cdc24 during yeast cell polarization
PLOS ONE 4:e6563.
https://doi.org/10.1371/journal.pone.0006563
- PubMed
- Google Scholar
1. Wild AC
2. Yu JW
3. Lemmon MA
4. Blumer KJ
(2004) The p21-activated protein kinase-related kinase Cla4 is a coincidence detector of signaling by Cdc42 and phosphatidylinositol 4-phosphate
Journal of Biological Chemistry 279:17101–17110.
https://doi.org/10.1074/jbc.M314035200
- PubMed
- Google Scholar
(2017) Cell cycle entry triggers a switch between two modes of Cdc42 activation during yeast polarization
eLife 6:e26722.
https://doi.org/10.7554/eLife.26722
- PubMed
- Google Scholar
1. Wu CF
2. Savage NS
3. Lew DJ
(2013) Interaction between bud-site selection and polarity-establishment machineries in budding yeast
Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 368:20130006.
https://doi.org/10.1098/rstb.2013.0006
- PubMed
- Google Scholar
1. Wu CF
2. Chiou JG
3. Minakova M
4. Woods B
5. Tsygankov D
6. Zyla TR
7. Savage NS
8. Elston TC
9. Lew DJ
(2015) Role of competition between polarity sites in establishing a unique front
eLife 4:e11611.
https://doi.org/10.7554/eLife.11611
- PubMed
- Google Scholar
1. Wu H
2. Brennwald P
(2010) The function of two rho family GTPases is determined by distinct patterns of cell surface localization
Molecular and Cellular Biology 30:5207–5217.
https://doi.org/10.1128/MCB.00366-10
- PubMed
- Google Scholar
1. Wu CF
2. Lew DJ
(2013) Beyond symmetry-breaking: competition and negative feedback in GTPase regulation
Trends in Cell Biology 23:476–483.
https://doi.org/10.1016/j.tcb.2013.05.003
- PubMed
- Google Scholar
1. Yang Z
2. Lavagi I
(2012) Spatial control of plasma membrane domains: rop GTPase-based symmetry breaking
Current Opinion in Plant Biology 15:601–607.
https://doi.org/10.1016/j.pbi.2012.10.004
- PubMed
- Google Scholar
1. Zhao ZS
2. Leung T
3. Manser E
4. Lim L
(1995) Pheromone signalling in Saccharomyces cerevisiae requires the small GTP-binding protein Cdc42p and its activator CDC24
Molecular and Cellular Biology 15:5246–5257.
https://doi.org/10.1128/MCB.15.10.5246
- PubMed
- Google Scholar
1. Ziman M
2. Johnson DI
(1994) Genetic evidence for a functional interaction between Saccharomyces cerevisiae CDC24 and CDC42
Yeast 10:463–474.
https://doi.org/10.1002/yea.320100405
- PubMed
- Google Scholar

Decision letter

Mohan K Balasubramanian

Reviewing Editor; University of Warwick, United Kingdom
Naama Barkai

Senior Editor; Weizmann Institute of Science, Israel

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

Your paper using genetics and imaging (with an embedded computational framework) very nicely examines how the number of polarity sites are established, using yeast as a model. The dissection of competition mechanism and the novel equalization that you describe will fuel further work in this field both in yeast and in other organisms, especially those which contain multiple polarity sites in normal physiology.

Decision letter after peer review:

[Editors’ note: the authors submitted for reconsideration following the decision after peer review. What follows is the decision letter after the first round of review.]

Thank you for submitting your work entitled "How cells determine the number of polarity sites" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and a Senior Editor. The reviewers have opted to remain anonymous.

Our decision has been reached after consultation between the reviewers. Based on these discussions and the individual reviews below, we regret to inform you that your work will not be considered further for publication in eLife.

The referees are enthusiastic about the topic and the question you are addressing, i.e. how polarity sites and their numbers are chosen. They also found a number of observations in the work interesting. However, all the three independent referees have raised a number of questions, both concerning the modeling as well as with the experiments, and also in citation of past work. In light of all these concerns, we are unable to publish this work in eLife. The referees comments are provided verbatim below.

Reviewer #1:

The manuscript entitled "How cells determine the number of polarity sites" by Chiou et al., compares theoretical models for polarity establishment in budding yeast, specifically their regulatory mechanisms, with experimental observations, in particular those that can lead to polarity cluster coexistence or equalization. After examining the implications of several models of increasing complexity the predictions of specific aspects of these models are explored, in particular alteration of cell size and polarity protein levels. While the findings presented are interesting, the overall message is not sufficiently clear and hence this obscures the significance of the work. Substantial rewriting is necessary together with refocusing to make the work more accessible to a broad audience.

1. The main findings of this work are not evident from the title, introduction and first paragraph of the Discussion. The Discussion talks about several classes of models, but does not indicate clearly which model best describes the observed behaviour. The title and abstract are somewhat general, overall appear descriptive and do not clearly indicate the findings. For example, in the Discussion section, page 25, it states, "Here we propose a novel mechanism for equalization that does not require negative feedback, but can account for the behavior of the more complex models that incorporate negative feedback," however it is not evident what this mechanism is.

2. Reference to and discussion of finding from several relevant and recent studies are lacking. For example, 3 studies, which use optogenetic systems to alter levels and/or clusters of active Cdc42 in fungi are not discussed, these findings are likely to be relevant to mechanism of polarity cluster control, see

-Witte et al., eLife 2017 e26722

-Lamas et al., Plos Biol 2020 18: e3000600

-Silva et al., Cell Rep 2019 28: 2231

Note that while the latter two are carried out in different yeast, the approaches involve temporal recruitment of active Cdc42 to the plasma membrane and hence are relevant to this work.

Furthermore the Discussion section (to some extent also the Introduction section, see also below), including the last subsection of "Implications for other systems" unfortunately does not put this study into the context of what is known about polarity determination outside of the budding yeast perspective, which limits its general interest. For example, I am surprised there is no mention or discussion of the recent work from the Goehring laboratory entitled "A Cell Size Threshold Limits Cell Polarity and Asymmetric Division Potential" (Hubatsch et al., Nat Phys 2019 15:1075) which would appear to be very relevant.

Similarly, the introduction seems to be overly focused on budding yeast with little indication of other systems and the more recent findings, including those from fission yeast (as opposed to cursory mention of an old S. pombe review) and other fungi, such as Neurospora crassa, among others. Furthermore, other reviews cited are quite old.

3. Throughout, the terminology 'protein content' is used which is imprecise. Are the authors referring to total protein amount or amount divided by volume, i.e. an effective concentration? This ambiguity is confusing, in particular in the Discussion section. It is unclear whether larger cells (page 20) have a higher amount or effective concentration of polarity proteins. It is surprising that this aspect of polarity would be cell size dependent given different sizes of haploid and diploid yeast cells.

4. Figures should be organised more clearly, with panels in left to right, top to bottom order (Figure 1-3), graph axes indicated (lacking in many panels including 1D, 2D, E, G, H), color schemes unclear (1G and 1H compared to 1I and 1J; green color used for different species), what is shown in different panels is not indicated (2D, 2H), in some scatter plots means and standard deviation should be indicated (3G, 5A, 5G), in several graphs error bars should be indicated (5B, 5E, 5I) and Figure 6 can be substantially simplified with at most 2 examples of each behaviour shown in A, together with an indication of what the lines refer to (the rest can go in the supporting figure). In addition, it is not clear in 6A if competed (note mix of past tense verbs and nouns for description, better to indicate 'competition, coexistence and equal) is actually different than equalized, in which the initial intensities are inversed, i.e. red higher than blue (A, i).

5. The analysis and interpretation of the cytoplasmic connection in Figure 3D-F and presented on page 14 (and mentioned again on pages 21 and 23) appears over-simplified. Firstly, diffusion of relatively small cytoplasmic GFP is unlikely to be directly relevant with respect to larger proteins and complexes, as well as those which can associate with membranes. Indeed this same septin mutant allele (cdc12-6) has been used to show that septins play an important role in cell cortex compartmentalization (Barral et al., 2000 Mol Cell 5:8410). Secondly, the photobleaching experiments were single photon, i.e. not limited to a small focal volume and hence a substantial region above and below the focal plane was bleached. It is unclear, in this situation, how differences between bud and mother cell geometry affects fluorescence recovery. As a result, attributing the outcomes to cell size appears to be an overly strong conclusion (page 14 and bottom of 15). Indeed the word cell geometry may be more appropriate than size. In the data presented in Figure 3H do the 2-budded cells form buds simultaneously or subsequently? This should be indicated and shown in a supporting figure.

Reviewer #2:

In this manuscript the authors study the concepts and cellular mechanisms that allow formation of multiple polarization sites. They focus on the S. cerevisiae model system and combine theoretical models with quantitative image data as validation of their predictions. They interpret formation of multiple polarization sites as a shift from competition to co-existence in a mass conserved reaction-diffusion system (MCAS). They conclude that a key feature in this scenario is the amount of available substrate in the system, determined by parameters such as cell size and expression levels.

My key conceptual criticism is that while the authors discuss several variants of reaction diffusion models in detail they completely ignore two fundamental aspects of cellular polarity systems: the cycling of the GTPase and in particular the link between activity cycling and physical cycling via GDI, and the role of vesicular transport in recycling of membrane-bound proteins and in supporting the polarization process. This is particularly striking as the role of these parameters has been studied in detail regarding their effects on formation of multiple polarization sites. As one key conclusion from previous work was that yeast cell were not able to form multiple polarization sites in the absence of actin I would have expected a convincing argument to ignore this point in the current study. Previous data also showed that the levels of active Cdc42 (by overexpressing Cdc24 or using a slow cycling mutant) directly increased the number of polarization sites formed through its limiting effect on GDI-based recycling. By ignoring those fundamental aspects of the polarity system the authors made it very hard for me to accept or follow the arguments provided in this study.

1. All citations for interactions between Cdc42, PAK Bem1 and Cdc24 are very selective – several of the postulated interactions are far from being established and open questions should be clearly stated. Lacks all referrals to pertinent studies by Li, McCusker and Wedlich-Söldner labs.

2. Page 6 third paragraph: in scenarios of two linked substrates isn't it obvious that the one with lower abundance will be limiting? Not really fitting to a Results section in my mind.

3. Page 10, third paragraph: Freisigner et al. is cited for the lack of effect of Cdc42 OE, but all the results in this study showing that OE of Cdc24 or increasing the activity of Cdc42 (deletion of Bem2 or fast cycling mutant of Cdc42) leads to formation of multiple polarization sites are ignored – those would be far more relevant here.

4. The image series in Figure 3A does not show two buds growing simultaneously from one cell segment – does this ever happen or are the buds only formed from distant segments? If diffusion is indeed not limiting shouldn't the distance between two forming buds be random – hence also occur within a single segment?

5. In general I have fundamental issues with the chosen method of generating larger cells – the cdc12 defective cells have not been sufficiently characterized and have man additional parameter changes beyond the simple increase in volume. Effects on cell cycle, attachment of formins (Bnr1 is recruited through septins), PM organization (what happens to eisosomes, lipid composition etc.) and many more. The cell is simply too complex to use such crude methods to validate mechanistic models. I didn't understand why they did not simply go with cell cycle arrest and larger cells. Even with the reported cytosolic dilution they could perform tests where they relate their conditions to the corresponding controls.

6. They should definitely show how actin is distributed in the cell chains and perform the basic tests of polarization in LatA treated cells. While Bem1 or Cdc24 might not be limited by diffusion – actin nucleators, vesicles or actin filaments will likely be. Of course bud formation will be stopped but polarized patches should still be able to form. The effect of 37{degree sign}C shift is also of particular relevance in this context as it has been linked to actin disruption in previous studies.

7. Please provide the bud-number analysis for the correct test strain with Drsr1 and expressed polarity marker – is this equivalent to the numbers in 3B? Please provide images for bud scars to exclude effects of those (even in rsr1D) on polarization.

8. Formation of Bem1-clusters will likely depend on local lipid composition – images often not good enough to distinguish between local micro clusters and polarized accumulation but the clusters often seem to be at the base of the bud and not at the bud tip – please clarify.

9. Panels in Figure 4 are too small – nearly impossible to follow. Blue patch in lower series of 4B seems to move from right to left – possible issues with projection or deconvolution? Why is patch not at bud tip? Same in lower series of 4C: patch seems to be at base of bud – very confusing.

10. Figure 5I: those three proteins cannot be thrown together – OE of Cdc42 and Cdc24 should result in very different outcomes (change in substrate or activator) – provide effects for each protein separately and show actual images as well as quantification of protein levels (western or GFP fluorescence). Again, this has been done in similar way in Freisinger et al. and showed link between Cdc42 GTPase cycle and number of polarity sites.

Reviewer #3:

This is a dense and quite technical manuscript pertaining to the mechanism of cell polarization in budding yeast which relies on a Rho family GTPase, Cdc42, that is known to exhibit positive feedback and in wild-type cells. The focus of this work is to identify whether these same biochemical circuit can also generate two foci that do not undergo competition as is the norm in this pathway, and if so, to identify such conditions and to provide a conceptual framework for the absence of competition.

In its present state, I do not find that this manuscript provides compelling evidence to support the underlying conceptual argument, namely that patch saturation can allow to foci to co-exist. Furthermore, the manuscript is challenging to follow, the figures are sparsely annotated so they are not self-explanatory and the text, while readable, is to lengthy (almost 10K words) not well organized, diluting the authors message.

Comments related to modeling:

1. It is not clear why the authors discuss the minimalistic model in this paper. It is discussed in their earlier work, which is probably essential for many readers to understand this manuscript (or superfluous for those fully conversant in these models). I understand that it is for simplicity, but it is a distraction that does not apply to the in vivo situation. In addition, in figure 2C, the indirect substrate is a theoretical construct that alters the behavior of the model but lacks a mechanistic counterpart. Along these lines, there is some overlap with the Chiou, 2018 PLOS comp bio paper.

2. Does the authors model predict that equivalent cells would form variable numbers of patches (eg Figure 5B)? And that these patches would resolve with different outcomes (eg Figure 5E)? If not, what are the implications of this mismatch?

3. There is no direct experimental evidence to suggest the existence of an "indirect substrate" with differential mobility.

Comments related to experimental data:

1. The coexistence of multiple sites is predicated on the concept of saturation which has been shown to exist in simplified computational models. Based on that model, the authors explore some of the predictions of this model, namely that cell size and protein levels will enhance co-existence of multiple sites. However, the authors do not directly document saturation, which is the key predicate of the model. The predictions that are tested to support this model may not be unique to the proposed model.

2. The use of GFP and its diffusion as a model for all the relevant species in the model is not well substantiated. The relevant proteins are much larger, in variably stable protein-protein complexes, and associate with cortical factors, lipids, proteins etc. This is a critical point, because slower diffusion of key components could prevent patches positioned at a distance from effectively competing with one another. The diffusion rates of the relevant proteins would need to be measured directly, when expressed at their normal levels. Perhaps the authors could FRAP Bem1 at one patch and measure the rate at which the other patch dims.

3. Related to the previous point, in Figure 6 in the author's 2018 modeling paper, they suggest that when saturation is operative, an increase in cell size rapidly limits competition between patches (black curve). The change in behavior with increasing cell size is far less striking in vivo than would be predicted.

4. The authors provide evidence that the situation in vivo is far more complex that their model would predict. Pools of "cytokinetic Bem1" are documented and the position of bud sites is not random ("the locations at which patches formed were non-random, with a preference for bud tips and mother cell locations (Figure 5C)"). These phenomena indicate that distinct mechanisms may be operable in vivo raising doubts that the in silico version can be directly applied in vivo.

5. In the model, the authors appear to assume that all Bem1 is bound to Cdc24 and Cla4? This is not well supported by the evidence in the literature (page 14 refs).

6. The authors "utilized cytokinesis-defective yeast mutants to obtain large connected cells that continue cycling and presumably retain a normal overall protein composition." the underlying presumption is important for the analysis of the data, yet it is assumed, not tested.

7. For some of the cells in the second row of figure 6A, the linear "interpolation" does not match the data well. What is the basis for this "interpolation"?

It would be useful to indicate the distance between the patches for the 20 cells in Figure 6.

8. Inhibition of actin polymerization could be used to inhibit budding and cytokinesis and might allow the authors to obtain cells that continue to cycle but retain a simple geometry.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

Thank you for resubmitting your work entitled "How cells determine the number of polarity sites" for further consideration by eLife. Your revised article has been evaluated by Naama Barkai (Senior Editor) and a Reviewing Editor (Mohan Balasubramanian).

The manuscript has been improved but there are some remaining issues that need to be addressed, as outlined below. Please note that one experiment has been suggested (point 5 below). If you have the data readily available, please do add it.

The rest of the points raised can be addressed through rewriting.

1. The text related to the portion regarding saturation requires further editing:

Line 76 "However, recent studies have shown that the growth rate of a peak "saturates" as the activator in the peak exceeds a threshold." Given that saturation is not shown empirically, this sentence should refer to "modeling studies".

This paragraph also refers to the possibility of equalization and explicitly states on line 83 "it has not yet been determined whether equalization occurs in cells". Given that saturation has also not been empirically demonstrated in cells, this too should be explicitly stated.

2. The authors observe that some cells also exhibit equalization, which the authors indicate is not possible in the "mechanistic model" as written. They further show that this becomes possible if an "indirect substrate" is incorporated into the model. This is an interesting finding even though the "indirect substrate" remains hypothetical/speculative. However, it does reveal that the mechanistic model based on MCAS does not provide a fully accurate description of the in vivo situation. Given that the reader was previously led to believe that the mechanistic MCAS model was supported by the available data, this apparent shortcoming is a bit jarring. The authors state (line 333) "Our conclusions from analysis of the simple indirect substrate model can explain the outcomes from all of the models discussed above and in previous studies (Figure 5-Figure supp. 1)." This sentence suggests that models with an indirect substrate would also predict that the increase in protein concentration would also lead to multibudding in this regime and figure 5 supports this interpretation. Nevertheless, it would help the reader to even more explicitly state that indirect substrate models is fully consistent with the findings up to that point in the manuscript.

More broadly, this manuscript begins as a Figure 1 Theory paper in the Phillips vernacular (PMID 26584768), but transitions to a "Figure 7 Theory paper". It would behove the reader to more clearly foreshadow the revision to the model in a subsequent figure.

3. Moreover, the description of the indirect substrate is unclear: line 280ff "The GAP and the inhibited GEFi are neither substrates nor activators, and appear to play different roles in the polarity circuit. However, we noticed that they both provide a source of substrate: the GAP converts local GTP-Cdc42 into the substrate GDP-Cdc42, while the inhibited GEFi turns into the substrate GEF upon dephosphorylation. Thus, in both cases a new species produced by the activator is highly mobile and generates a substrate in the cytoplasm."

In particular, the phrase "the inhibited GEFi turns into the substrate GEF upon dephosphorylation" is unclear. While it is evident that the inhibited GEF turns into a GEF upon dephosphorylation, this active GEF is not a substrate and thus does not fit the descriptor of being "highly mobile and generates a substrate in the cytoplasm." particularly as the GEF is unlikely to be active until it reaches the membrane. The confusion appears to arise from a conflation of the minimalistic model with a semi-mechanistic one. Whereas the activator and substrate are interconvertible in the minimalistic model, the same is not true in the semi-mechanistic one. This requires clarification.

4. Along these lines, it would be appropriate for the authors to discuss in this context the paper from Rodriguez et al., PMID 28781174 which demonstrates that the anterior PAR complex proteins PAR-6 and aPKC are induced to dissociate from PAR-3 by Cdc42 binding, which is analogous to this principle.

5. This study also raises the question as to whether the presence of multiple initial polarity sites described in Howell, 2012 and subsequent papers from the lab results from the hydroxyurea treatment which, by creating a cell cycle delay, would be expected to increase the amount of polarity proteins that exist in cells, thereby facilitating such behavior as shown here. It would be quite interesting to determine whether the strain overexpressing Bem1, Cdc42, and Cdc24 generate more nascent sites in otherwise unperturbed G1 cells as compared to their WT counterparts.

https://doi.org/10.7554/eLife.58768.sa1

Author response

[Editors’ note: The authors appealed the original decision. What follows is the authors’ response to the first round of review.]

Reviewer #1:

The manuscript entitled "How cells determine the number of polarity sites" by Chiou et al., compares theoretical models for polarity establishment in budding yeast, specifically their regulatory mechanisms, with experimental observations, in particular those that can lead to polarity cluster coexistence or equalization. After examining the implications of several models of increasing complexity the predictions of specific aspects of these models are explored, in particular alteration of cell size and polarity protein levels. While the findings presented are interesting, the overall message is not sufficiently clear and hence this obscures the significance of the work. Substantial rewriting is necessary together with refocusing to make the work more accessible to a broad audience.

We apologize for not making our main findings clearer, and hope the revised version makes the overall messages clearer and more accessible.

1. The main findings of this work are not evident from the title, introduction and first paragraph of the Discussion. The Discussion talks about several classes of models, but does not indicate clearly which model best describes the observed behaviour. The title and abstract are somewhat general, overall appear descriptive and do not clearly indicate the findings. For example, in the Discussion section, page 25, it states, "Here we propose a novel mechanism for equalization that does not require negative feedback, but can account for the behavior of the more complex models that incorporate negative feedback," however it is not evident what this mechanism is.

To address these concerns, we have (i) reworked the Abstract to highlight the two main advances: testing MCAS model predictions in yeast, and elucidating a novel equalization mechanism in multi-component MCAS models. (ii) In the last paragraph of the Introduction, and the first paragraph of the Discussion, we summarize our main findings and indicate that our findings favor coexistence as the dominant reason for two-budded cells. (iii) We have explored model behaviors over a broad range of key parameters (see new bifurcation analysis in Figure 5), allowing a more accurate and insightful analysis of the basis for equalization. In the third section of the Discussion, which has been extensively re-written, we now provide a specific description of the key features of the indirect substrate that enable equalization. We hope that the equalization mechanism is now clear.

2. Reference to and discussion of finding from several relevant and recent studies are lacking. For example, 3 studies, which use optogenetic systems to alter levels and/or clusters of active Cdc42 in fungi are not discussed, these findings are likely to be relevant to mechanism of polarity cluster control, see

-Witte et al., eLife 2017 e26722

-Lamas et al., Plos Biol 2020 18: e3000600

-Silva et al., Cell Rep 2019 28: 2231

Note that while the latter two are carried out in different yeast, the approaches involve temporal recruitment of active Cdc42 to the plasma membrane and hence are relevant to this work.

These studies are indeed relevant, and they are now cited in the penultimate paragraph of the Introduction as well as the Results.

Furthermore the Discussion section (to some extent also the Introduction section, see also below), including the last subsection of "Implications for other systems" unfortunately does not put this study into the context of what is known about polarity determination outside of the budding yeast perspective, which limits its general interest. For example, I am surprised there is no mention or discussion of the recent work from the Goehring laboratory entitled "A Cell Size Threshold Limits Cell Polarity and Asymmetric Division Potential" (Hubatsch et al., Nat Phys 2019 15:1075) which would appear to be very relevant.

We have expanded the “Implications…” section of the Discussion to include more references including a discussion of Hubatsch et al.

Similarly, the introduction seems to be overly focused on budding yeast with little indication of other systems and the more recent findings, including those from fission yeast (as opposed to cursory mention of an old S. pombe review) and other fungi, such as Neurospora crassa, among others. Furthermore, other reviews cited are quite old.

The Introduction is focused on mathematical models of pattern formation: budding yeast are introduced in the last paragraph as one well-studied system in which experimental tests of model predictions can be carried out. Other fungal systems are mentioned in the last section of the Discussion.

3. Throughout, the terminology 'protein content' is used which is imprecise. Are the authors referring to total protein amount or amount divided by volume, i.e. an effective concentration? This ambiguity is confusing, in particular in the Discussion section. It is unclear whether larger cells (page 20) have a higher amount or effective concentration of polarity proteins. It is surprising that this aspect of polarity would be cell size dependent given different sizes of haploid and diploid yeast cells.

We apologize for not making this clear. We have revised the text to use unambiguous terms like “total amount of X in the system”. We now explicitly show using Western blots (Figure 4—Figure supp 1) that the concentration of polarity proteins does not change with cell size, and therefore that larger cells have a higher total amount of polarity proteins per cell.

4. Figures should be organised more clearly, with panels in left to right, top to bottom order (Figure 1-3), graph axes indicated (lacking in many panels including 1D, 2D, E, G, H), color schemes unclear (1G and 1H compared to 1I and 1J; green color used for different species), what is shown in different panels is not indicated (2D, 2H), in some scatter plots means and standard deviation should be indicated (3G, 5A, 5G), in several graphs error bars should be indicated (5B, 5E, 5I) and Figure 6 can be substantially simplified with at most 2 examples of each behaviour shown in A, together with an indication of what the lines refer to (the rest can go in the supporting figure). In addition, it is not clear in 6A if competed (note mix of past tense verbs and nouns for description, better to indicate 'competition, coexistence and equal) is actually different than equalized, in which the initial intensities are inversed, i.e. red higher than blue (A, i).

We have re-organized the Figures as suggested, added axis labels for all graphs, indicated the color scheme in the labels or Figure Legends, and added mean and standard deviations for scatter plots. We prefer to keep several examples in Figure 6; we have added more in a new Figure 6—Figure supp 1. The orange and blue in Figure 6 track intensities at different locations, so we can clearly distinguish whether initial inequalities between sites narrowed (implying equalization) or widened (implying competition). This is now explicitly stated in the Figure Legend.

5. The analysis and interpretation of the cytoplasmic connection in Figure 3D-F and presented on page 14 (and mentioned again on pages 21 and 23) appears over-simplified. Firstly, diffusion of relatively small cytoplasmic GFP is unlikely to be directly relevant with respect to larger proteins and complexes, as well as those which can associate with membranes. Indeed this same septin mutant allele (cdc12-6) has been used to show that septins play an important role in cell cortex compartmentalization (Barral et al., 2000 Mol Cell 5:8410). Secondly, the photobleaching experiments were single photon, i.e. not limited to a small focal volume and hence a substantial region above and below the focal plane was bleached. It is unclear, in this situation, how differences between bud and mother cell geometry affects fluorescence recovery. As a result, attributing the outcomes to cell size appears to be an overly strong conclusion (page 14 and bottom of 15). Indeed the word cell geometry may be more appropriate than size. In the data presented in Figure 3H do the 2-budded cells form buds simultaneously or subsequently? This should be indicated and shown in a supporting figure.

Our conclusion from the bleaching experiment is that diffusion across the neck is mildly impaired, to the same degree as would be predicted from the geometry (i.e. the narrowing at the neck). To make this clear, we now present the 3D simulation of the experiment first, and then the data (New Figure 2-Figure supp 2). Our goal with this experiment was not to extract the diffusion constant, but to determine whether some blockage occurred at the neck. The match between result and model expectation indicates that there are no additional unexpected barriers to diffusion across the neck. Barral et al., (2000) concluded that septins retard diffusion of cortical proteins and that cdc12-6 removed this barrier, which is fully consistent with our NOT finding a barrier in cdc12-6 cells.

With respect to attributing the outcomes to cell size: Even the small effect of neck geometry on the diffusional connection between compartments has the potential to promote 2-budded outcomes. In distinguishing whether retarded diffusion through the neck or cell size was the dominant factor in promoting 2-budded outcomes, we relied on the comparison between haploid (smaller neck, smaller cell) and diploid cells (larger neck, larger cell). Smaller necks (haploid) would retard diffusion more effectively, yet haploids produced fewer 2-budded outcomes, leading us to favor size as the main contributor. To clarify these points we moved the bleaching experiment to a supplementary Figure and highlighted the haploid/diploid comparison in the text.

We have added Video 1 to show that the buds of 2-budded cells form simultaneously (within the resolution of our time-lapse). This is explicitly stated in the text.

Reviewer #2:

In this manuscript the authors study the concepts and cellular mechanisms that allow formation of multiple polarization sites. They focus on the S. cerevisiae model system and combine theoretical models with quantitative image data as validation of their predictions. They interpret formation of multiple polarization sites as a shift from competition to co-existence in a mass conserved reaction-diffusion system (MCAS). They conclude that a key feature in this scenario is the amount of available substrate in the system, determined by parameters such as cell size and expression levels.

My key conceptual criticism is that while the authors discuss several variants of reaction diffusion models in detail they completely ignore two fundamental aspects of cellular polarity systems: the cycling of the GTPase and in particular the link between activity cycling and physical cycling via GDI, and the role of vesicular transport in recycling of membrane-bound proteins and in supporting the polarization process. This is particularly striking as the role of these parameters has been studied in detail regarding their effects on formation of multiple polarization sites. As one key conclusion from previous work was that yeast cell were not able to form multiple polarization sites in the absence of actin I would have expected a convincing argument to ignore this point in the current study. Previous data also showed that the levels of active Cdc42 (by overexpressing Cdc24 or using a slow cycling mutant) directly increased the number of polarization sites formed through its limiting effect on GDI-based recycling. By ignoring those fundamental aspects of the polarity system the authors made it very hard for me to accept or follow the arguments provided in this study.

With regard to GTPase cycling and GDI: we agree that these are major key parameters—they are incorporated into ALL of the models we discussed and referenced in the papers now cited, including the optogenetic papers suggested by reviewer #1.

With regard to the role of vesicular transport in recycling Cdc42 to support polarization: we did not focus on historical differences in findings and interpretations between our lab and the labs of Rong Li and Roland Wedlich-Soldner, as we believe that they have been largely addressed by prior work (as discussed for instance in (Woods and Lew, 2017)). Some of those are relevant to the reviewer<milestone-start />’<milestone-end />s comments, and we discuss them briefly below.

While there is agreement on the presence of two-budded cells in rdi1 mutants lacking the GDI, the origin of the two-budded cells has been controversial. Our interpretation is that deleting the GDI slows, but does not stop, membrane-cytoplasm exchange of Cdc42 (Woods et al., 2016), that slowed exchange slows the competition between polarity sites (Wu et al., 2015), and that slowed competition allows polarity sites to persist past bud emergence, yielding >1 bud. Consistent with that view, artificially slowing membrane-cytoplasm exchange of Bem1 or Cdc24 also slowed competition and led to the appearance of cells with two or more buds (Wu et al., 2015).

Wedlich-Soldner and Li were the first to show that Cdc42 recycling was slowed in rdi1 mutants, but they assumed that in those mutants the Cdc42 was unable to detach from the membrane, and hence that all remaining recycling was due to actin-mediated vesicle traffic (Freisinger et al., 2013; Slaughter et al., 2009). Consistent with that view, they reported that cells were unable to polarize Cdc42 in the combined absence of Rdi1 and F-actin (Freisinger et al., 2013; Smith et al., 2013). Freisinger et al. concluded that two-budded cells arose from reliance on actin-mediated traffic in rdi1 mutants, which was reasonable given their findings and assumptions at the time.

However, our subsequent findings argue strongly that even in rdi1 mutants, F-actin is not required to polarize Cdc42 or Bem1 or Cdc24, that actin cables do not affect the timing or efficiency of polarization, and that Cdc42 can still exchange (albeit more slowly) between membrane and cytoplasm (Woods et al., 2016). These findings as well as several earlier findings led us to conclude that F-actin is not important for polarizing Cdc42 (Dyer et al., 2013; Howell et al., 2012; Howell et al., 2009; Irazoqui et al., 2003; Layton et al., 2011; Savage et al., 2012), reviewed in (Chiou et al., 2017; Johnson et al., 2011; Woods and Lew, 2017).

1. All citations for interactions between Cdc42, PAK Bem1 and Cdc24 are very selective – several of the postulated interactions are far from being established and open questions should be clearly stated. Lacks all referrals to pertinent studies by Li, McCusker and Wedlich-Söldner labs.

We have added citations for the direct interaction between Cdc42 and PAKs (Bose et al., 2001; Cvrckova et al., 1995; Lamson et al., 2002; Zhao et al., 1995), PAKs and Bem1 (Bose et al., 2001; Leeuw et al., 1995), and Bem1 and Cdc24 (Bose et al., 2001; Butty et al., 2002; Ito et al., 2001; Peterson et al., 1994)(Rapali et al., 2017) in the penultimate paragraph of the Introduction. We are not aware of any controversy or open questions regarding these interactions.

2. Page 6 third paragraph: in scenarios of two linked substrates isn't it obvious that the one with lower abundance will be limiting? Not really fitting to a Results section in my mind.

We have moved those panels to the new Figure 1—supp Figure 1. Our point in showing the results of those simulations was in part that a substrate can become limiting even if it is not the one with lower abundance (note the different axis labels for the concentrations of Cdc42 or Bem1-GEF). Which substrate is limiting depends on the reaction parameters as well as abundance.

3. Page 10, third paragraph: Freisigner et al. is cited for the lack of effect of Cdc42 OE, but all the results in this study showing that OE of Cdc24 or increasing the activity of Cdc42 (deletion of Bem2 or fast cycling mutant of Cdc42) leads to formation of multiple polarization sites are ignored – those would be far more relevant here.

Actually Freisinger did not see an effect of OE of Cdc24 unless they also deleted BEM2 , and even then the effect was marginal, though it could be enhanced by Latrunculin treatment/washout (see their Figure 7E)(Freisinger et al., 2013). We have added new experiments that individually doubled the gene dosage for CDC42, CDC24, or BEM1, and found that this did not necessarily increase multibudded outcomes (new Figure 4-supp Figure 2). We now cite Freisinger as being consistent with that result. Doubling the dosage for all three genes was more effective, and we have added our reasoning that this is expected because adding a single gene may alter the stoichiometry and make a different species limiting.

4. The image series in Figure 3A does not show two buds growing simultaneously from one cell segment – does this ever happen or are the buds only formed from distant segments? If diffusion is indeed not limiting shouldn't the distance between two forming buds be random – hence also occur within a single segment?

This is a good point. The two-budded cells we document have all emerged from different cell lobes (and in non-random locations, as we discussed). We suspect that the effect of cell geometry on diffusional connectivity, although too small to explain the existence of two-budded cells, may influence the placement of the buds and account for this phenomenon. This is now mentioned in the second section of the Discussion.

5. In general I have fundamental issues with the chosen method of generating larger cells – the cdc12 defective cells have not been sufficiently characterized and have man additional parameter changes beyond the simple increase in volume. Effects on cell cycle, attachment of formins (Bnr1 is recruited through septins), PM organization (what happens to eisosomes, lipid composition etc.) and many more. The cell is simply too complex to use such crude methods to validate mechanistic models. I didn't understand why they did not simply go with cell cycle arrest and larger cells. Even with the reported cytosolic dilution they could perform tests where they relate their conditions to the corresponding controls.

We acknowledge that any method to generate larger cells might inadvertently introduce unanticipated parameter changes, although we do not understand why the reviewer should feel that cdc12-6 mutants are uniquely suspect in that regard. We have experimentally tested our assumption that overall concentrations of Cdc42, Cdc24, and Bem1 are unchanged by making cells larger in this way (new Figure 4-supp Figure 1).

With regard to cell cycle: we focus on initial polarization in late G1, so we do not believe that the extended G2 should affect the outcome. We found similar multi-budding in iqg1 depletion cells that still have intact septins and do not affect G2 (Figure 2-supp Figure 1B).

6. They should definitely show how actin is distributed in the cell chains and perform the basic tests of polarization in LatA treated cells. While Bem1 or Cdc24 might not be limited by diffusion – actin nucleators, vesicles or actin filaments will likely be. Of course bud formation will be stopped but polarized patches should still be able to form. The effect of 37{degree sign}C shift is also of particular relevance in this context as it has been linked to actin disruption in previous studies.

We see no reason to doubt that actin is polarized towards the same sites as Cdc42 in cdc12-6 cells. With regard to Latrunculin: we view this as a much more disruptive treatment than cdc12-6. We note that Lat inhibits all endocytosis (Ayscough et al., 1997), so that plasma membrane composition changes a lot as material is added with no recycling. Furthermore, Lat treatment induces the cell wall integrity stress response (Harrison et al., 2001), which itself can cause depolarization. In fission yeast, Sawin and colleagues showed that the effects of Lat on Cdc42 (which are far more severe in that organism) are all mediated by a stress response (Mutavchiev et al., 2016). Thus, we believe that interpretation of Lat treatment is far more complex that generally assumed.

7. Please provide the bud-number analysis for the correct test strain with Drsr1 and expressed polarity marker – is this equivalent to the numbers in 3B? Please provide images for bud scars to exclude effects of those (even in rsr1D) on polarization.

The bud-number data for cdc12-6rsr1D mutants expressing the Bem1 probe is now shown in Figure 3-supp Figure 1. Like cdc12-6 RSR1 strains, these exhibit multipolar outcomes as they grow larger. As expected from previous work showing that RSR1 retards competition (Wu et al., 2013), cdc12-6rsr1D strains display fewer multipolar outcomes than cdc12-6 RSR1 strains.

We did not understand how bud scar images would be informative. We note that septins are known to be essential for axial budding (Flescher et al., 1993), so axial budding is disabled with or without Rsr1 in our strains.

8. Formation of Bem1-clusters will likely depend on local lipid composition – images often not good enough to distinguish between local micro clusters and polarized accumulation but the clusters often seem to be at the base of the bud and not at the bud tip – please clarify.

We fully agree that lipid composition would affect the parameters of reaction-diffusion models and hence could impact competition between polarity sites. Detecting nanoclusters requires super-resolution methods: our spinning-disc confocal microscopy can detect protein-rich polarity sites but does not distinguish whether or not they are composed of nanoclusters. To remove this ambiguity, we no longer use the word <milestone-start />“<milestone-end />cluster” to describe polarity sites.

With regard to bud base or bud tip: once a bud is growing, the polarity site is always at the bud tip. This is now explicitly stated in the new Figure 6 Legend.

9. Panels in Figure 4 are too small – nearly impossible to follow. Blue patch in lower series of 4B seems to move from right to left – possible issues with projection or deconvolution? Why is patch not at bud tip? Same in lower series of 4C: patch seems to be at base of bud – very confusing.

We apologize for the small size and confusing display: the patches are always at the bud tips, but projection from 3D to 2D can create a misleading impression when the bud does not grow in the focal plane. In the new Figure 3 and associated supporting Figures the images are larger and explanatory cartoons have been added.

10. Figure 5I: those three proteins cannot be thrown together – OE of Cdc42 and Cdc24 should result in very different outcomes (change in substrate or activator) – provide effects for each protein separately and show actual images as well as quantification of protein levels (western or GFP fluorescence). Again, this has been done in similar way in Freisinger et al. and showed link between Cdc42 GTPase cycle and number of polarity sites.

We now show Western blots to quantify the expression levels of the proteins (new Figure 4-supp Figure 1), and examine the effect of doubling the dose for each protein individually (new Figure 4-supp Figure 2). This did not affect the frequency of multipolar outcomes much for any of the proteins. Overexpressing one component of a multi-component polarity system might fail to yield multi-polar outcomes because a non-overexpressed component becomes limiting. As noted above, Freisinger also did not observe any effect of doubling CDC24 dose unless combined with bem2 deletion.

Reviewer #3:

This is a dense and quite technical manuscript pertaining to the mechanism of cell polarization in budding yeast which relies on a Rho family GTPase, Cdc42, that is known to exhibit positive feedback and in wild-type cells. The focus of this work is to identify whether these same biochemical circuit can also generate two foci that do not undergo competition as is the norm in this pathway, and if so, to identify such conditions and to provide a conceptual framework for the absence of competition.

In its present state, I do not find that this manuscript provides compelling evidence to support the underlying conceptual argument, namely that patch saturation can allow to foci to co-exist. Furthermore, the manuscript is challenging to follow, the figures are sparsely annotated so they are not self-explanatory and the text, while readable, is to lengthy (almost 10K words) not well organized, diluting the authors message.

We have addressed these issues as follows:

– To reduce the density and length, we moved some sections to supplemental Figures, and reorganized the text to streamline the flow and remove unnecessary material.

– We summarized our main arguments and novel conclusions in the Abstract, the last paragraph of the Introduction, and the first paragraph of the Discussion. The conceptual argument identified by the reviewer, that “patch saturation can allow two foci to co-exist”, was actually the take-home from our previous paper on minimalistic models (Chiou et al., 2018). Here, our main advances are to show experimentally that yeast cells exhibit multipolar outcomes in a manner consistent with the MCAS models, to elucidate another mechanism (equalization) that can yield multipolar outcomes, and to distinguish which of the different model-based phenomena (periodic polarity peaks, slow competition/co-existence, or equalization) account for the multipolar outcomes in this system.

– We have better annotated the Figures and added explanatory cartoons to make them easier to follow.

Comments related to modeling:

1. It is not clear why the authors discuss the minimalistic model in this paper. It is discussed in their earlier work, which is probably essential for many readers to understand this manuscript (or superfluous for those fully conversant in these models). I understand that it is for simplicity, but it is a distraction that does not apply to the in vivo situation. In addition, in figure 2C, the indirect substrate is a theoretical construct that alters the behavior of the model but lacks a mechanistic counterpart. Along these lines, there is some overlap with the Chiou, 2018 PLOS comp bio paper.

We discuss the minimalistic model precisely because it is essential for many readers to understand this manuscript. A basic run-down seemed advisable so that readers could understand the novel aspects of this paper, and devoting 50% of Figure 1 to such introductory material seemed appropriate. Based on our findings we do believe that it is applicable to the in vivo situation.

With regard to the indirect substrate: there are many potential mechanistic counterparts. We have extensively revised the section on equalization and now emphasize that the key is a pathway that indirectly converts activator to substrate. The last paragraph of the Discussion section on equalization now explicitly presents various examples of known candidates that could act in this manner. Our analysis does not overlap with Chiou, 2018, which dealt exclusively with 2-component models that lacked an indirect pathway from activator to substrate.

2. Does the authors model predict that equivalent cells would form variable numbers of patches (eg Figure 5B)? And that these patches would resolve with different outcomes (eg Figure 5E)? If not, what are the implications of this mismatch?

All of the models considered here are deterministic, and the outcomes would depend on initial conditions. Noise (fluctuations) in the spatial distribution of starting protein concentrations would determine how many initial patches form, so seeing different numbers of initial patches is entirely consistent with expectation. If 2 initial patches form, the rate of competition depends on model parameters and the (noise-based) initial asymmetry between the patches. These points are now explicitly discussed in the Results.

3. There is no direct experimental evidence to suggest the existence of a "indirect substrate" with differential mobility.

We now discuss several known polarity components that are candidates that could act as indirect substrates (last paragraph of the Discussion section on equalization).

Comments related to experimental data:

1. The coexistence of multiple sites is predicated on the concept of saturation which has been shown to exist in simplified computational models. Based on that model, the authors explore some of the predictions of this model, namely that cell size and protein levels will enhance co-existence of multiple sites. However, the authors do not directly document saturation, which is the key predicate of the model. The predictions that are tested to support this model may not be unique to the proposed model.

The reviewer is correct that while our data indicate co-existence (rather than equalization) is the predominant reason for multipolar outcomes in yeast, we have not been able to demonstrate saturation from the fluorescent intensity profiles of the patches or the cytoplasm. A major issue is that when there are multiple species (as opposed to just one as in the minimalistic models), then which species is limiting depends on parameters, and modeling explains why the concentration profiles don’t show clear saturation (Figure 1-supp Figure 1). The more definitive changes in cytoplasmic concentrations (Figure 1) are unfortunately too minuscule to detect experimentally.

2. The use of GFP and its diffusion as a model for all the relevant species in the model is not well substantiated. The relevant proteins are much larger, in variably stable protein-protein complexes, and associate with cortical factors, lipids, proteins etc. This is a critical point, because slower diffusion of key components could prevent patches positioned at a distance from effectively competing with one another. The diffusion rates of the relevant proteins would need to be measured directly, when expressed at their normal levels. Perhaps the authors could FRAP Bem1 at one patch and measure the rate at which the other patch dims.

We note that because the dynamics of Bem1 coming on and off a patch are dominated by the relatively slow unbinding reaction, bleaching a patch would not provide any information about the relatively fast process of diffusion. Because competition between patches in different compartments is a frequent outcome, we do not doubt that Bem1 (and other polarity proteins) can travel between compartments. We do agree that Bem1 diffusion would be slower than that of GFP, but to do the analogous experiment (bleaching/recovery of cytoplasmic spot, not patch) with Bem1-GFP would require significant overexpression in order to get a decent signal:noise. We now clarify that our main conclusion from this experiment is simply that as predicted, neck geometry provides a minor but detectable impediment to diffusional communication.

3. Related to the previous point, in Figure 6 in the author's 2018 modeling paper, they suggest that when saturation is operative, an increase in cell size rapidly limits competition between patches (black curve). The change in behavior with increasing cell size is far less striking in vivo than would be predicted.

Figure 6 in Chiou et al., 2018 describes the deterministic outcome of competition between two standardized initial peaks containing 60% and 40% of the polarized proteins. However, the asymmetry of initial polarity sites in vivo is stochastic, and can range from 50:50 to 80:20. Stochasticity can obscure the effect of saturation, as in a deterministic model 80:20 sites can compete under the same parameters where 60:40 sites coexist. Another issue is that simulations on 2D surfaces (Figure 8A in Chiou, 2018 and Figure 1I in the current paper) show a more gradual increase in competition time than simulations of the same model in 1D domains (Figure 6 in Chiou, 2018). This is primarily because a secondary competition mechanism in 2D is still in effect even when peaks saturate, as discussed in Chiou, 2018. Thus, the in vivo behavior we observed is consistent with the 2D modeling predictions when one takes stochasticity of starting conditions into account.

4. The authors provide evidence that the situation in vivo is far more complex that their model would predict. Pools of "cytokinetic Bem1" are documented and the position of bud sites is not random ("the locations at which patches formed were non-random, with a preference for bud tips and mother cell locations (Figure 5C)"). These phenomena indicate that distinct mechanisms may be operable in vivo raising doubts that the in silico version can be directly applied in vivo.

Agreed! This is always an issue when trying to extract fundamental principles underlying complex phenomena, but we would argue that it does not invalidate the effort, and that conclusions that explain a large part (though not all) of the behavior are valuable.

5. In the model, the authors appear to assume that all Bem1 is bound to Cdc24 and Cla4? This is not well supported by the evidence in the literature (page 14 refs).

Agreed. This choice has a historical origin: in his foundational work Goryachev (Goryachev and Pokhilko, 2008) tested the effects of modeling separate species for Bem1 and GEF that could associate and dissociate, and concluded that the overall model behavior didn<milestone-start />’<milestone-end />t change (explained in the supplement of that paper), and we have followed his lead in simplifying the complex. More recently, Frey and colleagues (Klunder et al., 2013) also investigated a model with separate Bem1 and Cdc24 species; when examined in comparable parameter regimes (Wu et al., 2015), that model also predicts the same qualitative behavior. However, it is possible that in some parameter regimes, introducing separate PAK, Bem1, and GEF species would lead to equalization instead of competition, as the separate species have potential to act as indirect substrates. This is now addressed in the Discussion where the potential of separate GEF, Bem1, and PAK to act as indirect substrates is mentioned. In the Methods section providing a detailed description of the mechanistic model, we now clarify the historical reason for the use of a single species as well as the potential for more complex models with multiple species to behave differently.

6. The authors "utilized cytokinesis-defective yeast mutants to obtain large connected cells that continue cycling and presumably retain a normal overall protein composition." the underlying presumption is important for the analysis of the data, yet it is assumed, not tested.

Agreed. We now provide Western blot data confirming this assumption for Bem1, Cdc42, and Cdc24 (Figure 4-supp Figure 1).

7. For some of the cells in the second row of figure 6A, the linear "interpolation" does not match the data well. What is the basis for this "interpolation"?

It would be useful to indicate the distance between the patches for the 20 cells in Figure 6.

We did not mean to imply that the process is linear. We have removed the linear trend lines to avoid confusion. And, we now indicate the distance between patches as an inset in each panel. We also added more example cells and plotted the distances between patches for all examples, showing that the outcome appears uncorrelated with inter-patch distance (Figure 6—supp Figure 1).

8. Inhibition of actin polymerization could be used to inhibit budding and cytokinesis and might allow the authors to obtain cells that continue to cycle but retain a simple geometry.

Latrunculin treatment causes cell cycle arrest in G2 (McMillan et al., 1998), so the cells would not continue cycling. Moreover, as mentioned in our response to reviewer 2 point 6, Latrunculin inhibits all endocytosis (Ayscough et al., 1997), so that plasma membrane composition changes a lot as material is added with no recycling. Furthermore, Lat treatment induces the cell wall integrity stress response (Harrison et al., 2001), which itself can cause depolarization. In fission yeast, Sawin and colleagues showed that the effects of Lat on Cdc42 (which are far more severe in that organism) are all mediated by a stress response (Mutavchiev et al., 2016). Thus, we believe that interpretation of Lat treatment is far more complex than generally assumed.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

The manuscript has been improved but there are some remaining issues that need to be addressed, as outlined below. Please note that one experiment has been suggested (point 5 below). If you have the data readily available, please do add it.

The rest of the points raised can be addressed through rewriting.

1. The text related to the portion regarding saturation requires further editing:

Line 76 "However, recent studies have shown that the growth rate of a peak "saturates" as the activator in the peak exceeds a threshold." Given that saturation is not shown empirically, this sentence should refer to "modeling studies".

Good point. Edited as suggested.

This paragraph also refers to the possibility of equalization and explicitly states on line 83 "it has not yet been determined whether equalization occurs in cells". Given that saturation has also not been empirically demonstrated in cells, this too should be explicitly stated.

Agreed. Now edited.

2. The authors observe that some cells also exhibit equalization, which the authors indicate is not possible in the "mechanistic model" as written. They further show that this becomes possible if an "indirect substrate" is incorporated into the model. This is an interesting finding even though the "indirect substrate" remains hypothetical/speculative. However, it does reveal that the mechanistic model based on MCAS does not provide a fully accurate description of the in vivo situation. Given that the reader was previously lead to believe that the mechanistic MCAS model was supported by the available data, this apparent shortcoming is a bit jarring. The authors state (line 333) "Our conclusions from analysis of the simple indirect substrate model can explain the outcomes from all of the models discussed above and in previous studies (Figure 5-Figure supp. 1)." This sentence suggests that models with an indirect substrate would also predict that the increase in protein concentration would also lead to multibudding in this regime and figure 5 supports this interpretation. Nevertheless, it would help the reader to even more explicitly state that indirect substrate models is fully consistent with the findings up to that point in the manuscript.

More broadly, this manuscript begins as a Figure 1 Theory paper in the Phillips vernacular (PMID 26584768), but transitions to a "Figure 7 Theory paper". It would behoove the reader to more clearly foreshadow the revision to the model in a subsequent figure.

We were not entirely sure what the editor had in mind here. Is the idea that the equalization instances in Figure 6D negate the mechanistic model in Figure 1F, necessitating an indirect substrate? That may be true, but the evidence for equalization is quite weak (only 3 cells, and only one timepoint in each instance distinguishes equalization from coexistence). We have changed the labeling in Figure 6D and added a sentence to the text (p. 9, bottom) to make this clear.

3. Moreover, the description of the indirect substrate is unclear: line 280ff "The GAP and the inhibited GEFi are neither substrates nor activators, and appear to play different roles in the polarity circuit. However, we noticed that they both provide a source of substrate: the GAP converts local GTP-Cdc42 into the substrate GDP-Cdc42, while the inhibited GEFi turns into the substrate GEF upon dephosphorylation. Thus, in both cases a new species produced by the activator is highly mobile and generates a substrate in the cytoplasm."

In particular, the phrase "the inhibited GEFi turns into the substrate GEF upon dephosphorylation" is unclear. While it is evident that the inhibited GEF turns into a GEF upon dephosphorylation, this active GEF is not a substrate and thus does not fit the descriptor of being "highly mobile and generates a substrate in the cytoplasm." particularly as the GEF is unlikely to be active until it reaches the membrane. The confusion appears to arise from a conflation of the minimalistic model with a semi-mechanistic one. Whereas the activator and substrate are interconvertible in the minimalistic model, the same is not true in the semi-mechanistic one. This requires clarification.

Thank you for pointing out the lack of clarity in our discussion. In our view, the key features of an “activator” are that (i) the species has low mobility; and (ii) it can promote accumulation of more activator via positive feedback. Similarly, the key features of a “substrate” are that (i) the species has high mobility; and (ii) it can be converted into an activator. Using these criteria, the mechanistic model of Figure 1F has two species that could be considered as activators and two species that can be considered as corresponding substrates:

Activators: GTP-Cdc42 and Bem1-GEF-Cdc42. Both have low mobility and promote their own accumulation by positive feedback. There is no reason to distinguish only one of these as the “activator”.
Substrates: GDP-Cdc42 and Bem1-GEF in the cytoplasm. Both have high mobility and can be converted into activators (GDP-Cdc42 is converted to the activator GTP-Cdc42, and Bem1-GEF is converted into the activator Bem1-GEF-Cdc42 when it binds GTP-Cdc42).

Accordingly, we believe it is correct to refer to the dephosphorylated GEF (cytoplasmic Bem1-GEF) as a substrate in Figure 5. We have edited the Results text (p. 4, top) to make this clearer. We have also edited the cartoon in Figure 5Aiii and corresponding text (p. 7) and Figure legend to enhance clarity.

4. Along these lines, it would be appropriate for the authors to discuss in this context the paper from Rodriguez et al. PMID 28781174 which demonstrates that the anterior PAR complex proteins PAR-6 and aPKC are induced to dissociate from PAR-3 by Cdc42 binding, which is analogous to this principle.

This is an interesting paper, whose model includes one species analogous to an activator (Cdc42-PAR6-aPKC at the membrane) and another analogous to a substrate (cytoplasmic PAR6-aPKC) as well as an intermediate species (PAR3-PAR6-aPKC) that is neither an activator nor a substrate. However, that species does not appear to be analogous to an indirect substrate. Note that the indirect substrate in our models is a species generated by an activator that can then create a substrate, whereas PAR3-PAR6-aPKC is generated from a substrate (PAR6-aPKC) and can then generate an activator (Cdc42-PAR6-aPKC). Moreover, the indirect substrate species we considered must have higher mobility than the activator (Figure 5), whereas the PAR3-PAR6-aPKC species has lower mobility than the activator. We have not explored models with these characteristics. As the key role of the PAR3-PAR6-aPKC species is to couple the reactant distribution to actomyosin flows, which are absent from all of the models we discuss, it seemed that comparison of that model with the ones we discuss is perhaps best left to a review.

5. This study also raises the question as to whether the presence of multiple initial polarity sites described in Howell, 2012 and subsequent papers from the lab results from the hydroxyurea treatment which, by creating a cell cycle delay, would be expected to increase the amount of polarity proteins that exist in cells, thereby facilitating such behavior as shown here. It would be quite interesting to determine whether the strain overexpressing Bem1, Cdc42, and Cdc24 generate more nascent sites in otherwise unperturbed G1 cells as compared to their WT counterparts.

This is an interesting question but we have not imaged that strain. We note that we have also seen multiple foci competing in mating cells (not treated with hydroxyurea), reported in a new paper: https://www.molbiolcell.org/doi/pdf/10.1091/mbc.E20-12-0757.

https://doi.org/10.7554/eLife.58768.sa2

Article and author information

Author details

Jian-geng Chiou

Department of Pharmacology and Cancer Biology, Duke University Medical Center, Durham, United States

Contribution
Conceptualization, Resources, Data curation, Software, Formal analysis, Investigation, Visualization, Methodology, Writing - original draft, Project administration, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-3246-5841
Kyle D Moran

Department of Pharmacology and Cancer Biology, Duke University Medical Center, Durham, United States

Contribution
Data curation, Formal analysis, Investigation, Validation, Visualization, Writing - review and editing

Competing interests
No competing interests declared
Daniel J Lew

Department of Pharmacology and Cancer Biology, Duke University Medical Center, Durham, United States

Contribution
Conceptualization, Resources, Supervision, Funding acquisition, Validation, Writing - original draft, Project administration, Writing - review and editing

For correspondence
daniel.lew@duke.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-7482-3585

Funding

National Institutes of Health (MIRA R35GM122488)

Daniel J Lew

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank Tim Elston, Erwin Frey, Nick Buchler, Stefano Di Talia, Amy Gladfelter, Masayuki Onishi, and members of the Lew lab for comments on the manuscript. Thanks to Trevin Zyla for help with yeast strain construction. This work was funded by NIH/NIGMS grant R35GM122488 to DJL.

Senior Editor

Naama Barkai, Weizmann Institute of Science, Israel

Reviewing Editor

Mohan K Balasubramanian, University of Warwick, United Kingdom

Publication history

Received: May 10, 2020
Accepted: April 23, 2021
Accepted Manuscript published: April 26, 2021 (version 1)
Version of Record published: May 12, 2021 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.