Research Article

Defining hierarchical protein interaction networks from spectral analysis of bacterial proteomes

Department of Pathology and Immunology, Washington University School of Medicine, United States
Duchossois Family Institute, University of Chicago, United States
Department of Genetics, Washington University School of Medicine, United States
Department of Developmental Biology, Washington University School of Medicine, United States
The Edison Family Center for Genome Sciences and Systems Biology, Washington University School of Medicine, United States
Department of Pathology, University of Chicago, Chicago, United States
Center for the Physics of Evolving Systems, University of Chicago, Chicago, United States

Aug 17, 2022

https://doi.org/10.7554/eLife.74104

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

1,201 views

Version of Record published: August 30, 2022 (This version)
Accepted: August 17, 2022
Accepted Manuscript published: August 17, 2022 (Go to version)
Preprint posted: September 28, 2021 (Go to version)
Received: September 21, 2021

1. Of interest
A comprehensive model of Drosophila epithelium reveals the role of embryo geometry and cell topology in mechanical responses

Mohamad Ibrahim Cheikh, Joel Tchoufag ... Konstantin Doubrovinski

Research Article Oct 2, 2023
Further reading

Abstract
Editor's evaluation
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Cellular behaviors emerge from layers of molecular interactions: proteins interact to form complexes, pathways, and phenotypes. We show that hierarchical networks of protein interactions can be defined from the statistical pattern of proteome variation measured across thousands of diverse bacteria and that these networks reflect the emergence of complex bacterial phenotypes. Our results are validated through gene-set enrichment analysis and comparison to existing experimentally derived databases. We demonstrate the biological utility of our approach by creating a model of motility in Pseudomonas aeruginosa and using it to identify a protein that affects pilus-mediated motility. Our method, SCALES (Spectral Correlation Analysis of Layered Evolutionary Signals), may be useful for interrogating genotype-phenotype relationships in bacteria.

Editor's evaluation

Since the inception of comparative genomics, mining phyletic patterns has been a powerful approach for the discovery of previously unknown biological interactions. The authors use a combination of singular value decomposition of the phyletic pattern matrix and random forests classification method to uncover potential protein-protein interactions. The work illustrates the utility of such methods, which are finding increasing application in addressing various computational biological problems, such as predicting protein-protein interactions from genomic information.

https://doi.org/10.7554/eLife.74104.sa0

Introduction

A fundamental problem in biology is to understand how proteins interact to create a complex phenotype (Barabási and Oltvai, 2004; Chuang et al., 2010; Hartwell et al., 1999; Costanzo et al., 2016). Biochemical and genetic studies have illustrated that complex behaviors emerge from layers of protein interactions: proteins interact to form complexes, complexes interact to form pathways, and pathways interact to create phenotypes (Papin et al., 2004; Ravasz, 2009; Nurse, 2008). Current strategies for identifying protein-protein interactions (PPIs) span both experiment and computation. Experimental methods are rapidly becoming more high-throughput and comprehensive (Rajagopala et al., 2014; Schoenrock et al., 2017; Häuser et al., 2014; Koo et al., 2017; Luck et al., 2017). Computational methods based on statistical patterns of co-occurrence or co-proximity of functionally related genes first appeared shortly after publication of whole genome sequences and are an active area of research (Eisen, 2017; Pellegrini et al., 2017; Enright et al., 2017; Valencia and Pazos, 2002). More recent efforts have advanced the state-of-the-art in computational methods by incorporating evolutionary models (phylogenomics), interaction models borrowed from statistical physics, or spectral methods borrowed from signal processing (Nagy et al., 2020; Franceschini et al., 2016; Moi et al., 2020; Croce et al., 2019; Cong et al., 2019; Green et al., 2021).

Understanding how a phenotype emerges from a collection of proteins requires the ability to relate different ‘scales’ of interactions, from pairwise to higher-order. While higher-order interactions can be inferred from pairwise interactions, recent experimental evidence shows that such inferences are incomplete (Kuzmin et al., 2018). Using bacteria as a model, here we show that both pairwise and higher-order interactions can be extracted from coevolutionary statistics to create a single multi-scale hierarchical model describing the emergence of complex phenotypes.

Results

Global patterns of covariation between bacterial orthologs arise from phylogeny

The power of using the kingdom bacteria as a model for evolutionary analysis is the availability of thousands of high-quality proteomes originating from diverse organisms. To broadly sample extant bacterial diversity, we downloaded all bacterial proteomes from the UniProt Reference Proteome Database (UniProt Consortium, 2019; downloaded May 20, 2020). Each proteome was annotated using orthologous gene groups (OGGs)—a robust and computationally tractable way of inferring orthologs—and rare OGGs present in less than 1% of proteomes were filtered (Overbeek et al., 1999). The resulting data matrix, D^OGG, consisted of 7047 proteomes (rows) and 10,177 OGGs (columns), where each entry is the number of times an OGG was observed in a proteome (Figure 1A, Materials and methods; Huerta-Cepas et al., 2017; Huerta-Cepas et al., 2019).

Figure 1

Download asset Open asset

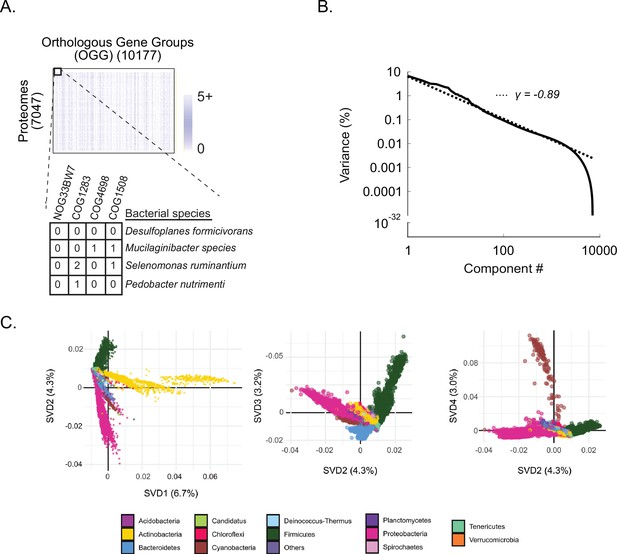
Shallow components of covariation measured across bacterial orthologs reflect broad phylogenetic relationships.

(A) D^OGG. Rows are 7047 bacterial proteomes, columns are 10,177 orthologous gene groups (OGGs), entries are the number of annotations of an OGG within a bacterial proteome (Figure 1—source data 1). (B) Percent variance explained versus spectral component (singular value decomposition [‘SVD] component’) number; fit is to a power-law distribution with the indicated exponent (γ). (C) Contributions of bacterial proteomes (colored dots) onto SVD components 1 through 4 (percent variance indicated in parenthesis on axis labels). Dots are colored according to phylum designation (color key).

Figure 1—source data 1 D^OGG matrix shown in Figure 1A.: https://cdn.elifesciences.org/articles/74104/elife-74104-fig1-data1-v2.zip
Download elife-74104-fig1-data1-v2.zip

To explore the structure of ortholog covariation across bacteria, we analyzed D^OGG using a technique called singular value decomposition (SVD), a generalized form of principal components analysis (PCA; Klema and Laub, 1980). SVD defines a spectrum of components of covariation (an ‘SVD spectrum’) where component 1 (SVD₁) explains more data variance than any other component, SVD₂ the second most, and so on (Figure 1B). We observed that bacteria sharing the same phylum clustered together on SVD₁ through SVD₄ suggesting that the most dominant patterns of bacterial variation arise from phylogeny (Figure 1C). These observations are consistent with prior reports that strong phylogenetic signals confound PPI inference using comparative genomics (Schäfer and Strimmer, 2005; Sul et al., 2018). Taken together, SVD₁ to SVD₄ explained only 17% of the overall data variance, motivating us to ask what information lies in the remaining data variance—more phylogenetic signal, functional signal, or noise?

Global to local patterns of bacterial covariation progressively reveal phylogeny, pathways, and protein complexes

We analyzed the SVD spectrum for information regarding (i) phylogeny, (ii) indirect interactions between proteins reflecting biological pathways, and (iii) direct (physical) interactions between proteins reflecting protein complexes. The workflow for our analysis was as follows. SVD applied to D^OGG output three separate matrices: bacterial projections onto left-singular vectors (U^OGG), a set of singular values, and OGG projections onto right-singular vectors (V^OGG; Figure 2A). We determined the statistical similarity of two bacterial proteomes across the SVD spectrum by dividing U^OGG into five-component spectral windows and computing the correlated SVD projections (‘spectral correlations’) for all pairs of proteomes within a spectral window (Figure 2B and C). We determined the extent to which two proteins in a proteome statistically interact across the SVD spectrum by (i) approximating projections of proteins onto right-singular vectors by averaging their constituent OGG content to create V^protein, (ii) dividing V^protein into five-component spectral windows, and (iii) computing protein-protein spectral correlations (Figure 2—figure supplement 1, Figure 2D and E). We then measured the information shared between spectral correlations and the three categories of biological benchmarks using mutual information (MI) and boostrap statistical support (Figure 2F; Materials and methods). For an estimation of the background MI attributed to finite sampling, we shuffled the SVD projections by random permutation across a row of V^OGG or U^OGG and computed the MI of the shuffled projections with the benchmark (Figure 2—figure supplement 2). This operation maintained the distribution of SVD projections while destroying spectral correlations arising from biology, thereby providing a null expectation for MI arising solely from sampling constraints. Collections of biological benchmarks were created from curating publicly available databases and previously published results (Materials and methods) (NCBI Resource Coordinators, 2018; Szklarczyk et al., 2019; Gene Ontology Consortium, 2021; Keseler et al., 2017; Cong et al., 2019). We focused our analysis of protein interactions on the proteome of Escherichia coli K12 because of the wealth of existing data regarding indirect and direct PPIs for this organism.

Figure 2 with 2 supplements see all

Download asset Open asset

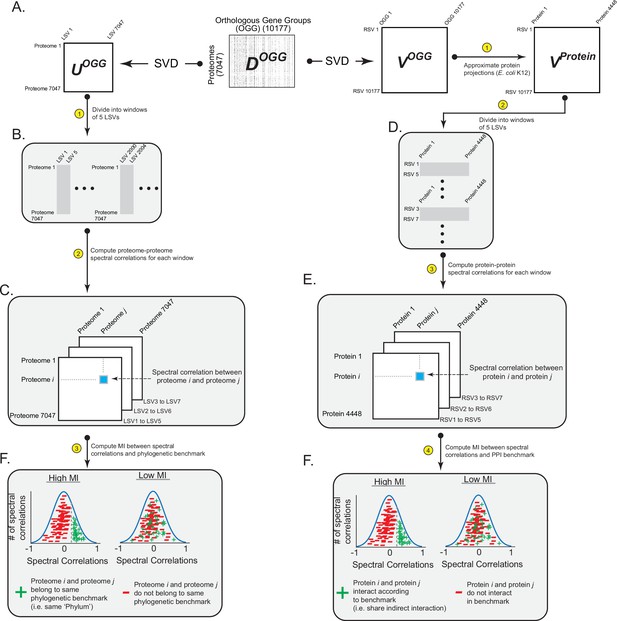
Workflow for relating patterns of ortholog covariation with phylogeny and protein interactions.

(A) Singular value decomposition (SVD) performed on ***D^OGG*** yields ***U^OGG*** (rows are proteomes, columns are ‘left singular vectors’ [LSVs]) and ***V^OGG*** (columns are OGGs, rows are ‘right singular vectors’ [RSVs]). ***U^OGG*** is used to relate information in the SVD spectrum with phylogenetic benchmarks. ***V^OGG*** is used to relate information in the SVD spectrum with protein interaction benchmarks. (**B,C**) Spectral correlations between bacterial proteomes are calculated by defining spectral windows of five LSVs each (panel A) and computing correlated projections between proteomes across all spectral windows (panel B). (**D,E**) Spectral correlations between proteins within a proteome are calculated by (i) approximating the projections of proteins onto RSVs, (ii) defining spectral windows of five RSVs each (panel C), and (iii) computing correlated projections between proteins across all spectral windows (panel D). (F) The final step is to compute the information shared between spectral correlations and biological benchmarks of phylogenetic relationships (left panel) or protein interactions (right panel). Shown are example distributions of spectral correlations that have ‘high’ and ‘low’ amounts of MI with a benchmark.

We found that the information for the different types of benchmarks was distributed distinctly across the SVD spectrum. The top tens of components contained phylogenetic information, the top hundreds contained indirect PPI information, and the top thousands contained direct PPI information (Figure 3A). Even SVD components 2996 through 3000 harboring 0.025% data variance contain non-random biological information reflecting direct PPIs (Figure 3B). Beyond component 3000, the MI shared between protein spectral correlations and PPIs converged to the estimation of background MI. Comparing the relative distributions of these different types of information across the SVD spectrum, we observed an order of phylum, class, order, family, genus, indirect PPIs, mixed indirect/direct PPIs, and direct PPIs (Figure 3C, Materials and methods). The ordering of these distributions across the SVD spectrum was robust to subsampling D^OGG to account for uneven phylogenetic distributions of bacterial strains in the UniProt database (Figure 3—figure supplement 1). These results show that global to local patterns of bacterial covariation reflect an intuitive hierarchy of biological scale—phylogeny, pathway, protein complex.

Figure 3 with 1 supplement see all

Download asset Open asset

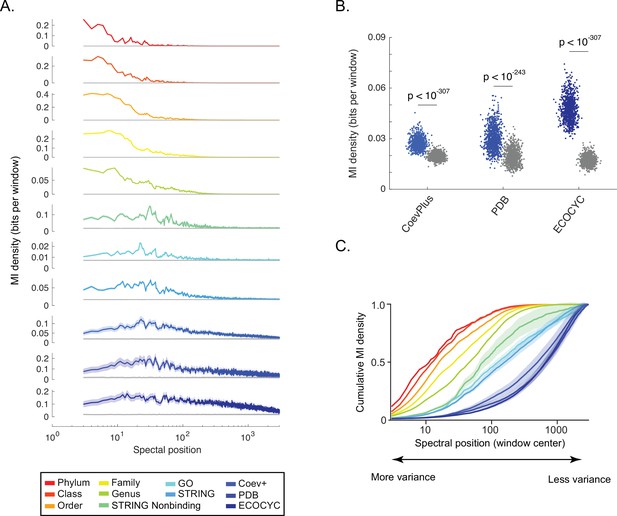
Shallow to deep spectral components of ortholog covariation reflect global to local biological ‘scales’.

(A) Distribution of information (y-axis, ‘mutual information [MI] density’) for each benchmark (see legend) measured across the singular value decomposition (SVD) spectrum (x-axis, ‘spectral position’). Gray line in each plot is the distribution of background MI (see Figure 2—figure supplement 2). Lines and shaded contours represent the mean±2 standard deviations for bootstraps of each benchmark. (B) Information shared between three benchmarks of direct protein-protein interactions (PPIs) (x-axis) and spectral correlations computed across SVD₂₉₉₆ to SVD₃₀₀₀. Each dot is the MI value for a single bootstrap of the indicated benchmark. Colored dots are non-random MI, gray dots are MI values for background spectral correlations. Values of statistical significance are shown above each distribution (p-value, Student’s t-test). (C) The degree to which information within the SVD spectrum reflects a biological benchmark, reported by the ‘cumulative density of MI’ (y-axis). As a curve for a benchmark approaches a value of ‘1’, deeper spectral components contain progressively less information regarding the benchmark. Colors follow those of panel A. Shaded regions are ±2 standard deviations of the mean MI value.

Figure 3—source data 1 NCBI taxonomic strings for each organism used to generate phylogenetic benchmarks.: https://cdn.elifesciences.org/articles/74104/elife-74104-fig3-data1-v2.xlsx
Download elife-74104-fig3-data1-v2.xlsx
Figure 3—source data 2 Benchmarks of protein-protein interactions (PPIs) in Escherichia coli K12.: https://cdn.elifesciences.org/articles/74104/elife-74104-fig3-data2-v2.xlsx
Download elife-74104-fig3-data2-v2.xlsx

A statistical approach for predicting the organization of emergent phenotype

Given the results shown in Figure 3, we hypothesized that by relating deep and shallow SVD components, we could create a statistical representation of emergence—the integration of local scales of protein interactions into global scales reflecting collective biological functions. Operationally, the way we related statistical information across shallow and deeper SVD components involved five steps. First, we removed SVD components enriched for phylogenetic signal and noise (components 1–33 and 3001–7047) (Figure 4A). Second, we computed spectral correlations between all proteins in a proteome across the remaining components (Figure 4B). Third, we removed spurious spectral correlations by developing a model of statistical significance. The model defined an optimal spectral window of 100 components for computing spectral correlations as well as a threshold for what constitutes ‘statistically significant’ spectral correlations (Figure 4—figure supplement 1, Materials and methods). Fourth, we defined the position in the SVD spectrum at which the spectral correlation between two proteins first dropped below the significance threshold; we term this position the ‘spectral depth’ of correlation between two proteins. Fifth, we discard all spectral correlations, significant or not, deeper than the spectral depth (Figure 4C). The effect of the last step is to condition spectral correlations found in deep regions of the SVD spectrum upon those found in shallow regions. Our rationale was that for a local interaction, like that in a protein complex, to contribute to a biological hierarchy, it must also contribute to a more global interaction network like a pathway.

Figure 4 with 1 supplement see all

Download asset Open asset

Workflow for computing the ‘spectral depth’ between pairs of proteins.

(A) Spectral components enriched for indirect and direct protein interactions (25th to 75th interquartile range of cumulative mutual information [MI] density) are selected, thereby filtering components enriched for phylogeny and noise. (B) Spectral correlations are computed for all pairs of proteins within a proteome; spurious spectral correlations introduced by finite sampling are filtered. Plotted here are spectral correlations (y-axis) as a function of spectral position (x-axis) for two pairs of proteins in *Escherichia coli* K12: MotA-MotB and MotA-CheR. Dashed line reflects the threshold defining statistically significant spectral correlations. (C) ‘Spectral depth’ is the spectral position at which the correlation value first reaches the threshold of statistical significance. Spectral depths of MotA-MotB and MotA-CheR are shown.

Following this five-step approach, we attempted to statistically re-derive the pathway of directed motility in E. coli K12. We chose to study this pathway because (i) there is a wealth of previous biological data regarding its constituent parts and interactions and (ii) it is an illustrative example of a global phenotype that emerges from several layers of protein interactions. From the KEGG hierarchy of directed motility in E. coli K12 (KEGG hierarchy, BRITE ECO:02035), there are three levels of molecular interactions. At the lowest levels, physical interactions between proteins create small units of collective structure and function, such as a basal body, rod, ring, motor, and filament. Integration of these structures and their individual functions produces the flagellum, a machine that turns to move the cell. Integration of the flagellum and the chemotaxis system produces directed motility—the ability to move purposefully along a chemical gradient. We used the flagellar filament, FliC, as a ‘bait’ for identifying spectrally correlated proteins in E. coli K12 putatively related to motility. Aside from this, no other biological knowledge was used: that is, no information regarding components or interactions producing complexes or collective structures contributing to directed motility. We found that 75 proteins were spectrally correlated with FliC (Figure 5A). We computed the spectral depth across all pairs of proteins (Figure 5B). We observed that the pattern of spectral depths was heterogeneous: a majority of protein pairs exhibited shallow spectral depths while sparse groups of proteins exhibited deeper spectral depths (Figure 5B). To depict the structure of spectral depths across all pairs of proteins, we thresholded spectral depth at three different levels: 50, 300, and 1000. These thresholds were chosen to reflect areas of the SVD spectrum found to be enriched for different types of biological information per Figure 3C. If two proteins had a spectral depth deeper than the threshold, they were considered to ‘statistically interact’ (Figure 5C, Supplementary file 1). Network graphs at each thresholded spectral depth were created where nodes are proteins and edges between nodes represent a statistically significant spectral correlation between two proteins.

Figure 5

Download asset Open asset

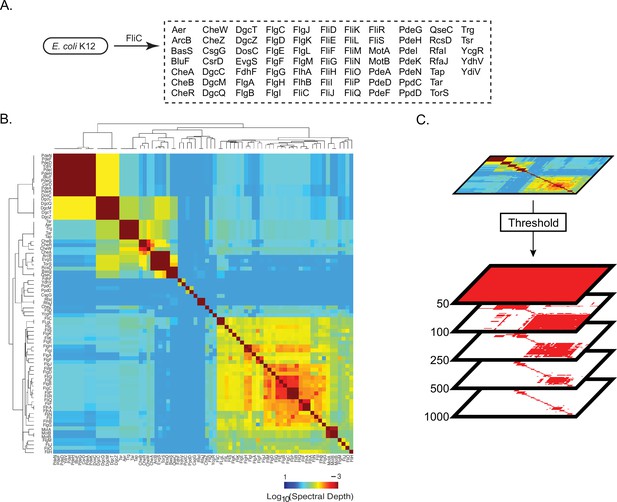
Pattern of spectral correlations with flagellar filament, FliC, in *Escherichia coli* K12.

(A) Proteins that shared significant spectral correlations with FliC after filtering for phylogeny and noise. (B) Hierarchically clustered spectral depth matrix for all pairs of proteins in panel A. (C) Set of matrices derived from thresholding the spectral depth matrix. Red pixels indicate that two proteins have a spectral depth deeper than the indicated threshold and therefore ‘statistically interact’. White pixels indicate that two proteins have a spectral depth of interaction shallower than the indicated threshold and therefore do not statistically interact.

At a spectral depth of 50, we observed a single densely connected network devoid of obvious substructure (Figure 6A, top panel). Gene-set enrichment analysis (GSEA) indicated that this network was enriched for functional terms related to ‘flagellar system’ (p<10^–45; Huang et al., 2009a; Huang et al., 2009b, Materials and methods). Progressing to spectral depth of 300, we observed that the network at 50 fractured into four discrete subnetworks (Figure 6A, middle panel). These subnetworks were significantly enriched for terms related to ‘chemotaxis signaling’ (p<10^–15), ‘flagellum’ (p<10^–56), ‘LPS biosynthesis’ (p<10^–3), or ‘cyclic di-GMP signaling’ (p<10^–21). Progressing to spectral depth of 1000, the subnetworks at 300 fractured further yielding 9 discrete subnetworks. Each subnetwork was significantly enriched for terms related to a specific function such as ‘cyclic di-GMP catabolism’ (p<10^–25) and ‘cyclic di-GMP synthesis’ (p<10^–13) or ‘chemotransmission’ (p<10^–4) and ‘chemoreception’ (p<10^–12 ; Figure 6A, bottom panel). Notably, considering additional spectral depths revealed further details of relevant hierarchical functional relationships within this pathway (Figure 6—figure supplement 1). Taken together the three network diagrams derived at spectral depths 50, 300, and 1000 depict a hierarchy of structure and function. Subnetworks observed at deeper spectral depths integrate to form the subnetworks observed at shallower spectral depths. As the subnetworks coalesced, the p-value associated with GSEA remained highly significant while the ontology of the significantly enriched terms changed. We interpret these observations to mean that as we ascend the statistical hierarchy, collective structures corresponding to new biological functions emerge from the integration of functional units at lower levels.

Figure 6 with 4 supplements see all

Download asset Open asset

A statistically derived hierarchical model of *Escherichia coli* K12 motility.

(A) Statistical interaction networks defined at spectral depths 50 (top), 300 (middle), and 1000 (bottom). Nodes (yellow circles) are proteins; edges (red lines) reflect statistical interactions between proteins; contours are drawn around groups of connected proteins; assignment of function associated with contours is based on gene-set enrichment analysis (GSEA) with p-value of most-enriched GSEA term in parenthesis (Supplementary file 1). (B) Comparison of the statistically derived model (left) to the KEGG model (BR:eco02035, right) of *E. coli* K12 motility. Venn diagrams represent the overlap between the sets of proteins in the indicated subnetwork of panel A (left) and the indicated KEGG category (right).

To validate our statistical model of motility, we compared it to the experimentally derived model of E. coli K12 motility detailed within the KEGG database (BR:eco02035; Kanehisa and Goto, 2000; Kanehisa, 2019; Kanehisa et al., 2021; Figure 6B). The two models were similar in several ways. First, 44 of 55 of the proteins listed in the KEGG hierarchy also appeared in the statistical hierarchy. Second, 7 of the 12 categories listed in the KEGG hierarchy had a one-to-one correspondence with a subnetwork of the statistical model sharing an overlapping set of proteins and similar descriptive label. Finally, both hierarchies shared a conserved architecture consisting of the integration of chemoreception and chemotransmission into chemotaxis signaling, the integration of flagellar substructures into the flagellum, and at the most global level the integration of chemotaxis and the flagellum. The most striking difference was that our statistical hierarchy included subnetworks related to cyclic-di-GMP signaling and LPS biosynthesis which were absent from the KEGG hierarchy. Prior experimental studies have provided direct genetic evidence that these systems are involved in E. coli K12 motility (Paul et al., 2010; Walker et al., 2004). Overall, of the 75 proteins in our hierarchical model of E. coli K12 motility, 44 (59%) were represented in the KEGG hierarchy, 28 (37%) were missing from the KEGG hierarchy but supported by prior experimental evidence in the literature, and only 3 (4%) remained unvalidated (CsgG, PpdD, TorS; Supplementary file 1). Taken together, these results illustrate that our approach for extracting a hierarchy of spectral correlations from the SVD spectrum produced a valid multi-scale, hierarchical model of directed motility in E. coli K12.

We performed four additional analyses to test the robustness and generalizability of our approach. First, we produced a hierarchical model of motility in E. coli K12 using MotB, the flagellar motor protein, as a query. We found a similar architecture as observed using FliC as the query with chemotaxis signaling, flagellum, and cyclic-di-GMP signaling modules appearing at spectral depth 300, and more fine-grained subnetworks appearing in deeper layers (Figure 6—figure supplement 2 Supplementary file 2). To test generalizability across different bacteria, we created a model of motility in Bacillus subtilis 168 using its flagellar filament protein as a query (Hag). This analysis again produced a hierarchical model of motility that (i) recapitulated the corresponding KEGG hierarchy, (ii) identified proteins missing from the KEGG hierarchy that are known effectors of B. subtilis motility, and (iii) identified a small number of putative motility effectors (Figure 6—figure supplement 3 Supplementary file 3). Next, we tested if our method could generalize to non-physically coupled pathways. We produced a model of amino acid metabolism in E. coli K12 using the query protein HisG, an enzyme involved in histidine biosynthesis. The resultant hierarchical model identified 130 proteins that were densely connected at spectral depth of 50. Progressing to deeper spectral depths revealed modules corresponding to specific functions, such as amino acid and nucleotide biosynthesis. At yet deeper spectral depths, modules enriched for proteins involved in the synthesis of specific amino acids became evident (Figure 6—figure supplement 4 Supplementary file 4). Taken together, these analyses demonstrated that our approach of defining a hierarchy of spectral correlations produced valid hierarchical models of biological pathways across different query proteins, organisms, and pathways.

Inferring functions for an uncharacterized protein from a model of emergent organization

We hypothesized that our statistical models could be used to assign general and specific functions to previously uncharacterized proteins in bacteria. To test this idea, we applied our approach to Pseudomonas aeruginosa, an organism with many uncharacterized proteins. We defined a hierarchical protein interaction network using PilA, a core structural element of the pilus, as a query; 141 proteins were spectrally correlated with PilA. At a spectral depth of 50, these proteins were found to collectively associate with motility of P. aeruginosa (Figure 7—figure supplement 1A Supplementary file 5; Burrows, 2004). Progressing to the spectral depth of 300, the global structure fractured into subnetworks associated with specific functions. Two major subnetworks related to specific types of motility, ‘pilus motility’ (p<10^–17) and ‘bacterial flagellum’ (p<10^–21), were evident, consistent with the ability of P. aeruginosa to use pilus or flagellar-based mechanisms of movement (Kearns et al., 2004; Rashid and Kornberg, 2004; Figure 7A, Figure 7—figure supplement 1B). Four uncharacterized proteins (Q9I5G6, Q9I5R2, Q9I0G2, Q9I0G1) were included in the pilus subnetwork that had not previously been associated with PilA in P. aeruginosa (Figure 7B Supplementary file 6). Our hierarchical models suggested that these proteins may contribute to the general function of directed motility by affecting the specific function of pilus-based motility but not flagellar-based motility.

Figure 7 with 1 supplement see all

Download asset Open asset

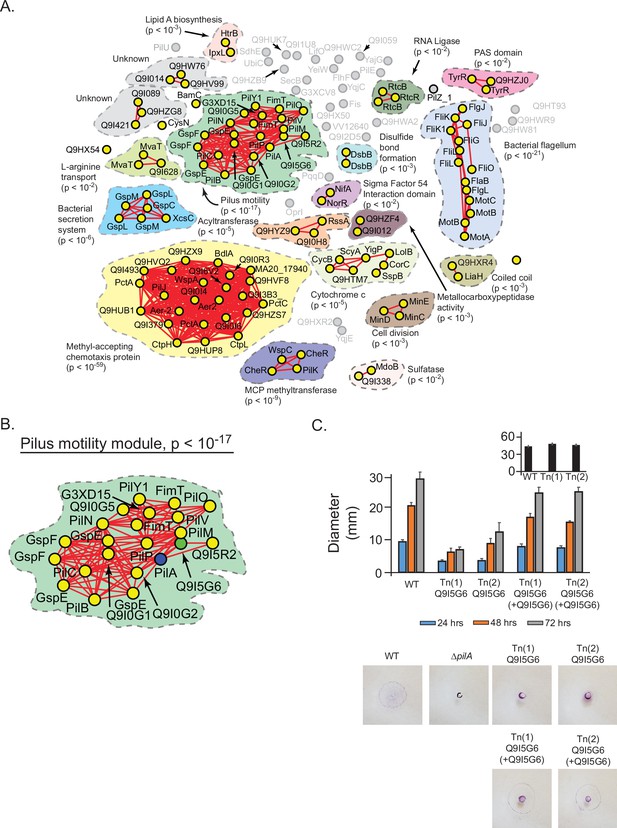
Prediction and validation of a novel effector of twitch motility in *Pseudomonas aeruginosa*.

(A) Statistical network derived by applying a spectral depth threshold of 300 to the set of 141 protein in *P. aeruginosa* (strain PAO1) that were significantly correlated with PilA across SVD₃₄ to SVD₁₃₄ (see Figure 7—figure supplement 1). Nodes, edges, shaded contours, gene-set enrichment analysis (GSEA) enrichment terms, and p-values are defined in the same manner as in Figure 6A. (B) The pilus motility subnetwork from panel A. Nodes representing PilA and Q9I5G6 are colored blue and green, respectively. (C) Time-course of pilus-based motility for parent (WT), two transposon mutants of Q9I5G6 (Tn(1) Q9I5G6, Tn(2) Q9I5G6), and transposon mutants complemented with Q9I5G6 (Tn(1) Q9I5G6+Q9I5G6, Tn(2) Q9I5G6+Q9I5G6). Inset shows results of flagellar motility for the parent strain (WT), and the two transposon mutants of Q9I5G6 (Tn(1), Tn(2)) 24 hr post-inoculation. Representative images of the crystal-violet stained plates are shown. SVD, singular value decomposition.

To test these predictions, we assayed single-gene transposon mutants of P. aeruginosa (PAO1) for twitch-based motility mediated by the pilus or flagellar-based motility (Materials and methods) (Kearns et al., 2004; Rashid and Kornberg, 2004; Little et al., 2018). Transposon mutants of Q9I5R2, Q9I0G2, and Q9I0G1 exhibited motility that was not significantly different from the parent strain in both assays (Supplementary file 7). In contrast, we found that two different transposon mutants of Q9I5G6 exhibited significantly reduced pilus-based motility over 24, 48, and 72 hr compared to the parent strain (Figure 7C, p<10^–4 by Dunnett’s multiple comparisons test). This phenotype resembled that of a knockout strain of PilA and was reversed upon trans-complementation. In contrast, flagellar-based motility of the transposon mutants in Q9I5G6 was not significantly different from that of the parent strain (Figure 7C—inset, p>0.05). These results illustrate that Q9I5G6 is a previously unappreciated effector of directed motility in P. aeruginosa that specifically impacts twitch-based motility. Compared to the background expectation of finding a protein that affects twitch motility (22 ‘pilus assembly proteins’ in BRITE KO02035 out of 5564 proteins in the PAO1 proteome equating to a 0.4% background rate of association), our experimental results represent a statistically significant enrichment (25% association rate, p<10^–4 by chi-squared). Moreover, the results of our statistical approach shown in Figure 7B illustrate a far higher enrichment of functional association with identifying 19 effectors of twitch motility out of 22 proteins in the ‘pilus motility module’. Overall, these experiments provide a proof of concept of how our hierarchical models may aid in discovering novel genotype-phenotype relationships.

Using spectral correlations to predict proteome-wide functional and physical protein interaction networks

Microbiome science has taught us that diverse bacteria affect human and environmental health. Therefore, there is a critical need to expand our knowledge of biology more broadly beyond the few well-studied model organisms. Comparative genomics has been critical to inferring functionally relevant interaction networks in newly sequenced organisms. However, these methods are limited in their ability to isolate functional and physical interaction networks from each other as well as from the admixed phylogenetic signal and noise due to finite sampling (Schäfer and Strimmer, 2005; Sul et al., 2018; Nagy et al., 2020). Our spectral approach offers a unique opportunity to isolate interactions arising at a specific biological scale. We hypothesized that spectral correlations could be used to accurately predict proteome-wide functional and physical interaction networks across diverse bacteria.

To test this hypothesis, we classified all possible pairs of proteins in the E. coli K12 proteome as functionally interacting (indirect PPI), physically interacting (direct PPI), or not-interacting (Materials and methods). These predictions were based on protein-protein spectral correlations across three different spectral windows chosen to isolate phylogenetic, indirect PPI, and direct PPI information, respectively (Figure 8—figure supplement 1). For comparison, we predicted the same interaction classes using quantitative features of various existing computational and experimental methods. To compare the various methods, we computed F-scores for each interaction class using a composite gold-standard benchmark as well as three individual database-wide benchmarks (Figure 8—figure supplement 2; Rajagopala et al., 2014; Babu et al., 2014; Babu et al., 2018; Hu et al., 2009). F-score is the harmonic mean of precision and recall; to achieve an F-score of 1, the predictions must be both accurate and complete.

We found that our predictions based on windowed spectral correlations produced significantly greater F-scores for all three interaction classes compared to 18 alternative methods in all four validation tasks (Figure 8A, Figure 8—figure supplement 3, statistical comparisons by Wilcoxon rank-sum test). Of the alternative methods tested, the most mathematically similar to ours is SVD-phy (Franceschini et al., 2016). SVD-phy is a PCA-based approach that also uses SVD but assumes that only the top (most global) components are useful for predicting PPIs. In contrast our approach to selecting specific SVD components is data-driven, guided by the results shown in Figure 3C. We found that the performance of SVD-phy depended on how many of the top components were retained. Including the most shallow SVD components yielded predictions at or below the median rank of all methods across all three interaction classes. Including the shallowest 100 SVD components yielded better indirect PPI prediction without improvement of predicting direct PPIs. Including components beyond SVD₁₀₀ improved the prediction of direct PPIs while decreasing F-scores for indirect PPIs. These results show that SVD-phy can be tuned for predicting either indirect or direct interactions, but not both simultaneously. In addition, the tuned performance on either class was inferior compared to our method of windowed spectral correlations.

Figure 8 with 3 supplements see all

Download asset Open asset

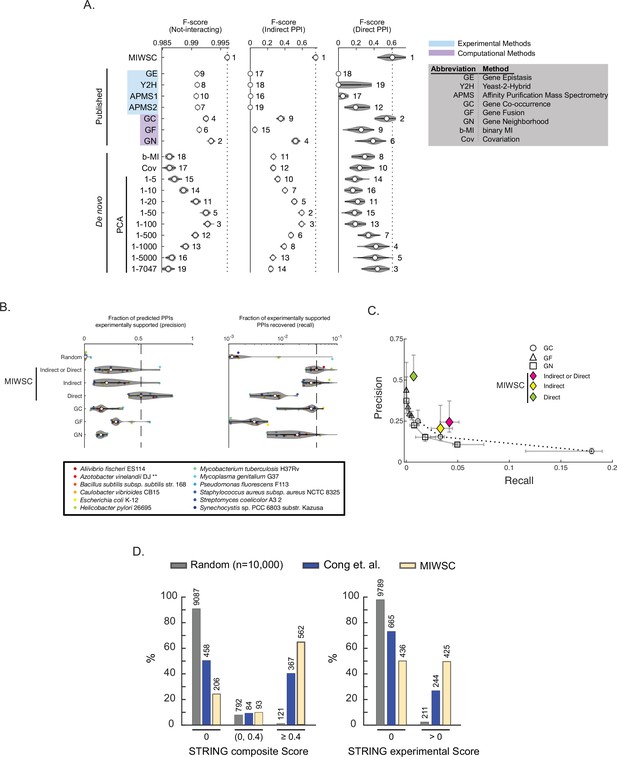
Mutual information (MI) windowed spectral correlations (MIWSCs) enable accurate classification of indirect and direct protein-protein interactions (PPIs).

See Figure 8—figure supplement 1 for definition of ‘MIWSCs’. (A) F-scores for predicting interaction classes for *Escherichia coli* K12 protein pairs using random forest (RF) models trained on MIWSCs or features from several different methods (see legend). Violin plots show distribution of F-scores for models trained and validated on 50 random partitions of the gold-standard dataset. Numbering indicates the rank of the median F-score for models trained on each feature (Figure 8—source data 1). (B) Precision (left) and recall (right) for predictions of any (indirect or direct), direct, or indirect PPIs in 12 bacteria using RF models trained on the MIWSCs of *E. coli* K12 proteins benchmarked against the experimentally supported PPIs in the STRING database (experimental score > 0). Comparisons are made to a set of 10,000 randomly selected pairs and to the ‘medium confidence’ predictions (score > 400) in the STRING database subchannels for GC, GN, and GF. Vertical dashed line indicates the median value for the best performing method. ** in legend indicates an organism that was not part of the input dataset ***D^OGG*** (Figure 8—source data 1). (C) Precision-recall curves were constructed for the methods of GC, GN, GF by thresholding the subchannel scores at 150 (‘low confidence’), 400 (‘medium confidence’), 700 (‘high confidence’), and 900 (‘highest confidence’). The precision versus recall is plotted for any (indirect or direct), direct, or indirect PPIs predicted using the RF models trained on MIWSCs. Symbols and whiskers represent the median and 25–75 percentile range, respectively, for the predictions produced for the 12 organisms in panel B (Figure 8—source data 1). (D) Percent of predicted direct PPIs in *Mycobacterium tuberculosis* H37Rv supported by an absent (0), low (0–0.4), or high (>0.4) composite score (left) or an absent (0) or present (>0) experimental subchannel score (right) in the STRING database. Comparisons were made between the methods of random selection (Random), amino acid coevolution (Cong et al., 2019), or RF models trained on MIWSC features of *E. coli* K12 proteins (MIWSC). Numbers of predicted interactions in each bin are indicated (Figure 8—source data 1).

Figure 8—source data 1 Data and statistical support for random forest (RF) model validation studies, related to Figure 8Figure 8.: https://cdn.elifesciences.org/articles/74104/elife-74104-fig8-data1-v2.xlsx
Download elife-74104-fig8-data1-v2.xlsx

Our choice of SVD windows used to compute spectral correlations was guided by MI distributions generated using known E. coli K12 PPIs. This observation led to the concern that our approach to PPI prediction may not generalize well to other organisms. On the other hand, the underlying spectral correlations were defined from a large ensemble of bacterial proteomes, suggesting that our approach may accurately predict PPIs across diverse bacteria. To test this idea, we predicted proteome-wide direct PPIs for 11 additional phylogenetically diverse bacteria, including one organism (Azotobacter vinelandii) that was not represented in D^OGG (Materials and methods). We computed the precision and recall for our predictions of any (indirect or direct), indirect, or direct PPIs using the experimentally supported PPIs in the STRING database as a benchmark (score > 0 in the STRING ‘experimental’ subchannel). We compared these results to those produced by the well-established methods of gene co-occurrence, gene neighborhood, and gene fusion by thresholding the corresponding STRING subchannel scores at different confidence levels (low, medium, high, highest). Figure 8B shows this comparison at the ‘medium’ confidence level. Figure 8C summarizes the entire analysis showing the precision-recall curves across all thresholds tested. We found that the sets of any indirect or direct PPIs produced by our method exhibited a higher precision for a given recall compared to the established methods. These results show that though the SVD windows used to compute spectral correlations were chosen based on analysis of PPIs in the E. coli K12 proteome, our approach for predicting PPIs performs as well or better than established methods across different organisms.

The state-of-the-art PPI prediction method is that produced by Cong and colleagues (Coev+) that infers direct PPIs from proteome-wide amino acid coevolution (AA Coev) (Cong et al., 2019). Briefly, they predict direct PPIs from primary sequence using a method called ‘direct coupling analysis’ (DCA) borne out of the field of statistical physics. Using the direct PPIs for Mycobacterium tuberculosis H37Rv found in the STRING database as a benchmark, we found that our approach exhibited significantly greater precision and recall whether using the STRING composite score (as done by Cong et al.) or the STRING experimental subscores (Figure 8D, Materials and methods). While we limited our comparative analysis to only M. tuberculosis, these results illustrate that our spectral approach to purifying biological information arising from a specific scale can produce predictions that are on par or better than a more computationally expensive alternative that leverages a higher-resolution genomic feature.

Discussion

We developed a statistical method that predicts hierarchical protein interaction networks reflecting the emergence of complex functions in bacteria. This method involves two aspects: (i) spectral decomposition of variation across bacterial proteomes into components enriched for specific biological scales, (ii) relating covariation structure across components to define hierarchical statistical networks. These hierarchical networks closely resembled the known organization for several well-studied bacterial phenotypes. We call our approach SCALES—Spectral Correlation Analysis of Layered Evolutionary Signals. Having shown that SCALES can be useful for guiding biological discovery, we have developed the following resources: (i) a precomputed database of proteome-wide indirect (122,725,727) and direct (19,546,063) PPI predictions for all 7047 UniProt reference bacterial proteomes; (ii) a tool for predicting indirect and direct PPIs for a user-input proteome; (iii) a tool for generating and interrogating a hierarchical model for a query protein of interest. All of these can be found at scales.cri.uchicago.edu.

The challenge of recovering functional interactions using comparative genomics

The admixture of signals arising from phylogeny, function, and noise negatively impact the accuracy of PPI predictions using comparative genomics (Schäfer and Strimmer, 2005; Sul et al., 2018). One approach to address this problem is to use PCA which assumes that only global covariation is not statistical noise (Wigner, 1967; Franceschini et al., 2016). A known source of variability between orthologs is phylogenetic relatedness. As SVD achieves spectral clustering and phylogenetic reconstruction achieves hierarchical clustering, we do expect some level of coherence between the two approaches. However, our results also illustrate that relevant biological signal is contained throughout the SVD spectrum, including components harboring a minutiae of data variance. Components in different regions of the spectrum contained information about different biological scales—shallow components phylogeny, deeper components pathways, even deeper components protein complexes, and the very deepest noise, thereby signifying a ‘cross-over’ from phylogenetic to functional information. Our interpretation of these results is that while statistical variance reflecting large-scale properties can be ‘compressed’ into just a few shallow components, information about ‘local’ biological scales is distributed broadly across the spectrum. As a result, discarding global components enriched for phylogeny improved prediction of functionally relevant interactions. These results demonstrate that percent variance per component is not a good proxy for relevant biological signal. In the absence of a suitable alternative, we used knowledge in public databases to define the information content of each component. Future work will be needed to provide a theoretical basis for finding relevant signal in cases where such prior knowledge is not available.

Extracting a multi-scale, hierarchical model of biology from coevolutionary statistics

Understanding the origins of complex biological functions requires defining hierarchical relationships describing how protein interactions integrate to create scales of biological organization. While the use of SVD is fundamental to our method, SVD itself does not define hierarchical relationships; SVD defines orthogonal components of variance ordered according to the amount of variance explained. Two results of our study were key for being able to use the SVD spectrum to produce hierarchical models. First, different components contain information regarding different biological scales. Second, the information in different components could be related by tracking the persistence of spectral correlations across components (‘spectral depth’). These two results enabled extracting hierarchical statistical relationships that predict the integration of PPIs into complex structures approximating pathways and phenotypes. To our knowledge, this is a fundamentally new way of constructing hierarchical models. Instead of predicting pairwise interaction networks and then inferring higher-order networks, we infer an entire hierarchy directly from coevolutionary statistics.

Comparison of our results with AA Coev

Recently, Cong and colleagues reported a method, AA Coev, for inferring direct PPIs from bacterial genome sequences. Their method represented a significant advance for two reasons: (i) it considered coevolution at the resolution of amino acids and (ii) it applied DCA, to entire bacterial proteomes. Like our method, AA Coev tries to extract signal related to a specific scale of biology from admixed signals of phylogeny and noise using coevolutionary statistics of genomes. Specifically, DCA is a statistical physical approach that isolates local (i.e. direct) interactions. However, we observed significant differences in quality and breadth of direct PPI inferences, scalability, and ability to reconstruct hierarchical networks.

When we compared our direct PPI predictions in M. tuberculosis with those of AA Coev, we predicted significantly more interactions with significantly greater precision. This was a surprising result given that our approach considers lower-information features—OGGs versus amino acid sequence-level information. One explanation may be that our predictions were derived by explicitly using correlations across three different spectral windows that provided information about three different scales of biology: phylogeny, indirect PPIs, and direct PPIs. In contrast, AA Coev discards signal unrelated to direct PPIs. It may be the case that phylogenetic and pathway-level information provides context clues for enhancing subtle statistical signals related to direct PPIs. In other words, the confidence in assigning a putative physical interaction is increased by additional signals suggesting that the interaction also contributes to a pathway-level function among phylogenetically related bacteria. The power of our method may lie in its ability to simultaneously deconvolute yet leverage information related to these different scales. Further work is needed to better understand the differences between our method and AA Coev and to determine if the observed difference in PPI prediction is consistent across additional organisms outside of M. tuberculosis.

A striking difference between the two approaches is related to computational scalability. AA Coev is computationally expensive and, as a result, has been applied to just two organisms thus far. In contrast, we note that our approach can compute proteome-wide PPIs in a matter of minutes, enabling us to provide predictions for all 7047 UniProt Reference Proteomes. As identifying and characterizing different strains of bacteria is becoming increasingly important, scalable computational tools becomes a necessity.

A final difference between the two methods is how a hierarchy can be constructed. Cong et al. predicted collective units of structure, using a ‘bottom-up’ approach by putting together their direct PPI predictions. However, compared to the networks produced by SCALES, these networks tended to be smaller and less representative of higher-order collective structure, reinforcing results reported by Kuzmin et al. illustrating that building collective organization from pairwise networks results in incomplete hierarchical descriptions of biology. We therefore pose that though SCALES does not consider as information-rich of a feature as AA Coev, it may prove to be a useful framework to extract hierarchical relationships for connecting bacterial genotype with phenotype.

Limitations

We observed two major limitations related to our use of OGGs as orthologous feature. First, many proteins have no annotated OGG—for example, 295 of the ~4000 E. coli K12 proteins (6.7%). These proteins cannot be assigned to interactions or units of function by our method. Second, many proteins share the same OGGs and appear to interact at all spectral depths. These putative interactions may or may not be related to biological function. We anticipate that ortholog annotations will continue to improve with additional bacterial genome sequences, helping to alleviate these limitations. Moreover, the use of phylogenomic methods that incorporate models of the phylogenetic history of proteins to improve ortholog definition might create superior inputs for the methods developed here (Nagy et al., 2020).

Another limitation of the methods developed here is that they are inherently ‘mechanism-free’: they leverage evolutionary constraint without knowledge of the specific pressures driving the selection of interactions. As a result, our methods identify functionally relevant interactors but cannot reveal their collective function or the detailed molecular basis of the interactions.

The potential of generalizing SCALES to other biological systems

To what degree are the approaches developed here applicable to other biological systems? Practically, we note that the spectral properties of any given dataset will be unique. As such, re-application of these methods to a new dataset will require following the steps outlined in this work: creating a diverse ensemble, identifying relevant benchmarks, using the benchmarks to find different scales of interactions in the SVD spectrum, and enforcing the necessary statistical constraints to define hierarchical relationships. Sufficient diversity and suitable benchmarks may not currently be available for other systems as they were for bacteria. Moreover, the parameters used in this work to enable analysis—width of spectral windows, bin width for MI calculations, threshold of spectral correlation value used to define spectral depth—likely need to be derived de novo for other datasets. However, aside from these practical considerations, SCALES represents a statistical way to describe emergence—the integration of individual components into layers of collective units of function. The property of emergence spans biological systems, from proteins to ecosystems. Thus, while it remains to be tested, it may be true that SCALES is a generally useful approach to learning the hierarchical architecture of biological systems.

Materials and methods

Generating D^OGG

Request a detailed protocol

All bacterial proteomes (n=7047) in the 2020_02 release of the Uniprot Reference Proteome database were downloaded on May 20, 2020 (UniProt Consortium, 2019). OGGs were annotated using eggNOG-mapper V2 at the level of bacteria (‘@2’; Huerta-Cepas et al., 2017; Huerta-Cepas et al., 2019). An OGG count matrix was assembled (D^OGG, Figure 1A) where rows were defined as proteomes, columns were defined as OGGs, and the value in each cell was the number of annotations an OGG in a proteome. The number of annotations was used to preserve as much information as possible versus the strategy of considering binary occurrence. All OGGs present in fewer than 1% of the proteomes were removed leaving 10,177 unique columns in D^OGG.

Assembling benchmarks described in Figure 3A

The various benchmarks described within this section can be found in Figure 3—source data 1, Figure 3—source data 2.

Phylogeny benchmarks

Request a detailed protocol

NCBI phylogenetic strings were mapped to the NCBI taxonometric IDs for each of the 7047 bacteria represented in D^OGG using taxonkit 5.0 (https://bioinf.shenwei.me/taxonkit/). Five different benchmarks were generated corresponding to pairs of proteomes that share identical phylogenetic substrings down to the level of phylum (n=5,841,696), class (n=2,460,194), order (n=807,338), family (n=434,753), or genus (n=267,794).

STRING Nonbinding benchmark

Request a detailed protocol

STRING database annotations were downloaded for the E. coli K12 proteome (STRING ID 511145) on July 22, 2019. A benchmark was assembled to include all protein pairs (n=14,793) with a non-zero combined STRING score that did not share a ‘binding’ action annotation. This benchmark was expected to be enriched for indirect PPIs.

GO terms benchmark

Request a detailed protocol

‘Biological function’ GO term annotations were mapped for the 4391 proteins in the E. coli K12 proteome through the UniProtKB API. A benchmark was assembled containing the 79,794 protein pairs that share at least one GO term annotation. This benchmark likely contained a mixture of indirect and direct PPIs.

STRING benchmark

Request a detailed protocol

STRING database annotations were downloaded for the E. coli K12 proteome (STRING ID 511145). A benchmark was assembled comprised of all (n=20,216) protein pairs with a non-zero combined STRING score. This benchmark included a mixture of pairs with (n=14,793) and without (n=5423) a ‘binding’ annotation and therefore is presumed to contain a mixture of direct and indirect PPIs.

ECOCYC benchmark

Request a detailed protocol

A previously published benchmark included 915 pairs of E. coli K12 proteins selected from the set of complexes in the ECOCYC database after intentionally excluding large complexes with greater than 10 proteins to enrich for directly interacting pairs of proteins (Keseler et al., 2017). This benchmark is assumed to primarily represent direct PPIs.

Coev+ benchmark

Request a detailed protocol

A previously published set of 1600 direct PPIs in E. coli K12 identified by a hybrid method combining the results of AA Coev and prior experimental data (Cong et al., 2019).

PDB benchmark

Request a detailed protocol

A previously published set of 809 direct PPIs in E. coli K12 selected by the criteria that they, or closely homologous proteins, have been observed to interact in a crystal structure in the PDB (Cong et al., 2019).

Computing proteome-proteome spectral correlations

Request a detailed protocol

A row vector in the matrix U^OGG contains the projections of a single proteome onto each of the left singular vectors.

[ω_{i} | 1 > \cdot \cdot \cdot ω_{i} | n > \cdot \cdot \cdot ω_{i} | N >]

where $ω_{i}$ is proteome $i$ , $ω_{i} ∣ n >$ is the projection of $ω_{i}$ onto the left singular vector n 1 ≤n ≤N, and N is the total number of left singular vectors. The ‘spectral correlation’ is computed as the Pearson correlation between proteome $ω_{i}$ and proteome $ω_{j}$ within the window of left singular vectors spanning SVD components $a$ to $b$ (‘spectral window’):

ρ_{ω_{i} ω_{j}}^{a : b} = c o r r (ω_{i, [a : b]}, ω_{j, [a : b]})

Computing protein-protein spectral correlations

Request a detailed protocol

A row vector in the matrix V^OGG contains the projections of a single OGG onto each of the right singular vectors:

[f_{i} | 1 > \cdot \cdot \cdot f_{i} | m > \cdot \cdot \cdot f_{i} | M >]

where f_i is the OGG in row i of matrix V^OGG, $f_{i} ∣ m >$ is the projection of f_i onto right singular vector m (1 ≤m ≤M), and M is the total number of SVD components. Each protein in a proteome may comprise up to several OGGs:

P_{l}^{ω} = {f_{i}, \dots, f_{j}}

where $P_{l}^{ω}$ is the $l$ th protein in proteome $ω$ ; $f_{i}$ is OGG $i$ and $f_{j}$ is OGG $j$ . The contribution of a protein onto each right singular vector was estimated by averaging the contributions of each constituent OGG on each right singular vector. An example of this process is illustrated in Figure 2—figure supplement 1A-F. The ‘spectral correlation’ is computed as the Pearson correlation between protein $l$ and protein $m$ within the window of right singular vectors spanning SVD components $a$ to $b$ (‘spectral window’):

ρ_{l m}^{a : b} = c o r r (P_{l, [a : b]}^{ω}, P_{m, [a : b]}^{ω})

An example of this process is illustrated in Figure 2—figure supplement 1G.

Computing MI between spectral correlations and benchmarks of biological knowledge

Request a detailed protocol

Spectral correlations were computed by first segmenting the top 3000 SVD components into windows comprised of five components each and calculating spectral correlations across all pairs of variables (either proteome-proteome or protein-protein) within each window. Computing the MI between the distribution of spectral correlations within a window and a biological benchmark quantitates how much knowing the distribution of spectral correlations reduces uncertainty about the benchmark. Because spectral correlations within a window comprise a finite distribution (i.e. not infinite), there exists intrinsic uncertainty due to the need to define a bin width in the distribution. The process of computing this uncertainty has been formalized and is calculated as the ‘differential entropy’ (Cover and Thomas, 2005):

H (ρ^{a : b}) = - \sum_{i} ∆ p (ρ_{i}^{a : b}) {l o g}_{2} p (ρ_{i}^{a : b}) - {l o g}_{2} (Δ)

$ρ^{a : b}$ is the vector of spectral correlations over the window ranging from SVD components a to b, $H (ρ^{a : b})$ is the differential entropy of $ρ^{a : b}$ , $ρ_{i}^{a : b}$ is the ith set of correlation values, $p (ρ_{i}^{a : b})$ is the probability of observing a correlation value within $ρ_{i}^{a : b}$ , and $Δ$ is the width of the quantization bins. In the present study $Δ$ = 0.25.

MI is the difference between the intrinsic uncertainty in spectral correlations, $H (ρ^{a : b})$ , and the uncertainty computed given a benchmark c, $H (ρ^{a : b} | c)$ .

I (ρ^{a : b}, c) = H (ρ^{a : b}) - H (ρ^{a : b} | c)

The uncertainty in spectral correlations given knowledge of a benchmark is evaluated in the following way. A benchmark c can be either ‘1’ if two variables share the benchmark (i.e. two proteins share the same phylogenetic classification or two proteins are found to interact in a database) or ‘0’ if two variables do not share the benchmark. The ‘conditional entropy’ of spectral correlations is the differential entropy conditioned on knowledge of the probability distribution of benchmarks. So, $H (ρ^{a : b} | c)$ is mathematically defined as:

H (ρ^{a : b} | c) = p (c = 1) H (ρ^{a : b} | c = 1) + p (c = 0) H (ρ^{a : b} | c = 0)

where p(c=1) and p(c=0) are the probability of observing a ‘1’ or ‘0’ in c respectively; and $H (ρ^{a : b}| c = 1)$ and $H (ρ^{a : b}| c = 0)$ are the differential entropies of spectral correlations conditioned upon variables that share (c=1) and do not share (c=0) a benchmark, respectively. A model of random MI was generated by computing the MI shared between the spectral correlations within row-shuffled versions of U^OGG or V^OGG and the benchmarks of phylogeny and protein interactions, respectively (Figure 2—figure supplement 2).

For each phylogenetic benchmark, 100 bootstraps were generated consisting of equal numbers of randomly selected pairs of proteomes that do or do not share an identical phylogenetic substring annotation in the benchmark. For each protein interaction benchmark, 1000 bootstraps were generated consisting of equal numbers of randomly selected pairs of proteins that do or do not share an interaction annotation in the benchmark. For bootstraps of both phylogenetic and protein interaction benchmarks, the number of pairs sharing an annotation was equal to the number of pairs indicated for each respective benchmark in the section ‘Assembling benchmarks described in Figure 3A’.

Calculation of MI cumulative distribution functions shown in Figure 3C

Request a detailed protocol

Each point in the MI cumulative distribution functions (cdfs) shown in Figure 3C was computed as following for the window centered on component w of the SV

{c d f}_{w} = \frac{\sum_{i = 1}^{w} ({M I}_{i}^{d a t a} - {M I}_{i}^{r a n d o m})}{\sum_{i = 1}^{W} (M I_{i}^{d a t a} - {M I}_{i}^{r a n d o m})}

where cdf_w is the value of the cdf at spectral position w, MI_i^data is the MI observed in window i, MI_i^random is the MI produced by random correlations in window i, W is the total number of windows, and 1≤w ≤ W. Because we considered five-component spectral windows within the first 3000 components, W=2997.

A model of spectral correlations between non-interacting proteins

Request a detailed protocol

To define a model of spectral correlations between non-interacting proteins, we first considered the distribution of all pairwise spectral correlations centered on SVD₁₀₀₀ for the proteins encoded in the proteome of E. coli K12. Our rationale was that since the vast majority of proteins do not interact, the distribution of all-by-all spectral correlations approximates correlations between proteins that do not functionally interact. The variance of this distribution decreased rapidly as the correlation window widened until a width of 100 components. This motivated our choice of computing spectral correlations over sets of 100 components (Figure 4—figure supplement 1A, B). We computed distributions of all-by-all spectral correlations between E. coli K12 proteins across windows centered on different regions of the SVD spectrum and found them to be superimposable (Figure 4—figure supplement 1C). Additionally, we computed such distributions for proteins from other diverse bacteria and found them to be superimposable with those derived from E. coli K12 (Figure 4—figure supplement 1D). These properties enabled defining a constant threshold for significant spectral correlations between two proteins across any 100-component SVD window. The p-value derived from the empirical cumulative distribution function of this model decreased rapidly until a threshold value of 0.29 (Figure 4—figure supplement 1E). Therefore, we chose the value of 0.29 associated with a p-value of 0.018 as the threshold of spectral correlations signifying functional interactions between proteins derived from any bacterial proteome within any region of the SVD spectrum.

GSEA performed on statistical model of E. coli K12 motility

Request a detailed protocol

GSEA was performed on the sets of proteins defined by the statistical networks and subnetworks using DAVID analysis (v6.8). The ontological term with the lowest p-value is indicated for each statistical module shown in Figure 6A. A full list of significant ontological terms and their associated p-values for each statistical module is listed in Supplementary file 1.

Assaying strains of P. aeruginosa for pilus and flagellar motility

Request a detailed protocol

All P. aeruginosa strains used in this study were ordered from the Manoil Lab. All strains were grown at 37°C on LB supplemented with 25 µg/ml irgasan and gentamicin (75 µg/ml) as necessary. E. coli XL1-Blue was maintained on LB agar plates with gentamicin (15 µg/ml) as necessary.

P. aeruginosa growth was at 37°C on LB supplemented with 25 µg/ml irgasan and gentamicin (75 µg/ml) as necessary. Strains were assayed for subsurface twitching motility as previously described (Alm and Mattick, 1995, Little et al., 2018). Strains were grown overnight and stab inoculated in the interstitial space between the basal surface of 1.0% LB agar and a plastic Petri dish. Plates were incubated for 48 hr at 37°C. Agar was removed and cells attached to the plate were stained with 0.5% crystal violet; twitch zone diameter was measured and plates were imaged.

Surface twitching motility assays were performed as previously described (Little et al., 2018; Kearns et al., 2004). P. aeruginosa strains of interest were grown overnight and concentrated in morpholinepropanesulfonic acid (MOPS) buffer (10 mM MOPS, 8 mM MgSO₄, pH 7.6). A 2.5 µl volume of the MOPS buffered bacterial suspension was spotted onto buffered twitching motility plates (10 mM Tris, 8 mM MgSO₄, 1 mM NaPO₄, 0.5% glucose, 1.5% agar, pH 7.6) and was incubated for 24 hr at 37°C. The twitching zone was measured and imaged.

Swimming motility was performed as previously described (Rashid and Kornberg, 2004). Overnight cultures were stab inoculated into the surface of LB-0.3% bacto agar and were incubated for 24 hr at 37°C. The resulting swimming zone was measured.

For complementation of genes of interest into P. aeruginosa strains, the complementation vector pBBR1-MCS5-PA0769 was created using Gibson assembly. The vector was transferred to P. aeruginosa by electroporation using 2.2 kV in a 2 mm gap cuvette and subsequent selection using gentamicin.

Training and validating RF models for predicting PPIs in E. coli K12 using MIWSCs

Assembling a ‘gold-standard’ dataset

Request a detailed protocol

Predicting PPIs is challenging in part because of the inherent class imbalance in biological systems: the number of non-interacting pairs greatly outnumber true interactors. We tried to design a relevant task by modeling this class imbalance using a previously published estimate of the ratio of these classes (Rajagopala et al., 2014). A ‘gold-standard’ dataset for E. coli K12 PPIs was assembled and consisted of 72,000 not-interacting, 1226 indirect PPIs, and 72 direct PPIs. All pairs defined as ‘direct PPI’ satisfied three criteria: they shared amino acid level coevolution (Coev+ benchmark), were annotated in the same protein complex in the ECOCYC benchmark, and interacted in the PDB benchmark. All indirect PPIs were selected based on the following criteria: they shared a ‘non-binding’ type interaction annotation in the STRING Nonbinding benchmark, shared a ‘biological function’ interaction in the GO benchmark, and did not share an interaction annotation in any of the benchmarks of direct PPIs (Coev+, ECOCYC, or PDB). The ‘not-interacting’ pairs did not share an interaction annotation in any of the benchmarks (GO, STRING Nonbinding, STRING, Coev+, ECOCYC, or PDB). The not-interacting set was subsampled to exceed the number of physically interacting pairs by 1000-fold (Rajagopala et al., 2014; Cong et al., 2019).

The gold-standard pairs were randomly partitioned into training (60%) and validation (40%) datasets. Fifty such random partitions were generated to assess the reproducibility of the results of the machine-learning task described below. Our rationale in partitioning the entire dataset randomly, instead of independent partitioning for each interaction class, was to produce fluctuations in the number of positives and degree of class imbalance.

Training and validating RF models

Request a detailed protocol

The workflow of training and validating RF models on MIWSCs is depicted in Figure 8—figure supplement 1. RF models consisting of 100 decision trees were trained to classify pairs of proteins in E. coli K12 as not-interacting, indirect PPIs, or direct PPIs by feeding the labeled training set examples to the TreeBagger algorithm (Matlab, v2020a). This process was repeated for each random partition of the gold-standard dataset yielding an ensemble of 50 RF models per feature. Each trained RF model was subjected to three validation tasks of classifying interaction types for unlabeled pairs of E. coli K12 proteins in the validation portion of the gold standard (40%). The model performance was evaluated by computing an F-score for each interaction type (not-interacting, indirect PPIs, direct PPIs), where F-score is the harmonic mean of precision and recall, precision is the ratio of the number of correctly predicted interactions within a class to the total number of predicted interactions in a class, and recall is the ratio of the number of correctly predicted interactions within a class to the total number of interactions of that class. F-scores for RF models trained on MIWSCs and used to predict the validation portion of the gold standard are shown in Figure 8A.

Training and validating RF models on quantitative features of existing methods

For each feature extracted from existing methods described below, RF models were trained and validated using the identical protocol as for MIWSCs (described in the section ‘Training and validating RF models’ for predicting PPIs in E. coli K12 using MIWSCs).

Existing experimental features

Request a detailed protocol

Previously published datasets derived from large-scale experimental PPI screens in E. coli K12 were used to generate a set of four different experimental features including: gene interaction scores from a gene epistasis screen (epistasis, n=41,820), sum log-likelihood scores from an affinity purification mass spectrometry screen (APMS1, n=12,801), protein interaction scores from an affinity purification mass spectrometry screen (APMS2, n=291), and binary pairs from a yeast-two hybrid screen (Y2H, n=1766) (Rajagopala et al., 2014; Babu et al., 2014; Babu et al., 2018; Hu et al., 2009).

Existing computational features

Request a detailed protocol

Gene co-occurrence, gene fusion, and gene neighborhood subscores for E. coli K12 (STRING ID 511145) were extracted from the STRING database (Szklarczyk et al., 2019; Rajagopala et al., 2014; Babu et al., 2014; Babu et al., 2018; Hu et al., 2009). Any pairs without an interaction annotation in the STRING database were assigned a subscore of zero.

Binary MI feature

Request a detailed protocol

The binary MI (b-MI) feature was modeled after the popular phylogenetic profiling method of Pellegrini et al., 2017. First, a binary OGG content matrix was defined as follows:

B^{O G G} = {\begin{cases} 1, D^{O G G} > 0. \\ 0, o t h e r w i s e . \end{cases}

where B^OGG is the binary OGG content matrix and has the same dimensions as D^OGG.

The phylogenetic profile of an OGG across all 7047 proteomes was defined as:

{p p}_{i} = {B^{O G G}}_{i}

where ${p p}_{i}$ is the phylogenetic profile of OGG $i$ . The degree to which phylogenetic profiles for a pairs of proteins in the E. coli K12 were similar was computed by averaging the MI between phylogenetic profiles of the OGGs encoded in the protein pair. The MI shared between two phylogenetic profiles was computed using Shannon’s formulation for the MI between two discrete random variables (, ; Cover and Thomas, 2005).

Covariation feature

Request a detailed protocol

The covariation between a pair of OGGs was described by:

C o v_{i j} = \frac{1}{Ω} \sum_{ω = 1}^{Ω} (f_{i}^{ω} - < f_{i} >) (f_{j}^{ω} - < f_{i} >)

where ${C o v}_{i j}$ is the covariation between OGGs $i$ and $j$ , $Ω$ is the total number of proteomes (rows) in D^OGG, $f_{i}^{ω}$ is the number of OGG $i$ in proteome $ω$ , $f_{j}^{ω}$ is the number of OGG $j$ in proteome $ω$ , and $< f_{i} >$ is the average number of OGG $i$ across all proteomes.

PCA-based spectral correlations features

Request a detailed protocol

These features were inspired by the approach of Franceschini and colleagues and the typical use of SVD to produce a low rank approximation of the initial data matrix in an effort to ‘denoise’ the data (Franceschini et al., 2016). For each pair of proteins in the E. coli K12 proteome spectral correlations were computed as described in the section ‘Computing protein-protein spectral correlations’ over windows ranging from component 1 to component k, where k=5, 10, 20, 50, 100, 500, 1000, 5000, or 7047.

F-scores for RF models trained on various experimental or computational features and used to predict the validation portion of the gold standard are shown in Figure 8A.

Validating RF models in two additional validation tasks

Training dataset task

Request a detailed protocol

Each decision tree within an RF model was tasked with predicting interaction classes for the out-of-bag examples from the training datasets. F-scores were computed for the consensus predictions of each model.

Comprehensive benchmark task

Request a detailed protocol

Biological interactions are typically sparse: the number of not-interacting pairs of proteins vastly outnumber the number of interacting pairs. As such, we desired to challenge each of the RF models in a validation task reflective of this asymmetry. To do so, each RF model was tasked with predicting classes for all pairs of proteins in the E. coli K12 proteome after exclusion of pairs used in the gold-standard dataset. These predictions were validated against four different comprehensive benchmarks: the indirect PPIs in the STRING Nonbinding benchmark (n=5423 indirect PPIs, 9,637,213 not-interacting), the mixed indirect/direct PPIs in the GO (n=79,794 indirect or direct PPIs, 9,562,842 not-interacting) and STRING benchmarks (n=20,216 indirect or direct PPIs, 9,622,420 not-interacting), and the direct PPIs in the entire PDB benchmark (n=809 direct PPIs, 9,614,827 not-interacting).

F-scores for RF models trained on MIWSCs, published experimental, or published computational features and used to predict the out-of-bag examples of non-interacting proteins, indirect PPIs, or direct PPIs are shown in Figure 8—figure supplement 3.

Predicting proteome-wide direct PPIs for 11 phylogenetically unrelated bacteria

Proteomes represented in D^OGG

Request a detailed protocol

Each of the 50 RF models trained to classify interactions in E. coli K12 using MIWSCs were used to predict proteome-wide indirect and direct PPIs in the following bacteria (Uniprot Proteome ID, NCBI taxonomy ID in parentheses): Aliivibrio fischeri ES114 (UP000000537, 312309), A. vinelandii DJ (UP000002424, 322710), B. subtilis 168 (UP000001570, 224308), Caulobacter vibrioides (UP000053705, 155892), Helicobacter pylori 26695 (UP000000429, 85962), M. tuberculosis H37Rv (UP000001584, 83332), Mycoplasma genitalium G37 (UP000000807, 243273), Pseudomonas fluorescens F113 (UP000005437, 1114970), Staphylococcus aureus NCTC 8325 (UP000008816, 93061), Streptomyces coelicolor A3(2) (UP000001973, 100226), Synechocystis sp. PCC 6803 (UP000001425, 1111708). For each proteome, a set of consensus PPIs was defined as those for which a majority of the models (>25) produced the same classification of ‘indirect PPI’ or ‘direct PPI’.

Proteomes not represented in D^OGG

Request a detailed protocol

To predict interactions for a proteome that was not represented in D^OGG (e.g. A. vinelandii DJ, UP000002424, 322710), OGGs were mapped using EggNOG mapper V2 and MIWSCs were extracted using the OGG projections in V^OGG (Huerta-Cepas et al., 2017; Huerta-Cepas et al., 2019). These features were used to predict proteome-wide indirect and direct PPIs as described for the Uniprot Reference Proteomes above.

Validating direct PPI predictions against experimental evidence in the STRING database

Request a detailed protocol

The predicted direct PPIs were benchmarked against the sets of interactions in the STRING database with a non-zero experimental subchannel score for E. coli K12 and the 11 additional organisms described above.

A head-to-head comparison with the approach of Cong and colleagues

Request a detailed protocol

Cong and colleagues have provided proteome-wide PPI predictions for E. coli K12 and M. tuberculosis H37Rv (Cong et al., 2019). Their predictions of E. coli PPIs were based on AA Coev supplemented with existing knowledge (‘Coev+’). In contrast, their predictions of PPIs in M. tuberculosis were based on AA Coev alone (‘Coev’). Therefore, for a head-to-head comparison, we compared the predictions produced by our RF models trained on MIWSCs with their PPI predictions in M. tuberculosis. We benchmarked these interactions using two strategies. The first strategy mirrored that used by Cong and colleagues, computing the fraction of interactions assigned a STRING combined score of 0, 0–0.4, or >0.4. The second strategy used orthogonal experimental evidence by computing the fraction of interactions assigned a STRING experimental subchannel score of 0 and >0.

Data availability

All data relevant to this manuscript can be downloaded, in Table format, at https://www.github.com/arjunsraman/Zaydman_et_al copy archived at swh:1:rev:b2c1091aafb726d88a925ad16e07f617a44c8cdc. All tables are available for download in .zip format. All code used for analyses contained within the manuscript can also be found within the same github repository; please refer to Readme.m and Supplemental_Code_9_23_2020.m for relevant Matlab scripts and to reproduce results.

References

1. Alm RA
2. Mattick JS
(1995) Identification of a gene, pilv, required for type 4 fimbrial biogenesis in pseudomonas aeruginosa, whose product possesses a pre-pilin-like leader sequence
Molecular Microbiology 16:485–496.
https://doi.org/10.1111/j.1365-2958.1995.tb02413.x
- PubMed
- Google Scholar
1. Babu M
2. Arnold R
3. Bundalovic-Torma C
4. Gagarinova A
5. Wong KS
6. Kumar A
7. Stewart G
8. Samanfar B
9. Aoki H
10. Wagih O
11. Vlasblom J
12. Phanse S
13. Lad K
14. Yeou Hsiung Yu A
15. Graham C
16. Jin K
17. Brown E
18. Golshani A
19. Kim P
20. Moreno-Hagelsieb G
21. Greenblatt J
22. Houry WA
23. Parkinson J
24. Emili A
(2014) Quantitative genome-wide genetic interaction screens reveal global epistatic relationships of protein complexes in Escherichia coli
PLOS Genetics 10:e1004120.
https://doi.org/10.1371/journal.pgen.1004120
- PubMed
- Google Scholar
1. Babu M
2. Bundalovic-Torma C
3. Calmettes C
4. Phanse S
5. Zhang Q
6. Jiang Y
7. Minic Z
8. Kim S
9. Mehla J
10. Gagarinova A
11. Rodionova I
12. Kumar A
13. Guo H
14. Kagan O
15. Pogoutse O
16. Aoki H
17. Deineko V
18. Caufield JH
19. Holtzapple E
20. Zhang Z
21. Vastermark A
22. Pandya Y
23. Lai CCL
24. El Bakkouri M
25. Hooda Y
26. Shah M
27. Burnside D
28. Hooshyar M
29. Vlasblom J
30. Rajagopala SV
31. Golshani A
32. Wuchty S
33. F Greenblatt J
34. Saier M
35. Uetz P
36. F Moraes T
37. Parkinson J
38. Emili A
(2018) Global landscape of cell envelope protein complexes in Escherichia coli
Nature Biotechnology 36:103–112.
https://doi.org/10.1038/nbt.4024
- PubMed
- Google Scholar
1. Barabási AL
2. Oltvai ZN
(2004) Network biology: understanding the cell’s functional organization
Nature Reviews. Genetics 5:101–113.
https://doi.org/10.1038/nrg1272
- PubMed
- Google Scholar
1. Burrows LL
(2004) Pseudomonas aeruginosa twitching motility: type IV pili in action
Annual Review of Microbiology 66:493–520.
https://doi.org/10.1146/annurev-micro-092611-150055
- PubMed
- Google Scholar
(2010) A decade of systems biology
Annual Review of Cell and Developmental Biology 26:721–744.
https://doi.org/10.1146/annurev-cellbio-100109-104122
- PubMed
- Google Scholar
(2019) Protein interaction networks revealed by proteome coevolution
Science 365:185–189.
https://doi.org/10.1126/science.aaw6718
- PubMed
- Google Scholar
1. Costanzo M
2. VanderSluis B
3. Koch EN
4. Baryshnikova A
5. Pons C
6. Tan G
7. Wang W
8. Usaj M
9. Hanchard J
10. Lee SD
11. Pelechano V
12. Styles EB
13. Billmann M
14. van Leeuwen J
15. van Dyk N
16. Lin ZY
17. Kuzmin E
18. Nelson J
19. Piotrowski JS
20. Srikumar T
21. Bahr S
22. Chen Y
23. Deshpande R
24. Kurat CF
25. Li SC
26. Li Z
27. Usaj MM
28. Okada H
29. Pascoe N
30. San Luis BJ
31. Sharifpoor S
32. Shuteriqi E
33. Simpkins SW
34. Snider J
35. Suresh HG
36. Tan Y
37. Zhu H
38. Malod-Dognin N
39. Janjic V
40. Przulj N
41. Troyanskaya OG
42. Stagljar I
43. Xia T
44. Ohya Y
45. Gingras AC
46. Raught B
47. Boutros M
48. Steinmetz LM
49. Moore CL
50. Rosebrock AP
51. Caudy AA
52. Myers CL
53. Andrews B
54. Boone C
(2016) A global genetic interaction network maps A wiring diagram of cellular function
Science 353:aaf1420.
https://doi.org/10.1126/science.aaf1420
- PubMed
- Google Scholar
Book
1. Cover TM
2. Thomas JA
(2005) Elements of Information Theory (2nd)
John Wiley & Sons.
https://doi.org/10.1002/047174882X
- Google Scholar
1. Croce G
2. Gueudré T
3. Ruiz Cuevas MV
4. Keidel V
5. Figliuzzi M
6. Szurmant H
7. Weigt M
(2019) A multi-scale coevolutionary approach to predict interactions between protein domains
PLOS Computational Biology 15:e1006891.
https://doi.org/10.1371/journal.pcbi.1006891
- PubMed
- Google Scholar
1. Eisen JA
(2017) Phylogenomics: improving functional predictions for uncharacterized genes by evolutionary analysis
Genome Research 8:163–167.
https://doi.org/10.1101/gr.8.3.163
- PubMed
- Google Scholar
(2017) Protein interaction maps for complete genomes based on gene fusion events
Nature 402:86–90.
https://doi.org/10.1038/47056
- PubMed
- Google Scholar
(2016) SVD-phy: improved prediction of protein functional associations through singular value decomposition of phylogenetic profiles
Bioinformatics 32:1085–1087.
https://doi.org/10.1093/bioinformatics/btv696
- PubMed
- Google Scholar
1. Gene Ontology Consortium
(2021) The gene ontology resource: enriching a gold mine
Nucleic Acids Research 49:D325–D334.
https://doi.org/10.1093/nar/gkaa1113
- PubMed
- Google Scholar
(2021) Large-scale discovery of protein interactions at residue resolution using co-evolution calculated from genomic sequences
Nature Communications 12:1396.
https://doi.org/10.1038/s41467-021-21636-z
- PubMed
- Google Scholar
(1999) From molecular to modular cell biology
Nature 402:C47–C52.
https://doi.org/10.1038/35011540
- PubMed
- Google Scholar
1. Häuser R
2. Ceol A
3. Rajagopala SV
4. Mosca R
5. Siszler G
6. Wermke N
7. Sikorski P
8. Schwarz F
9. Schick M
10. Wuchty S
11. Aloy P
12. Uetz P
(2014) A second-generation protein-protein interaction network of helicobacter pylori
Molecular & Cellular Proteomics 13:1318–1329.
https://doi.org/10.1074/mcp.O113.033571
- PubMed
- Google Scholar
1. Hu P
2. Janga SC
3. Babu M
4. Díaz-Mejía JJ
5. Butland G
6. Yang W
7. Pogoutse O
8. Guo X
9. Phanse S
10. Wong P
11. Chandran S
12. Christopoulos C
13. Nazarians-Armavil A
14. Nasseri NK
15. Musso G
16. Ali M
17. Nazemof N
18. Eroukova V
19. Golshani A
20. Paccanaro A
21. Greenblatt JF
22. Moreno-Hagelsieb G
23. Emili A
(2009) Global functional atlas of Escherichia coli encompassing previously uncharacterized proteins
PLOS Biology 7:e100096.
https://doi.org/10.1371/journal.pbio.1000096
- PubMed
- Google Scholar
(2009a) Bioinformatics enrichment tools: paths toward the comprehensive functional analysis of large gene lists
Nucleic Acids Research 37:1–13.
https://doi.org/10.1093/nar/gkn923
- PubMed
- Google Scholar
(2009b) Systematic and integrative analysis of large gene lists using DAVID bioinformatics resources
Nature Protocols 4:44–57.
https://doi.org/10.1038/nprot.2008.211
- PubMed
- Google Scholar
(2017) Fast genome-wide functional annotation through orthology assignment by eggnog-mapper
Molecular Biology and Evolution 34:2115–2122.
https://doi.org/10.1093/molbev/msx148
- PubMed
- Google Scholar
1. Huerta-Cepas J
2. Szklarczyk D
3. Heller D
4. Hernández-Plaza A
5. Forslund SK
6. Cook H
7. Mende DR
8. Letunic I
9. Rattei T
10. Jensen LJ
11. von Mering C
12. Bork P
(2019) EggNOG 5.0: a hierarchical, functionally and phylogenetically annotated orthology resource based on 5090 organisms and 2502 viruses
Nucleic Acids Research 47:D309–D314.
https://doi.org/10.1093/nar/gky1085
- PubMed
- Google Scholar
1. Kanehisa M
2. Goto S
(2000) KEGG: kyoto encyclopedia of genes and genomes
Nucleic Acids Research 28:27–30.
https://doi.org/10.1093/nar/28.1.27
- PubMed
- Google Scholar
1. Kanehisa M
(2019) Toward understanding the origin and evolution of cellular organisms
Protein Science 28:1947–1951.
https://doi.org/10.1002/pro.3715
- PubMed
- Google Scholar
(2021) KEGG: integrating viruses and cellular organisms
Nucleic Acids Research 49:D545–D551.
https://doi.org/10.1093/nar/gkaa970
- PubMed
- Google Scholar
(2004) Pseudomonas aeruginosa exhibits directed twitching motility up phosphatidylethanolamine gradients
Journal of Bacteriology 183:763–767.
https://doi.org/10.1128/JB.183.2.763-767.2001
- PubMed
- Google Scholar
(2017) The ecocyc database: reflecting new knowledge about Escherichia coli K-12
Nucleic Acids Research 45:D543–D550.
https://doi.org/10.1093/nar/gkw1003
- PubMed
- Google Scholar
1. Klema V
2. Laub A
(1980) The singular value decomposition: its computation and some applications
IEEE Transactions on Automatic Control 25:164–176.
https://doi.org/10.1109/TAC.1980.1102314
- Google Scholar
1. Koo BM
2. Kritikos G
3. Farelli JD
4. Todor H
5. Tong K
6. Kimsey H
7. Wapinski I
8. Galardini M
9. Cabal A
10. Peters JM
11. Hachmann AB
12. Rudner DZ
13. Allen KN
14. Typas A
15. Gross CA
(2017) Construction and analysis of two genome-scale deletion libraries for Bacillus subtilis
Cell Systems 4:291–305.
https://doi.org/10.1016/j.cels.2016.12.013
- PubMed
- Google Scholar
1. Kuzmin E
2. VanderSluis B
3. Wang W
4. Tan G
5. Deshpande R
6. Chen Y
7. Usaj M
8. Balint A
9. Mattiazzi Usaj M
10. van Leeuwen J
11. Koch EN
12. Pons C
13. Dagilis AJ
14. Pryszlak M
15. Wang JZY
16. Hanchard J
17. Riggi M
18. Xu K
19. Heydari H
20. San Luis BJ
21. Shuteriqi E
22. Zhu H
23. Van Dyk N
24. Sharifpoor S
25. Costanzo M
26. Loewith R
27. Caudy A
28. Bolnick D
29. Brown GW
30. Andrews BJ
31. Boone C
32. Myers CL
(2018) Systematic analysis of complex genetic interactions
Science 360:eaao1729.
https://doi.org/10.1126/science.aao1729
- PubMed
- Google Scholar
1. Little AS
2. Okkotsu Y
3. Reinhart AA
4. Damron FH
5. Barbier M
6. Barrett B
7. Oglesby-Sherrouse AG
8. Goldberg JB
9. Cody WL
10. Schurr MJ
11. Vasil ML
12. Schurr MJ
13. Collier RJ
14. Wozniak D
15. Pier G
(2018) Pseudomonas aeruginosa algr phosphorylation status differentially regulates pyocyanin and pyoverdine production
MBio 9:e02318-17.
https://doi.org/10.1128/mBio.02318-17
- PubMed
- Google Scholar
1. Luck K
2. Kim DK
3. Lambourne L
4. Spirohn K
5. Begg BE
6. Bian W
7. Brignall R
8. Cafarelli T
9. Campos-Laborie FJ
10. Charloteaux B
11. Choi D
12. Coté AG
13. Daley M
14. Deimling S
15. Desbuleux A
16. Dricot A
17. Gebbia M
18. Hardy MF
19. Kishore N
20. Knapp JJ
21. Kovács IA
22. Lemmens I
23. Mee MW
24. Mellor JC
25. Pollis C
26. Pons C
27. Richardson AD
28. Schlabach S
29. Teeking B
30. Yadav A
31. Babor M
32. Balcha D
33. Basha O
34. Bowman-Colin C
35. Chin SF
36. Choi SG
37. Colabella C
38. Coppin G
39. D’Amata C
40. De Ridder D
41. De Rouck S
42. Duran-Frigola M
43. Ennajdaoui H
44. Goebels F
45. Goehring L
46. Gopal A
47. Haddad G
48. Hatchi E
49. Helmy M
50. Jacob Y
51. Kassa Y
52. Landini S
53. Li R
54. van Lieshout N
55. MacWilliams A
56. Markey D
57. Paulson JN
58. Rangarajan S
59. Rasla J
60. Rayhan A
61. Rolland T
62. San-Miguel A
63. Shen Y
64. Sheykhkarimli D
65. Sheynkman GM
66. Simonovsky E
67. Taşan M
68. Tejeda A
69. Tropepe V
70. Twizere JC
71. Wang Y
72. Weatheritt RJ
73. Weile J
74. Xia Y
75. Yang X
76. Yeger-Lotem E
77. Zhong Q
78. Aloy P
79. Bader GD
80. De Las Rivas J
81. Gaudet S
82. Hao T
83. Rak J
84. Tavernier J
85. Hill DE
86. Vidal M
87. Roth FP
88. Calderwood MA
(2017) A reference map of the human binary protein interactome
Nature 580:402–408.
https://doi.org/10.1038/s41586-020-2188-x
- PubMed
- Google Scholar
(2020) Scalable phylogenetic profiling using minhash uncovers likely eukaryotic sexual reproduction genes
PLOS Computational Biology 16:e1007553.
https://doi.org/10.1371/journal.pcbi.1007553
- PubMed
- Google Scholar
(2020) Novel phylogenetic methods are needed for understanding gene function in the era of mega-scale genome sequencing
Nucleic Acids Research 48:2209–2219.
https://doi.org/10.1093/nar/gkz1241
- PubMed
- Google Scholar
1. NCBI Resource Coordinators
(2018) Database resources of the national center for biotechnology information
Nucleic Acids Research 46:D8–D13.
https://doi.org/10.1093/nar/gkx1095
- PubMed
- Google Scholar
1. Nurse P
(2008) Life, logic and information
Nature 454:424–426.
https://doi.org/10.1038/454424a
- PubMed
- Google Scholar
(1999) The use of gene clusters to infer functional coupling
PNAS 96:2896–2901.
https://doi.org/10.1073/pnas.96.6.2896
- PubMed
- Google Scholar
(2004) Hierarchical thinking in network biology: the unbiased modularization of biochemical networks
Trends in Biochemical Sciences 29:641–647.
https://doi.org/10.1016/j.tibs.2004.10.001
- PubMed
- Google Scholar
1. Paul K
2. Nieto V
3. Carlquist WC
4. Blair DF
5. Harshey RM
(2010) The c-di-GMP binding protein ycgr controls flagellar motor direction and speed to affect chemotaxis by a “backstop brake” mechanism
Molecular Cell 38:128–139.
https://doi.org/10.1016/j.molcel.2010.03.001
- PubMed
- Google Scholar
(2017) Assigning protein functions by comparative genome analysis: protein phylogenetic profiles
PNAS 96:4285–4288.
https://doi.org/10.1073/pnas.96.8.4285
- PubMed
- Google Scholar
1. Rajagopala SV
2. Sikorski P
3. Kumar A
4. Mosca R
5. Vlasblom J
6. Arnold R
7. Franca-Koh J
8. Pakala SB
9. Phanse S
10. Ceol A
11. Häuser R
12. Siszler G
13. Wuchty S
14. Emili A
15. Babu M
16. Aloy P
17. Pieper R
18. Uetz P
(2014) The binary protein-protein interaction landscape of Escherichia coli
Nature Biotechnology 32:285–290.
https://doi.org/10.1038/nbt.2831
- PubMed
- Google Scholar
1. Rashid MH
2. Kornberg A
(2004) Inorganic polyphosphate is needed for swimming, swarming, and twitching motilities of Pseudomonas aeruginosa
PNAS 97:4885–4890.
https://doi.org/10.1073/pnas.060030097
- PubMed
- Google Scholar
1. Ravasz E
(2009) Detecting hierarchical modularity in biological networks
Methods in Molecular Biology 541:145–160.
https://doi.org/10.1007/978-1-59745-243-4_7
- PubMed
- Google Scholar
1. Schäfer J
2. Strimmer K
(2005) An empirical bayes approach to inferring large-scale gene association networks
Bioinformatics 21:754–764.
https://doi.org/10.1093/bioinformatics/bti062
- PubMed
- Google Scholar
1. Schoenrock A
2. Burnside D
3. Moteshareie H
4. Pitre S
5. Hooshyar M
6. Green JR
7. Golshani A
8. Dehne F
9. Wong A
(2017) Evolution of protein-protein interaction networks in yeast
PLOS ONE 12:e0171920.
https://doi.org/10.1371/journal.pone.0171920
- PubMed
- Google Scholar
1. Sul JH
2. Martin LS
3. Eskin E
(2018) Population structure in genetic studies: confounding factors and mixed models
PLOS Genetics 14:e1007309.
https://doi.org/10.1371/journal.pgen.1007309
- PubMed
- Google Scholar
1. Szklarczyk D
2. Gable AL
3. Lyon D
4. Junge A
5. Wyder S
6. Huerta-Cepas J
7. Simonovic M
8. Doncheva NT
9. Morris JH
10. Bork P
11. Jensen LJ
12. Mering CV
(2019) STRING v11: protein-protein association networks with increased coverage, supporting functional discovery in genome-wide experimental datasets
Nucleic Acids Research 47:D607–D613.
https://doi.org/10.1093/nar/gky1131
- PubMed
- Google Scholar
1. UniProt Consortium
(2019) UniProt: a worldwide hub of protein knowledge
Nucleic Acids Research 47:D506–D515.
https://doi.org/10.1093/nar/gky1049
- PubMed
- Google Scholar
1. Valencia A
2. Pazos F
(2002) Computational methods for the prediction of protein interactions
Current Opinion in Structural Biology 12:368–373.
https://doi.org/10.1016/s0959-440x(02)00333-0
- PubMed
- Google Scholar
(2004) Role of cell surface lipopolysaccharides in Escherichia coli k12 adhesion and transport
Langmuir : The ACS Journal of Surfaces and Colloids 20:7736–7746.
https://doi.org/10.1021/la049511f
- PubMed
- Google Scholar
1. Wigner EP
(1967) Random matrices in physics
SIAM Review 9:1–23.
https://doi.org/10.1137/1009001
- Google Scholar

Decision letter

Nir Ben-Tal

Reviewing Editor; Tel Aviv University, Israel
Aleksandra M Walczak

Senior Editor; CNRS LPENS, France

Our editorial process produces two outputs: (i) public reviews designed to be posted alongside the preprint for the benefit of readers; (ii) feedback on the manuscript for the authors, including requests for revisions, shown below. We also include an acceptance summary that explains what the editors found interesting or important about the work.

Decision letter after peer review:

Thank you for submitting your article "Defining hierarchical protein interaction networks from spectral analysis of bacterial proteomes" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and Aleksandra Walczak as the Senior Editor. The reviewers have opted to remain anonymous.

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission.

Essential revisions:

1) The basic predictive power of their MIWSC approach is demonstrated in Figure 2C. However, we were surprised by the extremely low recall shown in the right panel. A recall of 10e-5 is very low indeed, and would preclude this method from having much practical value. We went ahead and recomputed both panels in Figure 2C, based on the author's raw prediction data that we downloaded for E. coli from their 'scales' website (14429 predictions). We could by-and-large confirm the left panel, but for the right panel we got recall values in the 10e-02 range, which is about 1000 times higher. Is this perhaps a mislabeled axis in the plot, or a misunderstanding on our part?

2) Also related to Figure 2C: this panel demonstrates specificity and sensitivity, but only for the author's prediction class of "direct" associations. The authors, however, also predict "indirect" associations … these in fact outnumber their "direct" predictions. Is it possible to also show specificity and sensitivity for those, similar to Figure 2C, for the same set of organisms? This could be done by taking KEGG-pathway membership or GO terms as the benchmark; in our own testing we found that the overall prediction power of their "indirect MIWSC" class is less impressive – more in line with previous efforts, which might be of interest to the reader.

3) Bacteria tree is not uniformly sequenced. There is an overrepresentation of certain lineages, e.g., of gammaproteobacteria and terrabacteria (Bacillus group) in the starting matrix. This could potentially bias the quality of the correlations that are obtained in the ``mid-range' SVD components.

4) The actual biological inferences drawn for the role of the tested gene in twitching mobility might be over-interpreted. Briefly, the authors recover 4 uncharacterized proteins (Q9I5G6, Q9I5R2, Q9I0G2, Q9I0G1) as part of their T4 pilus sub-graph and infer a general function for them in the twitching mobility. They chose Q9I5G6 because it was the only one with a supposed domain of unknown function (DUF4845). However, it should be noted that Q9I5R2 also contains another such domain DUF805 along with a Zn-ribbon domain. Further, Q9I0G2 is a T2SS secretion platform protein and Q9I0G1i is the ATPase engine for the pilus. Genomic neighborhood analysis by this referee revealed that DUF4845 likely functions with the signal peptidase in secretion. Thus, given the role of the pilus in secretion and mobility, the best one could infer is a role for DUF4845 in pilus function perhaps with a greater intersection with secretion. This could even indirectly affect the mobility function which the authors' experiments are said to support. However, the authors state right in the abstract they have uncovered a twitching mobility effector. At best they could say they have uncovered a potential component that might be functionally linked to the T4 pilus which might affect secretion or twitching mobility. Indeed, the phyletic pattern of DUF4845 does not immediately suggest that all organisms with it also possess definitive twitching mobility.

5) The authors found 4 proteins of unknown function associated with pilus motility in P. aeruginosa. Only one shows positive experimental results. It would be nice to have some idea how general this is, i.e. how many times proteins get associated by the approach, even if they have biologically known but totally distinct functions.

6) The authors might experiment with using a matrix that removes closely related gammaproteobacterial, actinobacterial and terrabacterial lineages to see its effects on their training and predictions.

7) When the manuscript speaks of scales of protein interactions represented in the spectrum, is this visible in the singular vectors? We would imagine that large-scale properties should correspond to distributed vectors (and not only large singular values), while local scales should intuitively correspond to localised vectors.

8) It is quite evident that the first singular vectors are related to phylogeny, which is known to be a major source of variability between orthologs (at the end SVD achieves spectral clustering, and phylogeny reconstruction hierarchical clustering, which are expected to show some level of coherence). What is more interesting is the crossover from phylogenetic to functional information.

9) The MI is not really well defined, it would be hard to reproduce on the basis of what is written in the Methods section.

10) We have some doubts concerning the gold standard. If non-interacting pairs are randomly chosen, and fractions of interacting and non-interacting pairs are given in their approximate true proportions, the non-interacting set should contain about the same number of actually interacting pairs as given in the positive examples. The choice of so many random pairs to represent non-interacting pairs is therefore dangerous and potentially misleading. It remains also unclear how the extreme bias towards non-interacting pairs in the dataset is handled (most machine-learning algorithms run into problems in this case). When partitioning into training and validation sets, is this done independently for each class, or for the entire dataset? In the latter case, the number of positive examples might fluctuate a lot in the training set.

11) The comparison with Cong et al., might be potentially spectacular, but it is hard to understand it from the little paragraph. This should be explained better. One should also keep in mind that Cong et al., use an unsupervised approach as compared to the supervised in the present manuscript.

12) The notation in Materials and methods requires revision. To give an example (beyond the MI part already mentioned), n is the number of proteomes in the first paragraph, and the number of OGGs in the second. Please use consistent notations!

13) Is Figure 1S2B really showing normalized columns? They appear optically to have very different variances, even if they all should be normalized to variance 1.

14) The code should be made available.

Presentation:

1) The paper is very hard to read and to understand. It is written in a semi-technical jargon mixing spectral analysis, machine learning and information theory. Even having expertise in these fields, we had to continuously jump between the main text, the methods and the figure (including the supplementary figures – a total of 86 pages) to follow the argumentation of the paper. This style is not suitable for a journal with a broad and interdisciplinary readership. The authors should make a serious effort to clean up their presentation, such that the main messages become accessible. Currently, even for disciplinary journals in computational biology or bioinformatics, the presentation would require simplifications.

2) The general reader would benefit from an opening figure that clearly lays out the steps in the workflow starting with SVD (giving some general background) to random forest training. It can augment what is shown in the current figure 1 and one of the supplements to figure 2.

3) The abstract repeats 8 times the word "hierarchy" or "hierarchical". Avoid such excessive repetitions.

4) The introduction was a bit short in giving credit to previous efforts in this area. Yes, the founding papers from the 90s are cited, but there have been quite a number of studies in the meantime, including the use of SVD, reviewed for example here: Nagy et al., NAR 2020, https://doi.org/10.1093/nar/gkz1241 or Moi et al., PLoS computational biology 2020, 16 (7), e1007553

5) The results on motility are really nice. We suggest placing them much earlier in the paper, and do the more technical stuff with random forest etc. later. It could come directly after Figure 1C has been explained.

[Editors’ note: further revisions were suggested prior to acceptance, as described below.]

Thank you for resubmitting your work entitled "Defining hierarchical protein interaction networks from spectral analysis of bacterial proteomes" for further consideration by eLife. Your revised article has been evaluated by Aleksandra Walczak (Senior Editor) and a Reviewing Editor.

The manuscript has been improved but there are some remaining issues that need to be addressed, as outlined below:

Reviewer #1 (Recommendations for the authors):

General Summary:

While the authors have made clearly visible efforts to improve the presentation of their manuscript, the major problem remains: while the results are very interesting, the presentation of the technical details is cumbersome, and reading the paper without massive reference to the huge number of supplementary figures is hardly possible. I think another round of simplification is unavoidable.

Detailed report:

I am still convinced that this paper has very interesting results, which fully merit publication. But in particular, the initial part of the paper is hard to read. In a nutshell, the method is quite simple: (a) extract a large matrix of phylogenetic profiles (here many proteomes annotated via OGGs), (b) perform a standard SVD, and represent OGGs via their projection to the singular vectors, (c) extract proteins having correlated projections in small spectral windows. The innovative part of the paper is a clever use of these spectral windows going from the singular values/vectors describing the large-scale organisation of the data, to smaller and smaller singular values, far beyond the few typically used in PCA, showing that these deep parts of the spectrum contain finer and finer information – here going from large functional categories via pathways to PPI. It should be possible to present this in a simple way.

I would like to make a number of more specific points:

1. The reading is impossible without the massive use of supplementary figures. To give one example (out of many), the singular vectors in U^OGG and V^OGG are used in methods but introduced only in Figure 1 Supp. 1. In addition, the left and right singular values are denoted equally as |n>, which is a bit confusing (even more since as mentioned, the matrices are not defined in the text). In general, the authors should revise the paper such that the supplement gives supplementary information, and the paper can be read without having ~50 pages of supplement in your hands.

2. The method heavily relies on subjective hyperparameters and thresholds: For the number of singular values considered, for the bin size in the MI calculation, for the size of the spectral window, for the used cutoffs of the spectral depth. Together with the somewhat anecdotal results (concentration mostly on motility), this gives the impression that the biological system and parameters are hand selected to show nicely interpretable results. I sincerely hope this is not the case, but if the authors would, e.g., show the tree generated by changing spectral depth from largest to smallest values, the different levels of organisation could become more evident (in case well-separated levels exist).

3. In some cases, it is hard to understand if the results are significant. If one considers Figure 1E, even a uniform MI distribution would have a similar shape as the blue curves, since the cumulative would be linear, and represented with a log-scale of the spectral position.

4. In some places, results imposed by the analysis are presented as astonishing findings. The most evident case is the hierarchical structure when changing spectral depth. Since spectral depth is defined as the depth where correlations are for the first time non-significant, the edge set of the graphs at higher spectral depth is necessarily proper subsets of those at lower spectral depth, and thus connected components are proper subsets, too. If all statistically significant correlations in each spectral window would have been taken into account, edges between proteins might disappear at some depth, and reappear at a deeper one, making the network potentially non-hierarchical.

5. Heavy but somewhat random statements like "Understanding the molecular basis of a phenotype requires (i) defining interactions that create units of collective function at different biological scales and (ii) relating these scales to create a hierarchical model of emergent phenotype." should be avoided.

https://doi.org/10.7554/eLife.74104.sa1

Author response

Essential revisions:

1) The basic predictive power of their MIWSC approach is demonstrated in Figure 2C. However, we were surprised by the extremely low recall shown in the right panel. A recall of 10e-5 is very low indeed, and would preclude this method from having much practical value. We went ahead and recomputed both panels in Figure 2C, based on the author's raw prediction data that we downloaded for E. coli from their 'scales' website (14429 predictions). We could by-and-large confirm the left panel, but for the right panel we got recall values in the 10e-02 range, which is about 1000 times higher. Is this perhaps a mislabeled axis in the plot, or a misunderstanding on our part?

We thank the reviewer for bringing attention to this point and recalculating the recall. We indeed found an error in our plot. We have corrected this error and observe similar results as the reviewer with recall on the order of 10^-2 (Figure 4B).

2) Also related to Figure 2C: this panel demonstrates specificity and sensitivity, but only for the author's prediction class of "direct" associations. The authors, however, also predict "indirect" associations … these in fact outnumber their "direct" predictions. Is it possible to also show specificity and sensitivity for those, similar to Figure 2C, for the same set of organisms? This could be done by taking KEGG-pathway membership or GO terms as the benchmark; in our own testing we found that the overall prediction power of their "indirect MIWSC" class is less impressive – more in line with previous efforts, which might be of interest to the reader.

We thank the reviewer for this excellent suggestion. We have now repeated the same analysis for our indirect predictions as well as the combined set of indirect and direct predictions to provide the reader with a more comprehensive understanding of the accuracy of our method. In addition, we considered that applying different confidence thresholds to the established methods might produce different results and therefore have considered various thresholds and reconstructed complete precision-recall (PR) curves for the methods of GC, GN, and GF. These analyses provide a more fair and complete evaluation of our predictions in comparison with standard prediction tools. We have added text in the manuscript to reflect these points (lines 296-308):

“We computed the precision and recall for our predictions of any (indirect or direct), indirect, or direct PPIs using the experimentally supported PPIs in the STRING database as a benchmark (score > 0 in the STRING ‘experimental’ subchannel). We compared these results to those produced by the well-established methods of gene co-occurrence, gene neighborhood, and gene fusion by thresholding the corresponding STRING subchannel scores at different confidence levels (low, medium, high, highest). Figure 4B shows this comparison at the ‘medium’ confidence level. Figure 4C summarizes the entire analysis showing the precision-recall curves across all thresholds tested. We found that the sets of any indirect or direct PPIs produced by our method exhibited a higher precision for a given recall compared to the established methods. These results show that though the SVD windows used to compute spectral correlations were chosen based on analysis of PPIs in the E. coli K12 proteome, our approach for predicting PPIs performs as well or better than established methods across different organisms.”

3) Bacteria tree is not uniformly sequenced. There is an overrepresentation of certain lineages, e.g., of gammaproteobacteria and terrabacteria (Bacillus group) in the starting matrix. This could potentially bias the quality of the correlations that are obtained in the ``mid-range' SVD components.

We appreciate this comment regarding the over-representation of certain clades in the original matrix. We performed a sensitivity analysis of our results by randomly downsampling the top 4 Phyla represented in the input dataset by 50%. We have included results of our analysis in the manuscript and have added a supplemental figure (Figure 1—figure supplement 5) to summarize our findings. Below is the text (lines 102-109).

“Comparing the relative distributions of these different types of information across the SVD spectrum, we observed an order of Phylum, Class, Order, Family, Genus, indirect PPIs, mixed indirect/direct PPIs, and direct PPIs. The ordering of these distributions across the SVD spectrum was robust to sub-sampling D^OGG to account for uneven phylogenetic distributions of bacterial strains in the input data (Figure 1—figure supplement 5). These results show that global to local patterns of bacterial covariation reflect an intuitive hierarchy of biological scale—phylogeny, pathway, protein complex (Figure 1E, Materials and methods).”

With respect to the quality of ‘mid-range’ SVD components, we did not observe a striking difference in the MI density when comparing the subsampled matrix versus the initial matrix. However, we did observe more overlap between the ‘Indirect PPI’ benchmark (STRING NB) and the ‘Mixed indirect and direct PPI’ benchmarks (GO, STRING). This difference may arise from having fewer SVD components over which information regarding the ‘Indirect PPI’ benchmark can be spread. We interpret these results to indicate that curating an optimally diverse dataset is a difficult problem that warrants future investigation.

4) The actual biological inferences drawn for the role of the tested gene in twitching mobility might be over-interpreted. Briefly, the authors recover 4 uncharacterized proteins (Q9I5G6, Q9I5R2, Q9I0G2, Q9I0G1) as part of their T4 pilus sub-graph and infer a general function for them in the twitching mobility. They chose Q9I5G6 because it was the only one with a supposed domain of unknown function (DUF4845).

We believe the text in our manuscript was unclear with respect to how these proteins were selected. We selected these proteins because they were labeled as ‘uncharacterized’ in UniProt. The modified text is found in lines 221-223:

“Four uncharacterized proteins (Q9I5G6, Q9I5R2, Q9I0G2, Q9I0G1) were identified in the pilus subnetwork that have not previously been associated with PilA in P. aeruginosa (Figure 3B, Supplementary File 6).”

We found that these proteins were connected to proteins that collectively reflect the global function of ‘motility’ at a spectral depth of 50. At a spectral depth of 300, these proteins shared connections with proteins that collectively reflect the specific function of ‘pilus-based motility’ but not other proteins that collectively reflect ‘flagellar motility’. We then experimentally interrogated genetic ablation of the genes encoding all four proteins individually to look for an effect on both pilus and flagellar motility. Our data revealed that Q9I5G6 affected pilus motility and not flagellar motility. We presented the results of our experiments for all four proteins (Figure 3C, Supplementary File 7).

However, it should be noted that Q9I5R2 also contains another such domain DUF805 along with a Zn-ribbon domain. Further, Q9I0G2 is a T2SS secretion platform protein and Q9I0G1i is the ATPase engine for the pilus. Genomic neighborhood analysis by this referee revealed that DUF4845 likely functions with the signal peptidase in secretion. Thus, given the role of the pilus in secretion and mobility, the best one could infer is a role for DUF4845 in pilus function perhaps with a greater intersection with secretion. This could even indirectly affect the mobility function which the authors' experiments are said to support. However, the authors state right in the abstract they have uncovered a twitching mobility effector. At best they could say they have uncovered a potential component that might be functionally linked to the T4 pilus which might affect secretion or twitching mobility.

We agree with the reviewer. Our approach does not infer a mechanism for Q9I5G6. We believe the key takeaway from our results is that there was a measurable effect of Tn-Q9I5G6 on pilus-based motility and not on flagellar motility. Neither our experiments nor our statistical approach were designed to address the nature (i.e. direct/physical or indirect/functional interaction) of Q9I5G6 with the pilus. We have included text in the manuscript (lines 424-427) to reflect this concept.

“Another limitation of the methods developed here is that they are inherently ‘mechanism-free’: they leverage evolutionary constraint without knowledge of the specific pressures driving the selection of interactions. As a result, our methods identify functionally relevant interactors but cannot reveal their collective function or the detailed molecular basis of the interactions.”

Indeed, the phyletic pattern of DUF4845 does not immediately suggest that all organisms with it also possess definitive twitching mobility.

We agree, merely having DUF4845 does not necessarily mean that the organism has twitching mobility. The phenotype of ‘twitching mobility’ is likely complex and dependent on the interactions between many proteins within individual organisms. Thus, the effect of Tn-Q9I5G6, conditional on the pattern of genetic interactions of strain PAO1, is to affect twitching motility. SCALES predicts an organism-specific, not domain-specific, hierarchical interaction map for Q9I5G6.

5) The authors found 4 proteins of unknown function associated with pilus motility in P. aeruginosa. Only one shows positive experimental results.

We appreciate the reviewer’s concern about the predictive value of our approach. It is worth noting that a ¼ rate of true positives is impressive given the background expectation. Consider that there are 5564 proteins in the P. aeruginosa PA01 strain, of which 25 appear in the ‘pilus-assembly module’ within the KEGG database (BRITE KO02035, ‘pilus assembly proteins’) equating to a 0.4% background rate of association. Thus, a hit rate of 25% is substantially statistically significant (p-value = 0.0001 by Chi-squared). However, we note that the hit-rate of our statistical approach is in fact much higher than 25%. We identified 22 proteins that significantly associated with Pilus-motility, 19 of which were validated by prior experiments in the literature or our own experiments (p < 0.0001 by Chi-squared) (Figure 3B). We posit that the three proteins that did not show a phenotype in our experimental conditions might in fact affect pilus-based motility but may require different assay conditions to be revealed.

We have incorporated our response into discussion within the main text found in lines 236-246:

“These results illustrate that Q9I5G6 is a previously unappreciated effector of directed motility in P. aeruginosa that specifically impacts twitch-based motility. Compared to the background expectation of finding a protein that affects twitch motility (22 ‘pilus assembly proteins’ in BRITE KO02035 out of 5,564 proteins in the PA01 proteome equating to a 0.4% background rate of association), our experimental results represent a statistically significant enrichment (25% association rate, p < 10^-4 by Chi-squared). Moreover, the results of our statistical approach shown in Figure 3B illustrate a far higher enrichment of association with identifying 19 effectors of twitch motility out of 22 proteins in the ‘Pilus motility module’. As such, these experiments provide a proof of concept of how our hierarchical models may aid in discovering novel genotype-phenotype relationships.”

It would be nice to have some idea how general this is, i.e. how many times proteins get associated by the approach, even if they have biologically known but totally distinct functions.

We agree with the reviewer’s point; it would be useful to know the overall false-positive rate of our method. However, our data show that a protein can have distinct functions at a lower scale of interaction and share a collective function at higher scales. Thus, a one-to-one mapping between protein identity and its function is not possible—our results illustrate the concept that biological ‘function’ maps onto emergent networks of protein interactions not individual proteins. Nonetheless, we point to our results in Figure 2, Figure 2—supplemental figures 4, 5, and 6, Figure 5, and Figure 5—supplemental figure 1, where all of the statistical modules characterized by GSEA show a statistically significant association with a known biological function. Moreover, the validation of our proteome-wide interaction predictions across diverse organisms (Figure 4B) revealed a consistently high precision. Together, we interpret that these results provide a general sense of a low false-positive rate for our statistically connected proteins.

6) The authors might experiment with using a matrix that removes closely related gammaproteobacterial, actinobacterial and terrabacterial lineages to see its effects on their training and predictions.

We agree with the reviewer’s comment. We have addressed this in our response to Comment #3.

7) When the manuscript speaks of scales of protein interactions represented in the spectrum, is this visible in the singular vectors? We would imagine that large-scale properties should correspond to distributed vectors (and not only large singular values), while local scales should intuitively correspond to localised vectors.

We thank the reviewers for bringing up this important point. While the reviewer’s intuition was shared by the authors as well, our data illustrate a different trend. We find that large-scale properties (i.e. protein interactions that reflect broad differences in phylogeny) are highly localized to the shallow components of variation (vectors with large singular values) while local scales are distributed across the entire spectrum of vectors. This is shown in the curves reflecting the relative distributions of mutual information across the spectrum of vectors shown in Figure 1—figure supplement 4.

What is the interpretation of this data? Large-scales properties can be ‘compressed’ into just a few variables while ‘local’ properties cannot. Thus, information regarding large-scale properties is increasingly ‘filtered out’ in deeper vectors thereby enriching for more local information. Hence, one of the main results of our analysis is that the order of the spectrum of vectors corresponds to a hierarchy of protein interactions.

We have added the above interpretation of our results into the main text in lines 345-352:

“Components in different regions of the spectrum were enriched for information about different biological scales—shallow components phylogeny, deeper components pathways, even deeper components protein complexes, and the very deepest noise, thereby signifying a ‘cross-over’ from phylogenetic to functional information. Our interpretation of these results is that while statistical variance reflecting large-scale properties can be ‘compressed’ into just a few shallow components, information about ‘local’ biological scales is distributed broadly across the spectrum. As a result, discarding global components enriched for phylogeny improved prediction of functionally relevant interactions.”

8) It is quite evident that the first singular vectors are related to phylogeny, which is known to be a major source of variability between orthologs (at the end SVD achieves spectral clustering, and phylogeny reconstruction hierarchical clustering, which are expected to show some level of coherence). What is more interesting is the crossover from phylogenetic to functional information.

We are in complete agreement with the reviewer in regard to this point. We have added text in the manuscript to reflect this distinction and explicitly point out the interesting nature of the cross-over from phylogenetic information into functional information (lines 339-348):

“One approach to address this problem is to use PCA which assumes that only global covariation is not statistical noise (Wigner, 1967; Franceschini et al., 2016). A known source of variability between orthologs is phylogenetic relatedness. As SVD achieves spectral clustering and phylogenetic reconstruction hierarchical clustering, we do expect some level of coherence between the two approaches. However, our results also illustrate that relevant biological signal is contained throughout the SVD spectrum, including components harboring a minutiae of data-variance. Components in different regions of the spectrum were enriched for information about different biological scales—shallow components phylogeny, deeper components pathways, even deeper components protein complexes, and the very deepest noise, thereby signifying a ‘cross-over’ from phylogenetic to functional information.”

9) The MI is not really well defined, it would be hard to reproduce on the basis of what is written in the Methods section.

We agree that the strategy we used to compute MI is critical to explain in the manuscript and was unclear in our initial submission. To address this we have added a supplemental figure (Figure 1—figure supplement 1) that illustrates the process of computing MI between spectral correlations and biological benchmarks step-by-step; we have also rewritten the Methods section to be more readable. The new text can be found in lines 518-562.

10) We have some doubts concerning the gold standard. If non-interacting pairs are randomly chosen, and fractions of interacting and non-interacting pairs are given in their approximate true proportions, the non-interacting set should contain about the same number of actually interacting pairs as given in the positive examples. The choice of so many random pairs to represent non-interacting pairs is therefore dangerous and potentially misleading.

We agree with the reviewer’s comment that our random sampling of non-interacting pairs may lead to imperfections in the gold-standard dataset, specifically the mis-classification of true interactors as non-interactors. The strategy we took was an attempt to mimic the true interaction class imbalance noted in biological PPI studies. As we do not know the true class imbalance, we used a previous estimate provided by Rajagopala and colleagues (Rajagopala et al., 2014). While we acknowledge that our gold-standard dataset is not perfect, we do not believe that it is misleading for the following reasons. First, false negatives in the gold-standard benchmark will manifest as false positives in our predictions and the imperfections of the gold-standard benchmark will only decrease model performance. Thus, the F-scores presented in Figure 4B can be interpreted as a conservative estimate. Second, the comparison of methods was performed using the same gold-standard dataset. Because the gold-standard was not selected to favor any one method, we believe the differences in relative performances are valid.

It remains also unclear how the extreme bias towards non-interacting pairs in the dataset is handled (most machine-learning algorithms run into problems in this case). When partitioning into training and validation sets, is this done independently for each class, or for the entire dataset? In the latter case, the number of positive examples might fluctuate a lot in the training set.

As the reviewer notes, class imbalance problems are challenging for many machine-learning algorithms. We purposely made a random partitioning across the whole dataset, not a partitioning independently performed for each class (i.e. stratified random sampling). Our intention was to introduce fluctuations in the number of positives across each iteration of partitioning the dataset and training models. In this way, we could ascertain the sensitivity of the performance estimates to the model class imbalance, addressing the reviewer’s concern above. In addition, we chose to report F-score as this is a valid metric for class imbalance problems. Finally, we computed F-scores for each class individually to ensure that the model accuracy is not limited to the majority class.

We agree with the reviewer that these points are critical and have included the following text in the Methods (lines 635-638 and 652-654):

“Predicting PPIs is challenging in part because of the inherent class imbalance in biological systems: the number of non-interacting pairs greatly outnumber true interactors. We tried to design a relevant task by modeling this class imbalance using a previously published estimate of the ratio of these classes (Rajagopala et al., 2014)…Our rationale in partitioning the entire dataset randomly, instead of independent partitioning for each interaction class, was to produce fluctuations in the number of positives and degree of class imbalance.”

11) The comparison with Cong et al., might be potentially spectacular, but it is hard to understand it from the little paragraph. This should be explained better. One should also keep in mind that Cong et al., use an unsupervised approach as compared to the supervised in the present manuscript.

We agree. We have added a section in the Discussion to discuss a comparison between our results and those of Cong et al., The new text can be found in lines 373-412:

“Comparison of our results with AA Coev

Recently, Cong and colleagues reported a method, AA Coev, for inferring direct PPIs from bacterial genome sequences. Their method represented a significant advance for two reasons: (i) it considered co-evolution at the resolution of amino acids and (ii) it applied Direct Coupling Analysis, to entire bacterial proteomes. […] We therefore pose that though SCALES does not consider as information-rich of a feature as AA Coev, it may prove to be a useful framework to extract hierarchical relationships for connecting bacterial genotype with phenotype.”

12) The notation in Materials and methods requires revision. To give an example (beyond the MI part already mentioned), n is the number of proteomes in the first paragraph, and the number of OGGs in the second. Please use consistent notations!

We apologize for this error. We have revised the Methods section and now use consistent notations in the resubmitted manuscript. If the reviewers and referees find any more errors, please alert us and we will correct the Methods section immediately.

13) Is Figure 1S2B really showing normalized columns? They appear optically to have very different variances, even if they all should be normalized to variance 1.

We verified that this matrix is column normalized, however decided that this figure supplement was unnecessary and have removed it from the new version of the manuscript. The column-normalized matrix can be found in Figure 1-source data 1.

14) The code should be made available.

We agree. The code is publicly available and can be found at https://github.com/arjunsraman/Zaydman_et_al

This information is in lines 814-815 in the manuscript.

Presentation:

1) The paper is very hard to read and to understand. It is written in a semi-technical jargon mixing spectral analysis, machine learning and information theory. Even having expertise in these fields, we had to continuously jump between the main text, the methods and the figure (including the supplementary figures – a total of 86 pages) to follow the argumentation of the paper. This style is not suitable for a journal with a broad and interdisciplinary readership. The authors should make a serious effort to clean up their presentation, such that the main messages become accessible. Currently, even for disciplinary journals in computational biology or bioinformatics, the presentation would require simplifications.

We deeply appreciate this feedback. In the resubmitted version, we have attempted to decrease jargon and focus on a single main message: extracting a hierarchy of PPIs from statistics of evolutionary variation. To this aim, we have rehauled the entire manuscript. This revision includes (i) rewriting the main text to appeal to a broader audience, (ii) reordering the main arguments of the paper, (iii) including three workflow figures (Figure 1—figure supplement 1, Figure 2—figure supplement 1, Figure 4—figure supplement 1) to explain analytical steps pictorially, and (iv) cutting material that was not salient to the main message of the paper. With respect to the latter, we have removed the entire section on domain-based analysis because in the re-written version, it felt unnecessary. We have also consolidated Supplemental Figures from the previous submission to focus on key ideas in the manuscript, decreasing the length of the manuscript from 86 pages to 60. We hope that the reviewer agrees we have taken their feedback seriously and these revisions have improved the readability and presentation of our manuscript.

2) The general reader would benefit from an opening figure that clearly lays out the steps in the workflow starting with SVD (giving some general background) to random forest training. It can augment what is shown in the current figure 1 and one of the supplements to figure 2.

We agree. We have included text describing SVD in a general way (lines 71-75):

“To explore the structure of extant bacterial variation, we analyzed D^OGG using a technique called Singular Value Decomposition (SVD), a generalized form of Principal Components Analysis (PCA) (Klema and Laub, 1980). SVD defines a spectrum of components of covariation (an ‘SVD spectrum’) where component 1 (SVD₁) explains more data-variance than any other component, SVD₂ the second most, and so on (Figure 1B).”

3) The abstract repeats 8 times the word "hierarchy" or "hierarchical". Avoid such excessive repetitions.

We have edited the abstract to remove unnecessary repetitions. The abstract (lines 22-31) reads:

“Cellular phenotypes emerge from layers of molecular interactions: proteins interact to form complexes, pathways, and phenotypes. We show that hierarchical networks of protein interactions can be extracted from the statistical pattern of proteome variation as measured across thousands of bacteria and that these networks reflect the emergence of complex bacterial phenotypes. We validate our results through gene-set enrichment analysis and comparison to existing experimentally-derived databases. We demonstrate the biological utility of our approach by creating a model of motility in Pseudomonas aeruginosa and using it to identify a protein that affects pilus-mediated motility. We anticipate that our method, SCALES (Spectral Correlation Analysis of Layered Evolutionary Signals), will be useful for interrogating genotype-phenotype relationships in bacteria.”

4) The introduction was a bit short in giving credit to previous efforts in this area. Yes, the founding papers from the 90s are cited, but there have been quite a number of studies in the meantime, including the use of SVD, reviewed for example here: Nagy et al., NAR 2020, https://doi.org/10.1093/nar/gkz1241 or Moi et al., PLoS computational biology 2020, 16 (7), e1007553

We thank the reviewer for this point. We have revised the manuscript to acknowledge that this is an evolving field and have included additional relevant references including those cited by the reviewer. [Lines: 35-48]

“Biochemical and genetic studies have illustrated that complex behaviors emerge from layers of protein interactions: proteins interact to form complexes, complexes interact to form pathways, and pathways interact to create phenotypes (Papin et al., 2004; Ravasz 2009; Nurse 2008). Current strategies for identifying protein-protein interactions (PPIs) span both experiment and computation. Experimental methods are rapidly becoming more high-throughput and comprehensive (Rajagopala et al., 2014; Schoenrock et al., 2017; Hauser et al., 2014; Koo et al., 2017; Luck et al., 2020). Computational methods based on statistical patterns of co-occurrence or co-proximity of functionally related genes first appeared shortly after publication of whole genome sequences (Eisen, 1998; Pellegrini et al., 1999; Enrich et al., 1999; Valencia and Pazos, 2002). More recent efforts have advanced the state-of-the-art in computational methods by incorporating evolutionary models (phylogenomics), interaction models borrowed from statistical physics, or spectral methods borrowed from signal processing (Nagy et al., 2020; Franceschini et al., 2016; Moi et al., 2020; Croce et al., 2019; Cong et al., 2019; Green et al., 2021).”

5) The results on motility are really nice. We suggest placing them much earlier in the paper, and do the more technical stuff with random forest etc. later. It could come directly after Figure 1C has been explained.

We thank the reviewer for this suggestion which we believe has dramatically improved the presentation of our results. To this end, we have reconfigured the order of the manuscript and the figures. The result of a statistically derived hierarchy of PPIs describing bacterial motility is now Figure 2. Figure 3 is the experimental validation of our approach. Figure 4 describes the results of predicting PPIs using RF models. This reconfiguration of the paper serves not only to highlight the motility results earlier on, but also emphasize the main thrust of the study.

[Editors’ note: further revisions were suggested prior to acceptance, as described below.]

Reviewer #1 (Recommendations for the authors):

General Summary:

While the authors have made clearly visible efforts to improve the presentation of their manuscript, the major problem remains: while the results are very interesting, the presentation of the technical details is cumbersome, and reading the paper without massive reference to the huge number of supplementary figures is hardly possible. I think another round of simplification is unavoidable.

We appreciate the reviewer’s feedback on improving the presentation of our manuscript, specifically in regard to the need of referencing many supplemental figures while navigating main figures and text. In the resubmitted version, we made several changes to ensure that (i) the main figures reflected results as well as operational processes of how we arrived at the results and (ii) the supplemental figures were not critical for understanding key messages in the manuscript. Specific changes are listed below

1. We remade Figure 1 to only show that shallow modes of variance are enriched for phylogenetic information.

2. We made a new Figure 2 to describe our statistical workflow.

3. What used to be a supplemental figure for showing that deep spectral components are enriched for physical PPIs is now Figure 3A and Figure 3B. These results are grouped together with the finding that deep to shallow spectral components collectively illustrate a progression of biological scale from phylogenetic to functional information (Figure 3C).

4. Figure 4 describes the process of computing spectral depth.

5. What used to be a supplemental figure for describing how we create hierarchical graphs of protein interaction networks is now Figure 5.

Together, the incorporation of supplemental figures from the previous version into main figures has demonstrably changed the flow of the manuscript with respect to needing reference to supplemental materials.

I would like to make a number of more specific points:

1. The reading is impossible without the massive use of supplementary figures. To give one example (out of many), the singular vectors in U^OGG and V^OGG are used in methods but introduced only in Figure 1 Supp. 1. In addition, the left and right singular values are denoted equally as |n>, which is a bit confusing (even more since as mentioned, the matrices are not defined in the text). In general, the authors should revise the paper such that the supplement gives supplementary information, and the paper can be read without having ~50 pages of supplement in your hands.

We thank the reviewer for this helpful suggestion. We have reconfigured several of the figures as well as incorporated previous supplemental figures into main figures to address the reviewer’s comment and make our manuscript more accessible (see our response to ‘General Summary’ above). In addition, we have attempted to further simplify text to make transitions easier to follow. Specifically, we have introduced simpler transition to help the reader connect between section of the manuscript. Importantly, all the matrices, including the input data matrix and those resulting from SVD, are now described in the main text, please see the specific description below.

– In the section: ‘Global to ‘local’ patterns of bacterial covariation progressively reveal phylogeny, pathways, and protein complexes’, we have edited the first paragraph to read (lines 85-90):

“We analyzed the SVD spectrum for information regarding (i) phylogenetic information, (ii) indirect interactions between proteins reflecting biological pathways, and (iii) direct (physical) interactions between proteins reflecting protein complexes. The workflow for our analysis was as follows. SVD applied to D^OGG output three separate matrices: bacterial projections onto left-singular vectors (U^OGG), a set of singular values, and OGG projections onto right-singular vectors (V^OGG) (Figure 2A).”

2. The method heavily relies on subjective hyperparameters and thresholds: For the number of singular values considered, for the bin size in the MI calculation, for the size of the spectral window, for the used cutoffs of the spectral depth.

We agree with the reviewer’s assessment. As our workflow is mostly statistical, several parameters and thresholds needed to be instantiated to conduct our analysis. However, whenever possible, we derived these parameters in a data-driven manner or performed some sensitivity analysis to show the robustness of the chosen parameter. In addition, once these parameters were set, no additional parameter tuning – i.e. the same set of parameter was used for motility and non-motility systems as well analysis of the E. coli proteome and proteomes from organisms distantly related to E. coli. Regarding the reviewer’s specific concerns:

– ‘For the number of singular values considered’:

We considered the top 3000 singular values because singular values beyond this point were not significantly enriched for biological information compared to our random model. We have edited the text to reflect this point (line 116-117).

“Beyond component 3000, the MI shared between protein spectral correlations and PPIs rapidly converged to the estimation of background MI.”

– ‘for the bin size in the MI calculation’:

Estimating the information content from a sample is practically difficult because we do not have access to the complete underlying distribution. This creates a tradeoff between a high-resolution bin size, capturing all entries of the distribution, and a low resolution bin size ensuring that all bins have more than one entry. We selected the bin width of 0.25 because it seemed to provide a balance. While we have not performed a formal sensitivity analysis on this parameter choice, we point out the following: (1) we did not adjust the bin size on a case-by-case basis and (2) the quantitative value of the MI estimate is not relevant to our conclusions, but rather the relative distribution of MI across the SVD spectrum. It is therefore unlikely that the choice of bin size will have a significant impact on our main findings.

– ‘for the size of the spectral window’:

The choice for size of the spectral window was not arbitrary. Rather, we performed a comprehensive analysis to find an optimal point that balanced resolution and signal detection, as described in Figure 4—figure supplement 1A-D. Importantly, once we decided on this window size, no further adjustment was made to this parameter. We have edited the text to clarify this point (lines 134-137).

“Third, we removed spurious spectral correlations by developing a model of statistical significance. The model defined an optimal spectral window of 100 components for computing spectral correlations as well as a threshold for what constitutes ‘statistically significant’ spectral correlations (Figure 4—figure supplement 1, Materials and methods).”

– ‘for the used cutoffs of the spectral depth’:

The depicted cutoffs for spectral depth were chosen to reflect areas of the SVD spectrum we found to be enriched for different types of biological information: 50 for the center of the shallowest 100-component spectral window, 300 for a window enriched for indirect PPI information, and 1000 for a window enriched for direct PPI information. We have edited the text to clarify this point (lines 163-166).

“To depict the structure of spectral depths across all pairs of proteins, we thresholded spectral depth at three different levels: 50, 300, and 1000. These thresholds were chosen to reflect areas of the SVD spectrum found to be enriched for different types of biological information per Figure 3C.”

Together with the somewhat anecdotal results (concentration mostly on motility), this gives the impression that the biological system and parameters are hand selected to show nicely interpretable results.

In response to the reviewer’s point, we note a few important aspects:

First, our statement that biological information is spread across the SVD spectrum (Figure 3C) was based on a comprehensive interrogation of multiple different databases containing the same type of information: GO and STRING for indirect interactions, the PDB, ECOCYC and Coev+ for direct interactions. Our rationale behind using several databases was to ensure that our results were not specific to a single database or a single type of data.

Second, while we concentrated on motility to show that we could create a hierarchical protein interaction graph, we also presented several supplemental figures demonstrating that our results are robust across (i) query protein, (ii) organism, and (iii) specific pathway. In particular, Figure 6—figure supplement 4 illustrates that our approach defines a relevant hierarchical decomposition of amino acid metabolism in E. coli K12. Our motivation for pursuing these analyses was to ensure that our hierarchical networks were not a result of ‘overfitting’ to specifically directed motility in E. coli K12 using FliC as a query.

Third, we tested the predictive potential of our approach by conducting an experiment testing whether uncharacterized proteins could be characterized using our hierarchical models (Figure 7, Figure 7—figure supplement 1). These experiments were performed in Pseudomonas aeruginosa, an organism unrelated to E. coli K12, within the context of a different type of motility thereby highlighting the generality of our approach.

Finally, the last section of our paper addresses using spectral correlations to infer protein interactions across a diversity of sequenced bacteria. Using several types of analyses, we demonstrate that our approach for inferring interactions at different biological scales produces predictions that are superior to those of current methods. Our motivation behind performing this analysis was to enable interrogation of pathways and organisms that are not currently well studied. This motivation is emphasized in the first paragraph of the section ‘Using spectral correlations to predict proteome-wide functional and physical interaction networks’ (lines 272-274):

“Microbiome science has taught us that diverse bacteria affect human and environmental health. Therefore, there is a critical need to expand our knowledge of biology more broadly beyond the few well-studied model organisms.”

We would like to reemphasize that, while there are several parameters that had to be chosen, at no point in the manuscript did we adjust our parameters to optimize the results for a specific database, organism, or pathway. In addition, we deliberately challenged our methods by predicting results across diverse databases, organisms, and pathways to ensure that our parameter choices were robust and generalizable.

I sincerely hope this is not the case, but if the authors would, e.g., show the tree generated by changing spectral depth from largest to smallest values, the different levels of organisation could become more evident (in case well-separated levels exist).

We thank the reviewer for this suggestion. We find that changing spectral depth from largest to smallest thresholds reveals a continuum of organization. To make the above point clear, we have added a new supplemental figure showing spectral depths 225, 500, and 750 for directed motility in E. coli K12 (Figure 6—figure supplement 1).

3. In some cases, it is hard to understand if the results are significant. If one considers Figure 1E, even a uniform MI distribution would have a similar shape as the blue curves, since the cumulative would be linear, and represented with a log-scale of the spectral position.

We thank the reviewer for this insightful question. We agree that the cumulative distribution function for a uniform MI distribution might have a similar shape. However, we clarify that the curves in Figure 1E (now Figure 3C) are the cumulative ‘specific’ MI, that is the cumulative difference between the MI produced by the data and that produced by a randomized matrix (see Methods section titled ‘Calculation of MI cumulative distribution functions (cdfs) shown in Figure 3C'). The specific MI for a uniform distribution would be expected to be zero thereby giving a distinct CDF curve compared to those in Figure 3C. To further clarify the question of significance, we have created a new Figure 3 where panels A and B highlight the non-random nature of the MI between protein spectral correlations and whether two proteins physically interact. We have included text to clarify this point (lines 112-116):

“The top tens of components contained phylogenetic information, the top hundreds contained indirect PPI information, and the top thousands contained direct PPI information (Figure 3A). Even SVD components 2996 through 3000 harboring 0.025% data-variance contain non-random biological information reflecting direct PPIs (Figure 3B).”

4. In some places, results imposed by the analysis are presented as astonishing findings. The most evident case is the hierarchical structure when changing spectral depth. Since spectral depth is defined as the depth where correlations are for the first time non-significant, the edge set of the graphs at higher spectral depth is necessarily proper subsets of those at lower spectral depth, and thus connected components are proper subsets, too. If all statistically significant correlations in each spectral window would have been taken into account, edges between proteins might disappear at some depth, and reappear at a deeper one, making the network potentially non-hierarchical.

The reviewer brings up a very good point: our approach does not consider spectral correlations that are significant deeper than the spectral depth of correlation. Our approach to only consider the spectral depth of correlation was to enforce a hierarchy: our definition of spectral depth is predicated on the pair of proteins being significantly spectrally correlated at all windows shallower than the spectral depth. Our intention in making this choice was to see whether we could extract a hierarchy of interactions from the SVD spectrum through a defined process, not whether the SVD spectrum naturally provides a hierarchy of interactions. We highlight this point in two separate places in the text: lines (127-129) and lines (380-387):

“Given the results shown in Figure 3, we hypothesized that by relating deep and shallow SVD components, we could create a statistical representation of emergence—the integration of local scales of protein interactions into global scales reflecting collective biological functions.”

“Understanding the origins of complex biological functions requires defining hierarchical relationships describing how protein interactions integrate to create scales of biological organization. While the use of SVD is fundamental to our method, SVD itself does not define hierarchical relationships; SVD defines orthogonal components of variance ordered according to the amount of variance explained. Two results of our study were key for being able to use the SVD spectrum to produce hierarchical models. First, different components contain information regarding different biological scales. Second, the information in different components could be related by tracking the persistence of spectral correlations across components (‘spectral depth’).”

6. Heavy but somewhat random statements like "Understanding the molecular basis of a phenotype requires (i) defining interactions that create units of collective function at different biological scales and (ii) relating these scales to create a hierarchical model of emergent phenotype." should be avoided.

We thank the reviewer for this comment. We have edited the manuscript to remove several such statements, with particular care given transitions from one section to another. These changes can be viewed in the document comparing the previously submitted version with the current resubmission.

https://doi.org/10.7554/eLife.74104.sa2

Article and author information

Author details

Mark A Zaydman

Department of Pathology and Immunology, Washington University School of Medicine, St Louis, United States

Contribution
Conceptualization, Resources, Data curation, Formal analysis, Supervision, Validation, Investigation, Visualization, Methodology, Writing – original draft, Project administration, Writing – review and editing

Contributed equally with
Arjun S Raman

For correspondence
zaydmanm@wustl.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-4236-1459
Alexander S Little

Duchossois Family Institute, University of Chicago, Chicago, United States

Contribution
Investigation

Competing interests
No competing interests declared
Fidel Haro

Duchossois Family Institute, University of Chicago, Chicago, United States

Contribution
Investigation

Competing interests
No competing interests declared
Valeryia Aksianiuk

Duchossois Family Institute, University of Chicago, Chicago, United States

Contribution
Investigation

Competing interests
No competing interests declared
William J Buchser

Department of Genetics, Washington University School of Medicine, St Louis, United States

Contribution
Manuscript edits and guidance

Competing interests
No competing interests declared
Aaron DiAntonio

Department of Developmental Biology, Washington University School of Medicine, St Louis, United States

Contribution
Manuscript edits and guidance

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-7262-0968
Jeffrey I Gordon
1. Department of Pathology and Immunology, Washington University School of Medicine, St Louis, United States
2. The Edison Family Center for Genome Sciences and Systems Biology, Washington University School of Medicine, St Louis, United States
Contribution
Manuscript edits and guidance

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-8304-3548
Jeffrey Milbrandt

Department of Genetics, Washington University School of Medicine, St Louis, United States

Contribution
Manuscript edits and guidance

Competing interests
No competing interests declared
Arjun S Raman
1. Duchossois Family Institute, University of Chicago, Chicago, United States
2. Department of Pathology, University of Chicago, Chicago, Chicago, United States
3. Center for the Physics of Evolving Systems, University of Chicago, Chicago, Chicago, United States
Contribution
Conceptualization, Resources, Data curation, Formal analysis, Supervision, Funding acquisition, Validation, Investigation, Visualization, Methodology, Writing – original draft, Project administration, Writing – review and editing

Contributed equally with
Mark A Zaydman

For correspondence
araman@bsd.uchicago.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-0070-1953

Funding

No external funding was received for this work.

Acknowledgements

We thank Robert Y Chen, Adam Bailey, Nima Mosammaparast, and Jacqueline Payton for substantial discussion regarding this manuscript. We thank Rama Ranganathan for a critical reading of the manuscript as well as in-depth discussion. We thank Dinanath Sulakhe (Center for Research Informatics [CRI], University of Chicago) for assisting in producing the web application tools described in this manuscript. We thank Sam Light, Sampriti Mukherjee, and Eric Pamer for helpful discussions regarding experiments performed.

Senior Editor

Aleksandra M Walczak, CNRS LPENS, France

Reviewing Editor

Nir Ben-Tal, Tel Aviv University, Israel

Version history

Received: September 21, 2021
Preprint posted: September 28, 2021 (view preprint)
Accepted: August 17, 2022
Accepted Manuscript published: August 17, 2022 (version 1)
Version of Record published: August 30, 2022 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.