A biophysical threshold for biofilm formation

Abstract
Editor's evaluation
Introduction
Results
Discussion
Materials and methods
Appendix 1
Appendix 2
Data availability
References
Article and author information
Metrics

Abstract

Bacteria are ubiquitous in our daily lives, either as motile planktonic cells or as immobilized surface-attached biofilms. These different phenotypic states play key roles in agriculture, environment, industry, and medicine; hence, it is critically important to be able to predict the conditions under which bacteria transition from one state to the other. Unfortunately, these transitions depend on a dizzyingly complex array of factors that are determined by the intrinsic properties of the individual cells as well as those of their surrounding environments, and are thus challenging to describe. To address this issue, here, we develop a generally-applicable biophysical model of the interplay between motility-mediated dispersal and biofilm formation under positive quorum sensing control. Using this model, we establish a universal rule predicting how the onset and extent of biofilm formation depend collectively on cell concentration and motility, nutrient diffusion and consumption, chemotactic sensing, and autoinducer production. Our work thus provides a key step toward quantitatively predicting and controlling biofilm formation in diverse and complex settings.

Editor's evaluation

In this work, the authors develop a continuum description of biofilm formation from initially planktonic cells. The coupled partial differential equations that encode the dynamics of the cell populations, nutrients and autoinducers contain many parameters, but it is shown that only two dimensionless combinations of them are needed to understand the threshold for biofilm formation. This work should be of broad interest to a wide range of researchers in biophysics and cell biology.

https://doi.org/10.7554/eLife.76380.sa0

Introduction

Dating back to their discovery by van Leeuwenhoek over three centuries ago, it has been known that bacteria typically exist in one of two phenotypic states: either as motile, planktonic cells that self-propel using e.g., flagella or pili (“animalcules … moving among one another”; Van Leewenhoeck, 1677), or as immobilized, surface-attached biofilms (“little white matter … in the scurf of the teeth”; Leewenhoeck, 1684). These different states have critical functional implications for processes in agriculture, environment, industry, and medicine. For example, motility-mediated dispersal of planktonic cells enables populations to escape from harmful conditions and colonize new terrain (Adler, 1966a; Adler, 1966b; Saragosti et al., 2011; Fu et al., 2018; Cremer et al., 2019; Bhattacharjee et al., 2021)—underlying infection progression, drug delivery to hard-to-reach spots in the body, food spoilage, interactions with plant roots in agriculture, and bioremediation of environmental contaminants (Balzan et al., 2007; Chaban et al., 2015; Datta et al., 2016; Harman et al., 2012; Ribet and Cossart, 2015; Siitonen and Nurminen, 1992; Lux et al., 2001; O’Neil and Marquis, 2006; Gill and Penney, 1977; Shirai et al., 2017; Thornlow et al., 2015; Toley and Forbes, 2012; Dechesne et al., 2010; Souza et al., 2015; Turnbull et al., 2001; Watt et al., 2006; Babalola, 2010; Adadevoh et al., 2016; Adadevoh et al., 2018; Ford and Harvey, 2007; Wang et al., 2008; Reddy and Ford, 1996; Martínez-Calvo et al., 2021). In addition, the formation of immobilized biofilms can initiate antibiotic-resistant infections, foul biomedical devices and industrial equipment, or conversely, help sequester and remove contaminants in dirty water (Davey and O’toole, 2000; Hall-Stoodley et al., 2004; Mah et al., 2003; O’Toole and Stewart, 2005; Fux et al., 2005; Nicolella et al., 2000; Donlan and Costerton, 2002; Davies et al., 1998). Hence, extensive research has focused on understanding bacterial behavior in either the planktonic or biofilm state.

For example, studies of planktonic cells have provided important insights into bacterial motility—which can be either undirected (Berg, 2018; Berg, 2004; Bhattacharjee and Datta, 2019a; Bhattacharjee and Datta, 2019b) or directed in response to e.g., a chemical gradient via chemotaxis (Adler, 1966b; Adler, 1966a; Saragosti et al., 2011; Fu et al., 2018; Cremer et al., 2019; Bhattacharjee et al., 2021; Keller and Segel, 1971; Odell and Keller, 1976; Keller and Odell, 1975; Lauffenburger, 1991; Seyrich et al., 2019; Croze et al., 2011; Amchin et al., 2022). These processes are now known to be regulated not just by intrinsic cellular properties, such as swimming kinematics and the amplitude and frequency of cell body reorientations, but also by the properties of their environment, such as cellular concentration, chemical/nutrient conditions, and confinement by surrounding obstacles (Berg, 2018; Berg, 2004; Bhattacharjee and Datta, 2019a; Bhattacharjee and Datta, 2019b; Adler, 1966b; Adler, 1966a; Saragosti et al., 2011; Fu et al., 2018; Cremer et al., 2019; Bhattacharjee et al., 2021; Keller and Segel, 1971; Odell and Keller, 1976; Keller and Odell, 1975; Lauffenburger, 1991; Seyrich et al., 2019; Croze et al., 2011; Amchin et al., 2022). Thus, the manner in which planktonic bacteria disperse can strongly vary between different species and environmental conditions.

Similarly, studies of biofilms under defined laboratory conditions have also provided key insights—such as by revealing the pivotal role of intercellular chemical signaling in biofilm formation (Nadell et al., 2008; Bassler and Losick, 2006; Davey and O’toole, 2000; Hall-Stoodley et al., 2004). In this process, termed quorum sensing, individual cells produce, secrete, and sense freely diffusible autoinducer molecules, thereby enabling different bacteria to coordinate their behavior (Davies et al., 1998; Sakuragi and Kolter, 2007; Bassler and Losick, 2006; Miller and Bassler, 2001; Herzberg et al., 2006; Laganenka et al., 2018; McLean et al., 1997; Paul et al., 2009). For example, in many cases, quorum sensing positively controls biofilm formation (Herzberg et al., 2006; Laganenka et al., 2018; Davies et al., 1998; Sakuragi and Kolter, 2007; McLean et al., 1997; González Barrios et al., 2006; Yarwood et al., 2004; Koutsoudis et al., 2006; Waters and Bassler, 2005; Parsek and Greenberg, 2005; Jayaraman and Wood, 2008; Hentzer et al., 2003; Kirisits and Parsek, 2006): autoinducer accumulation above a threshold concentration upregulates the expression of genes involved in biofilm formation, ultimately driving a transition from the planktonic to the biofilm state (Nadell et al., 2008). Again, however, the cellular factors that control this transition, such as the autoinducer production rate, diffusivity, and threshold concentration, can strongly vary between different species and environmental conditions.

Because planktonic dispersal and biofilm formation both depend on a dizzyingly complex array of factors, these distinct processes are typically studied in isolation. Thus, while each is well understood on its own, quantitative prediction of the conditions under which a population of planktonic bacteria transitions to the biofilm state—or instead, continues to disperse away and remains in the planktonic state—remains challenging. Here, we address this challenge by developing a mathematical model that describes essential features of motility-mediated dispersal of planktonic cells and autoinducer-mediated biofilm formation together. Using numerical simulations of this model, we systematically examine the influence of cellular concentration, motility, and chemotactic sensing; nutrient availability, diffusion, and consumption; and autoinducer production, diffusion, and accumulation on biofilm formation. Guided by these results, we establish a potentially-universal biophysical threshold that unifies the influence of all these factors in predicting the onset and extent of biofilm formation across different species and environmental conditions. Our work therefore provides a theoretical foundation for the prediction and control of biofilm formation in diverse and complex settings, and yields new quantitative predictions to guide future experiments.

Results

Development of the governing equations

As an illustrative example, and to connect our model to recent experiments of bacterial dispersal (Bhattacharjee et al., 2021), we consider a rectilinear geometry with a starting inoculum of planktonic cells at a maximal concentration $b_{1, 0}$ and of width $x_{0}$ . In general, the continuum variable $b (x, t)$ describes the number concentration of bacteria, where $x$ is the position coordinate and $t$ is time, and the subscripts ${1, 2}$ represent planktonic or biofilm-associated cells, respectively. Following previous work (Lauffenburger, 1991; Keller and Segel, 1971; Adler, 1966a; Croze et al., 2011; Fu et al., 2018; Bhattacharjee et al., 2021), we consider a sole diffusible nutrient that also acts as the chemoattractant, with a number concentration represented by the continuum variable $c (x, t)$ with diffusivity $D_{c}$ . Initially, nutrient is replete throughout the system at a constant concentration $c_{0}$ . The bacteria then consume the nutrient at a rate $b_{1} κ_{1} g (c)$ , where $κ_{1}$ is the maximum consumption rate per cell and the Michaelis-Menten function $g (c) \equiv \frac{c}{c + c_{c h a r}}$ quantifies the nutrient dependence of consumption relative to the characteristic concentration $c_{c h a r}$ (Croze et al., 2011; Monod, 1949; Cremer et al., 2019; Woodward et al., 1995; Shehata and Marr, 1971; Schellenberg and Furlong, 1977; Cremer et al., 2016).

As time progresses, the bacteria thereby establish a local nutrient gradient that they respond to via chemotaxis (Figure 1A). In particular, planktonic cells disperse through two processes: undirected active diffusion with a constant diffusivity $D_{1}$ (Berg, 2018), and directed chemotaxis with a drift velocity ${\vec{v}}_{c} \equiv χ_{1} \nabla \log (\frac{1 + c / c_{-}}{1 + c / c_{+}})$ that quantifies the ability of the bacteria to sense and respond to the local nutrient gradient (Keller and Segel, 1970; Keller and Segel, 1971; Odell and Keller, 1976; Keller and Odell, 1975) with characteristic bounds $c_{-} a n d c_{+}$ (Cremer et al., 2019; Sourjik and Wingreen, 2012; Shimizu et al., 2010; Tu et al., 2008; Kalinin et al., 2009; Shoval et al., 2010; Lazova et al., 2011; Celani et al., 2011; Fu et al., 2018; Dufour et al., 2014; Yang et al., 2015; Cai et al., 2016; Chen and Jin, 2011) and a chemotactic coefficient $χ_{1}$ . The planktonic cells also proliferate at a rate $b γ_{1} g (c)$ , where $γ_{1}$ is the maximal proliferation rate per cell. Finally, as the planktonic bacteria consume nutrients, they produce and secrete a diffusible autoinducer, with a number concentration represented by $a (x, t)$ and with diffusivity $D_{a}$ , at a maximal rate $k_{1}$ per cell. Motivated by some previous work (Hense et al., 2012; Hense and Schuster, 2015; Kirisits et al., 2007; Bollinger et al., 2001; Duan and Surette, 2007; Mellbye and Schuster, 2014; De Kievit et al., 2001; Pérez-Osorio et al., 2010), we take this process (hereafter referred to as ‘production’ for brevity) to also be nutrient-dependent via the same Michaelis-Menten function $g (c)$ for the results presented in the main text, but we also consider the alternate case of ‘protected’ nutrient-independent production in the supplementary materials. Following previous work (Koerber et al., 2002; Ward et al., 2001; Ward et al., 2003), we also model natural degradation of autoinducer as a first-order process with a rate constant λ.

Figure 1 with 2 supplements see all

Download asset Open asset

Competition between motility-mediated dispersal and autoinducer-mediated biofilm formation.

(A) Schematic of chemotactic dispersal: planktonic bacteria (green) consume nutrient (purple) and establish a local gradient that they, in turn, direct their motion in response to. (B) Schematic of positive quorum sensing-controlled biofilm formation: accumulation of produced autoinducer (red) above a threshold concentration causes cells to transition to the biofilm state (blue). (C) Results of an example simulation of Equations 1–4 showing the dynamics of the nutrient, planktonic cells, autoinducer, and biofilm cells from top to bottom, quantified by the normalized concentrations $c / c_{0}$ , $b_{1} / b_{1, 0}$ , $a / a^{*}$ , $b_{2} / b_{1, 0}$ , respectively; $c_{0}$ , $b_{1, 0}$ , and $a^{*}$ represent the initial nutrient concentration, initial bacterial concentration, and autoinducer threshold for biofilm formation, respectively. The position coordinate is represented by the normalized position $x / x_{0}$ , where $x_{0}$ is the width of the initial cellular inoculum. Different shades indicate different time points as listed. The inoculum initially centered about the origin consumes nutrient (purple), establishing a gradient that drives outward dispersal by chemotaxis (outward moving green curves); the cells also produce autoinducer (red) concomitantly. At $t \approx 13 h$ , sufficient autoinducer has been produced to trigger biofilm formation at the origin; at even longer times ( $t ≳ 16 h$ ), nutrient depletion limits autoinducer production at this position. However, accumulation of autoinducer by the dispersing planktonic cells triggers partial biofilm formation at $x / x_{0} \approx 6$ as well. This competition between dispersal and biofilm formation leads to a final biofilm fraction of $f = 21 %$ at the final time of $t = 20 h$ . An animated form of this figure is shown in Video 1. The values of the simulation parameters are given in Supplementary file 2.

Figure 1—source data 1: https://cdn.elifesciences.org/articles/76380/elife-76380-fig1-data1-v2.xlsx
Download elife-76380-fig1-data1-v2.xlsx

As autoinducer is produced, it binds to receptors on the surfaces of the planktonic cells with a second-order rate constant $α$ , as established previously (Koerber et al., 2002; Ward et al., 2001; Ward et al., 2003). Motivated by experiments on diverse bacteria, including the prominent and well-studied species Escherichia coli, Pseudomonas putida, and Pseudomonas aeruginosa (Davies et al., 1998; Sakuragi and Kolter, 2007; Bassler and Losick, 2006; Miller and Bassler, 2001; Herzberg et al., 2006; Laganenka et al., 2018; McLean et al., 1997; Paul et al., 2009; González Barrios et al., 2006; Yarwood et al., 2004; Koutsoudis et al., 2006; Waters and Bassler, 2005; Parsek and Greenberg, 2005; Jayaraman and Wood, 2008; Hentzer et al., 2003; Kirisits and Parsek, 2006), we assume that planktonic cells transition to the biofilm state at a rate $τ^{- 1}$ when the local autoinducer concentration exceeds a threshold value $a^{*}$ (Figure 1B). Because our focus is on this transition, we assume that it is irreversible, and that cells in the biofilm lose motility. However, they still continue to consume nutrient, proliferate, and produce autoinducer with maximal rates $κ_{2}$ , $γ_{2}$ , and $k_{2}$ per cell, respectively; additional behaviors such as subsequent production of extracellular polymeric substances or transitioning back to the planktonic state can be incorporated as future extensions to this model.

Hence, while planktonic cells can disperse via active diffusion and chemotaxis, their dispersal is hindered—and biofilm formation is instead promoted—when autoinducer accumulates sufficiently, as schematized in Figure 1A–B. The central goal of this paper is to examine the processes underlying this competition between dispersal and biofilm formation. Our model is thus summarized as:

\begin{array}{ll} P l a n k t o n i c : \frac{\partial b_{1}}{\partial t} & = \underset{M o t i l i t y}{\underset{⏟}{D_{1} \nabla^{2} b_{1} - \nabla \cdot (b_{1} {\vec{v}}_{c})}} + \underset{P r o l i f e r a t i o n}{\underset{⏟}{b_{1} γ_{1} g (c)}} \\ - \underset{B i o f i l m f o r m a t i o n}{\underset{⏟}{b_{1} τ^{- 1} H (a - a^{*})}} \end{array}

B i o f i l m : \frac{\partial b_{2}}{\partial t} = \underset{P r o l i f e r a t i o n}{\underset{⏟}{b_{2} γ_{2} g (c)}} + \underset{B i o f i l m f o r m a t i o n}{\underset{⏟}{b_{1} τ^{- 1} H (a - a^{*})}}

N u t r i e n t : \frac{\partial c}{\partial t} = \underset{D i f f u s i o n}{\underset{⏟}{D_{c} \nabla^{2} c}} - \underset{C o n s u m p t i o n}{\underset{⏟}{(b_{1} κ_{1} + b_{2} κ_{2}) g (c)}}

\begin{array}{ll} A u t o i n d u c e r : \frac{\partial a}{\partial t} & = \underset{D i f f u s i o n}{\underset{⏟}{D_{a} \nabla^{2} a}} + \underset{P r o d u c t i o n}{\underset{⏟}{(b_{1} k_{1} + b_{2} k_{2}) g (c)}} \\ - \underset{L o s s}{\underset{⏟}{a (λ + α b_{1})}} \end{array}

where $ℋ$ is the Heaviside step function describing the transition from the planktonic to biofilm state. To explore the competition between motility-mediated dispersal and autoinducer-mediated biofilm formation, we then numerically solve this system of coupled equations using values of all parameters—which are either intrinsic descriptors of cellular physiology or are solely/additionally influenced by the local environment—that are derived from experiments (Supplementary file 1). Further details are provided in the Materials and methods. Additional simulations indicate that the results obtained are not appreciably influenced by variations in the exact nature of how our model treats the arrest in planktonic cell motility while transitioning to the biofilm state (Figure 1—figure supplement 1) or the initial inoculum shape (Figure 1—figure supplement 2).

Representative numerical simulations

The results of a prototypical example are shown in Figure 1C and Video 1. Consumption by the planktonic cells (green curves) rapidly establishes a steep nutrient gradient (purple) at the leading edge of the inoculum. This gradient forces the planktonic cells to then move outward via chemotaxis. In particular, they self-organize into a coherent front that expands from the initial inoculum and continually propagates, sustained by continued consumption of the surrounding nutrient—consistent with the findings of previous studies of planktonic bacteria (Bhattacharjee et al., 2021). In this case, however, the cells also concomitantly produce autoinducer that accumulates into a growing plume (red). In some locations, the autoinducer eventually exceeds the threshold $a^{*}$ , thus driving the formation of an immobilized biofilm (blue). Hence, at long times, $f = 21 %$ of the overall population is biofilm-associated, while the remaining $1 - f = 79 %$ continues to disperse in the planktonic state.

Video 1

Download asset

posterframe for video — Animated form of Figure 1C: Results of an example simulation of Equations 1–4 showing the dynamics of the nutrient, planktonic cells, autoinducer, and biofilm cells from top to bottom, quantified by the normalized concentrations $c / c_{0}$ , $b_{1} / b_{1, 0}$ , $a / a^{*}$ , and $b_{2} / b_{1, 0}$ , respectively; $c_{0}$ , $b_{1, 0}$ , and $a^{*}$ represent the initial nutrient concentration, initial bacterial concentration, and autoinducer threshold for biofilm formation, respectively.

The position coordinate is represented by the normalized position $x / x_{0}$ , where $x_{0}$ is the width of the initial cellular inoculum. The inoculum initially centered about the origin consumes nutrient (purple), establishing a gradient that drives outward dispersal by chemotaxis (outward moving green curves); the cells also produce autoinducer (red) concomitantly. At $t \approx 13 h$ , sufficient autoinducer has been produced to trigger biofilm formation at the origin; at even longer times ( $t ≳ 16 h$ ), nutrient depletion limits autoinducer production at this position. However, accumulation of autoinducer by the dispersing planktonic cells triggers partial biofilm formation at $x / x_{0} \approx 4$ as well. This competition between dispersal and biofilm formation leads to a final biofilm fraction of $f = 21 %$ at the final time of $t = 20 h$ . The values of the simulation parameters are given in Supplementary file 2. The video displays the profiles every $30 m i n$ , to retain a manageable file size; however, the temporal step size in the actual simulations is $0.1 s$ .

Because the processes underlying motility-mediated dispersal and autoinducer-mediated biofilm formation are highly species- and environment-dependent, the values of the parameters in Equations 1–4 can span broad ranges—giving rise to different emergent behaviors under different conditions. Our simulations provide a way to examine how these behaviors depend on cellular concentration and motility, quantified by ${b_{1, 0}, D_{1}, χ_{1}, c_{-}, c_{+}}$ , nutrient availability and consumption, quantified by ${D_{c}, c_{0}, κ_{1}, κ_{2}, c_{char}}$ , cellular proliferation, quantified by ${γ_{1}, γ_{2}}$ , and autoinducer production, availability, and sensing, quantified by ${D_{a}, k_{1}, k_{2}, λ, α, τ, a^{*}}$ . For example, implementing the same simulation as in Figure 1C, but for cells with faster nutrient consumption, yields a population that completely disperses in the planktonic state (the fraction of the population in the biofilm state at the final time of $t = 20 h$ is $f = 0 %$ , as shown in Figure 2 and Video 2). Conversely, when cells consume nutrient slower, a larger fraction of the population forms an immobilized biofilm ( $f = 52 %$ , Figure 2—figure supplement 1 and Video 3).

Figure 2 with 1 supplement see all

Download asset Open asset

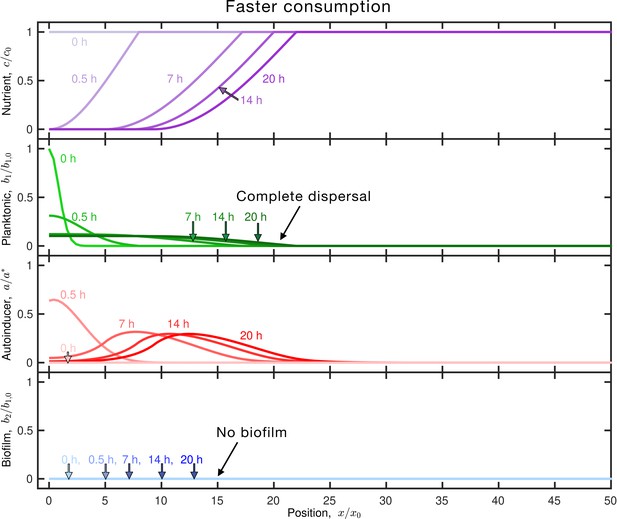
Faster nutrient consumption limits autoinducer production, leading to complete dispersal.

Retion as in Figure 1C, but for planktonic cells with faster nutrient consumption (larger $κ_{1}$ ). Panels and colors show the same quantities as in Figure 1C. The inoculum initially centered about the origin consumes nutrient (purple), establishing a gradient that drives outward dispersal by chemotaxis (outward moving green curves); the cells also produce autoinducer (red) concomitantly. However, nutrient is depleted at this position more rapidly, limiting autoinducer production; as a result, the population continues to disperse in the planktonic state and the final biofilm fraction is $f = 0 %$ . An animated form of this figure is shown in Video 2. The values of the simulation parameters are given in Supplementary file 2.

Figure 2—source data 1: https://cdn.elifesciences.org/articles/76380/elife-76380-fig2-data1-v2.xlsx
Download elife-76380-fig2-data1-v2.xlsx

Video 2

Download asset

Video 3

Download asset

Given that the competition between motility-mediated dispersal and autoinducer-mediated biofilm formation depends sensitively on such a bewildering array of cellular and environmental factors, we ask whether these dependencies can be captured by simple, generalizable, biophysical rules. Nondimensionalization of Equations 1–4 yields characteristic quantities and dimensionless groups that can parameterize these dependencies, as detailed in Appendix 1; however, given the large number of such groups, we seek an even simpler representation of the underlying processes that could unify the influence of all these different factors. To do so, we examine the fundamental processes underlying biofilm formation in our model.

Availability of nutrient for autoinducer production

When autoinducer production is nutrient-dependent, we expect that a necessary condition for biofilm formation is that enough nutrient is available for sufficient autoinducer to be produced to eventually exceed the threshold $a^{*}$ . To quantify this condition, we estimate two time scales: $τ_{d}$ , the time taken by the population of planktonic cells to deplete all the available nutrient locally, and $τ_{a}$ , the time at which produced autoinducer reaches the threshold for biofilm formation. While $τ_{d}$ and $τ_{a}$ can be directly obtained in each simulation, we seek a more generally-applicable analytical expression for both, solely using parameters that act as inputs to the model. In particular, for simplicity, we consider nutrient consumption and autoinducer production, both occurring at their maximal rates $κ_{1}$ and $k_{1}$ , respectively, by an exponentially-growing population of planktonic cells that are uniformly distributed in a well-mixed and fixed domain. Integrating Equations 3 and 4 then yields (Appendix 2)

τ_{d} = γ_{1}^{- 1} \ln (1 + {\tilde{β}}_{1, 0})

τ_{a} = γ_{1}^{- 1} \ln [1 - {\tilde{ζ}}_{1, 0}^{- 1} \ln (1 - \tilde{η})] .

Three key dimensionless quantities, denoted by the tilde $(\tilde{})$ notation, emerge from this calculation. The first, ${\tilde{β}}_{1, 0} \equiv γ_{1} / (b_{1, 0} κ_{1} / c_{0})$ , describes the yield of new cells produced as the population consumes nutrient—quantified by the rates of cellular proliferation and nutrient consumption, $γ_{1}$ and $b_{1, 0} κ_{1} / c_{0}$ , respectively (Amchin et al., 2022). The second, $\tilde{η} \equiv α a^{*} / k_{1}$ , describes the competition between autoinducer loss and production, quantified by their respective rates $α a^{*}$ and $k_{1}$ , at the single-cell scale. The third, ${\tilde{ζ}}_{1, 0} \equiv α b_{0} / γ_{1}$ , describes the loss of autoinducer due to cell-surface binding as the population continues to grow, quantified by the population-scale rates of autoinducer loss and cellular proliferation, $α b_{0}$ and $γ_{1}$ , respectively; for simplicity, this quantity neglects natural degradation of autoinducer, given that the degradation rate is relatively small, with $λ ≪ α b_{0}$ .

The ratio between Equations 5 and 6 then defines a nutrient availability parameter, $\tilde{D} \equiv τ_{d} / τ_{a}$ . When $\tilde{D}$ is large, produced autoinducer rapidly reaches the threshold for biofilm formation before the available nutrient is depleted; by contrast, when $\tilde{D}$ is small, nutrient depletion limits autoinducer production. Hence, we hypothesize that $\tilde{D} ≳ {\tilde{D}}^{*}$ specifies a necessary condition for biofilm formation, where ${\tilde{D}}^{*}$ is a threshold value of order unity. The simulations shown in Figures 1C and 2 and Figure 2—figure supplement 1 enable us to directly test this hypothesis. Consistent with our expectation, the simulation in Figure 1C is characterized by $\tilde{D} = 0.33$ , near the expected threshold for biofilm formation; as a result, $f = 21 %$ . When consumption is faster as in Figure 2 ( $\tilde{D} = 0.033$ ), the available nutrient is rapidly depleted; thus, cells disperse away before sufficient autoinducer is produced to initiate biofilm formation, and $f = 0 %$ . Conversely, when nutrient consumption is slow as in Figure 2—figure supplement 1 ( $\tilde{D} = 3.1$ ), nutrient continues to be available for autoinducer production, eventually driving biofilm formation, with a larger fraction $f = 52 %$ .

Taken together, these results support our hypothesis that $\tilde{D} ≳ {\tilde{D}}^{*} \sim 1$ is a necessary condition for biofilm formation. It is not, however, a sufficient condition: repeating the simulation of Figure 1C but for faster-moving cells yields a population that rapidly disperses without forming a biofilm at all ( $f = 0 %$ , Figure 3A and Video 4)—despite having the same value of $\tilde{D} = 0.33$ . Thus, our mathematical description of the conditions that determine biofilm formation is, as yet, incomplete.

Figure 3 with 1 supplement see all

Download asset Open asset

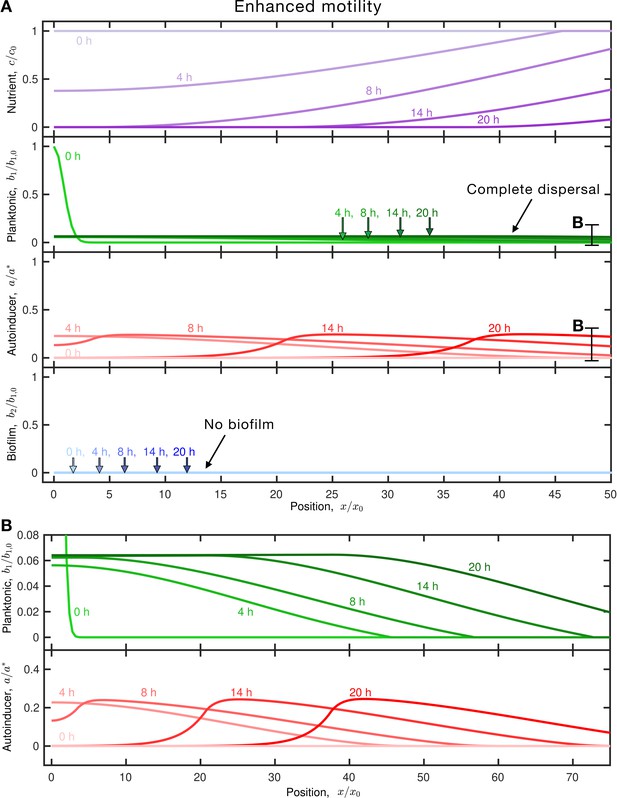
Enhanced motility enables cells to disperse before sufficient autoinducer accumulates, leading to complete dispersal.

(A) Results of the same simulation as in Figure 1C, but for faster-moving planktonic cells (larger $D_{1}$ and $χ_{1}$ ). Panels and colors show the same quantities as in Figure 1C. The inoculum initially centered about the origin consumes nutrient (purple), establishing a gradient that drives outward dispersal by chemotaxis (outward moving green curves); the cells also produce autoinducer (red) concomitantly. More rapid dispersal enables the planktonic cells to ‘outrun’ the growing autoinducer plume, as shown by the extended and magnified view in (B). As a result, the population continues to disperse in the planktonic state and the final biofilm fraction is $f = 0 %$ . An animated form of this figure is shown in Video 4. The values of the simulation parameters are given in Supplementary file 2.

Figure 3—source data 1: https://cdn.elifesciences.org/articles/76380/elife-76380-fig3-data1-v2.xlsx
Download elife-76380-fig3-data1-v2.xlsx

Video 4

Download asset

Competition between motility-mediated dispersal and autoinducer accumulation

The results shown in Figure 3 indicate that the ability of planktonic bacteria to move, which is not incorporated in the nutrient consumption parameter $\tilde{D}$ , also plays a key role in regulating whether a biofilm forms. Indeed, close inspection of Figure 3A hints at another necessary condition for biofilm formation: as shown by the magnified view in Figure 3B (e.g., at $t = 4 h$ ), the leading edge of the dispersing planktonic cells extends beyond the plume of produced autoinducer. Therefore, we expect that even when sufficient nutrient is available for autoinducer production ( $\tilde{D} ≳ {\tilde{D}}^{*} \sim 1$ ), autoinducer production must be rapid enough to reach the threshold for biofilm formation before cells have dispersed away. To quantify this condition, we estimate the the time $τ_{c}$ at which the motile planktonic cells begin to ‘outrun’ the growing autoinducer plume. Specifically, we quantify the dynamics of the leading edge positions of the chemotactic front of planktonic cells and the autoinducer plume, $x_{1, edge} (t)$ and $x_{a, edge} (t)$ , respectively. The front position $x_{1, edge} (t)$ is known to depend on cellular motility, nutrient diffusion, and nutrient consumption in a non-trivial manner (Berg, 2004; Cremer et al., 2019; Fu et al., 2018; Amchin et al., 2022), and we are not aware of a way to compute this quantity a priori from input parameters; instead, we extract this sole quantity from each simulation by identifying the largest value of $x$ at which $b_{1} \geq 10^{- 4} b_{1, 0}$ . While the plume position $x_{a, edge} (t)$ can also be directly obtained in each simulation, we again develop a more generally applicable analytical expression by assuming that the autoinducer continually diffuses from the initial inoculum: $x_{a, edge} (t) = x_{0} + \sqrt{2 D_{a} t}$ . Then, $τ_{c}$ can be directly determined as the time at which $x_{1, edge} (t)$ begins to exceed $x_{a, edge} (t)$ .

The ratio between $τ_{c}$ thereby determined and $τ_{a}$ , the time required for produced autoinducer to reach the threshold for biofilm formation (Equation 6), then defines a cellular dispersal parameter, $\tilde{J} \equiv τ_{c} / τ_{a}$ . When $\tilde{J}$ is large, autoinducer accumulation is sufficiently rapid to drive biofilm formation; by contrast, when $\tilde{J}$ is small, the planktonic cells rapidly disperse without forming a biofilm. Hence, we hypothesize that $\tilde{J} ≳ {\tilde{J}}^{*}$ specifies another necessary condition for biofilm formation, where ${\tilde{J}}^{*}$ is, again, a threshold value of order unity. The simulations shown in Figures 1C and 3A enable us to directly test this hypothesis. Consistent with our expectation, the simulations in Figure 1C and Figure 2—figure supplement 1 are characterized by $\tilde{J} = 1.6$ , near the expected threshold for biofilm formation; as a result, $f > 0$ in both cases. Furthermore, implementing the same simulation as Figure 1C (with the same $\tilde{D} = 0.33$ ) but for slower-moving cells, characterized by a larger $\tilde{J} = 120$ , yields a population that forms an even larger biofilm fraction $f = 82 %$ (Figure 3—figure supplement 1 and Video 5). Conversely, when cellular dispersal is faster as in Figure 3, characterized by a smaller $\tilde{J} = 0.1$ , the cells disperse away before sufficient autoinducer is produced to initiate biofilm formation, and $f = 0 %$ . Taken together, these results support our hypothesis that $\tilde{J} ≳ {\tilde{J}}^{*} \sim 1$ is another necessary condition for biofilm formation.

Video 5

Download asset

A universal biophysical threshold for biofilm formation

Thus far, we have shown that the two conditions $\tilde{D} ≳ {\tilde{D}}^{*}$ and $\tilde{J} ≳ {\tilde{J}}^{*}$ are both necessary for biofilm formation. Is the combination of both sufficient to fully specify the conditions required for biofilm formation? To test this possibility, we implement 10,983 numerical simulations of Equations 1–4 exploring the full physiological ranges of the input parameters that describe cellular, nutrient, and autoinducer properties for diverse bacterial species/strains and environmental conditions (Supplementary file 1). For each simulation, we compute $\tilde{D}$ , $\tilde{J}$ , and $f$ . Remarkably, despite the extensive variability in the values of the underlying parameters, all the results cluster between two states parameterized by $\tilde{D}$ and $\tilde{J}$ , as shown in Figure 4A: motility-mediated dispersal without biofilm formation ( $f = 0 %$ , green points) when either $\tilde{D} < {\tilde{D}}^{*}$ or $\tilde{J} < {\tilde{J}}^{*}$ , and biofilm formation without dispersal ( $f = 100 %$ , blue points) when both $\tilde{D} > {\tilde{D}}^{*}$ and $\tilde{J} > {\tilde{J}}^{*}$ . Many different combinations of the input parameters yield the same $(\tilde{D}$ , $\tilde{J})$ ; yet, no matter the input values of these parameters, which vary over broad ranges for different cells and environmental conditions, $(\tilde{D}$ , $\tilde{J})$ uniquely specify the resulting biofilm fraction $f$ for all points, as shown in Figure 4B–C—indicating that these two dimensionless parameters reasonably encompass all the factors determining biofilm formation within our model. We observe some exceptions at the boundary between these two states, likely because the simplifying assumptions underlying the derivation of the $\tilde{D}$ and $\tilde{J}$ parameters begin to break down. Nevertheless, the boundary between both states, summarized by the relation ${\tilde{D}}^{*} / \tilde{D} + {\tilde{J}}^{*} / \tilde{J} \sim 1$ with ${\tilde{D}}^{*}$ and ${\tilde{J}}^{*}$ both $\sim 1$ (black curve), thus specifies a universal biophysical threshold for biofilm formation.

Figure 4 with 2 supplements see all

Download asset Open asset

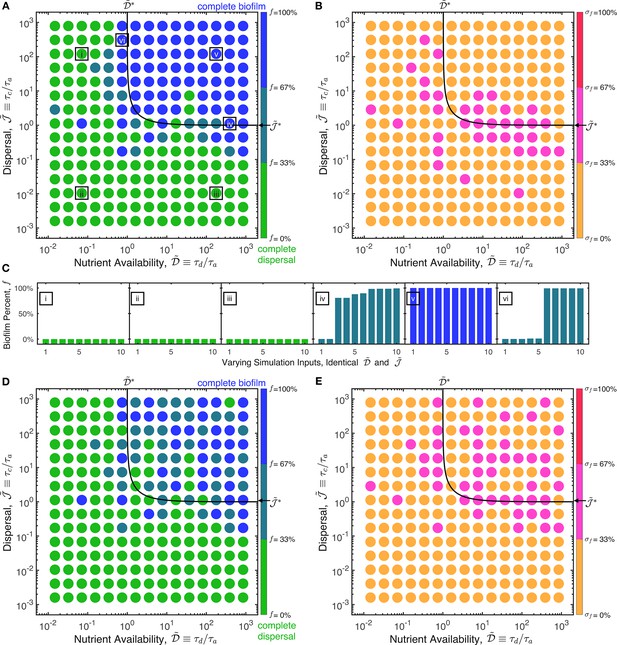
The two states of complete dispersal by planktonic cells (green) and complete formation of a biofilm (blue) can be universally described by three dimensionless parameters.

(A) State diagram showing the fraction of biofilm formed, $f$ , at the final time ( $t = 20 h$ ) for different values of the nutrient availability and cellular dispersal parameters, $\tilde{D}$ and $\tilde{J}$ , respectively. The state diagram summarizes the results of 10,983 simulations of Equations 1–4 exploring the full range of parameter values describing different bacterial species/strains and different environmental conditions (Supplementary file 1). Each point represents the mean value of $f$ obtained from multiple simulations with different parameter values, but with similar $\tilde{D}$ and $\tilde{J}$ (identical within each bin defined by the spacing between points). (B) represents the same data, but each point represents the standard deviation of the values of $f$ obtained from the same simulations. Despite the vastly differing conditions explored in each simulation, they cluster into the two states of planktonic dispersal (green) and biofilm formation (blue) when parameterized by $\tilde{D}$ and $\tilde{J}$ . The boundary between the two states can be described by the relation ${\tilde{D}}^{*} / \tilde{D} + {\tilde{J}}^{*} / \tilde{J} \sim 1$ , as shown by the black line; this relation combines the transition between the two states that occurs at both ${\tilde{D}}^{*} \sim 1$ and ${\tilde{J}}^{*} \sim 1$ . Away from this boundary, all simulations for the same $\tilde{D}$ and $\tilde{J}$ collapse to have the same biofilm fraction $f$ , as shown by the points in (B) and examples (i)–(iii) and (v) in (C)—confirming the universality of our parameterization. Near the boundary, we observe some slight differences between simulations, as shown in (B) and examples (iv) and (vi) in (C). The values of the simulation parameters for the examples in (C) are given in Source Data file 1. The data in (A–C) correspond to a fixed value of the third dimensionless parameter $\tilde{S} = 50$ , which describes the case of biofilm cells that produce autoinducer rapidly; repeating these simulations for the opposite case of slow autoinducer production by biofilm cells ( $\tilde{S} = 1 / 50$ ) yields the state diagram shown in (D), but for 14,351 simulation runs; again, (E) shows the standard deviation of the corresponding values of $f$ . As shown by (D–E), while the transition between the two states (black line) is unaffected by the change in $\tilde{S}$ , the transition to complete biofilm formation is more gradual. Together, the three parameters $\tilde{D}$ , $\tilde{J}$ , and $\tilde{S}$ provide a full description of the onset and extent of biofilm formation across vastly different conditions.

Figure 4—source data 1: https://cdn.elifesciences.org/articles/76380/elife-76380-fig4-data1-v2.xlsx
Download elife-76380-fig4-data1-v2.xlsx
Figure 4—source data 2: https://cdn.elifesciences.org/articles/76380/elife-76380-fig4-data2-v2.xlsx
Download elife-76380-fig4-data2-v2.xlsx
Figure 4—source data 3: https://cdn.elifesciences.org/articles/76380/elife-76380-fig4-data3-v2.xlsx
Download elife-76380-fig4-data3-v2.xlsx

Discussion

The transition from the planktonic to biofilm state is known to depend on a large array of factors that describe cellular concentration, motility, and proliferation; nutrient availability and consumption; and autoinducer production, availability, and sensing—all of which can vary considerably for different strains/species of bacteria and environmental conditions. Therefore, quantitative prediction of the onset of biofilm formation is challenging. The biophysical model presented here provides a key step toward addressing this challenge. In particular, for the illustrative case we consider—in which cells can either disperse through active motility, retaining them in the planktonic state, or form an immobilized biofilm when exposed to sufficient autoinducer—we have shown that the onset of biofilm formation is uniquely specified by a biophysical threshold set by the two dimensionless parameters $\tilde{D}$ (quantifying nutrient availability) and $\tilde{J}$ (quantifying bacterial dispersal). Importantly, within the formulation of our model, this threshold is universal: many different combinations of cellular and environmental factors are described by the same $(\tilde{D}, \tilde{J})$ , and thus, yield the same onset of biofilm formation. Therefore, given a bacterial strain and set of environmental conditions, extensions of our model could help provide a way to predict whether a biofilm will form a priori. Indeed, because the factors that define $\tilde{D}$ and $\tilde{J}$ can be directly measured, our work now provides quantitative principles and predictions (as summarized in Figure 4) to guide future experiments.

For generality, our model also incorporates proliferation, nutrient consumption, and autoinducer production by cells after they have transitioned to the biofilm state. Hence, within our model, biofilm-produced autoinducer could also drive surrounding planktonic cells to transition to the biofilm state. In this case, we expect that the long-time fraction of the population in the biofilm state, $f$ , will also depend on nutrient depletion and autoinducer production by the growing biofilm. Indeed, performing a similar calculation as that underlying the nutrient availability parameter, $\tilde{D}$ , yields a third dimensionless parameter, $\tilde{S} \equiv τ_{d, 2} / τ_{a, 2}$ ; here, $τ_{d, 2}$ and $τ_{a, 2}$ describe the times at which biofilm cells have depleted all the available nutrient and produced enough autoinducer to reach the threshold for biofilm formation, respectively (Appendix 2). Thus, we hypothesize that, while the onset of biofilm formation is specified by $(\tilde{D}, \tilde{J})$ , the final extent of biofilm that has formed will also be described by $\tilde{S}$ . The results shown in Figures 1—4 have a fixed $\tilde{S} = 50$ , which describes the case of a biofilm that produces autoinducer rapidly; repeating these simulations for the opposite case of slow autoinducer production by biofilm cells, with $\tilde{S} = 1 / 50$ , yields the state diagram shown in Figure 4D. In agreement with our hypothesis, while the transition to the biofilm state (black line) is not appreciably altered by the change in $\tilde{S}$ , the transition to complete biofilm formation ( $f = 1$ ) is more gradual in this case (compare Figure 4A,B,D,E). Moreover, we note that our analysis thus far has focused on the case in which autoinducer production is nutrient-dependent; however, this process may sometimes be nutrient-independent (Narla et al., 2021). In this case, we expect that our overall analysis still applies, but with the onset of biofilm formation specified by only the dispersal parameter $\tilde{J}$ —as confirmed in Figure 4—figure supplement 1.

Possible extensions of our work

The transition from the planktonic to biofilm state is highly complex and, in many cases, has features that are unique to different species of bacteria. Nevertheless, our model provides a minimal description that can capture many of the essential features of biofilm formation more generally—thereby providing a foundation for future extensions of our work, some of which are described below.

For simplicity, our model considers only one spatial dimension; however, fascinating new effects may arise in higher-dimensional implementations of our model. For example, in our prior work modeling the collective migration of planktonic bacteria in the absence of quorum sensing-mediated biofilm formation, we found that variations in the shape of the cellular front orthogonal to the main propagation direction ‘smooth out’ over time (Alert et al., 2022; Bhattacharjee et al., 2022). In particular, cells at outward-bulging parts of the front are exposed to more nutrient, which diminishes their ability to respond to the nutrient gradient via chemotaxis and thus slows them down. As a result, the migrating front eventually smooths to a flat shape whose subsequent dynamics can then be described using just one spatial dimension, just as in our treatment here. However, we expect that this behavior could be altered in interesting new ways when the cells can additionally produce and sense autoinducer and thereby transition to the biofilm state, as is the case here. In this case, we speculate that because cells at outward-bulging parts of the front are exposed to more nutrients and have a weaker chemotactic response, autoinducer production and accumulation will be more rapid relative to cellular dispersal. That is, at these parts of the front, $τ_{a}$ and $τ_{c}$ will be shorter and longer, respectively, causing the dispersal parameter $\tilde{J}$ to be larger locally. Thus, our model would predict biofilm formation to occur first at these parts of the front, potentially also influencing subsequent dispersal and biofilm formation at other locations along the front. Therefore, while our conclusions here could be the same locally at different parts of the front, the global behavior of the population could be different—potentially giving rise to e.g., spatially-heterogeneous biofilm formation.
As an illustrative example, our model considers the case in which cells produce a single autoinducer; however, some quorum sensing systems utilize multiple autoinducers (Miller and Bassler, 2001; Miller et al., 2002; Pesci et al., 1997), which could be described using additional field variables and equations similar to Equation 4. Moreover, while we take the nutrient to be the sole chemoattractant, in some cases, autoinducers can also act as chemoattractants (Laganenka et al., 2016), which could also be described in our framework by e.g., introducing autoinducer-dependent chemotaxis in the drift velocity in Equation 1.
Our model considers positive quorum sensing control in which planktonic cells transition to the biofilm state in a step-like fashion when the local autoinducer concentration exceeds a threshold value. That is, when planktonic cells encounter sufficiently concentrated autoinducer, the diffusivity and chemotactic coefficient transition in a step-like fashion from the constant values $D_{1}$ and $χ_{1}$ , respectively, to zero after the time duration $τ$ , for simplicity. In real systems, the change in cellular motility may not be as temporally abrupt. Future work could address a more gradual loss of motility in our theoretical framework by, for example, considering a cellular diffusivity and chemotactic coefficient that gradually transition from their planktonic values to zero over a non-zero time scale. Given that the same cells would be transitioning from the motile planktonic to immotile biofilm state—but in this case with the introduction of a time-varying diffusivity and chemotactic coefficient—we expect that the long-time biofilm fraction $f$ will be similar, and only the spatial profile of the biofilm population may be altered. Hence, we expect that our main findings summarized in Figure 4 will be unaffected by such a change. Indeed, performing the same representative simulation shown in Figure 1C, but with both motility parameters $D_{1}$ and $χ_{1}$ smoothly transitioning to zero in time, shows nearly identical results (Figure 1—figure supplement 1)—confirming our expectation that the temporal nature of the arrest in motility does not appreciably influence our model results and conclusions.
While we take the transition to the biofilm state as being irreversible, this is often not the case (Barraud et al., 2006; Kaplan, 2010; Abdel-Aziz, 2014). Longer-time transitions back to the planktonic state could be described using additional terms similar to the last terms of Equations 1; 2, but with the opposite sign. Similar modifications could be made to describe other species of bacteria (e.g., Vibrio cholerae) that utilize the opposite case of negative quorum sensing control, in which biofilm cells instead transition to the planktonic state when the autoinducer accumulates above a threshold value (Hammer and Bassler, 2003; Bridges and Bassler, 2019).
Biofilms are often formed by multiple different microbial species, whereas our model describes biofilm formation by a single species, for simplicity. Nevertheless, we expect that our theoretical framework can be extended by following reasoning similar to that described in this paper, but with the introduction of additional equations and variables in the governing Equations 1–4 to describe the distinct cell and chemical types, as appropriate. For example, if the different species i consume and respond to distinct nutrients $c_{i}$ , and secrete and respond to distinct autoinducers $a_{i}$ , each species could be described in isolation using our same governing Equations 1–4, but now extended to incorporate the distinct variables $c_{i}$ , $a_{i}$ , $b_{1, i}$ , and $b_{2, i}$ . Then, directly following our approach, each species would be described by its own dimensionless parameters ${\tilde{D}}_{i}$ and ${\tilde{J}}_{i}$ , with ${\tilde{D}}^{*} / {\tilde{D}}_{i} + {\tilde{J}}^{*} / {\tilde{J}}_{i} \sim 1$ again specifying the threshold for biofilm formation for each. We hypothesize that the composition of the final two-species biofilm community would then be given by the combination of each single-species biofilm. Alternatively, in the case that the different species consume and respond to the same nutrient $c$ , and secrete and respond to the same autoinducer $a$ , our Equations 1–4 could again be extended to consider the cellular parameters specific to each species i. In this approach, however, biofilm formation by each of the species cannot be described in isolation, because they are coupled through the nutrient and autoinducer dynamics. Instead, the calculations of the characteristic time scales $τ_{d}$ , $τ_{a}$ , and $τ_{c}$ would need to be extended, following our approach, to now reflect contributions from all the different species. We hypothesize that the overall multi-species community would then be described by one set of governing dimensionless parameters $(\tilde{D}, \tilde{J})$ , and ${\tilde{D}}^{*} / \tilde{D} + {\tilde{J}}^{*} / \tilde{J} \sim 1$ would again specify a universal biophysical threshold for the onset of biofilm formation for the overall community—but the composition of the final multi-species biofilm that results above this threshold may not be uniquely specified by $(\tilde{D}, \tilde{J})$ .
Biofilm formation may be regulated by other, non-quorum sensing-based, processes not considered in our model. For example, the intracellular accumulation of secondary signaling molecules such as cyclic di-GMP can also regulate biofilm formation (Valentini and Filloux, 2016; Simm et al., 2004; Jenal et al., 2017; Römling et al., 2013; Hengge, 2009; Krasteva et al., 2010; Baraquet and Harwood, 2013; Trampari et al., 2015; Davis et al., 2013; Boehm et al., 2010; Russell et al., 2013). In some cases, this process may be controlled by quorum sensing (Waters et al., 2008) and thus could be described by our model, while in others, it is controlled by other cues such as e.g., contact with surfaces, which would need to additionally be incorporated into our theoretical framework.
Finally, we note that our model is deterministic—describing the cellular processes of motility, nutrient consumption, proliferation, and autoinducer production, availability, and sensing using the parameters ${D_{1}, χ_{1}, c_{-}, c_{+}, κ_{1}, κ_{2}, c_{char}, γ_{1}, γ_{2}, k_{1}, k_{2}, α, τ, a^{*}}$ , respectively. Each of these is taken to be single-valued in each of our simulations. However, these parameters can have a distribution of values arising from e.g., inherent cell-to-cell variability. Because these values define the governing $\tilde{D}$ and $\tilde{J}$ that specify the threshold for biofilm formation in our model, we expect that variability in the parameter values would broaden the planktonic-to-biofilm transition predicted by our model. That is, we expect the transition specified by the black curve in Figure 4A to be smeared out, similar to what is seen in Figure 4D, though due to a fundamentally different reason—with biofilm formation arising in some cases at lower $(\tilde{D}, \tilde{J})$ than predicted by the black curve. Indeed, similar behavior was recently observed in a distinct model of biofilm formation on flat surfaces (Sinclair et al., 2022). Exploring the influence of such variations by using a more probabilistic approach in our theoretical framework will thus be a useful direction for future research.

Materials and methods

To numerically solve the continuum model described by Equations 1–4, we follow the experimentally validated approach used in our previous work (Bhattacharjee et al., 2021; Amchin et al., 2022). Specifically, we use an Adams-Bashforth-Moulton predictor-corrector method in which the order of the predictor and corrector are 3 and 2, respectively. Because the predictor-corrector method requires past time points to inform future steps, the starting time points must be found with another method; we choose the Shanks starter of order 6 as described previously (Rodabaugh and Wesson, 1965; Shanks, 1966). For the first and second derivatives in space, we use finite difference equations with central difference forms in rectilinear coordinates. The temporal and spatial resolution of the simulations are $δ t = 0.1 s$ and $δ x = 20 μ m$ , respectively; furthermore, we constrain our analysis to simulations for which the peak of the overall bacteria population moves slower than $δ x / δ t$ . Repeating representative simulations with different spatial and temporal resolution indicates that even finer discretization does not appreciably alter the results (Figure 4—figure supplement 2). Thus, our choice of discretization is sufficiently finely-resolved such that the results in the numerical simulations are not appreciably influenced by discretization. Furthermore, performing the same representative simulation shown in Figure 1C, but with the shape of the initial inoculum changed from a Gaussian profile to a step function with the same maximum cellular concentration and width, shows nearly identical results (Figure 1—figure supplement 2)—suggesting that our results are robust to variations in this initial condition chosen. Further probing the mathematical structure of our biophysical model to examine additional influences of initial conditions and explore the possibility of oscillatory solutions, closed orbits, or singularities would be a fascinating direction for future work.

To connect the simulations to our previous experiments (Bhattacharjee et al., 2021), we choose a total extent of $1.75 \times 10^{4} μ m$ for the size of the entire simulated system, with no-flux conditions for the field variables $b_{1}$ , $b_{2}$ , $c$ , and $a$ applied to both boundaries at $x = 0$ and $1.75 \times 10^{4} μ m$ . As in the experiments, we initialize each simulation with a starting inoculum of planktonic cells with a Gaussian profile defined by the maximum concentration $b_{1, 0}$ at $x = 0 µ m$ and a full width at half maximum of $100 μ m$ . Nutrient is initially uniform at a fixed concentration $c_{0}$ , and the autoinducer and biofilm concentrations are initially zero, throughout. Furthermore, following previous work (Amchin et al., 2022; Dell’Arciprete et al., 2018; Volfson et al., 2008; Farrell et al., 2013; Klapper and Dockery, 2002; Head, 2013), we also incorporate jammed growth expansion of the population in which growing cells push outward on their neighbors when the total concentration of bacteria is large enough. In particular, whenever the total concentration of bacteria (planktonic and biofilm) exceeds the jamming limit of $0.95 c e l l s μ m^{- 3}$ at a location $x_{i}$ , the excess cell concentration is removed from $x_{i}$ and added to the neighboring location, $x_{i} + δ x$ , where $δ x$ represents the spatial resolution of the simulation, retaining the same ratio of planktonic to biofilm cells in the new location. We repeat this process for every location in the simulated space for each time step.

We run each simulation for a total simulated duration of $t_{sim} = 20 h$ . At this final time, we use the simulation data to directly compute $f \equiv \frac{\int b_{2} d x}{\int b_{2} d x + \int b_{1} d x}$ , the total fraction of the population in the biofilm state. We also compute the values of the dimensionless parameters $\tilde{D}$ , $\tilde{J}$ , and $\tilde{S}$ using the equations presented in the main text. We note that the autoinducer production time $τ_{a}$ (Equation 6) is only finite for $\tilde{η} \equiv α a^{*} / k_{1} < 1$ ; when $\tilde{η} \geq 1$ , the rate of autoinducer loss exceeds that of autoinducer production, and thus the time required to reach the threshold for biofilm formation diverges. Because both $\tilde{D}$ and $\tilde{J}$ are defined as $τ_{d} / τ_{a}$ and $τ_{c} / τ_{a}$ , respectively, for simulations with $\tilde{η} \geq 1$ , we represent them on the state diagrams in Figure 4 and Figure 4—figure supplement 1 at $(D, J) = (10^{- 2}, 10^{- 3})$ , the smallest values shown on the diagrams. All of these simulations have $f = 0$ , as expected. Furthermore, to ensure that $t_{sim}$ is sufficiently long, we (i) only perform simulations with $τ_{a}$ and $τ_{a, 2}$ smaller than $t_{sim}$ , and (ii) do not include simulations with $f = 0$ but $τ_{c} = τ_{s i m}$ , for which sufficient time has not elapsed for planktonic cells to chemotactically disperse.

Appendix 1

Nondimensionalizing the governing equations

The governing equations Equations 1–4 are described by six variables: those describing the concentrations of planktonic bacteria ( $b_{1}$ ), biofilm bacteria ( $b_{2}$ ), nutrient ( $c$ ), autoinducer molecules ( $a$ ), as well as the one-dimensional space ( $x$ ), and time ( $t$ ) coordinates. Additional constants for our equations are highlighted in Supplementary file 1, with initial conditions $b_{1} (t = 0) = b_{1, 0}$ , $c (t = 0) = c_{0}$ , and $x_{0}$ as the width of the initial planktonic inoculum. We define the dimensionless variables ${\tilde{b}}_{1} \equiv \frac{b_{1}}{B_{1}}$ , ${\tilde{b}}_{2} \equiv \frac{b_{2}}{B_{2}}$ , $\tilde{c} \equiv \frac{c}{C}$ , $\tilde{a} \equiv \frac{a}{A}$ , $\tilde{x} \equiv \frac{x}{X}$ , and $\tilde{t} \equiv \frac{t}{T}$ , where the tilde $(\tilde{})$ notation indicates a dimensionless quantity and the dimensional quantities $B_{1}$ , $B_{2}$ , $C$ , $A$ , $X$ , and $T$ are not specified a priori. Thus, in nondimensional form, Equations 1–4 can be represented as:

\begin{array}{ll} P l a n k t o n i c : \frac{\partial {\tilde{b}}_{1}}{\partial \tilde{t}} & = \frac{D_{1}}{(X^{2} / T)} {\tilde{\nabla}}^{2} {\tilde{b}}_{1} - \frac{χ_{1}}{(X^{2} / T)} \tilde{\nabla} \cdot ({\tilde{b}}_{1} \tilde{\nabla} \log (\frac{1 + \tilde{c} / {\tilde{c}}_{-}}{1 + \tilde{c} / {\tilde{c}}_{+}})) \\ + {\tilde{b}}_{1} (γ_{1} T) g (\tilde{c}) - {\tilde{b}}_{1} (τ^{- 1} T) H (\tilde{a} - a^{*} / A) \end{array}

B i o f i l m : \frac{\partial {\tilde{b}}_{2}}{\partial \tilde{t}} = (γ_{2} T) {\tilde{b}}_{2} g (\tilde{c}) + (B_{1} / B_{2}) (τ^{- 1} T) {\tilde{b}}_{1} H (\tilde{a} - a^{*} / A)

N u t r i e n t : \frac{\partial \tilde{c}}{\partial \tilde{t}} = \frac{D_{c}}{(X^{2} / T)} {\tilde{\nabla}}^{2} \tilde{c} - ((B_{1} / C) κ_{1} T {\tilde{b}}_{1} + (B_{2} / C) κ_{2} T {\tilde{b}}_{2}) g (\tilde{c})

X^{2} / D_{1}, X^{2} / c h i_{1}, X^{2} / D_{c}, X^{2} / D_{a} γ_{1}^{- 1}, γ_{2}^{- 1}, τ, \frac{c_{o}}{b_{1},_{0} k_{1}}, \frac{c_{o}}{b_{1},_{0} k_{2}}, \frac{a^{*}}{b_{1},_{0} k_{1}}, \frac{a^{*}}{b_{1},_{0} k_{2}}, ⋋^{- 1}, (α β_{1, 0})^{- 1}

where $g (\tilde{c}) \equiv \frac{\tilde{c}}{\tilde{c} + {\tilde{c}}_{c h a r}}$ . Given that the characteristic autoinducer concentration $a^{*}$ arises in the argument of the Heaviside step function in Equations S1 and S2, we choose $A = a^{*}$ . Moreover, given that the planktonic cells have a characteristic concentration $b_{1, 0}$ defined by the initial inoculum, we choose $B_{1} = b_{1, 0}$ . The fraction of the population in the biofilm state is defined as $f = b_{2} / (b_{2} + b_{1})$ ; thus, to ensure that $\tilde{f} = f$ for simplicity, we also choose $B_{2} = B_{1} = b_{1, 0}$ . Finally, given that the nutrient has a characteristic concentration c₀ defined by the initial saturation, we choose $C = c_{0}$ . With these choices of characteristic quantities, multiple length and time scales emerge as possible choices for $X$ and $T$ , respectively:

Length scale: $\sqrt{T D_{1}}, \sqrt{T D_{a}}, \sqrt{T D_{c}}, \sqrt{T D_{a}}$

Time scale: $\begin{array}{ll} X^{2} / D_{1}, X^{2} / c h i_{1}, X^{2} / D_{c}, X^{2} / D_{a}, γ_{1}^{- 1}, γ_{2}^{- 1}, τ, \\ \frac{c_{o}}{b_{1},_{0} k_{1}}, \frac{c_{o}}{b_{1},_{0} k_{2}}, \frac{a^{*}}{b_{1},_{0} k_{1}}, \frac{a^{*}}{b_{1},_{0} k_{2}}, ⋋^{- 1}, (α β_{1, 0})^{- 1} \end{array}$

Each such choice will lead to the emergence of many different dimensionless groups characterizing this problem. Nevertheless, all these different groupings are accounted for in the dimensionless parameters $\tilde{D}$ , $\tilde{J}$ , and $\tilde{S}$ described in the main text, with the exception of quantities involving the nutrient diffusivity $D_{c}$ , planktonic-to-biofilm transition rate $τ^{- 1}$ , and the natural autoinducer degradation rate $λ$ , which have corresponding time scales that are much smaller than the other time scales of the systems considered here and are neglected from our analysis for simplicity.

Appendix 2

Derivation of the dimensionless parameters $\tilde{D}$ and $\tilde{S}$

We first estimate the time $τ_{d}$ taken for cells to deplete available nutrient through consumption. To do so, for simplicity, we consider a population of planktonic cells exponentially growing at the maximal rate $γ_{1}$ , uniformly distributed in a well-mixed and fixed domain (i.e., neglecting motility-mediated spreading), and consuming nutrient at the maximal rate $κ_{1}$ . Thus, $\frac{d c}{d t} = - κ_{1} b_{1, 0} e^{t γ_{1}}$ ; integrating this equation from $t = 0$ (with $c = c_{0}$ ) to $t = τ_{d}$ (with $c = 0$ ) yields Equation 5 of the main text.

We use a similar approach to estimate the time $τ_{a}$ taken for produced autoinducer to reach the threshold for biofilm formation $a^{*}$ . In particular, we consider the same population of planktonic cells secreting autoinducer at the maximal rate $k_{1}$ . We neglect natural degradation of autoinducer, given that the degradation rate is relatively small compared to binding to the cell surface receptors with a second-order rate constant $α$ , that is, $λ ≪ α b_{0}$ . The rate of autoinducer production and loss are then given by $b_{1, 0} e^{t γ_{1}} \times k_{1}$ and $b_{1, 0} e^{t γ_{1}} \times α a$ , respectively, ultimately yielding $\frac{d a}{d t} = b_{1, 0} e^{t γ_{1}} (k_{1} - α a)$ . Integrating this equation from $t = 0$ (with $a = 0$ ) to $t = τ_{a}$ (with $a = a^{*}$ ) then yields Equation 6 of the main text. Notably, this analytical solution for the time scale $τ_{a}$ is only defined for $\tilde{η} \equiv α a^{*} / k_{1} < 1$ ; when $\tilde{η} \geq 1$ , the rate of autoinducer loss exceeds that of autoinducer production and secretion, and thus the time required to reach the threshold for biofilm formation diverges. Finally, the ratio of $τ_{d}$ and $τ_{a}$ thus derived yields the nutrient availability parameter $\tilde{D}$ as described in the main text.

Thus far, we have only considered nutrient consumption by planktonic bacteria. However, cellular proliferation, autoinducer production, and nutrient consumption can also occur for cells after they have transitioned to the biofilm state, causing biofilm-produced autoinducer to also drive surrounding planktonic cells to transition to the biofilm state. Hence, we repeat the same calculations for $τ_{a}$ and $τ_{d}$ as described above, but now for a population of cells in the biofilm state (still with the characteristic concentration $b_{1, 0}$ defined in our model), exponentially growing at the maximal rate $γ_{2}$ and consuming nutrient at the maximal rate $κ_{2}$ . In this case, $\frac{d c}{d t} = - κ_{2} b_{1, 0} e^{t γ_{2}}$ , and integrating this equation from $t = 0$ (with $c = c_{0}$ ) to $t = τ_{d, 2}$ (with $c = 0$ ) yields $τ_{d, 2} = γ_{2}^{- 1} \ln (1 + {\tilde{β}}_{2, 0})$ , where ${\tilde{β}}_{2, 0} \equiv γ_{2} / (b_{1, 0} κ_{2} / c_{0})$ describes the yield of new biofilm cells produced as the population consumes nutrient. For the calculation of autoinducer production, we adopt a similar approach as that described above to calculate $τ_{a}$ , but now assuming that the biofilm surface receptors are saturated (i.e., neglecting autoinducer loss). As a result, $\frac{d a}{d t} = b_{1, 0} k_{2} e^{t γ_{2}}$ . Integrating this equation from $t = 0$ (with $a = 0$ ) to $t = τ_{a, 2}$ (with $a = a^{*}$ ) finally yields $τ_{a, 2} = γ_{2}^{- 1} \ln (1 + {\tilde{θ}}_{2, 0})$ , where ${\tilde{θ}}_{2, 0} \equiv \frac{γ_{2}}{b_{1, 0} k_{2} / a^{*}}$ . The ratio of $τ_{d, 2}$ and $τ_{a, 2}$ thus derived then yields the parameter $\tilde{S}$ as described in the main text.

Data availability

All data generated or analyzed during this study are included in the manuscript and supporting file; source data files have been provided for all figures.

References

1. Abdel-Aziz S
(2014) Bacterial Biofilm: Dispersal and Inhibition Strategies
Scholarena Journal of Biotechnology 10:105.

https://doi.org/10.18875/2375-6713.1.105
- Google Scholar
(2016) Chemotaxis Increases the Residence Time of Bacteria in Granular Media Containing Distributed Contaminant Sources
Environmental Science & Technology 50:181–187.

https://doi.org/10.1021/acs.est.5b03956
- PubMed
- Google Scholar
(2018) Chemotaxis Increases the Retention of Bacteria in Porous Media with Residual NAPL Entrapment
Environmental Science & Technology 52:7289–7295.

https://doi.org/10.1021/acs.est.8b01172
- PubMed
- Google Scholar
1. Adler J
(1966a) Chemotaxis in bacteria
Science 153:708–716.

https://doi.org/10.1126/science.153.3737.708
- PubMed
- Google Scholar
1. Adler J
(1966b) Effect of amino acids and oxygen on chemotaxis in Escherichia coli
Journal of Bacteriology 92:121–129.

https://doi.org/10.1128/jb.92.1.121-129.1966
- PubMed
- Google Scholar
(2022) Cellular Sensing Governs the Stability of Chemotactic Fronts
Physical Review Letters 128:148101.

https://doi.org/10.1103/PhysRevLett.128.148101
- PubMed
- Google Scholar
(2022) Influence of confinement on the spreading of bacterial populations
PLOS Computational Biology 18:e1010063.

https://doi.org/10.1371/journal.pcbi.1010063
- PubMed
- Google Scholar
1. Babalola OO
(2010) Beneficial bacteria of agricultural importance
Biotechnology Letters 32:1559–1570.

https://doi.org/10.1007/s10529-010-0347-0
- PubMed
- Google Scholar
(2007) Bacterial translocation: overview of mechanisms and clinical impact
Journal of Gastroenterology and Hepatology 22:464–471.

https://doi.org/10.1111/j.1440-1746.2007.04933.x
- PubMed
- Google Scholar
1. Baraquet C
2. Harwood CS
(2013) Cyclic diguanosine monophosphate represses bacterial flagella synthesis by interacting with the Walker A motif of the enhancer-binding protein FleQ
PNAS 110:18478–18483.

https://doi.org/10.1073/pnas.1318972110
- PubMed
- Google Scholar
1. Barraud N
2. Hassett DJ
3. Hwang SH
4. Rice SA
5. Kjelleberg S
6. Webb JS
(2006) Involvement of nitric oxide in biofilm dispersal of Pseudomonas aeruginosa
Journal of Bacteriology 188:7344–7353.

https://doi.org/10.1128/JB.00779-06
- PubMed
- Google Scholar
1. Bassler BL
2. Losick R
(2006) Bacterially speaking
Cell 125:237–246.

https://doi.org/10.1016/j.cell.2006.04.001
- PubMed
- Google Scholar
Book
1. Berg HC
(2004) E. coli in Motion
Springer-Verlag.

https://doi.org/10.1007/b97370
- Google Scholar
Book
1. Berg HC
(2018) Random Walks in Biology
Princeton University Press.

https://doi.org/10.2307/j.ctv7r40w6
- Google Scholar
1. Bhattacharjee T
2. Datta SS
(2019a) Bacterial hopping and trapping in porous media
Nature Communications 10:2075.

https://doi.org/10.1038/s41467-019-10115-1
- PubMed
- Google Scholar
1. Bhattacharjee T
2. Datta SS
(2019b) Confinement and activity regulate bacterial motion in porous media
Soft Matter 15:9920–9930.

https://doi.org/10.1039/c9sm01735f
- PubMed
- Google Scholar
1. Bhattacharjee T
2. Amchin DB
3. Ott JA
4. Kratz F
5. Datta SS
(2021) Chemotactic migration of bacteria in porous media
Biophysical Journal 120:3483–3497.

https://doi.org/10.1016/j.bpj.2021.05.012
- PubMed
- Google Scholar
1. Bhattacharjee T
2. Amchin DB
3. Alert R
4. Ott JA
5. Datta SS
(2022) Chemotactic smoothing of collective migration
eLife 11:e71226.

https://doi.org/10.7554/eLife.71226
- PubMed
- Google Scholar
1. Boehm A
2. Kaiser M
3. Li H
4. Spangler C
5. Kasper CA
6. Ackermann M
7. Kaever V
8. Sourjik V
9. Roth V
10. Jenal U
(2010) Second messenger-mediated adjustment of bacterial swimming velocity
Cell 141:107–116.

https://doi.org/10.1016/j.cell.2010.01.018
- PubMed
- Google Scholar
(2001) Gene expression in Pseudomonas aeruginosa: evidence of iron override effects on quorum sensing and biofilm-specific gene regulation
Journal of Bacteriology 183:1990–1996.

https://doi.org/10.1128/JB.183.6.1990-1996.2001
- PubMed
- Google Scholar
1. Bridges AA
2. Bassler BL
(2019) The intragenus and interspecies quorum-sensing autoinducers exert distinct control over Vibrio cholerae biofilm formation and dispersal
PLOS Biology 17:e3000429.

https://doi.org/10.1371/journal.pbio.3000429
- PubMed
- Google Scholar
1. Cai Q
2. Li Z
3. Ouyang Q
4. Luo C
5. Gordon VD
(2016) Singly Flagellated Pseudomonas aeruginosa Chemotaxes Efficiently by Unbiased Motor Regulation
MBio 7:e00013.

https://doi.org/10.1128/mBio.00013-16
- PubMed
- Google Scholar
(2011) Molecular and Functional Aspects of Bacterial Chemotaxis
Journal of Statistical Physics 144:219–240.

https://doi.org/10.1007/s10955-011-0251-6
- Google Scholar
(2015) The flagellum in bacterial pathogens: For motility and a whole lot more
Seminars in Cell & Developmental Biology 46:91–103.

https://doi.org/10.1016/j.semcdb.2015.10.032
- PubMed
- Google Scholar
1. Chen J
2. Jin Y
(2011) Motility of Pseudomonas aeruginosa in saturated granular media as affected by chemoattractant
Journal of Contaminant Hydrology 126:113–120.

https://doi.org/10.1016/j.jconhyd.2011.08.001
- PubMed
- Google Scholar
1. Cremer J
2. Segota I
3. Yang CY
4. Arnoldini M
5. Sauls JT
6. Zhang Z
7. Gutierrez E
8. Groisman A
9. Hwa T
(2016) Effect of flow and peristaltic mixing on bacterial growth in a gut-like channel
PNAS 113:11414–11419.

https://doi.org/10.1073/pnas.1601306113
- PubMed
- Google Scholar
1. Cremer J
2. Honda T
3. Tang Y
4. Wong-Ng J
5. Vergassola M
6. Hwa T
(2019) Chemotaxis as a navigation strategy to boost range expansion
Nature 575:658–663.

https://doi.org/10.1038/s41586-019-1733-y
- PubMed
- Google Scholar
(2011) Migration of chemotactic bacteria in soft agar: role of gel concentration
Biophysical Journal 101:525–534.

https://doi.org/10.1016/j.bpj.2011.06.023
- PubMed
- Google Scholar
(2016) Polymers in the gut compress the colonic mucus hydrogel
PNAS 113:7041–7046.

https://doi.org/10.1073/pnas.1602789113
- Google Scholar
1. Davey ME
2. O’toole GA
(2000) Microbial biofilms: from ecology to molecular genetics
Microbiology and Molecular Biology Reviews 64:847–867.

https://doi.org/10.1128/MMBR.64.4.847-867.2000
- PubMed
- Google Scholar
(1998) The involvement of cell-to-cell signals in the development of a bacterial biofilm
Science 280:295–298.

https://doi.org/10.1126/science.280.5361.295
- PubMed
- Google Scholar
1. Davis NJ
2. Cohen Y
3. Sanselicio S
4. Fumeaux C
5. Ozaki S
6. Luciano J
7. Guerrero-Ferreira RC
8. Wright ER
9. Jenal U
10. Viollier PH
(2013) De- and repolarization mechanism of flagellar morphogenesis during a bacterial cell cycle
Genes & Development 27:2049–2062.

https://doi.org/10.1101/gad.222679.113
- PubMed
- Google Scholar
1. De Kievit TR
2. Gillis R
3. Marx S
4. Brown C
5. Iglewski BH
(2001) Quorum-sensing genes in Pseudomonas aeruginosa biofilms: their role and expression patterns
Applied and Environmental Microbiology 67:1865–1873.

https://doi.org/10.1128/AEM.67.4.1865-1873.2001
- PubMed
- Google Scholar
1. Dechesne A
2. Wang G
3. Gülez G
4. Or D
5. Smets BF
(2010) Hydration-controlled bacterial motility and dispersal on surfaces
PNAS 107:14369–14372.

https://doi.org/10.1073/pnas.1008392107
- PubMed
- Google Scholar
(2018) A growing bacterial colony in two dimensions as an active nematic
Nature Communications 9:4190.

https://doi.org/10.1038/s41467-018-06370-3
- PubMed
- Google Scholar
1. Donlan RM
2. Costerton JW
(2002) Biofilms: survival mechanisms of clinically relevant microorganisms
Clinical Microbiology Reviews 15:167–193.

https://doi.org/10.1128/CMR.15.2.167-193.2002
- PubMed
- Google Scholar
1. Duan K
2. Surette MG
(2007) Environmental regulation of Pseudomonas aeruginosa PAO1 Las and Rhl quorum-sensing systems
Journal of Bacteriology 189:4827–4836.

https://doi.org/10.1128/JB.00043-07
- PubMed
- Google Scholar
(2014) Limits of feedback control in bacterial chemotaxis
PLOS Computational Biology 10:e1003694.

https://doi.org/10.1371/journal.pcbi.1003694
- PubMed
- Google Scholar
(2013) Mechanically driven growth of quasi-two-dimensional microbial colonies
Physical Review Letters 111:168101.

https://doi.org/10.1103/PhysRevLett.111.168101
- PubMed
- Google Scholar
1. Ford RM
2. Harvey RW
(2007) Role of chemotaxis in the transport of bacteria through saturated porous media
Advances in Water Resources 30:1608–1617.

https://doi.org/10.1016/j.advwatres.2006.05.019
- Google Scholar
1. Fu X
2. Kato S
3. Long J
4. Mattingly HH
5. He C
6. Vural DC
7. Zucker SW
8. Emonet T
(2018) Spatial self-organization resolves conflicts between individuality and collective migration
Nature Communications 9:e4.

https://doi.org/10.1038/s41467-018-04539-4
- Google Scholar
(2005) Survival strategies of infectious biofilms
Trends in Microbiology 13:34–40.

https://doi.org/10.1016/j.tim.2004.11.010
- PubMed
- Google Scholar
1. Gill CO
2. Penney N
(1977) Penetration of bacteria into meat
Applied and Environmental Microbiology 33:1284–1286.

https://doi.org/10.1128/aem.33.6.1284-1286.1977
- PubMed
- Google Scholar
(2006) Autoinducer 2 Controls Biofilm Formation in Escherichia coli through a Novel Motility Quorum-Sensing Regulator (MqsR, B3022)
Journal of Bacteriology 188:305–316.

https://doi.org/10.1128/JB.188.1.305-316.2006
- PubMed
- Google Scholar
(2004) Bacterial biofilms: from the natural environment to infectious diseases
Nature Reviews. Microbiology 2:95–108.

https://doi.org/10.1038/nrmicro821
- PubMed
- Google Scholar
1. Hammer BK
2. Bassler BL
(2003) Quorum sensing controls biofilm formation in Vibrio cholerae
Molecular Microbiology 50:101–104.

https://doi.org/10.1046/j.1365-2958.2003.03688.x
- PubMed
- Google Scholar
(2012) The heterogeneous motility of the Lyme disease spirochete in gelatin mimics dissemination through tissue
PNAS 109:3059–3064.

https://doi.org/10.1073/pnas.1114362109
- PubMed
- Google Scholar
1. Head DA
(2013) Linear surface roughness growth and flow smoothening in a three-dimensional biofilm model
Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics 88:032702.

https://doi.org/10.1103/PhysRevE.88.032702
- PubMed
- Google Scholar
1. Hengge R
(2009) Principles of c-di-GMP signalling in bacteria
Nature Reviews. Microbiology 7:263–273.

https://doi.org/10.1038/nrmicro2109
- PubMed
- Google Scholar
(2012) Spatial heterogeneity of autoinducer regulation systems
Sensors 12:4156–4171.

https://doi.org/10.3390/s120404156
- PubMed
- Google Scholar
1. Hense BA
2. Schuster M
(2015) Core principles of bacterial autoinducer systems
Microbiology and Molecular Biology Reviews 79:153–169.

https://doi.org/10.1128/MMBR.00024-14
- PubMed
- Google Scholar
1. Hentzer M
2. Eberl L
3. Nielsen J
4. Givskov M
(2003) Quorum Sensing
BioDrugs 17:241–250.

https://doi.org/10.2165/00063030-200317040-00003
- PubMed
- Google Scholar
1. Herzberg M
2. Kaye IK
3. Peti W
4. Wood TK
(2006) YdgG (TqsA) controls biofilm formation in Escherichia coli K-12 through autoinducer 2 transport
Journal of Bacteriology 188:587–598.

https://doi.org/10.1128/JB.188.2.587-598.2006
- PubMed
- Google Scholar
1. Jayaraman A
2. Wood TK
(2008) Bacterial quorum sensing: signals, circuits, and implications for biofilms and disease
Annual Review of Biomedical Engineering 10:145–167.

https://doi.org/10.1146/annurev.bioeng.10.061807.160536
- PubMed
- Google Scholar
(2017) Cyclic di-GMP: second messenger extraordinaire
Nature Reviews. Microbiology 15:271–284.

https://doi.org/10.1038/nrmicro.2016.190
- PubMed
- Google Scholar
1. Kalinin YV
2. Jiang L
3. Tu Y
4. Wu M
(2009) Logarithmic sensing in Escherichia coli bacterial chemotaxis
Biophysical Journal 96:2439–2448.

https://doi.org/10.1016/j.bpj.2008.10.027
- PubMed
- Google Scholar
1. Kaplan JB
(2010) Biofilm dispersal: mechanisms, clinical implications, and potential therapeutic uses
Journal of Dental Research 89:205–218.

https://doi.org/10.1177/0022034509359403
- PubMed
- Google Scholar
1. Keller EF
2. Segel LA
(1970) Initiation of slime mold aggregation viewed as an instability
Journal of Theoretical Biology 26:399–415.

https://doi.org/10.1016/0022-5193(70)90092-5
- PubMed
- Google Scholar
1. Keller EF
2. Segel LA
(1971) Traveling bands of chemotactic bacteria: a theoretical analysis
Journal of Theoretical Biology 30:235–248.

https://doi.org/10.1016/0022-5193(71)90051-8
- PubMed
- Google Scholar
1. Keller EF
2. Odell GM
(1975) Necessary and sufficient conditions for chemotactic bands
Mathematical Biosciences 27:309–317.

https://doi.org/10.1016/0025-5564(75)90109-1
- Google Scholar
1. Kirisits MJ
2. Parsek MR
(2006) Does Pseudomonas aeruginosa use intercellular signalling to build biofilm communities?
Cellular Microbiology 8:1841–1849.

https://doi.org/10.1111/j.1462-5822.2006.00817.x
- PubMed
- Google Scholar
(2007) Influence of the hydrodynamic environment on quorum sensing in Pseudomonas aeruginosa biofilms
Journal of Bacteriology 189:8357–8360.

https://doi.org/10.1128/JB.01040-07
- PubMed
- Google Scholar
1. Klapper I
2. Dockery J
(2002) Finger Formation in Biofilm Layers
SIAM Journal on Applied Mathematics 62:853–869.

https://doi.org/10.1137/S0036139900371709
- Google Scholar
1. Koerber A
2. King J
3. Ward J
4. Williams P
5. Croft J
6. Sockett R
(2002) A Mathematical Model of Partial-thickness Burn-wound Infection by Pseudomonas aeruginosa: Quorum Sensing and the Build-up to Invasion
Bulletin of Mathematical Biology 64:239–259.

https://doi.org/10.1006/bulm.2001.0272
- PubMed
- Google Scholar
(2006) Quorum-sensing regulation governs bacterial adhesion, biofilm development, and host colonization in Pantoea stewartii subspecies stewartii
PNAS 103:5983–5988.

https://doi.org/10.1073/pnas.0509860103
- PubMed
- Google Scholar
(2010) Vibrio cholerae VpsT regulates matrix production and motility by directly sensing cyclic di-GMP
Science 327:866–868.

https://doi.org/10.1126/science.1181185
- PubMed
- Google Scholar
(2016) Chemotaxis towards autoinducer 2 mediates autoaggregation in Escherichia coli
Nature Communications 7:12984.

https://doi.org/10.1038/ncomms12984
- PubMed
- Google Scholar
(2018) Autoinducer 2-Dependent Escherichia coli Biofilm Formation Is Enhanced in a Dual-Species Coculture
Applied and Environmental Microbiology 84:e02638-17.

https://doi.org/10.1128/AEM.02638-17
- PubMed
- Google Scholar
1. Lauffenburger DA
(1991) Quantitative studies of bacterial chemotaxis and microbial population dynamics
Microbial Ecology 22:175–185.

https://doi.org/10.1007/BF02540222
- PubMed
- Google Scholar
1. Lazova MD
2. Ahmed T
3. Bellomo D
4. Stocker R
5. Shimizu TS
(2011) Response rescaling in bacterial chemotaxis
PNAS 1:13870–13875.

https://doi.org/10.1073/pnas.1108608108
- PubMed
- Google Scholar
1. Leewenhoeck A
(1684) An abstract of a letter from Mr. Anthony Leevvenhoeck at Delft, dated Sep. 17. 1683. Containing some microscopical observations, about animals in the scurf of the teeth, the substance call’d worms in the nose, the cuticula consisting of scales
Philosophical Transactions of the Royal Society of London 14:568–574.

https://doi.org/10.1098/rstl.1684.0030
- Google Scholar
1. Lux R
2. Miller JN
3. Park NH
4. Shi W
(2001) Motility and chemotaxis in tissue penetration of oral epithelial cell layers by Treponema denticola
Infection and Immunity 69:6276–6283.

https://doi.org/10.1128/IAI.69.10.6276-6283.2001
- PubMed
- Google Scholar
1. Mah T-F
2. Pitts B
3. Pellock B
4. Walker GC
5. Stewart PS
6. O’Toole GA
(2003) A genetic basis for Pseudomonas aeruginosa biofilm antibiotic resistance
Nature 426:306–310.

https://doi.org/10.1038/nature02122
- PubMed
- Google Scholar
Preprint
(2021) Active Transport in Complex Environments
arXiv.

https://arxiv.org/abs/2108.07011
- Google Scholar
(1997) Evidence of autoinducer activity in naturally occurring biofilms
FEMS Microbiology Letters 154:259–263.

https://doi.org/10.1111/j.1574-6968.1997.tb12653.x
- PubMed
- Google Scholar
1. Mellbye B
2. Schuster M
(2014) Physiological framework for the regulation of quorum sensing-dependent public goods in Pseudomonas aeruginosa
Journal of Bacteriology 196:1155–1164.

https://doi.org/10.1128/JB.01223-13
- PubMed
- Google Scholar
1. Miller MB
2. Bassler BL
(2001) Quorum sensing in bacteria
Annual Review of Microbiology 55:165–199.

https://doi.org/10.1146/annurev.micro.55.1.165
- PubMed
- Google Scholar
(2002) Parallel quorum sensing systems converge to regulate virulence in Vibrio cholerae
Cell 110:303–314.

https://doi.org/10.1016/s0092-8674(02)00829-2
- PubMed
- Google Scholar
1. Monod J
(1949) The growth of bacterial cultures
Annual Review of Microbiology 3:371–394.

https://doi.org/10.1146/annurev.mi.03.100149.002103
- Google Scholar
(2008) The evolution of quorum sensing in bacterial biofilms
PLOS Biology 6:e14.

https://doi.org/10.1371/journal.pbio.0060014
- PubMed
- Google Scholar
(2021) A biophysical limit for quorum sensing in biofilms
PNAS 118:118.

https://doi.org/10.1073/pnas.2022818118
- PubMed
- Google Scholar
(2000) Wastewater treatment with particulate biofilm reactors
Journal of Biotechnology 80:1–33.

https://doi.org/10.1016/s0168-1656(00)00229-7
- PubMed
- Google Scholar
1. Odell GM
2. Keller EF
(1976) Letter: traveling bands of chemotactic bacteria revisited
Journal of Theoretical Biology 56:243–247.

https://doi.org/10.1016/s0022-5193(76)80055-0
- PubMed
- Google Scholar
1. O’Neil HS
2. Marquis H
(2006) Listeria monocytogenes flagella are used for motility, not as adhesins, to increase host cell invasion
Infection and Immunity 74:6675–6681.

https://doi.org/10.1128/IAI.00886-06
- PubMed
- Google Scholar
1. O’Toole GA
2. Stewart PS
(2005) Biofilms strike back
Nature Biotechnology 23:1378–1379.

https://doi.org/10.1038/nbt1105-1378
- PubMed
- Google Scholar
1. Parsek MR
2. Greenberg EP
(2005) Sociomicrobiology: the connections between quorum sensing and biofilms
Trends in Microbiology 13:27–33.

https://doi.org/10.1016/j.tim.2004.11.007
- PubMed
- Google Scholar
1. Paul D
2. Kim YS
3. Ponnusamy K
4. Kweon JH
(2009) Application of Quorum Quenching to Inhibit Biofilm Formation
Environmental Engineering Science 26:1319–1324.

https://doi.org/10.1089/ees.2008.0392
- Google Scholar
(2010) Heterogeneous rpoS and rhlR mRNA levels and 16S rRNA/rDNA (rRNA gene) ratios within Pseudomonas aeruginosa biofilms, sampled by laser capture microdissection
Journal of Bacteriology 192:2991–3000.

https://doi.org/10.1128/JB.01598-09
- PubMed
- Google Scholar
(1997) Regulation of las and rhl quorum sensing in Pseudomonas aeruginosa
Journal of Bacteriology 179:3127–3132.

https://doi.org/10.1128/jb.179.10.3127-3132.1997
- PubMed
- Google Scholar
1. Reddy HL
2. Ford RM
(1996) Analysis of biodegradation and bacterial transport: Comparison of models with kinetic and equilibrium bacterial adsorption
Journal of Contaminant Hydrology 22:271–287.

https://doi.org/10.1016/0169-7722(95)00095-X
- Google Scholar
1. Ribet D
2. Cossart P
(2015) How bacterial pathogens colonize their hosts and invade deeper tissues
Microbes and Infection 17:173–183.

https://doi.org/10.1016/j.micinf.2015.01.004
- PubMed
- Google Scholar
Report
1. Rodabaugh D
2. Wesson JR
(1965)
On the Efficient Use of Predictor-Corrector Methods in the Numerical Solution of Differential Equations. NASA-TN-D-2946

WashingtonWASHINGTON, D.C: National Aeronautics and Space AdministrationNATIONAL AERONAUTICS AND SPACE ADMINISTRATION.
- Google Scholar
(2013) Cyclic di-GMP: the first 25 years of a universal bacterial second messenger
Microbiology and Molecular Biology Reviews 77:1–52.

https://doi.org/10.1128/MMBR.00043-12
- PubMed
- Google Scholar
1. Russell MH
2. Bible AN
3. Fang X
4. Gooding JR
5. Campagna SR
6. Gomelsky M
7. Alexandre G
(2013) Integration of the second messenger c-di-GMP into the chemotactic signaling pathway
MBio 4:e00001.

https://doi.org/10.1128/mBio.00001-13
- PubMed
- Google Scholar
1. Sakuragi Y
2. Kolter R
(2007) Quorum-sensing regulation of the biofilm matrix genes (pel) of Pseudomonas aeruginosa
Journal of Bacteriology 189:5383–5386.

https://doi.org/10.1128/JB.00137-07
- PubMed
- Google Scholar
(2011) Directional persistence of chemotactic bacteria in a traveling concentration wave
PNAS 108:16235–16240.

https://doi.org/10.1073/pnas.1101996108
- PubMed
- Google Scholar
1. Schellenberg GD
2. Furlong CE
(1977) Resolution of the multiplicity of the glutamate and aspartate transport systems of Escherichia coli
The Journal of Biological Chemistry 252:9055–9064.

https://doi.org/10.1016/S0021-9258(17)38344-8
- PubMed
- Google Scholar
(2019) Traveling concentration pulses of bacteria in a generalized Keller–Segel model
New Journal of Physics 21:103001.

https://doi.org/10.1088/1367-2630/ab4522
- Google Scholar
1. Shanks EB
(1966) Solutions of differential equations by evaluations of functions
Mathematics of Computation 20:21–38.

https://doi.org/10.1090/S0025-5718-1966-0187406-1
- Google Scholar
1. Shehata TE
2. Marr AG
(1971) Effect of nutrient concentration on the growth of Escherichia coli
Journal of Bacteriology 107:210–216.

https://doi.org/10.1128/jb.107.1.210-216.1971
- PubMed
- Google Scholar
1. Shimizu TS
2. Tu Y
3. Berg HC
(2010) A modular gradient-sensing network for chemotaxis in Escherichia coli revealed by responses to time-varying stimuli
Molecular Systems Biology 6:382.

https://doi.org/10.1038/msb.2010.37
- PubMed
- Google Scholar
(2017) Penetration of aerobic bacteria into meat: A mechanistic understanding
Journal of Food Engineering 196:193–207.

https://doi.org/10.1016/j.jfoodeng.2016.10.012
- Google Scholar
1. Shoval O
2. Goentoro L
3. Hart Y
4. Mayo A
5. Sontag E
6. Alon U
(2010) Fold-change detection and scalar symmetry of sensory input fields
PNAS 107:15995–16000.

https://doi.org/10.1073/pnas.1002352107
- PubMed
- Google Scholar
1. Siitonen A
2. Nurminen M
(1992) Bacterial motility is a colonization factor in experimental urinary tract infection
Infection and Immunity 60:3918–3920.

https://doi.org/10.1128/iai.60.9.3918-3920.1992
- PubMed
- Google Scholar
1. Simm R
2. Morr M
3. Kader A
4. Nimtz M
5. Römling U
(2004) GGDEF and EAL domains inversely regulate cyclic di-GMP levels and transition from sessility to motility
Molecular Microbiology 53:1123–1134.

https://doi.org/10.1111/j.1365-2958.2004.04206.x
- PubMed
- Google Scholar
Preprint
(2022) A Model for Quorum-Sensing Mediated Stochastic Biofilm Nucleation
bioRxiv.

https://doi.org/10.1101/2022.03.23.485488
- Google Scholar
1. Sourjik V
2. Wingreen NS
(2012) Responding to chemical gradients: bacterial chemotaxis
Current Opinion in Cell Biology 24:262–268.

https://doi.org/10.1016/j.ceb.2011.11.008
- PubMed
- Google Scholar
(2015) Plant growth-promoting bacteria as inoculants in agricultural soils
Genetics and Molecular Biology 38:401–419.

https://doi.org/10.1590/S1415-475738420150053
- PubMed
- Google Scholar
(2015) Persistent enhancement of bacterial motility increases tumor penetration
Biotechnology and Bioengineering 112:2397–2405.

https://doi.org/10.1002/bit.25645
- PubMed
- Google Scholar
1. Toley BJ
2. Forbes NS
(2012) Motility is critical for effective distribution and accumulation of bacteria in tumor tissue
Integrative Biology 4:165–176.

https://doi.org/10.1039/c2ib00091a
- PubMed
- Google Scholar
(2015) Bacterial rotary export ATPases are allosterically regulated by the nucleotide second messenger cyclic-di-GMP
The Journal of Biological Chemistry 290:24470–24483.

https://doi.org/10.1074/jbc.M115.661439
- PubMed
- Google Scholar
1. Tu Y
2. Shimizu TS
3. Berg HC
(2008) Modeling the chemotactic response of Escherichia coli to time-varying stimuli
PNAS 105:14855–14860.

https://doi.org/10.1073/pnas.0807569105
- PubMed
- Google Scholar
(2001) The role of bacterial motility in the survival and spread of Pseudomonas fluorescens in soil and in the attachment and colonisation of wheat roots
FEMS Microbiology Ecology 36:21.

https://doi.org/10.1111/j.1574-6941.2001.tb00822.x
- PubMed
- Google Scholar
1. Valentini M
2. Filloux A
(2016) Biofilms and Cyclic di-GMP (c-di-GMP) Signaling: Lessons from Pseudomonas aeruginosa and Other Bacteria
The Journal of Biological Chemistry 291:12547–12555.

https://doi.org/10.1074/jbc.R115.711507
- PubMed
- Google Scholar
1. Van Leewenhoeck A
(1677) Observations, communicated to the publisher by Mr. Antony van Leewenhoeck, in a dutch letter of the 9th Octob. 1676. here English’d: concerning little animals by him observed in rain-well-sea- and snow water; as also in water wherein pepper had lain infused
Philosophical Transactions of the Royal Society of London 12:821–831.

https://doi.org/10.1098/rstl.1677.0003
- Google Scholar
(2008) Biomechanical ordering of dense cell populations
PNAS 105:15346–15351.

https://doi.org/10.1073/pnas.0706805105
- Google Scholar
1. Wang M
2. Ford RM
3. Harvey RW
(2008) Coupled effect of chemotaxis and growth on microbial distributions in organic-amended aquifer sediments: observations from laboratory and field studies
Environmental Science & Technology 42:3556–3562.

https://doi.org/10.1021/es702392h
- PubMed
- Google Scholar
1. Ward JP
2. King JR
3. Koerber A
4. Williams P
5. Croft J
6. Sockett R
(2001) Mathematical modelling of quorum sensing in bacteria
Mathematical Medicine and Biology 18:263–292.

https://doi.org/10.1093/imammb/18.3.263
- PubMed
- Google Scholar
1. Ward JP
2. King JR
3. Koerber AJ
4. Croft JM
5. Sockett RE
6. Williams P
(2003) Early development and quorum sensing in bacterial biofilms
Journal of Mathematical Biology 47:23–55.

https://doi.org/10.1007/s00285-002-0190-6
- PubMed
- Google Scholar
1. Waters CM
2. Bassler BL
(2005) Quorum sensing: cell-to-cell communication in bacteria
Annual Review of Cell and Developmental Biology 21:319–346.

https://doi.org/10.1146/annurev.cellbio.21.012704.131001
- PubMed
- Google Scholar
(2008) Quorum sensing controls biofilm formation in Vibrio cholerae through modulation of cyclic di-GMP levels and repression of vpsT
Journal of Bacteriology 190:2527–2536.

https://doi.org/10.1128/JB.01756-07
- PubMed
- Google Scholar
(2006) Rhizosphere biology and crop productivity—a review
Soil Research 44:299.

https://doi.org/10.1071/SR05142
- Google Scholar
(1995) Spatio-temporal patterns generated by Salmonella typhimurium
Biophysical Journal 68:2181–2189.

https://doi.org/10.1016/S0006-3495(95)80400-5
- PubMed
- Google Scholar
1. Yang Y
2. M Pollard A
3. Höfler C
4. Poschet G
5. Wirtz M
6. Hell R
7. Sourjik V
(2015) Relation between chemotaxis and consumption of amino acids in bacteria
Molecular Microbiology 96:1272–1282.

https://doi.org/10.1111/mmi.13006
- PubMed
- Google Scholar
(2004) Quorum sensing in Staphylococcus aureus biofilms
Journal of Bacteriology 186:1838–1850.

https://doi.org/10.1128/JB.186.6.1838-1850.2004
- PubMed
- Google Scholar

Article and author information

Author details

Jenna A Moore-Ott

Department of Chemical and Biological Engineering, Princeton University, Princeton, United States

Contribution
Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-6832-0658
Selena Chiu

Department of Chemical and Biological Engineering, Princeton University, Princeton, United States

Contribution
Data curation, Investigation, Software

Competing interests
No competing interests declared
Daniel B Amchin

Department of Chemical and Biological Engineering, Princeton University, Princeton, United States

Contribution
Methodology, Software

Competing interests
No competing interests declared
Tapomoy Bhattacharjee

Andlinger Center for Energy and the Environment, Princeton University, Princeton, United States

Contribution
Methodology

Competing interests
No competing interests declared
Sujit S Datta

Department of Chemical and Biological Engineering, Princeton University, Princeton, United States

Contribution
Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Visualization, Writing – original draft, Writing – review and editing

For correspondence
ssdatta@princeton.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-2400-1561

Funding

National Science Foundation (CBET-1941716)

Sujit S Datta

National Science Foundation (EF-2124863)

Sujit S Datta

National Science Foundation (DMR-2011750)

Sujit S Datta

Pew Charitable Trusts (Pew Biomedical Scholars Program)

Sujit S Datta

National Science Foundation (DGE-1656466)

Jenna A Moore-Ott

Princeton University (Eric and Wendy Schmidt Transformative Technology Fund)

Sujit S Datta

Princeton University (Princeton Catalysis Initiative)

Sujit S Datta

Princeton University (Reiner G. Stoll Undergraduate Summer Fellowship)

Selena Chiu

Princeton University (Princeton University Library Open Access Fund)

Jenna A Moore-Ott

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

It is a pleasure to acknowledge R Kōnane Bay, Vernita Gordon, Anna M Hancock, Andrej Košmrlj, Alejandro Martínez-Calvo, JTN Moore-Ott, PG-A Moore-Ott, NA Moore-Ott, Howard Stone, Carolina Trenado-Yuste, and Ned Wingreen for stimulating discussions. This work was supported by NSF grants CBET-1941716 and EF-2124863, the Eric and Wendy Schmidt Transformative Technology Fund at Princeton, the Princeton Catalysis Initiative, a Reiner G Stoll Undergraduate Summer Fellowship (to SC), in part by funding from the Princeton Center for Complex Materials, a Materials Research Science and Engineering Center supported by NSF grant DMR-2011750, and the Pew Charitable Trusts through the Pew Biomedical Scholars Program. This material is also based upon work supported by the National Science Foundation Graduate Research Fellowship Program (to JAM-O) under Grant No. DGE-1656466. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. This publication was supported by the Princeton University Library Open Access Fund.

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

2,462

views
767

downloads
20

citations

Views, downloads and citations are aggregated across all versions of this paper published by eLife.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Jenna A Moore-Ott
Selena Chiu
Daniel B Amchin
Tapomoy Bhattacharjee
Sujit S Datta

(2022)

A biophysical threshold for biofilm formation

eLife 11:e76380.

https://doi.org/10.7554/eLife.76380

Share this article

Cite this article

Competition between motility-mediated dispersal and autoinducer-mediated biofilm formation.

Figure 1—source data 1

Faster nutrient consumption limits autoinducer production, leading to complete dispersal.

Figure 2—source data 1

Animated form of Figure 2: Results of the same simulation as in Video 1, but for planktonic cells with faster nutrient consumption (larger κ1).

Animated form of Figure 2—figure supplement 1: Results of the same simulation as in Video 1, but for planktonic cells with slower nutrient consumption (smaller κ1).

Enhanced motility enables cells to disperse before sufficient autoinducer accumulates, leading to complete dispersal.

Figure 3—source data 1

Animated form of Figure 3: Results of the same simulation as in Video 1, but for faster-moving planktonic cells (larger D1 and χ1).

Animated form of Figure 3—figure supplement 1: Results of the same simulation as in Video 1, but for slower-moving planktonic cells (smaller D1 and χ1).

The two states of complete dispersal by planktonic cells (green) and complete formation of a biofilm (blue) can be universally described by three dimensionless parameters.

Figure 4—source data 1

Figure 4—source data 2

Figure 4—source data 3

Author details

Jenna A Moore-Ott

Contribution

Competing interests

Selena Chiu

Contribution

Competing interests

Daniel B Amchin

Contribution

Competing interests

Tapomoy Bhattacharjee

Contribution

Competing interests

Sujit S Datta

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Further reading

Animated form of Figure 2: Results of the same simulation as in Video 1, but for planktonic cells with faster nutrient consumption (larger $κ_{1}$ ).

Animated form of Figure 2—figure supplement 1: Results of the same simulation as in Video 1, but for planktonic cells with slower nutrient consumption (smaller $κ_{1}$ ).

Animated form of Figure 3: Results of the same simulation as in Video 1, but for faster-moving planktonic cells (larger $D_{1}$ and $χ_{1}$ ).

Animated form of Figure 3—figure supplement 1: Results of the same simulation as in Video 1, but for slower-moving planktonic cells (smaller $D_{1}$ and $χ_{1}$ ).