Inter-species population dynamics enhance microbial horizontal gene transfer and spread of antibiotic resistance

Abstract
eLife digest
Introduction
Results
Discussion
Materials and methods
References
Article and author information
Metrics

Abstract

Horizontal gene transfer (HGT) plays a major role in the spread of antibiotic resistance. Of particular concern are Acinetobacter baumannii bacteria, which recently emerged as global pathogens, with nosocomial mortality rates reaching 19–54% (Centers for Disease Control and Prevention, 2013; Joly Guillou, 2005; Talbot et al., 2006). Acinetobacter gains antibiotic resistance remarkably rapidly (Antunes et al., 2014; Joly Guillou, 2005), with multi drug-resistance (MDR) rates exceeding 60% (Antunes et al., 2014; Centers for Disease Control and Prevention, 2013). Despite growing concern (Centers for Disease Control and Prevention, 2013; Talbot et al., 2006), the mechanisms underlying this extensive HGT remain poorly understood (Adams et al., 2008; Fournier et al., 2006; Imperi et al., 2011; Ramirez et al., 2010; Wilharm et al., 2013). Here, we show bacterial predation by Acinetobacter baylyi increases cross-species HGT by orders of magnitude, and we observe predator cells functionally acquiring adaptive resistance genes from adjacent prey. We then develop a population-dynamic model quantifying killing and HGT on solid surfaces. We show DNA released via cell lysis is readily available for HGT and may be partially protected from the environment, describe the effects of cell density, and evaluate potential environmental inhibitors. These findings establish a framework for understanding, quantifying, and combating HGT within the microbiome and the emergence of MDR super-bugs.

https://doi.org/10.7554/eLife.25950.001

eLife digest

Every year, antibiotics save millions of lives, but this may not last forever. The bacteria that cause infections are getting smarter and continuously evolve genes to become resistant to antibiotics, which makes it harder to kill them. In many cases, using stronger drugs can bypass this problem, but some 'super-bugs' are developing resistance to every drug we have. For example, the bacterium Acinetobacter baumannii has recently been classified as a global threat that kills thousands of people every year, which placed it on a top six 'most wanted' list for multi drug-resistant bacteria. Worryingly, this drug resistance seems to develop faster than 'standard' evolution would allow, making it difficult to keep up with developing new effective drugs.

One way bacteria can shortcut the evolution of resistance is through a process called horizontal gene transfer, in which they collect resistance genes from other bacteria. Some bacteria can speed up this gene transfer by actively killing their neighbors to extract their DNA. However, until now, this process has not been observed directly, and it was not fully understood where and when killing neighbors becomes important for gene transfer.

Now, Cooper, Tsimring and Hasty have studied a relative of A. baumannii called A. baylyi. Together with another type of bacteria that contained green fluorescence genes, A. baylyi was placed onto a surface that allowed both species to grow. As the two types of bacteria grew together, A. baylyi started to kill the other one and stole their genes. This happened so often that some started to become fluorescent, which could be observed in real time under a microscope. A. baylyi also stole genes for antibiotic resistance, and when an antibiotic was added, the bacteria with the stolen resistance genes kept growing and dividing, while the others were killed.

Cooper et al. then developed a mathematical model to quantify and simulate this killing-enhanced horizontal gene transfer. The results showed that killing other bacteria made gene transfer more effective when the number of A. baylyi was high and the number of 'victims' was low – and also when they were together for a shorter period.

This work may help to explain how Acinetobacter and similar bacteria develop drug resistance so quickly. A next step will be to measure and compare gene transfer parameters in different types of bacteria. A better understanding of how, where, and when gene transfer happens, may in the future help to guide strategies to fight resistance.

https://doi.org/10.7554/eLife.25950.002

Introduction

The spread of antibiotic resistance among pathogenic microbes is a major and growing threat to public health. Gram-negative Acinetobacter spp. are a particularly worrisome example - these bacteria thrive in hospital settings, causing around 9% of nosocomial infections, particularly in the respiratory tract (Joly-Guillou, 2005). This prevalence, combined with high levels of antibiotic resistance (Antunes et al., 2014), has led the Infectious Diseases Society of America to designate Acinetobacter baumanii one of six particularly problematic multidrug-resistant (MDR) pathogens (Talbot et al., 2006) and the US Centers for Disease Control to assign it threat level ‘Serious’ (Centers for Disease Control and Prevention (CDC), 2013).

Much of the threat posed by Acinetobacter stems from its ability to acquire drug resistance via horizontal gene transfer (HGT) (Peleg et al., 2012). Acinetobacter has a remarkably high rate of HGT (Touchon et al., 2014), and many antibiotic resistance genes in clinical isolates appear to have been recently acquired from other human pathogens (Adams et al., 2008; Fournier et al., 2006; Imperi et al., 2011). Although A. baumanii can be naturally competent in vitro under some conditions (Ramirez et al., 2010; Wilharm et al., 2013), it is not understood at the population level how Acinetobacter acquires foreign genes at such high rates in real-world conditions, particularly considering that extracellular DNA is rapidly degraded or sequestered (Nielsen et al., 2007). For example, DNA lost its transforming ability with a half life of around 1 hr in soil (Nielsen et al., 2000) and 1 min in saliva (Mercer et al., 1999), and ingested DNA was unable to transform even highly competent A. baylyi within the mouse gut (Nordgård et al., 2007).

Many Streptococcus species also actively exchange genetic material in natural environments. Some of these species use quorum sensing to enhance HGT by co-regulating competence (the ability to take up extracellular DNA) with secretion of diffusible bacteriocins (small protein toxins) (Steinmoen et al., 2002). These toxins cause the release of potential donor DNA by lysing nearby sister cells (fratricide) or closely related species (sobrinocide) (Johnsborg et al., 2008; Kreth et al., 2005; Wei and Håvarstein, 2012), thereby making their genes available for uptake. However, fratricide-enhanced HGT has not been observed outside Streptococcus, and the narrow target range of bacteriocins limits potential DNA donors. Another killing mechanism, the contact-dependent type-VI secretion system (T6SS), is conserved across a much broader range of bacteria (Schwarz et al., 2010a). Recently, Vibrio cholera was shown to similarly co-regulate T6SS expression with competence, also enhancing HGT within biofilms (Borgeaud et al., 2015).

In this work, we extend the observation of killing-enhanced HGT to Acinetobacter, and we develop an experimental and modeling framework to quantify the population dynamics of this phenomenon within microbial communities. As a model system, we used Acinetobacter baylyi, which is closely related to A. baumannii (Touchon et al., 2014), because it is genetically tractable, fully sequenced, and well-studied (Elliott and Neidle, 2011). The two also share the key features of T6SS-mediated killing (Weber et al., 2013; Carruthers et al., 2013) and natural competence (Ramirez et al., 2010; Wilharm et al., 2013), and they are similar enough that standard phenotypic assays used in the clinic often fail to distinguish between them (Chen et al., 2007).

We show that A. baylyi uses its T6SS to lyse and acquire genes from neighboring E. coli cells, and that this process is frequent enough to observe functional and adaptive HGT from prey to predator cells in real time. Prey cell DNA released by predator cells is also available for uptake by other nearby, non-killing cells, highlighting the importance of polymicrobial population dynamics in HGT and the emergence of MDR. To understand the population dynamics of killing-enhanced HGT, we develop a model quantifying both neighbor killing and natural transformation. HGT parameters fit using naked DNA predict transfer of genes released via neighbor killing surprisingly well, suggesting DNA released from cell lysis in situ is readily available for uptake. Using this model, we characterize the impact of neighbor killing on HGT in a wide range of environmental conditions and evaluate potential inhibition strategies, and we experimentally confirm the key predictions. Contact-dependent neighbor killing may be a widespread contributor to HGT among gram-negative bacteria, and for Acinetobacter in particular, killing-enhanced HGT may play a key role in the emergence of clinically pervasive MDR ‘super-bug’ strains. In this context, our dynamic model should be useful for predicting and combating HGT of antibiotic resistance.

Results

Killing-enhanced horizontal gene transfer in Acinetobacter

To study the population dynamics generated by contact-dependent cell killing, we designed a custom microfluidic device (Figure 1—figure supplement 1) enabling visualization of spatially structured communities at single-cell resolution in a monolayer. We seeded the device with a simplified community consisting of predator A. baylyi strain ADP1 (Elliott and Neidle, 2011) (the predator) that kill directly adjacent, GFP-expressing Escherichia coli (the prey) (Basler et al., 2013). As expected, we observed spontaneous lysis of individual E. coli adjacent to Acinetobacter cells. Serendipitously, a few Acinetobacter cells spontaneously began expressing GFP, suggesting that they had acquired the GFP gene via HGT from DNA released by lysed E. coli.

In our initial experiments, the GFP-expressing plasmid in E. coli had a ColE1 origin of replication that does not stably replicate in Acinetobacter (Palmen et al., 1993). To better observe HGT, we constructed the broad-host plasmid pBAV1k-GFP (Bryksin and Matsumura, 2010), which can replicate in both Acinetobacter and E. coli. Expression of the GFP gene from this plasmid is repressed in E. coli by LacI, which is absent in Acinetobacter. We transformed E. coli with this plasmid and then seeded them in our microfluidic device alongside mCherry-expressing Acinetobacter (Figure 1a–d, Videos 1–6). After 3 hr, Acinetobacter had lysed a large number of E. coli cells, and multiple independent HGT events were visible within the device’s approximately 10 $^{4}$ um $^{2}$ traps (Figure 1b–d). Importantly, horizontally acquired GFP was stably maintained during cell division, giving rise to clumps of cells that were both red and green. In the movies, note that although GFP expression in E. coli was repressed by LacI, some E. coli appeared green due to incomplete repression (see also Supplementary Note 1).

Figure 1 with 1 supplement see all

Download asset Open asset

Real-time observation of functional HGT in microfluidic traps.

(**a–d**) *Acinetobacter* expressing mCherry were mixed with *E. coli* carrying LacI-repressed pBAV1k-GFP inside a microfluidic device (frames captured from Video 3, see also Supplementary Note 1). (a) t = 1:08, both *Acinetobacter* (Ab) and *E. coli* (Ec) were present, and no HGT had occurred. (**b–d**) t = 3:18, all *E. coli* in the field had been lysed, and several independent lineages of GFP-expressing *Acinetobacter* deriving from HGT were visible (circled). (**e–k**) HGT renders *Acinetobacter* resistant to antibiotic treatment (frames captured from Video 7). Kanamycin was added 11:42 after seeding the device. Still images were captured at indicated times after kanamycin addition, after several independent HGT events had already occurred (arrows in e-g). (**h–k**) Newly kanamycin-resistant *Acinetobacter* began outcompeting both *E. coli* and the sensitive parent (h), and by 13 hr after kanamyin addition (**i–k**), they dominated the environment.

https://doi.org/10.7554/eLife.25950.003

Video 1

Download asset

posterframe for video — Real-time observation of HGT from *E. coli* to *Acinetobacter.*

*E. coli* carrying pBAV1k-PLac-GFP were mixed with *Acinetobacter* expressing mCherry in a microfluidic device. Most *E. coli* were rapidly killed, and multiple HGT events were observed across several traps (circled). PLac-GFP was not fully repressed within *E. coli*, despite the presence of LacI (not found in *Acinetobacter*), so some *E. coli* expressed GFP as well. Expression of mCherry in *Acinetobacter* faded toward the end of the movies (see also Supplemental Note 1). Individual movies are physically separated traps within the same microfluidic chip.

https://doi.org/10.7554/eLife.25950.005

Video 2

Download asset

Video 3

Download asset

Video 4

Download asset

Video 5

Download asset

Video 6

Download asset

HGT of antibiotic resistance allows pathogenic bacteria to survive treatment with antibiotics that would kill the parental strain. In our experiments, the transferring plasmid, pBAV1k-GFP, contained a kanamycin resistance gene in addition to GFP. Therefore, expression of GFP should indicate a newly kanamycin-resistant strain of Acinetobacter, whose de novo appearance would demonstrate the potential clinical relevance of HGT within a microbial community. To test whether this directly observed HGT would be enough to provide a population-level selective advantage, we used our microfluidic chip to visualize functional HGT of antibiotic resistance in real time. We seeded the microfluidic device with mCherry-expressing Acinetobacter alongside E. coli carrying pBAV1k-GFP, grew them for just under 12 hr to allow E. coli lysis and HGT to occur, and then added kanamycin (Videos 7,S8). Within about 7 hr of kanamycin addition, multiple HGT events could be visibly identified by the emergence of GFP-expressing Acinetobacter (arrows in Figure 1e–g). Only those Acinetobacter that were expressing GFP, indicating horizontal transfer of kanamycin resistance, continued to grow (Figure 1h, Videos 7,8), while the parental GFP-negative Acinetobacter cells became smaller and stopped dividing. The red and green, dual-labeled Acinetobacter quickly dominated the device, lysing neighboring E. coli (dark) and pushing the non-dividing, GFP-negative Acinetobacter cells out of the trap (Figure 1i–k). To our knowledge, these experiments represent the first real-time observation of adaptive, cross-species HGT via natural competence that rapidly enables invading cells to thrive in a new niche.

Video 7

Download asset

Video 8

Download asset

The type VI secretion system (T6SS) of Vibrio cholera was recently shown to enhance HGT by promoting the release of DNA from lysed prey cells, thereby making it available for uptake (Borgeaud et al., 2015). We hypothesized that T6SS-mediated killing was similarly contributing to the high rate of HGT we observed with Acinetobacter. To test this, we quantified HGT from E. coli to Acinetobacter using bulk experiments, in which we dried small spots of liquid culture onto agar plates. These experiments involve surface-attached cells that are developing spatially-structured communities. This is a qualitatively different condition from growth in shaking culture tubes and more similar to biofilm dynamics, although we did not study true biofilms, which take longer to mature.

In these bulk experiments, we co-cultured Acinetobacter carrying genomic spectinomycin (spect) resistance and E. coli carrying both a genomic chloramphenicol (cm) resistance marker and the ‘bait’ kanamycin (kan) resistance plasmid pBAV1k. We placed the cm resistance gene in a region of the E. coli genome with minimal homology to Acinetobacter to preclude its horizontal transfer, enabling us to quantify the remaining E. coli and thereby measure killing efficiency.

We co-cultured Acinetobacter (spect) and E. coli (cm+kan), seeded together at roughly equal concentrations, on agar plates at 30 $^{\circ}$ C overnight to allow for T6SS-mediated killing and HGT. We also cultured each species alone as controls. We quantified the efficiency of E. coli lysis and HGT of kanamycin resistance by resuspending the initial spots, spotting serial dilutions of that resuspension onto selective agar plates (spect, cm+kan, and spect+kan), and counting colony-forming units (CFUs). As expected, Acinetobacter dramatically reduced E. coli numbers during co-culture (Figure 2a, cm+kan). Simultaneously, a novel spect+kan double antibiotic-resistant phenotype appeared. We picked three clones with this novel spect+kan phenotype and confirmed them to be Acinetobacter by microscopy and 16S sequencing. Transfer of the genomic cm E. coli marker to Acinetobacter was below our limit of detection (2500 CFUs in this case), as we did not recover any spect+cm resistant cells.

Figure 2 with 2 supplements see all

Download asset Open asset

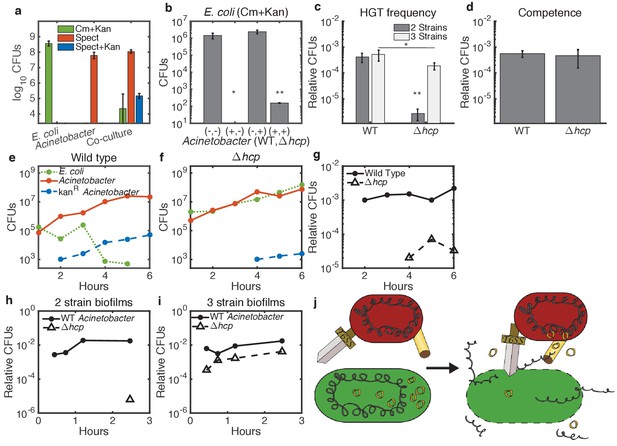
Enhancement of HGT efficiency by neighbor killing.

Communities were seeded with 2 ul droplets containing indicated strains of *Acinetobacter* with genomic spect resistance, mixed with genomically cm-resistant *E. coli* carrying the kan-resistant donor plasmid pBAV1k. Spots were incubated at 30°C overnight (a) or at 37°C for 150 min (**b–d**) or for the indicated time (**e–i**). Lower limits on y-axes are the limits of detection. (a) *E. coli* (cm+kan, green bars), *Acinetobacter* (spect, orange bars), and newly double-resistant *Acinetobacter* (spect+kan, blue bars) present after growth either alone or in co-culture. (b) Survival of *E. coli* after growth alone (-,-) or with wild type (+,-), non-killing $Δ$ *hcp* (-,+), or both (+,+) strains of *Acinetobacter*. Spots were seeded with *Acinetobacter* at optical density (OD) five and *E. coli* at OD 1. (c) HGT during the experiment shown in b, measured as the proportion of wild type (WT - spect, left bar group) or $Δ$ *hcp* (tetracycline, right bar group) CFUs that were also resistant to kan. Two-strain cultures (dark bars) correspond to the center two bars in b, while the three-strain cultures (light bars) corresponds to the rightmost bar in b. (d) Transformation efficiency of *Acinetobacter* as in c, but mixed with purified pBAV1k DNA just before spotting. (**e–g**) Time course showing CFUs of *E. coli* (dotted green), total *Acinetobacter* (solid orange) and double-resistant *Acinetobacter* (dashed blue) in two-strain cultures (wild-type *Acinetobacter* in e and $Δ$ *hcp Acinetobacter* in f). (g) The proportion of wild type (solid line) and $Δ$ *hcp* (dashed line) *Acinetobacter* cells that have acquired kan resistance during the experiment in e-f. (**h,i**) Time course showing HGT complementation by killing in trans. The proportion of double-resistant cells is shown for wild type (solid lines) and $Δ$ *hcp* (dashed lines) *Acinetobacter* grown with *E. coli* either separately in two-strain (h) or together in three-strain (i) cultures. (j) A conceptual model for killing-enhanced HGT to *Acinetobacter*. Statistical significance levels are: $* = p < 0.05$ with significance calculated using raw data, and $* * = p < 0.001$ , with significance calculated on log10-transformed data (see Materials and methods for sample sizes and statistical analysis, and see main text for exact p-values).

https://doi.org/10.7554/eLife.25950.013

Next, we confirmed the role of T6SS-mediated killing in HGT to Acinetobacter by replacing the T6SS structural gene hcp (Carruthers et al., 2013; Basler et al., 2013) with tetracycline resistance. To compare these non-killing Acinetobacter $Δ$ hcp with the wild type (WT), we incubated E. coli carrying pBAV1k on agar plates at 37°C for 150 min either alone or mixed with WT, $Δ$ hcp, or both strains of Acinetobacter, with Acinetobacter at optical density (OD) five and E. coli at OD 1 (Figure 2b,c). No E. coli were detected after co-incubation with WT Acinetobacter (Figure 2b, second bar). The limit of detection was 10 CFUs, which was significantly different from all other conditions at $p = 0.011$ (see Materials and methods for statistical tests). In contrast, survival of E. coli mixed with Acinetobacter $Δ$ hcp was not different from cultures containing E. coli alone ( $p = 0.063$ ), confirming a dramatic reduction of killing efficiency for Acinetobacter $Δ$ hcp (Figure 2b, third bar). At the same time, elimination of killing impaired HGT by about 100-fold (Figure 2c, dark bars, $p < 0.001$ ). Impaired HGT was not due to a competence defect, since WT and $Δ$ hcp Acinetobacter had equal competence for purified plasmid DNA (Figure 2d, $p = 0.57$ ). Furthermore, in a time course experiment with each Acinetobacter strain co-cultured at 37°C with approximately equal concentrations of E. coli (Figure 2e–g), we detected the spect+kan dual drug-resistant phenotype (indicating HGT) 2 hr earlier for WT cells (Figure 2e) than for non-killing $Δ$ hcp cells (Figure 2f, also compare solid to dashed lines in Figure 2g for fraction of transformed Acinetobacter cells). Presumably, the residual HGT to Acinetobacter $Δ$ hcp results from slow, but continued, spontaneous DNA release from E. coli, possibly from spontaneous cell lysis.

Together, these results and those reported for Vibrio cholera (Borgeaud et al., 2015) support a model in which the T6SS of Acinetobacter promotes HGT by killing neighboring E. coli, which then releases its DNA for subsequent uptake by Acinetobacter. If this model is correct, then WT Acinetobacter would complement HGT to the killing-defective $Δ$ hcp Acinetobacter strain in trans by lysing neighboring E. coli, thereby releasing their DNA into an extracellular pool accessible to all competent cells. To test this, we mixed the tetracycline (tet)-resistant Acinetobacter $Δ$ hcp with the spect-resistant WT Acinetobacter and co-cultured them in a ‘3-strain’ spot along with E. coli, seeding Acinetobacter at total OD = 5 and E. coli at OD = 1. Survival of E. coli in the three-strain culture was reduced by about 10⁴-fold (Figure 2b fourth bar, $p < 0.001$ ), although their survival was improved relative to E. coli mixed with only WT Acinetobacter, where E. coli were reduced below the 10 CFUs limit of detection ( $p = 0.011$ ), presumably due to the lower fraction of killing cells in the three-strain culture.

Consistent with the model, killing of E. coli by WT Acinetobacter in three-strain cultures was sufficient to increase HGT to co-cultured Acinetobacter $Δ$ hcp by about 100-fold (Figure 2c, compare two- to three-strain communities in right bar group, $p < 0.001$ ), while HGT to the WT remained unchanged relative to a two-strain community (Figure 2c, left bar group, $p = 0.68$ ). We found similar results for a time course experiment comparing HGT in two-strain (Figure 2h) and three-strain (Figure 2i) communities: co-culture with WT Acinetobacter dramatically increased HGT from E. coli to non-killing Acinetobaceter $Δ$ hcp. Interestingly, even in three-strain communities, HGT to Acinetobacter $Δ$ hcp was slightly less than HGT to the WT (Figure 2c light bars, $p < 0.014$ , and Figure 2i). This likely indicates a spatial effect - actively killing predator cells will be physically closest to the DNA released from their lysed prey. Together with experiments below showing HGT inhibition by extracellular DNase (Figure 7e), these results support a model in which the T6SS releases DNA into the extracellular environment via lysis of neighboring cells, thereby making it available for uptake by any nearby cell, but the T6SS is not directly involved in DNA uptake (Figure 2j).

To further characterize killing-enhanced HGT in Acinetobacter, we analyzed the effect of genetic context. Previous experiments have shown that A. baylyi is competent to take up and replicate plasmids with a limited set of origins of replication, they require genomic homology for efficient recombination into their genome, and both genomic and plasmid DNA can serve as a source for recombination (Palmen et al., 1993). However, those experiments were done using chemically purified, exogenously added DNA. Therefore, we experimentally confirmed them for the specific case of killing-enhanced HGT.

We co-cultured Acinetobacter on agar plates with E. coli containing each of three different bait plasmids conferring kan resistance: pBAV1k that replicates in both species, pRC03 that cannot replicate in Acinetobacter, and pRC03H - a derivative of pRC03 containing 3 kb of Acinetobacter genomic homology to promote genomic integration (de Vries and Wackernagel, 2002). Acinetobacter acquired the kan resistance gene from either pBAV1k or pRC03H, but not from pRC03 (Figure 2—figure supplement 1a). We also tested whether contact-dependent killing enables Acinetobacter to efficiently acquire genes from the E. coli genome. To do so, we created a bait plasmid containing kan resistance adjacent to 22 kb of Acinetobacter genomic homology. We transformed this plasmid into E. coli to create a plasmid bait strain, and then we integrated it into the E. coli genome to create a genomic bait strain (see Materials and methods). Acinetobacter acquired the kan resistance gene regardless of its location (Figure 2—figure supplement 1b), but HGT was approximately 100-fold lower when the kan gene was in the E. coli genome. Considering that the bait plasmid had a pBR322 origin of replication, with 10–20 plasmids per cell, the per-copy difference was only about 5- to 10-fold.

Finally, we picked three double-resistant Acinetobacter clones each that had acquired either the replicating or homology plasmid for further analysis, isolated both plasmid and genomic DNA, and confirmed that the replicating plasmid pBAV1k had transferred as an episomal unit, whereas the homology plasmid pRC03H had integrated into the genome (Figure 2—figure supplement 2). These results do not rule out additional lower frequency mechanisms, but they indicate that previous characterizations of competence using purified DNA are equally applicable to in situ HGT within spatially structured microbial communities.

Quantifying microbial population dynamics of killing-enhanced gene transfer

While killing-enhanced HGT has now been observed in multiple genera, little is known about the population dynamics of this process, its efficiency, or how that efficiency is influenced by environmental conditions. This lack of understanding is largely due to the absence of a quantitative method to measure mechanistic HGT parameters. Currently, HGT is generally quantified using the fraction of transformed CFUs or transformed CFUs per ng of DNA. This is problematic, because results depend on multiple parameters extrinsic to inherent competence, including cell concentration, DNA concentration, and incubation time. This makes results difficult to compare across experiments, conditions, strains, or even labs. A more useful approach would be to quantify transformation using variables intrinsic to the cells and the DNA, such as the DNA uptake rate and transformation efficiency per molecule of DNA. To this end, we developed a population dynamic model of spatially structured microbial communities that couples transformation via natural competence and contact-dependent killing (summarized in Box 1 and explained in more detail in the Materials and methods).

Box 1.

\begin{array}{ll} S p e c i e s \\ A_{1} = P a r e n t A c i n e t o b a c t e r \\ A_{2} = T r a n s f o r m e d A c i n e t o b a c t e r \\ A_{T} = A_{1} + A_{2} \\ E = E . c o l i \\ D = P l a s m i d D N A \\ D_{G} = G e n o m i c D N A \\ N^{*} = N u m b e r o f c e l l s (A o r E) o n t h e p e r i m e t e r o f m i c r o - c o l o n i e s \\ N_{0} = I n i t i a l n u m b e r o f c e l l s (A o r E) \\ P a r a m e t e r s \\ γ_{A, E} = G r o w t h r a t e s \\ K_{A, E} = G r o w t h s a t u r a t i o n \\ r_{k i l l} = K i l l i n g r a t e \\ K_{k i l l} = K i l l i n g s a t u r a t i o n \\ K_{E_k i l l} = P r e y k i l l i n g s a t u r a t i o n f a c t o r \\ c = D N A u p t a k e r a t e \\ K_{D N A} = D N A s a t u r a t i o n \\ ϵ = H G T e f f i c i e n c y \\ p = P l a s m i d s p e r c e l l \\ G = D_{G} p e r c e l l \\ r_{l e a k} = S p o n t a n e o u s D N A r e l e a s e r a t e \\ R e a c t i o n s \\ D + A_{-} 19 \overset{c ϵ}{\to} A_{2} \\ D + A_{1} \overset{c (1 - ϵ)}{\to} A_{1} \\ D + A_{2} \overset{c}{\to} A_{2} \\ D_{G} + A_{T} \overset{c}{\to} A_{T} \\ A_{T} + E \overset{r_{k i l l}}{\to} A_{T} + p D + G \\ E \overset{r_{l e a k}}{\to} E + p D + G \\ E q u a t i o n s \\ \begin{array}{ll} \frac{d A_{1}}{d t} = γ_{A} A_{1} - c ϵ \frac{A_{1} D}{K_{D N A} + D + D_{G}} \\ \frac{d A_{2}}{d t} = γ_{A} A_{2} + c ϵ \frac{A_{1} D}{K_{D N A} + D + D_{G}} \\ \frac{d E}{d t} = γ_{E} E - r_{k i l l} \frac{A_{T}^{*} E^{*}}{K_{k i l l} + A_{T}^{*} + K_{E_k i l l} E^{*}} \\ \frac{d D}{d t} = - c \frac{A_{T} D}{K_{D N A} + D + D_{G}} + p (r_{k i l l} \frac{A_{T}^{*} E^{*}}{K_{k i l l} + A_{T}^{*} + K_{E_k i l l} E^{*}} + r_{l e a k} E) \\ \frac{d D_{G}}{d t} = - c \frac{A_{T} D_{G}}{K_{D N A} + D + D_{G}} + G (r_{k i l l} \frac{A_{T}^{*} E^{*}}{K_{k i l l} + A_{T}^{*} + K_{E_k i l l} E^{*}} + r_{l e a k} E) \end{array}} (1 - \frac{A_{T}}{K_{A}}) (1 - \frac{E}{K_{E}}) \\ N^{*} = N (\frac{1}{1 + {(\frac{N}{5 N_{0}})}^{2}}) + π N_{0} (\sqrt{\frac{N}{N_{0}}} - 1) (\frac{{(\frac{N}{5 N_{0}})}^{2}}{1 + {(\frac{N}{5 N_{0}})}^{2}}) \end{array}

https://doi.org/10.7554/eLife.25950.016

The model parameters pertaining to growth, transformation, and killing can each be measured sequentially in simplified conditions (Figure 3, Figure 3—figure supplements 1–3, Table 1). For all parameter fitting, we incubated cells in spots on agar plates, the same condition used to measure HGT in dual-species communities (see Materials and methods). First, we measured growth parameters for each species separately (Figure 3—figure supplements 1–2, and see Materials and methods). Second, we fit the natural transformation parameters using data obtained by mixing Acinetobacter with known concentrations of the genomically integrating kan resistance plasmid pRC03H-2S, derived from pRC03H used earlier, with higher efficiency integration via fully homolgous recombination (HR) (Palmen et al., 1993), rather than homology-facilitated illegitimate recombination (de Vries and Wackernagel, 2002) as in Figure 2, see Materials and methods. We incubated the cell-DNA mixtures on agar plates, and then we counted the number of cells that had acquired kan resistance. To obtain values for the HGT parameters, we simultaneously fit data from time courses with either limiting (Figure 3a) or saturating (Figure 3b) DNA, and from DNA dilution series with cells harvested at different time points (Figure 3c). Third, we fit parameters for T6SS-mediated killing by mixing different concentrations of E. coli and Acinetobacter, incubating them together on agar plates, and counting the cells of each type that were present upon harvesting. As with DNA uptake, we fit killing parameters simultaneously for several time courses (Figure 3d–i and Figure 3—figure supplement 3) and dilution series (Figure 3j). Finally, to determine the ‘leak’ rate of DNA from E. coli, we measured HGT to non-killing Acinetobacter $Δ$ hcp and found the best fit for $r_{l e a k}$ , with the killing rate $r_{k i l l}$ set to 0 in the model (Figure 3k,l). The leak rate may be due to spontaneous E. coli cell death, but we do not include spontaneous death in the differential equation for E. coli because it is inherently included when measuring the bulk growth rate $γ_{E}$ .

Figure 3 with 5 supplements see all

Download asset Open asset

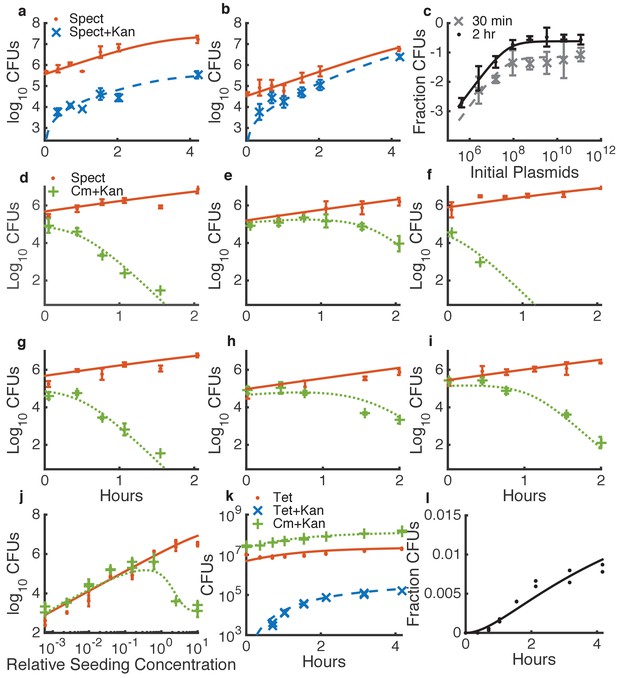
Determining quantitative parameters for natural transformation and contact-dependent neighbor killing.

Error bars indicate measurement standard deviations of experimental data for a single spot harvested from an agar plate, and lines represent simulations using the shared best fit parameters (Table 1). Note all y-axes are log scale except for l. Orange lines indicate *Acinetobacter* (spect-, or in k, tet-resistant), blue lines indicate transformed *Acinetobacter* (additionally kan-resistant), green lines indicate *E. coli* (cm-resistant), and black or grey lines indicate the fraction of *Acinetobacter* that have been transformed. (**a–c**) Transformation of *Acinetobacter* via homologous recombination of exogenous DNA (pRC03H-2S) added just before spotting the cells. (**a,b**) Time courses of transformation of *Acinetobacter* mixed with limiting (a) or saturating (b) plasmid DNA. (c) Fraction of *Acinetobacter* transformed by a DNA dilution series, harvested after either 30 min or 2 hr. (**d–j**) Measuring killing of *E. coli* by *Acinetobacter*. (**d–i**) A selection of independent time courses seeded with varying densities of *E. coli* and *Acinetobacter* (see also Figure 3—figure supplement 3). (j) A contact-dependent killing assay using a dilution series of *Acinetobacter* mixed with *E. coli* at the same ratio, but varying total concentration. (**k,l**) Time series of the number of CFUs (k) and fraction of transformed killing-deficient *Acinetobacter* $Δ$ *hcp* (l) after growth with *E. coli* on agar plates, used to fit DNA ‘leakage’.

https://doi.org/10.7554/eLife.25950.017

Table 1

Microbial community growth, killing, and horizontal gene transfer parameters.

See Materials and methods and main text for details.

https://doi.org/10.7554/eLife.25950.023

Parameter	Description	Value	Source
$γ$ _A	Acinetobacter growth rate	1.34 hr^∧−1	Figure 3—figure supplement 1
$γ$ _E	E. coli growth rate	1.51 hr^-1	Figure 3—figure supplement 2
K_A	Acinetobacter growthsaturation	2.6 x 10⁷	Figure 3—figure supplement 1
K_E	E. coli growth saturation	1.7 x 10⁸	Figure 3—figure supplement 2
r_kill	Killing rate	15 hr^-1	Figure 3d–j
K_kill	Killing saturation	9.3 x 10⁵	Figure 3d–j
K_{E_kill}	Killing saturationprey factor	17	Figure 3d–j
r_leak	Spontaneous E. colilysis rate	9.9 x 10^-4 hr^-1	Figure 3k,l
c	DNA uptake rate	60 bp/s	(Mao and Lu, 2016)
K_DNA	DNA uptake saturation	6.7 x 10⁸ kb	Figure 3a–c
ε	Plasmid transformationefficiency	6.7 x 10^-3	Figure 3a–c
p	Plasmids per E. colicell	162	See Materials and methods
G	Plasmid equivalents ofgenomic DNA per cell	506	= 3.6x10⁶ /9093

Using this experimentally parameterized model, we asked how well the transformation parameters that we measured using purified DNA would predict killing-enhanced HGT in dual-species microbial communities. The model closely matched experimental results, suggesting that DNA released from cells in situ is equivalently available for uptake as DNA purified in vitro (Figure 4). Note that counting CFUs in a spot on an agar plate is a destructive measurement, as it requires harvesting and resuspending the entire spot, so successive data points in a time course are actually from different individual spots that were seeded at the same time from the same cell mixture.

Figure 4

Download asset Open asset

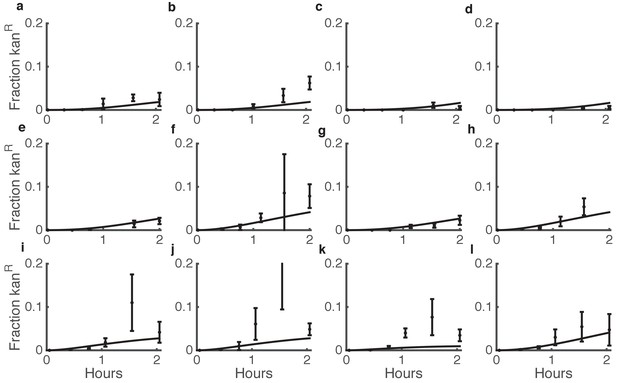
Comparison between predicted and actual killing-enhanced HGT in microbial communities.

Plotted is the fraction of *Acinetobacter* that have become double antibiotic-resistant due to HGT of kan resistance from *E. coli*. Data are from the same experiments as Figure 3d–i and Figure 3—figure supplement 3, which shows the total CFUs. Solid lines are model predictions, and error bars are standard deviations of experimental results. Each row of plots is from a different day, and plots within a row are for varying seeding densities of the two species (shown in the Figure Supplement at time 0).

https://doi.org/10.7554/eLife.25950.024

Exploration of environmental impacts on HGT

Experimental measurement of HGT is time-consuming and labor-intensive, limiting the study of how it is affected by environmental conditions. However, our experimentally parameterized, mechanistic model allows us to simulate a much wider variety of conditions. This allows us to predict the most conducive conditions for HGT, the conditions in which contact-dependent killing plays an important role, and what strategies are most likely to inhibit HGT, and thus the spread of MDR.

First, to determine the effect of bacterial seeding density on the fraction of transformed Acinetobacter, we simulated surfaces seeded with varying densities of the two species and incubated for two hours. Wild-type Acinetobacter had the highest transformation frequency when both species were seeded at higher densities, allowing maximal contact (Figure 5a). This can be understood by considering that the killing rate, and thus DNA release, depends on the product of the cell counts of both species (Box 1), so the most DNA is released when both species are at high density. In contrast, the transformation frequency of killing-deficient Acinetobacter was mainly dependent on only the E. coli seeding density (Figure 5b), because DNA release from spontaneous lysis depends only on the number of E. coli.

Figure 5

Download asset Open asset

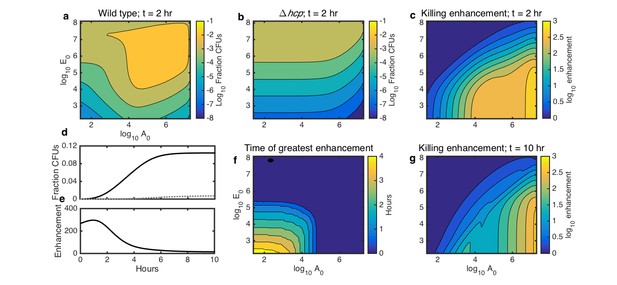
Simulations showing the effects of initial species density and interaction time on HGT, and the degree to which contact-dependent killing enhances HGT.

The axes in a-c,f,g indicate the initial cell count ( $A_{0}$ and $E_{0}$ ) relative to the carrying capacity ( $K_{A}$ and $K_{E}$ ) for *Acinetobacter* and *E. coli*, respectively. Contour levels indicate 10-fold changes in a,b, two-fold changes in c,g, and 30 min changes in f. (a) Simulated HGT frequency to wild-type *Acinetobacter* grown with *E. coli* at varying seeding densities for 2 hr. (b) Simulated HGT frequency as in a, but for killing-deficient *Acinetobacter* $Δ$ *hcp*. (c) The HGT enhancement factor provided by killing depending on seeding density; that is, the ratio of HGT to the wild type (a) divided by HGT to the killing mutant (b). (d) HGT frequency over time for agar surfaces seeded with both species at 10⁻³ of their respective carrying capacity. Solid line: wild type *Acinetobacter*, dotted gray line: killing mutant $Δ$ *hcp Acinetobacter*. (e) HGT enhancement factor provided by killing over time for the simulation in d. (f) Incubation time at which killing provides the greatest HGT enhancement, for varying seeding densities. (g) HGT enhancement as in c, but after 10 hr, by which time even sparsely seeded communities had approached simulated growth saturation.

https://doi.org/10.7554/eLife.25950.025

From these results, we calculated how the relative importance of killing for HGT depends on seeding density. We defined the degree to which killing of E. coli increases HGT to Acinetobacter - that is, the enhancement factor - as the ratio of HGT to WT Acinetobacter divided by HGT to the killing mutant Acinetobacter in the same condition. This killing enhancement was greatest when Acinetobacter was seeded at high density and E. coli at low density, in which case killing enhanced HGT by nearly 1000-fold (Figure 5c).

Next, we used our model to explore how killing-enhanced HGT interacts with incubation time. We simulated a surface seeded with both Acinetobacter and E. coli at 10⁻³ of their respective carrying capacities and calculated HGT to either killing or non-killing Acinetobacter over time. HGT increased with time for both the WT and the killing mutant Acinetobacter (Figure 5d), but the enhancement of HGT provided by killing was greatest within the first few hours (Figure 5e). Varying the initial seeding density (Figure 5f) revealed that at higher densities, the enhancement factor was greatest immediately after seeding, whereas at lower seeding densities, the enhancement factor did not peak until up to 4 hr after seeding. Killing still enhanced HGT by more than 10-fold for a wide range of seeding densities even after 10 hr (Figure 5g), which is long enough to reach the carrying capacity. Overall, these results show that the degree to which contact-dependent killing increases HGT to predatory bacteria is influenced by the total initial cell density, the ratio of the two species, and the length of time that the community has to grow.

In the case of transferring antibiotic resistance genes, it would be desirable to inhibit HGT. Therefore, we used our model to explore how well killing-enhanced HGT could be blocked by two potential environmental perturbations: either degradation by DNase or competitive inhibition with added DNA. First, we determined the DNA degradation rate and amount of competing DNA that would be required to inhibit HGT. We simulated surfaces seeded with both species at 10⁻³ of their respective carrying capacities and grown for 2 hr. At this seeding density, DNase was effective when it reduced DNA half life to less than about 2–3 min (Figure 6a), and competing DNA was effective at about 10⁹ kb or greater (Figure 6e).

Figure 6

Download asset Open asset

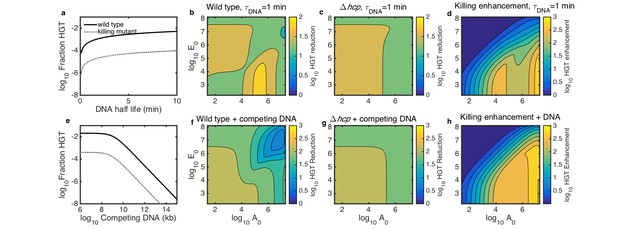
Simulated inhibition of HGT by DNase (**a–d**) or competing DNA (**e–h**) in simulated microbial communities seeded with both *Acinetobacter* and *E. coli* at 10⁻³ of their respective carrying capacities and grown for 2 hr.

All contour levels indicate two-fold differences, and all axis and colorbar scales are log10, except DNA half life in a. (a) Fraction of wild type (solid line) and non-killing (dotted grey line) *Acinetobacter* that have undergone HGT as a function of DNA half life in the extracellular space. (**b,c**) Fraction of wild type (b) and killing mutant (c) *Acinetobacter* that have undergone HGT with the half life of extracellular DNA set to 1 min, for varying initial cell counts. The axes indicate the initial cell count $A_{0}$ and $E_{0}$ for *Acinetobacter* and *E. coli*, respectively. (d) The degree to which killing increases HGT as a function of seeding density, with DNA half life set to 1 min; i.e., the ratio of HGT to the wild type (b) divided by HGT to the killing mutant (c). (e) HGT efficiency as in a, but with the addition of varying amounts of competing DNA rather than a finite DNA lifetime. (**f,g**) Efficiency of HGT as in b,c, but with the addition of 10¹¹ kb of competing DNA at time 0 rather than DNA decay. (h) Enhancement of HGT provided by killing, as in d, but with 10¹¹ kb of competing DNA at time 0 and no DNA degradation.

https://doi.org/10.7554/eLife.25950.026

We then explored how well each condition would inhibit HGT in microbial communities seeded at different cell densities and species ratios. We simulated surfaces seeded with varying numbers of E. coli mixed with either killing or non-killing Acinetobacter, either with DNA half life fixed to 1 min (Figure 6b–d) or with 10¹¹ kb of competing DNA added at time 0 (Figure 6f–h). To quantify the efficacy of each inhibition strategy, we calculated the HGT reduction factor, defined as the ratio of HGT without inhibition to HGT with inhibition. The HGT reduction factor depended on seeding density to varying degrees for both WT and non-killing ( $Δ$ hcp) Acinetobacter for both strategies - degradation with DNAse (Figure 6b,c) and competitive inhibition (Figure 6f,g). Our model had previously predicted contact-dependent killing-enhanced HGT to WT Acinetobacter to occur most frequently when both species begin at high density (see Figure 5a), so that may be the most important condition in which to inhibit HGT. Importantly, our model predicted DNAse to remain effective even at high initial cell density (Figure 6b), whereas competing DNA was predicted to dramatically lose efficacy in that condition (Figure 6f). This suggests that DNase may better inhibit HGT in dense communities such as biofilms than competitive inhibition with exogenous DNA. Regardless of the inhibition strategy, killing consistently increased HGT to the wild type relative to the killing mutant, even in the presence of the inhibitors (Figure 6d,h).

Finally, we experimentally tested the predictions from our model, focusing on cases with relatively high cell numbers where HGT events are detectable. With respect to seeding density, the model predicted experimental results quite well (see Figure 5a–c). For WT Acinetobacter mixed with E. coli carrying pRC03H-2S, HGT was greatest when both species were at high initial density, and it decreased along with seeding counts of either species (Figure 7a). In contrast, for non-killing Acinetobacter $Δ$ hcp, the HGT frequency was mainly dependent on the initial number of E. coli (Figure 7b). The HGT enhancement factor was greatest when the predator was seeded at high density, while the prey was at low density (Figure 7c). Also consistent with the model, the HGT enhancement decreased for all seeding densities after overnight growth (compare Figure 7c to Figure 7d).

Figure 7

Download asset Open asset

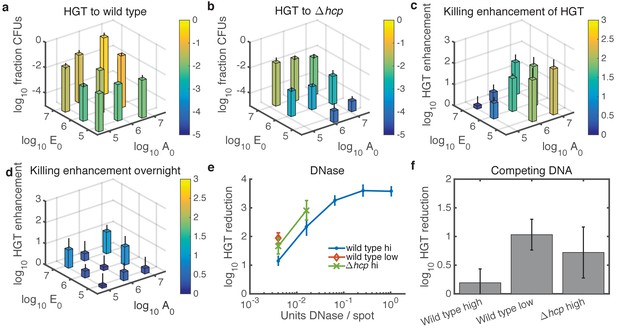
Experimental tests of model predictions.

(**a–d**) Dependence of HGT on cell seeding density. a HGT frequency to wild-type *Acinetobacter* spotted together with *E. coli* at the indicated cell counts ( $A_{0}$ and $E_{0}$ , respectively) and grown for 2 hr at 37°C. b HGT frequency as in a, but for *Acinetobacter* $Δ$ *hcp*. The missing bar at the bottom indicates data below detection. (c) HGT enhancment provided by killing; i.e., the ratio of data in a to that in (b) . (d) Same as in c but after overnight growth. (e) Reduction of HGT to wild type (blue dot) or $Δ$ *hcp* (green X) *Acinetobacter* seeded with *E. coli* at equal high density (approximately 3x10⁶ CFUs each), or to wild type with both species seeded at low density (3x10⁴ CFUs each, orange diamond), all mixed with the indicated amount of DNase before spotting and grown for 2 hr. Missing data points indicate HGT was below detection (5 CFUs), and HGT to *Acinetobacter* $Δ$ *hcp* was below detection (5 CFUs) for all tested levels of DNase. Reduction is relative to the same experiment with no DNase added. (f) HGT reduction as in e, but adding 10¹¹ kb of competing DNA before spotting. Error bars indicate the propagated standard error.

https://doi.org/10.7554/eLife.25950.027

Units of DNase are not easily converted to DNA half life on an agar substrate, so we tested a four-fold DNase dilution series (Figure 7e) with the two species seeded at approximately equal numbers. As predicted, DNase effectively inhibited HGT even to the wild type at high seeding density (approximately 3 × 10⁶ CFUs of each species). When cells were seeded at 100-fold lower density, or Acinetobacter was killing-deficient, DNase reduced HGT to an even greater extent. All tested levels of DNase reduced HGT below detection (5 CFUs) for Acinetobacter $Δ$ hcp seeded at the lower density.

In contrast, 10¹¹ kb of competing DNA was ineffective against HGT to WT Acinetobacter at high seeding density (Figure 7f). At 100-fold lower seeding density, or when Acinetobacter was unable to kill E. coli, competing DNA did inhibit HGT. The standard error for these HGT reductions appears relatively large because calculating HGT reduction requires four measurements - total CFUs and transformed CFUs for each of two conditions - and the Poisson-distributed measurement error compounds with each additional measurement (see Materials and methods). Nevertheless, the results were repeatable over 3 separate days, and the figure shows their average.

While our model predicted the key qualitative features of cell seeding density, extracellular DNase, and competing DNA, there were some discrepancies. In particular, HGT inhibition by DNase leveled off above 0.1 units per spot, suggesting a sub-population of Acinetobacter with privileged access to released DNA, and inhibition by competing DNA was less than predicted in all conditions. This may be a result of the fact that our model does not capture spatial heterogeneity in DNA concentrations. Lysed E. coli release DNA at a locally high concentration, which may provide privileged access for directly adjacent Acinetobacter. The discrepancies may also reflect the technical difficulty of delivering molecules evenly to real-world communities, which would be exacerbated for mature biofilms.

Discussion

Humanity’s dwindling arsenal of antibiotics is a significant and growing concern. This threat stems from pathogens such as Acinetobacter that are able to rapidly accumulate multiple resistance genes, which can make them nearly impossible to treat. High-throughput sequencing has revealed evidence for widespread horizontal gene transfer, but unlike conjugation and phage transduction, we still know relatively little about the microbial dynamics underlying HGT via natural competence (Mao and Lu, 2016; Johnsborg et al., 2007). It has been observed qualitatively that killing of nearby cells - via fratricide (Kreth et al., 2005; Wei and Håvarstein, 2012), sobrinocide (Johnsborg et al., 2008), or contact-dependent killing (Borgeaud et al., 2015) - can enhance HGT, but a lack of quantitative methods has precluded a fuller understanding of the importance of microbial combat in the horizontal spread of genes.

In this paper, we showed that contact-dependent killing by Acinetobacter can increase HGT rates from E. coli by up to 3 orders of magnitude, making it frequent enough to observe multiple events in real time within microfluidic chips. By subsequently adding kanamycin to our chips, we observed functionally adaptive emergence of newly drug-resistant bacteria in situ. Significantly, we also showed that killing by one strain in a spatially-structured community makes DNA available for uptake by nearby, non-killing cells. This highlights the role that polymicrobial interactions can play in facilitating HGT. We then developed population dynamic models for both natural transformation and contact-dependent killing, and we fit them to experimental data to obtain biologically relevant parameters. Interestingly, DNA uptake and transformation parameters fit using purified plasmid DNA accurately predicted HGT by DNA released in situ. This was not obvious a priori, particularly given that previous experiments have shown extracellular DNA to rapidly lose its transforming ability in real-world conditions (Mercer et al., 1999; Nielsen et al., 2000; Nielsen et al., 2007; Nordgård et al., 2007).

For contact-dependent killing, predation can occur only at the perimeter of micro-colonies, where there is contact between predator and prey cells (Schwarz et al., 2010a; Borenstein et al., 2015; Hood et al., 2010; Schwarz et al., 2010b; MacIntyre et al., 2010; LeRoux et al., 2012) (see also Supplemental Videos 9–12). In our model, we derived an approximation for the number of cells at the perimeter of their respective colonies, N^* (see Box 1 and Materials and methods). This allowed us to approximately account for the difference between interior and exterior prey cells, while maintaining the simplicity of a system of ordinary differential equations. This use of N^* to represent perimeter cells yielded a slightly better optimal fit to our data than assuming all cells are equally vulnerable, but the difference was not dramatic. Using all cells N rather than perimeter cells N^*, the optimal fit was $r_{k i l l} = 17$ hr⁻¹, $K_{k i l l} = 1.3$ x $10^{6}$ , $K_{E_k i l l} = 21$ (compare to values in Table 1), and the best fit sum of squares of residuals increased from 87.0 to 93.9 (calculated using log10-transformed data). See also Figure 3—figure supplement 4 for a comparison of simulations using the same parameters, fit using the restriction of killing to perimeter cells and shown in Table 1, simulated with and without that restriction. The difference between the total number of cells and the number of perimeter cells only becomes significant when the population has grown much greater than the initial cell number (compare solid blue to dashed orange lines in Figure 3—figure supplement 5), so we would expect it to be more important in longer time courses. The model presented here can be modified for the case when killing is mediated by diffusible molecules, where there is no distinction between interior and exterior cells in a micro-colony, by simply replacing N^* with N.

Video 9

Download asset

Video 10

Download asset

Video 11

Download asset

Video 12

Download asset

Using our experimentally parameterized model, we characterized contact-dependent killing-enhanced HGT in a wide range of simulated conditions. Our model revealed that killing is most important for HGT when the prey is at low density, the predator is at high density, and the interaction time is short (Figure 5c,f), which was confirmed by experimental data (Figure 7a–d). Killing is less important for HGT when the prey outnumbers the predator, because enough prey DNA is released by spontaneous lysis that the additional DNA released by killing no longer provides much advantage. Similarly, killing provides less HGT enhancement when the interaction time is longer, because killing Acinetobacter deplete their donor DNA source by killing neighboring prey E. coli, whereas the non-killing mutants have a slower, but exponentially growing, source of DNA from spontaneously lysing E. coli.

Interestingly, this seeding ratio at which contact-dependent killing most enhances HGT - when the predator outnumbers the prey - is the same condition in which it provides the strongest competitive advantage in terms of cell growth (Borenstein et al., 2015). High predator cell density is also the condition that induces fratricide-mediated HGT in Streptococci (Steinmoen et al., 2002) and simultaneously induces both T6SS expression and competence in V. cholera (Borgeaud et al., 2015). However, T6SS regulation does not always depend on high cell density, and it can be quite complex and varied, even within strains of the same species, likely reflecting the wide range of ecological contexts and functions performed by the T6SS (Miyata et al., 2013; Bernard et al., 2010; Weber et al., 2013; Weber et al., 2015). Given that the only demonstrated advantages are at high cell density, it remains an open question what, if any, selective advantages the T6SS may provide at lower cell density. While T6SS regulation in A. baylyi has not been extensively characterized with respect to cell density (Weber et al., 2016), it is active and functional in standard in vitro conditions (Weber et al., 2013; Basler et al., 2013), and we observed T6SS-mediated killing of E. coli at all times in the Supplemental Videos 1–6.

We also used our model to evaluate the effect of two conditions that may inhibit HGT: addition of either competing DNA or DNAse. Although our model predicted neither condition would eliminated the HGT enhancement provided by killing in our model, both strategies were predicted to reduce HGT when at realistic levels. DNA degradation began to reduce HGT when DNA half life was less than 2–3 min (Figure 6a), which is just longer than the half life of free DNA in saliva, about 1 min (Mercer et al., 1999). Competing DNA began to reduce HGT at about 10⁹ kb or greater (Figure 6e), and given that our agar spots could support 10⁷–10⁸ cells, that would be 10–100 kb of extracellular DNA per cell at carrying capacity.

Importantly, DNase was predicted to be more effective than competing DNA at high cell seeding densities, which is the condition where contact-dependent killing-enhanced HGT is most efficient. Our experimental results supported this, showing that DNase can reduce HGT to wild type Acinetobacter by nearly 10⁴-fold even at high seeding densities, whereas 10¹¹ kb of competing DNA was ineffective at high cell density. The reduced efficacy of competing DNA in this condition is likely because the high initial killing rate releases a large amount of prey DNA at once, overcoming competitive inhibition.

Interestingly, competing DNA was nearly 10-fold less effective than predicted, which may reflect its physical exclusion from dense microbial communities, or the fact that our model does not reflect the spatial heterogeneity of DNA released from lysing E. coli. The potential importance of non-isotropic DNA concentration is also suggested by the observation that there appears to be a small sub-population of Acinetobacter with access to prey cell DNA protected from DNase (Figure 7e), and the observation that even in three-strain communities, HGT to Acinetobacter $Δ$ hcp remains slightly lower than HGT to WT cells (Figure 2c,i). Spatial dependence of DNA concentration would be a valuable limitation to address in future work; nevertheless, the qualitative trends predicted by our model show its usefulness in guiding experiments and intuition. Additionally, the observation that contact-dependent killing appears to provide a sub-population of cells with privileged access to DNA that is protected from DNase may help explain how HGT can occur so frequently in real-world environments where DNA is quickly degraded.

While we used A. baylyi as a model for the more clinically threatening A. baumannii, the two are closely enough related that they are difficult to distinguish with standard phenotypic tests used in the clinic (Chen et al., 2007). Indeed, careful re-examination of clinical isolates recently revealed that A. baylyi can also opportunistically infect humans, including case clusters in hospitals (Chen et al., 2008). It was a clinical A. baylyi isolate that contained the first blaSIM-1 carbapenemase reported in China (Zhou et al., 2011), and the difficulty of distinguishing between the two suggests that A. baylyi may in fact be causing additional infections that are either misidentified as A. baumannii or identified nonspecifically as Acinetobacter (Chen et al., 2007, 2008). Perhaps more importantly, A. baylyi may serve as an easily sampled reservoir of genetic diversity for A. baumannii, due to the extremely high transformability of A. baylyi coupled to the ease with which Acinetobacter species exchange DNA. For example, another carbapenemase gene, blaOXA23, has been found in multiple Acinetobacter species isolated from both humans and animals, including both A. baumannii and A. baylyi (Smet et al., 2012; Nigro and Hall, 2016).

In addition to helping to explain, predict, and combat the rapid spread of multi drug-resistance, particularly among Acinetobacter, the population dynamics revealed here are likely important in the microbiome and microbial evolution more broadly. Both the T6SS (Schwarz et al., 2010a) and natural competence (Johnsborg et al., 2007) are widespread among gram-negative bacteria, and both competence and other neighbor killing mechanisms are found in both gram-negatives and gram-positives. Therefore, our results are likely broadly generalizable and may contribute to understanding the known increase of HGT within biofilms (Madsen et al., 2012). The method presented here for quantifying natural competence with standardized parameters may also help researchers address other outstanding questions about microbial evolution (Vos et al., 2015). In the light of a growing threat from antibiotic resistance, the quantitative methods presented here should greatly aid study of the mechanisms by which bacteria swap genes, shortcut evolution, and outsmart our drugs.

Materials and methods

Cell growth, strains, plasmids, CFU counting, and HGT characterization

View detailed protocol

We obtained Acinetobacter baylyi sp. ADP1 from the ATCC and used a lab strain of E. coli MG1655. We inserted spectinomycin resistance and mCherry into a putative prophage region of the Acinetobacter genome, as described previously (Murin et al., 2012). To give E. coli genomic chloramphenicol resistance, we first inserted a short ‘landing pad’ from pTKS/CS, including tetracycline resistance, into a neutral site on the genome (between atpI and gidB), using the recombineering helper plasmid pTKRED (Kuhlman and Cox, 2010). We then replaced this landing pad with the chloramphenicol marker from donor plasmid pTKIP-cat, as described previously (Kuhlman and Cox, 2010). We cured the cells of pTKRED by growing them overnight with saturating IPTG and arabinose and then screening for spectinomycin sensitivity.

For a replicating bait plasmid, we used the broad-host plasmid pBAV1k (Bryksin and Matsumura, 2010), to which we introduced a GFP gene. We derived our genomically integrating plasmids from and the ColE1 origin plasmid pRC03, which replicates in E. coli but not in Acinetobacter. To add Acinetobacter homology to pRC03, we inserted 7 kb of Acinetobacter genomic sequence (covering genes ACIAD3424 to ACIAD3429) adjacent to the kanamycin marker, yielding pRC03H. To make a higher efficiency integrating plasmid with genomic homology on both sides of the marker (pRC03H-2S), we moved the kanamycin marker into the middle of the Acinetobacter sequence.

To compare acquisition of plasmid vs. genomic resistance genes, we inserted 22 kb of Acinetobacter genomic sequence (covering genes ACIAD2681 to ACIAD2697) into the donor plasmid pTKIP-neo and transformed this into the landing pad-containing strain described above. We then used the helper plasmid pTKRED to integrate this sequence in place of the landing pad and finally cured the integrants of pTKRED (Kuhlman and Cox, 2010).

We constructed the the non-killing Acinetobacter $Δ$ hcp by first fusing the tetracycline resistance marker from pTKS/CS to approximately 400 bp homology arms amplified from either side of hcp (ACIAD2689) in the A. baylyi genome.

For microfluidic experiments, we seeded a custom microfluidic device (Figure 1—figure supplement 1) with both Acinetobacter and E. coli and imaged it on a Nikon TI microscope with an incubated stage set to 37°C and a gravity-driven nutrient flow (LB broth) (Ferry et al., 2011). We imaged the experiment shown in Figure 1a–d with a 40x objective and that shown in Figure 1e–k with a 60x objective. Note that microfluidics with A. baylyi are extremely challenging technically, due to its propensity to adhere to and clog the feeding channels (see the horizontal channels at the tops and bottoms of Videos 1-S6).

We grew spatially structured communities on LB agar plates (1.5%) in an incubator at 30 $^{\circ}$ C overnight or 37°C for the indicated time. We seeded the communities with 2 ul spots of cell culture, being careful not to introduce bubbles, which can spray aerosolized cells across the plates when they burst. Before seeding, we grew the cells overnight, resuspended them at 1:50 into fresh media, grew them again for 2–3 hr, washed them, and then resuspended again in fresh media. For time-course experiments, the initial cell density can be seen from the CFUs at time 0.

We harvested spots by cutting out spots with a razor blade and resuspending them in 500 ul of PBS buffer. To count CFUs, we made serial ten-fold dilutions of the resuspended cells, spotted 2 ul of each dilution onto selective plates, and counted colonies after incubation overnight. The limit of detetion by this method is $\frac{500}{2} = 250$ CFUs. To lower our limit of detection (Figure 2b bars 2 and 4, Figure 2c bar 3), we also spread 50 ul of resuspended cells across selective plates, achieving a theoretical limit of detection of 10 CFUs.

To characterize the genomic result of HGT, we picked three clones each of Acinetobacter that had acquired kan resistance via either pBAV1k or pRC03H. We isolated any plasmid DNA from these clones and from the bait E. coli carrying pBAV1k using a standard miniprep kit (Qiagen, Hilden, Germany), digested with SspI, which should cut twice, and ran the result on a gel (Figure 2—figure supplement 2a). To verify genomic integration of the kan gene from pRC03H, we isolated genomic DNA and performed inverse PCR from the kan gene. In particular, we digested the genomic DNA with SalI, diluted to 2 ng/ul, and used T4 DNA ligase to circularize the resulting fragments. Next, we performed PCR using primers pointing outward from the kan gene to amplify the circularized, surrounding genomic region. All three clones had the same PCR pattern (Figure 2—figure supplement 2b), and sequencing confirmed that the surrounding region was Acinetobacter genome. All enzymes used for cloning were from New England Biolabs (Ipswitch, Massachusetts).

When DNA or DNase was added to the cells, we added it to the cell mixture on ice just before spotting. We used PureLink DNase, resuspended in water at the recommended concentration (2.7 units/ul), frozen in aliquots, and diluted to the desired concentration when needed. For competitive inhibition, we used a high-copy, ampicillin resistance plasmid with a ColE1 origin of replication, which cannot replicate in Acinetobacter and does not provide resistance to any of the antibiotics in our experiments (pBest, Promega, Madison, Wisconsin). We grew this in E. coli, extracted it with a maxiprep kit, and concentrated it using ethanol precipitation.

Statistical analysis

Request a detailed protocol

Error bars in Figure 2b–d indicate the standard deviations of measurements pooled across two culture replicates, each with three measurement replicates. Culture replicates refer to distinct spots seeded with the same cell mixture at the same time. Each resuspended culture was then serially diluted, and these 10-fold dilutions were themselves spotted onto selective plates to count CFUs (measurement spots), as described above. However, the CFUs in each of these measurement spots are expected to be Poisson-distributed, so we spotted each dilution three times, to obtain measurement replicates. Error bars in Figure 2a are for three measurement replicates of one culture each. Where data was less than 250 CFUs, only one (larger volume) measurement replicate was counted for each community, as described above. To calculate the pooled variance of HGT frequency across both types of replicates, we followed the following procedure.

For each selective antibiotic condition a and each culture replicate c, calculate the sample variance of the CFU counts x across measurement replicates, $s_{a, c}^{2}$ .
For each culture replicate c, calculate the variance of the HGT frequency $f_{c} = \frac{x_{2, c}}{x_{1, c}}$ using the error propagation formula $s_{c}^{2} = f_{c}^{2} (s_{2, c}^{2} + s_{1, c}^{2})$ .
Calculate the pooled variance across all culture replicates as $s^{2} = \frac{\sum_{c} [(n_{c} - 1) s_{c}^{2} + n_{c} {(f_{c} - f)}^{2}]}{(\sum_{c} n_{c}) - 1}$ , where the sum is over all culture replicates, $n_{c}$ is the number of measurement replicates for culture replicate c, and f indicates the overall mean of the HGT frequency across culture replicates.

To calculate statistical significance, we performed analysis of variance (ANOVA). In particular, we calculated p-values with the MATLAB function multcompare, using the condition means and variances calculated above. Spotting serial dilutions to count CFUs measures data on a log base 10 scale, so to compare data separated by more than one order of magnitude, we first calculated the log base 10 value of each data point (Figure 2b, survival of E. coli with both strains of Acinetobacter, Figure 2c, HGT to Acinetobacter $Δ$ hcp in 2-strain communities). To test for significance where data was below the limit of detection (Figure 2b, survival of E. coli with WT Acinetobacter), we used one-tailed t-tests to determine whether each of the other conditions were significantly greater than that limit of detection (not log-transformed), reporting the largest p-value.

Modeling HGT in spatially structured communities

Request a detailed protocol

In our model (Box 1, Figure 2j, Table 1), both E. coli and Acinetobacter grow according to the logistic growth equation $\frac{d N}{d t} = γ_{N} N (1 - \frac{N}{K_{N}})$ , where $N$ is the number of cells of one species, $γ_{N}$ is the growth rate, and $K_{N}$ is the carrying capacity for 2 ul spots, and we multiplied the two saturation terms $(1 - \frac{N}{K_{N}})$ to couple the growth saturation of the two species. Acinetobacter takes up DNA with maximal rate $c$ and saturation constant $K_{D N A}$ , this DNA transforms Acinetobacter from species $A_{1}$ to $A_{2}$ with efficiency $ϵ$ , Acinetobacter kills E. coli, thereby releasing DNA, and E. coli leaks DNA at a basal level $r_{l e a k}$ . All variables are absolute numbers, not concentrations. We modeled the DNA uptake and E. coli killing terms using Michaelis-Menton kinetics. Since we did all experiments on equal-sized agar spots (resulting from evaporation of 2 ul droplets), we assumed constant volume and combined $V$ with the Michaelis constant $K_{M_{D N A}}$ to obtain a new parameter $K_{D N A}$ , with units kb, as demonstrated below for the DNA uptake term:

\frac{d D}{d t} = - c A \frac{\frac{D}{V}}{K_{M_{D N A}} + \frac{D}{V}}

\frac{d D}{d t} = - c A \frac{D}{K_{D N A} + D}; K_{D N A} \equiv K_{M_{D N A}} V

Analogously, the killing term $- r_{k i l l} \frac{A \frac{E}{V}}{K_{M_{k i l l}} + \frac{A}{V} + K_{E_{k i l l}} \frac{E}{V}}$ becomes $- r_{k i l l} \frac{A E}{K_{k i l l} + A + K_{E_{k i l l}} E}$ , where $K_{k i l l} \equiv K_{M_{k i l l}} V$ is unitless.

For contact-dependent killing, predation can occur only at the perimeter of micro-colonies where there is contact between predator and prey cells (Schwarz et al., 2010a; Borenstein et al., 2015; Hood et al., 2010; Schwarz et al., 2010b; MacIntyre et al., 2010; LeRoux et al., 2012) (see also Supplemental Videos 9–12), and that perimeter grows proportionally to the square root of the total cell count. Therefore, the relevant quantities in the killing terms are the numbers of perimeter cells, A^* and E^*, not the total numbers of cells, A and E. Consider a large micro-colony i with Ni cells of radius r and total colony radius Ri, where $N_{i} ≫ 1$ . The number of cells in the micro-colony is the area of the colony divided by the area of a single cell, $N_{i} = \frac{π R_{i}^{2}}{π r^{2}}$ , so the colony radius is $R_{i} = r \sqrt{N_{i}}$ . The number of perimeter cells is $N_{i}^{*} = \frac{2 π (R_{i} - r)}{2 r}$ , and substituting for $R_{i}$ , we find $N_{i}^{*} = π (\sqrt{N_{i}} - 1)$ . Each micro-colony grows from a single cell, so assuming equal distribution of cells across micro-colonies and initial number of cells N₀, we have $N_{i} = \frac{N}{N_{0}}$ , so $N_{i}^{*} = π (\sqrt{\frac{N}{N_{0}}} - 1)$ . Since there are N₀ micro-colonies, the total number of perimeter cells is:

N^{*} = π N_{0} (\sqrt{\frac{N}{N_{0}}} - 1)

Equation 3 is valid for large micro-colonies ( $N_{i} ≫ 1$ ), but when colonies consist of only one cell each; that is, N $\leq$ N₀, all cells are perimeter cells, so

N^{*} = N

Therefore, we define a function for the number of perimeter cells that transitions smoothly between the two limits of Equation 3 and Equation 4 at a threshold micro-colony size of 5 (Figure 3—figure supplement 5), which we used in the killing term for both A^* and E^*:

N^{*} = N (\frac{1}{1 + {(\frac{N}{5 N_{0}})}^{2}}) + π N_{0} (\sqrt{\frac{N}{N_{0}}} - 1) (\frac{{(\frac{N}{5 N_{0}})}^{2}}{1 + {(\frac{N}{5 N_{0}})}^{2}})

A. baylyi natural competence is largely proportional to its growth rate (Palmen et al., 1993), so we assumed the DNA uptake slows with the same saturation factor as cell growth. Over a longer time scale, communities on agar plates will continue to grow slowly as fresh nutrients diffuse in and to replace dying cells, but this model focuses on the early dynamics of a growing community in the very early stages of biofilm development.

Parameter fitting

Request a detailed protocol

Transformation of Acinetobacter by homologous recombination (HR) is more efficient than via replicating plasmids (Palmen et al., 1993), so it allows measurement of HGT with higher sensitivity. Therefore, we measured HGT parameters using pRC03H-2S, which cannot replicate in Acinetobacter but contains homology to the Acinetobacter genome, allowing Acinetobacter to integrate the kan gene via HR.

All parameter fitting (Table 1) was performed using the least squares nonlinear optimization function lsqnonlin in MATLAB. We fit each component of the model sequentially using simplified experiments. To determine the growth parameters, we measured growth curves for monoculture cell spots on agar and fit them using the logistic growth equation $N (t) = \frac{K_{N} N_{0} e^{γ_{N} t}}{K_{N} + N_{0} (e^{γ_{N} t} - 1)}$ , where $N$ is the number of cells, $γ_{N}$ is the growth rate, and $K_{N}$ is the saturation level for 2 ul spots (Figure 3—figure supplements 1 and 2). Using these growth parameters, we then fit the killing rate by measuring CFUs in co-cultured communities over time and using that data to fit the model as integrated using ode23 in MATLAB (Figure 3d–j). For simultaneous fitting of data from multiple experiments (Figure 3, Figure 3—figure supplement 3), we defined custom objective functions to calculate the prediction error for all data points, and then minimized the total sum of squares with lsqnonlin.

For DNA uptake rate $c$ , we used the previously measured 60 bp/s (Palmen et al., 1993). To measure the other key HGT parameters $K_{D N A}$ and transformation efficiency $ϵ$ , we seeded monoculture Acinetobacter spots on agar with known numbers of plasmids, and measured HGT over time. We simultaneously fit the HGT curves for time course and serial dilution data to the model as integrated using ode23 (Figure 3a–c). We measured plasmids per E. coli cell by growing a shaking tube of cells to exponential phase, counting cell density by spotting serial dilutions, isolating plasmid DNA with a standard miniprep kit, measuring obtained DNA density with a spectrophotometer, and converting ng of DNA to plasmids per cell. While plasmid copy number may vary as conditions change (e.g. growth phase and liquid vs. solid media), most of our results present log-scale effects, so this should not affect the qualitative conclusions. For genomic DNA per cell G, we divided the E. coli genome (3.6 Mb) by the plasmid length (9093 bp) to obtain the number of plasmid equivalents of genomic DNA.

Simulations

Request a detailed protocol

Full simulations of contact-dependent killing and HGT in microbial communities were performed by integrating the population dynamic model with the MATLAB function ode23, using parameters measured as described above for pRC03H-2S. For DNA, we defined D to be the number of plasmids, so we converted the units of c and KD using the conversion factor 9093 bp/plasmid.

Supplemental note 1

Request a detailed protocol

In Videos 1–6 and 9–12, GFP expression in E. coli is poorly repressed early in the movies, and mCherry expression in Acinetobacter becomes bleached later in the movies. We believe both of these phenomena are likely due to nutrient restriction, caused by Acinetobacter adhesion, growth, and eventual clogging in the channels meant to supply nutrients (see the top and bottom strips in the Supplemental Movies). Indeed, in our experience, the stickiness of Acinetobacter makes microfluidic experiments much more challenging than with only lab E. coli strains.

LacI repression in E. coli is less complete when nutrients are limiting (Grossman et al., 1998). The E. coli in Videos 1–6 are likely nutrient-deprived because Acinetobacter are coating the channels, both consuming nutrients and reducing flow rate. In Videos 7–8, on the other hand, the media had been switched to include kanamycin, which inhibited all Acinetobacter that had not acquired resistance via HGT from E. coli. This is likely why the GFP repression in E. coli is less complete in Videos 1–6 than in Videos 7–8.

Conversely, Acinetobacter appear to reduce expression of mCherry as they become more nutrient-limited. We speculate that mCherry fluorescence fades while GFP remains visible in Acinetobacter because (i) the mCherry gene is single-copy on the genome while the GFP plasmid is multi-copy, (ii) mCherry bleaches more readily and has lower intrinsic brightness than GFP (Shaner et al., 2005), and (iii) there may be promoter, ribosome-binding site, and codon usage effects affecting expression in A. baylyi, which is not nearly as well-characterized as E. coli in these respects.

Regardless, in the Supplemental Videos 1–6, it is clear when and where all E. coli are killed, because the GFP disappears suddenly within a single time-frame, indicating lysis as opposed to gradual bleaching. For GFP to re-emerge in an area where all E. coli have been killed (white circles in Videos 1–6), it must be expressed by the remaining Acinetobacter.

References

1. Adams MD
2. Goglin K
3. Molyneaux N
4. Hujer KM
5. Lavender H
6. Jamison JJ
7. MacDonald IJ
8. Martin KM
9. Russo T
10. Campagnari AA
11. Hujer AM
12. Bonomo RA
13. Gill SR
(2008) Comparative genome sequence analysis of multidrug-resistant Acinetobacter baumannii
Journal of Bacteriology 190:8053–8064.

https://doi.org/10.1128/JB.00834-08
- PubMed
- Google Scholar
(2014) Acinetobacter baumannii: evolution of a global pathogen
Pathogens and Disease 71:292–301.

https://doi.org/10.1111/2049-632X.12125
- PubMed
- Google Scholar
(2013) Tit-for-tat: type VI secretion system counterattack during bacterial cell-cell interactions
Cell 152:884–894.

https://doi.org/10.1016/j.cell.2013.01.042
- PubMed
- Google Scholar
(2010) Nooks and crannies in type VI secretion regulation
Journal of Bacteriology 192:3850–3860.

https://doi.org/10.1128/JB.00370-10
- PubMed
- Google Scholar
(2015) Established microbial colonies can survive type VI secretion assault
PLOS Computational Biology 11:e1004520.

https://doi.org/10.1371/journal.pcbi.1004520
- PubMed
- Google Scholar
(2015) The type VI secretion system of Vibrio cholerae fosters horizontal gene transfer
Science 347:63–67.

https://doi.org/10.1126/science.1260064
- PubMed
- Google Scholar
1. Bryksin AV
2. Matsumura I
(2010) Rational design of a plasmid origin that replicates efficiently in both gram-positive and gram-negative bacteria
PLoS One 5:e13244.

https://doi.org/10.1371/journal.pone.0013244
- PubMed
- Google Scholar
(2013) Acinetobacter baumannii utilizes a type VI secretion system for bacterial competition
PLoS One 8:e59388.

https://doi.org/10.1371/journal.pone.0059388
- PubMed
- Google Scholar
Website
1. Centers for Disease Control and Prevention (CDC)
(2013) Antibiotic resistance threats in the United States
Accessed 2013.

http://scholar.google.com/scholar?q=related:usYIUSMZp_QJ:scholar.google.com/&hl=en&num=20&as_sdt=1,5
1. Chen TL
2. Siu LK
3. Lee YT
4. Chen CP
5. Huang LY
6. Wu RC
7. Cho WL
8. Fung CP
(2008) Acinetobacter baylyi as a pathogen for opportunistic infection
Journal of Clinical Microbiology 46:2938–2944.

https://doi.org/10.1128/JCM.00232-08
- PubMed
- Google Scholar
1. Chen TL
2. Siu LK
3. Wu RC
4. Shaio MF
5. Huang LY
6. Fung CP
7. Lee CM
8. Cho WL
(2007) Comparison of one-tube multiplex PCR, automated ribotyping and intergenic spacer (ITS) sequencing for rapid identification of Acinetobacter baumannii
Clinical Microbiology and Infection 13:801–806.

https://doi.org/10.1111/j.1469-0691.2007.01744.x
- PubMed
- Google Scholar
1. de Vries J
2. Wackernagel W
(2002) Integration of foreign DNA during natural transformation of Acinetobacter sp. by homology-facilitated illegitimate recombination
PNAS 99:2094–2099.

https://doi.org/10.1073/pnas.042263399
- PubMed
- Google Scholar
1. Elliott KT
2. Neidle EL
(2011) Acinetobacter baylyi ADP1: transforming the choice of model organism
IUBMB Life 63:1075–1080.

https://doi.org/10.1002/iub.530
- PubMed
- Google Scholar
(2011) Microfluidics for synthetic biology: from design to execution
Methods in Enzymology 497:295-372.

https://doi.org/10.1016/B978-0-12-385075-1.00014-7
- PubMed
- Google Scholar
1. Fournier PE
2. Vallenet D
3. Barbe V
4. Audic S
5. Ogata H
6. Poirel L
7. Richet H
8. Robert C
9. Mangenot S
10. Abergel C
11. Nordmann P
12. Weissenbach J
13. Raoult D
14. Claverie JM
(2006) Comparative genomics of multidrug resistance in Acinetobacter baumannii
PLoS Genetics 2:e7.

https://doi.org/10.1371/journal.pgen.0020007
- PubMed
- Google Scholar
(1998) Spontaneous cAMP-dependent derepression of gene expression in stationary phase plays a role in recombinant expression instability
Gene 209:95–103.

https://doi.org/10.1016/S0378-1119(98)00020-1
- PubMed
- Google Scholar
1. Hood RD
2. Singh P
3. Hsu F
4. Güvener T
5. Carl MA
6. Trinidad RR
7. Silverman JM
8. Ohlson BB
9. Hicks KG
10. Plemel RL
11. Li M
12. Schwarz S
13. Wang WY
14. Merz AJ
15. Goodlett DR
16. Mougous JD
(2010) A type VI secretion system of Pseudomonas aeruginosa targets a toxin to bacteria
Cell Host & Microbe 7:25–37.

https://doi.org/10.1016/j.chom.2009.12.007
- PubMed
- Google Scholar
1. Imperi F
2. Antunes LC
3. Blom J
4. Villa L
5. Iacono M
6. Visca P
7. Carattoli A
(2011) The genomics of Acinetobacter baumannii: insights into genome plasticity, antimicrobial resistance and pathogenicity
IUBMB Life 63:1068–1074.

https://doi.org/10.1002/iub.531
- PubMed
- Google Scholar
(2008) A predatory mechanism dramatically increases the efficiency of lateral gene transfer in Streptococcus pneumoniae and related commensal species
Molecular Microbiology 69:245–253.

https://doi.org/10.1111/j.1365-2958.2008.06288.x
- PubMed
- Google Scholar
(2007) Natural genetic transformation: prevalence, mechanisms and function
Research in Microbiology 158:767–778.

https://doi.org/10.1016/j.resmic.2007.09.004
- PubMed
- Google Scholar
1. Joly-Guillou ML
(2005) Clinical impact and pathogenicity of Acinetobacter
Clinical Microbiology and Infection 11:868–873.

https://doi.org/10.1111/j.1469-0691.2005.01227.x
- PubMed
- Google Scholar
1. Kreth J
2. Merritt J
3. Shi W
4. Qi F
(2005) Co-ordinated bacteriocin production and competence development: a possible mechanism for taking up DNA from neighbouring species
Molecular Microbiology 57:392–404.

https://doi.org/10.1111/j.1365-2958.2005.04695.x
- PubMed
- Google Scholar
1. Kuhlman TE
2. Cox EC
(2010) Site-specific chromosomal integration of large synthetic constructs
Nucleic Acids Research 38:e92.

https://doi.org/10.1093/nar/gkp1193
- PubMed
- Google Scholar
1. LeRoux M
2. De Leon JA
3. Kuwada NJ
4. Russell AB
5. Pinto-Santini D
6. Hood RD
7. Agnello DM
8. Robertson SM
9. Wiggins PA
10. Mougous JD
(2012) Quantitative single-cell characterization of bacterial interactions reveals type VI secretion is a double-edged sword
PNAS 109:19804–19809.

https://doi.org/10.1073/pnas.1213963109
- PubMed
- Google Scholar
(2010) The Vibrio cholerae type VI secretion system displays antimicrobial properties
PNAS 107:19520–19524.

https://doi.org/10.1073/pnas.1012931107
- PubMed
- Google Scholar
(2012) The interconnection between biofilm formation and horizontal gene transfer
FEMS Immunology & Medical Microbiology 65:183–195.

https://doi.org/10.1111/j.1574-695X.2012.00960.x
- PubMed
- Google Scholar
1. Mao J
2. Lu T
(2016) Population-dynamic modeling of bacterial horizontal gene transfer by natural transformation
Biophysical Journal 110:258–268.

https://doi.org/10.1016/j.bpj.2015.11.033
- PubMed
- Google Scholar
(1999)
Fate of free DNA and transformation of the oral bacterium Streptococcus gordonii DL1 by plasmid DNA in human saliva

Applied and environmental microbiology 65:6–10.
- PubMed
- Google Scholar
(2013) Type VI secretion system regulation as a consequence of evolutionary pressure
Journal of Medical Microbiology 62:663–676.

https://doi.org/10.1099/jmm.0.053983-0
- PubMed
- Google Scholar
(2012) Expression vectors for Acinetobacter baylyi ADP1
Applied and Environmental Microbiology 78:280–283.

https://doi.org/10.1128/AEM.05597-11
- PubMed
- Google Scholar
(2007) Release and persistence of extracellular DNA in the environment
Environmental Biosafety Research 6:37–53.

https://doi.org/10.1051/ebr:2007031
- PubMed
- Google Scholar
(2000) Natural transformation of Acinetobacter sp. strain BD413 with cell lysates of Acinetobacter sp., Pseudomonas fluorescens, and Burkholderia cepacia in soil microcosms
Applied and Environmental Microbiology 66:206–212.

https://doi.org/10.1128/AEM.66.1.206-212.2000
- PubMed
- Google Scholar
1. Nigro SJ
2. Hall RM
(2016) Structure and context of Acinetobacter transposons carrying the oxa23 carbapenemase gene
Journal of Antimicrobial Chemotherapy 71:1135–1147.

https://doi.org/10.1093/jac/dkv440
- PubMed
- Google Scholar
1. Nordgård L
2. Nguyen T
3. Midtvedt T
4. Benno Y
5. Traavik T
6. Nielsen KM
(2007) Lack of detectable DNA uptake by bacterial gut isolates grown in vitro and by Acinetobacter baylyi colonizing rodents in vivo
Environmental Biosafety Research 6:149–160.

https://doi.org/10.1051/ebr:2007029
- PubMed
- Google Scholar
(1993) Physiological characterization of natural transformation in Acinetobacter calcoaceticus
Journal of General Microbiology 139:295–305.

https://doi.org/10.1099/00221287-139-2-295
- PubMed
- Google Scholar
1. Peleg AY
2. de Breij A
3. Adams MD
4. Cerqueira GM
5. Mocali S
6. Galardini M
7. Nibbering PH
8. Earl AM
9. Ward DV
10. Paterson DL
11. Seifert H
12. Dijkshoorn L
(2012) The success of acinetobacter species; genetic, metabolic and virulence attributes
PLoS One 7:e46984.

https://doi.org/10.1371/journal.pone.0046984
- PubMed
- Google Scholar
(2010) Naturally competent Acinetobacter baumannii clinical isolate as a convenient model for genetic studies
Journal of Clinical Microbiology 48:1488–1490.

https://doi.org/10.1128/JCM.01264-09
- PubMed
- Google Scholar
(2010a) What is type VI secretion doing in all those bugs?
Trends in Microbiology 18:531–537.

https://doi.org/10.1016/j.tim.2010.09.001
- PubMed
- Google Scholar
1. Schwarz S
2. West TE
3. Boyer F
4. Chiang WC
5. Carl MA
6. Hood RD
7. Rohmer L
8. Tolker-Nielsen T
9. Skerrett SJ
10. Mougous JD
(2010b) Burkholderia type VI secretion systems have distinct roles in eukaryotic and bacterial cell interactions
PLoS Pathogens 6:e1001068.

https://doi.org/10.1371/journal.ppat.1001068
- PubMed
- Google Scholar
(2005) A guide to choosing fluorescent proteins
Nature Methods 2:905–909.

https://doi.org/10.1038/nmeth819
- PubMed
- Google Scholar
1. Smet A
2. Boyen F
3. Pasmans F
4. Butaye P
5. Martens A
6. Nemec A
7. Deschaght P
8. Vaneechoutte M
9. Haesebrouck F
(2012) OXA-23-producing Acinetobacter species from horses: a public health hazard?
Journal of Antimicrobial Chemotherapy 67:3009–3010.

https://doi.org/10.1093/jac/dks311
- PubMed
- Google Scholar
(2002) Induction of natural competence in Streptococcus pneumoniae triggers lysis and DNA release from a subfraction of the cell population
PNAS 99:7681–7686.

https://doi.org/10.1073/pnas.112464599
- PubMed
- Google Scholar
(2006) Bad bugs need drugs: an update on the development pipeline from the Antimicrobial Availability Task Force of the Infectious Diseases Society of America
Clinical Infectious Diseases 42:657–668.

https://doi.org/10.1086/499819
- PubMed
- Google Scholar
1. Touchon M
2. Cury J
3. Yoon EJ
4. Krizova L
5. Cerqueira GC
6. Murphy C
7. Feldgarden M
8. Wortman J
9. Clermont D
10. Lambert T
11. Grillot-Courvalin C
12. Nemec A
13. Courvalin P
14. Rocha EP
(2014) The genomic diversification of the whole Acinetobacter genus: origins, mechanisms, and consequences
Genome Biology and Evolution 6:2866–2882.

https://doi.org/10.1093/gbe/evu225
- PubMed
- Google Scholar
(2015) Rates of lateral gene transfer in prokaryotes: high but why?
Trends in Microbiology 23:598–605.

https://doi.org/10.1016/j.tim.2015.07.006
- PubMed
- Google Scholar
1. Weber BS
2. Hennon SW
3. Wright MS
4. Scott NE
5. de Berardinis V
6. Foster LJ
7. Ayala JA
8. Adams MD
9. Feldman MF
(2016) Genetic dissection of the type VI secretion system in Acinetobacter and identification of a novel peptidoglycan hydrolase, tagX, required for its biogenesis
mBio 7:e01253-16.

https://doi.org/10.1128/mBio.01253-16
- PubMed
- Google Scholar
1. Weber BS
2. Ly PM
3. Irwin JN
4. Pukatzki S
5. Feldman MF
(2015) A multidrug resistance plasmid contains the molecular switch for type VI secretion in Acinetobacter baumannii
PNAS 112:9442–9447.

https://doi.org/10.1073/pnas.1502966112
- PubMed
- Google Scholar
1. Weber BS
2. Miyata ST
3. Iwashkiw JA
4. Mortensen BL
5. Skaar EP
6. Pukatzki S
7. Feldman MF
(2013) Genomic and functional analysis of the type VI secretion system in Acinetobacter
PLoS One 8:e55142.

https://doi.org/10.1371/journal.pone.0055142
- PubMed
- Google Scholar
1. Wei H
2. Håvarstein LS
(2012) Fratricide is essential for efficient gene transfer between pneumococci in biofilms
Applied and Environmental Microbiology 78:5897–5905.

https://doi.org/10.1128/AEM.01343-12
- PubMed
- Google Scholar
1. Wilharm G
2. Piesker J
3. Laue M
4. Skiebe E
(2013) DNA uptake by the nosocomial pathogen Acinetobacter baumannii occurs during movement along wet surfaces
Journal of Bacteriology 195:4146–4153.

https://doi.org/10.1128/JB.00754-13
- PubMed
- Google Scholar
1. Zhou Z
2. Du X
3. Wang L
4. Yang Q
5. Fu Y
6. Yu Y
(2011) Clinical carbapenem-resistant Acinetobacter baylyi strain coharboring blaSIM-1 and blaOXA-23 from China
Antimicrobial Agents and Chemotherapy 55:5347–5349.

https://doi.org/10.1128/AAC.00425-11
- PubMed
- Google Scholar

Article and author information

Author details

Robert M Cooper

BioCircuits Institute, University of California, San Diego, San Diego, United States

Contribution
Conceptualization, Data curation, Software, Formal analysis, Funding acquisition, Validation, Investigation, Visualization, Methodology, Writing—original draft, Writing—review and editing

For correspondence
rcooper@ucsd.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-2136-0403
Lev Tsimring
1. BioCircuits Institute, University of California, San Diego, San Diego, United States
2. San Diego Center for Systems Biology, University of California, San Diego, San Diego, United States
Contribution
Resources, Formal analysis, Supervision, Funding acquisition, Project administration, Writing—review and editing

Competing interests
No competing interests declared
Jeff Hasty
1. BioCircuits Institute, University of California, San Diego, San Diego, United States
2. San Diego Center for Systems Biology, University of California, San Diego, San Diego, United States
3. Molecular Biology Section, Division of Biological Science, University of California, San Diego, San Diego, United States
4. Department of Bioengineering, University of California, San Diego, San Diego, United States
Contribution
Resources, Formal analysis, Supervision, Funding acquisition, Project administration

For correspondence
jhasty@eng.ucsd.edu

Competing interests
No competing interests declared

Funding

Hartwell Foundation

Robert M Cooper

National Institute of General Medical Sciences (San Diego Center for Systems Biology (P50 GM085764))

Robert M Cooper
Lev Tsimring
Jeff Hasty

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

RMC was supported by a fellowship from the Hartwell Foundation. The authors would like to thank Bart Borek for valuable discussion regarding modeling, Ameen Rahimi for assistance in constructing the integrating plasmid pRC03H-2S, and Life Science Editors for assistance in editing the manuscript.

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

11,294

views
1,469

downloads
111

citations

Views, downloads and citations are aggregated across all versions of this paper published by eLife.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Robert M Cooper
Lev Tsimring
Jeff Hasty

(2017)

Inter-species population dynamics enhance microbial horizontal gene transfer and spread of antibiotic resistance

eLife 6:e25950.

https://doi.org/10.7554/eLife.25950

Categories and tags

Research organism

E. coli

Share this article

Cite this article

Real-time observation of functional HGT in microfluidic traps.

Real-time observation of HGT from E. coli to Acinetobacter.

Real-time observation of HGT from E. coli to Acinetobacter.

Real-time observation of HGT from E. coli to Acinetobacter.

Real-time observation of HGT from E. coli to Acinetobacter.

Real-time observation of HGT from E. coli to Acinetobacter.

Real-time observation of HGT from E. coli to Acinetobacter.

Killing-enhanced HGT enables Acinetobacter to dynamically adapt to new environments.

Killing-enhanced HGT enables Acinetobacter to dynamically adapt to new environments.

Enhancement of HGT efficiency by neighbor killing.

Box 1.

Determining quantitative parameters for natural transformation and contact-dependent neighbor killing.

Microbial community growth, killing, and horizontal gene transfer parameters.

Comparison between predicted and actual killing-enhanced HGT in microbial communities.

Simulations showing the effects of initial species density and interaction time on HGT, and the degree to which contact-dependent killing enhances HGT.

Simulated inhibition of HGT by DNase (a–d) or competing DNA (e–h) in simulated microbial communities seeded with both Acinetobacter and E. coli at 10−3 of their respective carrying capacities and grown for 2 hr.

Experimental tests of model predictions.

E. coli lysis is concentrated at the periphery of micro-colonies.

E. coli lysis is concentrated at the periphery of micro-colonies.

E. coli lysis is concentrated at the periphery of micro-colonies.

E. coli lysis is concentrated at the periphery of micro-colonies.

Author details

Robert M Cooper

Contribution

For correspondence

Competing interests

Lev Tsimring

Contribution

Competing interests

Jeff Hasty

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Research organism

Further reading

Simulated inhibition of HGT by DNase (a–d) or competing DNA (e–h) in simulated microbial communities seeded with both Acinetobacter and E. coli at 10⁻³ of their respective carrying capacities and grown for 2 hr.