Research Article

Electrocorticography is superior to subthalamic local field potentials for movement decoding in Parkinson’s disease

Movement Disorder and Neuromodulation Unit, Department of Neurology, Charité - Universitätsmedizin Berlin, corporate member of Freie Universität Berlin and Humboldt Universität zu Berlin, Germany
Brain Modulation Lab, Department of Neurosurgery, Massachusetts General Hospital, United States
Harvard Medical School, United States
Department of Neurobiology, University of Pittsburgh, United States
Department of Computer Science, Technische Universität Berln, Germany

May 27, 2022

https://doi.org/10.7554/eLife.75126

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: May 27, 2022 (This version)
Accepted: May 15, 2022
Received: October 29, 2021
Preprint posted: April 26, 2021 (Go to version)

1. Of interest
Task-dependent optimal representations for cerebellar learning

Marjorie Xie, Samuel P Muscinelli ... Ashok Litwin-Kumar

Research Article Sep 29, 2023
Further reading

Abstract
Editor's evaluation
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Brain signal decoding promises significant advances in the development of clinical brain computer interfaces (BCI). In Parkinson’s disease (PD), first bidirectional BCI implants for adaptive deep brain stimulation (DBS) are now available. Brain signal decoding can extend the clinical utility of adaptive DBS but the impact of neural source, computational methods and PD pathophysiology on decoding performance are unknown. This represents an unmet need for the development of future neurotechnology. To address this, we developed an invasive brain-signal decoding approach based on intraoperative sensorimotor electrocorticography (ECoG) and subthalamic LFP to predict grip-force, a representative movement decoding application, in 11 PD patients undergoing DBS. We demonstrate that ECoG is superior to subthalamic LFP for accurate grip-force decoding. Gradient boosted decision trees (XGBOOST) outperformed other model architectures. ECoG based decoding performance negatively correlated with motor impairment, which could be attributed to subthalamic beta bursts in the motor preparation and movement period. This highlights the impact of PD pathophysiology on the neural capacity to encode movement vigor. Finally, we developed a connectomic analysis that could predict grip-force decoding performance of individual ECoG channels across patients by using their connectomic fingerprints. Our study provides a neurophysiological and computational framework for invasive brain signal decoding to aid the development of an individualized precision-medicine approach to intelligent adaptive DBS.

Editor's evaluation

This paper evaluates movement decoding from intracranial brain recordings in patients with Parkinson's disease. Interestingly, the authors demonstrate that cortical recordings (electrocorticography) outperform subthalamic nucleus in decoding grip force. This work will be of interest to brain computer interface, movement disorder, motor control, and general neurophysiology communities.

https://doi.org/10.7554/eLife.75126.sa0

Introduction

Subthalamic deep brain stimulation (DBS) for Parkinson’s disease (PD) is one of the most successful neurotechnological advances in translational neuroscience to date. In addition to its clinical utility, DBS has provided unique insight into the neurophysiology of movement disorders (Cagnan et al., 2019; Krauss et al., 2021). PD has been associated with increased beta synchronization and beta bursts in the basal ganglia (Kühn et al., 2006; Neumann et al., 2016; Kehnemouyi et al., 2021) and exaggerated phase amplitude coupling and waveform sharpness asymmetry in cortex (de Hemptinne et al., 2015; Cole et al., 2017). Symptom severity in the OFF medication state was shown to correlate with resting beta power in the STN across patients (Kühn et al., 2006; Neumann et al., 2016). Such observations have inspired the idea of adaptive DBS (aDBS), where electrophysiological signals are used to change stimulation parameters in response to evolving clinical states (Little et al., 2013; Beudel and Brown, 2016; Tinkhauser et al., 2017; Swann et al., 2018; Piña-Fuentes and van Dijk, 2019; Velisar et al., 2019; Hwang et al., 2020; Petrucci et al., 2020). In a series of seminal papers it was shown that significant clinical benefit and reduced side-effects could be achieved, when stimulation was triggered by beta power (Little et al., 2013; Velisar et al., 2019). Machine-learning for aDBS applications can integrate multivariate feature sets for adaptive DBS control beyond beta power. First trials on machine learning based movement classification to trigger adaptive DBS either using electrocorticography (ECoG) or subcortical local field potentials (LFP) in essential tremor have shown promising results (Opri et al., 2020; He et al., 2021). In the future, smart implants may become available that combine invasive brain signal decoding with real-time stimulation adaptation, toward a precision medicine approach to adaptive DBS in PD and other brain disorders. However, the identification of optimal decoding strategies and the characterization of relevant factors with impact on decoding performance remains and unmet need. With the present study, we address this by a thorough investigation grip-force decoding that is motivated by the well-described relationship of vigor, movement velocity, bradykinesia, and dopamine in Parkinson’s disease (Turner and Desmurget, 2010; Yttri and Dudman, 2016; Lofredi et al., 2018). We use state-of-art machine learning algorithms with multimodal invasive neurophysiology and whole-brain connectomics in PD patients undergoing DBS electrode implantation. Our results highlight the utility of cortical vs. subcortical signals to accurately decode grip-force and establish a link between decoding performance and motor impairment in PD. Finally, we investigate brain networks from ECoG recording locations with normative structural and functional connectomics and demonstrate the predictive power of connectomic fingerprints for brain signal decoding.

Results

Real-time processing and feature definition

We analyzed sensorimotor ECoG and subthalamic LFP data recorded intraoperatively from 11 PD patients undergoing DBS implantation during performance of a Go/No-Go based cued grip-force task (Figure 1A). Individual electrode localizations in Montreal Neurological institute (MNI) space are shown in Figure 1B with typical responses (Kühn et al., 2004; Androulidakis et al., 2007; Kondylis et al., 2016; Lofredi et al., 2018) in Figure 1C aligned to onset of grip force (total n=2685, on average n=244 ± 149 STD movements per patient, see Figure 1—figure supplement 1 for more detail on grip-force variability). For the use in machine-learning models, band power feature time-series were extracted in a real-time BCI compatible implementation (Figure 1D) streamed in virtual packets of 100ms length at a sampling rate of 1000 Hz to mimic the online application. Variance as a measure of amplitude of rereferenced, band-pass filtered raw data segments was extracted at 10 Hz with an adaptive window length from 1000 to 100ms of past data for eight oscillatory features [θ (4–8 Hz), α (8–12 Hz), β (13–35 Hz), low β (13–20 Hz), high β (20–35 Hz), low γ (60–80 Hz), high-frequency activity (HFA) (90–200 Hz) and all γ (60–200 Hz)]. All features were normalized to the median of the past 10 s to compensate for potential signal changes over time. The target variable was continuously measured grip-force (z-scored for each recording session), which was cleaned from noise and baseline drift (Xie et al., 2018).

Figure 1 with 1 supplement see all

Download asset Open asset

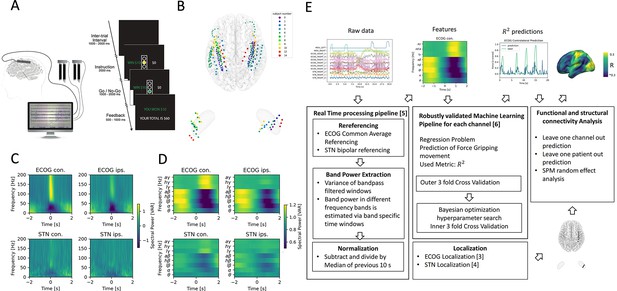
Movement induced spectral changes are more dominant for ECoG than STN-LFP signals for a grip force task before and after a machine learning feature signal processing pipeline.

(A) ECoG, STN, and gripping force were recorded simultaneously during performance of a Go / No-Go task. (B) Individual ECoG and STN electrodes were localized and transformed into in Montreal Neurological Institute (MNI) space (Figure 1—source data 1). Note that ECoG strip designs varied slightly between patients (see Supplementary file 1a), leading to varying dimensions of overall input feature matrices. The number of ECoG channels (average n=9.45 ± 11.15 STD per hemisphere) is higher compared to the number of STN LFP channels (n=3). (C) Mean spectral power of all ECoG and STN channels for contra- and ipsilateral movements showed typical movement induced spectral changes (Figure 1—source data 2). (D) Virtual streaming of data packets secured real-time compatible processing and normalization to extract time-frequency modulations into discrete feature time-series. Mean features of all ECoG and STN channels are visualized (Figure 1—source data 3). (E) Schematic flow chart of the implemented real-time enabled feature extraction, machine learning evaluation and functional and structural connectivity analysis pipeline.

Figure 1—source data 1 ECoG and STN electrode localizations.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig1-data1-v1.csv
Download elife-75126-fig1-data1-v1.csv
Figure 1—source data 2 Mean ECoG and STN spectral power.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig1-data2-v1.zip
Download elife-75126-fig1-data2-v1.zip
Figure 1—source data 3 Mean ECoG and STN features.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig1-data3-v1.zip
Download elife-75126-fig1-data3-v1.zip

Including preceding signals up to 500 ms before the decoded sample improves grip-force decoding performance

A linear model analysis of all eight oscillatory features per channel was used to investigate the contributing band power correlations for time-points simultaneous to and preceding target samples of continuous grip-force measurements. Figure 2A shows the weight distributions of multivariable linear models of the best performing channels per subject. Since each cortical or STN electrode has multiple channels, only the best channel per electrode is selected for this visualization. As the interpretability of coefficients in multivariable models is limited (Haufe et al., 2014), we have further visualized the normalized coefficients of univariate models for each relative time-point and frequency band in Figure 2B. Next, to investigate the cumulative performance contribution of preceding time points for optimal feature construction, all frequency bands were concatenated while continuously increasing the cumulative number of premovement time-points (from –100 to –1000ms) and each set was subjected to training a Wiener Filter. The respective best channel $R^{2}$ performances are shown in Figure 2C. A performance saturation becomes visible when concatenating 5 time-points from 500ms (prior to target sample) to 0ms (target sample), resulting in an optimal input vector of 8 frequency bands with 5 time-points (=40 features) for further analyses.

Figure 2

Download asset Open asset

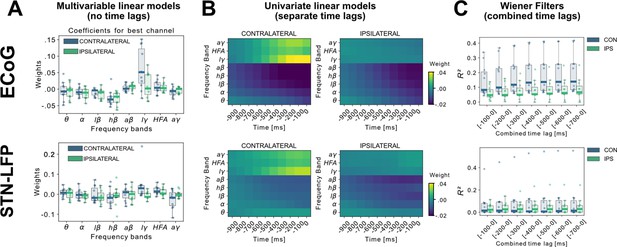
Linear Models and Wiener Filters reveal temporally and spectrally specific coefficient distributions with grip-force decoding performance gain by including signals preceding the target sample by up to 500ms.

(A) Multivariable linear model coefficients trained only from the instantaneous sample (0 time lag with respect to decoded target sample) including all frequency bands from best channels per patient resemble movement induced spectral changes with beta desynchronization and gamma synchronization (Figure 2—source data 1). ECoG derived coefficients yield higher absolute values than STN-LFP derived coefficients. (B) Univariate frequency and time lag specific Linear Models were trained and visualized to improve interpretability of average coefficients in the absence of interactions (Figure 2—source data 2). Low γ (60–80 Hz), HFA (90–200 Hz), and all γ (60–200 Hz) bands show stronger positive associations for contralateral over ipsilateral movements. Moreover, stronger associations are visible for ECoG over STN-LFP signals for $β$ , HFA, and $γ$ bands. (C) Wiener Filters can integrate multiple time-steps in Linear Models leading to an incremental performance gain when signals are included preceding the current target sample by up to 500ms (Figure 2—source data 3).

Figure 2—source data 1 Best channel Linear Model coefficients trained from instantaneous sample.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig2-data1-v1.csv
Download elife-75126-fig2-data1-v1.csv
Figure 2—source data 2 Univariate Linear Model coefficients of single frequency band and time lag.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig2-data2-v1.zip
Download elife-75126-fig2-data2-v1.zip
Figure 2—source data 3 Wiener Filter multiple time-step comparison.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig2-data3-v1.csv
Download elife-75126-fig2-data3-v1.csv

XGBOOST outperforms other machine learning models for grip-force decoding

In order to build a grip-force decoder, different machine learning (ML) algorithms were tested in a large-scale Bayesian Optimization hyperparameter search (see Supplementary file 1B for a list of hyperparameters for each model). Elastic - Net regularized Linear Models, Neural Networks and Gradient Boosted trees (XGBOOST) (Chen and Guestrin, 2016) were tested for each channel for contra- and ipsilateral movements. XGBOOST was included as it can learn non-linearities and has advantages over other models with respect to feature selection. To further utilize potential information derived from spatial patterns, the Source Power Comodulation (SPoC) framework (Dähne et al., 2014) was used in combination with Elastic - Net or XGBOOST predictors. Each model was informed by 40 features (8 specific frequency bands concatenated at 5 time-points ranging from t = –500ms to t=0ms to the target sample) per channel and evaluated via rigorously cross-validated test-set predictions ranked by $R^{2}$ coefficients of determination. Figure 3 shows performance outcomes for the different machine learning methods, with overall best results achieved by XGBOOST from ECoG signals (see Supplementary file 1c for further details). Contralateral ECoG strips had significantly higher decoding performances than ipsilateral ones (contralateral $R^{2}$ = 0.31 ± 24, ipsilateral $R^{2}$ = 0.13 ± 0.16, p=0.02). Given the relatively low decoding performances for STN-LFP, we applied permutation tests to confirm that performance was above chance (contralateral p=0.025, ipsilateral p=0.028). Corroborating the model choice in previous literature, highest STN performances were achieved with the Wiener Filter method for contra- and ipsilateral movements (Shah et al., 2018). Importantly, varying combinations of multiple ECoG and/or STN channels did not lead to significant performance advantages (Figure 3 C+D), which is important for the utility and design of machine learning enabled implantables.

Figure 3

Download asset Open asset

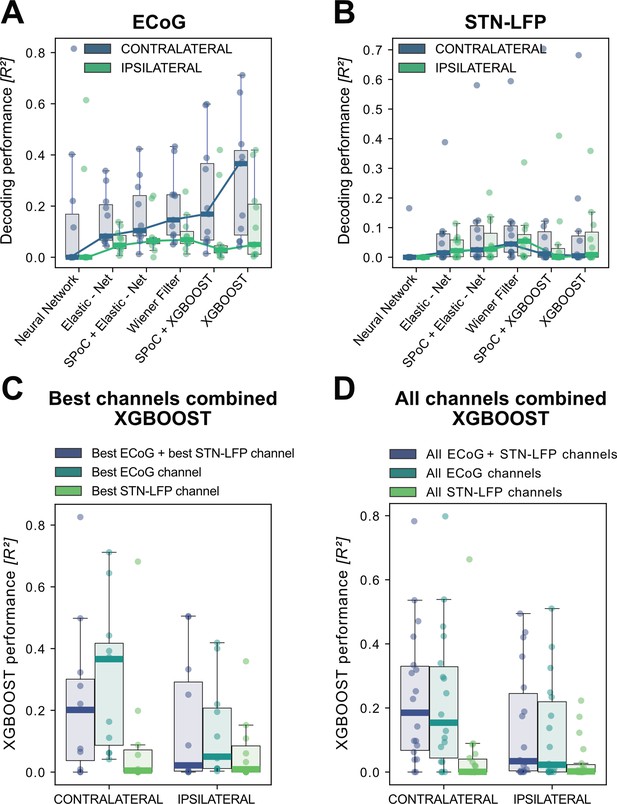
XGBOOST outperforms other machine learning methods for ECoG based grip-force decoding.

Based on the presented real-time compatible signal processing pipeline Neural Networks, Elastic - Net regularized Linear Models, Wiener Filters and extreme Gradient Boosting (XGBOOST) regression models were tested. Mean $R^{2}$ test-set grip-force decoding performances are shown for the best channel per patient after 10 rounds of Bayesian Optimization of hyperparameters with nested cross-validation for ECoG (A) and STN-LFP (B) (Figure 3—source data 1). The same pipeline was subjected to spatial feature extraction approach using all available channels of an electrode for each patient with Source Power Comodulation (SPoC). Best ECoG (A) performances were obtained by XGBOOST regressors. STN-LFP signals (B) did not exhibit performance gain when applying advanced machine learning methods. The mean ECoG vs. STN XGBOOST performance differences of contralateral ${∆ R}^{2}$ = 0.21 ± 0.18 and ipsilateral ${∆ R}^{2}$ = 0.069 ± 0.08 movements, indicate the higher grip-force decoding performance of ECoG over STN signals. The mean test-set prediction performances were higher for ECoG than for STN-LFP signals across all patients, for both contra- and ipsilateral movements. Best ECoG channels outperformed best STN-LFP channels and the combination of best channels from both ECoG and STN-LFP (C) (Figure 3—source data 2). When combining multiple channels, performances improve through the combination of ECoG and STN-LFPs (D), but the performances remain below individual best ECoG channels as depicted in (C). For combined ECoG +STN – LFP training, the model learned specific combinations between both feature locations and failed to select only the best ECoG features due to overfitting.

Figure 3—source data 1 Cross-validated ECoG and STN machine learning model performances for single channels.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig3-data1-v1.csv
Download elife-75126-fig3-data1-v1.csv
Figure 3—source data 2 Cross-validated combined and best-channel XGBOOST performances for best ECoG and STN channels.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig3-data2-v1.csv
Download elife-75126-fig3-data2-v1.csv
Figure 3—source data 3 Cross-validated XGBOOST performances for multichannel models based on ECoG, LFP and combined ECoG-LFP channels.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig3-data3-v1.csv
Download elife-75126-fig3-data3-v1.csv

Grip-force decoding performance is correlated with PD motor impairment and subthalamic beta burst dynamics

To investigate potential sources of bias from patient specific information on grip-force decoding performance, we performed Spearman’s correlations with the grand average from all contra -and ipsilateral decoding performances. Averaging was necessary to obtain one value per patient. Age (ρ=–0.16, p=0.32), disease duration in years (ρ=0.31, p=0.17) and number of movements (ρ=–0.41, p=0.11) and movement variability (Rho = –0.49, p=0.06) did not reveal significant correlations. We further investigated whether motor impairment related to the hypodopaminergic state in PD can explain differences in grip-force decoding across patients. Therefore, we correlated preoperative OFF medication total UPDRS-III scores, which revealed negative correlations for best ECoG (ρ=–0.55, p=0.039) and STN-LFP (ρ=–0.55, p=0.042) channels (Figure 4 A+B). Combined ECoG and STN channel performance also showed significant correlations ( $ρ$ =–0.54, p=0.045), as well as combined ECoG ( $ρ$ =–0.55, p=0.045) and combined STN-LFP performances ( $ρ$ =–0.61, p=0.024). To test whether the correlation measure was corrupted by outliers, we repeated the analysis using the robust percentage-bend correlation (Pernet et al., 2012) which replicated the significant association between UPDRS total score and mean contra -and ipsilateral channel performance for ECoG (r=–0.62, p=0.04) and STN (r=–0.7, p=0.016). This correlation was temporally specific to decoding of ongoing grip-force, indicative of the models’ underestimation of motor output (Figure 4C). Thus, the lower decoding performance in patients with more severe symptom severity could not be attributed to changes in decoder output in the absence of movement or temporal imprecision. This has practical implications and highlights the importance of investigating interactions between disease and machine learning approach for neural implants.

Figure 4

Download asset Open asset

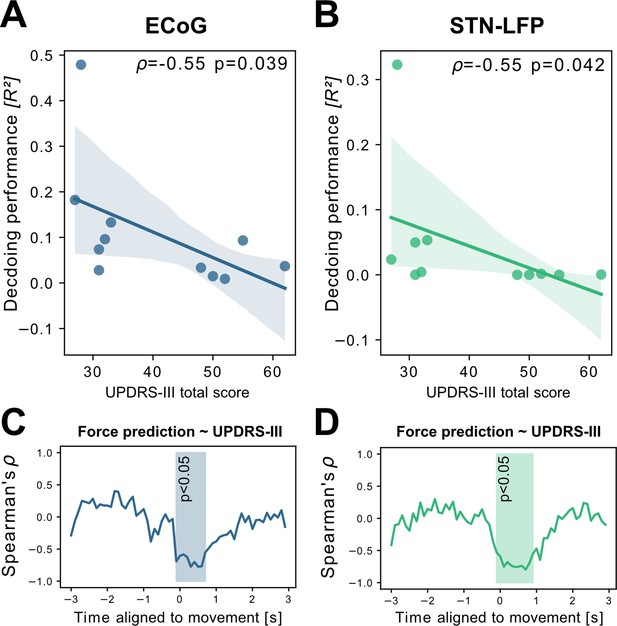
Grand average grip-force decoding performances correlate inversely with preoperative PD motor sign severity.

UPDRS-III scores show significant negative correlations with patient-wise XGBOOST grip-force decoding performance averages for (A) ECoG (ρ=–0.55, p=0.039) and (B) STN-LFP signals (ρ=–0.55, p=0.042) (Figure 4—source data 1). The temporal specificity of this correlation is revealed through movement aligned sample-wise correlations of average force prediction model output with UPDRS-III scores across patients (cluster based corrected significant segments are displayed shaded) (C+D) (Figure 4—source data 2).

Figure 4—source data 1 ECoG and STN single channel performances and UPDRS ratings.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig4-data1-v1.csv
Download elife-75126-fig4-data1-v1.csv
Figure 4—source data 2 ECoG and STN Force prediction UPDRS correlation.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig4-data2-v1.csv
Download elife-75126-fig4-data2-v1.csv

To better understand the relationship of PD pathophysiology and grip-force decoding performance, we have further investigated associations between cortical and subthalamic beta burst dynamics. We follow the methodology of previous reports that demonstrated that the time spent in beta burst correlates with impairment of movement kinematics (Torrecillos et al., 2018). Beta bursts were defined as threshold crossings of the beta feature vector above the 75th percentile of the baseline period. Following the previous finding that specifically the time-spent in low-beta but not high-beta bursts was correlated with PD motor impairment (Lofredi et al., 2019), we investigated these bands separately for the motor preparation period (−1–0 s with respect to movement onset) and movement execution period (0–1 s following movement onset). To uncover a potential relationship of the beta-burst metric with PD pathophysiology, we performed correlations with UPDRS-III total scores. Significant correlations were found between UPDRS-III and low-beta bursts in STN-LFP signals during motor preparation ( $ρ$ =0.63, p=0.02; Figure 5A) and movement execution ( $ρ$ =0.56, p=0.04; data not shown), but not for the high-beta band (p>0.05). Conversely, for ECoG high-beta but not low-beta burst dynamics during motor preparation but not movement periods were significantly correlated with UPDRS-III total scores ( $ρ$ =0.55, p=0.04). In summary, we provide evidence that both subthalamic and cortical beta burst dynamics relate to PD motor sign severity with subthalamic low-beta bursts showing the most robust correlations, both during motor preparation and movement periods.

Figure 5

Download asset Open asset

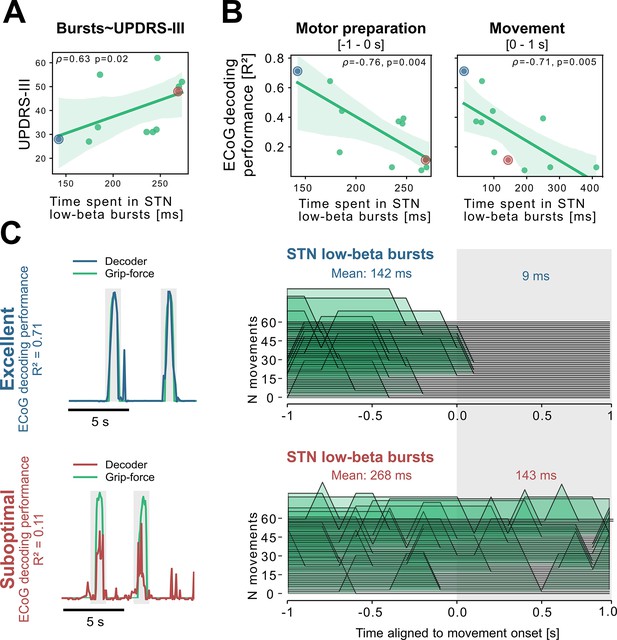
Subthalamic low-beta bursts relate to PD motor impairment and are associated with lower ECoG decoding performance.

UPDRS-III scores are significantly correlated with time spent in subthalamic low-beta bursts in the motor preparation period (A) and during movement (not shown). Average XGBOOST decoding performance correlated inversely with time spent in subthalamic low-beta bursts during motor preparation and movement performance (B) (Figure 5—source data 1). Patient examples with excellent (R²=0.71; blue) and suboptimal (R²=0.11; red) performances are highlighted in (B) and shown in further detail in (C) (Figure 5—source data 2). Note the difference in decoder output with respect to the original grip-force trace (left panel) and the differences in burst frequencies and durations across movement repetitions (right panel) in the motor preparation and movement execution (grey shaded area) period.

Figure 5—source data 1 Time spend in low-beta burst performance and UPDRS correlation.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig5-data1-v1.csv
Download elife-75126-fig5-data1-v1.csv
Figure 5—source data 2 Movement onset aligned low-beta bursts for two subjects.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig5-data2-v1.zip
Download elife-75126-fig5-data2-v1.zip

To relate these findings to movement decoding performance from cortex, we correlated the grand average XGBOOST grip-force decoding performances from ECoG channels (as above for UPDRS-III) with high- and low-beta burst dynamics in both ECoG and STN-LFP signals. ECoG based grip-force decoding performance was significantly correlated with subthalamic low-beta burst dynamics during motor preparation ( $ρ$ =–0.76, p=0.004) and movement execution ( $ρ$ =–0.71, p=0.005; Figure 5B). Subthalamic burst dynamics in the high-beta band also correlated with ECoG decoding performances during movement ( $ρ$ =0.71, p=0.007) but not motor preparation. Cortical burst dynamics from ECoG signals did not reveal significant correlations with ECoG-based grip-force decoding performances. Relevant correlations alongside exemplar burst visualizations and corresponding grip-force decoding traces are shown in Figure 5.

Brain mapping of grip-force decoding performance from invasive cortical and subthalamic recordings

The spatial distributions of decoding performance on cortex and STN for contra- and ipsilateral movements are shown in Figure 6. To evaluate the relevance of recording location with respect to decoding performance, we calculated correlations of performance measures with a priori defined implantation targets, namely the dorsolateral STN (Caire et al., 2013; Horn et al., 2017a) and the hand-knob of the precentral gyrus (Mayka et al., 2006). Linear mixed effects models showed a significant within-subject relation for contralateral ECoG decoding performances (β=−0.002, Lower CI = −0.003, upper CI = −0.001, $R^{2}$ = 0.57, p<0.001), but not STN locations (p>0.05). The dependent variable was the decoding performance, the fixed effect was the distance to hand knob area or dorsolateral STN respectively, and the random effect the subject. Repeating the analyses across electrodes and patients in a cross-validated manner revealed no significant predictive value (p>0.05). Thus, Euclidean distance to hand knob area for ECoG and therapeutic target for STN was significantly correlated with decoding performance within patients, but could not predict decoding performance across channels or patients.

Figure 6

Download asset Open asset

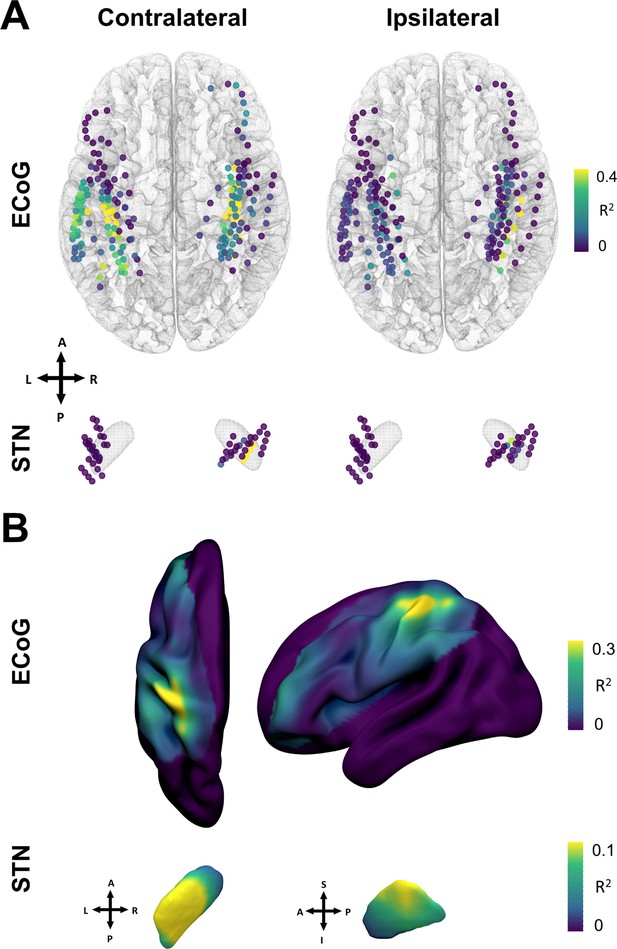
Grip-force decoding performances spatially peak in sensorimotor cortex and the dorsolateral STN.

(A) Channels are color coded for individual XGBOOST grip-force regression performances per channel. Performance differences shown are in favor of ECoG over STN and contralateral over ipsilateral recording locations for movement decoding. (Figure 6—source data 1) (B) Spatial interpolation across all contacts projected to the left hemisphere shows peak performances in sensorimotor cortex. STN interpolated decoding performance peaks in the dorsolateral portion of the STN, in proximity to the best therapeutic target (Caire et al., 2013).

Figure 6—source data 1 Single channel XGBOOST coordinates and performances.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig6-data1-v1.csv
Download elife-75126-fig6-data1-v1.csv

Whole-brain connectomics can aid the discovery of brain networks underlying the neural encoding of grip-force

The ability to account for decoding performances for invasive electrodes may soon become as important as accounting for variance in stimulation effects, as bidirectional clinical brain computer interfaces will rely both on electrical sensing and stimulation. Recently, network mapping of neurostimulation targets has shown utility to predict variance in clinical outcomes following DBS (Horn et al., 2017b; Horn and Fox, 2020; Li et al., 2020). Here, we extended the same framework to predict variance in grip-force decoding performance observed from single channels, using the XGBOOST grip-force decoding results. In this approach – termed prediction network mapping – we calculated functional and structural connectivity fingerprints by projecting each recording location to a group connectome that was acquired in a cohort of PD patients. These fingerprints denote to which other brain areas each site is connected to. Using a discriminative fiber tracking analysis, (Baldermann et al., 2019; Li et al., 2020) we analyzed the predictive value of structural connectivity from ECoG recording locations (for an exemplar case see Figure 7A) for XGBOOST decoding performance. Therefore, diffusion imaging derived whole-brain fiber connectome data traversing to more than 20% of recording locations were used (Figure 7B). The specific fiber distributions included structural projections spanning sensory, motor and prefrontal cortex, and could significantly predict decoding performance of left out channels (ρ=0.38, p<0.0001; thresholded at a false discovery rate α=0.05) and patients (ρ=0.37, p<0.0001) in a cross validated manner (Figure 7D). Next, we created spatial models of optimal decoding performance for functional connectivity (R-Maps are shown in Figure 7C). This model led to significant predictions of decoding performance in leave-one-channel-out ( $ρ$ =0.37, p<0.0001) and leave-one-subject-out cross validations (functional connectivity $ρ$ = 0.37, p<0.0001) (Figure 7E). The results were further validated with voxel-wise correlations using the statistical parametric mapping (SPM) framework (see Materials and methods for further details). Models such as the two presented here could be generalized to all BCI applications and used to identify brain networks that encode specific behavioral and clinical target variables.

Figure 7 with 1 supplement see all

Download asset Open asset

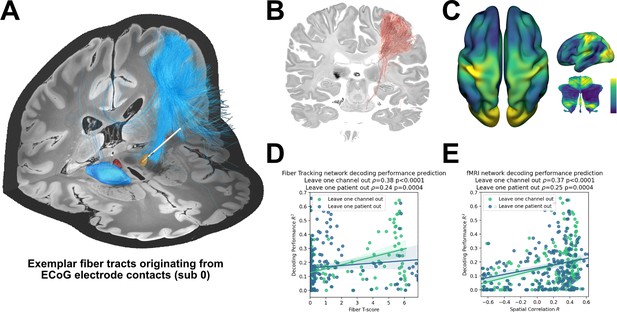
Structural and functional movement decoding network analysis reveals cerebellar as well as sensorimotor cortical decoding capacity.

(A) Visualization of fibers originating from the ECoG recording locations of subject 1. (B) Decoding performance across all subjects and channels significant fiber tracts are displayed. All ECoG contacts were projected to the left hemisphere. For every fiber a t-test statistic between connected and unconnected brain regions was calculated. Only significant fibers, indicating structural connectivity to grip-force decoding performance, are shown. (C) The optimal R-Map is shown for the cortical surface as well as cerebellum for fMRI functional connectivity. Fingerprints were calculated between the functional connectivity of every electrode contact to all other voxels. The R-Map was then calculated as a correlation between individual contact fingerprints and the contact specific $R^{2}$ decoding performance. (D) Fiber tracking connectivity predicts grip-force decoding performance (leave one channel out cross validation ρ=0.38, p<0.0001, leave one patient out cross validation ρ=0.24, p=0.0004) (Figure 7—source data 1). Here, each individual point represents a statistic of connected and unconnected fibers of each contact or patient. The previously calculated fiber statistic within each cross-validation fold could thus predict the channel or patient specific performance. (E) Functional connectivity predicts decoding performance (leave one channel out cross validation ρ=0.37, p<0.0001, leave one patient out cross validation ρ=0.25, p=0.0004) (Figure 7—source data 2). The spatial correlation between individual fingerprints and the cross-validation specific R-Map, predicts left out decoding performances.

Figure 7—source data 1 Fiber Tracking network decoding performance prediction.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig7-data1-v1.zip
Download elife-75126-fig7-data1-v1.zip
Figure 7—source data 2 fMRI network decoding performance prediction.: https://cdn.elifesciences.org/articles/75126/elife-75126-fig7-data2-v1.zip
Download elife-75126-fig7-data2-v1.zip

Discussion

Bidirectional brain computer interfaces will revolutionize the treatment of previously intractable brain disorders with brain signal decoding based adaptive neuromodulation. DBS provides a unique platform to trailblaze neurophysiological approaches, disease-specific modulation and computational strategies for brain signal decoding for next-generation brain implants. Here, we investigated clinical and computational strategies for grip-force decoding as a representative and pathophysiologically relevant behavioral target variable. We used multimodal invasive neurophysiology time-series data in PD patients undergoing DBS electrode implantation. Our findings can be broken down into four advances to the field: (1) we developed a new decoding approach based on multispectral time-concatenated band-power measures, subjected to Bayesian optimized extreme gradient boosted ensembles (XGBOOST): this outperformed traditional linear model-based methods and may be generalized to all brain signal-based regression problems. (2) Next, we demonstrate that electrocorticography signals outperform subthalamic LFP for grip-force decoding, supporting the utility of additional ECoG in adaptive DBS research for PD patients. (3) Our findings link PD motor impairment, PD pathophysiology with deterioration in decoding performance, highlighting a potential impairment in movement coding capacity through subthalamic low-beta bursts during motor preparation and execution periods. (4) Finally, we could significantly predict how well a specific recording site would perform to decode grip force based on brain connectivity. This novel framework (termed prediction network mapping) can be used in future implants to identify connectomic networks from which brain sensing can predict symptoms and behavior.

Limitations

Our analysis is retrospective in nature and the data were obtained in context of a Go/No-Go task, which may have implications on the generalizability of the findings in the application during naturalistic behavior. All model training and evaluations were conducted offline. Nevertheless, we took meticulous care to exclude any circularity in processing and machine learning applications. To this date, such circularities are overlooked in some movement decoding papers with filtering, normalization and time frequency transformation across entire sessions, thus reaching into the future from the point of the individually decoded sample. Ridding our analysis from data that would be unavailable in a real-time setting as reported in this study, leads to worse performances, but gives a more realistic estimate of model performance in the clinical use-case. While gripping is a relevant motor skill for human behavior, our findings are restricted to the decoding of grip-force and may have limited generalizability to other movements. The overall number of patients in this study is low. This may have limited a more detailed analysis of bias and other factors, beyond the described correlation of clinical symptom severity, subthalamic beta burst dynamics, electrode location and connectomics. Most importantly, the signal to noise ratio may further impact decoding accuracies differently for ECoG and LFP signals. This could in part explain why decoding from ECoG signals may benefit more from complex and non-linear model architectures. The comparability of ECoG and LFP recordings was further affected by the higher number of available ECoG channels, when compared to only three bipolar LFP channels. However, the large effect size of superior decoding performances with ECoG may indicate that this bias does not relevantly impact the interpretation of our findings. An additional limitation was the relatively small amount of available data per patient, which was constrained by the intraoperative setting (see Table 1). For deep learning approaches, we expect better performances with increased dataset sizes, which may become available, either through externalized extraoperative recordings (He et al., 2021) or sensing enabled implantable devices (Opri et al., 2020; Gilron et al., 2021). Importantly, our finding that decoding performances from single contacts outperform multi-electrode models may be a consequence of a combination of short recording durations in this study, suboptimal computational model selection and the fact that sensorimotor cortex and STN are part of the same circuit that is synchronized in oscillations. While we have made an effort to accommodate models that are optimized for spatio-spectral feature learning, and we are confident that these cannot outperform single channel approaches in this dataset, future studies should cautiously reinterrogate this issue in larger datasets, for example by implementing neural networks optimized for this purpose (Peterson et al., 2021). Finally, we should acknowledge that the exploration of the neural feature space in this study was non-exhaustive, and further raw data features, such as the local motor potential (Mehring et al., 2004), waveform shape features (Cole and Voytek, 2017), and aperiodic signal components (Wilson et al., 2022) could further improve decoding performances in future movement decoding studies.

Table 1

Subject characteristics.

N	Gender	UPDRS total	Hemisphere	Age	Movements	Disease duration [years]	ECoG Strip Contact Number Left	ECoG Strip Contact Number Right
0	Male	28	R	60.3	128	10.7	0	6
1	Male	27	L+R	51.2	464	14	28	28
2	Male	33	L+R	53.8	213	7.2	8	8
3	Male	31	L+R	44.2	285	10.1	8	8
4	Male	32	2L+2 R	63.6	381	13.1	28+8	28+8
5	Male	52	L	59.6	84	5.9	6	0
6	Male	55	L	71.6	161	1.4	6	0
7	Male	50	L	52.5	131	8.7	6	0
8	Male	62	L+R	66.8	547	9.8	6	6
9	Male	48	L	67.9	86	17.1	6	0
10	Female	31	R	69	205	10.4	0	6

Decoding grip force based on invasive electrophysiology

Our study defines a novel computational strategy to decode grip-force based on ECoG and LFP in patients undergoing DBS for PD. It explores defined oscillatory feature sets and compares machine-learning models with varying complexity, from linear models to artificial neural networks and regression trees. ECoG-based movement decoding of varying movement types has been previously investigated in epilepsy patients that underwent electrophysiological monitoring (Leuthardt et al., 2004) through which local motor potentials and gamma band activity were highlighted as informative features (Gunduz et al., 2016). First analyses based on STN-LFPs in PD patients have shown that Wiener Filter architectures can be successfully used for grip-force decoding (Tan et al., 2016; Shah et al., 2018). The present study extends these previous reports to a continuous non-trial-based decoding approach. Furthermore, a direct comparison of ECoG and LFP performance with relation to systematic machine learning methods was lacking. Our findings indicate that sensorimotor ECoG recordings are more informative than LFP recordings from the STN for grip-force decoding. While this finding is robust, we should acknowledge that the size and shape of electrodes (see Supplementary file 1a) and the spatial orientation and size of the neural architectures that are sampled are not directly comparable across these methods. Thus, it is difficult to derive the relative importance of the different brain regions for grip-force and vigor processing in motor control from this comparison. Instead, we interpret our result as a practical demonstration of the greater utility of ECoG signals for movement decoding. The results in this study are based on extracted band-power features and show superior performances with XGBOOST, when compared to other model architectures and algorithms. More specifically, best performances were obtained for Bayesian optimized XGBOOST models trained on data from single ECoG channels without additional benefit from channel combinations or combined ECoG and STN channel sets. In the future, this machine learning approach can be adopted to extend the clinical utility of invasive brain stimulation approaches for other brain disorders, e.g. through decoding of tics or obsessive compulsive behavior in neuropsychiatric DBS indications.

Towards machine-learning-based adaptive stimulation in Parkinson’s disease

Adaptive DBS (aDBS) has the potential for significant innovation in movement disorders (Starr, 2018). For Parkinson’s disease, different control policies of subthalamic beta band activity are now tested in clinical trials to improve the treatment for patients with akinetic rigid dominant PD (https://clinicaltrials.gov/ Identifier: NCT04681534, NCT04547712) (Little et al., 2013; Arlotti et al., 2018; Velisar et al., 2019). Beyond subthalamic beta power, ECoG recordings were previously used to successfully decode the presence of dyskinesia through elevated levels of gamma band synchronization. This could be used to reduce stimulation intensity to alleviate medication and stimulation induced dyskinesia (Swann et al., 2018). Such single biomarker approaches have the advantage that pathophysiological mechanisms may be the direct target of intervention, while machine learning based decoding methods derive correlates of symptoms and behavior indirectly through learning potentially noisy correlations (Neumann et al., 2019). Therefore, single biomarker based aDBS presents an optimal starting point for investigating the clinical utility of aDBS in controlled study designs. However, single biomarkers alone cannot account for the diverse and complex set of clinical signs of PD and behavior, for example during gait (Molina et al., 2021; Thenaisie et al., 2022), speech, and tremor (Hirschmann et al., 2013; Hirschmann et al., 2017). Here, a versatile decoding based control algorithm may further improve clinical outcome for these patients in the future (Neumann et al., 2019; Merk et al., 2022a). Indeed, machine learning-based decoding has been successfully described in first translational breakthrough studies (Opri et al., 2020; Gilron et al., 2021; He et al., 2021). In a complementary approach, we focused on direct grip-force decoding, motivated by the hypothesis that future aDBS studies increasing DBS amplitude during periods of higher movement vigor may advance the successful treatment of bradykinesia in PD. While our previous findings indicate that relative amounts of beta can still signal bradykinesia during movement, (Lofredi et al., 2019; Feldmann et al., 2021) further positive control parameters could keep stimulation proportional to intended movement vigor. Moreover, recent reports that beta power correlates negatively with phasic dopamine release may further substantiate the idea of movement/kinematics based STN stimulation to support intrinsic movement related dopamine signals (Schwerdt et al., 2020). We may speculate that DBS constitutes a network modulation that is similar to dopamine transients by suppressing local firing of the subthalamic nucleus (Milosevic et al., 2018) and shifting the balance of basal ganglia from indirect to direct pathway activity. As highlighted above it was recently shown in non-human primates that phasic decreases in beta in the basal ganglia are correlated to phasic dopamine signals during movement (Schwerdt et al., 2020). Thus, in order to support the intrinsic dopaminergic capacity of PD patients, future machine learning based aDBS approaches could be complemented by algorithms that inform the stimulation on behavioral and motor adjustments to mimic intrinsic phasic dopamine signals. Previous studies have successfully decoded the presence of movement using cortical beta activity (Opri et al., 2020) which could also become a viable treatment option in PD. However, getting an estimate of movement vigor that is through the prediction of grip-force may complement advanced aDBS control policies, as multivariate models emerge for the next-generation of neurotherapeutics.

Notably, the proposed adaptive stimulation would require a fast algorithmic adaptation of stimulation to ongoing behavior. This could be combined with additional slower adaptations in response to medication or sleep cycles. Specifically for PD, beta-activity-based adaptive stimulation can be well suited to track the patient’s overall symptom state (Tinkhauser and Moraud, 2021) while more rapid stimulation adaptations based on vigor can follow fast kinematic changes. The utility of vigor-based stimulation and the combination of this approach with additional slower adaptation algorithms, require further proof-of-concept studies before the clinical utility can be foreseen. In our study, we demonstrate that motor symptom severity itself can have direct and negative effects on decoding performance, which we should keep in mind during clinical decision making. Previous studies have shown that the presence of beta bursts correlated with motor performance in cortex (Little, 2019) and STN (Torrecillos et al., 2018), which could degrade decoding performance (Khawaldeh et al., 2020). Our study replicates and extends these findings, as we show a direct correlation between movement related beta burst dynamics and PD motor sign severity. More importantly, our results show that the amount of time the STN is bursting in the low-beta band, during motor preparation and movement execution is inversely correlated with ECoG based grip-force decoding performance. An obvious interpretation of this finding is that excessive synchronization in the STN may impair flexible motor control by decreasing information coding capacity and neural entropy as previously suggested in animal studies (Mallet et al., 2008; Cruz et al., 2009) and recently suggested for subthalamic beta bursts (Velasco et al., 2022). Again based on the inverse relationship of beta activity and dopamine (Schwerdt et al., 2020), we may speculate that beta bursts may relate to transient dips in dopamine signaling. Dopamine was shown to precede and invigorate future movement (da Silva et al., 2018). If subthalamic beta bursts indicate phasic decreases in dopaminergic innervation, we could expect a loss of invigoration and reinforcement of ongoing neural population activity in the cortex – basal ganglia – thalamic loop, which offers an elegant explanation for the lower decoding performance from ECoG signals in the absence of obvious cortical activity patterns.

Beyond beta bursts our findings indicate general impact of motor symptoms in the hypodopaminergic state on machine learning based kinematic decoding capacity. This highlights the conceptual relevance of disease specific interactions with computational models. Interestingly, in the hypodopaminergic state, the model output underestimated the grip force extent produced by the patients. This could reflect a loss of neural vigor representations related to insufficient dopaminergic modulation (Turner and Desmurget, 2010). In the future, we will have to account for the individual impact of disease specific changes in brain signals that affect decoding performance. Further, our results corroborate the notion that dopamine plays a key role in coding and modulating neural representations of movement kinematics in the human brain.

Connectomics can aid the discovery of brain networks underlying encoding of clinical and behavioral target variables

Decoding performance for clinical BCI may be drastically improved when adjusting brain signal recording sites to the underlying interconnected network that is relevant for encoding of the specific target behavior. For instance, when decoding language or speech, one could envision that recordings at either Broca’s or Wernicke’s region could be helpful, but a combination of both could be optimal. The two regions form a network with direct connections via the Arcuate Fascicle. In the present study, we have leveraged multisite recordings from various electrode locations across patients to identify the network that would be most informative for grip force decoding. For this endeavor, we adapted two existing methods that are able to isolate (i) connected voxels and (ii) connected fiber tracts (Horn et al., 2017b; Li et al., 2020) associated with a specific target metric (such as grip-force decoding performance in the present case). While Euclidean distance to motor target, i.e. hand knob area for ECoG and therapeutic target for STN, was significantly correlated with decoding performance within-subject, this simplistic notion could not predict decoding performance across channels or patients. Thus, proximity to landmarks alone does not reliably help the identification of optimal recording sites. Given the complexity and vast distribution of movement related brain areas, from cerebellum to frontal cortex to parietal cortex, it may not be surprising that whole-brain connectomics outperform single region of interest based distance metrics for predicting informative recording locations. The development of a connectomic identification of optimal decoding locations has important implications in clinical adoptions of BCI technology. Preoperative identification of brain networks would allow the design of optimal electrode architectures and targeted implantation to cover strategic nodes of distributed networks for decoding of clinical variables and behavior. Moreover, connectomic approaches can inform the optimal spatial feature selection of pretrained machine learning models to facilitate brain signal decoding without the requirement for individual (re-)training. Importantly, the connectomic models that we used can be trained based on multiple dimensions of input-output relationships, for example for decoding of behavior like grip-force, but also for decoding clinical signs, such as tremor or mood disturbances. Thus, when implanting a high-density ECoG grid, connectomic analyses can generate target specific contact combinations, for example focusing on primary cortex for tremor and supplementary motor area for motor intention and bradykinesia. Our results highlight the utility of whole-brain connectomics to predict machine learning-based brain signal decoding performance that can be generalized to any bidirectional clinical brain-computer interface use-case. In the future, neurosurgeons may not target individual sensing locations in isolation, but instead determine optimal implant trajectories in accordance with whole-brain connectomic fingerprints for optimal BCI performance.

Conclusion

Our analysis from PD patients undergoing DBS implantation showed that ECoG recordings outperform STN-LFP recordings for grip-force decoding throughout different machine learning methods, with XGBOOST showing the highest performance. Parkinsonian motor sign severity and subthalamic low-beta bursts were associated with loss of decoding performance, indicating a specific link between PD pathophysiology, kinematic coding capacity and motor impairment. To investigate the spatial relationship of ECoG decoding performances in the brain, we have formalized a connectomic framework that could cross-predict decoding performances across recording sites and patients, based on underlying whole brain MRI connectivity patterns. Our findings highlight the utility of ECoG for intelligent adaptive stimulation in PD, corroborate the role of PD symptom severity in kinematic coding and pave the way for connectomic neurosurgery for machine learning-based brain signal decoding. We hypothesize that future neurotechnological treatments may have the potential to outperform traditional drug regimes, due to a key advantage in the temporal and spatial precision of therapeutic delivery towards a precision medicine approach for intelligent adaptive DBS (Neumann et al., 2019; Neumann and Rodriguez-Oroz, 2021; Merk et al., 2022a).

Materials and methods

Participants

The current study is based on previously published data (Alhourani et al., 2020). In brief, subthalamic LFP and subdural ECoG recordings were simultaneously acquired from 11 PD patients. The patients were subjected to bilateral STN-DBS lead implantation, as proposed by standard clinical indications criteria. In accordance with protocol #PRO13110420, approved by the Institutional Review Board of the University of Pittsburgh, informed consent for all patients was obtained prior to any surgical procedure. The subject characteristics are detailed in Table 1. UPDRS Part III scores for the off-medication conditions were collected in a time period of 1–3 months prior to surgery by movement disorder neurologists. Dopaminergic medications were withheld for at least 12 hr before intraoperative testing.

Behavioral paradigm

Request a detailed protocol

The behavioral task performed for this study was previously described (Kondylis et al., 2016; Alhourani et al., 2020; Fischer et al., 2020) and it is schematically shown in Figure 1A. The task included Go/No-Go cues with randomized inter-trial interval durations. Feedback durations were adjusted based on grip force reaction times. In the present analyses, time-series were virtually streamed as continuous data to simulate real-time grip-force decoding, irrespective of task trials. Subjects were fully awake, and no anesthetic agents were administered for at least 1 hr before the task procedure. No medication was given during the task. The task paradigm was implemented using the Psychophysics Toolbox (Brainard, 1997) on a portable computer. The trials consisted of a simultaneous presentation of a yellow traffic light in the center of a screen, and a cue on one side indicating which hand the subject should use for the subsequent response of squeezing the handgrip. The cue remained on screen for 1000–2000ms, followed by the traffic light changing either green or red, signaling a ‘go cue’ and ‘no-go cue’, respectively. Subjects performed the task for a cumulative total time of 10–25 min. As the present study focuses on grip-force decoding performance based on the electrophysiological signals, all sessions containing valid movements were merged per subject for further analysis. To validate that the used grip-force label in our data varies not only between two movement states, but constitutes a relevant regression problem with varying force amplitude and velocity, all movement maximum amplitudes and velocity traces are visualized in the Figure 1—figure supplement 1.

Electrophysiological recordings

Request a detailed protocol

Subdural electrode strips were implanted temporarily through standard frontal burr holes located near the coronal suture and aimed posteriorly to the hand knob motor cortex region. Strip targeting has been previously described and was based on markings of stereotactically defined overlying scalp locations (Kondylis et al., 2016). STN-DBS electrodes were implanted bilaterally, targeting the dorsolateral motor area of the STN. ECoG data were recorded intra-operatively using six-contact (left n=5 patients, right n=3), eight-contact (left n=3, right n=3) and twenty-eight-contact (left n=2, right n=2) strip electrodes. The electrode details are shown in Supplementary file 1a and all ECoG and STN electrodes are plotted in Figure 1B (mean number of electrode contacts were 10.18±11.29 for left and 8.9±12 for right hemispheres). A referential montage was used in which the reference electrode was placed in the scalp and a ground electrode was placed in the skin overlying the acromion process. ECoG and STN signals were filtered (0.3–7.5 kHz), amplified, and digitized at 30 kHz using a Grapevine neural interface processor (Ripple Inc). Force signals were digitally recorded simultaneously with the ECoG and STN-LFP signals. LFPs from the STN were recorded using the clinical DBS lead (model 3389, Medtronic) from all four contacts and referenced offline in a bipolar montage. All signals were resampled to 1 kHz for offline analysis. To investigate the variability of grip-force as a potential bias for decoding performance, we calculated the variance of peak force across movement repetitions.

Electrode localization

Request a detailed protocol

Subdural electrode reconstructions were obtained by aligning pre-operative MRI, intra-operative fluoroscopy, and postoperative CT. Representative images of this technique were previously shown in detail (Randazzo et al., 2016). In short, the CT and MRI were co-registered using mutual information using the SPM software library and rendered onto 3D skull and brain surfaces using Osirix (v7.5) (Rosset et al., 2004) and Freesurfer (v5.3) software packages (Dale et al., 1999), respectively. These surfaces and the fluoroscopy images were then aligned according to common points: stereotactic frame pins, implanted depth electrodes, and skull outline positions (Randazzo et al., 2016). The parallax effect of the fluoroscopic images was accounted for using the obtained distance from the radiation source to the subject’s skull. Succeeding the surface-to-fluoroscopic image orientation alignment, a 3D location for each electrode contact was projected from the fluoroscopic image to the cortical surface. Deep brain stimulation electrode locations were reconstructed using the advanced neuroimaging pipeline defined by Lead-DBS using default settings (Horn et al., 2019). In brief, preoperative MRI and postoperative CT scans were co-registered and normalized to MNI 2009b NLIN ASYM space. Electrode artefacts were visually identified and marked to obtain MNI coordinates of DBS electrode contacts. All electrode localizations are visualized in Figure 1B.

ECoG and LFP preprocessing and feature extraction

Request a detailed protocol

The entire preprocessing pipeline used in the present study was optimized for real-time performance and inspired by the Berlin Brain Computer Interface (Blankertz, 2006). Processing was performed in Python using custom code based on MNE-python (Gramfort et al., 2013), mne_bids (Appelhoff et al., 2019) and pybv (https://pybv.readthedocs.io/en/stable/). All raw data files were saved in the iEEG-BIDS structure (Holdgraf et al., 2019). To account for baseline drifts, the force traces were cleaned using a normalization approach presented for previous ECoG finger trajectory decoding (Xie et al., 2018). A real-time data stream of untouched electrophysiological raw data was emulated to ensure that all processing that can impact decoding is performed in a real-time compatible manner. Referencing was performed online (i.e. after streaming virtual data packets). All LFP recordings were referenced bipolarly, against the adjacent contacts (0–1, 1–2, 2–3 with contact 0 being the lowest by convention of the manufacturer). Throughout the manuscript, we adopt the clinical usage of electrodes (also named ‘leads’) and contacts from the DBS realm. During preprocessing (in pseudo real time), we derive three bipolar STN-LFP channels from four adjacent contacts in one DBS electrode (also called ‘lead’). We also follow this nomenclature for ECoG, where we call the entire strip an ‘electrode’. ECoG electrodes in our dataset can have varying number of contacts (see Supplementary file 1a). ECoG recordings were referenced by subtracting the common average of all ECoG electrodes, therefore the number of channels per ECoG electrode is equal to the number of contacts per strip. To facilitate computationally efficient real-time enabled algorithms, time frequency decomposition for the machine learning analysis was conducted by bandpass filtering in the $θ$ (4–8 Hz), $α$ (8–12 Hz), $β$ (13–35 Hz), low $β$ (13–20 Hz), high $β$ (20–35 Hz), all $γ$ (60–200 Hz), low $γ$ (60–80 Hz) and high-frequency activity, (90–200 Hz) frequency bands. Overlapping broad $β$ and $γ$ bands were added in addition to subbands to enable the investigation of distinct interactions within these frequency bands (Figure 1C). To estimate band specific activity, different time durations were used for band-pass filtering with longer time segments for lower frequencies, and shorter time segments for higher frequencies ( $θ$ =1000ms, α and β bands = 500ms, γ = 100ms). To get an estimate of amplitude of the activity in the filtered signals, variance was extracted in intervals of 1 s in a sliding window of 100ms resulting in a time resolution of 10 Hz. All variance estimates were normalized by subtracting and dividing by the median in a sliding window of 10 s to account for differences in impedance and proximity to the source before subjecting the data to the machine learning analysis. All features were clipped as an artifact rejection mechanism when they exceeded a normalized value of [–2 2]. The used normalization is fully compatible with a real-time prediction approach, as data acquired in the future do not influence the present predictions. See Figure 1E for an outline of the methods pipeline. For the purpose of visualization, Morlet wavelets (7 cycles) were used to demonstrate the entire time-frequency decomposition (Figure 1C).

Machine learning training and evaluation

Request a detailed protocol

A rigorous nested cross-validation approach was implemented. An outer threefold cross validation split the data into folds of two third training and one third test set. For each individual channel, a Bayesian Optimization hyperparameter search (Frazier, 2018) was then conducted for 10 rounds using the training set only. For each round the training data was trained and tested in an inner threefold cross-validation with 80% training size. Post-hoc assessment confirmed convergence in performance after a maximum of 5 rounds in all recordings. The mean $R^{2}$ coefficient of determination of every test set estimate of the outer cross-validation was used as the performance measure as defined below:

R^{2} (y, \hat{y}) = 1 - \frac{\sum_{i = 1}^{n} (y_{i} - \hat{y_{i}})^{2}}{\sum_{i = 1}^{n} (y_{i} - \bar{y})^{2}}

Since the $R^{2}$ metric can be lower than zero for predictions that are worse than constant predictions, we used a lower threshold at zero to make performances comparable for the purpose of visualization. The input features for every model were all eight previously described frequency bands. In order to test the contribution of time points preceding the decoded target sample, frequency band features of different time points were concatenated and compared with respect to their decoding performance. The present study investigated commonly used and promising linear and non-linear machine learning algorithms, specifically elastic net regularized linear models, linear Wiener filters, neural networks, gradient boosted decision trees (XGBOOST) and source power comodulation.

Linear models

Request a detailed protocol

Linear models can capture underlying feature dependencies and reveal those as correlations in each weight parameter. Input features are multiplied by a weight coefficient. The dot product of the weight vector $w$ and feature vector $x$ is then shifted by the bias $b$ . The feature vector in this analysis is the vector of all frequency bands for a single time point. The prediction label $y$ is the baseline corrected gripping force. For a linear regression the activation function is linear, is defined as follows:

y = w x + b

To prevent overfitting, regularization in the form of $l_{1}$ and $l_{2}$ norm is commonly used. Here we tested different parameters of the elastic-net (enet) regularization (Zou and Hastie, 2005), which is a combination of the $l_{1}$ and $l_{2}$ norm specified by the regularization hyperparameters $α$ and $ρ$ , respectively. The objective function of the enet model follows:

\underset{w}{m i n} \frac{1}{2 n_{s a m p l e s}} {‖X w - y‖}_{2}^{2} + α ρ {‖w‖}_{1} + \frac{α (1 - p)}{2} {‖w‖}_{2}^{2}

where $X$ is a matrix of dimension $n$ x $m$ whom i^th row is the feature vector $x$ of size $m$ and $w$ is the solution vector, which, due to the $l_{1}$ sparse regularization term, most of the coefficient will be expected to be zero. For hyperparameter-search, $α$ and $ρ$ were both sampled from a uniform distribution ranging from zero to one. Since elastic nets are solved using gradient descent, the maximum training iteration also needs to be specified. Here an iteration number of 1000 has been used. The implementation was done using the scikit learn Python package (Pedregosa, 2011).

Wiener filters

Request a detailed protocol

Tan et al. described the use Wiener filters in the application of force estimation from STN-LFP signals (Shah et al., 2018). Here, the output $y$ is a weighted sum of features in the time and frequency domain in the weight matrix $W$ . $I$ frequency band features are used together with $J$ lags. For the regression analysis the activation function is kept linear, as follows:

y (n) = \sum_{j = 0}^{J} \sum_{i = 0}^{I} w_{i j} x_{i} (n - j)

This equation has a closed form solution, known as the normal equation (Proakis and Monolakis, 1996). Wiener filters essentially implement a multivariable linear model with multiple time-steps. Using Wiener filters, we tested the contribution of different concatenated time-steps of brain signals preceding the decoded target sample. This provides insight about the optimal feature length in the time domain.

Neural networks

Request a detailed protocol

We have further investigated the utility of artificial neural networks. While linear models and Wiener filters may underfit the data, neural networks can be very complex and have a higher risk to overfit with increasing complexity. The ideal model architecture finds a balance between under and over- fitting to the training dataset. In this context not only single weight correlations of band features could contribute to force decoding performances, but a richer representation of feature invariances in combinations of different frequency bands may be learned by additional layers and units of the model. The architecture of neural networks is derived from linear models with non-linear activation functions, which are referred to in this context as units. Multiple units are combined in different layers with different activation functions.

Explicitly, the output $y$ of the i^th unit in layer $l$ is the weighted sum of activations of the previous layer units $y_{k}^{l - 1}$ with weights $w_{i k}^{l}$ ,

y_{i}^{l} = f^{l} (\sum_{k} w_{i k}^{l} y_{k}^{l - 1} + b_{i}^{l})

Neural networks are trained through a cost function using a gradient descent algorithm. Hyperparameters were adjusted in order to prevent over -and underfitting (Geman et al., 1992). Here, neural networks were tested with at least one hidden layer. The input nodes of this layer were in the hyperparameter search uniformly sampled in a range of 1–10. The number of hidden dense layers were sampled from a range of 1–3 layers. The hidden dense layer neurons were uniformly sampled in a range of 1–10. Sigmoidal and hyperbolic tangent activation functions were tested in the hidden layers. After each hidden layer a batch normalization layer and a dropout layer with a factor of 0.2 was added. The output activation function was set linear. The used training algorithm was the Adam optimizer (the learning rate was sampled from a log uniform distribution from 0.0001 to 0.01, $β_{1}$ was set to 0.9, $β_{2}$ to 0.999 and $ε$ to 0.999). The Adam optimizer improves backpropagation such that each weight parameter is adapted according to its first and second momentum (Kingma and Ba, 2015). Each neural network was trained using 1,000 epochs with a batch size of 100. The loss function was set to the mean squared error. To prevent overfitting, the training set was further split into train and validation set with 80% train. The validation dataset was then used for early stopping with a patience parameter of 10 epochs. The model with lowest validation error is then used for test set prediction. Due to poor performances, the inner cross-validation was left out for the neural network training sequence. Neural Networks were implemented using the TensorFlow framework (Abadi, 2016).

Gradient boosted trees using the XGBOOST framework

Request a detailed protocol

A common problem with neural networks is the high dependency on the provided set of features and potential to learn spurious input-output associations. In this analysis, a feature vector of all 8 frequency bands concatenated for 5 time points requires a Wiener Filter with 40 weights. In an architecture-like neural networks all these features are contributing to the overall force prediction, nevertheless not all weight parameters are promising. Decision Tree algorithms overcome this problem naturally by implementing optimization of input feature use in their architecture. Thus, decision trees and random forests, first described by Breiman, 2001, were proven to be a robust, accurate and successful tool for solving machine learning tasks, including classification, regression, density estimation and manifold learning or semi-supervised learning (Gall and Lempitsky, 2013). Random forests are an ensemble method consisting of many decision trees. A decision tree is a statistical optimal data segregation method, that is only controlled by conditional sequences. Different implementations were proposed on top of Decision Trees. AdaBoost (Schapire, 2009) is an adaptive learning algorithm that builds up successive decision trees iteratively. By that an ensemble of multiple weighted weak learners are combined to yield a strong estimator. Gradient Boosting is built using the same concept. According to Empirical Risk Minimization it fits each decision tree based on the residuals of a defined objective function. This objective function is typically based on an error loss and a regularization term. The model is initialized using a constant value. In an iterative process, the new trees are added to the model up till the maximum defined estimators are reached. Here, the scalable tree boosting framework XGBOOST (Chen and Guestrin, 2016) was used. In this analysis the number of boosting rounds is set to 10. The depth of each tree is sampled uniformly in a range from 1 to 100. When adding new trees to the model the parameter learning rate $η$ is scaling the contribution of each tree prediction and is sampled here log uniformly from of the range [ $10^{- 5}$ , 1]. Regularization in Gradient Boosted Trees is controlled by different factors. One of the factors is the minimum splitting loss $γ$ . For every decision tree, new nodes were added only if the gain metric was above $γ$ . It is here sampled from a uniform distribution between 1 and 10. Hyperparameters for all used machine learning methods are listed in detail in Supplementary file 1b.

Source power comodulation

Request a detailed protocol

A state-of-the-art movement prediction approach is the source separating framework called Source Power Comodulation (SPoC) (Dähne et al., 2014). Oscillatory sources are here extracted based on their power comodulation with the force gripping target. SPoC was implemented using the MNE framework (Gramfort et al., 2013). Thus, discriminant neural sources are made visible. In this context, the band-power at each frequency band of interest was calculated by taking the logarithm of the variance of the projected signal in the source space. For sake of comparison, only one spatial filter was used for feature computation at each frequency band. In the same manner as before, a Wiener filter was then applied in order to resample time lags up to 500ms. Here again, the band power features are then used as input features. A Bayesian Optimization hyperparameter search was also here implemented for both the enet model as well as the XGBOOST framework with the aforementioned parameters.

Hyperparameter search: Bayesian optimization

Request a detailed protocol

All models underwent an extensive hyperparameter search using Bayesian optimization. A common problem using machine-learning algorithms is finding the optimal hyperparameter settings given a certain architecture. Grid search exhaustively tries out all provided hyperparameters while Random search only draws random parameters from the given hyperparameter distributions. Sampling the error loss function can be computationally expensive. Bayesian Optimization formulates this problem into an optimization problem. Here, a cost function is minimized given a set of hyperparameters. Instead of sampling from the objective cost function, a probabilistic model is defined. The hyperparameters minimizing the negative expected improvement are selected given a multinomial Gaussian process using a Matern kernel. Those parameters are then used to sample from the respective regressor in the given dataset. The resulting error is used to update the gaussian process distribution and given the maximum expected improvement, the next best hyperparameter set is drawn. This process is repeated for the elastic net, neural networks and XGBOOST architecture for 10 iterations. For every round, a threefold cross validation is used in order to prevent overfitting. Given log-uniform distributions a wide range of hyperparameters can thus be sampled in a computationally efficient manner. The implementation was done using the scikit-optimize framework (https://scikit-optimize.github.io/stable/). Supplementary file 1b lists the hyperparameters subjected to Bayesian optimization. The chosen methodology is non-exhaustive and primarily serves the comparison of variance in decoding explained by the recording location of the signal (ECoG vs. STN), motor symptom severity (UPDRS-III), beta bursts and brain networks. It further gives an intuition about the potential of more complex and elaborate machine learning methods for brain computer interfaces.

Definition of best model and best channels

Request a detailed protocol

Previous studies have repeatedly demonstrated that using a single optimal channel in the STN is advantageous over using all available channels (Shah et al., 2018). Most importantly, addition of more channels leads to decreased generalization and higher risk of overfitting with little performance benefit. Based on these results and to account for varying numbers of available electrode contacts, one channel with optimal decoding performance on the cross-validation test set was chosen per patient to quantify and compare decoding performance for the ECoG and STN analysis across patients. Since hyperparameter optimization is implemented only within each inner cross validation fold, any circularity and data leakage is circumvented. A robust decoding performance estimate is thus obtained through left out testing data only.

Analysis of beta bursts during motor preparation and movement execution periods

Request a detailed protocol

To investigate a potential relationship between grip-force decoding performance and beta burst activity, we have adopted a previously validated approach to movement related burst analyses (Torrecillos et al., 2018; Lofredi et al., 2019). Therefore, the beta feature time-series were used and a threshold constituting the 75th percentile of the rest periods were calculated. Next, threshold crossings of at least 100ms lengths in the motor preparation (−1–0 s with respect to movement) and movement execution (0–1 s with respect to movement execution) were marked as bursts. In previous reports, the most informative metric was the ‘time spent in burst’ which is calculated as the sum of burst durations in the time period of interest. This metric is directly proportional to the burst probability at a given time-point. All burst analyses were repeated for the low-beta and high-beta bands in ECoG and STN-LFP. The times spent in bursts were correlated with UPDRS-III and ECoG based decoding performances.

Prediction Network Mapping with whole-brain connectomics

Request a detailed protocol

To investigate whether decoding performance from different recording locations can cross-predict decoding performances across patients, we developed a whole-brain connectomics based approach. Therefore, ECoG electrode recording locations were projected to normative structural and functional MRI data (Parkinson’s Progression Markers Initiative [PPMI]; https://www.ppmi-info.org/) using Lead-DBS software in Matlab (https://www.lead-dbs.org/). (Horn et al., 2019) The PPMI connectomes of patients with PD (n = 74) was priorly computed (Ewert et al., 2018) and has been used in context of DBS multiple times (Horn et al., 2017c; Neumann et al., 2018; de Almeida Marcelino et al., 2019; Lofredi et al., 2021). No patient-specific diffusion or functional MRI was required for this analysis. Seeding from each recording site resulted in connectivity profiles (fingerprints) that were expressed as voxel-wise whole-brain volumes for functional and structural connectivity and a set of streamline connections for structural connectivity. We have adapted three previously published methods leveraging normative connectomes as predictive models.

First, fiber streamlines representative of structural connectivity between ECoG channels and all other brain areas were isolated and assigned with a ‘Fiber T-score’, associating XGBOOST decoding performance with the fiber tracts connectivity from respective ECoG recording locations across patients using mass-univariate two-sample t-tests between $R^{2}$ scores in connected vs. unconnected recording locations. Only fibers with significant t-scores surviving FDR correction at an alpha level 0.05 were considered further. Next, T-values were used as weights in an aggregated fiber score to predict out of training sample channel and patients’ performances. Next, functional connectivity maps were used to generate an ‘R-Map’, a connectivity model which is associated with optimal decoding performance, by performing voxel-wise correlations of connectivity and decoding performance from recording locations. The connectomic fingerprint from each recording location can then be assigned a spatial correlation coefficient that may have predictive value for the underlying decoding performance. The predictive value of these two methods were confirmed using ‘leave-one-channel-out’ and ‘leave-one-subject-out’ cross-validation. Finally, statistical parametric mapping was used to confirm the described correlations of structural and functional connectivity using linear-mixed effects models. In a voxel-wise approach, structural connectivity between ECoG channels and all other brain areas was calculated using Lead Mapper (https://www.lead-dbs.org/). Statistical voxel-wise correlation between decoding performance and structural and functional connectivity, separate mixed effects models, with a subject based random effect, were corrected for multiple comparisons with random field theory as implemented in the Statistical parametric mapping (SPM12) toolbox (https://www.fil.ion.ucl.ac.uk/spm/). Functional connectivity strengths between recording sites and sensorimotor cortex (peak coordinate x = –38, y = –22, z=72), parietal lobe (x=6, y = –32, z=82), striatum (x = –34, y = –24, z=26). and cerebellum (x=18, y = –50, z = –50 and x = –22, y = –52, z = –54) accounted for decoding performance. Similarly, for structural connectivity, a significant cluster in the sensorimotor region (x = –44, y = –18, z=70) correlated with high decoding performance. All connectivity analyses were performed using ECoG recording locations with contralateral $R^{2}$ performances (Figure 1E). A schematic illustrating the different steps of functional and structural prediction network mapping can be found in Figure 7—figure supplement 1.

Statistical analysis

Request a detailed protocol

Results are stated as mean ± standard deviation. All significance testing was performed using two-sided Monte-Carlo permutation tests and bootstrapping. p-Values were obtained by shuffling value positions and determining the resulting original rho value percentile in the distribution of surrogate combinations. Spearman’s correlations were performed because of small sample size and varying distributions. Clinical correlations were performed using preoperative UPDRS-III total scores. To test for the temporal specificity of the clinical correlation with decoding performance, we performed sample-wise correlations of decoding output with UPDRS-III total scores across subjects. Multiple comparisons were corrected by adjusting the significance threshold α to the false discovery rate (Benjamini and Hochberg, 2016).

Data availability

Request a detailed protocol

All raw data in BIDS for iEEG format are openly available through the Harvard Dataverse (https://doi.org/10.7910/DVN/IO2FLM). Code and derived source data for the reproduction of all figures and the machine learning and statistical analysis are provided through GitHub (https://github.com/neuromodulation/ECoG_vs_STN; Merk, 2022b; copy archived at swh:1:rev:09d3ea5b846681d28edb26943b4315ae5f5a37dd).

Data availability

All raw data in BIDS for iEEG format are openly available through the Harvard Dataverse (https://doi.org/10.7910/DVN/IO2FLM). Code and derived source data for the reproduction of all figures and the machine learning and statistical analysis are provided through GitHub (https://github.com/neuromodulation/ECoG_vs_STN, copy archived at swh:1:rev:09d3ea5b846681d28edb26943b4315ae5f5a37dd).

The following data sets were generated

1. Merk T
2. Peterson V
3. Lipski W
4. Blankertz B
5. Turner RS
6. Li N
7. Horn A
8. Richardson RM
9. Neumann WJ
(2022) Harvard Dataverse
Replication Data for: Electrocorticography is superior to subthalamic local field potentials for movement decoding in Parkinson’s disease.
https://doi.org/10.7910/DVN/IO2FLM

References

Conference
1. Abadi M
(2016)
TensorFlow: A system for large-scale machine learning

Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, OSDI 2016.
- Google Scholar
(2020) Subthalamic Nucleus Activity Influences Sensory and Motor Cortex during Force Transduction
Cerebral Cortex (New York, N.Y 30:2615–2626.
https://doi.org/10.1093/cercor/bhz264
- PubMed
- Google Scholar
1. Androulidakis AG
2. Kühn AA
3. Chen CC
4. Blomstedt P
5. Kempf F
6. Kupsch A
7. Schneider G-H
8. Doyle L
9. Dowsey-Limousin P
10. Hariz MI
11. Brown P
(2007) Dopaminergic therapy promotes lateralized motor activity in the subthalamic area in Parkinson’s disease
Brain 130:457–468.
https://doi.org/10.1093/brain/awl358
- PubMed
- Google Scholar
1. Appelhoff S
2. Sanderson M
3. Brooks T
4. van Vliet M
5. Quentin R
6. Holdgraf C
7. Chaumon M
8. Mikulan E
9. Tavabi K
10. Höchenberger R
11. Welke D
12. Brunner C
13. Rockhill A
14. Larson E
15. Gramfort A
16. Jas M
(2019) MNE-BIDS: Organizing electrophysiological data into the BIDS format and facilitating their analysis
Journal of Open Source Software 4:1896.
https://doi.org/10.21105/joss.01896
- Google Scholar
1. Arlotti M
2. Marceglia S
3. Foffani G
4. Volkmann J
5. Lozano AM
6. Moro E
7. Cogiamanian F
8. Prenassi M
9. Bocci T
10. Cortese F
11. Rampini P
12. Barbieri S
13. Priori A
(2018) Eight-hours adaptive deep brain stimulation in patients with Parkinson disease
Neurology 90:e971–e976.
https://doi.org/10.1212/WNL.0000000000005121
- PubMed
- Google Scholar
1. Baldermann JC
2. Melzer C
3. Zapf A
4. Kohl S
5. Timmermann L
6. Tittgemeyer M
7. Huys D
8. Visser-Vandewalle V
9. Kühn AA
10. Horn A
11. Kuhn J
(2019) Connectivity Profile Predictive of Effective Deep Brain Stimulation in Obsessive-Compulsive Disorder
Biological Psychiatry 85:735–743.
https://doi.org/10.1016/j.biopsych.2018.12.019
- PubMed
- Google Scholar
1. Benjamini Y
2. Hochberg Y
(2016) On the Adaptive Control of the False Discovery Rate in Multiple Testing With Independent Statistics
Journal of Educational and Behavioral Statistics 25:60–83.
https://doi.org/10.3102/10769986025001060
- Google Scholar
1. Beudel M
2. Brown P
(2016) Adaptive deep brain stimulation in Parkinson’s disease
Parkinsonism & Related Disorders 22 Suppl 1:S123–S126.
https://doi.org/10.1016/j.parkreldis.2015.09.028
- PubMed
- Google Scholar
1. Blankertz B
(2006)
‘The Berlin Brain-Computer Interface: Machine Learning Based Detection of User Specific Brain States

Journal of Universal Computer Science 12:581–607.
- Google Scholar
1. Brainard DH
(1997) The Psychophysics Toolbox
Spatial Vision 10:433–436.
https://doi.org/10.1163/156856897X00357
- PubMed
- Google Scholar
1. Breiman L
(2001) Random Forests
Machine Learning 45:324.
https://doi.org/10.1023/A:1010933404324
- Google Scholar
1. Cagnan H
2. Denison T
3. McIntyre C
4. Brown P
(2019) Emerging technologies for improved deep brain stimulation
Nature Biotechnology 37:1024–1033.
https://doi.org/10.1038/s41587-019-0244-6
- PubMed
- Google Scholar
1. Caire F
2. Ranoux D
3. Guehl D
4. Burbaud P
5. Cuny E
(2013) A systematic review of studies on anatomical position of electrode contacts used for chronic subthalamic stimulation in Parkinson’s disease
Acta Neurochirurgica 155:1647–1654.
https://doi.org/10.1007/s00701-013-1782-1
- PubMed
- Google Scholar
Conference
1. Chen T
2. Guestrin C
(2016) XGBoost: A Scalable Tree Boosting System
Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. pp. 785–794.
https://doi.org/10.1145/2939672.2939785
- Google Scholar
(2017) Nonsinusoidal Beta Oscillations Reflect Cortical Pathophysiology in Parkinson’s Disease
The Journal of Neuroscience 37:4830–4840.
https://doi.org/10.1523/JNEUROSCI.2208-16.2017
- PubMed
- Google Scholar
1. Cole S.R.
2. Voytek B
(2017) Brain Oscillations and the Importance of Waveform Shape
Trends in Cognitive Sciences 21:137–149.
https://doi.org/10.1016/j.tics.2016.12.008
- PubMed
- Google Scholar
1. Cruz AV
2. Mallet N
3. Magill PJ
4. Brown P
5. Averbeck BB
(2009) Effects of dopamine depletion on network entropy in the external globus pallidus
Journal of Neurophysiology 102:1092–1102.
https://doi.org/10.1152/jn.00344.2009
- PubMed
- Google Scholar
(2018) Dopamine neuron activity before action initiation gates and invigorates future movements
Nature 554:244–248.
https://doi.org/10.1038/nature25457
- PubMed
- Google Scholar
1. Dähne S
2. Meinecke FC
3. Haufe S
4. Höhne J
5. Tangermann M
6. Müller K-R
7. Nikulin VV
(2014) SPoC: a novel framework for relating the amplitude of neuronal oscillations to behaviorally relevant parameters
NeuroImage 86:111–122.
https://doi.org/10.1016/j.neuroimage.2013.07.079
- PubMed
- Google Scholar
(1999) Cortical surface-based analysis. I. Segmentation and surface reconstruction
NeuroImage 9:179–194.
https://doi.org/10.1006/nimg.1998.0395
- PubMed
- Google Scholar
(2019) Subthalamic neuromodulation improves short-term motor learning in Parkinson’s disease
Brain 142:2198–2206.
https://doi.org/10.1093/brain/awz152
- PubMed
- Google Scholar
(2015) Therapeutic deep brain stimulation reduces cortical phase-amplitude coupling in Parkinson’s disease
Nature Neuroscience 18:779–786.
https://doi.org/10.1038/nn.3997
- PubMed
- Google Scholar
1. Ewert S
2. Plettig P
3. Li N
4. Chakravarty MM
5. Collins DL
6. Herrington TM
7. Kühn AA
8. Horn A
(2018) Toward defining deep brain stimulation targets in MNI space: A subcortical atlas based on multimodal MRI, histology and structural connectivity
NeuroImage 170:271–282.
https://doi.org/10.1016/j.neuroimage.2017.05.015
- PubMed
- Google Scholar
(2021) Subthalamic beta band suppression reflects effective neuromodulation in chronic recordings
European Journal of Neurology 28:2372–2377.
https://doi.org/10.1111/ene.14801
- PubMed
- Google Scholar
1. Fischer P
2. Lipski WJ
3. Neumann W-J
4. Turner RS
5. Fries P
6. Brown P
7. Richardson RM
(2020) Movement-related coupling of human subthalamic nucleus spikes to cortical gamma
eLife 9:e51956.
https://doi.org/10.7554/eLife.51956
- PubMed
- Google Scholar
Preprint
1. Frazier PI
(2018) A Tutorial on Bayesian Optimization
arXiv.

https://arxiv.org/abs/1807.02811
- Google Scholar
Book
1. Gall J
2. Lempitsky V
(2013) Decision Forests for Computer Vision and Medical Image Analysis
Springer.
https://doi.org/10.1007/978-1-4471-4929-3
- Google Scholar
(1992) Neural Networks and the Bias/Variance Dilemma
Neural Computation 4:1–58.
https://doi.org/10.1162/neco.1992.4.1.1
- Google Scholar
1. Gilron R
2. Little S
3. Perrone R
4. Wilt R
5. de Hemptinne C
6. Yaroshinsky MS
7. Racine CA
8. Wang SS
9. Ostrem JL
10. Larson PS
11. Wang DD
12. Galifianakis NB
13. Bledsoe IO
14. San Luciano M
15. Dawes HE
16. Worrell GA
17. Kremen V
18. Borton DA
19. Denison T
20. Starr PA
(2021) Long-term wireless streaming of neural recordings for circuit discovery and adaptive stimulation in individuals with Parkinson’s disease
Nature Biotechnology 39:1078–1085.
https://doi.org/10.1038/s41587-021-00897-5
- PubMed
- Google Scholar
1. Gramfort A
2. Luessi M
3. Larson E
4. Engemann DA
5. Strohmeier D
6. Brodbeck C
7. Goj R
8. Jas M
9. Brooks T
10. Parkkonen L
11. Hämäläinen M
(2013) MEG and EEG data analysis with MNE-Python
Frontiers in Neuroscience 7:267.
https://doi.org/10.3389/fnins.2013.00267
- PubMed
- Google Scholar
1. Gunduz A
2. Brunner P
3. Sharma M
4. Leuthardt EC
5. Ritaccio AL
6. Pesaran B
7. Schalk G
(2016) Differential roles of high gamma and local motor potentials for movement preparation and execution
Brain-Computer Interfaces 3:88–102.
https://doi.org/10.1080/2326263X.2016.1179087
- Google Scholar
1. Haufe S
2. Meinecke F
3. Görgen K
4. Dähne S
5. Haynes J-D
6. Blankertz B
7. Bießmann F
(2014) On the interpretation of weight vectors of linear models in multivariate neuroimaging
NeuroImage 87:96–110.
https://doi.org/10.1016/j.neuroimage.2013.10.067
- PubMed
- Google Scholar
1. He S
2. Baig F
3. Mostofi A
4. Pogosyan A
5. Debarros J
6. Green AL
7. Aziz TZ
8. Pereira E
9. Brown P
10. Tan H
(2021) Closed-Loop Deep Brain Stimulation for Essential Tremor Based on Thalamic Local Field Potentials
Movement Disorders 36:863–873.
https://doi.org/10.1002/mds.28513
- PubMed
- Google Scholar
1. Hirschmann J
2. Hartmann CJ
3. Butz M
4. Hoogenboom N
5. Ozkurt TE
6. Elben S
7. Vesper J
8. Wojtecki L
9. Schnitzler A
(2013) A direct relationship between oscillatory subthalamic nucleus-cortex coupling and rest tremor in Parkinson’s disease
Brain : A Journal of Neurology 136:3659–3670.
https://doi.org/10.1093/brain/awt271
- PubMed
- Google Scholar
(2017) Parkinsonian rest tremor can be detected accurately based on neuronal oscillations recorded from the subthalamic nucleus
Clinical Neurophysiology 128:2029–2036.
https://doi.org/10.1016/j.clinph.2017.07.419
- PubMed
- Google Scholar
1. Holdgraf C
2. Appelhoff S
3. Bickel S
4. Bouchard K
5. D’Ambrosio S
6. David O
7. Devinsky O
8. Dichter B
9. Flinker A
10. Foster BL
11. Gorgolewski KJ
12. Groen I
13. Groppe D
14. Gunduz A
15. Hamilton L
16. Honey CJ
17. Jas M
18. Knight R
19. Lachaux JP
20. Lau JC
21. Lee-Messer C
22. Lundstrom BN
23. Miller KJ
24. Ojemann JG
25. Oostenveld R
26. Petridou N
27. Piantoni G
28. Pigorini A
29. Pouratian N
30. Ramsey NF
31. Stolk A
32. Swann NC
33. Tadel F
34. Voytek B
35. Wandell BA
36. Winawer J
37. Whitaker K
38. Zehl L
39. Hermes D
(2019) iEEG-BIDS, extending the Brain Imaging Data Structure specification to human intracranial electrophysiology
Scientific Data 6:102.
https://doi.org/10.1038/s41597-019-0105-7
- PubMed
- Google Scholar
1. Horn A
2. Kühn AA
3. Merkl A
4. Shih L
5. Alterman R
6. Fox M
(2017a) Probabilistic conversion of neurosurgical DBS electrode coordinates into MNI space
NeuroImage 150:395–404.
https://doi.org/10.1016/j.neuroimage.2017.02.004
- PubMed
- Google Scholar
1. Horn A
2. Reich M
3. Vorwerk J
4. Li N
5. Wenzel G
6. Fang Q
7. Schmitz-Hübsch T
8. Nickl R
9. Kupsch A
10. Volkmann J
11. Kühn AA
12. Fox MD
(2017b) Connectivity Predicts deep brain stimulation outcome in Parkinson disease
Annals of Neurology 82:67–78.
https://doi.org/10.1002/ana.24974
- PubMed
- Google Scholar
1. Horn A
2. Neumann WJ
3. Degen K
4. Schneider GH
5. Kühn AA
(2017c) Toward an electrophysiological “sweet spot” for deep brain stimulation in the subthalamic nucleus
Human Brain Mapping 38:3377–3390.
https://doi.org/10.1002/hbm.23594
- PubMed
- Google Scholar
1. Horn A
2. Li N
3. Dembek TA
4. Kappel A
5. Boulay C
6. Ewert S
7. Tietze A
8. Husch A
9. Perera T
10. Neumann WJ
11. Reisert M
12. Si H
13. Oostenveld R
14. Rorden C
15. Yeh FC
16. Fang Q
17. Herrington TM
18. Vorwerk J
19. Kühn AA
(2019) Lead-DBS v2: Towards a comprehensive pipeline for deep brain stimulation imaging
NeuroImage 184:293–316.
https://doi.org/10.1016/j.neuroimage.2018.08.068
- PubMed
- Google Scholar
1. Horn A
2. Fox MD
(2020) Opportunities of connectomic neuromodulation
NeuroImage 221:117180.
https://doi.org/10.1016/j.neuroimage.2020.117180
- PubMed
- Google Scholar
(2020) Perspective: Phase Amplitude Coupling-Based Phase-Dependent Neuromodulation in Parkinson’s Disease
Frontiers in Neuroscience 14:558967.
https://doi.org/10.3389/fnins.2020.558967
- PubMed
- Google Scholar
(2021) Modulation of beta bursts in subthalamic sensorimotor circuits predicts improvement in bradykinesia
Brain 144:473–486.
https://doi.org/10.1093/brain/awaa394
- PubMed
- Google Scholar
1. Khawaldeh S
2. Tinkhauser G
3. Shah SA
4. Peterman K
5. Debove I
6. Nguyen TAK
7. Nowacki A
8. Lachenmayer ML
9. Schuepbach M
10. Pollo C
11. Krack P
12. Woolrich M
13. Brown P
(2020) Subthalamic nucleus activity dynamics and limb movement prediction in Parkinson’s disease
Brain 143:582–596.
https://doi.org/10.1093/brain/awz417
- PubMed
- Google Scholar
Conference
1. Kingma DP
2. Ba JL
(2015)
Adam: A method for stochastic optimization

’, in 3rd International Conference on Learning Representations, ICLR 2015 - Conference Track Proceedings.
- Google Scholar
1. Kondylis ED
2. Randazzo MJ
3. Alhourani A
4. Lipski WJ
5. Wozny TA
6. Pandya Y
7. Ghuman AS
8. Turner RS
9. Crammond DJ
10. Richardson RM
(2016) Movement-related dynamics of cortical oscillations in Parkinson’s disease and essential tremor
Brain 139:2211–2223.
https://doi.org/10.1093/brain/aww144
- PubMed
- Google Scholar
1. Krauss JK
2. Lipsman N
3. Aziz T
4. Boutet A
5. Brown P
6. Chang JW
7. Davidson B
8. Grill WM
9. Hariz MI
10. Horn A
11. Schulder M
12. Mammis A
13. Tass PA
14. Volkmann J
15. Lozano AM
(2021) Technology of deep brain stimulation: current status and future directions
Nature Reviews. Neurology 17:75–87.
https://doi.org/10.1038/s41582-020-00426-z
- PubMed
- Google Scholar
1. Kühn AA
2. Williams D
3. Kupsch A
4. Limousin P
5. Hariz M
6. Schneider G-H
7. Yarrow K
8. Brown P
(2004) Event-related beta desynchronization in human subthalamic nucleus correlates with motor performance
Brain 127:735–746.
https://doi.org/10.1093/brain/awh106
- PubMed
- Google Scholar
(2006) Reduction in subthalamic 8-35 Hz oscillatory activity correlates with clinical improvement in Parkinson’s disease
The European Journal of Neuroscience 23:1956–1960.
https://doi.org/10.1111/j.1460-9568.2006.04717.x
- PubMed
- Google Scholar
(2004) A brain-computer interface using electrocorticographic signals in humans
Journal of Neural Engineering 1:63–71.
https://doi.org/10.1088/1741-2560/1/2/001
- PubMed
- Google Scholar
1. Li N
2. Baldermann JC
3. Kibleur A
4. Treu S
5. Akram H
6. Elias GJB
7. Boutet A
8. Lozano AM
9. Al-Fatly B
10. Strange B
11. Barcia JA
12. Zrinzo L
13. Joyce E
14. Chabardes S
15. Visser-Vandewalle V
16. Polosan M
17. Kuhn J
18. Kühn AA
19. Horn A
(2020) A unified connectomic target for deep brain stimulation in obsessive-compulsive disorder
Nature Communications 11:3364.
https://doi.org/10.1038/s41467-020-16734-3
- PubMed
- Google Scholar
1. Little S
2. Pogosyan A
3. Neal S
4. Zavala B
5. Zrinzo L
6. Hariz M
7. Foltynie T
8. Limousin P
9. Ashkan K
10. FitzGerald J
11. Green AL
12. Aziz TZ
13. Brown P
(2013) Adaptive deep brain stimulation in advanced Parkinson disease
Annals of Neurology 74:449–457.
https://doi.org/10.1002/ana.23951
- PubMed
- Google Scholar
1. Little S
(2019) Human motor cortical beta bursts relate to movement planning and response errors
PLOS Biology 17:e3000479.
https://doi.org/10.1371/journal.pbio.3000479
- Google Scholar
1. Lofredi R
2. Neumann W-J
3. Bock A
4. Horn A
5. Huebl J
6. Siegert S
7. Schneider G-H
8. Krauss JK
9. Kühn AA
(2018) Dopamine-dependent scaling of subthalamic gamma bursts with movement velocity in patients with Parkinson’s disease
eLife 7:e31895.
https://doi.org/10.7554/eLife.31895
- PubMed
- Google Scholar
1. Lofredi R
2. Tan H
3. Neumann W-J
4. Yeh C-H
5. Schneider G-H
6. Kühn AA
7. Brown P
(2019) Beta bursts during continuous movements accompany the velocity decrement in Parkinson’s disease patients
Neurobiology of Disease 127:462–471.
https://doi.org/10.1016/j.nbd.2019.03.013
- PubMed
- Google Scholar
1. Lofredi R
2. Auernig GC
3. Irmen F
4. Nieweler J
5. Neumann W-J
6. Horn A
7. Schneider G-H
8. Kühn AA
(2021) Subthalamic stimulation impairs stopping of ongoing movements
Brain : A Journal of Neurology 144:44–52.
https://doi.org/10.1093/brain/awaa341
- PubMed
- Google Scholar
1. Mallet N
2. Pogosyan A
3. Sharott A
4. Csicsvari J
5. Bolam JP
6. Brown P
7. Magill PJ
(2008) Disrupted dopamine transmission and the emergence of exaggerated beta oscillations in subthalamic nucleus and cerebral cortex
The Journal of Neuroscience 28:4795–4806.
https://doi.org/10.1523/JNEUROSCI.0123-08.2008
- PubMed
- Google Scholar
(2006) Three-dimensional locations and boundaries of motor and premotor cortices as defined by functional brain imaging: a meta-analysis
NeuroImage 31:1453–1474.
https://doi.org/10.1016/j.neuroimage.2006.02.004
- PubMed
- Google Scholar
(2004) Comparing information about arm movement direction in single channels of local and epicortical field potentials from monkey and human motor cortex
Journal of Physiology, Paris 98:498–506.
https://doi.org/10.1016/j.jphysparis.2005.09.016
- PubMed
- Google Scholar
1. Merk T
2. Peterson V
3. Köhler R
4. Haufe S
5. Richardson RM
6. Neumann WJ
(2022a) Machine learning based brain signal decoding for intelligent adaptive deep brain stimulation
Experimental Neurology 351:113993.
https://doi.org/10.1016/j.expneurol.2022.113993
- PubMed
- Google Scholar
Software
1. Merk T
(2022b) ECoG_vs_STN, version swh:1:rev:09d3ea5b846681d28edb26943b4315ae5f5a37dd
Software Heritage.

https://archive.softwareheritage.org/swh:1:dir:bf9ce2c55744e0ace1623bbb156804998a8909db;origin=https://github.com/neuromodulation/ECoG_vs_STN;visit=swh:1:snp:ff5ae9fee05224d3ed4640fd630021063a80d441;anchor=swh:1:rev:09d3ea5b846681d28edb26943b4315ae5f5a37dd
1. Milosevic L
2. Kalia SK
3. Hodaie M
4. Lozano AM
5. Fasano A
6. Popovic MR
7. Hutchison WD
(2018) Neuronal inhibition and synaptic plasticity of basal ganglia neurons in Parkinson’s disease
Brain 141:177–190.
https://doi.org/10.1093/brain/awx296
- PubMed
- Google Scholar
1. Molina R
2. Hass CJ
3. Cernera S
4. Sowalsky K
5. Schmitt AC
6. Roper JA
7. Martinez-Ramirez D
8. Opri E
9. Hess CW
10. Eisinger RS
11. Foote KD
12. Gunduz A
13. Okun MS
(2021) Closed-Loop Deep Brain Stimulation to Treat Medication-Refractory Freezing of Gait in Parkinson’s Disease
Frontiers in Human Neuroscience 15:633655.
https://doi.org/10.3389/fnhum.2021.633655
- PubMed
- Google Scholar
1. Neumann W-J
2. Degen K
3. Schneider G-H
4. Brücke C
5. Huebl J
6. Brown P
7. Kühn AA
(2016) Subthalamic synchronized oscillatory activity correlates with motor impairment in patients with Parkinson’s disease
Movement Disorders 31:1748–1751.
https://doi.org/10.1002/mds.26759
- PubMed
- Google Scholar
1. Neumann W-J
2. Schroll H
3. de Almeida Marcelino AL
4. Horn A
5. Ewert S
6. Irmen F
7. Krause P
8. Schneider G-H
9. Hamker F
10. Kühn AA
(2018) Functional segregation of basal ganglia pathways in Parkinson’s disease
Brain : A Journal of Neurology 141:2655–2669.
https://doi.org/10.1093/brain/awy206
- PubMed
- Google Scholar
(2019) Toward Electrophysiology-Based Intelligent Adaptive Deep Brain Stimulation for Movement Disorders
Neurotherapeutics 16:105–118.
https://doi.org/10.1007/s13311-018-00705-0
- PubMed
- Google Scholar
1. Neumann W-J
2. Rodriguez-Oroz MC
(2021) Machine Learning Will Extend the Clinical Utility of Adaptive Deep Brain Stimulation
Movement Disorders 36:796–799.
https://doi.org/10.1002/mds.28567
- PubMed
- Google Scholar
1. Opri E
2. Cernera S
3. Molina R
4. Eisinger RS
5. Cagle JN
6. Almeida L
7. Denison T
8. Okun MS
9. Foote KD
10. Gunduz A
(2020) Chronic embedded cortico-thalamic closed-loop deep brain stimulation for the treatment of essential tremor
Science Translational Medicine 12:eaay7680.
https://doi.org/10.1126/scitranslmed.aay7680
- PubMed
- Google Scholar
1. Pedregosa F
(2011)
Scikit-learn: Machine learning in Python

Journal of Machine Learning 1:.
- Google Scholar
(2012) Robust correlation analyses: false positive and power validation using a new open source matlab toolbox
Frontiers in Psychology 3:606.
https://doi.org/10.3389/fpsyg.2012.00606
- PubMed
- Google Scholar
(2021) Generalized neural decoders for transfer learning across participants and recording modalities
Journal of Neural Engineering 18:026014.
https://doi.org/10.1088/1741-2552/abda0b
- PubMed
- Google Scholar
(2020) Neural closed-loop deep brain stimulation for freezing of gait
Brain Stimulation 13:1320–1322.
https://doi.org/10.1016/j.brs.2020.06.018
- PubMed
- Google Scholar
1. Piña-Fuentes D
2. van Dijk JMC
(2019) Adaptive DBS in Parkinson’s disease: Headlines, perspectives and challenges
Brain Stimulation 12:1091–1092.
https://doi.org/10.1016/j.brs.2019.04.014
- PubMed
- Google Scholar
Book
1. Proakis JG
2. Monolakis DG
(1996)
Digital Signal Processing: Principles, Algorithms, and Applications

Pentice Hall.
- Google Scholar
(2016) Three-dimensional localization of cortical electrodes in deep brain stimulation surgery from intraoperative fluoroscopy
NeuroImage 125:515–521.
https://doi.org/10.1016/j.neuroimage.2015.10.076
- PubMed
- Google Scholar
(2004) OsiriX: an open-source software for navigating in multidimensional DICOM images
Journal of Digital Imaging 17:205–216.
https://doi.org/10.1007/s10278-004-1014-6
- PubMed
- Google Scholar
1. Schapire RE
(2009) A Short Introduction to Boosting
Society 1:912.
https://doi.org/10.1088/0004-637X/720/1/912
- Google Scholar
1. Schwerdt HN
2. Amemori K
3. Gibson DJ
4. Stanwicks LL
5. Yoshida T
6. Bichot NP
7. Amemori S
8. Desimone R
9. Langer R
10. Cima MJ
11. Graybiel AM
(2020) Dopamine and beta-band oscillations differentially link to striatal value and motor control
Science Advances 6:eabb9226.
https://doi.org/10.1126/sciadv.abb9226
- PubMed
- Google Scholar
1. Shah SA
2. Tan H
3. Tinkhauser G
4. Brown P
(2018) Towards Real-Time, Continuous Decoding of Gripping Force From Deep Brain Local Field Potentials
IEEE Transactions on Neural Systems and Rehabilitation Engineering 26:1460–1468.
https://doi.org/10.1109/TNSRE.2018.2837500
- PubMed
- Google Scholar
1. Starr PA
(2018) Totally Implantable Bidirectional Neural Prostheses: A Flexible Platform for Innovation in Neuromodulation
Frontiers in Neuroscience 12:619.
https://doi.org/10.3389/fnins.2018.00619
- PubMed
- Google Scholar
1. Swann NC
2. de Hemptinne C
3. Thompson MC
4. Miocinovic S
5. Miller AM
6. Gilron R
7. Ostrem JL
8. Chizeck HJ
9. Starr PA
(2018) Adaptive deep brain stimulation for Parkinson’s disease using motor cortex sensing
Journal of Neural Engineering 15:046006.
https://doi.org/10.1088/1741-2552/aabc9b
- PubMed
- Google Scholar
1. Tan H
2. Pogosyan A
3. Ashkan K
4. Green AL
5. Aziz T
6. Foltynie T
7. Limousin P
8. Zrinzo L
9. Hariz M
10. Brown P
(2016) Decoding gripping force based on local field potentials recorded from subthalamic nucleus in humans
eLife 5:e19089.
https://doi.org/10.7554/eLife.19089
- PubMed
- Google Scholar
Preprint
1. Thenaisie Y
2. Lee K
3. Moerman C
4. Scafa S
5. Gálvez A
6. Pirondini E
7. Burri M
8. Ravier J
9. Puiatti A
10. Accolla E
11. Wicki B
12. Zacharia A
13. Jiménez MC
14. Bally JF
15. Courtine G
16. Bloch J
17. Moraud EM
(2022) Principles of Gait Encoding in the Subthalamic Nucleus of People with Parkinson’s Disease
medRxiv.
https://doi.org/10.1101/2022.02.08.22270370
- Google Scholar
1. Tinkhauser Gerd
2. Pogosyan A
3. Little S
4. Beudel M
5. Herz DM
6. Tan H
7. Brown P
(2017) The modulatory effect of adaptive deep brain stimulation on beta bursts in Parkinson’s disease
Brain 140:1053–1067.
https://doi.org/10.1093/brain/awx010
- PubMed
- Google Scholar
1. Tinkhauser G.
2. Moraud EM
(2021) Controlling Clinical States Governed by Different Temporal Dynamics With Closed-Loop Deep Brain Stimulation: A Principled Framework
Frontiers in Neuroscience 15:734186.
https://doi.org/10.3389/fnins.2021.734186
- PubMed
- Google Scholar
1. Torrecillos F
2. Tinkhauser G
3. Fischer P
4. Green AL
5. Aziz TZ
6. Foltynie T
7. Limousin P
8. Zrinzo L
9. Ashkan K
10. Brown P
11. Tan H
(2018) Modulation of Beta Bursts in the Subthalamic Nucleus Predicts Motor Performance
The Journal of Neuroscience 38:8905–8917.
https://doi.org/10.1523/JNEUROSCI.1314-18.2018
- PubMed
- Google Scholar
1. Turner RS
2. Desmurget M
(2010) Basal ganglia contributions to motor control: a vigorous tutor
Current Opinion in Neurobiology 20:704–716.
https://doi.org/10.1016/j.conb.2010.08.022
- PubMed
- Google Scholar
1. Velasco S
2. Branco L
3. Abosch A
4. Ince NF
(2022) The Entropy of Adaptively Segmented Beta Oscillations Predict Motor Improvement in Patients with Parkinsons Disease
IEEE Transactions on Bio-Medical Engineering PP:1.
https://doi.org/10.1109/TBME.2022.3142716
- PubMed
- Google Scholar
(2019) Dual threshold neural closed loop deep brain stimulation in Parkinson disease patients
Brain Stimulation 12:868–876.
https://doi.org/10.1016/j.brs.2019.02.020
- PubMed
- Google Scholar
Preprint
(2022) Time-Resolved Parameterization of Aperiodic and Periodic Brain Activity
bioRxiv.
https://doi.org/10.1101/2022.01.21.477243
- Google Scholar
(2018) Decoding of finger trajectory from ECoG using deep learning
Journal of Neural Engineering 15:036009.
https://doi.org/10.1088/1741-2552/aa9dbe
- PubMed
- Google Scholar
1. Yttri EA
2. Dudman JT
(2016) Opponent and bidirectional control of movement velocity in the basal ganglia
Nature 533:402–406.
https://doi.org/10.1038/nature17639
- PubMed
- Google Scholar
1. Zou H
2. Hastie T
(2005) Regularization and variable selection via the elastic net
Journal of the Royal Statistical Society 67:301–320.
https://doi.org/10.1111/j.1467-9868.2005.00503.x
- Google Scholar

Decision letter

Nicole C Swann

Reviewing Editor; University of Oregon, United States
Michael J Frank

Senior Editor; Brown University, United States
Kevin Wilkins

Reviewer; Stanford University, United States

Our editorial process produces two outputs: i) public reviews designed to be posted alongside the preprint for the benefit of readers; ii) feedback on the manuscript for the authors, including requests for revisions, shown below. We also include an acceptance summary that explains what the editors found interesting or important about the work.

Decision letter after peer review:

Thank you for submitting your article "Electrocorticography is superior to subthalamic local field potentials for movement decoding in Parkinson's disease" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and Michael Frank as the Senior Editor. The following individual involved in review of your submission has agreed to reveal their identity: Kevin Wilkins (Reviewer #1).

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission.

Essential revisions:

1) The paper reports best performance with single channel ECoG inputs and no additional benefit from channel combinations or combined ECoG and STN channel sets (summarized from lines 322-324, and shown in Figure 4). This result requires further discussion – does it truly suggest that using a single channel is optimal (as seems to be suggested by the authors) or does it rather speak to a need for models which more appropriately combine information from separate sources? While these specific XGBOOST models may have failed to benefit from larger feature combinations, the usefulness and generalizability of that knowledge is limited without more exhaustive testing and discussion. Theoretically, any new features added to an existing model should be capable of benefiting the combined model, provided those features both contain some amount of information about the predicted variable and are being optimally integrated. This is related to the topics of ensemble learning, boosting, and regularization, which are a part of the current paper. We recommend the authors further develop this aspect.

2) A primary weakness of the paper is that some of the results and ideas are underdeveloped. While identifying a relationship between motor symptom severity and decoder performance is interesting on its own, there is no further investigation of this result for providing better intuition about why the relationship exists and what can or should be done about it. The authors discuss the potential impact β bursts might have on decoder performance but do not pursue any analysis of their own data to determine whether those proposed hypotheses are supported. We encourage the authors to explore this space a little more either with additional analyses or at least additional discussion. For instance, the authors report a relationship between UPDRS scores and decoding performance, which they suggest may be valuable to clinical decision making and may be explained by an association between β bursts and motor performance (summarized from lines 367-372). Elaborating on these points would be of great value to the manuscript. The authors could assess whether β bursts are necessary for their observed relationship between decoding performance and UPDRS scores by removing β features from their decoders and re-testing (however, this would only test for direct effects that β-band activity makes as a regressor). Additionally, if β bursts are necessary for producing this observation, are there any adjustments to the models that could accommodate the changes in how β-band activity is temporally distributed? Finally, a more thorough description of how this relationship would be valuable to clinical decision making would be quite nice. Whether in terms of computational modelling, dopamine replacement therapy, or other routes – it would benefit the reader to have some commentary on precisely how this might change the trajectory of a patient's treatment.

3) A wide-range of decoding performance is seen across participants with a group of good performers and a group of low-performers. The findings from the secondary analyses on impairment levels and electrode location/connectivity may explain some of these differences, but it is unclear to what extent or if other factors are at play. Further, the cohort is notably small, especially considering the heterogeneity of electrode location. Although this does not limit the major finding of the superiority of sensorimotor ECoG over STN signals, it does limit the ability to understand the observed individual differences in decoding performance. These limitations should be noted/discussed.

4) When comparing cortical and subthalamic electrodes the size and structure of the probe may be different. This means that instead of comparing apples to apples, it is more like comparing apples to oranges. This does not completely undermine the result because the difference in decoding between the areas, even given experimental differences, is likely to be of interest to clinical researchers studying DBS. If the surface area of the electrode is different between the two regions, then this could be a factor in decoding performance that does not have to do with brain region. Additionally, the electrodes in the subthalamus nucleus are circular, which are likely targeting very different neural populations across the probe within the small nucleus, which is different from the cortical electrodes which are on the surface targeting neural populations which are adjacent. Both of these factors (e.g. size and shape) could contribute to differences in decoding performance regardless of brain region. We did not see details of the electrodes in the method section, but this would be important to report as surface area is related to the number of neurons/dendrites summing to create the LFP, and this might lead to qualitatively different results for something like hand gripping irrespective of area. Similarly, with the shape of the electrode. These details will be an important addition to the paper and something that others can continue to investigate (e.g., researchers who have different size or shape of electrodes in the STN). We are sympathetic that this is not a variable that the researchers can change given the clinical nature of DBS, but the surface area of electrodes in each area should be mentioned in the method section, and if the surface area of the electrodes are different, then it should also be mentioned as a limitation in the Discussion section.

5) We wonder whether you have fully explored the neural feature space. One suggestion is that you also include the time domain data as a feature along with your frequency bands. Some papers have shown pretty good decoding with this feature – sometimes called the local motor potential. Here are some papers which discuss this feature in more detail. This could be an interesting addition especially if it performs well as it requires little preprocessing for studies doing online preprocessing and decoding.

Flint, R. D., Wang, P. T., Wright, Z. A., King, C. E., Krucoff, M. O., Schuele, S. U.,.… & Slutzky, M. W. (2014). Extracting kinetic information from human motor cortical signals. Neuroimage, 101, 695-703.

Mehring, C., Nawrot, M. P., de Oliveira, S. C., Vaadia, E., Schulze-Bonhage, A., Aertsen, A., & Ball, T. (2004). Comparing information about arm movement direction in single channels of local and epicortical field potentials from monkey and human motor cortex. Journal of Physiology-Paris, 98(4-6), 498-506.

Schalk, G., Kubanek, J., Miller, K. J., Anderson, N. R., Leuthardt, E. C., Ojemann, J. G.,.… & Wolpaw, J. R. (2007). Decoding two-dimensional movement trajectories using electrocorticographic signals in humans. Journal of neural engineering, 4(3), 264.

6) With respect to Figure 2, given how similar the descriptive power plots are, we were surprised that low γ has much larger weights compared to high γ or HFA. It looks like you aren't using regularization for your linear regression model. If your features (band pass filters) are highly correlated, the interpretation of the weights might not be meaningful. Have you thought about using ridge regression or lasso to deal with your seemingly highly correlated features? If not, then I don't believe it makes sense to try and interpret the weights. It looks like you do use regularized regression later but looking at the method section for your linear regression model there is no regularization term – so based on that it seems like for this first section it is just standard linear regression. We would suggest also using regularized regression for these analyses as interpreting the weights of linear regression with highly correlated features may be problematic.

7) The R2 plots all appear to have a lower limit of 0. This, combined with some of the descriptions in the Methods, suggest that these performance metrics are the squared correlation coefficient. The computational form of the coefficient of determination R2, which is 1 – sum[(y_true – y_pred)^2] / sum[(y_true – y_mean)^2], is a more appropriate metric to use for evaluating decoder performance in cross-validated settings. The squared correlation coefficient is not equivalent in this case, as illustrated by the fact that it cannot be negative. Using the computational form of R2 allows the reader to readily compare predictions against a naïve estimator that predicts the sample mean – if the decoder being evaluated has an R2 below zero, then it is worse than simply predicting the mean. The correlation coefficient is also invariant to scale and translation, which are important features of decoder performance that are captured by the computational form of R2. If in fact the computational form of R2 has been used, please explicitly state that it has been (by simply including the equation in methods), since the results presented in the paper do appear to show otherwise.

8) We had a difficult time understanding the logic and the methods of your last section which relates decoding performance with connectivity maps. For example, after reading the methods section, I was still unclear how you determined if a fiber was significant or not. I believe that this section needs more detail and clarity. For example, you have analyses for structural and functional connectivity, but for the functional connectivity we could not find anything in the method section about what the patient was doing when this was computed – were the patients at rest, were they doing the same gripping task? These details are important for understanding the analyses and interpretation.

9) Similarly, the prediction network mapping methods would be more clear if represented schematically and/or with accompanying equations. These methods were very difficult to understand given the current descriptions in the Results text and Methods.

10) The authors are unable to fully rule-out that the superiority of ECoG signals is not dependent on the task performed (i.e., grip force). The authors claim that the findings support the utility of additional ECoG in adaptive DBS research for PD patients. Although it is certainly expected that sensorimotor ECoG would provide a richer signal compared to STN LFPs due to both signal size, complexity, and relation to movement, the data in this paper is inherently limited to the grip task performed. This limitation should be noted/discussed.

11) The results of the paper are all centered on decoding grip-force. The authors suggest that this decoding could be used as a control signal for adaptive deep brain stimulation in patients with Parkinson's disease, increasing stimulation when higher movement "vigor" is predicted (summarized from lines 346-348). It seems that this would entail a fast algorithmic approach to adapting stimulation, making adjustments in response to frequently changing movement states. A comparison to different algorithmic approaches (for example, tracking slower fluctuations in medication state) would be helpful to have in the Discussion.

12) A Go/No-Go task is also used in the paper. This is potentially problematic, given that there may be modulation in the neural recordings associated with response inhibition. While the decoders are trained only to predict actual force production, it is possible that inhibitory responses could influence the decoder readout and impact the performance metrics on which every analysis of the paper hinges. It is also plausible that such inhibitory responses would asymmetrically affect the subthalamic decoders and the cortical decoders. Comparison of those two signal locations is the main topic of the paper, so this is a critical aspect to consider and discuss.

13) The results identify a stark difference in the way model "complexity" impacts decoding in the STN and cortex, yet this concept is not well-developed or discussed. What does this say about the nature of the information content in each area such that allowing for non-linear relationships benefits decoders based on one area, but harms decoders based on the other? Please discuss further.

14) The Bayesian Optimization hyperparameter search was run for a fixed number of iterations according to line 637. Were enough iterations used to reach convergence in performance? This would be a useful supplementary analysis.

15) In line 648, it is stated that a single best channel was chosen for each patient and brain area (STN, cortex) in part to "account for varying numbers of available electrode contacts". There seem to be far more ECoG channels than STN channels – does this introduce a bias in the results when taking the "best" performing channel from a larger candidate pool of ECoG channels as compared to the STN? The authors should elaborate on this and make any necessary corrections for bias.

16) The significantly connected fibers are shown in Figure 7B. However, due to the small nature of this sub-figure and only 1 slice shown, it is difficult to fully understand where these fibers tend to go (appears to be a combination of M1 and SMA/PM?). It may be helpful to describe in the text of the results where these fibers are going. For instance, Figure 7C gives a great look into the visualization of the topography of decoding performance. Although that type of figure may not be possible with the fiber tract analysis, at least a text description would be helpful for the reader and allow further interpretation of those results.

17) The supplementary figure provides transparency regarding the variability of observed grip performances. One remaining question was whether the observed variability in decoding performance across individuals and the observed correlation between decoding performance and impairment level may actually be related to the observed variability in grip force production. Do the more impaired individuals display greater variability across trials in grip force production compared to those with less impairment? And is this then creating a more difficult decoding problem for those individuals with more extreme variability compared to individuals who have consistent force production curves?

https://doi.org/10.7554/eLife.75126.sa1

Author response

Essential revisions:

1) The paper reports best performance with single channel ECoG inputs and no additional benefit from channel combinations or combined ECoG and STN channel sets (summarized from lines 322-324, and shown in Figure 4). This result requires further discussion – does it truly suggest that using a single channel is optimal (as seems to be suggested by the authors) or does it rather speak to a need for models which more appropriately combine information from separate sources? While these specific XGBOOST models may have failed to benefit from larger feature combinations, the usefulness and generalizability of that knowledge is limited without more exhaustive testing and discussion. Theoretically, any new features added to an existing model should be capable of benefiting the combined model, provided those features both contain some amount of information about the predicted variable and are being optimally integrated. This is related to the topics of ensemble learning, boosting, and regularization, which are a part of the current paper. We recommend the authors further develop this aspect.

We thank the reviewers for raising this important point. The fact that single channels outperform channel combinations has led to extensive discussion among the study team over the course of the analyses. We agree with the reviewers that the finding is counterintuitive from a theoretical perspective. Therefore, we have spent significant time and effort into understanding this specific issue and have trained models that make optimal use of both spatial and spectral information. Our results showed lower performances of combined sources compared to single contact models. To test for combined models of multiple contacts, we tested the Source Power Comodulation (SPoC) model by Dähne et al. 2014 https://doi.org/10.1016/j.neuroimage.2013.07.079. This method utilizes spatial information and has been widely used in EEG regression analysis. We trained linear models as well as XGBOOST decoders on top of SPoC extracted features to account for linear and non-linear interactions. But both models were outperformed by XGBOOST using a single best cross validated contact (see Figure 3 and Supplementary File 1c for decoding performance comparisons). We hypothesize that the small dataset size in the intraoperative recording setting is a limiting factor to generalize performances of multichannel models. We are confident that our findings are robust for the present dataset but believe that extending this section of the article with the limited data available is beyond the interest of the general readership of eLife. We conclude that there are two primary reasons for this finding, (a) the limited amount of data at hand, that is inherently restricted by the intraoperative recording setting, which is decisive for the risk of overfitting more complex models, and (b) the fact that the brain signals that are most informative for grip-force decoding all originate from the same cortex-basal ganglia-thalamic circuit. The positive side of this finding is that the channel count of emerging neurotechnology is often defined and limited by hardware manufacturers, and it appears that even devices with limited channel numbers may have a potential for good decoding performances. Nevertheless, we agree that our manuscript with the presented data cannot extrapolate towards all potential settings for invasive movement decoding and therefore discuss this topic more cautiously. Finally, we currently work on the implementation of convolutional and recurrent neural networks for movement decoding similar to Peterson et al., 2021 https://doi.org/10.1088/1741-2552/abda0b but our preliminary decoding performanes remain below the presented results in this paper and require further optimization and validation.

The limitations section of the discussion now reads:

“An additional limitation was the relatively small amount of available data per patient, which was constrained by the intraoperative setting (see Table 1). For deep learning approaches we expect better performances with increased dataset sizes, which may become available, either through externalized extra operative recordings (He et al., 2021) or sensing enabled implantable devices (Opri et al., 2020; Gilron et al., 2021). Importantly, our finding that decoding performances from single contacts outperform multi-electrode models may be a consequence of a combination of short recording durations in this study, suboptimal computational model selection and the fact that sensorimotor cortex and STN are part of the same circuit that is synchronized in oscillations. While we have made an effort to accommodate models that are optimized for spatio-spectral feature learning, and we are confident that these cannot outperform single channel approaches in this dataset, future studies should cautiously reinterrogate this issue in larger datasets, e.g. by implementing neural networks optimized for this purpose (Peterson et al., 2021).”

2) A primary weakness of the paper is that some of the results and ideas are underdeveloped. While identifying a relationship between motor symptom severity and decoder performance is interesting on its own, there is no further investigation of this result for providing better intuition about why the relationship exists and what can or should be done about it. The authors discuss the potential impact β bursts might have on decoder performance but do not pursue any analysis of their own data to determine whether those proposed hypotheses are supported. We encourage the authors to explore this space a little more either with additional analyses or at least additional discussion. For instance, the authors report a relationship between UPDRS scores and decoding performance, which they suggest may be valuable to clinical decision making and may be explained by an association between β bursts and motor performance (summarized from lines 367-372). Elaborating on these points would be of great value to the manuscript. The authors could assess whether β bursts are necessary for their observed relationship between decoding performance and UPDRS scores by removing β features from their decoders and re-testing (however, this would only test for direct effects that β-band activity makes as a regressor). Additionally, if β bursts are necessary for producing this observation, are there any adjustments to the models that could accommodate the changes in how β-band activity is temporally distributed? Finally, a more thorough description of how this relationship would be valuable to clinical decision making would be quite nice. Whether in terms of computational modelling, dopamine replacement therapy, or other routes – it would benefit the reader to have some commentary on precisely how this might change the trajectory of a patient's treatment.

This is a very relevant point, and we agree with the reviewer that the provided insight in the initial version of the paper was limited. Therefore, we have significantly extended the analyses on this topic for the revision. Before expanding on the new analyses, we would like to highlight some caveats when discussing the relationship of pathological β oscillations and movement decoding that β activity is one of the most potent features for prediction of movement. Also, when visualizing coefficients from linear models, we observe that strong β desynchronization is an important feature for movement decoding. Consequently, β power in the resting period is a requirement for the desynchronization, which means that removing these features from a model is expected to significantly deteriorate decoding performance. As by suggestion of the reviewer we have now analysed the performance changes by removing β activity from ECoG and STN decoding performances as shown in Author response image 1.

Author response image 1

Download asset Open asset

This should remind us of the fact that β activity per se is a physiological signal and it can be challenging to differentiate pathological and physiological aspects of it. Therefore, we have tried to conceptualize a new analysis that (a) abstains from manipulation of model features because of the direct and often hardly interpretable effects on decoding performance, (b) provides pathophysiological insight into PD and (c) is embedded into a physiologically plausible line of reasoning from previous literature. Upon reflection on these points, we realized that we could investigate the relationship of subthalamic β burst dynamics on ECoG based grip-force decoding performance. This is relevantly embedded in previous works, that have demonstrated that “time spent in β burst” in the subthalamic nucleus can be associated with worsening of movement performance (Torrecillos et al., 2018, J Neurosci, https://doi.org/10.1523/jneurosci.1314-18.2018). The “time spent in burst” metric was used in various previous publications on the relationship of β bursts and motor performance beyond the abovementioned one (Lofredi et al., 2019, Tinkhauser et al., 2020, Khawaldeh et al., 2020) and essentially reflects the likelihood of β bursts occurring in the STN during movement preparation and/or performance. It is practical for this purpose as it is easy to compute and sensitive even during periods of low average β activity even when the threshold is defined by the resting β measures. Note that all of the previous studies were restricted to subthalamic LFP recordings and none had the opportunity to compare burst dynamics with ECoG signals or decoding. Thus, we have adopted the methodology of these studies and analyzed the impact of β bursts on ECoG decoding performance, by identifying threshold crossings above the 75^th percentile of the resting low-β power feature vector of at least 100 ms length. We have focused on the low-β (13-20 Hz) band, because it was shown to be the primary relevant frequency band in our previous works (Lofredi et al., 2019) but also compared the correlation to the high-β frequency band (20-35 Hz) further in Author response image 2. We found a significant negative correlation of ECoG decoding performance (best performance with XGBOOST as highlighted in the manuscript before) and STN burst dynamics (time spent in burst as explained above and reported in previous studies). Specifically, we found robust significant correlations for STN time spent in β burst during motor preparation (Rho = -0.76, P = 0.001; -1 s to 0 s with relation to movement onset) and during movement execution (Rho = -0.71, P = 0.008; 0 s to 1 s after movement onset).

Author response image 2

Download asset Open asset

Importantly, the correlations were specific to the STN and did not yield significant results for bursts in cortex (all P>0.05). To uncover a potential relationship of PD symptom severity and burst measures we calculated correlations with UPDRS-III scores and found significant correlations for time spent in burst for STN during motor preparation (Rho = 0.63, P = 0.02) and movement (Rho = 0.56 P = 0.05) but not for time spent in burst from ECoG activity (P>0.05).Interestingly, the negative correlation of time spent in burst with motor preparation was specific for the low-β band and not significant for the high-β band (p>0.05), while the correlation during movement was significant but lower than for low β (Rho = -0.71 p = 0.007). Again, correlations of time spent in burst in the high-β frequency band in cortex with decoding performance were not significant (p>0.05) for neither motor preparation nor movement phase.

We believe that these findings add significant value to the manuscript, and we are truly thankful to the reviewers who have motivated us to dive deeper into this analysis. We have thus decided to merge previous figures 3 and 4 and include an additional figure (now figure 5) and added the required methods and results to the manuscript as will be highlighted below. As always with interesting scientific findings, they spark new questions, e.g. the question whether β bursts can impair corticosubthalamic communication, e.g. by suppressing neural phase locking of subthalamic neurons to cortical γ (see Fischer et al., 2020 eLife https://elifesciences.org/articles/51956) or modulating coherence and granger causality. Finally, the question arises whether dopaminergic medication suppresses β bursts and improves movement decoding. We will address these relevant questions in future studies for which we are now collecting data from externalized leads in Berlin, but unfortunately recruitment is going slow during the pandemic.

Finally, we want to further address the reviewers comments with respect to a discussion on potential practical implications. Foremost, we want to reinstate our original argument that our findings should spark a general awareness that the pathophysiology of brain disorders will have significant impact on machine learning models for clinical brain computer interfaces, beyond obvious / direct changes in the input features themselves. This general statement will be important beyond deep brain stimulation and could also hold value for first application of other brain computer interfaces, such as Neuralink or similar.

In the particular case of Parkinson’s disease and grip-force decoding, we demonstrate that subthalamic but not cortical β burst synchronization even before movement execution is associated with deterioration of decoding performance from cortex. An obvious interpretation of this finding is that excessive synchronization in the STN may impair flexible motor control by decreasing information coding capacity and neural entropy as previously suggested in animal studies (Mallet et al. 2008, https://doi.org/10.1523/JNEUROSCI.0123-08.2008; Cruz et al., 2009 https://doi.org/10.1152/jn.00344.2009) and recently suggested for subthalamic β bursts (Velasco et al. 2022, https://doi.org/10.1109/TBME.2022.3142716).

More generally, we speculate that β activity can be anticorrelated with phasic dopamine release (Schwerdt et al., 2020 https://doi.org/10.1126/sciadv.abb9226). If this holds true also for the STN, we may associate β bursts with phasic dips in dopamine signalling. Dopamine was shown to precede and invigorate future movement (da Silva et al., 2018; https://doi.org/10.1038/nature25457). If subthalamic β bursts indicate phasic decreases in dopaminergic innervation, we could expect a loss of invigoration and reinforcement of ongoing neural population activity in the cortex – basal ganglia – thalamic loop, which offers an elegant explanation for the lower decoding performance from ECoG signals in the absence of pathological cortical activity patterns. In the future, this could be further investigated through direct recordings of cortical neural population activity with Neuropixels that we and our collaborators have previously implanted in first human cases during epilepsy surgery (Paulk et al., 2022; https://doi.org/10.1038/s41593-021-00997-0) optimally coupled with electrochemical sensing of dopamine (Schwerdt et al., 2018; https://doi.org/10.1038/s42003-018-0147-y) when it becomes available for human application. On a more short-term perspective, we may investigate changes in patterning and amplitude of γ band activity with dopaminergic medication during externalized recordings. We are currently working on this and found preliminary unpublished evidence that cortical γ power is increased with dopaminergic medication when compared to OFF medication, which resembles previous work shown for the STN (Lofredi et al., 2018, https://doi.org/10.7554/eLife.31895).

While the practical clinical requirement for brain signal decoding beyond pathological signals remains distant, we finally want to state shortly, how we believe our results could affect clinical decision making: In general, our findings may suggest that patients with earlier disease stages or lower symptom severity may be better suited for clinical brain computer interfaces that rely on movement decoding. Another intuitive conclusion would be that decoding performance can be improved with dopaminergic medication. However, we should be cautious with this speculation, as the UPDRS-III in the OFF state reflects concurrent clinical state severity but is also correlated with chronic dopaminergic degeneration. Thus, neurodegeneration could lead to chronic loss of cortical information coding capacity that is not reversible with medication. We will address this important question in future studies from externalized recordings. To compensate, computational methods to improve decoding performance could account for presence of β bursts and increase model output in an adaptive way. More work is required to conceptualize this further, but we believe that such ideas could be interesting to follow up on. We hope that the editorial team recognizes our appreciation of the discussion. We have now substantially revised abstract, methods, results and discussion to accommodate the new analyses and have included a new Figure 5.

Abstract:

“ECoG based decoding performance negatively correlated with motor impairment, which could be attributed to subthalamic β bursts in the motor preparation and movement period. This highlights the impact of PD pathophysiology on the neural capacity to encode movement kinematics.”

Results:

“To better understand the relationship of PD pathophysiology and grip-force decoding performance we have further investigated associations between cortical and subthalamic β burst dynamics. We follow the methodology of previous reports that demonstrated that the time spent in β burst correlates with impairment of movement kinematics (Torrecillos et al., 2018). Β bursts were defined as threshold crossings of the β feature vector above the 75^th percentile of the baseline period. Following the previous finding that specifically the time-spent in low-β but not high-β bursts was correlated with PD motor impairment (Lofredi et al., 2019), we investigated these bands separately for the motor preparation period (-1 to 0 s with respect to movement onset) and movement execution period (0 to 1 s following movement onset). To uncover a potential relationship of the β-burst metric with PD pathophysiology, we performed correlations with UPDRS-III total scores. Significant correlations were found between UPDRS-III and low-β bursts in STN-LFP signals during motor preparation (ρ = 0.63, p = 0.02; Figure 5A) and movement execution (ρ = 0.56, p = 0.04; data not shown), but not for the high-β band (p>0.05). Conversely, for ECoG highbeta but not low-β burst dynamics during motor preparation but not movement periods were significantly correlated with UPDRS-III total scores (ρ = 0.55, p = 0.04). In summary, we provide evidence that both subthalamic and cortical β burst dynamics relate to PD motor sign severity with subthalamic low-β bursts showing the most robust correlations, both during motor preparation and movement periods.

To relate these findings to movement decoding performance from cortex, we correlated the grand average XGBOOST grip-force decoding performances from ECoG channels (as above for UPDRS-III) with high- and low-β burst dynamics in both ECoG and STN-LFP signals. ECoG based grip-force decoding performance was significantly correlated with subthalamic low-β burst dynamics during motor preparation (ρ = -0.76, p = 0.004) and movement execution (ρ = -0.71, p = 0.005; Figure 5B). Subthalamic burst dynamics in the high-β band also correlated with ECoG decoding performances during movement (ρ = 0.71, p = 0.007) but not motor preparation. Cortical burst dynamics from ECoG signals did not reveal significant correlations with ECoG based grip-force decoding performances. Relevant correlations alongside exemplar burst visualizations and corresponding grip-force decoding traces are shown in Figure 5.”

Discussion:

Our study replicates and extends these findings, as we show a direct correlation between movement related β burst dynamics and PD motor sign severity. More importantly, our results show that the amount of time the STN is bursting in the low-β band, during motor preparation and movement execution is inversely correlated with ECoG based grip-force decoding performance. An obvious interpretation of this finding is that excessive synchronization in the STN may impair flexible motor control by decreasing information coding capacity and neural entropy as previously suggested in animal studies (Mallet et al., 2008; Cruz et al., 2009) and recently suggested for subthalamic β bursts (Velasco et al., 2022). Again, based on the inverse relationship of β activity and dopamine (Schwerdt et al., 2020), we may speculate that β bursts may relate to transient dips in dopamine signaling. Dopamine was shown to precede and invigorate future movement (da Silva et al., 2018). If subthalamic β bursts indicate phasic decreases in dopaminergic innervation, we could expect a loss of invigoration and reinforcement of ongoing neural population activity in the cortex – basal ganglia – thalamic loop, which offers an elegant explanation for the lower decoding performance from ECoG signals in the absence of obvious cortical activity patterns.

Methods:

Analysis of β bursts during motor preparation and movement execution periods.

To investigate a potential relationship between grip-force decoding performance and β burst activity, we have adopted a previously validated approach to movement related burst analyses (Torrecillos et al., 2018; Lofredi et al., 2019). Therefore, the β feature time-series were used and a threshold constituting the 75th percentile of the rest periods were calculated. Next, threshold crossings of at least 100 ms lengths in the motor preparation (-1 to 0 s with respect to movement) and movement execution (0 to 1 s with respect to movement execution) were marked as bursts. In previous reports, the most informative metric was the “time spent in burst” which is calculated as the sum of burst durations in the time period of interest. This metric is directly proportional to the burst probability at a given time-point. All burst analyses were repeated for the low-β and high-β bands in ECoG and STN-LFP. The times spent in bursts were correlated with UPDRS-III and ECoG based decoding performances.

3) A wide-range of decoding performance is seen across participants with a group of good performers and a group of low-performers. The findings from the secondary analyses on impairment levels and electrode location/connectivity may explain some of these differences, but it is unclear to what extent or if other factors are at play. Further, the cohort is notably small, especially considering the heterogeneity of electrode location. Although this does not limit the major finding of the superiority of sensorimotor ECoG over STN signals, it does limit the ability to understand the observed individual differences in decoding performance. These limitations should be noted/discussed.

We fully agree with the reviewers. Although we believe we have further addressed this issue we are constantly dissatisfied with one source of additional bias, which is signal to noise ratio. Signal to noise ratio in (intracranial) EEG can be measured by assessing the presence of periodic activity over the 1/f aperiodic component or over the amplifier noise floor. The issue we have with this approach is that again, the presence of these activity patterns are direct features to our models and their relevance can be indirectly assessed through visualization of the correlation coefficients shown in Figure 2 of the original submission. On the other hand, presence of β activity can be affected by Parkinson’s disease and again it can be hard to disentangle the relationship of these activity patterns with physiology and pathophysiology of movement in an isolated way. Therefore, we have made an alternative effort in addition to the reflection on disease severity above and functional and structural connectivity profiles (Figure 7), we investigate an alternative measure of physiological signal to noise ratio. In brief, we hypothesize that higher noise contaminated signals contain higher amounts of uncorrelated components. In turn, less noisy signals contain most of the explained variance in fewer uncorrelated components. We used Principal Component Analysis (PCA) to project rest data to n uncorrelated components, where n is the number of features. We demonstrate that an increased amount of information content in higher order components is associated with lower decoding performance.

Author response image 3

Download asset Open asset

This may indirectly indicate that detrimental effect of signal noise. Upon reflection and in conjunction with our response to comment 2 however, it still remains unclear whether this increased “noise” reflects pathophysiology or differences in noise contamination from external signals. Therefore, we refrain from adding this to the manuscript. Instead, we highlight the limited amount of data and the potential impact of signal to noise ratio on decoding performance in the limitations section of the discussion, which now reads:“The overall number of patients in this study is low. This may have limited a more detailed analysis of bias and other factors, beyond the described correlation of clinical symptom severity, subthalamic β burst dynamics, electrode location and connectomics. Most importantly, the signal to noise ratio may further impact decoding accuracies differently for ECoG and LFP signals.”

4) When comparing cortical and subthalamic electrodes the size and structure of the probe may be different. This means that instead of comparing apples to apples, it is more like comparing apples to oranges. This does not completely undermine the result because the difference in decoding between the areas, even given experimental differences, is likely to be of interest to clinical researchers studying DBS. If the surface area of the electrode is different between the two regions, then this could be a factor in decoding performance that does not have to do with brain region. Additionally, the electrodes in the subthalamus nucleus are circular, which are likely targeting very different neural populations across the probe within the small nucleus, which is different from the cortical electrodes which are on the surface targeting neural populations which are adjacent. Both of these factors (e.g. size and shape) could contribute to differences in decoding performance regardless of brain region. We did not see details of the electrodes in the method section, but this would be important to report as surface area is related to the number of neurons/dendrites summing to create the LFP, and this might lead to qualitatively different results for something like hand gripping irrespective of area. Similarly, with the shape of the electrode. These details will be an important addition to the paper and something that others can continue to investigate (e.g., researchers who have different size or shape of electrodes in the STN). We are sympathetic that this is not a variable that the researchers can change given the clinical nature of DBS, but the surface area of electrodes in each area should be mentioned in the method section, and if the surface area of the electrodes are different, then it should also be mentioned as a limitation in the Discussion section.

We follow the line of argumentation regarding the lack of comparability of ECoG and LFP signals. In fact, we do not necessarily believe and did not state that the subthalamic nucleus does not encode grip-force or vigor signals or does this less than cortex. We have previously demonstrated that movement velocity scales with subthalamic γ band activity (Lofredi et al., 2018, https://doi.org/10.7554/eLife.31895). Thus, our assumptions in fact are quite the opposite and follows the vigorous tutor paradigm (Turner & Desmurget 2010; https://doi.org/10.1016/j.conb.2010.08.022). Thus, the comparison of ECoG and LFP signals was more practically motivated, to highlight the utility of ECoG in brain computer interfaces research in movement disorders and justify its use for further research. While widely adopted in the US, our own group is the first to implant ECoG electrodes in PD patients in Europe. There is ethical concern regarding safety (which was recently addressed by us in a retrospective analysis on 367 patients (Sisterson et al., 2021; https://doi.org/10.1093/neuros/nyaa592)) and practical concern regarding its utility which we clearly demonstrate in this paper. We now acknowledge the different nature of ECoG and LFP signals with respect to hardware in the discussion.

It now reads:

“Our findings indicate that sensorimotor ECoG recordings are more informative than LFP recordings from the STN for grip-force decoding. While this finding is robust, we should acknowledge that the size and shape of electrodes (see Supplementary File 1a) and the spatial orientation and size of the neural architectures that are sampled are not directly comparable across these methods. Thus, it is difficult to derive the relative importance of the different brain regions for grip-force and vigor processing in motor control from this comparison. Instead, we interpret our result as a practical demonstration of the greater utility of ECoG signals for movement decoding.”

Furthermore, beyond the differences in shape of ECoG vs. DBS electrodes, we realized that we further did not sufficiently highlight differences in shape of ECoG strip designs across patients. Size, shape and contact area of cortical strip and DBS electrodes are now listed in the Supplementary File 1a where we have added a table with these details:

5) We wonder whether you have fully explored the neural feature space. One suggestion is that you also include the time domain data as a feature along with your frequency bands. Some papers have shown pretty good decoding with this feature – sometimes called the local motor potential. Here are some papers which discuss this feature in more detail. This could be an interesting addition especially if it performs well as it requires little preprocessing for studies doing online preprocessing and decoding.

Flint, R. D., Wang, P. T., Wright, Z. A., King, C. E., Krucoff, M. O., Schuele, S. U.,.… & Slutzky, M. W. (2014). Extracting kinetic information from human motor cortical signals. Neuroimage, 101, 695-703.

Mehring, C., Nawrot, M. P., de Oliveira, S. C., Vaadia, E., Schulze-Bonhage, A., Aertsen, A., & Ball, T. (2004). Comparing information about arm movement direction in single channels of local and epicortical field potentials from monkey and human motor cortex. Journal of Physiology-Paris, 98(4-6), 498-506.

Schalk, G., Kubanek, J., Miller, K. J., Anderson, N. R., Leuthardt, E. C., Ojemann, J. G.,.… & Wolpaw, J. R. (2007). Decoding two-dimensional movement trajectories using electrocorticographic signals in humans. Journal of neural engineering, 4(3), 264.

The reason we excluded raw signals was our main background in oscillations research where we typically disregarded any activity below 3 Hz as potentially contaminated by movement artifacts in these movement disorders patients. For the sake of expectation management we would like to state first, that we have decided not to include the local motor potential in the main manuscript, because changing the preprocessing and raw data feature set would affect every single result of the paper, which was beyond of what we could accomplish in a revision. Nevertheless, we realized that excluding that feature was indeed a loss, as we have run some tests with XGBOOST (for pragmatic reasons without Bayesian optimization leading to slightly lower performances overall) and found a relevant increase in decoding performance from inclusion of the local motor potential.

Author response image 4

Download asset Open asset

While this difference in our exemplary analysis was not significant, we will now add the local motor potential in all future movement decoding applications and we are thankful for the suggestion to asses it. We further highlight its potential in the limitations section of the discussion and use this to further mention other features that we are exploring in the development of our decoding toolbox (https://github.com/neuromodulation/py_neuromodulation):“Finally, we should acknowledge that the exploration of the neural feature space in this study was non-exhaustive, and further raw data features, such as the local motor potential (Mehring et al., 2004), waveform shape features (Cole and Voytek, 2017) and aperiodic signal components (Wilson, Castanheira and Baillet, 2022) could further improve decoding performances in future movement decoding studies.”

6) With respect to Figure 2, given how similar the descriptive power plots are, we were surprised that low γ has much larger weights compared to high γ or HFA. It looks like you aren't using regularization for your linear regression model. If your features (band pass filters) are highly correlated, the interpretation of the weights might not be meaningful. Have you thought about using ridge regression or lasso to deal with your seemingly highly correlated features? If not, then I don't believe it makes sense to try and interpret the weights. It looks like you do use regularized regression later but looking at the method section for your linear regression model there is no regularization term – so based on that it seems like for this first section it is just standard linear regression. We would suggest also using regularized regression for these analyses as interpreting the weights of linear regression with highly correlated features may be problematic.

We thank the reviewers for this important point. We realize that our figure was not explained clearly enough in the figure legend. Therefore, we would like to start with a more thorough explanation of the figure itself before replying specifically to the point with respect to regularization. First, we would like to reconcile the frequency bands: Low γ (60-80 Hz), HFA (90-200 Hz) and all γ (60-200 Hz). Figure 2A shows the model coefficients of the multivariable ordinary least squares linear regression model without regularization. Figure 2B in contrast shows coefficients from multiple univariable models that were trained separately with just one frequency band and time-point with respect to current decoded sample (not movement onset). We have done that to allow a direct comparison of individual features without interactions. We interpret that instantaneous low γ activity has the strongest individual positive association and instantaneous high-β has the strongest negative association with grip-force.

To address the comment about regularization we have further tested the following steps to investigate weight changes:

We retrained linear models similar to Figure 1A but added LASSO regularization and optimized the α regularization parameter, such that slight performance deterioration occurs. With this method only relevant features would remain in the regularized model, and others get penalized towards zero.

The top row of Author response image 5 demonstrates that regularization did not qualitatively affect coefficients. The lower left panel shows that the performance with regularization deteriorated. The lower right panel shows the individual data points and box plots of univariate models from single frequency band features similar to the x-axis time-point 0 in the original Figure 2B. These additional analyses corroborate our initial finding that indeed low γ (60-80 Hz) activity can have the strongest positive association with grip-force.We would also like to note that this figure was solely serving the purpose of feature visualization. The comparison of machine learning model performances in Figure 3 an Elastic Net Regression Model was chosen, which contains LASSO and RIDGE regression parameters that were obtained using a Bayesian Optimization hyperparameter search.

Author response image 5

Download asset Open asset

We now further clarify this issue in the figure legend of Figure 2, which now reads:

“Figure 2: Linear Models and Wiener Filters reveal temporally and spectrally specific coefficient distributions with grip-force decoding performance gain by including signals preceding the target sample by up to 500 ms. Multivariable linear model coefficients trained only from the instantaneous sample (0 time lag with respect to decoded target sample) including all frequency bands from best channels per patient resemble movement induced spectral changes with β desynchronization and γ synchronization (A). ECoG derived coefficients yield higher absolute values than STN-LFP derived coefficients. (B) Univariate frequency and time lag specific Linear Models were trained and visualized to improve interpretability of average coefficients in the absence of interactions. Low γ (60 – 80 Hz), HFA (90 – 200 Hz) and all γ (60 – 200 Hz) bands show stronger positive associations for contralateral over ipsilateral movements. Moreover, stronger associations are visible for ECoG over STN-LFP signals for β, HFA and γ bands. (C) Wiener Filters can integrate multiple time-steps in Linear Models leading to an incremental performance gain when signals are included preceding the current target sample by up to 500 ms.”

7) The R2 plots all appear to have a lower limit of 0. This, combined with some of the descriptions in the Methods, suggest that these performance metrics are the squared correlation coefficient. The computational form of the coefficient of determination R2, which is 1 – sum[(y_true – y_pred)^2] / sum[(y_true – y_mean)^2], is a more appropriate metric to use for evaluating decoder performance in cross-validated settings. The squared correlation coefficient is not equivalent in this case, as illustrated by the fact that it cannot be negative. Using the computational form of R2 allows the reader to readily compare predictions against a naïve estimator that predicts the sample mean – if the decoder being evaluated has an R2 below zero, then it is worse than simply predicting the mean. The correlation coefficient is also invariant to scale and translation, which are important features of decoder performance that are captured by the computational form of R2. If in fact the computational form of R2 has been used, please explicitly state that it has been (by simply including the equation in methods), since the results presented in the paper do appear to show otherwise.

We thank the reviewers for this important note. The computational form of the coefficient of determination was calculated, but clipped at 0 for the purpose of axis standardization. We further clarify this in the methods section, which now reads:

“The mean R² coefficient of determination of every test set estimate of the outer cross validation was used as the performance measure as defined below:

$R^{2} (y, \hat{y}) = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\overset{⏞}{y}}_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}$ Since the R² metric can be lower than zero for prediction that are worse than constant predictions, we used a lower threshold at zero to make performances comparable for visualization purpose of visualizations.”

8) We had a difficult time understanding the logic and the methods of your last section which relates decoding performance with connectivity maps. For example, after reading the methods section, I was still unclear how you determined if a fiber was significant or not. I believe that this section needs more detail and clarity. For example, you have analyses for structural and functional connectivity, but for the functional connectivity we could not find anything in the method section about what the patient was doing when this was computed – were the patients at rest, were they doing the same gripping task? These details are important for understanding the analyses and interpretation.

Before diving into the details of this analysis, we would like to state that the used methods all rely on normative connectomes, in this case from a cohort of patients with Parkinson’s disease outside of the study sample. Thus, no patient individual diffusion or functional MRI was required. The methods are relatively new and have been developed for the use of clinical outcome prediction for deep brain stimulation network targets and were derived from Mike Fox’s approach to lesion network mapping (Fox MD, 2018; https://doi.org/10.1056/nejmra1706158). The idea is to use a normative connectome as a wiring diagram to reveal the shared network of distributed locations in the brain. This has led to numerous high-impact publications on the relevance of brain networks for neural disorders and neuromodulation targets, e.g. for a recent update in the field of deep brain stimulation see Hollunder et al., 2022 https://doi.org/10.1016/j.pneurobio.2021.102211. The present manuscript represents the first use of this method in the context of brain signal decoding. In this context we named it “Prediction Network Mapping” to indicate that we are using the network to estimate the predictive performance of a recording location. Thus, generally speaking, it allows the identification of a shared network connecting recording locations associated with good decoding performance. Specifically, in the present use case, it reveals the whole-brain network that connects ECoG recording locations that had good decoding performances. Even though in the case of movement decoding the result may look trivial, the method itself has impactful implications, as we demonstrate that it can be used to perform out-of-sample predictions on the expected decoding performance of a certain brain location. We are currently validating this method for across-patient brain signal decoding, where the right contact can be selected just based on the underlying network architecture of its location in the brain. We believe that this method will soon be adopted for other decoding purposes and believe it is a relevant novelty factor in this paper. The specific fiber tract method mentioned in the reviewers comment is named fiber filtering or discriminative tractography is a relatively new addition to the connectomics toolkit reported in Li et al., 2021 https://doi.org/10.1038/s41467-020-16734-3 to determine connectivity associated with response to DBS for OCD. Results are obtained by calculating the tract models from all ECoG recording locations and generate coefficients termed fiber T scores, that indicate the associated the association of the target variable for the recording location (in this case gripforce decoding performance) with the tract across all recording locations that share the tract. The relevant fiber bundle across all training subjects is determined by mass univariate Ttests FDR corrected for multiple comparisons. If this bundle is determined in a training group, its predictive performance can be validated on a test case through leave-one-subject or leave-one-electrode out cross-validation to predict decoding performance in an out-of-sample fashion, solely based on recording locations.

After rereading the paragraph we felt that it will be hard to explain the method more thoroughly without significantly extending the methods section. Given that the described methods are popular among DBS neuroimaging enthusiasts and are now frequently used by many groups and because they are not central to the present manuscript, we have decided to keep the methods section concise but add an explanatory schematic in response to comment 9 and a more clear statement regarding the absence of patient individual diffusion and functional MRI:

“To investigate whether decoding performance from different recording locations can cross predict across patients, we developed a whole-brain connectomics based approach. Therefore, ECoG electrode recording locations were projected to normative structural and functional MRI data (Parkinson's Progression Markers Initiative [PPMI]; www.ppmi-info.org) using Lead-DBS software in Matlab (www.lead-dbs.org).(Horn et al., 2019) The PPMI connectomes of patients with PD (n = 74) was priorly computed (Ewert et al., 2018) and has been used in context of DBS multiple times (de Almeida Marcelino et al., 2019; Horn et al., 2017b; Lofredi et al., 2021; Neumann et al., 2018). No patient specific diffusion or functional MRI was required for this analysis.”

9) Similarly, the prediction network mapping methods would be more clear if represented schematically and/or with accompanying equations. These methods were very difficult to understand given the current descriptions in the Results text and Methods.

We agree with the reviewers that the methods used for the connectomics analysis are quite dense and benefit from a schematic, which we have now added as an additional supplementary figure to the manuscript:

In the methods section we reference to the Figure:

“A schematic illustrating the different steps of functional and structural prediction network mapping can be found in Figure 7—figure supplement 1.”

10) The authors are unable to fully rule-out that the superiority of ECoG signals is not dependent on the task performed (i.e., grip force). The authors claim that the findings support the utility of additional ECoG in adaptive DBS research for PD patients. Although it is certainly expected that sensorimotor ECoG would provide a richer signal compared to STN LFPs due to both signal size, complexity, and relation to movement, the data in this paper is inherently limited to the grip task performed. This limitation should be noted/discussed.

We agree that the data presented is only limited to the single movement type of gripforce. And we expect the reviewers point would hold true for any kind of task, as the human ability to move is virtually infinite and can never be fully captured by repetition of certain aspects of movement. We now acknowledge the fact that our findings are not generalizable to movement per se, but are limited to grip-force in the limitations section of the discussion, which now reads:

“While gripping is a relevant motor skill for human behavior, our findings are restricted to the decoding of grip-force and may have limited generalizability to other movements.”

Nevertheless, to convince the reviewers that the findings may have some general worth in the context of movement we have performed further analyses on a dataset from an additional PD patient recruited at the Charité in Berlin, Germany. This subject was recorded with a cortical strip electrode (N=6 contacts) covering the sensorimotor cortex targeted as in the present cohort from Pittsburgh, as well as segmented DBS electrodes (N=8 contacts) in the STN. Here we recorded movements with a rotational handle, previously described by Lofredi et al. 2019, Neurobiology of Disease https://doi.org/10.1016/j.nbd.2019.03.013. The task instruction was to perform a voluntary self-paced rotational hand movement at an interval of approximately 10 s. The XGBOOST validation pipeline was the same as in the present manuscript. The target variable in this case was not grip force, but rotation amplitude.

Author response image 6

Download asset Open asset

We observe excellent decoding performances that are higher than on average than in the present manuscript. But more importantly, ECoG contacts are still outperforming recordings from the STN. In fact, the worst ECoG contact showed higher performances than the best STN contact, suggesting that the obtained grip force decoding results may hold at least in one other movement modality. Finally, we observe very similar results for a button press task in a different cohort from collaborators in Beijing. From our perspective, the question of specificity may be more relevant than the generalizability. Here, we believe that the primary source of specificity can be obtained through a denser coverage of somatotopy with higher density strips, e.g. as used in Chrabaszcz et al., 2019 https://doi.org/10.1523/jneurosci.284218.2019 where we showed lip vs. tongue specific activity during speech production. With low density strips with large surface areas and low impedances and with common DBS electrodes, we believe that the main signal that we can decode is movement vigor.

11) The results of the paper are all centered on decoding grip-force. The authors suggest that this decoding could be used as a control signal for adaptive deep brain stimulation in patients with Parkinson's disease, increasing stimulation when higher movement "vigor" is predicted (summarized from lines 346-348). It seems that this would entail a fast algorithmic approach to adapting stimulation, making adjustments in response to frequently changing movement states. A comparison to different algorithmic approaches (for example, tracking slower fluctuations in medication state) would be helpful to have in the Discussion.

We appreciate this comment and try to address it without delving too deep into speculation. Before that, we would like to state that we are convinced that adaptive neuromodulation will improve clinical outcome in DBS patients and that brain signal decoding will extend the clinical utility of adaptive DBS, and that ECoG signals outperform LFP from DBS electrodes (e.g. see Merk et al., 2022 https://doi.org/10.1016/j.expneurol.2022.113993 on the topic or Neumann & Rodriguez-Oroz https://doi.org/10.1002/mds.28567 for a short movement disorders editorial). Therefore, we are confident that the present paper is a relevant albeit indirect contribution towards the implementation of intelligent adaptive DBS beyond the present use case of PD and grip-force. In the discussion we tried to highlight the general relevance of the paper, while also trying to sketch the potential specific utility of our findings in PD. Here, it is our personal belief that stimulation proportional to movement vigor may have merit in the treatment of Parkinson’s disease as it could mimic the invigorating effects of phasic dopamine signals that are lost to neurodegeneration (see reply to comment 2). However, we want to be transparent that there is currently no clinical evidence for this use-case. Now the reviewers are right that indeed this use of vigor decoding for adaptive DBS would be a fast algorithmic adaptation to concurrent behaviour. This could be combined with a slower adaptation algorithm, e.g. based on subthalamic β activity or corticosubthalamic coherence, to rebalance tonic fluctuations of dopamine with medication cycles and or additional decoding applications, similar to the overlapping temporal scales for closedloop DBS pictured in Tinkhauser & Moraud, 2021 https://doi.org/10.3389/fnins.2021.734186. Our vision is that in the future, multiple decoders will decode concurrent symptoms, sideeffects and behaviours that are relevant for DBS adaptation in PD, e.g. bradykinesia, gait freezing, voluntary movements, dyskinesia, tremor, speech, dysarthria, dystonia and more. This vision is discussed in a previous review paper in Neumann et al., 2019 https://doi.org/10.1007/s13311-018-00705-0.

The Discussion section now reads:

“Notably, the proposed adaptive stimulation would require a fast algorithmic adaptation of stimulation to ongoing behavior. This could be combined with additional slower adaptations in response to medication or sleep cycles. Specifically for PD, β activity based adaptive stimulation can be well suited to track the patient’s overall symptom state (Tinkhauser and Moraud, 2021) while more rapid stimulation adaptations based on vigor can follow fast kinematic changes. The utility of vigor-based stimulation and the combination of this approach with additional slower adaptation algorithms, require further proof-of-concept studies before the clinical utility can be foreseen.”

12) A Go/No-Go task is also used in the paper. This is potentially problematic, given that there may be modulation in the neural recordings associated with response inhibition. While the decoders are trained only to predict actual force production, it is possible that inhibitory responses could influence the decoder readout and impact the performance metrics on which every analysis of the paper hinges. It is also plausible that such inhibitory responses would asymmetrically affect the subthalamic decoders and the cortical decoders. Comparison of those two signal locations is the main topic of the paper, so this is a critical aspect to consider and discuss.

We acknowledge the general relevance of this comment, but are convinced that the implications for the validity of our study remain limited. The absence of specific differential dynamics of EEG vs. STN recodings were addressed in a Go/No-Go task in Klostermann et al., 2007 https://doi.org/10.1111/j.1460-9568.2007.05417.x. The only specific difference reported for cortex vs. STN was an increased β rebound synchronization after movement termination, which is generally also observed in cortex. More recently and based on the same dataset and the same task the interplay of STN and cortex were evaluated, indicating an interplay of both structures during motor preparation and performance (Alhourani et al., 2020 https://doi.org/10.1093/cercor/bhz264; Fischer et al., 2020 https://doi.org/10.7554/eLife.51956). Finally, if decoding should work in naturalistic settings, the decoders would be required to be even more robust to distraction and additional information coding. Thus, we believe this could be interpreted to support the utility of our decoding framework during complex human behavior. Moreover, the preliminary analysis on new data outside of a Go/No-Go task shown in comment 10 can further serve as validation that the task is not required for the demonstration of higher decoding performances from ECoG recordings when compared to subthalamic LFP. Nevertheless, we now note this point as a limitation in our Discussion section, which now reads:

” Our analysis is retrospective in nature and the data were obtained in context of a Go/NoGo task, which may have implications on the generalizability of the findings in the application during naturalistic behavior.”

13) The results identify a stark difference in the way model "complexity" impacts decoding in the STN and cortex, yet this concept is not well-developed or discussed. What does this say about the nature of the information content in each area such that allowing for non-linear relationships benefits decoders based on one area, but harms decoders based on the other? Please discuss further.

In the present analysis we found that XGBOOST outperforms linear methods, such as Wiener Filters or linear regression of spatial features obtained with Source Power Comodulation (SPoC). Since XGBOOST makes use of highly non-linear feature interactions, we show that ECoG band power features encode grip force non-linearly. In the STN however linear methods seem to outperform non-linear methods, with Wiener Filters demonstrating best performances. As mentioned in our reply to comment 4, it is difficult to state a clear difference in the underlying representation of grip-force in the respective neural population, given the difference in electrode shape and the relation to the neural architecture that is recorded with ECoG vs. STN. Therefore, we like to refrain from such speculations and limit our interpretation to the empirical finding that the more complex XGBOOST models in combination with ECoG signals outperformed decoding from Wiener Filters with STN signals. We are afraid that signal to noise ratio may pose a bias that is difficult to control for. This was acknowledged in the discussion as part of our reply to comment 3 above. We have now extended this to:

“Most importantly, the signal to noise ratio may further impact decoding accuracies differently for ECoG and LFP signals. This could in part explain why decoding from ECoG signals may benefit more from complex and non-linear model architectures.

14) The Bayesian Optimization hyperparameter search was run for a fixed number of iterations according to line 637. Were enough iterations used to reach convergence in performance? This would be a useful supplementary analysis.

We thank the reviewers for identifying this important methodological aspect. Bayesian optimization was run for 10 rounds in total. We have now performed the requested supplementary analysis as shown in Author response image 7.

Author response image 7

Download asset Open asset

Author response image 7 shows the normalized XGBOOST performance change with incremental Bayesian optimization rounds for ECoG and STN contacts for contra – and ipsilateral movements. Importantly, the optimal hyperparameters have been found for every contact after 5 rounds. We have now added this information to the methods section, which now reads:“Post-hoc assessment confirmed convergence in performance after a maximum of 5 rounds in all recordings.”

15) In line 648, it is stated that a single best channel was chosen for each patient and brain area (STN, cortex) in part to "account for varying numbers of available electrode contacts". There seem to be far more ECoG channels than STN channels – does this introduce a bias in the results when taking the "best" performing channel from a larger candidate pool of ECoG channels as compared to the STN? The authors should elaborate on this and make any necessary corrections for bias.

We acknowledge the potential bias arising from the difference in number of ECoG and STN-LFP contacts. After bipolar rereferencing there were 3 STN channels, while on average 10.18±11.29 left and 8.9±12 right hemispheric ECoG channels. To account for this difference, we repeated the analysis by randomly selecting n=3 ECoG channels for every subject. After selecting the best cross-validated performance contact per subject for ECoG and STN-LFP, ECoG still outperforms STN-LFP recordings.

Author response image 8

Download asset Open asset

We have decided to abstain from including this additional analysis because we feel that for the main manuscript a more systematic approach comparing all machine learning architectures would be adequate but clutter the manuscript with technical details. Nevertheless, our results are further supported by the preliminary analysis on the Berlin subject where 6 ECoG contacts were compared to 8 STN contacts. Here, even the weakest ECoG channel outperformed the best STN LFP channel. We have now noted the potential bias in the limitations section of the discussion, which now reads:“The comparability of ECoG and LFP recordings was further affected by the higher number of available ECoG channels, when compared to only three bipolar LFP channels. However, the large effect size of superior decoding performances with ECoG may indicate that this bias does not relevantly impact the interpretation of our findings.”

16) The significantly connected fibers are shown in Figure 7B. However, due to the small nature of this sub-figure and only 1 slice shown, it is difficult to fully understand where these fibers tend to go (appears to be a combination of M1 and SMA/PM?). It may be helpful to describe in the text of the results where these fibers are going. For instance, Figure 7C gives a great look into the visualization of the topography of decoding performance. Although that type of figure may not be possible with the fiber tract analysis, at least a text description would be helpful for the reader and allow further interpretation of those results.

We appreciate the interest of the reviewers in the network topography associated with decoding performance in figure 7. The fiber tracts depicted in panel B indeed reflect projections spanning sensory, motor and prefrontal cortical regions and include descending fibers of the corticospinal tract. However, SMA even though expected from its known contribution to motor control and relevance in EEG based brain computer interfaces, was not particularly highlighted in this network. However, SMA but not preSMA is part of the functional network shown in figure 7C. Differences may arise from the limitations of diffusion MRI methodology or from the fact that fMRI better captures polysynaptic connections.

We have now added a short description of the fiber tracts to the Results section as suggested:

“The specific fiber distributions included structural projections spanning sensory, motor and prefrontal cortex, and could significantly predict decoding performance of left out channels (ρ = 0.38, p < 0.0001; thresholded at a false discovery rate α = 0.05) and patients (ρ = 0.37, p < 0.0001) in a cross validated manner (Figure 7D).”

17) The supplementary figure provides transparency regarding the variability of observed grip performances. One remaining question was whether the observed variability in decoding performance across individuals and the observed correlation between decoding performance and impairment level may actually be related to the observed variability in grip force production. Do the more impaired individuals display greater variability across trials in grip force production compared to those with less impairment? And is this then creating a more difficult decoding problem for those individuals with more extreme variability compared to individuals who have consistent force production curves?

We thank the reviewers for this important comment. It addresses a common chicken and egg problem in the field of movement disorders neurophysiology. In brief, pathophysiologically relevant changes in brain signals are expected to produce symptoms but the observed neurophysiological correlates could be cause or consequence of motor symptoms. For example, it remains unresolved whether excessive β activity in the STN is cause, epiphenomenon or consequence of bradykinesia. The conclusion of our reply to comment 2 is that PD pathophysiology may impair movement coding capacity. If this was true, we would expect a change in motor performance, otherwise it would defy its own logic or would at least require creative argumentation along the lines of magical neuromuscular compensatory mechanisms that are not captured by our analysis. Therefore, we have realized the potential impact of this comment and have tried to further substantiate our interpretation through correlation analyses of grip-force variability. To this end, we calculated the variance of maximum grip-force across all movements for every patient. Next, we correlated the resulting grip-force variability with UPDRS-III scores and decoding performances across patients. Grip force variability showed net negative yet insignificant correlations with decoding performance (Rho = -0.49, p = 0.06) and UPDRS-III (Rho = 0.48 p = 0.07). Thus, grip-force variability was unlikely the sole factor, as the strongest correlation was indeed obtained for the direct association of decoding performance with UPDRS-III (Rho = -0.55, p = 0.04) as previously reported. Our claim that pathophysiology can impair decoding performance was further substantiated through the revision and our reply to comment 2 for which we analysed time spent in β bursts. We found that time spent in β bursts in the subthalamic nucleus was inversely correlated with decoding performances even in the motor preparation period (-1 – 0) before movement onset. Interestingly, increased movement variability was specifically associated with increased subthalamic β bursts in the motor preparation period (Rho = 0.72, p = 0.004) but not during movement (Rho = 0.37; p = 0.13). Notably, subthalamic β bursts for both the motor preparation period and the movement periods were also correlated with UPDRS-III (Rho = 0.63/0.56, p = 0.02/0.05). Finally, the strongest correlations of all were found for time spent in β bursts in the subthalamic nucleus with ECoG based grip-force decoding performance during motor preparation (Rho = -0.76, p = 0.004). We conclude that grip-force variability is non-significantly but positively associated with symptom severity but does not solely explain deterioration of decoding performance with PD pathophysiology. Instead, excessive synchronization of the subthalamic nucleus in low-β bursts appears to be the strongest negative predictor for grip-force decoding performance in this study. We have now added a short comment on movement variability to the methods and results of the manuscript:

Methods

“To investigate the variability of grip-force as a potential bias for decoding performance, we calculated the variance of peak force across movement repetitions.”

Results

“To investigate potential sources of bias from patient specific information on grip-force decoding performance, we performed Spearman’s correlations with the grand average from all contra -and ipsilateral decoding performances. Averaging was necessary to obtain one value per patient. Age (ρ = -0.16, p = 0.32), disease duration in years (ρ = 0.31, p = 0.17) and number of movements (ρ = -0.41, p = 0.11) and movement variability (Rho = -0.49, p = 0.06) did not reveal significant correlations.”

https://doi.org/10.7554/eLife.75126.sa2

Article and author information

Author details

Timon Merk

Movement Disorder and Neuromodulation Unit, Department of Neurology, Charité - Universitätsmedizin Berlin, corporate member of Freie Universität Berlin and Humboldt Universität zu Berlin, Berlin, Germany

Contribution
Conceptualization, Formal analysis, Funding acquisition, Methodology, Software, Visualization, Writing – original draft, Writing – review and editing

For correspondence
timon.merk@charite.de

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-3011-2612
Victoria Peterson
1. Brain Modulation Lab, Department of Neurosurgery, Massachusetts General Hospital, Boston, United States
2. Harvard Medical School, Boston, United States
Contribution
Formal analysis, Methodology, Software, Writing – review and editing

Competing interests
No competing interests declared
Witold J Lipski

Department of Neurobiology, University of Pittsburgh, Pittsburgh, United States

Contribution
Investigation, Methodology, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-1499-6569
Benjamin Blankertz

Department of Computer Science, Technische Universität Berln, Berlin, Germany

Contribution
Funding acquisition, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-2437-4846
Robert S Turner

Department of Neurobiology, University of Pittsburgh, Pittsburgh, United States

Contribution
Funding acquisition, Supervision, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-6074-4365
Ningfei Li

Movement Disorder and Neuromodulation Unit, Department of Neurology, Charité - Universitätsmedizin Berlin, corporate member of Freie Universität Berlin and Humboldt Universität zu Berlin, Berlin, Germany

Contribution
Software, Writing – review and editing

Competing interests
No competing interests declared
Andreas Horn

Movement Disorder and Neuromodulation Unit, Department of Neurology, Charité - Universitätsmedizin Berlin, corporate member of Freie Universität Berlin and Humboldt Universität zu Berlin, Berlin, Germany

Contribution
Methodology, Resources, Software, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-0695-6025
Robert Mark Richardson
1. Brain Modulation Lab, Department of Neurosurgery, Massachusetts General Hospital, Boston, United States
2. Harvard Medical School, Boston, United States
Contribution
Conceptualization, Data curation, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Writing – review and editing

Contributed equally with
Wolf-Julian Neumann

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-2620-7387
Wolf-Julian Neumann

Movement Disorder and Neuromodulation Unit, Department of Neurology, Charité - Universitätsmedizin Berlin, corporate member of Freie Universität Berlin and Humboldt Universität zu Berlin, Berlin, Germany

Contribution
Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – review and editing

Contributed equally with
Robert Mark Richardson

For correspondence
julian.neumann@charite.de

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-6758-9708

Funding

National Institutes of Health (R01NS110424)

Robert S Turner
Robert Mark Richardson
Wolf-Julian Neumann

Bundesministerium für Bildung und Forschung (FKZ01GQ1802)

Wolf-Julian Neumann

Deutsche Forschungsgemeinschaft (410169619)

Andreas Horn

Deutsche Forschungsgemeinschaft (Project-ID 424778381 – TRR 295)

Andreas Horn
Wolf-Julian Neumann

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

The present manuscript was supported through a US-German Collaborative Research in Computational Neuroscience (CRCNS) grant to RST, RMR and WJN with funding from the German Federal Ministry for Research and Education and NIH (R01NS110424). Further funding was provided through Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 424778371 – TRR 295 to AH and WJN AH was supported by the German Research Foundation (Deutsche Forschungsgemeinschaft, Emmy Noether Stipend 410169619 and 424778371 – TRR 295) as well as Deutsches Zentrum für Luft- und Raumfahrt (DynaSti grant within the EU Joint Programme Neurodegenerative Disease Research, JPND). Some data used in the preparation of this article were obtained from the PPMI database (https://www.ppmi-info.org/). For up-to-date information on the study, visit https://www.ppmi-info.org/. PPMI, a public–private partnership, is funded by the Michael J Fox Foundation for Parkinson’s Research. For funding partners, see https://www.ppmi-info.org/fundingpartners.

Ethics

Human subjects: The patients were subjected to bilateral STN DBS lead implantation, as proposed by standard clinical indications criteria. In accordance with protocol #PRO13110420, approved by the Institutional Review Board of the University of Pittsburgh, informed consent for all patients was obtained prior to any surgical procedure.

Senior Editor

Michael J Frank, Brown University, United States

Reviewing Editor

Nicole C Swann, University of Oregon, United States

Reviewer

Kevin Wilkins, Stanford University, United States

Version history

Preprint posted: April 26, 2021 (view preprint)
Received: October 29, 2021
Accepted: May 15, 2022
Version of Record published: May 27, 2022 (version 1)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.