1. Neuroscience

The aperiodic exponent of subthalamic field potentials reflects excitation/inhibition balance in Parkinsonism

  1. Christoph Wiest
  2. Flavie Torrecillos
  3. Alek Pogosyan
  4. Manuel Bange
  5. Muthuraman Muthuraman
  6. Sergiu Groppa
  7. Natasha Hulse
  8. Harutomo Hasegawa
  9. Keyoumars Ashkan
  10. Fahd Baig
  11. Francesca Morgante
  12. Erlick A Pereira
  13. Nicolas Mallet
  14. Peter J Magill
  15. Peter Brown
  16. Andrew Sharott
  17. Huiling Tan  Is a corresponding author
  1. Medical Research Council Brain Network Dynamics Unit, Nuffield Department of Clinical Neurosciences, University of Oxford, United Kingdom
  2. Movement Disorders and Neurostimulation, Biomedical Statistics and Multimodal Signal Processing Unit, Department of Neurology, University Medical Center of the Johannes Gutenberg University Mainz, Germany
  3. Department of Neurosurgery, King's College London, United Kingdom
  4. Neurosciences Research Centre, Molecular and Clinical Sciences Institute, St. George' s, University of London, United Kingdom
  5. Institut des Maladies Neurodégénératives, CNRS UMR5293, Université de Bordeaux, France
https://doi.org/10.7554/eLife.82467
Share this article
Cite this article
  1. Christoph Wiest
  2. Flavie Torrecillos
  3. Alek Pogosyan
  4. Manuel Bange
  5. Muthuraman Muthuraman
  6. Sergiu Groppa
  7. Natasha Hulse
  8. Harutomo Hasegawa
  9. Keyoumars Ashkan
  10. Fahd Baig
  11. Francesca Morgante
  12. Erlick A Pereira
  13. Nicolas Mallet
  14. Peter J Magill
  15. Peter Brown
  16. Andrew Sharott
  17. Huiling Tan
(2023)
The aperiodic exponent of subthalamic field potentials reflects excitation/inhibition balance in Parkinsonism
eLife 12:e82467.
https://doi.org/10.7554/eLife.82467
  2. Download BibTeX
  3. Download .RIS

Abstract

Periodic features of neural time-series data, such as local field potentials (LFPs), are often quantified using power spectra. While the aperiodic exponent of spectra is typically disregarded, it is nevertheless modulated in a physiologically relevant manner and was recently hypothesised to reflect excitation/inhibition (E/I) balance in neuronal populations. Here, we used a cross-species in vivo electrophysiological approach to test the E/I hypothesis in the context of experimental and idiopathic Parkinsonism. We demonstrate in dopamine-depleted rats that aperiodic exponents and power at 30–100 Hz in subthalamic nucleus (STN) LFPs reflect defined changes in basal ganglia network activity; higher aperiodic exponents tally with lower levels of STN neuron firing and a balance tipped towards inhibition. Using STN-LFPs recorded from awake Parkinson’s patients, we show that higher exponents accompany dopaminergic medication and deep brain stimulation (DBS) of STN, consistent with untreated Parkinson’s manifesting as reduced inhibition and hyperactivity of STN. These results suggest that the aperiodic exponent of STN-LFPs in Parkinsonism reflects E/I balance and might be a candidate biomarker for adaptive DBS.

Editor's evaluation

This important work provides compelling evidence for the relationship between aperiodic components of spectral signals in the subthalamic nucleus and changes in neural firing. The manuscript is particularly notable because the authors used a unique cross-species approach in human patients and rats. The mechanistic insight this work provides will be especially impactful given the current interest in considering aperiodic components of electrophysiological signals.

https://doi.org/10.7554/eLife.82467.sa0

Introduction

Power spectral densities (PSDs) of neural time series, such as electroencephalography (EEG), electrocorticography (ECoG), or local field potentials (LFPs), tend to follow a 1/f power law distribution, where f is frequency, meaning that power is greatest at low frequencies and diminishes rapidly as frequencies increase (He et al., 2010). In this study, we will refer to the slope of the PSD as the aperiodic exponent. For decades, the aperiodic exponent has been deemed unimportant and was often removed from analyses to emphasise brain oscillations (He, 2014). Only recently did the aperiodic exponent gain more attention and was attributed a physiological meaning. Aperiodic exponents in LFP, EEG, and ECoG recordings vary by age (He et al., 2019; Schaworonkow and Voytek, 2021; Voytek et al., 2015), cortical depth (Halgren et al., 2021), psychiatric disorders (Adelhöfer et al., 2021; Molina et al., 2020; Robertson et al., 2019; Veerakumar et al., 2019), and Parkinson’s disease (PD) (Mostile et al., 2019). They track sensory stimuli (Waschke et al., 2021) and change with movement (Belova et al., 2021). Moreover, the aperiodic exponent was suggested to reflect neuronal spiking (Manning et al., 2009; Ray and Maunsell, 2011), synaptic currents (Baranauskas et al., 2012; Buzsáki et al., 2012), and excitation-inhibition (E/I) balance, which describes the delicate balance of inhibitory and excitatory synaptic inputs to neurons (Chini et al., 2022; Gao et al., 2017; Trakoshis et al., 2020). The latter is supported by multiple studies showing that aperiodic exponents in non-invasive EEG and invasive LFP measurements were modulated by sleep and anaesthesia, with lower exponents, corresponding to slower decay of power with increasing frequencies, during the conscious state, which is linked with increased excitation. Inversely, higher aperiodic exponents, corresponding to faster decay of power with increasing frequencies, were observed during the unconscious state (NREM sleep, anaesthesia), which is linked with more inhibition (Colombo et al., 2019; Huang et al., 2020; Lendner et al., 2020; Miskovic et al., 2019; Niethard et al., 2016; Waschke et al., 2021). In addition, Gao and colleagues found that theta cycle-modulated E/I changes in the rat hippocampus are reflected in the per-cycle PSD exponent of hippocampal LFPs calculated at different theta phases (peaks or troughs) confirming the E/I hypothesis for LFPs (Gao et al., 2017).

In our study, we seek to test whether the aperiodic exponent of LFPs recorded in the subthalamic nucleus (STN) tracks changes in E/I balance. To this end, we take advantage of the well-characterised rhythmic changes in neuronal firing patterns within the basal ganglia during slow-wave activity (SWA, see Figure 1A) induced in dopamine-depleted rats by general anaesthesia. STN and external globus pallidus (GPe) neurons are rhythmically active in time with cortical SWA in rats rendered Parkinsonian by lesion of midbrain dopamine neurons with 6-hydroxydopamine (6-OHDA) (Figure 1A). STN neurons are predominantly active during the active phase of cortical slow (~1 Hz) oscillations (Magill et al., 2001; Mallet et al., 2008a). Inversely, STN neurons reduce their firing around the inactive phase when GPe-Ti (‘type-inactive’) neurons tend to fire most. GPe-Ti neurons largely correspond to prototypic GPe neurons that are GABAergic and project to and inhibit STN (Abdi et al., 2015; Mallet et al., 2012); the GPe is considered the primary source of inhibitory inputs to the STN (Smith et al., 1998). Based on single-unit activity, we extracted separate periods with high levels of STN excitation or inhibition, and applied the FoooF algorithm to parameterise PSDs of LFPs during both states (Donoghue et al., 2020). Aperiodic exponents of STN-LFPs were consistently modulated with expected differences of the E/I ratio of STN in these states.

Figure 1 with 2 supplements see all
Download asset Open asset
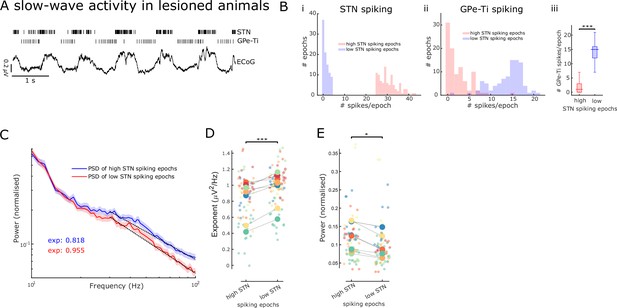
Aperiodic exponents and power of subthalamic nucleus-local field potentials (STN-LFPs) between 30 and 100 Hz reflect STN excitation and inhibition in lesioned animals.

(A) Example traces of electrocorticography (ECoG) and single-unit spiking activity of STN and GPe-Ti neurons during slow-wave activity (SWA) in anaesthetised 6-hydroxydopamine (6-OHDA)-lesioned animals. Note the rhythmic spiking pattern of both neuron types, which either aligns with peaks or troughs of cortical slow (~1 Hz) oscillations. (B) We identified 250 ms epochs of relatively high spiking (>75th percentile) and epochs of low spiking (<25th percentile) based on STN neuron activity during cortical SWA. The distribution of STN (i) and GPe-Ti (ii) spiking activity is shown for one example animal, which confirms that spiking rates are clearly differentiable for the two high and low STN spiking states. GPe-Ti neurons are most active when STN neurons are relatively inactive and vice versa (iii; ***p<.001, Wilcoxon rank-sum test). (C) Average power spectral densities (PSDs) of STN-LFPs in the two states identified above (mean ± SEM, n = 8 animals). The black dotted lines denote the aperiodic fits (exponent values [exp] are colour-coded) for the respective PSDs between 30 and 100 Hz. (D) Aperiodic exponents are high during low STN spiking epochs corresponding to more GPe-Ti activity and, by inference, more inhibition of STN. Inversely, aperiodic exponents are low during high STN spiking epochs associated with less GPe-Ti activity and, by inference, disinhibition (LME: estimate = 0.12, t = 3.92, p<0.001). (E) Average power between 30 and 100 Hz in the STN-LFPs is higher when STN neurons are highly active than when STN spiking is low (LME: estimate = –0.02, t = –2.34, p=0.02). (D, E) Large dots denote the mean per animal and are colour-coded. Small dots denote individual LFP channels. n = 8 animals, *p<0.05, **p<0.01, ***p<.001, LME.

In a second step, we tested whether similar findings can be obtained in human STN-LFP recordings from awake patients with PD. In PD, STN shows exaggerated and synchronised oscillatory activity in the beta range (Bergman et al., 1994; Brown et al., 2001; Levy et al., 2000). Dopaminergic medication and deep brain stimulation (DBS) desynchronise STN in the beta range (Eusebio et al., 2011; Kühn et al., 2008; Whitmer et al., 2012) and reduce STN single-unit activity (Filali et al., 2004). Here, we compare aperiodic exponents of the STN-LFP ON and OFF dopaminergic medication and ON and OFF DBS. We show that aperiodic exponents of the STN-LFP were increased with both therapies, and these results from PD patients are also consistent with the E/I hypothesis.

Results

Establishing the validity of STN-LFP aperiodic exponents as a marker of E/I balance

To validate the aperiodic exponent of STN activity as an estimate for E/I changes, we first took advantage of the distinct rhythmic changes in neuronal firing patterns within the basal ganglia during SWA in 6-OHDA-lesioned rats under anaesthesia. During SWA, STN neurons exhibit distinct periodic changes in firing rates, which are tightly linked with the phase of cortical slow (~1 Hz) oscillations that dominate SWA (Figure 1A; Magill et al., 2001). These changes in STN firing rates have been defined, by us and others, in relation to their major excitatory and inhibitory inputs (Abdi et al., 2015; Magill et al., 2001; Mallet et al., 2008a).

To contrast STN activity during opposing conditions of E/I balance, we first distinguished 250 ms epochs of ‘high’ and ‘low’ levels of spiking of STN single units during SWA (Figure 1—figure supplement 1B). Because STN and GPe-Ti neurons fire in a near anti-phase relationship during cortical SWA (Mallet et al., 2008a), high- and low-spiking epochs of STN neurons tend to occur in time with, respectively, low and high levels of GPe-Ti spiking (Figure 1B). We assume that, during low and high levels of GPe-Ti spiking, STN neurons receive low and high levels of inhibitory input from the GPe, respectively. Previous studies have shown that during SWA, excitatory input from cortical projection neurons would be in-phase with the high-spiking epochs of STN neurons, and thus, anti-phase to inhibitory inputs from GPe (Parr-Brownlie et al., 2007). First, we computed PSDs of STN-LFPs for the two states (high and low STN spiking epochs, Figure 1C) and extracted both aperiodic exponents and average power between 30 and 100 Hz. Aperiodic exponents were smaller in high compared to low STN spiking epochs, consistent with small exponents being generated in conditions of more excitation/less inhibition and vice versa (LME: estimate = 0.12, t = 3.92, p<0.001; Figure 1D). The total power of activities between 30 and 100 Hz in STN-LFP was smaller during low STN spiking epochs compared to high STN spiking epochs (LME: estimate = –0.02, t = –2.34, p=0.02; Figure 1E). Furthermore, the lack of correlations between power and aperiodic exponents suggests that both power and exponents from the same frequency range are dissociable and might contain different information (Spearman; ρ = –0.07, p=0.56 and ρ = –0.18, p=0.14 for high and low STN spiking epochs, respectively). When pooling aperiodic exponents and power from high and low STN spiking epochs, we still did not observe a significant correlation (ρ = –0.15, p=.07).

Overall, these results from 6-OHDA-lesioned rats suggest that the aperiodic exponent of STN-LFPs is altered according to different levels of STN spiking. The high- and low-spiking epochs of single STN neurons can in turn be ascribed with confidence to an E/I balance that is tipped in favour of excitation and inhibition, respectively. As such, these results support the notion that STN-LFP aperiodic exponents may become valid markers of overall E/I balance in STN.

Aperiodic exponents from 40 to 90 Hz separate levodopa medication states in PD patients

After corroborating the link between aperiodic exponents in STN-LFPs and changes in E/I balance in the STN in an animal model under anaesthesia, we sought to apply the same concept to clinical data from awake PD patients. According to the classical direct/indirect pathways model of basal ganglia functional organisation, the Parkinsonian STN is overactive (reduced inhibition), which is alleviated by dopaminergic stimulation (Albin et al., 1989; DeLong, 1990). Therefore, we hypothesised that aperiodic exponents of STN-LFPs are relatively low in the untreated Parkinsonian state and would be increased with dopaminergic medication. To test this hypothesis, we estimated aperiodic exponents in STN-LFPs recorded from 30 hemispheres in 17 patients both ON and OFF levodopa (Figure 2A and B). Aperiodic exponents at 40–90 Hz successfully distinguished dopaminergic medication states (paired samples permutation t-test; t = –3.31, p=0.0015, Cohen’s d: 0.60) and were larger ON medication (in 66% of hemispheres), suggesting a faster drop of power with increasing frequencies and in keeping with more inhibition of STN (Figure 2C). The levodopa effect on aperiodic exponents was robust against different settings for FoooF parameterisation (Figure 2—figure supplement 1). Note that for human data, the frequency range was adjusted to 40–90 Hz (the lower bound due to high-amplitude beta peaks crossing the fitting range and the upper bound due to the harmonic of mains interference; see section ‘Signal processing’ for more details).

Figure 2 with 2 supplements see all
Download asset Open asset
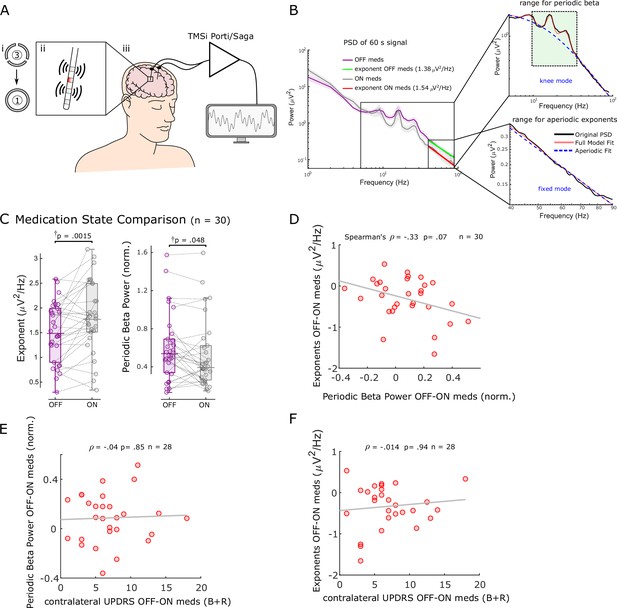
Aperiodic exponents between 40 and 90 Hz of subthalamic nucleus-local field potentials (STN-LFPs) distinguish medication states in externalised recordings from Parkinson’s patients.

(A) We analysed 60 s segments of bipolar STN-LFP recorded from Parkinson’s patients at rest while leads were externalised (iii). Recordings were performed ON and OFF dopaminergic medication. Directional contacts were fused (i) and bipolar recordings were conducted from contacts adjacent to the stimulation contact (red; ii). (B) Average power spectral densities (PSDs) from 30 hemispheres (17 patients) ON and OFF medication of 60 s recordings using Morlet wavelet transforms (mean ± SEM). Aperiodic exponents were computed between 40 and 90 Hz (fixed mode, bottom-right subplot) to avoid high-amplitude beta peaks and harmonics of mains noise at 100 Hz and the fixed mode was used since the PSD was relatively linear in log-log space within this range. To obtain periodic beta power, we fit the FoooF algorithm between 5 and 90 Hz (knee mode, top-right subplot) and picked the power of the largest oscillatory component within the beta range (13–35 Hz, green rectangle). (C) Aperiodic exponents and periodic beta power differ between medication states (p=0.0015 and p=0.048). †p-Values were computed using a paired samples permutation t-test with multiple comparison correction on 30 hemispheres recorded from 17 Parkinson’s disease (PD) patients. (D) Aperiodic exponent and periodic beta power changes with levodopa are not correlated (Spearman; ρ = –0.33, p=0.07, n = 30). (E, F) Neither periodic beta power (E) nor the aperiodic exponent (F) changes with medication are correlated with contralateral appendicular bradykinesia and rigidity UPDRS part III sub-scores OFF-ON levodopa (Spearman: ρ = –0.04, p=0.85, n = 28 hemispheres for periodic beta; Spearman: ρ = –0.014, p=0.94, n = 28 hemispheres for aperiodic exponents).

In addition, we quantified periodic beta power identified using the FoooF parameterisation (Figure 2B) and average power of six different frequency bands and compared them between conditions ON and OFF levodopa. Periodic beta power differed between the two medication states (paired samples permutation t-test, t = 2.08, p=0.048), with higher power in the OFF medication state consistent with previous studies (Brown et al., 2001; Neumann et al., 2017; Figure 2C). Of the six frequency ranges, only beta power distinguished medication states (Figure 2—figure supplement 2A). However, neither average (Spearman; ρ = –0.08, p=0.67), low (ρ = –0.20, p=0.28), nor high beta power (ρ = 0.004, p=0.99) correlated with aperiodic exponents (Figure 2—figure supplement 2B). In 10 of 20 cases in which the aperiodic exponent was higher ON medication, there was either no clear beta peak in the OFF state or no clear beta reduction with levodopa. This underlines the benefit of multi-biomarker adaptive DBS compared to an algorithm that only relies on beta power as a feedback signal. In 8 of 10 hemispheres in which aperiodic exponents were not higher ON medication, exponents were either very similar and the difference between medication states was <0.1 (four cases) or beta power was not affected by levodopa either ( four cases).

Medication-induced changes of aperiodic exponents and periodic beta power displayed a trend for a negative correlation (Spearman; ρ = –0.33, p=0.07, n = 30; Figure 2D), indicating that they may contain similar information on levodopa-induced changes in the STN. This may also hint at a physiological meaning of aperiodic exponents. Furthermore, neither levodopa-induced changes of periodic beta power (Spearman; ρ = –0.04, p=0.85, n = 28; Figure 2E) nor aperiodic exponents (Spearman; ρ = –0.014, p=0.94, n = 28; Figure 2F) were correlated with contralateral appendicular bradykinesia and rigidity UPDRS part III sub-scores OFF-ON levodopa in this cohort.

These results suggest that aperiodic exponents of STN-LFPs may be a useful measure to distinguish and track medication states.

Aperiodic exponents of STN-LFPs from 10 to 50 Hz distinguish periods ON and OFF DBS

High-frequency DBS was thought to induce functional inactivation of the neurons in the stimulated area (Aziz et al., 1991; Benabid et al., 1994; Bergman et al., 1990; Limousin et al., 1995). Furthermore, the inactivation hypothesis was corroborated when suppression of neuronal activity was recorded surrounding STN-DBS leads in patients, non-human primates, and rodents (Filali et al., 2004; Meissner et al., 2005; Shi et al., 2006) in line with the classical rate model of movement disorders. Here, we compared aperiodic exponents at 10–50 Hz of STN-LFPs ON and OFF high-frequency DBS in 26 hemispheres from 17 PD patients. Compared to previous analyses, we lowered the frequency range for parameterisation to avoid a spectral plateau starting >50 Hz when stimulation was on (Figure 3A). We found increased aperiodic exponents ON DBS (paired samples permutation t-test; t = –6.27, p<0.001, Cohen’s d: 1.23, Figure 3B), a similar effect as levodopa, in keeping with the E/I hypothesis and of the notion that DBS supresses STN firing to some degree.

Figure 3 with 1 supplement see all
Download asset Open asset
The aperiodic exponent between 10 and 50 Hz of subthalamic nucleus-local field potential (STN-LFP) distinguishes stimulation states in externalised recordings from Parkinson’s disease (PD) patients.

(A) Average power spectral densities (PSDs) and linear fitting in the exponential scale of 60 s segments of bipolar STN-LFPs ON and OFF 130 Hz STN-DBS recorded from externalised electrodes in 26 hemispheres from 17 PD patients (mean ± SEM). PSDs during DBS (red) display a spectral plateau >50 Hz, hence, exponents were isolated between 10 and 50 Hz (black rectangle). Linear fitting of the aperiodic exponents between 10 and 50 Hz for no DBS and DBS is shown in black and yellow, respectively. While the dotted extension of the black line is still a relatively good fit for the no DBS PSD, the yellow dotted line deviates from the DBS PSD due to the plateau at around 50 Hz. (B) Aperiodic exponents differ between periods of no DBS and periods of 130 Hz STN-DBS (paired samples permutation t-test, n = 26, p<0.001). (C) Periodic beta power was compared before and during 130 Hz STN-DBS (paired samples permutation t-test, n = 26, p=0.007).

When the average power of six different frequency ranges and periodic beta power was compared immediately before and during 130 Hz STN-DBS, beta power (primarily high beta) and low gamma power were suppressed with DBS (Figure 3C, Figure 2—figure supplement 2C) in accordance with our previous work (Wiest et al., 2020). The power increase of the high gamma band (51–90 Hz) was driven by artefacts of stimulation in that range (Figure 3A). Aperiodic exponent changes with DBS were not correlated with spectral changes of any frequency (Figure 2—figure supplement 2D). Again, this implies that the aperiodic exponent is independent of spectral changes averaged over pre-defined frequency ranges or periodic beta power and might provide additional information.

Discussion

In this study, we validated the aperiodic exponent of STN-LFPs as a marker of E/I balance using single-unit activity from the basal ganglia in 6-OHDA-lesioned animals, under conditions of where the activity levels of neurons providing major excitatory and inhibitory inputs to STN neurons are well defined. Having validated the approach with single-unit activities under these controlled conditions in rodents, we found that the aperiodic exponent of STN-LFPs recorded from awake PD patients distinguishes medication and stimulation states. Its sensitivity to levodopa and DBS underlines the notion that the aperiodic exponent of the STN-LFP may indicate pathological states of PD and can potentially serve as a feedback signal for adaptive DBS.

The aperiodic exponent as a marker of E/I balance

Our results support that the aperiodic exponent of STN-LFPs changes with excitatory and inhibitory inputs to STN in both a rodent PD model and patients with PD. STN dendrites are innervated by glutamatergic inputs from ipsilateral somatomotor and frontal cortical areas (Monakow et al., 1978), glutamatergic intralaminar thalamic nuclei (Kita et al., 2016), and GABAergic inputs from prototypic GPe neurons (Mallet et al., 2012). In lesioned animals, on the active phase of the cortical slow oscillation (here referred to as high STN spiking epochs), STN neurons are expected to receive intense excitatory input from cortical and thalamic afferents and decreased inhibitory input from prototypic GPe neurons (Mallet et al., 2012), conditions that lead to vigorous STN spiking. In contrast, during the inactive phase of the cortical slow oscillation, inhibition from prototypic GPe neurons should be high and excitation from cortex and thalamus is relatively low, conditions that can completely prevent STN spiking (Mallet et al., 2012). We found clear differences in the aperiodic exponents of STN-LFPs between these extreme states of local excitation and inhibition (Figure 1).

The majority of previous studies into the relationship between the aperiodic exponent and neuronal activity have been investigated in cortex (Waschke et al., 2021). However, the anatomy and physiology of STN differs significantly from cortex in that it is made up of relatively homogenous, glutamatergic projection neurons that fire action potentials autonomously and receive tonic inhibition from prototypic GPe neurons. Cortical circuits, in contrast, comprise a vast array of neuron types and activity of cortical projection neurons is predominantly input driven. Thus, our findings provide important validation that aperiodic exponents reflect changes in E/I balance at the synaptic (LFP) levels, specifically in STN. In addition, in contrast to these previous efforts examining the E/I hypothesis (Gao et al., 2017; Lendner et al., 2020; Waschke et al., 2021), we directly link aperiodic exponents to single-neuron spiking and predefined parameters of the dynamic E/I balance that specifically relate to the majority of neurons in the recorded structure (Figure 1). This approach provided a platform for understanding changes in the aperiodic exponent in STN-LFP recordings from humans.

Building on these findings, our clinical results hold up against the E/I hypothesis as well (Figures 2 and 3). Aperiodic exponents of STN-LFPs recorded from awake PD patients are increased ON medication and ON DBS when STN local activity is believed to be decreased according to the classical direct/indirect pathways model (Albin et al., 1989; DeLong, 1990). The increased exponents ON dopaminergic medication in PD are consistent with a recent study that reported higher aperiodic exponents in dopamine-intact compared to lesioned animals (Kim et al., 2022). Furthermore, our results indicate that periodic beta power differs between the two dopaminergic medication states (Figure 2C), consistent with previous findings (Kim et al., 2022; Kühn et al., 2006; Neumann et al., 2017; Ray et al., 2008). Finally, the missing correlation between medication-induced changes of aperiodic exponents and average beta power suggests that aperiodic exponents capture changes with medication that are not reflected by beta power alone and might be complimentary in an adaptive DBS algorithm ( Figure 2—figure supplement 2).

Can the aperiodic exponent be useful as a feedback signal in adaptive DBS?

Beta-band oscillations were identified as the most promising feedback signal for adaptive DBS considering their strong relationship with motor impairment in PD (Kühn et al., 2006; Priori et al., 2004). However, the correlation between beta and contralateral appendicular bradykinesia and rigidity UPDRS scores was not significant in our cohort, and abnormal beta activity is not observed in all patients (Giannicola et al., 2010) nor is it correlated with tremor, freezing of gait, or dyskinesia (Marceglia et al., 2021). It is therefore unlikely that a beta-only feedback model will address all PD symptoms. Several factors point towards the aperiodic exponent as a candidate feedback signal. First, it changes with medication and DBS (Figures 2 and 3), similar characteristics which brought beta oscillations into the spotlight and which may suggest a link to clinical improvement (Kühn et al., 2006; Kühn et al., 2008). Second, we observed medication-related changes of the aperiodic exponent in hemispheres without clear beta peaks or medication-related beta changes. Third, we estimate the aperiodic exponent between 40 and 90 Hz, when studying the effect of levodopa, avoiding lower frequencies, which are particularly susceptible to movement-related artefacts (van Rheede et al., 2022).

However, there are some obstacles to its use as a feedback marker. First, we could not show a direct link between the aperiodic exponent and clinical symptoms, but a trend for a negative correlation with periodic beta power (Figure 2D) and in our data set UPDRS part III scores were not correlated with periodic beta power either (Figure 2E and F). To unequivocally assess clinical relevance of aperiodic exponents, motor tests with higher discriminatory power than UPDRS motor sub-scores such as the BRAIN TEST may be useful (Giovannoni et al., 1999). Second, the aperiodic exponent would present a feedback signal with low temporal resolution. We averaged PSDs over 60 s to isolate exponents of STN-LFPs. Shortening this time window will introduce noise into the PSD and increase the error of aperiodic estimates. While these temporal dynamics prevent aperiodic exponents from targeting beta bursts, they may provide additional information about the E/I balance with slower temporal dynamics. Third, the frequency range is critical for isolating the aperiodic exponent and results may vary considerably depending on this. Moreover, for some PSDs with large oscillatory components and a spectral plateau at low frequencies, it may even be impossible to obtain an unequivocal linear fit (Gerster et al., 2022). Fourth, it is unclear if a miniaturised implantable device will have the computational power to parameterise PSDs in real time and what effects this may have on battery longevity. Whether aperiodic exponents can be combined with other LFP parameters to improve optimal DBS settings will depend on whether they can add additional clinical information than beta power alone, which our results imply (see section ‘Aperiodic exponents from 40 to 90 Hz separate levodopa medication states in PD patients’). In this cohort, we did not find correlations between levodopa-induced changes of aperiodic exponents and average beta power of three different frequency ranges (Figure 2—figure supplement 2B), but a trend for a negative correlation with periodic beta power, which comprises a measure similar to beta peaks that were used before (Darcy et al., 2022; Neumann et al., 2017). It is therefore possible that aperiodic exponents extract similar information than beta power, but may aid in subjects where no beta peaks are present or beta peaks are not affected by levodopa.

Limitations

The chosen frequency band for linear fitting can affect FoooF parameterisation. In the past, many different fitting ranges were applied to extract the aperiodic exponent (reviewed in Gerster et al., 2022). Most of these frequency ranges comprise low-frequency oscillations and start in the delta, theta, alpha, or beta range. If prominent low-frequency oscillations are present, this may lead to steepening of the spectrum and error-prone aperiodic fits (Gerster et al., 2022). In this study, when parameterising PSDs from rodent data recorded using high-impedance microelectrodes, we chose the frequency band from 30 to 100 Hz to avoid false-high exponents due to high power in the lower frequency bands. The lower fitting bound of 30 Hz was chosen to exclude overlap of the lower fitting bound with the rising or falling arm of alpha or beta oscillations. A similar frequency range has been recommended to estimate the E/I ratio before (from 30 to 70 Hz, if this range is uncorrupted by oscillatory peaks) (Gao et al., 2017; Trakoshis et al., 2020). To asses differences with medication in clinical data recorded using macro-electrodes, we narrowed the fitting range to 40–90 Hz to avoid overlap and false-high estimates due to peaks in the high beta range (Figure 2B), and to avoid the harmonic of mains interference. These results are robust as long as the selected frequency range covers 40–70 Hz (Figure 2—figure supplement 1). For DBS data analysis, we adapted the fitting range to avoid a spectral plateau (Figure 3A) which would have resulted in false-low exponents had we used the same fitting range as for the previous analysis. We observed this prominent plateau at frequencies larger than 50 Hz when DBS was switched ON in addition to prominent peaks at half stimulation frequency and other harmonics (Figure 3A). However, we did observe reduced power in the high beta and low gamma frequency bands (21–50 Hz) with stimulation, suggesting that the signal-to-noise ratio is sufficient to detect physiological signals in this frequency band. Therefore, we have focused on the lower frequency bands (10–50 Hz) for quantifying aperiodic exponents ON and OFF stimulation. In addition, in our dataset we did not see a link between medication-induced changes of either the aperiodic exponent or periodic beta power and contralateral bradykinesia and rigidity scores OFF-ON levodopa (Figure 2E and F) and further studies will be required to investigate if and to what extent aperiodic exponents of STN-LFPs correlate with Parkinsonian symptoms.

Conclusions

We showed that aperiodic exponents of STN-LFPs reflect STN excitation and inhibition as evinced by single-neuron activity in states of extreme spiking differences in rodents. We further showed that aperiodic exponents of STN-LFP in PD patients are larger ON dopaminergic medication and ON DBS reflecting more inhibition of STN compared to the dopamine-depleted and OFF DBS states. Our results corroborate that the aperiodic exponent contains information with respect to E/I balance and our clinical results give reason to believe the aperiodic component may be useful in a closed-loop feedback algorithm for PD.

Methods

Rodent data

Experiments were performed on adult male Sprague–Dawley rats (Charles River) and were conducted in accordance with the Animals (Scientific Procedures) Act, 1986 (UK). Animal data that was analysed in this paper has been generated under the project licence numbers 30/2131 and 30/2629. All details on the 6-OHDA lesion and electrophysiological recordings were published before (Mallet et al., 2008a).

6-Hydroxydopamine lesion of dopaminergic neurons

Unilateral 6-OHDA lesion was performed as described in Magill et al., 2001; Mallet et al., 2008a. Then, 25 min before injection, animals received desipramine i.p. to minimise uptake of 6-OHDA by noradrenergic neurons. 6-OHDA was dissolved in NaCl to a concentration of 4 mg/ml of which 3 μl were injected medial to the substantia nigra pars compacta to target the medial forebrain bundle, which results in widespread loss of midbrain dopaminergic neurons. The extent of the dopamine lesion was assessed 14–15 days after injection by apomorphine challenge. Lesions were considered successful if animals made >80 contraversive rotations in 20 min. Electrophysiological recordings were performed ipsilateral to 6-OHDA lesion 21–45 days after surgery when pathophysiological changes in the basal ganglia have likely reached their maxima.

Electrophysiological recordings

Data was recorded as described in Mallet et al., 2008a from eight 6-OHDA-lesioned rats. Here, we summarise key steps of the experimental procedure and data acquisition. Anaesthesia was induced with isoflurane and maintained with urethane, ketamine, and xylazine throughout the recording (Magill et al., 2006). Animals were placed in a stereotaxic frame where their body temperature was maintained at 37°C. ECoG, electrocardiograms (ECG), and respiration rate were monitored to ensure animal well-being. ECoG was recorded via a 1 mm steel screw juxtaposed to the dura mater above the frontal cortex and referenced against another screw in the skull above the ipsilateral cerebellum (Figure 1—figure supplement 1A). Raw ECoG traces were bandpass filtered (0.3–1500 Hz) and amplified (2000×) before acquisition. Extracellular recordings of unit activity and LFPs in the external globus pallidus (GPe) and STN were simultaneously made using silicon probes with high-impedance microelectrodes (Figure 1—figure supplement 1A). Each probe had one or two vertical arrays (500 μm apart) with 16 recording contacts along the arrays with 100 μm spacing. Monopolar probe signals were referenced against a screw above the contralateral cerebellum. Probes were advanced into the brain under stereotaxic control and extracellular signals were lowpass filtered (6000 Hz). ECoG and probe signals were each sampled at 17.9 kHz using a Power 1401 Analog-Digital converter. Recording locations were verified after experiments using histological procedures. STN was identified by comparison of recorded unit activity with the known characteristics of STN neurons in urethane anaesthesia (Magill et al., 2001).

The ECoG measurements were used to assess whether the rodent was in SWA state, which accompanies deep anaesthesia and is similar to activity observed during natural sleep (Steriade, 2000). We analysed a total of 28 extracellular LFP channels within STN during SWA (3.5 ± 0.18 channels per animal [mean ± SEM]). STN single-unit activity was isolated from 20 of these channels (2.5 ± 0.07 per animal).

Signal processing

Extraction of single-unit activity

Data analysis was performed using custom-written scripts in MATLAB (R2020b). Periods of robust SWA were selected according to previously described characteristics of these brain states (Magill et al., 2006; Magill et al., 2001). Analyses were performed on 97.61 ± 2.17 s of data during SWA in 6-OHDA-lesioned animals. After offline bandpass filtering (500–6000 Hz) of the probe signals, single-unit activity was isolated with standard spike sorting procedures including template matching, principal component analysis, and supervised clustering (Spike2) as described in Mallet et al., 2008a. Isolation of single units was verified by the presence of a distinct refractory period. Only neurons in which <1% of interspike intervals were <2 ms were analysed in this study. For further analysis, single-unit activity was converted such that each spike was represented by a single digital event. To analyse aperiodic exponents of STN-LFPs, raw signals were lowpass filtered at 300 Hz (third-order Butterworth filter; Oostenveld et al., 2011). A similar procedure to analyse LFPs from silicon probe electrodes was described before (Mallet et al., 2008b).

Re-referencing

LFPs were downsampled to 2048 Hz. Target channels within STN were re-referenced by subtracting the mean signal across the six neighbouring channels to reduce volume conduction (Figure 1—figure supplement 1C). We computed wavelet magnitude squared coherence between the target LFP channel in STN and ECoG to control for volume conduction and opted for the above re-referencing approach with coherence <0.1 for all frequencies >10 Hz (Figure 1—figure supplement 1C).

Spectral decomposition

Spectral parameters were evaluated using continuous complex Morlet wavelet convolution. The entire 100 s time series was decomposed from 1 to 100 Hz with a frequency resolution of 1 Hz (frequencies increased linearly) before epoching to reduce the edge effect on each epoch. Morlet wavelets of 50 cycles were used which did not change as a function of frequency. We counted the spike events per consecutive non-overlapping 250 ms epoch for all unit activity channels (Figure 1—figure supplement 1B). The epoch duration was chosen such that it captures the rhythmic dynamics during SWA. For every unit channel, we defined epochs with a spike rate >75th percentile as ‘high spiking’ and all epochs with a spike rate <25th percentile as ‘low spiking’ (Figure 1—figure supplement 1B). We computed the mean PSD for every 250 ms epoch and normalised it by dividing through the mean power from 1 to 100 Hz (Figure 1—figure supplement 1D).

FoooF parameterisation

For every LFP channel within STN, we computed the mean PSD of all high- and all low-spiking epochs separately. To isolate the aperiodic component from these spectra, we used the open-source FoooF algorithm (version 1.0.0) (Donoghue et al., 2020). Settings for the algorithm were set as peak width limits: 2–12; max number of peaks: infinite; minimum peak height: 0; peak threshold: 2; and aperiodic mode: fixed. Power spectra were parameterised across the frequency range 30–100 Hz. The lower bound was selected to avoid the impact of low-frequency oscillations, the upper bound was selected to avoid the impact of spectral plateaus (Gerster et al., 2022). Moreover, PSDs were linear across this frequency range in log-log space assuming a single 1/f like characteristic and did not contain overlapping periodic components (Figure 1—figure supplement 1E and F). Hence, higher aperiodic exponents indicate steeper power reduction with increasing frequencies in the PSD and vice versa as shown in Figure 1—figure supplement 1F. We evaluated the goodness of fit (R2) for all data used in this study (Figure 3—figure supplement 1). In addition, we evaluated and compared the goodness of fit using either ‘fixed’ mode or ‘knee’ mode in the FoooF fitting. Results show that using the ‘knee’ mode for parameterisation did not improve aperiodic fitting (Figure 1—figure supplement 2). Therefore, we opted to use the ‘fixed’ mode for parameterisation within the selected frequency range. To compare power across different spiking states, we computed the mean power between 30 and 100 Hz of the average PSD of all high or low-spiking epochs.

Human data

This protocol was approved by the Health Research Authority UK, the National Research Ethics Service local Research Ethics Committee (IRAS: 46576), and the local ethics committee at the University of Mainz (837.208.17 [11042]). Patients were recruited at St. George’s University Hospital NHS Foundation Trust, London, King’s College Hospital NHS Foundation Trust, London, and the University Medical Center Mainz. Written informed consent, and consent to publish, was obtained before surgery in line with the Declaration of the Principles of Helsinki. We analysed data from 24 patients from these three centres. Data from 17 patients were previously published (Wiest et al., 2021; Wiest et al., 2020).

Patients and surgery

Study participants were evaluated by an interdisciplinary team of movement disorder neurologists and functional neurosurgeons and met the UK Parkinson’s Disorder Society Brain Bank Diagnostic Criteria for diagnosis of PD. Baseline motor function in the ON and OFF medication state was assessed pre-operatively using the part III of the Unified Parkinson’s disease rating scale motor subscale (UPDRS-III). When UPDRS part III scores were reported in Figure 2, we used the contralateral appendicular categories (bradykinesia and rigidity scores only). The surgical target was STN. Five models of DBS leads were used: quadripolar (model 3389) or directional (SenSight) leads from Medtronic Inc, Neurological Division, USA, directional (Vercise model DB-2202) or non-directional (model DB-2201) leads from Boston Scientific, USA, and directional leads (Infinity model 6172ANS) from Abbott Inc, USA. DBS implantation was guided either by magnetic resonance imaging alone (St. George’s University Hospital) or with additional intra-operative microelectrode recordings and stimulation (King’s College Hospital and University Medical Center Mainz). The subthalamic leads were connected to temporary extension leads and these were externalised. Assessment of contact localisation was made through co-registration of immediate post-operative CT with pre-operative MRI by an experienced neurosurgeon or neurologist specialising in deep brain stimulation. Assessment was blinded to the electrophysiological data and made using Lead-DBS (Horn et al., 2019).

Data recording and lead localisation determination

Recordings were made between 3 and 6 days post-operatively, while lead extensions were still externalised and before implantation of the subcutaneous pulse generator. In total, 24 patients (37 hemispheres) were recorded for this study; 17 patients (30 hemispheres) were recorded ON and OFF dopaminergic medication and 17 patients (26 hemispheres) ON and OFF stimulation. In patients with directional leads, the three directional contacts were joined to form a ring contact (Figure 2Ai). All LFPs were amplified and sampled at either 2048 Hz using a TMSi Porti (TMS International, Netherlands) or at 4096 Hz using a TMSi Saga32 (TMS International, Netherlands). The ground electrode was placed on the non-dominant forearm. High-frequency stimulation at 130 Hz was only tested at the middle contacts to allow bipolar LFP recordings from the two surrounding contacts (Figure 2Aii). A self-adhesive electrode attached to the patient’s back served as a reference for stimulation, which was delivered using a custom-built highly configurable in-house neurostimulator. Stimuli comprised symmetric constant-current biphasic pulses (60 μs pulse width, negative phase first). The stimulation current was started at 0.5 mA and increased in increments of 0.5 mA until first a benefit in Parkinsonian motor symptoms was observed and second side-effect threshold was reached. The contact and current associated with the best clinical improvement were selected. If no stimulation was applied and multiple bipolar configurations were available, we selected the bipolar channel with the largest beta peak at rest. If only one hemisphere was recorded per patient, it was the hemisphere contralateral to the most affected upper limb.

Signal processing

Analyses were performed on 60 s of data while patients were awake and at rest. LFP time series were highpass filtered at 1 Hz. Complex Morlet wavelet convolution was used for time-frequency decomposition with 50 wavelet cycles between 1 and 90 Hz as described in section ‘Spectral decomposition’. To exclude artefacts from mains interference at 50 Hz before isolating the aperiodic component, frequencies between 47 and 53 Hz were removed and the gap was linearly interpolated using the fillmissing function. To run the FoooF algorithm, the same settings were used as described in ‘FoooF parameterisation’, and power spectra were parameterised across the frequency range 40–90 Hz. The lower bound was increased to avoid high-amplitude beta peaks crossing the fitting range (see Figure 2B). The upper bound was lowered to avoid the harmonic of mains interference. When a broad frequency band (e.g. 1–100 Hz) was considered, the PSD was not linear in log-log space. However, within the selected frequency band, the power spectrum followed an almost perfect linear line as illustrated in Figure 2B (bottom-right plot). Therefore, we used the ‘fixed’ mode for parameterisation of the selected frequency range. To isolate periodic beta activity, the PSD was parameterised using FoooF between 5 and 90 Hz (‘knee’ mode in this case as such a wide frequency range is unlikely to only have a single aperiodic component, all other FoooF settings were identical to what was used in animal data). After removing the aperiodic component, the largest peak within the canonical beta range from 8 to 35 Hz was selected (Figure 2B). All other FoooF fittings presented elsewhere in this study were performed using the ‘fixed’ mode. In the stimulation ON condition, stimulation artefacts led to a plateau at frequencies >50 Hz in the spectra (Figure 3A). Therefore, aperiodic exponents were estimated between 10 and 50 Hz to evaluate the effect of DBS. A similar frequency range (5–45 Hz) was used in a previous study (Chini et al., 2022). Beta (13–35 Hz), low beta (13–20 Hz), high beta (21–35 Hz), gamma (35–90 Hz), low gamma (35–50 Hz), and high gamma (51–90 Hz) power were computed as the mean power of the normalised (divided by the mean power from 1 to 90 Hz), 50 Hz removed and 1/F-corrected PSD across the respective frequency range.

Statistics

Statistical analyses were performed using custom-written scripts in MATLAB (R2020b). To perform paired comparisons between the two medication or stimulation conditions, we used a paired samples permutation t-test with multiple comparison correction (50,000 permutations each) as implemented in Groppe, 2022. When correlations were reported, we calculated Spearman’s rank coefficients because the non-baseline-transformed power data are non-normally distributed and contain outliers. When multiple channels within one animal were available, hierarchical comparisons of aperiodic exponents and power across different epochs was performed using linear mixed-effects models to take repeated measures from multiple electrodes for each animal into account. The exponent or power data was set as dependent variable and different STN spiking conditions (e.g. high STN spiking epochs, low STN spiking epochs) as fixed effects. The normal distribution of each variable and the residuals were visually inspected with quantile-quantile plots and histograms of distribution. All models were estimated by the method of maximum likelihood and included random intercept for subjects to allow different intercepts for each subject, thereby capturing individual differences. Multiple statistical tests were performed in this study under FDR control at 5% using the adaptive linear step-up procedure, a modification of the original Benjamini and Hochberg procedure (Duchet et al., 2021). This ensures that the expectation of the number of false positives over the total number of positives is less than 5% when many statistical tests are performed. When histograms of distribution are shown, the optimal number of histogram bins was determined using the Freedman–Diaconis rule (Freedman and Diaconis, 1981). All data are shown as mean ± standard error of the mean (SEM) unless mentioned otherwise.

Sample size estimation, replicates, and group allocation

Due to the explorative nature of this study, we did not perform prospective sample size estimations but included all animal data with wideband recordings from STN that were available to us (n = 8). Since 6-OHDA-lesion was performed unilaterally, only one STN was recorded per animal. Similarly, we did not perform prospective sample size calculations for human data, but included all STN recordings we had available (37 STNs from 24 patients). This approach was chosen as postoperative LFP recordings from DBS electrodes are rare research opportunities. Fortunately, due to the relatively high signal-to-noise ratio of LFP recordings, a small number of patients between 7 and 12 is considered sufficient to detect robust effects in LFP studies (Alegre et al., 2013; Brittain et al., 2012; Wessel et al., 2016).

In our study, each STN was treated as one independent sample. In doing so, we follow the definition that ‘biological replicates are parallel measurements of biologically distinct samples that capture random biological variation’ (Blainey et al., 2014). It should be recognised that the variations we observed in our sample can be caused by variability in the phenotype of PD, of the target location of the electrode, or in the temporary lesion effect of DBS surgery.

This was not a clinical study. We used a within-subject design to test the effects of DBS and dopaminergic medication. All available animal and human data recordings were included in the analysis (no attrition).

Data availability

The code is included in Source Code 1 and in addition can be found here https://doi.org/10.5287/bodleian:rJ7jyjX97. The animal data used for this project is available at the Medical Research Council Brain Network Dynamics Unit (MRC BNDU) Data Sharing Platform at the University of Oxford https://data.mrc.ox.ac.uk/stn-rat and https://doi.org/10.5287/bodleian:wx6D7oenk. The human data is also available at the MRC BNDU Data Sharing Platform https://data.mrc.ox.ac.uk/stn-lfp-on-off-and-dbs and https://doi.org/10.5287/bodleian:mzJ7YwXvo.

The following data sets were generated
    1. Wiest C
    2. Torrecillos F
    3. Pogosyan A
    4. Baig F
    5. Pereira E
    6. Morgante F
    7. Ashkan K
    8. Tan H
    (2022) Oxford University Research Archive
    STN local field potential recordings from awake patients with Parkinson’s, ON and OFF meds, and during 130 Hz DBS.
    https://doi.org/10.5287/bodleian:mzJ7YwXvo
    1. Wiest C
    2. Tan H
    (2022) Oxford University Research Archive
    Analysis code for publication: 'The aperiodic exponent of subthalamic field potentials reflects excitation/inhibition balance in Parkinsonism'.
    https://doi.org/10.5287/bodleian:rJ7jyjX97
    1. Mallet N
    2. Sharott A
    3. Brown P
    4. Maghill P
    (2022) Oxford University Research Archive
    Wideband recordings from silicon probes in the subthalamic nucleus of 6-OHDA hemi-lesioned rats during anaesthesia.
    https://doi.org/10.5287/bodleian:wx6D7oenk

References

    1. Freedman D
    2. Diaconis P
    (1981) On the histogram as a density estimator:L 2 theory
    Zeitschrift Für Wahrscheinlichkeitstheorie Und Verwandte Gebiete 57:453–476.
    https://doi.org/10.1007/BF01025868

Decision letter

  1. Nicole C Swann
    Reviewing Editor; University of Oregon, United States
  2. Floris P de Lange
    Senior Editor; Donders Institute for Brain, Cognition and Behaviour, Netherlands
  3. Bradley Voytek
    Reviewer; University of California, San Diego, United States

Our editorial process produces two outputs: (i) public reviews designed to be posted alongside the preprint for the benefit of readers; (ii) feedback on the manuscript for the authors, including requests for revisions, shown below. We also include an acceptance summary that explains what the editors found interesting or important about the work.

Decision letter after peer review:

Thank you for submitting your article "The aperiodic exponent of subthalamic field potentials reflects excitation/inhibition balance in Parkinsonism: a cross-species study in vivo" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and Floris de Lange as the Senior Editor. The following individual involved in review of your submission has agreed to reveal their identity: Bradley Voytek (Reviewer #2).

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission.

Essential revisions:

1) Our biggest concern was with some of the methodological choices, elaborated on in Reviewer #1's first point. In particular, the rationale with respect to the choice of frequency band used to fit the 1/f, and the inconsistency between experiments was unclear to us. Related, the modeling choices at times fail to account for some aspects of the spectra, which, for some cases, may impact results. The authors should respond to this, either by explaining the rationale or perhaps some re-analysis. One possibility is using a Lorentzian fit ("knee mode"). Please see Reviewer 1's main first point.

2) To elaborate a bit on the point above, as Reviewer #1 highlights in their public review, there was concern that the assumption of a monolithic model of the 1/f pattern (and its representation with a single exponent) fails to capture nuanced/fine-grained aspects of the spectrum, and might confuse an overall elevation of broadband γ power with a change of 1/f exponent. In such cases, observed changes in 1/f exponents would result from improper model fitting and be spurious findings. This issue needs to be carefully addressed.

3) Line 80-83. Is it possible the null result is due to the authors' choice of analyzing the two conditions separately? If the data were pooled between high and low spiking epochs, presumably a significant correlation between power and exponent would be found here. Could the authors please address this?

4) The authors conducted many bivariate correlation analyses, but it would be worthwhile to run a multiple linear regression analysis to see whether and to what degree the different electrophysiological features relate to clinical status.

5) In Figure 3, why do the authors not also show the aperiodic-adjusted β oscillation features?

Reviewer #1 (Recommendations for the authors):

Specific issues:

1) Line 5-7, the authors' terminology here confuses the exponent, which is measured from the power spectrum, with the activity that contributes to that power spectrum. In other words, 1/f exponent or aperiodic exponent should not be in the same status as the other terms. It is probably also safe to say that the term "1/f noise" is no longer used in the literature due to the increased recognition that this activity is not noise.

Reviewer #2 (Recommendations for the authors):

– The authors perform permutation tests, but report t-values and p-values. Are the p-values the empirical p-values derived from the permutation measure, or are they the inferred p-values from the t-test itself?

– Relatedly, 50,000 permutations seem excessive! Not problematic in any way, just probably overkill.

– The authors should look at Chini et al., eLife 2022 as optogenetic support that aperiodic activity indexes EI balance.

– In Figures 1D and E, the individual datapoints are difficult to see. Maybe they can be offset a bit, or the α adjusted so they're not as faint. This is especially true when the figures are printed.

– Across the Figures, the visual language isn't consistent. For example, in Figure 1 red and blue mean low- and high-spiking epochs, respectively. In Figure 2 red and blue mean on and off meds. In Figure 3 red and blue mean on or off DBS. In these cases they're somewhat consistent in the humans (on/off meds is similar to on/off DBS), and theoretically related to low- and high-spiking, but I think different colors should be used to make them better stand apart.

– In Figure 2B, the exponent fit lines in black and yellow are –very– difficult to see, especially in print.

Reviewer #3 (Recommendations for the authors):

– The motivation for selecting frequency ranges for analysis is not clear/convincing enough from my point of view, eg. why is it starting at 30 / 40 Hz only?

Potential β band activity below 30 / 40 Hz seems like a weak argument as strong β activity can appear at much lower frequencies or not really at all.

– Chapter 4.2.2: The last sentence appears redundant to me, is it?

– Just a typo on p. 12: SNc needs to be Substantia nigra pars compacta.

– Please double-check the citation Oostenveld et al. 2011. The Journal name is missing.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

Thank you for resubmitting your work entitled "The aperiodic exponent of subthalamic field potentials reflects excitation/inhibition balance in Parkinsonism" for further consideration by eLife. Your revised article has been evaluated by Floris de Lange (Senior Editor) and a Reviewing Editor.

The manuscript has been very much improved but there are some remaining issues that need to be addressed, as outlined below:

Upon discussion between the reviewers we have identified the following points which we would like the authors to address.

1) The reviewers felt the authors had not clearly indicated when a "knee" was included in the fit and when it was not included. The manuscript would be strengthened by clarifying this and also explaining how the decision was made.

2) We are concerned that the authors used the fact that a correlation yielded a p-value greater than 0.05 as justification for the idea that no correlation was present. The authors should include a clear discussion of this and consideration of alternative interpretations.

3) With respect to Figure 2B, we would like the authors to perform an analysis on the narrowband β peak (in addition to the analysis looking at the broader β range already included) and discuss any differences in the on vs off findings.

Below are the individual reviewer comments.

Reviewer #1 (Recommendations for the authors):

This revised manuscript is much improved. However, there are still some significant issues that are left unaddressed, which in my opinion precludes publication in the present form.

1. Essential revision Point 1, author point 2. FOOOF fitting with a new parameter.

The authors suggest that "PSDs in log-log space were almost linear (Figure 1C + Figure 2B + Figure 1—figure supplement 1E+F + Figure 3A)." However, a knee is evident in Figure 1C, Figure 2B, and Figure 3A, no-DBS condition. So, this sentence does not fit with the data presented in the figures.

Overall, from reading the response letter, I'm missing a principled approach to decide whether the knee fitting is used or not used in each case. If there was a consistent and objective criterion, the authors should clarify it in the paper.

2. Essential revision Point 3. You can't use a trend-level correlation (p = 0.07) to support a lack of correlation! This correlation is at trend-level, and you might just lack sufficient statistical power for it to cross the arbitrary p = 0.05 threshold.

3. Reviewer #1, point 2. The authors' response here is entirely unconvincing. Their response does not solve the salient issue that Figure 2B and Figure 2C are intuitively contradictory. The authors' response is essentially that a modification of their analysis pipeline yields the same result, even though this result is contrary to the impression one gets from looking at the power spectrum. Instead of believing that the method cannot fail, when the result from a multi-level complicated analysis does not fit the impression from the raw data, it would be prudent to at least consider the possibility that one's tools might be problematic. At the very least, no satisfactory answer is given here about why the statistics do not fit with the raw impression by examining the power spectrum in Figure 2B.

Reviewer #2 (Recommendations for the authors):

I've reviewed all of the author's comments and changes, and they have done a fine job addressing all of my concerns.

Reviewer #3 (Recommendations for the authors):

In their responses the authors have addressed all my comments convincingly. I also would consider the aspects raised by the other two reviewers as well addressed.

The additional data analyses did not change the nature of the work but confirmed the robustness of the results nicely. The manuscript and the figures have further improved through the revisions. I have no further comments.

https://doi.org/10.7554/eLife.82467.sa1

Author response

Essential revisions:

1) Our biggest concern was with some of the methodological choices, elaborated on in Reviewer #1's first point. In particular, the rationale with respect to the choice of frequency band used to fit the 1/f, and the inconsistency between experiments was unclear to us. Related, the modeling choices at times fail to account for some aspects of the spectra, which, for some cases, may impact results. The authors should respond to this, either by explaining the rationale or perhaps some re-analysis. One possibility is using a Lorentzian fit ("knee mode"). Please see Reviewer 1's main first point.

Choosing an acceptable frequency range is indeed a challenge of quantifying the aperiodic exponent. As the authors of Gerster et al., 2022 put it very accurately: “There is not one-fits-all fitting range”. The choice of the optimal fitting range is mostly driven by prominent oscillatory peaks and spectral plateaus in the PSD. Different electrodes, amplifier and recording systems, as used in this study for animal and human recordings, can also have an impact. Hence, all aperiodic fits were visually inspected as a quality check. In addition, we also tested different fitting ranges to assess how sensitive the results are to changes of the fitting parameters (Figure 2—figure supplement 1).

1. Choice of the fitting range

Despite this heterogeneity in the data, we found fitting ranges in Figure 1 and 2 that largely overlap (30-100 Hz for animal data and 40-90 Hz for the medication comparison in PD patients). We now confirmed that our results in animals data (Figure 1D+E) hold up if the same fitting range is used as for human data (40-90 Hz, shown in Author response image 1). Vice versa, the ON/OFF medication comparison in PD patients holds up if PSDs are parameterised from 30-95 Hz (Figure 2—figure supplement 1A). Harmonics of mains interferences, which were more prominent in human data did not allow to extend the fitting range to 100 Hz. In summary, the results stand for both animal data and human data with a frequency range from 30 to 90 Hz.

Author response image 1
Download asset Open asset
Aperiodic exponent and average γ power changes in animal data between 40 and 90 Hz are consistent with those reported in Figure 1 for a slightly different fitting range.

For the ON/OFF stimulation comparison in human data, we had to adapt the fitting range due to the presence of a spectral flattening/plateau around 50 Hz and prominent stimulation artefacts during stimulation (Figure 3A). Spectral plateaus are regularly present in electrophysiological data and potential sources are discussed in Gerster et al., 2022. Here, we hypothesise that the increased electrical noise floor during stimulation pushed the plateau to frequencies around 50 Hz.

In addition to the spectral plateau around 50 Hz, we could observe artefacts as clear peaks at half stimulation frequency (65 Hz) and some other harmonics in the PSD (e.g. at 80 Hz) at high intensity (Figure 3). While FOOOF will identify these peaks as oscillatory components and exclude them from the aperiodic fit, especially when higher DBS currents are used, there will be many overlapping peaks and little ‘clean’ frequency bands > 50 Hz, which will make a faithful parameterisation impossible (Gerster et al., 2022). Therefore, we would not feel comfortable about any inference from signals above 50 Hz when stimulation is ON.

As we mentioned previously, we are more confident about the signal to noise ratio at frequencies below 50 Hz, since DBS reduces power at 10-50 Hz. Β and low-γ power suppression during DBS are well described in literature (e.g. Wiest et al., 2020). We show in Figure 3A that PSDs of STN-LFPs show a spectral plateau ~ 50 Hz and β/γ power suppression when DBS is switched on. Importantly, power is suppressed in the full 10-50 Hz range and not just a single oscillatory component such as a β peak. The upper frequency bound (at 50 Hz) was determined by the plateau, the lower bound was set at 10 Hz to avoid the effect of low-frequency oscillations (Gerster et al., 2022) after verifying that oscillatory peaks did not overlap with the 10 Hz fitting bound.

2. FOOOF fitting with a knee parameter

We opted against introducing a “knee” in our aperiodic fits, since PSDs in log-log space were almost linear (Figure 1C + Figure 2B + Figure 1—figure supplement 1E+F + Figure 3A). Selecting the “knee mode” will force the algorithm to detect a knee in the given frequency range even when there is none. This will in many cases lead to spurious model fits. To illustrate this, we calculated the PSD of pink noise and performed FOOOF parameterisation with either the settings used in this manuscript (fitting range 40-90 Hz) or knee mode (Author response image 2). While the fixed mode yields an aperiodic exponent close to the ground truth, interpreting the fit results when using knee fits is more complex. When using the knee mode, the exponent reflects the aperiodic component past the knee inflecting point and as shown in this example can then deviate quite considerably from the ground truth (the PSD of pink noise has an exponent of 1). After visual inspection of all PSDs and parameterisations in this study, we decided that the fixed mode will be a good enough fit in the respective fitting ranges and its interpretation as the slope in log-log space is clearer. Also, see a recent study that parameterised power spectra over a frequency range of similar length (4-45 Hz) with the fixed mode (Chini et al., 2022).

Author response image 2
Download asset Open asset
FOOOF parameterisation of pink noise with the same settings used in this manuscript (left) and a knee parameter (right).

2) To elaborate a bit on the point above, as Reviewer #1 highlights in their public review, there was concern that the assumption of a monolithic model of the 1/f pattern (and its representation with a single exponent) fails to capture nuanced/fine-grained aspects of the spectrum, and might confuse an overall elevation of broadband γ power with a change of 1/f exponent. In such cases, observed changes in 1/f exponents would result from improper model fitting and be spurious findings. This issue needs to be carefully addressed.

We agree with the reviewer that broad frequency ranges, such as the one we use to extract periodic β power (5-90 Hz), are unlikely to only have a single aperiodic component. Thus, we now use the knee mode for this frequency range (see Figure 2B).

We changed this in the methods accordingly: “To isolate periodic β activity, the PSD was parameterised using FoooF between 5-90 Hz (knee mode as such a wide frequency range is unlikely to only have a single aperiodic component), otherwise using the same settings, and the largest peak within the canonical β range from 8-35 Hz was selected (Figure 2B).” (lines 419-422)

We have tried to include a knee in the fitting settings for the frequency range from 30 to 100 Hz in Figure 1. However, using the knee mode did not improve the goodness of fit or the fitting error and, in fact, made both parameters slightly worse (Figure 1—figure supplement 2). Based on this, we think the fixed mode would provide the most economical model for the PSDs in Figure 1C. We have now added this analysis in Figure 1—figure supplement 2 to justify the choice of the fixed mode. We added to the manuscript: “Using the ‘knee’ mode for parameterisation did not improve aperiodic fitting (Figure 1—figure supplement 2).” (lines 358-359)

As the reviewer pointed out and as we have shown in Figure 1C, broad γ power is increased when STN spiking is higher in animal data, which impacts the aperiodic exponent. Whether this broad γ power increase can be trivially explained by increases in STN spiking is less clear (see comments to reviewer 1). Previous experimental and modelling work showed an overall shift of the spectra to higher power values with increased spiking, while in Figure 1C the spectra are almost identical from 10-20 Hz and only drift apart > 20 Hz. Ray and Maunsell, 2011 show that the positive correlation between LFP power and spiking is less clear for frequencies below 100 Hz. In addition, we do not see any γ power difference between ON and OFF medication states in human data (Figure 2—figure supplement 2A), while aperiodic exponents separate both conditions suggesting that aperiodic exponents reflect more than just γ power changes.

3) Line 80-83. Is it possible the null result is due to the authors' choice of analyzing the two conditions separately? If the data were pooled between high and low spiking epochs, presumably a significant correlation between power and exponent would be found here. Could the authors please address this?

When pooling exponents and power of high and low STN spiking epochs, we still did not find a significant correlation (Spearman; ρ = -.15, p = .07 see Author response image 3). We added this information to our manuscript: “When pooling aperiodic exponents and power from high and low STN spiking epochs, we still did not observe a significant correlation (ρ = -.15, p = .07).” (lines 79-81)

This supports that aperiodic exponents and average power of the same frequency range carry complementary information.

Author response image 3
Download asset Open asset
Pooled correlation between power and exponents of high and low STN spiking epochs.

4) The authors conducted many bivariate correlation analyses, but it would be worthwhile to run a multiple linear regression analysis to see whether and to what degree the different electrophysiological features relate to clinical status.

Medication-induced changes of the aperiodic exponent were positively correlated with changes in the γ band (Figure 2—figure supplement 2B), and also showed a tendency for a negative correlation with periodic β power (Figure 2D). However, none of these electrophysiological features related to clinical state. We also used MATLAB’s fitlm function to perform a multiple linear regression analysis using the electrophysiological features from Figure 2—figure supplement 2A and Figure 2C (changes between ON and OFF medication) as predictors and the UPDRS score difference between both medication states as response variable (see Author response table 1). Because the R2 value of 0.117 is very low, and the p-value of 0.842 is far above the significance level of 0.05, we did not observe a significant linear regression relationship between the response (UPDRS changes with meds) and the predictor variables (electrophysiological differences between medication states). In addition, we tested linear regression models with just a subset of the electrophysiological predictor variables but did not find a significant linear regression relationship (Author response table 1). This is not as surprising as in another manuscript with 106 patients, the highest correlation between medication-induced spectral changes and UPDRS part III scores was in a more finely-tuned low β frequency band (13-20 Hz) with an ρ value of 0.361 (Lofredi et al., 2022). The relatively low ρ value of this previous study and the lower sample size and the broader β range used in this study may explain the lack of significance in these correlations.

Author response table 1
Results of linear regression models.
PredictorVariablesR2p-value
periodic β0.0020.821
β (13-35 Hz)0.0270.405
γ (15-35 Hz)0.0620.203
β + γ + 1/F0.1110.411
β + γ0.0710.399
all frequencies fromFigure 2—figure supplement 2A + 1/F0.1170.842

5) In Figure 3, why do the authors not also show the aperiodic-adjusted β oscillation features?

We have now moved the aperiodic-adjusted β oscillation features with and without DBS from Figure 2—figure supplement 2C to Figure 3C. Periodic β power, like the aperiodic exponent, was modulated by medication and DBS, consistent with previous studies (Brown et al., 2001; Kühn et al., 2008; Whitmer et al., 2012)

Reviewer #1 (Recommendations for the authors):

Specific issues:

1) Line 5-7, the authors' terminology here confuses the exponent, which is measured from the power spectrum, with the activity that contributes to that power spectrum. In other words, 1/f exponent or aperiodic exponent should not be in the same status as the other terms. It is probably also safe to say that the term "1/f noise" is no longer used in the literature due to the increased recognition that this activity is not noise.

We removed this section of the introduction and replaced it with: “In this study, we will refer to the slope of the PSD as aperiodic exponent.” (lines 4-5)

Reviewer #2 (Recommendations for the authors):

– The authors perform permutation tests, but report t-values and p-values. Are the p-values the empirical p-values derived from the permutation measure, or are they the inferred p-values from the t-test itself?

We report the empirical p-values derived from the permutation measure (adjusted for multiple comparisons) as implemented in:

David Groppe (2022). mult_comp_perm_t1(data,n_perm,tail,α_level,mu,reports,seed_state) (https://www.mathworks.com/matlabcentral/fileexchange/29782-mult_comp_perm_t1-data-n_perm-tail-α_level-mu-reports-seed_state), MATLAB Central File Exchange. Retrieved November 8, 2022.

For clarification, we made an addition to the methods section: “To perform paired comparisons between the two medication or stimulation conditions, we used a paired samples permutation t-test with multiple comparison correction (50,000 permutations each) as implemented in (Groppe, 2022).” (lines 431-434)

– Relatedly, 50,000 permutations seem excessive! Not problematic in any way, just probably overkill.

Manly, B.F.J., 1997 suggest using at least 1,000 permutations for a significance level of 0.05 and at least 5,000 permutations for a significance level of 0.01. We chose 50,000 permutations and a significance level of 0.05 as in the example by Groppe 2022. As the reviewer points out, lowering the number of permutations will not affect results.

– The authors should look at Chini et al., eLife 2022 as optogenetic support that aperiodic activity indexes EI balance.

We thank the reviewer for this hint and added Chini et al., 2022 and Trakoshis et al., 2020 in several places throughout the manuscript, for example:

“Moreover, the aperiodic exponent was suggested to reflect neuronal spiking (Manning et al., 2009; Ray and Maunsell, 2011), synaptic currents (Baranauskas et al., 2012; Buzsáki et al., 2012) and excitation-inhibition (E/I) balance, which describes the delicate balance of inhibitory and excitatory synaptic inputs to neurons (Chini et al., 2022; Gao et al., 2017; Trakoshis et al., 2020).” (lines 12-15)

“A similar frequency range (5-45 Hz) was used in a previous study (Chini et al., 2022).” (lines 424-425)

– In Figures 1D and E, the individual datapoints are difficult to see. Maybe they can be offset a bit, or the α adjusted so they're not as faint. This is especially true when the figures are printed.

We have now offset the individual data points and increased the opacity to make them easier to distinguish.

– Across the Figures, the visual language isn't consistent. For example, in Figure 1 red and blue mean low- and high-spiking epochs, respectively. In Figure 2 red and blue mean on and off meds. In Figure 3 red and blue mean on or off DBS. In these cases they're somewhat consistent in the humans (on/off meds is similar to on/off DBS), and theoretically related to low- and high-spiking, but I think different colors should be used to make them better stand apart.

We now changed the colours in Figures 1-3 to clearly distinguish high (blue) and low (red) STN spiking activity (Figure 1), OFF (purple) and ON (grey) levodopa (Figure 2) and OFF (green) and ON (orange) stimulation (Figure 3).

– In Figure 2B, the exponent fit lines in black and yellow are –very– difficult to see, especially in print.

We increased the line width and changed the colours for better contrast.

Reviewer #3 (Recommendations for the authors):

– The motivation for selecting frequency ranges for analysis is not clear/convincing enough from my point of view, eg. why is it starting at 30 / 40 Hz only?

Potential β band activity below 30 / 40 Hz seems like a weak argument as strong β activity can appear at much lower frequencies or not really at all.

As there is no “one-range-fits-all” frequency range, we adjust the fitting range for parameterisation based on oscillatory components and spectral plateaus of the respective spectra (Gerster et al., 2022). When comparing aperiodic exponents between high and low STN spiking states in rodent data, we chose the 30-100 Hz range. This exact range (Trakoshis et al., 2020) or a similar range (Gao et al., 2017) were used in the past to extract the aperiodic component and to make inferences on the E/I balance. In a complementary analysis, we show in this revision that results are not going to change if the 40-90 Hz range (as applied for clinical data in Figure 2) is chosen for this analysis (Author response image 1). Inversely, our findings in clinical data (Figure 2) hold up if a broader frequency range (30-95 Hz) is selected (Figure 2—figure supplement 1A).

As recommended by Gerster et al., 2022, we chose the lower frequency bound such that it avoids overlap with oscillatory peaks in the α and β range. As can be seen in Author response image 4 for clinical data and Author response image 5 for animal data, such peaks can very well appear between 30 and 40 Hz and therefore affect aperiodic fits. Hence, we decided to avoid overlap with such prominent oscillatory components and increased the lower fitting bound to 30 Hz in animals and 40 Hz in human data. In addition, as suggested by Gerster et al., 2022, we avoided the very low frequency range (1-10 Hz) as this will vary considerably with low frequency oscillations, which dominate the slow-wave sleep in 6-OHDA-lesioned animals (Figure 1A and Magill et al., 2001).

Author response image 4
Download asset Open asset
PSDs from all 30 hemispheres ON and OFF medication.

Aperiodic fits are shown between 5-90 Hz (knee mode), which was used to calculate the power of β peaks, and between 40-90 Hz (fixed mode), which was used to estimate the aperiodic exponent of the spectrum.

Author response image 5
Download asset Open asset
Power spectrum of STN LFPs recorded from anaesthetised 6-OHDA-lesioned rats during cortical activation.

Note the prominent peak in the β range. The black box designated the frequency range from 30-100 Hz.

The ON and OFF stimulation comparison was performed on the 10-50 Hz frequency range given the prominent spectral plateau that is most likely caused by increased noise in the amplifier/recording system during high-frequency stimulation (Figure 3). In addition, a very similar frequency range (4-45 Hz) was used to extract aperiodic exponents and make inferences on the E/I balance in a recent study Chini et al., 2022.

– Chapter 4.2.2: The last sentence appears redundant to me, is it?

We agree and removed this sentence.

– Please double-check the citation Oostenveld et al. 2011. The Journal name is missing.

Thanks for the hint, we corrected this.

References

Baranauskas, G., Maggiolini, E., Vato, A., Angotzi, G., Bonfanti, A., Zambra, G., Spinelli, A., Fadiga, L., 2012. Origins of 1/f2 scaling in the power spectrum of intracortical local field potential. J. Neurophysiol. 107, 984–994. https://doi.org/10.1152/jn.00470.2011

Brown, P., Oliviero, A., Mazzone, P., Insola, A., Tonali, P., Di Lazzaro, V., 2001. Dopamine dependency of oscillations between subthalamic nucleus and pallidum in Parkinson’s disease. J. Neurosci. 21, 1033–1038. https://doi.org/10.1523/JNEUROSCI.21-03-01033.2001

Buzsáki, G., Anastassiou, C.A., Koch, C., 2012. The origin of extracellular fields and currents — EEG, ECoG, LFP and spikes. Nat. Rev. Neurosci. 13, 407.

Chini, M., Pfeffer, T., Hanganu-Opatz, I., 2022. An increase of inhibition drives the developmental decorrelation of neural activity. ELife 11. https://doi.org/10.7554/eLife.78811

Donoghue, T., Haller, M., Peterson, E.J., Varma, P., Sebastian, P., Gao, R., Noto, T., Lara, A.H., Wallis, J.D., Knight, R.T., Shestyuk, A., Voytek, B., 2020. Parameterizing neural power spectra into periodic and aperiodic components. Nat. Neurosci. 23, 1655–1665. https://doi.org/10.1038/s41593-020-00744-x

Gao, R., Peterson, E.J., Voytek, B., 2017. Inferring synaptic excitation/inhibition balance from field potentials. Neuroimage 158, 70–78. https://doi.org/10.1016/j.neuroimage.2017.06.078

Gerster, M., Waterstraat, G., Litvak, V., Lehnertz, K., Schnitzler, A., Florin, E., Curio, G., Nikulin, V., 2022. Separating Neural Oscillations from Aperiodic 1/f Activity: Challenges and Recommendations. Neuroinformatics. https://doi.org/10.1007/s12021-022-09581-8

Groppe, D., 2022. mult_comp_perm_t1(data,n_perm,tail,α_level,mu,reports,seed_state) [WWW Document]. MATLAB Cent. File Exch. URL https://www.mathworks.com/matlabcentral/fileexchange/29782-mult_comp_perm_t1-data-n_perm-tail-α_level-mu-reports-seed_state (accessed 11.8.22).

Kim, J., Lee, J., Kim, E., Choi, J.H., Rah, J.-C., Choi, J.-W., 2022. Dopamine depletion can be predicted by the aperiodic component of subthalamic local field potentials. Neurobiol. Dis. 168, 105692. https://doi.org/10.1016/j.nbd.2022.105692

Kühn, A.A., Kempf, F., Brücke, C., Doyle, L.G., Martinez-Torres, I., Pogosyan, A., Trottenberg, T., Kupsch, A., Schneider, G.H., Hariz, M.I., Vandenberghe, W., Nuttin, B., Brown, P., 2008. High-frequency stimulation of the subthalamic nucleus suppresses oscillatory β activity in patients with Parkinson’s disease in parallel with improvement in motor performance. J. Neurosci. 28, 6165–6173. https://doi.org/10.1523/JNEUROSCI.0282-08.2008

Kühn, A.A., Kupsch, A., Schneider, G.H., Brown, P., 2006. Reduction in subthalamic 8-35 Hz oscillatory activity correlates with clinical improvement in Parkinson’s disease. Eur. J. Neurosci. 23, 1956–1960. https://doi.org/10.1111/j.1460-9568.2006.04717.x

Lofredi, R., Okudzhava, L., Irmen, F., Brücke, C., Huebl, J., Krauss, J.K., Schneider, G.-H., Faust, K., Neumann, W.-J., Kühn, A.A., 2022. Subthalamic β bursts correlate with dopamine-dependent motor symptoms in 106 Parkinson’s patients. bioRxiv 2022.05.06.490913. https://doi.org/10.1101/2022.05.06.490913

Manning, J.R., Jacobs, J., Fried, I., Kahana, M.J., 2009. Broadband shifts in local field potential power spectra are correlated with single-neuron spiking in humans. J. Neurosci. 29, 13613–13620. https://doi.org/10.1523/JNEUROSCI.2041-09.2009

Neumann, W.-J., Staub-Bartelt, F., Horn, A., Schanda, J., Schneider, G.-H., Brown, P., Kühn, A.A., 2017. Long term correlation of subthalamic β band activity with motor impairment in patients with Parkinson’s disease. Clin. Neurophysiol. Off. J. Int. Fed. Clin. Neurophysiol. 128, 2286–2291. https://doi.org/10.1016/j.clinph.2017.08.028

Ray, N.J., Jenkinson, N., Wang, S., Holland, P., Brittain, J.S., Joint, C., Stein, J.F., Aziz, T., 2008. Local field potential β activity in the subthalamic nucleus of patients with Parkinson’s disease is associated with improvements in bradykinesia after dopamine and deep brain stimulation. Exp. Neurol. 213, 108–113. https://doi.org/10.1016/j.expneurol.2008.05.008

Ray, S., Maunsell, J.H.R., 2011. Different origins of γ rhythm and high-γ activity in macaque visual cortex. PLoS Biol. 9, e1000610. https://doi.org/10.1371/journal.pbio.1000610

Trakoshis, S., Martínez-Cañada, P., Rocchi, F., Canella, C., You, W., Chakrabarti, B., Ruigrok, A.N., Bullmore, E.T., Suckling, J., Markicevic, M., Zerbi, V., Baron-Cohen, S., Gozzi, A., Lai, M.-C., Panzeri, S., Lombardo, M. V, 2020. Intrinsic excitation-inhibition imbalance affects medial prefrontal cortex differently in autistic men versus women. ELife 9. https://doi.org/10.7554/eLife.55684

Whitmer, D., de Solages, C., Hill, B., Yu, H., Henderson, J.M., Bronte-Stewart, H., 2012. High frequency deep brain stimulation attenuates subthalamic and cortical rhythms in Parkinson’s disease. Front. Hum. Neurosci. 6, 155. https://doi.org/10.3389/fnhum.2012.00155

Wiest, C., Tinkhauser, G., Pogosyan, A., Bange, M., Muthuraman, M., Groppa, S., Baig, F., Mostofi, A., Pereira, E.A., Tan, H., Brown, P., Torrecillos, F., 2020. Local field potential activity dynamics in response to deep brain stimulation of the subthalamic nucleus in Parkinson’s disease. Neurobiol. Dis. 143, 105019. https://doi.org/10.1016/j.nbd.2020.105019

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

The manuscript has been very much improved but there are some remaining issues that need to be addressed, as outlined below:

Upon discussion between the reviewers we have identified the following points which we would like the authors to address.

1) The reviewers felt the authors had not clearly indicated when a "knee" was included in the fit and when it was not included. The manuscript would be strengthened by clarifying this and also explaining how the decision was made.

We only used the ‘knee’ mode to isolate periodic β activity in Figure 2B+C. As suggested by Gerster et al., 2022: “If the purpose is not to obtain the 1/f exponent but rather the removal of the aperiodic component for better periodic power assessment, a broadband range (such as 1-100 Hz) should be chosen.” (Gerster et al., 2022) Due to this, we parameterised spectra between 5-90 Hz. This very broad fitting range is unlikely to consist of a single 1/f component (see bend in Figure 2B top right plot and the recommendations for aperiodic component fitting https://fooof-tools.github.io/fooof/auto_tutorials/plot_05-AperiodicFitting.html#sphx-glr-auto-tutorials-plot-05-aperiodicfitting-py) and, hence, we chose the knee parameter.

We clarified this in the revised version of the manuscript: “To isolate periodic β activity, the PSD was parameterised using FoooF between 5-90 Hz (‘knee’ mode in this case as such a wide frequency range is unlikely to only have a single aperiodic component, all other FoooF settings were identical to what was used in animal data). After removing the aperiodic component, the largest peak within the canonical β range from 8-35 Hz was selected (Figure 2B). All other FoooF fittings presented elsewhere in this study were performed using the ‘fixed’ mode.” (lines 436-441)

All other analyses in Figures 1-3 were performed using the ‘fixed’ mode as the PSD within the selected frequency ranges looked linear in log-log space.

In some complementary analyses (in figure supplements) we also tried the knee mode (Figure 2—figure supplement 1 D and Figure 1—figure supplement 2 B) to confirm if the ‘knee mode’ is necessary, and in both cases it is clearly labelled that ‘knee mode’ was used. The results shown in Figure 1—figure supplement 2 suggest that using the ‘knee mode’ did not improve the goodness of fit (quantified by the R2 value), and did not reduce the fitting error. These results support the decision of using the ‘fixed’ mode. The rationale for using ‘fixed mode’ can also be found in our manuscript: “Moreover, PSDs were linear across this frequency range in log-log space assuming a single 1/f like characteristic and did not contain overlapping periodic components (Figure 1—figure supplement 1E+F). Hence, higher aperiodic exponents indicate steeper power reduction with increasing frequencies in the PSD and vice versa as shown in Figure 1—figure supplement 1F. We evaluated the goodness of fit (R2) for all data used in this study (Figure 3—figure supplement 1). In addition, we evaluated and compared the goodness of fit using either ‘fixed’ mode or ‘knee’ mode in the FoooF fitting. Results show that using the ‘knee’ mode for parameterisation did not improve aperiodic fitting (Figure 1—figure supplement 2). Therefore, we opted to use the ‘fixed’ mode for parameterisation within the selected frequency range.” (lines 365-373)

2) We are concerned that the authors used the fact that a correlation yielded a p-value greater than 0.05 as justification for the idea that no correlation was present. The authors should include a clear discussion of this and consideration of alternative interpretations.

We agree that a p-value of 0.07 shows a trend and cannot be used to justify a lack of correlation. Here, the negative trend is expected given the inverse changes of periodic β power and aperiodic exponents with medication in Figure 2C. We revised the manuscript accordingly: “Medication-induced changes of aperiodic exponents and periodic β power displayed a trend for a negative correlation (Spearman; ρ = -.33, p = .07, n = 30; Figure 2D) indicating that they may contain similar information on levodopa-induced changes in the STN. This may also hint at a physiological meaning of aperiodic exponents.” (lines 122-125)

We deleted the following passage: “… and might add complimentary information to a β activity-based feedback algorithm.” and updated the p-values for correlations between average β power of three different frequency bands and aperiodic exponent changes with levodopa: “However, neither average (Spearman; ρ = -.08, p = .67), low (ρ = -.20, p = .28) nor high β power (ρ = .004, p = .99) correlated with aperiodic exponents (Figure 2—figure supplement 2B).” (lines 112-114)

We also revised our discussion: “First, we could not show a direct link between the aperiodic exponent and clinical symptoms, but a trend for a negative correlation with periodic β power (Figure 2D) and in our data set UPDRS part III scores were not correlated with periodic β power either (Figure 2E+F).” (lines 220-223)

and “In this cohort, we did not find correlations between levodopa-induced changes of aperiodic exponents and average β power of three different frequency ranges (Figure 2—figure supplement 2B), but a trend for a negative correlation with periodic β power, which comprises a measure similar to β peaks that were used before (Darcy et al., 2022; Neumann et al., 2017). It is therefore possible that aperiodic exponents extract similar information than β power, but may aid in subjects where no β peaks are present or β peaks are not affected by levodopa.” (lines 237-242)

3) With respect to Figure 2B, we would like the authors to perform an analysis on the narrowband β peak (in addition to the analysis looking at the broader β range already included) and discuss any differences in the on vs off findings.

When analysing periodic β power, we extract a measure that is very similar to narrowband β peaks. As described in the methods, we parameterise the power spectrum between 5 and 90 Hz, subtract the aperiodic component and select the power of the largest β peak between 8 and 35 Hz (largest oscillatory component obtained by FoooF in that range). In Figure 2C we are not showing broad β power, but periodic β power.

This question likely relates to the comment by reviewer 1 that Figures 2B and C seem to contradict each other such that β peaks seem more prominent ON medication in Figure 2B, while their power is higher OFF medication in Figure 2C. The most likely explanation for this disparity is that Figure 2B shows a group average. Plots for individual hemispheres (see Author response image 4) show that the precise frequency of β peaks varies across patients. When averaging across hemispheres, peaks will not line up but merge to a broader β peak (with finer β peaks superimposed, see purple spectrum in Figure 2B). In the ON medication condition, we do not observe the same phenomenon since β peaks are suppressed by levodopa in most hemispheres. However, in some hemispheres β peaks are almost unaffected by medication, which may have caused the prominent β peaks in Figure 2B. When a statistical analysis is performed (Figure 2C), periodic β peak power is larger in the OFF medication state (p = .048). Β peak power is reduced by medication in 18 of 30 hemispheres.

Below are the individual reviewer comments.

Reviewer #1 (Recommendations for the authors):

This revised manuscript is much improved. However, there are still some significant issues that are left unaddressed, which in my opinion precludes publication in the present form.

1. Essential revision Point 1, author point 2. FOOOF fitting with a new parameter.

The authors suggest that "PSDs in log-log space were almost linear (Figure 1C + Figure 2B + Figure 1—figure supplement 1E+F + Figure 3A)." However, a knee is evident in Figure 1C, Figure 2B, and Figure 3A, no-DBS condition. So, this sentence does not fit with the data presented in the figures.

We would like to clarify that when we say the ‘PSD in log-log space was almost linear’, we are referring to the PSD in the selected frequency range. We acknowledge that when a very broad frequency range is considered (e.g. 1-100 Hz), there are bends and knees.

We have now clarified this: “When a broad frequency band (e.g. 1-100 Hz) was considered, the PSD was not linear in log-log space. However, within the selected frequency band, the power spectrum followed an almost perfect linear line as illustrated in Figure 2B (bottom right plot). Therefore, we used the ‘fixed’ mode for parameterisation of the selected frequency range.” (lines 433-436)

In Figure 1C, using the ‘knee’ mode actually worsened the goodness of fit and increased the error (Figure 1—figure supplement 2). Furthermore, the potential ‘knee’ in the group plot (Figure 1C) is not apparent when PSDs from all 8 animals are evaluated individually. To illustrate this, we attached see author response image 6. PSDs from 30 to 100 Hz seem almost perfectly linear.

Author response image 6
Download asset Open asset

Overall, from reading the response letter, I'm missing a principled approach to decide whether the knee fitting is used or not used in each case. If there was a consistent and objective criterion, the authors should clarify it in the paper.

Please see response to Essential Revisions Point 1.

2. Essential revision Point 3. You can't use a trend-level correlation (p = 0.07) to support a lack of correlation! This correlation is at trend-level, and you might just lack sufficient statistical power for it to cross the arbitrary p = 0.05 threshold.

Please see response to Essential Revisions Point 2.

3. Reviewer #1, point 2. The authors' response here is entirely unconvincing. Their response does not solve the salient issue that Figure 2B and Figure 2C are intuitively contradictory. The authors' response is essentially that a modification of their analysis pipeline yields the same result, even though this result is contrary to the impression one gets from looking at the power spectrum. Instead of believing that the method cannot fail, when the result from a multi-level complicated analysis does not fit the impression from the raw data, it would be prudent to at least consider the possibility that one's tools might be problematic. At the very least, no satisfactory answer is given here about why the statistics do not fit with the raw impression by examining the power spectrum in Figure 2B.

Please see response to Essential Revisions Point 3. We do not argue that a modification of our analysis pipeline yields the same result, but that the visual illusion that is described by the reviewer is due to the summing of β peaks at different frequencies in the OFF medication state.

References

Darcy, N., Lofredi, R., Al-Fatly, B., Neumann, W.-J., Hübl, J., Brücke, C., Krause, P., Schneider, G.-H., Kühn, A., 2022. Spectral and spatial distribution of subthalamic β peak activity in Parkinson’s disease patients. Exp. Neurol. 114150. https://doi.org/10.1016/j.expneurol.2022.114150

Gerster, M., Waterstraat, G., Litvak, V., Lehnertz, K., Schnitzler, A., Florin, E., Curio, G., Nikulin, V., 2022. Separating Neural Oscillations from Aperiodic 1/f Activity: Challenges and Recommendations. Neuroinformatics. https://doi.org/10.1007/s12021-022-09581-8

Neumann, W.-J., Staub-Bartelt, F., Horn, A., Schanda, J., Schneider, G.-H., Brown, P., Kühn, A.A., 2017. Long term correlation of subthalamic β band activity with motor impairment in patients with Parkinson’s disease. Clin. Neurophysiol. Off. J. Int. Fed. Clin. Neurophysiol. 128, 2286–2291. https://doi.org/10.1016/j.clinph.2017.08.028

https://doi.org/10.7554/eLife.82467.sa2

Article and author information

Author details

  1. Christoph Wiest

    Medical Research Council Brain Network Dynamics Unit, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom
    Contribution
    Conceptualization, Formal analysis, Investigation, Visualization, Writing - original draft, Writing – review and editing
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0001-5728-3951

  2. Flavie Torrecillos

    Medical Research Council Brain Network Dynamics Unit, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom
    Contribution
    Conceptualization, Supervision, Investigation, Writing – review and editing
    Competing interests
    No competing interests declared

  3. Alek Pogosyan

    Medical Research Council Brain Network Dynamics Unit, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom
    Contribution
    Software
    Competing interests
    No competing interests declared

  4. Manuel Bange

    Movement Disorders and Neurostimulation, Biomedical Statistics and Multimodal Signal Processing Unit, Department of Neurology, University Medical Center of the Johannes Gutenberg University Mainz, Mainz, Germany
    Contribution
    Data curation
    Competing interests
    received grants from the German Research Council (DFG) grant number DFG CRC-TR-128. The author has no other competing interests to declare

  5. Muthuraman Muthuraman

    Movement Disorders and Neurostimulation, Biomedical Statistics and Multimodal Signal Processing Unit, Department of Neurology, University Medical Center of the Johannes Gutenberg University Mainz, Mainz, Germany
    Contribution
    Data curation
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0001-6158-2663

  6. Sergiu Groppa

    Movement Disorders and Neurostimulation, Biomedical Statistics and Multimodal Signal Processing Unit, Department of Neurology, University Medical Center of the Johannes Gutenberg University Mainz, Mainz, Germany
    Contribution
    Data curation
    Competing interests
    has received funding from BMBF, UM Mainz, Boehringer Foundation, Precisis, DFG, Abbott, Magventure and Innovationsfond GBA. The author received consulting fees from Abbott and Boston Scientific, and received payment or honoraria for lectures from Abbott, Bial, IPSEN, Abbvie, BVDN, BVDN and UCB. The author has no other competing interests to declare

  7. Natasha Hulse

    Department of Neurosurgery, King's College London, London, United Kingdom
    Contribution
    Resources
    Competing interests
    No competing interests declared

  8. Harutomo Hasegawa

    Department of Neurosurgery, King's College London, London, United Kingdom
    Contribution
    Resources
    Competing interests
    No competing interests declared

  9. Keyoumars Ashkan

    Department of Neurosurgery, King's College London, London, United Kingdom
    Contribution
    Resources
    Competing interests
    received funding from Medtronic and Abbott, and received support for attending meetings and/or travel from Medtronic and Abbott. The author has no other competing interests to declare

  10. Fahd Baig

    Neurosciences Research Centre, Molecular and Clinical Sciences Institute, St. George' s, University of London, London, United Kingdom
    Contribution
    Resources
    Competing interests
    No competing interests declared

  11. Francesca Morgante

    Neurosciences Research Centre, Molecular and Clinical Sciences Institute, St. George' s, University of London, London, United Kingdom
    Contribution
    Resources
    Competing interests
    has received research support from NIHR, consulting fees from Boston Scientific and royalties from Springer for the book "Disorders of Movement. The author has received speaking honoraria from Abbvie, Medtronic, Bial, Merz, International Parkinson's disease and Movement Disorder Society, and Advisory board fees from Merz, Abbvie, Boston Scientific. The author has no other competing interests to declare

  12. Erlick A Pereira

    Neurosciences Research Centre, Molecular and Clinical Sciences Institute, St. George' s, University of London, London, United Kingdom
    Contribution
    Resources
    Competing interests
    has received grants from Life after Paralysis, and royalties and licenses from Elsevier. The author has received consulting fees from Boston Scientific. The author has no other competing interests to declare

  13. Nicolas Mallet

    Institut des Maladies Neurodégénératives, CNRS UMR5293, Université de Bordeaux, Bordeaux, France
    Contribution
    Resources
    Competing interests
    No competing interests declared

  14. Peter J Magill

    Medical Research Council Brain Network Dynamics Unit, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom
    Contribution
    Resources, Data curation, Funding acquisition, Writing – review and editing
    Competing interests
    has received funding from the MRC Programme Grant MC_UU_00003/5 and Parkinson's UK (grant G-0806). The author has no other competing interests to declare

  15. Peter Brown

    Medical Research Council Brain Network Dynamics Unit, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom
    Contribution
    Conceptualization, Resources, Supervision, Funding acquisition, Project administration
    Competing interests
    is a named inventor on the following patent applications: Fischer P He S Tan H Brown P Patent Application: Treatment of gait impairment using deep brain stimulation 2021. WO/2021/250398; Debarros J Brown P Tan H Denison T Patent Application: Emulation of electrophysiological signals derived by stimulation of a body 2020. WO/2020/165591; Debarros J Brown P Tan H Patent Application: Measurement of electrophysiological signals during stimulation of a target area of a body 2020. WO/2020/070492. The author has no other competing interests to declare
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-5201-3044

  16. Andrew Sharott

    Medical Research Council Brain Network Dynamics Unit, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom
    Contribution
    Conceptualization, Resources, Supervision, Funding acquisition, Project administration, Writing – review and editing
    Competing interests
    has received funding from the MRC Programme Grant MC_UU_00003/6. The author has a pending patent application unrelated to the subject matter of this paper (Patent WO/2020/183152). The author participates on the Grant Advisory Panel for Aligning Science Across Parkinson's (ASAP). The author has no other competing interests to declare

  17. Huiling Tan

    Medical Research Council Brain Network Dynamics Unit, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom
    Contribution
    Conceptualization, Resources, Data curation, Supervision, Funding acquisition, Project administration, Writing – review and editing
    For correspondence
    huiling.tan@ndcn.ox.ac.uk
    Competing interests
    has received funding from the MRC Programme Grant MC_UU_00003/2, the National Institute for Health Research (NIHR) Oxford Biomedical Research Centre (BRC) and Rosetrees Trust. The author is a named inventor in the following patent applications: Fischer P He S Tan H Brown P Patent Application: Treatment of gait impairment using deep brain stimulation 2021. WO/2021/250398; Debarros J Brown P Tan H Denison T Patent Application: Emulation of electrophysiological signals derived by stimulation of a body 2020. WO/2020/165591; Debarros J Brown P Tan H Patent Application: Measurement of electrophysiological signals during stimulation of a target area of a body 2020. WO/2020/070492. The author has no other competing interests to declare
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0001-8038-3029

Funding

Medical Research Council (MC_UU_00003/2)

  • Huiling Tan

Medical Research Council (MC_UU_00003/5)

  • Peter J Magill

Medical Research Council (MC_UU_00003/6)

  • Andrew Sharott

National Institute for Health Research Oxford Biomedical Research Centre

  • Huiling Tan

Rosetrees Trust

  • Huiling Tan

Parkinson's UK (G-0806)

  • Peter J Magill

Medical Research Council (MR/V00655X/1)

  • Huiling Tan

Medical Research Council (MR/P012272/1)

  • Huiling Tan

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

This work was supported by the Medical Research Council (MC_UU_00003/2, MC_UU_00003/5, MC_UU_00003/6, MR/V00655X/1, MR/P012272/1), the National Institute for Health Research (NIHR) Oxford Biomedical Research Centre (BRC), Rosetrees Trust, and Parkinson’s UK (G-0806).

Ethics

This protocol was approved by the Health Research Authority UK, the National Research Ethics Service local Research Ethics Committee (IRAS: 46576) and the local ethics committee at the University of Mainz (837.208.17(11042)). Patients were recruited at St. George's University Hospital NHS Foundation Trust, London, King's College Hospital NHS Foundation Trust, London, and the University Medical Center Mainz. Written informed consent, and consent to publish, was obtained before surgery in line with the Declaration of the Principles of Helsinki. We analysed data from 24 patients from these 3 centres.

Experiments were performed on adult male Sprague Dawley rats (Charles River), and were conducted in accordance with the Animals (Scientific Procedures) Act, 1986 (UK). Animal data that was analysed in this paper has been generated under the project licence numbers 30/2131 and 30/2629. All details on the 6-OHDA lesion and electrophysiological recordings were published before (Mallet et al., 2008a).

Senior Editor

  1. Floris P de Lange, Donders Institute for Brain, Cognition and Behaviour, Netherlands

Reviewing Editor

  1. Nicole C Swann, University of Oregon, United States

Reviewer

  1. Bradley Voytek, University of California, San Diego, United States

Publication history

  1. Received: August 4, 2022
  2. Preprint posted: August 23, 2022 (view preprint)
  3. Accepted: February 22, 2023
  4. Accepted Manuscript published: February 22, 2023 (version 1)
  5. Version of Record published: March 10, 2023 (version 2)

Copyright

© 2023, Wiest et al.

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

  • 671
    Page views
  • 154
    Downloads
  • 1
    Citations

Article citation count generated by polling the highest count across the following sources: PubMed Central, Crossref, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Christoph Wiest
  2. Flavie Torrecillos
  3. Alek Pogosyan
  4. Manuel Bange
  5. Muthuraman Muthuraman
  6. Sergiu Groppa
  7. Natasha Hulse
  8. Harutomo Hasegawa
  9. Keyoumars Ashkan
  10. Fahd Baig
  11. Francesca Morgante
  12. Erlick A Pereira
  13. Nicolas Mallet
  14. Peter J Magill
  15. Peter Brown
  16. Andrew Sharott
  17. Huiling Tan
(2023)
The aperiodic exponent of subthalamic field potentials reflects excitation/inhibition balance in Parkinsonism
eLife 12:e82467.
https://doi.org/10.7554/eLife.82467

Categories and tags

Research organisms

Further reading

    1. Neuroscience

    Schema-based predictive eye movements support sequential memory encoding

    Jiawen Huang, Isabel Velarde ... Christopher Baldassano
    Research Article

    When forming a memory of an experience that is unfolding over time, we can use our schematic knowledge about the world (constructed based on many prior episodes) to predict what will transpire. We developed a novel paradigm to study how the development of a complex schema influences predictive processes during perception and impacts sequential memory. Participants learned to play a novel board game ('4-in-a-row') across six training sessions, and repeatedly performed a memory test in which they watched and recalled sequences of moves from the game. We found that participants gradually became better at remembering sequences from the game as their schema developed, driven by improved accuracy for schema-consistent moves. Eye tracking revealed that increased predictive eye movements during encoding, which were most prevalent in expert players, were associated with better memory. Our results identify prediction as a mechanism by which schematic knowledge can improve episodic memory.

    1. Neuroscience

    Extra-hippocampal contributions to pattern separation

    Tarek Amer, Lila Davachi
    Review Article

    Pattern separation, or the process by which highly similar stimuli or experiences in memory are represented by non-overlapping neural ensembles, has typically been ascribed to processes supported by the hippocampus. Converging evidence from a wide range of studies, however, suggests that pattern separation is a multistage process supported by a network of brain regions. Based on this evidence, considered together with related findings from the interference resolution literature, we propose the ‘cortico-hippocampal pattern separation’ (CHiPS) framework, which asserts that brain regions involved in cognitive control play a significant role in pattern separation. Particularly, these regions may contribute to pattern separation by (1) resolving interference in sensory regions that project to the hippocampus, thus regulating its cortical input, or (2) directly modulating hippocampal processes in accordance with task demands. Considering recent interest in how hippocampal operations are modulated by goal states likely represented and regulated by extra-hippocampal regions, we argue that pattern separation is similarly supported by neocortical–hippocampal interactions.

    1. Medicine
    2. Neuroscience

    The role of expectations, control and reward in the development of pain persistence based on a unified model

    Christian Büchel
    Review Article

    Chronic, or persistent pain affects more than 10% of adults in the general population. This makes it one of the major physical and mental health care problems. Although pain is an important acute warning signal that allows the organism to take action before tissue damage occurs, it can become persistent and its role as a warning signal thereby inadequate. Although per definition, pain can only be labeled as persistent after 3 months, the trajectory from acute to persistent pain is likely to be determined very early and might even start at the time of injury. The biopsychosocial model has revolutionized our understanding of chronic pain and paved the way for psychological treatments for persistent pain, which routinely outperform other forms of treatment. This suggests that psychological processes could also be important in shaping the very early trajectory from acute to persistent pain and that targeting these processes could prevent the development of persistent pain. In this review, we develop an integrative model and suggest novel interventions during early pain trajectories, based on predictions from this model.