Point of View: Is cell size a spandrel?

Ariel Amir

Harvard University, United States

Jan 19, 2017

Open access
Copyright information

Download
Cite
CommentOpen annotations (there are currently 0 annotations on this page).
Share

Article
Figures and data
Abstract
Main text
References
Decision letter
Author response
Article and author information
Metrics

Abstract

All organisms control the size of their cells. We focus here on the question of size regulation in bacteria, and suggest that the quantitative laws governing cell size and its dependence on growth rate may arise as byproducts of a regulatory mechanism which evolved to support multiple DNA replication forks. In particular, we show that the increase of bacterial cell size during Lenski’s long-term evolution experiments is a natural outcome of this proposal. This suggests that, in the context of evolution, cell size may be a 'spandrel'

https://doi.org/10.7554/eLife.22186.001

Main text

The question of how cells control their sizes has a long history (Haldane, 1926). The observation that cells of a given type often have a narrow size distribution suggests that cell size is tightly controlled, and one can try to rationalize this observation in various ways (Young, 2006; Ginzberg et al., 2015). For instance, one may speculate that diffusion will limit the supply of nutrients in large cells due to their small surface-area-to-volume ratio: however, many microbes are order of magnitudes smaller than any limit imposed by diffusion (Landy, 2014). Here I discuss the control of cell size in bacteria, which has been shown to manifest several size-related quantitative laws.

Cell size can be measured accurately, both on a population level and at the single-cell level. For several bacterial species it has been reported that the cell volume depends on its growth rate via a quantitative dependence known as the Schaechter-Maaløe–Kjeldgaard (SMK) growth law (Schaechter et al., 1958). For example, in Escherichia coli and its close relative Salmonella typhimurium, it is known that $V \propto e^{λ T}$ , where $V$ is the cell volume, $λ$ is the cell growth rate, and $T$ is constant and equals 60 minutes at 37°C. (The growth rate is defined as $λ = l o g (2) / t_{d}$ , where $t_{d}$ is the time taken for the number of cells in the sample to double).

Discovered in the 1950s, the SMK growth law is often interpreted in terms of cells adapting to their conditions: cells are larger at faster growth rates to accommodate more genetic material (Wang and Levin, 2009; Chien et al., 2012) or more ribosomes (Valgepea et al., 2013). Here we will refute this interpretation and suggest that, in certain cases, size may be a 'spandrel' in the sense coined by Gould and Lewontin (Gould and Lewontin, 1979): in other words, cell size may be a "phenotypic characteristic that is a byproduct of the evolution of some other characteristic, rather than a direct product of adaptive selection" (to use the definition given by Wikipedia). The dependence of cell size on growth conditions, we shall argue, is not an adaptation but a causal consequence of a particular regulation scheme, whose primary purpose is otherwise.

We will outline a particular model of regulation in which the control of cell size occurs at the initiation of DNA replication. Within this model, which appears to capture many experimental results, a new round of DNA replication is initiated when the cell has accumulated a critical biomass (or volume) per each origin of replication from the previous initiation. This 'adder per origin' model has the virtue of tightly regulating the number of replication forks, and we will suggest that this should have more significant implications on cell fitness than changes in cellular dimensions. We also briefly discuss the potential molecular mechanisms for implementing this control strategy.

Multiple replication forks and their regulation

In rich media, bacteria such as E. coli and Bacillus subtilis may have a doubling time shorter than the duration of DNA replication. This remarkable feat is achieved by having several ongoing rounds of DNA replication, each initiating from the single oriC locus on the chromosome, most of which will only terminate in a future generation (Yoshikawa and Sueoka, 1963; Yoshikawa et al., 1964). In contrast to eukaryotes, bacteria initiate new rounds of DNA replication in a synchronous fashion: that is, the number of origins of replications double within a time frame that is short compared to the cell cycle duration (Skarstad et al., 1986). This implies that the number of origins on the circular chromosome will be of the form 2ⁿ with n an integer (see Zaritsky et al., 2011) for a schematric illustration of the chromosome in fast growth conditions, and Figure 6 of Hill et al., 2012 for examples of the origin number distributions at different growth conditions).

In a seminal result, Helmstetter and Cooper showed that over quite a broad range of doubling times (between 20 and 60 minutes), the time from the initiation of DNA replication to division is approximately T = 60 minutes (Helmstetter et al., 1968; Cooper and Helmstetter, 1968) (note that this is not true for slow growth conditions (Adiciptaningrum et al., 2015; Wallden et al., 2016), which we do not discuss here). This result was obtained using the 'baby machine' (Helmstetter and Cummings, 1964; Helmstetter, 2015), a clever experimental technique which approximately synchronizes the bacterial population. It may seem like a strange coincidence for this number to be identical to that appearing in the SMK growth law. Indeed, shortly after this discovery, Donachie published an elegant model which links these two observations (Donachie, 1968).

Donachie’s main insight was to infer what the average cell size at the initiation of DNA replication is, based on the known value for the cell size at division (dictated by the SMK growth law). In order to make this extrapolation, additional information is necessary. First, what is the dependence of cell volume on time, at the single-cell level? Donachie assumed that cells grow exponentially over time. Later works verified that protein synthesis increases exponentially with time (Cooper, 1988), and more recently it was directly verified that the buoyant mass of cells also increases exponentially with time (Godin et al., 2010). These observations are consistent with the notion that the composition of the cytoplasm is approximately constant during the cell cycle. Taken together with the constancy of the length of time between initiation of DNA replication and cell division, these results provide sufficient information to calculate the cell size at DNA replication initiation. The fact that $T = 60$ minutes appears in both the SMK growth law and in the context of DNA replication led Donachie to an intriguing conclusion: at the moment of initiation of DNA replication, the average cell size is proportional to the number of origins per cell in that growth condition. This has since been observed in other bacterial species (Sharpe et al., 1998), and has recently been directly verified in experiments where cell volume was measured at the time of DNA replication initiation (Wallden et al., 2016). Note that all of these experiments were done at relatively fast growth rates, though, and the results do not seem to hold for slow growth.

All this may naturally lead one to envision a mechanistic model, at the single-cell level. Cells can ‘measure’ their size, and initiate DNA replication at a critical size proportional to the number of origins in the cell. A constant time $T$ later, the cell divides. Note that in fast growing conditions, there would have already been several additional divisions between the initiation event and the consequent division events a time $T$ later. Hence this might correspond to division of the daughter or grand-daughter cell, rather than the same generation when initiation occurred. This model couples DNA replication, growth and division robustly, while elucidating the SMK growth law, which would be a causal consequence of the model. Nonetheless, we will suggest that there is a logical flaw in going between the population-level experiments which inspired the model, and the single-cell level proposed mechanism, and that it is inconsistent with additional experiments.

Challenging Donachie’s model

Recently, several studies have revealed an inconsistency between Donachie’s model and experimental data, building on single-cell level data (Amir, 2014; Osella et al., 2014; Campos et al., 2014; Taheri-Araghi et al., 2015; Soifer et al., 2016). These experiments rely on the study of correlations. For instance, one may consider the Pearson correlation coefficient between mother and daughter cell sizes at birth (Amir, 2014); this coefficient is defined as the average of the product of the fluctuations of two variables around their means, normalized by the product of their standard deviations. It is 1 for perfectly correlated variables, −1 for perfectly anti-correlated variables, and 0 for independent variables. Assuming a constant growth rate (which is a good approximation in many cases, including E. coli in fast growth conditions), it can be shown that a critical cell size for division will eliminate any correlations between cell size at birth and division (Amir, 2014). This is illustrated schematically in Figure 1. More generally, a critical cell size for entering a new cell cycle stage which precedes division by a constant time (as in Donachie’s model) will also lead to vanishing correlations between birth and division size, i.e., a cell that is born smaller than average will take longer to reach that threshold size, but there will be no systematic bias for it to divide smaller than average – the memory of the initial conditions is ‘washed away’ by thresholding.

This prediction is in sharp contrast to numerous experimental findings on E. coli (Koppes et al., 1980; Osella et al., 2014; Campos et al., 2014; Taheri-Araghi et al., 2015; Soifer et al., 2016), where such correlations were measured and found to be significant and reproducible. In fact, these suggested that a cell that was born smaller than average by a volume $Δ V$ , will also be smaller than average by the same amount at division: in other words, when pooling all cells of a given size at birth together, their average size at division is related to that at birth by the quantitative law $V_{b} = V_{d} + Δ$ . This law may, once again, be interpreted at the single-cell level as implying that a cell ‘attempts’ to add a constant volume from birth to division: that is, it implies that the cue for division is the accumulation of sufficient volume from cell birth. This scenario is referred to as the incremental or adder model. Recent work proposed a similar model, in which a constant surface area is added between birth and division (Harris and Theriot, 2016). Clearly, these models are different than Donachie’s – yet they both stem from empirical findings. How can we reconcile Donachie’s analysis with the observed correlations?

Figure 1

Download asset Open asset

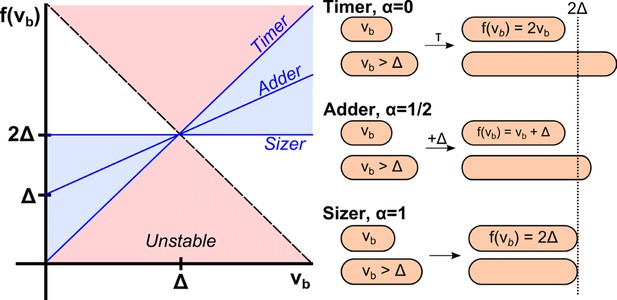
Phenomenological models for cell size control in bacteria.

This graph shows how the size at division, $f (v_{b})$ , depends on the size at birth (x-axis) in three different models. The parameter $α$ is related to the slope of the function, and can continuously interpolate across different models. Its value can be determined from single-cell level correlations (Amir, 2014; see Marantan and Amir, 2016 for a recent generalization of this phase diagram). As $α$ increases from 0 to 1, the correlations between mother and daughter cell sizes become weaker, yet the size distribution becomes narrower. The prevailing model for a critical size at initiation is effectively a ‘sizer’, and is inconsistent with recent experimental data supporting an ‘adder’.

https://doi.org/10.7554/eLife.22186.002

There is a simple way to resolve this apparent contradiction. The key point is to get away from the 'birth-centric' picture, where the cell is attempting to add the constant volume increment from birth to division, and replace it with a model where the volume is added between two DNA replication initiation events. Such a model recovers identical correlations between the various cell cycle events (Ho and Amir, 2015), while at the same time reproducing the exponential dependence of size on growth-rate, and hence is consistent with Donachie’s observations.

Implementing size control at DNA replication initiation

What does it mean to add a volume between two DNA replication initiation events? Sompayrac and Maaloe, 1973 provide a hypothetical model where an 'initiator' protein is accumulated as the cell volume grows, and where initiation of DNA replication occurs when sufficient copies of that initiator are accumulated, thereby providing a proof-of-principle that a cell may indeed add a constant volume increment without measuring its absolute size at any point in time. Note that this model assumes that the accumulation of the initiator does not depend on the status of the chromosome, but only on the increase in volume: this is accomplished by a mechanism involving two genes on the same operon. The first encodes an autorepressing protein, whose concentration will thus be fixed and independent of growth rate (or gene dosage effects), while the second is the initiator, whose copy number reflects the relative increase in volume.

In fact, there are two variants of this model which we may consider: in the first, the initiator protein localizes at some point within the cell, and initiation of DNA replication occurs when its copy number reaches some threshold. This implies that the cell will add the same volume regardless of the number of replication forks (Campos et al., 2014). In a related model, the initiator is localized at the (potentially numerous) origins of replication (or some locus close to it), and hence for conditions of multiple replication forks the cell has to accumulate more volume – in proportion to the number of origins of replication.

Despite their deceiving similarity, these models are very different from each other, and their differences are crucial with regards to the question of cell cycle regulation. The first model does not lead to a narrow size distribution – in fact, it does not even lead to a stable size distribution, as was first noted in 2014 (Campos et al., 2014)! The reason for this is that when the noise occasionally leads to a cell cycle where no initiations occur – or two initiations occur – there is no feedback in the mechanism to allow the cell to recover the correct number of origins.

However, the second model (Ho and Amir, 2015), which we refer to as the 'adder per origin' model, leads to stable size distributions, and appears to explain all experimental findings discussed above. Within this model, division still occurs a constant time $T$ after initiation of DNA replication – as it does in the Helmstetter-Cooper model – but the trigger for initiation of a new round of DNA replication is accumulation of a constant volume per origin of replication. This seemingly innocuous change of the model of Campos et al., 2014 is what provides the necessary feedback to recover from a faulty cell cycle not having a single initiation event. One should be cautious regarding interpreting this model as necessarily involving the accumulation of an initiator protein. While this is a possible mechanism, it is not the only way to implement this phenomenological model; in fact, it can be shown that other biophysical models based on inhibition rather than accumulation of a protein are mathematically equivalent and can also implement the incremental model (Soifer et al., 2016), thus the phenomenological observation of the 'adder per origin' model cannot unveil the structure of the particular molecular network that operates in vivo. Interestingly, it is the inhibition-based model that was first proposed (Pritchard et al., 1969), and provided the inspiration for the accumulation-based model.

Is size the driver or passenger?

The adder per origin model has another appealing feature – it regulates the number of multiple replication forks. If the cell has the wrong number of origins of replication for the given growth condition, the number of replication forks will automatically adjust until the appropriate number is achieved. If a cell has too many origins of replication, the accumulation of the initiator at each origin will slow down (since the volume increment is effectively divided between all origins of replication), and hence the frequency of initiation will decrease until the number of origins per cell reaches the correct value. Note that all of the control occurs at the level of DNA replication initiation, with division occurring deterministically a time $T$ later – regardless of the cell size – in line with recent experimental findings (Wallden et al., 2016).

Within this model, both the number of origins and cell size scale exponentially with the growth rate, and hence are proportional to each other. Yet size and the number of replication forks play a very different role in the bacterial cell cycle: in steady-state growth bacteria must have an exponential dependence of origin number on growth rate (Bremer and Churchward, 1977; Ho and Amir, 2015), in order to guarantee that DNA replication will not become a bottleneck for cell proliferation – which is why multiple replication forks presumably evolved in the first place. (Note that although the number of origins is an integer power of 2 in every cell, the aforementioned exponential dependence is a result of averaging over the entire population and thus is not restricted to take integer values). Changing this dependence will no doubt have significant consequences on fitness. Yet changes in cell size do not have that effect, and we may change cell size by tens or hundreds of percent without any measurable effect on the doubling time (which can typically be determined to accuracy within a few percent). For instance, thymine-limitation slows down the replication rate: this extends the duration of DNA replication, which is known as the C period, and leads to significantly larger cells with unperturbed doubling times (Pritchard and Zaritsky, 1970; Zaritsky and Pritchard, 1973; Zaritsky et al., 2011). Similarly, in ftsZ mutants the time between termination of replication and cell division (known as the D period) is changed: this leads to changes in the cell volume but does not change the doubling time (Palacios et al., 1996; Hill et al., 2012; Zheng et al., 2016). This raises the possibility that this control mechanism evolved in the first place not in order to tightly control size but, rather, as a means to control the number of multiple replication forks. Within this model, the exponential dependence of cell size on growth rate is not an adaptation of any sort but, rather, is a causal consequence of this particular regulation scheme.

What consequences does this interpretation lead to? It is known that many mutations affect cell size (Chien et al., 2012; Yao et al., 2012). Often, observing a large phenotypic response to a particular mutation is used as evidence supporting the role of a particular gene in the regulatory pathway. This logic may be problematic, however. Within the model’s framework, any mutation that would affect the growth rate $λ$ (say, by affecting metabolism or the ribosome efficiency) or the duration of the $C$ and $D$ periods (thus affecting $T = C + D$ ), would affect cell size. Moreover, the effect can be quantified, since cell size should be proportional to $e^{λ T}$ . Comparing this prediction with experimental data on various mutants shows quantitative agreement (Ho and Amir, 2015), as well as experiments where $T$ is systematically perturbed by controlling the expression level of proteins associated with cell division (Zheng et al., 2016).

A different class of experiments where this idea can be tested are the laboratory evolution experiments pioneered by Lenski and co-workers, in which bacteria are grown over thousands of generations, and their fitness is observed to continuously increase over time (Lenski and Travisano, 1994; Lenski and Mongold, 2000; Lenski, 2004; Wiser et al., 2013). In these experiments fitness should be strongly correlated with the growth rate, and inversely proportional to the doubling time (this would be precise in the case where cell growth is in exponential phase and is not affected by growth of other cells in the culture). It is observed that together with the fitness increase, cell size also increases, see Figure 2. According to our model, this is not an adaptation of the cell to the growth conditions, but a causal consequence of the increase in growth rate, which is presumably what is being selected for. Note that we expect the growth rate to be under strong selection, and not $T$ . While the latter affects the number of DNA replication forks, it should not have much impact on the growth rate – since the essence of multiple replication forks is precisely in bypassing the constraint imposed by DNA replication on the cell’s doubling time. It would be interesting to study the dynamics of the duration $T$ in these evolution experiments, which previous results suggest might even increase over time (Mongold and Lenski, 1996), enhancing further the effect on cell size.

Figure 2

Download asset Open asset

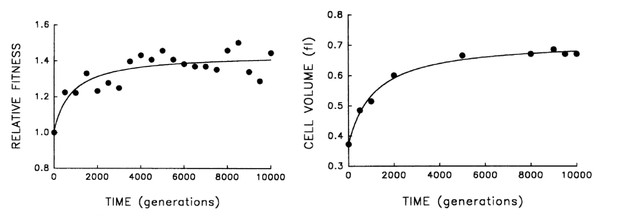
Bacterial evolution and growth regulation.

*E. coli* cells evolving in a culture tube show both increasing fitness over time as well as increasing size. This can be naturally explained by a simple, specific regulation strategy, consistent with additional experiments. Figure adapted from Lenski and Travisano, 1994, with permission.

https://doi.org/10.7554/eLife.22186.003

Discussion

Although it is intuitive to put bacterial cell size center stage in light of the various quantitative laws which it has been shown to follow, we suggest here a different view, that the main constraints on the cell cycle architecture, in fast growing bacteria, stem from the necessity of correctly controlling the number of multiple replication forks. We discussed a model in which control occurs over the initiation of DNA replication – rather than cell division. The model is able to reconcile observations regarding the bacterial cell size which a priori seem to be contradictory. Importantly, the very same model regulates not only size, but also the number of replication forks – allowing the cell to efficiently proliferate in differing environmental conditions.

Cell size correlations similar to those seen in bacteria have also been observed in the budding yeast Saccharomyces cerevisiae (Soifer et al., 2016). In the case of budding yeast, recent work enhances our molecular-level understanding of cell size control (Schmoller et al., 2015), and some progress was made relating this molecular mechanism to phenomenological models (Soifer et al., 2016). It is also known that budding yeast cell volume is dependent on the growth rate (Tyson et al., 1979). It would be interesting to explore whether this dependence could arise from cell cycle 'architecture' (since the term spandrel has its origins in architecture). The numerous differences between the eukaryotic and bacterial cell cycles (for instance, that initiation occurs from many origins on each chromosome, asynchronously) suggests that a different kind of spandrel – yet to be determined – might be needed to elucidate this observation. In any case, it seems that being cautious in our interpretation of such dependencies (that is, interpreting cell size dependence on growth rate as cellular adaption) could potentially be a lesson more broadly applicable.

All of the above discussion hinged on phenomenological observations at the single-cell level, yet hardly any mention of particular molecular mechanisms was made. Ultimately, further work should be able to bridge the gap between our improving phenomenological understanding of the coupling between cell growth, division and DNA replication, and our understanding of the molecular mechanism underlying these processes. The two approaches, molecular level and phenomenological studies, are complementary, and may supplement and benefit each other. The various quantitative laws discovered in bacteria are, in many ways, microscopes that provide us with new insights into the cell cycle. What we see with them should also inform and enhance our understanding at other levels, putting major constraints on the potential molecular mechanisms.

References

(2015) Stochasticity and homeostasis in the E. coli replication and division cycle
Scientific Reports 5:18261.

https://doi.org/10.1038/srep18261
- PubMed
- Google Scholar
1. Amir A
(2014) Cell size regulation in bacteria
Physical Review Letters 112:208102.

https://doi.org/10.1103/PhysRevLett.112.208102
- Google Scholar
1. Bremer H
2. Churchward G
(1977) An examination of the Cooper-Helmstetter theory of DNA replication in bacteria and its underlying assumptions
Journal of Theoretical Biology 69:645–654.

https://doi.org/10.1016/0022-5193(77)90373-3
- PubMed
- Google Scholar
(2014) A constant size extension drives bacterial cell size homeostasis
Cell 159:1433–1446.

https://doi.org/10.1016/j.cell.2014.11.022
- PubMed
- Google Scholar
(2012) Cell size control in bacteria
Current Biology 22:R340–R349.

https://doi.org/10.1016/j.cub.2012.02.032
- PubMed
- Google Scholar
1. Cooper S
2. Helmstetter CE
(1968) Chromosome replication and the division cycle of Escherichia coli B/r
Journal of Molecular Biology 31:519–540.

https://doi.org/10.1016/0022-2836(68)90425-7
- PubMed
- Google Scholar
1. Cooper S
(1988) Leucine uptake and protein synthesis are exponential during the division cycle of Escherichia coli B/r
Journal of Bacteriology 170:436–438.

https://doi.org/10.1128/jb.170.1.436-438.1988
- PubMed
- Google Scholar
1. Donachie WD
(1968) Relationship between cell size and time of initiation of DNA replication
Nature 219:1077–1079.

https://doi.org/10.1038/2191077a0
- PubMed
- Google Scholar
(2015) On being the right (cell) size
Science 348:1245075.

https://doi.org/10.1126/science.1245075
- Google Scholar
1. Godin M
2. Delgado FF
3. Son S
4. Grover WH
5. Bryan AK
6. Tzur A
7. Jorgensen P
8. Payer K
9. Grossman AD
10. Kirschner MW
11. Manalis SR
(2010) Using buoyant mass to measure the growth of single cells
Nature Methods 7:387–390.

https://doi.org/10.1038/nmeth.1452
- PubMed
- Google Scholar
1. Gould SJ
2. Lewontin RC
(1979) The spandrels of San Marco and the panglossian paradigm: A critique of the adaptationist programme
Proceedings of the Royal Society B: Biological Sciences 205:581–598.

https://doi.org/10.1098/rspb.1979.0086
- Google Scholar
1. Haldane JB
(1926)
On being the right size

Harpers Magazine 152:424–427.
- Google Scholar
1. Harris LK
2. Theriot JA
(2016) Relative rates of surface and volume synthesis set bacterial cell size
Cell 165:1479–1492.

https://doi.org/10.1016/j.cell.2016.05.045
- PubMed
- Google Scholar
(1968) On the bacterial life sequence
Cold Spring Harbor Symposia on Quantitative Biology 33:809–822.

https://doi.org/10.1101/SQB.1968.033.01.093
- PubMed
- Google Scholar
1. Helmstetter CE
2. Cummings DJ
(1964) An improved method for the selection of bacterial cells at division
Biochimica et Biophysica Acta 82:608–610.

https://doi.org/10.1016/0304-4165(64)90453-2
- Google Scholar
1. Helmstetter CE
(2015) A ten-year search for synchronous cells: obstacles, solutions, and practical applications
Frontiers in Microbiology 6:238.

https://doi.org/10.3389/fmicb.2015.00238
- PubMed
- Google Scholar
(2012) Cell size and the initiation of DNA replication in bacteria
PLoS Genetics 8:e1002549.

https://doi.org/10.1371/journal.pgen.1002549
- PubMed
- Google Scholar
1. Ho PY
2. Amir A
(2015) Simultaneous regulation of cell size and chromosome replication in bacteria
Frontiers in Microbiology 6:662.

https://doi.org/10.3389/fmicb.2015.00662
- PubMed
- Google Scholar
1. Koppes LJ
2. Meyer M
3. Oonk HB
4. de Jong MA
5. Nanninga N
(1980)
Correlation between size and age at different events in the cell division cycle of Escherichia coli

Journal of Bacteriology 143:1241–1252.
- PubMed
- Google Scholar
1. Landy J
(2014) Shape-dependent bounds on cell growth rates
EPL 105:68002.

https://doi.org/10.1209/0295-5075/105/68002
- Google Scholar
1. Lenski R
(2004)
Plant Breeding Reviews

225–265, Phenotypic and genomic evolution during a 20,000-generation experiment with the bacterium escherichia coli, Plant Breeding Reviews.
- Google Scholar
Book
1. Lenski RE
2. Mongold JA
(2000)
Cell Size, Shape, and Fitness in Evolving Populations of Bacteria

Oxford University Press.
- Google Scholar
1. Lenski RE
2. Travisano M
(1994) Dynamics of adaptation and diversification: a 10,000-generation experiment with bacterial populations
PNAS 91:6808–6814.

https://doi.org/10.1073/pnas.91.15.6808
- Google Scholar
1. Marantan A
2. Amir A
(2016) Stochastic modeling of cell growth with symmetric or asymmetric division
Physical Review E 94:012405.

https://doi.org/10.1103/PhysRevE.94.012405
- PubMed
- Google Scholar
1. Mongold JA
2. Lenski RE
(1996) Experimental rejection of a nonadaptive explanation for increased cell size in Escherichia coli
Journal of Bacteriology 178:5333–5334.

https://doi.org/10.1128/jb.178.17.5333-5334.1996
- PubMed
- Google Scholar
(2014) Concerted control of Escherichia coli cell division
PNAS 111:3431–3435.

https://doi.org/10.1073/pnas.1313715111
- Google Scholar
(1996) Dependency of Escherichia coli cell-division size, and independency of nucleoid segregation on the mode and level of ftsZ expression
Molecular Microbiology 20:1093–1098.

https://doi.org/10.1111/j.1365-2958.1996.tb02549.x
- PubMed
- Google Scholar
(1969)
Control of DNA synthesis in bacteria

Symposium of the Society for General Microbiology 19:263–297.
- Google Scholar
1. Pritchard RH
2. Zaritsky A
(1970) Effect of thymine concentration on the replication velocity of DNA in a thymineless mutant of Escherichia coli
Nature 226:126–131.

https://doi.org/10.1038/226126a0
- PubMed
- Google Scholar
(1958) Dependency on medium and temperature of cell size and chemical composition during balanced grown of Salmonella typhimurium
Journal of General Microbiology 19:592–606.

https://doi.org/10.1099/00221287-19-3-592
- PubMed
- Google Scholar
(2015) Dilution of the cell cycle inhibitor Whi5 controls budding-yeast cell size
Nature 526:268–272.

https://doi.org/10.1038/nature14908
- PubMed
- Google Scholar
(1998)
Bacillus subtilis cell cycle as studied by fluorescence microscopy: constancy of cell length at initiation of DNA replication and evidence for active nucleoid partitioning

Journal of Bacteriology 180:547–555.
- PubMed
- Google Scholar
(1986)
Timing of initiation of chromosome replication in individual Escherichia coli cells

EMBO Journal 5:1711.
- PubMed
- Google Scholar
1. Soifer I
2. Robert L
3. Amir A
(2016) Single-Cell analysis of growth in budding yeast and bacteria reveals a common size regulation strategy
Current Biology 26:356–361.

https://doi.org/10.1016/j.cub.2015.11.067
- Google Scholar
1. Sompayrac L
2. Maaloe O
(1973) Autorepressor model for control of DNA replication
Nature New Biology 241:133–135.

https://doi.org/10.1038/newbio241133a0
- Google Scholar
1. Taheri-Araghi S
2. Bradde S
3. Sauls JT
4. Hill NS
5. Levin PA
6. Paulsson J
7. Vergassola M
8. Jun S
(2015) Cell-size control and homeostasis in bacteria
Current Biology 25:385–391.

https://doi.org/10.1016/j.cub.2014.12.009
- PubMed
- Google Scholar
(1979)
Dependency of size of Saccharomyces cerevisiae cells on growth rate

Journal of Bacteriology 138:92–98.
- PubMed
- Google Scholar
1. Valgepea K
2. Adamberg K
3. Seiman A
4. Vilu R
(2013) Escherichia coli achieves faster growth by increasing catalytic and translation rates of proteins
Molecular BioSystems 9:2344–2358.

https://doi.org/10.1039/c3mb70119k
- PubMed
- Google Scholar
1. Wallden M
2. Fange D
3. Lundius EG
4. Baltekin Ö
5. Elf J
(2016) The synchronization of replication and division cycles in individual E. coli cells
Cell 166:729–739.

https://doi.org/10.1016/j.cell.2016.06.052
- PubMed
- Google Scholar
1. Wang JD
2. Levin PA
(2009) Metabolism, cell growth and the bacterial cell cycle
Nature Reviews Microbiology 7:822–827.

https://doi.org/10.1038/nrmicro2202
- PubMed
- Google Scholar
(2013) Long-term dynamics of adaptation in asexual populations
Science 342:1364–1367.

https://doi.org/10.1126/science.1243357
- PubMed
- Google Scholar
1. Yao Z
2. Davis RM
3. Kishony R
4. Kahne D
5. Ruiz N
(2012) Regulation of cell size in response to nutrient availability by fatty acid biosynthesis in Escherichia coli
PNAS 109:E2561–E2568.

https://doi.org/10.1073/pnas.1209742109
- PubMed
- Google Scholar
(1964) Sequential replication of the bacillus subtilis chromosome, III. Regulation of initiation
PNAS 52:973–980.

https://doi.org/10.1073/pnas.52.4.973
- PubMed
- Google Scholar
1. Yoshikawa H
2. Sueoka N
(1963) Sequential replication of Bacillus subtilis chromosome. I. Comparison of marker frequencies in exponential and stationary growth phases
PNAS 49:559–566.

https://doi.org/10.1073/pnas.49.4.559
- PubMed
- Google Scholar
1. Young KD
(2006) The selective value of bacterial shape
Microbiology and Molecular Biology Reviews 70:660–703.

https://doi.org/10.1128/MMBR.00001-06
- PubMed
- Google Scholar
1. Zaritsky A
2. Pritchard RH
(1973)
Changes in cell size and shape associated with changes in the replication time of the chromosome of escherichia coli

Journal of Bacteriology 114:824–837.
- PubMed
- Google Scholar
(2011) Instructive simulation of the bacterial cell division cycle
Microbiology 157:1876–1885.

https://doi.org/10.1099/mic.0.049403-0
- PubMed
- Google Scholar
1. Zheng H
2. Ho PY
3. Jiang M
4. Tang B
5. Liu W
6. Li D
7. Yu X
8. Kleckner NE
9. Amir A
10. Liu C
(2016) Interrogating the Escherichia coli cell cycle by cell dimension perturbations
PNAS 113:15000–15005.

https://doi.org/10.1073/pnas.1617932114
- Google Scholar

Decision letter

Naama Barkai

Reviewing Editor; Weizmann Institute of Science, Israel

In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.

Thank you for submitting your article "Is cell size a spandrel?" to eLife for consideration as a Feature Article. Your article has been reviewed by three peer reviewers, and the evaluation has been overseen by Naama Barkai as the Reviewing and Senior Editor. One of the reviewers, Stephen Cooper (Reviewer 1), has revealed his identity.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Summary:

The manuscript puts forward the suggestion that the well-studied mechanisms that regulate cell size in bacteria did not evolve for size-regulation. Rather, size regulation is a 'by-product' of the need to regulate the number of on-going replication forks. This conclusion is based on recent advances in single-cell experiments and theoretical approaches, which have led to new understanding of the size control mechanism.

Main Suggestion:

As reviewer #3 noted, the differences between classical ideas and the new model is not emphasized clearly enough. This should be fixed. In the discussion between reviewers, it was suggested to add a simple drawing that shows the difference in birth volumes predicted by the two models ('old' model and 'new' one, please see main comment Reviewer #3) during what is referred to as a noisy or faulty cell cycle. For instance, one could show that if a cell happened to initiate at some time after it had reached the critical volume/origin and then produced larger-than-average progeny, the timing and volume increase for the subsequent division would differ in the two models, with the new model being consistent with the recent findings with single cells. This type of drawing is thought to better clarify the main thrust of this manuscript.

Reviewer #1:

At the outset I want to apologize for the unremitting negative tone of this review. There are some positive points in the submitted article, but for the most part I feel that this paper is wrong on so many issues that I will try to be as detailed as possible in why I find these proposals most problematic.

Perhaps the best way to begin is to state clearly what I believe is the currently correct view of how the bacterial cell controls its size and progression through the division cycle. I believe that initiation of DNA synthesis occurs when there is an amount of "initiation mass" present for each origin and at that time initiations of DNA replication take place. Throughout the cell cycle I believe that mass is made simply and exponentially with mass increasing in proportion to extant mass at each time during bacterial growth during the cell cycle. I also believe that there are no variations in the composition of the "cytoplasm" of the cell during the cell cycle and that mass grows simply and exponentially during the cell cycle. I do not know precisely how initiation occurs, but following initiation of DNA replication over a range of growth rates the rate of DNA replication is relatively invariant and the time after termination of a round of replication till cell division is also relatively invariant. As pointed out by Dr. Amir in his review (which in that part is quite good) the size variation of cells as a function of growth rate is simply determined by this invariance of DNA replication and time from termination to division. The data from 1958 and 1968 fit these ideas extremely well.

In contrast to this simple model I feel that many of the suggestions made by Dr. Amir are akin to the Ptolmaic system of Astronomy. Whenever there a deviation from the predictions of the Ptolmaic system arose, a new epicycle is added to the extant cycles and more and more epicycles are used to make the observations fit to the Ptolmaic system. Analogously, I find the papers cited in Dr. Amir's paper, and in the submitted paper, an attempt to take weak data based on single cell measurements which are questionable (in my viewpoint) to fit the data by adding more and more slight variations in order to accommodate some published data.

I must admit that I have tried to look up a number of the papers referred to in the submitted paper, and I have tried to analyze these deeply, but time constraints have made it impossible for me to write a complete analysis of the papers used in this review to support the proposals made by Dr. Amir-Specifically the "Adder" system-and that is what I find problematic about this paper.

…

Reviewer #2:

I think this piece is worth publishing as front matter to make a more people realize that bacteria do not really care about their size. This is important in the light of recent high profile papers with a focus on bacterial cell size. I mainly like the spandrel analogy, but otherwise the observation that cell-size is a passenger and not driver is clear already from Cooper-Helmstetter-Donachi and more recently Wallden et al.

Reviewer #3:

The fundamental idea presented in this manuscript adds an important element to our understanding of bacterial cell cycle regulation and cell size determination. It basically states that the timing of a chromosomal initiation-of-replication event is determined by processes that take place subsequent to the previous initiation event, possibly but not necessarily, accumulation of an "initiator". As a consequence, the model places cell size control in the hands of initiation, and demands new thinking as to how initiation, and as a consequence the cell cycle, are controlled. It is a very satisfying idea because it is consistent with decades of information on the relationship between replication initiation and cell size, and with recent findings that cells growing at a specific rate add, on average, a constant volume from birth to division.

My one concern is whether the very important distinction between the Amir's proposal and previous proposals has been presented forcefully enough for readers to grasp its importance, especially those who may not be intimately familiar with the literature in this field. For instance, the essence of the model, which forms the basis for this manuscript and the entire cell cycle/size control idea, isn't presented until the middle of subsection “Challenging Donachie's model”: "…the volume is added between two DNA replication initiation events." After that model statement, there are comments regarding his proposal such as "…accumulation of a constant volume per origin of replication", "…accumulation of an initiator protein.", and "…multiple origins accumulation model…". These latter statements, taken alone, read too much like the old ideas that were proposed almost 50 years ago and still repeated even in papers published this year, i.e., that initiation takes place whenever a fixed active unit of initiator has accumulated per chromosomal origin (which is reflected in a fixed size/origin), and then cells divide C+D min later. That old proposal, as satisfying as it has been all these years, is wrong if taken literally and not modified, as proposed by the author, to state that it matters when the accumulation takes place, in order to be consistent with current data on cell size at division. I simply suggest that Amir make some changes in the manuscript so that the novelty of his ideas and their significance stand out better. In my opinion, this should also include changing the description of his model from "multiple origins accumulation" to something that reflects when this accumulation takes place. Whether or not Amir's model is correct, it is the most interesting idea on the overall picture of cell cycle control to appear in some time and needs to be promoted as a new way to think about the molecular basis of the initiation process.

https://doi.org/10.7554/eLife.22186.005

Author response

Main Suggestion:

Reviewer #1:

I would like to thank Prof. Cooper for his thorough review. I have made the following changes to the manuscript to address his comments:

1) Replaced “Growth-law” with “Schaechter’s growth-law throughout”.

2) Added additional references.

3) Added definition of Pearson correlation coefficient, and Figure 1 to explain the different correlations associated with the different models.

Reviewer #2:

I thank the reviewer for his positive review, and for the correction they suggested, which was implemented in the revised version.

Reviewer #3:

I would like to thank the reviewer for his thoughtful comments and useful suggestions.

In the revised version I try to make the distinction between the previous models and the recent ones clearer (and earlier in the paper), and added Figure 1 to emphasize this distinction. I also changed “Multiple origins accumulation” to the hopefully clearer “adder per origin”.

https://doi.org/10.7554/eLife.22186.006

Article and author information

Author details

Ariel Amir

School of Engineering and Applied Sciences, Harvard University, Cambridge, United States

For correspondence
arielamir@seas.harvard.edu

Competing interests
The author declares that no competing interests exist.

"This ORCID iD identifies the author of this article:" 0000-0003-2611-0139

Funding

No external funding was received for this work.

Acknowledgements

We thank Richard Lenski, Pankaj Mehta, Andrew Murray and Nancy Kleckner for useful discussions. We thank Arieh Zaritsky and the reviewers for careful reading of the manuscript and for their important comments, and Po-Yi Ho for help with Figure 1.

Publication history

Received: October 7, 2016
Accepted: December 21, 2016
Version of Record published: January 19, 2017

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.