Quantifying the impact of quarantine duration on COVID-19 transmission

Cited 4
Views 3,316
Annotations

Cite this article as: eLife 2021;10:e63704 doi: 10.7554/eLife.63704

Article
Figures and data
Abstract
eLife digest
Introduction
Results
Discussion
Materials and methods
Appendix 1
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

The large number of individuals placed into quarantine because of possible severe acute respiratory syndrome coronavirus 2 (SARS CoV-2) exposure has high societal and economic costs. There is ongoing debate about the appropriate duration of quarantine, particularly since the fraction of individuals who eventually test positive is perceived as being low. We use empirically determined distributions of incubation period, infectivity, and generation time to quantify how the duration of quarantine affects onward transmission from traced contacts of confirmed SARS-CoV-2 cases and from returning travellers. We also consider the roles of testing followed by release if negative (test-and-release), reinforced hygiene, adherence, and symptoms in calculating quarantine efficacy. We show that there are quarantine strategies based on a test-and-release protocol that, from an epidemiological viewpoint, perform almost as well as a 10-day quarantine, but with fewer person-days spent in quarantine. The findings apply to both travellers and contacts, but the specifics depend on the context.

eLife digest

The COVID-19 pandemic has led many countries to impose quarantines, ensuring that people who may have been exposed to the SARS-CoV-2 virus or who return from abroad are isolated for a specific period to prevent the spread of the disease. These measures have crippled travel, taken a large economic toll, and affected the wellbeing of those needing to self-isolate. However, there is no consensus on how long COVID-19 quarantines should be.

Reducing the duration of quarantines could significantly decrease the costs of COVID-19 to the overall economy and to individuals, so Ashcroft et al. decided to examine how shorter isolation periods and test-and-release schemes affected transmission. Existing data on how SARS-CoV-2 behaves in a population were used to generate a model that would predict how changing quarantine length impacts transmission for both travellers and people who may have been exposed to the virus. The analysis predicted that shortening quarantines from ten to seven days would result in almost no increased risk of transmission, if paired with PCR testing on day five of isolation (with people testing positive being confined for longer). The quarantine could be cut further to six days if rapid antigen tests were used.

Ashcroft et al.’s findings suggest that it may be possible to shorten COVID-19 quarantines if good testing approaches are implemented, leading to better economic, social and individual outcomes.

Introduction

Quarantining individuals with high risk of recent infection is one of the pillars of the non-pharmaceutical interventions to control the ongoing severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) pandemic (Kucharski et al., 2020). Owing to the large fraction of transmission of SARS-CoV-2 that is pre-symptomatic or asymptomatic (Ashcroft et al., 2020; Buitrago-Garcia et al., 2020; Ferretti et al., 2020b; He et al., 2020), quarantine can prevent a substantial fraction of onward transmission that would not be detected otherwise. In mathematical modelling studies, it was estimated that thermal screening at airports would allow more than 50% of infected travellers to enter the general population (Quilty et al., 2020; Gostic et al., 2020), which could have been prevented by mandatory quarantine. Quarantine is also a fundamental part of the test–trace–isolate–quarantine (TTIQ) intervention strategy to break chains of transmission within a community (Salathé et al., 2020). With the high or increasing case numbers that are observed in many places around the globe, however, more and more people are being placed into quarantine.

There is ongoing public debate about the appropriateness of quarantine and its duration. Quarantine lowers onward transmission in two ways: first, preventing transmission prior to symptom onset (with the assumption that symptomatic individuals will isolate) and decreasing overall transmission from persistently asymptomatic individuals. The appropriate length of quarantine thus depends on both incubation period and the temporal profile of infectiousness. In theory, quarantine periods could be avoided altogether through widespread and regular testing programmes, but the low sensitivity of reverse transcriptase PCR (RT-PCR) tests, particularly in early infection (Kucirka et al., 2020), as well as limitations on testing capacity in most countries preclude this approach. Quarantine has high economic, societal, and psychological costs (Nicola et al., 2020; Brooks et al., 2020). It restricts individual freedoms (Parmet and Sinha, 2020), although the level of restriction imposed is generally judged to be proportionate, given the severity of coronavirus disease 2019 (COVID-19). The low number of individuals placed in quarantine that turn out to be infected is another argument that is given against quarantine.

Individuals are generally placed into quarantine for one of two reasons: either they have been identified as a recent close contact of a confirmed SARS-CoV-2 case by contact tracing, or they have returned from recent travel to an area with community transmission that has been assessed to pose significant epidemiological risk (WHO, 2020). These groups of quarantined individuals differ in two important ways: compared with traced contacts, travel returners may have lower probability of being infected and have less precise information about the likely time of exposure. This raises the question whether the duration of quarantine should be the same for these two groups of individuals.

To our knowledge, there are no published analyses of surveillance data that directly assess the impact of duration of quarantine on SARS-CoV-2 transmission (Nussbaumer-Streit et al., 2020). In this study, we present a mathematical model that allows quantification of the effects of changing quarantine duration. We use the distributions of incubation time (time from infection to onset of symptoms), infectivity (infectiousness as a function of days since symptom onset), and generation time (difference of timepoints of infection between infector and infectee). These distributions have been estimated by Ferretti et al., 2020b, combining multiple empirical studies of documented SARS-CoV-2 transmission pairs (Ferretti et al., 2020a; Xia et al., 2020; Cheng et al., 2020; He et al., 2020).

Using the model, we explore the effect of duration of quarantine for both traced contacts of confirmed SARS-CoV-2 cases and for returning travellers on the fraction of prevented onward transmission. We assess the effects of test-and-release strategies and the time delay between test and result. These considerations are particularly important given that multiple testing has been shown to be of little benefit (Clifford, 2020). We also address the role of pre-symptomatic patients becoming symptomatic and therefore being isolated independent of quarantine. Furthermore, as one of the arguments for shortening the duration of quarantine is to increase the number of people complying with the recommendation, we investigate by how much adherence needs to increase to offset the increased transmission due to earlier release from quarantine. Finally, we assess the role of reinforced individual-level prevention measures, such as mask wearing, for those released early from quarantine.

Making policy decisions about the duration of quarantine fundamentally requires specifying how the effectiveness of quarantine relates to its costs. The effectiveness can be measured in terms of the overall reduction of transmission, while economic, societal, and individual costs are likely a function of the number of days spent in quarantine. In addition to the epidemiological outcome, which considers only the reduction in transmission, we also present results based on the ratio of transmission prevented to the average number of days spent in quarantine.

Results

Model description

In the absence of quarantine, individuals that are infected with SARS-CoV-2 can infect further individuals in the population. In the model, the timing of onward transmission from an infected individual is determined by the generation time distribution, which describes the time interval between the infection of an infector and infectee (see Figure 1—figure supplement 1). To quantify how much transmission is prevented by quarantining individuals who have been infected with SARS-CoV-2, we need to know the time at which the individual was exposed ( $t_{_} E$ ), as well as when they enter ( $t_{_} Q$ ) and are released from ( $t_{_} R$ ) quarantine. The fraction of transmission that is prevented by quarantine is then the total transmission probability (i.e. the area under the curve) that lies between $t_{_} Q$ and $t_{_} R$ (Figure 1). We refer to this fraction of prevented transmission as quarantine efficacy and is defined in Equation (1) in 'Materials and methods'. Unless otherwise stated, we assume that adherence to quarantine is 100%.

Figure 1 with 1 supplement see all

Download asset Open asset

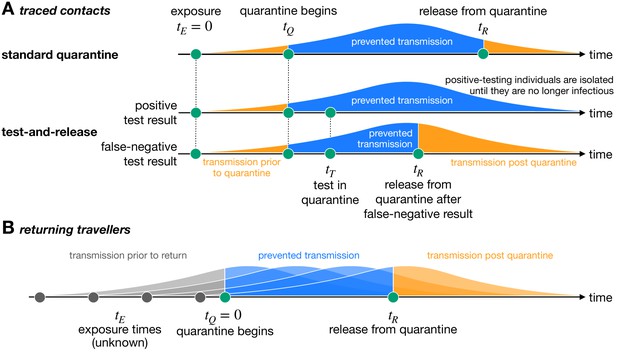
Quantifying the impact of quarantine using a mathematical model.

Here the y-axis represents the probability of transmission. These infectivity curves are a schematic representation of the generation time distribution shown in Figure 1—figure supplement 1. (A) Traced contacts are exposed to an infector at a known time $t_{_} E = 0$ and then enter quarantine at time $t_{_} Q$ . Some transmission can occur prior to quarantine. Under the standard quarantine protocol, the contact is quarantined until time $t_{_} R$ , and no transmission is assumed to occur during this time. The area under the infectivity curve between $t_{_} Q$ and $t_{_} R$ (blue) is the fraction of transmission that is prevented by quarantine. Transmission can occur after the individual leaves quarantine. Under the test-and-release protocol, quarantined individuals are tested at time $t_{_} T$ and released at time $t_{_} R$ if they receive a negative test result. Otherwise the individual is isolated until they are no longer infectious. The probability that an infected individual returns a false-negative test result, and therefore is prematurely released, depends on the timing of the test relative to infection ( $t_{_} T - t_{_} E$ ) (Kucirka et al., 2020). (B) For returning travellers, the time of exposure $t_{_} E$ is unknown and we assume that infection could have occurred on any day of the trip. The travellers enter quarantine immediately upon return at time $t_{_} Q = 0$ , and then leave quarantine at time $t_{_} R$ under the standard quarantine protocol. Test-and-release quarantine proceeds as in panel A.

Under the standard quarantine strategy, all potentially exposed individuals are quarantined for the same duration. An alternative approach is the test-and-release strategy, which uses virological testing during quarantine to release individuals with a negative test result earlier. Individuals with a positive test result are isolated until they are no longer infectious. The timing of the test ( $t_{_} T$ ) is important due to the substantial false-negative rate of the RT-PCR test in the early stages of infection (Kucirka et al., 2020). A false-negative test result would release an infected individual into the community prematurely, leading to further transmission (Figure 1A). In this case, quarantine efficacy is defined as the expected fraction of transmission that is prevented by quarantine across false-negative and positive testing individuals, as defined in Equation (2) in 'Materials and methods'.

As well as the epidemiological benefit of quarantine (i.e. the fraction of transmission prevented by quarantining an infected individual), we can also quantify the economic and societal costs in terms of the expected number of person-days spent in quarantine. We can then define the utility of a quarantine strategy as the ratio between the quarantine efficacy and the average time spent in quarantine, that is, the transmission prevented per day spent in quarantine, as defined in Equation (4) in 'Materials and methods'. This utility measure is dependent on the fraction of individuals in quarantine that are infected. This definition of utility should be considered as an example of such a utility function, but this may not be the best way to quantify quarantine utility.

Details of the calculations used can be found in 'Materials and methods'. Further extensions to the model, including the role of reinforced hygiene measures, asymptomatic infections, and adherence to quarantine, are described in Appendix 1.

Quarantining traced contacts of confirmed SARS-CoV-2 cases

Traced contacts have a known (last) time of exposure to a confirmed case. There is usually a delay between this exposure time and the start of quarantine. Under the standard quarantine protocol, traced contacts are released from quarantine once a number of days have passed after the last exposure time. In Switzerland, for example, quarantine lasts until 10 days after the last exposure.

Any shortening of a traced contact’s quarantine duration will lead to an increase in transmission from that individual if they are infected, but the degree of increase depends on the extent of the shortening. The expected onward transmission that is prevented by quarantine shows the diminishing return of increasing the quarantine duration (black line in Figure 2A). Increasing quarantine duration beyond 10 days shows almost no additional benefit (Figure 2—figure supplement 1A): the standard quarantine protocol (here with a 3-day delay between exposure and the start of quarantine) can maximally prevent 90.8% [95% CI: 79.6%,97.6%] of onward transmission from an infected traced contact, while release on day 10 prevents 90.1% [CI: 76.0%,97.5%].

Figure 2 with 2 supplements see all

Download asset Open asset

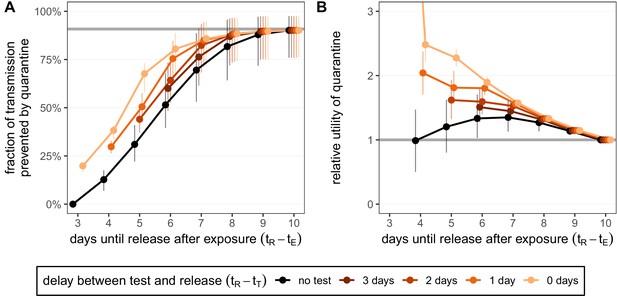
Quantifying the impact of quarantine for traced contacts.

(A) The fraction of transmission that is prevented by quarantining an infected contact. Quarantine begins at time $t_{_} Q = 3$ after exposure at time $t_{_} E = 0$ , that is, there is a 3-day delay between exposure and the start of quarantine. Under the standard quarantine protocol (black), individuals are released without being tested [Equation (1)]. The test-and-release protocol (colours) requires a negative test result before early release, otherwise individuals remain isolated until they are no longer infectious (day 10) [Equation (2)]. Colour intensity represents the delay between test and release (from 0 to 3 days). The grey line represents the maximum attainable prevention by increasing the time of release while keeping $t_{_} Q = 3$ fixed. (B) The relative utility of the quarantine scenarios in A compared to the standard protocol 10-day quarantine [Equation (6)]. Utility is defined as the fraction of transmission prevented per day spent in quarantine. The grey line represents equal utilities (relative utility of 1). We assume that the fraction of individuals in quarantine that are infected is 10%, and that there are no false-positive test results. Error bars reflect the uncertainty in the generation time distribution.

Figure 2—source data 1 Fraction of transmission prevented by quarantine (contacts; test-and-release).: https://cdn.elifesciences.org/articles/63704/elife-63704-fig2-data1-v2.zip
Download elife-63704-fig2-data1-v2.zip
Figure 2—source data 2 Relative utility of quarantine (contacts; test-and-release).: https://cdn.elifesciences.org/articles/63704/elife-63704-fig2-data2-v2.zip
Download elife-63704-fig2-data2-v2.zip

The maximum attainable prevention also applies to the test-and-release strategy: the onward transmission prevented under a test-and-release strategy will always be below this level (coloured lines in Figure 2A). This is because of the chance of prematurely releasing an infectious individual who received a false-negative test result. On the other hand, it is always better to test a person prior to release from quarantine so that individuals with asymptomatic and pre-symptomatic infections can be detected and prevented from being released. Hence, these scenarios provide upper and lower bounds for the efficacy of the test-and-release strategy. The fraction of transmission that is prevented increases if we test later in quarantine because we not only increase the duration of quarantine but also reduce the false-negative probability.

The delay between testing and release from quarantine can have a substantial effect on the efficacy. Current laboratory-based RT-PCR tests have a typical turnaround of 24–48 hr (Quilty et al., 2021). This delay is primarily operational, and so could be reduced by increasing test throughput. There are also rapid antigen-detection tests, which can provide same-day results, but with lower sensitivity and specificity than RT-PCR tests (Guglielmi, 2020). Here we assume that tests have the same sensitivity and specificity regardless of the delay to result. Compared to a test with 2-day delay until result, we observe that using a rapid test with same-day release can reduce the quarantine duration of individuals with a negative test result by 1 day while maintaining the same efficacy (Figure 2A): the extra accuracy gained by waiting one extra day until testing balances the increased transmission caused by reducing the duration. For example, a rapid test on day 6 has roughly the same efficacy (80.5% [CI: 67.9%,88.7%]) as testing on day 5 and releasing on day 7 (82.3% [CI: 68.2%,93.4%]) while shortening the quarantine duration of individuals with a negative test result from 7 to 6 days.

In Figure 2 we have assumed a fixed delay of 3 days between exposure and the start of quarantine. Shortening this delay increases the maximum efficacy of quarantine because pre-quarantine transmission is reduced (Figure 2—figure supplement 1A). If the duration of quarantine is longer than 10 days, then little can be gained in terms of prevention by quarantining for longer, but reducing the delay between exposure and quarantine does lead to increased efficacy.

Note that we have assumed that the contact was infected at the last time of exposure. If there have been multiple contacts between them and the index case, then transmission may have occurred earlier and we would overestimate the efficacy of quarantine.

For the standard quarantine strategy, the duration of quarantine is independent of whether individuals in quarantine are infected. Therefore, the utility of the standard quarantine strategy (i.e. the ratio of efficacy to duration) is directly proportional to the fraction of individuals in quarantine that are infected. By comparing two different standard quarantine strategies through their relative utility (i.e. the ratio of the utilities), we can eliminate the dependence on the fraction of infecteds in quarantine (see 'Materials and methods'). Therefore, the argument that we should shorten quarantine because of the low probability of quarantined individuals being infected is misguided in this situation. By calculating the relative utility for the standard quarantine strategy compared to the baseline 10-day quarantine, we observe that there is a quarantine strategy (release after 7 days) which maximises the ratio between the fraction of transmission prevented and the number of days spent in quarantine (black line in Figure 2B). The optimal strategy lies between 6 and 8 days if we vary the delay between exposure and the start of quarantine (Figure 2—figure supplement 1B).

Under the test-and-release quarantine protocol, the average time spent in quarantine is dependent on the fraction of infecteds in quarantine; only the infected individuals can test positive and face a longer period of isolation (i.e. we assume there are no false-positive test results). Hence the utility of the test-and-release strategy, as well as the relative utility of test-and-release compared to the standard quarantine protocol, is dependent on the fraction of individuals in quarantine that are infected. In Figure 2B, we fix the fraction of infecteds in quarantine to 10%. By calculating the relative utility for the test-and-release quarantine strategies shown in Figure 2A compared to the baseline 10-day quarantine, we see that testing-and-releasing before day 10 always increases the utility (Figure 2B). Testing on day 5 and releasing test-negative individuals on day 7 has a relative utility of 1.53 [CI: 1.45,1.62] compared to a standard 10-day quarantine. Reducing the delay between test and result leads to a corresponding increase in utility: a rapid test (zero delay between test and result) on day 6 has a relative utility of 1.90 [CI: 1.83,1.98] for an almost equivalent efficacy.

In Figure 2, we have made the following assumptions: (i) individuals released from quarantine have – in the post-quarantine phase – the same transmission probability as individuals who were not quarantined; (ii) adherence to quarantine is 100%; and (iii) the transmission prevented by quarantine for cases who develop symptoms is attributed to quarantine. We now relax these assumptions to assess their impact on quarantine efficacy.

Reinforced prevention measures post-quarantine, where individuals who are released from quarantine must adhere to strict hygiene and social distancing protocols until 10 days after exposure have passed, can reduce post-quarantine transmission. Considering a 50% reduction of post-quarantine transmission leads to large increases in both efficacy and utility for early testing strategies, but with diminishing returns as the release date is increased towards day 10 (Figure 2—figure supplement 2; see 'Appendix 1: Reinforced prevention measures after early release'). Note that we assume no contribution to the number of days spent in quarantine in the utility function due to mask wearing and social distancing in the post-release phase.

Adherence to quarantine is unlikely to be 100% and could depend on the proposed duration of quarantine. For simplicity we treat adherence to quarantine as a binary variable: a fraction of individuals adhere to quarantine completely for the proposed duration, while the remaining fraction do not undergo any quarantine. We now ask: by how much would the fraction of those who adhere to quarantine have to increase to maintain the efficacy of quarantine if the duration is shortened? In the absence of testing during quarantine, shortening from 10 to 5 days would require almost three times as many individuals to adhere to the quarantine guidelines in order to maintain the same overall efficacy (relative adherence 2.90 [CI: 2.15,4.36]; black line in Figure 3A). This threefold increase is not possible if adherence to the 10-day strategy is already above 33% as the maximum adherence cannot exceed 100%; the required increase in adherence grows rapidly as quarantine is shortened and soon becomes infeasible. Hence the argument of shortening quarantine to increase adherence is of limited use. Shortening to 7 days (without testing) may be effective provided that adherence can increase by 30% (relative adherence 1.30 [CI: 1.08,1.55]). Under the test-and-release strategy, however, the efficacy of the standard 10-day quarantine can be matched with release on day 5 or 6 if adherence is also increased by 30%. Releasing earlier than day 5 would seemingly be infeasible given the sharp increase in adherence required.

Figure 3 with 1 supplement see all

Download asset Open asset

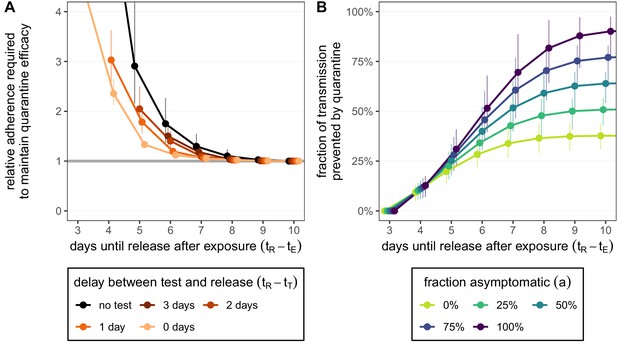
How adherence and symptoms affect quarantine efficacy for traced contacts.

(A) The fold-change in adherence to a new quarantine strategy that is required to maintain efficacy of the baseline 10-day standard strategy. Quarantine strategies are the same as in Figure 2 (standard = black, test-and-release = colours). The grey line represents equal adherence (relative adherence of 1). (B) The impact of symptomatic cases on the fraction of total onward transmission per infected traced contact that is prevented by standard (no test) quarantine [Equation (A9)]. We assume that symptomatic individuals will immediately self-isolate at symptom onset. The time of symptom onset is determined by the incubation period distribution (see Figure 1—figure supplement 1D). The curve for 100% asymptomatic cases corresponds to the black curve in Figure 2A. As in Figure 2, we fix the time of exposure at $t_{_} E = 0$ and the time of entering quarantine at $t_{_} Q = 3$ days. Error bars reflect the uncertainty in the generation time distribution.

Figure 3—source data 1 Relative adherence (contacts; test-and-release).: https://cdn.elifesciences.org/articles/63704/elife-63704-fig3-data1-v2.zip
Download elife-63704-fig3-data1-v2.zip
Figure 3—source data 2 Role of asymptomatic cases (contacts; zero delay).: https://cdn.elifesciences.org/articles/63704/elife-63704-fig3-data2-v2.zip
Download elife-63704-fig3-data2-v2.zip

As a final consideration, we note that our quantification of the fraction of transmission prevented by quarantine is more relevant to individuals with persistently asymptomatic SARS-CoV-2 infection than to those who develop symptoms during quarantine and are subsequently isolated. If symptomatic cases go into isolation once symptoms appear, then quarantine has no further impact on transmission after symptom onset as these cases would anyway be isolated. To account for this, we can modify the model such that cases are removed from the infectious pool upon symptom onset (see Appendix 1). For example, in a fully asymptomatic population a 10-day quarantine can prevent 90.1% [CI: 76.0%,97.5%] of transmission. However, if 25% of cases are asymptomatic, then only 50.8% [CI: 42.8%,56.5%] of transmission is prevented by quarantine, while 39.3% is prevented by the self-isolation of symptomatic cases (Figure 3B). We assume that self-isolation occurs immediately after symptom onset, but any delay between symptom onset and self-isolation would mean that more transmission is prevented by quarantine (Figure 3—figure supplement 1). The fraction of transmission prevented by quarantine is an increasing function of the fraction of asymptomatic cases (Figure 3B). This means that we likely overestimate the efficacy of quarantine as we are also counting transmission that could be prevented by isolation following symptom onset. Furthermore, we have assumed that the false-negative rate is the same between symptomatic and asymptomatic cases. If the test is less sensitive (higher false-negative probability) for asymptomatic cases, then quarantine efficacy would be further reduced.

Quarantining returning travellers

The rules for whether travellers returning from abroad are quarantined are frequently changed according to the epidemiological scenario in the travel destination and/or in the home country. A high risk of infection while abroad due to high prevalence, or the possibility of returning with a new virological variant, can lead to the imposition or reinstatement of quarantine measures (Russell et al., 2021). Countries that have already eliminated the infection may be even stricter in their quarantine approach to prevent new community-transmission clusters from being seeded. Here we do not discuss these scenarios or the concept of relative risk, we simply quantify how effective quarantine strategies would be at preventing transmission if the returning traveller was infected while abroad. Should quarantine rules be instated or modified, these results can help determine the optimal quarantine duration and/or testing strategy.

The timing of infection of a traveller during a trip abroad is generally unknown. We assume that infection could have happened on each day of the trip with equal probability. Quarantine begins immediately upon return, which we refer to as day 0, and lasts for a number of days (e.g. currently 10 days in Switzerland) from this timepoint (Figure 1B). We consider the fraction of local transmission that is prevented by quarantine. That is, the fraction of the transmission that could occur in the local country that is prevented by quarantine [Equation (8)]. For a 7-day trip, as in Figure 4, the maximum transmission that could occur in the local country is 73.3% [CI: 65.7%,80.3%]. The remaining infectivity potential was already used up before arrival.

Figure 4 with 3 supplements see all

Download asset Open asset

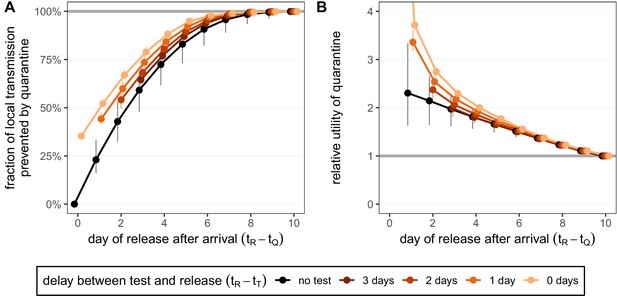
Quantifying the impact of quarantine for returning travellers.

(A) The fraction of *local* transmission that is prevented by quarantining an infected traveller returning from a 7-day trip. Quarantine begins upon return at time $t_{_} Q = 0$ , and we assume that exposure could have occurred at any time during the trip, that is, $- 7 \leq t_{_} E \leq 0$ . Under the standard quarantine protocol (black), individuals are released without being tested [Equation (9)]. The test-and-release protocol (colours) requires a negative test result before early release, otherwise individuals remain isolated until they are no longer infectious (day 10). Colour intensity represents the delay between test and release (from 0 to 3 days). While extended quarantine can prevent 100% of *local* transmission (grey line), this represents 73.3% [CI: 65.7%,80.3%] of the *total* transmission potential (see Figure 4—figure supplement 1A). The remaining transmission occurred before arrival. (B) The relative utility of the quarantine scenarios in A compared to the standard protocol 10-day quarantine [Equation 6]. Utility is defined as the *local* fraction of transmission that is prevented per day spent in quarantine. The grey line represents equal utilities (relative utility of 1). We assume that the fraction of individuals in quarantine that are infected is 10%, and that there are no false-positive test results. Error bars reflect the uncertainty in the generation time distribution.

Figure 4—source data 1 Fraction of transmission prevented by quarantine (travellers; local; test-and-release).: https://cdn.elifesciences.org/articles/63704/elife-63704-fig4-data1-v2.zip
Download elife-63704-fig4-data1-v2.zip
Figure 4—source data 2 Relative utility of quarantine (travellers; local; test-and-release).: https://cdn.elifesciences.org/articles/63704/elife-63704-fig4-data2-v2.zip
Download elife-63704-fig4-data2-v2.zip

A standard (no test) 10-day quarantine will prevent 99.9% [CI: 98.0%,100.0%] of local transmission if the individual was infected during a 7-day trip (Figure 4A). There is little benefit to gain by increasing the duration of quarantine beyond 10 days. On the other hand, standard quarantine efficacy decreases quickly as the duration is shortened.

The test-and-release strategy can improve the efficacy of shorter-duration quarantines. Testing on day 5 and releasing on day 7 (to account for test processing delays) performs similarly to 10-day quarantine, preventing 98.5% [CI: 95.5%,99.6%] of local transmission (Figure 4A). Testing and releasing on day 6 (i.e. no delay between test and result) still prevents 97.8% [CI: 94.4%,99.0%] of local transmission. Hence, if the rapid test has the same sensitivity and specificity as the laboratory-based RT-PCR test, then the duration of quarantine of individuals with a negative test result can be shortened by 1 day with minimal loss in efficacy compared to a test with a 48 hr turnaround.

The timing of the test can have a significant impact on prevented transmission; late testing reduces the false-negative probability but increases the stay in quarantine. An important consequence of this is that testing on arrival is a poor strategy for limiting transmission: testing and releasing on day 0 would prevent only 35.2% [CI: 35.1%,35.3%] of local transmission, while testing on arrival and releasing after 2 days prevents only 54.1% [CI: 49.5%,59.4%]. As was the case for the traced contacts, the fraction of local transmission prevented by standard quarantine bounds the efficacy of the test-and-release quarantine strategy from below (Figure 4A).

We again measure the utility of quarantine by calculating the efficacy (local transmission prevented across all individuals in quarantine, assuming 100% adherence) per day spent in quarantine, and then comparing these utilities for different quarantine strategies to the utility of the standard 10-day quarantine through the relative utility (Figure 4B).

In the absence of testing, the duration of quarantine, and hence the relative utility, is independent of the fraction of individuals in quarantine that are infected. For travellers returning from a 7-day trip, the relative utility is a decreasing function of quarantine duration (black line in Figure 4B). The maximum utility strategy would then be to shorten quarantine as much as possible.

As was the case for traced contacts, under the test-and-release quarantine protocol the average time spent in quarantine, the utility, and the relative utility compared to the standard 10-day quarantine will depend on the fraction of individuals in quarantine that are infected. This fraction may change depending on disease prevalence at the travel destination and the duration of travel. For example, the infected fraction of travellers returning from a long stay in a high-risk country is likely to be higher than the infected fraction of travellers returning from a short stay to a low-risk country. In Figure 4B, we keep this fraction fixed at 10%. Early testing greatly reduces the average duration of quarantine and hence leads to increased utility despite the low fraction of transmission that is prevented (coloured lines in Figure 4B).

The average quarantine duration increases linearly with the fraction of infecteds in quarantine [Equation (3) in 'Materials and methods']. The ratio of quarantine efficacy to the average quarantine duration will also increase, such that quarantine is of higher utility if the fraction of infecteds is higher. However, the relative utility of test-and-release quarantine compared to the standard 10-day protocol will decrease and approach 1 as the fraction of infecteds increases. Hence, if the disease prevalence among those returning from travel abroad is high, then test-and-release may not bring substantial benefits over the standard 10-day protocol.

Our assumption that infection occurs with uniform probability across each day of a trip leads to some interesting results. Returning travellers that have been infected on a short journey will have, on average, used up less of their infectivity potential by the time they return than a traveller who was infected on a long journey. Hence, the total transmission that can be prevented by a long quarantine period (e.g. 10 days) upon arrival is greater for short trips (Figure 4—figure supplement 1A). When considering the fraction of local transmission that can be prevented by quarantine, then shorter quarantine durations have a greater impact on long than short trips (Figure 4—figure supplement 1C). Again, this is because, on average, the traveller on a long trip would have been exposed earlier and they will be infectious for a shorter time period after arrival.

If an individual traveller is to be quarantined, then the optimum duration of quarantine, based on our metric of utility, would depend on the duration of their travel, with shorter journeys requiring longer quarantine (Figure 4—figure supplement 1B, D). This might be counterintuitive because individuals who have been on longer journeys to high-risk countries have a higher probability of being infected. The absolute utility (transmission prevented by quarantine across all individuals in quarantine divided by the average quarantine duration) of quarantining such individuals could indeed be higher than for individuals returning from shorter journeys. However, here, we are not considering the question of whether to quarantine or not, but we are assuming that the individual is quarantined and are trying to optimise the duration of quarantine in response to the expected infection dynamics.

We observe an almost-linear response between quarantine duration and the relative utility of the standard (no test) quarantine: for every day that quarantine is shortened, we see the same additive increase in relative utility (black line in Figure 4B). This almost-linear response is coincidental to the 7-day trip duration: longer or shorter trips show non-linear responses (Figure 4—figure supplement 1D). Trips shorter than 7 days have a maximum relative utility of between 4 and 7 days, while trips longer than 7 days have maximum utility for maximally shortened quarantine durations.

Enforcing additional hygiene and social distancing guidelines post-quarantine can increase both efficacy and utility, but with diminishing returns as the release date is increased (Figure 4—figure supplement 2).

As discussed for traced contacts, the loss of efficacy due to shortening quarantine could be offset by increasing quarantine adherence. Shortening from 10 to 5 days would require adherence to increase by 20% (relative adherence 1.20 [CI: 1.12,1.35]) in order to maintain the same overall efficacy (Figure 4—figure supplement 3A). With test-and-release this required increase in adherence is even smaller. We note that the change in adherence required to balance a change in efficacy for shortened quarantine durations is dependent on the travel duration, with short travel durations requiring a greater increase in adherence compared with longer travel durations.

Discussion

Quarantine is one of the most important measures in controlling the ongoing SARS-CoV-2 epidemic due to the large fraction of pre-symptomatic and asymptomatic transmission. A quarantine period of 10 days from exposure, as currently implemented in Switzerland, is long enough to prevent almost all onward transmission from infected contacts of confirmed cases from the point of entering quarantine: increasing the duration of quarantine beyond 10 days has no extra benefit. Reducing the delay to quarantining individuals increases the fraction of total transmission that is preventable. The same 10-day quarantine duration will prevent almost all local onward transmission from infected travel returners from the time of arrival, independent of their travel duration.

Any decrease in the duration of quarantine of an infected individual will result in increased onward transmission. Furthermore, our analyses suggest that this increase in transmission cannot realistically be compensated by increased adherence for significantly shortened quarantine (fewer than 5 days). However, there are diminishing returns for each day that we add to quarantine: increasing the duration from 10 days has a negligible effect in terms of reduced transmission. One therefore has to assess how much human cost, measured in terms of days spent in quarantine, we are willing to spend to prevent disease transmission. By comparing the ratio of prevented transmission to quarantine duration, we have shown that maximal utility strategies can exist. This ratio is maximised for quarantine durations of 6–8 days after exposure for traced contacts, and potentially less for returning travellers depending on their duration of travel. Importantly, under this metric the fraction of individuals in quarantine that are infected does not affect the optimal duration of quarantine. Therefore, the argument that we should shorten quarantine because of the low probability of being infected is misguided under our definition of utility and in the absence of testing during quarantine.

A test-and-release strategy will lead to a lower average quarantine duration across infected and non-infected individuals. However, due to the considerable false-negative probability of the RT-PCR test (Kucirka et al., 2020), this strategy also leads to increased transmission as infectious individuals are prematurely released. Nevertheless, test-and-release strategies prevent more transmission than releasing without testing, and hence test-and-release increases the utility of quarantine. Reducing the delay between test and result leads to further reduced transmission and increased utility, and reinforcing individual prevention measures after release is also effective for short quarantine periods.

The ratio of transmission prevented versus days spent in quarantine is only one possible definition of utility. Defining the appropriate function is ultimately a policy question: the economic, societal, and individual costs are likely a function of the number of days spent in quarantine, but we cannot determine the shape of this function. Furthermore, the local epidemiological situation will dictate which metric of quarantine efficacy is to be optimised. In situations where the goal is to prevent the (re)introduction of SARS-CoV-2, one should focus on maximising the reduction of transmission (and hence minimising the transmission risk). If the virus is already endemic, then considering the trade-off between transmission reduction and quarantine duration could determine the optimum strategy. Another perspective is that the utility of preventing transmission is crucially dependent on whether it brings the effective reproductive number under 1.

Ultimately, bringing the reproductive number below 1 requires a combination of effective measures including isolation, physical distancing, hygiene, contact tracing, and quarantine (Kucharski et al., 2020). Effective quarantine is only possible in the presence of efficient contact tracing to find the potentially exposed individuals in a short time, as well as surveillance of disease prevalence to identify high-risk travel. Further reducing the time taken to quarantine a contact after exposure and reducing the delay between test and result will allow average quarantine durations to be shorter, which increases the benefit-to-cost ratio of quarantine.

The scenarios of returning travellers and traced contacts of confirmed SARS-CoV-2 cases differ in the probability of having been exposed and infected and on the information available about the likely window of exposure. The impact of quarantining returning travellers depends on the duration of travel and whether we consider the local prevention of transmission or the total transmission prevented by quarantine. However, a single test done immediately after return can only prevent a small fraction of the transmission from a returning traveller because of the false-negative rate of the RT-PCR test early in infection. Therefore testing should be postponed until as late as possible, and utilising rapid tests could be crucial if their performance characteristics are acceptable. This same principle also applies to traced contacts. Our findings are aligned with those of two recent simulation studies which estimate the role that quarantine plays in limiting transmission from returning travellers (Clifford, 2020) and from traced contacts (Quilty et al., 2021).

Our results are based on the latest estimates of the generation time distribution of COVID-19 (Ferretti et al., 2020b). Potential limitations to our approach could be that these distributions may change throughout the epidemic, particularly depending on how people respond to symptoms (Ali et al., 2020). Furthermore, these distributions, and also the test sensitivity profile, could be different between persistently asymptomatic and symptomatic individuals (Buitrago-Garcia et al., 2020), which ultimately lead to an overestimation of how much transmission is prevented by quarantine. In addition, we have primarily assumed that symptom onset during quarantine has no impact on quarantine efficacy. However, this symptomatic transmission should not be counted towards the efficacy of quarantine as the infected individual should already self-isolate after symptom onset. We have quantified this effect and have shown that this assumption leads us to overestimate quarantine efficacy.

For travellers, another consideration is that lengthy quarantine is seen as a deterrent to travel to high-risk areas (IATA, 2020). Any shortening of quarantine may lead to an increase in travel volume, potentially leading to a compounded increase in disease transmission.

In the absence of empirical data about the effectiveness of different durations of quarantine, mathematical modelling can be used objectively to explore the fraction of onward transmission by infected contacts or returning travellers that can be prevented. However, determining the optimal quarantine strategy to implement depends on the impact that shortening the duration of quarantine has on individuals, society, and the economy versus how much weight is assigned to a consequential increase in transmission. Both the individual, societal, and economic impact, as well as the weight of transmission increase, will have to be considered based on the current epidemiological situation. We have shown that there are quarantine strategies based on a test-and-release protocol that, from an epidemiological viewpoint, perform almost as well as the standard 10-day quarantine, but with a lower cost in terms of person-days spent in quarantine. This applies to both travellers and contacts, but the specifics depend on the context.

Materials and methods

Quantifying the benefit of quarantine

Request a detailed protocol

For an infected individual who was exposed at time $t_{_} E$ , the fraction of transmission that is prevented by the standard quarantine strategy is given by the area under the generation time distribution, $q (t)$ (Figure 1—figure supplement 1B), between the times at which the individual enters ( $t_{_} Q$ ) and leaves ( $t_{_} R$ ) quarantine (Grantz et al., 2020), that is,

F_{_} qs (t_{_} E, t_{_} Q, t_{_} R) = \int_{_} t_{_} Q^{t_{_} R} d t q (t - t_{_} E) .

The duration of time that the individual spends in quarantine is then $D_{_} qs = t_{_} R - t_{_} Q$ .

The test-and-release strategy uses virological testing during quarantine to release individuals with a negative test result and to place those with a positive test result into isolation. As illustrated in Figure 1A, test is issued at time $t_{_} T \geq t_{_} Q$ . If the test is negative, the individual is released when the test result arrives at time $t_{_} R$ . Otherwise, the individual is isolated until they are no longer infectious. One challenge with this strategy is the high probability of a false-negative RT-PCR test result (i.e. an infectious individual is prematurely released into the community). As reported by Kucirka et al., 2020, the false-negative rate is 100% on days 0 and 1 post-infection, falling to 67% (day 4), 38% (day 5), 25% (day 6), 21% (day 7), 20% (day 8), and 21% (day 9), before rising to 66% on day 21. We use linear interpolation and label this function $f (t)$ , the false-negative probability on day t after infection. The fraction of transmission prevented by quarantining an infected individual under the test-and-release strategy is

F_{_} qtr (t_{_} E, t_{_} Q, t_{_} T, t_{_} R) = f (t_{_} T - t_{_} E) \int_{_} t_{_} Q^{t_{_} R} d t q (t - t_{_} E) + [1 - f (t_{_} T - t_{_} E)] \int_{_} t_{_} Q^{t_{_} end} d t q (t - t_{_} E),

where the first term captures the fraction of individuals who receive a false-negative test result and are released at time $t_{_} R$ , and the second term captures individuals who return a positive test and are subsequently isolated until they are no longer infectious at time $t_{_} end$ . A further challenge with this false-negative rate is that it was calculated by Kucirka et al., 2020 from symptomatic cases only. Here we assume that this test sensitivity profile also applies to asymptomatic cases.

Quarantine is applied pre-emptively, such that we do not know the infection status of individuals when they enter quarantine. If only a fraction s of the individuals that are quarantined are infected, then the average reduction in transmission across all individuals in quarantine is $s F$ , where F is the fraction of transmission prevented when an infected individual is quarantined [i.e. Equation (1) or (2)]. For the standard quarantine protocol, the average number of days spent in quarantine is independent of s: all individuals are quarantined for the same duration. However, under the test-and-release protocol, only the individuals who are actually infected can test positive and remain isolated after $t_{_} R$ . All non-infected individuals ( $1 - s$ ) will receive a negative test result and are released at time $t_{_} R$ . Among the infected individuals in quarantine (s), a fraction $f (t_{_} T - t_{_} E)$ will receive a false-negative test result and will be released at time $t_{_} R$ , while the remaining fraction [ $1 - f (t_{_} T - t_{_} E)$ ] will receive a positive test result and are isolated until they are no longer infectious. Hence the average number of days spent in quarantine for test-and-release is

\begin{array}{ll} D_{q t r} & = (1 - s) (t_{R} - t_{Q}) + s [f (t_{T} - t_{E}) (t_{R} - t_{Q}) + [1 - f (t_{T} - t_{E})] (t_{e n d} - t_{Q})] \\ = (t_{R} - t_{Q}) + s [1 - f (t_{T} - t_{E})] (t_{e n d} - t_{R}), \end{array}

where $s [1 - f (t_{_} T - t_{_} E)]$ is the fraction of quarantined individuals who return a positive test result. We see that the average test-and-release quarantine duration increases linearly with the fraction of individuals in quarantine that are infected (s).

Model parameters and timepoints are summarised in Table 1.

Table 1

Summary of terms used in the mathematical model.

Value	Definition	Notes
$q (t)$	Generation time distribution	Weibull distribution: shape = 3.277, scale = 6.127
$t_{_} E$	Time of exposure	$t_{_} E = 0$ for traced contacts
$t_{_} Q$	Time at which quarantine begins	$t_{_} Q = 0$ for returning travellers
$t_{_} R$	Time of release from quarantine	-
$t_{_} T$	Time of test	-
$t_{_} end$	End of infectiousness	$t_{_} end = t_{_} E + 10$ days
$g (t)$	Incubation period distribution	Meta-log-normal distribution ('Appendix 1: Distribution parameters')
$t_{_} S$	Time of symptom onset	$t_{_} S = t_{_} E +$ incubation period
$D_{_} qs$	Realised average duration of standard quarantine	$D_{_} qs = t_{_} R - t_{_} Q$
$D_{_} qtr$	Realised average duration of test-and-release quarantine	See Equation (3)
$F_{_} qs (\cdot)$ , $F_{_} qtr (\cdot)$	Quarantine efficacy; the fraction of transmission prevented by quarantining an infected individual	See Equations (1) and (2)
y	Duration of travel journey (days)	-
s	Fraction of individuals in quarantine that are infected	-
$f (t)$	Probability of returning a false-negative test result if tested t days after exposure	From Kucirka et al., 2020
r	Reduction of transmission under reinforced prevention measures post-quarantine	-
$α (D)$	Probability to adhere to quarantine of duration D	-
a	Fraction of persistently asymptomatic cases	-
$Δ$	Delay between symptom onset and isolation (days)	See 'Appendix 1: Persistently asymptomatic infections and the role of self-isolation'

Transmission reduction versus days spent in quarantine

Request a detailed protocol

One possible metric to relate the effectiveness of quarantine to its negative impact on society is to consider the ratio between the amount of overall transmission prevented and the number of person-days spent in quarantine. We refer to this ratio as the utility of quarantine. Concretely, for an efficacy F [ $F_{_} qs$ or $F_{_} qtr$ as defined by Equation (1) or (2), respectively], fraction of individuals in quarantine that are infected s, and average time spent in quarantine D ( $D_{_} qs$ or $D_{_} qtr$ ), we define the utility as

U (s, F, D) = \frac{s F}{D} .

We can then compare the utility of two quarantine strategies by calculating the relative utility, that is, the ratio between the two utilities:

R U (s, F, D, F^{*}, D^{*}) = \frac{s F / D}{s F^{*} / D^{*}} = \frac{F / D}{F^{*} / D^{*}},

where F and D are the efficacy and duration of quarantine of a new strategy, and $F^{*}$ and $D^{*}$ are the efficacy and duration of the baseline quarantine strategy to which we compare.

The efficacies F and $F^{*}$ in Equation (5) are independent of fraction of individuals in quarantine that are infected s. For the standard quarantine strategy, the durations $D = D_{_} qs$ and $D^{*} = D_{_} {qs}^{*}$ are also independent of s, and hence the relative utility of the standard quarantine strategy is independent of s. For the test-and-release strategy, however, the duration is a linearly increasing function of s [ $D = D_{_} qtr (s)$ ; Equation (3)]. Hence the relative utility of the test-and-release strategy is dependent on s:

RU [s, F_{_} qtr, D_{_} qtr (s), F_{_} {qs}^{*}, D_{_} {qs}^{*}] = \frac{F_{_} qtr / D_{_} qtr (s)}{F_{_} {qs}^{*} / D_{_} {qs}^{*}} .

In Appendix 1 we show that the relative utility of the test-and-release quarantine strategy is a decreasing function of s.

Traced contacts versus returning travellers

We consider the scenarios of a traced contact and a returning traveller differently because the values of $t_{_} E$ , $t_{_} Q$ , and $t_{_} R$ are implemented differently in each case.

Traced contacts

Request a detailed protocol

Following a positive test result, a confirmed index case has their recent close contacts traced. From contact tracing interviews, we know the date of last exposure between index case and a contact ( $t_{_} E$ ), which we assume is the time of infection of the contact. The contacts begin quarantine at time $t_{_} Q \geq t_{_} E$ . The delay between exposure and the start of quarantine represents the sum of the delay to the index case receiving a positive test result and the further delay to tracing the contacts. Under the standard quarantine protocol, the traced contacts are quarantined for a number of days after their last exposure. For example, in Switzerland quarantine lasts until $t_{_} R = t_{_} E + 10$ days, but may be longer or shorter depending on individual states’ regulations. Note that the actual time spent in quarantine is $D_{_} qs = t_{_} R - t_{_} Q$ days, which is typically shorter than 10 days due to the delay between exposure and the start of quarantine. For convenience, we set $t_{_} E = 0$ for the traced contacts, without loss of generality.

Returning travellers

Request a detailed protocol

Unlike traced contacts, we generally do not know when travellers were (potentially) exposed. This means that quarantine starts from the date that they return ( $t_{_} Q = 0$ ) and lasts until time $t_{_} R$ (Figure 1B). For simplicity, we assume that a traveller was infected with uniform probability at some time over a travel period of duration y days.

For each possible exposure time $- y \leq t_{_} E \leq 0$ during the trip, we can compute the fraction of transmission prevented using Equation (1) and then take the average over the possible exposure times. This represents the average fraction of the total transmission potential that is prevented by quarantining this traveller:

{\bar{F}}_{q s}^{(t o t a l)} (y, t_{R}) = \frac{1}{y + 1} \sum_{t_{E} = - y}^{0} \int_{0}^{t_{R}} d t q (t - t_{E}),

where we have used $t_{_} Q = 0$ .

For each exposure time $- y \leq t_{_} E \leq 0$ , we can also compute the local fraction of transmission prevented by quarantine, which is the fraction of transmission prevented by quarantine divided by the maximum amount of transmission that could occur in the local country, that is,

F_{q s}^{(l o c a l)} (t_{E}, t_{R}) = \frac{\int_{0}^{t_{R}} d t q (t - t_{E})}{\int_{0}^{\infty} d t q (t - t_{E})},

where we have again used $t_{_} Q = 0$ . Taking the average over the possible exposure times $- y \leq t_{_} E \leq 0$ , we have

{\bar{F}}_{q s}^{(l o c a l)} (y, t_{R}) = \frac{1}{y + 1} \sum_{t_{E} = - y}^{0} F_{q s}^{(l o c a l)} (t_{E}, t_{R}) .

Interactive app

Request a detailed protocol

To complement the results in this paper, and to allow readers to investigate different quarantine scenarios, we have developed an online interactive application. This can be found at https://ibz-shiny.ethz.ch/covidDashboard/quarantine.

Appendix 1

Utility and relative utility of test-and-release quarantine

From Equation (4) of 'Materials and methods', we can write the utility of the test-and-release strategy as

U (s, F_{_} qtr, D_{_} qtr (s)) = \frac{s F_{_} qtr}{D_{_} qtr (s)},

where $F_{_} qtr$ is the quarantine efficacy [Equation (2) in 'Materials and methods'], s is the fraction of individuals in quarantine that are infected, and $D_{_} qtr (s)$ is the average time spent in quarantine [Equation (3) in 'Materials and methods']. The duration $D_{_} qtr (s)$ is a linear function of s, which we can write simply as $D_{_} qtr (s) = m s + b$ [from Equation 3 in 'Materials and methods', we have $m = [1 - f (t_{_} T - t_{_} E)] (t_{_} end - t_{_} R)$ and $b = (t_{_} R - t_{_} Q)$ ].

We now ask, how does this utility change if we increase s? Taking the derivative of Equation (A1) with respect to s, we recover

\frac{d U}{d s} = \frac{d}{d s} (\frac{s F_{_} qtr}{m s + b}) = \frac{b F_{_} qtr}{{(m s + b)}^{2}} > 0 .

Hence, any increase in s leads to an increase in utility.

The relative utility of the test-and-release quarantine strategy to the standard quarantine strategy is defined in Equation (6) in 'Materials and methods'. Again taking the derivative with respect to s, we recover

\frac{d RU}{d s} = \frac{d}{d s} (\frac{F_{_} qtr / (m s + b)}{F_{_} {qs}^{*} / D_{_} {qs}^{*}}) = \frac{- m D_{_} {qs}^{*} F_{_} qtr}{F_{_} {qs}^{*} {(m s + b)}^{2}} < 0 .

Hence, any increase in s leads to a decrease in the relative utility of the test-and-release strategy compared to the standard quarantine strategy.

Reinforced prevention measures after early release

We further consider the possibility that individuals who are released early from quarantine are asked to strengthen hygiene, mask wearing, and social distancing protocols until the end of the infectious period. We assume that these practices reduce transmission by a fraction r such that the onward transmission prevented by quarantining an infected individual and reinforcing hygiene measures is

F_{_} {qs}^{(reduced)} (t_{_} E, t_{_} Q, t_{_} R) = F_{_} qs (t_{_} E, t_{_} Q, t_{_} R) + r \int_{_} t_{_} R^{t_{_} end} d t q (t - t_{_} E),

for the standard quarantine protocol, and

F_{q t r}^{(r e d u c e d)} (t_{E}, t_{Q}, t_{T}, t_{R}) = F_{q t r} (t_{E}, t_{Q}, t_{T}, t_{R}) + r f (t_{T} - t_{E}) \int_{t_{R}}^{t_{e n d}} d t q (t - t_{E}),

for the test-and-release protocol.

Adherence to quarantine

For the majority of our results, we have assumed that quarantine is completely adhered too. Because of this assumption we will overestimate the efficacy of quarantine at the level of the population as it is likely that adherence will be less than 100%.

Adherence could be included as a time-varying property of an individual such that the probability that an individual follows the quarantine guidelines is high at the beginning of quarantine, but is waning as the duration spent in quarantine increases. However, for simplicity, we assume that adherence is binary; either an individual completes the full duration of quarantine or they do not enter quarantine at all. We denote the probability to adhere to quarantine as $α (D)$ , which depends on the quarantine duration D. The average fraction of transmission prevented by (standard) quarantine is then $s α (t_{_} R - t_{_} Q) F_{_} qs (t_{_} E, t_{_} Q, t_{_} R)$ , where s is the fraction of individuals in quarantine that are infected, which we assume is independent of quarantine duration, and we have used $D = D_{_} qs = t_{_} R - t_{_} Q$ .

We do not know the adherence probabilities $α (D)$ . However, for two quarantine strategies with release dates $t_{_} R$ and $t_{_} R^{*}$ to have the same efficacy they must satisfy

\begin{array}{cc} s α (t_{R} - t_{Q}) F_{q s} (t_{E}, t_{Q}, t_{R}) = s α (t_{R}^{*} - t_{Q}) F_{q s} (t_{E}, t_{Q}, t_{R^{*}}) \\ \Rightarrow \frac{α (t_{R} - t_{Q})}{α (t_{R}^{*} - t_{Q})} = \frac{F_{q s} (t_{E}, t_{Q}, t_{R}^{*})}{F_{q s} (t_{E}, t_{Q}, t_{R})} . \end{array}

That is to say, the change in the fraction of transmission prevented by quarantine must be compensated by an inverse change in the adherence: a strategy which prevents half as much transmission as another would require adherence to be doubled to be equally effective. We therefore define the required relative adherence as

{RA}_{_} qs (t_{_} E, t_{_} Q, t_{_} R, t_{_} R^{*}) = \frac{F_{_} qs (t_{_} E, t_{_} Q, t_{_} R^{*})}{F_{_} qs (t_{_} E, t_{_} Q, t_{_} R)} .

This definition of relative adherence is directly extended to the test-and-release strategy, which we compare to the baseline standard protocol:

{R A}_{q t r} (t_{E}, t_{Q}, t_{T}, t_{R}, t_{R}^{*}) = \frac{F_{q s} (t_{E}, t_{Q}, t_{R}^{*})}{F_{q t r} (t_{E}, t_{Q}, t_{T}, t_{R})} .

Persistently asymptomatic infections and the role of self-isolation

If an individual develops symptoms, is tested, and ultimately tests positive while in quarantine, we can remove them from the infectious pool as they would have to isolate themselves. Importantly, this symptomatic individual would be removed from the infectious pool whether they have been placed in quarantine or not. Therefore, this symptomatic transmission should not be counted towards the efficacy of quarantine.

Let a be the fraction of asymptomatic cases who will be quarantined using the standard strategy from time $t_{_} Q$ until $t_{_} R$ . The symptomatic cases (which make up a fraction $1 - a$ of cases) will develop symptoms at time $t_{_} S$ , as described by the incubation period distribution shown in Figure 1—figure supplement 1D. We assume that the symptomatic cases would be isolated shortly after they develop symptoms at time $t_{_} S + Δ$ , so these individuals are effectively quarantined until time $\min (t_{_} R, t_{_} S + Δ)$ . We further assume equal transmissibility of persistently asymptomatic and symptomatic infections and that both are described by the same generation time distribution. This assumption might be an overestimate as onward transmission from persistently asymptomatic cases is less than onward transmission from symptomatic cases (Buitrago-Garcia et al., 2020). For each traced contact who is put into quarantine, the fraction of infections that would be prevented by quarantine is

\begin{array}{ll} F_{q s}^{(a s y m p)} (t_{E}, t_{Q}, t_{R}, a, Δ) & = a \int_{t_{Q}}^{t_{R}} d t q (t - t_{E}) \\ + (1 - a) \int_{t_{E}}^{\infty} d t_{S} g (t_{S} - t_{E}) \int_{t_{Q}}^{min (t_{R}, t_{S} + Δ)} d t q (t - t_{E}), \end{array}

where $g (t)$ is the incubation period distribution, and the outer integral over $t_{_} S$ is the averaging over the possible times of symptom onset. Note that this formulation assumes that the timing of onward transmission is independent of the incubation period (see Ferretti et al., 2020b and Lehtinen et al., 2021 for further discussion of this assumption). Unless otherwise stated, we assume $a = 1$ and $Δ = 0$ .

Confidence intervals

The primary source of uncertainty in the outcomes of this model comes from the generation time distribution, which is inferred from the empirical serial interval distribution combined with the incubation period distribution (Ferretti et al., 2020b). Following Ferretti et al., 2020b, we use a likelihood ratio test to extract sample parameter sets for the generation time distribution that lie within the 95% confidence interval.

Concretely, we first identify the parameter set $\hat{θ}$ for the generation time distribution which maximises the likelihood of observing the empirical serial interval distribution. The likelihood function and fitting process are described in detail by Ferretti et al., 2020b. The generation time distribution is described by a Weibull distribution (with $n = 2$ parameters). We then randomly sample the parameter space of the generation time distribution and keep 1000 parameter sets whose likelihood satisfies $\ln ℒ (θ) > \ln ℒ (\hat{θ}) - λ_{_} 2 / 2$ , where $λ_{_} 2$ is the 95% quantile of a $χ^{2}$ distribution with $n = 2$ degrees of freedom. These parameter sets, as shown in Appendix 1—figure 1, define the 95% confidence interval for the generation time distribution (Figure 1—figure supplement 1B).

Appendix 1—figure 1

Download asset Open asset

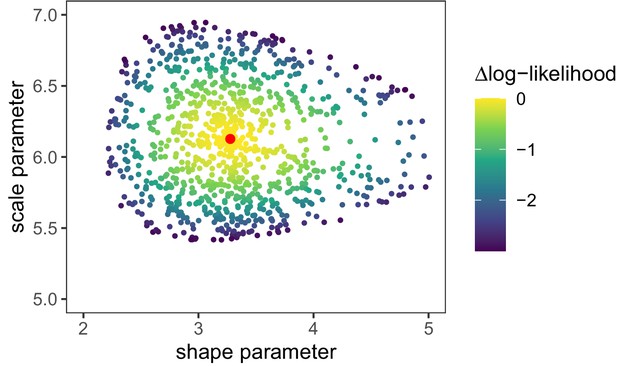
Log-likelihood values [ $\ln ℒ (θ) - \ln ℒ (\hat{θ})$ ] for random parameter samples of the generation time distribution.

These samples define the 95% confidence interval for the generation time distribution parameters. Red dot is the maximum likelihood parameter combination as shown in Appendix 1—table 1.

Appendix 1—figure 1—source data 1 Generation time distribution parameters versus likelihood.: https://cdn.elifesciences.org/articles/63704/elife-63704-app1-fig1-data1-v2.zip
Download elife-63704-app1-fig1-data1-v2.zip

We then use these sampled parameter sets to calculate quarantine efficacy, and the extrema of these efficacies across all of these parameter sets determines the 95% confidence interval of the efficacy.

Distribution parameters

The parameters that define the incubation period distribution, generation time distribution, and infectivity profile are shown in Appendix 1—table 1.

Appendix 1—table 1

Parameters of the distributions used in this work.

The meta-log-normal distribution is the average of seven reported log-normal distributions (Ferretti et al., 2020b). The shifted Student’s t distribution for the infectivity profile is defined in R by dt((x-shift)/scale, df)/scale (Ferretti et al., 2020b).

Distribution	Shape	Parameters	Properties
Incubation period	Meta-log-normal	meanlog = 1.570, sdlog = 0.650 (Bi)	mean = 5.723, sd = 3.450, median = 4.936
		meanlog = 1.621, sdlog = 0.418 (Lauer)
		meanlog = 1.434, sdlog = 0.661 (Li)
		meanlog = 1.611, sdlog = 0.472 (Linton)
		meanlog = 1.857, sdlog = 0.547 (Ma)
		meanlog = 1.540, sdlog = 0.470 (Zhang)
		meanlog = 1.530, sdlog = 0.464 (Jiang)
Generation time	Weibull	shape = 3.277, scale = 6.127	mean = 5.494, sd = 1.845, median = 5.479
Infectivity profile	Shifted Student's t	shift = -0.078, scale = 1.857, df = 3.345	mean = -0.042, sd = 2.876, median = -0.078

Data availability

All data generated or analysed during this study are included in the manuscript and supporting files. These files are available on github https://github.com/ashcroftp/COVID-quarantine/ (copy archived at https://archive.softwareheritage.org/swh:1:rev:7492ec296dab70e3eda5479fedc56f8310cc4417/) and archived at https://doi.org/10.5281/zenodo.4580232.

The following data sets were generated

1. Ashcroft P
2. Lehtinen S
3. Angst DC
4. Low N
5. Bonhoeffer S
(2021) Zenodo
ashcroftp/quarantine2020.
https://doi.org/10.5281/zenodo.4580232

The following previously published data sets were used

1. Ferretti L
(2020) Zenodo
Code & data for "The timing of COVID-19 transmission".
https://doi.org/10.5281/zenodo.4033022

References

1. Ali ST
2. Wang L
3. Lau EHY
4. Xu XK
5. Du Z
6. Wu Y
7. Leung GM
8. Cowling BJ
(2020) Serial interval of SARS-CoV-2 was shortened over time by nonpharmaceutical interventions
Science 369:1106–1109.
https://doi.org/10.1126/science.abc9004
- PubMed
- Google Scholar
(2020) COVID-19 infectivity profile correction
Swiss Medical Weekly 150:w20336.
https://doi.org/10.4414/smw.2020.20336
- PubMed
- Google Scholar
1. Bi Q
2. Wu Y
3. Mei S
4. Ye C
5. Zou X
6. Zhang Z
7. Liu X
8. Wei L
9. Truelove SA
10. Zhang T
11. Gao W
12. Cheng C
13. Tang X
14. Wu X
15. Wu Y
16. Sun B
17. Huang S
18. Sun Y
19. Zhang J
20. Ma T
21. Lessler J
22. Feng T
(2020) Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: a retrospective cohort study
The Lancet Infectious Diseases 20:911–919.
https://doi.org/10.1016/S1473-3099(20)30287-5
- PubMed
- Google Scholar
1. Brooks SK
2. Webster RK
3. Smith LE
4. Woodland L
5. Wessely S
6. Greenberg N
7. Rubin GJ
(2020) The psychological impact of quarantine and how to reduce it: rapid review of the evidence
The Lancet 395:912–920.
https://doi.org/10.1016/S0140-6736(20)30460-8
- PubMed
- Google Scholar
1. Buitrago-Garcia D
2. Egli-Gany D
3. Counotte MJ
4. Hossmann S
5. Imeri H
6. Ipekci AM
7. Salanti G
8. Low N
(2020) Occurrence and transmission potential of asymptomatic and presymptomatic SARS-CoV-2 infections: a living systematic review and meta-analysis
PLOS Medicine 17:e1003346.
https://doi.org/10.1371/journal.pmed.1003346
- PubMed
- Google Scholar
(2020) Contact tracing assessment of COVID-19 transmission dynamics in Taiwan and risk at different exposure periods before and after symptom onset
JAMA Internal Medicine 180:1156–1163.
https://doi.org/10.1001/jamainternmed.2020.2020
- PubMed
- Google Scholar
Preprint
1. Clifford S
(2020) Strategies to reduce the risk of SARS-CoV-2 re-introduction from international travellers
medRxiv.
https://doi.org/10.1101/2020.07.24.20161281
- Google Scholar
1. Ferretti L
2. Wymant C
3. Kendall M
4. Zhao L
5. Nurtay A
6. Abeler-Dörner L
7. Parker M
8. Bonsall D
9. Fraser C
(2020a) Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing
Science 368:eabb6936.
https://doi.org/10.1126/science.abb6936
- PubMed
- Google Scholar
Preprint
1. Ferretti L
2. Ledda A
3. Wymant C
4. Zhao L
5. Ledda V
6. Abeler-Dorner L
7. Kendall M
8. Nurtay A
9. Cheng H-Y
10. T-C N
11. Lin H-H
12. Hinch R
13. Masel J
14. Kilpatrick AM
15. Fraser C
(2020b) The timing of COVID-19 transmission
medRxiv.
https://doi.org/10.1101/2020.09.04.20188516
- Google Scholar
(2020) Estimated effectiveness of symptom and risk screening to prevent the spread of COVID-19
eLife 9:e55570.
https://doi.org/10.7554/eLife.55570
- PubMed
- Google Scholar
Preprint
1. Grantz KH
2. Lee EC
3. McGowan LD
4. Lee KH
5. Metcalf CJE
6. Gurley ES
7. Lessler J
(2020) Maximizing and evaluating the impact of test-trace-isolate programs
medRxiv.
https://doi.org/10.1101/2020.09.02.20186916
- Google Scholar
1. Guglielmi G
(2020) Fast coronavirus tests: what they can and can't do
Nature 585:496–498.
https://doi.org/10.1038/d41586-020-02661-2
- PubMed
- Google Scholar
1. He X
2. Lau EHY
3. Wu P
4. Deng X
5. Wang J
6. Hao X
7. Lau YC
8. Wong JY
9. Guan Y
10. Tan X
11. Mo X
12. Chen Y
13. Liao B
14. Chen W
15. Hu F
16. Zhang Q
17. Zhong M
18. Wu Y
19. Zhao L
20. Zhang F
21. Cowling BJ
22. Li F
23. Leung GM
(2020) Temporal dynamics in viral shedding and transmissibility of COVID-19
Nature Medicine 26:672–675.
https://doi.org/10.1038/s41591-020-0869-5
- PubMed
- Google Scholar
Website
1. IATA
(2020) Traveler survey reveals COVID-19 concerns
Accessed July 7, 2020.

https://www.iata.org/en/pressroom/pr/2020-07-07-01/
Preprint
1. Jiang X
2. Niu Y
3. Li X
4. Li L
5. Cai W
6. Chen Y
7. Liao B
8. Wang E
(2020) Is a 14-day quarantine period optimal for effectively controlling coronavirus disease 2019 (COVID-19)?
medRxiv.
https://doi.org/10.1101/2020.03.15.20036533
- Google Scholar
(2020) Effectiveness of isolation, testing, contact tracing, and physical distancing on reducing transmission of SARS-CoV-2 in different settings: a mathematical modelling study
The Lancet Infectious Diseases 20:1151–1160.
https://doi.org/10.1016/S1473-3099(20)30457-6
- PubMed
- Google Scholar
(2020) Variation in False-Negative rate of reverse transcriptase polymerase chain Reaction-Based SARS-CoV-2 tests by time since exposure
Annals of Internal Medicine 173:262–267.
https://doi.org/10.7326/M20-1495
- PubMed
- Google Scholar
1. Lauer SA
2. Grantz KH
3. Bi Q
4. Jones FK
5. Zheng Q
6. Meredith HR
7. Azman AS
8. Reich NG
9. Lessler J
(2020) The incubation period of coronavirus disease 2019 (COVID-19) From publicly reported confirmed cases: estimation and application
Annals of Internal Medicine 172:577–582.
https://doi.org/10.7326/M20-0504
- PubMed
- Google Scholar
(2021) On the relationship between serial interval, infectiousness profile and generation time
Journal of the Royal Society Interface 18:20200756.
https://doi.org/10.1098/rsif.2020.0756
- PubMed
- Google Scholar
1. Li Q
2. Guan X
3. Wu P
4. Wang X
5. Zhou L
6. Tong Y
7. Ren R
8. Leung KSM
9. Lau EHY
10. Wong JY
11. Xing X
12. Xiang N
13. Wu Y
14. Li C
15. Chen Q
16. Li D
17. Liu T
18. Zhao J
19. Liu M
20. Tu W
21. Chen C
22. Jin L
23. Yang R
24. Wang Q
25. Zhou S
26. Wang R
27. Liu H
28. Luo Y
29. Liu Y
30. Shao G
31. Li H
32. Tao Z
33. Yang Y
34. Deng Z
35. Liu B
36. Ma Z
37. Zhang Y
38. Shi G
39. Lam TTY
40. Wu JT
41. Gao GF
42. Cowling BJ
43. Yang B
44. Leung GM
45. Feng Z
(2020) Early transmission dynamics in Wuhan, China, of novel Coronavirus-infected pneumonia
New England Journal of Medicine 382:1199–1207.
https://doi.org/10.1056/NEJMoa2001316
- PubMed
- Google Scholar
1. Linton N
2. Kobayashi T
3. Yang Y
4. Hayashi K
5. Akhmetzhanov A
6. Jung S
7. Yuan B
8. Kinoshita R
9. Nishiura H
(2020) Incubation period and other epidemiological characteristics of 2019 novel coronavirus infections with right truncation: a statistical analysis of publicly available case data
Journal of Clinical Medicine 9:538.
https://doi.org/10.3390/jcm9020538
- PubMed
- Google Scholar
Preprint
1. Ma S
2. Zhang J
3. Zeng M
4. Yun Q
5. Guo W
6. Zheng Y
7. Zhao S
8. Wang MH
9. Yang Z
(2020) Epidemiological parameters of coronavirus disease 2019: a pooled analysis of publicly reported individual data of 1155 cases from seven countries
medRxiv.
https://doi.org/10.1101/2020.03.21.20040329
- Google Scholar
1. Nicola M
2. Alsafi Z
3. Sohrabi C
4. Kerwan A
5. Al-Jabir A
6. Iosifidis C
7. Agha M
8. Agha R
(2020) The socio-economic implications of the coronavirus pandemic (COVID-19): A review
International Journal of Surgery 78:185–193.
https://doi.org/10.1016/j.ijsu.2020.04.018
- PubMed
- Google Scholar
1. Nussbaumer-Streit B
2. Mayr V
3. Dobrescu AI
4. Chapman A
5. Persad E
6. Klerings I
7. Wagner G
8. Siebert U
9. Christof C
10. Zachariah C
11. Gartlehner G
(2020) Quarantine alone or in combination with other public health measures to control COVID-19: a rapid review
The Cochrane Database of Systematic Reviews 4:CD013574.
https://doi.org/10.1002/14651858.CD013574
- PubMed
- Google Scholar
1. Parmet WE
2. Sinha MS
(2020) Covid-19 - The law and limits of quarantine
New England Journal of Medicine 382:e28.
https://doi.org/10.1056/NEJMp2004211
- PubMed
- Google Scholar
(2020) Effectiveness of airport screening at detecting travellers infected with novel coronavirus (2019-nCoV)
Eurosurveillance 25:2000080.
https://doi.org/10.2807/1560-7917.ES.2020.25.5.2000080
- PubMed
- Google Scholar
(2021) Quarantine and testing strategies in contact tracing for SARS-CoV-2: a modelling study
The Lancet Public Health 6:e175–e183.
https://doi.org/10.1016/S2468-2667(20)30308-X
- PubMed
- Google Scholar
(2021) Effect of internationally imported cases on internal spread of COVID-19: a mathematical modelling study
The Lancet. Public Health 6:e12-e20.
https://doi.org/10.1016/S2468-2667(20)30263-2
- PubMed
- Google Scholar
1. Salathé M
2. Althaus CL
3. Neher R
4. Stringhini S
5. Hodcroft E
6. Fellay J
7. Zwahlen M
8. Senti G
9. Battegay M
10. Wilder-Smith A
11. Eckerle I
12. Egger M
13. Low N
(2020) COVID-19 epidemic in Switzerland: on the importance of testing, contact tracing and isolation
Swiss Medical Weekly 150:w20225.
https://doi.org/10.4414/smw.2020.20225
- PubMed
- Google Scholar
Report
1. WHO
(2020)
Considerations for Quarantine of Contacts of COVID-19 Cases

WHO.
- Google Scholar
Preprint
1. Xia W
2. Liao J
3. Li C
4. Li Y
5. Qian X
6. Sun X
7. Xu H
8. Mahai G
9. Zhao X
10. Shi L
11. Liu J
12. Yu L
13. Wang M
14. Wang Q
15. Namat A
16. Li Y
17. Qu J
18. Liu Q
19. Lin X
20. Cao S
21. Huan S
22. Xiao J
23. Ruan F
24. Wang H
25. Xu Q
26. Ding X
27. Fang X
28. Qiu F
29. Ma J
30. Zhang Y
31. Wang A
32. Xing Y
33. Xu S
(2020) Transmission of Corona virus disease 2019 during the incubation period may lead to a quarantine loophole
medRxiv.
https://doi.org/10.1101/2020.03.06.20031955
- Google Scholar
1. Zhang J
2. Litvinova M
3. Wang W
4. Wang Y
5. Deng X
6. Chen X
7. Li M
8. Zheng W
9. Yi L
10. Chen X
11. Wu Q
12. Liang Y
13. Wang X
14. Yang J
15. Sun K
16. Longini IM
17. Halloran ME
18. Wu P
19. Cowling BJ
20. Merler S
21. Viboud C
22. Vespignani A
23. Ajelli M
24. Yu H
(2020) Evolving epidemiology and transmission dynamics of coronavirus disease 2019 outside Hubei Province, China: a descriptive and modelling study
The Lancet Infectious Diseases 20:793–802.
https://doi.org/10.1016/S1473-3099(20)30230-9
- PubMed
- Google Scholar

Decision letter

Deborah Cromer

Reviewing Editor; University of New South Wales, Australia
Miles P Davenport

Senior Editor; University of New South Wales, Australia
Mirjam Kretzschmar

Reviewer

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

This work provides a detailed look into the potential benefits of a test and release quarantine strategy. By using quantitative models of the timing of quarantine, testing, release and transmission, the authors are able to show that testing people during quarantine, and releasing them after a negative test, could provide similar efficacy in terms of reducing transmission, while shortening the burden on quarantines individuals. This is relevant to policy decisions as balances are sought between efficacy and societal cost of quarantine.

Decision letter after peer review:

Thank you for submitting your article "Quantifying the impact of quarantine duration on COVID-19 transmission" for consideration by eLife. Your article has been reviewed by four peer reviewers, one of whom is a guest Reviewing Editor and the evaluation has been overseen by Miles Davenport as the Senior Editor. The following individual involved in review of your submission has agreed to reveal their identity: Mirjam Kretzschmar (Reviewer #2).

The Reviewing Editor has drafted this decision to help you prepare a revised submission.

In this paper the authors compare a standard quarantine scenario with a test and release quarantine scenario, and look at the efficacy and utility of each. This is a timely and important analysis, however as it is presented it is very technical, and not well explained for a general audience. It should therefore be revised, and technical details placed in an appendix.

The authors have successfully summarised both the advantages and disadvantages of a test and release quarantine strategy, as well as quarantine for different durations, and have shown that in some circumstances this may be preferable to a standard strategy.

At the moment, the paper does not clearly explain some of the more technical aspects, despite having many equations. It would be better served by explaining well, in plain language the approaches taken, and leaving the mathematics for a technical appendix.

Essential Revisions:

1) Equations must be tidied and there must be a consistency of notation. Many of them should be removed to a technical appendix, and explained in a more intuitive way in the text so the manuscript can be read by a more general audience.

2) Figures should be combined and edited to make paper accessible to a more general audience.

3) Assumptions made must be contextualised and explained. Specifically (but not exclusively):

a) Why do the authors repeatedly state that someone with a positive test is released on day tR+ when in actual fact they would be in isolation – please amend text and clarify.

b) Discuss how the local community transmission level impacts on the conclusions that can be drawn about returned travellers.

c) Consider how the likelihood that symptomatic individuals (not in already in quarantine) will isolate impacts the conclusions.

Reviewer #1:

This paper is well thought through and presents a very nice analysis of the benefits (and disadvantages) of a test and release quarantine strategy, as well as considering different durations of quarantine. I have some concerns however, with the presentation and the assumptions made, as well as the context in which these strategies are undertaken.

In regards to presentation, there are many mathematical equations presented throughout the manuscript, however in many cases these are confusing. As an example, Equations 2, 3 and 4 have no parameters for the function F, and do not contain an n in them, but F is repeatedly used with the parameter n. The relationship between n, t_R, t_Q, t_E etc should be explained and the functions parameterised more clearly.

Additionally, there are 5 result figures presented, which are difficult to interpret. The authors should consider alternative ways of representing their results to make them easier to understand for a non-technical reader.

Regarding assumptions made, the comments in section “Persistently asymptomatic infections” that state that symptomatic individuals would be removed from the population (N.B. this should read infectious pool rather than population) regardless of their quarantine status are only true if ALL people self-isolate on the day of symptom onset. Since this is unlikely to be the case, there will only be a probability of isolation occurring x days after symptom onset, p(x). Presumably p(x) will increase after (a) testing and (b) a positive result, but we cannot assume it will be 1 on the day of symptom onset. This needs to be addressed.

In section “Adherence to quarantine” a function α(n) is introduced, but α(n) is not shown in the paper, and it is not clear whether subsequent calculations include this α(n) or not. This must be clarified. Also, the authors do not consider the possibility that α may wane over time (i.e. for a fixed duration of quarantine, people may quarantine effectively for the first half and but less effectively for the second half). This should be either commented on, or addressed.

It is not clear from the text what is meant by "the test-and-release strategy always performs better than not testing if the release time is the same as the quarantine duration". This must be clarified, and can be done by stating "It will always be better to test a person prior to release from quarantine, as that way asymptomatic and pre-symptomatic infections are more likely to be detected and prevented from being released".

Finally, the context of this manuscript is not made clear. Early on, the authors state that quarantine of returning travellers occurs when "they have returned from recent travel to a high-risk area with levels of community transmission that are higher than in the home country" however in many countries that is not the strategy that is being implemented. Many countries are requiring quarantine after travel to countries with similar or slightly less community transmission. Therefore, the assumption that returning travellers must have contracted their infection overseas is incorrect. This only works in regions where there is little community transmission in the home country. Therefore, if this is to be presented as an argument, these results need to be stratified by cases where the visited country has either much more, similar or much less community transmission than the home country.

Reviewer #2:

In this manuscript the authors develop a computational approach to determine the impact of test sensitivity and duration of quarantine on onward transmission of COVID-19. Based on the generation time distribution, the authors estimate what part of onward transmission can be prevented, given test sensitivity per day since exposure, and delays in testing. They also introduce a utility measure for quarantine, that takes into account the average time spent in quarantine. Overall this is a well written paper with a clear approach and useful results on various quarantining strategies.

There are a few ways in which this paper could be made more accessible for the reader. The notation is mathematical, and notation of variables not always very intuitive. As many quantities have similar names, it would help the reader to have a table with explanation of the variable names, so that one can look back quickly while reading to check how a variable was defined. Alternatively (of in addition), the graphs in Figure 1 could be extended to include more variables, for example a similar graph could be made for the traced contacts, and for returning travellers.

Reviewer #3:

Quantifying the impact of quarantine is an important topic, where the literature is currently lacking. This piece is very timely and tackles some very important questions in the space. At the moment, I feel this paper is somewhat lacking and requires some revision. I think the biggest issue is that it seems to be tailored for the situation in Switzerland. In itself, that's fine, but if the paper stays that way, the title should be altered to specify "in Switzerland", and the Introduction should give some more detail about the local situation. If the authors made that change, I have only a few technical queries that need to be addressed. I will also give some comments and suggestions about the differences between quarantine for close contacts compared to returned travellers, and what should be done to make the analysis more useful globally.

1) I'm concerned that the calculations in this paper are incorrect. Specifically, I'm looking the second paragraph in subsection “Quantifying the benefit of quarantine” and Equation 1. If q(_t) is the probability density of the generation time (and generation time is the time from exposure until the person becomes infectious), then the integral in Equation 1 is the probability that the person becomes infectious while in quarantine. I don't see how this is equal to the fraction of transmission prevented. I thought you would need the function to be the probability that someone is infectious at time t? Which I think is the convolution of Figure 2A and 2B. I am not too concerned about this, as if it is an error it shouldn't be hard to fix.

2) The other technical issue is about returned travellers, and how the trip duration affects the transmission reduction through quarantine. I'm not convinced by the argument that short trips need longer quarantine. I think the calculations are ok, and the result comes from the assumptions themselves. The authors are assuming that a traveller contracts covid while away, so on a 1 day trip, they must have caught it recently, and therefore need more time for symptoms to develop and to test positive. However, I don't think the authors should rule out a traveller catching covid before leaving, and becoming infectious after returning. I understand that the authors want to split the paper up into locally acquired cases, and international, but I don't think it works. If the situation was one where the country had no covid, then this claim about short trips needing longer quarantine makes sense. But in general it's a more nuanced question and certainly doesn't seem to fit Switzerland. I guess it could also work if you assume all local transmissions can be contact-traced, but I don't think the authors claimed this either.

3) On to the more general point about applicability globally, which is specific to returning travellers (apart from the notes above, I think the close contact part of this work look good). I think the authors have missed explaining the decision context clearly (where the decision is about length of quarantine), and how differing values, objectives and system states affect things (see Baker et al., 2020 for a general discussion on decision making). The point I want to get to is, what is the objective of quarantine for returned travellers? The paper focusses on reduction of spread, which seems reasonable for countries with ongoing community transmission. However, it would be important to be clear about how much transmission in the country is coming through airports, relative to the community spread.

There are many countries and jurisdictions that have either no ongoing transmission, or very well contained clusters. Quarantine in these areas is completely different, as the aim isn't about getting some percentage reduction is transmission. Instead, the aim is to have 100% reduction, and the metric of interest is the probability that an infection escapes quarantine and seeds a cluster of cases in the community. I think many people would be very interested in an analysis that looked at quarantine length and testing strategy in this context, to get towards a trade-off between length of stay, costs and importation risk.

Overall, I think this paper has made some good steps. However, the message needs to be refined, and the context of the paper needs to be clarified. I think quarantine is a very important topic, and in its current state, the manuscript is only applicable to regions with active transmission. I think the current scope is acceptable at this journal, but it needs to be clear that it is aiming for that. Even without analysis suited to low/no prevalence scenarios, at a minimum there should be some discussion about how the local epidemiological situation is driving the results and the analysis, and how quarantine may need to be approached differently elsewhere.

I wish the authors all the best in their revisions. As I said, it's an important topic and there needs to be more literature about it. I would happily review this paper again. I also commend the authors for making everything available on Github. This was useful during my review.

References:

Baker, C.M., Campbell, P.T., Chades, I., Dean, A.J., Hester, S.M., Holden, M.H., McCaw, J.M., McVernon, J., Moss, R., Shearer, F.M. & Possingham, H.P. (2020). From climate change to pandemics: decision science can help scientists have impact. ArXiv200713261 Phys.

Reviewer #4:

Ashcroft et al. discussed the appropriate duration of quarantine for travellers and close-contacts by estimating the fraction of transmission that can be avoided under a range of scenario and their relative utility. The study also explored the impact of testing, reinforced hygiene, adherence, and symptom presentation on transmission. This is an important and policy relevant topic. The article is nicely written, and I only have a few comments.

Cases included in Kucirka et al. are all symptomatic, and they back calculated time from exposure assuming incubation period of 5 days. The authors here seem to assume that the sensitivity of the RT-PCR test found in symptomatic individuals can be applied to asymptomatic individuals. Please state this assumption (if that's correct) and discuss how this assumption impacts the outcome.

Figure 4 and other figures, can the authors state how the upper and lower bounds are estimated?

https://doi.org/10.7554/eLife.63704.sa1

Author response

Essential Revisions:

1) Equations must be tidied and there must be a consistency of notation. Many of them should be removed to a technical appendix, and explained in a more intuitive way in the text so the manuscript can be read by a more general audience.

We have followed the Editor’s recommendation and have removed all equations from the main text. To explain our approach in a more intuitive way, we have reworked Figure 1 which now graphically captures our methodology. We have added a verbal description of the model at the start of the Results section to complement this schematic.

All notation has now been streamlined by removing a number of terms (n,x,t_R±,∆_Q,∆_T).

In the main text we now only refer to the timepoints of exposure (t_E), quarantine

entry (t_Q), testing (t_T), and release (t_R), which are introduced in the revised Figure 1.

All equations describing the fraction of transmission prevented, utility, and relative utility in Materials and methods and in the Appendix now have explicit and consistent arguments based on these timepoints.

Finally, we have added a glossary of terms (Table 1 in Materials and methods) which can be used as a reference guide for our notation.

2) Figures should be combined and edited to make paper accessible to a more general audience.

Following our revisions, the main text now only contains four figures: one schematic figure and three figures containing the main results. We have combined the figures for standard quarantine and test-and-release for traced contacts into a single figure (now Figure 2). This now allows for direct comparison between the alternate quarantine strategies. We have repeated this for the returning travellers too (now Figure 4). We have modified the result figure that shows the impact of adherence (now Figure 3A) to also include test-and-release, which as pointed out by reviewer 2 (comment 2.9) contains an important result relating to minimum quarantine durations.

In all figures we have tried to reduce the information content and increase clarity, which we hope makes our results more accessible. As a consequence, we have added extra supplemental figures, all of which are referred to in the main text. Further details are described in the response to reviewer 1.

3) Assumptions made must be contextualised and explained. Specifically (but not exclusively):

a) Why do the authors repeatedly state that someone with a positive test is released on day tR+ when in actual fact they would be in isolation – please amend text and clarify.

b) Discuss how the local community transmission level impacts on the conclusions that can be drawn about returned travellers.

c) Consider how the likelihood that symptomatic individuals (not in already in quarantine) will isolate impacts the conclusions.

We thank the Editor for pointing this out. While streamlining our notation, we have removed the timepoints t_R±. Now we state explicitly that the infected individual who receives a positive test result while in quarantine is isolated until they are no longer infectious. In the Model description section of Results, we write: “Under the standard quarantine strategy, all potentially-exposed individuals are quarantined for the same duration. An alternative approach is the test-and-release strategy, which uses virological testing during quarantine to release individuals with a negative test result earlier. Individuals with a positive test result are isolated until they are no longer infectious.”. This point is reiterated in the Materials and methods section: “If the test is negative, the individual is released when the test result arrives at time t_R. Otherwise, the individual is isolated until they are no longer infectious.”.

Based on the generation time distribution, the infectious period lasts for 10 days after exposure, so we fix the release time to day 10, as noted in the captions of Figures 2 and 4, and in the glossary in Table 1.

b) This point was raised by reviewer 1 and reviewer 3. In this paper we focus on quantifying how much transmission is prevented by different quarantine durations and test-and-release strategies. This quantification is not affected by the relative risk of local community transmission versus import from travellers. What determines the optimal quarantine strategy ultimately depends on the local epidemiological situation and the goal of the authorities: Preventing (re)introduction of the virus would correspond maximising the transmission prevented by quarantine. However, if the virus is already endemic then we could be looking for trade-offs between transmission prevention and quarantine duration.

We have now expanded these points regarding what defines the optimal quarantine strategy at the beginning of the Results section for returning travellers: “The rules for whether travellers returning from abroad are quarantined are frequently changed according to the epidemiological scenario in the travel destination and/or in the home country. A high risk of infection while abroad due to high prevalence, or the possibility of returning with a new virological variant, can lead to the imposition or reinstatement of quarantine measures. Countries that have already eliminated the infection may be even stricter in their quarantine approach to prevent new community-transmission clusters from being seeded. Here we do not discuss these scenarios or the concept of relative risk, we simply quantify how effective quarantine strategies would be at preventing transmission if the turning traveller was infected while abroad. Should quarantine rules be instated or modified, these results can help determine the optimal quarantine duration and/or testing strategy.”.

c) Reviewers 1 and 2 have brought up points surrounding the role that symptom onset plays in our results. In addition to the existing results in Figures 3B and 4—figure supplement 3B, we have now included an additional supplementary figure (Figure 3—figure supplement 1) describing how delays between symptom onset and isolation further affect the results. We have clarified that we assume self-isolation occurs immediately in Figures 3B and 4—figure supplement 3B. We have also improved the description and equations describing these results in the Appendix. Finally, we have added this point as a limitation in our Discussion: “In addition, we have primarily assumed that symptom onset during quarantine has no impact on quarantine efficacy. However, this symptomatic transmission should not be counted towards the efficacy of quarantine as the infected individual should already self-isolate after symptom onset. We have quantified this effect and have shown that this assumption leads us to overestimate quarantine efficacy.”.

We hope it is now clear that self-isolation after symptom onset is only considered in Figures 3B, 3—figure supplement 1, and 4—figure supplement 3B, and that its impact is to reduce the fraction of transmission that is prevented by quarantine.

Reviewer #1:

This paper is well thought through and presents a very nice analysis of the benefits (and disadvantages) of a test and release quarantine strategy, as well as considering different durations of quarantine. I have some concerns however, with the presentation and the assumptions made, as well as the context in which these strategies are undertaken.

In regards to presentation, there are many mathematical equations presented throughout the manuscript, however in many cases these are confusing. As an example, Equations 2, 3 and 4 have no parameters for the function F, and do not contain an n in them, but F is repeatedly used with the parameter n. The relationship between n, t_R, t_Q, t_E etc should be explained and the functions parameterised more clearly.

We apologise for the confusion caused by our notation. Upon revision, we have streamlined our notation to focus only on the defined timepoints t_E, t_Q, t_T, and t_R(respectively time of exposure, start of quarantine, time of test, and time of release). These timepoints are now annotated in the new schematic figure (Figure 1). The equations (now located in Materials and methods and the Appendix) now have explicit arguments based on these timepoints. Furthermore, we have removed a number of terms (n,x,t_R±,∆_Q,∆_T) that can be described by the previously-mentioned timepoints. We hope with the introduction of the schematic figure and the simplified notation that any confusion/ambiguity has been removed.

Additionally, there are 5 result figures presented, which are difficult to interpret. The authors should consider alternative ways of representing their results to make them easier to understand for a non-technical reader.

In the revised manuscript we now have only four figures: one schematic and three containing the results. We believe this improves the accessibility and readability of our study. To make our result figures more interpretable, we have tried to reduce the information content of the figures, while making it easier to make comparisons between the standard quarantine strategy and test-and-release.

To this end, in the main results for traced contacts we have focussed on only one delay-to-quarantine value (3 days), and combined Figures 3 and 4 into a single figure (now Figure 2) containing the no-test scenario and test-and-release. The previous Figure 3 (varying the delay-to-quarantine) has moved to Figure 2—figure supplement 1, and so have the dashed lines from previous Figure 4 (now Figure 2—figure supplement 2) for the reduced post-quarantine transmission scenario.

Adherence and the role of symptoms are still discussed in Figure 3 (previously Figure 5), but with the same quarantine strategies (standard + test-and-release) as presented in Figure 2 and rescaled axes for visual clarity.

In the same fashion as Figures 3 and 4, we have combined Figures 6 and 7 for the returning travellers (now Figure 4). We now focus only on a travel duration of 7 days, and move Figure 6 with the impact of travel duration to Figure 4—figure supplement 1.

Regarding assumptions made, the comments in section “Persistently asymptomatic infections” that state that symptomatic individuals would be removed from the population (N.B. this should read infectious pool rather than population) regardless of their quarantine status are only true if ALL people self-isolate on the day of symptom onset. Since this is unlikely to be the case, there will only be a probability of isolation occurring x days after symptom onset, p(x). Presumably p(x) will increase after (a) testing and (b) a positive result, but we cannot assume it will be 1 on the day of symptom onset. This needs to be addressed.

In response to this point, we have investigated the impact of adding a delay between symptom onset and self-isolation (Figure 3—figure supplement 1). For the main results we stick with self-isolation immediately after symptom onset (zero delay). This zero-delay scenario is informative as it corresponds to the minimum efficacy of quarantine; any transmission that would occur between symptom onset and self-isolation would be prevented by quarantine, leading to an increase in efficacy. We now clarify this assumption in the Results section: “We assume self-isolation occurs immediately after symptom onset, but any delay here would mean more transmission is prevented by quarantine (Figure 3—figure supplement 1).”. The corresponding equation is written and described in the Appendix section “Persistently asymptomatic infections and the role of self-isolation”.

Thank you for pointing out our poor phrasing, we have replaced “remove them from the population” with “remove the symptomatic cases from the infectious pool”, and likewise in the Appendix.

In section “Adherence to quarantine” a function α(n) is introduced, but α(n) is not shown in the paper, and it is not clear whether subsequent calculations include this α(n) or not. This must be clarified. Also, the authors do not consider the possibility that α may wane over time (i.e. for a fixed duration of quarantine, people may quarantine effectively for the first half and but less effectively for the second half). This should be either commented on, or addressed.

We acknowledge that the adherence function α was not sufficiently or consistently described in the original submission. In response, we have removed α completely from the main text. This function now only features in the glossary table and in the Appendix (section “Adherence to quarantine”), where we define the relative adherence measure [Appendix 1—equation (3)].

We now explicitly state that we have assumed 100% adherence in the Model description: “Unless otherwise stated, we assume that adherence to quarantine is 100%.”; and that this assumption is relaxed for Figure 3A: “In Figure 2 have made the following assumptions: (i) individuals released from quarantine have – in the post-quarantine phase – the same transmission probability as individuals who were not quarantined; (ii) quarantine is 100% adhered to; and (iii) the transmission prevented by quarantine for cases who develop symptoms is attributed to quarantine. We now relax these assumptions to assess their impact on quarantine efficacy.”. In the Results text before Figure 3, we introduce the concept of adherence and clarify that we treat it as a binary variable: “Adherence to quarantine is unlikely to be 100% and could depend on the proposed duration of quarantine. For simplicity we treat adherence to quarantine as a binary variable: a fraction of individuals adhere to quarantine completely for the proposed duration, while the remaining fraction do not undergo any quarantine. We now ask: by how much would the fraction of those who adhere to quarantine have to increase to maintain the efficacy of quarantine if the duration is shortened?”. This is expanded in the Appendix: “Adherence could be included as a time-varying property of an individual, such that the probability that an individual follows the quarantine guidelines is high at the beginning of quarantine, but is waning as the duration spent in quarantine increases. However, for simplicity, we assume adherence is binary; either an individual completes the full duration of quarantine, or they do not enter quarantine at all.”.

We believe that with our verbal description of adherence and the assumptions, and the expanded Appendix (section “Adherence to quarantine”), that the confusion introduced around adherence has been clarified.

It is not clear from the text what is meant by "the test-and-release strategy always performs better than not testing if the release time is the same as the quarantine duration". This must be clarified, and can be done by stating "It will always be better to test a person prior to release from quarantine, as that way asymptomatic and pre-symptomatic infections are more likely to be detected and prevented from being released".

We thank the reviewer for their suggested explanation, which we have incorporated into the text: “On the other hand, it is always better to test a person prior to release from quarantine, so that individuals with asymptomatic and pre-symptomatic infections can be detected and prevented from being released.”.

Finally, the context of this manuscript is not made clear. Early on, the authors state that quarantine of returning travellers occurs when "they have returned from recent travel to a high-risk area with levels of community transmission that are higher than in the home country" however in many countries that is not the strategy that is being implemented. Many countries are requiring quarantine after travel to countries with similar or slightly less community transmission. Therefore, the assumption that returning travellers MUST have contracted their infection overseas is incorrect. This only works in regions where there is little community transmission in the home country. Therefore, if this is to be presented as an argument, these results need to be stratified by cases where the visited country has either much more, similar or much less community transmission than the home country.

We thank the reviewer for this comment and for helping us to sharpen the point of our manuscript. In our work we follow the guidelines of the World Health Organtion (WHO) who say: “There are two scenarios in which quarantine may be implemented: (1) for travellers from areas with community transmission and (2) for contacts of known cases.” (WHO, 2020). They then go on to say: “If Member States choose to implement quarantine measures for travellers on arrival at their destination, they should do so based on a risk assessment and consideration of local circumstances.” (WHO, 2020). In our work we are not considering the question of whether quarantine should be imposed on returning travellers or not: we do not consider the risk of introduction or the relative risk of infection abroad versus at home. Such an analysis was recently published by Russell et al., 2020. In our work we want to quantify how quarantine duration (and testing) impacts the amount of transmission if quarantine is implemented for returning travellers. We then assume that the returning traveller was infected during their trip, and that potential transmission is prevented by quarantine. The relative risk of infection could feature in a measure of utility, but that is beyond the scope of our paper.

In response, we have generalised our introductory statement about the circumstances under which returning travellers should be quarantined, using the guide lines from the WHO: “Individuals are generally placed into quarantine for one of two reasons: either they have been identified as a recent close contact of a confirmed SARS-CoV-2 case by contact tracing, or they have returned from recent travel to an area with community transmission that has been assessed to pose significant epidemiological risk (WHO, 2020).”.

We have expanded on this further in Results section “Quarantining returning travellers”: “The rules for whether travellers returning from abroad are quarantined are frequently changed according to the epidemiological scenario in the travel destination and/or in the home country. A high risk of infection while abroad due to high prevalence, or the possibility of returning with a new virological variant, can lead to the imposition or reinstatement of quarantine measures. Countries that have already eradicated the disease may be even stricter in their quarantine approach to prevent new community-transmission clusters from being seeded. Here we do not discuss these scenarios or the concept of relative risk, but we simply quantify how effective quarantine strategies would be at preventing transmission if the returning traveller was infected while abroad. Should quarantine rules be instated or modified, these results can help determine the optimal quarantine duration and/or testing strategy.”.

We hope these modifications have now clarified the message of our paper.

Reviewer #2:

In this manuscript the authors develop a computational approach to determine the impact of test sensitivity and duration of quarantine on onward transmission of COVID-19. Based on the generation time distribution, the authors estimate what part of onward transmission can be prevented, given test sensitivity per day since exposure, and delays in testing. They also introduce a utility measure for quarantine, that takes into account the average time spent in quarantine. Overall this is a well written paper with a clear approach and useful results on various quarantining strategies.

There are a few ways in which this paper could be made more accessible for the reader. The notation is mathematical, and notation of variables not always very intuitive. As many quantities have similar names, it would help the reader to have a table with explanation of the variable names, so that one can look back quickly while reading to check how a variable was defined. Alternatively (of in addition), the graphs in Figure 1 could be extended to include more variables, for example a similar graph could be made for the traced contacts, and for returning travellers.

We thank the reviewer for their positive comments about the project, and for their constructive suggestions. We believe these changes have greatly improved the quality and accessibility of the manuscript.

We have decided to follow both advices suggested here. We have redrawn Figure 1 to include more clearly the relevant variables for each case of traced contacts and returning travellers. This figure now also illustrates graphically how we compute the fraction of transmission that is prevented by quarantine. We have also included a glossary table (Table 1 in Materials and methods) with a description of all variable names and their relationships.

Reviewer #3:

Quantifying the impact of quarantine is an important topic, where the literature is currently lacking. This piece is very timely and tackles some very important questions in the space. At the moment, I feel this paper is somewhat lacking and requires some revision. I think the biggest issue is that it seems to be tailored for the situation in Switzerland. In itself, that's fine, but if the paper stays that way, the title should be altered to specify "in Switzerland", and the Introduction should give some more detail about the local situation. If the authors made that change, I have only a few technical queries that need to be addressed. I will also give some comments and suggestions about the differences between quarantine for close contacts compared to returned travellers, and what should be done to make the analysis more useful globally.

We thank the reviewer for their positive description of our project, and for the suggestions made. We feel the manuscript quality has greatly increased following these revisions.

With regards to the focus on Switzerland, the only country-specific statement that we make is that the baseline duration of quarantine to which we compare is 10 days. Other countries may use higher values, such as 14 or even 21 days, but under our framework we see that increasing quarantine beyond 10 days has very little (<1%) effect on transmission prevention.

For returning travellers, we are not considering the risk of being infected abroad versus at home. This risk should undoubtedly be included in an assessment of

whether to impose quarantine or not, as performed by Russell et al., 2020. But this is not the question we are asking. What we want to quantify is that given an individual is infected and that they have to go into quarantine, how do the different quarantine strategies perform? This question is independent of risk at home versus abroad. However, when it comes to choosing the optimal quarantine strategy, then the local epidemiological scenario will have an impact. We respond to this point in detail below.

1) I'm concerned that the calculations in this paper are incorrect. Specifically, I'm looking the second paragraph in subsection “Quantifying the benefit of quarantine” and Equation 1. If q(t) is the probability density of the generation time (and generation time is the time from exposure until the person becomes infectious), then the integral in Equation 1 is the probability that the person becomes infectious while in quarantine. I don't see how this is equal to the fraction of transmission prevented. I thought you would need the function to be the probability that someone is infectious at time t? Which I think is the convolution of Figure 2A and 2B. I am not too concerned about this, as if it is an error it shouldn't be hard to fix.

We apologise that the original text has caused some confusion between the generation time (the time interval between infection of an infector and the infection of a subsequent infectee) and the incubation period (the time interval between infection and symptom onset in the same individual). The generation time interval is exactly the probability density that an individual is infectious at time t, and this is what we use in our calculations of quarantine efficacy. Through clarifications to our notation, our new Figure 1, and the information content of the Materials and methods section, we hope that further confusion will be prevented.

In the Model description we now explicitly state: “In the model, the timing of onward transmission from an infected individual is determined by the generation time distribution, which describes the time interval between the infection of an infector and infectee (see Figure 1—figure supplement 1).”.

2) The other technical issue is about returned travellers, and how the trip duration affects the transmission reduction through quarantine. I'm not convinced by the argument that short trips need longer quarantine. I think the calculations are ok, and the result comes from the assumptions themselves. The authors are assuming that a traveller contracts covid while away, so on a 1 day trip, they must have caught it recently, and therefore need more time for symptoms to develop and to test positive. However, I don't think the authors should rule out a traveller catching covid before leaving, and becoming infectious after returning. I understand that the authors want to split the paper up into locally acquired cases, and international, but I don't think it works. If the situation was one where the country had no covid, then this claim about short trips needing longer quarantine makes sense. But in general it's a more nuanced question and certainly doesn't seem to fit Switzerland. I guess it could also work if you assume all local transmissions can be contact-traced, but I don't think the authors claimed this either.

We agree with the reviewer that the result about the relationship between the duration of the trip and the optimal duration of quarantine depends on the assumption that the infection is acquired during travel. This assumption is necessary because the concept of travel quarantines itself depends on the assumption. If local transmission rates are comparable to the travel destination, travel quarantines do not make sense. We now highlight in the Introduction that travel quarantine only applies to individuals who “have returned from recent travel to an area with community transmission that has been assessed to pose significant epidemiological risk (WHO, 2020).”, as specified in the WHO’s guidelines (WHO, 2020).

3) On to the more general point about applicability globally, which is specific to returning travellers (apart from the notes above, I think the close contact part of this work look good). I think the authors have missed explaining the decision context clearly (where the decision is about length of quarantine), and how differing values, objectives and system states affect things (see Baker et al., 2020 for a general discussion on decision making). The point I want to get to is, what is the objective of quarantine for returned travellers? The paper focusses on reduction of spread, which seems reasonable for countries with ongoing community transmission. However, it would be important to be clear about how much transmission in the country is coming through airports, relative to the community spread.

There are many countries and jurisdictions that have either no ongoing transmission, or very well contained clusters. Quarantine in these areas is completely different, as the aim isn't about getting some percentage reduction is transmission. Instead, the aim is to have 100% reduction, and the metric of interest is the probability that an infection escapes quarantine and seeds a cluster of cases in the community. I think many people would be very interested in an analysis that looked at quarantine length and testing strategy in this context, to get towards a trade-off between length of stay, costs and importation risk.

What we think the reviewer is saying is that the optimal quarantine strategy depends on the goal you want to achieve, and in turn this goal depends on the current epidemiological scenario both at home and abroad.

In this work we have computed two measures of the usefulness of quarantine; firstly is the reduction of transmission, and secondly is this reduction divided by quarantine duration. In situations where we want to prevent the (re)introduction of SARS-CoV-2, we should focus on maximising the reduction of transmission (and hence minimising the transmission risk). If the disease is already endemic then we could be looking for trade-offs between transmission reduction and quarantine duration. Hence our two measures can be used to describe these scenarios. We have expanded on these points in the Discussion: “The ratio of transmission prevented versus days spent in quarantine is only one possible definition of utility. Defining the appropriate function is ultimately a policy question: the economic, societal, and individual costs are likely a function the days spent in quarantine, but we cannot determine the shape of this function. Furthermore, the local epidemiological situation will dictate which metric of quarantine efficacy is to be optimised. In situations where the goal is to prevent the (re)introduction of SARS-CoV-2, one should focus on maximising the reduction of transmission (and hence minimising the transmission risk). If the virus is already endemic then considering the trade-off between transmission reduction and quarantine duration could determine the optimum strategy. Another perspective is that the utility of preventing transmission is crucially dependent on whether it brings the effective reproductive number under one.”.

Overall, I think this paper has made some good steps. However, the message needs to be refined, and the context of the paper needs to be clarified. I think quarantine is a very important topic, and in its current state, the manuscript is only applicable to regions with active transmission. I think the current scope is acceptable at this journal, but it needs to be clear that it is aiming for that. Even without analysis suited to low/no prevalence scenarios, at a minimum there should be some discussion about how the local epidemiological situation is driving the results and the analysis, and how quarantine may need to be approached differently elsewhere.

I wish the authors all the best in their revisions. As I said, it's an important topic and there needs to be more literature about it. I would happily review this paper again. I also commend the authors for making everything available on Github. This was useful during my review.

We thank the reviewer for their support, and we believe the message has been sharpened thanks to the combined comments of the Editor and reviewers. We are also happy to always share code and to be transparent about our methodology, sometimes even too transparent by including too many equations. The reviewer has made great points which have particularly improved the discussion and the overall message of this manuscript.

We have added the following paragraph to Results section where we begin to analyse returning travellers: “The rules for whether travellers returning from abroad are quarantined are frequently changed according to the epidemiological scenario in the travel destination and/or in the home country. A high risk of infection while abroad due to high prevalence, or the possibility of returning with a new virological variant, can lead to the imposition or reinstatement of quarantine measures. Countries that have already eliminated the infection may be even stricter in their quarantine approach to prevent new community-transmission clusters from being seeded. Here we do not discuss these scenarios or the concept of relative risk, we simply quantify how effective quarantine strategies would be at preventing transmission if the returning traveller was infected while abroad. Should quarantine rules be instated or modified, these results can help determine the optimal quarantine duration and/or testing strategy.”.

Furthermore, we have added the following paragraph to the Discussion to describe how the epidemiological scenario drives the choice of metric that defines the optimal quarantine strategy: “The ratio of transmission prevented versus days spent in quarantine is only one possible definition of utility. Defining the appropriate function is ultimately a policy question: the economic, societal, and individual costs are likely a function the days spent in quarantine, but we cannot determine the shape of this function. Furthermore, the local epidemiological situation will dictate which metric of quarantine efficacy is to be optimised. In situations where the goal is to prevent the (re)introduction of SARS-CoV-2, one should focus on maximising the reduction of transmission (and hence minimising the transmission risk). If the virus is already endemic then considering the trade-off between transmission reduction and quarantine duration could determine the optimum strategy. Another perspective is that the utility of preventing transmission is crucially dependent on whether it brings the effective reproductive number under one.”.

Reviewer #4:

Ashcroft et al. discussed the appropriate duration of quarantine for travelers and close-contacts by estimating the fraction of transmission that can be avoided under a range of scenario and their relative utility. The study also explored the impact of testing, reinforced hygiene, adherence, and symptom presentation on transmission. This is an important and policy relevant topic. The article is nicely written, and I only have a few comments.

Cases included in Kucirka et al. are all symptomatic, and they back calculated time from exposure assuming incubation period of 5 days. The authors here seem to assume that the sensitivity of the RT-PCR test found in symptomatic individuals can be applied to asymptomatic individuals. Please state this assumption (if that's correct) and discuss how this assumption impacts the outcome.

We thank the reviewer for clarifying how the sensitivity is calculated through the back calculation from symptom onset, as opposed to directly from the time of infection. The incubation period we use (from Ferretti et al., 2020) also has a median incubation period of 5 days, as used by Kucirka et al., 2020. We do assume the false-negative profile is the same across symptomatic and asymptomatic cases, which may not be the case. It is likely, although we couldn’t find any data on this, that the sensitivity is lower for asymptomatic cases, and hence we would be overestimating the efficacy of quarantine as the asymptomatic infections could be released earlier due to a more-probable false-negative test result.

This assumption is now stated when we describe the false negative rate in Materials and methods: “A further challenge with this false-negative rate is that it was calculated by Kucirka et al., 2020 from symptomatic cases only. Here we assume that this test sensitivity profile also applies to asymptomatic cases.”.

The impact of this assumption is discussed in the Results when we consider the role that symptomatic cases play in quarantine efficacy: “Furthermore, we have assumed that the false-negative rate is the same between symptomatic and asymptomatic cases. If the test is less sensitive (higher false-negative probability) for asymptomatic cases, then quarantine efficacy would be further reduced.”.

Finally, we acknowledge that this assumption is a limitation to our study in the Discussion: “Furthermore, these distributions, and also the test sensitivity profile, could be different between persistently asymptomatic and symptomatic individuals (Buitrago-Garcia et al., 2020), which ultimately lead to an overestimation of how much transmission is prevented by quarantine.”.

Figure 4 and other figures, can the authors state how the upper and lower bounds are estimated?

The bounding lines are now clearly described in all figure legends. By combining the standard quarantine with test-and-release in the results figures, we hope it is now clear that the standard quarantine protocol provides the lower bounds in Figures 2 and 4.

https://doi.org/10.7554/eLife.63704.sa2

Article and author information

Author details

Peter Ashcroft

Institute of Integrative Biology, ETH Zürich, Zürich, Switzerland

Contribution
Conceptualization, Data curation, Software, Formal analysis, Validation, Investigation, Visualization, Methodology, Writing - original draft, Project administration, Writing - review and editing

For correspondence
peter.ashcroft@env.ethz.ch

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-4067-7692
Sonja Lehtinen

Institute of Integrative Biology, ETH Zürich, Zürich, Switzerland

Contribution
Conceptualization, Data curation, Formal analysis, Methodology, Writing - original draft, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-4236-828X
Daniel C Angst

Institute of Integrative Biology, ETH Zürich, Zürich, Switzerland

Contribution
Data curation, Software, Validation, Visualization, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-6512-4595
Nicola Low

Institute of Social and Preventive Medicine, University of Bern, Bern, Switzerland

Contribution
Supervision, Funding acquisition, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-4817-8986
Sebastian Bonhoeffer

Institute of Integrative Biology, ETH Zürich, Zürich, Switzerland

Contribution
Conceptualization, Formal analysis, Supervision, Funding acquisition, Methodology,Writing - original draft, Project administration, Writing - review and editing

For correspondence
seb@env.ethz.ch

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-8052-3925

Funding

H2020 European Research Council (EpiPose 101003688)

Nicola Low

Swiss National Science Foundation (176233)

Nicola Low

Swiss National Science Foundation (176401)

Sebastian Bonhoeffer

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Senior Editor

Miles P Davenport, University of New South Wales, Australia

Reviewing Editor

Deborah Cromer, University of New South Wales, Australia

Reviewer

Mirjam Kretzschmar

Publication history

Received: October 2, 2020
Accepted: February 4, 2021
Accepted Manuscript published: February 5, 2021 (version 1)
Version of Record published: March 16, 2021 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.